Bài giảng phương trình mặt phẳng Toán 12

Bài giảng phương trình mặt phẳng Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

19 10 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

TOANMATH.com

Trang 1

BÀI 2. PHƯƠNG TRÌNH MẶT PHẲNG

Mục tiêu

 Kiến thức

+ Nắm được cách xác định mặt phẳng, vectơ pháp tuyến của mặt phẳng.

+ Nắm được công thức tính khoảng cách từ điểm đến mặt phẳng, góc giữa hai mặt phẳng.

+ Nhận biết được vị trí tương đối giữa đường thẳng với mặt phẳng, giữa mặt phẳng với mặt cầu.

 Kĩ năng

+ Viết được phương trình tổng quát của mặt phẳng.

+ Xác định được vectơ pháp tuyến trong các trường hợp.

+ Tính được khoảng cách và góc.

+ Xác định được vị trí tương đối và vận dụng vào giải bài tập.

I. LÍ THUYẾT TRỌNG TÂM

1. Phương trình mặt phẳng

Vectơ pháp tuyến

Vectơ



 

là vectơ pháp tuyến của







nếu giá của



vuông góc với







Cặp vectơ chỉ phương của mặt phẳng

Hai vectơ

a b

 

không cùng phương là cặp vectơ chỉ phương của







nếu các giá của chúng song song

hoặc nằm trên







Chú ý:

 Nếu



là một vectơ pháp tuyến của







thì





kn k





cũng là vectơ pháp tuyến của







 Nếu

a b

 

là một cặp vectơ chỉ phương của







thì

n a b

 



 

  

là một vectơ pháp tuyến của







Phương trình tổng quát của mặt phẳng

Ax By Cz D

   

với

2 2 2

A B C

  

 Nếu

( )



có phương trình

Ax By Cz D

   

thì

( ; ; )

n A B C





là một vectơ pháp tuyến của

( )



 Phương trình mặt phẳng đi qua





0 0 0 0

; ;

M x y z

và có một vectơ pháp tuyến

( ; ; )

n A B C





là:













0 0 0

A x x B y y C z z

     

Các trường hợp đặc biệt

Các hệ số

Phương trình mặt phẳng







Tính chất mặt phẳng









Ax By Cz

  







đi qua gốc tọa độ O



By Cz D

  





/ / Ox

 hoặc





 

TOANMATH.com

Trang 2



Ax Cz D

  





/ /

 hoặc





 



Ax By D

  





/ /

 hoặc





 

A B

 

Cz D

 









/ /

Oxy

 hoặc









Oxy

 

A C

 

By D

 









/ /

Oxz

 hoặc









Oxz

 

B C

 

Ax D

 









/ /

Oyz

 hoặc









Oyz

 

Nếu

( )



cắt các trục toạ độ tại các điểm

( ;0;0),(0; ;0),(0;0; )

a b c

với

abc



thì ta có phương trình mặt

phẳng theo đoạn chắn

( ) : 1

x y z

a b c

  



Chú ý: Nếu trong phương trình

( )



không chứa ẩn nào thì

( )



song song hoặc chứa trục tương ứng.

2. Khoảng cách từ một điểm tới mặt phẳng

Trong không gian

Oxyz

cho điểm





; ;

A A A

A x y z

và mặt phẳng

( ) : 0

Ax By Cz D

   



Khi đó khoảng cách từ điểm A đến mặt phẳng

( )



được tính theo công thức:

2 2 2

d( ,( ))

A A A

Ax By Cz D

A B C

  



 



3. Vị trí tương đối

Vị trí tương đối giữa hai mặt phẳng

Trong không gian

Oxyz

cho hai mặt phẳng

1 1 1 1 2 2 2 2

( ): 0; ( ) : 0

A x B y C z D A x B y C z D

       

 

1 1 1 1

2 2 2 2

( ) ( )

A B C D

    

 

1 1 1 1

2 2 2 2

( ) / /( )

A B C D

   

 

1 1

2 2

( ) ( )

A B

  

 

hoặc

1 1

2 2

B C



1 2 1 2 1 2

( ) ( ) 0

A A B B C C

    

 

Vị trí tương đối giữa mặt phẳng và mặt cầu

Trong không gian

Oxyz

cho mặt phẳng và mặt cầu

TOANMATH.com

Trang 3

( ) : 0

Ax By Cz D

   



;

2 2 2 2

( ) : ( ) ( ) ( )

S x a y b z c R

     

Để xét vị trí của

( )



và

( )

ta làm như sau:

+) Nếu









d I R





thì

( )



không cắt

( )

+) Nếu









d I R

 

thì







tiếp xúc





tại

Khi đó

được gọi là

tiếp điểm đồng thời

là hình chiếu vuông góc của

lên







và







được gọi là tiếp diện.

+) Nếu









d I R

 

thì







cắt





theo đường tròn có phương trình



2 2 2

( ) ( )

( ) :

x a y b z c R

Ax By Cz D



     





   





Bán kính của





là

2 2

d [ ,( )]

r R I 



Tâm J của (C) là hình chiếu vuông góc của

trên







4. Góc giữa hai mặt phẳng

Trong không gian

Oxyz

cho hai mặt phẳng

1 1 1 1

( ): 0

A x B y C z D

   



và

2 2 2 2

( ) : 0

A x B y C z D

   



Góc giữa

( )



và

( )



bằng hoặc bù với góc giữa hai vectơ pháp tuyến

, .

n n

 

 

Tức là

   

 



1 2 1 2 1 2

2 2 2 2 2 2

1 1 1 2 2 2

cos , cos , .

n n

A A B B C C

n n

A B C A B C

 

  



    

 

 

Chùm mặt phẳng

 Tập hợp tất cả các mặt phẳng qua giao tuyến của hai mặt phẳng

( )



và

( )



được gọi là một chùm mặt phẳng.

 Gọi





là giao tuyến của hai mặt phẳng

1 1 1 1

2 2 2 2

( ) : 0

A x B y C z D

   





Khi đó nếu





là mặt phẳng chứa





thì mặt phẳng





có dạng









1 1 1 1 2 2 2 2

m A x B y C z D n A x B y C z D

         

với

2 2

m n

 

SƠ ĐỒ HỆ THỐNG HÓA

TOANMATH.com

Trang 4

II. CÁC DẠNG BÀI TẬP

Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng

Bài toán 1. Viết phương trình mặt phẳng biết một điểm thuộc mặt phẳng và tìm được một vectơ

pháp tuyến

Phương pháp giải

Mặt phẳng







đi qua điểm





0 0 0

; ;

M x y z

có vectơ pháp tuyến





; ;

n A B C





là













0 0 0

A x x B y y C z z

     

Ví dụ: Phương trình mặt phẳng đi qua điểm





1;2;3

A và có vectơ pháp tuyến





1;2;1

v 



là:













1 1 2 2 1 3 0

2 6 0.

x y z

      

    

Ví dụ mẫu

Ví dụ 1: Trong không gian

Oxyz

một vectơ pháp tuyến của mặt phẳng

2 1 3

x y z

  

 

là





3;6; 2 .

 







2; 1;3 .

n  







3; 6; 2 .

   







2; 1;3 .

n   



Hướng dẫn giải

Ta có phương trình

1 1

1 1 0 3 6 2 6 0.

2 1 3 2 3

x y z

x y z x y z



            

 

Một vectơ pháp tuyến của mặt phẳng





3;6; 2 .

 



Chọn A.

TOANMATH.com

Trang 5

Ví dụ 2: Cho ba điểm













2;1; 1 , 1;0;4 , 0; 2; 1 .

A B C

   

Phương trình mặt phẳng đi qua

và vuông

góc với

là

2 5 5 0.

x y z

   

2 5 5 0.

x y z

   

2 5 0.

x y

  

2 5 5 0.

x y z

   

Hướng dẫn giải

Mặt phẳng





đi qua





2;1; 1



và vuông góc với

nên nhận





1; 2; 5

  



làm vectơ pháp

tuyến. Vì vậy ta viết được phương trình mặt phẳng





là:









2 2 1 5 1 0 2 5 5 0.

x y z x y z

          

Chọn A.

Chú ý: Mặt phẳng







đi qua một điểm

vuông góc với đường thẳng





khi đó vectơ chỉ phương



của đường thẳng





là một vectơ pháp tuyến của







Ví dụ 3: Trong không gian với hệ toạ độ

Oxyz

cho hai điểm









1; 3;2 , 3;5; 2 .

A B

 

Phương trình mặt

phẳng trung trực của đoạn thẳng

có dạng

x ay bz c

   

Khi đó

a b c

 

bằng



D. 2.

Hướng dẫn giải

Gọi

là trung điểm của đoạn thẳng

ta có

(2;1;0)

M và

(2;8; 4) 2(1;4; 2) 2

AB n

    





Mặt phẳng trung trực của đoạn thẳng

đi qua

và có một vectơ pháp tuyến là



nên có phương

trình:

4 2 6 0

x y z

   

Suy ra

4, 2, 6

a b c

    

Vậy

a b c

   

Chọn B.

Ví dụ 4: Trong không gian

Oxyz

mặt phẳng song song với mặt phẳng





Oxy

và đi qua điểm

(1;1;1)

có

phương trình là

1 0

 

. B.

1 0

x y z

   

. C.

1 0

 

. D.

1 0

 

Hướng dẫn giải

Mặt phẳng song song với mặt phẳng

( )

Oxy

và đi qua

(1;1;1)

nhận

(0;0;1)

k 



làm vectơ pháp tuyến

nên có phương trình là

1 0

 

Chọn D.

Ví dụ 5: Cho mặt phẳng





: 2 2 0.

Q x y z

   

Viết phương trình mặt phẳng

( )

song song với mặt

phẳng





đồng thời cắt các trục

Ox Oy

lần lượt tại các điểm

M N

sao cho

2 2

MN  .

( ) : 2 2 0

P x y z

   

. B.

( ) : 2 0

P x y z

  

( ) : 2 2 0.

P x y z

   

( ) : 2 2 0

P x y z

   

Hướng dẫn giải

TOANMATH.com

Trang 6

( ) / /( )

P Q

nên phương trình mặt phẳng

( )

có dạng

2 0 ( 2).

x y z D D

     

Khi đó mặt phẳng

( )

cắt các trục

Ox Oy

lần lượt tại các điểm

( ;0;0)

M D



(0; ;0)

N D

Từ giả thiết:

2 2 2 2 2 2 (do 2).

MN D D D

      

Vậy phương trình mặt phẳng

( ) : 2 2 0

P x y z

   

Chọn A.

Chú ý: Mặt phẳng







đi qua điểm





0 0 0

; ;

M x y z

và song song với mặt phẳng

( ) : 0

Ax By Cz D

   



thì







có phương trình là













0 0 0

A x x B y y C z z

     

Ví dụ 6: Cho điểm

(1;2;5).

Mặt phẳng

( )

đi qua điểm

cắt trục tọa độ

, ,

Ox Oy Oz

tại

, ,

A B C

sao

cho

là trực tâm tam giác

ABC

Phương trình mặt phẳng

( )

là

8 0

x y z

   

. B.

2 5 30 0

x y z

   

. C.

5 2 1

x y z

  

. D.

5 2 1

x y z

  

Hướng dẫn giải

Ta có

( ) ( ) (1)

OA BC

OA OBC BC OAM BC OM

AM BC





     







Tương tự

(2)

AB OM



Từ (1) và (2) suy ra

( )

OM ABC



hay

( )

OM P



Suy ra

(1;2;5)

OM 



là vectơ pháp tuyến của

( )

Vậy phương trình mặt phẳng





là









1 2 2 5 5 0 2 5 30 0.

x y z x y z

          

Chọn B.

Ví dụ 7: Cho tứ diện

ABCD

có đỉnh

(8; 14; 10); , ,

A AD AB AC

 

lần lượt song song với

, , .

Ox Oy Oz

Phương trình mặt phẳng





BCD

đi qua

(7; 16; 15)

 

là trực tâm

BCD



có phương trình là

2 5 100 0

x y z

   

. B.

2 5 100 0

x y z

   

7 16 15

x y z

  

 

. D.

7 16 15

x y z

  

 

Hướng dẫn giải

Theo đề ra, ta có

( )

BCD

đi qua

(7; 16; 15),

 

nhận

(1;2;5)

HA 



là vectơ pháp tuyến. Phương trình

mặt phẳng





BCD

là

( 7) 2( 16) 5( 15) 0

2 5 100 0.

x y z

     

    

Vậy

( ) : 2 5 100 0

BCD x y z

   

Chọn B.

TOANMATH.com

Trang 7

Bài toán 2. Viết phương trình mặt phẳng biết một điểm thuộc mặt phẳng và tìm được một cặp

vectơ chỉ phương

Phương pháp giải

Mặt phẳng

( )



đi qua điểm





0 0 0

; ;

M x y z

có cặp vectơ chỉ phương

, .

a b



Khi đó một vectơ pháp tuyến

của

( )



là

[ , ].

n a b





 

Ví dụ: Mặt phẳng

( )

đi qua điểm

(0;2; 2)



và nhận vectơ

(2,0,1), ( 1,1,0)

a b 



là hai vectơ chỉ

phương.

Suy ra





có vectơ pháp tuyến là:

[ , ] (1;1; 2)

n a b

  



 

Từ đó ta có

( ) : 2 6 0

P x y z

   

Ví dụ mẫu

Ví dụ 1: Cho hai điểm

(1; 1;5), (0;0;1)

A B



. Mặt phẳng

( )

chứa

A B

và song song với trục

có

phương trình là

4 1 0

x z

  

. B.

4 1 0

x y z

   

. C.

2 5 0

x z

  

. D.

4 1 0

x z

  

Hướng dẫn giải

Do mặt phẳng

( )

chứa

A B

và song song với trục

nên vectơ pháp tuyến của

( )

là

[ ; ] (4;0; 1)

n AB j

  





Phương trình mặt phẳng

( )

là:

4( 0) 0( 0) 1( 1) 0 4 1 0

x y z x z

         

Chọn A.

Ví dụ 2: Trong không gian với hệ tọa độ

Oxyz

cho hai điểm









1;2; 1 ; 2;1;0

A B và mặt phẳng

( ) : 2 3 1 0.

P x y z

   

Gọi

( )

là mặt phẳng chứa

;

A B

và vuông góc với

( ).

Phương trình mặt phẳng

( )

là

2 5 3 9 0

x y z

   

. B.

2 3 7 0

x y z

   

2 5 0

x y z

   

. D.

2 6 0

x y z

   

Hướng dẫn giải

Phương trình mặt phẳng





chứa

và vuông góc với mặt phẳng

( )

nên có cặp vectơ chỉ phương

là

(1; 1;1)

AB  



và

(2;1; 3)

 



Suy ra

[ ; ] (2;5;3)

Q P

n AB n 

  

Mặt phẳng

( )

đi qua

(1;2; 1)



nên

2( 1) 5( 2) 3( 1) 0

x y z

     

2 5 3 9 0

x y z

    

Chọn A.

Chú ý: Mặt phẳng

( )



chứa một đường thẳng





và vuông góc với một mặt phẳng







+) Xác định vectơ chỉ phương



của

( )

và vectơ pháp tuyến





của







TOANMATH.com

Trang 8

Một vectơ pháp tuyến của

( )



là:

n u n

 



 



  

+) Lấy một điểm M thuộc d thì

( )





Ví dụ 3: Mặt phẳng

( )



đi qua gốc tọa độ

và vuông góc với hai mặt phẳng

( ) : 7 0,( ) :3 2 12 5 0

P x y z Q x y z

       

có phương trình là

2 3 0

x y z

  

. B.

10 15 5 2 0

x y z

   

. C.

10 15 5 2 0

x y z

   

. D.

2 3 0

x y z

  

Hướng dẫn giải

Ta có

( ) : 7 0

P x y z

   

có vectơ pháp tuyến là

(1; 1;1)

 



và

( ) : 3 2 12 5 0

Q x y z

   

có vectơ pháp tuyến là

(3;2; 12)

n  



( ) ( )





và

( ) ( )





nên

( )



có vectơ pháp tuyến là

1 2

[ ; ] (10;15;5)

n n n 

 



Vậy

( )



có phương trình

10 15 5 0 2 3 0

x y z x y z

      

Chọn D.

Chú ý: Mặt phẳng







đi qua điểm

và vuông góc với hai mặt phẳng cắt nhau









, :

 

Chọn vectơ

pháp tuyến của







là:

n n n

 



 





  

Ví dụ 4: Trong không gian với hệ tọa độ

Oxyz

cho ba điểm

(0;1;2), (2; 2;1)

A B



( 2;1;0).



Khi đó,

phương trình mặt phẳng

( )

ABC

là

ax y z d

   

Hãy xác định

và

1, 1

a d

 

. B.

6, 6

a d

  

. C.

1, 6

a d

   

. D.

6, 6

a d

  

Hướng dẫn giải

Ta có:









2; 3; 1 ; 2;0; 2 .

AB AC

     

 

 

3 1 1 2 2 3

; ; ; 6;6; 6 .

0 2 2 2 2 0

AB AC

     

 

  

 

 

   

 

 

Chọn

 

; 1;1; 1

n AB AC

 

  

 

  

là một vectơ pháp tuyến của mặt phẳng





ABC

Ta có phương trình mặt phẳng





ABC

là:

1 2 0 1 0.

x y z x y z

         

Vậy

1, 1.

a d

 

Chọn A.

Chú ý: Mặt phẳng







đi qua ba điểm không thẳng hàng

, , .

A B C

Khi đó ta có thể xác định một vectơ

pháp tuyến của







là:

, .

n AB AC

 



 

  

TOANMATH.com

Trang 9

Ví dụ 5: Trong không gian

Oxyz

biết mặt phẳng

5 0

ax by cz

   

qua hai điểm

(3;1; 1), (2; 1;4)

A B

 

và vuông góc với

( ) : 2 3 4 0

P x y z

   

Giá trị của

a b c

 

bằng

A. 9. B. 12. C. 10. D. 8.

Hướng dẫn giải

Gọi

( ) : 5 0.

ax by cz

   



Ta có

( 1; 2;5), (2; 1;3)

AB n    

 

Mặt phẳng

( )



nhận

[ , ] ( 1;13;5)

n AB n  

 



làm vectơ pháp tuyến nên

( )



có dạng

13 5 0

x y z D

    

Mặt phẳng

( )



qua

(3;1; 1)



nên

3 13.1 5.( 1) 0 5

D D

        

( ) : 13 5 5 0

x y z

     



hay

( ) : 13 5 5 0

x y z

   



Suy ra

1; 13; 5

a b c

    

Vậy

a b c

  

Chọn A.

Bài toán 3. Lập phương trình mặt phẳng liên quan đến khoảng cách

Phương pháp giải

Sử dụng các công thức liên quan đến khoảng cách:

Khoảng cách từ điểm





0 0 0

, ,

M x y z

đến mặt phẳng

( ) : 0

ax by cz d

   



là

0 0 0

2 2 2

d( ,( ))

ax by cz d

a b c

  



 



Chú ý: Khoảng cách giữa hai mặt phẳng song song: d

[( ),( )] d[ ,( )]



  

trong đó điểm

( )





Ví dụ mẫu

Ví dụ 1: Trong không gian với hệ tọa độ

Oxyz

lập phương trình của các mặt phẳng song song với mặt

phẳng

( ) : 3 0

x y z

   



và cách

( )



một khoảng bằng

6 0; 0

x y z x y z

      

. B.

6 0

x y z

   

6 0; 0

x y z x y z

      

. D.

6 0; 0

x y z x y z

      

Hướng dẫn giải

Gọi

( )



là mặt phẳng cần tìm. Ta có

(0;0;3) ( )





( ) / /( )

 

nên phương trình của mặt phẳng

( )



có dạng:

x y z m

   

với



Ta có

| 3|

d(( ),( )) 3 d( ,( )) 3 3



    

  

| 3| 3





   







(thỏa mãn).

Vậy phương trình của các mặt phẳng cần tìm là

TOANMATH.com

Trang 10

6 0

x y z

   

và

x y z

  

Chọn A.

Ví dụ 2: Trong không gian

Oxyz

cho hai mặt phẳng

( ) : 3 2 0,( ) : 3 4 0

P x z Q x z

     

Mặt phẳng song song và cách đều

( )

và

( )

có phương trình là:

3 1 0

x z

  

. B.

3 2 0

x z

  

. C.

3 6 0

x z

  

. D.

3 6 0

x z

  

Hướng dẫn giải

Điểm

( ; ; )

M x y z

bất kỳ cách đều

( )

và

( ) ( ;( )) ( ;( ))

Q d M P d M Q

 

3 2 3 4

| 3 2 | | 3 4 |

3 2 3 4

1 9 1 9

2 4

3 1 0.

3 1 0

x z x z

x z

    



   

  



     

 



 



    



  



Vậy

thuộc

( ) : 3 1 0.

x z

  



Nhận thấy

( )



song song với

( )

và

( )

Chọn A.

Ví dụ 3: Trong không gian với hệ tọa độ

Oxyz

cho hai điểm









1;2;1 , 3;4;0

A B và mặt phẳng

( ) : 46 0

P ax by cz

   

. Biết rằng khoảng cách từ

A B

đến mặt phẳng

( )

lần lượt bằng 6 và 3. Giá trị

của biểu thức

T a b c

  

bằng



C. 3. D. 6.

Hướng dẫn giải

Gọi

H K

lần lượt là hình chiếu của

A B

trên mặt phẳng

( )

Theo giả thiết, ta có:

3, 6, 3

AB AH BK

  

Do đó

A B

ở cùng phía với mặt phẳng

( )

Lại có:

AB BK AK AH

  

Mà

AB BK AH

 

nên

H K



Suy ra

, ,

A B H

là ba điểm thẳng hàng và

là trung điểm của

nên tọa độ

(5;6; 1)



Vậy mặt phẳng

( )

đi qua

(5;6; 1)



và nhận

(2;2; 1)

 



là vectơ pháp tuyến nên có phương

trình là

2( 5) 2( 6) 1( 1) 0 2 2 23 0

x y z x y z

          

Theo bài ra, ta có

( ) : 4 4 2 46 0

P x y z

    

nên

4, 4, 2

a b c

    

Vậy

T a b c

    

Chọn B.

Bài toán 4. Viết phương trình mặt phẳng liên quan đến mặt cầu

Phương pháp giải

Viết phương trình mặt phẳng







tiếp xúc với mặt cầu (S) tại điểm

Giả sử mặt cầu





có tâm

và bán kính

khi đó ta viết được phương trình mặt phẳng

( )



đi qua

và có một vectơ pháp tuyến là

n IH







Ví dụ: Trong không gian với hệ trục

Oxyz

cho mặt cầu

2 2 2

( ) : ( 1) ( 2) 9

S x y z

    

TOANMATH.com

Trang 11

Gọi

( )



là mặt phẳng tiếp xúc với mặt cầu tại điểm

(1;3;2)

và

(1;0;2)

là tâm của mặt cầu

( ).

Mặt

phẳng

( )



nhận

(0;3;0)

IA 



làm vectơ pháp tuyến. Mặt khác, mặt phẳng

( )



đi qua điểm

(1;3;2)

nên

có phương trình tổng quát là

3 0

 

Ví dụ mẫu

Ví dụ 1: Trong không gian với hệ tọa độ

Oxyz

cho mặt cầu





có phương trình

2 2 2

( 1) ( 2) ( 3) 12

x y z

     

và mặt phẳng

( ) : 2 2 3 0.

P x y z

   

Viết phương trình mặt phẳng song

song với

( )

và cắt

( )

theo thiết diện là đường tròn

( )

sao cho khối nón có đỉnh là tâm mặt cầu và

đáy là hình tròn (C) có thể tích lớn nhất.

2 2 2 0

x y z

   

hoặc

2 2 8 0

x y z

   

2 2 1 0

x y z

   

hoặc

2 2 11 0

x y z

   

2 2 6 0

x y z

   

hoặc

2 2 3 0

x y z

   

2 2 2 0

x y z

   

hoặc

2 2 2 0

x y z

   

Hướng dẫn giải

Ta có

( ) / /( )



nên

( ) : 2 2 0 ( 3).

x y z d d

     



Mặt cầu





có tâm

(1; 2;3),



bán kính

2 3

R  .

Gọi





là khối nón thỏa mãn đề bài với đường sinh

2 3.

IM R 

Đặt

( ,( )).

x h d I

 



Khi đó bán kính đường tròn đáy hình nón là

r x

 

Thể tích khối nón là

 

( )

V x x

 



với

0 2 3

x  .

Xét hàm số:

 

( ) 12

f x x x

 



với

0 2 3

x  .

Khi đó

( )

f x

đạt giá trị lớn nhất tại



hay

( ,( )) 2

d I





Ta có

2 2 2

5 6 11

| 2.1 2 ( 2) 3 |

( ,( )) 2 2

5 6 1

2 2 ( 1)

d d

d I

d d



  



    

    



    

  





Chọn B.

Chú ý: Công thức tính thể tích hình nón:

TOANMATH.com

Trang 12

1 1

.2 .

3 3

V hS R h

 



Trong đó

là bán kính đáy, h là chiều cao.

Ví dụ 2: Trong không gian

Oxyz

cho mặt cầu (S):

2 2 2

( 1) 4

x y z

   

và điểm

(2;2;2).

Từ

kẻ ba

tiếp tuyến

, ,

AB AC AD

với mặt cầu

( , ,

B C D

là các tiếp điểm). Phương trình mặt phẳng





BCD

là

2 2 1 0

x y z

   

. B.

2 2 3 0

x y z

   

2 2 1 0

x y z

   

. D.

2 2 5 0

x y z

   

Hướng dẫn giải

Ta có mặt cầu





có tâm

(0;0;1) và bán kính



, ,

AB AC AD

là ba tiếp tuyến của mặt cầu

( )

với

, ,

B C D

là các tiếp điểm nên

AB AC AD

IB IC ID R

 







  



là trục của đường tròn ngoại tiếp

BCD



( )

IA BCD

 

Khi đó mặt phẳng





BCD

có một vectơ pháp tuyến

(2;2;1)

n IA 





Gọi

là tâm của đường tròn ngoại tiếp

BCD J IA

  

và

IJ BJ



Ta có

IBA



vuông tại

và

BJ IA



nên

4 4

3 9

IB IJ IA IJ IJ IA

     

 

Đặt

( ; ; ).

J x y z

Ta có

( ; ; 1); (2;2;1)

IJ x y z IA  

 

Từ

IJ IA



 

suy ra

8 8 13

; ;

9 9 9

 

 

 

Mặt phẳng

( )

BCD

đi qua

8 8 13

; ;

9 9 9

 

 

 

và nhận vectơ pháp tuyến

(2;2;1)





có phương trình:

8 8 13

2 2 0 2 2 5 0

9 9 9

x y z x y z

     

          

     

     

Chọn D.

Ví dụ 3: Trong không gian

Oxyz

cho mặt cầu





2 2 2

( 1) ( 1) ( 1) 12

x y z

     

và mặt phẳng

( ) : 2 2 11 0.

P x y z

   

Xét điểm

di động trên

( )

và các điểm

, ,

A B C

phân biệt di động trên





sao cho

, ,

AM BM CM

là các tiếp tuyến của





Mặt phẳng





ABC

luôn đi qua điểm cố định nào dưới

đây?

1 1 1

; ;

4 2 2

 

 

 

 

. B.

(0; 1;3)



. C.

;0;2

 

 

 

. D.





0;3; 1



Hướng dẫn giải

Mặt cầu





có tâm

(1;1;1) và bán kính

2 3

R  .

TOANMATH.com

Trang 13

Xét điểm

( ; ; ) ( ); ( ; ; ) ( )

M a b c P A x y z S

 

nên ta có hệ điều kiện:

2 2 2

( 1) ( 1) ( 1) 12

2 2 11 0

x y z

AI AM IM

a b c



     



 





   



2 2 2

2 2 2 2 2 2

( 1) ( 1) ( 1) 12 (1)

12 ( ) ( ) ( ) ( 1) ( 1) ( 1) (2)

2 2 11 0 (3)

x y z

x a y b z c a b c

a b c

     

           

 



 











Lấy (1)

(2)



ta có:

2 2 2 2 2 2

( 1) ( 1) ( 1) 12 ( ) ( ) ( )

x y z x a y b z c

 

           

 

2 2 2

12 ( 1) ( 1) ( 1)

a b c

 

      

 

( 1) ( 1) ( 1) 9 0

a x b y c z a b c

          

Vậy mặt phẳng đi qua ba tiếp điểm là:

( ) : ( 1) ( 1) ( 1) 9 0

Q a x b y c z a b c

         

Kết hợp với (3) suy ra mặt phẳng này luôn đi qua điểm cố định (0;3;-1).

Chọn D.

Bài toán 5. Phương trình mặt phẳng đoạn chắn

Phương pháp giải

Phương trình mặt phẳng

( )



đi qua ba điểm

( ;0;0), (0; ;0)

A a B b

và

(0;0; )

C c

với

abc



là:

x y z

a b c

  

Ví dụ: Phương trình mặt phẳng

( )



đi qua ba điểm

(1;0;0), (0;2;0)

A B

và

(0;0;3)

là:

1 2 3

x y z

  

Ví dụ mẫu

Ví dụ 1: Trong không gian

Oxyz

cho điểm M

(1;2;3)

. Gọi

, ,

A B C

lần lượt là hình chiếu vuông góc của

điểm M lên các trục

, , .

Ox Oy Oz

Phương trình mặt phẳng

( )

ABC

là

1 2 3

x y z

  

. B.

1 2 3

x y z

  

. C.

1 2 3

x y z

  

. D.

1 2 3

x y z

   

Hướng dẫn giải

Ta có

(1;0;0), (0;2;0), (0;0;3)

A B C

lần lượt là hình chiếu của

lên

, , .

Ox Oy Oz

Phương trình mặt

phẳng

( )

ABC

có dạng

1 2 3

x y z

  

Chọn A.

Ví dụ 2: Trong không gian với hệ trục tọa độ

Oxyz

cho hai điểm

(3;0;0), (2;2;2)

M N

. Mặt phẳng

( )

thay đổi qua

M N

cắt các trục

Oy Oz

lần lượt tại

(0; ;0), (0;0; )

B b C c

với

, 0.

b c



Hệ thức nào dưới đây

là đúng?

TOANMATH.com

Trang 14

b c

 

. B.

3( )

bc b c

 

. C.

bc b c

 

. D.

1 1 1

b c

 

Hướng dẫn giải

Mặt phẳng

( )

đi qua

(3;0;0), (0; ;0), (0;0; )

M B b C c

với

, 0

b c



nên phương trình mặt phẳng

( )

theo đoạn chắn là:

x y z

b c

  

Mặt phẳng

( )

đi qua

(2;2;2)

suy ra

2 2 2 1 1 1

3 6

b c b c

     

Chọn D.

Ví dụ 3: Trong không gian

Oxyz

cho điểm





1;4;3 .

G Phương trình mặt phẳng cắt các trục tọa độ

, ,

Ox Oy Oz

lần lượt tại

, ,

A B C

sao cho

là trọng tâm tứ diện

OABC

là

3 12 9

x y z

  

. B.

4 16 12

x y z

  

3 12 9 78 0

x y z

   

. D.

4 16 12 104 0

x y z

   

Hướng dẫn giải

Giả sử

( ,0,0); (0, ,0); (0;0; )

A a B b C c

(1;4;3)

là trọng tâm tứ diện

A B C D

x x x x

y y y y

OABC y

z z z z

  







  



 





  









0 0 0 4.1 4

0 0 0 4.4 16

0 0 0 4.3 12

a a

b b

c c



    



 

      

 

 

    



Ta có phương trình mặt phẳng

( )

ABC

là:

4 16 12

x y z

  

Chọn B.

Ví dụ 4: Trong không gian với hệ tọa độ

Oxyz

Viết phương trình mặt phẳng





đi qua điểm

(1;2;3)

và cắt các trục

, ,

Ox Oy Oz

lần lượt tại ba điểm

, ,

A B C

khác với gốc tọa độ

sao cho biểu thức

2 2 2

1 1 1

OA OB OC

  có giá trị nhỏ nhất.

( ) : 2 14 0

P x y z

   

. B.

( ) : 2 3 14 0

P x y z

   

( ) : 2 3 11 0

P x y z

   

. D.

( ) : 3 14 0

P x y z

   

Hướng dẫn giải

Gọi

là trực tâm

ABC



Ta có

 

( ) 1 .

BH AC

AC OBH AC OH

OB AC





   







TOANMATH.com

Trang 15

Chứng minh tương tự, ta có:

BC OH







Từ (1), (2) ta có

( )

OH ABC



Suy ra

2 2 2 2

1 1 1 1

OA OB OC OH

   .

Vậy để biểu thức

2 2 2

1 1 1

OA OB OC

 

đạt giá trị nhỏ nhất thì

đạt giá trị lớn nhất. Mà

OH OM



nên

đạt giá lớn nhất bằng

hay

H M



Khi đó

( )

OM ABC



nên

( )

có một vectơ pháp tuyến là

(1;2;3)

OM 



Phương trình mặt phẳng

( )

là

1( 1) 2( 2) 3( 3) 0 2 3 14 0

x y z x y z

          

Chọn B.

Ví dụ 5: Trong không gian

Oxyz

có bao nhiêu mặt phẳng qua điểm





4; 4;1

M  và chắn trên ba trục tọa

độ

, ,

Ox Oy Oz

theo ba đoạn thẳng có độ dài theo thứ tự lập thành cấp số nhân có công bội bằng

A. 1. B. 2. C. 3. D. 4.

Hướng dẫn giải

Gọi

( ;0;0), (0; ;0), (0;0; )

A a B b C c

với

abc



là giao điểm của mặt phẳng

( )

và các trục toạ độ. Khi

đó

( )

có phương trình là

x y z

a b c

  

Theo giả thiết ta có:

4 4 1

8, 4, 2

( )

8, 4, 2

1 1

| | | | | |

16, 8, 4

2 4

a b c

M P

a b c

OC OB OA

c b a

a b c



    





  



 



      

 



 

 

 



   







Vậy có ba mặt phẳng thỏa mãn.

Chọn C.

Ví dụ 6: Trong không gian với hệ toạ độ

Oxyz

cho các điểm









1;0;0 , 0;1;0 .

A B Mặt phẳng

x ay bz c

   

đi qua các điểm

A B

đồng thời cắt tia

tại

sao cho tứ diện

OABC

có thể tích

bằng

Giá trị của

3 2

a b c

 

là

A. 16. B. 1. C. 10. D. 6.

Hướng dẫn giải

Mặt phẳng đi qua các điểm

A B

đồng thời cắt tia

tại





0;0;

C t

với



có phương trình là

1 1

x y z

  

Mặt khác:

OABC

1 1

6 6

V  

OA.OB.OC

  

Vậy phương trình mặt phẳng cần tìm có dạng

1 1 0

1 1 1

x y z

       

TOANMATH.com

Trang 16

Vậy

1, 1

a b c

   

Suy ra

3 2 1 3.1 2 6

a b c

     

Chọn D.

Bài tập tự luyện dạng 1

Câu 1: Trong không gian

Oxyz

cho mặt phẳng





có phương trình

2 3 0

x y z

   

. Vectơ pháp

tuyến của mặt phẳng





là





1;1; 2 .

  



(1;1; 2)

 



. C.

( 1;2; 3)

  



. D.

(1;2; 3)

 



Câu 2: Cho ba điểm

(2;1; 1), ( 1;0;4), (0; 2; 1).

A B C

   

Phương trình mặt phẳng đi qua

và vuông góc

với

là

2 5 5 0

x y z

   

. B.

2 5 5 0

x y z

   

2 5 0

x y

  

. D.

2 5 5 0

x y z

   

Câu 3: Trong không gian với hệ tọa độ

Oxyz

cho điểm





3;2;1 .

M Mặt phẳng





đi qua

và cắt các

trục tọa độ

, ,

Ox Oy Oz

lần lượt tại các điểm

, ,C

A B

không trùng với gốc tọa độ sao cho

là trực tâm

tam giác

ABC

Trong các mặt phẳng sau, mặt phẳng song song với mặt phẳng





là

3 2 14 0

x y z

   

. B.

2 9 0

x y z

   

3 2 14 0

x y z

   

. D.

2 3 9 0

x y z

   

Câu 4: Trong không gian với hệ trục tọa độ

Oxyz

cho mặt phẳng

( ) : 2 2 5 0

P x y z

   

và hai điểm

( 3;0;1), (0; 1;3).

A B

 

Phương trình mặt phẳng

( )

đi qua

và song song với mặt phẳng

( )

là

2 2 1 0

x y z

   

. B.

2 2 1 0

x y z

   

. C.

2 2 1 0

x y z

   

. D.

2 2 1 0

x y z

   

Câu 5: Trong không gian

Oxyz

cho

(0;1;1), (1;0;0)

A B

và mặt phẳng

( ) : 3 0. ( )

P x y z Q

   

là mặt

phẳng song song với

( )

đồng thời đường thẳng

cắt

( )

tại

sao cho

CA CB



. Mặt phẳng





có phương trình là:

x y z

   

hoặc

x y z

  

. B.

x y z

  

x y z

   

. D.

2 0

x y z

   

hoặc

x y z

  

Câu 6: Trong không gian

Oxyz

phương trình mặt phẳng





song song và cách mặt phẳng

( ) : 2 2 3 0

Q x y z

   

một khoảng bằng 1 đồng thời

( )

không đi qua

là

2 2 1 0

x y z

   

. B.

2 2 0

x y z

  

2 2 6 0

x y z

   

. D.

2 2 3 0

x y z

   

Câu 7: Trong không gian

Oxyz

cho

(2;0;0), (0;4;0), (0;0;6), (2;4;6).

A B C D

Gọi

( )

là mặt phẳng song

song với

( )

ABC

, cách đều

và mặt phẳng

( )

ABC

. Phương trình của

( )

là

6 3 2 24 0

x y z

   

. B.

6 3 2 12 0

x y z

   

6 3 2 0

x y z

  

. D.

6 3 2 36 0

x y z

   

TOANMATH.com

Trang 17

Câu 8: Trong không gian

Oxyz

cho ba điểm













3;2;3 , 2;1;2 , 4;1;6 .

A B C Phương trình mặt phẳng

( )

ABC

là

2 1 0

x y z

   

. B.

2 0

x y z

   

2 7 0

x y z

   

. D.

2 0

x y z

   

Câu 9: Trong không gian

Oxyz

cho điểm





1;2;3 .

M Viết phương trình mặt phẳng





đi qua

cắt

các trục

, ,

Ox Oy Oz

lần lượt tại

, ,

A B C

sao cho

là trọng tâm tam giác

ABC

( ) : 6 3 2 18 0

P x y z

   

. B.

( ) : 6 3 2 6 0

P x y z

   

( ) : 6 3 2 18 0

P x y z

   

. D.

( ) : 6 3 2 6 0

P x y z

   

Câu 10: Trong không gian

Oxyz

cho điểm





1; 3; 2 .

M  Hỏi có bao nhiêu mặt phẳng đi qua

và cắt

các trục toạ độ tại

, ,

A B C

mà

OA OB OC

  

A. 3. B. 1. C. 4. D. 2.

Câu 11: Trong không gian

Oxyz

cho mặt cầu

2 2 2

( ) : 2 4 6 2 0.

S x y z x y z

      

Viết phương trình

mặt phẳng

( )



chứa

cắt mặt cầu

( )

theo thiết diện là đường tròn có chu vi bằng

8 .



( ) :3 0

x z

 



. B.

( ) :3 0

x z

 



. C.

( ) : 3 0

x z

 



. D.

( ) :3 2 0

x z

  



Bài tập nâng cao

Câu 12: Cho điểm









4; 7; 5 , 3; 9; 10

M N



    và các đường thẳng

1 2 3

, ,

d d

cùng đi qua điểm

và

lần lượt song song với

, , .

Ox Oy Oz

Mặt phẳng







đi qua



cắt

1 2 3

, ,

d d d

lần lượt tại

, ,

A B C

  

sao cho



là trực tâm

A B C

  



Phương trình mặt phẳng







là

2 5 35 0

x y z

   

. B.

2 5 35 0

x y z

   

4 7 5

x y z

  

 

. D.

4 7 5

x y z

  

 

Câu 13: Trong không gian với hệ tọa độ

Oxyz

cho các điểm













1;0;0 , 0;2;0 , 0;0;1 .

A B C Xét ba mặt

cầu tiếp xúc ngoài đôi một với nhau và tiếp xúc với mặt phẳng





ABC

lần lượt tại

, , .

A B C

Tổng diện tích

của ba mặt cầu trên là:



. B.



. C.



. D.



Câu 14: Trong không gian tọa độ

Oxyz

cho mặt phẳng

( ) : 2 1 0

P x y z

   

, các điểm

(0;1;1), (1;0;0)

A B

với

và

nằm trên mặt phẳng

( )

và mặt cầu

2 2 2

( ) : ( 2) ( 1) ( 2) 4.

S x y z

     

là một đường kính thay đổi của

( )

sao cho

/ /( )

CD P

và bốn điểm

, , ,

A B C D

tạo thành một tứ diện.

Giá trị lớn nhất của thể tích tứ diện

ABCD

bằng

2 2

. B.

2 3

. C.

2 5

. D.

2 6

Dạng 2. Vị trí tương đối giữa hai mặt phẳng, giữa mặt cầu và mặt phẳng

Bài toán 1. Vị trí tương đối giữa hai mặt phẳng

Phương pháp giải

Cho hai mặt phẳng:

( ) : 0

P Ax By Cz D

   

;

TOANMATH.com

Trang 18





: 0

P A x B y C z D

    

   

Khi đó:



( )

cắt





: : : : .

P A B C A B C

   

 



 

( ) / /

A B C D

P P

A B C D



   

   



 

( )

A B C D

P P

A B C D



    

   







   

( ) ( )

( ) 0

P P

P P n n n n

 



    

   

AA BB CC

  

   

Chú ý:

 Nếu



thì tương ứng





 Nếu



thì tương ứng





 Nếu



thì tương ứng





Ví dụ: Trong không gian với hệ trục toạ độ

Oxyz

cho hai mặt phẳng

( ) : 2 1 0

x y z

   



và

( ) : 2 4 2 0

x y mz

   



Tìm

để







và







song song với nhau.

Hướng dẫn giải

Ta có

1 2 1 1

( ) / /( )

2 4 2

 

   

 

 

(vô lý vì

2 4 2

1 2 1



 



Vậy không tồn tại

để hai mặt phẳng









 

song song với nhau.

Ví dụ mẫu

Ví dụ 1: Trong không gian

Oxyz

mặt phẳng

( ) : 2 2 0

P x y z

   

vuông góc với mặt phẳng nào dưới

đây?

2 2 0

x y z

   

. B.

2 0

x y z

   

. C.

2 0

x y z

   

. D.

2 2 0

x y z

   

Hướng dẫn giải

Mặt phẳng

( )

có một vectơ pháp tuyến là

(2;1;1)

n 



Mặt phẳng

( ) : 2 0

Q x y z

   

có một vectơ pháp tuyến

(1; 1; 1)

  



Mà

2 1 1 0 ( ) ( )

P Q P Q

n n n n P Q

        

   

Vậy mặt phẳng

2 0

x y z

   

là mặt phẳng cần tìm.

Chọn B.

Ví dụ 2: Trong không gian với hệ tọa độ

Oxyz

cho mặt phẳng





có phương trình

( 1) 10 0

mx m y z

    

và mặt phẳng

( ) : 2 2 3 0

Q x y z

   

Với giá trị nào của

thì

( )

và

( )

vuông góc với nhau?

TOANMATH.com

Trang 19

 

. B.



. C.



. D.

 

Hướng dẫn giải

( ) : ( 1) 10 0

P mx m y z

    

có vectơ pháp tuyến

( ; 1;1)

n m m

 



( ) : 2 2 3 0

Q x y z

   

có vectơ pháp tuyến

(2;1; 2)

 



1 2

( ) ( ) 0 2 1 2 0 1

P Q n n m m m

          

 

Chọn C.

Bài toán 2. Vị trí tương đối giữa mặt cầu và mặt phẳng

Phương pháp giải

Cho mặt phẳng

( ) : 0

Ax By Cz D

   



và mặt cầu tâm

;

bán kính



( )



và

( )

không có điểm chung

( ,( ))

d I R

 





( )



tiếp xúc với

( ) ( ,( )) .

S d I R

 



Khi đó

( )



là tiếp diện.



( )



và

( )

cắt nhau

( ;( ))

d I R

 



Khi đó





có tâm là hình chiếu của

trên







và bán kính

2 2

( ;( ))

r R d I 



Ví dụ mẫu

Ví dụ 1: Trong không gian

Oxyz

cho mặt cầu

2 2 2

( ) : 6 4 12 0

S x y z x y

     

Mặt phẳng nào cắt





theo một đường tròn có bán kính



4 3 4 26 0

x y z

   

. B.

2 2 12 0

x y z

   

3 4 5 17 20 2 0

x y z

    

. D.

3 0

x y z

   

Hướng dẫn giải

Phương trình mặt cầu





là

2 2 2

6 4 12 0.

x y z x y

     

Suy ra tâm





3; 2;0

I  và bán kính



Ta gọi khoảng cách từ tâm

của mặt cầu tới các mặt phẳng ở các đáp án là h, khi đó để mặt phẳng cắt

mặt cầu





theo một đường tròn có bán kính



thì

2 2

25 9 4

h R r

    

Đáp án A loại vì

|18 4 26 |



 

Đáp án B loại vì

 

Chọn đáp án C vì



Đáp án D loại vì

1 3



 

Chọn C.

Ví dụ 2: Trong không gian với hệ tọa độ

Oxyz

cho điểm





1;2; 2



và mặt phẳng

TOANMATH.com

Trang 20

( ) : 2 2 5 0.

P x y z

   

Phương trình mặt cầu tâm

cắt mặt phẳng

( )

theo giao tuyến là một đường

tròn có diện tích bằng



là

2 2 2

( 2) ( 2) ( 1) 36

x y z

     

2 2 2

( 1) ( 2) ( 2) 9

x y z

     

2 2 2

( 1) ( 2) ( 2) 25

x y z

     

2 2 2

( 1) ( 2) ( 2) 16

x y z

     

Hướng dẫn giải

Ta có

2 2 2

| 2.1 2.2 2 5 |

( ;( )) 3

2 2 1

a d I P

  

  

 

Bán kính của đường tròn giao tuyến là:

16 4

  



Mặt cầu tâm

cắt mặt phẳng





theo giao tuyến là một đường tròn nên ta có

2 2 2

9 16 25 5

R a r R

      

Vậy phương trình mặt cầu tâm

, bán kính



là:

2 2 2

( 1) ( 2) ( 2) 25

x y z

     

Chọn C.

Ví dụ 3: Trong không gian

Oxyz

cho mặt cầu





có phương trình

2 2 2

2 4 6 2 0

x y z x y z

      

và

mặt phẳng

( ) : 4 3 12 10 0.

x y z

   



Tìm phương trình mặt phẳng







thỏa mãn đồng thời các điều

kiện: tiếp xúc với





; song song với

( )



và cắt trục

ở điểm có cao độ dương.

4 3 12 78 0

x y z

   

. B.

4 3 12 26 0

x y z

   

4 3 12 78 0

x y z

   

. D.

4 3 12 26 0

x y z

   

Hướng dẫn giải

Mặt cầu

( )

có tâm

(1;2;3),

bán kính

2 2 2

1 2 3 2 4

    

Vì

( ) / /( )

 

nên phương trình

( )



có dạng:

4 3 12 0, 10

x y z d d

    

Vì

( )



tiếp xúc mặt cầu

( )

nên

( ,( ))

2 2 2

| 4.1 3.2 12.3 |

4 | 26 | 52

4 3 ( 12)

d R d

 



  

      





  





( )



cắt trục

ở điểm có cao độ dương nên chọn



Vậy phương trình mặt phẳng

( ) : 4 3 12 78 0

x y z

   



Chọn C.

Bài tập tự luyện dạng 2

Bài tập cơ bản

Câu 1: Trong không gian

Oxyz

mặt phẳng nào dưới đây song song với mặt phẳng





Oxz





: 3 0.

P x

 

( ) : 2 0

Q y

 

. C.

( ) : 1 0

R z

 

. D.

( ) : 3 0

S x z

  

TOANMATH.com

Trang 21

Câu 2: Trong không gian

Oxyz

cho hai mặt phẳng







1 0

x y z

   

và

( ) : 2 1 0

x y mz m

    



với

là tham số thực. Giá trị của

để

( ) ( )



 

là



. B. 0. C. 1. D.



Câu 3: Trong không gian

Oxyz

có bao nhiêu số thực

để mặt phẳng (

) : 2 2 1 0

P x y z

   

song

song với mặt phẳng

( ) : 2 ( 2) 2 0?

Q x m y mz m

    

A. 1. B. 0. C. Vô số. D. 2.

Câu 4: Cho mặt cầu





có đường kính 10 cm và mặt phẳng





cách tâm mặt cầu một khoảng 4 cm.

Khẳng định nào sau đây sai?

( )

và

( )

có vô số điểm chung.

( )

tiếp xúc với

( )

cắt

( )

theo một đường tròn bán kính 3 cm.

( )

cắt

( )

Câu 5: Trong không gian

Oxyz

cho mặt cầu





2 2 2

( 2) ( 1) ( 1) 12.

x y z     

Mặt phẳng nào sau

đây cắt mặt cầu





theo giao tuyến là một đường tròn?





: 2 0

P x y z

   

. B.





: 5 0

P x y z

   





: 10 0

P x y z

   

. D.





: 10 0

P x y z

   

Câu 6: Trong không gian

Oxyz

cho mặt cầu





có phương trình

2 2 2

( 2) ( 1) ( 2) 4

x y z

     

và mặt

phẳng

( )

có phương trình

4 3 0.

x y m

  

Tìm tất cả các giá trị thực của tham số

để mặt phẳng

( )

và mặt cầu





có đúng một điểm chung.



. B.

 

hoặc

 



hoặc



. D.

 

hoặc



Câu 7: Trong không gian

Oxyz

cho mặt cầu





có phương trình

2 2 2

( 2) ( 4) ( 1) 4

x y z

     

và mặt

phẳng

( )

có phương trình

3 1 0

x my z m

    

. Tìm tất cả các giá trị thực của tham số

để mặt

phẳng

( )

cắt mặt cầu

( )

theo giao tuyến là đường tròn có đường kính bằng 2.



. B.

 

hoặc

 



hoặc



. D.

 

Bài tập nâng cao

Câu 8: Biết rằng trong không gian với hệ toạ độ

Oxyz

có hai mặt phẳng





và





cùng thoả mãn các

điều kiện sau: đi qua hai điểm





1;1;1

A và





0; 2;2

B  đồng thời cắt các trục toạ độ

Ox Oy

tại hai điểm

cách đều

Giả sử





có phương trình

1 1 1

x b y c z d

   

và





có phương trình

2 2 2

x b y c z d

   

Giá trị biểu thức

1 2 1 2

b b c c



bằng

A. 7. B.



D. 9.

TOANMATH.com

Trang 22

Câu 9: Trong không gian tọa độ

Oxyz

cho mặt phẳng













2 2

: 2 1 1 10 0

P mx m y m z

     

và điểm





2;11; 5 .



Biết khi

thay đổi thì luôn tồn tại hai mặt cầu cố định tiếp xúc với mặt phẳng





và đi

qua

Tổng bán kính hai mặt cầu đó bằng

7 2.

15 2.

5 2.

12 2.

Câu 10: Trong không gian

Oxyz

cho mặt cầu

       

2 2 2

: 1 1 1 9

S x y z

     

tiếp xúc với hai mặt

phẳng





: 2 2 4 0

P x y z

   

và





: 2 2 4 0

Q x y z

   

lần lượt tại các điểm

, .

A B

Độ dài đoạn

là

3 2.

2 3.

Dạng 3. Khoảng cách từ một điểm đến mặt phẳng

Phương pháp giải

Khoảng cách từ điểm





0 0 0 0

; ;

M x y z

đến mặt phẳng





: 0

Ax By Cz D

    

là

 

0 0 0

2 2 2

, .

Ax By Cz D

d M

A B C

  

 

 

Ví dụ: Trong không gian

Oxyz

khoảng cách từ điểm





1; 2;3

A  đến mặt phẳng





có phương trình

3 4 9 0

x y z

   

là

 





 

2 2

1 3. 2 4.3 9

4 26

, .

1 3 4

d A P

   

 

  

Ví dụ mẫu

Ví dụ 1: Trong không gian

Oxyz

khoảng cách giữa hai mặt phẳng





: 2 2 10 0

P x y z

   

và





: 2 2 3 0

Q x y z

   

bằng

B. 3. C.

Hướng dẫn giải

Vì









/ /

P Q

nên





















, ,

d P Q d A Q

 với





A P



Chọn









0;0;5

A P

 thì

 

2 2 2

0 2.0 2.5 3

1 2 2

d A Q

  

 

 

Chọn D.

Chú ý: Khoảng cách giữa hai mặt phẳng song song bằng khoảng cách từ một điểm bất kì trên mặt phẳng

này đến mặt phẳng kia.

Nếu hai mặt phẳng không song song thì khoảng cách giữa chúng bằng 0.

Ví dụ 2: Trong không gian với hệ trục toạ độ

Oxyz

cho









1;2;3 , 3;4;4 .

A B Tìm tất cả các giá trị của

tham số

sao cho khoảng cách từ điểm

đến mặt phẳng





: 2 1 0

P x y mz

   

bằng độ dài đoạn

thẳng



 

 

TOANMATH.com

Trang 23

Hướng dẫn giải

Ta có

   

2 2 2

2;2;1 2 2 1 3 1 .

AB AB     



Khoảng cách từ

đến mặt phẳng





là

2 2 2 2

| 2.1 2 3 1| | 3 3|

( ,( ))

2 1 5

m m

d A P

m m

    

 

  

(2).

Vì

 

2 2

| 3 3 |

( ,( )) 3 9 5 9( 1) 2

AB d A P m m m



        



Chọn A.

Ví dụ 3: Trong không gian

Oxyz

cho tứ diện

ABCD

với





1;2;1 ,

A 





2;1;3 ,

B 

(3;2;2), (1;1;1)

C D

 

. Độ dài chiều cao

của tứ diện bằng

3 14

. B.

. C.

4 14

. D.

3 14

Hướng dẫn giải

Ta có

(1; 1;2), (2;0;1) [ ; ] ( 1;3;2)

AB AC AB AC     

   

là một vectơ pháp tuyến của mặt phẳng

( )

ABC

Vậy phương trình mặt phẳng

( )

ABC

là

1( 1) 3( 2) 2( 1) 0 3 2 7 0

x y z x y z

            

Độ dài chiều cao

của tứ diện

ABCD

là khoảng cách từ

đến

( )

ABC

Suy ra

2 2 2

| 1.1 3.1 2.1 7 | 3 14

( ,( ))

( 1) 3 2

DH d D ABC

   

  

  

Chọn A.

Ví dụ 4: Trong không gian tọa độ

Oxyz

cho điểm





; ;

A a b c

với

, , 0.

a b c



Xét





là mặt phẳng thay

đổi đi qua điểm

. Khoảng cách lớn nhất từ điểm

đến mặt phẳng

( )

bằng

2 2 2

a b c

 

. B.

2 2 2

a b c

 

. C.

2 2 2

a b c

 

. D.

2 2 2

a b c

 

Hướng dẫn giải

Gọi

là hình chiếu vuông góc của

lên mặt phẳng





Khi đó

2 2 2

( ,( ))

d O P OH OA a b c

    

Chọn A.

Bài tập tự luyện dạng 3

Câu 1: Trong không gian

Oxyz

cho hai mặt phẳng

( ) : 2 2 10 0

P x y z

   

và

( ) : 2 2 3 0

Q x y z

   

Điểm M là giao điểm của mặt phẳng





với trục

. Khoảng cách từ

tới mặt phẳng





bằng

. B.

. C. 3. D.

TOANMATH.com

Trang 24

Câu 2: Trong không gian cho hệ trục tọa độ

Oxyz

tất cả các điểm

nằm trên

có khoảng cách đến

mặt phẳng

( ) : 2 2 2 0

P x y z

   

bằng 2 là

(0;0; 4)



. B.

(0;0;0), (0;0; 2)

M M



(0;0;2)

. D.

(0;0;2), (0;0; 4)

M M



Câu 3: Trong không gian với hệ toạ độ

Oxyz

cho mặt phẳng





: 2 2 3 0

P x y z

   

và điểm





1; 2;3 .

A  Gọi









; ;

M a b c P

 sao cho



Giá trị của

a b c

 

bằng

B. 2. C.

D. 12.

Bài tập nâng cao

Câu 4: Trong không gian với hệ toạ độ

Oxyz

cho hai điểm

 

3 3 1

1;2; 3 , ; ; .

2 2 2

A B

 

 

 

 

Gọi





là mặt

cầu tâm

bán kính bằng 3 và





là mặt cầu tâm

bán kính bằng

Gọi





là mặt phẳng tiếp xúc

với cả hai mặt cầu









1 2

, .

S S

Khoảng cách lớn nhất từ gốc toạ độ

đến mặt phẳng





bằng

58 36 61

127



11 3 61



11 2 61



63 61 89

169



Dạng 4. Góc giữa hai mặt phẳng

Phương pháp giải

Cho hai mặt phẳng









 

có phương trình:





 

1 1 1 1

2 2 2 2

: 0

: 0.

A x B y C z D

    

    

Góc giữa









 

bằng hoặc bù với góc giữa hai vectơ pháp tuyến

1 2

, .

n n

 

   







1 2

cos ,

n n

  

 

1 2 1 2 1 2

2 2 2 2 2 2

1 1 1 2 2 2

A A B B C C

A B C A B C

 



   

Chú ý:

   







0 , 90 .

o o

   

Ví dụ: Trong không gian với hệ toạ độ

Oxyz

cho mặt phẳng





có phương trình là

3 0.

x z

  

Tính

góc giữa





và mặt phẳng





Oxy

Hướng dẫn giải

Mặt phẳng





: 3 0

P x z

  

có vectơ pháp tuyến





1;0; 1

 



và mặt phẳng





Oxy

có vectơ pháp tuyến





0;0;1 .

n 



Gọi



là góc giữa mặt phẳng





và mặt phẳng





Oxy

Ta có

1 2

cos 45 .

n n

     

 

TOANMATH.com

Trang 25

Ví dụ mẫu

Ví dụ: Trong không gian

Oxyz

biết hình chiếu của

lên mặt phẳng





là điểm





2; 1; 2 .

 

Số đo góc giữa mặt phẳng





với mặt phẳng





: 5 0

Q x y

  

là

A. 30

. B. 90

. C. 60

. D. 45

Hướng dẫn giải

Gọi



là góc giữa mặt phẳng





với mặt phẳng





Ta có





2; 1; 2

  



là vectơ pháp tuyến của mặt phẳng





và





1; 1;0

n  



là vectơ pháp tuyến

của mặt phẳng





Ta có

 

. 1

cos cos , 45 .

OH n

      

 

Chọn D.

Bài tập tự luyện dạng 4

Bài tập cơ bản

Câu 1: Trong hệ trục toạ độ

Oxyz

cho điểm





2;1;2 .

H Điểm

là hình chiếu vuông góc của gốc toạ độ

xuống mặt phẳng





số đo góc giữa mặt phẳng





và mặt phẳng





: 11 0

Q x y

  

là

A. 90

. B. 30

. C. 60

. D. 45

Câu 2: Trong không gian với hệ toạ độ

Oxyz

cho mặt phẳng





có phương trình:

1 0

ax by cz

   

với



đi qua 2 điểm









0;1;0 , 1;0;0

A B và tạo với mặt phẳng





Oyz

một góc 60





5;8 .





8;11 .





0;3 .





3;5 .

Bài tập nâng cao

Câu 3: Cho khối chóp

S ABCD

có đáy là hình bình hành





120 .

BAD 

Cạnh bên

2 3

SA  vuông góc với mặt phẳng đáy





ABCD

Gọi

, ,

M N P

lần lượt là trung điểm các cạnh

SA SD

và



là góc giữa hai mặt phẳng





SAC

và





MNP

Chọn khẳng định đúng trong các khẳng định sau

đây:





60 ;90 .

o o

 B.





0 ;30 .

o o

 C.





30 ;45 .

o o

 D.





45 ;60 .

o o



Dạng 5. Một số bài toán cực trị

Ví dụ mẫu

Ví dụ 1: Trong không gian

Oxyz

cho ba điểm













1;1;1 , 1;2;0 , 3; 1;2

A B C  và

là điểm thuộc mặt

phẳng





: 2 2 7 0.

x y z

    

Tính giá trị nhỏ nhất của

3 5 7 .

P MA MB MC

  

  

min

20.



min



min

25.



min

27.



Hướng dẫn giải

TOANMATH.com

Trang 26

Gọi điểm





; ;

I x y z

sao cho

3 5 7 0.

IA IB IC

  

   

Khi đó













     

 

3 1 5 1 7 3 0

3 1 5 2 7 1 0 20 23;20; 11 .

3 1 5 0 7 2 0

x x x

y y y y I

z z z

      

 





           

 

 

 

     



Xét













3 5 7 3 5 7 .

P MA MB MC MI IA MI IB MI IC

        

        





3 5 7 .

MI IA IB IC MI MI

     

    

min

khi

ngắn nhất hay

là hình chiếu vuông góc của

lên mặt phẳng







Khi đó:

 









 

min

2 2

2. 23 20 2. 11 7

, 27.

2 1 2

P d I

    

   

  

Chọn D.

Ví dụ 2: Trong không gian với hệ trục tọa độ

Oxyz

cho hai điểm









3;5; 5 , 5; 3;7

A B   và mặt phẳng

( ) : 0.

P x y z

  

Tìm toạ độ điểm

trên mặt phẳng

( )

sao cho

2 2

MA MB



lớn nhất.

( 2;1;1)



. B.

(2; 1;1)



. C.

(6; 18;12)



. D.

( 6;18;12)



Hướng dẫn giải

Gọi

thỏa mãn

2 0.

IA IB

 

 



Khi đó

2( ) 0 2 (13; 11;19).

IO OA IO OB OI OB OA I        

      



Ta có

















 

2 2 2 2

2 2 2 2 2

2 2 2 2 .

MA MB MA MB MI IA MI IB MI IA IB

          

     

2 2

MA MB



lớn nhất khi

nhỏ nhất. Khi đó

là hình chiếu vuông góc của

lên

( )

Ta tìm được

(6; 18;12)



Chọn C.

Ví dụ 3: Trong không gian

Oxyz

cho các điểm

( ;0;0), (0; ;0), (0;0; )

M m N n P p

không trùng với gốc tọa

độ và thỏa mãn

2 2 2

m n p

  

. Giá trị lớn nhất của khoảng cách từ

đến mặt phẳng





MNP

bằng

. B.

. C.

. D.

Hướng dẫn giải

, ,

M N P

không trùng với gốc tọa độ nên

0, 0, 0

m n p

  

Phương trình mặt phẳng

( )

MNP

là:

1 1 1

1 1 0

x y z

m n p m n p

       

Suy ra

2 2 2

( ,( ))

1 1 1

d O MNP

m n p



 

Áp dụng bất đẳng thức Cô-si cho ba số dương

2 2 2

, ,

m n p

và ba số dương

2 2

1 1

n p

ta có:

TOANMATH.com

Trang 27

2 2 2 2 2 2

m n p m n p

   và

2 2 2 2 2 2

1 1 1 1

m n p m n p

   .

Suy ra

 

2 2 2

1 1 1

m n p

 

    

 

 

 

2 2 2

1 1 1

3 9 do 3

m n p

 

       

 

 

2 2 2 2 2 2

2 2 2

1 1 1 1 1 1 1 1

3 3

1 1 1 3

m n p m n p

m n p

         

 

Vậy

( ,( )) .

d O MNP 

Dấu "=" xảy ra khi và chỉ khi

2 2 2

m n p

  

Vậy giá trị lớn nhất của khoảng cách từ

đến mặt phẳng





MNP

là

Chọn C.

Ví dụ 4: Trong không gian với hệ tọa độ

Oxyz

cho mặt phẳng

( ) : 2 2 3 0

P x y z

   

và mặt cầu

2 2 2

( ) : 2 4 2 5 0.

S x y z x y z

      

Giả sử

( )

M P



và

( )

N S



sao cho



cùng phương với vectơ

(1;0;1)





và khoảng cách giữa

và

lớn nhất. Tính



. B.

1 2 2

MN  

. C.

3 2

MN 

. D.



Hướng dẫn giải





có tâm

( 1;2;1)



và bán kính



Ta có:

2 2 2

| 1 2.2 2.1 3 |

( ,( )) 2

1 2 2

d I P R

   

  

 

Gọi

là hình chiếu vuông góc của

trên mặt phẳng





và



là góc giữa

và

Vì



cùng phương với



nên góc



có số đo không đổi.

MNH



vuông tại

có



HNM

  nên

.cos .

cos

HN MN MN HN

  



Do đó

lớn nhất



lớn nhất

( ,( )) 3.

HN d I P R

   

Có

cos cos( , )

u n 







nên

3 2

cos

MN HN 



Chọn C.

Ví dụ 5: Trong không gian với hệ toạ độ

Oxyz

gọi





: 3 0

P ax by cz

   

(với

, ,

a b c

là các số nguyên

không đồng thời bằng 0) là mặt phẳng đi qua hai điểm









0; 1;2 , 1;1;3

M N  và không đi qua điểm

(0;0;2).

H Biết rằng khoảng cách từ

đến mặt phẳng

( )

đạt giá trị lớn nhất. Giá trị của tổng

2 3 12

T a b c

   

bằng



. B. 8. C. 12. D. 16.

Hướng dẫn giải

Gọi

là hình chiếu của

lên

( ),

là hình chiếu của

lên

TOANMATH.com

Trang 28

Ta có

( ;( ))

d H P HK



và

( ; ) ,

d H MN HE HK HE

 

(không đổi).

Vậy

( ;( ))

d H P

lớn nhất khi

K E



với

là hình chiếu của

lên

Suy ra

1 1 7

; ;

3 3 3

 

 

 

 

Vậy mặt phẳng

( )

cần tìm là mặt phẳng nhận

1 1 1

; ;

3 3 3

 

  

 

 



làm vectơ pháp tuyến và đi qua

có phương trình là

3 0

x y z

    

Suy ra

 





 









Vậy



Chọn D.

Bài tập tự luyện dạng 5

Bài tập cơ bản

Câu 1: Trong không gian với hệ trục toạ độ

Oxyz

cho tam giác

ABC

với





2;1;3 ,





1; 1;2 ,

B 





3; 6;1 .

C  Điểm





; ;

M x y z

thuộc mặt phẳng





Oyz

sao cho

2 2 2

MA MB MC

 

đạt giá trị nhỏ nhất.

Tính giá trị biểu thức

P x y z

  



 

Câu 2: Cho









4;5;6 ; 1;1;2 ,

A B M

là một điểm di động trên mặt phẳng





: 2 2 1 0.

P x y z

   

Khi đó

MA MB

 nhận giá trị lớn nhất là

77.

41.

C. 7. D.

85.

Câu 3: Trong không gian

Oxyz

cho mặt phẳng





:3 5 0

P x y z

   

và hai điểm









1;0;2 , 2; 1;4 .

A B 

Tập hợp các điểm

nằm trên mặt phẳng





sao cho tam giác

MAB

có diện tích nhỏ nhất.

7 4 7 0

3 5 0.

x y z

   





   



7 4 14 0

3 5 0.

x y z

   





   



7 4 7 0

3 5 0.

x y z

   





   



7 4 5 0

3 5 0.

x y z

   





   



Bài tập nâng cao

Câu 4: Trong không gian với hệ toạ độ

Oxyz

cho điểm





3; 2;4

A  và mặt phẳng

















2 2 2

: 2 4 1 2 3 1 1 0.

P m m x m m y m z m

        

Tìm giá trị lớn nhất của khoảng cách từ

đến mặt phẳng





A. 5. B.

29.

33.

21.

TOANMATH.com

Trang 29

Câu 5: Trong không gian

Oxyz

cho mặt cầu

     

2 2

: 3 6 45

S x y z

    

và





1;4;5 .

M Ba đường

thẳng thay đổi

1 2 3

, ,

d d d

nhưng luôn đôi một vuông góc với nhau tại

và cắt mặt cầu tại điểm thứ hai lần

lượt là

, , .

A B C

Khoảng cách lớn nhất từ

đến mặt phẳng





ABC

là

A. 3. B.

C. 4. D.

ĐÁP ÁN VÀ LỜI GIẢI BÀI TẬP TỰ LUYỆN

Dạng 1. Xác định vectơ pháp tuyến và viết phương trình mặt phẳng

1-A 2-A 3-A 4-D 5-A 6-C 7-A 8-A 9-C 10-A

11-A 12-B 13-A 14-A

Dạng 2. Vị trí tương đối giữa hai mặt phẳng, giữa hai mặt phẳng và mặt cầu

1-B 2-A 3-B 4-C 5-A 6-C 7-A 8-B 9-D 10-C

Dạng 3. Khoảng cách từ một điểm đến mặt phẳng

1-B 2-D 3-A 4-C

Dạng 4. Góc giữa hai mặt phẳng

1-D 2-C 3-A

Dạng 5. Một số bài toán cực trị

1-A 2-B 3-C 4-B 5-D

Bấm Tải xuống để xem toàn bộ.

| 1/29

| | Tải xuống

Preview text:

BÀI 2. PHƯƠNG TRÌNH MẶT PHẲNG Mục tiêu  Kiến thức
+ Nắm được cách xác định mặt phẳng, vectơ pháp tuyến của mặt phẳng.
+ Nắm được công thức tính khoảng cách từ điểm đến mặt phẳng, góc giữa hai mặt phẳng.
+ Nhận biết được vị trí tương đối giữa đường thẳng với mặt phẳng, giữa mặt phẳng với mặt cầu.  Kĩ năng
+ Viết được phương trình tổng quát của mặt phẳng.
+ Xác định được vectơ pháp tuyến trong các trường hợp.
+ Tính được khoảng cách và góc.
+ Xác định được vị trí tương đối và vận dụng vào giải bài tập. I. LÍ THUYẾT TRỌNG TÂM
1. Phương trình mặt phẳng Vectơ pháp tuyến   
Vectơ n  0 là vectơ pháp tuyến của  nếu giá của n vuông góc với .
Cặp vectơ chỉ phương của mặt phẳng  
Hai vectơ a,b không cùng phương là cặp vectơ chỉ phương của  nếu các giá của chúng song song hoặc nằm trên . Chú ý:  
 Nếu n là một vectơ pháp tuyến của  thì knk  0 cũng là vectơ pháp tuyến của .     
 Nếu a,b là một cặp vectơ chỉ phương của  thì n  a,b 
 là một vectơ pháp tuyến của .
Phương trình tổng quát của mặt phẳng
Ax  By  Cz  D  0 với 2 2 2 A  B  C  0 .  
Nếu ( ) có phương trình Ax  By  Cz  D  0 thì n  ( ; A ;
B C) là một vectơ pháp tuyến của ( ) .  
Phương trình mặt phẳng đi qua M x ; y ; z và có một vectơ pháp tuyến n  ( ; A B;C) là: 0  0 0 0 
A x  x  B y  y  C z  z  0 . 0   0   0 
Các trường hợp đặc biệt Các hệ số
Phương trình mặt phẳng 
Tính chất mặt phẳng  D  0 . Ax  By  Cz  0
 đi qua gốc tọa độ O A  0 By  Cz  D  0
 / / Ox hoặc   Ox TOANMATH.com Trang 1 B  0 Ax  Cz  D  0
 / /Oy hoặc   Oy C  0 Ax  By  D  0
 / /Oz hoặc   Oz A  B  0 Cz  D  0  / /Oxy hoặc   Oxy A  C  0 By  D  0  / /Oxzhoặc   Oxz B  C  0 Ax  D  0  / /Oyz hoặc   Oyz
Nếu ( ) cắt các trục toạ độ tại các điểm ( ; a 0;0),(0; ;
b 0), (0;0;c) với abc  0 thì ta có phương trình mặt x y z
phẳng theo đoạn chắn ( ) :    1. a b c
Chú ý: Nếu trong phương trình ( ) không chứa ẩn nào thì ( ) song song hoặc chứa trục tương ứng.
2. Khoảng cách từ một điểm tới mặt phẳng
Trong không gian Oxyz, cho điểm A x ; y ; z và mặt phẳng A A A 
( ) : Ax  By  Cz  D  0 .
Khi đó khoảng cách từ điểm A đến mặt phẳng ( ) được tính theo công thức: Ax  By  Cz  D d( , A ( )) A A A  2 2 2 A  B  C 3. Vị trí tương đối
Vị trí tương đối giữa hai mặt phẳng
Trong không gian Oxyz, cho hai mặt phẳng
( ) : A x  B y  C z  D  0; ( ) : A x  B y  C z  D  0 1 1 1 1 2 2 2 2 A B C D +) 1 1 1 1 ( )  ( )     . A B C D 2 2 2 2 A B C D +) 1 1 1 1 ( ) / /( )     . A B C D 2 2 2 2 A B B C +) 1 1 ( )  ( )   hoặc 1 1  . A B B C 2 2 2 2
+) ( )  ( )  A A  B B  C C  0 . 1 2 1 2 1 2
Vị trí tương đối giữa mặt phẳng và mặt cầu
Trong không gian Oxyz, cho mặt phẳng và mặt cầu TOANMATH.com Trang 2
( ) : Ax  By  Cz  D  0 ; 2 2 2 2
(S) : (x  a)  ( y  b)  (z  c)  R .
Để xét vị trí của ( ) và (S) ta làm như sau:
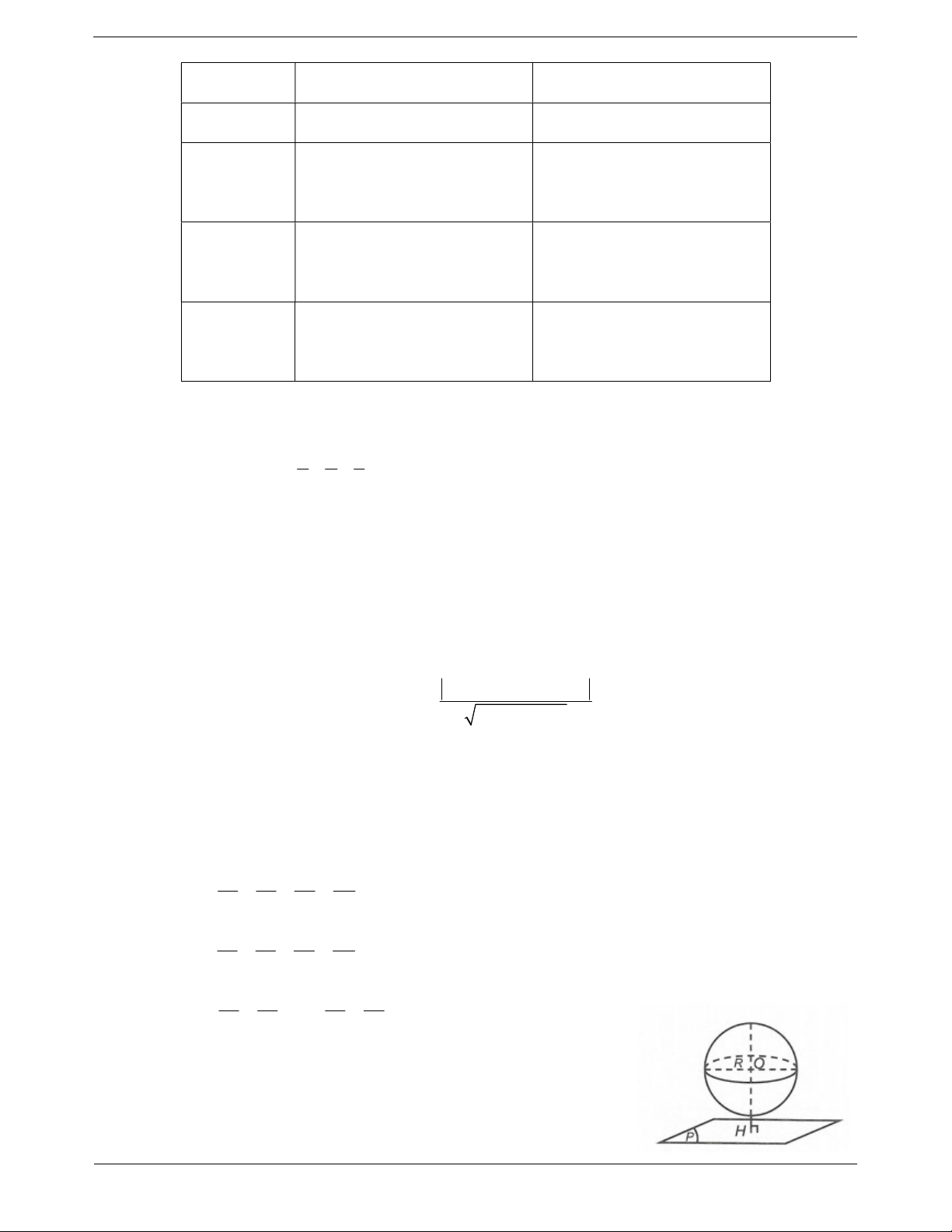
+) Nếu d I,   R thì () không cắt (S) .
+) Nếu d I,  R thì  tiếp xúc S  tại H. Khi đó H được gọi là
tiếp điểm đồng thời H là hình chiếu vuông góc của I lên  và 
được gọi là tiếp diện.
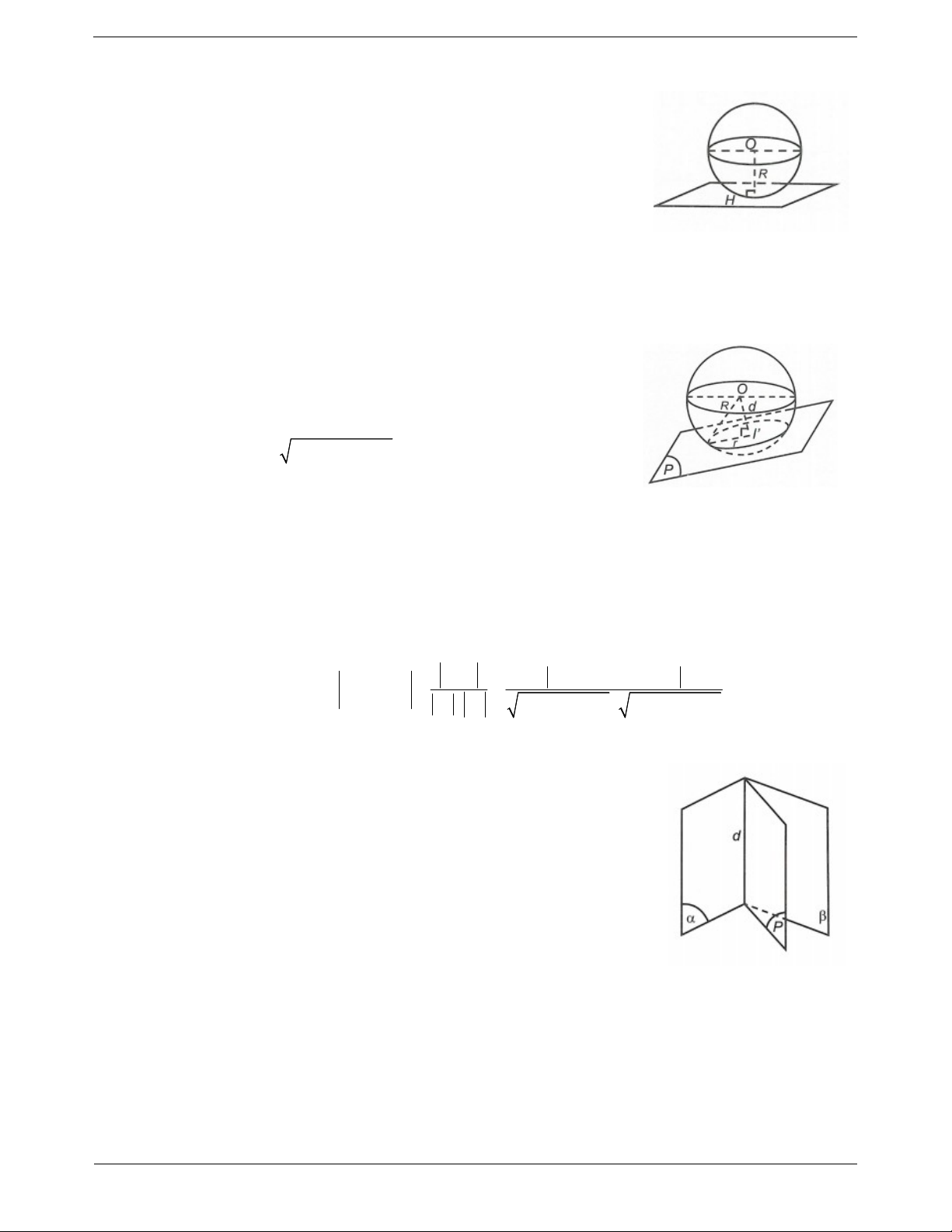
+) Nếu d I,  R thì  cắt S  theo đường tròn có phương trình
 x  a  y b  z  c2 2 2 2 ( ) ( )  R (C) : 
Ax  By  Cz  D  0.  Bán kính của C là 2 2 r  R  d [I,( )] .
Tâm J của (C) là hình chiếu vuông góc của I trên  .
4. Góc giữa hai mặt phẳng
Trong không gian Oxyz, cho hai mặt phẳng
( ) : A x  B y  C z  D  0 và ( ) : A x  B y  C z  D  0 . 1 1 1 1 2 2 2 2  
Góc giữa ( ) và ( ) bằng hoặc bù với góc giữa hai vectơ pháp tuyến n , n .   Tức là     n n   A A  B B  C C
cos  ,   1 2 1 2 1 2  cos n , n   .   2 2 2 2 2 2 n  n  
A  B  C  A  B  C 1 1 1 2 2 2 Chùm mặt phẳng
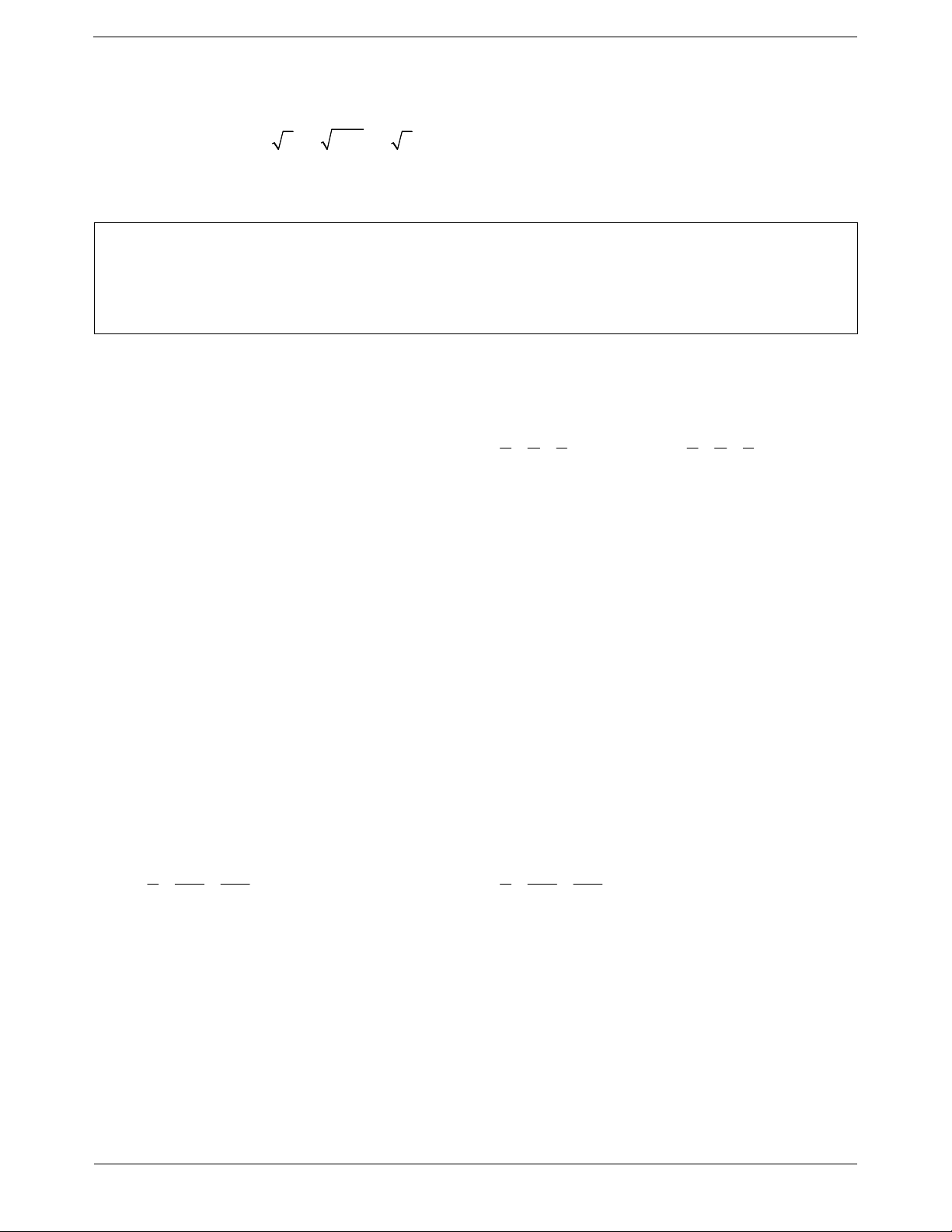
 Tập hợp tất cả các mặt phẳng qua giao tuyến của hai mặt phẳng ( )
và ( ) được gọi là một chùm mặt phẳng.
 Gọi d  là giao tuyến của hai mặt phẳng
( ) : A x  B y  C z  D  0 1 1 1 1
( ) : A x  B y  C z  D  0 2 2 2 2
Khi đó nếu P là mặt phẳng chứa d  thì mặt phẳng P có dạng
m  A x  B y  C z  D  n  A x  B y  C z  D  0 với 2 2 m  n  0 1 1 1 1   2 2 2 2  SƠ ĐỒ HỆ THỐNG HÓA TOANMATH.com Trang 3 II. CÁC DẠNG BÀI TẬP
Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng
Bài toán 1. Viết phương trình mặt phẳng biết một điểm thuộc mặt phẳng và tìm được một vectơ pháp tuyến Phương pháp giải 
Mặt phẳng  đi qua điểm M  x ; y ; z có vectơ pháp tuyến n   ; A ; B C  là 0 0 0 
A x  x  B y  y  C z  z  0. 0   0   0  
Ví dụ: Phương trình mặt phẳng đi qua điểm A1;2;3 và có vectơ pháp tuyến v 1  ; 2;  1 là: 1 x  
1  2 y  2 1 z  3  0
 x  2y  z  6  0. Ví dụ mẫu x y z
Ví dụ 1: Trong không gian Oxyz, một vectơ pháp tuyến của mặt phẳng    1 là 2  1 3     A. n  3;6; 2  . B. n  2; 1  ;3. C. n  3; 6  ;2. D. n  2;1;3. Hướng dẫn giải Ta có phương trình x y z 1 1    1 
x  y  z 1  0  3x  6 y  2z  6  0. 2  1  3 2 3 
Một vectơ pháp tuyến của mặt phẳng n  3;6; 2  . Chọn A. TOANMATH.com Trang 4
Ví dụ 2: Cho ba điểm A2;1;  1 , B  1
 ;0;4,C 0;2; 
1 . Phương trình mặt phẳng đi qua A và vuông góc với BC là
A. x  2 y  5z  5  0.
B. 2x  y  5z  5  0. C. x  2 y  5  0.
D. x  2 y  5z  5  0. Hướng dẫn giải 
Mặt phẳng P đi qua A2;1; 
1 và vuông góc với BC nên nhận BC  1; 2  ; 5   làm vectơ pháp
tuyến. Vì vậy ta viết được phương trình mặt phẳng P là: x  2  2 y   1  5z  
1  0  x  2y  5z  5  0. Chọn A.
Chú ý: Mặt phẳng  đi qua một điểm M , vuông góc với đường thẳng d , khi đó vectơ chỉ phương
u của đường thẳng d là một vectơ pháp tuyến của .
Ví dụ 3: Trong không gian với hệ toạ độ Oxyz, cho hai điểm A1;3;2, B3;5;2. Phương trình mặt
phẳng trung trực của đoạn thẳng AB có dạng x  ay  bz  c  0. Khi đó a  b  c bằng A. 2. B. 4. C. 3  . D. 2. Hướng dẫn giải  
Gọi M là trung điểm của đoạn thẳng AB, ta có M (2;1;0) và AB  (2;8; 4)  2(1; 4; 2)  2n . 
Mặt phẳng trung trực của đoạn thẳng AB đi qua M và có một vectơ pháp tuyến là n nên có phương
trình: x  4y  2z  6  0
Suy ra a  4,b  2,c  6 .
Vậy a  b  c  4 . Chọn B.
Ví dụ 4: Trong không gian Oxyz, mặt phẳng song song với mặt phẳng Oxy và đi qua điểm ( A 1;1;1) có phương trình là A. y 1  0 . B. x  y  z 1  0 . C. x 1  0 . D. z 1  0 . Hướng dẫn giải 
Mặt phẳng song song với mặt phẳng (Oxy) và đi qua (
A 1;1;1) nhận k  (0;0;1) làm vectơ pháp tuyến
nên có phương trình là z 1  0 . Chọn D.
Ví dụ 5: Cho mặt phẳng Q : x  y  2z  2  0. Viết phương trình mặt phẳng (P) song song với mặt
phẳng Q, đồng thời cắt các trục Ox, Oy lần lượt tại các điểm M , N sao cho MN  2 2 .
A. (P) : x  y  2z  2  0 .
B. (P) : x  y  2z  0 .
C. (P) : x  y  2z  2  0.
D. (P) : x  y  2z  2  0 . Hướng dẫn giải TOANMATH.com Trang 5
(P) / /(Q) nên phương trình mặt phẳng (P) có dạng x  y  2z  D  0 (D  2  ).
Khi đó mặt phẳng (P) cắt các trục Ox,Oy lần lượt tại các điểm M ( ; D 0;0) , N(0; ; D 0) . Từ giả thiết: 2
MN  2 2  2D  2 2  D  2 (do D  2).
Vậy phương trình mặt phẳng (P) : x  y  2z  2  0 . Chọn A.
Chú ý: Mặt phẳng  đi qua điểm M  x ; y ; z và song song với mặt phẳng ( ) : Ax  By  Cz  D  0 0 0 0 
thì  có phương trình là
A x  x  B y  y  C z  z  0 0   0   0 
Ví dụ 6: Cho điểm M (1; 2;5). Mặt phẳng (P) đi qua điểm M cắt trục tọa độ Ox,Oy,Oz tại , A B,C sao
cho M là trực tâm tam giác ABC. Phương trình mặt phẳng (P) là x y z x y z
A. x  y  z  8  0 .
B. x  2y  5z  30  0 . C.    0 . D.    1. 5 2 1 5 2 1 Hướng dẫn giải OA  BC  Ta có OA  (OBC) 
  BC  (OAM )  BC  OM (1) AM  BC Tương tự AB  OM (2) .
Từ (1) và (2) suy ra OM  (ABC) hay OM  (P) . 
Suy ra OM  (1; 2;5) là vectơ pháp tuyến của (P) .
Vậy phương trình mặt phẳng P là
x 1 2 y  2  5 z  5  0  x  2 y  5z  30  0. Chọn B.
Ví dụ 7: Cho tứ diện ABCD có đỉnh ( A 8; 1  4; 1
 0); AD, AB, AC lần lượt song song với Ox,Oy,Oz.
Phương trình mặt phẳng BCD đi qua H (7;16;15) là trực tâm BCD có phương trình là
A. x  2y  5z 100  0 .
B. x  2y  5z 100  0 . x y z x y z C.    0 . D.    1. 7 16 15 7 16 15 Hướng dẫn giải 
Theo đề ra, ta có (BCD) đi qua H (7; 16; 1
 5), nhận HA  (1;2;5) là vectơ pháp tuyến. Phương trình mặt phẳng BCD là
(x  7)  2( y 16)  5(z 15)  0
 x  2y  5z 100  0.
Vậy (BCD) : x  2y  5z 100  0 . Chọn B. TOANMATH.com Trang 6
Bài toán 2. Viết phương trình mặt phẳng biết một điểm thuộc mặt phẳng và tìm được một cặp vectơ chỉ phương Phương pháp giải  
Mặt phẳng ( ) đi qua điểm M  x ; y ; z có cặp vectơ chỉ phương a,b. Khi đó một vectơ pháp tuyến 0 0 0     của ( ) là n  [a,b].  
Ví dụ: Mặt phẳng (P) đi qua điểm M (0; 2; 2
 ) và nhận vectơ a(2,0,1),b( 1
 ,1,0) là hai vectơ chỉ phương.
Suy ra P có vectơ pháp tuyến là:    n  [a,b]  (1;1; 2  ) .
Từ đó ta có (P) : x  y  2z  6  0 . Ví dụ mẫu Ví dụ 1: Cho hai điểm (
A 1;1;5), B(0;0;1) . Mặt phẳng (P) chứa ,
A B và song song với trục Oy có phương trình là A. 4x  z 1  0 .
B. 4x  y  z 1  0 . C. 2x  z  5  0 . D. x  4z 1  0 . Hướng dẫn giải Do mặt phẳng (P) chứa ,
A B và song song với trục Oy nên vectơ pháp tuyến của (P) là    n  [AB; j]  (4;0; 1  ) .
Phương trình mặt phẳng (P) là:
4(x  0)  0( y  0) 1(z 1)  0  4x  z 1  0 Chọn A.
Ví dụ 2: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A1;2; 
1 ; B 2;1;0 và mặt phẳng
(P) : 2x  y  3z 1  0. Gọi (Q) là mặt phẳng chứa ;
A B và vuông góc với (P). Phương trình mặt phẳng (Q) là
A. 2x  5y  3z  9  0 .
B. 2x  y  3z  7  0 .
C. 2x  y  z  5  0 .
D. x  2 y  z  6  0 . Hướng dẫn giải
Phương trình mặt phẳng Q chứa AB và vuông góc với mặt phẳng (P) nên có cặp vectơ chỉ phương   là AB  (1; 1  ;1) và n  (2;1; 3  ) . P
  
Suy ra n  [AB; n ]  (2;5;3) . Q P Mặt phẳng (Q) đi qua (
A 1; 2;1) nên 2(x 1)  5( y  2)  3(z 1)  0
 2x  5y  3z  9  0 Chọn A.
Chú ý: Mặt phẳng ( ) chứa một đường thẳng d  và vuông góc với một mặt phẳng  :  
+) Xác định vectơ chỉ phương u của (d) và vectơ pháp tuyến n của . TOANMATH.com Trang 7   
Một vectơ pháp tuyến của ( ) là: n  u, n     .
+) Lấy một điểm M thuộc d thì M  ( ) .
Ví dụ 3: Mặt phẳng ( ) đi qua gốc tọa độ O và vuông góc với hai mặt phẳng
(P) : x  y  z  7  0,(Q) : 3x  2 y 12z  5  0 có phương trình là A. 2x  3y  z  0 .
B. 10x 15y  5z  2  0 . C. 10x 15y  5z  2  0 . D. 2x  3y  z  0 . Hướng dẫn giải 
Ta có (P) : x  y  z  7  0 có vectơ pháp tuyến là n  (1; 1  ;1) và 1 
(Q) : 3x  2 y 12z  5  0 có vectơ pháp tuyến là n  (3; 2; 12) 2
Do ( )  (P) và ( )  (Q) nên ( ) có vectơ pháp tuyến là    n  [n ;n ]  (10;15;5) . 1 2
Vậy ( ) có phương trình 10x 15y  5z  0  2x  3y  z  0 . Chọn D.
Chú ý: Mặt phẳng  đi qua điểm M và vuông góc với hai mặt phẳng cắt nhau , : Chọn vectơ
pháp tuyến của  là:    n  n , n      .
Ví dụ 4: Trong không gian với hệ tọa độ Oxyz, cho ba điểm ( A 0;1; 2), B(2; 2
 ;1) , C(2;1;0). Khi đó,
phương trình mặt phẳng (ABC) là ax  y  z  d  0. Hãy xác định a và d. A. a  1, d  1. B. a  6, d  6 . C. a  1, d  6  . D. a  6  , d  6 . Hướng dẫn giải  
Ta có: AB  2;3;  1 ; AC  2;0; 2  .    3 1  1  2 2 3   A ; B AC   ; ;   6;6; 6.   0 2  2  2 2  0    1   Chọn n   A ; B AC  1;1; 
1 là một vectơ pháp tuyến của mặt phẳng  ABC . 6  
Ta có phương trình mặt phẳng  ABC là: x  y 1 z  2  0  x  y  z 1  0. Vậy a  1, d  1. Chọn A.
Chú ý: Mặt phẳng  đi qua ba điểm không thẳng hàng ,
A B,C. Khi đó ta có thể xác định một vectơ
pháp tuyến của  là:    n   AB, AC.   TOANMATH.com Trang 8
Ví dụ 5: Trong không gian Oxyz, biết mặt phẳng ax  by  cz  5  0 qua hai điểm ( A 3;1; 1  ), B(2; 1  ; 4)
và vuông góc với (P) : 2x  y  3z  4  0 .
Giá trị của a  b  c bằng A. 9. B. 12. C. 10. D. 8. Hướng dẫn giải  
Gọi ( ) : ax  by  cz  5  0. Ta có AB  ( 1  ;2;5),n  (2; 1  ;3) . P   
Mặt phẳng ( ) nhận n  [AB, n ]  ( 1
 ;13;5) làm vectơ pháp tuyến nên ( ) có dạng P
x 13y  5z  D  0 . Mặt phẳng ( ) qua (
A 3;1;1) nên 3 13.1 5.(1)  D  0  D  5 .
 ( ) : x 13y  5z  5  0 hay ( ) : x 13y  5z  5  0 . Suy ra a  1;b  1  3;c  5. Vậy a  b  c  9 . Chọn A.
Bài toán 3. Lập phương trình mặt phẳng liên quan đến khoảng cách Phương pháp giải
Sử dụng các công thức liên quan đến khoảng cách:
Khoảng cách từ điểm M  x , y , z đến mặt phẳng ( ) : ax  by  cz  d  0 là 0 0 0  ax  by  cz  d 0 0 0 d(M ,( ))  . 2 2 2 a  b  c
Chú ý: Khoảng cách giữa hai mặt phẳng song song: d [( ),( )]  d[M ,( )] trong đó điểm M  ( ) . Ví dụ mẫu
Ví dụ 1: Trong không gian với hệ tọa độ Oxyz, lập phương trình của các mặt phẳng song song với mặt
phẳng ( ) : x  y  z  3  0 và cách ( ) một khoảng bằng 3 .
A. x  y  z  6  0; x  y  z  0 .
B. x  y  z  6  0 .
C. x  y  z  6  0; x  y  z  0 .
D. x  y  z  6  0; x  y  z  0 . Hướng dẫn giải
Gọi ( ) là mặt phẳng cần tìm. Ta có ( A 0;0;3)  ( ) .
Do ( ) / /( ) nên phương trình của mặt phẳng ( ) có dạng:
x  y  z  m  0 với m  3 . | m  3 |
Ta có d(( ),( ))  3  d( , A ( ))  3   3 . 3 m  6 |  m  3| 3   (thỏa mãn). m   0
Vậy phương trình của các mặt phẳng cần tìm là TOANMATH.com Trang 9
x  y  z  6  0 và x  y  z  0 . Chọn A.
Ví dụ 2: Trong không gian Oxyz, cho hai mặt phẳng
(P) : x  3z  2  0, (Q) : x  3z  4  0 .
Mặt phẳng song song và cách đều (P) và (Q) có phương trình là: A. x  3z 1  0 . B. x  3z  2  0 . C. x  3z  6  0 . D. x  3z  6  0 . Hướng dẫn giải Điểm M ( ;
x y; z) bất kỳ cách đều (P) và (Q)  d (M ;(P))  d(M ;(Q))
| x  3z  2 | | x  3z  4 |
x  3z  2  x  3z  4     1 9 1 9 x
  3z  2  x  3z  4 2  4    x  3z 1  0. x   3z 1  0
Vậy M thuộc ( ) : x  3z 1  0. Nhận thấy ( ) song song với (P) và (Q) . Chọn A.
Ví dụ 3: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A1;2; 
1 , B 3;4;0 và mặt phẳng
(P) : ax  by  cz  46  0 . Biết rằng khoảng cách từ ,
A B đến mặt phẳng (P) lần lượt bằng 6 và 3. Giá trị
của biểu thức T  a  b  c bằng A. 3. B. 6. C. 3. D. 6. Hướng dẫn giải
Gọi H , K lần lượt là hình chiếu của , A B trên mặt phẳng (P) .
Theo giả thiết, ta có: AB  3, AH  6, BK  3. Do đó ,
A B ở cùng phía với mặt phẳng (P) .
Lại có: AB  BK  AK  AH. Mà AB  BK  AH nên H  K . Suy ra ,
A B, H là ba điểm thẳng hàng và B là trung điểm của AH nên tọa độ H (5;6;1) . 
Vậy mặt phẳng (P) đi qua H (5;6; 1) và nhận AB  (2; 2; 1
 ) là vectơ pháp tuyến nên có phương
trình là 2(x  5)  2( y  6) 1(z 1)  0  2x  2 y  z  23  0 Theo bài ra, ta có (P) : 4
 x  4 y  2z  46  0 nên a  4,b  4  ,c  2 .
Vậy T  a  b  c  6  . Chọn B.
Bài toán 4. Viết phương trình mặt phẳng liên quan đến mặt cầu Phương pháp giải
Viết phương trình mặt phẳng  tiếp xúc với mặt cầu (S) tại điểm H.
Giả sử mặt cầu S  có tâm I và bán kính R, khi đó ta viết được phương trình mặt phẳng ( ) đi qua H  
và có một vectơ pháp tuyến là n  IH .
Ví dụ: Trong không gian với hệ trục Oxyz, cho mặt cầu 2 2 2
(S) : (x 1)  y  (z  2)  9 . TOANMATH.com Trang 10
Gọi ( ) là mặt phẳng tiếp xúc với mặt cầu tại điểm (
A 1;3; 2) và I (1;0; 2) là tâm của mặt cầu (S). Mặt 
phẳng ( ) nhận IA  (0;3;0) làm vectơ pháp tuyến. Mặt khác, mặt phẳng ( ) đi qua điểm ( A 1;3; 2) nên
có phương trình tổng quát là y  3  0 . Ví dụ mẫu
Ví dụ 1: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S  có phương trình 2 2 2
(x 1)  ( y  2)  (z  3)  12 và mặt phẳng (P) : 2x  2y  z  3  0. Viết phương trình mặt phẳng song
song với (P) và cắt (S) theo thiết diện là đường tròn (C) sao cho khối nón có đỉnh là tâm mặt cầu và
đáy là hình tròn (C) có thể tích lớn nhất.
A. 2x  2 y  z  2  0 hoặc 2x  2 y  z  8  0 .
B. 2x  2 y  z 1  0 hoặc 2x  2 y  z 11  0.
C. 2x  2 y  z  6  0 hoặc 2x  2 y  z  3  0 .
D. 2x  2 y  z  2  0 hoặc 2x  2 y  z  2  0 . Hướng dẫn giải
Ta có ( ) / /(P) nên ( ) : 2x  2y  z  d  0 (d  3).
Mặt cầu S  có tâm I(1; 2
 ;3), bán kính R  2 3 .
Gọi H  là khối nón thỏa mãn đề bài với đường sinh IM  R  2 3.
Đặt x  h  d(I, ( )). Khi đó bán kính đường tròn đáy hình nón là 2 r  12  x . 1 Thể tích khối nón là V  
 x x với 0  x  2 3 . H  2 12 ( )  3 1
Xét hàm số: f (x)    2
12  x  x với 0  x  2 3 . 3
Khi đó f (x) đạt giá trị lớn nhất tại x  2 hay d (I ,( ))  2 . | 2.1 2 ( 2  )  3  d | d  5  6 d  11 Ta có d (I ,( ))  2   2     . 2 2 2    d  5  6  d  1 2 2 ( 1)   Chọn B.
Chú ý: Công thức tính thể tích hình nón: TOANMATH.com Trang 11 1 1 V  hS  .2 . R h 3 3
Trong đó R là bán kính đáy, h là chiều cao.
Ví dụ 2: Trong không gian Oxyz, cho mặt cầu (S): 2 2 2
x  y  (z 1)  4 và điểm ( A 2; 2; 2). Từ A kẻ ba
tiếp tuyến AB, AC, AD với mặt cầu (B,C, D là các tiếp điểm). Phương trình mặt phẳng BCD là
A. 2x  2 y  z 1  0 .
B. 2x  2 y  z  3  0 .
C. 2x  2 y  z 1  0 .
D. 2x  2 y  z  5  0 . Hướng dẫn giải
Ta có mặt cầu S  có tâm I (0;0;1) và bán kính R  2 .
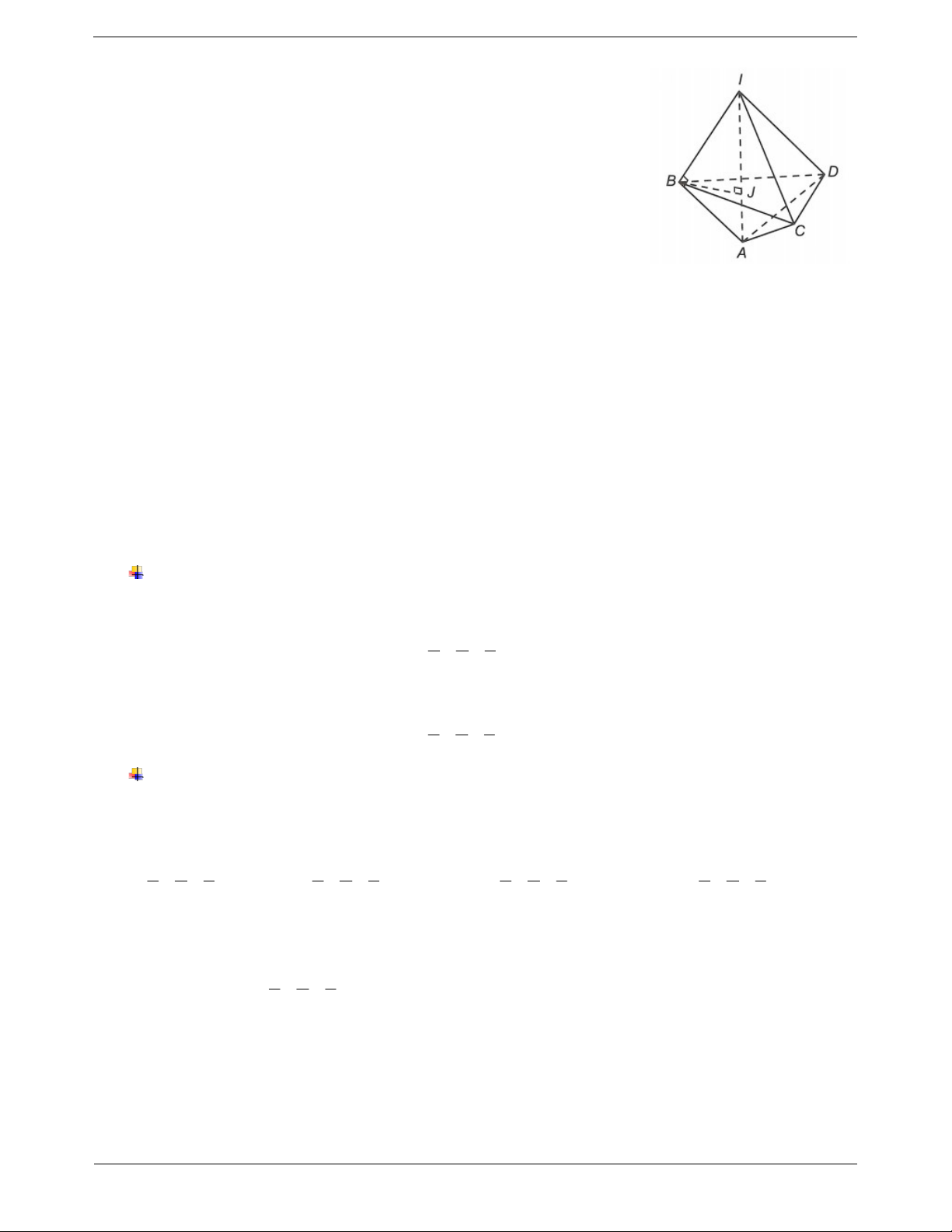
Do AB, AC, AD là ba tiếp tuyến của mặt cầu (S) với B,C, D là các tiếp điểm nên AB  AC  AD 
 IA là trục của đường tròn ngoại tiếp BC . D IB   IC  ID  R  IA  (BCD) .  
Khi đó mặt phẳng BCD có một vectơ pháp tuyến n  IA  (2;2;1).
Gọi J là tâm của đường tròn ngoại tiếp BCD  J  IA và IJ  BJ.
Ta có IBA vuông tại B và BJ  IA nên 2   2 IB 4 4 IB  IJ.IA  IJ    IJ  IA . IA 3 9   Đặt J ( ; x y; z). Ta có IJ  ( ;
x y; z 1); IA  (2; 2;1) .  4   8 8 13  Từ IJ  IA suy ra J ; ;   . 9  9 9 9   8 8 13   Mặt phẳng (BCD) đi qua J ; ; 
 và nhận vectơ pháp tuyến n  (2;2;1) có phương trình:  9 9 9   8   8   13  2 x   2 y   z 
 0  2x  2y  z  5  0       .  9   9   9  Chọn D.
Ví dụ 3: Trong không gian Oxyz, cho mặt cầu S  : 2 2 2
(x 1)  ( y 1)  (z 1)  12 và mặt phẳng
(P) : x  2 y  2z 11  0. Xét điểm M di động trên (P) và các điểm ,
A B,C phân biệt di động trên S 
sao cho AM , BM ,CM là các tiếp tuyến của S . Mặt phẳng  ABC luôn đi qua điểm cố định nào dưới đây?  1 1 1   3  A. ;  ;   . B. (0; 1  ;3) . C. ;0; 2   . D. 0;3;  1  .  4 2 2   2  Hướng dẫn giải
Mặt cầu S  có tâm I (1;1;1) và bán kính R  2 3 . TOANMATH.com Trang 12 Xét điểm M (a; ; b c)  (P); (
A x; y; z)  (S) nên ta có hệ điều kiện: 2 2 2
(x 1)  ( y 1)  (z 1)  12  2 2 2 AI  AM  IM a  2b  2c 11 0  2 2 2
(x 1)  ( y 1)  (z 1)  12 (1)  2 2 2 2 2 2  1
 2  (x  a)  ( y  b)  (z  c)  (a 1)  (b 1)  (c 1) (2)
a  2b  2c 11 0 (3)  Lấy (1)  (2) ta có: 2 2 2 2 2 2
(x 1)  ( y 1)  (z 1)  1
 2  (x  a)  (y  b)  (z  c)    2 2 2
 12  (a 1)  (b 1)  (c 1)   
 (a 1)x  (b 1)y  (c 1)z  a  b  c  9  0
Vậy mặt phẳng đi qua ba tiếp điểm là:
(Q) : (a 1)x  (b 1) y  (c 1)z  a  b  c  9  0
Kết hợp với (3) suy ra mặt phẳng này luôn đi qua điểm cố định (0;3;-1). Chọn D.
Bài toán 5. Phương trình mặt phẳng đoạn chắn Phương pháp giải
Phương trình mặt phẳng ( ) đi qua ba điểm ( A a;0;0), B(0; ;
b 0) và C(0;0; c) với abc  0 là: x y z   1. a b c
Ví dụ: Phương trình mặt phẳng ( ) đi qua ba điểm (
A 1;0; 0), B(0; 2;0) và C(0;0;3) là: x y z   1. 1 2 3 Ví dụ mẫu
Ví dụ 1: Trong không gian Oxyz, cho điểm M (1; 2;3) . Gọi ,
A B,C lần lượt là hình chiếu vuông góc của
điểm M lên các trục Ox,Oy,O .
z Phương trình mặt phẳng (ABC) là x y z x y z x y z x y z A.    1. B.    1. C.    0 . D.     1. 1 2 3 1 2 3 1 2 3 1 2 3 Hướng dẫn giải Ta có (
A 1;0;0), B(0; 2;0),C(0;0;3) lần lượt là hình chiếu của M lên Ox,Oy,Oz. Phương trình mặt x y z
phẳng (ABC) có dạng    1. 1 2 3 Chọn A.
Ví dụ 2: Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm M (3;0;0), N (2; 2; 2) . Mặt phẳng (P)
thay đổi qua M , N cắt các trục Oy,Oz lần lượt tại B(0; ;
b 0),C(0;0;c) với b, c  0. Hệ thức nào dưới đây là đúng? TOANMATH.com Trang 13 1 1 1 A. b  c  6. B. bc  3(b  c) . C. bc  b  c . D.   . b c 6 Hướng dẫn giải
Mặt phẳng (P) đi qua M (3;0;0), B(0; ;
b 0),C(0;0;c) với b, c  0 nên phương trình mặt phẳng (P) x y z
theo đoạn chắn là:    1 3 b c 2 2 2 1 1 1
Mặt phẳng (P) đi qua N(2; 2; 2) suy ra    1    . 3 b c b c 6 Chọn D.
Ví dụ 3: Trong không gian Oxyz, cho điểm G 1;4;3. Phương trình mặt phẳng cắt các trục tọa độ Ox,Oy,Oz lần lượt tại ,
A B,C sao cho G là trọng tâm tứ diện OABC là x y z x y z A.    1. B.    1. 3 12 9 4 16 12
C. 3x 12y  9z  78  0 .
D. 4x 16y 12z 104  0 . Hướng dẫn giải Giả sử ( A a,0,0); B(0,b,0);C(0;0;c) .  x  x  x  x A B C D x   G 4   y  y  y  y
G(1; 4;3) là trọng tâm tứ diện A B C D OABC  y  G 4   z  z  z  z A B C D x   G  4 0  a  0  0  4.1 a  4  
 0  0  b  0  4.4  b  16 . 0 0 0 c 4.3      c  12   x y z
Ta có phương trình mặt phẳng (ABC) là:    1. 4 16 12 Chọn B.
Ví dụ 4: Trong không gian với hệ tọa độ Oxyz. Viết phương trình mặt phẳng P đi qua điểm M (1;2;3)
và cắt các trục Ox,Oy,Oz lần lượt tại ba điểm ,
A B,C khác với gốc tọa độ O sao cho biểu thức 1 1 1   có giá trị nhỏ nhất. 2 2 2 OA OB OC
A. (P) : x  2y  z 14  0 .
B. (P) : x  2 y  3z 14  0 .
C. (P) : x  2y  3z 11  0 .
D. (P) : x  y  3z 14  0 . Hướng dẫn giải
Gọi H là trực tâm ABC. BH  AC Ta có 
 AC  (OBH )  AC  OH   1 . OB   AC TOANMATH.com Trang 14
Chứng minh tương tự, ta có: BC  OH 2 .
Từ (1), (2) ta có OH  (ABC) . 1 1 1 1 Suy ra    . 2 2 2 2 OA OB OC OH 1 1 1 Vậy để biểu thức  
đạt giá trị nhỏ nhất thì OH đạt giá trị lớn nhất. Mà OH  OM 2 2 2 OA OB OC
nên OH đạt giá lớn nhất bằng OM hay H  M . 
Khi đó OM  (ABC) nên (P) có một vectơ pháp tuyến là OM  (1; 2;3) .
Phương trình mặt phẳng (P) là
1(x 1)  2( y  2)  3(z  3)  0  x  2 y  3z 14  0 . Chọn B.
Ví dụ 5: Trong không gian Oxyz, có bao nhiêu mặt phẳng qua điểm M 4; 4  ; 
1 và chắn trên ba trục tọa 1
độ Ox,Oy,Oz theo ba đoạn thẳng có độ dài theo thứ tự lập thành cấp số nhân có công bội bằng ? 2 A. 1. B. 2. C. 3. D. 4. Hướng dẫn giải Gọi ( A a;0;0), B(0; ;
b 0),C(0;0;c) với abc  0 là giao điểm của mặt phẳng (P) và các trục toạ độ. Khi x y z
đó (P) có phương trình là    1. a b c Theo giả thiết ta có:   4 4 1 M  (P)    1 a  8  ,b  4,c  2    a b c   1 1    a  8,b  4,c  2  OC OB OA 1 1     2 4 |  c | | b | | a | a  16,b  8,c  4   2 4  
Vậy có ba mặt phẳng thỏa mãn. Chọn C.
Ví dụ 6: Trong không gian với hệ toạ độ Oxyz, cho các điểm A1;0;0, B 0;1;0. Mặt phẳng
x  ay  bz  c  0 đi qua các điểm ,
A B đồng thời cắt tia Oz tại C sao cho tứ diện OABC có thể tích 1
bằng . Giá trị của a  3b  2c là 6 A. 16. B. 1. C. 10. D. 6. Hướng dẫn giải
Mặt phẳng đi qua các điểm ,
A B đồng thời cắt tia Oz tại C 0;0;t  với t  0 có phương trình là x y z    1. 1 1 t 1 1 1 Mặt khác: V
  . OA.OB.OC   t  1. OABC 6 6 6 x y z
Vậy phương trình mặt phẳng cần tìm có dạng    1  x  y  z 1  0 . 1 1 1 TOANMATH.com Trang 15
Vậy a  b  1,c  1.
Suy ra a  3b  2c  1 3.1 2  6 . Chọn D.
Bài tập tự luyện dạng 1
Câu 1: Trong không gian Oxyz, cho mặt phẳng P có phương trình x  y  2z  3  0 . Vectơ pháp
tuyến của mặt phẳng P là     A. n   1  ;1;2. B. n  (1;1; 2) . C. n  (1; 2; 3) . D. n  (1; 2;3) . Câu 2: Cho ba điểm ( A 2;1; 1  ), B(1;0;4),C(0; 2
 ;1). Phương trình mặt phẳng đi qua A và vuông góc với BC là
A. x  2 y  5z  5  0 .
B. 2x  y  5z  5  0 . C. x  2y  5  0 .
D. x  2y  5z  5  0 .
Câu 3: Trong không gian với hệ tọa độ Oxyz, cho điểm M 3;2; 
1 . Mặt phẳng P đi qua M và cắt các
trục tọa độ Ox,Oy,Oz lần lượt tại các điểm ,
A B,C không trùng với gốc tọa độ sao cho M là trực tâm
tam giác ABC. Trong các mặt phẳng sau, mặt phẳng song song với mặt phẳng P là
A. 3x  2y  z 14  0 .
B. 2x  y  z  9  0 .
C. 3x  2 y  z 14  0 .
D. 2x  y  3z  9  0 .
Câu 4: Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) : x  2y  2z  5  0 và hai điểm ( A 3;0;1), B(0; 1
 ;3). Phương trình mặt phẳng (Q) đi qua A và song song với mặt phẳng (P) là
A. x  2 y  2z 1  0 . B. x  2 y  2z 1  0 .
C. x  2 y  2z 1  0 .
D. x  2 y  2z 1  0 .
Câu 5: Trong không gian Oxyz, cho (
A 0;1;1), B(1;0;0) và mặt phẳng (P) : x  y  z  3  0. (Q) là mặt
phẳng song song với (P) đồng thời đường thẳng AB cắt (Q) tại C sao cho CA  2CB . Mặt phẳng Q có phương trình là: 4
A. x  y  z   0 hoặc x  y  z  0 . B. x  y  z  0 . 3 4 C. x  y  z   0 .
D. x  y  z  2  0 hoặc x  y  z  0 . 3
Câu 6: Trong không gian Oxyz, phương trình mặt phẳng P song song và cách mặt phẳng
(Q) : x  2 y  2z  3  0 một khoảng bằng 1 đồng thời (P) không đi qua O là
A. x  2y  2z 1  0 . B. x  2y  2z  0 .
C. x  2 y  2z  6  0 .
D. x  2 y  2z  3  0 .
Câu 7: Trong không gian Oxyz, cho (
A 2;0;0), B(0; 4;0),C(0;0;6), D(2; 4; 6). Gọi (P) là mặt phẳng song
song với (ABC) , cách đều D và mặt phẳng (ABC) . Phương trình của (P) là
A. 6x  3y  2z  24  0 .
B. 6x  3y  2z 12  0 . C. 6x  3y  2z  0 .
D. 6x  3y  2z  36  0 . TOANMATH.com Trang 16
Câu 8: Trong không gian Oxyz, cho ba điểm A3;2;3, B 2;1;2,C 4;1;6. Phương trình mặt phẳng (ABC) là
A. 2x  y  z 1  0 .
B. x  y  z  2  0 .
C. x  y  2z  7  0 .
D. x  y  z  2  0 .
Câu 9: Trong không gian Oxyz, cho điểm M 1;2;3. Viết phương trình mặt phẳng P đi qua M cắt
các trục Ox,Oy,Oz lần lượt tại ,
A B,C sao cho M là trọng tâm tam giác ABC.
A. (P) : 6x  3y  2z 18  0 .
B. (P) : 6x  3y  2z  6  0 .
C. (P) : 6x  3y  2z 18  0 .
D. (P) : 6x  3y  2z  6  0 .
Câu 10: Trong không gian Oxyz, cho điểm M 1; 3
 ; 2. Hỏi có bao nhiêu mặt phẳng đi qua M và cắt
các trục toạ độ tại ,
A B,C mà OA  OB  OC  0? A. 3. B. 1. C. 4. D. 2.
Câu 11: Trong không gian Oxyz, cho mặt cầu 2 2 2
(S) : x  y  z  2x  4 y  6z  2  0. Viết phương trình
mặt phẳng ( ) chứa Oy cắt mặt cầu (S) theo thiết diện là đường tròn có chu vi bằng 8 .  A. ( ) : 3x  z  0 . B. ( ) : 3x  z  0 . C. ( ) : x  3z  0 .
D. ( ) : 3x  z  2  0 . Bài tập nâng cao
Câu 12: Cho điểm M 4;7;5, N 3; 9
 ;10 và các đường thẳng d ,d ,d cùng đi qua điểm N và 1 2 3
lần lượt song song với Ox,Oy,Oz. Mặt phẳng P đi qua M  cắt d ,d , d lần lượt tại A , B ,C sao cho 1 2 3
M  là trực tâm AB C
 . Phương trình mặt phẳng P là
A. x  2y  5z  35  0 .
B. x  2y  5z  35  0 . x y z x y z C.    0 . D.    1. 4 7 5  4 7 5 
Câu 13: Trong không gian với hệ tọa độ Oxyz, cho các điểm A1;0;0, B 0;2;0, C 0;0;  1 . Xét ba mặt
cầu tiếp xúc ngoài đôi một với nhau và tiếp xúc với mặt phẳng  ABC lần lượt tại , A B,C. Tổng diện tích
của ba mặt cầu trên là: 33 31 A. . B. 36 . C. . D. 54 . 2 2
Câu 14: Trong không gian tọa độ Oxyz, cho mặt phẳng (P) : x  y  2z 1  0 , các điểm (
A 0;1;1), B(1;0;0) với A và B nằm trên mặt phẳng (P) và mặt cầu 2 2 2
(S) : (x  2)  ( y 1)  (z  2)  4.
CD là một đường kính thay đổi của (S) sao cho CD / /(P) và bốn điểm ,
A B,C, D tạo thành một tứ diện.
Giá trị lớn nhất của thể tích tứ diện ABCD bằng A. 2 2 . B. 2 3 . C. 2 5 . D. 2 6 .
Dạng 2. Vị trí tương đối giữa hai mặt phẳng, giữa mặt cầu và mặt phẳng
Bài toán 1. Vị trí tương đối giữa hai mặt phẳng Phương pháp giải Cho hai mặt phẳng:
(P) : Ax  By  Cz  D  0 ; TOANMATH.com Trang 17
P: A x  B y C z  D  0 . Khi đó:
 (P) cắt P  A: B :C  A: B:C .  A B C D (P) / / P     . A B C D  A B C D (P)  P     . A B C D     
(P)  P  n  n  n n  0 . (P) P (P) P
 AA  BB  CC  0. Chú ý:
 Nếu A  0 thì tương ứng A  0 .
 Nếu B  0 thì tương ứng B  0 .
 Nếu C  0 thì tương ứng C  0 .
Ví dụ: Trong không gian với hệ trục toạ độ Oxyz, cho hai mặt phẳng ( ) : x  2 y  z 1  0 và
( ) : 2x  4 y  mz  2  0 .
Tìm m để  và  song song với nhau. Hướng dẫn giải 1 2 1 1  Ta có ( ) / /( )     2 4 m 2  2 4 2 (vô lý vì   ). 1 2 1 
Vậy không tồn tại m để hai mặt phẳng , song song với nhau. Ví dụ mẫu
Ví dụ 1: Trong không gian Oxyz, mặt phẳng (P) : 2x  y  z  2  0 vuông góc với mặt phẳng nào dưới đây?
A. 2x  y  z  2  0 . B. x  y  z  2  0 .
C. x  y  z  2  0 .
D. 2x  y  z  2  0 . Hướng dẫn giải 
Mặt phẳng (P) có một vectơ pháp tuyến là n  (2;1;1) . P 
Mặt phẳng (Q) : x  y  z  2  0 có một vectơ pháp tuyến n  (1; 1  ;1) . Q    
Mà n  n  2 11  0  n  n  (P)  (Q) . P Q P Q
Vậy mặt phẳng x  y  z  2  0 là mặt phẳng cần tìm. Chọn B.
Ví dụ 2: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P có phương trình
mx  (m 1) y  z 10  0 và mặt phẳng (Q) : 2x  y  2z  3  0 .
Với giá trị nào của m thì (P) và (Q) vuông góc với nhau? TOANMATH.com Trang 18 A. m  2 . B. m  2 . C. m  1. D. m  1. Hướng dẫn giải 
(P) : mx  (m 1) y  z 10  0 có vectơ pháp tuyến n  ( ; m m 1;1) . 1 
(Q) : 2x  y  2z  3  0 có vectơ pháp tuyến n  (2;1;2) . 2  
(P)  (Q)  n  n  0  2m  m 1 2  0  m  1. 1 2 Chọn C.
Bài toán 2. Vị trí tương đối giữa mặt cầu và mặt phẳng Phương pháp giải
Cho mặt phẳng ( ) : Ax  By  Cz  D  0 và mặt cầu tâm I; bán kính . R
 ( ) và (S) không có điểm chung  d(I,( ))  R .
 ( ) tiếp xúc với (S)  d(I,( ))  .
R Khi đó ( ) là tiếp diện.
 ( ) và (S) cắt nhau  d(I;())  R .
Khi đó O có tâm là hình chiếu của I trên  và bán kính 2 2 r  R  d (I;( )) . Ví dụ mẫu
Ví dụ 1: Trong không gian Oxyz, cho mặt cầu 2 2 2
(S) : x  y  z  6x  4y 12  0 .
Mặt phẳng nào cắt S  theo một đường tròn có bán kính r  3?
A. 4x  3y  z  4 26  0 .
B. 2x  2 y  z 12  0 .
C. 3x  4 y  5z 17  20 2  0 .
D. x  y  z  3  0 . Hướng dẫn giải
Phương trình mặt cầu S  là 2 2 2
x  y  z  6x  4y 12  0. Suy ra tâm I 3; 2
 ;0 và bán kính R  5.
Ta gọi khoảng cách từ tâm I của mặt cầu tới các mặt phẳng ở các đáp án là h, khi đó để mặt phẳng cắt
mặt cầu S  theo một đường tròn có bán kính r  3 thì 2 2
h  R  r  25  9  4 . |18  4 26 | Đáp án A loại vì h   4 . 26 14 Đáp án B loại vì h   4 . 3
Chọn đáp án C vì h  4 . 1 3 Đáp án D loại vì h   4 . 3 Chọn C.
Ví dụ 2: Trong không gian với hệ tọa độ Oxyz, cho điểm I 1;2; 2   và mặt phẳng TOANMATH.com Trang 19
(P) : 2x  2y  z  5  0. Phương trình mặt cầu tâm I cắt mặt phẳng (P) theo giao tuyến là một đường
tròn có diện tích bằng 16 là A. 2 2 2
(x  2)  ( y  2)  (z 1)  36 . B. 2 2 2
(x 1)  ( y  2)  (z  2)  9 . C. 2 2 2
(x 1)  ( y  2)  (z  2)  25 . D. 2 2 2
(x 1)  ( y  2)  (z  2)  16 . Hướng dẫn giải | 2.1 2.2  2  5 | Ta có a  d (I; (P))   3 . 2 2 2 2  2 1 S
Bán kính của đường tròn giao tuyến là: r   16  4 . 
Mặt cầu tâm I cắt mặt phẳng P theo giao tuyến là một đường tròn nên ta có 2 2 2
R  a  r  9 16  25  R  5 .
Vậy phương trình mặt cầu tâm I , bán kính R  5 là: 2 2 2
(x 1)  ( y  2)  (z  2)  25. Chọn C.
Ví dụ 3: Trong không gian Oxyz, cho mặt cầu S  có phương trình 2 2 2
x  y  z  2x  4y  6z  2  0 và
mặt phẳng ( ) : 4x  3y 12z 10  0. Tìm phương trình mặt phẳng  thỏa mãn đồng thời các điều
kiện: tiếp xúc với S  ; song song với ( ) và cắt trục Oz ở điểm có cao độ dương.
A. 4x  3y 12z  78  0 .
B. 4x  3y 12z  26  0 .
C. 4x  3y 12z  78  0 .
D. 4x  3y 12z  26  0 . Hướng dẫn giải
Mặt cầu (S) có tâm I (1; 2;3), bán kính 2 2 2
R  1  2  3  2  4 .
Vì ( ) / /( ) nên phương trình ( ) có dạng: 4x  3y 12z  d  0, d  10 .
Vì ( ) tiếp xúc mặt cầu (S) nên | 4.1 3.2 12.3  d | d  2  6 d  R   4 |  d  26 | 52  (I ,( . ))  2 2 2    d  78 4 3 ( 12)
Do ( ) cắt trục Oz ở điểm có cao độ dương nên chọn d  78 .
Vậy phương trình mặt phẳng ( ) : 4x  3y 12z  78  0 . Chọn C.
Bài tập tự luyện dạng 2 Bài tập cơ bản
Câu 1: Trong không gian Oxyz, mặt phẳng nào dưới đây song song với mặt phẳng Oxz? A. P : x  3  0. B. (Q) : y  2  0 . C. (R) : z 1  0 .
D. (S) : x  z  3  0 . TOANMATH.com Trang 20
Câu 2: Trong không gian Oxyz, cho hai mặt phẳng  : x  y  z 1  0 và ( ) : 2x  y  mz  m 1  0 ,
với m là tham số thực. Giá trị của m để ( )  ( ) là A. 1. B. 0. C. 1. D. 4  .
Câu 3: Trong không gian Oxyz, có bao nhiêu số thực m để mặt phẳng ( P) : x  2y  2z 1  0 song
song với mặt phẳng (Q) : 2x  (m  2) y  2mz  m  0? A. 1. B. 0. C. Vô số. D. 2.
Câu 4: Cho mặt cầu S  có đường kính 10 cm và mặt phẳng P cách tâm mặt cầu một khoảng 4 cm.
Khẳng định nào sau đây sai?
A. (P) và (S) có vô số điểm chung.
B. (P) tiếp xúc với (S) .
C. (P) cắt (S) theo một đường tròn bán kính 3 cm. D. (P) cắt (S) .
Câu 5: Trong không gian Oxyz, cho mặt cầu S  : 2 2 2
(x  2)  ( y 1)  (z 1)  12. Mặt phẳng nào sau
đây cắt mặt cầu S  theo giao tuyến là một đường tròn?
A. P : x  y  z  2  0 .
B. P : x  y  z  5  0 . 2  1 
C. P : x  y  z 10  0 .
D. P : x  y  z 10  0 . 4  3 
Câu 6: Trong không gian Oxyz, cho mặt cầu S  có phương trình 2 2 2
(x  2)  ( y 1)  (z  2)  4 và mặt
phẳng (P) có phương trình 4x  3y  m  0. Tìm tất cả các giá trị thực của tham số m để mặt phẳng (P)
và mặt cầu S  có đúng một điểm chung. A. m  1.
B. m  1 hoặc m  21. C. m  1 hoặc m  21.
D. m  9 hoặc m  31.
Câu 7: Trong không gian Oxyz, cho mặt cầu S  có phương trình 2 2 2
(x  2)  ( y  4)  (z 1)  4 và mặt
phẳng (P) có phương trình x  my  z  3m 1  0 . Tìm tất cả các giá trị thực của tham số m để mặt
phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn có đường kính bằng 2. A. m  1.
B. m  1 hoặc m  2 . C. m  1 hoặc m  2 . D. m  1. Bài tập nâng cao
Câu 8: Biết rằng trong không gian với hệ toạ độ Oxyz có hai mặt phẳng P và Q cùng thoả mãn các
điều kiện sau: đi qua hai điểm A1;1;  1 và B 0; 2
 ;2 đồng thời cắt các trục toạ độ Ox,Oy tại hai điểm cách đều .
O Giả sử P có phương trình x  b y  c z  d  0 và Q có phương trình 1 1 1
x  b y  c z  d  0. Giá trị biểu thức b b  c c bằng 2 2 2 1 2 1 2 A. 7. B. 9. C. 7  . D. 9. TOANMATH.com Trang 21
Câu 9: Trong không gian tọa độ Oxyz, cho mặt phẳng P mx   2 m   y   2 : 2 1 m   1 z 10  0 và điểm A2;11; 5
 . Biết khi m thay đổi thì luôn tồn tại hai mặt cầu cố định tiếp xúc với mặt phẳng P và đi qua .
A Tổng bán kính hai mặt cầu đó bằng A. 7 2. B. 15 2. C. 5 2. D. 12 2.
Câu 10: Trong không gian Oxyz, cho mặt cầu S   x  2   y  2   z  2 : 1 1
1  9 tiếp xúc với hai mặt
phẳng P : 2x  2y  z  4  0 và Q : 2x  y  2z  4  0 lần lượt tại các điểm , A . B Độ dài đoạn AB là A. 3 2. B. 3. C. 2. D. 2 3.
Dạng 3. Khoảng cách từ một điểm đến mặt phẳng Phương pháp giải
Khoảng cách từ điểm M x ; y ; z đến mặt phẳng  : Ax  By  Cz  D  0 là 0  0 0 0   Ax  By  Cz  D d M , 0 0 0  . 0 2 2 2 A  B  C
Ví dụ: Trong không gian Oxyz, khoảng cách từ điểm A1; 2
 ;3 đến mặt phẳng P có phương trình
x  3y  4z  9  0 là    
d  A P 1 3. 2 4.3 9 4 26 ,   .    2 2 2 13 1 3 4 Ví dụ mẫu
Ví dụ 1: Trong không gian Oxyz, khoảng cách giữa hai mặt phẳng P : x  2y  2z 10  0 và
Q: x  2y  2z 3  0 bằng 4 8 7 A. . B. 3. C. . D. . 3 3 3 Hướng dẫn giải
Vì P / / Q nên d P,Q  d  ,
A Q với AP. 0  2.0  2.5  3 7
Chọn A0;0;5P thì d  AQ   . 2 2 2 1  2  2 3 Chọn D.
Chú ý: Khoảng cách giữa hai mặt phẳng song song bằng khoảng cách từ một điểm bất kì trên mặt phẳng
này đến mặt phẳng kia.
Nếu hai mặt phẳng không song song thì khoảng cách giữa chúng bằng 0.
Ví dụ 2: Trong không gian với hệ trục toạ độ Oxyz, cho A1;2;3, B3;4;4. Tìm tất cả các giá trị của
tham số m sao cho khoảng cách từ điểm A đến mặt phẳng P : 2x  y  mz 1  0 bằng độ dài đoạn thẳng A . B A. m  2. B. m  2. C. m  3. D. m  2. TOANMATH.com Trang 22 Hướng dẫn giải  Ta có AB    2 2 2
2; 2;1  AB  2  2 1  3   1 .
Khoảng cách từ A đến mặt phẳng P là | 2.1 2  m 3 1| | 3m  3 | d ( , A (P))   (2). 2 2 2 2 2 1  m 5  m | 3m  3 | Vì AB  d ( , A (P))  3   9 2 5  m  2  9(m 1)  m  2. 2 5  m Chọn A.
Ví dụ 3: Trong không gian Oxyz, cho tứ diện ABCD với A  1;2;  1 , B  2;1;3,
C  (3; 2; 2), D  (1;1;1) . Độ dài chiều cao DH của tứ diện bằng 3 14 14 4 14 3 14 A. . B. . C. . D. . 14 14 7 7 Hướng dẫn giải    
Ta có AB  (1; 1; 2), AC  (2;0;1)  [A ; B AC]  ( 1
 ;3;2) là một vectơ pháp tuyến của mặt phẳng (ABC) .
Vậy phương trình mặt phẳng (ABC) là
1(x 1)  3(y  2)  2(z 1)  0  x  3y  2z  7  0.
Độ dài chiều cao DH của tứ diện ABCD là khoảng cách từ D đến (ABC) . | 1
 .1 3.1 2.1 7 | 3 14 Suy ra DH  d(D,(ABC))   . 2 2 2 (1)  3  2 14 Chọn A.
Ví dụ 4: Trong không gian tọa độ Oxyz, cho điểm A ; a ; b c với a, ,
b c  0. Xét P là mặt phẳng thay
đổi đi qua điểm A . Khoảng cách lớn nhất từ điểm O đến mặt phẳng (P) bằng A. 2 2 2 a  b  c . B. 2 2 2 2 a  b  c . C. 2 2 2 3 a  b  c . D. 2 2 2 4 a  b  c . Hướng dẫn giải
Gọi H là hình chiếu vuông góc của O lên mặt phẳng P . Khi đó 2 2 2
d (O,(P))  OH  OA  a  b  c . Chọn A.
Bài tập tự luyện dạng 3
Câu 1: Trong không gian Oxyz, cho hai mặt phẳng (P) : x  2 y  2z 10  0 và (Q) : x  2y  2z  3  0 .
Điểm M là giao điểm của mặt phẳng P với trục Oz . Khoảng cách từ M tới mặt phẳng Q bằng 8 7 4 A. . B. . C. 3. D. . 3 3 3 TOANMATH.com Trang 23
Câu 2: Trong không gian cho hệ trục tọa độ Oxyz, tất cả các điểm M nằm trên Oz có khoảng cách đến
mặt phẳng (P) : 2x  y  2z  2  0 bằng 2 là A. M (0; 0;4) .
B. M (0; 0;0), M (0; 0;2) . C. M (0; 0;2) . D. M (0; 0;2), M (0;0; 4  ) .
Câu 3: Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng P : 2x  2y  z  3  0 và điểm A1; 2  ;3. Gọi M  ; a ;
b cP sao cho AM  4. Giá trị của a  b  c bằng 2 8 A. . B. 2. C. . D. 12. 3 3 Bài tập nâng cao  
Câu 4: Trong không gian với hệ toạ độ Oxyz, cho hai điểm A   3 3 1 1; 2; 3 , B ; ;  .   Gọi S là mặt 1   2 2 2  3 cầu tâm ,
A bán kính bằng 3 và S là mặt cầu tâm B, bán kính bằng . Gọi P là mặt phẳng tiếp xúc 2  2
với cả hai mặt cầu S , S . Khoảng cách lớn nhất từ gốc toạ độ O đến mặt phẳng P bằng 1   2  58  36 61 11 3 61 11 2 61 63 61  89 A. . B. . C. . D. . 127 9 9 169
Dạng 4. Góc giữa hai mặt phẳng Phương pháp giải
Cho hai mặt phẳng , có phương trình:
: A x  B y C z  D  0 1 1 1 1 
 : A x  B y  C z  D  0. 2 2 2 2  
Góc giữa , bằng hoặc bù với góc giữa hai vectơ pháp tuyến n ,n . 1 2   n .n A A  B B  C C cos ,    1 2    1 2 1 2 1 2  . n . n 2 2 2 2 2 2 A  B  C . A  B  C 1 2 1 1 1 2 2 2 Chú ý: 0o  ,     90 .o    
Ví dụ: Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng P có phương trình là x  z  3  0. Tính
góc giữa P và mặt phẳng Oxy. Hướng dẫn giải 
Mặt phẳng P : x  z  3  0 có vectơ pháp tuyến n  1;0;1 và mặt phẳng Oxy có vectơ pháp tuyến 1    n  0;0;1 . 2  
Gọi  là góc giữa mặt phẳng P và mặt phẳng Oxy.   n .n 1 Ta có 1 2
cos         45 .o n . n 2 1 2 TOANMATH.com Trang 24 Ví dụ mẫu
Ví dụ: Trong không gian Oxyz, biết hình chiếu của O lên mặt phẳng P là điểm H 2; 1  ;2.
Số đo góc giữa mặt phẳng P với mặt phẳng Q : x  y  5  0 là A. 30o. B. 90o. C. 60o. D. 45o. Hướng dẫn giải
Gọi  là góc giữa mặt phẳng P với mặt phẳng Q.   Ta có OH  2;1; 2
  là vectơ pháp tuyến của mặt phẳng P và n  1;1;0 là vectơ pháp tuyến của mặt phẳng Q.     OH n Ta có   OH n . 1 cos cos ,        45 .o OH . n 2 Chọn D.
Bài tập tự luyện dạng 4 Bài tập cơ bản
Câu 1: Trong hệ trục toạ độ Oxyz, cho điểm H 2;1;2. Điểm H là hình chiếu vuông góc của gốc toạ độ
O xuống mặt phẳng P, số đo góc giữa mặt phẳng P và mặt phẳng Q : x  y 11  0 là A. 90o. B. 30o. C. 60o. D. 45o.
Câu 2: Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng P có phương trình: ax  by  cz 1  0
với c  0 đi qua 2 điểm A0;1;0, B1;0;0 và tạo với mặt phẳng Oyz một góc 60o. A. 5;8. B. 8;1  1 . C. 0;3. D. 3;5. Bài tập nâng cao
Câu 3: Cho khối chóp S.ABCD có đáy là hình bình hành AB  3, AD  4,  120 .o BAD  Cạnh bên
SA  2 3 vuông góc với mặt phẳng đáy  ABCD. Gọi M , N, P lần lượt là trung điểm các cạnh S , A SD
và BC,  là góc giữa hai mặt phẳng SAC  và MNP. Chọn khẳng định đúng trong các khẳng định sau đây: A. 60o;90o   . B. 0o;30o   . C. 30o;45o   . D. 45o;60o   .
Dạng 5. Một số bài toán cực trị Ví dụ mẫu
Ví dụ 1: Trong không gian Oxyz, cho ba điểm A1;1;  1 , B  1  ;2;0,C 3; 1
 ;2 và M là điểm thuộc mặt
phẳng  : 2x  y  2z  7  0.   
Tính giá trị nhỏ nhất của P  3MA  5MB  7MC . A. P  20. B. P  5. C. P  25. D. P  27. min min min min Hướng dẫn giải TOANMATH.com Trang 25     Gọi điểm I  ;
x y; z sao cho 3IA  5IB  7IC  0. 3  1 x  5 1
  x  73 x  0 x  23   Khi đó 3
 1 y  52  y  71 y  0  y  20  I  2  3;20; 1   1 .  
31 z  50  z  72  z  0 z  11           
Xét P  3MA  5MB  7MC  3MI  IA  5MI  IB  7MI  IC .     
 MI  3IA 5IB  7IC  MI  MI.
P khi MI ngắn nhất hay M là hình chiếu vuông góc của I lên mặt phẳng . min 2. 23  20  2. 1  1  7 Khi đó: P  d I,    27. min        2   2 2 2 1  2 Chọn D.
Ví dụ 2: Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A3;5;5, B5; 3  ;7 và mặt phẳng
(P) : x  y  z  0. Tìm toạ độ điểm M trên mặt phẳng (P) sao cho 2 2 MA  2MB lớn nhất. A. M ( 2  ;1;1) . B. M (2; 1  ;1) . C. M (6; 1  8;12) . D. M ( 6  ;18;12) .
Hướng dẫn giải   
Gọi I thỏa mãn IA  2IB  0.        
Khi đó IO  OA  2(IO  OB)  0  OI  2OB  OA  I (13; 1  1;19).  2  2   2   2 Ta có 2 2
MA  MB  MA  MB  MI  IA  MI  IB 2  MI   2 2 2 2 2 IA  2IB . 2 2
MA  2MB lớn nhất khi MI nhỏ nhất. Khi đó I là hình chiếu vuông góc của M lên (P) . Ta tìm được M (6; 1  8;12) . Chọn C.
Ví dụ 3: Trong không gian Oxyz, cho các điểm M ( ; m 0; 0), N (0; ;
n 0), P(0; 0; p) không trùng với gốc tọa độ và thỏa mãn 2 2 2
m  n  p  3 . Giá trị lớn nhất của khoảng cách từ O đến mặt phẳng MNP bằng 1 1 1 A. . B. 3 . C. . D. . 3 3 27 Hướng dẫn giải
Do M , N, P không trùng với gốc tọa độ nên m  0, n  0, p  0 . x y z 1 1 1
Phương trình mặt phẳng (MNP) là:    1  x  y  z 1  0 . m n p m n p 1 Suy ra d (O,(MNP))  . 1 1 1   2 2 2 m n p 1 1 1
Áp dụng bất đẳng thức Cô-si cho ba số dương 2 2 2 m , n , p và ba số dương , ta có: 2 m 2 2 n p TOANMATH.com Trang 26 1 1 1 1 2 2 2 3 2 2 2 m  n  p  3 m n p và    33 . 2 2 2 2 2 2 m n p m n p  1 1 1  Suy ra  2 2 2 m  n  p     9  2 2 2   m n p   1 1 1   3    9    2 2 2 do m  n  p  3 2 2 2   m n p  1 1 1 1 1 1 1 1     3     3   2 2 2 2 2 2 m n p m n p 1 1 1 3   2 2 2 m n p 1 Vậy d (O, (MNP)) 
. Dấu "=" xảy ra khi và chỉ khi 2 2 2 m  n  p  1. 3 1
Vậy giá trị lớn nhất của khoảng cách từ O đến mặt phẳng MNP là . 3 Chọn C.
Ví dụ 4: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) : x  2y  2z  3  0 và mặt cầu  2 2 2
(S) : x  y  z  2x  4y  2z  5  0. Giả sử M  (P) và N  (S) sao cho MN cùng phương với vectơ
u  (1;0;1) và khoảng cách giữa M và N lớn nhất. Tính MN. A. MN  3. B. MN  1 2 2 . C. MN  3 2 . D. MN  14 . Hướng dẫn giải S có tâm I( 1
 ;2;1) và bán kính R 1. | 1   2.2  2.1 3 | Ta có: d (I ,(P))   2  R . 2 2 2 1  2  2
Gọi H là hình chiếu vuông góc của N trên mặt phẳng P và  là góc giữa MN và NH.  
Vì MN cùng phương với u nên góc  có số đo không đổi.  1 MNH vuông tại H có 
  HNM nên HN  MN.cos  MN  .HN cos
Do đó MN lớn nhất  HN lớn nhất  HN  d(I, (P))  R  3.   1 1 Có cos  cos(u, n )  nên MN  HN  3 2 . P 2 cos Chọn C.
Ví dụ 5: Trong không gian với hệ toạ độ Oxyz, gọi P : ax  by  cz  3  0 (với a, , b c là các số nguyên
không đồng thời bằng 0) là mặt phẳng đi qua hai điểm M 0; 1  ;2, N  1
 ;1;3 và không đi qua điểm
H (0;0; 2). Biết rằng khoảng cách từ H đến mặt phẳng (P) đạt giá trị lớn nhất. Giá trị của tổng
T  a  2b  3c 12 bằng A. 16 . B. 8. C. 12. D. 16. Hướng dẫn giải
Gọi K là hình chiếu của H lên (P), E là hình chiếu của H lên MN. TOANMATH.com Trang 27
Ta có d (H;(P))  HK và d (H ; MN )  HE, HK  HE (không đổi).
Vậy d (H;(P)) lớn nhất khi K  E, với E là hình chiếu của H lên MN .  1 1 7  Suy ra E ; ;   .  3 3 3    1 1 1
Vậy mặt phẳng (P) cần tìm là mặt phẳng nhận HE   ; ; 
 làm vectơ pháp tuyến và đi qua M  3 3 3 
có phương trình là x  y  z  3  0 . a  1   Suy ra b   1 . c 1  Vậy T  16 . Chọn D.
Bài tập tự luyện dạng 5 Bài tập cơ bản
Câu 1: Trong không gian với hệ trục toạ độ Oxyz, cho tam giác ABC với A2;1;3, B1; 1  ; 2, C 3; 6  ;  1 . Điểm M  ;
x y; z thuộc mặt phẳng Oyz sao cho 2 2 2
MA  MB  MC đạt giá trị nhỏ nhất.
Tính giá trị biểu thức P  x  y  z. A. P  0. B. P  2. C. P  6. D. P  2  .
Câu 2: Cho A4;5;6; B1;1;2, M là một điểm di động trên mặt phẳng P : 2x  y  2z 1  0. Khi đó
MA  MB nhận giá trị lớn nhất là A. 77. B. 41. C. 7. D. 85.
Câu 3: Trong không gian Oxyz, cho mặt phẳng P :3x  y  z  5  0 và hai điểm A1;0;2, B 2;1;4.
Tập hợp các điểm M nằm trên mặt phẳng P sao cho tam giác MAB có diện tích nhỏ nhất. x  7y  4z  7  0 x  7y  4z 14  0 A.  B.  3  x  y  z  5  0. 3  x  y  z  5  0. x  7y  4z  7  0 x  7y  4z  5  0 C.  D.  3  x  y  z  5  0. 3  x  y  z  5  0. Bài tập nâng cao
Câu 4: Trong không gian với hệ toạ độ Oxyz, cho điểm A3;2;4 và mặt phẳng P  2 m  m x   2
m  m   y   m   2 : 2 4 1 2 3
1 z  m 1  0. Tìm giá trị lớn nhất của khoảng cách từ A đến mặt phẳng P. A. 5. B. 29. C. 33. D. 21. TOANMATH.com Trang 28
Câu 5: Trong không gian Oxyz, cho mặt cầu S  x   y  2   z  2 2 : 3
6  45 và M 1;4;5. Ba đường
thẳng thay đổi d , d , d nhưng luôn đôi một vuông góc với nhau tại O và cắt mặt cầu tại điểm thứ hai lần 1 2 3 lượt là ,
A B,C. Khoảng cách lớn nhất từ M đến mặt phẳng  ABC là A. 3. B. 5. C. 4. D. 6.
ĐÁP ÁN VÀ LỜI GIẢI BÀI TẬP TỰ LUYỆN
Dạng 1. Xác định vectơ pháp tuyến và viết phương trình mặt phẳng 1-A 2-A 3-A 4-D 5-A 6-C 7-A 8-A 9-C 10-A 11-A 12-B 13-A 14-A
Dạng 2. Vị trí tương đối giữa hai mặt phẳng, giữa hai mặt phẳng và mặt cầu 1-B 2-A 3-B 4-C 5-A 6-C 7-A 8-B 9-D 10-C
Dạng 3. Khoảng cách từ một điểm đến mặt phẳng 1-B 2-D 3-A 4-C
Dạng 4. Góc giữa hai mặt phẳng 1-D 2-C 3-A
Dạng 5. Một số bài toán cực trị 1-A 2-B 3-C 4-B 5-D TOANMATH.com Trang 29

Bài giảng phương trình mặt phẳng Toán 12

Thông tin :

Tài liệu liên quan:

Bài giảng vectơ và hệ trục tọa độ trong không gian Toán 12 KNTTVCS

Toán ứng dụng thực tế vectơ và hệ trục toạ độ trong không gian

Chuyên đề hình học giải tích không gian – Lưu Huy Thưởng Toán 12

Chuyên đề HH giải tích không gian – Trung tâm LTĐH Vĩnh Viễn Toán 12

Bài tập tọa độ không gian phân theo dạng có lời giải chi tiết – Trần Sĩ Tùng Toán 12