









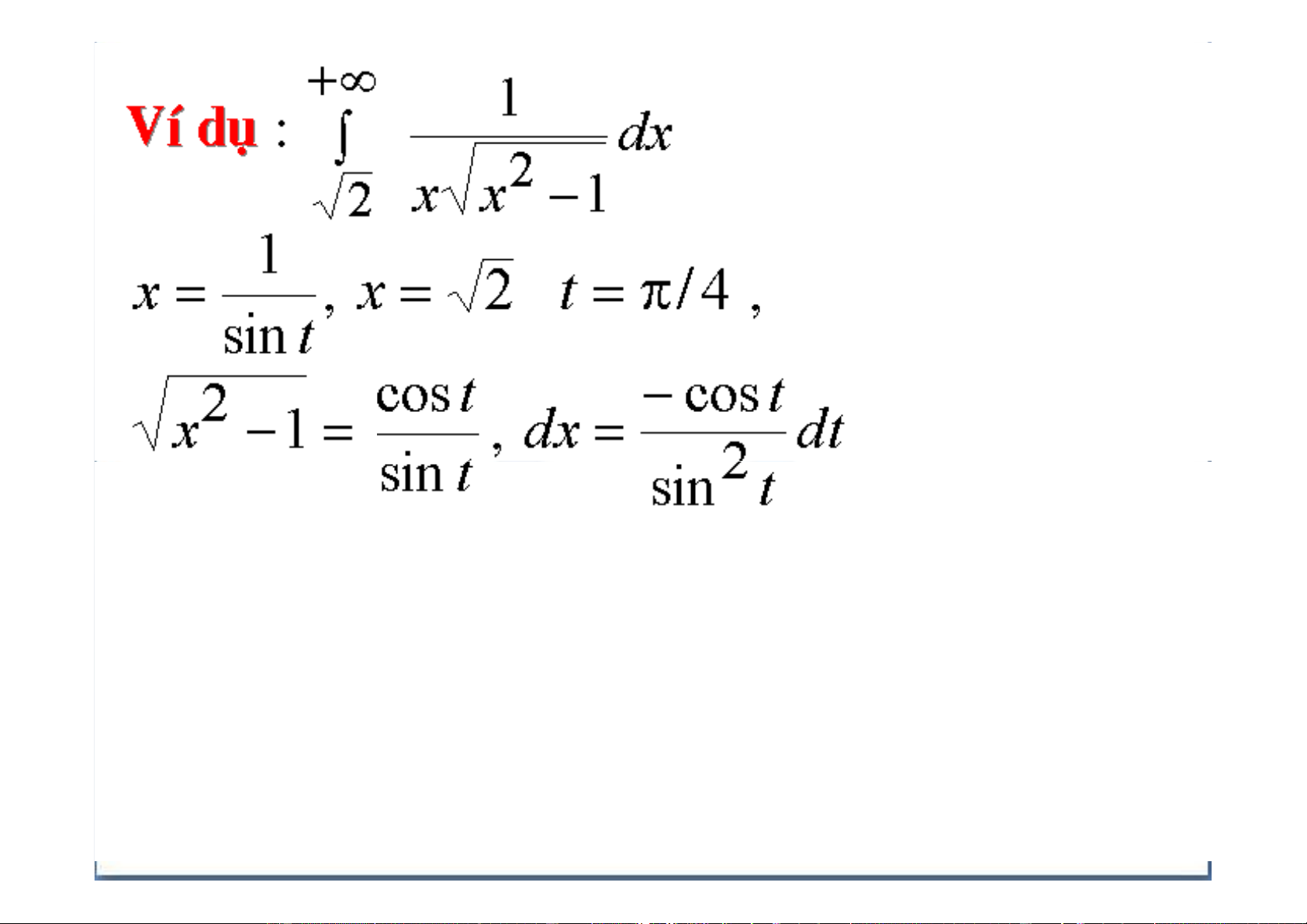
Preview text:
Ch C ươn ơ g I I – Ph P ép Tí T nh Tí T ch c P h P ân Bà B i 15 - Tí T ch c P h P ân Suy R ộng Cá ác c tí t ch c h p hân â n sa s u a đ ây ây gọ g i i là l à tí t ch c h ph p ân â su s y y rộng ( lo l ại i 1 1 )
( tích phân có cận là vô hạn ) +∞
∫ f (x) dx d (1 ( ) 1 a a
∫ f (x) dx (2) −∞ +∞
∫ f (x) dx (3) −∞ (a là hằng số)
Ngô Thu Lương- Ôn tập Cao Học Ch C ươn ơ g I I – Ph P ép Tí T nh Tí T ch c P h P ân Bà B i 15 - Tí T ch c P h P ân Suy R ộng Gi G á i á trị r ị củ c a tích c h ph p ân â su s y y rộng : g +∞ b
∫ f (x) dx = lim
∫ f (x) dx b→+∞ a a
Nếu giới hạn khi lấy lim là số A hữu hạ h n , tích phân gọi là hội i tụ
t , giá trị của nó là A Nếu giới hạn kh k ông t g ồn
n tại hoặc bằng vô hạn ,
tích phân gọi là phân â kỳ k
Ngô Thu Lương- Ôn tập Cao Học Ch C ươn ơ g I I – Ph P ép Tí T nh Tí T ch c P h P ân Bà B i 15 - Tí T ch c P h P ân Suy R ộng
Ngô Thu Lương- Ôn tập Cao Học Ch C ươn ơ g I I – Ph P ép Tí T nh Tí T ch c P h P ân Bà B i 15 - Tí T ch c P h P ân Suy R ộng +∞ 1 Ví í d ụ ụ 1 : Xét tích phân suy rộng ∫ dx 2 1 x b 1 1 − b 1 − ∫ dx = = +1 2 b 1 x 1 x +∞ 1 b 1 1 − ∫ dx = lim ∫ dx = lim +1 =1 2 2 →∞ 1 x b→+∞ 1 x b b +∞ 1 Vậy ta có tích phân ∫ dx hội i tụ 2 1 x
và giá trị của nó là 1
Ngô Thu Lương- Ôn tập Cao Học Ch C ươn ơ g I I – Ph P ép Tí T nh Tí T ch c P h P ân Bà B i 15 - Tí T ch c P h P ân Suy R ộng +∞ 1 Ví í d ụ ụ 22:: Xét tích phân suy rộng ∫ dx 1 x b 1 b ∫ dx = ln x =ln b 1 x 1 +∞ 1 ∫
dx = lim ln b = ∞ 1 x b→+∞ +∞ 1 Vậy ta có tích phân ∫ dx phân â n kỳ k ỳ 1 x
Ngô Thu Lương- Ôn tập Cao Học Ch C ươn ơ g I I – Ph P ép Tí T nh Tí T ch c P h P ân Bà B i 15 - Tí T ch c P h P ân Suy R ộng Hai H ai bài i toá oán n đ ối i với i tí t ch c h ph p ân â su s y y rộng : g Tính giá trị tích phân Khả h o ả sá s t á t sự s ự hộ h i ộ itụ t ụ củ c a ủ a tí t c í h c phâ ph n â
Ngô Thu Lương- Ôn tập Cao Học Ch C ươn ơ g I I – Ph P ép Tí T nh Tí T ch c P h P ân Bà B i 15 - Tí T ch c P h P ân Suy R ộng *) Tí T nh n h giá trị tích ph p â h n
Để tính giá trị tích phân suy rộng ta có thể dùng công thức Newt w on-Le L i e b i nit i z +∞ b + +∞ +b
∫ f (x) dx = F (x) a a
= F(+∞) − F(a)
= lim F(x) − F(a) x→+∞
Ngô Thu Lương- Ôn tập Cao Học Ch C ươn ơ g I I – Ph P ép Tí T nh Tí T ch c P h P ân Bà B i 15 - Tí T ch c P h P ân Suy R ộng
hoặc công thức tích c p hân â n từng n ph p ần +∞ b + ∞ +∞ b b
∫u(x)dv(x) = u(x)v(x)
− ∫ v(x)du (x) a a a +∞
u(x)v(x)
= lim u(x)v(x) x→+∞
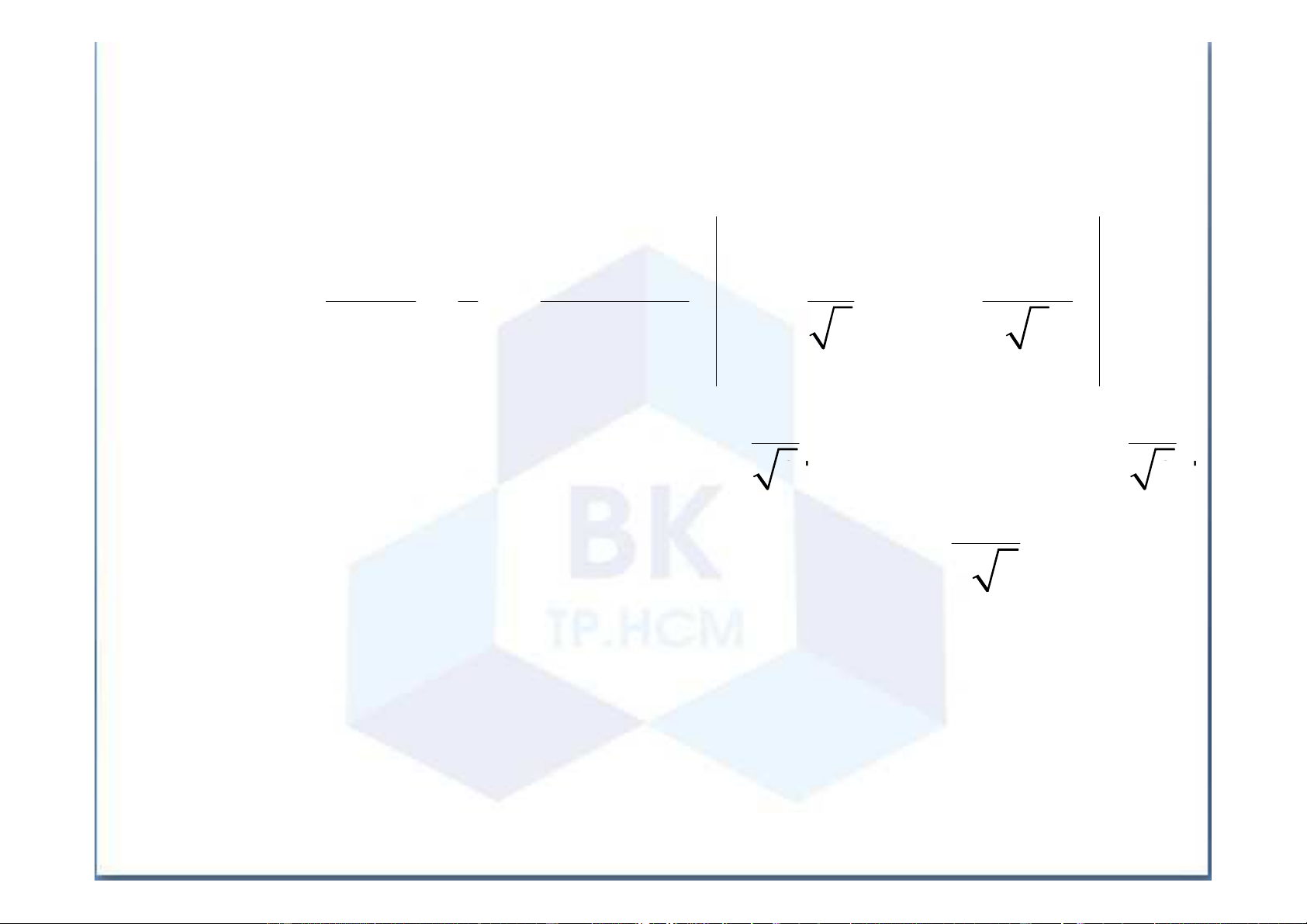
hoặc công thức đổi i b iến n thí h ch c h ợp
Ngô Thu Lương- Ôn tập Cao Học Ch C ươn ơ g I I – Ph P ép Tí T nh Tí T ch c P h P ân Bà B i 15 - Tí T ch c P h P ân Suy R ộng +∞ 1 Ví í d ụ ụ 3 : ∫ dx 2 1 1 + x dùng công thức Newt w on o -Le L i e b i ni n t i z +∞ + 1 +∞ + ∫ dx = arctan x 2 1 1 1 + x = arctan(+∞) − arctan(1) π π π = − = 2 4 4
Ngô Thu Lương- Ôn tập Cao Học Ch C ươn ơ g I I – Ph P ép Tí T nh Tí T ch c P h P ân Bà B i 15 - Tí T ch c P h P ân Suy R ộng +∞ dx Ví í d ụ ụ 4 : ∫ 3 0 1 + x 1 A Bx + C = + 1 / 3 x / 3 + 2 / 3 = − + 3 2 x + x +1 1 x x 1 1 − x +1 2 x 1 +1 x 1 − x +1 dx 1 1 2 1 2x −1 ∫
= ln | x +1| − ln | x − x +1| + arctan + C 3 6 1 3 x 3 3 + +∞ +∞ dx − ∫ 1 1 2 1 2x 1
= ln | x +1| − ln | x − x +1| + arctan 3 + 3 6 3 3 0 1 x 0 (∞ − ∞)
Ngô Thu Lương- Ôn tập Cao Học Ch C ươn ơ g I I – Ph P ép Tí T nh Tí T ch c P h P ân Bà B i 15 - Tí T ch c P h P ân Suy R ộng +∞ dx Ví í d ụ ụ 4 : ∫ 3 0 1 + x 1 A Bx + C = + 1 / 3 x / 3 + 2 / 3 = − + 3 2 x + x +1 1 x x 1 1 − x +1 2 x 1 +1 x 1 − x +1 dx 1 1 2 1 2x −1 ∫
= ln | x +1| − ln | x − x +1| + arctan + C 3 6 1 3 x 3 3 + 1 (x + )2 1 1 2x −1 = ln + arctan + C 2 6 x x 1 3 3 − +
Ngô Thu Lương- Ôn tập Cao Học Ch C ươn ơ g I I – Ph P ép Tí T nh Tí T ch c P h P ân Bà B i 15 - Tí T ch c P h P ân Suy R ộng +∞ +∞ +∞ dx 1 (x + )2 1 1 2x −1 ∫ = ln + arctan 3 2 0 6 1+ x x − x +1 3 3 0 0 1 −1 = ar a c r t c an a + ∞ − ar a c r t c an a 3 3 2π = 3 3
Ngô Thu Lương- Ôn tập Cao Học Ch C ươn ơ g I I – Ph P ép Tí T nh Tí T ch c P h P ân Bà B i 15 - Tí T ch c P h P ân Suy R ộng +∞ − Ví í d ụ ụ 5 : ∫ e xdx 0 − +∞ x = − e 0 −∞ 0 = − (e − e ) = − (0 −1) =1
Ngô Thu Lương- Ôn tập Cao Học Ch C ươn ơ g I I – Ph P ép Tí T nh Tí T ch c P h P ân Bà B i 15 - Tí T ch c P h P ân Suy R ộng +∞ − Ví dụ 6 : ∫ xe x Ví dụ dx 0 +∞ − = ∫ ( x x d −e ) 0 − +∞ +∞ − + +∞ x −x = x(− ) − ∫ (− e e ) dx 0 0 +∞ −x
= ∫ e dx =1 (vidu5) 0
Ngô Thu Lương- Ôn tập Cao Học Ch C ươn ơ g I I – Ph P ép Tí T nh Tí T ch c P h P ân Bà B i 15 - Tí T ch c P h P ân Suy R ộng +∞ 6 −x Bà Bài i tập : ∫ x e dx 0 +∞ 2 ∫ 7 − ∫ x e x e dx 0
Ngô Thu Lương- Ôn tập Cao Học Ch C ươn ơ g I I – Ph P ép Tí T nh Tí T ch c P h P ân Bà B i 15 - Tí T ch c P h P ân Suy R ộng +∞ − Ví í d ụ ụ 7 : ∫ e xdx 0 x = 0 ,t = 0 2 x = t x = t dx = 2t dt
x = +∞ t = +∞ +∞ + − +∞ − + x −t ∫ e
dx = ∫ e 2tdt 0 0 +∞ − = 2 t ∫ t e dt = 2 0 +∞ 3 − x Bà B i t ập ∫ e dx 0
Ngô Thu Lương- Ôn tập Cao Học Ch C ươn ơ g I I – Ph P ép Tí T nh Tí T ch c P h P ân Bà B i 15 - Tí T ch c P h P ân Suy R ộng +∞ = du 1 ∫ = 2 2 2 u +∞ du − +∞ = ∫ 1 1 = = 2 u ln 2 ln 2 ln 2 u
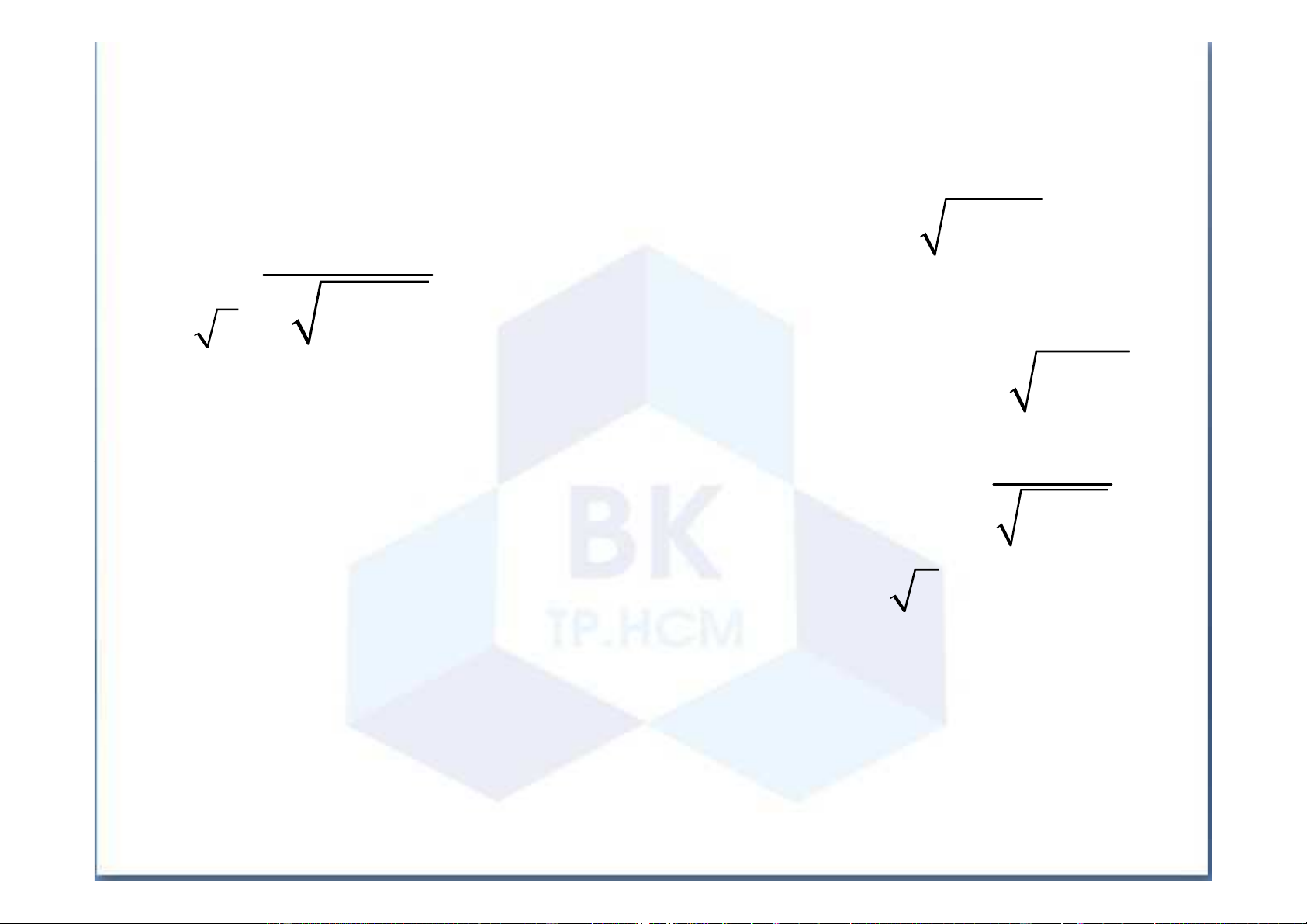
Ngô Thu Lương- Ôn tập Cao Học Ch C ươn ơ g I I – Ph P ép Tí T nh Tí T ch c P h P ân Bà B i 15 - Tí T ch c P h P ân Suy R ộng +∞ 2 dx x −1 = t ∫ Cá ách c t h t ứ ứ 1 2 2 2 x = 1 + t 2 x x −1 2 x = 1 + t t dx d = dt d 2 1 + t x = 2 → t = 1 x = +∞ → t = +∞
Ngô Thu Lương- Ôn tập Cao Học Cá ách c t h t ứ ứ 2
Ngô Thu Lương- Ôn tập Cao Học Ch C ươn ơ g I I – Ph P ép Tí T nh Tí T ch c P h P ân Bà B i 15 - Tí T ch c P h P ân Suy R ộng 1 = t (t ≥ 0) x Cá ách c t h t ứ ứ 3 1 x = t 1 − dx = dt 2 t 2 1 x −1 = −1 = 2 t 2 2 1− t 1− t = = 2 t t
Ngô Thu Lương- Ôn tập Cao Học




