Bài giảng toán cao cấp | Trường Đại học Bách Khoa Hà Nội

Bài giảng toán cao cấp | Trường Đại học Bách Khoa Hà Nội. Tài liệu gồm 54 trang, giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

119 60 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Toán cao cấp

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

54 trang 4 tháng trước

Tác giả:

Profile Sang
0 Ths.NGUYỄN QUỐC TIẾN
NGUYỄN QUỐC TIẾN
BÀI GIẢNG TOÁN
CAO CẤP
THÀNH PHỐ HỒ CHÍ MINH-2011
1
1 Ths.NGUYỄN QUỐC TIẾN
CHƯƠNG 1. GIỚI HẠN-TÍNH LIÊN TỤC CỦA HÀM SỐ
1.1 Giới hạn hàm số
1.1.1 Định nghĩa
Cho hàm số
( )
f x
xác định trong một lân cận của
0
x
(có thể trừ tại
0
x
). Số
L
được gọi là
giới hạn của hàm số
( )
f x
khi x dần đến
0
x
nếu:
0
0, 0, :(0 ( ) )
x D x x f x L
và được kí hiệu
0
lim ( )
x x
f x L
hay ( )
f x L
khi
0
x x
.
Giới hạn của hàm số
( )
f x
khi x dần đến
0
x
còn có thể định nghĩa thông qua giới hạn của dãy
số như sau:
0
0
lim ( ) ( ):
n n n
x x
f x x x f x
L x L
1.1.2 Định lí
Cho
( ), ( ), ( )
f x u x v x
xác định trong một lân cận của
0
x
có thể trừ tại
0
x
.
Nếu
( ) ( ) ( )
u x f x v x
với mọi x thuộc lân cận đó và
0 0
lim ( ) lim ( )
x x x x
u x v x L
thì
0
lim ( )
x x
f x L
Ví dụ. Chứng minh
0
sin
lim 1
x
x
x
Thật vậy
:0
2
x x
ta có bất đẳng thức
sin
cos 1
x
x
x
, mà
0
limcos 1
x
x
suy ra
0
sin
lim 1
x
x
x
1.1.3 Một số tính chất của giới hạn hàm số
i) Nếu
0
lim ( )
x x
f x L
thì giới hạn đó là duy nhất
ii)
0
lim
x x
C C
(C : hằng số)
iii) Nếu
( ) ( ),
f x g x x
thuộc một lân cận nào đó của
0
x
hoặc ở vô cực thì
0 0
lim ( ) lim ( )
x x x x
f x g x
(nếu các giới hạn này tồn tại).
2 Ths.NGUYỄN QUỐC TIẾN
iv) Nếu
( ) ( ) ( ),
f x g x h x x
thuộc một lân cận nào đó của
0
x
hoặc ở vô cực và
0 0
lim ( ) lim ( )
x x x x
f x L h x
thì
0
lim ( )
x x
g x L
v) Giả sử các hàm số
( ), ( )
f x g x
có giới hạn khi
0
x x
khi đó ta có các kết quả sau :
0 0 0
lim ( ( ) ( )) lim ( ) lim ( )
x x x x x x
f x g x f x g x
lim ( ) lim ( )
x x x x
o o
kf x k f x
lim ( ). ( ) lim ( ). lim ( )
x x x x x x
o o o
f x g x f x g x
0
0 0
0
,
lim ( )
( )
lim lim ( ) 0
( ) lim ( )
x x
x x x x
x x
f x
f x
g x
g x g x
1.2 Vô cùng bé
Giả sử ta xét các hàm trong cùng một quá trình, chẳng hạn khi
o
x x
. (Những kết quả đạt
được vẫn đúng trong một quá trình khác)
1.2.1 Định nghĩa
Hàm
( )
x
được gọi là một vô cùng bé (VCB) trong quá trình
o
x x
nếu
0
lim ( ) 0
x x
x
Ví dụ.
sin , , 1 cos
x tgx x
là những VCB khi
0
x
, còn
2
1
2
x
x
là VCB khi
x
1.2.2 So sánh hai VCB
Cho
( )
x
và
( )
x
là hai VCB trong một quá trình nào đó (chẳng hạn khi
o
x x
). Khi đó
tốc độ tiến về 0 của chúng đôi khi có ý nghĩa quan trọng. Cụ thể ta có các định nghĩa:
Nếu
( )
lim 0
( )
x
x
thì ta nói
( )
x
là VCB bậc cao hơn VCB
( )
x
trong quá trình đó (
( )
x
dần tới 0 nhanh hơn
( )
x
khi
o
x x
)
Nếu
( )
lim 0
( )
x
L
x
thì ta nói
( )
x
và
( )
x
là hai VCB ngang cấp trong quá trình đó (
( )
x
và
( )
x
dần tới 0 ngang nhau khi
o
x x
.
Đặc biệt khi
1
L
ta nói
( )
x
và
( )
x
là hai VCB tương đương, kí hiệu là
( ) ( )
x x
.
1.2.3 Một số VCB tương đương cơ bản khi
0
x
sin
x x
tgx x
arcsin
x x
;
arctgx x
3 Ths.NGUYỄN QUỐC TIẾN
2
( )
1 cos
2
ax
ax
1
log (1 )
ln
x x
a
a
1 1
x x
ln(1 )
x x
-1 ln
x
a x a
-1
x
e x
1
1
... ,( , 0)
n n p p
n n p p p
a x a x a x a x n p a
Sinh viên có thể tự kiểm tra các tương đương này (xem như bài tập)
Ví dụ. So sánh cấp của các VCB:
( ) sin ; ( ) 1 cos
x x tgx x x
, khi
0
x
Ta có:
0 0 0 0
1
sin 1
( ) sin sin
cos
lim lim lim lim 0
( ) 1 cos 1 cos cos
x x x x
x
x x tgx x
x
x x x x
Do đó,
( )
x
là VCB cấp cao hơn
( )
x
Ví dụ. So sánh cấp của các VCB:
2
( ) 1 cos , ( ) , 0
x x x x x
Ta có:
2
0 0
( ) 1 cos 1
lim lim 0
( ) 2
x x
x x
x x
Do đó,
( )
x
và
( )
x
là hai VCB cùng cấp.
1.2.4 Quy tắc ngắt bỏ VCB cấp cao
i) Nếu
1
( ) ( )
x x
và
1
( ) ( )
x x
trong cùng một quá trình thì trong quá trình ấy
1
1
( )
( )
lim lim
( ) ( )
x
x
x x
ii) Cho
( )
x
và
( )
x
là hai VCB trong một quá trình và
( )
x
có cấp cao hơn
( )
x
. Khi đó
( ) ( ) ( )
x x x
.
Từ hai kết quả trên ta suy ra quy tắc ngắt bỏ VCB cấp cao:
Giả sử
( )
x
và
( )
x
là hai VCB trong một quá trình nào đó.
( )
x
và
( )
x
đều là tổng của
nhiều VCB . Khi đó giới hạn của tỉ số
( )
( )
x
x
bằng giới hạn của tỉ số hai VCB cấp thấp nhất
trong
( )
x
và
( )
x
.
Ví dụ. Tìm các giới hạn sau:
1)
2 3
3 8
0
3sin 4sin
lim
5
x
x x x
x x x
Ta có
2 3
3 8
0 0
3sin 4sin 1
lim lim
5 5 5
x x
x x x x
x x x x
2)
3
0
1 1
lim
1 1
x
x
x
.
4 Ths.NGUYỄN QUỐC TIẾN
Khi
0
x
ta có
1
2
1
1 1 (1 ) 1
2
x x x
;
3
1
3
1
1 1 (1 ) 1
3
x x x
Suy ra
3
1 1 3
2
1 1
x
x
. Vậy
3
0
1 1 3
lim
2
1 1
x
x
x
3)
0
sin
lim
x
tgx x
x
Khi
0
x , ta có:
sin
2 khi 0
tgx x x x
x
x x
. Do đó
0
sin
lim 2
x
tgx x
x
4) Tính
3
3
0
sin sin
lim
x
tgx x x
x
.
Ta có
2
3
1
.
sin (1 cos ) 1
2
sin
cos 1 2
x x
x x
tgx x x
x
khi
0
x
Do đó
3 3 3 3
1 3
sin sin
2 2
tgx x x x x x
khi
0
x
Suy ra
3
3
3 3
3
sin sin 3
2
2
x
tgx x x
x x
khi
0
x
Vậy
0
3
3
sin sin 3
lim
2
x x
tgx x x
x
1.3 Hàm số liên tục
1.3.1 Các định nghĩa
Hàm số
( )
y f x
được gọi là liên tục tại
o
x D
nếu
0
0
lim ( ) ( )
x x
f x f x
. Khi đó
0
x
gọi là
điểm liên tục của hàm
( )
f x
.
Hàm số
( )
y f x
được gọi là liên tục trên
( , )
a b
nếu
( )
f x
liên tục tại mọi điểm thuộc
( , )
a b
.
Hàm số
( )
y f x
được gọi là liên tục bên trái (bên phải)
0
x D
nếu
0
0
lim ( ) ( )
x x
f x f x
(
0
0
lim ( ) ( )
x x
f x f x
).
Hàm
( )
f x
được gọi là liên tục trên
[ , ]
a b
nếu
( )
f x
liên tục trên
( , )
a b
và liên tục bên phải tại
a, bên trái tại b.
1.3.2 Tính chất của hàm số liên tục
Giả sử
( ), ( )
f x g x
là hai hàm liên tục trên
[ , ]
a b
. Khi đó:
5 Ths.NGUYỄN QUỐC TIẾN
i)
( ) ( )
f x g x
và
( ) ( )
f x g x
liên tục trên
[ , ]
a b
, nếu
( ) 0
g x
thì
( )
( )
f x
g x
liên tục trên
[ , ]
a b
.
ii)
( )
f x
liên tục trên
[ , ]
a b
.
iii) Nếu
( )
u x
liên tục tại
0
x
và
( )
f u
liên tục tại
0 0
( )
u u x
thì hàm
0
( )
f u x
liên tục tại
0
x
.
iv)
( )
f x
liên tục trên
[ , ]
a b
thì đạt giá trị lớn nhất, giá trị bé nhất trên đoạn đó.
1.3.3 Điểm gián đoạn
Nếu
( )
f x
không liên tục tại
0
x D
thì ta nói
( )
f x
gián đoạn tại
0
x
và điểm
0
x
gọi là điểm
gián đoạn.
Hàm
( )
f x
gián đoạn tai
0
x
nhưng tồn tại giới hạn của f(x) tại
0 0
,
x x
thì
0
x
được gọi là điểm
gián đoạn loại 1. Các điểm gián đoạn khác gọi là điểm gián đoạn loại 2.
Ví dụ. Xét tính liên tục của hàm
1)
1, 0
( )
sin 2
, 0
2
x
f x
x
x
Ta có
0 0
sin 2
lim ( ) lim (0) 1
2
x x
x
f x f
x
.
Vậy
( )
f x
gián đoạn tại
0
x
,và
0
x
là điểm gián đoạn loại 1
2)
1 , 0
( )
-1 , 0
x x
f x
x x
Hàm số gián đoạn tại
0
x
và
0 0
lim ( ) 1, lim ( ) 1
x x
f x f x
nên
0
x
là điểm gián đoạn loại 1
3)
2 3
( )
2
x
f x
x
, có điểm gián đoạn tại
0
2
x
Ta có
2
lim ( )
x
f x

và
2
lim ( )
x
f x

Suy ra
0
2
x
là điểm gián đoạn loại 2.
BÀI TẬP CHƯƠNG I
Câu 1. Tìm miền xác định của hàm số
6 Ths.NGUYỄN QUỐC TIẾN
a)
2
ln 1
y x
b)
1
arctan
1
y
x
c)
2
1
1
x
x x
d)
2
1
x x
e
c)
2
sin
2 3
x
x x
f)
2
1
2
x
x x
Câu 2. Tính giới hạn của các dãy số sau:
a)
2
lim ( )
n
n n n

; ds
1
2
b)
4
2
lim
1
n
n n n
n

;ds
1
c)
3 4
lim
2 7
n n
n n
n
;ds
0
d)
1 1 1
lim ...
1.2 2.3 .( 1)
n
n n
Câu 3. Tính giới hạn của các hàm số sau:
a)
2
2
2 1
lim
2 3
x
x x x
x x

b)
2
2
1
1
lim
4 3
x
x
x x
d)
3
2
1
1
lim
1
x
x
x
e)
4 4
3 3
lim
x a
x a
x a
f)
2
lim( 2 )
x
x x x
g)
2
lim(2 2 )
x
x x x
a)
4
2 1 3
lim
4
x
x
x
b)
2
4
2
lim
3 4
x
x
x x
d)
3
4
1
1
lim
1
x
x
x
Câu 4. Tính giới hạn của các hàm số sau:
a)
2
2
0
(1 cos )
lim
sin tan
x
x
x x x
; ds 1/4 b)
2
0
1 cos2
lim
sin
x
x
x
; ds 1
c)
0
sin3
lim
ln(2 1)
x
x
x
; ds 3/2 d)
3
0
sin
lim
x
tgx x
x
; ds ½
Câu 5. Tính giới hạn của các hàm số sau:
a)
cot
0
lim(sin cos )
x
x
x x
; ds e b)
0
lim ln
x
x x
; ds 0
c)
lim
x
x
xe

; ds 0 d)
1
2( 1)
1
lim
x
x
x
; ds
e
e)
3 5
2 6
0
sin tan
lim
3 9
x
x x x
x x x
;ds 1/3 f)
2
1
0
lim(cos )
x
x
x
Câu 6. Tìm
a
để các hàm số sau liên tục trên tập xác định của chúng.
a)
2
1
( 0)
( 0)
x
y
x
a x
b)
2
2
1 cos
( 0)
2 ( 0)
2
x
x
x
y
a
x x
c)
2
ln ( 0)
( 0)
x x x
y
a x
Câu 7. Tìm các điểm gián đoạn của hàm số và chúng thuộc loại nào
a)
1
2 5
x
y
x
b)
2
2
2
x x
y
x
c)
0 0
1 0
x
y
x
sin
( 0)
( 0)
x
x
x
y
a x
7 Ths.NGUYỄN QUỐC TIẾN
2 CHƯƠNG 2. PHÉP TÍNH VI PHÂN HÀM MỘT BIẾN
2.1 Đạo hàm
2.1.1 Đạo hàm tại một điểm
Cho hàm số
( )
y f x
xác định tại
0
x
và tại lân cận
0
x
. Khi đó nếu tỉ số
0
0
( ) ( )
f x f x
x x
có giới hạn khi
0
x x
thì ta nói
( )
f x
khả vi tại
0
x
hay
( )
f x
có đạo hàm tại
0
x
và giới
hạn đó được gọi là đạo hàm của
( )
f x
tại
0
x
. Ký hiệu là
0
'( )
f x
hay
0
'( )
y x
.Vậy
0
0
0
( ) ( )
'( ) lim
f x f x
f x
x x
x x
.
Nếu đặt
0
0
0
0
x x x
x x x
x x x
Lúc đó
0 0
0
0
( ) ( )
'( ) lim
x
f x x f x
f x
x
Hàm số
( )
y f x
được gọi là có đạo hàm trên khoảng
( , )
a b
nếu nó có đạo hàm tại
mọi điểm
0
( , )
x a b
. Khi đó đạo hàm của hàm số
( )
f x
là một hàm số xác định trên
( , )
a b
. Cho nên ký hiệu của đạo hàm của
( )
y f x
trên
( , )
a b
là
'( )
f x
hoặc
'
y
Vậy
0
( ) ( )
' '( ) lim
x
f x x f x
y f x
x
Ví dụ. Xét hàm số
2
( )
y f x x
Ta có miền xác định của hàm số là
R
. Đạo hàm của hàm số trên tập xác định là
2 2
0 0
0 0
( ) ( ) ( )
' lim lim
( )( )
lim lim(2 ) 2
x x
x x
f x x f x x x x
y
x x
x x x x x x
x x x
x
Do đó
2
' '( ) ( )' 2
y f x x x
8 Ths.NGUYỄN QUỐC TIẾN
2.1.2 Bảng các đạo hàm cơ bản
'
1
1
' 0 ( )
1
( )' ,
1
ln '
1
(log )'
ln
( )'
n
n
n
a
x
C C const
x x R x
n x
x
x
x
x a
e e
2
2
2
2
(sin )' cos
(cos )' -sin
1
( )' 1
cos
1
(cot )' (1 cot )
sin
x x
x x
tgx tg x
x
gx g x
x
2.1.3 Các quy tắc tính đạo hàm
Nếu hai hàm
( )
u x
và
( )
v x
có đạo hàm tại điểm
x
thì tổng, hiệu, tích, thương của chúng
cũng có đạo hàm tại điểm
x
và:
2
( )' ' '
( )' ',
( . )' ' '
' - '
( ) ' , 0
u v u v
ku ku k R
u v u v uv
u u v uv
v
v v
2.1.4 Đạo hàm của hàm hợp
Xét hàm hợp
( )
y y u x
nếu hàm
( )
y y u
có đạo hàm đối với
u
và
( )
u u x
có đạo
hàm đối với
x
thì
( )
y y u x
có đạo hàm đối với
x
và
'( ) '( ). '( )
y x y u u x
Ví dụ. Xét hàm số
3 10
(1 )
xy
Ta có
3 9 3
3 9 2 2 3 9
' 10(1 ) (1 )'
10(1 ) 3 30 (1 )
y x x
x x x x
Ví dụ. Giả sử
( ), ( )
x x
có đạo hàm với mọi
x R
. Tính đạo hàm của hàm
2 2
( ) ( )
y x x
Đặt
2 2
( ) ( )
u x x
khi đó
y u
Ta có
9 Ths.NGUYỄN QUỐC TIẾN
2 2
'( ) '( ). '( )
( ) ( )
1
2 ( ) '( ) 2 ( ) '( )
2
( ) '( ) ( ) '( )
y x y u u x
x x
x x x x
u
x x x x
Ví dụ. Tính các đạo hàm của hàm số sau:
1
1
x
y
x
Ta có
1
ln ln(1 )
y x
x
Lấy đạo hàm hai vế ta được:
' 1 1
ln(1 )
1
y
y x x
Suy ra
1 1 1
' 1 ln(1 )
1
x
y
x x x
2.1.5 Đạo hàm cấp cao
Cho hàm số
( )
f x
có đạo hàm
'( )
f x
. Hàm số
'( )
f x
được gọi là đạo hàm cấp một của
( )
f x
. Nếu
'( )
f x
khả vi thì đạo hàm của
'( )
f x
được gọi là đạo hàm cấp hai của
( )
f x
và
ký hiệu là
''( )
f x
. Vậy
''( ) '( ) '
f x f x
Tổng quát, đạo hàm của đạo hàm cấp
1
n
của
( )
f x
được gọi là đạo hàm cấp
n
của
( )
f x
ký hiệu
( )
( )
n
f x
vậy
( ) ( 1)
( ) ( ) '
n n
f x f x
Ví dụ. Tìm đạo hàm cấp
n
của ( )
x
y f x xe
Ta có
' (1 )
" (1 ) (2 )
...
x x x
x x x
y e xe x e
y e x e x e
Chứng minh bằng quy nạp ta đi đến kết quả sau
( )
( )
n x
y n x e
2.1.6 Vi phân
Cho hàm số
( )
y f x
xác định trên
( , )
a b
và
( , )
x a b
, nếu hàm số
( )
y f x
khả vi
tại điểm
x
thì số gia của hàm số tại
x
có thể viết được dưới dạng
( ) ( ) - ( ) '( ) ( )
f x f x x f x f x x o x
với
( )
o x
là VCB cấp cao hơn
x
khi
0
x
.
Biểu thức
'( ).
f x x
được gọi là vi phân của
( )
f x
tại
x
. Ký hiệu:
( )
df x
hoặc
( )
dy x
tức
là
( ) '( ).
df x f x x
Xét hàm ( )
y f x x
ta có
'( ) 1
f x
nên ( ) 1.
df x dx x x
từ đó ta có
10 Ths.NGUYỄN QUỐC TIẾN
( ) '( ). '( ).
df x f x x f x dx
. Để ngắn gọn ta viết
'( ).
df f x dx
Giả sử
( ), ( )
y f x x t
là các hàm số khả vi, khi đó vi phân hàm
( )
y f t
là
( ( ) )' '( ) '( ) '( )
df f t dt f x x t dt f x dx
. Vậy dạng vi phân của hàm
( )
y f x
không
thay đổi dù
x
là biến độc lập hay là
x
là hàm khả vi theo biến
t
. Tính chất này
gọi là tính bất biến của dạng vi phân.
Ví dụ.. Tìm vi phân của hàm
ln
y x
Áp dụng định nghĩa dạng vi phân ta được
(ln )
dx
dy d x
x
2.1.7 Ứng dụng của vi phân để tính gần đúng
Cho hàm
( )
y f x
khả vi tại
0
x
. Theo định nghĩa vi phân ta có số gia của hàm tại
0
x
là :
0 0 0
( ) - ( ) '( ) ( )
f f x x f x f x x o x
Do đó khi
x
khá bé ta có công thức gần đúng.
0 0 0
( ) '( ) ( )
f x x f x x f x
Ví dụ. Tính gần đúng
122
Ta thấy
122 121 1
Xét hàm
( )
y f x x
Áp đụng công thức gần đúng
0 0 0
( ) '( ) ( )
f x x f x x f x
suy ra
0 0
0
1
.
2
x x x x
x
. Chọn
0
121, 1
x x
ta được
1
122 .1 121 0,0454 11 11,0454
2 121
Ví dụ. Tính gần đúng
sin 29
o
Ta thấy
0
sin 29 sin
6 180
. Xét hàm
( ) sin
y f x x
Ta có
0 0 0
sin( ) cos . sin
x x x x x
, áp dụng cho
0
, -
6 180
x x
ta được
1 3
sin 29 sin sin cos . . 0,484
6 180 6 6 180 2 2 180
o
11 Ths.NGUYỄN QUỐC TIẾN
2.2 Ứng dụng đạo hàm
2.2.1 Định lí ( Quy tắc L’Hospital).
i) Cho
( ), ( ) 0
f x g x
là hai hàm liên tục và khả vi tại lân cận
0
x
(
0
x
hữu hạn hoặc
). Giả sử
lim ( ) lim ( ) 0
o o
x x x x
f x g x
và
'( ) 0
g x
với mọi
x
thuộc lân cận
0
x
. Khi đó nếu
'( )
'( )
lim
o
x x
f x
L
g x
thì
( )
( )
lim
o
x x
f x
L
g x
.
ii) Cho
( ), ( ) 0
f x g x
là hai hàm liên tục và khả vi tại lân cận
0
x
. Giả sử
lim ( ) lim ( )
o o
x x x x
f x g x
và
'( ) 0
g x
, với mọi
x
thuộc lân cận
0
x
. Khi đó:
Nếu
'( )
lim
'( )
o
x x
f x
L
g x
thì
( )
lim
( )
o
x x
f x
L
g x
Ví dụ. Tính lim
x a
x a
a x
x a
(dạng
0
0
)
Ta có:
1
ln
lim lim ln
1
( )'
( )'
x a
a a
x a
x a x a
a a ax
a a a
a x
x a
.
Vậy
lim ln
x a
a a
x a
a x
a a a
x a
Ví dụ.. Tính
lim
x
x
x
e

(dạng
)
Ta có:
' 1
lim lim 0
( )'
x x
x x
x
e e
 
. Vậy
lim 0
x
x
x
e

Chú ý : Khi
x
tiến tới một quá trình nào đó (chẳng hạn
x
tiến tới
0
x
), nếu
0
'( )
'( )
lim
x x
f x
g x
không tồn tại thì không kết luận được cho
0
( )
( )
lim
x x
f x
g x
. Nếu áp dụng quy tắc L’Hospital mà
giới hạn vẫn còn dạng vô định
0
0
hoặc
thì có thể áp dụng quy tắc L’Hospital một lần
nữa và tiếp tục cho đến hết dạng vô định.
Ví dụ. Tính
2
1
1 cos
lim
2 1
x
x
x x
Áp dụng liên tiếp hai lần quy tắc L’Hospital ta được
2
1 1 1
sin sin cos
lim lim lim
2 2 2 1 2 1 2
x x x
x x x
x x
.
Vậy
2
2
1
1 cos
lim
2 1 2
x
x
x x
12 Ths.NGUYỄN QUỐC TIẾN
Ví dụ. Tính
3
0
lim
sin
x
x
x x
Áp dụng liên tiếp quy tắc L’Hospital ta có:
3 2
0 0 0 0
3 6 6
lim lim lim lim 6
sin 1 cos sin cos
x x x x
x x x
x x x x x
Vậy
3
0
lim 6
sin
x
x
x x
Đối với các dạng vô định
0 0
, 0. , 0 ,
và
1
ta phải đưa các dạng vô định đó về
một trong hai dạng
0
0
hoặc
sau đó lại áp dụng quy tắc L’Hospital.
Ví dụ.
Tính
0
lim .ln
x
x x
( dạng 0. )
Ta biến đổi để đưa giới hạn về dạng
0 0 0 0
2
1
ln
lim ln lim lim lim 0
1 1x x x x
x
x
x x x
x x
Ví dụ. Tính
0
1 1
lim
1
x
x
x e
(dạng
-
)
Ta biến đổi giới hạn để đưa về dạng
0
0
sau đó áp dụng liên tiếp quy tắc L’Hospital
0 0 0 0
1 1 1 1 1
lim lim lim lim
1 ( 1) 1 2 2
x x x
x x x x x x
x x x x
e x e e
x e x e e xe e xe
Ví dụ. Tính
3
lim ln
x
x x

(dạng
-
)
Ta có:
3
3
ln
ln (1- )
x
x x x
x
và
2
3 2
1
3ln .
ln ln 6ln 1
lim lim lim 3 lim lim 6 0
1
x x x x x
x
x x x
x
x x x x
    
Vậy:
3
3
ln
lim ln lim 1- .1
x x
x
x x x
x
 
Ví dụ. Tính
2
lim
x
x
x

( dạng
0
)
Ta có
2
0
1
2 ln
lim ln 2 lim 2 lim
1
lim 1
x
x
x
x
x
x x
x x x
x e e e e

  
13 Ths.NGUYỄN QUỐC TIẾN
2.2.2 Sự biến thiên của hàm số
Cho hàm số
( )
y f x
liên tục trên
[ , ]
a b
và có đạo hàm hữu hạn trên
( , )
a b
, khi đó ta có
các kết quả sau :
Nếu
( )
f x
luôn tăng (giảm) trên
[ , ]
a b
thì
'( ) 0, ( , )
f x x a b
(
'( ) 0, ( , )
f x x a b
)
Nếu
'( ) 0, ( , )
f x x a b
(
'( ) 0, ( , )
f x x a b
) thì trên
[ , ]
a b
hàm
( )
f x
đơn điệu tăng
(giảm)
Việc chứng minh hai kết quả trên dựa vào định nghĩa hàm số tăng (giảm), định nghĩa đạo
hàm và định lí Lagrange. Sinh viên tự chứng minh như bài tập.
Từ hai kết quả trên ta có nhận xét : Nếu hàm
( )
f x
có đạo hàm đồng nhất bằng 0 trên
[ , ]
a b
thì
( )
f x
là hàm hằng trên
[ , ]
a b
.
2.2.3 Định lí .
Giả sử
( )
f x
liên tục trên một lân cận của
0
x
có đạo hàm trong lân cận đó (có thể trừ
0
x
)
và
0
x
là điểm tới hạn của
( )
f x
. Khi đó :
i) Nếu
'( )
f x
đổi dấu từ âm sang dương khi
x
đi qua
0
x
thì
( )
f x
đạt cực tiểu tại
0
x
ii) Nếu
'( )
f x
đổi dấu từ dương sang âm khi
x
đi qua
0
x
thì
( )
f x
đạt cực đại tại
0
x
iii) Nếu
'( )
f x
không đổi dấu khi
x
đi qua
0
x
thì
( )
f x
không đạt cực trị tại
0
x
Ví dụ. Tìm cực trị của hàm số
3
2
( ) ( 1)
y f x x x
Miền xác định của hàm số là
R
Bảng xét dấu của đạo hàm :
3
5 -2
'
3
x
y
x
, với các điểm tới hạn là :
2
0,
5
x x
Ta có hàm số đạt cực đại
0
x
và đạt cực tiểu tại
2
5
x
2.2.4 Định lí .
Cho hàm số
( )
y f x
liên tục trên
[ , ]
a b
và khả vi liên tục đến cấp hai trên
( , )
a b
, khi đó:
i) Nếu tại
0 0
( , ), '( ) 0
x a b f x
và
0
''( ) 0
f x
thì
( )
f x
đạt cực đại tại
0
x
ii) Nếu tại
0 0
( , ), '( ) 0
x a b f x
và
0
''( ) 0
f x
thì
( )
f x
đạt cực tiểu tại
0
x
Ví dụ. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
3
2
4
x
y
x
Ta có :
\ 0
TXD R
3
2
0
4
lim
x
x
x
: đường cong có tiệm cận đứng
0
x
3
2
4
lim
x
x
x
: đường cong không có tiệm cận ngang
14 Ths.NGUYỄN QUỐC TIẾN
3
3
( ) 4
lim lim 1
x x
f x x
a
x x

3
2
4
lim ( ) lim 0
x x
x
b f x ax x
x

đường cong có tiệm cận xiên
y x
3
8
' 1 , ' 0 2
y y x
x
4
24
'' 0
y
x
: đường cong luôn lõm.
Ta có bảng biến thiên
Hàm số đạt cực tiểu tại
2
x
và
min
3
y
Giao điểm của đồ thi với trục hoành
3
( 4,0)
Vẽ đồ thị
BÀI TẬP CHƯƠNG II
Câu 1. Tính đạo hàm của các hàm số sau:
a)
2
sin
y x
b)
2
cos( 3 )
y x x
c)
2
ln( 3 )
y x x
d)
2
1
y x x
e)
sin
x
y e
f)
x
y x
g)
sin
x
y x
h)
2
ln 3
y x x
i)
2
1
x x
y
x
Câu 2. Tính đạo hàm cấp
3
của các hàm số sau
a)
sin
y ax
b)
1
y
ax b
c)
2
sin
y x
d)
ln
y x x
Câu 3. Khảo sát sự biến thiên của các hàm số sau
a)
2
ln
2
x
y x b)
1 arctan
y x
c)
x
y xe
d)
2
1
2
y
x x
e)
2
4 3
y x x
f)
2
4
x
y e
Câu 4. Tìm cực trị của các hàm số sau
a)
ln
y x x
b)
2
3 2sin
y x x
c)
2
2
x
y e
Câu 4. Tính các giới hạn sau bằng quy tắc L’hospital
15 Ths.NGUYỄN QUỐC TIẾN
a)
0
2
lim
sin
x x
x
e e x
x x
b)
0
ln(cos2 )
lim
sin
x
x
x
c)
2
0
1 1
lim
sin
x
x x x
d)
1
1
lim
ln ln
x
x
x x
e)
ln
0
lim 1
x
x
x
f)
sin
0
lim
x
x
x
16 Ths.NGUYỄN QUỐC TIẾN
3 CHƯƠNG 3. PHÉP TÍNH TÍCH PHÂN HÀM MỘT BIẾN
3.1 Nguyên hàm
3.1.1 Định nghĩa (Nguyên hàm)
Hàm
( )
F x
được gọi là một nguyên hàm của
( )
f x
trên
( , )
a b
nếu
'( ) ( ), ,
F x f x x a b
.
Ví dụ.
( )
tg x
là một nguyên hàm của
2
1
tg x
trên
\ 2 1
2
R n
,
sin 100
x
là một nguyên
hàm của
cos
x
…
Có thể chứng minh được: nếu
( )
F x
là một nguyên hàm của
( )
f x
trên
( , )
a b
thì mọi
nguyên hàm của
( )
f x
trên khoảng đó đều có dạng ( )
F x C
với
C
là một hằng số. Họ vô số
các nguyên hàm đó được gọi là tích phân bất định của hàm
( )
f x
ký hiệu
( )
f x dx
. Vậy
( ) ( )f x dx
F x C
trong đó dấu
được gọi là dấu tích phân,
( )
f x
là hàm dưới dấu tích phân,
( )
f x dx
là biểu
thức dưới dấu tích phân và
x
là biến số tích phân.
3.1.2 Một số tính chất của tích phân bất định
'
( ) ( )
)
f x dx f x
i
. ( ) . ( )
)
C f x dx C f x dx
ii
,
C
là hằng số
( ) ( ) ( ) ( )
)
f x g x dx f x dx g x dx
iii
Việc chứng minh các tính chất trên xem như bài tập.
3.1.3 Tích phân bất định của một số hàm số cơ bản.
kdx kx C
1
, ( 1)
1
x
x dx C
1
1
, ( 1)
1
dx
C
x x
ln | |
dx
x C
x
, ( 0, 1)
ln
x
x
a
a dx C a a
a
, ( 0)
x
x
e
e dx C
1
cos( ) sin( )
ax b dx ax b C
a
1
sin( ) cos( )
ax b dx ax b C
a
2
(1 )
tg x dx tgx C
2
(1 cot ) cot
g x dx gx C
17 Ths.NGUYỄN QUỐC TIẾN
2
1
arcsin
1
,
dx x C
x
2 2
1
arcsin ( 0)
,
x
dx a
a
a x
C
2
1
1
dx arctgx
x
C
2 2
1 1
( 0)
,
x
dx arctg a
a x a a
C
1
lndx a x
a x
C
2 2
1 1
ln
2
x a
dx
x a a x a
C
1
ln
cos 2 4
x
dx tg C
x
1
ln
sin 2
x
dx tg C
x
2
1 1
( )
cos ( )
dx tg ax b C
ax b a
1
, ( 0)
ax b ax b
e d e C a
a
x
2
1 1
( )
sin ( )
dx cotg ax b C
ax b a
1 1
ln , ( 0)
dx ax b C a
ax b a
3.2 Tích phân xác định
3.2.1 Định nghĩa
Cho hàm số
( )
f x
liên tục trên
,
a b
và
( )
F x
là một nguyên hàm của
( )
f x
trên đoạn đó.
Khi đó giá trị
( ) ( )
F b F a
được gọi là tích phân xác định của hàm
( )
f x
trên
,
a b
. Kí hiệu
( )
b
a
f x dx
. Người ta thường viết
( ) ( ) ( )
b
a
F x F b F a
. Vậy
( ) ( ) ( ) ( )
b
b
a
a
f x dx F x F b F a
.
Nhận xét. Tích phân xác định không phụ thuộc vào ký hiệu của biến dưới dấu tích phân,
nghĩa là
( ) ( ) ...
b b
a a
f x dx f u du
Ví dụ. Tính
1
2
0
x dx
Ta có
3
3
x
là một nguyên hàm của
2
( )
f x x
, do đó
1
1
3
2
0
0
1
3 3
x
x dx
Ví dụ. Tính
4
0
tgxdx
Ta có trên đoạn
[0, ]
4
hàm số
ln(cos )
x
là một nguyên hàm của
tgx
nên
18 Ths.NGUYỄN QUỐC TIẾN
4
0
4
0
2
ln(cos ) ln( ) ln(1) ln 2
2
tgxdx x
.
3.2.2 Các tính chất của tích phân xác định
Giả sử
( ), ( )
f x g x
là các hàm khả tích trên
,
a b
khi đó:
) ( ) ( ) ( )
b b
a a
i kf x dx k f x dx k const
) [ ( ) ( )] ( ) ( )
b b b
a a a
ii f x g x dx f x dx g x dx
) ( ) ( ), [ , ] ( ) ( )
b b
a a
iii f x g x x a b f x dx g x dx
) ( ) ( ) ( ) , ,
b c b
a a c
iv f x dx f x dx f x dx c a b
) ( )
v f x
khả tích trên
,
a b
và
( ) ( )
b b
a a
f x dx f x dx
Khi đi tìm nguyên hàm hay tính tích phân xác định trong nhiều trường hợp hàm dưới dấu
tích phân không đơn giản, không có dạng như những hàm cơ bản nêu trên, ta phải biến đổi
hàm dưới dấu tích phân sao cho có thể áp dụng được các tích phân cơ bản. Có hai phương
pháp để biến đổi tích phân trong trường hợp này.
3.3 Hai phương pháp tính tích phân cơ bản
3.3.1 Phương pháp đổi biến số
Phương pháp đổi biến trong tích phân bất định có thể chia làm hai dạng
Dạng 1: Đặt
( )
x t
, trong đó
( )
t
là hàm khả vi và đơn điệu đối với biến
t
. Ta có:
( ) [ ( )] '( )
f x dx f t t dt
Ví dụ. Tính
3
3 2
sin
x
dx
x
Đặt
3
x t
,
x
khả vi và đơn điệu với mọi
t
, suy ra
2
'( ) 3
dx x t dt t dt
2
3
3
2
3 2
sin 3 sin
3 sin 3cos 3cos
x t t
dx tdt t C x C
t
x
Ví dụ. Tính
2
1
x dx
Đặt
sin , arcsin ,( 1 1)
2 2
x t t t x x
. Ta có
'( ) cos
dx x t dt tdt
19 Ths.NGUYỄN QUỐC TIẾN
2 2 2
1 1 sin cos cos
cos (cos 0 )
2 2
x t t t
t t do t
Suy ra
2 2
1 cos2 1
1 cos sin 2
2 2 4
t t
x dx tdt dt t C
thay
2 2
1 1
arcsin 1 arcsin 1
2 2
t x x dx x x x C
Dạng 2: Đặt
( )
u u x
trong đó
( )
u x
là hàm khả vi. Ta có
( ) [ ( )] '( ) ( )
f x dx f u x u x dx f u du
Ví dụ. Tính
5
2
1
x
x
e dx
e
Đặt '( )
x x
u e du u x dx e dx
. Suy ra
5 4
2
2 2 2
3 3
1
( 1 )
1 1 1
( )
3 3
x
x
x
x x
e dx u du
u du
e u u
u e
u arctg u e arctg e C
Ví dụ. Tính
4
sin 2
cos 4
xdx
x
Đặt
2
cos '( ) 2sin cos
u x du u x dx x xdx
. Suy ra
4 2
2
2
sin2 1 2
ln
cos 4 4 4 2
1 cos 2
ln
4 cos 2
xdx du u
C
x u u
x
C
x
Ví dụ. Tính
2
1
4
2 1
1
x x
I dx
x
Đặt
2
2
u x du xdx
, khi đó:
2 2 2
2
4 2
2 1
1 1 2 1
2 1 2 1 2 1
1 1
ln( 1)
2 2
1 1
ln( 1) ( )
2 2
u
udu du
I du
u u u
u arctgu C
x arctg x C
Áp dụng phương pháp trên khi tính tích phân xác định ta có thể thực hiện như sau:
Đối với dạng 1:
| 1/54
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

NGUYỄN QUỐC TIẾN BÀI GIẢNG TOÁN CAO CẤP
THÀNH PHỐ HỒ CHÍ MINH-2011 1 0 Ths.NGUYỄN QUỐC TIẾN
CHƯƠNG 1. GIỚI HẠN-TÍNH LIÊN TỤC CỦA HÀM SỐ
1.1 Giới hạn hàm số 1.1.1 Định nghĩa
Cho hàm số f (x) xác định trong một lân cận của x (có thể trừ tại x ). Số L được gọi là 0 0
giới hạn của hàm số f (x) khi x dần đến x nếu: 0
  0, 0, x
  D : (0  x x f (x)  L ) 0 và được kí hiệu
lim f (x)  L hay f (x)  L khi x x . 0 x 0 x
Giới hạn của hàm số f (x) khi x dần đến x còn có thể định nghĩa thông qua giới hạn của dãy 0 số như sau:
lim f (x)  L       x x x f x L n  : ( ) n 0 n x x0 1.1.2 Định lí
Cho f (x), u(x), v(x) xác định trong một lân cận của x có thể trừ tại x . 0 0
Nếu u(x)  f (x)  v(x) với mọi x thuộc lân cận đó và lim u(x)  lim v(x)  L thì x  0 x x 0 x
lim f (x)  L x x0 sin x
Ví dụ. Chứng minh lim  1 x0 x x Thật vậy x
 :0  x  ta có bất đẳng thức sin cos x
 1, mà lim cos x 1 suy ra 2 x x0 sin x lim  1 x 0 x
1.1.3 Một số tính chất của giới hạn hàm số
i) Nếu lim f (x)  L thì giới hạn đó là duy nhất xx0
ii) lim C C (C : hằng số) xx0
iii) Nếu f (x)  g(x), x
 thuộc một lân cận nào đó của x hoặc ở vô cực thì 0
lim f (x)  lim g(x) (nếu các giới hạn này tồn tại). xx xx 0 0 1 Ths.NGUYỄN QUỐC TIẾN
iv) Nếu f (x)  g(x)  h(x), x
 thuộc một lân cận nào đó của x hoặc ở vô cực và 0
lim f (x)  L  lim h (x) thì lim g(x)  L xx xx  0 0 x x0
v) Giả sử các hàm số f (x), g(x) có giới hạn khi x x khi đó ta có các kết quả sau : 0
lim ( f (x)  g(x))  lim f (x)  lim g(x) xx xx xx 0 0 0
lim kf (x)  k lim f (x) xx xx o o
lim f (x).g(x)  lim f (x). lim g(x) xx xx xx o o o lim f (x) f (x)  x 0 lim x  , lim g(x)  0 x  0 x g(x)
lim g( x)  x 0xx 0 x 1.2 Vô cùng bé
Giả sử ta xét các hàm trong cùng một quá trình, chẳng hạn khi x x . (Những kết quả đạt o
được vẫn đúng trong một quá trình khác) 1.2.1 Định nghĩa
Hàm (x) được gọi là một vô cùng bé (VCB) trong quá trình x x nếu lim (x)  0 o x 0 x x 1
Ví dụ. sin x, tgx, 1 cos x là những VCB khi x  0 , còn 2
x  là VCB khi x   2 1.2.2 So sánh hai VCB
Cho (x) và (x) là hai VCB trong một quá trình nào đó (chẳng hạn khi x x ). Khi đó o
tốc độ tiến về 0 của chúng đôi khi có ý nghĩa quan trọng. Cụ thể ta có các định nghĩa:  x Nếu ( ) lim  0
thì ta nói (x) là VCB bậc cao hơn VCB (x) trong quá trình đó ( (x) (x)
dần tới 0 nhanh hơn (x) khi x x ) o  x Nếu ( ) lim  L  0
thì ta nói (x) và (x) là hai VCB ngang cấp trong quá trình đó ( (x) (x)
và (x) dần tới 0 ngang nhau khi x x . o
Đặc biệt khi L  1 ta nói (x) và (x) là hai VCB tương đương, kí hiệu là (x)  (x) .
1.2.3 Một số VCB tương đương cơ bản khi x  0 sin x x tgx x arcsin x x arctgx  ; x 2 Ths.NGUYỄN QUỐC TIẾN 2 (ax) 1 1 cos ax  log (1 x)  x
1 x 1x
ln(1 x)  x 2 a ln a x
a -1  x ln a x e -1  x n n 1
a x a x   ... p p
a x a x ,(n p,a  0) n n 1  p p p
Sinh viên có thể tự kiểm tra các tương đương này (xem như bài tập)
Ví dụ. So sánh cấp của các VCB:
(x)  sin x tg ;x (x) 1cos x , khi x  0 Ta có: 1   sin x 1    (x) sin x tgx  cos x sin x  lim  lim  lim  lim  0 x0 x0 x0 x 0 (x) 1 cos x 1  cos x cos x
Do đó, (x) là VCB cấp cao hơn (x)
Ví dụ. So sánh cấp của các VCB: 2
(x) 1cos x, (x)  x , x  0 (x) 1  cos x 1 Ta có: lim  lim   0 2 x 0 x0 (x) x 2
Do đó, (x) và (x) là hai VCB cùng cấp.
1.2.4 Quy tắc ngắt bỏ VCB cấp cao
i) Nếu (x)  (x) và (x)  (x) trong cùng một quá trình thì trong quá trình ấy 1 1 (x) (x) 1 lim  lim (x) (x) 1
ii) Cho (x) và (x) là hai VCB trong một quá trình và (x) có cấp cao hơn (x) . Khi đó
(x)  (x)  (x) .
Từ hai kết quả trên ta suy ra quy tắc ngắt bỏ VCB cấp cao:
Giả sử (x) và (x) là hai VCB trong một quá trình nào đó. (x) và (x) đều là tổng của  x
nhiều VCB . Khi đó giới hạn của tỉ số ( ) bằng giới hạn của tỉ số hai VCB cấp thấp nhất (x)
trong (x) và (x) .
Ví dụ. Tìm các giới hạn sau: 2 3
x  3sin x  4sin x 1) lim 3 8 x0
5x x x 2 3
x  3sin x  4 sin x x 1 Ta có lim  lim  3 8 x0 x0
5x x x 5x 5 1  x 1 2) lim . 3 x0 1  x 1 3 Ths.NGUYỄN QUỐC TIẾN 1 1 1 1 Khi x  0 ta có 2
1 x 1  (1 x) 1  x ; 3 3
1 x 1  (1 x) 1  x 2 3 1  x 1 3 1  x 1 3 Suy ra  . Vậy lim  3 1  x 1 2 3 x0 1  x 1 2 tgx  sin x 3) lim x0 x Khi x  0 , ta có: tgx  sin x x x tgx  sin x
 2 khi x  0 . Do đó lim  2 x x x 0  x 3
tgx  sin x  sin x 4) Tính lim . 3 x0 x Ta có 1 2 . x x
sin x(1 cos x) 1 2 3
tgx  sin x  
x khi x  0 cos x 1 2 Do đó 1 3 3 3 3 3
tgx  sin x  sin x x x x khi x  0 2 2 3 3 3 x
tgx  sin x  sin x 3 Suy ra 2   khi x  0 3 3 x x 2 3
tgx  sin x  sin x 3 Vậy lim  3 x 0 x x 2
1.3 Hàm số liên tục
1.3.1 Các định nghĩa
Hàm số y f (x) được gọi là liên tục tại x D
lim f (x)  f (x ) . Khi đó x gọi là o nếu 0 0 x 0 x
điểm liên tục của hàm f (x) .
Hàm số y f (x) được gọi là liên tục trên (a,b) nếu f (x) liên tục tại mọi điểm thuộc (a,b) .
Hàm số y f (x) được gọi là liên tục bên trái (bên phải) x D nếu 0
lim f (x)  f (x ) ( lim f (x)  f (x ) ). 0 0 x     0 x x 0 x
Hàm f (x) được gọi là liên tục trên [a,b] nếu f (x) liên tục trên (a,b) và liên tục bên phải tại
a, bên trái tại b.
1.3.2 Tính chất của hàm số liên tục
Giả sử f (x), g(x) là hai hàm liên tục trên [a,b]. Khi đó: 4 Ths.NGUYỄN QUỐC TIẾN f ( x)
i) f (x)  g(x) và f (x)g(x) liên tục trên [a,b], nếu g(x)  0 thì
liên tục trên [a,b] . g (x)
ii) f (x) liên tục trên [a,b].
iii) Nếu u(x) liên tục tại x và f (u) liên tục tại u u(x ) thì hàm f u(x) liên tục tại x . 0 0 0 0 0
iv) f (x) liên tục trên [a,b] thì đạt giá trị lớn nhất, giá trị bé nhất trên đoạn đó.
1.3.3 Điểm gián đoạn
Nếu f (x) không liên tục tại x D thì ta nói f (x) gián đoạn tại x và điểm x gọi là điểm 0 0 0 gián đoạn.
Hàm f (x) gián đoạn tai x nhưng tồn tại giới hạn của f(x) tại x , x thì x được gọi là điểm 0 0 0 0
gián đoạn loại 1. Các điểm gián đoạn khác gọi là điểm gián đoạn loại 2.
Ví dụ. Xét tính liên tục của hàm 1, x   0 
1) f (x)  sin 2x , x  0  2 Ta có sin 2 x
lim f (x)  lim  2  f (0)  1. x0 x0 x
Vậy f (x) gián đoạn tại x  0 ,và x  0 là điểm gián đoạn loại 1 1
  x, x  0 2) f (x)   -1
  x, x  0
Hàm số gián đoạn tại x  0 và
lim f (x)  1, lim f (x)  1  x 0 x 0  
nên x  0 là điểm gián đoạn loại 1 2x  3 3) f (x) 
, có điểm gián đoạn tại x  2 0 x  2
Ta có lim f (x)   và lim f (x)     x 2 x 2
Suy ra x  2 là điểm gián đoạn loại 2. 0 BÀI TẬP CHƯƠNG I
Câu 1. Tìm miền xác định của hàm số 5 Ths.NGUYỄN QUỐC TIẾN 1 1 x a) 2
y  ln 1 x b) y  arctan c) x 1 2 x x  1 2 sin x 1 x d) x x 1 e   c) f) 2
x  2x  3 2 x x  2
Câu 2. Tính giới hạn của các dãy số sau: 1 4
n n n a) 2
lim ( n n n) ; ds b) lim n 2 2 n 1 ;ds 1 n 3n  4n  1 1 1  c) lim lim   ...  2n  ;ds 0 d) 7n n n 1.2 2.3 . n (n  1) 
Câu 3. Tính giới hạn của các hàm số sau: 2 x x  2x 1 2 x 1 3 x 1 a) lim b) lim lim 2 x 2x x  3 2 x 1
x  4x  d) 3 2 x 1  x  1 4 4 x a e) lim
x x x g) 2
lim(2x x  2x) 3 3 xa x  f) 2 lim( 2 ) a x x 2x 1  3 x  2 3 x 1 a) lim lim lim x4 x  b) 4 2
x4 x  3x  d) 4 4 x 1  x 1
Câu 4. Tính giới hạn của các hàm số sau: 2 (1 cos x) 1 cos 2x a) lim ; ds 1/4 b) lim ; ds 1 2
x0 x sin x tan x 2 x0 sin x sin 3x tgx  sin x c) lim lim ; ds ½ x0 ln(2x  ; ds 3/2 d) 1) 3 x0 x
Câu 5. Tính giới hạn của các hàm số sau: a) cot
lim(s in x  cos x) x ; ds e
b) lim x ln x ; ds 0 x0 x 0  1 c) lim x xe ; ds 0 d) 2( 1) lim x x  ; ds e x x 1  3 5 1
x  sin x  tan x e) lim lim(cos x) x 2 6 x0 3x x  ;ds 1/3 f) 2 9x x0
Câu 6. Tìm a để các hàm số sau liên tục trên tập xác định của chúng.  1   cos x 1 (x  0) ( x   0) 2  2 x
xln x (x  0) a) 2 y   x b) y   c) y    a a ( x   0) a (x   0) 2
  2x (x  0) 2
Câu 7. Tìm các điểm gián đoạn của hàm số và chúng thuộc loại nào sin x x 1 2 x x  2 0 x  0 (x   0) a) y y y   y x  2x  b) 5 x  c) 2 1 x   0 a (x   0) 6 Ths.NGUYỄN QUỐC TIẾN
2 CHƯƠNG 2. PHÉP TÍNH VI PHÂN HÀM MỘT BIẾN 2.1 Đạo hàm
2.1.1 Đạo hàm tại một điểm
f ( x)  f (x )
Cho hàm số y f (x) xác định tại x và tại lân cận x . Khi đó nếu tỉ số 0 0 0 x x0
có giới hạn khi x x thì ta nói f (x) khả vi tại x hay f (x) có đạo hàm tại x và giới 0 0 0
hạn đó được gọi là đạo hàm của f (x) tại x . Ký hiệu là f '(x ) hay y '(x ) .Vậy 0 0 0
f (x)  f (x ) 0 f '(x)  lim . x   x x x 0 0 Nếu đặt
x x x  0
x x x   0 x
  x  x  0 0 Lúc đó
f ( x  x)  f (x ) 0 0 f '( x )  lim 0 x  0 x
Hàm số y f (x) được gọi là có đạo hàm trên khoảng (a,b) nếu nó có đạo hàm tại
mọi điểm x  (a,b) . Khi đó đạo hàm của hàm số f (x) là một hàm số xác định trên 0
(a,b) . Cho nên ký hiệu của đạo hàm của y f (x) trên (a,b) là f '(x) hoặc y '
f (x x  )  f (x)
Vậy y '  f '(x)  lim x  0 x
Ví dụ. Xét hàm số 2
y f (x)  x
Ta có miền xác định của hàm số là R . Đạo hàm của hàm số trên tập xác định là 2 2
f (x x  )  f (x) (x x  )  x y '  lim  lim x  0 x  0   x x
(x  x x)(x x   x)  lim  lim(2x x  )  2xx0 x  0 x  Do đó 2
y '  f '(x)  (x ) '  2x 7 Ths.NGUYỄN QUỐC TIẾN
2.1.2 Bảng các đạo hàm cơ bản
C '  0 ( Cconst)
(x ) '  x
 , R  n x' 1 1  n n 1 n x   x  1 ln '  x 1 (log x ) '  a x ln a (e) '  x e (sin x) '  cos x
(cos x) '  -sin x 1 2 (tgx) '  1tg x 2 cos x 1 2 (cot gx) '    (1 cot g x) 2 sin x
2.1.3 Các quy tắc tính đạo hàm
Nếu hai hàm u(x) và v(x) có đạo hàm tại điểm x thì tổng, hiệu, tích, thương của chúng
cũng có đạo hàm tại điểm x và:
(u v) '  u ' v '
(ku) '  ku ', k   R
(u.v) '  u 'v uv ' u
u ' v - uv ' ( ) '  , v  0 2 v v
2.1.4 Đạo hàm của hàm hợp
Xét hàm hợp y yu(x) nếu hàm y y(u) có đạo hàm đối với u và u u(x) có đạo
hàm đối với x thì y yu(x)có đạo hàm đối với x và y'(x)  y'(u).u'(x)
Ví dụ. Xét hàm số 3 10 y  (1 x ) Ta có 3 9 3
y '  10(1 x ) (1 x ) ' 3 9 2 2 3 9
 10(1 x ) 3x  30x (1 x )
Ví dụ. Giả sử (x), (x) có đạo hàm với mọi x R . Tính đạo hàm của hàm 2 2
y (x) (x) Đặt 2 2
u (x) (x) khi đó y u Ta có 8 Ths.NGUYỄN QUỐC TIẾN 1
y '(x)  y '(u).u '(x) 
2(x)'(x) 2(x)'(x) 2 u
(x)'(x) (x)'(x)  2 2
(x) (x) x  1 
Ví dụ. Tính các đạo hàm của hàm số sau: y  1    x   1
Ta có ln y x ln(1 ) x y
Lấy đạo hàm hai vế ta được: ' 1 1  ln(1 )  y x x  1 x  1   1 1  Suy ra y '  1   ln(1   )    x x x    1
2.1.5 Đạo hàm cấp cao
Cho hàm số f (x) có đạo hàm f '(x) . Hàm số f '(x) được gọi là đạo hàm cấp một của
f (x) . Nếu f '(x) khả vi thì đạo hàm của f '(x) được gọi là đạo hàm cấp hai của f (x) và
ký hiệu là f '(x) . Vậy f '(x)   f '(x)'
Tổng quát, đạo hàm của đạo hàm cấp n 1 của f (x) được gọi là đạo hàm cấp n của
f (x) ký hiệu (n) f (x) vậy (n) (n 1  ) f (x)   f (x) '  
Ví dụ. Tìm đạo hàm cấp n của  ( ) x y f x xe Ta có y ' x x
e xe  (1 x) x e y " x
e  (1 x) x
e  (2  x) x e ...
Chứng minh bằng quy nạp ta đi đến kết quả sau (n)  (  ) x y n x e 2.1.6 Vi phân
Cho hàm số y f (x) xác định trên (a,b) và x  (a, b) , nếu hàm số y f (x) khả vi
tại điểm x thì số gia của hàm số tại x có thể viết được dưới dạng f
 (x)  f (x  x) - f (x)  f '(x) x   o( x  )
với o(x) là VCB cấp cao hơn x khi x  0 .
Biểu thức f '(x).x được gọi là vi phân của f (x) tại x . Ký hiệu: df (x) hoặc dy(x) tức là
df (x)  f '(x). x
Xét hàm y f (x)  x ta có f '(x)  1nên df (x)  dx 1.x  x từ đó ta có 9 Ths.NGUYỄN QUỐC TIẾN
df (x)  f '(x).x f '(x).dx . Để ngắn gọn ta viết df f '(x).dx
Giả sử y f (x), x (t) là các hàm số khả vi, khi đó vi phân hàm y f (t) là
df  ( f (t)) 'dt f '(x)x '(t)dt f '(x)dx . Vậy dạng vi phân của hàm y f (x) không
thay đổi dù x là biến độc lập hay là x là hàm khả vi theo biến t . Tính chất này
gọi là tính bất biến của dạng vi phân.
Ví dụ.. Tìm vi phân của hàm y  ln x dx
Áp dụng định nghĩa dạng vi phân ta được dy d (ln x)  x
2.1.7 Ứng dụng của vi phân để tính gần đúng
Cho hàm y f (x) khả vi tại x . Theo định nghĩa vi phân ta có số gia của hàm tại x là : 0 0
f f (x  x) - f (x )  f '(x )x o( x) 0 0 0
Do đó khi x khá bé ta có công thức gần đúng.
f (x  x)  f '(x ) x   f (x ) 0 0 0
Ví dụ. Tính gần đúng 122 Ta thấy 122  121 1 
Xét hàm y f (x)  x
Áp đụng công thức gần đúng f (x  x)  f '(x ) x
  f (x ) suy ra 0 0 0 1 x  x  . x
  x . Chọn x 121, x 1 ta được 0 0 0 2 x0 1 122 
.1 121  0, 0454 11  11, 0454 2 121
Ví dụ. Tính gần đúng sin 29o  Ta thấy 0 sin 29  sin  
 . Xét hàm y f (x)  sin x  6 180 
Ta có sin(x x
 )  cos x . x
  sin x , áp dụng cho x  , x  - ta được 0 0 0 0 6 180  o 1 3 sin 29  sin     sin  cos .     .  0,484  6 180  6 6  180  2 2 180 10 Ths.NGUYỄN QUỐC TIẾN
2.2 Ứng dụng đạo hàm
2.2.1 Định lí ( Quy tắc L’Hospital).
i) Cho f (x), g(x)  0 là hai hàm liên tục và khả vi tại lân cận x ( x hữu hạn hoặc 0 0
 ). Giả sử lim f (x)  lim g(x)  0 và g '(x)  0 với mọi x thuộc lân cận x . Khi đó nếu 0 x  o x x o x f '(x) f (x) lim  L thì lim  L . x  o x g '( x) x o x g( x)
ii) Cho f (x), g (x)  0 là hai hàm liên tục và khả vi tại lân cận x . Giả sử 0
lim f (x)  lim g(x)   và g '(x)  0 , với mọi x thuộc lân cận x . Khi đó: 0 x  o x x o x f x f (x) Nếu '( ) lim  L thì lim  L xx xx o g '( x) o g(x) x a a x Ví dụ. Tính lim (dạng 0 ) xa x a 0 x a x a 1 (a x ) '
a ln a ax  Ta có: lim  lim aa ln a a a xa (x  . a) ' xa 1 x a a x Vậy lim aa ln a a a xa x a x Ví dụ.. Tính lim (dạng  x x  e  ) x ' 1 x Ta có: lim  lim  0 . Vậy lim  0  ( x e ) ' x x x e x x  e f '( x)
Chú ý : Khi x tiến tới một quá trình nào đó (chẳng hạn x tiến tới x ), nếu lim 0
xx0 g '(x) f (x)
không tồn tại thì không kết luận được cho lim
. Nếu áp dụng quy tắc L’Hospital mà
x x0 g( x)
giới hạn vẫn còn dạng vô định 0 hoặc  0
 thì có thể áp dụng quy tắc L’Hospital một lần
nữa và tiếp tục cho đến hết dạng vô định. 1 cos x Ví dụ. Tính lim 2 x 1
x  2x 1
Áp dụng liên tiếp hai lần quy tắc L’Hospital ta được 2  sin x  sin  x cos x  lim  lim  lim  . x 1  x 1  x 1 2x  2 2 x 1 2  1 2 2 1 cos x Vậy lim  2 x 1
x  2x 1 2 11 Ths.NGUYỄN QUỐC TIẾN 3 x Ví dụ. Tính lim
x0 x  sin x
Áp dụng liên tiếp quy tắc L’Hospital ta có: 3 2 x 3x 6x 6 lim  lim  lim  lim  6 x0 x 0 x0 x0 x  sin x 1  cos x sin x cos x 3 x Vậy lim  6
x0 x  sin x
Đối với các dạng vô định 0 0
  , 0., 0 ,  và 1 ta phải đưa các dạng vô định đó về
một trong hai dạng 0 hoặc  sau đó lại áp dụng quy tắc L’Hospital. 0  Ví dụ. Tính lim .
x ln x ( dạng 0. ) x 0 
Ta biến đổi để đưa giới hạn về dạng   1 ln x lim ln  lim  lim x x x   lim x  0     x 0 x0 1 x0 1 x 0  2 x x 1 1  
Ví dụ. Tính lim    (dạng - ) x
x0  x e 1 
Ta biến đổi giới hạn để đưa về dạng 0 sau đó áp dụng liên tiếp quy tắc L’Hospital 0 1 1 x e   1 xx e 1 x e 1 lim     lim  lim  lim  x x x x x x x0 x0 x0 x0  x e 1 x(e 1) e 1 xe 2e xe 2 Ví dụ. Tính  (dạng  -  )   3 lim x ln x x  3 ln x Ta có: 3
x  ln x x(1- ) và x 1 2 3 3ln . x 2 ln x ln x 6 ln x 1 lim  lim x  lim 3  lim  lim 6  0 x x x  1 x x x x x  x  ln x  Vậy: lim           x ln x  3 3 lim x 1- .1 x x x   2
Ví dụ. Tính lim x x ( dạng 0) x  1 2 ln x 2 lim ln 2 lim 2 lim x x Ta có x x 1 0 lim x x x x x e e e      e 1 x  12 Ths.NGUYỄN QUỐC TIẾN
2.2.2 Sự biến thiên của hàm số
Cho hàm số y f (x) liên tục trên [a,b] và có đạo hàm hữu hạn trên (a,b) , khi đó ta có các kết quả sau :
Nếu f (x) luôn tăng (giảm) trên [a,b] thì f '(x)  0, x
 (a,b) ( f '(x)  0, x  (a,b) )
Nếu f '(x)  0, x
 (a,b) ( f '(x)  0, x
 (a,b) ) thì trên [a,b] hàm f (x) đơn điệu tăng (giảm)
Việc chứng minh hai kết quả trên dựa vào định nghĩa hàm số tăng (giảm), định nghĩa đạo
hàm và định lí Lagrange. Sinh viên tự chứng minh như bài tập.
Từ hai kết quả trên ta có nhận xét : Nếu hàm f (x) có đạo hàm đồng nhất bằng 0 trên [a,b]
thì f (x) là hàm hằng trên [a,b] . 2.2.3 Định lí .
Giả sử f (x) liên tục trên một lân cận của x có đạo hàm trong lân cận đó (có thể trừ x ) 0 0
và x là điểm tới hạn của f (x) . Khi đó : 0
i) Nếu f '(x) đổi dấu từ âm sang dương khi x đi qua x thì f (x) đạt cực tiểu tại x 0 0
ii) Nếu f '(x) đổi dấu từ dương sang âm khi x đi qua x thì f (x) đạt cực đại tại x 0 0
iii) Nếu f '(x) không đổi dấu khi x đi qua x thì f (x) không đạt cực trị tại x 0 0
Ví dụ. Tìm cực trị của hàm số 3 2
y f (x)  (x 1) x
Miền xác định của hàm số là R 5x - 2 2
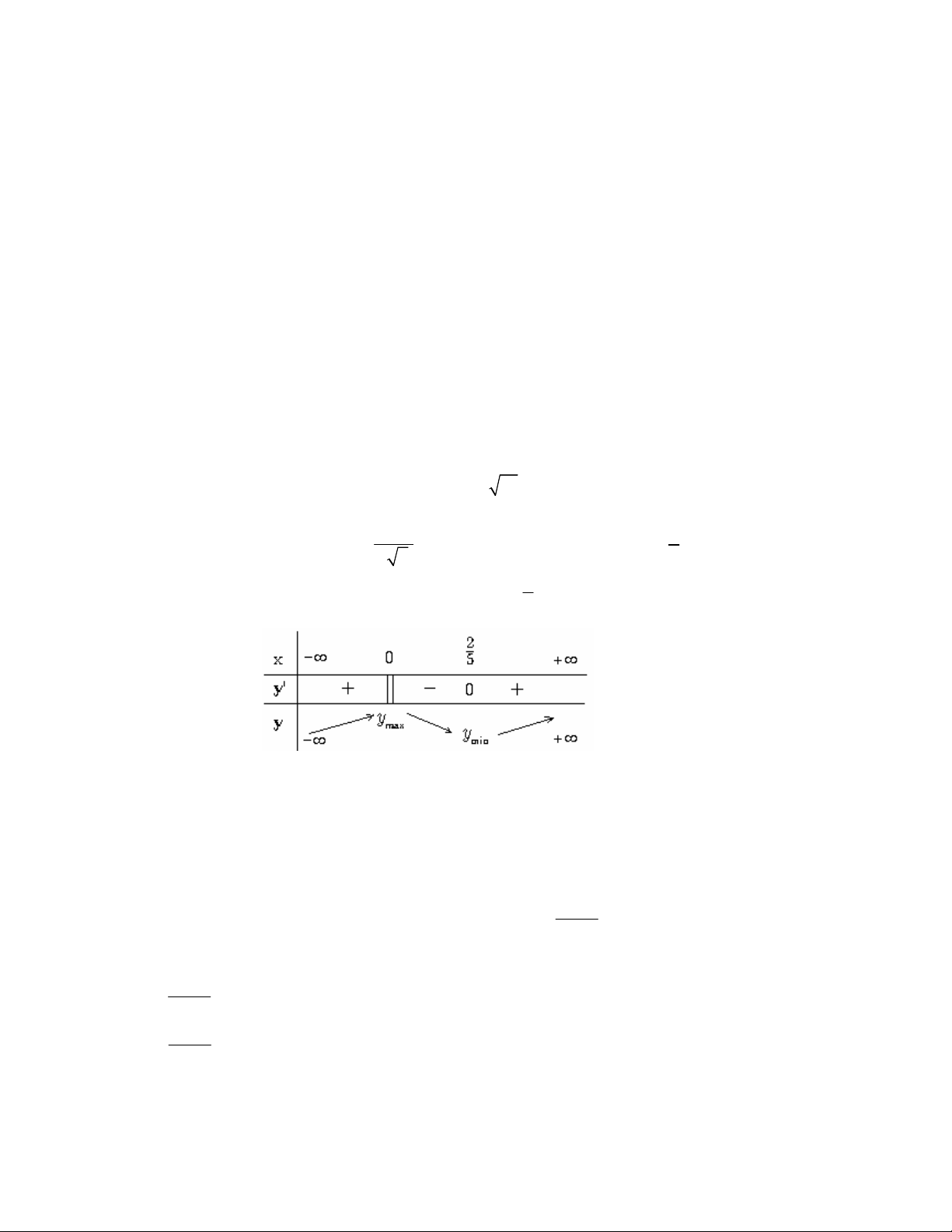
Bảng xét dấu của đạo hàm : y ' 
, với các điểm tới hạn là : x  0, x  3 3 x 5
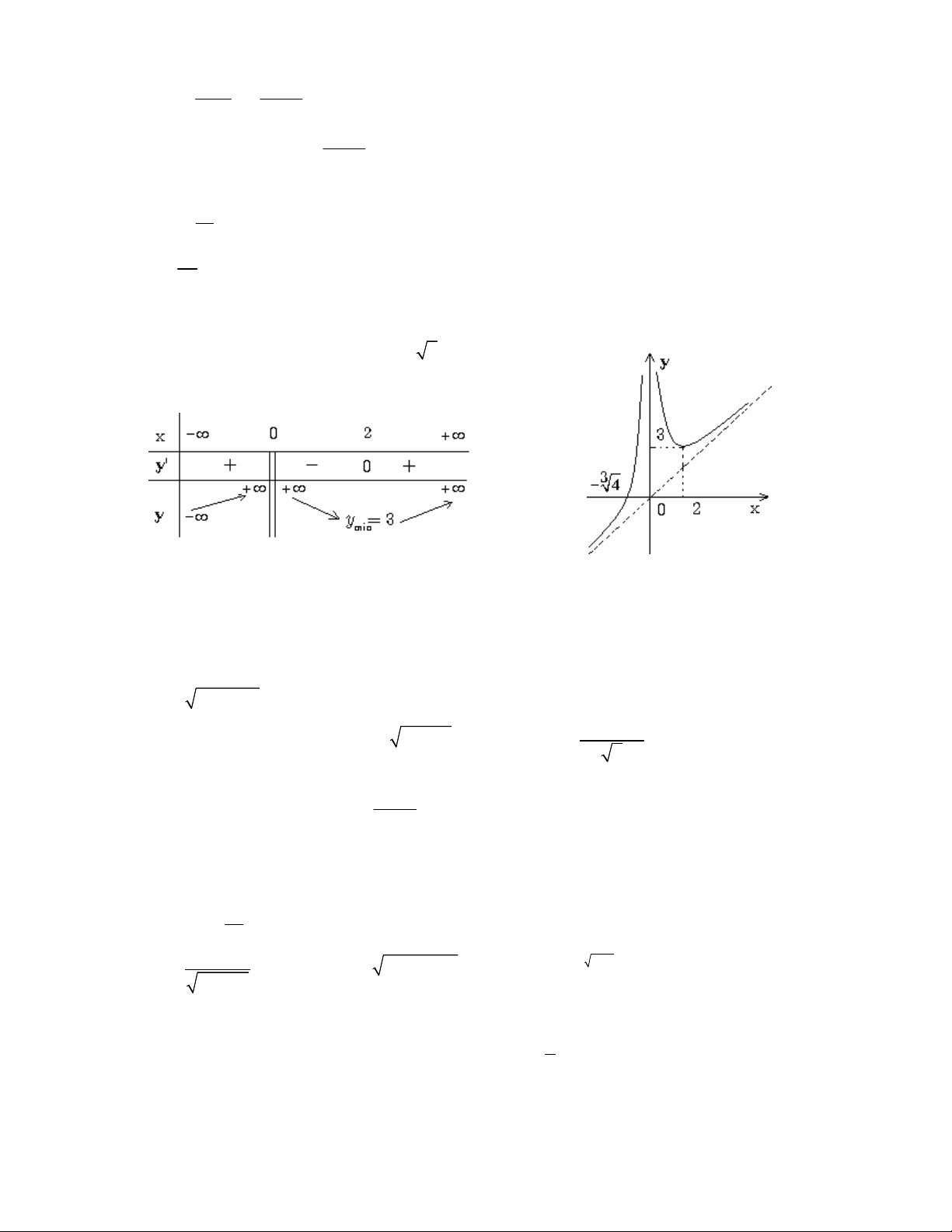
Ta có hàm số đạt cực đại x  0 và đạt cực tiểu tại 2 x  5 2.2.4 Định lí .
Cho hàm số y f (x) liên tục trên [a,b] và khả vi liên tục đến cấp hai trên (a,b) , khi đó:
i) Nếu tại x  (a,b), f '(x )  0 và f ' (x )  0 thì f (x) đạt cực đại tại x 0 0 0 0
ii) Nếu tại x  (a,b), f '(x )  0 và f ' (x )  0 thì f (x) đạt cực tiểu tại x 0 0 0 0 3 x  4
Ví dụ. Khảo sát sự biến thiên và vẽ đồ thị của hàm số y  2 x
Ta có : TXD R \  0 3 x  4 lim
  : đường cong có tiệm cận đứng x  0 2 x0 x 3 x  4 lim
  : đường cong không có tiệm cận ngang 2 x x 13 Ths.NGUYỄN QUỐC TIẾN 3 f ( x) x  4 a  lim lim 1 3 x x x  xx   b f x ax    x  x   3 4 lim ( ) lim 0 2  x x  
đường cong có tiệm cận xiên y x 8 y '  1
, y '  0  x  2 3 x 24 y ' 
 0: đường cong luôn lõm. 4 x Ta có bảng biến thiên
Hàm số đạt cực tiểu tại x  2 và y  3 min
Giao điểm của đồ thi với trục hoành 3 ( 4,0) Vẽ đồ thị BÀI TẬP CHƯƠNG II
Câu 1. Tính đạo hàm của các hàm số sau: a) 2 y  sin x b) 2
y  cos(x  3x) c) 2
y  ln(x  3x) d) 2
y x x 1 e) s in x y e  f) x y x 2 x x 1 g) sin x y x h) 2
y  ln x  3x i) y x
Câu 2. Tính đạo hàm cấp 3 của các hàm số sau 1
a) y  sin ax b) y ax b c) 2 y  sin x
d) y x ln x
Câu 3. Khảo sát sự biến thiên của các hàm số sau 2 x
a) y  ln x
b) y  1 arctan x c) x y xe 2 1 2 d) y  e) 2
y x  4x  3 f) x 4 y e   2 x  2x
Câu 4. Tìm cực trị của các hàm số sau 2 x
a) y x ln x b) 2
y  3x  2sin x c) 2 y e
Câu 4. Tính các giới hạn sau bằng quy tắc L’hospital 14 Ths.NGUYỄN QUỐC TIẾN xx
e e  2x ln(cos 2x)  1 1  a) lim lim c) lim    x0 x  b) sin x x0 sin x 2
x0  x sin x x   1 x x d) lim    e) lim 1 x f) sin lim x x  ln x 1
  ln x ln x x0 x 0  15 Ths.NGUYỄN QUỐC TIẾN
3 CHƯƠNG 3. PHÉP TÍNH TÍCH PHÂN HÀM MỘT BIẾN 3.1 Nguyên hàm
3.1.1 Định nghĩa (Nguyên hàm)
Hàm F(x) được gọi là một nguyên hàm của f (x) trên (a,b) nếu
F '(x)  f (x), x
 a,b.
Ví dụ. tg(x) là một nguyên hàm của 2
1 tg x trên R \ 2n
 1 , sin x 100 là một nguyên 2   hàm của cos x …
Có thể chứng minh được: nếu F (x) là một nguyên hàm của f (x) trên (a,b) thì mọi
nguyên hàm của f (x) trên khoảng đó đều có dạng F (x)  C với C là một hằng số. Họ vô số
các nguyên hàm đó được gọi là tích phân bất định của hàm f (x) ký hiệu f (x)dx  . Vậy
f (x)dx F(x)  C
trong đó dấu  được gọi là dấu tích phân, f (x) là hàm dưới dấu tích phân, f (x)dx là biểu
thức dưới dấu tích phân và x là biến số tích phân.
3.1.2 Một số tính chất của tích phân bất định '
i)  f (x)dx  f (x)  
ii) C. f (x)dx C. f (x)dx   , C là hằng số
iii)  f (x)  g(x)dx f (x)dx g(x)dx  
Việc chứng minh các tính chất trên xem như bài tập.
3.1.3 Tích phân bất định của một số hàm số cơ bản. 1 x
kdx kx Cx dx
C, ( 1)   1 dx 1     dx    ln | x | Cx  C, ( 1) 1 1 x x x a  x e x a dx
C, (a  0, a 1)   x e dx
C, ( 0)  ln a 1 1
cos(ax b)dx  sin(ax b)  C
sin(ax b)dx   cos(ax b)  Ca a 2
(1 tg x)dx tgx C  2
(1 cot g x)dx  cot gx C 16 Ths.NGUYỄN QUỐC TIẾN 1 1 x
dx  arcsin x C, 
dx  arcsin  C, (a  0)  2 1 x 2 2 a a x 1 1 1 x
dx arctgx Cdx arctgC,( a  0)  2 1  x 2 2 a x a a 1 1 1 x a
dx  ln a x Cdx  ln Ca x 2 2 x a 2a x a 1  x   1 x dx  ln tg      C dx  ln tgC  cos x  2 4  sin x 2 1 1 1  
dx tg(ax b)  Cax b ax b e dx eC, (a  0)  2 cos (ax b) a a 1 1 1 1
dx   cotg(ax b)  C
dx  ln ax b C, (a  0)  2 sin (ax b) a ax b a
3.2 Tích phân xác định 3.2.1 Định nghĩa
Cho hàm số f (x) liên tục trên a,bvà F(x) là một nguyên hàm của f (x) trên đoạn đó.
Khi đó giá trị F(b)  F(a) được gọi là tích phân xác định của hàm f (x) trên a,b. Kí hiệu b b f (x)dx
. Người ta thường viết F(x)  F(b)  F(a) . Vậy a a b
b f (x)dx F(x)  F(b)  F(a)  . a a
Nhận xét. Tích phân xác định không phụ thuộc vào ký hiệu của biến dưới dấu tích phân, nghĩa là b b
f (x)dx
f (u)du  ...   a a 1 Ví dụ. Tính 2 x dx  0 1 3 x 1 3 x 1 Ta có là một nguyên hàm của 2
f (x)  x , do đó 2 x dx    3 3 3 0 0 4
Ví dụ. Tính tgxdx  0 Ta có trên đoạn [0,
] hàm số  ln(cos x) là một nguyên hàm của tgx nên 4 17 Ths.NGUYỄN QUỐC TIẾN 4 4 2
tgxdx   ln(cos x)   ln( )  ln(1)  ln 2  . 0 2 0
3.2.2 Các tính chất của tích phân xác định
Giả sử f (x), g(x) là các hàm khả tích trên a,b khi đó: b b i)
kf (x)dx k
f (x)dx (k const)   a a b b b ii)
[ f (x)  g(x)]dx
f (x)dx g(x)dx    a a a b b
iii) f (x)  g(x), x
 [a,b]  f (x)dx g(x)dx   a a b c b iv)
f (x)dx
f (x)dx
f (x)dx, c   a b    a a c  ,  b b
v) f ( x) khả tích trên a,b và f (x)dx f (x) dx   a a
Khi đi tìm nguyên hàm hay tính tích phân xác định trong nhiều trường hợp hàm dưới dấu
tích phân không đơn giản, không có dạng như những hàm cơ bản nêu trên, ta phải biến đổi
hàm dưới dấu tích phân sao cho có thể áp dụng được các tích phân cơ bản. Có hai phương
pháp để biến đổi tích phân trong trường hợp này.
3.3 Hai phương pháp tính tích phân cơ bản
3.3.1 Phương pháp đổi biến số
Phương pháp đổi biến trong tích phân bất định có thể chia làm hai dạng
Dạng 1: Đặt x (t) , trong đó (t) là hàm khả vi và đơn điệu đối với biến t . Ta có:
f (x)dx f [(t)]'(t)dt   3 sin x Ví dụ. Tính dx  3 2 x Đặt 3
x t , x khả vi và đơn điệu với mọi t , suy ra 2
dx x '(t)dt  3t dt 3 2 sin x 3t sin t 3 dx
 3 sintdt  3cost C  3cos x C    2 3 2 t x Ví dụ. Tính 2 1 x dx  Đặt 
x  sin t,   t    t  arcsin x,(1 x 1) . Ta có dx x'(t)dt  costdt  2 2  18 Ths.NGUYỄN QUỐC TIẾN 2 2 2
1 x  1 sin t  cos t  cost
 cost (cost  0 do   t  ) 2 2 1 cos 2t t 1 Suy ra 2 2
1  x dx  cos tdt
dt   sin 2t C    2 2 4 1 1 thay 2 2
t  arcsin x
1 x dx  arcsin x x 1 x C  2 2
Dạng 2: Đặt u u(x) trong đó u(x) là hàm khả vi. Ta có
f (x)dx f [u(x)]u '(x)dx f (u)du    5 x e dx Ví dụ. Tính  2x e 1 Đặt x    '( ) x u e du
u x dx e dx . Suy ra 5x 4 e dx u du 1 2   (u 1 )du    2 x 2 2 e 1 u 1 u 1 3 3x u e
 u arctg ux
e arctg ( x e )  C 3 3 sin 2xdx Ví dụ. Tính  4 cos x  4 Đặt 2
u  cos x du u '(x)dx  2sin x cos xdx . Suy ra sin 2xdx du 1 u  2     ln C 4 2   cos x  4 u  4 4 u  2 2 1 cos x  2   ln C 2 4 cos x  2  2 2x   1 x
Ví dụ. Tính I dx 1 4 x  1 Đặt 2
u x du  2xdx , khi đó: 1 2u   1 1 2udu 1 du I du      2 2 2 2 u 1
2 u 1 2 u 1 1 1 2
 ln(u 1)  arctgu C 2 2 1 1 4 2
 ln(x 1)  arctg(x )  C 2 2
Áp dụng phương pháp trên khi tính tích phân xác định ta có thể thực hiện như sau: Đối với dạng 1: 19 Ths.NGUYỄN QUỐC TIẾN