Bài giảng tuần 5: Các nội dung trọng tâm và hướng dẫn học tập môn Xác suất thống kê | Đại học Bách Khoa Hà Nội

2. BÀI TẬP ÁP DỤNG Bài tập 4. Đề bài.
Từ một hộp chứa 5 quả bóng màu xanh, 4 quả bóng màu đỏ và 2 quả
bóng màu vàng, lấy ngẫu nhiên có hoàn lại lần lượt từng quả bóng ra 3
quả bóng. Gọi X là số quả bóng màu đỏ trong 3 quả được lấy ra. (a) Lập
bảng phân phối xác suất của X . (b) Tìm P(0 < X ≤ 2). Lời giải.
(a) X là biến ngẫu nhiên rời rạc và SX = {0, 1, 2, 3}.
■ Gọi A là sự kiện chọn được quả màu đỏ trong mỗi lần lấy quả bóng. Ta có P(A) = 4/11.
■ Theo công thức Bernoulli,
P(X = k) = C k (4/11)k (7/11)3−k với k ∈ {0, 1, 2, 3}. 3 18 / 30 2. BÀI TẬP ÁP DỤNG Bài tập 4. Lời giải.
■ Bảng phân phối xác suất của X : X 0 1 2 3 P(X = k)
343/1331 588/1331 336/1331 64/1331
(b) Xác suất cần tính được cho bởi:
P(0 < X ≤ 2) = P(X = 1) + P(X = 2) = 588/1331 + 336/1331 = 84/121. 19 / 30 Lời giải.
■ Ký hiệu D là thẻ màu đỏ, X là thẻ màu xanh, V là thẻ màu vàng.
■ S = {{D , D }, {D , V }, {V , V }, {D , X }, {V , X }, {X , X }}.
■ Z là biến ngẫu nhiên rời rạc và SZ = {−2, −1, 0, 1, 2, 4}. 2. BÀI TẬP ÁP DỤNG Bài tập 5. Đề bài.
Một hộp chứa 8 thẻ màu đỏ, 4 thẻ màu xanh và 2 thẻ màu vàng. Một
người chơi trò chơi lấy ngẫu nhiên không hoàn lại hai thẻ từ hộp đó.
Người đó sẽ mất 1$ cho mỗi thẻ màu đỏ lấy được và sẽ nhận được 2$ cho
mỗi thẻ màu xanh lấy được; người đó sẽ không nhận được tiền hay mất
tiền cho bất kỳ thẻ màu vàng nào lấy được. Gọi Z là tiền thắng cuộc của
người chơi ($).Lập bảng phân phối xác suất của Z . 20 / 30 2. BÀI TẬP ÁP DỤNG Bài tập 5. Đề bài.
Một hộp chứa 8 thẻ màu đỏ, 4 thẻ màu xanh và 2 thẻ màu vàng. Một
người chơi trò chơi lấy ngẫu nhiên không hoàn lại hai thẻ từ hộp đó.
Người đó sẽ mất 1$ cho mỗi thẻ màu đỏ lấy được và sẽ nhận được 2$ cho
mỗi thẻ màu xanh lấy được; người đó sẽ không nhận được tiền hay mất
tiền cho bất kỳ thẻ màu vàng nào lấy được. Gọi Z là tiền thắng cuộc của
người chơi ($).Lập bảng phân phối xác suất của Z . Lời giải.
■ Ký hiệu D là thẻ màu đỏ, X là thẻ màu xanh, V là thẻ màu vàng.
■ S = {{D , D }, {D , V }, {V , V }, {D , X }, {V , X }, {X , X }}.
■ Z là biến ngẫu nhiên rời rạc và SZ = {−2, −1, 0, 1, 2, 4}. 21 / 30 2. BÀI TẬP ÁP DỤNG Bài tập 5. Lời giải.
■ Phân phối xác suất của Z được cho bởi:
P(Z = −2) = P({D, D}) = C 2/C 2 = 28/91, 8 14
P(Z = −1) = P({D, V }) = C 1C 1/C 2 = 16/91, 8 2 14
P(Z = 0) = P({V , V }) = C 2/C 2 = 1/91, 2 14
P(Z = 1) = P({D, X }) = C 1C 1/C 2 = 32/91, 8 4 14
P(Z = 2) = P({V , X }) = C 1C 1/C 2 = 8/91, 2 4 14
P(Z = 4) = P({X , X }) = C 2/C 2 = 6/91. 4 14
■ Bảng phân phối xác suất của Z : Z −2 −1 0 1 2 4 P(Z = zi ) 28/91 16/91 1/91 32/91 8/91 6/91 22 / 30 Lời giải.
■ Gọi X là số sản phẩm tốt có trong 2 sản phẩm lấy ra từ kiện II.
■ X là biến ngẫu nhiên rời rạc và SX = {0, 1, 2}.
■ Gọi Ai là sự kiện lấy được i sản phẩm tốt từ kiện I bỏ sang kiện II, với i ∈ {0, 1, 2}. 2. BÀI TẬP ÁP DỤNG Bài tập 6. Đề bài.
Có hai kiện hàng. Kiện thứ nhất có 8 sản phẩm tốt và 2 sản phẩm xấu.
Kiện thứ hai có 5 sản phẩm tốt và 3 sản phẩm xấu. Lấy ngẫu nhiên 2 sản
phẩm từ kiện I bỏ sang kiện II. Sau đó từ kiện II lấy ngẫu nhiên ra 2 sản
phẩm. Lập bảng phân phối xác suất của biến ngẫu nhiên chỉ số sản phẩm
tốt có trong 2 sản phẩm lấy ra từ kiện II. 23 / 30 2. BÀI TẬP ÁP DỤNG Bài tập 6. Đề bài.
Có hai kiện hàng. Kiện thứ nhất có 8 sản phẩm tốt và 2 sản phẩm xấu.
Kiện thứ hai có 5 sản phẩm tốt và 3 sản phẩm xấu. Lấy ngẫu nhiên 2 sản
phẩm từ kiện I bỏ sang kiện II. Sau đó từ kiện II lấy ngẫu nhiên ra 2 sản
phẩm. Lập bảng phân phối xác suất của biến ngẫu nhiên chỉ số sản phẩm
tốt có trong 2 sản phẩm lấy ra từ kiện II. Lời giải.
■ Gọi X là số sản phẩm tốt có trong 2 sản phẩm lấy ra từ kiện II.
■ X là biến ngẫu nhiên rời rạc và SX = {0, 1, 2}.
■ Gọi Ai là sự kiện lấy được i sản phẩm tốt từ kiện I bỏ sang kiện II, với i ∈ {0, 1, 2}. 24 / 30 2. BÀI TẬP ÁP DỤNG Bài tập 6. Lời giải.
■ {A0, A1, A2} là một hệ đầy đủ các sự kiện. ■ Ta có: P(A0) = C 0C 2/C 2 = 1/45; 8 2 10 P(A1) = C 1C 1/C 2 = 16/45; 8 2 10 P(A2) = C 2C 0/C 2 = 28/45. 8 2 10
■ Với k ∈ {0, 1, 2}, áp dụng công thức xác suất đầy đủ,
P(X = k) = P(A0)P(X = k|A0) + P(A1)P(X = k|A1) + P(A2)P(X = k|A2). 25 / 30 2. BÀI TẬP ÁP DỤNG Bài tập 6. Lời giải. ■ Khi đó: P(X = 0) = 1/45 × C 0 5 C 2 5 /C 2 10 + 16/45 × C 0 6 C 2 4 /C 2 10 + 28/45 × C 0 7 C 2 3 /C 2 10 = 38/405; P(X = 1) = 1/45 × C 1 5 C 1 5 /C 2 10 + 16/45 × C 1 6 C 1 4 /C 2 10 + 28/45 × C 1 7 C 1 3 /C 2 10 = 997/2025; P(X = 2) = 1/45 × C 2 5 C 0 5 /C 2 10 + 16/45 × C 2 6 C 0 4 /C 2 10 + 28/45 × C 2 7 C 0 3 /C 2 10 = 838/2025. 26 / 30 2. BÀI TẬP ÁP DỤNG Bài tập 6. Lời giải.
■ Bảng phân phối xác suất của X : X 0 1 2 P(X = xi ) 38/405 997/2025 838/2025 27 / 30 2. BÀI TẬP ÁP DỤNG Bài tập 1. Đề bài.
Một kiện hàng có 12 sản phẩm, trong đó có 7 sản phẩm loại I và 5 sản
phẩm loại II. Khi bán được một sản phẩm loại I thì được lãi 50 ngàn đồng;
còn nếu bán được một sản phẩm loại II thì được lãi 20 ngàn đồng. Lấy
ngẫu nhiên từ kiện hàng ra 3 sản phẩm. (a) Viết hàm phân phối xác suất
của số tiền lãi thu được khi bán 3 sản phẩm đó và (b) vẽ đồ thị của nó. Lời giải.
(a) Gọi X là số sản phẩm loại I có trong 3 sản phẩm lấy ra. Khi đó, X là
biến ngẫu nhiên rời rạc có SX = {0, 1, 2, 3}. 9 / 30 2. BÀI TẬP ÁP DỤNG Bài tập 1. Lời giải.
■ Gọi Y (ngàn đồng) là số tiền lãi thu được khi bán 3 sản phẩm. Khi
đó, Y là biến ngẫu nhiên rời rạc được xác định bởi
Y = 50X + 20(3 − X ) = 30X + 60.
■ Ta có SY = {60, 90, 120, 150}.
■ Phân phối xác suất của Y được cho bởi
P(Y = 60) = P(X = 0) = C 3/C 3 = 1/22; 5 12
P(Y = 90) = P(X = 1) = C 1C 2/C 3 = 7/22; 7 5 12
P(Y = 120) = P(X = 2) = C 2C 1/C 3 = 21/44; 7 5 12
P(Y = 150) = P(X = 3) = C 3/C 3 = 7/44. 7 12 10 / 30 2. BÀI TẬP ÁP DỤNG Bài tập 1. Lời giải.
■ Bảng phân phối xác suất của Y Y 60 90 120 150
P(Y = yi ) 1/22 7/22 21/44 7/44
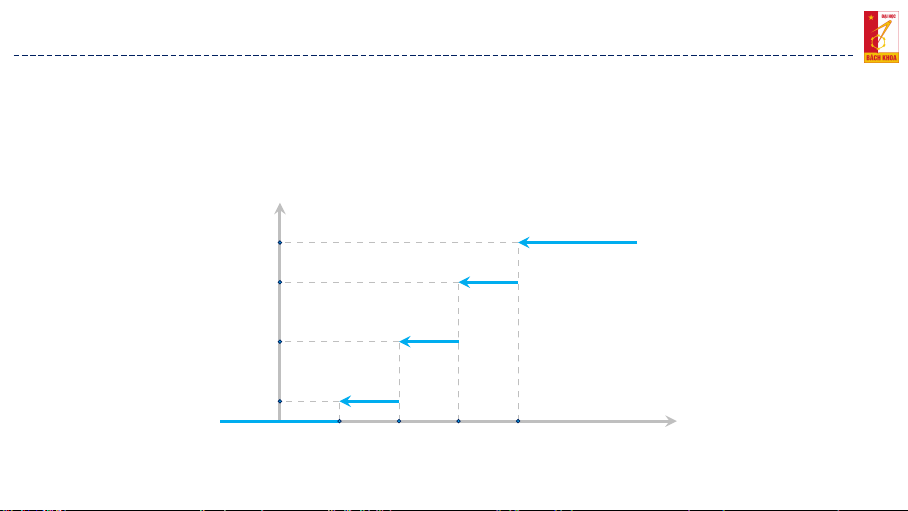
■ Hàm phân phối xác suất của Y 0, nếu y ≤ 60    1/22, nếu 60 < y ≤ 90   FY (y ) = 1/22 + 7/22 = 4/11, nếu 90 < y ≤ 120 
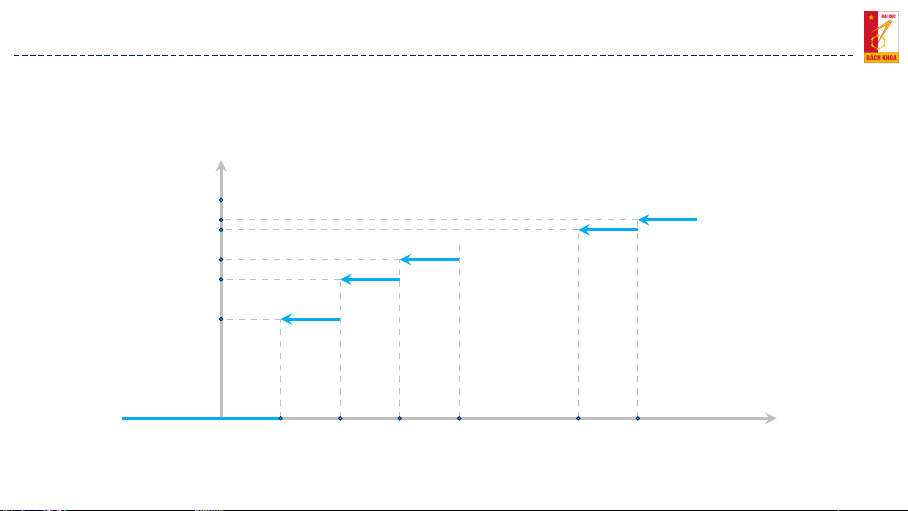
1/22 + 7/22 + 21/44 = 37/44, nếu 120 < y ≤ 150    1, nếu y > 150. 11 / 30 2. BÀI TẬP ÁP DỤNG Bài tập 1. Lời giải. (b) Đồ thị của FY (y ) FY (y ) 1 37/44 4/11 1/22 0 60 90 120 150 y
Hình 1: Hàm phân phối xác suất của biến ngẫu nhiên Y 12 / 30 2. BÀI TẬP ÁP DỤNG Bài tập 2. Đề bài.
Cho X là biến ngẫu nhiên rời rạc có SX = {1, 2, 3, . . .}. Giả sử rằng phân
phối xác suất của X được cho bởi P(X = k) = 1/2k với k ∈ SX .
(a) Viết hàm phân phối xác suất của X và vẽ đồ thị của nó.
(b) Tìm các xác suất P(2 ≤ X < 5) và P(X ≥ 4). 13 / 30 2. BÀI TẬP ÁP DỤNG Bài tập 2. Lời giải. (a) Chú ý rằng +∞ +∞ X X P(X = k) = 1/2k = 1. k=1 k=1
■ Bảng phân phối xác suất của X X 1 2 3 . . . n . . . P(X = xi ) 1/2 1/22 1/23 . . . 1/2n . . . 14 / 30 2. BÀI TẬP ÁP DỤNG Bài tập 2. Lời giải.
■ Hàm phân phối xác suất của X 0, nếu x ≤ 1    1/2, nếu 1 < x ≤ 2     1/2 + 1/22 = 3/4, nếu 2 < x ≤ 3  FX (x) = 1/2 + 1/22 + 1/23 = 7/8, nếu 3 < x ≤ 4  . . .   Pn  1/2k = (2n − 1)/2n, nếu  n < x ≤ n + 1,  k=1  . . . 15 / 30 2. BÀI TẬP ÁP DỤNG Bài tập 2. Lời giải. FX (x) 1 (2n − 1)/2n 7/8 3/4 1/2 0 1 2 3 4 n n + 1 x
Hình 2: Hàm phân phối xác suất của biến ngẫu nhiên X 16 / 30 2. BÀI TẬP ÁP DỤNG Bài tập 2. Lời giải.
(b) Các xác suất cần tính được cho bởi:
■ P (2 ≤ X < 5) = FX (5) − FX (2) = 15/16 − 1/2 = 7/16.
■ P (X ≥ 4) = 1 − P (X < 4) = 1 − FX (4) = 1 − 7/8 = 1/8. 17 / 30 2. BÀI TẬP ÁP DỤNG Bài tập 3. Đề bài.
Giả sử thời gian (đơn vị phút) mà mỗi khách hàng xếp hàng tại một bưu
điện để được nhân viên phục vụ là biến ngẫu nhiên liên tục T có hàm phân phối xác suất 0, nếu t < 0,  FT (t) = ct(243 − t2), nếu 0 ≤ t ≤ 9, 1, nếu t > 9.
(a) Xác định hằng số c.
(b) Tìm xác suất để một khách hàng xếp hàng nhiều hơn 3 phút. 18 / 30