Bài tập cá nhân môn Kinh tế vĩ mô ứng dụng | Đại học Kinh tế Thành phố Hồ Chí Minh

lOMoAR cPSD| 46988474 Họ và tên : Nguyễn Phương Thịnh Lớp : 23C1ECO50113804 Môn : Kinh tế vi mô ứng dụng
Mã số sinh viên : 3122102386 BÀI TẬP CÁ NHÂN
Môn: Kinh tế vi mô Ứng Dụng Bài làm : Câu 1 :
Dựa vào hàm số sau:
QD= 171 - 20P + 20Pb + 3Pc + 2I QS= 178 + 40P - 60Ph
a. Ý nghĩa của các hệ số đứng trước P, Pb, Pc Ph
- Hệ số -20 trước P thể hiện mối quan hệ nghịch biến giữa lượng cầu xúc xích heo và giá xúc
xích heo. Điều này có nghĩa là khi giá xúc xích heo tăng lên, lượng cầu xúc xích heo sẽ giảm xuống và ngược lại.
- Hệ số 20 trước Pb thể hiện mối quan hệ thuận biến giữa lượng cầu xúc xích heo và giá thịt bò. Điều
này có nghĩa là khi giá thịt bò tăng lên, lượng cầu xúc xích heo sẽ tăng lên và ngược lại.
- Hệ số 3 trước Pc thể hiện mối quan hệ thuận biến giữa lượng cầu xúc xích heo và giá thịt gà. Điều
này có nghĩa là khi giá thịt gà tăng lên, lượng cầu xúc xích heo sẽ tăng lên và ngược lại.
- Hệ số 2 trước I thể hiện mối quan hệ thuận biến giữa lượng cầu xúc xích heo và thu nhập. Điều này
có nghĩa là khi thu nhập tăng lên, lượng cầu xúc xích heo sẽ tăng lên và ngược lại.
- Xúc xích heo là hàng hóa thông thường
- Vì hệ số đứng trước P là âm, nên xúc xích heo là hàng hóa thông thường. Hàng hóa thông
thường là hàng hóa mà khi thu nhập của người tiêu dùng tăng lên, họ sẽ mua nhiều hàng hóa đó hơn.
b. Lượng cầu xúc xích heo sẽ thay đổi như thế nào khi giá thịt bò tăng thêm 6 nghìn đồng/kg
- Khi giá thịt bò tăng thêm 6 nghìn đồng/kg, lượng cầu xúc xích heo sẽ giảm đi 20*0,6 = 12 nghìn kg.
- Cụ thể, lượng cầu xúc xích heo sẽ giảm từ 171 nghìn kg xuống còn 159 nghìn kg. *Giải thích
- Khi giá thịt bò tăng thêm 6 nghìn đồng/kg, người tiêu dùng sẽ chuyển sang tiêu thụ thịt gà thay
vì xúc xích heo. Điều này dẫn đến lượng cầu xúc xích heo giảm đi. Số lượng giảm đi là: Δ QD = -20.Pb. Δ Pb = -20*0,6*6 = -12
=> Vì vậy, lượng cầu xúc xích heo sẽ giảm từ 171 nghìn/kg xuống còn 159 nghìn/kg. c.
Hàm cầu và cung xúc xích heo theo giá
- Tại mức giá thịt bò Pb =4; Pc=3.1/3; Ph=1,5; I=12,5, hàm cầu xúc xích heo được viết như sau: lOMoAR cPSD| 46988474
QD = 171 - 20P + 20*4 + 3*3*1/3 + 2*12,5 QD = 171 + 104 QD = 275
- Hàm cung xúc xích heo được viết như sau: Qs = 178 + 40P - 60*1,5 Qs = 178 - 90 Qs = 88
* Giá và lượng xúc xích heo cân bằng
Tại điểm cân bằng, lượng cầu bằng lượng cung: QD = Qs 275 = 88 P = 275/88 = 3,13
=> Vậy, giá và lượng xúc xích heo cân bằng là:
Giá: 3,13 chục nghìn đồng/kg Lượng: 275 nghìn kg
d. Độ co giãn của cầu xúc xích heo theo giá thịt bò tại điểm cân bằng
- Độ co giãn của cầu theo giá là một đại lượng đo lường sự thay đổi của lượng cầu theo một thay
đổi của giá. Độ co giãn của cầu theo giá được tính theo công thức sau:
Ed = (% thay đổi của lượng cầu)/(% thay đổi của giá)
- Tại điểm cân bằng, lượng cầu là 275 nghìn kg và giá là 3,13 chục nghìn đồng/kg.
- Khi giá thịt bò tăng thêm 6 nghìn đồng/kg, lượng cầu xúc xích heo sẽ giảm đi 12 nghìn kg.
Vậy, % thay đổi của lượng cầu là: (12/275)*100 = 4,34%
Và % thay đổi của giá là: (6/3,13)*100 = 19,4%
=> Do đó, độ co giãn của cầu theo giá thịt bò tại điểm cân bằng là: Ed = (4,34)/(19,4) = 0,22
* Độ co giãn cầu theo giá thịt bò tại điểm cân bằng là 0,22. Độ co giãn cầu < 1, nên cầu xúc
xích heo là cầu co giãn theo giá thịt bò.
e. Sự thay đổi trong giá và lượng xúc xích heo cân bằng
- Khi giá thịt bò tăng thêm denta P =0,60, thì lượng cầu xúc xích heo sẽ giảm đi: Δ QD = -20*Pb*ΔPb = -20*0,6*0,6 = 7,2
=> Vậy, lượng cầu xúc xích heo giảm từ 275 nghìn kg xuống còn 267,8 nghìn kg.
Giá cân bằng mới là: P = (275 - 7,2)/267,8 = 3,16
=> Vậy, giá cân bằng mới là 3,16 chục nghìn đồng/kg.
Như vậy, khi giá thịt bò tăng thêm Δ P =0,60, thì giá cân bằng mới tăng lên 0,03 chục
nghìn đồng/kg và lượng cầu cân bằng giảm xuống 7,2 nghìn kg. lOMoAR cPSD| 46988474 * Chú thích:
- Giá xúc xích heo : chục nghìn đồng/kg.
- Do giá thịt bò tăng thêm 0,6 chục nghìn đồng/kg, => ΔPb = 0,6.
Mà, Độ co giãn của cầu theo giá thịt bò được tính bằng công thức: Ed =
Giá và lượng xúc xích heo cân bằng được tính bằng cách giải phương trình Qd = Qs. Câu 2:
a) Đường ngân sách
- Do thu nhập của người tiêu dùng được giới hạn bởi giá cả của hai hàng hóa, nên người tiêu
dùng chỉ có thể lựa chọn các tập hợp hàng hóa nằm trên đường ngân sách. Đường ngân sách
được xác định bằng cách biểu thị quan hệ giữa số lượng của hai hàng hóa mà người tiêu dùng
có thể mua được với giá cả của chúng.
- Trong trường hợp này, đường ngân sách của người tiêu dùng được xác định bởi phương trình: 1.020 = 10c + 10f
- Giải phương trình này, ta có: c = 102 - f
- Vẽ đường ngân sách trên đồ thị, ta được đường thẳng có dạng: y = -x + 102
- Độ dốc của đường ngân sách là -1, có nghĩa là người tiêu dùng phải hy sinh một đơn vị quần áo
để có được một đơn vị thực phẩm.
=>Ý nghĩa kinh tế của độ dốc của đường ngân sách là nó cho thấy chi phí cơ hội của việc
tiêu thụ một hàng hóa. Trong trường hợp này, chi phí cơ hội của việc tiêu thụ một bộ quần
áo là một kg thực phẩm.
b) Tỷ lệ thay thế biên
Tỷ lệ thay thế biên giữa hai hàng hóa C, F (MRScf = MUf/MUc) cho thấy số lượng hàng
hóa F mà người tiêu dùng sẵn sàng từ bỏ để có được một đơn vị hàng hóa C mà vẫn giữ
nguyên mức độ thỏa dụng.
- Trong trường hợp này, hàm hữu dụng của người tiêu dùng là U(c,f)=c+2f. Do đó, MUc = 1 và MUf = 2.
- Tỷ lệ thay thế biên là:
MRScf = MUf/MUc = 2/1 = 2 -
Tỷ lệ thay thế biên bằng 2 cho thấy người tiêu dùng sẵn sàng từ bỏ hai kg thực phẩm
để có được một bộ quần áo mà vẫn giữ nguyên mức độ thỏa dụng. -
Mối quan hệ giữa hai hàng hóa này là bổ sung, vì tỷ lệ thay thế biên dương.
Ý nghĩa kinh tế của tỷ lệ thay thế biên MRScf là nó cho thấy mức độ thay thế
giữa hai hàng hóa. Trong trường hợp này, hai hàng hóa C và F có thể thay thế cho nhau,
vì tỷ lệ thay thế biên dương. lOMoAR cPSD| 46988474
c) Hàng hóa mà người tiêu dùng lựa chọn để tối đa hóa hữu dụng
Để tối đa hóa hữu dụng, người tiêu dùng cần lựa chọn một tập hợp hàng hóa mà tại đó MRScf = P(F)/Pc.
Trong trường hợp này, MRScf = 2, P(F) = 10 và Pc = 10. Do đó, người tiêu dùng sẽ lựa
chọn một tập hợp hàng hóa mà tại đó: ( ) = MRScf
Điều này có nghĩa là người tiêu dùng sẽ lựa chọn một tập hợp hàng hóa mà tại đó số
lượng quần áo và thực phẩm bằng nhau.
d) Đường ngân sách sau khi nhận trợ cấp
Sau khi nhận trợ cấp, người tiêu dùng có thêm 100 nghìn đồng để mua thực phẩm. Do đó,
đường ngân sách của người tiêu dùng sẽ di chuyển sang phải một đoạn 10 đơn vị thực phẩm.
Đường ngân sách mới được xác định bởi phương trình: 1.120 = 10c + 10(f + 10)
Giải phương trình này, ta có: c = 112 - f - 10
Vẽ đường ngân sách mới trên đồ thị, ta được đường thẳng có dạng: y = -x + 122
Như vậy, sau khi nhận trợ cấp, đường ngân sách của người tiêu dùng sẽ di chuyển sang
phải một đoạn 10 đơn vị thực phẩm và độ dốc của đường ngân sách vẫn giữ nguyên. Câu 3 :
a) Đường giới hạn ngân sách Không có trợ cấp
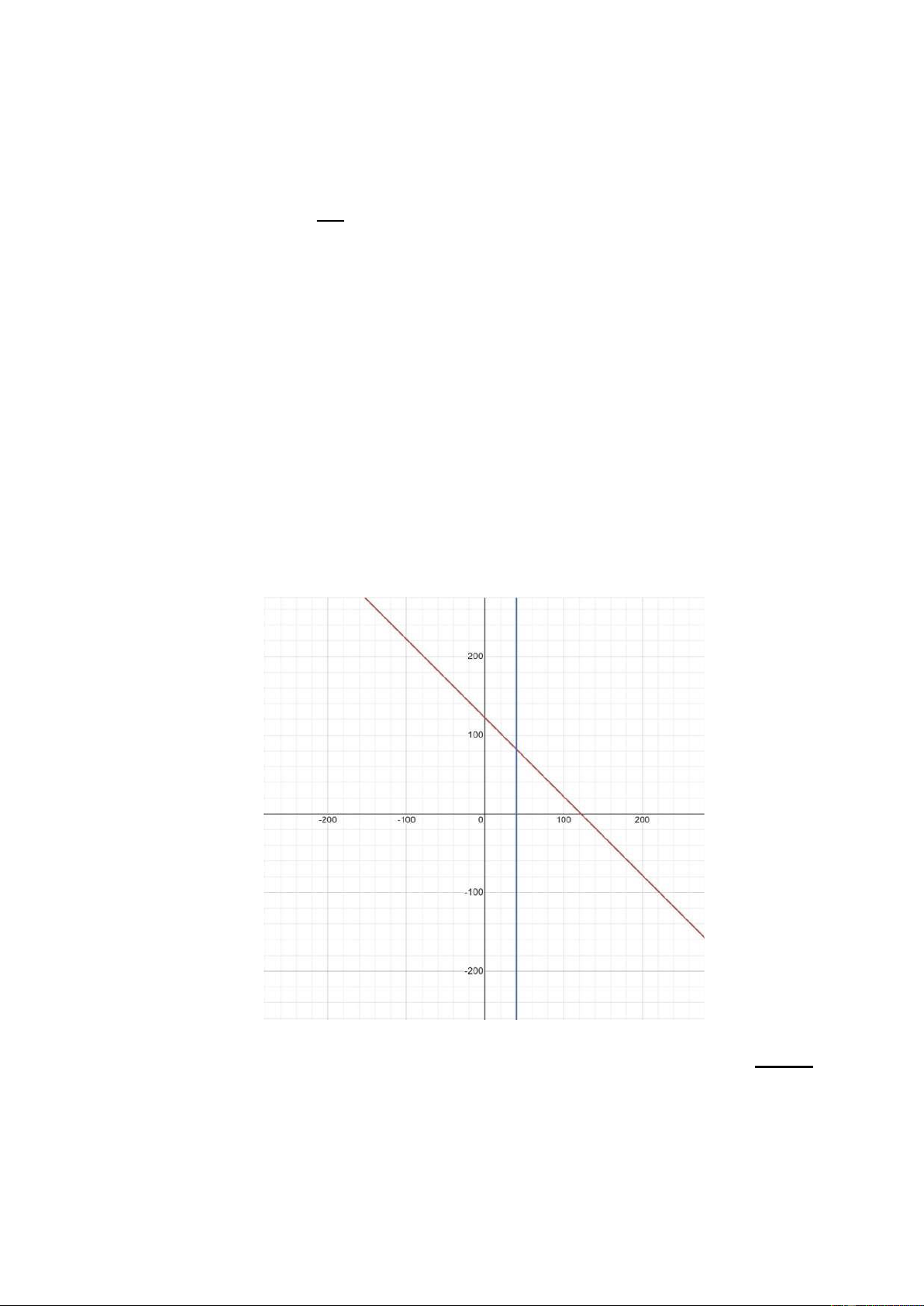
Tổng kinh phí của Khoa Kinh tế phát triển là 150 triệu đồng. Do đó, đường giới
hạn ngân sách của Khoa trong trường hợp không có trợ cấp là một đường thẳng đi qua
điểm (0, 150) và (150, 0). lOMoAR cPSD| 46988474
Trợ cấp không ràng buộc
Khi nhận được trợ cấp không ràng buộc, Khoa Kinh tế phát triển có thêm 50 triệu
đồng để chi cho bất cứ hoạt động nào của Khoa. Do đó, đường giới hạn ngân sách trong
trường hợp này sẽ di chuyển ra xa trục tung thêm 50 triệu đồng. Đường giới hạn ngân
sách mới đi qua điểm (0, 150) và (150, 200).
Trợ cấp có ràng buộc
Trong trường hợp này, Khoa Kinh tế phát triển chỉ được phép chi 50 triệu đồng
cho việc mua sách và tạp chí. Do đó, đường giới hạn ngân sách trong trường hợp này sẽ
di chuyển ra xa trục hoành thêm 50 triệu đồng. Đường giới hạn ngân sách mới đi qua
điểm (50, 0) và (150, 50).
Trợ cấp có yêu cầu chi đối ứng
Trong trường hợp này, Khoa Kinh tế phát triển phải chi đối ứng 100% cho việc
mua sách và tạp chí. Do đó, đường giới hạn ngân sách trong trường hợp này sẽ di chuyển
ra xa trục hoành và trục tung đều thêm 50 triệu đồng. Đường giới hạn ngân sách mới đi
qua điểm (50, 50) và (150, 150). Vẽ đường giới hạn ngân sách trên đồ thị Trên đồ thị, ta có:
x: Kinh phí mua sách và tạp chí y: Kinh
phí chi cho các hoạt động khác
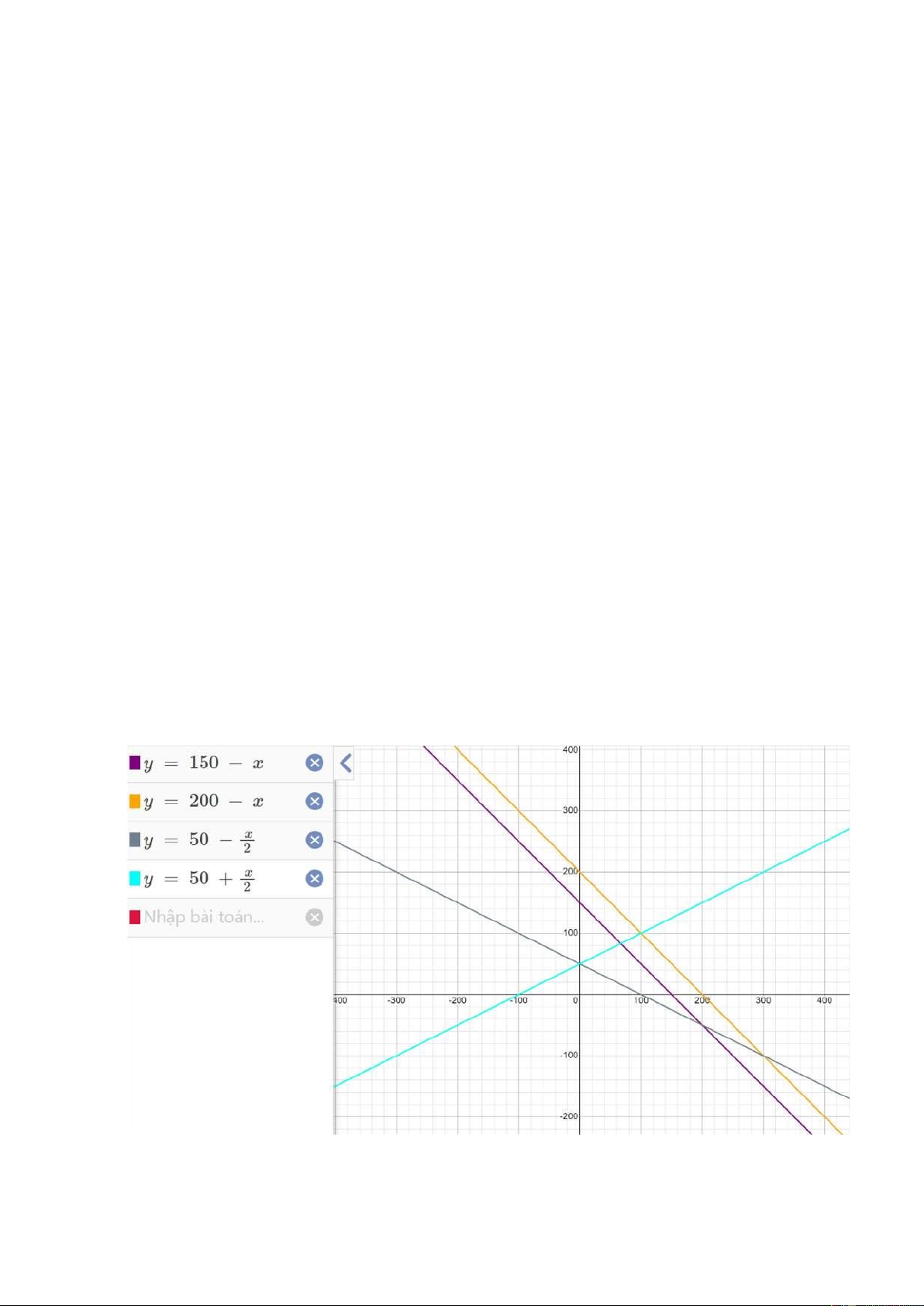
Không có trợ cấp: y = 150 - x
Trợ cấp không ràng buộc: y = 200 - x
Trợ cấp có ràng buộc: y = 50 - x/2
Trợ cấp có yêu cầu chi đối ứng: y = 50 + x/2
Vẽ các đường giới hạn ngân sách trên đồ thị, ta được hình sau:
b) Tư vấn cho Trưởng Khoa Kinh tế phát triển
Nếu Trưởng Khoa Kinh tế phát triển dự kiến mua sách và tạp chí trong năm học
20052006 dưới 45 triệu thì Trưởng khoa nên chọn chương trình trợ cấp không ràng
buộc. Trong trường hợp này, Trưởng Khoa Kinh tế phát triển có thể linh hoạt chi tiêu cho
các hoạt động khác của Khoa. lOMoAR cPSD| 46988474
c) Tư vấn cho Trưởng Khoa Kinh tế phát triển
Nếu Trưởng Khoa Kinh tế phát triển dự kiến mua sách và tạp chí với khoản tiền là 90
triệu thì trưởng khoa nên chọn chương trình trợ cấp có ràng buộc. Trong trường hợp
này, Trưởng Khoa Kinh tế phát triển vẫn có thể mua sách và tạp chí với số tiền mong
muốn mà vẫn có thể chi tiêu cho các hoạt động khác của Khoa. d) Tư vấn cho Trưởng
Khoa Kinh tế phát triển
Nếu Trưởng Khoa Kinh tế phát triển nhận thấy còn nhiều sách và tạp chí hay, cần thiết
cho sinh viên mà thư viện khoa chưa có và muốn chi đáng kể cho mua sách và tạp chí
trong năm học 2005-2006. Số tiền tối thiểu mà ông ta định mua sách và tạp chí là 120
triệu. Với trường hợp này, Trưởng Khoa Kinh tế phát triển nên chọn chương trình trợ
cấp có yêu cầu chi đối ứng. Trong trường hợp này, Trưởng Khoa Kinh tế phát triển có
thể mua sách và tạp chí với số tiền mong muốn mà vẫn tiết kiệm được một khoản tiền so
với chương trình trợ cấp không ràng buộc.
Tóm lại, chương trình trợ cấp phù hợp nhất cho Trưởng Khoa Kinh tế phát triển phụ
thuộc vào dự kiến chi tiêu cho mua sách và tạp chí của Trưởng khoa. Câu 4 :
a. Năng suất tăng theo quy mô
Hàm sản xuất Q= căn bậc 2(KL) là hàm sản xuất Cobb-Douglas với hệ số kỹ thuật α =
1/2. Do đó, hàm sản xuất này có năng suất tăng theo quy mô.
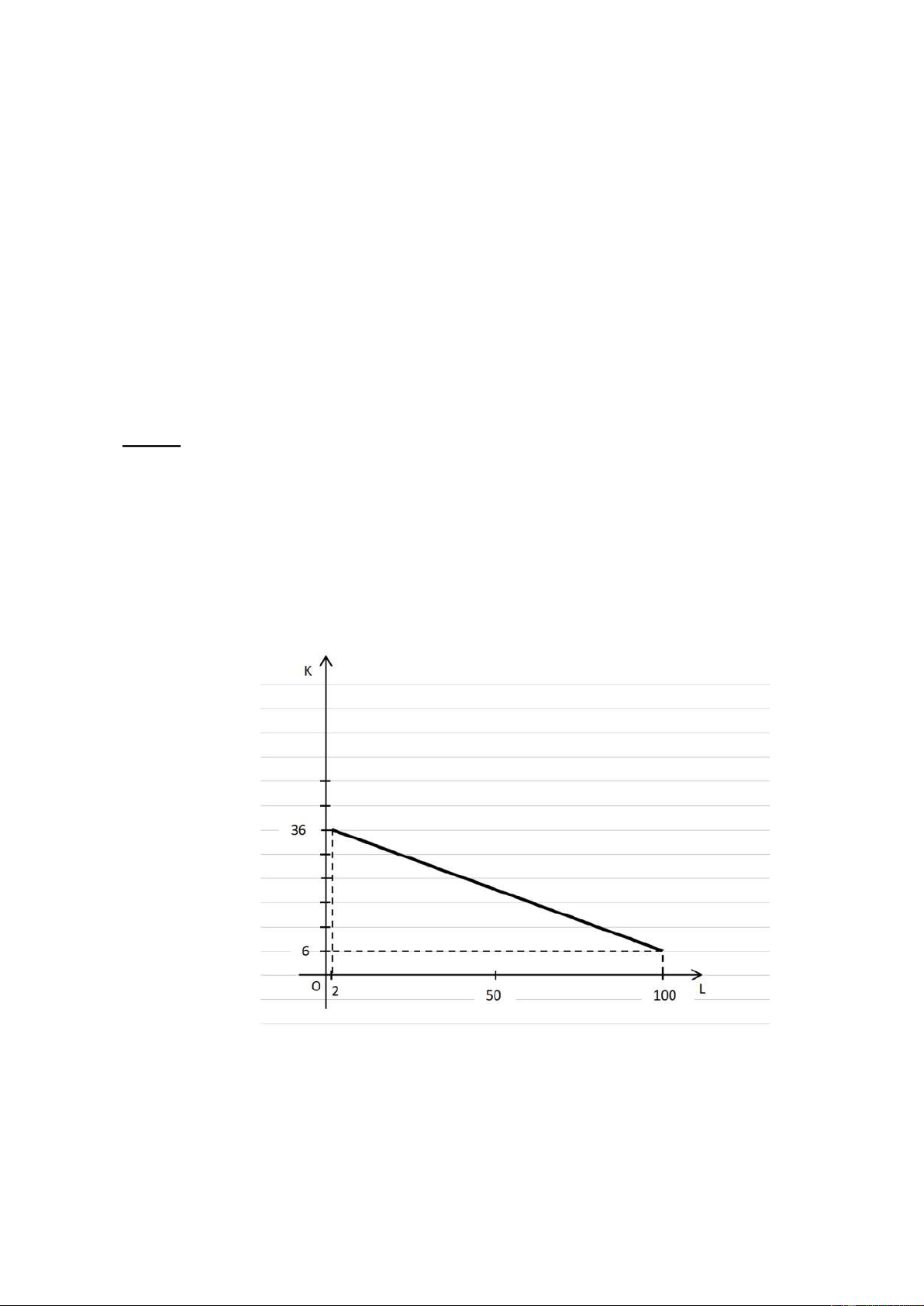
b. Đường đẳng lượng ứng với mức sản lượng Q = 6000 lốp/tháng
Đường đẳng lượng ứng với mức sản lượng Q = 6000 lốp/tháng là đường thẳng đi qua điểm (K,
L) = (6, 100) và (36, 2) trên mặt phẳng (K, L).
Tỷ lệ thay thế kỹ thuật biên của lao động đối với vốn (MRTSLK) tại A (K = 12, L = 3) là:
MRTSLK = -Q/KL = -6000/12*3 = -50 Ý nghĩa của MRSTSLK là:
Nếu công ty muốn tăng sản lượng thêm 1 đơn vị, công ty cần giảm lượng vốn sử dụng đi
50 đơn vị và tăng lượng lao động sử dụng lên 1 đơn vị.
MRSTSLK là âm vì lao động và vốn là hai yếu tố sản xuất bổ sung cho nhau. lOMoAR cPSD| 46988474
c. Quy mô để đáp ứng lượng cầu trên thị trường là 6000 chiếc lốp/tháng trong tương lai với
chi phí thấp nhất
Để đáp ứng lượng cầu trên thị trường là 6000 chiếc lốp/tháng trong tương lai với chi phí
thấp nhất, công ty nên lựa chọn quy mô K = 36.
Với quy mô K = 36, tổng chi phí sản xuất là: TC = 12*100 + 36*400 = 19200
Với quy mô K = 24, tổng chi phí sản xuất là: TC = 24*100 + 24*400 = 19200
Với quy mô K = 12, tổng chi phí sản xuất là: TC = 12*100 + 12*400 = 12000
Với quy mô K = 6, tổng chi phí sản xuất là: TC = 6*100 + 6*400 = 4200
Như vậy, quy mô K = 36 có tổng chi phí sản xuất thấp nhất.
d. Lựa chọn trên thay đổi nếu nhà máy được đặt tại một vùng khác với giả thiết lương công
nhân chỉ còn là 100 đô la/tháng và bỏ qua chi phí vận chuyển
Nếu lương công nhân chỉ còn là 100 đô la/tháng và bỏ qua chi phí vận chuyển, thì công ty
nên lựa chọn quy mô K = 60.
Với quy mô K = 60, tổng chi phí sản xuất là: TC = 60*100 + 60*100 = 12000
Với quy mô K = 36, tổng chi phí sản xuất là: TC = 36*100 + 36*400 = 25200
Với quy mô K = 24, tổng chi phí sản xuất là: TC = 24*100 + 24*400 = 20160
Với quy mô K = 12, tổng chi phí sản xuất là: TC = 12*100 + 12*400 = 12000
Với quy mô K = 6, tổng chi phí sản xuất là: TC = 6*100 + 6*400 = 4200
Như vậy, quy mô K = 60 có tổng chi phí sản xuất thấp nhất.
e)Đường tổng chi phí dài hạn (LTC) là đường cong đi qua các điểm tổng chi phí ứng với các
quy mô sản xuất khác nhau. LTC = 12*100 + 400*sqrt(L) lOMoAR cPSD| 46988474
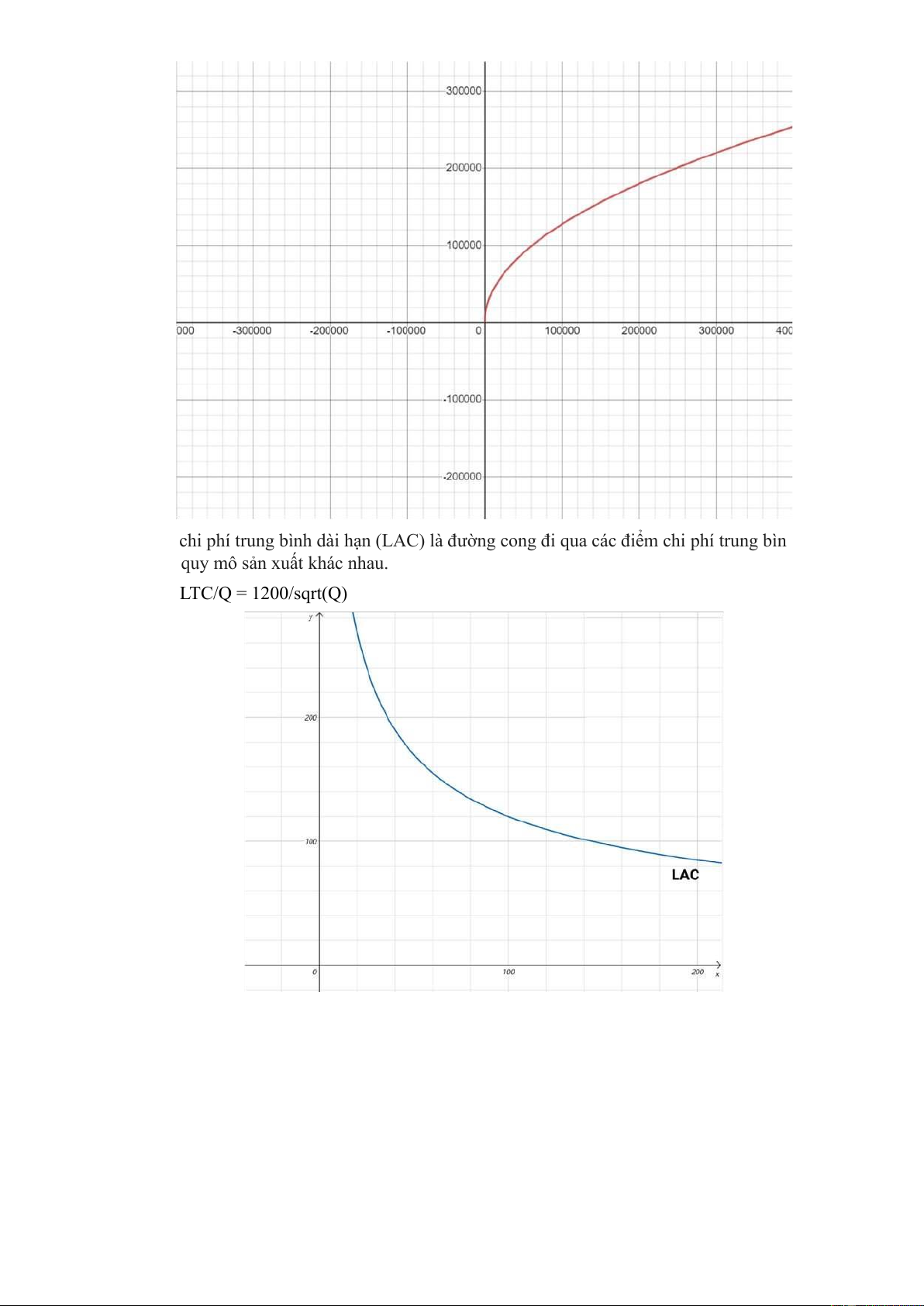
Đường chi phí trung bình dài hạn (LAC) là đường cong đi qua các điểm chi phí trung bình ứng
với các quy mô sản xuất khác nhau. LAC = LTC/Q = 1200/sqrt(Q)
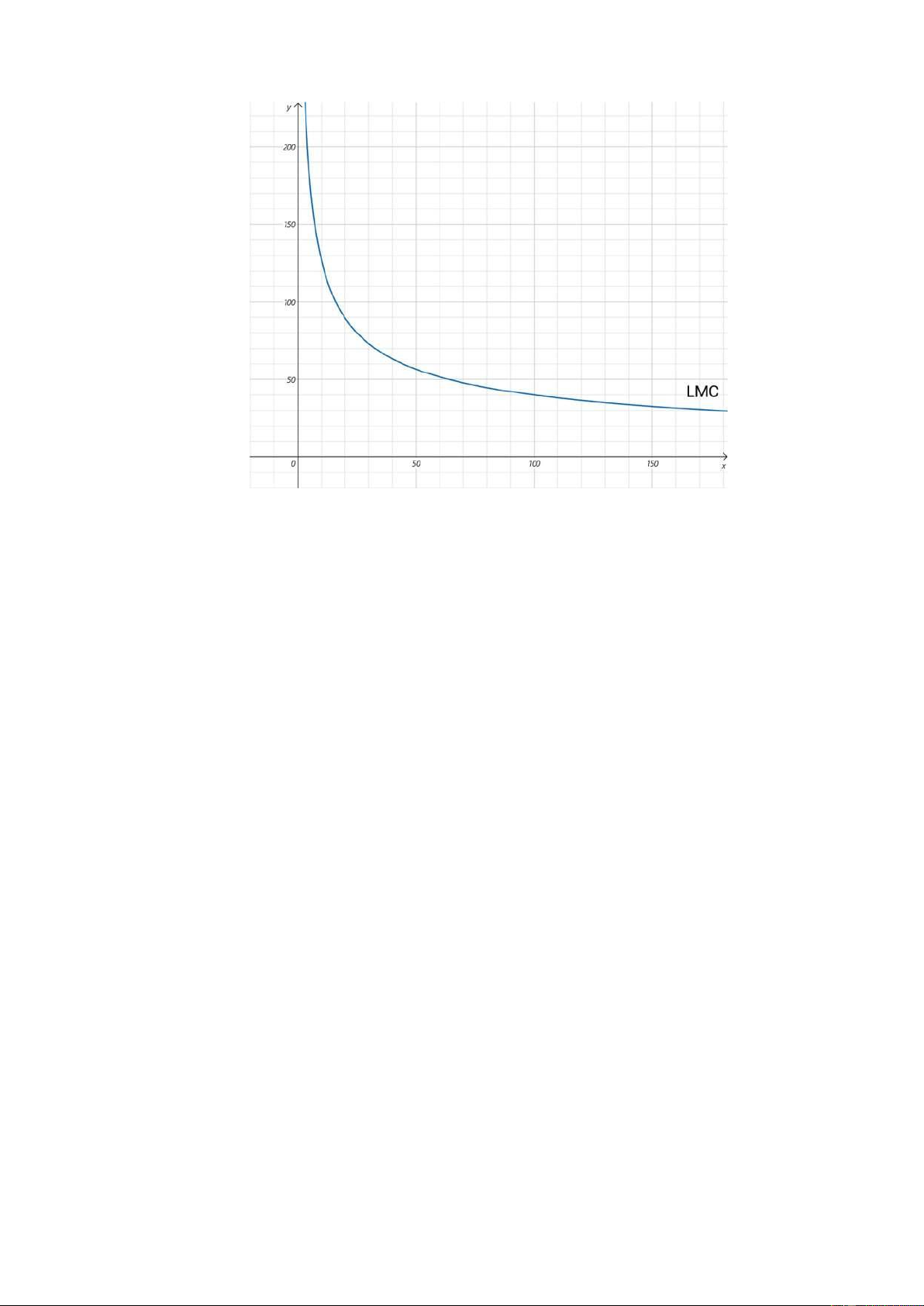
Đường chi phí biên dài hạn (LMC) là đường cong đi qua các điểm chi phí biên ứng với các quy mô sản xuất khác nhau. LMC = 400/sqrt(Q) lOMoAR cPSD| 46988474
Như vậy, đường tổng chi phí dài hạn là một đường tăng dần. Đường chi phí trung bình dài hạn
giảm dần đến khi đạt giá trị thấp nhất tại quy mô sản xuất tối ưu, sau đó tăng dần lên. Đường chi
phí biên dài hạn giảm dần đến khi đạt giá trị bằng chi phí trung bình dài hạn tại quy mô sản xuất
tối ưu, sau đó tăng dần lên.
g. Đường tổng chi phí, chi phí trung bình, chi phí biên trong ngắn hạn.
Tổng chi phí trong ngắn hạn được tính như sau: TC = wL + rK
Tại mức sản lượng 24 nghìn lốp mỗi tháng, tổng chi phí, chi phí trung bình và chi phí biên trong
ngắn hạn lần lượt là 1.920, 80 và 120. Đường chi phí biên cắt đường chi phí trung bình tại mức sản lượng 16. h.
Nếu giả sử rằng giá của mỗi lốp xe trên thị trường là 1 đô la. Hãy cho biết lượng lốp xe
mà công ty sẵn sàng cung cấp là bao nhiêu để tối đa hóa lợi nhuận? Lợi nhuận công ty lúc này là bao nhiêu?
Để tối đa hóa lợi nhuận, công ty sẽ sản xuất tại mức sản lượng mà tại đó chi phí biên bằng giá
thị trường. Theo giả thiết, giá thị trường là 1 đô la, do đó công ty sẽ sản xuất 24 nghìn lốp xe để
tối đa hóa lợi nhuận. Lợi nhuận công ty lúc này là: π = TR - TC = 24000 - 1920 = 4800 i.
Nếu công ty muốn tối thiểu hóa chi phí sản xuất trong ngắn hạn, mức sản lượng nên phân
bổ như thế nào giữa hai nhà máy?
Để tối thiểu hóa chi phí sản xuất trong ngắn hạn, công ty nên phân bổ sản lượng sao cho chi phí
biên của mỗi nhà máy bằng nhau. Giả sử công ty phân bổ sản lượng như sau: Q1 = x Q2 = 24000 - x
Tại mức sản lượng này, chi phí biên của mỗi nhà máy như sau: MPK1 = K1/L1 MPK2 = K2/L2
Để chi phí biên của mỗi nhà máy bằng nhau, ta có phương trình: K1/L1 = K2/L2
Với giả thiết công ty mua thêm một nhà máy sản xuất lốp xe khác với cùng công nghệ và quy
mô (K) lớn gấp bốn lần nhà máy hiện thời, ta có: lOMoAR cPSD| 46988474 K1 = 12 K2 = 48
Với giá trị K1 và K2, ta có: L1 = 48 L2 = 12
Do đó, lượng sản lượng mà công ty nên phân bổ cho mỗi nhà máy như sau: Q1 = 48 Q2 = 19200
j. Tổng chi phí, chi phí trung bình và chi phí biên
Với giả thiết công ty phân bổ sản lượng giữa hai nhà máy để tối thiểu hóa chi phí sản xuất, thì
tổng chi phí trong ngắn hạn của công ty là: TC = 2 * MC * Q
Thay Q = 12 nghìn lốp/tháng, ta có:
TC = 2 * MC * 12 nghìn lốp/tháng
Chi phí trung bình trong ngắn hạn của công ty là: AC = TC / Q
Thay TC = 2 * MC * 12 nghìn lốp/tháng và Q = 12 nghìn lốp/tháng, ta có: AC = 2 * MC
Chi phí biên trong ngắn hạn của công ty là: MC = AC' Thay AC = 2 * MC, ta có: MC = 2 * MC
Vậy, tổng chi phí, chi phí trung bình và chi phí biên trong ngắn hạn của công ty ứng với các mức
sản lượng là 24 nghìn lốp/tháng là: Mức sản lượng T ổng chi phí
Chi phí trung bình Chi phí biên 24 nghìn lốp/tháng 48 nghìn lốp/tháng 4 nghìn lốp/tháng 4 nghìn lốp/tháng Chú thích
Trong bài toán này, chúng ta giả sử rằng chi phí cố định của công ty không đổi khi công ty mở rộng quy mô sản xuất. Câu 5 :
a. Mức giá thấp nhất mà doanh nghiệp sẵn sang cung ứng sản phẩm ra thị trường trong ngắn hạn
Để xác định mức giá thấp nhất mà doanh nghiệp sẵn sang cung ứng sản phẩm ra thị trường trong
ngắn hạn, chúng ta cần xác định điểm giao nhau giữa đường chi phí biên (MC) và đường giá thị trường (P).
Từ hàm tổng chi phí, ta có thể suy ra hàm chi phí biên như sau: MC = q^2 - 4q + 6
Thay P = 213 - Q vào hàm chi phí biên, ta có:
q^2 - 4q + 6 = 213 - Q Giải phương trình trên, ta được: lOMoAR cPSD| 46988474 Q = 9,333
Tại mức sản lượng này, chi phí biên bằng giá thị trường:
MC = P = 213 - Q = 213 - 9,333 = 203,667
Vậy, mức giá thấp nhất mà doanh nghiệp sẵn sang cung ứng sản phẩm ra thị trường trong
ngắn hạn là 203,667.
b. Mức sản lượng tương ứng
Mức sản lượng tương ứng với mức giá thấp nhất là 9,333.
c. Số lượng doanh nghiệp hoạt động trên thị trường
Giả sử có n doanh nghiệp hoạt động trên thị trường. Tổng sản lượng của thị trường là Q = n * 9,333.
Để thị trường đạt được cân bằng, tổng cung phải bằng tổng cầu. Ta có:
n * 9,333 = 213 - Q Giải phương trình trên, ta được: n = 10
Vậy, có 10 doanh nghiệp hoạt động trên thị trường khi thị trường đạt được cân bằng. Câu 6:
a. Doanh thu của nhà độc quyền là tổng giá bán sản phẩm.
Doanh thu = Giá bán * Số lượng bán = P * Q = (140 - 2Q) * Q = 140Q - 2Q^2
b. Doanh thu biên là sự thay đổi của doanh thu khi lượng bán sản phẩm thay đổi một đơn vị.
Doanh thu biên = (d/dQ)(140Q - 2Q^2) = 140 - 4Q
c. Chi phí biên là sự thay đổi của chi phí khi lượng bán sản phẩm thay đổi một đơn vị.
Chi phí biên = (d/dQ)(5Q^2) = 10Q
d. Mức sản lượng tối đa lợi nhuận của nhà độc quyền là mức sản lượng mà doanh thu biên bằng chi phí biên. 140 - 4Q = 10Q => 14Q = 140 => Q = 10
Vậy mức sản lượng tối đa lợi nhuận của nhà độc quyền là mức sản lượng mà doanh thu biên bằng chi phí biên là 10
e. Mức lợi nhuận của nhà độc quyền là tổng doanh thu trừ tổng chi phí.
Lợi nhuận = TR - TC = (140Q - 2Q^2) - (5Q^2) Lợi nhuận = 140Q - 7Q^2
Lợi nhuận = (140 * 10) - 7(10^2) = 1400 - 700 = 700
f. Mức sản lượng tối ưu sẽ không thay đổi.
Mức sản lượng tối ưu được xác định bởi điểm giao nhau của đường doanh thu biên và
đường chi phí biên. Khi nhà độc quyền phải trả mức phí hàng năm $150, tổng chi phí của nó sẽ
tăng thêm $150. Tuy nhiên, đường chi phí biên vẫn sẽ có dạng tuyến tính với hệ số góc là 10.
Do đó, đường chi phí biên vẫn sẽ cắt đường doanh thu biên tại mức sản lượng 10. Vậy,
câu trả lời là Không. Câu 7 : lOMoAR cPSD| 46988474 Câu a
Nếu không phân biệt giá, hãng Nha Trang Airlines sẽ tối đa hóa lợi nhuận bằng cách bán vé với
giá bằng chi phí biên, tức là $100.
Với giá vé $100, hãng sẽ bán được tổng số 260 + 240 = 500 vé.
Lợi nhuận của hãng là:
Lợi nhuận = Doanh thu - Chi phí
= (100 * 500) - (30.000 + 100 * 500) = 50.000 - 180.000 = -130.000 $
Như vậy, nếu không phân biệt giá, hãng Nha Trang Airlines sẽ chịu lỗ $130.000. Câu b
Theo Ông Vinh, một chính sách giá phân biệt áp dụng cho từng loại hành khách có thể làm tăng lợi nhuận của hãng.
Để kiểm tra nhận xét này, ta cần tính toán lợi nhuận của hãng khi áp dụng chính sách giá phân biệt.
Giá vé cho hành khách doanh nhân là:
Pd = (260 - 0,4 * Pd) - (260 - 0,4 * Pd) => Pd = 325
Giá vé cho hành khách thông thường là:
Pt = (240 - 0,6 * P_t) - (240 - 0,6 * P_t) => Pt = 200
Với giá vé này, hãng sẽ bán được tổng số 200 vé cho hành khách doanh nhân và 300 vé cho hành khách thông thường.
Lợi nhuận của hãng là: Lợi nhuận
= (325 * 200) + (200 * 300) - (30.000 + 100 * (200 + 300)) = 65.000 - 80.000 = -15.000 $
Như vậy, khi áp dụng chính sách giá phân biệt, hãng Nha Trang Airlines vẫn chịu lỗ, nhưng mức
lỗ giảm xuống còn $15.000 so với mức lỗ $130.000 khi không phân biệt giá.
Như vậy, nhận xét của Ông Vinh là đúng. Chính sách giá phân biệt có thể làm tăng lợi nhuận của
hãng Nha Trang Airlines, mặc dù mức tăng không đáng kể.
Câu c. Sự gia tăng chi phí cố định cho mỗi chuyến bay có ảnh hưởng đến hoạt động của hãng Nha Trang Airlines.
Nếu không phân biệt giá, hãng sẽ phải bán vé với giá $100 để tối đa hóa lợi nhuận. Tuy nhiên,
với chi phí cố định tăng thêm 40%, hãng sẽ bị lỗ $190.000 khi bán vé với giá $100.
Để bù đắp cho chi phí cố định tăng thêm, hãng Nha Trang Airlines cần phải bán vé với giá cao
hơn $100. Giá vé tối thiểu mà hãng cần phải bán là: P = 30.000 + 100 * 500 = 280
Tuy nhiên, nếu hãng bán vé với giá $280, hãng sẽ chỉ bán được 260 vé, thấp hơn so với số lượng
500 vé mà hãng bán được khi không có sự gia tăng chi phí cố định.
Do đó, hãng Nha Trang Airlines có thể phải áp dụng chính sách giá phân biệt để bù đắp cho chi
phí cố định tăng thêm.