Bài tập chương 3 kinh tế vi mô có đáp án | Đại học Kinh tế kỹ thuật công nghiệp

Câu 3.1: Một người tiêu dùng có thu nhập hàng tháng là 200 nghìn đồng để phân bổ cho hai hàng hóa X và Y.
a. Gỉa sử hàng hóa X là 4 nghìn một đơn vị và giá hàng hóa Y là 2 nghìn một đơn vị. Hãy
vẽ đường ngân sách cho người này.
b. Gỉa sử hàm hợi ích tiêu dùng của người tiêu dùng này được cho bởi U(x,y) = 2X +
Y. Người này nên chọn kết hợp X, Y nào để tối đa hóa lợi ích?
c. Cửa hàng nơi người này thường mua có sự khuyến khích đặc biệt. Nếu mua 20 đơnvị
Y ở giá 2 nghìn sẽ được thêm 10 đơn vị nữa không mất tiền. Điều này chỉ áp dụng cho
20 đơn vị Y đầu tiên, tất cả các đơn vị sau vẫn phải mua ở giá 2 nghìn (trừ số được
thưởng). Hãy vẽ đường ngân sách cho người này.
d. Vì cung hàng hóa Y giảm nên giá của nó tăng thành 4 nghìn đồng một đơn vị. Cửahàng
này không khuyến khích mua như trước nữa. Bây giờ đường ngân sách của người này
thay đổi như thế nào? Kết hợp X, Y nào tối đa hóa ích lợi của người đó?
Câu 3.2. Bạn có 40 nghìn để chi tiêu cho hai hàng hóa. Hàng hóa thứ nhất X giá 10
nghìn một đơn vị, hàng hóa thứ 2 Y giá 5 nghìn một đơn vị. Hàm tổng lợi ích là TU=2XY
a. Hãy viết phương trình đường ngân sách của bạn.
b. Tính tỷ lệ thay thế cận biên
c. Để tối đa hóa lợi ích bạn sẽ chọn mua bao nhiêu X, bao nhiêu Y? Tính tổng lợi ích tối đa đó
d. Gỉa sử giá hàng hóa thứ nhất tăng lên thành 20 nghìn và thu nhập của bạn tăng lên
thành 60 nghìn. Hãy vẽ đường ngân sách mới của bạn. Kết hợp tiêu dùng sẽ thay đổi như thế nào?
e. Gỉa sử giá của hàng hóa Y tăn lên thành 6 nghìn đồng. Tìm ra cách kết hợp tiêu dùng tối ưu mới
Câu 3.3. Kết hợp tiêu dùng của một người A được cho dưới đây Y(nghìnđ) 200 I 2 0 100 X(nghìnđ) I 1 I 0
a. Nếu giá của hàng hoá X là 15.000 thì ngân sách của người tiêu dùng này là bao
nhiêu? Giá của hàng hoá Y là bao nhiêu? Viết pt đường ngân sách
b. Người tiêu dùng phân bố thu nhập cho hai hàng hóa X và Y với giá như trên.Giả sử
hàm lợi ích của người tiêu dùng này là U(X,Y) = X(2+Y).
b1. Hãy xác định tỷ lệ thay thế biên?
b2. Xác định số lượng hàng hóa X và Y để người tiêu dùng này tối đa hóa lợi ích?
Tính tổng lợi ích tối đa đó?
c. Nhân ngày kỷ niệm đặc biệt,cửa hàng này có sự khuyến mại cho khách hàng
muahàng. Nếu mua 50 đơn vị X đầu tiên sẽ được khuyến mãi 10 đơn vị X , tất cả các đơn
vị sau vẫn phải mua với giá như cũ. Hãy vẽ đường ngân sách cho người này.
d. Nếu ngân sách của người này tăng thêm gấp đôi, giá hàng hóa X và Y không đổithì
sự kết hợp hàng hóa nào sẽ tối đa sự thỏa mãn của người tiêu dùng?
e. Vì cung hàng hóa Y giảm nên giá của nó tăng thành 30.000đ. Cửa hàng này khôngcó
sự khuyến mại. Đường ngân sách của người này thay đổi như thế nào? Sự kết hợp X và Y
nào để người tiêu dùng tối đa hóa lợi ích?
Câu 3.4 Mỗi tuần Hoa dùng 200.000đ để mua 2 hàng hóa X và Y, giá lần lượt của 2
sản phẩm này là 20.000đ/sp và 10.000đ/sp.Tổng lợi ích mà Hoa nhận được khi tiêu dùng 2 sản
phẩm này thể hiện ở bảng dưới đây: Sản phẩm X Sản phẩm Y X TUx Y TUy 1 50 1 70 2 80 2 100 3 100 3 120 4 110 4 130 5 110 5 130 6 100 6 120
a) Hãy xác định phương án tiêu dùng tối ưu của Hoa. Khi đó tổng lợi ích là baonhiêu?
b) Nếu giá của Y tăng lên gấp đôi thì phương án tiêu dùng tối ưu sẽ thay đỏi như thếnào?
c) Thu nhập của Hoa tăng, Hoa bổ sung số tiền dùng để tiêu dùng 2 hàng hóa X và
Ythêm 40.000đ. Xác định số lượng hàng hóa A, B mà Hoa tiêu dùng để tối đa hóa lợi ích.
Câu 3.5. Hàm ích lợi của một người tiêu dùng cho bởi U(x,y) = XY
a. Gỉa sử rằng lúc đầu người này tiêu dùng 4 đơn vị X và 12 đơn vị Y. Nếu việc tiêudùng
hàng hóa Y giảm xuống còn 8 đơn vị thì người này phải có bao nhiêu đơn vị X để vẫn thỏa mãn như lúc đầu?
b. Người này thích tập hợp nào hơn trong hai tập hợp sau:
3 đơn vị X và 10 đơn vị Y; 4 đơn vị X và 8 đơn vị Y
c. Hãy xét 2 tập hợp sau: (8,12) và (16,6), người này có bàng quan giữa hai tập hợp này không? ĐÁP ÁN Câu 3.1. I = 200 nghìnđ
a. Px = 4 nghìnđ, Py = 2 nghìnđ
Phương trình đường ngân sách có dạng: I = X.Px + Y.Py → pt đường ngân sách: X.4 + Y.2 = 200 Y 100 50 0 50 100 X c. U(x,y) = 2X + Y MUx = U’(x) = 2 MUy = U’(y) = 1 X=0, Y=100 Y=0, X = 50
Để tối đa hóa lợi ích người tiêu dùng sẽ lựa chọn X, Y sao cho: →
→ Như vậy mọi kết hợp (X,Y) thỏa mãn phương trình (2) đề tối đa hóa lợi ích người tiêu dùng. Y
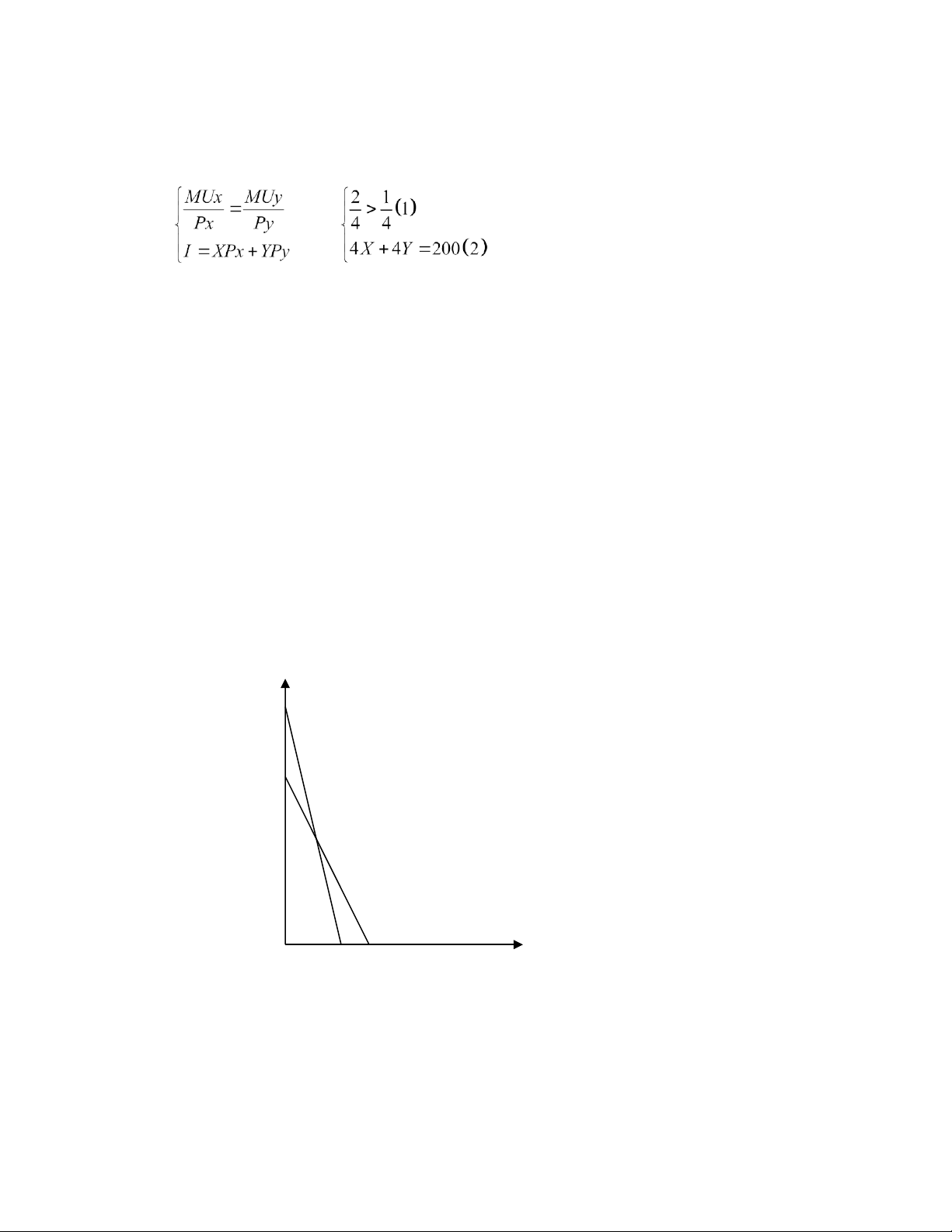
c. Cửa hàng có sự khuyến mại, vẽ đg ngân sách mới 100 Y 50 100 50 50 30 0 50 100 20 Mua 20Y được + 10Y
→ người này sẽ mua 20Y, 40X và được 30Y, 40X 0 50 100 X Nếu X = 0 → Y = 110 Y = 0 → X = 50 Đường
ngân sách mới là đường gãy
d. Gía y tăng P’y = 4 nghìnđ Ta có pt đường ngân khúc như hình bên sách mới 200 = 4X + 4Y X=0, Y=50 Y=0, X = 50
Để tối đa hóa lợi ích người tiêu dùng sẽ lựa chọn X, Y sao cho: →
Như vậy để tối đa hóa lợi ích người tiêu dùng này sẽ dành hết số tiền trong ngân
sách để mua X. Và kết hợp tiêu dùng sẽ là X = 5, Y = 0 Câu 3.2 I = 40, Px = 10, Py = 5
Phương trình đường ngân sách có dạng: I = X.Px + Y.Py → pt đường ngân sách: X.10 + Y.5 = 40 Y 12 Y=0, X = 4 8 4 0 3 4 8 X X=0, Y=8 b. TU = 2XY MUx = U’(x) = 2Y MUy = U’(y) = 2X
MRSx/y = MUx/MUy = 2Y/2X = Y/X
c. Để tối đa hóa lợi ích người tiêu dùng sẽ lựa chọn X, Y sao cho: → → X = 2, Y = 4 TU = 2X.Y = 2.2.4 = 16
d. Gía hàng hóa X tăn lê Px = 20, ngân sách tăng lên I = 60
Ta có phương trình đường ngân sách mới 60 = 20X + 5Y
Để tối đa hóa lợi ích người tiêu dùng sẽ lựa chọn X, Y sao cho: → → X = 1,5, Y = 6
e. Gía Y tăng lên Py = 6 nghìn đ
Ta có phương trình đường ngân sách mới 40 = 10X + 6Y
Để tối đa hóa lợi ích người tiêu dùng sẽ lựa chọn X, Y sao cho: → → X = 2, Y = 10/3 Câu 3.3.
a. Phương trình đường ngân sách có dạng: I = X.Px + Y.Py
Nhìn vào đồ thị ta thấy: với X = 0, Y= I/Py = 200 (1)
với Y = 0, X=I/Px = 100 (2)
Nếu Px = 15 nghìn, từ pt (2) → I = 1500 nghìn
Thay I = 1500 vào pt (1) → Py = 1500/200 = 7,5 nghìn Phương
trình đường ngân sách là: 1500 = 15X + 7,5Y
b. TU = X(2+Y)b1. Xác định MRSx/y MUx = TU’x = 2+Y MUy = TU’y = X MRSx/y = MUx/MUy = (2+Y)/X
b2. Để tối đa hóa lợi ích người tiêu dùng sẽ lựa chọn X, Y sao cho: → → X = 50,5; Y = 101
TU = X(2+Y) = 50,5(2+101) = 5201,2
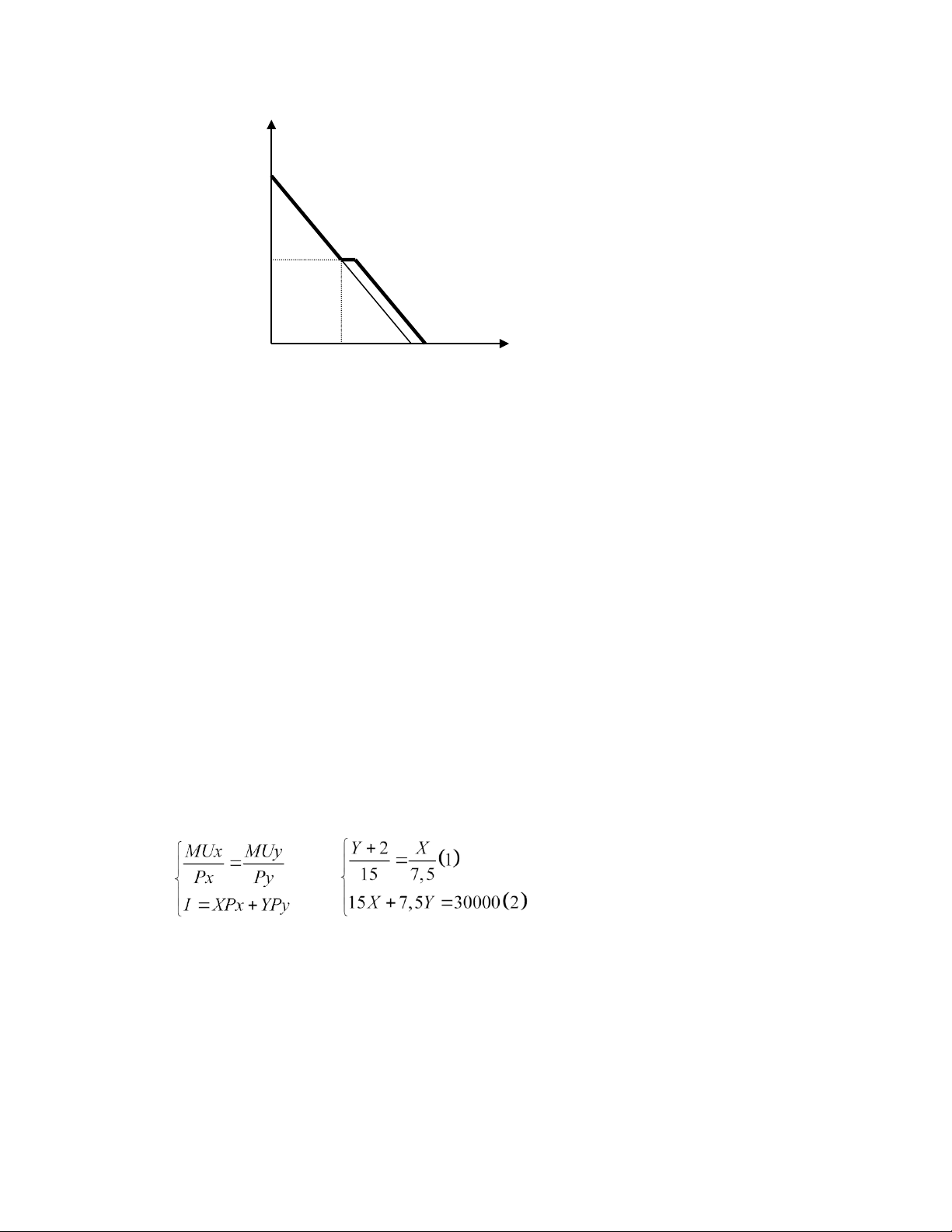
c. Mua 50 đơn vị X đầu tiên sẽ được 10 đơn vị X không mất tiền 50 0 100 110 X Y Mua 50X được + 10X
200→ người này vẫn sẽ mua 50,5X
và 101Y được 10X nữa là 60,5X, 50Nếu X = 0 → Y = 200 Y = 0 → X = 100 +10=110
30Đường ngân sách mới là đường 20gãy khúc như hình bên
TU’ = 60,5(2+101) =6231,5>TU
d. Ngân sách tăng lên gấp đôi I = 30000 đ
Ta có phương trình đường ngân sách mới 30000 = 15X + 7,5Y
Để tối đa hóa lợi ích người tiêu dùng sẽ lựa chọn X, Y sao cho: → → X = 100,5; Y = 199
e. Gía Y tăng Py = 30 nghìnđ
Để tối đa hóa lợi ích người tiêu dùng sẽ lựa chọn X, Y sao cho: → → X = 52; Y = 24 Câu 3.4
a. Để xác định phương án tiêu dùng tối ưu ta đi so sánh MUx/Px và MUy/Py Sản phẩm X Sản phẩm Y X TUx MUx MUx/Px Y TUy MUy MUy/Py 1 50 50 2,5 1 70 70 7 2 80 30 1,5 2 100 30 3 3 100 20 1 3 120 20 2 4 110 10 0,5 4 130 10 1 5 110 0 0 5 130 0 0 6 100 -10 -0,5 6 120 -10 -1
Nguyên tắc lựa chọn là sẽ lựa chọn chi phí cận biên tính trên một đồng chi mua lớn hơn.
I = 100 nghìn ta chia làm 5 lần lựa chọn, mỗi lần sẽ mua được 1X và 2Y - Lần 1: Ta so sánh MUx/Px(X=1) = 2,5 <
MUy/Py(Y=1)+MUy/Py(Y=2) = 10. Vậy lần này Hoa sẽ chọn mua 2Y - Lần 2: Ta so sánh MUx/Px(X=1) = 2,5 <
MUy/Py(Y=3)+MUy/Py(Y=4) = 3. Vậy lần này Hoa vấn sẽ chọn mua 2Y - Lần 3: Ta so sánh MUx/Px(X=1) = 2,5 >
MUy/Py(Y=5)+MUy/Py(Y=6) = -1. Vậy lần này Hoa vấn sẽ chọn mua 1X - Lần 4: Ta so sánh MUx/Px(X=2) = 1,5 >
MUy/Py(Y=5)+MUy/Py(Y=6) = -1. Vậy lần này Hoa vấn sẽ chọn mua 1X
- Lần 5, Ta so sánh MUx/Px(X=3) = 1 > MUy/Py(Y=5)+MUy/Py(Y=6)
= -1 Vậylần này Hoa vấn sẽ chọn mua 1X
Đến đây vửa hết ngân sách
Vậy qua 5 lần lựa chọn Hoa chọn 3X, 4Y
TU = 70 + 100 + 120 + 130 + 50 + 80 + 100 = 650
b. Nếu giá của Y tăng lên là 20 nghìnđ ta có biểu sau: Sản phẩm X Sản phẩm Y X TUx MUx MUx/Px Y TUy MUy MUy/Py 1 50 50 2,5 1 70 70 3,5 2 80 30 1,5 2 100 30 1,5 3 100 20 1 3 120 20 1 4 110 10 0,5 4 130 10 0,5 5 110 0 0 5 130 0 0 6 100 -10 -0,5 6 120 -10 -0,5
I = 100 nghìn ta chia làm 5 lần lựa chọn, mỗi lần sẽ mua được 1X và 1Y
- Lần 1: Ta so sánh MUx/Px(X=1) = 2,5 < MUy/Py(Y=1)= 3,5. Vậy lần này Hoasẽ chọn mua 1Y
- Lần 2: Ta so sánh MUx/Px(X=1) = 2,5 > MUy/Py(Y=2)= 1,5. Vậy lần này Hoasẽ chọn mua 1X
- Lần 3: Ta so sánh MUx/Px(X=2) = 1,5 = MUy/Py(Y=2)= 1,5. Vậy lần
này Hoavấn sẽ chọn mua cả X và Y (vì giá X = giá Y)
- Lần 4: Ta so sánh MUx/Px(X=3) = 1 = MUy/Py(Y=3)=1. Vậy lần này
Hoa vấnsẽ chọn mua 1Y (vì giá X = Y mà Tux< TUy)
Lần này vừa hết ngân sách, vậy qua 4 lần lựa chọn Hoa sẽ mua 2X và 3Y
TU = 70 + 50 + 100+80+120 = 420
c. Vơi bảng tổng lợi ích và lợi ích cận biên như câu a
Lúc này thu nhập của Hoa tăng thêm 40 nghìn đ.Với 40 nghìn đồng Hoa có thể chia
thêm ra làm 2 lần lựa chọn nữa, mỗi lần mua được 1X hoặc 2Y Tiếp tục các lần lựa chọn ở câu a - Lần 6: Ta so sánh MUx/Px(X=4) = 0,5 >
MUy/Py(Y=5)+MUy/Py(Y=6) = -1. Lần này Hoa sẽ chọn 1X - Lân 7: Ta so sánh MUx/Px(X=5) = 0 >
MUy/Py(Y=5)+MUy/Py(Y=6) = -1 Vậy lần này Hoa vẫn sẽ chọn 1X.
Đến đây vừa hết ngân sách tăng thêm TU = 650 + 110 + 110 =870 Câu 3.5. Có U(x,y) = X.Y
a. X = 4, Y=12 → U(x,y) = 4.12 = 48
Khi Y giảm xuống còn Y=8, để U(x,y)= 48 X = U(x,y)/Y = 48/8 = 6
Như vậy nếu Y giảm xuống còn 8, để thỏa mãn như lúc đầu thì X=6
b. X1=3, Y1=10 → U(x,y)1 = 3.10 = 30 X2=4, Y2=8 → U(x,y)2 = 4.8 = 32 → U(x,y)1< U(x,y)1
→ Người này thích tập hợn X = 4, Y=8 hơn c. Hai tập (8,12) và (16,6)
X3=8, Y3=12 → U(x,y)1 = 8.12 = 96
X4=16, Y4=6 → U(x,y)2 = 16.6 = 96 → U(x,y)3= U(x,y)4
→ Anh ta bàng quan giữa 2 tập hợp này