
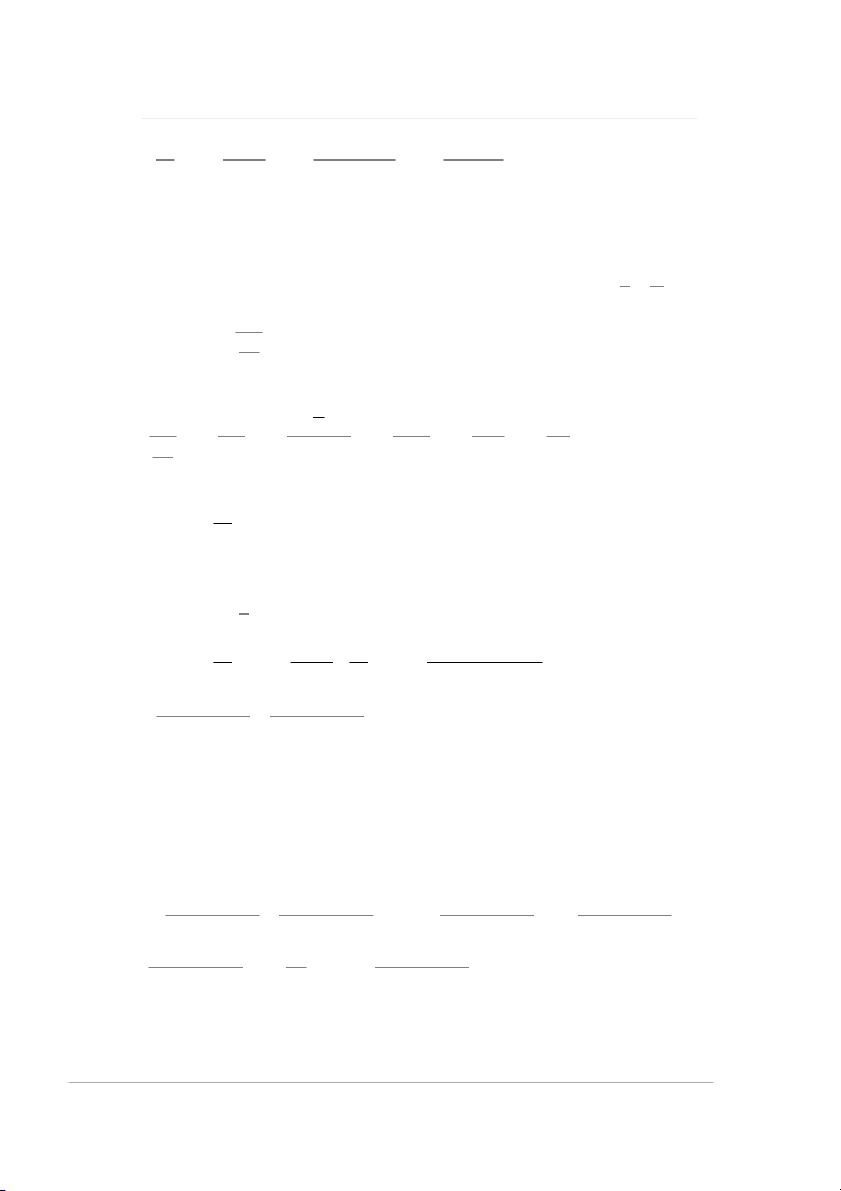
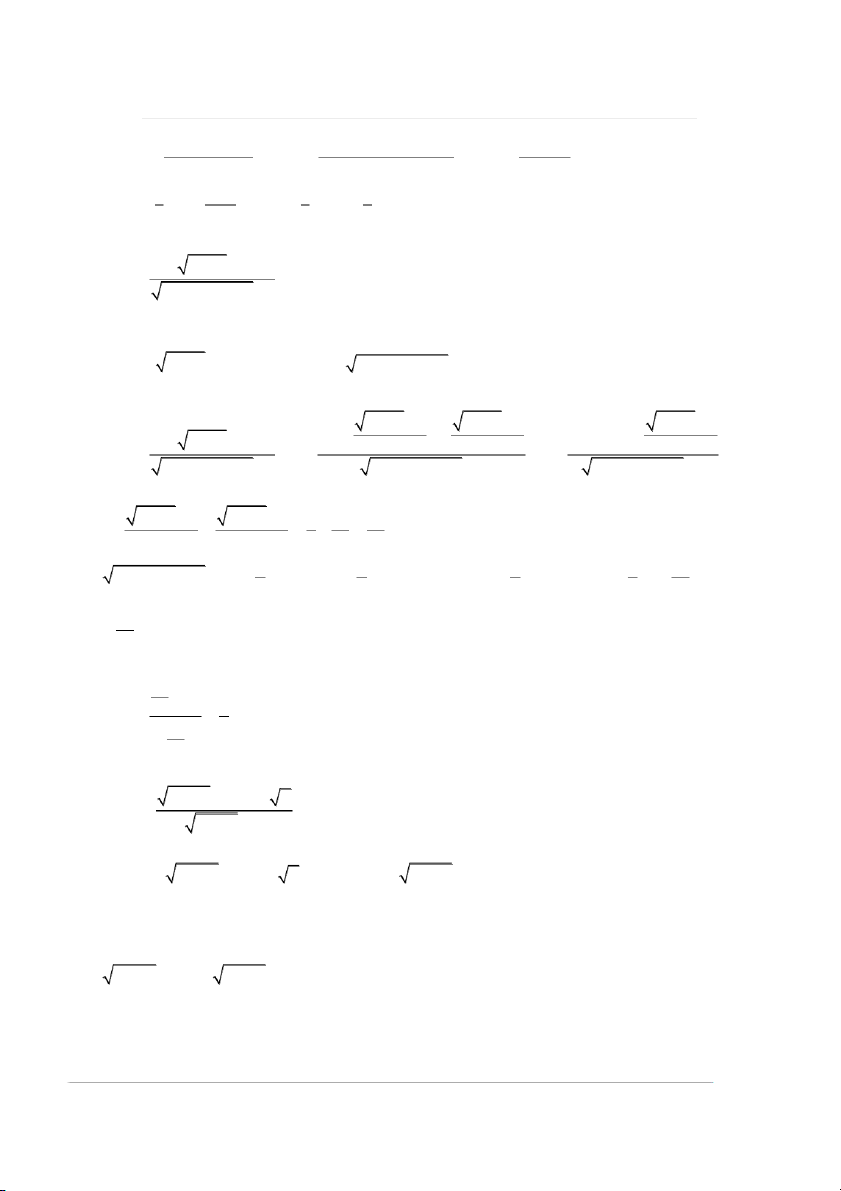




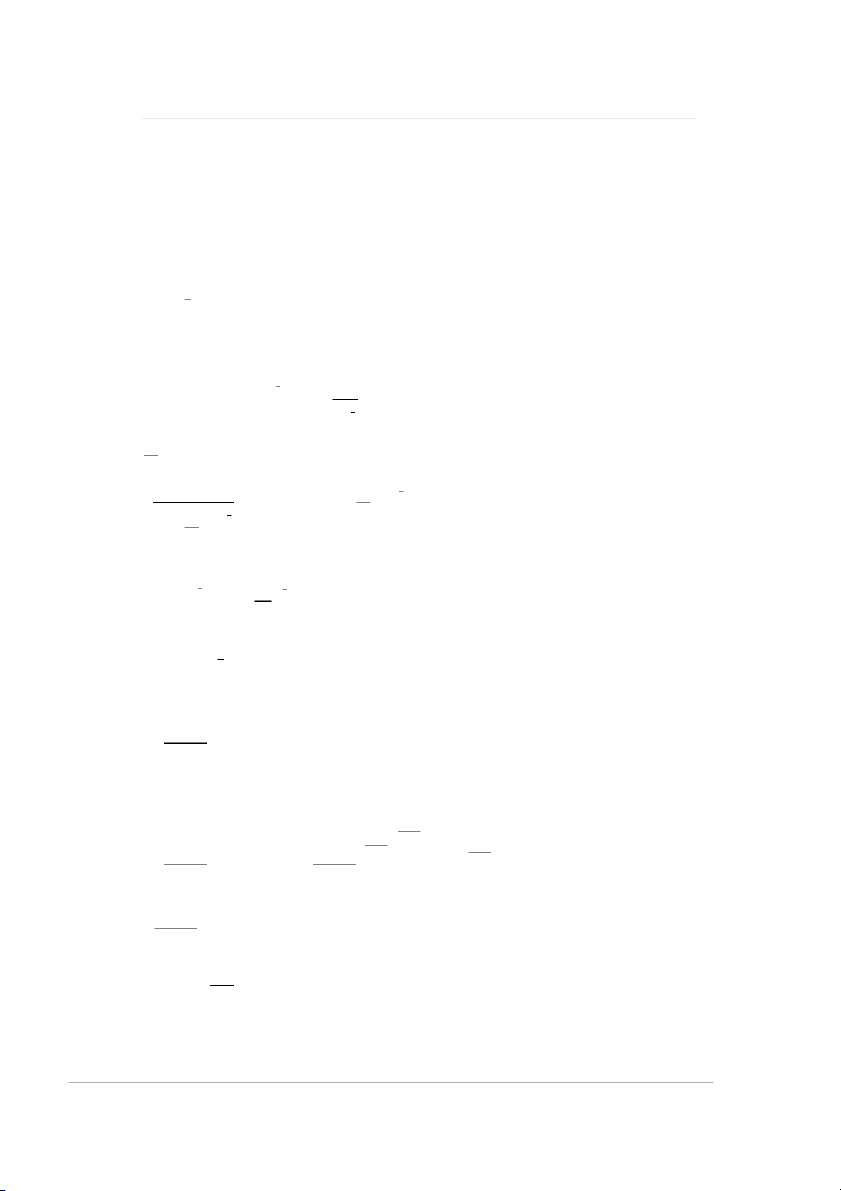
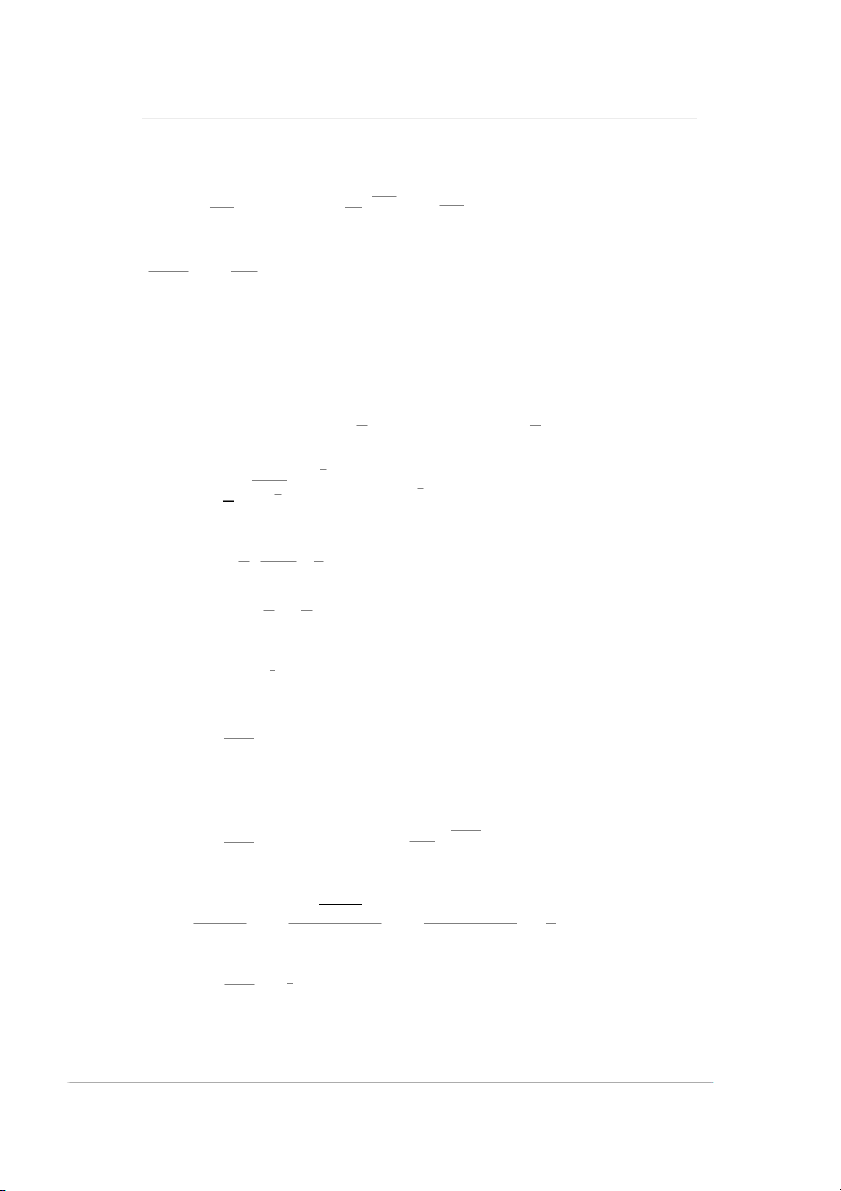


Preview text:
1 | B À I T Ậ P G I Ớ I H Ạ N H À M S Ố
Bài 1: Tính giới hạn của hàm sau: tan x x I lim x 0 x sin x 0
Giải bài 1: Thấy khi x 0 thì giới hạn đã cho có dạng bất định là . 0
Áp dụng quy tắc L’Hospital: 1 1 2 tan x x cos x 1 cosx1 cosx 1 cos x 2 lim lim lim x sin x 1 cos x 1 cosx lim 2 2 2 x 0 x 0 x 0 x 0 cos x cos x 1
Bài 2: Tính giới hạn sau đây: 1 x e 1 I lim x 1 x
Giải bài 2: 0
Khi x thì giới hạn đã cho có dạng bất định là . 0
Áp dụng quy tắc L’Hospital 1 1 1 x e x 2 e 1 x 0 I lim lim e 1 x 1 x 1 2 x x
Bài 3: Tính giới hạn sau đây: ln x I lim x 0 1 x
Giải bài 3:
Khi x 0 thì giới hạn đã cho có dạng bất định là .
Áp dụng quy tắc L’Hospital 1 ln x x I lim lim 0 x 0 1 x 0 1 2 x x
Bài 4: Tính giới hạn khi n N , a 1 n x I lim x x a
Giải bài 4:
Khi x thì giới hạn có dạng bất định là
Áp dụng quy tắc L’Hospital
2 | B À I T Ậ P G I Ớ I H Ạ N H À M S Ố n n 1 n2 x nx n(n 1)x n! I lim lim lim lim
0 (vì n là một số) x x x 2 x n x x x x a a ln a a (ln a) a (lna)
Bài 5: Tính giới hạn sau đây khi 0 I lim x ln x x0
Giải bài 5: 0
Khi x0, giới hạn đã cho có dạng bất định là 0. , ta đưa về dạng bất định 0 ln x I lim x ln x lim x 0 x 0 1 x
Áp dụng quy tắc L’Hospital 1 ( 1 ) ln x ln x x x x x x I lim lim lim lim lim lim 0 ( 1 ) x0 1 x0 x0 x0 x0 x0 x x x x x
Bài 6: Tính giới hạn sau: 1 2 I lim cot x 2 x0 x
Giải bài 6:
Khi x 0 thì giới hạn đã cho có dạng bất định là 0 Đưa về dạng 0 2 2 2 2 1 cos x 1 x cos x sin x 2 I limcot x lim lim 2 2 2 2 2 x0 x0 x0 x sin x x x sin x
x cos x sin x x cos x sin x lim 2 x 0 x sin x sin x
Tới đây tiến hành thay thế VCB tương đương Khi x 0 thì ta có: xcosx ~ x sinx ~ x x2sinx ~ x3
Vậy xcosx + sinx ~ x + x = 2x
xcosx – sinx không thay được VCB tương đương vì x – x = 0x
x cos x sin x x cos x sin x x cos x sin x x cos x sin x I lim lim lim 2 2 x0 x0 x0 x sin x sin x x sin x sin x x cos x sin x 2x x cos x sin x lim lim 2lim 3 3 x 0 x 0 x 0 x x x
Áp dụng quy tắc L’Hospital
3 | B À I T Ậ P G I Ớ I H Ạ N H À M S Ố x cos x sin x
cos x x sin x cos x xsin x I 2lim 2lim 2lim 3 2 2 x 0 x 0 x 0 x 3x 3x 1 sin x 1 2 2 lim 2 1 x0 3 x 3 3
Bài 7: Tính giới hạn sau đây: 3 sin 1 x sin1 I lim 5 x0 1 2x ln cos x 1
Giải bài 7: Nhận xét, vì: lim
và lim 5 1 2xlncosx 1 0 ta mới tiến hành thay thế VCB x 0 3 sin 1 x sin1 0 x 0 tương đương được. 3 3 3 1 x 1 1 x 1 1 x 1 3 2cos sin 2cos1 sin sin 1 x sin1 2 2 2 I lim lim lim 5 5 5 x0 x0 x0 1 2xln cos x 1 1 2x lncosx 1 1 2x lncosx 1 Khi x 0, ta có: 3 3 3 3 1 x 1 1 x 1 1 x x sin ~ ~ 2 2 2 2 4 2 2 2 2 2 x
5 1 2x lncosx 1 ~ x lncosx x ln(1 cosx 1) ~ x(cosx 1) ~ x 5 5 5 5 2 3 x 5 Vậy: 3 x cos1 5 2 I lim cos1 3 x0 x 2 5
Bài 8: Tính giới hạn sau đây: 2 x 4 2x 3 x I lim x 2 x 4 x
Giải bài 8: Vì lim
nên ta tiến hành thay VCL 2 x 4 2x 3 x lim 2 x 4 x x x tương đương được.
Khi x ta tiến hành lượt bỏ các VCL có bậc thấp hơn, chỉ chọn những VCL có bậc cao
nhất của cả tử và mẫu. 2 x 4 ~ x và 2 x 4 ~ x Như vậy, ta có:
4 | B À I T Ậ P G I Ớ I H Ạ N H À M S Ố 3x 3 I lim x 2x 2
Bài 9: Tính giới hạn sau đây: l n 1 x tan x I lim 2 3 x0 x sin x
Giải bài 9:
Vì, limln1 x tan x 0 lim 2 3
x sin x 0 nên ta thay được các VCB tương đương. x 0 x 0
Khi x 0, ta tiến hành thay các VCB tương đương: 2 ln 1 x tanx ~ x tan x ~ x 3 3 sin x ~ x Dưới mẫu được 2 3
x x , lượt bỏ VCB có bậc cao hơn, như vậy dưới mẫu ta được x2 Như vậy: 2 x I lim 1 2 x0 x
Bài 10: Tính giới hạn sau đây: l n cosx I lim 2 x0 ln(1 x )
Giải bài 10: Vì limlncosx 2
0 limln(1 x ) 0 nên thay VCB tương đương được. x 0 x 0 Khi x 0, ta được: 2 x
ln(cosx) ln(1 cosx 1) ~ cosx 1 ~ 2 2 2 ln(1 x ) ~ x Như vậy: 2 x 1 2 I lim 2 x0 x 2
Bài 11: Tính giới hạn sau đây: si x1 n e 1 I lim x 1 ln x
Giải bài 11: Vì limsin x 1 e
1 0 limln x 0 nên thay VCB tương đương được. x 1 x 1 si x1 n e 1 si x1 n e 1 I lim lim x 1 x 1 ln x ln(1 x 1) Khi x 1, ta có: x 1 x 1 sin e 1 ~ e 1~ x 1
5 | B À I T Ậ P G I Ớ I H Ạ N H À M S Ố ln(1 x 1) ~ x 1 Vậy, x 1 I lim 1 x 1 x 1
Bài 12: Tính giới hạn sau đây: xe 1cosx 1 I lim 3 4 x0 sin x 2x
Giải bài 12: Vì lim xe 1 cosx 1 0 lim 3 4
sin x 2x 0 nên ta thay VCB tương đương được. x 0 x 0 Khi x0, ta có: 2 x x e 1~ x và cos x 1~ và 3 3 sin x ~ x 2 Như vậy, 3 x 1 2 I lim 3 x0 x 2
Bài 13: Tính giới hạn sau: 2 sin 2x 2arctan3x 3x I lim ln 2 1 3x sin x x x 0 xe
Giải bài 13: Vì l 2
im sin2x 2arctan3x 3x 0 limln 2 1 3x sin x x xe 0 x 0 x 0 nên thay VCB tương đương được. Khi x0, ta có:
sin2x ~ 2x; 2arctan3x ~ 6x ; 2 2 2
ln 1 3x sin x ~ 3x sin x ~ 3x x x xe ~ x.1 x Như vậy, ta được: 8x I lim 2 x 0 4x
Bài 14: Tính giới hạn sau đây: 2 x 4 2x 3 x I lim x 2 x 4 x
Giải bài 14: Vì lim
nên thay VCL tương đương 2 x 4 2x 3 x lim 2 x 4 x x x được. Khi x , ta có: 2 x 4 ~ x ; 2 x 4 ~ x
6 | B À I T Ậ P G I Ớ I H Ạ N H À M S Ố
Nhận thấy VCL bậc cao nhất của tử và mẫu là bậc 1, nên các VCL có bậc < 1 sẽ bị giản lược
đi bớt. Như vậy, ta có: 3x 3 I lim x 2x 2
Bài 15: Tính giới hạn sau đây: 2 x 14 x I lim x 2 x 2 x
Giải bài 15: Vì lim
nên ta thay VCL tương đương được. 2 x 14 x lim 2 x 2 x x x Khi x , ta có: Ta thấy: lim và lim
. Nên ta mới tiến hành thay VCL tương 2 x 2 x x 2 x 14 x x đương được. 2 x 14 ~ x 2 x 2 ~ x Như vậy, 2x I lim 1 x 2x
Bài 16: Tính giới hạn sau đây: 2 x 14 x I lim x 2 x 2 x
Giải bài 16: Vì lim
nên ta không thể thay thế VCL tương 2 x 14 x 0 lim 2 x 2 x 0 x x
đương được mà chỉ có thể tính bằng các giới hạn cơ bản hoặc thay bằng VCB tương đương
bằng cách biến đổi biểu thức. #CÁCH 1: 14 14 2 x 1 x 1 1 2 2 x 14 x x x I lim lim lim x 2 x x x 2 x 2 2 2 x x x 1 1 2 2 x x Khi x , ta có: 14 1 14 7 2 1 2 1 1 1~ ; 1 1~ 2 2 2 x 2 x x 2 2 2 x 2 x x Như vậy,
7 | B À I T Ậ P G I Ớ I H Ạ N H À M S Ố 7 2 x I lim 7 x 1 2 x # CÁCH 2: Đặt t x
Như vậy, giới hạn đã cho trở thành: 2 2 2 2 t 14 t t 14 t t 2 t t 14 t I lim lim t 2 t 2 2 2 t 2 t t 2 t t 2 t t 14 t 2 14 t 2 t lim t 2 2 t 14 t
Khi t , ta được: 2 t 2 ~ t và 2 t 14 ~ t Như vậy, 14 2t 14 I lim 7 t 2 2t 2
Bài 17: VCL nào sau đây có bậc cao nhất khi x : 3 3x ln x , xln x, 3x, 4 x(2 sin x)
Giải bài 17:
(Phương pháp: Giống như thuật toán tìm giá trị Max, thì đầu tiên ta gán một phần tử bất kì
xem như là nó max ban đầu, sau đó so sánh tiếp với các phần tử khác. Nếu có phần tử nào mà
lớn hơn phần tử đã gán ban đầu thì giá trị Max sẽ gán cho phần tử mới đó. Tương tự, so sánh
dần dần và ta được giá trị Max nhất trong dãy) Chọn 3 3x ln x Khi x thì 3 3x ln x ~ 3x xln x ln x
So sánh với hàm kế tiếp là xlnx: lim lim x x 3x 3
Như vậy: xlnx có bậc cao hơn 3x + ln3x 1 Có 2
3x 3x . Như vậy 3x + ln3x có bậc cao nhất là 1 bé hơn bậc của xlnx đã bị loại. Trong
khi 3x có bậc là 1/2 < 1 nên cũng bị loại.
Ta đem hàm xlnx so sánh với x(2 + sin4x): 4
x(2 sin x) ~ 2x (do hàm sinx là hàm bị chặn) 2x 2 lim lim
0 xlnx có bậc cao hơn x(2 + sin4x) x x xln x ln x
Vậy: VCL có bậc cao nhất là xlnx
Bài 18: VCL nào sau đây có bậc cao nhất khi x : 2x, x2, x2 + sin4x, xlnx
Giải bài 18: Tương tự bài 17.
8 | B À I T Ậ P G I Ớ I H Ạ N H À M S Ố
Nhận định đầu tiên là giữa 2x và x2 thì ta thấy 2x là VCL có bậc cao hơn vì 2x tiến ra vô cùng nhanh hơn x2. Xét 2 4 2
x sin x ~ x (do hàm sinx là hàm bị chặn)
Nên 2x là VCL có bậc cao hơn x2 + sin4x
Tương tự, ta thấy xlnx tiến ra vô cùng chậm hơn 2x, như vậy:
2x là VCL có bậc cao nhất khi x
Bài 19: Tính giới hạn sau đây: 1 x x I lim xe x
Giải bài 19:
Đặt t = -x, ta được giới hạn s au: 1 t #CÁCH 1: t t I lim te lim 1 t t t t e Dạng
. Tiến hành dùng L’Hospital 1 1 t 1 I lim 0 . Do t lim 1 e 1 t t 1 2 t t t 1 e 2 t #CÁCH 2: 1 1 t t t t I lim te lim
e 0 (Do 0.1 = 0 vì hàm t chạy ra vô cùng chậm hơn so với hàm et t t t e nên –t/et = 0) 1 x Vậy x I lim xe 0 x
Bài 20: Tính giới hạn sau đây: 2 x 2 x 4 I lim 2 x x 4
Giải bài 20: Dạng bất định 1 2 8x 2 2 2 x 4 x 4 x 2 2 8x 8 lim x 4 8 2 x x 4 8 I lim lim 1 e e 2 2 x x x 4 x 4 2 8x Vì lim 8 2 x x 4
Bài 21: Tính giới hạn sau đây: I lim1 2x 1 4 2 sin x x0
9 | B À I T Ậ P G I Ớ I H Ạ N H À M S Ố
Giải bài 21: Dạng bất định 1 4 2x 4 1 1 2x I lim1 2x sin x lim 4 2 sin x lim 4 1 2x 2 4 2 x 0 2x sin x e 1 x0 x0 4 4 2x 2x Vì lim lim 0 2 2 x 0 x 0 sin x x
Bài 22: Tính giới hạn sau đây:
I limln e xcotx x0
Giải bài 22: Dạng bất định 1 cot x cot x cotx x x I lim ln e x limln e 1 lim 1 ln 1 x0 x0 x0 e e x ln 1 cot x 1 e x x lim ln 1 cot x x ln 1 x 0 e 2 I e lim 1 ln 1 e e x 0 e x cos x 1 Tính I limln 1 2 x 0 e sin x e x x Vì khi x 0 thì ln 1 ~ ; cosx ~ 1; sinx ~ x e e Như vậy: 1
I limlne xcotx e e x 0
Bài 23: Tính giới hạn sau; I lim1 tan x 1 2 2 sin 2x x0
Giải bài 23: Dạng bất định 1 2 tan x I lim 2 1 tan x 1 1 sin 2x 2
sin 2x lim 1 tan x e x0 x0 2 2 2 tan x 2 I 2 sin x 2 2 2 tan x sin x 1 Tính cos x I lim lim lim 2 2 2 2 2 4 x 0 x 0 x 0 sin 2x 4sin x cos x 4sin x cos x 4 Như vậy, I lim 2 1 tan x 1 1 2 sin 2x 4 e x 0
Bài 24: Tính giới hạn sau đây:
10 | B À I T Ậ P G I Ớ I H Ạ N H À M S Ố I limcosx 12x x0
Giải bài 24: Dạng bất định 1 cos x 1 cos x1 I limcosx 1 1 x lim 2 x
I lim 1 cosx 2 2 x 0 I x 2 cos x 1 1 e e x0 x0 Tính: cos x 1 I lim 2 2 x 0 x
Khi x 0, cosx – 1 ~ -x2/ 2 2 x cos x 1 1 2 I lim lim 2 2 2 x 0 x 0 x x 2 1 I limcosx 12 2 x e x 0
Bài 25: Tính giới hạn sau đây: 2 x 2 2x 3 I lim 2 x 2x 1
Giải bài 25: Dạng bất định 1 2 4x 2 2 2 2x 1 2x 1 x 2 2x 3 4 4 2 I lim lim 1 e 2 2 x x 2x 1 2x 1 2 4x Vì lim 2 2 x 2x 1
Bài 26: Tính giới hạn sau đây: x 1 1 x I lim e x x
Giải bài 26: Dạng bất định 1
Đặt t = 1/x, ta được giới hạn sau I lim te t1 1 t lim ln(e t) t t 0t I2 e e t 0 Tính I2
11 | B À I T Ậ P G I Ớ I H Ạ N H À M S Ố 1 I lim ln 1 1 t t e t lim ln t e t t lim lne 1 2 t t 0 t 0 t 0 t t t e 1 t t 1 t 1 lim ln e ln 1 lim t lim 1 2 t t t t 0 t 0 t 0 t e t e e Như vậy, x 1 1 2 x
I lim e e x x




