Bài Tập Hình 8 Bài Đa Giác-Đa Giác Đều Có Lời Giải

1. ĐA GIÁC – ĐA GIÁC ĐỀU
I. KIẾN THỨC CƠ BẢN
1. Đa giác: A A ...A
A A ; A A ; ...; A A 1 2
n là hình gồm n đoạn thẳng 1 2 2 3
n 1 trong đó bất kì hai đoạn
thẳng nào đó có một điểm chung cũng không cùng nằm trên một đường thẳng
2. Đa giác lồi: là đa giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa
bất kì cạnh nào của đa giác.
Lưu ý: Trong chương trình THCS, chúng ta sẽ chỉ xét các đa giác lồi. Vì vậy, nếu không giải
thích gì thêm, chúng ta viết “đa giác” để thay cho “đa giác lồi”.
3. Các khái niệm khác
 Một đa giác có n đỉnh được gọi là n – giác.
Ví dụ: tam giác, tứ giác, ngũ giác, thập giác,…, 100 – giác.
 Đường chéo của đa giác là các đoạn thẳng nối hai đỉnh không kề nhau của đa giác đó.
 Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau III. BÀI TẬP
Bài 1: Tính số đo của mỗi góc của ngũ giác đều, lục giác đều, bát giác đều ( đa giác đều 8 cạnh).
Bài 2: a) Tính tổng các góc của đa giác 15 cạnh.
b) Đa giác nào có tổng các góc bằng 1620 ?
Bài 3: Tìm số cạnh của một đa giác biết số đường chéo hơn số cạnh là 7.
Bài 4: Tính số cạnh cảu một đa giác đều, biết mỗi góc của nó bằng 135 .
Bài 5: Góc ngoài của đa giác là góc kề bù với một góc của đa giác. Ta coi ở mỗi đỉnh của đa
giác có một góc ngoài. Chứng minh rằng tổng các góc ngoài của đa giác bằng 3600.
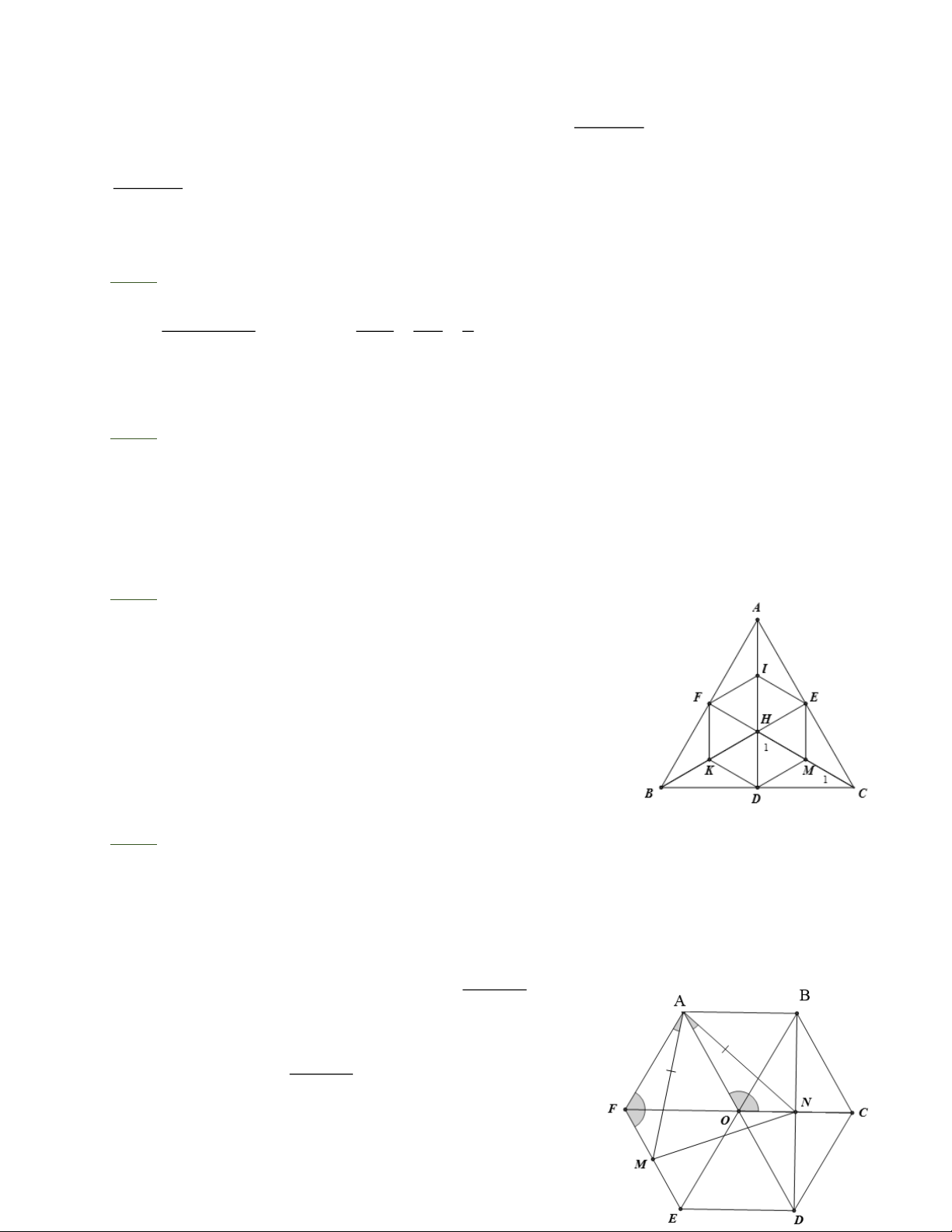
Bài 6: Cho tam giác đều ABC , các đường cao AD , BE , CF cắt nhau tại H . Gọi I , K , M
theo thứ tự là trung điểm của HA , HB , HC . Chứng minh rằng DKFIEM là lục giác đều.
Bài 7: a) Tính số đường chéo của đa giác n cạnh.
b) Đa giác nào có số đường chéo bằng số cạnh?
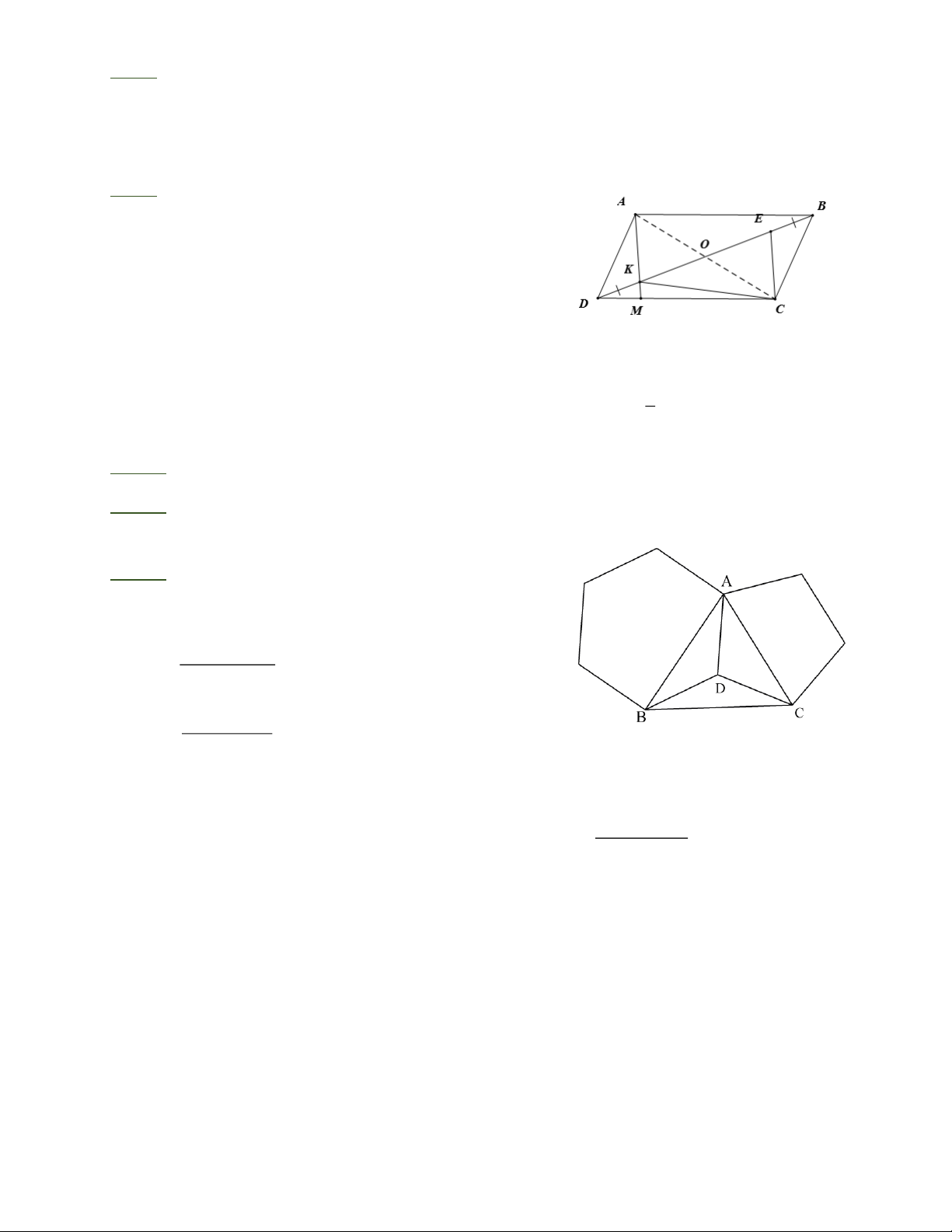
Bài 8: Cho lục giác đều ABCDEF . Gọi M là trung điểm của EF , N là trung điểm của
BD . Chứng minh rằng AMN là tam giác đều. Trang 1
Bài 9: Cho hình bình hành A B CD . Trên đường chéo BD, lấy các điểm E và K sao cho BE = DK .
a) Chứng minh rằng A K CE là hình bình hành.
b) Hình bình hành A B CD có điều kiện gì thì A K CE là hình thoi.
c) Gọi M là giao điểm của AK và CD. Xác định vị trí của điểm K để M là trung điểm của CD. Tự luyện
Bài 10: Lục giác ABCDEF có các cạnh đối song song và bằng nhau. Chứng minh rằng
đường chéo AD , BE , CF đồng quy.
Bài 11: Cho lục giác đều ABCDEF . Trên cạnh AB , BC , CD , DE , EF , FA lấy các điểm
A , B , C , D , E , F sao cho AA = BB = CC = DD = EE = FF . Chứng minh rằng A B  C  D  E  F
  là một lục giác đều.
Bài 12: Một lục giác đều và một ngũ giác đều chung cạnh AD (như hình vẽ). Tính các góc của tam giác ABC.
KẾT QUẢ - ĐÁP SỐ
III. BÀI TẬP TỰ LUẬN 0 (5 - 2).180
Bài 1: Mỗi góc của ngũ giác đều bằng: 0 = 108 5 0 (6 - 2).180
Mỗi góc của ngũ lục đều bằng: 0 = 120 6 0 (8 - 2).180
Mỗi góc của bát giác đều bằng: 0 = 135 8
Bài 2: a) 26 v. (Tạo được 13 tam giác)
b) Đa giác có 11 cạnh (Số cạnh: 1620 : 180 + 2 = 11 )
Bài 3: Tìm cách giải. Bài này biết mối liên hệ giữa số đường chéo và số cạnh nên hiển n (n - ) 3
nhiên chúng ta đặt số cạnh của đa giác là n biểu thị số đường chéo là từ đó ta tìm 2 được số cạnh. Trang 2
Trình bày lời giải n (n - ) 3
Đặt số cạnh của đa giác là n (n ≥ 3) thì số đường chéo là theo đề bài ta có: 2 n (n - ) 3 2
- n = 7 Û n - 5n - 14 = 0 Û (n + ) 2 (n - 7)= 0 2
Vì n ³ 3 nên n - 7 = 0 Û n = 7 Vậy số cạnh của đa giác là 7.
Bài 4: Gọi n là số cạnh của đa giác đều. (n−2).180 n − 2 135 3 Ta có = 135 nên = = . n n 180 4
Do đó 4 (n − 2) = 3n . Vậy n = 8 .
Bài 5: Tổng các góc trong và ngoài của đa giác tại một đỉnh bằng 2v , tại n đỉnh bằng 2nv
Ta đã biết tổng các góc trong của đa giác bằng (n − 2).2 . v
Vậy tổng các góc ngoài của đa giác bằng: 2nv − (n − 2).2v = 4 . v
Bài 6: Xét HDC vuông tại D , DM là đường trung tuyến
ứng với cạnh huyền nên DM = HM . Ta lại có C = 30 nên 1
H = 60. Do đó HDM là tam giác đều. 1
Tương tự các tam giác HME , HEI , HIF , HFK , HKD là các tam giác đều.
Lục giác DKFIEM có các cạnh bằng nhau và các góc bằng
nhau (bằng 120 ) nên là lục giác đều.
Bài 7: a) Từ mỗi đỉnh của hình n – giác lồi. kẻ được n −1 đoạn thẳng đến các đỉnh còn lại,
trong đó có hai đoạn thẳng là cạnh của đa giác, n − 3 đoạn thẳng là đường chéo.
Đa giác có n đỉnh nên kẻ được n (n − 3) đường chéo, trong đó mỗi đường chéo tính 2 lần. n (n − 3)
Vậy số đường chéo của hình n - giác lồi là . 2 n(n − 3) b) Giải phường trình
= n . Ta được n = 5 2 Trang 3
Bài 8: Gọi O là giao điểm của AD , BE , CF . Dễ dàng chứng minh N là trung điểm của OC , AF  M = AO  N (c.g.c).
Từ đó AM = AN và MAN = 60 nên AMN là tam giác đều.
Bài 9: a) Tứ giác A K CE có các đường chéo cắt nhau
tại trung điểm của mỗi đường nên là hình bình hành.
b) Hình bình hành K A CE là hình thoi.  AC ⊥ KE
 hình bình hành A BCD là hình thoi
c) M là trung điểm của CD  K là trọng tâm của  1
ADC  DK = D . B 3
Bài 10: HD: Chứng minh rằng FBCE và ACDF là hình bình hành.
Bài 11: HD: Chứng minh rằng các tam giác AA F  , BB A   , CC B   , DD C   , EE D   , FF E  bằng nhau. Bài 12:
Theo công thức tính góc của đa giác đều, ta có: 0 · (6 - ) 2 .180 0 · · 0 A DB =
= 120 Þ DA B = DBA = 30 ; 6 0 · (5 - ) 2 180 0 · · 0 A DC =
= 108 Þ DA C = DCA = 36 ; 5 Suy ra 0 0 0 0
BDC = 360 −120 −108 = 132 . · · 0 0 180 - 132
Ta có ∆BDC (DB = DC ) cân tại D. Do đó 0 DBC = DCB = = 24 . 2 · 0 0 0 · 0 0 0 · Suy ra 0 0 0
BA C = 30 + 36 = 66 ; A BC = 30 + 24 = 54 ; BCA = 24 + 36 = 60 Trang 4