Bài Tập Hình 8 Bài Diện Tích Hình Thang Có Lời Giải

4. DIỆN TÍCH HÌNH THANG
I. KIẾN THỨC CƠ BẢN
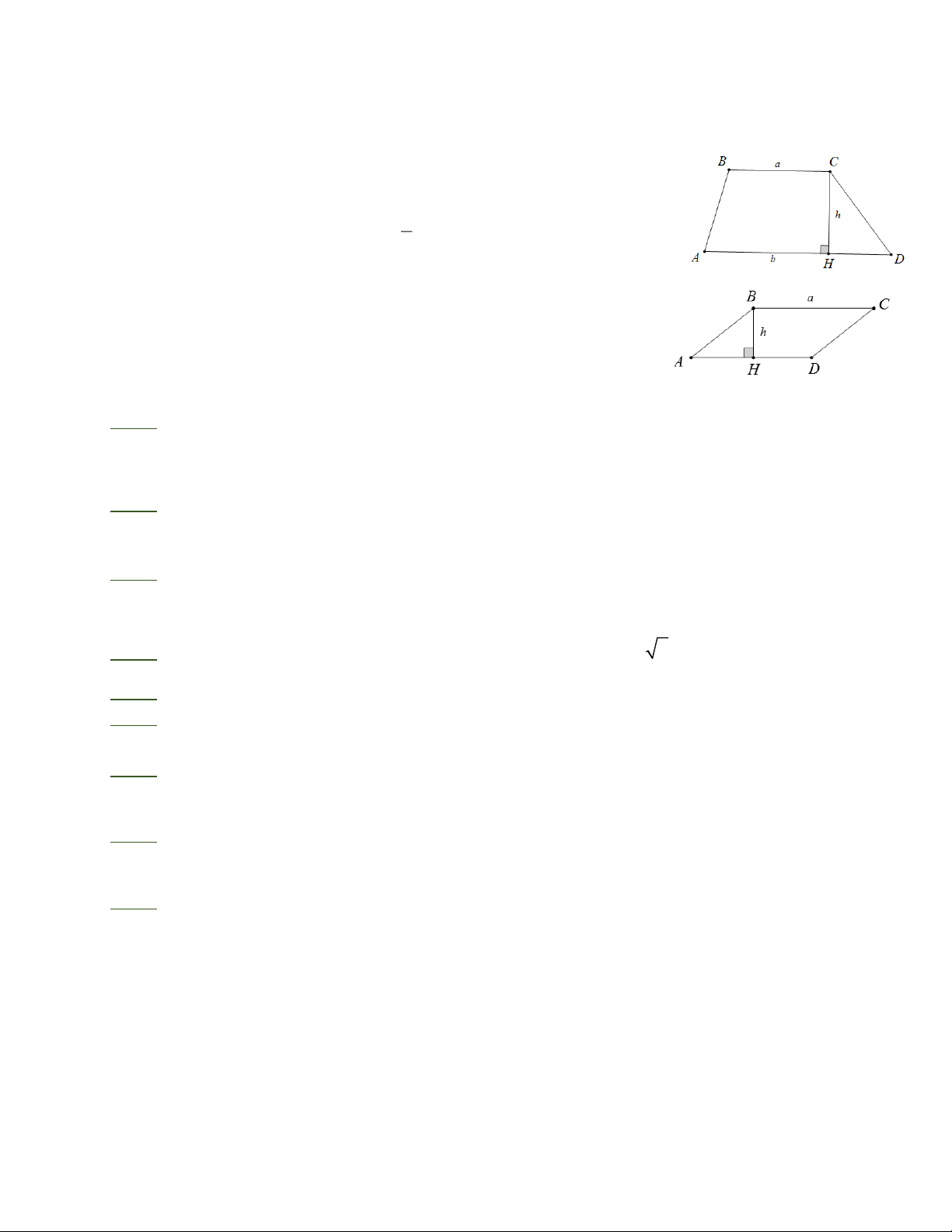
 Diện tích hình thang bằng nửa tích của tổng hai đáy với chiều cao: 1
S = (a + b). . h 2
 Diện tích hình bình hành bằng tích của một cạnh với chiều cao ứng với cạnh đó: S = . a . h II. BÀI TẬP Bài 1:
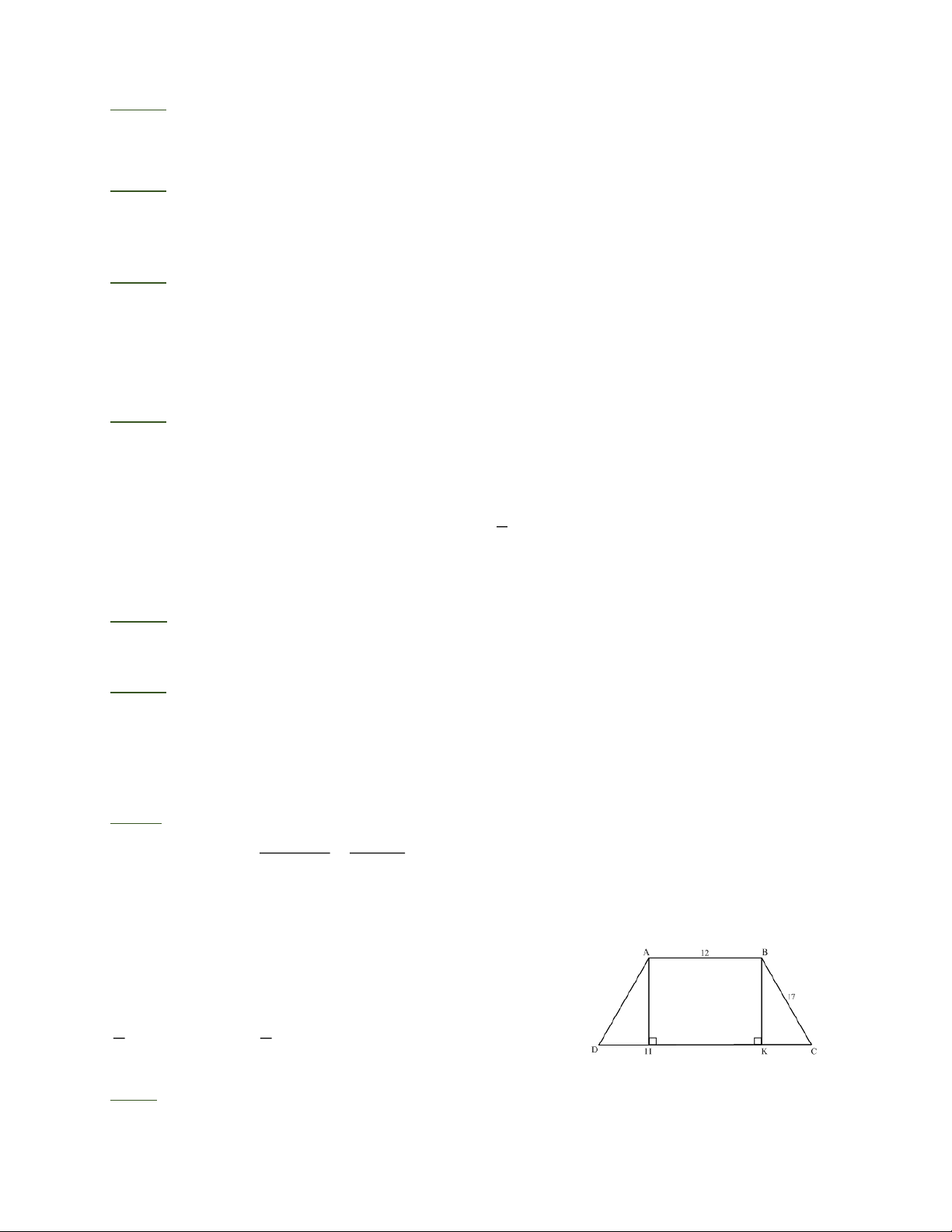
Hình thang cân ABCD (AB / / CD) có AB = 12cm, CD = 28cm, AD = BC = 17cm . Tính diện tích hình thang.
Bài 2: Tính diện tích hình thang vuông ABCD ( = = 90o A B
) , biết AB = 5cm, CD = 12cm, BC = 25 . cm
Bài 3: Tính diện tích hình thang ABCD (AB / / CD) , biết AB = 5cm, CD = 13cm, BC = 8cm, C = 30 . 
Bài 4: Tính diện tích hình bình hành ABCD, biết = 135o A
, AD = 2dm, CD = 3dm .
Bài 5: Tính diện tích hình bình hành ABCD, biết AD = 6cm, AC = 8cm, CD = 10 . cm
Bài 6: Hình bình hành ABCD có AB = 54cm, AD = 36cm, một chiều cao bằng 30cm. Tính chiều cao còn lại.
Bài 7: Tính diện tích hình thang ABCD (AB / / CD) , biết AB = 4cm, CD = 14cm,
AD = 6cm, BC = 8cm
Bài 8: Tính các góc của một hình bình hành có diện tích bằng 2
27cm . Hai cạnh kề bằng 6 cm và 9 cm.
Bài 9: Cho hình thang ABCD (AB // CD), E là trung điểm của AD. Gọi H là hình chiếu của
E trên đường thẳng BC. Qua E vẽ đường thẳng song song với BC, cắt các đường thẳng AB
và CD theo thứ tự ở I và K.
a) Chứng minh rằng D A EI = D DEK
b) Cho biết BC = 8cm, EH = 5cm. Tính diện tích tứ giác IB CK ; A B CD Trang 1
Bài 10: Cho hình thang ABCD có hai đáy AB = 5 c ,
m CD = 15 cm và hai đường chéo là AC = 16 c , m BD = 12 .
cm Tính diện tích hình thang ABC . D
Bài 11: Hình thang cân ABCD (AB //CD) có hai đường chéo vuông góc, AB = 40 cm,
CD = 60cm. Tính diện tích hình thang.
Bài 12: Cho tứ giác ABCD có diện tích 40 cm2. Gọi E , F , G , H thứ tự là trung điểm của
các cạnh AB , BC , CD , DA .
a) Tứ giác EFGH là hình gì?
b) Tính diện tích tứ giác EFGH .
Bài 13: Cho hình bình hành ABCD . Gọi E , F , G , H thứ tự là trung điểm của AB , BC ,
CD , DA . Các đoạn thẳng AG , CE , BH , DF cắt nhau tạo thành một tứ giác.
a) Tứ giác đó là hình gì? 1
b) Chứng minh rằng diện tích tứ giác đó bằng diện tích hình bình hành ABCD . 5 Tự luyện
Bài 14: Cho hình thang ABCD ( AB//CD), E là trung điểm của .
AD Đường thẳng qua E
và song song với BC cắt AB và CD ở I và K. Chứng minh S = S . ABCD BIKC
Bài 15: Cho hình bình hành ABCD, M là trung điểm của AD, qua M kẻ đường thẳng d
cắt AB, CD lần lượt tại E và F. Kẻ MH ⊥ BC tại H. Chứng minh S = MH.BC. EBCF
KẾT QUẢ - ĐÁP SỐ
Bài 1: Kẻ AH, BK vuông góc với CD. CD − AB 28 − 12
Ta có: DH = CK = = = 8(c ) m 2 2
Áp dụng định lý Py – ta – go vào tam giác vuông BKC có: 2 2 2 2 2 2
BK = BC − CK = 17 − 8 = 15 nên BK = 15cm
Diện tích hình thang ABCD bằng: 1 1 2
(AB + CD). BK = (12 + 28).15 = 300(cm ) 2 2
Bài 2: Chiều cao hình thang bằng 24cm. Đáp số: 2 204cm . Trang 2
Bài 3: Chiều cao hình thang bằng 4cm. Đáp số: 2 36cm .
Bài 4: Chiều cao AH = 1dm . Đáp số: 2 3dm .
Bài 5: Chứng minh rằng 90o CAD = . Đáp số: 2 48cm .
Bài 6: Nếu chiều cao 30cm ứng với cạnh 54cm thì diện tích hình bình hành bằng 2
30.54 = 1620(cm ) , chiều cao còn lại bằng 1620 : 36 = 45( ) cm .
Nếu chiều cao 30cm ứng với cạnh 36cm thì chiều cao còn lại bằng 30.36 : 54 = 20(cm)
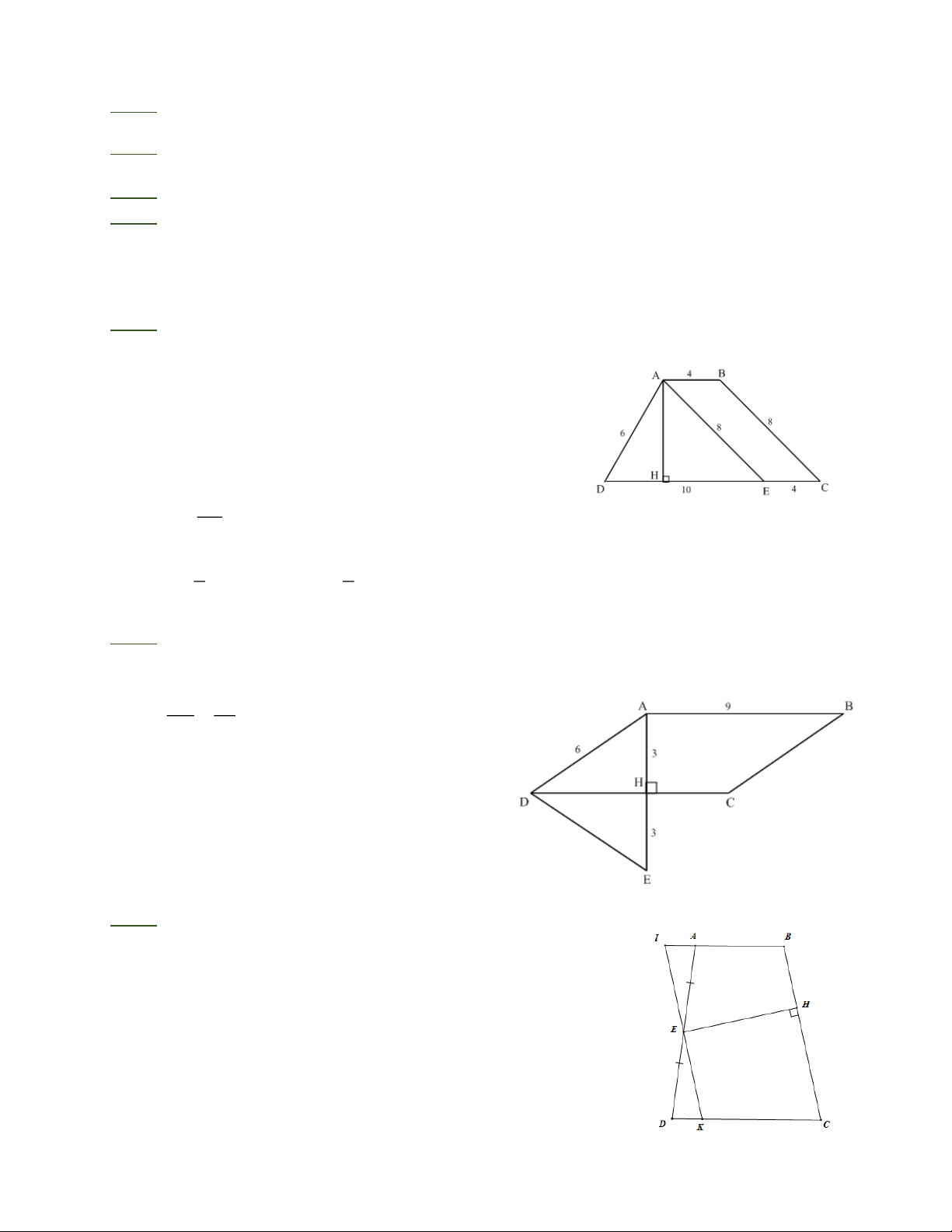
Bài 7: Kẻ AE / /BC . Tứ giác ABCE là hình bình hành nên AE = BC = 8cm, EC = AB = 4cm,
DE = DC − EC = 14 − 4 = 10(cm) Tam giác ADE có 2 2 2
AD + AE = DE (vì 2 2 2 6 + 8 = 10 ) nên 90o DAE = .
Kẻ AH ⊥ CD , ta có AH.DE = AD = AE (bằng 2.S ) ADE 6.8 nên AH = = 4,8(c ) m . 10 1 1 2
SABCD = (AB + CD).AH = (4 + 14).4,8 = 43, 2(cm ) 2 2
Bài 8: Giả sử hình bình hàng ABCD có AD = 6cm, AB = 9cm diện tích 2
27cm ( A là góc tù). Kẻ AH ⊥ C . D S 27 AH = = = 3(c ) m . AB 9
Tam giác vuông AHD có AD = 2AH nên 30o ADH =
(Chứng minh: Lấy E đối xứng
với A qua H, để chứng minh ADE đều). Do đó = = 30o , = = 150o ADH B DAB C .
Bài 9: a) AEI = DEK (c.g.c)
b) IBCK là hình bình hành, 2 S = BC.EH = 8.5 = 40(cm ) IBCK Ta có AEI = DEK  S = S  S = S . AEI DEK ABCD IBCK Vậy 2 S = 40cm ABCD Trang 3
Bài 10: Qua A kẻ AE // BD (ECD).
 AE = BD = 12cm,DE = AB = 5 . cm
 ΔAEC vuông tại A (Định lý Pytago đảo). A . E AC 12.16  AH = = = 9,6c . m EC 20 2  S = 96cm . ABCD
Bài 11: Kẻ BE / / AC(E  DC)
Ta có: CE= AB= 40 cm  DE = 100 cm
Ta lại có: BE = AC = BD Þ D BDE cân ở B .
Kẻ BH ⊥ DE thì BH cũng là trung tuyến. 1
Do AC ⊥ BD, AC//BE nên BD ⊥ BE △ BDE vuông ở E  BH = DE = 50cm 2 S = ( + ) = ( 2 40 60 .50 : 2 2500 cm ABCD ) . Bài 12:
a) EFGH là hình bình hành.
b) Gọi I , K là các giao điểm của EF ,GH và BD .
Kẻ EE ' , A A' vuông góc với BD 1 1
Xét hình bình hành EHKI , ta có EH =
BD, E E ' = A A' 2 2 1 1  S
= EH.EE ' = B . D AA' = S EHKI 4 2 ABD Trang 4 1
Xét hình bình hành FGKI và chứng minh tương tự: S = S FGKI (2) 2 BCD 1 Từ (1) và (2) suy ra 2 S = S = 20cm . EFGH 2 ABCD
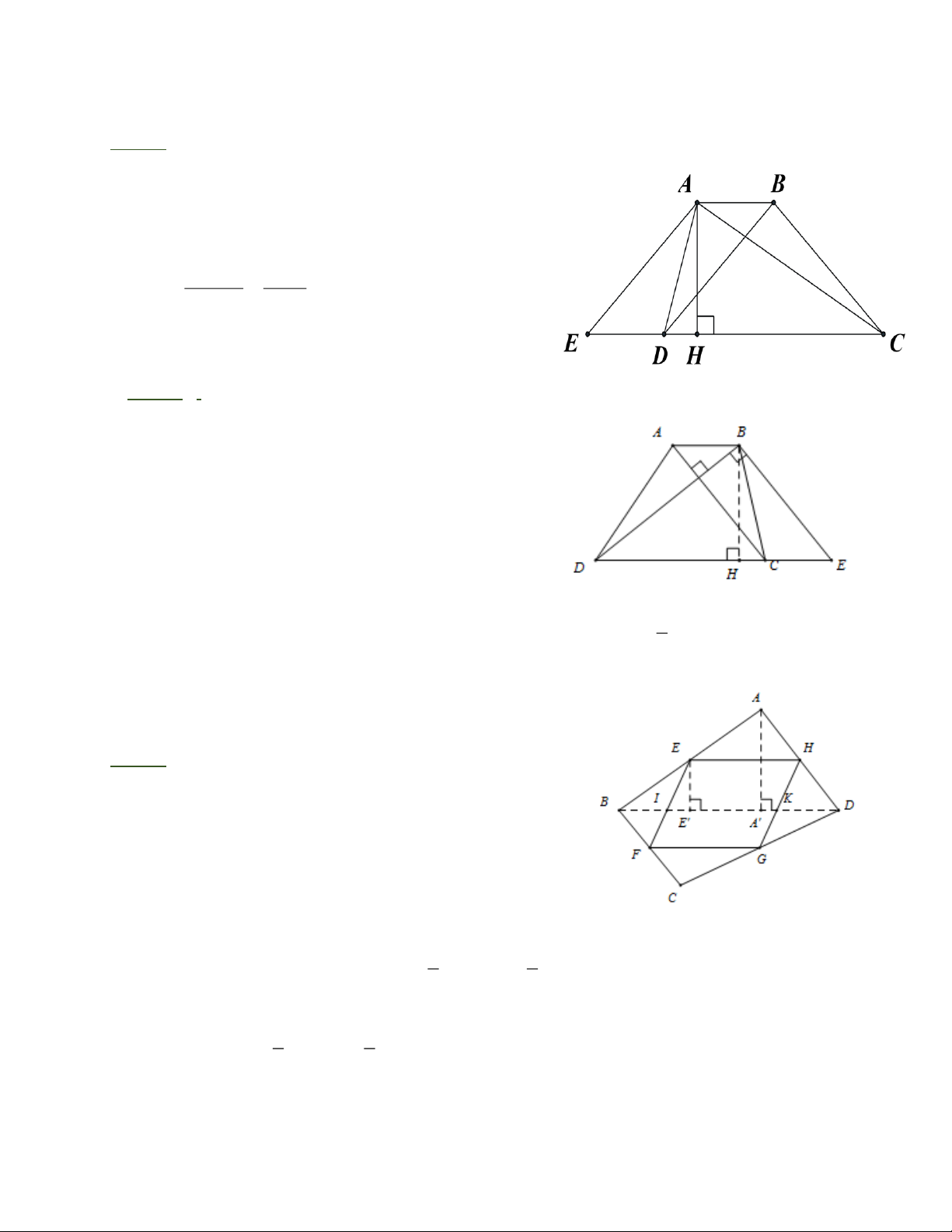
Bài 13: a) Gọi tứ giác tạo thành là MNPQ như trên hình 207.
Dễ dàng chứng minh A G / / CE ,
BH// DF nên MNPQ là hình bình hành.
b) ADQ có AH = HD ,
HM / /DQ  AM = M .
Q Tương tự: NP = PC, mà
MQ = NP nên AM = MQ = PC. 1 1 2 Ta lại có QG =
PC nên QG = M .
Q Vậy MQ = A . G 2 2 5 2 1 1 Suy ra S = S S = S . S = S . MNPQ , mà Do đó 5 AECG AECG 2 ABCD MNPQ 2 ABCD Trang 5