Bài tập kinh tế vi mô

lOMoARc PSD|17327243 BT KTVM1
Bài 1: Viết phương trình đường cầu
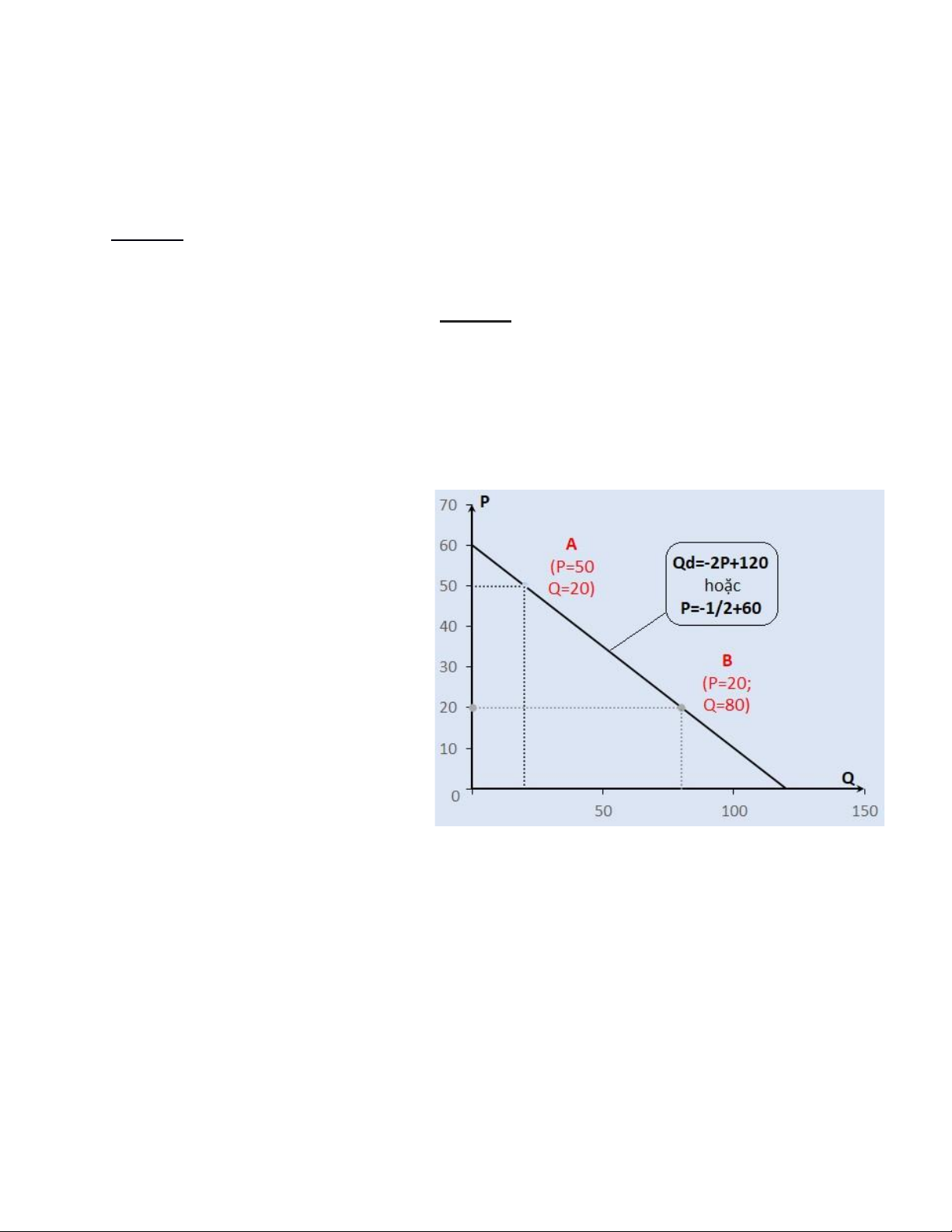
Yêu cầu: Một đường cầu đi qua tọa độ 2 điểm như sau: A (P=50 và Q=20); B
(P=20 và Q=80). Xác định phương trình của đường cầu theo 2 dạng: Q=f(P) và P=f(Q) Lời giải
Đường cầu đi qua 2 điểm thể hiện dạng đường thẳng hay tuyến tính. Phương trình
đường cầu có dạng tuyến tính Qd=aP+b. Mục tiêu cần xác định là tìm hệ số gốc a
và hoành độ gốc b. Có 2 cách để tìm phương trình của đường cầu
Cách 1: Giải hệ phương trình
Đường cầu đi qua 2 điểm (P=50, Q=20) và (P=20, Q=80) nên ta có hệ phương trình sau: 20 = a*50+b (1) 80 = a*20+b (2) Lấy (1) – (2) <=> 30*a = -60
<=> a = -2, thế vào (1) <=> b = 120
Vậy phương trình đường cầu là Qd = -2*P+120 hay P =-1/2*Q + 60
Cách 2: Xác định dựa vào công thức hệ số a
Ta có công thức hệ số gốc a = ∆Q/∆P
Dựa vào dữ liệu, lấy hai giá trị
lượng và hai giá trị giá trừ nhau ta có: ∆Q=-60 và ∆P=30
<=> a = -60/30 = -2; thế giá trị a, và P, Q của bất kỳ điểm nào vào phương trình QD= aP+b => b = 120
Vậy phương trình đường cầu là Qd = -2*P+120 hay P =-1/2*Q + 60
Bài 2: Tính hệ số co giãn của cầu theo giá (co giãn điểm) lOMoARc PSD|17327243
Có hàm số cầu một hàng hóa A như sau: Q=-2*P+120 (có thế viết thành P=- 1/2Q+60) Yêu cầu:
1. Hãy xác định hệ số co giãn của cầu tại 3 mức giá: P= 40, P=30 và P=20, và
cho biết xu hướng thay đổi của mức độ co giãn khi giá càng thấp?
2. Tại ba mức giá này, muốn tăng doanh thu, người bán nên tăng hay giảm giá? Lời giải Câu 1:
a) Tại mức giá P=40, ta xác định được mức sản lượng Q=40 (thế vào phương trình
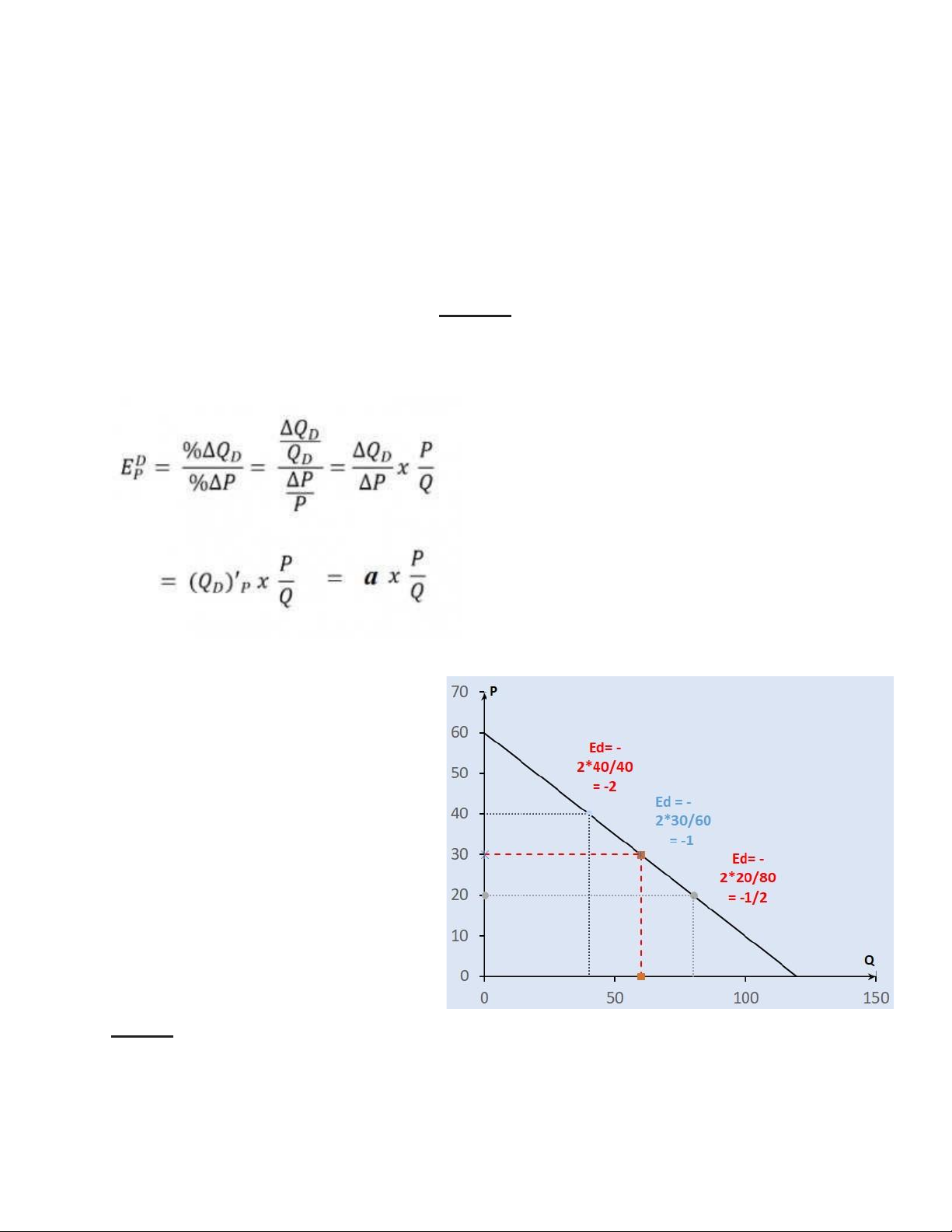
đường cầu). Dựa vào công thức dưới đây
Hệ số co giãn tại mức giá P=40: ED=a*P/Q = -2*40/40 = -2
b) Tại mức giá P=30, ta xác định
được mức sản lượng Q=60 (thế vào
phương trình đường cầu)
Hệ số co giãn ED=a*P/Q = -2*30/60 = -1
c) Tại mức giá P=20, ta xác định
được mức sản lượng Q=80 (thế vào
phương trình đường cầu)
Hệ số co giãn ED=a*P/Q = -2*20/80 = -1/2
Vậy khi mức giá càng cao thì mức
độ co giãn càng cao (trị tuyệt đối của hệ số co giãn) Câu 2: a)
Tại mức giá P=40, ta xác định được ED=a*P/Q = -2*40/40 = -2 như kết quả
câu trên. Vì │ED│>1 nên cầu co giãn nhiều tại mức giá này. Trong trường hợp này,
người bán cần giảm giá để tăng doanh thu (theo lý thuyết). lOMoARc PSD|17327243
Kiểm chứng: Khi P=40, Q=40 => TR = 1600. Nếu giảm giá P từ 40 xuống còn 30,
khi đó lượng tăng lên đến 60 (Q=60) => TR = 1800 (30*60) b)
Tại mức giá P=30, ta xác định được ED=a*P/Q = -2*30/60 = -1 như kết quả
câu trên. Vì │ED│=1 nên cầu co giãn đơn vị tại mức giá này. Trong trường hợp
này, người bán cần giữ giá để giữ doanh thu ở mức cao nhất (theo lý thuyết). c)
Tại mức giá P=20, ta xác định được ED=a*P/Q = -2*20/80 = -1/2 như kết
quả câu trên. Vì │ED│<1 nên cầu co giãn ít tại mức giá này. Trong trường hợp này,
người bán cần tăng giá để tăng doanh thu (theo lý thuyết).
Kiểm chứng: Khi P=20, Q=80 => TR = 1600. Nếu tăng giá P từ 20 lên 25, khi đó
lượng cầu giảm còn 70 (Q=70) => TR = 1750 (25*70)
Như vậy để tăng doanh thu, người bán cần biết hàng hóa mình đang bán co giãn
nhiều hay ít trước khi quyết định. Nếu co giãn nhiều thì nên giảm giá, ngược lại
nếu cầu co giãn ít thì nên tăng giá.
Bài 3: Tính hệ số co giãn cầu theo giá (co giãn khoảng)
Người ta khảo sát và ước lượng được rằng: Khi giá mặt hàng A là 20.000 đồng/kg,
lượng cầu là 300 tấn. Nếu giá A tăng lên 25.000 đồng/kg, lượng cầu hàng A sẽ
giảm xuống còn 280 tấn. Yêu cầu:
1. Hãy tính hệ số co giãn cầu theo giá của mặt hàng A trong khoảng giá dao động trên.
2. Nhận định mặt hàng này thuộc nhóm hàng thiết yếu hay xa xỉ với giả định hàng
xa xỉ là hàng mức độ co giãn lEdl >1.
3. Với kết quả này, người bán có nên tăng giá để tăng doanh thu? Lời giải
Câu 1: Dựa vào công thức tính hệ số co giãn khoảng như được thể hiện trong hình,
thế các số liệu vào, kết quả hệ số co giãn được xác định sau: lOMoARc PSD|17327243
Câu 2: Kết quả trên cho thấy mặt hàng A có trị
số tuyệt đối hệ số co giãn cầu theo giá nhỏ hơn 1, thể hiện cầu co giãn ít theo giá.
Nói khác đi là lượng cầu ít nhạy cảm với sự biến đổi của giá. Từ kết quả này, có
thể kết luận đây là mặt hàng thuộc nhóm hàng thiết yếu.
Câu 3: Với những mặt hàng thiết yếu có mức độ co giãn thấp, theo lý thuyết,
người bán nên tăng giá nếu muốn tăng doanh thu.
Thực tế số liệu trên cũng cho thấy điều đó. Cụ thế,
Khi P=20.000 và Q=300 tấn => Tổng doanh thu TR = 6 tỷ (20.000đ/kg*300.000kg).
Khi P=25.000 và Q=280 tấn =? Tổng doanh thu TR = 7 tỷ (25.000 đ/kg*280.000kg).
Bài 4: Xác định mức giá tại điểm cầu co giãn đơn vị
Có hàm số cầu một hàng hóa X như sau: Q=-0,2*P+80 (có thế viết thành P=- 5Q+400) Yêu cầu:
Xác định mức giá tại điểm cầu co giãn đơn vị?
Khuyến cáo người bán nên tăng hay giảm giá để tăng doanh thu trong trường hợp này. Lời giải
Câu 1: Dựa vào 2 dạng phương trình đường cầu, thế lần lượt Q=0 và P=0 và
phương trình đường cầu, có thể xác định được đường cầu cắt trục tung (trục giá) tại
mức giá 400 và cắt trục hoành (trục lượng) tại mức sản lượng 80. Do vậy, theo lý lOMoARc PSD|17327243
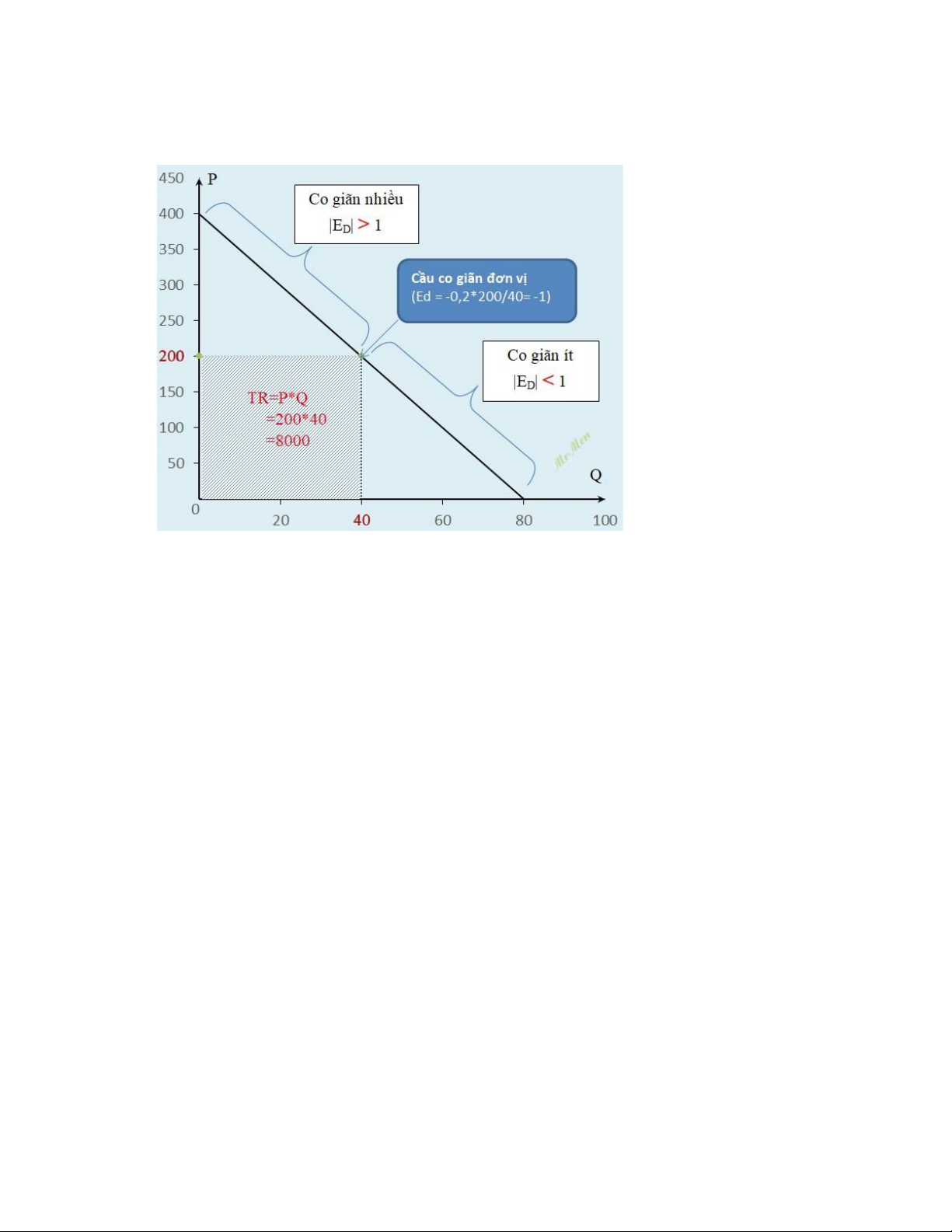
thuyết, cầu co giãn đơn vị tại điểm giữa với mức giá P=200 và lượng Q= 40. Ngoài
cách trên, có thể giải bằng cách khác như sau:
Cầu co giãn đơn vị nên ta có a*P/Q = -1, mà a = -0,2 => P=5Q
Thế vào phương trình đường cầu ta có Q = -0,2*(5Q)+80 <=> 2Q = 80 <=> Q = 40, thế vào => P=200
Vậy tại mức giá P=200 và mức sản lượng Q=40 cầu co giãn đơn vị
Câu 2: Khi cầu co giãn đơn vị, doanh thu đạt cực đại. Điều này có thể thấy trong
hình vẽ với hình chữ nhật gạch chéo là lớn nhất, so với bất kỳ diện tích hình chữ
nhật nào khi có sự thay đổi đến một điểm khác nào trên đường cầu.
Nếu thử nghiệm bằng cách thế số, cũng không có giá trị doanh thu nào lớn hơn con số 8000 được tính.
Do vậy, một khi doanh thu đã đạt tối đa thì không nên có bất kỳ sự điều chỉnh giá
tăng/giảm nếu không muốn doanh thu bị giảm. lOMoARc PSD|17327243
Bài 5: Hệ số co giãn của cầu theo thu nhập
Giả sử có số liệu về mối tương quan giữa thu nhập bình quân và cầu một hàng hóa
như sau: Tại mức thu nhập I=5 triệu đồng/tháng, lượng tiêu dùng hàng hóa A là
800 (đvsp). Khi thu nhập giảm xuống còn 4 triệu đồng/tháng, lượng tiêu dùng hàng hóa A là 900 (đvsp). Yêu cầu:
1. Tính hệ số co giãn của cầu theo thu nhập.
2. Cho biết hàng hóa A thuộc nhóm hàng hóa nào? Xa xỉ, thông thường hay cấp thấp?
3. Bài học ứng dụng gì có thể được rút ra từ bài tập này?Lời giải
Câu 1: Ta có công thức tính hệ số co giãn của cầu theo thu nhập
Thay số vào ta tính được
Câu 2: Vì EI= -0,53 <0, nên ta có thể kết luận đây là mặt cấp thấp.
Câu 3 – Ứng dụng: Bài tập này là một ví dụ minh họa cho thấy có những mặt
hàng thuộc nhóm hàng cấp thấp hay thứ cấp, mà lượng cầu của nó nghịch biến với
sự thay đổi của thu nhập. Nói khác đi, khi thu nhập người tiêu dùng tăng thì người
ta ít sử dụng mặt hàng thuộc nhóm này.
Bài 6: Hệ số co giãn chéo, theo giá hàng hóa liên quan
Giả sử có số liệu về mối tương quan giữa giá hàng hóa Y và cầu một hàng hóa X
như sau: Khi giá hàng hóa Y là 200 (đv giá), lượng tiêu dùng hàng hóa X là 1500
(đvsp). Khi giá hàng hóa Y là 220 (đv giá), lượng tiêu dùng hàng hóa X là 1300 (đvsp). Yêu cầu:
Tính hệ số co giãn chéo của cầu hàng hóa X theo giá hàng hóa Y.
Cho biết mối liên quan giữa hay loại hàng hóa này? Bổ sung, thay thế hay độc lập? lOMoARc PSD|17327243
Bài tập này để lại lưu ý gì cho người kinh doanh? Lời giải
Câu 1: Ta có công thức tính hệ số co giãn chéo như sau
Thay số vào ta tính được
Câu 2: Vì EXY < 0 hay xu hướng thay đổi của 2 đại lượng này nghịch chiều nhau,
nên ta có thể kết luận X và Y là 2 mặt hàng bổ sung
Câu 3: Bài tập này đề cập đến mối quan hệ giữa những hàng hóa khác nhau, theo
đó sự thay đổi giá mặt hàng này có thể ảnh hưởng đến hàng hóa kia. Đề bài này thể
hiện X và Y là cặp hàng hóa bổ sung và thể hiện sự tăng giá mặt hàng Y tác động
làm giảm cầu mặt hàng X. Nhớ đến đây, người đọc cũng sẽ gợi nhớ đến mối quan
hệ thay thế một khi đã tìm hiểu hiểu về hai mối liên quan khác nhau giữa hai hàng
hóa; đó là những cặp hàng hóa mà khi mua hàng này mà không cần phải mua hàng
kia, chẳng hạn thịt – cá, nước mía – nước rau má, bia tiger – bia 333…
Bài 7: Viết phương trình đường cung
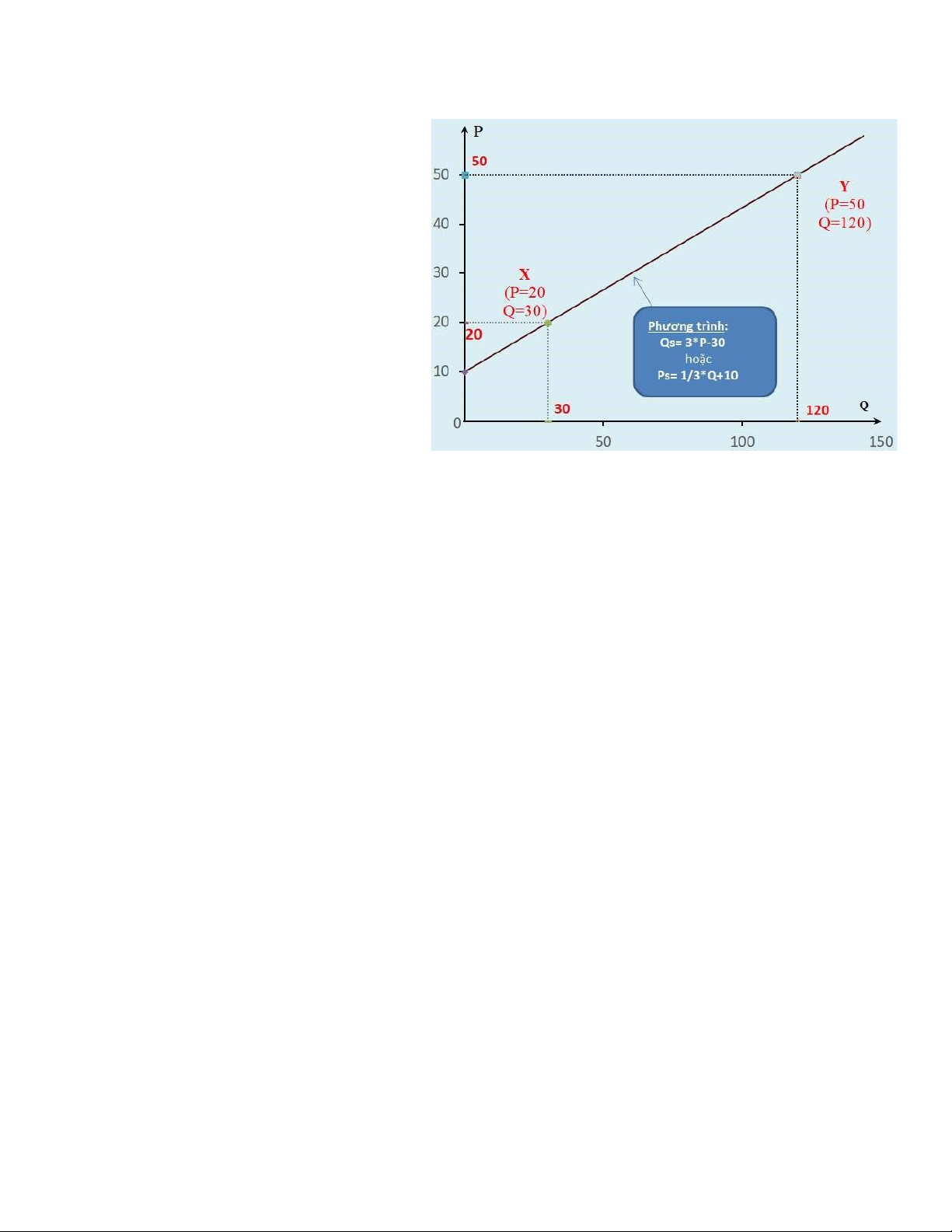
Một đường cung đi qua tọa độ 2 điểm như sau: X (P=20 và Q=30); Y (P=50 và Q=120).
Yêu cầu: Xác định phương trình của đường cung theo 2 dạng: Q=f(P) và P=f(Q) Lời giải
Đường cung đi qua 2 điểm thể hiện dạng đường thẳng hay tuyến tính. Phương
trình đường cung có dạng tuyến tính QS=cP+d. Mục tiêu cần xác định là tìm hệ số
gốc c và hoành độ gốc d. Có 2 cách để tìm phương trình của đường cung lOMoARc PSD|17327243
Cách 1: Giải hệ phương trình
Đường cung đi qua 2 điểm X (P=20 và Q=30); Y (P=50 và
Q=120) nên ta có hệ phương trình sau: 30 = c*20+d (1) 120 = c*50+d (2) Lấy (2) – (1) <=> 30*c = 90
<=> c = 3, thế vào (1) <=> d = -30
Vậy phương trình đường cung là
QS = 3*P – 30 hay P = 1/3*Q +10 (chuyển vế)
Cách 2: Xác định dựa vào công thức hệ số c
Ta có công thức hệ số gốc c = ∆Q/∆P
Dựa vào dữ liệu, lấy hai giá trị lượng và hai giá trị giá trừ nhau ta có: ∆Q=90 và ∆P=30
<=> c = 90/30 = 3; thế giá trị c, và P, Q của bất kỳ điểm nào vào phương trình Qs=c*P+d => d = -30
Qs = 3*P-30 hay P = 1/3*Q + 10 (chuyển vế)
Bài 8: Hệ số co giãn cung theo giá Đề bài
Có hàm số cung một hàng hóa A như sau: QS = 3*P-30 hay P = 1/3*Q + 10 (chuyển vế) Yêu cầu:
Hãy xác định hệ số co giãn của cung theo giá tại 2 mức giá riêng biệt P=20 và P=50
Hãy xác định hệ số co giãn của cung theo giá trong khoảng giá từ 20 đến 50 Giá
thị trường hàng hóa thường dao động trong khoảng 20-50. Hãy nhận định về tính
khan hiếm của nguồn lực trong ngành sản xuất mặt hàng này ở thời điểm hiện tại. Lời giải Câu 1: lOMoARc PSD|17327243
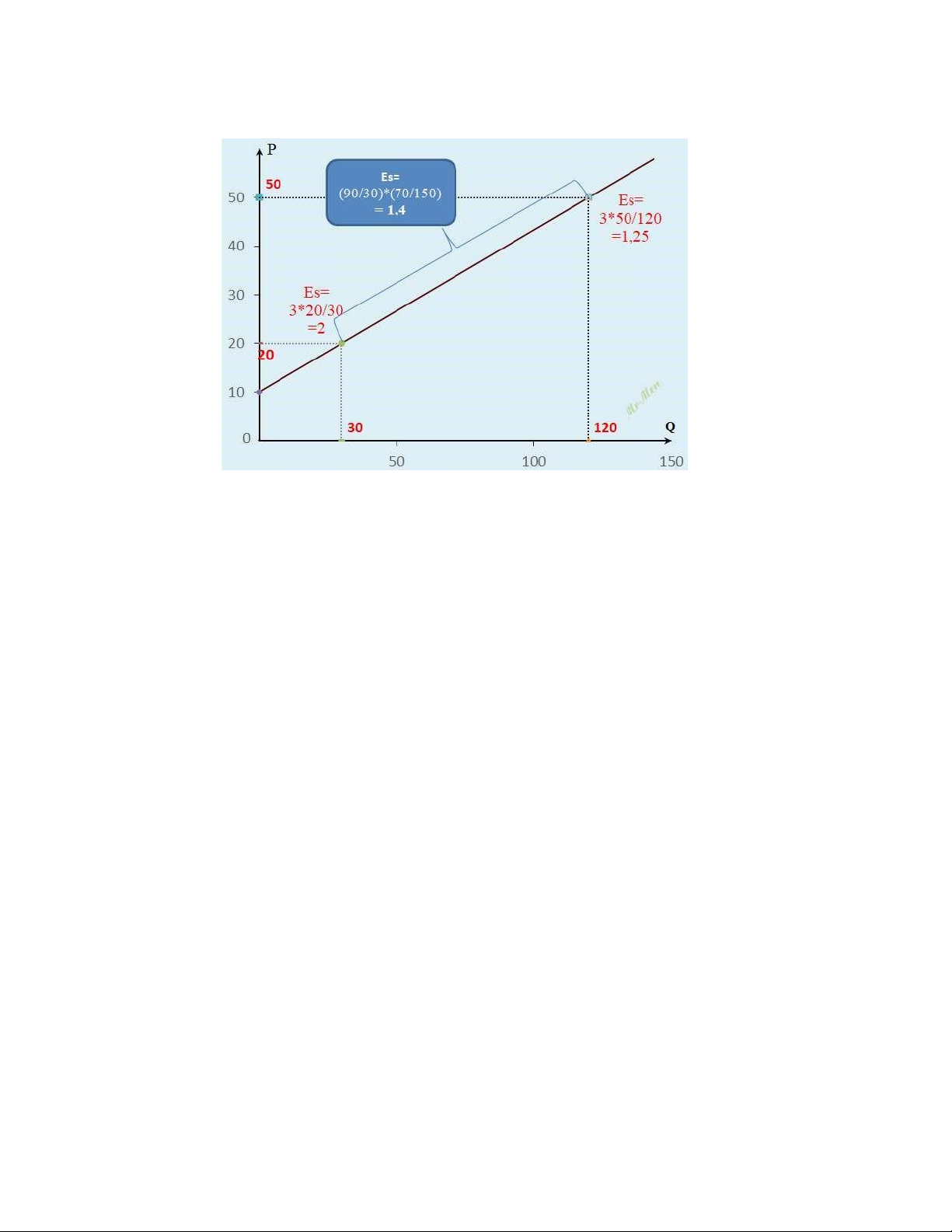
Tại mức giá P=20, ta xác định được sản lượng cung Q=30 (thế vào phương trình đường cung)
Hệ số co giãn ES=c*P/Q = 3*20/30 = 2
Tại mức giá P=50, ta xác định được sản lượng cung Q=150 (thế vào phương trình đường cung)
Hệ số co giãn ES=c*P/Q = 3*50/120 = 5/4 = 1,25 Câu 2:
Tại mức giá P=20, ta xác định được sản lượng cung Q=30
Tại mức giá P=50, ta xác định được sản lượng cung Q=120
Áp dụng công thức co giãn khoảng (giống công thức tính hệ số co giãn cầu trong
bài 3 – https://mr-men.top/2020/04/01/bai-3-tinh-he-so-co-gian-cau-theo-gia-
cogian-khoang), tính được ES=(90/30)*(70/150) = 1,4 Câu 3:
Từ kết quả tính được ở trên, có thế thấy cung khá co giãn với sự biến động của giá,
Es>1. Kết quả trên có nghĩa là nếu giá tăng 1% thì lượng cung tăng đến 1,4%. Điều
này cho thấy nguồn lực để sản xuất ra hàng hóa A không quá khan hiếm. Nhà sản
xuất dễ dàng tăng sản lượng sản xuất khi nhu cầu thì trường tăng và giá hàng hóa tăng.