











Preview text:
lOMoAR cPSD| 47879361 BÀI TẬP LỚN
DỰ BÁO THEO PHƯƠNG PHÁP NGOẠI SUY XU THẾ [Nhóm 8]
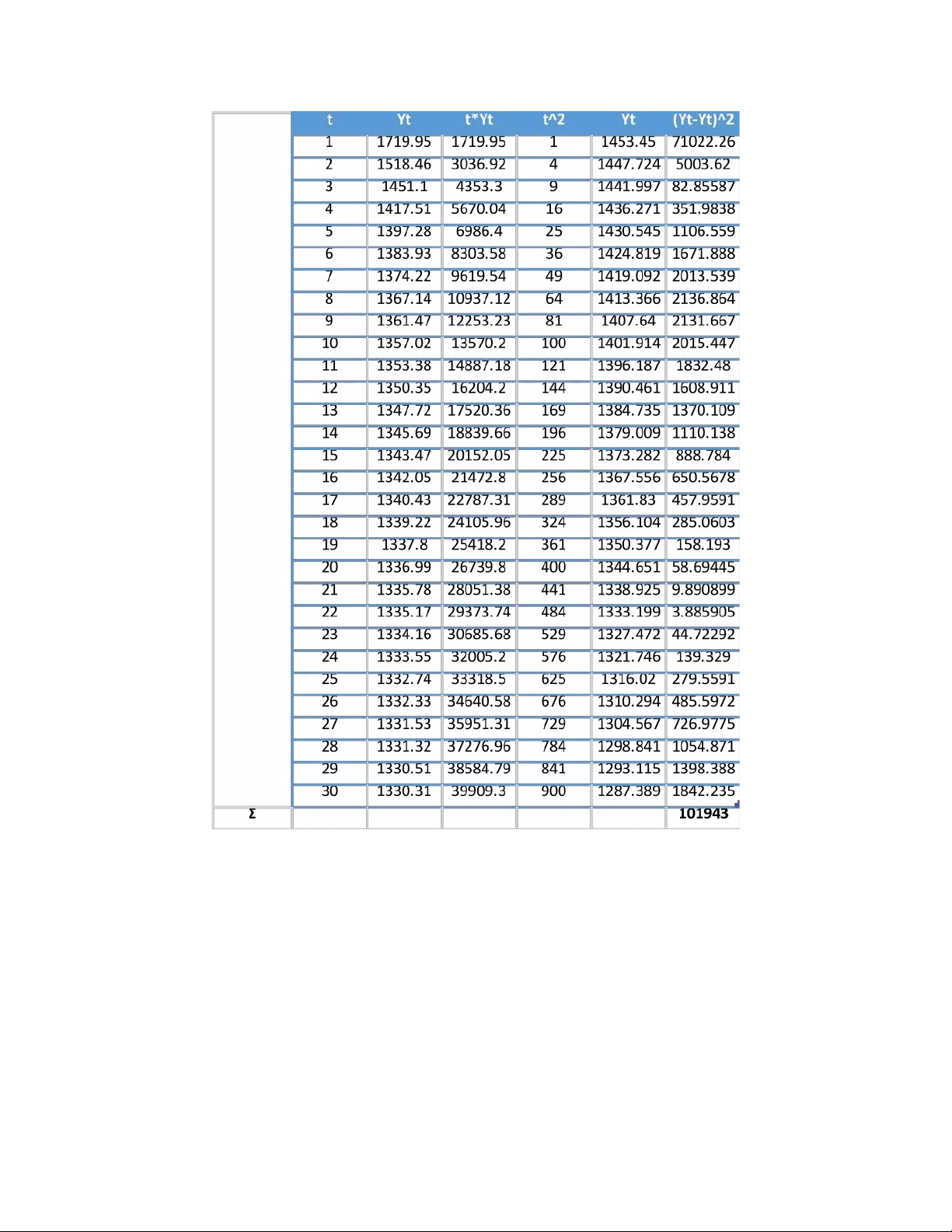
Bảng số liệu (Bảng 8): t Yt t Yt t Yt 1 1719.95 11 1353.38 21 1335.78 2 1518.46 12 1350.35 22 1335.17 3 1451.1 13 1347.72 23 1334.16 4 1417.51 14 1345.69 24 1333.55 5 1397.28 15 1343.47 25 1332.74 6 1383.93 16 1342.05 26 1332.33 7 1374.22 17 1340.43 27 1331.53 8 1367.14 18 1339.22 28 1331.32 9 1361.47 19 1337.8 29 1330.51 10 1357.02 20 1336.99 30 1330.31
I. Xác định hàm xu thế:
1. Phương pháp phân tích đồ thị:
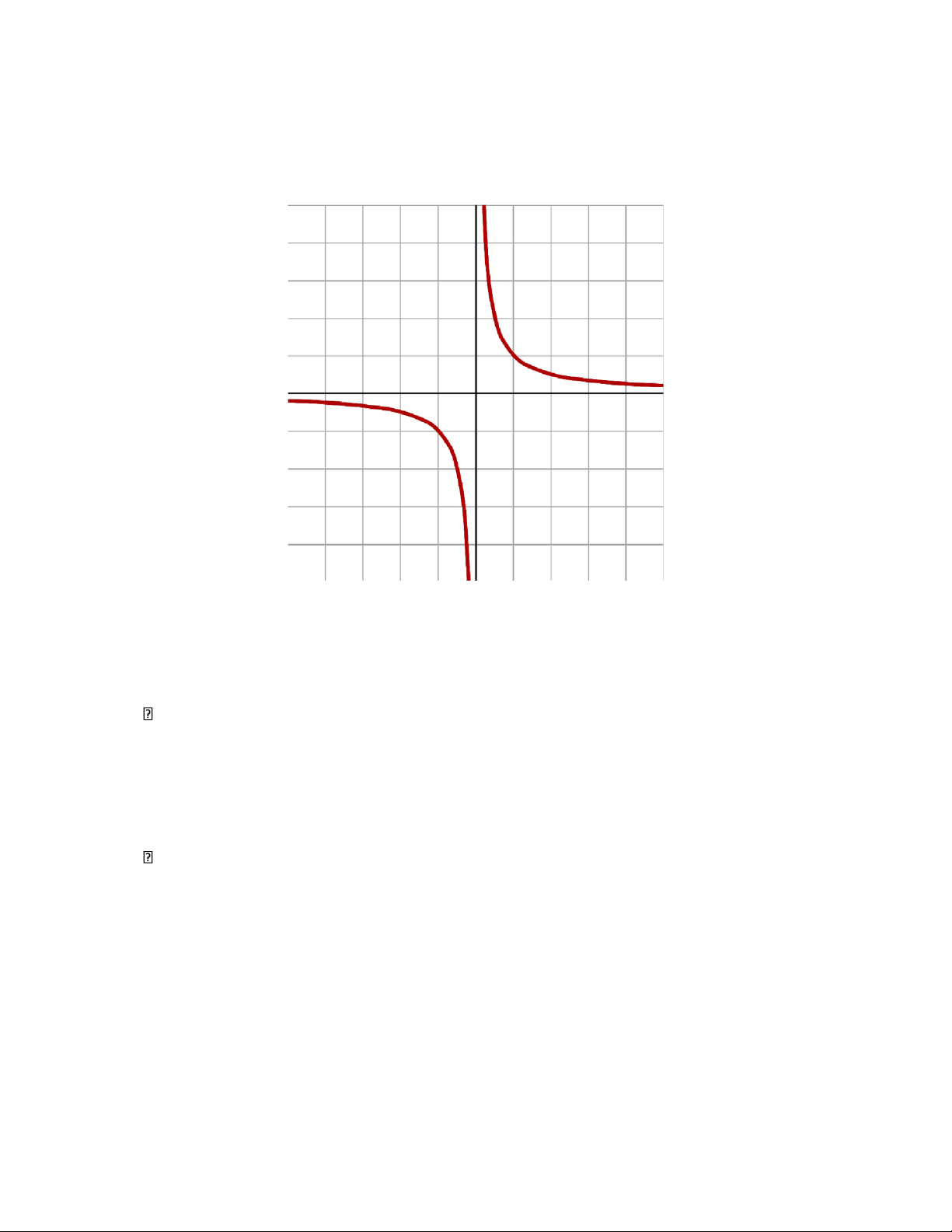
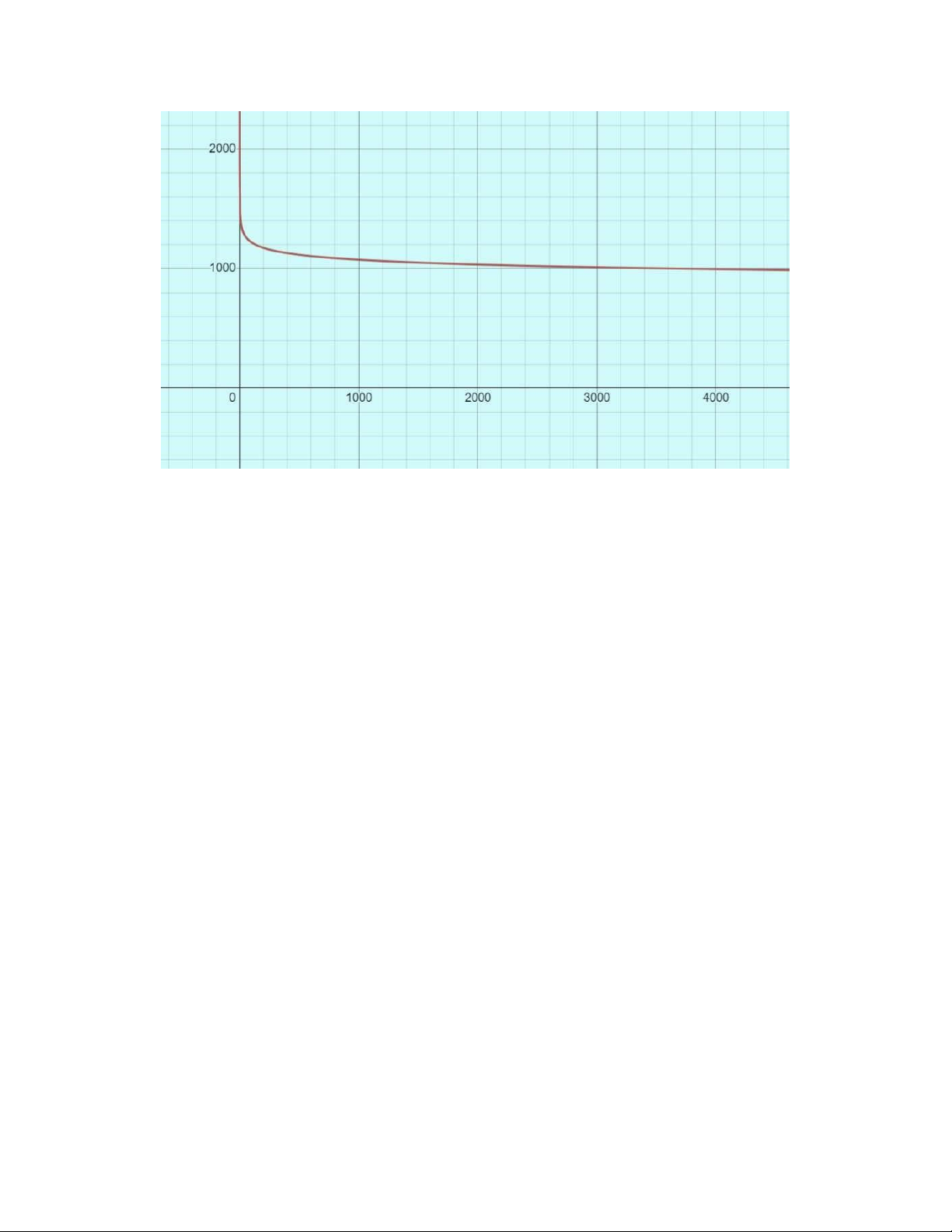
Biểu diễn chuỗi thời gian nêu trên lên hệ trục toạ độ. Ta được biểu đồ sau: 1 lOMoAR cPSD| 47879361
Nhận xét: Sự phân bố các điểm trên biểu đồ là giảm dần (nhưng không đều) - Trong bảng số liệu
đã cho, các giá trị của y giảm đáng kể khi x tăng, càng về sau thì độ giảm giá trị càng nhỏ. Ta
nhận thấy biểu đồ này có sự tương đồng với hàm Hypebole. Vì vậy, ta sẽ chọn hàm Hypebole là
dạng hàm tương ứng với bảng số liệu trên.
Biểu đồ 1. Minh hoạ.
Hàm số đó sẽ có dạng: Ŷ = 0 + .
2. Phương pháp phân tích chuỗi thời gian:
Mặc dù các giá trị t sắp xếp theo qui luật cấp số cộng. Tuy nhiên, thực hiện tính toán ta sẽ
thấy các sai số giữa các giá trị của Y không bằng nhau, do đó ta không thể kết luận được
rằng các giá trị của Y sắp xếp theo quy luật cấp số cộng. Vì vậy, hàm xu thế không thể có dạng tuyến tính: Ŷt = 1 + 2*t.
Để kiểm tra xem các giá trị của Y có sắp xếp theo quy luật cấp số nhân không, chúng ta
cần tính tỷ số giữa mỗi giá trị và giá trị trước đó. Nếu các tỷ số này bằng nhau, thì ta có
thể kết luận rằng các giá trị của Y sắp xếp theo quy luật cấp số nhân.
Thực hiện tính toán, ta có thể tính được tỷ số giữa các giá trị: lOMoAR cPSD| 47879361
Nhận thấy rằng các tỷ số này gần bằng nhau (trong khoảng
0,99 - 1), do đó ta có thể kết luận rằng các giá trị của Y có
thể sắp xếp theo quy luật cấp số nhân.
Do đó, các giá trị t sắp xếp theo qui luật cấp số cộng, và các
giá trị Yt sắp xếp theo qui luật cấp số nhân, thì hàm xu thế
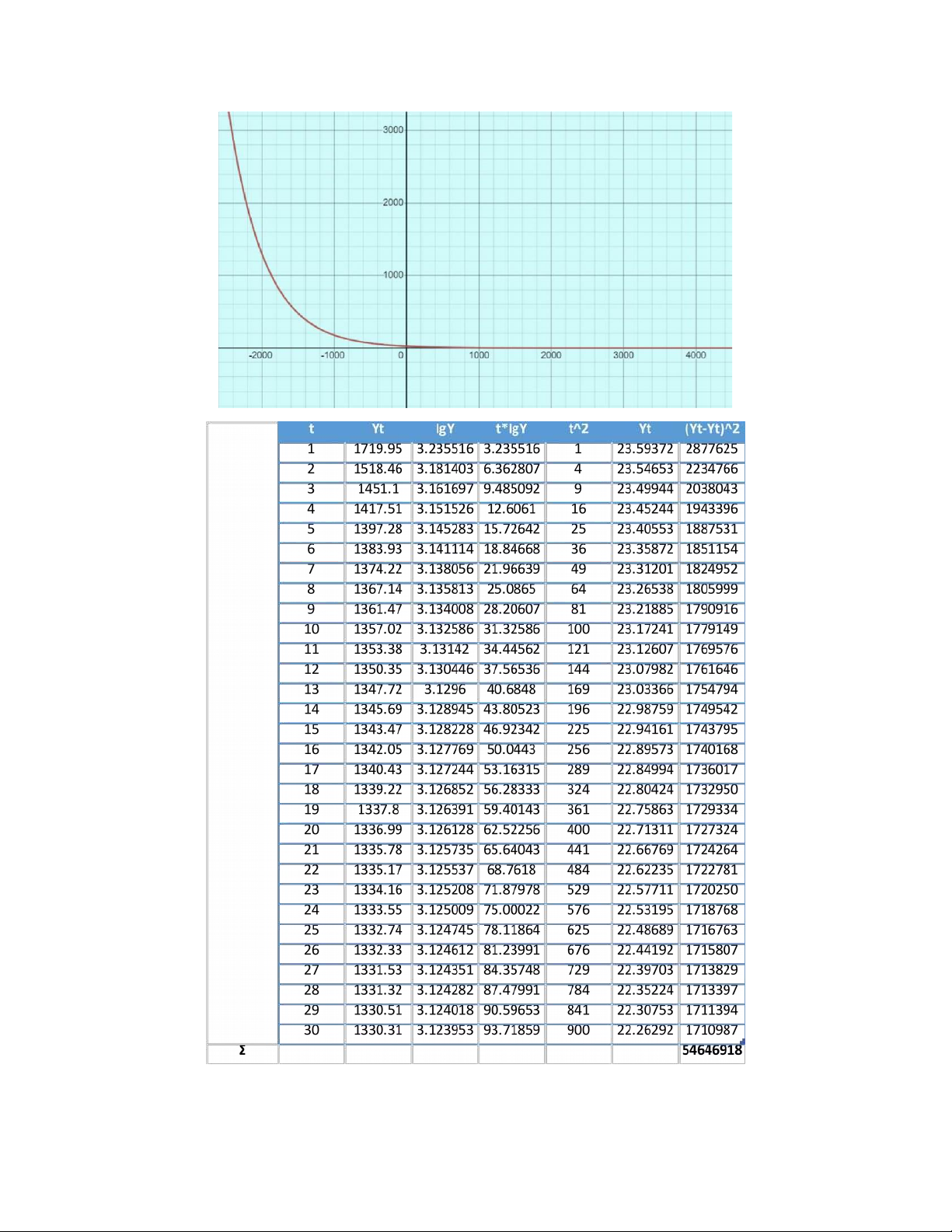
có thể có dạng hàm mũ: Ŷ = 0 * 1^t. 3 lOMoAR cPSD| 47879361 Ta xét bảng số liệu: r
Trong đó, các giá trị trong cột 3 và 4 (lgt và lgY) lần lượt là giá trị logarit nepe của t và Y.
Lgt và lgY là hai cột thể hiện giá trị của hai đại lượng t và Y tương ứng. Hàm mũ được biểu
diễn dưới dạng a^x (a là số cơ sở và x là số mũ), và hàm đảo ngược của hàm mũ đó chính
là hàm logarithm, được biểu diễn dưới dạng logarit tự nhiên (log nepe) trong trường hợp này.
Chúng ta có thể thấy rằng Y tăng/giảm theo hàm mũ khi tăng/giảm giá trị của t, có nghĩa là
khi tăng/giảm một lượng nhất định thì Y sẽ tăng/giảm theo một nguyên tắc cụ thể của hàm mũ. lOMoAR cPSD| 47879361
Vì vậy, nếu chúng ta lấy logarit tự nhiên của Y (giá trị nằm trong cột lgY) thì giá trị logarit
tự nhiên này sẽ tăng/giảm theo cùng một nguyên tắc của hàm mũ mà Y đang tăng/giảm
theo đó. Tương tự, nếu chúng ta lấy logarit tự nhiên của t (giá trị nằm trong cột lgt) thì giá
trị logarit này sẽ cũng tăng/giảm theo cùng một nguyên tắc của hàm mũ mà t đang tăng/giảm theo đó.
Vì vậy, hai cột lgt và lgY đều thể hiện quá trình tăng/giảm của hai đại lượng t và Y theo
cùng một nguyên tắc của hàm mũ, và do đó hai cột này có liên quan tuyến tính với nhau.
Nói cách khác, khi giá trị của lgt tăng/giảm một lượng nhất định, giá trị của lgY cũng sẽ
tăng/giảm theo một lượng tương tự. Vì vậy, cặp giá trị (lgt, lgY) thể hiện mối quan hệ tuyến
tính giữa các giá trị này.
Vì vậy, hàm xu thế tổng quát trong trường hợp này có thể có dạng: t = 0 * t ^1 lOMoAR cPSD| 47879361
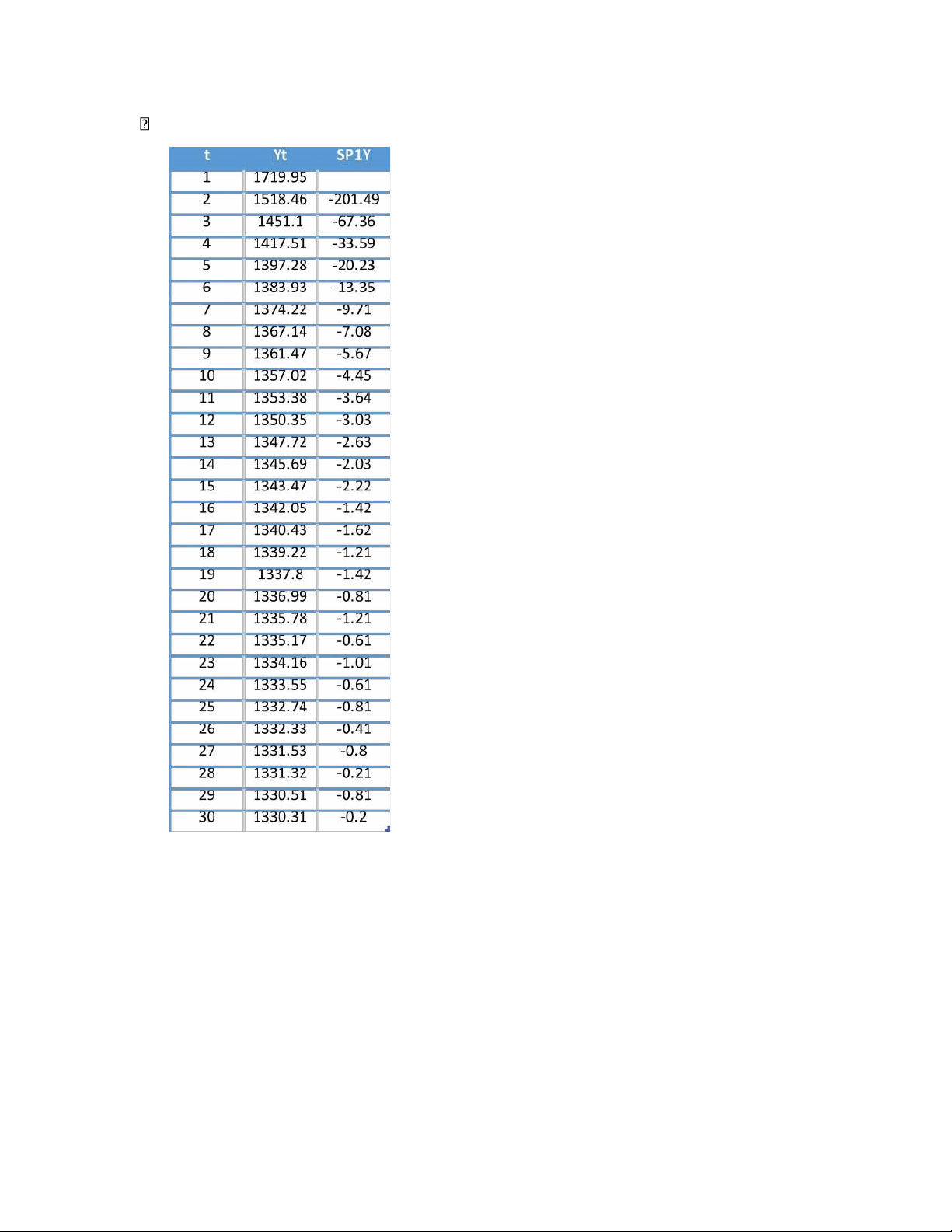
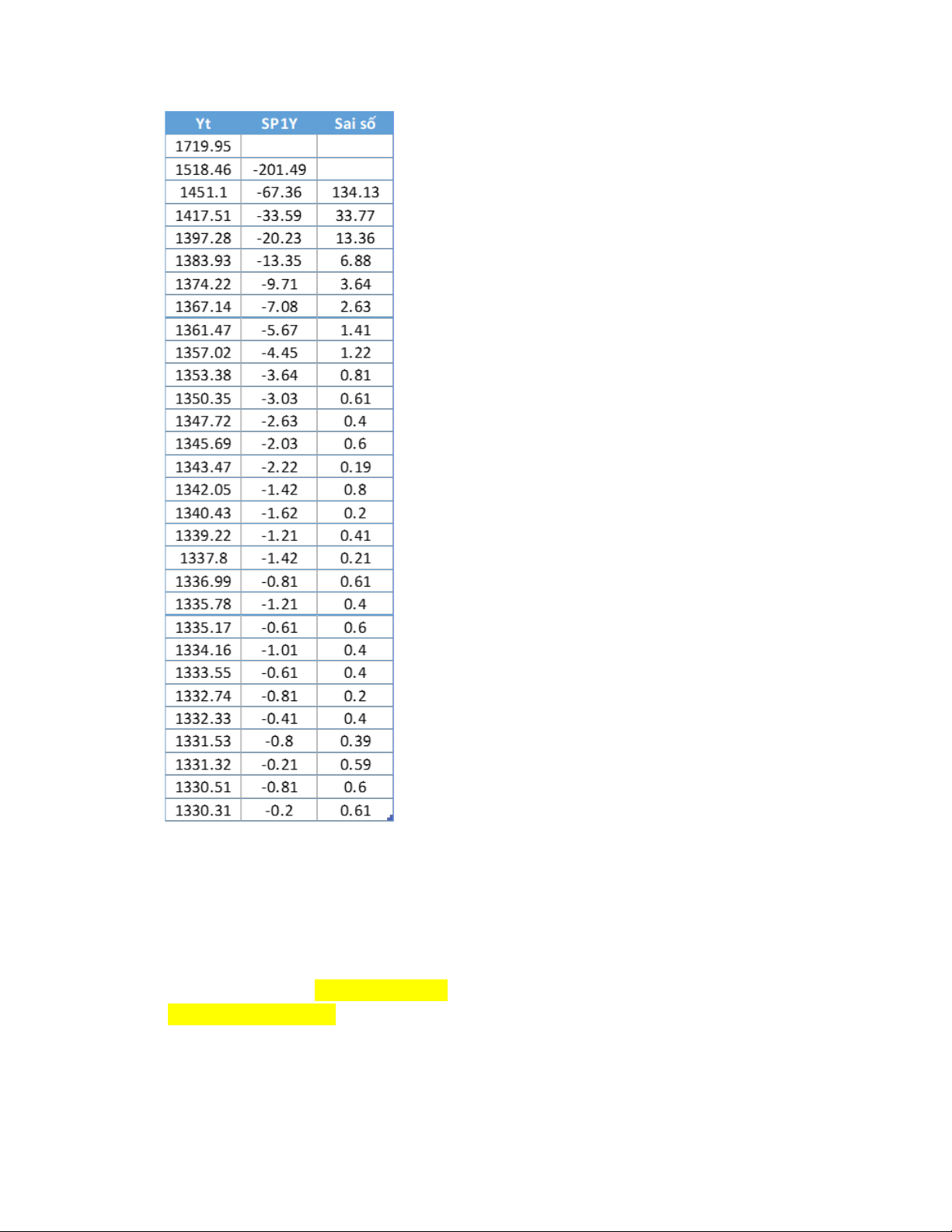
Xét bảng dữ liệu, với cột SP1Y là các giá trị sai phân bậc 1 của Y:
Để kiểm tra xem các giá trị của cột SP1Y có giảm đều hay
không, ta cần tính sai số giữa mỗi giá trị và giá trị trước đó.
Nếu các sai số này bằng nhau hoặc gần bằng nhau, thì ta
có thể kết luận rằng các giá trị của SP1Y giảm đều.
Thực hiện tính toán, ta có thể tính được sai số giữa các giá trị: lOMoAR cPSD| 47879361
Ta nhận thấy khoảng cách giữa các giá trị không bẳng nhau.
Ví dụ: |(-201,49)-(-67,36)| = 134,13 và |(-67,36)-(-33,59)| = 33,77.
Như vậy, (độ lớn) sai phân bậc 1 của
Y giảm không đều, hàm xu thế không thể có dạng Hypebole. t = 0 +
3. Phương pháp so sánh sai số: lOMoAR cPSD| 47879361
Dựa vào chuỗi thời gian (bảng số liệu đã cho), ta xây dựng một loạt các hàm tương ứng với các
khả năng có thể xảy ra. Sau đó tính sai số trung bình của từng hàm theo công thức:
Dùng tiêu chuẩn cực tiểu Sai số trung bình để lựa chọn hàm xu thế phù hợp.
a. Xây dựng hàm tuyến tính:
Xét hàm cần ước lượng có dạng: Ŷ = 1 + 2*t. lOMoAR cPSD| 47879361
Để ước lượng hàm số trên, ta sử dụng hệ phương trình chuẩn: = n*1 + 2* = 1* + 2*
Thay số vào hệ phương trình, ta được kết quả: 1 = 1459,17623 ; 2 = -5,72625.
Vậy, hàm tuyến tính ước lượng có dạng: Ŷ = 1459,17623 - 5,72625*t. lOMoAR cPSD| 47879361
Ta có sai số trung bình của hàm tuyến tính: SYt = 60,339. b.
Xây dựng hàm mũ (exponential growth model):
Xét hàm cần ước lượng có dạng: Ŷ = 0 * 1^t. lOMoAR cPSD| 47879361
Để ước lượng hàm số trên, ta sử dụng hệ phương trình chuẩn: ΣlgY = n*lg0 + lg1*Σt Σt*lgY = lg0*Σt + lg1*Σt²
Thay số vào hệ phương trình, ta được kết quả: lg0 = 3,163 => 0 = 23,641; lg1 = -1,725*10^-3 => 1 = 0,998.
Vậy, hàm tuyến tính ước lượng có dạng: Ŷ = 23,641* 0,998^t. lOMoAR cPSD| 47879361 lOMoAR cPSD| 47879361
Ta có sai số trung bình của hàm mũ: SYt = 1397,024.
c. Xây dựng hàm mũ có cơ số thay đổi (power law growth model):
Xét hàm cần ước lượng có dạng: Yt = β0 * t ^β1 ln(Yt)
= ln(0) + 1 * ln(t) Đặt ln(Yt) = ’t; ln(t) = t’; ln(0) = 0’. ’t = 0’ + 1*t’.
Ta sẽ tiến hành ước lượng hàm xu thế trên: Ŷ’t = 0’ + 1*t’
Hàm xu thế lúc này đã có dạng tương tự như hàm tuyến tính, ta có thể áp dụng hệ phương trình
chuẩn để ước lượng các tham số, hệ phương trình có dạng: t = n*0’ + 1* t* t’ = 0’ * + 1* lOMoAR cPSD| 47879361
Thay số vào biểu thức, ta được: 0’ = 7,3579; 1 = -0,0548 0 = = 1568,4646; 1 = -0,0548
Hàm xu thế trong trường hợp này có dạng: t = 1568,4646 * . lOMoAR cPSD| 47879361
Ta có sai số trung bình của hàm mũ: SYt = 36,3728. lOMoAR cPSD| 47879361
d. Xây dựng hàm Hypebole:
Xét hàm cần ước lượng có dạng: Ŷ = 0 + . lOMoAR cPSD| 47879361
Để ước lượng hàm số trên, ta sử dụng hệ phương trình: ΣY = n*0 + 1*Σ Σ = 0* Σ +1*Σ
Thay số vào hệ phương trình, ta được: 0 = 1316,72 ; 1 = 403,2435.
Vậy, hàm tuyến tính ước lượng có dạng: Ŷ = 1316,72 + . lOMoAR cPSD| 47879361
Ta có sai số trung bình của hàm Hypebole: SYt = 0,1035.
Vì hàm Hypebole là hàm xu thế có sai số trung bình tương ứng nhỏ nhất nên ta sẽ chọn nó là dạng
hàm xu thế tương ứng với dữ liệu của bài toán.
II. Xây dựng hàm dự báo:
1. Phương pháp bình phương bé nhất: (OLS)
2. Phương pháp điểm chọn: lOMoAR cPSD| 47879361
III. Kiểm định hàm xu thế:
1. Tiêu chuẩn hệ số biến phân: 2. Tiêu chuẩn lô:
IV. Tính kế quả dự báo:




