
Preview text:
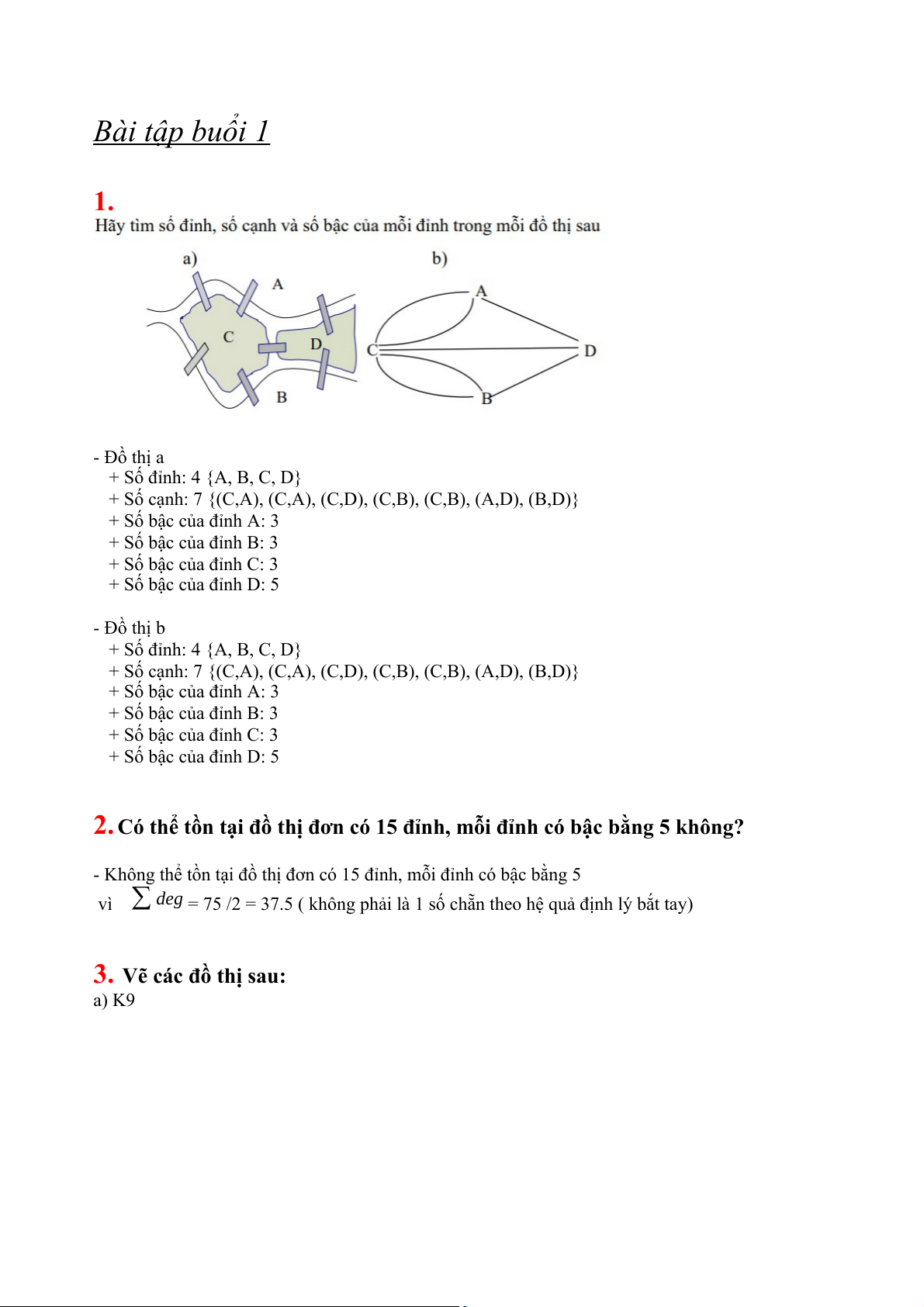
Bài tập buổi 1 1. - Đồ thị a + Số đỉnh: 4 {A, B, C, D}
+ Số cạnh: 7 {(C,A), (C,A), (C,D), (C,B), (C,B), (A,D), (B,D)}
+ Số bậc của đỉnh A: 3
+ Số bậc của đỉnh B: 3
+ Số bậc của đỉnh C: 3
+ Số bậc của đỉnh D: 5 - Đồ thị b + Số đỉnh: 4 {A, B, C, D}
+ Số cạnh: 7 {(C,A), (C,A), (C,D), (C,B), (C,B), (A,D), (B,D)}
+ Số bậc của đỉnh A: 3
+ Số bậc của đỉnh B: 3
+ Số bậc của đỉnh C: 3
+ Số bậc của đỉnh D: 5
2. Có thể tồn tại đồ thị đơn có 15 đỉnh, mỗi đỉnh có bậc bằng 5 không?
- Không thể tồn tại đồ thị đơn có 15 đỉnh, mỗi đỉnh có bậc bằng 5
vì ∑ deg = 75 /2 = 37.5 ( không phải là 1 số chẵn theo hệ quả định lý bắt tay)
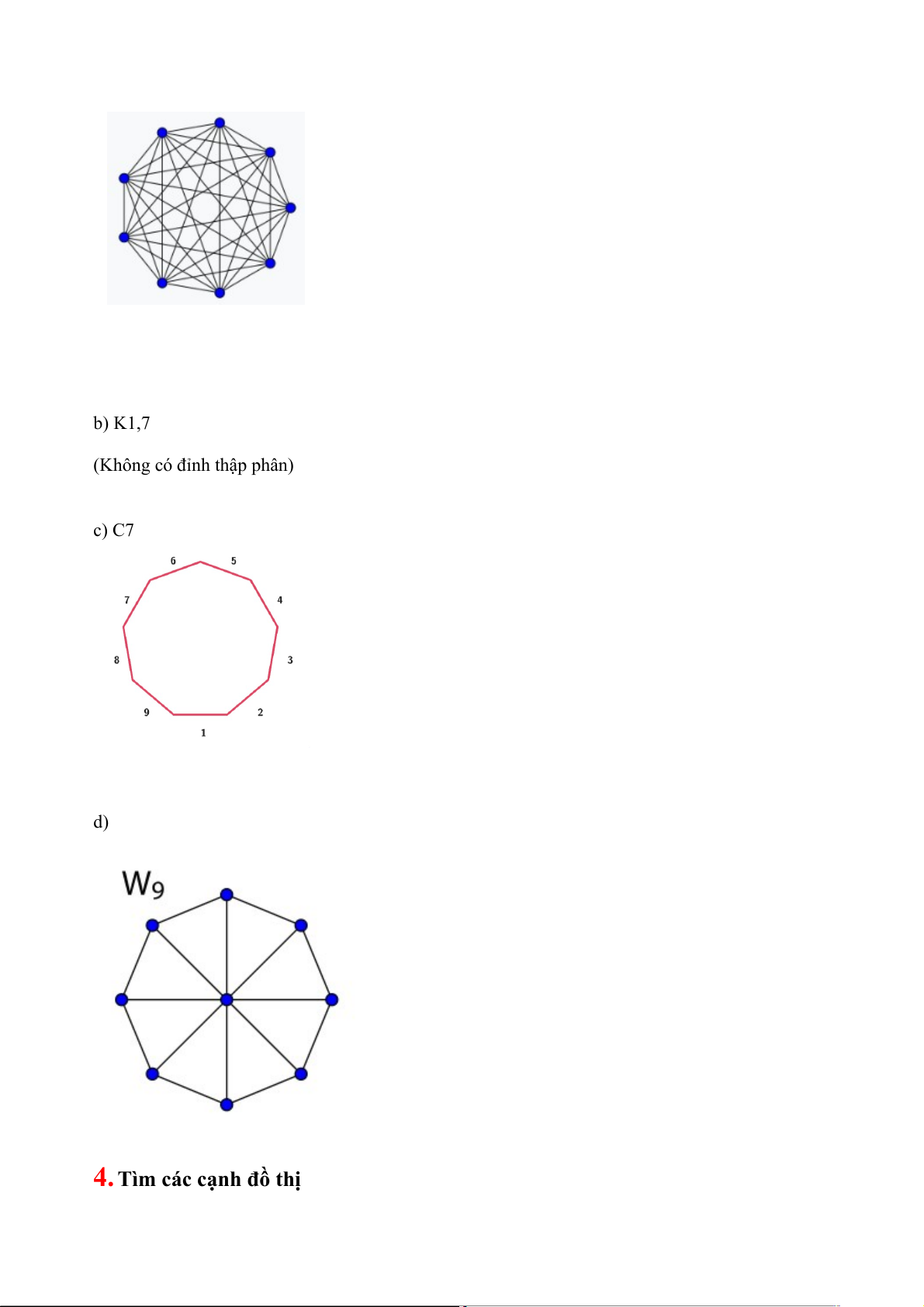
3. Vẽ các đồ thị sau: a) K9 b) K1,7
(Không có đỉnh thập phân) c) C7 d)
4. Tìm các cạnh đồ thị
- Số cạnh trong các đồ thị: a) K8: 28 cạnh b) C12: 12 cạnh c) W15: 30 cạnh
d) K3,4:( không có đỉnh thập phân)
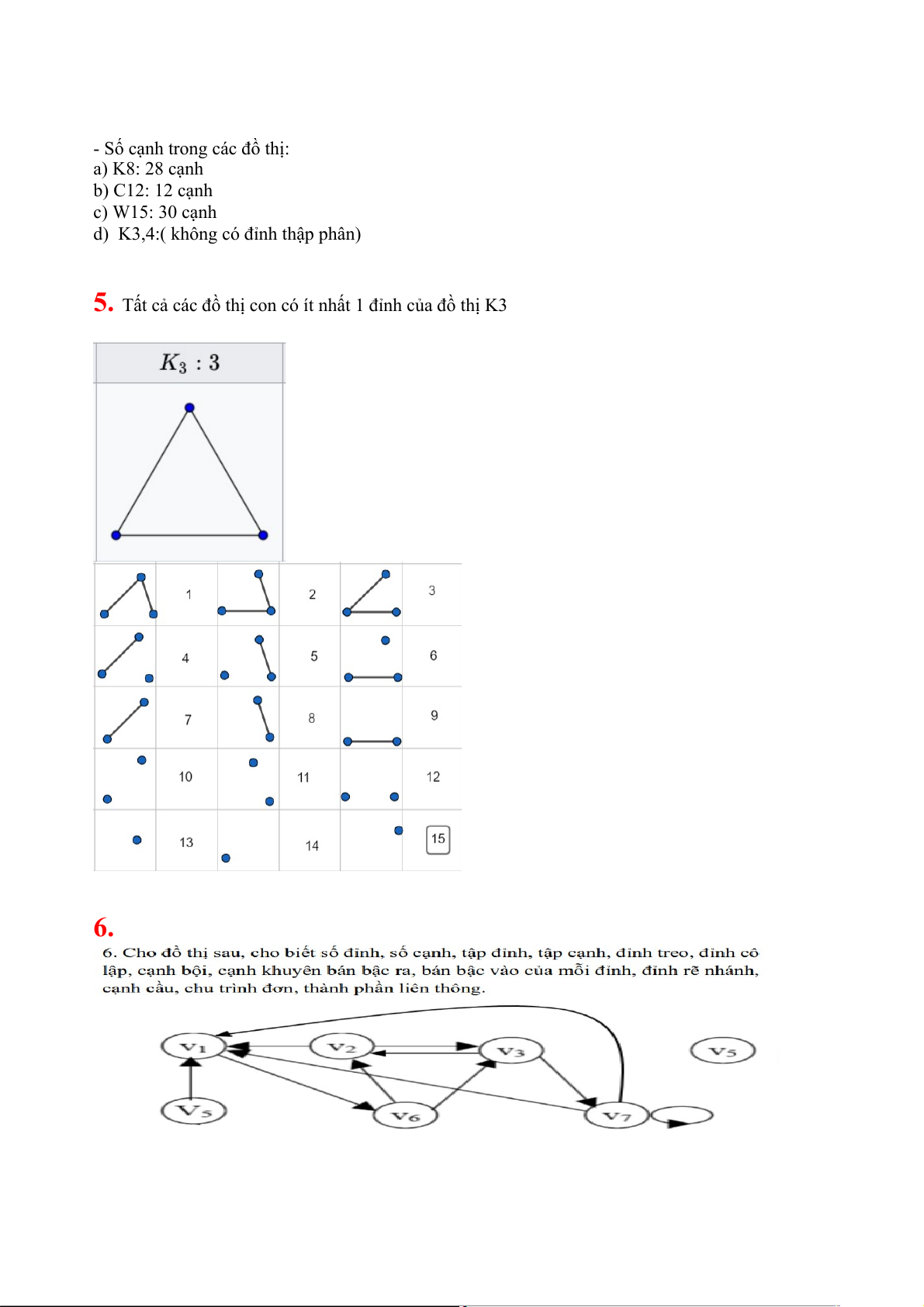
5. Tất cả các đồ thị con có ít nhất 1 đỉnh của đồ thị K3 6. - Số đỉnh: 7 - Số cạnh: 11
- Tập đỉnh: {V1, V2, V3, V4, V5, V6, V7} - Tập cạnh: {(1,6)} - Đỉnh treo: 1 {V5} - Đỉnh cô lập: 1 {V4}
- Cạnh bội:1 {(V1,V7),(V1,V7)} - Cạnh khuyên: 1 {V7}
- Bán bậc ra của đỉnh V1: 1 {(V1,V6)}
-Bán bậc ra của đỉnh V2: 2 {(V2,V1), (V2,V3)}
-Bán bậc ra của đỉnh V3: 2 {(V3,V2), (V3,V7)}
-Bán bậc ra của đỉnh V4: 0
-Bán bậc ra của đỉnh V5: 1 {(V5,V1)}
-Bán bậc ra của đỉnh V6: 2 {(V6,V2), (V6,V3)}
-Bán bậc ra của đỉnh V7: 3 {(V7,V1), (V7,V1), (V7,V7)}
- Bán bậc vào của đỉnh V1: 4 {(V5,V1), (V7,V1), (V7,V1), (V2,V1)}
-Bán bậc vào của đỉnh V2: 2 {(V6,V2),(V3,V2)}
-Bán bậc vào của đỉnh V3: 2 {(V6,V3),(V2,V4)}
-Bán bậc vào của đỉnh V4: 0
-Bán bậc vào của đỉnh V5: 0
-Bán bậc vào của đỉnh V6: 1 {(V1,V6)}
-Bán bậc vào của đỉnh V7: 2 {(V3,V7), (V7,V7)}
- Đỉnh rẽ nhánh: V1, V2, V3, V6
- Cạnh cầu: (V1,V6), (V5,V1) - Chu trình đơn: + V1,V6,V3,V2,V1 +V1,V6,V3,V7,V1 +V1,V6,V2,V3,V7,V1 +V1,V6,V2,V1 +V2,V3,V2 - Thành phần liên thông: + V1,V2,V3,V6,7 +V4 +V5




