Bài Tập Mô Hình Đo Lường Rủi Ro | Môn Quản trị rủi ro - Đại học Kinh Tế Quốc Dân

lOMoAR cPSD| 61401654
MỘT SỐ BÀI TẬP QUẢN TRỊ RỦI RO ĐỊNH LƯỢNG
CHƯƠNG 2: CÁC MÔ HÌNH ĐO LƯỜNG RỦI RO Bài 1.
Một công ty tính được giá trị rủi ro (VaR) của danh mục đầu tư của mình là 10 triệu
đồng (xét về độ lớn) với chu kỳ 1 ngày và độ tin cậy 99%. Các bạn cho biết giải
thích nào dưới đây về VaR là đúng:
a.Với xác suất 99%, danh mục đầu tư của công ty đó sẽ lỗ 10 triệu đồng ở ngày tiếp theo.
b.Với xác suất 99%, danh mục đầu tư của công ty đó có thể lỗ tối đa là 10 triệu đồng
ở ngày tiếp theo. Đúng, giải thích theo ý nghĩa của VaR: Tổn thất tối đa của 1
danh mục đầu tư nếu nắm giữ trong một ngày và độ tin cậy 99% Bài 2.
Cho bảng véc tơ trung bình và ma trận hiệp phương sai của 2 chuỗi lợi suất (chu kỳ 1 ngày) RBVH và RDPM: Trung bình Ma trận hiệp phương sai RBVH RDPM 0.001162 RBVH 0.000908 0.000276 -0.000769 RDPM 0.000276 0.000498
Xét danh mục (P) của 2 chuỗi lợi suất trên với trọng số (0.3; 0.7). Giả thiết
(RBVH, RDPM) có phân phối chuẩn 1.
Có thể cho rằng cổ phiếu BVH rủi ro hơn cổ phiếu DPM không? 2.
Tính trung bình và phương sai của danh mục P.
Trung bình của danh mục P= 0.3*0.001162 + 0.7*(-0.000769) =−1.897×10^(−4)
Phương sai danh mục P= 0.3^2*var(BVH) + 2*0.3*0.7*cov(BVH,DPM) + 0.7^2*var(DPM)
= 0.3^2* 0.000908+ 2*0.3*0.7* 0.000276+ 0.7^2*0.000498= 4.4166×10^(−4) lOMoAR cPSD| 61401654 3.
Tính VaR(1 ngày, 99%) của danh mục P. Nêu ý nghĩa của giá trị tính được.
VaR(1 ngày, 99%)= 1* MEAN + 1^(1/2)*N^(-1)(0.01)*Std.(P)
=1*(−1.897×10^(−4)) + 1^(1/2)*(-2.33)* 4.4166×10^(−4)
Tổn thất tối đa của 1 danh mục đầu tư nếu nắm giữ trong một ngày và độ tin cậy
99% là một khoản bằng… 4.
Tính VaR(10 ngày, 99%) của danh mục P và cho nhận xét.
=10*(−1.897×10^(−4)) + 10^(1/2)*(-2.33)* 4.4166×10^(−4)
Tổn thất tối đa của 1 danh mục đầu tư nếu nắm giữ trong một ngày và độ tin cậy
99% là một khoản bằng… Bài 3.
Cho bảng véc tơ trung bình và ma trận hiệp phương sai của 2 chuỗi lợi suất (chu kỳ 1 ngày) RCTG và RVCB: Trung bình Ma trận hiệp phương sai RCTG RVCB -0.00112 RCTG 0.000493 0.000247 -0.00164 RVCB 0.000247 0.000461
Giả thiết (RCTG, RVCB) có phân phối chuẩn.
1. Tính VaR(99%, 1 ngày) của R1= 0.5*RCTG và R2=0.5*RVCB.
R1: VaR(99%, 1 ngày)= 1* (0.5*(-0.00112)) + 1^(1/2)*(-2.33)* 0.000493 = −0.00170869
R2: VaR(99%, 1 ngày)= 1* (0.5*(-0.00164)) + 1^(1/2)*(-2.33)* 0.000461 = −0.00189413
2. Xét danh mục (P) của 2 chuỗi lợi suất trên với trọng số (0.5; 0.5). Tính VaR (99%, 1 ngày) của P. lOMoAR cPSD| 61401654
Trung bình của danh mục P= 0.5*(-0.00112)+ 0.5*(-0.00164)= −0.00138
Phương sai danh mục P
= 0.5^2* 0.000493+ 2*0.5*0.5* 0.000247+ 0.5^2*0.000461= 3.62×10−4
VaR(99%, 1 ngày)= 1* (-0.00138) + 1^(1/2)*(-2.33)* 3.62×10−4= −0.00222346
3. So sánh giá trị rủi ro của danh mục P với tổng giá trị rủi ro của R1 và giá trị rủi
ro của R2. Qua đó có nhận xét gì?
Tổng giá trị rủi ro của R1 và giá trị rủi ro của R2= (−0.00170869) +
(−0.00189413)= −0.00360282 Bài 4.
Tính toán lợi suất của danh mục (theo ngày) cho 100 ngày, sau khi sắp xếp các giá
trị lợi suất từ nhỏ đến lớn, ta lấy ra 7 giá trị lợi suất nhỏ nhất:
-0.0019, -0.0017, -0.004, -0.002, -0.0016, -0.0018, -0.0015
Tính giá trị rủi ro với độ tin cậy 95% bằng phương pháp mô phỏng lịch sử. K=1 ngày alpha=0.05 n= 100 ngày
5% của 100 ngày là 5 (=> giá trị nguyên => chọn giá trị đứng thứ 5 trong dãy)
Dãy (min-max): −0.004,−0.002,−0.0019,−0.0018,−0.0017,−0.0016,−0.0015
Kết luận: −0.0017 Bài 5.
Dựa trên phương pháp mô phỏng Monte Carlo, tạo ra 1000 giá trị lợi suất của danh
mục. Sau khi sắp xếp các giá trị lợi suất từ nhỏ đến lớn và chọn ra 15 giá trị lợi suất nhỏ nhất:
-0.0018, -0.0011, -0.0020, -0.0012, -0.0015, -0.0013, -0.0014, -0.0024, -0.0021,
0.0019, -0.0022, -0.0017, -0.0016, -0.0010, -0.0023.
Tính giá trị rủi ro với độ tin cậy 99% bằng phương pháp mô phỏng Monte Carlo 1000*1%=10 lOMoAR cPSD| 61401654 Bài 6.
Thực hiện hậu kiểm mô hình VaR (1 ngày, 99%) của một danh mục cho 250 ngày
của 3 phương pháp ước lượng: Phân phối chuẩn, Phương pháp mô phỏng lịch sử,
Phương pháp mô phỏng Monte Carlo. Ta xác định được số ngày thua lỗ thực tế vượt
quá giá trị rủi roc ho mỗi phương pháp tương ứng là: 9, 7, 4. Trong 3 phương pháp
ước lượng VaR (1 ngày, 99%) của danh mục trên thì phương pháp nào phù hợp? Nháp
Để xác định phương pháp nào phù hợp nhất trong ba phương pháp ước lượng VaR
(1 ngày, 99%), ta thực hiện hậu kiểm (backtesting) bằng cách so sánh số ngày mà
lỗ thực tế vượt quá VaR với kỳ vọng lý thuyết.
Với mức tin cậy 99% trong 250 ngày, ta kỳ vọng rằng số ngày mà lỗ thực tế vượt quá VaR là:
Điều này có nghĩa là, lý thuyết dự đoán có khoảng 2–3 ngày lỗ thực tế sẽ vượt quá
mức VaR. So sánh kết quả thực tế của từng phương pháp: •
Phân phối chuẩn: 9 ngày vượt quá VaR •
Mô phỏng lịch sử: 7 ngày vượt quá VaR •
Mô phỏng Monte Carlo: 4 ngày vượt quá VaR Đánh giá
So với dự đoán lý thuyết (khoảng 2–3 ngày), phương pháp nào có số ngày vượt quá
gần với 2–3 nhất sẽ được coi là phù hợp nhất. •
Phương pháp mô phỏng Monte Carlo (4 ngày): gần nhất với dự đoán lý
thuyết, chỉ vượt hơn một chút so với 3 ngày kỳ vọng. •
Phương pháp mô phỏng lịch sử (7 ngày) và phân phối chuẩn (9 ngày) đều có
số lần vượt quá cao hơn dự đoán, cho thấy chúng có thể đã đánh giá thấp
mức độ rủi ro thực tế của danh mục. lOMoAR cPSD| 61401654 Kết luận
Trong ba phương pháp ước lượng VaR trên, phương pháp mô phỏng Monte Carlo
là phương pháp phù hợp nhất cho danh mục, vì số ngày vượt quá VaR gần với giá
trị kỳ vọng lý thuyết nhất. lOMoAR cPSD| 61401654 lOMoAR cPSD| 61401654
CHƯƠNG 3: RỦI RO LÃI SUẤT Mô hình ARIMA
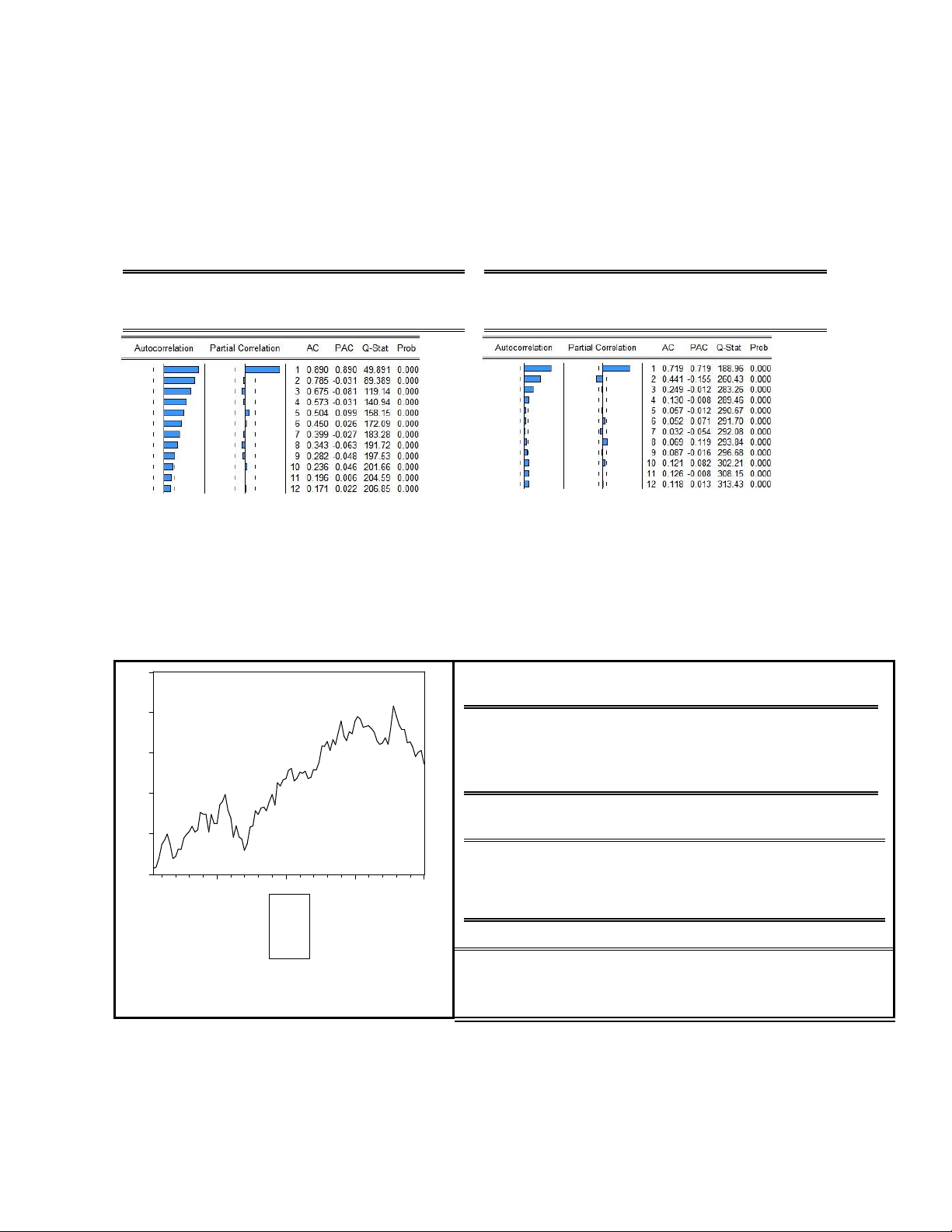
Bài 1. Cho kết quả kiểm định ADF và lược đồ tự tương quan của chuỗi lãi suất 1 tháng (Rt) và
sai phân của nó là D(Rt) như sau Biến Rt Biến D(Rt)
Test Stat 0.931 1% Critical Value* -3.541
Test Stat 5.451 1% Critical Value* -4.036 5% Critical Value -2.910 5% Critical Value -2.816 10% Critical Value -2.592 10% Critical Value -2.92
(a) Kiểm định tính dừng với chuỗi lãi suất và sai phân của lãi suất
(b) Lược đồ tự tương quan cho biết thông tin gì về chuỗi lãi suất và sai phân của nó
(c) Với lược đồ tự tương quan của chuỗi D(Rt), hãy nêu một mô hình phù để dự báo cho D(Rt), giải thích?
Bài 2. Cho đồ thị và kết quả kiểm định với chuỗi lãi suất như sau 20
Kiểm định không hệ số chặn, không xu thế 16 Test Statistic -0.371583 1% Critical Value* -2.6026 5% Critical Value -1.9462 12 10% Critical Value -1.6187 8
Kiểm định có hệ số chặn, không có xu thế 4 Test Statistic -3.961119 1% Critical Value* -3.5457 0 5% Critical Value -2.9118 25 50 75 100 10% Critical Value -2.5932 X Kiểm định có xu thế Test Statistic -3.901491 1% Critical Value* -4.1219 5% Critical Value -3.4875 10% Critical Value -3.1718
(a) Trong ba kiểm định trên, nên dùng kiểm định nào, vì sao ? (3) vì kiểm định chuỗi có xu
thế tăng và có hệ số chặn
(b) Với kiểm định đã lựa chọn, cho kết luận về tính dừng của chuỗi Rt ? lOMoAR cPSD| 61401654
(c) Có thể dùng mô hình nào để mô hình hóa và dự báo cho chuỗi Rt ? Bài 3.
Cho kết quả ước lượng sau với chuỗi lãi suất Dependent Variable: R
Method: ARMA Maximum Likelihood (BFGS) Sample: 2008M03 2013M08 Variable Coefficient Std. Error t-Statistic Prob. C 10.79052 1.824261 5.915011 0.0000 AR(1) 0.894128 0.058073 15.39663 0.0000 MA(1) 0.320842 0.113649 2.823092 0.0064
Lược đồ tương quan và kiểm định ADF của chuỗi phần dư: Autocorrelation Partial Correlation AC PAC Q-Stat Prob 1 0.095 0.095 0.6179 2 0.300 0.293 6.9172 3 -0.031 -0.087 6.9848 0.008 4 0.042 -0.041 7.1130 0.029 5 -0.217 -0.203 10.584 0.014 6 -0.099 -0.080 11.317 0.023
7 -0.176 -0.045 13.679 0.018 8 0.044 0.117 13.828 0.032 9 0.041 0.117 13.960 0.052 10 -0.013 -0.126 13.973 0.082 11 -0.006 -0.094 13.976 0.123 12 -0.038 -0.073 14.095 0.169
13 -0.041 -0.006 14.236 0.220 Null Hypothesis: RESID01 has a unit root t-Statistic Prob.*
Augmented Dickey-Fuller test statistic -3.869508 0.0038 Test critical values: 1% level -3.536587 5% level -2.907660 10% level -2.591396
(a) Viết mô hình ước lượng và cho biết mô hình này có nên sử dụng để dự báo không ?
(b) Nếu lãi suất tháng 8/2013 là 7.5% và sai số ước lượng tháng 8/2013 là -0.22%. Hãy dự
báo lãi suất tháng 9/2013 và 10/2013 là bao nhiêu % ? Bài 4.
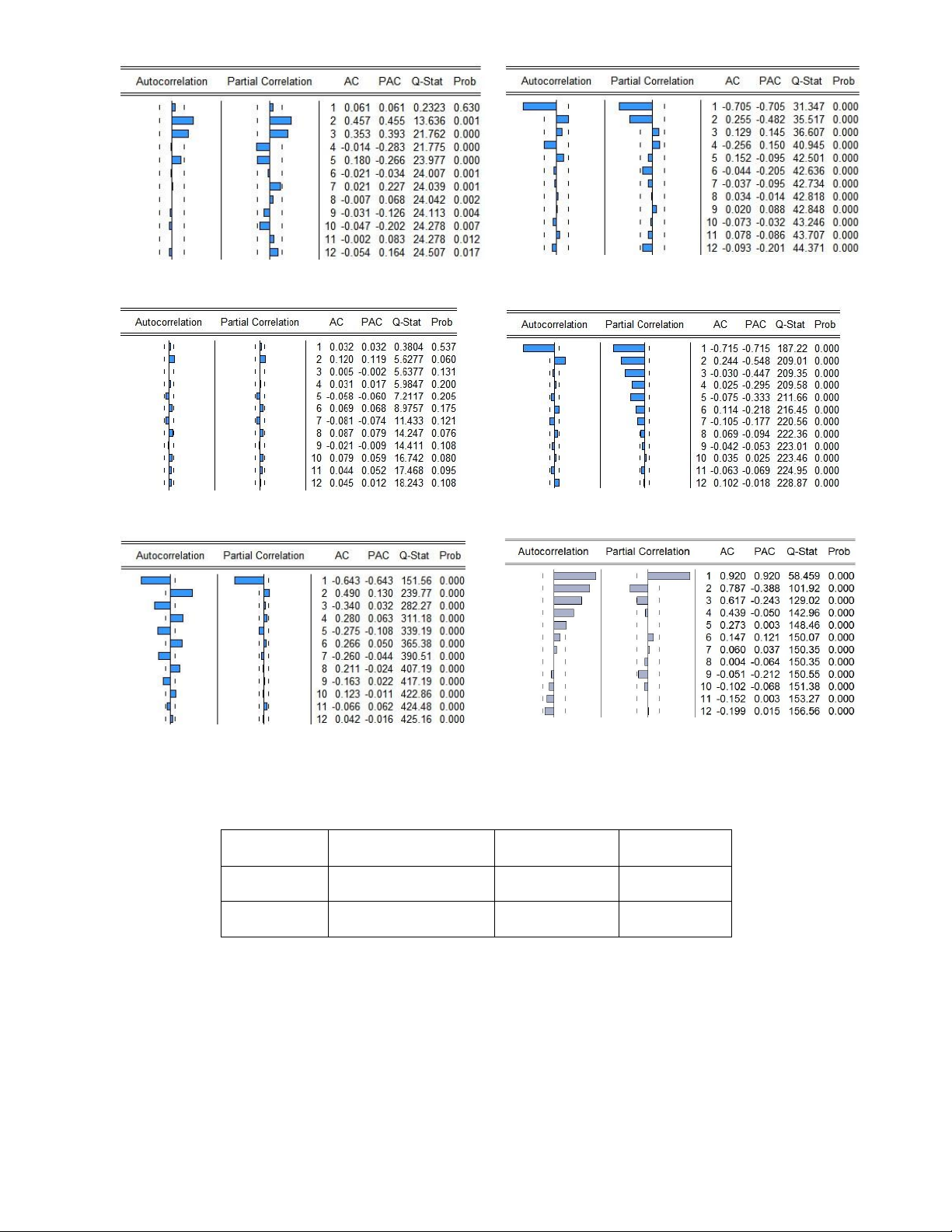
Nhận xét về định dạng bậc ARIMA qua các lược đồ của các dừng sau : Lược đồ 4.1 Lược đồ 4.2 lOMoAR cPSD| 61401654 Lược đồ 4.3 Lược đồ 4.4 Lược đồ 4.5 Lược đồ 4.6
CHƯƠNG 4: RỦI RO TỶ GIÁ
Bài 1. Cho bảng véc tơ trung bình và ma trận hiệp phương sai của 2 chuỗi lợi suất
(chu kỳ 1 ngày) RUSD và RJPY: Tỷ giá Tỷ trọng Trung bình Phương sai JPY 0,43 0,0012 0,0053 USD 0,57 0,0002 0,001
1. Xác định VaR(7 ngày, 95%) biết hiệp phương sai 2 chuỗi lợi suất xấp xỉ bằng 0. Giả
thiết lợi suất có phân phối chuẩn. Cho U0,05 = 1,645
Trung bình của danh mục P= 0.43*(0.0012)+ 0.57*(0.0002)= 6.3*10^-4
Phương sai danh mục P lOMoAR cPSD| 61401654
= 0.43^2* 0.0053+ 2*0.43*0.57* 0+ 0.53^2*0.001= 1.26087^-3
VaR(95%, 7 ngày)= 7* (6.3*10^-4) + 7^(1/2)*(-1.645)* 1.26087^-3
= -1.077 *10^-3 = -0.107%
2. Tính toán lợi suất trung bình (theo tuần) của danh mục P cho 100 tuần, ta lấy ra 10
giá trị lợi suất nhỏ nhất:
0,0022; 0,0045; 0,0024; 0,0067; 0,0054; 0,0041; 0,0061; 0,0040; 0,0038; 0,0037; 0,0015
Tính VaR(7 ngày, 95%) của lợi suất tỷ giá bằng phương pháp mô phỏng lịch sử. K=7
ngày=1 tuần alpha=0.05n= 100 tuần
5% của 100 ngày là 5
(=> giá trị nguyên => chọn giá trị đứng thứ 5 trong dãy)
Dãy (min-max): 0.0015, 0.0022, 0.0024, 0.0037, 0.0038, 0.0040, 0.0041, 0.0045, 0.0054, 0.0061, 0.0067 Kết luận: 0.0038
3. Các định được số ngày thua lỗ thực tế vượt quá giá trị rủi ro cho hai phương pháp
tương ứng là: 9 và 4. Trong 2 phương pháp trên thì phương pháp nào phù hợp? Giải thích.
Ngày thua lỗ vượt quá nhiều hơn = phương pháp kém hiệu quả hơn?
Bài 2. Cho kiểm định tính dừng của chuỗi lợi suất tỷ giá RUSD và kết quả ước lượng mô hình ARIMA như sau: ADF Test Statistic
-14,53 5% Critical Value -2,94109 Dependent Variable: RUSD
Method: ARMA Maximum Likelihood (OPG - BHHH)
Included observations: 2019/03/01 2019/09/01 Variable
Coefficient Std. Error t-Statistic Prob. C -1,27 0,0011 -1181 0,0002 AR(1) -0,152 0,0753 -2,018 0,0348 AR(3) 0,121 0,0754 -1,605 0,0414 lOMoAR cPSD| 61401654
1. Cho kiểm định tính dừng của chuỗi lợi suất tỷ giá RUSD. Từ kết quả sau đây có thể
kết luận chuỗi dừng với mức ý nghĩa 5% không ? |tqs|=14.53
Với 5% level: |tqs|=14.53 > |talpha|=2.94109 => chuỗi DR dừng
2. Từ bảng kết quả, hãy viết phương trình dự báo lợi suất tỷ giá và tính lợi suất tỷ giá
ngày 02/3/2019 khi biết tỷ giá VND/USD ngày 27.2, 28.2, 29.2.2019 và 1.3.2019 lần
lượt là 23.334, 23.354, 23.346 và 23.340 Ước lượng R:
^R=-1.27 – 0.152DRt-1 +0.121DRt-3
3. Đề xuất một ứng dụng cho kết quả dự báo phương trình ARIMA nói trên
CHƯƠNG 5: RỦI RO TÍN DỤNG Mô hình Logit
Bài 1. Giả sử rằng ước lượng được mô hình xác suất tuyến tính sau:
PD = 0.3X1 + 0.2X2 – 0.5X3 ,
trong đó X1 là tỉ số nợ trên vốn chủ sở hữu của khách hàng vay, X2 là độ biến động
thu nhập của khách hàng vay, X3 là chỉ số lợi nhuận của khách hàng vay
1. Tính xác suất vỡ nợ - PD của khách hàng khi X1 = 0.75, X2 = 0.25, X3 = 0.1?
Thay số tính: PD= 0.3*0.75 + 0.2* 0.25 – 0.5*0.1 = 0.225
2. Tính xác suất vỡ nợ nếu tỉ số nợ trên vốn chủ sở hữu là 2.5? Trong trường hợp
này điều kiện rằng buộc giữa X2 và X3 như thế nào? PD = 0.3*2.5 + 0.2X2 –
0.5X3 = 0.75 + 0.2X2 – 0.5X3
Điều kiện là X2, X3 không tương quan với nhau?
3. Hạn chế của mô hình xác suất tuyến tính là gì?
Bài 2. Chạy mô hình logit ngành thương mại có kết quả Dependent Variable: BADFLAG lOMoAR cPSD| 61401654
Method: ML - Binary Logit (Quadratic hill climbing) Sample: 1 738 Variable Coefficient Std. Error z-Statistic Prob. X1 -0.024368 0.010658 -2.286371 0.0222 X2 -0.004168 0.002227 -1.871268 0.0613 C -1.437857 0.543966 -2.643285 0.0082 Mean dependent var 0.035278 S.D. dependent var 0.184607 S.E. of regression 0.183066
Akaike info criterion 0.296190 Obs with Dep=0 711 Total obs 737 Obs with Dep=1 26
Trong đó: X1: là tỷ số tài sản lỏng / tổng tài sản
X2: là tỷ số doanh thu trên tổng tài sản
a.Cho các chỉ tiêu: X1 = 0.32, X2 = 2.3. Tính PD ¿PD=exp
(¿−1.437857−0.024368 X 1– 0.004168 X 2) ¿
1+exp(¿−1.437857−0.024368 X1 –0.004168 X 2)¿ Thay số vô tính
b. Khi tỷ số doanh thu trên tổng tài sản tăng 1 đơn vị (các chỉ tiêu khác không đổi) thì PD giảm bao nhiêu? Bài 3.
Cho một số thông tin của ma trận xác suất chuyển hạng sau 1 năm: Hạng Aaa Baa Caa Default Aaa 90% 10% 0% 0% Baa 10% 80% 5% 5% lOMoAR cPSD| 61401654 Caa 1% 4% 80% 15%
a.Giải thích ý nghĩa của các con số trong bảng trên.
Đang ở hạng Aaa thì 90% giữ nguyên hạng, 10% xuống Baa và 0% xuống Caa hoặc phá sản.
Tương tự với Baa và Caa
b.Có nhận xét gì về các giá trị xác suất trên mỗi hàng trong bảng trên.
Đa số hạng của doanh nghiệp/cá nhân ổn định và chỉ biến động nhỏ quanh hạng
năm trước, chứ ít có sự biến đổi về hạng. Bài 4.
Giả sử rằng 1 ngân hàng đang có 1 danh mục cho vay gồm 2 khoản vay với các đặc trưng sau: Khoản vay Tỷ trọng (Wi) Lãi suất tb(Ri) Độ biến động ( ) 1 0.4 10% 0.007344 2 0.6 12% 0.009604
1. Tính lãi suất của danh mục
R= 0.4*10%+0.6*12%= 0.112= 11.2%
2. Xác định độ biến động của danh mục biết rằng hệ số tương quan về lãi suất
giữa 2 khoản vay là -0.84.
Phương sai của danh mục
= 0.4^2* 0.007344^2+ 2*0.4*0.6* 0.007344*0.009604*(-0.84)+ 0.6^2*0.009604 = 1.3387* 10^-5
Độ biến động (Độ lệch chuẩn) của danh mục
= căn bậc hai của Phương sai = 3.66*10^-3 Bài 5. lOMoAR cPSD| 61401654
Mô hình z-Altman: z = 1,2X1 + 1,4X2 + 3,3X3 + 0,6X4 + 1,0X5 Trong đó:
X1 = tỷ số “vốn lưu động ròng/tổng tài sản”, X2 = tỷ số “lợi nhuận giữ lại/tổng tài
sản”, X3 = tỷ số “lợi nhuận trước thuế và tiền lãi/tổng tài sản”, X4 = tỷ số “thị giá
cổ phiếu/giá trị ghi sổ của nợ dài hạn”, X5 = tỷ số “doanh thu/tổng tài sản”,
Giả sử các chỉ số tài chính của 1 doanh nghiệp vay vốn tại ngân hàng như sau: X1 =
0.2; X2 = 0; X3 = -0.2; X4 = 0.1; X5 = 2.0. Nêu nhận xét về các chỉ số tài chính của
doanh nghiệp nào? Tính điểm số Z và đánh giá.
X1 (Vốn lưu động ròng / Tổng tài sản = 0.2): Tỷ số này cho thấy khả năng thanh
toán ngắn hạn của doanh nghiệp. Với X1=0.2, doanh nghiệp có một mức vốn lưu
động ròng chiếm 20% tổng tài sản, cho thấy doanh nghiệp có khả năng thanh toán
ngắn hạn ở mức trung bình.
X2 (Lợi nhuận giữ lại / Tổng tài sản = 0): Đây là chỉ tiêu về tích lũy lợi nhuận.
X2=0 cho thấy doanh nghiệp không có lợi nhuận giữ lại hoặc có rất ít tích lũy từ
hoạt động kinh doanh trước đó. Điều này có thể chỉ ra khả năng sinh lời kém hoặc
việc phân phối hết lợi nhuận cho cổ đông.
X3 (Lợi nhuận trước thuế và lãi vay / Tổng tài sản = -0.2): Tỷ số này đo lường
hiệu quả sinh lời của tài sản. Với X3=−0.2, doanh nghiệp đang lỗ trước thuế và lãi
vay, nghĩa là khả năng sinh lợi từ tài sản là rất kém, có thể khiến doanh nghiệp gặp
khó khăn trong việc chi trả các khoản nợ và chi phí khác.
X4 (Thị giá cổ phiếu / Giá trị ghi sổ của nợ dài hạn = 0.1): Tỷ số này đo lường
độ an toàn của vốn cổ đông so với nợ dài hạn. Với X4=0.1, doanh nghiệp có thị giá
cổ phiếu thấp hơn nhiều so với nợ dài hạn, điều này cho thấy khả năng tài trợ vốn
bằng vốn chủ sở hữu khá yếu.
X5 (Doanh thu / Tổng tài sản = 2.0): Đây là tỷ số về hiệu quả sử dụng tài sản để
tạo ra doanh thu. Với X5=2.0, doanh nghiệp có doanh thu gấp đôi tổng tài sản, cho
thấy doanh nghiệp có khả năng tạo ra doanh thu tốt từ tài sản của mình, mặc dù vẫn không sinh lợi.
Thay số vào mô hình z-Altman: lOMoAR cPSD| 61401654
z = 1,2*0.2 + 1,4*0 + 3,3*(-0,2) + 0,6*0,1 + 1,0*2,0 = 1,64
Dựa trên điểm số Z: •
Nếu Z>2.99: Doanh nghiệp thuộc nhóm an toàn, ít có nguy cơ phá sản. •
Nếu 1.81Doanh nghiệp thuộc nhóm "xám" với rủi ro trung bình. •
Nếu Z<1.81: Doanh nghiệp thuộc nhóm nguy cơ cao có thể phá sản.
Với Z=1.64, doanh nghiệp này nằm dưới ngưỡng 1.81, thuộc nhóm có nguy cơ
phá sản cao. Điều này cảnh báo rằng ngân hàng cần thận trọng khi cấp tín dụng
cho doanh nghiệp này, vì các chỉ số tài chính cho thấy doanh nghiệp có hiệu quả
sinh lợi kém và không có tích lũy từ lợi nhuận giữ lại, trong khi khả năng thanh
toán và tỷ số an toàn vốn cổ đông cũng ở mức thấp.
Bài 6. Ngân hàng A nắm giữ 1 danh mục gồm 10 trái phiếu xếp hạng AA với tổng
giá trị là 200 triệu đồng. Xác suất vỡ nợ trong 1 năm của mỗi nhà phát hành trái
phiếu là 5% và tỷ lệ thu hồi tiền mặt của mỗi nhà phát hành bằng 40% a.Tính EL.
EL = PD * LGD * EAD = 0.05 * 0.6 * 200 = 6 (triệu đồng) Giải thích
PD: xác suất vỡ nợ của nhà phát hành trái phiếu (5%)
LGD: phần tổn thất nếu vỡ nợ = 1 – tỷ lệ thu hồi tiền mặt = 1 – 40% = 0.6
EAD: Giá trị tài sản tại thời điểm vỡ nợ = 200 triệu đồng
b.Giải thích ý nghĩa của “vốn kinh tế”.
Vốn kinh tế là mức vốn mà một tổ chức tài chính, như ngân hàng, cần duy trì để bảo vệ
chống lại rủi ro tổn thất có thể xảy ra do các rủi ro tín dụng, thị trường và hoạt động. Nó
được xác định dựa trên xác suất các tổn thất vượt quá tổn thất kỳ vọng trong một khoảng
thời gian nhất định và thường được dùng để:
1. Giảm thiểu rủi ro vỡ nợ: Đảm bảo rằng ngân hàng có đủ vốn để đối phó với các
rủi ro không mong muốn, giảm nguy cơ mất khả năng thanh toán. lOMoAR cPSD| 61401654
2. Tăng cường ổn định tài chính: Củng cố lòng tin của cổ đông và nhà đầu tư vào
khả năng tồn tại và khả năng chi trả của ngân hàng.
3. Tuân thủ quy định: Các cơ quan quản lý yêu cầu các ngân hàng phải giữ mức
vốn tối thiểu, chẳng hạn như Basel II và Basel III, để đảm bảo tính ổn định của hệ thống tài chính.