Bài tập nâng cao chuyên đề hình học không gian

Tuyển tập 99 bài tập nâng cao chuyên đề hình học không gian, có đáp án và lời giải chi tiết, dành cho giáo viên và học sinh ôn thi học sinh giỏi, học sinh năng khiếu và chuyên Toán..Mời bạn đọc đón xem.

24 12 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 1

BÀI TẬP CHUYÊN ĐỀ HÌNH HỌC KHÔNG GIAN

(Dành cho giáo viên ôn thi học sinh giỏi, học sinh năng khiếu và chuyên toán)

 Câu 1: (HSG NAM ĐỊNH 2014-2015) Cho tứ diện đều

ABCD

có cạnh bằng 1, hai điểm

và

lần lượt nằm trên các đoạn

và

, sao cho

BN DN



a) Chứng minh rằng

AD BC



. Tìm điểm

cách đều 4 đỉnh của tứ diện

ABC

b) Khi

lần lượt là trung điểm của

và

, gọi







là mặt phẳng chứa

và song song

với

Tính chu vi thiết diện tạo bởi







và tứ diện

ABC

c) Tìm giá trị lớn nhất và giá trị nhỏ nhất của

khi

thay đổi trên các đoạn

và C

 Lời giải

a) +) Gọi

là trực tâm tam giác

ABC

, suy ra

( )

DH ABC



Chứng minh được

( )

BC ADH BC AD

  

+) Trong (

ADH

) dựng đường trung trực của đoạn

cắt

tại

, suy ra IA=I

(1)

Mặt khác

IHA IHB IHC

    

suy ra

IA IB IC

 

. (2)

Từ (1), (2)

IA IB IC ID

   

hay I là điểm cách đều 4 đỉnh của tứ diện ABC

b) Trong mặt phẳng (

DMC

) kẻ

(

K DM



) suy ra

( )



chính là (

BNK

Trong mặt phẳng (

ABD

) gọi

P BK AD

 

suy ra

( )



cắt tứ diện

ABCD

theo thiết diện là tam

giác

BNP

Vì

lần lượt là trung điểm của

và

1 1

3 3

PD AD

  

Áp dụng định lý côsin trong các tam giác

; ;

BDP PDN BDN

  

ta có

7 7 3

; ;

3 6 2

PB PN BN  

Vậy chu vi

BNP



là

7 3

BNP





c) +) Đặt



, với

0 1

 

 

. Khi đó ta có:

BM x BA



 

và

DN x DC



 

Ta có:

. ( ) . (1 ).

DN x DC BN BD x BC BD BN x BC x BD

        

        

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 2

Do đó:

. (1 ). .

MN BN BM x BC x BD x BA

     

     

2 2 2 2 2 2 2 2

(1 ) 2 (1 ) . 2 . 2 (1 ) .

MN x BC x BD x BA x x BC BD x BC BA x x BD BA

        

     

2 2 1

x x

  

+) Xét





2 2 1

f x x x

  

trên đoạn





0;1

, ta có:

       

1 1

max 0 1 1, min

2 2

f x f f f x f

 

    

 

 

Vậy,

đạt giá trị nhỏ nhất bằng

khi

lần lượt là trung điểm của

đạt giá trị lớn nhất bằng 1

khi



hoặc



 Câu 2: (HSG ĐÀ NẴNG NĂM 2011-2012) Cho hình hộp

. ' ' ' '.

ABCD A B C D

Trên cạnh

lấy điểm

khác

và

Gọi (

) là mặt phẳng đi qua

và song song với mặt phẳng

( ').

ACD

a) Trình bày cách dựng thiết diện của hình hộp và mặt phẳng (

b) Xác định vị trí của

để thiết diện nói trên có diện tích lớn nhất.

 Lời giải

Trong mp(

ABCD

), qua

vẽ đường thẳng song song với

cắt

DB, BC

lần lượt tại

E, N

Trong mp(

BDD’B’

), qua

vẽ đường thẳng song song với

D’O

(

O=AC



) cắt

B’D’

tại

Trong mp(

A’B’C’D’

), qua

vẽ đường thẳng song song với

cắt

A’D’, D’C’

lần lượt tại

R, Q

Trong mp(

AA’D’D

), qua

vẽ đường thẳng song song với

AD’

cắt

AA’

tại

Trong mp(

CC’D’D

), qua

vẽ đường thẳng song song với

CD’

cắt

CC’

tại

Thiết diện là lục giác

MNPQRS

b. Do các mặt đối diên của hình hộp song song nên các cạnh đối của lục giác thiết diện

MNPQRS

song song và 3 cặp cạnh đó lần lượt song song với các cạnh tam giác

ACD’

 Các tam giác

JKI

ACD’

RQI

JMS

NKP

đồng dạng



' '

MJ MA NC NK PC PK QD QI

MN MB NB NM PC PQ QC QP

      



MJ=NK

và

PK=QI

 Các tam giác

RQI

JMS

NKP

bằng nhau (gọi diện tích của chúng là

và gọi diện tích các tam

giác

JKI

ACD’

lần lượt là

)

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 3

Đặt

;



ta có điều kiện

0 1

 

và có:

2 2 2

S JM AM AM

S AC DC AB

     

   

 

 



= k

 

2 2 2

S JK JM MK JM MK

S AC AC AC AC



     

     

     

     



(

+1)

 Diện tích thiết diện:

2 1

S S S

 

1 3 1 3

2 ( ) 2

2 4 2 2

S S k k S k

 

 

       

 

 

 

 

 

(dấu bằng xảy ra 



)

lớn nhất 





là trung điểm của

 Câu 3: (HSG ĐÀ NẴNG NĂM 2011-2012) Cho hình chóp

S.ABCD

có đáy

ABCD

là hình

bình hành và

là trung điểm của

Một mặt phẳng (

) chứa

và lần lượt cắt các cạnh

tại các điểm

khác

. Chứng minh rằng:

4 ' ' 3

3 2

SB SD

  

 Lời giải

Lấy



B'D'

và



ta có:

S, O, I

là các điểm chung của 2 mặt phẳng (

SAC

) và (

SBD

)



thẳng hàng.Và

là trọng tâm các mặt chéo

SAC





Vẽ

BP // B'I

và

DN // D'I





P N SO





OP ON



. Đặt

;

' '

SD SB

x y

SD SB

 



2 3

' ' 2

SB SD SP SN SO

x y

SB SD SI SI SI

       



, [1;2]

x y



(*)

Suy ra:

1 1 3 2 4

x y xy x y

 

   

 



 

Từ (*):

1 2

 



3 2 0

x x

  



(3 ) 2

x x

 



x y

 

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 4



3 3





x y







1 1 3

x y

 

 Câu 4: (HSG ĐỀ 046) Cho lăng trụ tam giác

. ’ ’ ’.

ABC A B C

Trên tia đối của tia

lấy điểm

sao cho

Gọi

là trung điểm của

a) Xác định thiết diện của lăng trụ cắt bởi mặt phẳng (

MEB’

)

b) Gọi

D = BC



(

MEB’),

K = AA’



(MEB

’). Tính tỷ số

và

 Lời giải

a) Ta có D =



; K





Suy ra thiết diện là tứ giác DEKB’

b, Xét tam giác MBB’ có

1 1

' 3 ' 3

AK MA AK

BB MB AA

   

+) Trong (ABC). Dựng EN // AB (N



BC), khi đó EN=

+) Xét tam giác DBM có:

1 1

3 2

DN NE

DN BN

DB BM

   

Suy ra D là trung điểm CN. Vậy



 Câu 5: (HSG ĐỀ 046) Cho tứ diện

ABCD

Tìm M trong không gian sao cho

2 2 2 2

MA MB MC MD

  

đạt giá trị nhỏ nhất

 Lời giải

Gọi G là trọng tâm của tứ diện ta có:

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 5

       

      

       

        

    

 

   

       

    

2 2 2 2

2 2 2 2 2

2 2

4 2 ( )

MA M B M C M D M A M B M C M D

M G GA M G GB M G G C MG GD

M G M G GA GB G C GD GA GB GC G D

M G GA GB GC G D

GA GB

 

2 2

GC G D

Dấu “=” xảy ra khi và chỉ khi M



G. Vậy:

  

2 2 2 2

MA MB MC MD

đạt giá trị nhỏ nhất khi M

là trọng tâm của tứ diện.

 Câu 6: (HSG ĐỀ 047) Cho hình chóp tứ giác

S ABCD

có đáy

ABCD

là hình vuông cạnh

bằng

, các cạnh bên bằng nhau và bằng





3 , 0

a a



. Hãy xác định điểm

sao cho

cách đều

tát cả các đỉnh của hình chóp

S ABCD

và tính độ dài

. Lời giải

Gọi

I AC BD

 

. Do

SA SB SC SD

  

nên các tam

giác

SAC, SBD

cân tại đỉnh

nên

vuông góc với

suy ra

vuông góc với mặt phẳng (

ABCD

Dễ thấy mọi điểm nằm trên đường thẳng

cách đều

các đỉnh

A, B, C,

Trong tam giác

SIC

, dựng trung trực của cạnh

cắt

đường thẳng

tại

suy ra

OS OA OB OC OD

   

Ta có:

2 2 2 2

. 3 .3 9 9 2

. .

2 2 9

SM SC a a a a

SM SC SO SI SO

SA IA a a

     

 

. Vậy

9 2

SO 

 Câu 7: (HSG ĐỀ 047) Cho hình chóp

S.ABC

có đường thẳng

vuông góc với mặt phẳng

(

SBC

). Gọi

là hình chiếu của

lên mặt phẳng

(ABC)

. Chứng minh rằng đường thẳng

vuông

góc với đường thẳng

, biết rằng

2 2 2 2

1 1 1 1

SH SA SB SC

  

. tứ giác

S ABCD

có đáy

ABCD

là hình

vuông cạnh bằng

, các cạnh bên

. Lời giải

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 6

Gọi

là giao điểm của đường thẳng

và

; trong mặt

phẳng (

SBC

) gọi

là giao điểm của đường thẳng qua

vuông góc với

Ta có

vuông góc với

và

nên

vuông góc với mặt

phẳng (

SAH

) suy ra

vuông góc với

Trong tam giác vuông

SAK

ta có

2 2 2

1 1 1

SH SA SK

 

, kết hợp

với giả thiết ta được

2 2 2

1 1 1

SK SB SC

 

(1)

Trong tam giác vuông

SDC

ta có

2 2 2

1 1 1

SK SD SC

 

(2)

Từ (1) và (2) ta được

SB SD



, từ đó suy ra

B D



hay suy ra

vuông góc với

 Câu 8: (HSG ĐỀ 047) Cho tứ diện

ABCD

thỏa mãn điều kiện

, ,

AB CD BC AD AC BD

  

và một điểm

thay đổi trong không gian. Tìm vị trí của điểm

sao cho tổng

XA XB XC XD

  

đạt giá trị nhỏ nhất.

. Lời giải

Gọi

là trọng tâm của tứ diện;

M, N, P, Q

lần lượt là

trung điểm của các cạnh

AB, CD, BC,

Ta có tam giác

ACD

bằng tam giác

BCD

nên

AN BN



suy ra

MN AB



, tương tự ta chứng minh được

MN CD



và đường thẳng

vuông góc với cả

hai đường thẳng

BC,

Từ đó suy

GA GB GC GD

  

Ta có

. . . .

XA GA XB GB XC GC XD GD

XA XB XC XD

  

   

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 7

. . . .

XA GA XB GB XC GC XD GD

  



       





. 4.

XG GA GB GC GD GA

   

 

    

Dấu bằng xảy ra khi và chỉ khi

trùng với điểm

. Vậy

XA XB XC XD

  

nhỏ nhất khi và

chỉ khi

là trọng tâm của tứ diện

ABCD

 Câu 9: (HSG ĐỀ 048) Cho hình chóp

S ABCD

, có đáy

ABCD

là hình thang cân





/ /

AD BC

và





2 ; , 0

BC a AB AD DC a a

    

Mặt bên

SBC

là tam giác đều. Gọi

là giao điểm của

và

. Biết

vuông góc với

a) Tính

b) Mặt phẳng







qua điểm

thuộc đoạn

(

khác

O D

) và song song với hai đường thẳng

và

. Xác định thiết diện của hình chóp

S ABCD

cắt bởi mặt phẳng

( )



). Biết

MD x



Tìm

để diện tích thiết diện lớn nhất.

 Lời giải

a) Dễ thấy đáy ABCD là nữa hình lục

giác đều cạnh a.

Kẻ DT//AC (T thuộc BC). Suy ra CT

= AD = a và DT vuông góc S

Ta có: DT = AC =

Xét tam giác SCT có SC=2a, CT=a,



120

SCT 

ST a

 

Xét tam giác vuông SDT có DT=

7 2

ST a SD a

  

b) Qua M kẻ đường thẳng song song

với AC cắt AD, DC lần lượt tại N,P.

Qua M, N, P kẻ các đường thẳng song song với SD cắt SB, SA, SC lần lượt tại K, J, Q. Thiết

B C

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 8

diện là ngũ giác NPQKJ.

Ta có: NJ, MK, PQ cùng vuông góc với NP.

NPQKJ NMKJ MPQK

S S S  

1 1

(NJ MK)MN (MK PQ)MP

2 2

  

( ).

NJ MK NP 

(do

NJ=PQ).

Ta có:

. . 3

NP MD AC MD x a

NP x

AC OD OD

    

2 .

2( 3)

a x

NJ AN OM SD OM

NJ a x

SD AD OD OD

 



 

 

      

 

2 . 3

. 2

( 3 )

3 3

a a x

KM BM SD BM

KM a x

SD BD BD



     

Suy ra:

NPQKJ

1 2

2( 3) ( 3 ) 3 2(3 2 3 )

a x a x x a x x

 

    

 

 

1 1 3 3

(3 2 3 )2 3 (3 2 3 ) 2 3

3 4 3

a x x a x x a

 

     

 

Diện tích NPQKJ lớn nhất bằng

3 3

khi

x a

 Câu 10: (HSG ĐỀ 049) Cho hình chóp đều

.S ABCD

cạch đáy bằng

, chiều cao bằng

Tính diện tích thiết diện của hình chóp bị cắt bởi mặt phẳng

 



chứa

và vuông góc với mặt

phẳng

 

SAB

 Lời giải

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 9

Gọi

là tâm hình vuông

ABCD

M N

lần lượt là trung điểm của

và

. Khi đó

là trung

điểm của

và

vuông góc





SMN

. Kẻ

vuông góc



vuông góc mp





SAB









CDI



 

Từ

kẻ đường thẳng song song với

cắt

SB SA

lần lượt tại

,E F



EF / / / /

AB CD

.Thiết diện

là hình thang

CDEF

Ta có +)

17a

OMSOSM



;

MN.SO

IN 

172

a15

INSNSI



a15

AB.SI



Diện tích thiết diện:

1717

a64

IN)EFCD(

CDEF



 Câu 11: (HSG HÀ NAM) Cho hình lập phương

ABC

A’B’C’D’

có cạnh

. Gọi

là tâm

của hình vuông

CDD’C’

là trung điểm của cạnh

a. Dựng thiết diện của hình lập phương

ABC

A’B’C’D’

cắt bởi mặt phẳng (

AKI

). Tính diện tích

của thiết diện theo

b. Tính góc tạo bởi hai đường thẳng

A’D’

và

với

là giao điểm của (

AKI

) và

CC’

 Lời giải

a, +) Gọi

là giao điểm của

và

là giao điểm của

và

CC’

là giao điểm của

và

DD’

Thiết diện là tứ giác

AKQN

Chứng minh được

AKQN

là hình thang có 2 đáy là

+) Chứng minh được

là trung điểm của

là trung điểm

là trung điểm của

1 1 1

. . 3 .

2 2 4

JKQ

AKQN JAN JKQ JKQ

JAN

JK JQ

S S S S

S JA JN



  



      

1 1 1

2 ' 3 3

CQ ND QC CQ a

     

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 10

+) Tính được

13 5 10

; ;

6 2 3

a a a

KQ JK JQ  

2 2 2

cos

2 .

sin 1 cos

1 14

. .sin

2 12

3 .

JKQ

AKQN JKQ

JQ JQ KQ

KJQ

JK JQ

KJQ KJQ

S JK JQ KJQ

S S



 

 

  

 

b, Vì

A’D’

nên góc tạo bởi

A’D’

bằng góc tạo bởi

Có

2 2 2

AC AB AD AA a

 

   

Tính được

19 10

; ; .

3 3

a a

AQ AD a QD  

2 2 2

cos .

2 .

AQ AD QD

QAD

AQ AD

 

 

 Câu 12: (HSG ĐỀ 052) Cho hình chóp

S ABC

có





SA ABC



và

SA a



, đáy

ABC

là tam

giác vuông tại

với

AB a





BAC

 

. Gọi

là điểm di động trên cạnh

là hình chiếu

vuông góc của

trên

a) Chứng minh

vuông góc với

b) Đặt

AI x



(

0 3

x a

 

). Tính khoảng cách từ

đến

theo

và

. Tìm các giá trị của

để khoảng cách này có giá trị lớn nhất, nhỏ nhất.

 Lời giải

a) Ta có

là hình chiếu của

trên mặt phẳng





ABC

SJ BI



AJ BI

 

(định lí ba đường vuông góc).

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 11

SJ BI



tại

nên





SJ d S BI





cos 2 .cos30 3

AC AB BAC a a

  



sin 2 .sin 30

BC AB BAC a a

  





2 2 2 2 2 2

3 4 2 3

BI BC CI a a x a x ax

       

2 2

4 2 3

BI a x ax

   

* Hai tam giác vuông

AJI

và

BCI

có



AIJ BIC



(đối đỉnh) nên chúng đồng dạng, suy ra

AJ AI

BC BI



2 2

. .

4 2 3

BC AI a x

a x ax

  

 

* Xét tam giác vuông

SAJ

ta có:

2 2 4 3 2 2

2 2 2 2

16 8 3 5

4 2 3 4 2 3

a x a a x a x

SJ SA AJ a

a x ax a x ax

 

    

   

Vậy

 

4 3 2 2

2 2

16 8 3 5

4 2 3

a a x a x

d B SI

a x ax

 



 

+) Tìm

để

đạt min, max:

Trong mặt phẳng





ABC

AJ JB



nên

thuộc đường tròn





đường kính

chứa trong mặt

phẳng này. Rõ ràng

cũng thuộc





Mặt khác

là giao điểm thứ hai của

với





nên khi

di động trên

thì

di động trên

cung nhỏ

của





Do đó:

đạt min



đạt min

I A

 

 

đạt max



đạt max

I C

 

x a

 

 Câu 13: (HSG ĐỀ 053) Cho hình lập phương

ABC

A’B’C’D’

cạnh

. Gọi

M, N, P

lần lượt

là trung điểm của các đoạn thẳng

AD, BB’, C’D’

. Xác định thiết diện cắt bởi mặt phẳng (

MNP

) với

hình lập phương

ABC

A’B’C’D’

. tính theo

diện tích thiết diện đó.

 Lời giải

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 12

Gọi

là trung điểm của

, khi đó

/ / / /( ')

MS BD MS BDC



và

/ / ' / /( ')

NS C D NS BDC



suy ra





/ /( ')

MNS BDC

. Do





/ / '

MNS BC

nên (

MNS

) cắt (

BCC’B’

) theo giao tuyến qua

song song với

BC’

cắt

B’C’

tại





/ / / / ' '

MNS BD B D

nên (

MNS

) cắt (

A’B’C’D’

) theo giao tuyến qua

song song với

B’D’

cắt

D’C’

tại

P’

, do

P’

là trung điểm của

C’D’

nên

P’

trùng với

. Do





/ / ' '

MNS C D

nên (

MNS

) cắt

(

CDD’C’

) theo giao tuyến qua

song song với

C’D

cắt

DD’

tại

Do đó thiết diện cắt bởi (

MNP

) với hình lập phương

ABC

A’B’C’D’

là lục giác đều

MSNQPR

cạnh

MR 

và có tâm là

. Suy ra:

OMS

1 3 3

6 6. . .sin 60

2 4

MSNQPR

S S OM OS  

. Vậy

3 3

MSNQPR

S 

 Câu 14: (HSG ĐỀ 053) Cho hình chóp

S.ABCD

có đáy

ABCD

là hình thang vuông tại

và

= 2

. Các mặt phẳng (

SAC

) và (

SBD

) cùng vuông góc với mặt phẳng đáy.

Biết góc giữa hai mặt phẳng (

SAB

) và (

ABCD

) bằng 60

. Tính khoảng cách giữa hai đường thẳng

và

 Lời giải

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 13

Gọi

H AC BD

 

( ) ( )

SH SAC SBD

  





SH ABCD

 

và

BH BD



Kẻ

HE AB







AB SHE

 



góc giữa hai mặt phẳng (

SAB

) và (

ABCD

) là



SHE

nên



SHE 

Mà

1 2

3 3

HE AD 

2 3

SH 

Gọi

là trung điểm



ABCO

là hình vuông cạnh

BO AC

 

, mà

BO SH







BO SAC

 

Gọi

I AC BO

 

, kẻ

CK SI



mà

CK BO



(do





BO SAC



)







CK SBD



Có

CD BO













, ,( ) ,( )

d CD SB d CD SBD d C SBD CK

   

Nhận thấy

là trọng tâm tam giác

BCO

1 2

3 6

IH IC  

2 2

5 2

IS IH HS   

Trong tam giác

SIC

có:

1 1 . 2 3

. .

2 2 5

SIC

SH IC a

S SH IC SI CK CK

    

Vậy

 

2 3

d CD SB 

 Câu 15: (ĐỀ THI OLYMPIC 11 – BIM SON 2012) Cho hình chóp

S ABCD

có đáy là hình

vuông tâm

, cạnh

và

vuông góc với mặt

phẳng





ABCD

. Gọi

M N

là trung điểm của

và

. Biết góc giữa đường thẳng

và mặt

phẳng





ABCD

bằng



1. Tính độ dài các đoạn thẳng

và

theo

2. Tính cosin của góc giữa đường thẳng

với mặt phẳng





SBD

 Lời giải

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 14

Gọi

là trung điểm của



MI SO

( )

 

MI ABCD

. Do đó góc giữa

và





ABCD

là góc



MNI



 MNI

2 2 2 0

2 . .cos 45

  IN IC NC IC NC

3 2 3 2 2 5

2. . .

4 2 4 2 2 8

 

   

 

 

a a a a a

 

cos60 2

 

NI a

.tan 60

  

MI NI

  

SO MI

2. Ta có

( )





 







AC BD

AC SBD

AC SO

. Gọi

H K

là trung điểm của

và

// // ( ), ( )

   

MH KN AC MH SBD KN SBD

Do đó

là hình chiếu của

lên





SBD

Gọi

 

E MN HK

suy ra góc



giữa

và





SBD

là góc



MEH

+) Do

1 1 2

2 2 4

   

MH OA OC KN

, nên

MHNK

là hình bình hành.



là trung điểm của

1 10

2 4

  

ME MN

Do tam giác

MHE

vuông tại

nên

2 10 1

sin :

4 4

  

MH a a





cos 1 sin

  

 

 Câu 16: (ĐỀ THI HSGTPDN - Toan11 - 2013) Cho hình chóp

S ABCD

có đáy

ABCD

là

hình bình hành tâm

và

là trung điểm của

. Một mặt phẳng





chứa

và lần lượt cắt

các cạnh

SB SD

tại các điểm

 

B D

khác

. Chứng minh rằng:

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 15

 

 

SB SD

. b)

4 3

3 2

 

  

SB SD

 Lời giải

Lấy

 

 

I AM B D

và

 

O AC BD

Ta có:

, ,

S O I

là các điểm chung của

mặt phẳng





SAC

và





SBD



, ,

S O I

thẳng hàng.

Và

là trọng tâm các mặt chéo

 

+ Vẽ



BP B I

và



DN D I





, 

P N SO

 

OP ON

. Đặt

; 

 

SD SB

x y

SD SB



2 3

       

 

SB SD SP SN SO

x y

SB SD SI SI SI

, [1;2]

 

x y

(*)

+ Suy ra:

1 1 3 2 4

 

   

 



 

x y xy x y

+ Từ (*):

1 2

 

3 2 0

   

x x

(3 ) 2

  

x x

 

3 3

 



 

x y

1 1 3

  

x y

 Câu 17: (ĐỀ THI OLYMPIC 11 – BIM SON 2013) Cho hình chóp

S ABCD

có đáy là hình

bình hành tâm

là điểm di động trên

và





là mặt phẳng qua

và song song với

. Tìm các giao điểm

và

của





với

và

. Chứng minh

 

SB SD SC

SH SK SM

là một hằng số.

 Lời giải

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 16

Gọi

là trung điểm của

;

 

I HK AM

Ta có

// , //

HK BD OJ AM

do đó

2   

SB SD SC SO SC

SH SK SM SI SM

 

 

SI IO SM MC

SI SM

2 2 1   

IO MJ

SI SM

1 2 2 1

   

IO IO

SI SI

 Câu 18: (ĐỀ THI OLYMPIC 11 – BIM SON 2013) Cho lăng trụ đứng

  

ABC A B C

có đáy

là tam giác vuông tại

, , 2 ,

 

B AB a AC a

góc giữa

đường thẳng



và mặt phẳng





 

BCC B

bằng



. Gọi

M N

lần lượt là trung điểm của

và



. Tính khoảng cách từ



tới mặt phẳng





AMN

 Lời giải

2 2

  

BC AC AB a

Ta có

, ( )

  

   

AB BC AB BB AB BCC B

Nên góc giữa



và





’ ’

BCC B

là góc





AB B



' 30

 AB B

cot 30 3



   

BB AB a

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 17

Gọi

  

   I AN A B O AB A B

Khi đó

là trọng tâm tam giác



ABB

nên

2 1

3 3

 

   BI BO A B A I BI

( )



 I A B AMN

nên

( ,( )) 2 ( , ( )) 2



 d A AMN d B AMN h

BAMN

là tứ diện vuông tại

nên

2 2 2 2

1 1 1 1

  

h AB BM BN

2 2 2 2

1 4 4 11 33

3 3 3 11

     

a a a a

Vậy

2 33

( , ( ))





d A AMN

 Câu 19: (ĐỀ THI OLYMPIC 11 – BIM SON 2015) Cho hình chóp

.S ABCD

có đáy là hình

vuông cạnh

6SA a

vuông góc với mặt

phẳng

 

ABCD

a) Tính góc giữa đường thẳng

với mặt phẳng

 

SCD

b) Gọi

là điểm bất kì trong không gian, tìm giá trị nhỏ nhất của biểu thức

2 2 2 2 2

     MA MB MC MD MS

 Lời giải

a) Gọi

là tâm của hình vuông,

là trung điểm của

suy ra

//OE SB

Ta có

CD AD

CD SA

suy ra

 

CD SAD

Kẻ

AH SD

H SD  AH CD

Gọi

là trung điểm của

suy ra

//OF AH

( ) OF SCD

nên

là hình chiếu vuông góc

của

lên mp

 

SCD

( ) AH SCD

Gọi



là góc giữa

và

 

SCD

, khi đó



( , ) OE EF OEF



Ta có

2 2

1 7

2 2

     

SB SA AB a OE SB



 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 18

2 2 2 2

1 1 1 7 42 1 42

6 7 2 14

       

a a

AH OF AH

AH SA AD a

6 6

sin arcsin

7 7

    

 

b) Với điểm

bất kì ta luôn có

2 2 2 2 2

     

    

MA MB MC MD MS

2 2 2 2 2

( ) ( ) ( ) ( ) ( )

         

         

MI IA MI IB MI IC MI ID MI IS

2 2 2 2 2 2

5 2 ( )

          

     

MI IA IB IC ID IS MI IA IB IC ID IS

Chọn

thỏa mãn

0 4 0 4

          

         

IA IB IC ID IS IO IS IS IO

Suy ra

là điểm thuộc đoạn

sao cho



IS IO

Khi đó

2 2 2 2 2 2 2 2 2 2 2

5           

MI IA IB IC ID IS IA IB IC ID IS

Suy ra



nhỏ nhất khi



M I

Ta có

2 2 2

  

SO SA OA

Suy ra

2 2

2 2 2 2 2 2 2 2

2 2

2 2 25

        

BD AC

IA IB IC ID IS IO IO SO

2 2 2 2 2 2 2 2

16 4 16 4 36

25 25 25 5 5

        

IO AC SO SO AC SO SO AC

Vậy



nhỏ nhất bằng

khi



M I

 Câu 20: (ĐỀ THI OLYMPIC 11 – BIM SON 2014) Cho hình chóp

S.ABC

là trọng tâm

của tam giác

Một mặt phẳng

( )



cắt các tia

 , , ,

SA SB SC SG

theo thứ tự tại

, , ,

   

A B C G

Chứng minh rằng

3  

   

SA SB SC SG

 Lời giải

Đặt

, , ,

   

   

SA SB SC SG

a b c d

SA SB SC SG

. Theo bài ra ta suy ra





 

SA aSA





 

SB bSB





 

SC cSC





 

SG d SG

là trọng tâm của tam giác

ABC

nên

( )

  

   

SG SA SB SC

Suy ra

( )

   

  

   

SG aSA bSB cSC

Mặt khác do

, , ,

   

A B C G

đồng phẳng nên từ đẳng thức trên ta có

1 3

3 3 3

      

a b c

a b c d

d d d

3   

   

SA SB SC SG

 Câu 21: (ĐỀ THI OLYMPIC 11 – BIM SON 2014) Cho lăng trụ đứng

  

ABC A B C

có đáy

ABC

là tam giác cân,

 

AB AC a

, góc



120

 

BAC





BB a

là trung điểm của



. Tính cosin

của góc giữa hai mặt phẳng





ABC

và







AB I

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 19

 Lời giải

Gọi



 

K BC B I

Suy ra

( ) ( )



 

AK ABC AB I

Kẻ

 

AH AK H BC

Kẻ

/ / ,

 



HE BB E B I

, do

( )





BB ABC

nên

( )



HE ABC

 

HE AK

Khi đó

( )



AK AHE

Góc giữa hai mặt phẳng





ABC

và







AB I

là



( , ) 

AH AE HAE



2 2 2 0 2

2 . .cos120 3 3

     

BC AB AC AB AC a BC a

+) Ta thấy

là đường trung bình của tam giác



KBB

nên

là trung điểm của

, do đó

2 2 3

 

BK BC a

2 2 2 0 2

2 . .cos 30 7 7

     

AK AB BK AB BK a AK a



2 2 2

9 14 3

cos

2 . 9

2 21

cos

 

    

AK BK AB AK a

AKB HK

AK BK

AKB

2 2

  

AH HK AK

+) Ta có

. 7



   



HE KH BB KH a

BB KB KB



tan tan

  

HAE



1 7 10 30

1 tan 1 cos

cos 3 3 10

       

 



 Câu 22: (HSG ĐỀ 059) Cho hình chóp

SABC

có





SC ABC



và tam giác

ABC

vuông tại

Biết

,aAB



3aAC  và góc giữa hai mặt phẳng

(SAB), (SAC)

bằng



với

sin





. Tính

độ dài

theo a.

 Lời giải

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 20

Gọi

là hình chiếu của

lên

Ta chứng minh được

)(),( CHKSASABCK 

Suy ra

CHK

vuông tại

và

KHSA 

Do đó

.CHK



Đặt

0 xSC

. Trong tam giác vuông

SAC

ta có

3111

222

CSCACH 



Tương tự, trong tam giác vuông

SBC

ta có





Ta có

13 13

sin

19 19



  

2 2

2(3 ) 13

3(2 ) 19

a x



 



ax 6

, vì

> 0. Vậy

6SC a

 Câu 23: (HSG ĐỀ 059) Cho khối lăng trụ tam giác

. ' ' 'ABC A B C

có đáy là tam giác đều cạnh

, điểm

cách đều ba điểm

Góc giữa

'AA

và mặt phẳng (

ABC

) bằng

. Tính khoảng

cách giữa hai đường thẳng

’ theo

 Lời giải

là trọng tâm



Ta có

 

'A G ABC

và

 



';( ) ' 60AA ABC A AG 

AG 

. Xét

'A AG

có

' .tan 60A G AG a 

Kẻ

'//'' AACCHACK 

C A

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 21

CKBBAACCdAACCd





))''(,'()','(

Ta có

2 2

' . 3 3 39 13

. : ' :

' 2 2 6 13

A G CH a a a a

CK a A G HG

A H

    

 Câu 24: (HSG THPT LÊ VĂN HƯU LỚP 11) Cho hình hộp cố định. Trên

các đoạn lần lượt lấy các điểm sao cho . Chứng minh đường

thẳng song song với mặt phẳng .

 Lời giải

Gọi D(m ;m-4) Sử dụng điều kiện

. 0 4 (4;0)

HD HN m D   

 

Nhận xét H và C đối xứng qua DN tìm được

(1; 4)



Từ đó tìm được :

(0;3), ( 3; 1)

A B

 

Chứng minh

Gọi E là trung điểm của BB

Vì

1 1

EB PB

AA PA

 

nên

, ,

A P E

theo thứ tự đó thẳng hàng và



Tương tự,

, ,

C Q E

theo thứ tự đó thẳng hàng và



Xét tam giác có P, Q lần lượt thuộc các cạnh EA

và EC đồng thời

Mặt khác

 Câu 25: (HSG THPT LÊ VĂN HƯU LỚP 11) Cho hình hộp cố định. Trên

các đoạn lần lượt lấy các điểm sao cho . Gọi là điểm thay

đổi trên cạnh ( khác và ). cắt tại , cắt tại và cắt tại .

Chứng minh mặt phẳng luôn chứa một đường thẳng cố định.

 Lời giải

1 1 1 1

ABCD A B C D

1 1

AB C B

P Q

1 1

2 , 2

AP PB C Q QB

 





ACC





PQ ACC

EAC

PE QE

PA QC



PQ A C











1 1 1

AC ACC PQ ACC

 

1 1 1 1

ABCD A B C D

1 1

AB C B

P Q

1 1

2 , 2

AP PB C Q QB

 





A NI

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 22

Chứng minh mặt phẳng luôn chứa một đường thẳng cố định

Trong mặt phẳng (ABCD), gọi .

Vì AB//CD nên:

; .

Mặt khác

Qua A

kẻ đường thẳng d song song với IN. Suy ra d song song với BD và nằm trong mặt phẳng

. Vậy mp chứa đường thẳng d cố định.

 Câu 26: (HSG NÔNG CÔNG 4 – THANH HÓA NĂM 2017-2018) Cho tứ diện

OABC

có

, ,

OA OB OC

đôi một vuông góc. Gọi

, ,

  

lần lượt là góc giữa các đường thẳng với mặt phẳng





ABC

. Tính giá trị nhỏ nhất của biểu thức













2 2 2

3 cot 3 cot 3 cot

  

   

 Lời giải

Gọi

là chân đường cao hạ từ

xuống mặt phẳng





ABC

. Khi đó ta chứng minh:

2 2 2 2

1 1 1 1

OH OA OB OC

  

2 2 2

1 sin sin sin 1

OH OH OH

OA OB OC

  

       





A NI

K DM AB

 

MB BN NK NK CD

MJ CJ CD NB CJ

   

AB IB IK

CJ IC ID

 

NK IK

AB CD IN BD

NB ID

   





A NI





A NI

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 23

Khi đó:

   

2 2 2

1 1 1

3 cot 3 cot 3 cot 2 2 2

sin sin sin

  

  

 

       

 

  

 

  

Đặt

2 2 2

sin ,sin b,sin

a c

  

  

với

, , 0

a b c





Dạng

1 1 1

2 2 2M

a b c

   

   

   

   

với

1 27

a b c

abc

    

Biến đổi:

1 1 1 1 1 1 1

8 4 2M

a b c ab bc ca abc

   

       

   

   

Áp dụng bất đẳng thức AM-GM ta có:

1 1 1

8 4.3. 2.3. 125

abc abc abc

 

    

 

 

Vậy

min

125

M 

khi

a b c

  

hay

sin sin sin

  

  

 Câu 27: (HSG NÔNG CÔNG 4 – THANH HÓA NĂM 2017-2018) Cho hình chóp

S ABCD

có đáy là hình vuông cạnh

và các cạnh bên đều bằng

. Gọi

là điểm trên

sao cho

SM SB



 

và

là một điểm thay đổi trên cạnh

. Xác định vị trí điểm

để

vuông góc

với

 Lời giải

Đặt

CE xCA



Kẻ





, / /

EH CD H CD EH AD

  

nên

CH xCD



Suy ra

CH xCD



 

2 1

3 3

MH CH CM xCD CS CB

 

    

 

 

     

Do:

 

1 2 1 2 1

3 3 3 3 3

CM CS SM CS SB CS CS SB CS CB

        

         

ME MH HE

 

  

Để

vuông góc với

điều kiện là:

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 24





. 0 . 0 . 0

ME CD MH HE CD MH CD

     

      

HE CD



2 1 2

. 0 . 0

3 3 3

xCD CS CB CD xCD CS CD

 

 

      

 

 

 

 

      

CB CD



SCD



đều nên

0 2

. . .cos60

CS CD CS CD a

 

 

Do đó

2 2 2

2 1 1 1

. . 0 0

3 2 3 3

x a a a x x

 

      

 

 

Vậy

thuộc đoạn

sao cho

CE CA

 Câu 28: (HSG NÔNG CÔNG 4 – THANH HÓA NĂM 2017-2018) Cho hình hộp chữ nhật

1 1 1 1

ABCD A B C D

có

AB AD a AA b

  

. Gọi

là trung điểm của

. Xác định tỷ số

để hai

mặt phẳng





A BD

và





MBD

vuông góc với nhau.

 Lời giải

Gọi

là tâm hình vuông

ABCD

Ta có:

     

1 1 1

AC BD

BD A BD MBD ACC A BD

AA BD





   







Vậy:





   

1 1

1 1 1 1

1 1

ACC A BD

ACC A A BD OA

ACC A MBD OM







 





 



do đó góc giữa hai đường thẳng

và

là góc giữa hai mặt

phẳng





A BD

và





MBD

Ta có:

2 2 2

2 2

2 2 2

AB AD AA

a b

 



  

D1 C1

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 25

2 2 2 2

1 1

OA AO AA b

   

;

2 2 2 2

1 1 1 1

MA A C MC a   

Hai mặt phẳng





A BD

và





MBD

vuông góc với nhau

OMA

  vuông tại

2 2 2

1 1

OM OA MA

  

2 2 2 2

2 5

4 2 4

a b a b a

b a a b

 



        

 

 

 Câu 29: (HSG NÔNG CÔNG 4 – THANH HÓA NĂM 2017-2018) Cho hình chóp

S ABC

có



0 0 0

, 60 , 90 , 120

SA SB SC a ASB CSB ASC     

. Gọi

M N

là hai điểm thay đổi trên cạnh

và

sao cho

CN AM

SC AB



. Tìm giá trị nhỏ nhất của đoạn thẳng

 Lời giải

Đặt

, ,

SC c SB b SA a

  

     

 

0 1

CN AM

m m

SC AB

   





NC mSC mc AM m AB m b a

     

      





   

1 1

MN MA AS SC CN m b a a c mc m a mb m c

              

            

2 2

. , . 0, .

2 2

a a

a b b c a c

   

     

nên





2 2 2

3 5 3

MN m m a

  

 

2 2 2

5 11 11 33

3 0;1

6 12 12 12

a m a a MN m

 

       

 

 

Dấu đẳng thức xảy ra khi



. Vậy giá trị nhỏ nhất của

là

 Câu 30: (HSG THPT TĨNH GIA 1 NĂM 2018-2019) Cho hình hộp

. ’ ’ ’ ’

ABCD A B C D

. Gọi

M N

lần lượt là trung điểm của

và

’

. Chứng minh rằng





/ / ’

MN A BD

 Lời giải

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 26

Gọi

là trung điểm

     

/ /

/ / / / '

/ / '

ME BD

MNE A BD MN A BD

NE A B



  







 Câu 31: (HSG THPT TĨNH GIA 1 NĂM 2018-2019) Cho hình chóp tứ giác





có đáy là

hình vuông cạnh

3 2, 2

n n

u u n













   



Tam giác





là tam giác đều và nằm trong mặt phẳng

vuông góc với mặt đáy. Gọi

lần lượt là trung điểm của các cạnh

ABC

Gọi

là trung điểm của

là chân đường vuông góc hạ từ

lên

Chứng minh





MN SAB



và tính diện tích thiết diện

của hình chóp cắt bởi mặt phẳng

2 2 .

OM OA OB OC

  

   

 Lời giải

+ Đặt

, ,

HA x HK y HS z

  

     

(

là trung điểm

)

+ Ta có





AM AS AB

 

  





AM HS HA HK

   

   





AM z x y

   

   





1 1 3 1

2 2 2 2

MN MA AD DN z x y x y x z

           

          

SB SH HA AB z x y

      

      

+ Suy ra

 

2 2

3 1 3 1 3

. 0 1

4 4 4 2 4 2

a a

MN AM x z MN AM

 

      

 

 

   

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 27

 

2 2

3 1 3 1 3

. 0 2

2 2 2 2 2 2

a a

MN SB x z MN SB

 

        

 

 

   

+ Từ





và





ta suy ra





MN SAB



+ Mặt khác

2 2 2

3 1 9 1 9 3 3 3

2 2 4 4 16 16 4 2

a a a a

MN x z x z MN

 

         

 

 

    

Dựng thiết diện :

+ Qua

kẻ đường thẳng

song song với

và









CD d SAB SCD

  

+ Trong mặt phẳng





SCD

kéo dài

NE d I

 

+ Trong mặt phẳng





SAB

kéo dài

IM AB F

 

+ Tứ giác

MENF

là thiết diện cần tìm

+ Ta có

SC SH HD DC z x y

      

      

+ Giả sử





SE k SC SE k z x y

     

     





HE HS SE k z k x k y

     

     

+ Do

HE SC



nên

 

2 2 2

. 0 1 0

HE SC k z k x k y

     

    





3 1

4 4 8

k k



     

, từ đây suy ra



+ Ta có

3 3 3

5 5 10

BF SI ES CN a

CN CN EC

     

+ Do đó

2 5

a a

NF a BF

 

   

 

 

và

2 2

MF NF MN  

+ Diện tích tam giác

INF

là

 

dt INF MN MF 

+ Gọi

là đường cao kẻ qua

của tam giác

IEM

h IE SE

MN IN SC

  

3 3 3

8 16

MN a

h  

+ Diện tích tam giác

IEM

là

 

1 1 3 87

. .

2 2 320

dt IEM h IM h MF  

+ Vậy diện tích của thiết diện là

 

13 87

320

dt MENF 

 Câu 32: (HSG THPT CẨM THỦY 1) Cho tứ diện đều

ABCD

cạnh

. Gọi

và

là hai

điểm di động trên các cạnh

và

sao cho

,(0 ).

AM CP x x a

   

Một mặt phẳng

( )



đi

qua

và song song với

cắt tứ diện

ABCD

theo một thiết diện.

a. Thiết diện trên là hình gì?

b. Tìm

để thiết diện có diện tích nhỏ nhất.

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 28

 Lời giải

a. Ta có:

( ) ( )

( ) / /

( ) ( ) / / ( )

M ABCD

ABCD MN CD N AC



 







   

Tương tự

( ) ( ) / / ( )

BCD PQ CD Q BD



  

( ) ( )

BAD MQ



 

;

( ) ( )

ABC PN



 

Vậy thiết diện của

( )



với tứ diện

ABCD

là tứ giác

MNPQ

Vì

/ / / /

MN PQ CD

nên MNPQ là hình thang.

Hai tam giác

CNP

và

DMQ

bằng nhau vì

CP DQ

CN DM

PCN QDN













   



Suy ra

NP MQ



hay thiết diện là hình thang cân.

b. Ta có

,  –

MN AM x PQ BP a x

   

Áp dụng định lý hàm cosin trong tam giác

MDQ

ta có:

2 2 2

2 2 2 2

2 . .cos

( ) 2 ( ) 3 3

MQ DQ DM DQ DM MDQ

x a x x a x x ax a

   

       

Dựng đường cao

ta có:

2 2 2 2 2 2

2 2 2 2

2 2 2

3 3 ( )

8 8 3 8 8 3

3 3 ( )

2 4 2

PQ MN

ME MQ QE x ax a

a x x x ax a x ax a

x ax a ME



     

     

      

Diện tích thiết diện

MNPQ

là:

2 2 2 2

( ).

8 8 3 8( )

2 4 4 2 4

MN PQ ME a a a a

S x ax a x a



       

4 2

a a

MinS x

  

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 29

 Câu 33:

(HSG THPT TRIỆU SƠN 2 NĂM 2018-2019) Cho hình chóp

S ABCD

. Gọi

là

giao điểm của

và

là giao điểm của

và

. Mặt phẳng







không qua

, song

song với mặt phẳng

( )

SEF

cắt các cạnh

của hình chóp lần lượt tại

. Chứng minh rằng

SM SP SN SQ

SA SC SB SD

  

 Lời giải









SEF











SAB MN



 





MN SE SAB



nên suy ra

MN SE









SEF











SAD MQ



 





MQ SF SAD



nên suy ra

MN SF









SEF











SBC NP



 





NP SF SBC



nên suy ra

NP SF









SEF











SCD PQ



 





PQ SE SCD



nên suy ra

PQ SE

Vậy

MNPQ

là hình bình hành.

Suy ra

SM SP SN SQ

  

   

SM SP SN SQ

SA SC SB SD

   

   

SM SP SN SQ

SA SC SB SD

    

   

SA SP SN SQ

SA SC SB SD

SM SC SB SD

 

    

 

 

   

Vì bốn điểm

đồng phẳng nên ta có

SA SP SN SQ

SM SC SB SD

 

   

 

 

SP SN SQ SM

SC SB SD SA

    

SM SP SN SQ

SA SC SB SD

   

 Câu 34: (HSG THPT TRIỆU SƠN 2 NĂM 2018-2019) Cho hai nửa đường thẳng

chéo nhau. Hai điểm

thay đổi lần lượt ở trên

và

sao cho

1 2 3

AC BD AB

 



là điểm

thứ tư của hình bình hành

ABDD







là mặt phẳng chứa

và song song với





là mặt

phẳng chứa

và song song với

. Chứng minh rằng





luôn luôn đi qua một điểm cố định

trong mặt phẳng





. Tìm vị trí của

và

sao cho diện tích

của tam giác

AD C



nhỏ nhất.

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 30

 Lời giải

Dựng

Ay By



trên



sao cho

AD BD









là mặt phẳng





CDD







là mặt phẳng





Ax Ay



Với

tùy ý trên



. Gọi

là các điểm trên



sao cho

/ /

MI Ax

/ /

NI Ay



.Ta có:

' '

1(1)

' ' ' '

AM AN CI D I CI ID

AD AC CD D C CD



    

1 2 3 : 3 2 : 3

1(2)

AB AB

AC BD AB AC AD

    

Với

là hai điểm tùy ý thỏa mãn giả thiết. Trên



tồn tại điểm

sao cho

' : 3

D I AB

D C AC



Ta được:

' : 3

(3)

' 3

AN D I AB AB

AC D C AC

   

và

' : 3 2 : 3 2

1 1 (4)

' ' ' ' 3

AM CI D I AB AB AB

AD CD D C AC AD

       

Từ (3) và (4) suy ra

cố định nên

cố định. Do đó





luôn đi qua điểm cố định

trong





1 1

. sin . sin

2 2

S AC AD A AC BD A



 

nên

nhỏ nhất

AC BD



nhỏ nhất.

Áp dụng bất đẳng thức Côsi cho hai số dương:

ta có:

3 1 2 1 2 8

2 . .

AC BD AB

AB AC BD AC BD

    

Dấu bằng xảy ra khi và chỉ khi

1 2 3 2

2 3

AC BD AB

   

và

BD 

Vậy

nhỏ nhất khi và chỉ khi

BD 

AC 

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 31

 Câu 35: (THPT ĐÔNG SƠN 1 NĂM 2018-2019) Cho hình chóp

S ABC

có





SC ABC



và

tam giác

ABC

vuông tại

.Biết

AB a



AC a



và góc giữa hai mặt phẳng





SAB

và





SAC

bằng



với

sin





. Tính

 Lời giải

Gọi

H K

lần lượt là hình chiếu của

lên

SA SB

. Ta chứng minh được

(SAB),







SA CKH



, suy ra tam giác

CHK

vuông tại

và

SA KH



Do đó



CHK





. Đặt

SC x



Trong tam giác vuông

SAC

ta có

2 2

2 2 2 2 2

1 1 1 3

a x

CH CA CS a x

   



Tương tự, trong tam giác vuông

SBC

ta có

2 2

a x





Ta có





 

2 2

2 3

13 13 13

sin 6

19 19 19

3 2

a x

x a

a x





      



. Vậy

SC a



 Câu 36: (THPT ĐÔNG SƠN 1 NĂM 2018-2019) Cho hình chóp

S ABCD

có đáy

ABCD

là

hình thang





/ / , 2

AB CD AB CD



. Gọi

và

lần lượt là điểm thuộc cạnh

và

thoả mãn

SMA P

MD PC

 

. Xác định thiết diện của hình chóp cắt bởi mặt phẳng

( )



chứa

và song song

với

. Tìm

để diện tích thiết diện bằng một nửa diện tích tam giác

SAB

 Lời giải

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 32

Ta có:

( ) ( )

( ) ( ) / / ( )

( ) / /

M ABCD

ABCD MQ AB Q BC



 



   





Tương tự

( ) ( ) / / ( )

SCD PN AB N SD



  

Vậy thiết diện của

( )



với hình chóp là tứ giác MNPQ. Vì

/ / / /

MQ NP AB

nên MNPQ là hình

thang

Gọi

T MN PQ

 

. Ta có:

 

 1 2

  1 1 2 1

MD AM x x

QM AB C AB CD AB

AD AD x x x



    

  

Vì

S S

/ / , / / S

MA QB P N

PQ SB MN SA AB TMQ

MD QC PC N

      

Do đó

 

S 2 1

TMQ

MQ x

AB x

 



 

 

 



 

Vì

 

D SD AD 1 1 2 1 2

NP N AM x x x NP x

NP C AB

C x x x QM x

       

   

Do đó

     

2 2

2 2 2

x x 4 4

S S

x 2 x 2 2

MNPQ

TPN

TMQ TMQ

NP x

 



     

 

  

 

Từ (1) và (2) suy ra

S 1

MNPQ

TMQ





Vậy



ta có

1 1 1

S 2 1 2

MNPQ

TMQ

    



 Câu 37:

(HSG THPT HẬU LẬU 2 NĂM 2018-2019) Cho hình hộp . Trên

cạnh lấy điểm

khác và . Gọi là mặt phẳng đi qua và song song với mặt phẳng

a. Trình bày cách dựng thiết diện của hình hộp và mặt phẳng .

b. Xác định vị trí của để thiết diện nói trên có diện tích lớn nhất.

 Lời giải

ABCD A B C D

   









ACD







 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 33

a. Trong mp(

ABCD

), qua

vẽ đường thẳng song song với

cắt

DB, BC

lần lượt tại

E, N

Trong mp(

BDD’B’

), qua

vẽ đường thẳng song song với

D’O

(

O=AC



) cắt

B’D’

tại

Trong mp(

A’B’C’D’

), qua

vẽ đường thẳng song song với

cắt

A’D’, D’C’

lần lượt tại

R, Q

Trong mp(

AA’D’D

), qua

vẽ đường thẳng song song với

AD’

cắt

AA’

tại

Trong mp(

CC’D’D

), qua

vẽ đường thẳng song song với

CD’

cắt

CC’

tại

Thiết diện là lục giác

MNPQRS

b. Do các mặt đối diên của hình hộp song song nên các cạnh đối của lục giác thiết diên

MNPQRS

song song và 3 cặp cạnh đó lần lượt song song với các cạnh tam giác

ACD’

 Các tam giác

JKI

ACD’

RQI

JMS

NKP

đồng dạng

 

MJ=NK

và

PK=QI

 Các tam giác

RQI

JMS

NKP

bằng nhau (gọi diện tích của chúng là

và gọi diện tích các

tam giác

JKI

ACD’

lần lượt là

)

Đặt ta có điều kiện và có:



= k



(

+1)

 Diện tích thiết diện:

(dấu bằng xảy ra  )

lớn nhất  

là trung điểm của

 Câu 38: (ĐỀ HSG NÔNG CÔNG – THANH HÓA NĂM 2017-2018) Cho hình chóp

S.ABCD

có đáy là hình vuông cạnh



SA a

vuông góc với mặt phẳng (

ABCD

). Gọi

là điểm bất

kì trong không gian, tìm giá trị nhỏ nhất của biểu thức:

2 2 2 2 2

     

MA MB MC MD MS

' '

MJ MA NC NK PC PK QD QI

MN MB NB NM PC PQ QC QP

      

;



0 1

 

2 2 2

S JM AM AM

S AC DC AB

     

   

 

 

 

2 2 2

S JK JM MK JM MK

S AC AC AC AC



     

     

     

     

2 1

S S S

 

1 3 1 3

2 ( ) 2

2 4 2 2

S S k k S k

 

 

       

 

 

 

 

 



 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 34

 Lời giải

Với điểm

bất kì ta luôn có

2 2 2 2 2

     

    

MA MB MC MD MS

2 2 2 2 2

( ) ( ) ( ) ( ) ( )         

         

MI IA MI IB MI IC MI ID MI IS

2 2 2 2 2 2

5 2 ( )          

     

MI IA IB IC ID IS MI IA IB IC ID IS

Chọn

thỏa mãn

0 4 0 4          

         

IA IB IC ID IS IO IS IS IO

Suy ra

là điểm thuộc đoạn

sao cho

= 4

với

tâm đáy

ABC

Khi đó

2 2 2 2 2 2 2 2 2 2 2

5           MI IA IB IC ID IS IA IB IC ID IS

Suy ra



nhỏ nhất khi

M I

Ta có

2 2 2

  

SO SA OA

Suy ra

2 2

2 2 2 2 2 2 2 2

2 2

2 2 25

        

BD AC

IA IB IC ID IS IO IO SO

2 2 2 2 2 2 2 2

16 4 16 4 36

25 25 25 5 5

        

IO AC SO SO AC SO SO AC

Vậy



nhỏ nhất bằng

khi

M I

 Câu 39: (HSG ĐỀ 075) Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật và

vuông

góc với mặt phẳng

 

ABCD

. Biết

, 3 AB a BC a

và 5.SD a

a) Đường thẳng qua

vuông góc với

cắt các đường thẳng

,CB CD

lần lượt tại

,I J

. Gọi

là

hình chiếu vuông góc của

trên

. Hãy xác định các giao điểm

,K L

của

,SB SD

với

 

HIJ

và

chứng minh rằng

 

.AK SBC

b) Tính diện tích tứ giác

.AKHL

 Lời giải

Trong

 

SCD

gọi

 

IJ    L SD JH L SD H

Trong

 

SBC

gọi

 

IJ    K SB IH K SB H

Ta có

 

IJ AC

IJ SAC IJ SC

IJ SA





   







, mà

AH SC

. Suy ra

 

.SC IJH

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 35

Suy ra



AK SC

. Mà





  

BC SAB BC AK

.Vậy







AK SBC

b) Ta có

2 2

  

SA SD AD a

;

2 2

. 2

 



SA AC a

SA AC

;

2 2

. 2

 



SA AB a

SA AB





  

AK SBC AK KH

, do đó

2 2

  

KH AH AK

Tương tự phần (a) thì





  

AL SCD AL HL

. Từ đó tính được

2 2

  

LH AH AL

Suy ra

1 1 8

. . .

2 2 15

    

AKHL AKH ALH

S S S AK KH AL LH

 Câu 40: (HSG THPT CẨM THỦY 1 NĂM 2018-2019) Cho tứ diện đều

ABCD

cạnh

. Gọi

và

là hai điểm di động trên các cạnh

và

sao cho

,(0 ).

AM CP x x a

   

Một mặt

phẳng

( )



đi qua

và song song với

cắt tứ diện

ABCD

theo một thiết diện.

1. Thiết diện trên là hình gì?

2. Tìm

để thiết diện có diện tích nhỏ nhất.

 Lời giải

( ) ( )

( ) ( ) / / ( )

( ) / /

M ABCD

ABCD MN CD N AC



 



   





Tương tự

( ) ( ) / / ( )

BCD PQ CD Q BD



  

( ) ( )

BAD MQ



 

;

( ) ( )

ABC PN



 

Vậy thiết diện của

( )



với tứ diện ABCD là tứ giác MNPQ.

Vì

/ / / /

MN PQ CD

nên MNPQ là hình thang. Hai tam giác CNP và DMQ bằng nhau vì

CP DQ

CN DM

PCN QDN













   



Suy ra NP = MQ hay thiết diện là hình thang cân.

2. Ta có

,  –

MN AM x PQ BP a x

   

. Áp dụng định lý hàm cosin trong tam giác MDQ ta có:

2 2 2 2 2 2 2

2 . .cos ( ) 2 ( ) 3 3

MQ DQ DM DQ DM MDQ x a x x a x x ax a

           

Dựng đường cao ME ta có:

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 36

2 2 2 2 2 2

2 2 2 2

2 2 2

3 3 ( )

8 8 3 8 8 3

3 3 ( )

2 4 2

PQ MN

ME MQ QE x ax a

a x x x ax a x ax a

x ax a ME



     

     

      

Diện tích thiết diện MNPQ là:

2 2 2 2

( ).

8 8 3 8( )

2 4 4 2 4

MN PQ ME a a a a

S x ax a x a



       

min

4 2

a a

S x

  

 Câu 41: (THPT TRIỆU SƠN 2 NĂM 2018-2019) Cho hình chóp

S ABCD

. Gọi

là giao

điểm của

và

là giao điểm của

và

. Mặt phẳng







không qua

, song song

với mặt phẳng

( )

SEF

cắt các cạnh

của hình chóp lần lượt tại

Chứng minh rằng

SM SP SN SQ

SA SC SB SD

  

 Lời giải









SEF











SAB MN



 





MN SE SAB



nên suy ra

MN SE









SEF











SAD MQ



 





MQ SF SAD



nên suy ra

MN SF









SEF











SBC NP



 





NP SF SBC



nên suy ra

NP SF









SEF











SCD PQ



 





PQ SE SCD



nên suy ra

PQ SE

Vậy

MNPQ

là hình bình hành.

Suy ra

SM SP SN SQ

  

   

SM SP SN SQ

SA SC SB SD

   

   

SM SP SN SQ

SA SC SB SD

    

   

SA SP SN SQ

SA SC SB SD

SM SC SB SD

 

    

 

 

   

Vì bốn điểm

đồng phẳng nên ta có

SA SP SN SQ

SM SC SB SD

 

   

 

 

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 37

SP SN SQ SM

SC SB SD SA

    

SM SP SN SQ

SA SC SB SD

   

 Câu 42: (THPT TRIỆU SƠN 2 NĂM 2018-2019) Cho hai nửa đường thẳng

chéo

nhau. Hai điểm

thay đổi lần lượt ở trên

và

sao cho

1 2 3

AC BD AB

 



là điểm thứ

tư của hình bình hành

ABDD







là mặt phẳng chứa

và song song với





là mặt

phẳng chứa

và song song với

. Chứng minh rằng





luôn luôn đi qua một điểm cố định

trong mặt phẳng





. Tìm vị trí của

và

sao cho diện tích

của tam giác

AD C



nhỏ nhất.

 Lời giải

Dựng

Ay By



trên



sao cho

AD BD









là mặt phẳng





CDD







là mặt phẳng





Ax Ay



Với

tùy ý trên



. Gọi

là các điểm trên



sao cho

/ /

MI Ax

/ /

NI Ay



.Ta có:

' '

1(1)

' ' ' '



    

AM AN CI D I CI ID

AD AC CD D C CD

1 2 3 : 3 2 : 3

1(2)

    

AB AB

AC BD AB AC AD

Với

là hai điểm tùy ý thỏa mãn giả thiết. Trên



tồn tại điểm

sao cho

' : 3



D I AB

D C AC

Ta được:

' : 3

(3)

' 3

   

AN D I AB AB

AC D C AC

và

' : 3 2 : 3 2

1 1 (4)

' ' ' ' 3

       

AM CI D I AB AB AB

AD CD D C AC AD

Từ (3) và (4) suy ra

cố định nên

cố định. Do đó





luôn đi qua điểm cố định

trong





1 1

. sin . sin

2 2

S AC AD A AC BD A



 

nên

nhỏ nhất

AC BD



nhỏ nhất.

Áp dụng bất đẳng thức Côsi cho hai số dương:

ta có:

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 38

3 1 2 1 2 8

2 . .

    

AC BD AB

AB AC BD AC BD

Dấu bằng xảy ra khi và chỉ khi

1 2 3 2

2 3

   

AC BD AB

và



Vậy

nhỏ nhất khi và chỉ khi



 Câu 43: (HSG ĐỀ 078) Cho hình lăng trụ

ABⒸ.A'B'C'

có đáy là tam giác đều cạnh

a. AA'

vuông góc với

(ABC).

Đường chéo

BC'

của mặt bên

BCC'B'

hợp với

(ABB'A')

một góc bằng

Gọi

M, N

lần lượt là trung điểm của

và

BB'

. Tính góc giữa

và

(BA'C').

Lời gải

Ta tính được AA' = BB' =CC’= a

. Gọi J là trung điểm của C’A’, H là hình chiếu của M lên

BJ. Gọi



là góc giữa MN và (BA'C') thì ta có

















BJMNMKH ,



, K là giao điểm của MN và

BJ (Với qui ước lấy góc nhọn).

+ Ta có:









'..'..'.

BBBNBNBMBBMBBMMBBBBMBNMBBJMN 

,cos..

BJMNBJMN 

















+ Áp dụng hệ thức lượng trong các tam giác vuông BMN và BMJ tính được

5 a

MN 

arccos0

,cos 



















BJMN

 Câu 44: (HSG ĐỀ 079) Cho hình chóp

ABCD

có đáy là hình vuông tâm

, cạnh

và

vuông góc với mặt phẳng (

ABCD

). Gọi

là trung điểm của

và

Biết góc giữa đường

thẳng

và mặt phẳng (

ABCD

) bằng 60

. Tính độ dài các đoạn thẳng

và tính cosin của

góc giữa đường thẳng

với mặt phẳng (

SBD

 Lời giải

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 39

Gọi

là trung điểm của



)(ABCDMI 

. Do đó góc giữa

và (

ABCD

) là góc



MNI



MNI 60 

0222

45cos..2 NCICNCICIN 

aaaaa































10a

NI 

60cos

aNI

MN 

60tan.

NIMI 

MISO 

Ta có )(SBDAC

SOAC

BDAC











. Gọi

là trung điểm của

và

)(),(//// SBDKNSBDMHACKNMH 

Do đó

là hình chiếu của

lên (

SBD

). Gọi

HKMNE 

suy ra góc



giữa

và (

SBD

)

là góc

MEH

1 a

KNOCOAMH 

, nên

MHNK

là hình bình hành



là trung điểm của

1 a

MNME 

Do tam giác

MHE

vuông tại

nên

sin 





sin1cos





 Câu 45: (HSG ĐỀ 080) Cho hình chóp tam giác đều

.S ABC

cạnh đáy

, đường cao

2SO a

. Gọi

là điểm thuộc đường cao



của tam giác

ABC

. Xét mặt phẳng

 

đi qua

và vuông

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 40

góc với



. Đặt

AM x



(

3 3

3 2

a a

x 

). Tìm

để thiết diện của hình chóp khi cắt bởi mặt

phẳng





có diện tích lớn nhất.

 Lời giải

Vì

3 3

3 2

a a

x 

nên

thuộc



Ta có





SO ABC



SO AA



 

, tam giác

ABC

đều nên

BC AA





. Vậy





qua

song song với

và

Xét





và





ABC

có

chung. Do





P BC



nên kẻ qua

đường thẳng song song với

cắt

AB AC

tại

E F

Tương tự kẻ qua

đường thẳng song song với

cắt



tại

, qua

kẻ đường thẳng song

song với

cắt

tại

. Ta có thiết diện là tứ giác

EFGH

Ta có

EF BC GH

 

M N

là trung điểm

EF GH

và

MN F



nên

EFGH

là hình thang cân đáy

EF GH

Khi đó:

( ).

EFGH

S EF GH MN

 

Ta có

3 3

' ,

2 3

a a

AA AO 

nên

2 3





2 3

' '

HG SN OM

HG x a

BC SA OA

    





2 3 2 3

MN MA

MN a x

SO OA

   









EFGH

1 2

S = (EF + GH).MN = 4 3 3 3 2 3

2 3

x a a x 

  

EFGH

1 1 3 3

S = 4 3 3 6 4 3 . ( )

3 3 2 4

a a

x a a x theoCosi

 

   

 

 

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 41

EFGH

đạt giá trị lớn nhất bằng

khi và chỉ khi

3 3

x 

Vậy giá trị lớn nhất của diện tích thiết diện bằng

khi

3 3

x 

 Câu 46: (HSG ĐỀ 080) Cho hình thoi

ABCD

có



60 , 2 .

BAD AB a 

Gọi

là trung điểm

. Trên đường thẳng

vuông góc với mặt phẳng

 

ABCD

tại

lấy điểm

thay đổi khác

Trên tia đối của tia

lấy điểm

sao cho

BM BC

a. Khi

SH 

Chứng minh đường thẳng

vuông góc với mặt phẳng

 

SAD

b. Tính theo

độ dài của

để góc giữa

và

 

SAD

có số đo lớn nhất.

 Lời giải

a. Ta có



1 1

, 60

4 2 2

MB BC HB HBM HAD    

HBM 

vuông tại

.sin 60 .

HM HB  

Gọi

là giao của

và

Ta có:

HN HM SH  

SMN 

vuông tại

( ( ))

( )

( / / )

SH AD SH ABCD

AD SMN AD SM

MN DA AD BC

 



   







Kết hợp với

( )SM SN SM SAD  

b. Gọi



là góc giữa

và

 

SAD

;

là hình chiếu vuông góc của

lên

;

là giao của

với

Lấy

đối xứng với

qua

Vì

( )AD SMN AD HK  

. Kết hợp với

( )HK SN KH SAD  

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 42

Mà

là đường trung bình của tam giác

ICE

nên

HK CE

Suy ra

( )

CE SAD



tại

. Suy ra

SEC



vuông tại

và

là hình chiếu của

trên





SAD

. Ta

có



CSE





Đặt

( 0)

x SH x

 

. Tam giác

SHN

vuông tại

và

là đường cao nên

2 2 2 2

. 3 2 3

3 4 3 4

SH HN ax ax

HK CE

a x a x

   

 

2 2

2 2 2 2

25 3

4 4

a a

CH CM MC a

    

Tam giác

SHC

vuông tại

nên

2 2 2 2

SC SH CH x a

   

2 2 2 2 4 4 2 2

2 3 2 3

sin

(4 3 )( 7 ) (4 21 ) 31

EC ax ax

x a x a x a a x

  

   



2 2 2 2

2 3 12

sin sin .

4 21 31

4 21. 31.

a x a x

   



 

Dấu đẳng thức xảy ra khi

x a



Vậy



lớn nhất khi và chỉ khi

sin



lớn nhất khi và chỉ khi

. .

SH a



 Câu 47: (HSG ĐỀ 081) Cho tứ diện

ABCD

, có

, .

AB AC AB BD

 

Gọi

P Q

lần lượt chia

đoạn

và

theo cùng tỉ số

Chứng minh hai đường thẳng

và

vuông góc với nhau.

 Lời giải

Ta có:

. . 0

AB AC a b

 

   

;





. . 0 .

AB BD a c a a c a

    

       

Ta có:

1 1

AA k AB k

PA k PB AP a

k k



    

 

 

   

. .

1 1 1

AC k AD k

QC kQD AQ b c

k k k



    

  

 

    





1 1

. . . .

1 1 1 1 1

k k k

PQ AQ AP a b c a c b

k k k k k

       

    

        

Chọn hệ cơ sở

, ,

AB a AC b AD c

  

     

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 43

Vậy hai đường thẳng

và

vuông góc với nhau.

 Câu 48: (HSG ĐỀ 081) Cho tứ diện đều

ABCD

Mọi

, ,

M N P

lần lượt là trung điểm của các

cạnh

, ,

AB BC AD

và

là trọng tâm tam giác

BCD

Tính góc giữa hai đường thẳng

và

 Lời giải

Và

. . .

a b b c c a

  

     

   

1 1 1

2 2 2 2

6 6 2

MG AG AM a b c MG a b c

           

         

   

1 1 2

2 2 2

PN AN AP a b c PN a b c         

         

 

2 2

cos = cos , ar os

6 6

MG PN

MG PN cc

MG PN

 

   

 

 Câu 49: (HSG ĐỀ 082) Cho hình chóp

S.ABCD

có đáy

ABCD

là hình thang





/ / , 2

AB CD AB CD



. Gọi

và

lần lượt là điểm thuộc cạnh

và

thoả mãn

SMA P

MD PC

 

a. Xác định thiết diện của hình chóp cắt bởi mặt phẳng

( )



chứa

và song song với

b.Tìm

để diện tích thiết diện bằng một nửa diện tích tam giác

 Lời giải

 





1 1

. . . . . 0

1 1 1 1

k k

AB PQ a a c b a a c a b

k k k k

 

       

 

   

 

       

Đặt

, ,

AB a AC b AD c

  

     

là các véctơ không đồng phẳng và





AG a b c

  

   

Vì

ABCD

là tứ diện đều nên giả sử

a b c

  

  

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 44

a. Ta có:

( ) ( )

( ) ( ) / / ( )

( ) / /

M ABCD

ABCD MQ AB Q BC



 



   





Tương tự

( ) ( ) / / ( )

SCD PN AB N SD



  

Vậy thiết diện của

( )



với hình chóp là tứ giác MNPQ. Vì

/ / / /

MQ NP AB

nên MNPQ là hình

thang

b. Gọi

T MN PQ

 

. Ta có:

 

 1 2

  1 1 2 1

MD AM x x

QM AB C AB CD AB

AD AD x x x



    

  

Vì

S S

/ / , / / S

MA QB P N

PQ SB MN SA AB TMQ

MD QC PC N

      

Do đó

 

S 2 1

TMQ

MQ x

AB x

 



 

 

 



 

Vì

 

D SD AD 1 1 2 1 2

NP N AM x x x NP x

NP C AB

C x x x QM x

       

   

Do đó

     

2 2

2 2 2

x x 4 4

S S

x 2 x 2 2

MNPQ

TPN

TMQ TMQ

NP x

 



     

 

  

 

Từ (1) và (2) suy ra

S 1

MNPQ

TMQ





Vậy

1 1 1

S 2 1 2

MNPQ

TMQ

    



 Câu 50:

(HSG ĐỀ 083) Cho hình hộp

. ' ' ' '.

ABCD A B C D

Trên cạnh

lấy điểm

khác

và

. Gọi

( )

là mặt phẳng đi qua

và song song với mặt phẳng

( ').

ACD

a. Xác định thiết diện của hình hộp khi cắt bởi mặt phẳng

( )

b. Tìm vị trí của điểm

để thiết diện đó có diện tích lớn nhất.

 Lời giải

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 45

a.Trong mp(

ABCD

), qua

vẽ đường thẳng song song với

cắt

DB, BC

lần lượt tại

E, N

Trong mp(

BDD’B’

), qua

vẽ đường thẳng song song với

D’O

(

O=AC



) cắt

B’D’

tại

Trong mp(

A’B’C’D’

), qua

vẽ đường thẳng song song với

cắt

A’D’, D’C’

lần lượt tại

R, Q

Trong mp(

AA’D’D

), qua

vẽ đường thẳng song song với

AD’

cắt

AA’

tại

Trong mp(

CC’D’D

), qua

vẽ đường thẳng song song với

CD’

cắt

CC’

tại

Thiết diện là lục giác

MNPQRS

b. Do các mặt đối diên của hình hộp song song nên các cạnh đối của lục giác thiết diên

MNPQRS

song song và 3 cặp cạnh đó lần lượt song song với các cạnh tam giác

ACD’

, Các đường thẳng RS,

MN, AD đồng quy tại J, các đường thẳng

MN, DC, QP đồng quy tại K, Các đường thẳng DD

’

, RS, QP đồng quy tại I

 Các tam giác

JKI

ACD’

RQI

JMS

NKP

đồng dạng



' '

MJ MA NC NK PC PK QD QI

MN MB NB NM PC PQ QC QP

      



MJ=NK

và

PK=QI

 Các tam giác

RQI

JMS

NKP

bằng nhau (gọi diện tích của chúng là

và gọi diện tích các

tam giác

JKI

ACD’

lần lượt là

)

Đặt

;



ta có điều kiện

0 1

 

và có:

2 2 2

S JM AM AM

S AC DC AB

     

   

 

 



= k

 

2 2 2

S JK JM MK JM MK

S AC AC AC AC



     

     

     

     



(

+1)

 Diện tích thiết diện:

2 1

S S S

 

1 3 1 3

2 ( ) 2

2 4 2 2

S S k k S k

 

 

       

 

 

 

 

 

(dấu bằng xảy ra 



)

lớn nhất 





là trung điểm của

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 46

 Câu 51: (HSG THPT LAM KINH THANH HÓA NĂM 2018-2019) Cho hình chóp

S.ABCD

có đáy

ABCD

là hình thang cân (

) và

BC a







 0

AB AD DC a a

   

. Gọi

là giao

điểm của

và

Biết

vuông góc với

và mặt bên

SBC

là tam giác đều. Tính

 Lời giải

Trong (ABCD), kẻ DT//AC (T thuộc BC)



CT=AD=a và DT



Ta có: DT=AC=



SCT có SC=2a, CT=a,



120

SCT 

ST a

 



SDT có



SDT  , DT=

7 2

ST a SD a

   .

 Câu 52: (HSG THPT LAM KINH THANH HÓA NĂM 2018-2019) Cho hình chóp

S.ABCD

có đáy

ABCD

là hình thang cân (

) và

BC a







 0

AB AD DC a a

   

. Gọi

là giao

điểm của

và

Biết

vuông góc với

và mặt bên

SBC

là tam giác đều. Mặt phẳng (



)

qua điểm

thuộc đoạn

(

không trùng

) và song song với hai đường thẳng

và

Xác định thiết diện của hình chóp

S.ABCD

cắt bởi mặt phẳng (



). Biết

. Tìm

để diện

tích thiết diện lớn nhất.

 Lời giải

Trong (ABCD), qua M kẻ đường thẳng song song với AC cắt AD, DC lần lượt tại N,P.

Trong (SBD), qua M kẻ đường thẳng song song với SD cắt SB tại K.

Trong (SAD), qua N kẻ đường thẳng song song với SD cắt SA tại J.

Trong (SDC), qua P kẻ đường thẳng song song với SD cắt SC tại Q.

Thiếtdiện là ngũ giác NPQKJ.

Ta có :

NJ NP



;

MK NP



;

PQ NP



; NJ=PQ

1 1 1

( ) ( ) ( )

2 2 2

NPQKJ NMKJ MPQK

S S S NJ MK MN MK PQ MP NJ MK NP

       

Xét



ACD có

. . 3

NP MD AC MD x a

NP x

AC OD OD

    

B C

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 47

Xét



ASD và



AOD có

2 .

2( 3)

a x

NJ AN OM SD OM

NJ a x

SD AD OD OD

 



 

 

      

Xét



BSD có





2 . 3

. 2

( 3 )

3 3

a a x

KM BM SD BM

KM a x

SD BD BD



     

2(3 2 3 )

NPQKJ

S a x x

 

1 1 3 3

(3 2 3 )2 3 (3 2 3 ) 2 3

3 4 3

a x x a x x a

 

     

 

3 3

NPQKJ

Max S a



khi

x a



 Câu 53: (HSG THPT LÊ LỢI NĂM 2018-2019) Cho hình chóp S.ABCD có đáy ABCD là

hình thang cân với AD // BC, AB = BC = a, AD = 2a tam giác SAD vuông cân tại S và SB =

. Gọi M là trung điểm của SA, G là trọng tâm của tam giác SCD, H là giao điểm của BG và

mp(SAC).

Chứng minh rằng BM // (SCD) và tính tỉ số

 Lời giải

Gọi

là trung điểm của

ta có

= a và

tứ giác

BCDN

là hình bình hành

/ / .

BN CD

Vì

lần lượt là trung điểm của

và

nên

mà

*) Gọi

là trung điểm của

. Gọi J là

giao điểm của

và

, vì tứ giác

BCNA

là hình bình hành nên

là trung điểm của

mà

nên

là trung điểm của

*) Trong tam giác

SBP

vẽ

, ta có:

(do

là trọng tâm của tam giác

SCD

)

 Câu 54: (HSG THPT LÊ LỢI NĂM 2018-2019) Cho tứ diện đều ABCD cạnh a. Hai điểm

M, N chạy tương ứng trên các đoạn AB và CD sao cho BM = DN. Tìm giá trị lớn nhất, nhỏ nhất

của MN.

 Lời giải



( ) / /( )

BMN SCD



( ) / /( )

BM BMN BM SCD

 

;   H=BG (SAC)

I AC BP H SI BG

     

HB IB IP SP

HG IK IK SG

   

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 48

Đặt , với . Khi đó ta có: và

Ta có:

Do đó:

= (2x

– 2x + 1)

Xét hàm số

(

) = 2x

– 2x + 1 trên đoạn ta có:

MN đạt giá trị nhỏ nhất bằng khi M, N lần lượt là trung điểm của

, .AB CD

MN đạt giá trị lớn nhất bằng

khi M B, N D hoặc M A,N

 Câu 55: (TRƯỜNG THPT LÊ LỢI NĂM 2017 - 2018) Cho hình chóp , đáy

là nửa lục giác đều ,

Mặt bên là tam giác đều, vuông góc với , O là giáo điểm của AC, B

Mặt phẳng

qua điểm thuộc đoạn ( không trùng với ), song song với và . Xác định

thiết diện của hình chóp với mặt phẳng và tìm

để diện tích thiết diện đó lớn

nhất biết .

 Lời giải

Xác định thiết diện của hình chóp

ABCD

với mặt phẳng

+) Xác định được thiết diện là tam giác

NPQ

(với

lần lượt nằm trên các cạnh

)

+) Ta có:

Diện tích thiết diện:

Gọi J là điểm nằm trên BC sao cho ACJD là hình bình hành.



0 1

 

 

BM x BA



 

DN x DC



 

. ( ) . (1 ).

DN x DC BN BD x BC BD BN x BC x BD

        

        

. (1 ). .

MN BN BM x BC x BD x BA

     

     

2 2 2

2 2 2 2 2 2 2

(1 ) 2 (1 ) 2 . 2 (1 )

2 2 2

a a a

x a x a x a x x x x x       

2 2 2 2

(1 ) (1 ) (1 )

x x x x x x x x

 

       

 

 





0;1

1 1

max ( ) (0) (1) 1, min ( ) ( )

2 2

f x f f f x f

    



S ABCD

ABCD

AB AD DC a

   

BC a



SBC

( )



S ABCD







BM x



( ).



/ / , / /MQ SD NP AC

NP MQ

SD AC



 









NPQ

S NP MQ



 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 49

Trong tam giác SCJ có

Trong tam giác ABC vuông tại A có:

Trong tam giác SDJ vuông tại D vì SD vuông góc A

Trong tam giác ABC có:

ABC

 

+) Trong tam giác :

Trong tam giác

+) Diện tích thiết diện:

+) Vì thuộc đoạn ( ) nên

Do đó, . Vậy, .

 Câu 56: (THPT NÔNG CỐNG - NHƯ THANH NĂM HỌC 2018 - 2019) Cho hình lăng trụ

đứng có . Mặt phẳng (

) cắt các đường thẳng lần lượt

tại sao cho tam giác

MNP

đều. Tính cosin góc tạo bởi (

) và (

ABC

)

 Lời giải

Từ

dựng

song song với

thuộc

AA’, CF

song song với

PN, F

thuộc

BB’

. Ta có (

CEF

)

// (

PMN

) nên

EF // MN

và tam giác

CEF

là một tam giác đều. Đặt

AE = x, BF= y, CE = CF =

EF = a

Ta có hệ

Từ (1) và (2) suy ra: . Kết hợp (3) suy ra

Từ (1) và (2) suy ra: . Do đó:

Giải được: . Suy ra



2 ; ; 120

SC a CJ a SCJ  

2 2

2. . .cos 7

SJ SC CJ SC CJ C a

   

2 2

AC BC AB a

  

2 2

SD SJ DJ a

  

SBD

BM MQ

MQ x

BD SD

  

BAC

NP BM

NP x

AC BO

  

NP x



3 3

NPQ

S 



M B



2 3 2

0 3 0

3 3

a a

x BO x     

3 3 2 2 3

2 3 3

NPQ

a a

 

 

 

 

2 3

min

NPQ

S 

. ' ' '

ABC A B C

2, 1

AB CB AC

  

', ', '

AA BB CC

, ,

M N P

2 2

1 (1)

4 (2)

( ) 4 (3)

x a

y a

x y a



 



 





  



2 2 2

2 5

x y a

  





2 2 2 2

( 1)( 4)

x y a a

  

2 2 2

( ) ( 1)( 4)

a a



  

2 2

1( ), 5

a l a

 

5 3

CEF





( )( )( )

ABC

S p p a p b p c



    

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 50

Gọi là góc cần tìm. Theo định lí hình chiếu ta có . Vậy

góc của (

) và (

ABC

) là

 Câu 57: (THPT NÔNG CỐNG - NHƯ THANH NĂM HỌC 2018 - 2019) Cho hình hộp chữ

nhật có tâm

và . Mặt phẳng đi qua

và cắt các tia

tương ứng tại ba điểm phân biệt . Tìm giá trị lớn nhất của biểu thức

 Lời giải

Đặt . Ta có

Vì

M, N, P, O

đồng phẳng nên

Ta có:

. Suy ra

BĐT Cauchy:

Vậy minT = . Khi

 Câu 58: Cho hình chóp tứ giác

S ABCD

có đáy là hình vuông cạnh

Tam giác

SAD

là tam

giác

đều và nằm trong mặt phẳng vuông góc với mặt đáy. Gọi

M N

lần lượt là trung điểm của các cạnh

, .

SB CD

Gọi

là trung điểm của

AD E

là chân đường vuông góc hạ từ

lên

Chứng minh





MN SAB



và tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng





MNE

 Lời giải



15 / 4 5

cos

5 3 / 4

ABC

CEF





  

arccos( )

ABCD A B C D

   

3 , 4



  

AB a AD AA a





', , '

AB AC AD

, ,

M N P

. .



T AM AN AP

' , ,

AA a AB b AD d

  

     

AC a b c

  

   

. . .

AO x AM y AN z AP

x y z



   



  





   

. ' ( ), . ( ), ( ).

AM m AB m a b AN n AC n b d AP p a d

       

          

1 1

' ( )

2 2

AO AC a b d

   

    

1 1 1 1

mx ny pz

m n p

      

' ' 5 5 4 2 1 1 4 2 4

4 4

' 5 ' 5

AB AC AD a a a

AM AN AP AM AN AD AM AN AD

           

4 4 2 675 2

5 5 16

  

675 2

, ' 3 2

AM AN AD  

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 51

+ Đặt

, ,

HA x HK y HS z

  

     

(K là trung điểm BC)

+ Ta có

 

AM AS AB

 

  

 

AM HS HA HK

   

   

 

AM z x y

   

   





1 1 3 1

2 2 2 2

MN MA AD DN z x y x y x z

           

          

SB SH HA AB z x y

      

      

+ Suy ra

 

2 2

3 1 3 1 3

. 0 1

4 4 4 2 4 2

a a

MN AM x z MN AM

 

      

 

 

   

 

2 2

3 1 3 1 3

. 0 2

2 2 2 2 2 2

a a

MN SB x z MN SB

 

        

 

 

   

+ Từ





và





ta suy ra





MN SAB



+ Mặt khác

2 2 2

3 1 9 1 9 3 3 3

2 2 4 4 16 16 4 2

a a a a

MN x z x z MN

 

         

 

 

    

Dựng thiết diện :

+ Qua

kẻ đường thẳng

song song với

và









CD d SAB SCD

  

+ Trong mặt phẳng





SCD

kéo dài

NE d I

 

+ Trong mặt phẳng





SAB

kéo dài

IM AB F

 

+ Tứ giác

MENF

là thiết diện cần tìm

+ Ta có

SC SH HD DC z x y

      

      

+ Giả sử





SE k SC SE k z x y

     

     





HE HS SE k z k x k y

     

     

+ Do

HE SC



nên

 

2 2 2

. 0 1 0

HE SC k z k x k y

     

    





3 1

4 4 8

k k



     

, từ đây suy ra



+ Ta có

3 3 3

5 5 10

BF SI ES CN a

CN CN EC

     

+ Do đó

2 5

a a

NF a BF

 

   

 

 

và

2 2

MF NF MN  

+ Diện tích tam giác

INF

là

 

dt INF MN MF 

+ Gọi

là đường cao kẻ qua

của tam giác

IEM

h IE SE

MN IN SC

  

3 3 3

8 16

MN a

h  

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 52

+ Diện tích tam giác

IEM

là

 

1 1 3 87

. .

2 2 320

dt IEM h IM h MF  

+ Vậy diện tích của thiết diện là

 

13 87

320

dt MENF 

 Câu 59: (HSG ĐỀ 095)

Cho hình lăng trụ đứng

ABCD A B C D

   

đáy là nửa lục giác đều với

AD a



AB BC CD a

  

Đường cao của hình lăng trụ là

, (P) là mặt phẳng qua



, cắt các cạnh

BB CC

 

lần lượt tại

1 1

B C

a) Thiết diện của hình lăng trụ cắt bởi (P) là hình gì? Tìm liên hệ giữa

và

và tìm vị trí của

điểm

1 1

B C

sao cho





P AD





b) Định vị trí của





để chu vi thiết diện nhỏ nhất. Tính giá trị nhỏ nhất ấy.

 Lời giải

Ta có









 

' ' ' '

' '

1 1

/ /

ADD A BCC B

P ADD A AD

P BCC B B C





 





 





1 1

/ /

AD B C



Qua

dựng đường thẳng song song với

, cắt



tại

. Hai tam giác

ADD

và

1 1

B IC

có các

cạnh song song từng từng đôi một nên chúng đồng dạng suy ra

1 1 1

AD AD AB

B C B I BC

 

( do

B I BC

 )

Mặt khác vì

AD BC



(do ABCD là nửa lục giác đều) suy ra

1 1

AD B C



Vậy thiết diện là hình thanh

1 1

AD C B

Tìm liên hệ giữa a và h và tìm vị trí

1 1

B C

sao cho

( ) '

P A D



Ta có

' '

ADD A

là hình chữ nhật nên khi

( )

P A D



thì

' '

A D AD



suy ra

' '

ADD A

là hình vuông.

Suy ra



tức

h a



Hơn nữa theo tính chất của nửa lục giác đều ta có:

BD AB AC CD

 

Do đó

 

' '

1 1

BD AB

BD ABB A BD AB AB A B

BD AA





     







vì

AB A D



 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 53

 

' '

1 1

CD AC

CD ACC A CD AC AC A C

CD AA





     







vì

AC A D

 .

Vậy khi

2h a

AC A C

AB A B

















thì

( ) '

P A D



Xác định vị trí của (P) để chu vi thiết diện nhỏ nhất.

Gọi p là chu vi của thiết diện, ta có:

' ' ' '

1 1 1 1 1 1

p AD B C AB D C AD AB D C

      

Vì

có độ dài không đổi nên chu vi nhỏ nhất khi và chỉ khi

1 1

AB D C



nhỏ nhất.

Đặt

BB x



, khi đó

2 2

DD h

CI x C I

  

Ta có

 

1 1

2 2

h h

CC CC C I CI h x x

 

       

 

 

Ta có

1 1

AB D C



2 2 ' 2 ' 2 2 2 2

1 1

AB BB C D C C a h a x

 

        

 

 

Đặt

 

; , ;

u a x v a x

 



 

 

 

thì

2 ;

u v a

 

 

 

 

 

u v u v a    

   

a 

u v



 

cùng hướng

2 4

a h h

x x x

a x



      

2 2

2 2 2 2

4 min 4 4

4 2 4

h h

T a p a h a      

đạt được khi



Vậy giá trị nhỏ nhất đạt được khi (P) cắt

tại

với



 Câu 60: (HSG ĐỀ 095) Cho hình lăng trụ tứ giác ABC

. Một mặt phẳng (P) thay

đổi song song với hai đáy của lăng trụ, cắt các đoạn thẳng AB

, BC

, CD

, DA

tương ứng lần lượt

các điểm M, N, P, Q. Hãy xác định vị trí của mặt phẳng (P) sao cho tứ giác MNPQ có diện tích

lớn nhất.

 Lời giải

Giả sử mặt phẳng

( )

cắt

1111

,,, DDCCBBAA

tương ứng tại A’, B’, C’, D’. Khi đó ta có



 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 54

Đặt

MNPQ

S S



Theo định lí Ta- lét ta có



 1

Do đó ta được

' ' '

' ' ' '

' ' ' ' ' ' '

( )

. (1 ) ( ) (1 ).S( )

( )

s A MQ A M A Q

x x S A MQ x x A B D

s A B D A B A D

     

(1)

Chứng minh tương tự ta có:

' ' ' '

S( ) (1 ).S( )

B MN x x B A C

  (2)

' ' ' '

S( ) (1 ). ( )

C NP x x s C B D

 

(3)

' ' ' '

S( ) (1 ).S( )

D PQ x x D C A

  (4)

Từ (1), (2), (3), (4) ta có

S(MNPQ) = S(A’B’C’D’)- S(A’MQ)-S(B’MN)-S(C’NP)-S(D’PQ) =

S -x(1-x)

' ' '

(S( )

A B D

' ' '

( )

S B A C



' ' '

S( )

C B D

' ' '

S( )

D C A

) = S -x(1-x).2S = S(2x

- 2x +1)

SxS .

)

(2.

















Vậy diện tích tứ giác

MNPQ

bằng





M là trung điểm AA



(P) song song và cách

đều hai đáy.

 Câu 61: (HSG ĐỀ 098) Cho hình lập phương

ABCD

A’B’C’D’ có cạnh

. Gọi I là tâm của

hình vuông CDD’C’, K là trung điểm của cạnh C

1. Dựng thiết diện của hình lập phương

ABCD

A’B’C’D’ cắt bởi mặt phẳng (AKI). Tính diện tích

của thiết diện theo

2. Tính góc tạo bởi hai đường thẳng A’D’ và AQ với Q là giao điểm của (AKI) và CC’.

 Lời giải

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 55

1). Gọi J là giao điểm của AK và C

Q là giao điểm của JI và CC’; N là giao điểm của IJ và DD’.

Thiết diện là tứ giác AKQN.

Chứng minh được AKQN là hình thang có 2 đáy là KQ, AN.

Chứng minh được C là trung điểm của JD, K là trung điểm JA, Q là trung điểm của JN.

1 1 1

. . 3 .

2 2 4

JKQ

AKQN JAN JKQ JKQ

JAN

JK JQ

S S S S

S JA JN



  



      

1 1 1

2 ' 3 3

CQ ND QC CQ a

     

Tính được

13 5 10

; ;

6 2 3

a a a

KQ JK JQ  

2 2 2

2 2

6 7

osKJQ= ,sin 1 os

2 . 5

1 14 14

. .sin , 3 .

2 12 4

JKQ AKQN JKQ

JQ JQ KQ

c KJQ c KJQ

JK JQ

a a

S JK JQ KJQ S S

 

 

   

   

2). Vì A’D’//AD nên góc tạo bởi A’D’, AQ bằng góc tạo bởi AQ, AD

' ' ' 3.

AC AB AD AA AC a    

   

Tính được

19 10

; ; .

3 3

a a

AQ AD a QD  

2 2 2

cos .

2 .

AQ AD QD

QAD

AQ AD

 

 

 Câu 62: Cho tứ diện

ABCD

, các điểm

M N

xác định bởi

MA xMC NB y ND

 

   





, 1

x y



Tìm điều kiện giữa

và

để ba đường thẳng

, ,

AB CD MN

cùng song song với một mặt phẳng.

 Lời giải

C D

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 56

+) Chọ hệ véc tơ:

, ,

a DA b DB c DC

  

     

thì

, ,

a b c

  

không đồng phẳng.

+) Ta có





MA xMC DA DM x DC DM

    

     

 

 1

1 1 1

DA xDC x

DM a c

x x x



    

  

 

  

Lại có

 

1 1

 2

1 1

NB yND DN DB b

y y

   

 

    

+) Từ





và





suy ra

1 1

1 1 1

MN DN DM a b c

x y x



    

  

     

(3)

+) Ta có

AB DB DA b a CD c

     

      

;



và



là hai véc tơ không cùng phương nên ba

đường thẳng

, ,

AB CD MN

cùng song song với một mặt phẳng khi và chỉ khi ba véc tơ

, ,

AB CD MN

  

đồng phẳng







MN mAB nCD m b a nc ma mb nc

        

        

(4)

+) Do

, ,

a b c

  

không đồng phẳng nên từ (3) và (4) ta có hệ:

m x y











  







 







Vậy ba đường thẳng

, ,

AB CD MN

cùng song song với một mặt phẳng khi và chỉ khi

x y



 Câu 63: Cho lăng trụ

ABD

có tất cả các mặt bên là hình vuông cạnh bằng 1. Gọi D,

E, F lần lượt là trung điểm của các cạnh BC, A

, B

. Tính côsin của góc giữa hai đường thẳng

F, DE.

 Lời giải

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 57

+) Chọn hệ véc tơ

1 1 1 1 1

, ,

a A A b A B c A C

  

     

. Khi đó:

a b c

  

  

và

. . 0

a b a c

 

   

b c



 

+) Ta có





1 1 1 1 1

1 1 1

2 2 2

A F A B A C b c

   

    

1 1

DE DC CC C E a b

     

     

+) Tính





cos ,

A F DE

1 1

1 1 3

2 2 2

A F A F b c

 

   

 

 

  

1 5

2 2

DE DE a b

 

    

 

 

  

1 1 1 3

. .

2 2 2 8

A F DE b c a b

   

     

   

   

     

Suy ra:

 

1 1

cos , cos ,

. 10

A F DE

A F DE A F DE

A F DE

  

 

 Câu 64: Cho tứ diện

ABCD

và các điểm

xác định bởi

2 3

AM AB AC

 

  

;

DN DB xDC

 

  

. Tìm

để các đường thẳng

,  , 

AD BC MN

cùng song song với một mặt phẳng.

 Lời giải

Yêu cầu bài toán tương đương với tìm

để ba vectơ

,  , 

MN AD BC

  

đồng phẳng.

Hệ thức









1 2 3 3

AM AB AB BC AM AB BC

       

      

Hệ thức









AN AD AB AD x DA AB BC

      

      

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 58





AN x AB xAD xBC

    

   

Từ





và





, suy ra









2 3

MN AN AM x AB xAD x BC

      

     

Vậy ba vectơ

,  , 

MN AD BC

  

đồng phẳng khi

2 0 2

x x

    

Ta có:

( ) ( )

( ) ( ) / / ( )

( ) / /

M ABCD

ABCD MQ AB Q BC



 



   





Tương tự

( ) ( ) / / ( )

SCD PN AB N SD



  

Vậy thiết diện của

( )



với hình chóp là tứ giác MNPQ. Vì

/ / / /

MQ NP AB

nên MNPQ là hình

thang

 Câu 65: Cho hình chóp

S.ABCD

có đáy

ABCD

là hình thang





/ / , 2

AB CD AB CD



. Gọi

và

lần lượt là điểm thuộc cạnh

và

thoả mãn

SMA P

MD PC

 

. Xác định thiết diện của hình

chóp cắt bởi mặt phẳng

( )



chứa

và song song với

Tìm

để diện tích thiết diện bằng một

nửa diện tích tam giác

 Lời giải

Gọi

T MN PQ

 

. Ta có:

 

 1 2

  1 1 2 1

MD AM x x

QM AB C AB CD AB

AD AD x x x



    

  

Vì

S S

/ / , / / S

MA QB P N

PQ SB MN SA AB TMQ

MD QC PC N

      

Do đó

 

S 2 1

4 1

TMQ

MQ x

AB x

 



 

  

 



 



 

Vì

 

D SD AD 1 1 2 1 2

NP N AM x x x NP x

NP C AB

C x x x QM x

       

   

Do đó

   

 

2 2

2 2 2

4 1

x x

S S

x 2 x 2 2

MNPQ

TPN

TMQ TMQ



 

     

 

  

 

(2)

Từ (1) và (2) suy ra

S 1

MNPQ

SAB





Vậy

1 1 1

S 2 1 2

MNPQ

SAB

    



 Câu 66: Cho hình chóp

. 

S ABCD

có đáy

ABCD

là hình bình hành. Gọi

là điểm thỏa mãn:

GS GA GB GC GD

    

     

Một mặt phẳng đi qua

cắt các cạnh

,  , 

SB SC SD

lần lượt tại

,  , 

M N P

. Chứng minh rằng:

BM CN DP

SM SN SP

  

 Lời giải

Gọi

là giao điểm của hai đường chéo

và

. Ta có:

OA OB OC OD

   

    

suy ra

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 59





SO SA SB SC SD

   

    

GS GA GB GC GD

    

     

suy ra





4 1

4 0 4

5 5

GS GO SG GO SG SO SA SB SC SD

          

          

SB SC SD

SA SM SN SP

SM SN SP

 

   

 

 

   

Vì

, , , ,

A G M N P

đồng phẳng nên ta có

1 5 4 1.

SB SC SD SM BM SN CN SP DP BM CN DP

SM SN SP SM SN SP SM SN SP

  

           

 Câu 67: Cho tứ diện

ABCD

là một điểm bất kỳ trong tam giác

ABC

. Các đường thẳng

đi qua

song song với

CDBDAD ,,

tương ứng cắt các mặt phẳng

)(),(),( ABDACDBCD

tại

'''

,, CBA

. Tìm vị trí

sao cho

'''

.. MCMBMA

đạt giá trị lớn nhất.

 Lời giải

+ Trong mặt phẳng (ABC), gọi













111

,, CABCMBACBMABCAM 

+Trong (DAA

), kẻ đường thẳng qua M song song với AD cắt DA

tại A

’

Xét tam giác DAA

có MA

’

// AD nên

ABC

MBC





Tương tự có

ABC

MAC



ABC

MAB



)(1

'''

ABCMABMACMBC

SSSSDo



+ Ta có:

DCDBDAMCMBMA

....3

'''

''''''



(không đổi)



’

.MB

’

.MC

’

đạt giá trị lớn nhất là

DCDBDA ..

khi

'''



hay M là trọng tâm tam giác

ABC

Vậy

'''

.. MCMBMA

đạt giá trị lớn nhất khi M là trọng tâm tam giác

ABC

 Câu 68: Cho hình chóp

S ABCD

có đáy là hình vuông cạnh

Đường thẳng

vuông góc

với mặt đáy, góc giữa

và mặt đáy bằng

60 .

Gọi

là trung điểm của

1. Tính cosin của góc giữa hai đường thẳng

và

2. Gọi là hai điểm lần lượt thuộc các đường thẳng và

sao cho

Tính độ dài đoạn theo

 Lời giải

H K

, .

HK SB HK DN

 

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 60

+ Đặt với và

+ Ta có và

Suy ra và

Vậy

Suy ra

+ Ta có và

o nên

Suy ra

Vậy

, ,

AB a AD b AS c

  

     

. . . 0

a b b c c a

  

     

, 3

a b a c a

  

  

SD b c

 

  

AN a b

 

  

2 2 2 2

1 5

2 ,

4 2

SD b c a AN a b     

     

2 2

SD AN b 

  

 

cos , 0

5 2 5

2 .

SD AN

  

 

 

cos , .

2 5

SD AN 

SB a c

 

  

DN a b

 

  

 

1 1

2 2

HK HB BN NK xSB BN yDN x a c b y a b

 

          

 

 

           

 

HK HB BN NK x y a b xc



       

      

HK SB

HK DN











 

2 2

x y a xc

x y a b



  







  





 





 

2 2

3 0

x y a xa

x y a a



  









  





4 0

4 5 1

x y



 



 





 

 

 











3 3 1 3 3 1 3

16 8 16 16 8 16 4

HK a b c HK a b c

     

       

     

     

      

HK 

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 61

 Câu 69: Cho tứ diện có

. Biết chu vi tam giác

ABC

bằng 3. Gọi S là diện tích toàn phần của tứ diện

ABCD

Tìm giá trị lớn

nhất của S.

 Lời giải

Cắt tứ diện

ABCD

theo các cạnh

DC, BC, AC

và trải tứ diện xuống mặt phẳng

như sau:

Ta có: nên thẳng hàng.

nên thẳng hàng.

suy ra tứ giác nội tiếp .

Suy ra .

Diện tích toàn phần của tứ diện bằng diện tích tứ giác .

Đặt theo định lý Cosin, suy ra . Do chu vi tam giác ABC bằng

3 nên

Ta có

Lại có nên kết hợp với (*) ta được

Vậy giá trị lớn nhất của S là đạt tại

 Câu 70: Cho khối chóp

S.ABC

có

= 6;

= 2,

= 4,

= và góc

Mặt phẳng (

) đi qua

và trung điểm

của cạnh

đồng thời vuông góc

với (

SAC

), cắt

tại

. Tính tỷ số

 Lời giải

ABCD



180 ;

ACD BCD CAD BAD BAC CBD ABD ABC ACB      

   

ABCD





ABD

1 2 3

; ; .

ACB AC B ACD AC B DCB DC B

      



2 1

180

 

   

CAD BAD BAC C AD BAD BAC

2 1

, ,

C A C



3 1

180

  



C BD ABD ABC

1 3

, ,

C B C





2 3

180

    

ACD BCD AC D BC D

1 2 3

C C DC



2 3 1

180 180 120

    

  

C DC AC B ACB

ABCD

1 2 3

C C DC

;

 

CA x CB y

2 2

AB x y xy

  

2 2

3 (*)

x y x y xy    

1 2 3 1 2 3 2 3

0 2

2 3

1 1 1

2 .2 sin 60 . ( )

2 2

C C DC C C C DC C

S S S x y C C DH x y

     

2 2

( )

x y xy x y

   

x y

 

x y

 

2 10



0 0

90 , 120 .

SBC ASC 

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 62

Ta có , dựng hình bình hành

SBCD

thì Mặt cắt

chính là mặt qua

và vuông góc với (

SAC

Từ

kẻ

vuông góc với

, kẻ

vuông góc với

thì

vuông góc với (

SAC

), như vậy

(

DBH

) vuông góc với (

SAC

) nên

là giao của

với

 .SA

Tính được ,

Vậy tỷ số cần tìm là

 Câu 71: (HSG THPT YÊN ĐỊNH 1 NĂM 2017-2018) Cho hình lập phương ABC

A’B’C’D’

cạnh bằng a. Lấy điểm M thuộc đoạn AD’, điểm N thuộc đoạn BD sao cho

a. Tìm độ dài đoạn MN.

b. Tìm theo a để đoạn MN ngắn nhất.

 Lời giải

2 2 2

;

SB BC SB SA AB SB SA

    

( ).

CD SAD



2 3; 2; 76; 4

SD BC CD AC BD

    



có 90 6 2 cos

ACD ADC AD ASD      

2 2 2; 2 3 2

CH CD HE

SE DE CE

CE CE HC

         

Menelauyt . 1 2

NC MS HE MS

MS SE

NS ME HC ME

      

2 1

6 3

  



, 0

AM DN x x   

 

 

 

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 63

 Câu 72: (HSG THPT YÊN ĐỊNH 1 NĂM 2017-2018) Cho hình chóp tứ giác có

đáy là hình vuông tâm cạnh bằng Gọi là mặt phẳng đi qua và

vuông góc với mặt phẳng kéo dài cắt mặt phẳng tại

Chứng minh

Biết Tính độ dài đoạn thẳng

 Lời giải

+ Vì

+ Mặt khác theo giao tuyến

mà

+ Từ và suy ra hay

S ABCD



, 90 .

a ASB ASD 









ABCD







AEB 

SA SO



   

SA SB

SA SBD BE SA

SA SD





   















P ABCD











AD AB AD P BE AD    













BE SAD BE AE

  



AEB 

Gọi M’, N’ lần lượt là hình chiếu của M, N lên AD

Ta có

Tam giác M’AM vuông cân tại M’ nên có ;

Tam giác N’DN vuông cân tại N’ nên có

Khi đó

Vậy MN ngắn nhất bằng đạt được khi

2 2 2 2 2 2

' ' ' ' ' '

MN M M M N M M M N N N

    

' '

M A M M 

' '

N D N N 

' ' ' ' 2

M N AD M A N D a x

    

 

2 2

2 2 2

2 3 2 2 .

2 2

x x

a x x a x a



     

2 2

2 3

3 3 3 3

a a a

x a MN

 

     

 

 

x 

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 64

+ Ta có

+ Vì vuông cân tại nên

+ Dễ thấy

+ Khi đó

+ Vậy

 Câu 73: Cho hình chóp S.ABCD, có đáy ABCD là hình thang cân (AD//BC) và BC = 2a, AB

= AD = DC = a (a > 0). Mặt bên SBC là tam giác đều. Gọi O là giao điểm của AC và B

Biết

SD vuông góc với A

a) Tính S

b) Mặt phẳng ( ) qua điểm M thuộc đoạn OD (M khác O, D) và song song với hai đường thẳng

SD và A

Tìm x để diện tích thiết diện lớn nhất.

 Lời giải

a) Dễ thấy đáy ABCD là nữa hình lục giác đều cạnh a.

Kẻ DT//AC (T thuộc BC). Suy ra CT=AD=a và DT vuông góc S

Ta có: DT=AC= .

Xét tam giác SCT có SC=2a, CT=a,

Xét tam giác vuông SDT có DT= ,

b) Qua M kẻ đường thẳng song song với AC cắt AD, DC lần lượt tại N,P.

Qua M, N, P kẻ các đường thẳng song song với SD cắt SB, SA, SC lần lượt tại K, J, Q. Thiết diện

là ngũ giác NPQKJ.

Ta có: NJ, MK, PQ cùng vuông góc với NP.

dt(NPQKJ)=dt(NMKJ)+dt(MPQK)=

AC a AO  

SA SO SAO

  

AO a

 

2 2

AE SA

SAE ADE AE AE a

DE AD

       



AE 

2 2 2

BE AB AE  

2 2 2

2 15

3 3

a a

CE BC BE a    



B C

120

SCT 

ST a

 

7 2

ST a SD a

  

1 1

( ) ( )

2 2

NJ MK MN MK PQ MP

  

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 65

(do NJ=PQ).

Ta có:

Suy ra: dt(NPQKJ)=

Diện tích NPQKJ lớn nhất bằng khi

 Câu 74: (HSG THPT TRIỆU SƠN 2 NĂM 2017) Cho tứ diện có SA, SB,SC đôi một

vuông góc. Gọi lần lượt là các góc giữa các mặt phẳng với .

Chứng minh rằng:

 Lời giải

Chứng minh

Đẳng thức xảy ra khi

 Câu 75: (THPT HÀM RỔNG THANH HÓA)

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, ,

và SA (ABCD). Gọi M, N, K lần lượt là trung điểm của AB, SB, S

1/ Tính góc hợp bởi giữa đường thẳng SB và DM.

2/ Tính diện tích thiết diện của hình chóp khi cắt bởi (ANK).

 Lời giải

( ).

NJ MK NP

 

. . 3

NP MD AC MD x a

NP x

AC OD OD

    

2 .

2( 3)

a x

NJ AN OM SD OM

NJ a x

SD AD OD OD

 



 

 

      





2 . 3

. 2

( 3 )

3 3

a a x

KM BM SD BM

KM a x

SD BD BD



     

1 2

2( 3) ( 3 ) 3 2(3 2 3 )

a x a x x a x x

 

    

 

 

1 1 3 3

(3 2 3 )2 3 (3 2 3 ) 2 3

3 4 3

a x x a x x a

 

     

 

3 3

x a



SABC

, ,

  













, ,

SAB SBC SCA





ABC

2 2 2

2 2 2 2 2 2

cos cos cos 3

sin sin sin sin sin sin

  

     

  

  

2 2 2

cos cos cos 1

  

   

2 2 2

sin sin sin 2

  

  

2 2 2 2 2 2

2 2 2 2 2 2 2 2 2

2 2 2

2 2 2 2 2 2

cos cos cos cos cos cos 3

2 2 2 4

cos cos cos 1 1 1 9 3

3 3

1 os 1 os 1 os 1 os 1 os 1 os 4 4

sin sin sin sin sin sin sin sin sin

c c c c c c

     

        

  

     

     

     

 

         

 

     

 

  

 

AB AD CD a

  

SA a





 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 66

1/ Kẻ BE//DM. Ta tính được:

+ Áp dụng định lí cosin trong tam giác SBE ta có:

2/ Cách dựng thiết diện:

Gọi . Trong (SAC), . Thiết diện là ANHK

Ta có: đều

 Câu 76: (HSG THPT HẬU LỘC 1 NĂM 2017-2018) Cho hình chóp tứ giác có đáy

là hình vuông tâm cạnh bằng Gọi là mặt phẳng đi qua và vuông

góc với mặt phẳng kéo dài cắt mặt phẳng tại

Chứng minh

Biết Tính độ dài đoạn thẳng

 Lời giải

5, 2 2, 3

BE MD AE a SB a SE a

    

2 2 2

cos 0

2.SB.BE

SB BE SE

SBE

 

  

   

, , arccos

SB MD SB BE SBE

 

    

 

 

O AC BD F SO NK

   

H SC

 

2, 2

2 2

SD BD

AN AK a NK a ANK

      

 

1 3

2 sin 60

2 2

ANK

S a  

2 2

1 3 3 3

2 4 4

HNK ANK TD

a a

S S S   

S ABCD



, 90 .

a ASB ASD 









ABCD







AEB 

SA SO



 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 67

+ Vì

+ Mặt khác theo giao tuyến

mà

+ Từ và suy ra hay

+ Ta có

+ Vì vuông cân tại nên

+ Dễ thấy

+ Khi đó

+ Vậy

 Câu 77: (HSG THPT HẬU LỘC 3 NĂM 2017-2018)

Cho tứ diện

ABCD

có

AB = a

CD = b

. Gọi

I, J

lần lượt là trung điểm

và

Giả sử



nằm trên đoạn

sao cho . Tính diện tích thiết diện tạo bởi mặt phẳng () qua

song song với

và tứ diện

ABC

 Lời giải

Xác định thiết diện của (ABCD)

   

SA SB

SA SBD BE SA

SA SD





   















P ABCD











AD AB AD P BE AD    













BE SAD BE AE

  



AEB 

AC a AO  

SA SO SAO

  

AO a

 

2 2

AE SA

SAE ADE AE AE a

DE AD

       



AE 

2 2 2

BE AB AE  

2 2 2

2 15

3 3

a a

CE BC BE a    

IM IJ



 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 68

với mặt phẳng ()

: Ta có:

 EF // AB (1)

Tương tự:

 HG // AB (2)

Từ (1) và (2), suy ra EF // HG // AB (3)

Ta có:

 FG // CD (4)

Tương tự:  EH // CD (5)

Từ (4) và (5), suy ra FG // EH // CD (6)

Từ (3) và (6), suy ra EFGH là hình bình hành

Mà AB  CD (*)

Từ (3), (6) và (*), suy ra EFGH là hình chữ nhật

Tính diện tích thiết diện của huình chữ nhật biết IM = IJ

Ta có:

Tính LN:

Xét tam giác ICD: Ta có: LN // CD  (7)

Xét tam giác IJD: Ta có: MN // JD  (8)

Từ (7) và (8), suy ra

Tương tự:  Vậy:

 Câu 78: (HSG THPT HẬU LỘC 3 NĂM 2017-2018) Cho tứ diện

ABCD

có

AB = a

CD =

. Gọi

I, J

lần lượt là trung điểm

và

Giả sử



nằm trên đoạn

sao cho

. Tính diện tích thiết diện tạo bởi mặt phẳng () qua

song song với

và tứ diện

ABCD















)()(

)(

//)(

ABCL

ABCAB

















)()(

)(

//)(

ABDN

ABDAB

















)()(

)(

//)(

ACDP

ACDCD

















)()(

)(

//)(

BCDQ

BCDCD



LNPQFGEFS

EFGH

.. 



1 bCD





aABPQ .



2ab

EFGH



IM IJ



 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 69

 Lời giải

Xác định thiết diện của (ABCD)

với mặt phẳng ()

: Ta có:

 EF // AB (1)

Tương tự:

 HG // AB (2)

Từ (1) và (2), suy ra EF // HG // AB (3)

Ta có:

 FG // CD (4)

Tương tự:  EH // CD (5)

Từ (4) và (5), suy ra FG // EH // CD (6)

Từ (3) và (6), suy ra EFGH là hình bình hành

Mà AB  CD (*)

Từ (3), (6) và (*), suy ra EFGH là hình chữ nhật

Tính diện tích thiết diện của huình chữ nhật biết IM = IJ















)()(

)(

//)(

ABCL

ABCAB

















)()(

)(

//)(

ABDN

ABDAB

















)()(

)(

//)(

ACDP

ACDCD

















)()(

)(

//)(

BCDQ

BCDCD



 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 70

Ta có:

Tính LN:

Xét tam giác ICD: Ta có: LN // CD  (7)

Xét tam giác IJD: Ta có: MN // JD  (8)

Từ (7) và (8), suy ra

Tương tự:  Vậy:

 Câu 79: (HSG THPT BA ĐÌNH NĂM 2017-2018) Cho tứ diện đều

SABC

có độ dài cạnh

bằng 1, gọi

là trung điểm của các cạnh

và

Trên các đường thẳng

và

lấy các

điểm

sao cho

song song với

. Tính độ dài đoạn thẳng

 Lời giải

Kẻ KJ // BI (J thuộc SI), P là giao của CJ với SA, kẻ PQ // JK (Q thuộc CK) thì đươch PQ

thỏa mãn P thuộc SA, Q thuộc CK và PQ//BI.

Ta có đều cạnh 1 nên

Qua cách dựng PQ thì J là trung điểm của SI nên

Xét với 3 điểm P, J, C thẳng hàng ta có

Xét với 3 điểm thẳng hàng S, J, I ta có

Suy ra

LNPQFGEFS

EFGH

.. 



1 bCD





aABPQ .



2ab

EFGH



ABC



BI 

1 3

2 4

KJ BI 

SAI



1 . . .2.1

PS CA JI PS PS

PA CI JS PA PA

   

APC



1 . . .1.3

JP IC SA JP JP

JC IA SP JC JC

   



3 4 4 3 3

4 3 3 4 3

PQ JK

    

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 71

Vậy

 Câu 80: (HSG THPT BA ĐÌNH NĂM 2017-2018) Cho hình chóp

ABCD

có đáy

ABCD

là

hình thoi tâm

với

= 2

và

vuông góc với đáy (

ABCD

). Mặt phẳng qua

vuông góc với

cắt

lần lượt tại

B’

C’

D’

. Tính côsin góc giữa (

SAB)

với biết

đều.

 Lời giải

trong đó E đối xứng với C qua B và F đối xứng với C qua D, E đối xứng với

F qua A và . Tam giác B’C’D’ đều nên tam giác EFC’ đều.

;

Hạ ;

;

Từ đó ta có .

 Câu 81: (HSG THPT SẦM SƠN NĂM 2017-2018) Cho

OABC

là tứ diện có OA,OB,OC đôi

một vuông góc.

là trực tâm của tam giác

Gọi lần lượt là góc tạo bởi

với

OA,OB,

Chứng minh rằng

 Lời giải

PQ 

( )



( )



' ' '

B C D



( ) ( )

ABCD EF



 

2 4

EF BD a

 

2 2

' ' 20 4 2

CC x C F a x EF a x a

       

2 2 2 2

' ' 16 4 2 3

AC AC CC a a a

    

2 2 2 2 2 2

' ' ' ( ')

SC SA AC SC AC SC CC

     

2 2 2 2 2

12 ( 2 ) 16 4 .

SC a SC a a a SC SC

      

4 2 3

SC a SO a

   

 



' ' ' ( ' ) ( );( ' ') '

C I AB AB SC I SAB AB C SIC

    

2 4 3

' '

3 3

AO AC 



2 '

' ' cot ' 2 3

3 ' '

a AO

O B IAC

O B

   

 

1 2 39

sin ' ' '.sin '

IAC IC AC IAC    



' 13 3

tan tan ' cos

' 4

SIC

 

    

, ,

  

2 2 2

cos cos cos 1

  

  

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 72

Chứng minh OH vuông góc với mặt phẳng (ABC)

Chứng minh

Ta có . Tương tự: . Nên

 Câu 82: (HSG THPT SẦM SƠN NĂM 2017-2018) Cho hình chóp có vuông góc

với mặt phẳng đáy. Gọi là trung điểm của và là trung điểm của

Biết

, ; góc giữa mặt phẳng và mặt phẳng bằng . Tính

SA và cosin của góc giữa đường thẳng và mặt phẳng .

 Lời giải

Gọi

là hình chiếu vuông góc của

trên

Ta có

2 2 2 2

1 1 1 1

OH OA OB OC

  

cos cos

OH OH

OC OC

    

2 2

cos ;cos

OH OH

OA OB

   

2 2 2

2 2 2 2

2 2 2 2 2 2

1 1 1

cos cos cos 1

OH OH OH

OA OB OC OA OB OC

 

           

 

 

S ABC

HB HC a

 

30HBC





SHC





HBC





SHC

60°

30°

0 0

sin 30 .sin 60

2 4

a a

AH HM HB AK AH     

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 73

Góc giữa (

SHC

)

và (

ABC

) là

* Gọi

B’

là hình chiếu của

trên (

SHC

), suy ra góc giữa

và (

SHC

) là . Gọi

là hình

chiếu của

trên

*Ta có .

Trong tam giác vuông

SAK,

ta có

Do đó .

Vậy

 Câu 83: (HSG THPT THƯỜNG XUÂN) Cho tứ diện

ABCD

, hai mặt

ABC

và

ABD

là hai

tam giác đều cạnh .

a. Chứng minh rằng

và

vuông góc với nhau. Gọi

M, N, P, Q

lần lượt là trung điểm của các

cạnh

AC, BC, BD, D

Chứng minh rằng tứ giác

MNPQ

là hình chữ nhật.

b. Tính góc giữa hai đường thẳng

và

, biết

c. Gọi

là độ dài đường cao của tam giác

BCD

nằm trên

sao cho

theo thứ

tự lập thành một cấp số nhân. Tìm công bội của cấp số nhân đó và tính độ dài đoạn

 Lời giải

Ta có:

Vậy



* Ta có:

và

Nên tứ giác

MNPQ

là hình bình hành

Vì

và

mà



nên hình bình hành

MNPQ

là hình chữ nhật.

b. Gọi

là trung điểm của

60tan.60

AKSASKA 

BCB

( )

AI SHC

 

' ( ,( )) 2 ( ,( )) 2 ( , ( )) 2

BB d B SHC d M SHC d A SHC AI

   

2 2

. 3 3 2 3 3

. ' .

16 8 4

AK AS a a a

AI BB

AK AS

    



cos

sin



BCB

1cos

BCB

MP a







. . .

CD AB AD AC AB AD AB AC AB

   

        

. . cos 60 . cos 60 0

o o

CD AB AD AB AC AB

  

     

MN PQ 

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 74

Ta có: .

Xét tam giác

IMP

có: .

Do đó,

Vậy:

c. Theo bài ra:

theo thứ tự lập thành cấp số nhân.

Gọi

là công bội của cấp số nhân trên,

>0.

Khi đó ta có:

(Vì tam giác

BCD

cân tại B).

Trong tam giác

BHD

vuông tại

nên ta có: Khi đó:

Vậy .

Khi đó: .

 Câu 84: (HSG 11 THPT THIỆU HÓA THANH HÓA)

Cho hình hộp

. ’ ’ ’ '.

ABCD A B C D

Trên

cạnh

lấy điểm

khác

và

Gọi (

) là mặt phẳng đi qua

và song song với mặt phẳng

(ACD’).

a) Trình bày cách dựng thiết diện của hình hộp và mặt phẳng (

b) Xác định vị trí của

để thiết diện nói trên có diện tích lớn nhất.

c) Gọi C

là trung điểm của CC’. Mặt phẳng (Q) đi qua AC

cắt C’B, C’D lần lượt tại B

, D

khác

C’. Chứng minh rằng:

 Lời giải

/ /

( , ) ( , )

/ /

IP AD

CB AD IM IP

IM BC



 





, 3

IM IP a MP a

  

 

2 2 2 2 2

2 3 1

cos 120

2. . 2 2

IM IP MP a a

MIP MIP

IM IP a

  

     

0 0 0

( , ) 180 120 60

CB AD   

D. ; D D.

BH C q B C q

 

HC H 

BD 2a 4a

1 2 1 2

  

 

2 2 2 2 2 2 . 2 2 2

2 4 2 2 4 2

CD CD

BD BH HD BD ( ) BH (CD .q ) (CD.q)

2 4

1 2

CD .q CD .q 4q 4q 1 0

1 2

       









       











1 2 1 2

q q

2 2

 

  

1 2





BD 2a 4a

1 2 1 2

  

 

1 1

4 ' ' 3

3 ' ' 2

C B C D

  

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 75

a) Trong mp(

ABCD

), qua

vẽ đường thẳng song song với

cắt

DB, BC

lần lượt tại

E, N

Trong mp(

BDD’B’

), qua

vẽ đường thẳng song song với

D’O

(

O=AC



) cắt

B’D’

tại

Trong mp(

A’B’C’D’

), qua

vẽ đường thẳng song song với

cắt

A’D’, D’C’

lần lượt tại

R, Q

Trong mp(

AA’D’D

), qua

vẽ đường thẳng song song với

AD’

cắt

AA’

tại

Trong mp(

CC’D’D

), qua

vẽ đường thẳng song song với

CD’

cắt

CC’

tại

Thiết diện là lục giác

MNPQRS

 Do các mặt đối diên của hình hộp song song nên các cạnh đối của lục giác thiết diên

MNPQRS

song song và 3 cặp cạnh đó lần lượt song song với các cạnh tam giác

ACD’

 Các tam giác

JKI

ACD’

RQI

JMS

NKP

đồng dạng

 

MJ=NK

và

PK=QI

 Các tam giác

RQI

JMS

NKP

bằng nhau (gọi diện tích của chúng là

và gọi diện tích các tam

giác

JKI

ACD’

lần lượt là

)

Đặt ta có điều kiện và có:



= k



(

+1)

 Diện tích thiết diện:

(dấu bằng xảy ra  )

lớn nhất  

là trung điểm của

' '

MJ MA NC NK PC PK QD QI

MN MB NB NM PC PQ QC QP

      

;



0 1

 

2 2 2

S JM AM AM

S AC DC AB

     

   

 

 

 

2 2 2

JK JM MK JM MK

S AC AC AC AC



     

     

     

     

2 1

S S S

 

1 3 1 3

2 ( ) 2

2 4 2 2

S S k k S k

 

 

       

 

 

 

 

 



 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 76

)Lấy



và



ta có: C’

, O, G

là các điểm chung của 2 mặt phẳng (

C’AC

) và (

C’BD

)

 C’,

thẳng hàng.

Và G

là trọng tâm của tam giác C’



Vẽ BH

//G B

và

DL // D

 . Đặt

  (*)

 Suy ra: (1)

Từ (*):   

   (2); Từ (1) và (2) đpcm

 Câu 85: (TRƯỜNG THPT TĨNH GIA 1-2017-2018) Cho hình chóp

có đáy

là hình thang cân và , cắt tại điểm . Cạnh

bên . Gọi mặt phẳng ( ) là mặt phẳng đi qua điểm thuộc đoạn ( khác )

và song song với hai đường thẳng . Mặt phẳng ( ) cắt lần lượt tại và .

a. Xác định thiết diện của hình chóp cắt bởi mặt phẳng ( ).

b. Đặt . Tìm để diện tích thiết diện lớn nhất, biết vuông góc với .

 Lời giải

a) Qua M kẻ đường thẳng song song với AC cắt AD, DC lần lượt tại N,P.

Qua M, N, P kẻ các đường thẳng song song với SD cắt SB, SA, SC lần lượt tại K, J, Q. Thiết diện

là ngũ giác NPQKJ.

b) Ta có: NJ, MK, PQ cùng vuông góc với NP.

' 2

' 3

C G

C O







, '

H L C O



OH OL



1 1

' '

;

' '

C D C B

x y

C D C B

 

1 1

' ' ' ' 2 ' 3

2 3

' ' ' ' ' 2

C D C B C L C H C O

x y

C D C B C G C G C G

       

, [1; 2]

x y



1 1 3 2 4

x y xy x y

 

   

 



 

1 2

 

3 2 0

x x

  

(3 ) 2

x x

 

x y

 

3 3



x y





1 1 3

x y

 

ABCDS. ABCD

)//( BCAD )0(,2





aaDCADABaBC

aSD 2





DO,

ACSD,



SAAD,

ABCDS.



)0(





xxMD

MN NI

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 77

dt(NPQKJ)=dt(NMKJ)+dt(MPQK)=

(do NJ=PQ).

Ta có:

Suy ra: dt(NPQKJ)=

Diện tích NPQKJ lớn nhất bằng khi

 Câu 86: (HSG THPT SẦM SƠN NĂM HỌC 2017-2018) Cho tứ diện đều ABCD có độ dài

cạnh bằng 1. Gọi M, N lần lượt là hai điểm thuộc các cạnh AB, AC sao cho mặt phẳng (DMN)

vuông góc với mặt phẳng (ABC). Đặt . Chứng minh rằng .Tìm

để diện tích toàn phần của tứ diện DAMN nhỏ nhất.

 Lời giải

Kẻ DH MN, do (DMN) (ABC) suy ra DH (ABC).

Ta có: S

AMN

= .AM.AN.sin60

= ; S

AMN

= S

AMH

+ S

ANH

= .AM.AH.sin30

+ .AN.AH.sin30

= (x+y).

Mà ABCD là tứ diện đều, nên suy ra H là tâm của tam giác đều ABC

Suy ra = (x+y) x+y= 3xy (0 x,y 1 ).

Diện tích toàn phần của tứ diện DAMN:

S = S

AMD

+ S

AND

+ S

DMN

+ S

AMN

= A

AM.sin60

+ A

. AN.sin60

1 1

( ) ( )

2 2

NJ MK MN MK PQ MP

  

( ).

NJ MK NP

 

. . 3

NP MD AC MD x a

NP x

AC OD OD

    

2 .

2( 3)

a x

NJ AN OM SD OM

NJ a x

SD AD OD OD

 



 

 

      





2 . 3

. 2

( 3 )

3 3

a a x

KM BM SD BM

KM a x

SD BD BD



     

1 2

2( 3) ( 3 ) 3 2(3 2 3 )

a x a x x a x x

 

    

 

 

1 1 3 3

(3 2 3 )2 3 (3 2 3 ) 2 3

3 4 3

a x x a x x a

 

     

 

3 3

x a



AM x



AN y



x y 3xy

 

x y







 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 78

+ DH.MN + AM.AN.sin60

= xy + .

Từ

Suy ra khi

 Câu 87: (HSG THPT SẦM SƠN NĂM HỌC 2017-2018) Cho hình chóp đều S.ABC đỉnh S,

chiều cao h, đáy ABC là tam giác đều cạnh a. Qua AB dựng mp (P) vuông góc với S

1. Xác định thiết diện của hình chóp khi cắt bởi (P).

2. Tính diện tích thiết diện theo a và h.

 Lời giải

)1xy3(xy3



2 4

3 2 .

3 9

xy x y xy xy xy

      

3(4 2)

min ,





x y

 

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 79

Gọi O là trọng tâm tam giác ABC ta có khi đó , gọi M là trung điểm AB

do tam giác ABC đều nên vậy .

Trong mp(SMC) kẻ MH  SC ta có mặt phẳng (AHB)  S

Thiết diện là tam giác

AHB

Ta có: .

Theo giả thiết AB = a. ta có , ,

SO = h,

Ta có: MH.SC = SO.MC

 Câu 88: (HSG THPT TRIỆU SƠN 5 NĂM 2017-2018) Cho hình chóp SABC có ABC là tam

giác đều. Gọi H,O lần lượt là trực tâm của các tam giác ABC và

SBC

OH cắt SA tại N.

1. Giả sử SA(ABC). Chứng minh OH(SBC) và tứ diện BCSN có các cặp cạnh đối diện vuông

góc với nhau.

2. Giả sử SH(ABC). Gọi  là góc giữa mặt bên và mặt đáy;  là góc giữa hai mặt bên kề

nhau.Chứng minh rằng .

 Lời giải

SO ABC



( )

SO AB



CM AB



AB SMC



( )

AHB

S MH AB





MC 

OC 

2 2 2

SC SO OC h   

2 2 2

2 3

a h a

  



2 2

1 3

4 3

AHB

a h

S MH AB

h a



 



2cos = 3sin

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 80

Chứng minh OH(SBC)

+ AO cắt BC tại I. BCAO( ABC đều)

BCSA

nên BC( SAI) BCAI nên H nằm trên

đường AI. OH nằm trong (SAI)BCOH(1)

+ Có BOAC; BOSABO(SAC)

BOSC

BHSC SC(BOH) ACOH (2)

Từ (1) và (2) ta được OH(SBC)

+) Chứng minh BCSN có các cặp cạnh đối

vuông góc với nhau

SA(ABC) SNBC

SC(BOH) SCBN( vì N nằm trên OH)

Chứng minh tương tự ta có

SB(COH) SBCN( N nằm trên OH)

 Câu 89: (HSG THPT VĨNH LỘC NĂM 2017-2018) Cho điểm cố định và một số thực

không đổi. Một hình chóp thay đổi thỏa mãn

Chứng minh

rằng:

là tam giác vuông.

Khoảng cách không thay đổi.



S ABC



0 0 0

, , , , 90 , 60 , 120 .

OA OB OC a SA OA SB OB SC OC ASB BSC CSA        

ABC



 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 81

 Lời giải

+ Đặt

+ Vì các tam giác lần lượt vuông tại nên

+ Tam giác vuông tại nên

+ Xét tam giác ta có đều nên

+ Xét tam giác ta có

+ So sánh và ta thấy vuông tại

+ Gọi là trung điểm của

+ Vì là tam giác vuông tại nên

+ Mặt khác và

+ Từ và suy ra là hình chiếu của lên

+ Từ đây suy ra tại . Do đó là đường cao của tam giác vuông

+ Vậy đpcm.

 Câu 90: (HSG SGD&ĐT HÀ TĨNH NĂM 2006-2007) Hình chóp S.ABC có đáy ABC là tam

giác vuông tại A, và cạnh BC = a. Mặt bên SBC vuông góc với đáy, hai mặt bên còn

lại đều tạo với đáy góc . Các góc SBC và SCB đều nhọn.

a) Cho và , hãy xác định tâm và tính bán kính mặt cầu nội tiếp hình chóp

S.ABC theo a.

SO x



, ,

SAO SBO SCO

, ,

A B C

2 2

SA SB SC x a

   

SAB









2 2 2 2 2

2 1

AB SA SB x a   

SBC



BSC SBC

  





2 2 2

BC x a 

SCA









2 2 2 0 2 2

2 . .cos120 3 3

CA SC SA SC SA x a    









1 , 2





2 2 2

CA AB BC ABC

   

ABC





MA MB MC 





SA SB SC 





OA OB OC 













ABC













ABC





SO ABC



SAO

   

2 2 2 2 2 2 2

2 2 2 2

1 1 1 4 1 1 4 1 1

AM SA OA CA SA OA a

x a x a

       

 

 

2 2 2 2

2 2

1 1 4 2

a a

x a a x x

x a

        



 

ACB



 











 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 82

b) Khi a và không đổi, tìm giá trị của để đường cao SH của hình chóp có độ dài lớn nhất.

 Lời giải

Do mp(SBC) vuông góc với đáy ABC và các góc SBC, SCB đều nhọn nên H thuộc cạnh BC của

tam giác AB

Vẽ suy ra nên do đó

2 tam giác vuông: SMH,SNH bằng nhau, suy ra MH=NH, từ đó ta có tứ giác AMHN là hình

vuông.

a) Khi thì tam giác ABC vuông cân tại A nên .

Vẽ tia phân giác của góc SMH cắt SH tại K thì mp(KAC) và mp(KAB) thứ tự là mặt phẳng phân

giác của các góc nhị diện cạnh AC,AB của hình chóp S.AB

Dễ thấy giao tuyến của hai mặt

phẳng này là đường thẳng AK.

Vẽ tia phân giác của góc SHA cắt AK tại I thì I cách đều 4 mặt của hình chóp S.ABC nên nó là

tâm mặt cầu nội tiếp hình chóp.

Dễ thấy

Xét tam giác vuông KHM:

Vẽ thì với r là bán kính mặt cầu nội tiếp hình chóp S.AB

Ta có: ( vì mỗi vế cùng bằng 2 lần diện tích )





HM AC HN AB

 

AC SM AB SN

 

SMH SNH



   







AH BC AH

 

.sin 45

2 2

a a

HM  



.tan 30 . ( 30 )

2 2 3 2 6

a a

KH HM do KMH    

 

IE AH IF HK

 

IE IF r

 

. . .

IE AH IF HK AH HK

 

AHK



 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 83

b) Đặt . Xét tam giác vuông NBH: (1)

Xét tam giác vuông MCH: (2)

Từ (1) và (2) ta có:

Xét tam giác vuông SHM:

Do không đổi nên SH lớn nhất khi và chỉ khi lớn nhất.

Áp dụng bất đẳng thức Cô si cho 2 số dương ta được:

Dấu bằng xảy ra khi và chỉ khi

Gía trị thỏa mãn là

Vậy đường cao SH của hình chóp S.ABC lớn nhất khi và chỉ khi .

 Câu 91: (HSG ĐỀ 142) Cho hình chóp S.ABC với đáy ABC là tam giác nhọn, cạnh SA vuông

cắt đường thẳng SA tại P.

a) Chứng minh tứ diện SPBC có các cặp cạnh đối vuông góc.

b) Tam giác ABC cố định có BC = a, , điểm S di động. Tìm độ dài đoạn

thẳng SA trong trường hợp diện tích tam giác SPC đạt giá trị nhỏ nhất.

 Lời giải

2 6

2( 6 1)

2 6

a a

AH HK a

a a

AH HK

   



HM HN x

 

cos cos

NH x

BH BH

 

  

sin sin

HM x

HC HC

 

  

(sin cos ) a .cos .sin

cos .sin sin cos

a x

   



  



a .sin .cos

.tan .tan

sin cos

SH x

 

 

 

 





sin .cos

sin cos

 



sin cos

( )

sin .cos 1 2

(sin cos ) .

sin cos sin cos 4 4

 

   



   

 



sin cos

sin cos 2

 



 













ABC ACB

 

   

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 84

a)  (do )



 Trong (SPC) K là trực tâm tam giác SPC



 Tứ diện SPBC có

Tứ diện SPBC có các cặp cạnh đối vuông góc với nhau

b) Ta có (g.g) không đổi

Đẳng thức xảy ra

SP BC



( )

SA ABC



( ) ,

BK SA

BK SAC PC BK BK SC

BK AC





    







( ) ,

SC BI

SC BIK SC BP SC PI

SC BK





    







CK SP

PK SC













PC SK

 

( )

PC SK

PC SBK PC SB

PC BK





   







SP BC

SC BP

PC SB



















SAK CAP

 



. .

SA AK

SA AP AK AC

AC AP

   

1 1

.SP .( ) . . . .

2 2

SPC

S AC AC SA AP AC SA AP AC AC AK

     

SA AP AK AC

  

.cot(180 ).

sin(180 )

SA BK

 

   

 

.sin

.sin .cot(180 ).

sin(180 )

SA a



  

 

   

 

cos(180 )

.sin .sin .

sin ( )

SA a

 

 

 



 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 85

( )

Vậy khi

đạt giá nhỏ nhất thì

 Câu 92: (HSG ĐỀ 143) Cho hình chóp

S.ABCD

có đáy

ABCD

là hình bình hành và

là

trung điểm của

Một mặt phẳng (

) chứa

và lần lượt cắt các cạnh

tại các điểm

khác

. Chứng minh rằng

 Lời giải

Gọi là giao điểm của BD và AC, suy ra .

Gọi H là giao điểm của và . Ta có:

Áp dụng định lý Menelaus cho tam giác ta có:

Mà thuộc trung tuyến suy ra là trọng tâm tam giác

Xét mặt phẳng :

+Lấy sao cho . Suy ra ta có:

.sin( ). sin .sin .cos(180 )

SA a

     

    

CH AB H AB

 

SPC

.sin( ). sin .sin .cos(180 )

SA a

     

   

4 ' ' 3

3 2

SB SD

  









SO SBD SAC

 

' '

B D









 





' '

SBD SAC SO

B D SBD

H SO

AM SAC

B D AM H





 







 









 





SOC

. . 1 1.2. 1

SM AC OH OH OH

MC AO HS HS HS

    

SBD





SBD

E F SO



' '

BF DE B D

 

' ' 1 1 4 4 4

2 3

SB SD SH SH SH SH

SB SD SF SE SF SE SF SE SO

 







       













 

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 86

Vậy

+Vẽ trung tuyến của tam giác

Do vai trò của B và D là bình đẳng nhau nên vai trò B’ và D’ cũng bình đẳng nhau

Giả sử ( trường hợp ngược lại chứng minh tương tự)

Theo định lý Talet ta có

Lấy thuộc DM sao cho .Ta có

Mặt khác lại có

Suy ra

Vậy (dpcm)

 Câu 93: (HSG ĐỀ 145) Cho hình chóp có , diện tích tam

giác SBC là .Gọi M là điểm di động trên SB,N là trung điểm của B

Biết AN vuông góc với mặt

phẳng . Tìm giá trị nhỏ nhất của diện tích tam giác AMN theo a và .

 Lời giải

Cho hình chóp có , diện tích tam giác SBC là .

Gọi M là điểm di động trên SB,N là trung điểm của B

Biết AN vuông góc với mặt phẳng

Tìm giá trị nhỏ nhất của diện tích tam giác AMN theo a và .

 Ta có

Suy ra vuông tại S, do đó ta có và .

' ' 4

SB SD

 

SBD

' '

HD HB



1 ' '

D K HK

D K B M

B M HM

   

D K SB



' ' ' ' 3 ' '

SB SD SM MB SD DD DD MB

SB SD SB SB SD SD SD SB

     

  

  

  

       

  

  

  

  

  

     

' ' 2 ' ' ' '

DD D K D K MB DD MB

SD SM SB SB SD SB

     

' ' 3 ' ' 3

2 2

SB SD DD MB

SB SD SD SB

 







    











 

4 ' ' 3

3 2

SB SD

  

2 2 2 2

BN CN AB AN SA AN SN

     

SBC





2 4

2 2

S a

BC SC SB



  

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 87

 Xét vuông tại N ta có .

 Ta có

Vậy giá trị nhỏ nhất của diện tích tam giác AMN là .

 Câu 94: (HSG ĐỀ 147) Cho tam giác nhọn ABC cố định. Trên tia lấy điểm S

khác

Kẻ các đường cao BH của các tam giác BA

Gọi (P) là mặt phẳng qua C và vuông góc

với SB, giả sử (P) cắt tia đối của tia AS tại M. Đường thẳng MH cắt SC tại N.

a) Chứng minh tứ diện SMBC có các cặp cạnh đối vuông góc với nhau và

b)Biết cạnh BC = a, . Tìm giá trị nhỏ nhất của diện tích tam giác SPC

theo a khi S di động trên tia Ax (S khác A).

 Lời giải

a) Ta có (giả thiết) (1)

Mà (2)

Từ (1) và (2) suy ra S.MBC là tứ diện có 2 cặp cạnh đối vuông góc nên cặp thứ 3 cũng vuông góc

Ta có nên

Theo chứng minh trên thì , do đó ta có

b) Từ câu a ta có , do đó đồng dạng (g.g)

do đó

Có “ =” khi SA = AM

Theo định lý hàm số sin ta có

CAN



4 2

2 2 2 2

1 4

2 2

a S

AN AC CN a BC



    

4 2

1 1 1 1 1 2 4

. . ( , ) . . . .

2 2 2 2 4 2

o o

AMN

S a S

S AN MN AN d N SB AN SC

a a



   

4 2

2 2

o o

S a S

a a



( )

Ax ABC



( )

SC MBN



; ABC ACB

 

   

 

BC SM



MC SB



( )

BH SAC



SC HB



SC BM



( )

SC MBN



SC MN



AHM ASC

 

AH AM

SAAM AH AC

SA AC

  

1 1

. ( ) . . . .

2 2

SMC

S SM AC SA AM AC SA AM AC AH AC AC



    

sin sin

;

sin sin( ) sin sin( ) sin( )

AC a AB

AC a AB a

 

       

    

  

os( ) sin cot( )

AH ABc a

    

   

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 88

Có “=” khi

 Câu 95: (HSG HUẾ 2000-2001) Cho tứ diện có hai cạnh đối bằng và các cạnh

còn lại bằng

a/ Tìm giá trị nhỏ nhất của tổng các khoảng cách từ một điểm tùy ý trong không gian đến các đỉnh

của tứ diện.

b/ Giả sử tứ diện thay đổi vị trí trong không gian nhưng có ba đỉnh lần lượt ở

trên mặt cầu cố định và đồng tâm. Chứng minh rằng đỉnh luôn ở trong một hình cầu cố định

khi độ dài thay đổi thỏa các giả đã cho.

 Lời giải

a) Ta có thể giả sử và các cạnh còn lại bằng . Gọi lần lượt là trung điểm

của các cạnh Ta dễ dàng suy ra vuông góc với và và chính là trục đối

xứng của tứ diện.

Lấy tùy ý trong không gian, là điểm đối xứng của qua suy ra trung điểm của

chính là hình chiếu của trên đường thẳng và ta có:

Do tính chất: trung tuyến của một tam giác thì bé hơn nửa tổng của hai cạnh cùng xuất phát từ

một đỉnh của nó).

Do đó: Bài toán trở thành tìm điểm trên

sao cho bé nhất.

sin

. . sin sin os( )

sin ( )

SMC

S AH AC AC c



   

 



  



. sin sin cos( )

2 2sin( )

SA AH AC

   

 

  



ABCD

b c

ABCD

, ,

A B C

, ,

a b c

AD b BC c

 

I J

, .

AD B

’





       





2 ’ ’ ’ ’

’ ’ ’ ’

2 2 2 2 1 .

MA MB MC MD MA MB MC MD M A M B M C M D

MA M A MB M B MC M C MD M D

KA KB KC KD

          

       

   

MA MB MC MD KA KB KC KD

      

KA KB KC KD

  

D’

A’

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 89

Trong mặt phẳng dựng hình thang sao cho là trung điểm của hai đáy và

Ta thấy rằng: với tùy ý trên thì và Do đó:

Vậy nhỏ nhất khi chính là giao điểm của hai đường chéo và

Tính .

Tính : .

Tổng các khoảng cách nhỏ nhất là: .

b) Gọi là bán kính các mặt cầu tâm O và lần lượt đi qua các đỉnh Ta có:

Do đó ở trong hình cầu cố định

tâm O, bán kính

 Câu 96: (HSG HUẾ 1998-1999) Cho hình chóp đáy là hình chữ nhật có

. là hình chiếu vuông góc của xuống

a/ Tính độ dài đoạn vuông góc chung của và

b/ Gọi lần lượt là trung điểm của đoạn thẳng và Chứng minh: Các đường thẳng

và vuông góc nhau.

 Lời giải

Câu a / (2.5 điểm)

+ Theo giả thiết ta được:

Mà và

+ Gọi H là hình chiếu của K xuống SA

và ( vì )





BCI

’ ’

BCD A

’, ’.

IA IA ID ID

 

’

KA KA



’.

KD KD











’ ’

’ ’ ’ ’.

KA KB KC KD KA KB KC KD

KA KC KB KD AC BD

      

     

KA KB KC KD

  

’

’.

2 2

2 2 2

2 2 22 2 2

– –

4 4 4 4

–IJ DJ ID DC JC ID a

c b c b

IJ a      

’

2 2

2 2 2 2

' '

2 2 4 4 2

BC A D b c c b bc

BD IJ a a

   

 

 

 

 

       

 

 

 

 

 

   

’

a b

d BD

 



1 2 3

, ,

r r r

, , .

A B C

1 2 3

OD OC DC OC AB OC OA OB r r r

         

1 2 3

R r r r

  

. ,

S ABCD

ABCD

, ,

AB a BC b SA SB SC SD c

     

M N

SO (ABCD) (SAC) (ABCD)

  







BK SAC

  

BK AC BK SA

HK SA

 



HK BK







HK SAC

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 90

là đoạn vuông góc chung của và

Suy ra được: BH  SA và vuông tại K.

+ Do vuông đỉnh nên: .

+ cân đỉnh là đường cao nên

+ Do vuông tại nên:

Câu b (2.5 điểm)

+ ( vì là trung điểm của )

+ .

+ Do đó:

Vậy:

( Có thể tính và áp dụng định lý Pythagor).

 Câu 97: (HSG SỞ GD&ĐT NGHỆ AN NĂM 2017-2018) Cho hình chóp

S.ABC

, mặt phẳng

(P) di động luôn cắt các cạnh

tại

A’

B’

C’

. Gọi

là trọng tâm tam giác

a) Tìm giao điểm của

với mp

(P)

b) Biết rằng

Chứng minh rằng mp (P) luôn đi qua một điểm cố định.

 Lời giải





HBK



ABC

2 2

2 2 2 2 2

1 1 1

   



a b

BK AB BC a b



SAB

S BH



 

c a

SI AB

SA c



HBK

2 2 2 2 2

2 2 2

(4 )



   



c a a a b

HK HB BK

c a b

2 2 2 4 2 2 2 2

2 2 2 2 2

(4 ) (4 )

4 ( ) ( )

   

  

 

c a b a a c a b

HK HK

c a b a b

 

  

BM BA BK

1 1

MN MB BC CN (AB KB) BC BA

2 2

      

       

 

  

MN KB BC

4 . ( ).( 2 )= BA. 2 . . 2 .

= BA. . 2 . = KB.( 2. )

BM MN BA BK KB BC KB BA BC BK KB BK BC

KB BK KB BK BC BA BK BC

     

   

         

    

         

= KB.( )= KB.( ) KB. . 0

BA BC BK BC CA CK CA KB CK

      

           



BM MN

2 8.

' ' '

SA SB SC

  

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 91

a. Gọi I là giao của AG và BC nên I là trung điểm của B

SI cắt B’C’ tại I’

Trong tam giác SAI: A’I’ cắt SG tại G’

Khi đó G’ là giao của SG và mặt phẳng (P)

b. Ta có

Thật vậy: từ B kẻ BM//B’C’ cắt SI tại M, từ C kẻ CN// B’C’ cắt SI tại N

Khi đó vì I là trung điểm BC nên SM+SN=2SI

Gọi O là trung điểm AI, A’I’ cắt SO tại O’ khi đó mặt phẳng (P) đi qua O’

Mặt khác từ (*) ta chứng minh tương tự (1) có

vậy O’ là trung điểm của SO.

Hay O’ là điểm cố định nên (P ) luôn đi qua điểm cố định là O’

 Câu 98: (HSG SỞ GD&ĐT NGHỆ AN NĂM 2018-2019) Cho hình chóp có đáy

là hình thang cân nội tiếp đường tròn tâm và Gọi là

trung điểm của cạnh

a) Chứng minh rằng

b) Gọi là góc giữa hai đường thẳng và Chứng minh rằng

 Lời giải

2 (1)

' ' '

SB SC SI

 

' ' ' ' ' '

SB SC SM SN SM SN SI

SB SC SI SI SI SI



    

2 8 2 2 8(*)

' ' ' ' '

SA SB SC SA SI

      

2 4

' ' '

SA SI SO

  

S ABCD

ABCD





/ /

AB CD



90 .

SBA SCA 





MO ABCD





cos .





 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 92

a.Gọi là hình chiếu vuông góc của điểm trên mặt phẳng

Xét các tam giác có

chung

Suy ra nên

Do đó vì vậy

b. Vì nên góc giữa hai đường thẳng và là góc giữa hai đường thẳng và

suy ra

Gọi điểm là hình chiếu vuông góc của điểm lên mặt phẳng

Ta có nên vuông tại

Mặt khác lại có suy ra là tâm đường tròn ngoại tiếp Khi đó

(vì vuông tại nên )

Từ (*) suy ra

(đpcm)

 Câu 99: (HSG NAM ĐỊNH NĂM 2015-2016) Cho hình chóp có đáy là hình

thang vuông tại A và B;

Tam giác SAB đều và nằm trong mặt phẳng vuông góc với

mặt phẳng (ABCD). Gọi H là trung điểm của AB, biết khoảng cách từ C đến mặt phẳng (SHD)

bằng . Tính thể tích của khối chóp S.HBCD và cosin của góc giữa hai đường thẳng SC và

 Lời giải





ABCD

, ,

MHA MHB MHC

  



MHA MHB MHC  

MA MB MC SA

  

MHA MHB MHC

    

HA HB HC

 

H O







MO ABCD



/ /

AB CD



cos cos 1 sin (*)

SCD SCD



  





SCD

MD MC SA

 

SDA



MS MD MC

 

SCD





sin

2 2

SD SD SD

SCD

ID MD SA

  

MID



ID MD





2 2 2 2

2 2 2

cos 1 sin 1

SD SA SD AD AD BC

SCD

SA SA SA SA SA





       

cos





S ABCD

ABCD

4 .

AB BC a

 

 BÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 93

+) Tam giác SAB cân nên

+) Kẻ mà

Do đó

+ Tính được . Do đó tam giác CHK vuông cân tại K

Nên

+) Tam giác ABH vuông tại B nên

Mà . Do đó

Ta có

Vậy

Tính cosin của góc giữa hai đường thắng SC và HD

Tam giác SHC vuông tại H nên

+) Gọi

+) Khi đó AEBD là hình bình hành nên

+) AD//EC nên

+) Trong mặt phẳng (ABCD), kẻ CN//HD với N thuộc đường AB

Do đó góc giữa SC và HD là góc giữa CN và SC

SH AB

 

) ( )

( ) ( ) ( )

SAB ABCD

SAB ABCD AB SH ABCD

SH AB







   









CK HD K HD

 

( )

SH ABCD SH CK

  

( ) ( , ( )) 10

CK SHD d C SHD CK a   

20 10

CH a HK a CK

   



45 45 tan 1

KHC DHC DHC

 

    



tan 2

BHC





tan tan

tan tan( ) 3

1 tan .tan

BHC CHD

BHD BHC CHD

BHC CHD



    





180

BHD AHD



 



tan 3 3 6

AHD AD a

    

( ).

ABCD

AD BC AB

S a



 

2 2 2

20 6 14

HBCD ABCD AHD

S S S a a a

    

1 28 3

3 3

S HBCD HBCD

V SH S 

SC a

;

M AC HD E BC HD

   

4 10

EB AD a EC a

   

6 3 3 3 3 3 2

. 32

10 5 5 8 8 2

AD AM a a

AM MC AC a

EC MC a

       

 B

ÀI TẬP ÔN THI HSG TOÁN 11  WEB: toanthaycu.com

GV: Trần Đình Cư –Zalo: 0834332133 94

a có:

Ta có:

+) Áp dụng định lý Côsin trong tam giác SCN, ta có

Vậy

10 4

3 3

AH HN HN a BN a

    

2 2 2

208 4 10

;

SH HN a CN BN BC a



    



2 2

s .

. 4

SC CN SN

SCN

C CN

 

 



os( , ) cos( , ) cos

HD CN SC SCN





cos(

, ) cos .

HD SCN 

Bấm Tải xuống để xem toàn bộ.

| 1/94

| | Tải xuống

Preview text:

 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
BÀI TẬP CHUYÊN ĐỀ HÌNH HỌC KHÔNG GIAN
(Dành cho giáo viên ôn thi học sinh giỏi, học sinh năng khiếu và chuyên toán)  Câu 1:
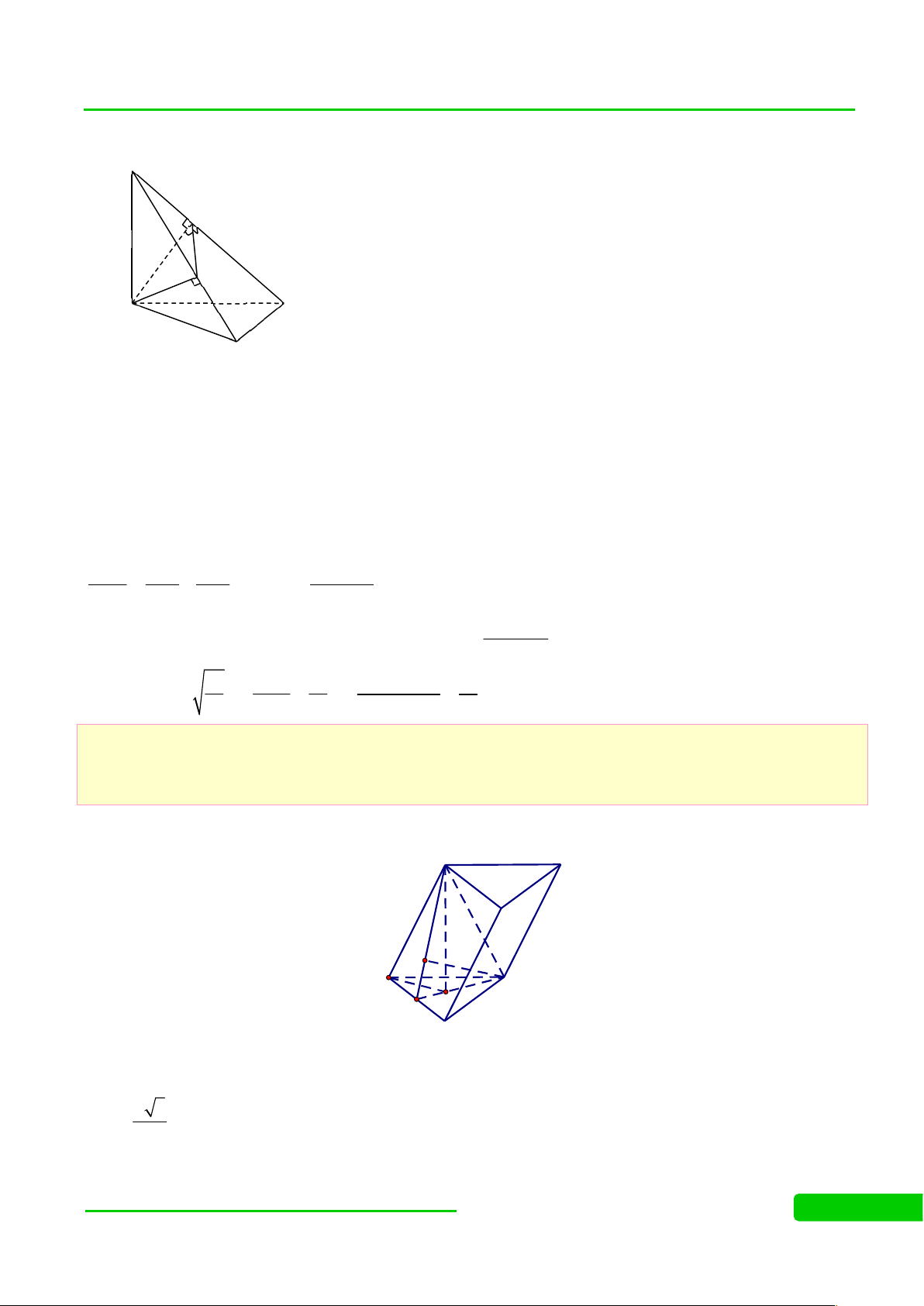
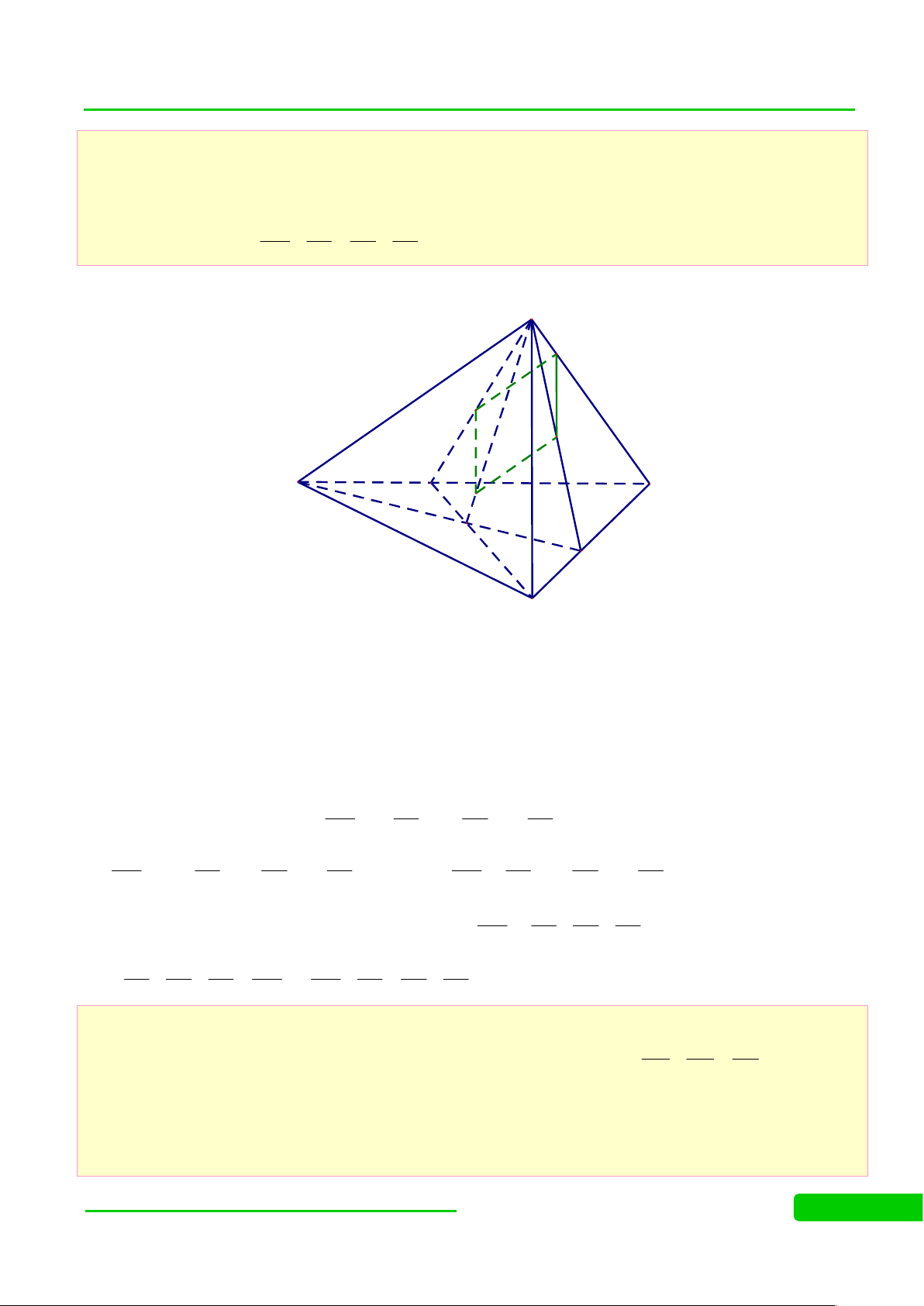
(HSG NAM ĐỊNH 2014-2015) Cho tứ diện đều ABCD có cạnh bằng 1, hai điểm M
và N lần lượt nằm trên các đoạn AB và CD, sao cho BN  DN .
a) Chứng minh rằng AD  BC . Tìm điểm I cách đều 4 đỉnh của tứ diện ABCD
b) Khi M, N lần lượt là trung điểm của AB và CD, gọi   là mặt phẳng chứa BN và song song với M .
C Tính chu vi thiết diện tạo bởi   và tứ diện ABCD
c) Tìm giá trị lớn nhất và giá trị nhỏ nhất của MN khi M, N thay đổi trên các đoạn AB và C D.  Lời giải D P K J N I M B A H C
a) +) Gọi H là trực tâm tam giác ABC, suy ra DH  ( ABC) .
Chứng minh được BC  (ADH )  BC  AD .
+) Trong (ADH) dựng đường trung trực của đoạn AD cắt DH tại I, suy ra IA=I D. (1) Mặt khác I
 HA  IHB  I
 HC suy ra IA  IB  IC . (2)
Từ (1), (2)  IA  IB  IC  ID hay I là điểm cách đều 4 đỉnh của tứ diện ABC . D
b) Trong mặt phẳng (DMC) kẻ NK//MC ( K  DM ) suy ra ( ) chính là (BNK).
Trong mặt phẳng (ABD) gọi P  BK  AD suy ra ( ) cắt tứ diện ABCD theo thiết diện là tam giác BNP. 1 1
Vì M, K lần lượt là trung điểm của AB và DM  PD  AD  . 3 3 7 7 3
Áp dụng định lý côsin trong các tam giác B  ; DP P  DN; B
 DN ta có PB  ; PN  ; BN  . 3 6 2 7  3 Vậy chu vi B  NP là C  . BNP 2 BM DN     c) +) Đặt
 x , với 0  x  1 
 x . Khi đó ta có: BM  .
x BA và DN  . x DC . BA DC          Ta có: DN  .
x DC  BN  BD  x(BC  BD)  BN  .
x BC  (1 x).BD .
GV: Trần Đình Cư –Zalo: 0834332133 1
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
     
Do đó: MN  BN  BM  .
x BC  (1 x).BD  . x BA .       2 2 2 2 2 2 2 2
MN  x BC  (1 x) BD  x BA  2x(1 x)BC.BD  2x BC.BA  2x(1  x)B . D BA 2
 2x  2x 1.  1  1
+) Xét f  x 2
 2x  2x 1 trên đoạn 0 
;1 , ta có: max f  x  f 0  f  
1  1, min f  x  f     2  2 2
Vậy, MN đạt giá trị nhỏ nhất bằng
khi M, N lần lượt là trung điểm của AB, C . D 2
MN đạt giá trị lớn nhất bằng 1 khi M  B, N  D hoặc M  A, N  C.  Câu 2:
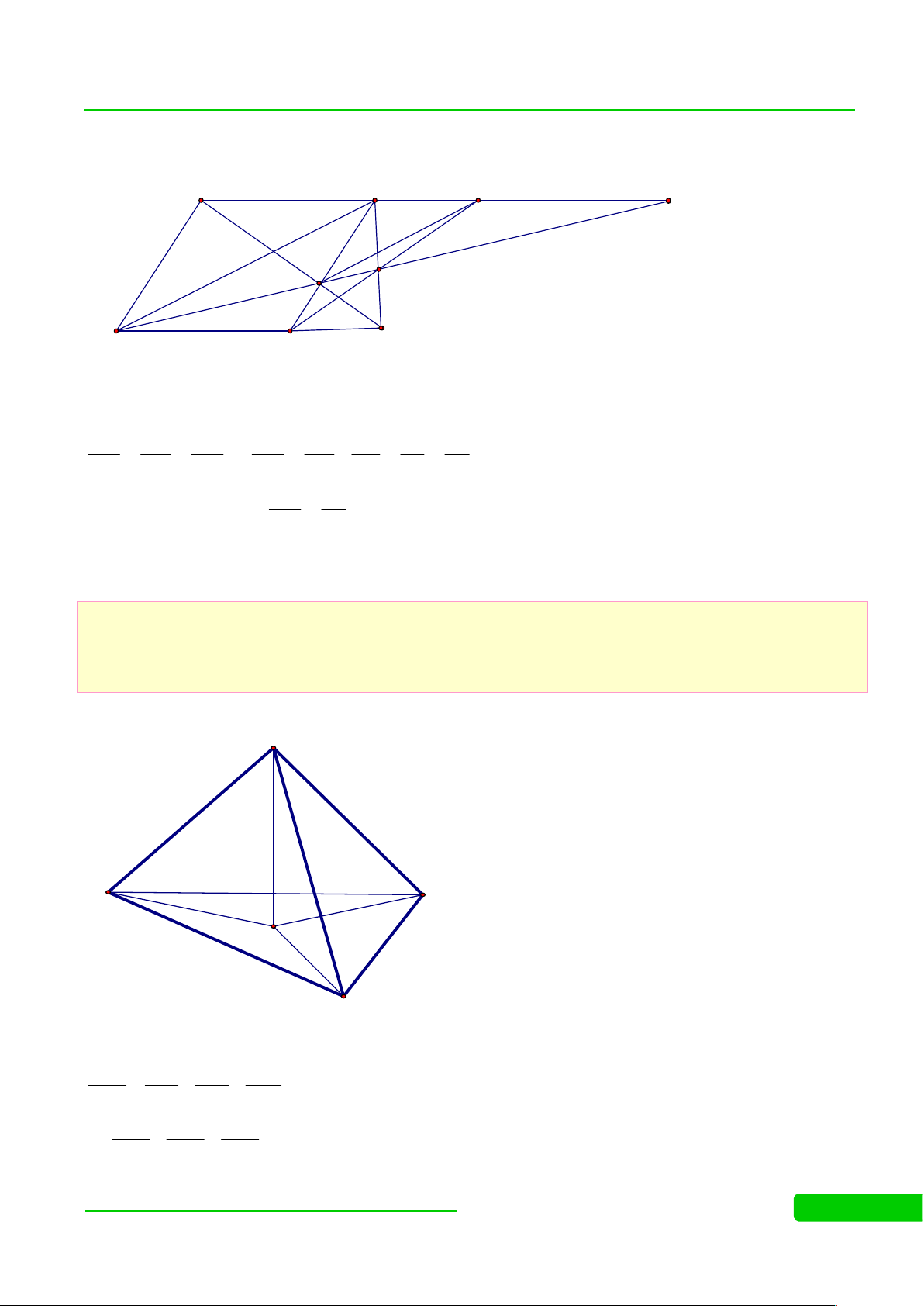
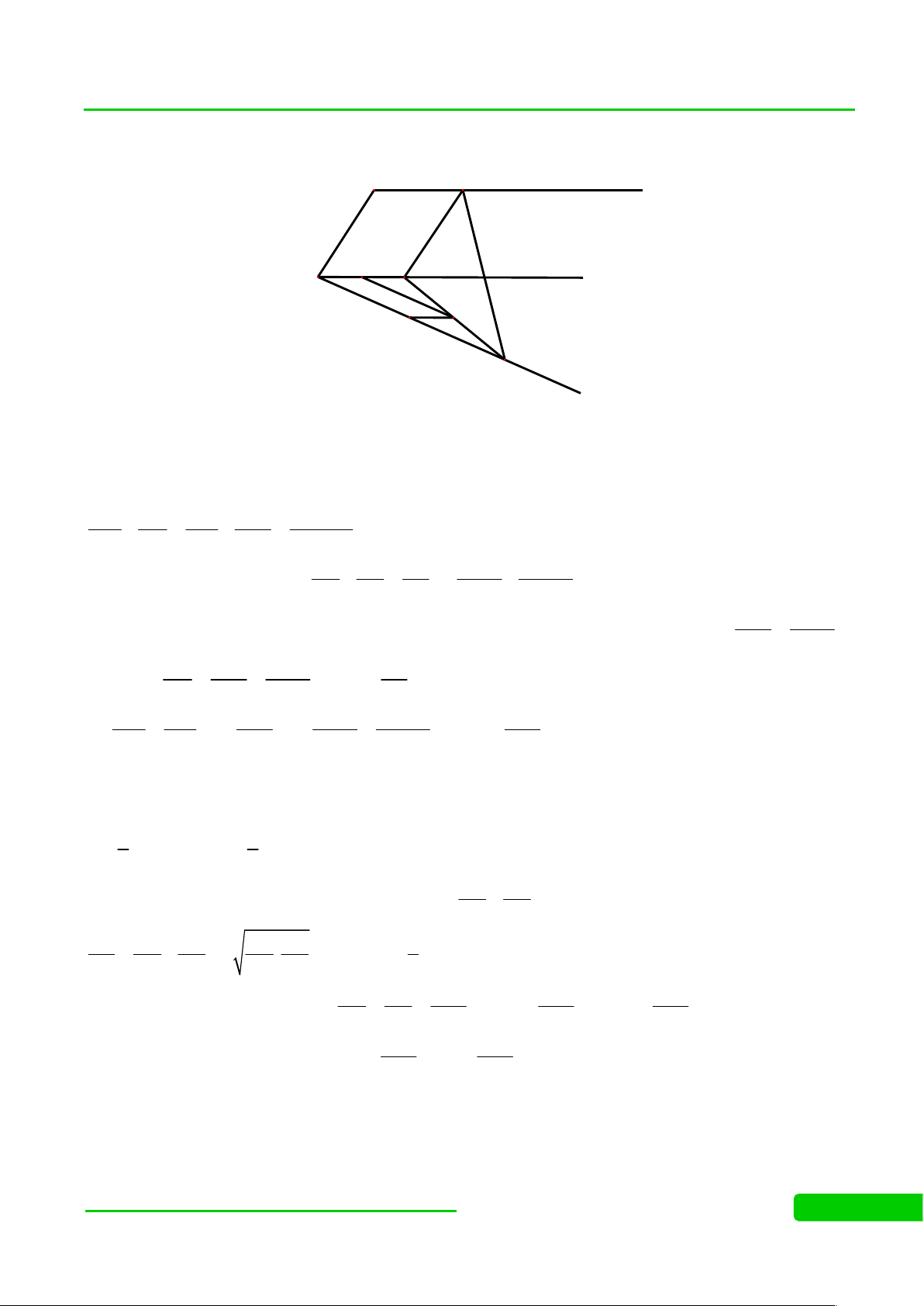
(HSG ĐÀ NẴNG NĂM 2011-2012) Cho hình hộp .
ABCD A' B 'C ' D '. Trên cạnh AB lấy điểm M khác A và .
B Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (ACD ').
a) Trình bày cách dựng thiết diện của hình hộp và mặt phẳng (P).
b) Xác định vị trí của M để thiết diện nói trên có diện tích lớn nhất.  Lời giải a. I D' Q C' R F A' P D B' C S K O A N E J M B
Trong mp(ABCD), qua M vẽ đường thẳng song song với AC cắt DB, BC lần lượt tại E, N.
Trong mp(BDD’B’), qua E vẽ đường thẳng song song với D’O (O=ACBD) cắt B’D’ tại F.
Trong mp(A’B’C’D’), qua F vẽ đường thẳng song song với AC cắt A’D’, D’C’ lần lượt tại R, Q.
Trong mp(AA’D’D), qua R vẽ đường thẳng song song với AD’ cắt AA’ tại S.
Trong mp(CC’D’D), qua Q vẽ đường thẳng song song với CD’ cắt CC’ tại P.
Thiết diện là lục giác MNPQRS.
b. Do các mặt đối diên của hình hộp song song nên các cạnh đối của lục giác thiết diện MNPQRS
song song và 3 cặp cạnh đó lần lượt song song với các cạnh tam giác ACD’.
 Các tam giác JKI, ACD’, RQI, JMS, NKP đồng dạng MJ MA NC NK PC PK QD ' QI          MJ=NK và PK=QI MN MB NB NM PC ' PQ QC ' QP
 Các tam giác RQI, JMS, NKP bằng nhau (gọi diện tích của chúng là S1 và gọi diện tích các tam
giác JKI, ACD’ lần lượt là S2, S)
GV: Trần Đình Cư –Zalo: 0834332133 2
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com AM Đặt
 k; ta có điều kiện 0  k  1 và có: AB 2 2 2 S  JM   AM   AM  1 2        
  k  S1 = k2S S  AC   DC   AB  2 2 2 S  JK 
 JM  MK   JM MK             k  2 2 1  S2 =( k2 + 2k +1)S S  AC   AC   AC AC 
 Diện tích thiết diện: S  S  3S td 2 1 2 1  3 1    3S 1 2
S  2S (k  k  )  2S   k     
(dấu bằng xảy ra  k  ) td 2 4   2  2   2 S 1
lớn nhất  k   M là trung điểm của A . B 2  Câu 3:
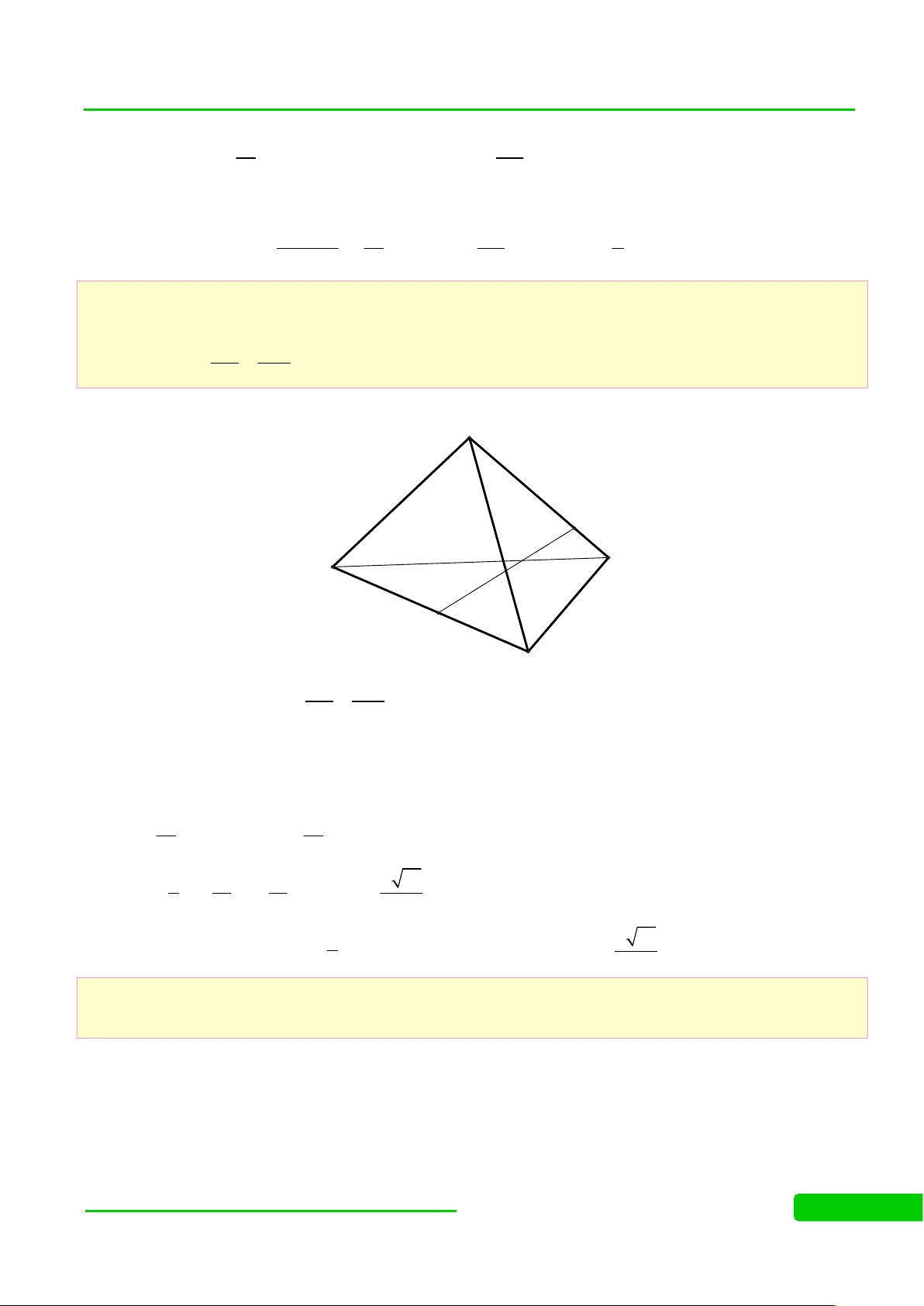
(HSG ĐÀ NẴNG NĂM 2011-2012) Cho hình chóp S.ABCD có đáy ABCD là hình
bình hành và M là trung điểm của S C. Một mặt phẳng (P) chứa AM và lần lượt cắt các cạnh SB, SD 4 SB ' SD ' 3
tại các điểm B', D' khác S. Chứng minh rằng:    3 SB SD 2  Lời giải S D' M I D P C O B' A N B
Lấy I = AMB'D' và O = ACBD,
ta có: S, O, I là các điểm chung của 2 mặt phẳng (SAC) và (SBD) SI 2
 S, O, I thẳng hàng.Và I là trọng tâm các mặt chéo SAC  SO 3 SD SB
Vẽ BP // B'I và DN // D'I P, N  SO  OP  ON . Đặt x  ; y  SD ' SB ' SB SD SP SN 2SO 3  x  y       2
 3  x, y [1; 2] (*) SB ' SD ' SI SI SI 2 2 1 1 3  2  4 Suy ra:    3    x y xy x  y 3  
Từ (*): 1  x  2  2
x  3x  2  0  x(3  x)  2  x  y  2
GV: Trần Đình Cư –Zalo: 0834332133 3
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com 3 3 x  y 3 1 1 3        xy 2 xy 2 x y 2  Câu 4:
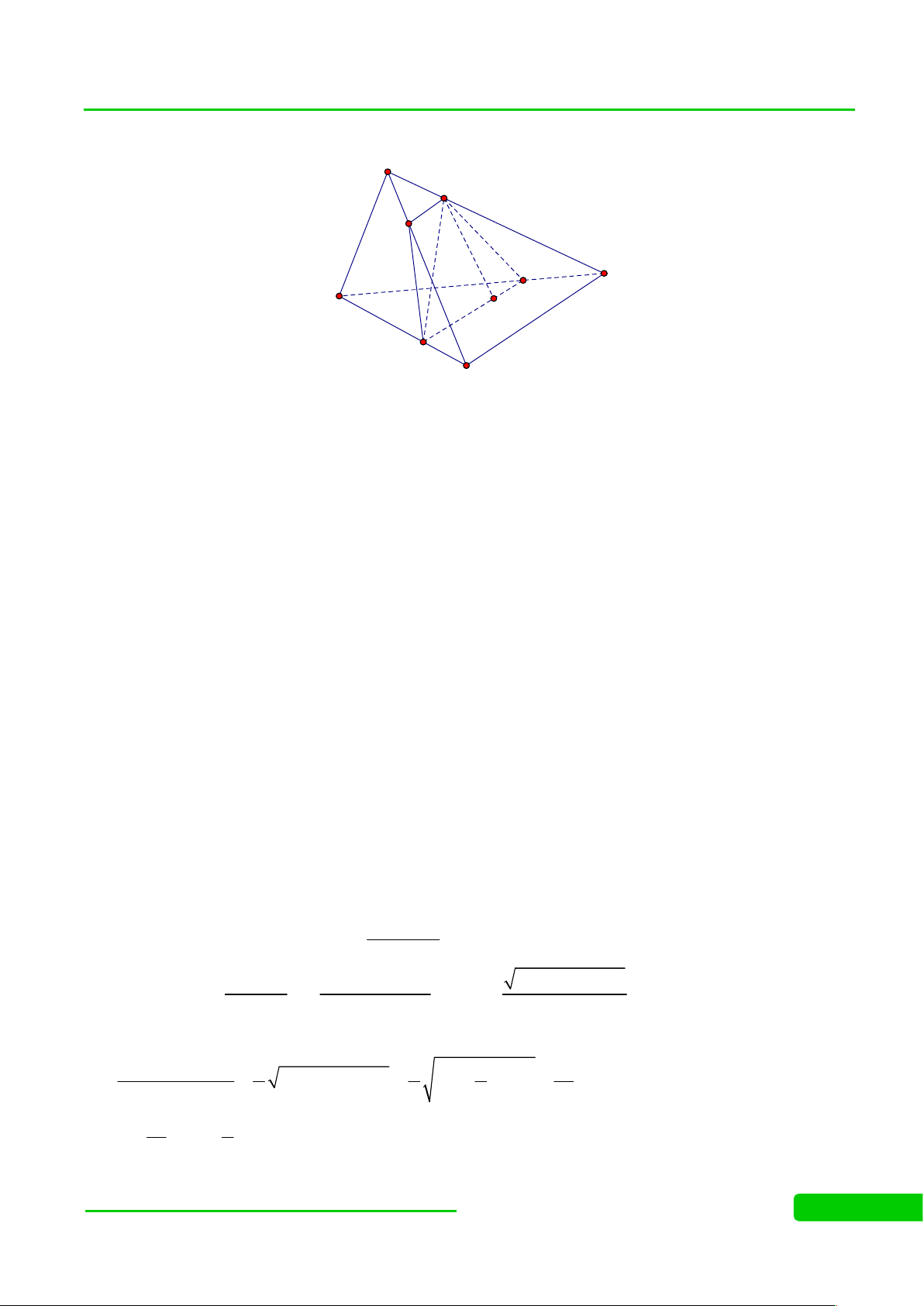
(HSG ĐỀ 046) Cho lăng trụ tam giác ABC. ’ A ’
B C’.Trên tia đối của tia AB lấy điểm 1 M sao cho AM = A .
B Gọi E là trung điểm của . CA 2
a) Xác định thiết diện của lăng trụ cắt bởi mặt phẳng (MEB’) CD AK
b) Gọi D = BC  (MEB’), K = AA’  (MEB’). Tính tỷ số và . CB ' AA  Lời giải
a) Ta có D = ME  BC ; K  MB' '
AA Suy ra thiết diện là tứ giác DEKB’ M A E C D B K A' C' B'
b, Xét tam giác MBB’ có AK MA 1 AK 1     BB ' MB 3 AA' 3
+) Trong (ABC). Dựng EN // AB (NBC), khi đó EN= 1 AB 2
+) Xét tam giác DBM có: DN NE 1 1    DN  BN DB BM 3 2 CD 1
Suy ra D là trung điểm CN. Vậy  CB 4  Câu 5:
(HSG ĐỀ 046) Cho tứ diện ABC .
D Tìm M trong không gian sao cho 2 2 2 2
MA  MB  MC  MD đạt giá trị nhỏ nhất  Lời giải
Gọi G là trọng tâm của tứ diện ta có:
GV: Trần Đình Cư –Zalo: 0834332133 4
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com 2 2 2 2 2 MA  2 M B  2 MC  2
MD  M A  MB  M C  M D   2   2   2   2
 MG  GA    MG  GB   MG  GC    MG  GD        2
4 M G  2 MG (GA  GB  GC  GD )  2 GA  2 GB  2 GC  2 GD  2 4 M G  2 GA  2 GB  2 GC  2 GD  2 GA  2 GB  2  2 GC GD
Dấu “=” xảy ra khi và chỉ khi M  G. Vậy: 2  2  2  2 MA MB MC
MD đạt giá trị nhỏ nhất khi M
là trọng tâm của tứ diện.  Câu 6:
(HSG ĐỀ 047) Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh
bằng a 2 , các cạnh bên bằng nhau và bằng 3a,a  0 . Hãy xác định điểm O sao cho O cách đều
tát cả các đỉnh của hình chóp S.ABCD và tính độ dài SO . Lời giải S M O D C I A B
Gọi I  AC  BD . Do SA  SB  SC  SD nên các tam
giác SAC, SBD cân tại đỉnh S nên SI vuông góc với AC,
BD suy ra SI vuông góc với mặt phẳng (ABCD).
Dễ thấy mọi điểm nằm trên đường thẳng SI cách đều các đỉnh A, B, C, . D
Trong tam giác SIC, dựng trung trực của cạnh SC cắt
đường thẳng SI tại O suy ra OS  OA  OB  OC  OD . Ta có: 2 SM .SC 3 . a 3a 9a 9 2a 9 2a SM .SC  . SO SI  SO     . Vậy SO  . 2 2 2 2 SI 8 2 SA  IA 2 9a  a 8  Câu 7:
(HSG ĐỀ 047) Cho hình chóp S.ABC có đường thẳng SA vuông góc với mặt phẳng
(SBC). Gọi H là hình chiếu của S lên mặt phẳng (ABC). Chứng minh rằng đường thẳng SB vuông 1 1 1 1
góc với đường thẳng SC, biết rằng   
. tứ giác S.ABCD có đáy ABCD là hình 2 2 2 2 SH SA SB SC
vuông cạnh bằng a 2 , các cạnh bên . Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 5
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com A H S C K B D
Gọi K là giao điểm của đường thẳng AH và BC; trong mặt
phẳng (SBC) gọi D là giao điểm của đường thẳng qua S, vuông góc với SC.
Ta có BC vuông góc với SH và SA nên BC vuông góc với mặt
phẳng (SAH) suy ra BC vuông góc với SK. 1 1 1
Trong tam giác vuông SAK ta có   , kết hợp 2 2 2 SH SA SK 1 1 1
với giả thiết ta được   (1) 2 2 2 SK SB SC 1 1 1
Trong tam giác vuông SDC ta có   (2) 2 2 2 SK SD SC
Từ (1) và (2) ta được SB  SD , từ đó suy ra B  D hay suy ra SB vuông góc với SC.  Câu 8:
(HSG ĐỀ 047) Cho tứ diện ABCD thỏa mãn điều kiện AB  CD, BC  AD, AC  BD
và một điểm X thay đổi trong không gian. Tìm vị trí của điểm X sao cho tổng XA  XB  XC  XD
đạt giá trị nhỏ nhất. . Lời giải
Gọi G là trọng tâm của tứ diện; M, N, P, Q lần lượt là A
trung điểm của các cạnh AB, CD, BC, AD.
Ta có tam giác ACD bằng tam giác BCD nên AN  BN M Q
suy ra MN  AB , tương tự ta chứng minh được
MN  CD và đường thẳng PQ vuông góc với cả G
hai đường thẳng BC, AD. D B
Từ đó suy GA  GB  GC  GD . Ta có P N . XA GA  X .
B GB  XC.GC  . XD GD
XA  XB  XC  XD  C GA
GV: Trần Đình Cư –Zalo: 0834332133 6
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
        X . A GA  X .
B GB  XC.GC  . XD GD  GA
    
XG GA  GB  GC  GD 2 .  4.GA   4GA . GA
Dấu bằng xảy ra khi và chỉ khi X trùng với điểm G. Vậy XA  XB  XC  XD nhỏ nhất khi và
chỉ khi X là trọng tâm của tứ diện ABC . D .  Câu 9:
(HSG ĐỀ 048) Cho hình chóp S.ABCD , có đáy ABCD là hình thang cân  AD / /BC 
và BC  2a; AB  AD  DC  a,a  0 Mặt bên SBC là tam giác đều. Gọi O là giao điểm của AC
và BD . Biết SD vuông góc với AC . a) Tính SD .
b) Mặt phẳng   qua điểm M thuộc đoạn OD ( M khác O, D ) và song song với hai đường thẳng
SD và AC . Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng ( ) ). Biết M MD  x .
Tìm x để diện tích thiết diện lớn nhất.  Lời giải S K Q B C T J P O M A D N
a) Dễ thấy đáy ABCD là nữa hình lục giác đều cạnh a.
Kẻ DT//AC (T thuộc BC). Suy ra CT
= AD = a và DT vuông góc S D.
Ta có: DT = AC = a 3 .
Xét tam giác SCT có SC=2a, CT=a,  0
SCT  120  ST  a 7
Xét tam giác vuông SDT có DT= a 3
, ST  a 7  SD  2a
b) Qua M kẻ đường thẳng song song
với AC cắt AD, DC lần lượt tại N,P.
Qua M, N, P kẻ các đường thẳng song song với SD cắt SB, SA, SC lần lượt tại K, J, Q. Thiết
GV: Trần Đình Cư –Zalo: 0834332133 7
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
diện là ngũ giác NPQKJ.
Ta có: NJ, MK, PQ cùng vuông góc với NP. 1 1 1 S  S  S  (NJ  MK)MN  (MK  PQ)MP 
(NJ  MK ).NP (do NPQKJ NMKJ MPQK 2 2 2 NJ=PQ). NP MD AC.MD . x a 3 Ta có:   NP    3x AC OD OD a 3  a  2 . a  x NJ AN OM . SD OM    3     NJ  
 2(a  x 3) SD AD OD OD a 3 2 . a a 3 .  x KM BM SD BM  2   KM    (a 3  x) SD BD BD a 3 3 1  2  Suy ra: S = 2(a  x 3) 
(a 3  x) 3x  2(3a  2 3x)x NPQKJ   2  3  2 1 1 3 3 2 
(3a  2 3x)2 3x 
(3a  2 3x)  2 3x  a 3 4 3   4 3 3 3
Diện tích NPQKJ lớn nhất bằng 2 a khi x  a 4 4
 Câu 10: (HSG ĐỀ 049) Cho hình chóp đều S.ABCD cạch đáy bằng a , chiều cao bằng 2a .
Tính diện tích thiết diện của hình chóp bị cắt bởi mặt phẳng   chứa CD và vuông góc với mặt phẳng SAB .  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 8
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
Gọi O là tâm hình vuông ABCD . M , N lần lượt là trung điểm của CD và AB . Khi đó O là trung
điểm của MN và AB vuông góc SMN . Kẻ IN vuông góc SM  IN vuông góc mp SAB
    CDI  .
Từ I kẻ đường thẳng song song với AB cắt SB, SA lần lượt tại E, F  EF / / AB / /CD .Thiết diện là hình thang CDEF . SO MN 4a 2 2 a 17 Ta có +) SM  SO  OM  ; IN   2 SM 17 2 2 a 15 EF SI SI AB . 15a +) SI  SN  IN  .   EF   2 17 AB SM SM 17 1 64a2 Diện tích thiết diện: S  (CD  EF)IN  CDEF 2 17 17
 Câu 11: (HSG HÀ NAM) Cho hình lập phương ABC D.A’B’C’D’ có cạnh a . Gọi I là tâm
của hình vuông CDD’C’, K là trung điểm của cạnh C . B
a. Dựng thiết diện của hình lập phương ABC D.A’B’C’D’ cắt bởi mặt phẳng (AKI). Tính diện tích
của thiết diện theo a .
b. Tính góc tạo bởi hai đường thẳng A’D’ và AQ với Q là giao điểm của (AKI) và CC’.  Lời giải C' D' A' B' N I Q J D C K B A
a, +) Gọi J là giao điểm của AK và CD, Q là giao điểm của JI và CC’, N là giao điểm của IJ và DD’.
Thiết diện là tứ giác AKQN.
Chứng minh được AKQN là hình thang có 2 đáy là KQ, AN.
+) Chứng minh được C là trung điểm của JD, K là trung điểm JA, Q là trung điểm của JN. SJKQ JK JQ 1 1 1  .  .   S  S  S  3S . S JA JN 2 2 4 AKQN J  AN J  KQ J  KQ JAN  1 CQ 1 1 +) CQ  ND  QC '    CQ  a . 2 CC ' 3 3
GV: Trần Đình Cư –Zalo: 0834332133 9
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com a 13 a 5 a 10
+) Tính được KQ  ; JK  ; JQ  . 6 2 3 2 2 2
JQ  JQ  KQ 6 cos KJQ   2JK.JQ 50 7 2
sin KJQ  1 cos KJQ  5 2 1 14a S  JK. . JQ sin KJQ  JKQ  2 12 2 14a S  3S  . AKQN JKQ  4
b, Vì A’D’//AD nên góc tạo bởi A’D’, AQ bằng góc tạo bởi AQ, A D. Có 2 2 2 AC 
AB  AD  AA  a 3. a 19 a 10 Tính được AQ  ; AD  ; a QD  . 3 3 2 2 2
AQ  AD  QD 3 cos QAD   . 2A . Q AD 19
 Câu 12: (HSG ĐỀ 052) Cho hình chóp S.ABC có SA   ABC và SA  2a , đáy ABC là tam 
giác vuông tại C với AB  2a , BAC  30 . Gọi I là điểm di động trên cạnh AC , J là hình chiếu
vuông góc của S trên BI .
a) Chứng minh AJ vuông góc với BI .
b) Đặt AI  x ( 0  x  a 3 ). Tính khoảng cách từ S đến BI theo a và x . Tìm các giá trị của x
để khoảng cách này có giá trị lớn nhất, nhỏ nhất.  Lời giải S 2a 2a A B x I J C
a) Ta có AJ là hình chiếu của SJ trên mặt phẳng  ABC  , SJ  BI
 AJ  BI (định lí ba đường vuông góc).
GV: Trần Đình Cư –Zalo: 0834332133 10
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
b) SJ  BI tại J nên SJ  d S, BI  . +)  0
AC  AB cos BAC  2 .
a cos 30  a 3  0
BC  AB sin BAC  2 . a sin 30  a
BI  BC  CI  a  a  x2 2 2 2 2 2 2 3
 4a  x  2ax 3 2 2  BI 
4a  x  2ax 3 . AJ AI
* Hai tam giác vuông AJI và BCI có  
AIJ  BIC (đối đỉnh) nên chúng đồng dạng, suy ra  BC BI BC.AI . a x  AJ   . 2 2 BI
4a  x  2ax 3
* Xét tam giác vuông SAJ ta có: 2 2 4 3 2 2 a x
16a  8a x 3  5a x 2 2 2 2
SJ  SA  AJ  4a   . 2 2 2 2
4a  x  2ax 3
4a  x  2ax 3 4 3 2 2
16a  8a x 3  5a x
Vậy d B, SI   . 2 2
4a  x  2ax 3
+) Tìm x để SJ đạt min, max:
Trong mặt phẳng  ABC  , AJ  JB nên J thuộc đường tròn C  đường kính AB chứa trong mặt
phẳng này. Rõ ràng C cũng thuộc C  .
Mặt khác J là giao điểm thứ hai của BI với C  nên khi I di động trên AC thì J di động trên
cung nhỏ AC của C  .
Do đó: SJ đạt min  AJ đạt min  I  A  x  0 .
SJ đạt max  AJ đạt max  I  C  x  a 3 .
 Câu 13: (HSG ĐỀ 053) Cho hình lập phương ABC D.A’B’C’D’ cạnh a. Gọi M, N, P lần lượt
là trung điểm của các đoạn thẳng AD, BB’, C’D’. Xác định thiết diện cắt bởi mặt phẳng (MNP) với hình lập phương ABC .
D A’B’C’D’. tính theo a diện tích thiết diện đó.  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 11
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com A M D S C B R N D' A' P B' Q C'
Gọi S là trung điểm của AB, khi đó MS / / BD  MS / /(BDC ') và NS / /C ' D  NS / /(BDC ') suy ra
MNS  / /(BDC ') . Do MNS  / /BC ' nên (MNS) cắt (BCC’B’) theo giao tuyến qua N song song với BC’ cắt B’C’ tại Q.
Do MNS  / /BD / /B ' D ' nên (MNS) cắt (A’B’C’D’) theo giao tuyến qua Q song song với B’D’ cắt
D’C’ tại P’, do P’ là trung điểm của C’D’ nên P’ trùng với P. Do MNS  / /C ' D ' nên (MNS) cắt
(CDD’C’) theo giao tuyến qua P song song với C’D cắt DD’ tại R.
Do đó thiết diện cắt bởi (MNP) với hình lập phương ABC .
D A’B’C’D’ là lục giác đều MSNQPR a 2 cạnh MR  và có tâm là O. Suy ra: 2 2 1 3 3a 2 3 3a 0 S  6S
 6. OM .OS.sin 60  . Vậy S  . MSNQPR OMS 2 4 MSNQPR 4
 Câu 14: (HSG ĐỀ 053) Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và
B, AB = BC = a, AD = 2a. Các mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng đáy.
Biết góc giữa hai mặt phẳng (SAB) và (ABCD) bằng 600. Tính khoảng cách giữa hai đường thẳng CD và S . B  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 12
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com S O A D K I E H B C 1
Gọi H  AC  BD  SH  (SAC)  (SBD)  SH   ABCD và BH  BD . 3
Kẻ HE  AB  AB  SHE  góc giữa hai mặt phẳng (SAB) và (ABCD) là  SHE nên  0 SHE  60 . 1 2a 2a 3 Mà HE  AD   SH  . 3 3 3
Gọi O là trung điểm AD  ABCO là hình vuông cạnh a  BO  AC , mà BO  SH
 BO  SAC  .
Gọi I  AC  BO , kẻ CK  SI mà CK  BO (do BO  SAC  )  CK  SBD .
Có CD//BO  d CD, SB  d CD,(SBD)  d C, (SBD)  CK . 1 a 2
Nhận thấy H là trọng tâm tam giác BCO  IH  IC  3 6 5 2a 2 2  IS  IH  HS  . 6 1 1 SH .IC 2 3a
Trong tam giác SIC có: S  SH .IC 
SI.CK  CK   . SIC 2 2 SI 5 2 3a
Vậy d CD, SB  . 5
 Câu 15: (ĐỀ THI OLYMPIC 11 – BIM SON 2012) Cho hình chóp S.ABCD có đáy là hình
vuông tâm O , cạnh a và SO vuông góc với mặt
phẳng  ABCD . Gọi M, N là trung điểm của SA và BC . Biết góc giữa đường thẳng MN và mặt
phẳng  ABCD bằng 60 .
1. Tính độ dài các đoạn thẳng SO và MN theo a .
2. Tính cosin của góc giữa đường thẳng MN với mặt phẳng SBD .  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 13
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
Gọi I là trung điểm của OA  MI // SO  MI  (ABCD) . Do đó góc giữa MN và  ABCD là góc   MNI 0  MNI  60 2 2 2  3 2a   a  3 2a a 2 5a +) 2 2 2 0
IN  IC  NC  2IC.N . C cos 45      2. . .     4   2  4 2 2 8   a 10 NI a 10  NI  , MN   . 4 0 cos 60 2 a 30 a 30
+) MI  NI.tan 60 
 SO  2MI  4 2  AC  BD 2. Ta có 
 AC  (SBD) . Gọi
H , K là trung điểm của SO và OB AC   SO
 MH // KN // AC  MH  (SB )
D , KN  (SB ) D .
Do đó HK là hình chiếu của MN lên SBD. Gọi E  MN  HK suy ra góc  giữa MN và SBD là góc  MEH . 1 1 a 2
+) Do MH  OA  OC  KN 
, nên MHNK là hình bình hành. 2 2 4 1 a 10
 E là trung điểm của MN  ME  MN  . 2 4 MH a 2 a 10 1
Do tam giác MHE vuông tại H nên sin   :  ME 4 4 5 2  2 cos  1 sin   . 5
 Câu 16: (ĐỀ THI HSGTPDN - Toan11 - 2013) Cho hình chóp S.ABCD có đáy ABCD là
hình bình hành tâm O và M là trung điểm của SC . Một mặt phẳng  P chứa AM và lần lượt cắt các cạnh S ,
B SD tại các điểm B ,  
D khác S . Chứng minh rằng:
GV: Trần Đình Cư –Zalo: 0834332133 14
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com SB SD 4 SB SD 3 a)   3 . b)    . SB SD 3 SB SD 2  Lời giải S D' M I D P C O B' A N B
Lấy I  AM  BDvà O  AC  BD , Ta có: S, ,
O I là các điểm chung của 2 mặt phẳng SAC  và SBD .  S, , O I thẳng hàng. SI 2
Và I là trọng tâm các mặt chéo SA   . SO 3 SD SB + Vẽ BP // 
B I và DN // 
D I  P, N  SO  OP  ON . Đặt x  ; y  SD SB SB SD SP SN 2SO 3  x  y       2  3  , x y [1; 2] (*) SB SD SI SI SI 2 2 1 1 3  2  4 + Suy ra:    3    . x y xy x  y 3   3 3 x  y 3 1 1 3
+ Từ (*): 1  x  2 2
 x  3x  2  0  x(3  x)  2  xy  2        . xy 2 xy 2 x y 2
 Câu 17: (ĐỀ THI OLYMPIC 11 – BIM SON 2013) Cho hình chóp S.ABCD có đáy là hình
bình hành tâm O , M là điểm di động trên SC và
P là mặt phẳng qua AM và song song với BD . Tìm các giao điểm H và K của P với SB và SB SD SC SD . Chứng minh   là một hằng số. SH SK SM  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 15
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
Gọi J là trung điểm của MC ; I  HK  AM Ta có HK // B ,
D OJ // AM do đó SB SD SC SO SC SI  IO SM  MC IO 2MJ IO IO    2   2   2  2 1   1  2  2  1. SH SK SM SI SM SI SM SI SM SI SI
 Câu 18: (ĐỀ THI OLYMPIC 11 – BIM SON 2013) Cho lăng trụ đứng ABC. 
A BC có đáy là tam giác vuông tại , B AB  , a AC  2 , a góc giữa
đường thẳng AB và mặt phẳng BCCB bằng 30 . Gọi M , N lần lượt là trung điểm của BC và
BB . Tính khoảng cách từ 
A tới mặt phẳng  AMN .  Lời giải 2 2 BC 
AC  AB  a 3
Ta có AB  BC, AB  B 
B  AB  (BCCB ) 
Nên góc giữa AB và BCC’ ’ B  là góc  A  B B  0
 AB ' B  30  BB  AB cot 30  a 3 .
GV: Trần Đình Cư –Zalo: 0834332133 16
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
Gọi I  AN   A , B O  A  B   A B . 2 1
Khi đó I là trọng tâm tam giác ABB nên BI  BO   A B   A I  2BI . 3 3 Do I  
A B  ( AMN) nên d( A ,
 (AMN))  2d( ,
B ( AMN))  2h
Do BAMN là tứ diện vuông tại B nên 1 1 1 1 1 4 4 11 a 33         h  . 2 2 2 2 h AB BM BN 2 2 2 2 a 3a 3a 3a 11 2 33a
Vậy d (A , (AMN))  . 11
 Câu 19: (ĐỀ THI OLYMPIC 11 – BIM SON 2015) Cho hình chóp S.ABCD có đáy là hình
vuông cạnh a , SA  a 6 , SA vuông góc với mặt phẳng  ABCD .
a) Tính góc giữa đường thẳng SB với mặt phẳng SCD .
b) Gọi M là điểm bất kì trong không gian, tìm giá trị nhỏ nhất của biểu thức 2 2 2 2 2
  MA  MB  MC  MD  MS .  Lời giải S H E F A I D B O C
a) Gọi O là tâm của hình vuông, E là trung điểm của SD suy ra OE // SB .
Ta có CD  AD , CD  SA suy ra CD  SAD .
Kẻ AH  SD , H  SD  AH  CD .
Gọi F là trung điểm của HC suy ra OF // AH  OF  (SC )
D nên EF là hình chiếu vuông góc
của OE lên mp SCD  AH  (SCD) .
Gọi  là góc giữa SB và SCD , khi đó  
  (OE, EF )  OEF . 1 a 7 Ta có 2 2
SB  SA  AB  a 7  OE  SB  . 2 2
GV: Trần Đình Cư –Zalo: 0834332133 17
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com 1 1 1 7 a 42 1 a 42     AH   OF  AH  . 2 2 2 2 AH SA AD 6a 7 2 14 OF 6 6  sin       arcsin . OE 7 7      2 2 2 2 2
b) Với điểm I bất kì ta luôn có   MA  MB  MC  MD  MS           2 2 2 2 2  (MI  ) IA
 (MI  IB)  (MI  IC)  (MI  ID)  (MI  IS )
      2 2 2 2 2 2
 5MI  IA  IB  IC  ID  IS  2MI (IA  IB  IC  ID  IS ) .
         
Chọn I thỏa mãn IA  IB  IC  ID  IS  0  4IO  IS  0  IS  4  IO
Suy ra I là điểm thuộc đoạn SO sao cho IS  4IO . Khi đó 2 2 2 2 2 2 2 2 2 2 2
  5MI  IA  IB  IC  ID  IS  IA  IB  IC  ID  IS .
Suy ra  nhỏ nhất khi M  I . 2 13a Ta có 2 2 2
SO  SA  OA  . 2 2 2 BD AC 16 Suy ra 2 2 2 2 2 2 2 2
IA  IB  IC  ID  IS  2IO   2IO   SO . 2 2 25 2 16 4 16 4 36a 2 2 2 2 2 2 2 2
 4IO  AC  SO  SO  AC  SO  SO  AC  . 25 25 25 5 5 2 36a Vậy  nhỏ nhất bằng khi M  I . 5
 Câu 20: (ĐỀ THI OLYMPIC 11 – BIM SON 2014) Cho hình chóp S.ABC, G là trọng tâm
của tam giác AB C. Một mặt phẳng () cắt các tia S , A S ,
B SC, SG theo thứ tự tại A ,
 B ,C ,  G . SA SB SC SG Chứng minh rằng    3 . S  A SB SC SG  Lời giải SA SB SC SG       Đặt  a,  b,  c,
 d . Theo bài ra ta suy ra SA  a 
SA , SB  bSB , SC  cSC , S  A SB SC SG  
SG  d SG .  1   
Do G là trọng tâm của tam giác ABC nên SG  (SA  SB  SC) . 3  1    Suy ra SG  (aS 
A  bSB  cSC )  . 3d
Mặt khác do A , B ,C , 
G đồng phẳng nên từ đẳng thức trên ta có a b c SA SB SC SG  
 1  a  b  c  3d     3 . 3d 3d 3d S  A SB SC SG
 Câu 21: (ĐỀ THI OLYMPIC 11 – BIM SON 2014) Cho lăng trụ đứng ABC. 
A BC có đáy 
ABC là tam giác cân, AB  AC  a , góc BAC  120 , BB  a , I là trung điểm của CC . Tính cosin
của góc giữa hai mặt phẳng  ABC  và  ABI  .
GV: Trần Đình Cư –Zalo: 0834332133 18
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com  Lời giải
Gọi K  BC  BI .
Suy ra AK  (ABC)  (A  B I ) .
Kẻ AH  AK, H  BC .
Kẻ HE / /BB , E   B I , do B 
B  (ABC) nên HE  (ABC)  HE  AK
Khi đó AK  (AHE)
Góc giữa hai mặt phẳng  ABC  và  ABI  là 
  ( AH , AE)  HAE . 2 2 2 0 2
BC  AB  AC  2A .
B AC.cos120  3a  BC  a 3
+) Ta thấy CI là đường trung bình của tam giác KBB nên C là trung điểm của BK , do đó
BK  2BC  2a 3 . 2 2 2 0 2
AK  AB  BK  2 .
AB BK.cos 30  7a  AK  a 7  2 2 2
AK  BK  AB 9 AK 14 3a cos AKB    HK    2 AK.BK 2 21 cos AKB 9 21a 2 2
AH  HK  AK  . 9 HE KH BB .KH 7a HE +) Ta có   HE   ,  7 tan  tan HAE   . BB KB KB 9 AH 3 1 7 10 30 2   1 tan   1   cos  . 2 cos  3 3 10
 Câu 22: (HSG ĐỀ 059) Cho hình chóp SABC có SC   ABC  và tam giác ABC vuông tại 13 .
B Biết AB  a, AC  a 3 và góc giữa hai mặt phẳng (SAB), (SAC) bằng  với sin  . Tính 19 độ dài SC theo a.  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 19
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com S H x K C A a B
Gọi H, K là hình chiếu của C lên SA, S . B Ta chứng minh được
CK  (SAB), SA  (CHK ) . Suy ra CHK 
vuông tại K và SA  KH .
Do đó   CHK.
Đặt SC  x  0 . Trong tam giác vuông SAC ta có 1 1 1 a x 2 3 2 2    CH  . 2 2 2 CH CA CS 3 2 2 a  x a x 2 2 2 2
Tương tự, trong tam giác vuông SBC ta có CK  . 2 2 2 a  x 2 13 CK 13 2 2 2(3a  x ) 13 Ta có sin     
 x  6a , vì x > 0. Vậy SC  6a . 2 19 CH 19 2 2 3(2a  x ) 19
 Câu 23: (HSG ĐỀ 059) Cho khối lăng trụ tam giác ABC.A' B 'C ' có đáy là tam giác đều cạnh
a, điểm A' cách đều ba điểm A, B, C.Góc giữa AA' và mặt phẳng (ABC) bằng 0 60 . Tính khoảng
cách giữa hai đường thẳng AB, CC’ theo a.  Lời giải A' C' B' K C A G H B
G là trọng tâm  AB C. Ta có A'G   ABC  và  AA ABC    0 '; (
)  A' AG  60 a 3 AG  . Xét A  ' AG có 0
A 'G  A . G tan 60  a 3 Kẻ CK  '
A H  CC'// A ' A
GV: Trần Đình Cư –Zalo: 0834332133 20
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com  d CC ( ', AA')  d CC (
',( AA' B' B))  CK 2 A ' . G CH a 3 a 3 a 39 a 13 Ta có 2 2 CK   . a :
A 'G  HG  :  A' H 2 2 6 13
 Câu 24: (HSG THPT LÊ VĂN HƯU LỚP 11) Cho hình hộp ABC .
D A B C D cố định. Trên 1 1 1 1
các đoạn AB ,C B lần lượt lấy các điểm P,Q sao cho AP  2PB ,C Q  2QB . Chứng minh đường 1 1 1 1
thẳng PQ song song với mặt phẳng  ACC1 .  Lời giải  
Gọi D(m ;m-4) Sử dụng điều kiện H .
D HN  0  m  4  D(4;0)
Nhận xét H và C đối xứng qua DN tìm được C(1; 4) Từ đó tìm được : (
A 0;3), B(3; 1  )
Chứng minh PQ //  ACC1 A B D C Q E P A B 1 1 D1 C1
Gọi E là trung điểm của BB1. EB PB 1 PE 1 Vì 1 1  
nên A , P, E theo thứ tự đó thẳng hàng và  AA PA 2 1 PA 2 1 1 QE 1
Tương tự, C,Q, E theo thứ tự đó thẳng hàng và  QC 2 PE QE
Xét tam giác EA C có P, Q lần lượt thuộc các cạnh EA1 và EC đồng thời  1 PA QC 1  PQ // A C 1
Mặt khác A C  ACC  PQ // ACC 1  1   1 
 Câu 25: (HSG THPT LÊ VĂN HƯU LỚP 11) Cho hình hộp ABC .
D A B C D cố định. Trên 1 1 1 1
các đoạn AB ,C B lần lượt lấy các điểm P,Q sao cho AP  2PB ,C Q  2QB . Gọi I là điểm thay 1 1 1 1
đổi trên cạnh BC ( I khác B và C ). AI cắt CD tại J , DI cắt BJ tại M và CM cắt AB tại N .
Chứng minh mặt phẳng  A NI 1
 luôn chứa một đường thẳng cố định.  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 21
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
Chứng minh mặt phẳng  A NI 1
 luôn chứa một đường thẳng cố định A B N K M I D J C
Trong mặt phẳng (ABCD), gọi K  DM  AB . Vì AB//CD nên: MB BN NK NK CD AB IB IK     ;   . MJ CJ CD NB CJ CJ IC ID NK IK
Mặt khác AB  CD    IN // BD NB ID
Qua A1 kẻ đường thẳng d song song với IN. Suy ra d song song với BD và nằm trong mặt phẳng  A NI  A NI 1  1  . Vậy mp
chứa đường thẳng d cố định.
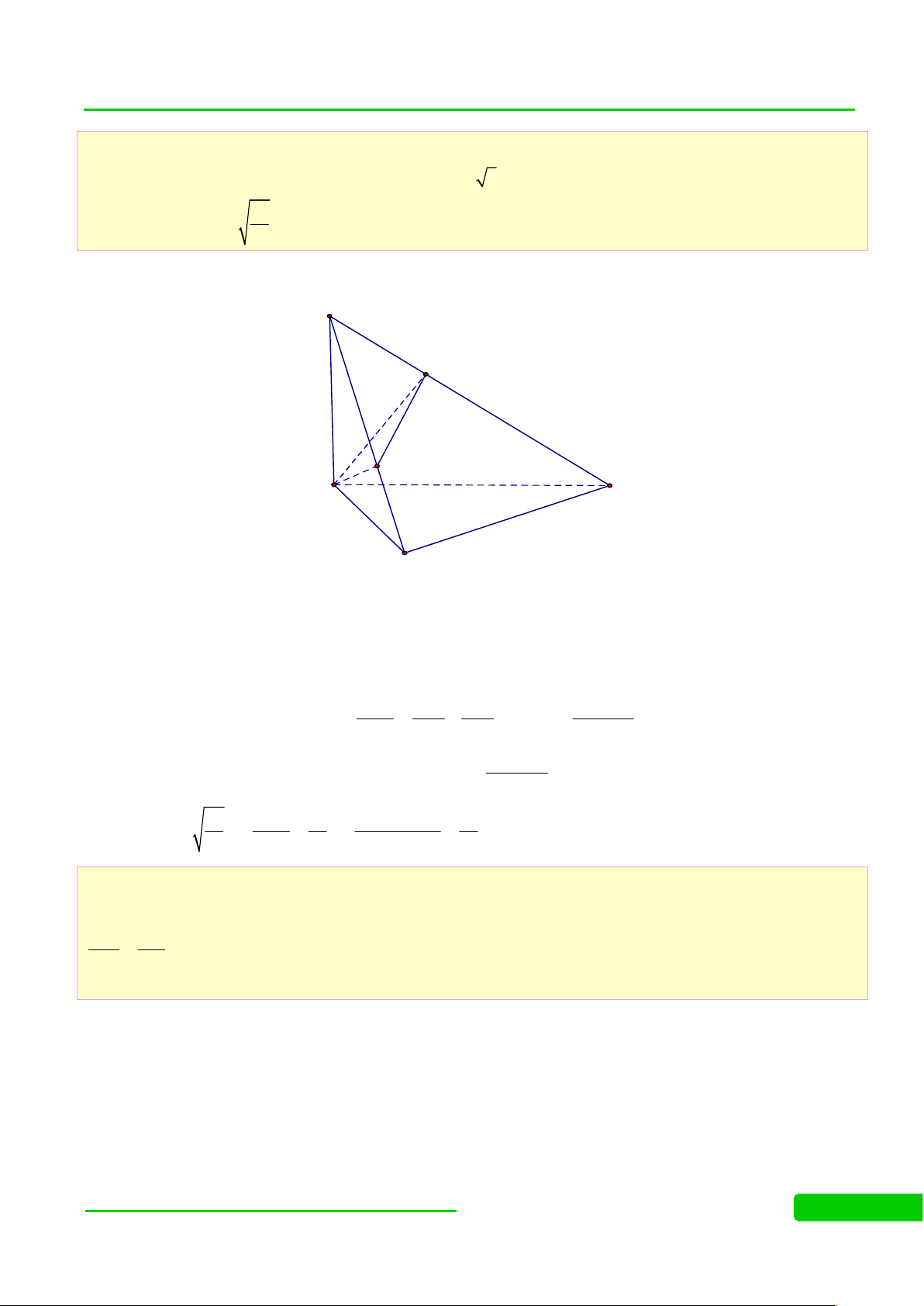
 Câu 26: (HSG NÔNG CÔNG 4 – THANH HÓA NĂM 2017-2018) Cho tứ diện OABC có ,
OA OB, OC đôi một vuông góc. Gọi  ,  , lần lượt là góc giữa các đường thẳng với mặt phẳng
 ABC  . Tính giá trị nhỏ nhất của biểu thức M   2    2    2 3 cot 3 cot 3  cot    Lời giải O A C H B
Gọi H là chân đường cao hạ từ O xuống mặt phẳng  ABC  . Khi đó ta chứng minh: 1 1 1 1    2 2 2 2 OH OA OB OC 2 2 2 OH OH OH 2 2 2   
 1  sin   sin   sin   1 2 2 2 OA OB OC
GV: Trần Đình Cư –Zalo: 0834332133 22
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com  1   1   1  Khi đó: M   2 3  cot   2 3  cot   2 3  cot    2  2  2   2   2   2   sin   sin  sin      Đặt 2 2 2
sin   a,sin   b, sin   c với a,b, c  0  1  1  1  1  Dạng M  2  2  2      
 với a  b  c  1   27  a  b  c  abc  1 1 1   1 1 1  1
Biến đổi: M  8  4    2         a b c   ab bc ca  abc
Áp dụng bất đẳng thức AM-GM ta có: 2 1  1  1 3 3 M  8  4.3.  2.3.   125   abc  abc  abc 1 1 Vậy M
 125 khi a  b  c 
hay sin  sin   sin   min 3 3
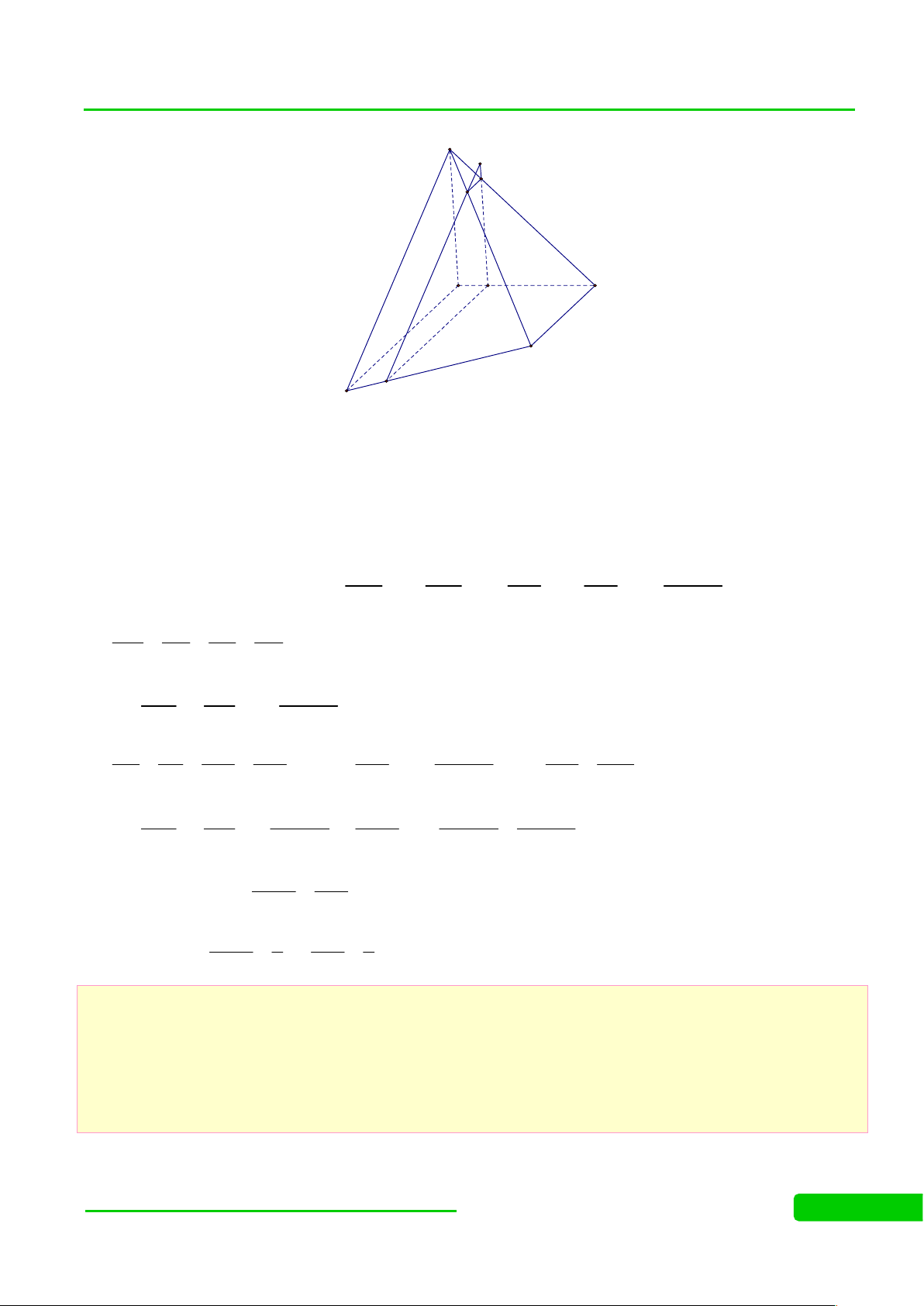
 Câu 27: (HSG NÔNG CÔNG 4 – THANH HÓA NĂM 2017-2018) Cho hình chóp S.ABCD
có đáy là hình vuông cạnh a và các cạnh bên đều bằng a . Gọi M là điểm trên SB sao cho  1  SM 
SB và E là một điểm thay đổi trên cạnh AC . Xác định vị trí điểm E để ME vuông góc 3 với CD .  Lời giải S M D A H E C B
Đặt CE  xC .
A Kẻ EH  CD,  H CD  EH / / AD nên CH  xCD  
Suy ra CH  xCD
  
  2  1  
MH  CH  CM  xCD  CS  CB    3 3 
    1  2  1   2  1 
Do: CM  CS  SM  CS  SB  CS  CS  SB  CS  CB 3 3 3 3 3
  
ME  MH  HE
Để ME vuông góc với CD điều kiện là:
GV: Trần Đình Cư –Zalo: 0834332133 23
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
 
    
ME.CD  0  MH  HE.CD  0  MH.CD  0 do HE  CD
   2  1       2 2  xCD  CS  CB
.CD  0  xCD  CS.CD  0    do CB  CD 3 3     3    1 Do S  CD đều nên 0 2
CS.CD  CS. . CD cos 60  a . 2 2 1  1  1 Do đó 2 2 2 .
x a  . a  0  a x   0  x    3 2  3  3 1
Vậy E thuộc đoạn AC sao cho CE CA. 3
 Câu 28: (HSG NÔNG CÔNG 4 – THANH HÓA NĂM 2017-2018) Cho hình hộp chữ nhật a A .
BCD A B C D có AB  AD  a, AA  b . Gọi M là trung điểm của CC . Xác định tỷ số để hai 1 1 1 1 1 1 b
mặt phẳng  A BD và MBD vuông góc với nhau. 1   Lời giải A1 B1 D1 C1 M A B O D C
Gọi O là tâm hình vuông ABCD .  AC  BD
Ta có: BD   A BD  MBD , 
 ACC A  BD 1     1 1  AA  BD  1   ACC A  BD 1 1   Vậy: 
 ACC A  A BD  OA do đó góc giữa hai đường thẳng OM và OA là góc giữa hai mặt 1 1   1  1 1 
 ACC A  MBD  OM  1 1   
phẳng  A BD và MBD . 1  2 2 2 2 2 AC
AB  AD  AA 2a  b Ta có: 1 1 OM    2 2 2
GV: Trần Đình Cư –Zalo: 0834332133 24
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com 2 a 2 5b 2 2 2 2
OA  AO  AA   b ; 2 2 2 2
MA  A C  MC  a  1 1 2 1 1 1 1 4
Hai mặt phẳng  A BD và MBD vuông góc với nhau  OMA  vuông tại O 1  1 2 2 2 2 2a  b  a  5b a 2 2 2
 OM  OA  MA 2 2 2 2    b  a   a  b   1 1 1   4 2 4 b  
 Câu 29: (HSG NÔNG CÔNG 4 – THANH HÓA NĂM 2017-2018) Cho hình chóp S.ABC có  0  0  0
SA  SB  SC  a, ASB  60 , CSB  90 , ASC  120 . Gọi M , N là hai điểm thay đổi trên cạnh AB CN AM và SC sao cho 
. Tìm giá trị nhỏ nhất của đoạn thẳng MN . SC AB  Lời giải S N C A M B
      CN AM Đặt SC  , c SB  , b SA  a , 
 m 0  m   1 SC AB       
 NC  mSC  mc, AM  m AB  m b  a
            
MN  MA  AS  SC  CN  m b  a  a  c  mc  m  
1 a  mb  1 m c 2 2   a     a Do . a b  , . b c  0, . a c   nên 2 MN   2
m  m   2 3 5 3 a 2 2 2  5  11 11 a 33 2 2 2  3a m   a  a  MN  m     0  ;1  6  12 12 12 5 a 33
Dấu đẳng thức xảy ra khi m  . Vậy giá trị nhỏ nhất của MN là . 6 6
 Câu 30: (HSG THPT TĨNH GIA 1 NĂM 2018-2019) Cho hình hộp ABC . D ’ A ’ B C’ ’ D . Gọi
M , N lần lượt là trung điểm của BC và D ’
D . Chứng minh rằng MN / /  ’ A BD .  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 25
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com  ME / / BD
Gọi E là trung điểm CD  
 MNE  / /  ABD  MN / /  A' BD
NE / / A ' B 
 Câu 31: (HSG THPT TĨNH GIA 1 NĂM 2018-2019) Cho hình chóp tứ giác u có đáy là n   3 u   hình vuông cạnh 1 2 
Tam giác u là tam giác đều và nằm trong mặt phẳng n  u   3u  2, n   2  n n 1 
vuông góc với mặt đáy. Gọi a. lần lượt là trung điểm của các cạnh ABC Gọi .
O là trung điểm của
I là chân đường vuông góc hạ từ AC lên M Chứng minh MN  SAB và tính diện tích thiết diện    
của hình chóp cắt bởi mặt phẳng OM  2OA  OB  2OC.  Lời giải S I d M E A B F H D N C . 
    
+ Đặt HA  x, HK  y, HS  z ( K là trung điểm BC )  1    1     1   
+ Ta có AM   AS  AB  AM  HS  HA  HK   AM  z  x  y 2 2 2
    1       
MN  MA  AD  DN    z  x  y 1 3 1  2x  y   x  z 2 2 2 2 
     
SB  SH  HA  AB  z  x  y 2 2
    2 2 3 1 3  a  1  a 3 
+ Suy ra MN.AM  x  z     
  0  MN  AM   1 4 4 4 2 4  2     
GV: Trần Đình Cư –Zalo: 0834332133 26
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com 2 2     2 2 3 1 3 a 1  a 3    MN.SB   x  z      
  0  MN  SB 2 2 2 2 2 2  2      + Từ  
1 và 2 ta suy ra MN  SAB. 2 2 2 2      2  3 1  9 2 1 2 9a 3a 3a a 3
+ Mặt khác MN   x  z  x  z     MN     2 2  4 4 16 16 4 2 Dựng thiết diện :
+ Qua S kẻ đường thẳng d song song với AB và CD  d  SAB  SCD
+ Trong mặt phẳng SCD kéo dài NE  d  I
+ Trong mặt phẳng SAB kéo dài IM  AB  F
+ Tứ giác MENF là thiết diện cần tìm 
     
+ Ta có SC  SH  HD  DC  z  x  y      
+ Giả sử SE  k SC  SE  k z  x  y
     
+ HE  HS  SE  1 k  z  k x  k y      2 2 2
+ Do HE  SC nên HE.SC  0  k  
1 z  k x  k y  0 3k   1 k 3 ES 3  
 k  0  k  , từ đây suy ra  4 4 8 EC 5 BF SI ES 3 3CN 3a + Ta có     BF   CN CN EC 5 5 10 2  a  a 26 a 29 + Do đó 2 NF  a   BF    và 2 2 MF  NF  MN   2  5 10 2 a 87
+ Diện tích tam giác INF là dt INF   MN.MF  20 h IE SE 3
+ Gọi h là đường cao kẻ qua E của tam giác IEM    MN IN SC 8 3MN 3a 3  h   8 16 2 1 1 3a 87
+ Diện tích tam giác IEM là dt IEM   . h IM  . h MF  2 2 320 2 13a 87
+ Vậy diện tích của thiết diện là dt MENF   320
 Câu 32: (HSG THPT CẨM THỦY 1) Cho tứ diện đều ABCD cạnh a . Gọi M và P là hai
điểm di động trên các cạnh AD và BC sao cho AM  CP  x ,(0  x  a). Một mặt phẳng () đi
qua MP và song song với CD cắt tứ diện ABCD theo một thiết diện.
a. Thiết diện trên là hình gì?
b. Tìm x để thiết diện có diện tích nhỏ nhất.
GV: Trần Đình Cư –Zalo: 0834332133 27
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com  Lời giải A M N Q D B E P C a. Ta có:
M  ( )  ( ABCD) () / /CD 
 ( )  ( ABCD)  MN / /CD(N  AC)
Tương tự ()  (BC )
D  PQ / /C ( D Q  B ) D ()  (BA )
D  MQ ; ()  (ABC)  PN
Vậy thiết diện của () với tứ diện ABCD là tứ giác MNPQ .
Vì MN / /PQ / /CD nên MNPQ là hình thang. C  P  DQ Hai tam giác 
CNP và DMQ bằng nhau vì C  N  DM  0 P  CN  QDN   60 
Suy ra NP  MQ hay thiết diện là hình thang cân.
b. Ta có MN  AM  ,
x PQ  BP  a – x
Áp dụng định lý hàm cosin trong tam giác MDQ ta có: 2 2 2
MQ  DQ  DM  2 . DQ DM .cos MDQ  2 2 2 2
 x  (a  x)  2x(a  x)  3x  3ax  a
Dựng đường cao ME ta có: PQ  MN 2 2 2 2 2 2
ME  MQ  QE  3x  3ax  a  ( ) 2 2 2 2 2
a  x  x
8x  8ax  3a
8x  8ax  3a 2 2 2
 3x  3ax  a  ( )   ME  2 4 2
Diện tích thiết diện MNPQ là: 2
(MN  PQ).ME a a a a 2 2 2 2 S  
8x  8ax  3a 
8(x  )  a  . 2 4 4 2 4 2 a a MinS   x  4 2
GV: Trần Đình Cư –Zalo: 0834332133 28
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
 Câu 33: - (HSG THPT TRIỆU SƠN 2 NĂM 2018-2019) Cho hình chóp S.ABCD . Gọi E là
giao điểm của AB và CD , F là giao điểm của AD và BC . Mặt phẳng   không qua S , song
song với mặt phẳng (SEF ) cắt các cạnh SA , SB , SC , SD của hình chóp lần lượt tại M , N , P , SM SP SN SQ
Q . Chứng minh rằng    . SA SC SB SD  Lời giải S Q M P F D A N B C E
  // SEF  ,    SAB  MN , MN, SE  SAB nên suy ra MN //SE .
  // SEF  ,    SAD  MQ , MQ, SF  SAD nên suy ra MN //SF .
  // SEF  ,    SBC   NP , NP, SF  SBC nên suy ra NP//SF .
  // SEF  ,   SCD  PQ , PQ, SE  SCD nên suy ra PQ //SE .
Vậy MNPQ là hình bình hành.
    SM  SP  SN  SQ 
Suy ra SM  SP  SN  SQ  SA  SC  SB  SD SA SC SB SD SM  SP  SN  SQ  
SA  SP  SN  SQ    SA   SC  SB  SD  SA   SC  SB  SD   SA SC SB SD SM  SC SB SD  SA  SP SN SQ Vì bốn điểm 
A , B , C , D đồng phẳng nên ta có     1   SM  SC SB SD  SP SN SQ SM SM SP SN SQ          SC SB SD SA SA SC SB SD
 Câu 34: (HSG THPT TRIỆU SƠN 2 NĂM 2018-2019) Cho hai nửa đường thẳng Ax , By 1 2 3
chéo nhau. Hai điểm C , D thay đổi lần lượt ở trên Ax và By sao cho   , D là điểm AC BD AB
thứ tư của hình bình hành ABDD .  P là mặt phẳng chứa CD và song song với AB , Q là mặt
phẳng chứa Ax và song song với By . Chứng minh rằng  P luôn luôn đi qua một điểm cố định I
trong mặt phẳng Q . Tìm vị trí của C và D sao cho diện tích S của tam giác AD C  nhỏ nhất.
GV: Trần Đình Cư –Zalo: 0834332133 29
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com  Lời giải B D y M D' y' A I N C x
Dựng Ay//By . D trên Ay sao cho AD  BD .  P là mặt phẳng CDD , Q là mặt phẳng
 Ax, Ay
Với I tùy ý trên CD . Gọi M , N là các điểm trên Ay , Ax sao cho MI / / Ax , NI / / Ay .Ta có: AM AN CI D ' I CI  ID '      1 (1) AD ' AC CD ' D 'C CD ' 1 2 3 AB : 3 2 AB : 3      1 (2) . AC BD AB AC AD ' D ' I AB : 3
Với C , D là hai điểm tùy ý thỏa mãn giả thiết. Trên CD tồn tại điểm I sao cho  . D 'C AC AN D ' I AB : 3 AB Ta được:    AN  (3) AC D 'C AC 3 AM CI D ' I AB : 3 2 AB : 3 2 AB và   1  1   AM  (4) AD ' CD ' D 'C AC AD ' 3
Từ (3) và (4) suy ra M , N cố định nên I cố định. Do đó  P luôn đi qua điểm cố định I trong Q . 1 1 S 
AC.ADsin A 
AC.BD sin A nên S nhỏ nhất  AC.BD nhỏ nhất. 2 2 1 1
Áp dụng bất đẳng thức Côsi cho hai số dương: , ta có: AC BD 3 1 2 1 2 8 2    2 .  AC.BD  AB AB AC BD AC BD 9 1 2 3 2 AB 4 AB
Dấu bằng xảy ra khi và chỉ khi    AC  và BD  . AC BD 2 AB 3 3 4 AB 2 AB
Vậy S nhỏ nhất khi và chỉ khi BD  , AC  . 3 3
GV: Trần Đình Cư –Zalo: 0834332133 30
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
 Câu 35: (THPT ĐÔNG SƠN 1 NĂM 2018-2019) Cho hình chóp S.ABC có SC   ABC và
tam giác ABC vuông tại B .Biết AB  a , AC  a 3 và góc giữa hai mặt phẳng SAB và SAC  13 bằng  với sin  . Tính SC . 19  Lời giải S H K C A B
Gọi H , K lần lượt là hình chiếu của C lên S ,
A SB . Ta chứng minh được
CK  (SAB), SA  CKH  , suy ra tam giác CHK vuông tại K và SA  KH Do đó 
  CHK . Đặt SC  x 2 2 1 1 1 3a x
Trong tam giác vuông SAC ta có 2    CH  2 2 2 2 2 CH CA CS 3a  x 2 2 2a x
Tương tự, trong tam giác vuông SBC ta có 2 CK  2 2 2a  x 2 2 2 2 3 13 13 a  x CK  13 Ta có sin     
 x  6a . Vậy SC  6a . 2 19 CH 19 3 2 2 2a  x  19
 Câu 36: (THPT ĐÔNG SƠN 1 NĂM 2018-2019) Cho hình chóp S.ABCD có đáy ABCD là
hình thang  AB / /CD, AB  2CD . Gọi M và P lần lượt là điểm thuộc cạnh AD và SC thoả mãn MA PS 
 x . Xác định thiết diện của hình chóp cắt bởi mặt phẳng ( ) chứa MP và song song MD PC
với AB . Tìm x để diện tích thiết diện bằng một nửa diện tích tam giác SAB .  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 31
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com S T N P A D M C Q B
M  ( )  ( ABCD) Ta có: 
 ( )  ( ABCD)  MQ / / AB(Q  BC) ( ) / / AB 
Tương tự ( )  (SCD)  PN / / AB(N  SD)
Vậy thiết diện của ( ) với hình chóp là tứ giác MNPQ. Vì MQ / / NP / / AB nên MNPQ là hình thang MD AM 1 x x  2
Gọi T  MN  PQ . Ta có: QM  AB  D C  AB  CD  AB AD AD 1 x 1 x 2 x   1 MA QB S P S N Vì   
 PQ / /SB, MN / /SA  S  AB  T  MQ MD QC PC D N 2 2 S      TMQ MQ x 2 Do đó         1 S  AB   2 x 1   SAB     NP NS AM x x x NP x Vì     NP  CD  AB   CD SD AD x 1 x 1 2 x   1 QM x  2 2 2 2 S  NP  x SMNPQ x 4x  4 Do đó TPN     1    S MQ TMQ   x  22 STMQ x  22  x  22 SMNPQ 1 Từ (1) và (2) suy ra  S x 1 TMQ SMNPQ 1 1 1 Vậy x  1 ta có     x  1 S 2 x 1 2 TMQ
 Câu 37: (HSG THPT HẬU LẬU 2 NĂM 2018-2019) Cho hình hộp ABC . D AB C  D   . Trên
cạnh AB lấy điểm M khác A và B . Gọi P là mặt phẳng đi qua M và song song với mặt phẳng  ACD .
a. Trình bày cách dựng thiết diện của hình hộp và mặt phẳng P .
b. Xác định vị trí của M để thiết diện nói trên có diện tích lớn nhất.  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 32
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com I D' Q C' R F A' P D B' C S K O A N E J M B
a. Trong mp(ABCD), qua M vẽ đường thẳng song song với AC cắt DB, BC lần lượt tại E, N.
Trong mp(BDD’B’), qua E vẽ đường thẳng song song với D’O (O=ACBD) cắt B’D’ tại F.
Trong mp(A’B’C’D’), qua F vẽ đường thẳng song song với AC cắt A’D’, D’C’ lần lượt tại R, Q.
Trong mp(AA’D’D), qua R vẽ đường thẳng song song với AD’ cắt AA’ tại S.
Trong mp(CC’D’D), qua Q vẽ đường thẳng song song với CD’ cắt CC’ tại P.
Thiết diện là lục giác MNPQRS
b. Do các mặt đối diên của hình hộp song song nên các cạnh đối của lục giác thiết diên MNPQRS
song song và 3 cặp cạnh đó lần lượt song song với các cạnh tam giác ACD’.
 Các tam giác JKI, ACD’, RQI, JMS, NKP đồng dạng MJ MA NC NK PC PK QD ' QI          MJ=NK và PK=QI MN MB NB NM PC ' PQ QC ' QP
 Các tam giác RQI, JMS, NKP bằng nhau (gọi diện tích của chúng là S1 và gọi diện tích các
tam giác JKI, ACD’ lần lượt là S2, S) AM Đặt
 k; ta có điều kiện 0  k  1 và có: AB 2 2 2 1 S  JM   AM   AM  2        
  k  S1 = k2S S  AC   DC   AB  2 2 2 S  JK 
 JM  MK   JM MK             k  2 2 1  S2 =( k2 + 2k +1)S S  AC   AC   AC AC 
 Diện tích thiết diện: S  S  3S td 2 1 2 1  3 1    3S 1 2 S
 2S (k  k  )  2S   k     
(dấu bằng xảy ra  k  ) td 2 4   2  2   2 S 1 lớn nhất  k 
 M là trung điểm của AB 2
 Câu 38: (ĐỀ HSG NÔNG CÔNG – THANH HÓA NĂM 2017-2018) Cho hình chóp S.ABCD
có đáy là hình vuông cạnh a, SA  a 6 , SA vuông góc với mặt phẳng (ABCD). Gọi M là điểm bất
kì trong không gian, tìm giá trị nhỏ nhất của biểu thức: 2 2 2 2 2
  MA  MB  MC  MD  MS .
GV: Trần Đình Cư –Zalo: 0834332133 33
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com  Lời giải      2 2 2 2 2
Với điểm I bất kì ta luôn có   MA  MB  MC  MD  MS           2 2 2 2 2
 (MI  IA)  (MI  IB)  (MI  IC)  (MI  ID)  (MI  IS ) .
      2 2 2 2 2 2
 5MI  IA  IB  IC  ID  IS  2MI (IA  IB  IC  ID  IS )
         
Chọn I thỏa mãn IA  IB  IC  ID  IS  0  4IO  IS  0  IS  4  IO
Suy ra I là điểm thuộc đoạn SO sao cho IS = 4IO với O tâm đáy ABC D. Khi đó 2 2 2 2 2 2 2 2 2 2 2
  5MI  IA  IB  IC  ID  IS  IA  IB  IC  ID  IS Suy ra  nhỏ nhất khi M  I . 2 13a Ta có 2 2 2
SO  SA  OA  . 2 2 2 BD AC 16 Suy ra 2 2 2 2 2 2 2 2
IA  IB  IC  ID  IS  2IO   2IO   SO 2 2 25 2 16 4 16 4 36a 2 2 2 2 2 2 2 2
 4IO  AC  SO  SO  AC  SO  SO  AC  25 25 25 5 5 2 36a Vậy  nhỏ nhất bằng khi M  I 5
 Câu 39: (HSG ĐỀ 075) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA vuông
góc với mặt phẳng  ABCD . Biết AB  a, BC  a 3 và SD  a 5.
a) Đường thẳng qua A vuông góc với AC cắt các đường thẳng CB,CD lần lượt tại I , J . Gọi H là
hình chiếu vuông góc của A trên SC . Hãy xác định các giao điểm K, L của SB, SD với  HIJ  và
chứng minh rằng AK  SBC .
b) Tính diện tích tứ giác AKH . L S L H J K A D I B C  Lời giải
Trong SCD gọi L  SD  JH  L  SD  I H J
Trong SBC  gọi K  SB  IH  K  SB   I H J IJ  AC Ta có 
 IJ  SAC   IJ  SC , mà AH  SC . Suy ra SC   IJH . IJ  SA 
GV: Trần Đình Cư –Zalo: 0834332133 34
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
Suy ra AK  SC . Mà BC  SAB  BC  AK .Vậy AK  SBC . . SA AC 2a . SA AB 2a b) Ta có 2 2 SA 
SD  AD  a 2 ; AH   ; AK   . 2 2 SA  AC 3 2 2 SA  AB 6 2a
Do AK  SBC   AK  KH , do đó 2 2 KH  AH  AK  . 6
Tương tự phần (a) thì AL  SCD  AL  HL . Từ đó tính được a 2 2 2 LH  AH  AL  . 15 2 1 1 8a Suy ra S  S  S  AK.KH  A . L LH  . AKHL AKH ALH 2 2 15
 Câu 40: (HSG THPT CẨM THỦY 1 NĂM 2018-2019) Cho tứ diện đều ABCD cạnh a. Gọi
M và P là hai điểm di động trên các cạnh AD và BC sao cho AM  CP  x , (0  x  a). Một mặt
phẳng ( ) đi qua MP và song song với CD cắt tứ diện ABCD theo một thiết diện.
1. Thiết diện trên là hình gì?
2. Tìm x để thiết diện có diện tích nhỏ nhất.  Lời giải
M  ( )  ( ABCD) 1. 
 ( )  ( ABCD)  MN / /CD(N  AC) ( ) / /CD 
Tương tự ( )  (BCD)  PQ / /CD(Q  BD) , ( )  (BAD)  MQ ; ( )  ( ABC)  PN
Vậy thiết diện của ( ) với tứ diện ABCD là tứ giác MNPQ. A M N Q D B E P C
Vì MN / /PQ / /CD nên MNPQ là hình thang. Hai tam giác CNP và DMQ bằng nhau vì C  P  DQ C  N  DM
Suy ra NP = MQ hay thiết diện là hình thang cân.  0 P  CN  Q  DN  60 
2. Ta có MN  AM  x, PQ  BP  a – x . Áp dụng định lý hàm cosin trong tam giác MDQ ta có: 2 2 2 2 2 2 2
MQ  DQ  DM  2 . DQ DM .cos MDQ 
 x  (a  x)  2x(a  x)  3x  3ax  a
Dựng đường cao ME ta có:
GV: Trần Đình Cư –Zalo: 0834332133 35
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com PQ  MN 2 2 2 2 2 2
ME  MQ  QE  3x  3ax  a  ( ) 2 2 2 2 2
a  x  x
8x  8ax  3a
8x  8ax  3a 2 2 2
 3x  3ax  a  ( )   ME  2 4 2 2
(MN  PQ).ME a a a a
Diện tích thiết diện MNPQ là: 2 2 2 2 S  
8x  8ax  3a 
8(x  )  a  . 2 4 4 2 4 2 a a min S   x  4 2
 Câu 41: (THPT TRIỆU SƠN 2 NĂM 2018-2019) Cho hình chóp S.ABCD . Gọi E là giao
điểm của AB và CD , F là giao điểm của AD và BC . Mặt phẳng   không qua S , song song
với mặt phẳng (SEF ) cắt các cạnh SA , SB , SC , SD của hình chóp lần lượt tại M , N , P , Q . SM SP SN SQ Chứng minh rằng    . SA SC SB SD  Lời giải S Q M P F D A N B C E
  // SEF  ,    SAB  MN , MN, SE  SAB nên suy ra MN //SE .
  // SEF  ,    SAD  MQ , MQ, SF  SAD nên suy ra MN //SF .
  // SEF  ,    SBC  NP , NP, SF  SBC nên suy ra NP//SF .
  // SEF  ,    SCD  PQ , PQ, SE  SCD nên suy ra PQ //SE .
Vậy MNPQ là hình bình hành.
    SM  SP  SN  SQ 
Suy ra SM  SP  SN  SQ  SA  SC  SB  SD SA SC SB SD SM  SP  SN  SQ  
SA  SP  SN  SQ    SA   SC  SB  SD  SA   SC  SB  SD   SA SC SB SD SM  SC SB SD  SA  SP SN SQ Vì bốn điểm 
A , B , C , D đồng phẳng nên ta có     1   SM  SC SB SD 
GV: Trần Đình Cư –Zalo: 0834332133 36
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com SP SN SQ SM SM SP SN SQ          . SC SB SD SA SA SC SB SD
 Câu 42: (THPT TRIỆU SƠN 2 NĂM 2018-2019) Cho hai nửa đường thẳng Ax , By chéo 1 2 3
nhau. Hai điểm C , D thay đổi lần lượt ở trên Ax và By sao cho  
, D là điểm thứ AC BD AB
tư của hình bình hành ABDD .  P là mặt phẳng chứa CD và song song với AB , Q là mặt
phẳng chứa Ax và song song với By . Chứng minh rằng  P luôn luôn đi qua một điểm cố định I
trong mặt phẳng Q . Tìm vị trí của C và D sao cho diện tích S của tam giác AD C  nhỏ nhất.  Lời giải B D y M D' y' A I N C x
Dựng Ay//By . D trên Ay sao cho AD  BD .  P là mặt phẳng CDD , Q là mặt phẳng
 Ax, Ay
Với I tùy ý trên CD . Gọi M , N là các điểm trên Ay, Ax sao cho MI / / Ax , NI / / Ay .Ta có: AM AN CI D ' I CI  ID '      1 (1) AD ' AC CD ' D 'C CD ' 1 2 3 AB : 3 2 AB : 3      1 (2) . AC BD AB AC AD ' D ' I AB : 3
Với C , D là hai điểm tùy ý thỏa mãn giả thiết. Trên CD tồn tại điểm I sao cho  . D 'C AC AN D ' I AB : 3 AB Ta được:    AN  (3) AC D 'C AC 3 AM CI D ' I AB : 3 2 AB : 3 2 AB và   1  1   AM  (4) AD ' CD ' D 'C AC AD ' 3
Từ (3) và (4) suy ra M , N cố định nên I cố định. Do đó  P luôn đi qua điểm cố định I trong Q . 1 1 S 
AC.ADsin A 
AC.BD sin A nên S nhỏ nhất  AC.BD nhỏ nhất. 2 2 1 1
Áp dụng bất đẳng thức Côsi cho hai số dương: , ta có: AC BD
GV: Trần Đình Cư –Zalo: 0834332133 37
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com 3 1 2 1 2 8 2    2 .  AC.BD  AB AB AC BD AC BD 9 1 2 3 2 AB 4 AB
Dấu bằng xảy ra khi và chỉ khi    AC  và BD  . AC BD 2 AB 3 3 4 AB 2 AB
Vậy S nhỏ nhất khi và chỉ khi BD  , AC  . 3 3
 Câu 43: (HSG ĐỀ 078) Cho hình lăng trụ ABⒸ.A'B'C' có đáy là tam giác đều cạnh a. AA'
vuông góc với (ABC). Đường chéo BC' của mặt bên BCC'B' hợp với (ABB'A') một góc bằng 300.
Gọi M, N lần lượt là trung điểm của AC và BB'. Tính góc giữa MN và (BA'C'). Lời gải
Ta tính được AA' = BB' =CC’= a 2 . Gọi J là trung điểm của C’A’, H là hình chiếu của M lên    
BJ. Gọi  là góc giữa MN và (BA'C') thì ta có   MKH   MN, BJ  , K là giao điểm của MN và    
BJ (Với qui ước lấy góc nhọn). 2 a
+ Ta có: MN.BJ  MB  BN BM  BB' . MB BM  .
MB BB'  BM .BN  BN.BB'  4 E A B M A K C N H F B' A' J  2   a
 MN.BJ.cos MN , BJ   C'   4   a 5 a 11
+ Áp dụng hệ thức lượng trong các tam giác vuông BMN và BMJ tính được MN  , BJ  2 2    1 1
 cos MN , BJ    0    arccos .   55 55  
 Câu 44: (HSG ĐỀ 079) Cho hình chóp S.ABCD có đáy là hình vuông tâm O, cạnh a và SO
vuông góc với mặt phẳng (ABCD). Gọi M, N là trung điểm của SA và BC.Biết góc giữa đường
thẳng MN và mặt phẳng (ABCD) bằng 600. Tính độ dài các đoạn thẳng SO , MN và tính cosin của
góc giữa đường thẳng MN với mặt phẳng (SBD).  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 38
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com S H M E D C O I N K A B
Gọi I là trung điểm của OA  MI // SO  MI  (ABCD) . Do đó góc giữa MN và (ABCD) là góc   MNI 0  MNI  60 2 2 2 0
IN  IC  NC  2 . IC . NC cos45 2 2
3 2a a 3 2a a 2 5 2 a      . 2 . .   4  2 4 2 2 8   a 10 NI a 10  NI  , MN   4 cos 600 2 a a 30 0 30
MI  NI.tan 60 
 SO  2MI  4 2 AC  BD Ta có 
 AC  (SBD) . Gọi H, K là trung điểm của SO và O . B AC  SO 
 MH // KN // AC  MH  (SBD), KN  (SBD) .
Do đó HK là hình chiếu của MN lên (SBD). Gọi E  MN  HK suy ra góc  giữa MN và (SBD) là góc MEH. 1 1 a 2
Do MH  OA  OC  KN 
, nên MHNK là hình bình hành 2 2 4 1 a 10
 E là trung điểm của MN  ME  MN  . 2 4 MH a 2 a 10 1
Do tam giác MHE vuông tại H nên sin   :  ME 4 4 5 2 2
 cos  1 sin   . 5
 Câu 45: (HSG ĐỀ 080) Cho hình chóp tam giác đều S.ABC cạnh đáy a , đường cao SO  2a
. Gọi M là điểm thuộc đường cao AA của tam giác ABC . Xét mặt phẳng  P đi qua M và vuông
GV: Trần Đình Cư –Zalo: 0834332133 39
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com a 3 a 3
góc với AA . Đặt AM  x (  x 
). Tìm x để thiết diện của hình chóp khi cắt bởi mặt 3 2
phẳng  P có diện tích lớn nhất.  Lời giải S G N H A C F O M A' E B a 3 a 3 Vì  x 
nên M thuộc OA . 3 2
Ta có SO   ABC   SO  AA, tam giác ABC đều nên BC  AA . Vậy  P qua M song song với SO và BC .
Xét  P và  ABC  có M chung. Do  P  BC nên kẻ qua M đường thẳng song song với BC cắt
AB, AC tại E, F .
Tương tự kẻ qua M đường thẳng song song với SO cắt SA tại N , qua N kẻ đường thẳng song
song với BC cắt SB , SC tại H , Q . Ta có thiết diện là tứ giác EFGH .
Ta có EF  BC  GH . M , N là trung điểm EF,GH và MN  EF nên EFGH là hình thang cân đáy EF , GH 1 Khi đó: S 
(EF  GH ).MN EFGH 2 a 3 a 3 2x 3 Ta có AA'  , AO  nên EF = 2 3 3 HG SN OM  
 HG  2  x 3  a BC SA ' OA ' MN MA ' 
 MN  2 3a  2x 3 SO OA ' 1 2 S = (EF + GH).MN =
4x 3  3a 3a  2x 3 EFGH    2 3 2 2 1 1  3a  3a S =
4x 3  3a 6a  4x 3  .  (theo Cosi) EFGH      3 3  2  4
GV: Trần Đình Cư –Zalo: 0834332133 40
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com 2 3a 3a 3 S
đạt giá trị lớn nhất bằng
khi và chỉ khi x  . EFGH 4 8 2 3a 3a 3
Vậy giá trị lớn nhất của diện tích thiết diện bằng khi x  . 4 8
 Câu 46: (HSG ĐỀ 080) Cho hình thoi ABCD có   60o BAD , AB  2 .
a Gọi H là trung điểm
AB . Trên đường thẳng d vuông góc với mặt phẳng  ABCD tại H lấy điểm S thay đổi khác H . 1
Trên tia đối của tia BC lấy điểm M sao cho BM  BC. 4 a 3 a. Khi SH 
. Chứng minh đường thẳng SM vuông góc với mặt phẳng SAD . 2
b. Tính theo a độ dài của SH để góc giữa SC và SAD có số đo lớn nhất.  Lời giải S B M C K H I A N D 1 a 1 a. Ta có   0 MB  BC  
HB, HBM  HAD  60 4 2 2  H
 BM vuông tại M . a o 3  HM  . HB sin 60  . 2
Gọi N là giao của HM và AD . a 3
Ta có: HN  HM  SH 
 SMN vuông tại S . 2
SH  AD (SH  ( ABCD)) 
 AD  (SMN )  AD  SM
MN  DA( AD / / BC) 
Kết hợp với SM  SN  SM  (SAD)
b. Gọi là góc giữa SC và SAD ; K là hình chiếu vuông góc của H lên SN ; I là giao của HC với AD .
Lấy E đối xứng với I qua K .
Vì AD  (SMN )  AD  HK . Kết hợp với HK  SN  KH  (SAD) .
GV: Trần Đình Cư –Zalo: 0834332133 41
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
Mà HK là đường trung bình của tam giác ICE nên HK // CE .
Suy ra CE  (SAD) tại E . Suy ra SEC vuông tại E và SE là hình chiếu của SC trên SAD . Ta có    CSE .
Đặt x  SH (x  0) . Tam giác SHN vuông tại H và HK là đường cao nên SH.HN 3ax 2 3ax HK    CE  . 2 2 2 2 SN 3a  4x 3a  4x 2 2 25a 3a 2 2 2 2
CH  CM  MC    7a 4 4
Tam giác SHC vuông tại H nên 2 2 2 2 SC  SH  CH  x  7a . EC 2 3ax 2 3ax sin     . 2 2 2 2 4 4 2 2 SC
(4x  3a )(x  7a )
(4x  21a )  31a x 2 3ax 12  sin   sin  . 2 2 2 2 4 21  31
4 21.a x  31.a x 21
Dấu đẳng thức xảy ra khi 4 x  .a . 4 21
Vậy  lớn nhất khi và chỉ khi sin  lớn nhất khi và chỉ khi 4 SH  . . a 4
 Câu 47: (HSG ĐỀ 081) Cho tứ diện ABCD , có AB  AC, AB  B .
D Gọi P,Q lần lượt chia
đoạn AB và CD theo cùng tỉ số k. Chứng minh hai đường thẳng AB và PQ vuông góc với nhau.  Lời giải A P D B Q C      
           
Chọn hệ cơ sở AB  a, AC  b, AD  c Ta có: A . B AC  .
a b  0 ; AB BD  a c  a 2 . .  0  . a c  a      AA  k AB k 
Ta có: PA  k PB  AP    .a 1 k 1 k      AC  k AD 1  k 
QC  kQD  AQ   .b  .c 1 k 1 k 1 k
   k  1  k  k   
PQ  AQ  AP  a  b  c  a c 1 . . .  .b 1 k 1 k 1 k 1 k 1 k
GV: Trần Đình Cư –Zalo: 0834332133 42
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com         2  k 1  k 1
Vậy hai đường thẳng AB và PQ . AB PQ  . a  a c b   
a  .ac . . a b  0 1 k 1 k  1 k 1 k vuông góc với nhau.
 Câu 48: (HSG ĐỀ 081) Cho tứ diện đều ABC .
D Mọi M , N, P lần lượt là trung điểm của các
cạnh AB, BC, AD và G là trọng tâm tam giác B .
CD Tính góc giữa hai đường thẳng MG và NP.  Lời giải A M M B D N G C        1   
Đặt AB  a, AC  b, AD  c là các véctơ không đồng phẳng và AG  a  b  c 3   
Vì ABCD là tứ diện đều nên giả sử a  b  c  1       1 Và . a b  . b c  . c a  2
         
MG  AG  AM 
a  b  c  MG 
a  b  c2 1 1 1 2 2 2 2  6 6 2
         
PN  AN  AP 
a b c  PN 
a  b c2 1 1 2  2 2 2     M . G PN  MG PN  2 2 cos = cos ,
       arc os c MG . PN 6 6
 Câu 49: (HSG ĐỀ 082) Cho hình chóp S.ABCD có đáy ABCD là hình thang MA S P
 AB / /CD, AB  2CD . Gọi M và P lần lượt là điểm thuộc cạnh AD và SC thoả mãn   x MD PC .
a. Xác định thiết diện của hình chóp cắt bởi mặt phẳng () chứa MP và song song với A . B
b.Tìm x để diện tích thiết diện bằng một nửa diện tích tam giác SA B .  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 43
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com S T N P A D M C Q B a. Ta có:
M ( )  ( ABCD) 
 ( )  ( ABCD)  MQ / / A ( B Q  BC) ( ) / / AB 
Tương tự ()  (SC )
D  PN / / AB(N  S ) D
Vậy thiết diện của () với hình chóp là tứ giác MNPQ. Vì MQ / /NP / / AB nên MNPQ là hình thang MD AM 1 x x  2
b. Gọi T  MN  PQ . Ta có: QM  AB  D C  AB  CD  AB AD AD 1 x 1 x 2 x   1 MA QB S P S N Vì   
 PQ / /SB, MN / /SA  S  AB  TM  Q MD QC PC D N 2 2 S      TMQ MQ x 2 Do đó         1 S  AB   2 x 1   SAB     NP S N AM x x x NP x Vì     NP  D C  AB   D C SD AD x 1 x 1 2 x   1 QM x  2 2 2 2 S  NP  x SMNPQ x 4x  4 TPN Do đó     1    S MQ TMQ   x  22 STMQ
x  22  x  22 SMNPQ 1 Từ (1) và (2) suy ra  S x 1 TMQ SMNPQ 1 1 1 Vậy     x  1 S 2 x 1 2 TMQ
 Câu 50: (HSG ĐỀ 083) Cho hình hộp .
ABCD A' B 'C ' D '. Trên cạnh AB lấy điểm M khác
A và B . Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng ( ACD ').
a. Xác định thiết diện của hình hộp khi cắt bởi mặt phẳng (P) .
b. Tìm vị trí của điểm M để thiết diện đó có diện tích lớn nhất.  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 44
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com I D' Q C' R F A' P D B' C S K O A N E J M B
a.Trong mp(ABCD), qua M vẽ đường thẳng song song với AC cắt DB, BC lần lượt tại E, N.
Trong mp(BDD’B’), qua E vẽ đường thẳng song song với D’O (O=ACBD) cắt B’D’ tại F.
Trong mp(A’B’C’D’), qua F vẽ đường thẳng song song với AC cắt A’D’, D’C’ lần lượt tại R, Q.
Trong mp(AA’D’D), qua R vẽ đường thẳng song song với AD’ cắt AA’ tại S.
Trong mp(CC’D’D), qua Q vẽ đường thẳng song song với CD’ cắt CC’ tại P
Thiết diện là lục giác MNPQRS
b. Do các mặt đối diên của hình hộp song song nên các cạnh đối của lục giác thiết diên MNPQRS
song song và 3 cặp cạnh đó lần lượt song song với các cạnh tam giác ACD’, Các đường thẳng RS,
MN, AD đồng quy tại J, các đường thẳng
MN, DC, QP đồng quy tại K, Các đường thẳng DD’, RS, QP đồng quy tại I
 Các tam giác JKI, ACD’, RQI, JMS, NKP đồng dạng MJ MA NC NK PC PK QD ' QI          MJ=NK và PK=QI MN MB NB NM PC ' PQ QC ' QP
 Các tam giác RQI, JMS, NKP bằng nhau (gọi diện tích của chúng là S1 và gọi diện tích các
tam giác JKI, ACD’ lần lượt là S2, S) AM Đặt
 k; ta có điều kiện 0  k  1 và có: AB 2 2 2 S  JM   AM   AM  1 2        
  k  S1 = k2S S  AC   DC   AB  2 2 2 S  JK 
 JM  MK   JM MK             k  2 2 1  S2 =( k2 + 2k +1)S S  AC   AC   AC AC 
 Diện tích thiết diện: S  S  3S td 2 1 2 1  3 1    3S 1 2
S  2S(k  k  )  2S   k     
(dấu bằng xảy ra  k  ) td 2 4   2  2   2 1
S lớn nhất  k   M là trung điểm của AB 2
GV: Trần Đình Cư –Zalo: 0834332133 45
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
 Câu 51: (HSG THPT LAM KINH THANH HÓA NĂM 2018-2019) Cho hình chóp S.ABCD
có đáy ABCD là hình thang cân (AD//BC) và BC  2a AB  AD  DC  a a  0 . Gọi O là giao điểm của AC và .
BD Biết SD vuông góc với AC và mặt bên SBC là tam giác đều. Tính S D.  Lời giải S K Q B C T J P O M A D N
Trong (ABCD), kẻ DT//AC (T thuộc BC)  CT=AD=a và DT  S . D Ta có: DT=AC= a 3 .  SCT có SC=2a, CT=a,  0
SCT  120  ST  a 7 .  SDT có  0
SDT  90 , DT= a 3 , ST  a 7  SD  2a .
 Câu 52: (HSG THPT LAM KINH THANH HÓA NĂM 2018-2019) Cho hình chóp S.ABCD
có đáy ABCD là hình thang cân (AD//BC) và BC  2a AB  AD  DC  a a  0 . Gọi O là giao điểm của AC và B .
D Biết SD vuông góc với AC và mặt bên SBC là tam giác đều. Mặt phẳng ( )
qua điểm M thuộc đoạn OD (M không trùng O, D) và song song với hai đường thẳng SD và AC.
Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng ( ). Biết MD = x. Tìm x để diện
tích thiết diện lớn nhất.  Lời giải
Trong (ABCD), qua M kẻ đường thẳng song song vớ
i AC cắt AD, DC lần lượt tại N,P.
Trong (SBD), qua M kẻ đường thẳng song song với SD cắt SB tại K.
Trong (SAD), qua N kẻ đường thẳng song song với SD cắt SA tại J.
Trong (SDC), qua P kẻ đường thẳng song song với SD cắt SC tại Q.
Thiếtdiện là ngũ giác NPQKJ.
Ta có : NJ  NP ; MK  NP ; PQ  NP ; NJ=PQ 1 1 1 S  S  S 
(NJ  MK )MN 
(MK  PQ)MP 
(NJ  MK )NP NPQKJ NMKJ MPQK 2 2 2 NP MD AC.MD . x a 3 Xét  ACD có   NP    3x AC OD OD a 3
GV: Trần Đình Cư –Zalo: 0834332133 46
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com  a  2 . a  x   NJ AN OM S . D OM  3 Xét   ASD và  AOD có    NJ  
 2(a  x 3) SD AD OD OD a 3 2 . a a 3 .  x KM BM SD BM  2 Xét  BSD có   KM   
(a 3  x) S
 2(3a  2 3x)x SD BD BD NPQKJ a 3 3 2 1 1 3 3 3 3 3 2 
(3a  2 3x)2 3x 
(3a  2 3x)  2 3x  a 2 Max S  a khi x  a NPQKJ 3 4 3   4 4 4
 Câu 53: (HSG THPT LÊ LỢI NĂM 2018-2019) Cho hình chóp S.ABCD có đáy ABCD là
hình thang cân với AD // BC, AB = BC = a, AD = 2a tam giác SAD vuông cân tại S và SB =
a 3 . Gọi M là trung điểm của SA, G là trọng tâm của tam giác SCD, H là giao điểm của BG và mp(SAC). HB
Chứng minh rằng BM // (SCD) và tính tỉ số HG  Lời giải
Gọi N là trung điểm của AD S
ta có BC = DN = a và BC // DN
 tứ giác BCDN là hình bình hành  BN / / . CD M
Vì M, N lần lượt là trung điểm của SA và G
AD nên MN // SD  (BMN ) / /(SCD) N A D
mà BM  (BMN )  BM / /(SCD) J H K P *) Gọi P là trung điểm của CD, I
I  AC  BP; H  SI  BG  H=BG  (SAC) . Gọi J là B C
giao điểm của BN và AC, vì tứ giác BCNA là hình bình hành nên J là trung điểm của BN mà IJ //
NP nên I là trung điểm của BP
*) Trong tam giác SBP vẽ GK // SI, ta có: HB IB IP SP 3    
(do G là trọng tâm của tam giác SCD) HG IK IK SG 2
 Câu 54: (HSG THPT LÊ LỢI NĂM 2018-2019) Cho tứ diện đều ABCD cạnh a. Hai điểm
M, N chạy tương ứng trên các đoạn AB và CD sao cho BM = DN. Tìm giá trị lớn nhất, nhỏ nhất của MN.  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 47
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com BM     Đặt
 x , với 0  x  DN 1 
 x . Khi đó ta có: BM  .
x BA và DN  . x DC BA DC          Ta có: DN  .
x DC  BN  BD  x(BC  BD)  BN  .
x BC  (1 x).BD      
Do đó: MN  BN  BM  .
x BC  (1 x).BD  . x BA 2 2 2 a a a MN2 = 2 2 2 2 2 2 2
x a  (1 x) a  x a  2x(1 x)  2x .  2x(1 x) 2 2 2 = a2 2 2 2 2 x (1 x) x x(1 x) x x(1 x)         = (2x2 – 2x + 1)a2  
Xét hàm số f(x) = 2x2 – 2x + 1 trên đoạn 0;  1 ta có: 1 1
max f (x)  f (0)  f (1)  1, min f (x)  f ( )  2 2 a 2
MN đạt giá trị nhỏ nhất bằng
khi M, N lần lượt là trung điểm của AB, . CD 2
MN đạt giá trị lớn nhất bằng a khi M B, N  D hoặc M A,N C.
 Câu 55: (TRƯỜNG THPT LÊ LỢI NĂM 2017 - 2018) Cho hình chóp S.ABCD , đáy ABCD
là nửa lục giác đều AB  AD  DC  a  0 , BC  2a
Mặt bên SBC là tam giác đều, SD vuông góc với AC , O là giáo điểm của AC, B D.Mặt phẳng
() qua điểm M thuộc đoạn OB ( M không trùng với B ), song song với SD và AC . Xác định
thiết diện của hình chóp S.ABCD với mặt phẳng   và tìm x để diện tích thiết diện đó lớn
nhất biết BM  x 3 .  Lời giải
Xác định thiết diện của hình chóp S.ABCD với mặt phẳng ().
+) Xác định được thiết diện là tam giác NPQ (với N, P, Q lần lượt nằm trên các cạnh BA, BC, BS)
MQ / /SD, NP / / AC +) Ta có:  NP  MQ SD  AC  1
 Diện tích thiết diện: S  N . P MQ NPQ 2
Gọi J là điểm nằm trên BC sao cho ACJD là hình bình hành.
GV: Trần Đình Cư –Zalo: 0834332133 48
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com Trong tam giác SCJ có  0 SC  2 ; a CJ  ; a SCJ  120 2 2 SJ 
SC  CJ  2.SC.CJ.cos C  a 7
Trong tam giác ABC vuông tại A có: 2 2 AC 
BC  AB  a 3
Trong tam giác SDJ vuông tại D vì SD vuông góc A C. 2 2 SD 
SJ  DJ  2a 2S a 3 Trong tam giác ABC có: ABC BO   AC 2 BM MQ
+) Trong tam giác SBD :   MQ  2x BD SD NP BM 3 3 Trong tam giác BAC   NP  x 3 NP  x 3 AC BO 2 2 2 3 3x
+) Diện tích thiết diện: S  NPQ 2 2a 3 2a
+) Vì M thuộc đoạn BO ( M  B ) nên 0  x 3  BO   0  x  3 3 2 2 3 3 2  2a  2a 3 2a 3 Do đó, S  .  . Vậy, min S  . NPQ   2 NPQ  3  3 3
 Câu 56: (THPT NÔNG CỐNG - NHƯ THANH NĂM HỌC 2018 - 2019) Cho hình lăng trụ
đứng ABC.A'B'C ' có AB  CB  2, AC  1 . Mặt phẳng (P) cắt các đường thẳng AA',BB ',CC ' lần lượt
tại M, N ,P sao cho tam giác MNP đều. Tính cosin góc tạo bởi (P) và (ABC)  Lời giải
Từ C dựng CE song song với PM, E thuộc AA’, CF song song với PN, F thuộc BB’. Ta có (CEF)
// (PMN) nên EF // MN và tam giác CEF là một tam giác đều. Đặt AE = x, BF= y, CE = CF = EF = a. 2 2
x 1  a (1)  Ta có hệ 2 2
y  4  a (2)  2 2
(x  y)  4  a (3)  2 a 1 Từ (1) và (2) suy ra: 2 2 2
x  y  2a  5. Kết hợp (3) suy ra xy  2 2 a 1 Từ (1) và (2) suy ra: 2 2 2 2
x y  (a 1)(a  4). Do đó: 2 2 2 (
)  (a 1)(a  4) 2 5 3 Giải được: 2 2
a  1(l),a  5 . Suy ra S  CE  F 4 15 S  (
p p  a)( p  b)( p  c)  A  BC 4
GV: Trần Đình Cư –Zalo: 0834332133 49
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com S 15 / 4 5
Gọi  là góc cần tìm. Theo định lí hình chiếu ta có cos ABC      . Vậy S CE  F 5 3 / 4 5 5
góc của (P) và (ABC) là arccos( ) 5
 Câu 57: (THPT NÔNG CỐNG - NHƯ THANH NĂM HỌC 2018 - 2019) Cho hình hộp chữ
nhật ABCD.AB C  D
  có tâm O và AB  3a, AD  A 
A  4a . Mặt phẳng  P  đi qua O và cắt các tia
AB', AC, AD' tương ứng tại ba điểm phân biệt M , N , P . Tìm giá trị lớn nhất của biểu thức
T  AM .AN .AP .  Lời giải          
Đặt AA'  a, AB  b, AD  d . Ta có AC '  a  b  c     
 AO  x.AM  y.AN  . z AP
Vì M, N, P, O đồng phẳng nên x  yz 1             Ta có: AM  . m AB'  (
m a  b), AN  . n AC  (
n b  d), AP  ( p a  d).  1  1    1 1 1 1 AO 
AC '  (a  b  d) . Suy ra mx  ny  pz      4 2 2 4 m n p AB' AC AD ' 5a 5a 4a 2 1 1 4 2 4     4     4     AM AN AP AM AN AD ' AM AN 5AD ' 5 4 4 2 675 2 BĐT Cauchy: 3  3  T  5 5T 16 675 2 15 Vậy minT =
. Khi AM  AN  , AD '  3 2 16 4
 Câu 58: Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh .
a Tam giác SAD là tam giác
đều và nằm trong mặt phẳng vuông góc với mặt đáy. Gọi M , N lần lượt là trung điểm của các cạnh SB, C .
D Gọi H là trung điểm của AD, E là chân đường vuông góc hạ từ H lên SC. Chứng minh
MN  SAB và tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng MNE .  Lời giải S I d M E A B F H D N C
GV: Trần Đình Cư –Zalo: 0834332133 50
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com      
+ Đặt HA  x, HK  y, HS  z (K là trung điểm BC)  1    1     1    + Ta có AM 
 AS  AB  AM  HS  HA  HK   AM  z  x  y 2 2 2 
   1       
MN  MA  AD  DN  
z  x  y 1 3 1  2x  y   x  z 2 2 2 2 
     
SB  SH  HA  AB  z  x  y 2 2
    2 2 3 1 3 a 1  a 3   
+ Suy ra MN.AM  x  z     
  0  MN  AM   1 4 4 4  2  4 2   2 2     2 2 3 1 3 a 1  a 3    MN.SB   x  z      
  0  MN  SB 2 2 2 2  2  2 2   + Từ  
1 và 2 ta suy ra MN  SAB. 2 2 2 2      2 2 2  3 1  9 1 9a 3a 3a a 3
+ Mặt khác MN   x  z  x  z     MN     2 2  4 4 16 16 4 2 Dựng thiết diện :
+ Qua S kẻ đường thẳng d song song với AB và CD  d  SAB  SCD
+ Trong mặt phẳng SCD kéo dài NE  d  I
+ Trong mặt phẳng SAB kéo dài IM  AB  F
+ Tứ giác MENF là thiết diện cần tìm 
     
+ Ta có SC  SH  HD  DC  z  x  y      
+ Giả sử SE  k SC  SE  k z  x  y
     
+ HE  HS  SE  1  k  z  k x  k y      2 2 2
+ Do HE  SC nên HE.SC  0  k  
1 z  k x  k y  0 3k   1 k 3 ES 3  
 k  0  k  , từ đây suy ra  4 4 8 EC 5 BF SI ES 3 3CN 3a + Ta có     BF   CN CN EC 5 5 10 2  a  a 26 a 29 + Do đó 2 NF  a   BF    và 2 2 MF  NF  MN   2  5 10 2 a 87
+ Diện tích tam giác INF là dt  INF   MN.MF  20 h IE SE 3
+ Gọi h là đường cao kẻ qua E của tam giác IEM    MN IN SC 8 3MN 3a 3  h   8 16
GV: Trần Đình Cư –Zalo: 0834332133 51
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com 2 1 1 3a 87
+ Diện tích tam giác IEM là dt  IEM   . h IM  . h MF  2 2 320 2 13a 87
+ Vậy diện tích của thiết diện là dt MENF   . 320  Câu 59: (HSG ĐỀ 095)
Cho hình lăng trụ đứng A . BCD AB C  D
  đáy là nửa lục giác đều với AD  2a , AB  BC  CD  a .
Đường cao của hình lăng trụ là h , (P) là mặt phẳng qua AD , cắt các cạnh BB ,CC lần lượt tại B ,C . 1 1
a) Thiết diện của hình lăng trụ cắt bởi (P) là hình gì? Tìm liên hệ giữa a và h và tìm vị trí của
điểm B ,C sao cho P  AD . 1 1
b) Định vị trí của  P để chu vi thiết diện nhỏ nhất. Tính giá trị nhỏ nhất ấy.  Lời giải A' D' B' H C' C1 D A J B I 1 C B  ' '  ADD A  / /  ' ' BCC B   '  Ta có  '  P   ' ' ADD A  '
 AD  AD / / B C 1 1 P ' '
BCC B   B C 1 1 
Qua B dựng đường thẳng song song với BC , cắt CC tại I . Hai tam giác '
ADD và B IC có các 1 1 1 AD AD AB
cạnh song song từng từng đôi một nên chúng đồng dạng suy ra  
( do B I  BC ) B C B I BC 1 1 1 1
Mặt khác vì AD  2BC (do ABCD là nửa lục giác đều) suy ra ' AD  2B C . 1 1
Vậy thiết diện là hình thanh ' AD C B . 1 1
Tìm liên hệ giữa a và h và tìm vị trí B ,C sao cho (P)  A' D . 1 1 Ta có ' '
ADD A là hình chữ nhật nên khi '
(P)  A D thì ' '
A D  AD suy ra ' '
ADD A là hình vuông. Suy ra '
AA  AD tức h  2a .
Hơn nữa theo tính chất của nửa lục giác đều ta có: BD  AB, AC  CD BD  AB Do đó   BD   ' '
ABB A   BD  AB  AB  A' B vì AB  A' D 1 1 ' 1 BD  AA 
GV: Trần Đình Cư –Zalo: 0834332133 52
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com C  D  AC   CD   ' '
ACC A   CD  AC  AC  A'C vì AC  A' D . 1 1 ' 1 CD  AA  h  2a  Vậy khi '
 AC  A C thì (P)  A ' D . 1  ' AB  A B  1
Xác định vị trí của (P) để chu vi thiết diện nhỏ nhất.
Gọi p là chu vi của thiết diện, ta có: 3 ' ' ' '
p  AD  B C  AB  D C 
AD  AB  D C 1 1 1 1 1 1 2 Vì '
AD có độ dài không đổi nên chu vi nhỏ nhất khi và chỉ khi '
AB  D C nhỏ nhất. 1 1 ' DD h
Đặt BB  x , khi đó CI  x,C I   . 1 1 2 2  h  h Ta có '
CC  CC  C I  CI  h   x   x 1  1     2  2 2  h Ta có '  AB  D C 2 2 ' 2 ' 2 2 2 2 
AB  BB  C D  C C 
a  h  a   x 1 1 1 1    2     h    h Đặt   u  ;
a x, v a;  x 
 thì u  v  2a;    2   2  2     h 2
u  v  u  v  4a  4 h 2  a a   a h h 2 4a 
 u, v cùng hướng 2    x   x  x  4 a x 2 4 2 2 h 3 h 2 2 2 2 h T  4a   min p 
4a  h  4a 
đạt được khi x  4 2 4 4 h
Vậy giá trị nhỏ nhất đạt được khi (P) cắt '
BB tại B với BB  . 1 1 4
 Câu 60: (HSG ĐỀ 095) Cho hình lăng trụ tứ giác ABC .
D A1B1C1D1. Một mặt phẳng (P) thay
đổi song song với hai đáy của lăng trụ, cắt các đoạn thẳng AB1, BC1, CD1, DA1 tương ứng lần lượt
các điểm M, N, P, Q. Hãy xác định vị trí của mặt phẳng (P) sao cho tứ giác MNPQ có diện tích lớn nhất.  Lời giải
Giả sử mặt phẳng (P) cắt AA , BB ,CC , DD D C 1 1 1 1
tương ứng tại A’, B’, C’, D’. Khi đó ta có A D' P B AA' BB ' CC ' DD' Q C'     x A' AA BB CC DD N 1 1 1 1 D M B' C A B
GV: Trần Đình Cư –Zalo: 0834332133 53
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com S  S MNPQ Đặt
Theo định lí Ta- lét ta có A'M AM AA'    x A' B' AB AA 1 1 A'Q A Q A A'  1  1  1  x A' D' A D A A 1 1 Do đó ta được ' ' ' s( A MQ) A M A Q ' ' ' '  .
 x(1 x)  S( A MQ)  x(1 x).S( A B D ) (1) ' ' ' ' ' ' ' s( A B D ) A B A D
Chứng minh tương tự ta có: ' ' ' '
S(B MN )  x(1 x).S(B A C ) (2) ' ' ' '
S(C NP)  x(1 x).s(C B D ) (3) ' ' ' '
S(D PQ)  x(1 x).S(D C A ) (4)
Từ (1), (2), (3), (4) ta có
S(MNPQ) = S(A’B’C’D’)- S(A’MQ)-S(B’MN)-S(C’NP)-S(D’PQ) = S -x(1-x) ' ' ' (S( A B D ) ' ' ' S (B A C ) + ' ' ' S(C B D ) + ' ' '
S(D C A ) ) = S -x(1-x).2S = S(2x2- 2x +1)  1 2 1  1 = S. ( 2 x  )   S .   2 2  2 S 1
Vậy diện tích tứ giác MNPQ bằng  x 
 M là trung điểm AA1  (P) song song và cách 2 2 đều hai đáy.
 Câu 61: (HSG ĐỀ 098) Cho hình lập phương ABC .
D A’B’C’D’ có cạnh a . Gọi I là tâm của
hình vuông CDD’C’, K là trung điểm của cạnh C . B
1. Dựng thiết diện của hình lập phương ABC .
D A’B’C’D’ cắt bởi mặt phẳng (AKI). Tính diện tích
của thiết diện theo a .
2. Tính góc tạo bởi hai đường thẳng A’D’ và AQ với Q là giao điểm của (AKI) và CC’.  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 54
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com C' D' B' A' N I Q J C D K B A
1). Gọi J là giao điểm của AK và C D.
Q là giao điểm của JI và CC’; N là giao điểm của IJ và DD’.
Thiết diện là tứ giác AKQN.
Chứng minh được AKQN là hình thang có 2 đáy là KQ, AN.
Chứng minh được C là trung điểm của JD, K là trung điểm JA, Q là trung điểm của JN. S JKQ  JK JQ 1 1 1  .  .   S  S  S  3S . S JA JN 2 2 4 AKQN J  AN JKQ  J  KQ JAN  1 CQ 1 1 CQ  ND  QC '    CQ  a 2 CC ' 3 3 a 13 a 5 a 10 Tính được KQ  ; JK  ; JQ  6 2 3 2 2 2
JQ  JQ  KQ 6 7 2 o c sKJQ=  , sin KJQ  1 os c KJQ  2JK.JQ 50 5 2 2 1 14a 14a S  JK.J . Q sin KJQ  , S  3S  . JKQ  2 12 AKQN J  KQ 4
2). Vì A’D’//AD nên góc tạo bởi A’D’, AQ bằng góc tạo bởi AQ, AD
   
AC '  AB  AD  AA '  AC '  a 3. a 19 a 10 Tính được AQ 
; AD  a; QD  . 3 3 2 2 2
AQ  AD  QD 3 cos QAD   . 2A . Q AD 19    
 Câu 62: Cho tứ diện ABCD , các điểm M , N xác định bởi MA  xMC, NB  yND  x, y   1 .
Tìm điều kiện giữa x và y để ba đường thẳng AB,CD, MN cùng song song với một mặt phẳng.  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 55
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com A B N D M C         
+) Chọ hệ véc tơ: a  D ,
A b  DB, c  DC thì a, b, c không đồng phẳng.      
+) Ta có MA  xMC  DA  DM  x DC  DM     DA  xDC 1  x   DM    a  c   1 1 x x 1 x 1    1  1 
Lại có NB  yND  DN  DB  b 2 1 y 1 y
   1   1  x  +) Từ  
1 và 2 suy ra MN  DN  DM  a  b  c (3) 1 x 1 y 1 x
        
+) Ta có AB  DB  DA  b  a, CD  c ; AB và CD là hai véc tơ không cùng phương nên ba
  
đường thẳng AB,CD, MN cùng song song với một mặt phẳng khi và chỉ khi ba véc tơ AB, CD, MN         
đồng phẳng  MN  mAB  nCD  m b  a  nc  ma  mb  nc (4)  1 m   1 x      1
+) Do a,b, c không đồng phẳng nên từ (3) và (4) ta có hệ: m   x  y 1 y   x n    1 x
Vậy ba đường thẳng AB,CD, MN cùng song song với một mặt phẳng khi và chỉ khi x  y .
 Câu 63: Cho lăng trụ AB .
D A1B1C1 có tất cả các mặt bên là hình vuông cạnh bằng 1. Gọi D,
E, F lần lượt là trung điểm của các cạnh BC, A1C1, B1C1. Tính côsin của góc giữa hai đường thẳng A1F, DE.  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 56
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
               1
+) Chọn hệ véc tơ a  A ,
A b  A B , c  A C . Khi đó: a  b  c  1 và . a b  . a c  0 , . b c  . 1 1 1 1 1 2  1   1  1  +) Ta có A F  A B  A C  b  c 1  1 1 1 1 2 2 2
     1 
DE  DC  CC  C E  a  b 1 1 2 2    2    2  1 1  3 2  1  5
+) Tính cos  A F, DE : A F  A F  b  c  , DE  DE  a  b  1  1 1      2 2  2  2  2
   1  1    1   3 , A F.DE  b  c . a  b   . 1      2 2   2  8     A F.DE 15
Suy ra: cos  A F, DE  cos A F, DE 1   . 1 1 A F.DE 10 1   
 Câu 64: Cho tứ diện ABCD và các điểm M , N xác định bởi AM  2AB  3AC ;   
DN  DB  xDC . Tìm x để các đường thẳng AD, BC, MN cùng song song với một mặt phẳng.  Lời giải S T N P A D M C Q B
  
Yêu cầu bài toán tương đương với tìm x để ba vectơ MN, AD, BC đồng phẳng.        Hệ thức  
1  AM  2 AB  3 AB  BC  AM  AB  3BC .
   
  
Hệ thức 2  AN  AD  AB  AD  x DA AB  BC
GV: Trần Đình Cư –Zalo: 0834332133 57
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com    
 AN  1 x AB  x AD  xBC .
      Từ  
1 và 2 , suy ra MN  AN  AM  2  x AB  x AD   x  3 BC .
  
Vậy ba vectơ MN, AD, BC đồng phẳng khi 2  x  0  x  2  .
M  ( )  ( ABCD) Ta có: 
 ( )  ( ABCD)  MQ / / AB(Q  BC) ( ) / / AB 
Tương tự ( )  (SCD)  PN / / AB(N  SD)
Vậy thiết diện của ( ) với hình chóp là tứ giác MNPQ. Vì MQ / / NP / / AB nên MNPQ là hình thang
 Câu 65: Cho hình chóp S.ABCD có đáy ABCD là hình thang  AB / /CD, AB  2CD . Gọi M MA S P
và P lần lượt là điểm thuộc cạnh AD và SC thoả mãn 
 x . Xác định thiết diện của hình MD PC
chóp cắt bởi mặt phẳng ( ) chứa MP và song song với A .
B Tìm x để diện tích thiết diện bằng một
nửa diện tích tam giác SA B .  Lời giải MD AM 1 x x  2
Gọi T  MN  PQ . Ta có: QM  AB  D C  AB  CD  AB AD AD 1 x 1 x 2 x   1 MA QB S P S N Vì   
 PQ / /SB, MN / /SA  S  AB  TM  Q MD QC PC D N 2 2 S  MQ   x   x  TMQ 2  22 Do đó        1 2   S  AB   2 x 1   SAB   4 x     1 NP NS AM x x x NP x Vì     NP  CD  AB   D C SD AD x 1 x 1 2 x   1 QM x  2 2 2 2 S  NP  x S x  MNPQ x 4   1 TPN Do đó     1    S MQ (2) TMQ   x  22 STMQ x  22  x  22 SMNPQ 1 Từ (1) và (2) suy ra  S x 1 SAB SMNPQ 1 1 1 Vậy     x  1 S 2 x 1 2 SAB
 Câu 66: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là điểm thỏa mãn:
     
GS  GA  GB  GC  GD  0. Một mặt phẳng đi qua AG cắt các cạnh SB, SC, SD lần lượt tại BM CN DP
M , N, P . Chứng minh rằng:    1. SM SN SP  Lời giải
    
Gọi O là giao điểm của hai đường chéo AC và BD . Ta có: OA  OB  OC  OD  0 suy ra
GV: Trần Đình Cư –Zalo: 0834332133 58
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
 1     SO 
SA SB SC  SD. 4
     
Do GS  GA  GB  GC  GD  0.     
 4  1    
suy ra GS  4GO  0  SG  4GO  SG 
SO  SA SB  SC  SD  5 5 1   SB  SC  SD    SA  SM  SN  SP .   5  SM SN SP  Vì ,
A G, M , N , P đồng phẳng nên ta có SB SC SD SM  BM SN  CN SP  DP BM CN DP 1    5     4     1. SM SN SP SM SN SP SM SN SP
 Câu 67: Cho tứ diện ABCD , M là một điểm bất kỳ trong tam giác ABC . Các đường thẳng
đi qua M song song với AD, BD,CD tương ứng cắt các mặt phẳng (BCD), ( ACD), ( ABD) tại ' ' '
A , B , C . Tìm vị trí M sao cho ' ' '
MA .MB .MC đạt giá trị lớn nhất.  Lời giải
+ Trong mặt phẳng (ABC), gọi AM  BC  A , BM  AC  B , CM  AB  C 1  1  1
+Trong (DAA1), kẻ đường thẳng qua M song song với AD cắt DA1 tại A’ MA' MA S Xét tam giác DAA 1 MBC  1 có MA’ // AD nên   DA AA S 1 AB  C MB' MB S MC ' MC S Tương tự có 1 MAC   , 1 MAB   BD BB S DC CC S 1 ABC 1 ABC ' ' ' MA MB MC     1 (Do S  S  S  S ) MBC MAC MAB ABC DA DB DC MA' MB' MC '
MA' MB' MC ' ' ' ' 1 + Ta có:    3 3 . .  MA MB . MC .  DA DB . DC . (không đổi) DA DB DC DA DB DC 27 1
 MA’.MB’.MC’ đạt giá trị lớn nhất là DA DB . DC . khi 27 ' ' ' MA MB MC 1   
hay M là trọng tâm tam giác ABC. DA DB DC 3 Vậy ' ' '
MA .MB .MC đạt giá trị lớn nhất khi M là trọng tâm tam giác ABC.
 Câu 68: Cho hình chóp S.ABCD có đáy là hình vuông cạnh .
a Đường thẳng SA vuông góc
với mặt đáy, góc giữa SB và mặt đáy bằng 0
60 . Gọi N là trung điểm của BC.
1. Tính cosin của góc giữa hai đường thẳng SD và AN.
2. Gọi H , K là hai điểm lần lượt thuộc các đường thẳng SB và DN sao cho HK  SB, HK  DN.
Tính độ dài đoạn HK theo . a  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 59
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com S H A B K N D C 1.               
+ Đặt AB  a, AD  b, AS  c với . a b  . b c  .
c a  0 và a  b  a, c  a 3      1 
+ Ta có SD  b  c và AN  a  b 2       2    2 2 2 2 1 a 5 2 1 a
Suy ra SD  b  c  2a, AN  a  b  và . SD AN  b  4 2 2 2 2 a   1 Vậy SD AN  2 cos ,    0 a 5 2 5 2 . a 2 1
Suy ra cos SD, AN   . 2 5 2.      1 
+ Ta có SB  a  c và DN  a  b 2 
            
HK  HB  BN  NK  xSB  BN  y DN  x a  c  b  y a  b   1 1   2  2  
    1 y  
 HK  HB  BN  NK   x  y a  b  xc 2   2 2   2 2
x  y a  xc  0 
 x  y a  3xa  0 HK  SB   o  nên      y  1 HK  DN 2 2 y  1   2 2
 x  y a  b  0  x  y   a  a  0  4  4  1 x  
4x  y  0   16     4x  5y  1 1   y    4 2  3  3  1   3    3    1   a 3 Suy ra HK  a  b  c  HK  a  b  c        16 8 16  16   8   16  4 a 3 Vậy HK  4
GV: Trần Đình Cư –Zalo: 0834332133 60
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
 Câu 69: Cho tứ diện         
ABCD có ACD  BCD  CAD  BAD  BAC  CBD  ABD  ABC  180 ;  ACB  60
. Biết chu vi tam giác ABC bằng 3. Gọi S là diện tích toàn phần của tứ diện ABCD . Tìm giá trị lớn nhất của S.  Lời giải
Cắt tứ diện ABCD theo các cạnh DC, BC, AC và trải tứ diện ABCD xuống mặt phẳng  ABD như sau: AC  B  AC ; B A
 CD  AC B; DCB  DC . B 1 2 3 Ta có:       0
CAD  BAD  BAC  C AD  BAD  BAC  180 nên C , , A C thẳng hàng. 2 1 2 1   
C BD  ABD  ABC  180 nên C , B, C thẳng hàng. 3 1 1 3    
 ACD  BCD  AC D  BC D  180 suy ra tứ giác nội tiếp C C DC . 2 3 1 2 3 Suy ra   
C DC  180  AC B  180  ACB  120 . 2 3 1
Diện tích toàn phần của tứ diện ABCD bằng diện tích tứ giác C C DC . 1 2 3
Đặt CA  x; CB  y theo định lý Cosin, suy ra 2 2 AB 
x  y  xy . Do chu vi tam giác ABC bằng 3 nên 2 2 x  y 
x  y  xy  3 (*) 1 1 1 Ta có 0 2 S  S  S  2 . x 2 y sin 60  C C .DH  (x  y) C C DC C C C DC C 2 3 1 2 3 1 2 3 2 3 2 2 3 1 Lại có 2 2
x  y  xy 
(x  y) nên kết hợp với (*) ta được x  y  2. 2 4
Vậy giá trị lớn nhất của S là
, đạt tại x  y  1. 3
 Câu 70: Cho khối chóp S.ABC có SA = 6; SB = 2, SC = 4, AB = 2 10 và góc  0  0
SBC  90 , ASC  120 . Mặt phẳng (P) đi qua B và trung điểm N của cạnh SC đồng thời vuông góc SM
với (SAC), cắt SA tại M. Tính tỷ số . SA  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 61
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com Ta có 2 2 2
SB  BC; SB  SA  AB  SB  SA , dựng hình bình hành SBCD thì CD  (SAD). Mặt cắt
chính là mặt qua DB và vuông góc với (SAC).
Từ D kẻ DE vuông góc với SA, kẻ DH vuông góc với CE thì DH vuông góc với (SAC), như vậy
(DBH) vuông góc với (SAC) nên M là giao của NH với S . A
Tính được SD  BC  2 3;CD  2; AC  76; BD  4 ,  1 0  A
 CD có ADC  90  AD  6 2  cos ASD   3 2 CH CD 1 HE
 SE  2  DE  2 2; CE  2 3      2 . 2 CE CE 3 HC NC MS HE MS 1 Menelauyt  .  1  
 MS  SE  2 NS ME HC ME 2 SM 2 1    . SA 6 3 SM 1
Vậy tỷ số cần tìm là  . SA 3
 Câu 71: (HSG THPT YÊN ĐỊNH 1 NĂM 2017-2018) Cho hình lập phương ABC D.A’B’C’D’
cạnh bằng a. Lấy điểm M thuộc đoạn AD’, điểm N thuộc đoạn BD sao cho  a 2 
AM  DN  x, 0  x  .   2  
a. Tìm độ dài đoạn MN.
b. Tìm x theo a để đoạn MN ngắn nhất.  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 62
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
 Câu 72: (HSG THPT YÊN ĐỊNH 1 NĂM 2017-2018) Cho hình chóp tứ giác S.ABCD có
Gọi M’, N’ lần lượt là hình chiếu của M, N lên AD 2 2 2 2 2 2
Ta có MN  M ' M  M ' N  M ' M  M ' N '  N ' N x 2
Tam giác M’AM vuông cân tại M’ nên có M ' A  M ' M  ; 2 x 2
Tam giác N’DN vuông cân tại N’ nên có N ' D  N ' N  2
M ' N '  AD  M ' A  N ' D  a  x 2 2 2 x x MN   a  x 2 2 2 2 2   3x  2 2 . a x  a Khi đó 2 2 2 2 2  2  a a a 3 2
MN  3 x  a     MN  3 3 3 3   a 3 a 2 Vậy MN ngắn nhất bằng
đạt được khi x  3 3
đáy là hình vuông tâm O cạnh bằng   0
a, ASB  ASD  90 . Gọi  P là mặt phẳng đi qua AB và
vuông góc với mặt phẳng  ABCD , kéo dài SD cắt mặt phẳng  P tại E. a. Chứng minh  0 AEB  90 b. Biết SA  .
SO Tính độ dài đoạn thẳng CE.  Lời giải E S A D O B C a. SA  SB + Vì 
 SA  SBD  BE  SA   1 SA  SD 
+ Mặt khác P   ABCD theo giao tuyến AB
mà AD  AB  AD   P  BE  AD 2 + Từ  
1 và 2 suy ra BE  SAD  BE  AE hay  0 AEB  90 b.
GV: Trần Đình Cư –Zalo: 0834332133 63
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com a 2
+ Ta có AC  a 2  AO  2 AO a
+ Vì SA  SO  S
 AO vuông cân tại S nên SA   2 2 AE SA 1 2 a + Dễ thấy 2 2 S
 AE  ADE     2 AE  AE  a 2  AE  DE AD 2 3 2 2a + Khi đó 2 2 2
BE  AB  AE  3 2 2a a 15 + Vậy 2 2 2 CE  BC  BE  a   3 3
 Câu 73: Cho hình chóp S.ABCD, có đáy ABCD là hình thang cân (AD//BC) và BC = 2a, AB
= AD = DC = a (a > 0). Mặt bên SBC là tam giác đều. Gọi O là giao điểm của AC và B D. Biết
SD vuông góc với A C. a) Tính S D .
b) Mặt phẳng ( ) qua điểm M thuộc đoạn OD (M khác O, D) và song song với hai đường thẳng
SD và A C.Ⓒ. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng ( ). Biết MD = x.
Tìm x để diện tích thiết diện lớn nhất.  Lời giải S K Q B C T J P O M A D N
a) Dễ thấy đáy ABCD là nữa hình lục giác đều cạnh a.
Kẻ DT//AC (T thuộc BC). Suy ra CT=AD=a và DT vuông góc S . D Ta có: DT=AC= a 3 .
Xét tam giác SCT có SC=2a, CT=a, 0
SCT  120  ST  a 7
Xét tam giác vuông SDT có DT= a 3 , ST  a 7  SD  2a
b) Qua M kẻ đường thẳng song song với AC cắt AD, DC lần lượt tại N,P.
Qua M, N, P kẻ các đường thẳng song song với SD cắt SB, SA, SC lần lượt tại K, J, Q. Thiết diện là ngũ giác NPQKJ.
Ta có: NJ, MK, PQ cùng vuông góc với NP. dt(NPQKJ)=dt(NMKJ)+dt(MPQK)= 1 1
(NJ  MK )MN 
(MK  PQ)MP 2 2
GV: Trần Đình Cư –Zalo: 0834332133 64
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com 1 
(NJ  MK ).NP (do NJ=PQ). 2 Ta có: NP MD AC.MD . x a 3   NP    3x AC OD OD a 3  a  2 . a  x NJ AN OM . SD OM    3     NJ    2(a  x 3) SD AD OD OD a 3 2 . a a 3 .  x KM BM SD BM  2   KM    (a 3  x) SD BD BD a 3 3 Suy ra: dt(NPQKJ)= 1  2  2(a  x 3) 
(a 3  x) 3x  2(3a  2 3x)x   2  3  2 1 1 3 3 2 
(3a  2 3x)2 3x 
(3a  2 3x)  2 3x  a 3 4 3   4
Diện tích NPQKJ lớn nhất bằng 3 3 3 2 a khi x  a 4 4
 Câu 74: (HSG THPT TRIỆU SƠN 2 NĂM 2017) Cho tứ diện SABC có SA, SB,SC đôi một
vuông góc. Gọi  ,  , lần lượt là các góc giữa các mặt phẳng SAB,SBC,SCA với  ABC. Chứng minh rằng: 2 2 2 cos  cos  cos  3    . 2 2 2 2 2 2
sin   sin 
sin   sin 
sin   sin  4  Lời giải Chứng minh 2 2 2
cos   cos   cos   1  2 2 2
sin   sin   sin   2 2 2 2 2 2 2 cos  cos  cos  cos  cos  cos  3       2 2 2 2 2 2 2 2 2
sin   sin 
sin   sin 
sin   sin  2  sin  2  sin  2  sin  4 2 2 2 cos  cos  cos   1 1 1  9 3     3     3   2 2 2  2 2 2  1 os c  1 os c  1 os c  1 os c   1 os c  1 os c  4 4 
Đẳng thức xảy ra khi     
 Câu 75: (THPT HÀM RỔNG THANH HÓA) 1
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB  AD  CD  2a , 2
SA  2a và SA  (ABCD). Gọi M, N, K lần lượt là trung điểm của AB, SB, S . D
1/ Tính góc hợp bởi giữa đường thẳng SB và DM.
2/ Tính diện tích thiết diện của hình chóp khi cắt bởi (ANK).  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 65
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com S 2a A 2a D a M E B 3a C
1/ Kẻ BE//DM. Ta tính được: BE  MD  AE  a 5, SB  2a 2, SE  3a
+ Áp dụng định lí cosin trong tam giác SBE ta có: 2 2 2
SB  BE  SE 1 cos SBE    0 2.SB.BE 10  1 
 SB, MD  SB, BE   SBE   arccos    10 
2/ Cách dựng thiết diện:
Gọi O  AC  BD, F  SO  NK . Trong (SAC), H  SC  AF . Thiết diện là ANHK SD BD 2 2 1 a 3
Ta có: AN  AK   a 2, NK 
 a 2  ANK đều 0  S  a 2 sin 60  ANK   2 2 2 2 2 2 1 a 3 3a 3 S  S   S  HNK 2 ANK 4 TD 4
 Câu 76: (HSG THPT HẬU LỘC 1 NĂM 2017-2018) Cho hình chóp tứ giác S.ABCD có đáy
là hình vuông tâm O cạnh bằng   0
a, ASB  ASD  90 . Gọi  P là mặt phẳng đi qua AB và vuông
góc với mặt phẳng  ABCD , kéo dài SD cắt mặt phẳng  P tại E. a. Chứng minh  0 AEB  90
b. Biết SA  S .
O Tính độ dài đoạn thẳng CE.  Lời giải E S A D O B C a.
GV: Trần Đình Cư –Zalo: 0834332133 66
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com SA  SB + Vì 
 SA  SBD  BE  SA   1 SA  SD 
+ Mặt khác P   ABCD theo giao tuyến AB
mà AD  AB  AD   P  BE  AD 2 + Từ  
1 và 2 suy ra BE  SAD  BE  AE hay  0 AEB  90 b. a 2
+ Ta có AC  a 2  AO  2 AO a
+ Vì SA  SO  SA 
O vuông cân tại S nên SA   2 2 AE SA 1 2 a + Dễ thấy 2 2 S
 AE  ADE     2 AE  AE  a 2  AE  DE AD 2 3 2 2a + Khi đó 2 2 2
BE  AB  AE  3 2 2a a 15 + Vậy 2 2 2 CE  BC  BE  a   3 3
 Câu 77: (HSG THPT HẬU LỘC 3 NĂM 2017-2018)
Cho tứ diện ABCD có AB = a, CD = b. Gọi I, J lần lượt là trung điểm AB và C D. Giả sử AB  CD 1
, M nằm trên đoạn IJ sao cho IM  IJ . Tính diện tích thiết diện tạo bởi mặt phẳng () qua 3
M song song với AB, CD và tứ diện ABC D .  Lời giải A G P I F N M L B H D Q E J C
Xác định thiết diện của (ABCD)
GV: Trần Đình Cư –Zalo: 0834332133 67
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com ( ) // AB với mặt phẳng ( 
): Ta có: AB  ( ABC)  
L  ( )  ( ABC)  EF // AB (1) ( ) // AB 
Tương tự: AB  (ABD) 
N  ( )  ( ABD)  HG // AB (2)
Từ (1) và (2), suy ra EF // HG // AB (3) ( ) // CD 
Ta có: CD  (ACD) 
P  ( )  ( ACD)  FG // CD (4) ( ) // CD 
Tương tự: CD  (BCD)   EH // CD (5) 
Q  ( )  (BCD)
Từ (4) và (5), suy ra FG // EH // CD (6)
Từ (3) và (6), suy ra EFGH là hình bình hành Mà AB  CD (*)
Từ (3), (6) và (*), suy ra EFGH là hình chữ nhật
Tính diện tích thiết diện của huình chữ nhật biết IM = 1 IJ: 3 Ta có: S  EF FG .  PQ LN . EFGH Tính LN: LN IN
Xét tam giác ICD: Ta có: LN // CD   (7) CD ID IN IM
Xét tam giác IJD: Ta có: MN // JD   (8) ID IJ LN IM 1 CD b Từ (7) và (8), suy ra    LN   CD IJ 3 3 3 PQ JM 2 2 2 2ab Tương tự:    PQ  .AB  a . Vậy: S  AB JI 3 3 3 EFGH 9
 Câu 78: (HSG THPT HẬU LỘC 3 NĂM 2017-2018) Cho tứ diện ABCD có AB = a, CD =
b. Gọi I, J lần lượt là trung điểm AB và CD. Giả sử AB  CD, M nằm trên đoạn IJ sao cho 1 IM 
IJ . Tính diện tích thiết diện tạo bởi mặt phẳng () qua M song song với AB, CD và tứ diện 3 ABC . D
GV: Trần Đình Cư –Zalo: 0834332133 68
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com  Lời giải A G P I F N M L B H D Q E J C
Xác định thiết diện của (ABCD) ( ) // AB với mặt phẳng ( 
): Ta có: AB  ( ABC)  
L  ( )  ( ABC)  EF // AB (1) ( ) // AB 
Tương tự: AB  ( ABD)  
N  ( )  ( ABD)  HG // AB (2)
Từ (1) và (2), suy ra EF // HG // AB (3) ( ) // CD 
Ta có: CD  (ACD)  
P  ( )  ( ACD)  FG // CD (4) ( ) // CD 
Tương tự: CD  (BCD)   EH // CD (5) 
Q  ( )  (BCD)
Từ (4) và (5), suy ra FG // EH // CD (6)
Từ (3) và (6), suy ra EFGH là hình bình hành Mà AB  CD (*)
Từ (3), (6) và (*), suy ra EFGH là hình chữ nhật
Tính diện tích thiết diện của huình chữ nhật biết IM = 1 IJ: 3
GV: Trần Đình Cư –Zalo: 0834332133 69
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com Ta có: S  EF FG .  PQ LN . EFGH Tính LN: LN IN
Xét tam giác ICD: Ta có: LN // CD   (7) CD ID IN IM
Xét tam giác IJD: Ta có: MN // JD   (8) ID IJ LN IM 1 CD b Từ (7) và (8), suy ra    LN   CD IJ 3 3 3 PQ JM 2 2 2 2ab Tương tự:    PQ  .AB  a . Vậy: S  AB JI 3 3 3 EFGH 9
 Câu 79: (HSG THPT BA ĐÌNH NĂM 2017-2018) Cho tứ diện đều SABC có độ dài cạnh
bằng 1, gọi I, K là trung điểm của các cạnh AC và S .
B Trên các đường thẳng AS và CK lấy các
điểm P, Q sao cho PQ song song với BI. Tính độ dài đoạn thẳng PQ.  Lời giải
Kẻ KJ // BI (J thuộc SI), P là giao của CJ với SA, kẻ PQ // JK (Q thuộc CK) thì đươch PQ
thỏa mãn P thuộc SA, Q thuộc CK và PQ//BI. 3
Ta có ABC đều cạnh 1 nên BI  2 1 3
Qua cách dựng PQ thì J là trung điểm của SI nên KJ  BI  2 4 PS CA JI PS PS 1
Xét SAI với 3 điểm P, J, C thẳng hàng ta có 1  . .  .2.1   PA CI JS PA PA 2 JP IC SA JP JP 1
Xét APC với 3 điểm thẳng hàng S, J, I ta có 1  . .  .1.3   JC IA SP JC JC 3 CJ 3 Suy ra  CP 4 JK 3 4 4 3 3 Suy ra   PQ  JK  .  PQ 4 3 3 4 3
GV: Trần Đình Cư –Zalo: 0834332133 70
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com 3 Vậy PQ  3
 Câu 80: (HSG THPT BA ĐÌNH NĂM 2017-2018) Cho hình chóp S.ABCD có đáy ABCD là
hình thoi tâm O với OA = 2OB = 2a và SO vuông góc với đáy (ABCD). Mặt phẳng () qua A
vuông góc với SC cắt SB, SC, SD lần lượt tại B’, C’, D’. Tính côsin góc giữa (SAB) với () biết
B 'C ' D ' đều.  Lời giải
( )  ( ABCD)  EF trong đó E đối xứng với C qua B và F đối xứng với C qua D, E đối xứng với
F qua A và EF  2BD  4a . Tam giác B’C’D’ đều nên tam giác EFC’ đều. 2 2
CC '  x  C ' F 
20a  x  EF  4a  x  2a ; 2 2 2 2 AC ' 
AC  CC '  16a  4a  2a 3 2 2 2 2 2 2
SC  SA  AC '  SC '  AC '  (SC  CC ') 2 2 2 2 2
 SC  12a  (SC  2a)  16a  4 .
a SC  SC  SC  4a  SO  2a 3
Hạ C I  AB  AB  SC I   SAB AB C    ' ' ' ( ' ) ( ); ( ' ')  SIC ' ; 2 4a 3 2a AO ' AO '  AC '  ;  O ' B '   cot IAC '   2 3 3 3 3 O ' B '  1  2a 39  sin IAC ' 
 IC '  AC '.sin IAC '  13 13 SC Từ đó ta có  ' 13 3
tan   tan SIC '    cos  . IC ' 39 4
 Câu 81: (HSG THPT SẦM SƠN NĂM 2017-2018) Cho OABC là tứ diện có OA,OB,OC đôi
một vuông góc. H là trực tâm của tam giác AB C . Gọi  ,  , lần lượt là góc tạo bởi OH với OA,OB,
O C . Chứng minh rằng 2 2 2
cos   cos   cos   1  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 71
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com C Z c H γ b B O a K A
Chứng minh OH vuông góc với mặt phẳng (ABC) 1 1 1 1 Chứng minh    2 2 2 2 OH OA OB OC 2 OH OH 2 2 OH OH Ta có 2 cos    cos   . Tương tự: 2 2 cos   ; cos   . Nên 2 OC OC 2 2 OA OB 2 2 2 OH OH OH  1 1 1 2 2 2 2 
cos   cos   cos      OH    1 2 2 2  2 2 2  OA OB OC  OA OB OC 
 Câu 82: (HSG THPT SẦM SƠN NĂM 2017-2018) Cho hình chóp S.ABC có SA vuông góc
với mặt phẳng đáy. Gọi M là trung điểm của BC và H là trung điểm của AM. Biết
HB  HC  a , 0 0
HBC  30 ; góc giữa mặt phẳng  SHC  và mặt phẳng  HBC  bằng 60 . Tính
SA và cosin của góc giữa đường thẳng BC và mặt phẳng SHC .  Lời giải S B C I A H B' C 60° M K 30° B
Gọi K là hình chiếu vuông góc của A trên H C. a a 3 Ta có 0 0
AH  HM  HB sin 30 
 AK  AH.sin 60  2 4
GV: Trần Đình Cư –Zalo: 0834332133 72
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com a 0 0 3
Góc giữa (SHC) và (ABC) là SKA  60  SA  AK.tan 60  4
* Gọi B’ là hình chiếu của B trên (SHC), suy ra góc giữa BC và (SHC) là ' B
 CB . Gọi I là hình
chiếu của A trên SK  AI  (SHC) .
*Ta có BB '  d (B, (SHC))  2d(M , (SHC))  2d ( ,
A (SHC))  2AI . 2 AK.AS 3 3a 2 3a 3a
Trong tam giác vuông SAK, ta có AI   .   BB '  . 2 2 16 AK  AS a 3 8 4 ' BB a a ' 3 3 3 Do đó sin BCB     . BC 2 . 4 BM . 8 . HB cos 300 4 3 13 Vậy cos ' BCB  1   16 4
 Câu 83: (HSG THPT THƯỜNG XUÂN) Cho tứ diện ABCD, hai mặt ABC và ABD là hai
tam giác đều cạnh 2a .
a. Chứng minh rằng AB và CD vuông góc với nhau. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AC, BC, BD, D .
A Chứng minh rằng tứ giác MNPQ là hình chữ nhật.
b. Tính góc giữa hai đường thẳng BC và AD, biết MP  a 3
c. Gọi BH là độ dài đường cao của tam giác BCD, H nằm trên CD sao cho CD, BH, BD theo thứ
tự lập thành một cấp số nhân. Tìm công bội của cấp số nhân đó và tính độ dài đoạn C . D  Lời giải a. C N M H B P I 60o 60o D Q A  
       Ta có: .
CD AB  AD  AC AB  .
AD AB  AC.AB         .  . cos 60o  . cos 60o CD AB AD AB AC AB  0 Vậy CD  AB AB
* Ta có: MN // PQ // AB và MN  PQ  2
Nên tứ giác MNPQ là hình bình hành
Vì MN // AB và NP // CD mà AB  CD nên hình bình hành MNPQ là hình chữ nhật.
b. Gọi I là trung điểm của A . B
GV: Trần Đình Cư –Zalo: 0834332133 73
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com IP / / AD  Ta có:
  (CB, AD)  (IM , IP) . IM / / BC 
Xét tam giác IMP có: IM  IP  , a MP  a 3 . 2 2 2 2 2
IM  IP  MP 2a  3a 1 Do đó,   0 cos MIP      MIP  120 2 2.IM .IP 2a 2 Vậy: 0 0 0
(CB, AD)  180 120  60
c. Theo bài ra: CD, BH, BD theo thứ tự lập thành cấp số nhân.
Gọi q là công bội của cấp số nhân trên, q >0. Khi đó ta có: 2 BH  CD. ; q D B  CD.q D C HC  D H 
(Vì tam giác BCD cân tại B). 2 BD 2a 4a
Trong tam giác BHD vuông tại H nên ta có: Khi đó: CD    2 q 1  2 1  2 2 2 CD CD 2 2 2 2 2 2 . 2 2 2 BD  BH  HD  BD  ( )  BH  (CD .q )   (CD.q) 2 4  1 2 2 q  2  CD 2 4 2 2 4 2 2  CD .q 
 CD .q  4q  4q 1  0   4  1 2 2 q   2 1  2 1  2 Do 2 q   q  2 2 1  2 Vậy q  . 2 BD 2a 4a Khi đó: CD    . 2 q 1 2 1 2 2
 Câu 84: (HSG 11 THPT THIỆU HÓA THANH HÓA) Cho hình hộp ABCD. ’ A ’ B C’D '.Trên
cạnh AB lấy điểm M khác A và .
B Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (ACD’).
a) Trình bày cách dựng thiết diện của hình hộp và mặt phẳng (P).
b) Xác định vị trí của M để thiết diện nói trên có diện tích lớn nhất.
c) Gọi C1 là trung điểm của CC’. Mặt phẳng (Q) đi qua AC1 cắt C’B, C’D lần lượt tại B1, D1 khác 4 C ' B C ' D 3 C’. Chứng minh rằng: 1 1    3 C ' B C ' D 2  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 74
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com I D' Q C' R F A' P D B' C S K O A N E J M B
a) Trong mp(ABCD), qua M vẽ đường thẳng song song với AC cắt DB, BC lần lượt tại E, N.
Trong mp(BDD’B’), qua E vẽ đường thẳng song song với D’O (O=ACBD) cắt B’D’ tại F.
Trong mp(A’B’C’D’), qua F vẽ đường thẳng song song với AC cắt A’D’, D’C’ lần lượt tại R, Q.
Trong mp(AA’D’D), qua R vẽ đường thẳng song song với AD’ cắt AA’ tại S.
Trong mp(CC’D’D), qua Q vẽ đường thẳng song song với CD’ cắt CC’ tại P.
Thiết diện là lục giác MNPQRS
b)  Do các mặt đối diên của hình hộp song song nên các cạnh đối của lục giác thiết diên MNPQRS
song song và 3 cặp cạnh đó lần lượt song song với các cạnh tam giác ACD’.
 Các tam giác JKI, ACD’, RQI, JMS, NKP đồng dạng MJ MA NC NK PC PK QD ' QI          MJ=NK và PK=QI MN MB NB NM PC ' PQ QC ' QP
 Các tam giác RQI, JMS, NKP bằng nhau (gọi diện tích của chúng là S1 và gọi diện tích các tam
giác JKI, ACD’ lần lượt là S2, S) AM Đặt
 k; ta có điều kiện 0  k  1 và có: AB 2 2 2 1 S  JM   AM   AM  2        
  k  S1 = k2S S  AC   DC   AB  2 2 2 S  JK 
 JM  MK   JM MK             k  2 2 1  S2 =( k2 + 2k +1)S S  AC   AC   AC AC 
 Diện tích thiết diện: S  S  3S td 2 1 2 1  3 1    3S 1 2 S
 2S (k  k  )  2S   k     
(dấu bằng xảy ra  k  ) td 2 4   2  2   2 1
S lớn nhất  k 
 M là trung điểm của AB 2 c.
GV: Trần Đình Cư –Zalo: 0834332133 75
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com D' C' B' C1 D1 G B1 D H C O A B L
)Lấy G= AC1B1D1 và O = ACBD,
ta có: C’, O, G là các điểm chung của 2 mặt phẳng (C’AC) và (C’BD)  C’, O, G thẳng hàng.
Và G là trọng tâm của tam giác C’AC C 'G 2   C 'O 3 C ' D C ' B
Vẽ BH //G B1 và DL // D1G H , L C 'O OH  OL . Đặt x  ; y  C ' D C ' B 1 1 C ' D C ' B C ' L C ' H 2C 'O 3  x  y       2
 3  x, y [1; 2] (*) C ' D C ' B C 'G C 'G C 'G 2 1 1 2 1 1 3  2  4  Suy ra:    3  (1)   x y xy x  y 3  
Từ (*): 1  x  2  2
x  3x  2  0  x(3  x)  2  x  y  2 3 3 x  y 3 1 1 3       
(2); Từ (1) và (2) đpcm xy 2 xy 2 x y 2
 Câu 85: (TRƯỜNG THPT TĨNH GIA 1-2017-2018) Cho hình chóp S.ABCD , có đáy ABCD
là hình thang cân ( AD // BC) và BC  2a, AB  AD  DC  a (a  )
0 , AC cắt BD tại điểm O . Cạnh
bên SD  2a . Gọi mặt phẳng ( ) là mặt phẳng đi qua điểm M thuộc đoạn OD ( M khác O, D )
và song song với hai đường thẳng SD, AC . Mặt phẳng ( ) cắt AD, SA lần lượt tại N và I .
a. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng ( ).
b. Đặt MD  x (x  0) . Tìm x để diện tích thiết diện lớn nhất, biết MN vuông góc với NI .  Lời giải
a) Qua M kẻ đường thẳng song song với AC cắt AD, DC lần lượt tại N,P.
Qua M, N, P kẻ các đường thẳng song song với SD cắt SB, SA, SC lần lượt tại K, J, Q. Thiết diện là ngũ giác NPQKJ.
b) Ta có: NJ, MK, PQ cùng vuông góc với NP.
GV: Trần Đình Cư –Zalo: 0834332133 76
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com 1 1
dt(NPQKJ)=dt(NMKJ)+dt(MPQK)= (NJ  MK )MN  (MK  PQ)MP 2 2 1 
(NJ  MK ).NP (do NJ=PQ). 2 NP MD AC.MD . x a 3 Ta có:   NP    3x AC OD OD a 3  a  2 . a  x NJ AN OM . SD OM    3 NJ      
 2(a  x 3) SD AD OD OD a 3 2 . a a 3 .  x KM BM SD BM  2   KM    (a 3  x) SD BD BD a 3 3 1  2  Suy ra: dt(NPQKJ)= 2(a  x 3) 
(a 3  x) 3x  2(3a  2 3x)x   2  3  2 1 1 3 3 2 
(3a  2 3x)2 3x 
(3a  2 3x)  2 3x  a 3 4 3   4 3 3 3
Diện tích NPQKJ lớn nhất bằng 2 a khi x  a 4 4
 Câu 86: (HSG THPT SẦM SƠN NĂM HỌC 2017-2018) Cho tứ diện đều ABCD có độ dài
cạnh bằng 1. Gọi M, N lần lượt là hai điểm thuộc các cạnh AB, AC sao cho mặt phẳng (DMN)
vuông góc với mặt phẳng (ABC). Đặt AM  x, AN  y . Chứng minh rằng x  y  3xy .Tìm x, y
để diện tích toàn phần của tứ diện DAMN nhỏ nhất.  Lời giải
Kẻ DH  MN, do (DMN)  (ABC) suy ra DH  (ABC). 1 3 Ta có: SAMN = .AM.AN.sin600 = xy ; SAMN = SAMH + SANH 2 4 1 1 1 3 = .AM.AH.sin300+ .AN.AH.sin300 = . (x+y). 2 2 4 3
Mà ABCD là tứ diện đều, nên suy ra H là tâm của tam giác đều ABC 3 1 3 Suy ra xy = .
(x+y)  x+y= 3xy (0  x,y  1 ). 4 4 3
Diện tích toàn phần của tứ diện DAMN: S = SAMD + SAND + SDMN + SAMN 1 1 =
A D.AM.sin600+ A D . AN.sin600 2 2
GV: Trần Đình Cư –Zalo: 0834332133 77
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com 1 1 + DH.MN + AM.AN.sin600 2 2 6 = 3 xy + xy 3 3 ( xy  ) 1 . 6 2 4
Từ 3xy  x  y  2 xy  xy   xy  . 3 9 3(4  2) 2 Suy ra min S 
, khi x  y  . 9 3 D C B H N M A
 Câu 87: (HSG THPT SẦM SƠN NĂM HỌC 2017-2018) Cho hình chóp đều S.ABC đỉnh S,
chiều cao h, đáy ABC là tam giác đều cạnh a. Qua AB dựng mp (P) vuông góc với SC.
1. Xác định thiết diện của hình chóp khi cắt bởi (P).
2. Tính diện tích thiết diện theo a và h.  Lời giải S H A C O M B
GV: Trần Đình Cư –Zalo: 0834332133 78
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
Gọi O là trọng tâm tam giác ABC ta có SO  ( ABC) khi đó SO  AB , gọi M là trung điểm AB
do tam giác ABC đều nên CM  AB vậy AB  (SMC) .
Trong mp(SMC) kẻ MH  SC ta có mặt phẳng (AHB)  S C.
Thiết diện là tam giác AH . B 1 Ta có: S  MH.AB . A  HB 2 a 3 a 3
Theo giả thiết AB = a. ta có MC  , OC  , 2 3 2 a SO = h, 2 2 2
SC  SO  OC  h  3 a 3 h. 3ah Ta có: MH.SC = SO.MC 2  MH   2 2 2 a 2 3h  a 2 h  3 2 1 3a h S 
MH .AB  . AH  B 2 2 2 4 3h  a
 Câu 88: (HSG THPT TRIỆU SƠN 5 NĂM 2017-2018) Cho hình chóp SABC có ABC là tam
giác đều. Gọi H,O lần lượt là trực tâm của các tam giác ABC và SBC.OH cắt SA tại N.
1. Giả sử SA(ABC). Chứng minh OH(SBC) và tứ diện BCSN có các cặp cạnh đối diện vuông góc với nhau.
2. Giả sử SH(ABC). Gọi  là góc giữa mặt bên và mặt đáy;  là góc giữa hai mặt bên kề β
nhau.Chứng minh rằng 2cos = 3sinα . 2  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 79
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com S H C A O I B N Chứng minh OH(SBC)
+ AO cắt BC tại I. BCAO(  ABC đều) BCSA
nên BC( SAI) BCAI nên H nằm trên
đường AI. OH nằm trong (SAI)BCOH(1)
+ Có BOAC; BOSABO(SAC) BOSC
BHSC SC(BOH) ACOH (2)
Từ (1) và (2) ta được OH(SBC)
+) Chứng minh BCSN có các cặp cạnh đối vuông góc với nhau SA(ABC) SNBC
SC(BOH) SCBN( vì N nằm trên OH)
Chứng minh tương tự ta có
SB(COH) SBCN( N nằm trên OH)
 Câu 89: (HSG THPT VĨNH LỘC NĂM 2017-2018) Cho điểm O cố định và một số thực a không đổi. Một hình chóp S.ABC thay đổi thỏa mãn  0  0  0
OA  OB  OC  a, SA  O ,
A SB  OB, SC  OC, ASB  90 , BSC  60 , CSA  120 . Chứng minh rằng: a. A
 BC là tam giác vuông.
b. Khoảng cách SO không thay đổi.
GV: Trần Đình Cư –Zalo: 0834332133 80
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com  Lời giải S M A C B a a a O a. + Đặt SO  . x
+ Vì các tam giác SAO, SBO, SCO lần lượt vuông tại , A B, C nên 2 2
SA  SB  SC  x  a
+ Tam giác SAB vuông tại S nên 2 2 2
AB  SA  SB   2 2 2 x  a    1
+ Xét tam giác SBC ta có  0
BSC  60  SBC  đều nên 2 2 2
BC  x  a 2
+ Xét tam giác SCA ta có 2 2 2 0
CA  SC  SA  SC SA   2 2 2 . . cos120 3 x  a  3 + So sánh  
1 , 2 và 3 ta thấy 2 2 2
CA  AB  BC  ABC vuông tại . B b.
+ Gọi M là trung điểm của AC
+ Vì ABC là tam giác vuông tại B nên MA  MB  MC 4
+ Mặt khác SA  SB  SC
5 và OA  OB  OC 6
+ Từ 4 và 5 suy ra M là hình chiếu của S lên  ABC
+ Từ 4 và 6 suy ra M là hình chiếu của O lên  ABC
+ Từ đây suy ra SO   ABC tại M . Do đó AM là đường cao của tam giác vuông SAO 1 1 1 4 1 1 4 1 1         2 2 2 2 2 2 AM SA OA CA SA OA 3 2 2 x  a   2 2 x  a  2 a 2 1 1 4a 2a    3 x  a  a  x   x  2 2 2  2 2  2 2 3 x  a  a 3 3 2a + Vậy SO   đpcm. 3
 Câu 90: (HSG SGD&ĐT HÀ TĨNH NĂM 2006-2007) Hình chóp S.ABC có đáy ABC là tam
giác vuông tại A, ACB   và cạnh BC = a. Mặt bên SBC vuông góc với đáy, hai mặt bên còn
lại đều tạo với đáy góc  . Các góc SBC và SCB đều nhọn. a) Cho 0   45 và 0
  60 , hãy xác định tâm và tính bán kính mặt cầu nội tiếp hình chóp S.ABC theo a.
GV: Trần Đình Cư –Zalo: 0834332133 81
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
b) Khi a và  không đổi, tìm giá trị của  để đường cao SH của hình chóp có độ dài lớn nhất.  Lời giải
Do mp(SBC) vuông góc với đáy ABC và các góc SBC, SCB đều nhọn nên H thuộc cạnh BC của tam giác ABC.
Vẽ HM  AC, HN  AB suy ra AC  SM , AB  SN nên SMH  SNH   do đó
2 tam giác vuông: SMH,SNH bằng nhau, suy ra MH=NH, từ đó ta có tứ giác AMHN là hình vuông.  a
a) Khi   45 thì tam giác ABC vuông cân tại A nên AH  BC, AH  . 2
Vẽ tia phân giác của góc SMH cắt SH tại K thì mp(KAC) và mp(KAB) thứ tự là mặt phẳng phân
giác của các góc nhị diện cạnh AC,AB của hình chóp S.AB C.Dễ thấy giao tuyến của hai mặt
phẳng này là đường thẳng AK.
Vẽ tia phân giác của góc SHA cắt AK tại I thì I cách đều 4 mặt của hình chóp S.ABC nên nó là
tâm mặt cầu nội tiếp hình chóp. a  a Dễ thấy HM  .sin 45  2 2 2  a 1 a 
Xét tam giác vuông KHM: KH  HM . tan 30  . 
(doKMH  30 ) 2 2 3 2 6
Vẽ IE  AH , IF  HK thì IE  IF  r với r là bán kính mặt cầu nội tiếp hình chóp S.AB C.
Ta có: IE.AH  IF.HK  AH .HK ( vì mỗi vế cùng bằng 2 lần diện tích AHK )
GV: Trần Đình Cư –Zalo: 0834332133 82
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com a a . AH .HK 2 2 6 a  r    AH  HK a a 2( 6 1)  2 2 6 NH x
b) Đặt HM  HN  x . Xét tam giác vuông NBH: BH   BH  (1) cos cos HM x
Xét tam giác vuông MCH: HC   HC  (2) sin  sin  x(sin   cos ) a .cos.sin 
Từ (1) và (2) ta có: a   x  cos.sin sin   cos Xét tam giác vuông SHM: a .sin .cos SH  . x tan   . tan  sin   cos sin .cos
Do a,  không đổi nên SH lớn nhất khi và chỉ khi lớn nhất. sin   cos
Áp dụng bất đẳng thức Cô si cho 2 số dương ta được: sin   cos 2 ( ) sin.cos 1 2 2   (sin  cos )  . sin   cos sin   cos 4 4 sincos
Dấu bằng xảy ra khi và chỉ khi sin cos  2 
Gía trị thỏa mãn là   45 
Vậy đường cao SH của hình chóp S.ABC lớn nhất khi và chỉ khi   45 .
 Câu 91: (HSG ĐỀ 142) Cho hình chóp S.ABC với đáy ABC là tam giác nhọn, cạnh SA vuông
góc với đáy. Gọi I, K lần lượt là chân đường cao kẻ từ B của tam giác BSC, BAⒸ. Đường thẳng IK
cắt đường thẳng SA tại P.
a) Chứng minh tứ diện SPBC có các cặp cạnh đối vuông góc.
b) Tam giác ABC cố định có BC = a, ABC  ,
 ACB   , điểm S di động. Tìm độ dài đoạn
thẳng SA trong trường hợp diện tích tam giác SPC đạt giá trị nhỏ nhất.  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 83
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com BK  SA
a)  SP  BC (do SA  ( ABC) ) 
 BK  (SAC)  PC  BK , BK  SC BK  AC  SC  BI  
 SC  (BIK )  SC  BP, SC  PI SC  BK  CK   SP  Trong (SPC)
 K là trực tâm tam giác SPC  PC  SK PK  SC  PC  SK  
 PC  (SBK )  PC  SB PC  BK  SP  BC 
 Tứ diện SPBC có SC  BP PC  SB 
 Tứ diện SPBC có các cặp cạnh đối vuông góc với nhau SA AK b) Ta có S  AK  C  AP (g.g)    S .
A AP  AK.AC không đổi AC AP 1 1  S  AC.SP 
AC.(SA  AP)  AC. .
SA AP  AC. AC.AK SPC 2 2
Đẳng thức xảy ra  SA  AP  AK.AC CH  SA 
BK.cot(180o     ).
sin(180o     ) a  o .sin  SA  .
a sin  .cot(180     ).
sin(180o     )
cos(180o     ) 2
 SA  a .sin .sin . 2 sin (   )
GV: Trần Đình Cư –Zalo: 0834332133 84
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com 
 .sin(  ). sin .sin .cos(180o SA a         )
( CH  AB, H  AB ) Vậy khi S đạt giá nhỏ nhất thì  .sin(  ). sin .sin .cos(180o SA a         ) SPC .
 Câu 92: (HSG ĐỀ 143) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và M là
trung điểm của S C. Một mặt phẳng (P) chứa AM và lần lượt cắt các cạnh SB, SD tại các điểm B',
D' khác S. Chứng minh rằng 4 SB ' SD ' 3    . 3 SB SD 2  Lời giải
Gọi O là giao điểm của BD và AC, suy ra SO  SBD  SAC .
Gọi H là giao điểm của B ' D ' và AM . Ta có: SBD 
SAC  SO B  'D '   SBD   H  SO A  M   SAC B
 'D ' AM  H 
Áp dụng định lý Menelaus cho tam giác SOC ta có: SM AC OH OH OH 1 . .  1  1.2.  1   MC AO HS HS HS 2
Mà H thuộc trung tuyến AO suy ra H là trọng tâm tam giác SBD
Xét mặt phẳng SBD:
+Lấy E, F  SO sao cho BF  DE  B ' D ' . Suy ra ta có: SB ' SD ' SH SH  1 1    4SH 4SH 4     SH       SB SD SF SE
SF SE  SF  SE 2SO 3
GV: Trần Đình Cư –Zalo: 0834332133 85
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com SB ' SD ' 4 Vậy   SB SD 3
+Vẽ trung tuyến DM của tam giác SBD
Do vai trò của B và D là bình đẳng nhau nên vai trò B’ và D’ cũng bình đẳng nhau
Giả sử HD '  HB ' ( trường hợp ngược lại chứng minh tương tự) D ' K HK Theo định lý Talet ta có 
 1  D ' K  B ' M B ' M HM
Lấy K thuộc DM sao cho D ' K  SB .Ta có SB ' SD ' SM MB '
SD DD ' 3 DD ' MB '                     SB SD  SB SB    SD SD  2  SD SB  DD ' D ' K 2D ' K MB ' DD ' MB ' Mặt khác lại có       0 SD SM SB SB SD SB SB ' SD ' 3 DD ' MB '   3 Suy ra        SB SD 2  SD SB  2 4 SB ' SD ' 3 Vậy    (dpcm) 3 SB SD 2
 Câu 93: (HSG ĐỀ 145) Cho hình chóp có , diện tích tam
giác SBC là .Gọi M là điểm di động trên SB,N là trung điểm của BC.Biết AN vuông góc với mặt phẳng
. Tìm giá trị nhỏ nhất của diện tích tam giác AMN theo a và .  Lời giải Cho hình chóp có
, diện tích tam giác SBC là .
Gọi M là điểm di động trên SB,N là trung điểm của BC. Biết AN vuông góc với mặt phẳng .
Tìm giá trị nhỏ nhất của diện tích tam giác AMN theo a và .  Ta có 2 2 2 2
BN  CN  AB  AN  SA  AN  SN. 2S 2 4 4S  a
Suy ra SBC vuông tại S, do đó ta có o SC  và 2 2 o
BC  SC  SB  . a 2 a
GV: Trần Đình Cư –Zalo: 0834332133 86
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com 4 2 1 a  4S
 Xét CAN vuông tại N ta có 2 2 2 2 o
AN  AC CN  a  BC  . 2 2 2a 4 2 1 1 1 1 1 2S a  4S  Ta có S
 AN.MN  AN.d(N,SB)  AN. SC  . o . o . AMN 2 2 2 2 2 4 a 2a 4 2 S a  4S
Vậy giá trị nhỏ nhất của diện tích tam giác AMN là o . o . 2 2a 2a
 Câu 94: (HSG ĐỀ 147) Cho tam giác nhọn ABC cố định. Trên tia Ax  (ABC) lấy điểm S khác .
A Kẻ các đường cao BH của các tam giác BA C.Gọi (P) là mặt phẳng qua C và vuông góc
với SB, giả sử (P) cắt tia đối của tia AS tại M. Đường thẳng MH cắt SC tại N.
a) Chứng minh tứ diện SMBC có các cặp cạnh đối vuông góc với nhau và SC  (MBN)
b)Biết cạnh BC = a, A
 BC  ; A
 CB   . Tìm giá trị nhỏ nhất của diện tích tam giác SPC
theo a ,  khi S di động trên tia Ax (S khác A).  Lời giải S N A B H M C
a) Ta có BC  SM (giả thiết) (1)
Mà MC  SB (2)
Từ (1) và (2) suy ra S.MBC là tứ diện có 2 cặp cạnh đối vuông góc nên cặp thứ 3 cũng vuông góc
Ta có BH  (SAC) nên SC  HB
Theo chứng minh trên thì SC  BM , do đó ta có SC  (MBN)
b) Từ câu a ta có SC  MN , do đó A  HM , A
 SC đồng dạng (g.g) AH AM do đó 
 SAAM  AH.AC SA AC 1 1 S  SM .AC 
(SA  AM ) AC  . SA AM .AC 
AH.AC .AC SM  C 2 2 Có “ =” khi SA = AM
Theo định lý hàm số sin ta có AC a AB sin  sin     AC  a ; AB  a sin sin(   ) sin  sin(   ) sin(   ) AH  AB o
c s(   )  a sin  cot(   )
GV: Trần Đình Cư –Zalo: 0834332133 87
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com 2 a sin S 
AH.AC.AC  sin sin  os c (   ) SMC  2 sin (   ) 1 a Có “=” khi SA  AH.AC 
s insin cos(   ) 2 2 sin(   )
 Câu 95: (HSG HUẾ 2000-2001) Cho tứ diện ABCD có hai cạnh đối bằng ,
b c và các cạnh còn lại bằng a.
a/ Tìm giá trị nhỏ nhất của tổng các khoảng cách từ một điểm tùy ý trong không gian đến các đỉnh của tứ diện.
b/ Giả sử tứ diện ABCD thay đổi vị trí trong không gian nhưng có ba đỉnh ,
A B, C lần lượt ở
trên mặt cầu cố định và đồng tâm. Chứng minh rằng đỉnh D luôn ở trong một hình cầu cố định khi độ dài a, ,
b c thay đổi thỏa các giả đã cho.  Lời giải D D’ I A’ K0 C A J B
a) Ta có thể giả sử AD  ,
b BC  c và các cạnh còn lại bằng a . Gọi I, J lần lượt là trung điểm của các cạnh A , D B .
C Ta dễ dàng suy ra IJ vuông góc với AD và BC và IJ chính là trục đối xứng của tứ diện.
Lấy M tùy ý trong không gian, M’ là điểm đối xứng của M qua IJ suy ra trung điểm K của
MM’ chính là hình chiếu của M trên đường thẳng IJ và ta có:
2MA  MB  MC  MD  MA  MB  MC  MD  M’A  M’B  M’C  M’D
 MA  M’ 
A  MB  M’B  MC  M’C   MD  M’D
 2KA  2KB  2KC  2KD   1 .
Do tính chất: trung tuyến của một tam giác thì bé hơn nửa tổng của hai cạnh cùng xuất phát từ một đỉnh của nó).
Do đó: MA  MB  MC  MD  KA  KB  KC  KD. Bài toán trở thành tìm điểm K trên
IJ sao cho KA  KB  KC  KD bé nhất.
GV: Trần Đình Cư –Zalo: 0834332133 88
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
Trong mặt phẳng BCI  dựng hình thang BCD’ ’
A sao cho IJ là trung điểm của hai đáy và IA  I ’,
A ID  ID’. Ta thấy rằng: với K tùy ý trên IJ thì KA  ’
KA và KD  KD’. Do đó:
KA  KB  KC  KD  ’
KA  KB  KC  ’ KD  K ’
A  KC   KB  KD ’  ’ AC  ’. BD
Vậy KA  KB  KC  KD nhỏ nhất khi K chính là giao điểm K của hai đường chéo ’ AC và 0 BD’. 2 2 2 2 c b c b Tính IJ : 2 2 2 2 2 2 2 2
IJ  DJ – ID  DC – JC – ID  a    IJ  a   . 4 4 4 4 2 2 2 2 BC A'D '   b  c      c b bc Tính BD’ : 2 2 2 2 BD '     IJ     a    a  .  2     2  4 4 2
Tổng các khoảng cách nhỏ nhất là: 2 d  2B ’
D  4a  2bc .
b) Gọi r , r , r là bán kính các mặt cầu tâm O và lần lượt đi qua các đỉnh ,
A B,C . Ta có: 1 2 3
OD  OC  DC  OC  AB  OC OA OB  r  r  r . Do đó D ở trong hình cầu cố định 1 2 3
tâm O, bán kính R  r  r  r . 1 2 3
 Câu 96: (HSG HUẾ 1998-1999) Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật có
AB  a, BC  ,
b SA  SB  SC  SD  c . K là hình chiếu vuông góc của P xuống AC.
a/ Tính độ dài đoạn vuông góc chung của SA và BK.
b/ Gọi M, N lần lượt là trung điểm của đoạn thẳng AK và CD. Chứng minh: Các đường thẳng
BM và MN vuông góc nhau.  Lời giải _ S _ D _ N _ C _ K _ M _ O _ A _ B Câu a / (2.5 điểm)
+ Theo giả thiết ta được: SO  (ABCD)  (SAC)  (ABCD)
Mà BK  SAC  và BK  AC  BK  SA
+ Gọi H là hình chiếu của K xuống SA
 HK  SA và HK  BK ( vì HK  SAC )
GV: Trần Đình Cư –Zalo: 0834332133 89
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com
 HK là đoạn vuông góc chung của SA và BK.
Suy ra được: BH  SA và HBK vuông tại K. 2 2 1 1 1 a b
+ Do ABC vuông đỉnh A nên: 2    BK  . 2 2 2 2 2 BK AB BC a  b 2 2 a c  .a SI.AB
+ SAB cân đỉnh S, BH là đường cao nên 4 HB   SA c
+ Do HBK vuông tại K nên: 2 2 2 2 2
(4c a )a a b 2 2 2
HK  HB  BK   2 2 2 4c a  b 2 2 2 4 2 2 2 2
(4c  a b )a a
(4c a b ) 2 HK   HK  2 2 2 2 2
4c (a  b ) 2c (a  b ) Câu b (2.5 điểm)   
+ 2BM  BA  BK ( vì M là trung điểm của AK )
    1    1 
+ MN  MB  BC  CN  (AB  KB)  BC  BA 2 2  1   + MN  KB  BC . 2 + Do đó:              
4BM.MN  (BA  BK).(KB  2BC )= BA.KB  2B .
A BC  BK.KB  2BK.BC          
= BA.KB  BK.KB  2BK.BC = KB.(BA  BK  2.BC )            
= KB.(BA  BC  BK  BC )= KB.(CA CK)  KB.CA  KB.CK  0
Vậy: BM  MN .
( Có thể tính và áp dụng định lý Pythagor).
 Câu 97: (HSG SỞ GD&ĐT NGHỆ AN NĂM 2017-2018) Cho hình chóp S.ABC, mặt phẳng
(P) di động luôn cắt các cạnh SA, SB,SC tại A’, B’, C’. Gọi G là trọng tâm tam giác AB C.
a) Tìm giao điểm của SG với mp(P) SA SB SC b) Biết rằng 2  
 8. Chứng minh rằng mp (P) luôn đi qua một điểm cố định. SA ' SB ' SC '  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 90
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com S A' C' G' I' B' A C G I B
a. Gọi I là giao của AG và BC nên I là trung điểm của B C. SI cắt B’C’ tại I’
Trong tam giác SAI: A’I’ cắt SG tại G’
Khi đó G’ là giao của SG và mặt phẳng (P) SB SC SI b. Ta có   2 (1) SB ' SC ' SI '
Thật vậy: từ B kẻ BM//B’C’ cắt SI tại M, từ C kẻ CN// B’C’ cắt SI tại N
Khi đó vì I là trung điểm BC nên SM+SN=2SI SB SC SM SN SM  SN 2.SI      SB ' SC ' SI ' SI ' SI ' SI ' SA SB SC SA SI  2    8  2  2  8 (*) SA ' SB ' SC ' SA ' SI '
Gọi O là trung điểm AI, A’I’ cắt SO tại O’ khi đó mặt phẳng (P) đi qua O’
Mặt khác từ (*) ta chứng minh tương tự (1) có SA SI SO   2
 4 vậy O’ là trung điểm của SO. SA ' SI ' SO '
Hay O’ là điểm cố định nên (P ) luôn đi qua điểm cố định là O’
 Câu 98: (HSG SỞ GD&ĐT NGHỆ AN NĂM 2018-2019) Cho hình chóp S.ABCD có đáy
ABCD là hình thang cân  AB / /CD nội tiếp đường tròn tâm O và   0
SBA  SCA  90 . Gọi M là
trung điểm của cạnh S . A
a) Chứng minh rằng MO   ABCD. BC
b) Gọi  là góc giữa hai đường thẳng AB và SC. Chứng minh rằng cos  . SA  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 91
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com S M I A B O D C
a.Gọi H là hình chiếu vuông góc của điểm M trên mặt phẳng  ABCD
Xét các tam giác MH ,
A MHB, MHC có    0
MHA  MHB  MHC  90 1
MH chung MA  MB  MC  SA 2 Suy ra M  HA  M  HB  M
 HC nên HA  HB  HC
Do đó H  O, vì vậy MO   ABCD.
b. Vì AB / /CD nên góc giữa hai đường thẳng AB và SC là góc giữa hai đường thẳng CD và SC, suy ra  2 
cos  cos SCD  1 sin SCD (*)
Gọi điểm I là hình chiếu vuông góc của điểm M lên mặt phẳng SCD 1
Ta có MD  MC  SA nên S
 DA vuông tại D 2
Mặt khác lại có MS  MD  MC suy ra I là tâm đường tròn ngoại tiếp SC  . D Khi đó  SD SD SD sin SCD   
(vì MID vuông tại I nên ID  MD ) 2ID 2MD SA Từ (*) suy ra  2 2 2 2 SD SA  SD AD AD BC 2
cos  1 sin SCD  1     2 2 2 SA SA SA SA SA BC cos  (đpcm) SA
 Câu 99: (HSG NAM ĐỊNH NĂM 2015-2016) Cho hình chóp S.ABCD có đáy ABCD là hình
thang vuông tại A và B; AB  BC  4 .
a Tam giác SAB đều và nằm trong mặt phẳng vuông góc với
mặt phẳng (ABCD). Gọi H là trung điểm của AB, biết khoảng cách từ C đến mặt phẳng (SHD)
bằng a 10 . Tính thể tích của khối chóp S.HBCD và cosin của góc giữa hai đường thẳng SC và H . D  Lời giải
GV: Trần Đình Cư –Zalo: 0834332133 92
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com S A D K M H E B C N
+) Tam giác SAB cân nên  SH  AB SAB)  ( ABCD)  
+) (SAB)  ( ABCD)  AB  SH  (ABCD) SH AB   
+) Kẻ CK  HD, K  HD mà SH  (ABCD)  SH  CK
Do đó CK  (SHD)  d (C,(SHD))  CK  a 10
+ Tính được CH  a 20  HK  a 10  CK . Do đó tam giác CHK vuông cân tại K Nên     
KHC  45  DHC  45  tan DHC  1
+) Tam giác ABH vuông tại B nên  tan BHC  2  
tan BHC  tan CHD +)   
tan BHD  tan(BHC  CHD)   3   
1 tan BHC.tan CHD AD Mà   BHD AHD 180   . Do đó  tan AHD  3 
 3  AD  6a AH
( AD  BC).AB Ta có 2 S   20a ABCD 2 2 2 2 S  S  S
 20a  6a  14a HBCD ABCD AHD 3 1 28a 3 Vậy V  SH .S  S.HBCD 3 HBCD 3
Tính cosin của góc giữa hai đường thắng SC và HD
Tam giác SHC vuông tại H nên SC  a 32
+) Gọi M  AC  HD; E  BC  HD
+) Khi đó AEBD là hình bình hành nên EB  AD  4a  EC  10a AD AM 6a 3 3 3 3 3a 2 +) AD//EC nên     AM  MC  AC  .a 32  EC MC 10a 5 5 8 8 2
+) Trong mặt phẳng (ABCD), kẻ CN//HD với N thuộc đường AB
Do đó góc giữa SC và HD là góc giữa CN và SC
GV: Trần Đình Cư –Zalo: 0834332133 93
 BÀI TẬP ÔN THI HSG TOÁN 11
 WEB: toanthaycu.com 3 10 4
Ta có: AH  HN  HN  a  BN  . a 5 3 3 208 4 10 Ta có: 2 2 2 2
SN  SH  HN  ; a CN  BN  BC  . a 3 3
SC  CN  SN
+) Áp dụng định lý Côsin trong tam giác SCN, ta có  2 2 2 5 cos SCN   . 2SC.CN 4 +) 
cos(SC, HD)  cos(CN , SC)  cos SCN Vậy  5
cos(SC, HD)  cos SCN  . 4
GV: Trần Đình Cư –Zalo: 0834332133 94

Bài tập nâng cao chuyên đề hình học không gian

Thông tin :

Tài liệu liên quan:

Chuyên Đề Thể Tích Khối Đa Diện Có Yếu Tố Góc Ôn Thi Tốt Nghiệp THPT Có Đáp Án Và Lời Giải

10 Đề Trắc Nghiệm Ôn Tập Chương Khối Đa Diện Hình 12 Có Đáp Án

TOP 600 bài tập chọn lọc khối tròn xoay – Lê Minh Tâm Toán 12

Phương pháp giải các bài toán HH không gian trong đề thi Quốc gia Toán 12

Các bài tập khối đa diện trong đề thi Đại học Toán 12