Bài tập nhóm ôn tập | Microeconomics | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh

https://www.facebook.com/profile.php?id=100014611920740Problem 1: a. The complete table belike: Quantity Price Total
Marginal Total cost Averange Marginal revenue revenue total cost cost 0 8.5 0 5 1 8.0 8.0 8.0 9 9 4.0 2 7.5 15.0 7.0 11.5 5.75 2.5 3 7.0 21.0 6.0 12.5 4.167 1.0 4 6.5 26.0 5.0 13.5 3.375 1.0 5 6.0 30.0 4.0 14.0 2.8 0.5 6 5.5 33.0 3.0 16.0 2.67 2.0 7 5.0 35.0 2.0 20.0 2.86 4.0 8 4.5 36.0 1.0 25.0 3.125 5.0 9 4.0 36.0 0 32.0 3.56 7.0 10 3.5 35.0 -1.0 40.0 4.0 8.0
b. Let’s take a look at the line that the quantity is 6. At this point, the marginal
revenue is still bigger than the marginal cost, but at the time the quantity is 7, this happens in reverse.
So, stop produce at the last time MR > MC is reasonable. The monopolist should produce 6 products only.
c. The quantity is 6, according to the table, the price will be $5.5
d. The profit at this price is: �㔋 = ĄĂ 2 Ąÿ = 33.0 2 16.0 = 17.0 (�㕑Āýý�㕎ÿĀ) Problem 2:
a. This firm is not a perfect competitive firm. As you can see, the demand function Ā = 100 2 ā
is a downward demand curve of a monopoly firm.
b. To maximize total revenue (TC), āĂ = 0
ĄĂ = Ā × ā = (100 2 ā)ā = 2ā2 + 100ā
→ āĂ = ĄĂ′ = 22ā + 100 = 0 → ā = 50 → ĄĂ = 2500
c. �㔋 þ�㕎�㕥 ↔ āĂ = āÿ
→ 22ā + 100 = (500 + 4ā + ā2)′ = 4 + 2ā → 4ā = 96 → ā = 24
�㔋 þ�㕎�㕥 = ĄĂ 2 Ąÿ = 24 × (100 2 24) 2 (500 + 4 × 24 + 242) = 652
d. Assume government imposes a tax of 8 $ per unit of good sold (ā = 8),
āÿā = āÿ + ā = 4 + 2ā + 8 = 2ā + 12
To maximum profit: āÿā = āĂ → 100 – 2ā = 2ā + 12 ↔ ā = ā ā = 22 (Ăÿ�㕖āĀ)
→ Ā = Āā = 100 – 22 = 78 ($)
→ �㔋ā = ĄĂ 2 Ąÿ = 644 ($)
e. When government imposes a fixed tax of 100 $ (T = $100), the quantity and the
price of the good don’t change Ā ∗ = 76$ and ā ∗ = 24 Ăÿ�㕖āĀ
The only thing that will change is the profit
The profit will decrease by a fixed tax amount (T)
�㔋′ = �㔋 ∗ 2Ą = 625 2 100 = 525( $) Problem 3: a. We have:
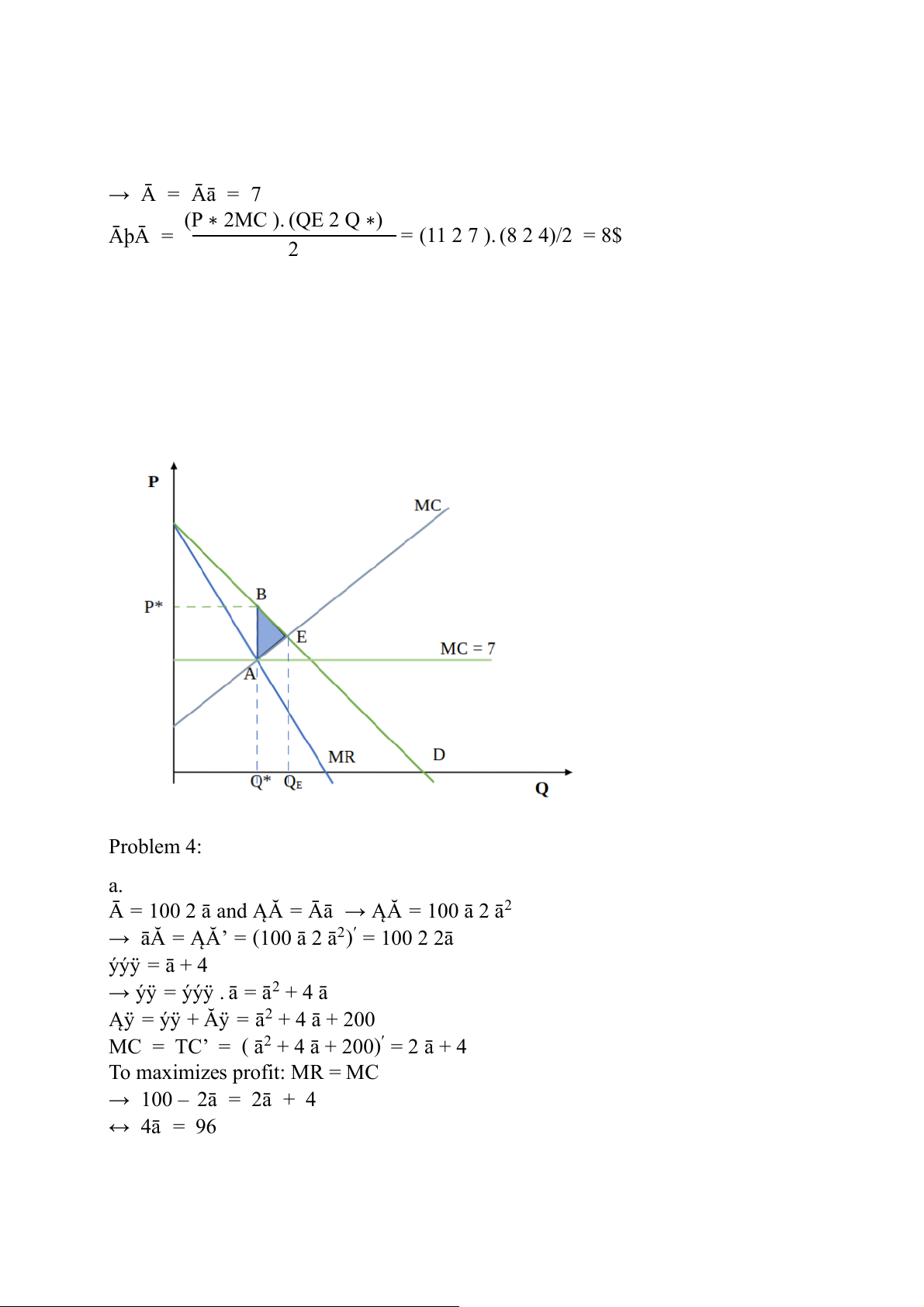
P = 15 2 Q and ĄĂ = Ā . ā → ĄĂ = 15ā 2 ā2
→ āĂ = Ą Ă′ = (15ā 2 ā2)′ = 15 2 2ā āÿ = Ąÿ′ = (7Q)′ = 7
The firm has maximum profit when MR = MC → 15 – 2ā = 7
↔ ā = ā ∗ = 4(Ăÿ�㕖āĀ) → Ā = Ā ∗ = 11($) → Ā = P 2 MC 11 2 7 P = = 0,36 11
b. In perfect competitive market, to have optimal quantity for society: MC = P → 15 – ā = 7
↔ ā = āā = 8(Ăÿ�㕖āĀ) → Ā = Āā = 7 (P ∗ 2MC ). (QE 2 Q ∗) ĀþĀ = = (11 2 7 ). (8 2 4)/2 = 8$ 2 Problem 4: a.
Ā = 100 2 ā and ĄĂ = Āā → ĄĂ = 100 ā 2 ā2
→ āĂ = ĄĂ’ = (100 ā 2 ā2)′ = 100 2 2ā ýýÿ = ā + 4
→ ýÿ = ýýÿ . ā = ā2 + 4 ā
Ąÿ = ýÿ + Ăÿ = ā2 + 4 ā + 200
MC = TC’ = ( ā2 + 4 ā + 200)′ = 2 ā + 4 To maximizes profit: MR = MC → 100 – 2ā = 2ā + 4 ↔ 4ā = 96
↔ ā = ā ∗ = 24 (Ăÿ�㕖āĀ)
→ Ā = Ā ∗ = 100 – 24 = 76 ($)
→ Profit = π ∗= TR 2 TC = (100.24 – 24^2) – (24^2 + 4.24 + 200) = 952 ($) b. When ā = 0 → M C = 2.0 + 4 = 4 �㕎ÿ� 㕑 Ā = 100 2 0 = 100
Consumer surplus equals ăý㥠= ( (100 2 76).24)/2 = 288 $
Assume this firm applies perfect price discrimination, to maximize profit: āÿ = Ā → 2ā + 4 = 100 – ā
→ ā = āā = 32 (Ăÿ�㕖āĀ) → Ā = Āā = 68 ($)
When ā ∗ = 24 → āÿ ∗ = 24.2 + 4 = 52 ($) (P ∗ 2MC ). (QE 2 Q ∗) (76 2 52 ). (32 2 24) ĀĀ = ăýāþ = = = 96 ($) 2 2
c. Assume this firm applies perfect price discrimination, (100 2 68). 32 ýÿ’ = ăāÿă = = 512 ($) 2 (68 2 4). 32 Āă’ = ăāÿÿ = = 1024($) 2
d. Āă = ăýþÿĄ = [(76252)+(7624)].24 = 1152($) 2 At first, PS =HABK
After applying perfect price discrimination, Āă’ = Āă – ýāÿĄ, ý ’ ÿ = ýÿ + ýāÿĄ → π′ = π + DL