HỌC PHẦN XÁC SUẤT VÀ THỐNG KÊ
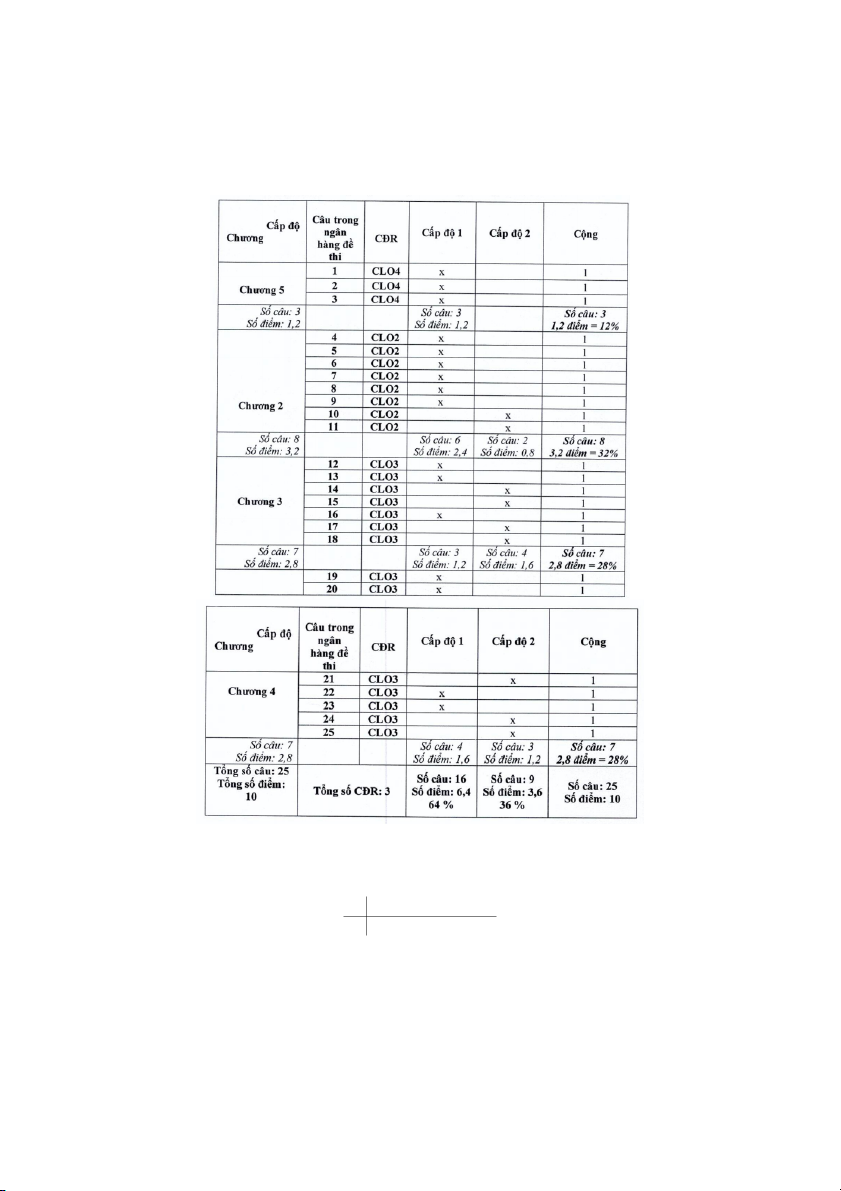
Cấu trúc đề thi gồm 25 câu CÂU HỎI THAM KHẢO
Câu 1: Cho BNN rời rạc X có bảng phân phối xác suất: X 1 2 3 4 P 0.15 0.25 0.4 0.2 1
Giá trị kỳ vọng của X là: A. 2.6; B. 2.8; C. 2.65; D. 0.9275
Câu 2: Cho BNN rời rạc X có bảng phân phối xác suất: X 1 2 3 4 P 0.15 0.25 0.4 0.2
Giá trị phương sai của X là: A. 5,3; B. 7,0225; C. 7,95; D. 0,9275
Câu 3: Kiện hàng I có 3 sản phẩm tốt và 2 phế phẩm, kiện hàng II có 2 sản phẩm tốt và 4 phế phẩm. Chọn
ngẫu nhiên từ kiện hàng I ra 1 sản phẩm và từ kiện hàng II ra 1 sản phẩm. Gọi X là số phế phẩm chọn được.
Hàm phân phối xác suất F (x) = P (X < x) của X là:   0, nếu x < 0 0, nếu x   ≤ 0          1  1  , nếu 0 ≤ x < 1  , nếu 0 < x ≤ 1 A. 5 B. 5 11 11  , nếu 1  , nếu 1 < x  ≤ x < 2  ≤ 2  15  15         1, nếu 2 < x 1, nếu 2 < x   0, nếu x < 0 0, nếu x ≤ 0            1  1  , nếu 0 ≤ x < 1  , nếu 0 < x ≤ 1 C. 5 B. 5 8 8  , nếu 1  , nếu 1 < x  ≤ x < 2  ≤ 2  15  15         1, nếu 2 < x 1, nếu 2 < x  3  x2, x ∈ (−2, 2)
Câu 4: Biến ngẫu nhiên X có hàm mật độ xác suất f(x) = 16 0, x / ∈ (−2, 2) √ √ √
Giá trị của P ( 2 < Y < 5) với Y = X2 + 1 là: A. 0,3125; B. 0,4375; C. 0,875; D. 0,625
Câu 5: Theo thống kê trung bình cứ 1.000 người dân ở độ tuổi 40 thì sau 1 năm có 996 người còn sống. Một
công ty bảo hiểm nhân thọ bán bảo hiểm 1 năm cho những người ở độ tuổi này với giá 1,5 triệu đồng, nếu
người mua bảo hiểm chết thì số tiền bồi thường là 300 triệu đồng. Giả sử công ty bán được 40.000 hợp đồng
bảo hiểm loại này (mỗi hợp đồng ứng với 1 người mua bảo hiểm) trong 1 năm.
Hỏi trong 1 năm lợi nhuận trung bình thu được của công ty về loại bảo hiểm này là bao nhiêu ? A. 1,2 tỉ đồng; B. 1,5 tỉ đồng; C. 12 tỉ đồng; D. 15 tỉ đồng
Câu 6: Theo thống kê trung bình cứ 1.000 người đi xe máy thì có 25 người bị tai nạn trong 1 năm.
Một công ty bảo hiểm bán bảo hiểm loại này cho 20.000 người trong 1 năm với giá 98 ngàn đồng và mức chi
trả khi bị tai nạn là 3 triệu đồng. Hỏi trong 1 năm lợi nhuận trung bình thu được của công ty về loại bảo hiểm này là bao nhiêu ? A. 445 triệu đồng; B. 450 triệu đồng; C. 455 triệu đồng; D. 460 triệu đồng
Câu 7: Một cửa hàng điện máy bán 1 chiếc máy lạnh A thì lời 850.000 đồng nhưng nếu chiếc máy lạnh đó 2
phải bảo hành thì lỗ 1.000.000 đồng. Biết xác suất máy lạnh A phải bảo hành của cửa hàng là p = 15% ,
tính mức lời trung bình khi bán 1 chiếc máy lạnh A ? A. 722.500 đồng; B. 75.500 đồng; C. 605.500 đồng; D. 572.500 đồng
Câu 8: Một cửa hàng điện máy bán 1 chiếc tivi thì lời 500.000 đồng nhưng nếu chiếc tivi đó phải bảo
hành thì lỗ 700.000 đồng. Tính xác suất tivi phải bảo hành của cửa hàng để mức lời trung bình khi bán 1
chiếc tivi là 356.000 đồng ? A. 10%; B. 12%; C. 15%; D. 23%  a(3x − x2), 0 ≤ x ≤ 3, Câu 9: 
Cho BNN liên tục X có hàm mật độ xác suất f(x) = , 0, x / ∈ [0, 3]
Giá trị trung bình của Y với Y = 3X2 là: A.EY = 8,1; B. EY = 7,9; C. EY = 4,5; D. EY = 5,4 
a(3x − x2), 0 ≤ x ≤ 3,
Câu 10: Cho BNN liên tục X có hàm mật độ xác suất f(x) = , 0, x / ∈ [0, 3]
Giá trị phương sai của Y với Y = 3X2 là: A.VarY = 38,0329 ; B. VarY = 38,5329; C. VarY = 38,9672; D. VarY = 39,0075 
a(3x − x2), 0 ≤ x ≤ 3,
Câu 11: Cho BNN liên tục X có hàm mật độ xác suất f(x) = , 0, x / ∈ [0, 3]
Giá trị của xác suất p = P (1 < X ≤ 2) là: A.p = 0,4815; B. p = 0,4915; C. p = 0,5015; D. p = 0,5115  0, x ≤ 1     Câu 12: x
BNN liên tục X có hàm phân phối xác suất − 1 F (x) = , 1 < x ≤ 3 2     1, 3 < x
Giá trị phương sai của X là: A. V arX = 1; B. V arX = 1; C. V arX = 1 ; D. V arX = 1 4 6 2 3
Câu 13: Chủ vườn lan đã để nhầm 10 chậu lan có hoa màu đỏ với 10 chậu lan có hoa màu tím (lan
chưa nở hoa). Một khách hàng chọn ngẫu nhiên 7 chậu từ 20 chậu lan đó. Xác suất khách chọn được nhiều
hơn 5 chậu lan có hoa màu đỏ là: A. 0,0586; B. 0,0486; C. 10,0386; D. 0,0286
Câu 14: Chủ vườn lan đã để nhầm 20 chậu lan có hoa màu đỏ với 100 chậu lan có hoa màu tím (lan
chưa nở hoa). Một khách hàng chọn ngẫu nhiên 15 chậu từ 120 chậu lan đó. Gọi X là số chậu lan có hoa
màu tím khách chọn được. Giá trị của EX và VarX là: 36 25 135 A.EX = 3, V ar(X) = B.EX = , V ar(X) = . 17 2 68 25 125 5 135 C.EX = , V ar(X) = D.EX = , V ar(X) = .4 2 68 2 68 3
Câu 15: Một hiệu sách bán 40 cuốn truyện A, trong đó có 12 cuốn in lậu. Một khách hàng chọn ngẫu
nhiên 4 cuốn truyện A. Hỏi khả năng cao nhất khách chọn được bao nhiêu cuốn truyện A không phải in lậu ? A. 1 cuốn; B. 2 cuốn; C. 3 cuốn; D. 4 cuốn
Câu 16: Một hộp chứa 100 viên phấn trong đó có 10 viên màu đỏ. Hỏi nếu không nhìn vào hộp bốc
tùy ý 1 lần bao nhiêu viên để xác suất có 4 viên màu đỏ là 0,0272 ? A. 10 viên; B. 12 viên; C. 14 viên; D. 16 viên
Câu 17: Xác suất có bệnh của những người chờ khám bệnh tại 1 bệnh viện là 12%. Khám lần lượt 20
người này, xác suất có ít hơn 2 người bị bệnh là: A. 0,2891; B. 0,7109; C. 0,3891; D. 0,6109
Câu 18: Xác suất có bệnh của những người chờ khám bệnh tại 1 bệnh viện là 72%, khám lần lượt 61
người này, hỏi khả năng cao nhất có mấy người bị bệnh là: A. 41 người; B. 42 người; C. 43 người; D. 44 người
Câu 19: Một gia đình nuôi gà mái đẻ với xác suất đẻ trứng của mỗi con gà trong 1 ngày là 0,75. Để
trung bình mỗi ngày có nhiều hơn 122 con gà mái đẻ trứng thì số gà tối thiểu gia đình đó phải nuôi là: A. 151 con; B. 162 con; C. 163 con; D. 175 con
Câu 20: Tại bệnh viện A trung bình 3 giờ có 8 ca mổ. Hỏi số ca mổ chắc chắn nhất sẽ xảy ra tại bệnh viện
A trong 10 giờ là bao nhiêu ? A. 25 ca; B. 26 ca; C. 27 ca; D. 28 ca
Câu 21: Một bến xe khách trung bình có 70 xe xuất bến trong 1 giờ. Xác suất để trong 5 phút có từ
4 đến 6 xe xuất bến là: A. 0,2133; B. 0,2792; C. 0,3209; D. 0,4663
Câu 22: Cho biến biến ngẫu nhiên X, N ∈ (4; 2, 25). Giá trị của xác suất P (X > 5, 5) là: A. 0,1587; B. 0,3413; C. 0,1916; D. 0,2707
Câu 23: Thời gian X (tháng) từ lúc vay đến lúc trả tiền của 1 khách hàng tại ngân hàng A là biến
ngẫu nhiên có phân phối N(18; 16). Tính tỉ lệ khách hàng trả tiền cho ngân hàng A trong khoảng từ 12 đến 16 tháng ? A. 24,17%; B. 9,63%; C. 25,17%; D. 10,63%
Câu 24: Chiều cao của nam giới đã trưởng thành là biến ngẫu nhiên X (cm) có phân phối N(165; 25).
Tỉ lệ nam giới đã trưởng thành cao từ 1,65m đến 1,75m là: A. 1,6%;; B. 42,75%; C. 45,96%; D. 47,73%
Câu 25: Trong một kho lúa giống có tỉ lệ hạt lúa lai tạp là 2%. Tính xác suất sao cho khi chọn lần 4
lượt 1000 hạtlúa giống trong kho thì có từ 17 đến 19 hạt lúa lai tạp ? A. 0,2492; B. 0,3492; C. 0,0942; D. 0,0342
Câu 26: Một khách sạn nhận đặt chỗ của 585 khách hàng cho 500 phòng vào ngày 2/9 vì theo kinh
nghiệm củanhững năm trước cho thấy có 15% khách đặt chỗ nhưng không đến. Biết mỗi khách đặt 1 phòng,
tính xác suất có từ 494 đến 499 khách đặt chỗ và đến nhận phòng vào ngày 2/9 ? A. 0,0273; B. 0,1273; C. 0,2273; D. 0,3273
Câu 27: Tỉ lệ thanh niên đã tốt nghiệp THPT của quận A là 75%. Trong đợt tuyển quân đi nghĩa vụ
quân sự năm nay, quận A đã gọi ngẫu nhiên 325 thanh niên. Tính xác suất để có từ 80 đến 84 thanh niên bị
loại do chưa tốt nghiệp THPT ? A. 13,79%; B. 20,04%; C. 26,32%; D. 28,69%
Câu 28:: Giá trị có số lần xuất hiện từ 2 trở lên và xuất hiện nhiều nhất trong tập dữ liệu gọi là: A. Mốt B. Trung bình C. Phương sai D. Độ lệch chuẩn.
Câu 29: Gọi X là lợi nhuận của công ty A (nghìn USD). Giả sử X có bảng phân phối xác suất như sau: X -10 0 5 10 15 P 0.1 0.15 0.35 0.3 0.1
Xác suất để công ty A có lợi nhuận không dưới 5 (nghìn USD) là: A. 0,25; B. 0,35; C. 0,4; D. 0,75%
Câu 30: Gọi X là tỷ suất lợi nhuận (%) của một loại cổ phiếu. Giả sử X có bảng phân phối xácsuất như sau: X(%) -3 2 4 P 0.2 0.5 0.3
Tìm tỷ suất lợi nhuận trung bình. A. 0%; B. 1%; C. 1.6%, D. 2%
Câu 31: Một cửa hàng cho rằng xác suất bán được hàng trong 1 tuần là 0,4. Nếu bán được hàng thì
lãi 10 triệu đồng; nếu không bán được hàng thì lỗ 1 triệu đồng. Phương sai của số tiền lãi là A. 40,6 (triệu đồng). B. 29,04 (triệu đồng). C. 27,84 (triệu đồng). D. 5,39 (triệu đồng)
Câu 32: Một người môi giới thực hiện giao dịch với 10 người độc lập nhau trong 1 ngày. Xác suất giao 5
dịch thành công đều bằng 0,3. Số giao dịch thành công có khả năng cao nhất là A. 10 B. 4 C. 3,8 D. 3
Câu 33: Một biến số mà trong kết quả của phép thử nó nhận đúng một giá trị mà giá trị đó là bất kì
số nào trong khoảng (0; 1) thì gọi là:
A. Biến ngẫu nhiên rời rạc; B. Biến cố;
C. Biến ngẫu nhiên liên tục;
D. Biến ngẫu nhiên phân phối Không – một.
Câu 34: Giả sử thu nhập là biến ngẫu nhiên phân phối Chuẩn với trung bình là 10 (triệu đồng) và phương
sai là 9 (triệu đồng). Xác suất thu nhập dưới 4 triệu đồng bằng? A. 0,0228 B. 0,1327 C. 0,3446 D. 0,9772
Câu 35: Cân nặng một loại sản phẩm là biến ngẫu nhiên phân phối Chuẩn với trung bình là 200g và
độ lệch chuẩn 10g. Sản phẩm nhẹ hơn 190g thì không đạt tiêu chuẩn. Kiểm tra 3 sản phẩm thì xác suất đúng
1 sản phẩm không đạt tiêu chuẩn gần bằng: A. 0,0658 B. 0,1123 C. 0,1587 D. 0,3370 Câu 36: Trung bình mẫu X
A. Là một biến ngẫu nhiên. B. Là một giá trị.
C. Bằng trung bình tổng thể.
D. Luôn có phân phối Chuẩn.
Câu 37: Tiền lương của một nhân viên phân phối Chuẩn với trung bình là 200$, độ lệch chuẩnlà 50$.
Chọn một mẫu ngẫu nhiên 100 nhân viên thì xác suất để lương trung bình của 100 nhân viên này nằm trong
khoảng 195$ đến 205$ là bao nhiêu? Xác suất cần tìm bằng: 205 − 200 195 − 200 A.ϕ( ) − ϕ( ) 50 50 5 B.2 × ϕ( √ ). 50/ 100 205 − 200 195 − 200 C.ϕ( √ ) − ϕ( √ ) 50/ 100 50/ 100 6 205 − 200 195 − 200 D.ϕ( ) − ϕ( ) p50/100 p50/100
Câu 38: Tỷ lệ phế phẩm của một lô hàng là 10%. Nếu lấy mẫu ngẫu nhiên 400 sản phẩm từ lô hàng
thì xác suất tỷ lệ phế phẩm của mẫu đó vượt quá 12% gần bằng: A. 0,0918 B. 0,0968 C. 0,9082 D. 0,4721
Câu 39: Cho chiều cao của sinh viên phân phối Chuẩn, chưa biết trung bình (µ) và chưa biết phương
sai (σ2). Với độ tin cậy (1 − α), muốn ước lượng chiều cao trung bình tối đa của sinh viên thì dùng công thức nào? s A. n− µ < X + t( 1) α . n s B. n− X − t( 1) α < µ. n s s C. n− n− X − t( 1) α < µ < X + t( 1) . n α n s D. µ < X + t(n−1) . α/2 n
Câu 40: Kiểm tra 200 sản phẩm của nhà máy thì có 20 phế phẩm. Với độ tin cậy 90%, khi ước alượng
khoảng tin cậy đối xứng cho tỷ lệ phế phẩm của nhà máy thì độ dài khoảng tin cậy là: A. 0,0349 B. 0,0698 C. 0,0832 D. 0,0416
Câu 40: Cân nặng một loại sản phẩm có phân phối Chuẩn. Cân 100 sản phẩm tìm được trung bình
mẫu là 175g và độ lệch chuẩn mẫu là 40g. Với độ tin cậy 95%, đâu là khoảng tin cậy đối xứng của cân nặng trung bình? A. (167,16; 182,84) B. (171; 179) C. (174,2; 175,8) D. (167; 179)
Câu 41: Gọi X là điểm thi môn Toán của học sinh lớp 12, giả sử X ∼ N(µ, σ2). Muốn kiểm định điểm thi
trung bình có vượt quá 6 hay không thì cặp giả thuyết cần kiểm định là:
A. H0 : ¯x = 6, H1 : ¯x > 6.
B. H0 : µ = 6, H1 : µ > 6.
C. H0 : µ > 6, H1 : µ ≤ 6. D. H0 : µ = 6, H1 : µ = 6 6.
Câu 42: Kiểm tra 200 sản phẩm của máy A thì có 28 phế phẩm. Khi kiểm định xem tỷ lệ phế phẩm
của máy A có vượt quá 10% hay không thì giá trị quan sát của tiêu chuẩn kiểm định là: 7 A. 1,886 B. -1,886 C. 1,630 D. -1,630
Câu 43: Giả sử chiều cao của sinh viên có phân phối Chuẩn. Có ý kiến cho rằng: chiều cao trung bình
của sinh viên thấp hơn 163cm. Đo chiều cao của 40 sinh viên thì tìm được trung bình là 161cm và độ lệch
chuẩn mẫu là 7 cm. Với mức ý nghĩa 5%, lựa chọn nào đúng?
A. H0 : µ = 163, H1 : µ > 163; ý kiến đúng
B. H0 : µ > 163, H1 : µ ≤ 163; ý kiến đúng
C. H0 : µ = 163, H1 : µ < 163; ý kiến đúng
D. H0 : µ = 163, H1 : µ < 163; ý kiến sai  H0 : µ = µ Câu 44: 0
Giả sử BNN có phân phối chuẩn. Khi cặp giả thuyết H1 : µ < µ0
Với mẫu có kích thước n thì tìm được p-value = 0.085. Với mức ý nghĩa nào thì bác bỏ H0 khi: A. 10% B. 3% C. 5% D. 8%
Câu 45: Cho 3 biến ngẫu nhiên độc lập X, Y, Z biết X ∼ N(5, 4), Y ∼ P (3) và Z ∼ B(6, 0.3). Tính
phương sai của T = 4X − 3Y + Z + 1 A. 50.26 B. 92.26 C. 8.26 D. 26.26
Câu 46: Trước đây định mức tiêu dùng điện cho một hộ gia đình trong một thánglà 140 KW. Do hệ
thống cấp điện được nâng cấp, người ta theo dõi 100 hộ gia đình và thu được các số liệu sau: Lượng tiêu dùng 100-120 120-140 140-160 160-180 180-200 Số hộ gia đình 14 25 30 20 11
Với mức ý nghĩa 5%, tính giá trị của tiêu chuẩn kiểm định và kết luận.
A. z = -3,23607 ; Kết luận: Cần thay đổi định mức.
B. z = 3,23607 ; Kết luận: Không cần thay đổi định mức.
C. z = 3,23607 ; Kết luận: Cần thay đổi định mức.
D. z = 3,23607 ; Kết luận: Không cần thay đổi định mức.
Câu 47: Thống kê 10650 trẻ sơ sinh ở một địa phương người ta thấy có 5410 con trai. Với mức ý nghĩa 1%,
hỏi tỷ lệ sinh con trai có thực sự cao hơn tỷ lệ sinh congái không? Yêu cầu tính giá trị của tiêu chuẩn kiểm
định và đưa ra kết luận.
A. z = -1.747; Tỉ lệ sinh con trai cao hơn tỉ lệ sinh con gái. 8
B. z =1,647; Tỉ lệ sinh con trai cao hơn tỉ lệ sinh con gái.
C. z =1,747; Tỉ lệ sinh con trai và con gái là như nhau.
D, z =1,647; Chưa có cơ sở cho rằng tỉ lệ sinh con trai thực sự cao hơn tỉ lệ sinh con gái.
Câu 48: Theo dõi mức đầu tư (Y) và lợi nhuận (X) của 10 xí nghiệp khác nhau trong cùng một ngành,
người ta thu được bảng số liệu sau: Y 1 1 2 3 3 5 6 7 8 8 X 2,3 2,5 2,6 3 3,1 3,5 3,7 4 4,5 5
Tính hệ số tương quan giữa Y và X A. 0,98694 B. 0,94879 C. 0,97406 D. 0,97604
Câu 49: Các giá trị sau đây thu được từ một mẫu các quan sát của hai đại lượng Xvà Y: X X X X Xi = 125, X2i = 295, Yi = 1160, XiYi = 2730, n = 70
Phương trình hồi quy tuyến tính thực nghiệm của Y theo X là A. Y = 9, 174X − 0, 189. B. Y = 9, 174 + 0, 189X. A. Y = −9, 174X + 0, 189. A. Y = 9, 174X + 0, 189.
Câu 50: Theo dõi mức đầu tư (Y) và lợi nhuận (X) của 10 xí nghiệp khác nhau trong cùng một ngành,
người ta thu được bảng số liệu sau: Y 1 1 2 3 3 5 6 7 8 8 X 2,3 2,5 2,6 3 3,1 3,5 3,7 4 4,5 5
Phương trình hồi quy tuyến tính thực nghiệm của Y theo X là A. Y = −3, 01569X + 5, 91368 B. Y = 3, 01569 + 5, 91368X
C. Y = −3, 01569X − 5, 91368 D. Y = 3, 01569X − 5, 91368
Câu 51: Các giá trị sau đây thu được từ một mẫu các quan sát của hai đại lượng Xvà Y: X X X X X n = 8, Xi = 80, X2i = 836, Yi = 7100, Y 2i = 6890000, XiYi = 75500
Tìm hệ số tương quan và phương trình hồi quy tuyến tính thực nghiệm của Y theo X.
A. r = −0, 97745, Y = −125X + 362.5
B. r = −0, 97745, Y = 125X − 362.5
C. r = −0, 97745, Y = 125X + 362.5 9
D. r = 0, 97745, Y = 125X − 362.5
Câu 52: Bảng số liệu sau đây là kết quả thu thập của một công ty về số tiền dành hoạt động quảng
cáo (X) và doanh thu (Y) sau một số tháng X (triệu đồng) 45 60 75 90 80 100 110 Y (tỉ đồng) 6 7 8 11 10 14 16
Giả sử một tháng nào đó công ty đầu tư 130 triệu đồng cho hoạt động quảng cáo, hãy dự đoán doanh thu của tháng đó. A. 18,15 tỉ đồng. B. 17,25 triệu đồng. C. 17,25 tỉ đồng. D. 18,15 triệu đồng.
Câu 53: Bảng sau đây là số liệu của một công ty về số tiền dành hoạt động chăm sóc khách hàng (X) và doanh thu (Y) sau 8 năm X (triệu đồng) 8 9 7 10 9 11 16 22 Y (tỉ đồng) 600 700 500 1200 800 1180 1720 2440
Giả sử một năm nào đó công ty đầu tư 24 tỉ đồng dành cho hoạt động chăm sóc khách hàng, dự đoán doanh thu của năm đó là A. 2748,54 tỉ đồng. B. 2848,54 tỉ đồng. C. 2948,54 tỉ đồng. D. 2648,54 tỉ đồng.
Câu 54: Đo chiều cao (X: m) và khối lượng (Y: kg) của 5 học sinh nam, ta có kết quả sau X 1,45 1,6 1,5 1,65 1,55 Y 50 55 45 60 55
Dự đoán nếu một học sinh cao 1,62m thì cân nặng khoảng bao nhiêu kg? A. 57,2012 kg B. 57 kg C. 50 kg D. 52,5 kg.
Câu 55: Từ một mẫu gồm 42 quan sát của hai đại lượng X và Y, người ta thu được hệ số tương quan
r = 0, 22. Với mức ý nghĩa 5% . Yêu cầu tính giá trị của tiêu chuẩn kiểm định và đưa ra kết luận
A. T=2,43; Có cơ sở để khẳng định X và Y có tương quan.
B. T=1,43; Chưa có cơ sở để khẳng định X và Y có tương quan.
C. T=1,53; Chưa có cơ sở để khẳng định X và Y có tương quan.
D. T=2,34; Có cơ sở để khẳng định X và Y có tương quan. 10