Bài tập Phân tích hồi quy và kiểm định giả thuyết môn Kinh tế lượng | Đại học Kinh tế Thành phố Hồ Chí Minh

BÀI TẬP – KINH TẾ LƯỢNG
Bài 1. Bảng sau đây chứa điểm ACT (điểm tuyển sinh đại học) và GPA (điểm trung bình) của 8 sinh viên đại
học. GPA được tính theo thang điểm 4 và được làm tròn đến một số thập phân.
1. Ước lượng mối quan hệ giữa GPA và ACT bằng cách dùng OLS; nghĩa là, tìm hệ số chặn và hệ số góc
trong phương trình hồi quy sau 𝐺𝑃𝐴̂ = 𝛽̂ 0 + 𝛽̂ 1𝐴̂𝐶𝑇.
Nhận xét về chiều hướng của mối quan hệ. Hệ số chặn có ý nghĩa thực tế trong ví dụ này không? Hãy giải
thích. Nếu ACT tăng thêm 5 điểm, hãy dự đoán GPA sẽ tăng thêm bao nhiêu?
2. Tính các giá trị ước lượng và các phần dư đối với mỗi quan sát, và kiểm chứng rằng các tổng các phần dư
(gần đúng) là bằng không.
3. Giá trị dự đoán của GPA khi ACT = 20 là bao nhiêu?
4. ACT đã giải thích được bao nhiêu phần trăm sự thay đổi GPA của 8 học sinh?
Bài 2. Sử dụng dữ liệu của Kiel và McClain (1995) từ năm 1988 về lượng nhà đã bán tại Andover,
Massachusetts, phương trình thể hiện mối liên hệ giữa giá nhà (price) với khoảng cách từ nhà đến lò đốt rác
thải được xây dựng gần đây (dist) như sau: 1.
Nêu ý nghĩa hệ số hồi quy của log(dist). Dấu của ước lượng này có phù hợp với kỳ vọng của bạn hay không? 2.
Bạn có cho rằng hồi quy đơn trong trường hợp này đã mang lại ước lượng không chệch cho hệ số
co dãn của price theo dist, trong điều kiện các yếu tố khác không đổi, hay không? (Hãy nghĩ đến quyết định
của thành phố về nơi để đặt các lò đốt.) 3.
Những yếu tố nào khác của ngôi nhà có thể tác động đến giá của nó? Các yếu tố này có thể có
tương quan với khoảng cách đến lò đốt rác hay không?
Bài 3. Xét phương trình giải thích tiền lương của các CEO theo doanh thu hàng năm, tỷ suất lợi nhuận
trên vốn chủ sở hữu (roe, dạng phần trăm), và tỷ suất lợi nhuận trên cổ phiếu (ros, dạng phần trăm), và số
năm nắm giữ chức vụ tại công ty (tenure, năm) log(salary) = 0 + 1log(sales) + 2roe + 3ros +
4tenure + u Sử dụng dữ liệu thu thập được, kết quả ước lượng phương trình bằng OLS như sau:
1. Phát biểu ý nghĩa của hệ số hồi quy đứng trước biến log(sales), biến roe.
2. Kiểm định giả thuyết không rằng ros không có tác động lên salary. Tiến hành kiểm định với mức ý nghĩa 10%.
3. Kiểm định giả thuyết cho rằng tỷ suất lợi nhận trên vốn chủ sở hữu càng cao thì tiền lương của CEO càng
cao. Kết luận với mức ý nghĩa 5%.
4. Có nhận định cho rằng “Nếu doanh thu tăng 10% sẽ làm tăng 3,6% tiền lương của CEO”, nhận định này
có đúng không? Kết luận với mức ý nghĩa 10%.
5. Có nhận định cho rằng “Thời gian nắm giữ chức vụ của CEO tăng thêm 1 năm thì tiền lương của CEO sẽ
tăng 1,2%”, nhận định này có đúng không? Kết luận với mức ý nghĩa 5%.
6. Có nhận định cho rằng “Nếu tỷ suất lợi nhuận trên vốn chủ sở hữu tăng 10 điểm phần trăm sẽ làm tăng
2% tiền lương của CEO”, nhận định này có đúng không? Kết luận với mức ý nghĩa 5%.
7. Hãy kiểm định giả thuyết cho rằng các biến giải thích đồng thời không có ý nghĩa tại mức ý nghĩa 5%. 8.
Loại bỏ hai biến ros và roe ra khỏi phương trình, ta được kết quả ước lượng
log( 𝑠𝑎𝑙𝑎𝑟𝑦) = 4,82 + 0,257log(𝑠𝑎𝑙𝑒𝑠) + 0,014 𝑡𝑒𝑛𝑢𝑟𝑒 n = 209, R2 = 0,211
Biến ros và roe có ý nghĩa đồng thời tại mức ý nghĩa 5% trong phương trình ban đầu hay không?
9. Gọi ro_sum là tổng ros và roe: ro_sum = ros + roe. Dùng ro_sum thay cho roe được kết quả
log( 𝑠𝑎𝑙𝑎𝑟𝑦) = 4,31 + 0,280log(𝑠𝑎𝑙𝑒𝑠) + 0,017 𝑟𝑜_𝑠𝑢𝑚 − 0,013𝑟𝑜𝑠 + 0.012 𝑡𝑒𝑛𝑢𝑟𝑒
(0,32) (0,035) (0,004) (0.003) (0,007)
Bạn có thể bác bỏ H0: 𝛽̂𝑟𝑜𝑒 = 𝛽̂𝑟𝑜𝑠 hay không, với mức ý nghĩa 1%?
Bài 4. Mô hình sau đây là một phiên bản đơn giản của mô hình hồi quy bội được xây dựng bởi Biddle và
Hamermesh (1990) nghiên cứu sự đánh đổi giữa thời gian dành cho ngủ với thời gian làm việc và xem xét
các yếu khác ảnh hưởng đến giấc ngủ:
trong đó sleep (tổng
thời gian ngủ) và totwrk (tổng thời gian làm việc) tính bằng phút/tuần và educ và age được đo theo năm.
Từ mẫu thu thập được, phương trình ước lượng là
1. Liệu từng biến educ và age có ý nghĩa riêng lẻ tại mức ý nghĩa 5% với giả thuyết đối 2 phía hay không?
2. Có nhận định cho rằng “Tổng thời gian làm việc tăng thì tổng thời gian ngủ sẽ giảm ”, nhận định này có
đúng không? Kết luận với mức ý nghĩa 5%.
3. Có nhận định cho rằng “Tổng thời gian làm việc tăng 1 giờ/tuần thì thì tổng thời gian ngủ sẽ giảm 15
phút/tuần”, nhận định này có đúng không? Kết luận với mức ý nghĩa 5%.
4. Hãy kiểm định xem các biến giải thích có ý nghĩa đồng thời tại mức ý nghĩa 5% hay không?
5. Loại bỏ hai biến educ và age ra khỏi phương trình, ta được kết quả ước lượng
Biến educ và age có ý nghĩa đồng thời tại mức ý nghĩa 5% trong phương trình ban đầu hay không?
6. Viết lại hàm hồi quy mẫu, nếu tổng thời gian làm việc có đơn vị là giờ/ngày.
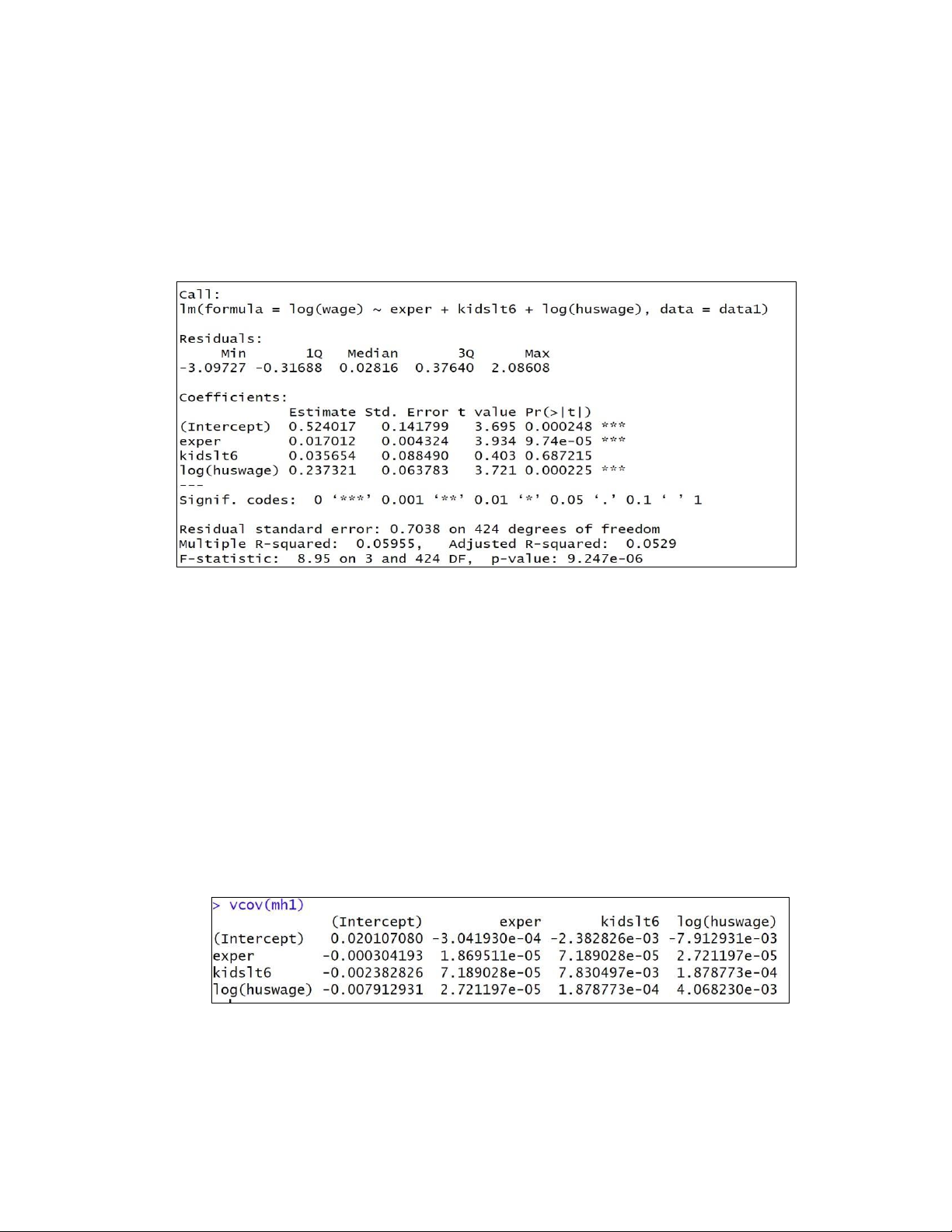
Bài 5. Xét phương trình giải thích thu nhập của người vợ (wage, USD/giờ) theo số năm kinh nghiệm (exper,
năm), số trẻ dưới 6 tuổi (kidslt6, trẻ) và thu nhập của người chồng (huswage, USD/giờ):
(𝐦𝐡𝟏): log(𝑤𝑎𝑔𝑒) = 𝛽̂0 + 𝛽̂1𝑒𝑥𝑝𝑒𝑟 + 𝛽̂2𝑘𝑖𝑑𝑠𝑙𝑡6 + 𝛽̂3 log(ℎ𝑢𝑠𝑤𝑎𝑔𝑒) + 𝑢 Dựa
trên bộ dữ liệu có sẵn, kết quả hồi quy từ phần mềm R như sau:
1. Viết hàm hồi quy mẫu. Nêu ý nghĩa của hệ số hồi quy trước biến kidslt6, log(huswage).
2. Thu nhập của người chồng có ảnh hưởng đến thu nhập của người vợ không, với mức ý nghĩa 5%?
3. Có ý kiến:”Khi kinh nghiệm tăng thì tiền lương của người vợ tăng.” Kết luận với mức ý nghĩa 10%.
4. Có ý kiến: “Khi có thêm 1 đứa trẻ 6 tuổi thì tiền lương của người vợ sẽ tăng 3%.” Kết luận ý kiến trên với mức ý nghĩa 5%.
5. Có ý kiến: “Khi thu nhập người chồng tăng 1% thì tiền lương người vợ tăng thấp hơn 0.3%.” Kết luận với mức ý nghĩa 5%.
6. Tìm khoảng tin cậy của hệ số hồi quy đứng trước biến kidsl6, với độ tin cậy 95%.
7. Kiểm định ý định đồng thời của tất cả các biến độc lập trong mô hình trên, với mới ý nghĩa 3%.
8. Viết lại hàm hồi quy mẫu, khi thu nhập của người vợ và người chồng đều có đơn vị là USD/tuần.
9. Kiểm định giả thuyết sau, với mức ý nghĩa 5%:
H0: 𝛽̂2 = 2𝛽̂1 H1: 𝛽̂2 ≠ 2𝛽̂1
Biết ma trận phương sai, hiệp phương sai của các hệ số hồi quy như sau:
10. Có k ế t qu ả ki ể m đ ị nh như sau:
Viết giả thuyết H0 và H1 tương ứng với bảng trên? Phát biểu bằng lời về mục đích của kiểm định, Nêu kết
luận với mức ý nghĩa 5%?
11. Các bảng kết quả sau dùng để kiểm định vi phạm nào? Nêu kết luận với mức ý nghĩa 5%.
Bài 6. Có các biến sau:
wage : tiền lương (USD/tháng) exper: kinh nghiệm (năm) educ: số năm đi học (năm)
Câu 1: Sử dụng OLS để ước lượng mô hình: log(wage) = β0 + β1 educ + β2exper + β3exper2 + u.
Kết quả ước lượng từ R như sau:
1. Viết hàm hồi quy mẫu. Biến exper2 có ý nghĩa thống kê ở mức ý nghĩa 1% không?
2. Chứng tỏ rằng: từ đó xác định mức tăng tiền lương của năm kinh
nghiệm thứ 5, năm kinh nghiệm thứ 20.
3. Tại giá trị nào của exper thì số năm kinh nghiệm tăng thêm sẽ làm giảm giá trị dự đoán của log(wage)?
4. Mô hình trên có đa cộng tuyến không?
Trình bày một hậu quả của hiện tượng đa cộng tuyến.
Câu 2: Sử dụng OLS để ước lượng mô hình: log(wage) = β0 + β1 educ + β2exper + β3 educ∙exper + u. Kết quả từ R:
1. Viết biểu thức thể hiện ảnh hưởng của một năm đi học tăng thêm lên tiền lương, trong điều kiện exper không đổi.
2. Với mức ý nghĩa 2%, có thể cho rằng ảnh hương của của một năm đi học tăng thêm lên tiền lương không
phụ thuộc vào exper hay không?
3. Gọi là ký hiệu mức tăng tiền lương khi số năm đi học tăng lên 1, với exper = 10. Hãy tính . Có kết
quả hồi quy mẫu như sau:
log( 𝑤𝑎𝑔𝑒) = 5.9495 + 0.0761educ − 0.0215exper + 0.0032(𝑒𝑑𝑢𝑐 ∗ 𝑒𝑥𝑝𝑒𝑟 − 10𝑒𝑑𝑢𝑐)
(0.2408) (0.0066) (0.0200) (0.0015)
Dựa trên kết quả trên, hãy tìm khoảng tin cậy 95% cho .
4. Kiểm định sau dùng để làm gì? Nêu kết luận với mức ý nghĩa 2%.
Câu 3: Xét hàm hồi quy:
wage = β0 + β1 educ + β2exper + u.
Để ước lượng tiền lương trung bình của một cá nhân có 12 năm đi học và 6 năm kinh nghiệm, người ta thực hiện hàm hồi quy sau:
Với độ tin cậy 95%, tìm khoảng tin cậy cho tiền lương trung bình của một cá nhân có 12 năm đi học và 6 năm kinh nghiệm.
Bài 7. Có kết quả hồi quy mẫu như sau: trong đó, sleep là
tổng số giờ ngủ buổi tối trong tuần được tính bằng phút, totwrk là tổng số phút làm việc trong tuần, educ
và age số năm đi học và tuổi (tính bằng năm), male = 1 nếu là nam giới.
1. Trong điều kiện tất cả các yếu tố khác như nhau, có bằng chứng thống kê để chứng tỏ nam giới ngủ
nhiều hơn nữ giới hay không? Kết luận với mức ý nghĩa 5%?
2. Trong điều kiện các yếu tố khác là như nhau, có bằng chứng thống kê để chứng tỏ nam giới ngủ
nhiều hơn nữ giới 2 giờ mỗi tuần không? Kết luận với mức ý nghĩa 10%?
3. Viết lại hàm hồi quy mẫu khi biến giả giới tính được đặt female = 1 nếu là nữ giới.
4. Nếu chúng ta muốn kiểm định giả thuyết không về việc tuổi tác không tác động đến thời gian ngủ,
trong điều kiện các yếu tố khác không đổi, chúng ta cần xây dựng mô h.nh hồi quy như thế nào?
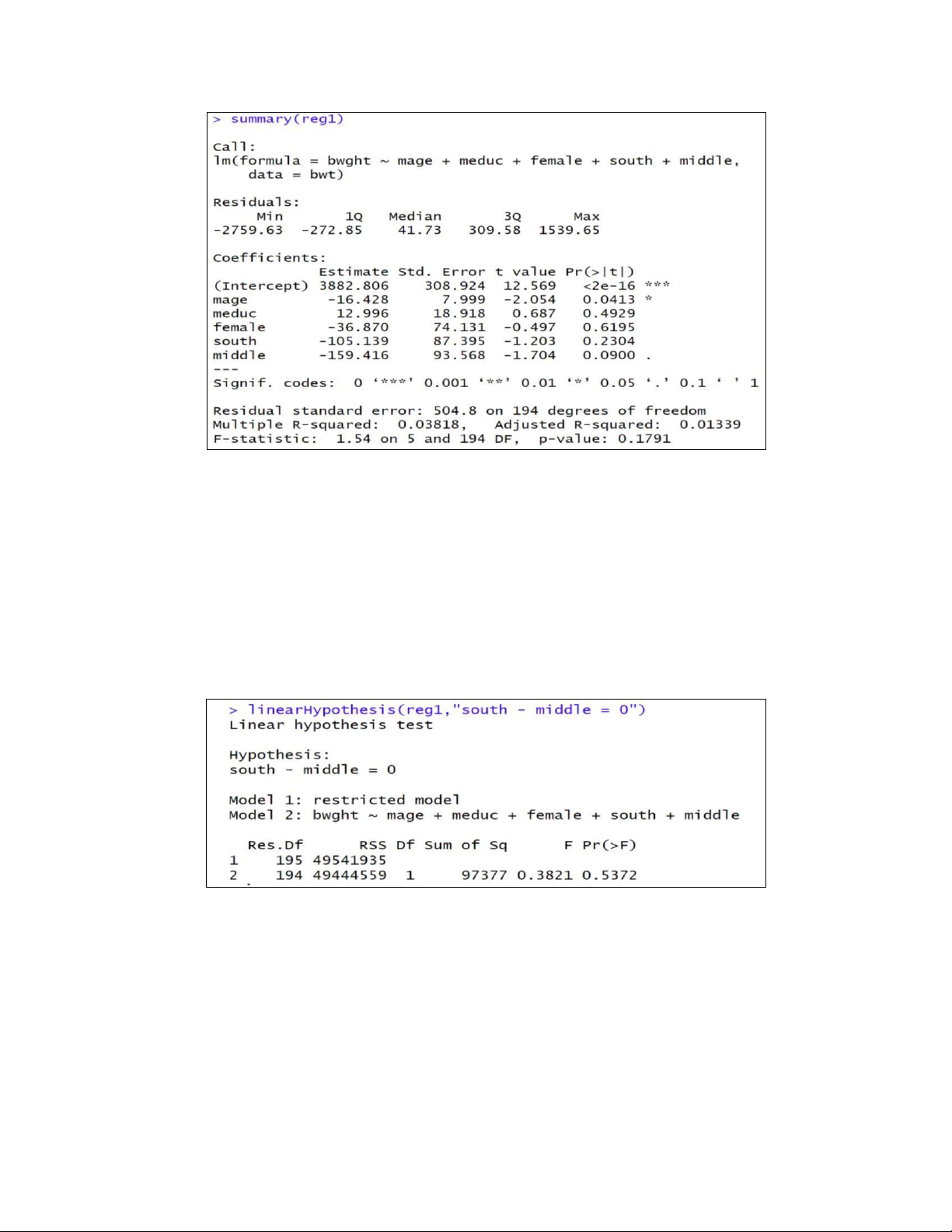
Bài 8. Tập dữ liệu gồm 200 thông tin của trẻ mới sinh tại 3 vùng (Bắc, Trung, Nam) gồm các biến sau:
- bwght (gram): cân nặng của trẻ
- mage (năm) : tuổi của người mẹ
- meduc (năm): số năm đi học của người mẹ
- female = 1: nếu trẻ là bé gái
- south = 1 nếu trẻ được sinh ở miền Nam, middle = 1 nếu trẻ được sinh ở miền Trung.
1. Giải thích ý nghĩa của hệ số hồi quy đứng trước biến female, biến south.
2. Trong điều kiện các yếu tố khác là như nhau, sự chênh lệch cân nặng giữa bé trai và gái có ý nghĩa
thống kê hay không? Kết luận với mức ý nghĩa 5%.
3. Loại bỏ hai biến south và middle ra khỏi mô hình, được mô hình mới có R2 = 0.02317.
Kiểm định giả thuyết cho rằng cân nặng của trẻ không phụ thuộc vào vùng miền, với mức ý nghĩa 1%.
4. Trong điều kiện các yếu tố khác là như nhau, có thể kết luận bé trai sinh ở miền Bắc có cân nặng hơn bé
trai sinh ở miền Trung không? Kết luận với mức ý nghĩa 2%.
5. Trong điều kiện các yếu tố khác là như nhau, có thể kết luận bé trai sinh ở miền Bắc có cân nặng hơn
bé trai sinh ở miền Trung 200gram không? Kết luận với mức ý nghĩa 2%
6. Có kết quả kiểm định như sau:
Viết giả thuyết của kiểm định? Ý nghĩa của kiểm định này là gì? Nêu kết luận với mức ý nghĩa 1%.
7. Nếu biến giả vùng miền được định nghĩa như sau: north = 1 nếu trẻ được sinh ở miền Bắc, middle = 1
nếu trẻ được sinh ở miền Trung. Viết lại hàm hồi quy mẫu nếu sử dụng biến giả north và middle thay vì
south và middle,
8. Kiểm định sau dùng để làm gì? Nêu kết luận với mức ý nghĩa 5%.
9 . Ki ể m đ ị nh sau dùng đ ể làm gì? Nêu k ế t lu ậ n v ớ i m ứ c ý nghĩa 1 %.
B ài 9 . Có các biến sau:
colgpa = điểm trung bình học tập sau học kỳ đầu tiên ở đại học (theo thang điểm 10)
act = điểm thi tuyển đại học skipped = số buổi vắng trung bình mỗi
tuần income = thu nhập trung bình của gia đình trong một tháng (triệu đồng/tháng) urban = 1 nếu
sinh viên có hộ khẩu tại khu vực thành thị Ước lượng mô hình:
Kết quả hồi quy như sau:
1. Kiểm định giả thuyết 2 phía H0: β5 = 0, với mức ý nghĩa 7%? Nêu ý nghĩa của kiểm định này?
2. Để kiểm định giả thuyết cho rằng, đối với sinh viên có hộ khẩu tại khu vực thành thị, điểm
thi tuyển đại học (act) không ảnh hưởng đến kết quả học kỳ đầu tiên; người ta thực hiện kiểm định sau
Hãy viết giả thuyết 2 phía H0 và H1 tương ứng dựa vào bảng kết quả trên?
Giải thích tại sao cần kiểm định giả thuyết H0 như vậy? Nêu kết luận của bạn, với mức ý nghĩa 4%?
Bài 10. Xét mô hình tuyến tính để giải thích sự tiêu thụ bia hàng tháng
beer = 0 + 1inc + 2price + 3educ + u
E(u|inc, price, educ, female) = 0
Var(u|inc, price, educ, female) = 2inc2
Hay viết phương trinh biến đổi để sai số có phương sai thuần nhất.