Tài liệu học tập môn Kinh tế lượng | Đại học Kinh tế Thành phố Hồ Chí Minh

TRƯỜNG ĐẠI HỌC KINH TẾ TP.HCM
KHOA TOÁN – THỐNG KÊ BỘ
MÔN TOÁN KINH TẾ

TÀI LIỆU HỌC TẬP MÔN KINH TẾ LƯỢNG 2019 Các tác giả: Phạm Trí Cao Nguyễn Thành Cả Hoàng Thị Diễm Hương Ngô Thị Tường Nam Bùi Thị Lệ Thủy I MỤC LỤC
CHƯƠNG 1. BẢN CHẤT CỦA KINH TẾ LƯỢNG VÀ DỮ LIỆU KINH TẾ 1
1.1. Kinh tế lượng là gì? 1
1.2. Các bước thực hiện phân tích kinh tế lượng 1
1.3. Cấu trúc của dữ liệu kinh tế 2
1.3. Cấu trúc của dữ liệu kinh tế 2
1.4. Quan hệ nhân quả và khái niệm về các iều kiện khác không ổi 5
trong kinh tế lượng
CHƯƠNG 2. MÔ HÌNH HỒI QUY ĐƠN 7
2.1. Định nghĩa mô hình hồi quy ơn 7
2.2. Phương pháp ước lượng bình phương bé nhất 8
2.3. Các tính chất của OLS trên mẫu dữ liệu bất kỳ 9
2.4. Vấn ề ơn vị o của biến và dạng hàm 11
2.5. Giá trị kỳ vọng và phương sai của ước lượng OLS 12
2.6. Hồi quy qua gốc tọa ộ 15
CHƯƠNG 3. PHÂN TÍCH HỒI QUY BỘI: VẤN ĐỀ ƯỚC LƯỢNG 17
3.1. Sự cần thiết của mô hình hồi quy bội 17
3.2. Mô hình hồi quy tuyến tính bội và phương pháp OLS 17
3.3. “ Ý nghĩa riêng phần” trong hồi quy bội 19
3.4. Ước lượng hồi quy bội khi bỏ sót biến 20
3.5. Mức ộ phù hợp của mô hình 21
3.6. Hồi quy qua gốc tọa ộ 23
3.7. Các giả thiết Gauss-Markov 23
3.8. Phương sai của ước lượng OLS 25
3.9. Vấn ề ịnh dạng thừa mô hình và chệch do bỏ sót biến 27 II
3.10. Vấn ề a cộng tuyến 32
CHƯƠNG 4. PHÂN TÍCH HỒI QUY BỘI: VẤN ĐỀ SUY DIỄN 35
4.1. Phân phối mẫu của các ước lượng OLS 35
4.2. Kiểm ịnh giả thuyết ơn về tham số tổng thể (t-Test) 37
4.3. Khoảng tin cậy của hệ số hồi quy riêng 40
4.4. Kiểm ịnh giả thuyết về một kết hợp tuyến tính của các tham số 40
4.5. Kiểm ịnh nhiều ràng buộc tuyến tính (Wald-Test) 42
CHƯƠNG 5. PHÂN TÍCH HỒI QUY BỘI:
TÍNH TIỆM CẬN CỦA ƯỚC LƯỢNG OLS 49 5.1. Ước lượng vững 49 5.2. Tính vững 49
5.3. Tính tiệm cận chuẩn và vấn ề suy diễn với mẫu lớn 51
5.4. Tính hiệu quả tiệm cận của ước lượng OLS 52
CHƯƠNG 6. PHÂN TÍCH HỒI QUY BỘI: MỘT SỐ VẤN ĐỀ MỞ RỘNG 55
6.1. Vấn ề ơn vị tính trong hồi quy OLS 55
6.2. Bàn thêm về dạng hàm hồi quy 56
6.3. Bàn thêm về hệ số xác ịnh và vấn ề lựa chọn biến ộc lập 60
6.4. Phân tích về dự oán và sai số dự oán 61
CHƯƠNG 7. PHÂN TÍCH HỒI QUY BỘI VỚI BIẾN ĐỊNH TÍNH 65
7.1. Mô tả thông tin ịnh tính 65
7.2. Trường hợp biến ịnh tính có hai lựa chọn 65
7.3. Trường hợp biến ịnh tính có nhiều lựa chọn 67
7.4. Tương tác với biến giả 69
7.5. Biến phụ thuộc nhị phân: Mô hình xác suất tuyến tính 71
7.6. Diễn giải kết quả hồi quy với biến phụ thuộc rời rạc 73 III
CHƯƠNG 8. PHƯƠNG SAI THAY ĐỔI 75
8.1. Hậu quả của phương sai thay ổi ối với OLS 75
8.2. Kiểm ịnh phương sai thay ổi 75
8.3. Xử lý khi có phương sai thay ổi 76
CHƯƠNG 9. MỘT SỐ VẤN ĐỀ MỞ RỘNG VỀ DẠNG HÀM VÀ DỮ LIỆU 79
9.1. Vấn ề xác ịnh sai dạng hàm 79
9.2. Sử dụng biến ại diện cho các biến giải thích không quan sát ược 81
9.3. Mô hình với hệ số góc ngẫu nhiên 83
9.4. Các tính chất của OLS khi có sai số trong o lường 84
9.5. Dữ liệu bị khuyết , mẫu phi ngẫu nhiên 85
Chương 1. BẢN CHẤT CỦA KINH TẾ LƯỢNG VÀ DỮ LIỆU KINH TẾ
Học xong chương 1 sinh viên cần nắm ược các kiến thức sau:
- Khái niệm kinh tế lượng, mục tiêu và các bước phân tích kinh tế lượng.
- Mô hình kinh tế và mô hình kinh tế lượng.
- Các loại dữ liệu kinh tế.
- Quan hệ nhân quả và khái niệm “các iều kiện khác không ổi”.
1.1 Kinh tế lượng là gì?
Kinh tế lượng là sử dụng các công cụ thống kê ể phân tích dữ liệu kinh tế.
Các mục tiêu ặc trưng của phân tích kinh tế lượng
• Ước lượng các mối quan hệ giữa các biến kinh tế.
• Kiểm ịnh các lý thuyết và các giả thuyết kinh tế.
• Dự báo các biến số kinh tế.
• Đánh giá hiệu quả thực thi chính sách của chính phủ và các quyết ịnh của người làm kinh doanh.
1.2 Các bước thực hiện phân tích kinh tế lượng
Bước 1: Xác ịnh vấn ề nghiên cứu.
Bước 2: Xác ịnh mô hình kinh tế.
Bước 3: Chuyển thành mô hình kinh tế lượng.
Bước 4: Thu thập dữ liệu liên quan.
Bước 5: Ước lượng mô hình.
Bước 6: Diễn giải kết quả.
Mô hình kinh tế
• Có thể là các mô hình kinh tế vi mô hoặc kinh tế vĩ mô.
• Thường sử dụng mô hình hành vi tối ưu, mô hình cân bằng,…
• Giúp thiết lập mối quan hệ giữa các biến số kinh tế. Ví dụ 1.1
y = f x x x x x x x( 1, 2, 3, 4, 5, 6, 7) Trong ó:
y = số giờ tiêu tốn cho các hoạt ộng phạm tội, x1 = số
tiền nhận ược cho 1 giờ thực hiện hoạt ộng phạm tội, x2 = tiền
lương mỗi giờ khi làm việc hợp pháp, x3 = thu nhập khác
ngoài hoạt ộng phạm tội hay việc làm chính, x4 = xác suất bị bắt,
x5 = xác suất bị kết án nếu bị bắt,
x6 = mức án dự kiến nếu bị kết án, x7 = tuổi. Ví dụ 1.2
wage = f educ exper training( , , ) Trong ó:
wage = tiền lương theo giờ,
educ = số năm i học chính thức,
exper = số năm kinh nghiệm lao ộng,
training = số tuần tham gia khóa huấn luyện.
Mô hình kinh tế lượng
• Dạng hàm phải ược xác ịnh trước.
• Các biến có thể phải xấp xỉ bởi các ại lượng khác.
Ví dụ 1.3 (tiếp theo Ví dụ 1.1)
crime = + 0 1wagem + 2othinc+ 3freqarr + 4 freqconv+ 5avgsen+ 6age
u+ Trong ó: crime = ại lượng o lường cho mức ộ hoạt ộng phạm tội, wagem = mức
lương có thể ạt ược khi làm việc hợp pháp, othinc = thu nhập từ các nguồn khác
(tài sản, thừa kế,…), freqarr = số lần bị bắt của các lần phạm tội trước ó, freqconv
= số lần bị kết án, avgsen = ộ dài trung bình của bản án nếu bị kết án, age = tuổi
Thành phần u chứa các yếu tố không quan sát ược, chẳng hạn như số
tiền nhận ược từ hoạt ộng phạm tội, tư cách ạo ức, nền tảng gia ình,…
Ví dụ 1.4 (tiếp theo Ví dụ 1.2)
wage = + 01educ+ 2exper + 3training +u Trong ó:
wage = tiền lương theo giờ,
educ = số năm i học chính thức,
exper = số năm kinh nghiệm lao ộng,
training = số tuần tham gia khóa huấn luyện,
Thành phần u chứa các yếu tố không quan sát ược, chẳng hạn như năng
lực bẩm sinh, chất lượng giáo dục, nền tảng gia ình,…
1.3 Cấu trúc của dữ liệu kinh tế
Các loại dữ liệu kinh tế
• Dữ liệu chéo (Cross-sectional data).
• Dữ liệu chuỗi thời gian (Time series data).
• Dữ liệu chéo gộp (Pooled cross-sectional data).
• Dữ liệu bảng/dữ liệu dọc (Panel data/longitudinal data).
1.3.1 Dữ liệu chéo
• Một tập dữ liệu chéo bao gồm 1 mẫu của các cá nhân, các hộ gia ình, các doanh
nghiệp, các tỉnh thành, các quốc gia, hay các ối tượng khác tại một thời iểm cụ
thể hoặc trong một khoảng thời gian ã cho (không nhất thiết trùng khớp hoàn toàn).
• Dữ liệu chéo thường giả ịnh thu ược bằng cách lấy mẫu ngẫu nhiên từ tổng thể
cần nghiên cứu. Do ó, các quan sát chéo thường ộc lập với nhau.
• Đôi khi việc lấy mẫu ngẫu nhiên bị vi phạm. Ví dụ: các ơn vị từ chối trả lời
trong các cuộc khảo sát, hay nếu việc lấy mẫu ược phân theo cụm.
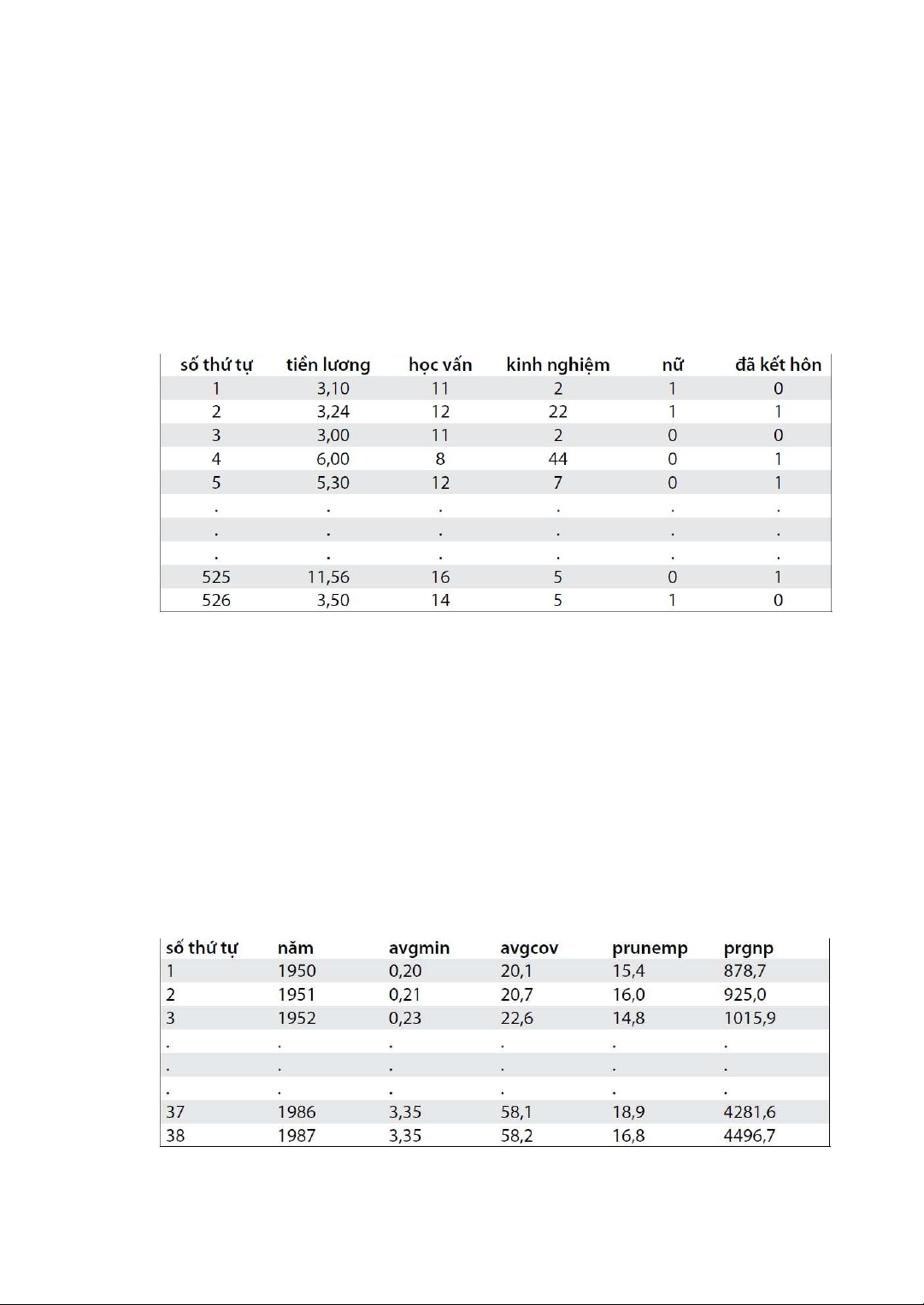
• Dữ liệu chéo thường gặp trong kinh tế vi mô ứng dụng. Ví dụ 1.5
Bảng sau chứa một tập dữ liệu chéo về 526 cá nhân làm việc trong năm 1976 (trong tập tin WAGE1.XLS)
1.3.2 Dữ liệu chuỗi thời gian
• Một tập dữ liệu chuỗi thời gian bao gồm các quan sát của một hay nhiều biến
theo thời gian. Ví dụ: giá chứng khoán, cung tiền, chỉ số giá tiêu dùng, tổng
sản phẩm trong nước, doanh số bán xe hơi,…
• Thứ tự của các quan sát cũng truyền tải những thông tin quan trọng.
• Các quan sát chuỗi thời gian thường gặp vấn ề tương quan chuỗi.
• Tần suất dữ liệu: hàng ngày, hàng tuần, hàng tháng, hàng quý, hàng năm,…
• Đặc iểm tiêu biểu của chuỗi thời gian: xu thế và thời vụ.
• Các ứng dụng thường gặp : Kinh tế vĩ mô và tài chính ứng dụng. Ví dụ 1.6
Bảng sau chứa một tập dữ liệu chuỗi thời gian về tác ộng của lương tối thiểu ở Puerto
Rico (từ Castillo-Freeman and Freeman (1992))
1.3.3 Dữ liệu chéo gộp
• Hai hay nhiều bộ dữ liệu chéo ược kết hợp thành một tập dữ liệu chéo gộp.
• Dữ liệu chéo gộp thường ược dùng ể ánh giá các thay ổi chính sách. Ví dụ 1.7
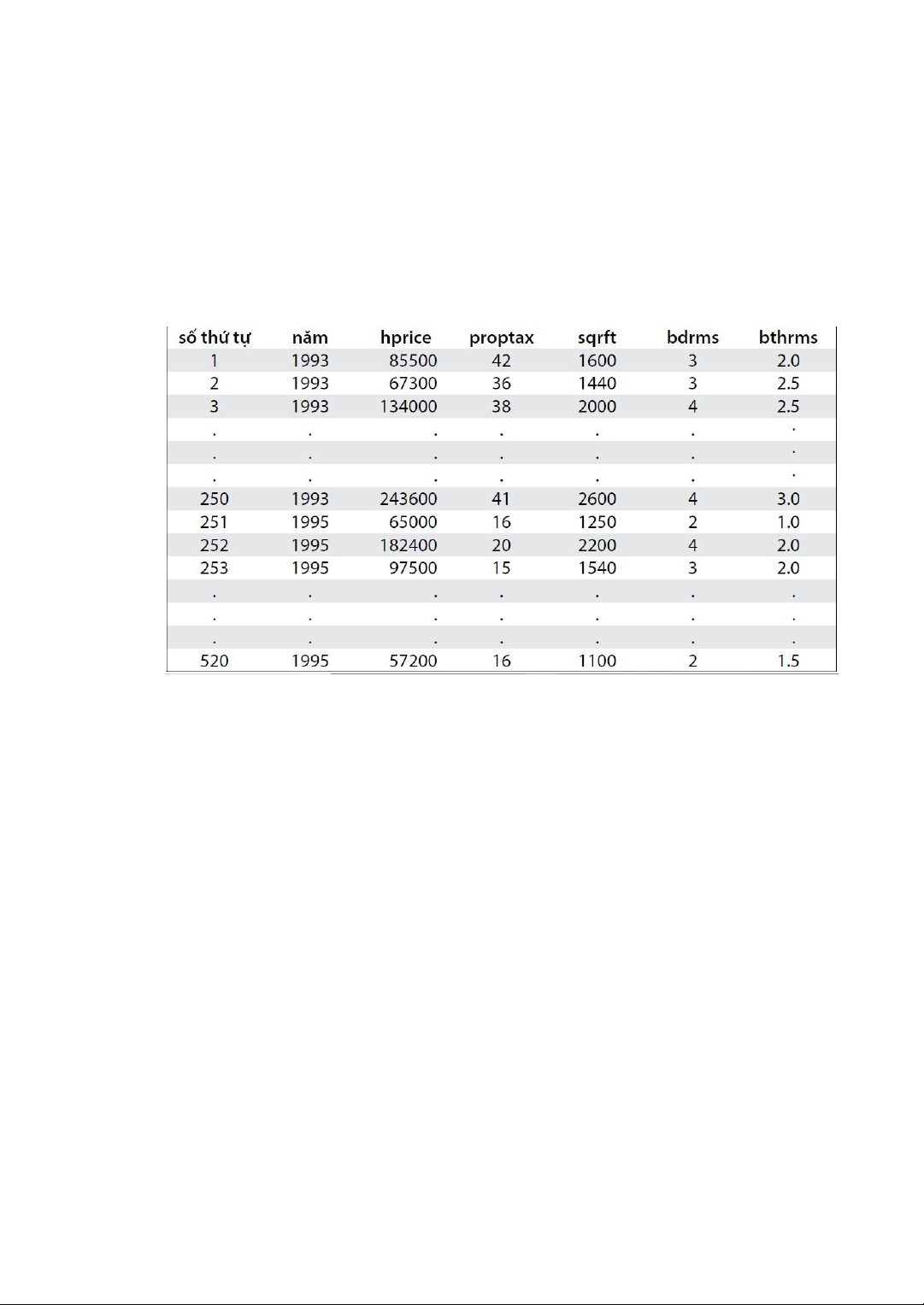
Bảng sau chứa tập dữ liệu dùng ể ánh giá tác ộng của thay ổi thuế tài sản lên giá nhà, gồm:
• Mẫu ngẫu nhiên về giá nhà trong năm 1993.
• Mẫu ngẫu nhiên khác của giá nhà trong năm 1995.
• So sánh trước/sau (1993: trước thay ổi, 1995: sau thay ổi).
1.3.4 Dữ liệu bảng (dữ liệu dọc)
• Cùng các ơn vị chéo ược quan sát theo thời gian.
• Dữ liệu bảng có chiều thời gian và chiều dữ liệu chéo.
• Dữ liệu bảng có thể ược dùng ể kiểm soát những yếu tố không quan sát ược
nhưng không ổi theo thời gian.
• Dữ liệu bảng có thể ược dùng ể lập mô hình trong trường hợp có biến trễ của biến phụ thuộc. Ví dụ 1.8
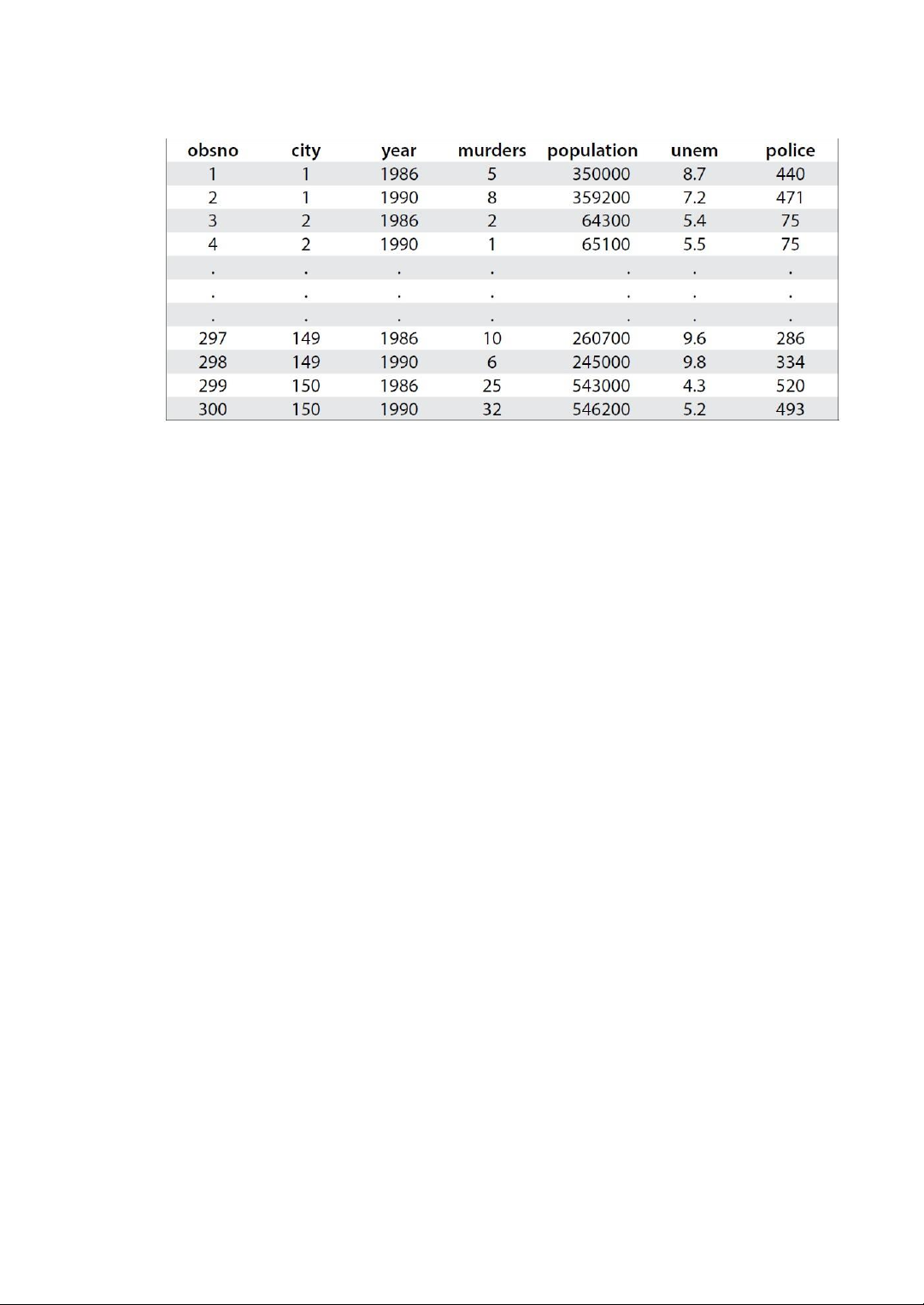
Bảng sau chứa dữ liệu bảng về tội phạm trong hai năm của 150 thành phố ở nước Mỹ
• Thống kê tội phạm trong thành phố; mỗi thành phố ược quan sát trong hai năm.
• Các ặc iểm không quan sát ược nhưng không thay ổi theo thời gian của
thành phố có thể ược kiểm soát trong mô hình.
• Tác ộng của cảnh sát ến tỷ lệ tội phạm có thể có tính trễ theo thời gian.
1.4 Quan hệ nhân quả và khái niệm về các iều kiện khác
không ổi trong kinh tế lượng
Tác ộng nhân quả của một biến x ến một biến y là cách thức biến y thay ổi khi
biến x thay ổi trong iều kiện các yếu tố khác không ổi. Khái niệm các yếu tố khác
không ổi có nghĩa là “các yếu tố khác có liên quan là như nhau, hay ược giữ nguyên”.
• Đa số các câu hỏi kinh tế là câu hỏi phân tích trong iều kiện các yếu tố khác không ổi.
• Điều quan trọng là xác ịnh tác ộng nhân quả nào mà người ta quan tâm.
• Cần thiết phải mô tả cách thiết kế một thí nghiệm ể có thể suy diễn ược về quan
hệ nhân quả mà câu hỏi nghiên cứu ặt ra. Ví dụ 1.9
Tác ộng của phân bón ến sản lượng cây trồng
• Câu hỏi: “Sản lượng ậu nành sẽ tăng lên bao nhiêu nếu tăng lượng phân bón cho ất?“
• Giả thiết ngầm: tất cả các yếu tố khác tác ộng ến năng suất cây trồng như
chất lượng ất, lượng mưa, sự hiện diện của ký sinh trùng,... ược giữ cố ịnh.
• Cách thí nghiệm: Chọn các thửa ất có diện tích một mẫu; gán ngẫu nhiên số
lượng phân bón khác nhau cho các thửa khác nhau; so sánh sản lượng.
• Cách thí nghiệm này áp dụng ược khi lượng phân bón sử dụng không liên
quan ến các yếu tố khác có tác ộng ến năng suất cây trồng.
Chương 2. MÔ HÌNH HỒI QUY ĐƠN
Học xong chương 2 sinh viên cần nắm ược các kiến thức sau:
- Mô hình hồi quy ơn: hàm hồi quy tổng thể và hồi quy mẫu, dạng xác ịnh và ngẫu nhiên.
- Phương pháp ước lượng bình phương bé nhất OLS.
- Các tính chất của ước lượng OLS. - Hệ số xác ịnh.
- Thay ổi ơn vị tính và các dạng hàm hồi quy thông dụng.
- Các giả thiết của mô hình và ịnh lý liên quan.
- Hồi quy qua gốc tọa ộ và hồi quy theo một hằng số.
2.1 Định nghĩa mô hình hồi quy ơn
Mô hình hồi quy tuyến tính ơn ứng với tổng thể có dạng sau:
Hàm hồi quy tổng thể dạng ngẫu nhiên (PRF ngẫu nhiên) y= + + (2.1) 0 1x u Với các giả ịnh E u( ) = 0 (2.2)
E u x( | ) =E u( ) thì ta có (2.3) E u x( | ) = 0 (2.4)
Lúc ó, ta có hàm hồi quy tổng thể dạng xác ịnh (PRF)
E y x( | ) = E( + + + (2.5) 0 1xu x| ) = E(
0 1x x| )+E u x( | ) = + 0 1x
Ứng với một mẫu cụ thể, hàm hồi quy mẫu tương ứng:
Hàm hồi quy mẫu dạng ngẫu nhiên (SRF ngẫu nhiên) y = + ˆ (2.6) 0ˆ1x+uˆ
Hàm hồi quy mẫu dạng xác ịnh (SRF) yˆ = + ˆ ˆ (2.7) 0 1x Trong ó:
y: biến phụ thuộc x: biến ộc lập
0, 1 : các hệ số hồi quy
1: hệ số góc (hệ số ộ dốc)
0 : hệ số chặn (hệ số tự do, tung ộ gốc)
u: sai số ngẫu nhiên, nhiễu uˆ : phần dư (thặng dư)
yˆ : là ước lượng của E(y/x)
ˆ0 , ˆ1 , uˆ là ước lượng của 0, 1, u
2.2 Phương pháp ước lượng bình phương bé nhất
Ta có nhiều phương pháp ể ước lượng β0, β1 từ hàm PRF, ví dụ như: phương pháp
bình phương bé nhất OLS, phương pháp ước lượng hợp lý cực ại, phương pháp mô
men. Chương này trình bày phương pháp ước lượng bình phương bé nhất.
Xét một mẫu ngẫu nhiên có cỡ mẫu n, {(x yi, i ),i =1,...,n}. Hàm hồi quy PRF ngẫu
nhiên ứng với quan sát thứ i là y = + + i 01xi ui (2.8)
Hàm hồi quy mẫu ứng với quan sát thứ i là
yˆi = + ˆ0ˆ1xi (2.9)
Sai số giữa giá trị thực tế y ˆ ˆ
i và giá trị ước lượng tính toán y i là u i : y ˆ i = +
ˆ0 1xi + = + = −uˆi yˆi uˆi uˆi yi yˆi (2.10)
Một hàm hồi quy mẫu ược gọi là “phù hợp tốt” với mẫu khảo sát sai số uˆi có giá
trị tuyệt ối nhỏ, với mọi i n uˆ 2i nhỏ i=1 Ta mong muốn n uˆ 2 2
i càng nhỏ càng tốt, tức là n uˆi min i=1 i=1 Ta xét: f ( ˆ 2 0 , ˆ1) =
n uˆi = n (yi − − ˆ0 ˆ1xi )2 min i=1 i=1 Lấy ạo hàm riêng: f ˆ' = n 2(y x 0 i − −
ˆ0ˆ1xi )( 1)− = 0 n ˆ0 + ˆ1 i = yi (2.11) i=1 f ˆ' = n 2(y x 2 = x y 1 i − −
ˆ0ˆ1xi )(− =xi )0 ˆ0 i + ˆ1xi i i (2.12) i=1 Giải hệ trên ta ược
ˆ1 = ( xi −( xi −)(xyi)2− y) (2.13) x
ˆ0 = −yˆ1.x (2.14)
Giải thích ý nghĩa của 1:
y = + + 01x u = + y 1. x u
Với iều kiện “các yếu tố khác không ổi” ta có =u 0, do ó: = y 1. x (2.15) Ví dụ 2.1
Tiền lương và học vấn wage = + 0 1educ+u
(2.16) Sử dụng dữ liệu trong tập tin WAGE1.XLS ta có kết quả
wage =−0,90+0,54educ (2.17)
Vậy nếu số năm i học tăng lên 1 (năm) thì tiền lương tăng lên 0,54 (USD/giờ), trong
iều kiện các yếu tố khác cố ịnh.
Cách nói khác: Vậy nếu số năm i học tăng lên 2 (năm) thì tiền lương tăng lên 0,54*2
= 1,08 (USD/giờ), trong iều kiện các yếu tố khác cố ịnh.
Giá trị -0,90 không có ý nghĩa trong thực tế. Ví dụ 2.2
Trọng lượng trẻ sơ sinh và sự hút thuốc lá của người mẹ mang thai
bwght = + 01cigs+u (2.18)
Sử dụng dữ liệu trong tập tin BWGHT.XLS ta có kết quả
bwght =119,77−0,514cigs (2.19)
Vậy nếu số iếu thuốc lá trung bình bà mẹ mang thai hút mỗi ngày tăng lên 1 ( iếu) thì
trọng lượng trẻ sơ sinh giảm xuống 0,514 (ounce), trong iều kiện các yếu tố khác cố ịnh.
Vậy nếu bà mẹ mang thai không hút thuốc lá thì trọng lượng trẻ sơ sinh là 119,77 ounce.
2.3 Các tính chất của OLS trên mẫu dữ liệu bất kỳ
Tính chất ại số của các thống kê OLS
1) Trung bình mẫu của các phần dư luôn bằng 0 uˆi = 0 (2.20)
2) Hiệp phương sai mẫu giữa biến ộc lập x và phần dư uˆ luôn bằng 0 x ui.ˆi = 0 (2.21)
3) Hiệp phương sai mẫu giữa giá trị ước lượng yˆ và phần dư uˆ luôn bằng 0
y uˆ ˆi. i = 0 (2.22)
4) Hàm hồi quy mẫu luôn i qua iểm ứng với giá trị trung bình (x y, ) (2.23)
5) Với biến phụ thuộc, trung bình thực tế luôn bằng trung bình ước lượng y y= ˆ (2.24)
Mức ộ phù hợp của mô hình Định nghĩa các tổng:
SST = (yi − y)2 (2.25)
SST: tổng bình phương toàn phần, SST cho biết tổng mức ộ biến ộng trong mẫu của yi
SSE = (yˆi − y)2
(2.26) SSE: tổng bình
phương hồi quy, SSE cho biết tổng mức ộ biến ộng của ˆ y i SSR = (y 2
i − yˆi )2 = uˆi (2.27)
SSE: tổng bình phương phần dư, SSR cho biết tổng mức ộ biến ộng của ˆ u i Lưu ý:
Một số sách viết TSS thay cho SST, tương tự cho 2 ký hiệu còn lại
Ứng với một mẫu cho trước, ta có: SST là cố ịnh
SSE và SSR thay ổi theo dạng hàm ta chọn, tuy nhiên ta có kết quả (xem chứng minh trong sách):
SST = SSE + SSR (2.28)
Chia 2 vế cho SST cố ịnh: 1= SSE SSR+ (2.29) SST SST
Một hàm hồi quy mẫu ược gọi là “phù hợp tốt” với mẫu khảo sát sai số uˆi
n có giá trị tuyệt ối nhỏ, với mọi i uˆ 2i
nhỏ SSR nhỏ SSE lớn tỷ số i=1 SSE/SST lớn Định nghĩa:
R2 = SSE = −1 SSR (2.30) SST SST
R2 gọi là hệ số xác ịnh
Vậy hàm hồi quy mẫu phù hợp tốt với mẫu khảo sát khi R2 lớn Lưu ý: SSE= (y yˆ 2 i − )2 = ˆ1 . (x xi − )2 (2.31)
R2 = (ry y, ˆ )2 (2.32)
trong ó ry y, ˆ là hệ số tương quan tuyến tính giữa y và yˆ Tính chất: 0 R2 1 (2.33)
Ta xét một vài trường hợp ặc biệt:
R2 =1 : ta suy ra y i
yˆi, i , tất cả sự thay ổi của y ều ược giải thích bởi hàm SRF, hàm
SRF gọi là phù hợp “hoàn hảo”. ˆ
R2 = 0 : ta suy ra y i
y, i , tất cả sự thay ổi của y ều không ược giải thích bởi hàm
SRF, hàm SRF gọi là không phù hợp.
2.4 Vấn ề ơn vị o của biến và dạng hàm
2.4.1 Thay ổi ơn vị o của các biến Mô hình hồi quy y = + + 0 1x u (2.34)
Bây giờ y với ơn vị o mới là y*, x với ơn vị o mới là x*. Hàm hồi quy với ơn vị o mới y*= + * * 0 1 x*+u* (2.35)
Mối liên hệ giữa ơn vị o cũ và mới của các biến là: y* = k0.y và x* = k1.x (2.36)
Mối liên hệ giữa ơn vị o cũ và mới của các hệ số hồi quy là: = k * * 0 0 =k0. 0 (2.37) 1 1 (2.38) k1 Lưu ý:
Hệ số xác ịnh R2 không phụ thuộc vào ơn vị o của x và y.
2.4.2 Các dạng hàm hồi quy 2 biến thông dụng
Ta có bảng các mô hình hồi quy 2 biến thông dụng ở trang sau: Ví dụ 2.3
Khảo sát thời gian ngủ ban êm theo thời gian làm việc, tập tin SLEEP75.XLS.
sleep: thời gian ngủ vào ban êm (phút/tuần) totwrk:
thời gian làm việc (phút/tuần)
Hàm hồi quy mẫu trong các dạng hàm thông dụng và ý nghĩa của hệ số góc:
1)sleep =3586,377 −0,1507totwrk
Khi thời gian làm việc tăng lên 1 phút/tuần thì thời gian ngủ ban êm giảm 0,1507
phút/tuần, với các yếu tố khác cố ịnh
2) sleep =5022,8−232,6log(totwrk)
Khi thời gian làm việc tăng lên 1 % thì thời gian ngủ ban êm giảm 232,6/100 =
2,326 phút/tuần, với các yếu tố khác cố ịnh
3) log(sleep) =8,184−4,867 10 −5totwrk
Khi thời gian làm việc tăng lên 1 phút/tuần thì thời gian ngủ ban êm giảm
(4,867 10 ) 100 −5 = 4,867 10 −3 %, với các yếu tố khác cố ịnh
4) log(sleep) =8,6375−0,0737log(totwrk)
Khi thời gian làm việc tăng lên 1 % thì thời gian ngủ ban êm giảm 0,0737 %, với các yếu tố khác cố ịnh Tên Dạng hàm
Biên tế Dẫn xuất từ biên tế Hệ số Ý nghĩa gọi co giãn của hệ số góc
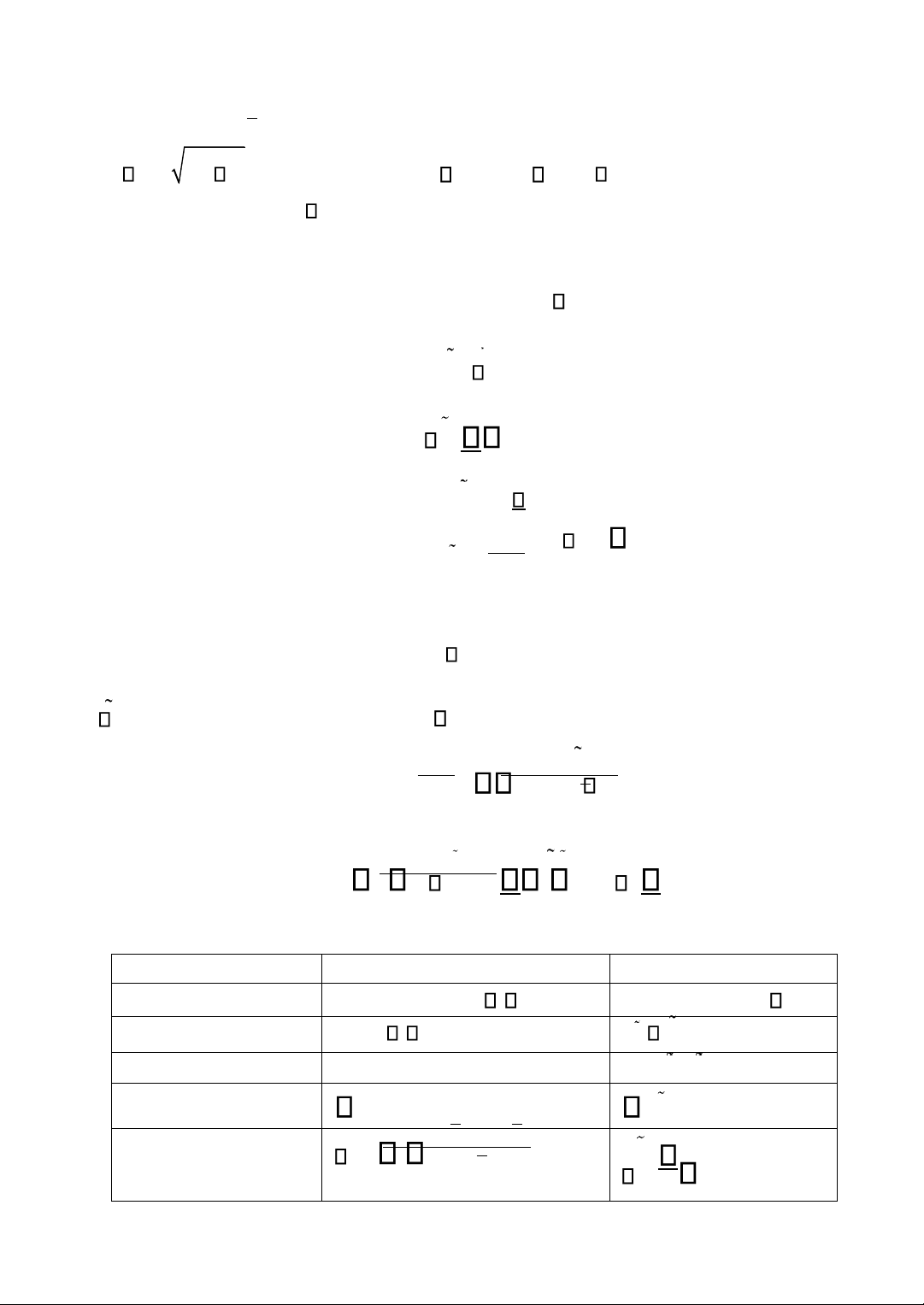
Tuyến y = + 0 1x β1 =y ( 1)( x)
β1 .(x/y) Khi x tính- tăng 1 Tuyến ơn vị tính thì y thay ổi β1 ơn vị
Tuyến y = + 0 1 log( )x β1 (1/x) =y ( 1 /100)(100 x x/ ) β1 .(1/y) Khi x tính - tăng 1 % log thì y thay ổi (β1 /100) ơn vị Log -
log( )y = + 0 1x β1 (y)
100 y y/ = (100 1)( x) β1 .(x) Khi x Tuyến tăng 1 tính ơn vị thì y thay ổi (100β1) % Log -
log( )y = + 0 1 l og( )β1x 100 y y/ = ( 1)(100 x x/ ) β1 Khi x Log (y/x) tăng 1% thì y thay ổi β1 % Lưu ý:
Mô hình Log-Log còn gọi là mô hình hệ số co giãn không ổi.
2.5 Giá trị kỳ vọng và phương sai của ước lượng OLS Hàm hồi quy tổng thể y = + + 0 1x u
Với giả ịnh E u x( | ) = 0
ˆ0 , ˆ1 là ước lượng của β0, β1 theo phương pháp OLS.
Với mẫu ngẫu nhiên thì ˆ0 , ˆ1 là các biến ngẫu nhiên. Ta khảo sát tính chất của phân phối của ˆ0 , ˆ1.
Tính không chệch của OLS.
Ta có các giả thiết sau:
Giả thiết SLR1. Tuyến tính theo tham số Mô hình hồi quy y = + + 0 1x u Trong ó:
y, x là biến số β0, β1 là tham số
Mô hình hồi quy ược gọi là tuyến tính khi tuyến tính theo tham số. Không có ràng
buộc về dạng xuất hiện của y và x trong mô hình.
Giả thiết SLR2. Mẫu ngẫu nhiên
Mẫu ược chọn là mẫu ngẫu nhiên ại diện cho tổng thể.
Giả thiết SLR3. Sự biến ộng trong mẫu của biến ộc lập
Các giá trị của x trong mẫu cụ thể không ược nhận cùng 1 giá trị. Điều này là cần thiết
ể cho công thức sau có nghĩa
ˆ1 = ( xi −x)(yi 2− y) (xi −x)
Giả thiết SLR4. Trung bình có iều kiện bằng 0 E u x( | ) = 0
Giả thiết này có nghĩa là biến ộc lập x và nhiễu u không có tương quan nhau ở bất cứ dạng hàm nào.
Định lý 2.1 Tính không chệch của ước lượng OLS Dưới
các giả thiết SLR1-4, thì
E( ˆ0 ) = 0 và E( ˆ1) = 1 (2.39)
Tính không chệch sẽ không còn úng nữa nếu bất kỳ giả thiết nào trong 4 giả thiết trên
bị vi phạm. Giả thiết quan trọng nhất là SLR4. Nếu u chứa các yếu tố ảnh hưởng ến
y mà các yếu tố này có tương quan với x thì u và x có tương quan với nhau. Ví dụ 2.6
Mô hình hồi quy tiền lương theo số năm i học
wage = + 01educ u+
Trong u có chứa các yếu tố có tương quan với educ, ví dụ như năng lực (ability). Do
ó u và educ có tương quan với nhau, dẫn ến ước lượng hệ số hồi quy bị chệch.
Phương sai của ước lượng OLS
Để xác ịnh ộ biến ộng của các giá trị ước lượng ˆ0 , ˆ1 qua các mẫu khác nhau, ta
cần tính phương sai var( ˆ0), var( ˆ1). Do ó ta cần giả thiết thứ 5.
Giả thiết SLR5. Phương sai thuần nhất (phương sai không ổi) var(u x| ) = 2 (2.40) Lưu ý: Nếu ta có var(u 2 i | xi ) =
i thì gọi là phương sai không thuần nhất (phương sai thay ổi)
Giả thiết SLR5 trong thực tế có thể sai, ví dụ sự biến ộng trong chi tiêu giữa nhóm
người có thu nhập thấp và thu nhập cao sẽ khác nhau, sự biến ộng trong tiền lương
giữa nhóm người có học vấn thấp và học vấn cao sẽ khác nhau. Định lý 2.2
Dưới các giả thiết SLR1-5, ta có công thức phương sai var( ˆ1) = 2 2 = 2 (2.41) (x xi − ) SSTx ˆ ) = ( i 2 2 . xi2 (2.42) var( 0 − x) n x
Ước lượng phương sai của sai số Ta
có 2 ước lượng của 2 là 2 = SSR (2.43) n ˆ2 =
SSR (2 là số tham số của mô hình hồi quy ơn) (2.44) n−2
Ta có 2 là ước lượng chệch của 2, còn ˆ2 là ước lượng không chệch của 2.
Định lý 2.3 Ước lượng không chệch của 2 Ta có: E( ˆ2) = 2 (2.45) ˆ = ˆ 2 (2.46)
ˆ gọi là sai số chuẩn hồi quy (SER) Lưu ý:
Với ˆ2 là ước lượng của 2
var( ˆ1) = ( ˆi 2− )2 là ước lượng của var( ˆ1) = ( x xi 2− )2 x x
se( ˆ1) = var( ˆ1) là ước lượng của sd( ˆ1) = var( ˆ1) se( ˆ1)
gọi là sai số chuẩn của ˆ1
2.6 Hồi quy qua gốc tọa ộ
Hàm PRF của hồi quy qua gốc tọa ộ: E y x( | ) = 1x
Hàm SRF của hồi quy qua gốc tọa ộ: y= 1x
Dùng phương pháp OLS, ta có công thức tính như sau: i 1 = x yi 2 (2.47) xi 2 = var( 1) 2 (2.48) xi 2 = SSR (2.49) n−1
2 là ước lượng không chệch của 2. Hệ số xác ịnh:
R2 = −1 SSR = −1
(y(iy−i − 1yx)i2)2 (2.50) SST
R2 có thể âm, do ó có thể ịnh nghĩa lại R2 như sau
R2 = −1 (y i − 21xi )2 =
yii22 = 12 2xi2 (2.51) yi y yi
So sánh hồi quy không qua gốc tọa ộ và hồi quy qua gốc tọa ộ
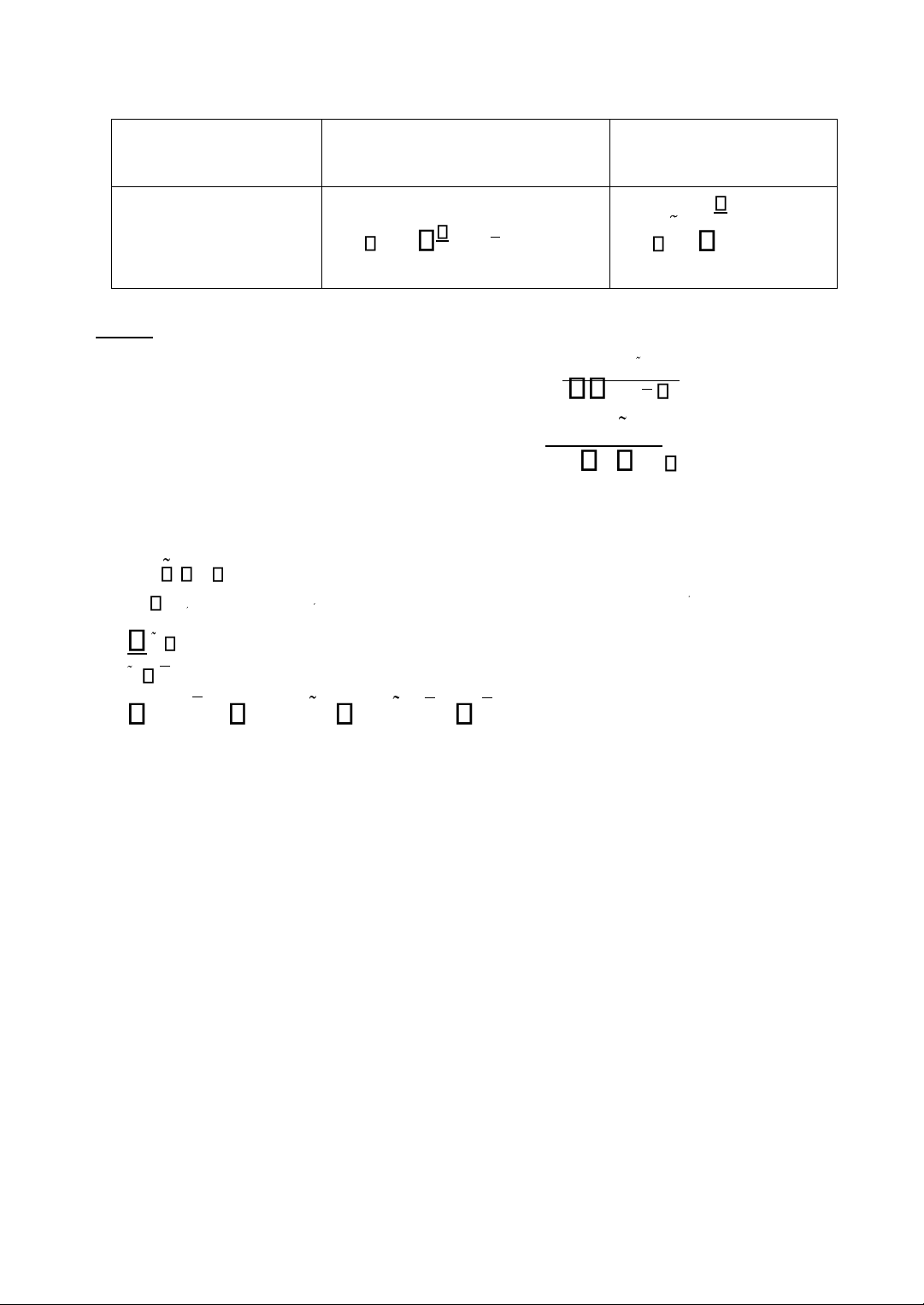
Hồi quy không qua gốc tọa ộ Hồi quy qua gốc tọa ộ Hàm PRF E y x( |) = + 0 1x E y x( | ) = 1x Hàm SRF
yˆ = + ˆ0 ˆ1x y= 1x
Hàm SRF ngẫu nhiên y y u= +ˆ ˆ y y u= + Phương pháp OLS uˆ 2 2 i → min ui → min Kết quả
ˆ1 = ( xi −xi −)(xyi)2− y) (x 1 = x yi 2i xi 2 var( ˆ1) = i 2− )2 var( 1) = 2 (x x xi Lưu ý: (
1) Trong phần mềm Eviews dùng công thức R2 = −1
y(iy−i 1xi2)2 −y) 2 = −1 (y i − 1 2 xi )2
Trong phần mềm R, Stata dùng công thức R yi 2) var( 1) var( ˆ1) 3) R2 r 2 2
y y , , trong ó ry y , là hệ số tương quan tuyến tính của y và y 4) ui 0 5) y y 6)
(yi − y)2 = (yi − yi )2 + (yi − y)2 −2y ui
Chương 3. PHÂN TÍCH HỒI QUY BỘI:
VẤN ĐỀ ƯỚC LƯỢNG
Học xong chương 3 sinh viên cần nắm ược các kiến thức sau:
- Phương pháp OLS và các tính chất cơ bản áp dụng cho mô hình hồi quy bội. - Ý
nghĩa riêng phần trong hồi quy bội.
- Hệ số xác ịnh: Số o mức ộ phù hợp của mô hình.
- Các giả thiết Gauss – Markov và tính chất BLUE của ước lượng OLS.
- Vấn ề ịnh dạng thừa mô hình và chệch do bỏ sót biến. - Vấn ề a cộng tuyến.
3.1 Sự cần thiết của mô hình hồi quy bội
• Việc có nhiều biến ộc lập/biến giải thích trong mô hình sẽ giải thích tốt hơn
cho sự biến ộng của biến phụ thuộc.
• Phân tích ược tác ộng riêng phần của từng biến ộc lập lên biến phụ thuộc, khi
giữ nguyên các biến/yếu tố khác không ổi.
• Mô hình hồi quy bội cho phép giữ nguyên giá trị của các biến ộc lập khác
không ổi, ngay cả khi trong thực tế các biến ộc lập này có thể tương quan với nhau.
• Lý tưởng thì trong mô hình hồi quy bội ta có sai số u ộc lập với các biến giải
thích, hay ít ra thì u không tương quan với các biến giải thích ể ạt ược phân
tích trong iều kiện các biến/yếu tố khác không ổi.
3.2 Mô hình hồi quy tuyến tính bội và phương pháp bình
phương bé nhất thông thường (OLS)
Xét hàm hồi quy tổng thể (PRF = Population Regression Function):
y = + 01 1x + + k xk +u Trong ó:
y là biến phụ thuộc/biến ược giải thích/biến phản ứng/biến ược dự báo/biến ược hồi quy.
x1, x2,…, xk là các biến ộc lập/biến giải thích/biến kiểm soát/biến dự báo/biến hồi quy.
u là sai số ngẫu nhiên hay nhiễu, biểu thị cho các biến chưa ược kiểm soát, tức là các
biến chưa ược liệt kê trong mô hình, và những biến/yếu tố không quan sát ược.
Ta có mẫu ngẫu nhiên kích thước n:
(y xi, i1,...,xik ),i =1,2,...,n (Các dãy số liệu chéo)
Tức là, mẫu ược chọn ngẫu nhiên theo phương thức lấy có hoàn lại; Nên các
(y xi, i1,...,xik ) là những véctơ ngẫu nhiên, ộc lập với nhau và có cùng phân phối xác
suất như véctơ ngẫu nhiên tổng thể (y x, 1,...,xk )
Các yi là những biến ngẫu nhiên ộc lập với nhau và có cùng phân phối xác xuất như
tổng thể y; Các xi1 là những biến ngẫu nhiên ộc lập với nhau và có cùng phân phối
xác xuất như tổng thể x1; Các xi2 là những biến ngẫu nhiên ộc lập với nhau và có cùng