Bài tập phương trình đường thẳng nâng cao Toán 12

Bài tập phương trình đường thẳng nâng cao Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

32 16 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Phương pháp tọa độ trong không gian

Môn: Toán 12

Thông tin:

62 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
PHƯƠNG TRÌNH ĐƯỜNG THẲNG NÂNG CAO
Câu 1: [2H3-3.2-3] Trong không gian với hệ tọa độ
Oxyz
, viết phương trình đường vuông góc chung
của hai đường thẳng
2 3 4
:
2 3 5
x y z
d
và
1 4 4
:
3 2 1
x y z
d
.
A.
1
1 1 1
x y z
. B.
2 2 3
2 3 4
x y z
.
C.
2 2 3
2 2 2
x y z
. D.
2 3
2 3 1
x y z
.
Câu 2: [2H3-3.2-3] Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
: 2 4 0
P x y z
và
đường thẳng
:
x y z
d
. Viết phương trình đường thẳng
nằm trong mặt phẳng
P
, đồng thời cắt và vuông góc với đường thẳng
d
.
A.
1 1 1
5 1 3
x y z
. B.
1 1 1
5 1 3
x y z
.
C.
1 1 1
5 1 2
x y z
. D.
1 3 1
5 1 3
x y z
.
Câu 3: [2H3-3.2-3] Trong không gian
Oxyz
, cho hai đường thẳng
1
3 3 2
:
1 2 1
x y z
d
;
2
5 1 2
:
3 2 1
x y z
d
và mặt phẳng
: 2 3 5 0
P x y z
. Đường thẳng vuông góc với
P
,
cắt
1
d
và
2
d
có phương trình là
A.
1 1
1 2 3
x y z
. B.
2 3 1
1 2 3
x y z
.
C.
3 3 2
1 2 3
x y z
. D.
1 1
3 2 1
x y z
.
Câu 4: [2H3-3.2-3] Phương trình đường thẳng song song với đường thẳng
1 2
:
1 1 1
x y z
d
và cắt
hai đường thẳng
1
1 1 2
:
2 1 1
x y z
d
;
2
1 2 3
:
1 1 3
x y z
d
là:
A.
x y z
. B.
1 1
1 1 1
x y z
.
C.
1 2 3
1 1 1
x y z
. D.
1 1
1 1 1
x y z
.
Câu 5: [2H3-3.2-3] Trong không gian
Oxyz
, cho ba điểm
1;1;1
A
,
1;2;0
B
,
2; 3;2
C
. Tập hợp
tất cả các điểm
M
cách đều ba điểm
A
,
B
,
C
là một đường thẳng
d
. Phương trình tham số
của đường thẳng
d
là:
A.
8 3
15 7
x t
y t
z t
. B.
8 3
15 7
x t
y t
z t
. C.
8 3
15 7
x t
y t
z t
. D.
8 3
15 7
x t
y t
z t
.
Câu 6: [2H3-3.2-3] Trong không gian cho đường thẳng
1 1 2
:
2 1 1
x y z
. Tìm hình chiếu vuông
góc của
trên mặt phẳng
Oxy
.
A.
0
1
0
x
y t
z
. B.
1 2
1
0
x t
y t
z
. C.
1 2
1
0
x t
y t
z
. D.
1 2
1
0
x t
y t
z
.
Câu 7: [2H3-3.2-3] Trong không gian với hệ tọa độ
Oxyz
, cho các điểm
2;0;0
A
;
0;3;0
B
;
0;0;4
C
. Gọi
H
là trực tâm tam giác
ABC
. Tìm phương trình tham số của đường thẳng
OH
.
A.
4
3
2
x t
y t
z t
. B.
3
4
2
x t
y t
z t
. C.
6
4
3
x t
y t
z t
. D.
4
3
2
x t
y t
z t
.
Câu 8: [2H3-3.2-3] Trong không gian
Oxyz
, cho ba đường thẳng
1
3 1 2
:
2 1 2
x y z
d
,
2
1 4
:
3 2 1
x y z
d
và
3
3 2
:
4 1 6
x y z
d
. Đường thẳng song song
3
d
, cắt
1
d
và
2
d
có
phương trình là
A.
3 1 2
4 1 6
x y z
. B.
3 1 2
4 1 6
x y z
.C.
1 4
4 1 6
x y z
. D.
1 4
4 1 6
x y z
.
Câu 9: [2H3-3.2-3] Trong không gian
Oxyz
, cho mặt phẳng
: 2 0
y z
và hai đường thẳng:
1
1
:
4
x t
d y t
z t
;
2
2
: 4 2
4
x t
d y t
z
. Đường thẳng
nằm trong mặt phẳng
và cắt hai đường
thẳng
1
d
;
2
d
có phương trình là
A.
1
7 8 4
x y z
. B.
1
7 8 4
x y z
. C.
1
7 8 4
x y z
. D.
1
7 8 4
x y z
.
Câu 10: [2H3-3.2-3] Trong không gian
Oxyz
, cho đường thẳng
1 2
:
1 1 1
x y z
d
và mặt phẳng
: 2 2 1 0
P x y z
. Đường thẳng nằm trong
P
, cắt và vuông góc với
d
có phương trình là
A.
2 1 3
3 4 1
x y z
. B.
2 1 3
3 4 1
x y z
.
C.
2 1 3
3 4 1
x y z
. D.
1 1 1
3 4 1
x y z
.
Câu 11: [2H3-3.2-3] Trong không gian với hệ tọa độ Descartes
Oxyz
, cho điểm
0; 1; 2
M
và hai
đường thẳng
1
1 2 3
:
1 1 2
x y z
d
,
2
1 4 2
:
2 1 4
x y z
d
. Phương trình đường thẳng đi qua
M
, cắt cả
1
d
và
2
d
là
A.
1 3
9 9
8
2 2
x y z
. B.
1 2
3 3 4
x y z
. C.
1 2
9 9 16
x y z
. D.
1 2
9 9 16
x y z
.
Câu 12: [2H3-3.2-3] Trong không gian
Oxyz
, cho ba đường thẳng
1
:
d
;
2
2 1
:
1 2 2
x y z
d
;
3
3 2 5
:
3 4 8
x y z
d
. Đường thẳng song song với
3
d
, cắt
1
d
và
2
d
có
phương trình là
A.
1 1
3 4 8
x y z
. B.
1 3
3 4 8
x y z
. C.
1 3
3 4 8
x y z
. D.
1 1
3 4 8
x y z
.
Câu 13: [2H3-3.2-3] Trong không gian với hệ trục tọa độ
Oxyz
, cho tam giác
ABC
biết điểm
1; 2; 3
A
, đường trung tuyến
BM
và đường cao
CH
có phương trình tương ứng là
5
0
1 4
x t
y
z t
và
4 2 3
16 13 5
x y z
. Viết phương trình đường phân giác góc
A
.
A.
1 2 3
7 1 10
x y z
. B.
1 2 3
4 13 5
x y z
.C.
1 2 3
2 3 1
x y z
.D.
1 2 3
2 11 5
x y z
.
Câu 14: [2H3-3.2-3] Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
d
:
3 2
2 1 3
x y z
và
mặt phẳng
P
:
2 6 0
x y z
. Đường thẳng nằm trong mặt phẳng
P
, cắt và vuông góc
với
d
có phương trình
A.
2 2 5
1 7 3
x y z
. B.
2 4 1
1 7 3
x y z
.
C.
2 2 5
1 7 3
x y z
. D.
2 4 1
1 7 3
x y z
.
Câu 15: [2H3-3.2-3] Trong không gian với hệ tọa độ
Oxyz
cho ba điểm
3; 2;4
A
,
5;3; 2
B
,
0;4;2
C
, đường thẳng
d
cách đều ba điểm
A
,
B
,
C
có phương trình là
A.
8
26
3
5
22
3
4
27
3
x t
y t
z t
. B.
4 26
2 22
9
27
4
x t
y t
z t
. C.
11
6
1
22
6
27
x
y t
z t
. D.
4 26
2 38
9
27
4
x t
y t
z t
.
Câu 16: [2H3-3.2-3] Trong không gian
Oxyz
, cho tam giác
ABC
với
3;0;0
A
,
0;6;0
B
,
0;0;6
C
.
Phương trình nào dưới đây là phương trình đường thẳng đi qua trực tâm của tam giác
ABC
và
vuông góc với mặt phẳng
ABC
.
A.
1 2 3
2 1 1
x y z
. B.
2 1 1
2 1 1
x y z
.C.
3 6 6
2 1 1
x y z
.D.
.
Câu 17: [2H3-3.2-3] Trong không gian
Oxyz
, cho hai điểm
2;1; 3
A
và
3;2;1
B
. Viết phương
trình đường thẳng
d
đi qua gốc toạ độ sao cho tổng khoảng cách từ
A
và
B
đến đường thẳng
d
lớn nhất.
A.
1 1 1
x y z
. B.
1 1 1
x y z
. C.
1 1 2
x y z
. D.
1 1 2
x y z
.
Câu 18: [2H3-3.2-3] Trong không gian
Oxyz
, cho hai đường thẳng cắt nhau
1
2
: 2 2
1
x t
y t
z t
,
2
1
:
2
x t
y t
z t
,t t
. Viết phương trình đường phân giác của góc nhọn tạo bởi
1
và
2
.
A.
1
2 3 3
x y z
. B.
1
1 1 1
x y z
. C.
1
2 3 3
x y z
. D.
1
1 1 1
x y z
.
Câu 19: [2H3-3.2-3] Trong không gian với hệ tọa độ
Oxyz
. Cho mặt phẳng
: 2 10 0,
P x y z
điểm
1;3;2
A
và đường thẳng
2 2
: 1
1
x t
d y t
z t
. Tìm phương trình đường thẳng
cắt
P
và
d
lần lượt tại hai điểm
M
và
N
sao cho
A
là trung điểm cạnh
MN
.
A.
6 1 3
7 4 1
x y z
. B.
6 1 3
7 4 1
x y z
.
C.
6 1 3
7 4 1
x y z
. D.
6 1 3
7 4 1
x y z
.
Câu 20: [2H3-3.2-3] Cho hai đường thẳng cắt nhau
1
2
: 2 2
1
x t
y t
z t
,
2
1
:
2
x t
y t
z t
,t t
. Viết
phương trình đường phân giác của góc nhọn tạo bởi
1
và
2
.
A.
1
2 3 3
x y z
. B.
1
1 1 1
x y z
. C.
1
2 3 3
x y z
. D. Cả A, B, C đều sai.
Câu 21: [2H3-3.2-3] Trong không gian
Oxyz
, Cho mặt phẳng
: 2 2 0
R x y z
và đường
thẳng
1
1
:
2 1 1
x y z
. Đường thẳng
2
nằm trong mặt phẳng
R
đồng thời cắt và vuông góc
với đường thẳng
1
có phương trình là
A.
3
1
x t
y t
z t
. B.
2
1
x t
y t
z t
. C.
2
1
x t
y t
z t
. D.
2 3
1
x t
y t
z t
.
Câu 22: [2H3-3.2-3] Trong không gian
Oxyz
, cho đường thẳng
1 3
: 1 4
1
x t
d y t
z
. Gọi
là đường thẳng đi
qua điểm
1;1;1
A
và có vectơ chỉ phương
1; 2;2
u
. Đường phân giác của góc nhọn tạo bởi
d
và
có phương trình là
A.
1 7
1
1 5
x t
y t
z t
. B.
1 2
10 11
6 5
x t
y t
z t
. C.
1 2
10 11
6 5
x t
y t
z t
. D.
1 3
1 4
1 5
x t
y t
z t
.
Câu 23: [2H3-3.2-3] Trong không gian
Oxyz
, cho đường thẳng
1 3
: 3
5 4
x t
d y
z t
. Gọi
là đường thẳng đi
qua điểm
1; 3;5
A
và có vectơ chỉ phương
1;2; 2
u . Đường phân giác của góc nhọn tạo bởi
d
và
có phương trình là
A.
1 2
2 5
6 11
x t
y t
z t
. B.
1 2
2 5
6 11
x t
y t
z t
. C.
1 7
3 5
5
x t
y t
z t
. D.
1
3
5 7
x t
y
z t
.
Câu 24: [2H3-3.2-3] Trong không gian
Oxyz
, cho đường thẳng
1
: 2 .
3
x t
d y t
z
Gọi
là đường thẳng đi
qua điểm
(1;2;3)
A
và có vectơ chỉ phương
(0; 7; 1).
u
Đường phân giác của góc nhọn tạo bởi
d
và
có phương trình là
A.
1 6
2 11 .
3 8
x t
y t
z t
B.
4 5
10 12 .
2
x t
y t
z t
C.
4 5
10 12 .
2
x t
y t
z t
D.
1 5
2 2 .
3
x t
y t
z t
Câu 25: [2H3-3.1-3] Trong không gian
,Oxyz
cho đường thẳng
2 1 2
:
4 4 3
x y z
d
và mặt phẳng
: 2 2 1 0
P x y z
. Đường thẳng
đi qua
2; 1; 2
E
, song song với
P
đồng thời tạo
với
d
góc bé nhất. Biết rằng
có một véctơ chỉ phương
; ; 1 .
u m n
Tính
2 2
T m n
.
A.
5
T
. B.
4T
. C.
3
T
. D.
4T
.
Câu 26: [2H3-3.1-3] Trong không gian với hệ tọa độ
Oxyz
, cho tam giác
ABC
có phương trình đường
phân giác trong góc
A
là:
6 6
1 4 3
x y z
. Biết rằng điểm
0;5;3
M
thuộc đường thẳng
AB
và điểm
1;1;0
N
thuộc đường thẳng
AC
. Vectơ nào sau đây là vectơ chỉ phương của đường
thẳng
AC
.
A.
1;2;3
u
. B.
0;1;3
u
. C.
0; 2;6
u
. D.
0;1; 3
u
.
Câu 27: [2H3-3.1-3] Cho
2
mặt cầu
2 2 2
1
: 3 2 2 4
S x y z
,
2 2
2
2
: 1 1 1
S x y z
.
Gọi
d
là đường thẳng đồng thời tiếp xúc với hai mặt cầu trên, cắt đoạn thẳng nối tâm hai mặt
cầu và cách gốc tọa độ
O
một khoảng lớn nhất. Nếu
; 1;u a b
là một vectơ chỉ phương của
d
thì tổng
2 3S a b
bằng bao nhiêu?
A.
2
S
. B.
1
S
. C.
0
S
. D.
4
S
.
Câu 28: [2H3-3.1-3] Trong không gian
Oxy
cho tam giác
ABC
có
2;3;3
A
, phương trình đường
trung tuyến kẻ từ
B
là
3 3 2
1 2 1
x y z
, phương trình đường phân giác trong góc
C
là
2 4 2
2 1 1
x y z
. Biết rằng
; ; 1
u m n
là một véc tơ chỉ phương của đường thẳng
AB
.
Tính giá trị biểu thức
2 2
T m n
.
A.
1T
. B.
5
T
. C.
2T
. D.
10
T
.
Câu 29: Suy ra
A B
2;5;1
B
0; 2;2
AB
2 0; 1;1
là một véc tơ của đường thẳng
AB
.
Vậy
2 2
2
T m n
.[2H3-3.1-3] Trong không gian với hệ toạ độ
Oxyz
, cho phương trình
đường phân giác trong của góc
A
là
6 6
1 4 3
x y z
. Biết
0;5;3
M
thuộc đường thẳng
AB
và
1;1;0
N
thuộc đường thẳng
AC
. Vector nào sau đây là vector chỉ phương của đường thẳng
AC
?
A.
0;1;3
u
. B.
0;1; 3
u
. C.
0; 2;6
u
. D.
1;2;3
u
.
Câu 30: [2H3-3.1-3] Trong không gian với hệ tọa độ
Oxyz
, cho hai đường thẳng
1
4 1 5
:
3 1 2
x y z
và
2
2 3
:
1 3 1
x y z
. Giả sử
1
M
,
2
N
sao cho
MN
là đoạn
vuông góc chung của hai đường thẳng
1
và
2
. Tính
MN
.
A.
5; 5;10
MN
. B.
2; 2;4
MN
. C.
3; 3;6
MN
. D.
1; 1;2
MN
.
Câu 31: [2H3-3.1-3] Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
:
2 1 1
x y z
d
, mặt
phẳng
: 2 5 0
P x y z
và
1; 1;2
A
. Đường thẳng
cắt
d
và
P
lần lượt tại
M
và
N
sao cho
A
là trung điểm của đoạn thẳng
MN
. Một vectơ chỉ phương của
là:
A.
2;3;2
u
. B.
1; 1; 2
u
. C.
3;5;1
u
. D.
4;5; 13
u
.
Câu 32: [2H3-3.1-4] Trong không gian
Oxyz
, cho tam giác
ABC
có
2;3;3
A
, phương trình đường
trung tuyến kẻ từ
B
là
3 3 2
1 2 1
x y z
, phương trình đường phân giác trong của góc
C
là
2 4 2
2 1 1
x y z
. Đường thẳng
AB
có một véc-tơ chỉ phương là
A.
3
2;1; 1
u
. B.
2
1; 1;0
u
. C.
4
0;1; 1
u
. D.
1
1;2;1
u
.
Câu 33: [2H3-3.1-4] Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
2; 2;1 ,
M
1;2; 3
A
và
đường thẳng
1 5
:
2 2 1
x y z
d
. Tìm một vectơ chỉ phương
u
của đường thẳng
đi qua
M
, vuông góc với đường thẳng
d
đồng thời cách điểm
A
một khoảng bé nhất.
A.
2;2; 1
u
. B.
1;7; 1
u
. C.
1;0;2
u
. D.
3;4; 4
u
.
Câu 34: [2H3-3.1-4] Trong không gian
Oxyz
, cho tam giác
ABC
có
2;3;3
A
, phương trình đường
trung tuyến kẻ từ
B
là
3 3 2
1 2 1
x y z
, phương trình đường phân giác trong của góc
C
là
2 4 2
2 1 1
x y z
. Đường thẳng
AB
có một véc-tơ chỉ phương là
A.
3
2;1; 1
u
. B.
2
1; 1;0
u
. C.
4
0;1; 1
u
. D.
1
1;2;1
u
.
Câu 35: [2H3-3.3-4] Trong không gian với hệ tọa độ
Oxyz
, cho tam giác
ABC
vuông tại
C
,
60
ABC
,
3 2,
AB
đường thẳng
AB
có phương trình
3 4 8
1 1 4
x y z
, đường thẳng
AC
nằm trên mặt phẳng
: 1 0
x z
. Biết
B
là điểm có hoành độ dương, gọi
; ;a b c
là
tọa độ điểm
C
, giá trị của
a b c
bằng
A.
3
. B.
2
. C.
4
. D.
7
.
Câu 36: [2H3-3.3-4] Trong không gian tọa độ
Oxyz
cho các điểm
1;5;0
A
,
3;3;6
B
và đường thẳng
1 1
:
2 1 2
x y z
. Gọi
; ;M a b c
sao cho chu vi tam giác
MAB
đạt giá trị nhỏ nhất. Tính
tổng
T a b c
?
A.
2T
. B.
3
T
. C.
4T
. D.
5
T
.
Câu 37: [2H3-3.3-4] Trong không gian với hệ tọa độ
Oxyz
cho ba điểm
2; 1;1
A
,
5;3;1
M
,
4;1;2
N
và mặt phẳng
: 27
P y z
. Biết rằng tồn tại điểm
B
trên tia
AM
, điểm
C
trên
P
và điểm
D
trên tia
AN
sao cho tứ giác
ABCD
là hình thoi. Tọa độ điểm
C
là
A.
15;21;6
. B.
21;21;6
. C.
15;7;20
. D.
21;19;8
.
Câu 38: [2H3-3.5-3] Trong không gian với hệ tọa độ
Oxyz
, cho
: 2 2 5 0
P x y z
,
3;0;1
A
,
1; 1;3
B
. Viết phương trình đường thẳng
d
đi qua
A
, song song với
P
sao cho khoảng
cách từ
B
đến
d
là lớn nhất.
A.
3 1
1 1 2
x y z
. B.
3 1
3 2 2
x y z
. C.
1 1
1 2 2
x y z
. D.
3 1
2 6 7
x y z
.
Câu 39: [2H3-3.5-3] Trong không gian
Oxyz
, cho mặt phẳng
: 2 2 2 0
x y z
, đường thẳng
1 2 3
:
1 2 2
x y z
d
và điểm
1
;1;1 .
2
A
Gọi
là đường thẳng nằm trong mặt phẳng
,
song song với
d
đồng thời cách
d
một khoảng bằng 3. Đường thẳng
cắt mặt phẳng
Oxy
tại điểm
.B
Độ dài đoạn thẳng
AB
bằng.
A.
7
2
. B.
21
2
. C.
7
3
. D.
3
2
.
Câu 40: [2H3-3.5-3] Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
đi qua gốc tọa độ
O
và
điểm
0;1;1
I
. Gọi
S
là tập hợp các điểm nằm trên mặt phẳng
Oxy
, cách đường thẳng
một khoảng bằng
6
. Tính diện tích hình phẳng giới hạn bởi
S
.
A.
36
. B.
36 2
. C.
18 2
. D.
18
.
Câu 41: [2H3-3.5-3]
Trong không gian với hệ trục toạ độ
Oxyz
, cho ba điểm
2;0;0
A
,
0;3;1
B
,
1;4;2
C
. Độ dài đường cao từ đỉnh
A
của tam giác
ABC
:
A.
6
. B.
2
. C.
3
2
. D.
3
.
Câu 42: [2H3-3.5-3] Trong không gian
Oxyz
cho mặt cầu
2 2 2
: 1 2 3 9
S x y z
và mặt
phẳng
:2 2 3 0
P x y z
. Gọi
; ;M a b c
là điểm trên mặt cầu sao cho khoảng cách từ
M
đến
P
lớn nhất. Khi đó:
A.
8
a b c
. B.
5
a b c
. C.
6
a b c
. D.
7
a b c
.
Câu 43: [2H3-3.5-3] Trong không gian
Oxyz
, cho hai điểm
2; 2;1
M
,
1;2; 3
A
và đường thẳng
1 5
:
2 2 1
x y z
d
. Tìm véctơ chỉ phương
u
của đường thẳng
đi qua
M
, vuông góc với
đường thẳng
d
, đồng thời cách điểm
A
một khoảng lớn nhất.
A.
4; 5; 2
u
. B.
1;0;2
u
. C.
8; 7;2
u
. D.
1;1; 4
u
.
Câu 44: [2H3-3.5-3] Trong không gian
Oxyz
cho hai đường thẳng
1
1
: 2
x
y t
z t
,
2
4
: 3 2
1
x t
y t
z t
. Gọi
S
là mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng
1
và
2
. Bán kính mặt
cầu
S
.
A.
10
2
. B.
11
2
. C.
3
2
. D.
2
.
Câu 45: [2H3-3.4-3] Trong không gian
Oxyz
cho tam giác
ABC
có
1;2; 1
A
,
2; 1;3
B
,
4;7;5
C
.
Tọa độ chân đường phân giác góc
ABC
của tam giác
ABC
là
A.
11
; 2;1
2
. B.
2 11 1
; ;
3 3 3
. C.
2;11;1
. D.
2 11
; ;1
3 3
.
Câu 46: [2H3-3.4-4] Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
2 2
2
: 1 2 4
S x y z
và đường thẳng
2
:
1
x t
d y t
z m t
. Gọi
T
là tập tất cả các giá trị của
m
để
d
cắt
S
tại hai
điểm phân biệt
A
,
B
sao cho các tiếp diện của
S
tại
A
và
B
tạo với nhau góc lớn nhất có
thể. Tính tổng các phần tử của tập hợp
T
.
A.
3
. B.
3
. C.
5
. D.
4
.
Câu 47: [2H3-3.6-3] Trong không gian với hệ tọa độ
,Oxyz
cho điểm
(0;1;2)
A
, mặt phẳng
( ) : 4 0
x y z
và mặt cầu
2 2 2
( ) : 3 1 2 16
S x y z
. Gọi
P
là mặt phẳng đi
qua
A
, vuông góc với
( )
và đồng thời
P
cắt mặt cầu
S
theo giao tuyến là một đường
tròn có bán kính nhỏ nhất. Tọa độ giao điểm
M
của
P
và trục
x Ox
là
A.
1
;0;0
2
M
. B.
1
;0;0
3
M
. C.
1;0;0
M
. D.
1
;0;0
3
M
.
Câu 48: [2H3-3.6-3] Trong không gian tọa độ
Oxyz
cho
1;1; 1
A
,
2;3;1
B
,
5;5;1
C
. Đường phân
giác trong góc
A
của tam giác
ABC
cắt mặt phẳng
Oxy
tại
; ;0M a b
. Tính
3
b a
.
A.
6
. B.
5
. C.
3
. D.
0
.
Câu 49: [2H3-3.6-3] Trong không gian với hệ trục tọa độ
Oxyz
, cho bốn đường thẳng:
1
3 1 1
:
1 2 1
x y z
d
,
2
1
:
1 2 1
x y z
d
,
3
1 1 1
:
2 1 1
x y z
d
,
4
1
:
1 1 1
x y z
d
. Số
đường thẳng trong không gian cắt cả bốn đường thẳng trên là:
A.
0
. B.
2
. C. Vô số. D.
1
.
Câu 50:
[2H3-3.6-3] Trong không gian
Oxyz
, cho bốn đường thẳng:
1
3 1 1
:
1 2 1
x y z
d
,
2
1
:
1 2 1
x y z
d
,
3
1 1 1
:
2 1 1
x y z
d
,
4
1 1
:
1 1 1
x y z
d
. Số đường thẳng trong
không gian cắt cả bốn đường thẳng trên là:
A.
0
. B.
2
. C. Vô số. D.
1
.
Câu 51: [2H3-3.6-3] Trong không gian
Oxyz
, cho đường thẳng
1 2 3
:
1 2 1
x y z
d
và mặt phẳng
: 2 0
x y z
. Trong các đường thẳng sau, đường thẳng nào nằm trong mặt phẳng
,
đồng thời vuông góc và cắt đường thẳng
d
?
A.
2
2 4 4
:
1 2 3
x y z
. B.
4
1 1
:
3 2 1
x y z
.
B.
3
5 2 5
:
3 2 1
x y z
. D.
1
2 4 4
:
3 2 1
x y z
.
Câu 52: [2H3-3.6-4] Trong không gian với hệ trục tọa độ
Oxyz
, cho bốn đường thẳng:
1
3 1 1
:
1 2 1
x y z
d
,
2
1
:
1 2 1
x y z
d
,
3
1 1 1
:
2 1 1
x y z
d
,
4
1
:
1 1 1
x y z
d
. Số đường
thẳng trong không gian cắt cả bốn đường thẳng trên là
A.
0
. B.
2
. C. Vô số. D.
1
.
Câu 53: [2H3-3.6-4] Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 3a
: 2
2 3a (1 )
x at
y t
x a t
.
Biết rằng khi
a
thay đổi luôn tồn tại một mặt cầu cố định qua điểm
1;1;1
M
và tiếp xúc với
đường thẳng
. Tìm bán kính mặt cầu đó.
A.
5 3
. B. 4
3
. C. 7
3
. D.
3 5
.
Câu 54: [2H3-3.6-4] Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
3 2 1
:
2 1 1
x y z
d
và
mặt phẳng
: 2 0
P x y z
. Đường thẳng
nằm trong mặt phẳng
P
, vuông góc với
đường thẳng
d
đồng thời khoảng cách từ giao điểm
I
của
d
với
P
đến
bằng
42
. Gọi
5; ;M b c
là hình chiếu vuông góc của
I
trên
. Giá trị của
bc
bằng
A.
10
. B.
10
. C.
12
. D.
20
.
Câu 55: [2H3-3.8-3] Trong không gian với hệ trục tọa độ
Oxyz
, cho hai điểm
2;1;1
A
,
0;3; 1
B
.
Điểm
M
nằm trên mặt phẳng
:2 4 0
P x y z
sao cho
MA MB
nhỏ nhất là
A.
1;0;2 .
B.
0;1;3 .
C.
1;2;0 .
D.
3;0;2 .
Câu 56: [2H3-3.8-3]
Trong không gian với hệ trục tọa độ
Oxyz
, cho ba điểm
0; 2; 1
A
,
2; 4;3
B
,
1;3; 1
C
và mặt phẳng
: 2 3 0
P x y z
. Tìm điểm
M P
sao cho
2
MA MB MC
đạt giá trị nhỏ nhất.
A.
1 1
; ; 1
2 2
M
. B.
1 1
; ;1
2 2
M
. C.
2;2; 4
M
. D.
2; 2;4
M
.
Câu 57: [2H3-3.8-3]
Trong không gian với hệ trục
Oxyz
, cho hai điểm
0; 1;2
M
,
1;1;3
N
. Một
mặt phẳng
P
đi qua
M
,
N
sao cho khoảng cách từ điểm
0;0;2
K
đến mặt phẳng
P
đạt
giá trị lớn nhất. Tìm tọa độ véctơ pháp tuyến
n
của mặt phẳng
P
.
1; 1;1
n
. B.
1;1; 1
n
. C.
2; 1;1
n
. D.
2;1; 1
n
.
Câu 58: [2H3-3.8-3] Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;2; 3
A
và mặt phẳng
: 2 2 9 0
P x y z
. Đường thẳng
d
đi qua
A
và có vectơ chỉ phương
3;4; 4
u
cắt
P
tại
B
. Điểm
M
thay đổi trong
P
sao cho
M
luôn nhìn đoạn
AB
dưới góc
o
90
. Khi độ dài
MB
lớn nhất, đường thẳng
MB
đi qua điểm nào trong các điểm sau?
A.
2; 1;3
H
. B.
1; 2;3
I
. C.
3;0;15
K
. D.
3;2;7
J
.
Câu 59: [2H3-3.8-3] Trong không gian
Oxyz
, cho hai điểm
1;2;1
A
,
1;2; 3
B
và đường thẳng
1 5
:
2 2 1
x y z
d
. Tìm vectơ chỉ phương
u
của đường thẳng
đi qua điểm
A
và vuông góc
với
d
đồng thời cách
B
một khoảng lớn nhất.
A.
4; 3;2
u
. B.
2;0; 4
u
. C.
2;2; 1
u
. D.
1;0;2
u
.
Câu 60: [2H3-3.8-3] Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
: 2 1 0
P x y z
và
điểm
0; 2;3
A
,
2;0;1
B
. Điểm
; ;M a b c
thuộc
P
sao cho
MA MB
nhỏ nhất. Giá trị của
2 2 2
a b c
bằng
A.
41
4
. B.
9
4
. C.
7
4
. D.
3
.
Câu 61: [2H3-3.8-3] Trong không gian với hệ toạ độ
Oxyz
, cho hai điểm
2; 3;2
A
,
3;5;4
B
. Tìm
toạ độ điểm
M
trên trục
Oz
so cho
2 2
MA MB
đạt giá trị nhỏ nhất.
A.
0;0;49
M
. B.
0;0;67
M
. C.
0;0;3
M
. D.
0;0;0
M
.
Câu 62:
[2H3-3.8-3] Trong không gian
Oxyz
, cho bốn đường thẳng:
1
3 1 1
:
1 2 1
x y z
d
,
2
1
:
1 2 1
x y z
d
,
3
1 1 1
:
2 1 1
x y z
d
,
4
1 1
:
1 1 1
x y z
d
. Số đường thẳng trong không
gian cắt cả bốn đường thẳng trên là
A.
0
. B.
2
. C. Vô số. D.
1
.
Câu 63: [2H3-3.8-3] Trong không gian với hệ trục toạ độ
Oxyz
, cho mặt cầu
2 2 2
: 1 2 3 9
S x y z
, điểm
0; 0; 2
A
. Phương trình mặt phẳng
P
đi qua
A
và
cắt mặt cầu
S
theo thiết diện là hình tròn
C
có diện tích nhỏ nhất là
A.
: 2 3 6 0
P x y z
. B.
: 2 2 0
P x y z
.
C.
: 2 6 0
P x y z
. D.
:3 2 2 4 0
P x y z
.
Câu 64: [2H3-3.8-3] Trong không gian với hệ tọa độ
Oxyz
cho các điểm
4;2;5
A
,
0;4; 3
B
,
2; 3;7
C
. Biết điểm
0 0 0
; ;M x y z
nằm trên mặt phẳng
Oxy
sao cho
MA MB MC
đạt giá
trị nhỏ nhất. Tính tổng
0 0 0
P x y z
.
A.
3
P
. B.
0
P
. C.
3
P
. D.
6
P
.
Câu 65: [2H3-3.8-3] Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
:
x y z
và hai
điểm
0; 1;3
A
,
1; 2;1
B
. Tìm tọa độ điểm
M
thuộc đường thẳng
sao cho
2 2
2MA MB
đạt giá trị nhỏ nhất.
A.
5;2; 4
M
. B.
1; 1; 1
M
. C.
1;0; 2
M
. D.
3;1; 3
M
.
Câu 66: [2H3-3.8-3] Trong không gian
Oxyz
, cho điểm
1 3
; ;0
2 2
M
và mặt cầu
2 2 2
: 8
S x y z
.
Một đường thẳng đi qua điểm
M
và cắt
S
tại hai điểm phân biệt
A
,
B
. Diện tích lớn nhất
của tam giác
OAB
bằng
A.
4
. B.
2 7
. C.
2 2
. D.
7
.
Câu 67: [2H3-3.8-3] Trong không gian
Oxyz
, cho đường thẳng
1 1
:
1 1 2
x y z m
d
và mặt cầu
2 2 2
: 1 1 2 9
S x y z
. Tìm
m
để đường thẳng
d
cắt mặt cầu
S
tại hai điểm
phân biệt
E
,
F
sao cho độ dài đoạn
EF
lớn nhất
A.
1
m
. B.
0
m
. C.
1
3
m
. D.
1
3
m
.
Câu 68: [2H3-3.8-3] Trong không gian
Oxyz
, cho hai đường thẳng
1
: 2
x t
d y t
z t
,
2
: 1
2
x t
d y t
z t
. Đường
thẳng
cắt
d
,
d
lần lượt tại các điểm
A
,
B
thỏa mãn độ dài đoạn thẳng
AB
nhỏ nhất.
Phương trình đường thẳng
là
A.
1 2
2 1 3
x y z
. B.
4 2
2 1 3
x y z
C.
3 1
2 1 3
x y z
. D.
2 1 1
2 1 3
x y z
.
Câu 69: [2H3-3.8-3] Trong không gian
Oxyz
, cho hình hộp
.
ABCD A B C D
biết
1;0;1
A
,
2;1;2
B
,
2; 2;2
D
,
3;0; 1
A
, điểm
M
thuộc cạnh
DC
. Giá trị nhỏ nhất của tổng các khoảng cách
AM MC
là
A.
17
. B.
17 4 6
. C.
17 8 3
. D.
17 6 2
.
Câu 70: [2H3-3.8-3] Trong không gian với hệ tọa độ
Oxyz
, cho các điểm
2;2; 3
M
và
4;2;1
N
.
Gọi
là đường thẳng đi qua
M
, nhận vecto
; ;u a b c
làm vectơ chỉ phương và song song
với mặt phẳng
: 2 0
P x y z
sao cho khoảng cách từ
N
đến
đạt giá trị nhỏ nhất. Biết
a
,
b
là hai số nguyên tố cùng nhau. Khi đó
a b c
bằng:
A.
15
. B.
13
. C.
16
. D.
14
.
Câu 71: [2H3-3.8-3] Trong không gian
,Oxyz
cho đường thẳng
2 1 2
:
4 4 3
x y z
d
và mặt phẳng
: 2 2 1 0
P x y z
. Đường thẳng
đi qua
2; 1; 2
E
, song song với
P
đồng thời tạo
với
d
góc bé nhất. Biết rằng
có một véctơ chỉ phương
; ; 1 .
u m n
Tính
2 2
T m n
.
A.
5
T
. B.
4T
. C.
3
T
. D.
4T
.
Câu 72: [2H3-3.8-3] Họ parabol
2
: 2 3 2
m
P y mx m x m
0
m
luôn tiếp xúc với đường
thẳng
d
cố định khi
m
thay đổi. Đường thẳng
d
đó đi qua điểm nào dưới đây?
A.
0; 2 .
B.
0;2 .
C.
1;8 .
D.
1; 8 .
Câu 73: [2H3-3.8-3] Trong không gian với hệ toạ độ
Oxyz
, cho hai điểm
2; 3;2
A
,
3;5;4
B
. Tìm
toạ độ điểm
M
trên trục
Oz
so cho
2 2
MA MB
đạt giá trị nhỏ nhất.
A.
0;0;49
M
. B.
0;0;67
M
. C.
0;0;3
M
. D.
0;0;0
M
.
Câu 74: [2H3-3.8-4] Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 3 1
x y z
và hai
điểm
1;2; 1
A
,
3; 1; 5
B
. Gọi
d
là đường thẳng đi qua điểm
A
và cắt đường thẳng
sao
cho khoảng cách từ điểm
B
đến đường thẳng
d
là lớn nhất. Phương trình đường thẳng
d
là:
A.
3 5
2 2 1
x y z
. B.
2
1 3 4
x y z
.
C.
2 1
3 1 1
x y z
. D.
1 2 1
1 6 5
x y z
.
Câu 75: [2H3-3.8-4] Trong không gian
Oxyz
, cho
2
điểm
3; 2;3
A
,
1;0;5
B
và đường thẳng
1 2 3
:
1 2 2
x y z
d
. Tìm tọa độ điểm
M
trên đường thẳng
d
để
2 2
MA MB
đạt giá trị nhỏ
nhất.
A.
1;2;3
M
. B.
2;0;5
M
. C.
3; 2;7
M
. D.
3;0;4
M
.
Câu 76: [2H3-3.8-4] Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
: 1 0
P x y z
, đường
thẳng
15 22 37
:
1 2 2
x y z
d
và mặt cầu
2 2 2
: 8 6 4 4 0
S x y z x y z
. Một đường
thẳng
thay đổi cắt mặt cầu
S
tại hai điểm
A
,
B
sao cho
8
AB
. Gọi
A
,
B
là hai điểm
lần lượt thuộc mặt phẳng
P
sao cho
AA
,
BB
cùng song song với
d
. Giá trị lớn nhất của
biểu thức
AA BB
là
A.
8 30 3
9
. B.
24 18 3
5
. C.
12 9 3
5
. D.
16 60 3
9
.
Câu 77: [2H3-3.8-4] Trong không gian
Oxyz
, cho ba điểm
1;0;1
A
,
3;2;1
B
,
5;3;7
C
. Gọi
; ;M a b c
là điểm thỏa mãn
MA MB
và
MB MC
đạt giá trị nhỏ nhất. Tính
P a b c
A.
4P
. B.
0
P
. C.
2P
. D.
5
P
.
Câu 78: [2H3-3.8-4] Trong không gian
Oxyz
, cho ba điểm
1;0;1
A
,
3;2;1
B
,
5;3;7
C
. Gọi
; ;M a b c
là điểm thỏa mãn
MA MB
và
MB MC
đạt giá trị nhỏ nhất. Tính
P a b c
A.
4P
. B.
0
P
. C.
2P
. D.
5
P
.
Câu 79: [2H3-3.8-4] Trong không gian với hệ trục tọa độ
Oxyz
cho mặt cầu
2 2 2
: 2 4 4 0
S x y z x y z
và điểm
1;2; 1
M
. Một đường thẳng thay đổi qua
M
và
cắt
S
tại hai điểm
A
,
B
. Tìm giá trị lớn nhất của tổng
MA MB
.
A.
8
. B.
10
. C.
2 17
. D.
8 2 5
.
Câu 80: [2H3-3.8-4] Trong không gian
Oxyz
, cho hai điểm
1;2;4
A
,
0;0;1
B
và mặt cầu
2 2
2
: 1 1 4.
S x y z
Mặt phẳng
: 3 0
P ax by cz
đi qua
A
,
B
và cắt mặt cầu
S
theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tính
T a b c
.
A.
3
4
T
. B.
33
5
T
. C.
27
4
T
. D.
31
5
T
.
Câu 81: [2H3-3.8-4] Trong không gian
Oxyz
, cho ba điểm
1; 2;1
A
,
5; 0; 1
B
,
3;1; 2
C
và mặt
phẳng
:3 3 0
Q x y z
. Gọi
; ;M a b c
là điểm thuộc
Q
thỏa mãn
2 2 2
2
MA MB MC
nhỏ nhất. Tính tổng
5a b c
.
A.
11
. B.
9
. C.
15
. D.
14
.
Câu 82: [2H3-3.8-4] Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
: 4 0
P x y z
, đường
thẳng
1 1 3
:
2 1 1
x y z
d
và điểm
1; 3; 1
A
thuộc mặt phẳng
P
. Gọi
là đường thẳng đi
qua
A
, nằm trong mặt phẳng
P
và cách đường thẳng
d
một khoảng cách lớn nhất. Gọi
; ; 1u a b
là một véc tơ chỉ phương của đường thẳng
. Tính
2a b
.
A.
2 3
a b
. B.
2 0
a b
. C.
2 4
a b
. D.
2 7
a b
.
Câu 83: [2H3-3.8-4] Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
3;0;1
A
,
1; 1;3
B
và mặt
phẳng
: 2 2 5 0
P x y z
. Viết phương trình chính tắc của đường thẳng
d
đi qua
A
, song
song với mặt phẳng
P
sao cho khoảng cách từ
B
đến
d
nhỏ nhất.
A.
3 1
:
26 11 2
x y z
d
. B.
3 1
:
26 11 2
x y z
d
.
C.
3 1
:
26 11 2
x y z
d
. D.
3 1
:
26 11 2
x y z
d
.
Câu 84: [2H3-3.8-4] Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
: 4 0
P x y z
, đường
thẳng
1 1 3
:
2 1 1
x y z
d
và điểm
1; 3; 1
A
thuộc mặt phẳng
P
. Gọi
là đường thẳng đi
qua
A
, nằm trong mặt phẳng
P
và cách đường thẳng
d
một khoảng cách lớn nhất. Gọi
; ; 1u a b
là một véc tơ chỉ phương của đường thẳng
. Tính
2a b
.
A.
2 3
a b
. B.
2 0
a b
. C.
2 4
a b
. D.
2 7
a b
.
Câu 85: [2H3-3.8-4] Trong không gian
Oxyz
, cho ba điểm
1; 2;1
A
,
5; 0; 1
B
,
3;1; 2
C
và mặt
phẳng
:3 3 0
Q x y z
. Gọi
; ;M a b c
là điểm thuộc
Q
thỏa mãn
2 2 2
2
MA MB MC
nhỏ nhất. Tính tổng
5a b c
.
A.
11
. B.
9
. C.
15
. D.
14
.
Câu 86: [2H3-3.8-4] Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
2 1
:
1 2 3
x y z
d
và hai
điểm
2;0;3
A
,
2; 2; 3
B
. Biết điểm
0 0 0
; ;M x y z
thuộc
d
thỏa mãn
4 4
MA MB
nhỏ nhất.
Tìm
0
x
.
A.
0
1
x
. B.
0
3
x
. C.
0
0
x
. D.
0
2
x
.
HƯỚNG DẪN GIẢI CHI TIẾT PHƯƠNG TRÌNH ĐƯỜNG THẲNG NÂNG CAO
Câu 1: [2H3-3.2-3] Trong không gian với hệ tọa độ
Oxyz
, viết phương trình đường vuông góc chung của
hai đường thẳng
2 3 4
:
2 3 5
x y z
d
và
1 4 4
:
3 2 1
x y z
d
.
A.
1
1 1 1
x y z
. B.
2 2 3
2 3 4
x y z
.
C.
2 2 3
2 2 2
x y z
. D.
2 3
2 3 1
x y z
.
Lời giải
Chọn A.
Ta có
M d
suy ra
2 2 ;3 3 ; 4 5
M m m m
. Tương tự
N d
suy ra
1 3 ;4 2 ;4
N n n n
.
Từ đó ta có
3 3 2 ;1 2 3 ;8 5
MN n m n m n m
.
Mà do
MN
là đường vuông góc chung của
d
và
d
nên
MN d
MN d
2 3 3 2 3. 1 2 3 5 8 5 0
3 3 3 2 2. 1 2 3 1 8 5 0
n m n m n m
n m n m n m
38 5 43
5 14 19
m n
m n
1
1
m
n
.
Suy ra
0;0;1
M
,
2;2;3
N
.
Ta có
2;2;2
MN nên đường vuông góc chung
MN
là
1
1 1 1
x y z
.
Câu 2: [2H3-3.2-3] Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
: 2 4 0
P x y z
và đường
thẳng
:
x y z
d
. Viết phương trình đường thẳng
nằm trong mặt phẳng
P
, đồng thời
cắt và vuông góc với đường thẳng
d
.
A.
1 1 1
5 1 3
x y z
. B.
1 1 1
5 1 3
x y z
.
C.
1 1 1
5 1 2
x y z
. D.
1 3 1
5 1 3
x y z
.
Lời giải
Chọn A.
Vectơ pháp tuyến của mặt phẳng
P
là
1;2;1
P
n .
Vectơ chỉ phương của đường thẳng
d
là
2;1;3
d
u
.
Phương trình tham số của đường thẳng
1 2
:
2 3
x t
d y t
z t
.
Xét phương trình:
1 2 2 2 3 4 0 7 7 0 1 t t t t t
.
Suy ra giao điểm của đường thẳng
d
và mặt phẳng
P
là
1;1;1
A
. Ta có:
A
.
Vectơ chỉ phương của đường thẳng
là
, 5; 1; 3
d
P
u n u .
Phương trình chính tắc của đường thẳng
1 1 1
:
5 1 3
x y z
.
Câu 3: [2H3-3.2-3] Trong không gian
Oxyz
, cho hai đường thẳng
1
3 3 2
:
1 2 1
x y z
d
;
2
5 1 2
:
3 2 1
x y z
d
và mặt phẳng
: 2 3 5 0
P x y z
. Đường thẳng vuông góc với
P
, cắt
1
d
và
2
d
có phương trình là
A.
1 1
1 2 3
x y z
. B.
2 3 1
1 2 3
x y z
.
C.
3 3 2
1 2 3
x y z
. D.
1 1
3 2 1
x y z
.
Lời giải
Chọn A.
Gọi
M
và
N
lần lượt là giao điểm của đường thẳng
d
cần tìm với
1
d
và
2
d
, khi đó
3 ;3 2 ; 2
M t t t
,
5 3 ; 1 2 ;2
N s s s
2 3 ; 4 2 2 ;4
MN s t s t s t
.
Đường thẳng
d
vuông góc với
P
suy ra
MN
cùng phương với
1;2;3
P
n
. Do đó
2 3 4 2 2 4
1 2 3
s t s t s t
2
1
t
s
1; 1;0
M
.
Vậy đường thẳng cần tìm qua
1; 1;0
M
và có vectơ chỉ phương là
1;2;3
u
là
1 1
1 2 3
x y z
.
Câu 4: [2H3-3.2-3] Phương trình đường thẳng song song với đường thẳng
1 2
:
1 1 1
x y z
d
và cắt hai
đường thẳng
1
1 1 2
:
2 1 1
x y z
d
;
2
1 2 3
:
1 1 3
x y z
d
là:
A.
x y z
. B.
1 1
1 1 1
x y z
.
C.
1 2 3
1 1 1
x y z
. D.
1 1
1 1 1
x y z
.
Lời giải
Chọn B.
Vectơ chỉ phương của
d
là
1;1; 1
u
.
Gọi
là đường thẳng cần tìm và
1
A d
,
2
B d
. Suy ra:
1 2 ; 1 ;2
1 ;2 ;3 3
A a a a
B b b b
.
Khi đó:
2 2; 3;3 1
AB b a b a b a
.
Vì đường thẳng
song song với đường thẳng
d
nên
AB
cùng phương với
u
.
Suy ra:
2 2 3 3 1
1 1 1
b a b a b a
1;0;1
1
1
2;1;0
A
a
b
B
.
Thay
1;0;1
A
vào đường thẳng
d
ta thấy
A d
.
Vậy phương trình đường thẳng
1 1
:
1 1 1
x y z
.
Câu 5: [2H3-3.2-3] Trong không gian
Oxyz
, cho ba điểm
1;1;1
A
,
1;2;0
B
,
2; 3;2
C
. Tập hợp tất
cả các điểm
M
cách đều ba điểm
A
,
B
,
C
là một đường thẳng
d
. Phương trình tham số của đường
thẳng
d
là:
A.
8 3
15 7
x t
y t
z t
. B.
8 3
15 7
x t
y t
z t
. C.
8 3
15 7
x t
y t
z t
. D.
8 3
15 7
x t
y t
z t
.
Lời giải
Chọn A.
Ta có
2;1; 1
AB
;
3; 5;2
BC
.
Ta thấy
AB
và
BC
không cùng phương nên ba điểm
A
,
B
,
C
không thẳng hàng.
M
cách đều hai điểm
A
,
B
nên điểm
M
nằm trên mặt trung trực của
AB
.
M
cách đều hai điểm
B
,
C
nên điểm
M
nằm trên mặt trung trực của
BC
.
Do đó tập hợp tất cả các điểm
M
cách đều ba điểm
A
,
B
,
C
là giao tuyến của hai mặt trung trực
của
AB
và
BC
.
Gọi
P
,
Q
lần lượt là các mặt phẳng trung trực của
AB
và
BC
.
3 1
0; ;
2 2
K
là trung điểm
AB
;
1 1
; ;1
2 2
N
là trung điểm
BC
.
P
đi qua
K
và nhận
2;1; 1
AB
làm véctơ pháp tuyến nên
3 1
: 2 0
2 2
P x y z
hay
: 2 1 0
P x y z
.
Q
đi qua
N
và nhận
3; 5;2
BC
làm véctơ pháp tuyến nên
1 1
: 3 5 2 1 0
2 2
Q x y z
hay
: 3 5 2 6 0
Q x y z
.
Ta có
2 1 0
:
3 5 2 6 0
x y z
d
x y z
Nên
d
có véctơ chỉ phương
, 3;1;7
u AB BC
.
Cho
0
y
ta sẽ tìm được
8
x
,
15
z
nên
8;0;15
d
.
Vậy
8 3
15 7
x t
y t
z t
.
Câu 6: [2H3-3.2-3] Trong không gian cho đường thẳng
1 1 2
:
2 1 1
x y z
. Tìm hình chiếu vuông góc
của
trên mặt phẳng
Oxy
.
A.
0
1
0
x
y t
z
. B.
1 2
1
0
x t
y t
z
. C.
1 2
1
0
x t
y t
z
. D.
1 2
1
0
x t
y t
z
.
Lời giải
Chọn B.
Đường thẳng
qua điểm
1; 1; 2
M
và có vectơ chỉ phương:
2; 1; 1
u
.
Mặt phẳng
Oxy
có vectơ pháp tuyến
0; 0; 1
k
.
Gọi
P
là mặt phẳng chứa
và vuông góc mặt phẳng
Oxy
, thì
P
qua
M
và có vectơ pháp
tuyến
; 1; 2; 0
n u k
.
Khi đó, phương trình mặt phẳng
P
là
2 3 0
x y
.
Gọi
d
là hình chiếu của
lên
Oxy
, thì
d
chính là giao tuyến của
P
với
Oxy
.
Suy ra
2 3 0
:
0
x y
d
z
hay
3 2
:
0
x t
d y t
z
. Với
1,
t
ta thấy
d
đi qua điểm
1; 1; 0
N
.
Câu 7: [2H3-3.2-3] Trong không gian với hệ tọa độ
Oxyz
, cho các điểm
2;0;0
A
;
0;3;0
B
;
0;0;4
C
.
Gọi
H
là trực tâm tam giác
ABC
. Tìm phương trình tham số của đường thẳng
OH
.
A.
4
3
2
x t
y t
z t
. B.
3
4
2
x t
y t
z t
. C.
6
4
3
x t
y t
z t
. D.
4
3
2
x t
y t
z t
.
Lời giải
Chọn D.
Do tứ diện
OABC
có ba cạnh
OA
,
OB
,
OC
đôi một vuông góc và
H
là trực tâm tam giác
ABC
nên
OH ABC
.
Phương trình mặt phẳng
ABC
là
1
2 3 4
x y z
, hay
6 4 3 12 0
x y z
.
Vì
OH ABC
nên đường thẳng
OH
có véc-tơ chỉ phương
6;4;3
u
.
Vậy, phương trình tham số của đường thẳng
OH
là
6
4
3
x t
y t
z t
.
Câu 8: [2H3-3.2-3] Trong không gian
Oxyz
, cho ba đường thẳng
1
3 1 2
:
2 1 2
x y z
d
,
2
1 4
:
3 2 1
x y z
d
và
3
3 2
:
4 1 6
x y z
d
. Đường thẳng song song
3
d
, cắt
1
d
và
2
d
có
phương trình là
A.
3 1 2
4 1 6
x y z
. B.
3 1 2
4 1 6
x y z
.
C.
1 4
4 1 6
x y z
. D.
1 4
4 1 6
x y z
.
Lời giải
Chọn B.
Ta có
1
3 2
: 1
2 2
x u
d y u
z u
,
2
1 3
: 2
4
x v
d y v
z v
.
Gọi
4
d
là đường thẳng cần tìm.
Gọi
4 1
A d d
3 2 ; 1 ;2 2A u u u
,
4 2
B d d
1 3 ; 2 ; 4
B v v v
.
4 3 2 ;1 2 ; 6 2AB v u v u v u
.
4
d
song song
3
d
nên
3
AB ku
với
3
4; 1;6
u
.
3
4 3 2 4 0
1 2 0
6 2 6 1
v u k v
AB ku v u k u
v u k k
.
Đường thẳng
4
d
đi qua
3; 1;2
A
và có vtcp là
3
4; 1;6
u
nên
4
3 1 2
:
4 1 6
x y z
d
.
Câu 9: [2H3-3.2-3] Trong không gian
Oxyz
, cho mặt phẳng
: 2 0
y z
và hai đường thẳng:
1
1
:
4
x t
d y t
z t
;
2
2
: 4 2
4
x t
d y t
z
. Đường thẳng
nằm trong mặt phẳng
và cắt hai đường thẳng
1
d
;
2
d
có phương trình là
A.
1
7 8 4
x y z
. B.
1
7 8 4
x y z
. C.
1
7 8 4
x y z
. D.
1
7 8 4
x y z
.
Lời giải
Chọn C.
Gọi
1
A d
suy ra
1 ; ;4A t t t
và
2
B d
suy ra
2 ;4 2 ;4B t t
.
Mặt khác
A
;
B
nên ta có
2.4 0
4 2 2.4 0
t t
t
0
6
t
t
Do đó
1;0;0
A
và
8; 8;4
B
.
Đường thẳng
đi qua
A
và nhận
7; 8;4
AB
làm vectơ chỉ phương có phương trình
1
7 8 4
x y z
.
Câu 10: [2H3-3.2-3] Trong không gian
Oxyz
, cho đường thẳng
1 2
:
1 1 1
x y z
d
và mặt phẳng
: 2 2 1 0
P x y z
. Đường thẳng nằm trong
P
, cắt và vuông góc với
d
có phương trình là
A.
2 1 3
3 4 1
x y z
. B.
2 1 3
3 4 1
x y z
.
C.
2 1 3
3 4 1
x y z
. D.
1 1 1
3 4 1
x y z
.
Lời giải
Chọn C.
Phương trình tham số của
1
:
2
x t
d y t
z t
. Gọi
M d P
.
Khi đó
M d
nên
1 ; ;2
M t t t
;
M P
nên
2 1 2 2 1 0 1t t t t
.
Vậy đường thẳng
d
cắt mặt phẳng
P
tại
2; 1;3
M
.
Gọi
1; 1;1
d
u
và
2; 1; 2
n
lần lượt là vectơ chỉ phương của
d
và vectơ pháp tuyến của mặt
phẳng
P
.
Khi đó một vectơ chỉ phương của đường thẳng cần tìm là
, 3;4;1
d
u u n
.
Vậy phương trình đường thẳng cần tìm là
2 1 3
3 4 1
x y z
.
Câu 11: [2H3-3.2-3] Trong không gian với hệ tọa độ Descartes
Oxyz
, cho điểm
0; 1; 2
M
và hai đường
thẳng
1
1 2 3
:
1 1 2
x y z
d
,
2
1 4 2
:
2 1 4
x y z
d
. Phương trình đường thẳng đi qua
M
, cắt cả
1
d
và
2
d
là
A.
1 3
9 9
8
2 2
x y z
. B.
1 2
3 3 4
x y z
. C.
1 2
9 9 16
x y z
. D.
1 2
9 9 16
x y z
.
Lời giải
Chọn C.
Gọi
là đường thẳng cần tìm.
1 1 1 1
1; 2; 2 3
d A t t t
;
2 2 2 2
2 1; 4; 4 2
d B t t t
.
1 1 1
1; 1; 2 1

MA t t t
;
2 2 2
2 1; 5; 4

MB t t t
.
Ta có:
,M
,A
B
thẳng hàng
1
1 2
1
1 2
2
1 2
2
7
2
1 2 1
7
1
1 5
2
2
4
2 1 4
2

t
t k t
t
MA k MB t k t k
t
t kt
kt
.
9; 9; 16

MB
.
Đường thẳng
đi qua
0; 1; 2
M
, một VTCP là
9; 9;16
u
có phương trình là:
1 2
:
9 9 16
x y z
.
Câu 12: [2H3-3.2-3] Trong không gian
Oxyz
, cho ba đường thẳng
1
:
d
;
2
2 1
:
1 2 2
x y z
d
;
3
3 2 5
:
3 4 8
x y z
d
. Đường thẳng song song với
3
d
, cắt
1
d
và
2
d
có
phương trình là
A.
1 1
3 4 8
x y z
. B.
1 3
3 4 8
x y z
.
C.
1 3
3 4 8
x y z
. D.
1 1
3 4 8
x y z
.
Lời giải
Chọn A.
Gọi
d
là đường thẳng song song với
3
d
, cắt
1
d
và
2
d
lần lượt tại các điểm
A
,
B
.
Gọi
1 2 ;3 ; 1
và
2 3; 2 3 1;2 1
AB b a b a b a
.
Đường thẳng
3
d
có véc-tơ chỉ phương
3; 4;8
u
.
Đường thẳng
d
song song với
3
d
nên
AB ku
2 3 3
2 3 1 4
2 1 8
b a k
b a k
b a k
0
3
2
1
2
a
b
k
.
Như vậy
1;0; 1
A
và
1
; 2;3
2
B
.
Phương trình đường thẳng
d
là:
1 1
3 4 8
x y z
.
Câu 13: [2H3-3.2-3] Trong không gian với hệ trục tọa độ
Oxyz
, cho tam giác
ABC
biết điểm
1; 2; 3
A
,
đường trung tuyến
BM
và đường cao
CH
có phương trình tương ứng là
5
0
1 4
x t
y
z t
và
4 2 3
16 13 5
x y z
. Viết phương trình đường phân giác góc
A
.
A.
1 2 3
7 1 10
x y z
. B.
1 2 3
4 13 5
x y z
.
C.
1 2 3
2 3 1
x y z
. D.
1 2 3
2 11 5
x y z
.
Lời giải
Chọn D.
Giả sử
5 ; 0; 1 4
B b b BM
,
4 16 ; 2 13 ; 3 5
C c c c CH
.
Ta có:
 Tọa độ trung điểm
M
của
AC
là
5 16 13 6 5
; ;
2 2 2
c c c
M
.
M BM
5 16
5
2
13
0
2
6 5
1 4
2
c
t
c
c
t
0
1
2
c
t
4; 2; 3
C
5 1; 2; 4 2
AB b b
Vectơ chỉ phương của
CH
là:
16; 13; 5
w
.
Do
AB CH
nên
. 0
AB u
16 5 1 13 2 5 4 2 0
b b
0
b
0; 0; 1
B
.
1; 2; 2
AB
,
3; 4; 0
AC
.
Đặt
1
1 2 2
; ;
3 3 3
AB
u
AB
,
2
3 4
; ; 0
5 5
u
,
1 2
4 22 2
; ;
15 15 3
u u u
.
Chọn
2; 11; 5
v
là vectơ chỉ phương của đường phân giác góc
A
.
Vậy phương trình đường phân giác góc
A
là:
1 2 3
2 11 5
x y z
.
Câu 14: [2H3-3.2-3] Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
d
:
3 2
2 1 3
x y z
và mặt
phẳng
P
:
2 6 0
x y z
. Đường thẳng nằm trong mặt phẳng
P
, cắt và vuông góc với
d
có
phương trình
A.
2 2 5
1 7 3
x y z
. B.
2 4 1
1 7 3
x y z
.
C.
2 2 5
1 7 3
x y z
. D.
2 4 1
1 7 3
x y z
.
Lời giải
Chọn A.
Tọa độ giao điểm
M
của
d
và
P
là nghiệm của hệ
3 2
2 1 3
2 6 0
x y z
x y z
2 6
3 11
2 6 0
x y
y z
x y z
2
2
5
x
y
z
2;2;5
M
.
P
:
2 6 0
x y z
có vtpt
1; 1;2
n
,
d
có vtcp
2;1; 3
u
Ta có
đi qua
2;2;5
M
nhận
, 1;7;3
k n u
là một vectơ chỉ phương có dạng
:
2 2 5
1 7 3
x y z
.
Câu 15: [2H3-3.2-3] Trong không gian với hệ tọa độ
Oxyz
cho ba điểm
3; 2;4
A
,
5;3; 2
B
,
0;4;2
C
,
đường thẳng
d
cách đều ba điểm
A
,
B
,
C
có phương trình là
A.
8
26
3
5
22
3
4
27
3
x t
y t
z t
. B.
4 26
2 22
9
27
4
x t
y t
z t
. C.
11
6
1
22
6
27
x
y t
z t
. D.
4 26
2 38
9
27
4
x t
y t
z t
.
Lời giải
Chọn B.
Gọi
I
là trung điểm của
AB
suy ra
1
4; ;1
2
I
và
P
là mặt phẳng trung trực của đoạn
AB
.
Mặt phẳng
P
đi qua
I
và nhận
2;5; 6
AB
làm vec tơ pháp tuyến có phương trình là:
1
2 4 5 6 1 0 4 10 12 9 0
2
x y z x y z
.
Gọi
J
là trung điểm của
AC
suy ra
3
;1;3
2
J
và
Q
là mặt phẳng trung trực của đoạn
AC
Mặt phẳng
Q
đi qua
J
và nhận
3;6; 2
AC
làm vec tơ pháp tuyến có phương trình là:
3
3 6 1 2 3 0 6 12 4 9 0
2
x y z x y z
.Khi đó
d P Q
Ta có
d
có vectơ chỉ phương
; 26;22;27
u AB AC
và đi qua
M
là nghiệm của hệ
4 10 12 9 0
6 12 4 9 0
x y z
x y z
, ta chọn
4
x
suy ra
2
y
và
9
4
z
. Vậy
9
4; 2;
4
M
.
Phương trình tham số của
d
là:
4 26
2 22
9
27
4
x t
y t
z t
.
Câu 16: [2H3-3.2-3] Trong không gian
Oxyz
, cho tam giác
ABC
với
3;0;0
A
,
0;6;0
B
,
0;0;6
C
.
Phương trình nào dưới đây là phương trình đường thẳng đi qua trực tâm của tam giác
ABC
và vuông
góc với mặt phẳng
ABC
.
A.
1 2 3
2 1 1
x y z
. B.
2 1 1
2 1 1
x y z
.
C.
3 6 6
2 1 1
x y z
. D.
.
Lời giải
Chọn B.
Ta có
; ;H a b c
là trực tâm tam giác
ABC
nên ta có
. 0
. 0
AH BC
BH AC
AB AC AH
.
Ta có
3; ;AH a b c
;
; 6;BH a b c
;
0; 6;6
BC
;
3;0;6
AC
;
3;6;0
AB
.
, 36;18;18
AB AC
.
. 0
. 0
AH BC
BH AC
AB AC AH
6 6 0
3 6 0
36 3 18 18 0
b c
a c
a b c
6 6 0
3 6 0
2 6
b c
a c
a b c
2
1
1
a
b
c
2;1;1
H
.
Đường thẳng đi qua trực tâm
2;1;1
H
của tam giác
ABC
và vuông góc với mặt phẳng
ABC
có
vecto chỉ phương
1
, 2;1;1
18
u AB AC
có phương trình là
2 1 1
2 1 1
x y z
.
Câu 17: [2H3-3.2-3] Trong không gian
Oxyz
, cho hai điểm
2;1; 3
A
và
3;2;1
B
. Viết phương trình
đường thẳng
d
đi qua gốc toạ độ sao cho tổng khoảng cách từ
A
và
B
đến đường thẳng
d
lớn nhất.
A.
1 1 1
x y z
. B.
1 1 1
x y z
. C.
1 1 2
x y z
. D.
1 1 2
x y z
.
Lời giải
Chọn A.
Ta có
; ;
d A d d B d OA OB
.
Dấu
" "
xảy ra
OA d
OB d
d
có VTCP là
; 7;7;7 7 1;1;1
u OA OB
.
Vậy
:
1 1 1
x y z
d
.
Câu 18: [2H3-3.2-3] Trong không gian
Oxyz
, cho hai đường thẳng cắt nhau
1
2
: 2 2
1
x t
y t
z t
,
2
1
:
2
x t
y t
z t
,t t
. Viết phương trình đường phân giác của góc nhọn tạo bởi
1
và
2
.
A.
1
2 3 3
x y z
. B.
1
1 1 1
x y z
. C.
1
2 3 3
x y z
. D.
1
1 1 1
x y z
.
Lời giải
Chọn C.
Thấy ngay
1 2
1;0;0
M
và các VTCP lần lượt là
1;2; 1
a
và
1; 1;2
b
.
Ta có
0;1;1
a b u
và
, 3; 1;1
a b v
.
Vì
. 4 0
a b
nên góc giữa hai vectơ là góc tù do đó đường phân giác của góc nhọn tạo bởi
1
và
2
có VTCP
, 2; 3;3
n u v
.
Vậy phương trình đường phân giác cần tìm:
1
2 3 3
x y z
.
Câu 19: [2H3-3.2-3] Trong không gian với hệ tọa độ
Oxyz
. Cho mặt phẳng
: 2 10 0,
P x y z
điểm
1;3;2
A
và đường thẳng
2 2
: 1
1
x t
d y t
z t
. Tìm phương trình đường thẳng
cắt
P
và
d
lần lượt
tại hai điểm
M
và
N
sao cho
A
là trung điểm cạnh
MN
.
A.
6 1 3
7 4 1
x y z
. B.
6 1 3
7 4 1
x y z
.
C.
6 1 3
7 4 1
x y z
. D.
6 1 3
7 4 1
x y z
.
Lời giải
Chọn D.
Ta có
M d M d
. Giả sử
2 2 ,1 ,1 ,M t t t t
Do
A
là trung điểm
MN
nên
4 2 ; 5 ; 3
N t t t
.
Mà
N P
nên ta có phương trình
2 4 2 5 3 10 0
t t t
2
t
.
Do đó,
6; 1;3
M
.
7; 4;1
AM
là vectơ chỉ phương của đường thẳng
.
Vậy phương trình đường thẳng cần tìm là
6 1 3
7 4 1
x y z
.
Câu 20: [2H3-3.2-3] Trong không gian
Oxyz
, cho hai đường thẳng cắt nhau
1
2
: 2 2
1
x t
y t
z t
,
2
1
:
2
x t
y t
z t
,t t
. Viết phương trình đường phân giác của góc nhọn tạo bởi
1
và
2
.
A.
1
2 3 3
x y z
. B.
1
1 1 1
x y z
. C.
1
2 3 3
x y z
. D. Cả A, B, C đều sai.
Hướng dẫn giải
Chọn A.
1 2
1;0;0I
.
1
và
2
có VTCP lần lượt là
1
1;2; 1
u
và
2
1; 1;2
u
.
Ta có:
1 2
1 2
1 2
. 5
cos ; 0
6
.
u u
u u
u u
1 2
;u u
là góc tù.
Gọi
u
là véc tơ đối của
2
u
1;1; 2
u
.
Khi đó đường phân giác của góc nhọn tạo bởi
1
và
2
có VTCP
1
2;3; 3
u u u
.
Vậy phương trình đường phân giác của góc nhọn tạo bởi
1
và
2
có dạng:
1
2 3 3
x y z
.
Câu 21: [2H3-3.2-3] Trong không gian
Oxyz
, Cho mặt phẳng
: 2 2 0
R x y z
và đường
thẳng
1
1
:
2 1 1
x y z
. Đường thẳng
2
nằm trong mặt phẳng
R
đồng thời cắt và vuông góc với
đường thẳng
1
có phương trình là
A.
3
1
x t
y t
z t
. B.
2
1
x t
y t
z t
. C.
2
1
x t
y t
z t
. D.
2 3
1
x t
y t
z t
.
Lời giải
Chọn A.
Phương trình tham số của đường thẳng
1
là
2
1
x t
y t
z t
.
Gọi
; ;I x y z
là giao điểm của
1
và
R
. Khi đó tọa độ của
I
là thỏa mãn
2
1
2 2 0
x t
y t
z t
x y z
0
0
1
x
y
z
0;0;1
I
.
Mặt phẳng
R
có VTPT
1;1; 2
n
; Đường thẳng
1
có VTCP
2;1; 1
u
.
Ta có
, 1; 3; 1
n u
.
Đường thẳng
2
nằm trong mặt phẳng
R
đồng thời cắt và vuông góc với đường thẳng
1
.
Do đó
2
đi qua
0;0;1
I
và nhận
,n u
làm một VTCP.
Vậy phương trình của
2
là
3
1
x t
y t
z t
.
Câu 22: [2H3-3.2-3] Trong không gian
Oxyz
, cho đường thẳng
1 3
: 1 4
1
x t
d y t
z
. Gọi
là đường thẳng đi qua
điểm
1;1;1
A
và có vectơ chỉ phương
1; 2;2
u
. Đường phân giác của góc nhọn tạo bởi
d
và
có phương trình là
A.
1 7
1
1 5
x t
y t
z t
. B.
1 2
10 11
6 5
x t
y t
z t
. C.
1 2
10 11
6 5
x t
y t
z t
. D.
1 3
1 4
1 5
x t
y t
z t
.
Lời giải
Chọn C.
Phương trình tham số đường thẳng
1
: 1 2
1 2
x t
y t
z t
.
Chọn điểm
2; 1;3B
,
3
AB
.
Điểm
14 17
; ;1
5 5
C
hoặc
4 7
; ;1
5 5
C
nằm trên
d
thỏa mãn
AC AB
.
Kiểm tra được điểm
4 7
; ;1
5 5
C
thỏa mãn
BAC
nhọn.
Trung điểm của
BC
là
3 6
; ; 2
5 5
I
. Đường phân giác cần tìm là
AI
có vectơ chỉ phương
2;11; 5
u
và có phương trình
1 2
10 11
6 5
x t
y t
z t
,
Câu 23: [2H3-3.2-3] Trong không gian
Oxyz
, cho đường thẳng
1 3
: 3
5 4
x t
d y
z t
. Gọi
là đường thẳng đi qua
điểm
1; 3;5
A
và có vectơ chỉ phương
1;2; 2
u . Đường phân giác của góc nhọn tạo bởi
d
và
có phương trình là
A.
1 2
2 5
6 11
x t
y t
z t
. B.
1 2
2 5
6 11
x t
y t
z t
. C.
1 7
3 5
5
x t
y t
z t
. D.
1
3
5 7
x t
y
z t
.
Hướng dẫn giải
Chọn B
Ta có điểm
1; 3;5
A
thuộc đường thẳng
d
, nên
1; 3;5
A
là giao điểm của
d
và
.
Một vectơ chỉ phương của đường thẳng
d
là
3;0; 4
v . Ta xét:
1
1
.
u u
u
1
1;2; 2
3
1 2 2
; ;
3 3 3
;
1
1
.
v v
v
1
3;0; 4
5
3 4
;0;
5 5
.
Nhận thấy
1 1
. 0
u v
, nên góc tạo bởi hai vectơ
1
u
,
1
v
là góc nhọn tạo bởi
d
và
.
Ta có
1 1
w
u v
4 10 22
; ;
15 15 15
15
2; 5;11
2
là vectơ chỉ phương của đường phân giác của
góc nhọn tạo bởi
d
và
hay đường phân giác của góc nhọn tạo bởi
d
và
có vectơ chỉ phương là
1
w 2; 5;11
. Do đó có phương trình:
1 2
2 5
6 11
x t
y t
z t
.
Câu 24: [2H3-3.2-3] Trong không gian
Oxyz
, cho đường thẳng
1
: 2 .
3
x t
d y t
z
Gọi
là đường thẳng đi qua
điểm
(1;2;3)
A
và có vectơ chỉ phương
(0; 7; 1).
u
Đường phân giác của góc nhọn tạo bởi
d
và
có phương trình là
A.
1 6
2 11 .
3 8
x t
y t
z t
B.
4 5
10 12 .
2
x t
y t
z t
C.
4 5
10 12 .
2
x t
y t
z t
D.
1 5
2 2 .
3
x t
y t
z t
Lời giải
Chọn B.
Đường thẳng
d
đi qua
(1;2;3)
A
và có VTCP
(1;1;0)
a
.
Ta có
. 1.0 1.( 7) 0.( 1) 7 0 ( , ) 90 .
a u a u
Đường phân giác của góc nhọn tạo bởi
d
và
có VTCP:
1
5;12;1 // 5;12;1
5 2
u a
b
u a
.
Phương trình đường thẳng cần tìm là
4 5
10 12 .
2
x t
y t
z t
Câu 25: [2H3-3.1-3] Trong không gian
,Oxyz
cho đường thẳng
2 1 2
:
4 4 3
x y z
d
và mặt phẳng
: 2 2 1 0
P x y z
. Đường thẳng
đi qua
2; 1; 2
E
, song song với
P
đồng thời tạo với
d
góc bé nhất. Biết rằng
có một véctơ chỉ phương
; ; 1 .
u m n
Tính
2 2
T m n
.
A.
5
T
. B.
4T
. C.
3
T
. D.
4T
.
Lời giải
Chọn D.
Mặt phẳng
P
có vec tơ pháp tuyến
2; 1;2
n
và đường thẳng
d
có vec tơ chỉ phương
4; 4;3
v
Vì
song song với mặt phẳng
P
nên
2 2 0 2 2
u n m n n m
.
Mặt khác ta có
.
cos ;
.
u v
d
u v
2
2 2 2 2
4 4 3
1. 4 4 3
m n
m n
2
4 5
41 5 8 5
m
m m
2
2
2 2
4 5
1 1 16 40 25
. .
5 8 5 5 8 5
41 41
m
m m
m m m m
.
Vì
0 ; 90
d
nên
;d
bé nhất khi và chỉ khi
cos ;d
lớn nhất
Xét hàm số
2
2
16 40 25
5 8 5
t t
f t
t t
2
2
2
72 90
5 8 5
t t
f t
t t
.
Bảng biến thiên
Dựa vào bảng biến thiên ta có
max 0 5
f t f
suy ra
;d
bé nhất khi
0 2
m n
. Do đó
2 2
4
T m n
.
Làm theo cách này thì không cần đến dữ kiện: đường thẳng
đi qua
2; 1; 2
E
.
Câu 26: [2H3-3.1-3] Trong không gian với hệ tọa độ
Oxyz
, cho tam giác
ABC
có phương trình đường phân
giác trong góc
A
là:
6 6
1 4 3
x y z
. Biết rằng điểm
0;5;3
M
thuộc đường thẳng
AB
và điểm
1;1;0
N
thuộc đường thẳng
AC
. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
AC
.
A.
1;2;3
u
. B.
0;1;3
u
. C.
0; 2;6
u
. D.
0;1; 3
u
.
Lời giải
Chọn B.
Phương trình tham số của đường phân giác trong góc
A
:
6 4
6 3
x t
y t
z t
.
d
Gọi
D
là điểm đối xứng với
M
qua
d
. Khi đó
D AC
đường thẳng
AC
có một
vectơ chỉ phương là
ND
.
Ta xác định điểm
D
.
Gọi
K
là giao điểm
MD
với
d
. Ta có
;6 4 ;6 3K t t t
;
;1 4 ;3 3MK t t t
.
Ta có
d
MK u
với
1; 4; 3
d
u
nên
4 1 4 3 3 3 0
t t t
1
2
t
.
1 9
;4;
2 2
K
.
K
là trung điểm
MD
nên
2
2
2
D K M
D K M
D K M
x x x
y y y
z z z
1
3
6
D
D
D
x
y
z
hay
1;3;6
D
.
Một vectơ chỉ phương của
AC
là
0; 2; 6
DN
. Hay
0;1;3
u
là vectơ chỉ phương.
Câu 27: [2H3-3.1-3] Cho
2
mặt cầu
2 2 2
1
: 3 2 2 4
S x y z
,
2 2
2
2
: 1 1 1
S x y z
.
Gọi
d
là đường thẳng đồng thời tiếp xúc với hai mặt cầu trên, cắt đoạn thẳng nối tâm hai mặt cầu và
cách gốc tọa độ
O
một khoảng lớn nhất. Nếu
; 1;u a b
là một vectơ chỉ phương của
d
thì tổng
2 3S a b
bằng bao nhiêu?
A.
2
S
. B.
1
S
. C.
0
S
. D.
4
S
.
Lời giải
Chọn A.
1
S
có tâm
1
3; 2; 2
I
, bán kính
1
2
R
.
2
S
có tâm
2
1; 0; 1
I
, bán kính
2
1
R
.
Ta có:
1 2 1 2
3
I I R R
, do đó
1
S
và
2
S
tiếp xúc ngoài với nhau tại điểm
5 2 4
; ;
3 3 3
A
.
Vì
d
tiếp xúc với hai mặt cầu, đồng thời cắt đoạn thẳng nối hai tâm
1 2
I I
nên
d
phải tiếp
xúc với hai mặt cầu tại
A
1 2
d I I
.
Mặt khác
;
d d O d OA
max
d OA
khi
d OA
.
Khi đó,
d
có một vectơ chỉ phương là
1 2
, 6; 3; 6
I I OA
2; 1; 2
u
.
Suy ra
2
a
,
2
b
.
Vậy
2
S
.
Câu 28: [2H3-3.1-3] Trong không gian
Oxy
cho tam giác
ABC
có
2;3;3
A
, phương trình đường trung
tuyến kẻ từ
B
là
3 3 2
1 2 1
x y z
, phương trình đường phân giác trong góc
C
là
2 4 2
2 1 1
x y z
. Biết rằng
; ; 1
u m n
là một véc tơ chỉ phương của đường thẳng
AB
. Tính
giá trị biểu thức
2 2
T m n
.
A.
1T
. B.
5
T
. C.
2T
. D.
10
T
.
Lời giải
Chọn C.
Gọi
M
là trung điểm
AC
. Trung tuyến
BM
có phương trình
3 3 2
1 2 1
x y z
suy ra
3 ;3 2 ;2
M m m m
4 2 ;3 4 ;1 2C m m m
.
Vì
C
nằm trên đường phân giác trong góc
C
nên
4 2 2 3 4 4 1 2 2
2 1 1
m m m
0
m
4;3;1
C
.
Gọi
A
là điểm đối xứng của
A
qua phân giác trong góc
C
, khi đó
2 4 ;5 2 ;1 2A a a a
và
A BC
.
Véc tơ chỉ phương của đường thẳng chứa phân giác trong góc
C
là
2; 1; 1
u
.
Ta có
. 0
AA u
4 .2 2 2 . 1 2 2 1 0
a a a
0
a
2;5;1
A BM
.
Câu 29: Suy ra
A B
2;5;1
B
0; 2;2
AB
2 0; 1;1
là một véc tơ của đường thẳng
AB
. Vậy
2 2
2
T m n
.[2H3-3.1-3] Trong không gian với hệ toạ độ
Oxyz
, cho phương trình đường phân
giác trong của góc
A
là
6 6
1 4 3
x y z
. Biết
0;5;3
M
thuộc đường thẳng
AB
và
1;1;0
N
thuộc đường thẳng
AC
. Vector nào sau đây là vector chỉ phương của đường thẳng
AC
?
A.
0;1;3
u
. B.
0;1; 3
u
. C.
0; 2;6
u
. D.
1;2;3
u
.
Lời giải
Chọn A.
1; 4; 3
MN
,
d
qua điểm
;6 4 ;6 3A t t t
và có
VTCP 1; 4; 3
u
.
Suy ra
//MN d
Giả sử
AK
là tia phân giác ngoài góc
A
cắt
MN
tại
K
K
là trung điểm của
MN
.
1 3
;3;
2 2
K
,
1 9
;3 4 ; 3
2 2
KA t t t
.
KA u
. 0
KA u
1 9
1. 4 3 4 3 3 0
2 2
t t t
1t
1;2;3
A
.
0;1;3
AN
.
Vậy
AC
có một vector chỉ phương là
0;1;3
AN
.
Câu 30: [2H3-3.1-3] Trong không gian với hệ tọa độ
Oxyz
, cho hai đường thẳng
1
4 1 5
:
3 1 2
x y z
và
2
2 3
:
1 3 1
x y z
. Giả sử
1
M
,
2
N
sao cho
MN
là đoạn vuông góc chung của hai đường
thẳng
1
và
2
. Tính
MN
.
A.
5; 5;10
MN
. B.
2; 2;4
MN
. C.
3; 3;6
MN
. D.
1; 1;2
MN
.
Lời giải
Chọn B.
1
có VTCP
1
3; 1; 2
u
và
2
có VTCP
2
1;3;1
u
.
Gọi
4 3 ;1 ; 5 2M t t t
và
2 ; 3 3 ;N s s s
.
Suy ra
2 3 ; 3 4;2 5
MN t s t s t s
.
Ta có
1
2
. 0
. 0
MN u
MN u
2 3 0
8 9 0
s t
s t
1
1
s
t
.
Vậy
2; 2;4
MN
.
Câu 31: [2H3-3.1-3] Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
:
2 1 1
x y z
d
, mặt
phẳng
: 2 5 0
P x y z
và
1; 1;2
A
. Đường thẳng
cắt
d
và
P
lần lượt tại
M
và
N
sao
cho
A
là trung điểm của đoạn thẳng
MN
. Một vectơ chỉ phương của
là:
A.
2;3;2
u
. B.
1; 1; 2
u
. C.
3;5;1
u
. D.
4;5; 13
u
.
Lời giải
Chọn A.
Điểm
M d
1 2 ; ;2
M t t t
,
A
là trung điểm của
MN
3 2 ; 2 ;2
N t t t
Điểm
N P
3 2 2 2 2 5 0
t t t
2t
3;2;4
M
,
1; 4;0
N
4; 6; 4
MN
2 2;3;2
.
Câu 32: [2H3-3.1-4] Trong không gian
Oxyz
, cho tam giác
ABC
có
2;3;3
A
, phương trình đường trung
tuyến kẻ từ
B
là
3 3 2
1 2 1
x y z
, phương trình đường phân giác trong của góc
C
là
2 4 2
2 1 1
x y z
. Đường thẳng
AB
có một véc-tơ chỉ phương là
A.
3
2;1; 1
u
. B.
2
1; 1;0
u
. C.
4
0;1; 1
u
. D.
1
1;2;1
u
.
Lời giải
Chọn C.
Phương trình tham số của đường phân giác trong góc
C
là
2 2
: 4
2
x t
CD y t
z t
.
Gọi
2 2 ;4 ;2
C t t t
, suy ra tọa độ trung điểm
M
của
AC
là
7 5
2 ; ;
2 2
t t
M t
. Vì
M BM
nên:
7 5
3 2
2 3
2 2
1 2 1
t t
t
1 1 1
1
1 4 2
t t t
t
.
Do đó
4;3;1
C
.
Phương trình mặt phẳng
P
đi qua
A
và vuông góc
CD
là
2. 2 1. 3 1. 3 0
x y z
hay
2 2 0
x y z
.
Tọa độ giao điểm
H
của
P
và
CD
là nghiệm
; ;x y z
của hệ
2 2
4
2
2 2 0
x t
y t
z t
x y z
2 2
4
2
2 2 2 4 2 2 0
x t
y t
z t
t t t
2
4
2
0
x
y
z
t
2;4;2
H
.
Gọi
A
là điểm đối xứng với
A
qua đường phân giác
CD
, suy ra
H
là trung điểm
AA
,
bởi vậy:
2 2.2 2 2
2 2.4 3 5
2 2.2 3 1
A H A
A H A
A H A
x x x
y y y
x z z
2;5;1
A
.
Do
A BC
nên đường thẳng
BC
có véc-tơ chỉ phương là
2;2;0 2 1;1;0
CA
,
nên phương trình đường thẳng
BC
là
4
3
1
x t
y t
z
.
Vì
B BM BC
nên tọa độ
B
là nghiệm
; ;x y z
của hệ
4
2
3
5
1
1
3 3
2
1
1 2
x t
x
y t
y
z
z
x y
t
2;5;1
B A
.
Đường thẳng
AB
có một véc-tơ chỉ phương là
0;2; 2 2 0;1; 1
AB
; hay
4
0;1; 1
u
là một véc-tơ chỉ của phương đường thẳng
AB
.
Câu 33: [2H3-3.1-4] Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
2; 2;1 ,
M
1;2; 3
A
và đường
thẳng
1 5
:
2 2 1
x y z
d
. Tìm một vectơ chỉ phương
u
của đường thẳng
đi qua
M
, vuông góc với đường thẳng
d
đồng thời cách điểm
A
một khoảng bé nhất.
A.
2;2; 1
u
. B.
1;7; 1
u
. C.
1;0;2
u
. D.
3;4; 4
u
.
Lời giải
Chọn C.
Gọi
P
là mp đi qua
M
và vuông góc với
d
, khi đó
P
chứa
.
Mp
P
qua
2; 2;1
M
và có vectơ pháp tuyến
2;2; 1
P d
n u
nên có phương trình:
: 2 2 9 0
P x y z
.
Gọi
,H
K
lần lượt là hình chiếu của
A
lên
P
và
. Khi đó:
:
AK AH const
nên
min
AK
khi
K H
. Đường thẳng
AH
đi qua
1,2, 3
A
và có vectơ chỉ phương
2;2; 1
d
u
nên
AH
có phương trình tham số:
1 2
2 2
3
x t
y t
z t
.
1 2 ;2 2 ; 3
H AH H t t t
.
2 1 2 2 2 2 3 9 0 2 3; 2; 1
H P t t t t H
.
Vậy
1;0;2
u HM
.
Câu 34: [2H3-3.1-4] Trong không gian
Oxyz
, cho tam giác
ABC
có
2;3;3
A
, phương trình đường trung
tuyến kẻ từ
B
là
3 3 2
1 2 1
x y z
, phương trình đường phân giác trong của góc
C
là
2 4 2
2 1 1
x y z
. Đường thẳng
AB
có một véc-tơ chỉ phương là
A.
3
2;1; 1
u
. B.
2
1; 1;0
u
. C.
4
0;1; 1
u
. D.
1
1;2;1
u
.
Lời giải
Chọn C.
Phương trình tham số của đường phân giác trong góc
C
là
2 2
: 4
2
x t
CD y t
z t
.
Gọi
2 2 ;4 ;2
C t t t
, suy ra tọa độ trung điểm
M
của
AC
là
7 5
2 ; ;
2 2
t t
M t
. Vì
M BM
nên:
7 5
3 2
2 3
2 2
1 2 1
t t
t
1 1 1
1
1 4 2
t t t
t
.
Do đó
4;3;1
C
.
Phương trình mặt phẳng
P
đi qua
A
và vuông góc
CD
là
2. 2 1. 3 1. 3 0
x y z
hay
2 2 0
x y z
.
Tọa độ giao điểm
H
của
P
và
CD
là nghiệm
; ;x y z
của hệ
2 2
4
2
2 2 0
x t
y t
z t
x y z
2 2
4
2
2 2 2 4 2 2 0
x t
y t
z t
t t t
2
4
2
0
x
y
z
t
2;4;2
H
.
Gọi
A
là điểm đối xứng với
A
qua đường phân giác
CD
, suy ra
H
là trung điểm
AA
,
bởi vậy:
2 2.2 2 2
2 2.4 3 5
2 2.2 3 1
A H A
A H A
A H A
x x x
y y y
x z z
2;5;1
A
.
Do
A BC
nên đường thẳng
BC
có véc-tơ chỉ phương là
2;2;0 2 1;1;0
CA
,
nên phương trình đường thẳng
BC
là
4
3
1
x t
y t
z
.
Vì
B BM BC
nên tọa độ
B
là nghiệm
; ;x y z
của hệ
4
2
3
5
1
1
3 3
2
1
1 2
x t
x
y t
y
z
z
x y
t
2;5;1
B A
.
Đường thẳng
AB
có một véc-tơ chỉ phương là
0;2; 2 2 0;1; 1
AB
; hay
4
0;1; 1
u
là một véc-tơ chỉ của phương đường thẳng
AB
.
Câu 35: [2H3-3.3-4] Trong không gian với hệ tọa độ
Oxyz
, cho tam giác
ABC
vuông tại
C
,
60
ABC
,
3 2,
AB
đường thẳng
AB
có phương trình
3 4 8
1 1 4
x y z
, đường thẳng
AC
nằm trên mặt
phẳng
: 1 0
x z
. Biết
B
là điểm có hoành độ dương, gọi
; ;a b c
là tọa độ điểm
C
, giá trị
của
a b c
bằng
A.
3
. B.
2
. C.
4
. D.
7
.
Lời giải
Chọn B.
Ta có
A
là giao điểm của đường thẳng
AB
với mặt phẳng
. Tọa độ điểm
A
là nghiệm của hệ
3 4 8
1 1 4
1 0
x y z
x z
1
2
0
x
y
z
. Vậy điểm
1;2;0
A
.
Điểm
B
nằm trên đường thẳng
AB
nên điểm
B
có tọa độ
3 ;4 ; 8 4B t t t
.
Theo giả thiết thì
3 0
t
3
t
.
Do
3 2
AB
, ta có
2 2 2
2 2 16 2 18
t t t
1
t
nên
2;3; 4
B
.
Theo giả thiết thì
3 6
sin 60
2
AC AB
;
3 2
.cos60
2
BC AB
.
Vậy ta có hệ
2 2
2
2 2 2
1
27
1 2
2
9
2 3 4
2
a c
a b c
a b c
2 2
2
1
2 2 8 9
27
1 2
2
a c
a b c
a b c
7
2
3
5
2
a
b
c
. Vậy
7 5
;3;
2 2
C
nên
2
a b c
.
Câu 36: [2H3-3.3-4] Trong không gian tọa độ
Oxyz
cho các điểm
1;5;0
A
,
3;3;6
B
và đường thẳng
1 1
:
2 1 2
x y z
. Gọi
; ;M a b c
sao cho chu vi tam giác
MAB
đạt giá trị nhỏ nhất. Tính
tổng
T a b c
?
A.
2T
. B.
3
T
. C.
4T
. D.
5
T
.
Lời giải
Chọn B.
Ta có
M
1 2 ;1 ;2M t t t
.
2 2 ;4 ; 2MA t t t
,
4 2 ;2 ;6 2MB t t t
.
Khi đó chu vi tam giác
MAB
đạt giá trị nhỏ nhất khi và chỉ khi
MA MB
nhỏ nhất.
Xét hàm số
f t MA MB
2 2
9 20 9 36 56
t t t
2 2 2
2 2
2
3 2 5 6 3 2 5 6 4 5 2 29
t t .
Dấu bằng đạt được khi và chỉ khi bộ số
3 ;6 3t t
và bộ số
2 5;2 5
tỉ lệ.
Suy ra
3 6 3 1t t t
. Suy ra
1;0;2
M
.
Chú ý ở đây có dùng bất đẳng thức Mincopski
2 2
2 2 2 2 2 2
1 1 2 2 1 2 1 2
... ... ...
n n n n
a b a b a b a a a b b b
, đúng với mọi
i
a
,
i
b
.
Dấu bằng xảy ra khi hai bộ số
1 2
, ,...,
n
a a a
và
1 2
, ,...,
n
b b b
tỉ lệ.
Câu 37: [2H3-3.3-4] Trong không gian với hệ tọa độ
Oxyz
cho ba điểm
2; 1;1
A
,
5;3;1
M
,
4;1;2
N
và
mặt phẳng
: 27
P y z
. Biết rằng tồn tại điểm
B
trên tia
AM
, điểm
C
trên
P
và điểm
D
trên
tia
AN
sao cho tứ giác
ABCD
là hình thoi. Tọa độ điểm
C
là
A.
15;21;6
. B.
21;21;6
. C.
15;7;20
. D.
21;19;8
.
Lời giải
Chọn B.
C
A
B
D
E
F
K
M
N
Cách 1: Ta có
3;4;0
AM
;
5
AM
. Gọi
E
là điểm sao cho
1 3 4
. ; ;0
5 5
AE AM
AM
, khi đó
E
thuộc tia
AM
và
1AE
.
Ta cũng có
2;2;1
AN
;
3
AN
. Gọi
F
là điểm sao cho
1 2 2 1
. ; ;
3 3 3
AF AN
AN
, khi đó
F
thuộc tia
AN
và
1AF
.
Do
ABCD
là hình thoi nên suy ra
19 22 1 1
; ; 19;22;5
15 15 3 15
AK AE AF

cùng hướng với
AC
, hay
19;22;5
u
là một véc-tơ chỉ phương của đường thẳng
AC
. Phương trình đường thẳng
AC
là
2 19
: 1 22
1 5
x t
AC y t
z t
.
Tọa độ điểm
C
ứng với
t
là nghiệm phương trình:
1 22 1 5 27 1t t t
.
Do đó
21;21;6
C
.
Cách 2:
3;4;0
AM
,
5
AM
.
2;2;1
AN
,
3
AN
.
Chọn điểm
1
3
AM AM
,
1
15
AM
và
1
3
AN AN
,
1
15
AN
. Khi đó tam giác
1 1
AM N
cân tại
A
.
Do tứ giác
ABCD
là hình thoi nên tam giác
ABD
cân tại
A
. Suy ra
BD
và
1 1
M N
song song.
Ta có
1 1 1 1
5 3 1; 2;5
M N AN AM AN AM
.
Cần có
1 1 1 1
. 0
AC BD AC M N AC M N
Với
; ;C x y z
, ta có
1 1
. 0
AC M N
2 5 9 0
x y z
.Thử đáp án thấy B thỏa mãn.
Câu 38: [2H3-3.5-3] Trong không gian với hệ tọa độ
Oxyz
, cho
: 2 2 5 0
P x y z
,
3;0;1
A
,
1; 1;3
B
. Viết phương trình đường thẳng
d
đi qua
A
, song song với
P
sao cho khoảng cách từ
B
đến
d
là lớn nhất.
A.
3 1
1 1 2
x y z
. B.
3 1
3 2 2
x y z
. C.
1 1
1 2 2
x y z
. D.
3 1
2 6 7
x y z
.
Lời giải
Chọn D.
Đường thẳng
d
đi qua
A
nên
;
d B d BA
, do đó khoảng cách từ
B
đến
d
lớn nhất khi
AB d
u AB
, với
u
là vectơ chỉ phương của
d
.
Lại có
d
song song với
P
nên
P
u n
.
4; 1;2
AB
,
1; 2;2
P
n
, chọn
, 2; 6; 7
P
u AB n
.
Do đó phương trình đường thẳng
d
là
3 1
2 6 7
x y z
.
Câu 39: [2H3-3.5-3] Trong không gian
Oxyz
, cho mặt phẳng
: 2 2 2 0
x y z
, đường thẳng
1 2 3
:
1 2 2
x y z
d
và điểm
1
;1;1 .
2
A
Gọi
là đường thẳng nằm trong mặt phẳng
, song
song với
d
đồng thời cách
d
một khoảng bằng 3. Đường thẳng
cắt mặt phẳng
Oxy
tại điểm
.B
Độ dài đoạn thẳng
AB
bằng.
A.
7
2
. B.
21
2
. C.
7
3
. D.
3
2
.
Lời giải
Chọn A.
Cách 1:
Ta có:
B Oxy
và
B
nên
;2 2 ;0 .
B a a
1 2 3
:
1 2 2
x y z
d
đi qua
1; 2; 3
M
và có một véctơ chỉ phương là
1;2;2
u
.
Ta có:
d
nên
d
và
song song với nhau và cùng nằm trong mặt phẳng
.
Gọi
C d Oxy
1 2 3
:
1 2 2
0
x y z
C
z
1
;1;0
2
C
.
Gọi
d Oxy
, suy ra
d
thỏa hệ
: 2 2 2 0
: 0
x y z
Oxy z
. Do đó,
d
qua
1
;1;0
2
C
và có
VTCP
1; 2;0
d
u
.
Gọi
, ,d d d
. Ta có:
1
cos cos ,
5
d d
u u
.
Gọi
H
là hình chiếu của
C
lên
. Ta có
3
CH
và
3 5
sin 2
CH
BC
.
Ta có
0;0; 1
AC
nên
AC Oxy
AC BC
.
Vậy
2 2
45 7
1
4 2
AB AC BC
.
Cách 2: Ta có:
1 2 3
:
1 2 2
x y z
d
đi qua
( 1; 2; 3)
M
và có một VTCP là
1;2;2
u
.
Ta có:
B Oxy
,
nên
B Oxy
;2 2 ;0 .
B a a
Ta có:
// d
và
, 3
d d
nên
; 3
d B d
;
3
u MB
u
Ta có:
1;4 2 ;3MB a a
;
; 4 2;2 1;2 4u MB a a a
.
Do đó
;
3
u MB
u
2
2
3 2 1
3 2 1 9.
3
a
a
Vậy
2
2
2
1 9 7
1 2 1 9 1 .
2 4 2
AB a a
Câu 40: [2H3-3.5-3] Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
đi qua gốc tọa độ
O
và
điểm
0;1;1
I
. Gọi
S
là tập hợp các điểm nằm trên mặt phẳng
Oxy
, cách đường thẳng
một
khoảng bằng
6
. Tính diện tích hình phẳng giới hạn bởi
S
.
A.
36
. B.
36 2
. C.
18 2
. D.
18
.
Lời giải
Chọn B.
Gọi
; ;0
M x y Oxy
2 2
,
2
,
2
OM OI
y x
d M
OI
Yêu cầu bài toán
2 2
2
6
2
y x
2 2
1
36 72
x y
Vậy quỹ tích
M
trên
Oxy
là hình Elip với
6
a
và
6 2
b
36 2 .
S ab
Câu 41: [2H3-3.5-3]
Trong không gian với hệ trục toạ độ
Oxyz
, cho ba điểm
2;0;0
A
,
0;3;1
B
,
1;4;2
C
. Độ dài đường cao từ đỉnh
A
của tam giác
ABC
:
A.
6
. B.
2
. C.
3
2
. D.
3
.
Lời giải
Chọn B.
Độ dài đường cao từ đỉnh
A
của tam giác
ABC
là
,
AH d A BC
.
Ta có đường thẳng
BC
đi qua điểm
0;3;1
B
và nhận vectơ
1; 1; 1
CB
làm vectơ chỉ phương
nên có phương trình
3
1
x t
y t
z t
.
Do đó:
,
AH d A BC
,
CB AB
CB
.
Với
1; 1; 1
CB
;
2;3;1
AB
, 2;1;1
CB AB
, 6
CB AB
.
3
CB
.
Vậy
,
AH d A BC
,
CB AB
CB
2
.
Câu 42: [2H3-3.5-3] Trong không gian
Oxyz
cho mặt cầu
2 2 2
: 1 2 3 9
S x y z
và mặt phẳng
:2 2 3 0
P x y z
. Gọi
; ;M a b c
là điểm trên mặt cầu sao cho khoảng cách từ
M
đến
P
lớn nhất. Khi đó:
A.
8
a b c
. B.
5
a b c
. C.
6
a b c
. D.
7
a b c
.
Hướng dẫn giải
Chọn D.
Mặt
S
cầu có tâm
1;2;3 , 3
I R
.
2
2 2
2.1 2.2 3 3
4
,
3
2 2 1
d I P R
mặt phẳng cắt mặt cầu theo một đường tròn
Gọi
; ;M a b c
là điểm trên mặt cầu sao cho khoảng cách từ
M
đến
P
lớn nhất.
Khi
M
thuộc đường thẳng
vuông đi qua
M
và vuông góc với
P
1 2
: 2 2
3
x t
y t
z t
. Thay vào mặt cầu
S
2 2 2
2
2 2 9 9 9 1
t t t t t
Với
2
2 2
2.3 2.0 4 3
10
1 3;0;4 ;
3
2 2 1
t M d M P
Với
2
2 2
2. 1 2.4 2 3
1
1 1;4;2 ;
3
2 2 1
t M d M P
Vậy
3;0;4
M
7
a b c
.
Câu 43: [2H3-3.5-3] Trong không gian
Oxyz
, cho hai điểm
2; 2;1
M
,
1;2; 3
A
và đường thẳng
1 5
:
2 2 1
x y z
d
. Tìm véctơ chỉ phương
u
của đường thẳng
đi qua
M
, vuông góc với đường
thẳng
d
, đồng thời cách điểm
A
một khoảng lớn nhất.
A.
4; 5; 2
u
. B.
1;0;2
u
. C.
8; 7;2
u
. D.
1;1; 4
u
.
Lời giải
Chọn A.
Gọi
H
là hình chiếu vuông góc của
A
lên
, ta có
;
d A AH
.
Mặt khác, vì
M
nên
AH AM
. Do đó,
max
AH AM
H M
.
Khi đó, đường thẳng
đi qua
M
, vuông góc với đường thẳng
d
và vuông góc với đường thẳng
AM
nên có véctơ chỉ phương là ;
d
u u AM
4; 5; 2
.
Câu 44: [2H3-3.5-3] Trong không gian
Oxyz
cho hai đường thẳng
1
1
: 2
x
y t
z t
,
2
4
: 3 2
1
x t
y t
z t
. Gọi
S
là mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng
1
và
2
. Bán kính mặt cầu
S
.
A.
10
2
. B.
11
2
. C.
3
2
. D.
2
.
Hướng dẫn giải
Chọn B.
1
A
1;2 ;A t t
,
2
B
4 ;3 2 ;1
B t t t
.
Ta có
3 ;1 2 ;1
AB t t t t t
VTCP của đường thẳng
1
là
1
0;1; 1
u
.
VTCP củả đường thẳng
2
là
2
1; 2; 1
u
.
Ta có
1
2
. 0
. 0
AB u
AB u
1 2 1 0
3 2 1 2 1 0
t t t t
t t t t t
2 0
6 0
t t
t t
0
t t
. Suy ra
3;1;1
AB
11
AB
.
Mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng
1
và
2
có đường kính bằng độ dài
đoạn
AB
nên có bán kính
11
2 2
AB
r
.
Câu 45: [2H3-3.4-3] Trong không gian
Oxyz
cho tam giác
ABC
có
1;2; 1
A
,
2; 1;3
B
,
4;7;5
C
. Tọa
độ chân đường phân giác góc
ABC
của tam giác
ABC
là
A.
11
; 2;1
2
. B.
2 11 1
; ;
3 3 3
. C.
2;11;1
. D.
2 11
; ;1
3 3
.
Lời giải
Chọn D.
Ta có phương trình đường thẳng
AC
là
1 5
2 5 ,
1 6
x t
y t t
z t
.
Gọi
I
là chân đường phân giác góc
ABC
của tam giác
ABC
.
1 5 ;2 5 ; 1 6I t t t
.
Lại có
1;3; 4
BA
,
6;8;2
BC
,
5 1;5 3;6 4
BI t t t
.
Vì
I
là chân đường phân giác góc
ABC
của tam giác nên
ABC
:
cos ; cos ;
BA BI BC BI
. .
. .
BA BI BC BI
BA BI BC BI
2 2 2
2 2 2
5 1 15 9 16 24 30 6 40 24 12 8
1 3 4 6 8 2
t t t t t t
4 26 82 22
26 104
t t
1
8 52 82 22
3
t t t
2 11
; ;1
3 3
I
.
Câu 46: [2H3-3.4-4] Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
2 2
2
: 1 2 4
S x y z
và
đường thẳng
2
:
1
x t
d y t
z m t
. Gọi
T
là tập tất cả các giá trị của
m
để
d
cắt
S
tại hai điểm phân
biệt
A
,
B
sao cho các tiếp diện của
S
tại
A
và
B
tạo với nhau góc lớn nhất có thể. Tính tổng các
phần tử của tập hợp
T
.
A.
3
. B.
3
. C.
5
. D.
4
.
Hướng dẫn giải
Chọn B.
(
S
)
d
H
M
I
A
B
Mặt cầu
S
có tâm
1;0; 2
I
và bán kính
2R
.
Đường thẳng
d
đi qua điểm
2;0; 1
N m
và có véc tơ chỉ phương
1;1;1
u
.
Điều kiện để
d
cắt
S
tại hai điểm phân biệt là
;
d I d R
;
2
IN u
u
2
2 6 6
2
3
m m
3 21 3 21
2 2
m
.
Khi đó, tiếp diện của
S
tại
A
và
B
vuông góc với
IA
và
IB
nên góc giữa chúng là góc
;IA IB
.
Ta có
o o
0 ; 90
IA IB
nên
o
max
; 90
IA IB
IA IB
.
Từ đó suy ra
1
;
2
d I d AB
2
2
2 6 6
2
3
m m
2
2 6 0
m m
0
3
m
m
.
Vậy
3;0
T
. Tổng các phần tử của tập hợp
T
bằng
3
.
Câu 47: [2H3-3.6-3] Trong không gian với hệ tọa độ
,Oxyz
cho điểm
(0;1;2)
A
, mặt phẳng
( ) : 4 0
x y z
và mặt cầu
2 2 2
( ) : 3 1 2 16
S x y z
. Gọi
P
là mặt phẳng đi qua
A
, vuông góc với
( )
và đồng thời
P
cắt mặt cầu
S
theo giao tuyến là một đường tròn có bán
kính nhỏ nhất. Tọa độ giao điểm
M
của
P
và trục
x Ox
là
A.
1
;0;0
2
M
. B.
1
;0;0
3
M
. C.
1;0;0
M
. D.
1
;0;0
3
M
.
Hướng dẫn giải
Chọn A.
Gọi
; ;n a b c
là một vec tơ pháp tuyến của mặt phẳng
P
.
Theo đề bài ta có mặt phẳng
P
vuông góc với mặt phẳng
( ) : 4 0
x y z
nên ta có
phương trình
0
a b c
b a c
; ;n a a c c
.
Phương trình mặt phẳng
P
đi qua
(0;1;2)
A
và có véc tơ pháp tuyến
; ;n a a c c
là
1 2 0
ax a c y c z
.
Khoảng cách từ tâm
3;1;2
I
đến mặt phẳng
P
là
2 2
3
,
2
a
d I P h
a ac c
.
Gọi
r
là bán kính của đường tròn giao tuyến giữa mặt cầu
S
và mặt phẳng
P
ta có
2 2
16
r h
r
nhỏ nhất khi
h
lớn nhất.
Khi
0
a
thì
0
h
.
Khi
0
a
thì
2
2
9
2 1
h
c c
a a
. Do
2
2
2
1 3 3
2 1 2
2 4 2
c c c
a a a
nên
2
2
9 2
9. 6
3
2 1
h
c c
a a
. Dấu
" "
xảy ra khi
2a c
.
một véc tơ pháp tuyến là
2;1; 1
n
phương trình mặt phẳng
P
là
2 1 0
x y z
.
Vậy tọa độ giao điểm
M
của
P
và trục
x Ox
là
1
;0;0
2
M
Câu 48: [2H3-3.6-3] Trong không gian tọa độ
Oxyz
cho
1;1; 1
A
,
2;3;1
B
,
5;5;1
C
. Đường phân giác
trong góc
A
của tam giác
ABC
cắt mặt phẳng
Oxy
tại
; ;0M a b
. Tính
3
b a
.
A.
6
. B.
5
. C.
3
. D.
0
.
Lời giải
Chọn B.
Ta có
3
AB
,
6
AC
. Gọi
; ;I x y z
là điểm thuộc cạnh
BC
sao cho
AI
là phân giác trong của
góc
A
Ta có
2
IC AC
IB AB
2IC IB
5 2 2
5 2 3
1 2 1
x x
y y
z z
3
11
3
1
x
y
z
11
3; ;1
3
I
.
Ta có
8
2; ;2
3
AI
.
Phương trình tham số của
AI
là:
1 2
8
1
3
1 2
x t
y t
z t
.
Phương trình mặt phẳng
Oxy
là:
0
z
.
Giao điểm của đường thẳng
AI
với mặt phẳng
Oxy
là
7
2; ;0
3
M
.
Vậy
3 5
b a
.
Câu 49: [2H3-3.6-3] Trong không gian với hệ trục tọa độ
Oxyz
, cho bốn đường thẳng:
1
3 1 1
:
1 2 1
x y z
d
,
2
1
:
1 2 1
x y z
d
,
3
1 1 1
:
2 1 1
x y z
d
,
4
1
:
1 1 1
x y z
d
. Số
đường thẳng trong không gian cắt cả bốn đường thẳng trên là:
A.
0
. B.
2
. C. Vô số. D.
1
.
Lời giải
Chọn A.
Ta có
1
d
song song
2
d
, phương trình mặt phẳng chứa hai
Hai đường thẳng
1
d
,
2
d
là
: 1 0
P x y z
.
Gọi
3
A d P
1; 1;1
A
,
1 2
,
A d A d
.
4
B d P
0;1;0
B
,
1 2
,
B d B d
.
Mà
1;2; 1
AB
cùng phương với véc-tơ chỉ phương của hai đường thẳng
1
d
,
2
d
nên không
tồn tại đường thẳng nào đồng thời cắt cả bốn đường thẳng trên.
Câu 50:
[2H3-3.6-3] Trong không gian
Oxyz
, cho bốn đường thẳng:
1
3 1 1
:
1 2 1
x y z
d
,
2
1
:
1 2 1
x y z
d
,
3
1 1 1
:
2 1 1
x y z
d
,
4
1 1
:
1 1 1
x y z
d
. Số đường thẳng trong không
gian cắt cả bốn đường thẳng trên là:
A.
0
. B.
2
. C. Vô số. D.
1
.
Lời giải
Chọn D.
Đường thẳng
1
d
đi qua điểm
1
3; 1; 1
M
và có một véctơ chỉ phương là
1
1; 2;1
u
.
P
A
B
1
d
2
d
3
d
4
d
Đường thẳng
2
d
đi qua điểm
2
0;0;1
M
và có một véctơ chỉ phương là
2
1; 2;1
u
.
Do
2
1
u u
và
1 1
M d
nên hai đường thẳng
1
d
và
2
d
song song với nhau.
Ta có
1 2
3;1;2
M M
,
1
1 2
, 5; 5; 5
u M M
5 1;1;1;
Gọi
là mặt phẳng chứa
1
d
và
2
d
khi đó
có một véctơ pháp tuyến là
1;1;1
n
.
Phương trình mặt phẳng
là
1 0
x y z
.
Gọi
3
A d
thì
1; 1;1
A
. Gọi
4
B d
thì
1;2;0
B
.
Do
2;3; 1
AB
không cùng phương với
1
1; 2;1
u
nên đường thẳng
AB
cắt hai
đường thẳng
1
d
và
2
d
.
Câu 51: [2H3-3.6-3] Trong không gian
Oxyz
, cho đường thẳng
1 2 3
:
1 2 1
x y z
d
và mặt phẳng
: 2 0
x y z
. Trong các đường thẳng sau, đường thẳng nào nằm trong mặt phẳng
, đồng
thời vuông góc và cắt đường thẳng
d
?
A.
2
2 4 4
:
1 2 3
x y z
. B.
4
1 1
:
3 2 1
x y z
.
B.
3
5 2 5
:
3 2 1
x y z
. D.
1
2 4 4
:
3 2 1
x y z
.
Lời giải
Chọn B.
Phương trình tham số của đường thẳng
1
: 2 2
3
x t
d y t
z t
.
1 ;2 2 ;3
I d I t t t
1 2 2 3 2 0 1
I t t t t
2;4;4
I
.
Vectơ chỉ phương của
d
là
1;2;1
u
Vectơ chỉ pháp tuyến của
là
1;1; 1
n
Ta có
, 3;2; 1
u n
.
Đường thẳng cần tìm qua điểm
2;4;4
I
, nhận một VTCP là
, 3;2; 1
u n
nên có PTTS
2 3
4 2
4
x t
y t
z t
.
Câu 52: [2H3-3.6-4] Trong không gian với hệ trục tọa độ
Oxyz
, cho bốn đường thẳng:
1
3 1 1
:
1 2 1
x y z
d
,
2
1
:
1 2 1
x y z
d
,
3
1 1 1
:
2 1 1
x y z
d
,
4
1
:
1 1 1
x y z
d
. Số đường
thẳng trong không gian cắt cả bốn đường thẳng trên là
A.
0
. B.
2
. C. Vô số. D.
1
.
Lời giải
Chọn A.
Ta có
1
d
song song
2
d
, phương trình mặt phẳng chứa hai
Hai đường thẳng
1
d
,
2
d
là
: 1 0
P x y z
.
Gọi
3
A d P
1; 1;1
A
,
1 2
,
A d A d
.
4
B d P
0;1;0
B
,
1 2
,
B d B d
.
Mà
1;2; 1
AB
cùng phương với véc-tơ chỉ phương của hai đường thẳng
1
d
,
2
d
nên không tồn
tại đường thẳng nào đồng thời cắt cả bốn đường thẳng trên.
Câu 53: [2H3-3.6-4] Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 3a
: 2
2 3a (1 )
x at
y t
x a t
. Biết
rằng khi
a
thay đổi luôn tồn tại một mặt cầu cố định qua điểm
1;1;1
M
và tiếp xúc với đường thẳng
. Tìm bán kính mặt cầu đó.
A.
5 3
. B. 4
3
. C. 7
3
. D.
3 5
.
Lời giải
Chọn A.
Từ đường thẳng
1 3a
: 2
2 3a (1 )
x at
y t
x a t
3 0
x y z
Ta có
luôn qua điểm
1; 5; 1
A
cố định và
nằm trong mặt phẳng
: 3 0
x yP z
Mặt cầu tiếp xúc với đường thẳng
vói mọi
a
. Nên mặt cầu tiếp xúc mặt phẳng
P
tại
A
.
Đường thẳng
IA
qua
A
và vuông góc
P
có phương trình
1
5
1
x t
y t
z t
(1 ; 5 ; 1 )I t t t
Mà
2 2 2 2 2 2
( 6) ( 2) 5IA IM t t t t t t t
vậy
(6;0; 6) 5 3
I R IM
Câu 54: [2H3-3.6-4] Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
3 2 1
:
2 1 1
x y z
d
và mặt
phẳng
: 2 0
P x y z
. Đường thẳng
nằm trong mặt phẳng
P
, vuông góc với đường thẳng
d
đồng thời khoảng cách từ giao điểm
I
của
d
với
P
đến
bằng
42
. Gọi
5; ;M b c
là hình
chiếu vuông góc của
I
trên
. Giá trị của
bc
bằng
A.
10
. B.
10
. C.
12
. D.
20
.
Lời giải
P
A
B
1
d
2
d
3
d
4
d
Chọn B.
d
Δ'
Δ
I
M
Mặt phẳng
P
có véc-tơ pháp tuyến
1;1;1
P
n
, đường thẳng
d
có véc-tơ chỉ phương
2;1; 1
d
u
.
Tọa độ giao điểm
I
d
với
P
là nghiệm của hệ phương trình:
3 2 1
2 1 1
2 0
x y z
x y z
1
3
0
x
y
z
1; 3;0
I
.
Đường thẳng
nằm trong mặt phẳng
P
, vuông góc với đường thẳng
d
nên có một véc-tơ chỉ
phương là
; 2;3; 1
P d
u n u

.
Đường thẳng
đi qua
I
, thuộc mặt phẳng
P
và vuông góc với đường thẳng
có véc-tơ chỉ
phương là:
; 4; 1;5
P
u n u

.
Phương trình đường thẳng
là:
1 4
3
5
x t
y t
z t
.
Hình chiếu
M
của
I
trên đường thẳng
là giao điểm của
và
1 4 ; 3 ;5M t t t
.
Khoảng cách từ
I
đến
bằng
42
nên
42
IM
2
42
IM
2 2 2
5
42
4t t t
1
t
.
Với
1t
thì
3; 4;5
M
.
Với
1
t
thì
5; 2; 5
M
.
Như vậy
2, 5 10
b c bc
.
Câu 55: [2H3-3.8-3] Trong không gian với hệ trục tọa độ
Oxyz
, cho hai điểm
2;1;1
A
,
0;3; 1
B
. Điểm
M
nằm trên mặt phẳng
:2 4 0
P x y z
sao cho
MA MB
nhỏ nhất là
A.
1;0;2 .
B.
0;1;3 .
C.
1;2;0 .
D.
3;0;2 .
Lời giải
Chọn C.
Khi đó Trước hết ta xét vị trí tương đối của hai điểm
2;1;1
A
và
0;3; 1
B
so với mặt phẳng
:2 4 0
P x y z
. Ta có
2.2 1 1 4 2.0 3 1 4 4 0.
Do đó
2;1;1
A
và
0;3; 1
A
nằm khác phía so với mặt phẳng
:2 4 0
P x y z
.
Theo bất đẳng thức tam giác ta có
MA MB AB
. Đẳng thức xảy ra khi và chỉ khi
, ,M A B
thẳng
hàng hay
.M AB P
Đường thẳng
AB
qua điểm
2;1;1
A
và có vec tơ chỉ phương
2 1; 1;1
AB
có phương trình
tham số
2
1
1 .
x t
y t
z t
Suy ra
2 ;1 ;1
M t t t
.
Vì
M P
nên ta có
2 2 1 1 4 0 2 2 1.
t t t t t
Vậy
1;2;0
M
.
Câu 56: ----------HẾT----------[2H3-3.8-3]
Trong không gian với hệ trục tọa độ
Oxyz
, cho ba điểm
0; 2; 1
A
,
2; 4;3
B
,
1;3; 1
C
và mặt phẳng
: 2 3 0
P x y z
. Tìm điểm
M P
sao
cho 2
MA MB MC
đạt giá trị nhỏ nhất.
A.
1 1
; ; 1
2 2
M
. B.
1 1
; ;1
2 2
M
. C.
2;2; 4
M
. D.
2; 2;4
M
.
Lời giải
Chọn A.
I
A
B
M
Gọi
I
,
O
lần lượt là trung điểm của
AB
và
IC
, khi đó với điểm
M
bất kỳ ta luôn có
2

MA MB MI IA MI IB MI
; tương tự
2
MI MC MO
.
Suy ra 2 2 2 4
d MA MB MC MI MC MO
nên
d
nhỏ nhất khi và chỉ khi
MO
nhỏ nhất
MO P
nên
M
là hình chiếu vuông góc của
O
lên
P
.
Có
0; 2; 1
A
,
2; 4;3
B
1; 3;1
I
, kết hợp với
1;3; 1
C
ta có
0;0;0
O
.
Đường thẳng qua
0;0;0
O
vuông góc với
P
có phương trình
:
2
x t
d y t
z t
.
Giao điểm của
d
và
P
chính là hình chiếu vuông góc
M
của
0;0;0
O
lên mặt phẳng
P
.
Giải hệ
2
2 3 0
x t
y t
z
x y z
t
ta được
1 1 1
, , , 1
2 2 2
t x y z
.
Vậy
1 1
; ; 1
2 2
M
.
* Nhận xét: Với 4 đáp án bài này học sinh chỉ làm phép thử đơn giản là thay tọa độ từng điểm vào
phương trình mặt phẳng
P
thôi cũng đủ chọn đáp án A, “mồi nhử” chưa tốt. Có lẽ tác giả chỉ quan
tâm cách giải tự luận!
Câu 57: [2H3-3.8-3]
Trong không gian với hệ trục
Oxyz
, cho hai điểm
0; 1;2
M
,
1;1;3
N
. Một mặt
phẳng
P
đi qua
M
,
N
sao cho khoảng cách từ điểm
0;0;2
K
đến mặt phẳng
P
đạt giá trị lớn
nhất. Tìm tọa độ véctơ pháp tuyến
n
của mặt phẳng
P
.
1; 1;1
n
. B.
1;1; 1
n
. C.
2; 1;1
n
. D.
2;1; 1
n
.
Lời giải
Chọn B.
Ta có:
1;2;1
MN
.
P
M
N
K
I
Đường thẳng
d
qua hai điểm
M
,
N
có phương trình tham số
1 2
2
x t
y t
z t
.
Gọi
I
là hình chiếu vuông góc của
K
lên đường thẳng
; 1 2 ;2
d I t t t
.
Khi đó ta có
; 1 2 ;KI t t t
.
Do
1 1 1 1 1
. 0 2 4 0 ; ; 1;1; 1
3 3 3 3 3
KI MN KI MN t t t t KI
.
Ta có
; ;
nax
d K P KI d K P KI KI P
1;1; 1
n
.
Câu 58: [2H3-3.8-3] Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;2; 3
A
và mặt phẳng
: 2 2 9 0
P x y z
. Đường thẳng
d
đi qua
A
và có vectơ chỉ phương
3;4; 4
u
cắt
P
tại
B
. Điểm
M
thay đổi trong
P
sao cho
M
luôn nhìn đoạn
AB
dưới góc
o
90
. Khi độ dài
MB
lớn
nhất, đường thẳng
MB
đi qua điểm nào trong các điểm sau?
A.
2; 1;3
H
. B.
1; 2;3
I
. C.
3;0;15
K
. D.
3;2;7
J
.
Lời giải
Chọn B.
+ Đường thẳng
d
đi qua
1;2; 3
A
và có vectơ chỉ phương
3;4; 4
u
có phương trình
là
1 3
2 4
3 4
x t
y t
z t
.
+ Ta có:
2 2 2
MB AB MA
. Do đó
max
MB
khi và chỉ khi
min
MA
.
+ Gọi
E
là hình chiếu của
A
lên
P
. Ta có:
AM AE
.
Đẳng thức xảy ra khi và chỉ khi
M E
.
Khi đó
min
AM AE
và
MB
qua
B
nhận
BE
làm vectơ chỉ phương.
+ Ta có:
B d
nên
1 3 ;2 4 ; 3 4B t t t
mà
B P
suy ra:
2 1 3 2 2 4 3 4 9 0 1
t t t t
2; 2;1
B
.
+ Đường thẳng
AE
qua
1;2; 3
A
, nhận
2;2; 1
P
n
làm vectơ chỉ phương có phương
trình là
1 2
2 2
3
x t
y t
z t
.
Suy ra
1 2 ;2 2 ; 3
E t t t
.
Mặt khác,
E P
nên
2 1 2 2 2 2 3 9 0 2
t t t t
3; 2; 1
E
.
+ Do đó đường thẳng.
MB
. qua
2; 2;1
B
, có vectơ chỉ phương
1;0; 2
BE

nên
có phương trình là
2
2
1 2
x t
y
z t
.
Thử các đáp án thấy điểm
1; 2;3
I
thỏa. Vậy chọn đáp án B.
Câu 59: [2H3-3.8-3] Trong không gian
Oxyz
, cho hai điểm
1;2;1
A
,
1;2; 3
B
và đường thẳng
1 5
:
2 2 1
x y z
d
. Tìm vectơ chỉ phương
u
của đường thẳng
đi qua điểm
A
và vuông góc với
d
đồng thời cách
B
một khoảng lớn nhất.
A.
4; 3;2
u
. B.
2;0; 4
u
. C.
2;2; 1
u
. D.
1;0;2
u
.
Lời giải
Chọn A.
Ta có
2; 0; 4
AB
,
2;2; 1
d
u
.
Gọi
H
là hình chiếu vuông góc của
B
lên
, lúc đó
,
.
Do đó
,
d B
lớn nhất khi
H A
d
và
AB
.
Ta có VTCP của
là
; 8; 6;4
d
u AB u

. Do đó chọn
4; 3;2
u
là VTCP của
.
Câu 60: [2H3-3.8-3] Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
: 2 1 0
P x y z
và điểm
0; 2;3
A
,
2;0;1
B
. Điểm
; ;M a b c
thuộc
P
sao cho
MA MB
nhỏ nhất. Giá trị của
2 2 2
a b c
bằng
A.
41
4
. B.
9
4
. C.
7
4
. D.
3
.
Lời giải
Chọn B.
A
B
A'
Ta có
,A B
cùng nằm về một phía của
P
. Gọi
A
đối xứng với
A
qua
P
suy ra
2;2;1
A
.
Ta có
MA MB
MA MB BA
. Dấu bằng xảy ra khi
M
là giao điểm của
BA
và
P
.
Xác định được
1
1; ;1
2
M
. Suy ra chọn B.
Câu 61: [2H3-3.8-3] Trong không gian với hệ toạ độ
Oxyz
, cho hai điểm
2; 3;2
A
,
3;5;4
B
. Tìm toạ độ
điểm
M
trên trục
Oz
so cho
2 2
MA MB
đạt giá trị nhỏ nhất.
A.
0;0;49
M
. B.
0;0;67
M
. C.
0;0;3
M
. D.
0;0;0
M
.
Lời giải
Chọn C.
Gọi
I
là trung điểm của
AB
5
;1;3
2
I
.
Ta có:
2 2
2 2
MA MB MA MB
2 2
MI IA MI IB
2 2 2
2MI IA IB
.
2 2
IA IB
không đổi nên
2 2
MA MB
đạt giá trị nhỏ nhất khi
MI
đạt giá trị nhỏ nhất.
M
là hình chiếu của
I
trên trục
Oz
.
0;0;3
M
.
Câu 62:
[2H3-3.8-3] Trong không gian
Oxyz
, cho bốn đường thẳng:
1
3 1 1
:
1 2 1
x y z
d
,
2
1
:
1 2 1
x y z
d
,
3
1 1 1
:
2 1 1
x y z
d
,
4
1 1
:
1 1 1
x y z
d
. Số đường thẳng trong không gian
cắt cả bốn đường thẳng trên là
A.
0
. B.
2
. C. Vô số. D.
1
.
Lời giải
Chọn D.
Đường thẳng
1
d
đi qua điểm
1
3; 1; 1
M
và có một véctơ chỉ phương là
1
1; 2;1
u
.
Đường thẳng
2
d
đi qua điểm
2
0;0;1
M
và có một véctơ chỉ phương là
2
1; 2;1
u
.
Do
2
1
u u
và
1 1
M d
nên hai đường thẳng
1
d
và
2
d
song song với nhau.
Ta có
1 2
3;1;2
M M
,
1
1 2
, 5; 5; 5
u M M
5 1;1;1;
Gọi
là mặt phẳng chứa
1
d
và
2
d
khi đó
có một véctơ pháp tuyến là
1;1;1
n
.
Phương trình mặt phẳng
là
1 0
x y z
.
Gọi
3
A d
thì
1; 1;1
A
. Gọi
4
B d
thì
1;2;0
B
.
Do
2;3; 1
AB
không cùng phương với
1
1; 2;1
u
nên đường thẳng
AB
cắt hai
đường thẳng
1
d
và
2
d
.
Câu 63: [2H3-3.8-3] Trong không gian với hệ trục toạ độ
Oxyz
, cho mặt cầu
2 2 2
: 1 2 3 9
S x y z
, điểm
0; 0; 2
A
. Phương trình mặt phẳng
P
đi qua
A
và
cắt mặt cầu
S
theo thiết diện là hình tròn
C
có diện tích nhỏ nhất là
A.
: 2 3 6 0
P x y z
. B.
: 2 2 0
P x y z
.
C.
: 2 6 0
P x y z
. D.
:3 2 2 4 0
P x y z
.
Lời giải
Chọn B.
Mặt cầu
2 2 2
: 1 2 3 9
S x y z
có tâm
1;2;3
I
, bán kính
3
R
.
6
IA R
nên
A
nằm trong mặt cầu.
Gọi
r
là bán kính đường tròn thiết diện, ta có
2 2
r R h
.
Trong đó
h
là khoảng cách từ
I
đến
P
.
Diện tích thiết diện là
2
r
2 2
R h
2 2
R IA
.
Vậy diện tích hình tròn
C
đạt nhỏ nhất khi
h IA
. Khi đó
IA
là véc tơ pháp tuyến của
P
.
Phương trình mặt phẳng
P
là
1 0 2 0 2 0
x y z
2 z 2 0
x y
.
Câu 64: [2H3-3.8-3] Trong không gian với hệ tọa độ
Oxyz
cho các điểm
4;2;5
A
,
0;4; 3
B
,
2; 3;7
C
. Biết điểm
0 0 0
; ;M x y z
nằm trên mặt phẳng
Oxy
sao cho
MA MB MC
đạt giá trị
nhỏ nhất. Tính tổng
0 0 0
P x y z
.
A.
3
P
. B.
0
P
. C.
3
P
. D.
6
P
.
Hướng dẫn giải
Chọn C.
Gọi
2;1;3
G
là trọng tâm
ABC
3 3
MA MB MC MG MG
Do đó
MA MB MC
nhỏ nhất khi
MG
nhỏ nhất
Mà
,
MG d G Oxy GH
nên
MG
nhỏ n hất khi
M H
khi đó
M
là hình chiếu vuông góc của
G
lên
Oxy
2;1;0
M
0 0 0
3
x y z
Câu 65: [2H3-3.8-3] Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
:
x y z
và hai
điểm
0; 1;3
A
,
1; 2;1
B
. Tìm tọa độ điểm
M
thuộc đường thẳng
sao cho
2 2
2MA MB
đạt
giá trị nhỏ nhất.
A.
5;2; 4
M
. B.
1; 1; 1
M
. C.
1;0; 2
M
. D.
3;1; 3
M
.
Hướng dẫn giải
Chọn B.
Vì
M
thuộc đường thẳng
nên
1 2 ; ; 2
M t t t
.
Ta có
2 2
2MA MB
2 2 2 2 2 2
2 1 1 5 2 2 2 3
t t t t t t
2
18 36 53
t t
2 2
2MA MB
2
18 1 35
t
35
,
t
.
Vậy
2 2
min 2 35
MA MB
1
t
hay
1; 1; 1
M
.
Câu 66: [2H3-3.8-3] Trong không gian
Oxyz
, cho điểm
1 3
; ;0
2 2
M
và mặt cầu
2 2 2
: 8
S x y z
. Một
đường thẳng đi qua điểm
M
và cắt
S
tại hai điểm phân biệt
A
,
B
. Diện tích lớn nhất của tam
giác
OAB
bằng
A.
4
. B.
2 7
. C.
2 2
. D.
7
.
Lời giải
Chọn. D.
Mặt cầu
S
có tâm
0;0;0
O
và bán kính
2 2
R
.
Ta có:
1 3
; ;0
2 2
OM
1
OM R
điểm
M
nằm trong mặt cầu
S
.
Gọi
H
là trung điểm
AB OH OM
.
Đặt
0 1OH x x
.
Đặt
2 2 2
8
sin
2 2
AH OA OH x
AOH
OA OA
;
cos
2 2
OH x
OA
.
Suy ra
2
8
sin 2sin cos
4
x x
AOB
.
Ta có:
2
1
. .sin 8
2
OAB
S OA OB AOB x x
với
0 1x
.
Xét hàm số
2
8
f x x x
trên đoạn
0;1
2 2
2
2 2
8 2
8 0, 0;1
8 8
x x
f x x x
x x
0;1
max 1 7
f x f
Vậy diện tích lớn nhất của tam giác
OAB
bằng
7
.
Câu 67: [2H3-3.8-3] Trong không gian
Oxyz
, cho đường thẳng
1 1
:
1 1 2
x y z m
d
và mặt cầu
2 2 2
: 1 1 2 9
S x y z
. Tìm
m
để đường thẳng
d
cắt mặt cầu
S
tại hai điểm phân
biệt
E
,
F
sao cho độ dài đoạn
EF
lớn nhất
A.
1
m
. B.
0
m
. C.
1
3
m
. D.
1
3
m
.
Lời giải
Chọn B.
Mặt cầu
S
có tâm
1;1;2
I
và bán kính
3
R
.
Gọi
H
là hình chiếu vuông góc của
I
trên
d
, khi đó
H
là trung điểm đoạn
EF
.
Ta có
2
2
2 2 ,EF EH R d I P . Suy ra
EF
lớn nhất khi
,
d I P
nhỏ nhất
Đường thẳng
d
qua
1; 1;A m
và có véc tơ chỉ phương
1;1;2
u
.
Ta có
0;2;2
AI m
,
, 2 ;2 ; 2
AI u m m
.
Suy ra
2
,
2 12
, 2
1 1 4
AI u
m
d I P
u
.
Do đó
,
d I P
nhỏ nhất khi
0
m
. Khi đó
2
2
2 2 , 2 7
EF EH R d I P .
Câu 68: [2H3-3.8-3] Trong không gian
Oxyz
, cho hai đường thẳng
1
: 2
x t
d y t
z t
,
2
: 1
2
x t
d y t
z t
. Đường
thẳng
cắt
d
,
d
lần lượt tại các điểm
A
,
B
thỏa mãn độ dài đoạn thẳng
AB
nhỏ nhất. Phương
trình đường thẳng
là
A.
1 2
2 1 3
x y z
. B.
4 2
2 1 3
x y z
.
C.
3 1
2 1 3
x y z
. D.
2 1 1
2 1 3
x y z
.
Lời giải
Chọn D.
1 ;2 ;d A t t t
,
2 ;1 ;2
d B t t t
.
. 0 2 1 1 2 0
4 2 2 1 2 0
. 0
AB u t t t t t t
t t t t t t
AB u
1
2 3 2
2
6 2 1
1
t t
t
t t
t
.
Suy ra
2;1;1
A
,
1 3
1; ;
2 2
AB
AB
ngắn nhất khi và chỉ khi
AB
là đoạn vuông góc chung của
d
,
d
.
Vậy
đi qua
2;1;1
A
có vectơ chỉ phương
2 2;1;3
u AB
2 1 1
:
2 1 3
x y z
.
Câu 69: [2H3-3.8-3] Trong không gian
Oxyz
, cho hình hộp
.
ABCD A B C D
biết
1;0;1
A
,
2;1;2
B
,
2; 2;2
D ,
3;0; 1
A
, điểm
M
thuộc cạnh
DC
. Giá trị nhỏ nhất của tổng các khoảng cách
AM MC
là
A.
17
. B.
17 4 6
. C.
17 8 3
. D.
17 6 2
.
Hướng dẫn giải
Chọn C.
B
(2;1;2)
C
A
(1;0;1)
D
(2;-2;2)
D'
A'
(3;0;-1)
C'
B'
M
Ta có
1;1;1
AB
;
2;0; 2
AA
;
1; 2;1
AD
.
Theo quy tắc hình hộp ta có
AB AD AA AC
5; 1;1
C
.
Phương trình đường thẳng
DC
đi qua
2; 2;2
D
và nhận
1;1;1
AB
làm véc tơ chỉ
phương là
2
2
2
x t
y t
z t
.
Gọi
2 ; 2 ;2
M t t t DC
.
Ta có
1; 2; 1
AM t t t
2
3 6
MA t
,
3; 1; 1
C M t t t
2
3 1 8
MC t
.
Xét vectơ
3 ; 6
u t
,
v t
.
Do
u v u v
nên
2 2
3 6 8
AM MC
17 8 3
AM MC
.
Dấu
" "
xảy ra khi
3 6
3 1 2 3
t
t
3
1 2
t
t
2 3 3
t
.
2 3 1;1 2 3;2 3 1
M
.
Vậy giá trị nhỏ nhất của tổng các khoảng cách
AM MC
là
17 8 3
.
Câu 70: [2H3-3.8-3] Trong không gian với hệ tọa độ
Oxyz
, cho các điểm
2;2; 3
M
và
4;2;1
N
. Gọi
là đường thẳng đi qua
M
, nhận vecto
; ;u a b c
làm vectơ chỉ phương và song song với mặt
phẳng
: 2 0
P x y z
sao cho khoảng cách từ
N
đến
đạt giá trị nhỏ nhất. Biết
a
,
b
là hai
số nguyên tố cùng nhau. Khi đó
a b c
bằng:
A.
15
. B.
13
. C.
16
. D.
14
.
Lời giải
Chọn A.
Gọi
Q
là mặt phẳng đi qua
2;2; 3
M
và song song với mặt phẳng
P
.
Suy ra
: 2 3 0
Q x y z
.
Do
//
P
nên
Q
.
,
d N
đạt giá trị nhỏ nhất
đi qua
N
, với
N
là hình chiếu của
N
lên
Q
.
Gọi
d
là đường thẳng đi qua
N
và vuông góc
P
,
4 2
: 2
1
x t
d y t
z t
.
Ta có
N d
4 2 ;2 ;1
N t t t
;
4
3
N Q t
4 10 7
; ;
3 3 3
N
.
; ;u a b c
cùng phương
10 4 16
; ;
3 3 3
MN
.
Do
a
,
b
nguyên tố cùng nhau nên chọn
5;2;8
u
.
Vậy
15
a b c
.
45-47 CHANH MUỐI
Câu 71: [2H3-3.8-3] Trong không gian
,Oxyz
cho đường thẳng
2 1 2
:
4 4 3
x y z
d
và mặt phẳng
: 2 2 1 0
P x y z
. Đường thẳng
đi qua
2; 1; 2
E
, song song với
P
đồng thời tạo với
d
góc bé nhất. Biết rằng
có một véctơ chỉ phương
; ; 1 .
u m n
Tính
2 2
T m n
.
A.
5
T
. B.
4T
. C.
3
T
. D.
4T
.
Lời giải
Chọn D.
Mặt phẳng
P
có vec tơ pháp tuyến
2; 1;2
n
và đường thẳng
d
có vec tơ chỉ phương
4; 4;3
v
Vì
song song với mặt phẳng
P
nên
2 2 0 2 2
u n m n n m
.
Mặt khác ta có
.
cos ;
.
u v
d
u v
2
2 2 2 2
4 4 3
1. 4 4 3
m n
m n
2
4 5
41 5 8 5
m
m m
2
2
2 2
4 5
1 1 16 40 25
. .
5 8 5 5 8 5
41 41
m
m m
m m m m
.
Vì
0 ; 90
d
nên
;d
bé nhất khi và chỉ khi
cos ;d
lớn nhất
Xét hàm số
2
2
16 40 25
5 8 5
t t
f t
t t
2
2
2
72 90
5 8 5
t t
f t
t t
.
Bảng biến thiên
Dựa vào bảng biến thiên ta có
max 0 5
f t f
suy ra
;d
bé nhất khi
0 2
m n
. Do đó
2 2
4
T m n
.
Làm theo cách này thì không cần đến dữ kiện : đường thẳng
đi qua
2; 1; 2
E
.
Câu 72: [2H3-3.8-3] Họ parabol
2
: 2 3 2
m
P y mx m x m
0
m
luôn tiếp xúc với đường thẳng
d
cố định khi
m
thay đổi. Đường thẳng
d
đó đi qua điểm nào dưới đây?
A.
0; 2 .
B.
0;2 .
C.
1;8 .
D.
1; 8 .
Lời giải
Chọn A.
Gọi
0 0
;H x y
là điểm cố định mà
m
P
luôn đi qua.
Khi đó ta có:
2
0 0 0
2 3 2
y mx m x m
2
0 0 0 0
2 1 6 2 0
m x x x y
,
0
m
.
2
0 0
0 0
2 1 0
6 2 0
x x
x y
.
Do
2
0 0
2 1 0
x x
có nghiệm kép nên
m
P
luôn tiếp xúc với đường thẳng
: 6 2
d y x
.
Ta thấy
0; 2
d
.
Câu 73: [2H3-3.8-3] Trong không gian với hệ toạ độ
Oxyz
, cho hai điểm
2; 3;2
A
,
3;5;4
B
. Tìm toạ độ
điểm
M
trên trục
Oz
so cho
2 2
MA MB
đạt giá trị nhỏ nhất.
A.
0;0;49
M
. B.
0;0;67
M
. C.
0;0;3
M
. D.
0;0;0
M
.
Lời giải
Chọn C.
Gọi
I
là trung điểm của
5
;1;3
2
AB I
.
Ta có:
2 2
2 2
2 2 2 2 2
2
MA MB MA MB MI IA MI IB MI IA IB
.
2 2
IA IB
không đổi nên
2 2
MA MB
đạt giá trị nhỏ nhất khi
MI
đạt giá trị nhỏ nhất.
M
là hình chiếu của
I
trên trục
Oz
.
0;0;3
M
.
Câu 74: [2H3-3.8-4] Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 3 1
x y z
và hai
điểm
1;2; 1
A
,
3; 1; 5
B
. Gọi
d
là đường thẳng đi qua điểm
A
và cắt đường thẳng
sao cho
khoảng cách từ điểm
B
đến đường thẳng
d
là lớn nhất. Phương trình đường thẳng
d
là:
A.
3 5
2 2 1
x y z
. B.
2
1 3 4
x y z
.
C.
2 1
3 1 1
x y z
. D.
1 2 1
1 6 5
x y z
.
Lời giải
Chọn D.
Gọi
I d
. Khi đó
1 2 ;3 ; 1
I t t t
.
Ta có:
2; 3; 4
AB
;
2 2;3 2;AI t t t
; 8 15 ;6 8;10 12AI AB t t t
.
Suy ra:
2
2
,
405 576 228
;
14 20 8
AI AB
t t
d B d
t t
AI
.
Xét hàm số
2 2
2 2
405 576 228 3 135 192 76
.
14 20 8 2 7 10 4
t t t t
f t
t t t t
2
2
2
3 6 16 8
.
2
7 10 4
t t
f t
t t
. Cho
2
0
2
3
t
f t
t
.
Bảng biến thiên:
Do đó
;d B d
nhỏ nhất khi
f t
đạt giá trị nhỏ nhất bằng 27 tại
2
3
t
.
Suy ra
1 5
;2;
3 3
AI
.
Chọn một vectơ chỉ phương của đường thẳng
d
là
3 1;6; 5
u AI
.
Vậy phương trình đường thẳng
1 2 1
:
1 6 5
x y z
d
.
Câu 75: [2H3-3.8-4] Trong không gian
Oxyz
, cho
2
điểm
3; 2;3
A
,
1;0;5
B
và đường thẳng
1 2 3
:
1 2 2
x y z
d
. Tìm tọa độ điểm
M
trên đường thẳng
d
để
2 2
MA MB
đạt giá trị nhỏ
nhất.
A.
1;2;3
M
. B.
2;0;5
M
. C.
3; 2;7
M
. D.
3;0;4
M
.
Lời giải
Chọn B.
Gọi
I
là trung điểm của
AB
, ta có
2; 1;4
I
.
Khi đó:
2 2
2 2
MA MB MA MB
2 2
MI IA MI IB
2 2 2
2 2 .
MI IA IB MI IA IB
2 2 2
2MI IA IB
2
6
MI
.
Do đó
2 2
MA MB
đạt giá trị nhỏ nhất khi và chỉ khi
MI
có độ dài ngắn nhất, điều này xảy ra khi và
chỉ khi
M
là hình chiếu vuông góc của
I
trên đường thẳng
d
.
Phương trình mặt phẳng
P
đi qua
I
và vuông góc với đường thẳng
d
là
1. 2 2. 1 2. 4 0
x y y
hay
: 2 2 12 0
P x y z
.
t

2
3
2

f t
0
0
f t
405
14
27
29
405
14
Phương trình tham số của đường thẳng
d
là
1
2 2
3 2
x t
y t
z t
.
Tọa độ điểm
M
cần tìm là nghiệm
; ;x y z
của hệ phương trình:
1
2 2
3 2
2 2 12 0
x t
y t
z t
x y z
2
0
5
1
x
y
z
t
. Vậy
2;0;5
M
.
Câu 76: [2H3-3.8-4] Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
: 1 0
P x y z
, đường
thẳng
15 22 37
:
1 2 2
x y z
d
và mặt cầu
2 2 2
: 8 6 4 4 0
S x y z x y z
. Một đường
thẳng
thay đổi cắt mặt cầu
S
tại hai điểm
A
,
B
sao cho
8
AB
. Gọi
A
,
B
là hai điểm lần
lượt thuộc mặt phẳng
P
sao cho
AA
,
BB
cùng song song với
d
. Giá trị lớn nhất của biểu thức
AA BB
là
A.
8 30 3
9
. B.
24 18 3
5
. C.
12 9 3
5
. D.
16 60 3
9
.
Lời giải
Chọn B.
Mặt cầu
S
có tâm
4;3; 2
I
và bán kính
5
R
.
Gọi
H
là trung điểm của
AB
thì
IH AB
và
3
IH
nên
H
thuộc mặt cầu
S
tâm
I
bán kính
3
R
.
Gọi
M
là trung điểm của
A B
thì
2AA BB HM
,
M
nằm trên mặt phẳng
P
.
Mặt khác ta có
4
;
3
d I P R
nên
P
cắt mặt cầu
S
và
5
sin ; sin
3 3
d P
. Gọi
K
là hình chiếu của
H
lên
P
thì
.sin
HK HM
.
Vậy để
AA BB
lớn nhất thì
HK
lớn nhất
HK
đi qua
I
nên
max
4 4 3 3
; 3
3 3
HK R d I P
.
Vậy
AA BB
lớn nhất bằng
4 3 3 3 3 24 18 3
2 .
5 5
3
.
Câu 77: [2H3-3.8-4] Trong không gian
Oxyz
, cho ba điểm
1;0;1
A
,
3;2;1
B
,
5;3;7
C
. Gọi
; ;M a b c
là điểm thỏa mãn
MA MB
và
MB MC
đạt giá trị nhỏ nhất. Tính
P a b c
A.
4P
. B.
0
P
. C.
2P
. D.
5
P
.
Lời giải
Gọi
I
là trung điểm của
AB
, suy ra
1;1;1
I
;
4;2;0
AB
.
Phương trình mặt phẳng trung trực của
AB
:
: 2 3 0
x y
.
Vì
2.3 1.2 3 . 2.5 1.3 3 50 0
nên
B
,
C
nằm về một phía so với
, suy ra
A
,
C
nằm
về hai phía so với
.
Điểm
M
thỏa mãn
MA MB
khi
M
. Khi đó
MB MC MA MC AC
.
MB MC
nhỏ nhất bằng
AC
khi
M AC
.
Phương trình đường thẳng
AC
:
1 2
1 2
x t
y t
z t
, do đó tọa độ điểm
M
là nghiệm của hệ phương trình
1 2
1 2
2 3 0
x t
y t
z t
x y
1
1
1
3
t
x
y
z
. Do đó
1;1;3
M
,
5
a b c
.
Câu 78: [2H3-3.8-4] Trong không gian
Oxyz
, cho ba điểm
1;0;1
A
,
3;2;1
B
,
5;3;7
C
. Gọi
; ;M a b c
là điểm thỏa mãn
MA MB
và
MB MC
đạt giá trị nhỏ nhất. Tính
P a b c
A.
4P
. B.
0
P
. C.
2P
. D.
5
P
.
Lời giải
Gọi
I
là trung điểm của
AB
, suy ra
1;1;1
I
;
4;2;0
AB
.
Phương trình mặt phẳng trung trực của
AB
:
: 2 3 0
x y
.
Vì
2.3 1.2 3 . 2.5 1.3 3 50 0
nên
B
,
C
nằm về một phía so với
, suy ra
A
,
C
nằm
về hai phía so với
.
Điểm
M
thỏa mãn
MA MB
khi
M
. Khi đó
MB MC MA MC AC
.
MB MC
nhỏ nhất bằng
AC
khi
M AC
.
Phương trình đường thẳng
AC
:
1 2
1 2
x t
y t
z t
, do đó tọa độ điểm
M
là nghiệm của hệ phương trình
1 2
1 2
2 3 0
x t
y t
z t
x y
1
1
1
3
t
x
y
z
. Do đó
1;1;3
M
,
5
a b c
.
Câu 79: [2H3-3.8-4] Trong không gian với hệ trục tọa độ
Oxyz
cho mặt cầu
2 2 2
: 2 4 4 0
S x y z x y z
và điểm
1;2; 1
M
. Một đường thẳng thay đổi qua
M
và cắt
S
tại hai điểm
A
,
B
. Tìm giá trị lớn nhất của tổng
MA MB
.
A.
8
. B.
10
. C.
2 17
. D.
8 2 5
.
Lời giải
Chọn C.
Mặt cầu
S
có tâm
1; 2; 2
I
, bán kính
3
R
.
Vì
17 3
IM
nên
M
nằm ngoài đường tròn,
Gọi
là góc tạo bởi
MB
và
MI
. Áp dụng định lí Côsin cho tam giác
MIA
và
MIB
ta có
2 2 2
2 . .cos 1
R MA MI MA MI
2 2 2
2 . .cos 2
R MB MI MB MI
Lấy
1
trừ cho
2
vế theo vế ta được
2 2
0 2 17. .cos
MA MB MA MB
2 17 cos
MA MB
Do đó
MA MB
lớn nhất bằng
2 17
khi
cos 1 0
.
Câu 80: [2H3-3.8-4] Trong không gian
Oxyz
, cho hai điểm
1;2;4
A
,
0;0;1
B
và mặt cầu
2 2
2
: 1 1 4.
S x y z
Mặt phẳng
: 3 0
P ax by cz
đi qua
A
,
B
và cắt mặt cầu
S
theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tính
T a b c
.
A.
3
4
T
. B.
33
5
T
. C.
27
4
T
. D.
31
5
T
.
Lời giải
Chọn A.
Mặt cầu
S
có tâm
1;1;0
I
và bán kính
2R
.
Đường thẳng
AB
đi qua điểm
B
, có một VTCP là
1;2;3
BA
: 2
1 3
x t
AB y t t
z t
1; 1;1
IB
3
IB R
P
luôn cắt mặt cầu
S
theo giao tuyến là đường tròn
C
C
có bán kính nhỏ nhất
,
d I P
lớn nhất.
Gọi
H
,
K
lần lượt là hình chiếu vuông góc của
I
lên
P
và
AB
, ta có:
,
d I P IH IK
Do đó
,
d I P
lớn nhất
H K
hay mặt phẳng
P
vuông góc với
IK
Tìm
: ;2 ;1 3 1;2 1;3 1
K K AB K t t t IK t t t
Ta có
1
. 0
7
IK AB IK AB t
6 9 4 1
; ; 6; 9;4
7 7 7 7
IK
Mặt phẳng
P
đi qua
0;0;1
B
, có một VTPT là
6; 9;4
n
9 27
: 6 9 4 4 0 3 3 0
2 4
P x y z x y z
. Vậy
3
4
T
.
Câu 81: [2H3-3.8-4] Trong không gian
Oxyz
, cho ba điểm
1; 2;1
A
,
5; 0; 1
B
,
3;1; 2
C
và mặt phẳng
:3 3 0
Q x y z
. Gọi
; ;M a b c
là điểm thuộc
Q
thỏa mãn
2 2 2
2
MA MB MC
nhỏ nhất.
Tính tổng
5a b c
.
A.
11
. B.
9
. C.
15
. D.
14
.
Lời giải
Chọn B.
Gọi
E
là điểm thỏa mãn
2 0
EA EB EC
3;0;1
E
.
Ta có:
2 2 2
2
S MA MB MC
2 2 2
2
MA MB MC
2 2 2
2
ME EA ME EB ME EC
2 2 2 2
4 2
ME EA EB EC
.
Vì
2 2 2
2
EA EB EC
không đổi nên
S
nhỏ nhất khi và chỉ khi
ME
nhỏ nhất.
M
là hình chiếu vuông góc của
E
lên
Q
.
Phương trình đường thẳng
:ME
3 3
1
x t
y t
z t
.
Tọa độ điểm
M
là nghiệm của hệ phương trình:
3 3
1
3 3 0
x t
y t
z t
x y z
0
1
2
1
x
y
z
t
.
0; 1;2
M
0
a
,
1
b
,
2
c
5 0 1 5.2
a b c
9
.
Câu 82: [2H3-3.8-4] Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
: 4 0
P x y z
, đường thẳng
1 1 3
:
2 1 1
x y z
d
và điểm
1; 3; 1
A
thuộc mặt phẳng
P
. Gọi
là đường thẳng đi qua
A
,
nằm trong mặt phẳng
P
và cách đường thẳng
d
một khoảng cách lớn nhất. Gọi
; ; 1u a b
là
một véc tơ chỉ phương của đường thẳng
. Tính
2a b
.
A.
2 3
a b
. B.
2 0
a b
. C.
2 4
a b
. D.
2 7
a b
.
Lời giải
Chọn A.
d
d
(Q)
(P)
A
I
A
K
H
Đường thẳng
d
đi qua
1; 1; 3
M
và có véc tơ chỉ phương
1
2; 1; 1
u
.
Nhận xét rằng,
A d
và
7; 3; 1
d P I
.
Gọi
Q
là mặt phẳng chứa
d
và song song với
. Khi đó
, , ,
d d d Q d A Q
.
Gọi
H
,
K
lần lượt là hình chiếu vuông góc của
A
lên
Q
và
d
. Ta có
AH AK
.
Do đó,
,d d
lớn nhất
,
d A Q
lớn nhất
max
AH
H K
. Suy ra
AH
chính là đoạn
vuông góc chung của
d
và
.
Mặt phẳng
R
chứa
A
và
d
có véc tơ pháp tuyến là
1
,
R
n AM u
2; 4; 8
.
Mặt phẳng
Q
chứa
d
và vuông góc với
R
nên có véc tơ pháp tuyến là
1
,
Q R
n n u
12; 18; 6
.
Đường thẳng
chứa trong mặt phẳng
P
và song song với mặt phẳng
Q
nên có véc tơ chỉ
phương là
,
P R
u n n
66; 42; 6
6 11; 7; 1
.
Suy ra,
11; 7
a b
. Vậy
2 3
a b
.
Câu 83: [2H3-3.8-4] Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
3;0;1
A
,
1; 1;3
B
và mặt
phẳng
: 2 2 5 0
P x y z
. Viết phương trình chính tắc của đường thẳng
d
đi qua
A
, song song
với mặt phẳng
P
sao cho khoảng cách từ
B
đến
d
nhỏ nhất.
A.
3 1
:
26 11 2
x y z
d
. B.
3 1
:
26 11 2
x y z
d
.
C.
3 1
:
26 11 2
x y z
d
. D.
3 1
:
26 11 2
x y z
d
.
Lời giải
Chọn A.
Gọi mặt phẳng
Q
là mặt phẳng đi qua
A
và song song với mặt phẳng
P
. Khi đó phương trình
của mặt phẳng
Q
là
1 3 2 0 2 1 0
x y z
2 2 1 0
x y z
.
Gọi
H
là hình chiếu của điểm
B
lên mặt phẳng
Q
, khi đó đường thẳng
BH
đi qua
1; 1;3
B
và
nhận
1; 2;2
Q
n
làm vectơ chỉ phương có phương trình tham số là
1
1 2
3 2
x t
y t
z t
.
Vì
H BH Q
H BH
1 ; 1 2 ;3 2H t t t
và
H Q
nên ta có
1 2 1 2 2 3 2 1 0
t t t
10
9
t
1 11 7
; ;
9 9 9
H
.
26 11 2
; ;
9 9 9
AH
1
26;11; 2
9
.
Gọi
K
là hình chiếu của
B
lên đường thẳng
d
, khi đó
Ta có
;
d B d BK BH
nên khoảng cách từ
B
đến
d
nhỏ nhất khi
BK BH
, do đó đường
thẳng
d
đi qua
A
và có vectơ chỉ phương
26;11; 2
u
có phương trình chính tắc:
3 1
:
26 11 2
x y z
d
.
Câu 84: [2H3-3.8-4] Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
: 4 0
P x y z
, đường thẳng
1 1 3
:
2 1 1
x y z
d
và điểm
1; 3; 1
A
thuộc mặt phẳng
P
. Gọi
là đường thẳng đi qua
A
,
nằm trong mặt phẳng
P
và cách đường thẳng
d
một khoảng cách lớn nhất. Gọi
; ; 1u a b
là
một véc tơ chỉ phương của đường thẳng
. Tính
2a b
.
A.
2 3
a b
. B.
2 0
a b
. C.
2 4
a b
. D.
2 7
a b
.
Lời giải
Chọn A.
d
d
(Q)
(P)
A
I
A
K
H
Đường thẳng
d
đi qua
1; 1; 3
M
và có véc tơ chỉ phương
1
2; 1; 1
u
.
Nhận xét rằng,
A d
và
7; 3; 1
d P I
.
Gọi
Q
là mặt phẳng chứa
d
và song song với
. Khi đó
, , ,
d d d Q d A Q
.
Gọi
H
,
K
lần lượt là hình chiếu vuông góc của
A
lên
Q
và
d
. Ta có
AH AK
.
Do đó,
,d d
lớn nhất
,
d A Q
lớn nhất
max
AH
H K
. Suy ra
AH
chính là đoạn
vuông góc chung của
d
và
.
Mặt phẳng
R
chứa
A
và
d
có véc tơ pháp tuyến là
1
,
R
n AM u
2; 4; 8
.
Mặt phẳng
Q
chứa
d
và vuông góc với
R
nên có véc tơ pháp tuyến là
1
,
Q R
n n u
12; 18; 6
.
Đường thẳng
chứa trong mặt phẳng
P
và song song với mặt phẳng
Q
nên có véc tơ chỉ
phương là
,
P R
u n n
66; 42; 6
6 11; 7; 1
.
Suy ra,
11; 7
a b
. Vậy
2 3
a b
.
Câu 85: [2H3-3.8-4] Trong không gian
Oxyz
, cho ba điểm
1; 2;1
A
,
5; 0; 1
B
,
3;1; 2
C
và mặt
phẳng
:3 3 0
Q x y z
. Gọi
; ;M a b c
là điểm thuộc
Q
thỏa mãn
2 2 2
2
MA MB MC
nhỏ
nhất. Tính tổng
5a b c
.
A.
11
. B.
9
. C.
15
. D.
14
.
Lời giải
Chọn B.
Gọi
E
là điểm thỏa mãn
2 0
EA EB EC

3;0;1
E
.
Ta có:
2 2 2
2
S MA MB MC
2 2 2
2
MA MB MC
2 2 2
2
ME EA ME EB ME EC

2 2 2 2
4 2
ME EA EB EC
.
Vì
2 2 2
2
EA EB EC
không đổi nên
S
nhỏ nhất khi và chỉ khi
ME
nhỏ nhất.
M
là hình chiếu vuông góc của
E
lên
Q
.
Phương trình đường thẳng
:ME
3 3
1
x t
y t
z t
.
Tọa độ điểm
M
là nghiệm của hệ phương trình:
3 3
1
3 3 0
x t
y t
z t
x y z
0
1
2
1
x
y
z
t
.
0; 1;2
M
0
a
,
1
b
,
2
c
.
5 0 1 5.2
a b c
9
.
Câu 86: [2H3-3.8-4] Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
2 1
:
1 2 3
x y z
d
và hai
điểm
2;0;3
A
,
2; 2; 3
B
. Biết điểm
0 0 0
; ;M x y z
thuộc
d
thỏa mãn
4 4
MA MB
nhỏ nhất.
Tìm
0
x
.
A.
0
1
x
. B.
0
3
x
. C.
0
0
x
. D.
0
2
x
.
Lời giải
Chọn D.
Gọi
I
là trung điểm của
AB
. Khi đó ta có
2 2
2 2
2
4 4 2 2 2 2 2 2
4 4
4 2 2 4 2 2
2
4 2
4 2 2 2 4
2 . 2 2
2 4
4 2 2
4 8
3 7
2 3 2
4 4 10
AB AB
MA MB MA MB MA MB MI MI
AB AB
MI MI AB MI MI AB
AB AB
MI MI AB MI AB
Do đó,
4 4
MA MB
đạt GTNN khi
MI
nhỏ nhất
M
là hình chiếu vuông góc của
I
lên
d
.
Điểm
2; 1;0
I
. Lấy
2 ; 1 2 ;3 d
M t t t
.
;2 ;3IM t t t
. 0 4 9 0 0
d d
IM u IM u t t t t
Suy ra
M I
.
Vậy
0
2
x
| 1/62
| | Tải xuống

Có thể bạn quan tâm:

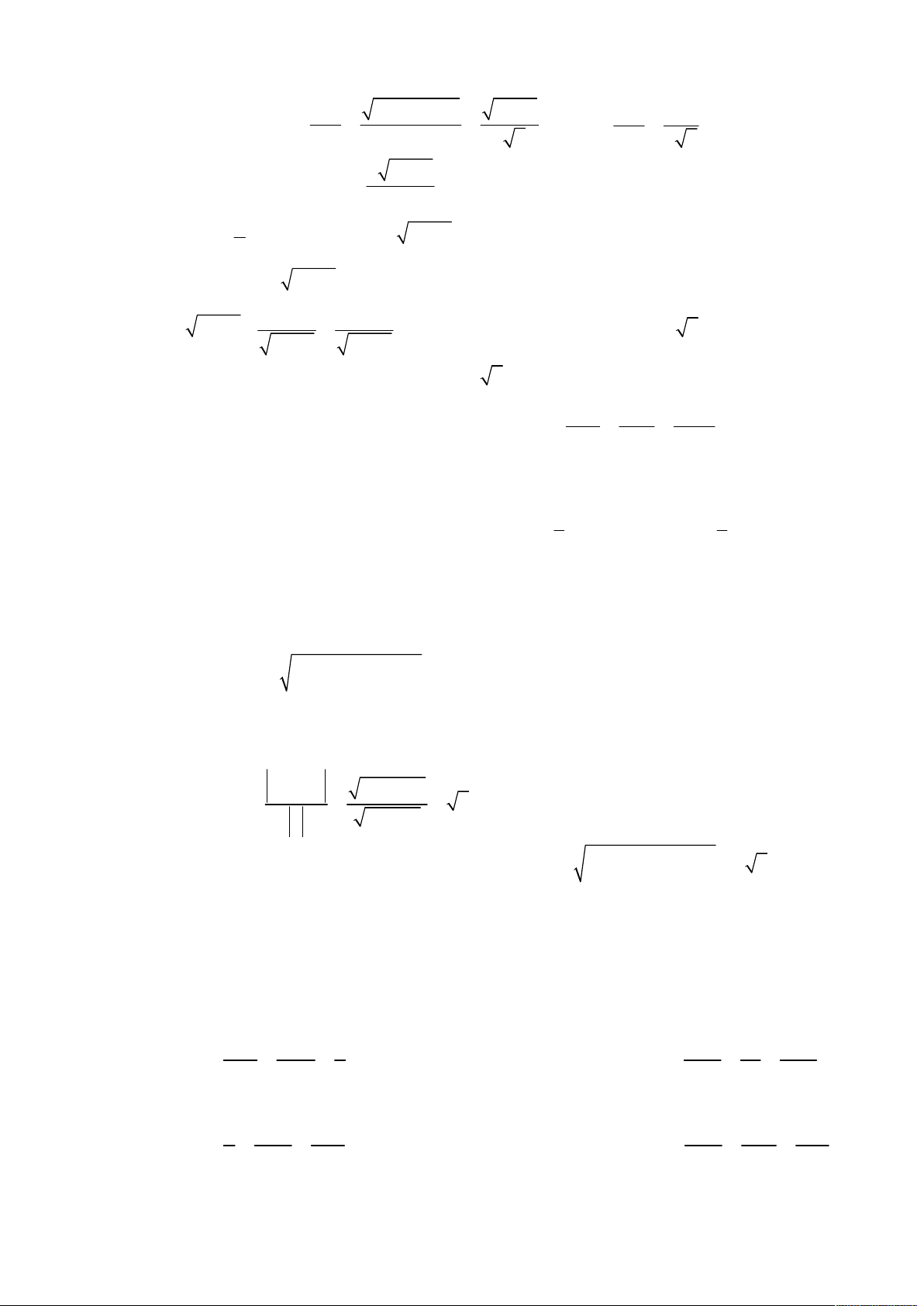
Preview text:

PHƯƠNG TRÌNH ĐƯỜNG THẲNG NÂNG CAO
Câu 1: [2H3-3.2-3] Trong không gian với hệ tọa độ Oxyz , viết phương trình đường vuông góc chung x  2 y  3 z  4 x 1 y  4 z  4
của hai đường thẳng d :   và d  :   . 2 3 5 3 2 1  x y z 1 x  2 y  2 z  3 A.   . B.   . 1 1 1 2 3 4 x  2 y  2 z  3 x y  2 z  3 C.   . D.   . 2 2 2 2 3 1 
Câu 2: [2H3-3.2-3] Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng  P : x  2 y z  4  0 và x 1 y z  2 đường thẳng d :  
. Viết phương trình đường thẳng  nằm trong mặt phẳng 2 1 3
P , đồng thời cắt và vuông góc với đường thẳng d . x 1 y 1 z 1 x 1 y 1 z 1 A.   . B.   . 5 1 3 5 1 3 x 1 y 1 z 1 x 1 y  3 z 1 C.   . D.   . 5 1  2 5 1 3 x  3 y  3 z  2
Câu 3: [2H3-3.2-3] Trong không gian Oxyz , cho hai đường thẳng d :   ; 1 1  2 1 x  5 y 1 z  2 d :  
và mặt phẳng  P : x  2 y  3z  5  0 . Đường thẳng vuông góc với  P , 2 3  2 1
cắt d và d có phương trình là 1 2 x 1 y 1 z x  2 y  3 z 1 A.   . B.   . 1 2 3 1 2 3 x  3 y  3 z  2 x 1 y 1 z C.   . D.   . 1 2 3 3 2 1 x 1 y  2 z
Câu 4: [2H3-3.2-3] Phương trình đường thẳng song song với đường thẳng d :   và cắt 1 1 1 x 1 y 1 z  2 x 1 y  2 z  3
hai đường thẳng d :   ; d :   là: 1 2 1 1 2 1 1 3 x 1 y 1 z  2 x 1 y z 1 A.   . B.   . 1 1 1 1 1 1 x 1 y  2 z  3 x 1 y z 1 C.   . D.   . 1 1 1 1 1  1
Câu 5: [2H3-3.2-3] Trong không gian Oxyz , cho ba điểm A1;1; 
1 , B 1;2;0 , C 2;  3;2 . Tập hợp
tất cả các điểm M cách đều ba điểm A , B , C là một đường thẳng d . Phương trình tham số
của đường thẳng d là:
x  8  3t
x  8  3t
x  8  3t
x  8  3t    
A. y t .
B. y t .
C. y  t .
D. y t .
z  15  7t     z  15  7t
z  15  7tz  15  7tx 1 y 1 z  2
Câu 6: [2H3-3.2-3] Trong không gian cho đường thẳng  :   . Tìm hình chiếu vuông 2 1 1
góc của  trên mặt phẳng Oxy . x  0 x  1 2tx  1   2tx  1   2t    
A. y  1 t .
B. y  1 t .
C. y  1 t .
D. y  1 t . z  0     z  0  z  0  z  0 
Câu 7: [2H3-3.2-3] Trong không gian với hệ tọa độ Oxyz , cho các điểm A2;0;0 ; B 0;3;0 ;
C 0;0; 4 . Gọi H là trực tâm tam giác ABC . Tìm phương trình tham số của đường thẳng OH .  x  4tx  3tx  6tx  4t    
A. y  3t .
B. y  4t .
C. y  4t .
D. y  3t . z  2t     z  2tz  3tz  2tx  3 y 1 z  2
Câu 8: [2H3-3.2-3] Trong không gian Oxyz , cho ba đường thẳng d :   , 1 2 1 2 x 1 y z  4 x  3 y  2 z d :   và d :  
. Đường thẳng song song d , cắt d và d có 2 3 2 1  3 4 1  6 3 1 2 phương trình là x  3 y 1 z  2 x  3 y 1 z  2 x 1 y z  4 x 1 y z  4 A.   . B.   .C.   . D.   . 4 1 6 4 1 6  4 1 6 4 1  6
Câu 9: [2H3-3.2-3] Trong không gian Oxyz , cho mặt phẳng   : y  2z  0 và hai đường thẳng: x  1 t
x  2  t  
d :  y t
; d :  y  4  2t . Đường thẳng  nằm trong mặt phẳng   và cắt hai đường 1 2 z  4t   z  4 
thẳng d ; d có phương trình là 1 2 x 1 y z x 1 y z x 1 y z x 1 y z A.   . B.   . C.   . D.   . 7 8 4 7 8 4 7 8 4 7 8 4 x 1 y z  2
Câu 10: [2H3-3.2-3] Trong không gian Oxyz , cho đường thẳng d :   và mặt phẳng 1 1  1
P : 2x y  2z 1  0 . Đường thẳng nằm trong  P , cắt và vuông góc với d có phương trình là x  2 y 1 z  3 x  2 y 1 z  3 A.   . B.   . 3 4 1 3 4 1  x  2 y 1 z  3 x 1 y 1 z 1 C.   . D.   . 3 4 1 3 4 1
Câu 11: [2H3-3.2-3] Trong không gian với hệ tọa độ Descartes Oxyz , cho điểm M 0; 1; 2 và hai x 1 y  2 z  3 x 1 y  4 z  2 đường thẳng d :   , d :  
. Phương trình đường thẳng đi qua 1 1 1 2 2 2 1 4
M , cắt cả d và d là 1 2 x y 1 z  3 x y 1 z  2 x y 1 z  2 x y 1 z  2 A.   . B.   . C.   . D.   . 9 9 8  3 3 4 9 9  16 9 9 16 2 2 x 1 y z 1
Câu 12: [2H3-3.2-3] Trong không gian Oxyz , cho ba đường thẳng d :   ; 1 2 3 1 x  2 y 1 z x  3 y  2 z  5 d :   ; d :  
. Đường thẳng song song với d , cắt d và d có 2 1 2 2 3 3 4 8 3 1 2 phương trình là x 1 y z 1 x 1 y  3 z x 1 y  3 z x 1 y z 1 A.   . B.   . C.   . D.   . 3 4 8 3 4 8 3 4 8 3 4  8
Câu 13: [2H3-3.2-3] Trong không gian với hệ trục tọa độ Oxyz , cho tam giác ABC biết điểm x  5t
A1; 2; 3 , đường trung tuyến BM và đường cao CH có phương trình tương ứng là  y  0 z  1 4tx  4 y  2 z  3 và  
. Viết phương trình đường phân giác góc A . 16 13 5 x 1 y  2 z  3 x 1 y  2 z  3 x 1 y  2 z  3 x 1 y  2 z  3 A.   . B.   .C.   .D.   . 7 1 10 4 13 5 2 3  1 2 11 5 x y  3 z  2
Câu 14: [2H3-3.2-3] Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và 2 1 3 
mặt phẳng  P : x y  2z  6  0 . Đường thẳng nằm trong mặt phẳng  P , cắt và vuông góc
với d có phương trình x  2 y  2 z  5 x  2 y  4 z 1 A.   . B.   . 1 7 3 1 7 3 x  2 y  2 z  5 x  2 y  4 z 1 C.   . D.   . 1 7 3 1 7 3
Câu 15: [2H3-3.2-3] Trong không gian với hệ tọa độ Oxyz cho ba điểm A3; 2
 ; 4 , B 5;3; 2   ,
C 0;4; 2 , đường thẳng d cách đều ba điểm A , B , C có phương trình là  8  11 x   26t   x   3  6 
x  4  26t
x  4  26t  5   1 
A. y   22t .
B. y  2  22t .
C. y   22t .
D. y  2  38t . 3   6 9   9  4 z   27tz  27tz   27t z   27t   4   4  3 
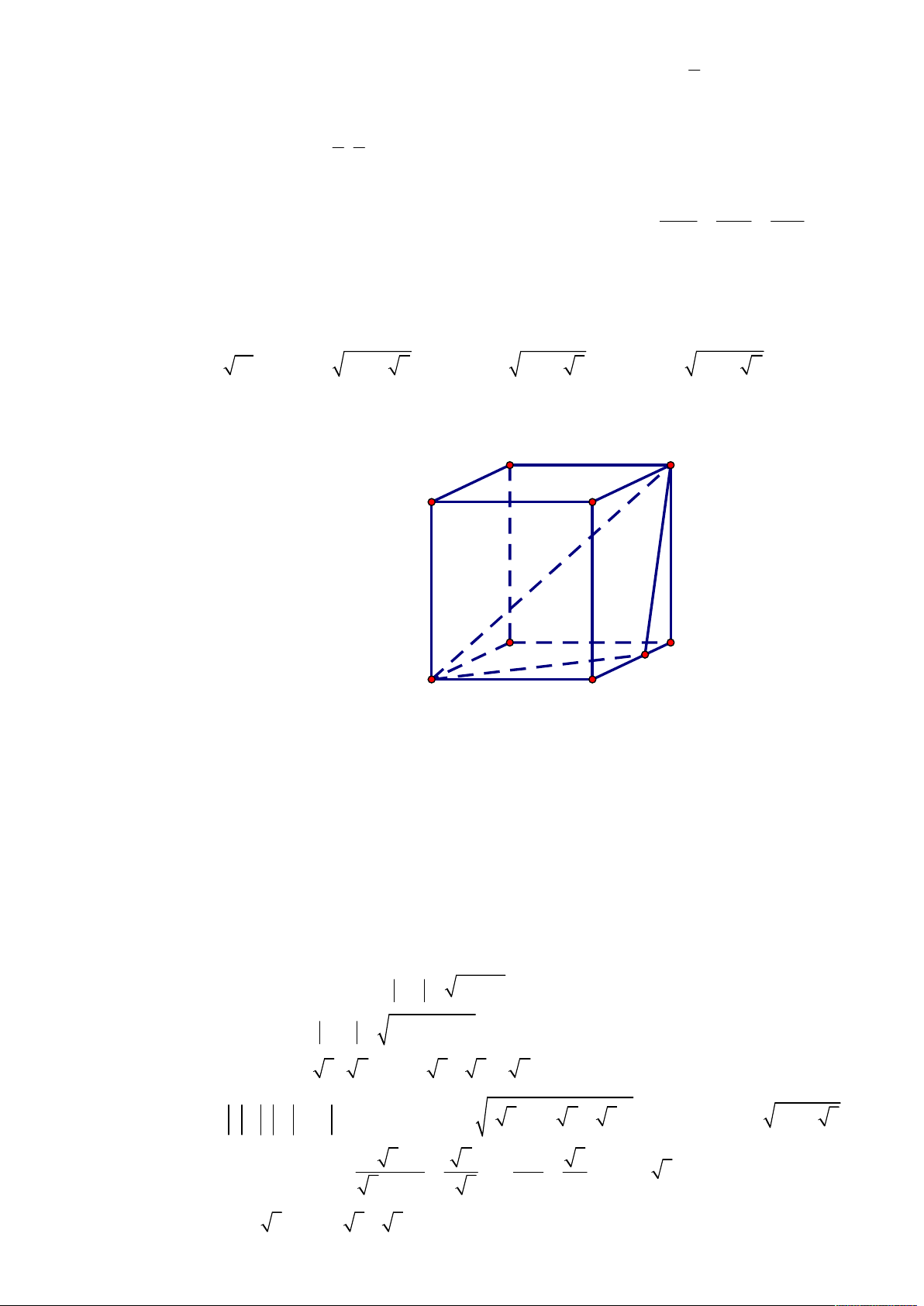
Câu 16: [2H3-3.2-3] Trong không gian Oxyz , cho tam giác ABC với A3;0;0 , B 0;6;0 , C 0;0;6 .
Phương trình nào dưới đây là phương trình đường thẳng đi qua trực tâm của tam giác ABC và
vuông góc với mặt phẳng  ABC  . x 1 y  2 z  3 x  2 y 1 z 1 x  3 y  6 z  6 x 1 y  3 z  3 A.   . B.   .C.   .D.   . 2 1 1 2 1 1 2 1 1 2 1 1
Câu 17: [2H3-3.2-3] Trong không gian Oxyz , cho hai điểm A2;1;  3 và B  3  ; 2  ;1 . Viết phương
trình đường thẳng d đi qua gốc toạ độ sao cho tổng khoảng cách từ A và B đến đường thẳng d lớn nhất. x y z x y z x y z x y z A.   . B.   . C.   . D.   . 1 1 1 1 1 1 1 1 2 1 1 2 x  2  t
Câu 18: [2H3-3.2-3] Trong không gian Oxyz , cho hai đường thẳng cắt nhau  :  y  2  2t , 1 z  1   t
x  1 t 
 :  y t
  t,t  . Viết phương trình đường phân giác của góc nhọn tạo bởi  và  . 2 1 2 z  2t  x 1 y z x 1 y z x 1 y z x 1 y z A.   . B.   . C.   . D.   . 2 3 3 1 1 1 2 3 3 1 1 1
Câu 19: [2H3-3.2-3] Trong không gian với hệ tọa độ Oxyz . Cho mặt phẳng  P : 2x y z 10  0,
x  2  2t
điểm A1;3; 2 và đường thẳng d :  y  1 t
. Tìm phương trình đường thẳng  cắt  P và z 1 t
d lần lượt tại hai điểm M và N sao cho A là trung điểm cạnh MN . x  6 y 1 z  3 x  6 y 1 z  3 A.   . B.   . 7 4 1 7 4 1  x  6 y 1 z  3 x  6 y 1 z  3 C.   . D.   . 7 4 1 7 4 1  x  2  t
x  1 t  
Câu 20: [2H3-3.2-3] Cho hai đường thẳng cắt nhau  :  y  2  2t ,  :  y  t t,t  . Viết 1 2 z  1   t   z  2t 
phương trình đường phân giác của góc nhọn tạo bởi  và  . 1 2 x 1 y z x 1 y z x 1 y z A.   . B.   . C.   .
D. Cả A, B, C đều sai. 2 3 3 1 1 1 2 3 3
Câu 21: [2H3-3.2-3] Trong không gian Oxyz , Cho mặt phẳng  R : x y  2z  2  0 và đường x y z 1 thẳng  :  
. Đường thẳng  nằm trong mặt phẳng  R đồng thời cắt và vuông góc 1 2 1 1  2
với đường thẳng  có phương trình là 1 x tx tx  2  t
x  2  3t     A. y  3  t . B. y  2  t .
C. y  1 t .
D. y  1 t . z  1 t     z  1 tz tz t  x  1 3t
Câu 22: [2H3-3.2-3] Trong không gian Oxyz , cho đường thẳng d :  y  1 4t . Gọi  là đường thẳng đi z 1  
qua điểm A1;1; 
1 và có vectơ chỉ phương u  1; 2
 ; 2 . Đường phân giác của góc nhọn tạo bởi
d và  có phương trình là x  1 7tx  1   2tx  1   2tx  1 3t    
A. y 1 t . B. y  1  0 11t . C. y  1  0 11t .
D. y 1 4t . z 1 5t     z  6   5tz  6  5tz  1 5t  x  1 3t
Câu 23: [2H3-3.2-3] Trong không gian Oxyz , cho đường thẳng d :  y  3
. Gọi  là đường thẳng đi z  5  4  t  qua điểm A1; 3
 ;5 và có vectơ chỉ phương u 1; 2; 2 . Đường phân giác của góc nhọn tạo bởi
d và  có phương trình là
x  1 2t
x  1 2tx  1 7tx  1 t    
A. y  2  5t .
B. y  2  5t . C. y  3   5t .
D. y  3 .  z  6 11     t z  6 11  t z  5   t z  5  7  tx  1 t
Câu 24: [2H3-3.2-3] Trong không gian Oxyz , cho đường thẳng d :  y  2  t . Gọi  là đường thẳng đi z  3   qua điểm (
A 1; 2;3) và có vectơ chỉ phương u  (0; 7  ; 1
 ). Đường phân giác của góc nhọn tạo bởi
d và  có phương trình là x  1 6t
x  4  5t
x  4  5tx  1 5t    
A. y  2 11t .
B. y  10 12t .
C. y  10 12t .
D. y  2  2t .
z  3  8t     z  2  tz  2  tz  3  tx  2 y 1 z  2
Câu 25: [2H3-3.1-3] Trong không gian Oxyz, cho đường thẳng d :   và mặt phẳng 4 4 3
P : 2x y  2z 1  0 . Đường thẳng  đi qua E 2; 1; 2 , song song với  P đồng thời tạo 
với d góc bé nhất. Biết rằng  có một véctơ chỉ phương u   ; m ; n  1 . Tính 2 2
T m n . A. T  5  . B. T  4 . C. T  3 . D. T  4  .
Câu 26: [2H3-3.1-3] Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có phương trình đường x y  6 z  6
phân giác trong góc A là:  
. Biết rằng điểm M 0;5;3 thuộc đường thẳng AB 1 4  3 
và điểm N 1;1;0 thuộc đường thẳng AC . Vectơ nào sau đây là vectơ chỉ phương của đường thẳng AC .    
A. u  1; 2;3 .
B. u  0;1;3 .
C. u  0;  2;6 .
D. u  0;1;  3 . 2 2 2 2 2
Câu 27: [2H3-3.1-3] Cho 2 mặt cầu S : x  3  y  2  z  2
 4 , S  : x   2
1  y z 1  1. 2   1       
Gọi d là đường thẳng đồng thời tiếp xúc với hai mặt cầu trên, cắt đoạn thẳng nối tâm hai mặt 
cầu và cách gốc tọa độ O một khoảng lớn nhất. Nếu u   ;
a 1; b là một vectơ chỉ phương của
d thì tổng S  2a  3b bằng bao nhiêu? A. S  2 . B. S  1 . C. S  0 . D. S  4 .
Câu 28: [2H3-3.1-3] Trong không gian Oxy cho tam giác ABC có A2;3;3 , phương trình đường x  3 y  3 z  2
trung tuyến kẻ từ B là  
, phương trình đường phân giác trong góc C là 1 2 1 x  2 y  4 z  2   
. Biết rằng u   ; m ; n  
1 là một véc tơ chỉ phương của đường thẳng AB . 2 1 1
Tính giá trị biểu thức 2 2
T m n . A. T  1. B. T  5 . C. T  2 . D. T  10 . 
Câu 29: Suy ra A  B B 2;5 
;1  AB  0; 2; 2  20; 1 
;1 là một véc tơ của đường thẳng AB . Vậy 2 2
T m n  2 .[2H3-3.1-3] Trong không gian với hệ toạ độ Oxyz , cho phương trình x y  6 z  6
đường phân giác trong của góc A là  
. Biết M 0;5;3 thuộc đường thẳng AB 1 4  3 
và N 1;1;0 thuộc đường thẳng AC . Vector nào sau đây là vector chỉ phương của đường thẳng AC ?    
A. u  0;1;3 .
B. u  0;1;  3 .
C. u  0;  2;6 .
D. u  1; 2;3 .
Câu 30: [2H3-3.1-3] Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng x  4 y 1 z  5 x  2 y  3 z  :   và  :  
. Giả sử M   , N   sao cho MN là đoạn 1 3 1 2 2 1 3 1 1 2 
vuông góc chung của hai đường thẳng  và  . Tính MN . 1 2    
A. MN  5; 5;10 .
B. MN  2; 2; 4 .
C. MN  3; 3;6 .
D. MN  1; 1; 2 . x 1 y z  2
Câu 31: [2H3-3.1-3] Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   , mặt 2 1 1
phẳng  P : x y  2z  5  0 và A1; 1
 ; 2 . Đường thẳng  cắt d và  P lần lượt tại M và N
sao cho A là trung điểm của đoạn thẳng MN . Một vectơ chỉ phương của  là:    
A. u  2; 3; 2 .
B. u  1; 1; 2 .
C. u  3; 5;1 .
D. u  4; 5; 13 .
Câu 32: [2H3-3.1-4] Trong không gian Oxyz , cho tam giác ABC có A2;3;3 , phương trình đường x  3 y  3 z  2
trung tuyến kẻ từ B là  
, phương trình đường phân giác trong của góc C là 1 2 1 x  2 y  4 z  2  
. Đường thẳng AB có một véc-tơ chỉ phương là 2 1 1    
A. u3  2;1;   1 .
B. u2  1; 1  ; 0 .
C. u4  0;1;   1 .
D. u1  1; 2  ;1 .
Câu 33: [2H3-3.1-4] Trong không gian với hệ tọa độ Oxyz , cho hai điểm M 2; 2  
;1 , A1; 2; 3 và x 1 y  5 z  đường thẳng d :  
. Tìm một vectơ chỉ phương u của đường thẳng  đi qua 2 2 1
M , vuông góc với đường thẳng d đồng thời cách điểm A một khoảng bé nhất.    
A. u  2; 2;   1 .
B. u  1;7;   1 .
C. u  1;0; 2 .
D. u  3; 4; 4   .
Câu 34: [2H3-3.1-4] Trong không gian Oxyz , cho tam giác ABC có A2;3;3 , phương trình đường x  3 y  3 z  2
trung tuyến kẻ từ B là  
, phương trình đường phân giác trong của góc C là 1 2 1 x  2 y  4 z  2  
. Đường thẳng AB có một véc-tơ chỉ phương là 2 1 1    
A. u3 2;1;   1 .
B. u2 1; 1;0 .
C. u4 0;1;   1 .
D. u1 1; 2  ;1 .
Câu 35: [2H3-3.3-4] Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC vuông tại C ,  x  3 y  4 z  8
ABC  60 , AB  3 2, đường thẳng AB có phương trình   , đường thẳng 1 1 4
AC nằm trên mặt phẳng   : x z 1  0 . Biết B là điểm có hoành độ dương, gọi  ; a ; b c là
tọa độ điểm C , giá trị của a b c bằng A. 3 . B. 2 . C. 4 . D. 7 .
Câu 36: [2H3-3.3-4] Trong không gian tọa độ Oxyz cho các điểm A1;5;0 , B 3;3;6 và đường thẳng x 1 y 1 z  :   . Gọi M  ; a ;
b c   sao cho chu vi tam giác MAB đạt giá trị nhỏ nhất. Tính 2 1 2
tổng T a b c ? A. T  2 . B. T  3 . C. T  4 . D. T  5 .
Câu 37: [2H3-3.3-4] Trong không gian với hệ tọa độ Oxyz cho ba điểm A2; 1  ;1 , M 5;3  ;1 ,
N 4;1; 2 và mặt phẳng  P : y z  27 . Biết rằng tồn tại điểm B trên tia AM , điểm C trên
P và điểm D trên tia AN sao cho tứ giác ABCD là hình thoi. Tọa độ điểm C là A.  15  ; 21; 6 . B. 21; 21;6 . C. 15;7; 20 . D. 21;19;8 .
Câu 38: [2H3-3.5-3] Trong không gian với hệ tọa độ Oxyz , cho  P : x  2 y  2z  5  0 , A 3  ; 0  ;1 ,
B 1; 1;3 . Viết phương trình đường thẳng d đi qua A , song song với  P sao cho khoảng
cách từ B đến d là lớn nhất. x  3 y z 1 x  3 y z 1 x 1 y z 1 x  3 y z 1 A.   . B.   . C.   . D.   . 1 1 2 3 2  2 1 2  2 2 6  7
Câu 39: [2H3-3.5-3] Trong không gian Oxyz , cho mặt phẳng   : 2x y  2z  2  0 , đường thẳng x 1 y  2 z  3  1  d :   và điểm A ;1;1 . 
 Gọi  là đường thẳng nằm trong mặt phẳng   , 1 2 2  2 
song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng  cắt mặt phẳng Oxy tại điểm .
B Độ dài đoạn thẳng AB bằng. 7 21 7 3 A. . B. . C. . D. . 2 2 3 2
Câu 40: [2H3-3.5-3] Trong không gian với hệ tọa độ Oxyz , cho đường thẳng  đi qua gốc tọa độ O và điểm I 0;1 
;1 . Gọi S là tập hợp các điểm nằm trên mặt phẳng Oxy , cách đường thẳng 
một khoảng bằng 6 . Tính diện tích hình phẳng giới hạn bởi S . A. 36 . B. 36 2 . C. 18 2 . D. 18 .
Câu 41: [2H3-3.5-3] Trong không gian với hệ trục toạ độ Oxyz , cho ba điểm A2;0;0 , B 0;3  ;1 ,
C 1; 4; 2 . Độ dài đường cao từ đỉnh A của tam giác ABC : 3 A. 6 . B. 2 . C. . D. 3 . 2 2 2 2
Câu 42: [2H3-3.5-3] Trong không gian Oxyz cho mặt cầu S  : x  
1   y  2   z  3  9 và mặt
phẳng  P :2x  2 y z  3  0 . Gọi M  ; a ;
b c là điểm trên mặt cầu sao cho khoảng cách từ M
đến  P lớn nhất. Khi đó:
A. a b c  8 .
B. a b c  5 .
C. a b c  6 .
D. a b c  7 .
Câu 43: [2H3-3.5-3] Trong không gian Oxyz , cho hai điểm M  2  ; 2  ;  1 , A1; 2; 3   và đường thẳng x 1 y  5 zd :  
. Tìm véctơ chỉ phương u của đường thẳng  đi qua M , vuông góc với 2 2 1
đường thẳng d , đồng thời cách điểm A một khoảng lớn nhất.    
A. u  4; 5; 2 .
B. u  1;0; 2 . C. u  8; 7  ; 2 .
D. u  1;1; 4 . x  1 x  4  t  
Câu 44: [2H3-3.5-3] Trong không gian Oxyz cho hai đường thẳng  :  y  2  t ,  :  y  3  2t . Gọi 1 2 z t    z  1 t
S  là mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng  và  . Bán kính mặt 1 2 cầu S  . 10 11 3 A. . B. . C. . D. 2 . 2 2 2
Câu 45: [2H3-3.4-3] Trong không gian Oxyz cho tam giác ABC có A1; 2;  
1 , B 2; 1;3 , C  4  ; 7;5 .
Tọa độ chân đường phân giác góc 
ABC của tam giác ABC là  11   2 11 1   2 11  A. ;  2;1   . B. ; ;   . C.  2  ;11;  1 . D.  ; ;1   .  2   3 3 3   3 3  2 2
Câu 46: [2H3-3.4-4] Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S   x   2 :
1  y   z  2  4 x  2  t
và đường thẳng d :  y t
. Gọi T là tập tất cả các giá trị của m để d cắt S  tại hai
z m 1 t
điểm phân biệt A , B sao cho các tiếp diện của S  tại A và B tạo với nhau góc lớn nhất có
thể. Tính tổng các phần tử của tập hợp T . A. 3 . B. 3 . C. 5 . D. 4 .
Câu 47: [2H3-3.6-3] Trong không gian với hệ tọa độ Oxyz, cho điểm (
A 0;1; 2) , mặt phẳng 2 2 2
( ) : x y z  4  0 và mặt cầu (S) :  x  3   y  
1   z  2  16 . Gọi  P là mặt phẳng đi
qua A , vuông góc với ( ) và đồng thời  P cắt mặt cầu S  theo giao tuyến là một đường
tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của  P và trục x Ox  là  1   1   1  A. M  ; 0; 0   . B. M  ; 0; 0   .
C. M 1;0;0 . D. M ; 0; 0   .  2   3   3 
Câu 48: [2H3-3.6-3] Trong không gian tọa độ Oxyz cho A1;1;   1 , B 2;3;  1 , C 5;5;  1 . Đường phân
giác trong góc A của tam giác ABC cắt mặt phẳng Oxy tại M  ; a ;
b 0 . Tính 3b a . A. 6 . B. 5 . C. 3 . D. 0 .
Câu 49: [2H3-3.6-3] Trong không gian với hệ trục tọa độ Oxyz , cho bốn đường thẳng: x  3 y  1 z  1 x y z 1 x 1 y  1 z 1 x y 1 zd :   , d :   , d :   , d :   . Số 4  3  2  1  1 2  1 1 2 1 2 1 1 1 1 1
đường thẳng trong không gian cắt cả bốn đường thẳng trên là: A. 0 . B. 2 . C. Vô số. D. 1. x  3 y 1 z 1
Câu 50: [2H3-3.6-3] Trong không gian Oxyz , cho bốn đường thẳng: d :   , 1  1 2 1 x y z 1 x 1 y 1 z 1 x y 1 z 1 d :   , d :   , d :  
. Số đường thẳng trong 4  3  2  1 2 1 2 1 1 1 1  1
không gian cắt cả bốn đường thẳng trên là: A. 0 . B. 2 . C. Vô số. D. 1. x 1 y  2 z  3
Câu 51: [2H3-3.6-3] Trong không gian Oxyz , cho đường thẳng d :   và mặt phẳng 1 2 1
  : x y z  2  0 . Trong các đường thẳng sau, đường thẳng nào nằm trong mặt phẳng   ,
đồng thời vuông góc và cắt đường thẳng d ? x  2 y  4 z  4 x 1 y 1 z A.  :   . B.  :   . 2 1 2 3 4 3 2 1 x  5 y  2 z  5 x  2 y  4 z  4 B.  :   . D.  :   . 3 3 2 1 1 3 2 1
Câu 52: [2H3-3.6-4] Trong không gian với hệ trục tọa độ Oxyz , cho bốn đường thẳng: x  3 y 1 z 1 x y z 1 x 1 y 1 z 1 x y 1 z d :   , d :   , d :   , d :   . Số đường 1 1 2  1 2 1 2 1 3 2 1 1 4 1 1 1 
thẳng trong không gian cắt cả bốn đường thẳng trên là A. 0 . B. 2 . C. Vô số. D. 1.
x  1 3a  at
Câu 53: [2H3-3.6-4] Trong không gian với hệ tọa độ Oxyz , cho đường thẳng  :  y  2   t .
x  2  3a  (1 a)t
Biết rằng khi a thay đổi luôn tồn tại một mặt cầu cố định qua điểm M 1;1  ;1 và tiếp xúc với
đường thẳng  . Tìm bán kính mặt cầu đó. A. 5 3 . B. 4 3 . C. 7 3 . D. 3 5 . x  3 y  2 z 1
Câu 54: [2H3-3.6-4] Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và 2 1 1
mặt phẳng  P : x y z  2  0 . Đường thẳng  nằm trong mặt phẳng  P , vuông góc với
đường thẳng d đồng thời khoảng cách từ giao điểm I của d với  P đến  bằng 42 . Gọi M 5; ;
b c là hình chiếu vuông góc của I trên  . Giá trị của bc bằng A. 10 . B. 10 . C. 12 . D. 20 .
Câu 55: [2H3-3.8-3] Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm A2;1  ;1 , B 0;3;   1 .
Điểm M nằm trên mặt phẳng  P :2x y z  4  0 sao cho MA MB nhỏ nhất là
A. 1;0; 2. B. 0;1;3.
C. 1; 2;0. D. 3;0; 2.
Câu 56: [2H3-3.8-3] Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm A0; 2;   1 , B  2  ; 4  ;3 , C 1;3;  1 
và mặt phẳng  P : x y  2z  3  0 . Tìm điểm M  P sao cho   
MA MB  2MC đạt giá trị nhỏ nhất.  1 1   1 1  A. M ; ; 1    .
B. M  ;  ;1   .
C. M 2; 2; 4 . D. M  2  ; 2; 4 .  2 2   2 2 
Câu 57: [2H3-3.8-3] Trong không gian với hệ trục Oxyz , cho hai điểm M 0; 1; 2 , N  1  ;1;3 . Một
mặt phẳng  P đi qua M , N sao cho khoảng cách từ điểm K 0;0; 2 đến mặt phẳng  P đạt 
giá trị lớn nhất. Tìm tọa độ véctơ pháp tuyến n của mặt phẳng  P .     n  1; 1 
;1 . B. n  1;1;   1 . C. n  2; 1  ;  1 .
D. n  2;1;   1 .
Câu 58: [2H3-3.8-3] Trong không gian với hệ tọa độ Oxyz , cho điểm A1; 2; 3 và mặt phẳng 
P : 2x  2y z  9  0 . Đường thẳng d đi qua A và có vectơ chỉ phương u  3;4; 4   cắt  P
tại B . Điểm M thay đổi trong  P sao cho M luôn nhìn đoạn AB dưới góc o 90 . Khi độ dài
MB lớn nhất, đường thẳng MB đi qua điểm nào trong các điểm sau? A. H  2  ; 1  ;3 . B. I 1; 2  ;3 .
C. K 3;0;15 . D. J  3  ; 2; 7 .
Câu 59: [2H3-3.8-3] Trong không gian Oxyz , cho hai điểm A1; 2 
;1 , B 1; 2;  3 và đường thẳng x 1 y  5 zd :  
. Tìm vectơ chỉ phương u của đường thẳng  đi qua điểm A và vuông góc 2 2 1
với d đồng thời cách B một khoảng lớn nhất.   
A. u  4;  3; 2 .
B. u  2; 0;  4 .
C. u  2; 2;   1 . D. u  1;0; 2 .
Câu 60: [2H3-3.8-3] Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng  P : x  2 y z 1  0 và
điểm A0; 2;3 , B 2;0  ;1 . Điểm M  ; a ;
b c thuộc  P sao cho MA MB nhỏ nhất. Giá trị của 2 2 2
a b c bằng 41 9 7 A. . B. . C. . D. 3 . 4 4 4
Câu 61: [2H3-3.8-3] Trong không gian với hệ toạ độ Oxyz , cho hai điểm A2; 3; 2 , B 3;5; 4 . Tìm
toạ độ điểm M trên trục Oz so cho 2 2
MA MB đạt giá trị nhỏ nhất.
A. M 0;0; 49 .
B. M 0;0;67 .
C. M 0;0;3 .
D. M 0;0;0 . x  3 y 1 z 1
Câu 62: [2H3-3.8-3] Trong không gian Oxyz , cho bốn đường thẳng: d :   , 1 1 2  1 x y z 1 x 1 y 1 z 1 x y 1 z 1 d :   , d :   , d :  
. Số đường thẳng trong không 2 1 2 1 3 2 1 1 4 1 1 1
gian cắt cả bốn đường thẳng trên là A. 0 . B. 2 . C. Vô số. D. 1.
Câu 63: [2H3-3.8-3] Trong không gian với hệ trục toạ độ Oxyz , cho mặt cầu
S   x  2   y  2   z  2 : 1 2 3
 9 , điểm A0; 0; 2 . Phương trình mặt phẳng  P đi qua A và
cắt mặt cầu S  theo thiết diện là hình tròn C  có diện tích nhỏ nhất là
A. P : x  2 y  3z  6  0 .
B. P : x  2 y z  2  0 .
C. P : x  2 y z  6  0 .
D. P : 3x  2 y  2z  4  0 .
Câu 64: [2H3-3.8-3] Trong không gian với hệ tọa độ Oxyz cho các điểm A4; 2;5 , B 0; 4; 3 ,
   C 2; 3
 ; 7 . Biết điểm M x ; y ; z nằm trên mặt phẳng Oxy sao cho MA MB MC đạt giá 0 0 0 
trị nhỏ nhất. Tính tổng P x y z . 0 0 0 A. P  3 . B. P  0 . C. P  3 . D. P  6 . x 1 y z  2
Câu 65: [2H3-3.8-3] Trong không gian với hệ tọa độ Oxyz , cho đường thẳng  :   và hai 2 1 1
điểm A0; 1;3 , B 1; 2 
;1 . Tìm tọa độ điểm M thuộc đường thẳng  sao cho 2 2 MA  2MB
đạt giá trị nhỏ nhất. A. M 5; 2; 4   . B. M 1; 1  ;   1 . C. M 1;0; 2   . D. M 3;1; 3   .  1 3 
Câu 66: [2H3-3.8-3] Trong không gian Oxyz , cho điểm M  ;
; 0  và mặt cầu S  2 2 2
: x y z  8 .  2 2   
Một đường thẳng đi qua điểm M và cắt  S  tại hai điểm phân biệt A , B . Diện tích lớn nhất
của tam giác OAB bằng A. 4 . B. 2 7 . C. 2 2 . D. 7 . x 1 y 1 z m
Câu 67: [2H3-3.8-3] Trong không gian Oxyz , cho đường thẳng d :   và mặt cầu 1 1 2
S   x  2   y  2   z  2 : 1 1 2
 9 . Tìm m để đường thẳng d cắt mặt cầu S  tại hai điểm
phân biệt E , F sao cho độ dài đoạn EF lớn nhất 1 1 A. m  1. B. m  0 . C. m   . D. m  . 3 3 x  1 tx  2t  
Câu 68: [2H3-3.8-3] Trong không gian Oxyz , cho hai đường thẳng d :  y  2  t , d :  y  1 t . Đường z t   z  2  t 
thẳng  cắt d , d  lần lượt tại các điểm A , B thỏa mãn độ dài đoạn thẳng AB nhỏ nhất.
Phương trình đường thẳng  là x 1 y  2 z x  4 y z  2 x y  3 z 1 x  2 y 1 z 1 A.   . B.   C.   . D.   . 2 1 3 2 1  3 2 1 3 2 1 3
Câu 69: [2H3-3.8-3] Trong không gian Oxyz , cho hình hộp ABC . D AB CD
  biết A1;0  ;1 , B 2;1; 2 , D 2; 2
 ; 2 , A3;0;  
1 , điểm M thuộc cạnh DC . Giá trị nhỏ nhất của tổng các khoảng cách
AM MC là A. 17 . B. 17  4 6 . C. 17  8 3 . D. 17  6 2 .
Câu 70: [2H3-3.8-3] Trong không gian với hệ tọa độ Oxyz , cho các điểm M 2; 2;  3 và N  4  ; 2  ;1 . 
Gọi  là đường thẳng đi qua M , nhận vecto u   ; a ;
b c làm vectơ chỉ phương và song song
với mặt phẳng  P : 2x y z  0 sao cho khoảng cách từ N đến  đạt giá trị nhỏ nhất. Biết
a , b là hai số nguyên tố cùng nhau. Khi đó a b c bằng: A. 15 . B. 13 . C. 16 . D. 14 . x  2 y 1 z  2
Câu 71: [2H3-3.8-3] Trong không gian Oxyz, cho đường thẳng d :   và mặt phẳng 4 4 3
P : 2x y  2z 1  0. Đường thẳng  đi qua E  2
 ; 1;  2 , song song với  P đồng thời tạo 
với d góc bé nhất. Biết rằng  có một véctơ chỉ phương u   ; m ; n  1 . Tính 2 2
T m n . A. T  5  . B. T  4 . C. T  3 . D. T  4  .
Câu 72: [2H3-3.8-3] Họ parabol  P y mx m x m
m  0 luôn tiếp xúc với đường m  2 :   2  3   2
thẳng d cố định khi m thay đổi. Đường thẳng d đó đi qua điểm nào dưới đây? A. 0; 2  . B. 0; 2. C. 1;8. D. 1; 8  .
Câu 73: [2H3-3.8-3] Trong không gian với hệ toạ độ Oxyz , cho hai điểm A2; 3
 ; 2 , B 3;5; 4 . Tìm
toạ độ điểm M trên trục Oz so cho 2 2
MA MB đạt giá trị nhỏ nhất.
A. M 0;0; 49 .
B. M 0;0;67 .
C. M 0;0;3 .
D. M 0;0;0 . x 1 y z 1
Câu 74: [2H3-3.8-4] Trong không gian với hệ tọa độ Oxyz , cho đường thẳng  :   và hai 2 3 1 
điểm A1; 2;   1 , B 3; 1  ; 5
  . Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng  sao
cho khoảng cách từ điểm B đến đường thẳng d là lớn nhất. Phương trình đường thẳng d là: x  3 y z  5 x y  2 z A.   . B.   . 2 2 1  1 3 4 x  2 y z 1 x 1 y  2 z 1 C.   . D.   . 3 1 1 1 6 5
Câu 75: [2H3-3.8-4] Trong không gian Oxyz , cho 2 điểm A3; 2
 ;3 , B 1;0;5 và đường thẳng x 1 y  2 z  3 d :  
. Tìm tọa độ điểm M trên đường thẳng d để 2 2
MA MB đạt giá trị nhỏ 1 2 2 nhất.
A. M 1; 2;3 . B. M 2;0;5 .
C. M 3; 2;7 .
D. M 3;0; 4 .
Câu 76: [2H3-3.8-4] Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng  P : x y z 1  0 , đường x 15 y  22 z  37 thẳng d :  
và mặt cầu S  2 2 2
: x y z  8x  6 y  4z  4  0 . Một đường 1 2 2
thẳng  thay đổi cắt mặt cầu  S  tại hai điểm A , B sao cho AB  8 . Gọi A , B là hai điểm
lần lượt thuộc mặt phẳng  P sao cho AA , BB cùng song song với d . Giá trị lớn nhất của
biểu thức AA  BB là 8  30 3 24 18 3 12  9 3 16  60 3 A. . B. . C. . D. . 9 5 5 9
Câu 77: [2H3-3.8-4] Trong không gian Oxyz , cho ba điểm A1;0  ;1 , B 3; 2; 
1 , C 5;3;7 . Gọi M  ; a ;
b c là điểm thỏa mãn MA MB và MB MC đạt giá trị nhỏ nhất. Tính P a b c A. P  4 . B. P  0 . C. P  2 . D. P  5 .
Câu 78: [2H3-3.8-4] Trong không gian Oxyz , cho ba điểm A1;0  ;1 , B 3; 2; 
1 , C 5;3;7 . Gọi M  ; a ;
b c là điểm thỏa mãn MA MB và MB MC đạt giá trị nhỏ nhất. Tính P a b c A. P  4 . B. P  0 . C. P  2 . D. P  5 .
Câu 79: [2H3-3.8-4]
Trong không gian với hệ trục tọa độ Oxyz cho mặt cầu S  2 2 2
: x y z  2x  4 y  4z  0 và điểm M 1; 2;  
1 . Một đường thẳng thay đổi qua M và
cắt S  tại hai điểm A , B . Tìm giá trị lớn nhất của tổng MA MB . A. 8 . B. 10 . C. 2 17 . D. 8  2 5 .
Câu 80: [2H3-3.8-4] Trong không gian Oxyz , cho hai điểm A1; 2; 4 , B 0;0  ;1 và mặt cầu
S   x  2   y  2 2 : 1
1  z  4. Mặt phẳng  P : ax by cz  3  0 đi qua A , B và cắt mặt cầu
S  theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tính T a b c . 3 33 27 31 A. T   . B. T  . C. T  . D. T  . 4 5 4 5
Câu 81: [2H3-3.8-4] Trong không gian Oxyz , cho ba điểm A1;  2;  1 , B 5; 0;  
1 , C 3;1; 2 và mặt
phẳng Q : 3x y z  3  0 . Gọi M  ; a ;
b c là điểm thuộc Q thỏa mãn 2 2 2
MA MB  2MC
nhỏ nhất. Tính tổng a b  5c . A. 11. B. 9 . C. 15 . D. 14 .
Câu 82: [2H3-3.8-4] Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng  P : x y  4z  0 , đường x 1 y 1 z  3 thẳng d :  
và điểm A1; 3; 
1 thuộc mặt phẳng  P . Gọi  là đường thẳng đi 2 1 1
qua A , nằm trong mặt phẳng  P và cách đường thẳng d một khoảng cách lớn nhất. Gọi
u   ;a ;b 1 là một véc tơ chỉ phương của đường thẳng . Tính a2b.
A. a  2b  3 .
B. a  2b  0 .
C. a  2b  4 . D.
a  2b  7 .
Câu 83: [2H3-3.8-4] Trong không gian với hệ tọa độ Oxyz , cho hai điểm A3;0; 
1 , B 1;1;3 và mặt
phẳng  P : x  2 y  2z  5  0 . Viết phương trình chính tắc của đường thẳng d đi qua A , song
song với mặt phẳng  P sao cho khoảng cách từ B đến d nhỏ nhất. x  3 y z  1 x  3 y z  1 A. d :   . B. d :   . 26 11 2 26 11 2 x  3 y z  1 x  3 y z  1 C. d :   . D. d :   . 26 11 2 26  11 2
Câu 84: [2H3-3.8-4] Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng  P : x y  4z  0 , đường x 1 y 1 z  3 thẳng d :  
và điểm A1; 3; 
1 thuộc mặt phẳng  P . Gọi  là đường thẳng đi 2 1  1
qua A , nằm trong mặt phẳng  P và cách đường thẳng d một khoảng cách lớn nhất. Gọi
u   ;a ;b 1 là một véc tơ chỉ phương của đường thẳng  . Tính a2b.
A. a  2b  3 .
B. a  2b  0 .
C. a  2b  4 .
D. a  2b  7 .
Câu 85: [2H3-3.8-4] Trong không gian Oxyz , cho ba điểm A1;  2;  1 , B 5; 0;  
1 , C 3;1; 2 và mặt
phẳng Q : 3x y z  3  0 . Gọi M  ; a ;
b c là điểm thuộc Q thỏa mãn 2 2 2
MA MB  2MC
nhỏ nhất. Tính tổng a b  5c . A. 11. B. 9 . C. 15 . D. 14 . x  2 y 1 z
Câu 86: [2H3-3.8-4] Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và hai 1 2 3
điểm A2;0;3 , B 2; 2; 3 . Biết điểm M x ; y ; z thuộc d thỏa mãn 4 4
MA MB nhỏ nhất. 0 0 0  Tìm x . 0 A. x  1. B. x  3 . C. x  0 . D. x  2 . 0 0 0 0
HƯỚNG DẪN GIẢI CHI TIẾT PHƯƠNG TRÌNH ĐƯỜNG THẲNG NÂNG CAO Câu 1:
[2H3-3.2-3] Trong không gian với hệ tọa độ Oxyz , viết phương trình đường vuông góc chung của x  2 y  3 z  4 x 1 y  4 z  4
hai đường thẳng d :   và d  :   . 2 3 5 3 2 1  x y z 1 x  2 y  2 z  3 A.   . B.   . 1 1 1 2 3 4 x  2 y  2 z  3 x y  2 z  3 C.   . D.   . 2 2 2 2 3 1  Lời giải Chọn A.
Ta có M d suy ra M 2  2 ; m 3  3 ; m 4
  5m . Tương tự N d suy ra N  1   3 ; n 4  2 ; n 4  n . 
Từ đó ta có MN  3  3n  2 ;1 m  2n  3 ;
m 8  n  5m . MN d
Mà do MN là đường vuông góc chung của d và d  nên  MN d   2
 3  3n  2m  3.1 2n  3m  58  n  5m  0
38m  5n  43 m  1        . 3   3
  3n  2m  2.1 2n  3m 18  n  5m  0 
5m 14n  19  n  1  Suy ra M 0;0  ;1 , N 2; 2;3 .  x y z 1
Ta có MN  2; 2; 2 nên đường vuông góc chung MN là   . 1 1 1 Câu 2:
[2H3-3.2-3] Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng  P : x  2 y z  4  0 và đường x 1 y z  2 thẳng d :  
. Viết phương trình đường thẳng  nằm trong mặt phẳng  P , đồng thời 2 1 3
cắt và vuông góc với đường thẳng d . x 1 y 1 z 1 x 1 y 1 z 1 A.   . B.   . 5 1 3 5 1 3 x 1 y 1 z 1 x 1 y  3 z 1 C.   . D.   . 5 1  2 5 1 3 Lời giải Chọn A. 
Vectơ pháp tuyến của mặt phẳng  P là n  . P 1;2  ;1   
Vectơ chỉ phương của đường thẳng d là u  . d 2;1;3 x  1   2t
Phương trình tham số của đường thẳng d :  y t . z  2  3  t
Xét phương trình: 1 2t  2t  2  3t  4  0  7t  7  0  t  1.
Suy ra giao điểm của đường thẳng d và mặt phẳng  P là A 
1;1;1 . Ta có: A  .   
Vectơ chỉ phương của đường thẳng  là u  n , u   . P d 5;1; 3       x 1 y 1 z 1
Phương trình chính tắc của đường thẳng  :   . 5 1  3 x  3 y  3 z  2 Câu 3:
[2H3-3.2-3] Trong không gian Oxyz , cho hai đường thẳng d :   ; 1 1  2 1 x  5 y 1 z  2 d :  
và mặt phẳng  P : x  2 y  3z  5  0 . Đường thẳng vuông góc với  P , cắt 2 3  2 1
d và d có phương trình là 1 2 x 1 y 1 z x  2 y  3 z 1 A.   . B.   . 1 2 3 1 2 3 x  3 y  3 z  2 x 1 y 1 z C.   . D.   . 1 2 3 3 2 1 Lời giải Chọn A.
 Gọi M và N lần lượt là giao điểm của đường thẳng d cần tìm với d và d , khi đó 1 2 
M 3  t;3  2t; 2
  t  , N 5  3s; 1 2s; 2  s  MN  2  3s t; 4
  2s  2t; 4  s t  .  
 Đường thẳng d vuông góc với  P suy ra MN cùng phương với n  1; 2;3 . Do đó P  2  3s t
4  2s  2t 4  s t t   2      M 1; 1  ; 0 . 1 2 3 s  1  
 Vậy đường thẳng cần tìm qua  M 1; 1
 ; 0 và có vectơ chỉ phương là u  1; 2;3 là x 1 y 1 z   . 1 2 3 x 1 y  2 z Câu 4:
[2H3-3.2-3] Phương trình đường thẳng song song với đường thẳng d :   và cắt hai 1 1 1 x 1 y 1 z  2 x 1 y  2 z  3 đường thẳng d :   ; d :   là: 1 2 1 1 2 1 1 3 x 1 y 1 z  2 x 1 y z 1 A.   . B.   . 1 1 1 1 1 1 x 1 y  2 z  3 x 1 y z 1 C.   . D.   . 1 1 1 1 1  1 Lời giải Chọn B. 
Vectơ chỉ phương của d là u  1;1;   1 .  A  1 2 ; a 1   ; a 2  a
Gọi  là đường thẳng cần tìm và A    d , B    d . Suy ra: . 1 2 B  1 ; b 2  ; b 3  3b  
Khi đó: AB  b  2a  2;b a  3;3b a   1 .  
Vì đường thẳng  song song với đường thẳng d nên AB cùng phương với u .
b  2a  2 b a  3 3b a 1 a  1  A  1; 0  ;1 Suy ra:       . 1 1 1  b  1  B   2;1; 0  Thay A1;0 
;1 vào đường thẳng d ta thấy A d . x 1 y z 1
Vậy phương trình đường thẳng  :   . 1 1 1  Câu 5:
[2H3-3.2-3] Trong không gian Oxyz , cho ba điểm A1;1; 
1 , B 1;2;0 , C 2; 3;2 . Tập hợp tất
cả các điểm M cách đều ba điểm A , B , C là một đường thẳng d . Phương trình tham số của đường thẳng d là:
x  8  3t
x  8  3t
x  8  3t
x  8  3t     A.  y t . B.  y t .
C.  y  t . D.  y t .
z  15  7t     z  15  7t
z  15  7tz  15  7t  Lời giải Chọn A.  
Ta có AB  2;1;  
1 ; BC  3;  5;2 .  
Ta thấy AB và BC không cùng phương nên ba điểm A , B , C không thẳng hàng.
M cách đều hai điểm A , B nên điểm M nằm trên mặt trung trực của AB .
M cách đều hai điểm B , C nên điểm M nằm trên mặt trung trực của BC .
Do đó tập hợp tất cả các điểm M cách đều ba điểm A , B , C là giao tuyến của hai mặt trung trực
của AB và BC .
Gọi  P , Q lần lượt là các mặt phẳng trung trực của AB và BC .  3 1   1 1  K 0; ; 
 là trung điểm AB ; N ;  ;1 
 là trung điểm BC .  2 2   2 2    3   1  
P đi qua K và nhận AB  2;1;  
1 làm véctơ pháp tuyến nên  P : 2x y   z   0      2   2 
hay  P : 2x y z  1  0 . 
Q đi qua N và nhận BC  3; 5;2 làm véctơ pháp tuyến nên  1   1   Q  : 3 x   5 y   2      z  
1  0 hay Q : 3x  5y  2z  6  0 .  2   2 
2x y z  1  0 Ta có d : 
3x  5 y  2z  6  0    
Nên d có véctơ chỉ phương u   AB, BC   3;1;7 .  
Cho y  0 ta sẽ tìm được x  8 , z  15 nên 8;0;15  d .
x  8  3t
Vậy  y t .
z  15  7tx 1 y 1 z  2 Câu 6:
[2H3-3.2-3] Trong không gian cho đường thẳng  :  
. Tìm hình chiếu vuông góc 2 1 1
của  trên mặt phẳng Oxy . x  0 x  1 2tx  1   2tx  1   2t    
A.  y  1 t .
B.  y  1 t .
C.  y  1 t .
D.  y  1 t . z  0     z  0  z  0  z  0  Lời giải Chọn B. 
Đường thẳng  qua điểm M 1; 1; 2 và có vectơ chỉ phương: u  .  2; 1;  1 
Mặt phẳng Oxy có vectơ pháp tuyến k  0; 0;  1 .
Gọi  P là mặt phẳng chứa  và vuông góc mặt phẳng Oxy , thì  P qua M và có vectơ pháp   
tuyến n  u ; k    .  1; 2; 0  
Khi đó, phương trình mặt phẳng  P là x  2 y  3  0 .
Gọi d là hình chiếu của  lên Oxy , thì d chính là giao tuyến của  P với Oxy .
x  3  2t
x  2 y  3  0  Suy ra d : 
hay d :  y t
. Với t  1, ta thấy d đi qua điểm N 1; 1; 0 . z  0  z  0  Câu 7:
[2H3-3.2-3] Trong không gian với hệ tọa độ Oxyz , cho các điểm A2;0;0 ; B 0;3;0 ; C 0;0; 4 .
Gọi H là trực tâm tam giác ABC . Tìm phương trình tham số của đường thẳng OH .  x  4tx  3tx  6tx  4t    
A.  y  3t .
B.  y  4t .
C.  y  4t .
D.  y  3t . z  2t     z  2tz  3tz  2t  Lời giải Chọn D.
Do tứ diện OABC có ba cạnh OA , OB , OC đôi một vuông góc và H là trực tâm tam giác ABC
nên OH   ABC  . x y z
Phương trình mặt phẳng  ABC  là  
 1 , hay 6x  4 y  3z 12  0 . 2 3 4 
Vì OH   ABC  nên đường thẳng OH có véc-tơ chỉ phương u  6; 4;3 .  x  6t
Vậy, phương trình tham số của đường thẳng OH là  y  4t .  z  3tx  3 y 1 z  2 Câu 8:
[2H3-3.2-3] Trong không gian Oxyz , cho ba đường thẳng d :   , 1 2 1 2 x 1 y z  4 x  3 y  2 z d :   và d :  
. Đường thẳng song song d , cắt d và d có 2 3 2 1  3 4 1  6 3 1 2 phương trình là x  3 y 1 z  2 x  3 y 1 z  2 A.   . B.   . 4 1 6 4 1 6  x 1 y z  4 x 1 y z  4 C.   . D.   . 4 1 6 4 1  6 Lời giải Chọn B.
x  3  2ux  1   3v  
Ta có d :  y  1
  u , d :  y  2  v . 1 2
z  2  2u   z  4   v
Gọi d là đường thẳng cần tìm. 4
Gọi A d d A3  2u; 1 u; 2  2u , B d d B  1   3 ; v  2 ;
v  4  v . 4 1 4 2  AB   4
  3v  2u;1 2v u;  6  v  2u  .   
d song song d nên AB ku với u  4; 1;6 . 3   4 3 3  4
  3v  2u  4kv  0     AB ku  1
  2v u  ku   0 . 3
 6 v 2u 6k      k  1     x  3 y 1 z  2
Đường thẳng d đi qua A3; 1; 2 và có vtcp là u  4; 1;6 nên d :   . 3   4 4 4 1 6 Câu 9:
[2H3-3.2-3] Trong không gian Oxyz , cho mặt phẳng   : y  2z  0 và hai đường thẳng: x  1 t
x  2  t  
d :  y t
; d :  y  4  2t . Đường thẳng  nằm trong mặt phẳng   và cắt hai đường thẳng 1 2 z  4t   z  4 
d ; d có phương trình là 1 2 x 1 y z x 1 y z x 1 y z x 1 y z A.   . B.   . C.   . D.   . 7 8 4 7 8 4 7 8 4 7 8 4 Lời giải Chọn C.
Gọi A d   suy ra A1 t;t; 4t  và B d   suy ra B 2  t ; 4  2t ; 4 . 1 2 t   2.4t  0 t   0
Mặt khác A   ; B   nên ta có   
4  2t  2.4  0  t  6  
Do đó A1;0;0 và B 8;  8; 4 . 
Đường thẳng  đi qua A và nhận AB  7;  8; 4 làm vectơ chỉ phương có phương trình x 1 y z   . 7 8 4 x 1 y z  2
Câu 10: [2H3-3.2-3] Trong không gian Oxyz , cho đường thẳng d :   và mặt phẳng 1 1  1
P : 2x y  2z 1  0 . Đường thẳng nằm trong  P , cắt và vuông góc với d có phương trình là x  2 y 1 z  3 x  2 y 1 z  3 A.   . B.   . 3 4 1 3 4 1  x  2 y 1 z  3 x 1 y 1 z 1 C.   . D.   . 3 4 1 3 4 1 Lời giải Chọn C. x  1 t
Phương trình tham số của d :  y t
. Gọi M d   P . z  2  t
Khi đó M d nên M 1 t; t; 2  t  ; M   P nên 21 t   t   2 2  t  1  0  t  1 .
Vậy đường thẳng d cắt mặt phẳng  P tại M 2; 1;3 .  
Gọi u  1; 1  ;1 và n  2; 1
 ; 2 lần lượt là vectơ chỉ phương của d và vectơ pháp tuyến của mặt d phẳng  P .   
Khi đó một vectơ chỉ phương của đường thẳng cần tìm là u  u , n  3; 4;  1 . d   x  2 y 1 z  3
Vậy phương trình đường thẳng cần tìm là   . 3 4 1
Câu 11: [2H3-3.2-3] Trong không gian với hệ tọa độ Descartes Oxyz , cho điểm M 0; 1; 2 và hai đường x 1 y  2 z  3 x 1 y  4 z  2 thẳng d :   , d :  
. Phương trình đường thẳng đi qua M , cắt cả 1 1 1 2 2 2 1 4 d và d là 1 2 x y 1 z  3 x y 1 z  2 x y 1 z  2 x y 1 z  2 A.   . B.   . C.   . D.   . 9 9 8  3 3 4 9 9  16 9 9 16 2 2 Lời giải Chọn C.
Gọi  là đường thẳng cần tìm.
  d A t 1;  t  2; 2t  3 ;   d B 2t 1;  t  4; 4t  2 . 2  2 2 2  1  1 1 1   
MA  t 1;  t 1; 2t 1 ; MB  2t 1;  t  5; 4t . 2 2 2  1 1 1   7 t  1  2
t 1  k 2t 1 1  2    7     1 t  Ta có: M , ,
A B thẳng hàng  MA k MB  t 1  k t  5 1
 k     2 . 1 2 2   t  4 2t 1  4kt  2 1 2  kt  2 2   
MB  9; 9; 16 . 
Đường thẳng  đi qua M 0; 1; 2 , một VTCP là u  9;  9;16 có phương trình là: x y 1 z  2  :   . 9 9 16 x 1 y z 1
Câu 12: [2H3-3.2-3] Trong không gian
Oxyz , cho ba đường thẳng d :   ; 1 2 3 1 x  2 y 1 z x  3 y  2 z  5 d :   ; d :  
. Đường thẳng song song với d , cắt d và d có 2 1 2 2 3 3 4 8 3 1 2 phương trình là x 1 y z 1 x 1 y  3 z A.   . B.   . 3 4 8 3 4 8 x 1 y  3 z x 1 y z 1 C.   . D.   . 3 4 8 3 4  8 Lời giải Chọn A.
Gọi d là đường thẳng song song với d , cắt d và d lần lượt tại các điểm A , B . 3 1 2  Gọi A1 2 ; a 3 ; a 1
  a và B 2  ;1 b  2 ;
b 2b  AB  b  2a  3; 2
b  3a 1; 2b a   1 . 
Đường thẳng d có véc-tơ chỉ phương u  3; 4;8 . 3
Đường thẳng d song song với d nên 3  a  0   b   2a  3  3  k    3
AB ku  2b  3a 1  4  k b   .  2
2b a 1  8k    1 k    2  1 
Như vậy A1;0;  
1 và B   ; 2;3   .  2  x 1 y z 1
Phương trình đường thẳng d là:   . 3 4 8
Câu 13: [2H3-3.2-3] Trong không gian với hệ trục tọa độ Oxyz , cho tam giác ABC biết điểm A1; 2; 3 , x  5t
đường trung tuyến BM và đường cao CH có phương trình tương ứng là  y  0 và z  1 4tx  4 y  2 z  3  
. Viết phương trình đường phân giác góc A . 16 13 5 x 1 y  2 z  3 x 1 y  2 z  3 A.   . B.   . 7 1 10 4 13 5 x 1 y  2 z  3 x 1 y  2 z  3 C.   . D.   . 2 3  1 2 11 5 Lời giải Chọn D. Giả sử B 5 ;
b 0; 1 4b  BM , C 4 16 ; c  2 13 ;
c 3  5c CH . Ta có:  5 16c 13c 6  5c
Tọa độ trung điểm M của AC là M ;  ;   .  2 2 2 
5 16c  5t  2  c  0  13  c
M BM    0  
1  C  4;  2; 3 2  t    2
6  5c 1 4t   2 
AB  5b 1;  2; 4b  2 
Vectơ chỉ phương của CH là: w  16; 13; 5 .  
Do AB CH nên .
AB u  0  165b   1 13 2
   54b  2  0  b  0  B 0; 0;  1 .  
AB  1;  2;  2 , AC  3;  4; 0 .   AB  1 2 2    3 4      4 22 2 
Đặt u     ;  ;  , u  ; 
; 0 , u u u  ;  ;  . 1   2   1 2   AB  3 3 3   5 5   15 15 3  
Chọn v  2; 11;  5 là vectơ chỉ phương của đường phân giác góc A . x 1 y  2 z  3
Vậy phương trình đường phân giác góc A là:   . 2 11 5 x y  3 z  2
Câu 14: [2H3-3.2-3] Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt 2 1 3 
phẳng  P : x y  2z  6  0 . Đường thẳng nằm trong mặt phẳng  P , cắt và vuông góc với d có phương trình x  2 y  2 z  5 x  2 y  4 z 1 A.   . B.   . 1 7 3 1 7 3 x  2 y  2 z  5 x  2 y  4 z 1 C.   . D.   . 1 7 3 1 7 3 Lời giải Chọn A.  x y  3 z  2   
Tọa độ giao điểm M của d và  P là nghiệm của hệ 2 1 3 
x y  2z  6  0 
x  2 y  6  x  2     3
y z  11
  y  2  M  2  ; 2;5 .
x y  2z  6  0   z  5   
P : x y  2z  6  0 có vtpt n  1; 1
 ; 2 , d có vtcp u  2;1;  3   
Ta có  đi qua M  2
 ; 2;5 nhận k  n,u  1;7;3 là một vectơ chỉ phương có dạng x  2 y  2 z  5 :   . 1 7 3
Câu 15: [2H3-3.2-3] Trong không gian với hệ tọa độ Oxyz cho ba điểm A3; 2
 ; 4 , B 5;3; 2
  , C 0;4; 2 ,
đường thẳng d cách đều ba điểm A , B , C có phương trình là  8  11 x   26t   x   3  6 
x  4  26t
x  4  26t  5   1 
A.  y   22t .
B.  y  2  22t .
C.  y   22t .
D.  y  2  38t . 3   6 9   9  4 z   27tz  27tz   27t z   27t   4   4  3  Lời giải Chọn B.  1 
Gọi I là trung điểm của AB suy ra I 4; ;1 
 và  P là mặt phẳng trung trực của đoạn AB .  2  
Mặt phẳng  P đi qua I và nhận AB  2;5; 6 làm vec tơ pháp tuyến có phương trình là:  1 
2  x  4  5 y   6    z  
1  0  4x 10 y 12z  9  0 .  2   3 
Gọi J là trung điểm của AC suy ra J ;1;3 
 và Q là mặt phẳng trung trực của đoạn AC  2  
Mặt phẳng Q đi qua J và nhận AC   3  ; 6; 2
  làm vec tơ pháp tuyến có phương trình là:  3  3 x   6    y  
1  2  z  3  0  6x 12 y  4z  9  0 .Khi đó d   P Q  2    
Ta có d có vectơ chỉ phương u   ;
AB AC   26; 22; 27 và đi qua M là nghiệm của hệ  
4x 10 y 12z  9  0 9  9  
, ta chọn x  4 suy ra y  2 và z  . Vậy M 4; 2;   .
6x 12 y  4z  9  0  4  4  
x  4  26t
Phương trình tham số của d là:  y  2  22t .  9 z   27t  4
Câu 16: [2H3-3.2-3] Trong không gian Oxyz , cho tam giác ABC với A3;0;0 , B 0;6;0 , C 0;0;6 .
Phương trình nào dưới đây là phương trình đường thẳng đi qua trực tâm của tam giác ABC và vuông
góc với mặt phẳng  ABC  . x 1 y  2 z  3 x  2 y 1 z 1 A.   . B.   . 2 1 1 2 1 1 x  3 y  6 z  6 x 1 y  3 z  3 C.   . D.   . 2 1 1 2 1 1 Lời giải Chọn B.    AH.BC  0    Ta có H  ; a ;
b c là trực tâm tam giác ABC nên ta có BH.AC  0 .
   
AB, AC  .AH  0        
Ta có AH  a  3; ;
b c ; BH   ;
a b  6; c ; BC  0; 6;6 ; AC   3
 ; 0; 6 ; AB  3;6;0 .  
  AB, AC   36;18;18 .      AH.BC  0
6b  6c  0
6b  6c  0 a  2       BH .AC  0
 3a  6c  0
 3a  6c  0  b
  1  H  2;1  ;1 .
      
AB, AC  .AH  0
36 a  3 18b 18c  0
2a b c  6 c  1      
Đường thẳng đi qua trực tâm H 2;1 
;1 của tam giác ABC và vuông góc với mặt phẳng  ABC  có 1    x  2 y 1 z 1
vecto chỉ phương u
AB, AC   2;1  ;1 có phương trình là   . 18   2 1 1
Câu 17: [2H3-3.2-3] Trong không gian Oxyz , cho hai điểm A2;1;  3 và B 3; 2  ;1 . Viết phương trình
đường thẳng d đi qua gốc toạ độ sao cho tổng khoảng cách từ A và B đến đường thẳng d lớn nhất. x y z x y z x y z x y z A.   . B.   . C.   . D.   . 1 1 1 1 1 1 1 1 2 1 1 2 Lời giải Chọn A. Ta có d  ;
A d   d  ;
B d   OA OB . OA   d    Dấu "  " xảy ra  
d có VTCP là u   ;
OA OB  7;7;7  71;1  ;1 . OB d    x y z Vậy d :   . 1 1 1 x  2  t      x 1 t
Câu 18: [2H3-3.2-3] Trong không gian Oxyz , cho hai đường thẳng cắt nhau  :  y  2  2t ,  :  y t   1 2 z  1   t  z  2t 
t,t  . Viết phương trình đường phân giác của góc nhọn tạo bởi  và  . 1 2 x 1 y z x 1 y z x 1 y z x 1 y z A.   . B.   . C.   . D.   . 2 3 3 1 1 1 2 3 3 1 1 1 Lời giải Chọn C.  
Thấy ngay     M 1; 0; 0 và các VTCP lần lượt là a  1; 2;  
1 và b  1; 1; 2 . 1 2        
Ta có a b  0;1 
;1  u và a,b  3; 1  ;  1  v .     Vì . a b  4
  0 nên góc giữa hai vectơ là góc tù do đó đường phân giác của góc nhọn tạo bởi  và 1   
 có VTCP n  u, v  2; 3  ;3 . 2   x 1 y z
Vậy phương trình đường phân giác cần tìm:   . 2 3 3
Câu 19: [2H3-3.2-3] Trong không gian với hệ tọa độ Oxyz . Cho mặt phẳng  P : 2x y z 10  0, điểm
x  2  2t
A1;3; 2 và đường thẳng d :  y  1 t
. Tìm phương trình đường thẳng  cắt  P và d lần lượt z 1 t
tại hai điểm M và N sao cho A là trung điểm cạnh MN . x  6 y 1 z  3 x  6 y 1 z  3 A.   . B.   . 7 4 1 7 4 1  x  6 y 1 z  3 x  6 y 1 z  3 C.   . D.   . 7 4 1 7 4 1  Lời giải Chọn D.
Ta có M  d     M  d  . Giả sử M 2  2t,1 t,1 t , t  
Do A là trung điểm MN nên N 4  2t; 5  t; t  3 .
Mà N   P nên ta có phương trình 24  2t   5  t   3  t  10  0  t  2 . Do đó, M  6  ; 1;3 . 
AM  7;  4 
;1 là vectơ chỉ phương của đường thẳng  . x  6 y 1 z  3
Vậy phương trình đường thẳng cần tìm là   . 7 4 1  x  2  t
x  1 t  
Câu 20: [2H3-3.2-3] Trong không gian Oxyz , cho hai đường thẳng cắt nhau  :  y  2  2t ,  :  y  t 1 2 z  1   t   z  2t 
t,t  . Viết phương trình đường phân giác của góc nhọn tạo bởi  và  . 1 2 x 1 y z x 1 y z x 1 y z A.   . B.   . C.   . D. Cả A, B, C đều sai. 2 3 3 1 1 1 2 3 3 Hướng dẫn giải Chọn A.
I 1;0;0     . 1 2  
 và  có VTCP lần lượt là u  1; 2; 1 và u  1  ; 1; 2 . 2   1   1 2     u .u 5  
Ta có: cos u ;u  1 2     
 0  u ;u là góc tù. 1 2  1 2 u . u 6 1 2   
Gọi u là véc tơ đối của u u  1;1; 2 . 2   
Khi đó đường phân giác của góc nhọn tạo bởi  và  có VTCP u u u  2;3; 3 . 1   1 2 x 1 y z
Vậy phương trình đường phân giác của góc nhọn tạo bởi  và  có dạng:   . 1 2 2 3 3
Câu 21: [2H3-3.2-3] Trong không gian Oxyz , Cho mặt phẳng  R : x y  2z  2  0 và đường x y z 1 thẳng  :  
. Đường thẳng  nằm trong mặt phẳng  R đồng thời cắt và vuông góc với 1 2 1 1  2
đường thẳng  có phương trình là 1 x tx tx  2  t
x  2  3t     A.  y  3  t . B.  y  2  t .
C.  y  1 t .
D.  y  1 t . z  1 t     z  1 tz tz t  Lời giải Chọn A. x  2t
Phương trình tham số của đường thẳng  là  y t . 1 z  1 t  Gọi I  ;
x y; z là giao điểm của  và  R . Khi đó tọa độ của I là thỏa mãn 1 x  2t  x  0  y t  
  y  0  I  0;0;  1 . z  1 t  z 1  
x y  2z  2  0   
Mặt phẳng  R có VTPT n  1;1; 2
  ; Đường thẳng  có VTCP u  2;1;  1 . 1  
Ta có n,u  1; 3  ;   1 .
Đường thẳng  nằm trong mặt phẳng  R đồng thời cắt và vuông góc với đường thẳng  . 2 1  
Do đó  đi qua I  0;0; 
1 và nhận n,u làm một VTCP. 2 x t
Vậy phương trình của  là  y  3  t . 2 z  1 t  x  1 3t
Câu 22: [2H3-3.2-3] Trong không gian Oxyz , cho đường thẳng d :  y  1 4t . Gọi  là đường thẳng đi qua z 1   điểm A1;1; 
1 và có vectơ chỉ phương u  1; 2
 ; 2 . Đường phân giác của góc nhọn tạo bởi d và  có phương trình là x  1 7tx  1   2tx  1   2tx  1 3t    
A.  y 1 t . B. y  1  0 11t . C. y  1  0 11t .
D.  y 1 4t . z 1 5t     z  6   5tz  6  5tz  1 5t  Lời giải Chọn C.
x  1 t 
Phương trình tham số đường thẳng  :  y  1 2t .
z 1 2t 
Chọn điểm B 2; 1
 ;3   , AB  3 .  14 17   4 7  Điểm C ; ;1 
 hoặc C  ;  ;1 
 nằm trên d thỏa mãn AC AB .  5 5   5 5   4 7 
Kiểm tra được điểm C  ;  ;1   thỏa mãn  BAC nhọn.  5 5   3 6 
Trung điểm của BC là I ;  ; 2 
 . Đường phân giác cần tìm là AI có vectơ chỉ phương  5 5  x  1   2t   u  2;11; 5
  và có phương trình y  1  0 11t , z  6 5t  x  1 3t
Câu 23: [2H3-3.2-3] Trong không gian Oxyz , cho đường thẳng d :  y  3
. Gọi  là đường thẳng đi qua z  5  4  t  điểm A1; 3
 ;5 và có vectơ chỉ phương u 1; 2; 2 . Đường phân giác của góc nhọn tạo bởi d và  có phương trình là
x  1 2t
x  1 2tx  1 7tx  1 t    
A.  y  2  5t .
B.  y  2  5t . C.  y  3   5t . D.  y  3 .  z  6 11     t z  6 11  t z  5   t z  5  7  t Hướng dẫn giải Chọn B Ta có điểm A1; 3
 ;5 thuộc đường thẳng d , nên A1; 3
 ;5 là giao điểm của d và  . 
Một vectơ chỉ phương của đường thẳng d là v  3  ; 0; 4 . Ta xét:  1  1  1 2 2  u   .u  1;2;2  ; ;  ; 1   u 3  3 3 3   1  1  3 4  v   .v
3;0;4   ;0; . 1   v 5  5 5     
Nhận thấy u .v  0 , nên góc tạo bởi hai vectơ u , v là góc nhọn tạo bởi d và  . 1 1 1 1
    4 10 22  15
Ta có w  u v   ; ;    2;5;1 
1 là vectơ chỉ phương của đường phân giác của 1 1    15 15 15  2
góc nhọn tạo bởi d và  hay đường phân giác của góc nhọn tạo bởi d và  có vectơ chỉ phương là 
x  1 2t
w  2; 5;11 . Do đó có phương trình:  y  2  5t . 1   z  6 11  tx  1 t
Câu 24: [2H3-3.2-3] Trong không gian Oxyz , cho đường thẳng d :  y  2  t . Gọi  là đường thẳng đi qua z  3   điểm (
A 1; 2;3) và có vectơ chỉ phương u  (0; 7  ; 1
 ). Đường phân giác của góc nhọn tạo bởi d và  có phương trình là x  1 6t
x  4  5t
x  4  5tx  1 5t    
A.  y  2 11t .
B.  y  10 12t .
C.  y  10 12t .
D.  y  2  2t .
z  3  8t     z  2  tz  2  tz  3  t  Lời giải Chọn B. 
Đường thẳng d đi qua (
A 1; 2;3) và có VTCP a  (1;1; 0) .     Ta có a.u 1.0 1.( 7) 0.( 1) 7 0 (a,u) 90 .            Đường phân giác của góc nhọn tạo bởi d và  có VTCP:    u a 1
b       5;12  ;1 // 5;12  ;1 . u a 5 2
x  4  5t
Phương trình đường thẳng cần tìm là  y  10 12t . z  2  tx  2 y 1 z  2
Câu 25: [2H3-3.1-3] Trong không gian Oxyz, cho đường thẳng d :   và mặt phẳng 4 4 3
P : 2x y  2z 1  0 . Đường thẳng  đi qua E  2
 ; 1;  2 , song song với  P đồng thời tạo với 
d góc bé nhất. Biết rằng  có một véctơ chỉ phương u   ; m ; n  1 . Tính 2 2
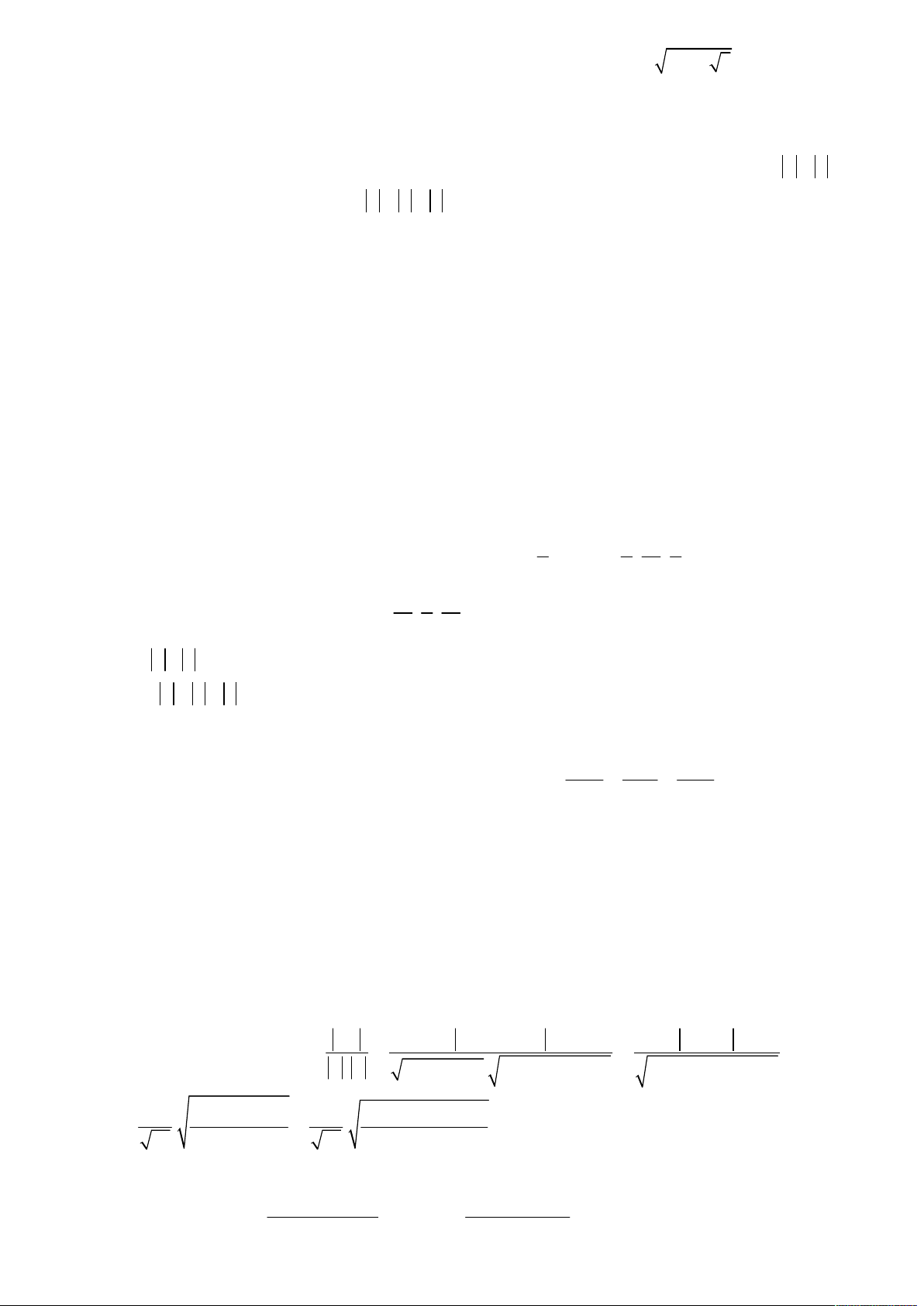
T m n . A. T  5  . B. T  4 . C. T  3 . D. T  4  . Lời giải Chọn D. 
Mặt phẳng  P có vec tơ pháp tuyến n  2; 1; 2 và đường thẳng d có vec tơ chỉ phương
v  4;4;3  
Vì  song song với mặt phẳng  P nên u n  2m n  2  0  n  2m  2 .   u v 4m  4n  3 4m  5 Mặt khác ta có  d   . cos ;      u . v
m n 1. 4  42 2 2 2 2  3 41 2
5m  8m  5 1 4m  52 2 1
16m  40m  25  .  . . 2 2 41 5m  8m  5 41 5m  8m  5
Vì    d   0 ;  90 nên   
; d bé nhất khi và chỉ khi    cos ; d lớn nhất 2
16t  40t  25 2 72t  90t
Xét hàm số f t  
f t   . 2 5t  8t  5
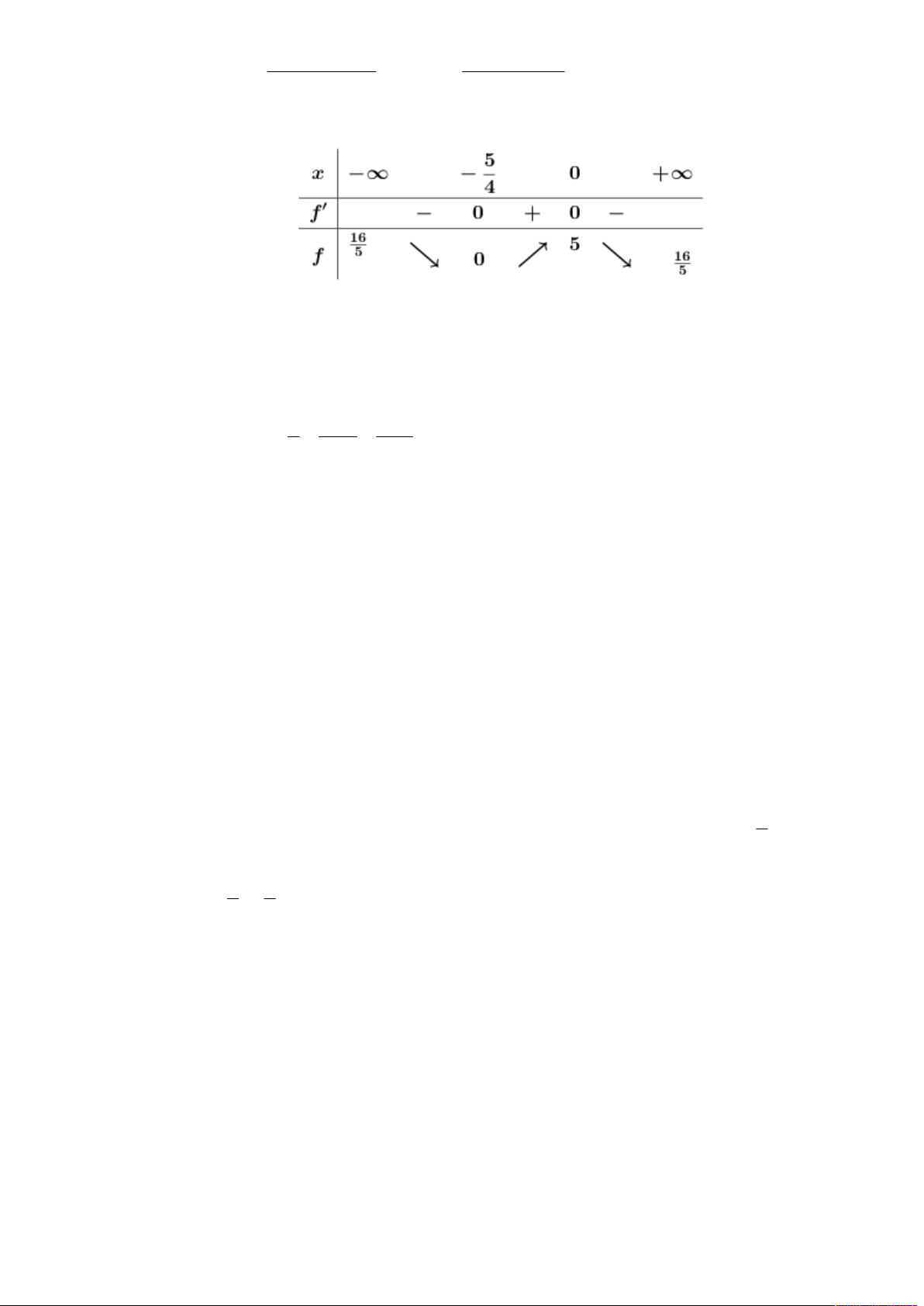
5t 8t  52 2 Bảng biến thiên
Dựa vào bảng biến thiên ta có max f t   f 0  5 suy ra   
; d bé nhất khi m  0  n  2 . Do đó 2 2
T m n  4 .
Làm theo cách này thì không cần đến dữ kiện: đường thẳng  đi qua E 2; 1;  2 .
Câu 26: [2H3-3.1-3] Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có phương trình đường phân x y  6 z  6
giác trong góc A là:  
. Biết rằng điểm M 0;5;3 thuộc đường thẳng AB và điểm 1 4  3 
N 1;1;0 thuộc đường thẳng AC . Vectơ nào sau đây là vectơ chỉ phương của đường thẳng AC .    
A. u  1; 2;3 . B. u  0;1;3 .
C. u  0;  2;6 .
D. u  0;1;  3 . Lời giải Chọn B. x t
Phương trình tham số của đường phân giác trong góc A :  y  6  4t . d
z  6  3t
Gọi D là điểm đối xứng với M qua d  . Khi đó D AC  đường thẳng AC có một 
vectơ chỉ phương là ND .
Ta xác định điểm D . 
Gọi K là giao điểm MD với d  . Ta có K t;6  4t;6  3t  ; MK  t;1 4t;3  3t  .    1
Ta có MK u với u  1;  4;  3 nên t  41 4t   33  3t   0  t  . dd 2
x  2x xx  1 D K M D  1 9    K ; 4; 
 . K là trung điểm MD nên  y  2 y y
  y  3 hay D 1;3;6 . D K M D  2 2 
z  2z z   z  6 D K MD  
Một vectơ chỉ phương của AC là DN  0;  2;  6 . Hay u  0;1;3 là vectơ chỉ phương. 2 2 2 2 2
Câu 27: [2H3-3.1-3] Cho 2 mặt cầu S : x  3  y  2  z  2
 4 , S  : x   2
1  y z 1  1. 2   1       
Gọi d là đường thẳng đồng thời tiếp xúc với hai mặt cầu trên, cắt đoạn thẳng nối tâm hai mặt cầu và 
cách gốc tọa độ O một khoảng lớn nhất. Nếu u   ;
a 1; b là một vectơ chỉ phương của d thì tổng
S  2a  3b bằng bao nhiêu? A. S  2 . B. S  1 . C. S  0 . D. S  4 . Lời giải Chọn A.
S có tâm I 3; 2; 2 , bán kính R  2 . 1   1  1
S có tâm I 1; 0; 1 , bán kính R  1. 2   2  2
Ta có: I I  3  R R , do đó S và S tiếp xúc ngoài với nhau tại điểm 2  1  1 2 1 2  5 2 4  A ; ;   .  3 3 3 
Vì d tiếp xúc với hai mặt cầu, đồng thời cắt đoạn thẳng nối hai tâm I I nên d phải tiếp 1 2
xúc với hai mặt cầu tại A d I I . 1 2
Mặt khác d d  ;
O d   OA d
OA khi d OA . max   
Khi đó, d có một vectơ chỉ phương là I I , OA  6;  3;  6  u   2  ; 1; 2 . 1 2    
Suy ra a  2 , b  2 . Vậy S  2 .
Câu 28: [2H3-3.1-3] Trong không gian Oxy cho tam giác ABC có A2;3;3 , phương trình đường trung x  3 y  3 z  2
tuyến kẻ từ B là  
, phương trình đường phân giác trong góc C là 1 2 1 x  2 y  4 z  2   
. Biết rằng u   ; m ; n  
1 là một véc tơ chỉ phương của đường thẳng AB . Tính 2 1 1 giá trị biểu thức 2 2
T m n . A. T  1. B. T  5 . C. T  2 . D. T  10 . Lời giải Chọn C. x  3 y  3 z  2
Gọi M là trung điểm AC . Trung tuyến BM có phương trình   suy ra 1 2 1 M 3  ; m 3  2 ;
m 2  m  C 4  2 ; m 3  4 ;1 m  2m .
Vì C nằm trên đường phân giác trong góc C nên 4  2m  2 3  4m  4 1 2m  2  
m  0  C 4;3  ;1 . 2 1  1
Gọi A là điểm đối xứng của A qua phân giác trong góc C , khi đó A2  4 ; a 5  2 ;1 a  2a và A  BC . 
Véc tơ chỉ phương của đường thẳng chứa phân giác trong góc C là u  2; 1;   1 .  
Ta có AA .u  0  4 .2
a  2  2a.  1   2
a  2 
1  0  a  0  A2;5  ;1  BM . 
Câu 29: Suy ra A  B B 2;5 
;1  AB  0; 2; 2  20; 1  
;1 là một véc tơ của đường thẳng AB . Vậy 2 2
T m n  2 .[2H3-3.1-3] Trong không gian với hệ toạ độ Oxyz , cho phương trình đường phân x y  6 z  6
giác trong của góc A là  
. Biết M 0;5;3 thuộc đường thẳng AB và N 1;1;0 1 4  3 
thuộc đường thẳng AC . Vector nào sau đây là vector chỉ phương của đường thẳng AC ?     A. u  0;1;3 .
B. u  0;1;  3 .
C. u  0;  2;6 .
D. u  1; 2;3 . Lời giải Chọn A. 
MN  1;  4;  3 , 
d qua điểm At;6  4t;6  3t  và có VTCP u  1;  4;  3 . Suy ra MN //d
Giả sử AK là tia phân giác ngoài góc A cắt MN tại K K là trung điểm của MN .  1 3    1 9   K ;3; 
 , KA t  ;3  4t;  3t   .  2 2   2 2       1   9  KA u  .
KA u  0  1. t   4   3  4t   3  3t  0  
t  1  A1; 2;3 .  2   2   AN  0;1;3 . 
Vậy AC có một vector chỉ phương là AN  0;1;3 . x  4 y 1 z  5
Câu 30: [2H3-3.1-3] Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng  :   và 1 3 1 2 x  2 y  3 z  :  
. Giả sử M   , N   sao cho MN là đoạn vuông góc chung của hai đường 2 1 3 1 1 2 
thẳng  và  . Tính MN . 1 2    
A. MN  5; 5;10 .
B. MN  2; 2; 4 .
C. MN  3; 3;6 .
D. MN  1; 1; 2 . Lời giải Chọn B.    có VTCP u  3; 1  ; 2 
và  có VTCP u  1;3;1 . 2   1   1 2
Gọi M 4  3t;1 t; 5
  2t  và N 2  ; s 3   3 ; s s . 
Suy ra MN  2  3t s;t  3s  4; 2t s  5 .    MN.u  0
2s t  3  0 s  1 Ta có 1       . MN.u  0
s  8t  9  0 t  1    2 
Vậy MN  2; 2; 4 . x 1 y z  2
Câu 31: [2H3-3.1-3] Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   , mặt 2 1 1
phẳng  P : x y  2z  5  0 và A1; 1
 ; 2 . Đường thẳng  cắt d và  P lần lượt tại M và N sao
cho A là trung điểm của đoạn thẳng MN . Một vectơ chỉ phương của  là:    
A. u  2; 3; 2 .
B. u  1; 1; 2 .
C. u  3; 5;1 .
D. u  4; 5; 13 . Lời giải Chọn A.
Điểm M d M  1
  2t;t; 2  t  , A là trung điểm của MN N 3 2t; 2
  t; 2  t
Điểm N  P  3 2t  2  t  22  t  5  0  t  2  M 3;2;4 , N  1  ; 4  ;0   MN   4  ; 6  ; 4    2  2;3;2 .
Câu 32: [2H3-3.1-4] Trong không gian Oxyz , cho tam giác ABC có A2;3;3 , phương trình đường trung x  3 y  3 z  2
tuyến kẻ từ B là  
, phương trình đường phân giác trong của góc C là 1 2 1 x  2 y  4 z  2  
. Đường thẳng AB có một véc-tơ chỉ phương là 2 1 1   
A. u3  2;1;   1 . B. u2  1; 1  ; 0 .
C. u4  0;1;   1 . D. u1  1;2  ;1 . Lời giải Chọn C.
x  2  2t
Phương trình tham số của đường phân giác trong góc C là CD :  y  4  t . z  2  t  Gọi
C  2  2t; 4  t; 2  t  , suy ra tọa độ trung điểm M của AC là 
7  t 5  t M  2  t; ; 
 . Vì M BM nên:  2 2   7  t   5  t   3  2 2 t  3        2   2  t 1 1 t 1 t       t  1. 1  2 1  1 4 2
Do đó C  4;3  ;1 .
Phương trình mặt phẳng  P đi qua A và vuông góc CD là
2. x  2 1. y  3 1. z  3  0 hay 2x y z  2  0 .
Tọa độ giao điểm H của  P và CD là nghiệm  ;
x y; z  của hệ
x  2  2t
x  2  2tx  2   
y  4  t y  4  t   y  4       H 2; 4; 2 . z  2  tz  2  tz  2 
2x y z  2  0 
22  2t   4  t   2  t  2  0   t  0 
Gọi A là điểm đối xứng với A qua đường phân giác CD , suy ra H là trung điểm AA , bởi vậy:
x  2x x  2.2  2  2 AH A
y  2 y y  2.4  3  5  A 2;5  ;1 . AH A
x  2z z  2.2  3 1  AH A 
Do A  BC nên đường thẳng BC có véc-tơ chỉ phương là CA  2; 2;0  21;1;0 , x  4  t
nên phương trình đường thẳng BC là  y  3  t . z  1 
Vì B BM BC nên tọa độ B là nghiệm  ;
x y; z  của hệ x  4  tx  2  y  3 t     y  5 z  1    B 2;5  ;1  A . z  1   x  3 y  3    1 t   2    1 2 
Đường thẳng AB có một véc-tơ chỉ phương là AB  0; 2; 2    20;1;   1 ; hay
u4  0;1; 1 là một véc-tơ chỉ của phương đường thẳng AB .
Câu 33: [2H3-3.1-4] Trong không gian với hệ tọa độ Oxyz , cho hai điểm M  2  ; 2   ;1 , A1; 2; 3   và đường x 1 y  5 z  thẳng d :  
. Tìm một vectơ chỉ phương u của đường thẳng  đi qua 2 2 1
M , vuông góc với đường thẳng d đồng thời cách điểm A một khoảng bé nhất.    
A. u  2; 2;   1 .
B. u  1;7;   1 .
C. u  1;0; 2 . D. u  3; 4; 4   . Lời giải Chọn C.
Gọi  P là mp đi qua M và vuông góc với d , khi đó  P chứa  .  
Mp  P qua M  2  ; 2  ; 
1 và có vectơ pháp tuyến n u  2; 2;   1 nên có phương trình: P d
P : 2x  2y z  9  0 .
Gọi H , K lần lượt là hình chiếu của A lên  P và  . Khi đó: AK AH : const nên AK min 
khi K H . Đường thẳng AH đi qua A1, 2, 3
  và có vectơ chỉ phương u  2; 2;   1 nên dx  1 2t
AH có phương trình tham số:  y  2  2t .
z  3 t
H AH H 1 2t; 2  2t; 3   t  .
H   P  21 2t   22  2t    3
  t   9  0  t  2  H  3  ; 2;   1 .  
Vậy u HM  1;0; 2 .
Câu 34: [2H3-3.1-4] Trong không gian Oxyz , cho tam giác ABC có A2;3;3 , phương trình đường trung x  3 y  3 z  2
tuyến kẻ từ B là  
, phương trình đường phân giác trong của góc C là 1 2 1 x  2 y  4 z  2  
. Đường thẳng AB có một véc-tơ chỉ phương là 2 1 1    A. u3 2;1;   1 .
B. u2 1; 1;0 . C. u4 0;1;   1 . D. u11;2  ;1 . Lời giải Chọn C.
x  2  2t
Phương trình tham số của đường phân giác trong góc C là CD :  y  4  t . z  2  t  Gọi
C  2  2t; 4  t; 2  t  , suy ra tọa độ trung điểm M của AC là 
7  t 5  t M  2  t; ; 
 . Vì M BM nên:  2 2   7  t   5  t   3  2 2 t  3        2   2  t 1 1 t 1 t       t  1. 1  2 1  1 4 2
Do đó C  4;3  ;1 .
Phương trình mặt phẳng  P đi qua A và vuông góc CD là
2. x  2 1. y  3 1. z  3  0 hay 2x y z  2  0 .
Tọa độ giao điểm H của  P và CD là nghiệm  ;
x y; z  của hệ
x  2  2t
x  2  2tx  2   
y  4  t y  4  t   y  4      z  2  tz  2  tz  2 
2x y z  2  0 
22  2t   4  t   2  t  2  0   t  0   H 2; 4; 2 .
Gọi A là điểm đối xứng với A qua đường phân giác CD , suy ra H là trung điểm AA , bởi vậy:
x  2x x  2.2  2  2 AH A
y  2 y y  2.4  3  5  A 2;5  ;1 . AH A
x  2z z  2.2  3 1  AH A 
Do A  BC nên đường thẳng BC có véc-tơ chỉ phương là CA  2; 2;0  21;1;0 , x  4  t
nên phương trình đường thẳng BC là  y  3  t . z  1 
Vì B BM BC nên tọa độ B là nghiệm  ;
x y; z  của hệ x  4  tx  2  y  3 t     y  5 z  1    B 2;5  ;1  A . z  1   x  3 y  3    1 t   2    1 2 
Đường thẳng AB có một véc-tơ chỉ phương là AB  0; 2; 2    20;1;   1 ; hay
u4 0;1; 1 là một véc-tơ chỉ của phương đường thẳng AB .
Câu 35: [2H3-3.3-4] Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC vuông tại C ,  ABC  60 , x  3 y  4 z  8
AB  3 2, đường thẳng AB có phương trình  
, đường thẳng AC nằm trên mặt 1 1 4
phẳng   : x z 1  0 . Biết B là điểm có hoành độ dương, gọi  ; a ;
b c là tọa độ điểm C , giá trị
của a b c bằng A. 3 . B. 2 . C. 4 . D. 7 . Lời giải Chọn B.
Ta có A là giao điểm của đường thẳng AB với mặt phẳng   . Tọa độ điểm A là nghiệm của hệ  x  3 y  4 z  8 x  1      1 1
4   y  2 . Vậy điểm A1; 2; 0 .
x z 1  0   z  0 
Điểm B nằm trên đường thẳng AB nên điểm B có tọa độ B 3  t; 4  t;  8  4t  .
Theo giả thiết thì t  3  0  t  3 . 2 2 2
Do AB  3 2 , ta có t  2  t  2 16t  2  18  t  1 nên B 2;3;  4 . 3 6 3 2
Theo giả thiết thì AC AB sin 60  ; BC  . AB cos 60  . 2 2  a c  1   a c  1  2 2 27  Vậy ta có hệ   a   1  b  2 2  c
 2a  2b  8c  9 2   27  9 2 2 2    a  
1  b  2  c
a  22  b  32  c  42    2  2  7 a   2   7 5   b   3 . Vậy C ;3;  
 nên a b c  2 .   2 2  5 c    2
Câu 36: [2H3-3.3-4] Trong không gian tọa độ Oxyz cho các điểm A1;5;0 , B 3;3;6 và đường thẳng x 1 y 1 z  :   . Gọi M  ; a ;
b c   sao cho chu vi tam giác MAB đạt giá trị nhỏ nhất. Tính 2 1 2
tổng T a b c ? A. T  2 . B. T  3 . C. T  4 . D. T  5 . Lời giải Chọn B.
Ta có M    M   1
  2t;1 t; 2t  .  
MA  2  2t; 4  t; 2
t  , MB  4  2t; 2  t;6  2t  .
Khi đó chu vi tam giác MAB đạt giá trị nhỏ nhất khi và chỉ khi MA MB nhỏ nhất.
Xét hàm số f t   MA MB 2 2
 9t  20  9t  36t  56 2 2 2   t 2  
    t2   2 3 2 5 6 3 2 5
 6  4 5  2 29 .
Dấu bằng đạt được khi và chỉ khi bộ số 3t;6  3t  và bộ số 2 5;2 5 tỉ lệ.
Suy ra 3t  6  3t t  1. Suy ra M  1;0; 2 .
Chú ý ở đây có dùng bất đẳng thức Mincopski
a b a b  ...  a b  a a  ...  a 2  b b  ...  b
, đúng với mọi a , b . n n n n 2 2 2 2 2 2 2 1 1 2 2 1 2 1 2 i i
Dấu bằng xảy ra khi hai bộ số a , a ,..., a và b ,b ,...,b tỉ lệ. 1 2 n  1 2 n
Câu 37: [2H3-3.3-4] Trong không gian với hệ tọa độ Oxyz cho ba điểm A2; 1   ;1 , M 5;3 
;1 , N 4;1; 2 và
mặt phẳng  P : y z  27 . Biết rằng tồn tại điểm B trên tia AM , điểm C trên  P và điểm D trên
tia AN sao cho tứ giác ABCD là hình thoi. Tọa độ điểm C là A.  15  ; 21; 6 . B. 21; 21;6 . C.  15  ; 7; 20 . D. 21;19;8 . Lời giải Chọn B. A F E N M D B K C   1   3 4 
Cách 1: Ta có AM  3; 4;0 ; AM  5 . Gọi E là điểm sao cho AE  .AM  ; ; 0   , khi đó AM  5 5 
E thuộc tia AM và AE  1 .   1   2 2 1 
Ta cũng có AN  2; 2 
;1 ; AN  3 . Gọi F là điểm sao cho AF  .AN  ; ;   , khi đó F AN  3 3 3 
thuộc tia AN và AF  1.
   19 22 1  1
Do ABCD là hình thoi nên suy ra AK AE AF  ; ;   
19;22;5 cùng hướng với  15 15 3  15  
AC , hay u  19; 22;5 là một véc-tơ chỉ phương của đường thẳng AC . Phương trình đường thẳng
x  2 19t
AC là AC :  y  1   22t . z  1 5t
Tọa độ điểm C ứng với t là nghiệm phương trình:  1
  22t   1 5t   27  t  1.
Do đó C 21; 21;6 . 
Cách 2: AM  3; 4;0 , AM  5 .  AN  2; 2  ;1 , AN  3 .    
Chọn điểm AM  3AM , AM  15 và AN  3AN , AN  15 . Khi đó tam giác AM N cân tại A . 1 1 1 1 1 1
Do tứ giác ABCD là hình thoi nên tam giác ABD cân tại A . Suy ra BD và M N song song. 1 1
    
Ta có M N AN AM  5AN  3AM  1; 2  ;5 . 1 1 1 1  
  Cần có
AC BD AC M N AC.M N  0 Với C  ; x y; z  , ta có 1 1 1 1
 
AC.M N  0  x  2 y  5z  9  0 .Thử đáp án thấy B thỏa mãn. 1 1
Câu 38: [2H3-3.5-3] Trong không gian với hệ tọa độ Oxyz , cho  P : x  2 y  2z  5  0 , A3;0  ;1 ,
B 1; 1;3 . Viết phương trình đường thẳng d đi qua A , song song với  P sao cho khoảng cách từ
B đến d là lớn nhất. x  3 y z 1 x  3 y z 1 x 1 y z 1 x  3 y z 1 A.   . B.   . C.   . D.   . 1 1 2 3 2  2 1 2  2 2 6  7 Lời giải Chọn D.
Đường thẳng d đi qua A nên d  ;
B d   BA , do đó khoảng cách từ B đến d lớn nhất khi AB d   
u AB , với u là vectơ chỉ phương của d .  
Lại có d song song với  P nên u n . P     
AB  4; 1; 2 , n  1; 2
 ; 2 , chọn u   AB, n   2;6;7 . PP        x  3 y z 1
Do đó phương trình đường thẳng d là   . 2 6  7
Câu 39: [2H3-3.5-3] Trong không gian Oxyz , cho mặt phẳng   : 2x y  2z  2  0 , đường thẳng x 1 y  2 z  3  1  d :   và điểm A ;1;1 . 
 Gọi  là đường thẳng nằm trong mặt phẳng   , song 1 2 2  2 
song với d đồng thời cách d một khoảng bằng 3. Đường thẳng  cắt mặt phẳng Oxy tại điểm . B
Độ dài đoạn thẳng AB bằng. 7 21 7 3 A. . B. . C. . D. . 2 2 3 2 Lời giải Chọn A. Cách 1:
Ta có: B Oxy và B    nên B  ; a 2  2 ; a 0. x 1 y  2 z  3  d :   đi qua M 1; 2  ; 3
  và có một véctơ chỉ phương là u  1; 2; 2 . 1 2 2
Ta có: d    nên d và  song song với nhau và cùng nằm trong mặt phẳng   .  x 1 y  2 z  3     1 
Gọi C d  OxyC :  1 2 2  C ;1; 0   .   2 z  0      
 : 2x y  2z  2  0  1 
Gọi d      Oxy , suy ra d thỏa hệ 
. Do đó, d  qua C ;1; 0 và có    Oxy   : z  0   2   VTCP u   .  1; 2;0 d    1
Gọi   , d  d, d . Ta có: cos  cos u ,u  . d d   5 CH 3 5
Gọi H là hình chiếu của C lên  . Ta có CH  3 và BC   . sin  2 
Ta có AC  0;0;  
1 nên AC  Oxy  AC BC . 45 7 Vậy 2 2 AB
AC BC  1  . 4 2 x 1 y  2 z  3  Cách 2: Ta có: d :   đi qua M ( 1
 ; 2; 3) và có một VTCP là u  1; 2; 2 . 1 2 2
Ta có: B    Oxy ,     nên B Oxy     B  ; a 2  2 ; a 0.   u; MB  
Ta có:  // d và d , d   3 nên d  ; B d   3    3 u   
Ta có: MB  a 1; 4  2 ;
a 3 ; u; MB  4a  2; 2a 1; 2  4a .     u; MB 2   3 2a   1 2 Do đó   3   3  2a   1  9. u 3 2  1  2 9 7 Vậy AB a     1 2a 2 1   9 1  .  2  4 2
Câu 40: [2H3-3.5-3] Trong không gian với hệ tọa độ Oxyz , cho đường thẳng  đi qua gốc tọa độ O và điểm I 0;1 
;1 . Gọi S là tập hợp các điểm nằm trên mặt phẳng Oxy , cách đường thẳng  một
khoảng bằng 6 . Tính diện tích hình phẳng giới hạn bởi S . A. 36 . B. 36 2 . C. 18 2 . D. 18 . Lời giải Chọn B. Gọi M  ;
x y; 0 Oxy     2 2 OM ,OI   y  2x
d M ,    OI 2 2 2 y  2x 2 2 x y Yêu cầu bài toán   6    1 2 36 72
Vậy quỹ tích M trên Oxy là hình Elip với a  6 và b  6 2  S   ab  36 2 .
Câu 41: [2H3-3.5-3] Trong không gian với hệ trục toạ độ Oxyz , cho ba điểm A2;0;0 , B 0;3  ;1 ,
C 1; 4; 2 . Độ dài đường cao từ đỉnh A của tam giác ABC : 3 A. 6 . B. 2 . C. . D. 3 . 2 Lời giải Chọn B.
Độ dài đường cao từ đỉnh A của tam giác ABC là AH d  , A BC  . 
Ta có đường thẳng BC đi qua điểm B 0;3 
;1 và nhận vectơ CB  1; 1;   1 làm vectơ chỉ phương x t
nên có phương trình  y  3  t . z  1 t    CB, AB  
Do đó: AH d  , A BC    . CB        
Với CB  1; 1;  
1 ; AB  2;3 
;1  CB, AB  2;1 
;1  CB, AB  6 .      CB  3 .     CB, AB  
Vậy AH d  , A BC     2 . CB   2 2 2
Câu 42: [2H3-3.5-3] Trong không gian Oxyz cho mặt cầu S  : x  
1   y  2   z  3  9 và mặt phẳng
P :2x  2y z  3  0 . Gọi M  ; a ;
b c là điểm trên mặt cầu sao cho khoảng cách từ M đến  P lớn nhất. Khi đó:
A. a b c  8 .
B. a b c  5 .
C. a b c  6 . D.
a b c  7 . Hướng dẫn giải Chọn D.
Mặt S  cầu có tâm I 1; 2;3, R  3 . 2.1 2.2  3  3 d  4
I ,  P  
R mặt phẳng cắt mặt cầu theo một đường tròn   2 2 2 3 2 2 1 Gọi M  ; a ;
b c là điểm trên mặt cầu sao cho khoảng cách từ M đến  P lớn nhất.
Khi M thuộc đường thẳng  vuông đi qua M và vuông góc với  P x  1 2t  2 2 2  : 2
y  2  2t . Thay vào mặt cầu  S    2t    2
t   t   9  9t  9  t  1  z  3  t  2.3  2.0  4  3 10
Với t  1  M 3;0; 4 d M ; P     2 2 2 3 2 2 1 2.  1  2.4  2  3 1
Với t  1  M 1; 4; 2  d M ; P     2 2 2 3 2 2 1
Vậy M 3;0; 4  a b c  7 .
Câu 43: [2H3-3.5-3] Trong không gian Oxyz , cho hai điểm M  2  ; 2;  1 , A1; 2; 3   và đường thẳng x 1 y  5 zd :  
. Tìm véctơ chỉ phương u của đường thẳng  đi qua M , vuông góc với đường 2 2 1
thẳng d , đồng thời cách điểm A một khoảng lớn nhất.    
A. u  4; 5; 2 .
B. u  1;0; 2 . C. u  8; 7  ; 2 .
D. u  1;1; 4 . Lời giải Chọn A.
Gọi H là hình chiếu vuông góc của A lên  , ta có d  ;
A   AH .
Mặt khác, vì M   nên AH AM . Do đó, AH
AM H M . max
Khi đó, đường thẳng  đi qua M , vuông góc với đường thẳng d và vuông góc với đường thẳng   
AM nên có véctơ chỉ phương là u  u ; AM   4; 5  ; 2 . d   x  1 x  4  t  
Câu 44: [2H3-3.5-3] Trong không gian Oxyz cho hai đường thẳng  :  y  2  t ,  :  y  3  2t . Gọi S  1 2 z t    z  1 t
là mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng  và  . Bán kính mặt cầu S  . 1 2 10 11 3 A. . B. . C. . D. 2 . 2 2 2 Hướng dẫn giải Chọn B.
A   A1; 2  t;  t  , B    B 4  t ;3  2t ;1   t . 1 2 
Ta có AB  3  t ;1
  2t  t;1 t  t  
VTCP của đường thẳng  là u  0;1; 1 . 1   1 
VTCP củả đường thẳng  là u  1;  2; 1 . 2   2     . AB u  0 1
  2t  t  
1 t  t  0 Ta có 1      . AB u  0  3  t  2 
1 2t  t   1 t  t   0 2 
t  2t  0   
t t  0 . Suy ra AB  3;1  ;1  AB  11 .
6t  t  0 
Mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng  và  có đường kính bằng độ dài 1 2 AB 11
đoạn AB nên có bán kính r   . 2 2
Câu 45: [2H3-3.4-3] Trong không gian Oxyz cho tam giác ABC có A1; 2;  
1 , B 2; 1;3 , C  4  ; 7;5 . Tọa
độ chân đường phân giác góc 
ABC của tam giác ABC là  11   2 11 1  A. ;  2;1   . B. ; ;   . C.  2  ;11;  1 . D.  2   3 3 3   2 11   ; ;1   .  3 3  Lời giải Chọn D. x  1 5t
Ta có phương trình đường thẳng AC là  y  2  5t ,t   .
z  1 6t
Gọi I là chân đường phân giác góc 
ABC của tam giác ABC .
I 1 5t; 2  5t; 1 6t  .    Lại có BA 1
 ;3;  4 , BC  6  ;8; 2 , BI  5
t 1;5t  3;6t  4 .
Vì I là chân đường phân giác góc 
ABC của tam giác nên ABC :         B . A BI BC.BI cos  ;
BA BI   cosBC; BI        BA . BI BC . BI
5t 115t  9 16  24t
30t  6  40t  24 12t  8 4  t  26 82t  22      2 1  3   4  2  6  2 2 2 2  8  2 26 104 1  2 11 
 8t  52  82t  22  t   I  ; ;1   . 3  3 3  2 2
Câu 46: [2H3-3.4-4] Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S   x   2 :
1  y   z  2  4 và x  2  t
đường thẳng d :  y t
. Gọi T là tập tất cả các giá trị của m để d cắt S  tại hai điểm phân
z m 1 t
biệt A , B sao cho các tiếp diện của S  tại A và B tạo với nhau góc lớn nhất có thể. Tính tổng các
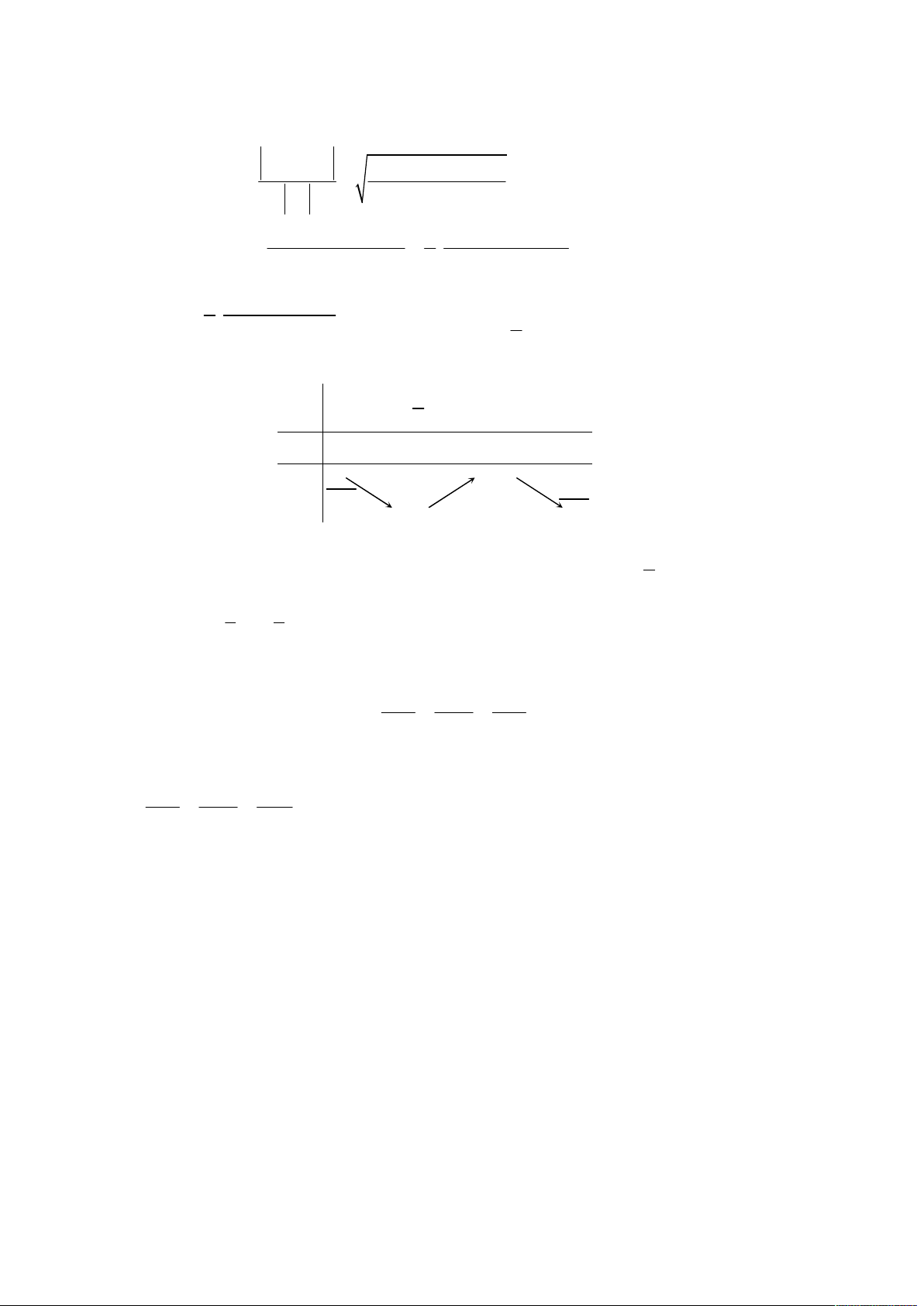
phần tử của tập hợp T . A. 3 . B. 3 . C. 5 . D. 4 . Hướng dẫn giải Chọn B. I (S) d A H B M
Mặt cầu S  có tâm I 1;0; 2 và bán kính R  2 . 
Đường thẳng d đi qua điểm N 2;0; m  
1 và có véc tơ chỉ phương u  1;1  ;1 .   IN;u  
Điều kiện để d cắt S  tại hai điểm phân biệt là d I;d   R    2 u 2 2m  6m  6 3   21 3  21   2   m  . 3 2 2
Khi đó, tiếp diện của S  tại A và B vuông góc với IA và IB nên góc giữa chúng là góc  I ; A IB .
Ta có o   IA IB o 0 ;  90 nên  I ; A IB o
 90  IA IB . max 2 2m  6m  6 m  0
Từ đó suy ra d I d  1 ;  AB  2   2  2
2m  6m  0   . 2 3 m  3 
Vậy T  3; 
0 . Tổng các phần tử của tập hợp T bằng 3 .
Câu 47: [2H3-3.6-3] Trong không gian với hệ tọa độ Oxyz, cho điểm (
A 0;1; 2) , mặt phẳng 2 2 2
( ) : x y z  4  0 và mặt cầu (S) :  x  3   y  
1   z  2  16 . Gọi  P là mặt phẳng đi qua
A , vuông góc với ( ) và đồng thời  P cắt mặt cầu S  theo giao tuyến là một đường tròn có bán
kính nhỏ nhất. Tọa độ giao điểm M của  P và trục x Ox  là  1   1  A. M  ; 0; 0   . B. M  ; 0; 0   . C. M 1;0;0 . D.  2   3   1  M ; 0; 0   .  3  Hướng dẫn giải Chọn A.  Gọi n   ; a ;
b c là một vec tơ pháp tuyến của mặt phẳng  P .
Theo đề bài ta có mặt phẳng  P vuông góc với mặt phẳng ( ) : x y z  4  0 nên ta có 
phương trình a b c  0  b a c n  a; a  ; c c . 
Phương trình mặt phẳng  P đi qua (
A 0;1; 2) và có véc tơ pháp tuyến n   ; a a  ; c c là
ax  a c y  
1  c z  2  0 . 3a
Khoảng cách từ tâm I 3;1; 2 đến mặt phẳng  P là d I, P  h  . 2 2 2
a ac c
Gọi r là bán kính của đường tròn giao tuyến giữa mặt cầu S  và mặt phẳng  P ta có 2 2
r  16  h r nhỏ nhất khi h lớn nhất.
Khi a  0 thì h  0 . 2 9 2  c c   c 1  3  3
Khi a  0 thì h  . Do 2 1   2          nên 2  c c  2 a a    a 2  4 2 2 1     2  a a   9 2 h   9.
 6 . Dấu "  " xảy ra khi a  2c .  một véc tơ pháp tuyến là 2  c c  3 2 1   2  a a  
n 2;1; 1  phương trình mặt phẳng P là 2xyz1 0.  1 
Vậy tọa độ giao điểm M của  P và trục x Ox  là M  ; 0; 0    2 
Câu 48: [2H3-3.6-3] Trong không gian tọa độ Oxyz cho A1;1;   1 , B 2;3;  1 , C 5;5;  1 . Đường phân giác
trong góc A của tam giác ABC cắt mặt phẳng Oxy tại M  ; a ;
b 0 . Tính 3b a . A. 6 . B. 5 . C. 3 . D. 0 . Lời giải Chọn B.
Ta có AB  3 , AC  6 . Gọi I  ;
x y; z  là điểm thuộc cạnh BC sao cho AI là phân giác trong của góc A 5
  x  2 2  x x  3  IC AC     11  11  Ta có   2  IC  2  IB  5   y  2
 3  y   y   I 3; ;1   . IB AB  3   3 
1 z  21 z  z  1    8  Ta có AI  2; ; 2   .  3  x  1 2t   8
Phương trình tham số của AI là:  y  1 t . 3  z  1   2t
Phương trình mặt phẳng Oxy là: z  0 .  7 
Giao điểm của đường thẳng AI với mặt phẳng Oxy là M 2; ;0   .  3 
Vậy 3b a  5 .
Câu 49: [2H3-3.6-3] Trong không gian với hệ trục tọa độ Oxyz , cho bốn đường thẳng: x  3 y  1 z  1 x y z 1 x 1 y  1 z 1 x y 1 zd :   , d :   , d :   , d :   . Số 4  3  2  1  1 2  1 1 2 1 2 1 1 1 1 1
đường thẳng trong không gian cắt cả bốn đường thẳng trên là: A. 0 . B. 2 . C. Vô số. D. 1. Lời giải Chọn A. d 4  d 3  A d 1  B d 2  P
Ta có d song song d , phương trình mặt phẳng chứa hai 2  1 
Hai đường thẳng d , d là  P : x y z 1  0 . 2  1 
Gọi A  d P A1; 1  
;1 ,  Ad , Ad . 1   2  3   
B  d P B 0;1;0 , B d , B d . 1   2  4     Mà AB   1  ; 2;  
1 cùng phương với véc-tơ chỉ phương của hai đường thẳng d , d nên không 2  1 
tồn tại đường thẳng nào đồng thời cắt cả bốn đường thẳng trên. x  3 y 1 z 1
Câu 50: [2H3-3.6-3] Trong không gian Oxyz , cho bốn đường thẳng: d :   , 1  1 2 1 x y z 1 x 1 y 1 z 1 x y 1 z 1 d :   , d :   , d :  
. Số đường thẳng trong không 4  3  2  1 2 1 2 1 1 1 1  1
gian cắt cả bốn đường thẳng trên là: A. 0 . B. 2 . C. Vô số. D. 1. Lời giải Chọn D. 
Đường thẳng d đi qua điểm M  3; 1; 1 và có một véctơ chỉ phương là u  1; 2;1 . 1   1   1 
Đường thẳng d đi qua điểm M  0; 0;1 và có một véctơ chỉ phương là u  1; 2;1 . 2   2   2  
Do u u2 và M d nên hai đường thẳng d và d song song với nhau. 1 1 1 1 2   
Ta có M M  3;1; 2 , u  1, M M  5  ; 5  ; 5   5  1;1;1; 1 2   1 2     
Gọi   là mặt phẳng chứa d và d khi đó   có một véctơ pháp tuyến là n  1;1  ;1 . 1 2
Phương trình mặt phẳng   là x y z 1  0 .
Gọi A d   thì A1; 1  
;1 . Gọi B d   thì B  1  ; 2; 0 . 4   3    
Do AB  2;3;  
1 không cùng phương với u  1; 2;1 nên đường thẳng AB cắt hai 1  
đường thẳng d và d . 1 2 x 1 y  2 z  3
Câu 51: [2H3-3.6-3] Trong không gian Oxyz , cho đường thẳng d :   và mặt phẳng 1 2 1
  : x y z  2  0 . Trong các đường thẳng sau, đường thẳng nào nằm trong mặt phẳng   , đồng
thời vuông góc và cắt đường thẳng d ? x  2 y  4 z  4 x 1 y 1 z A.  :   . B.  :   . 2 1 2 3 4 3 2 1 x  5 y  2 z  5 x  2 y  4 z  4 B.  :   . D.  :   . 3 3 2 1 1 3 2 1 Lời giải Chọn B. x  1 t
Phương trình tham số của đường thẳng d :  y  2  2t . z  3  t
I d I 1 t; 2  2t;3  t
I     1 t  2  2t  3  t   2  0  t  1  I 2; 4; 4 . 
Vectơ chỉ phương của d là u  1; 2  ;1 
Vectơ chỉ pháp tuyến của   là n  1;1;   1  
Ta có u, n   3  ; 2;   1 .    
Đường thẳng cần tìm qua điểm I 2; 4; 4 , nhận một VTCP là u, n   3  ; 2;   1 nên có PTTS  
x  2  3t
y  4  2t . z  4  t
Câu 52: [2H3-3.6-4] Trong không gian với hệ trục tọa độ Oxyz , cho bốn đường thẳng: x  3 y 1 z 1 x y z 1 x 1 y 1 z 1 x y 1 z d :   , d :   , d :   , d :   . Số đường 1 1 2  1 2 1 2 1 3 2 1 1 4 1 1 1 
thẳng trong không gian cắt cả bốn đường thẳng trên là A. 0 . B. 2 . C. Vô số. D. 1. Lời giải Chọn A. d4  d3  A B d1 d2  P
Ta có d song song d , phương trình mặt phẳng chứa hai 1 2
Hai đường thẳng d , d là  P : x y z 1  0 . 1 2
Gọi A d P A1; 1  
;1 ,  Ad , Ad . 1 2  3  
B d P B 0;1;0 ,  B d , B d . 1 2  4   
Mà AB  1; 2;  
1 cùng phương với véc-tơ chỉ phương của hai đường thẳng d , d nên không tồn 1 2
tại đường thẳng nào đồng thời cắt cả bốn đường thẳng trên.
x  1 3a  at
Câu 53: [2H3-3.6-4] Trong không gian với hệ tọa độ Oxyz , cho đường thẳng  :  y  2   t . Biết
x  2  3a  (1 a)t
rằng khi a thay đổi luôn tồn tại một mặt cầu cố định qua điểm M 1;1 
;1 và tiếp xúc với đường thẳng
 . Tìm bán kính mặt cầu đó. A. 5 3 . B. 4 3 . C. 7 3 . D. 3 5 . Lời giải Chọn A.
x  1 3a  at
Từ đường thẳng  :  y  2   t
x y z  3  0
x  2  3a  (1 a)t
Ta có  luôn qua điểm A1; 5;  
1 cố định và  nằm trong mặt phẳng  P : x y z  3  0
Mặt cầu tiếp xúc với đường thẳng  vói mọi a . Nên mặt cầu tiếp xúc mặt phẳng  P tại A . x  1 t
Đường thẳng IA qua A và vuông góc  P có phương trình  y  5
  t I (1 t; 5  t; 1 t) z  1   t  Mà 2 2 2 2 2 2
IA IM t t t t  (t  6)  (t  2)  t  5 vậy I (6; 0; 6
 )  R IM  5 3 x  3 y  2 z 1
Câu 54: [2H3-3.6-4] Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt 2 1 1
phẳng  P : x y z  2  0 . Đường thẳng  nằm trong mặt phẳng  P , vuông góc với đường thẳng
d đồng thời khoảng cách từ giao điểm I của d với  P đến  bằng 42 . Gọi M 5; ; b c là hình
chiếu vuông góc của I trên  . Giá trị của bc bằng A. 10 . B. 10 . C. 12 . D. 20 . Lời giải Chọn B. d Δ' M I Δ 
Mặt phẳng  P có véc-tơ pháp tuyến n  1;1 
;1 , đường thẳng d có véc-tơ chỉ phương P  u  2;1;   1 . d
Tọa độ giao điểm I d với  P là nghiệm của hệ phương trình:  x  3 y  2 z 1 x  1      2 1 1   y  3
  I 1; 3;0 .
x y z  2  0   z  0 
Đường thẳng  nằm trong mặt phẳng  P , vuông góc với đường thẳng d nên có một véc-tơ chỉ   
phương là u  n ;u     .   2;3;  1 P d  
Đường thẳng  đi qua I , thuộc mặt phẳng  P và vuông góc với đường thẳng  có véc-tơ chỉ   
phương là: u  n ;u     .    4; 1;5 P    x  1 4t
Phương trình đường thẳng  là:  y  3  t . z  5t
Hình chiếu M của I trên đường thẳng  là giao điểm của  và   M 1 4t; 3
  t;5t  .
Khoảng cách từ I đến  bằng 42 nên 2 2 2 IM  42 2
IM  42  4t    t
   5t   42  t  1 .
Với t  1 thì M  3  ; 4  ;5 .
Với t  1 thì M 5; 2  ; 5   . Như vậy b  2  , c  5   bc  10 .
Câu 55: [2H3-3.8-3] Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm A2;1  ;1 , B 0;3;   1 . Điểm
M nằm trên mặt phẳng  P :2x y z  4  0 sao cho MA MB nhỏ nhất là
A. 1;0; 2. B. 0;1;3. C. 1; 2;0. D. 3;0; 2. Lời giải Chọn C.
Khi đó Trước hết ta xét vị trí tương đối của hai điểm A2;1 
;1 và B 0;3;   1 so với mặt phẳng
P :2x y z  4  0 . Ta có  2.2 11 42.0  31 4  4
  0. Do đó A2;1  ;1 và A0;3;   1
nằm khác phía so với mặt phẳng  P :2x y z  4  0 .
Theo bất đẳng thức tam giác ta có MA MB AB . Đẳng thức xảy ra khi và chỉ khi M , , A B thẳng
hàng hay M AB   P. 
Đường thẳng AB qua điểm A2;1 
;1 và có vec tơ chỉ phương AB  21; 1  ;1 có phương trình x  2  t
tham số  y  1 t Suy ra M 2  t;1 t;1 t  . z 1 t. 
Vì M  P nên ta có 22  t  1 t 1 t  4  0  2t  2   t  1  . Vậy M 1; 2;0 .
Câu 56: ----------HẾT----------[2H3-3.8-3] Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm A0; 2;   1 , B  2  ; 4
 ;3 , C 1;3;  
1 và mặt phẳng  P : x y  2z  3  0 . Tìm điểm M  P sao   
cho MA MB  2MC đạt giá trị nhỏ nhất.  1 1   1 1  A. M ; ; 1    . B. M  ;  ;1   . C. M 2; 2; 4   .
D. M 2; 2; 4 .  2 2   2 2  Lời giải Chọn A. M A B I
Gọi I , O lần lượt là trung điểm của AB và IC , khi đó với điểm M bất kỳ ta luôn có          
MA MB  MI IA  MI IB  2MI ; tương tự MI MC  2MO .       
Suy ra d MA MB  2MC  2MI  2MC  4 MO nên d nhỏ nhất khi và chỉ khi MO nhỏ nhất
MO   P nên M là hình chiếu vuông góc của O lên  P .
Có A0; 2;   1 , B  2  ; 4  ;3  I  1  ; 3  
;1 , kết hợp với C 1;3;  1 
ta có O 0;0;0 . x t
Đường thẳng qua O 0;0;0 vuông góc với  P có phương trình d :  y t . z  2   t
Giao điểm của d và  P chính là hình chiếu vuông góc M của O 0;0;0 lên mặt phẳng  P . x t   y t 1 1 1 Giải hệ  ta được t  , x  , y  , z  1  . z  2   t 2 2 2
x y  2z  3 0    1 1  Vậy M ; ; 1    .  2 2 
* Nhận xét: Với 4 đáp án bài này học sinh chỉ làm phép thử đơn giản là thay tọa độ từng điểm vào
phương trình mặt phẳng  P thôi cũng đủ chọn đáp án A, “mồi nhử” chưa tốt. Có lẽ tác giả chỉ quan
tâm cách giải tự luận!
Câu 57: [2H3-3.8-3] Trong không gian với hệ trục Oxyz , cho hai điểm M 0; 1; 2 , N  1  ;1;3 . Một mặt
phẳng  P đi qua M , N sao cho khoảng cách từ điểm K 0;0; 2 đến mặt phẳng  P đạt giá trị lớn 
nhất. Tìm tọa độ véctơ pháp tuyến n của mặt phẳng  P .     n  1; 1 
;1 . B. n  1;1;   1 . C. n  2; 1  ;  1 .
D. n  2;1;   1 . Lời giải Chọn B. 
Ta có: MN  1; 2  ;1 . K N M I P   x t  
Đường thẳng d  qua hai điểm M , N có phương trình tham số  y  1 2t . z  2  t
Gọi I là hình chiếu vuông góc của K lên đường thẳng d   I t; 1
  2t; 2  t  . 
Khi đó ta có KI  t; 1 2t;t  . Do   1   1 1 1  1
KI MN KI.MN  0  t  2  4t t  0  t   KI   ;  ;   1;1;     1 . 3  3 3 3  3 
Ta có d K; P  KI d K; P
KI KI   P  n  1;1;   1 . nax
Câu 58: [2H3-3.8-3] Trong không gian với hệ tọa độ Oxyz , cho điểm A1; 2; 3   và mặt phẳng 
P : 2x  2y z  9  0 . Đường thẳng d đi qua A và có vectơ chỉ phương u  3;4; 4
  cắt  P tại
B . Điểm M thay đổi trong  P sao cho M luôn nhìn đoạn AB dưới góc o
90 . Khi độ dài MB lớn
nhất, đường thẳng MB đi qua điểm nào trong các điểm sau? A. H  2  ; 1  ;3 . B. I  1  ; 2  ;3 . C. K 3;0;15 . D. J  3  ; 2; 7 . Lời giải Chọn B. 
+ Đường thẳng d đi qua A1; 2; 3
  và có vectơ chỉ phương u  3; 4; 4   có phương trình là x  1 3t
y  2  4t . z  3   4t  + Ta có: 2 2 2
MB AB MA . Do đó MB
khi và chỉ khi MA . max min
+ Gọi E là hình chiếu của A lên  P . Ta có: AM AE .
Đẳng thức xảy ra khi và chỉ khi M E .  Khi đó  AM
AE và MB qua B nhận BE làm vectơ chỉ phương. min
+ Ta có: B d nên B 1 3t; 2  4t; 3
  4t  mà B  P suy ra:
21 3t   22  4t    3
  4t   9  0  t  1   B  2  ; 2   ;1 . 
+ Đường thẳng AE qua A1; 2; 3
  , nhận n  2; 2;  
1 làm vectơ chỉ phương có phương Px  1 2t
trình là  y  2  2t .
z  3 t
Suy ra E 1 2t; 2  2t; 3   t  .
Mặt khác, E   P nên 21 2t   22  2t    3
  t   9  0  t  2   E  3  ; 2  ;   1 . 
+ Do đó đường thẳng. MB . qua B2;2 
;1 , có vectơ chỉ phương BE  1; 0;2 nên
x  2t 
có phương trình là y  2  .
z 12t 
Thử các đáp án thấy điểm I  1  ; 2
 ;3 thỏa. Vậy chọn đáp án B.
Câu 59: [2H3-3.8-3] Trong không gian Oxyz , cho hai điểm A1; 2 
;1 , B 1; 2;  3 và đường thẳng x 1 y  5 zd :  
. Tìm vectơ chỉ phương u của đường thẳng  đi qua điểm A và vuông góc với 2 2 1
d đồng thời cách B một khoảng lớn nhất.   
A. u  4;  3; 2 .
B. u  2; 0;  4 .
C. u  2; 2;   1 . D.  u  1;0; 2 . Lời giải Chọn A.  
Ta có AB  2;  0;  4 , u  2; 2;   1 . d
Gọi H là hình chiếu vuông góc của B lên  , lúc đó d B,   BH BA .
Do đó d B,  lớn nhất khi H A    d và   AB .    
Ta có VTCP của  là u   ; AB u   
. Do đó chọn u  4;  3; 2 là VTCP của  8; 6;4 d     .
Câu 60: [2H3-3.8-3] Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng  P : x  2 y z 1  0 và điểm
A0; 2;3 , B 2;0  ;1 . Điểm M  ; a ;
b c thuộc  P sao cho MA MB nhỏ nhất. Giá trị của 2 2 2
a b c bằng 41 9 7 A. . B. . C. . D. 3 . 4 4 4 Lời giải Chọn B. A B A' Ta có ,
A B cùng nằm về một phía của  P . Gọi A đối xứng với A qua  P suy ra A2; 2  ;1 .
Ta có MA MB MA  MB BA . Dấu bằng xảy ra khi M là giao điểm của BA và  P .  1 
Xác định được M 1; ;1   . Suy ra chọn B.  2 
Câu 61: [2H3-3.8-3] Trong không gian với hệ toạ độ Oxyz , cho hai điểm A2; 3; 2 , B 3;5; 4 . Tìm toạ độ
điểm M trên trục Oz so cho 2 2
MA MB đạt giá trị nhỏ nhất. A. M 0;0; 49 . B. M 0;0;67 . C. M 0;0;3 . D. M 0;0;0 . Lời giải Chọn C.  5 
Gọi I là trung điểm của AB I ;1;3   .  2        2 2 2 2 Ta có: 2 2
MA MB MA MB  MI IA  MI IB 2 2 2
 2MI IA IB . 2 2
IA IB không đổi nên 2 2
MA MB đạt giá trị nhỏ nhất khi MI đạt giá trị nhỏ nhất.
M là hình chiếu của I trên trục Oz .  M 0;0;3 . x  3 y 1 z 1
Câu 62: [2H3-3.8-3] Trong không gian Oxyz , cho bốn đường thẳng: d :   , 1 1 2  1 x y z 1 x 1 y 1 z 1 x y 1 z 1 d :   , d :   , d :  
. Số đường thẳng trong không gian 2 1 2 1 3 2 1 1 4 1 1 1
cắt cả bốn đường thẳng trên là A. 0 . B. 2 . C. Vô số. D. 1. Lời giải Chọn D. 
Đường thẳng d đi qua điểm M  3; 1  ; 1 
và có một véctơ chỉ phương là u  1; 2;1 . 1   1   1 
Đường thẳng d đi qua điểm M  0;0;1 và có một véctơ chỉ phương là u  1; 2  ;1 . 2   2   2  
Do u u2 và M d nên hai đường thẳng d và d song song với nhau. 1 1 1 1 2   
Ta có M M  3;1; 2 , u  1, M M  5  ; 5  ; 5   5  1;1;1; 1 2   1 2     
Gọi   là mặt phẳng chứa d và d khi đó   có một véctơ pháp tuyến là n  1;1  ;1 . 1 2
Phương trình mặt phẳng   là x y z 1  0 .
Gọi A d   thì A1; 1  
;1 . Gọi B d   thì B  1  ; 2; 0 . 4   3    
Do AB  2;3;  
1 không cùng phương với u  1; 2;1 nên đường thẳng AB cắt hai 1  
đường thẳng d và d . 1 2
Câu 63: [2H3-3.8-3] Trong không gian với hệ trục toạ độ Oxyz , cho mặt cầu
S   x  2   y  2   z  2 : 1 2 3
 9 , điểm A0; 0; 2 . Phương trình mặt phẳng  P đi qua A và
cắt mặt cầu S  theo thiết diện là hình tròn C  có diện tích nhỏ nhất là
A.  P : x  2 y  3z  6  0 .
B.  P : x  2 y z  2  0 .
C.  P : x  2 y z  6  0 .
D.  P : 3x  2 y  2z  4  0 . Lời giải Chọn B. 2 2 2
Mặt cầu S  :  x  
1   y  2   z  3  9 có tâm I 1; 2;3 , bán kính R  3 .
IA  6  R nên A nằm trong mặt cầu.
Gọi r là bán kính đường tròn thiết diện, ta có 2 2 r R h .
Trong đó h là khoảng cách từ I đến  P .
Diện tích thiết diện là 2  r    2 2
R h     2 2 R IA  . 
Vậy diện tích hình tròn C  đạt nhỏ nhất khi h IA . Khi đó IA là véc tơ pháp tuyến của  P .
Phương trình mặt phẳng  P là 1 x  0  2 y  0   z  2  0  x  2 y  z  2  0 .
Câu 64: [2H3-3.8-3] Trong không gian với hệ tọa độ Oxyz cho các điểm A4; 2;5 , B 0; 4; 3 ,
   C 2; 3
 ; 7 . Biết điểm M x ; y ; z nằm trên mặt phẳng Oxy sao cho MA MB MC đạt giá trị 0 0 0 
nhỏ nhất. Tính tổng P x y z . 0 0 0 A. P  3 . B. P  0 . C. P  3 . D. P  6 . Hướng dẫn giải Chọn C.
   
Gọi G 2;1;3 là trọng tâm ABC MA MB MC  3MG  3MG
  
Do đó MA MB MC nhỏ nhất khi MG nhỏ nhất
Mà MG d G,Oxy  GH  
nên MG nhỏ n hất khi M H khi đó M là hình chiếu vuông góc của
G lên Oxy  M 2;1;0  x y z  3 0 0 0 x 1 y z  2
Câu 65: [2H3-3.8-3] Trong không gian với hệ tọa độ Oxyz , cho đường thẳng  :   và hai 2 1 1
điểm A0; 1;3 , B 1; 2  
;1 . Tìm tọa độ điểm M thuộc đường thẳng  sao cho 2 2
MA  2MB đạt giá trị nhỏ nhất.
A. M 5; 2; 4 . B. M  1  ; 1  ;   1 . C. M 1;0; 2   . D. M 3;1; 3   . Hướng dẫn giải Chọn B.
Vì M thuộc đường thẳng  nên M 1 2t;t;  2  t  . 2 2 2 2 2 2 Ta có 2 2 MA  2MB 2t  1 t  1 t 5 2 2t  t 2 t 3             2
 18t  36t  53    2 2 MA  2MB  t  2 18 1  35  35 , t    . Vậy  2 2
min MA  2MB   35  t  1 hay M  1  ; 1  ;   1 .  1 3 
Câu 66: [2H3-3.8-3] Trong không gian Oxyz , cho điểm M  ;
; 0  và mặt cầu S  2 2 2
: x y z  8 . Một  2 2   
đường thẳng đi qua điểm M và cắt  S  tại hai điểm phân biệt A , B . Diện tích lớn nhất của tam giác OAB bằng A. 4 . B. 2 7 . C. 2 2 . D. 7 . Lời giải Chọn. D.
Mặt cầu S  có tâm O 0;0; 0 và bán kính R  2 2 .   1 3  Ta có: OM   ;
; 0   OM  1  R  điểm M nằm trong mặt cầu S  .  2 2   
Gọi H là trung điểm AB OH OM .
Đặt OH x  0  x  1 .  2 2 2 AH OA OH 8  x OH x
Đặt AOH    sin    ; cos   . OA OA 2 2 OA 2 2 xx Suy ra  2 8
sin AOB  2 sin  cos  . 4 1 Ta có:  2 S  . OA O .
B sin AOB x 8  x với 0  x  1. OAB  2
Xét hàm số f x 2
x 8  x trên đoạn 0;  1 2 2 x 8  2x f  x 2  8  x    0, x  0 
;1  max f x  f   1  7 2 2 8  x 8  x 0;  1
Vậy diện tích lớn nhất của tam giác OAB bằng 7 . x 1 y 1 z m
Câu 67: [2H3-3.8-3] Trong không gian Oxyz , cho đường thẳng d :   và mặt cầu 1 1 2
S   x  2   y  2   z  2 : 1 1 2
 9 . Tìm m để đường thẳng d cắt mặt cầu S  tại hai điểm phân
biệt E , F sao cho độ dài đoạn EF lớn nhất 1 1 A. m  1. B. m  0 . C. m   . D. m  . 3 3 Lời giải Chọn B.
Mặt cầu S  có tâm I 1;1; 2 và bán kính R  3 .
Gọi H là hình chiếu vuông góc của I trên d , khi đó H là trung điểm đoạn EF .
Ta có EF EH
R  d I P2 2 2 2 ,
. Suy ra EF lớn nhất khi d I, P nhỏ nhất 
Đường thẳng d qua A1; 1
 ; m và có véc tơ chỉ phương u  1;1; 2 .   
Ta có AI  0; 2; 2  m ,  AI ,u  2  ; m 2  ; m 2 .      AI,u 2   2m 12
Suy ra d I,P     2 . u 11 4
Do đó d I, P nhỏ nhất khi m  0 . Khi đó EF EH
R  d I P2 2 2 2 ,  2 7 . x  1 tx  2t  
Câu 68: [2H3-3.8-3] Trong không gian Oxyz , cho hai đường thẳng d :  y  2  t , d :  y  1 t . Đường z t   z  2  t 
thẳng  cắt d , d  lần lượt tại các điểm A , B thỏa mãn độ dài đoạn thẳng AB nhỏ nhất. Phương
trình đường thẳng  là x 1 y  2 z x  4 y z  2 A.   . B.   . 2 1 3 2 1  3 x y  3 z 1 x  2 y 1 z 1 C.   . D.   . 2 1 3 2 1 3 Lời giải Chọn D.
  d A1 t; 2  t;t  ,   d B 2t ;1
  t ; 2  t .    1   . AB u  0
2t  t 1 t  t 1 t  t  2  0
2t  3t  2 t            2 .  
4t  2t  2  t  t 1 t  t  2  0 . AB u  0    6t  2t  1  t   1    1 3  Suy ra A2;1  ;1 , AB  1; ;    2 2 
AB ngắn nhất khi và chỉ khi AB là đoạn vuông góc chung của d , d  .   x  2 y 1 z 1
Vậy  đi qua A2;1 
;1 có vectơ chỉ phương u  2AB   2  ;1;3   :   . 2  1 3
Câu 69: [2H3-3.8-3] Trong không gian Oxyz , cho hình hộp ABC . D AB CD
  biết A1;0  ;1 , B 2;1; 2 , D 2; 2
 ; 2 , A3;0;  
1 , điểm M thuộc cạnh DC . Giá trị nhỏ nhất của tổng các khoảng cách
AM MC là A. 17 . B. 17  4 6 . C. 17  8 3 . D. 17  6 2 . Hướng dẫn giải Chọn C. B' C' A'(3;0;-1) D' B(2;1;2) C M A(1;0;1) D(2;-2;2)   
Ta có AB  1;1 
;1 ; AA  2;0; 2 ; AD  1; 2   ;1 .
   
Theo quy tắc hình hộp ta có AB AD AA  AC  C5; 1  ;1 . 
Phương trình đường thẳng DC đi qua D 2; 2
 ; 2 và nhận AB  1;1  ;1 làm véc tơ chỉ x  2  t
phương là  y  2  t . z  2  t
Gọi M 2  t; 2
  t; 2  t   DC . Ta có 
AM  t 1;t  2;t   1 2
MA  3t  6 ,  C M
 t  3;t 1;t   1  MC  t  2 3 1  8 .  
Xét vectơ u   3t; 6 , v   3  3t;2 2  .     2 2
Do u v u v nên AM MC   3   6  8  AM MC  17  8 3 . 3t 6 t 3 Dấu "  " xảy ra khi     t  2 3  3 . 3 1 t  2 3 1 t 2
M 2 3 1;1 2 3;2 3   1 .
Vậy giá trị nhỏ nhất của tổng các khoảng cách AM MC là 17  8 3 .
Câu 70: [2H3-3.8-3] Trong không gian với hệ tọa độ Oxyz , cho các điểm M 2; 2;  3 và N  4  ; 2  ;1 . Gọi 
 là đường thẳng đi qua M , nhận vecto u  a; ;
b c làm vectơ chỉ phương và song song với mặt
phẳng  P : 2x y z  0 sao cho khoảng cách từ N đến  đạt giá trị nhỏ nhất. Biết a , b là hai
số nguyên tố cùng nhau. Khi đó a b c bằng: A. 15 . B. 13 . C. 16 . D. 14 . Lời giải Chọn A.
Gọi Q là mặt phẳng đi qua M 2; 2;  3 và song song với mặt phẳng  P .
Suy ra Q : 2x y z  3  0 .
Do  //  P nên   Q .
d N,  đạt giá trị nhỏ nhất   đi qua N , với N là hình chiếu của N lên Q .
x  4  2t
Gọi d là đường thẳng đi qua N và vuông góc  P , d :  y  2  t . z 1 t  4  4 10 7 
Ta có N   d N  4
  2t; 2  t;1 t  ; NQ  t   N   ; ;   . 3  3 3 3  
  10 4 16  u   ; a ;
b c cùng phương MN   ; ;   .  3 3 3  
Do a , b nguyên tố cùng nhau nên chọn u  5;2;8 .
Vậy a b c  15 . 45-47 CHANH MUỐI x  2 y 1 z  2
Câu 71: [2H3-3.8-3] Trong không gian Oxyz, cho đường thẳng d :   và mặt phẳng 4 4 3
P : 2x y  2z 1  0. Đường thẳng  đi qua E 2; 1; 2 , song song với  P đồng thời tạo với 
d góc bé nhất. Biết rằng  có một véctơ chỉ phương u   ; m ; n  1 . Tính 2 2
T m n . A. T  5  . B. T  4 . C. T  3 . D. T  4  . Lời giải Chọn D. 
Mặt phẳng  P có vec tơ pháp tuyến n  2;1;2 và đường thẳng d có vec tơ chỉ phương
v  4; 4;3  
Vì  song song với mặt phẳng  P nên u n  2m n  2  0  n  2m  2 .   u v 4m  4n  3 4m  5 Mặt khác ta có  d   . cos ;      u . v
m n  1. 4   4  2 2 2 2 2  3  2
41 5m  8m  5 1 4m  52 2 1
16m  40m  25  .  . . 2 2 41 5m  8m  5 41 5m  8m  5
Vì    d   0 ;  90 nên   
; d bé nhất khi và chỉ khi    cos ; d lớn nhất 2
16t  40t  25 2 72t  90t
Xét hàm số f t  
f t   . 2 5t  8t  5
5t  8t  52 2 Bảng biến thiên
Dựa vào bảng biến thiên ta có max f t   f 0  5 suy ra   
; d bé nhất khi m  0  n  2 . Do đó 2 2
T m n  4 .
Làm theo cách này thì không cần đến dữ kiện : đường thẳng  đi qua E  2  ; 1;  2 .
Câu 72: [2H3-3.8-3] Họ parabol  P y mx m x m
m  0 luôn tiếp xúc với đường thẳng m  2 :   2  3   2
d cố định khi m thay đổi. Đường thẳng d đó đi qua điểm nào dưới đây? A. 0; 2  . B. 0; 2. C. 1;8. D. 1; 8  . Lời giải Chọn A.
Gọi H x ; y là điểm cố định mà  P luôn đi qua. m  0 0  Khi đó ta có: 2
y mx  2 m  3 x m  2  m  2
x  2x  1  6x y  2  0 , m   0 . 0 0  0 0   0 0 0 2 
x  2x  1  0 0 0   .
6x y  2  0  0 0 Do 2
x  2x  1  0 có nghiệm kép nên  P luôn tiếp xúc với đường thẳng d : y  6x  2 . m  0 0 Ta thấy 0; 2    d .
Câu 73: [2H3-3.8-3] Trong không gian với hệ toạ độ Oxyz , cho hai điểm A2; 3
 ; 2 , B 3;5; 4 . Tìm toạ độ
điểm M trên trục Oz so cho 2 2
MA MB đạt giá trị nhỏ nhất. A. M 0;0; 49 . B. M 0;0;67 . C. M 0;0;3 . D. M 0;0;0 . Lời giải Chọn C.  5 
Gọi I là trung điểm của AB I ;1;3   .  2        2 2 2 2 Ta có: 2 2
MA MB MA MB  MI IA  MI IB 2 2 2
 2MI IA IB . 2 2
IA IB không đổi nên 2 2
MA MB đạt giá trị nhỏ nhất khi MI đạt giá trị nhỏ nhất.
M là hình chiếu của I trên trục Oz .  M 0;0;3 . x 1 y z 1
Câu 74: [2H3-3.8-4] Trong không gian với hệ tọa độ Oxyz , cho đường thẳng  :   và hai 2 3 1 
điểm A1; 2;   1 , B 3; 1  ; 5
  . Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng  sao cho
khoảng cách từ điểm B đến đường thẳng d là lớn nhất. Phương trình đường thẳng d là: x  3 y z  5 x y  2 z A.   . B.   . 2 2 1  1 3 4 x  2 y z 1 x 1 y  2 z 1 C.   . D.   . 3 1 1 1 6 5 Lời giải Chọn D.
Gọi I    d . Khi đó I  1   2t;3t; 1   t  .    
Ta có: AB  2; 3; 4 ; AI  2t  2;3t  2; t    AI; AB  8 15t;6t  8;10 12t  .      AI , AB 2  
405t  576t  228 Suy ra: d  ; B d     . 2 AI
14t  20t  8 2 2
405t  576t  228
3 135t 192t  76
Xét hàm số f t    . 2 2
14t  20t  8 2 7t 10t  4 t  2 2
3 6t 16t  8
f t   .
. Cho f t  0     2 .
2 7t 10t  42 2 t   3 Bảng biến thiên: 2 t  2  3 f t   0  0  405 29
f t 405 14 27 14 2 Do đó d  ;
B d  nhỏ nhất khi f t  đạt giá trị nhỏ nhất bằng 27 tại t  . 3   1 5  Suy ra AI  ; 2;    .  3 3   
Chọn một vectơ chỉ phương của đường thẳng d là u  3AI  1;6; 5 . x 1 y  2 z 1
Vậy phương trình đường thẳng d :   . 1 6 5
Câu 75: [2H3-3.8-4] Trong không gian Oxyz , cho 2 điểm A3; 2
 ;3 , B 1;0;5 và đường thẳng x 1 y  2 z  3 d :  
. Tìm tọa độ điểm M trên đường thẳng d để 2 2
MA MB đạt giá trị nhỏ 1 2 2 nhất.
A. M 1; 2;3 . B. M 2;0;5 . C. M 3; 2;7 . D. M 3;0; 4 . Lời giải Chọn B.
Gọi I là trung điểm của AB , ta có I  2; 1  ; 4 .       2 2 2 2 Khi đó: 2 2
MA MB MA MB  MI IA  MI IB   
   2 2 2
 2MI IA IB  2MI.IA IB 2 2 2
 2MI IA IB 2  MI  6 . Do đó 2 2
MA MB đạt giá trị nhỏ nhất khi và chỉ khi MI có độ dài ngắn nhất, điều này xảy ra khi và
chỉ khi M là hình chiếu vuông góc của I trên đường thẳng d .
Phương trình mặt phẳng  P đi qua I và vuông góc với đường thẳng d là
1. x  2  2. y  
1  2. y  4  0 hay  P : x  2 y  2z 12  0 . x  1 t
Phương trình tham số của đường thẳng d là  y  2  2t .
z  3  2t
Tọa độ điểm M cần tìm là nghiệm  ;
x y; z  của hệ phương trình: x  1 tx  2  
y  2  2ty  0   
. Vậy M 2;0;5 . z  3  2tz  5 
x  2 y  2z 12  0  t   1 
Câu 76: [2H3-3.8-4] Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng  P : x y z 1  0 , đường x 15 y  22 z  37 thẳng d :  
và mặt cầu S  2 2 2
: x y z  8x  6 y  4z  4  0 . Một đường 1 2 2
thẳng  thay đổi cắt mặt cầu  S  tại hai điểm A , B sao cho AB  8 . Gọi A , B là hai điểm lần
lượt thuộc mặt phẳng  P sao cho AA , BB cùng song song với d . Giá trị lớn nhất của biểu thức
AA  BB là 8  30 3 24 18 3 12  9 3 16  60 3 A. . B. . C. . D. . 9 5 5 9 Lời giải Chọn B.
Mặt cầu  S  có tâm I 4;3; 2
  và bán kính R  5 .
Gọi H là trung điểm của AB thì IH AB và IH  3 nên H thuộc mặt cầu  S tâm I
bán kính R  3 .
Gọi M là trung điểm của AB thì AA  BB  2HM , M nằm trên mặt phẳng  P . Mặt khác ta có
d I P 4 ;   R nên
P cắt mặt cầu S  và 3 d P 5 sin ;  sin  
. Gọi K là hình chiếu của H lên  P thì HK HM.sin . 3 3
Vậy để AA  BB lớn nhất thì HK lớn nhất 4 4  3 3
HK đi qua I nên HK
R  d I; P  3   . max    3 3  4  3 3  3 3 24 18 3
Vậy AA  BB lớn nhất bằng 2  .  .  3  5 5  
Câu 77: [2H3-3.8-4] Trong không gian Oxyz , cho ba điểm A 1  ; 0  ;1 , B 3; 2; 
1 , C 5;3;7 . Gọi M  ; a ; b c
là điểm thỏa mãn MA MB và MB MC đạt giá trị nhỏ nhất. Tính P a b c A. P  4 . B. P  0 . C. P  2 . D. P  5 . Lời giải 
Gọi I là trung điểm của AB , suy ra I 1;1; 
1 ; AB  4; 2;0 .
Phương trình mặt phẳng trung trực của AB :   : 2x y  3  0 .
Vì 2.3 1.2  3.2.5 1.3  3  50  0 nên B , C nằm về một phía so với   , suy ra A , C nằm
về hai phía so với   .
Điểm M thỏa mãn MA MB khi M    . Khi đó MB MC MA MC AC .
MB MC nhỏ nhất bằng AC khi M AC    . x  1   2t
Phương trình đường thẳng AC :  y t
, do đó tọa độ điểm M là nghiệm của hệ phương trình z 1 2t
x  1 2t t   1    y tx  1   
. Do đó M 1;1;3 , a b c  5 . z  1 2ty  1 
2x y  3  0  z  3 
Câu 78: [2H3-3.8-4] Trong không gian Oxyz , cho ba điểm A 1  ; 0  ;1 , B 3; 2; 
1 , C 5;3;7 . Gọi M  ; a ; b c
là điểm thỏa mãn MA MB và MB MC đạt giá trị nhỏ nhất. Tính P a b c A. P  4 . B. P  0 . C. P  2 . D. P  5 . Lời giải 
Gọi I là trung điểm của AB , suy ra I 1;1; 
1 ; AB  4; 2;0 .
Phương trình mặt phẳng trung trực của AB :   : 2x y  3  0 .
Vì 2.3 1.2  3.2.5 1.3  3  50  0 nên B , C nằm về một phía so với   , suy ra A , C nằm
về hai phía so với   .
Điểm M thỏa mãn MA MB khi M    . Khi đó MB MC MA MC AC .
MB MC nhỏ nhất bằng AC khi M AC    . x  1   2t
Phương trình đường thẳng AC :  y t
, do đó tọa độ điểm M là nghiệm của hệ phương trình z 1 2t
x  1 2t t   1    y tx  1   
. Do đó M 1;1;3 , a b c  5 . z  1 2ty  1 
2x y  3  0  z  3  Câu 79: [2H3-3.8-4] Trong không gian với hệ trục tọa độ Oxyz cho mặt cầu S  2 2 2
: x y z  2x  4 y  4z  0 và điểm M 1; 2;  
1 . Một đường thẳng thay đổi qua M và cắt
S  tại hai điểm A , B . Tìm giá trị lớn nhất của tổng MA MB . A. 8 . B. 10 . C. 2 17 . D. 8  2 5 . Lời giải Chọn C.
Mặt cầu S  có tâm I 1; 2; 2 , bán kính R  3 .
Vì IM  17  3 nên M nằm ngoài đường tròn,
Gọi  là góc tạo bởi MB và MI . Áp dụng định lí Côsin cho tam giác MIA và MIB ta có 2 2 2
R MA MI  2 . MA MI.c os   1 2 2 2
R MB MI  2M . B MI.c os 2 Lấy  
1 trừ cho 2 vế theo vế ta được 2 2
0  MA MB  2 17.MA MB.cos  MA MB  2 17 cos
Do đó MA MB lớn nhất bằng 2 17 khi cos  1    0 .
Câu 80: [2H3-3.8-4] Trong không gian Oxyz , cho hai điểm A1; 2; 4 , B 0;0  ;1 và mặt cầu
S   x  2   y  2 2 : 1
1  z  4. Mặt phẳng  P : ax by cz  3  0 đi qua A , B và cắt mặt cầu S
theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tính T a b c . 3 33 27 31 A. T   . B. T  . C. T  . D. T  . 4 5 4 5 Lời giải Chọn A.
Mặt cầu S  có tâm I  1
 ;1; 0 và bán kính R  2 .  x t
Đường thẳng AB đi qua điểm B , có một VTCP là BA  1; 2;3  AB :  y  2tt   z 1 3t   IB  1; 1 
;1  IB  3  R   P luôn cắt mặt cầu S  theo giao tuyến là đường tròn C
C  có bán kính nhỏ nhất  d I,P lớn nhất.
Gọi H , K lần lượt là hình chiếu vuông góc của I lên  P và AB , ta có:
d I, P  IH IK
Do đó d I, P lớn nhất  H K hay mặt phẳng  P vuông góc với IK 
Tìm K : K AB K t; 2t;1 3t   IK  t 1; 2t 1;3t   1   1   6 9 4  1
Ta có IK AB IK.AB  0  t    IK ;  ;    6;9;4 7  7 7 7  7 
Mặt phẳng  P đi qua B 0;0 
;1 , có một VTPT là n  6; 9; 4 9 27 3
  P : 6x  9 y  4z  4  0   x
y  3z  3  0 . Vậy T   . 2 4 4
Câu 81: [2H3-3.8-4] Trong không gian Oxyz , cho ba điểm A1;  2;  1 , B 5; 0;  
1 , C 3;1; 2 và mặt phẳng
Q :3x y z  3  0 . Gọi M  ; a ;
b c là điểm thuộc Q thỏa mãn 2 2 2
MA MB  2MC nhỏ nhất.
Tính tổng a b  5c . A. 11. B. 9 . C. 15 . D. 14 . Lời giải Chọn B.    
Gọi E là điểm thỏa mãn EA EB  2EC  0  E 3;0  ;1 .    2 2 2 Ta có: 2 2 2
S MA MB  2MC MA MB  2MC      
 ME EA2  ME EB2  ME EC2 2 2 2 2 2
 4ME EA EB  2EC . Vì 2 2 2
EA EB  2EC không đổi nên S nhỏ nhất khi và chỉ khi ME nhỏ nhất.
M là hình chiếu vuông góc của E lên Q .
x  3  3t
Phương trình đường thẳng ME :  y t . z  1 t
x  3  3tx  0    y ty  1
Tọa độ điểm M là nghiệm của hệ phương trình:    . z  1 tz  2  3
x y z  3  0  t   1   M 0; 1
 ; 2  a  0 , b  1
 , c  2  a b  5c  0 1 5.2  9 .
Câu 82: [2H3-3.8-4] Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng  P : x y  4z  0 , đường thẳng x 1 y 1 z  3 d :  
và điểm A1; 3; 
1 thuộc mặt phẳng  P . Gọi  là đường thẳng đi qua A , 2 1 1 
nằm trong mặt phẳng  P và cách đường thẳng d một khoảng cách lớn nhất. Gọi u   ; a ; b  1 là
một véc tơ chỉ phương của đường thẳng  . Tính a  2b .
A. a  2b  3 .
B. a  2b  0 .
C. a  2b  4 . D. a  2b  7 . Lời giải Chọn A. d A d I H A K (P) (Q) 
Đường thẳng d đi qua M 1; 1; 3 và có véc tơ chỉ phương u  2; 1; 1 . 1  
Nhận xét rằng, A d và d   P  I 7; 3;   1 .
Gọi Q là mặt phẳng chứa d và song song với  . Khi đó d , d   d ,Q  d  , A Q .
Gọi H , K lần lượt là hình chiếu vuông góc của A lên Q và d . Ta có AH AK .
Do đó, d , d  lớn nhất  d  ,
A Q lớn nhất  AH
H K . Suy ra AH chính là đoạn max
vuông góc chung của d và .    
Mặt phẳng  R chứa A và d có véc tơ pháp tuyến là n
  AM , u    2  ; 4; 8 . R 1  
Mặt phẳng Q chứa d và vuông góc với  R nên có véc tơ pháp tuyến là    n
 n ,u   12; 18;  6 . Q  R 1  
Đường thẳng  chứa trong mặt phẳng  P và song song với mặt phẳng Q nên có véc tơ chỉ   
phương là u  n , n
  66;  42; 6  611;  7;  1 .  P R  
Suy ra, a  11; b  7
 . Vậy a  2b  3 .
Câu 83: [2H3-3.8-4] Trong không gian với hệ tọa độ Oxyz , cho hai điểm A3;0; 
1 , B 1;1;3 và mặt
phẳng  P : x  2 y  2z  5  0 . Viết phương trình chính tắc của đường thẳng d đi qua A , song song
với mặt phẳng  P sao cho khoảng cách từ B đến d nhỏ nhất. x  3 y z  1 x  3 y z  1 A. d :   . B. d :   . 26 11 2 26 11 2 x  3 y z  1 x  3 y z 1 C. d :   . D. d :   . 26 11 2 26  11 2 Lời giải Chọn A.
Gọi mặt phẳng Q là mặt phẳng đi qua A và song song với mặt phẳng  P . Khi đó phương trình
của mặt phẳng Q là 
1 x  3  2 y  0  2 z  
1  0  x  2 y  2z  1  0 .
Gọi H là hình chiếu của điểm B lên mặt phẳng Q , khi đó đường thẳng BH đi qua B 1;1;3 và x  1  t   nhận n
 1; 2;2 làm vectơ chỉ phương có phương trình tham số là  y  1  2t . Q   
z  3  2t  Vì
H BH  Q  H BH H 1  t;1  2t;3  2t  và H  Q nên ta có 10  1 11 7   1  t   2 1
  2t   23  2t  1  0  t    H  ; ;   . 9  9 9 9 
  26 11 2  1  AH  ; ;    26;11; 2 .  9 9 9  9
Gọi K là hình chiếu của B lên đường thẳng d , khi đó Ta có d  ;
B d   BK BH nên khoảng cách từ B đến d nhỏ nhất khi BK BH , do đó đường 
thẳng d đi qua A và có vectơ chỉ phương u  26;11; 2 có phương trình chính tắc: x  3 y z  1 d :   . 26 11 2
Câu 84: [2H3-3.8-4] Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng  P : x y  4z  0 , đường thẳng x 1 y 1 z  3 d :  
và điểm A1; 3; 
1 thuộc mặt phẳng  P . Gọi  là đường thẳng đi qua A , 2 1  1 
nằm trong mặt phẳng  P và cách đường thẳng d một khoảng cách lớn nhất. Gọi u   ; a ; b  1 là
một véc tơ chỉ phương của đường thẳng  . Tính a  2b .
A. a  2b  3 .
B. a  2b  0 .
C. a  2b  4 . D. a  2b  7 . Lời giải Chọn A. d A d I H A K (P) (Q) 
Đường thẳng d đi qua M 1; 1; 3 và có véc tơ chỉ phương u  2; 1; 1 . 1  
Nhận xét rằng, A d và d   P  I  7  ; 3;   1 .
Gọi Q là mặt phẳng chứa d và song song với  . Khi đó d , d   d ,Q  d  , A Q .
Gọi H , K lần lượt là hình chiếu vuông góc của A lên Q và d . Ta có AH AK . Do đó, d  ,
d  lớn nhất  d  ,
A Q lớn nhất  AH
H K . Suy ra AH chính là đoạn max
vuông góc chung của d và .    
Mặt phẳng  R chứa A và d có véc tơ pháp tuyến là n
  AM ,u    2  ; 4; 8 . R 1  
Mặt phẳng Q chứa d và vuông góc với  R nên có véc tơ pháp tuyến là    n  n
, u   12; 18;  6 . Q R 1  
Đường thẳng  chứa trong mặt phẳng  P và song song với mặt phẳng Q nên có véc tơ chỉ   
phương là u  n , n
  66;  42; 6  611;  7;  1 . P R  
Suy ra, a  11; b  7 . Vậy a  2b  3 .
Câu 85: [2H3-3.8-4] Trong không gian Oxyz , cho ba điểm A1;  2;  1 , B 5; 0;  
1 , C 3;1; 2 và mặt
phẳng Q : 3x y z  3  0 . Gọi M  ; a ;
b c là điểm thuộc Q thỏa mãn 2 2 2
MA MB  2MC nhỏ
nhất. Tính tổng a b  5c . A. 11. B. 9 . C. 15 . D. 14 . Lời giải Chọn B.    
Gọi E là điểm thỏa mãn EA EB  2EC  0  E 3;0  ;1 .    2 2 2 Ta có: 2 2 2
S MA MB  2MC MA MB  2MC      
 ME EA2  ME EB2  ME EC2 2 2 2 2 2
 4ME EA EB  2EC . Vì 2 2 2
EA EB  2EC không đổi nên S nhỏ nhất khi và chỉ khi ME nhỏ nhất.
M là hình chiếu vuông góc của E lên Q .
x  3  3t
Phương trình đường thẳng ME :  y t . z 1 t
x  3  3tx  0    y ty  1
Tọa độ điểm M là nghiệm của hệ phương trình:    . z  1 tz  2  3
x y z  3  0  t   1 
M 0; 1; 2  a  0 , b  1  , c  2 .
a b  5c  0 1 5.2  9 . x  2 y 1 z
Câu 86: [2H3-3.8-4] Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và hai 1 2 3
điểm A2;0;3 , B 2; 2; 3 . Biết điểm M x ; y ; z thuộc d thỏa mãn 4 4
MA MB nhỏ nhất. 0 0 0  Tìm x . 0 A. x  1. B. x  3 . C. x  0 . D. x  2 . 0 0 0 0 Lời giải Chọn D.
Gọi I là trung điểm của AB . Khi đó ta có 2 2 2 2    
MA MB  MA MB 2 AB AB 4 4 2 2 2 2 2 2
 2MA .MB  2MI   2 MI      2 4     4 4 AB AB 4 2 2 4 2 2
 4MI  2MI AB
 2MI MI AB  4 8 2 4 2 AB  3AB  7 4 2 2 2 4
 2MI  3MI AB   2 MI   AB   4 4 10   Do đó, 4 4
MA MB đạt GTNN khi MI nhỏ nhất  M là hình chiếu vuông góc của I lên d . 
Điểm I 2; 1;0 . Lấy M 2  t; 1
  2t;3t   d . IM  t; 2t;3t     
IM u IM .u  0  t  4t  9t  0  t  0 d d
Suy ra M I . Vậy x  2 0