Bài tập thành phần 2 môn kinh tế vĩ mô | Trường Đại học Kinh tế Thành phố Hồ Chí Minh
Ta có: dY= dC + dG + dI ; dC = 0,9 (dY – dT); dT = 0,2 dY; dI = -100dr; dL = dM; dL = 3,2dY – 100dr; dL = dM = 10dH; dH – dH-1 = dG – dT; dG = 1000. Đường IS: Y = C (Y-T) + G + I (r). dY = dC + dG + dI. dY = 0,9 (dY – 0,2 dY) + 1000 - 100dr. 0,28dY = 1000 – 100dr. Trong ngắn hạn: dH-1 = 0 . dH= dG – dT = 1000 - 0,2 dY. Đường LM: = L (Y,r). M = L = 3,2dY – 100dr. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem !
Môn: Kinh tế vĩ mô ( UEH)
Trường: Đại học Kinh tế Thành phố Hồ Chí Minh
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
lOMoAR cPSD| 46831624
Họ và tên: Tran Thị Bích Diễm Lớp: K43_QLK _ĐN1
BÀI TẬP THÀNH PHaN 2
Môn: Kinh tế vĩ mô Bài 1:
Ta có: dY= dC + dG + dI ; dC = 0,9 (dY – dT); dT = 0,2 dY; dI = -100dr; dL = dM;
dL = 3,2dY – 100dr; dL = dM = 10dH; dH – dH-1 = dG – dT; dG = 1000
Đường IS: Y = C (Y-T) + G + I (r) dY = dC +
dG + dI dY = 0,9 (dY – 0,2 dY) + 1000 - 100dr 0,28dY = 1000 – 100dr
Trong ngắn hạn: dH-1 = 0
dH= dG – dT = 1000 - 0,2 dY Đường LM: = L (Y,r) M = L = 3,2dY – 100dr 10dH = 3,2dY – 100dr
10(1000 - 0,2 dY) = 3,2dY – 100dr 5,2dY = 10000 +100dr Giải phương trình sau: 0,28 dY = 1000 - 100dr 5,2dY = 10000 +100dr Ta ược: dY = 2007,3
Vậy, trong ngắn hạn, sản lượng thay ổi 2007,3 tỷ ồng.
Trong dài hạn: dH – dH-1 = dG – dT = 0 lOMoAR cPSD| 46831624 1000 - 0,2 dY = 0 dY= 5000
Vậy, trong dài hạn, sản lượng thay ổi 5000 tỷ ồng. Bài 2:
Từ ề bài, ta có: dY = dC + dI + dG; dC = 0,8 (dY- dT); dI = -1000dr; dL = dM = 0;
= 0,1dY – 500dr; dT = -1000; dG = 0 Đường IS:
Y = C (Y-T) + G + I (r) dY = dC + dI + dG dY = 0,8 (dY+1000) -1000dr dY = 4000 – 5000dr Đường LM: = L (Y,r) = dL = 0 0,1dY – 500dr = 0 dY = 5000dr Giải phương trình sau: dY = 4000 – 5000dr dY = 5000dr Ta ược: dY = 2000
Như vậy, nếu Chính phủ giảm thuế 1.000 tỷ ồng thì sản lượng của nền kinh
tế sẽ tăng 2000 tỷ ồng. Bài 3:
Ta có: dY= dC + dI + dG + dEx - dIm
dY = 0,8 (dY – 0,2dY) + dI - 0,14dY lOMoAR cPSD| 46831624 0,5dY = dI Số nhân ầu tư k = = 2 Bài 4:
Từ ề bài, suy ra: dY = dC + dI + dG + dB; dC = 0,9dY, dI = -50dY; dB= -
0,1dY; dM = 0,8dY – 300dr; dM = 1000; dG = dT = 0
Ta thấy hàm ầu tư I không phụ thuộc vào lãi suất, do ó dr = 0 dM = 0,8dY – 300dr = 1000 dY = 1250
Như vậy, khi tăng lượng cung tiền thêm 1000 tỷ ồng, sản lượng tăng 1250 tỷ ồng. Bài 5:
Từ ề bài ta có: dY = dC + dI + dG + dB; dC= 0,9 (dY – dT); dI = -100dY, dB = -
0,05dY; dM = 0,05dY – 50dr, dM=dL = 0; dH = 0; dG = dT = 1000 Đường IS: dY =
dC + dI + dG + dB dY= 0,9 (dY – 1000) -100dY + 1000 - 0,05dY 100,15dY = 100 dY = = 0,999
Như vậy, khi Chính phủ tăng chỉ tiêu 1000 tỷ ồng ể bù ắp chi tiêu, sản lượng sẽ tăng 0,999 tỷ ồng.
BÀI TẬP MÔ HÌNH IS-LM Bài 1:
Cho nền kinh tế vĩ mô như sau: Y = C + G + I
Y : Sản lượng/ Thu nhập
C = 500 + 0,8(Y –T) C: Tiêu dùng của hộ gia ình
I = 7.000 - 500 r I : Đầu tư L = M
G: Tiêu dùng của Chính phủ lOMoAR cPSD| 46831624 L = Y - 500r T : Thuế M = 10H r : Lãi suất M : Lượng cung tiền
L : Lượng cầu về tiền H : Lượng tiền cơ sở
Trong mô hình này, Tiêu dùng của chính phủ (G), Thuế (T), Lượng tiền cơ
sở (H) và Lượng cung tiền (M) là các biến ngoại sinh. Tại iểm cân bằng ban ầu
của nền kinh tế, giá trị các biến ngoại sinh ược cho trước như sau: G = 1.000 T = 1.000 H = 430 M = 4.300 Yêu c¿u:
a. Tính toán sản lượng (Y), Lãi suất (r), Tiêu dùng của hộ gia ình (C), Đầu
tư (I) tại iểm cân bằng ban ầu của nền kinh tế.
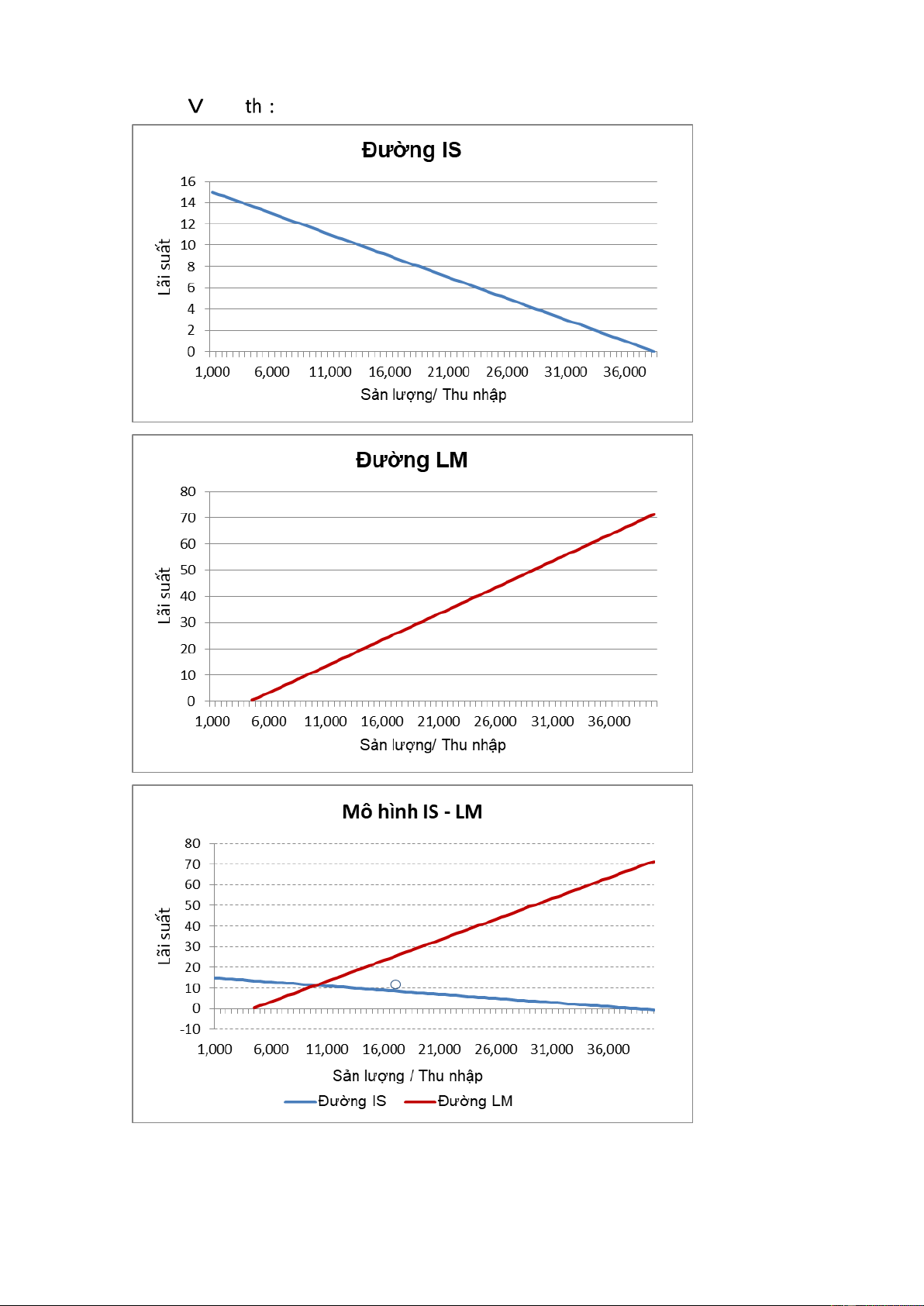
b. Sử dụng phần mềm Excel vẽ ồ thị ường IS, ường LM và Mô hình IS – LM.
c. So sánh kết quả tính toán ở Câu a với các giá trị ược biểu diễn trên ồ thị ở Câu b. Bài làm: Đường IS :
Y = 500 + 0,8(Y –T) + G + 7.000 - 500 r
Y = 500 + 0.8Y - 800 + 1.000 + 7.000 – 500r Y = 38.500 - 2.500r Đường LM : M = Y - 500r Y = M + 500r Y = 4.300 + 500r
Giải hệ phương trình biểu diễn ường IS và LM sau: Y = 38.500 - 2.500r Y = 4.300 + 500r Ta ược: lOMoAR cPSD| 46831624
Lãi xuất cân bằng r = 11,4 Y = 10.000
Từ ó xác ịnh ược C = 500 + 0,8 (10.000 – 1.000) = 7.700 I = 7.000 - 500*11,4 = 1.300 lOMoAR cPSD| 46831624 ẽ ồ ị
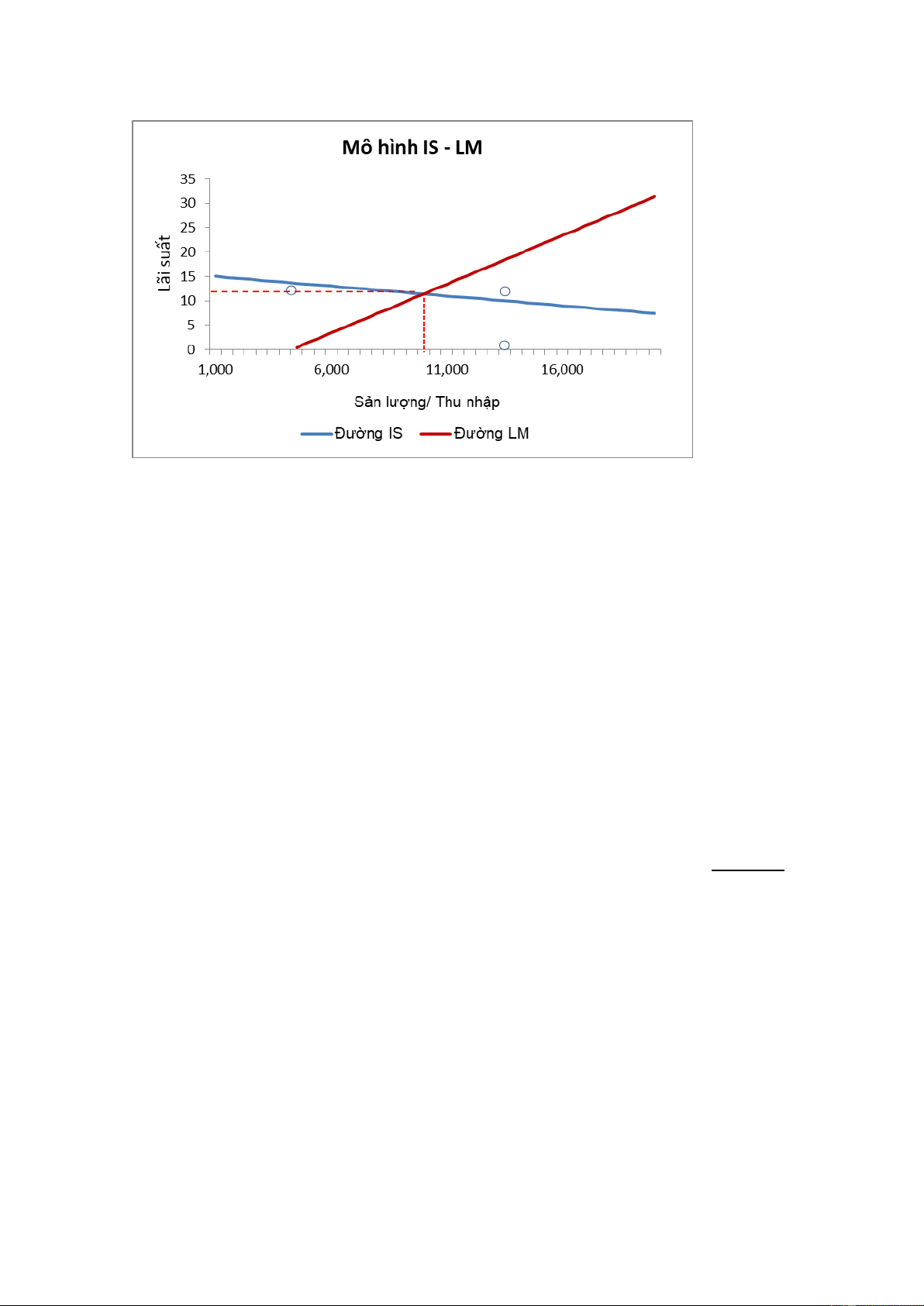
c. Để dễ So sánh kết quả tính toán ở Câu a với các giá trị ược biểu diễn
trên ồ thị ở Câu b, ta phóng to ồ thị mô hình IS – LM như sau: lOMoAR cPSD| 46831624
Quan sát ồ thị, ta thấy giao iểm của hai ường IS và LM chính là sản lượng
cân bằng (Y* = 10.000) và lãi suất cân bằng (r* = 11,4). Bài 2:
Cho nền kinh tế vĩ mô như ược trình bày ở Bài 1.
Khi chính phủ sử dụng 3 biện pháp dưới ây ể tăng chi tiêu của chính phủ
thêm 200 tỷ ồng thì sản lượng của nền kinh tế sẽ bị tác ộng như thế nào. a. Tăng thuế b.
Phát hành trái phiếu chính phủ bán cho người dân c.
Phát hành trái phiếu chính phủ bán cho NHTW Bài làm:
a. Tăng thuế 200 tỷ ể bù ắp chi tiêu của Chính phủ Ta có: dT = dG = 200
dY = dC + dG + dI dC = 0,8(dY – dT) dI = -
500 dr; dL = dM ; dL = dY – 500dr; dM = 10dH dH = 0, dL = dM = 0 Đường IS : Y = C + G + I dY = dC + dG + dI lOMoAR cPSD| 46831624 dY = 0,8(dY – 200) + 200 - 500dr dY = 200 – 2500dr Đường LM : M = L = Y - 500r dM = dY – 500dr = 0
Giải hệ phương trình sau: dY = 200 - 2.500dr dY= 500dr Ta ược: dr = = 0,067 dY = = 33,333
Như vậy, khi Chính phủ tăng thuế 200 tỷ ể bù ắp chi tiêu của Chính phủ, sản lượng sẽ tăng tỷ ồng.
b. Phát hành trái phiếu chính phủ bán cho người dân ể bù ắp cho tăng chi tiêu Chính phủ Ta có:
dY = dC + dG + dI ; dC = 0,8(dY – dT); dI = - 500 dr; dL = dM dL =
dY – 500dr; dM = 10dH ; dH = 0, dL = dM = 0 dG = 200, dT= 0 Đường IS : Y = C + G + I dY = dC + dG + dI
dY = 0,8(dY – 0) + 200 - 500dr dY = 1000 – 2500dr Đường LM : M = L = Y - 500r dM = dY – 500dr = 0 dY= 500dr
Giải hệ phương trình sau: dY = 1.000 - 2.500dr dY= 500dr Ta ược: dr = = 0,333 dY = = 166,667 lOMoAR cPSD| 46831624
Như vậy, khi Chính phủ phát hành trái phiếu bán cho người dân ể bù ắp chi
tiêu của Chính phủ, sản lượng sẽ tăng tỷ ồng.
c. Phát hành trái phiếu chính phủ bán cho NHTW Ta có: dY = dC + dG + dI dC = 0,8(dY – dT) dI = - 500 dr dL = dY – 500dr dM = 10dH , dH =
200, dL = dM = 2000 dG = 200, dT = 0 Đường IS : Y = C + G + I dY = dC + dG + dI
dY = 0,8(dY – 0) + 200 - 500dr dY = 1000 – 2500dr Đường LM : M = L = Y - 500r dM = dY – 500dr = 2000 dY= 2000 + 500dr
Giải hệ phương trình sau: dY = 1.000 - 2.500dr
dY= 2000 + 500dr Ta ược: dr = = -0,333 dY = = 1833,333
Như vậy, khi Chính phủ phát hành trái phiếu bán cho ngân hàng Trung ương
ể bù ắp chi tiêu của Chính phủ, sản lượng sẽ tăng 1833,333 tỷ ồng.