57 trang 34 lượt tải

Bài tập thể tích khối chóp có một cạnh bên vuông góc với đáy Toán 12

67

Giới thiệu đề bài và lời giải chi tiết 97 bài tập thể tích khối chóp có một cạnh bên vuông góc với đáy, với nhiều biến dạng và độ khó khác nhau, đây là các dạng bài thường gặp trong chương trình Hình học 12 và trong các đề thi THPT Quốc gia môn Toán.Mời bạn đọc đón xem.

Chủ đề: Chương 1: Khối đa diện 172 tài liệu

Môn: Toán 12 3.9 K tài liệu

Tác giả:

Profile

Lan Tường

1 năm trước
Danh sách Quiz
/57
https://toanmath.com/
THỂ TÍCH KHỐI CHÓP CÓ MỘT CẠNH BÊN VUÔNG GÓC VỚI ĐÁY
A. BÀI TẬP
Câu 1: Cho khối chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Biết
SA
vuông góc với
( )
ABCD
và
3SA a=
. Thể tích của khối chóp
.S ABCD
là:
A.
3
4
a
. B.
3
3a
. C.
3
3
6
a
. D.
3
3
3
a
.
Câu 2: Cho hình chóp tứ giác
.
S ABCD
có đáy là hình vuông cạnh
a
,
vuông góc với mặt phẳng đáy
và
2=SA a
. Thể tích khối chóp
.
S ABCD
bằng
A.
3
4
3
a
. B.
3
2a
. C.
. D.
3
2
3
a
.
Câu 3: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật
,2
AB a BC a= =
, cạnh bên
vuông
góc với đáy và
2SA a=
. Tính thể tích khối chóp
.S ABCD
.
A.
3
23
3
a
. B.
3
2a
. C.
3
22a
. D.
3
22
3
a
.
Câu 4: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Cạnh bên
vuông góc với đáy
và có độ dài bằng
2a
. Thể tích khối tứ diện
.S BCD
là:
A.
3
4
a
. B.
. C.
. D.
3
3
a
.
Câu 5: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông tâm
O
cạnh
2a
. Biết
vuông góc với
mặt phẳng đáy và
2.SA a=
Tính thể tích khối chóp
.S ABO
.
A.
3
2
3
a
. B.
3
22
12
a
. C.
3
2
12
a
. D.
3
42
3
a
.
Câu 6: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
2a
. Biết
6SA a=
và
vuông
góc với mặt phẳng đáy. Tính thể tích khối chóp
.S ABCD
.
A.
3
8a
. B.
3
63a
. C.
3
12 3a
. D.
3
24a
.
Câu 7: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông tâm
O
cạnh
2
a
. Biết
vuông góc với
mặt phẳng đáy và
2.SA a=
Tính thể tích khối chóp
.S ABO
.
A.
3
42
3
a
. B.
3
22
12
a
. C.
3
2
12
a
. D.
3
2
3
a
.
Câu 8: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật với
,2
AB a AD a= =
,
( )
SA ABCD⊥
và
3SA a=
. Thể tính khối chóp
.S ABC
bằng:
A.
3
3a
. B.
3
23a
. C.
3
23
3
a
. D.
3
3
3
a
.
Câu 9: Cho hình chóp tam giác
.S ABC
với
,
SB
,
SC
đôi một vuông góc và
SA SB SC a= = =
. Tính
thế tích của khối chóp
.S ABC
.
A.
3
1
2
a
. B.
3
1
6
a
. C.
3
2
3
a
. D.
3
1
3
a
.
Câu 10: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Cạnh
SA
vuông góc với mặt phẳng
đáy và có độ dài là
a
. Thể tích khối tứ diện
.S BCD
bằng.
A.
3
6
a
. B.
. C.
. D.
3
4
a
.
https://toanmath.com/
Câu 11: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật với
,2AB a AD a= =
,
SA
vuông góc với mặt
đáy và
3SA a=
. Thể tính khối chóp
.S ABCD
bằng
A.
3
2 3.a
B.
3
3
.
3
a
C.
3
3.a
D.
3
23
.
3
a
Câu 12: Cho tứ diện
OABC
có
OA
,
OB
,
OC
đôi một vuông góc với nhau tại
O
và
2OA =
,
4OB =
,
6OC =
. Thể tích khối tứ diện đã cho bằng.
A.
24
. B.
16
. C.
8
. D.
48
.
Câu 13: Cho khối chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
SA
vuông góc với mặt phẳng đáy và
2SA a=
. Tính thể tích khối chóp
.S ABC
.
A.
3
3
.
6
a
B.
3
3
.
2
a
C.
3
3
.
3
a
D.
3
3
.
12
a
Câu 14: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
2a
,
vuông góc với mặt phẳng đáy,
3SA a=
. Tính thể tích khối chóp
.S ABC
.
A.
2
.
S ABC
Va
=
(đvtt). B.
3
.S ABC
Va=
(đvtt).
C.
3
.
2
S ABC
a
V =
(đvtt). D.
3
.
3
S ABC
Va=
(đvtt).
Câu 15: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
B
,
AB a=
,
2BC a=
,
( )
SA ABC⊥
,
3SA a=
. Thể tích của khối chóp
.S ABC
bằng
A.
3
1
6
a
. B.
3
a
. C.
3
1
3
a
. D.
3
3a
.
Câu 16: Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
vuông góc
với mặt phẳng đáy và
2SA a=
. Tính thể tích
V
của khối chóp
.S ABCD
.
A.
3
2Va=
. B.
3
2
4
a
V =
. C.
3
2
6
a
V
=
. D.
3
2
3
a
V =
.
Câu 17: Cho hình chóp tứ giác
. S ABCD
có đáy là hình vuông cạnh
( )
8 cm
, chiều cao
SH
bằng
( )
3 cm
.
Tính thể tích khối chóp?
A.
( )
3
1 6
V cm=
. B.
( )
3
24V cm=
. C.
( )
3
48V cm=
.
D.
( )
3
64V cm=
.
Câu 18: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Biết
( )
SA ABCD⊥
và
3SA a=
.
Thể tích của khối chóp
.S ABCD
có giá trị là
A.
3
3
3
a
. B.
. C.
3
3
12
a
. D.
3
3
a
.
Câu 19: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
( )
SA ABC⊥
và
3SA a=
. Thể tích
khối chóp
.S ABC
là.
A.
3
3
6
a
. B.
. C.
3
3
4
a
. D.
3
3
8
a
.
Câu 20: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
AB a=
,
2BC a=
, đường thẳng
SA
vuông góc với mặt phẳng
( )
ABCD
và
3SA a=
. Thể tích của khối chóp
.S ABCD
bằng
A.
3
a
. B.
3
3a
. C.
3
6a
. D.
3
2a
.
Câu 21: Cho hình hình chóp
.S ABC
có cạnh
vuông góc với mặt đáy và
3SA a=
. Đáy
ABC
là tam
giác đều cạnh bằng
a
. Thể tích của khối chóp
.S ABC
bằng.
A.
3
12
a
V =
. B.
3
4
a
V
=
. C.
3
3Va=
. D.
3
3
12
a
V =
.
Câu 22: Đáy của hình chóp
.S ABCD
là một hình vuông cạnh
a
. Cạnh bên
SA
vuông góc với mặt phẳng
đáy và có độ dài là
a
. Thể tích khối tứ diện
.S BCD
bằng:
https://toanmath.com/
A.
3
4
a
. B.
3
3
a
. C.
3
6
a
. D.
3
8
a
.
Câu 23: Hình chóp
.S ABC
có
SA a=
,
SB b=
,
SC c=
đôi một vuông góc với nhau. Thể tích khối chóp
là.
A.
2
9
abc
. B.
6
abc
. C.
3
abc
. D.
9
abc
.
Câu 24: Cho tứ diện
ABCD
có
AD
vuông góc với mặt phẳng
( )
ABC
. Biết đáy
ABC
là tam giác vuông
tại
B
và
5,
AD =
5,
AB =
12BC =
. Tính thể tích
V
của tứ diện
ABCD
.
A.
50
V =
. B.
120V =
. C.
150V =
. D.
325
16
V =
.
Câu 25: Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
( )
SA ABCD⊥
và
6SA a=
. Thể tích của khối chóp
.S ABCD
bằng
A.
3
6
3
a
. B.
3
6
2
a
. C.
3
6
6
a
. D.
3
6a
.
Câu 26: Cho hình chóp
.
S ABCD
có
ABCD
là hình vuông cạnh
a
,
( )
SA ABCD⊥
và
3aSA =
. Thể tích
khối chóp
.
S ABCD
là.
A.
3
2a
. B.
3
a
. C.
. D.
3
2
a
.
Câu 27: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Biết
( ); 3.
SA ABCD SA a⊥=
Tính thể tích của khối chóp.
A.
3
3
3
a
. B.
3
3
12
a
. C.
. D.
3
3a
.
Câu 28: Cho hình chóp
.
S ABCD
có đáy hình vuông cạnh
a
;
SA
vuông góc mặt đáy; Góc giữa
SC
và mặt
đáy của hình chóp bằng
0
60
. Thể tích khối chóp
.S ABCD
là
A.
3
2
3
a
B.
3
3
a
C.
3
6
3
a
D.
3
3
3
a
Câu 29: Cho hình chóp
.S ABCD
đáy
ABCD
là hình vuông có cạnh
a
và
SA
vuông góc đáy
ABCD
và
mặt bên
( )
SCD
hợp với đáy một góc
60
°
. Tính thể tích hình chóp
.S ABCD
.
A.
3
3
3
a
. B.
3
3
6
a
. C.
3
3a
. D.
3
23
3
a
.
Câu 30: Cho hình chóp
.S ABCD
có
SA
vuông góc với mặt phẳng
( )
,ABCD
đáy
ABCD
là hình thang
vuông tại
A
và
B
có
, 3 , .AB a AD a BC a= = =
Biết
3,SA a=
tính thể tích khối chóp
.S BCD
theo
.a
A.
3
3
.
6
a
B.
3
23
.
3
a
C.
3
3
.
4
a
D.
3
23 .a
Câu 31: Cho hình chóp
.S ABC
có
vuông góc với đáy. Tam giác
ABC
vuông cân tại
B
, biết
2SA AC a= =
. Tính thể tích khối chóp
.S ABC
.
A.
3
2
3
a
. B.
3
1
3
a
. C.
3
22
3
a
. D.
3
4
3
a
.
Câu 32: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
.
SA
vuông góc với đáy và tạo với
đường thẳng
SB
một góc
45°
. Tính thể tích khối chóp
.S ABC
.
A.
3
3
12
a
. B.
3
3
4
a
. C.
3
3
24
a
. D.
3
3
6
a
.
https://toanmath.com/
Câu 33: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, hai mặt phẳng
( )
SAB
và
( )
SAD
cùng vuông góc với mặt phẳng
( )
ABCD
; góc giữa đường thẳng
SC
và mặt phẳng
( )
ABCD
bằng
60°
. Tính theo
a
thể tích khối chóp
.S ABCD
.
A.
3
6
9
a
. B.
3
6
3
a
. C.
3
32
a
. D.
3
3
a
.
Câu 34: Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, đường cao của một mặt bên là
3a
. Tính
thể tích
V
khối chóp đó.
A.
3
2
9
a
V =
. B.
3
2Va=
. C.
3
2
6
a
V =
.
D.
3
2
3
a
V =
.
Câu 35: Hình chóp
.
S ABC
có đáy là tam giác
ABC
vuông cân tại
,
B
2
;
2
a
AC =
SA
vuông góc với mặt
đáy. Góc giữa mặt bên
( )
SBC
và mặt đáy bằng
45 .°
Tính theo
a
thể tích khối chóp
.S ABC
.
A.
. B.
3
3
48
a
. C.
3
2
48
a
. D.
.
Câu 36: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh bằng
a
, cạnh bên
SB
vuông góc với mặt
phẳng
(
)
ABC
,
2=SB a
. Tính thể tích khối chóp
.S ABC
.
A.
3
3
2
a
. B.
. C.
3
3
6
a
. D.
3
3
4
a
.
Câu 37: Cho khối tứ diện
OABC
với
OA
,
OB
,
OC
vuông góc từng đôi một và
OA a=
,
2OB a
=
,
3OC a=
. Gọi
,MN
lần lượt là trung điểm của hai cạnh
,AC BC
. Thể tích của khối tứ diện
OCMN
tính
theo
a
bằng
A.
3
4
a
. B.
3
3
4
a
. C.
3
a
. D.
3
2
3
a
.
Câu 38: Cho hình chóp
.S ABC
có mặt phẳng
( )
SAC
vuông góc với mặt phẳng
( )
ABC
,
SAB
là tam giác
đều cạnh
3a
,
3BC a=
đường thẳng
SC
tạo với mặt phẳng
( )
ABC
góc
60°
. Thể tích của
khối chóp
.S ABC
bằng
A.
3
6
6
a
. B.
3
26a
. C.
3
3
3
a
. D.
3
6
2
a
.
Câu 39: Cho khối chóp
.S ABC
có
(
)
SA ABC
⊥
, tam giác
ABC
vuông tại
B
,
AB a=
,
3AC a=
. Tính
thể tích khối chóp
.S ABC
, biết rằng
5SB a=
.
A.
3
6
4
a
. B.
3
15
6
a
. C.
3
2
3
a
. D.
3
6
6
a
.
Câu 40: Cho hình chóp tứ giác
.S ABCD
, đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
vuông góc với
mặt đáy, góc giữa
SC
và
( )
ABCD
bằng
45°
. Thể tích khối chóp
.S ABCD
là
A.
3
2
6
a
. B.
3
2
4
a
. C.
3
2a
. D.
3
2
3
a
.
Câu 41: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
2a
,
( )
SA ABC⊥
. Góc giữa hai mặt phẳng
( )
SBC
và
( )
ABC
bằng
30°
. Thể tích khối chóp
.S ABC
là.
A.
3
3
8
a
. B.
3
3
6
a
. C.
3
3
12
a
. D.
3
3
3
a
.
https://toanmath.com/
Câu 42: Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
C
,
5AB a=
,
AC a=
. Cạnh bên
3SA a=
và vuông góc với mặt phẳng
( )
ABC
. Thể tích khối chóp
.S ABC
bằng:
A.
3
5
3
a
. B.
3
a
. C.
3
2a
. D.
3
3a
.
Câu 43: Cho khối chóp
.S ABC
có
( )
SA ABC⊥
, tam giác
ABC
vuông tại
B
,
AB a=
,
3AC a=
. Tính
thể tích khối chóp
.S ABC
biết rằng
5SB a
=
.
A.
3
2
3
a
. B.
3
6
4
a
. C.
3
6
6
a
. D.
3
15
6
a
.
Câu 44: Cho khối chóp tam giác
.S ABC
có
( )
SA ABC⊥
, tam giác
ABC
có độ dài
3
cạnh là
5AB a=
;
8BC a
=
;
7AC a
=
, góc giữa
SB
và
( )
ABC
là
45
°
. Tính thể tích khối chóp
.S ABC
.
A.
3
50
3
a
. B.
3
50 7
3
a
. C.
3
50 3a
. D.
3
50 3
3
a
.
Câu 45: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
D
,
AB AD a= =
,
3SA CD a= =
,
vuông góc với mặt phẳng
( )
ABCD
. Thể tích khối chóp
.
S ABCD
bằng.
A.
3
1
3
a
. B.
3
2a
. C.
3
6a
. D.
3
1
6
a
.
Câu 46: Cho hình chóp
.S ABC
có
( )
,SA ABC⊥
góc giữa
SB
và
( )
ABC
bằng
o
60
; tam giác
ABC
đều
cạnh
.a
Thể tích khối chóp
.S ABC
bằng
A.
3
a
. B.
3
3a
. C.
3
1
4
a
. D.
3
1
2
a
.
Câu 47: Cho tứ diện
ABCD
có các cạnh
,,BA BC BD
đôi một vuông góc với nhau:
3,BA a=
2BC BD a= =
. Gọi
M
và
N
lần lượt là trung điểm của
AB
và
AD
. Tính thể tích khối chóp
.C BDNM
.
A.
3
3
2
=
a
V
. B.
3
=
Va
. C.
3
2
3
=
a
V
. D.
3
8
=Va
.
Câu 48: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật, cạnh bên
SA
vuông góc với đáy
( )
ABCD
. Biết
AB a
=
,
2BC a=
và
3SC a
=
. Tính thể tích khối chóp
.S ABCD
.
A.
3
4
3
a
. B.
3
25
3
a
. C.
3
2a
. D.
3
a
.
Câu 49: Cho tứ diện
.S ABC
có
,SAB SCB
là các tam giác cân tại
S
và
,,SA SB SC
đôi một vuông góc với
nhau. Biết
2BA a=
, thể tích
V
của tứ diện
.S ABC
là.
A.
3
6
a
V
=
. B.
3
2
a
V =
. C.
3
22Va=
. D.
3
Va=
.
Câu 50: Cho khối chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
. Hai mặt bên
( )
SAB
và
(
)
SAC
cùng
vuông góc với đáy. Tính thể tích khối chóp biết
3SC a=
.
A.
3
6
12
a
.
B.
3
3
2
a
. C.
3
26
9
a
. D.
3
3
4
a
.
Câu 51: Cho hình chóp
.S ABCD
có
( )
SA ABCD⊥
,
ABCD
là hình chữ nhật,
SA a=
,
2AB a
=
,
4BC a=
. Gọi
M
,
N
lần lượt là trung điểm của
BC
,
CD
. Thể tích của khối chóp
.S MNC
là
A.
3
5
a
. B.
3
2
a
. C.
3
4
a
. D.
3
3
a
.
https://toanmath.com/
Câu 52: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật
AB a=
,
2BC a=
,
2SA a
=
,
vuông
góc với mặt phẳng
(
)
ABCD
. Tính thể tích khối chóp
.S ABCD
tính theo
a
.
A.
3
8
3
a
B.
3
4
3
a
C.
3
6
3
a
D.
3
4
a
Câu 53: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông, cạnh bên
2
SA a=
và
SA
vuông góc với
mặt phẳng đáy, tam giác
SBD
là tam giác đều. Thể tích của khối chóp
.S ABCD
bằng
A.
3
2.
a
B.
3
2 2.a
C.
3
2
.
3
a
D.
3
22
3
a
.
Câu 54: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh bằng 1. Cạnh bên
vuông góc với
mặt phẳng
( )
ABCD
và
5=
SC
. Tính thể tích khối chóp
.S ABCD
.
A.
15
3
V =
. B.
3V =
. C.
3
6
V =
. D.
3
3
V =
.
Câu 55: Hình chóp tứ giác
.
S ABCD
có đáy là hình chữ nhật cạnh
( )
, 2,AB a AD a SA ABCD= = ⊥
, góc
giữa
SC
và đáy bằng
60°
. Thể tích hình chóp
.S ABCD
bằng:
A.
3
6a
. B.
3
3a
. C.
32a
. D.
3
2a
.
Câu 56:
Hình chóp
.
S ABCD
có đáy hình vuông,
vuông góc với đáy và
3SA a=
,
2AC a=
. Khi đó
thể tích khối chóp
.
S ABCD
là
A.
3
2
3
a
B.
3
2
2
a
C.
3
3
3
a
D.
3
3
2
a
Câu 57: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác cân tại
A
,
2BC a=
,
120BAC = °
, biết
( )
SA ABC⊥
và mặt phẳng
( )
SBC
hợp với đáy một góc bằng
45°
. Tính thể tích khối chóp
.
S ABC
.
A.
3
2a
. B.
. C.
. D.
.
Câu 58: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Cạnh bên
SA
vuông góc với đáy
và có độ dài bằng
a
. Tính thể tích khối tứ diện
.S BCD
.
A.
. B.
. C.
. D.
.
Câu 59: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi cạnh
a
và góc
60BAD = °
,
( )
SA ABCD⊥
.
Biết rằng khoảng cách từ
A
đến cạnh
SC
bằng
a
. Thể tích khối chóp
.S ABCD
là
A.
3
2
4
a
. B.
3
2
12
a
. C.
3
3
6
a
. D.
3
3
a
.
Câu 60: Thể tích của tứ diện
OABC
có
,,OA OB OC
đôi một vuông góc,
=OA a
,
2=OB a
,
3=
OC a
là
A.
3
3a
. B.
3
2a
. C.
3
4
a
. D.
3
a
.
Câu 61: Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh a,
0
120 ,ABC =
( )
SA ABCD⊥
. Biết góc giữa hai
mặt phẳng
( )
SBC
và
( )
SCD
bằng
60°
. Tính
SA
A.
6
4
a
B.
6
.
2
a
C.
6a
D.
3
2
a
Câu 62: Cho hình chóp có vuông góc với mặt phẳng đáy, tam giác đều cạnh , góc giữa
mặt phẳng và đáy là . Thể tích khối chóp là.
A. . B. . C. . D. .
.S ABC
SA
SBC
a
( )
SBC
30°
.S ABC
3
3
24
a
V =
3
3
64
a
V
=
3
3
16
a
V =
3
3
32
a
V =
https://toanmath.com/
Câu 63: Cho khối chóp
.S ABCD
có đáy là hình chữ nhậ,
AB a=
,
3AD a=
,
SA
vuông góc với đáy và
mặt phẳng
( )
SBC
tạo với đáy một góc
60°
. Tính thể tích
V
của khối chóp
.
S ABCD
.
A.
3
3
a
V =
. B.
3
3Va=
. C.
3
3
3
a
V =
. D.
3
Va=
.
Câu 64: Hình chóp
.S ABC
có đáy là tam giác
ABC
vuông cân tại
B
,
2
2
=
a
AC
;
SA
vuông góc với mặt đáy.
Góc giữa mặt bên
(
)
SBC
và mặt đáy bằng
45 .°
Tính theo
a
thể tích khối chóp
..S ABC
A.
3
48
a
. B.
. C.
3
3
48
a
. D.
3
2
48
a
.
Câu 65: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
vuông góc với mặt phẳng đáy.
Gọi
I
là trung điểm của
BC
, góc giữa
( )
SBC
và
( )
ABC
bằng
30
°
. Thể tích khối chóp
.S ABC
bằng:
A.
3
6
24
a
. B.
3
6
8
a
. C.
3
3
24
a
. D.
3
3
8
a
.
Câu 66: Cho khối chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
.
vuông góc với
( )
ABCD
,
3SC a=
. Tính thể tích khối chóp
.S ABCD
theo
a
.
A.
3
.S ABCD
Va=
. B.
3
.
3
S ABCD
a
V
=
. C.
3
.
3
9
S ABCD
a
V =
. D.
3
.
3
3
S ABCD
a
V =
.
Câu 67: Cho hình chóp
SABC
có đáy
ABC
là tam giác vuông cân tại
B
,
AB a
, góc giữa mặt phẳng
SBC
và mặt phẳng
ABC
bằng
o
60
,
.SA ABC
Gọi
M
,
N
lần lượt là trung điểm của
SC
và
AC
. Tính thể tích khối chóp
MNBC
?
A.
3
4
a
. B.
3
3
24
a
. C.
3
6
18
a
. D.
3
3
12
a
.
Câu 68: Hình chóp tứ giác
.S ABCD
có đáy là hình chữ nhật cạnh
,2AB a AD a= =
,
( )
SA ABCD⊥
, góc
giữa
SC
và mặt phẳng đáy bằng
60°
. Thể tích khối chóp
.S ABCD
bằng:
A.
3
2a
. B.
3
6a
.
C.
3
3a
.
D.
3
32a
.
Câu 69: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
( )
SA ABCD⊥
,
SC
tạo với mặt
đáy một góc bằng
60
. Tính thể tích
V
của khối chóp đã cho.
A.
3
3
3
a
V =
. B.
3
6
6
a
V =
. C.
3
3
6
a
V =
. D.
3
6
3
a
V =
.
Câu 70: Hình chóp
.S ABC
có đáy là tam giác
ABC
vuông cân tại
,B
2
;
2
a
AC =
SA
vuông góc với mặt
đáy. Góc giữa mặt bên
( )
SBC
và mặt đáy bằng
45 .°
Tính theo
a
thể tích khối chóp
..S ABC
A.
3
2
.
48
a
B.
3
.
48
a
C.
3
3
.
48
a
D.
3
.
16
a
Câu 71: Cho hình chóp
.S ABCD
với
ABCD
là hình vuông cạnh
a
. Mặt bên
SAB
là tam giác cân tại
S
và nằm trên mặt phẳng vuông góc với mặt phẳng đáy. Cạnh bên
SC
tạo với đáy một góc
60°
.
Tính thể tích khối chóp
.S ABCD
.
A.
3
6
3
a
. B.
3
3
6
a
. C.
3
15
2
a
. D.
3
15
6
a
.
https://toanmath.com/
Câu 72: Cho hình chóp
.
S ABCD
có
(
)
SA ABCD⊥
,
ABCD
là hình chữ nhật.
2SA AD a= =
. Góc giữa
( )
SBC
và mặt đáy
( )
ABCD
là
60°
. Gọi
G
là trọng tâm tam giác
SBC
. Tính thể tích khối chóp
.S AGD
là
A.
3
32 3
27
a
. B.
3
83
27
a
. C.
3
43
9
a
. D.
3
16
93
a
.
Câu 73: Hình chóp
.S ABCD
có đáy là hình vuông,
a
là độ dài cạnh đáy. Cạnh bên
SA
vuông góc với đáy,
SC
tạo với
( )
SAB
góc
o
30
. Thể tích khối chóp
.S ABCD
là:
A.
3
2
2
a
B.
3
3
3
a
. C.
3
2
4
a
. D.
3
2
3
a
.
Câu 74: Cho hình chóp
.S ABCD
có
( )
SA ABCD⊥
,
2AC a=
,
2
3
2
ABCD
a
S
=
và góc giữa đường thẳng
SC
và mặt phẳng
ABCD
bằng
60°
. Gọi
H
là hình chiếu vuông góc của
A
trên
SC
. Tính theo
a
thể tích của khối chóp
.H ABCD
.
A.
3
36
4
a
. B.
3
6
2
a
. C.
3
6
4
a
. D.
3
6
8
a
.
Câu 75: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
vuông góc với mặt đáy
( )
,ABCD
,2AB a AD a= =
. Góc giữa cạnh bên
SB
và mặt phẳng
( )
ABCD
bằng
o
45
. Thể tích hình chóp
.
S ABCD
bằng.
A.
3
22
3
a
. B.
3
6
18
a
. C.
. D.
3
2
3
a
.
Câu 76: Cho hình chóp
.S ABC
có
AB a
=
,
3BC a
=
,
5AC a=
và
SA
vuông góc với mặt đáy,
SB
tạo với đáy góc
45°
. Thể tích của khối chóp
.S ABC
là:
A.
3
15
12
a
. B.
3
12
a
. C.
3
3
12
a
. D.
3
11
12
a
.
Câu 77: Hình chóp tứ giác
.S ABCD
có đáy là hình chữ nhật cạnh
AB a=
,
2
AD a=
;
( )
SA ABCD⊥
,
góc giữa
SC
và đáy bằng
60°
. Tính theo
a
thể tích khối chóp
.S ABCD
.
A.
3
32a
. B.
3
3
a
. C.
3
6a
. D.
3
2
a
.
Câu 78: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
,a SA
vuông góc với mặt phẳng đáy, góc
giữa
( )
SBC
và
( )
ABC
bằng
30 .°
Thể tích khối chóp
.
S ABC
là
A.
3
6
.
8
a
B.
3
3
.
24
a
C.
3
3
.
8
a
D.
3
6
.
24
a
Câu 79: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
, cạnh bên
vuông góc với đáy,
đường thẳng
SC
tạo với đáy một góc bằng
60°
. Thể tích của khối chóp
.S ABC
bằng
A.
3
3
4
a
. B.
. C.
. D.
.
Câu 80: Cho tứ diện
.O ABC
có
OA
,
OB
,
OC
đôi một vuông góc với nhau và
2OA a=
,
3OB a=
,
8OC a=
.
M
là trung điểm của
.OC
Tính thể tích
V
của khối tứ diện
.O ABM
.
A.
3
6Va
=
. B.
3
8Va=
. C.
3
4Va=
. D.
3
3Va=
.
Câu 81: Cho khối chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
. Hai mặt bên
( )
SAB
và
( )
SAC
cùng
vuông góc với đáy. Tính thể tích khối chóp biết
3SC a=
.
A.
3
3
2
a
B.
3
26
9
a
. C.
3
6
12
a
. D.
3
3
4
a
.
https://toanmath.com/
Câu 82: Cho khối chóp
.S ABC
có
()SA ABC⊥
,
ABC∆
vuông tại
B
,
2SB a=
,
5SC a=
. Thể tích khối
chóp
.S ABC
bằng
3
a
. Khoảng cách từ
A
đến
( )
SBC
là:
A.
2a
. B.
3
a
. C.
3a
. D.
6a
.
Câu 83: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
A
,
=AB a
,
2=AC a
,
3=SC a
,
vuông góc với đáy
( )
ABC
. Thể tích khối chóp
.S ABC
là.
A.
3
5
3
a
. B.
3
3
12
a
. C.
. D.
3
3
4
a
.
Câu 84: Cho hình chóp
.
S ABC
có
ABC
là tam giác đều cạnh
a
và
SA
vuông góc với đáy. Góc tạo bởi
mặt phẳng
( )
SBC
và mặt phẳng
( )
ABC
bằng
30°
. Thể tích của khối chóp
.S ABC
là
A. . B. . C. . D. .
Câu 85: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
. Cạnh bên
vuông góc với mặt phẳng
đáy, cạnh bên
SC
tạo với mặt phẳng
( )
SAB
một góc
30°
. Thể tích của khối chóp
.S ABCD
bằng:
A.
3
2
3
a
. B.
3
2
4
a
. C.
3
2
2
a
. D.
3
3
3
a
.
Câu 86: Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
a
. Cạnh bên
vuông góc với mặt phẳng
đáy, cạnh bên
SC
tạo với mặt phẳng
(
)
SAB
một góc
30°
. Thể tích của khối chóp đó bằng.
.
A.
3
2
2
a
. B.
3
3
3
a
. C.
3
2
4
a
. D.
3
2
3
a
.
Câu 87: Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
C
và
vuông góc với mặt phẳng
( )
ABC
. Biết
4AB a=
và góc giữa mặt phẳng
( )
SBC
và
( )
ABC
bằng
45°
. Tính thể tích
V
của
khối chóp
.
S ABC
.
A.
3
82
3
Va=
. B.
3
32
2
Va=
. C.
3
1
6
Va=
. D.
3
2
6
Va=
.
Câu 88: Cho hình chóp tứ giác
.S ABCD
có đáy là hình chữ nhật,
AB a=
,
2AD a=
. Biết
( )
SA ABCD⊥
và góc giữa đường thẳng
SC
với mặt phẳng đáy bằng
45°
. Thể tích khối chóp
.S ABCD
bằng:
A.
3
3a
. B.
3
6a
. C.
3
6
3
a
. D.
3
2a
.
Câu 89: Cho khối chóp
.S ABC
có đáy
ABC
là tam giác vuông cân có cạnh huyền
BC a=
và
vuông
góc với mặt phẳng đáy. Biết góc giữa mặt phẳng
( )
SBC
và mặt phẳng
( )
ABC
bằng
45°
. Thể tích
của hình chóp
.S ABC
là.
A.
3
.
2
24
S ABC
a
V =
. B.
3
.
8
S ABC
a
V
=
. C.
3
.
24
S ABC
a
V =
. D.
3
.
2
8
S ABC
a
V =
.
Câu 90: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
a
. Các mặt bên
( )
SAB
,
( )
SAC
cùng vuông
góc với mặt đáy
( )
ABC
; góc giữa
SB
và mặt
( )
ABC
bằng
60°
. Tính thể tích khối chóp
.S ABC
.
A.
3
12
a
. B.
3
3
4
a
. C.
3
2
a
. D.
3
4
a
.
Câu 91: Cho khối chóp
.S ABC
, có đáy
ABC
là tam giác đều cạnh
a
. Hai mặt bên
( )
SAB
và
( )
SAC
cùng
vuông góc với đáy. Tính thể tích khối chóp biết
3SC a=
.
3
3
24
a
3
4
a
3
12
a
3
3
8
a
https://toanmath.com/
A.
3
6
3
a
V =
. B.
3
6
6
a
V
=
. C.
3
6
12
a
V =
. D.
3
6
8
a
V =
.
Câu 92: Cho hình chóp
.S ABC
là tam giác vuông tại
A
,
30
o
ABC =
,
BC a
=
. Hai mặt bên
(
)
SAB
và
(
)
SAC
cùng vương góc với đáy
( )
ABC
, mặt bên
( )
SBC
tạo với đáy một góc
0
45
. Thể tích của
khối chóp
.S ABC
là:
A.
3
9
a
. B.
3
32
a
. C.
3
64
a
. D.
3
16
a
.
Câu 93: Cho khối chóp
.
S ABC
có
( )
SA ABC⊥
,
SA a=
,
AB a=
,
2AC a=
và
120BAC = °
. Tính thể tích
khối chóp
.S ABC
.
A.
3
3a
. B.
3
3
6
a
. C.
3
3
3
a
. D.
3
3
2
a
.
Câu 94: Tính thể tích khối chóp
.S ABC
có
AB a=
,
2AC a
=
,
120BAC = °
,
(
)
SA ABC⊥
, góc giữa
( )
SBC
và
( )
ABC
là
60°
.
A.
3
7
7
a
. B.
3
21
14
a
. C.
3
7
14
a
. D.
3
3 21
14
a
.
Câu 95: Hình chóp tứ giác
.S ABCD
có đáy là hình chữ nhật cạnh
AB a=
,
2AD a=
,
( )
SA ABCD⊥
,
góc giữa
SC
và đáy bằng
60°
. Thể tích hình chóp
.S ABCD
bằng
A.
3
32a
. B.
3
2a
. C.
3
3
a
. D.
3
6a
.
Câu 96: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng đáy
và cạnh bên
SD
hợp với đáy một góc
60
°
. Hỏi thể tích
V
của khối chóp
.
S ABCD
bằng bao
nhiêu?
A.
3
23
3
a
V =
. B.
3
3Va=
. C.
3
3
6
a
V =
. D.
3
3
3
a
V =
.
Câu 97: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
a
. Cạnh
SA
vuông góc với đáy
và
SA y=
. Trên cạnh
AD
lấy điểm
M
sao cho
AM x=
. Biết rằng
222
xya+=
. Tìm giá trị lớn
nhất của thể tích khối chóp
.
S ABCM
.
A.
. B.
3
3
8
a
. C.
3
3
2
a
. D.
3
3
4
a
.
https://toanmath.com/
THỂ TÍCH KHỐI CHÓP CÓ MỘT CẠNH BÊN VUÔNG GÓC VỚI ĐÁY
B. LỜI GIẢI CHI TIẾT
Câu 1: Cho khối chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Biết
SA
vuông góc với
( )
ABCD
và
3
SA a=
. Thể tích của khối chóp
.S ABCD
là:
A.
3
4
a
. B.
3
3a
. C.
3
3
6
a
. D.
3
3
3
a
.
Hướng dẫn giải
Chọn D
Thể tích khối chóp
3
.
13
.
33
S ABCD ABCD
a
V S SA= =
.
Câu 2: Cho hình chóp tứ giác
.S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng đáy
và
2=
SA a
. Thể tích khối chóp
.S ABCD
bằng
A.
3
4
3
a
. B.
3
2a
. C.
3
3
a
. D.
3
2
3
a
.
Hướng dẫn giải
Chọn D
3
2
.
1 12
2
3 33
S ABCD ABCD
a
V S SA a a
∆
= ⋅ =⋅⋅ =
.
Câu 3: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật
,2AB a BC a= =
, cạnh bên
SA
vuông
góc với đáy và
2SA a=
. Tính thể tích khối chóp
.S ABCD
.
A.
3
23
3
a
. B.
3
2a
. C.
3
22a
. D.
3
22
3
a
.
S
A
B
C
D
https://toanmath.com/
Hướng dẫn giải
Chọn D
Diện tích đáy:
2
.2
ABCD
S AB BC a
= =
.
Thể tích:
3
1 22
.
33
ABCD
a
V S SA= =
.
Câu 4: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Cạnh bên
SA
vuông góc với đáy
và có độ dài bằng
2a
. Thể tích khối tứ diện
.S BCD
là:
A.
3
4
a
. B.
3
8
a
. C.
3
6
a
. D.
3
3
a
.
Hướng dẫn giải
Chọn D
Ta có:
2
1
22
BCD ABCD
a
SS
∆
= =
. Suy ra
23
.
11
. .2 .
3 3 23
S ABCD BCD
aa
V SAS a
∆
= = =
.
Câu 5: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông tâm
O
cạnh
2a
. Biết
vuông góc với
mặt phẳng đáy và
2.
SA a=
Tính thể tích khối chóp
.S ABO
.
A.
3
2
3
a
. B.
3
22
12
a
. C.
3
2
12
a
. D.
3
42
3
a
.
Hướng dẫn giải
Chọn A
.
Ta có:
2
1
2 . 2 2 .OB a
22
OAB
AC
AC a OA OB a S OA= ⇒== = ⇒ = =
.
Vậy:
23
.
11 2
. . 2. .
33 3
S OAB OAB
V SAS a a a= = =
.
Câu 6: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
2a
. Biết
6SA a=
và
SA
vuông góc với mặt phẳng đáy. Tính thể tích khối chóp
.S ABCD
.
A.
3
8a
. B.
3
63a
. C.
3
12 3a
. D.
3
24a
.
Hướng dẫn giải
A
D
B
C
S
https://toanmath.com/
Chọn A
Ta có
2
4
ABCD
Sa=
. Do
SA
vuông góc với mặt phẳng đáy nên
.
1
..
3
S ABCD ABCD
V SA S=
3
8a=
.
Câu 7: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông tâm
O
cạnh
2
a
. Biết
SA
vuông góc với
mặt phẳng đáy và
2.SA a=
Tính thể tích khối chóp
.S ABO
.
A.
3
42
3
a
. B.
3
22
12
a
. C.
3
2
12
a
. D.
3
2
3
a
.
Hướng dẫn giải
Chọn D
.
Ta có:
2
1
2.2 2 .
22
= ⇒== = ⇒ = =
OAB
AC
AC a OA OB a S OAOB a
.
Vậy :
23
.
11 2
. . 2. .
33 3
S OAB OAB
V SA S a a a= = =
.
Câu 8: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật với
,2AB a AD a= =
,
( )
SA ABCD⊥
và
3SA a=
. Thể tính khối chóp
.S ABC
bằng:
A.
3
3a
. B.
3
23a
. C.
3
23
3
a
. D.
3
3
3
a
.
Hướng dẫn giải
Chọn D
Ta có
3
1 11 1 3
. . . 3. .2
3 32 6 3
ABC
a
V SA S SA AB BC a a a= = = =
.
Câu 9: Cho hình chóp tam giác
.S ABC
với
SA
,
SB
,
SC
đôi một vuông góc và
SA SB SC a= = =
. Tính
thế tích của khối chóp
.S ABC
.
A.
3
1
2
a
. B.
3
1
6
a
. C.
3
2
3
a
. D.
3
1
3
a
.
Hướng dẫn giải
Chọn B
Ta có
1
..
3
SBC
V S SA=
11
.. . .
32
SB SC SA=
3
1
.
6
a=
.
Câu 10: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Cạnh
vuông góc với mặt
phẳng đáy và có độ dài là
a
. Thể tích khối tứ diện
.S BCD
bằng.
A
D
B
C
S
https://toanmath.com/
A.
. B.
. C.
. D.
.
Hướng dẫn giải
Chọn A
3
2
.D . D
1 11
. .. .
2 23 6
S BC S ABC
a
V V aa= = =
.
Câu 11: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật với
,2AB a AD a= =
,
SA
vuông góc với mặt
đáy và
3SA a=
. Thể tính khối chóp
.S ABCD
bằng
A.
3
2 3.a
B.
3
3
.
3
a
C.
3
3.a
D.
3
23
.
3
a
Hướng dẫn giải
Chọn D
Ta có
3
1 1 23
. . 3. .2
33 3
ABCD
a
V SA S a a a= = =
.
Câu 12: Cho tứ diện
OABC
có
OA
,
OB
,
OC
đôi một vuông góc với nhau tại
O
và
2OA =
,
4OB =
,
6OC
=
. Thể tích khối tứ diện đã cho bằng.
A.
24
. B.
16
. C.
8
. D.
48
.
Hướng dẫn giải
Chọn C
Ta có
1
..
6
OABC
V OAOB OC=
1
.2.4.6 8
6
= =
.
Câu 13: Cho khối chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
SA
vuông góc với mặt phẳng đáy
và
2SA a=
. Tính thể tích khối chóp
.S ABC
.
A.
3
3
.
6
a
B.
3
3
.
2
a
C.
3
3
.
3
a
D.
3
3
.
12
a
Hướng dẫn giải
Chọn A
B
A
D
C
S
https://toanmath.com/
Ta có
3
.
1 11 11 3 3
. . .2 . . . .sin60 .2 . . . . .
3 32 32 2 6
S ABC ABC
a
V SA S a AB AC a a a= = °= =
Câu 14: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
2a
,
SA
vuông góc với mặt phẳng đáy,
3SA a=
. Tính thể tích khối chóp
.S ABC
.
A.
2
.
S ABC
Va=
(đvtt). B.
3
.S ABC
Va=
(đvtt).
C.
3
.
2
S ABC
a
V
=
(đvtt). D.
3
.
3
S ABC
Va=
(đvtt).
Hướng dẫn giải
Chọn B
Thể tích khối chóp là
1
.
3
ABC
V SA S=
1
. . .sin 60
6
SA AB AC= °
13
3.2 .2 .
62
a aa=
3
a=
.
Câu 15: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
B
,
AB a=
,
2BC a=
,
( )
SA ABC⊥
,
3SA a=
. Thể tích của khối chóp
.S ABC
bằng
A.
3
1
6
a
. B.
3
a
. C.
3
1
3
a
. D.
3
3
a
.
Hướng dẫn giải
Chọn B
Thể tích
.
1
.
3
S ABC ABC
V S SA=
11
. ..
32
BA BC SA=
3
1
.2 .3
6
aaa a= =
.
A
C
B
S
A
C
B
S
https://toanmath.com/
Câu 16: Cho hình chóp tứ giác
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
vuông góc
với mặt phẳng đáy và
2SA a=
. Tính thể tích
V
của khối chóp
.S ABCD
.
A.
3
2Va=
. B.
3
2
4
a
V =
. C.
3
2
6
a
V =
. D.
3
2
3
a
V =
.
Hướng dẫn giải
Chọn D
.
Ta có:
2SA a=
.
3
22
112
.S . 2 .
33 3
ABCD ABCD ABCD
a
S a V SA a a=⇒= = =
.
Câu 17: Cho hình chóp tứ giác
. S ABCD
có đáy là hình vuông cạnh
(
)
8
cm
, chiều cao
SH
bằng
(
)
3
cm
.
Tính thể tích khối chóp?
A.
(
)
3
1 6V cm
=
. B.
( )
3
24V cm=
. C.
( )
3
48V cm=
.
D.
( )
3
64V cm
=
.
Hướng dẫn giải
Chọn D
( )
3
1
. 64
3
ABCD
V SH S cm= =
.
Câu 18: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Biết
(
)
SA ABCD⊥
và
3SA a=
.
Thể tích của khối chóp
.
S ABCD
có giá trị là
A.
3
3
3
a
. B.
3
4
a
. C.
3
3
12
a
. D.
3
3a
.
Hướng dẫn giải
Chọn A
Vì
( )
SA ABCD⊥
nên
3
2
.
11 3
. . 3.
33 3
S ABCD ABCD
a
V SA S a a= = =
.
Câu 19: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
( )
SA ABC⊥
và
3SA a=
. Thể
tích khối chóp
.S ABC
là.
A.
3
3
6
a
. B.
. C.
3
3
4
a
. D.
3
3
8
a
.
Hướng dẫn giải
Chọn B
23
.
1 13
. .3
3 34 4
S ABC ABC
aa
V S SA a= = =
.
Câu 20: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
AB a=
,
2BC a=
, đường thẳng
SA
vuông góc với mặt phẳng
( )
ABCD
và
3SA a=
. Thể tích của khối chóp
.S ABCD
bằng
A.
3
a
. B.
3
3a
. C.
3
6a
. D.
3
2a
.
Hướng dẫn giải
Chọn D
B
C
D
A
S
https://toanmath.com/
16TÁp dụng công thức tính thể tích khối chóp ta có 16T34T
.
1
. .2 .3
3
S ABCD
V aaa
=
3
2
a=
16T34T.
Câu 21: Cho hình hình chóp
.S ABC
có cạnh
vuông góc với mặt đáy và
3
SA
a=
. Đáy
ABC
là tam
giác đều cạnh bằng
a
. Thể tích của khối chóp
.
S ABC
bằng.
A.
3
12
a
V
=
. B.
3
4
a
V =
. C.
3
3Va=
. D.
3
3
12
a
V =
.
Hướng dẫn giải
Chọn B
Ta có:
22
33
.
44
ABC
AB a
S
∆
= =
.
23
.
1 13
. . 3.
3 3 44
S ABC ABC
aa
V SA S a
∆
= = =
.
Câu 22: Đáy của hình chóp
.S ABCD
là một hình vuông cạnh
a
. Cạnh bên
SA
vuông góc với mặt phẳng
đáy và có độ dài là
a
. Thể tích khối tứ diện
.S BCD
bằng:
A.
3
4
a
. B.
3
3
a
. C.
3
6
a
. D.
3
8
a
.
Hướng dẫn giải
Chọn C
Thể tích
3
2
..
1 11 1
. . ..
2 23 6 6
S BCD S ABCD ABCD
a
V V SA S a a= = = =
.
Câu 23: Hình chóp
.S ABC
có
SA a=
,
SB b=
,
SC c=
đôi một vuông góc với nhau. Thể tích khối chóp
là.
A.
2
9
abc
. B.
6
abc
. C.
3
abc
. D.
9
abc
.
Hướng dẫn giải
Chọn B
1
.
36
SAB
abc
V SC S= =
.
Câu 24: Cho tứ diện
ABCD
có
AD
vuông góc với mặt phẳng
( )
ABC
. Biết đáy
ABC
là tam giác vuông
tại
B
và
5,AD =
5,AB =
12BC =
. Tính thể tích
V
của tứ diện
ABCD
.
A.
50V =
. B.
120
V =
. C.
150V =
. D.
325
16
V =
.
Hướng dẫn giải
Chọn A
11 1
. . .5.5.12 50.
32 6
V AD AB BC= = =
.
2a
a
3a
C
B
A
D
S
https://toanmath.com/
Câu 25: Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
( )
SA ABCD
⊥
và
6
SA a=
. Thể tích của khối chóp
.S ABCD
bằng
A.
3
6
3
a
. B.
3
6
2
a
. C.
3
6
6
a
. D.
3
6a
.
Hướng dẫn giải
Chọn A
3
2
.
11 6
. .6
33 3
S ABCD ABCD
a
V S SA a a= = =
.
Câu 26: Cho hình chóp
.
S ABCD
có
ABCD
là hình vuông cạnh
a
,
( )
SA ABCD⊥
và
3aSA
=
. Thể tích
khối chóp
.
S ABCD
là.
A.
3
2a
. B.
3
a
. C.
. D.
.
Hướng dẫn giải
Chọn B
.
Vì
(
)
SA ABCD⊥
SA⇒
là chiều cao hình chóp
.S ABCD
.
Ta có:
2
ABC
Sa
=
.
23
11
. . . .3a
33
ABC
V S SA a a= = =
.
Câu 27: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Biết
( ); 3.SA ABCD SA a⊥=
Tính thể tích của khối chóp.
A.
3
3
3
a
. B.
3
3
12
a
. C.
. D.
3
3a
.
Hướng dẫn giải
Chọn A
.
Câu 28: Cho hình chóp
.S ABCD
có đáy hình vuông cạnh
a
;
SA
vuông góc mặt đáy; Góc giữa
SC
và
mặt đáy của hình chóp bằng
0
60
. Thể tích khối chóp
.S ABCD
là
A.
3
2
3
a
B.
3
3
a
C.
3
6
3
a
D.
3
3
3
a
Hướng dẫn giải
Chọn C
= = =
3
2
11 3
. . . 3.
333
ABCD
a
V SA S a a
https://toanmath.com/
Ta có
( ) ( )
0
, , 60SC ABCD SC AC SCA
∧
= = =


.
0
.tan 60 2. 3 6SA AC a a
= = =
.
Vậy
3
2
11 6
.6
333
ABCD ABCD
a
V S SA a a= = =
.
Câu 29: Cho hình chóp
.S ABCD
đáy
ABCD
là hình vuông có cạnh
a
và
SA
vuông góc đáy
ABCD
và
mặt bên
(
)
SCD
hợp với đáy một góc
60
°
. Tính thể tích hình chóp
.S ABCD
.
A.
3
3
3
a
. B.
3
3
6
a
. C.
3
3a
. D.
3
23
3
a
.
Hướng dẫn giải
Chọn A
Do
( ) ( ) ( )
,
AD CD
CD SDA SCD ABC SDA
SA CD
⊥
⇒⊥ ⇒ =
⊥
Khi đó
tan60 3SA AD a= °=
.
Suy ra
3
.
13
.
33
S ABCD ABCD
a
V SA S= =
.
Câu 30: Cho hình chóp
.S ABCD
có
SA
vuông góc với mặt phẳng
( )
,ABCD
đáy
ABCD
là hình thang
vuông tại
A
và
B
có
, 3 , .AB a AD a BC a= = =
Biết
3,SA a=
tính thể tích khối chóp
.S BCD
theo
.a
A.
3
3
.
6
a
B.
3
23
.
3
a
C.
3
3
.
4
a
D.
3
23 .a
Hướng dẫn giải
Chọn A
a
a
60
A
B
C
D
S
https://toanmath.com/
Ta có
.
1
..
3
S BCD BCD
V SA S=
Lại có
BCD ABCD ABD
SS S= −
(
)
11
..
22
AB AD BC AB AD
= +−
2
11
..
22
AB BC a= =
Mà
23
.
13
3 3. .
3 26
S BCD
aa
SA a V a=⇒= =
Nhận xét: Nếu đề bài bỏ giả thiết
3AD a
=
thì sẽ giải như sau:
Ta có
( )
.
1 11
. . ,.
3 32
S BCD BCD
V SA S SA d D BC BC
= =
3
13
..
66
a
SA AB BC= =
.
Câu 31: Cho hình chóp
.S ABC
có
SA
vuông góc với đáy. Tam giác
ABC
vuông cân tại
B
, biết
2SA AC a= =
. Tính thể tích khối chóp
.
S ABC
.
A.
3
2
3
a
. B.
3
1
3
a
. C.
3
22
3
a
. D.
3
4
3
a
.
Hướng dẫn giải
Chọn A
Ta có
2
2
22
AC a
AB BC a= = = =
.
Thể tích khối chóp
.S ABC
là
(
)
2
23
1 11 1 2
. . . . 2 .2
3 32 6 3
ABC
V S SA AB SA a a a= = = =
.
Câu 32: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
.
SA
vuông góc với đáy và tạo với
đường thẳng
SB
một góc
45°
. Tính thể tích khối chóp
.S ABC
.
A.
3
3
12
a
. B.
3
3
4
a
. C.
3
3
24
a
. D.
3
3
6
a
.
Hướng dẫn giải
Chọn A
B
A
C
S
S
A
B
C
D
https://toanmath.com/
Ta có:
( )
SA ABC⊥
SA⇒
là chiều cao của hình chóp
SA AB⇒⊥
SAB⇒∆
vuông tại
A
.
( )
, 45SA SB ASB⇒==°
SAB
⇒∆
vuông cân tại
A
SA AB⇒=
a=
.
Vậy thể tích của khối chóp
.S ABC
là:
1
..
3
ABC
V S SA
=
2
13
..
34
a
a=
3
3
12
a
=
.
Câu 33: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, hai mặt phẳng
( )
SAB
và
( )
SAD
cùng vuông góc với mặt phẳng
( )
ABCD
; góc giữa đường thẳng
SC
và mặt phẳng
( )
ABCD
bằng
60°
. Tính theo
a
thể tích khối chóp
.S ABCD
.
A.
3
6
9
a
. B.
3
6
3
a
. C.
3
32a
. D.
3
3a
.
Hướng dẫn giải
Chọn B
Ta có
( )
( )
( ) ( )
( ) ( )
( )
SAB ABCD
SAD ABCD SA ABCD
SAB SAD SA
⊥
⊥ ⇒⊥
∩=
AC⇒
là hình chiếu vuông góc của
SC
lên mặt phẳng
( )
ABCD
(
)
(
)
, 60SC ABCD SCA⇒==°
Tam giác
SAC
vuông tại
A
có
.tan 60 6SA AC a= °=
.
Khi đó
3
2
11 6
. . . 6.
33 3
SABCD ABCD
a
V SA S a a= = =
.
Câu 34: Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, đường cao của một mặt bên là
3a
.
Tính thể tích
V
khối chóp đó.
a
A
B
C
S
https://toanmath.com/
A.
3
2
9
a
V =
. B.
3
2Va=
. C.
3
2
6
a
V =
.
D.
3
2
3
a
V =
.
Hướng dẫn giải:
Chọn D
Gọi các đỉnh của hình chóp tứ giác đều như hình vẽ bên và đặt cạnh bằng
2AB x=
. Khi đó
2,SO x OH x= =
suy ra
3SH x=
. Vậy
xa=
. Khi đó
3
2
12
.
33
a
V SO AB= =
.
Câu 35: Hình chóp
.S ABC
có đáy là tam giác
ABC
vuông cân tại
,B
2
;
2
a
AC =
SA
vuông góc với mặt
đáy. Góc giữa mặt bên
( )
SBC
và mặt đáy bằng
45 .°
Tính theo
a
thể tích khối chóp
.S ABC
.
A.
. B.
3
3
48
a
. C.
3
2
48
a
. D.
.
Hướng dẫn giải
Chọn D
.
Tam giác
ABC
vuông cân tại
,B
2
2
a
AC =
.
Nên
2
1
, . .
22 8
ABC
aa
AB BC S BA BC
∆
= = = =
.
Ta có:
( ) ( )
( )
( )
( ) ( )
( )
, , 45
,
SBC ABC BC
AB ABC AB BC ABC SBC SBA
SB SBC SB BC
∩=
⊂ ⊥⇒ = =°
⊂⊥
.
Tam giác
SAB
vuông cân tại
A
nên
2
a
SA AB= =
.
Vậy:
23
.
11
. . ..
3 3 2 8 48
S ABC ABC
aa a
V SA S
∆
= = =
.
Câu 36: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh bằng
a
, cạnh bên
SB
vuông góc với mặt
phẳng
( )
ABC
,
2=SB a
. Tính thể tích khối chóp
.S ABC
.
A.
3
3
2
a
. B.
3
4
a
. C.
3
3
6
a
. D.
3
3
4
a
.
Hướng dẫn giải
Chọn C
https://toanmath.com/
Thể tích khối chóp
.S ABC
là:
1
..
3
=
ABC
V S SB
2
13
. .2
34
=
a
a
3
3
6
=
a
.
Câu 37: Cho khối tứ diện
OABC
với
OA
,
OB
,
OC
vuông góc từng đôi một và
OA a=
,
2OB a
=
,
3OC a=
. Gọi
,
MN
lần lượt là trung điểm của hai cạnh
,
AC BC
. Thể tích của khối tứ diện
OCMN
tính theo
a
bằng
A.
3
4
a
. B.
3
3
4
a
. C.
3
a
. D.
3
2
3
a
.
Hướng dẫn giải
Chọn A
.
Ta có thể tích
3
11
..
32
OABC
V OAOB OC a

= =


(đvtt).
Diện tích tam giác
1 1 11 1
. .sin . .sin . .sin
2 22 2 42 4
CMN ABC
CA CB
S CM CN C C AC BC C S
∆Λ

= = = =


.
Vậy thể tích
3
1
44
OCMN OABC
a
VV= =
(đvtt).
Câu 38: Cho hình chóp
.S ABC
có mặt phẳng
(
)
SAC
vuông góc với mặt phẳng
( )
ABC
,
SAB
là tam giác
đều cạnh
3a
,
3BC a=
đường thẳng
SC
tạo với mặt phẳng
( )
ABC
góc
60°
. Thể tích của
khối chóp
.S ABC
bằng
A.
3
6
6
a
. B.
3
26a
. C.
3
3
3
a
. D.
3
6
2
a
.
2a
C
A
B
S
a
3a
2a
a
N
M
C
O
B
A
https://toanmath.com/
Hướng dẫn giải
Chọn A
Ta thấy tam giác
ABC
cân tại
B
, gọi
H
là trung điểm của
AB
suy ra
.BH AC⊥
Do
(
)
( )
SAC ABC
⊥
nên
( )
BH SAC⊥
.
Ta lại có
BA BC BS= =
nên
B
thuộc trục đường tròn ngoại tiếp tam giác
ABC
⇒
H
là tâm
đường tròn ngoại tiếp tam giác
SAC
⇒
SA SC
⊥
.
Do
AC
là hình chiếu của
SC
lên mặt phẳng
( )
ABC
⇒
0
60SCA =
.
Ta có
0
.cot 60
SC SA a= =
,
0
2
sin 60
SA
AC a= =
HC a⇒=
22
2BH BC HC a⇒= − =
.
.S ABC
V
1
.
3
SAC
BH S
=
1
..
6
BH SA SC=
3
6
6
a
=
.
Câu 39: Cho khối chóp
.S ABC
có
( )
SA ABC⊥
, tam giác
ABC
vuông tại
B
,
AB a=
,
3AC a
=
.
Tính thể tích khối chóp
.S ABC
, biết rằng
5SB a=
.
A.
3
6
4
a
. B.
3
15
6
a
. C.
3
2
3
a
. D.
3
6
6
a
.
Hướng dẫn giải
Chọn C
Ta có:
22 22
2; 2SA SB AB a BC AC AB a
= −= = −=
23
.
.2 1 2
.
22 3 3
ABC S ABC ABC
AB BC a a
S V SA S= =⇒= =
.
Câu 40: Cho hình chóp tứ giác
.S ABCD
, đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
SA
vuông góc với
mặt đáy, góc giữa
SC
và
( )
ABCD
bằng
45°
. Thể tích khối chóp
.S ABCD
là
A.
3
2
6
a
. B.
3
2
4
a
. C.
3
2a
. D.
3
2
3
a
.
Hướng dẫn giải
Chọn D
60
o
A
C
B
S
H
https://toanmath.com/
Ta có
( )
SA ABCD⊥
( )
( )
; 45
SC ABCD SCA
⇒==°
tan 45
SA
AC
⇒ °=
2SA AC a⇒= =
3
2
.
11 2
. 2.
33 3
S ABCD ABCD
a
V SA S a a⇒= = =
.
Câu 41: Cho hình chóp
.
S ABC
có đáy là tam giác đều cạnh
2a
,
( )
SA ABC⊥
. Góc giữa hai mặt phẳng
( )
SBC
và
(
)
ABC
bằng
30°
. Thể tích khối chóp
.S ABC
là.
A.
3
3
8
a
. B.
3
3
6
a
. C.
3
3
12
a
. D.
3
3
3
a
.
Hướng dẫn giải
Chọn D
.
Gọi
I
là trung điểm
BC
.
Góc giữa hai mặt phẳng
( )
SBC
và
(
)
ABC
là
30SIA = °
⇒
SIA∆
nửa tam giác đều nên
23
2
33
a
AI
SA a= = =
.
Thể tích khối chóp
.S ABC
là
1
.
3
ABC
V S SA=
=
( )
2
12 3
..
34
a
a
=
3
3
3
a
.
Câu 42: Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
C
,
5
AB a
=
,
AC a=
. Cạnh bên
3SA a=
và vuông góc với mặt phẳng
( )
ABC
. Thể tích khối chóp
.S ABC
bằng:
A.
3
5
3
a
. B.
3
a
. C.
3
2a
. D.
3
3a
.
Hướng dẫn giải
Chọn B
D
C
B
A
S
2a
2a
2a
30
o
I
A
B
C
S
https://toanmath.com/
Ta có
ABC
vuông tại
C
nên
22
2BC AB AC a= −=
.
Diện tích tam giác
ABC
là
2
1
.
2
ABC
S CACB a
∆
= =
.
Do cạnh bên
3SA a=
và vuông góc với mặt phẳng
( )
ABC
nên
SA
là đường cao của hình chóp
.S ABC
.
Thể tích của khối chóp
.S ABC
là
23
..
11
. 3.
33
S ABC ABC
V SAS a a a
∆
= = =
.
Câu 43: Cho khối chóp
.S ABC
có
( )
SA ABC⊥
, tam giác
ABC
vuông tại
B
,
AB a
=
,
3AC a=
.
Tính thể tích khối chóp
.S ABC
biết rằng
5SB a=
.
A.
3
2
3
a
. B.
3
6
4
a
. C.
3
6
6
a
. D.
3
15
6
a
.
Hướng dẫn giải
Chọn A
Cạnh
2 2 22
52SA SB AB a a a= − = −=
.
Cạnh
22
2BC AC AB a= −=
3
11 2
.2 . . . 2
32 3
a
V a aa⇒= =
.
S
B
C
A
https://toanmath.com/
Câu 44: Cho khối chóp tam giác
.S ABC
có
( )
SA ABC
⊥
, tam giác
ABC
có độ dài
3
cạnh là
5AB a=
;
8
BC a
=
;
7AC a
=
, góc giữa
SB
và
( )
ABC
là
45°
. Tính thể tích khối chóp
.S ABC
.
A.
3
50
3
a
. B.
3
50 7
3
a
. C.
3
50 3a
. D.
3
50 3
3
a
.
Hướng dẫn giải
Chọn D
Ta có nửa chu vi
ABC∆
là
10
2
AB AC BC
pa
++
= =
.
Diện tích
ABC
∆
là
2
10 .5 .3 .2 10 3
ABC
S aaaa a
∆
= =
.
( )
SA ABC⊥
nên
SAB∆
vuông, cân tại
A
nên
5SA AB= =
.
Thể tích khối chóp
.S ABC
là
.
1
.
3
S ABC ABC
V SA S
∆
=
2
1
5 .10 3
3
aa=
3
50 3
3
a=
.
Câu 45: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
D
,
AB AD a= =
,
3SA CD a
= =
,
SA
vuông góc với mặt phẳng
( )
ABCD
. Thể tích khối chóp
.S ABCD
bằng.
A.
3
1
3
a
. B.
3
2
a
. C.
3
6a
. D.
3
1
6
a
.
Hướng dẫn giải
Chọn B
Ta có
( )
( )
2
.3
2
22
ABCD
AB DC AD a a a
Sa
++
= = =
. Vậy
.
1
.
3
S ABCD ABCD
V SA S=
23
1
3 .2 2
3
aa a= =
.
Câu 46: Cho hình chóp
.S ABC
có
( )
,
SA ABC⊥
góc giữa
SB
và
(
)
ABC
bằng
o
60
; tam giác
ABC
đều
cạnh
.a
Thể tích khối chóp
.S ABC
bằng
3a
a
https://toanmath.com/
A.
3
a
. B.
3
3
a
. C.
3
1
4
a
. D.
3
1
2
a
.
Hướng dẫn giải
Chọn C
0
.tan 60 3
= =
SA AB a
23
.
1 13
. 3.
3 3 44
= = =
S ABC ABC
aa
V SAS a
.
Câu 47: Cho tứ diện
ABCD
có các cạnh
,,BA BC BD
đôi một vuông góc với nhau:
3,BA a
=
2BC BD a= =
. Gọi
M
và
N
lần lượt là trung điểm của
AB
và
AD
. Tính thể tích khối chóp
.C BDNM
.
A.
3
3
2
=
a
V
. B.
3
=Va
. C.
3
2
3
=
a
V
. D.
3
8=Va
.
Hướng dẫn giải
Chọn A
BG: Ta có
2
3
(2 ).
9
2
24
+
= =
MNBD
a
aa
a
S
;
2BC a= ⇒
23
19 3
. .2
34 2
= =
aa
Va
.
Câu 48: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật, cạnh bên
SA
vuông góc với đáy
( )
ABCD
. Biết
AB a=
,
2BC a=
và
3SC a=
. Tính thể tích khối chóp
.S ABCD
.
A.
3
4
3
a
. B.
3
25
3
a
.16T C. 16T
3
2a
16T.16T D.
3
a
.
Hướng dẫn giải
Chọn A
Ta có
AB a=
,
2BC a=
suy ra
5AC a=
.
Mà tam giác
SAC
vuông tại
A
suy ra
22
2SA SC AC a= −=
.
Vậy
3
.
1 14
. .2 . .2
3 33
S ABCD ABCD
V SA S a a a a= = =
.
Câu 49: Cho tứ diện
.S ABC
có
,SAB SCB
là các tam giác cân tại
S
và
,,SA SB SC
đôi một vuông góc
với nhau. Biết
2BA a
=
, thể tích
V
của tứ diện
.S ABC
là.
60
0
S
a
B
C
A
https://toanmath.com/
A.
3
6
a
V =
. B.
3
2
a
V
=
. C.
3
22Va=
. D.
3
Va=
.
Hướng dẫn giải
Chọn A
.
Các tam giác
, SAB SCB
là các tam giác vuông cân suy ra
SA SB SC a= = =
. Vậy
3
6
a
V =
.
Câu 50: Cho khối chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
. Hai mặt bên
( )
SAB
và
(
)
SAC
cùng
vuông góc với đáy. Tính thể tích khối chóp biết
3SC a=
.
A.
3
6
12
a
.
B.
3
3
2
a
. C.
3
26
9
a
. D.
3
3
4
a
.
Hướng dẫn giải
Chọn A
.
Ta có
2
3
4
=
ABC
a
S
.
Do
( )
( )
(
) ( )
⊥
⊥
SAB ABC
SAC ABC
nên
( )
⊥
SA ABC
.
2 2 22
32= − = −=SA SC AC a a a
.
3
16
.
3 12
= =
SABC ABC
a
V SA S
.
Câu 51: Cho hình chóp
.S ABCD
có
( )
SA ABCD⊥
,
ABCD
là hình chữ nhật,
SA a=
,
2AB a=
,
4BC a=
. Gọi
M
,
N
lần lượt là trung điểm của
BC
,
CD
. Thể tích của khối chóp
.S MNC
là
A.
3
5
a
. B.
3
2
a
. C.
3
4
a
. D.
3
3
a
.
Hướng dẫn giải
Chọn D
A
C
B
A
https://toanmath.com/
Ta có
3
1 1 11
. . . .2 .
3 2 32 3
a
V SA CM CN a a a= = =
.
Câu 52: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật
AB a=
,
2BC a=
,
2SA a
=
,
SA
vuông góc với mặt phẳng
(
)
ABCD
. Tính thể tích khối chóp
.S ABCD
tính theo
a
.
A.
3
8
3
a
B.
3
4
3
a
C.
3
6
3
a
D.
3
4
a
Hướng dẫn giải
Chọn B
Ta có
.
ABCD
S AB CD=
2
2
a=
.
Thể tích khối chóp
.S ABCD
là
.
1
.
3
S ABCD ABCD
V SA S=
3
2
14
2 .2
33
a
aa
= =
.
Câu 53: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông, cạnh bên
2SA a
=
và
SA
vuông góc
với mặt phẳng đáy, tam giác
SBD
là tam giác đều. Thể tích của khối chóp
.S ABCD
bằng
A.
3
2.a
B.
3
2 2.a
C.
3
2
.
3
a
D.
3
22
3
a
.
Hướng dẫn giải
Chọn D
https://toanmath.com/
Đặt
AB x=
,
ABD∆
vuông cân tại
2.A BD x⇒=
Do
SBD∆
là tam giác đều
2.SB SD BD x⇒== =
Lại có
SAB∆
vuông tại
A
( ) ( )
22
222 2
22SA AB SB a x x⇒ + = ⇔ +=
22
22
x a xa⇒ = ⇒=
( )
3
2
.
1 1 22
. . . 2. 2
33 3
S ABCD ABCD
a
V SA S a a⇒= = =
.
Câu 54: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh bằng 1. Cạnh bên
SA
vuông góc với
mặt phẳng
( )
ABCD
và
5=SC
. Tính thể tích khối chóp
.S ABCD
.
A.
15
3
V
=
. B.
3V =
. C.
3
6
V
=
. D.
3
3
V =
.
Hướng dẫn giải
Chọn D
.
Đường chéo hình vuông
2AC =
.
Xét tam giác
SAC
, ta có
22
3SA SC AC= −=
.
Chiều cao khối chóp là
3SA =
.
Diện tích hình vuông
ABCD
là
2
11
ABCD
S = =
.
Thể tích khối chóp
.S ABCD
là:
.
13
.
33
S ABCD ABCD
V S SA= =
(đvtt).
Câu 55: Hình chóp tứ giác
.S ABCD
có đáy là hình chữ nhật cạnh
( )
, 2,
AB a AD a SA ABCD= = ⊥
, góc
giữa
SC
và đáy bằng
60°
. Thể tích hình chóp
.S ABCD
bằng:
A.
3
6a
. B.
3
3a
. C.
32a
. D.
3
2a
.
Hướng dẫn giải
Chọn D
Phương pháp: + Dựng hình như hình vẽ.
O
B
A
D
C
S
https://toanmath.com/
.
+ Xác định được góc giữa
SC
và đáy.
Cách giải: + Góc giữa
SC
và mặt đáy là
60SCA =
.
( )
2
2
23
AD a a a
=+=
.
Suy ra
tan 60 3= °=SH AD a
.
3
11
. 3.. 2 2
33
ABCD
V SA S a a a a= = =
.
Câu 56:
Hình chóp
.S ABCD
có đáy hình vuông,
SA
vuông góc với đáy và
3
SA a=
,
2AC a=
. Khi
đó thể tích khối chóp
.
S ABCD
là
A.
3
2
3
a
B.
3
2
2
a
C.
3
3
3
a
D.
3
3
2
a
Hướng dẫn giải
Chọn C
Ta có
ABCD
là hình vuông có
2AC a=
suy ra
AB a=
.
2
.
11
. 3.
33
S ABCD ABCD
V SA S a a= =
3
3
3
a
=
.
Câu 57: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác cân tại
A
,
2BC a=
,
120BAC = °
, biết
( )
SA ABC⊥
và mặt phẳng
( )
SBC
hợp với đáy một góc bằng
45°
. Tính thể tích khối chóp
.S ABC
.
A.
3
2a
. B.
. C.
. D.
.
Hướng dẫn giải
Chọn B
Gọi
I
là trung điểm của
BC
. Vì tam giác
ABC
cân tại
A
nên
AI BC⊥
và góc
30ACI = °
.
https://toanmath.com/
Trong tam giác
AIC
vuông tại
I
ta có:
33
tan30 .tan 30 .
33
AI a
AI IC a
IC
°= ⇒ = °= =
.
Diện tích đáy:
2
1 1.3 3
. .2
2 23 3
ABC
aa
S AI BC a
= = =
.
Ta có:
( ) (
)
SBC ABC BC
AI BC
SI BC
∩=
⊥
⊥
.
Góc giữa
(
)
SBC
và
( )
ABC
là
45SIA = °
.
Suy ra tam giác
SAI
vuông cân tại
3
3
a
A SA AI
⇒==
.
Thể tích khối chóp là là:
23
1 1 33
.. . .
3 33 3 9
ABC
aa a
V SA S= = =
.
Câu 58: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Cạnh bên
vuông góc với đáy
và có độ dài bằng
a
. Tính thể tích khối tứ diện
.S BCD
.
A.
3
2
a
. B.
. C.
. D.
3
3
a
.
Hướng dẫn giải
Chọn C
Ta có
3
2
.
1 11
..
3 32 6
S BCD BCD
a
V SH S a a= = =
.
Câu 59: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi cạnh
a
và góc
60
BAD = °
,
( )
SA ABCD⊥
.
Biết rằng khoảng cách từ
A
đến cạnh
SC
bằng
a
. Thể tích khối chóp
.S ABCD
là
A.
3
2
4
a
. B.
3
2
12
a
. C.
3
3
6
a
. D.
3
3a
.
Hướng dẫn giải
Chọn A
Tam giác
ABD
đều, có cạnh bằng
a
.
Suy ra
22
33
2 2.
42
ABCD ABD
aa
SS= = =
.
Kẻ
( )
,AH SC H SC⊥∈
, ta có
( )
,d A SC AH a= =
.
Gọi
O AC BD= ∩
,
23AC AO a= =
.
2 2 22
1112 6
32
a
SA
SA AH AC a
= − = ⇒=
.
https://toanmath.com/
3
.
12
.
34
S ABCD ABC
a
V S SA
∆
= =
.
.
Câu 60: Thể tích của tứ diện
OABC
có
,,OA OB OC
đôi một vuông góc,
=
OA a
,
2
=OB a
,
3=
OC a
là
A.
3
3a
. B.
3
2a
. C.
3
4a
. D.
3
a
.
Hướng dẫn giải
Chọn D
.
3
1 .2 .3
..
66
aaa
V OAOB OC a= = =
.
Câu 61: Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh a,
0
120 ,ABC =
( )
SA ABCD⊥
. Biết góc giữa
hai mặt phẳng
( )
SBC
và
( )
SCD
bằng
60°
. Tính
SA
A.
6
4
a
B.
6
.
2
a
C.
6a
D.
3
2
a
Hướng dẫn giải
Chọn A
60
o
O
H
a
D
C
B
A
S
O
A
D
B
C
S
M
B
A
C
a
2a
3a
https://toanmath.com/
Ta có
ABCD
là hình thoi cạnh
a
có
0
120ABC =
nên
,3BD a AC a= =
.
Nhận xét
BD SC⊥⇒
kẻ
( )
OM SC BDM SC⊥⇒ ⊥
do đó góc giữa hai mặt phẳng
( )
SBC
và
( )
SCD
là
0
120BMD
=
hoặc
0
60BMD =
.
TH1: Nếu
0
120
BMD =
mà tam giác
BMD
cân tại
M
nên
00
3
60 . 60
6
a
BMO MO BO cot
=⇒= =
Mà tam giác
OCM
đồng dạng với tam giác
SCA
nên
.6
4
SACD a
OM SA
SC
= ⇒=
.
TH2: Nếu
0
60BMD =
thì tam giác
BMD
là tam giác đều nên
3
2
OM a=
.
OM OC⇒=
vô lý vì
OMC∆
vuông tại
M
.
Câu 62: Cho hình chóp có vuông góc với mặt phẳng đáy, tam giác đều cạnh , góc
giữa mặt phẳng và đáy là . Thể tích khối chóp là.
A. . B. . C. . D. .
Hướng dẫn giải
Chọn C
.
Vì tam giác đều nên suy ra . Gọi M là trung điểm của BC thì . Mà
nên . Do đó: .
Vì tam giác đều nên .
Xét tam giác vuông ta có: .
Vậy, thể tích khối chóp là: .
Câu 63: Cho khối chóp
.S ABCD
có đáy là hình chữ nhậ,
AB a=
,
3AD a=
,
SA
vuông góc với đáy và
mặt phẳng
( )
SBC
tạo với đáy một góc
60°
. Tính thể tích
V
của khối chóp
.S ABCD
.
A.
3
3
a
V =
. B.
3
3
Va=
. C.
3
3
3
a
V =
. D.
3
Va=
.
Hướng dẫn giải
Chọn D
.S ABC
SA
SBC
a
( )
SBC
30°
.S ABC
3
3
24
a
V =
3
3
64
a
V =
3
3
16
a
V =
3
3
32
a
V =
SBC
AB AC=
AM BC
⊥
BC SA⊥
BC SM⊥
( ) ( )
( )
0
, 30SBC ABC SMA
= =
SBC
3
2
SM a=
,SAM
0
0
3
.sin30
4
3
.co 3
4
s 0
SA SM a
a
AM SM
= =
= =
.S ABC
.
3
1 1 13 3 3
. . . ..
3 3 3 4 4 16
ACAB B
SC
aa
V S SA AM BC SA a a= = = =
https://toanmath.com/
Ta có
( ) ( )
( ) ( )
, 60
SBC ABCD BC
BC AB SBC ABCD
BC SB
∩=
⊥ ⇒=°
⊥
.
Suy ra
.tan 60 3SA a a= °=
.
Tính thể tích
V
của khối chóp
.S ABCD
là
3
11
.. .3..3
33
ABCD
V SAS a a a a
= = =
.
Câu 64: Hình chóp
.S ABC
có đáy là tam giác
ABC
vuông cân tại
B
,
2
2
=
a
AC
;
SA
vuông góc với mặt
đáy. Góc giữa mặt bên
( )
SBC
và mặt đáy bằng
45 .°
Tính theo
a
thể tích khối chóp
..S ABC
A.
3
48
a
. B.
3
16
a
. C.
3
3
48
a
. D.
3
2
48
a
.
Hướng dẫn giải
Chọn A
.
Tam giác
ABC
vuông cân tại
B
,
2
2
a
AC =
.
Nên
2
1
, . . .
22 8
ABC
aa
AB BC S BA BC
∆
= = = =
Ta có:
( ) ( )
( ) ( )
( )
( ), , 45
( ),
∩=
⊂ ⊥⇒ = =°
⊂⊥
SBC ABC BC
AB ABC AB BC ABC SBC SBA
SB SBC SB BC
.
Tam giác
SAB
vuông cân tại
A
nên
.
2
a
SA AB= =
Vậy:
23
.
11
. . ..
3 3 2 8 48
S ABC ABC
aa a
V SA S
∆
= = =
.
Câu 65: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
SA
vuông góc với mặt phẳng đáy.
Gọi
I
là trung điểm của
BC
, góc giữa
( )
SBC
và
( )
ABC
bằng
30
°
. Thể tích khối chóp
.S ABC
bằng:
A.
3
6
24
a
. B.
3
6
8
a
. C.
3
3
24
a
. D.
3
3
8
a
.
Hướng dẫn giải
Chọn C
https://toanmath.com/
Ta có
BC SA
BC AI
⊥
⊥
( )
BC SAI⇒⊥
BC SI⇒⊥
( ) ( )
( )
,ABC SBC SIA⇒=
30
°
=
.
Do tam giác
ABC
đều cạnh
a
nên
3
2
a
AI
=
.
Xét tam giác vuông
SAI
có
.tanSA AI SIA=
13
.
2
3
a
SA⇔=
2
a
=
.
Thể tích khối chóp
.
S ABC
là
.
11
.. . .
32
S ABC
V BC AI SA
=
13
.. .
6 22
aa
a=
3
3
24
a
=
.
Câu 66: Cho khối chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
.
SA
vuông góc với
( )
ABCD
,
3SC a=
. Tính thể tích khối chóp
.
S ABCD
theo
a
.
A.
3
.S ABCD
Va=
. B.
3
.
3
S ABCD
a
V =
. C.
3
.
3
9
S ABCD
a
V =
. D.
3
.
3
3
S ABCD
a
V =
.
Hướng dẫn giải
Chọn B
Xét tam giác vuông
SAC
có
2 2 22
32SA SC AC a a a= − = −=
.
Thể tích khối chóp
.S ABCD
là
3
2
.
1
..
33
S ABCD
a
V aa= =
.
Câu 67: Cho hình chóp
SABC
có đáy
ABC
là tam giác vuông cân tại
B
,
AB a
, góc giữa mặt phẳng
SBC
và mặt phẳng
ABC
bằng
o
60
,
.SA ABC
Gọi
M
,
N
lần lượt là trung điểm của
SC
và
AC
. Tính thể tích khối chóp
MNBC
?
I
A
C
B
S
A
B
C
D
S
https://toanmath.com/
A.
3
4
a
. B.
3
3
24
a
. C.
3
6
18
a
. D.
3
3
12
a
.
Hướng dẫn giải
Chọn B
.
Ta có:
( )
(SBC),(ABC) 60= = °SBA
.
0
tan 60 3
SA
SA a
AB
= ⇒=
;
3
.
1 11 3
. . 3. .
3 32 6
S ABC ABC
V SA S a a a a

= = =


.
3
.
.
11 3
.
4 4 24
MNBC
MNBC C SAB
C SAB
V
CM CN a
VV
V CS CA
= =⇒= =
.
Câu 68: Hình chóp tứ giác
.S ABCD
có đáy là hình chữ nhật cạnh
,2AB a AD a= =
,
( )
SA ABCD⊥
,
góc giữa
SC
và mặt phẳng đáy bằng
60
°
. Thể tích khối chóp
.S ABCD
bằng:
A.
3
2a
. B.
3
6
a
.
C.
3
3a
.
D.
3
32a
.
Hướng dẫn giải
Chọn A
.
( )
SA ABCD⊥
nên
AC
là hình chiếu vuông góc của
SC
lên mặt phẳng
( )
ABCD
.
Xét
ABC∆
vuông tại
B
, ta có.
2 2 22
23AC AB BC a a a= + =+=
.
Xét
SAC
∆
vuông tại
A
,
( )
( )
SA ABCD SA AC⊥ ⇒⊥
.
Ta có:
tan .tan .tan 60 3. 3 3
SA
SCA SA AC SCA AC a a
AC
= ⇒ = = °= =
.
Vậy thể tích hình chóp
.S ABCD
là
3
.
11
. . .3 . . 2 2
33
S ABCD ABCD
V SAS aaa a= = =
.
https://toanmath.com/
Câu 69: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
( )
SA ABCD⊥
,
SC
tạo với mặt
đáy một góc bằng
60
. Tính thể tích
V
của khối chóp đã cho.
A.
3
3
3
a
V =
. B.
3
6
6
a
V =
. C.
3
3
6
a
V =
. D.
3
6
3
a
V
=
.
Hướng dẫn giải
Chọn D
Diện tích đáy:
2
ABCD
Sa=
.
( )
SA ABCD⊥
nên góc giữa
SC
và mặt phẳng đáy là
60SCA =
.
Tam giác
SAC
vuông tại
A
nên
.tan 2.tan 60 6
SA AC SCA a a= = =
.
Vậy
3
16
.
33
ABCD
a
V SA S= =
.
Cho hình chóp
SABC
có đáy
ABC
là tam giác vuông cân tại
B
với
AC a=
biết
SA
vuông góc với đáy
ABC
và
SB
hợp với đáy một góc
60°
. Tính thể tích hình chóp.
A.
3
6
24
a
. B.
3
3
24
a
. C.
3
6
48
a
. D.
3
6
8
a
.
Hướng dẫn giải
Chọn A
https://toanmath.com/
.
Do tam giác
ABC
vuông cân tại
B
nên
22
= = =
AC a
AB BC
.
2
1
.
24
= =
ABC
a
S AB BC
.
Theo giả thiết
60= °SBA
nên
6
.tan 60
2
= °=
a
SA AB
.
3
16
.
3 24
= =
SABC ABC
a
V SA S
.
Câu 70: Hình chóp
.S ABC
có đáy là tam giác
ABC
vuông cân tại
,B
2
;
2
a
AC
=
SA
vuông góc với mặt
đáy. Góc giữa mặt bên
( )
SBC
và mặt đáy bằng
45 .°
Tính theo
a
thể tích khối chóp
..S ABC
A.
3
2
.
48
a
B.
3
.
48
a
C.
3
3
.
48
a
D.
3
.
16
a
Hướng dẫn giải
Chọn B
Tam giác
ABC
vuông cân tại
,B
2
2
a
AC =
Nên
2
1
, . . .
22 8
ABC
aa
AB BC S BA BC
∆
= = = =
Ta có:
( ) ( )
( ) ( )
(
)
0
( ), , 45
( ),
SBC ABC BC
AB ABC AB BC ABC SBC SBA
SB SBC SB BC
∩=
⊂ ⊥⇒ = =
⊂⊥
Tam giác
SAB
vuông cân tại
A
nên
.
2
a
SA AB= =
A
C
B
A
S
A
B
C
https://toanmath.com/
Vậy:
23
.
11
. . ..
3 3 2 8 48
S ABC ABC
aa a
V SA S
∆
= = =
.
Câu 71: Cho hình chóp
.S ABCD
với
ABCD
là hình vuông cạnh
a
. Mặt bên
SAB
là tam giác cân tại
S
và nằm trên mặt phẳng vuông góc với mặt phẳng đáy. Cạnh bên
SC
tạo với đáy một góc
60°
. Tính thể tích khối chóp
.S ABCD
.
A.
3
6
3
a
. B.
3
3
6
a
. C.
3
15
2
a
. D.
3
15
6
a
.
Hướng dẫn giải
Chọn D
Gọi
I
là trung điểm của
AB
.
Ta có:
SAB∆
cân tại
S
⇒
SI AB⊥
( )
1
Mặt khác:
( ) ( )
( ) ( )
SAB ABCD
SAB ABCD AB
⊥
∩=
( )
2
Từ
( )
1
và
( )
2
, suy ra:
( )
SI ABCD⊥
SI
⇒
là chiều cao của hình chóp
.S ABCD
⇒
IC
là hình chiếu của
SC
lên mặt phẳng
( )
ABCD
( )
( )
( )
, , 60SC ABCD SC IC SCI⇒===°
Xét
IBC∆
vuông tại
B
, ta có:
2
22 2
5
22
aa
IC IB BC a

= + = +=


Xét
SIC∆
vuông tại
I
, ta có:
5 15
.tan60 . 3
22
aa
SI IC= °= =
Vậy thể tích khối chóp
.S ABCD
là:
3
2
1 1 15 15
. . ..
3 32 6
ABCD
aa
V S SI a= = =
.
Câu 72: Cho hình chóp
.S ABCD
có
( )
SA ABCD⊥
,
ABCD
là hình chữ nhật.
2SA AD a= =
. Góc giữa
( )
SBC
và mặt đáy
( )
ABCD
là
60°
. Gọi
G
là trọng tâm tam giác
SBC
. Tính thể tích khối chóp
.S AGD
là
A
a
a
I
D
C
B
S
https://toanmath.com/
A.
3
32 3
27
a
. B.
3
83
27
a
. C.
3
43
9
a
. D.
3
16
93
a
.
Hướng dẫn giải
Chọn B
Vì góc giữa
( )
SBC
và mặt đáy
( )
ABCD
là
60°
nên
60SBA = °
2
tan 60
3
SA a
AB⇒= =
°
.
Khi đó:
2
2 43
. .2
3
3
ABCD
aa
S AB AD a= = =
.
Gọi
M
là trung điểm
BC
, khi đó:
2
1 23
23
ADM ABCD
a
SS= =
.
⇒
23
..
2 21 2 3 8 3
. .2 .
3 3 3 3 27
S ADG S ADM
aa
VV a= = =
.
Câu 73: Hình chóp
.S ABCD
có đáy là hình vuông,
a
là độ dài cạnh đáy. Cạnh bên
SA
vuông góc với
đáy,
SC
tạo với
( )
SAB
góc
o
30
. Thể tích khối chóp
.S ABCD
là:
A.
3
2
2
a
B.
3
3
3
a
. C.
3
2
4
a
. D.
3
2
3
a
.
Hướng dẫn giải
Chọn D
G
M
D
A
B
C
S
https://toanmath.com/
Ta có
2
ABCD
Sa
=
( )
CB AB
CB SAB
CB SA
⊥
⇒⊥
⊥
SB là hình chiếu vuông góc của SC lên
( )
SAB
( )
( )
( )
, , 30SC SAB SC SB CSB⇒===°
Xét
CSB∆
vuông tại B có
3
tan
BC
SB a
CSB
= =
22
2SA SB AB a= −=
3
.
12
.
33
S ABCD ABCD
a
V S SA= =
.
Câu 74: Cho hình chóp
.S ABCD
có
(
)
SA ABCD⊥
,
2AC a
=
,
2
3
2
ABCD
a
S =
và góc giữa đường thẳng
SC
và mặt phẳng
ABCD
bằng
60°
. Gọi
H
là hình chiếu vuông góc của
A
trên
SC
. Tính theo
a
thể tích của khối chóp
.H ABCD
.
A.
3
36
4
a
. B.
3
6
2
a
. C.
3
6
4
a
. D.
3
6
8
a
.
Hướng dẫn giải
Chọn D
Ta có
( )
SA ABCD⊥
⇒
Góc toạ bởi
SC
và mặt phẳng
( )
ABCD
là
60SCA = °
.
Lại có
tan 60 6SA AC a= °=
,
2 2 22
6 2 22
SC SA AC a a a= + = +=
.
Do đó
22
2
22
21
.
84
CH AC a
AC CH SC
SC SC a
= ⇒= ==
.
( )
( )
( )
( )
(
)
( )
,
36
,
44
,
d H ABCD
SH a
d H ABCD
SC
d H ABCD
==⇒=
.
Thể tích của khối chóp
.H ABCD
là
23
1 63 6
..
34 2 8
a aa
V = =
.
Câu 75: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
vuông góc với mặt đáy
( )
,ABCD
,2AB a AD a= =
. Góc giữa cạnh bên
SB
và mặt phẳng
( )
ABCD
bằng
o
45
. Thể tích hình chóp
.S ABCD
bằng.
https://toanmath.com/
A.
3
22
3
a
. B.
3
6
18
a
. C.
. D.
3
2
3
a
.
Hướng dẫn giải
Chọn D
3
1 12
. ...2
3 33
ABCD
a
V SA S a a a= = =
.
Câu 76: Cho hình chóp
.S ABC
có
AB a=
,
3BC a
=
,
5AC a=
và
SA
vuông góc với mặt đáy,
SB
tạo với đáy góc
45°
. Thể tích của khối chóp
.S ABC
là:
A.
3
15
12
a
. B.
3
12
a
. C.
3
3
12
a
. D.
3
11
12
a
.
Hướng dẫn giải
Chọn D
Góc
( )
(
)
( )
, , 45SB ABC SB AB SBA= = = °
.
SBA∆
vuông tại A có
45SBA SA AB a= ° → = =
222
3 5 55
cos sin
2. . 10 10
AB AC BC
BAC BAC
AB AC
+−
= =→=
.
2
1 11
. .sin
24
ABC
a
S AB AC BAC= =
23
.
1 1 11 11
..
3 3 4 12
S ABC ABC
aa
V S SA a= = =
.
Câu 77: Hình chóp tứ giác
.S ABCD
có đáy là hình chữ nhật cạnh
AB a
=
,
2AD a=
;
(
)
SA ABCD
⊥
,
góc giữa
SC
và đáy bằng
60°
. Tính theo
a
thể tích khối chóp
.S ABCD
.
A.
3
32a
. B.
3
3
a
. C.
3
6a
. D.
3
2a
.
Hướng dẫn giải
Chọn D
https://toanmath.com/
Ta có
( )
2
222
23AC AB BC a a a= +=+ =
( ,( )) 60SCA SC ABCD= = °
Vậy
.tan 3.tan 60 3SA AC SCA a a= = °=
. Ngoài ra
2
.2 2
ABCD
S aa a
= =
nên
23
.
11
. .3 . 2 2
33
S ABCD ABCD
V SA S a a a
= = =
.
Câu 78: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
,a SA
vuông góc với mặt phẳng đáy,
góc giữa
( )
SBC
và
( )
ABC
bằng
30 .°
Thể tích khối chóp
.S ABC
là
A.
3
6
.
8
a
B.
3
3
.
24
a
C.
3
3
.
8
a
D.
3
6
.
24
a
Hướng dẫn giải
Chọn B
Từ
A
kẻ
AM
⊥
BC
,
ta có:
()
()
SA ABC SA BC
BC SAM
BC AM
⊥ ⇒⊥
⇒⊥
⊥
( ) (ABC) BC
()
( )( ) ;( )( )
SBC
BC SAM
SAM SBC SM SAM ABC AM
∩=
⊥
∩= ∩ =
0
(( ),(ABC)) 30SBC SMA⇒==
Xét tam giác vuông
AMB
ta có
22 2
AM AB BM= −
2
2
2
a
a

= −


2
3
4
a
=
⇒
3
2
a
AM =
https://toanmath.com/
Xét tam giác vuông
SAM
ta có
.tanSA AM SMA=
0
3
tan30
2
a
=
2
a
=
Suy ra:
1
.
3
SABC
V SA S ABC
=
2
13
..
32 4
aa
=
3
3
24
a
=
.
Câu 79: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
, cạnh bên
SA
vuông góc với đáy,
đường thẳng
SC
tạo với đáy một góc bằng
60°
. Thể tích của khối chóp
.S ABC
bằng
A.
3
3
4
a
. B.
3
8
a
. C.
3
4
a
. D.
3
2
a
.
Hướng dẫn giải
Chọn C
Diện tích
ABC∆
là
2
3
4
ABC
a
S
∆
=
.
(
)
SA ABC⊥
nên
AC
là hình chiếu của
SC
lên
( )
ABC
.
( )
( )
( )
, , 60SC ABC SC AC SCA⇒===°
.
SAC∆
vuông tại
A
có
60SCA = °
, ta có
.tan 3SA AC SCA a= =
.
Thể tích khối chóp là
23
1 13
. . . .3
3 34 4
ABC
aa
V S SA a
∆
= = =
.
Câu 80: Cho tứ diện
.
O ABC
có
OA
,
OB
,
OC
đôi một vuông góc với nhau và
2OA a=
,
3OB a=
,
8OC a=
.
M
là trung điểm của
.OC
Tính thể tích
V
của khối tứ diện
.O ABM
.
A.
3
6Va=
. B.
3
8Va=
. C.
3
4Va=
. D.
3
3Va=
.
Hướng dẫn giải
Chọn C
https://toanmath.com/
.
Vì
( )
OB OA
OB OAC
OB OC
⊥
⇒⊥
⊥
.
.
1 11
. 3. .
3 32
OABM B AOM AOM
V V BO S a OAOM= = =
3
1
3 .2 .4 4
6
aaa a
= =
.
Câu 81: Cho khối chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
. Hai mặt bên
( )
SAB
và
(
)
SAC
cùng vuông góc với đáy. Tính thể tích khối chóp biết
3SC a=
.
A.
3
3
2
a
B.
3
26
9
a
. C.
3
6
12
a
. D.
3
3
4
a
.
Hướng dẫn giải
Chọn C
Ta có:
(
) ( )
( ) ( )
(
)
SAB ABC
SA ABC
SAC ABC
⊥
⇒⊥
⊥
+)
2
22
3
2;
4
ABC
a
SA SC AC a S= −= =
3
.
16
..
3 12
S ABC ABC
a
V SA S⇒= =
.
Câu 82: Cho khối chóp
.S ABC
có
()SA ABC⊥
,
ABC∆
vuông tại
B
,
2SB a=
,
5SC a=
. Thể tích khối
chóp
.S ABC
bằng
3
a
. Khoảng cách từ
A
đến
( )
SBC
là:
A.
2a
. B.
3a
. C.
3a
. D.
6a
.
Hướng dẫn giải
Chọn B
https://toanmath.com/
.
Ta có
SA BC
SB BC
AB BC
⊥
⇒⊥
⊥
.
SBC⇒∆
vuông tại
B
.
Do đó:
22 2 2
( 5) (2 )BC SC SB a a a= −= − =
.
2
1
.
2
SBC
S SB BC a
∆
= =
.
Vậy:
3
.
2
3
3.
( ,( )) 3
A SBC
SBC
V
a
d A SBC a
Sa
∆
= = =
.
Câu 83: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
A
,
=AB a
,
2=
AC a
,
3=SC a
,
SA
vuông góc với đáy
( )
ABC
. Thể tích khối chóp
.
S ABC
là.
A.
3
5
3
a
. B.
3
3
12
a
. C.
3
4
a
. D.
3
3
4
a
.
Hướng dẫn giải
Chọn A
Phân tích: Tam giác
SAC
vuông tại
A
nên
( ) ( )
22
22
32 5= −= − =SA SC AC a a a
.
Khi đó
3
.
1 11 5
. . . 5. .2
3 32 3
= = =
S ABCD ABC
a
V SA S a a a
.
Câu 84: Cho hình chóp
.S ABC
có
ABC
là tam giác đều cạnh
a
và
SA
vuông góc với đáy. Góc tạo bởi
mặt phẳng
( )
SBC
và mặt phẳng
( )
ABC
bằng
30°
. Thể tích của khối chóp
.S ABC
là
A. . B. . C. . D. .
3
3
24
a
3
4
a
3
12
a
3
3
8
a
2a
a
A
S
C
B
a
5
2a
A
B
C
S
https://toanmath.com/
Hướng dẫn giải
Chọn A
Gọi là trung điểm . Suy ra .
.
Câu 85: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
. Cạnh bên
SA
vuông góc với mặt phẳng
đáy, cạnh bên
SC
tạo với mặt phẳng
( )
SAB
một góc
30°
. Thể tích của khối chóp
.
S ABCD
bằng:
A.
3
2
3
a
. B.
3
2
4
a
. C.
3
2
2
a
. D.
3
3
3
a
.
Hướng dẫn giải
Chọn A
Ta có:
ABCD
là hình vuông cạnh
a
nên
2
ABCD
Sa
=
Vì hình chóp
.S ABCD
có đáy là hình vuông, cạnh bên
SA
vuông góc với mặt phẳng đáy
( )
BC SAB⇒⊥
.
Cạnh bên
SC
tạo với mặt phẳng
( )
SAB
một góc
30°
30CSB⇒=°
.
Tam giác
SBC
vuông tại
B
có
30CSB = °
,
60SCB = °
,
BC a
=
.
sin sin
SB BC
SCB CSB
⇒=
3SB a
⇒=
.
Từ giả thiết
SA AB⇒⊥
. Tam giác
SAB
có
22
2SA SB AB a= −=
.
3
12
.
33
SABCD ABCD
a
V SA S⇒= =
.
Câu 86: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
. Cạnh bên
vuông góc với mặt phẳng
đáy, cạnh bên
SC
tạo với mặt phẳng
( )
SAB
một góc
30°
. Thể tích của khối chóp đó bằng.
M
BC
30SMA = °
3
tan tan30
22
aa
SA AM SMA= = °=
23
.
1 1 33
. .. .
3 3 2 4 24
S ABC ABC
aa a
V SA S= = =
O
C
B
D
s
A
S
A
B
C
M
30°
https://toanmath.com/
.
A.
3
2
2
a
. B.
3
3
3
a
. C.
3
2
4
a
. D.
3
2
3
a
.
Hướng dẫn giải
Chọn D
( )
( )
( )
0
, , 30SC SAB SC SB BSC= = =
.
0 22
tan30 3 ; SA= 2
a
SB a SB AB a
SB
=⇔= − =
.
3
12
.
33
SABCD ABCD
a
V SA S= =
.
Câu 87: Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
C
và
SA
vuông góc với mặt phẳng
( )
ABC
. Biết
4AB a=
và góc giữa mặt phẳng
( )
SBC
và
( )
ABC
bằng
45°
. Tính thể tích
V
của
khối chóp
.
S ABC
.
A.
3
82
3
Va=
. B.
3
32
2
Va=
. C.
3
1
6
Va=
. D.
3
2
6
Va=
.
Hướng dẫn giải
Chọn A
.
( ) ( )
SBC ABC BC
AC BC
SC BC
∩=
⊥
⊥
suy ra góc giữa
( )
SBC
và
( )
ABC
là góc
45SCA∠=°
.
4
22
2
a
SA AC a⇒= = =
.
Thể tích khối chóp là
( )
3
2
1 1 1 82
.. .22..22
3 32 3
ABC
a
V SA S a a= = =
.
Câu 88: Cho hình chóp tứ giác
.S ABCD
có đáy là hình chữ nhật,
AB a=
,
2AD a=
. Biết
( )
SA ABCD⊥
và góc giữa đường thẳng
SC
với mặt phẳng đáy bằng
45°
. Thể tích khối chóp
.S ABCD
bằng:
A
D
B
C
S
4a
A
C
B
S
https://toanmath.com/
A.
3
3a
. B.
3
6a
. C.
3
6
3
a
. D.
3
2a
.
Hướng dẫn giải
Chọn C
Vì AC là hình chiếu vuông góc của SC trên mp
( )
ABCD
.
Suy ra
(
)
(
)
( )
, , 45SC ABCD SC AC SCA= = = °
.
Tam giác SAC vuông tại A, có
tan
SA
SCA SA AC
AC
= ⇒=
.
Tam giác ABC vuông tại A, có
22
3AC AB BC a= +=
.
Vậy thể tích khối chóp S.ABCD là
3
.
16
..
33
S ABCD ABCD
a
V SA S= =
.
Câu 89: Cho khối chóp
.S ABC
có đáy
ABC
là tam giác vuông cân có cạnh huyền
BC a=
và
vuông
góc với mặt phẳng đáy. Biết góc giữa mặt phẳng
( )
SBC
và mặt phẳng
( )
ABC
bằng
45°
. Thể
tích của hình chóp
.S ABC
là.
A.
3
.
2
24
S ABC
a
V =
. B.
3
.
8
S ABC
a
V
=
. C.
3
.
24
S ABC
a
V =
. D.
3
.
2
8
S ABC
a
V =
.
Hướng dẫn giải
Chọn C
.
Gọi M là trung điểm
BC AM
BC BC SM
BC SA
⊥
⇒ ⇒⊥
⊥
.
( ) ( )
(
)
( )
0
, , 45
22
BC a
SBC SAM SM AM SMA SA AM= = = ⇒= = =
.
2
2 1 122
.
2 2 22 2 4
2
ABC
BC a a a a
AB AC S AB AC
∆
===⇒= = =
.
a
A
B
C
S
M
https://toanmath.com/
23
.
1
..
3 2 4 24
S ABC
aa a
V
= =
(đvtt).
Câu 90: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
a
. Các mặt bên
( )
SAB
,
( )
SAC
cùng vuông
góc với mặt đáy
( )
ABC
; góc giữa
SB
và mặt
( )
ABC
bằng
60
°
. Tính thể tích khối chóp
.S ABC
.
A.
3
12
a
. B.
3
3
4
a
. C.
3
2
a
. D.
3
4
a
.
Hướng dẫn giải
Chọn D
Ta có
( ) ( )
( ) ( )
( )
SAB ABC
SA ABC
SAC ABC
⊥
⇒⊥
⊥
Ta có
( ) { }
SB ABC B∩=
và
( )
SA ABC⊥
( )
( )
(
)
, , 60
SB ABC SB AB SBA⇒===°
Mà
.tan60 3AB a SA a a= ⇒ = °=
Ta có
2
3
4
ABC
a
S =
23
.
1 13
. . 3.
3 3 44
S ABC ABC
aa
V SA S a⇒= = =
.
Câu 91: Cho khối chóp
.S ABC
, có đáy
ABC
là tam giác đều cạnh
a
. Hai mặt bên
( )
SAB
và
( )
SAC
cùng vuông góc với đáy. Tính thể tích khối chóp biết
3SC a=
.
A.
3
6
3
a
V =
. B.
3
6
6
a
V =
. C.
3
6
12
a
V =
. D.
3
6
8
a
V =
.
Hướng dẫn giải
Chọn C
.
A
C
B
S
https://toanmath.com/
Hai mặt bên
(
)
SAB
và
(
)
SAC
cùng vuông góc với đáy
( )
SA ABC⊥
.
Ta có
23
1 2. 3 6
.
3 12 12
ABC
aa a
V SA S
∆
= = =
.
Câu 92: Cho hình chóp
.
S ABC
là tam giác vuông tại
A
,
30
o
ABC =
,
BC a
=
. Hai mặt bên
( )
SAB
và
( )
SAC
cùng vương góc với đáy
( )
ABC
, mặt bên
( )
SBC
tạo với đáy một góc
0
45
. Thể tích của
khối chóp
.S ABC
là:
A.
3
9
a
. B.
3
32
a
. C.
3
64
a
. D.
3
16
a
.
Hướng dẫn giải
Chọn B
Ta có:
(
) (
)
(
) (
)
( )
( )
(
)
SAB ABC
SAC ABC SA ABC
SAB SAC SA
⊥
⊥ ⇒⊥
∩=
.
Kẻ
AH BC SH BC⊥⇒⊥
Khi đó:
( ) (
)
45
o
SBC ABC BC
BC AH SHA
BC SH
∩=
⊥ ⇒=
⊥
Mà
0
3
.cos30
2
a
AB BC= =
và
.sin30
2
o
a
AC BC= =
nên
0
3
.sin30
4
a
AH AB= =
Nên
3
4
a
SA =
Do đó:
3
11
. ..
3 6 32
ABC
a
V S SA AB AC SA= = =
.
Câu 93: Cho khối chóp
.S ABC
có
( )
SA ABC⊥
,
SA a=
,
AB a=
,
2AC a=
và
120
BAC = °
. Tính thể
tích khối chóp
.S ABC
.
A.
3
3a
. B.
3
3
6
a
. C.
3
3
3
a
. D.
3
3
2
a
.
Hướng dẫn giải
https://toanmath.com/
Chọn B
Ta có:
3
.
1 11 3
. . . .sin
3 32 6
S ABC ABC
a
V SA S SA AB AC BAC
∆
= = =
(đvtt).
Vậy thể tích khối chóp
.S ABC
là
3
3
6
a
.
Câu 94: Tính thể tích khối chóp
.S ABC
có
AB a=
,
2AC a=
,
120BAC = °
,
( )
SA ABC⊥
, góc giữa
( )
SBC
và
( )
ABC
là
60
°
.
A.
3
7
7
a
. B.
3
21
14
a
. C.
3
7
14
a
. D.
3
3 21
14
a
.
Hướng dẫn giải
Chọn C
+ Diện tích đáy
1
. .sin120
2
ABC
S AB AC= °
13
. .2 .
22
aa=
2
3
2
a=
+ Tính chiều cao
SA
:
• Dựng
AH BC⊥
(với
H BC∈
) suy ra
SH BC⊥
, do đó góc
( ) ( )
( )
, 60SBC ABC SHA= = °
,
suy ra
.tan 60
SA AH= °
A
C
B
S
60
o
120
o
2a
a
A
C
B
S
H
https://toanmath.com/
• Tính
AH
: ta có diện tích
1
.
2
ABC
S AH BC=
2.
ABC
S
AH
BC
⇒=
mà theo định lý hàm côsin thì
222
2. . .cosBC AB AC AB AC A=+−
22
1
4 2. .2 .
2
a a aa

=+− −


2
7a=
7BC a⇒=
, suy ra
2
3
2.
21
2
7
7
a
AH a
a
= =
.
+ KL: Thể tích khối chóp
.S ABC
là
1
.
3
ABC
V S SA=
2
1 3 21
..
32 7
aa=
3
7
14
a=
(đvtt).
Câu 95: Hình chóp tứ giác
.S ABCD
có đáy là hình chữ nhật cạnh
AB a=
,
2AD a=
,
(
)
SA ABCD
⊥
,
góc giữa
SC
và đáy bằng
60°
. Thể tích hình chóp
.S ABCD
bằng
A.
3
32a
. B.
3
2a
. C.
3
3a
. D.
3
6a
.
Hướng dẫn giải
Chọn B
Ta có
22
3AC AB BC a= +=
.
Góc giữa
SC
và đáy bằng góc
60SCA = °
. Suy ra
.tan 60 3SA AC a= °=
.
Thể tích hình chóp bằng
23
.
11
. 3. 2 2
33
S ABCD ABCD
V SA S a a a= = =
.
Câu 96: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng
đáy và cạnh bên
SD
hợp với đáy một góc
60
°
. Hỏi thể tích
V
của khối chóp
.S ABCD
bằng
bao nhiêu?
A.
3
23
3
a
V =
. B.
3
3Va=
. C.
3
3
6
a
V =
. D.
3
3
3
a
V =
.
Hướng dẫn giải
Chọn D
C
A
D
B
S
https://toanmath.com/
.
Theo đề có :
60 .tan60 3
= °⇒ = °=SDA SA AD a
.
Thể tích
V
của khối chóp
.S ABCD
:
. ..= = =
ABCD
a
V dt SA a a
3
2
11 3
3
33 3
.
Câu 97: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
a
. Cạnh
vuông góc với
đáy và
SA y
=
. Trên cạnh
AD
lấy điểm
M
sao cho
AM x=
. Biết rằng
222
xya+=
. Tìm giá trị
lớn nhất của thể tích khối chóp
.S ABCM
.
A.
. B.
3
3
8
a
. C.
3
3
2
a
. D.
3
3
4
a
.
Hướng dẫn giải
Chọn B
.
Ta có
0 xa<<
;
22
y ax= −
.
(
)
.
11
..
3 32
S ABCM ABCM
x aa
V SA S y
+
= =
( )
22
1
6
aa x x a= −+
.
Xét hàm số
( ) ( )
22
fx a x xa=−+
.
(
)
22
22
2
x ax a
fx
ax
− −+
′
=
−
.
( )
0
2
xa
fx
a
x
= −
′
= ⇔
=
nhận
2
a
x =
.
a
a
a
a
S
A
D
B
C
https://toanmath.com/
.
( )
2
33
24
aa
Max f x f

⇒==


.
3
.
3
8
S ABCM
a
MaxV
=
.

Tài liệu khác của Toán 12

Preview text:


THỂ TÍCH KHỐI CHÓP CÓ MỘT CẠNH BÊN VUÔNG GÓC VỚI ĐÁY A. BÀI TẬP Câu 1:
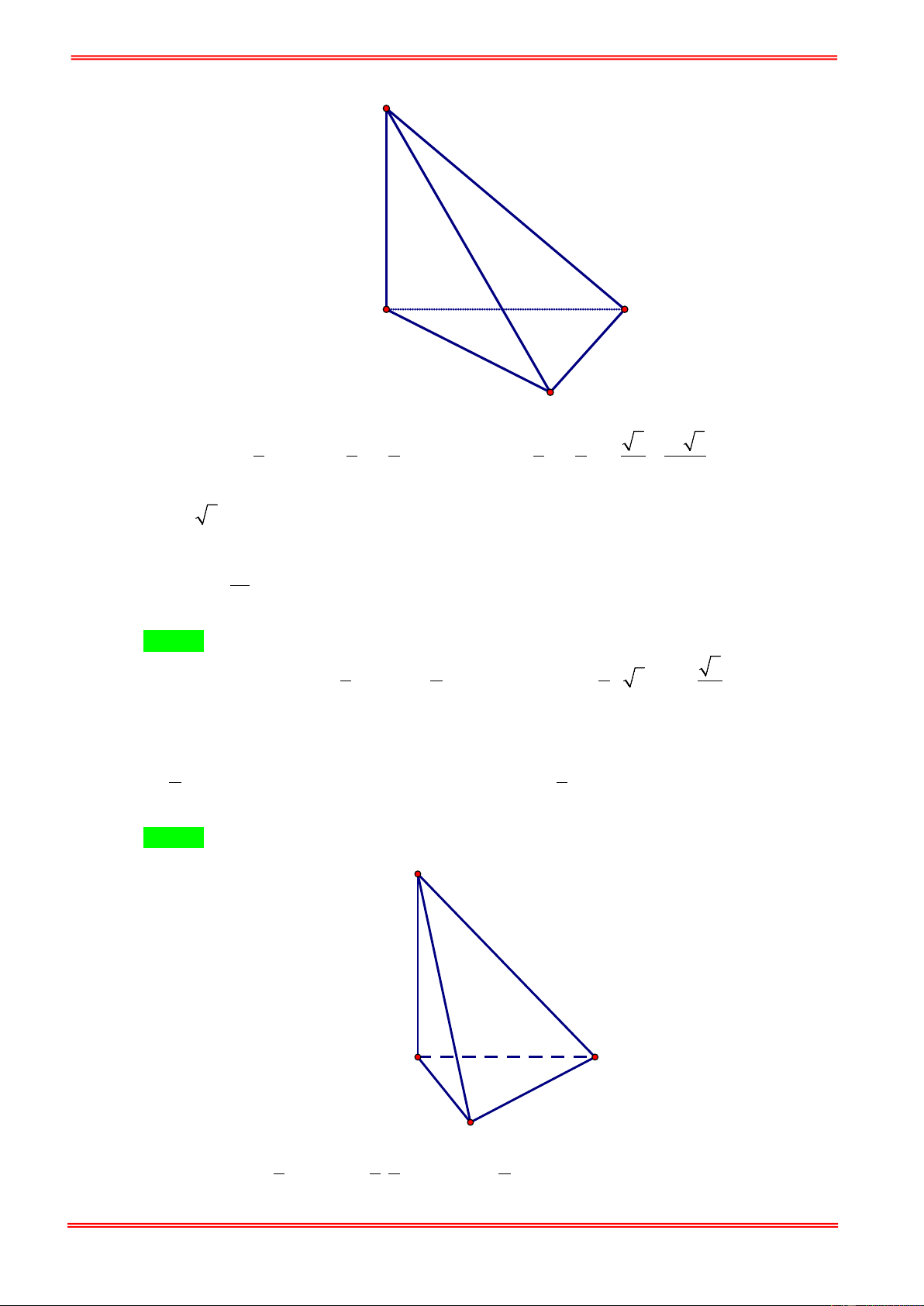
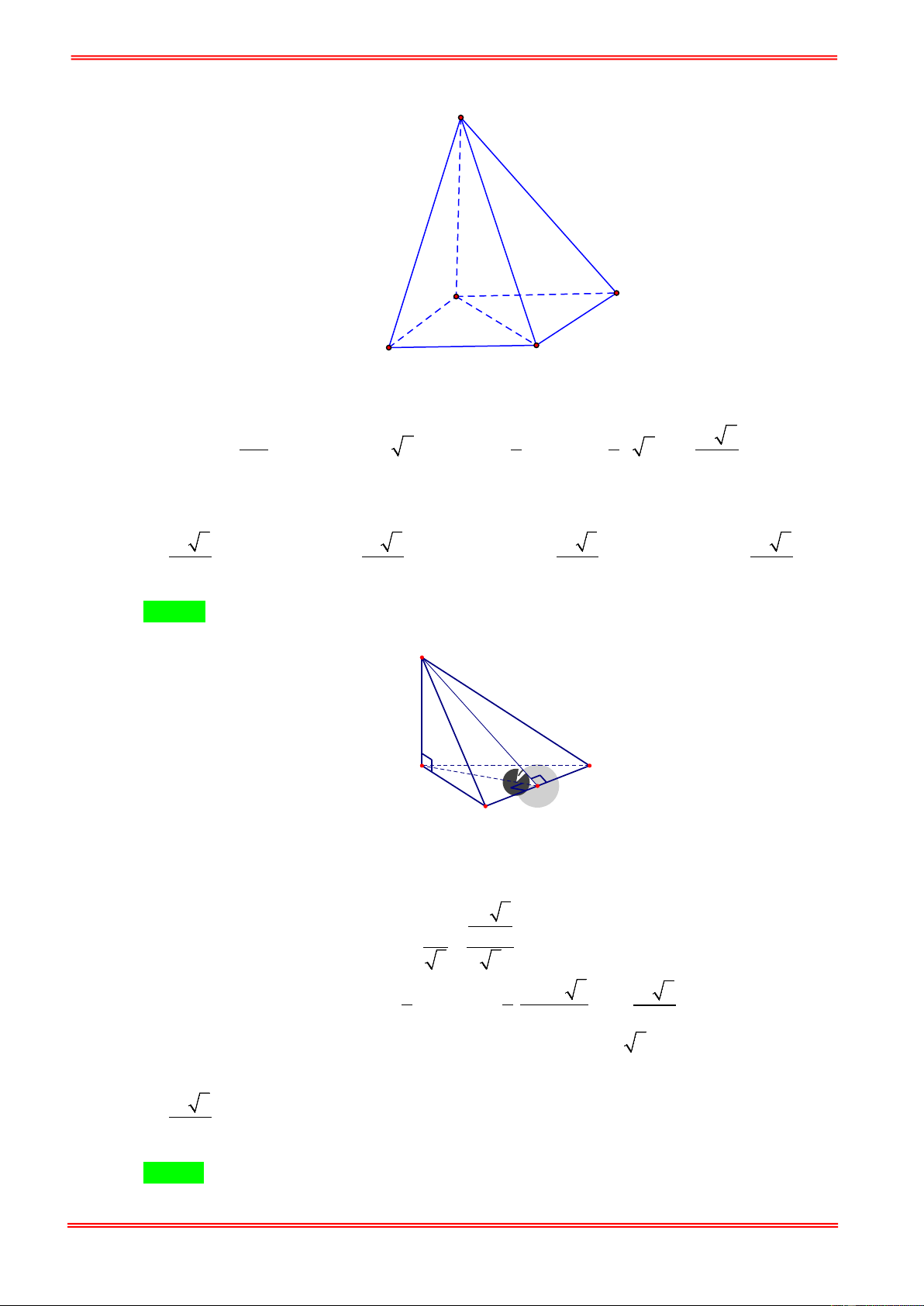
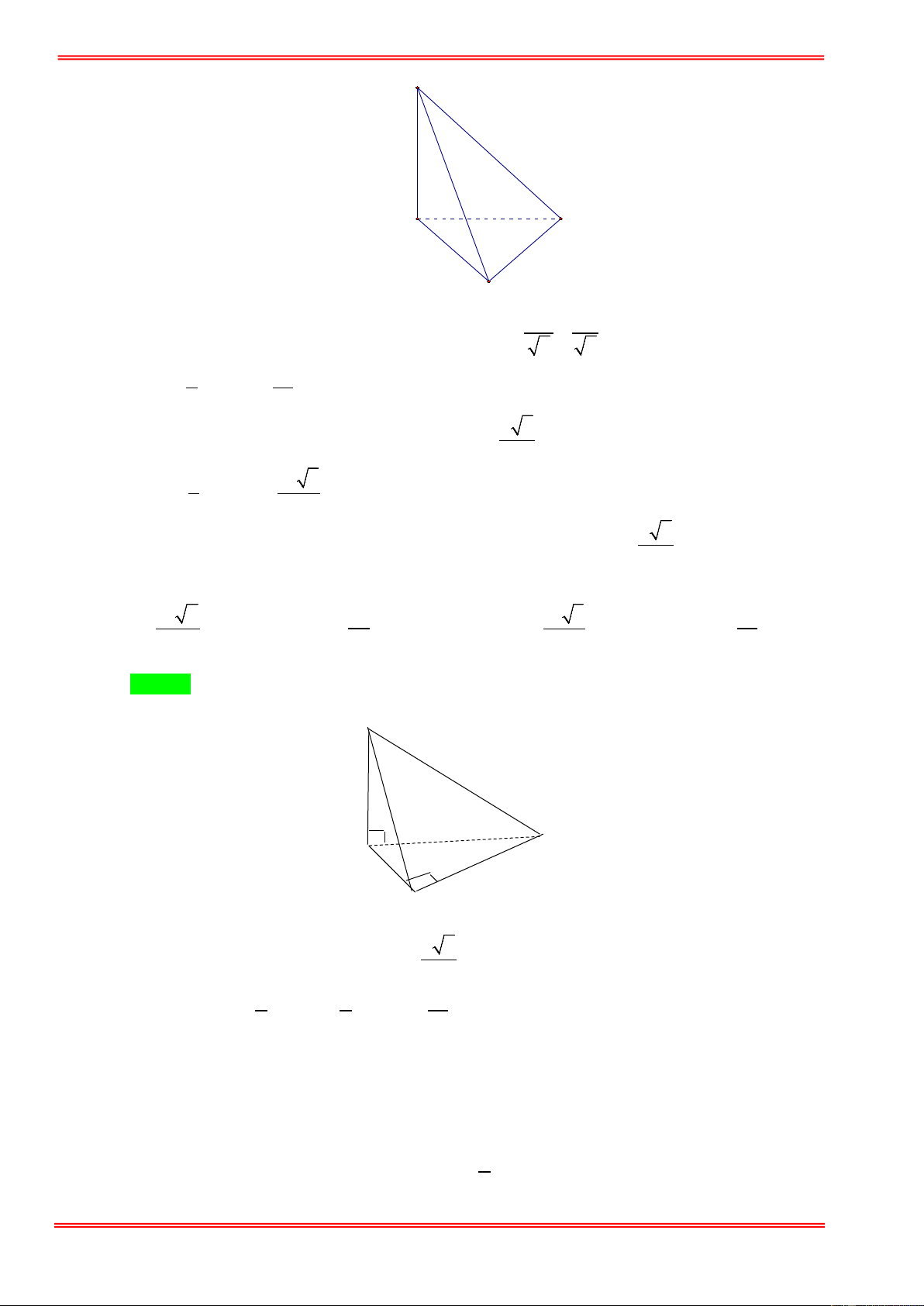
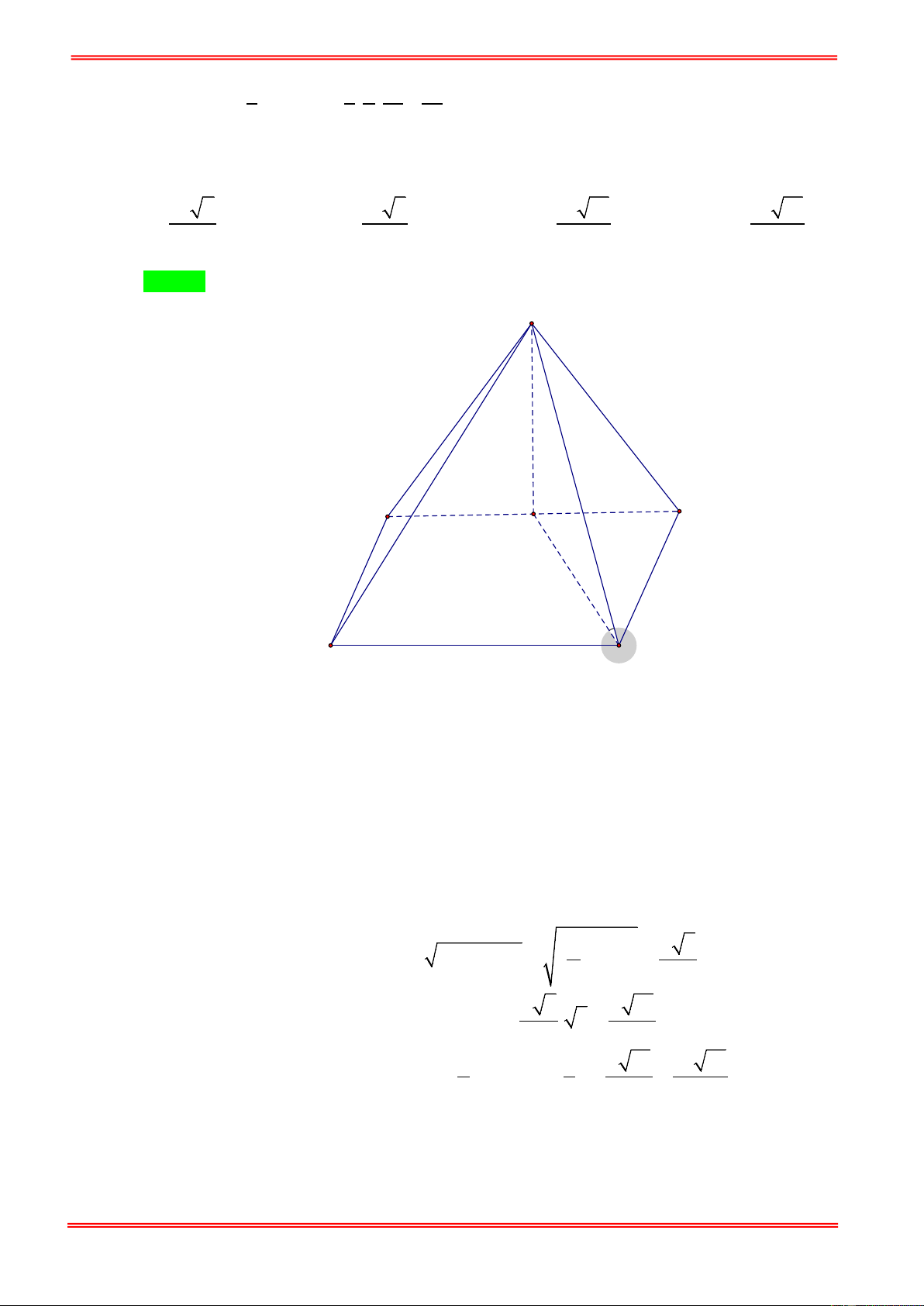
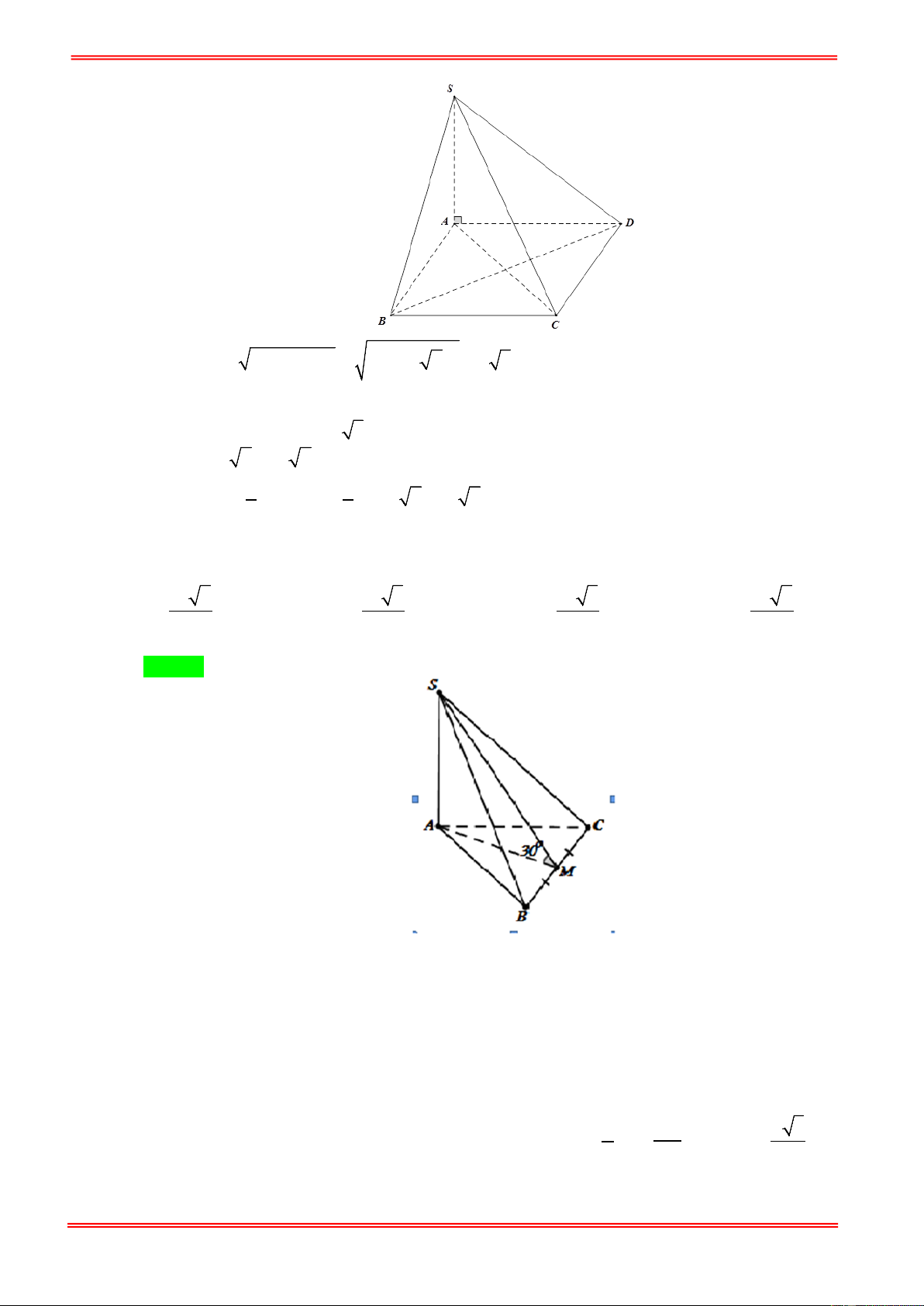
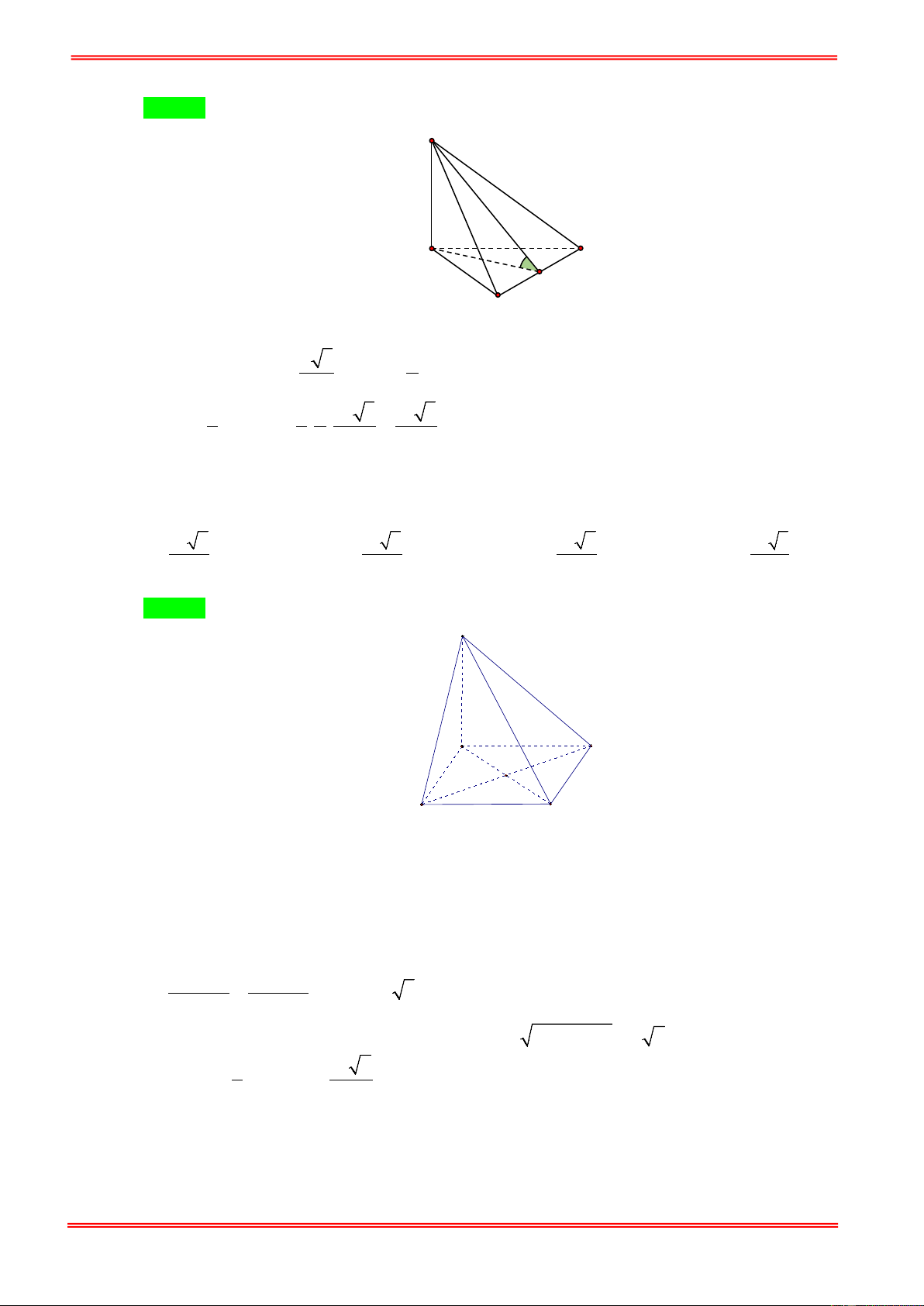
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Biết SA vuông góc với ( ABCD)
và SA = a 3 . Thể tích của khối chóp S.ABCD là: 3 a 3 a 3 3 a 3 A. . B. 3 a 3 . C. . D. . 4 6 3 Câu 2:
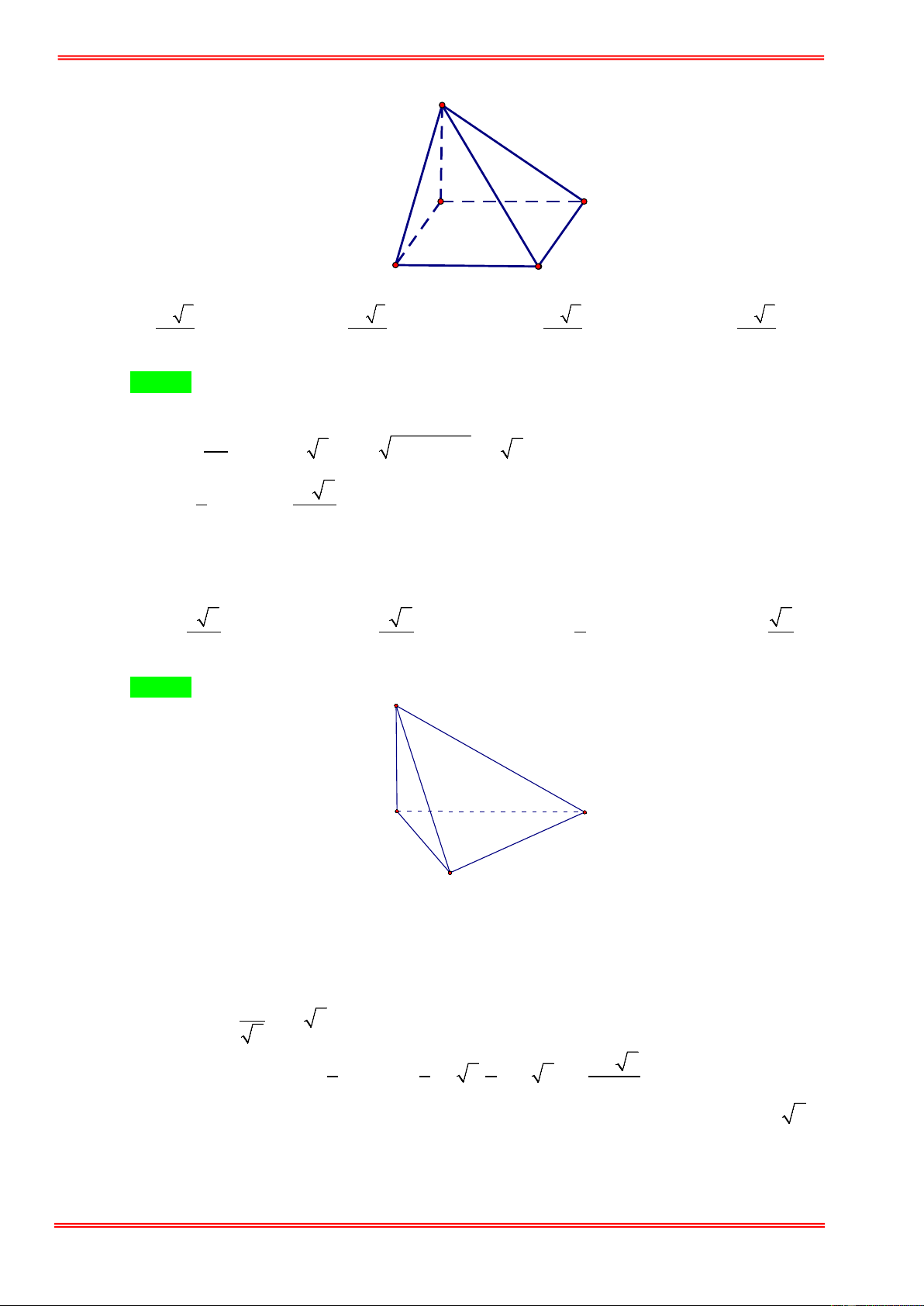
Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với mặt phẳng đáy
và SA = 2a . Thể tích khối chóp S.ABCD bằng 3 4a 3 a 3 2a A. . B. 3 2a . C. . D. . 3 3 3 Câu 3:
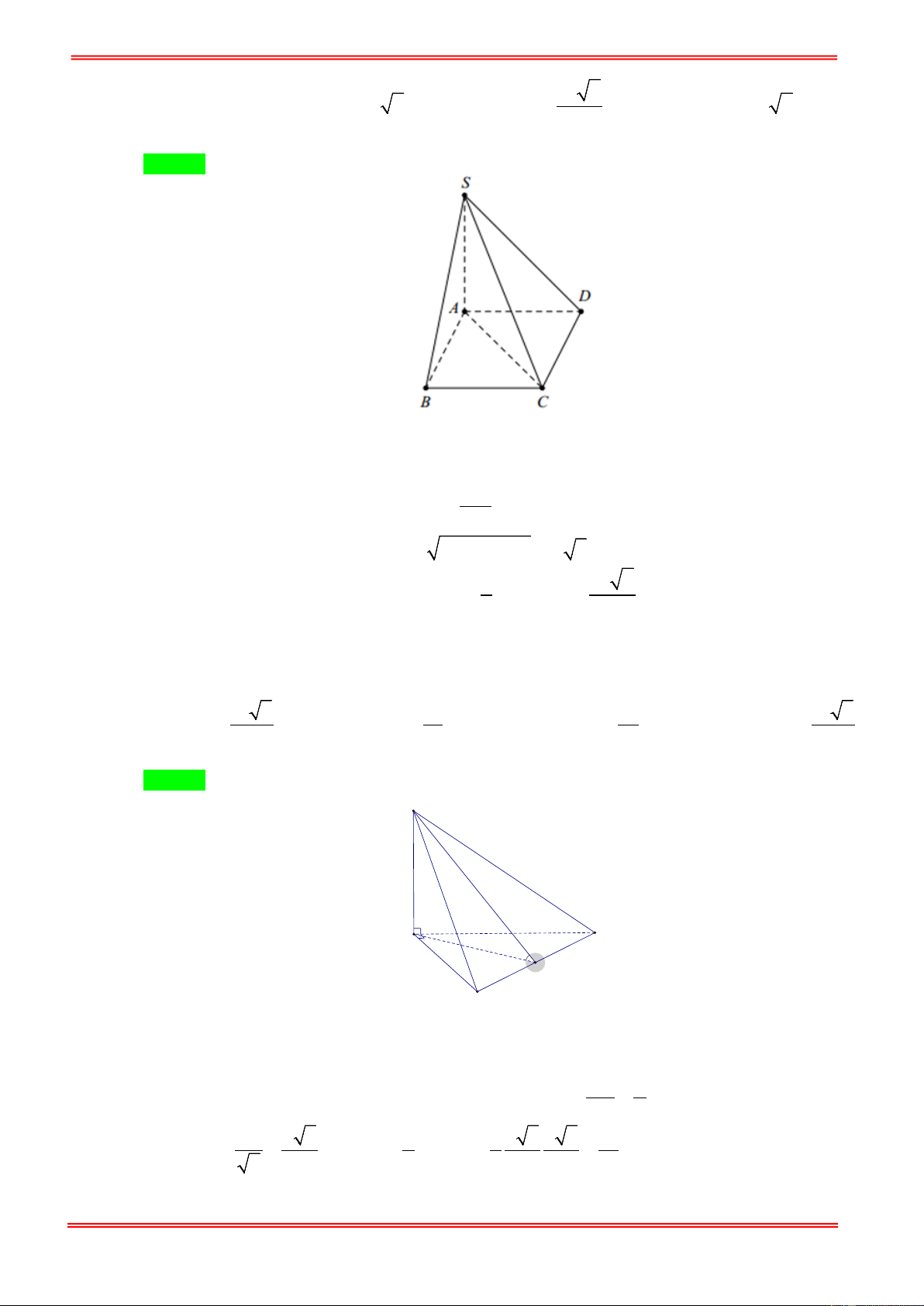
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a, BC = 2a , cạnh bên SA vuông
góc với đáy và SA = a 2 . Tính thể tích khối chóp S.ABCD . 3 2a 3 3 2a 2 A. . B. 3 a 2 . C. 3 2a 2 . D. . 3 3 Câu 4:
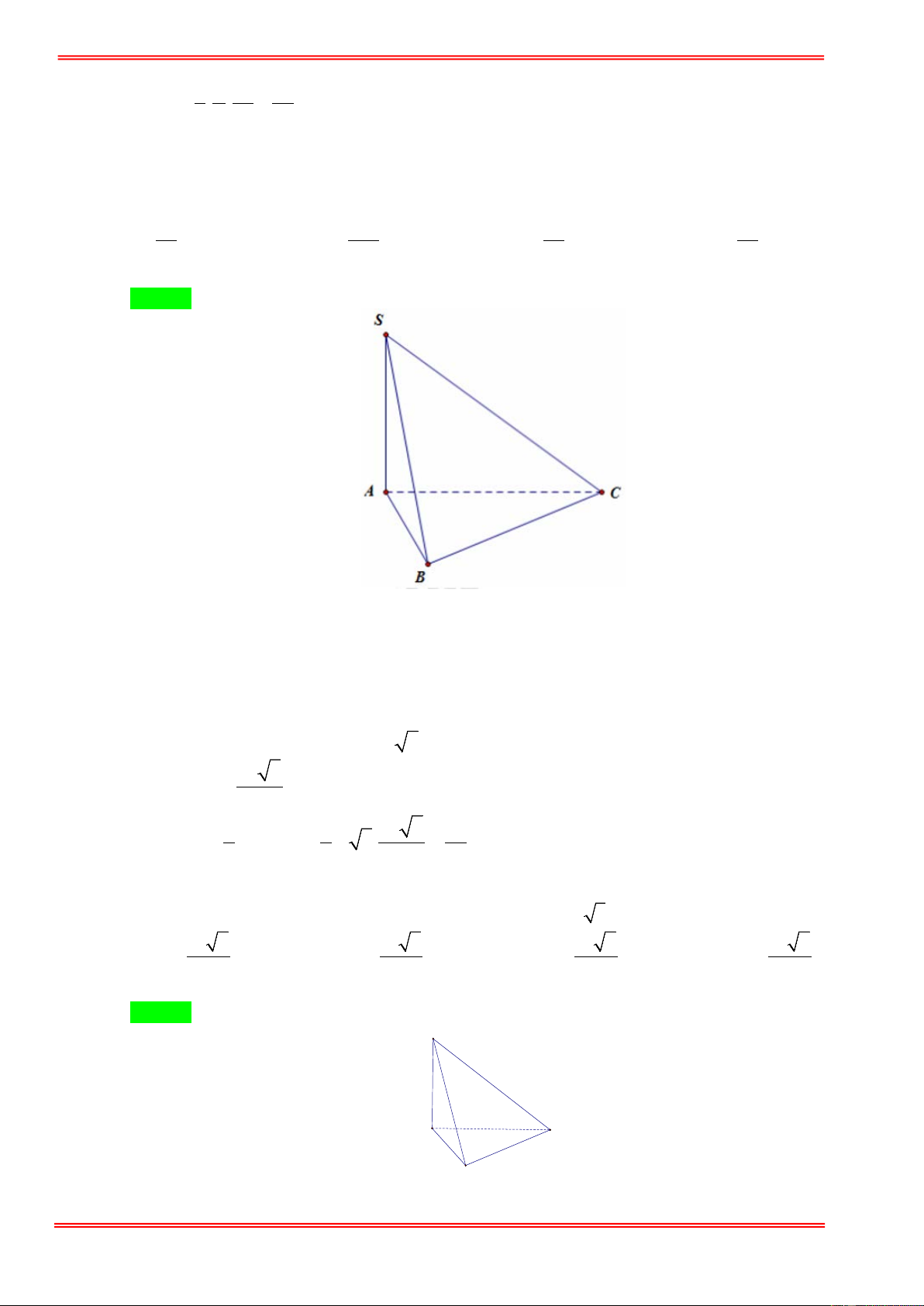
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh bên SA vuông góc với đáy
và có độ dài bằng 2a . Thể tích khối tứ diện S.BCD là: 3 a 3 a 3 a 3 a A. . B. . C. . D. . 4 8 6 3 Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a . Biết SA vuông góc với
mặt phẳng đáy và SA = a 2. Tính thể tích khối chóp S.ABO . 3 a 2 3 2a 2 3 a 2 3 4a 2 A. . B. . C. . D. . 3 12 12 3 Câu 6:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2a . Biết SA = 6a và SA vuông
góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD . A. 3 8a . B. 3 6 3a . C. 3 12 3a . D. 3 24a . Câu 7:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a . Biết SA vuông góc với
mặt phẳng đáy và SA = a 2. Tính thể tích khối chóp S.ABO . 3 4a 2 3 2a 2 3 a 2 3 a 2 A. . B. . C. . D. . 3 12 12 3 Câu 8:
Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = a, AD = 2a , SA ⊥ ( ABCD) và
SA = a 3 . Thể tính khối chóp S.ABC bằng: 3 2a 3 3 a 3 A. 3 a 3 . B. 3 2a 3 . C. . D. . 3 3 Câu 9:
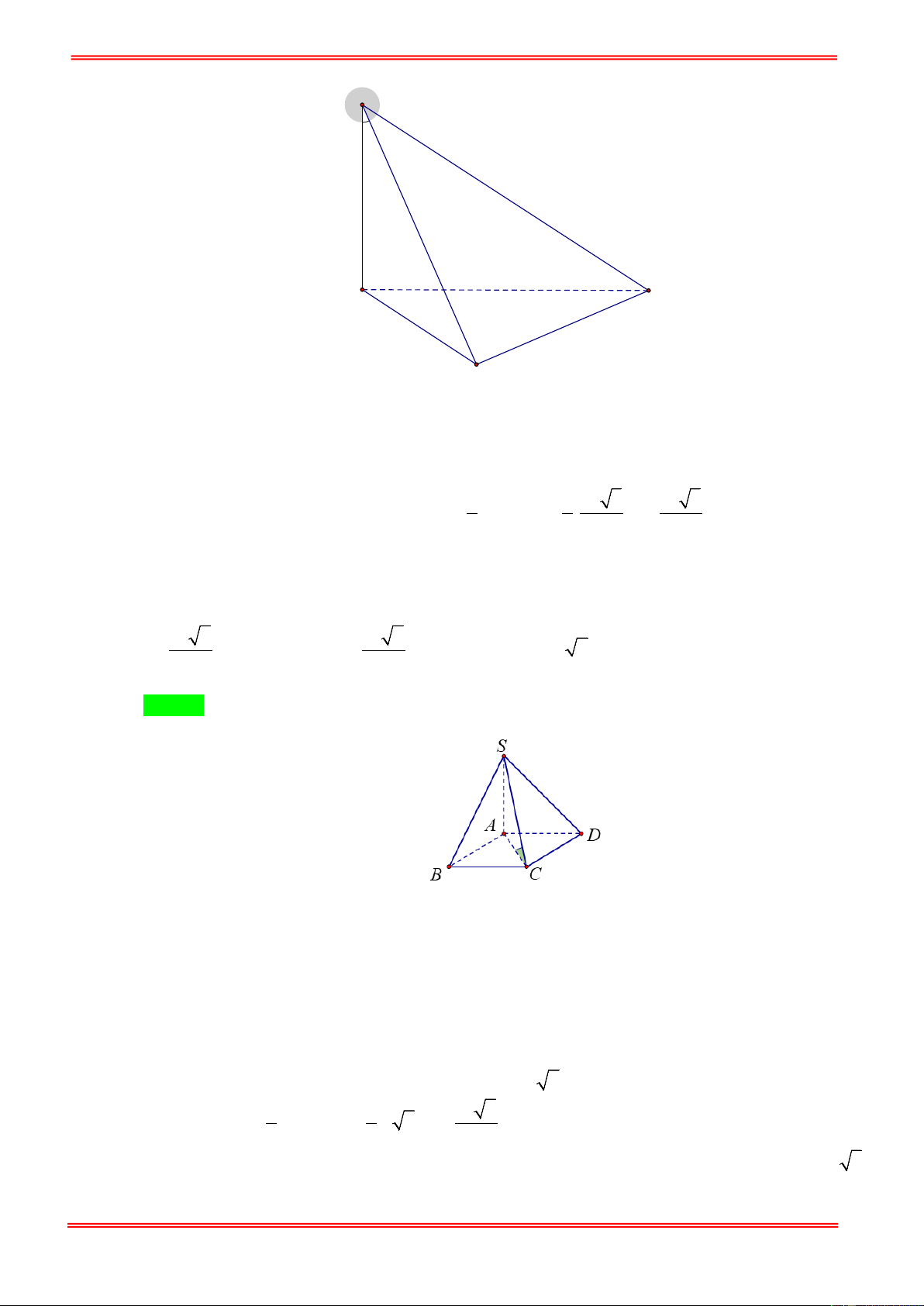
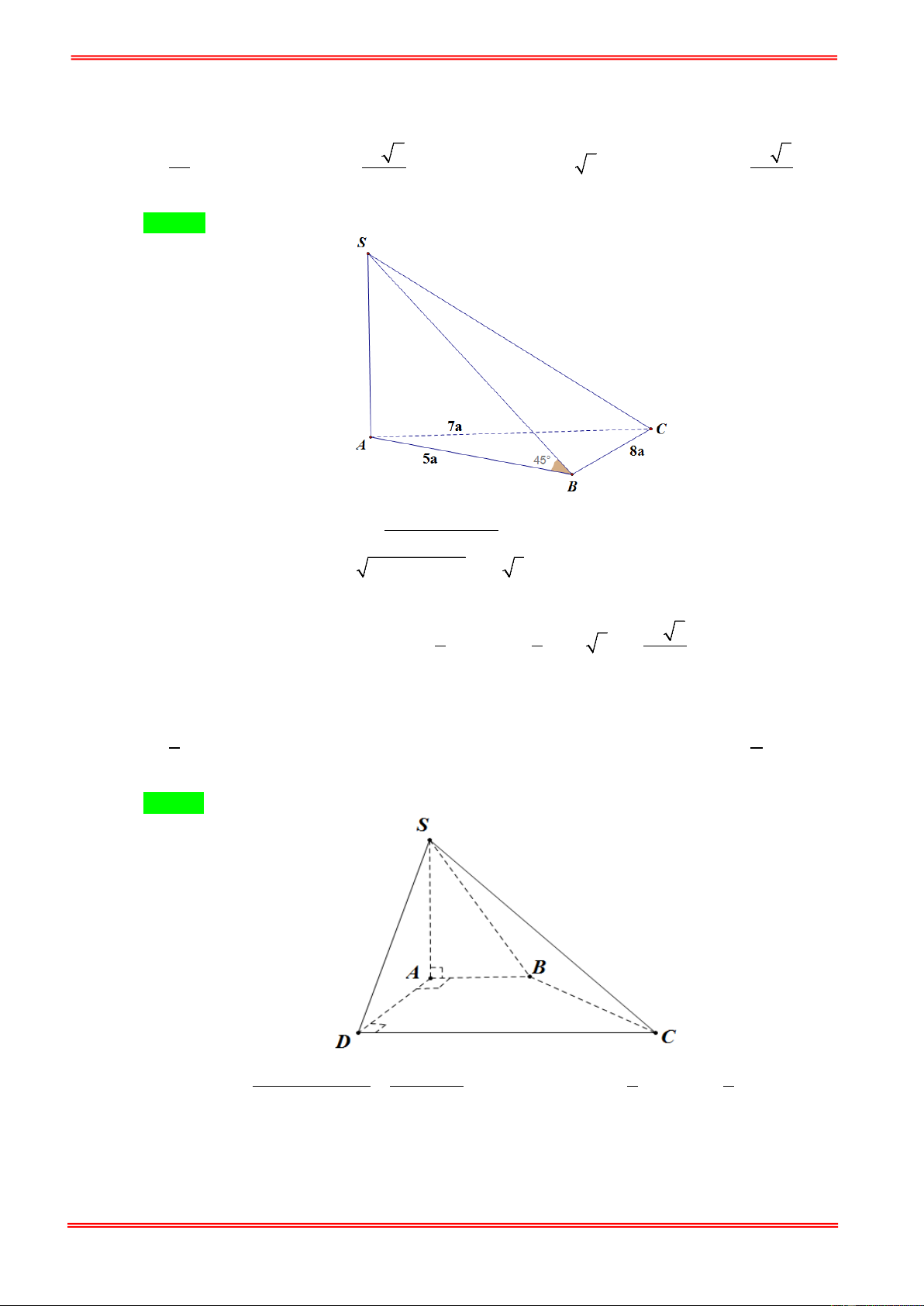
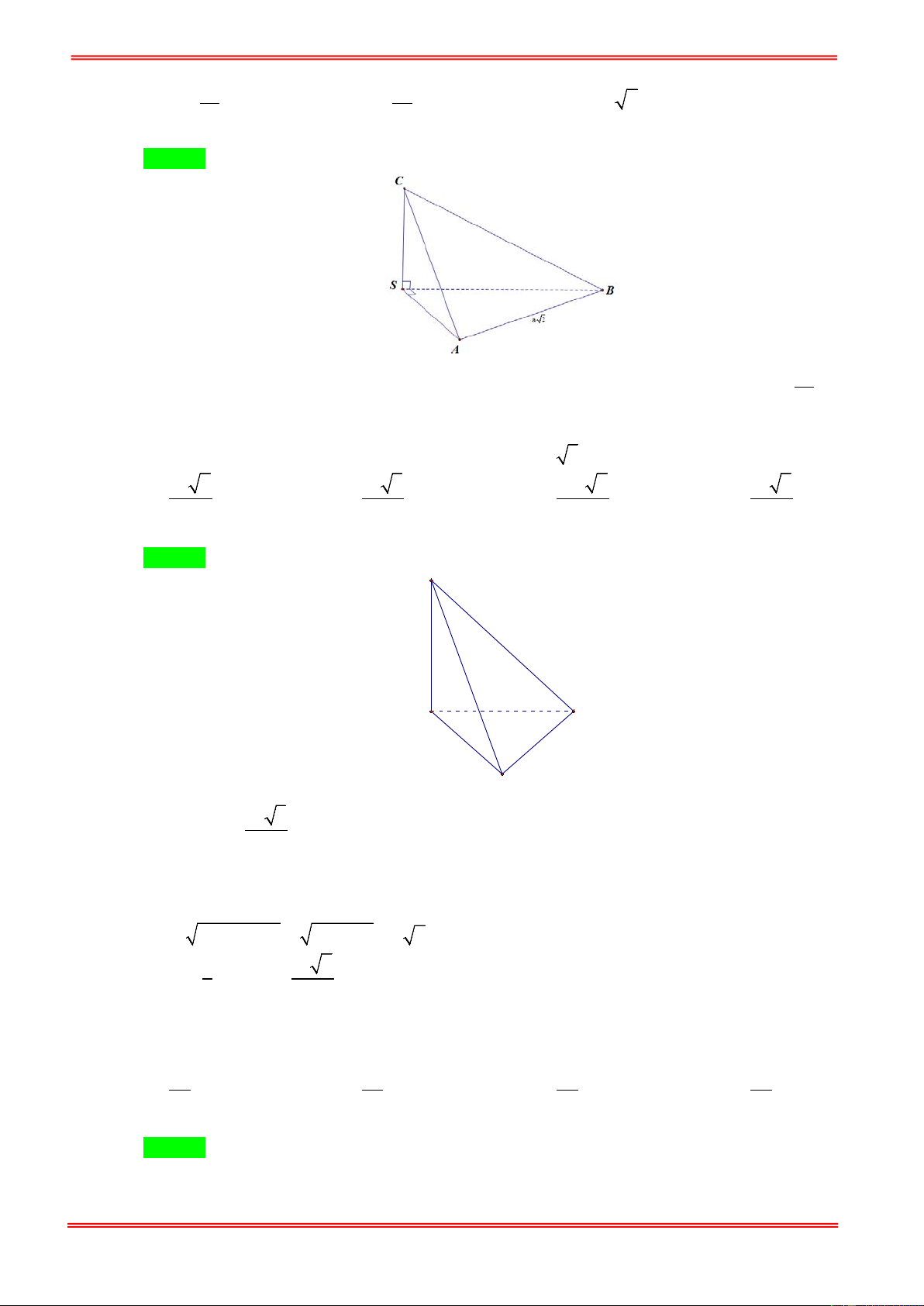
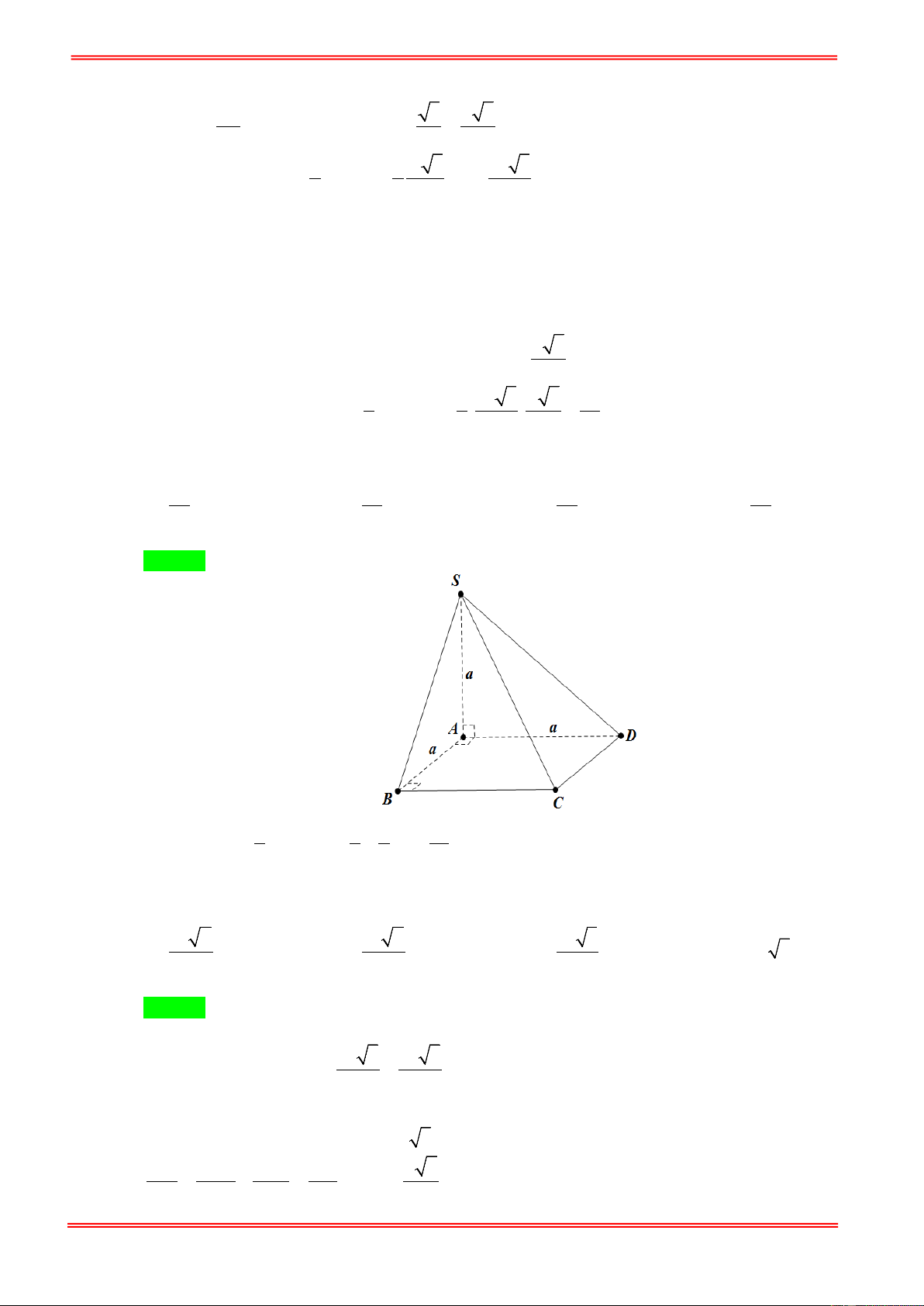
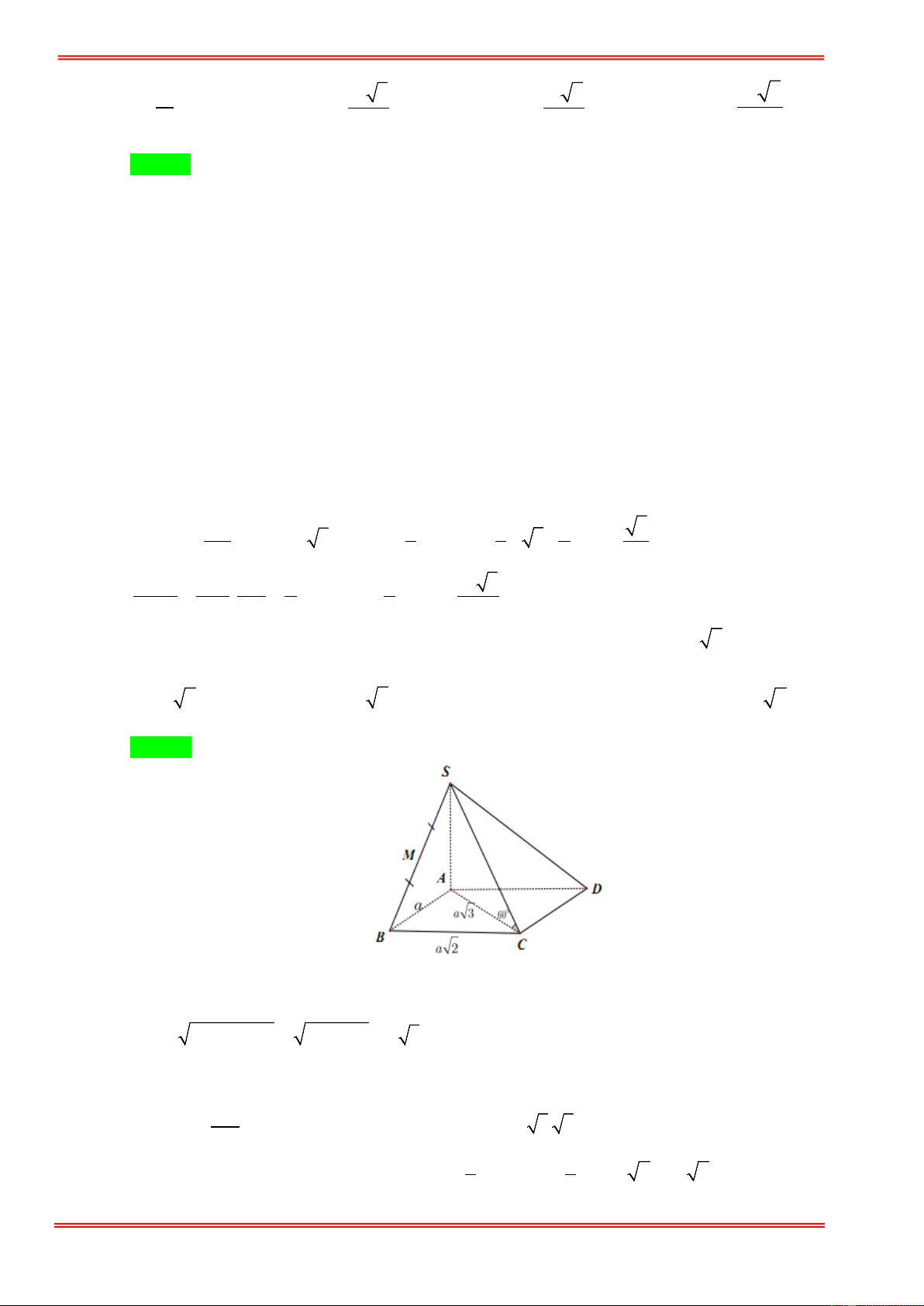
Cho hình chóp tam giác S.ABC với SA , SB , SC đôi một vuông góc và SA = SB = SC = a . Tính
thế tích của khối chóp S.ABC . 1 1 2 1 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 2 6 3 3
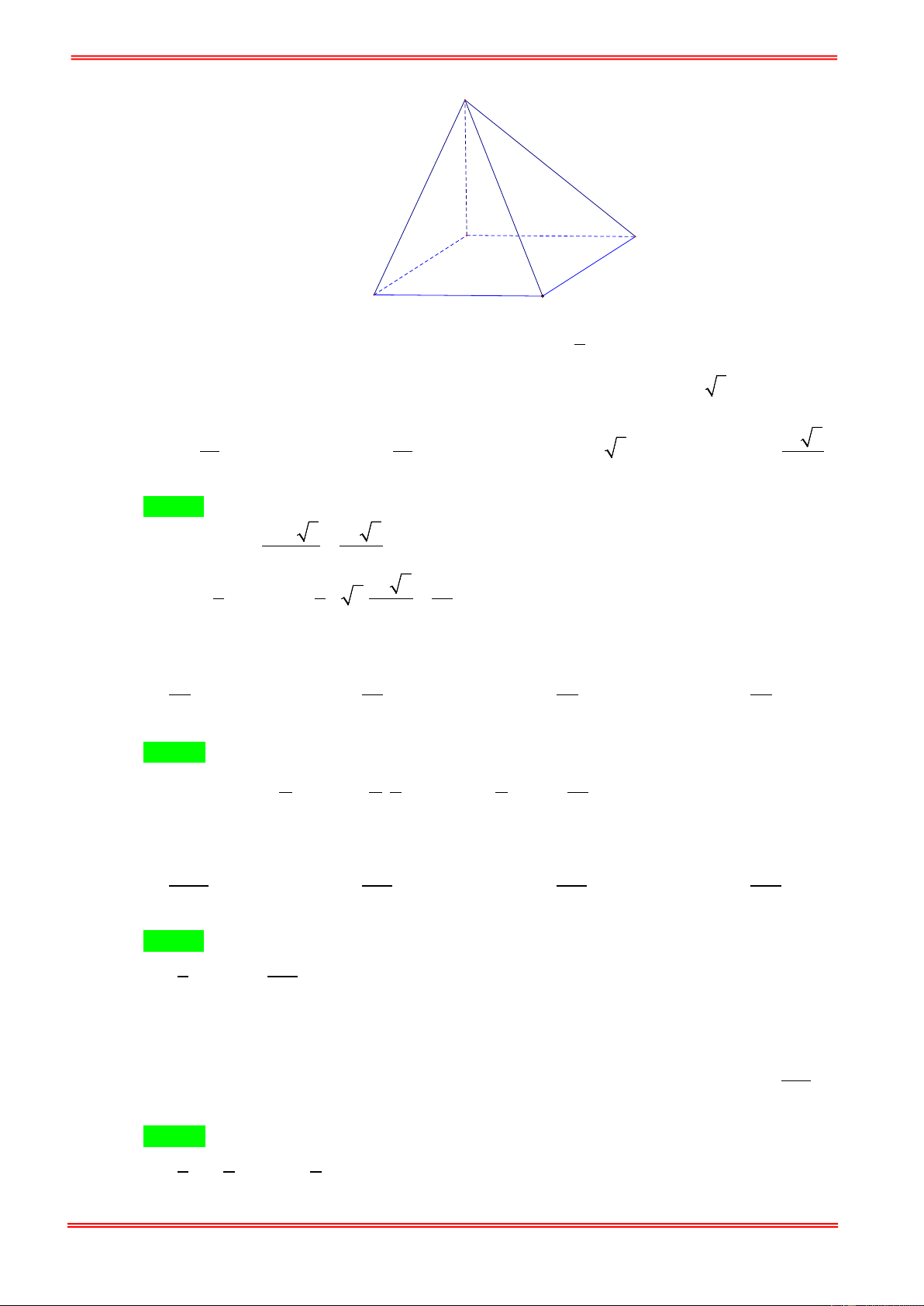
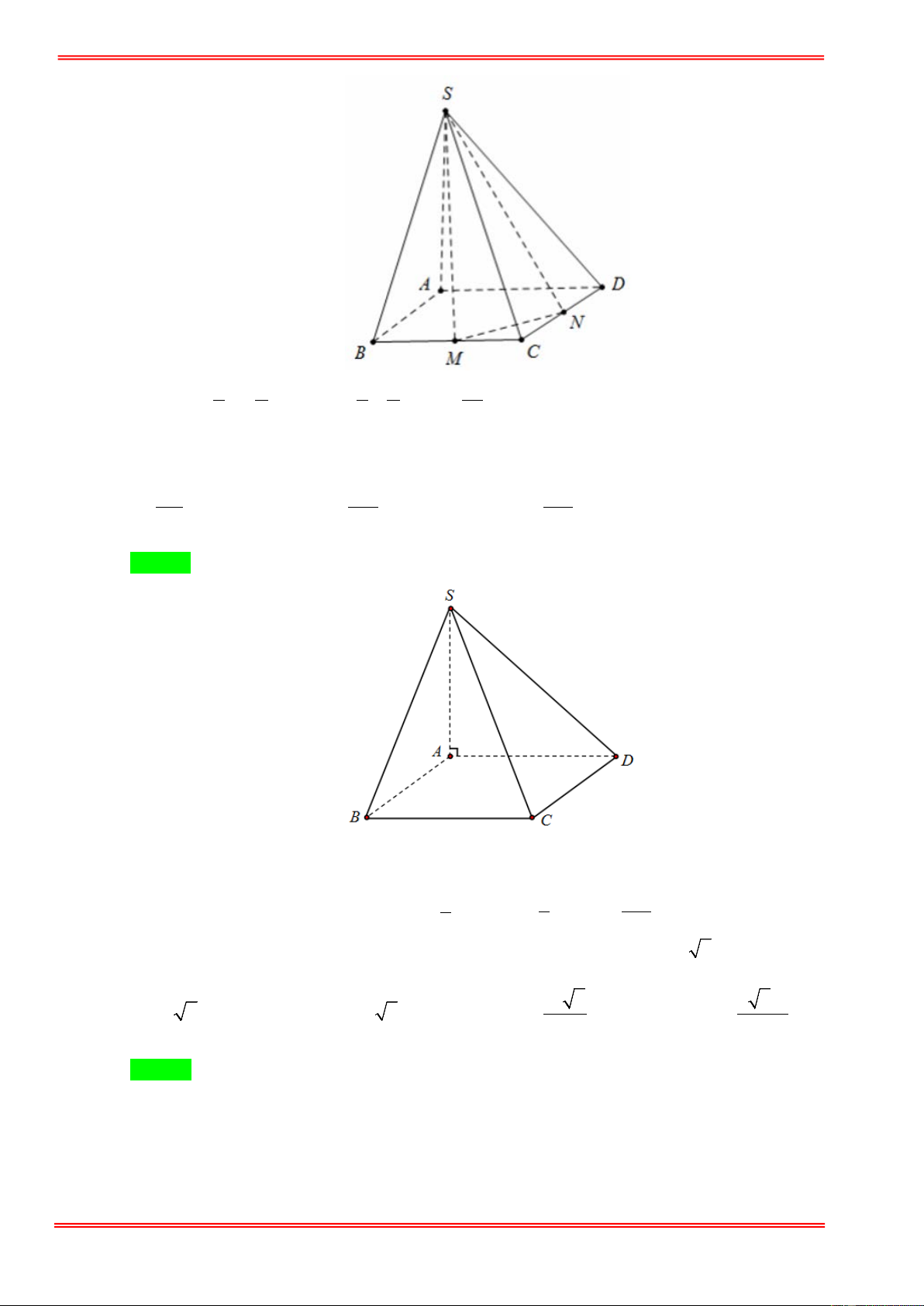
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh SA vuông góc với mặt phẳng
đáy và có độ dài là a . Thể tích khối tứ diện S.BCD bằng. 3 a 3 a 3 a 3 a A. . B. . C. . D. . 6 8 3 4 https://toanmath.com/
Câu 11: Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = a, AD = 2a , SA vuông góc với mặt
đáy và SA = a 3 . Thể tính khối chóp S.ABCD bằng 3 a 3 3 2a 3 A. 3 2a 3. B. . C. 3 a 3. D. . 3 3
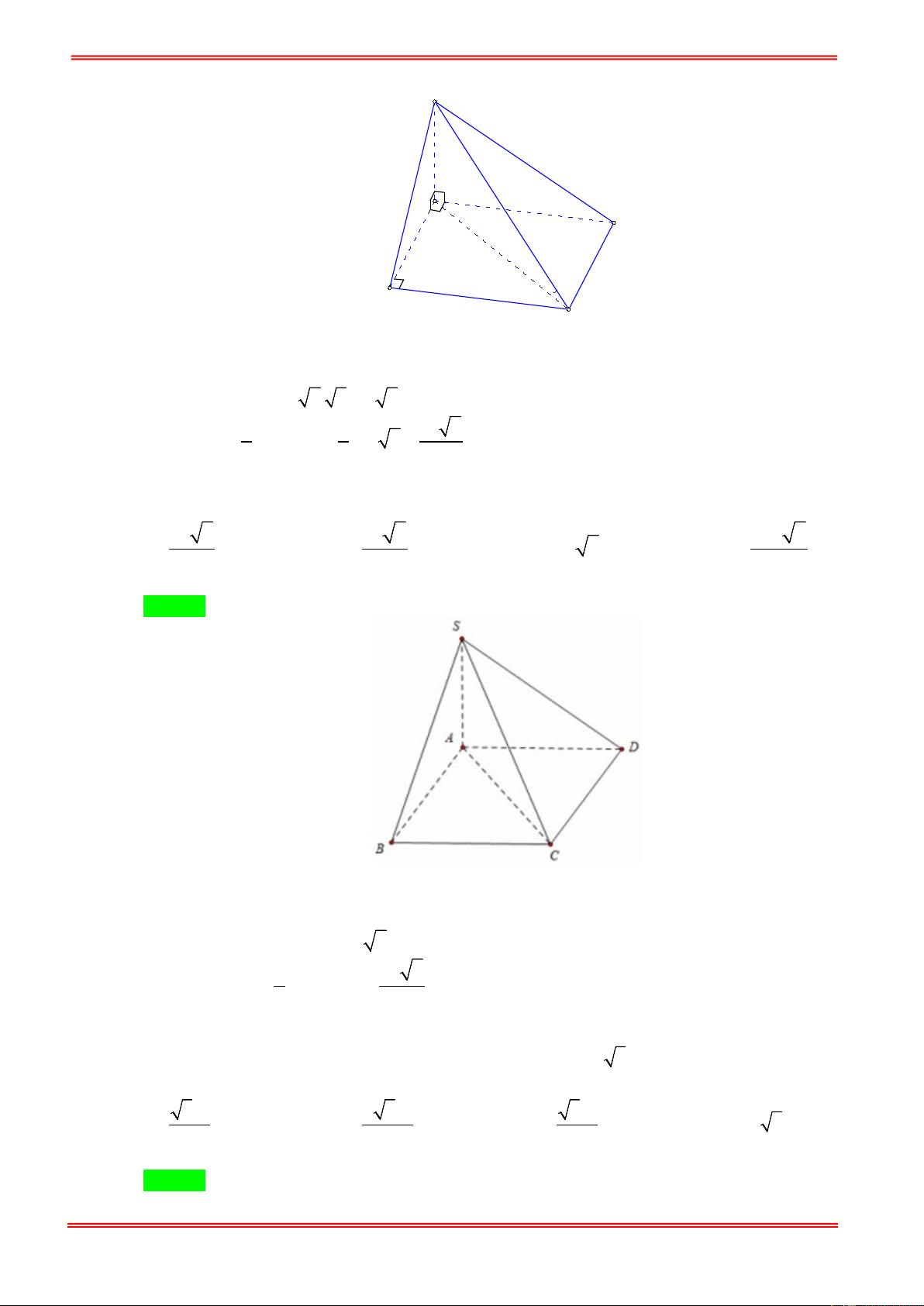
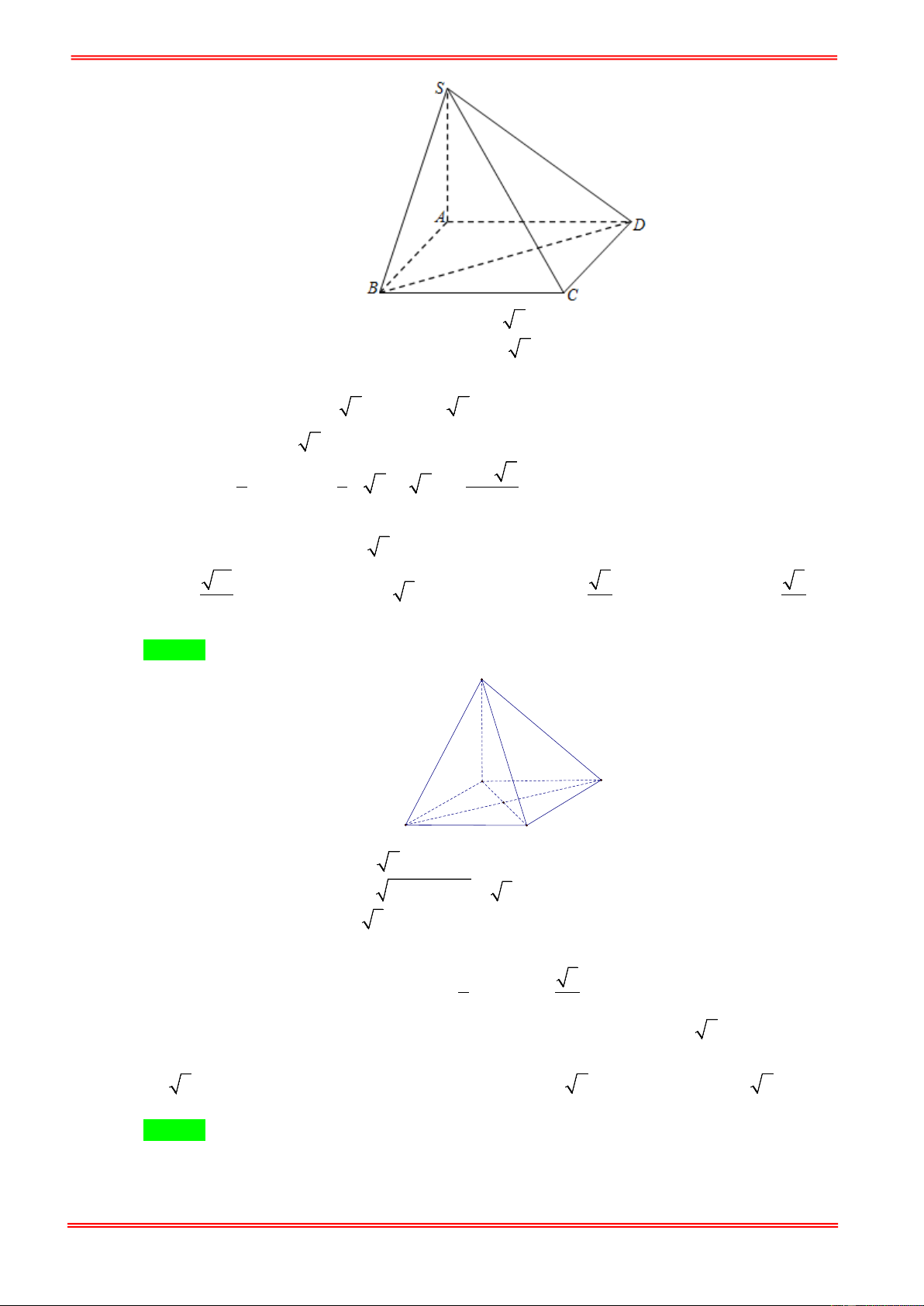
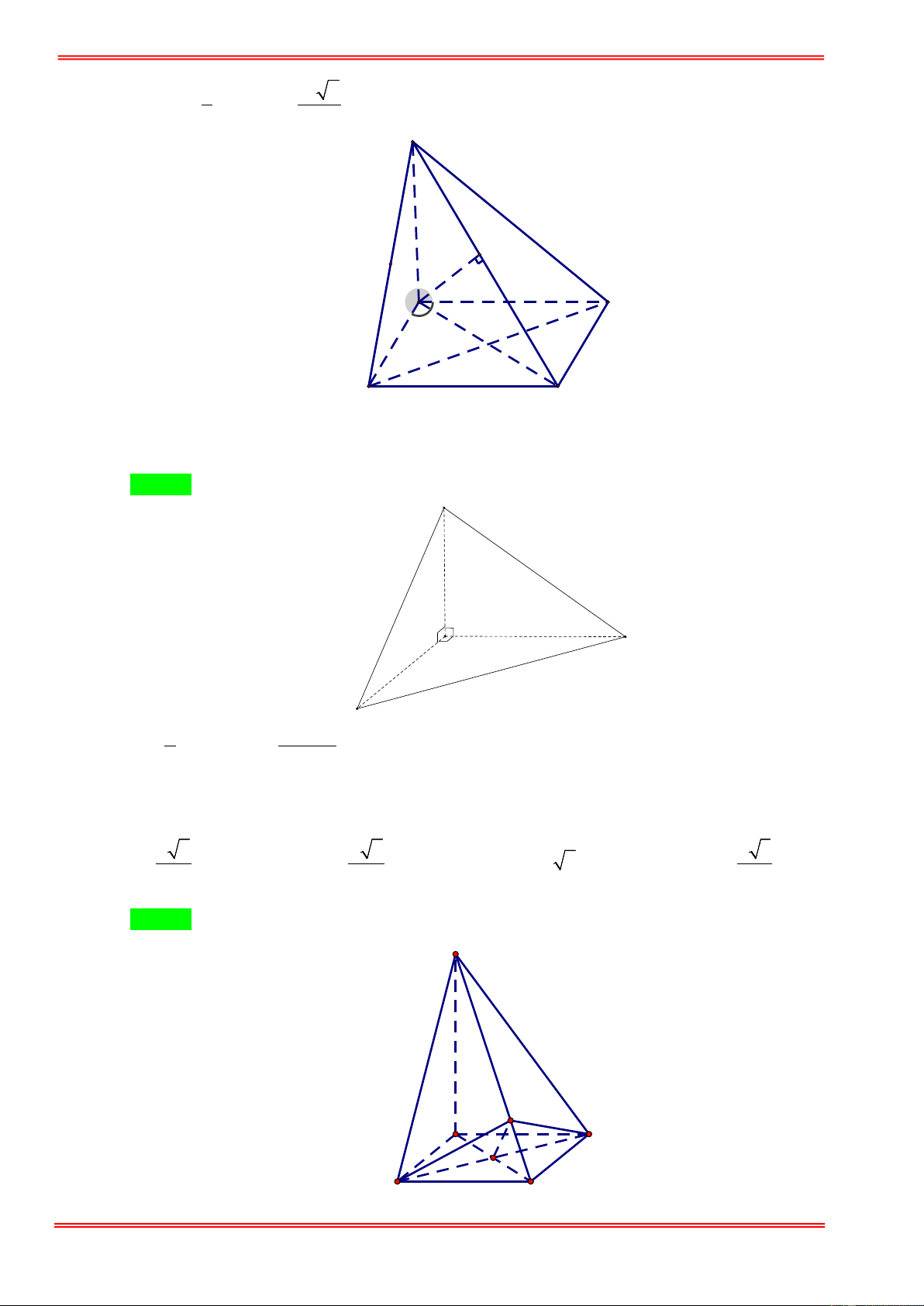
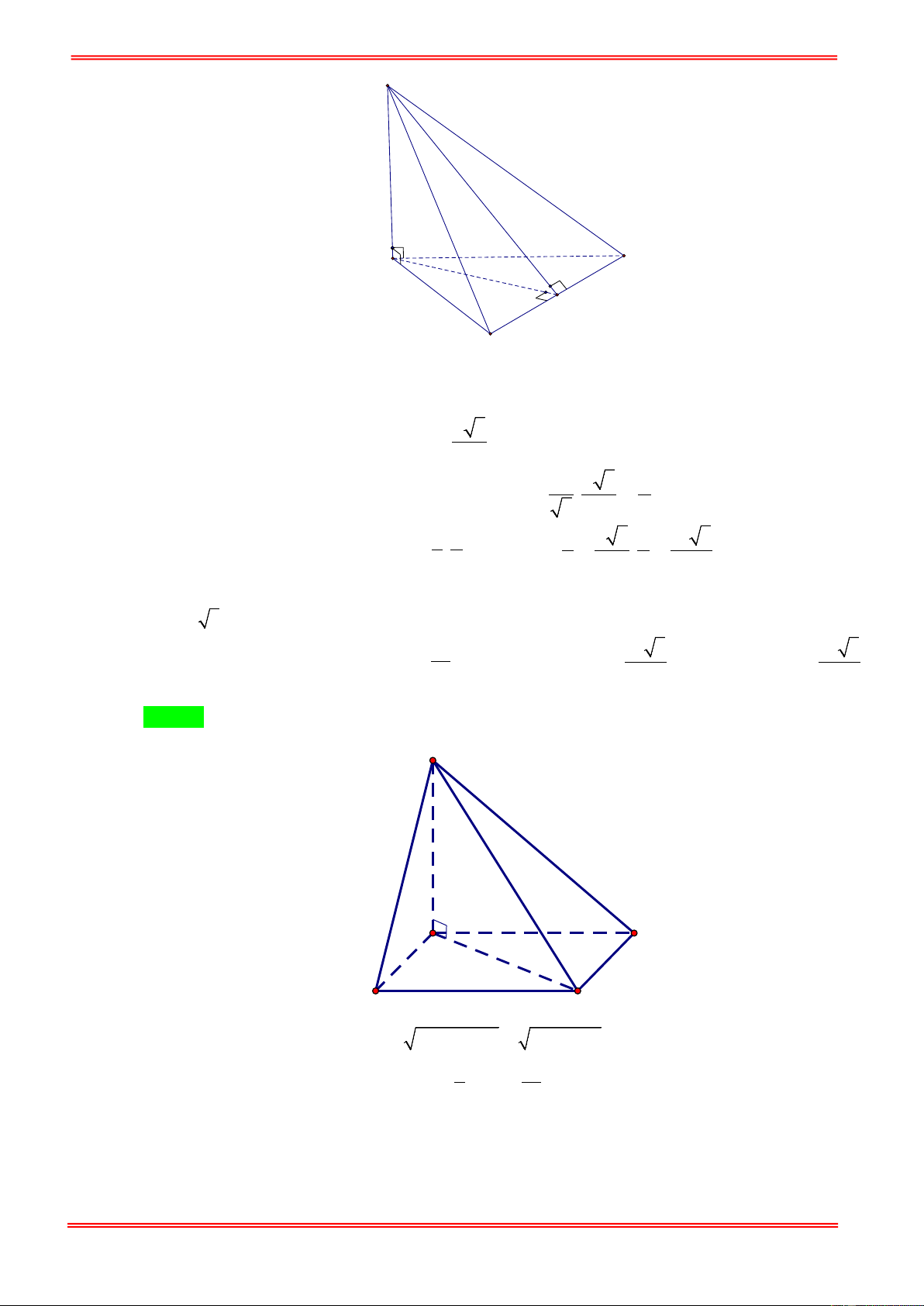
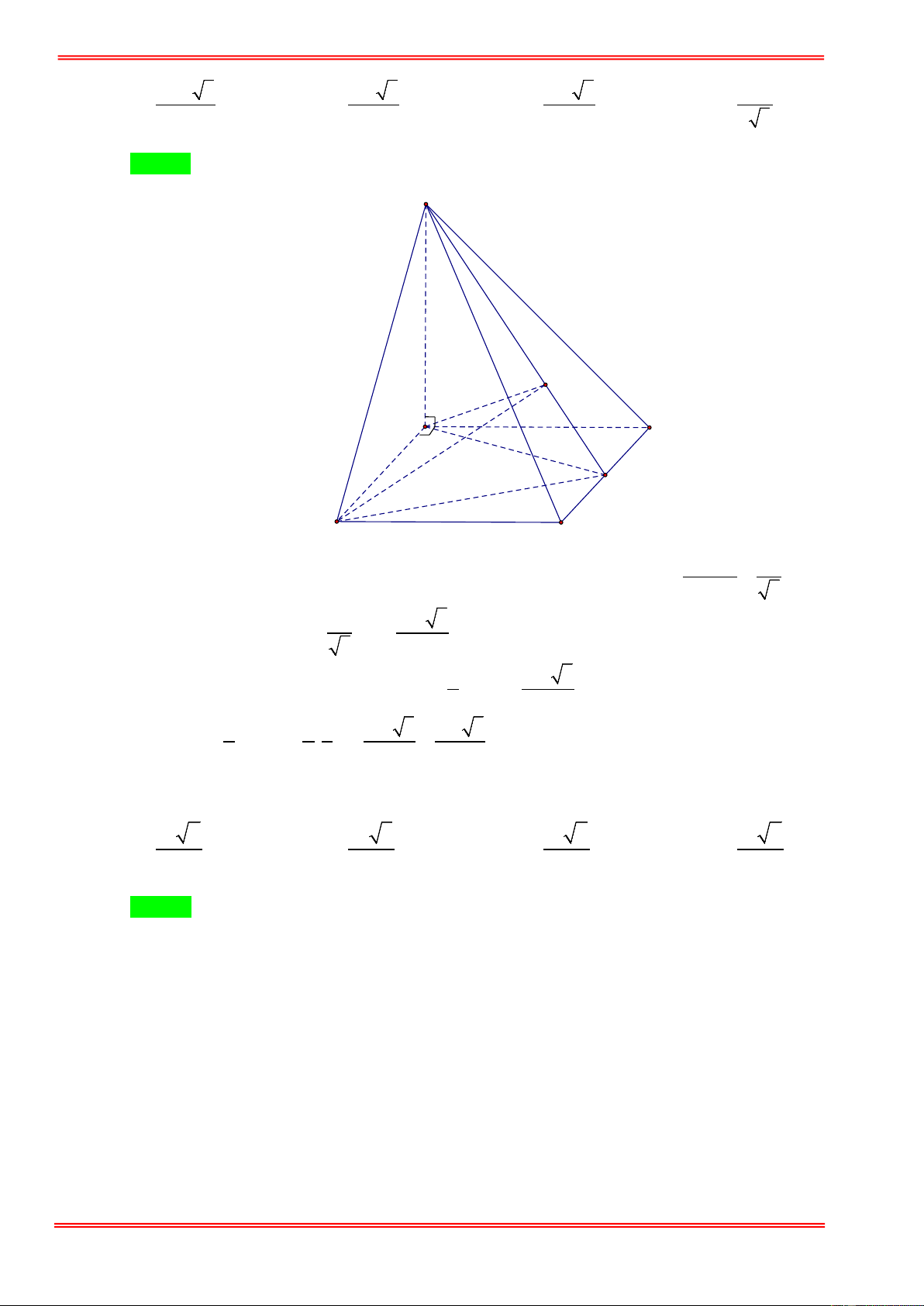
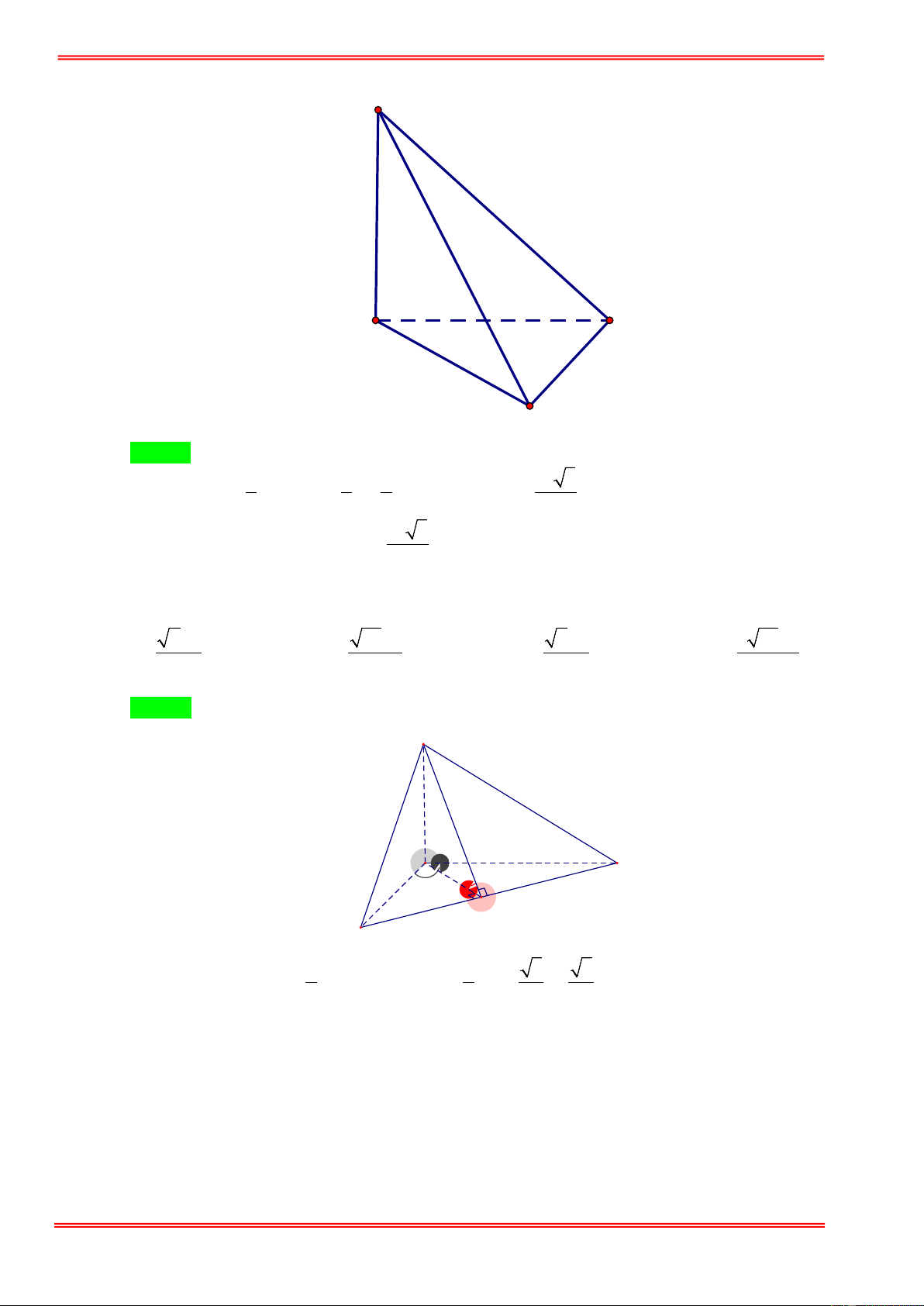
Câu 12: Cho tứ diện OABC có OA , OB , OC đôi một vuông góc với nhau tại O và OA = 2 , OB = 4 ,
OC = 6 . Thể tích khối tứ diện đã cho bằng. A. 24 . B. 16 . C. 8 . D. 48 .
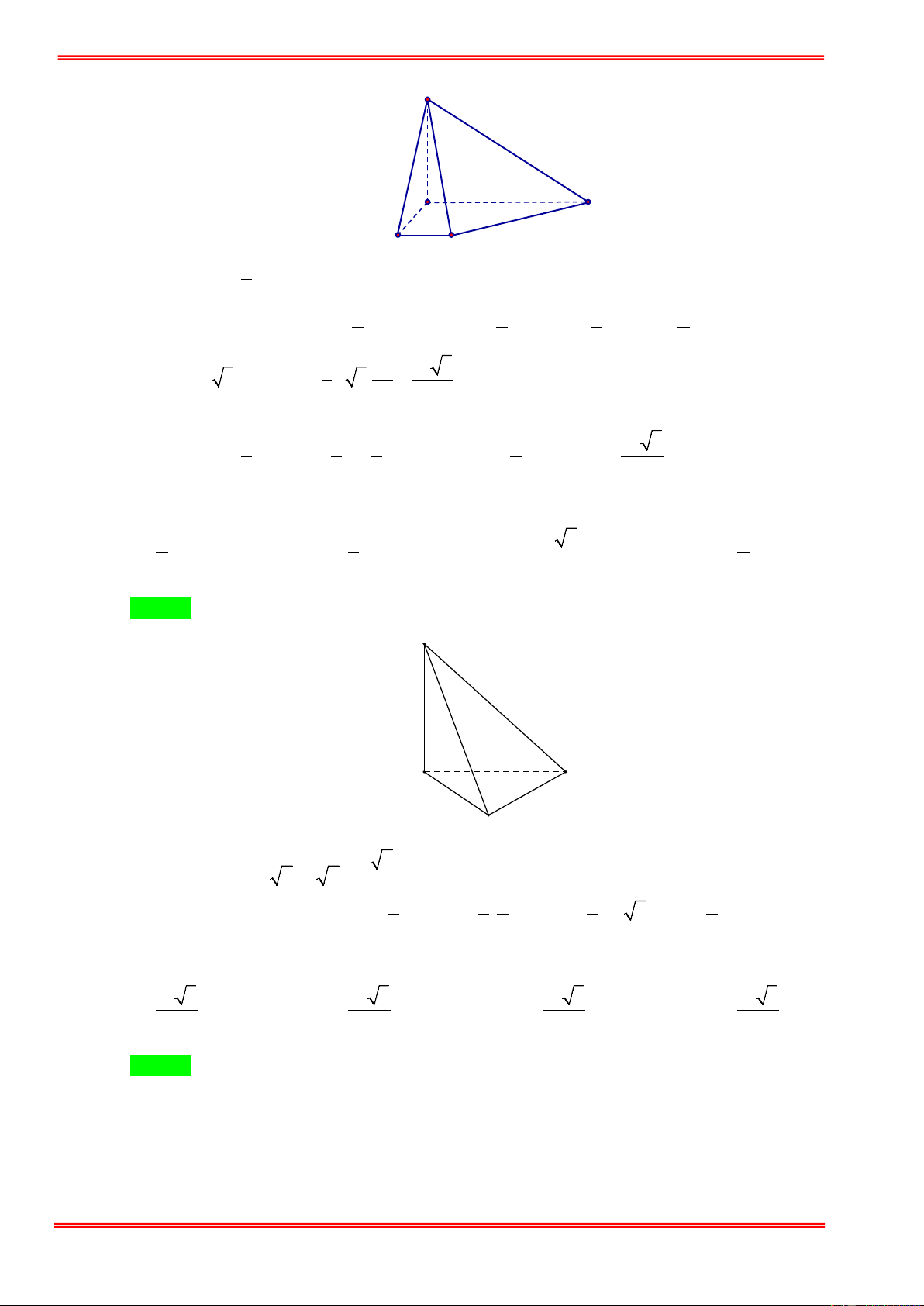
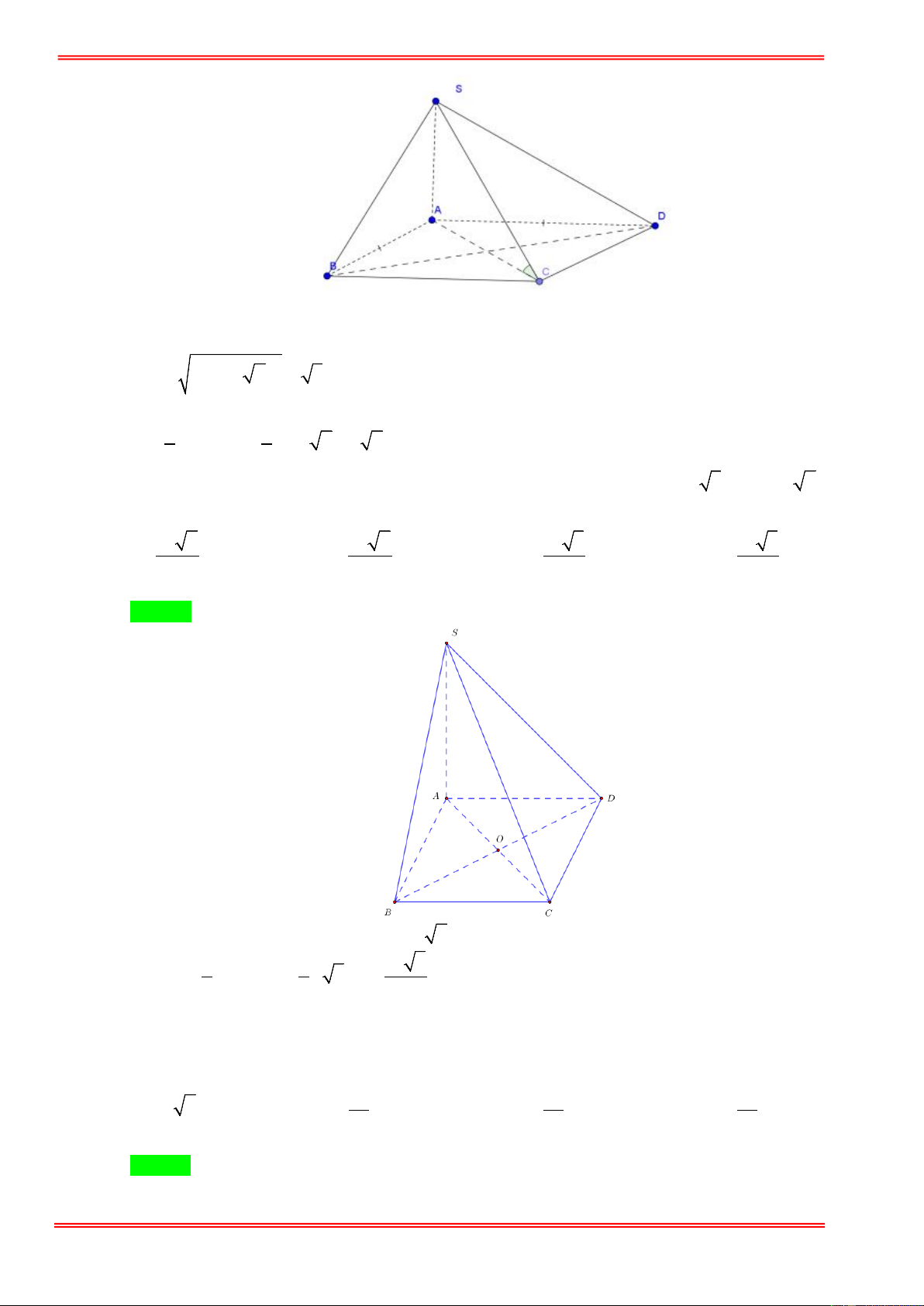
Câu 13: Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA vuông góc với mặt phẳng đáy và
SA = 2a . Tính thể tích khối chóp S.ABC . 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 2 3 12
Câu 14: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a , SA vuông góc với mặt phẳng đáy,
SA = a 3 . Tính thể tích khối chóp S.ABC . A. 2 V = a (đvtt). B. 3 V = a (đvtt). S . ABC S . ABC 3 a C. V = (đvtt). D. 3 V = 3a (đvtt). S . ABC 2 S . ABC
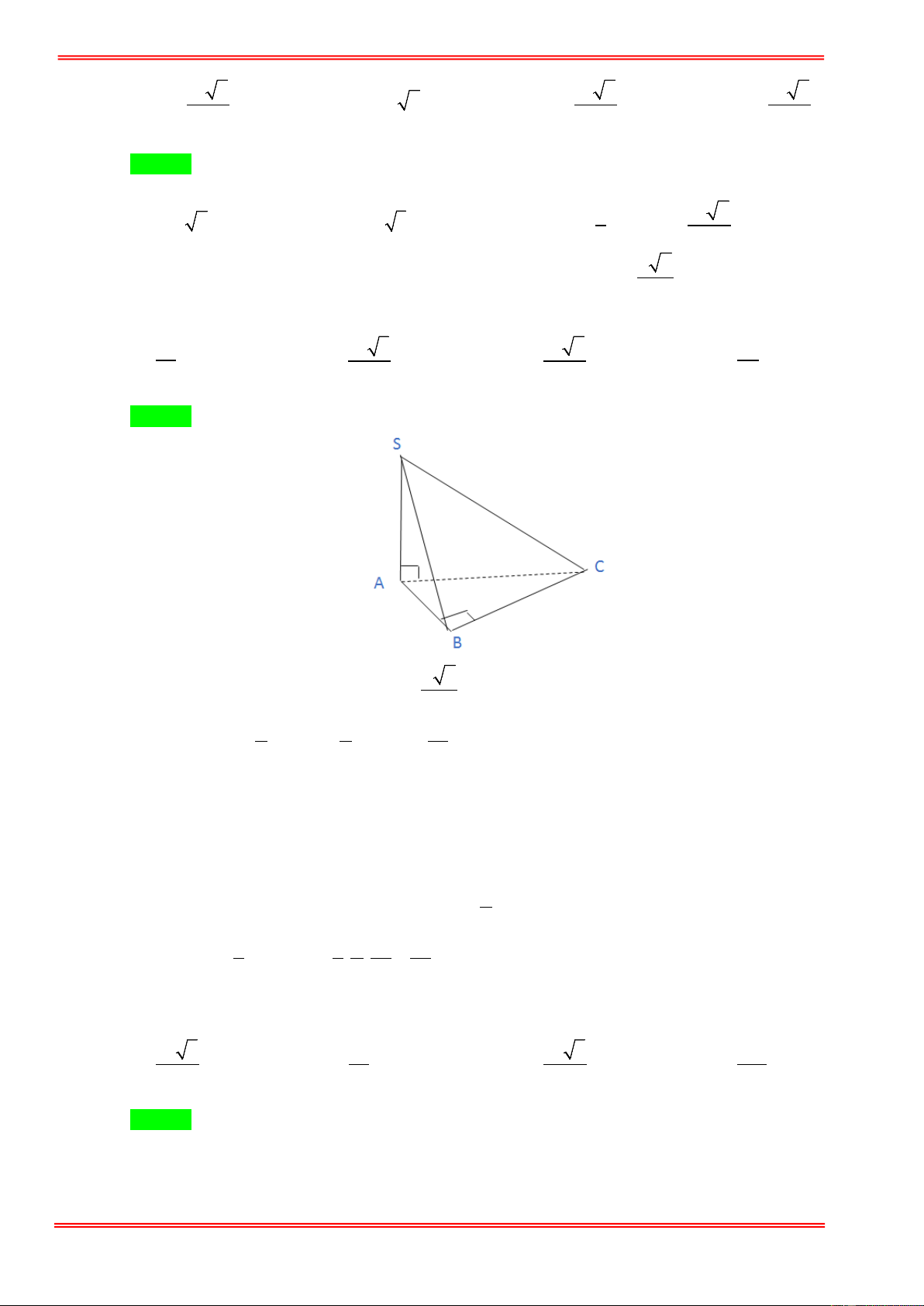
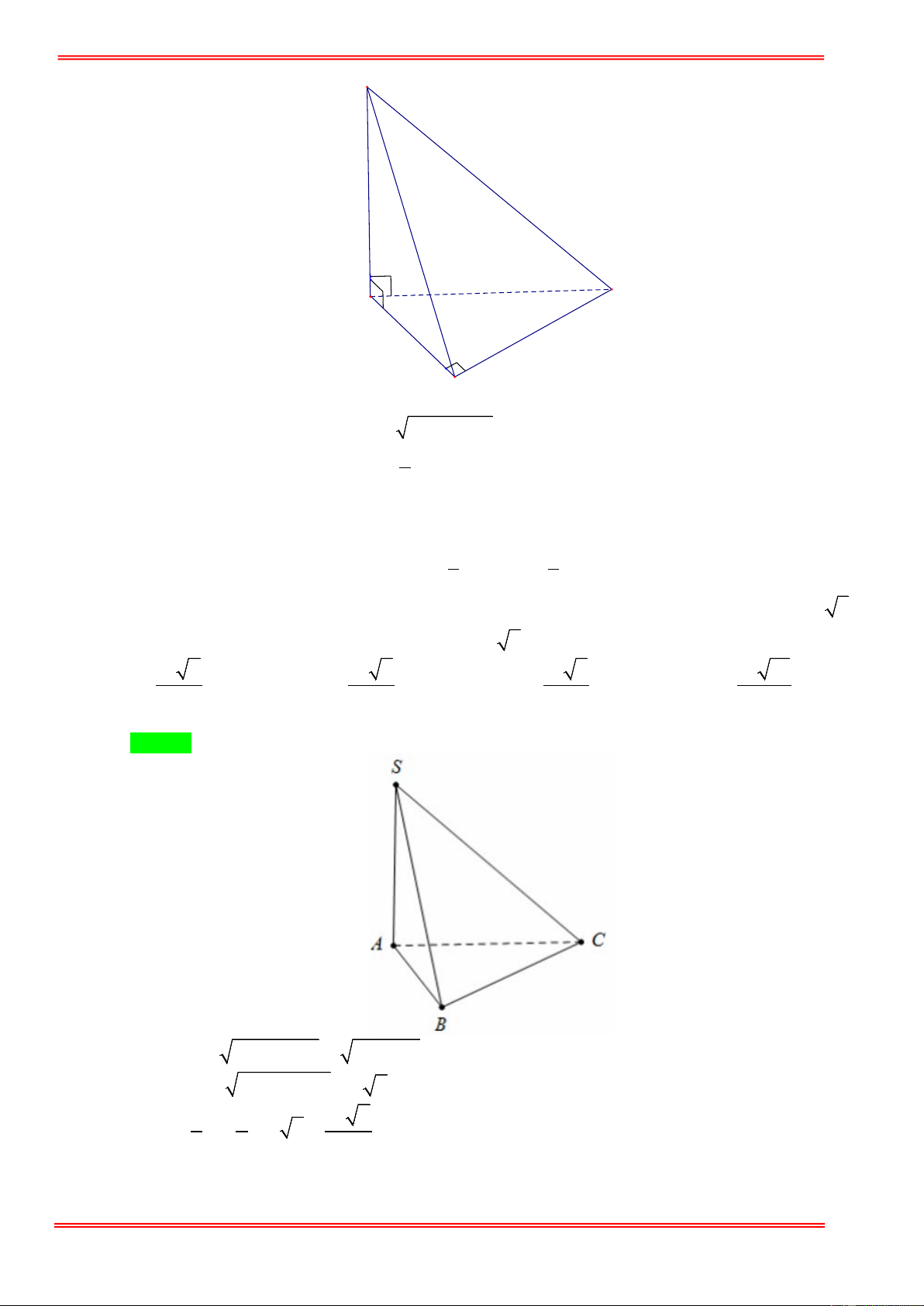
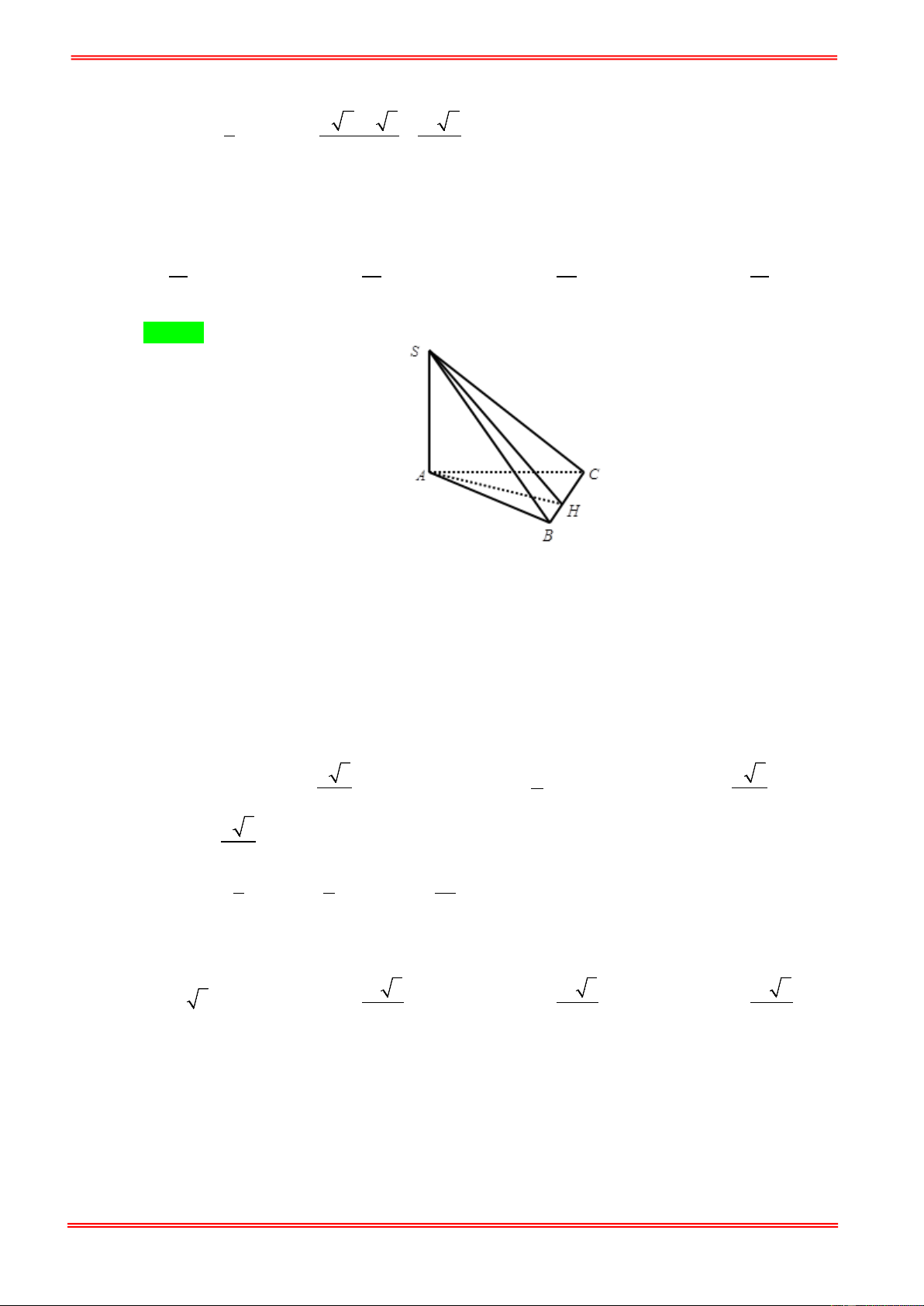
Câu 15: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB = a , BC = 2a , SA ⊥ ( ABC ) ,
SA = 3a . Thể tích của khối chóp S.ABC bằng 1 1 A. 3 a . B. 3 a . C. 3 a . D. 3 3a . 6 3
Câu 16: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc
với mặt phẳng đáy và SA = 2a . Tính thể tích V của khối chóp S.ABCD . 3 2a 3 2a 3 2a A. 3 V = 2a . B. V = . C. V = . D. V = . 4 6 3
Câu 17: Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh 8(cm) , chiều cao SH bằng 3(cm) .
Tính thể tích khối chóp? A. V = ( 3 1 6 cm ) . B. V = ( 3 24 cm ) . C. V = ( 3 48 cm ) . V = ( 3 64 cm ) D. .
Câu 18: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Biết SA ⊥ ( ABCD) và SA = a 3 .
Thể tích của khối chóp S.ABCD có giá trị là 3 a 3 3 a 3 a 3 A. . B. . C. . D. 3 a 3 . 3 4 12
Câu 19: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA ⊥ ( ABC ) và SA = a 3 . Thể tích
khối chóp S.ABC là. 3 3a 3 a 3 3a 3 3a A. . B. . C. . D. . 6 4 4 8
Câu 20: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a , BC = 2a , đường thẳng SA
vuông góc với mặt phẳng ( ABCD) và SA = 3a . Thể tích của khối chóp S.ABCD bằng A. 3 a . B. 3 3a . C. 3 6a . D. 3 2a .
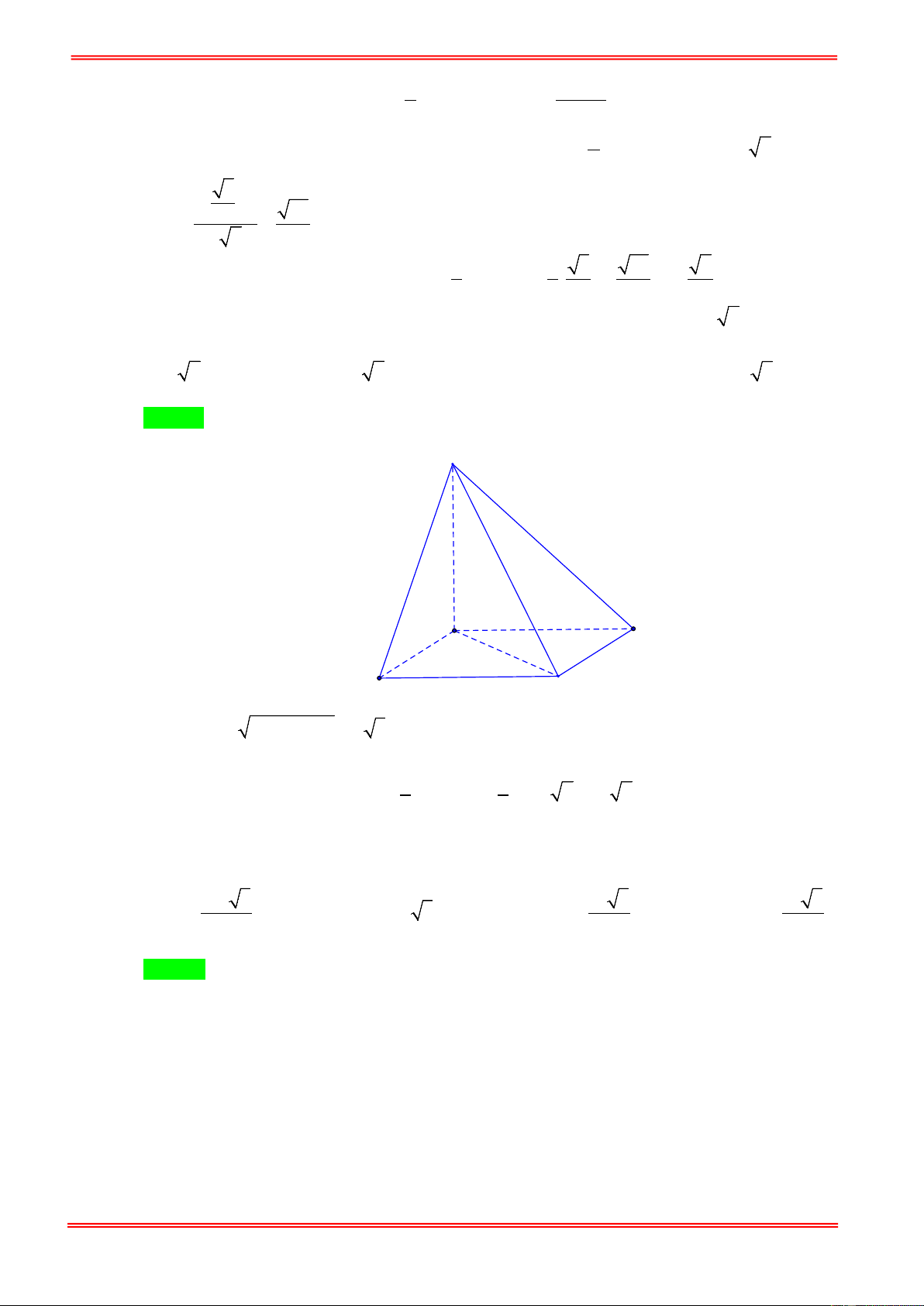
Câu 21: Cho hình hình chóp S.ABC có cạnh SA vuông góc với mặt đáy và SA = a 3 . Đáy ABC là tam
giác đều cạnh bằng a . Thể tích của khối chóp S.ABC bằng. 3 a 3 a 3 a 3 A. V = . B. V = . C. 3 V = a 3 . D. V = . 12 4 12
Câu 22: Đáy của hình chóp S.ABCD là một hình vuông cạnh a . Cạnh bên SA vuông góc với mặt phẳng
đáy và có độ dài là a . Thể tích khối tứ diện S.BCD bằng: https://toanmath.com/ 3 a 3 a 3 a 3 a A. . B. . C. . D. . 4 3 6 8
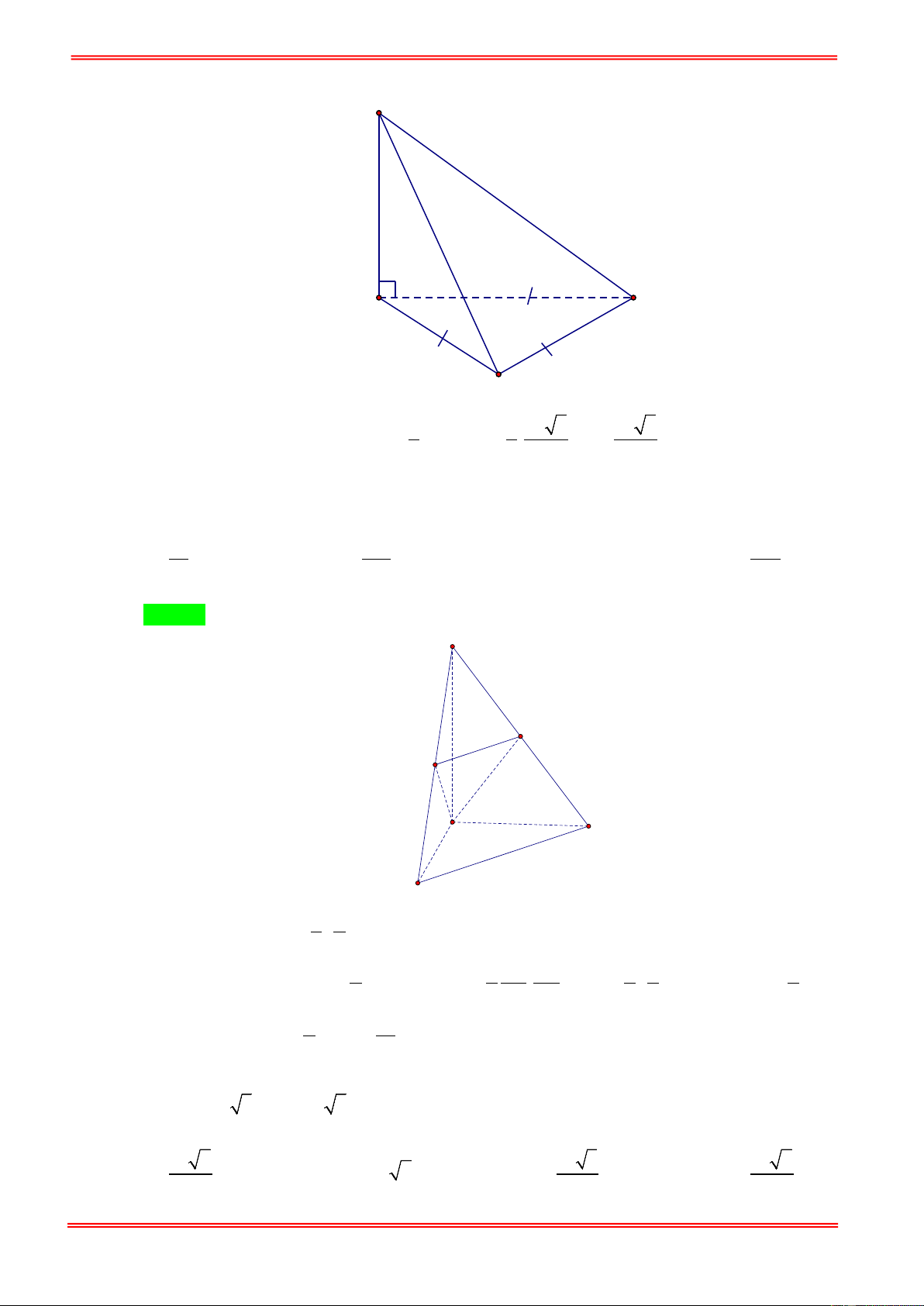
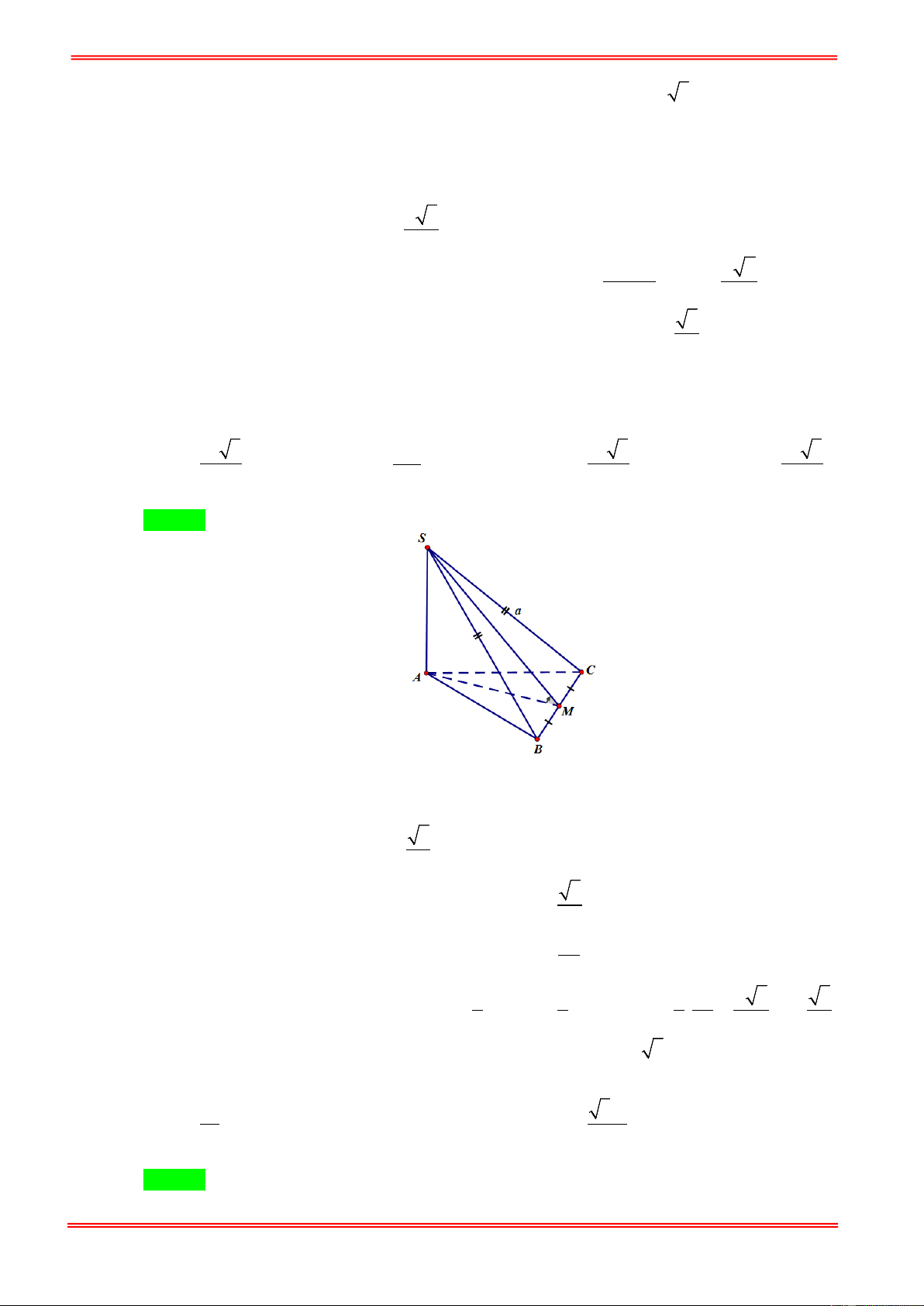
Câu 23: Hình chóp S.ABC có SA = a , SB = b , SC = c đôi một vuông góc với nhau. Thể tích khối chóp là. 2abc abc abc abc A. . B. . C. . D. . 9 6 3 9
Câu 24: Cho tứ diện ABCD có AD vuông góc với mặt phẳng ( ABC ) . Biết đáy ABC là tam giác vuông
tại B và AD = 5, AB = 5, BC =12 . Tính thể tích V của tứ diện ABCD . 325
A. V = 50 .
B. V = 120 .
C. V = 150 . D. V = . 16
Câu 25: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a , SA ⊥ ( ABCD) và
SA = a 6 . Thể tích của khối chóp S.ABCD bằng 3 a 6 3 a 6 3 a 6 A. . B. . C. . D. 3 a 6 . 3 2 6
Câu 26: Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a , SA ⊥ ( ABCD) và SA = 3a . Thể tích
khối chóp S.ABCD là. 3 a 3 a A. 3 2a . B. 3 a . C. . D. . 3 2
Câu 27: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Biết SA ⊥ ( ABCD); SA = a 3.
Tính thể tích của khối chóp. 3 a 3 3 a 3 3 a A. . B. . C. . D. 3 a 3 . 3 12 4
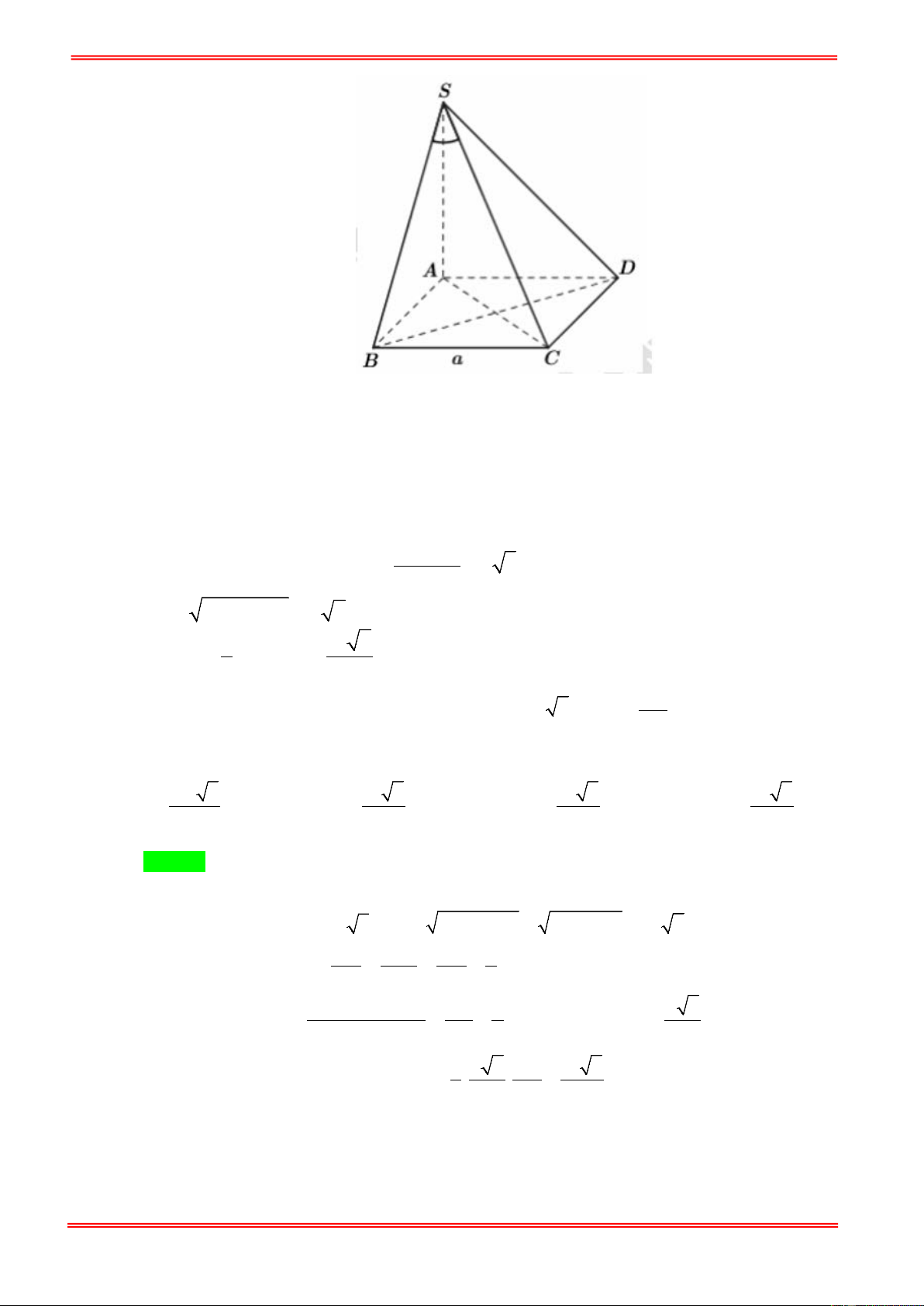
Câu 28: Cho hình chóp S.ABCD có đáy hình vuông cạnh a ; SA vuông góc mặt đáy; Góc giữa SC và mặt
đáy của hình chóp bằng 0
60 . Thể tích khối chóp S.ABCD là 3 a 2 3 a 3 a 6 3 a 3 A. B. C. D. 3 3 3 3
Câu 29: Cho hình chóp S.ABCD đáy ABCD là hình vuông có cạnh a và SA vuông góc đáy ABCD và
mặt bên (SCD) hợp với đáy một góc 60° . Tính thể tích hình chóp S.ABCD . 3 a 3 3 a 3 3 2a 3 A. . B. . C. 3 a 3 . D. . 3 6 3
Câu 30: Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng ( ABCD), đáy ABCD là hình thang
vuông tại A và B có AB = a, AD = 3a, BC = .
a Biết SA = a 3, tính thể tích khối chóp S.BCD theo . a 3 3a 3 2 3a 3 3a A. . B. . C. . D. 3 2 3a . 6 3 4
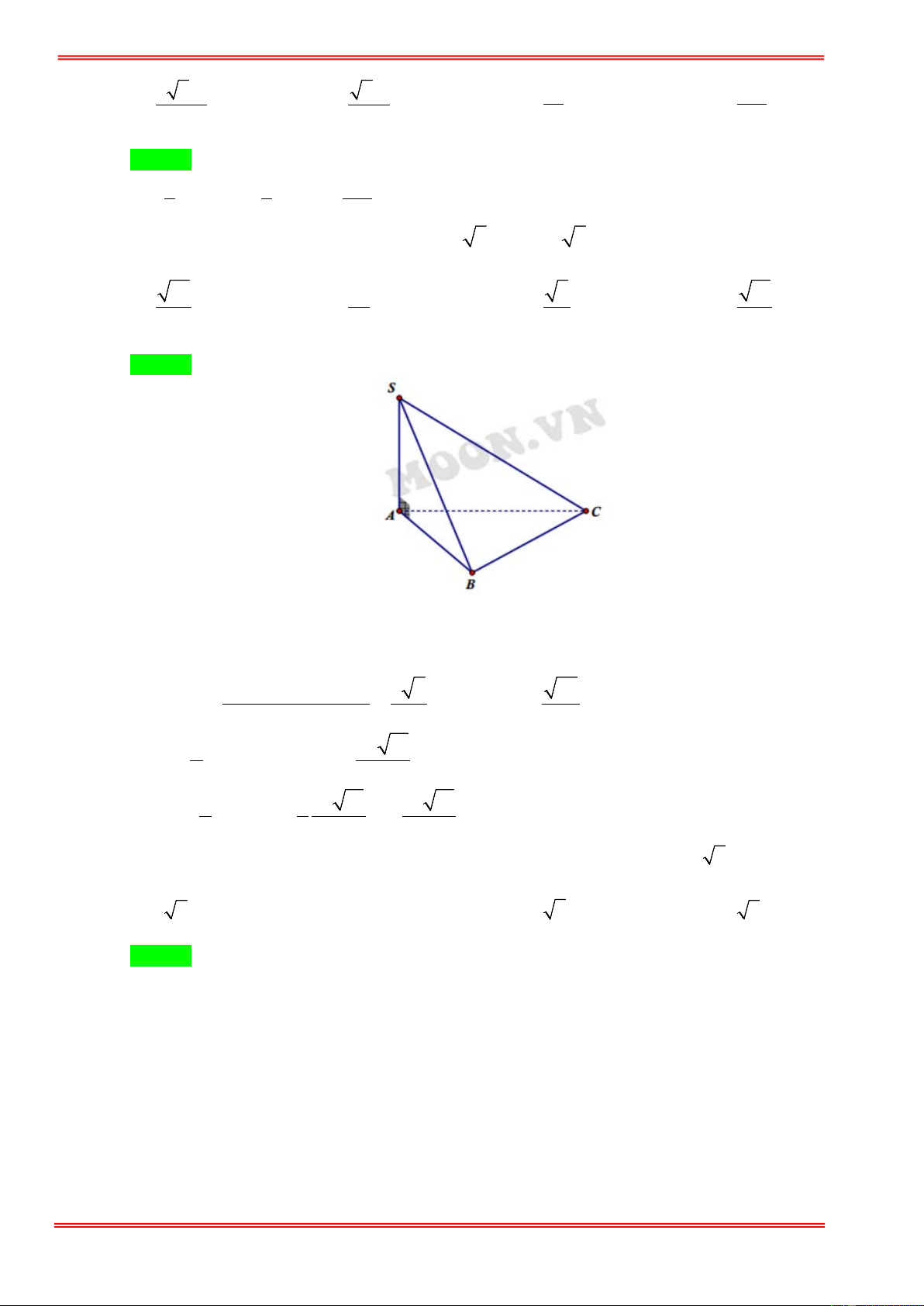
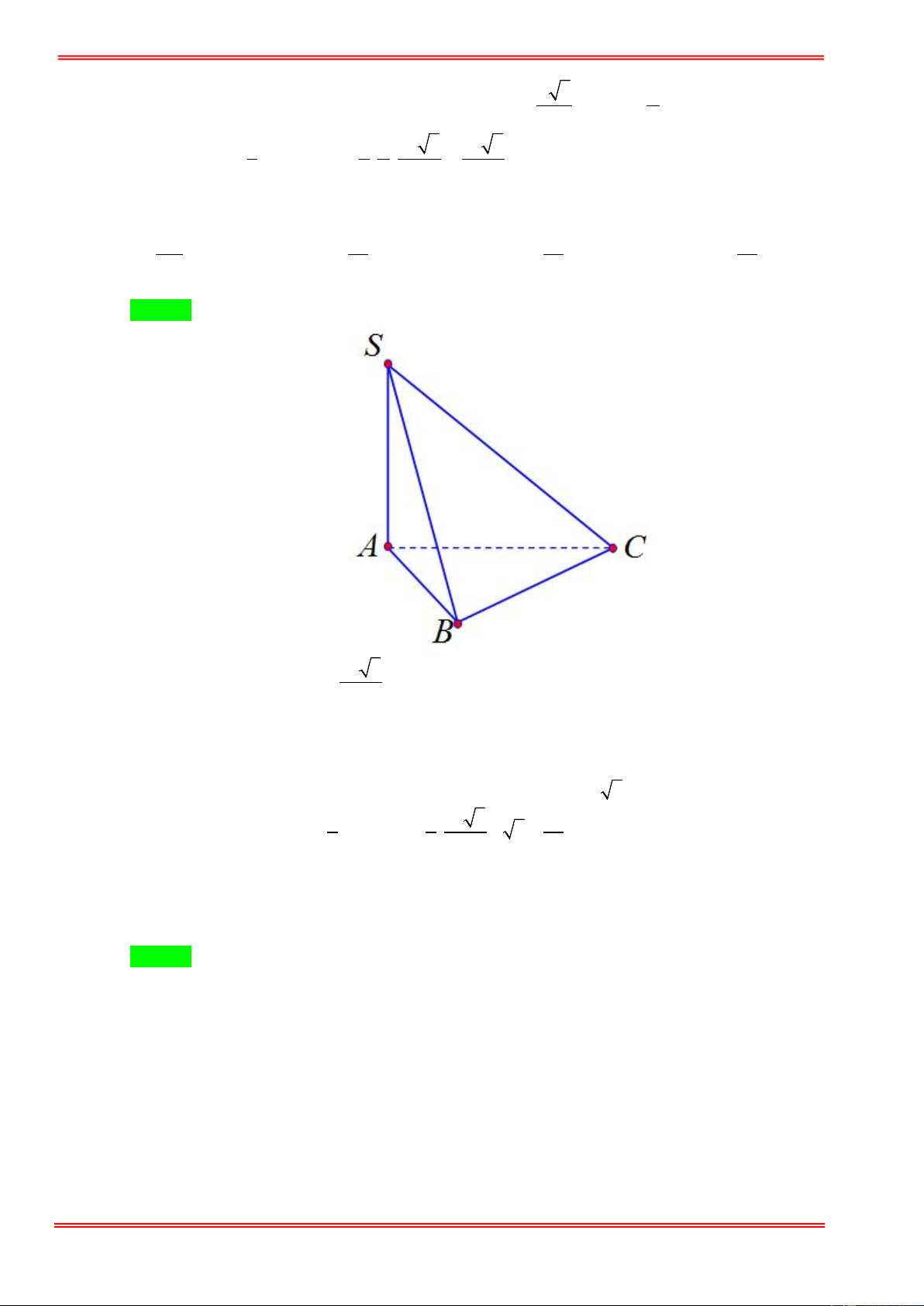
Câu 31: Cho hình chóp S.ABC có SA vuông góc với đáy. Tam giác ABC vuông cân tại B , biết
SA = AC = 2a . Tính thể tích khối chóp S.ABC . 2 1 2 2 4 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 3 3 3 3
Câu 32: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . SA vuông góc với đáy và tạo với
đường thẳng SB một góc 45°. Tính thể tích khối chóp S.ABC . 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 12 4 24 6 https://toanmath.com/
Câu 33: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , hai mặt phẳng (SAB) và (SAD)
cùng vuông góc với mặt phẳng ( ABCD) ; góc giữa đường thẳng SC và mặt phẳng ( ABCD) bằng
60° . Tính theo a thể tích khối chóp S.ABCD . 3 a 6 3 a 6 A. . B. . C. 3 3 2a . D. 3 3a . 9 3
Câu 34: Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, đường cao của một mặt bên là a 3 . Tính
thể tích V khối chóp đó. 3 a 2 3 a 2 3 a 2 A. V = . B. 3 V = a 2 . C. V = . V = 9 6 D. 3 . a 2
Câu 35: Hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AC =
; SA vuông góc với mặt 2
đáy. Góc giữa mặt bên (SBC) và mặt đáy bằng 45 .° Tính theo a thể tích khối chóp S.ABC . 3 a 3 a 3 3 a 2 3 a A. . B. . C. . D. . 16 48 48 48
Câu 36: Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng a , cạnh bên SB vuông góc với mặt
phẳng ( ABC), SB = 2a . Tính thể tích khối chóp S.ABC . 3 a 3 3 a 3 a 3 3 3a A. . B. . C. . D. . 2 4 6 4
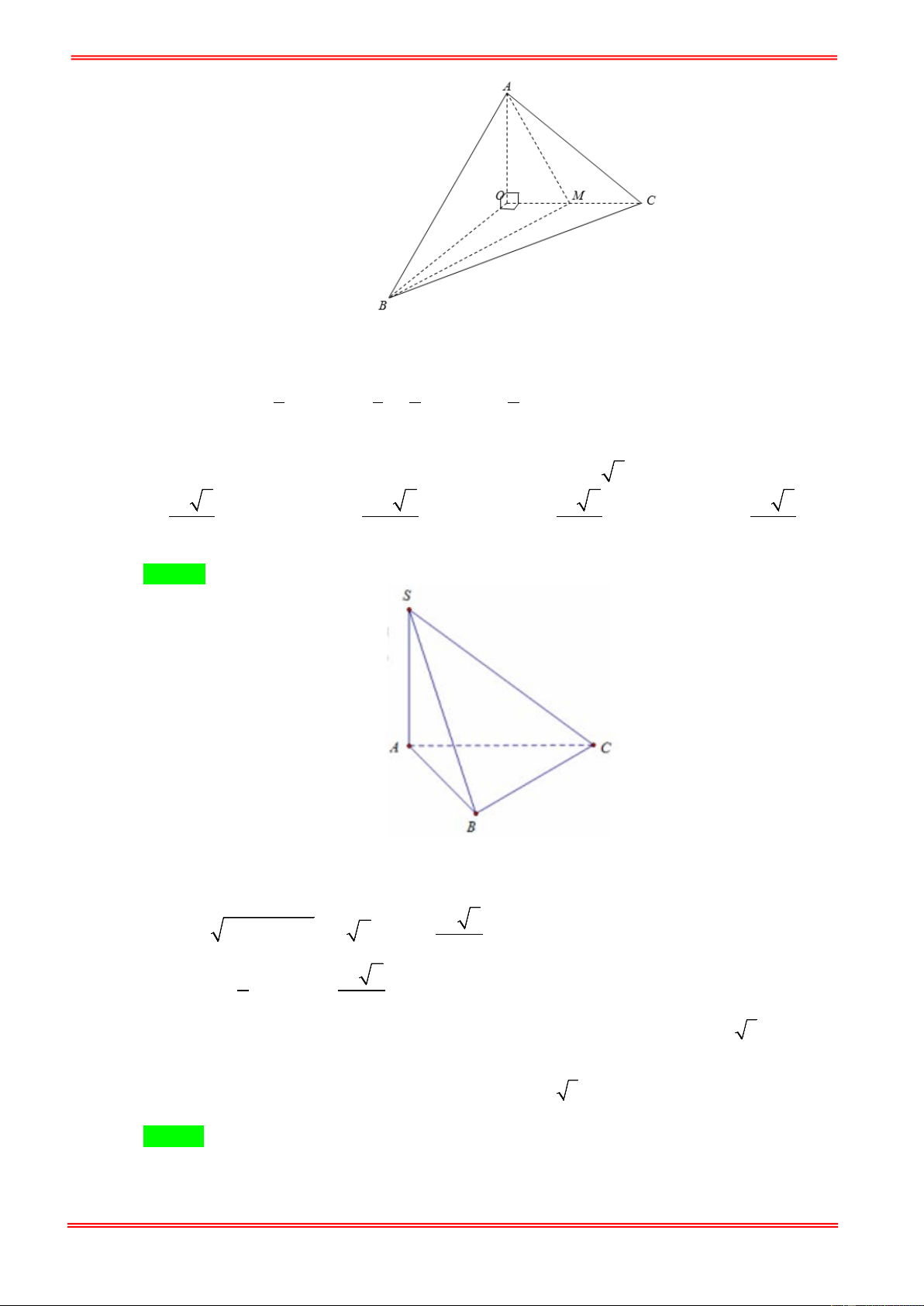
Câu 37: Cho khối tứ diện OABC với OA , OB , OC vuông góc từng đôi một và OA = a , OB = 2a , OC = 3a
. Gọi M , N lần lượt là trung điểm của hai cạnh AC, BC . Thể tích của khối tứ diện OCMN tính theo a bằng 3 a 3 3a 3 2a A. . B. . C. 3 a . D. . 4 4 3
Câu 38: Cho hình chóp S.ABC có mặt phẳng (SAC ) vuông góc với mặt phẳng ( ABC ) , SAB là tam giác
đều cạnh a 3 , BC = a 3 đường thẳng SC tạo với mặt phẳng ( ABC) góc 60°. Thể tích của
khối chóp S.ABC bằng 3 a 6 3 a 3 3 a 6 A. . B. 3 2a 6 . C. . D. . 6 3 2
Câu 39: Cho khối chóp S.ABC có SA ⊥ ( ABC ) , tam giác ABC vuông tại B , AB = a , AC = a 3 . Tính
thể tích khối chóp S.ABC , biết rằng SB = a 5 . 3 a 6 3 a 15 3 a 2 3 a 6 A. . B. . C. . D. . 4 6 3 6
Câu 40: Cho hình chóp tứ giác S.ABCD , đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với
mặt đáy, góc giữa SC và ( ABCD) bằng 45° . Thể tích khối chóp S.ABCD là 3 a 2 3 a 2 3 a 2 A. . B. . C. 3 a 2 . D. . 6 4 3
Câu 41: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a , SA ⊥ ( ABC ) . Góc giữa hai mặt phẳng
(SBC) và ( ABC) bằng 30°. Thể tích khối chóp S.ABC là. 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 8 6 12 3 https://toanmath.com/
Câu 42: Cho hình chóp S.ABC có đáy là tam giác vuông tại C , AB = a 5 , AC = a . Cạnh bên SA = 3a
và vuông góc với mặt phẳng ( ABC). Thể tích khối chóp S.ABC bằng: 3 a 5 A. . B. 3 a . C. 3 2a . D. 3 3a . 3
Câu 43: Cho khối chóp S.ABC có SA ⊥ ( ABC ) , tam giác ABC vuông tại B , AB = a , AC = a 3 . Tính
thể tích khối chóp S.ABC biết rằng SB = a 5 . 3 a 2 3 a 6 3 a 6 3 a 15 A. . B. . C. . D. . 3 4 6 6
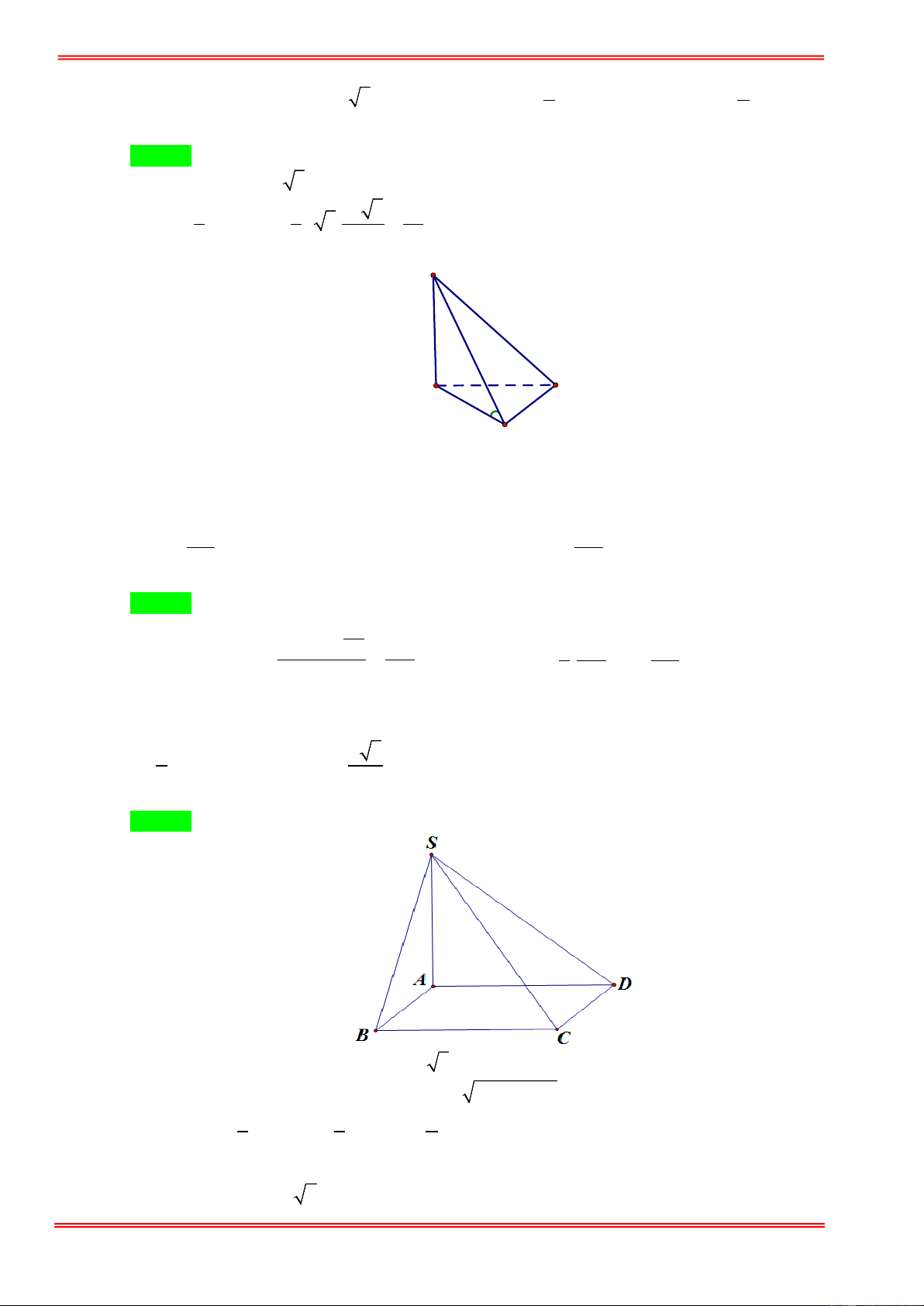
Câu 44: Cho khối chóp tam giác S.ABC có SA ⊥ ( ABC ) , tam giác ABC có độ dài 3 cạnh là AB = 5a ;
BC = 8a ; AC = 7a , góc giữa SB và ( ABC ) là 45° . Tính thể tích khối chóp S.ABC . 50 50 7 50 3 A. 3 a . B. 3 a . C. 3 50 3a . D. 3 a . 3 3 3
Câu 45: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D , AB = AD = a ,
SA = CD = 3a , SA vuông góc với mặt phẳng ( ABCD) . Thể tích khối chóp S.ABCD bằng. 1 1 A. 3 a . B. 3 2a . C. 3 6a . D. 3 a . 3 6
Câu 46: Cho hình chóp S.ABC có SA ⊥ ( ABC )
, góc giữa SB và ( ABC ) bằng o
60 ; tam giác ABC đều cạnh .
a Thể tích khối chóp S.ABC bằng 1 1 A. 3 a . B. 3 3a . C. 3 a . D. 3 a . 4 2
Câu 47: Cho tứ diện ABCD có các cạnh B ,
A BC, BD đôi một vuông góc với nhau: BA = 3a,
BC = BD = 2a . Gọi M và N lần lượt là trung điểm của AB và AD . Tính thể tích khối chóp C.BDNM . 3 3 3 2 A. = a V . B. 3 V = a . C. = a V . D. 3 V = 8a . 2 3
Câu 48: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy
( ABCD) . Biết AB = a , BC = 2a và SC = 3a . Tính thể tích khối chóp S.ABCD . 4 2 5 A. 3 a . B. 3 a . C. 3 2a . D. 3 a . 3 3
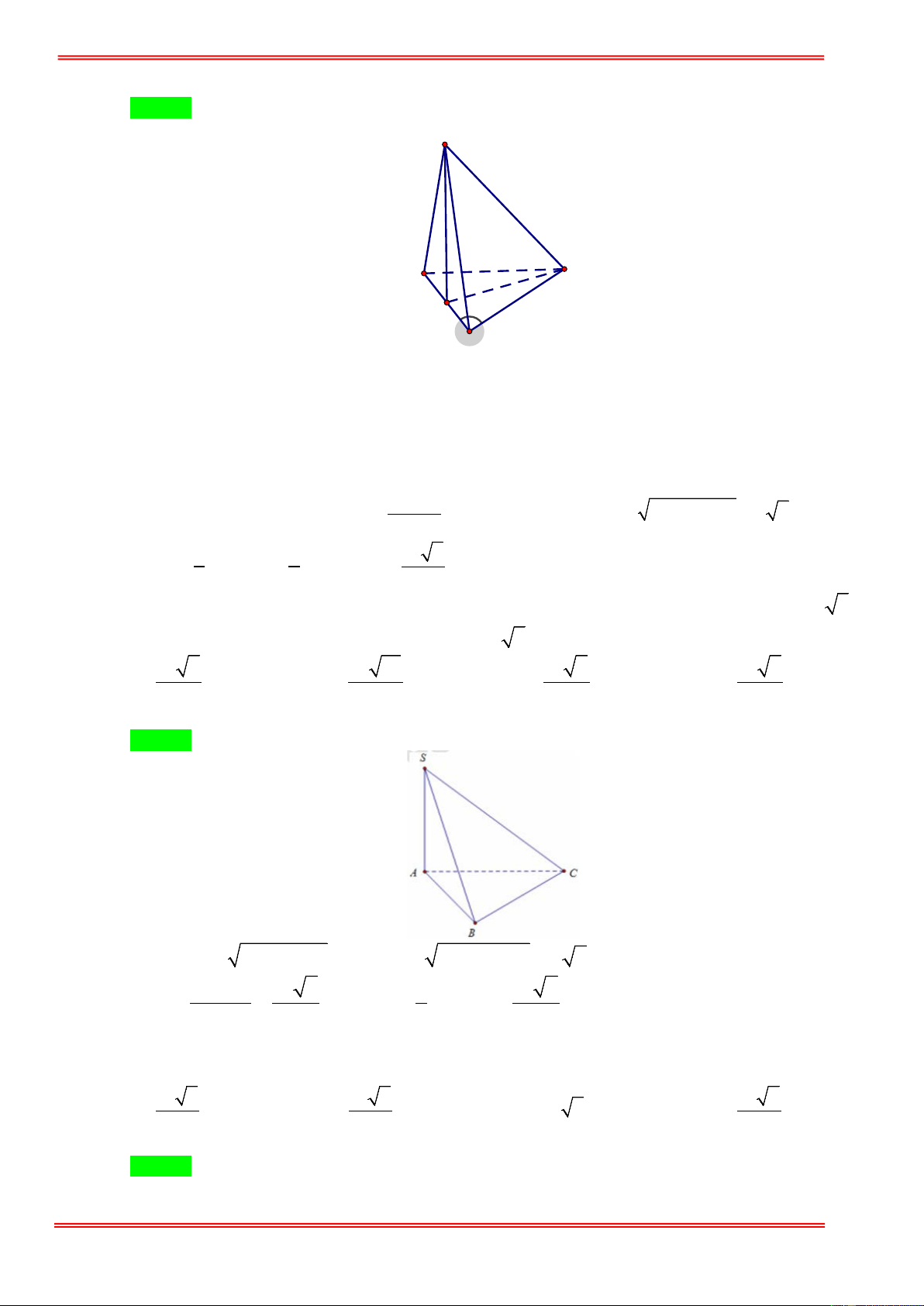
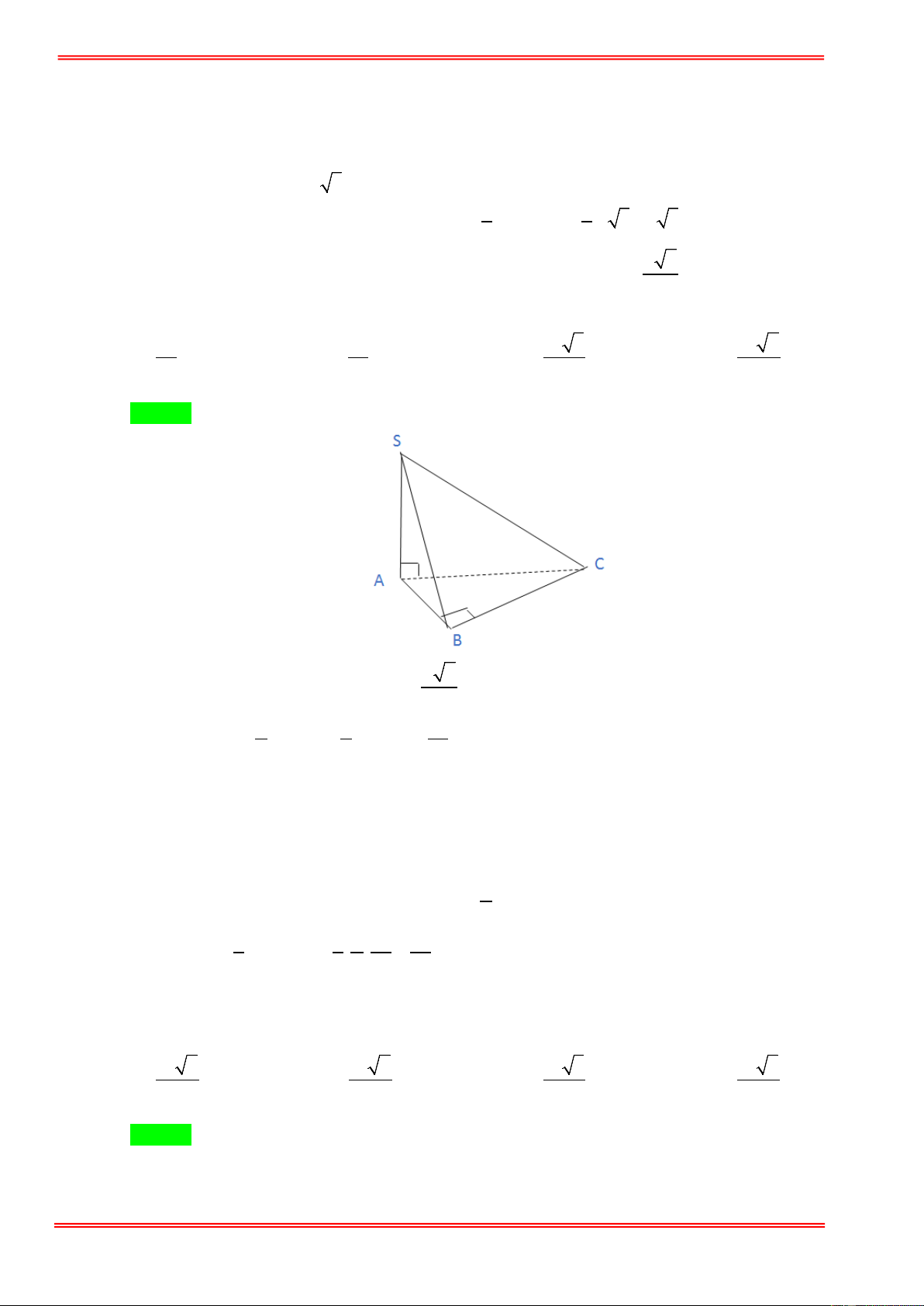
Câu 49: Cho tứ diện S.ABC có SAB, SCB là các tam giác cân tại S và ,
SA SB, SC đôi một vuông góc với
nhau. Biết BA = a 2 , thể tích V của tứ diện S.ABC là. 3 a 3 a A. V = . B. V = . C. 3 V = 2a 2 . D. 3 V = a . 6 2
Câu 50: Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a . Hai mặt bên (SAB) và (SAC ) cùng
vuông góc với đáy. Tính thể tích khối chóp biết SC = a 3 . 3 a 6 3 a 3 3 2a 6 3 a 3 B. . C. . D. . A. 12 . 2 9 4
Câu 51: Cho hình chóp S.ABCD có SA ⊥ ( ABCD) , ABCD là hình chữ nhật, SA = a , AB = 2a ,
BC = 4a . Gọi M , N lần lượt là trung điểm của BC , CD . Thể tích của khối chóp S.MNC là 3 a 3 a 3 a 3 a A. . B. . C. . D. . 5 2 4 3 https://toanmath.com/
Câu 52: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a , BC = 2a , SA = 2a , SA vuông
góc với mặt phẳng ( ABCD) . Tính thể tích khối chóp S.ABCD tính theo a . 3 8a 3 4a 3 6a A. B. C. D. 3 4a 3 3 3
Câu 53: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA = a 2 và SA vuông góc với
mặt phẳng đáy, tam giác SBD là tam giác đều. Thể tích của khối chóp S.ABCD bằng 3 a 2 3 2 2a A. 3 a 2. B. 3 2a 2. C. . D. . 3 3
Câu 54: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 1. Cạnh bên SA vuông góc với
mặt phẳng ( ABCD) và SC = 5 . Tính thể tích khối chóp S.ABCD . 15 3 3 A. V = .
B. V = 3 . C. V = . D. V = . 3 6 3
Câu 55: Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a, AD = a 2, SA ⊥ ( ABCD) , góc
giữa SC và đáy bằng 60° . Thể tích hình chóp S.ABCD bằng: A. 3 6a . B. 3 3a .
C. 3 2a . D. 3 2a .
Hình chóp S.ABCD có đáy hình vuông, SA vuông góc với đáy và SA = a 3 , AC = a 2 . Khi đó
Câu 56: thể tích khối chóp S.ABCD là 3 a 2 3 a 2 3 a 3 3 a 3 A. 3 B. 2 C. 3 D. 2
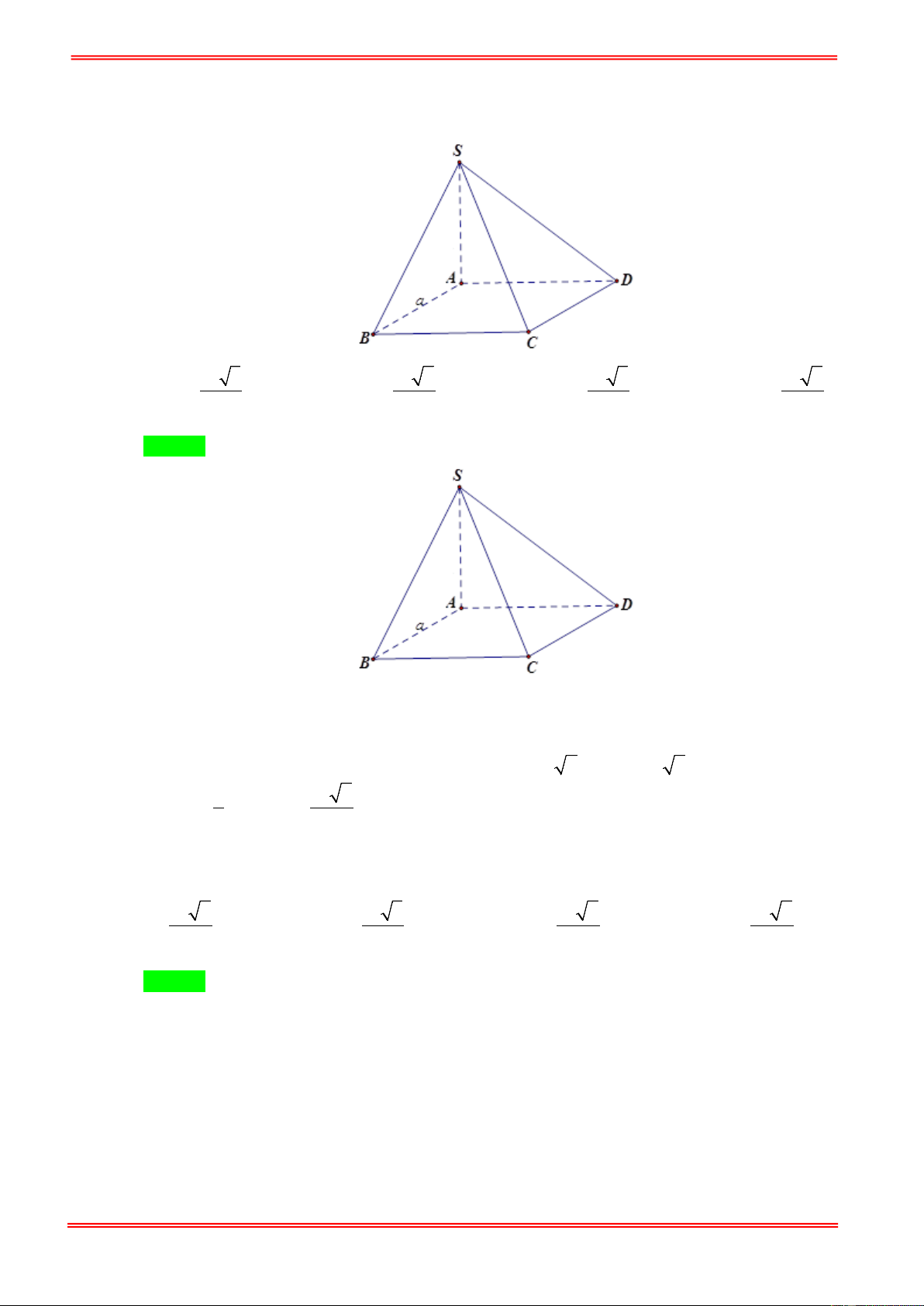
Câu 57: Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A , BC = 2a ,  BAC = 120° , biết
SA ⊥ ( ABC ) và mặt phẳng (SBC ) hợp với đáy một góc bằng 45° . Tính thể tích khối chóp S.ABC . 3 a 3 a 3 a A. 3 a 2 . B. . C. . D. . 9 2 3
Câu 58: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh bên SA vuông góc với đáy
và có độ dài bằng a . Tính thể tích khối tứ diện S.BCD . 3 a 3 a 3 a 3 a A. . B. . C. . D. . 2 4 6 3
Câu 59: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc 
BAD = 60° , SA ⊥ ( ABCD) .
Biết rằng khoảng cách từ A đến cạnh SC bằng a . Thể tích khối chóp S.ABCD là 3 a 2 3 a 2 3 a 3 A. . B. . C. . D. 3 a 3 . 4 12 6
Câu 60: Thể tích của tứ diện OABC có ,
OA OB, OC đôi một vuông góc, OA = a , OB = 2a , OC = 3a là A. 3 3a . B. 3 2a . C. 3 4a . D. 3 a .
Câu 61: Cho hình chóp S.ABCD có đáy là hình thoi cạnh a,  0
ABC = 120 , SA ⊥ ( ABCD) . Biết góc giữa hai
mặt phẳng (SBC)và (SCD) bằng 60°. Tính SA a 6 a 6 a 3 A. B. . C. a 6 D. 4 2 2
Câu 62: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng đáy, tam giác SBC đều cạnh a , góc giữa
mặt phẳng (SBC) và đáy là 30° . Thể tích khối chóp S.ABC là. 3 a 3 3 3a 3 a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . 24 64 16 32 https://toanmath.com/
Câu 63: Cho khối chóp S.ABCD có đáy là hình chữ nhậ, AB = a , AD = a 3 , SA vuông góc với đáy và
mặt phẳng (SBC) tạo với đáy một góc 60°. Tính thể tích V của khối chóp S.ABCD . 3 a 3 3a A. V = . B. 3 V = 3a . C. V = . D. 3 V = a . 3 3 2
Câu 64: Hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B , = a AC
; SA vuông góc với mặt đáy. 2
Góc giữa mặt bên (SBC) và mặt đáy bằng 45 .° Tính theo a thể tích khối chóp S.ABC. 3 a 3 a 3 a 3 3 a 2 A. . B. . C. . D. . 48 16 48 48
Câu 65: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA vuông góc với mặt phẳng đáy.
Gọi I là trung điểm của BC , góc giữa (SBC ) và ( ABC ) bằng 30° . Thể tích khối chóp S.ABC bằng: 3 a 6 3 a 6 3 a 3 3 a 3 A. . B. . C. . D. . 24 8 24 8
Câu 66: Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a . SA vuông góc với ( ABCD) ,
SC = a 3 . Tính thể tích khối chóp S.ABCD theo a . 3 a 3 a 3 3 a 3 A. 3 V = a . B. V = . C. V = . D. V = . S . ABCD S . ABCD 3 S . ABCD 9 S . ABCD 3
Câu 67: Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B , AB a , góc giữa mặt phẳng
SBC và mặt phẳng ABC bằng o
60 , SA  ABC. Gọi M , N lần lượt là trung điểm của SC
và AC . Tính thể tích khối chóp MNBC ? 3 a 3 a 3 3 a 6 3 a 3 A. . B. . C. . D. . 4 24 18 12
Câu 68: Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a, AD = a 2 , SA ⊥ ( ABCD) , góc
giữa SC và mặt phẳng đáy bằng 60°. Thể tích khối chóp S.ABCD bằng: A. 3 a 2 . B. 3 a 6 . 3 C. 3a . D. 3 3a 2 .
Câu 69: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA ⊥ ( ABCD) , SC tạo với mặt
đáy một góc bằng 60 . Tính thể tích V của khối chóp đã cho. 3 a 3 3 a 6 3 a 3 3 a 6 A. V = . B. V = . C. V = . D. V = . 3 6 6 3 a 2
Câu 70: Hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AC =
; SA vuông góc với mặt 2
đáy. Góc giữa mặt bên (SBC) và mặt đáy bằng 45 .° Tính theo a thể tích khối chóp S.ABC. 3 a 2 3 a 3 a 3 3 a A. . B. . C. . D. . 48 48 48 16
Câu 71: Cho hình chóp S.ABCD với ABCD là hình vuông cạnh a . Mặt bên SAB là tam giác cân tại S
và nằm trên mặt phẳng vuông góc với mặt phẳng đáy. Cạnh bên SC tạo với đáy một góc 60° .
Tính thể tích khối chóp S.ABCD . 3 a 6 3 a 3 3 a 15 3 a 15 A. . B. . C. . D. . 3 6 2 6 https://toanmath.com/
Câu 72: Cho hình chóp S.ABCD có SA ⊥ ( ABCD) , ABCD là hình chữ nhật. SA = AD = 2a . Góc giữa
(SBC) và mặt đáy ( ABCD) là 60°. Gọi G là trọng tâm tam giác SBC . Tính thể tích khối chóp
S.AGD là 3 32a 3 3 8a 3 3 4a 3 3 16a A. . B. . C. . D. . 27 27 9 9 3
Câu 73: Hình chóp S.ABCD có đáy là hình vuông, a là độ dài cạnh đáy. Cạnh bên SA vuông góc với đáy,
SC tạo với (SAB) góc o
30 . Thể tích khối chóp S.ABCD là: 3 a 2 3 a 3 3 a 2 3 a 2 A. B. . C. . D. . 2 3 4 3 2 3a
Câu 74: Cho hình chóp S.ABCD có SA ⊥ ( ABCD) , AC = a 2 , S =
và góc giữa đường thẳng ABCD 2
SC và mặt phẳng ABCD bằng 60° . Gọi H là hình chiếu vuông góc của A trên SC . Tính theo
a thể tích của khối chóp H.ABCD . 3 3a 6 3 a 6 3 a 6 3 a 6 A. . B. . C. . D. . 4 2 4 8
Câu 75: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy ( ABCD),
AB = a, AD = 2a . Góc giữa cạnh bên SB và mặt phẳng ( ABCD) bằng o 45 . Thể tích hình chóp
S.ABCD bằng. 3 2 2a 3 6a 3 a 3 2a A. . B. . C. . D. . 3 18 3 3
Câu 76: Cho hình chóp S.ABC có AB = a , BC = a 3 , AC = a 5 và SA vuông góc với mặt đáy, SB
tạo với đáy góc 45° . Thể tích của khối chóp S.ABC là: 15 3 a 3 11 A. 3 a . B. . C. 3 a . D. 3 a . 12 12 12 12
Câu 77: Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a , AD = a 2 ; SA ⊥ ( ABCD) ,
góc giữa SC và đáy bằng 60°. Tính theo a thể tích khối chóp S.ABCD . A. 3 3 2a . B. 3 3a . C. 3 6a . D. 3 2a .
Câu 78: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, S A vuông góc với mặt phẳng đáy, góc
giữa (SBC ) và ( ABC ) bằng 30 .
° Thể tích khối chóp S.ABC là 3 a 6 3 a 3 3 a 3 3 a 6 A. . B. . C. . D. . 8 24 8 24
Câu 79: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , cạnh bên SA vuông góc với đáy,
đường thẳng SC tạo với đáy một góc bằng 60°. Thể tích của khối chóp S.ABC bằng 3 3a 3 a 3 a 3 a A. . B. . C. . D. . 4 8 4 2
Câu 80: Cho tứ diện .
O ABC có OA , OB , OC đôi một vuông góc với nhau và OA = 2a , OB = 3a ,
OC = 8a . M là trung điểm của OC. Tính thể tích V của khối tứ diện . O ABM . A. 3 V = 6a . B. 3 V = 8a . C. 3 V = 4a . D. 3 V = 3a .
Câu 81: Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a . Hai mặt bên (SAB) và ( SAC ) cùng
vuông góc với đáy. Tính thể tích khối chóp biết SC = a 3 . 3 a 3 3 2a 6 3 a 6 3 a 3 A. B. . C. . D. . 2 9 12 4 https://toanmath.com/
Câu 82: Cho khối chóp S.ABC có SA ⊥ ( ABC) , A
∆ BC vuông tại B , SB = 2a , SC = a 5 . Thể tích khối
chóp S.ABC bằng 3
a . Khoảng cách từ A đến (SBC ) là: A. 2a . B. 3a . C. 3a . D. 6a .
Câu 83: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , AB = a , AC = 2a , SC = 3a , SA
vuông góc với đáy ( ABC). Thể tích khối chóp S.ABC là. 3 a 5 3 a 3 3 a 3 a 3 A. . B. . C. . D. . 3 12 4 4
Câu 84: Cho hình chóp S.ABC có ABC là tam giác đều cạnh a và SA vuông góc với đáy. Góc tạo bởi
mặt phẳng (SBC) và mặt phẳng ( ABC) bằng 30° . Thể tích của khối chóp S.ABC là 3 a 3 3 a 3 a 3 a 3 A. . B. . C. . D. . 24 4 12 8
Câu 85: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Cạnh bên SA vuông góc với mặt phẳng
đáy, cạnh bên SC tạo với mặt phẳng (SAB) một góc 30° . Thể tích của khối chóp S.ABCD bằng: 3 a 2 3 a 2 3 a 2 3 a 3 A. . B. . C. . D. . 3 4 2 3
Câu 86: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Cạnh bên SA vuông góc với mặt phẳng
đáy, cạnh bên SC tạo với mặt phẳng (SAB) một góc 30° . Thể tích của khối chóp đó bằng. . 3 a 2 3 a 3 3 a 2 3 a 2 A. . B. . C. . D. . 2 3 4 3
Câu 87: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C và SA vuông góc với mặt phẳng
(ABC). Biết AB = 4a và góc giữa mặt phẳng (SBC) và (ABC) bằng 45°. Tính thể tích V của
khối chóp S.ABC . 8 2 3 2 1 2 A. 3 V = a . B. 3 V = a . C. 3 V = a . D. 3 V = a . 3 2 6 6
Câu 88: Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật, AB = a , AD = a 2 . Biết
SA ⊥ ( ABCD) và góc giữa đường thẳng SC với mặt phẳng đáy bằng 45°. Thể tích khối chóp
S.ABCD bằng: 3 a 6 A. 3 3a . B. 3 a 6 . C. . D. 3 a 2 . 3
Câu 89: Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân có cạnh huyền BC = a và SA vuông
góc với mặt phẳng đáy. Biết góc giữa mặt phẳng (SBC) và mặt phẳng ( ABC) bằng 45°. Thể tích
của hình chóp S.ABC là. 3 a 2 3 a 3 a 3 a 2 A. V = . B. V = . C. V = . D. V = . S . ABC 24 S . ABC 8 S . ABC 24 S . ABC 8
Câu 90: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a . Các mặt bên (SAB) , ( SAC ) cùng vuông
góc với mặt đáy ( ABC ) ; góc giữa SB và mặt ( ABC ) bằng 60° . Tính thể tích khối chóp S.ABC . 3 a 3 3a 3 a 3 a A. . B. . C. . D. . 12 4 2 4
Câu 91: Cho khối chóp S.ABC , có đáy ABC là tam giác đều cạnh a . Hai mặt bên (SAB) và (SAC ) cùng
vuông góc với đáy. Tính thể tích khối chóp biết SC = a 3 . https://toanmath.com/ 3 a 6 3 a 6 3 a 6 3 a 6 A. V = . B. V = . C. V = . D. V = . 3 6 12 8
Câu 92: Cho hình chóp S.ABC là tam giác vuông tại A ,  30o ABC =
, BC = a . Hai mặt bên (SAB) và
(SAC) cùng vương góc với đáy (ABC), mặt bên (SBC) tạo với đáy một góc 0 45 . Thể tích của
khối chóp S.ABC là: 3 a 3 a 3 a 3 a A. . B. . C. . D. . 9 32 64 16
Câu 93: Cho khối chóp S.ABC có SA ⊥ ( ABC ) , SA = a , AB = a , AC = 2a và 
BAC = 120° . Tính thể tích
khối chóp S.ABC . 3 a 3 3 a 3 3 a 3 A. 3 a 3 . B. . C. . D. . 6 3 2
Câu 94: Tính thể tích khối chóp S.ABC có AB = a , AC = 2a , 
BAC = 120° , SA ⊥ ( ABC ) , góc giữa
(SBC) và ( ABC) là 60°. 3 7 a 3 21 a 3 7 a 3 3 21 a A. . B. . C. . D. . 7 14 14 14
Câu 95: Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a , AD = a 2 , SA ⊥ ( ABCD) ,
góc giữa SC và đáy bằng 60°. Thể tích hình chóp S.ABCD bằng A. 3 3 2a . B. 3 2a . C. 3 3a . D. 3 6a .
Câu 96: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với mặt phẳng đáy
và cạnh bên SD hợp với đáy một góc 60°. Hỏi thể tích V của khối chóp S.ABCD bằng bao nhiêu? 3 2a 3 3 a 3 3 a 3 A. V = . B. 3 V = a 3 . C. V = . D. V = . 3 6 3
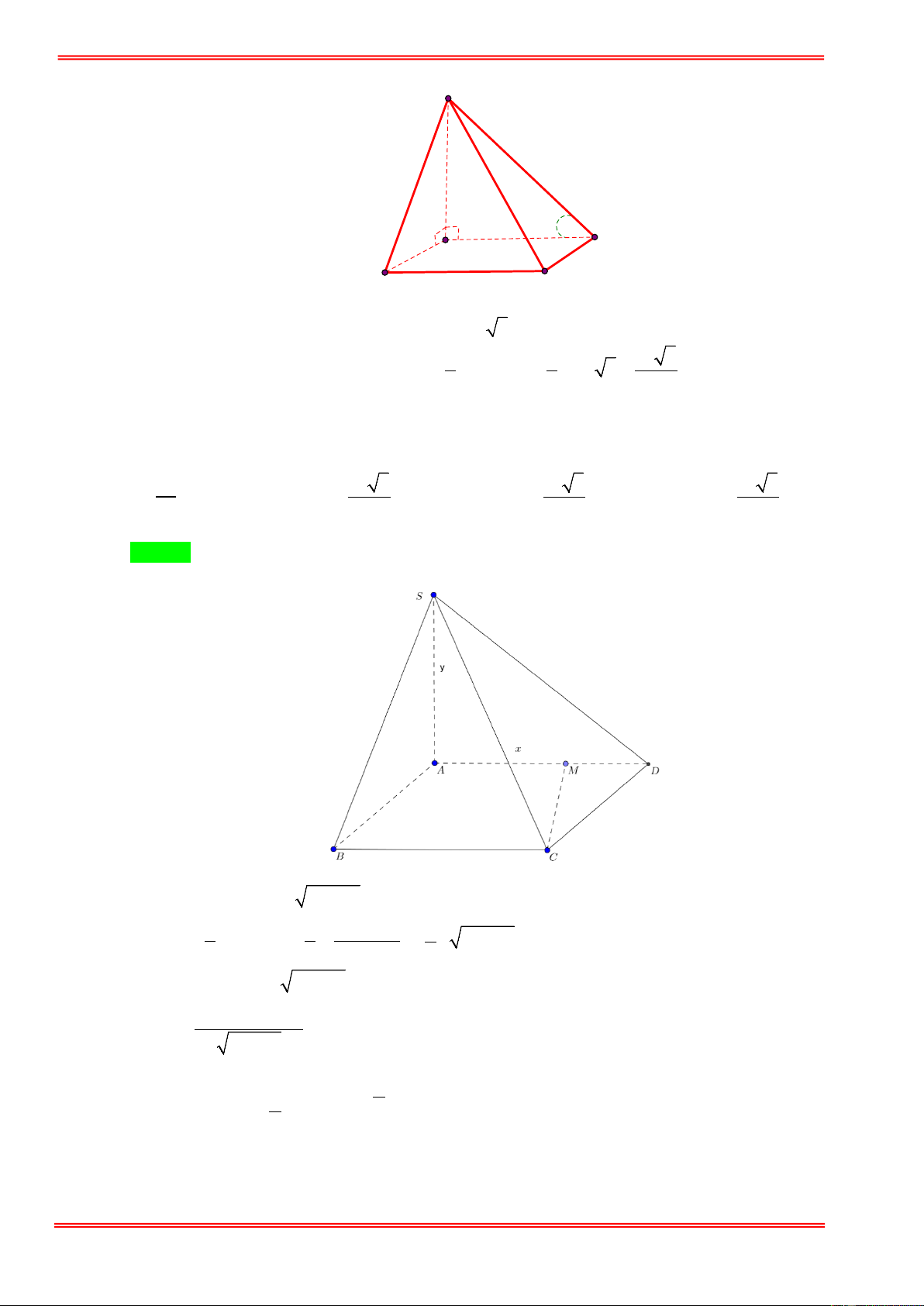
Câu 97: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a . Cạnh SA vuông góc với đáy
và SA = y . Trên cạnh AD lấy điểm M sao cho AM = x . Biết rằng 2 2 2
x + y = a . Tìm giá trị lớn
nhất của thể tích khối chóp S.ABCM . 3 a 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 8 8 2 4 https://toanmath.com/
THỂ TÍCH KHỐI CHÓP CÓ MỘT CẠNH BÊN VUÔNG GÓC VỚI ĐÁY B. LỜI GIẢI CHI TIẾT Câu 1:
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Biết SA vuông góc với ( ABCD)
và SA = a 3 . Thể tích của khối chóp S.ABCD là: 3 a 3 a 3 3 a 3 A. . B. 3 a 3 . C. . D. . 4 6 3 Hướng dẫn giải Chọn D S A D B C 3 Thể tích khối chóp 1 a 3 V = S .SA = . S . ABCD 3 ABCD 3 Câu 2:
Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với mặt phẳng đáy
và SA = 2a . Thể tích khối chóp S.ABCD bằng 3 4a 3 a 3 2a A. . B. 3 2a . C. . D. . 3 3 3 Hướng dẫn giải Chọn D 3 1 1 2a 2 V = S
⋅ SA = ⋅ a ⋅ 2a = . S . ABCD ∆ 3 ABCD 3 3 Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a, BC = 2a , cạnh bên SA vuông
góc với đáy và SA = a 2 . Tính thể tích khối chóp S.ABCD . 3 2a 3 3 2a 2 A. . B. 3 a 2 . C. 3 2a 2 . D. . 3 3 https://toanmath.com/ Hướng dẫn giải Chọn D Diện tích đáy: 2 S = A . B BC = 2a . ABCD 3 Thể tích: 1 2a 2 V = S .SA = . 3 ABCD 3 Câu 4:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh bên SA vuông góc với đáy
và có độ dài bằng 2a . Thể tích khối tứ diện S.BCD là: 3 a 3 a 3 a 3 a A. . B. . C. . D. . 4 8 6 3 Hướng dẫn giải Chọn D S A D B C 2 1 a 2 3 1 1 a a Ta có: S = S = . Suy ra V = . SA S = .2 . a = . BC ∆ D ∆ 2 ABCD 2 S . ABCD 3 BCD 3 2 3 Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a . Biết SA vuông góc với
mặt phẳng đáy và SA = a 2. Tính thể tích khối chóp S.ABO . 3 a 2 3 2a 2 3 a 2 3 4a 2 A. . B. . C. . D. . 3 12 12 3 Hướng dẫn giải Chọn A . AC 1 Ta có: 2 AC = 2 .
a 2 ⇒ OA = OB = = a 2 ⇒ S = . OA OB = a . 2 OAB 2 Vậy: 1 1 2 2 3 V = . SA S = .a 2.a = .a . S .OAB 3 OAB 3 3 Câu 6:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2a . Biết SA = 6a và SA
vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD . A. 3 8a . B. 3 6 3a . C. 3 12 3a . D. 3 24a . Hướng dẫn giải https://toanmath.com/ Chọn A S A D B C 1 Ta có 2 S
= 4a . Do SA vuông góc với mặt phẳng đáy nên V = . . SA S 3 = 8a . ABCD S . ABCD 3 ABCD Câu 7:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a . Biết SA vuông góc với
mặt phẳng đáy và SA = a 2. Tính thể tích khối chóp S.ABO . 3 4a 2 3 2a 2 3 a 2 3 a 2 A. . B. . C. . D. . 3 12 12 3 Hướng dẫn giải Chọn D . AC 1 Ta có: 2 AC = 2 .
a 2 ⇒ OA = OB = = a 2 ⇒ S = . OA OB = a . 2 OAB 2 Vậy : 1 1 2 2 3 V = . SA S = .a 2.a = .a . S .OAB 3 OAB 3 3 Câu 8:
Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = a, AD = 2a , SA ⊥ ( ABCD) và
SA = a 3 . Thể tính khối chóp S.ABC bằng: 3 2a 3 3 a 3 A. 3 a 3 . B. 3 2a 3 . C. . D. . 3 3 Hướng dẫn giải Chọn D 3 1 1 1 1 a 3 Ta có V = S . A S = S . A A . B BC = a 3. .2 a a = . 3 ABC 3 2 6 3 Câu 9:
Cho hình chóp tam giác S.ABC với SA , SB , SC đôi một vuông góc và SA = SB = SC = a . Tính
thế tích của khối chóp S.ABC . 1 1 2 1 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 2 6 3 3 Hướng dẫn giải Chọn B 1 1 1 1 Ta có V = .S .SA = . . . SB SC.SA 3 = .a . 3 SBC 3 2 6
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh SA vuông góc với mặt
phẳng đáy và có độ dài là a . Thể tích khối tứ diện S.BCD bằng. https://toanmath.com/ 3 a 3 a 3 a 3 a A. . B. . C. . D. . 6 8 3 4 Hướng dẫn giải Chọn A 3 1 1 1 a 2 V = V = . . . a a = . . S .BCD S . ABCD 2 2 3 6
Câu 11: Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = a, AD = 2a , SA vuông góc với mặt
đáy và SA = a 3 . Thể tính khối chóp S.ABCD bằng 3 a 3 3 2a 3 A. 3 2a 3. B. . C. 3 a 3. D. . 3 3 Hướng dẫn giải Chọn D S Ta có A D B C 3 1 1 2a 3 V = . SA S = .a 3. . a 2a = . 3 ABCD 3 3
Câu 12: Cho tứ diện OABC có OA , OB , OC đôi một vuông góc với nhau tại O và OA = 2 , OB = 4 ,
OC = 6 . Thể tích khối tứ diện đã cho bằng. A. 24 . B. 16 . C. 8 . D. 48 . Hướng dẫn giải Chọn C 1 Ta có V = 1 . OA . OB OC = .2.4.6 = 8 . OABC 6 6
Câu 13: Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA vuông góc với mặt phẳng đáy
và SA = 2a . Tính thể tích khối chóp S.ABC . 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 2 3 12 Hướng dẫn giải Chọn A https://toanmath.com/ S C A B 3 1 1 1 1 1 3 a 3 Ta có V = .S . A S = .2 . a .A . B AC.sin 60° = .2 . a . . a . a = . S . ABC 3 ABC 3 2 3 2 2 6
Câu 14: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a , SA vuông góc với mặt phẳng đáy,
SA = a 3 . Tính thể tích khối chóp S.ABC . A. 2 V = a (đvtt). B. 3 V = a (đvtt). S . ABC S . ABC 3 a C. V = (đvtt). D. 3 V = 3a (đvtt). S . ABC 2 S . ABC Hướng dẫn giải Chọn B 1
Thể tích khối chóp là V = 1 . SA S = S . A A . B AC.sin 60° 1 3 = a 3.2 .2 a . a 3 = a . 3 ABC 6 6 2
Câu 15: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB = a , BC = 2a , SA ⊥ ( ABC ) ,
SA = 3a . Thể tích của khối chóp S.ABC bằng 1 1 A. 3 a . B. 3 a . C. 3 a . D. 3 3a . 6 3 Hướng dẫn giải Chọn B S A C B Thể tích 1 1 1 1 V = S .SA = . B . A BC.SA 3 = .2 a .3
a a = a . S . ABC 3 ABC 3 2 6 https://toanmath.com/
Câu 16: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc
với mặt phẳng đáy và SA = 2a . Tính thể tích V của khối chóp S.ABCD . 3 2a 3 2a 3 2a A. 3 V = 2a . B. V = . C. V = . D. V = . 4 6 3 Hướng dẫn giải Chọn D S A D B C .
Ta có: SA = a 2 . 3 1 1 2a 2 2 S = a ⇒ V = .S SA = . 2 . a a = . ABCD ABCD 3 ABCD 3 3
Câu 17: Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh 8(cm) , chiều cao SH bằng 3(cm) .
Tính thể tích khối chóp? A. V = ( 3 1 6 cm ) . B. V = ( 3 24 cm ) . C. V = ( 3 48 cm ) . V = ( 3 64 cm ) D. . Hướng dẫn giải Chọn D 1 V = SH .S = 64( 3 cm ) . 3 ABCD
Câu 18: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Biết SA ⊥ ( ABCD) và SA = a 3 .
Thể tích của khối chóp S.ABCD có giá trị là 3 a 3 3 a 3 a 3 A. . B. . C. . D. 3 a 3 . 3 4 12 Hướng dẫn giải Chọn A 3 1 1 a 3
Vì SA ⊥ ( ABCD) nên 2 V = . SA S = .a 3.a = S . ABCD 3 ABCD 3 3 .
Câu 19: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA ⊥ ( ABC ) và SA = a 3 . Thể
tích khối chóp S.ABC là. 3 3a 3 a 3 3a 3 3a A. . B. . C. . D. . 6 4 4 8 Hướng dẫn giải Chọn B 2 3 1 1 a 3 a V = S .SA = .a 3 = . S . ABC 3 ABC 3 4 4
Câu 20: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a , BC = 2a , đường thẳng SA
vuông góc với mặt phẳng ( ABCD) và SA = 3a . Thể tích của khối chóp S.ABCD bằng A. 3 a . B. 3 3a . C. 3 6a . D. 3 2a . Hướng dẫn giải Chọn D https://toanmath.com/ S 3a D A a 2a B C 1 V = . .2 a .3 a a S . ABCD 3
Áp dụng công thức tính thể tích khối chóp ta có 3 = 2a . 1 6 T 1 6 T 3 4 1 6 T 3 4
Câu 21: Cho hình hình chóp S.ABC có cạnh SA vuông góc với mặt đáy và SA = a 3 . Đáy ABC là tam
giác đều cạnh bằng a . Thể tích của khối chóp S.ABC bằng. 3 a 3 a 3 a 3 A. V = . B. V = . C. 3 V = a 3 . D. V = . 12 4 12 Hướng dẫn giải Chọn B 2 2 AB 3 a 3 Ta có: S . ABC ∆ = = . 4 4 2 3 1 1 a 3 a V = . SA S = .a 3. = . S.ABC ABC ∆ 3 3 4 4
Câu 22: Đáy của hình chóp S.ABCD là một hình vuông cạnh a . Cạnh bên SA vuông góc với mặt phẳng
đáy và có độ dài là a . Thể tích khối tứ diện S.BCD bằng: 3 a 3 a 3 a 3 a A. . B. . C. . D. . 4 3 6 8 Hướng dẫn giải Chọn C 3 1 1 1 1 a Thể tích 2 V = V = . . SA S = . . a a = . S .BCD S . 2 ABCD 2 3 ABCD 6 6
Câu 23: Hình chóp S.ABC có SA = a , SB = b , SC = c đôi một vuông góc với nhau. Thể tích khối chóp là. 2abc abc abc abc A. . B. . C. . D. . 9 6 3 9 Hướng dẫn giải Chọn B 1 abc V = SC.S = . 3 SAB 6
Câu 24: Cho tứ diện ABCD có AD vuông góc với mặt phẳng ( ABC ) . Biết đáy ABC là tam giác vuông
tại B và AD = 5, AB = 5, BC =12 . Tính thể tích V của tứ diện ABCD . 325
A. V = 50 .
B. V = 120 .
C. V = 150 . D. V = . 16 Hướng dẫn giải Chọn A 1 1 1 V = A . D A . B BC = .5.5.12 = 50.. 3 2 6 https://toanmath.com/
Câu 25: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a , SA ⊥ ( ABCD) và
SA = a 6 . Thể tích của khối chóp S.ABCD bằng 3 a 6 3 a 6 3 a 6 A. . B. . C. . D. 3 a 6 . 3 2 6 Hướng dẫn giải Chọn A 3 1 1 a 6 2 V = S .SA = a .a 6 = . S . ABCD 3 ABCD 3 3
Câu 26: Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a , SA ⊥ ( ABCD) và SA = 3a . Thể tích
khối chóp S.ABCD là. 3 a 3 a A. 3 2a . B. 3 a . C. . D. . 3 2 Hướng dẫn giải Chọn B .
Vì SA ⊥ ( ABCD) ⇒ SA là chiều cao hình chóp S.ABCD . Ta có: 2 S = a . ABC 1 1 2 3 V = .S
.SA = .a .3a = a . 3 ABC 3
Câu 27: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Biết SA ⊥ ( ABCD); SA = a 3.
Tính thể tích của khối chóp. 3 a 3 3 a 3 3 a A. . B. . C. . D. 3 a 3 . 3 12 4 Hướng dẫn giải Chọn A 3 1 1 a 3 V = .S . A S = 2 .a 3.a = . 3 ABCD 3 3
Câu 28: Cho hình chóp S.ABCD có đáy hình vuông cạnh a ; SA vuông góc mặt đáy; Góc giữa SC và
mặt đáy của hình chóp bằng 0
60 . Thể tích khối chóp S.ABCD là 3 a 2 3 a 3 a 6 3 a 3 A. B. C. D. 3 3 3 3 Hướng dẫn giải Chọn C https://toanmath.com/ S A D a 60 B a C ∧ Ta có SC  ( ABCD) =  (SC AC) 0 , , = SCA = 60 . 0
SA = AC. tan 60 = a 2. 3 = a 6 . 3 Vậy 1 1 a 6 2 V = S .SA = a a 6 = . ABCD 3 ABCD 3 3
Câu 29: Cho hình chóp S.ABCD đáy ABCD là hình vuông có cạnh a và SA vuông góc đáy ABCD và
mặt bên (SCD) hợp với đáy một góc 60° . Tính thể tích hình chóp S.ABCD . 3 a 3 3 a 3 3 2a 3 A. . B. . C. 3 a 3 . D. . 3 6 3 Hướng dẫn giải Chọn A AD ⊥ CD Do 
⇒ CD ⊥ (SDA) ⇒ (SCD) ( ABC)  =  , SDA SA ⊥ CD
Khi đó SA = AD tan 60° = a 3 . 3 1 a 3 Suy ra V = . SA S = . S . ABCD 3 ABCD 3
Câu 30: Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng ( ABCD), đáy ABCD là hình thang
vuông tại A và B có AB = a, AD = 3a, BC = .
a Biết SA = a 3, tính thể tích khối chóp S.BCD theo . a 3 3a 3 2 3a 3 3a A. . B. . C. . D. 3 2 3a . 6 3 4 Hướng dẫn giải Chọn A https://toanmath.com/ S A D B C 1 Ta có V = . SA S . S .BCD 3 BCD 1 1 1 1 Lại có S = S − S = A .
B ( AD + BC ) − A . B AD 2 = A . B BC = a . BCD ABCD ABD 2 2 2 2 2 3 1 a a 3
Mà SA = a 3 ⇒ V = a 3. = . S .BCD 3 2 6
Nhận xét: Nếu đề bài bỏ giả thiết AD = 3a thì sẽ giải như sau: 1 1 1 3 1 a 3 Ta có V = S . A S = S . A
d D, BC .BC = S . A A . B BC = . S .BCD BCD ( ) 3 3 2 6 6
Câu 31: Cho hình chóp S.ABC có SA vuông góc với đáy. Tam giác ABC vuông cân tại B , biết
SA = AC = 2a . Tính thể tích khối chóp S.ABC . 2 1 2 2 4 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 3 3 3 3 Hướng dẫn giải Chọn A S A C B AC 2a Ta có AB = BC = = = a 2 . 2 2 Thể tích khối chóp 1 1 1 1 2
S.ABC là V = S .SA = . AB .SA = . a a = a . ABC ( 2)2 2 3 .2 3 3 2 6 3
Câu 32: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . SA vuông góc với đáy và tạo với
đường thẳng SB một góc 45°. Tính thể tích khối chóp S.ABC . 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 12 4 24 6 Hướng dẫn giải Chọn A https://toanmath.com/ S A C a B
Ta có: SA ⊥ ( ABC ) ⇒ SA là chiều cao của hình chóp ⇒ SA ⊥ AB ⇒ S
∆ AB vuông tại A . ⇒ (SA SB)  =  , ASB = 45° ⇒ S
∆ AB vuông cân tại A ⇒ SA = AB = a . 1 2 1 a 3 3 a 3
Vậy thể tích của khối chóp S.ABC là: V = .S .SA = . .a = . 3 ABC 3 4 12
Câu 33: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , hai mặt phẳng (SAB) và (SAD)
cùng vuông góc với mặt phẳng ( ABCD) ; góc giữa đường thẳng SC và mặt phẳng ( ABCD)
bằng 60° . Tính theo a thể tích khối chóp S.ABCD . 3 a 6 3 a 6 A. . B. . C. 3 3 2a . D. 3 3a . 9 3 Hướng dẫn giải Chọn B (
SAB) ⊥ ( ABCD)  Ta có (
SAD) ⊥ ( ABCD)
⇒ SA ⊥ ( ABCD) (  SAB  )∩(SAD) = SA
⇒ AC là hình chiếu vuông góc của SC lên mặt phẳng ( ABCD) ⇒ SC ( ABCD)  ( )=  , SCA = 60°
Tam giác SAC vuông tại A có SA = AC.tan 60° = a 6 . 3 Khi đó 1 1 a 6 2 V = . . SA S = .a 6.a = . SABCD 3 ABCD 3 3
Câu 34: Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, đường cao của một mặt bên là a 3 .
Tính thể tích V khối chóp đó. https://toanmath.com/ 3 a 2 3 a 2 3 a 2 A. V = . B. 3 V = a 2 . C. V = . V = 9 6 D. 3 . Hướng dẫn giải: Chọn D
Gọi các đỉnh của hình chóp tứ giác đều như hình vẽ bên và đặt cạnh bằng AB = 2x . Khi đó 3 1 a 2
SO = x 2, OH = x suy ra SH = x 3 . Vậy x = a . Khi đó 2 V = S . O AB = . 3 3 a 2
Câu 35: Hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AC =
; SA vuông góc với mặt 2
đáy. Góc giữa mặt bên (SBC) và mặt đáy bằng 45 .° Tính theo a thể tích khối chóp S.ABC . 3 a 3 a 3 3 a 2 3 a A. . B. . C. . D. . 16 48 48 48 Hướng dẫn giải Chọn D . a 2
Tam giác ABC vuông cân tại B, AC = . 2 2 a 1 a Nên AB = BC = , S = .B . A BC = ∆ . 2 ABC 2 8 Ta có: (
SBC) ∩( ABC) = BC
AB ⊂ ( ABC) AB ⊥ BC ⇒ (( ABC) (SBC)) =  , , SBA = 45° . SB ⊂ 
(SBC), SB ⊥ BC a
Tam giác SAB vuông cân tại A nên SA = AB = . 2 2 3 Vậy: 1 1 a a a V = . . SA S = . . = . S . ABC ∆ 3 ABC 3 2 8 48
Câu 36: Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng a , cạnh bên SB vuông góc với mặt
phẳng ( ABC), SB = 2a . Tính thể tích khối chóp S.ABC . 3 a 3 3 a 3 a 3 3 3a A. . B. . C. . D. . 2 4 6 4 Hướng dẫn giải Chọn C https://toanmath.com/ S 2a a C B A 2 3 Thể tích khối chóp 1 1 3 3
S.ABC là: V = .S .SB = a . .2a = a . 3 ABC 3 4 6
Câu 37: Cho khối tứ diện OABC với OA , OB , OC vuông góc từng đôi một và OA = a , OB = 2a ,
OC = 3a . Gọi M , N lần lượt là trung điểm của hai cạnh AC, BC . Thể tích của khối tứ diện
OCMN tính theo a bằng 3 a 3 3a 3 2a A. . B. . C. 3 a . D. . 4 4 3 Hướng dẫn giải Chọn A C 3a N M 2a O B a A . Ta có thể tích 1  1  3 V = .
OA OB .OC = a (đvtt). OABC   3  2  Diện tích tam giác 1 1 CA CB 1  1  1 S
= CM .CN.sin C = . .sin C =
AC.BC.sin C = S . C ∆ MN   Λ 2 2 2 2 4  2  4 ABC 3 Vậy thể tích 1 a V = V = (đvtt). OCMN 4 OABC 4
Câu 38: Cho hình chóp S.ABC có mặt phẳng (SAC ) vuông góc với mặt phẳng ( ABC ) , SAB là tam giác
đều cạnh a 3 , BC = a 3 đường thẳng SC tạo với mặt phẳng ( ABC) góc 60°. Thể tích của
khối chóp S.ABC bằng 3 a 6 3 a 3 3 a 6 A. . B. 3 2a 6 . C. . D. . 6 3 2 https://toanmath.com/ Hướng dẫn giải Chọn A B A S 60o H C
Ta thấy tam giác ABC cân tại B , gọi H là trung điểm của AB suy ra BH ⊥ AC.
Do (SAC ) ⊥ ( ABC ) nên BH ⊥ (SAC ) .
Ta lại có BA = BC = BS nên B thuộc trục đường tròn ngoại tiếp tam giác ABC ⇒ H là tâm
đường tròn ngoại tiếp tam giác SAC ⇒ SA ⊥ SC .
Do AC là hình chiếu của SC lên mặt phẳng ( ABC ) ⇒  0 SCA = 60 . SA Ta có 0 SC = .
SA cot 60 = a , AC =
= 2a ⇒ HC = a 2 2
⇒ BH = BC − HC = a 2 . 0 sin 60 1 3 a 6 V = 1 BH .S = BH. . SA SC = . S . ABC 3 SAC 6 6
Câu 39: Cho khối chóp S.ABC có SA ⊥ ( ABC ) , tam giác ABC vuông tại B , AB = a , AC = a 3 .
Tính thể tích khối chóp S.ABC , biết rằng SB = a 5 . 3 a 6 3 a 15 3 a 2 3 a 6 A. . B. . C. . D. . 4 6 3 6 Hướng dẫn giải Chọn C Ta có: 2 2 2 2 SA =
SB − AB = 2a; BC =
AC − AB = a 2 2 3 . AB BC a 2 1 a 2 S = = ⇒ V = . SA S = . ABC S . 2 2 ABC 3 ABC 3
Câu 40: Cho hình chóp tứ giác S.ABCD , đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với
mặt đáy, góc giữa SC và ( ABCD) bằng 45° . Thể tích khối chóp S.ABCD là 3 a 2 3 a 2 3 a 2 A. . B. . C. 3 a 2 . D. . 6 4 3 Hướng dẫn giải Chọn D https://toanmath.com/ S A D B C
Ta có SA ⊥ ( ABCD) ⇒ (SC ( ABCD))  =  ; SCA = 45° SA 3 ⇒ 1 1 a 2 tan 45° =
⇒ SA = AC = a 2 2 ⇒ V = . SA S = a 2.a = . AC S . ABCD 3 ABCD 3 3
Câu 41: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a , SA ⊥ ( ABC ) . Góc giữa hai mặt phẳng
(SBC) và ( ABC) bằng 30°. Thể tích khối chóp S.ABC là. 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 8 6 12 3 Hướng dẫn giải Chọn D S 2a A C 30o 2a 2a I B .
Gọi I là trung điểm BC .
Góc giữa hai mặt phẳng (SBC) 
và ( ABC ) là SIA = 30° 2a 3 ⇒ AI S
∆ IA nửa tam giác đều nên 2 SA = = = a . 3 3 1 (2a)2 3 Thể tích khối chóp 1 3 a 3
S.ABC là V = S .SA = . .a = . 3 ABC 3 4 3
Câu 42: Cho hình chóp S.ABC có đáy là tam giác vuông tại C , AB = a 5 , AC = a . Cạnh bên SA = 3a
và vuông góc với mặt phẳng ( ABC). Thể tích khối chóp S.ABC bằng: 3 a 5 A. . B. 3 a . C. 3 2a . D. 3 3a . 3 Hướng dẫn giải Chọn B https://toanmath.com/ S A B C
Ta có ABC vuông tại C nên 2 2 BC =
AB − AC = 2a . Diện tích tam giác 1 ABC là 2 S = . CA CB = a . ABC ∆ 2
Do cạnh bên SA = 3a và vuông góc với mặt phẳng ( ABC) nên SA là đường cao của hình chóp S.ABC .
Thể tích của khối chóp 1 1 S.ABC là 2 3 V = . SA S = 3 .
a a = a . S . ABC ∆. 3 ABC 3
Câu 43: Cho khối chóp S.ABC có SA ⊥ ( ABC ) , tam giác ABC vuông tại B , AB = a , AC = a 3 .
Tính thể tích khối chóp S.ABC biết rằng SB = a 5 . 3 a 2 3 a 6 3 a 6 3 a 15 A. . B. . C. . D. . 3 4 6 6 Hướng dẫn giải Chọn A Cạnh 2 2 2 2 SA =
SB − AB = 5a − a = 2a . Cạnh 2 2 BC =
AC − AB = a 2 3 1 1 a 2 ⇒ V = .2 . a . . a a 2 = . 3 2 3 https://toanmath.com/
Câu 44: Cho khối chóp tam giác S.ABC có SA ⊥ ( ABC ) , tam giác ABC có độ dài 3 cạnh là AB = 5a ;
BC = 8a ; AC = 7a , góc giữa SB và ( ABC ) là 45° . Tính thể tích khối chóp S.ABC . 50 50 7 50 3 A. 3 a . B. 3 a . C. 3 50 3a . D. 3 a . 3 3 3 Hướng dẫn giải Chọn D Ta có nửa chu vi
AB + AC + BC ABC ∆ là p = = 10a . 2 Diện tích ABC ∆ là 2 S
= 10a.5a.3a.2a = 10 3a ∆ . ABC
SA ⊥ ( ABC ) nên SA
∆ B vuông, cân tại A nên SA = AB = 5 . Thể tích khối 1 1 50 3
chóp S.ABC là V = . SA S 2 = 5a.10 3a 3 = a . S . ABC ∆ 3 ABC 3 3
Câu 45: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D , AB = AD = a ,
SA = CD = 3a , SA vuông góc với mặt phẳng ( ABCD) . Thể tích khối chóp S.ABCD bằng. 1 1 A. 3 a . B. 3 2a . C. 3 6a . D. 3 a . 3 6 Hướng dẫn giải Chọn B a 3a
( AB + DC).AD (a +3a)a 1 1 Ta có 2 S = = = 2a . Vậy V = . SA S 2 3 = 3 .2
a a = 2a . ABCD 2 2 S . ABCD 3 ABCD 3
Câu 46: Cho hình chóp S.ABC có SA ⊥ ( ABC )
, góc giữa SB và ( ABC ) bằng o
60 ; tam giác ABC đều cạnh .
a Thể tích khối chóp S.ABC bằng https://toanmath.com/ 1 1 A. 3 a . B. 3 3a . C. 3 a . D. 3 a . 4 2 Hướng dẫn giải Chọn C 0 SA = A . B tan 60 = a 3 2 3 1 1 a 3 = a V . SA S = a 3. = S . ABC  . 3 ABC 3 4 4 S A B 600 a C
Câu 47: Cho tứ diện ABCD có các cạnh B ,
A BC, BD đôi một vuông góc với nhau: BA = 3a,
BC = BD = 2a . Gọi M và N lần lượt là trung điểm của AB và AD . Tính thể tích khối chóp C.BDNM . 3 3 3 2 A. = a V . B. 3 V = a . C. = a V . D. 3 V = 8a . 2 3 Hướng dẫn giải Chọn A 3a (2a + a). 2 9a 2 3 1 9a 3a BG: Ta có 2 S = =
; BC = 2a ⇒ V = . .2a = . MNBD 2 4 3 4 2
Câu 48: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy
( ABCD) . Biết AB = a , BC = 2a và SC = 3a . Tính thể tích khối chóp S.ABCD . 4 2 5 A. 3 a . B. 3 a . C. 3 2a . D. 3 a . 1 6 T 1 6 T 1 6 T 1 6 T 3 3 Hướng dẫn giải Chọn A
Ta có AB = a , BC = 2a suy ra AC = a 5 .
Mà tam giác SAC vuông tại A suy ra 2 2 SA =
SC − AC = 2a . Vậy 1 1 4 3 V = . SA S = .2 . a .2 a a = a . S . ABCD 3 ABCD 3 3
Câu 49: Cho tứ diện S.ABC có SAB, SCB là các tam giác cân tại S và ,
SA SB, SC đôi một vuông góc
với nhau. Biết BA = a 2 , thể tích V của tứ diện S.ABC là. https://toanmath.com/ 3 a 3 a A. V = . B. V = . C. 3 V = 2a 2 . D. 3 V = a . 6 2 Hướng dẫn giải Chọn A . 3 a
Các tam giác SAB, SCB là các tam giác vuông cân suy ra SA = SB = SC = a . Vậy V = . 6
Câu 50: Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a . Hai mặt bên (SAB) và (SAC ) cùng
vuông góc với đáy. Tính thể tích khối chóp biết SC = a 3 . 3 a 6 3 a 3 3 2a 6 3 a 3 B. . C. . D. . A. 12 . 2 9 4 Hướng dẫn giải Chọn A A A C B . 2 a 3 Ta có S = . ABC 4 (
 SAB) ⊥ ( ABC) Do (
nên SA ⊥ ( ABC ) .
 SAC) ⊥ ( ABC) 2 2 2 2 SA =
SC − AC = 3a − a = a 2 . 3 1 a 6 V = . SA S = . SABC 3 ABC 12
Câu 51: Cho hình chóp S.ABCD có SA ⊥ ( ABCD) , ABCD là hình chữ nhật, SA = a , AB = 2a ,
BC = 4a . Gọi M , N lần lượt là trung điểm của BC , CD . Thể tích của khối chóp S.MNC là 3 a 3 a 3 a 3 a A. . B. . C. . D. . 5 2 4 3 Hướng dẫn giải Chọn D https://toanmath.com/ 3 1 1 1 1 a Ta có V = S . A CM .CN = . a .2 . a a = . 3 2 3 2 3
Câu 52: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a , BC = 2a , SA = 2a , SA
vuông góc với mặt phẳng ( ABCD) . Tính thể tích khối chóp S.ABCD tính theo a . 3 8a 3 4a 3 6a A. B. C. D. 3 4a 3 3 3 Hướng dẫn giải Chọn B Ta có S = A . B CD 2 = 2a . ABCD 3 Thể tích khối chóp 1 1 4a
S.ABCD là V = . SA S 2 = 2a.2a = . S . ABCD 3 ABCD 3 3
Câu 53: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA = a 2 và SA vuông góc
với mặt phẳng đáy, tam giác SBD là tam giác đều. Thể tích của khối chóp S.ABCD bằng 3 a 2 3 2 2a A. 3 a 2. B. 3 2a 2. C. . D. . 3 3 Hướng dẫn giải Chọn D https://toanmath.com/
Đặt AB = x , A
∆ BD vuông cân tại A ⇒ BD = x 2. Do S
∆ BD là tam giác đều ⇒ SB = SD = BD = x 2. Lại có S
∆ AB vuông tại A
⇒ SA + AB = SB ⇔ (a )2 + x = (x )2 2 2 2 2 2 2 2 2
⇒ x = 2a ⇒ x = a 2 1 1 a ⇒ V = SA S = a a = . S ABCD ABCD ( ) 3 2 2 2 . . . 2. 2 . 3 3 3
Câu 54: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 1. Cạnh bên SA vuông góc với
mặt phẳng ( ABCD) và SC = 5 . Tính thể tích khối chóp S.ABCD . 15 3 3 A. V = .
B. V = 3 . C. V = . D. V = . 3 6 3 Hướng dẫn giải Chọn D S A D O B C .
Đường chéo hình vuông AC = 2 .
Xét tam giác SAC , ta có 2 2 SA = SC − AC = 3 .
Chiều cao khối chóp là SA = 3 .
Diện tích hình vuông ABCD là 2 S = 1 = 1. ABCD Thể tích khối chóp 1 3
S.ABCD là: V = S .SA = (đvtt). S . ABCD 3 ABCD 3
Câu 55: Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a, AD = a 2, SA ⊥ ( ABCD) , góc
giữa SC và đáy bằng 60° . Thể tích hình chóp S.ABCD bằng: A. 3 6a . B. 3 3a .
C. 3 2a . D. 3 2a . Hướng dẫn giải Chọn D
Phương pháp: + Dựng hình như hình vẽ. https://toanmath.com/ .
+ Xác định được góc giữa SC và đáy.
Cách giải: + Góc giữa SC và mặt đáy là  SCA = 60 . AD = a + (a )2 2 2 = 3a .
Suy ra SH = AD tan 60° = 3a . 1 1 3 V = . SA S = 3 . a . a 2a = 2a . 3 ABCD 3
Hình chóp S.ABCD có đáy hình vuông, SA vuông góc với đáy và SA = a 3 , AC = a 2 . Khi
Câu 56: đó thể tích khối chóp S.ABCD là 3 a 2 3 a 2 3 a 3 3 a 3 A. 3 B. 2 C. 3 D. 2 Hướng dẫn giải Chọn C
Ta có ABCD là hình vuông có AC = a 2 suy ra AB = a . 1 1 3 a 3 2 V = . SA S = a 3.a = . S . ABCD 3 ABCD 3 3
Câu 57: Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A , BC = 2a ,  BAC = 120° , biết
SA ⊥ ( ABC ) và mặt phẳng (SBC ) hợp với đáy một góc bằng 45° . Tính thể tích khối chóp S.ABC . 3 a 3 a 3 a A. 3 a 2 . B. . C. . D. . 9 2 3 Hướng dẫn giải Chọn B
Gọi I là trung điểm của BC . Vì tam giác ABC cân tại A nên AI ⊥ BC và góc  ACI = 30° . https://toanmath.com/
Trong tam giác AIC vuông tại I ta có: AI 3 a 3 tan 30° =
⇒ AI = IC.tan 30° = . a = . IC 3 3 2 Diện tích đáy: 1 1 . a 3 a 3 S = AI.BC = .2a = . ABC 2 2 3 3 (
SBC) ∩( ABC) = BC
Ta có: AI ⊥ BC . SI ⊥ BC
Góc giữa (SBC) và ( ABC) là  SI A = 45° . a
Suy ra tam giác SAI vuông cân tại 3
A ⇒ SA = AI = . 3 2 3
Thể tích khối chóp là là: 1 1 a 3 a 3 a V = . . SA S = . . = . 3 ABC 3 3 3 9
Câu 58: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh bên SA vuông góc với đáy
và có độ dài bằng a . Tính thể tích khối tứ diện S.BCD . 3 a 3 a 3 a 3 a A. . B. . C. . D. . 2 4 6 3 Hướng dẫn giải Chọn C 3 1 1 1 a Ta có 2 V = SH.S = . a a = . S .BCD 3 BCD 3 2 6
Câu 59: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc 
BAD = 60° , SA ⊥ ( ABCD) .
Biết rằng khoảng cách từ A đến cạnh SC bằng a . Thể tích khối chóp S.ABCD là 3 a 2 3 a 2 3 a 3 A. . B. . C. . D. 3 a 3 . 4 12 6 Hướng dẫn giải Chọn A
Tam giác ABD đều, có cạnh bằng a . 2 2 a 3 a 3 Suy ra S = 2S = 2. = . ABCD ABD 4 2
Kẻ AH ⊥ SC, ( H ∈ SC ) , ta có d ( ,
A SC ) = AH = a .
Gọi O = AC ∩ BD , AC = 2AO = a 3 . 1 1 1 2 a 6 = − = ⇒ SA = . 2 2 2 2 SA AH AC 3a 2 https://toanmath.com/ 3 1 a 2 V = S .SA = . S . ABCD ∆ 3 ABC 4 S H a A B 60o O D C .
Câu 60: Thể tích của tứ diện OABC có ,
OA OB, OC đôi một vuông góc, OA = a , OB = 2a , OC = 3a là A. 3 3a . B. 3 2a . C. 3 4a . D. 3 a . Hướng dẫn giải Chọn D A a 3a C 2a B . 1 .2 a .3 a a 3 V = . OA . OB OC = = a . 6 6
Câu 61: Cho hình chóp S.ABCD có đáy là hình thoi cạnh a,  0
ABC = 120 , SA ⊥ ( ABCD) . Biết góc giữa
hai mặt phẳng (SBC) và (SCD) bằng 60°. Tính SA a 6 a 6 a 3 A. B. . C. a 6 D. 4 2 2 Hướng dẫn giải Chọn A S M A D O B C https://toanmath.com/
Ta có ABCD là hình thoi cạnh a có  0
ABC = 120 nên BD = a, AC = a 3 .
Nhận xét BD ⊥ SC ⇒ kẻ OM ⊥ SC ⇒ (BDM ) ⊥ SC do đó góc giữa hai mặt phẳng (SBC) và (SCD) là  0 BMD = 120 hoặc  0 BMD = 60 . TH1: Nếu  0
BMD = 120 mà tam giác BMD cân tại M nên  a 3 0 0
BMO = 60 ⇒ MO = B . O cot60 = 6 . SA CD a 6
Mà tam giác OCM đồng dạng với tam giác SCA nên OM = ⇒ SA = . SC 4 TH2: Nếu  0
BMD = 60 thì tam giác BMD là tam giác đều nên 3 OM = a . 2
⇒ OM = OC vô lý vì O
∆ MC vuông tại M .
Câu 62: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng đáy, tam giác SBC đều cạnh a , góc
giữa mặt phẳng (SBC) và đáy là 30° . Thể tích khối chóp S.ABC là. 3 a 3 3 3a 3 a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . 24 64 16 32 Hướng dẫn giải Chọn C .
Vì tam giác SBC đều nên suy ra AB = AC . Gọi M là trung điểm của BC thì AM ⊥ BC . Mà
BC ⊥ SA nên BC ⊥ SM . Do đó: ((SBC ) ( ABC )) =  0 , SMA = 30 . 3
Vì tam giác SBC đều nên SM = a . 2  3 0
SA = SM.sin 30 = a  4
Xét tam giác vuông SAM , ta có:  . 3a  0
AM = SM .cos 30 =  4
Vậy, thể tích khối chóp 1 1 1 3a a 3 3 S.ABC là: 3 V = S SA =
AM .BC.SA = . . . a = a . S . ABC 3 A C B 3 3 4 4 16
Câu 63: Cho khối chóp S.ABCD có đáy là hình chữ nhậ, AB = a , AD = a 3 , SA vuông góc với đáy và
mặt phẳng (SBC) tạo với đáy một góc 60°. Tính thể tích V của khối chóp S.ABCD . 3 a 3 3a A. V = . B. 3 V = 3a . C. V = . D. 3 V = a . 3 3 Hướng dẫn giải Chọn D https://toanmath.com/ (
SBC) ∩( ABCD) = BC
Ta có BC ⊥ AB
⇒ (SBC) ( ABCD)  , = 60°. BC ⊥ SB  Suy ra SA = .
a tan 60° = a 3 . Tính thể tích 1 1
V của khối chóp S.ABCD là 3 V = . . SA S = .a 3. .
a a 3 = a . 3 ABCD 3 2
Câu 64: Hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B , = a AC
; SA vuông góc với mặt 2
đáy. Góc giữa mặt bên (SBC) và mặt đáy bằng 45 .° Tính theo a thể tích khối chóp S.ABC. 3 a 3 a 3 a 3 3 a 2 A. . B. . C. . D. . 48 16 48 48 Hướng dẫn giải Chọn A . a 2
Tam giác ABC vuông cân tại B , AC = . 2 2 a 1 a Nên AB = BC = , S = .B . A BC = . ∆ 2 ABC 2 8 Ta có: (
SBC) ∩( ABC) = BC
AB ⊂ ABC AB ⊥ BC ⇒ (( ABC) (SBC)) =  ( ), , SBA = 45° .
SB ⊂ (SBC), SB ⊥  BC a
Tam giác SAB vuông cân tại A nên SA = AB = . 2 2 3 Vậy: 1 1 a a a V = . . SA S = . . = . S . ABC ∆ 3 ABC 3 2 8 48
Câu 65: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA vuông góc với mặt phẳng đáy.
Gọi I là trung điểm của BC , góc giữa (SBC ) và ( ABC ) bằng 30° . Thể tích khối chóp S.ABC bằng: 3 a 6 3 a 6 3 a 3 3 a 3 A. . B. . C. . D. . 24 8 24 8 Hướng dẫn giải Chọn C https://toanmath.com/ S C A I B BC ⊥ SA Ta có 
⇒ BC ⊥ (SAI ) ⇒ BC ⊥ SI ⇒ (( ABC) (SBC)) =  , SIA 30° = . BC ⊥ AI a 3
Do tam giác ABC đều cạnh a nên AI = . 2 a a
Xét tam giác vuông SAI có SA = 1 3
AI. tan SIA ⇔ SA = . = . 3 2 2 1 1 a a 3 a 3
Thể tích khối chóp S.ABC là V = 1 3
. .BC.AI.SA = . . a . = . S . ABC 3 2 6 2 2 24
Câu 66: Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a . SA vuông góc với ( ABCD) ,
SC = a 3 . Tính thể tích khối chóp S.ABCD theo a . 3 a 3 a 3 3 a 3 A. 3 V = a . B. V = . C. V = . D. V = . S . ABCD S . ABCD 3 S . ABCD 9 S . ABCD 3 Hướng dẫn giải Chọn B S A D B C
Xét tam giác vuông SAC có 2 2 2 2 SA =
SC − AC = 3a − 2a = a . 3 Thể tích khối chóp 1 a S.ABCD là 2 V = .a .a = . S . ABCD 3 3
Câu 67: Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B , AB a , góc giữa mặt phẳng
SBC và mặt phẳng ABC bằng o
60 , SA  ABC. Gọi M , N lần lượt là trung điểm của SC
và AC . Tính thể tích khối chóp MNBC ? https://toanmath.com/ 3 a 3 a 3 3 a 6 3 a 3 A. . B. . C. . D. . 4 24 18 12 Hướng dẫn giải Chọn B . Ta có: ( )  =  (SBC), (ABC) SBA = 60° . SA 1 1  1  3 0 tan 60 = ⇒ SA = a 3 ; 3 V = . SA S = .a 3. . a a = a   . AB S . ABC 3 ABC 3  2  6 3 V CM CN 1 1 a 3 MNBC = . = ⇒ V = V = . MNBC C. V CS CA 4 4 SAB 24 C.SAB
Câu 68: Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a, AD = a 2 , SA ⊥ ( ABCD) ,
góc giữa SC và mặt phẳng đáy bằng 60°. Thể tích khối chóp S.ABCD bằng: A. 3 a 2 . B. 3 a 6 . 3 C. 3a . D. 3 3a 2 . Hướng dẫn giải Chọn A .
SA ⊥ ( ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng ( ABCD) . Xét A
∆ BC vuông tại B , ta có. 2 2 2 2 AC =
AB + BC = a + 2a = a 3 . Xét S
∆ AC vuông tại A , (SA ⊥ ( ABCD)) ⇒ SA ⊥ AC . Ta có:  SA = ⇒ =  tan SCA SA
AC. tan SCA = AC. tan 60° = a 3. 3 = 3a . AC Vậy thể tích hình chóp 1 1 S.ABCD là 3 V = .S . A S = .3 . a . a a 2 = a 2 S . ABCD 3 ABCD 3 . https://toanmath.com/
Câu 69: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA ⊥ ( ABCD) , SC tạo với mặt
đáy một góc bằng 60 . Tính thể tích V của khối chóp đã cho. 3 a 3 3 a 6 3 a 3 3 a 6 A. V = . B. V = . C. V = . D. V = . 3 6 6 3 Hướng dẫn giải Chọn D Diện tích đáy: 2 S = a . ABCD
SA ⊥ ( ABCD) nên góc giữa SC và mặt phẳng đáy là  SCA = 60 .
Tam giác SAC vuông tại A nên =  SA
AC. tan SCA = a 2. tan 60 = a 6 . 3 Vậy 1 a 6 V = . SA S = . 3 ABCD 3
Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B với AC = a
biết SA vuông góc với đáy
ABC và SB hợp với đáy một góc 60° . Tính thể tích hình chóp. 3 a 6 3 a 3 3 a 6 3 a 6 A. . B. . C. . D. . 24 24 48 8 Hướng dẫn giải Chọn A https://toanmath.com/ A A C B . AC a
Do tam giác ABC vuông cân tại B nên AB = BC = = . 2 2 2 1 = a S A . B BC = . ABC 2 4 Theo giả thiết  6 SBA = 60° nên = . tan 60° = a SA AB . 2 3 1 a 6 V = . SA S = . SABC 3 ABC 24 a 2
Câu 70: Hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AC =
; SA vuông góc với mặt 2
đáy. Góc giữa mặt bên (SBC) và mặt đáy bằng 45 .° Tính theo a thể tích khối chóp S.ABC. 3 a 2 3 a 3 a 3 3 a A. . B. . C. . D. . 48 48 48 16 Hướng dẫn giải Chọn B S C A B a 2
Tam giác ABC vuông cân tại B, AC = 2 2 a 1 a Nên AB = BC = , S = .B . A B C = . ∆ 2 ABC 2 8 Ta có: (
SBC) ∩( ABC) = BC
AB ⊂ ABC AB ⊥ BC ⇒ (( ABC ) (SBC)) =  0 ( ), , SBA = 45
SB ⊂ (SBC), SB ⊥ BCa
Tam giác SAB vuông cân tại A nên SA = AB = . 2
https://toanmath.com/ 2 3 Vậy: 1 1 a a a V = . . SA S = . . = . S . ABC ∆ 3 ABC 3 2 8 48
Câu 71: Cho hình chóp S.ABCD với ABCD là hình vuông cạnh a . Mặt bên SAB là tam giác cân tại
S và nằm trên mặt phẳng vuông góc với mặt phẳng đáy. Cạnh bên SC tạo với đáy một góc
60° . Tính thể tích khối chóp S.ABCD . 3 a 6 3 a 3 3 a 15 3 a 15 A. . B. . C. . D. . 3 6 2 6 Hướng dẫn giải Chọn D S A I B a D a C
Gọi I là trung điểm của AB . Ta có: S
∆ AB cân tại S ⇒ SI ⊥ AB ( ) 1 (  SAB) ⊥  ( ABCD) Mặt khác: ( (2)  SAB  )∩( ABCD) = AB Từ ( )
1 và (2) , suy ra: SI ⊥ ( ABCD)
⇒ SI là chiều cao của hình chóp S.ABCD
⇒ IC là hình chiếu của SC lên mặt phẳng ( ABCD) ⇒ (SC ( ABCD))  = (SC IC)  =  , , SCI = 60° 2  a a 5 Xét IB
∆ C vuông tại B , ta có: 2 2 2 IC = IB + BC = + a =    2  2 a 5 a 15 Xét S
∆ IC vuông tại I , ta có: SI = IC.tan 60° = . 3 = 2 2 3
Vậy thể tích khối chóp 1 1 a 15 a 15 S.ABCD là: 2 V = .S .SI = .a . = . 3 ABCD 3 2 6
Câu 72: Cho hình chóp S.ABCD có SA ⊥ ( ABCD) , ABCD là hình chữ nhật. SA = AD = 2a . Góc giữa
(SBC) và mặt đáy ( ABCD) là 60°. Gọi G là trọng tâm tam giác SBC . Tính thể tích khối chóp
S.AGD là https://toanmath.com/ 3 32a 3 3 8a 3 3 4a 3 3 16a A. . B. . C. . D. . 27 27 9 9 3 Hướng dẫn giải Chọn B S G B A M D C Vì góc giữa ( SA 2a
SBC ) và mặt đáy ( ABCD) là 60° nên 
SBA = 60° ⇒ AB = = . tan 60° 3 2 Khi đó: 2a 4a 3 S = A . B AD = .2a = . ABCD 3 3 2 Gọi 1 2a 3
M là trung điểm BC , khi đó: S = S = . ADM 2 ABCD 3 2 3 ⇒ 2 2 1 2a 3 8a 3 V = V = . .2 . a = . S . ADG S . 3 ADM 3 3 3 27
Câu 73: Hình chóp S.ABCD có đáy là hình vuông, a là độ dài cạnh đáy. Cạnh bên SA vuông góc với
đáy, SC tạo với (SAB) góc o
30 . Thể tích khối chóp S.ABCD là: 3 a 2 3 a 3 3 a 2 3 a 2 A. B. . C. . D. . 2 3 4 3 Hướng dẫn giải Chọn D https://toanmath.com/ Ta có 2 S = a ABCD CB ⊥ AB
⇒ CB ⊥ (SAB) CB ⊥ SA
SB là hình chiếu vuông góc của SC lên (SAB) ⇒ (SC (SAB))  = (SC SB)  =  , , CSB = 30° BC Xét C
∆ SB vuông tại B có SB =  = a 3 tan CSB 2 2 SA =
SB − AB = a 2 3 1 a 2 V = S .SA = . S . ABCD 3 ABCD 3 2 3a
Câu 74: Cho hình chóp S.ABCD có SA ⊥ ( ABCD) , AC = a 2 , S =
và góc giữa đường thẳng ABCD 2
SC và mặt phẳng ABCD bằng 60° . Gọi H là hình chiếu vuông góc của A trên SC . Tính theo
a thể tích của khối chóp H.ABCD . 3 3a 6 3 a 6 3 a 6 3 a 6 A. . B. . C. . D. . 4 2 4 8 Hướng dẫn giải Chọn D
Ta có SA ⊥ ( ABCD) ⇒ Góc toạ bởi SC và mặt phẳng ( ABCD) là  SCA = 60° .
Lại có SA = AC tan 60° = a 6 , 2 2 2 2 SC =
SA + AC = 6a + 2a = 2a 2 . 2 2 Do đó CH AC 2a 1 2
AC = CH.SC ⇒ = = = . 2 2 SC SC 8a 4
d ( H ,( ABCD)) SH 3 a 6 = = ⇒ = . d (
d ( H , ABCD ) H , ( ABCD)) ( ) SC 4 4 2 3 1 a 6 3a a 6
Thể tích của khối chóp H.ABCD là V = . . = . 3 4 2 8
Câu 75: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy ( ABCD),
AB = a, AD = 2a . Góc giữa cạnh bên SB và mặt phẳng ( ABCD) bằng o 45 . Thể tích hình chóp
S.ABCD bằng. https://toanmath.com/ 3 2 2a 3 6a 3 a 3 2a A. . B. . C. . D. . 3 18 3 3 Hướng dẫn giải Chọn D 3 1 1 2a V = . SA S = . . a . a 2a = . 3 ABCD 3 3
Câu 76: Cho hình chóp S.ABC có AB = a , BC = a 3 , AC = a 5 và SA vuông góc với mặt đáy, SB
tạo với đáy góc 45° . Thể tích của khối chóp S.ABC là: 15 3 a 3 11 A. 3 a . B. . C. 3 a . D. 3 a . 12 12 12 12 Hướng dẫn giải Chọn D
Góc (SB ( ABC ))  = (SB AB)  =  , , SBA = 45° . S ∆ BA
vuông tại A có SBA = 45° 
→SA = AB = a  2 2 2
AB + AC − BC 3 5 = = →  55 cos BAC sin BAC = . 2. . AB AC 10 10 =  2 1 a 11 S . AB AC.sin BAC = ABC 2 4 2 3 1 1 a 11 a 11 V = S .SA = .a = . S . ABC 3 ABC 3 4 12
Câu 77: Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a , AD = a 2 ; SA ⊥ ( ABCD) ,
góc giữa SC và đáy bằng 60°. Tính theo a thể tích khối chóp S.ABCD . A. 3 3 2a . B. 3 3a . C. 3 6a . D. 3 2a . Hướng dẫn giải Chọn D https://toanmath.com/ Ta có AC = AB + BC = a + (a )2 2 2 2 2 = a 3  =  SCA
(SC, ( ABCD)) = 60° Vậy =  SA
AC. tan SCA = a 3. tan 60° = 3a . Ngoài ra 2 S = . a a 2 = a 2 ABCD 1 1 nên 2 3 V = . SA S = .3 . a a 2 = a 2 . S . ABCD 3 ABCD 3
Câu 78: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, S A vuông góc với mặt phẳng đáy,
góc giữa (SBC ) và ( ABC ) bằng 30 .
° Thể tích khối chóp S.ABC là 3 a 6 3 a 3 3 a 3 3 a 6 A. . B. . C. . D. . 8 24 8 24 Hướng dẫn giải Chọn B
Từ A kẻ AM ⊥ BC , ta có:
SA ⊥ ( ABC) ⇒ SA ⊥ BC ⇒ BC ⊥ (SAM) BC ⊥ AM  (SBC) ∩ (ABC) = BC   BC ⊥ (SAM )  ⇒  =  0 ((SBC), (ABC)) SMA = 30 
(SAM ) ∩ (SBC) = SM ; (SAM ) ∩ ( ABC) = AM  2  a  2 3a a 3
Xét tam giác vuông AMB ta có 2 2 2
AM = AB − BM 2 = a −   = ⇒ AM =  2  4 2 https://toanmath.com/ a 3 a
Xét tam giác vuông SAM ta có =  SA AM . tan SMA 0 = tan 30 = 2 2 1 2 1 a a 3 3 a 3 Suy ra: V = S . A S ABC = . . = . SABC  3 3 2 4 24
Câu 79: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , cạnh bên SA vuông góc với đáy,
đường thẳng SC tạo với đáy một góc bằng 60°. Thể tích của khối chóp S.ABC bằng 3 3a 3 a 3 a 3 a A. . B. . C. . D. . 4 8 4 2 Hướng dẫn giải Chọn C 2 Diện tích a 3 A ∆ BC là S = . ABC ∆ 4
SA ⊥ ( ABC ) nên AC là hình chiếu của SC lên ( ABC ) . ⇒ (SC ( ABC))  = (SC AC)  =  , , SCA = 60° . S
∆ AC vuông tại A có  SCA = 60° , ta có =  SA
AC. tan SCA = a 3 . 2 3 Thể tích khối chóp là 1 1 a 3 a V = .S .SA = . .a 3 = ∆ . 3 ABC 3 4 4
Câu 80: Cho tứ diện .
O ABC có OA , OB , OC đôi một vuông góc với nhau và OA = 2a , OB = 3a ,
OC = 8a . M là trung điểm của OC. Tính thể tích V của khối tứ diện . O ABM . A. 3 V = 6a . B. 3 V = 8a . C. 3 V = 4a . D. 3 V = 3a . Hướng dẫn giải Chọn C https://toanmath.com/ . OB  ⊥ OA Vì 
⇒ OB ⊥ (OAC) . OB  ⊥ OC 1 1 1 1 V = V = B . O S = 3 . a . OA OM 3 = 3 .2 a .4
a a = 4a . OABM B. AOM 3 AOM 3 2 6
Câu 81: Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a . Hai mặt bên (SAB) và ( SAC )
cùng vuông góc với đáy. Tính thể tích khối chóp biết SC = a 3 . 3 a 3 3 2a 6 3 a 6 3 a 3 A. B. . C. . D. . 2 9 12 4 Hướng dẫn giải Chọn C (  SAB) ⊥  ( ABC) Ta có: 
⇒ SA ⊥ ( ABC) (  SAC  ) ⊥ ( ABC) 2 a 3 +) 2 2 SA =
SC − AC = a 2; S = ABC 4 3 1 a 6 ⇒ V = . . SA S = . S . ABC 3 ABC 12
Câu 82: Cho khối chóp S.ABC có SA ⊥ ( ABC) , A
∆ BC vuông tại B , SB = 2a , SC = a 5 . Thể tích khối
chóp S.ABC bằng 3
a . Khoảng cách từ A đến (SBC ) là: A. 2a . B. 3a . C. 3a . D. 6a . Hướng dẫn giải Chọn B https://toanmath.com/ S a 5 2a A C B . SA ⊥ BC Ta có  ⇒ SB ⊥ BC . AB ⊥ BC ⇒ S
∆ BC vuông tại B . Do đó: 2 2 2 2 BC =
SC − SB = (a 5) − (2a) = a . 1 2 S = S . B BC = a . S ∆ BC 2 3 Vậy: 3V 3.a . d ( , A (SBC)) A SBC = = = 3a . 2 S a S ∆ BC
Câu 83: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , AB = a , AC = 2a , SC = 3a , SA
vuông góc với đáy ( ABC). Thể tích khối chóp S.ABC là. 3 a 5 3 a 3 3 a 3 a 3 A. . B. . C. . D. . 3 12 4 4 Hướng dẫn giải Chọn A S 2a A C a B 2 2
Phân tích: Tam giác SAC vuông tại A nên 2 2 SA =
SC − AC = (3a) − (2a) = a 5 . 3 Khi đó 1 1 1 a 5 V = . . SA S = .a 5. .2 a a = . S . ABCD 3 ABC 3 2 3
Câu 84: Cho hình chóp S.ABC có ABC là tam giác đều cạnh a và SA vuông góc với đáy. Góc tạo bởi
mặt phẳng (SBC) và mặt phẳng ( ABC) bằng 30° . Thể tích của khối chóp S.ABC là 3 a 3 3 a 3 a 3 a 3 A. . B. . C. . D. . 24 4 12 8 https://toanmath.com/ Hướng dẫn giải Chọn A S A C 30° M B
Gọi M là trung điểm BC . Suy ra  SMA = 30° . =  a 3 a SA AM tan SMA = tan 30° = . 2 2 2 3 1 1 a a 3 a 3 V = . SA S = . . = . S . ABC 3 ABC 3 2 4 24
Câu 85: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Cạnh bên SA vuông góc với mặt phẳng
đáy, cạnh bên SC tạo với mặt phẳng (SAB) một góc 30° . Thể tích của khối chóp S.ABCD bằng: 3 a 2 3 a 2 3 a 2 3 a 3 A. . B. . C. . D. . 3 4 2 3 Hướng dẫn giải Chọn A s A B O D C
Ta có: ABCD là hình vuông cạnh a nên 2 S = a ABCD
Vì hình chóp S.ABCD có đáy là hình vuông, cạnh bên SA vuông góc với mặt phẳng đáy
⇒ BC ⊥ (SAB) .
Cạnh bên SC tạo với mặt phẳng (SAB) một góc 30° ⇒  CSB = 30° .
Tam giác SBC vuông tại B có  CSB = 30° , 
SCB = 60° , BC = a . SB BC ⇒ ⇒ =  =  SB a 3 . sin SCB sin CSB
Từ giả thiết ⇒ SA ⊥ AB . Tam giác SAB có 2 2 SA =
SB − AB = a 2 . 3 1 a 2 ⇒ V = . SA S = . SABCD 3 ABCD 3
Câu 86: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Cạnh bên SA vuông góc với mặt phẳng
đáy, cạnh bên SC tạo với mặt phẳng (SAB) một góc 30° . Thể tích của khối chóp đó bằng. https://toanmath.com/ S A D B C . 3 a 2 3 a 3 3 a 2 3 a 2 A. . B. . C. . D. . 2 3 4 3 Hướng dẫn giải Chọn D
(SC (SAB)) = (SC SB) =  0 , , BSC = 30 . a 0 2 2 tan 30 =
⇔ SB = a 3 ; SA= SB − AB = a 2 . SB 3 1 a 2 V = . SA S = . SABCD 3 ABCD 3
Câu 87: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C và SA vuông góc với mặt phẳng
( ABC). Biết AB = 4a và góc giữa mặt phẳng (SBC) và (ABC) bằng 45°. Tính thể tích V của
khối chóp S.ABC . 8 2 3 2 1 2 A. 3 V = a . B. 3 V = a . C. 3 V = a . D. 3 V = a . 3 2 6 6 Hướng dẫn giải Chọn A S 4a A B C . (
SBC) ∩( ABC) = BC  AC ⊥ BC
suy ra góc giữa (SBC ) và ( ABC ) là góc SC ∠ A = 45° . SC ⊥ BC  4a ⇒ SA = AC = = 2a 2 . 2 Thể tích khối chóp là a V = SA S = a a = . ABC ( ) 3 2 1 1 1 8 2 . . .2 2. . 2 2 3 3 2 3
Câu 88: Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật, AB = a , AD = a 2 . Biết
SA ⊥ ( ABCD) và góc giữa đường thẳng SC với mặt phẳng đáy bằng 45°. Thể tích khối chóp
S.ABCD bằng: https://toanmath.com/ 3 a 6 A. 3 3a . B. 3 a 6 . C. . D. 3 a 2 . 3 Hướng dẫn giải Chọn C
Vì AC là hình chiếu vuông góc của SC trên mp ( ABCD) .
Suy ra (SC ( ABCD))  = (SC AC)  =  , , SCA = 45° . SA
Tam giác SAC vuông tại A, có  tan SCA = ⇒ SA = AC . AC
Tam giác ABC vuông tại A, có 2 2 AC =
AB + BC = a 3 . 3 1 a 6
Vậy thể tích khối chóp S.ABCD là V = . . SA S = . S . ABCD 3 ABCD 3
Câu 89: Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân có cạnh huyền BC = a và SA vuông
góc với mặt phẳng đáy. Biết góc giữa mặt phẳng (SBC) và mặt phẳng ( ABC) bằng 45°. Thể
tích của hình chóp S.ABC là. 3 a 2 3 a 3 a 3 a 2 A. V = . B. V = . C. V = . D. V = . S . ABC 24 S . ABC 8 S . ABC 24 S . ABC 8 Hướng dẫn giải Chọn C S A C a M B .  ⊥ Gọi M là trung điểm BC AM BC ⇒  ⇒ BC ⊥ SM . BC ⊥ SA (SBC) (SAM )  ( )=(SM AM)  =  BC a 0 , ,
SMA = 45 ⇒ SA = AM = = . 2 2 2 BC a 2 1 1 a 2 a 2 a AB = AC = = ⇒ S = A . B AC = = . ABC ∆ 2 2 2 2 2 2 4 https://toanmath.com/ 2 3 1 a a a V = . . = (đvtt). S . ABC 3 2 4 24
Câu 90: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a . Các mặt bên (SAB) , ( SAC ) cùng vuông
góc với mặt đáy ( ABC ) ; góc giữa SB và mặt ( ABC ) bằng 60° . Tính thể tích khối chóp S.ABC . 3 a 3 3a 3 a 3 a A. . B. . C. . D. . 12 4 2 4 Hướng dẫn giải Chọn D (  SAB) ⊥  ( ABC) Ta có 
⇒ SA ⊥ ( ABC) (  SAC  ) ⊥ ( ABC)
Ta có SB ∩ ( ABC ) = { }
B và SA ⊥ ( ABC ) ⇒ (SB ( ABC))  = (SB AB)  =  , , SBA = 60°
Mà AB = a ⇒ SA = .
a tan 60° = a 3 2 a 3 Ta có S = ABC 4 2 3 1 1 a 3 a ⇒ V = . SA S = .a 3. = . S . ABC 3 ABC 3 4 4
Câu 91: Cho khối chóp S.ABC , có đáy ABC là tam giác đều cạnh a . Hai mặt bên (SAB) và (SAC )
cùng vuông góc với đáy. Tính thể tích khối chóp biết SC = a 3 . 3 a 6 3 a 6 3 a 6 3 a 6 A. V = . B. V = . C. V = . D. V = . 3 6 12 8 Hướng dẫn giải Chọn C S A C B . https://toanmath.com/
Hai mặt bên (SAB) và (SAC) cùng vuông góc với đáy SA ⊥ ( ABC) . 2 3 1 a 2.a 3 a 6 Ta có V = . SA S = = ∆ . 3 ABC 12 12
Câu 92: Cho hình chóp S.ABC là tam giác vuông tại A ,  30o ABC =
, BC = a . Hai mặt bên (SAB) và
(SAC) cùng vương góc với đáy (ABC), mặt bên (SBC) tạo với đáy một góc 0 45 . Thể tích của
khối chóp S.ABC là: 3 a 3 a 3 a 3 a A. . B. . C. . D. . 9 32 64 16 Hướng dẫn giải Chọn B (
SAB) ⊥ ( ABC)  Ta có: (
SAC) ⊥ ( ABC)
⇒ SA ⊥ ( ABC) . (  SAB  )∩(SAC) = SA
Kẻ AH ⊥ BC ⇒ SH ⊥ BC (
SBC) ∩( ABC) = BC  Khi đó:  ⊥ ⇒  BC AH SHA = 45o BC ⊥ SHa 3 a a 3 Mà 0 AB = BC.cos30 =
và AC = BC.sin 30o = nên 0 AH = A . B sin 30 = 2 2 4 a 3 Nên SA = 4 3 Do đó: 1 1 a V = S .SA = A . B AC.SA = . 3 ABC 6 32
Câu 93: Cho khối chóp S.ABC có SA ⊥ ( ABC ) , SA = a , AB = a , AC = 2a và 
BAC = 120° . Tính thể
tích khối chóp S.ABC . 3 a 3 3 a 3 3 a 3 A. 3 a 3 . B. . C. . D. . 6 3 2 Hướng dẫn giải https://toanmath.com/ S C A B Chọn B 1 1 1 a 3 Ta có: = =  3 V S . A S S . A A . B AC.sin BAC = (đvtt). S . ABC ∆ 3 ABC 3 2 6 3
Vậy thể tích khối chóp a 3 S.ABC là . 6
Câu 94: Tính thể tích khối chóp S.ABC có AB = a , AC = 2a , 
BAC = 120° , SA ⊥ ( ABC ) , góc giữa
(SBC) và ( ABC) là 60°. 3 7 a 3 21 a 3 7 a 3 3 21 a A. . B. . C. . D. . 7 14 14 14 Hướng dẫn giải Chọn C S A 2a 120o C 60o a H B + Diện tích đáy 1 1 3 3 S = A . B AC.sin120° = . .2 a . a 2 = a ABC 2 2 2 2
+ Tính chiều cao SA : • ( SBC ABC )
Dựng AH ⊥ BC (với H ∈ BC ) suy ra SH ⊥ BC , do đó góc ( ) ( )  =  , SHA = 60° ,
suy ra SA = AH. tan 60° https://toanmath.com/ • 2.S
Tính AH : ta có diện tích 1 S = AH.BC ABC ⇒ AH =
mà theo định lý hàm côsin thì ABC 2 BC  1  2 2 2
BC = AB + AC − 2.A . B AC.cos A 2 2
= a + 4a − 2. .2 a . a  −  2 =
⇒ BC = a 7 , suy ra  7a 2  3 2 2. a 21 2 AH = = a . a 7 7 1 1 3 21 7
+ KL: Thể tích khối chóp S.ABC là V = S .SA 2 = . a . a 3 = a (đvtt). 3 ABC 3 2 7 14
Câu 95: Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a , AD = a 2 , SA ⊥ ( ABCD) ,
góc giữa SC và đáy bằng 60°. Thể tích hình chóp S.ABCD bằng A. 3 3 2a . B. 3 2a . C. 3 3a . D. 3 6a . Hướng dẫn giải Chọn B S D A B C Ta có 2 2 AC =
AB + BC = a 3 .
Góc giữa SC và đáy bằng góc 
SCA = 60° . Suy ra SA = AC. tan 60° = 3a .
Thể tích hình chóp bằng 1 1 2 3 V = . SA S = 3 . a a 2 = a 2 . S . ABCD 3 ABCD 3
Câu 96: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với mặt phẳng
đáy và cạnh bên SD hợp với đáy một góc 60°. Hỏi thể tích V của khối chóp S.ABCD bằng bao nhiêu? 3 2a 3 3 a 3 3 a 3 A. V = . B. 3 V = a 3 . C. V = . D. V = . 3 6 3 Hướng dẫn giải Chọn D https://toanmath.com/ S a D a A a B C a . Theo đề có : 
SDA = 60° ⇒ SA = A .
D tan 60° = a 3 . 3 Thể tích 1 1 3 2 a
V của khối chóp S.ABCD : V = dt
.SA = .a .a 3 = . ABCD 3 3 3
Câu 97: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a . Cạnh SA vuông góc với
đáy và SA = y . Trên cạnh AD lấy điểm M sao cho AM = x . Biết rằng 2 2 2
x + y = a . Tìm giá trị
lớn nhất của thể tích khối chóp S.ABCM . 3 a 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 8 8 2 4 Hướng dẫn giải Chọn B .
Ta có 0 < x < a ; 2 2 y = a − x . 1 1
(x + a)a 1 V = . SA S = . y 2 2
= a a − x (x + a) . S . ABCM 3 ABCM 3 2 6 Xét hàm số ( ) 2 2
f x = a − x ( x + a) . ′( ) 2 2 2
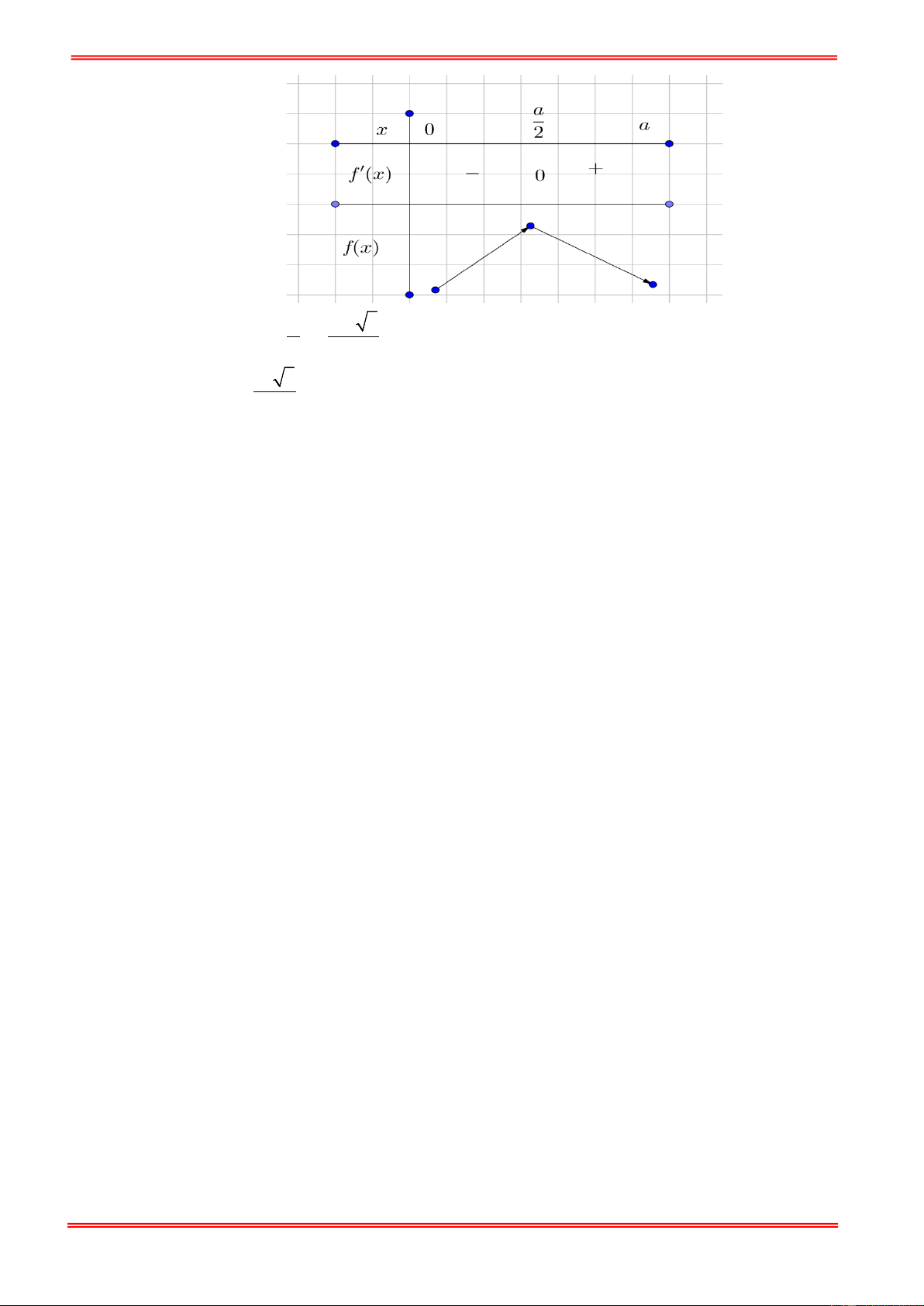
− x − ax + a f x = . 2 2 a − xx = −a a f ′( x) = 0  ⇔ a  nhận x = . x = 2  2 https://toanmath.com/ .   ⇒ Max f (x) 2 a 3a 3 = f =   .  2  4 3 a 3 MaxV = . S . ABCM 8 https://toanmath.com/
Document Outline

  • 2.1 BT KHỐI CHÓP CÓ CẠNH BÊN VUÔNG GÓC VỚI ĐÁY
    • THỂ TÍCH KHỐI CHÓP CÓ MỘT CẠNH BÊN VUÔNG GÓC VỚI ĐÁY
      • A. BÀI TẬP
  • 2.1 HDG KHỐI CHÓP CÓ CẠNH BÊN VUÔNG GÓC VỚI ĐÁY
    • THỂ TÍCH KHỐI CHÓP CÓ MỘT CẠNH BÊN VUÔNG GÓC VỚI ĐÁY
      • B. LỜI GIẢI CHI TIẾT

Tài liệu liên quan: