Bài tập thể tích khối chóp đều có lời giải chi tiết Toán 12

 Giới thiệu đến bạn đọc đề bài và hướng dẫn giải chi tiết 85 bài tập thể tích khối chóp đều, tài liệu gồm 55 trang.Mời bạn đọc đón xem.

Chủ đề:

Chương 1: Khối đa diện 172 tài liệu

Môn:

Toán 12 3.9 K tài liệu

Thông tin:
55 trang 1 năm trước
Tác giả:
L
Lan Tường
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Bài tập thể tích khối chóp đều có lời giải chi tiết Toán 12

 Giới thiệu đến bạn đọc đề bài và hướng dẫn giải chi tiết 85 bài tập thể tích khối chóp đều, tài liệu gồm 55 trang.Mời bạn đọc đón xem.

39 20 lượt tải Tải xuống

Chủ đề: Chương 1: Khối đa diện 172 tài liệu

Môn: Toán 12 3.9 K tài liệu

Thông tin:

55 trang 1 năm trước

Tác giả:

Profile Lan Tường
https://toanmath.com/
THỂ TÍCH KHỐI CHÓP ĐỀU
A. BÀI TẬP
Câu 1. Cho khối tứ diện đều
ABCD
cạnh bằng
a
,
M
là trung điểm
BC
. Thể tích
V
của khối chóp
.M ABC
bằng bao nhiêu?
A.
3
3
24
a
V =
. B.
3
2
a
V =
. C.
3
2
12
a
V =
. D.
3
2
24
a
V
=
.
Câu 2. Cho hình chóp đều
có cạnh đáy bằng
a
và cạnh bên tạo với đáy một góc
60°
. Thể tích
của hình chóp đều đó là:
A.
3
6
6
a
. B.
3
3
6
a
. C.
3
3
2
a
. D.
3
6
2
a
.
Câu 3. Thể tích hình tứ diện đều có cạnh bằng
a
là:
A.
3
2
3
a
. B.
3
2
12
a
. C.
3
2
6
a
. D.
3
52
12
a
.
Câu 4.Cho khối chóp tứ giác đều có cạnh đáy bằng
a
, cạnh bên gấp hai lần cạnh đáy. Tính thể tích
V
của
khối chóp tứ giác đã cho.
A.
3
2
2
a
. B.
3
2
6
a
. C.
3
14
6
a
. D.
3
14
2
a
.
Câu 5. Cho hình chóp tứ giác đều có cạnh đáy bằng
a
và cạnh bên bằng
3a
. Tính thể tích
V
của khối
chóp đó theo
a
.
A.
3
3
3
a
V =
. B.
3
2
a
V =
. C.
3
2
3
a
V =
. D.
3
10
6
a
V =
.
Câu 6. Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, đường cao của một mặt bên là
3
a
. Thể
tích
V
của khối chóp đó là:
A.
3
2
6
=Va
. B.
3
2
9
=Va
. C.
3
22
3
=
Va
. D.
3
42
3
=Va
.
Câu 7. Cho tứ diện đều
ABCD
cạnh bằng
2a
. Tính thể tích của khối tứ diện đó.
A.
3
2
12
a
V =
. B.
3
3
6
a
V =
.
C.
3
3
a
V =
.
D.
3
2
6
a
V =
.
Câu 8. Cho hình chóp đều
.S ABCD
có cạnh đáy bằng
2a
, khoảng cách giữa hai đường thẳng
SA
và
CD
bằng
3a
. Thể tích khối chóp đều
.S ABCD
bằng?
A.
3
43
a
. B.
3
3a
. C.
3
43
3
a
. D.
3
3
3
a
.
Câu 9. Cho khối chóp đều
.S ABC
có cạnh bên bằng
a
và các mặt bên hợp với đáy một góc
45°
. Tính thể
tích của khối chóp
.S ABC
theo
.a
.
A.
3
15
25
a
. B.
3
5
25
a
. C.
3
3
a
. D.
3
15
5
a
.
Câu 10. Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, đường cao của một mặt bên là
3a
. Tính
thể tích
V
của khối chóp đó.
A.
3
2
9
a
V =
. B.
3
42Va=
. C.
3
42
3
a
V =
. D.
3
2
6
a
V =
.
Câu 11. Cho hình chóp tam giác đều cạnh đáy bằng
a
và các mặt bên đều tạo với mặt phẳng đáy một góc
60 .°
Tính thể tích
V
của khối chóp.
https://toanmath.com/
A.
3
3
4
a
V =
. B.
3
3
24
a
V =
. C.
3
2
6
a
V =
. D.
3
3
8
a
V =
.
Câu 12. Cho hình chóp tứ giác đều có cạnh đáy bằng
a
, cạnh bên bằng
2a
(hình vẽ). Thể tích khối chóp
là
A.
3
3
6
a
. B.
3
22
3
a
. C.
3
6
3
a
. D.
3
6
6
a
.
Câu 13. [Sở GDĐT Lâm Đồng lần 07 - 2017] Cho
( )
H
là khối chóp tứ giác đều có tất cả các cạnh bằng
2a
. Thể tích của
( )
H
bằng:
A.
3
4
5
a
. B.
3
43
3
a
. C.
3
42
3
a
. D.
3
4
3
a
.
Câu 14. Một hình chóp tam giác đều có cạnh bên bằng
b
và cạnh bên tạo với mặt phẳng đáy một góc
α
.
Thể tích của hình chóp đó là
A.
3
3
cos sin
4
b
αα
. B.
32
3
sin cos
4
b
αα
.
C.
32
3
cos sin
4
b
αα
. D.
32
3
cos sin
4
b
αα
.
Câu 15.Cho hình chóp tứ giác đều
có thể tích
2
6
V =
. Gọi
M
là trung điểm của cạnh
SD
. Nếu
thì khoảng cách từ
B
đến mặt phẳng
( )
MAC
bằng:
A.
3
4
. B.
1
2
. C.
2
3
. D.
1
2
.
Câu 16. Khối chóp tam giác đều có tất cả các cạnh bằng
a
có thể tích bằng:
A.
3
3
12
a
. B.
3
3
4
a
. C.
3
2
6
a
. D.
3
3
a
.
Câu 17. Khi chiều cao của một hình chóp đều tăng lên
n
lần nhưng mỗi cạnh đáy giảm đi
n
lần thì thể tích
của nó.
A. Không thay đổi. B. Tăng lên
n
lần.
C. Tăng lên
1n −
lần. D. Giảm đi
n
lần.
Câu 18. Tính thể tích khối chóp tứ giác đều có tất cả các cạnh bằng
a
.
A.
3
23
3
a
. B.
3
2
6
a
. C.
3
3
4
a
. D.
3
3
2
a
.
Câu 19. Cho khối chóp đều
.S ABC
có cạnh đáy bằng
a
, tính thể tích khối chóp
.S ABC
biết cạnh bên bằng
a
là:
A.
3
.
4
S ABC
a
V =
. B.
3
.
2
12
S ABC
a
V =
. C.
3
.
3
6
S ABC
a
V =
. D.
3
.
12
S ABC
a
V =
.
https://toanmath.com/
Câu 20. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
, cạnh bên hợp với đáy một góc
60
. Thể
tích
V
của khối chóp
.S ABCD
bằng
A.
3
3
2
a
V =
. B.
3
3
3
a
V
=
. C.
3
6
6
a
V
=
. D.
3
6
3
a
V
=
.
Câu 21. Cho hình chóp tam giác đều cạnh đáy bằng
a
và các mặt bên đều tạo với mặt phẳng đáy một góc
0
60 .
Tính thể tích
V
của khối chóp.
A.
3
3
24
a
V
. B.
3
3
4
a
V
. C.
3
2
6
a
V
. D.
3
3
8
a
V
.
Câu 22. Thể tích của khối chóp tứ giác đều có chiều cao bằng
6
3
a
và cạnh đáy bằng
3a
bằng:
A.
3
32
2
a
. B.
3
32
4
a
. C.
3
6
3
a
. D.
3
36
2
a
.
Câu 23. Cho hình chóp tứ giác đều
có cạnh đáy bằng
a
. Gọi điểm
O
là giao điểm của
AC
và
BD
. Biết khoảng cách từ
O
đến
SC
bằng
6
a
. Tính thể tích khối chóp
.S ABC
.
A.
3
6
a
. B.
3
4
a
. C.
3
8
a
. D.
3
12
a
.
Câu 24. Cho hình chóp tam giác đều
.S ABC
có độ dài cạnh đáy bằng
a
, góc hợp bởi cạnh bên và mặt đáy
bằng
60°
. Thể tích của hình chóp đã cho.
A.
3
3
4
a
. B.
3
3
6
a
. C.
3
3
3
a
. D.
3
3
12
a
.
Câu 25. Cho hình chóp đều
.S ABCD
có
2AC a=
, mặt bên
( )
SBC
tạo với đáy
(
)
ABCD
một góc
45
°
.
Tính thể tích
V
của khối chóp
.
A.
3
2
a
V =
. B.
3
2
3
a
V =
. C.
3
23
3
a
V =
. D.
3
2Va=
.
Câu 26. Khối chóp tam giác đều có cạnh đáy bằng a và cạnh bên bằng
3a
có thể tích bằng:
A.
3
2
6
a
V =
. B.
3
6
6
aV =
. C.
3
6
2
aV =
. D.
3
3
1
aV =
.
Câu 27. Cho khối chóp tứ giác đều có cạnh đáy bằng
a
, cạnh bên bằng
2a
. Tính thể tích
V
của khối chóp
đã cho.
A.
3
2
2
a
V =
. B.
3
14
2
a
V =
. C.
3
14
6
a
V =
. D.
3
2
6
a
V =
.
Câu 28. Một hình chóp có đáy là tam giác đều cạnh bằng
2
và có chiều cao bằng
4.
Tính thể tích hình chóp
đó.
A.
23
. B.
2
. C.
4
. D.
43
3
.
Câu 29.] Cho hình chóp tứ giác đều có cạnh đáy bằng
x
. Diện tích xung quanh gấp đôi diện tích đáy. Khi
đó thể tích của khối chóp bằng:
A.
3
.3
3
x
. B.
3
.3
2
x
.
C.
3
.3
12
x
. D.
3
.3
6
x
.
Câu 30. Cho hình chóp tam giác đều
.S ABC
có cạnh đáy bằng
3a
. Gọi
,MN
lần lượt là trung điểm của
,SB BC
Tính thể tích khối chóp
.A BCNM
. Biết mặt phẳng
( )
AMN
vuông góc với mặt phẳng
( )
SBC
.
https://toanmath.com/
A.
3
3 15
48
a
. B.
3
15
32
a
. C.
3
3 15
32
a
. D.
3
3 15
16
a
.
Câu 31. Người ta gọt một khối lập phương gỗ để lấy khối tám mặt đều nội tiếp nó (tức là khối có các đỉnh là
các tâm của các mặt khối lập phương). Biết các cạnh của khối lập phương bằng
a
. Hãy tính thể
tích của khối tám mặt đều đó:
A.
3
8
a
. B.
3
6
a
. C.
3
4
a
. D.
3
12
a
.
Câu 32. Cho
( )
H
là khối chóp tứ giác đều có tất cả các cạnh bằng
a
. Thể tích của
( )
H
bằng.
A.
3
3
2
a
. B.
3
2
6
a
. C.
3
3
a
. D.
3
3
4
a
.
Câu 33. Một hình chóp tứ giác đều có đáy là hình vuông cạnh
a
, các mặt bên tạo với đáy một góc
α
. Thể
tích khối chóp đó là
A.
3
tan
6
a
α
. B.
3
tan
2
a
α
. C.
3
cot
6
a
α
. D.
3
sin
2
a
α
.
Câu 34.Cho khối chóp đều
có đáy
ABCD
là hình vuông cạnh
a
,
3SA a=
. Tính thể tích
V
của
khối chóp
.S ABCD
theo
a
.
A.
3
26
9
Va=
. B.
3
10
6
Va=
. C.
3
2
3
Va=
. D.
3
11
6
Va=
.
Câu 35. Thể tích của chóp tam giác đều có tất cả các cạnh đều bằng
a
là
A.
3
2
4
a
. B.
3
2
2
a
. C.
3
2
6
a
. D.
3
2
12
a
.
Câu 36. Cho hình chóp tứ giác đều có cạnh đáy bằng cạnh bên bằng
2a
. Tính thể tích khối chóp đã cho.
A.
3
2
4
a
. B.
3
42
3
a
. C.
3
3
12
a
. D.
3
2
6
a
.
Câu 37. Cho hình chóp đều
.S ABC
có
1=SA
. Gọi
,DE
lần lượt là trung điểm của hai cạnh
,SA SC
. Tính
thể tích khối chóp
.S ABC
, biết đường thẳng
BD
vuông góc với đường thẳng
AE
.
A.
.
2
12
=
S ABC
V
B.
.
21
54
=
S ABC
V
C.
.
12
4
=
S ABC
V
D.
.
21
18
=
S ABC
V
Câu 38. Tính thể tích khối tứ diện đều có cạnh
a
.
A.
3
a
. B.
3
3
4
a
. C.
3
2
12
a
. D.
3
3
12
a
.
Câu 39. Trong tất cả các khối chóp tứ giác đều ngoại tiếp mặt cầu bán kính bằng
a
, thể tích
V
của khối chóp
có thể tích nhỏ nhất.
A.
3
32
3
=
a
V
. B.
3
10
3
=
a
V
. C.
3
2
=Va
. D.
3
8
3
=
a
V
.
Câu 40. Cho hình chóp tam giác đều có cạnh đáy bằng
a
, góc giữa cạnh bên và mặt đáy bằng
o
60
. Thể tích
khối chóp
.S ABC
là:
A.
3
3
12
a
. B.
3
6
12
a
. C.
3
8
a
. D.
3
3
8
a
.
Câu 41. Cho hình chóp tam giác đều
.S ABC
có
=AB a
, cạnh bên
6
3
=SA a
. Tính thể tích
V
của khối
chóp
.S ABC
.
A.
3
3
36
=
a
V
. B.
3
4
=
a
V
. C.
3
24
=
a
V
. D.
3
12
=
a
V
.
https://toanmath.com/
Câu 42. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
. Gọi
SH
là đường cao của hình chóp.
Khoảng cách từ trung điểm của
SH
đến
(
)
SBC
bằng
b
. Thể tích khối chóp
là
A.
3
22
2
3 16
ab
ab−
. B.
3
22
3 16
ab
ab
−
. C.
3
22
2
16
ab
ab−
. D.
2
3
ab
.
Câu 43. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
. Gọi
M
,
N
lần lượt là trung điểm của
SA
và
CD
. Cho biết
MN
tạo với mặt đáy một góc bằng
30°
. Tính thể tích khối chóp
.S ABCD
.
A.
3
15
5
a
. B.
3
30
18
a
. C.
3
15
3
a
. D.
3
5
12
a
.
Câu 44. Cho hình chóp tam giác đều có cạnh đáy bằng
a
và cạnh bên bằng
b
.
Thể tích của khối chóp là
A.
2
22
3
6
a
ba−
. B.
2 22
3
a ba−
. C.
2
22
3
4
a
ba−
. D.
2
22
3
12
a
ba−
.
Câu 45. Cho hình chóp tứ giác đều có độ dài cạnh bên và cạnh đáy cùng bằng
a
. Khi đó, khoảng cách
h
giữa đường thẳng
AD
và mặt phẳng
( )
SBC
là:
A.
6
3
a
h =
. B.
2
a
h =
. C.
2
2
a
h =
. D.
2a 5
5
h
=
.
Câu 46. Cho hình chóp tam giác đều
.S ABC
đỉnh
S
, độ dài cạnh đáy là
a
, cạnh bên bằng
2a
. Gọi
I
là
trung điểm của cạnh
BC
. Tính thể tích
V
của khối chóp
.S ABI
.
A.
3
11
8
a
. B.
3
11
6
a
. C.
3
11
12
a
. D.
3
11
24
a
.
Câu 47. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
góc giữa cạnh bên và mặt phẳng đáy bằng
60°
. Tính thể tích khối chóp
.
A.
3
6
a
. B.
3
6
3
a
. C.
3
6
2
a
. D.
3
6
6
a
.
Câu 48. Xét tứ diện
ABCD
có các cạnh
2AC CD DB BA= = = =
và
AD
,
BC
thay đổi. Giá trị lớn nhất
của thể tích tứ diện
ABCD
bằng
A.
32 3
27
. B.
16 3
27
. C.
32 3
9
. D.
16 3
9
.
Câu 49. Cho hình chóp tứ giác đều
.S ABCD
, đáy
ABCD
có diện tích
2
16cm
, diện tích một mặt bên là
2
8 3cm .
Tính thể tích
V
của khối chóp
.S ABCD
.
A.
3
32 2
cm .
3
V =
B.
3
32 13
cm .
3
V =
C.
3
32 11
cm .
3
V =
D.
3
32 15
cm .
3
V =
Câu 50. Cho khối chóp tam giác đều. Nếu tăng cạnh đáy lên hai lần và giảm chiều cao đi bốn lần thì thể tích
của khối chóp đó sẽ:
A. Giảm đi hai lần. B. Không thay đổi.
C. Tăng lên hai lần. D. Giảm đi ba lần.
Câu 51. Hình chóp tứ giác đều có tất cả các cạnh bằng
a
. Thể tích khối chóp đó bằng:
A.
3
2
2
a
. B.
3
2
6
a
. C.
3
3
3
a
. D.
3
2
3
a
.
Câu 52. Khi chiều cao của một hình chóp đều tăng lên
n
lần nhưng mỗi cạnh đáy giảm đi
n
lần thì thể tích
của nó.
A. Không thay đổi. B. Tăng lên
n
lần.
C. Tăng lên
1n −
lần. D. Giảm đi
n
lần.
Câu 53. Cho hình chóp đều
.S ABCD
có đáy bằng
2a
, khoảng cách giữa hai đường thẳng
SA
và
CD
bằng
3a
. Thể tích khối chóp đều
bằng.
A.
3
3a
. B.
3
43a
. C.
3
3
3
a
. D.
3
43
3
a
.
https://toanmath.com/
Câu 54. Thể tích khối bát diện đều cạnh
a
là:
A.
3
2
3
a
. B.
3
2
2
a
. C.
3
2
6
a
. D.
3
2a
.
Câu 55. Cho hình chóp tứ giác đều
có đáy
ABCD
là hình vuông cạnh bằng
3a
và
2SA SB SC SD a= = = =
. Tính thể tích khối chóp
?
A.
3
2
2
a
. B.
3
3
3
a
. C.
3
6
6
a
. D.
3
2
6
a
.
Câu 56. Cho hình chóp tứ giác đều
có chiều cao bằng
h
, góc giữa hai mặt phẳng
( )
SAB
và
bằng
α
. Tính thể tích của khối chóp
.S ABCD
theo
h
và
α
.
A.
3
2
3
8tan
h
α
. B.
3
2
3
4tan
h
α
. C.
3
2
4
3tan
h
α
. D.
3
2
8
3tan
h
α
.
Câu 57. Cho tứ diện đều . Biết khoảng cách từ đến mặt phẳng bằng . Tính thể tích
của tứ diện .
A. . B. . C. . D. .
Câu 58. Cho hình chóp đều
có
2AC a=
, mặt bên
( )
SBC
tạo với đáy
( )
ABCD
một góc
45°
. Tính
thể tích
V
của khối chóp
.S ABCD
?
A.
3
2
a
V =
. B.
3
2
3
a
V =
. C.
3
2Va=
. D.
3
23
3
a
V =
.
Câu 59. Thể tích hình chóp tứ giác đều có tất cả các cạnh đều bằng
a
bằng
A.
3
2
3
a
B.
3
2
2
a
C.
3
6
a
D.
3
2
6
a
Câu 60. Cho hình chóp đều
.S ABCD
có chiều cao bằng
2
a
và độ dài cạnh bên bằng
6a
. Tính thể tích
khối chóp
.S ABCD
.
A.
3
83
3
a
. B.
3
10 3
3
a
. C.
3
82
3
a
. D.
3
10 2
3
a
.
Câu 61. Tính thể tích khối chóp tứ giác đều có tất cả các cạnh bằng
a
.
A.
3
2
6
a
. B.
3
23
3
a
. C.
3
3
4
a
. D.
3
3
2
a
.
Câu 62. Cho hình chóp tứ giác đều
có cạnh đáy bằng a và mặt bên tạo với đáy một góc 45P
0
P. Thể
tích
V
khối chóp
.S ABCD
là:
A.
3
6
a
V =
. B.
3
9
a
V =
. C.
3
2
a
V
=
. D.
3
1
24
Va=
.
Câu 63. Tính thể tích
V
của hình tứ diện đều có đường cao
ha=
.
A.
3
3
12
a
V =
. B.
3
3
6
a
V =
. C.
3
3
8
a
V =
. D.
3
3
4
a
V =
.
Câu 64. Cho hình chóp tứ giác đều
có cạnh đáy bằng
2a
cạnh bên bằng
3a
. Tính thể tích
V
của
khối chóp đã cho?
A.
3
47Va=
. B.
3
47
9
a
V =
. C.
3
4
3
a
V =
. D.
3
47
3
a
V =
.
Câu 65. Cho khối chóp tứ giác đều có cạnh đáy bằng
a
, cạnh bên bằng
3a
. Tính thể tích
V
của khối chóp
đã cho.
A.
3
34
.
6
a
V =
B.
3
2
.
6
a
V =
C.
3
2
.
2
a
V =
D.
3
34
.
2
a
V =
ABCD
A
( )
BCD
6
V
ABCD
93
2
V =
53V =
27 3V
=
27 3
2
V =
https://toanmath.com/
Câu 66. Một hình chóp tứ giác đều có đáy là hình vuông cạnh
a
, các mặt bên tạo với đáy một góc
α
. Thể
tích của khối chóp đó là
A.
3
sin
2
a
α
. B.
. C.
3
cot
6
a
α
. D.
3
tan
6
a
α
.
Câu 67.Tính thể tích của khối bát diện đều có cạnh bằng 2.
A.
82
3
. B.
16
3
. C.
42
3
. D.
16 2
3
.
Câu 68. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
. Gọi
SH
là chiều cao của hình chóp,
khoảng cách từ trung điểm
I
của
SH
đến mặt bên
( )
SBC
bằng
b
. Tính thể tích
V
của khối chóp
.S ABCD
.
A.
22
3 16
ab
V
ab
=
−
. B.
3
22
2
3 16
ab
V
ab
=
−
.
C.
22
16
ab
V
ab
=
−
. D.
22
2
16
ab
V
ab
=
−
.
Câu 69. Cho hình chóp đều
có cạnh đáy bằng
a
, góc giữa cạnh bên và mặt đáy bằng
o
60
. Tính thể tích
của khối chóp
theo
a
.
A.
3
6
2
a
B.
3
6
6
a
C.
3
3
6
a
D.
3
6
12
a
Câu 70. Thể tích của khối tứ diện đều có cạnh bằng
3
.
A.
22
. B.
42
9
. C.
92
4
. D.
2
.
Câu 71. Cho hình chóp tứ giác đều
.S ABCD
có đáy hợp với mặt bên một góc
45°
. Bán kính mặt cầu ngoại
tiếp hình chóp
.S ABCD
bằng
2
. Tính thể tích khối chóp
.
A.
32 2
9
. B.
64 2
27
. C.
64 2
81
. D.
128 2
81
.
Câu 72. Người ta cắt miếng bìa hình tam giác cạnh bằng
10cm
như hình bên và gấp theo các đường kẻ, sau
đó dán các mép lại để được hình tứ diện đều. Tính thể tích của khối tứ diện tạo thành.
A.
3
250 2 .V cm=
B.
3
125 2
.
12
V cm=
C.
3
1000 2
.
3
V cm=
D.
3
250 2
.
12
V cm=
Câu 73. Tính thể tích khối chóp tứ giác đều cạnh đáy bằng
a
, chiều cao bằng
3a
.
A.
3
a
. B.
3
3
4
a
. C.
3
3
a
. D.
3
3
12
a
.
Câu 74. Thể tích của khối bát diện đều cạnh
a
là:
A.
3
3
6
a
. B.
3
2
3
a
. C.
3
2
6
a
. D.
3
3
3
a
.
https://toanmath.com/
Câu 75. Thể tích của khối tứ diện đều cạnh
a
là
A.
3
6
12
a
. B.
3
3
12
a
. C.
3
2
12
a
. D.
3
2
24
a
.
Câu 76. Cho hình chóp tứ giác đều
có cạnh đáy bằng
a
,diện tích mỗi mặt bên bằng
2
2a
. Thể
tích khối nón có đỉnh là
S
và có đáy là đường tròn ngoại tiếp hình vuông
ABCD
bằng
A.
3
37
4
a
π
. B.
3
7
4
a
π
. C.
3
7
3
a
π
. D.
3
7
6
a
π
.
Câu 77.Cho tứ diện đều
ABCD
có cạnh bằng 3. Gọi
,MN
lần lượt là trung điểm các cạnh
,.
AD BD
Lấy
điểm không đổi
P
trên cạnh
AB
(khác
,AB
). Thể tích khối chóp
PMNC
bằng
A.
92
16
B.
83
3
C.
33
D.
27 2
12
Câu 78. Tính thể tích
V
của khối chóp tứ giác đều có chiều cao là
h
và bán kính mặt cầu nội tiếp là
r
( )
20
hr>>
.
A.
( )
22
4
2
rh
V
hr
=
+
. B.
( )
22
4
32
rh
V
hr
=
−
. C.
(
)
22
3
42
rh
V
hr
=
−
. D.
( )
22
4
32
rh
V
hr
=
+
.
Câu 79. Cho khối tứ diện đều
ABCD
có cạnh bằng
a
. Gọi
', '
BC
lần lượt là trung điểm của các cạnh
AB
và
AC
. Tính thể tích
V
của khối tứ diện
''
AB C D
theo
a
.
A.
3
24
a
V =
. B.
3
2
24
a
V
=
. C.
3
3
48
a
V =
. D.
3
2
48
a
V =
.
Câu 80. Thể tích khối tứ diện đều có cạnh bằng
2a
là.
A.
3
3
6
a
. B.
3
2
12
a
. C.
3
22a
. D.
3
22
3
a
.
Câu 81. Cho hình chóp đều
.S ABC
có đáy cạnh bằng
a
, góc giữa đường thẳng
SA
và mặt phẳng
( )
ABC
bằng
60°
. Gọi
A
′
,
B
′
,
C
′
tương ứng là các điểm đối xứng của
A
,
B
,
C
qua
S
. Thể tích của khối
bát diện có các mặt
,ABC
ABC
′′′
,
A BC
′
,
B CA
′
,
C AB
′
,
AB C
′′
,
BA C
′′
,
CA B
′′
là
A.
3
23
3
a
. B.
3
23a
. C.
3
3
2
a
. D.
3
43
3
a
.
Câu 82. Cho hình chóp tam giác đều
.S ABC
, cạnh đáy bằng
a
. Mặt bên tạo với mặt đáy một góc
o
60
. Tính
thể tích
V
của hình chóp
.S ABC
.
A.
3
3
2
a
V =
. B.
3
3
12
a
V =
. C.
3
3
24
a
V =
. D.
3
3
6
a
V =
.
Câu 83. Cho khối chóp đều
.S ABC
cạnh đáy bằng
a
, cạnh bên bằng
3a
. Tính thể tích khối chóp đó ?
A.
3
26
12
a
V =
. B.
3
11
6
a
V =
. C.
3
3
4
a
V =
. D.
3
11
12
a
V =
.
https://toanmath.com/
Câu 84.Cắt một miếng giấy hình vuông như hình bên và xếp thành hình một hình chóp tứ giác đều. Biết
các cạnh hình vuông bằng
20
cm
,
(
)
OM x cm
=
. Tìm
x
để hình chóp đều ấy có thể tích lớn nhất
A.
8
x cm
=
. B.
6x cm=
. C.
7x cm=
. D.
9x cm=
.
Câu 85. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
. Gọi
G
là trọng tâm của tam giác
SAC
và khoảng cách từ
G
đến mặt bên
( )
SCD
bằng
3
6
a
. Tính khoảng cách từ tâm
O
của đáy đến
mặt bên
( )
SCD
và thể tích của khối chóp
.
A.
( )
( )
,
3
2
O SCD
a
d =
và
3
.
3
6
S ABCD
a
V =
. B.
( )
( )
,
3
4
O SCD
a
d =
và
3
.
3
6
S ABCD
a
V =
.
C.
(
)
(
)
,
3
4
O SCD
a
d
=
và
3
.
3
2
S ABCD
a
V =
. D.
( )
(
)
,
3
2
O SCD
a
d =
và
3
.
3
2
S ABCD
a
V =
.
https://toanmath.com/
THỂ TÍCH KHỐI CHÓP ĐỀU
B. LỜI GIẢI CHI TIẾT
Câu 1. Cho khối tứ diện đều
ABCD
cạnh bằng
a
,
M
là trung điểm
BC
. Thể tích
V
của khối chóp
.M ABC
bằng bao nhiêu?
A.
3
3
24
a
V =
. B.
3
2
a
V =
. C.
3
2
12
a
V =
. D.
3
2
24
a
V
=
.
Hướng dẫn giải
Chọn D
Ta có
33
.
1 12 2
.
2 2 12 24
M ABC ABCD
aa
VV= = =
.
Câu 2. Cho hình chóp đều
có cạnh đáy bằng
a
và cạnh bên tạo với đáy một góc
60°
. Thể tích
của hình chóp đều đó là:
A.
3
6
6
a
. B.
3
3
6
a
. C.
3
3
2
a
. D.
3
6
2
a
.
Hướng dẫn giải
Chọn A
Gọi
( )
O AC BD SO ABCD=∩⇒⊥
60 tan60 3 . 3
2
SO a
SCO SO OC
OC
⇒ = °⇒ °= ⇒ = =
3
2
13 6
.
32 6
a
V aa⇒= =
.
Câu 3. Thể tích hình tứ diện đều có cạnh bằng
a
là:
A.
3
2
3
a
. B.
3
2
12
a
. C.
3
2
6
a
. D.
3
52
12
a
.
Hướng dẫn giải
Chọn B
https://toanmath.com/
Gọi
I
là trung điểm
,'BA A
là trọng tâm
ABC∆
.
Ta có
32
,BA'
23
3
aa
BI BI= = =
,.
diện tích tam giác
BCD
là
2
13
.
24
a
S CD AI= =
.
Trong tam giác
'ABA
vuông tại
'A
ta có:
2
2 22
2
''
3
3
aa
A A AB A B a= − = −=
Thể tích tứ diện là:
23
1 1 32 2
.' . .
3 3 4 12
3
x ABC
aa a
V S AA
∆
= = =
.
Câu 4.Cho khối chóp tứ giác đều có cạnh đáy bằng
a
, cạnh bên gấp hai lần cạnh đáy. Tính thể tích
V
của
khối chóp tứ giác đã cho.
A.
3
2
2
a
. B.
3
2
6
a
. C.
3
14
6
a
. D.
3
14
2
a
.
Hướng dẫn giải
Chọn C
Ta có
2AC a=
2
2
a
AO⇒=
22
SO SA OA⇒= −
14
2
a
=
.
Vậy
.
1
.
3
S ABCD ABCD
V SO S=
33
1 14 14
..
32 6
aa= =
.
Câu 5. Cho hình chóp tứ giác đều có cạnh đáy bằng
a
và cạnh bên bằng
3a
. Tính thể tích
V
của khối
chóp đó theo
a
.
A.
3
3
3
a
V =
. B.
3
2
a
V
=
. C.
3
2
3
a
V =
. D.
3
10
6
a
V =
.
Hướng dẫn giải
Chọn D
O
D
C
B
A
S
https://toanmath.com/
Gọi
h
là chiều cao hình chóp, ta có
2
2
10
3
22
aa
ha= −=
.
1
.
3
ABCD
VSh=
3
2
1 10 10
.
32 6
aa
a= =
.
Câu 6. Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, đường cao của một mặt bên là
3a
. Thể
tích
V
của khối chóp đó là:
A.
3
2
6
=
Va
. B.
3
2
9
=Va
. C.
3
22
3
=Va
. D.
3
42
3
=Va
.
Hướng dẫn giải
Chọn D
Ta có
3=
SM a
.
SCD∆
đều nên
2
SC CD a
= =
.
Suy ra:
22
2
22
AC a
SO a= = =
.
Vậy
3
2
1 1 42
. 2.4 .
33 3
= = =
ABCD
a
V SO S a a
Câu 7. Cho tứ diện đều
ABCD
cạnh bằng
2a
. Tính thể tích của khối tứ diện đó.
A.
3
2
12
a
V =
. B.
3
3
6
a
V =
.
C.
3
3
a
V =
.
D.
3
2
6
a
V =
.
Hướng dẫn giải:
Chọn C
.
D
A
B
C
S
https://toanmath.com/
Ta có
22
33
42
ABC
AB a
S = =
;
22
.
33
23
3
6
2
a
a
AH m
a
= = =
.
22
23
3
a
SH SA AH⇒= − =
.
3
1
.
33
ABC
a
V SH S⇒= =
.
Câu 8. Cho hình chóp đều
có cạnh đáy bằng
2a
, khoảng cách giữa hai đường thẳng
SA
và
CD
bằng
3a
. Thể tích khối chóp đều
.S ABCD
bằng?
A.
3
43a
. B.
3
3a
. C.
3
43
3
a
. D.
3
3
3
a
.
Hướng dẫn giải
Chọn C
Gọi
O AC BD= ∩
, hình chóp đều
.S ABCD
( )
SO ABCD⇒⊥
và tứ giác
ABCD
là hình vuông.
Ta có
//CD AB
( )
//CD SAB⇒
( )
;d CD SA⇒
( )
( )
;d C SAB=
( )
( )
2;d O SAB=
.
Bài ra
( )
;3d CD SA a=
(
)
( )
3
;
2
a
d O SAB
⇒=
.
Tứ diện vuông
.O SAB
2 222
11 1 1
h OS OA OB
⇒= + +
với
( )
( )
3
;
2
a
h d O SAB= =
.
Cạnh
2
2
AB
OA OB a
= = =
2 222
4 111
3 22a SO a a
⇒= ++
3SO a⇒=
.
Do đó
.
1
.
3
S ABCD ABCD
V SO S=
3
2
1 43
3.4
33
a
aa= =
.
Câu 9. Cho khối chóp đều
.S ABC
có cạnh bên bằng
a
và các mặt bên hợp với đáy một góc
45°
. Tính thể
tích của khối chóp
.S ABC
theo
.a
.
A.
3
15
25
a
. B.
3
5
25
a
. C.
3
3
a
. D.
3
15
5
a
.
Hướng dẫn giải
Chọn A
O
S
A
B
C
D
https://toanmath.com/
.
Gọi
O
là trọng tâm tam giác
( )
ABC SO ABC⇒⊥
.
I
là trung điểm của
( )
(
)
( )
, 45 .
BC SBC ABC SIO⇒==°
.
x
là độ dài cạnh của tam giác
ABC
(
0x >
).
Ta có:
2
22 2
13
;.
36 4
xx
OI AI SI SC IC a= = = −=−
.
Trong tam giác
SOI
có:
2
2 22
3 2 2 15
cos45 5 12 .
62 4 5
xx a
OI SI a x a x= °⇒ = − ⇔ = ⇒ =
.
Suy ra:
5
,
5
SO OI a= =
2
2
3 33
.
45
ABC
x
Sa
∆
= =
.
Vậy:
3
2
.
1 3 3 5 15
.. .
3 5 5 25
S ABC
a
V aa= =
.
Câu 10. Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, đường cao của một mặt bên là
3a
. Tính
thể tích
V
của khối chóp đó.
A.
3
2
9
a
V =
. B.
3
42Va=
. C.
3
42
3
a
V =
. D.
3
2
6
a
V =
.
Hướng dẫn giải
Chọn C
Gọi cạnh của hình chóp tứ giác đều là
x
.
Xét tam giác vuông
SCH
ta có
222
SC HC SH−=
2
22
3
4
x
xa⇔−=
2xa⇔=
.
Chiều cao
2 2 22
32SO SH HO a a a= − = −=
.
https://toanmath.com/
Thể tích khối chóp là
3
2
1 42
. 2.4
33
a
Vaa
= =
.
Câu 11. Cho hình chóp tam giác đều cạnh đáy bằng
a
và các mặt bên đều tạo với mặt phẳng đáy một góc
60 .°
Tính thể tích
V
của khối chóp.
A.
3
3
4
a
V =
. B.
3
3
24
a
V =
. C.
3
2
6
a
V =
. D.
3
3
8
a
V
=
.
Hướng dẫn giải
Chọn B
.
Gọi
M
là trung điểm của
BC
,
G
là trọng tâm
ABC∆
.
22
33
.
44
ABC
AB a
S
∆
= =
.
133
32 6
AB a
GM = =
.
Ta có: góc giữa mặt đáy và mặt bên bằng
60°
suy ra
60 .SMG = °
Xét tam giác vuông
SGM
:
tan .
SG
SMG
GM
=
.
Suy ra:
3
.tan60 . 3 .
62
aa
SG GM= °= =
.
Vậy
23
.
1 1 33
. ..
3 3 2 4 24
S ABC ABC
aa a
V SG S
∆
= = =
.
Câu 12. Cho hình chóp tứ giác đều có cạnh đáy bằng
a
, cạnh bên bằng
2a
(hình vẽ). Thể tích khối chóp
là
A.
3
3
6
a
. B.
3
22
3
a
. C.
3
6
3
a
. D.
3
6
6
a
.
Hướng dẫn giải
Chọn D
M
G
B
A
C
S
https://toanmath.com/
Xét hình chóp tứ giác đều
.S ABCD
.
Ta có:
2
2
a
OD =
,
2
22 2
6
2
22
aa
SO SD OD a= − = −=
.
3
2
.
1 16 6
.. . .
3 32 6
S ABCD ABCD
aa
V SO S a= = =
.
Câu 13. [Sở GDĐT Lâm Đồng lần 07 - 2017] Cho
( )
H
là khối chóp tứ giác đều có tất cả các cạnh
bằng
2a
. Thể tích của
( )
H
bằng:
A.
3
4
5
a
. B.
3
43
3
a
. C.
3
42
3
a
. D.
3
4
3
a
.
Hướng dẫn giải
Chọn C
ABCD
hình vuông cạnh 2a
2
2
a
22 2
.–
AO SO SA AO
=>= = ==>
2SO a=
.
23
1 42
(2 ) . 2
33
V aa a= =
.
Câu 14. Một hình chóp tam giác đều có cạnh bên bằng
b
và cạnh bên tạo với mặt phẳng đáy một góc
α
.
Thể tích của hình chóp đó là
A.
3
3
cos sin
4
b
αα
. B.
32
3
sin cos
4
b
αα
.
C.
32
3
cos sin
4
b
αα
. D.
32
3
cos sin
4
b
αα
.
Hướng dẫn giải
Chọn D
Gọi
M
là trung điểm
BC
,
H
là tâm tam giác
ABC
.
Ta có:
( )
SH ABC⊥
.
Xét tam giác
SHA∆
vuông tại
H
, ta có:
sin sin
cos cos
SH SA b
AH SA b
αα
αα
= =
= =
https://toanmath.com/
33
cos
22
AM AH b
α
⇒= =
.
Mà:
32
3 cos
2
3
AB AM
AM AB
α
= ⇔= =
.
( )
2
32
3 3 cos
11
. . . sin .
33 4
3
cos sin
4
SABC ABC
b
V SH S b
b
α
α
αα
= =
=
.
Câu 15.Cho hình chóp tứ giác đều
có thể tích
2
6
V
=
. Gọi
M
là trung điểm của cạnh
SD
. Nếu
thì khoảng cách từ
B
đến mặt phẳng
( )
MAC
bằng:
A.
3
4
. B.
1
2
. C.
2
3
. D.
1
2
.
Hướng dẫn giải
Chọn D
Giả sử hình chóp có đáy
ABCD
là hình vuông cạnh
a
. Khi đó,
2BD a=
.
Tam giác
SBD
vuông cân tại
S
nên
SD SB a= =
và
2
22
BD a
SO = =
.
Suy ra các tam giác
,SCD SAD
là các tam giác đều cạnh
a
và
( )
SD MAC⊥
tại
M
.
Thể tích khối chóp là
3
12
..
36
ABCD
a
V SO S= =
Mà
3
22
1
66
a
a= ⇒=
Vì
O
là trung điểm
BD
nên
( )
( )
( )
(
)
1
,,
2
d B MAC d D MAC DM= = =
.
Câu 16. Khối chóp tam giác đều có tất cả các cạnh bằng
a
có thể tích bằng:
A.
3
3
12
a
. B.
3
3
4
a
. C.
3
2
6
a
. D.
3
3
a
.
Hướng dẫn giải
Chọn A
Chiều cao của khối chóp là
2
2
23 6
.
32 3
aa
ha

=−=


mà
2
3
4
day
a
S =
.
O
M
A
S
D
C
B
https://toanmath.com/
Do đó thể tích khối chóp là
3
13
.
3 12
day
a
hS =
.
Câu 17. Khi chiều cao của một hình chóp đều tăng lên
n
lần nhưng mỗi cạnh đáy giảm đi
n
lần thì thể tích
của nó.
A. Không thay đổi. B. Tăng lên
n
lần.
C. Tăng lên
1n −
lần. D. Giảm đi
n
lần.
Hướng dẫn giải
Chọn D
Ta có:
1
..
3
V hS=
, với
h
là chiều cao,
S
là diện tích đáy
2
0
180
4tan
xa
S
a
=




với
x
là độ dài cạnh của đa giác đều,
a
là số đỉnh của đa giác đều.
Ycbt
2
1
0
1 11 1
. . . .. .
33
180
4tan
x
a
n
V nh h S V
nn
a



⇔= = =




.
Câu 18. Tính thể tích khối chóp tứ giác đều có tất cả các cạnh bằng
a
.
A.
3
23
3
a
. B.
3
2
6
a
. C.
3
3
4
a
. D.
3
3
2
a
.
Hướng dẫn giải
Chọn B
Giả sử cho hình chóp tứ giác đều
.S ABCD
có tất cả các cạnh bằng
a
.
Diện tích đáy
ABCD
:
2
ABCD
Sa=
.
11 2
2
22 2
a
AO AC AB= = =
;
2
222
22
22
aa
SO SA AO a

= −=− =



Vậy thể tích khối chóp tứ giác đều là:
3
2
1 122
. ..
3 32 6
ABCD
aa
V S SO a= = =
.
Câu 19. Cho khối chóp đều
.S ABC
có cạnh đáy bằng
a
, tính thể tích khối chóp
.S ABC
biết cạnh bên
bằng
a
là:
A.
3
.
4
S ABC
a
V =
. B.
3
.
2
12
S ABC
a
V =
. C.
3
.
3
6
S ABC
a
V
=
. D.
3
.
12
S ABC
a
V =
.
Hướng dẫn giải
Chọn B
O
C
A
B
D
S
https://toanmath.com/
Gọi H là trọng tâm
ABC∆
đều
( )
SH ABC → ⊥
.
23
33
a
AH AM= =
(M là trung điểm BC)
SAH∆
vuông tại H có
22
6
3
a
SH SA AH=−=
.
ABC∆
đều cạnh a nên
2
3
4
ABC
a
S =
.
Vậy
23
1 1 36 2
. ..
3 3 4 3 12
ABC
aa a
V S SH= = =
.
Câu 20. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
, cạnh bên hợp với đáy một góc
60
. Thể
tích
V
của khối chóp
.S ABCD
bằng
17T A. 17T
3
3
2
a
V =
17T.17T B.
3
3
3
a
V =
.17T C. 17T
3
6
6
a
V =
17T.17T D.
3
6
3
a
V =
.
Hướng dẫn giải
17TChọn C
Gọi
O AC BD= ∩
thì
(
)
SO ABCD⊥
.
Ta có góc giữa cạnh bên và mặt đáy là góc
60SDO =
.
Mà
ABCD
là hình vuông nên
22BD AB a= =
.
Tam giác
SBD
đều nên
36
.
22
a
SO BD= =
.
https://toanmath.com/
Vậy
3
2
.
1 16 6
.. . .
3 32 6
S ABCD ABCD
aa
V SO S a= = =
.
Câu 21. Cho hình chóp tam giác đều cạnh đáy bằng
a
và các mặt bên đều tạo với mặt phẳng đáy một góc
0
60 .
Tính thể tích
V
của khối chóp.
A.
3
3
24
a
V
. B.
3
3
4
a
V
. C.
3
2
6
a
V
. D.
3
3
8
a
V
.
Hướng dẫn giải
Chọn A
Gọi hình chóp tam giác đó là
.,S ABC
kẻ
( )
SH ABC⊥
tại
.
H
.
Gọi
', ', 'A B C
lần lượt là chân đường cao hạ từ
H
xuống BC, CA, AB.
.
Xét
', ', 'SHA SHB SHC∆∆∆
đều vuông tại
H
có
SH
chung.
0
' ' ' 60 ' ' 'SB H SC H SA H HSC HSA HSB= = =⇒==
.
( )
' ' ' ' ' '.SHA SHB SHC g g g HA HB HC⇒∆ =∆ =∆ − − ⇒ = =
.
Do đó
H
là tâm đường tròn nội tiếp tam giác
.ABC
.
Tam giác
ABC
đều cạnh
2
3
.'
42
ABC
AB BC CA
a S a HA
++
⇒= =
.
2
33 3
''.
42 6
a
a HA HA a⇒ = ⇒=
.
Tam giác
'SHA
vuông tại
H
và
0
' 60 '.tan60 .
2
a
HA S SH HA=⇒= =
.
Thể tích
23
1 13 3
. .. .
3 3 2 4 24
ABC
a
V SH S a a= = =
.
Câu 22. Thể tích của khối chóp tứ giác đều có chiều cao bằng
6
3
a
và cạnh đáy bằng
3a
bằng:
A.
3
32
2
a
. B.
3
32
4
a
. C.
3
6
3
a
. D.
3
36
2
a
.
Hướng dẫn giải
Chọn C
https://toanmath.com/
Ta có :
1
.
3
ABCD
V S SO
=
( )
2
16
. 3.
33
a
a=
3
6
3
a
=
.
Câu 23. Cho hình chóp tứ giác đều
có cạnh đáy bằng
a
. Gọi điểm
O
là giao điểm của
AC
và
BD
. Biết khoảng cách từ
O
đến
SC
bằng
6
a
. Tính thể tích khối chóp
.S ABC
.
A.
3
6
a
. B.
3
4
a
. C.
3
8
a
. D.
3
12
a
.
Hướng dẫn giải
Chọn C
H
là hình chiếu của
O
lên
SC
nên
6
a
OH =
,
ABCD
là hình vuông có
12
22
a
OC AC
= =
SOC∆
vuông tại
O
có
OH
là đường cao
222
1 11
2
a
SO
OH SO OC
→ = + → =
.
3
.
1 11
...
3 3 2 12
S ABCD ABC ABCD
a
V S SO S SO → = = =
.
Câu 24. Cho hình chóp tam giác đều
.
S ABC
có độ dài cạnh đáy bằng
a
, góc hợp bởi cạnh bên và mặt đáy
bằng
60°
. Thể tích của hình chóp đã cho.
A.
3
3
4
a
. B.
3
3
6
a
. C.
3
3
3
a
. D.
3
3
12
a
.
Hướng dẫn giải
Chọn D
https://toanmath.com/
Gọi
M
là trung điểm của cạnh
BC
,
O
là tâm của tam giác đều
ABC
.
Hình chóp tam giác đều
.S ABC
có góc giữa cạnh bên bên và mặt đáy bằng
60°
, nên
60SAM = °
.
Ta có:
3
2
a
AM
=
3
3
a
AO⇒=
.
Diện tích tam giác
ABC
:
2
3
4
ABC
a
S
=
.
Xét tam giác
SAO
vuông tại
O
có:
.tan 60SO AO= °
3
.3
3
a
a= =
.
Thể tích khối chóp tam giác đều
.S ABC
:
2
13
..
34
a
Va
= =
3
3
12
a
.
Câu 25. Cho hình chóp đều
.S ABCD
có
2AC a=
, mặt bên
( )
SBC
tạo với đáy
( )
ABCD
một góc
45°
.
Tính thể tích
V
của khối chóp
.
A.
3
2
a
V =
. B.
3
2
3
a
V =
. C.
3
23
3
a
V =
. D.
3
2Va=
.
Hướng dẫn giải
Chọn B
Gọi
M
là trung điểm của
BC OM BC → ⊥
mà
BC SO⊥
nên
( )
BC SOM⊥
BC SM → ⊥
.
( ) ( )
BC SBC ABCD=∩→
Góc
( ) ( )
, 45SBC ABCD SMO = = °

Do hình chóp đều nên đáy ABCD là hình vuông có
2
2
AC
AD a= =
SOM∆
vuông tại O có
45SMO = °
nên
12
22
a
SO OM AD= = =
.
Vậy
( )
3
2
.
1 1 22
. 2.
3 3 23
S ABCD ABCD
aa
V S SO a= = =
.
60
°
a
O
M
A
C
B
S
https://toanmath.com/
Câu 26. Khối chóp tam giác đều có cạnh đáy bằng a và cạnh bên bằng
3a
có thể tích bằng:
A.
3
2
6
aV =
. B.
3
6
6
a
V =
. C.
3
6
2
aV =
. D.
3
3
1
aV
=
.
Hướng dẫn giải:
Chọn C
.
ABC
đều cạnh
a AM=>=
2
3a
3
3a
.
2 2 22
–3
SO SA AO a= = −
2
3
a
=
3
8
2
a
.
12 2 1 3
.. .
3 22
3
a
V aa=
3
2
6
Va⇔=
.
Câu 27. Cho khối chóp tứ giác đều có cạnh đáy bằng
a
, cạnh bên bằng
2
a
. Tính thể tích
V
của khối chóp
đã cho.
A.
3
2
2
a
V =
. B.
3
14
2
a
V =
. C.
3
14
6
a
V
=
. D.
3
2
6
a
V =
.
Hướng dẫn giải
UChọn C
Ta có:
( )
2
2
22
2
2
2
a
SO SB OB a

= −= −



14
2
a
=
.
2
1 1 14
. . ..
3 32
ABCD
a
V S SO a= =
3
14
6
a
=
.
Câu 28. Một hình chóp có đáy là tam giác đều cạnh bằng
2
và có chiều cao bằng
4.
Tính thể tích hình
chóp đó.
O
A
B
D
C
S
https://toanmath.com/
A.
23
. B.
2
. C.
4
. D.
43
3
.
Hướng dẫn giải
Chọn D
Ta có diện tích tam giác đều cạnh
2
là
1
.2.2.sin 60
2
S = °
3=
.
Thể tích của khối chóp là
1
. 3.4
3
V =
43
3
=
.
Câu 29.] Cho hình chóp tứ giác đều có cạnh đáy bằng
x
. Diện tích xung quanh gấp đôi diện tích đáy. Khi
đó thể tích của khối chóp bằng:
A.
3
.3
3
x
. B.
3
.3
2
x
.
C.
3
.3
12
x
. D.
3
.3
6
x
.
Hướng dẫn giải:
Chọn D
.
2
; S 4. 2 .
ABCD xq SCD
S x S SI x= = =
.
Theo yêu cầu bài toán.
2
2.SI x x SI x=⇔=
.
2
22 2
3
42
x
SO SI OI x x= − = −=
.
3
2
1 1 3 .3
. ..
3 32 6
SABCD ABCD
x
V SO S x x= = =
.
Câu 30. Cho hình chóp tam giác đều
.S ABC
có cạnh đáy bằng
3a
. Gọi
,MN
lần lượt là trung điểm
của
,SB BC
Tính thể tích khối chóp
.A BCNM
. Biết mặt phẳng
( )
AMN
vuông góc với mặt
phẳng
( )
SBC
.
A.
3
3 15
48
a
. B.
3
15
32
a
. C.
3
3 15
32
a
. D.
3
3 15
16
a
.
Hướng dẫn giải
Chọn C
O
A
D
B
C
S
I
https://toanmath.com/
E
là trung điểm
BC
nên
,CB AE CB SH⊥⊥
( )
CB SAE CB SE → ⊥ → ⊥
.
SE vừa là trung tuyến vừa là đường cao nên
SBC∆
cân tại
S
F
là giao điểm của
MN
với
SE
1
,
2
SF MN SF SE → ⊥ =
.
Giả thiết
( ) ( )
( ) ( )
( )
SF MN
AMN SBC
SF AMN
AMN SBC MN
⊥
⊥
→ ⊥
∩=
SE AF→⊥
và
1
2
SF SE=
nên
SAE∆
cân tại
3
2
a
A AE AS→==
22
2 23 5
.
3 32 2
aa
AH AE a SH SA AH= = = → = − =
( )
3
2
.
1 1 3 5 15
. .3 .
3 3 42 8
S ABC ABC
aa
V S SH a= = =
.
3
.
.
.
1 15
.
4 32
S AMN
S AMN
S ABC
V
SM SN a
V
V SB SC
= = → =
.
Vậy
3
..
3 15
32
S ABC S AMN
a
VV V=−=
.
Câu 31. Người ta gọt một khối lập phương gỗ để lấy khối tám mặt đều nội tiếp nó (tức là khối có các đỉnh
là các tâm của các mặt khối lập phương). Biết các cạnh của khối lập phương bằng
a
. Hãy tính
thể tích của khối tám mặt đều đó:
A.
3
8
a
. B.
3
6
a
. C.
3
4
a
. D.
3
12
a
.
Hướng dẫn giải
Chọn B
Dựng được hình như hình bên.
https://toanmath.com/
.
+ Thấy được thể tích khối cần tính bằng
2
lần thể tích của hình chóp
.
S ABCD
.
+ Nhiệm vụ bây giờ đi tìm thể tích của
.
+
ABCD
là hình vuông có tâm
O
đồng thời chính là hình chiếu của
S
lên mặt đáy.
2
a
SO =
;
BD a
=
(cạnh của hình lập phương). Suy ra các cạnh của hình vuông
2
2
ABCD a
=
.
.
1
3
S ABCD
V Sh
=
3
11 2 2
32 2 2
a

=⋅⋅



3
12
a
=
.
đa di
ên .
2.
khôi S ABCD
VV=
3
6
a
=
.
Câu 32. Cho
( )
H
là khối chóp tứ giác đều có tất cả các cạnh bằng
a
. Thể tích của
( )
H
bằng.
A.
3
3
2
a
. B.
3
2
6
a
. C.
3
3
a
. D.
3
3
4
a
.
Hướng dẫn giải:
Chọn B
.
Tính diện tích
ABCD
:
2
ABCD
Sa=
.
Xác định chiều cao:
Gọi
DO AC B SO=∩⇒
là chiều cao của khối chóp.
SOA∆
vuông tại O cho ta
2
222
1
22
a
SO SA AO a a= − = −=
.
Vậy:
3
2
1 12 2
. ..
3 32 6
SABCD ABCD
aa
V S SO a= = =
.
Câu 33. Một hình chóp tứ giác đều có đáy là hình vuông cạnh
a
, các mặt bên tạo với đáy một góc
α
. Thể
tích khối chóp đó là
O
D
A
C
B
S
a
https://toanmath.com/
A.
3
tan
6
a
α
. B.
3
tan
2
a
α
. C.
3
cot
6
a
α
. D.
3
sin
2
a
α
.
Hướng dẫn giải
Chọn A
Gọi
h
là đường cao của hình chóp ta có
tan
2
a
h
α
=
,
Vậy
3
1
. tan
36
day
a
V hS
α
= =
.
42TCâu 34.Cho khối chóp đều 42T
42T có đáy 42T
ABCD
42T là hình vuông cạnh 42T
a
42T, 42T
3SA a=
42T. Tính thể tích 42T
V
42T của
khối chóp 42T
.S ABCD
42T theo 42T
a
42T.
A.
3
26
9
Va=
. B.
3
10
6
Va=
. C.
3
2
3
Va
=
. D.
3
11
6
Va
=
.
Hướng dẫn giải
Chọn B
Gọi
O
là tâm hình vuông
ABCD
( )
SO ABCD⇒⊥
42T.
2
22 2
10
3
22
aa
SO SA OA a= − = −=
42T.
Thể tích của khối chóp
.S ABCD
42T là 42T
1
..
3
ABCD
V SO S=
23
1 10 10
..
32 6
a
aa= =
.
Câu 35. Thể tích của chóp tam giác đều có tất cả các cạnh đều bằng
a
là
A.
3
2
4
a
. B.
3
2
2
a
. C.
3
2
6
a
. D.
3
2
12
a
.
Hướng dẫn giải
Chọn D
UCách 1: Theo tự luận
https://toanmath.com/
Gọi
O
là tâm mặt đáy
( )
ABC
và
I
là trung điểm cạnh
BC
.
.
S ABC
là hình chóp tam giác đều nên
( )
SO ABC⊥
.
SAO∆
vuông tại
O
có:
2 23 3
.
3 32 3
aa
AO AI= = =
22
SO SA AO⇒= −
2
3
a
=
.
2
3
4
ABC
a
S =
.
Vậy thể tích khối chóp cần tìm là:
.
1
.
3
S ABC ABC
V SO S
=
2
12 3
..
34
3
aa
=
3
2
12
a
=
.
UCách 2: Tính bằng công thức tính nhanh.
Hình chóp tam giác đều có tất cả các cạnh đều bằng
a
là hình tứ diện đều cạnh
a
.
3
2
12
a
V⇒=
.
Câu 36. Cho hình chóp tứ giác đều có cạnh đáy bằng cạnh bên bằng
2a
. Tính thể tích khối chóp đã cho.
A.
3
2
4
a
. B.
3
42
3
a
. C.
3
3
12
a
. D.
3
2
6
a
.
Hướng dẫn giải
Chọn B
Gọi khối chóp đó là S.ABCD có tâm O. Vẽ hình nhanh ta thấy
2
2
AC
OA a
= =
.
3
22 2
.
1 1 42
2 . .4 . 2
34 3
S ABCD ABCD
a
SO SA OA a V S SO a a= − = → = = =
.
Câu 37. Cho hình chóp đều
.S ABC
có
1=SA
. Gọi
,DE
lần lượt là trung điểm của hai cạnh
,SA SC
. Tính
thể tích khối chóp
.S ABC
, biết đường thẳng
BD
vuông góc với đường thẳng
AE
.
A.
.
2
12
=
S ABC
V
B.
.
21
54
=
S ABC
V
C.
.
12
4
=
S ABC
V
D.
.
21
18
=
S ABC
V
Hướng dẫn giải
I
O
C
B
A
S
https://toanmath.com/
Chọn B
Giả sử cạnh đáy có độ dài
a
;
SH h=
. Chọn hệ trục tọa độ như hình vẽ, ta có:
;
;0;0
2
a
A

−


;
;0;0
2
a
B



;
3
0; ;0
2
a
C




;
3
0; ;
6
a
Sh




;
3
;;
4 12 2
aa h
D

−



;
3
0; ;
32
ah
E




.
Lại có
BD AE⊥
6
.0
7
BD AE a h⇔ =⇒=
 
2
36
.
37
a−
=
27
33
ah⇒= ⇒=
.
Vậy
.
2
.3
1 7 21
3
..
3 3 4 54
S ABCD
V = =
.
Câu 38. Tính thể tích khối tứ diện đều có cạnh
a
.
A.
3
a
. B.
3
3
4
a
. C.
3
2
12
a
. D.
3
3
12
a
.
Hướng dẫn giải
Chọn C
17TTa có:
2
222
36
33
aa
SG SA AG a

= −=− =



.
17TVậy:
23
1 16 3 2
. ..
3 3 3 4 12
SABC ABC
aa a
V SG S
∆
= = =
.
17TÁp dụng công thức tính nhanh 17Tthể tích khối tứ diện đều có cạnh
a
bằng:
3
2
12
a
.
https://toanmath.com/
Câu 39. Trong tất cả các khối chóp tứ giác đều ngoại tiếp mặt cầu bán kính bằng
a
, thể tích
V
của khối
chóp có thể tích nhỏ nhất.
A.
3
32
3
=
a
V
. B.
3
10
3
=
a
V
. C.
3
2=Va
. D.
3
8
3
=
a
V
.
Hướng dẫn giải
Chọn A
Giả sử
=
SO x
ta có:
= −
SI x a
;
( )
2
22
2= − −= −SE x a a x ax
Xét
∆∆SEI SON∽
ta có:
=
SE IE
SO NO
2
.
2
⇒= =
−
IE SO ax
NO
SE
x ax
Thể tích khối chóp là:
( )
2
22
2
12 4
.
3 32
2

= =

−
−

ax a x
Vx
xa
x ax
Xét hàm số
(
)
2
2
=
−
x
fx
xa
( )
02<<ax
( )
( )
2
2
4
2
−
′
=
−
x ax
fx
xa
;
( )
0
′
=fx
4⇔=xa
(do
02
<<ax
)
Bảng biến thiên
Vậy giá trị nhỏ nhất của thể tích là:
3
32
3
=
a
V
.
Câu 40. Cho hình chóp tam giác đều có cạnh đáy bằng
a
, góc giữa cạnh bên và mặt đáy bằng
o
60
. Thể
tích khối chóp
.S ABC
là:
A.
3
3
12
a
. B.
3
6
12
a
. C.
3
8
a
. D.
3
3
8
a
.
Hướng dẫn giải
Chọn A
https://toanmath.com/
.
Gọi
O
trọng tâm tam giác
E
, khi đó
( )
SO ABC⊥
.
Ta có:
3
3
a
AO SO a= ⇒=
.
Suy ra:
23
1 133
. . ..
3 3 4 12
ABC
aa
V SO S a
∆
= = =
.
Câu 41. Cho hình chóp tam giác đều
.S ABC
có
=AB a
, cạnh bên
6
3
=SA a
. Tính thể tích
V
của khối
chóp
.S ABC
.
A.
3
3
36
=
a
V
. B.
3
4
=
a
V
. C.
3
24
=
a
V
. D.
3
12
=
a
V
.
Hướng dẫn giải
Chọn D
Gọi
O
là tâm của tam giác đều
ABC
khi đó
23 3
32 3
= =AO a a
.
Vì
SO
là đường cao của khối chóp nên
22
22
6 33
3 33

= −= − =



SO SA AO a a a
.
Diện tích
2
3
4
∆
=
ABC
Sa
, suy ra thể tích
3
2
.
1 33
3 4 3 12
= =
S ABC
a
V aa
.
Câu 42. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
. Gọi
SH
là đường cao của hình chóp.
Khoảng cách từ trung điểm của
SH
đến
( )
SBC
bằng
b
. Thể tích khối chóp
là
https://toanmath.com/
A.
3
22
2
3 16
ab
ab−
. B.
3
22
3 16
ab
ab−
. C.
3
22
2
16
ab
ab−
. D.
2
3
ab
.
Hướng dẫn giải
Chọn A
Hình chóp tứ giác đều
H AC BD= ∩
và tứ giác ABCD là hình vuông. Gọi I là trung điểm của
cạnh SH
( )
( )
( )
( )
,2,2d H SBC d I SBC b
⇒==
Tứ diện vuông
( )
2
22 2
1 111
2
SHBC
HS HB HC
b
⇒ =++
22
22
2 2 2 2 22
22
1 1 1 1 1 4 16
4 44
22
2
16
ab
aa
SH b b a a b
ab
SH
ab
−
⇒ = −−= −=
⇒=
−
3
2
.
22 22
1 12 2
.. .
33
16 3 16
S ABCD ABCD
ab a b
V SH S a
ab ab
⇒= = =
−−
.
Câu 43. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
. Gọi
M
,
N
lần lượt là trung điểm của
SA
và
CD
. Cho biết
MN
tạo với mặt đáy một góc bằng
30°
. Tính thể tích khối chóp
.S ABCD
.
42T A. 42T
3
15
5
a
42T. B. 42T
3
30
18
a
42T. C. 42T
3
15
3
a
42T. D. 42T
3
5
12
a
42T.
Hướng dẫn giải
Chọn B.
Gọi
O AC BD= ∩
, ta có
( )
SO ABCD⊥
.
Gọi
H
là trung điểm
OA
, ta có
//MH SO
( )
MH ABCD⇒⊥
.
Do đó
( )
( )
,
MN ABCD
(
)
,MN NH=
MNH=
30= °
.
Ta có:
22
2
31
44
NH AD CD

= +


2
5
8
a=
10
4
a
NH⇒=
.
a
H
N
M
O
B
C
A
D
S
H
O
N
D
A
B
C
https://toanmath.com/
tan
MH
MNH
NH
=
10
4
MH
a
=
3
3
=
30
12
a
MH
⇒=
.
Mặt khác:
30
2
6
a
SO MH
= =
.
Vậy thể tích khối chóp
là:
1
..
3
ABCD
V S SO=
2
1 30
..
36
a
a=
3
30
18
a
=
.
Câu 44. Cho hình chóp tam giác đều có cạnh đáy bằng
a
và cạnh bên bằng
b
.
Thể tích của khối chóp là
A.
2
22
3
6
a
ba−
. B.
2 22
3
a ba
−
. C.
2
22
3
4
a
ba−
. D.
2
22
3
12
a
ba−
.
Hướng dẫn giải
Chọn D
Gọi
.S ABC
là hình chóp tam giác đều và
G
là trọng tâm tam giác
ABC
. Khi đó
(
)
SG ABC
⊥
và
AB a=
,
SB b=
,
23 3
.
32 3
aa
AG = =
22
22
3
3
ba
SG SA AG
−
⇒= − =
.
Vậy
2 22 2
22
.
1 1 33
. .. 3
3 3 4 3 12
S ABC ABC
a ba a
V SG S b a
∆
−
= = = −
.
Câu 45. Cho hình chóp tứ giác đều có độ dài cạnh bên và cạnh đáy cùng bằng
a
. Khi đó, khoảng cách
h
giữa đường thẳng
AD
và mặt phẳng
( )
SBC
là:
A.
6
3
a
h =
. B.
2
a
h =
. C.
2
2
a
h =
. D.
2a 5
5
h =
.
Hướng dẫn giải:
Chọn A
( )
( )
( )
( )
( )
( )
, , 2,d AD SBC d A SBC d O SBC= =
với
O
là tâm hình vuông
ABCD
.
Gọi
I
là trung điểm
( ) ( ) (
)
BC OI
BC BC SOI SBC SOI
BC SO
⊥
⇒ ⇒⊥ ⇒ ⊥
⊥
.
Ta có
( ) ( )
SBC SOI SI∩=
, kẻ
OH SI⊥
tại
H
( ) ( )
( )
,OH SBC d O SBC OH⇒⊥ ⇒ =
.
.
22
22
,
22 2
AC a a
AO SO SA AO== = −=
.
2 2 22
2
.
.6
22
6
2
44
aa
SO OI a
OH
SO OI a a
= = =
+
+
.
( )
( )
6
,2
3
a
d AD SBC OH= =
.
a
a
O
B
A
D
C
S
I
H
https://toanmath.com/
Câu 46. Cho hình chóp tam giác đều
.S ABC
đỉnh
S
, độ dài cạnh đáy là
a
, cạnh bên bằng
2a
. Gọi
I
là
trung điểm của cạnh
BC
. Tính thể tích
V
của khối chóp
.S ABI
.
A.
3
11
8
a
. B.
3
11
6
a
. C.
3
11
12
a
. D.
3
11
24
a
.
Hướng dẫn giải
Chọn D
Gọi O là hình chiếu của S lên (ABC) ta có:
2
22 2
33
4
33
aa
SO SB BO a
= − = −=
23
1 1 3 33 11
. ..
3 3 8 3 24
ABI
aa a
V S SO
∆
⇒= = =
.
Câu 47. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
góc giữa cạnh bên và mặt phẳng đáy
bằng
60°
. Tính thể tích khối chóp
.S ABCD
.
A.
3
6
a
. B.
3
6
3
a
. C.
3
6
2
a
. D.
3
6
6
a
.
Hướng dẫn giải
Chọn D
Ta có:
60SBO = °
.
.tan60SO OB= °
2
.tan 60
2
a
= °
6
2
a
=
.
2
ABCD
Sa=
Suy ra
1
.
3
SABCD ABCD
V SO S=
2
16
..
32
a
a=
3
6
6
a
=
.
I
A
B
C
S
O
a
60
°
O
D
A
B
C
S
https://toanmath.com/
Câu 48. Xét tứ diện
ABCD
có các cạnh
2AC CD DB BA= = = =
và
AD
,
BC
thay đổi. Giá trị lớn nhất
của thể tích tứ diện
ABCD
bằng
A.
32 3
27
. B.
16 3
27
. C.
32 3
9
. D.
16 3
9
.
Hướng dẫn giải
Chọn A
Gọi
M
,
N
lần lượt là trung điểm
AD
và
BC
.
Theo giả thiết ta có:
ABD
và
ACD
là các tam giác cân có
M
là trung điểm của
AD
nên
BM AD⊥
và
CM AD⊥
( )
AD BMC⇒⊥
. Và có
BM CM=
MBC⇒∆
cân tại.
Trong tam giác
MBC∆
có
MN
vừa là đường cao vừa là trung tuyến nên
2
22
4
BC
MN MB
= −
22
22
44
AD BC
MN AB⇔ =−−
22
4
4
AD BC
MN
+
⇔=−
.
Khi đó diện tích tam giác
MBC
∆
là:
1
.
2
MBC
S MN BC
∆
=
22
1
.4
24
AD BC
BC
+
= −
Thể tích tứ diện
ABCD
là:
1
..
3
ABCD MBC
V AD S
∆
=
22
1
. . .4
34
AD BC
BC AD
+
= −
.
Đặt
AD x=
,
BC y=
ta có:
22
1
... 4
34
ABCD
xy
V xy
+
= −
.
Ta có:
22
2x y xy+≥
22
42
x y xy+
⇔≥
22
42
x y xy+
⇔− ≤−
.
Do đó:
1
... 4
32
ABCD
xy
V xy≤−
( ) ( )
2
2
8
6
ABCD
V xy xy⇔≤ −
. Dấu bằng xảy ra khi
xy
=
.
Ta lại có:
( ) ( )
2
8xy xy−
( )
4...8
22
xy xy
xy= −
3
8
22
4.
3
xy xy
xy

+ +−

≤



3
4.8
27
=
.
Dấu bằng xảy ra khi
8
2
xy
xy= −
16
3
xy⇔=
4
3
xy⇔==
.
Vậy giá trị lớn nhất của thể tích tứ diện
ABCD
là: tập xác định
3
m
2
ax
4.8
6 27
ABCD
V =
32 3
27
=
.
Câu 49. Cho hình chóp tứ giác đều
.
S ABCD
, đáy
ABCD
có diện tích
2
16cm
, diện tích một mặt bên là
2
8 3 cm .
Tính thể tích
V
của khối chóp
.S ABCD
.
N
M
A
B
C
D
https://toanmath.com/
A.
3
32 2
cm .
3
V =
B.
3
32 13
cm .
3
V =
C.
3
32 11
cm .
3
V =
D.
3
32 15
cm .
3
V
=
Hướng dẫn giải
Chọn C
Ta có
22
16cm 4cm 2 2 cm.
ABCD
S AB AB AO= = ⇒= ⇒=
Gọi
M
là trung điểm của
AB
. Khi đó
.SM AB⊥
2
1
. 8 3cm 4 3 cm.
2
SAB
S SM AB SM
= = ⇒=
22
2 13 cm.SA SM AM
= +=
22
2 11cm.SO SA AO= −=
3
1 1 32 11
. .16.2 11 cm .
33 3
ABCD
V S SO= = =
Câu 50. Cho khối chóp tam giác đều. Nếu tăng cạnh đáy lên hai lần và giảm chiều cao đi bốn lần thì thể
tích của khối chóp đó sẽ:
A. Giảm đi hai lần. B. Không thay đổi.
C. Tăng lên hai lần. D. Giảm đi ba lần.
Hướng dẫn giải
Chọn B
Nếu tăng cạnh đáy lên hai lần thì diện tích đáy tăng bốn lần. Vì giảm chiều cao đi bốn lần nên thể
tích khối chóp không thay đổi.
Câu 51. Hình chóp tứ giác đều có tất cả các cạnh bằng
a
. Thể tích khối chóp đó bằng:
A.
3
2
2
a
. B.
3
2
6
a
. C.
3
3
3
a
. D.
3
2
3
a
.
Hướng dẫn giải:
Chọn B
M
O
B
D
C
A
S
https://toanmath.com/
.
Gọi
O
là tâm của hình vuông
ABCD
, khi đó
( )
SO ABCD⊥
.
Ta có:
2
2
a
AO =
.
Suy ra:
22
2
2
a
SO SA AO= −=
.
Khi đó:
3
2
1 12 2
.. . .
3 32 6
ABCD
aa
V SO S a
= = =
.
Câu 52. Khi chiều cao của một hình chóp đều tăng lên
n
lần nhưng mỗi cạnh đáy giảm đi
n
lần thì thể tích
của nó.
A. Không thay đổi. B. Tăng lên
n
lần.
C. Tăng lên
1n −
lần. D. Giảm đi
n
lần.
Hướng dẫn giải
Chọn D
Ta có:
1
..
3
V hS
=
, với
h
là chiều cao,
S
là diện tích đáy
2
0
180
4tan
xa
S
a
=




với
x
là độ dài cạnh của đa giác đều,
a
là số đỉnh của đa giác đều.
Ycbt
2
1
0
1 11 1
. . . .. .
33
180
4tan
x
a
n
V nh h S V
nn
a



⇔= = =




.
Câu 53. Cho hình chóp đều
.S ABCD
có đáy bằng
2a
, khoảng cách giữa hai đường thẳng
SA
và
CD
bằng
3a
. Thể tích khối chóp đều
bằng.
A.
3
3a
. B.
3
43a
. C.
3
3
3
a
. D.
3
43
3
a
.
Hướng dẫn giải
Chọn D
https://toanmath.com/
.
Ta có
( )
// //CD AB CD SAB⇒
.
Suy ra
( ) ( )
( )
( )
( )
( )
( )
; ; ; 2;d CD AB d CD SAB d C SAB d O SAB= = =
( )
( )
3
;
2
a
d O SAB⇒=
.
Gọi I là trung điểm AB
SI AB⇒⊥
(tam giác SAB cân tại S).
Dựng
OH SI⊥
(với
H SI
∈
). Khi đó ta có:
( )
( )
( ) ( )
( )
3
;
2
OH AB AB SOI
a
OH SAB d O SAB OH
OH SI
⊥⊥
⇒⊥ ⇒ ==
⊥
.
Tam giác
SOI
vuông tại
O
ta có:
2 22
22 2
2
3
.a
1 11 .
2
3
3
4
a
OH OI
SO a
OH SO OI
OI OH a
a
= + ⇒= = =
−
−
.
Vậy
3
2
1 43
3.4
33
a
Vaa= =
.
Câu 54. Thể tích khối bát diện đều cạnh
a
là:
A.
3
2
3
a
. B.
3
2
2
a
. C.
3
2
6
a
. D.
3
2a
.
Hướng dẫn giải
Chọn A
O
A
B
C
D
E
F
https://toanmath.com/
Vì hình bát diện
ABCDEF
có các cạnh bằng
2a EF a⇒=
.
Khi đó
23
.
1 22 2
2 2. . . . .
3 32 3
ABCDEF E ABCD ABCD
a
V V EO S a a= = = =
.
Câu 55. Cho hình chóp tứ giác đều
có đáy
ABCD
là hình vuông cạnh bằng
3a
và
2SA SB SC SD a= = = =
. Tính thể tích khối chóp
?
A.
3
2
2
a
. B.
3
3
3
a
. C.
3
6
6
a
. D.
3
2
6
a
.
Hướng dẫn giải
Chọn A
Có:
2
ABCD
S AB=
( )
2
3a
=
2
3a=
. Gọi
O
là tâm của hình vuông
ABCD
.
1
2
BO BD=
1
. 3. 2
2
a=
6
2
a
=
.
Vì
là hình chóp đều nên
(
)
SO ABCD⊥
22
SO SB BO⇒= −
2
2
3
2
2
a
a
= −
2
a
=
.
.
1
..
3
S ABCD ABCD
V SO S=
2
1
. .3
3
2
a
a
=
3
2
2
a
=
(đvtt).
Câu 56. Cho hình chóp tứ giác đều
có chiều cao bằng
h
, góc giữa hai mặt phẳng
( )
SAB
và
bằng
α
. Tính thể tích của khối chóp
.S ABCD
theo
h
và
α
.
A.
3
2
3
8tan
h
α
. B.
3
2
3
4tan
h
α
. C.
3
2
4
3tan
h
α
. D.
3
2
8
3tan
h
α
.
Hướng dẫn giải
Chọn C
Gọi
O
là tâm của đáy. Do
.S ABCD
là hình chóp tứ giác đều nên
( )
SO ABCD⊥
, các cạnh bên
bằng nhau và đáy là hình vuông. Gọi
I
là trung điểm của
AB
, ta có
SI AB⊥
suy ra góc giữa
hai mặt phẳng
( )
SAB
và
( )
ABCD
bằng
SIO
α
=
.
Ta có:
tan tan
SO h
OI
SIO
α
= =
suy ra
2
2
tan
h
AD OI
α
= =
. Vậy thể tích hình chóp
.S ABCD
:
2
3
2
1 12 4
. ..
3 3 tan 3tan
ABCD
hh
V SO S h
αα

= = =


.
https://toanmath.com/
Câu 57. Cho tứ diện đều . Biết khoảng cách từ đến mặt phẳng bằng . Tính thể tích
của tứ diện .
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn A
.
Gọi cạnh của tứ diện đều
ABCD
là
a
.
Gọi
M
là trung điểm cạnh
CD
và
G
là trọng tâm tam giác
BCD
.
Ta có
2
2 2 22 22 2
2 23
6 36 . 3
3 32
AG BG AB BM a a a a


+ = ⇔ + = ⇔ + = ⇒=





.
Khi đó
93
4
BCD
S
∆
=
.
Thể tích của tứ diện
ABCD
là
1 193 93
. . .6
3 34 2
BCD
V S AG
∆
= = =
.
Câu 58. Cho hình chóp đều
có
2AC a=
, mặt bên
( )
SBC
tạo với đáy
( )
ABCD
một góc
45°
.
Tính thể tích
V
của khối chóp
?
A.
3
2
a
V =
. B.
3
2
3
a
V =
. C.
3
2Va=
. D.
3
23
3
a
V =
.
Hướng dẫn giải
ABCD
A
(
)
BCD
6
V
ABCD
93
2
V =
53V =
27 3V =
27 3
2
V =
6
a
M
G
D
C
B
A
https://toanmath.com/
Chọn B
Ta có
ABCD
là hình vuông nên
2AC AB=
2
2
AC
AB a⇒= =
.
Gọi
M
là trung điểm
BC
Ta có góc giữa mặt bên
( )
SBC
và đáy chính là góc giữa
SM
và
MO
hay
45
SMO = °
.
Do đó
SOM∆
vuông cân tại
O
2
22
AB a
SO OM⇒= = =
.
Ngoài ra
22
2
ABCD
S AB a= =
.
Vậy
3
2
1 12 2
. . . .2
3 32 3
ABCD ABCD
aa
V SO S a
= = =
.
Câu 59. Thể tích hình chóp tứ giác đều có tất cả các cạnh đều bằng
a
bằng
A.
3
2
3
a
B.
3
2
2
a
C.
3
6
a
D.
3
2
6
a
Hướng dẫn giải
Chọn D
12
22
AO AC= =
;
22
SO SA AO
= −
2
2
2
a
a= −
2
2
a
=
.
1
..
3
ABCD
V SO S=
2
12
..
32
a
a=
3
2
6
a
=
.
Câu 60. Cho hình chóp đều
.S ABCD
có chiều cao bằng
2a
và độ dài cạnh bên bằng
6a
. Tính thể tích
khối chóp
.S ABCD
.
O
A
D
B
C
S
https://toanmath.com/
A.
3
83
3
a
. B.
3
10 3
3
a
. C.
3
82
3
a
. D.
3
10 2
3
a
.
Hướng dẫn giải.
Chọn C
Ta có
22
2BO SA SO a= −=
. Vậy
, suy ra
22AB a=
.
Vậy
2
1 1 82
..
33 3
= = =
ABCD
a
V S SO AB SO
Câu 61. Tính thể tích khối chóp tứ giác đều có tất cả các cạnh bằng
a
.
A.
3
2
6
a
. B.
3
23
3
a
. C.
3
3
4
a
. D.
3
3
2
a
.
Hướng dẫn giải
Chọn A
Giả sử cho hình chóp tứ giác đều
.S ABCD
có tất cả các cạnh bằng
a
.
Diện tích đáy
ABCD
:
2
ABCD
Sa=
.
11 2
2
22 2
a
AO AC AB= = =
;
2
222
22
22
aa
SO SA AO a

= −=− =



.
Vậy thể tích khối chóp tứ giác đều là:
3
2
1 122
. ..
3 32 6
ABCD
aa
V S SO a= = =
.
.
Câu 62. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng a và mặt bên tạo với đáy một góc 45P
0
P. Thể
tích
V
khối chóp
.S ABCD
là:
A.
3
6
a
V =
. B.
3
9
a
V =
. C.
3
2
a
V =
. D.
3
1
24
Va=
.
Hướng dẫn giải:
O
C
A
B
D
S
https://toanmath.com/
Chọn A
Gọi
H
là hình chiếu vuông góc của
A
trên
( )
,ABCD
M
là trung điểm của
BC
.
3
0
.
45
26
S ABCD
aa
SMH SH HM V
=⇒= =⇒ =
.
Câu 63. Tính thể tích
V
của hình tứ diện đều có đường cao
ha=
.
A.
3
3
12
a
V =
. B.
3
3
6
a
V =
. C.
3
3
8
a
V =
. D.
3
3
4
a
V =
.
Hướng dẫn giải:
Chọn C
.
Gọi
x
là độ dài một cạnh của tứ diện. Ta có chiều cao.
2
2
23 2 3 6
.
32 3 2 2
xa
hx xx h

= − = ⇔= =



.
Suy ra diện tích tam giác đáy là.
22
33 3
48
xa
S = =
. Vậy
23
13 3 3
..
38 8
aa
Va= =
.
Câu 64. Cho hình chóp tứ giác đều
có cạnh đáy bằng
2a
cạnh bên bằng
3a
. Tính thể tích
V
của
khối chóp đã cho?
A.
3
47
Va=
. B.
3
47
9
a
V =
. C.
3
4
3
a
V =
. D.
3
47
3
a
V
=
.
Hướng dẫn giải
Chọn D
Trong mặt phẳng
ABCD
, gọi
O AC BD= ∩
, do hình chóp
.S ABCD
đều nên
( )
SO ABCD⊥
.
Đáy là hình vuông vạnh
2a
2
2
AC
AO a⇒==
Trong tam giác vuông
SAO
có
22
7SO SA AO a= −=
x
x
a
https://toanmath.com/
Thể tích
V
của khối chóp trên là
3
2
1 1 47
. 74
33 3
ABCD
a
V SO S a a= = =
.
Câu 65. Cho khối chóp tứ giác đều có cạnh đáy bằng
a
, cạnh bên bằng
3a
. Tính thể tích
V
của khối chóp
đã cho.
A.
3
34
.
6
a
V
=
B.
3
2
.
6
a
V =
C.
3
2
.
2
a
V =
D.
3
34
.
2
a
V =
Hướng dẫn giải
Chọn A
Gọi
O
là tâm mặt đáy
của hình chóp tứ giác đều
.S ABCD
.
Ta có
( )
SO ABCD⊥
SO⇒
là đường cao của hình chóp.
Tam giác
SAO
vuông tại
O
có
12
22
a
OA AC= =
,
3SA a
=
22
34
2
a
SO SA OA
⇒= − =
.
Khi đó thể tích khối chóp tứ giác đều là
3
1 34
.
36
ABCD
a
V S SO= =
.
Câu 66. Một hình chóp tứ giác đều có đáy là hình vuông cạnh
a
, các mặt bên tạo với đáy một góc
α
.
Thể tích của khối chóp đó là
A.
3
sin
2
a
α
. B.
. C.
3
cot
6
a
α
. D.
3
tan
6
a
α
.
Hướng dẫn giải
Chọn C
Xét hình chóp tứ giác đều S.ABCD, có đáy ABCD là hình vuông tâm O.
Gọi M là trung điểm của AB suy ra
( )
OM AB
AB SMO
SO AB
⊥
⇒⊥
⊥
.
Khi đó
( ) ( )
( )
,,SAB ABCD SM OM SMO
α
= = =
.
S
A
B
C
D
O
https://toanmath.com/
Tam giác SMO vuông tại O, có
.tan
tan
2
SO a
SMO SO
MO
α
= ⇒=
.
Thể tích khối chóp S.ABCD là
3
.
1
. . .tan
36
S ABCD ABCD
a
V SO S
α
= =
.
Câu 67.Tính thể tích của khối bát diện đều có cạnh bằng 2.
A.
82
3
. B.
16
3
. C.
42
3
. D.
16 2
3
.
Hướng dẫn giải
Chọn A
Gọi
ABCDEF
là hình bát diện đều có tâm
H
(như hình vẽ) có cạnh bằng
2
.
Ta có
22
2
22
AC
EH AH= = = =
.
Thể tích của bát diện đều đã cho là
.
2
E ABCD
VV=
1
2. . .
3
ABCD
S EH=
2
1 82
2. .2 . 2
33
= =
.
Câu 68. Cho hình chóp tứ giác đều
có cạnh đáy bằng
a
. Gọi
SH
là chiều cao của hình chóp,
khoảng cách từ trung điểm
I
của
SH
đến mặt bên
( )
SBC
bằng
b
. Tính thể tích
V
của khối
chóp
.S ABCD
.
A.
22
3 16
ab
V
ab
=
−
. B.
3
22
2
3 16
ab
V
ab
=
−
.
C.
22
16
ab
V
ab
=
−
. D.
22
2
16
ab
V
ab
=
−
.
Hướng dẫn giải:
Chọn B
E
A
B
D
F
C
H
https://toanmath.com/
.
Vì
.S ABCD
là hình chóp tứ giác đều suy ra
H
là tâm của hình vuông
ABCD
.
Gọi
M
là trung điểm
BC
,
K
là hình chiếu vuông góc của
H
lên
SM
.
Ta có:
( )
BC SH
BC SHM
BC HM
⊥
⇒⊥
⊥
.
( ) ( )
SBC SHM⇒⊥
, mà
( )
HK SM HK SBC⊥⇒⊥
.
Suy ra
22
HK IJ b
= =
, ta có.
22
22
22
.2
16
HK HM ab
SH
HM HK
ab
= =
−
−
. Vậy
3
22
2
3 16
ab
V
ab
=
−
.
Câu 69. Cho hình chóp đều
.S ABCD
có cạnh đáy bằng
a
, góc giữa cạnh bên và mặt đáy bằng
o
60
. Tính thể
tích của khối chóp
theo
a
.
A.
3
6
2
a
B.
3
6
6
a
C.
3
3
6
a
D.
3
6
12
a
Hướng dẫn giải
Chọn B
Gọi
O
là tâm của mặt đáy
( )
(
)
,SO ABCD⇒
SBO=
60= °
.
Ta có
.3SO BO=
6
2
a
SO⇒=
. Vậy thể tích khối chóp
1
..
3
ABCD
V SO S=
3
6
6
a
=
.
Câu 70. Thể tích của khối tứ diện đều có cạnh bằng
3
.
A.
22
. B.
42
9
. C.
92
4
. D.
2
.
Hướng dẫn giải
Chọn C
Cách 1: Áp dụng công thức tính nhanh thể tích khối tứ diện đều:
3
3 2 92
12 4
V = =
.
H
A
D
C
S
B
M
K
I
J
https://toanmath.com/
Cách 2: Khối tứ diện đều
.S ABC
có đáy là tam giác đều và đường cao
SG
.
2
3 93
44
ABC
AB
S
∆
= =
,
22
23
3 9 3 6.
32
AB
AG SG SA AG= = ⇒ = − = −=
Vậy
.
1 92
..
34
S ABC ABC
V S SG
∆
= =
.
Câu 71. Cho hình chóp tứ giác đều
có đáy hợp với mặt bên một góc
45°
. Bán kính mặt cầu
ngoại tiếp hình chóp
.S ABCD
bằng
2
. Tính thể tích khối chóp
.S ABCD
.
A.
32 2
9
. B.
64 2
27
. C.
64 2
81
. D.
128 2
81
.
Hướng dẫn giải
Chọn C
.
Đặt
AB a=
. Gọi
O
là tâm
ABCD
,
E
là trung điểm
AB
. Khi đó
( )
, 45SAB ABCD SEO= = °
.
Suy ra
2
a
SO OE= =
và
22
3
24 2
aa a
SA = +=
.
Mà
2
2
.
3
3 42
4
2
24 3
2.
2
S ABCD
a
SA a
Ra
a
SO
= = = = ⇒=
.
Nên
.
1 1 2 2 32 64 2
.
3 3 3 9 81
S ABCD ABCD
V SO S= = =
.
Câu 72. Người ta cắt miếng bìa hình tam giác cạnh bằng
10cm
như hình bên và gấp theo các đường kẻ, sau
đó dán các mép lại để được hình tứ diện đều. Tính thể tích của khối tứ diện tạo thành.
E
O
B
C
A
D
S
https://toanmath.com/
A.
3
250 2 .V cm=
B.
3
125 2
.
12
V cm=
C.
3
1000 2
.
3
V cm=
D.
3
250 2
.
12
V cm=
Hướng dẫn giải
Chọn B
Tứ diện đều tạo thành là tứ diện đều
ABCD
có tất cả các cạnh bằng
5cm
.
Diện tích đáy là
2
2
3 25 3
44
a
S cm= =
.
Đường cao
2
2 22
253 56
5
32 3
AH AD DH

= − = −⋅ =



, với
H
là tâm đáy.
Thể tích
1 25 3 5 6 125 2
3 4 3 12
V =⋅ ⋅=
.
Ghi nhớ: Thể tích khối tứ diện đều cạnh
a
là
3
2
12
a
V =
Câu 73. Tính thể tích khối chóp tứ giác đều cạnh đáy bằng
a
, chiều cao bằng
3a
.
A.
3
a
. B.
3
3
4
a
. C.
3
3
a
. D.
3
3
12
a
.
Hướng dẫn giải
Chọn A
Ta có:
23
.
11
. .3 .
33
S ABCD ABCD
V hS aa a= = =
Câu 74. Thể tích của khối bát diện đều cạnh
a
là:
A.
3
3
6
a
. B.
3
2
3
a
. C.
3
2
6
a
. D.
3
3
3
a
.
Hướng dẫn giải
Chọn B
https://toanmath.com/
Khối bát diện đều là khối ghép bởi 2 khối chóp tứ giác S.ABCD đều cạnh a, với O là tâm đáy.
2
3
22 2
.
22 2 2
2. . .
22 3 3
S ABCD ABCD
aa a
SO SA OA a V V S SO

= − = − = → = = =


.
Câu 75. Thể tích của khối tứ diện đều cạnh
a
là
A.
3
6
12
a
. B.
3
3
12
a
. C.
3
2
12
a
. D.
3
2
24
a
.
Hướng dẫn giải
Chọn C
Gọi tứ diện đều cạnh
a
là
ABCD
.
Gọi
G
là trọng tâm của tam giác
ABC
.
Ta có:
( )
AG ABC⊥
.
Xét
ABG
∆
vuông tại
G
, ta có:
22
AG AB BG= −
2
2
23
.
32
a
a

= −



6
3
a
=
.
Thể tích của khối tứ diện đều là:
1
..
3
BCD
V S AG=
2
1 36
..
34 3
aa
=
3
2
12
a
=
.
Câu 76. Cho hình chóp tứ giác đều
có cạnh đáy bằng
a
,diện tích mỗi mặt bên bằng
2
2a
. Thể
tích khối nón có đỉnh là
S
và có đáy là đường tròn ngoại tiếp hình vuông
ABCD
bằng
A.
3
37
4
a
π
. B.
3
7
4
a
π
. C.
3
7
3
a
π
. D.
3
7
6
a
π
.
Hướng dẫn giải
Chọn B
Ta có
2
22
1 63
. 2 4 ; 16
2 42
SCD
aa
S a SI a SI a SO a= = ⇒= = − =
Khối nón có
.3 7 2
;
22
aa
h SO r= = =
23
1 37 7
.
32 2 4
aa a
V
π
π
= =
Câu 77.Cho tứ diện đều
ABCD
có cạnh bằng 3. Gọi
,MN
lần lượt là trung
điểm các cạnh
,.AD BD
Lấy điểm không đổi
P
trên cạnh
AB
(khác
,AB
). Thể tích khối chóp
PMNC
bằng
A.
92
16
B.
83
3
C.
33
D.
27 2
12
Hướng dẫn giải
Chọn A
a
a
B
C
D
A
G
O
I
A
D
B
C
S
https://toanmath.com/
Do
(
)
AB CMN
nên
(
)
( )
( )
( )
(
)
( )
,A,D,d P CMN d CMN d CMN= =
Vậy
1
4
PCMN DPMN MCND ABCD
VVV V= = =
(Do diện tích đáy và chiều cao đều bằng một nửa).
Mặt khác
2
23
2
1 3 2 27 2
.
3 4 12 12
3
ABCD
a aa
Va

= −==


nên
1 27 2 9 2
.
4 12 16
MCND
V = =
Câu 78. Tính thể tích
V
của khối chóp tứ giác đều có chiều cao là
h
và bán kính mặt cầu nội tiếp là
r
( )
20hr>>
.
A.
( )
22
4
2
rh
V
hr
=
+
. B.
(
)
22
4
32
rh
V
hr
=
−
. C.
( )
22
3
42
rh
V
hr
=
−
. D.
( )
22
4
32
rh
V
hr
=
+
.
Hướng dẫn giải
Chọn B
Gọi
I
là giao điểm ba đường phân giác trong tam giác
'SMM∆
. Nên
I
là tâm đường tròn nội
tiếp tam giác
'SMM
∆
. Mặt khác, do
.S ABCD
là hình chóp tứ giác đều nên
I
là tâm mặt cầu nội
tiếp hình chóp.
Xét
SMO∆
có
MI
là đường phân giác ta có:
SM SI
MO IO
=
22
h x hr
xr
+−
⇒=
(với
x MO=
).
2
2
2
hr
x
hr
⇒=
−
2
2
4
2
hr
AB
hr
⇒=
−
Vậy thể tích cần tìm là
( )
22
2
14
.4.
3 32
hr
V hx
hr
= =
−
.
Câu 79. Cho khối tứ diện đều
ABCD
có cạnh bằng
a
. Gọi
', 'BC
lần lượt là trung điểm của các cạnh
AB
và
AC
. Tính thể tích
V
của khối tứ diện
''AB C D
theo
a
.
A.
3
24
a
V =
. B.
3
2
24
a
V =
. C.
3
3
48
a
V =
. D.
3
2
48
a
V =
.
Hướng dẫn giải
Chọn D
N
M
B
D
C
A
P
x
I
M
O
C
B
A
D
S
M’
https://toanmath.com/
Ta có
''
11
.
44
′′
′′
= =⇒=
AB C D
AB C D ABCD
ABCD
V
AB AC
VV
V AB AC
Khối tứ diện đều
ABCD
có cạnh bằng
a
thì
33
''
22
12 48
ABCD AB C D
aa
VV
=⇒=
.
Câu 80. Thể tích khối tứ diện đều có cạnh bằng
2a
là.
A.
3
3
6
a
. B.
3
2
12
a
. C.
3
22a
. D.
3
22
3
a
.
Hướng dẫn giải:
Chọn D
Giả sử khối tứ diện đều là
ABCD
như hình bên.
Tam giác đều
ABC
cạnh
a
có.
2
3
ABC
Sa
.
2 22323
3 32 3
aa
AO AM
.
.
Tam giác
SAO
vuông tại
O
có.
2
22 2
4 26
4
33
aa
SO SA AO a 
.
Thể tích cần tìm.
3
2
12 6 2 2
. .3
33 3
aa
Va
.
Câu 81. Cho hình chóp đều
.S ABC
có đáy cạnh bằng
a
, góc giữa đường thẳng
SA
và mặt phẳng
( )
ABC
bằng
60°
. Gọi
A
′
,
B
′
,
C
′
tương ứng là các điểm đối xứng của
A
,
B
,
C
qua
S
. Thể tích của
khối bát diện có các mặt
,ABC
ABC
′′′
,
A BC
′
,
B CA
′
,
C AB
′
,
AB C
′′
,
BA C
′′
,
CA B
′′
là
A.
3
23
3
a
. B.
3
23a
. C.
3
3
2
a
. D.
3
43
3
a
.
Hướng dẫn giải
Chọn A
https://toanmath.com/
Cách 1: Ta tính thể tích khối chóp
.S ABC
:
Gọi H là tâm tam giác ABC đều cạnh a
3
3
a
CH⇒=
. Góc giữa đường thẳng SA và mặt phẳng
(ABC) bằng
0
60
23
.
1 133
60 .S . . .
3 3 4 12
o
S ABC ABC
aa
SCH SH a V H S a⇒ =⇒=⇒ = = =
3
. ' ' .ACS .
23
2 2.4 8
3
B ACA C B S ABC
a
VV V V= = = =
.
Cách 2: Ta có thể tích khối chóp
.
S ABC
là:
3
.
3
12
S ABC
a
V =
.
Diện tích tam giác
SBC
là:
2
39
12
SBC
a
S
∆
=
.
Khoảng cách từ
A
đến mặt phẳng
(
)
SBC
là:
( )
( )
3
,
13
a
d A SBC =
.
Tứ giác
''BCB C
là hình chữ nhật vì có hai đường chéo bằng nhau và cắt nhau tại trung điểm
mỗi đường.
Có
23 23 39
''
33 3
a aa
SB BB B C= ⇒= ⇒ =
.
Diện tích
''BCB C
là:
2
''
39
3
BCB C
a
S =
.
Thể tích khối 8 mặt cần tìm là:
( )
( )
3
''
1 23
2. , . .
33
BCB C
a
V d A SBC S= =
Cách 3 (Tham khảo Hướng dẫn giải của Ngọc HuyềnLB).
Thể tích khối bát diện đã cho là
' ' ' '. .
1
2 2.4 8 8. .
3
A B C BC A SBC S ABC ABC
V V V V SG S= = = =
.
Ta có:
(
)
( )
0
; 60 .SA ABC SAG= =
Xét
SGA∆
vuông tại
G
:
tan .tan .
SG
SAG SG AG SAG a
AG
= ⇔= =
Vậy
23
1 1 3 23
8. . 8. . . .
3 34 3
ABC
aa
V SG S a= = =
H
B'
A'
C'
C
A
B
S
https://toanmath.com/
Câu 82. Cho hình chóp tam giác đều
.S ABC
, cạnh đáy bằng
a
. Mặt bên tạo với mặt đáy một góc
o
60
.
Tính thể tích
V
của hình chóp
.S ABC
.
A.
3
3
2
a
V =
. B.
3
3
12
a
V =
. C.
3
3
24
a
V =
. D.
3
3
6
a
V =
.
Hướng dẫn giải
Chọn C
.
Gọi các điểm như hình vẽ. Theo đề suy ra
0
60SIA =
.
Ta có
33
2 62
aa a
AI HI SH= ⇒= ⇒ =
.
Vậy
3
3
24
a
V
=
.
Câu 83. Cho khối chóp đều
.S ABC
cạnh đáy bằng
a
, cạnh bên bằng
3a
. Tính thể tích khối chóp đó ?
A.
3
26
12
a
V
=
. B.
3
11
6
a
V =
. C.
3
3
4
a
V =
. D.
3
11
12
a
V
=
.
Hướng dẫn giải
Chọn A
Gọi
G
là trọng tâm của tam giác
ABC
.
1
.
3
ABC
V SG S
∆
=
(do khối chóp
.S ABC
đều).
Ta có
23 3
.
32 3
aa
AG = =
22
26
3
a
SG SA AG⇒= − =
;
2
3
4
ABC
a
S
∆
=
;
H
A
B
C
S
I
a
a
a
3a
3a
3a
H
N
M
A
C
B
S
https://toanmath.com/
Suy ra
23
1 26 3 26
..
3 4 12
3
aa a
V = =
(đvtt).
Câu 84.Cắt một miếng giấy hình vuông như hình bên và xếp thành hình một hình chóp tứ giác đều. Biết
các cạnh hình vuông bằng
20cm
,
( )
OM x cm=
. Tìm
x
để hình chóp đều ấy có thể tích lớn nhất
A.
8x cm
=
. B.
6x cm=
. C.
7x cm=
. D.
9x cm=
.
Hướng dẫn giải
Chọn A
Giả sử được hình chóp tứ giác đều như hình vẽ
Ta có
OM x=
2
x
OH HM⇒= =
10 2
2
x
SH
⇒= −
nên
(
)
22
22
10 2 20 10
22
xx
SO SH OH x

= −= − − = −


. Suy ra cạnh đáy bằng
2x
.
Thể tích
1
..
3
MNPQ
V S SO=
( )
2
1
.2 . 20 10
3
xx= −
2
20
. . 40 4
3
xx= −
, (với
0 10x≤≤
).
Tìm GTLN của
V
ta được
max
90,51V =
khi
8x =
* Cách 1 – tìm GTLN: Áp dụng BĐT Cauchuy cho 4 số không âm, ta có:
4
40 4
404....
4
xxxxx
xxxxx
− ++++

−≤


24
40 4 . 10xx⇔− ≤
24
20 20
. 40 4 .10
33
xx⇔ −≤
. Dấu bằng xảy ra khi
40 4 8xx x− =⇔=
.
* Cách 2 – tìm GTLN: Có thể sử dụng máy tính – phần bảng (mode 7) để tìm GTLN cho nhanh:
x
H
O
N
Q
M
P
S
https://toanmath.com/
Câu 85. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
. Gọi
G
là trọng tâm của tam giác
SAC
và khoảng cách từ
G
đến mặt bên
( )
SCD
bằng
3
6
a
. Tính khoảng cách từ tâm
O
của đáy đến
mặt bên
( )
SCD
và thể tích của khối chóp
.S ABCD
.
A.
( )
( )
,
3
2
O SCD
a
d =
và
3
.
3
6
S ABCD
a
V =
. B.
( )
(
)
,
3
4
O SCD
a
d =
và
3
.
3
6
S ABCD
a
V =
.
C.
( )
( )
,
3
4
O SCD
a
d =
và
3
.
3
2
S ABCD
a
V =
. D.
( )
(
)
,
3
2
O SCD
a
d
=
và
3
.
3
2
S ABCD
a
V =
.
Hướng dẫn giải
Chọn B
.
Gọi
I
là trung điểm của
CD
.
( ) ( ) ( )
OI CD SOI CD SOI SCD⇒⊥⇒ ⊥⇒ ⊥
.
Kẻ
( ) ( )
,GH SI ,OK OK SCD GH SCD⊥⇒ ⊥ ⊥
.
(
)
( )
0, SCD
d OK⇒=
, mà
33
24
a
OK GH OK= ⇒=
.
22
22
.3
2
OI OK a
SO
OI OK
= =
−
. Vậy
3
.
3
6
S ABCD
a
V =
.
| 1/55

Tài liệu khác của Toán 12

Preview text:


THỂ TÍCH KHỐI CHÓP ĐỀU A. BÀI TẬP Câu 1.
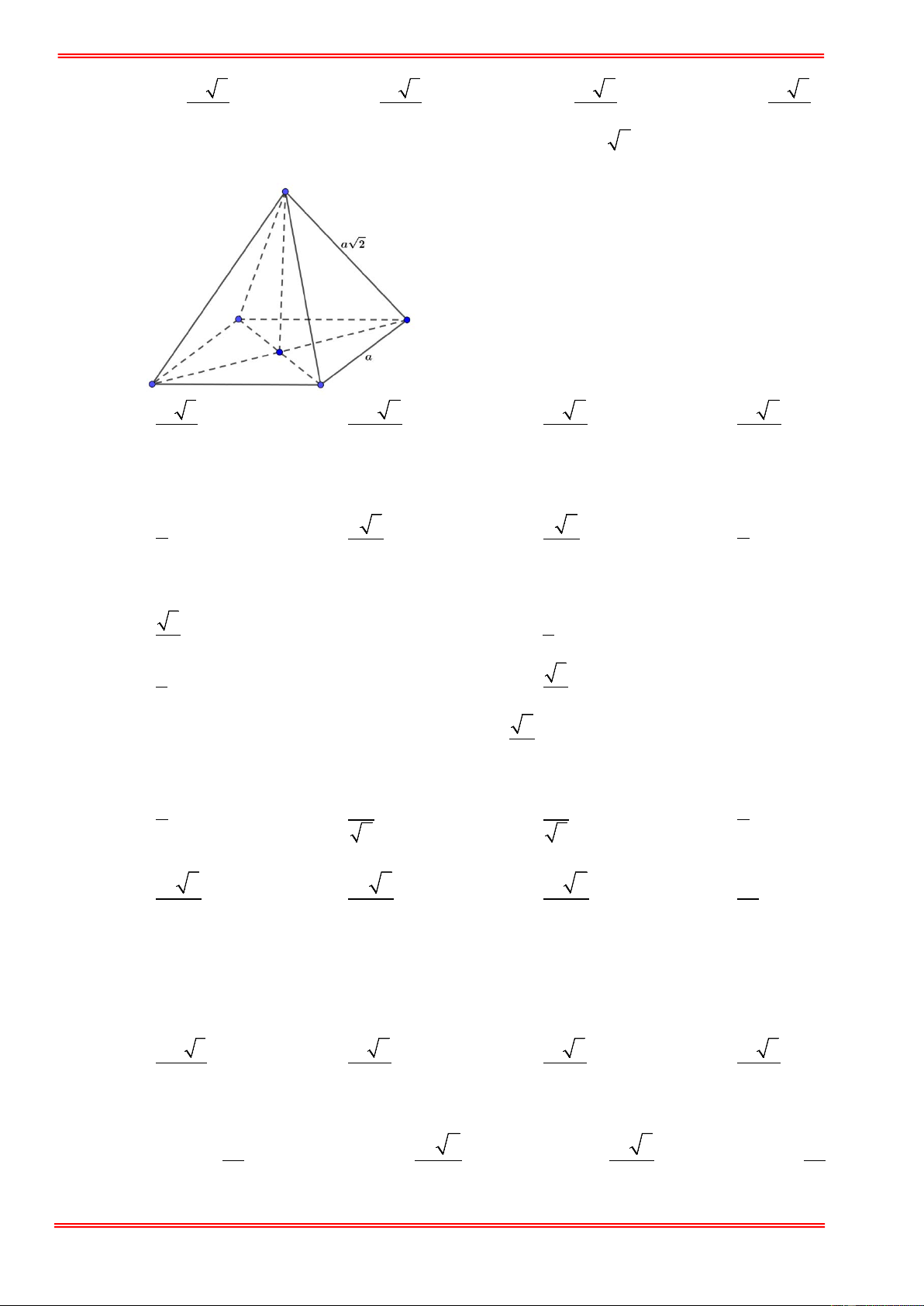
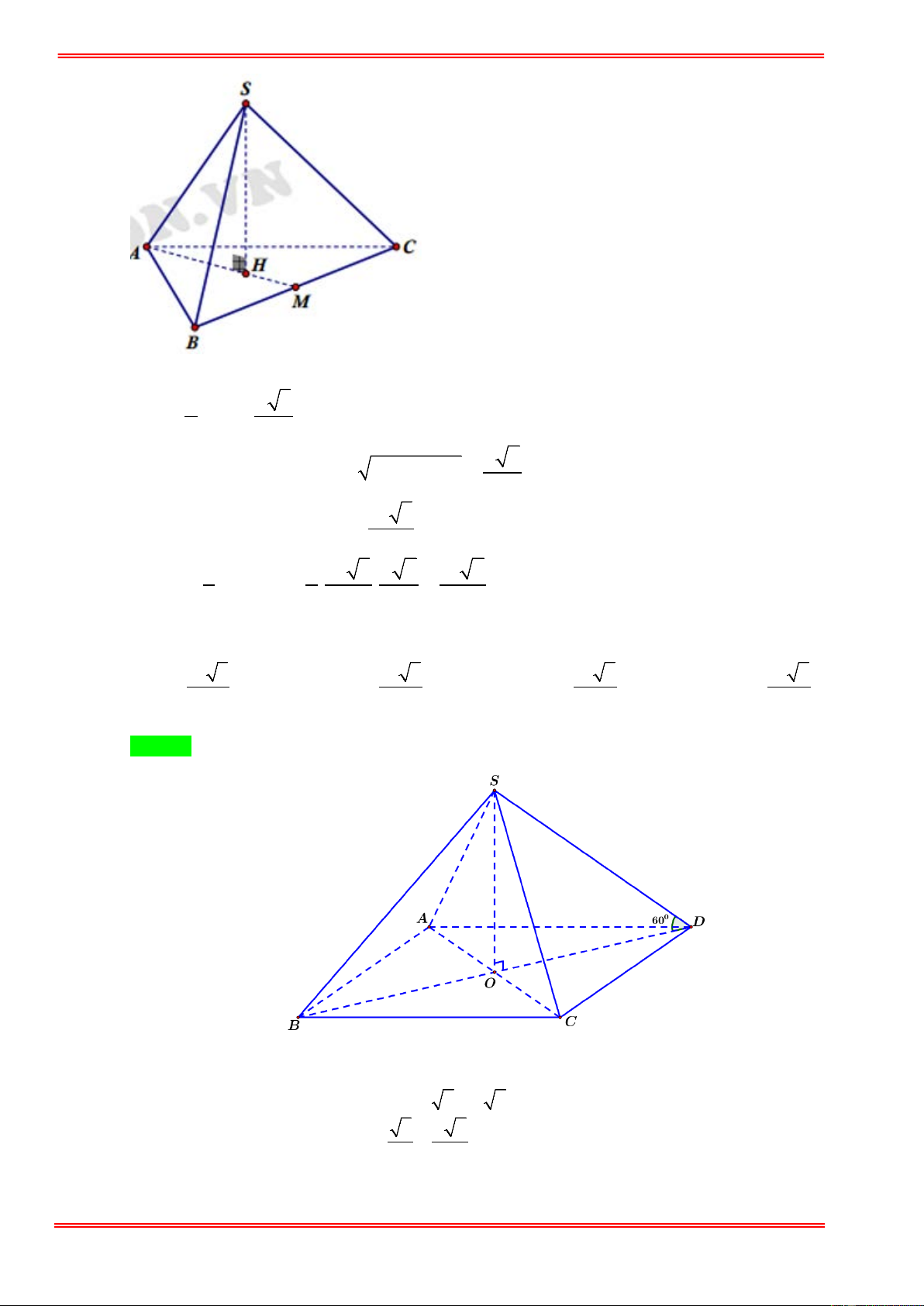
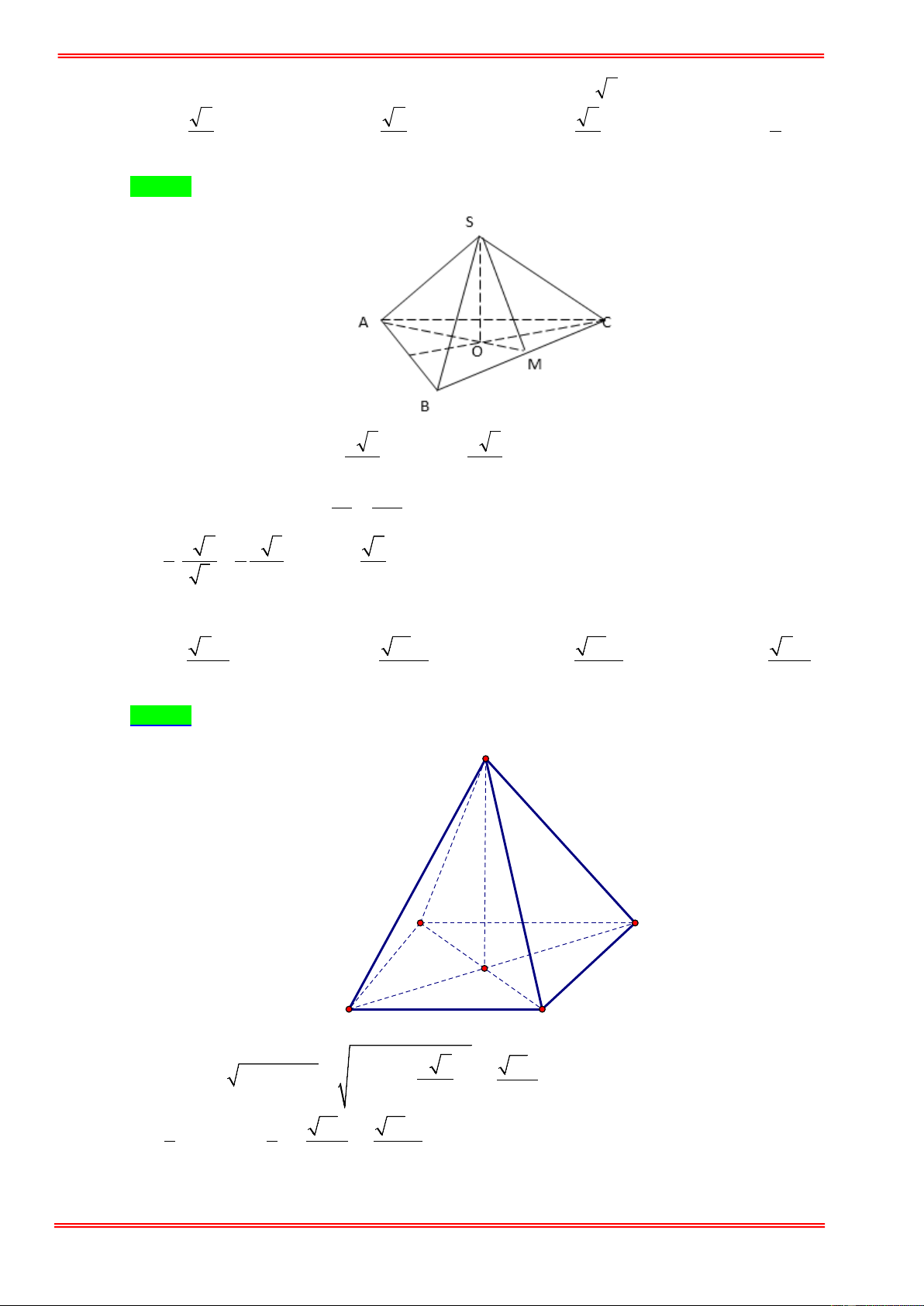
Cho khối tứ diện đều ABCD cạnh bằng a , M là trung điểm BC . Thể tích V của khối chóp
M .ABC bằng bao nhiêu? 3 3a 3 a 3 2a 3 2a A. V = . B. V = . C. V = . D. V = . 24 2 12 24 Câu 2.
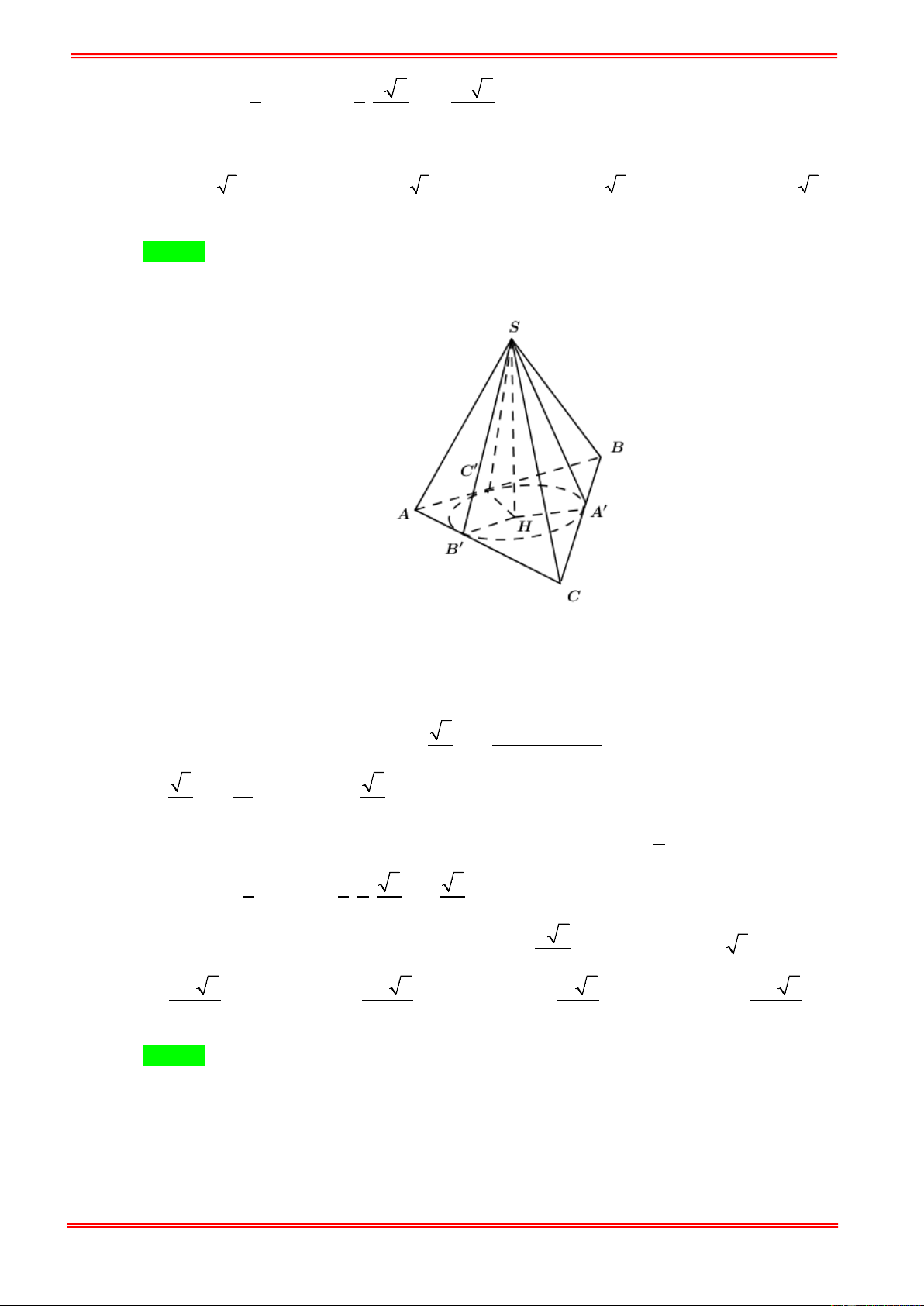
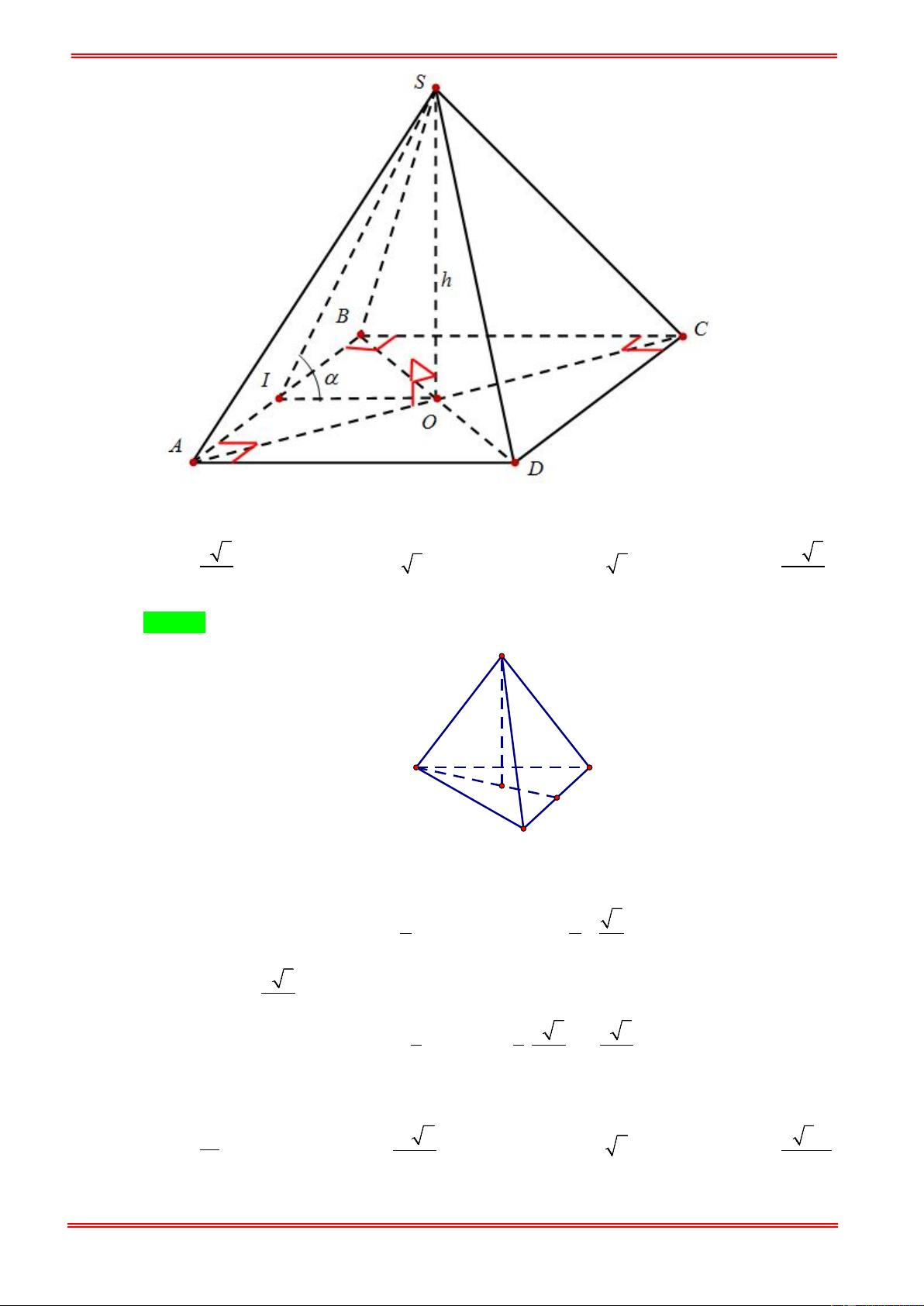
Cho hình chóp đều S.ABCD có cạnh đáy bằng a và cạnh bên tạo với đáy một góc 60°. Thể tích
của hình chóp đều đó là: 3 a 6 3 a 3 3 a 3 3 a 6 A. . B. . C. . D. . 6 6 2 2
Câu 3. Thể tích hình tứ diện đều có cạnh bằng a là: 3 a 2 3 a 2 3 a 2 3 5a 2 A. . B. . C. . D. . 3 12 6 12
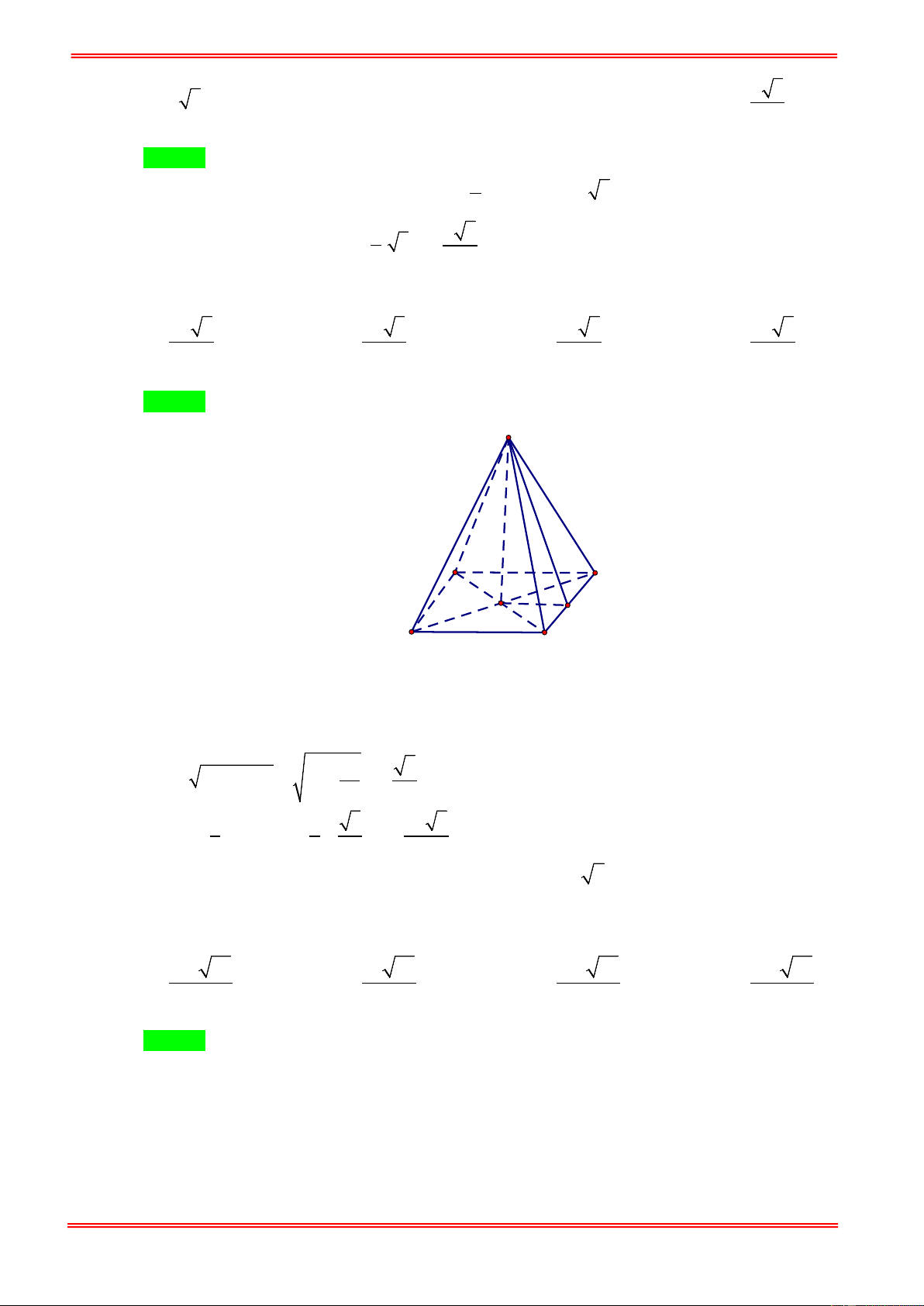
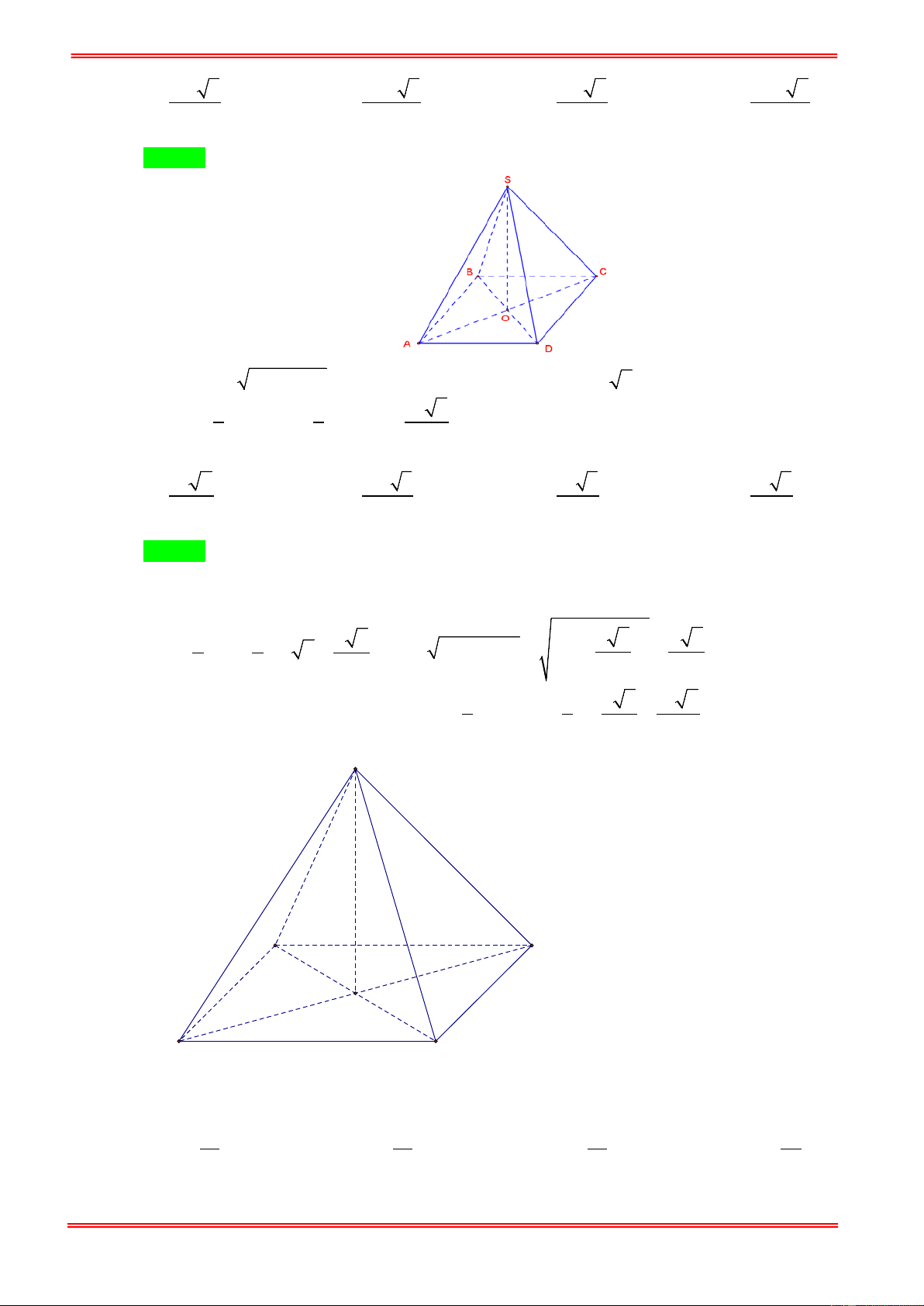
Câu 4.Cho khối chóp tứ giác đều có cạnh đáy bằng a , cạnh bên gấp hai lần cạnh đáy. Tính thể tích V của
khối chóp tứ giác đã cho. 3 2a 3 2a 3 14a 3 14a A. . B. . C. . D. . 2 6 6 2
Câu 5. Cho hình chóp tứ giác đều có cạnh đáy bằng a và cạnh bên bằng a 3 . Tính thể tích V của khối
chóp đó theo a . 3 a 3 3 a 3 a 2 3 a 10 A. V = . B. V = . C. V = . D. V = . 3 2 3 6
Câu 6. Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, đường cao của một mặt bên là a 3 . Thể
tích V của khối chóp đó là: 2 2 2 2 4 2 A. 3 V = a . B. 3 V = a . C. 3 V = a . D. 3 V = a . 6 9 3 3
Câu 7. Cho tứ diện đều ABCD cạnh bằng 2a . Tính thể tích của khối tứ diện đó. 3 a 2 3 a 3 3 a 3 a 2 A. V = . B. V = . V = D. V = . 12 6 C. 3 . 6
Câu 8. Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a , khoảng cách giữa hai đường thẳng SA và CD
bằng a 3 . Thể tích khối chóp đều S.ABCD bằng? 3 4a 3 3 a 3 A. 3 4a 3 . B. 3 a 3 . C. . D. . 3 3
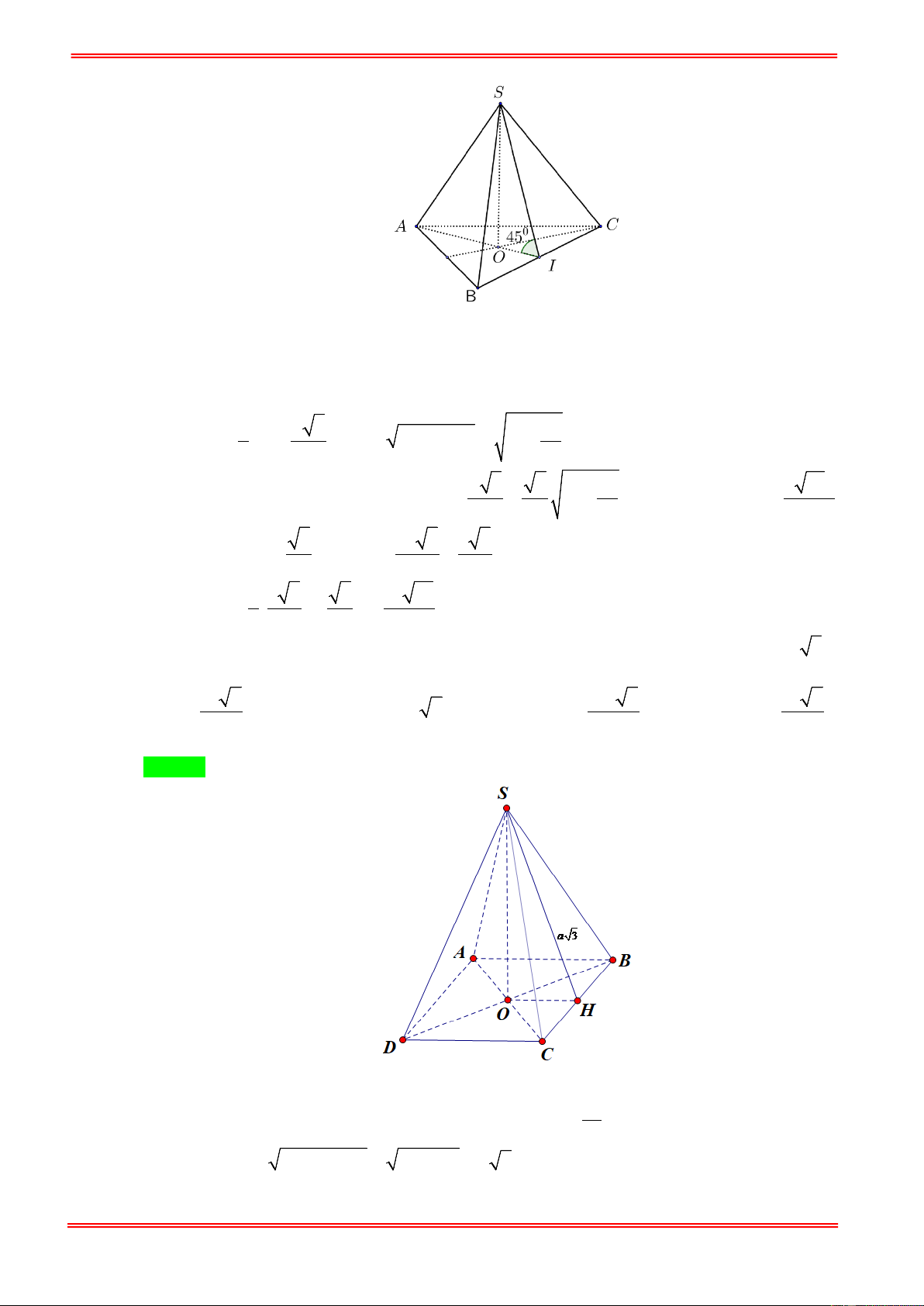
Câu 9. Cho khối chóp đều S.ABC có cạnh bên bằng a và các mặt bên hợp với đáy một góc 45° . Tính thể
tích của khối chóp S.ABC theo . a . 3 a 15 3 a 5 3 a 3 a 15 A. 25 . B. 25 . C. 3 . D. 5 .
Câu 10. Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, đường cao của một mặt bên là a 3 . Tính
thể tích V của khối chóp đó. 3 a 2 3 4a 2 3 a 2 A. V = . B. 3 V = 4a 2 . C. V = . D. V = . 9 3 6
Câu 11. Cho hình chóp tam giác đều cạnh đáy bằng a và các mặt bên đều tạo với mặt phẳng đáy một góc 60 .
° Tính thể tích V của khối chóp. https://toanmath.com/ 3 a 3 3 a 3 3 a 2 3 a 3 A. V = . B. V = . C. V = . D. V = . 4 24 6 8
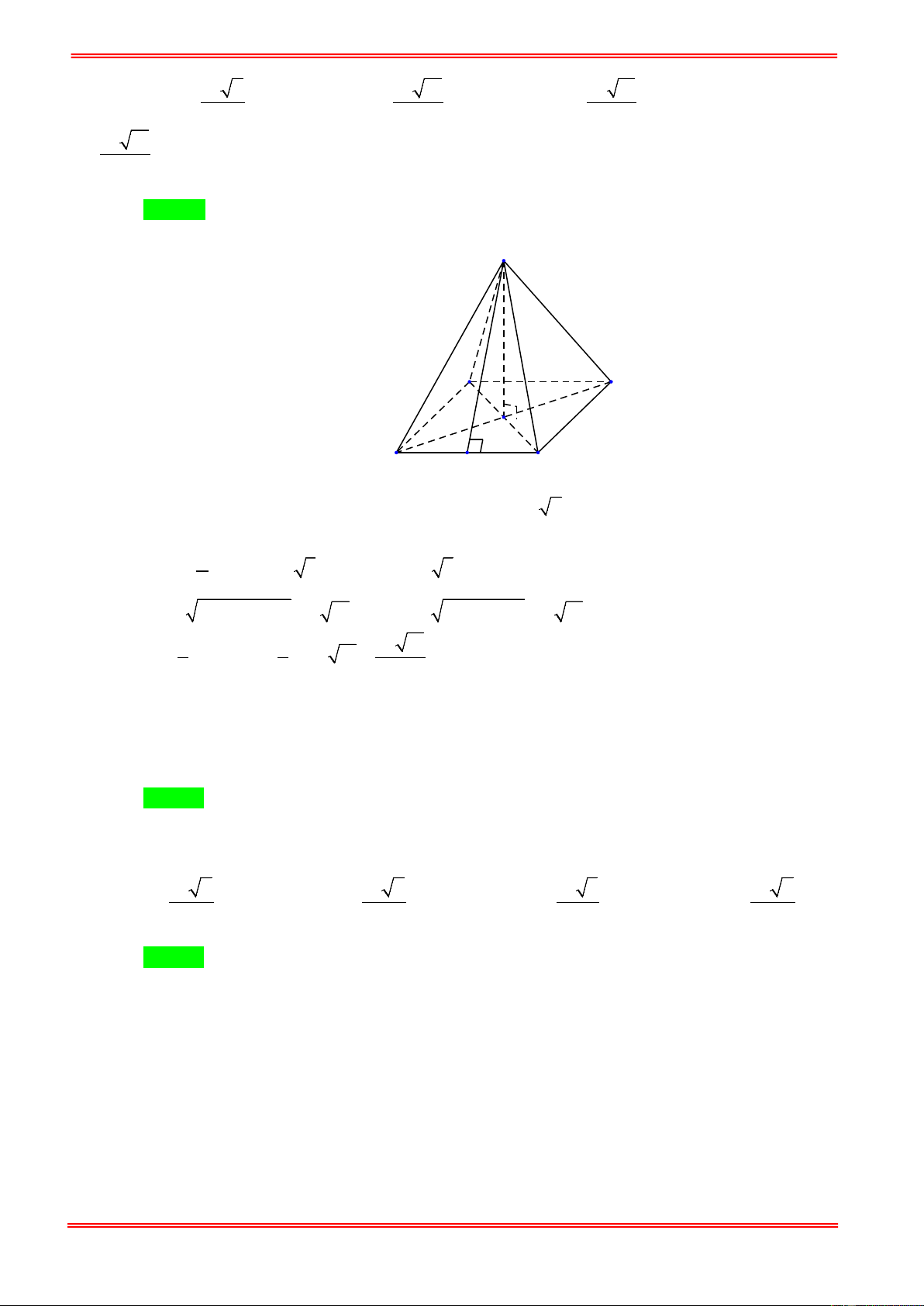
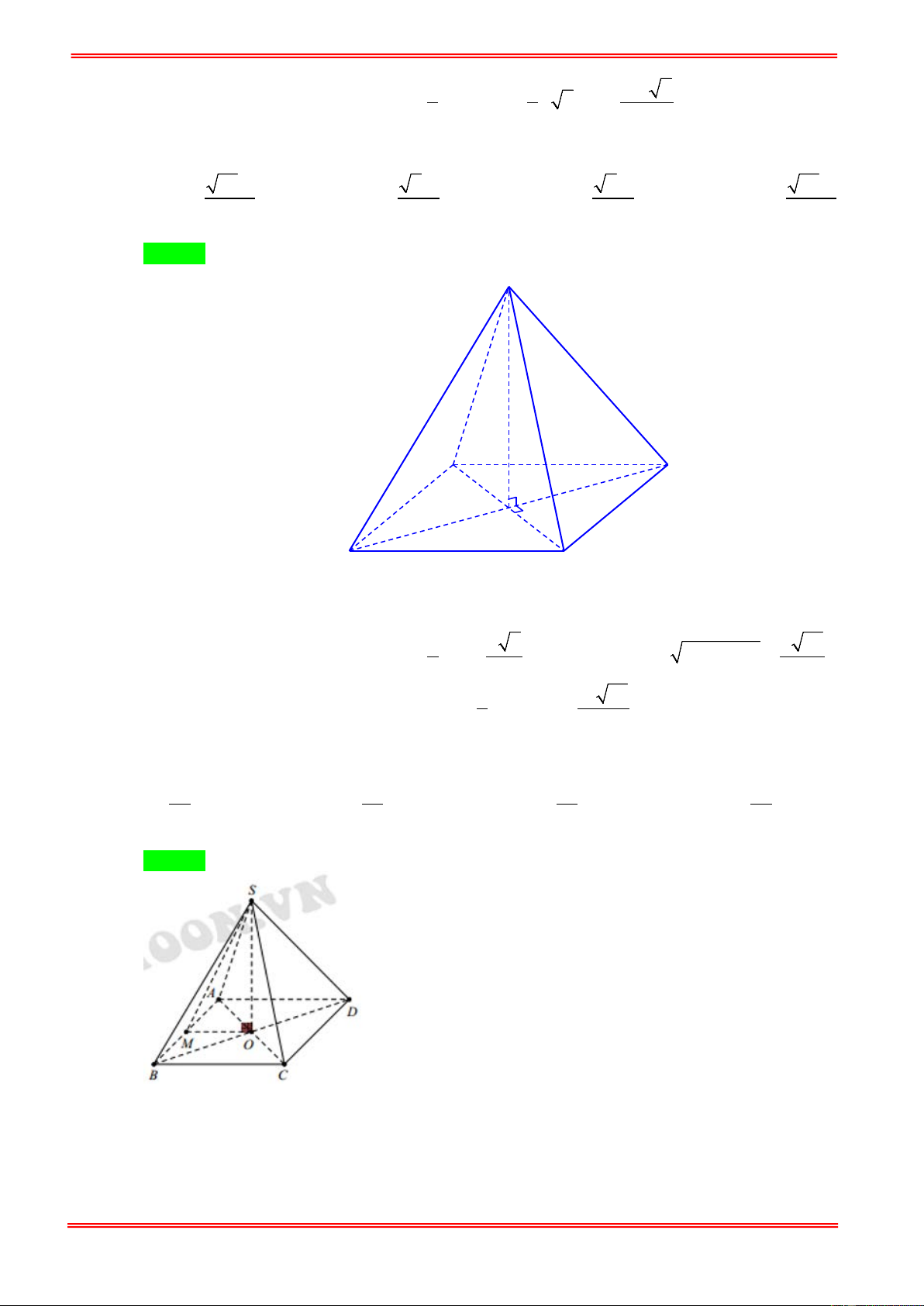
Câu 12. Cho hình chóp tứ giác đều có cạnh đáy bằng a , cạnh bên bằng a 2 (hình vẽ). Thể tích khối chóp là 3 a 3 3 2a 2 3 a 6 3 a 6 A. . B. . C. . D. . 6 3 3 6 Câu 13.
[Sở GDĐT Lâm Đồng lần 07 - 2017] Cho (H ) là khối chóp tứ giác đều có tất cả các cạnh bằng
2a . Thể tích của ( H ) bằng: 4 4 3 4 2 4 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 5 3 3 3
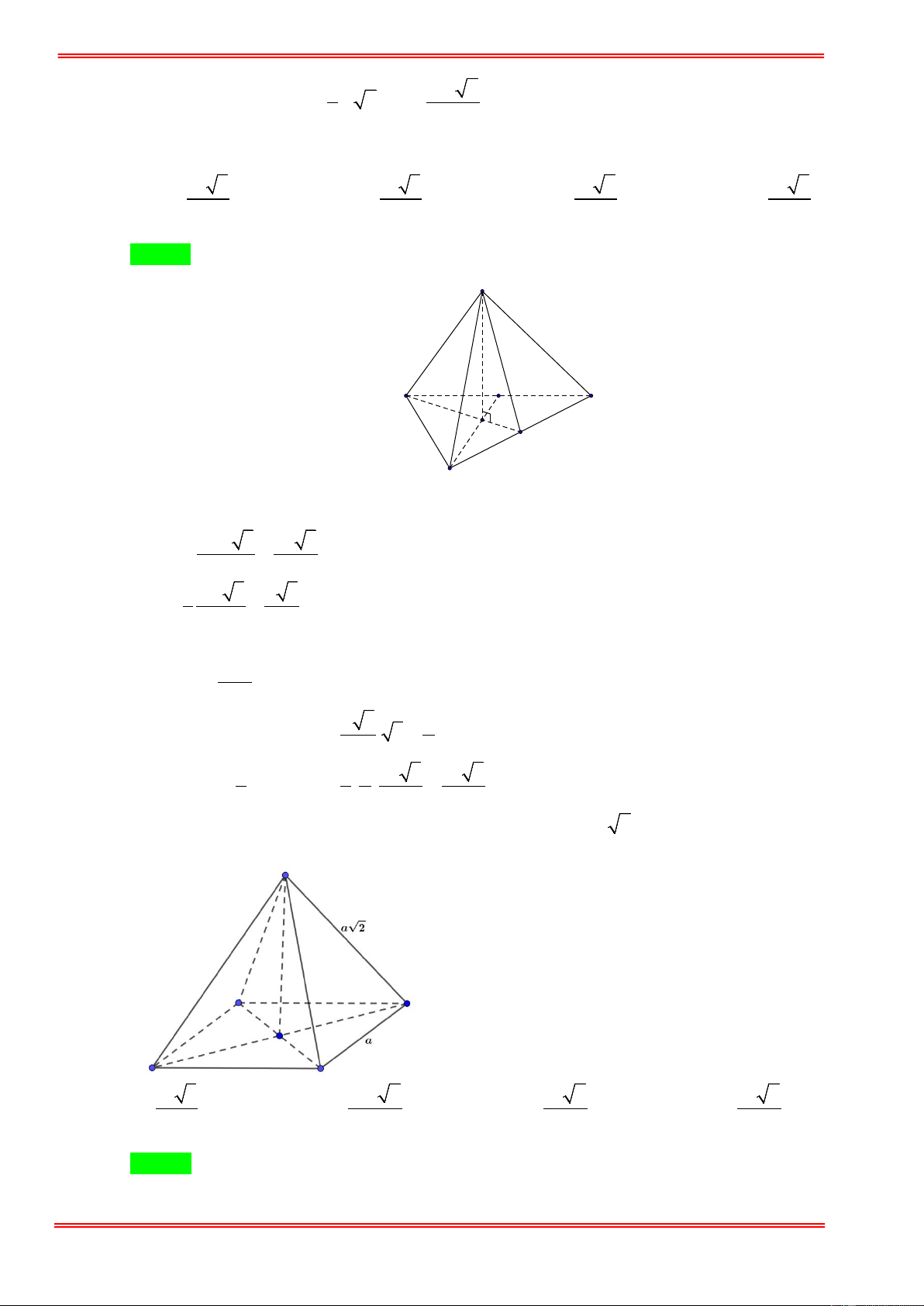
Câu 14. Một hình chóp tam giác đều có cạnh bên bằng b và cạnh bên tạo với mặt phẳng đáy một góc α .
Thể tích của hình chóp đó là 3 3 A. 3
b cosα sin α . B. 3 2
b sin α cosα . 4 4 3 3 C. 3 2
b cos α sin α . D. 3 2
b cos α sin α . 4 4 2
Câu 15.Cho hình chóp tứ giác đều S.ABCD có thể tích V =
. Gọi M là trung điểm của cạnh SD . Nếu 6
SB ⊥ SD thì khoảng cách từ B đến mặt phẳng ( MAC ) bằng: 3 1 2 1 A. . B. . C. . D. . 4 2 3 2
Câu 16. Khối chóp tam giác đều có tất cả các cạnh bằng a có thể tích bằng: 3 a 3 3 a 3 3 a 2 3 a A. . B. . C. . D. . 12 4 6 3
Câu 17. Khi chiều cao của một hình chóp đều tăng lên n lần nhưng mỗi cạnh đáy giảm đi n lần thì thể tích của nó.
A. Không thay đổi.
B. Tăng lên n lần.
C. Tăng lên n −1 lần.
D. Giảm đi n lần.
Câu 18. Tính thể tích khối chóp tứ giác đều có tất cả các cạnh bằng a . 3 2a 3 3 a 2 3 a 3 3 a 3 A. . B. . C. . D. . 3 6 4 2
Câu 19. Cho khối chóp đều S.ABC có cạnh đáy bằng a , tính thể tích khối chóp S.ABC biết cạnh bên bằng a là: 3 a 3 a 2 3 a 3 3 a A. V = . B. V = . C. V = . D. V = . S . ABC 4 S . ABC 12 S . ABC 6 S . ABC 12 https://toanmath.com/
Câu 20. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , cạnh bên hợp với đáy một góc 60 . Thể
tích V của khối chóp S.ABCD bằng 3 3 a 3 a 3 3 a 6 3 a 6 V = V = V = V = A. 2 . B. 3 . C. 6 . D. 3 .
Câu 21. Cho hình chóp tam giác đều cạnh đáy bằng a và các mặt bên đều tạo với mặt phẳng đáy m ột góc 0
60 . Tính thể tích V của khối chóp. 3 a 3 3 a 3 3 a 2 3 a 3 A. V  . B. V  . C. V  . D. V  . 24 4 6 8 a
Câu 22. Thể tích của khối chóp tứ giác đều có chiều cao bằng
6 và cạnh đáy bằng a 3 bằng: 3 3 3a 2 3 3a 2 3 a 6 3 3a 6 A. . B. . C. . D. . 2 4 3 2
Câu 23. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a . Gọi điểm O là giao điểm của AC và a
BD . Biết khoảng cách từ O đến SC bằng
. Tính thể tích khối chóp S.ABC . 6 3 a 3 a 3 a 3 a A. . B. . C. . D. . 6 4 8 12
Câu 24. Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bằng a , góc hợp bởi cạnh bên và mặt đáy
bằng 60°. Thể tích của hình chóp đã cho. 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 4 6 3 12
Câu 25. Cho hình chóp đều S.ABCD có AC = 2a , mặt bên (SBC ) tạo với đáy ( ABCD) một góc 45° .
Tính thể tích V của khối chóp S.ABCD . 3 a 3 a 2 3 2 3a A. V = . B. V = . C. V = . D. 3 V = a 2 . 2 3 3
Câu 26. Khối chóp tam giác đều có cạnh đáy bằng a và cạnh bên bằng a 3 có thể tích bằng: 6 6 2 1 A. 3 V = a . B. 3 V = a . C. 3 V = a . D. 3 V = a . 2 6 6 3
Câu 27. Cho khối chóp tứ giác đều có cạnh đáy bằng a , cạnh bên bằng 2a . Tính thể tích V của khối chóp đã cho. 3 2a 3 14a 3 14a 3 2a A. V = . B. V = . C. V = . D. V = . 2 2 6 6
Câu 28. Một hình chóp có đáy là tam giác đều cạnh bằng 2 và có chiều cao bằng 4. Tính thể tích hình chóp đó. 4 3 A. 2 3 . B. 2 . C. 4 . D. . 3
Câu 29.] Cho hình chóp tứ giác đều có cạnh đáy bằng x . Diện tích xung quanh gấp đôi diện tích đáy. Khi
đó thể tích của khối chóp bằng: 3 x . 3 3 x . 3 3 x . 3 3 x . 3 A. . B. . 3 2 C. 12 . D. 6 .
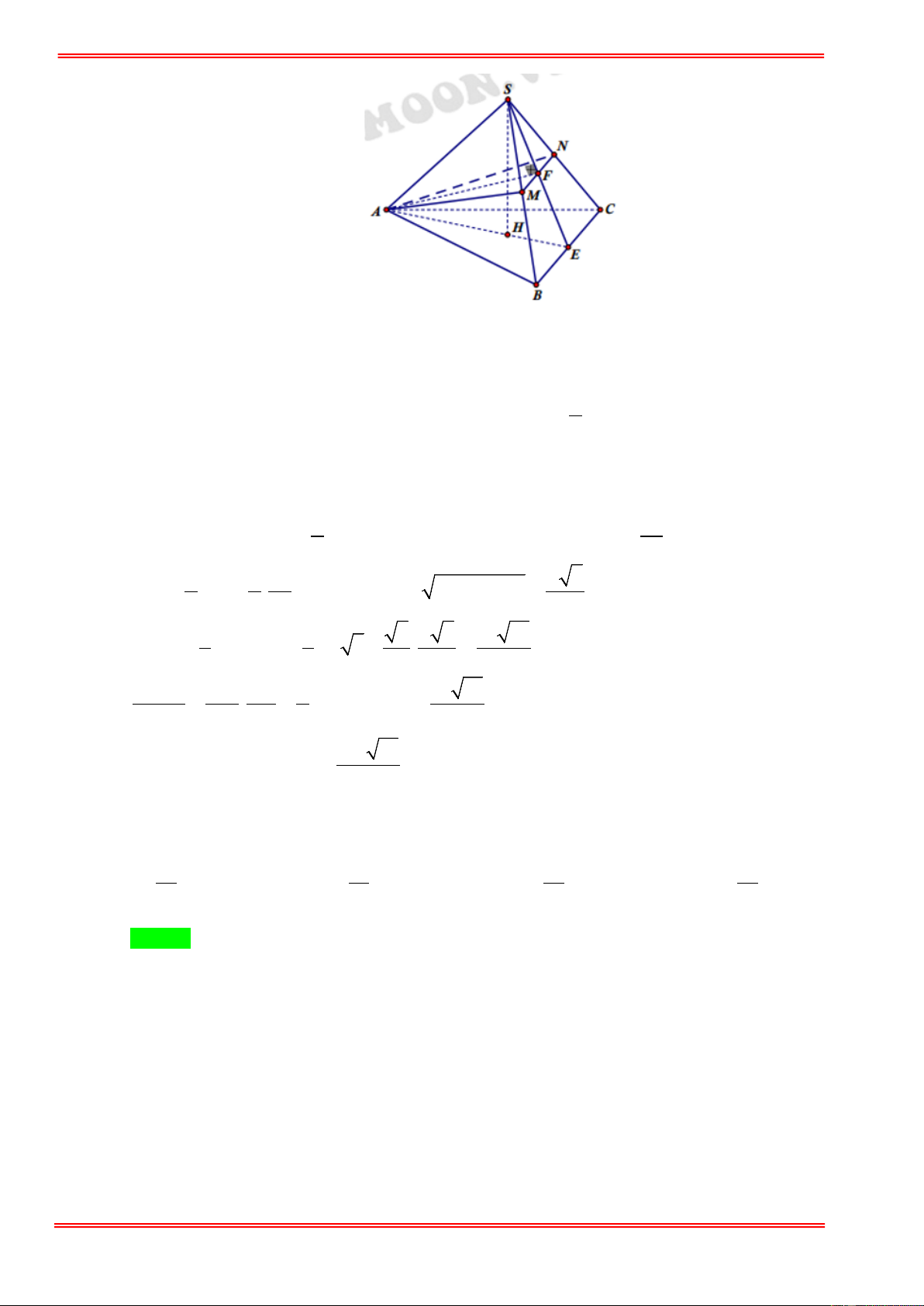
Câu 30. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a 3 . Gọi M , N lần lượt là trung điểm của
SB, BC Tính thể tích khối chóp .
A BCNM . Biết mặt phẳng ( AMN ) vuông góc với mặt phẳng (SBC) . https://toanmath.com/ 3 3a 15 3 a 15 3 3a 15 3 3a 15 A. . B. . C. . D. . 48 32 32 16
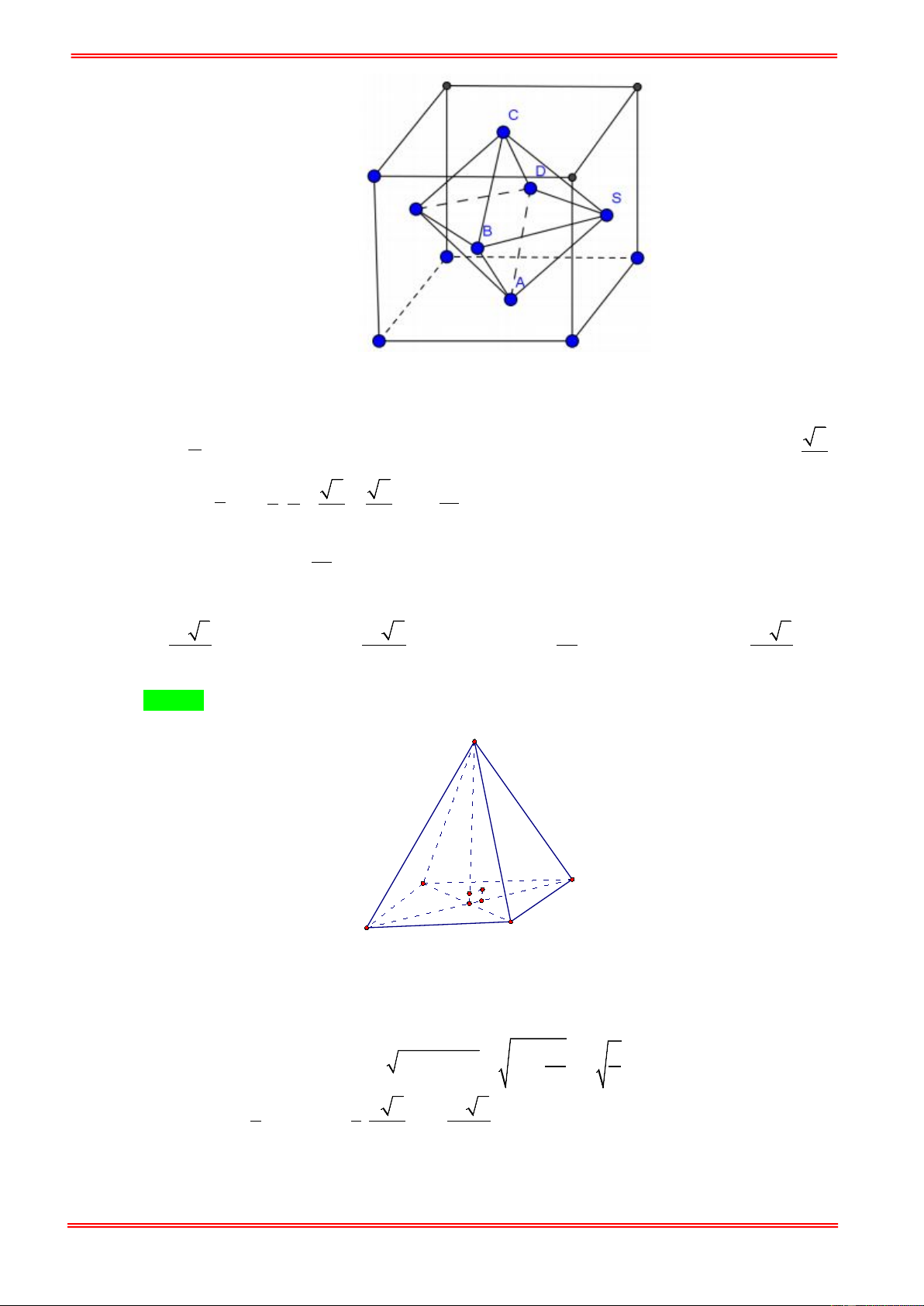
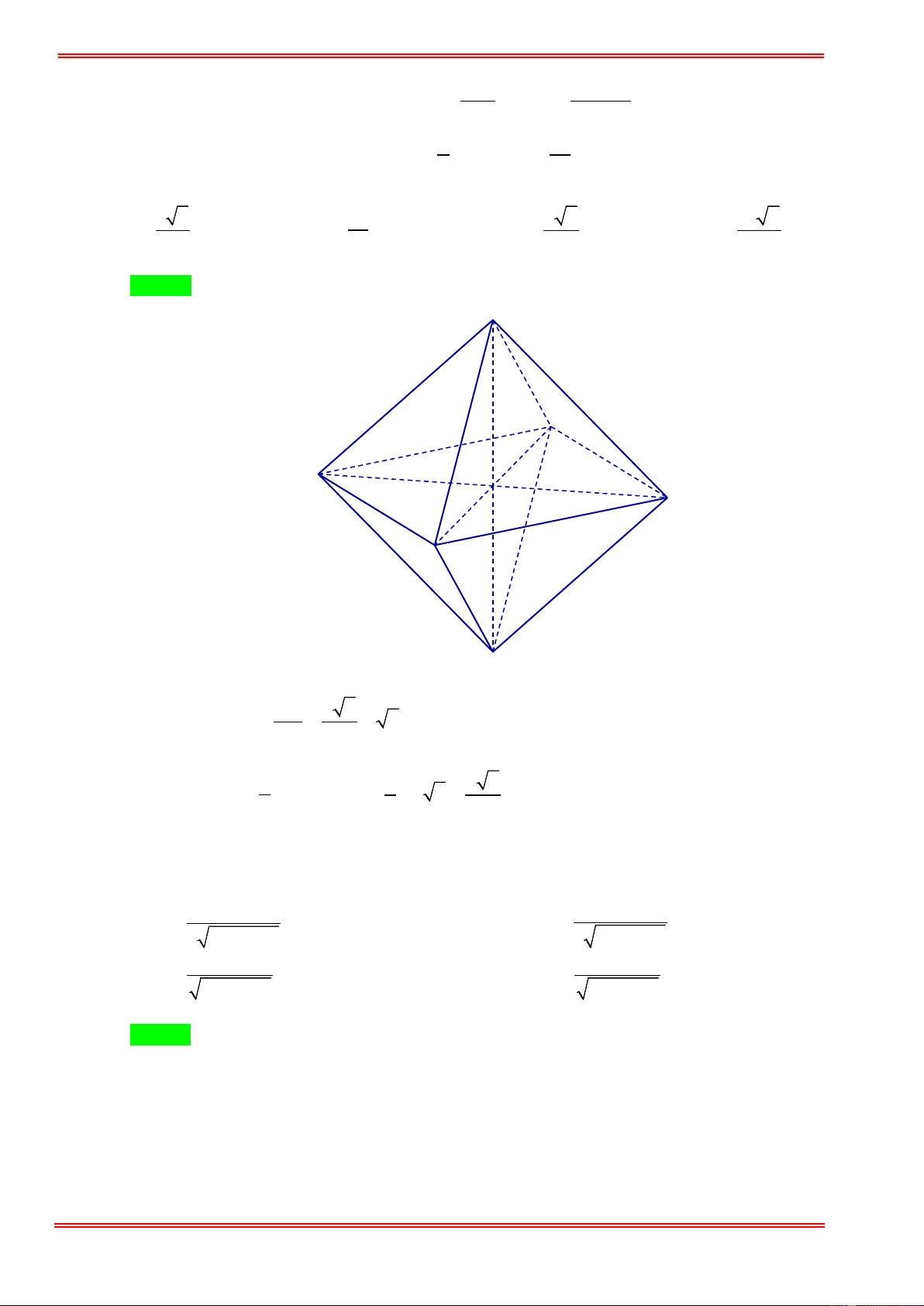
Câu 31. Người ta gọt một khối lập phương gỗ để lấy khối tám mặt đều nội tiếp nó (tức là khối có các đỉnh là
các tâm của các mặt khối lập phương). Biết các cạnh của khối lập phương bằng a . Hãy tính thể
tích của khối tám mặt đều đó: 3 a 3 a 3 a 3 a A. . B. . C. . D. . 8 6 4 12
Câu 32. Cho ( H ) là khối chóp tứ giác đều có tất cả các cạnh bằng a . Thể tích của ( H ) bằng. 3 a 3 3 a 2 3 a 3 a 3 A. . B. . C. . D. . 2 6 3 4
Câu 33. Một hình chóp tứ giác đều có đáy là hình vuông cạnh a , các mặt bên tạo với đáy một góc α . Thể
tích khối chóp đó là 3 a 3 a 3 a 3 a A. tan α . B. tan α . C. cot α . D. sin α . 6 2 6 2 =
Câu 34.Cho khối chóp đều S.ABCD có đáy ABCD là hình vuông cạnh a , SA a 3 . Tính thể tích V của
khối chóp S.ABCD theo a . 2 6 10 2 11 A. 3 V = a . B. 3 V = a . C. 3 V = a . D. 3 V = a . 9 6 3 6
Câu 35. Thể tích của chóp tam giác đều có tất cả các cạnh đều bằng a là 3 a 2 3 a 2 3 a 2 3 a 2 A. . B. . C. . D. . 4 2 6 12
Câu 36. Cho hình chóp tứ giác đều có cạnh đáy bằng cạnh bên bằng 2a . Tính thể tích khối chóp đã cho. 3 a 2 3 4a 2 3 a 3 3 a 2 A. . B. . C. . D. . 4 3 12 6
Câu 37. Cho hình chóp đều S.ABC có SA = 1. Gọi D, E lần lượt là trung điểm của hai cạnh , SA SC . Tính
thể tích khối chóp S.ABC , biết đường thẳng BD vuông góc với đường thẳng AE . 2 21 12 21 A. V = B. V = C. V = D. V = S . ABC 12 S . ABC 54 S . ABC 4 S . ABC 18
Câu 38. Tính thể tích khối tứ diện đều có cạnh a . 3 a 3 3 a 2 3 a 3 A. 3 a . B. . C. . D. . 4 12 12
Câu 39. Trong tất cả các khối chóp tứ giác đều ngoại tiếp mặt cầu bán kính bằng a , thể tích V của khối chóp
có thể tích nhỏ nhất. 3 32 3 10 3 8 A. = a V . B. = a V . C. 3 V = 2a . D. = a V . 3 3 3
Câu 40. Cho hình chóp tam giác đều có cạnh đáy bằng a , góc giữa cạnh bên và mặt đáy bằng o 60 . Thể tích
khối chóp S.ABC là: 3 a 3 3 a 6 3 a 3 a 3 A. . B. . C. . D. . 12 12 8 8
Câu 41. Cho hình chóp tam giác đều S.ABC có AB = a , cạnh bên 6 SA = a
. Tính thể tích V của khối 3
chóp S.ABC . 3 3 3 3 3 A. = a V . B. = a V . C. = a V . D. = a V . 36 4 24 12 https://toanmath.com/
Câu 42. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a . Gọi SH là đường cao của hình chóp.
Khoảng cách từ trung điểm của SH đến (SBC) bằng b . Thể tích khối chóp S.ABCD là 3 2a b 3 a b 3 2a b 2ab A. . B. . C. . D. . 2 2 3 a −16b 2 2 3 a −16b 2 2 a −16b 3
Câu 43. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a . Gọi M , N lần lượt là trung điểm của
SA và CD . Cho biết MN tạo với mặt đáy một góc bằng 30° . Tính thể tích khối chóp S.ABCD . 3 a 15 3 a 30 3 a 15 3 a 5 A. . B. . C. . D. . 5 18 3 12
Câu 44. Cho hình chóp tam giác đều có cạnh đáy bằng a và cạnh bên bằng b . Thể tích của khối chóp là 2 a 2 a 2 a A. 2 2
3b − a . B. 2 2 2 a
3b − a . C. 2 2
3b − a . D. 2 2
3b − a . 6 4 12
Câu 45. Cho hình chóp tứ giác đều có độ dài cạnh bên và cạnh đáy cùng bằng a . Khi đó, khoảng cách h
giữa đường thẳng AD và mặt phẳng (SBC) là: a 6 a a 2 2a 5 A. h = . B. h = . C. h = . D. h = . 3 2 2 5
Câu 46. Cho hình chóp tam giác đều S.ABC đỉnh S , độ dài cạnh đáy là a , cạnh bên bằng 2a . Gọi I là
trung điểm của cạnh BC . Tính thể tích V của khối chóp S.ABI . 3 a 11 3 a 11 3 a 11 3 a 11 A. . B. . C. . D. . 8 6 12 24
Câu 47. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a góc giữa cạnh bên và mặt phẳng đáy bằng
60° . Tính thể tích khối chóp S.ABCD . 3 a 3 a 6 3 a 6 3 a 6 A. . B. . C. . D. . 6 3 2 6
Câu 48. Xét tứ diện ABCD có các cạnh AC = CD = DB = BA = 2 và AD , BC thay đổi. Giá trị lớn nhất
của thể tích tứ diện ABCD bằng 32 3 16 3 32 3 16 3 A. . B. . C. . D. . 27 27 9 9
Câu 49. Cho hình chóp tứ giác đều S.ABCD , đáy ABCD có diện tích 2
16 cm , diện tích một mặt bên là 2
8 3 cm . Tính thể tích V của khối chóp S.ABCD . 32 2 32 13 32 11 32 15 A. 3 V = cm . B. 3 V = cm . C. 3 V = cm . D. 3 V = cm . 3 3 3 3
Câu 50. Cho khối chóp tam giác đều. Nếu tăng cạnh đáy lên hai lần và giảm chiều cao đi bốn lần thì thể tích
của khối chóp đó sẽ:
A. Giảm đi hai lần.
B. Không thay đổi.
C. Tăng lên hai lần.
D. Giảm đi ba lần.
Câu 51. Hình chóp tứ giác đều có tất cả các cạnh bằng a . Thể tích khối chóp đó bằng: 3 a 2 3 a 2 3 a 3 3 a 2 A. . B. . C. . D. . 2 6 3 3
Câu 52. Khi chiều cao của một hình chóp đều tăng lên n lần nhưng mỗi cạnh đáy giảm đi n lần thì thể tích của nó.
A. Không thay đổi.
B. Tăng lên n lần.
C. Tăng lên n −1 lần.
D. Giảm đi n lần.
Câu 53. Cho hình chóp đều S.ABCD có đáy bằng 2a , khoảng cách giữa hai đường thẳng SA và CD bằng
a 3 . Thể tích khối chóp đều S.ABCD bằng. 3 a 3 3 4a 3 A. 3 a 3 . B. 3 4a 3 . C. . D. . 3 3 https://toanmath.com/
Câu 54. Thể tích khối bát diện đều cạnh a là: 2 3 2a 3 2a A. 3 a . B. . C. . D. 3 2a . 3 2 6
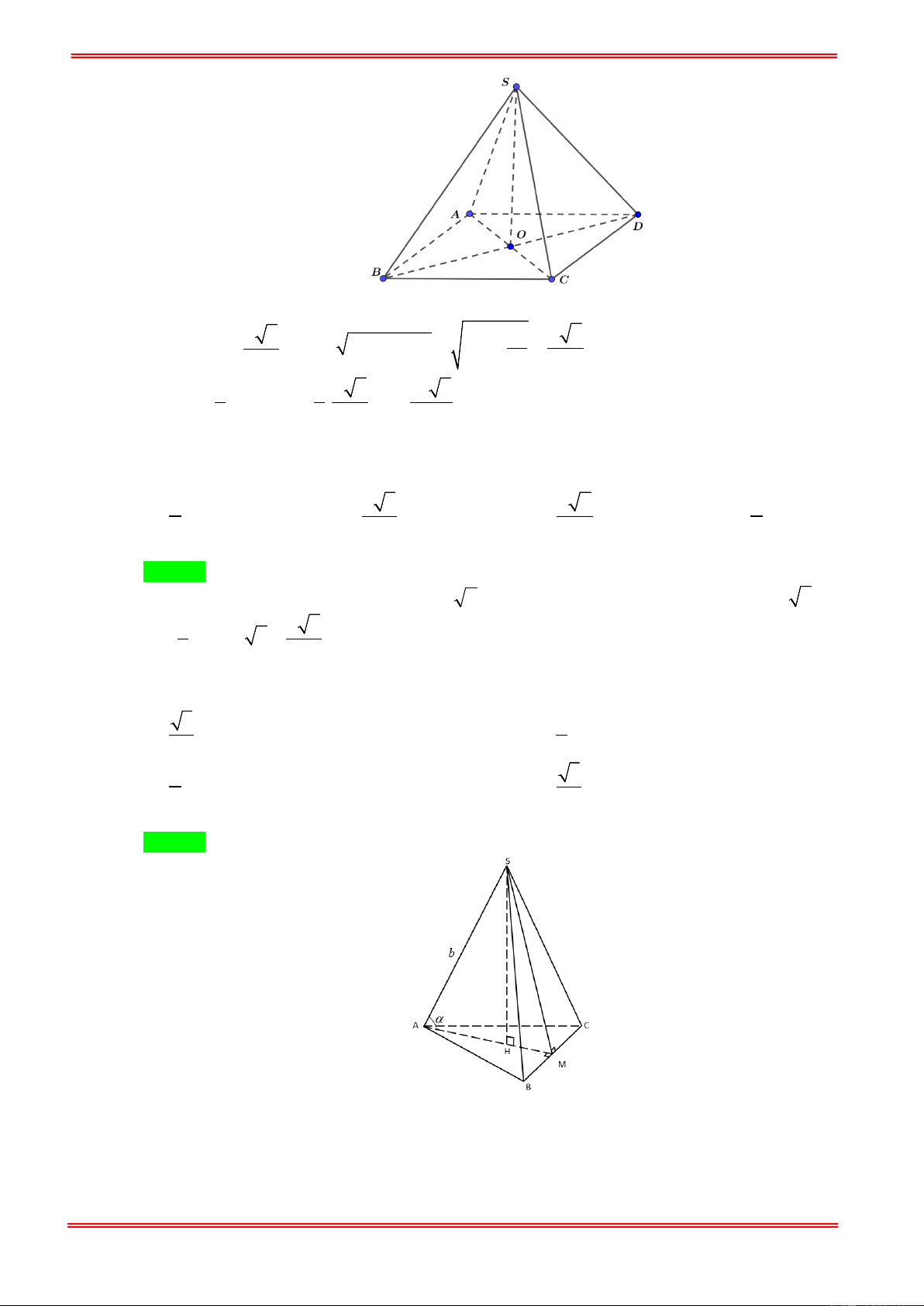
Câu 55. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh bằng a 3 và
SA = SB = SC = SD = 2a . Tính thể tích khối chóp S.ABCD ? 3 2a 3 3a 3 6a 3 2a A. . B. . C. . D. . 2 3 6 6
Câu 56. Cho hình chóp tứ giác đều S.ABCD có chiều cao bằng h , góc giữa hai mặt phẳng (SAB) và
( ABCD) bằng α . Tính thể tích của khối chóp S.ABCD theo h và α . 3 3h 3 3h 3 4h 3 8h A. 2 8 tan α . B. 2 4 tan α . C. 2 3 tan α . D. 2 3 tan α .
Câu 57. Cho tứ diện đều ABCD . Biết khoảng cách từ A đến mặt phẳng ( BCD) bằng 6 . Tính thể tích V
của tứ diện ABCD . 9 3 A. V = .
B. V = 5 3 . C. V = 27 3 27 3 . D. V = . 2 2
Câu 58. Cho hình chóp đều S.ABCD có AC = 2a , mặt bên (SBC ) tạo với đáy ( ABCD) một góc 45° . Tính
thể tích V của khối chóp S.ABCD ? 3 a 3 a 2 3 2 3a A. V = . B. V = . C. 3 V = a 2 . D. V = . 2 3 3
Câu 59. Thể tích hình chóp tứ giác đều có tất cả các cạnh đều bằng a bằng 3 a 2 3 a 2 3 a 3 a 2 A. B. C. D. 3 2 6 6
Câu 60. Cho hình chóp đều S.ABCD có chiều cao bằng a 2 và độ dài cạnh bên bằng a 6 . Tính thể tích
khối chóp S.ABCD . 3 8a 3 3 10a 3 3 8a 2 3 10a 2 A. . B. . C. . D. . 3 3 3 3
Câu 61. Tính thể tích khối chóp tứ giác đều có tất cả các cạnh bằng a . 3 a 2 3 2a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 3 4 2
Câu 62. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và mặt bên tạo với đáy một góc 450. Thể P P
tích V khối chóp S.ABCD là: 3 a 3 a 3 a 1 A. V = . B. V = . C. V = . D. 3 V = a . 6 9 2 24
Câu 63. Tính thể tích V của hình tứ diện đều có đường cao h = a . 3 a 3 3 a 3 3 a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . 12 6 8 4
Câu 64. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a cạnh bên bằng 3a . Tính thể tích V của khối chóp đã cho? 3 4 7a 3 4a 3 4 7a A. 3
V = 4 7a . B. V = . C. V = . D. V = . 9 3 3
Câu 65. Cho khối chóp tứ giác đều có cạnh đáy bằng a , cạnh bên bằng 3a . Tính thể tích V của khối chóp đã cho. 3 34a 3 2a 3 2a 3 34a A. V = . B. V = . C. V = . D. V = . 6 6 2 2 https://toanmath.com/
Câu 66. Một hình chóp tứ giác đều có đáy là hình vuông cạnh a , các mặt bên tạo với đáy một góc α . Thể
tích của khối chóp đó là 3 a 3 a 3 a 3 a A. sinα . B. tanα . C. cotα . D. tanα . 2 2 6 6
Câu 67.Tính thể tích của khối bát diện đều có cạnh bằng 2. 8 2 16 4 2 16 2 A. . B. . C. . D. . 3 3 3 3
Câu 68. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a . Gọi SH là chiều cao của hình chóp,
khoảng cách từ trung điểm I của SH đến mặt bên (SBC) bằngb . Tính thể tích V của khối chóp S.ABCD . 3 ab 2a b A. V = . B. V = . 2 2 3 a −16b 2 2 3 a −16b ab 2ab C. V = . D. V = . 2 2 a −16b 2 2 a −16b
Câu 69. Cho hình chóp đều S.ABCD có cạnh đáy bằng a , góc giữa cạnh bên và mặt đáy bằng o 60 . Tính thể tích
của khối chóp S.ABCD theo a . 3 a 6 3 a 6 3 a 3 3 a 6 A. B. C. D. 2 6 6 12
Câu 70. Thể tích của khối tứ diện đều có cạnh bằng 3 . 4 2 9 2 A. 2 2 . B. . C. . D. 2 . 9 4
Câu 71. Cho hình chóp tứ giác đều S.ABCD có đáy hợp với mặt bên một góc 45° . Bán kính mặt cầu ngoại
tiếp hình chóp S.ABCD bằng 2 . Tính thể tích khối chóp S.ABCD . 32 2 64 2 64 2 128 2 A. . B. . C. . D. . 9 27 81 81
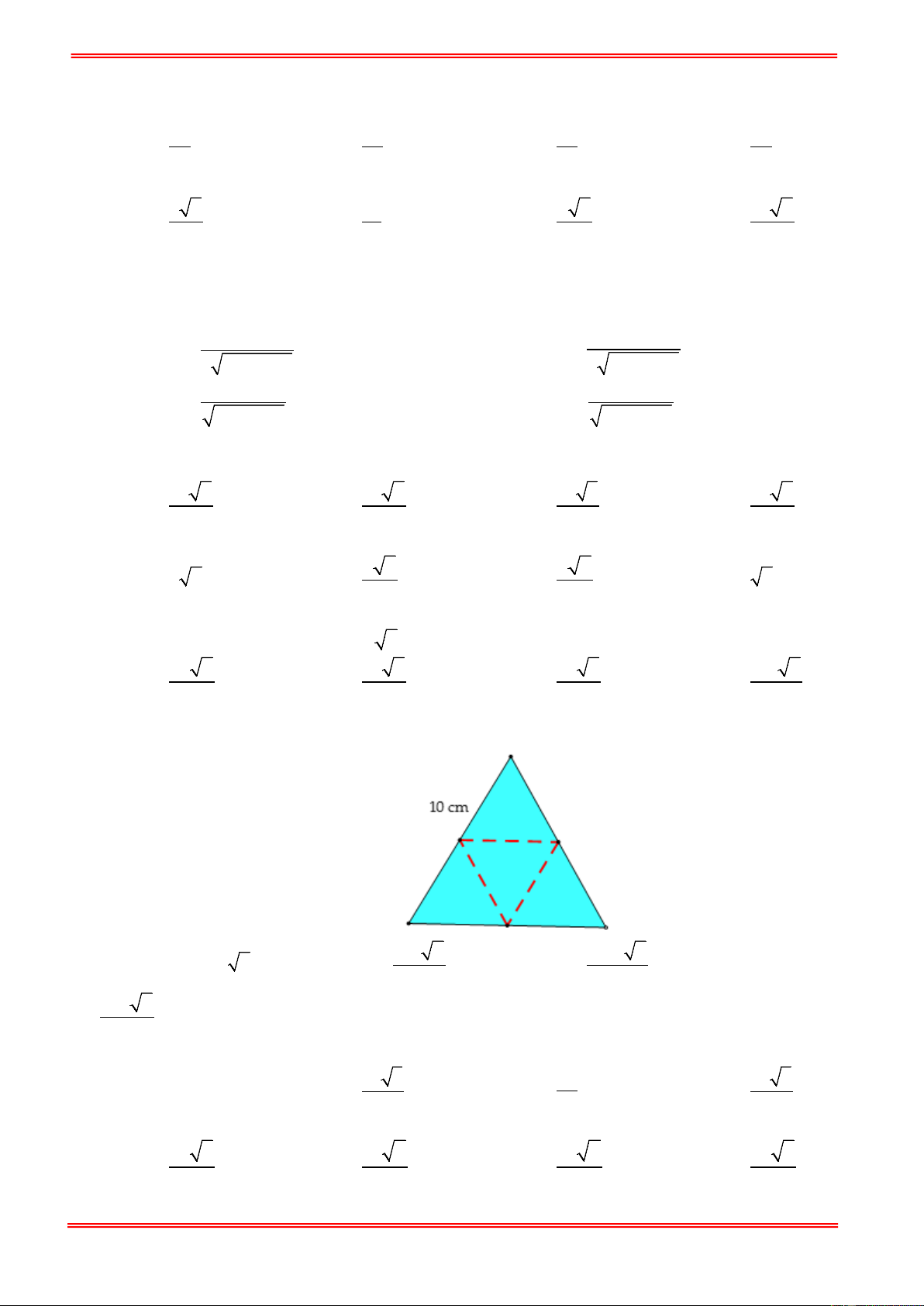
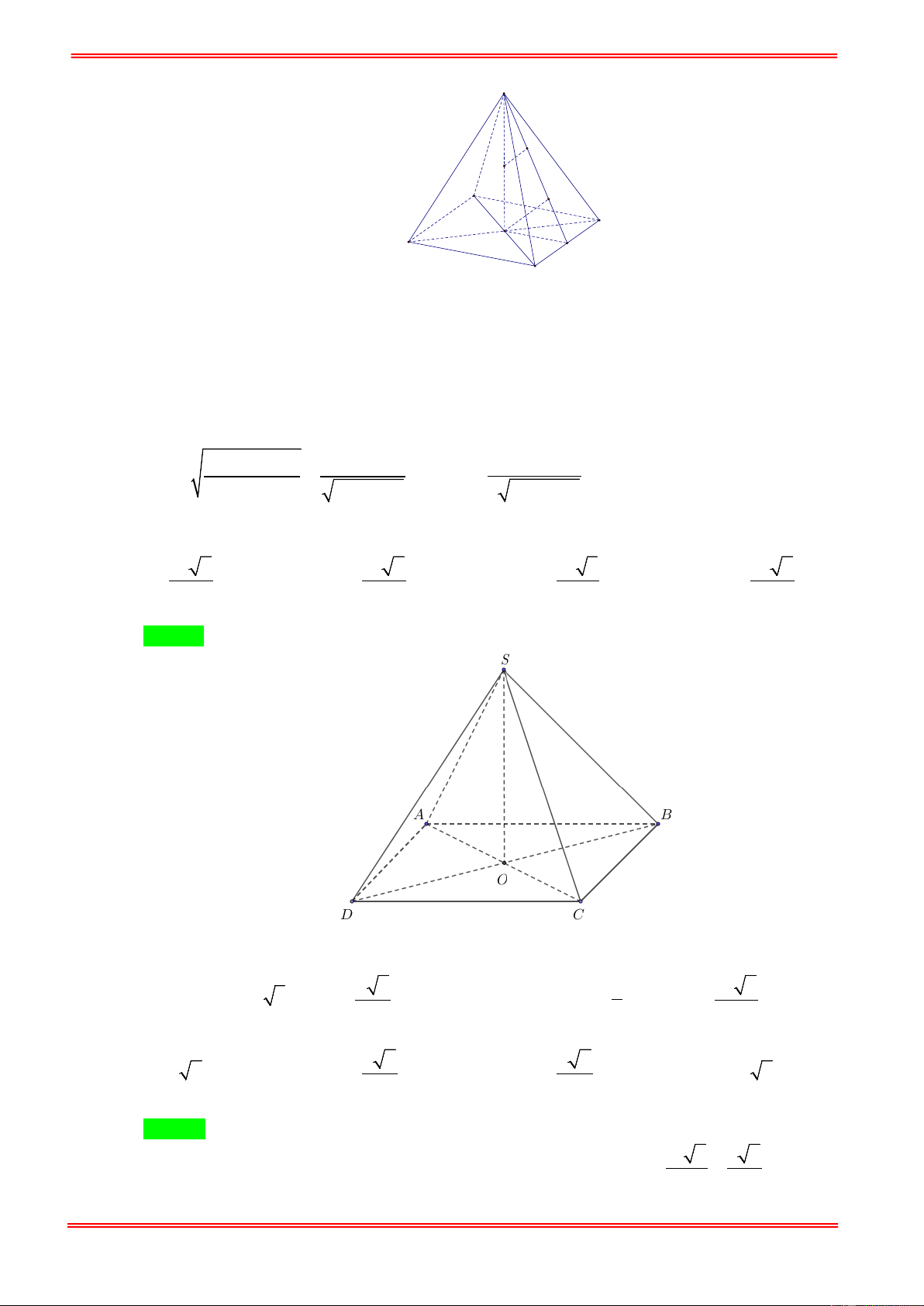
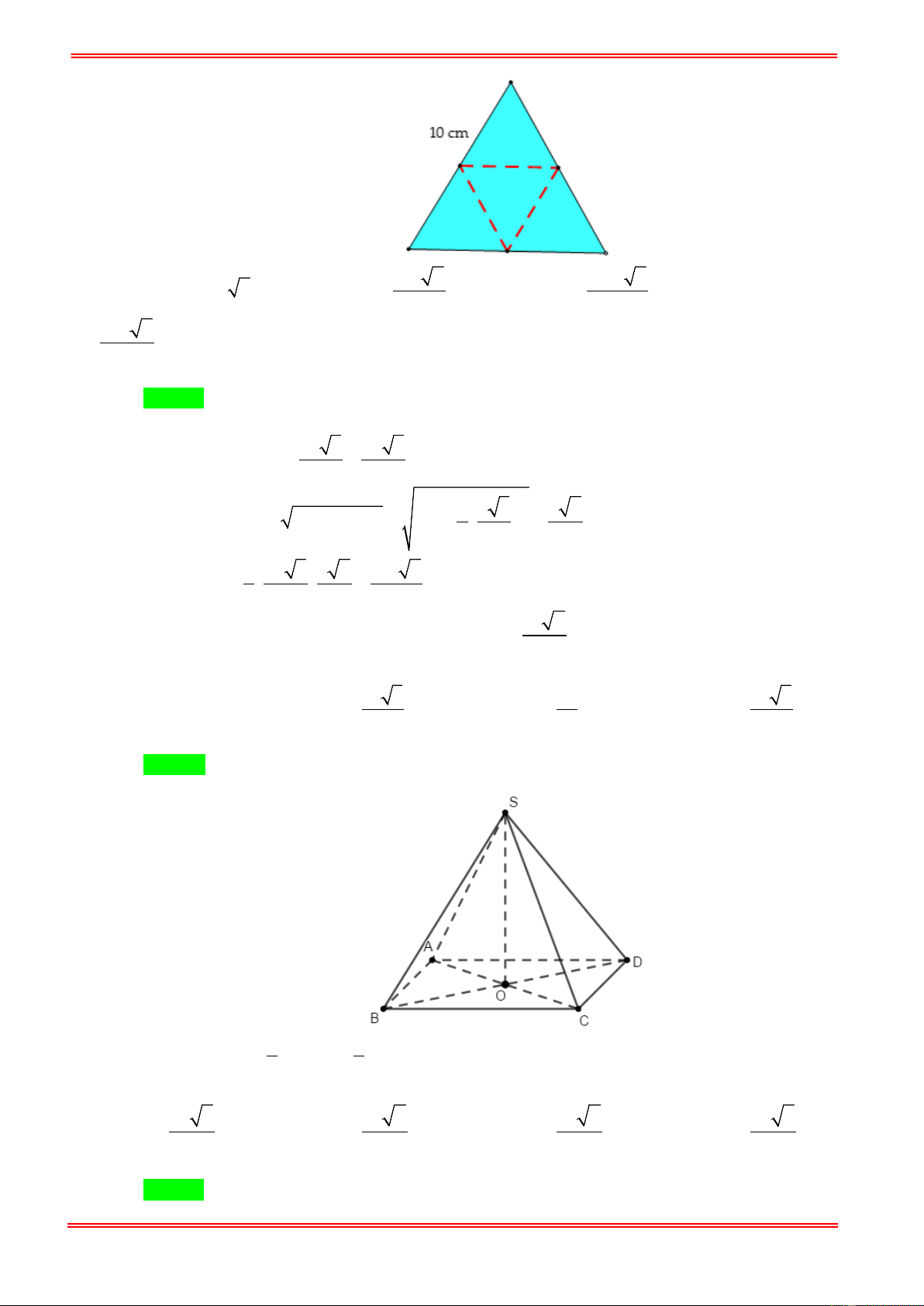
Câu 72. Người ta cắt miếng bìa hình tam giác cạnh bằng 10cm như hình bên và gấp theo các đường kẻ, sau
đó dán các mép lại để được hình tứ diện đều. Tính thể tích của khối tứ diện tạo thành. 125 2 1000 2 A. 3
V = 250 2cm . B. 3 V = cm . C. 3 V = cm . D. 12 3 250 2 3 V = cm . 12
Câu 73. Tính thể tích khối chóp tứ giác đều cạnh đáy bằng a , chiều cao bằng 3a . 3 a 3 3 a 3 a 3 A. 3 a . B. . C. . D. . 4 3 12
Câu 74. Thể tích của khối bát diện đều cạnh a là: 3 a 3 3 a 2 3 a 2 3 a 3 A. . B. . C. . D. . 6 3 6 3 https://toanmath.com/
Câu 75. Thể tích của khối tứ diện đều cạnh a là 3 6a 3 3a 3 2a 3 2a A. . B. . C. . D. . 12 12 12 24
Câu 76. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a ,diện tích mỗi mặt bên bằng 2 2a . Thể
tích khối nón có đỉnh là S và có đáy là đường tròn ngoại tiếp hình vuông ABCD bằng 3 7 3 π 7a 3 π 7a 3 π 7a A. 3 π a . B. . C. . D. . 4 4 3 6
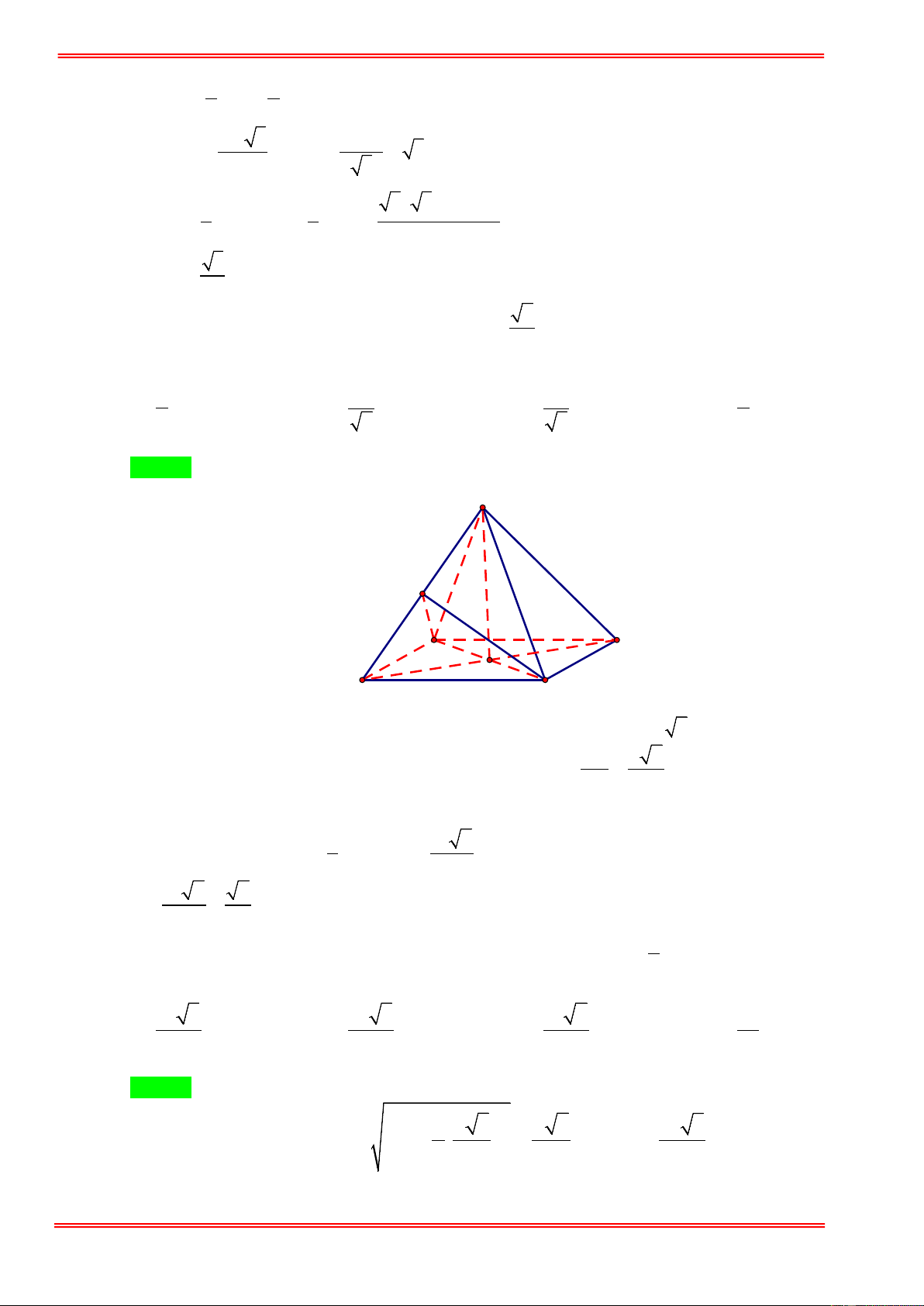
Câu 77.Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M , N lần lượt là trung điểm các cạnh AD, B . D Lấy
điểm không đổi P trên cạnh AB (khác ,
A B ). Thể tích khối chóp PMNC bằng 9 2 8 3 27 2 A. B. C. 3 3 D. 16 3 12
Câu 78. Tính thể tích V của khối chóp tứ giác đều có chiều cao là h và bán kính mặt cầu nội tiếp là r
(h > 2r > 0) . 2 2 4r h 2 2 4r h 2 2 3r h 2 2 4r h A. V = ( . B. V = . C. V = . D. V = . h + 2r ) 3(h − 2r ) 4 (h − 2r ) 3(h + 2r )
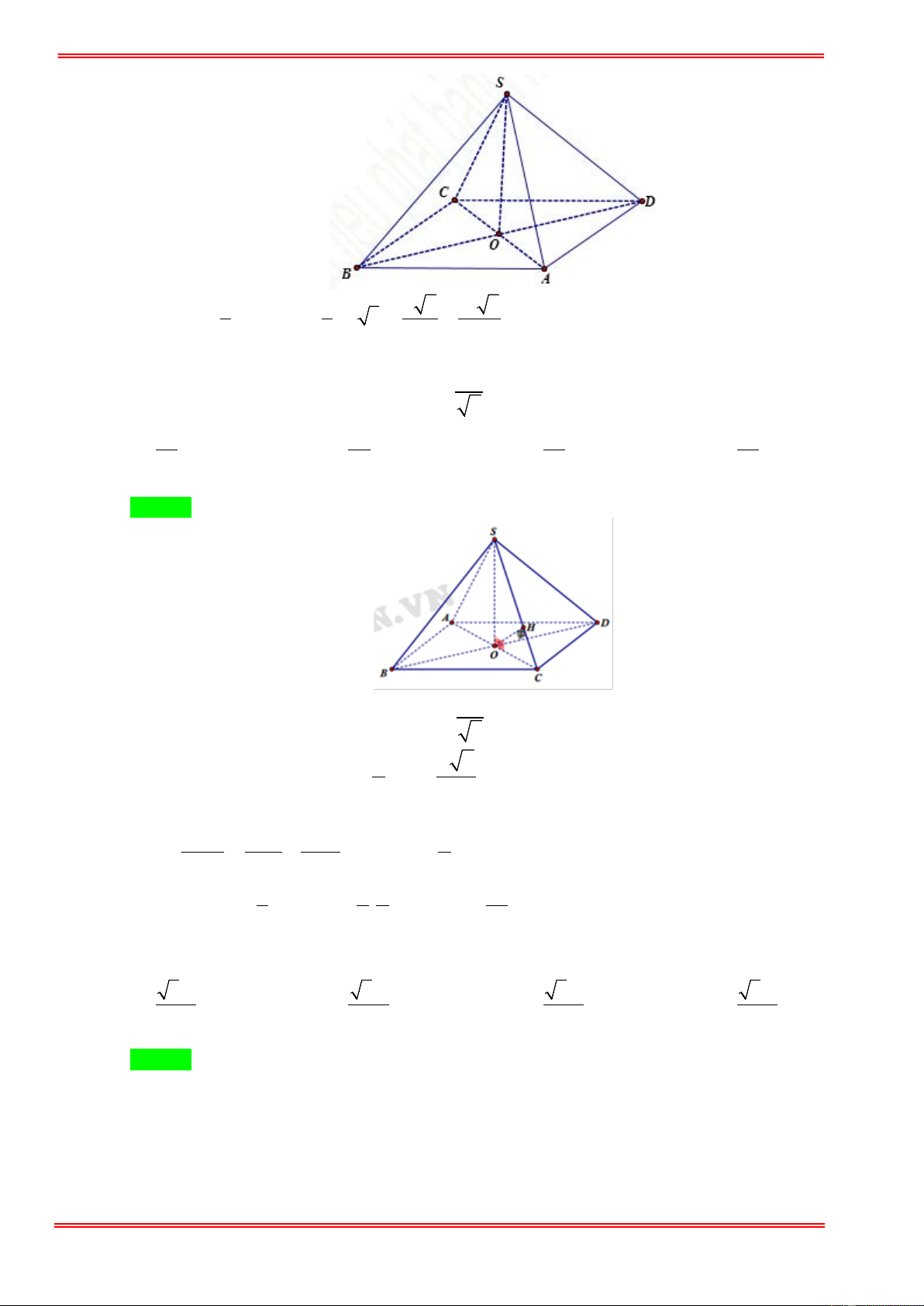
Câu 79. Cho khối tứ diện đều ABCD có cạnh bằng a . Gọi B ',C ' lần lượt là trung điểm của các cạnh AB
và AC . Tính thể tích V của khối tứ diện AB 'C ' D theo a . 3 a 3 a 2 3 a 3 3 a 2 A. V = . B. V = . C. V = . D. V = . 24 24 48 48
Câu 80. Thể tích khối tứ diện đều có cạnh bằng 2a là. 3 a 3 3 a 2 3 2a 2 A. . B. . C. 3 2a 2 . D. . 6 12 3
Câu 81. Cho hình chóp đều S.ABC có đáy cạnh bằng a , góc giữa đường thẳng SA và mặt phẳng ( ABC )
bằng 60°. Gọi A′, B′, C′ tương ứng là các điểm đối xứng của A , B , C qua S . Thể tích của khối
bát diện có các mặt ABC, A′B C
′ ′ , A′BC , B CA ′ , C A ′ B , AB C
′ ′, BA′C′ , CA′B′ là 3 2 3a 3 3a 3 4 3a A. . B. 3 2 3a . C. . D. . 3 2 3
Câu 82. Cho hình chóp tam giác đều S.ABC , cạnh đáy bằng a . Mặt bên tạo với mặt đáy một góc o 60 . Tính
thể tích V của hình chóp S.ABC . 3 a 3 3 a 3 3 a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . 2 12 24 6
Câu 83. Cho khối chóp đều S.ABC cạnh đáy bằng a , cạnh bên bằng 3a . Tính thể tích khối chóp đó ? 3 a 26 3 a 11 3 a 3 3 a 11 A. V = . B. V = . C. V = . D. V = . 12 6 4 12 https://toanmath.com/
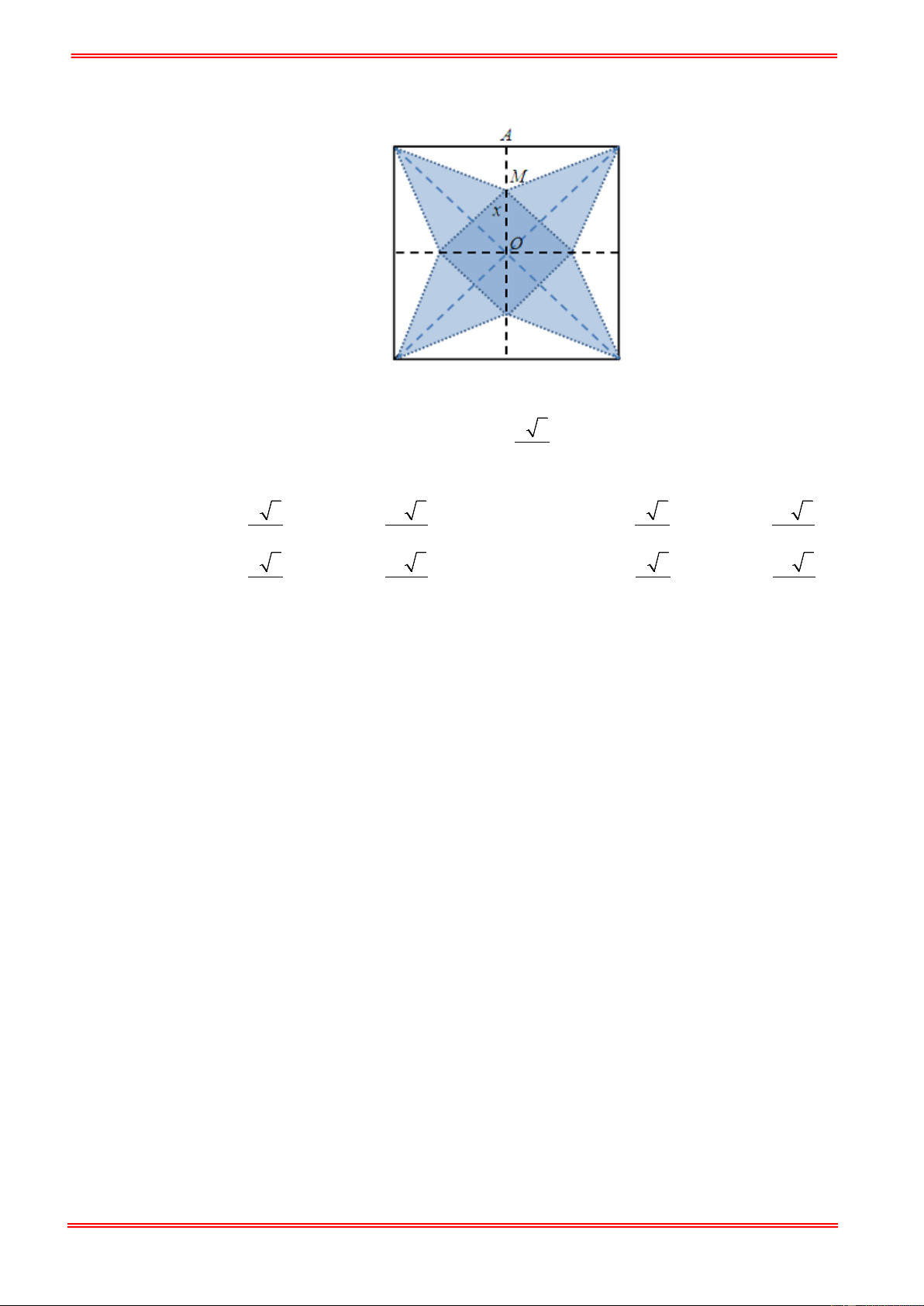
Câu 84.Cắt một miếng giấy hình vuông như hình bên và xếp thành hình một hình chóp tứ giác đều. Biết
các cạnh hình vuông bằng 20cm , OM = x(cm) . Tìm x để hình chóp đều ấy có thể tích lớn nhất
A. x = 8 cm .
B. x = 6 cm .
C. x = 7 cm .
D. x = 9 cm .
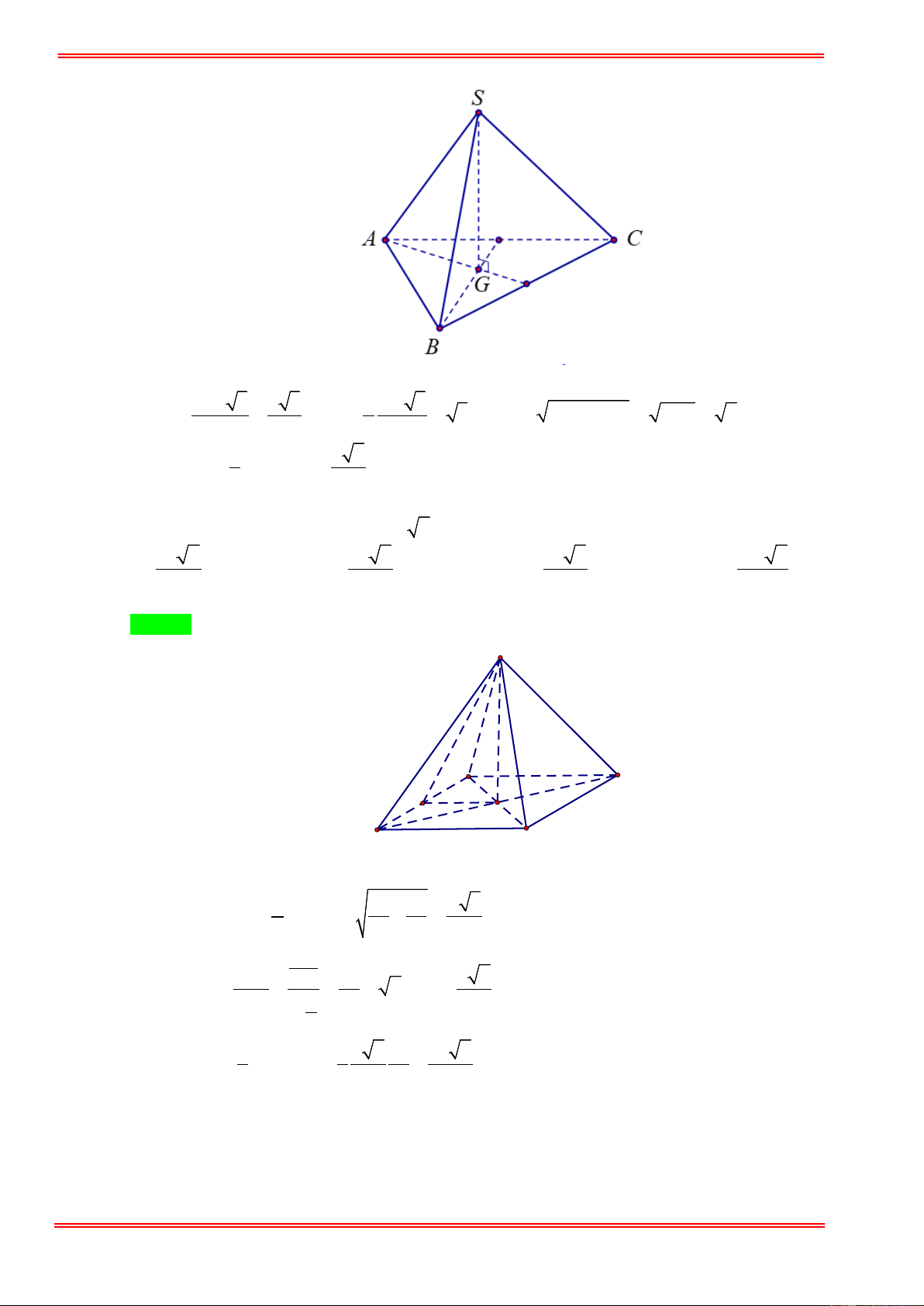
Câu 85. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a . Gọi G là trọng tâm của tam giác SAC và khoảng cách từ a
G đến mặt bên (SCD) bằng
3 . Tính khoảng cách từ tâm O của đáy đến 6
mặt bên (SCD) và thể tích của khối chóp S.ABCD . a 3 3 a 3 a 3 3 a 3 A. d( = và V = . B. d = và V = . O,(SCD)) (O,(SCD)) 2 S . ABCD 6 4 S . ABCD 6 a 3 3 a 3 a 3 3 a 3 C. d( = và V = . D. d = và V = . O,(SCD)) (O,(SCD)) 4 S . ABCD 2 2 S . ABCD 2 https://toanmath.com/
THỂ TÍCH KHỐI CHÓP ĐỀU B. LỜI GIẢI CHI TIẾT Câu 1.
Cho khối tứ diện đều ABCD cạnh bằng a , M là trung điểm BC . Thể tích V của khối chóp
M .ABC bằng bao nhiêu? 3 3a 3 a 3 2a 3 2a A. V = . B. V = . C. V = . D. V = . 24 2 12 24 Hướng dẫn giải Chọn D 3 3 1 1 a 2 a 2 Ta có V = V = . = . M . ABC 2 ABCD 2 12 24 Câu 2.
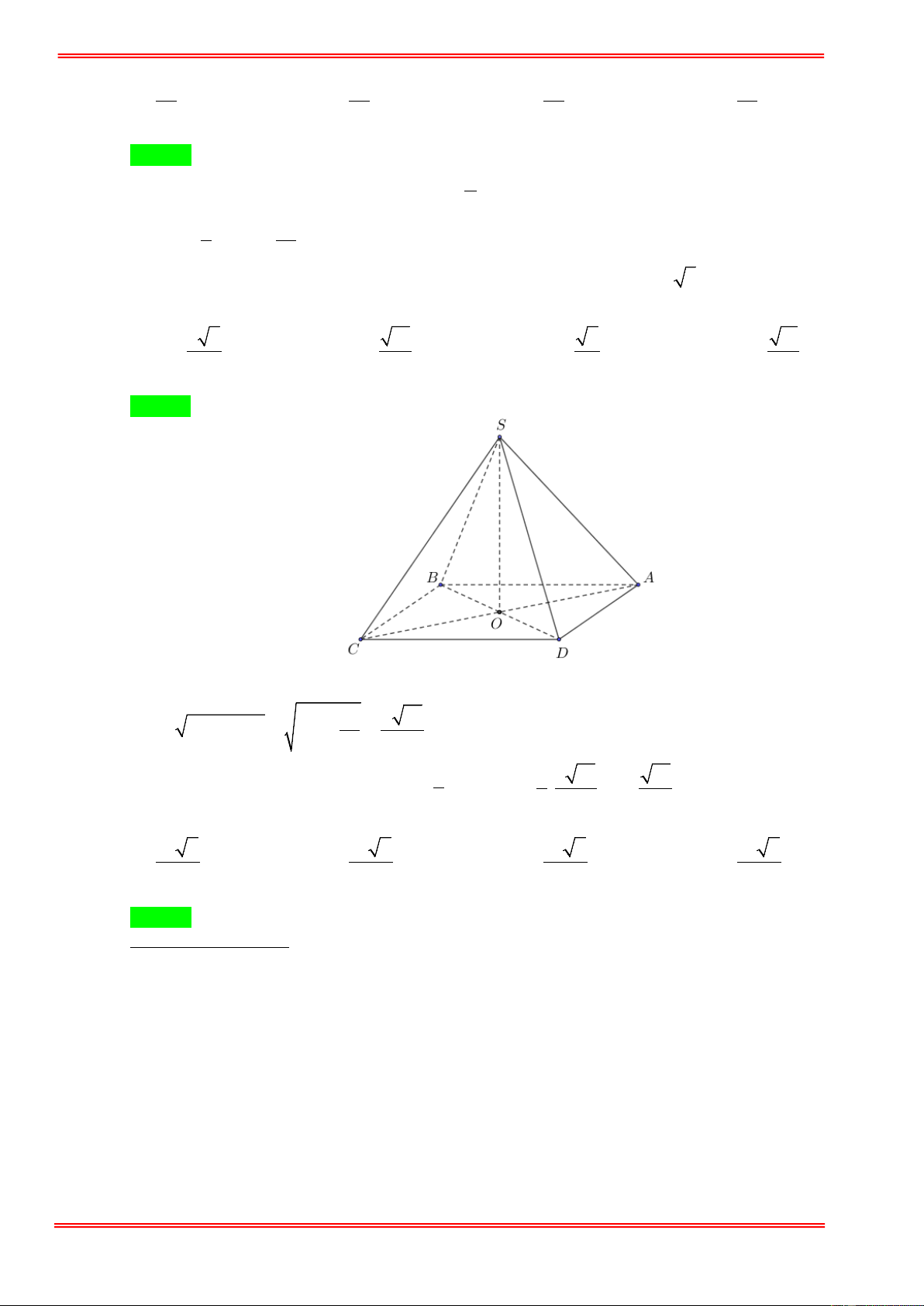
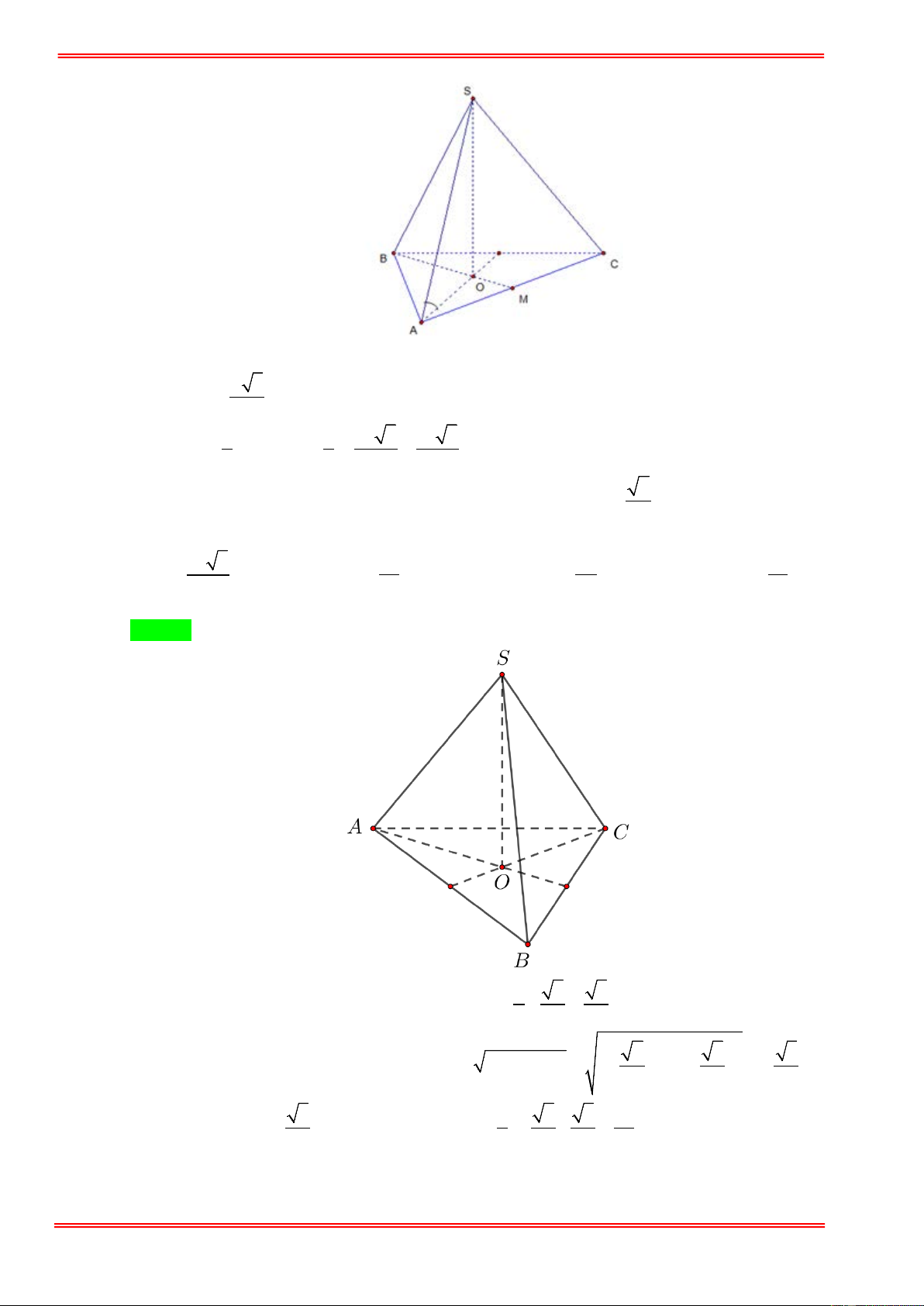
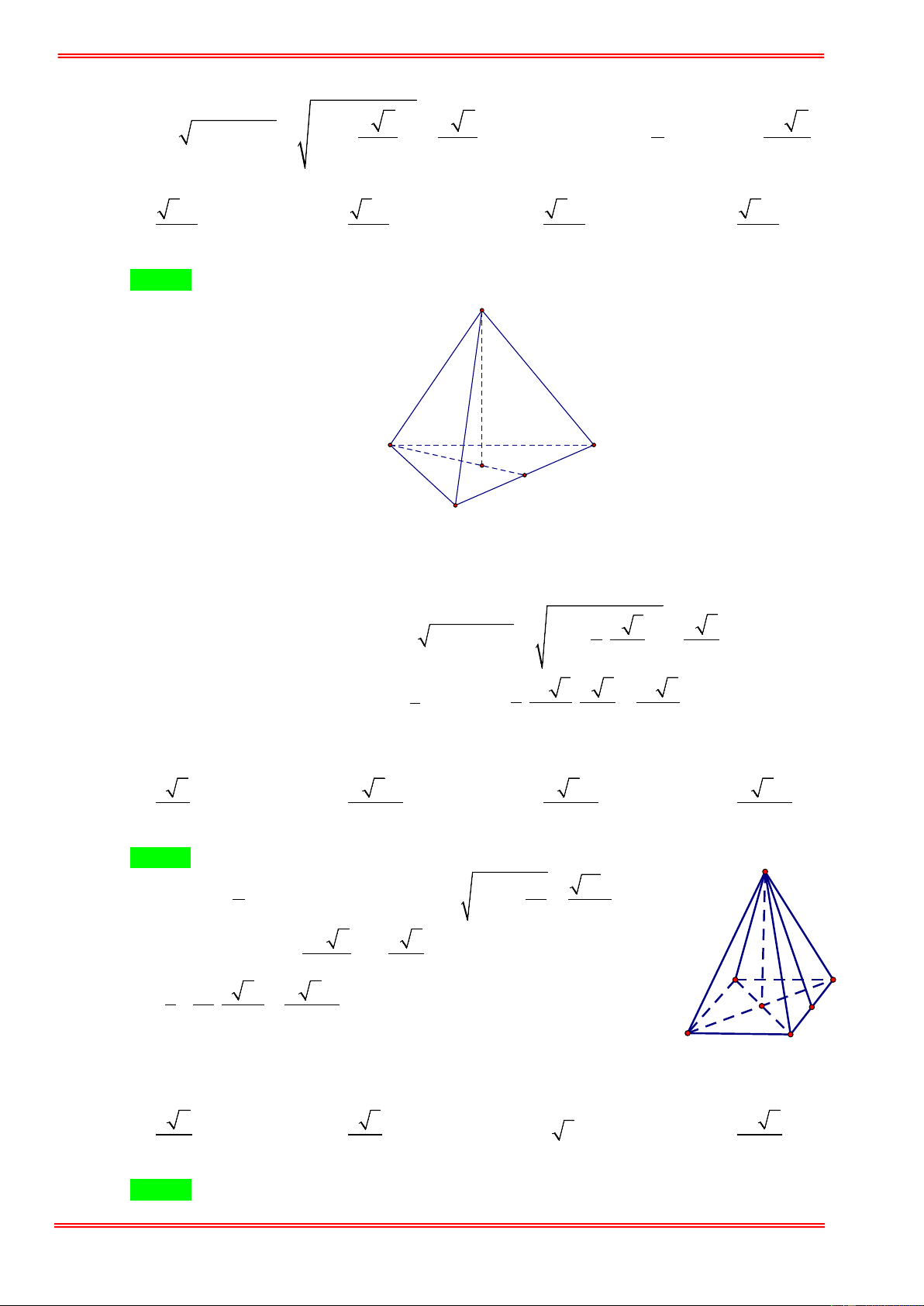
Cho hình chóp đều S.ABCD có cạnh đáy bằng a và cạnh bên tạo với đáy một góc 60°. Thể tích
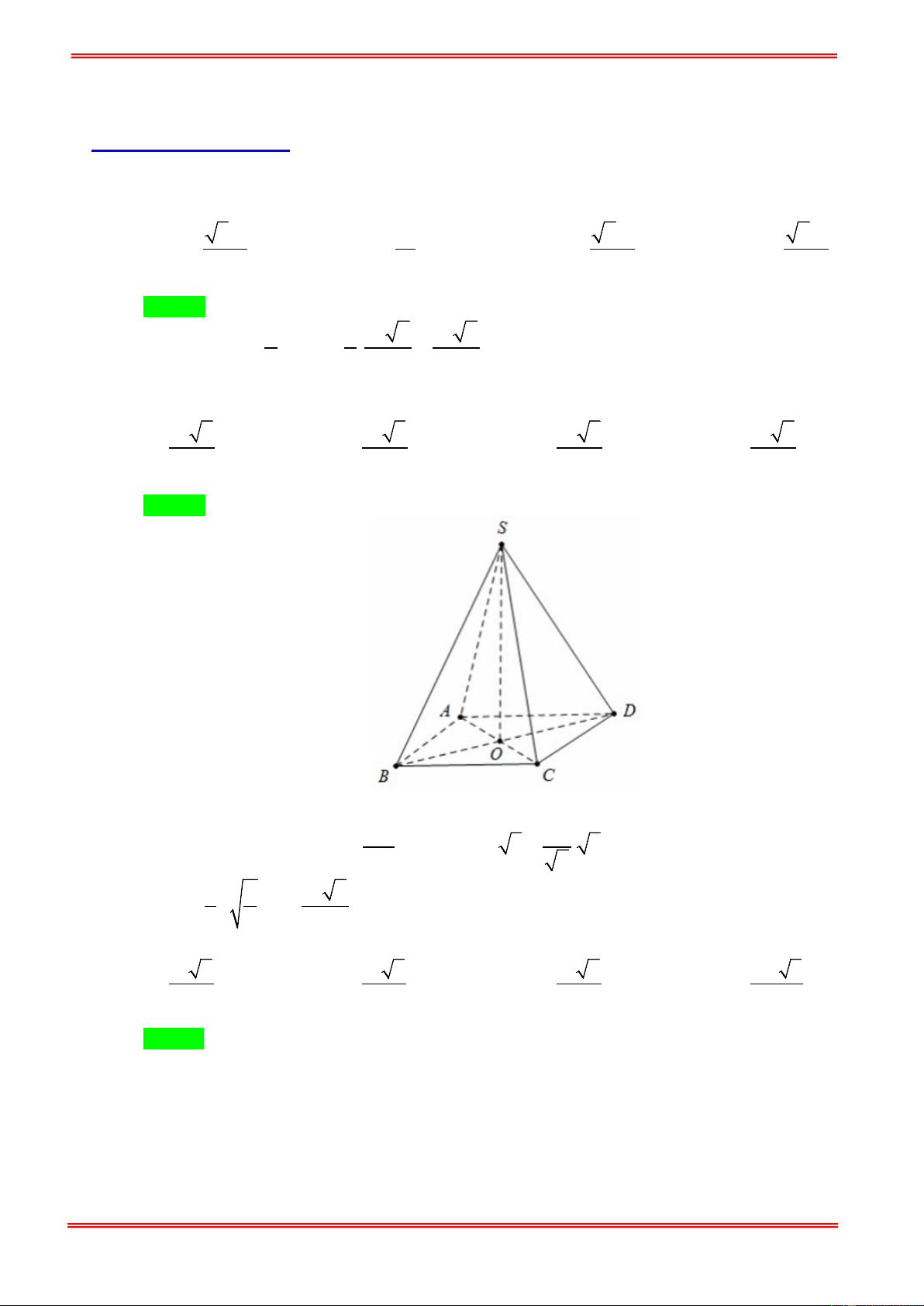
của hình chóp đều đó là: 3 a 6 3 a 3 3 a 3 3 a 6 A. . B. . C. . D. . 6 6 2 2 Hướng dẫn giải Chọn A
Gọi O = AC ∩ BD ⇒ SO ⊥ ( ABCD) ⇒  SO a
SCO = 60° ⇒ tan 60° = ⇒ SO = OC 3 = . 3 OC 2 3 1 3 a 6 2 ⇒ V = a .a = . 3 2 6
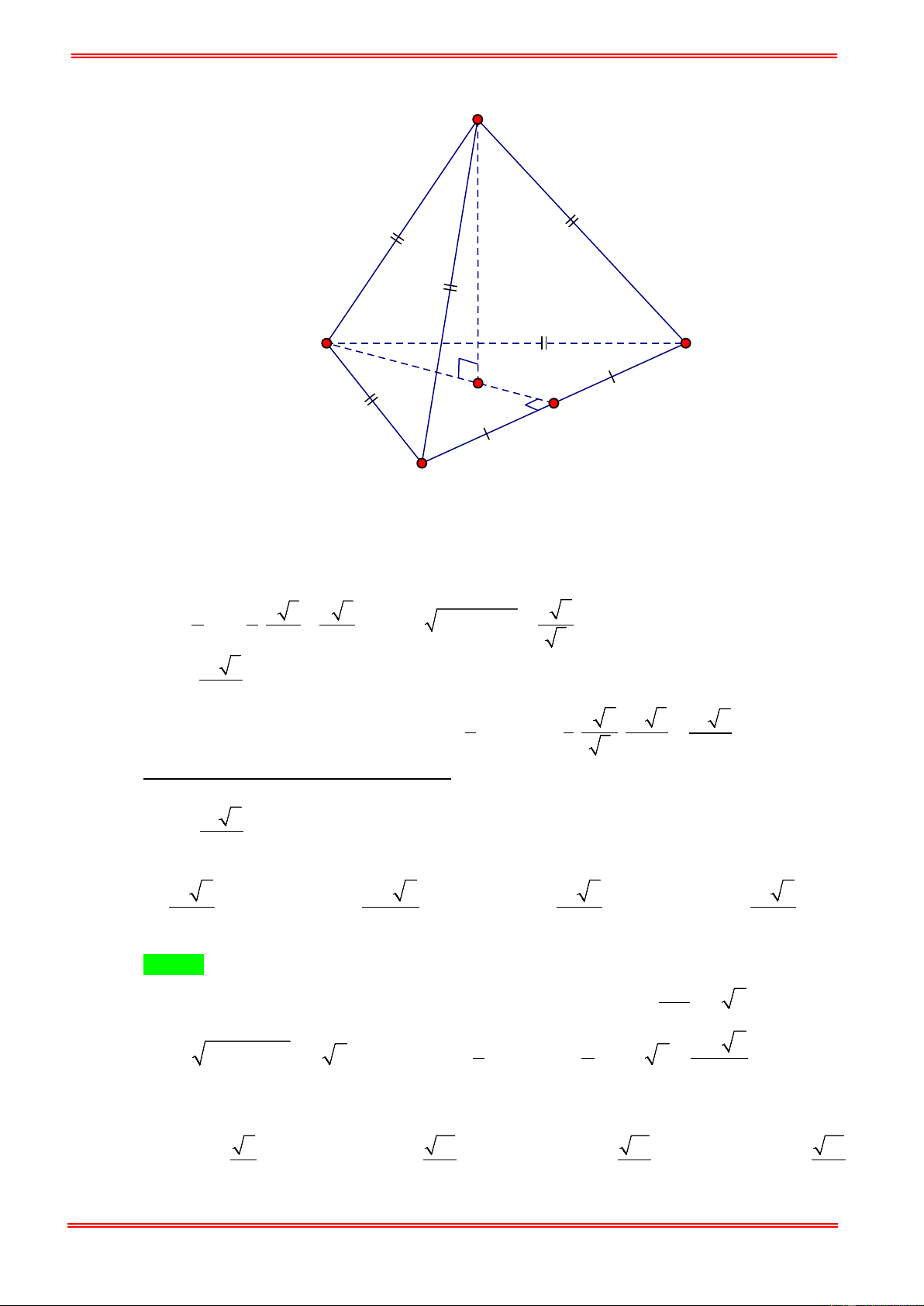
Câu 3. Thể tích hình tứ diện đều có cạnh bằng a là: 3 a 2 3 a 2 3 a 2 3 5a 2 A. . B. . C. . D. . 3 12 6 12 Hướng dẫn giải Chọn B https://toanmath.com/
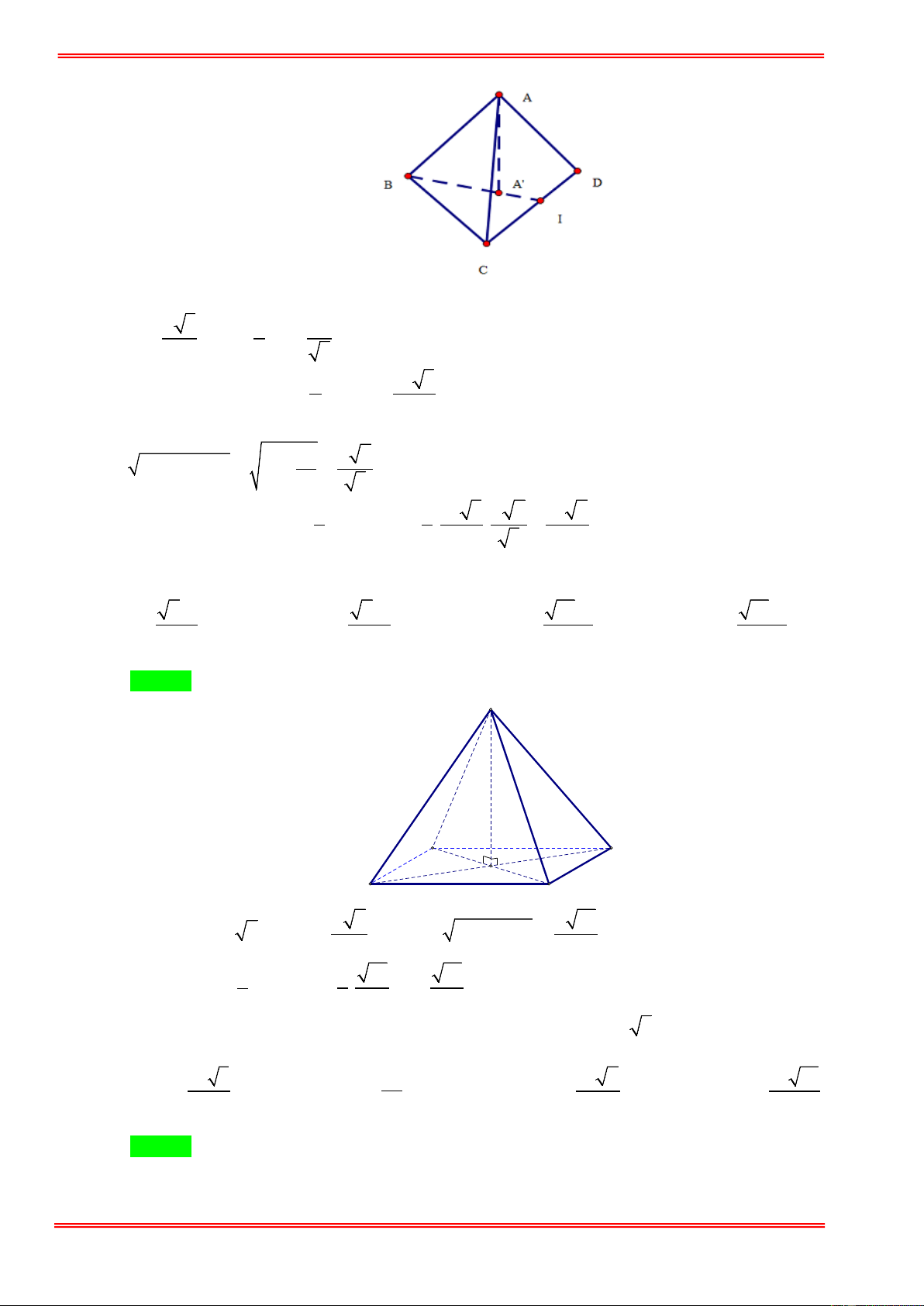
Gọi I là trung điểm B ,
A A' là trọng tâm A ∆ BC . a 3 2 a Ta có BI = , BA' = BI = ,. 2 3 3 2 diện tích tam giác 1 a 3 BCD là S = C . D AI = . 2 4
Trong tam giác ABA ' vuông tại A' ta có: 2 a a 2 2 2 2 A ' A =
AB − A ' B = a − = 3 3 2 3 Thể tích tứ diện là: 1 1 a 3 a 2 a 2 V = S .A ' A = . . = . x ∆ 3 ABC 3 4 3 12
Câu 4.Cho khối chóp tứ giác đều có cạnh đáy bằng a , cạnh bên gấp hai lần cạnh đáy. Tính thể tích V của
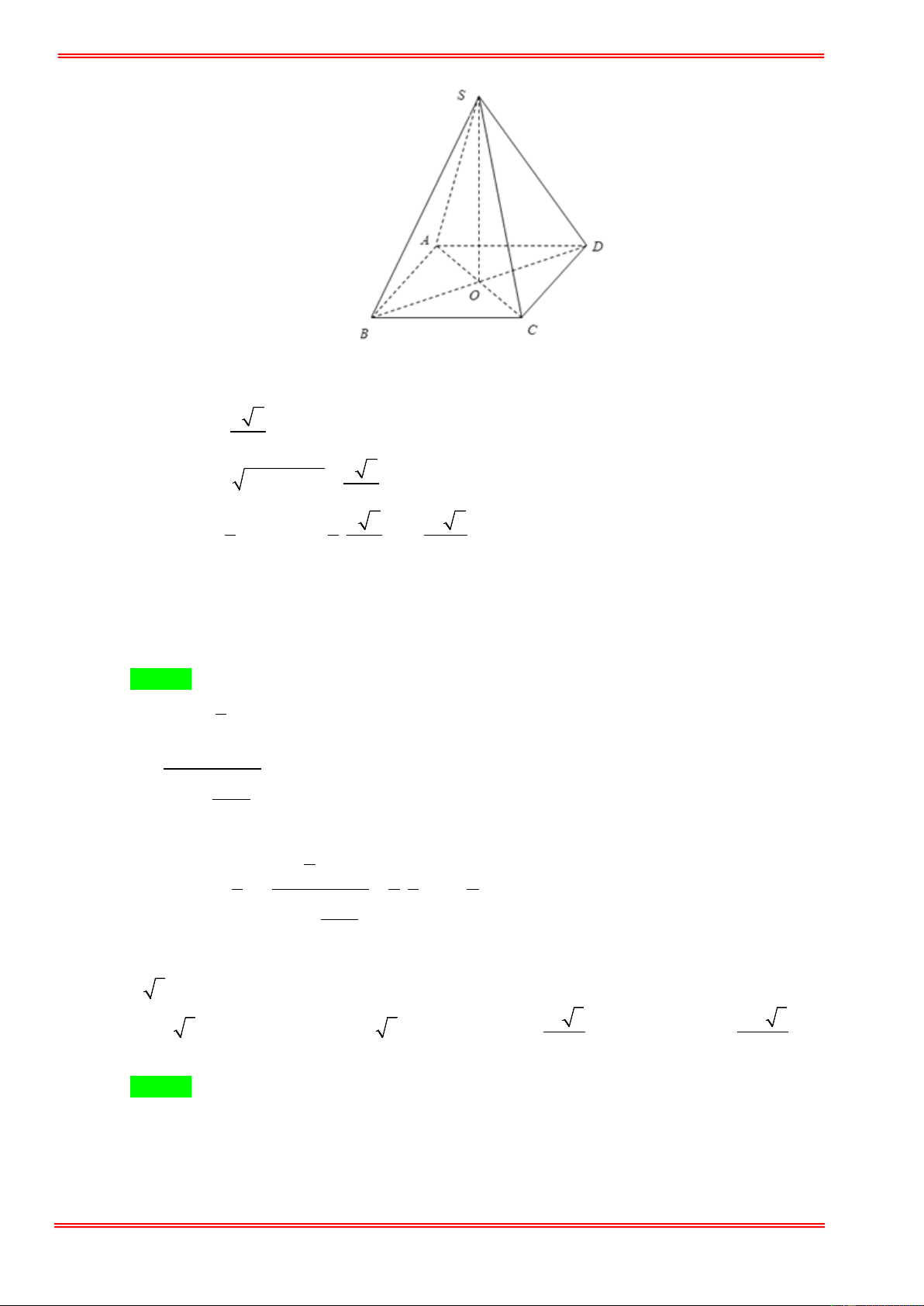
khối chóp tứ giác đã cho. 3 2a 3 2a 3 14a 3 14a A. . B. . C. . D. . 2 6 6 2 Hướng dẫn giải Chọn C S C B O D A a a Ta có AC = 2 a 2 ⇒ AO = 2 2 ⇒ SO = SA − 14 OA = . 2 2 Vậy 1 1 14 14 V = . SO S 3 3 = . .a = a . S . ABCD 3 ABCD 3 2 6
Câu 5. Cho hình chóp tứ giác đều có cạnh đáy bằng a và cạnh bên bằng a 3 . Tính thể tích V của khối
chóp đó theo a . 3 a 3 3 a 3 a 2 3 a 10 A. V = . B. V = . C. V = . D. V = . 3 2 3 6 Hướng dẫn giải Chọn D https://toanmath.com/ S D A B C 2 a a 10
Gọi h là chiều cao hình chóp, ta có 2 h = 3a − = . 2 2 1 3 1 a 10 a 10 V = S .h 2 = a . = . 3 ABCD 3 2 6
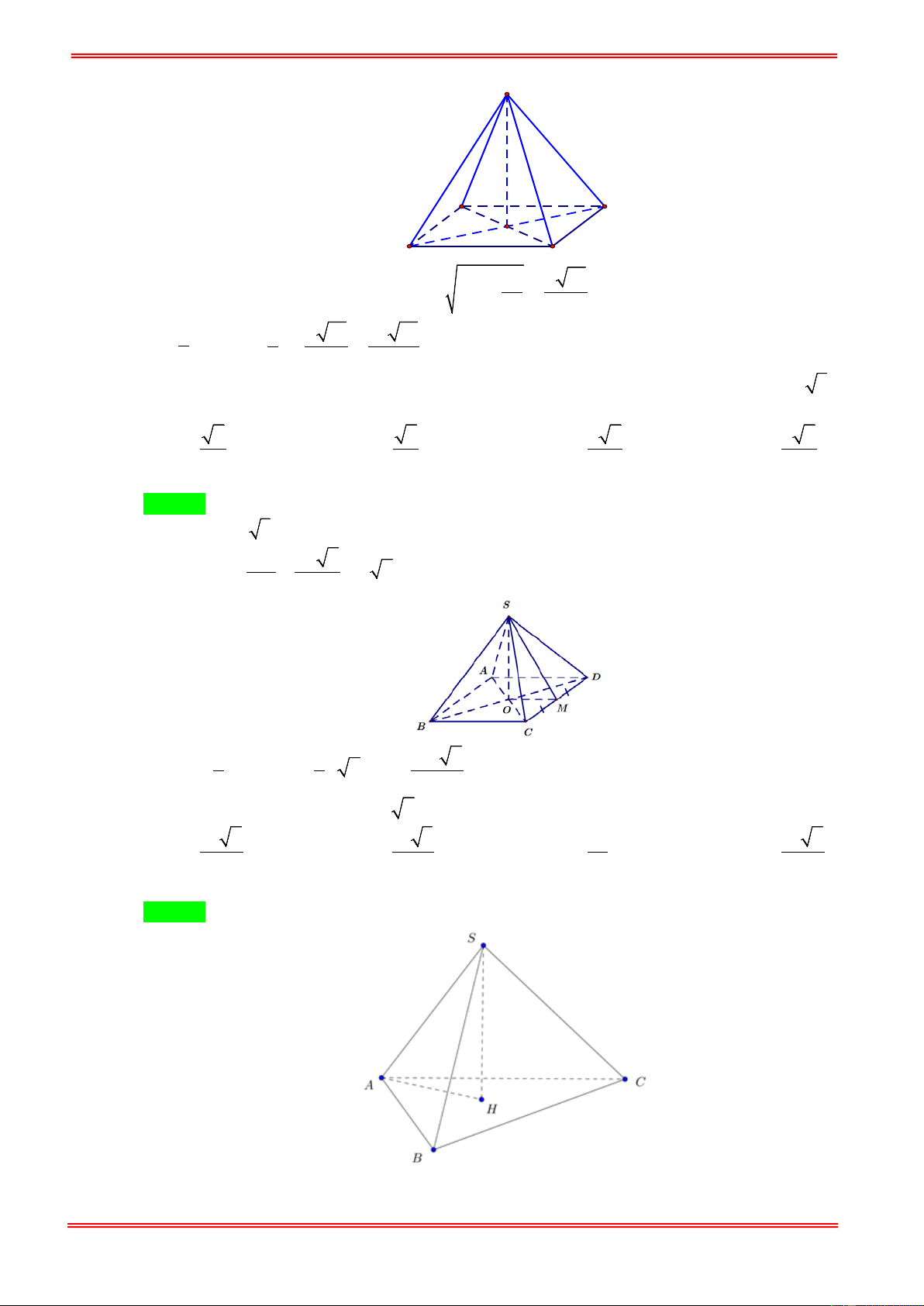
Câu 6. Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, đường cao của một mặt bên là a 3 . Thể
tích V của khối chóp đó là: 2 2 2 2 4 2 A. 3 V = a . B. 3 V = a . C. 3 V = a . D. 3 V = a . 6 9 3 3 Hướng dẫn giải Chọn D
Ta có SM = a 3 . SC
∆ D đều nên SC = CD = 2a . AC 2a 2 Suy ra: SO = = = a 2 . 2 2 3 Vậy 1 1 4a 2 2 V = . SO S = a 2.4a = . 3 ABCD 3 3
Câu 7. Cho tứ diện đều ABCD cạnh bằng 2a . Tính thể tích của khối tứ diện đó. 3 a 2 3 a 3 3 a 3 a 2 A. V = . B. V = . V = D. V = . 12 6 C. 3 . 6 Hướng dẫn giải: Chọn C . https://toanmath.com/ 2 2 AB 3 a 3 2 2 2a 3 a 6 Ta có S = = ; AH = m = . = . ABC 4 2 3 a 3 2 3 2a 3 2 2
⇒ SH = SA − AH = . 3 3 1 a
⇒ V = SH.S = . 3 ABC 3
Câu 8. Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a , khoảng cách giữa hai đường thẳng SA và CD
bằng a 3 . Thể tích khối chóp đều S.ABCD bằng? 3 4a 3 3 a 3 A. 3 4a 3 . B. 3 a 3 . C. . D. . 3 3 Hướng dẫn giải Chọn C S A D O B C
Gọi O = AC ∩ BD , hình chóp đều S.ABCD ⇒ SO ⊥ ( ABCD) và tứ giác ABCD là hình vuông.
Ta có CD//AB ⇒ CD// (SAB) ⇒ d (C ;
D SA) = d (C;(SAB)) = 2d ( ; O (SAB)) . a Bài ra d (C ;
D SA) = a 3 ⇒ d (O (SAB)) 3 ; = . 2 1 1 1 1 a Tứ diện vuông . O SAB ⇒ = + +
với h = d (O (SAB)) 3 ; = . 2 2 2 2 h OS OA OB 2 AB 4 1 1 1 Cạnh OA = OB = = a 2 ⇒ = + + ⇒ SO = a 3 . 2 2 2 2 2 3a SO 2a 2a 3 Do đó 1 1 4a 3 V = . SO S 2 = a 3.4a = . S . ABCD 3 ABCD 3 3
Câu 9. Cho khối chóp đều S.ABC có cạnh bên bằng a và các mặt bên hợp với đáy một góc 45° . Tính thể
tích của khối chóp S.ABC theo . a . 3 a 15 3 a 5 3 a 3 a 15 A. 25 . B. 25 . C. 3 . D. 5 . Hướng dẫn giải Chọn A https://toanmath.com/ .
Gọi O là trọng tâm tam giác ABC ⇒ SO ⊥ (ABC).
I là trung điểm của BC ⇒ ( SBC) (ABC))   , = SIO = 45 . ° .
x là độ dài cạnh của tam giác ABC ( x > 0 ). 2 1 x 3 x Ta có: 2 2 2 OI = AI =
; SI = SC − IC = a − . 3 6 4 . 2 x 3 2 x 2 15a
Trong tam giác SOI có: 2 2 2
OI = SIcos45° ⇒ = a −
⇔ 5x = 12a ⇒ x = . 6 2 4 5 . 5 2 x 3 3 3 2
Suy ra: SO = OI = , a S = = a . 5 ABC ∆ 4 5 . 3 1 3 3 5 a 15 Vậy: 2 V = . a . a = . S.ABC 3 5 5 25 .
Câu 10. Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, đường cao của một mặt bên là a 3 . Tính
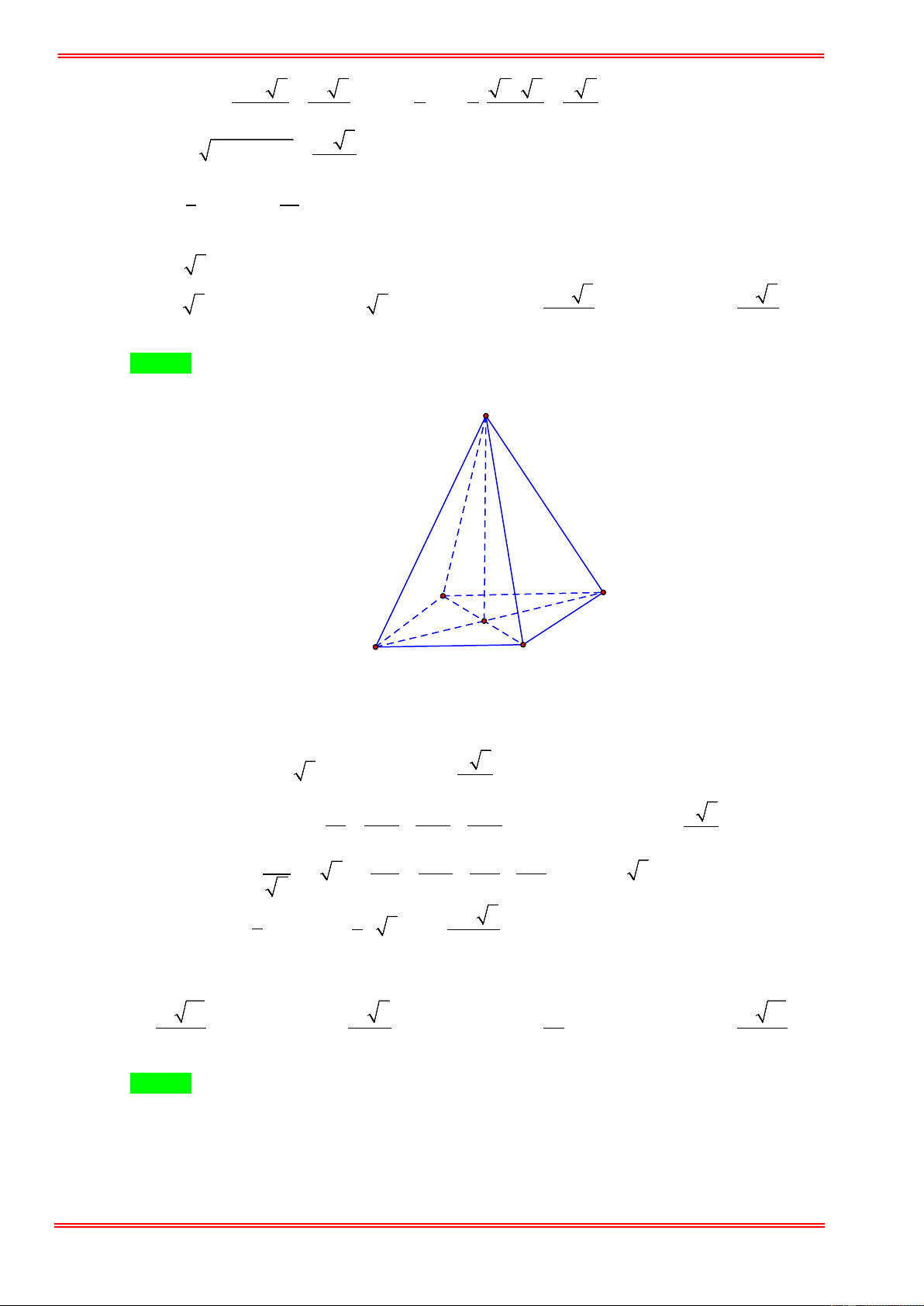
thể tích V của khối chóp đó. 3 a 2 3 4a 2 3 a 2 A. V = . B. 3 V = 4a 2 . C. V = . D. V = . 9 3 6 Hướng dẫn giải Chọn C
Gọi cạnh của hình chóp tứ giác đều là x . 2 x
Xét tam giác vuông SCH ta có 2 2 2
SC − HC = SH 2 2 ⇔ x −
= 3a ⇔ x = 2a . 4 Chiều cao 2 2 2 2 SO =
SH − HO = 3a − a = a 2 . https://toanmath.com/ 3 Thể tích khối chóp là 1 4a 2 2 V = .a 2.4a = . 3 3
Câu 11. Cho hình chóp tam giác đều cạnh đáy bằng a và các mặt bên đều tạo với mặt phẳng đáy một góc 60 .
° Tính thể tích V của khối chóp. 3 a 3 3 a 3 3 a 2 3 a 3 A. V = . B. V = . C. V = . D. V = . 4 24 6 8 Hướng dẫn giải Chọn B S A C G M B .
Gọi M là trung điểm của BC , G là trọng tâm ABC ∆ . 2 2 AB 3 a 3 S . ABC ∆ = = . 4 4 1 AB 3 a 3 GM = = . 3 2 6
Ta có: góc giữa mặt đáy và mặt bên bằng 60° suy ra  SMG = 60 .
° Xét tam giác vuông SGM :  SG tan SMG = .. GM a 3 a
Suy ra: SG = GM . tan 60° = . 3 = .. 6 2 2 3 Vậy 1 1 a a 3 a 3 V = . SG S = . . = . S.ABC ∆ 3 ABC 3 2 4 24
Câu 12. Cho hình chóp tứ giác đều có cạnh đáy bằng a , cạnh bên bằng a 2 (hình vẽ). Thể tích khối chóp là 3 a 3 3 2a 2 3 a 6 3 a 6 A. . B. . C. . D. . 6 3 3 6 Hướng dẫn giải Chọn D https://toanmath.com/
Xét hình chóp tứ giác đều S.ABCD . a 2 2 a a 6 Ta có: OD = , 2 2 2 SO =
SD − OD = 2a − = . 2 2 2 3 1 1 a 6 a 6 2 V = . . SO S = . .a = . S . ABCD 3 ABCD 3 2 6 Câu 13.
[Sở GDĐT Lâm Đồng lần 07 - 2017] Cho (H ) là khối chóp tứ giác đều có tất cả các cạnh
bằng 2a . Thể tích của (H ) bằng: 4 4 3 4 2 4 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 5 3 3 3 Hướng dẫn giải Chọn C
ABCD hình vuông cạnh 2a => AC = 2a 2 2 2 2
=> AO = .SO = SA – AO ==> SO = a 2 . 1 4 2 2 3 V = (2a) .a 2 = a . 3 3
Câu 14. Một hình chóp tam giác đều có cạnh bên bằng b và cạnh bên tạo với mặt phẳng đáy một góc α .
Thể tích của hình chóp đó là 3 3 A. 3
b cosα sin α . B. 3 2
b sin α cosα . 4 4 3 3 C. 3 2
b cos α sin α . D. 3 2
b cos α sin α . 4 4 Hướng dẫn giải Chọn D
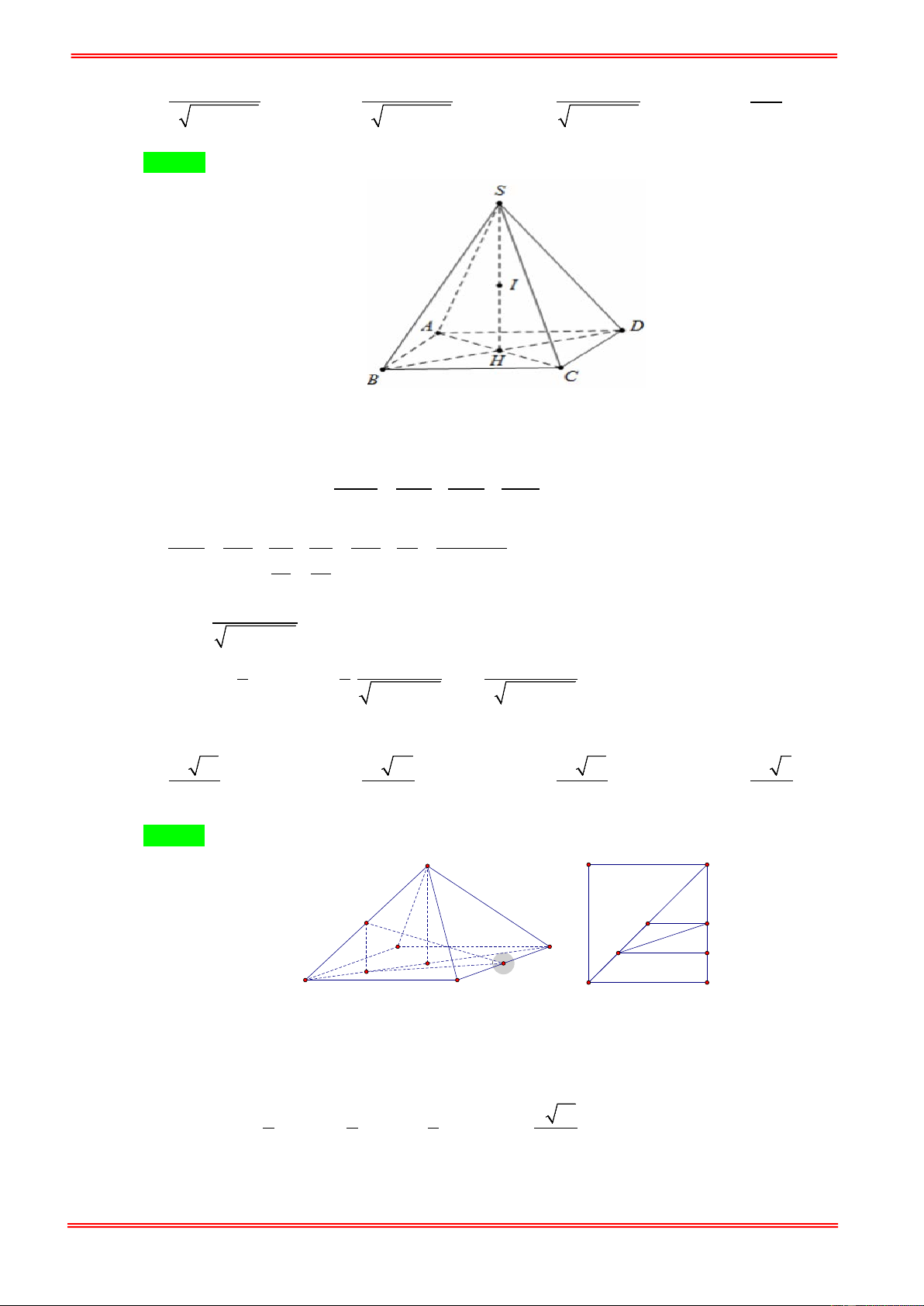
Gọi M là trung điểm BC , H là tâm tam giác ABC .
Ta có: SH ⊥ ( ABC ) .
SH = SAsinα = bsinα Xét tam giác S
∆ HA vuông tại H , ta có: 
AH = SAcosα = b cosα https://toanmath.com/ 3 3
⇒ AM = AH = b cosα . 2 2 AB 3 2 AM Mà: AM = ⇔ AB = = 3 cosα . 2 3 3 ( 3b cosα 1 1 )2 V = .SH.S = .bsinα. SABC ABC 3 3 4 . 3 3 2 = b cos α sin α 4 2
Câu 15.Cho hình chóp tứ giác đều S.ABCD có thể tích V =
. Gọi M là trung điểm của cạnh SD . Nếu 6
SB ⊥ SD thì khoảng cách từ B đến mặt phẳng ( MAC ) bằng: 3 1 2 1 A. . B. . C. . D. . 4 2 3 2 Hướng dẫn giải Chọn D S M D A O B C
Giả sử hình chóp có đáy ABCD là hình vuông cạnh a . Khi đó, BD = a 2 . BD a 2
Tam giác SBD vuông cân tại S nên SD = SB = a và SO = = . 2 2
Suy ra các tam giác SCD, SAD là các tam giác đều cạnh a và SD ⊥ (MAC ) tại M . 3 Thể tích khối chóp là 1 a 2 V = . . SO S = 3 ABCD 6 3 a 2 2 Mà = ⇒ a = 1 6 6
Vì O là trung điểm BD nên d ( B (MAC )) = d ( D (MAC )) 1 , , = DM = . 2
Câu 16. Khối chóp tam giác đều có tất cả các cạnh bằng a có thể tích bằng: 3 a 3 3 a 3 3 a 2 3 a A. . B. . C. . D. . 12 4 6 3 Hướng dẫn giải Chọn A 2  2 a 3  a 6 2 a 3
Chiều cao của khối chóp là 2 h = a −  .  = mà S = . 3 2 3   day 4 https://toanmath.com/ 3 Do đó thể 1 a 3 tích khối chóp là . h S = . 3 day 12
Câu 17. Khi chiều cao của một hình chóp đều tăng lên n lần nhưng mỗi cạnh đáy giảm đi n lần thì thể tích của nó.
A. Không thay đổi.
B. Tăng lên n lần.
C. Tăng lên n −1 lần.
D. Giảm đi n lần. Hướng dẫn giải Chọn D 1 Ta có: V = . .
h S , với h là chiều cao, S là diện tích đáy 3 2 x a S =
với x là độ dài cạnh của đa giác đều, a là số đỉnh của đa giác đều. 0 180  4 tan    a    2  x a   1  n  1 1 1 Ycbt ⇔ = = = 1 V . . nh . . . h S .V .  0 3  n 3 180 n 4 tan    a   
Câu 18. Tính thể tích khối chóp tứ giác đều có tất cả các cạnh bằng a . 3 2a 3 3 a 2 3 a 3 3 a 3 A. . B. . C. . D. . 3 6 4 2 Hướng dẫn giải Chọn B
Giả sử cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a .
Diện tích đáy ABCD : 2 S = a . ABCD 2 1 1 a 2  a 2  a 2 AO = AC = AB 2 = ; 2 2 2 SO =
SA − AO = a −   =   2 2 2 2 2   3 1 1 a 2 a 2
Vậy thể tích khối chóp tứ giác đều là: 2 V = S .SO = .a . = . 3 ABCD 3 2 6 S A B O D C
Câu 19. Cho khối chóp đều S.ABC có cạnh đáy bằng a , tính thể tích khối chóp S.ABC biết cạnh bên bằng a là: 3 a 3 a 2 3 a 3 3 a A. V = . B. V = . C. V = . D. V = . S . ABC 4 S . ABC 12 S . ABC 6 S . ABC 12 Hướng dẫn giải Chọn B https://toanmath.com/
Gọi H là trọng tâm ABC ∆ đều 
→ SH ⊥ ( ABC) . 2 a 3 AH = AM =
(M là trung điểm BC) 3 3 a 6 S
∆ AH vuông tại H có 2 2 SH = SA − AH = . 3 2 a 3 ABC ∆
đều cạnh a nên S = . ABC 4 2 3 1 1 a 3 a 6 a 2 Vậy V = S .SH = . . = . 3 ABC 3 4 3 12
Câu 20. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , cạnh bên hợp với đáy một góc 60 . Thể
tích V của khối chóp S.ABCD bằng 3 3 a 3 a 3 3 a 6 3 a 6 V = V = V = V = A. 2 . B. 3 . C. 6 . D. 3 . 1 7 T 1 7 T 1 7 T 1 7 T 1 7 T 1 7 T 1 7 T 1 7 T Hướng dẫn giải Chọn C 1 7 T
Gọi O = AC ∩ BD thì SO ⊥ ( ABCD) .
Ta có góc giữa cạnh bên và mặt đáy là góc  SDO = 60 .
Mà ABCD là hình vuông nên BD = AB 2 = a 2 . 3 a 6
Tam giác SBD đều nên SO = B . D = . 2 2 https://toanmath.com/ 3 Vậy 1 1 a 6 a 6 2 V = . . SO S = . .a = . S . ABCD 3 ABCD 3 2 6
Câu 21. Cho hình chóp tam giác đều cạnh đáy bằng a và các mặt bên đều tạo với mặt phẳng đáy một góc 0
60 . Tính thể tích V của khối chóp. 3 a 3 3 a 3 3 a 2 3 a 3 A. V  . B. V  . C. V  . D. V  . 24 4 6 8 Hướng dẫn giải Chọn A
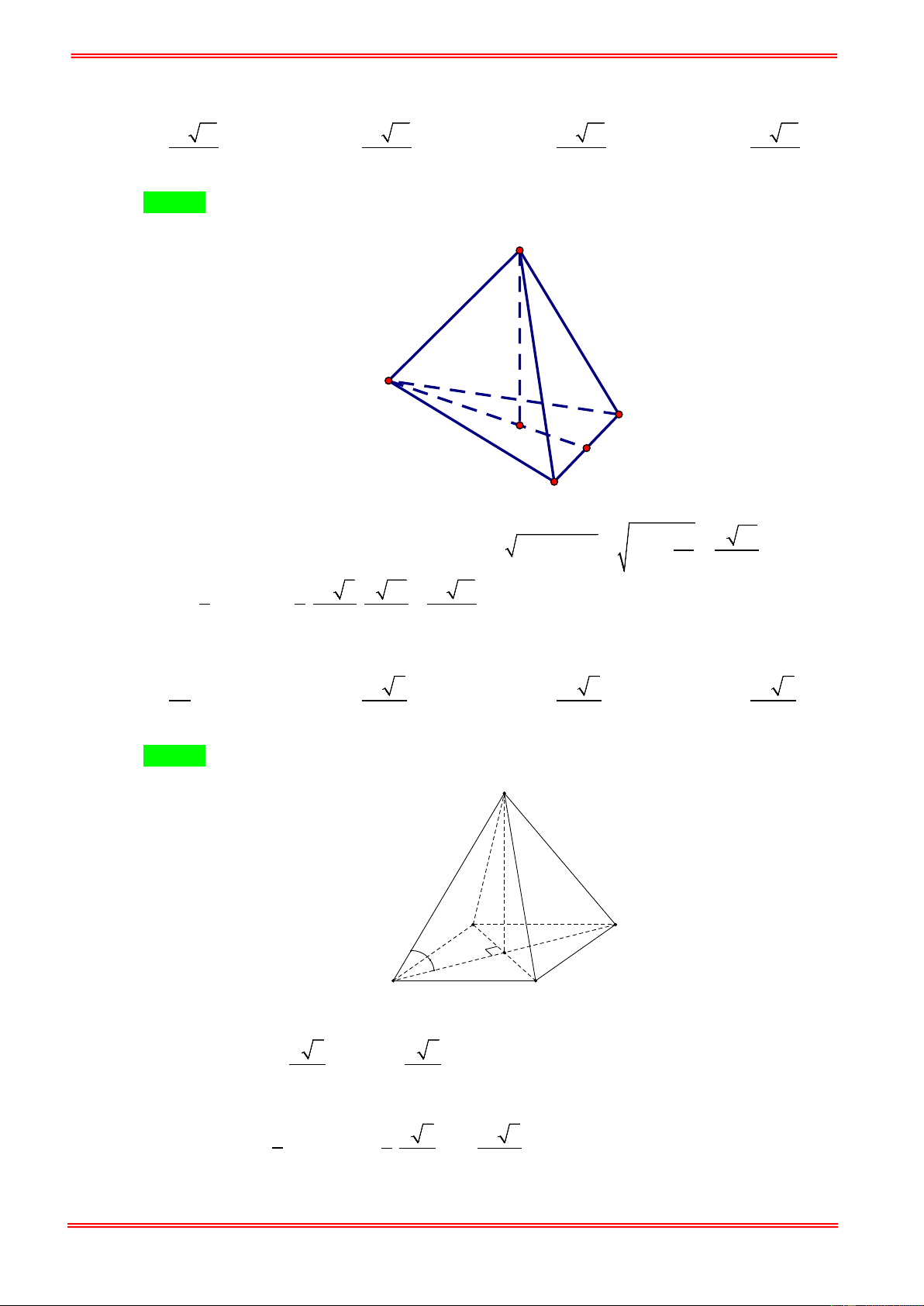
Gọi hình chóp tam giác đó là S.ABC, kẻ SH ⊥ ( ABC) tại H..
Gọi A', B ', C ' lần lượt là chân đường cao hạ từ H xuống BC, CA, AB. . Xét S ∆ HA', S ∆ HB ', S
∆ HC ' đều vuông tại H có SH chung.  =  =  0 = ⇒  =  =  SB ' H SC ' H SA' H 60 HSC ' HSA' HSB ' . ⇒ S ∆ HA' = S ∆ HB ' = S ∆ HC ' (
g − g − g ) ⇒ HA' = HB ' = HC '. .
Do đó H là tâm đường tròn nội tiếp tam giác ABC.. 3
AB + BC + CA
Tam giác ABC đều cạnh 2 a ⇒ S = a = .HA ' . ABC 4 2 3 3a 3 2 ⇒ a = HA ' ⇒ HA ' = . a . 4 2 6 a
Tam giác SHA ' vuông tại H và  0
HA ' S = 60 ⇒ SH = HA '. tan 60 = . . 2 Thể tích 1 1 a 3 3 2 3 V = SH .S = . . a = a .. 3 ABC 3 2 4 24 a
Câu 22. Thể tích của khối chóp tứ giác đều có chiều cao bằng
6 và cạnh đáy bằng a 3 bằng: 3 3 3a 2 3 3a 2 3 a 6 3 3a 6 A. . B. . C. . D. . 2 4 3 2 Hướng dẫn giải Chọn C https://toanmath.com/ 1 a 3 a 6 Ta có : V = S .SO = (a )2 1 6 . 3 . = . 3 ABCD 3 3 3
Câu 23. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a . Gọi điểm O là giao điểm của AC và a
BD . Biết khoảng cách từ O đến SC bằng
. Tính thể tích khối chóp S.ABC . 6 3 a 3 a 3 a 3 a A. . B. . C. . D. . 6 4 8 12 Hướng dẫn giải Chọn C a
H là hình chiếu của O lên SC nên OH = , 6 1 a 2
ABCD là hình vuông có OC = AC = 2 2 S
∆ OC vuông tại O có OH là đường cao 1 1 1 a  → = +  → SO = . 2 2 2 OH SO OC 2 3 1 1 1 a  →V = S .SO = . S .SO = . S . ABCD 3 ABC 3 2 ABCD 12
Câu 24. Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bằng a , góc hợp bởi cạnh bên và mặt đáy
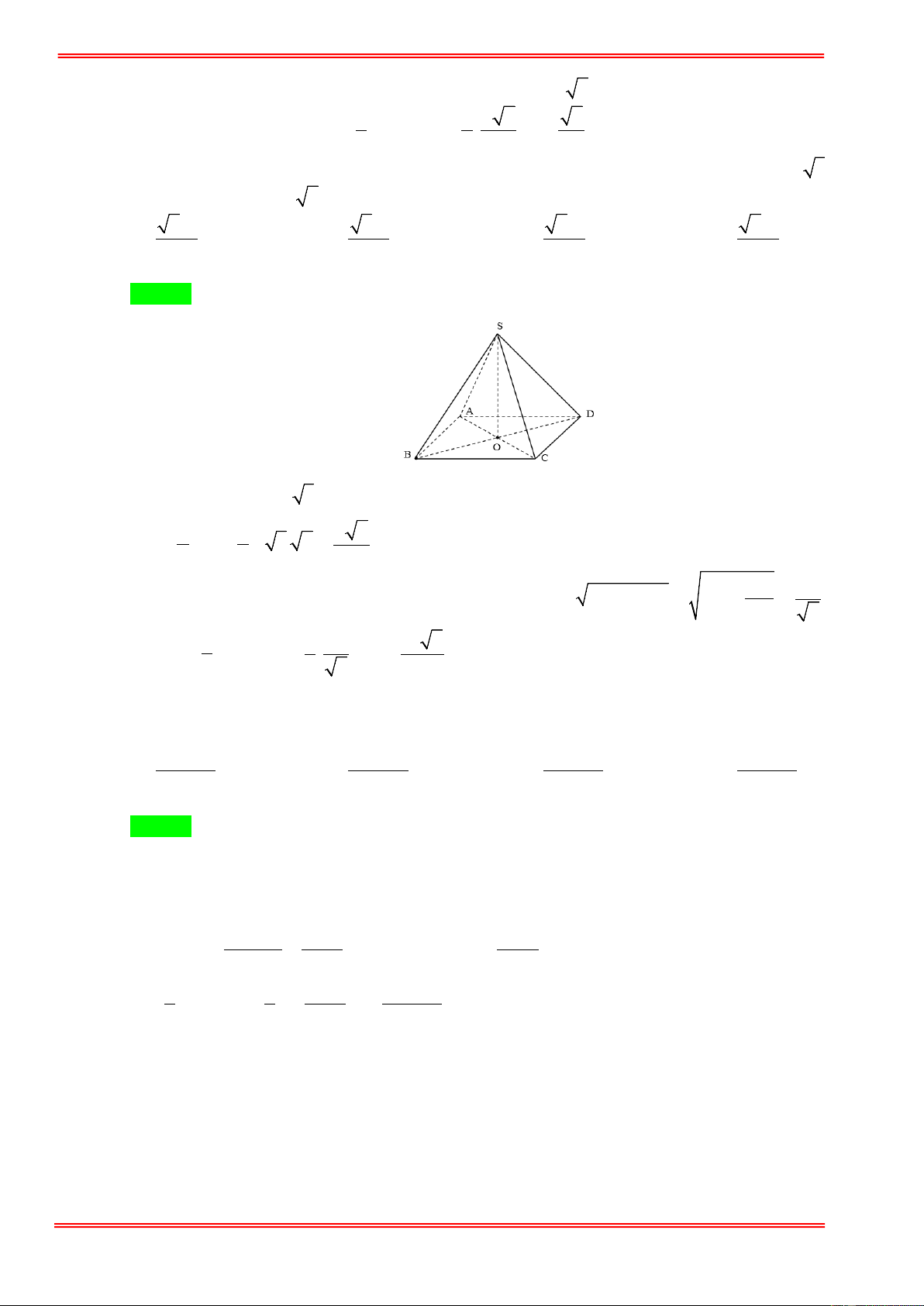
bằng 60°. Thể tích của hình chóp đã cho. 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 4 6 3 12 Hướng dẫn giải Chọn D https://toanmath.com/ S 60° A C O a M B
Gọi M là trung điểm của cạnh BC , O là tâm của tam giác đều ABC .
Hình chóp tam giác đều S.ABC có góc giữa cạnh bên bên và mặt đáy bằng 60°, nên  SAM = 60° . a 3 a Ta có: AM = 3 ⇒ AO = . 2 3 2 Diện tích tam giác a 3 ABC : S = . ABC 4 a
Xét tam giác SAO vuông tại O có: SO = A . O tan 60° 3 = . 3 = a . 3 2 3
Thể tích khối chóp tam giác đều 1 a 3 a 3
S.ABC : V = . .a = . 3 4 12
Câu 25. Cho hình chóp đều S.ABCD có AC = 2a , mặt bên (SBC ) tạo với đáy ( ABCD) một góc 45° .
Tính thể tích V của khối chóp S.ABCD . 3 a 3 a 2 3 2 3a A. V = . B. V = . C. V = . D. 3 V = a 2 . 2 3 3 Hướng dẫn giải Chọn B
Gọi M là trung điểm của BC 
→OM ⊥ BC mà BC ⊥ SO nên BC ⊥ (SOM )  → BC ⊥ SM .
BC = (SBC ) ∩ ( ABCD) → Góc (SBC ) ( ABCD) =  , SMO = 45°  
Do hình chóp đều nên đáy AC
ABCD là hình vuông có AD = = a 2 2 1 a 2 S
∆ OM vuông tại O có 
SMO = 45° nên SO = OM = AD = . 2 2 Vậy 1 1 a a V = S SO = a = . S ABCD ABCD ( ) 3 2 2 2 . 2 . . 3 3 2 3 https://toanmath.com/
Câu 26. Khối chóp tam giác đều có cạnh đáy bằng a và cạnh bên bằng a 3 có thể tích bằng: 6 6 2 1 A. 3 V = a . B. 3 V = a . C. 3 V = a . D. 3 V = a . 2 6 6 3 Hướng dẫn giải: Chọn C . a 3 a 3
ABC đều cạnh a => AM = => AO = . 2 3 2 2 2 2 2 a 8 2 a
SO = SA – AO = 3a − = . 3 3 1 2 2 1 a 3 2 V = . . a .a 3 ⇔ V = a . 3 3 2 2 6
Câu 27. Cho khối chóp tứ giác đều có cạnh đáy bằng a , cạnh bên bằng 2a . Tính thể tích V của khối chóp đã cho. 3 2a 3 14a 3 14a 3 2a A. V = . B. V = . C. V = . D. V = . 2 2 6 6 Hướng dẫn giải Chọn C U S A B O D C 2   2 a 2 14a Ta có: 2 2 SO =
SB − OB = (2a) −     = . 2   2 1 1 14a 3 14a 2 V = .S .SO = .a . = . 3 ABCD 3 2 6
Câu 28. Một hình chóp có đáy là tam giác đều cạnh bằng 2 và có chiều cao bằng 4. Tính thể tích hình chóp đó. https://toanmath.com/ 4 3 A. 2 3 . B. 2 . C. 4 . D. . 3 Hướng dẫn giải Chọn D 1
Ta có diện tích tam giác đều cạnh 2 là S = .2.2.sin 60° = 3 . 2
Thể tích của khối chóp là 1 V = 4 3 . 3.4 = . 3 3
Câu 29.] Cho hình chóp tứ giác đều có cạnh đáy bằng x . Diện tích xung quanh gấp đôi diện tích đáy. Khi
đó thể tích của khối chóp bằng: 3 x . 3 3 x . 3 3 x . 3 3 x . 3 A. . B. . 3 2 C. 12 . D. 6 . Hướng dẫn giải: Chọn D S A D O I B C . 2 S = x ; S = 4.S = 2SI.x . ABCD xq SCD Theo yêu cầu bài toán. 2
2SI.x = x ⇔ SI = x . 2 x 3 2 2 2 SO = SI − OI = x − = x . 4 2 3 1 1 3 x . 3 2 V = . SO S = .x .x = . SABCD 3 ABCD 3 2 6
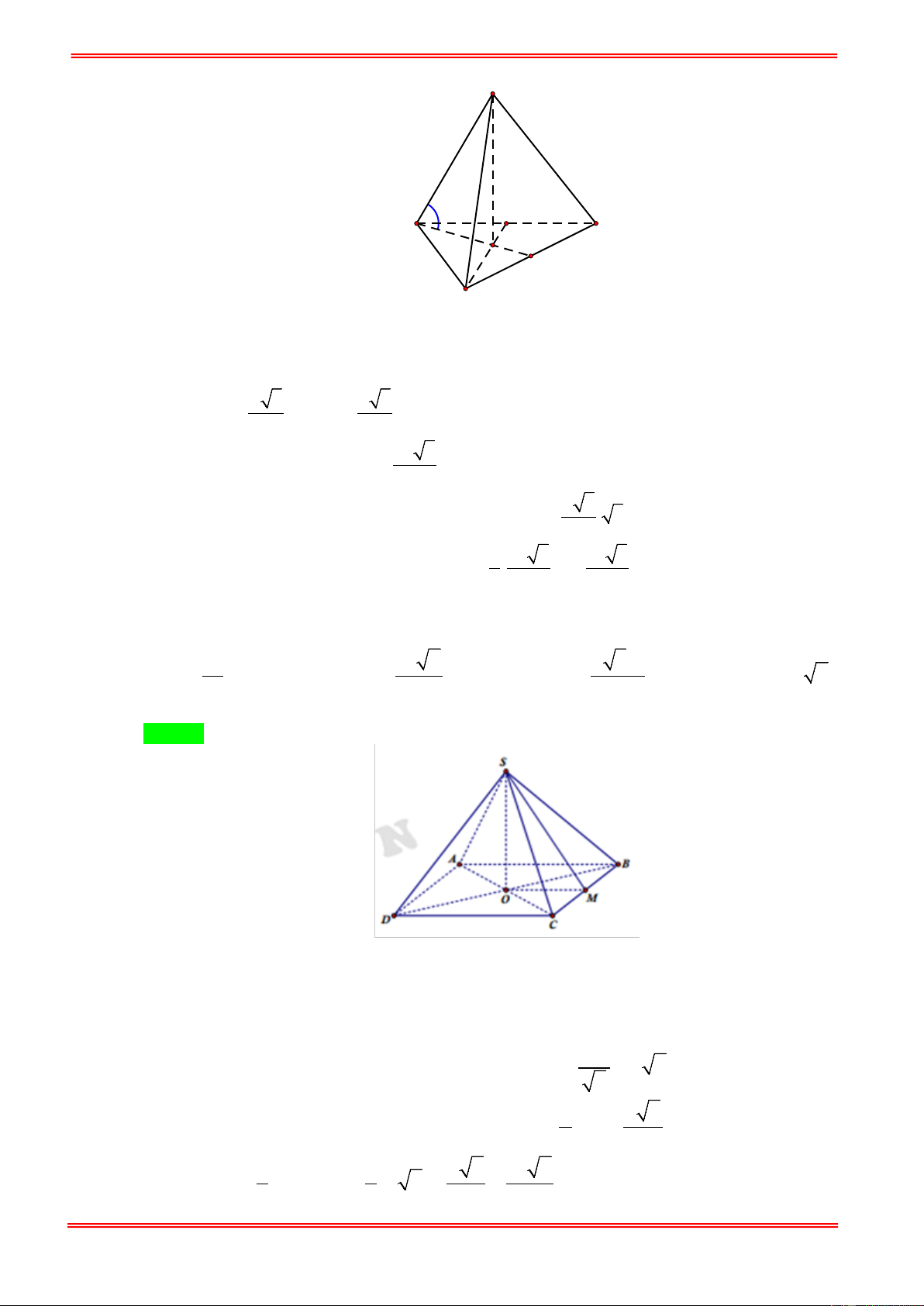
Câu 30. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a 3 . Gọi M , N lần lượt là trung điểm
của SB, BC Tính thể tích khối chóp .
A BCNM . Biết mặt phẳng ( AMN ) vuông góc với mặt phẳng (SBC) . 3 3a 15 3 a 15 3 3a 15 3 3a 15 A. . B. . C. . D. . 48 32 32 16 Hướng dẫn giải Chọn C https://toanmath.com/
E là trung điểm BC nên CB ⊥ AE,CB ⊥ SH 
→CB ⊥ (SAE) → CB ⊥ SE .
SE vừa là trung tuyến vừa là đường cao nên S
∆ BC cân tại S 1
F là giao điểm của MN với SE 
→ SF ⊥ MN, SF = SE . 2 (  AMN ) ⊥  (SBC) Giả thiết SF ⊥MN  
→ SF ⊥ ( AMN ) (  AMN  )∩(SBC) = MN → 1 a
SE ⊥ AF và SF = SE nên S ∆ AE cân tại 3
A → AE = AS = 2 2 2 2 3a a 5 2 2 AH = AE = . = a 
→SH = SA − AH = 3 3 2 2 1 1 a a V = S SH = a = . S ABC ABC ( ) 3 2 3 5 15 . . 3 . . 3 3 4 2 8 3 V SM SN 1 a 15 S . AMN = . =  →V = . S . V SB SC 4 AMN 32 S . ABC 3 Vậy 3a 15 V = V −V = . S . ABC S . AMN 32
Câu 31. Người ta gọt một khối lập phương gỗ để lấy khối tám mặt đều nội tiếp nó (tức là khối có các đỉnh
là các tâm của các mặt khối lập phương). Biết các cạnh của khối lập phương bằng a . Hãy tính
thể tích của khối tám mặt đều đó: 3 a 3 a 3 a 3 a A. . B. . C. . D. . 8 6 4 12 Hướng dẫn giải Chọn B
Dựng được hình như hình bên. https://toanmath.com/ .
+ Thấy được thể tích khối cần tính bằng 2 lần thể tích của hình chóp S.ABCD .
+ Nhiệm vụ bây giờ đi tìm thể tích của S.ABCD .
+ ABCD là hình vuông có tâm O đồng thời chính là hình chiếu của S lên mặt đáy. a 2 SO =
; BD = a (cạnh của hình lập phương). Suy ra các cạnh của hình vuông ABCD = a . 2 2 1 1 1  2   2  3 a V = Sh 3 = ⋅ ⋅   a = . S . ABCD 3    3 2 2 2    12 3 a V = 2.V = . khôi đa diên S . ABCD 6
Câu 32. Cho ( H ) là khối chóp tứ giác đều có tất cả các cạnh bằng a . Thể tích của ( H ) bằng. 3 a 3 3 a 2 3 a 3 a 3 A. . B. . C. . D. . 2 6 3 4 Hướng dẫn giải: Chọn B S A B O a C D .
Tính diện tích ABCD : 2 S = a . ABCD Xác định chiều cao:
Gọi O = AC ∩ D
B ⇒ SO là chiều cao của khối chóp. 2 a 1 S
∆ OA vuông tại O cho ta 2 2 2 SO =
SA − AO = a − = a . 2 2 3 Vậy: 1 1 a 2 a 2 2 V = S .SO = . .a = . SABCD 3 ABCD 3 2 6
Câu 33. Một hình chóp tứ giác đều có đáy là hình vuông cạnh a , các mặt bên tạo với đáy một góc α . Thể
tích khối chóp đó là https://toanmath.com/ 3 a 3 a 3 a 3 a A. tan α . B. tan α . C. cot α . D. sin α . 6 2 6 2 Hướng dẫn giải Chọn A a 2
Gọi h là đường cao của hình chóp ta có h = tan α , S = a day 2 3 1 a Vậy V = . h S = tan α . 3 day 6 =
Câu 34.Cho khối chóp đều S.ABCD có đáy ABCD là hình vuông cạnh a , SA a 3 . Tính thể tích V của 4 2 T 4 2 T 4 2 T 4 2 T 4 2 T 4 2 T 4 2 T 4 2 T 4 2 T 4 2 T 4 2 T
khối chóp S.ABCD theo a . 4 2 T 4 2 T 4 2 T 4 2 T 2 6 10 2 11 A. 3 V = a . B. 3 V = a . C. 3 V = a . D. 3 V = a . 9 6 3 6 Hướng dẫn giải Chọn B Gọi
⇒ SO ⊥ ( ABCD)
O là tâm hình vuông ABCD . 4 2 T 2 a a 10 2 2 2 SO =
SA − OA = 3a − = 2 2 . 4 2 T
Thể tích của khối chóp S.ABCD 1 1 a 10 10 là V = . . SO S 2 3 = . .a = a . 4 2 T 4 2 T 3 ABCD 3 2 6
Câu 35. Thể tích của chóp tam giác đều có tất cả các cạnh đều bằng a là 3 a 2 3 a 2 3 a 2 3 a 2 A. . B. . C. . D. . 4 2 6 12 Hướng dẫn giải Chọn D
Cách 1: Theo tự luận U https://toanmath.com/ S A C O I B
Gọi O là tâm mặt đáy ( ABC) và I là trung điểm cạnh BC .
S.ABC là hình chóp tam giác đều nên SO ⊥ ( ABC ) . S
∆ AO vuông tại O có: 2 2 a 3 a 3 a AO = AI = . = 2 2 ⇒ SO = SA − 2 AO = . 3 3 2 3 3 2 a 3 S = . ABC 4 2 3
Vậy thể tích khối chóp cần tìm là: 1 1 a 2 a 3 a 2 V = . SO S = . . = . S . ABC 3 ABC 3 3 4 12
Cách 2: Tính bằng công thức tính nhanh. U
Hình chóp tam giác đều có tất cả các cạnh đều bằng a là hình tứ diện đều cạnh a . 3 a 2 ⇒ V = . 12
Câu 36. Cho hình chóp tứ giác đều có cạnh đáy bằng cạnh bên bằng 2a . Tính thể tích khối chóp đã cho. 3 a 2 3 4a 2 3 a 3 3 a 2 A. . B. . C. . D. . 4 3 12 6 Hướng dẫn giải Chọn B AC
Gọi khối chóp đó là S.ABCD có tâm O. Vẽ hình nhanh ta thấy OA = = a 2 . 2 3 1 1 4a 2 2 2 2 SO =
SA − OA = a 2  →V = S .SO = .4a .a 2 = . S . ABCD 3 ABCD 4 3
Câu 37. Cho hình chóp đều S.ABC có SA = 1. Gọi D, E lần lượt là trung điểm của hai cạnh , SA SC . Tính
thể tích khối chóp S.ABC , biết đường thẳng BD vuông góc với đường thẳng AE . 2 21 12 21 A. V = B. V = C. V = D. V = S . ABC 12 S . ABC 54 S . ABC 4 S . ABC 18 Hướng dẫn giải https://toanmath.com/ Chọn B
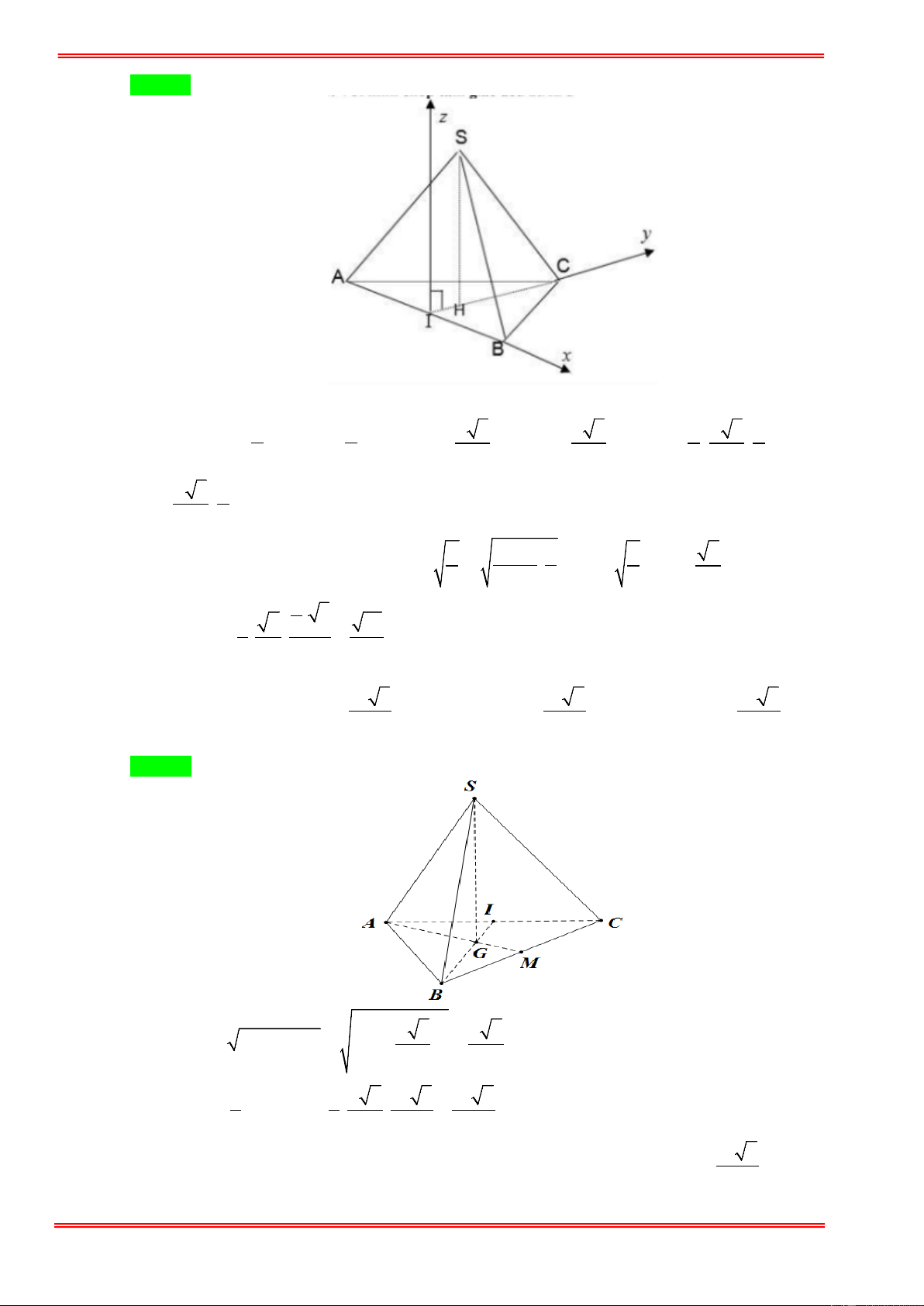
Giả sử cạnh đáy có độ dài a ; SH = h . Chọn hệ trục tọa độ như hình vẽ, ta có:  a   a   a 3   a 3   a a 3 h
I (0;0;0) ; A − ;0;0   ; B ; 0; 0   ; C  0; ; 0  ; S  0;
; h  ; D  − ; ;  ;  2   2        2   6   4 12 2    a 3 h E  0; ;    . 3 2     2 Lại có 3 − a 6 BD ⊥ 6 AE ⇔ B .
D AE = 0 ⇒ a = h = 2 7 . ⇒ a = ⇒ h = . 7 3 7 3 3 2 . 3 Vậy 1 7 21 3 V = . . = . S . ABCD 3 3 4 54
Câu 38. Tính thể tích khối tứ diện đều có cạnh a . 3 a 3 3 a 2 3 a 3 A. 3 a . B. . C. . D. . 4 12 12 Hướng dẫn giải Chọn C 2  a 3  a 6 2 2 2 SG =
SA − AG = a −   =   3 3   Ta có: . 1 7 T 2 3 1 1 a 6 a 3 a 2 V = . SG S = . . = SABC ABC ∆ Vậy: 3 3 3 4 12 . 1 7 T 3
Áp dụng công thức tính nhanh thể tích khối tứ diện đều có cạnh a 2 a bằng: . 1 7 T 1 7 T 12 https://toanmath.com/
Câu 39. Trong tất cả các khối chóp tứ giác đều ngoại tiếp mặt cầu bán kính bằng a , thể tích V của khối
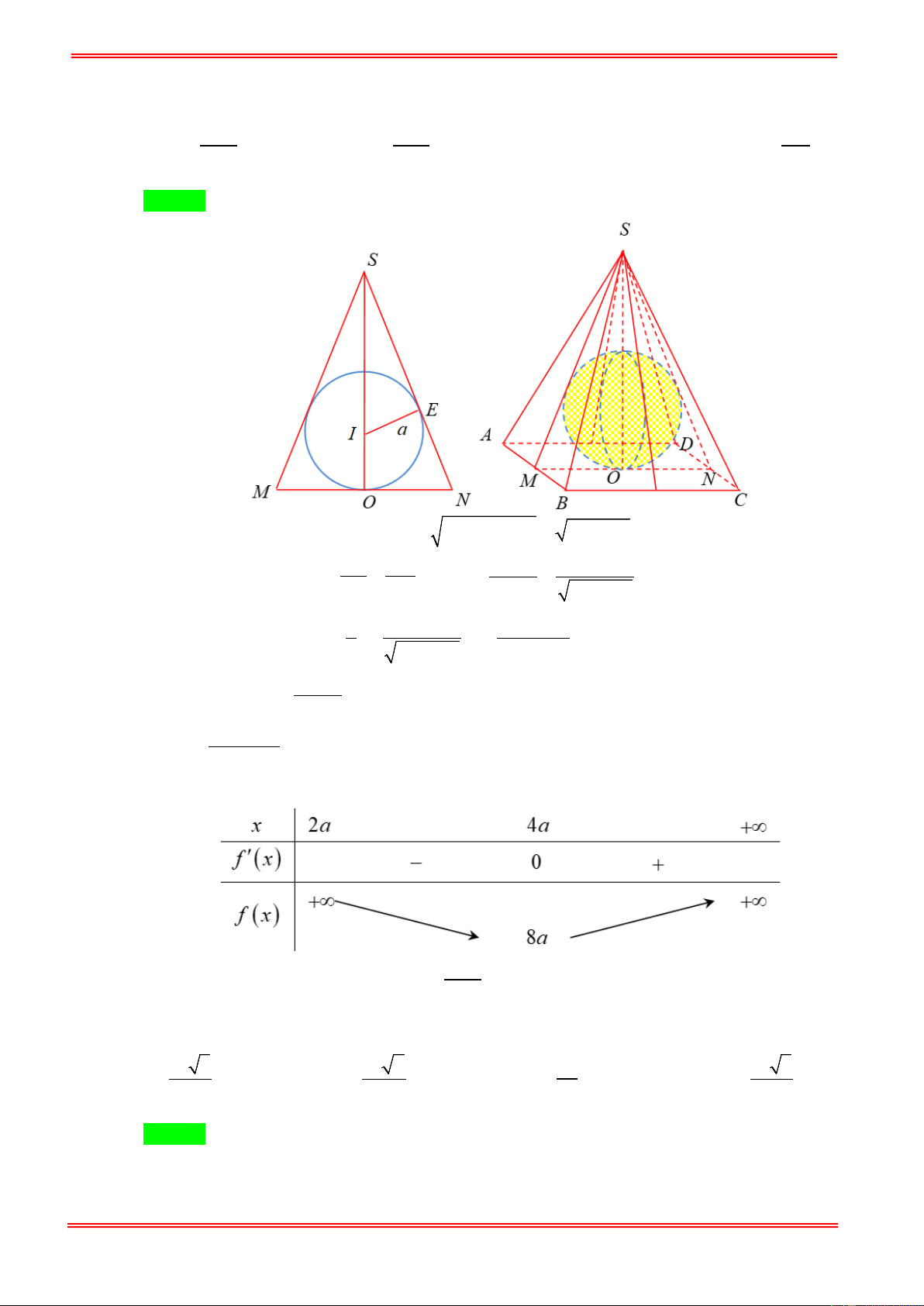
chóp có thể tích nhỏ nhất. 3 32 3 10 3 8 A. = a V . B. = a V . C. 3 V = 2a . D. = a V . 3 3 3 Hướng dẫn giải Chọn A
Giả sử SO = x ta có: SI = x − a ; SE = (x − a)2 2 2
− a = x − 2ax SE IE IE.SO ax
Xét ∆SEI ∽ ∆SON ta có: = ⇒ NO = = SO NO 2 SE x − 2ax 2 2 2  ax  Thể tích khối chóp là: 1 2 4 = a x V . x   = 2 3  − 3  (x − 2 2 a x ax ) Xét hàm số ( ) 2 = x f x
(0 < 2a < x) x − 2a ′( ) 2 x − 4 = ax f x f ′ x = ⇔ x = < a < ( ; ( ) 0 4a (do 0 2 x ) x − 2a)2 Bảng biến thiên 3
Vậy giá trị nhỏ nhất của thể tích là: 32 = a V . 3
Câu 40. Cho hình chóp tam giác đều có cạnh đáy bằng a , góc giữa cạnh bên và mặt đáy bằng o 60 . Thể
tích khối chóp S.ABC là: 3 a 3 3 a 6 3 a 3 a 3 A. . B. . C. . D. . 12 12 8 8 Hướng dẫn giải Chọn A https://toanmath.com/ .
Gọi O trọng tâm tam giác E , khi đó SO ⊥ ( ABC) . a 3 Ta có: AO = ⇒ SO = a . 3 2 3 1 1 a 3 a 3 Suy ra: V = . . SO S = . . a = ∆ . 3 ABC 3 4 12
Câu 41. Cho hình chóp tam giác đều S.ABC có AB = a , cạnh bên 6 SA = a
. Tính thể tích V của khối 3
chóp S.ABC . 3 3 3 3 3 A. = a V . B. = a V . C. = a V . D. = a V . 36 4 24 12 Hướng dẫn giải Chọn D
Gọi O là tâm của tam giác đều ABC khi đó 2 3 3 AO = a = a . 3 2 3 2 2  6   3  3
Vì SO là đường cao của khối chóp nên 2 2 SO =
SA − AO =  a  −  a  =     a . 3 3 3     3 Diện tích 3 1 3 3 a 2 S = 2 V = a a = ∆ a , suy ra thể tích . ABC 4 S . ABC 3 4 3 12
Câu 42. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a . Gọi SH là đường cao của hình chóp.
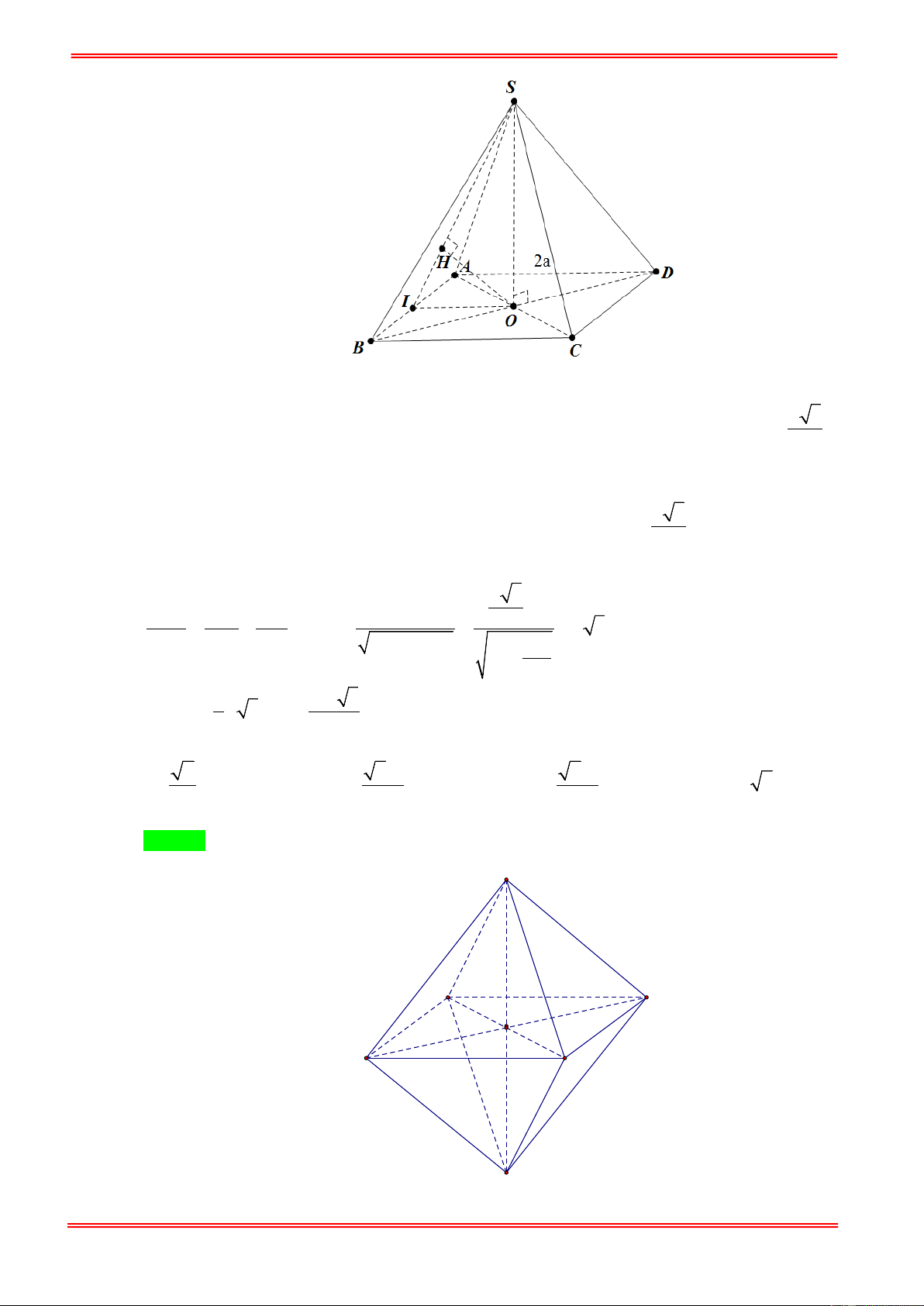
Khoảng cách từ trung điểm của SH đến (SBC) bằng b . Thể tích khối chóp S.ABCD là https://toanmath.com/ 3 2a b 3 a b 3 2a b 2ab A. . B. . C. . D. . 2 2 3 a −16b 2 2 3 a −16b 2 2 a −16b 3 Hướng dẫn giải Chọn A
Hình chóp tứ giác đều H = AC ∩ BD và tứ giác ABCD là hình vuông. Gọi I là trung điểm của cạnh SH
⇒ d (H,(SBC)) = 2d (I,(SBC)) = 2b Tứ diện vuông 1 1 1 1 SHBC ⇒ = + + ( 2b)2 2 2 2 HS HB HC 2 2 1 1 1 1 1 4 a −16b ⇒ = − − = − = 2 2 2 2 2 2 2 2 SH 4b a a 4b a 4a b 2 2 2ab ⇒ SH = 2 2 a −16b 3 1 1 2ab 2a b 2 ⇒ V = SH.S = . .a = . S . ABCD ABCD 2 2 2 2 3 3 a −16b 3 a −16b
Câu 43. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a . Gọi M , N lần lượt là trung điểm của
SA và CD . Cho biết MN tạo với mặt đáy một góc bằng 30° . Tính thể tích khối chóp S.ABCD . 3 a 15 3 a 30 3 a 15 3 a 5 A. . B. . C. . D. . 4 2 T 4 2 T 4 2 T 4 2 T 4 2 T 4 2 T 4 2 T 4 2 T 4 2 T 5 18 3 12 Hướng dẫn giải Chọn B. S B C M O N B C H H O N A a D A D
Gọi O = AC ∩ BD , ta có SO ⊥ ( ABCD) .
Gọi H là trung điểm OA, ta có MH // SO ⇒ MH ⊥ ( ABCD) .
Do đó (MN,( ABCD)) = (MN, NH ) =  MNH = 30° . 2 2  3   1  5 a Ta có: 2 NH = AD + CD     2 = 10 a ⇒ NH = .  4   4  8 4 https://toanmath.com/ MH MH a 30 tan MNH = = 3 = ⇒ MH = . NH a 10 3 12 4 Mặt khác: a 30 SO = 2MH = . 6 3
Vậy thể tích khối chóp 1 1 a 30 a 30
S.ABCD là: V = .S .SO 2 = .a . = . 3 ABCD 3 6 18
Câu 44. Cho hình chóp tam giác đều có cạnh đáy bằng a và cạnh bên bằng b . Thể tích của khối chóp là 2 a 2 a 2 a A. 2 2
3b − a . B. 2 2 2 a
3b − a . C. 2 2
3b − a . D. 2 2
3b − a . 6 4 12 Hướng dẫn giải Chọn D
Gọi S.ABC là hình chóp tam giác đều và G là trọng tâm tam giác ABC . Khi đó SG ⊥ ( ABC ) 2 2 2 a 3 a 3 3b − a
và AB = a , SB = b , AG = . = 2 2
⇒ SG = SA − AG = . 3 2 3 3 2 2 2 2 1 1 a 3 3b − a a Vậy 2 2 V = . SG S = . . =
3b − a . S . ABC ∆ 3 ABC 3 4 3 12
Câu 45. Cho hình chóp tứ giác đều có độ dài cạnh bên và cạnh đáy cùng bằng a . Khi đó, khoảng cách h
giữa đường thẳng AD và mặt phẳng (SBC) là: a 6 a a 2 2a 5 A. h = . B. h = . C. h = . D. h = . 3 2 2 5 Hướng dẫn giải: Chọn A
d ( AD,(SBC )) = d ( ,
A (SBC )) = 2d (O,(SBC )) với O là tâm hình vuông ABCD .  ⊥ Gọi BC OI
I là trung điểm BC ⇒ 
⇒ BC ⊥ (SOI ) ⇒ (SBC) ⊥ (SOI ) . BC ⊥ SO
Ta có (SBC ) ∩ (SOI ) = SI , kẻ OH ⊥ SI tại H ⇒ OH ⊥ (SBC ) ⇒ d (O,(SBC )) = OH . S a H A D O B I a C . AC a 2 a 2 2 2 AO = = , SO = SA − AO = . 2 2 2 a 2 a . S . O OI a 6 2 2 OH = = = . 2 2 2 2 + 6 SO OI 2a a + 4 4
d ( AD (SBC )) a 6 , = 2OH = . 3 https://toanmath.com/
Câu 46. Cho hình chóp tam giác đều S.ABC đỉnh S , độ dài cạnh đáy là a , cạnh bên bằng 2a . Gọi I là
trung điểm của cạnh BC . Tính thể tích V của khối chóp S.ABI . 3 a 11 3 a 11 3 a 11 3 a 11 A. . B. . C. . D. . 8 6 12 24 Hướng dẫn giải Chọn D S A C O I B 2 a a 33
Gọi O là hình chiếu của S lên (ABC) ta có: 2 2 2 SO = SB − BO = 4a − = 3 3 2 3 1 1 a 3 a 33 a 11 ⇒ V = S .SO = . . = ∆ . 3 ABI 3 8 3 24
Câu 47. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a góc giữa cạnh bên và mặt phẳng đáy
bằng 60°. Tính thể tích khối chóp S.ABCD . 3 a 3 a 6 3 a 6 3 a 6 A. . B. . C. . D. . 6 3 2 6 Hướng dẫn giải Chọn D S A D 60° O B a C Ta có:  SBO = 60° . a a SO = . OB tan 60° 2 = .tan 60° 6 = . 2 2 2 S = ABCD a 1 1 a 6 3 a 6 Suy ra V = . 2 = = SABCD SO SABCD . .a . 3 3 2 6 https://toanmath.com/
Câu 48. Xét tứ diện ABCD có các cạnh AC = CD = DB = BA = 2 và AD , BC thay đổi. Giá trị lớn nhất
của thể tích tứ diện ABCD bằng 32 3 16 3 32 3 16 3 A. . B. . C. . D. . 27 27 9 9 Hướng dẫn giải Chọn A A M B D N C
Gọi M , N lần lượt là trung điểm AD và BC .
Theo giả thiết ta có: ABD và ACD là các tam giác cân có M là trung điểm của AD nên BM ⊥ AD ⇒ AD ⊥ (BMC) và CM ⊥ AD
. Và có BM = CM ⇒ MB ∆ C cân tại. 2 BC Trong tam giác MB ∆ C 2 2
có MN vừa là đường cao vừa là trung tuyến nên MN = MB − 4 2 2 AD BC 2 2 AD + BC 2 2 ⇔ MN = AB − − ⇔ MN = 4 − . 4 4 4 2 2
Khi đó diện tích tam giác 1 1 AD + BC MB ∆ C là: S
= MN.BC = BC. 4 − MB ∆ C 2 2 4 2 2 Thể tích tứ diện 1 1 AD + BC ABCD là: V = .A . D S = .BC.A . D 4 − . ABCD ∆ 3 MBC 3 4 2 2 Đặt 1 x + y
AD = x , BC = y ta có: V = . . x . y 4 − ABCD . 3 4 2 2 + 2 2 + 2 2 x y xy x y xy
Ta có: x + y ≥ 2xy ⇔ ≥ ⇔ − ≤ − . 4 2 4 2 1 xy 2 Do đó: 2 V ≤ . . x . y 4 − ⇔ V ≤ xy
− xy . Dấu bằng xảy ra khi x = y ABCD ( ) (8 ) ABCD . 3 2 6 3  xy xy  + + 8 − xy xy xy   3 4.8
Ta lại có: (xy)2 (8 − xy) = 4. . .(8 − xy) 2 2 ≤ 4.  = . 2 2 3   27  
Dấu bằng xảy ra khi xy = 8 − 16 xy ⇔ xy = 4 ⇔ x = y = . 2 3 3 3
Vậy giá trị lớn nhất của thể tích tứ diện 2 4.8
ABCD là: tập xác định maxV = 32 3 = . ABCD 6 27 27
Câu 49. Cho hình chóp tứ giác đều S.ABCD , đáy ABCD có diện tích 2
16 cm , diện tích một mặt bên là 2
8 3 cm . Tính thể tích V của khối chóp S.ABCD . https://toanmath.com/ 32 2 32 13 32 11 A. 3 V = cm . B. 3 V = cm . C. 3 V = cm . D. 3 3 3 32 15 3 V = cm . 3 Hướng dẫn giải Chọn C S D C O A M B Ta có 2 2 S
= AB = 16cm ⇒ AB = 4cm ⇒ AO = 2 2 cm. ABCD
Gọi M là trung điểm của AB . Khi đó SM ⊥ A . B 1 2 S
= SM.AB = 8 3 cm ⇒ SM = 4 3 cm. SAB 2 2 2
SA = SM + AM = 2 13 cm. 2 2
SO = SA − AO = 2 11 cm. 1 1 32 11 3 V = S .SO = .16.2 11 = cm . 3 ABCD 3 3
Câu 50. Cho khối chóp tam giác đều. Nếu tăng cạnh đáy lên hai lần và giảm chiều cao đi bốn lần thì thể
tích của khối chóp đó sẽ:
A. Giảm đi hai lần.
B. Không thay đổi.
C. Tăng lên hai lần.
D. Giảm đi ba lần. Hướng dẫn giải Chọn B
Nếu tăng cạnh đáy lên hai lần thì diện tích đáy tăng bốn lần. Vì giảm chiều cao đi bốn lần nên thể
tích khối chóp không thay đổi.
Câu 51. Hình chóp tứ giác đều có tất cả các cạnh bằng a . Thể tích khối chóp đó bằng: 3 a 2 3 a 2 3 a 3 3 a 2 A. . B. . C. . D. . 2 6 3 3 Hướng dẫn giải: Chọn B https://toanmath.com/ .
Gọi O là tâm của hình vuông ABCD , khi đó SO ⊥ ( ABCD) . a 2 Ta có: AO = . 2 a 2 Suy ra: 2 2 SO = SA − AO = . 2 3 Khi đó: 1 1 a 2 a 2 2 V = . . SO S = . .a = . 3 ABCD 3 2 6
Câu 52. Khi chiều cao của một hình chóp đều tăng lên n lần nhưng mỗi cạnh đáy giảm đi n lần thì thể tích của nó.
A. Không thay đổi.
B. Tăng lên n lần.
C. Tăng lên n −1 lần.
D. Giảm đi n lần. Hướng dẫn giải Chọn D 1 Ta có: V = . .
h S , với h là chiều cao, S là diện tích đáy 3 2 x a S =
với x là độ dài cạnh của đa giác đều, a là số đỉnh của đa giác đều. 0 180  4 tan    a    2  x a   1  n  1 1 1 Ycbt ⇔ = = = 1 V . . nh . . . h S .V .  0 3  n 3 180 n 4 tan    a   
Câu 53. Cho hình chóp đều S.ABCD có đáy bằng 2a , khoảng cách giữa hai đường thẳng SA và CD bằng
a 3 . Thể tích khối chóp đều S.ABCD bằng. 3 a 3 3 4a 3 A. 3 a 3 . B. 3 4a 3 . C. . D. . 3 3 Hướng dẫn giải Chọn D https://toanmath.com/ .
Ta có CD / / AB ⇒ CD / / (SAB) . a Suy ra d (C ;
D AB) = d (C ;
D (SAB)) = d (C;(SAB)) = 2d ( ;
O (SAB)) ⇒ d (O (SAB)) 3 ; = . 2
Gọi I là trung điểm AB⇒ SI ⊥ AB (tam giác SAB cân tại S).
Dựng OH ⊥ SI (với H ∈ SI ). Khi đó ta có: OH 
⊥ AB ( AB ⊥ (SOI )) 
⇒ OH ⊥ (SAB) ⇒ d (O (SAB)) a 3 ; = OH = . OH  ⊥ SI 2
Tam giác SOI vuông tại O ta có: a 3 .a 1 1 1 OH .OI 2 = + ⇒ SO = = = a 3 . 2 2 2 2 2 2 OH SO OI OI − OH 3a 2 a − 4 3 Vậy 1 4a 3 2 V = a 3.4a = . 3 3
Câu 54. Thể tích khối bát diện đều cạnh a là: 2 3 2a 3 2a A. 3 a . B. . C. . D. 3 2a . 3 2 6 Hướng dẫn giải Chọn A E B C O A D F https://toanmath.com/
Vì hình bát diện ABCDEF có các cạnh bằng a ⇒ EF = a 2 . Khi đó 1 2 a 2 2 2 3 V = 2V = 2. .E . O S = . .a = a . ABCDEF E. ABCD 3 ABCD 3 2 3
Câu 55. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh bằng a 3 và
SA = SB = SC = SD = 2a . Tính thể tích khối chóp S.ABCD ? 3 2a 3 3a 3 6a 3 2a A. . B. . C. . D. . 2 3 6 6 Hướng dẫn giải Chọn A Có: 2 S = AB = (a )2 3 2
= 3a . Gọi O là tâm của hình vuông ABCD . ABCD 1 a BO = 1 BD = 6 .a 3. 2 = . 2 2 2 2 3a a
Vì S.ABCD là hình chóp đều nên SO ⊥ ( ABCD) 2 2
⇒ SO = SB − BO 2 = 2a − = . 2 2 1 1 a 3 a 2 V = . . SO S 2 = . .3a = (đvtt). S . ABCD 3 ABCD 3 2 2
Câu 56. Cho hình chóp tứ giác đều S.ABCD có chiều cao bằng h , góc giữa hai mặt phẳng (SAB) và
( ABCD) bằng α . Tính thể tích của khối chóp S.ABCD theo h và α . 3 3h 3 3h 3 4h 3 8h A. 2 8 tan α . B. 2 4 tan α . C. 2 3 tan α . D. 2 3 tan α . Hướng dẫn giải Chọn C
Gọi O là tâm của đáy. Do S.ABCD là hình chóp tứ giác đều nên SO ⊥ ( ABCD) , các cạnh bên
bằng nhau và đáy là hình vuông. Gọi I là trung điểm của AB , ta có SI ⊥ AB suy ra góc giữa
hai mặt phẳng (SAB) và ( ABCD) bằng  SIO = α . SO h 2h Ta có: OI = =
suy ra AD = 2OI =
. Vậy thể tích hình chóp S.ABCD : tan SIO tan α tan α 2 3 1 1  2h  4h V = . SO S = . . h = . ABCD   2 3 3  tanα  3 tan α https://toanmath.com/
Câu 57. Cho tứ diện đều ABCD . Biết khoảng cách từ A đến mặt phẳng ( BCD) bằng 6 . Tính thể tích V
của tứ diện ABCD . 9 3 A. V = .
B. V = 5 3 . C. V = 27 3 27 3 . D. V = . 2 2 Hướng dẫn giải: Chọn A A 6 B D G a M C .
Gọi cạnh của tứ diện đều ABCD là a .
Gọi M là trung điểm cạnh CD và G là trọng tâm tam giác BCD . 2  2   2 3  Ta có 2 2 2 2 2 2 2
AG + BG = AB ⇔ 6 + BM = a ⇔ 36 +    .a
 = a ⇒ a = 3   .  3  3 2   Khi đó 9 3 S = . BC ∆ D 4 Thể tích của tứ diện 1 1 9 3 9 3 ABCD là V = S .AG = . .6 = ∆ . 3 BCD 3 4 2
Câu 58. Cho hình chóp đều S.ABCD có AC = 2a , mặt bên (SBC ) tạo với đáy ( ABCD) một góc 45° .
Tính thể tích V của khối chóp S.ABCD ? 3 a 3 a 2 3 2 3a A. V = . B. V = . C. 3 V = a 2 . D. V = . 2 3 3 Hướng dẫn giải https://toanmath.com/ Chọn B AC
Ta có ABCD là hình vuông nên AC = AB 2 ⇒ AB = = a 2 . 2
Gọi M là trung điểm BC
Ta có góc giữa mặt bên (SBC) và đáy chính là góc giữa SM và MO hay  SMO = 45° . Do đó AB a 2 S
∆ OM vuông cân tại O ⇒ SO = OM = = . 2 2 Ngoài ra 2 2 S = AB = 2a . ABCD 3 Vậy 1 1 a 2 a 2 2 V = . . SO S = . .2a = . ABCD 3 ABCD 3 2 3
Câu 59. Thể tích hình chóp tứ giác đều có tất cả các cạnh đều bằng a bằng 3 a 2 3 a 2 3 a 3 a 2 A. B. C. D. 3 2 6 6 Hướng dẫn giải Chọn D S A D O B C 1 2 2 a a AO = AC = ; 2 2 SO = SA − AO 2 = a − 2 = . 2 2 2 2 1 1 a 2 3 a 2 V = . . SO S 2 = . .a = . 3 ABCD 3 2 6
Câu 60. Cho hình chóp đều S.ABCD có chiều cao bằng a 2 và độ dài cạnh bên bằng a 6 . Tính thể tích
khối chóp S.ABCD . https://toanmath.com/ 3 8a 3 3 10a 3 3 8a 2 3 10a 2 A. . B. . C. . D. . 3 3 3 3 Hướng dẫn giải. Chọn C Ta có 2 2 BO =
SA − SO = 2a . Vậy BD = 4a , suy ra AB = 2a 2 . Vậy 1 1 8a 2 2 V = S .SO = AB .SO = 3 ABCD 3 3
Câu 61. Tính thể tích khối chóp tứ giác đều có tất cả các cạnh bằng a . 3 a 2 3 2a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 3 4 2 Hướng dẫn giải Chọn A
Giả sử cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a .
Diện tích đáy ABCD : 2 S = a . ABCD 2 1 1 a 2  a 2  a 2 AO = AC = AB 2 = ; 2 2 2 SO = SA − AO = a −   =   . 2 2 2 2 2   3 1 1 a 2 a 2
Vậy thể tích khối chóp tứ giác đều là: 2 V = S .SO = .a . = . 3 ABCD 3 2 6 S A B O D C .
Câu 62. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và mặt bên tạo với đáy một góc 450. Thể P P
tích V khối chóp S.ABCD là: 3 a 3 a 3 a 1 A. V = . B. V = . C. V = . D. 3 V = a . 6 9 2 24 Hướng dẫn giải: https://toanmath.com/ Chọn A
Gọi H là hình chiếu vuông góc của A trên ( ABCD), M là trung điểm của BC .  3 a a 0
SMH = 45 ⇒ SH = HM = ⇒ V = . S . 2 ABCD 6
Câu 63. Tính thể tích V của hình tứ diện đều có đường cao h = a . 3 a 3 3 a 3 3 a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . 12 6 8 4 Hướng dẫn giải: Chọn C x a x .
Gọi x là độ dài một cạnh của tứ diện. Ta có chiều cao. 2  2 x 3  2 3 a 6 2 h = x −  .  = x ⇔ x = h =   . 3 2 3 2 2  
Suy ra diện tích tam giác đáy là. 2 2 x 3 3a 3 2 3 1 3a 3 a 3 S = = . Vậy V = . .a = . 4 8 3 8 8
Câu 64. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a cạnh bên bằng 3a . Tính thể tích V của khối chóp đã cho? 3 4 7a 3 4a 3 4 7a A. 3
V = 4 7a . B. V = . C. V = . D. V = . 9 3 3 Hướng dẫn giải Chọn D
Trong mặt phẳng ABCD , gọi O = AC ∩ BD , do hình chóp S.ABCD đều nên SO ⊥ ( ABCD) . Đáy là hình vuông vạnh AC 2a ⇒ AO = = a 2 2
Trong tam giác vuông SAO có 2 2 SO =
SA − AO = a 7 https://toanmath.com/ 3 Thể tích 1 1 4a 7
V của khối chóp trên là 2 V = . SO S = a 74a = . 3 ABCD 3 3
Câu 65. Cho khối chóp tứ giác đều có cạnh đáy bằng a , cạnh bên bằng 3a . Tính thể tích V của khối chóp đã cho. 3 34a 3 2a 3 2a 3 34a A. V = . B. V = . C. V = . D. V = . 6 6 2 2 Hướng dẫn giải Chọn A S B C O A D
Gọi O là tâm mặt đáy ( ABCD) của hình chóp tứ giác đều S.ABCD .
Ta có SO ⊥ ( ABCD) ⇒ SO là đường cao của hình chóp. 1 a 2 a 34
Tam giác SAO vuông tại O có OA = AC = , SA = 3a 2 2
⇒ SO = SA − OA = . 2 2 2 3
Khi đó thể tích khối chóp tứ giác đều là 1 a 34 V = S .SO = . 3 ABCD 6
Câu 66. Một hình chóp tứ giác đều có đáy là hình vuông cạnh a , các mặt bên tạo với đáy một góc α .
Thể tích của khối chóp đó là 3 a 3 a 3 a 3 a A. sinα . B. tanα . C. cotα . D. tanα . 2 2 6 6 Hướng dẫn giải Chọn C
Xét hình chóp tứ giác đều S.ABCD, có đáy ABCD là hình vuông tâm O. OM  ⊥ AB
Gọi M là trung điểm của AB suy ra 
⇒ AB ⊥ (SMO) . SO ⊥ AB
Khi đó (SAB) ( ABCD)  = (SM OM )  =  , , SMO = α . https://toanmath.com/ SO a α
Tam giác SMO vuông tại O, có  .tan tan SMO = ⇒ SO = . MO 2 3 1 a
Thể tích khối chóp S.ABCD là V = . . SO S = .tanα . S . ABCD 3 ABCD 6
Câu 67.Tính thể tích của khối bát diện đều có cạnh bằng 2. 8 2 16 4 2 16 2 A. . B. . C. . D. . 3 3 3 3 Hướng dẫn giải Chọn A E D A H C B F
Gọi ABCDEF là hình bát diện đều có tâm H (như hình vẽ) có cạnh bằng 2 . AC 2 2 Ta có EH = AH = = = 2 . 2 2
Thể tích của bát diện đều đã cho là 1 8 2 V = 1 2V = 2. .S .EH 2 = 2. .2 . 2 = . E .ABCD 3 ABCD 3 3
Câu 68. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a . Gọi SH là chiều cao của hình chóp,
khoảng cách từ trung điểm I của SH đến mặt bên (SBC) bằngb . Tính thể tích V của khối
chóp S.ABCD . 3 ab 2a b A. V = . B. V = . 2 2 3 a −16b 2 2 3 a −16b ab 2ab C. V = . D. V = . 2 2 a −16b 2 2 a −16b Hướng dẫn giải: Chọn B https://toanmath.com/ S J I D K C H A M B .
Vì S.ABCD là hình chóp tứ giác đều suy ra H là tâm của hình vuông ABCD .
Gọi M là trung điểm BC , K là hình chiếu vuông góc của H lên SM . BC ⊥ SH  Ta có:
 ⇒ BC ⊥ (SHM ). BC ⊥ HM
⇒ (SBC) ⊥ (SHM ) , mà HK ⊥ SM ⇒ HK ⊥ (SBC) .
Suy ra HK = 2IJ = 2b , ta có. 2 2 HK .HM 2ab 3 2a b SH = = . Vậy V = . 2 2 2 2 HM − HK a −16b 2 2 3 a −16b
Câu 69. Cho hình chóp đều S.ABCD có cạnh đáy bằng a , góc giữa cạnh bên và mặt đáy bằng o 60 . Tính thể
tích của khối chóp S.ABCD theo a . 3 a 6 3 a 6 3 a 3 3 a 6 A. B. C. D. 2 6 6 12 Hướng dẫn giải Chọn B
Gọi O là tâm của mặt đáy ⇒ =  SO, ( ABCD)  ( ) SBO =60°. a 1 3 a 6 Ta có SO = 6 B . O 3 ⇒ SO =
. Vậy thể tích khối chóp V = . . SO S = . 2 3 ABCD 6
Câu 70. Thể tích của khối tứ diện đều có cạnh bằng 3 . 4 2 9 2 A. 2 2 . B. . C. . D. 2 . 9 4 Hướng dẫn giải Chọn C 3 3 2 9 2
Cách 1: Áp dụng công thức tính nhanh thể tích khối tứ diện đều: V = = . 12 4 https://toanmath.com/
Cách 2: Khối tứ diện đều S.ABC có đáy là tam giác đều và đường cao SG . 2 AB 3 9 3 2 AB 3 S = = , 2 2 AG =
= 3 ⇒ SG = SA − AG = 9 − 3 = 6. ABC ∆ 4 4 3 2 Vậy 1 9 2 V = .S .SG = . S . ABC ∆ 3 ABC 4
Câu 71. Cho hình chóp tứ giác đều S.ABCD có đáy hợp với mặt bên một góc 45° . Bán kính mặt cầu
ngoại tiếp hình chóp S.ABCD bằng 2 . Tính thể tích khối chóp S.ABCD . 32 2 64 2 64 2 128 2 A. . B. . C. . D. . 9 27 81 81 Hướng dẫn giải Chọn C S A D E O B . C
Đặt AB = a . Gọi O là tâm ABCD , E là trung điểm AB . Khi đó (SAB, ABCD) = SEO = 45°. a 2 2 a a a 3 Suy ra SO = OE = và SA = + = . 2 2 4 2 2 3a 2 SA 3a 4 2 Mà 4 R = = = = 2 ⇒ a = . S . ABCD 2SO a 4 3 2. 2 1 1 2 2 32 64 2 Nên V = . SO S = = . S . ABCD 3 ABCD 3 3 9 81
Câu 72. Người ta cắt miếng bìa hình tam giác cạnh bằng 10cm như hình bên và gấp theo các đường kẻ, sau
đó dán các mép lại để được hình tứ diện đều. Tính thể tích của khối tứ diện tạo thành. https://toanmath.com/ 125 2 1000 2 A. 3
V = 250 2cm . B. 3 V = cm . C. 3 V = cm . D. 12 3 250 2 3 V = cm . 12 Hướng dẫn giải Chọn B
Tứ diện đều tạo thành là tứ diện đều ABCD có tất cả các cạnh bằng 5cm . 2 a 3 25 3 Diện tích đáy là 2 S = = cm . 4 4 2   Đườ 2 5 3 5 6 ng cao 2 2 2 AH =
AD − DH = 5 −  ⋅  =  
, với H là tâm đáy. 3 2 3   1 25 3 5 6 125 2 Thể tích V = ⋅ ⋅ = . 3 4 3 12 3 a 2
Ghi nhớ: Thể tích khối tứ diện đều cạnh a là V = 12
Câu 73. Tính thể tích khối chóp tứ giác đều cạnh đáy bằng a , chiều cao bằng 3a . 3 a 3 3 a 3 a 3 A. 3 a . B. . C. . D. . 4 3 12 Hướng dẫn giải Chọn A 1 1 Ta có: 2 3 V = . h S = .3 . a a = a S . ABCD 3 ABCD 3
Câu 74. Thể tích của khối bát diện đều cạnh a là: 3 a 3 3 a 2 3 a 2 3 a 3 A. . B. . C. . D. . 6 3 6 3 Hướng dẫn giải Chọn B https://toanmath.com/
Khối bát diện đều là khối ghép bởi 2 khối chóp tứ giác S.ABCD đều cạnh a, với O là tâm đáy. 2 3  a 2  a 2 2 a 2 2 2 2 SO = SA − OA = a −   =  →V = 2.V = .S .SO = . S . 2 2 ABCD 3 ABCD 3  
Câu 75. Thể tích của khối tứ diện đều cạnh a là 3 6a 3 3a 3 2a 3 2a A. . B. . C. . D. . 12 12 12 24 Hướng dẫn giải Chọn C A a B D G a C
Gọi tứ diện đều cạnh a là ABCD .
Gọi G là trọng tâm của tam giác ABC .
Ta có: AG ⊥ ( ABC ) . 2  2 a 3  a 6 Xét A
∆ BG vuông tại G , ta có: 2 2 AG = AB − BG 2 = a −  .    = . 3 2   3 2 3
Thể tích của khối tứ diện đều là: 1 1 a 3 a 6 a 2 V = .S .AG = . . = . 3 BCD 3 4 3 12
Câu 76. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a ,diện tích mỗi mặt bên bằng 2 2a . Thể
tích khối nón có đỉnh là S và có đáy là đường tròn ngoại tiếp hình vuông ABCD bằng 3 7 3 π 7a 3 π 7a 3 π 7a A. 3 π a . B. . C. . D. . 4 4 3 6 Hướng dẫn giải Chọn B S 2 1 a 63a Ta có 2 2 S = .
a SI = 2a ⇒ SI = 4 ; a SO = 16a − = SCD 2 4 2 Khối nón có .3 a 7 a 2 h = SO = ; r = 2 2 A D 2 3 1 a 3 7a π 7a V = π . = 3 2 2 4 O I
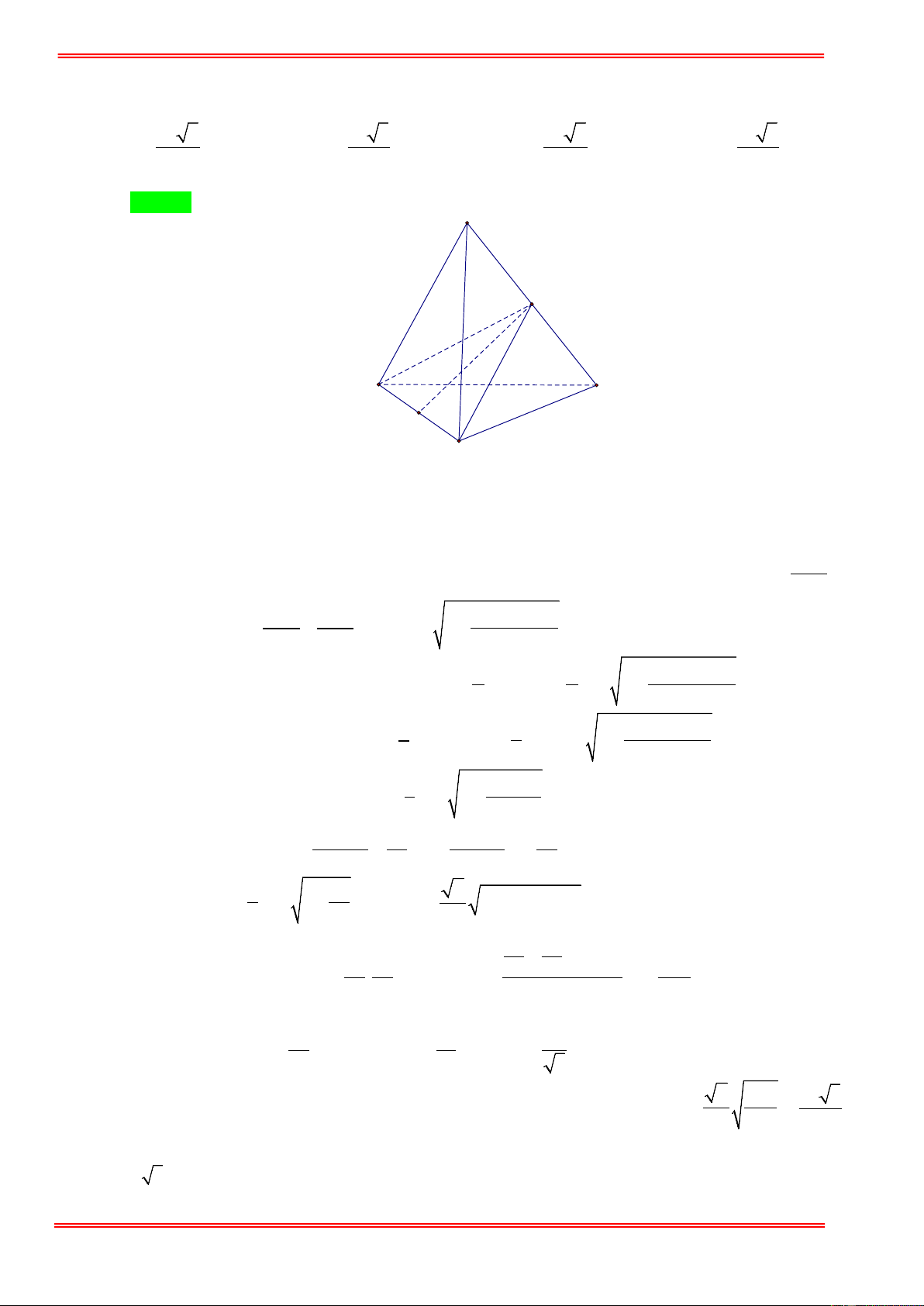
Câu 77.Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M , N lần lượt là trung B C
điểm các cạnh AD, B .
D Lấy điểm không đổi P trên cạnh AB (khác ,
A B ). Thể tích khối chóp PMNC bằng 9 2 8 3 27 2 A. B. C. 3 3 D. 16 3 12 Hướng dẫn giải Chọn A https://toanmath.com/ A M P N B D C
Do AB  (CMN ) nên d ( P,(CMN )) = d (A,(CMN )) = d (D,(CMN )) Vậy 1 V = V = V = V PCMN DPMN MCND 4 ABCD
(Do diện tích đáy và chiều cao đều bằng một nửa). 2 2 3 Mặt khác 1 a 3  a a 2 27 2 2 1 27 2 9 2 V = . a − = = nên V = . = ABCD   3 4  MCND 3  12 12 4 12 16
Câu 78. Tính thể tích V của khối chóp tứ giác đều có chiều cao là h và bán kính mặt cầu nội tiếp là
r (h > 2r > 0) . 2 2 4r h 2 2 4r h 2 2 3r h 2 2 4r h A. V = ( . B. V = . C. V = . D. V = . h + 2r ) 3(h − 2r ) 4 (h − 2r ) 3(h + 2r ) Hướng dẫn giải Chọn B
Gọi I là giao điểm ba đường phân giác trong tam giác S
∆ MM '. Nên I là tâm đường tròn nội tiếp tam giác S
∆ MM '. Mặt khác, do S.ABCD là hình chóp tứ giác đều nên I là tâm mặt cầu nội tiếp hình chóp. S I A D M’ x M O B C Xét S
∆ MO có MI là đường phân giác ta có: SM SI 2 2 + − 2 2 = h x h r ⇒ = hr hr
(với x = MO ). 2 ⇒ x = 2 ⇒ AB = 4 MO IO x r h − 2r h − 2r 2 2
Vậy thể tích cần tìm là 1 4h r 2 V = .4. h x = . 3 3(h − 2r )
Câu 79. Cho khối tứ diện đều ABCD có cạnh bằng a . Gọi B ',C ' lần lượt là trung điểm của các cạnh
AB và AC . Tính thể tích V của khối tứ diện AB 'C ' D theo a . 3 a 3 a 2 3 a 3 3 a 2 A. V = . B. V = . C. V = . D. V = . 24 24 48 48 Hướng dẫn giải Chọn D https://toanmath.com/ V AB′ AC′ AB′C′ 1 1 Ta có D = . = ⇒ V = V AB 'C ' V AB AC 4 D 4 ABCD ABCD 3 3
Khối tứ diện đều a 2 a 2
ABCD có cạnh bằng a thì V = ⇒ V = . ABCD AB 'C ' 12 D 48
Câu 80. Thể tích khối tứ diện đều có cạnh bằng 2a là. 3 a 3 3 a 2 3 2a 2 A. . B. . C. 3 2a 2 . D. . 6 12 3 Hướng dẫn giải: Chọn D
Giả sử khối tứ diện đều là ABCD như hình bên.
Tam giác đều ABC cạnh a có. 2 Sa 3 . ABC  2 2 2a 3 2a 3 AO AM   3 3 2 3 . .
Tam giác SAO vuông tại O có. 2 4a 2a 6 2 2 2
SO SA AO  4a   . 3 3 Thể tích cần tìm. 3 1 2a 6 2a 2 2 V  . .a 3  . 3 3 3
Câu 81. Cho hình chóp đều S.ABC có đáy cạnh bằng a , góc giữa đường thẳng SA và mặt phẳng ( ABC )
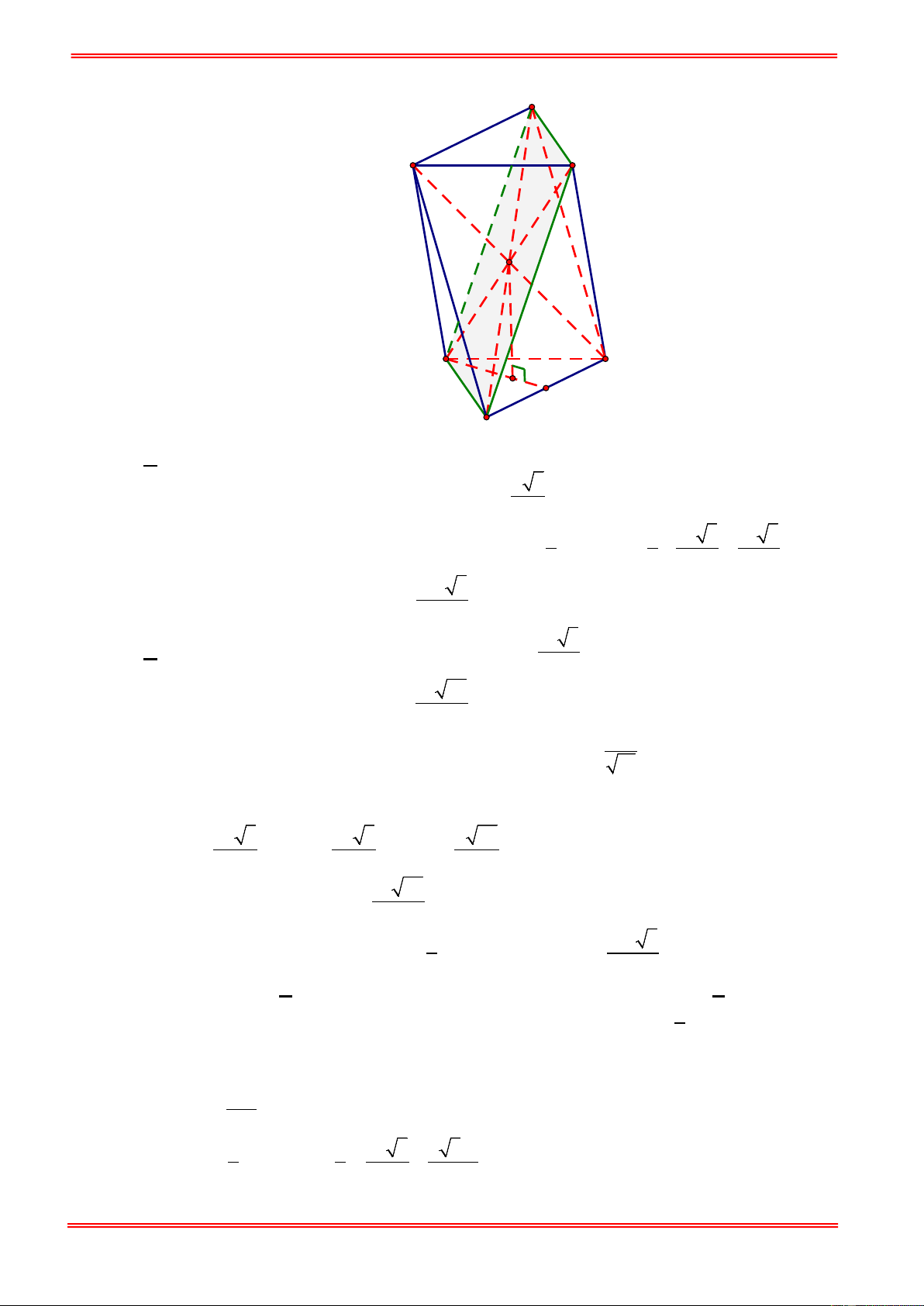
bằng 60°. Gọi A′, B′, C′ tương ứng là các điểm đối xứng của A , B , C qua S . Thể tích của
khối bát diện có các mặt ABC, A′B C
′ ′ , A′BC , B CA ′ , C A ′ B , AB C
′ ′, BA′C′ , CA′B′ là 3 2 3a 3 3a 3 4 3a A. . B. 3 2 3a . C. . D. . 3 2 3 Hướng dẫn giải Chọn A https://toanmath.com/ A' B' C' S C B H A
Cách 1: Ta tính thể tích khối chóp S.ABC :
Gọi H là tâm tam giác ABC đều cạnh a a 3 ⇒ CH =
. Góc giữa đường thẳng SA và mặt phẳng 3 a a o 1 1 3 3 (ABC) bằng 0 60 ⇒  2 3
SCH = 60 ⇒ SH = a ⇒ V = .S H.S = . a = . S . ABC 3 ABC 3 4 12 3 2a 3 V = 2V = 2.4V = 8V = .
B. ACA'C ' B.ACS S . ABC 3 3 a 3
Cách 2: Ta có thể tích khối chóp S.ABC là:V = . S . ABC 12 2 Diện tích tam giác a 39 SBC là: S = . S ∆ BC 12 Khoảng cách từ a
A đến mặt phẳng (SBC ) là: d ( A (SBC )) 3 , = . 13
Tứ giác BCB 'C ' là hình chữ nhật vì có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường. 2a 3 2a 3 a 39 Có SB = ⇒ BB ' = ⇒ B 'C = . 3 3 3 2 Diện tích a 39
BCB 'C ' là: S = . BCB 'C ' 3
Thể tích khối 8 mặt cần tìm là: 1 2a 3 V = 2. d ( , A (SBC )) 3 .S = . BCB 'C ' 3 3
Cách 3 (Tham khảo Hướng dẫn giải của Ngọc HuyềnLB).
Thể tích khối bát diện đã cho là 1 V = 2V = 2.4V = 8V = 8. . SG S .
A' B 'C ' BC A'.SBC S . ABC 3 ABC
Ta có: (SA ( ABC ))  =  0 ;
SAG = 60 . Xét S
∆ GA vuông tại G :  SG = ⇔ =  tan SAG SG A . G tan SAG = . a AG 2 3 Vậy 1 1 a 3 2 3a V = 8. . SG S = 8. . . a = . 3 ABC 3 4 3 https://toanmath.com/
Câu 82. Cho hình chóp tam giác đều S.ABC , cạnh đáy bằng a . Mặt bên tạo với mặt đáy một góc o 60 .
Tính thể tích V của hình chóp S.ABC . 3 a 3 3 a 3 3 a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . 2 12 24 6 Hướng dẫn giải Chọn C S A C H I B .
Gọi các điểm như hình vẽ. Theo đề suy ra  0 SIA = 60 . a 3 a 3 a Ta có AI = ⇒ HI = ⇒ SH = . 2 6 2 3 Vậy a 3 V = . 24
Câu 83. Cho khối chóp đều S.ABC cạnh đáy bằng a , cạnh bên bằng 3a . Tính thể tích khối chóp đó ? 3 a 26 3 a 11 3 a 3 3 a 11 A. V = . B. V = . C. V = . D. V = . 12 6 4 12 Hướng dẫn giải Chọn A S 3a 3a 3a a A C a H M N a B
Gọi G là trọng tâm của tam giác ABC . 1 V = . SG S∆
(do khối chóp S.ABC đều). 3 ABC 2 a 3 a 3 a 26 2 a 3 Ta có AG = . = 2 2
⇒ SG = SA − AG = ; S = ∆ ; 3 2 3 ABC 3 4 https://toanmath.com/ 2 3 1 a 26 a 3 a 26 Suy ra V = . . = (đvtt). 3 3 4 12
Câu 84.Cắt một miếng giấy hình vuông như hình bên và xếp thành hình một hình chóp tứ giác đều. Biết
các cạnh hình vuông bằng 20cm , OM = x(cm) . Tìm x để hình chóp đều ấy có thể tích lớn nhất
A. x = 8 cm .
B. x = 6 cm .
C. x = 7 cm .
D. x = 9 cm . Hướng dẫn giải Chọn A S Q M x O H P N
Giả sử được hình chóp tứ giác đều như hình vẽ x x Ta có OM = x ⇒ OH = HM = ⇒ SH = 10 2 − nên 2 2 2 2  x   x  2 2 SO = SH − OH = 10 2 − − = 20(10 − x)    
. Suy ra cạnh đáy bằng x 2 .  2   2  Thể tích 1 1 20 V = .S .SO 2
= .2x . 20(10 − x) 2 =
.x . 40 − 4x , (với 0 ≤ x ≤ 10 ). 3 MNPQ 3 3
Tìm GTLN của V ta được V = 90,51 khi x = 8 max
* Cách 1 – tìm GTLN: Áp dụng BĐT Cauchuy cho 4 số không âm, ta có: 4
 40 − 4x + x + x + x + x
40 − 4x. x. x. x. x ≤   2 4
⇔ 40 − 4x.x ≤10  4  20 20 2 4 ⇔ .x 40 − 4x ≤
.10 . Dấu bằng xảy ra khi 40 − 4x = x ⇔ x = 8 . 3 3
* Cách 2 – tìm GTLN: Có thể sử dụng máy tính – phần bảng (mode 7) để tìm GTLN cho nhanh: https://toanmath.com/
Câu 85. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a . Gọi G là trọng tâm của tam giác SAC và khoảng cách từ a
G đến mặt bên (SCD) bằng
3 . Tính khoảng cách từ tâm O của đáy đến 6
mặt bên (SCD) và thể tích của khối chóp S.ABCD . a 3 3 a 3 a 3 3 a 3 A. d( = và V = . B. d = và V = . O,(SCD)) (O,(SCD)) 2 S . ABCD 6 4 S . ABCD 6 a 3 3 a 3 a 3 3 a 3 C. d( = và V = . D. d = và V = . O,(SCD)) (O,(SCD)) 4 S . ABCD 2 2 S . ABCD 2 Hướng dẫn giải Chọn B .
Gọi I là trung điểm của CD .
⇒ OI ⊥ CD ⇒ (SOI ) ⊥ CD ⇒ (SOI ) ⊥ (SCD) .
Kẻ OK,GH ⊥ SI ⇒ OK ⊥ (SCD),GH ⊥ (SCD) . ⇒ 3 a 3 d(
= OK , mà OK = GH ⇒ OK = . 0,(SCD)) 2 4 2 2 OI .OK a 3 3 a 3 SO = = . Vậy V = . 2 2 OI − OK 2 S . ABCD 6 https://toanmath.com/
Document Outline

  • 2.3 BT KHỐI CHÓP ĐỀU
    • THỂ TÍCH KHỐI CHÓP ĐỀU
      • A. BÀI TẬP
  • 2.3 HDG KHỐI CHÓP ĐỀU
    • THỂ TÍCH KHỐI CHÓP ĐỀU
      • B. LỜI GIẢI CHI TIẾT