Bài tập thể tích khối lăng trụ đều có lời giải chi tiết Toán 12

Khối lăng trụ đều có đáy là đa giác đều và các cạnh bên vuông góc với đáy, do đó trong khối lăng trụ đều, ta có thể nhanh chóng xác định độ dài đường cao và diện tích mặt đáy. Các bài toán tính thể tích khối lăng trụ đều thường đi kèm với các giả thiết về độ dài đường chéo, góc giữa đường chéo và mặt đáy.Mời bạn đọc đón xem.

17 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

58 trang 8 tháng trước

Tác giả:

Profile Lan Tường
https://toanmath.com/
THỂ TÍCH KHỐI LĂNG TRỤ ĐỀU
Câu 1. Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng
3
. Thể tích khối lăng trụ đã cho bằng
A.
93
4
. B.
27 3
4
. C.
27 3
2
. D.
93
2
.
Câu 2. Cho lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
4cm
, diện tích tam giác
A BC
′
bằng
2
12cm
. Thể tích khối lăng trụ đó là:
A.
3
82V cm=
. B.
. C.
3
24V cm=
. D.
3
24 2V cm=
.
Câu 3. Cho hình lăng trụ đứng
.'' 'ABC A B C
có đáy
ABC
đều cạnh bằng
a
và chu vi của mặt bên
''ABB A
bằng
6a
. Thể tích của khối lăng trụ
.'' 'ABC A B C
bằng
A.
3
3
2
a
. B.
3
3a
. C.
3
3
3
a
. D.
3
3
6
a
.
Câu 4. Cho khối tứ giác đều
.S ABCD
có thể tích là
V
. Nếu giảm độ dài cạnh đáy xuống hai lần và tăng độ
dài đường cao lên ba lần thì ta được khối chóp mới có thể tích là:
A.
3
2
V
. B.
2
3
V
. C.
1
4
V
. D.
3
4
V
.
Câu 5. Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
và có thể tích
(
)
3
9
dm
4
V
=
Tính giá trị của
a
.
A.
( )
9 dma =
. B.
( )
3 dma
=
. C.
(
)
3 3 dm
a =
. D.
(
)
3 dma =
.
Câu 6. Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
và có thể tích
( )
3
9
4
V dm=
Tính giá trị của
a
.
A.
( )
3a dm
=
. B.
( )
33
a dm=
. C.
( )
3a dm=
. D.
( )
9a dm
=
.
Câu 7. Cho hình lăng trụ
.'' 'ABC A B C
có đáy là tam giác đều cạnh
3a
, hình chieus của
'A
trên mặt phẳng
( )
ABC
trùng với tâm đường tròn ngoại tiếp tam giác
ABC
. Cạnh
AA'
hợp với mặt phẳng đáy
một góc
0
45
. Thể tích của khối lăng trụ
.'' 'ABC A B C
tính theo
a
bằng.
A.
3
27
6
a
. B.
3
9
4
a
. C.
3
27
4
a
. D.
3
3
4
a
.
Câu 8. Cho lăng trụ đều
.ABC A B C
′′′
có cạnh đáy bằng
a
. Gọi
I
là trung điểm cạnh
BC
. Nếu góc giữa
đường thẳng
AI
′
và mặt phẳng
( )
ABC
bằng
60°
thì thể tích của lăng trụ đó là
A.
3
33
8
a
. B.
3
3
24
a
. C.
3
3
8
a
. D.
3
3
4
a
.
Câu 9. Cho hình lăng trụ tam giác đều có tất cả các cạnh đều bằng
a
. Tính theo
a
thể tích của khối lăng
trụ.
A.
3
3
4
a
. B.
3
2
3
a
. C.
3
3
12
a
. D.
3
3
a
.
Câu 10. Cho lăng trụ tam giác đều
.
ABC A B C
′′′
có cạnh đáy bằng
a
và cạnh bên bằng
3a
. Thể tích của khối
lăng trụ
.ABC A B C
′′′
bằng:
A.
3
8
a
. B.
3
3
8
a
. C.
3
4
a
. D.
3
3
4
a
.
Câu 11. Cho lăng trụ đứng có đáy là tam giác đều, biết rằng tất cả các cạnh của lăng trụ bằng
a
. Thể tích
của lăng trụ đó là.
A.
3
3
12
a
. B.
3
4
a
. C.
3
3
8
a
. D.
3
3
4
a
.
https://toanmath.com/
Câu 12. Cho khối lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
2
, diện tích tam giác
A BC
′
bằng
3
. Tính thể tích của khối lăng trụ.
A.
32
. B.
25
3
. C.
25
. D.
2
.
Câu 13. Tính thể tích
V
của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng
a
.
A.
3
2
4
a
V
B.
3
3
2
a
V
C.
3
3
4
a
V
D.
3
2
3
a
V
Câu 14. Cho lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
a
và
AB BC
′′
⊥
. Tính thể tích của khối
lăng trụ.
A.
3
6Va=
. B.
3
7
8
a
V
=
. C.
3
6
8
a
V =
. D.
3
6
4
a
V =
.
Câu 15. Nếu khối lăng trụ đứng có đáy là hình vuông cạnh
2a
và đường chéo mặt bên bằng
4a
thì khối
lăng trụ đó có thể tích bằng.
A.
3
4a
. B.
3
83a
. C.
3
12a
. D.
3
63a
.
Câu 16. Cho hình lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
2
a
, góc giữa hai đường thẳng
AB
′
và
BC
′
bằng
60°
. Tính thể tích
V
của khối lăng trụ đó.
A.
3
26Va=
. B.
3
23Va
=
. C.
3
26
3
a
V =
. D.
3
23
3
a
V =
.
Câu 17. Một khối lăng trụ tam giác có đáy là tam giác đều cạnh 3, cạnh bên bằng
23
và tạo với mặt phẳng
đáy một góc
30 .°
Khi đó thể tích khối lăng trụ là?
A.
27
.
4
B.
93
.
4
C.
9
.
4
D.
27 3
.
4
Câu 18. Cho hình lăng trụ tứ giác đều
.ABCD A B C D
′′′′
có cạnh đáy bằng
a
, khoảng cách từ
A
đến mặt
phẳng
( )
A BC
′
bằng
3
a
. Tính thể tích lăng trụ.
A.
3
2
4
a
. B.
3
33a
. C.
3
3
4
a
. D.
3
3
2
a
.
Câu 19. Thể tích của khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng
a
bằng:
A.
3
3
a
. B.
3
3
4
a
. C.
3
3
6
a
. D.
3
2
3
a
.
Câu 20. Cho khối lăng trụ đều
.ABC A B C
′′′
và
M
là trung điểm của cạnh
AB
. Mặt phẳng
( )
BCM
′′
chia
khối lăng trụ thành hai phần. Tính tỷ số thể tích của hai phần đó.
A.
3
8
B.
6
5
. C.
7
5
. D.
1
4
.
Câu 21. Cho hình lăng trụ tam giác đều
.ABC A B C
′′′
có
AB a=
, đường thẳng
AB
′
tạo với mặt phẳng
( )
BCC B
′′
một góc
30°
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
2
3
a
V
=
. B.
3
6
4
a
V =
. C.
3
6
12
a
V
=
. D.
3
3
4
a
V =
.
Câu 22. Cho lăng trụ đứng
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh
a
, góc tạo bởi hai mặt phẳng
( )
ABC
,
( )
A BC
′
bằng
60°
. Tính thể tích khối lăng trụ
.ABC A B C
′′′
.
A.
3
3
24
a
. B.
3
33
4
a
. C.
3
3
6
a
. D.
3
33
8
a
.
https://toanmath.com/
Câu 23. Khối lăng trụ tam giác đều có tất cả các cạnh bằng nhau và có thể tích là
9
4
thì độ dài mỗi cạnh
bằng.
A.
3
. B.
3
. C.
6
243
. D.
33
.
Câu 24. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
là.
A.
3
2
4
Va=
. B.
3
3
4
Va=
. C.
3
2
3
Va=
. D.
3
3
2
Va=
.
Câu 25. Tính thể tích của khối lăng trụ đều
.ABC A B C
′′′
có
AB AA a
′
= =
.
A.
3
3
12
a
. B.
3
3
4
a
. C.
3
3
6
a
. D.
3
a
.
Câu 26. Cho lăng trụ đứng
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Mặt phẳng
(
)
AB C
′′
tạo với mặt đáy
góc
60°
. Tính theo
a
thể tích khối lăng trụ
.ABC A B C
′′′
.
A.
3
3
.
8
a
V =
B.
3
33
.
8
a
V =
C.
3
3
.
2
a
V =
D.
3
33
.
4
a
V =
Câu 27. Tính thể tích
V
của khối lăng trụ đều
.'' 'ABC A B C
biết
AB a=
và
'2
AB a
=
.
A.
3
3
4
a
V =
. B.
3
3
2
a
V =
. C.
3
3
12
a
V =
. D.
3
3
4
a
V =
.
Câu 28. Cho hình lăng trụ tứ giác đều
.ABCD A B C D
′′′′
có cạnh đáy
( )
43 .m
Biết mặt phẳng
( )
D BC
′
hợp
với đáy một góc
60
ο
. Thể tích khối lăng trụ là.
A.
3
325m
. B.
3
648m
. C.
3
478m
. D.
3
576m
.
Câu 29. Cho lăng trụ đứng
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh
a
, góc tạo bởi hai mặt phẳng
( )
ABC
,
( )
A BC
′
bằng
60°
. Tính thể tích khối lăng trụ
.ABC A B C
′′′
.
A.
3
3
6
a
. B.
3
33
4
a
. C.
3
33
8
a
. D.
3
3
24
a
.
Câu 30. Cho hình chóp
.S ABC
có
( )
SA ABC⊥
, tam giác
ABC
vuông tại
C
,
2, 6
AC a AB a= =
. Tính
thể tích khối chóp
.S ABC
biết
3SC a=
A.
3
2 42
3
a
. B.
3
14a
. C.
3
6
3
a
. D.
3
14
3
a
.
Câu 31. Cho hình lăng trụ đều
.ABC A B C
′′′
. Biết khoảng cách từ điểm
C
đến mặt phẳng
( )
ABC
′
bằng
a
,
góc giữa hai mặt phẳng
(
)
ABC
′
và
( )
BCC B
′′
bằng
α
với
1
cos
23
α
=
(tham khảo hình vẽ bên).
Thể tích khối lăng trụ
.ABC A B C
′′′
là
A.
3
2
2
a
. B.
3
32
2
a
. C.
3
32
4
a
. D.
3
32
8
a
C
B
A
C'
B'
A'
https://toanmath.com/
Câu 32. Cho hình hộp đứng
.ABCD A B C D
′′′′
có đáy là hình vuông cạnh
a
, góc giữa mặt phẳng
(
)
D AB
′
và
mặt phẳng
( )
ABCD
bằng
30°
. Thể tích khối hộp
.ABCD A B C D
′′′′
bằng
A.
3
3a
. B.
3
3
3
a
. C.
3
3
9
a
. D.
3
3
18
a
.
Câu 33. Cho hình lăng trụ tam giác đều
ABCA B C
′′′
có
AB a
=
, đường thẳng
AB
′
tạo với mặt phẳng
( )
BCC B
′′
một góc
30°
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
6
12
a
V =
. B.
3
3
.
4
a
V =
. C.
3
6
4
a
V =
. D.
3
.
4
a
V =
.
Câu 34. Cho lăng trụ tam giác đều
.ABC A B C
′′′
có chiều cao bằng
2
. Biết góc giữa đường thẳng
AB
′
và
mặt phẳng
( )
ABC
′′′
bằng
α
thỏa
1
tan
2
α
=
. Tính thể tích khối lăng trụ
.ABC A B C
′′′
.
A.
43
. B.
43
3
. C.
43
9
. D.
23
3
.
Câu 35. Cho lăng trụ tam giác đều
.
ABC A B C
′′′
cạnh đáy bằng
a
, chiều cao bằng
2a
. Mặt phẳng
( )
P
qua
B
′
và vuông góc với
AC
′
chia lăng trụ thành hai khối. Biết thể tích của hai khối là
1
V
và
2
V
với
12
VV<
. Tỉ số
1
2
V
V
bằng
A.
1
7
B.
1
47
C.
1
23
D.
1
11
Câu 36. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng
2a
là.
A.
3
3
4
a
. B.
3
3
12
a
.
C.
3
23a
.
D.
3
4a
.
Câu 37. Cho lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
a
và
AB BC
′′
⊥
. Tính thể tích
V
của
khối lăng trụ đã cho.
A.
3
6
4
a
V =
. B.
3
7
8
a
V =
. C.
3
6Va=
. D.
3
6
8
a
V =
.
Câu 38. Cho lăng trụ
ABCDA B C D
′′′′
có đáy
ABCD
là hình thoi cạnh
a
, tâm
O
và
120ABC = °
. Các cạnh
AA
′
;
AB
′
;
AD
′
cùng tạo với mặt đáy một góc bằng
45°
. Tính theo
a
thể tích
V
của khối lăng trụ
đã cho.
A.
3
3
2
a
B.
3
2
a
C.
3
3
4
a
D.
3
3
2
a
Câu 39. Cho hình lăng trụ đứng
.ABC A B C
′′′
, biết đáy
ABC
là tam giác đều cạnh
a
. Khoảng cách từ tâm
O
của tam giác
ABC
đến mặt phẳng
( )
A BC
′
bằng
6
a
. Tính thể tích khối lăng trụ
.ABC A B C
′′′
.
A.
3
32
8
a
. B.
3
32
28
a
. C.
3
32
4
a
. D.
3
32
16
a
.
Câu 40. Cho lăng trụ tam giác đều
.ABC A B C
′′′
có độ dài cạnh đáy bằng
2a
, cạnh bên bằng
3a
. Tính thể
tích
V
của lăng trụ.
A.
3
32Va=
. B.
3
2Va=
. C.
3
3Va=
. D.
3
3Va=
.
Câu 41. Cho lăng trụ đều
.ABC A B C
′′′
có cạnh đáy bằng
2a
, diện tích xung quanh bằng
2
63a
. Thể tích
V
của khối lăng trụ.
A.
3
3Va
=
. B.
3
3
4
Va=
. C.
3
Va=
. D.
3
1
4
Va=
.
Câu 42. Tính thể tích của khối lăng trụ tam giác đều có cạnh đáy bằng
2a
và cạnh bên bằng
a
.
https://toanmath.com/
A.
3
3
4
a
. B.
3
3a
. C.
3
a
. D.
3
3
3
a
.
Câu 43. Cho hình lăng trụ đều
.ABC A B C
′′′
có cạnh đáy bằng
a
,
AC
′
hợp với mặt đáy
( )
ABC
một góc
60
°
. Thể tích của khối lăng trụ
.ABC A B C
′′′
bằng:
A.
3
3
8
a
. B.
3
4
a
. C.
3
2
3
a
. D.
3
3
4
a
.
Câu 44. Cho lăng trụ tam giác
.ABC A B C
′′′
có đáy là tam giác vuông cân, cạnh huyền
2
AC a=
. Hình chiếu
của
A
lên mặt phẳng
( )
ABC
′′′
là trung điểm
I
của
AB
′′
, góc giữa cạnh bên và mặt đáy bằng
60°
. Thể tích khối lăng trụ
.ABC A B C
′′′
là.
A.
3
6
2
a
. B.
3
2a
. C.
3
6
6
a
. D.
3
3
4
a
.
Câu 45..Cho lăng trụ tam giác
.ABC A B C
′′′
có đáy là tam giác vuông cân, cạnh huyền
2AC a=
. Hình chiếu
của
A
lên mặt phẳng
( )
ABC
′′′
là trung điểm
I
của
AB
′′
, góc giữa cạnh bên và mặt đáy bằng
60°
. Thể tích khối lăng trụ
.
ABC A B C
′′′
là.
A.
3
6
2
a
.
B.
3
6
6
a
.
C.
3
2a
.
D.
3
3
4
a
.
Câu 46. Cho hình lăng trụ đứng
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
, cạnh bên
2
AA a
′
=
. Thể tích
của khối lăng trụ là
A.
3
3
4
a
. B.
3
3
12
a
. C.
3
6
12
a
. D.
3
6
4
a
.
Câu 47. Cho lăng trụ tam giác đều
.ABC A B C
′′′
có tất cả các cạnh đều bằng
2a
. Tính thể tích của khối
lăng trụ.
A.
3
3
8
a
. B.
3
6
2
a
. C.
3
6
6
a
. D.
3
3
6
a
.
Câu 48. Thể tích
V
của khối lăng trụ tam giác đều có cạnh đáy bằng
2a
và cạnh bên bằng
a
là
A.
3
3
3
a
V =
. B.
3
3
2
a
V =
. C.
3
3Va=
. D.
3
3
4
a
V =
.
Câu 49. Tính thể tích
V
của khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
.
A.
3
3
2
a
V =
. B.
3
2
4
a
V =
. C.
3
3
4
a
V =
. D.
3
2
3
a
V =
.
Câu 50. Cho hình lăng trụ tam giác
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông tại
A
,
AB a=
,
3AC a=
. Hình chiếu vuông góc của
A
′
lên
( )
ABC
là trung điểm của
BC
. Góc giữa
AA
′
và
( )
ABC
bằng
60°
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
3
2
a
V =
. B.
3
3
2
a
V =
. C.
3
2
a
V =
. D.
3
33
2
a
V =
.
Câu 51. Cho hình lăng trụ đứng tam giác
.ABC A B C
′′′
có đáy là
∆ABC
đều cạnh
4=a
và biết
8
A BC
S
′
∆
=
.
Tính thể tích khối lăng trụ.
A.
23
. B.
43
. C.
63
. D.
83
.
Câu 52. Cho lăng trụ đứng
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh
a
, cạnh bên
AB
′
tạo với đáy
một góc
45
°
. Thể tích khối lăng trụ
.ABC A B C
′′′
là:
A.
3
.'''
3
4
ABC A B C
a
V =
. B.
3
.'''
3
ABC A B C
Va=
.
https://toanmath.com/
C.
. D.
3
.'''
2
3
ABC A B C
a
V =
.
Câu 53. Cho hình lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
a
, góc giữa mặt phẳng
(
)
A BC
′
và
mặt phẳng
(
)
ABC
bằng
45°
. Thể tích của khối lăng trụ
.ABC A B C
′′′
bằng
A.
3
3
2
a
. B.
3
3
8
a
. C.
3
3
8
a
. D.
3
3
4
a
.
Câu 54. Cho hình lăng trụ tứ giác đều
.ABCD A B C D
′′′′
có cạnh đáy bằng
a
. Biết đường chéo của mặt bên
là
3
a
. Khi đó, thể tích khối lăng trụ bằng:
A.
3
3a
. B.
3
2a
. C.
3
2
3
a
. D.
3
2
a
.
Câu 55. Cho hình lăng trụ đứng
.ABC A B C
′′′
có tam giác
ABC
là tam giác đều cạnh bằng
a
, góc giữa
( )
AB C
′′
và
()ABC
′′′
bằng
o
60
. Thể tích khối lăng trụ
.ABC A B C
′′′
là.
A.
3
3
24
a
. B.
3
3
8
a
. C.
3
33
8
a
. D.
3
24
a
.
Câu 56. Cho hình lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
a
. Góc giữa đường thẳng
AB
′
và
mặt phẳng
(
)
ABC
bằng
45°
. Tính thể tích của khối lăng trụ
.ABC A B C
′′′
.
A.
3
3
6
a
. B.
3
3
12
a
. C.
3
3
24
a
. D.
3
3
4
a
.
Câu 57. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng
a
là:
A.
3
3
3
a
. B.
3
3
4
a
. C.
3
2
3
a
. D.
3
2
2
a
.
Câu 58. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng
a
là:
A.
3
2
a
. B.
3
3
12
a
. C.
3
3
2
a
. D.
3
3
4
a
.
Câu 59. Cho hình lăng trụ đều
.ABC A B C
′′′
. Biết khoảng cách từ điểm
C
đến mặt phẳng
( )
ABC
′
bằng a,
góc giữa hai mặt phẳng
( )
ABC
′
và
( )
BCC B
′′
bằng
α
với
1
23
cos
α
=
(tham khảo hình vẽ dưới
đây). Thể tích khối lăng trụ
.ABC A B C
′′′
bằng
A.
3
2
3
4
a
. B.
3
2
2
a
. C.
3
2
3
2
a
. D.
3
2
3
8
a
.
Câu 60. Cho hình lăng trụ đứng
.'' 'ABC A B C
có đáy
ABC
đều cạnh bằng
a
và chu vi của mặt bên
''ABB A
bằng
6a
. Thể tích của khối lăng trụ
.'' 'ABC A B C
bằng
A.
3
3
2
a
. B.
3
3a
. C.
3
3
3
a
. D.
3
3
6
a
.
Câu 61. Cho lăng trụ đứng
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
và
AB
′
vuông góc với
BC
′
. Thể
tích của lăng trụ đã cho là.
A.
3
6
12
a
. B.
3
6
4
a
. C.
3
6
8
a
. D.
3
6
24
a
.
Câu 62. Cho hình lăng trụ tam giác đều
.ABC A B C
′′′
có tất cả các cạnh bằng
a
. Gọi
,MN
lần lượt là trung
điểm của các cạnh
AB
và
BC
′′
. Mặt phẳng
( )
A MN
′
cắt cạnh
BC
tại
.P
Thể tích khối đa diện
.MBPABN
′′
bằng.
A.
3
73
68
a
. B.
3
3
32
a
. C.
3
73
96
a
. D.
3
73
32
a
.
https://toanmath.com/
Câu 63. Cho
( )
H
là khối lăng trụ đứng tam giác đều có tất cả các cạnh đều bằng
a
. Thể tích của
( )
H
bằng:
A.
3
3
2
a
. B.
3
3
4
a
. C.
3
2
3
a
. D.
3
2
a
.
Câu 64. Cho khối lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
2a
và mỗi mặt bên có diện tích
bằng
2
4a
. Thể tích khối lăng trụ đó là
A.
3
26a
. B.
3
26
3
a
. C.
3
6
2
a
. D.
3
6a
.
Câu 65. Cho hình lăng trụ tứ giác đều
.
ABCD A B C D
′′′′
có cạnh đáy bằng
a
. Biết đường chéo của mặt bên
là
3a
. Khi đó, thể tích khối lăng trụ bằng:
A.
3
3a
. B.
3
2a
. C.
3
2
3
a
. D.
3
2
a
.
Câu 66.Khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
thì có thể tích bằng
A.
3
3
6
a
. B.
3
3
12
a
. C.
3
3
4
a
. D.
3
3
8
a
.
Câu 67. Từ một ảnh giấy hình vuông cạnh là
4cm
, người ta gấp nó thành bốn phần đều nhau rồi dựng lên
thành bốn mặt xung quanh của hình hình lăng trụ tứ giác đều như hình vẽ. Hỏi thể tích của khối
lăng trụ này là bao nhiêu.
A.
3
64
3
cm
B.
3
16cm
. C.
3
4
3
cm
D.
3
4cm
.
Câu 68. Cho lăng trụ tứ giác đều
.ABCD A B C D
′′′′
đáy hình có cạnh bằng
,a
đường chéo
AC
′
tạo với mặt
bên
( )
BCC B
′′
một góc
α
( )
0
0 45 .
α
<<
Tính thể tích của lăng trụ tứ giác đều
.ABCD A B C D
′′′′
.
A.
32
cot 1a
α
+
. B.
32
tan 1a
α
−
. C.
3
cos2a
α
. D.
32
cot 1a
α
−
.
Câu 69. Cho khối lăng trụ
.ABC A B C
′′′
có
,
6AC a=
. Hình chiếu vuông góc của
A
′
trên mặt
phẳng
( )
ABC
là trung điểm của
AB
và
133
2
a
AC
′
=
. Tính thể tích
V
của khối lăng trụ
.ABC A B C
′′′
theo
.a
.
A.
3
12 133Va=
.
B.
3
4 133Va=
.
C.
3
12Va=
. D.
3
36Va=
.
Câu 70. Cho hình lăng trụ đều
.'ABC A B C
′′
có cạnh đáy bằng
a
, cạnh bên
3a
. Thể tích của khối lăng trụ
là.
A.
3
3
7
a
. B.
3
3
4
a
. C.
3
7
5
a
.
D.
3
3
4
a
.
Câu 71. Cho khối lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy là
a
và khoảng cách từ
A
đến mặt phẳng
( )
A BC
′
bằng
2
a
. Tính thể tích của khối lăng trụ
.ABC A B C
′′′
.
A.
3
32
12
a
. B.
3
32
16
a
. C.
3
32
48
a
. D.
3
2
16
a
.
https://toanmath.com/
Câu 72. Cho lăng trụ tứ giác đều
.ABCD A B C D
′′′′
có cạnh đáy bằng
5a
. Khoảng cách từ
A
đến mặt
phẳng
(
)
'
A BC
bằng
5
2
a
. Thể tích khối lăng trụ là:
A.
3
5 15
3
a
. B.
3
63
5
a
. C.
3
22a
. D.
3
5
3
a
.
Câu 73. Cho lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
2
a
, khoảng cách từ
A
đến mặt phẳng
( )
A BC
′
bằng
6
2
a
. Khi đó thể tích lăng trụ bằng.
A.
3
43
3
Va=
. B.
3
4
3
Va
=
. C.
3
3Va=
. D.
3
Va=
.
Câu 74. Cho hình lăng trụ đều
.'ABC A B C
′′
có
AB a=
,
3
'
2
a
AA =
. Gọi
G
là trọng tâm tam giác
A BC
′
.
Tính thể tích tứ diện
GABC
theo
a
.
A.
3
3
16
a
. B.
3
3
12
a
.
C.
3
3
24
a
.
D.
3
33
8
a
.
Câu 75. Tính thể tích
V
của khối lăng trụ tam giác đều
.ABC A B C
′′′
có
AA BC a
′
= =
.
A.
3
3
4
a
V =
. B.
3
2
6
a
V =
. C.
3
3
12
a
V =
. D.
3
3
a
V =
.
Câu 76. Cho lăng trụ
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh
a
, cạnh bên tạo với mặt phẳng bằng
0
45
. Hình chiếu của
A
trên mặt phẳng
( )
ABC
′′′
trùng với trung điểm của
AB
′′
. Tính thể tích
V
của khối lăng trụ theo
a
.
A.
3
3
2
a
V =
. B.
3
3
24
a
V =
. C.
3
3
8
a
V =
. D.
3
3
16
a
V =
.
Câu 77. Cho lăng trụ
.ABC A B C
′′′
có cạnh bên bằng
2a
, đáy
ABC
là tam giác cân tại
;A
2 ; AB a=
0
120 .BAC =
Hình chiếu vuông góc của
A
′
trên
( )
mp ABC
trùng với trung điểm của cạnh
BC
.
Tính thể tích khối chóp
.A BB C C
′ ′′
?
A.
3
3a
. B.
3
2a
. C.
3
4a
. D.
3
4
3
a
.
Câu 78. Cho khối lăng trụ đứng có cạnh bên bằng
5
, đáy là hình vuông có cạnh bằng
4
. Hỏi thể tích khối
lăng trụ là:
A.
64
. B.
80
. C.
100
. D.
20
.
Câu 79. Cho hình lăng trụ tam giác đều
.ABC A B C
′′′
có tất cả các cạnh bằng
a
. Gọi
M
,
N
lần lượt là trung
điểm của các cạnh
AB
và
BC
′′
. Mặt phẳng
( )
A MN
′
cắt cạnh
BC
tại
P
. Tính thể tích của khối
đa diện
.MBPABN
′′
A.
3
3
24
a
. B.
3
3
12
a
. C.
3
73
96
a
. D.
3
73
32
a
.
Câu 80. Cho hình lăng trụ
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông tại
B
,
60ACB
°
=
,
BC a=
,
2AA a
′
=
. Cạnh bên tạo với mặt phẳng
( )
ABC
một góc
30°
.Thể tích khối lăng trụ
.ABC A B C
′′′
bằng.
A.
3
3
2
a
. B.
3
3
6
a
. C.
3
3a
. D.
3
3
3
a
.
https://toanmath.com/
Câu 81. Cho hình lăng trụ tam giác
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh bằng
a
, hình chiếu
vuông góc của
A
′
lên mặt phẳng
( )
ABC
là trung điểm
H
của cạnh
AB
, cạnh
10
2
a
AA
′
=
. Tính
theo
a
tích của khối lăng trụ
.ABC A B C
′′′
.
A.
3
3
.
8
a
B.
3
33
.
4
a
C.
3
3
.
12
a
V =
D.
3
33
.
8
a
V =
Câu 82. Cho hình lăng trụ tam giác đều có tất cả các cạnh đều bằng
a
. Tính theo
a
thể tích của khối lăng
trụ.
A.
3
2
3
a
. B.
3
3
a
. C.
3
3
4
a
. D.
3
3
12
a
.
Câu 83. Cho hình lăng trụ tam giác đều có các cạnh đều bằng
2a
.Thể tích khối lăng trụ đều là:
A.
3
2
3
a
. B.
3
23
3
a
. C.
3
23a
. D.
3
3
a
.
Câu 84. Một hình lăng trụ có đáy là tam giác đều cạnh bằng
a
, cạnh bên bằng
b
và tạo với mặt phẳng đáy
một góc
α
. Thể tích của khối lăng trụ đó là
A.
2
3
cos
12
ab
α
. B.
2
3
cos
4
ab
α
. C.
2
3
sin
12
ab
α
. D.
2
3
sin
4
ab
α
.
Câu 85.] Cho
()
H
là khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng
a
Thể tích của
()H
bằng:
A.
3
2
3
a
.
B.
3
3
4
a
.
C.
3
3
2
a
. D.
3
2
a
.
Câu 86. Cho hình lăng trụ
.’’’ABC A B C
có đáy là tam giác đều cạnh
a
. Hình chiếu của
A
′
trên mặt phẳng
( )
ABC
là trung điểm
H
của cạnh
BC
.
'7
AA a=
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
53
8
a
. B.
3
3
8
a
. C.
3
53
24
a
. D.
3
53
6
a
.
Câu 87. Cho lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
a
và
AB BC
′′
⊥
. Khi đó thể tích của khối
lăng trụ trên sẽ là:
A.
3
6
8
a
V =
. B.
3
7
8
a
V =
. C.
3
6Va=
. D.
3
6
4
a
V
=
.
Câu 88. Cho hình lăng trụ đều
.ABC A B C
′′′
có cạnh đáy bằng
a
.
M
,
N
là hai điểm thõa mãn
20MB MB
′
+=
 
;
3NB NC
′′
=
 
. Biết hai mặt phẳng
( )
MCA
và
( )
NAB
vuông góc với nhau. Tính
thể tích của hình lăng trụ.
A.
3
32
8
a
B.
3
92
8
a
C.
3
92
16
a
D.
3
32
16
a
Câu 89. Cho
( )
H
là hình lăng trụ xiên
.ABC A B C
′′′
có đáy là tam giác đều cạch
a
, hình chiếu vuông góc
A
′
lên đáy trùng với tâm đường tròn ngoại tiếp tam giác
ABC
và
AA
′
hợp đáy bằng
60°
. Thể
tích của
(
)
H
bằng.
A.
3
3
4
a
. B.
3
3
12
a
. C.
3
3
2
a
. D.
3
3
6
a
.
Câu 90. Cho lăng trụ tam giác đều
.ABC A B C
′′′
có độ dài cạnh đáy bằng
2a
, cạnh bên bằng
3a
. Tính thể
tích
V
của lăng trụ.
A.
3
32Va=
. B.
3
2Va=
. C.
3
3Va=
. D.
3
3Va=
.
Câu 91. Cho hình lăng trụ tam giác đều có các cạnh đều bằng
.a
Thể tích khối lăng trụ đều là
A.
3
2
.
3
a
B.
3
3
.
4
a
C.
3
22
.
3
a
D.
3
.
3
a
https://toanmath.com/
Câu 92. Cho hình lăng trụ đứng
.ABCD A B C D
′′′′
có đáy là hình vuông cạnh bằng
3
, đường chéo
AB
′
của
mặt bên
( )
ABB A
′′
có độ dài bằng
5
. Tính thể tích
V
của khối lăng trụ
.ABCD A B C D
′′′′
?
A.
18V =
. B.
48
V
=
. C.
36V =
. D.
45V =
.
Câu 93. Cho hình lăng trụ đều
.ABC A B C
′′′
có cạnh đáy bằng
a
. Đường thẳng
AB
′
tạo với mặt phẳng
( )
BCC B
′′
một góc
30°
. Thể tích khối lăng trụ
.ABC A B C
′′′
theo
a
.
A.
3
6
4
a
. B.
3
4
a
. C.
3
6
12
a
. D.
3
3
4
a
.
Câu 94. Cho khối lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
2
, diện tích tam giác
A BC
′
bằng
3
. Tính thể tích của khối lăng trụ.
A.
2
. B.
25
3
. C.
32
. D.
25
.
Câu 95. Cho hình lăng trụ đều
.ABC A B C
′′′
, biết khoảng cách từ điểm
C
đến mặt phẳng
( )
ABC
′
bằng
a
,
góc giữa hai mặt phẳng
( )
ABC
′
và
( )
BCC B
′′
bằng
α
với
1
cos
3
α
=
(tham khảo hình vẽ bên
dưới).Thể tích khối lăng trụ bằng
A.
3
9 15
20
a
. B.
3
3 15
20
a
. C.
3
3 15
10
a
. D.
3
9 15
10
a
.
Câu 96.Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông, các tam giác
SAB
và
SAD
là những tam
giác vuông tại
A
. Mặt phẳng
( )
P
qua
A
vuông góc với cạnh bên
SC
cắt
,,SB SC SD
lần lượt
tại các điểm
,,MNP
. Biết
8SC a=
,
0
60
ASC =
. Tính thể tích khối cầu ngoại tiếp đa diện
ABCDMNP
?
A.
3
6Va
π
=
. B.
3
24Va
π
=
. C.
3
32 3Va
π
=
. D.
3
18 3Va
π
=
.
Câu 97. Cho khối lăng trụ tam giác đều
.
ABC A B C
′′′
có cạnh đáy bằng
2
, diện tích tam giác
A BC
′
bằng
3
. Tính thể tích của khối lăng trụ
A.
32
. B.
25
. C.
2
. D.
25
3
.
Câu 98. Cho hình lăng trụ tứ giác
.ABCD A B C D
′′′′
có đáy
ABCD
là hình vuông cạnh
a
và thể tích bằng
2
3a
. Tính chiều cao
h
của hình lăng trụ đã cho.
A.
3
a
h =
. B.
9ha=
. C.
3ha=
. D.
ha=
.
Câu 99. Cho lăng trụ đứng
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Góc tạo bởi cạnh
BC
′
và mặt đáy
( )
ABC
′′′
bằng
o
30
. Tính thể tích khối lăng trụ.
A.
3
3
4
a
. B.
3
2
a
. C.
3
12
a
. D.
3
4
a
.
A
B
C
C'
B'
A'
https://toanmath.com/
Câu 100.] Cho lăng trụ đứng
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh
a
, cạnh bên
AB
′
tạo với đáy
một góc
0
45
Thể tích khối lăng trụ
.ABC A B C
′′′
là:
A.
3
.'''
2
3
ABC A B C
a
V =
. B.
3
.'''
3
ABC A B C
Va=
.
C.
. D.
3
.'''
3
4
ABC A B C
a
V =
.
Câu 101. Cho lăng trụ tam giác đều
.
ABC A B C

có tất cả các cạnh bằng
2a
. Tính thể tích khối lăng trụ
.ABC A B C
.
A.
3
23a
. B.
3
3a
. C.
3
3
4
a
. D.
3
3
2
a
.
https://toanmath.com/
THỂ TÍCH KHỐI LĂNG TRỤ ĐỀU
Câu 1. Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng
3
. Thể tích khối lăng trụ đã cho bằng
A.
93
4
. B.
27 3
4
. C.
27 3
2
. D.
93
2
.
Hướng dẫn giải.
Chọn B
Diện tích đáy:
1 93
.3.3.sin60
24
ABC
S
∆
= °=
. Thể tích
27 3
.
4
l ABCt
V S AA
∆
′
= =
.
Câu 2. Cho lăng trụ tam giác đều
.
ABC A B C
′′′
có cạnh đáy bằng
4
cm
, diện tích tam giác
A BC
′
bằng
2
12cm
. Thể tích khối lăng trụ đó là:
A.
3
82
V cm=
. B.
. C.
3
24V cm=
. D.
3
24 2V cm
=
.
Hướng dẫn giải
Chọn D
Kẻ
( )
'A P BC P BC BC AP⊥ ∈ ⇒⊥
.
Ta có
1 24
' . 12 ' 6
24
APBC AP=⇒==
.
Cạnh
3
2 3 ' 36 12 2 6
2
AB
AP A A= = ⇒ = −=
1
' . 2 6. .4.2 3 24 2
2
ABC
V A AS⇒= = =
.
Câu 3. Cho hình lăng trụ đứng
.'' 'ABC A B C
có đáy
ABC
đều cạnh bằng
a
và chu vi của mặt bên
''ABB A
bằng
6a
. Thể tích của khối lăng trụ
.'' 'ABC A B C
bằng
A.
3
3
2
a
. B.
3
3a
. C.
3
3
3
a
. D.
3
3
6
a
.
Hướng dẫn giải
Chọn A
https://toanmath.com/
Chu vi của hình chữ nhật
(
)
2 ' 6 '2AB AA a AA a
+ =⇒=
Thể tích khối lăng trụ
23
33
.2
42
aa
V Bh a
= = =
.
Câu 4. Cho khối tứ giác đều
.S ABCD
có thể tích là
V
. Nếu giảm độ dài cạnh đáy xuống hai lần và tăng độ
dài đường cao lên ba lần thì ta được khối chóp mới có thể tích là:
A.
3
2
V
. B.
2
3
V
. C.
1
4
V
. D.
3
4
V
.
Hướng dẫn giải
Chọn D
Gọi độ dài cạnh đáy và chiều cao của hình chóp tứ giác đều lần lượt là
và ah
. Thể tích khối
chóp sau khi đã giảm độ dài cạnh đáy và tăng chiều cao là:
2
2
1 31 3
.3 . .
32 4 3 4
a
h ah V

= =


.
Câu 5. Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
và có thể tích
( )
3
9
dm
4
V =
Tính giá trị
của
a
.
A.
( )
9 dma =
. B.
( )
3 dma =
. C.
( )
3 3 dma =
. D.
( )
3 dma
=
.
Hướng dẫn giải
Chọn B
Khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
có thể tích bằng.
23
33
..
44
aa
V Bh a
= = =
.
Mà
(
)
3
33
9 39
3 3 3( )
4 44
a
V dm a a dm= ⇒ = ⇔ = ⇔=
.
Câu 6. Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
và có thể tích
(
)
3
9
4
V dm=
Tính giá trị
của
a
.
A.
( )
3a dm=
. B.
( )
33a dm=
. C.
( )
3a dm=
. D.
( )
9a dm=
.
Hướng dẫn giải
Chọn A
Khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
có thể tích bằng
23
33
..
44
aa
V Bh a= = =
.
A
C
B
B'
C'
A'
https://toanmath.com/
Mà
(
)
3
33
9 39
3 3 3( )
4 44
a
V dm a a dm= ⇒ = ⇔ = ⇔=
.
Câu 7. Cho hình lăng trụ
.'' '
ABC A B C
có đáy là tam giác đều cạnh
3a
, hình chieus của
'A
trên mặt
phẳng
( )
ABC
trùng với tâm đường tròn ngoại tiếp tam giác
ABC
. Cạnh
AA'
hợp với mặt
phẳng đáy một góc
0
45
. Thể tích của khối lăng trụ
.'' 'ABC A B C
tính theo
a
bằng.
A.
3
27
6
a
. B.
3
9
4
a
. C.
3
27
4
a
. D.
3
3
4
a
.
Hướng dẫn giải
Chọn C
Gọi
AI
là đường cao,
H
là tâm của tam giác
ABC
( )
A H ABC
′
⇒⊥
.
Vì
( )
(
)
AA ABC A
A H ABC
′
∩=
⇒
′
⊥
góc giữa
AA
′
và
( )
ABC
là
45A AH A AH
′′
⇒=°
.
Ta có:
33 2
,3
23
a
AI AH AI a
= = =
,
( )
2
2
33
93
44
ABC
a
a
S = =
.
.tan 45 3A H AH AH a
′
= °= =
.
Thể tích của lăng trụ là:
23
9 3 27
. 3.
44
ABC
aa
V AHS a
′
= = =
.
.
Câu 8. Cho lăng trụ đều
.ABC A B C
′′′
có cạnh đáy bằng
a
. Gọi
I
là trung điểm cạnh
BC
. Nếu góc giữa
đường thẳng
AI
′
và mặt phẳng
( )
ABC
bằng
60°
thì thể tích của lăng trụ đó là
A.
3
33
8
a
. B.
3
3
24
a
. C.
3
3
8
a
. D.
3
3
4
a
.
Hướng dẫn giải
Chọn A
I
B'
C'
A
B
C
H
A'
https://toanmath.com/
Ta có
(
)
( )
( )
,,A I ABC A I AI
′′
=
60A IA
′
= = °
.
Suy ra
33
tan 60 .
22
aa
AA
′
= °=
.
Vậy
.
.
ABC A B C ABC
V S AA
′′′
∆
′
=
23
33 33
.
42 8
aaa
= =
.
Câu 9. Cho hình lăng trụ tam giác đều có tất cả các cạnh đều bằng
a
. Tính theo
a
thể tích của khối lăng
trụ.
A.
3
3
4
a
. B.
3
2
3
a
. C.
3
3
12
a
. D.
3
3
a
.
Hướng dẫn giải
Chọn A
23
33
..
44
ABC
aa
V AA S a
′
= = =
.
Câu 10. Cho lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
a
và cạnh bên bằng
3a
. Thể tích của
khối lăng trụ
.ABC A B C
′′′
bằng:
A.
3
8
a
. B.
3
3
8
a
. C.
3
4
a
. D.
3
3
4
a
.
Hướng dẫn giải
Chọn D
2 23
.'' '
3 33
; =AA'.S . 3
4 44
ABC ABC A B C ABC
a aa
SV a= = =
.
Câu 11. Cho lăng trụ đứng có đáy là tam giác đều, biết rằng tất cả các cạnh của lăng trụ bằng
a
. Thể tích
của lăng trụ đó là.
A.
3
3
12
a
. B.
3
4
a
. C.
3
3
8
a
. D.
3
3
4
a
.
Hướng dẫn giải
Chọn D
Câu 12. Cho khối lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
2
, diện tích tam giác
A BC
′
bằng
3
. Tính thể tích của khối lăng trụ.
A.
32
. B.
25
3
. C.
25
. D.
2
.
Hướng dẫn giải
Chọn A
60
C'
B'
I
A
B
C
A'
https://toanmath.com/
.
Gọi
M
là trung điểm của
BC
.
Vì
BC AM
BC A M
BC AA
⊥
′
⇒⊥
′
⊥
.
3
A BC
S
′
∆
=
1
.3
2
A M BC
′
⇔=
1
.2 3
2
AM
′
⇔=
3AM
′
⇔=
.
22
AA AM A M
′′
= −
(
)
2
2
33 6
=−=
.
2
.
23
.' .6 32
4
ABC A B C ABC
V S AA
′′′
∆
= = =
.
Câu 13. Tính thể tích
V
của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng
a
.
A.
3
2
4
a
V
B.
3
3
2
a
V
C.
3
3
4
a
V
D.
3
2
3
a
V
Hướng dẫn giải
Chọn C
.
aa
Va= =
23
33
44
.
Câu 14. Cho lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
a
và
AB BC
′′
⊥
. Tính thể tích của khối
lăng trụ.
A.
3
6Va=
. B.
3
7
8
a
V =
. C.
3
6
8
a
V =
. D.
3
6
4
a
V =
.
Hướng dẫn giải
Chọn C
A
′
B
′
C
′
A
B
C
M
https://toanmath.com/
.
Gọi
I
là trung điểm
AB
. Vì
'''ABCA B C
là lăng trụ tam giác đều nên.
( )
'' 'AI BB C C AI BC⊥ =>⊥
.
Lại có:
''AC BC⊥
nên suy ra
( )
' ' ''
BC AIB BC B I⊥ =>⊥
.
Gọi
''H B I BC= ∩
.
Ta có
BHI∆
đồng dạng
''C HB∆
=>
1
' 2 '3
' '' 2
HI BI
B H HI B I HI
BH BC
= ==> = =>=
.
Xét tam giác vuông
'B BI
có
22
22
3
.' 3
3 12 2
BI a a
BI HI B I HI HI= = =>= = =
.
Suy ra
2
2
22
32
''
2 22
a aa
BB B I BI


= −= − =





.
Vậy
3
2
32 6
.BB' a .
42 8
ABC
aa
VS
∆
= = =
.
Câu 15. Nếu khối lăng trụ đứng có đáy là hình vuông cạnh
2a
và đường chéo mặt bên bằng
4a
thì khối
lăng trụ đó có thể tích bằng.
A.
3
4a
. B.
3
83
a
. C.
3
12a
. D.
3
63a
.
Hướng dẫn giải
Chọn B
Đường cao của lăng trụ bằng
( ) (
)
22
4 2 23ha aa= −=
.
Thể tích khối lăng trụ bằng
( )
2
3
. 2 .2 3 8 3V Bh a a a
= = =
.
Câu 16. Cho hình lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
2a
, góc giữa hai đường thẳng
AB
′
và
BC
′
bằng
60°
. Tính thể tích
V
của khối lăng trụ đó.
A.
3
26Va=
. B.
3
23Va
=
. C.
3
26
3
a
V =
. D.
3
23
3
a
V =
.
Hướng dẫn giải
Chọn A
H
I
C'
B'
A'
A
B
C
https://toanmath.com/
Đặt
( )
0
AA x x
′
= >
.
Ta có:
( )( )
2
..
AB BC BB BA BC BB BA BC BB
′′ ′ ′ ′
=− +=− +
        
.
2 22 2
. .cos60 2BA BC BB x a
′
=− +=−
.
22
4AB BC x a
′′
= = +
.
Theo đề:
22
0
2222
.
2
1
cos60
.2
4. 4
AB BC
xa
AB BC
xaxa
′′
−
= ⇔=
′′
++
 
22 22
422
xa xa⇔+ = −
22 22
22 22
424
22
4 24
xa xa
xa
xa xa
+=−
⇔ ⇔=
+ =−+
.
Vậy
2
3
3
. 26
4
AB
V AA a
′
= =
.
Câu 17. Một khối lăng trụ tam giác có đáy là tam giác đều cạnh 3, cạnh bên bằng
23
và tạo với mặt
phẳng đáy một góc
30 .°
Khi đó thể tích khối lăng trụ là?
A.
27
.
4
B.
93
.
4
C.
9
.
4
D.
27 3
.
4
Hướng dẫn giải
Chọn A
Kẻ
( )
C H ABC
′
⊥
tại
( )
( )
;.H CC ABC C CH
′′
⇒=
Bài ra
( )
( )
; 30 30
CC ABC C CH
′′
= °⇒ = °
1 1 23
sin30 3.
2 22
CH
C H CC
CC
′
′′
⇒ °= = ⇒ = = =
′
A
B
C
H
A
′
B
′
C
′
https://toanmath.com/
Do đó
.
.
ABC A B C ABC
V CHS
′′′
′
=
1 1 3 27
. . .sin 60 3. .3.3. .
2 2 24
C H AB AC
′
= °= =
Câu 18. Cho hình lăng trụ tứ giác đều
.ABCD A B C D
′′′′
có cạnh đáy bằng
a
, khoảng cách từ
A
đến mặt
phẳng
( )
A BC
′
bằng
3
a
. Tính thể tích lăng trụ.
A.
3
2
4
a
. B.
3
33
a
. C.
3
3
4
a
. D.
3
3
2
a
.
Hướng dẫn giải
Chọn A
.
Ta có:
(
) ( )
( )
,BC AA BC AB BC ABA A BC ABA
′ ′′ ′
⊥ ⊥⇒⊥ ⇒ ⊥
.
Kẻ
( )
AH A B AH A BC
′′
⊥⇒⊥
(
)
( )
,
3
a
AH d A A BC
′
= =
.
Xét
A AB
′
∆
vuông tại
A
:
2 2 2 2 2 22
1 1 1 1 1 18
AH AB A A A A AH AB a
=+ ⇒ = −=
′′
.
2
4
a
AA
′
⇒=
3
.
2
4
ABCD A B C D
a
V
′′′′
⇒=
.
Câu 19. Thể tích của khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng
a
bằng:
A.
3
3
a
. B.
3
3
4
a
. C.
3
3
6
a
. D.
3
2
3
a
.
Hướng dẫn giải
Chọn B
Diện tích đáy là
23
33
44
aa
V⇒=
.
Câu 20. Cho khối lăng trụ đều
.ABC A B C
′′′
và
M
là trung điểm của cạnh
AB
. Mặt phẳng
( )
BCM
′′
chia khối lăng trụ thành hai phần. Tính tỷ số thể tích của hai phần đó.
A.
3
8
B.
6
5
. C.
7
5
. D.
1
4
.
Hướng dẫn giải
Chọn C
a
a
D
'
C
'
B
'
A
'
H
C
A
B
D
https://toanmath.com/
Qua M kẻ đường thẳng song song với BC cắt AC tại N khi đó thiết diện tạo bởi mặt phẳng
(
)
''BCM
và khối chóp là tứ giác
''B C NM
Khi đó thiết diện chia hình lăng trụ thành 2 phần là
''BCNMB C
và
'''
AMNA B C
Gọi S là giao điểm của
'CN
với
'AA
Ta có
'''
''"
111 1 1
. . ..
' ' ' 222 8 8
SAMN
SAMN SA B C
SA B C
V
SA SM SN
VV
V SA SB SC
= = =⇒=
''' ''' ''' '''
7 71 71
. . '. . .2 '.
8 83 83
AMNABC SABC ABC ABC
V V SAS AAS⇒== =
''' .''' '' .'''
77 5
'.
12 12 12
A B C ABC A B C BCNMB C ABC A B C
AA S V V V= = ⇒=
Do đó tỉ số thể tích hai phần là
75 7
:
12 12 5
=
.
Câu 21. Cho hình lăng trụ tam giác đều
.ABC A B C
′′′
có
AB a=
, đường thẳng
AB
′
tạo với mặt phẳng
( )
BCC B
′′
một góc
30°
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
2
3
a
V =
. B.
3
6
4
a
V =
. C.
3
6
12
a
V =
. D.
3
3
4
a
V =
.
Hướng dẫn giải
Chọn B
Gọi
M
là trung điểm của
AB AM BC⇒⊥
.
Vì
.
′′′
ABC A B C
là lăng trụ đứng
( )
′′
⇒⊥ ⇒⊥BB ABC BB AM
.
Suy ra
( ) ( )
( )
, 30
′′ ′ ′′ ′
⊥⇒ ==°AM BCC B AB BCC B AB M
.
Tam giác
′
AB M
vuông tại M, có
sin ' ' 3
'
AM
AB M AB a
AB
= ⇒=
.
https://toanmath.com/
Tam giác
′′
AA B
vuông tại
'
A
, có
22
2
′ ′ ′′
= −=AA AB A B a
.
Thể tích khối lăng trụ
.
′′′
ABC A B C
là
23
.
36
. 2.
44
′′′
∆
′
= = =
ABC A B C ABC
aa
V AA S a
.
Câu 22. Cho lăng trụ đứng
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh
a
, góc tạo bởi hai mặt phẳng
( )
ABC
,
( )
A BC
′
bằng
60°
. Tính thể tích khối lăng trụ
.ABC A B C
′′′
.
A.
3
3
24
a
. B.
3
33
4
a
. C.
3
3
6
a
. D.
3
33
8
a
.
Hướng dẫn giải
Chọn D
Gọi
K
là trung điểm cạnh
BC
.
Suy ra góc giữa mặt phẳng
( )
ABC
và
( )
A BC
′
là
60A KA
′
= °
.
3
2
a
AK
=
(đường trung tuyến trong tam giác đều).
3
.tan 60 .
2
a
AA AK
′
= °=
Thể tích khối lăng trụ
.ABC A B C
′′′
là:
23
1 3 33
. .sin 60 .
2 28
ABC
a
V S AA a a
∆
′
= = °=
.
Câu 23. Khối lăng trụ tam giác đều có tất cả các cạnh bằng nhau và có thể tích là
9
4
thì độ dài mỗi cạnh
bằng.
A.
3
. B.
3
. C.
6
243
. D.
33
.
Hướng dẫn giải
Chọn B
Gọi độ dài cạnh là
.a
.
1 39
. . . ..
2 44
a
V h S h BH AC a a
∆
= = = =
3
33 3aa⇒ = ⇒=
.
K
C
B
A'
B'
C'
A
https://toanmath.com/
.
Câu 24. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
là.
A.
3
2
4
Va=
. B.
3
3
4
Va=
. C.
3
2
3
Va=
. D.
3
3
2
Va=
.
Hướng dẫn giải
Chọn B
Đáy là tam giác đều cạnh a nên
2 23
3 33
..
4 44
a aa
B V Bh a= ⇒= = =
.
Câu 25. Tính thể tích của khối lăng trụ đều
.ABC A B C
′′′
có
AB AA a
′
= =
.
A.
3
3
12
a
. B.
3
3
4
a
. C.
3
3
6
a
. D.
3
a
.
Hướng dẫn giải
Chọn B
23
33
..
44
ABC
aa
V S AA a
′
= = =
.
Câu 26. Cho lăng trụ đứng
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Mặt phẳng
( )
AB C
′′
tạo với mặt
đáy góc
60
°
. Tính theo
a
thể tích khối lăng trụ
.ABC A B C
′′′
.
A.
3
3
.
8
a
V =
B.
3
33
.
8
a
V =
C.
3
3
.
2
a
V =
D.
3
33
.
4
a
V =
Hướng dẫn giải
Chọn B
Gọi
M
là trung điểm
''BC
. Ta có
' ''
''
' ''
AM BC
B C AM
AA B C
⊥
⇒⊥
⊥
nên góc giữa mặt phẳng
( )
''AB C
tạo với đáy là góc
' 60AMA = °
.
Tam giác
'AA M
vuông tại
'A
nên
0
3
' ' .tan 60
2
a
AA A M= =
Vậy thể tích khối lăng trụ
.'' 'ABC A B C
là
3
'''
33
'. .
8
ABC
a
V AA S= =
Câu 27. Tính thể tích
V
của khối lăng trụ đều
.'' 'ABC A B C
biết
AB a=
và
'2AB a=
.
H
C'
B'
A'
C
B
A
https://toanmath.com/
A.
3
3
4
a
V
=
. B.
3
3
2
a
V =
. C.
3
3
12
a
V =
. D.
3
3
4
a
V =
.
Hướng dẫn giải
Chọn A
.
Ta có:
2 2 22
43
BB AB AB a a a
′′
= − = −=
.
Vậy
23
.'''
33
. .3
44
ABC A B C ABC
aa
V S BB a
′
= = =
.
Câu 28. Cho hình lăng trụ tứ giác đều
.ABCD A B C D
′′′′
có cạnh đáy
(
)
43 .
m
Biết mặt phẳng
( )
D BC
′
hợp
với đáy một góc
60
ο
. Thể tích khối lăng trụ là.
A.
3
325m
. B.
3
648m
. C.
3
478m
. D.
3
576m
.
Hướng dẫn giải
Chọn D
.
Phân tích:
.ABCD A B C D
′′′′
là một hình lăng trụ tứ giác đều, cũng có nghĩa rằng nó là một hình
hộp đứng có đáy là hình vuông cạnh
(
)
43m
.
Ta có
( )
,BC CD BC DD BC CDD C BC CD
′ ′′ ′
⊥ ⊥ ⇒⊥ ⇒⊥
.
Suy ra
( ) ( )
(
)
(
)
, , 60D BC ABCD CD CD D CD
ο
′ ′′
= = =
.
Hướng dẫn giải:
D CD
′
∆
vuông tại D nên:
( )
0
tan 4 3.tan 60 12
DD
D CD DD m
CD
′
′′
=⇒= =
.
Vậy
( )
( )
2
2
.
. 12. 4 3 576
ABCD A B C D ABCD
V DD S m
′′′′
′
= = =
.
Câu 29. Cho lăng trụ đứng
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh
a
, góc tạo bởi hai mặt phẳng
( )
ABC
,
( )
A BC
′
bằng
60°
. Tính thể tích khối lăng trụ
.ABC A B C
′′′
.
A.
3
3
6
a
. B.
3
33
4
a
. C.
3
33
8
a
. D.
3
3
24
a
.
Hướng dẫn giải
C'
D'
B'
C
A
D
B
A'
A
B
C
A’
B’
C’
https://toanmath.com/
Chọn C
Gọi
K
là trung điểm cạnh
.BC
Suy ra góc giữa mặt phẳng
( )
ABC
và
( )
A BC
′
là
60A KA
′
= °
.
3
2
a
AK =
(đường trung tuyến trong tam giác đều).
3
.tan 60 .
2
a
AA AK
′
= °=
.
Thể tích khối lăng trụ
.ABC A B C
′′′
là:
23
1 3 33
. .sin 60 .
2 28
ABC
a
V S AA a a
∆
′
= = °=
.
Câu 30. Cho hình chóp
.
S ABC
có
( )
SA ABC⊥
, tam giác
ABC
vuông tại
C
,
2, 6AC a AB a= =
.
Tính thể tích khối chóp
.
S ABC
biết
3SC a=
A.
3
2 42
3
a
. B.
3
14a
. C.
3
6
3
a
. D.
3
14
3
a
.
Hướng dẫn giải
Chọn D
2222
.
11
... . .
66
S ABC
V CACB SA AC AB AC SC AC= = −−
3
1 14
2.2 . 7
63
a
a aa= =
.
Câu 31. Cho hình lăng trụ đều
.ABC A B C
′′′
. Biết khoảng cách từ điểm
C
đến mặt phẳng
( )
ABC
′
bằng
a
,
góc giữa hai mặt phẳng
( )
ABC
′
và
( )
BCC B
′′
bằng
α
với
1
cos
23
α
=
(tham khảo hình vẽ
bên). Thể tích khối lăng trụ
.ABC A B C
′′′
là
A.
3
2
2
a
. B.
3
32
2
a
. C.
3
32
4
a
. D.
3
32
8
a
Hướng dẫn giải
Chọn B
C
B
A
C'
B'
A'
https://toanmath.com/
Gọi
,
KJ
lần lượt là trung điểm của
,
AB BC
.
Gọi
x
là độ dài cạnh
AB
.
3
2
x
AJ CK= =
.
Ta có
( )
CH ABC
′
⊥
( )
( )
,d C ABC CH a
′
⇒==
.
Mặt khác
( )
AJ BCC B
′′
⊥
.
Nên
( ) ( )
(
)
,ABC BCC B
′ ′′
( )
,CH AJ=
=
α
( )
,CH AG=
(
cos sin
αϕ
=
).
Ta có
1
sin
23
MG
AG
ϕ
= =
23
AG
MG
⇔=
2
3
3.2
AJ
= =
3
6
2.3 3
xx
=
.
3 6 36
HC x a x
=⇔=
2xa⇔=
.
Mà
( )
( )
,d C ABC CH a
′
= =
.
22
.CH CK
CC
CK CH
′
⇒=
−
( )
2
2
23
2
3
a
a
aa
=
−
6
2
a
=
.
Vậy
2
3
.
4
x
V CC
′
=
( )
2
23
6
.
42
a
a
=
3
32
2
a
=
.
Câu 32. Cho hình hộp đứng
.ABCD A B C D
′′′′
có đáy là hình vuông cạnh
a
, góc giữa mặt phẳng
( )
D AB
′
và mặt phẳng
( )
ABCD
bằng
30°
. Thể tích khối hộp
.
ABCD A B C D
′′′′
bằng
A.
3
3a
. B.
3
3
3
a
. C.
3
3
9
a
. D.
3
3
18
a
.
Hướng dẫn giải
Chọn A
M
G
J
K
C
B
A
C'
B'
A'
H
https://toanmath.com/
Ta có
( ) (
)
ADD A AB
′′
⊥
nên góc giữa mặt phẳng
( )
D AB
′
và mặt phẳng
( )
ABCD
là góc
AD
′
và
AA
′
hay
30
A AD
′′
= °
. Suy ra
3
tan30
AD
AA a
′′
′
= =
°
. Vậy thể tích hộp
3
.
3
ABCD A B C D
Va
′′′′
=
.
Câu 33. Cho hình lăng trụ tam giác đều
ABCA B C
′′′
có
AB a=
, đường thẳng
AB
′
tạo với mặt phẳng
( )
BCC B
′′
một góc
30°
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
6
12
a
V =
. B.
3
3
.
4
a
V =
. C.
3
6
4
a
V
=
. D.
3
.
4
a
V =
.
Hướng dẫn giải
Chọn C
Gọi
M
là trung điểm, do tam giác
ABC
đều nên
AM BC⊥
, mà
AM BB
′
⊥
nên
( )
AM BCC B
′′
⊥
. Suy ra hình chiếu vuông góc của
AB
′
trên
( )
BCC B
′′
là
BM
′
.
Vậy góc giữa đường thẳng
AB
′
và mặt phẳng
( )
BCC B
′′
là góc
AB M
′
và
0
30AB M
′
=
.
22
3
3 2.
2
a
AM AB a AA AB A B a
′ ′ ′ ′′
= ⇒= ⇒= − =
.
3
6
4
a
V =
.
Câu 34. Cho lăng trụ tam giác đều
.ABC A B C
′′′
có chiều cao bằng
2
. Biết góc giữa đường thẳng
AB
′
và
mặt phẳng
( )
ABC
′′′
bằng
α
thỏa
1
tan
2
α
=
. Tính thể tích khối lăng trụ
.ABC A B C
′′′
.
A.
43
. B.
43
3
. C.
43
9
. D.
23
3
.
Hướng dẫn giải
Chọn A
https://toanmath.com/
.
Góc tạo bởi
AB
′
và
( )
ABC
′′′
.
là góc
AB A
α
′′
=
.
Ta có:
tan
AA
AB
α
′
=
′′
22
tan
AA
AB
α
′
′′
⇒= =
.
Vậy
( )
2
.
22 3
. .2 4 3
4
ABC A B C ABC
V S AA
′′′
′
= = =
.
Câu 35. Cho lăng trụ tam giác đều
.ABC A B C
′′′
cạnh đáy bằng
a
, chiều cao bằng
2a
. Mặt phẳng
( )
P
qua
B
′
và vuông góc với
AC
′
chia lăng trụ thành hai khối. Biết thể tích của hai khối là
1
V
và
2
V
với
12
VV<
. Tỉ số
1
2
V
V
bằng
16T A. 16T
1
7
16T B. 16T
1
47
16T C. 16T
1
23
16T D. 16T
1
11
16T Hướng dẫn giải
Chọn B
Gọi
H
là trung điểm của
AC
′′
, giác
ABC
′′′
∆
đều nên
BH AC
′ ′′
⊥
.
Trong
( )
A C CA
′′
, kẻ
HE A C
′
⊥
,
HE A A I
′
∩=
.
Ta có:
( )
BH AC
AC BHI
HI A C
′ ′′
⊥
′′ ′
⇒⊥
′′
⊥
( ) ( )
P B HI
′
⇒≡
.
A
C
B
A’
C’
B’
α
https://toanmath.com/
AEH ACC
′ ′′
∆∆#
AE AC
AH AC
′ ′′
⇒=
′′
.
AC AH
AE
AC
′′′
′
⇒=
′
5
10
a
=
.
AIH ACC
′ ′′
∆∆#
IH A C
AH CC
′
⇒=
′′
.ACAH
IH
CC
′′
⇒=
′
5
4
a
=
.
1
.
2
B HI
S B H HI
′
′
=
2
15
16
a
=
.
1
1
..
3
B HI
V S AE
′
′
=
2
1 15 5
..
3 16 10
aa
=
3
3
96
a
=
.
.
.
ABC A B C ABC
V S AA
′′′
′
=
2
3
.2
4
a
a=
3
3
2
a
=
.
3
2
47
3
96
Va=
do đó
1
2
1
47
V
V
=
.
Câu 36. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng
2a
là.
A.
3
3
4
a
. B.
3
3
12
a
.
C.
3
23a
.
D.
3
4a
.
Hướng dẫn giải
Chọn C
Giả sử khối lăng trụ đều là
.
ABC A B C
′′′
như hình bên.
Tam giác
ABC
đều cạnh
2a
có diện tích bằng
( )
2
2
23
3
4
a
Sa= =
.
.
Thể tích khối lăng trụ
23
. 2. 3 2 3
V AA S a a a
′
= = =
.
Câu 37. Cho lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
a
và
AB BC
′′
⊥
. Tính thể tích
V
của
khối lăng trụ đã cho.
A.
3
6
4
a
V =
. B.
3
7
8
a
V =
. C.
3
6Va=
. D.
3
6
8
a
V =
.
Hướng dẫn giải
Chọn D
Gọi
E
là điểm đối xứng của
C
qua điểm
B
. Khi đó tam giác
ACE
vuông tại
A
.
https://toanmath.com/
22
43AE a a a⇒ = −=
.
Mặt khác, ta có
BC B E AB
′′ ′
= =
nên tam giác
AB E
′
vuông cân tại
B
′
.
2
AE
AB
′
⇒=
3
2
a
=
6
2
a
=
.
Suy ra:
2
2
62
22
aa
AA a

′
= −=



.
Vậy
2
23
.
24
aa
V =
3
6
8
a
=
.
Câu 38. Cho lăng trụ
ABCDA B C D
′′′′
có đáy
ABCD
là hình thoi cạnh
a
, tâm
O
và
120
ABC = °
. Các
cạnh
AA
′
;
AB
′
;
AD
′
cùng tạo với mặt đáy một góc bằng
45°
. Tính theo
a
thể tích
V
của khối
lăng trụ đã cho.
A.
3
3
2
a
B.
3
2
a
C.
3
3
4
a
D.
3
3
2
a
Hướng dẫn giải
Chọn B
ABCD
là hình thoi cạnh
a
,
120ABC
= °
⇒
ABD∆
đều cạnh
a
,
2
3
4
ABD
a
S
∆
=
do đó
2
3
2
ABCD
a
S =
.
Các cạnh
AA
′
;
AB
′
;
AD
′
cùng tạo với mặt đáy một góc bằng
45°
nên chóp
A ABD
′
đều đỉnh
A
′
suy ra
3
3
a
AH =
.
Suy ra
3
.
2
ABCDA B C D ABCD
a
V AH S
′′′′
= =
.
Câu 39. Cho hình lăng trụ đứng
.ABC A B C
′′′
, biết đáy
ABC
là tam giác đều cạnh
a
. Khoảng cách từ tâm
O
của tam giác
ABC
đến mặt phẳng
( )
A BC
′
bằng
6
a
. Tính thể tích khối lăng trụ
.ABC A B C
′′′
.
A.
3
32
8
a
. B.
3
32
28
a
. C.
3
32
4
a
. D.
3
32
16
a
.
Hướng dẫn giải
Chọn D
Diện tích đáy là
2
3
4
ABC
a
BS
∆
= =
.
Chiều cao là
( ) ( )
( )
;h d ABC A B C AA
′′′ ′
= =
.
A
B
D
A'
H
C
D'
B'
C'
https://toanmath.com/
Do tam giác
ABC
là tam giác đều nên
O
là trọng tâm của tam giác
ABC
. Gọi
I
là trung điểm
của
BC
,
H
là hình chiếu vuông góc của
A
lên
AI
′
ta có
( ) ( )
(
)
;AH A BC d A A BC AH
′′
⊥⇒ =
( )
( )
(
)
(
)
;
1
3
;
d O A BC
IO
IA
d A A BC
′
= =
′
(
)
(
)
( )
(
)
;
;
3 36
d A A BC
AH a
d O A BC
′
′
⇒===
2
a
AH⇒=
Xét tam giác
A AI
′
vuông tại
A
ta có:
2 22
1 11
AH AA AI
= +
′
2 22
1 11
AA AH AI
⇒=−
′
3
22
a
AA
′
⇒=
3
22
a
h⇒=
3
.
32
16
ABC A B C
a
V
′′′
⇒=
.
Câu 40. Cho lăng trụ tam giác đều
.ABC A B C
′′′
có độ dài cạnh đáy bằng
2a
, cạnh bên bằng
3a
. Tính
thể tích
V
của lăng trụ.
A.
3
32Va=
. B.
3
2
Va=
. C.
3
3Va=
. D.
3
3Va=
.
Hướng dẫn giải
Chọn D
Diện tích đáy tam giác đều
( )
2
2
23
3
4
a
Sa= =
.
Thể tích lăng trụ
23
. 3. 3 3V Sh a a a= = =
.
Câu 41. Cho lăng trụ đều
.ABC A B C
′′′
có cạnh đáy bằng
2a
, diện tích xung quanh bằng
2
63a
. Thể tích
V
của khối lăng trụ.
A.
3
3Va=
. B.
3
3
4
Va=
. C.
3
Va
=
. D.
3
1
4
Va=
.
Hướng dẫn giải
Chọn A
Do
.ABC A B C
′′′
là lăng trụ đều nên
ABB A ACC A BCC B
SSS
′′ ′′ ′′
= =
⇒
2
''
3 3 . '6. '63 ' 3
xp ABB A
S S AB AA a AA a AA a
= = = = ⇔=
Do đó
( )
2
3
23
'. 3. 3
4
ABC
a
V AA S a a= = =
I
A'
B'
C'
A
B
C
H
O
K
https://toanmath.com/
Câu 42. Tính thể tích của khối lăng trụ tam giác đều có cạnh đáy bằng
2a
và cạnh bên bằng
a
.
A.
3
3
4
a
. B.
3
3a
. C.
3
a
. D.
3
3
3
a
.
Hướng dẫn giải
Chọn B
Vì lăng trụ đứng nên đường cao bằng
a
.
Vì đáy là tam giác đều nên diện tích đáy:
(
)
2
2
2 .3
3
4
ABC
a
Sa= =
.
Thể tích:
23
. 3. 3
ABC
VS aa aa= = =
.
Câu 43. Cho hình lăng trụ đều
.ABC A B C
′′′
có cạnh đáy bằng
a
,
AC
′
hợp với mặt đáy
( )
ABC
một góc
60°
. Thể tích của khối lăng trụ
.ABC A B C
′′′
bằng:
A.
3
3
8
a
. B.
3
4
a
. C.
3
2
3
a
. D.
3
3
4
a
.
Hướng dẫn giải
Chọn D
.
23
33
' . 3.
44
ABC
aa
V A AS a= = =
.
Câu 44. Cho lăng trụ tam giác
.ABC A B C
′′′
có đáy là tam giác vuông cân, cạnh huyền
2AC a=
. Hình
chiếu của
A
lên mặt phẳng
( )
ABC
′′′
là trung điểm
I
của
AB
′′
, góc giữa cạnh bên và mặt đáy
bằng
60°
. Thể tích khối lăng trụ
.ABC A B C
′′′
là.
A.
3
6
2
a
. B.
3
2a
. C.
3
6
6
a
. D.
3
3
4
a
.
Hướng dẫn giải
Chọn A
C'
B'
C
B
A
A'
a
a
A
C
B
C'
A'
B'
https://toanmath.com/
.
Góc giữa cạnh bên
AA
′
và mặt đáy
( )
ABC
′′′
bằng
60°
là góc
60AA I
′
= °
.
Ta có:
2AC a=
nên
2
2
AC
AB a= =
2
222
A B AB a
AI
′′
′
⇒= ==
.
Vậy
23
.
6
. .tan 60 .
22
ABC A B C ABC
AB a
V AI S A I
′′′
′
= = °=
.
Câu 45..Cho lăng trụ tam giác
.ABC A B C
′′′
có đáy là tam giác vuông cân, cạnh huyền
2
AC a=
. Hình
chiếu của
A
lên mặt phẳng
( )
ABC
′′′
là trung điểm
I
của
AB
′′
, góc giữa cạnh bên và mặt đáy
bằng
60
°
. Thể tích khối lăng trụ
.ABC A B C
′′′
là.
A.
3
6
2
a
.
B.
3
6
6
a
.
C.
3
2
a
.
D.
3
3
4
a
.
Hướng dẫn giải
Chọn A
.
Góc giữa cạnh bên
AA
′
và mặt đáy
( )
ABC
′′′
bằng
60°
là góc
60AA I
′
= °
.
Ta có:
2AC a=
nên
2
2
AC
AB a= =
2
222
A B AB a
AI
′′
′
⇒= ==
.
Vậy
23
.
6
. .tan 60 .
22
ABC A B C ABC
AB a
V AI S A I
′′′
′
= = °=
.
Câu 46. Cho hình lăng trụ đứng
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
, cạnh bên
2AA a
′
=
. Thể
tích của khối lăng trụ là
A.
3
3
4
a
. B.
3
3
12
a
. C.
3
6
12
a
. D.
3
6
4
a
.
Hướng dẫn giải
Chọn A
https://toanmath.com/
Ta có
23
36
. 2.
44
ABC
aa
V Bh S AA a
′
= = = =
.
Câu 47. Cho lăng trụ tam giác đều
.ABC A B C
′′′
có tất cả các cạnh đều bằng
2a
. Tính thể tích của khối
lăng trụ.
A.
3
3
8
a
. B.
3
6
2
a
. C.
3
6
6
a
. D.
3
3
6
a
.
Hướng dẫn giải
Chọn B
Đáy lăng trụ là tam giác đều cạnh
( )
2
2
23
3
2
44
day
a
a
aS → = =
23
36
. .2
22
′
⇒= = =
day
aa
V S AA a
.
Câu 48. 42TThể tích 42T
V
42T của khối lăng trụ tam giác đều có cạnh đáy bằng 42T
2a
42T và cạnh bên bằng 42T
a
42T là
A.
3
3
3
a
V =
. B.
3
3
2
a
V =
. C.
3
3Va=
. D.
3
3
4
a
V =
.
Hướng dẫn giải
Chọn C
Ta có
.
ABC
V S AA
′
=
( )
2
23
.
4
a
a=
3
3a=
.
Câu 49. Tính thể tích
V
của khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
.
A.
3
3
2
a
V =
. B.
3
2
4
a
V =
. C.
3
3
4
a
V =
. D.
3
2
3
a
V =
.
Hướng dẫn giải
Chọn C
C'
B'
A
C
B
A'
a
2a
A'
C'
B'
B
C
A
https://toanmath.com/
Ta có:
23
.
33
..
44
ABC A B C ABC
aa
V S AA a
′′′
∆
′
= = =
.
Câu 50. Cho hình lăng trụ tam giác
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông tại
A
,
AB a
=
,
3
AC a=
. Hình chiếu vuông góc của
A
′
lên
( )
ABC
là trung điểm của
BC
. Góc giữa
AA
′
và
( )
ABC
bằng
60°
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
3
2
a
V =
. B.
3
3
2
a
V =
. C.
3
2
a
V =
. D.
3
33
2
a
V
=
.
Hướng dẫn giải
Chọn B
.
Gọi
H
là trung điểm
( )
BC A H ABC
′
⇒⊥
.
22
2BC AB AC a= +=
2
BC
AH a⇒==
.
.tan 60 3A H AH a
′
= °=
;
2
13
.
22
ABC
a
S AB AC
∆
= =
Vậy,
23
33
3.
22
aa
Va= =
.
Câu 51. Cho hình lăng trụ đứng tam giác
.ABC A B C
′′′
có đáy là
∆ABC
đều cạnh
4=a
và biết
8
A BC
S
′
∆
=
.
Tính thể tích khối lăng trụ.
A.
23
. B.
43
. C.
63
. D.
83
.
Hướng dẫn giải
Chọn D
a
3
a
60
°
C'
B'
H
B
C
A
A'
https://toanmath.com/
Gọi
M
là trung điểm
BC
. Ta có
2
1 2.8
.4
24
A BC
A BC
S
S AMBC AM
BC


Vì
AM
là đường trung tuyến của tam giác đều cạnh bằng
4
nên
43
23
2
AM 
.
Trong tam giác vuông
A AM
ta có
22
16 12 2AA A M AM


.
Thể tích khối lăng trụ
2
43
. .2 8 3
4
ABC
V S AA

.
Câu 52. Cho lăng trụ đứng
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh
a
, cạnh bên
AB
′
tạo với đáy
một góc
45
°
. Thể tích khối lăng trụ
.ABC A B C
′′′
là:
A.
3
.'''
3
4
ABC A B C
a
V =
. B.
3
.'''
3
ABC A B C
Va=
.
C.
. D.
3
.'''
2
3
ABC A B C
a
V
=
.
Hướng dẫn giải
Chọn A
.
Tam giác
ABC
đều
2
3
4
ABC
a
S⇒=
.
Góc giữa
( )
(
)
0
, 45A B ABC A BA A AB
′′ ′
= = ⇒∆
vuông cân tại
A
.
A A AB a
′
⇒==
.
23
.'''
33
.' .
44
ABC A B C ABC
aa
V S AA a= = =
(đvtt).
Câu 53. Cho hình lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
a
, góc giữa mặt phẳng
( )
A BC
′
và
mặt phẳng
( )
ABC
bằng
45°
. Thể tích của khối lăng trụ
.ABC A B C
′′′
bằng
A
C
B
B'
C'
A'
https://toanmath.com/
A.
3
3
2
a
. B.
3
3
8
a
. C.
3
3
8
a
. D.
3
3
4
a
.
Hướng dẫn giải
Chọn B
Gọi
M
là trung điểm
BC
AM BC⇒⊥
( )
BC AMA
′
⇒⊥
BC MA
′
⇒⊥
Ta có
( ) ( )
ABC A BC BC
′
∩=
,
AM BC⊥
,
BC MA
′
⊥
( ) ( )
(
)
( )
,,ABC A BC AM A M
′′
⇒=
45AMA
′
= = °
3
2
a
AM AA
′
⇒==
.
Thể tích khối lăng trụ
.
ABC
V AA S
′
=
23
3 33
.
24 8
aa a
= =
.
Câu 54. Cho hình lăng trụ tứ giác đều
.ABCD A B C D
′′′′
có cạnh đáy bằng
a
. Biết đường chéo của mặt bên
là
3a
. Khi đó, thể tích khối lăng trụ bằng:
A.
3
3a
. B.
3
2
a
. C.
3
2
3
a
. D.
3
2a
.
Hướng dẫn giải
Chọn B
Ta có
AB a=
,
3AB a
′
=
2AA a
′
⇒=
.
( )
2
3
.
.2
ABCD A B C D
V AA AB a
′′′′
′
⇒==
.
Câu 55. Cho hình lăng trụ đứng
.ABC A B C
′′′
có tam giác
ABC
là tam giác đều cạnh bằng
a
, góc giữa
( )
AB C
′′
và
()ABC
′′′
bằng
o
60
. Thể tích khối lăng trụ
.ABC A B C
′′′
là.
A.
3
3
24
a
. B.
3
3
8
a
. C.
3
33
8
a
. D.
3
24
a
.
Hướng dẫn giải
Chọn C
Gọi
M
là trung điểm của
''BC
. Khi đó dễ dàng xác định được
0
' 60AMA =
.
Suy ra
0
33
' ' .tan60 . 3
22
aa
AA A M= = =
. Vậy
3
.'''
33
.
8
ABC A B C ABC
a
V AA S
′
= =
.
https://toanmath.com/
Câu 56. Cho hình lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
a
. Góc giữa đường thẳng
AB
′
và
mặt phẳng
(
)
ABC
bằng
45°
. Tính thể tích của khối lăng trụ
.ABC A B C
′′′
.
A.
3
3
6
a
. B.
3
3
12
a
. C.
3
3
24
a
. D.
3
3
4
a
.
Hướng dẫn giải
Chọn D
Theo giả thiết, ta có
( )
AA ABC
′
⊥
BA
⇒
là hình chiếu vuông góc của
AB
′
trên
( )
ABC
⇒
Góc giữa đường thẳng
AB
′
và mặt phẳng
( )
ABC
là
45
ABA
′
= °
Do
ABA
′
∆
vuông cân tại
A AA AB a
′
⇒==
Vậy thể tích của khối lăng trụ
.ABC A B C
′′′
.là
3
3
4
a
V =
.
Câu 57. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng
a
là:
A.
3
3
3
a
. B.
3
3
4
a
. C.
3
2
3
a
. D.
3
2
2
a
.
Hướng dẫn giải
Chọn B
Ta có
23
33
.
44
aa
V Bh a= = =
.
Câu 58. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng
a
là:
A.
3
2
a
. B.
3
3
12
a
. C.
3
3
2
a
. D.
3
3
4
a
.
Hướng dẫn giải
Chọn D
3
13 3
.. .
22 4
aa
Va a= =
.
Câu 59. Cho hình lăng trụ đều
.ABC A B C
′′′
. Biết khoảng cách từ điểm
C
đến mặt phẳng
( )
ABC
′
bằng a,
góc giữa hai mặt phẳng
( )
ABC
′
và
( )
BCC B
′′
bằng
α
với
1
23
cos
α
=
(tham khảo hình vẽ
dưới đây). Thể tích khối lăng trụ
.ABC A B C
′′′
bằng
A.
3
2
3
4
a
. B.
3
2
2
a
. C.
3
2
3
2
a
. D.
3
2
3
8
a
.
Hướng dẫn giải
Chọn C
https://toanmath.com/
Gọi
O
là trung điểm của
AB
,
E
là trung điểm của
BC
Trong
(
)
mp C CO
′
kẻ
CH C O
′
⊥
tại
H
Khi đó
( )
( )
,d C ABC CH a
′
= =
Chọn hệ trục tọa độ
Oxyz
như hình vẽ, gọi
2x
là độ dài cạnh của tam giác
ABC
ta có
2 22
1 11
'CH C C CO
= +
⇒
22
2
2 2 2 2 22
1 1 11 1 3
'3
23
2
xa
C C CH CO a a x
x
−
=−=− =



22
3
'
3
xa
CC
ax
−
⇒=
Khi đó,
( )
;0;0Ax−
,
( )
;0;0Bx
,
( )
0; 3;0Cx
,
22
3
' 0; 3;
3
xa
Cx
ax

−



,
3
; ;0
22
xx
E




VTPT của
mặt phẳng
( )
ABC
′
là
1
,n OC AB

′
= =

 
2
2
22
23
0; ;2 3
3
ax
x
xa

−


−

VTPT của
mặt phẳng
( )
BCC B
′′
là
2
33
; ;0
22
n AE
xx
=



=


1
23
cos
α
=
⇔
12
12
.
1
23
nn
nn
=


⇔
3
22
24 2 2
4
22
3
1
3
23
12 9 3
12 .
3 44
ax
xa
ax x x
x
xa
−
=
++
−
⇔
xa=
3
2
.
6 32
.S . 3
22
ABC A B C ABC
aa
V CC a
′′′
∆
′
= = =
.
https://toanmath.com/
Câu 60. Cho hình lăng trụ đứng
.'' 'ABC A B C
có đáy
ABC
đều cạnh bằng
a
và chu vi của mặt bên
''ABB A
bằng
6a
. Thể tích của khối lăng trụ
.'' 'ABC A B C
bằng
A.
3
3
2
a
. B.
3
3
a
. C.
3
3
3
a
. D.
3
3
6
a
.
Hướng dẫn giải
Chọn A
Chu vi của hình chữ nhật
( )
2 ' 6 '2AB AA a AA a+ =⇒=
Thể tích khối lăng trụ
23
33
.2
42
aa
V Bh a= = =
.
Câu 61. Cho lăng trụ đứng
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
và
AB
′
vuông góc với
BC
′
. Thể
tích của lăng trụ đã cho là.
A.
3
6
12
a
. B.
3
6
4
a
. C.
3
6
8
a
. D.
3
6
24
a
.
Hướng dẫn giải
Chọn C
.
Gọi
I
là trung điểm
BC
. Vì
'''ABCA B C
là lăng trụ tam giác đều nên.
( )
'' 'AI BB C C AI BC⊥ =>⊥
.
Lại có giả thiết
''
AC BC⊥
nên suy ra
( )
' ' ''BC AIB BC B I⊥ =>⊥
.
Gọi
''H B I BC= ∩
.
Ta có
BHI∆
đồng dạng
''C HB∆
=>
1
' 2 '3
' '' 2
HI BI
B H HI B I HI
BH BC
= ==> = =>=
.
A
C
B
B'
C'
A'
https://toanmath.com/
Xét tam giác vuông
'
B BI
có
22
22
3
.' 3
3 12 2
BI a a
BI HI B I HI HI
= = =>= = =
.
Suy ra
2
2
22
32
''
2 22
a aa
BB B I BI


= −= − =





.
Vậy
3
2
32 6
.BB' a .
42 8
ABC
aa
VS
∆
= = =
.
Câu 62. Cho hình lăng trụ tam giác đều
.ABC A B C
′′′
có tất cả các cạnh bằng
a
. Gọi
,MN
lần lượt là
trung điểm của các cạnh
AB
và
BC
′′
. Mặt phẳng
(
)
A MN
′
cắt cạnh
BC
tại
.P
Thể tích khối đa
diện
.MBPABN
′′
bằng.
A.
3
73
68
a
. B.
3
3
32
a
. C.
3
73
96
a
. D.
3
73
32
a
.
Hướng dẫn giải
Chọn C
.
Gọi
Q
là trung điểm của
.BC
Suy ra
AQ A N MP AQ P
′
⇒⇒

là trung điểm của
BQ
.
Ta có
,,BB A M NP
′′
đồng quy tại
S
và
B
là trung điểm của
BS
′
2SB a
′
⇒=
.
23
.
33
8 12
ABN S ABN
aa
SV
′′ ′′
=⇒=
.
1
8
SMNP SA B N
VV
′′
=
3
7 73
8 96
MBPABN SABN
a
VV
′′ ′′
⇒==
.
Câu 63. Cho
( )
H
là khối lăng trụ đứng tam giác đều có tất cả các cạnh đều bằng
a
. Thể tích của
( )
H
bằng:
A.
3
3
2
a
. B.
3
3
4
a
. C.
3
2
3
a
. D.
3
2
a
.
Hướng dẫn giải
Chọn B
P
M
Q
N
B
C
A'
C'
B'
S
A
https://toanmath.com/
* Đáy lăng trụ là tam giác đều cạnh
a
nên có diện tích là
2
3
4
=
a
S
, đường cao
=ha
.
* Vậy thể tích khối lăng trụ
3
3
.
4
= =
a
V Sh
.
Câu 64. Cho khối lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
2a
và mỗi mặt bên có diện tích
bằng
2
4a
. Thể tích khối lăng trụ đó là
A.
3
26a
. B.
3
26
3
a
. C.
3
6
2
a
. D.
3
6a
.
Hướng dẫn giải
Chọn D
Do
.ABC A B C
′′′
là khối lăng trụ tam giác đều nên
ABB A
′′
là hình chữ nhật.
Mặt khác mỗi mặt bên có diện tích bằng
2
4a
nên
2
.4
AB AA a
′
=
2
4a
AA
AB
′
⇔=
2
4
2
a
AA
a
′
⇔=
22AA a
′
⇔=
.
Thể tích khối lăng trụ
.
ABC A B C
′′′
là
.
1
. .sin 60 .
2
ABC A B C
V AB AB AA
′′′
′
= °
1
2. 2.sin 60 .2 2
2
aa a= °
3
6a=
.
[DS11.C5.2.D0.d](THPT Quảng Xương 1 - Thanh Hóa- Lần 1- 2017 - 2018 - BTN) Gọi
1
k
,
2
k
,
3
k
lần lượt là hệ số góc của tiếp tuyến của đồ thị các hàm số
( )
=y fx
,
( )
=y gx
,
( )
()
=
fx
y
gx
tại
2=x
và thỏa mãn
12 3
20= = ≠kk k
khi đó
A.
( )
1
2.
2
<f
.
B.
( )
1
2.
2
≤f
.
a
a
C'
B'
A'
A
B
C
https://toanmath.com/
C.
(
)
1
2.
2
≥
f
.
D.
(
)
1
2.
2
>f
Hướng dẫn giải
Chọn.
B.
Theo đề bài ta có
12
kk=
( )
2f
′
=
( )
2
g
′
=
.
(
)
( )
( )
(
)
(
)
3
2
22 22
2
fg gf
k
g
′′
−
=
.
Theo đề bài ta có
12 3
20kk k= = ≠
nên ta có phương trình
( ) ( ) ( )
( )
( )
2
22 2
1
2
22
fgf
f
g
′
−


′
=
(
) (
) (
)
2
22222 0
g gf
⇔−+ =
.
Do
( )
2g
là một giá trị thuộc tập giá trị của hàm số nên phương trình
( ) ( ) ( )
2
22222 0g gf−+ =
có nghiệm
0
′
⇔∆ ≥
( )
12 2 0f⇔− ≥
(
)
1
2
2
f
⇔≤
.
Câu 65. Cho hình lăng trụ tứ giác đều
.ABCD A B C D
′′′′
có cạnh đáy bằng
a
. Biết đường chéo của mặt bên
là
3a
. Khi đó, thể tích khối lăng trụ bằng:
A.
3
3a
. B.
3
2a
. C.
3
2
3
a
. D.
3
2a
.
Hướng dẫn giải
Chọn
B
.
Ta có
AB a=
,
3AB a
′
=
2
AA a
′
⇒=
( )
2
3
.
.2
ABCD A B C D
V AA AB a
′′′′
′
⇒==
.
Câu 66.Khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
thì có thể tích bằng
A.
3
3
6
a
. B.
3
3
12
a
. C.
3
3
4
a
. D.
3
3
8
a
.
Hướng dẫn giải
Chọn C
Thể tích khối lăng trụ tam giác đều:
23
33
..
44
aa
V hS a= = =
.
Câu 67. Từ một ảnh giấy hình vuông cạnh là
4cm
, người ta gấp nó thành bốn phần đều nhau rồi dựng lên
thành bốn mặt xung quanh của hình hình lăng trụ tứ giác đều như hình vẽ. Hỏi thể tích của khối
lăng trụ này là bao nhiêu.
A.
3
64
3
cm
B.
3
16cm
. C.
3
4
3
cm
D.
3
4cm
.
Hướng dẫn giải
Chọn D
Đáy là hình vuông có cạnh bằng 1 nên diện tích đáy:
2
1S cm=
.
Thể tích lăng trụ là:
3
.4V h S cm= =
https://toanmath.com/
Câu 68. Cho lăng trụ tứ giác đều
.ABCD A B C D
′′′′
đáy hình có cạnh bằng
,
a
đường chéo
AC
′
tạo với mặt
bên
( )
BCC B
′′
một góc
α
(
)
0
0 45 .
α
<<
Tính thể tích của lăng trụ tứ giác đều
.ABCD A B C D
′′′′
.
A.
32
cot 1a
α
+
. B.
32
tan 1a
α
−
. C.
3
cos2a
α
. D.
32
cot 1a
α
−
.
Hướng dẫn giải
Chọn D
.
Ta có ngay
'
AC B
α
=
.
Tam giác
'ABC
vuông tại
B
và
' ' cot .
tan
a
AC B BC a
αα
α
=⇒= =
.
Áp dụng định lý Pytago thì
22 2
' ' cot 1.CC BC BC a
α
= −= −
.
Thể tích khối lăng trụ
32
. . ' cot 1.V BC CD CC a
α
= = −
.
Câu 69. Cho khối lăng trụ
.ABC A B C
′′′
có
,
6AC a=
. Hình chiếu vuông góc của
A
′
trên
mặt phẳng
( )
ABC
là trung điểm của
AB
và
133
2
a
AC
′
=
. Tính thể tích
V
của khối lăng trụ
.ABC A B C
′′′
theo
.a
.
A.
3
12 133Va=
.
B.
3
4 133Va=
.
C.
3
12Va=
. D.
3
36Va=
.
Hướng dẫn giải
Chọn D
.
Gọi
H
là trung điểm của
AB
.
Tam giác
ABC∆
có
22 2 2
2
97
2 44
AC BC AB a
HC
+
= −=
.
Trong
A HC
′
∆
ta có
22
3AH AC HC AH a h
′′ ′
= −⇒==
.
Diện tích đáy
2
12Sa=
(dùng công thức Hê – rông).
Thể tích khối lăng trụ
.ABC A B C
′′′
là
23
6
. 12 . 36
2
a
V Sh a a= = =
.
Câu 70. Cho hình lăng trụ đều
.'ABC A B C
′′
có cạnh đáy bằng
a
, cạnh bên
3a
. Thể tích của khối lăng
trụ là.
a
133
2
5a
6a
5a
C
/
B
/
A
/
C
B
A
https://toanmath.com/
A.
3
3
7
a
. B.
3
3
4
a
. C.
3
7
5
a
.
D.
3
3
4
a
.
Hướng dẫn giải
Chọn D
Vì
.'ABC A B C
′′
là hình lăng trụ đều nên đáy
ABC
là tam giác đều cạnh
a
.
2
13
. .sin 60
24
ABC
a
S AB AC
∆
= °=
.
.
ABC
V S AA
∆
′
=
23
33
.3 .
44
aa
a= =
.
Câu 71. Cho khối lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy là
a
và khoảng cách từ
A
đến mặt
phẳng
( )
A BC
′
bằng
2
a
. Tính thể tích của khối lăng trụ
.ABC A B C
′′′
.
A.
3
32
12
a
. B.
3
32
16
a
. C.
3
32
48
a
. D.
3
2
16
a
.
Hướng dẫn giải
Chọn B
Gọi
M
là trung điểm
BC
,
H
là hình chiếu của
A
trên
AM
′
. Nhận xét
( )
( )
,d A A BC AH
′
=
.
Tam giác
AA M
′
vuông tại
A
nên có:
222
111
A A AM AH
+=
′
2 22
1 44
3AA a a
⇒ +=
′
22
18 3
3
22
a
AA
AA a
′
⇒ =⇒=
′
.
Thể tích của lăng trụ
.ABC A B C
′′′
là
23
3 33 2
.
4 16
22
aa a
V = =
.
Câu 72. Cho lăng trụ tứ giác đều
.ABCD A B C D
′′′′
có cạnh đáy bằng
5a
. Khoảng cách từ
A
đến mặt
phẳng
( )
'A BC
bằng
5
2
a
. Thể tích khối lăng trụ là:
A.
3
5 15
3
a
. B.
3
63
5
a
. C.
3
22a
. D.
3
5
3
a
.
Hướng dẫn giải
Chọn A
M
A
B
C
A'
B'
C'
H
https://toanmath.com/
Dựng
'
AH A B
⊥
. Do
( )
'
'
AH BC
AH A BC
AH A B
⊥
⇒⊥
⊥
Do đó
( )
( )
5
,'
2
a
d A A BC AH= =
.
Mặt khác
2 22
1 1 1 15
'
'3
a
AA
AH AA AB
= + ⇒=
.
Suy ra
3
.''' '
5 15
'.
3
ABCD A B C D ABCD
a
V AA S= =
.
Câu 73. Cho lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
2a
, khoảng cách từ
A
đến mặt phẳng
( )
A BC
′
bằng
6
2
a
. Khi đó thể tích lăng trụ bằng.
A.
3
43
3
Va=
. B.
3
4
3
Va=
. C.
3
3Va=
. D.
3
Va=
.
Hướng dẫn giải
Chọn C
.
Gọi I là trung điểm
BC
.
H
là hình chiếu của
A
lên
AI
′
.
( )
ˆ
( ) ( ) theo giao tuye n
; ( )
()
6
( ;( ))
2
AI BC
BC AA I A BC AA I A I
AA BC
AH A I AH AA I
AH A BC
a
d A A BC AH
⊥
′ ′ ′ ′′
⇒⊥ ⇒ ⊥
′
⊥
′′
⊥⊂
′
⇒⊥
′
⇒==
.
https://toanmath.com/
A AI
′
∆
vuông tại
A
:
( )
( )
22
22 2 2
2
3
111 1 1 1
3. 3
6
3
2
23
. . 3 3.
4
ABC
AA a
AH AI AA AA
a
a
a
V S AA a a
′
= + ⇒ = − ⇒=
′′



′
= = =
.
Câu 74. Cho hình lăng trụ đều
.'ABC A B C
′′
có
AB a
=
,
3
'
2
a
AA =
. Gọi
G
là trọng tâm tam giác
A BC
′
.
Tính thể tích tứ diện
GABC
theo
a
.
A.
3
3
16
a
. B.
3
3
12
a
.
C.
3
3
24
a
.
D.
3
33
8
a
.
Hướng dẫn giải
Chọn C
[ ]
.
1
. . ;( )
3
G ABC ABC
V S d G ABC
∆
=
[ ]
11
. . . ;( )
33
ABC
S d A ABC
∆
′
=
11
..
33
ABC
S AA
∆
′
=
3
3
24
a
=
.
Câu 75. Tính thể tích
V
của khối lăng trụ tam giác đều
.ABC A B C
′′′
có
AA BC a
′
= =
.
A.
3
3
4
a
V
=
. B.
3
2
6
a
V =
. C.
3
3
12
a
V =
. D.
3
3
a
V =
.
Hướng dẫn giải
Chọn A
.
2
3
4
ABC
a
S =
. Khi đó
3
.'''
3
4
ABC A B C
a
V =
.
https://toanmath.com/
Câu 76. Cho lăng trụ
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh
a
, cạnh bên tạo với mặt phẳng
bằng
0
45
. Hình chiếu của
A
trên mặt phẳng
( )
ABC
′′′
trùng với trung điểm của
AB
′′
. Tính thể
tích
V
của khối lăng trụ theo
a
.
A.
3
3
2
a
V =
. B.
3
3
24
a
V =
. C.
3
3
8
a
V =
. D.
3
3
16
a
V =
.
Hướng dẫn giải
Chọn C
.
Gọi
H
là trung điểm của
'AB
, theo đề ta suy ra:
( )
'''AH A B C⊥
.
0
' 45AA H⇒=
khi đó
0
' .tan 45
2
a
AH A H
= =
.
Vậy
3
3
8
a
V =
.
Câu 77. Cho lăng trụ
.ABC A B C
′′′
có cạnh bên bằng
2a
, đáy
ABC
là tam giác cân tại
;A
2 ; AB a=
0
120 .
BAC =
Hình chiếu vuông góc của
A
′
trên
( )
mp
ABC
trùng với trung điểm của
cạnh
BC
. Tính thể tích khối chóp
.
A BB C C
′ ′′
?
A.
3
3a
. B.
3
2a
. C.
3
4
a
. D.
3
4
3
a
.
Hướng dẫn giải
Chọn B
Gọi là
H
trung điểm của cạnh
.
BC
.
Xét tam giác
.ABC
có
2 .sin60 3;BH a a= =
2 .cos60 ;AH a a= =
.
Xét tam giác
.A HA
′
vuông tại
H
có
(
)
2
2
2 3.AH a a a
′
= −=
.
Ta có:
lt
V hS= ⋅
.
Trong đó
3h AH a
′
= =
.
2
1
3
2
ABC
S AH BC a
∆
= ⋅=
.
Vậy
3
3.
lt
Va
=
33
.
1
3
3
A ABC
V aa
′
⇒ =⋅=
.
Mặt khác
33 3
..
32
A BCB C lt A ABC
V VV aa a
′ ′′ ′
=− = −=
.
Câu 78. Cho khối lăng trụ đứng có cạnh bên bằng
5
, đáy là hình vuông có cạnh bằng
4
. Hỏi thể tích khối
lăng trụ là:
A.
64
. B.
80
. C.
100
. D.
20
.
Hướng dẫn giải
Chọn B
Lăng trụ đứng có cạnh bên bằng
5
nên có chiều cao
5h =
.
Thể tích khối lăng trụ là:
2
. 4 .5 80
ABCD
VS h= = =
.
A
B
C
A'
B'
C'
H
https://toanmath.com/
Câu 79. Cho hình lăng trụ tam giác đều
.ABC A B C
′′′
có tất cả các cạnh bằng
a
. Gọi
M
,
N
lần lượt là
trung điểm của các cạnh
AB
và
BC
′′
. Mặt phẳng
( )
A MN
′
cắt cạnh
BC
tại
P
. Tính thể tích của
khối đa diện
.MBPABN
′′
A.
3
3
24
a
. B.
3
3
12
a
. C.
3
73
96
a
. D.
3
73
32
a
.
Hướng dẫn giải
Chọn C
Gọi
S
là giao điểm của
AM
′
và
BB
′
, khi đó
P
là giao điểm
SN
và
BC
.
Ta có
1
..
8
SMBP
SABN
V
SM SB SP
V SA SB SN
′′
= =
′′
.
77
88
MBPABN SABN
VV
′′ ′′
⇒==
.
1
.
3
SABN ABN
V SB S
′′ ′′
∆
′
=
11
. . sin 60
32
SB AB BN
′ ′′ ′
= °
1
2 . . sin60
62
a
aa= °
3
3
12
a
=
.
3
.
7 73
8 96
MBPABN SABN
a
VV
′′ ′′
⇒==
.
Câu 80. Cho hình lăng trụ
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông tại
B
,
60ACB
°
=
,
BC a=
,
2AA a
′
=
. Cạnh bên tạo với mặt phẳng
( )
ABC
một góc
30°
.Thể tích khối lăng trụ
.ABC A B C
′′′
bằng.
A.
3
3
2
a
. B.
3
3
6
a
. C.
3
3a
. D.
3
3
3
a
.
Hướng dẫn giải
Chọn A
Trong tam giác
ABC
vuông tại
B
ta có:
tan 60 . 3 3
AB
AB BC a
BC
°= ⇒ = =
.
Diện tích đáy:
2
1 .3
.
22
ABC
a
S AB BC= =
.
Gọi
H
là hình chiếu của
A
′
lên mặt phẳng
( )
ABC
. Góc giữa cạnh bên
AA
′
và đáy là
30A AH
′
= °
.
Trong tam giác vuông
A HA
′
ta có:
1
.sin30 2 .
2
A H AA a a
′′
= °= =
.
Thể tích lăng trụ là:
23
3 .3
..
22
ABC
aa
V AH S a
′
= = =
.
P
S
M
N
C
B
A'
B'
C'
A
https://toanmath.com/
Câu 81. Cho hình lăng trụ tam giác
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh bằng
a
, hình chiếu
vuông góc của
A
′
lên mặt phẳng
( )
ABC
là trung điểm
H
của cạnh
AB
, cạnh
10
2
a
AA
′
=
.
Tính theo
a
tích của khối lăng trụ
.ABC A B C
′′′
.
A.
3
3
.
8
a
B.
3
33
.
4
a
C.
3
3
.
12
a
V =
D.
3
33
.
8
a
V =
Hướng dẫn giải
Chọn D
H
là trung điểm của
AB
và
AB a=
nên
2
a
AH =
.
Trong
AA H
′
∆
có
22
A H AA AH
′′
= −
22
10 3
4 42
aa a
= −=
.
Suy ra
23
.
33 3 3
.
42 8
ABC A B C
a aa
V
′′′
= =
.
Câu 82. Cho hình lăng trụ tam giác đều có tất cả các cạnh đều bằng
a
. Tính theo
a
thể tích của khối lăng
trụ.
A.
3
2
3
a
. B.
3
3
a
. C.
3
3
4
a
. D.
3
3
12
a
.
Hướng dẫn giải
Chọn C
23
33
..
44
ABC
aa
V AA S a
′
= = =
.
Câu 83. Cho hình lăng trụ tam giác đều có các cạnh đều bằng
2a
.Thể tích khối lăng trụ đều là:
A.
3
2
3
a
. B.
3
23
3
a
. C.
3
23a
. D.
3
3
a
.
Hướng dẫn giải
Chọn C
2
3
(2 ) 3
. .(2 ) 2 3
4
a
V Bh a a= = =
.
Câu 84. Một hình lăng trụ có đáy là tam giác đều cạnh bằng
a
, cạnh bên bằng
b
và tạo với mặt phẳng đáy
một góc
α
. Thể tích của khối lăng trụ đó là
A.
2
3
cos
12
ab
α
. B.
2
3
cos
4
ab
α
. C.
2
3
sin
12
ab
α
. D.
2
3
sin
4
ab
α
.
Hướng dẫn giải
https://toanmath.com/
Chọn D
Gọi
H
là hình chiếu của
A
′
lên
( )
ABC
.
Lúc đó góc giữa
AA
′
với
( )
ABC
là
A AH
α
′
=
.
Trong
A AH
′
∆
có
sin sin
AH
AH b
AA
αα
′
′
=⇒=
′
.
22
.
33
. sin . sin
44
ABC A B C ABC
a ab
V AHS b
αα
′′′
∆
′
= = =
.
Câu 85.] Cho
()H
là khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng
a
Thể tích của
()H
bằng:
A.
3
2
3
a
.
B.
3
3
4
a
.
C.
3
3
2
a
. D.
3
2
a
.
Hướng dẫn giải
Chọn B
.
Thể tích của
()H
bằng
23
33
.
44
aa
Va= =
.
Câu 86. Cho hình lăng trụ
.’’’ABC A B C
có đáy là tam giác đều cạnh
a
. Hình chiếu của
A
′
trên mặt phẳng
( )
ABC
là trung điểm
H
của cạnh
BC
.
'7AA a=
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
53
8
a
. B.
3
3
8
a
. C.
3
53
24
a
. D.
3
53
6
a
.
Hướng dẫn giải
Chọn A
+ Diện tích đáy:
2
3
4
a
S =
.
+ Chiều cao
22
5
''
2
a
A H AA AH= −=
.
23
35 53
.
42 8
aaa
V = =
.
Câu 87. Cho lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
a
và
AB BC
′′
⊥
. Khi đó thể tích của
khối lăng trụ trên sẽ là:
A
C
B
A'
C'
B'
H
B
A
C
′
a
A
′
B
′
C
https://toanmath.com/
A.
3
6
8
a
V =
. B.
3
7
8
a
V =
. C.
3
6
Va=
. D.
3
6
4
a
V =
.
Hướng dẫn giải
Chọn A
Ta có
( ) ( )
..
AB BC AB BB BC CC
′′ ′ ′
=++
     
22
1
0
2
ax=− +=
2
2
a
x AA
′
⇔= =
.
Vậy thể tích lăng trụ là
2
32
.
42
aa
V =
3
6
8
a
=
.
Câu 88. Cho hình lăng trụ đều
.ABC A B C
′′′
có cạnh đáy bằng
a
.
M
,
N
là hai điểm thõa mãn
20MB MB
′
+=
 
;
3NB NC
′′
=
 
. Biết hai mặt phẳng
( )
MCA
và
( )
NAB
vuông góc với nhau. Tính
thể tích của hình lăng trụ.
A.
3
32
8
a
B.
3
92
8
a
C.
3
92
16
a
D.
3
32
16
a
Hướng dẫn giải
Chọn C
x
C'
B'
A
B
C
A'
https://toanmath.com/
Chọn hệ tọa độ
Oxyz
như hình vẽ
Ta có
0; ;0
2
a
A

−


,
3
;0;0
2
a
B




,
0; ;0
2
a
C



,
32
;0;
23
ah
M




,
3
;;
4 43
a ah
I




3
; ;0
22
aa
AB

=




,
3
;;
4 43
a ah
BI

= −




2
33
, ;;
66 4
ah ah a
n AB BI


⇒= =




 
( )
0; ;0AC a=

,
32
;;
2 23
a ah
AM

=




2
2
23
, ;0;
32
ah a
n AC AM

−

⇒= =




 
Ta có
( ) ( )
22 4
12
2 3 36
.0 0
6.3 8 4
ah a a
NAB MAC n n h⊥ ⇔ =⇔ − =⇔=

3
.
3 61 3 9 2
. ...
4 2 2 16
ABC A B C
aa
V aa
′′′
= =
.
Câu 89. Cho
(
)
H
là hình lăng trụ xiên
.ABC A B C
′′′
có đáy là tam giác đều cạch
a
, hình chiếu vuông góc
A
′
lên đáy trùng với tâm đường tròn ngoại tiếp tam giác
ABC
và
AA
′
hợp đáy bằng
60°
. Thể
tích của
(
)
H
bằng.
A.
3
3
4
a
. B.
3
3
12
a
. C.
3
3
2
a
. D.
3
3
6
a
.
Hướng dẫn giải
Chọn A
2
3
4
ABC
a
S
∆
=
.
Gọi
O
là hình chiếu của
A
′
lên
( )
mp ABC
,
I
là trung điểm của
BC
.
Góc giữa
AA
′
và
( )
mp ABC
là góc
60A AO
′
= °
.
https://toanmath.com/
23
33
a
AO AI
= =
,
.tan 60A O AO a
′
= °=
.
( )
3
3
.
4
ABC
H
a
V S AO
∆
′
= =
.
.
Câu 90. Cho lăng trụ tam giác đều
.ABC A B C
′′′
có độ dài cạnh đáy bằng
2a
, cạnh bên bằng
3a
. Tính
thể tích
V
của lăng trụ.
A.
3
32Va=
. B.
3
2
Va=
. C.
3
3Va=
. D.
3
3Va=
.
Hướng dẫn giải
Chọn D
Diện tích đáy tam giác đều
( )
2
2
23
3
4
a
Sa
= =
.
Thể tích lăng trụ
23
. 3. 3 3
V Sh a a a= = =
.
Câu 91. Cho hình lăng trụ tam giác đều có các cạnh đều bằng
.a
Thể tích khối lăng trụ đều là
A.
3
2
.
3
a
B.
3
3
.
4
a
C.
3
22
.
3
a
D.
3
.
3
a
Hướng dẫn giải
Chọn B
Ta có hình lăng trụ tam giác đều là hình lăng trụ đứng có đáy là tam giác đều. Gọi hình lăng trụ
cần tính thể tích là ABCA’B’C’.
Ta có:
1
. sinA
2
ABC
S AB AC=
2
3
4
a
=
'B'C'
'.
ABCA ABC
V AA S=
2
3
.
4
a
a=
3
3
4
a
=
Câu 92. Cho hình lăng trụ đứng
.ABCD A B C D
′′′′
có đáy là hình vuông cạnh bằng
3
, đường chéo
AB
′
của
mặt bên
( )
ABB A
′′
có độ dài bằng
5
. Tính thể tích
V
của khối lăng trụ
.ABCD A B C D
′′′′
?
A.
18V =
. B.
48V =
. C.
36V
=
. D.
45V =
.
Hướng dẫn giải
Chọn C
O
C
B
A
C'
B'
A'
60
o
https://toanmath.com/
.
Xét tam giác vuông
AA B
′′
có:
22
4
AA AB A B
′ ′ ′′
= −=
và có
2
39
ABCD
S = =
.
.
4.9 36
ABCD A B C D
V
′′′′
= =
.
Câu 93. Cho hình lăng trụ đều
.ABC A B C
′′′
có cạnh đáy bằng
a
. Đường thẳng
AB
′
tạo với mặt phẳng
( )
BCC B
′′
một góc
30°
. Thể tích khối lăng trụ
.ABC A B C
′′′
theo
a
.
A.
3
6
4
a
. B.
3
4
a
. C.
3
6
12
a
. D.
3
3
4
a
.
Hướng dẫn giải
Chọn A
Gọi
M
là trung điểm của cạnh
BC
. Do
.ABC A B C
′′′
là hình lăng trụ tam giác đều nên ta có
( )
AM BCC B
′′
⊥
⇒
(
)
(
)
,
AB BCC B AB M
′ ′′ ′
=
30= °
.
Xét tam giác vuông
AB M
′
ta có
tan30
AM
AB
°=
′
tan30
AM
AB
′
⇔=
°
3
2
a
AB
′
⇔=
.
Xét tam giác vuông
B BM
′
ta có
22
BB B M BM
′′
= −
22
9
44
aa
= −
2a=
.
Thể tích khối lăng trụ
.ABC A B C
′′′
là
.
1
. .sin 60 .
2
ABC A B C
V AB AC BB
′′′
′
= °
3
6
4
a
=
.
Câu 94. Cho khối lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
2
, diện tích tam giác
A BC
′
bằng
3
. Tính thể tích của khối lăng trụ.
A.
2
. B.
25
3
. C.
32
. D.
25
.
Hướng dẫn giải
Chọn C
3
5
B'
A'
C'
C
D
A
B
D'
M
B'
A'
A
C
B
https://toanmath.com/
.
Gọi
M
là trung điểm của
BC
.Vì
BC AM
BC A M
BC AA
⊥
′
⇒⊥
′
⊥
.
1
3 .3
2
A BC
S A M BC
′
∆
′
=⇔=
1
.2 3 3
2
AM AM
′′
⇔ =⇔=
.
22
AA AM A M
′′
= −
(
)
2
2
33 6=−=
.
2
.
23
. .6 32
4
ABC A B C ABC
V S AA
′′′
∆
′
= = =
.
Câu 95. Cho hình lăng trụ đều
.ABC A B C
′′′
, biết khoảng cách từ điểm
C
đến mặt phẳng
( )
ABC
′
bằng
a
,
góc giữa hai mặt phẳng
( )
ABC
′
và
( )
BCC B
′′
bằng
α
với
1
cos
3
α
=
(tham khảo hình vẽ bên
dưới).Thể tích khối lăng trụ bằng
A.
3
9 15
20
a
. B.
3
3 15
20
a
. C.
3
3 15
10
a
. D.
3
9 15
10
a
.
Hướng dẫn giải
Chọn A
A
′
B
′
C
′
A
B
C
M
A
B
C
C'
B'
A'
H
K
O
A'
B'
C'
C
B
A
https://toanmath.com/
Gọi
2x
là cạnh của tam giác đều, Gọi
,OK
lần lượt là trung điểm của
,AB BC
Kẻ
O
CK C
′
⊥
Ta có
CH C O
′
⊥
và
CH AB
⊥
nên
( )
CH ABC
′
⊥
và
( )
( )
,'d C ABC CH a= =
Suy ra:
2 22
1 11
CH CC CO
= +
′
hay
2 22
111
3a CC x
= +
′
(1)
Ta có hình chiếu vuông góc của tam giác
ABC
′
lên mặt phẳng
( )
BCC B
′′
là tam giác
'KBC
Do đó
'
'
1
cos
3
KBC
ABC
S
S
α
∆
= =
Ta có:
'
1
..
2
KBC
S x CC
′
=
và
2 2 22
'
11
.. .. 3
22
ABC
S AB C O AB CC CO x CC x
∆
′′ ′
= = += +
Do đó
22 22 2 2
11
.. 332 35 12
23
xCC x CC x CC CC x CC x
′ ′ ′′ ′
= +⇔ = +⇔ =
(2)
Từ
( ) ( )
1,2
ta có
22
22 2
11 4 3
59
5
5
a
CC a CC
a CC CC
′′
= + ⇔ =⇔=
′′
Suy ra
3
2
a
x =
Vậy thể tích khối lăng trụ là
23
3 3 3 9 15
..
4 20
5
ABC
aa a
V S CC
′
= = =
.
Câu 96.Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông, các tam giác
SAB
và
SAD
là những tam
giác vuông tại
A
. Mặt phẳng
( )
P
qua
A
vuông góc với cạnh bên
SC
cắt
,,SB SC SD
lần lượt
tại các điểm
,,MNP
. Biết
8
SC a=
,
0
60
ASC
=
. Tính thể tích khối cầu ngoại tiếp đa diện
ABCDMNP
?
A.
3
6Va
π
=
. B.
3
24Va
π
=
. C.
3
32 3Va
π
=
. D.
3
18 3Va
π
=
.
Hướng dẫn giải
Chọn C
Mặt phẳng
( )
( )
0
90 1 ,AMNP SC ANC SC AM⊥⇒ = ⊥
.
Do
( ) ( )
( )
0
90 2SAB BC BC AM AM SBC AM MC AMC⊥⇒⊥⇒⊥ ⇒⊥⇒ =
Tương tự ta có
( )
0
90 3APC =
https://toanmath.com/
Do
ABCD
là hình vuông nên từ
( ) ( ) ( )
1, 2, 3
suy ra
AC
là đường kính mặt cầu ngoại tiếp đa
diện
ABCDMNP
.
Xét tam giác
SAC
có
( )
3
03
4
sin60 43 23 23 323
3
AC
AC a R a V a a
SC
ππ
= ⇒ = ⇒= ⇒= =
.
Câu 97. Cho khối lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
2
, diện tích tam giác
A BC
′
bằng
3
. Tính thể tích của khối lăng trụ
A.
32
. B.
25
. C.
2
. D.
25
3
.
Hướng dẫn giải
Chọn A
Gọi
M
là trung điểm của
BC
.
Vì
BC AM
BC A M
BC AA
⊥
′
⇒⊥
′
⊥
.
1
3 .3
2
A BC
S A M BC
′
∆
′
=⇔=
1
.2 3 3
2
AM AM
′′
⇔ =⇔=
.
22
AA AM A M
′′
= −
( )
2
2
33 6=−=
.
2
.
23
.' .6 32
4
ABC A B C ABC
V S AA
′′′
∆
= = =
Câu 98. Cho hình lăng trụ tứ giác
.ABCD A B C D
′′′′
có đáy
ABCD
là hình vuông cạnh
a
và thể tích bằng
2
3a
. Tính chiều cao
h
của hình lăng trụ đã cho.
A.
3
a
h =
. B.
9ha=
. C.
3ha=
. D.
ha=
.
Hướng dẫn giải
Chọn C
Ta có
2
ABCD
Sa=
.
Suy ra:
2
.
2
3
3
ABCD A B C D
ABCD
V
a
ha
Sa
′′′′
= = =
.
Câu 99. Cho lăng trụ đứng
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Góc tạo bởi cạnh
BC
′
và mặt đáy
( )
ABC
′′′
bằng
o
30
. Tính thể tích khối lăng trụ.
A.
3
3
4
a
. B.
3
2
a
. C.
3
12
a
. D.
3
4
a
.
Hướng dẫn giải
Chọn D
https://toanmath.com/
.
( )
0
, 30BC A B C BC B
′ ′′′ ′′
= =


.
2
3
4
ABC
a
S =
;
0
3
tan30 .
3
a
BB B C
′ ′′
= =
3
4
a
V⇒=
.
Câu 100.] Cho lăng trụ đứng
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh
a
, cạnh bên
AB
′
tạo với đáy
một góc
0
45
Thể tích khối lăng trụ
.ABC A B C
′′′
là:
A.
3
.'''
2
3
ABC A B C
a
V
=
. B.
3
.'''
3
ABC A B C
Va=
.
C.
. D.
3
.'''
3
4
ABC A B C
a
V =
.
Hướng dẫn giải
Chọn D
Ta có
AB
là hình chiếu vuông góc của
AB
′
lên
mp( )
ABC
.
.
( )
0
,( ) 45A B ABC ABA
′′
⇒==
.
Khi đó tam giác
ABA
′
vuông cân tại
A AA AB a
′
⇒==
.
Vậy
23
ABC.A B C
33
.
44
aa
Va
′′′
= = ⇒
chọn phương án.
D.
Câu 101. Cho lăng trụ tam giác đều
.ABC A B C
có tất cả các cạnh bằng
2a
. Tính thể tích khối lăng trụ
.ABC A B C

.
A.
3
23a
. B.
3
3a
. C.
3
3
4
a
. D.
3
3
2
a
.
Hướng dẫn giải
Chọn D
Ta có
( )
2
3
23
. .2 2 3
4
ABC
a
V S AA a a= ′= =
.
------------- HẾT -------------
45
0
A
B
C
A
′
B
′
C
′
| 1/58
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


THỂ TÍCH KHỐI LĂNG TRỤ ĐỀU
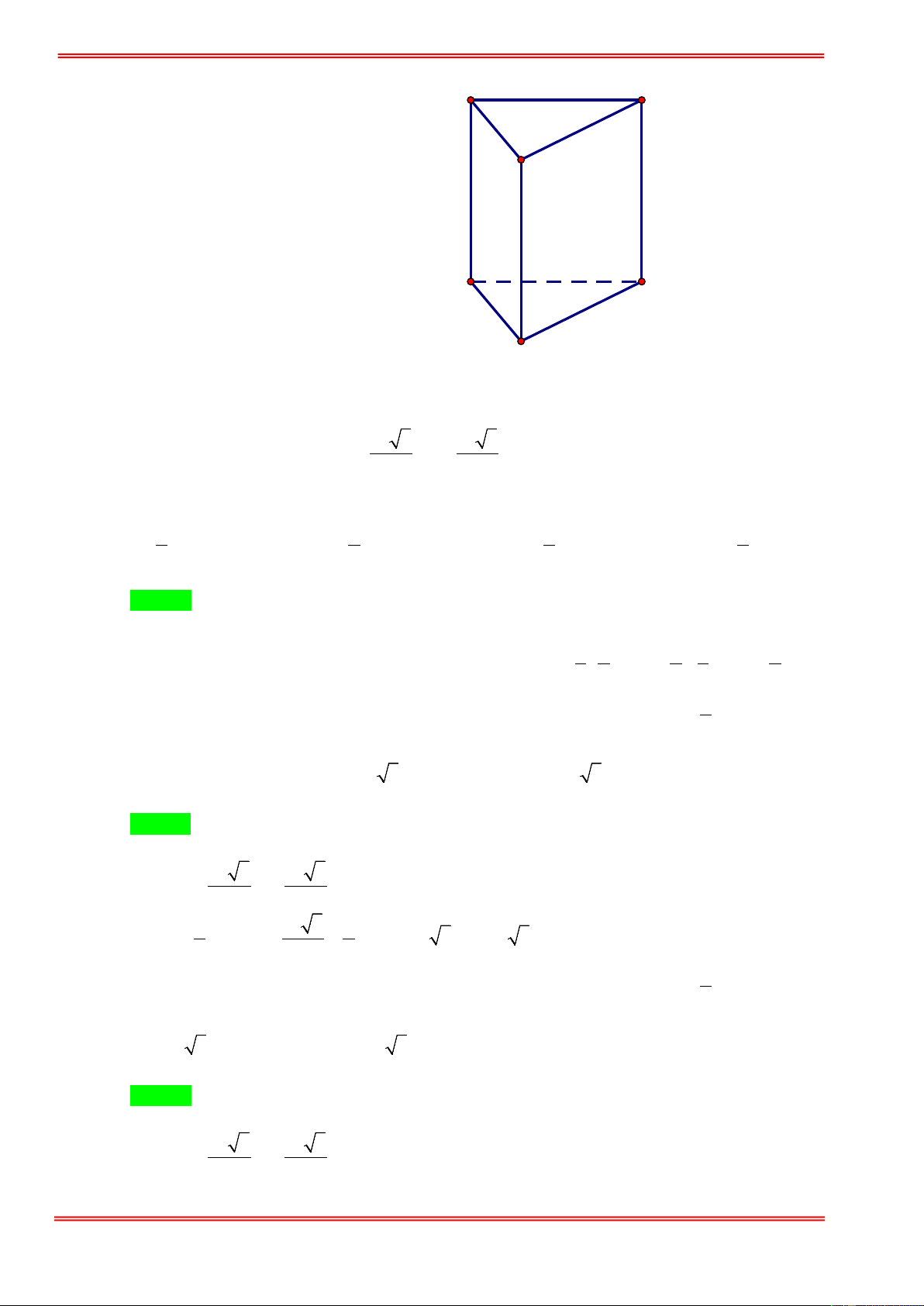
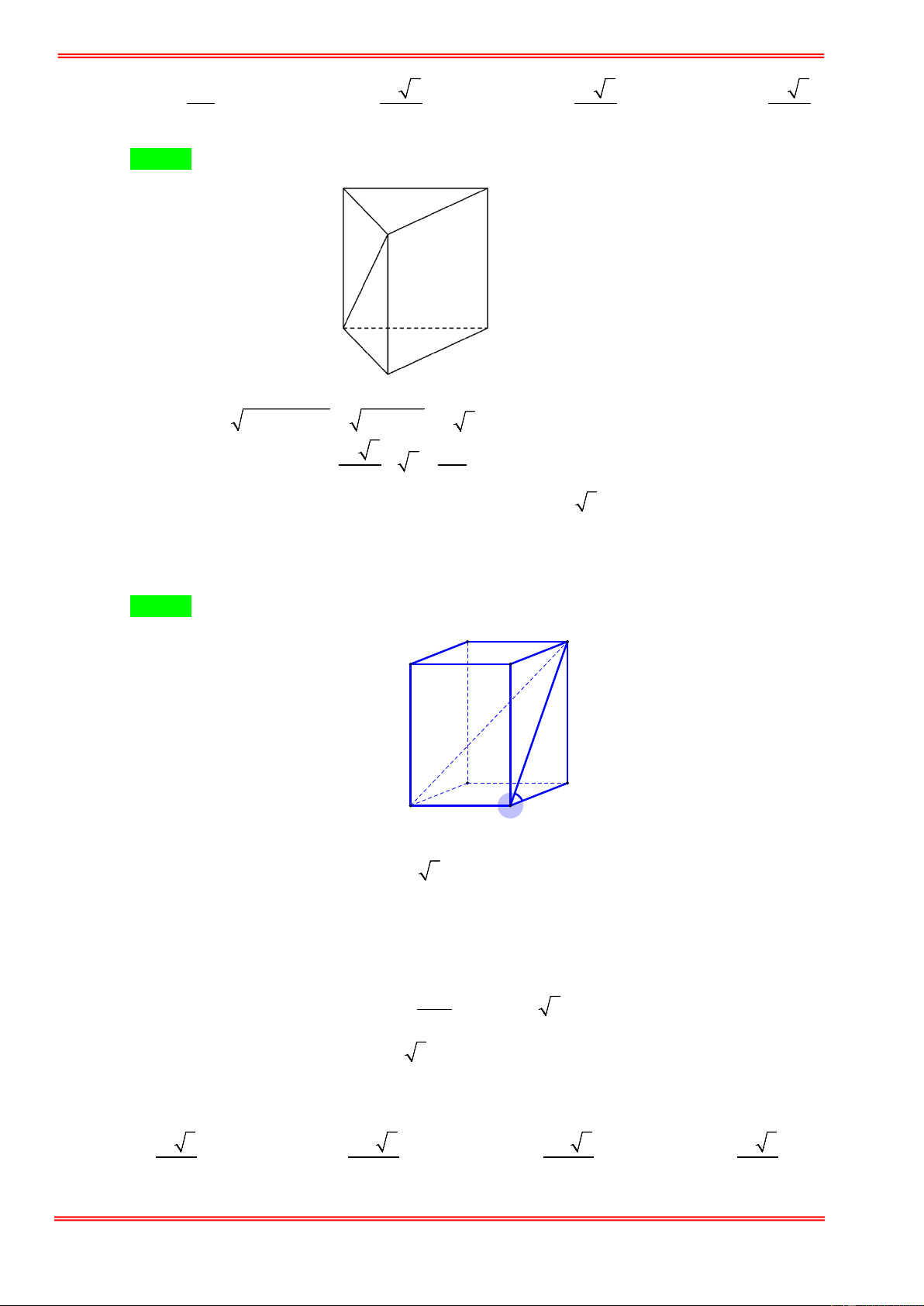
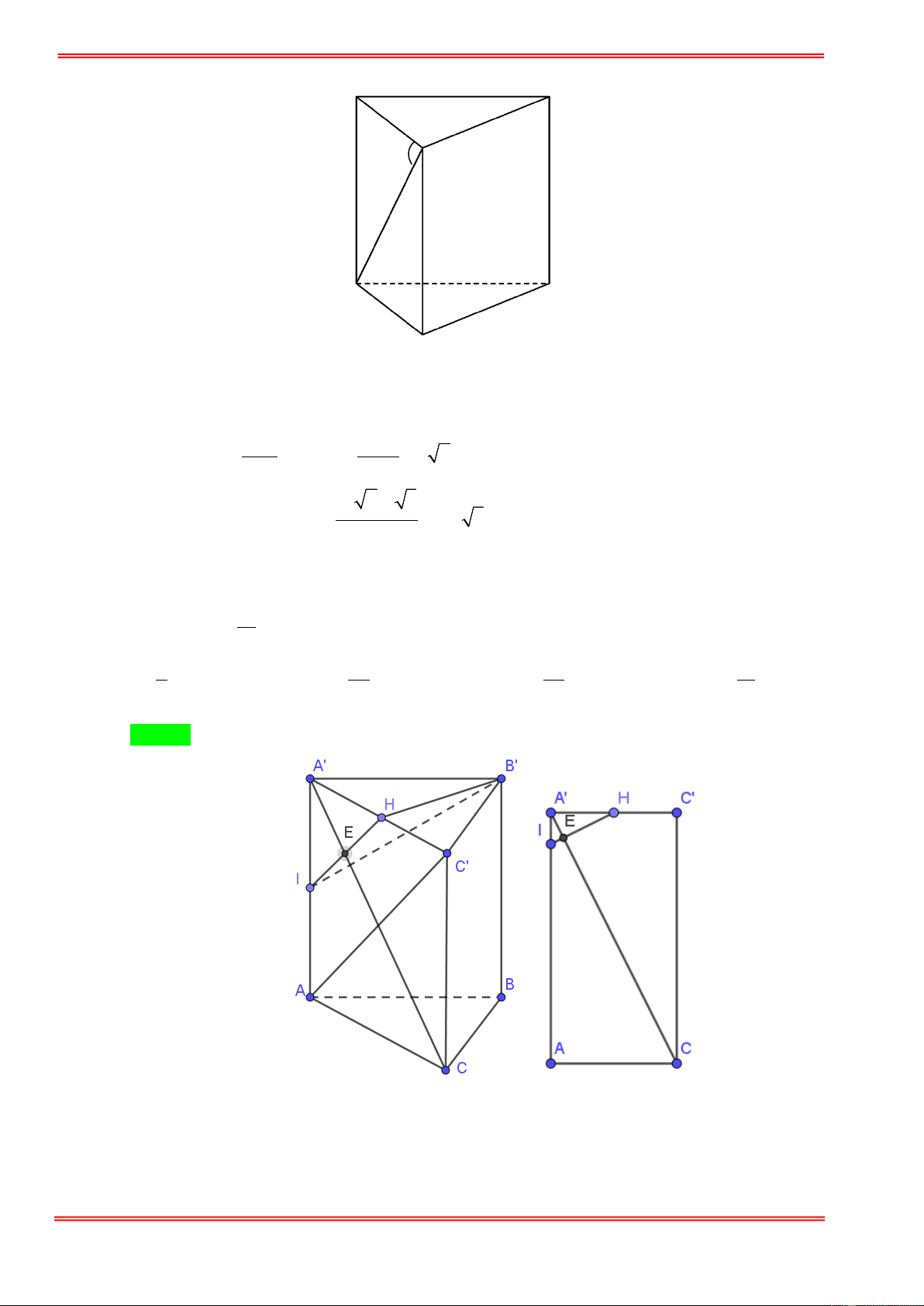
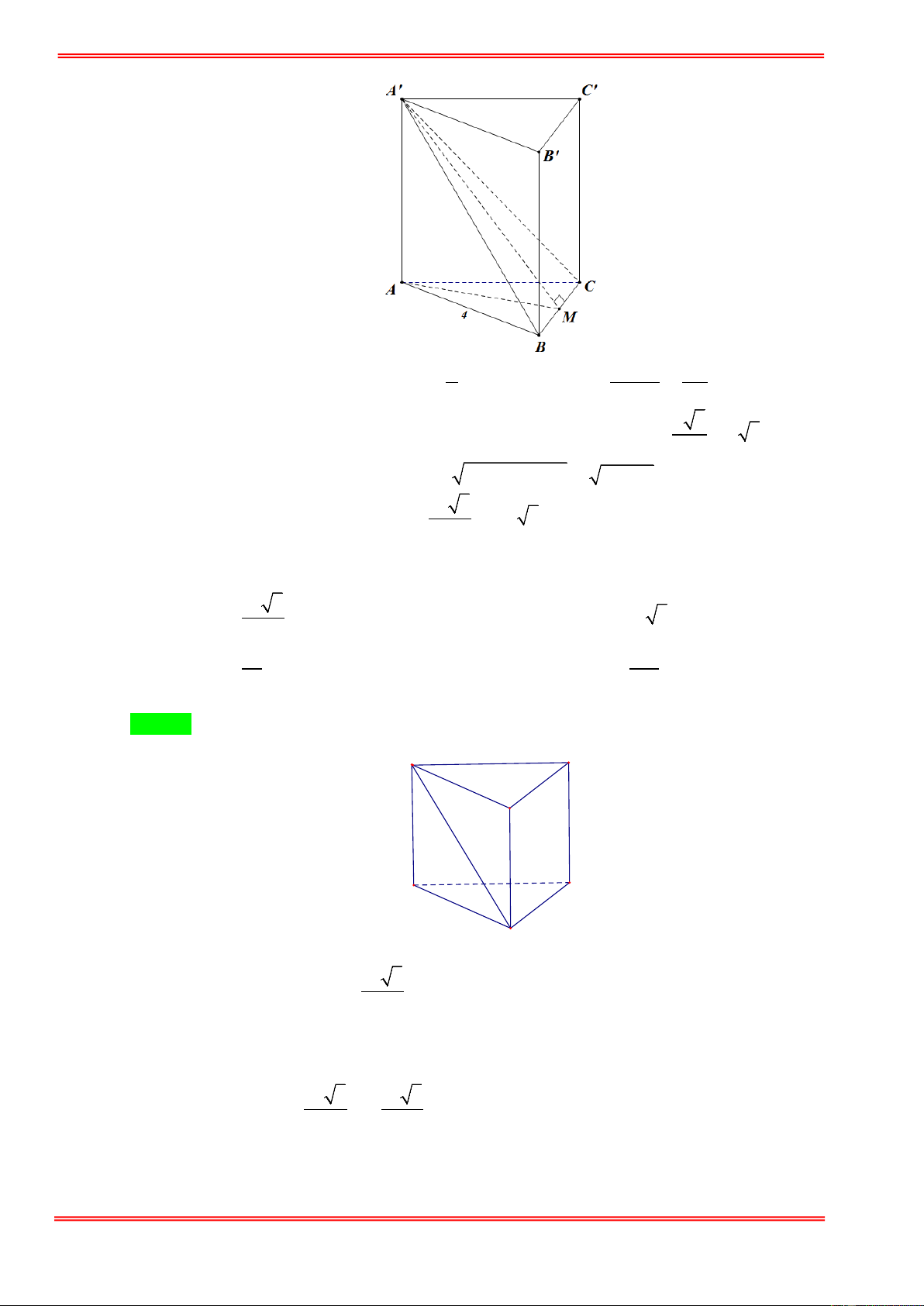
Câu 1. Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3 . Thể tích khối lăng trụ đã cho bằng 9 3 27 3 27 3 9 3 A. . B. . C. . D. . 4 4 2 2 Câu 2.
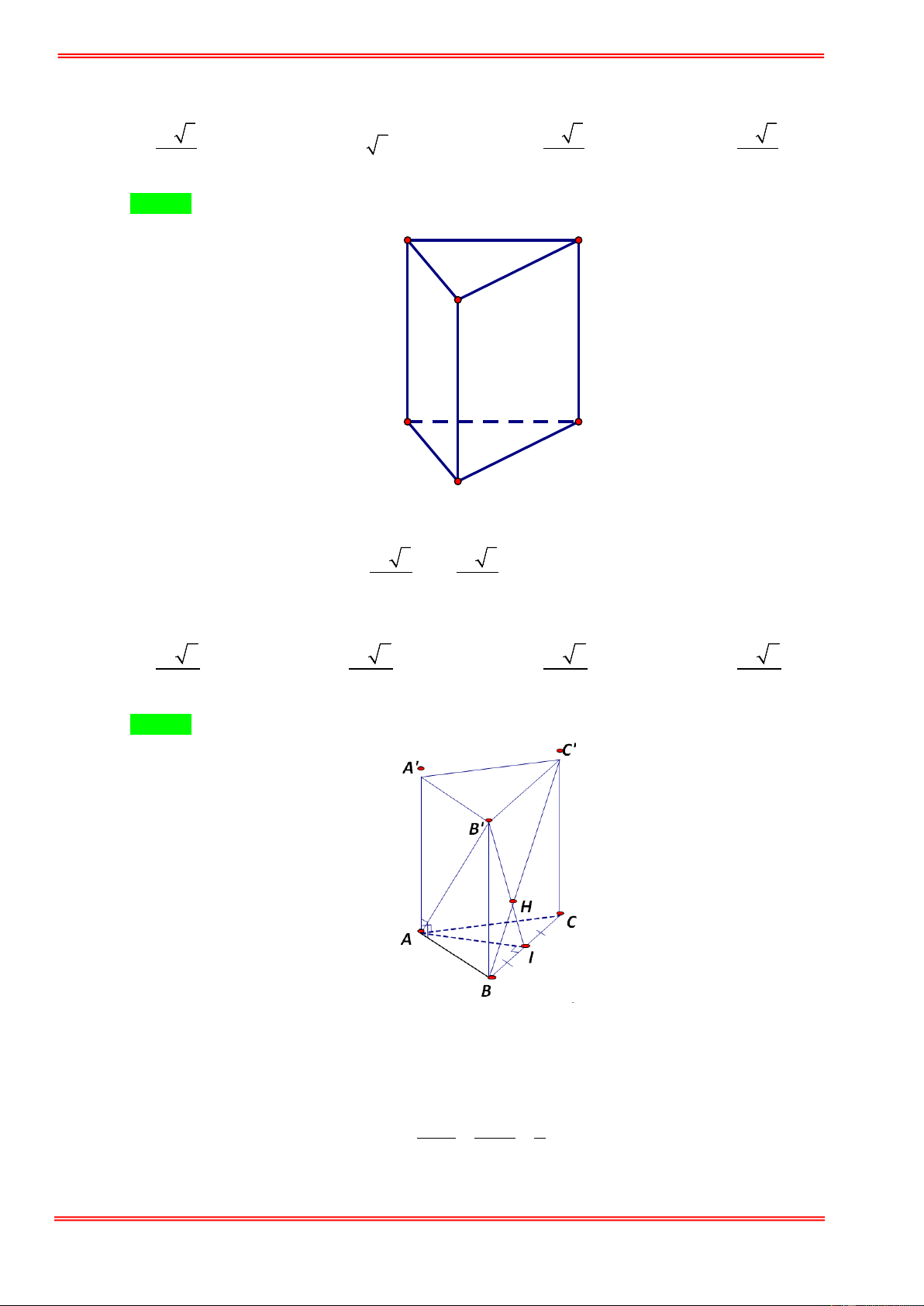
Cho lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng 4cm , diện tích tam giác A′BC bằng 2
12cm . Thể tích khối lăng trụ đó là: A. 3
V = 8 2cm . B. 3
V = 24 3cm . C. 3
V = 24cm . D. 3
V = 24 2cm .
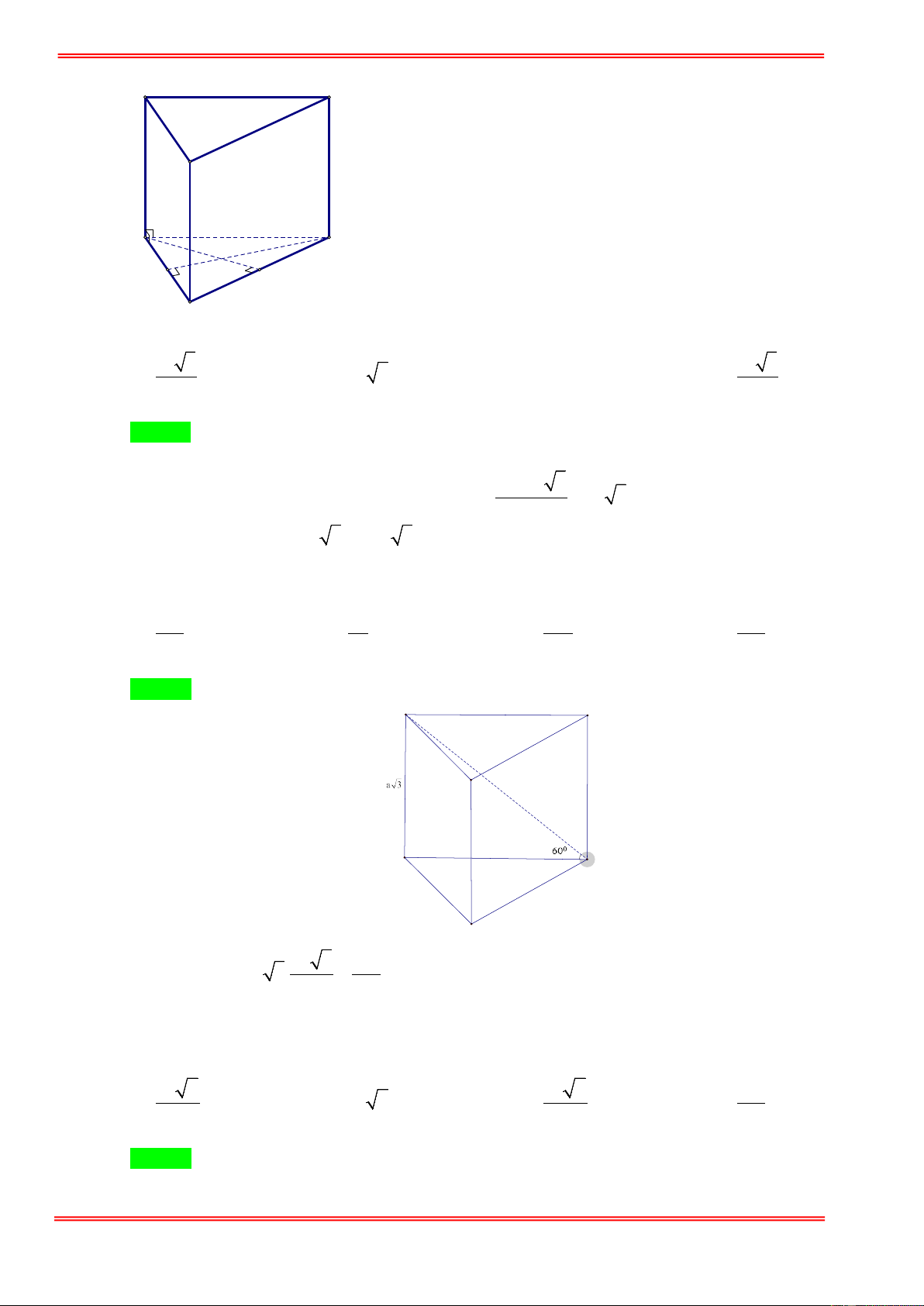
Câu 3. Cho hình lăng trụ đứng ABC.A' B 'C ' có đáy ABC đều cạnh bằng a và chu vi của mặt bên ABB ' A'
bằng 6a . Thể tích của khối lăng trụ ABC.A' B 'C ' bằng 3 a 3 3 a 3 3 a 3 A. . B. 3 a 3 . C. . D. . 2 3 6
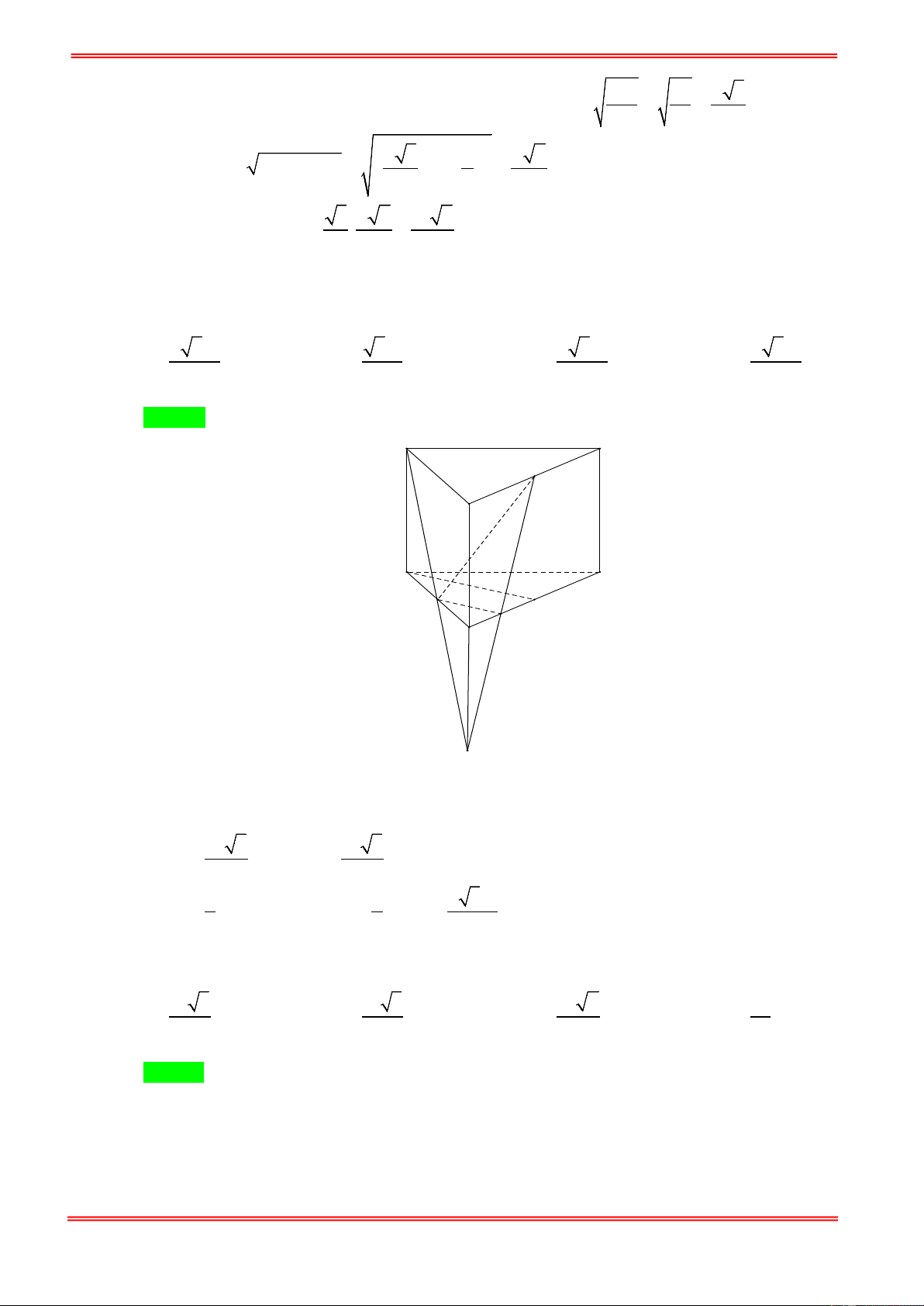
Câu 4. Cho khối tứ giác đều S.ABCD có thể tích là V . Nếu giảm độ dài cạnh đáy xuống hai lần và tăng độ
dài đường cao lên ba lần thì ta được khối chóp mới có thể tích là: 3 2 1 3 A. V . B. V . C. V . D. V . 2 3 4 4 9
Câu 5. Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng a 3
và có thể tích V = (dm ) Tính giá trị của 4 a .
A. a = 9 (dm) .
B. a = 3 (dm) .
C. a = 3 3 (dm) .
D. a = 3 (dm) . 9
Câu 6. Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng a 3
và có thể tích V =
(dm ) Tính giá trị của 4 a .
A. a = 3 (dm) .
B. a = 3 3 (dm) .
C. a = 3 (dm) .
D. a = 9 (dm) .
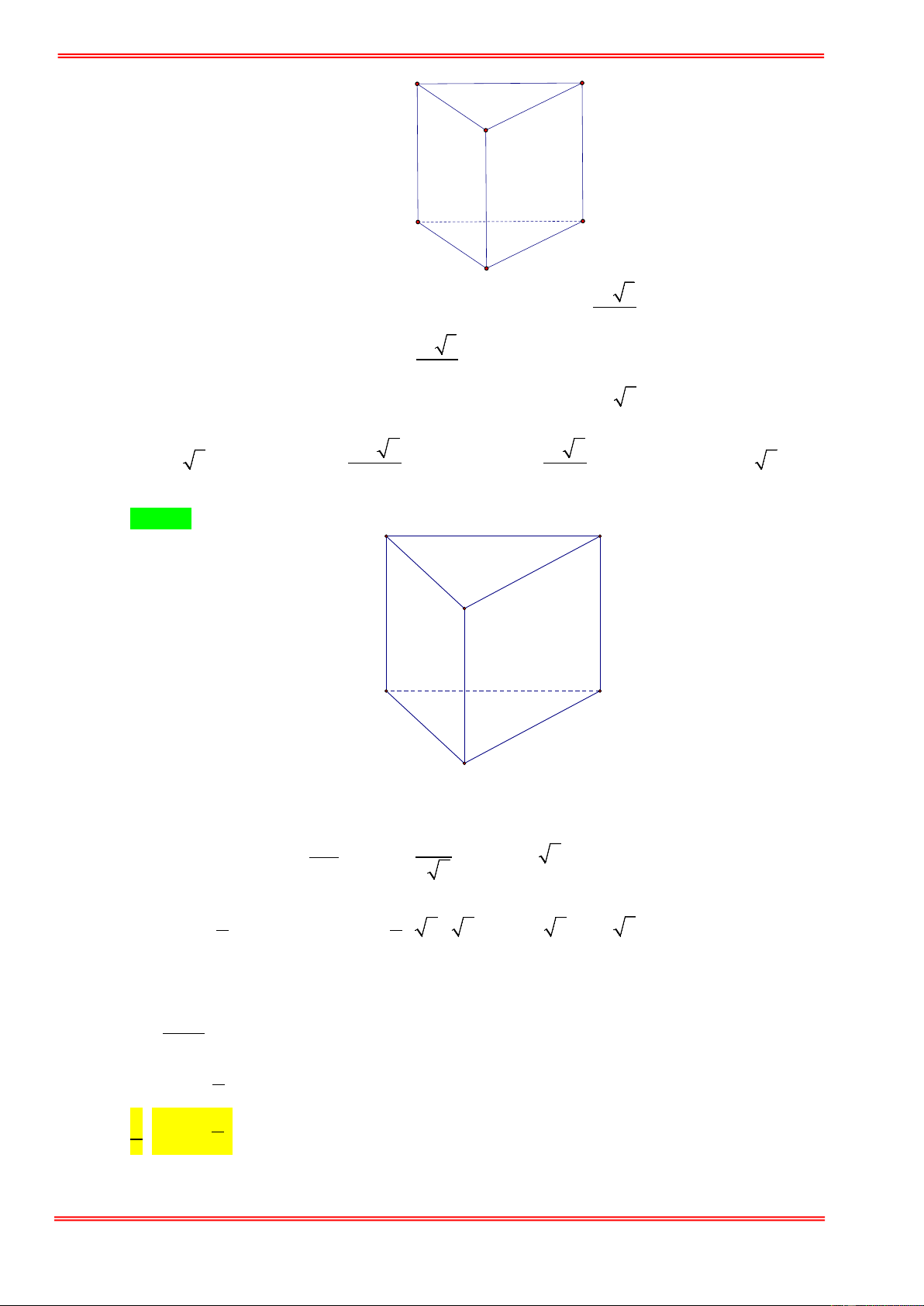
Câu 7. Cho hình lăng trụ ABC.A' B 'C ' có đáy là tam giác đều cạnh 3a , hình chieus của A' trên mặt phẳng
( ABC) trùng với tâm đường tròn ngoại tiếp tam giác ABC . Cạnh AA' hợp với mặt phẳng đáy một góc 0
45 . Thể tích của khối lăng trụ ABC.A' B 'C ' tính theo a bằng. 3 27a 3 9a 3 27a 3 3a A. . B. . C. . D. . 6 4 4 4
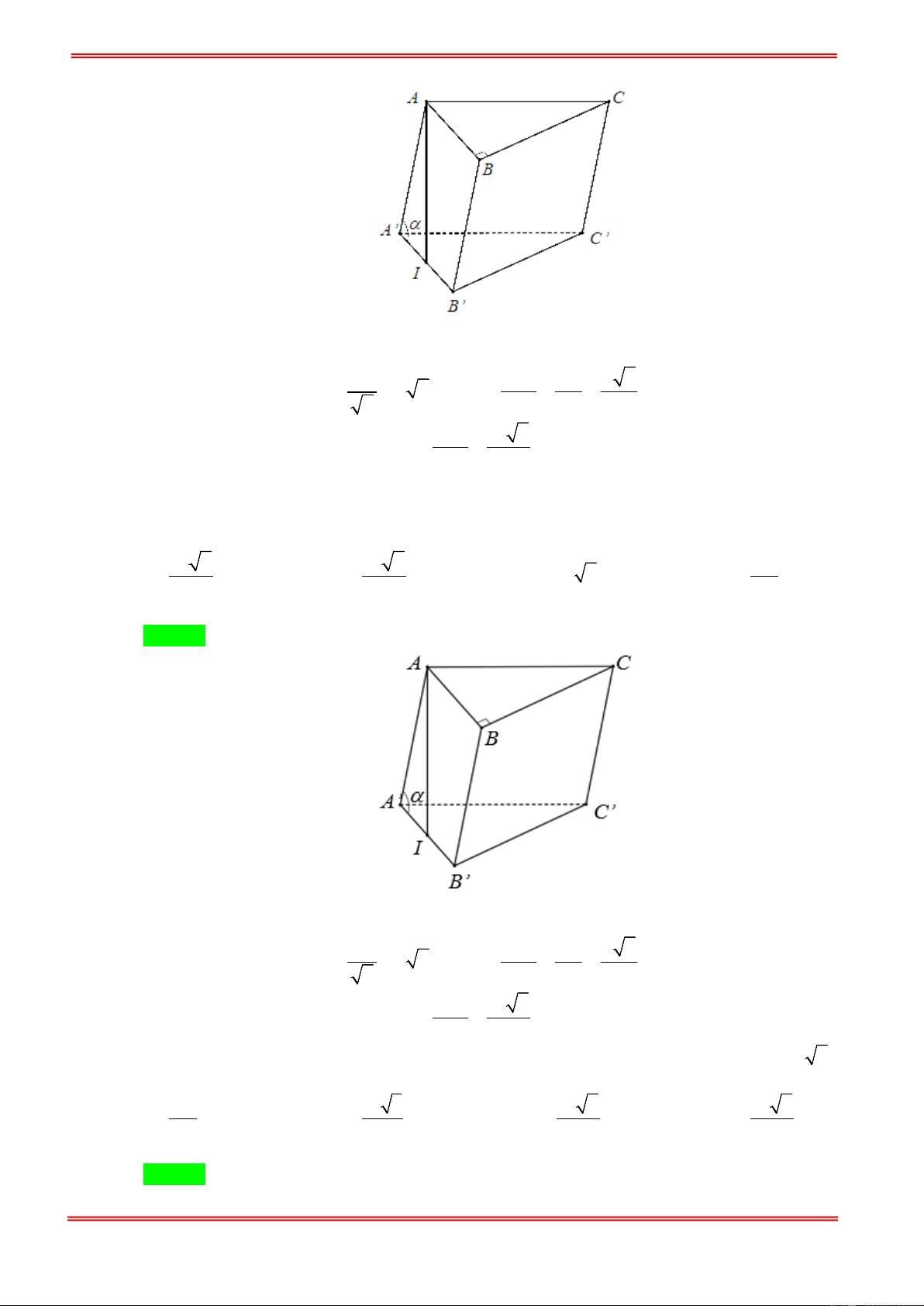
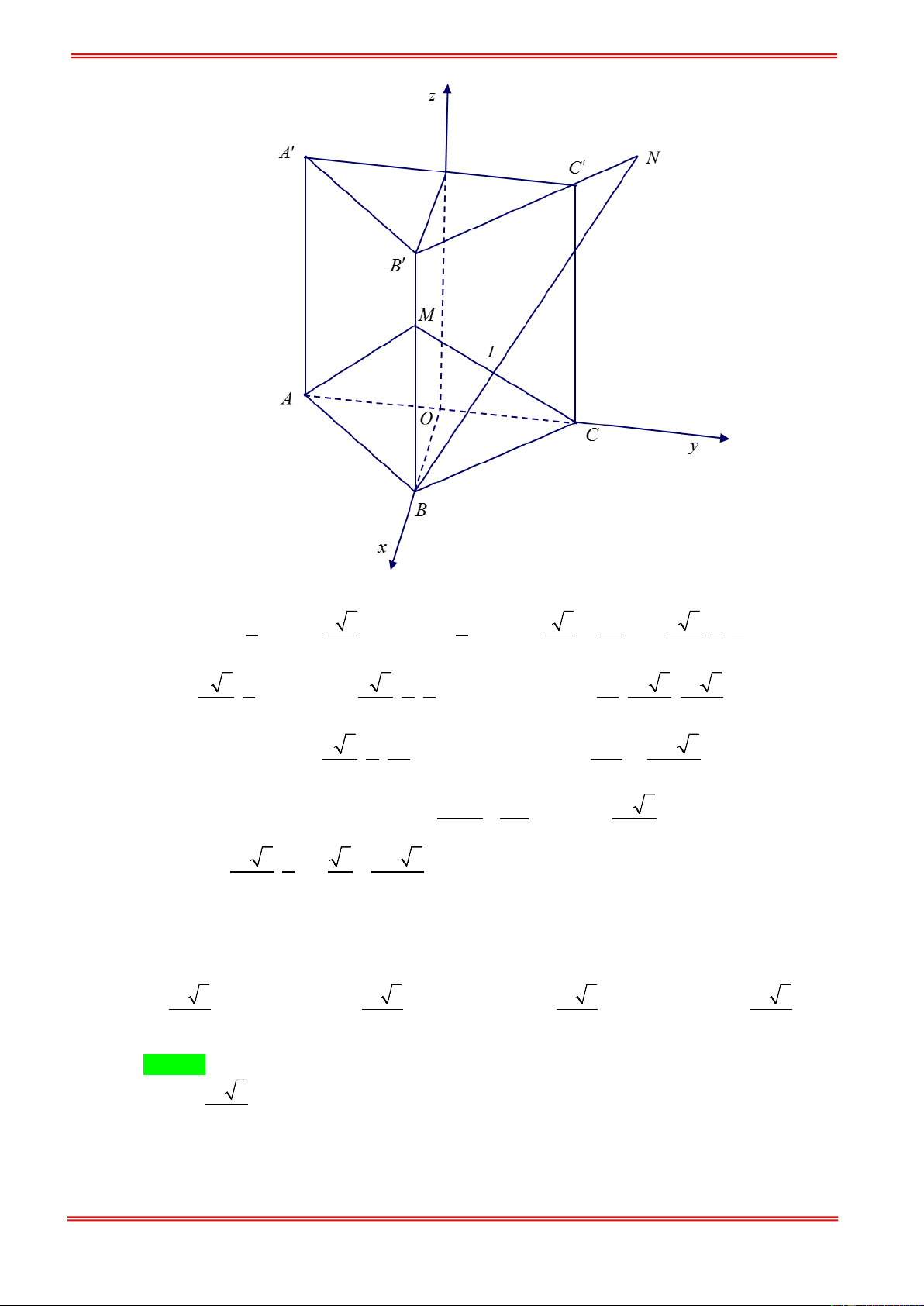
Câu 8. Cho lăng trụ đều ABC.A′B C
′ ′ có cạnh đáy bằng a . Gọi I là trung điểm cạnh BC . Nếu góc giữa
đường thẳng A′I và mặt phẳng ( ABC) bằng 60° thì thể tích của lăng trụ đó là 3 3a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 8 24 8 4 Câu 9.
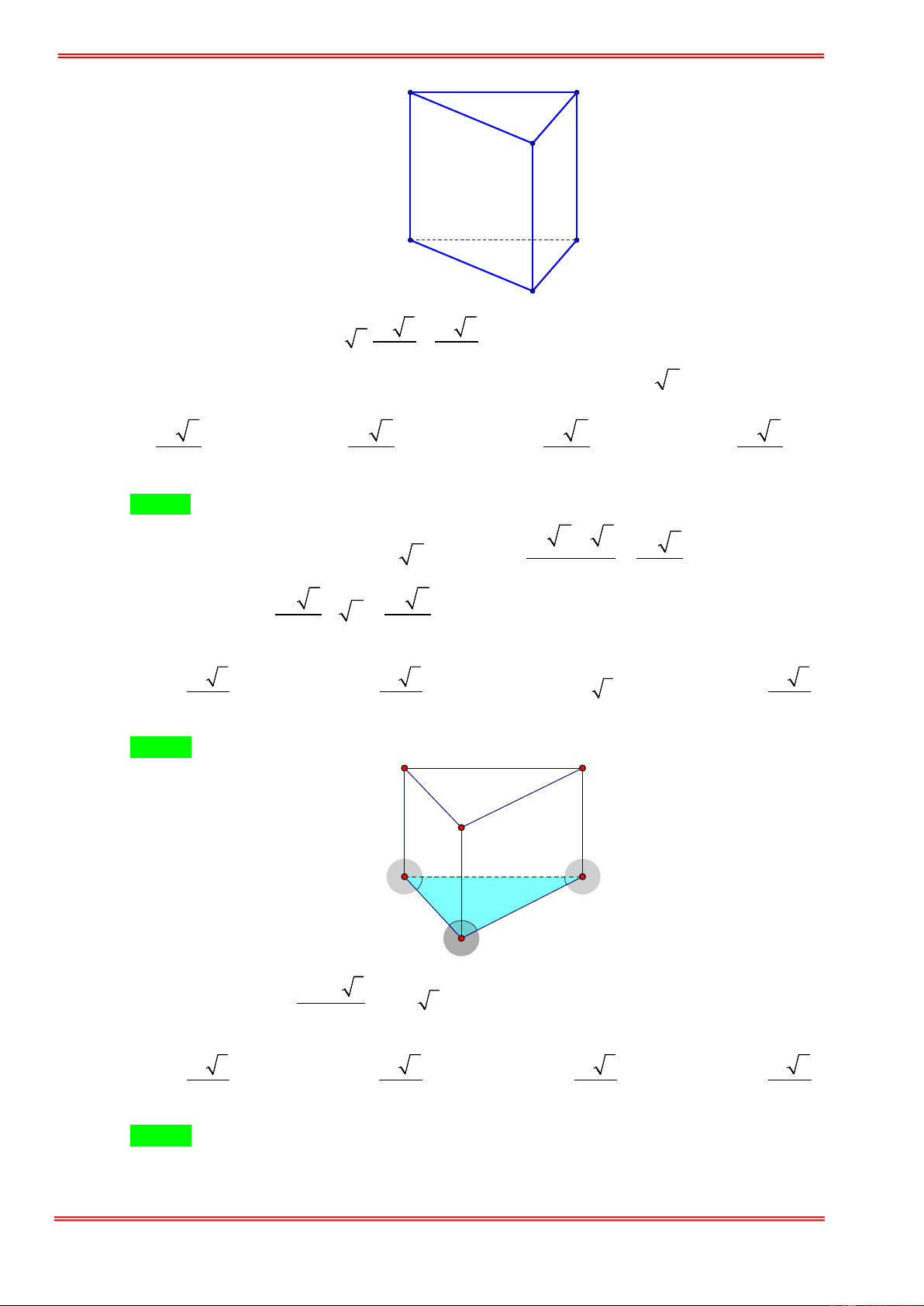
Cho hình lăng trụ tam giác đều có tất cả các cạnh đều bằng a . Tính theo a thể tích của khối lăng trụ. 3 a 3 3 2a 3 a 3 3 a A. . B. . C. . D. . 4 3 12 3
Câu 10. Cho lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng a và cạnh bên bằng a 3 . Thể tích của khối
lăng trụ ABC.A′B C ′ ′ bằng: 3 a 3 3a 3 a 3 3a A. . B. . C. . D. . 8 8 4 4
Câu 11. Cho lăng trụ đứng có đáy là tam giác đều, biết rằng tất cả các cạnh của lăng trụ bằng a . Thể tích
của lăng trụ đó là. 3 a 3 3 a 3 a 3 3 a 3 A. . B. . C. . D. . 12 4 8 4 https://toanmath.com/
Câu 12. Cho khối lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng 2 , diện tích tam giác A′BC bằng 3
. Tính thể tích của khối lăng trụ. 2 5 A. 3 2 . B. . C. 2 5 . D. 2 . 3
Câu 13. Tính thể tích V của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a . 3 2a 3 3a 3 3a 3 2a A. V B. V C. V D. V 4 2 4 3
Câu 14. Cho lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng a và AB′ ⊥ BC′ . Tính thể tích của khối lăng trụ. 3 7a 3 6a 3 6a A. 3 V = 6a . B. V = . C. V = . D. V = . 8 8 4
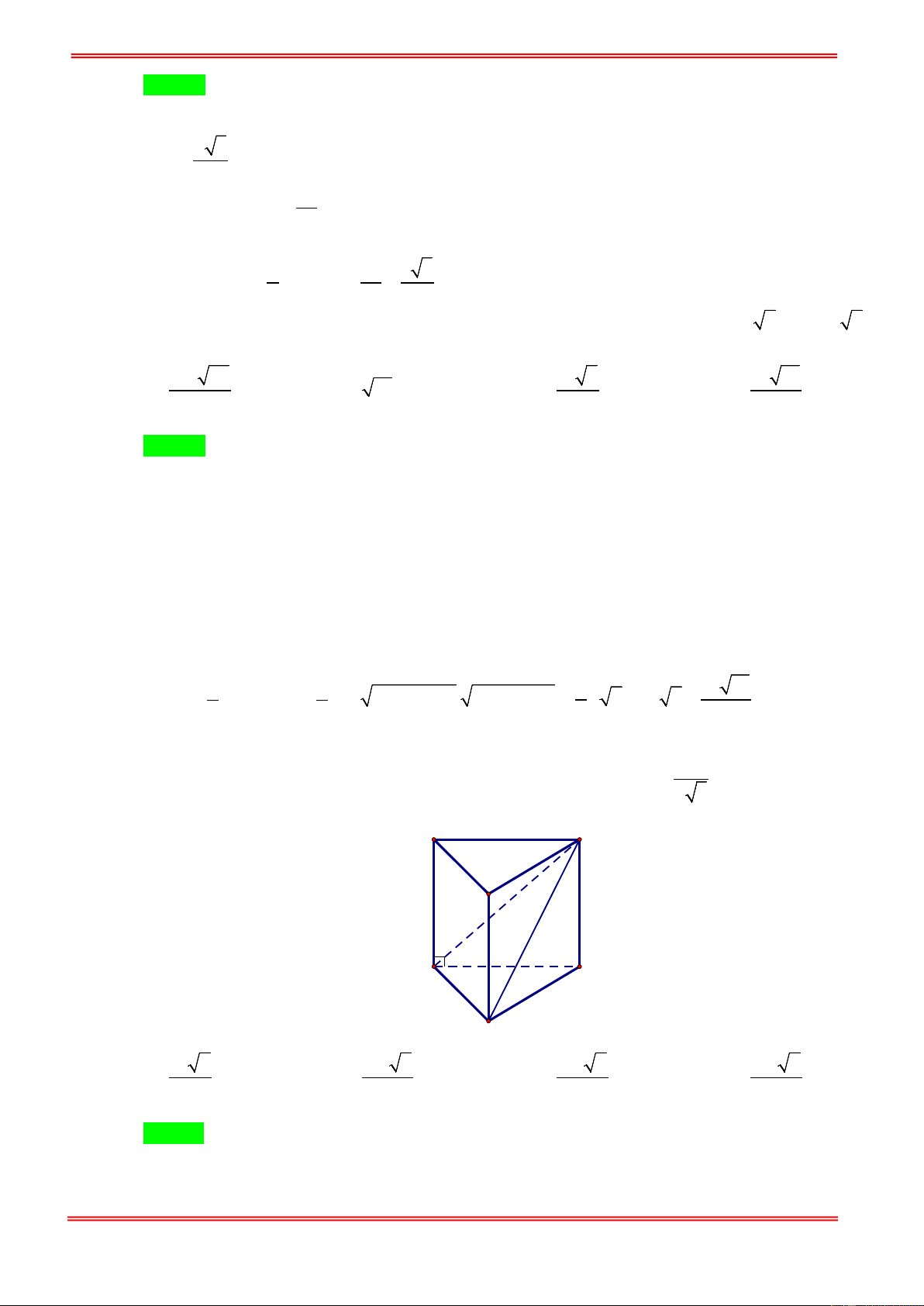
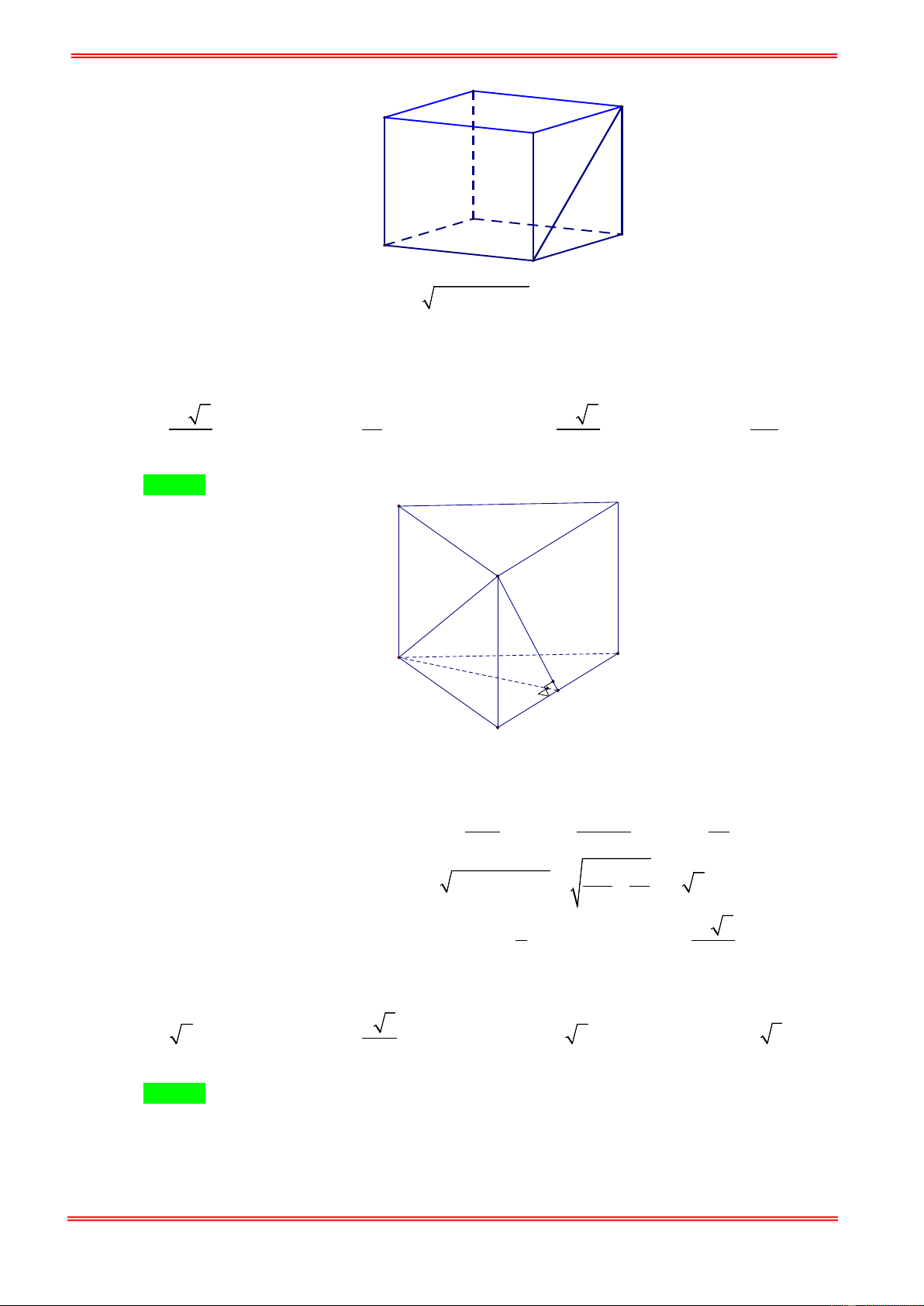
Câu 15. Nếu khối lăng trụ đứng có đáy là hình vuông cạnh 2a và đường chéo mặt bên bằng 4a thì khối
lăng trụ đó có thể tích bằng. A. 3 4a . B. 3 8 3a . C. 3 12a . D. 3 6 3a .
Câu 16. Cho hình lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng 2a , góc giữa hai đường thẳng AB′
và BC′ bằng 60° . Tính thể tích V của khối lăng trụ đó. 3 2 6a 3 2 3a A. 3
V = 2 6a . B. 3
V = 2 3a . C. V = . D. V = . 3 3
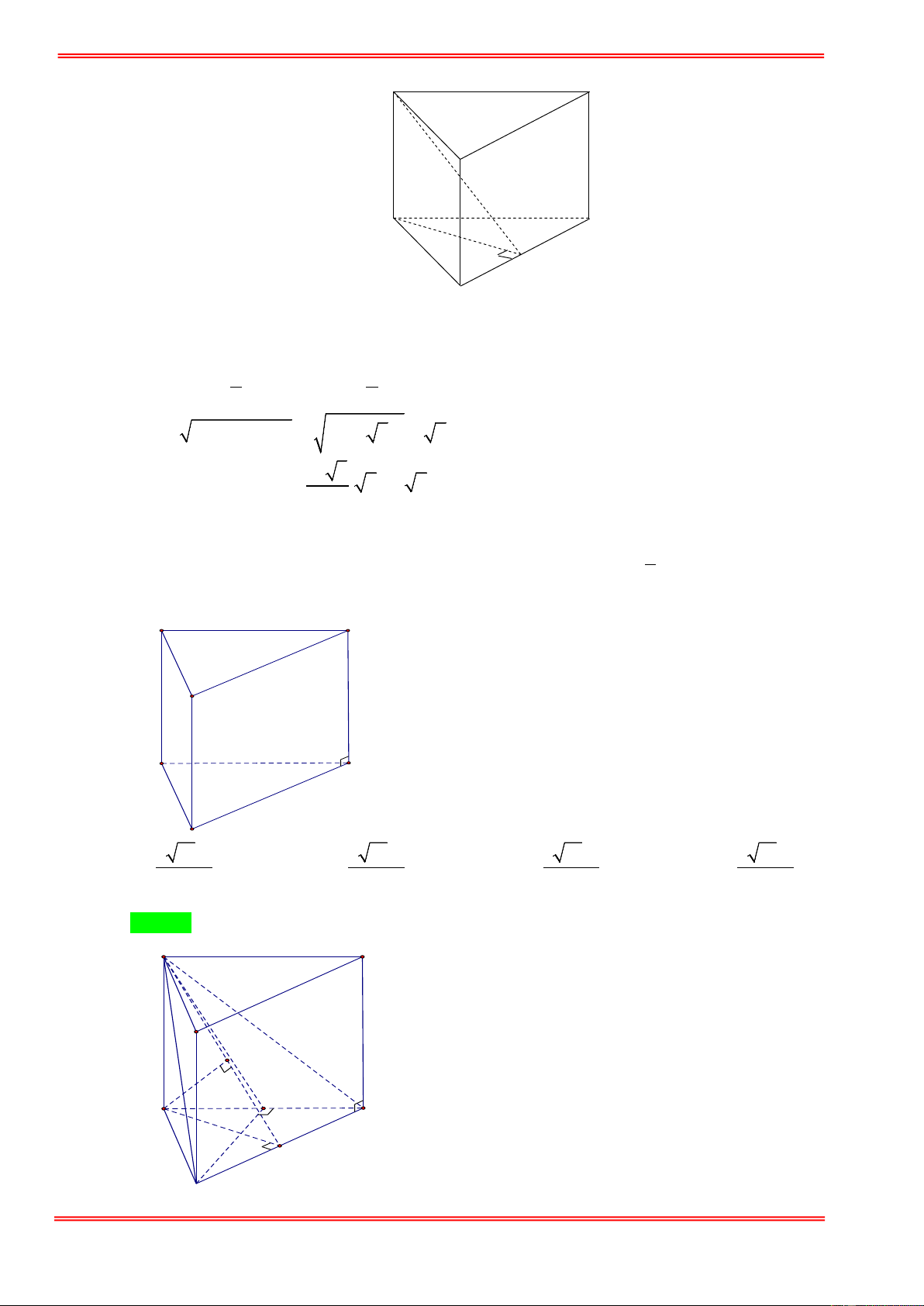
Câu 17. Một khối lăng trụ tam giác có đáy là tam giác đều cạnh 3, cạnh bên bằng 2 3 và tạo với mặt phẳng
đáy một góc 30 .° Khi đó thể tích khối lăng trụ là? 27 9 3 9 27 3 A. . B. . C. . D. . 4 4 4 4
Câu 18. Cho hình lăng trụ tứ giác đều ABC . D A′B C ′ D
′ ′ có cạnh đáy bằng a , khoảng cách từ A đến mặt phẳng ( a A′BC ) bằng
. Tính thể tích lăng trụ. 3 3 2a 3 3a 3 3a A. . B. 3 3 3a . C. . D. . 4 4 2
Câu 19. Thể tích của khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng a bằng: 3 a 3 a 3 3 a 3 3 a 2 A. . B. . C. . D. . 3 4 6 3
Câu 20. Cho khối lăng trụ đều ABC.A′B C
′ ′ và M là trung điểm của cạnh AB . Mặt phẳng (B C ′ M ′ ) chia
khối lăng trụ thành hai phần. Tính tỷ số thể tích của hai phần đó. 3 6 7 1 A. B. . C. . D. . 8 5 5 4
Câu 21. Cho hình lăng trụ tam giác đều ABC.A′B C
′ ′ có AB = a , đường thẳng AB′ tạo với mặt phẳng
(BCC B′′) một góc 30°. Tính thể tích V của khối lăng trụ đã cho. 3 a 2 3 a 6 3 a 6 3 3a A. V = . B. V = . C. V = . D. V = . 3 4 12 4
Câu 22. Cho lăng trụ đứng ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh a , góc tạo bởi hai mặt phẳng
( ABC), ( A′BC) bằng 60°. Tính thể tích khối lăng trụ ABC.A′B C ′ ′. 3 a 3 3 3a 3 3 a 3 3 3a 3 A. . B. . C. . D. . 24 4 6 8 https://toanmath.com/
Câu 23. Khối lăng trụ tam giác đều có tất cả các cạnh bằng nhau và có thể tích là 9 thì độ dài mỗi cạnh 4 bằng. A. 3 . B. 3 . C. 6 243 . D. 3 3 .
Câu 24. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng a là. 2 3 2 3 A. 3 V = a . B. 3 V = a . C. 3 V = a . D. 3 V = a . 4 4 3 2
Câu 25. Tính thể tích của khối lăng trụ đều ABC.A′B C
′ ′ có AB = AA′ = a . 3 3a 3 3a 3 3a A. . B. . C. . D. 3 a . 12 4 6
Câu 26. Cho lăng trụ đứng ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Mặt phẳng ( AB C
′ ′) tạo với mặt đáy
góc 60° . Tính theo a thể tích khối lăng trụ ABC.A′B C ′ ′ . 3 a 3 3 3a 3 3 a 3 3 3a 3 A. V = . B. V = . C. V = . D. V = . 8 8 2 4
Câu 27. Tính thể tích V của khối lăng trụ đều ABC.A' B 'C ' biết AB = a và AB ' = 2a . 3 3a 3 a 3 3 a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . 4 2 12 4
Câu 28. Cho hình lăng trụ tứ giác đều ABC . D A′B C ′ D
′ ′ có cạnh đáy 4 3(m). Biết mặt phẳng (D B ′ C) hợp với đáy một góc ο
60 . Thể tích khối lăng trụ là. A. 3 325 m . B. 3 648 m . C. 3 478 m . D. 3 576 m .
Câu 29. Cho lăng trụ đứng ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh a , góc tạo bởi hai mặt phẳng
( ABC), (A′BC) bằng 60°. Tính thể tích khối lăng trụ ABC.A′B C ′ ′. 3 a 3 3 3a 3 3 3a 3 3 a 3 A. . B. . C. . D. . 6 4 8 24
Câu 30. Cho hình chóp S.ABC có SA ⊥ ( ABC ) , tam giác ABC vuông tại C , AC = a 2, 6 AB = a . Tính
thể tích khối chóp S.ABC biết SC = 3a 3 2a 42 3 a 6 3 a 14 A. . B. 3 14a . C. . D. . 3 3 3
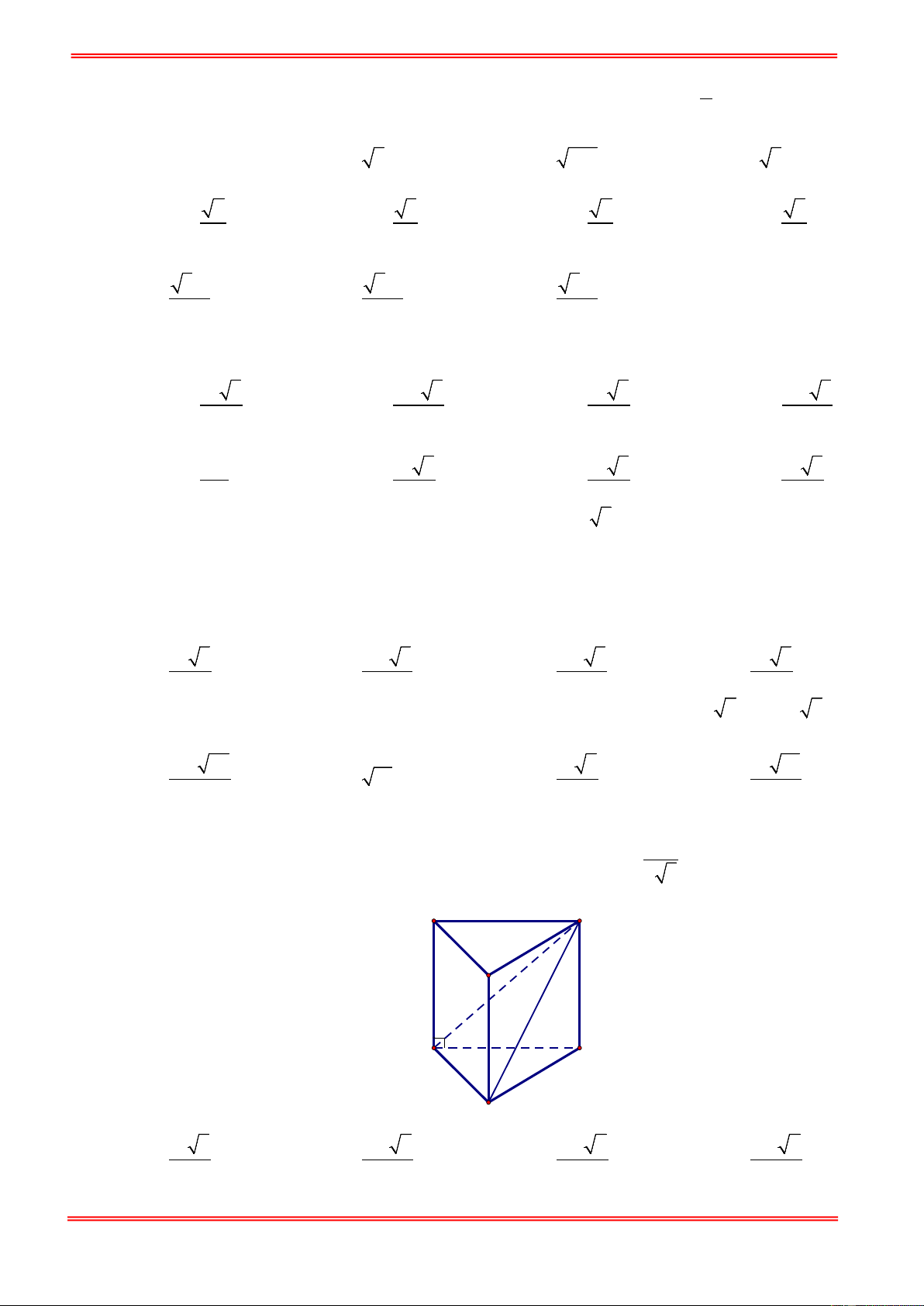
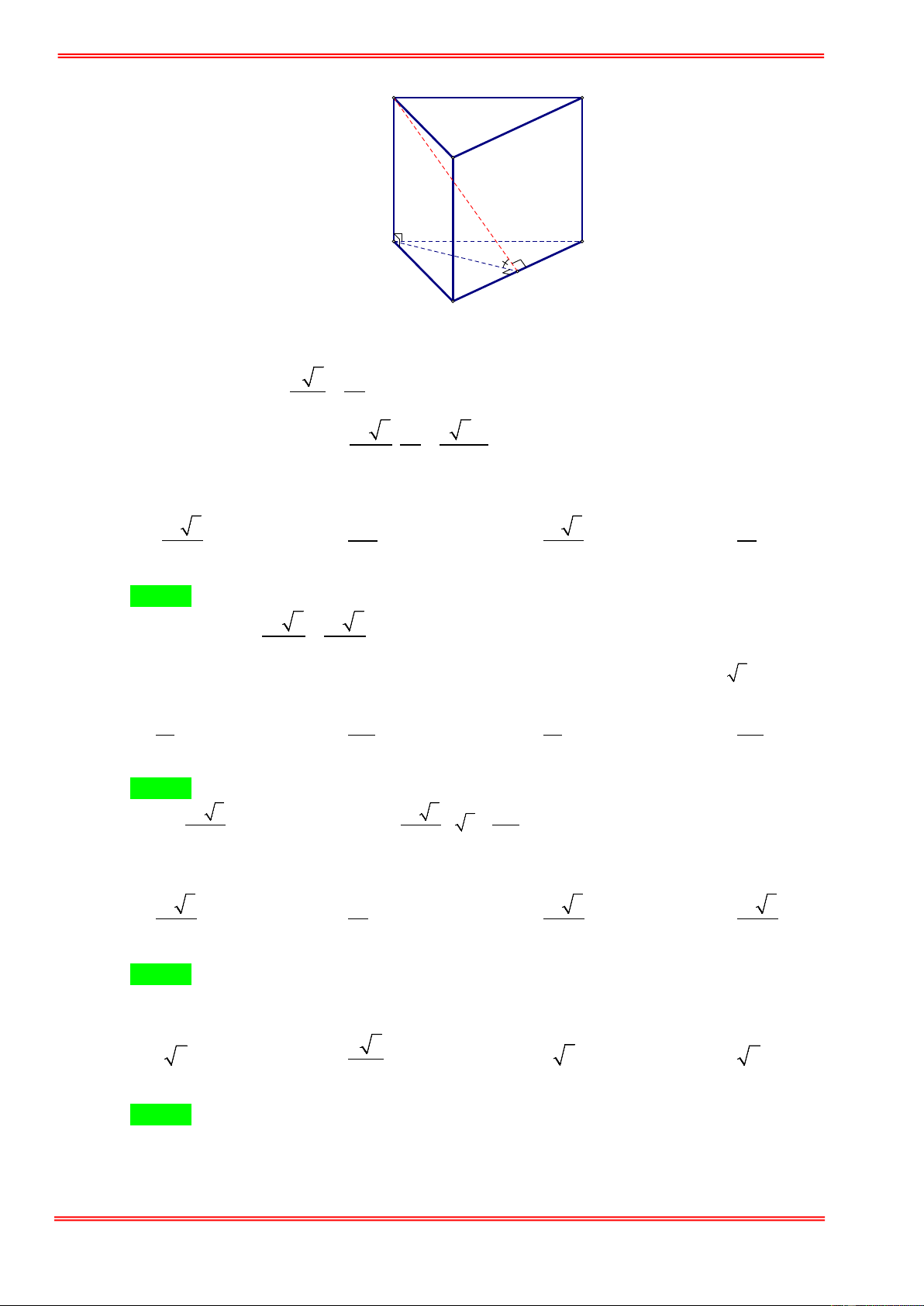
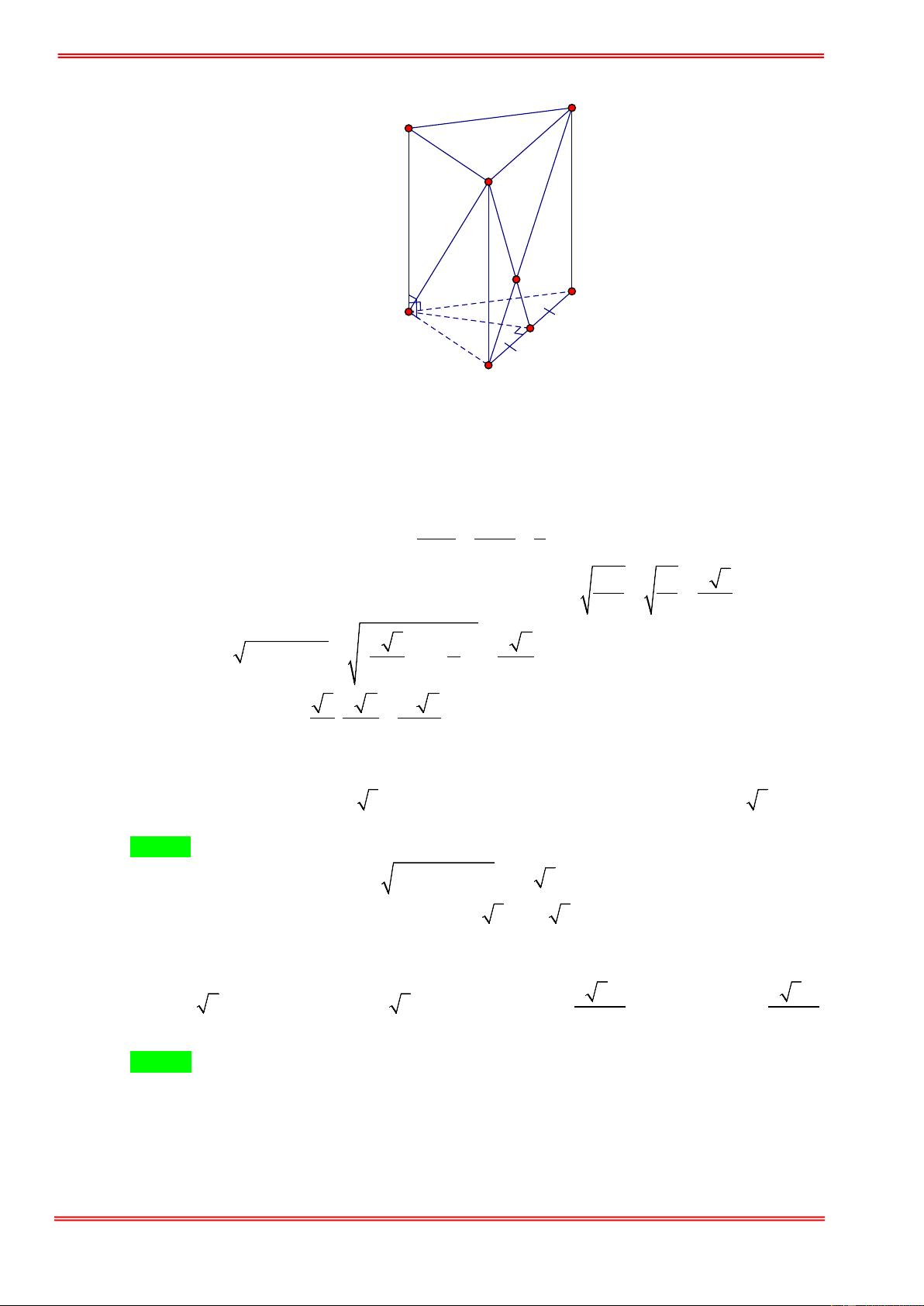
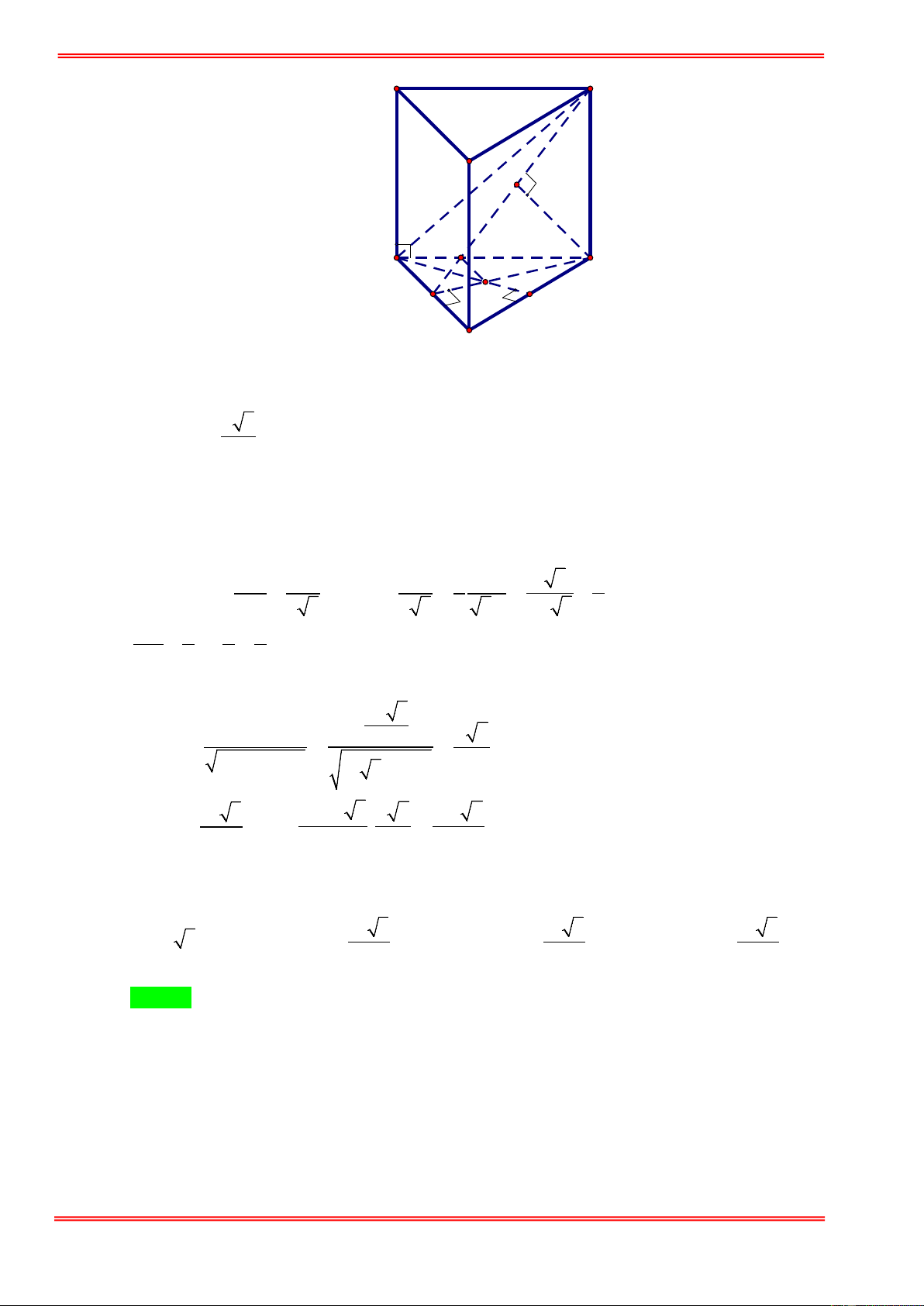
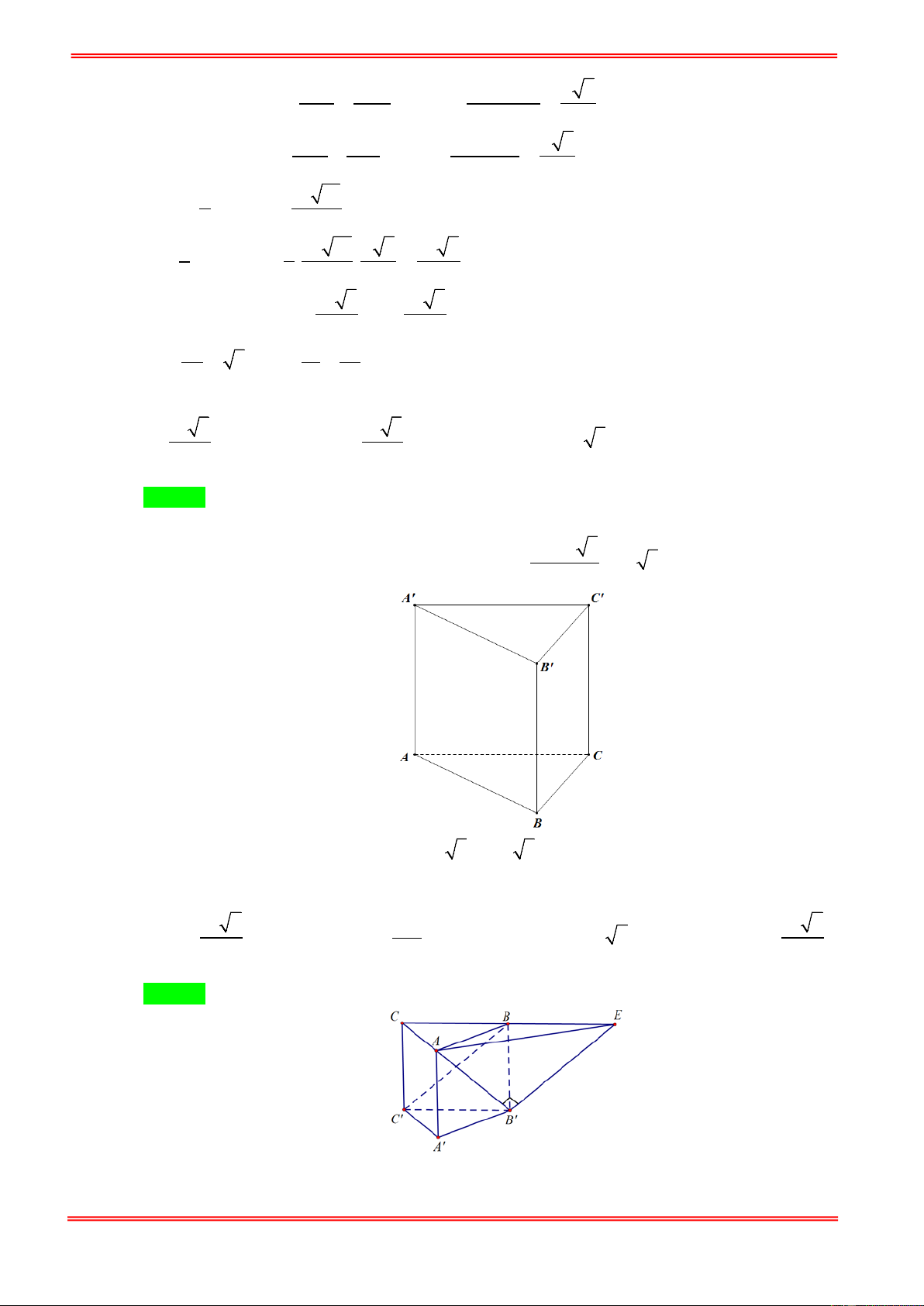
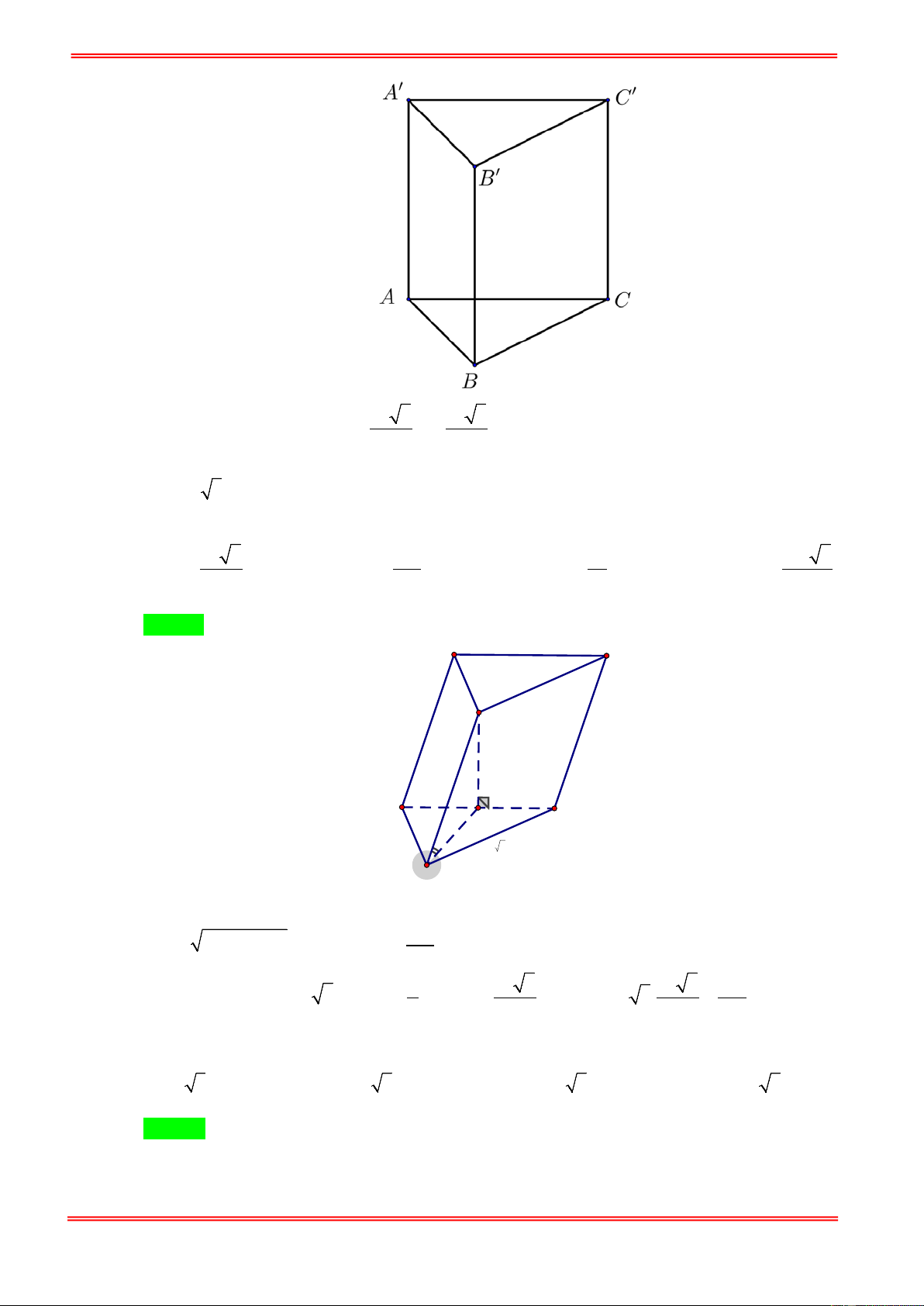
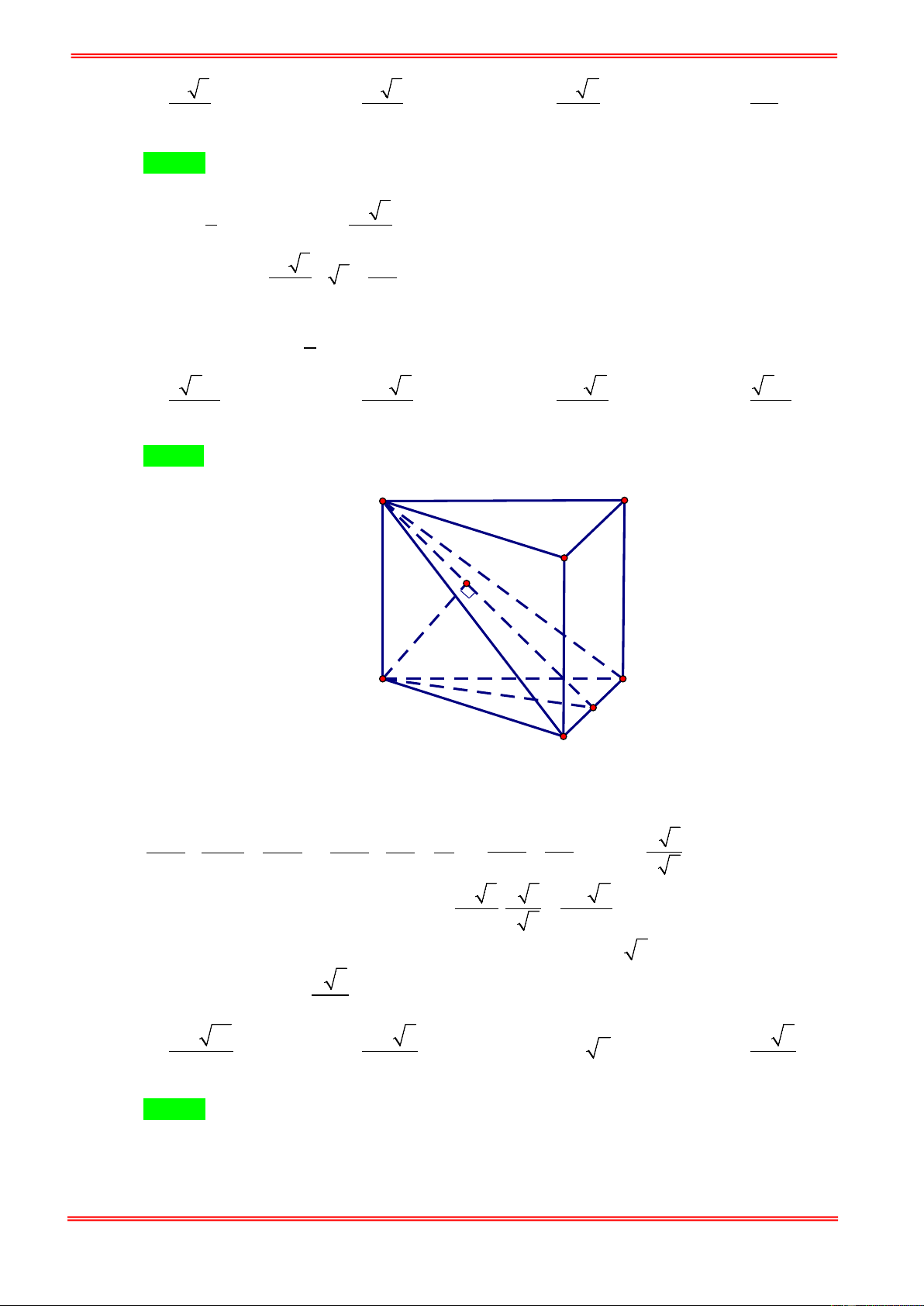
Câu 31. Cho hình lăng trụ đều ABC.A′B C
′ ′. Biết khoảng cách từ điểm C đến mặt phẳng ( ABC′) bằng a ,
góc giữa hai mặt phẳng ( ABC′) và (BCC B ′ ′) bằng α với 1 cosα =
(tham khảo hình vẽ bên). 2 3
Thể tích khối lăng trụ ABC.A′B C ′ ′ là A' C' B' A C B 3 a 2 3 3a 2 3 3a 2 3 3a 2 A. . B. . C. . D. 2 2 4 8 https://toanmath.com/
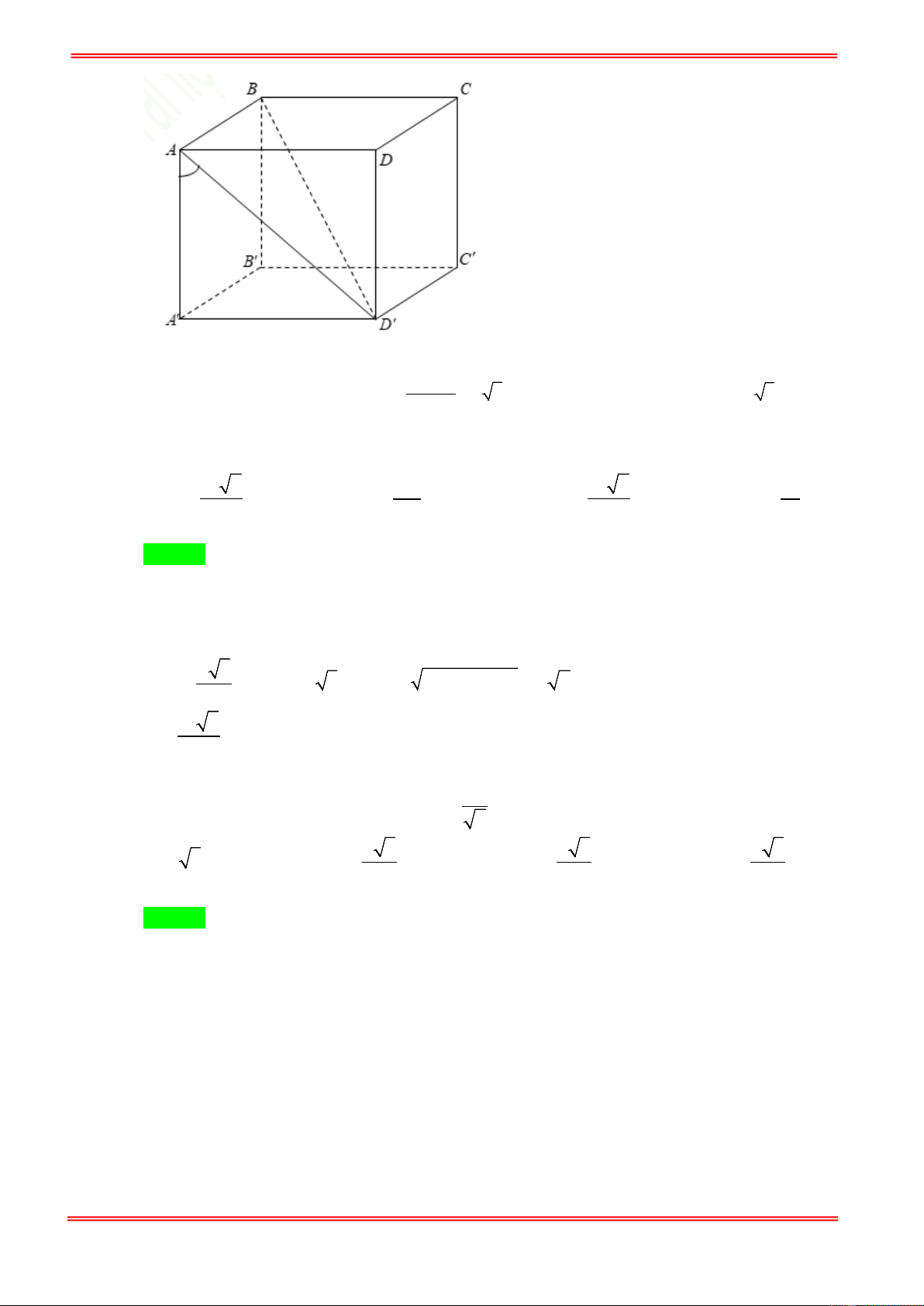
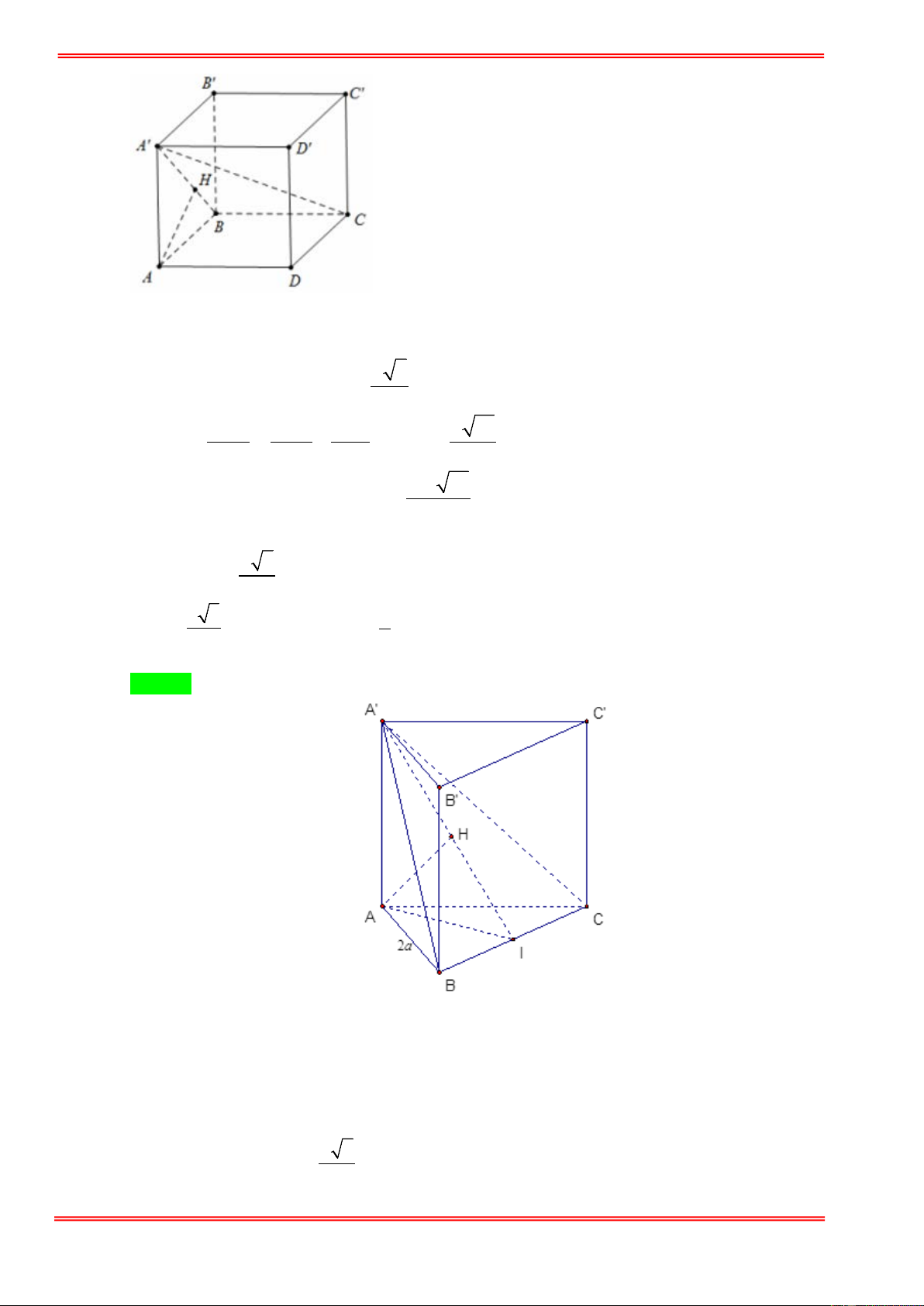
Câu 32. Cho hình hộp đứng ABC . D A′B C ′ D
′ ′ có đáy là hình vuông cạnh a , góc giữa mặt phẳng (D A ′ B) và
mặt phẳng ( ABCD) bằng 30° . Thể tích khối hộp ABC . D A′B C ′ D ′ ′ bằng 3 a 3 3 a 3 3 a 3 A. 3 a 3 . B. . C. . D. . 3 9 18
Câu 33. Cho hình lăng trụ tam giác đều ABCA′B C
′ ′ có AB = a , đường thẳng AB′ tạo với mặt phẳng
(BCC B′′) một góc 30°. Tính thể tích V của khối lăng trụ đã cho. 3 a 6 3 3a 3 a 6 3 a A. V = . B. V = .. C. V = . D. V = . . 12 4 4 4
Câu 34. Cho lăng trụ tam giác đều ABC.A′B C
′ ′ có chiều cao bằng 2 . Biết góc giữa đường thẳng AB′ và mặt phẳng ( 1 A′B C
′ ′) bằng α thỏa tanα =
. Tính thể tích khối lăng trụ ABC.A′B C ′ ′. 2 4 3 4 3 2 3 A. 4 3 . B. . C. . D. . 3 9 3
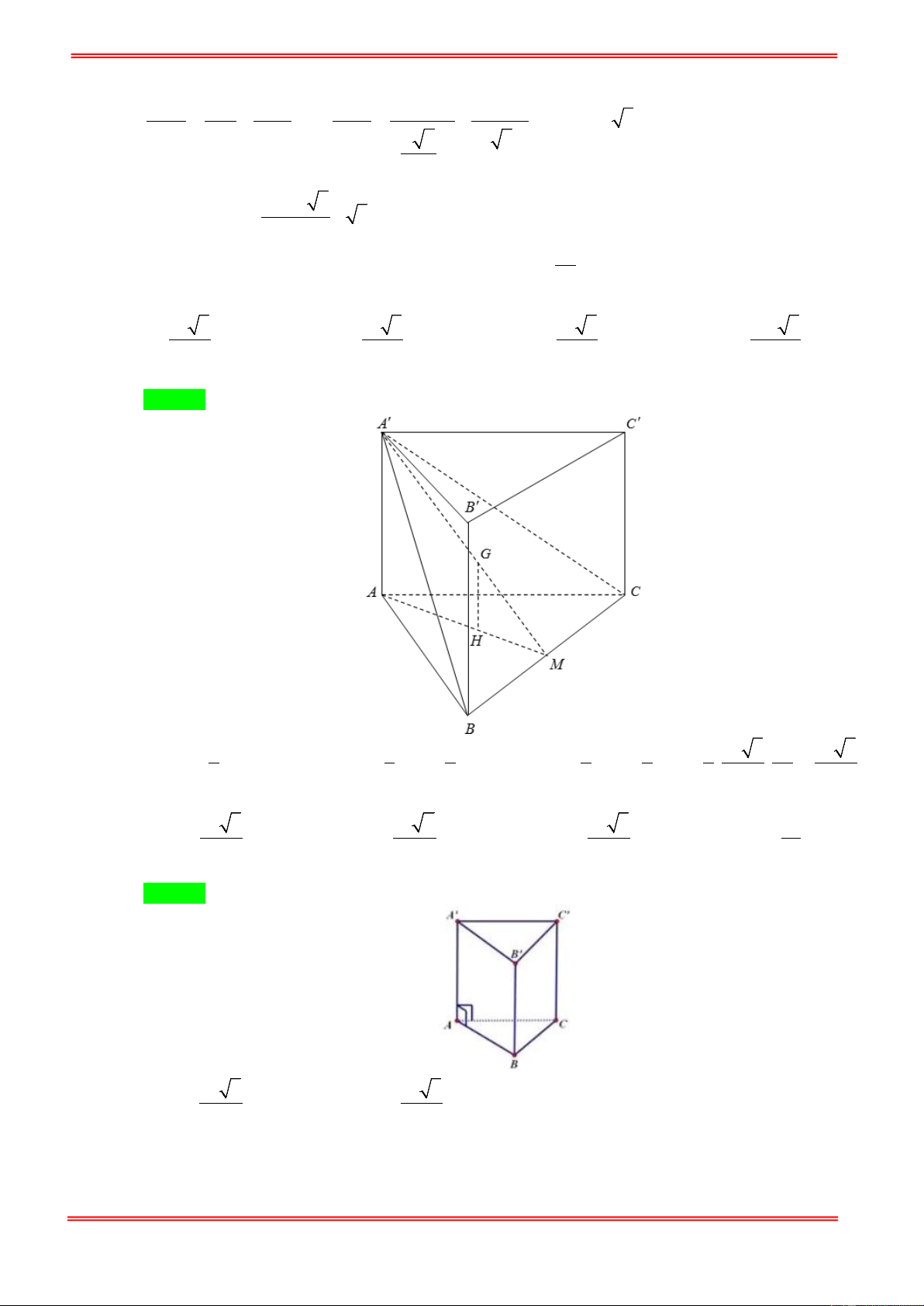
Câu 35. Cho lăng trụ tam giác đều ABC.A′B C
′ ′ cạnh đáy bằng a , chiều cao bằng 2a . Mặt phẳng (P) qua
B′ và vuông góc với A′C chia lăng trụ thành hai khối. Biết thể tích của hai khối là V và V với 1 2 V
V < V . Tỉ số 1 bằng 1 2 V2 1 1 1 1 A. B. C. D. 7 47 23 11
Câu 36. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng 2a là. 3 a 3 3 a 3 A. . B. . 3 C. 2a 3 . D. 3 4a . 4 12
Câu 37. Cho lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng a và AB′ ⊥ BC′ . Tính thể tích V của
khối lăng trụ đã cho. 3 a 6 3 7a 3 a 6 A. V = . B. V = . C. 3 V = a 6 . D. V = . 4 8 8
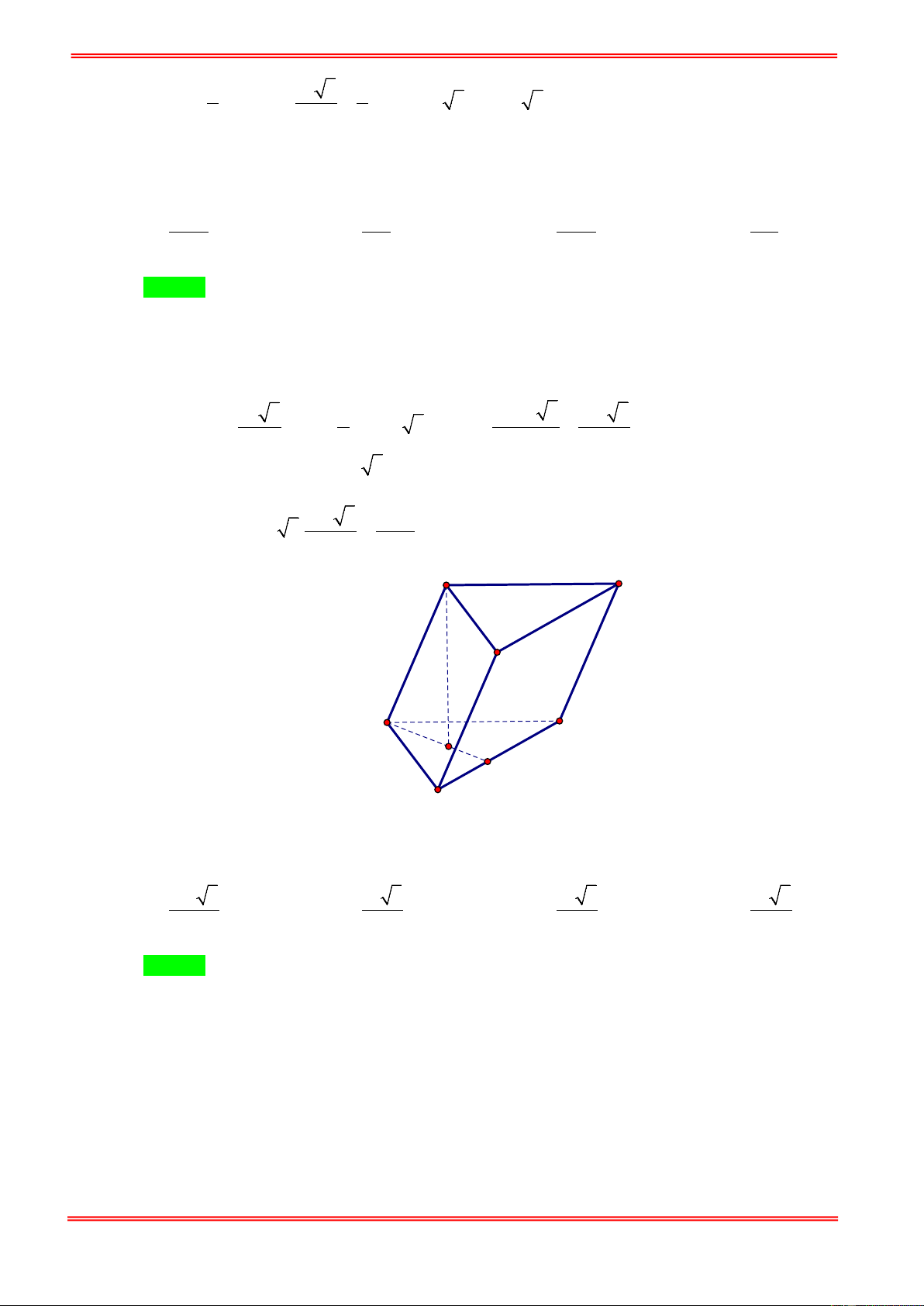
Câu 38. Cho lăng trụ ABCDA′B C ′ D
′ ′ có đáy ABCD là hình thoi cạnh a , tâm O và 
ABC = 120° . Các cạnh
A′A ; A′B ; A′D cùng tạo với mặt đáy một góc bằng 45° . Tính theo a thể tích V của khối lăng trụ đã cho. 3 a 3 3 a 3 3a 3 3a A. B. C. D. 2 2 4 2
Câu 39. Cho hình lăng trụ đứng ABC.A′B C
′ ′, biết đáy ABC là tam giác đều cạnh a . Khoảng cách từ tâm a
O của tam giác ABC đến mặt phẳng ( A′BC ) bằng . Tính thể tích khối lăng trụ ABC.A′B C ′ ′. 6 3 3a 2 3 3a 2 3 3a 2 3 3a 2 A. . B. . C. . D. . 8 28 4 16
Câu 40. Cho lăng trụ tam giác đều ABC.A′B C
′ ′ có độ dài cạnh đáy bằng 2a , cạnh bên bằng a 3 . Tính thể
tích V của lăng trụ. A. 3 V = 2a 3 . B. 3 V = 2a . C. 3 V = a 3 . D. 3 V = 3a .
Câu 41. Cho lăng trụ đều ABC.A′B C
′ ′ có cạnh đáy bằng 2a , diện tích xung quanh bằng 2 6 3a . Thể tích
V của khối lăng trụ. 3 1 A. 3 V = 3a . B. 3 V = a . C. 3 V = a . D. 3 V = a . 4 4
Câu 42. Tính thể tích của khối lăng trụ tam giác đều có cạnh đáy bằng 2a và cạnh bên bằng a . https://toanmath.com/ 3 a 3 3 a 3 A. . B. 3 a 3 . C. 3 a . D. . 4 3
Câu 43. Cho hình lăng trụ đều ABC.A′B C
′ ′ có cạnh đáy bằng a , A′C hợp với mặt đáy ( ABC) một góc
60° . Thể tích của khối lăng trụ ABC.A′B C ′ ′ bằng: 3 3a 3 a 3 2a 3 3a A. . B. . C. . D. . 8 4 3 4
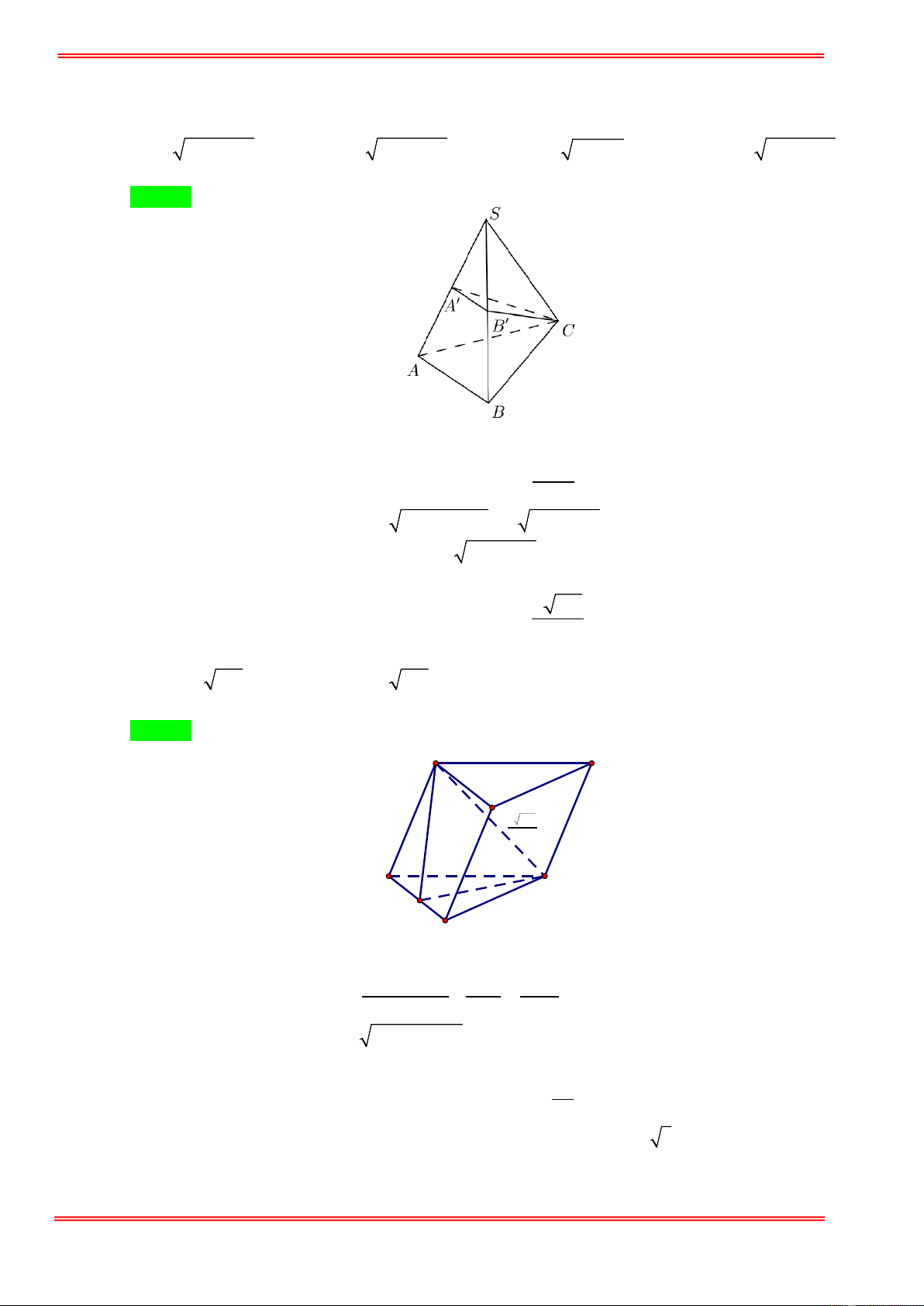
Câu 44. Cho lăng trụ tam giác ABC.A′B C
′ ′ có đáy là tam giác vuông cân, cạnh huyền AC = 2a . Hình chiếu
của A lên mặt phẳng ( A′B C
′ ′) là trung điểm I của A′B′ , góc giữa cạnh bên và mặt đáy bằng
60° . Thể tích khối lăng trụ ABC.A′B C ′ ′ là. 3 a 6 3 a 6 3 3a A. . B. 3 a 2 . C. . D. . 2 6 4
Câu 45..Cho lăng trụ tam giác ABC.A′B C
′ ′ có đáy là tam giác vuông cân, cạnh huyền AC = 2a . Hình chiếu
của A lên mặt phẳng ( A′B C
′ ′) là trung điểm I của A′B′ , góc giữa cạnh bên và mặt đáy bằng
60° . Thể tích khối lăng trụ ABC.A′B C ′ ′ là. 3 a 6 3 a 6 3 3a A. . 3 C. a 2 . 2 B. 6 . D. 4 .
Câu 46. Cho hình lăng trụ đứng ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a , cạnh bên AA′ = a 2 . Thể tích
của khối lăng trụ là 3 3a 3 a 3 3 a 6 3 a 6 A. . B. . C. . D. . 4 12 12 4
Câu 47. Cho lăng trụ tam giác đều ABC.A′B C
′ ′ có tất cả các cạnh đều bằng a 2 . Tính thể tích của khối lăng trụ. 3 a 3 3 a 6 3 a 6 3 a 3 A. . B. . C. . D. . 8 2 6 6
Câu 48. Thể tích V của khối lăng trụ tam giác đều có cạnh đáy bằng 2a và cạnh bên bằng a là 3 a 3 3 a 3 3 a 3 A. V = . B. V = . C. 3 V = a 3 . D. V = . 3 2 4
Câu 49. Tính thể tích V của khối lăng trụ tam giác đều có tất cả các cạnh bằng a . 3 a 3 3 a 2 3 a 3 3 a 2 A. V = . B. V = . C. V = . D. V = . 2 4 4 3
Câu 50. Cho hình lăng trụ tam giác ABC.A′B C
′ ′ có đáy ABC là tam giác vuông tại A , AB = a , AC = a 3
. Hình chiếu vuông góc của A′ lên ( ABC ) là trung điểm của BC . Góc giữa AA′ và ( ABC ) bằng
60° . Tính thể tích V của khối lăng trụ đã cho. 3 a 3 3 3a 3 a 3 3a 3 A. V = . B. V = . C. V = . D. V = . 2 2 2 2
Câu 51. Cho hình lăng trụ đứng tam giác ABC.A′B C
′ ′ có đáy là ∆ABC đều cạnh a = 4 và biết S = ∆ ′ 8 . A BC
Tính thể tích khối lăng trụ. A. 2 3 . B. 4 3 . C. 6 3 . D. 8 3 .
Câu 52. Cho lăng trụ đứng ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh a , cạnh bên A′B tạo với đáy
một góc 45° . Thể tích khối lăng trụ ABC.A′B C ′ ′là: 3 a 3 A. V = . B. 3 V = a 3 .
ABC. A' B 'C ' 4
ABC. A' B 'C ' https://toanmath.com/ 3 a 3 2a C. V = . D. V = .
ABC. A' B 'C ' 6
ABC. A' B 'C ' 3
Câu 53. Cho hình lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng a , góc giữa mặt phẳng ( A′BC) và
mặt phẳng ( ABC) bằng 45°. Thể tích của khối lăng trụ ABC.A′B C ′ ′ bằng 3 a 3 3 3a 3 a 3 3 a 3 A. . B. . C. . D. . 2 8 8 4
Câu 54. Cho hình lăng trụ tứ giác đều ABC . D A′B C ′ D
′ ′ có cạnh đáy bằng a . Biết đường chéo của mặt bên
là a 3 . Khi đó, thể tích khối lăng trụ bằng: 3 a 2 A. 3 a 3 . B. 3 a 2 . C. . D. 3 2a . 3
Câu 55. Cho hình lăng trụ đứng ABC.A′B C
′ ′ có tam giác ABC là tam giác đều cạnh bằng a , góc giữa ( AB C
′ ′) và (A′B C ′ )′ bằng o
60 . Thể tích khối lăng trụ ABC.A′B C ′ ′ là. 3 3a 3 3a 3 3 3a 3 a A. . B. . C. . D. . 24 8 8 24
Câu 56. Cho hình lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng a . Góc giữa đường thẳng A′B và
mặt phẳng ( ABC) bằng 45°. Tính thể tích của khối lăng trụ ABC.A′B C ′ ′. 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 12 24 4
Câu 57. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a là: 3 a 3 3 a 3 3 a 2 3 a 2 A. . B. . C. . D. . 3 4 3 2
Câu 58. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a là: 3 a 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 2 12 2 4
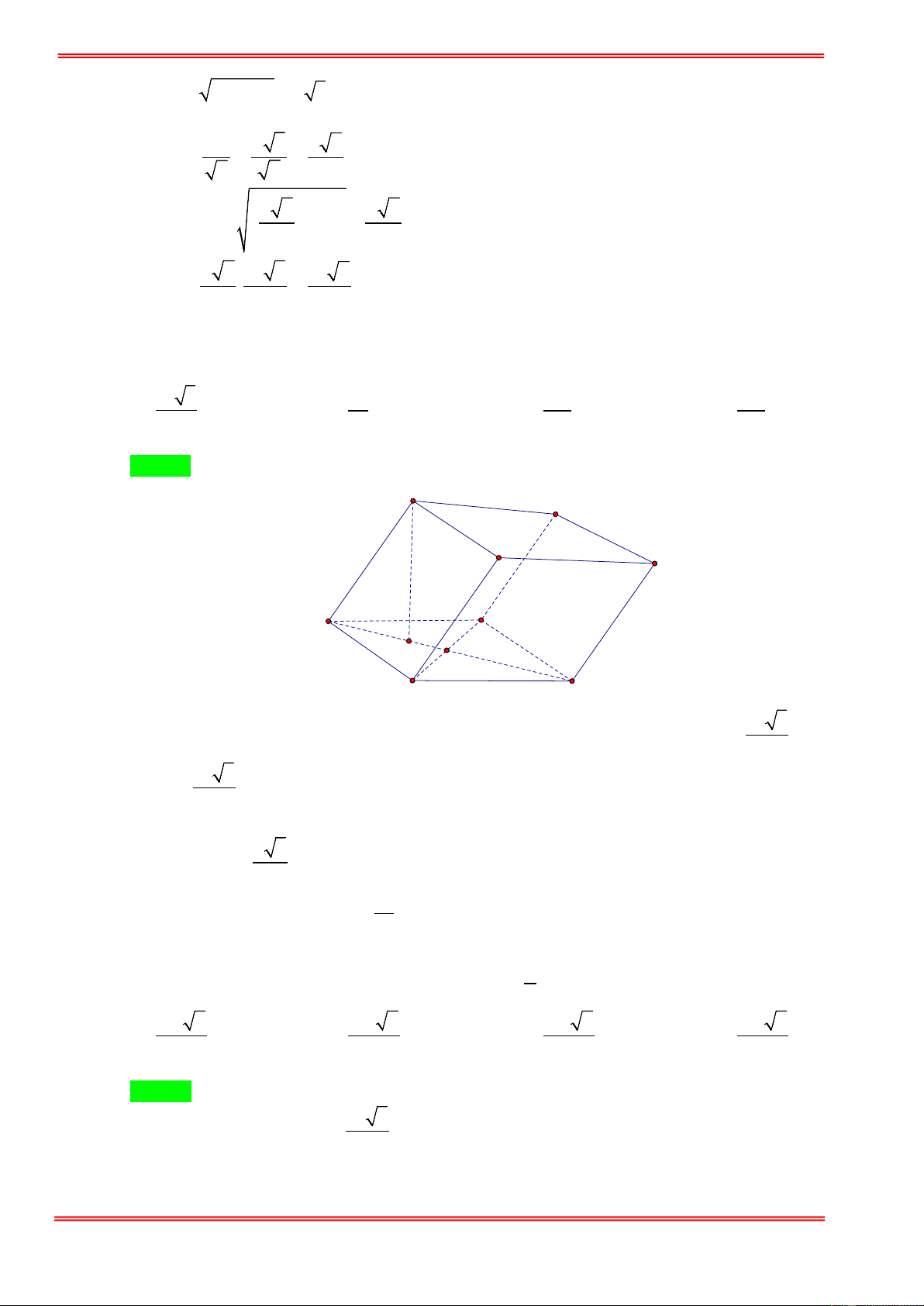
Câu 59. Cho hình lăng trụ đều ABC.A′B C
′ ′. Biết khoảng cách từ điểm C đến mặt phẳng ( ABC′) bằng a,
góc giữa hai mặt phẳng ( ABC′) và (BCC B ′ ′) bằng α với 1 cosα =
(tham khảo hình vẽ dưới 2 3
đây). Thể tích khối lăng trụ ABC.A′B C ′ ′ bằng 2 2 2 2 A. 3 3a . B. 3 a . C. 3 3a . D. 3 3a . 4 2 2 8
Câu 60. Cho hình lăng trụ đứng ABC.A' B 'C ' có đáy ABC đều cạnh bằng a và chu vi của mặt bên ABB ' A'
bằng 6a . Thể tích của khối lăng trụ ABC.A' B 'C ' bằng 3 a 3 3 a 3 3 a 3 A. . B. 3 a 3 . C. . D. . 2 3 6
Câu 61. Cho lăng trụ đứng ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a và AB′ vuông góc với BC′ . Thể
tích của lăng trụ đã cho là. 3 a 6 3 a 6 3 a 6 3 a 6 A. . B. . C. . D. . 12 4 8 24
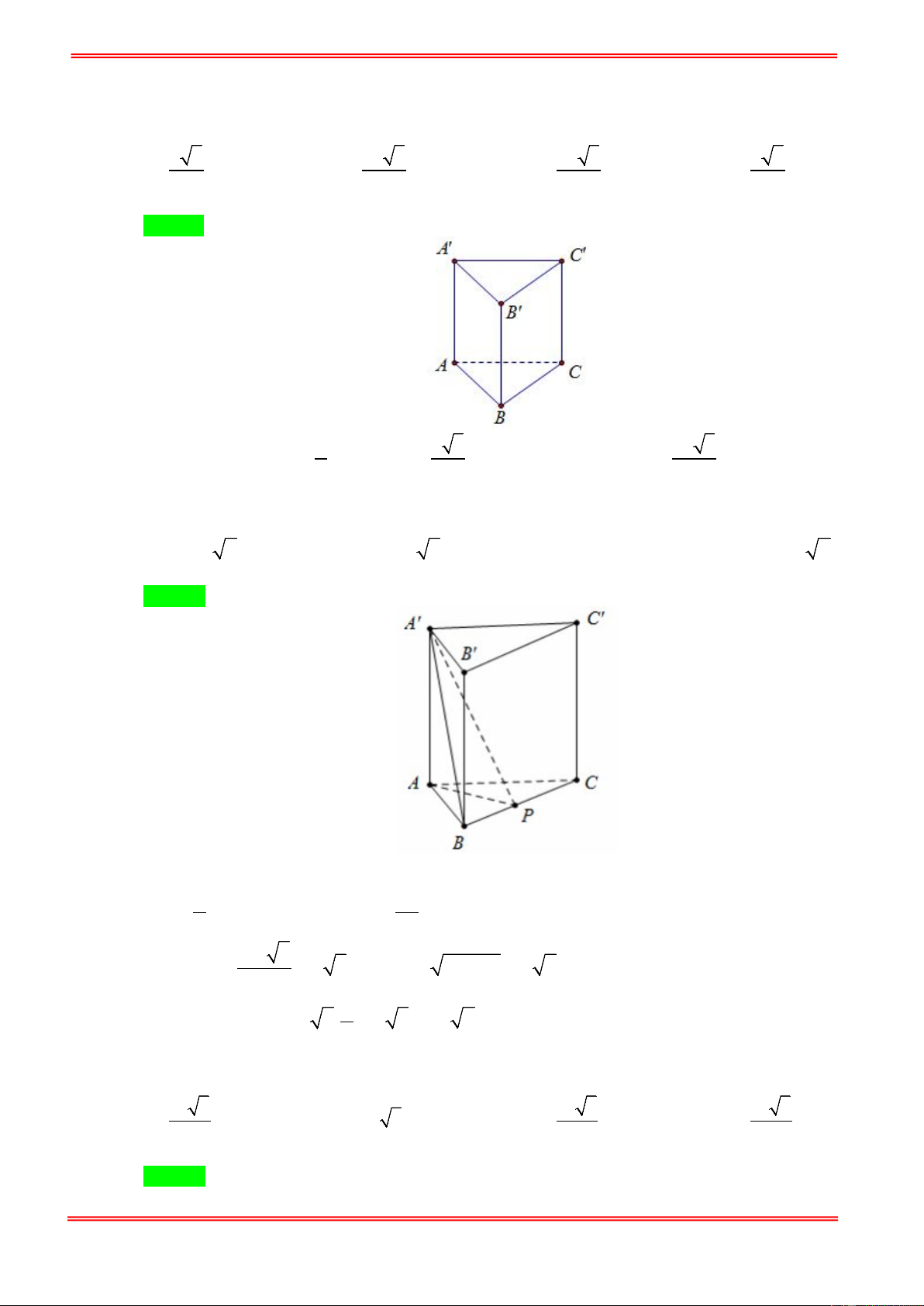
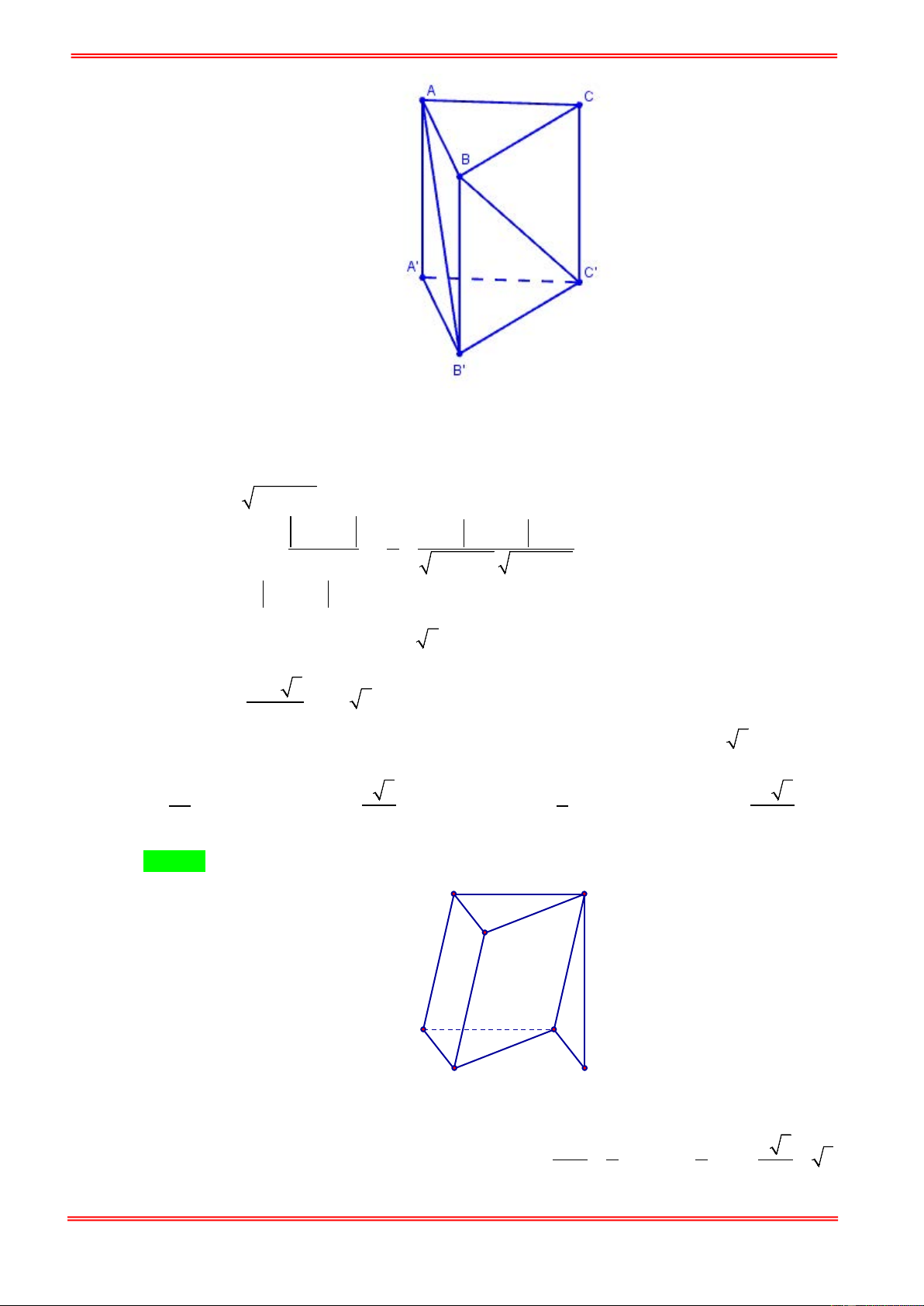
Câu 62. Cho hình lăng trụ tam giác đều ABC.A′B C
′ ′ có tất cả các cạnh bằng a . Gọi M , N lần lượt là trung
điểm của các cạnh AB và B C
′ ′. Mặt phẳng ( A′MN ) cắt cạnh BC tại .
P Thể tích khối đa diện MB . P A′B N ′ bằng. 3 7 3a 3 3a 3 7 3a 3 7 3a A. . B. . C. . D. . 68 32 96 32 https://toanmath.com/
Câu 63. Cho ( H ) là khối lăng trụ đứng tam giác đều có tất cả các cạnh đều bằng a . Thể tích của ( H ) bằng: 3 a 3 3 a 3 3 a 2 3 a A. . B. . C. . D. . 2 4 3 2
Câu 64. Cho khối lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng a 2 và mỗi mặt bên có diện tích bằng 2
4a . Thể tích khối lăng trụ đó là 3 2a 6 3 a 6 A. 3 2a 6 . B. . C. . D. 3 a 6 . 3 2
Câu 65. Cho hình lăng trụ tứ giác đều ABC . D A′B C ′ D
′ ′ có cạnh đáy bằng a . Biết đường chéo của mặt bên
là a 3 . Khi đó, thể tích khối lăng trụ bằng: 3 a 2 A. 3 a 3 . B. 3 a 2 . C. . D. 3 2a . 3
Câu 66.Khối lăng trụ tam giác đều có tất cả các cạnh bằng a thì có thể tích bằng 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 12 4 8
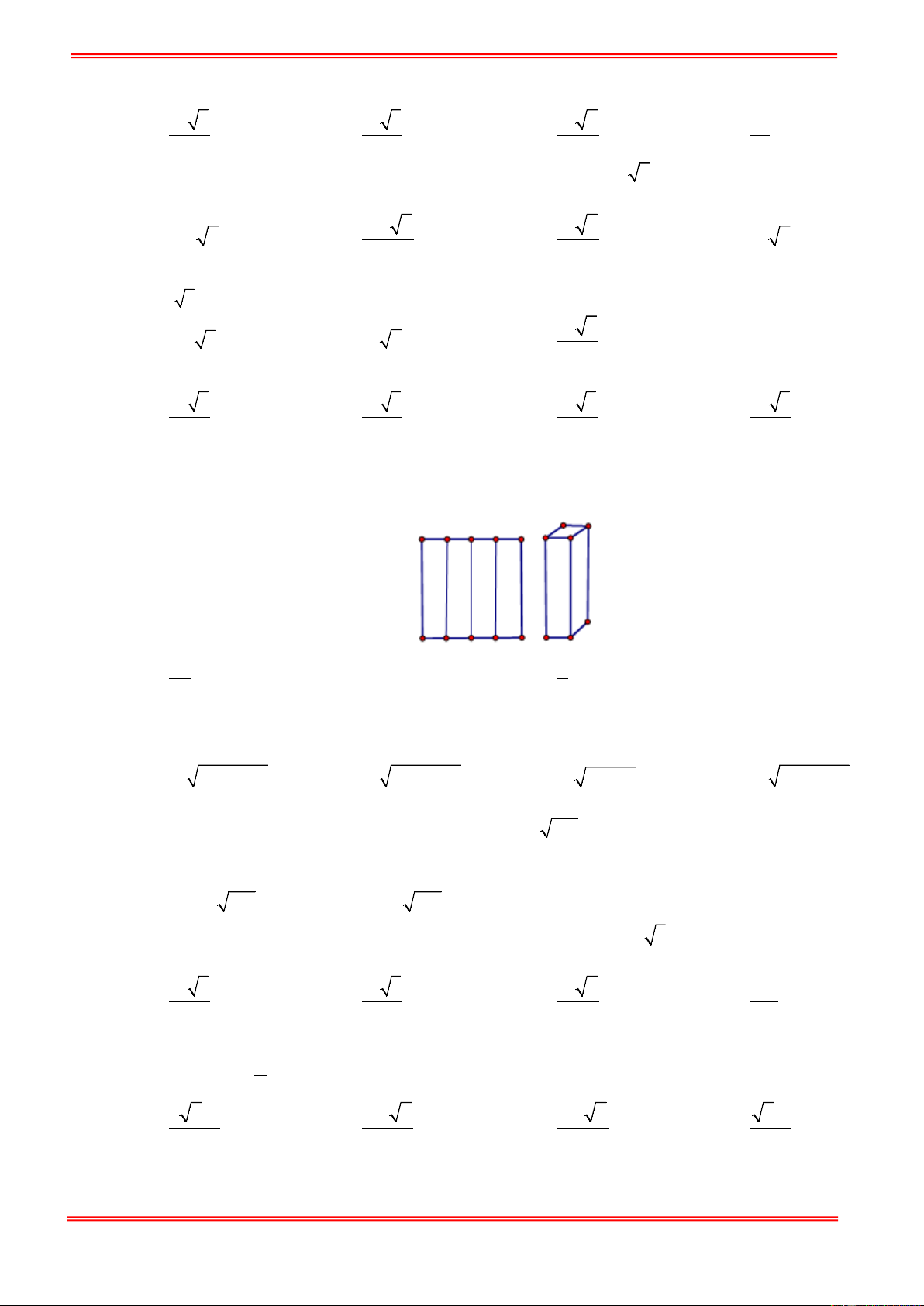
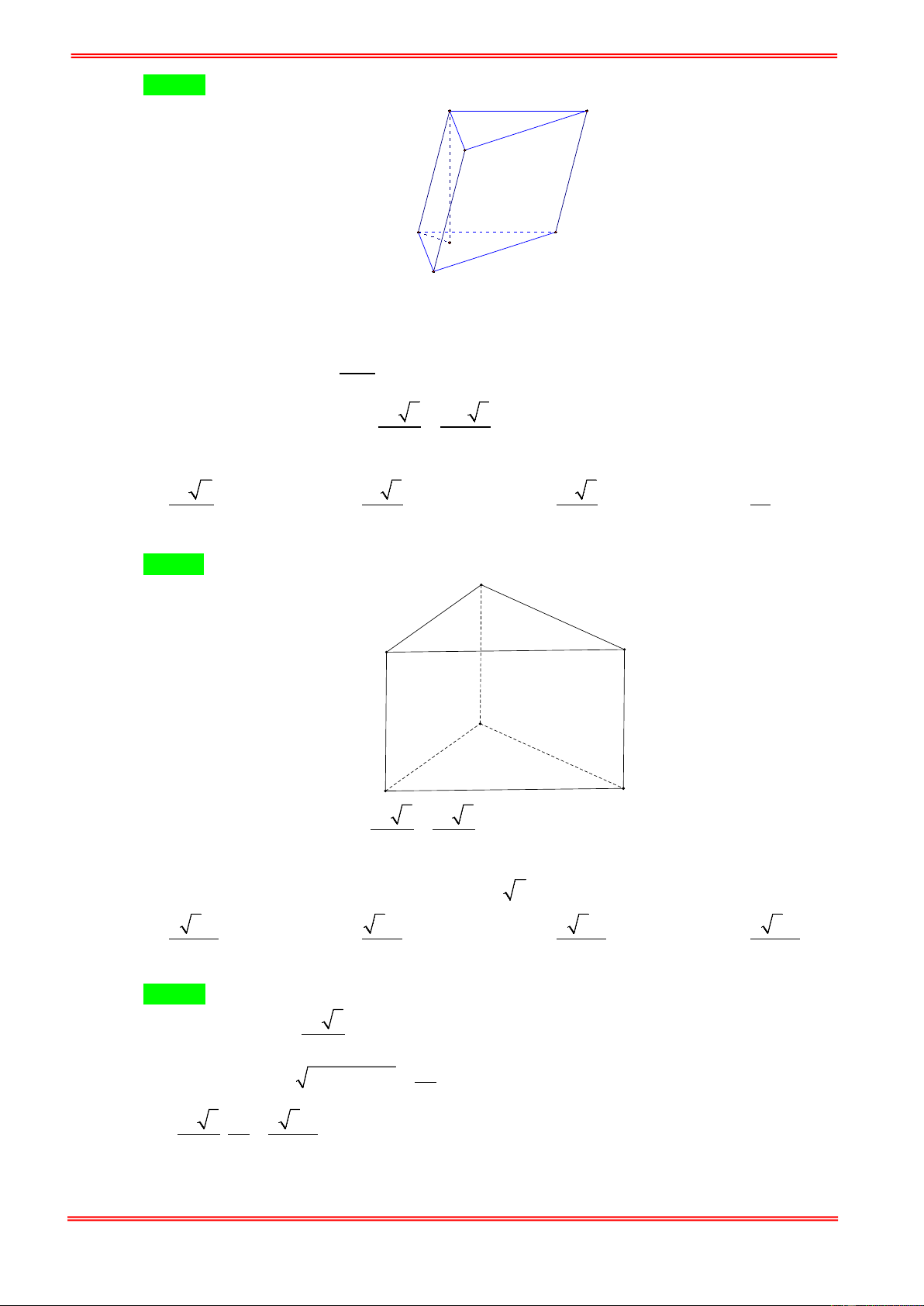
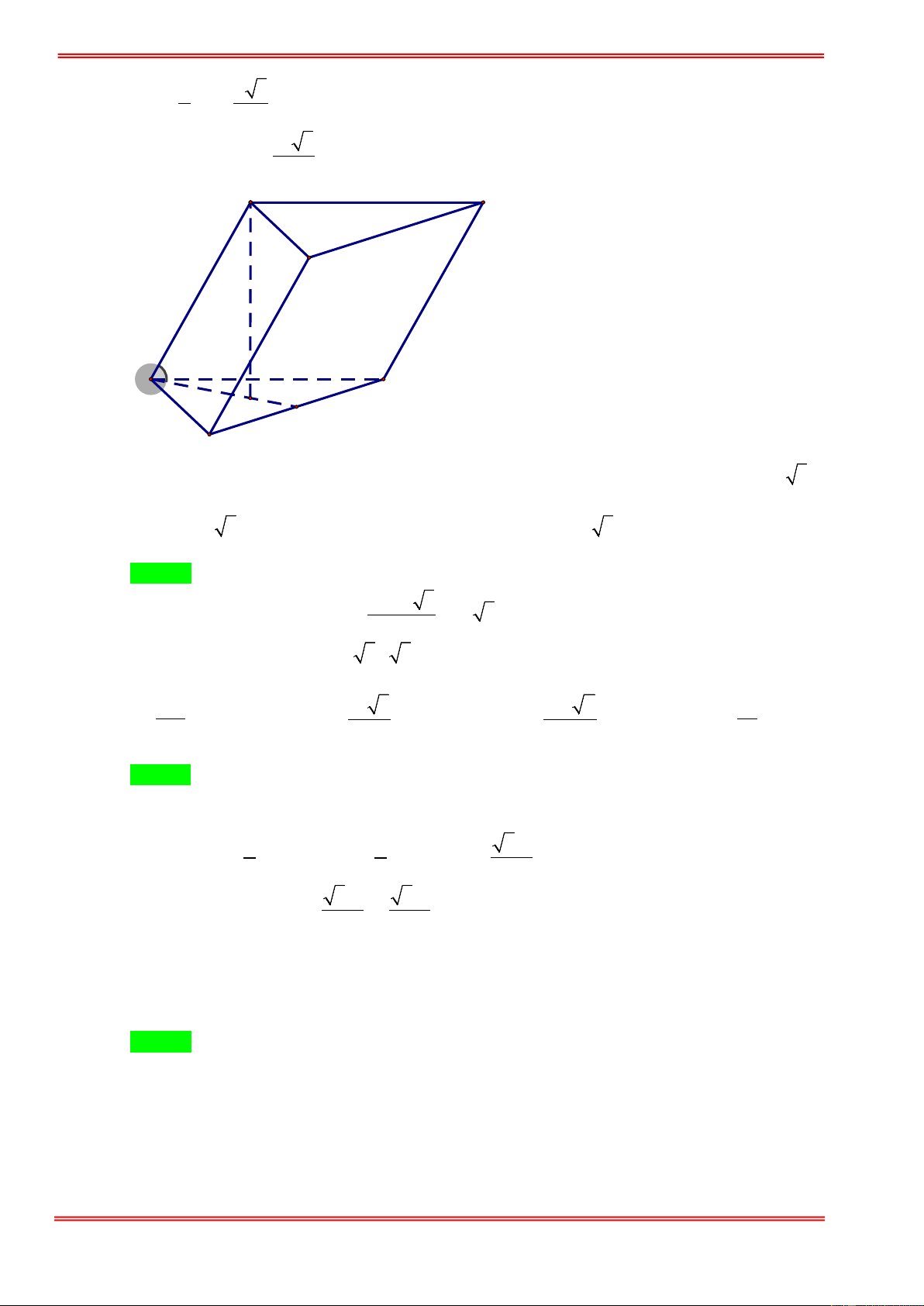
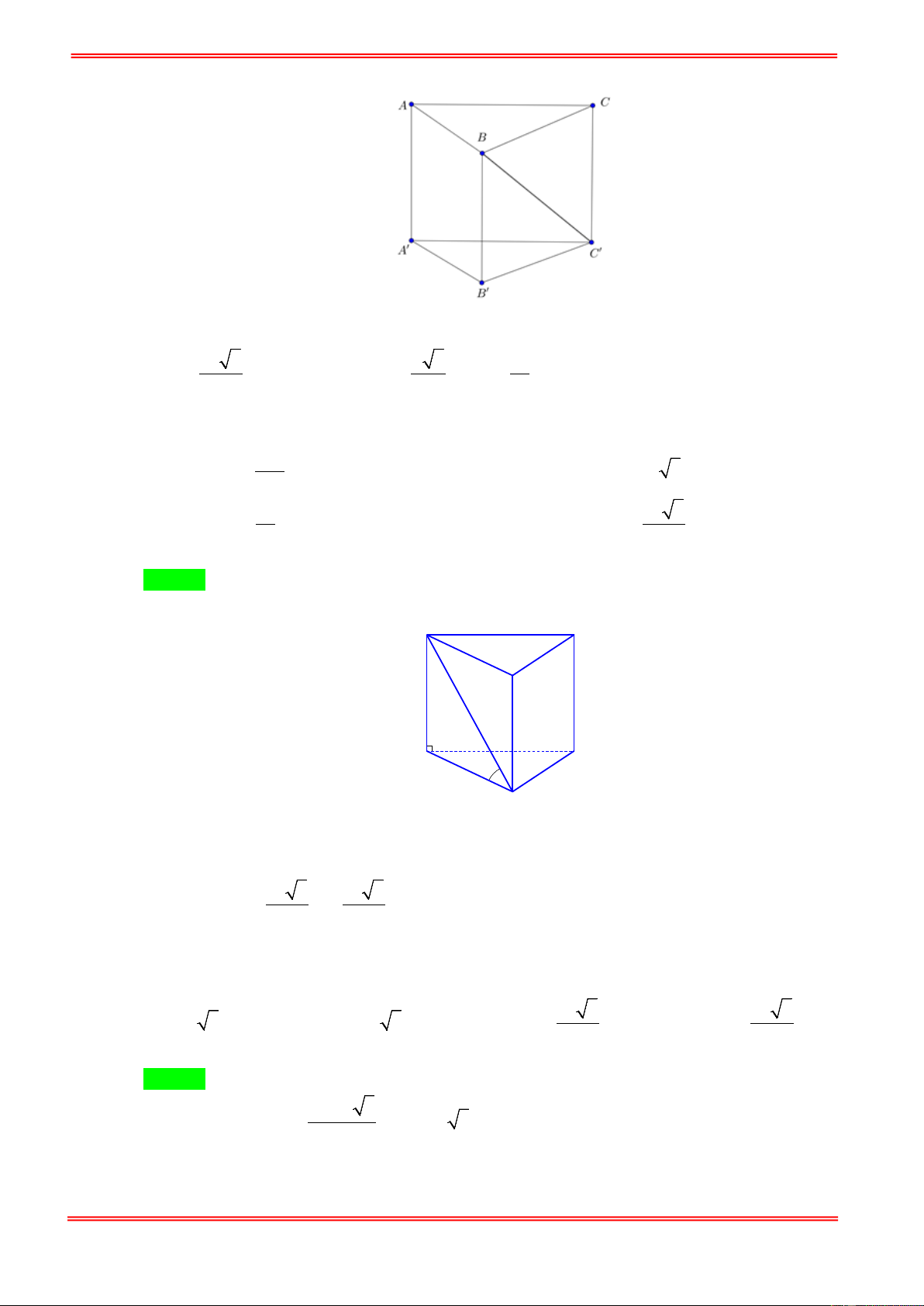
Câu 67. Từ một ảnh giấy hình vuông cạnh là 4cm , người ta gấp nó thành bốn phần đều nhau rồi dựng lên
thành bốn mặt xung quanh của hình hình lăng trụ tứ giác đều như hình vẽ. Hỏi thể tích của khối
lăng trụ này là bao nhiêu. 64 4 A. 3 cm B. 3 16cm . C. 3 cm D. 3 4cm . 3 3
Câu 68. Cho lăng trụ tứ giác đều ABC . D A′B C ′ D
′ ′ đáy hình có cạnh bằng a, đường chéo AC′ tạo với mặt bên ( BCC B ′ ′) một góc α ( 0
0 < α < 45 ). Tính thể tích của lăng trụ tứ giác đều ABC . D A′B C ′ D ′ ′ . A. 3 2 a cot α +1 . B. 3 2 a tan α −1 . C. 3 a cos 2α . D. 3 2 a cot α −1 .
Câu 69. Cho khối lăng trụ ABC.A′B C
′ ′ có AB = BC = 5a , AC = 6a . Hình chiếu vuông góc của A′ trên mặt phẳng ( a 133
ABC ) là trung điểm của AB và A′C =
. Tính thể tích V của khối lăng trụ 2
ABC.A′B C ′ ′ theo . a . A. 3 V = 12 133a . 3 = = = B. V 4 133a . C. 3 V 12a . D. 3 V 36a .
Câu 70. Cho hình lăng trụ đều ABC.A′B 'C′ có cạnh đáy bằng a , cạnh bên a 3 . Thể tích của khối lăng trụ là. 3 a 3 3 a 3 3 a 7 3 3a A. . B. . C. . 7 4 5 D. 4 .
Câu 71. Cho khối lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy là a và khoảng cách từ A đến mặt phẳng ( a
A′BC ) bằng . Tính thể tích của khối lăng trụ ABC.A′B C ′ ′. 2 3 3 2a 3 3a 2 3 3a 2 3 2a A. . B. . C. . D. . 12 16 48 16 https://toanmath.com/
Câu 72. Cho lăng trụ tứ giác đều ABC . D A′B C ′ D
′ ′ có cạnh đáy bằng a 5 . Khoảng cách từ A đến mặt a 5
phẳng ( A' BC ) bằng
. Thể tích khối lăng trụ là: 2 3 5a 15 3 6a 3 3 a 5 A. . B. . C. 3 2a 2 . D. . 3 5 3
Câu 73. Cho lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng 2a , khoảng cách từ A đến mặt phẳng ( a A′BC ) bằng
6 . Khi đó thể tích lăng trụ bằng. 2 4 3 4 A. 3 V = a . B. 3 V = a . C. 3 V = 3a . D. 3 V = a . 3 3 3a
Câu 74. Cho hình lăng trụ đều ABC.A′B 'C′ có AB = a , AA' =
. Gọi G là trọng tâm tam giác A′BC . 2
Tính thể tích tứ diện GABC theo a . 3 a 3 3 a 3 3 a 3 3 3a 3 A. . B. . D. . 16 12 C. 24 . 8
Câu 75. Tính thể tích V của khối lăng trụ tam giác đều ABC.A′B C
′ ′ có AA′ = BC = a . 3 a 3 3 a 2 3 a 3 3 a A. V = . B. V = . C. V = . D. V = . 4 6 12 3
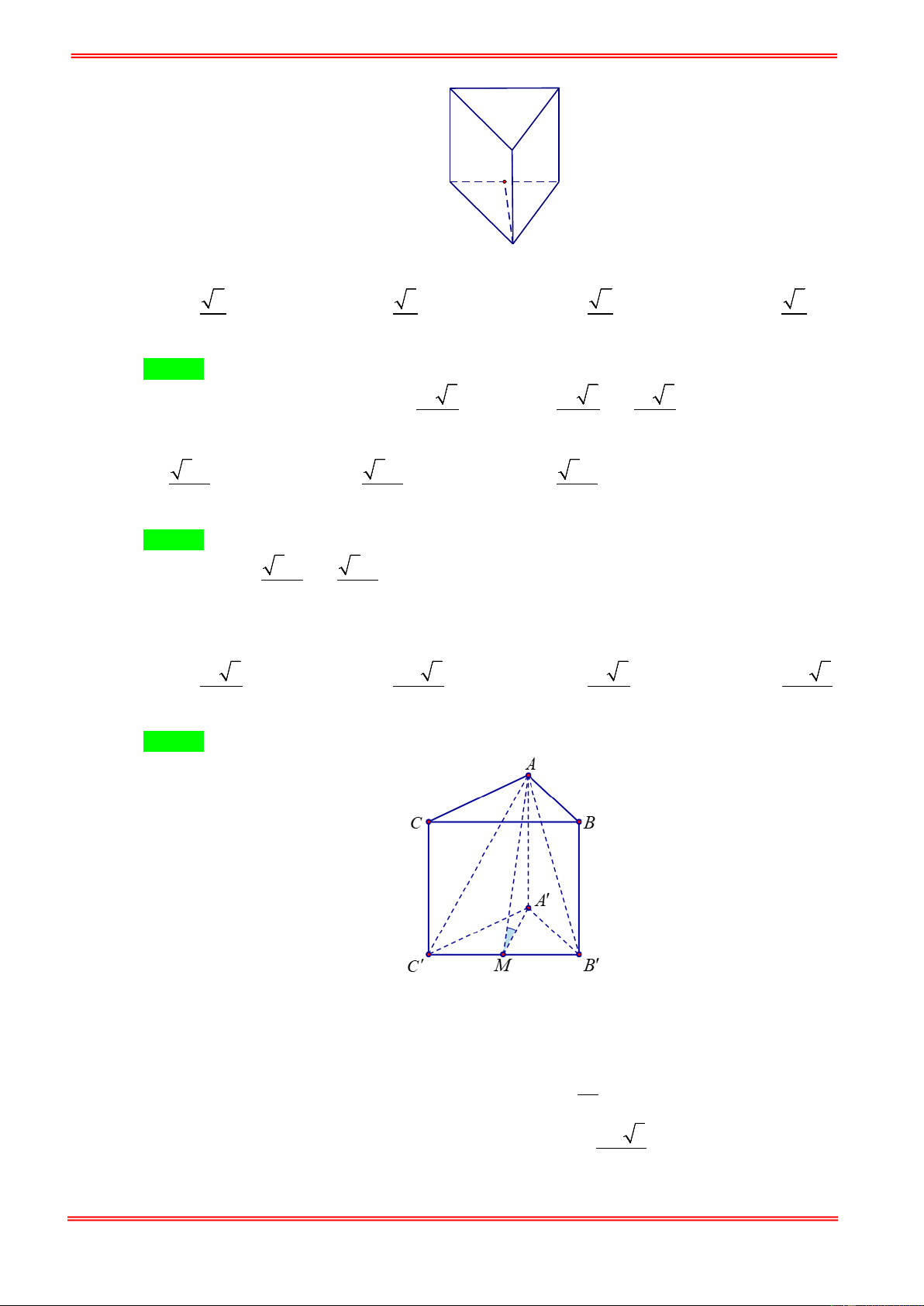
Câu 76. Cho lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh a , cạnh bên tạo với mặt phẳng bằng 0
45 . Hình chiếu của A trên mặt phẳng ( A′B C
′ ′) trùng với trung điểm của A′B′ . Tính thể tích V
của khối lăng trụ theo a . 3 a 3 3 a 3 3 a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . 2 24 8 16
Câu 77. Cho lăng trụ ABC.A′B C
′ ′ có cạnh bên bằng 2a , đáy ABC là tam giác cân tại ; A AB = 2 ; a  0
BAC = 120 . Hình chiếu vuông góc của A′ trên mp ( ABC ) trùng với trung điểm của cạnh BC .
Tính thể tích khối chóp A .′BB C ′ C ′ ? 3 4a A. 3 3a . B. 3 2a . C. 3 4a . D. . 3
Câu 78. Cho khối lăng trụ đứng có cạnh bên bằng 5 , đáy là hình vuông có cạnh bằng 4 . Hỏi thể tích khối lăng trụ là: A. 64 . B. 80 . C. 100 . D. 20 .
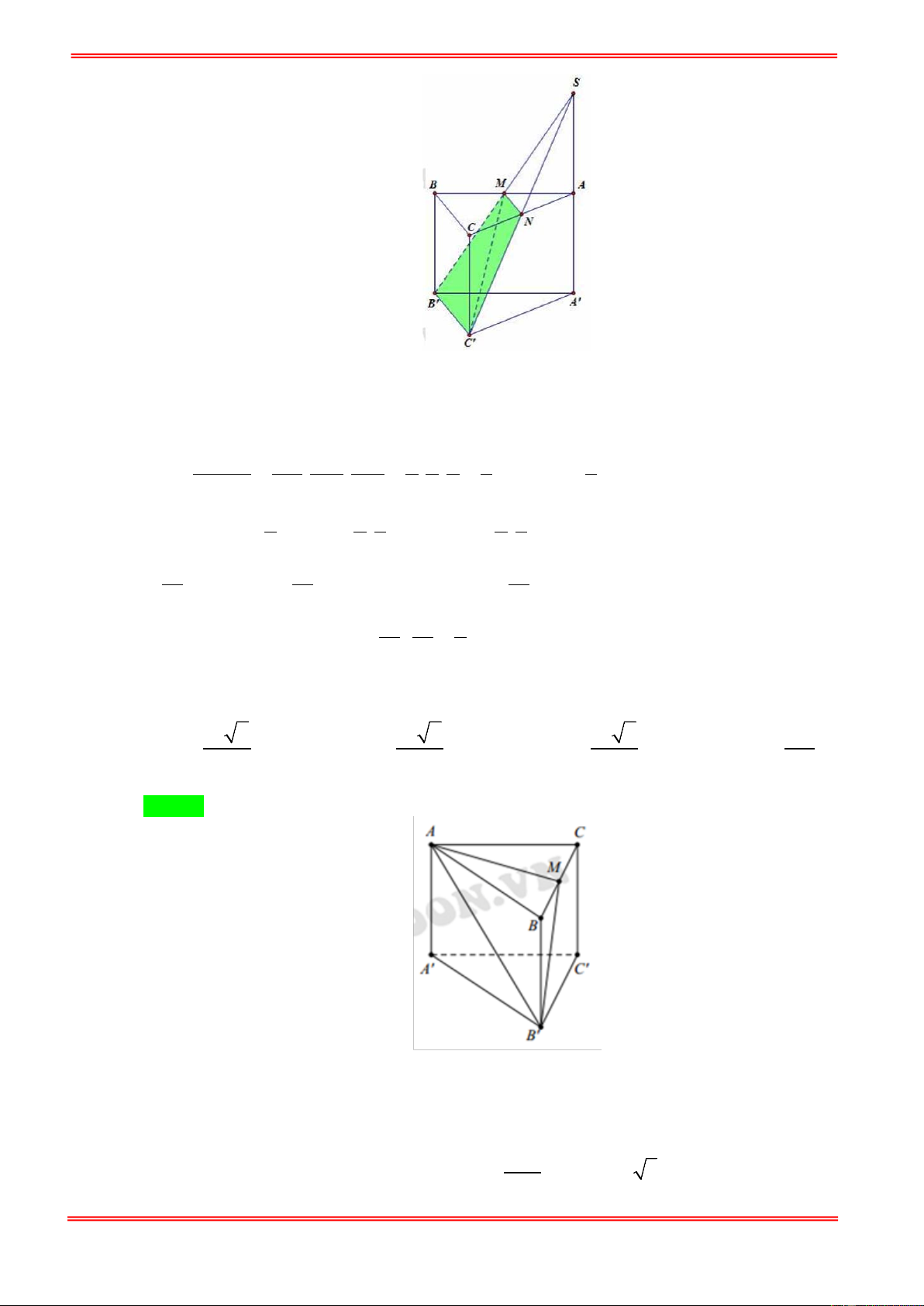
Câu 79. Cho hình lăng trụ tam giác đều ABC.A′B C
′ ′ có tất cả các cạnh bằng a . Gọi M , N lần lượt là trung
điểm của các cạnh AB và B C
′ ′. Mặt phẳng ( A′MN ) cắt cạnh BC tại P . Tính thể tích của khối đa diện MB . P A′B N ′ 3 3a 3 3a 3 7 3a 3 7 3a A. . B. . C. . D. . 24 12 96 32 °
Câu 80. Cho hình lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác vuông tại B , 
ACB = 60 , BC = a ,
AA′ = 2a . Cạnh bên tạo với mặt phẳng ( ABC ) một góc 30° .Thể tích khối lăng trụ ABC.A′B C ′ ′ bằng. 3 a 3 3 a 3 3 a 3 A. . B. . C. 3 a 3 . D. . 2 6 3 https://toanmath.com/
Câu 81. Cho hình lăng trụ tam giác ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh bằng a , hình chiếu vuông góc của a
A′ lên mặt phẳng ( ABC ) là trung điểm H của cạnh AB , cạnh 10 AA′ = . Tính 2
theo a tích của khối lăng trụ ABC.A′B C ′ ′. 3 a 3 3 3a 3 3 a 3 3 3a 3 A. . B. . C. V = . D. V = . 8 4 12 8
Câu 82. Cho hình lăng trụ tam giác đều có tất cả các cạnh đều bằng a . Tính theo a thể tích của khối lăng trụ. 3 2a 3 a 3 a 3 3 a 3 A. . B. . C. . D. . 3 3 4 12
Câu 83. Cho hình lăng trụ tam giác đều có các cạnh đều bằng 2a .Thể tích khối lăng trụ đều là: 3 2a 3 2a 3 3 a A. . B. . C. 3 2a 3 . D. . 3 3 3
Câu 84. Một hình lăng trụ có đáy là tam giác đều cạnh bằng a , cạnh bên bằng b và tạo với mặt phẳng đáy
một góc α . Thể tích của khối lăng trụ đó là 3 3 3 3 A. 2 a b cosα . B. 2 a b cosα . C. 2 a b sin α . D. 2 a b sin α . 12 4 12 4
Câu 85.] Cho (H ) là khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng a Thể tích của (H ) bằng: 3 a 2 3 a 3 3 a 3 3 a A. . C. . D. . 3 B. 4 . 2 2
Câu 86. Cho hình lăng trụ ABC. ’ A ’
B C’ có đáy là tam giác đều cạnh a . Hình chiếu của A′ trên mặt phẳng
( ABC) là trung điểm H của cạnh BC . AA' = a 7 . Tính thể tích V của khối lăng trụ đã cho. 3 5 3a 3 3a 3 5 3a 3 5 3a A. . B. . C. . D. . 8 8 24 6
Câu 87. Cho lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng a và AB′ ⊥ BC′ . Khi đó thể tích của khối
lăng trụ trên sẽ là: 3 6a 3 7a 3 6a A. V = . B. V = . C. 3 V = 6a . D. V = . 8 8 4
Câu 88. Cho hình lăng trụ đều ABC.A′B C
′ ′ có cạnh đáy bằng a . M , N là hai điểm thõa mãn 
   
MB + 2MB′ = 0 ; NB′ = 3NC′ . Biết hai mặt phẳng (MCA) và ( NAB) vuông góc với nhau. Tính
thể tích của hình lăng trụ. 3 3a 2 3 9a 2 3 9a 2 3 3a 2 A. B. C. D. 8 8 16 16
Câu 89. Cho ( H ) là hình lăng trụ xiên ABC.A′B C
′ ′ có đáy là tam giác đều cạch a , hình chiếu vuông góc
A′ lên đáy trùng với tâm đường tròn ngoại tiếp tam giác ABC và A′A hợp đáy bằng 60° . Thể
tích của (H ) bằng. 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 4 12 2 6
Câu 90. Cho lăng trụ tam giác đều ABC.A′B C
′ ′ có độ dài cạnh đáy bằng 2a , cạnh bên bằng a 3 . Tính thể
tích V của lăng trụ. A. 3 V = 2a 3 . B. 3 V = 2a . C. 3 V = a 3 . D. 3 V = 3a .
Câu 91. Cho hình lăng trụ tam giác đều có các cạnh đều bằng .
a Thể tích khối lăng trụ đều là 3 2a 3 a 3 3 2a 2 3 a A. . B. . C. . D. . 3 4 3 3 https://toanmath.com/
Câu 92. Cho hình lăng trụ đứng ABC . D A′B C ′ D
′ ′ có đáy là hình vuông cạnh bằng 3, đường chéo AB′ của mặt bên ( ABB A
′ ′) có độ dài bằng 5. Tính thể tích V của khối lăng trụ ABC . D A′B C ′ D ′ ′ ?
A. V = 18 .
B. V = 48 .
C. V = 36 .
D. V = 45 .
Câu 93. Cho hình lăng trụ đều ABC.A′B C
′ ′ có cạnh đáy bằng a . Đường thẳng AB′ tạo với mặt phẳng
(BCC B′′) một góc 30°. Thể tích khối lăng trụ ABC.A′B C
′ ′ theo a . 3 a 6 3 a 3 a 6 3 3a A. . B. . C. . D. . 4 4 12 4
Câu 94. Cho khối lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng 2 , diện tích tam giác A′BC bằng 3
. Tính thể tích của khối lăng trụ. 2 5 A. 2 . B. . C. 3 2 . D. 2 5 . 3
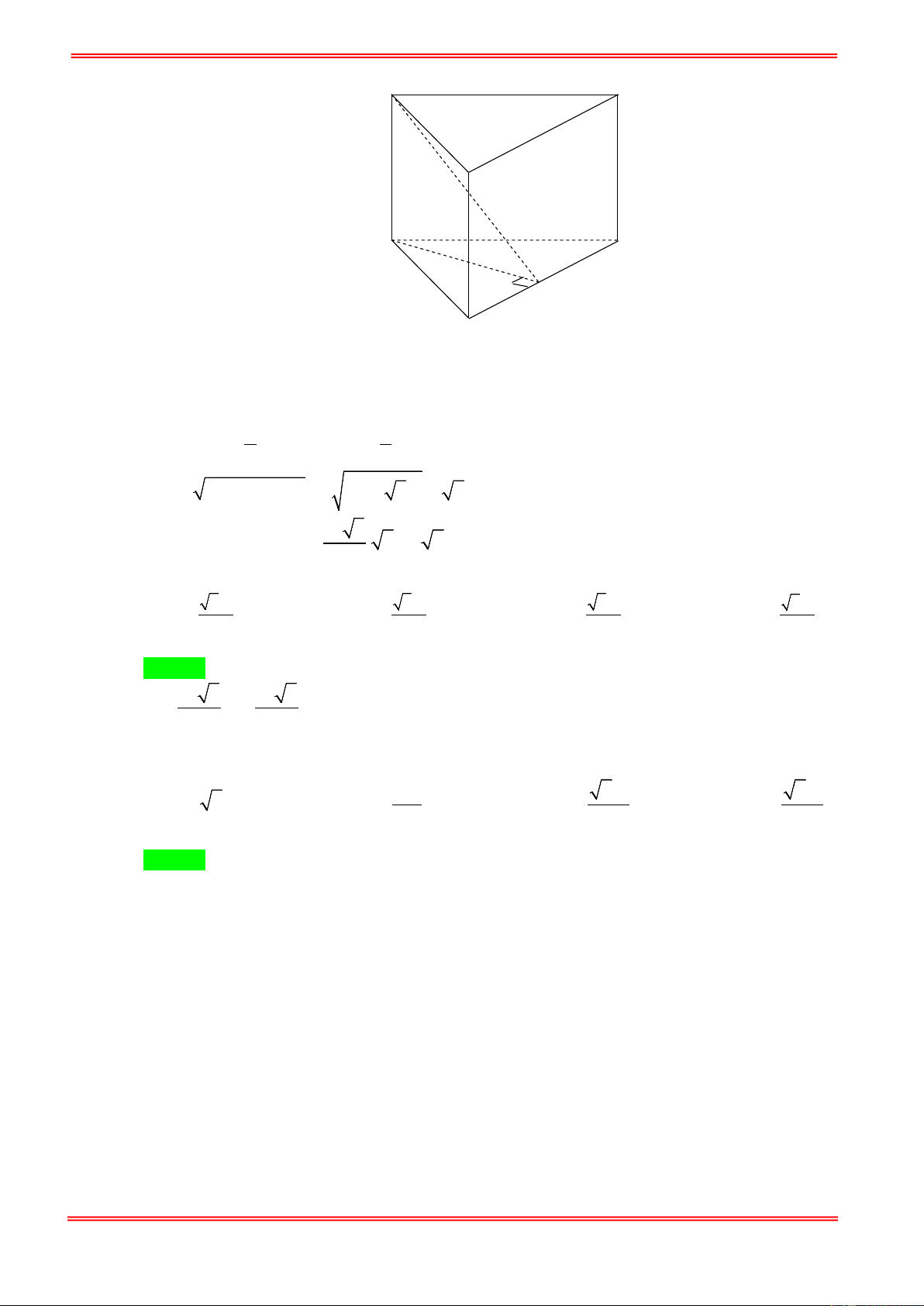
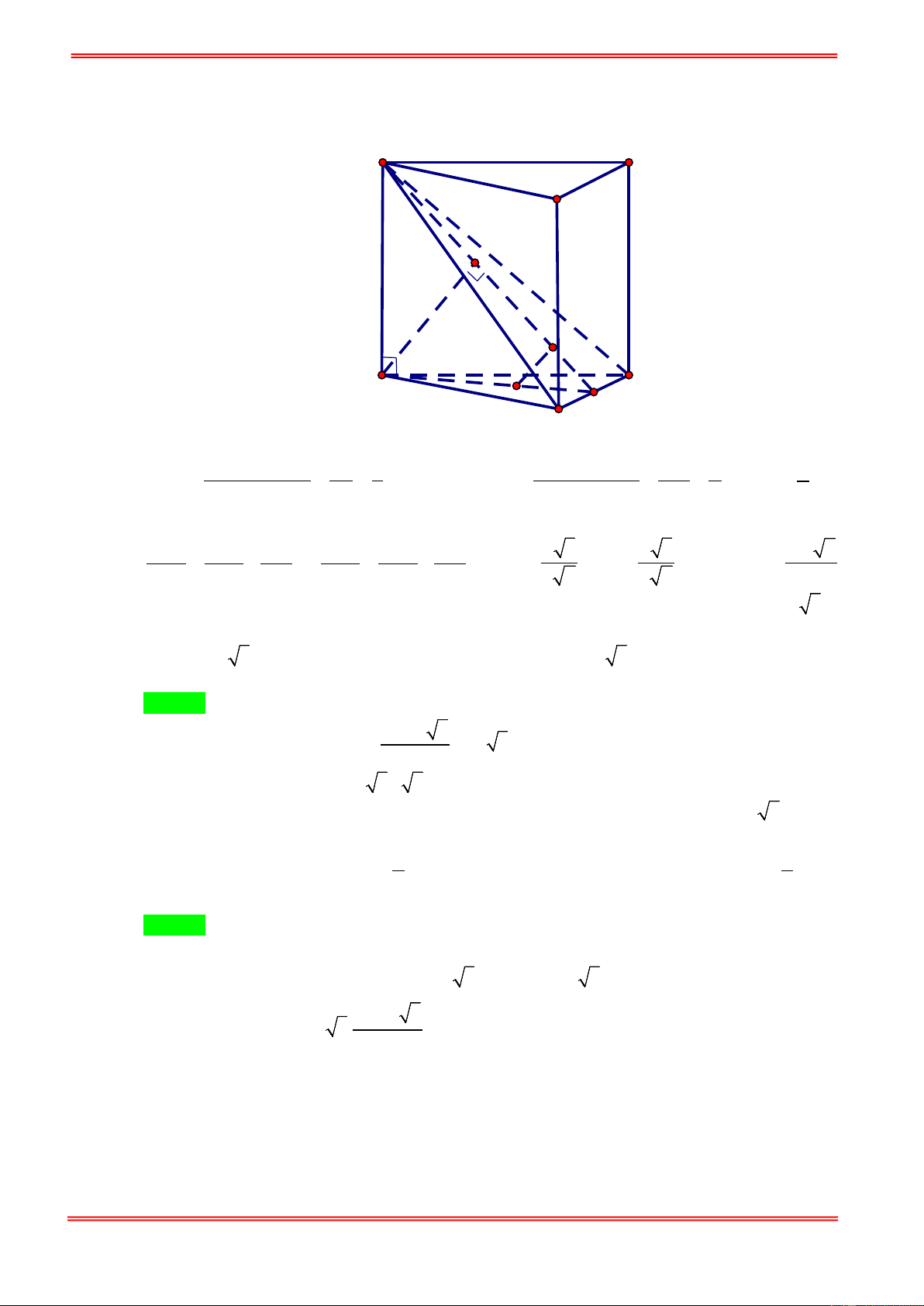
Câu 95. Cho hình lăng trụ đều ABC.A′B C
′ ′, biết khoảng cách từ điểm C đến mặt phẳng ( ABC′) bằng a ,
góc giữa hai mặt phẳng ( ABC′) và (BCC B ′ ′) bằng α với 1 cosα =
(tham khảo hình vẽ bên 3
dưới).Thể tích khối lăng trụ bằng C' B' A' C B A 3 9 15a 3 3 15a 3 3 15a 3 9 15a A. . B. . C. . D. . 20 20 10 10
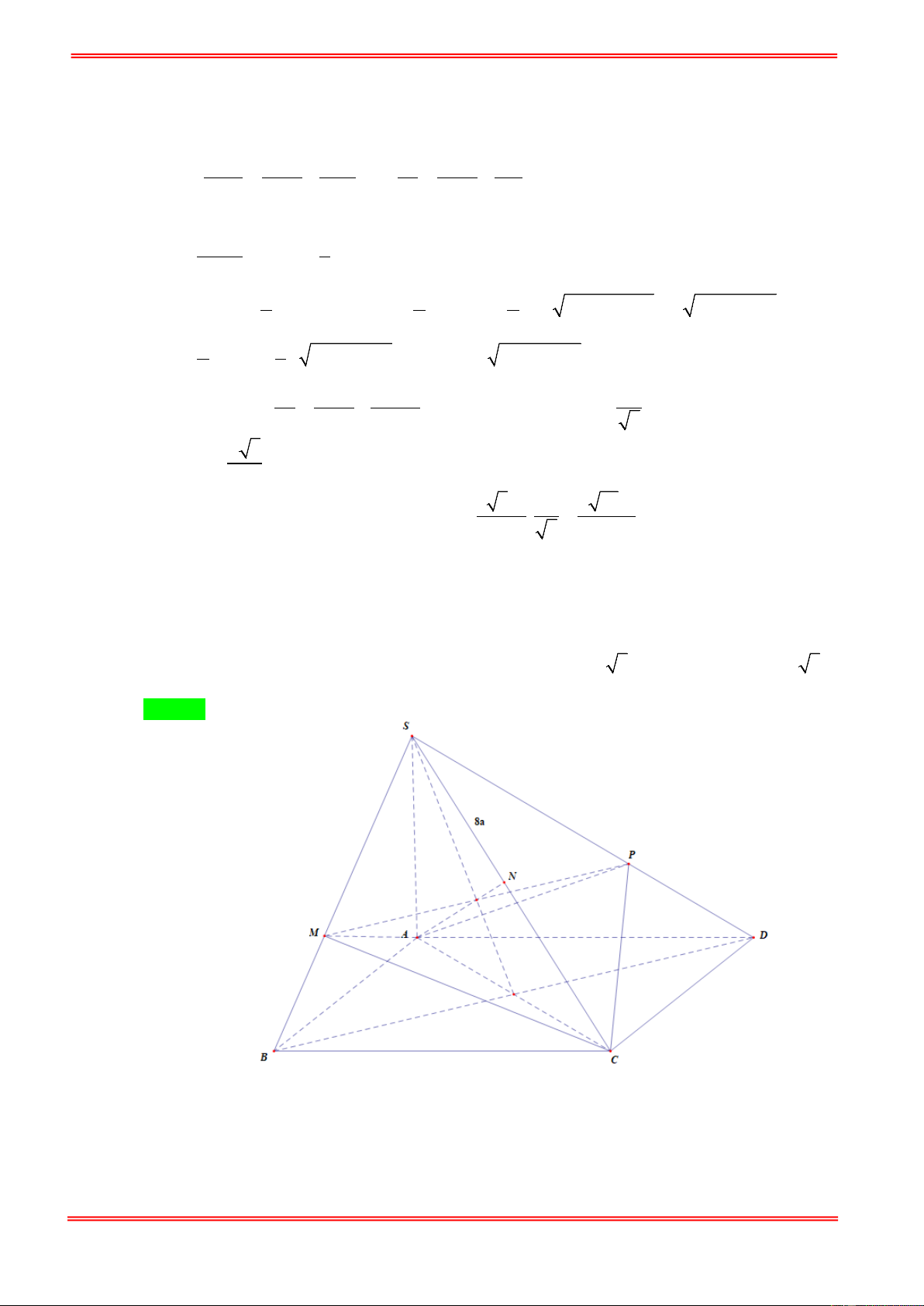
Câu 96.Cho hình chóp S.ABCD có đáy ABCD là hình vuông, các tam giác SAB và SAD là những tam
giác vuông tại A . Mặt phẳng (P) qua A vuông góc với cạnh bên SC cắt SB, SC, SD lần lượt
tại các điểm M , N, P . Biết SC = 8a ,  0
ASC = 60 . Tính thể tích khối cầu ngoại tiếp đa diện ABCDMNP ? A. 3
V = 6π a . B. 3
V = 24π a . C. 3
V = 32 3π a . D. 3
V = 18 3π a .
Câu 97. Cho khối lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng 2 , diện tích tam giác A′BC bằng
3 . Tính thể tích của khối lăng trụ 2 5 A. 3 2 . B. 2 5 . C. 2 . D. . 3
Câu 98. Cho hình lăng trụ tứ giác ABC . D A′B C ′ D
′ ′ có đáy ABCD là hình vuông cạnh a và thể tích bằng 2
3a . Tính chiều cao h của hình lăng trụ đã cho. a A. h = .
B. h = 9a .
C. h = 3a .
D. h = a . 3
Câu 99. Cho lăng trụ đứng ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Góc tạo bởi cạnh BC′ và mặt đáy ( A′B C ′ ′) bằng o
30 . Tính thể tích khối lăng trụ. 3 3a 3 a 3 a 3 a A. . B. . C. . D. . 4 2 12 4 https://toanmath.com/
Câu 100.] Cho lăng trụ đứng ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh a , cạnh bên A′B tạo với đáy một góc 0
45 Thể tích khối lăng trụ ABC.A′B C ′ ′ là: 3 2a A. V = . B. 3 V = a 3 .
ABC. A' B 'C ' 3
ABC. A' B 'C ' 3 a 3 a 3 C. V = . D. V = .
ABC. A' B 'C ' 6
ABC. A' B 'C ' 4
Câu 101. Cho lăng trụ tam giác đều ABC.ABC có tất cả các cạnh bằng 2a . Tính thể tích khối lăng trụ
ABC.ABC . 3 a 3 3 a 3 A. 3 2a 3 . B. 3 a 3 . C. . D. . 4 2 https://toanmath.com/
THỂ TÍCH KHỐI LĂNG TRỤ ĐỀU
Câu 1. Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3 . Thể tích khối lăng trụ đã cho bằng 9 3 27 3 27 3 9 3 A. . B. . C. . D. . 4 4 2 2
Hướng dẫn giải. Chọn B Diện tích đáy: 1 9 3 S = .3.3.sin 60° = . Thể tích 27 3 V = S .AA′ = . ABC ∆ ∆ 2 4 lt ABC 4 Câu 2.
Cho lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng 4cm , diện tích tam giác A′BC bằng 2
12cm . Thể tích khối lăng trụ đó là: A. 3
V = 8 2cm . B. 3
V = 24 3cm . C. 3
V = 24cm . D. 3
V = 24 2cm . Hướng dẫn giải Chọn D
Kẻ A' P ⊥ BC ( P ∈ BC ) ⇒ BC ⊥ AP . 1 24 Ta có A' .
P BC = 12 ⇒ A' P = = 6 . 2 4 AB 3 Cạnh AP =
= 2 3 ⇒ A' A = 36 −12 = 2 6 2 1 ⇒ V = A' . A S = 2 6. .4.2 3 = 24 2 . ABC 2
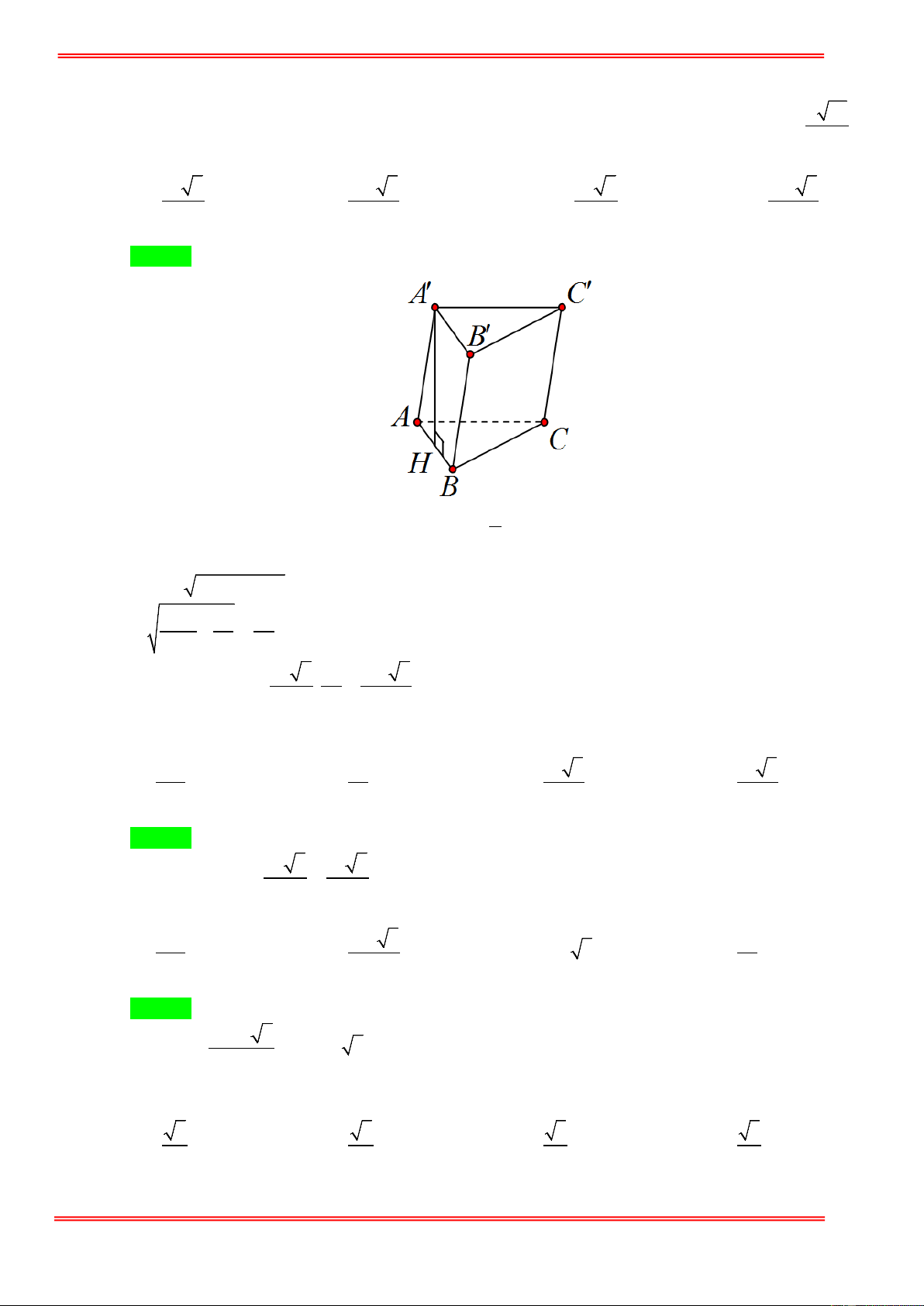
Câu 3. Cho hình lăng trụ đứng ABC.A' B 'C ' có đáy ABC đều cạnh bằng a và chu vi của mặt bên
ABB ' A ' bằng 6a . Thể tích của khối lăng trụ ABC.A' B 'C ' bằng 3 a 3 3 a 3 3 a 3 A. . B. 3 a 3 . C. . D. . 2 3 6 Hướng dẫn giải Chọn A https://toanmath.com/ A' C' B' A C B
Chu vi của hình chữ nhật 2( AB + AA') = 6a ⇒ AA' = 2a 2 3 a 3 a 3
Thể tích khối lăng trụ V = Bh = .2a = . 4 2
Câu 4. Cho khối tứ giác đều S.ABCD có thể tích là V . Nếu giảm độ dài cạnh đáy xuống hai lần và tăng độ
dài đường cao lên ba lần thì ta được khối chóp mới có thể tích là: 3 2 1 3 A. V . B. V . C. V . D. V . 2 3 4 4 Hướng dẫn giải Chọn D
Gọi độ dài cạnh đáy và chiều cao của hình chóp tứ giác đều lần lượt là a và h . Thể tích khối 2
chóp sau khi đã giảm độ dài cạnh đáy và tăng chiều cao là: 1  a  3  1  3 2 .3h = . a .h = V     . 3  2  4  3  4 9
Câu 5. Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng a 3
và có thể tích V = (dm ) Tính giá trị 4 của a .
A. a = 9 (dm) .
B. a = 3 (dm) .
C. a = 3 3 (dm) .
D. a = 3 (dm) . Hướng dẫn giải Chọn B
Khối lăng trụ tam giác đều có tất cả các cạnh bằng a có thể tích bằng. 2 3 a 3 a 3 V = . B h = .a = . 4 4 9 a 3 9 Mà V = (dm ) 3 3 3 ⇒
= ⇔ a = 3 3 ⇔ a = 3 (dm) . 4 4 4 9
Câu 6. Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng a 3
và có thể tích V = (dm ) Tính giá trị 4 của a .
A. a = 3 (dm) .
B. a = 3 3 (dm) .
C. a = 3 (dm) .
D. a = 9 (dm) . Hướng dẫn giải Chọn A
Khối lăng trụ tam giác đều có tất cả các cạnh bằng a có thể tích bằng 2 3 a 3 a 3 V = . B h = .a = . 4 4 https://toanmath.com/ 9 a 3 9 Mà V = (dm ) 3 3 3 ⇒
= ⇔ a = 3 3 ⇔ a = 3 (dm) . 4 4 4
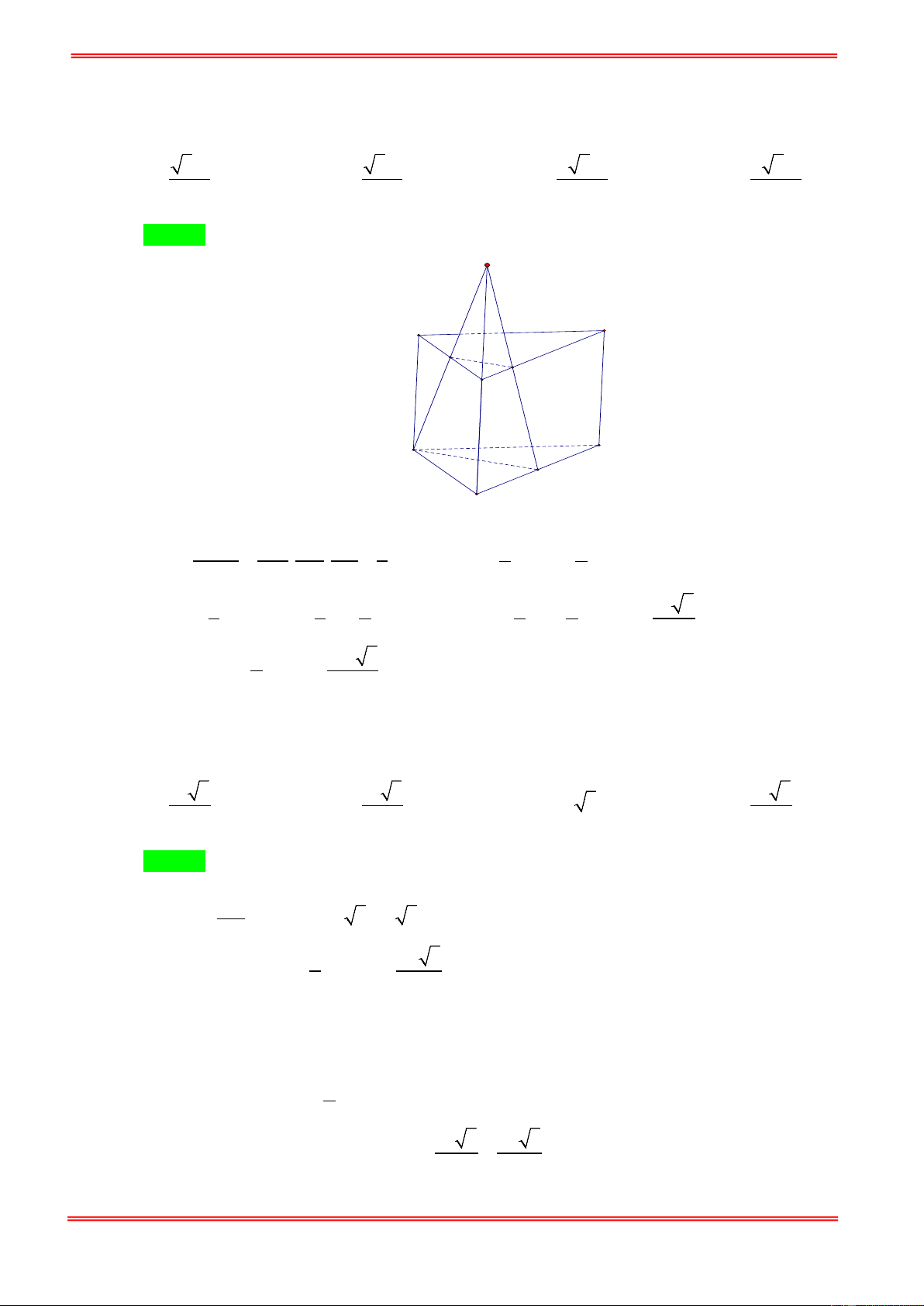
Câu 7. Cho hình lăng trụ ABC.A' B 'C ' có đáy là tam giác đều cạnh 3a , hình chieus của A' trên mặt
phẳng ( ABC) trùng với tâm đường tròn ngoại tiếp tam giác ABC . Cạnh AA' hợp với mặt phẳng đáy một góc 0
45 . Thể tích của khối lăng trụ ABC.A' B 'C ' tính theo a bằng. 3 27a 3 9a 3 27a 3 3a A. . B. . C. . D. . 6 4 4 4 Hướng dẫn giải Chọn C
Gọi AI là đường cao, H là tâm của tam giác ABC ⇒ A′H ⊥ ( ABC) . AA′ ∩  ( ABC) = A Vì 
⇒ góc giữa AA′ và ( ABC) là  ′ ⇒  A AH A′AH = 45° . A′H ⊥  ( ABC) 3a 3 2 ( a)2 2 3 3 9a 3 Ta có: AI = , AH =
AI = a 3 , S = = . 2 3 ABC 4 4
A′H = AH.tan 45° = AH = a 3 .
Thể tích của lăng trụ là: 2 3 9a 3 27a
V = A′H .S = a 3. = . ABC 4 4 A' B' C' A B H I C .
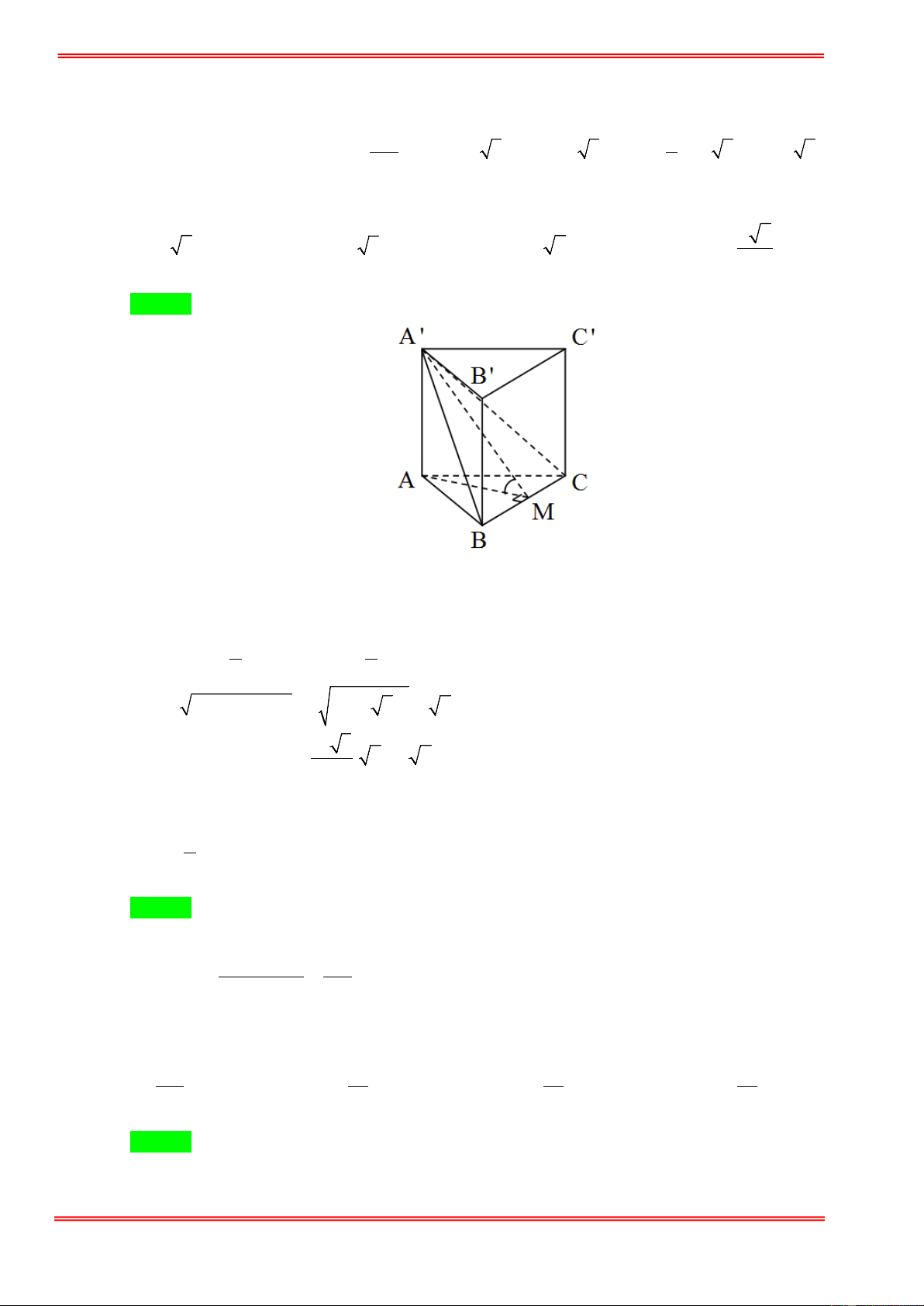
Câu 8. Cho lăng trụ đều ABC.A′B C
′ ′ có cạnh đáy bằng a . Gọi I là trung điểm cạnh BC . Nếu góc giữa
đường thẳng A′I và mặt phẳng ( ABC) bằng 60° thì thể tích của lăng trụ đó là 3 3a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 8 24 8 4 Hướng dẫn giải Chọn A https://toanmath.com/ A' C' B' A C 60 I B
Ta có ( A′I ( ABC ))  = (A′I AI)  , , =  A′IA = 60° . a 3 3a
Suy ra A′A = tan 60 . ° = . 2 2 2 3 Vậy a 3 3a 3 3a V = ′ = = ′ ′ ′ S .A A . . ABC. A B C ABC ∆ 4 2 8 Câu 9.
Cho hình lăng trụ tam giác đều có tất cả các cạnh đều bằng a . Tính theo a thể tích của khối lăng trụ. 3 a 3 3 2a 3 a 3 3 a A. . B. . C. . D. . 4 3 12 3 Hướng dẫn giải Chọn A 2 3 a 3 a 3
V = AA .′S = . a = . ABC 4 4
Câu 10. Cho lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng a và cạnh bên bằng a 3 . Thể tích của
khối lăng trụ ABC.A′B C ′ ′ bằng: 3 a 3 3a 3 a 3 3a A. . B. . C. . D. . 8 8 4 4 Hướng dẫn giải Chọn D 2 2 3 a 3 a 3 3a S = ;V =AA'.S = .a 3 = . ABC
ABC.A ' B 'C ' ABC 4 4 4
Câu 11. Cho lăng trụ đứng có đáy là tam giác đều, biết rằng tất cả các cạnh của lăng trụ bằng a . Thể tích
của lăng trụ đó là. 3 a 3 3 a 3 a 3 3 a 3 A. . B. . C. . D. . 12 4 8 4 Hướng dẫn giải Chọn D
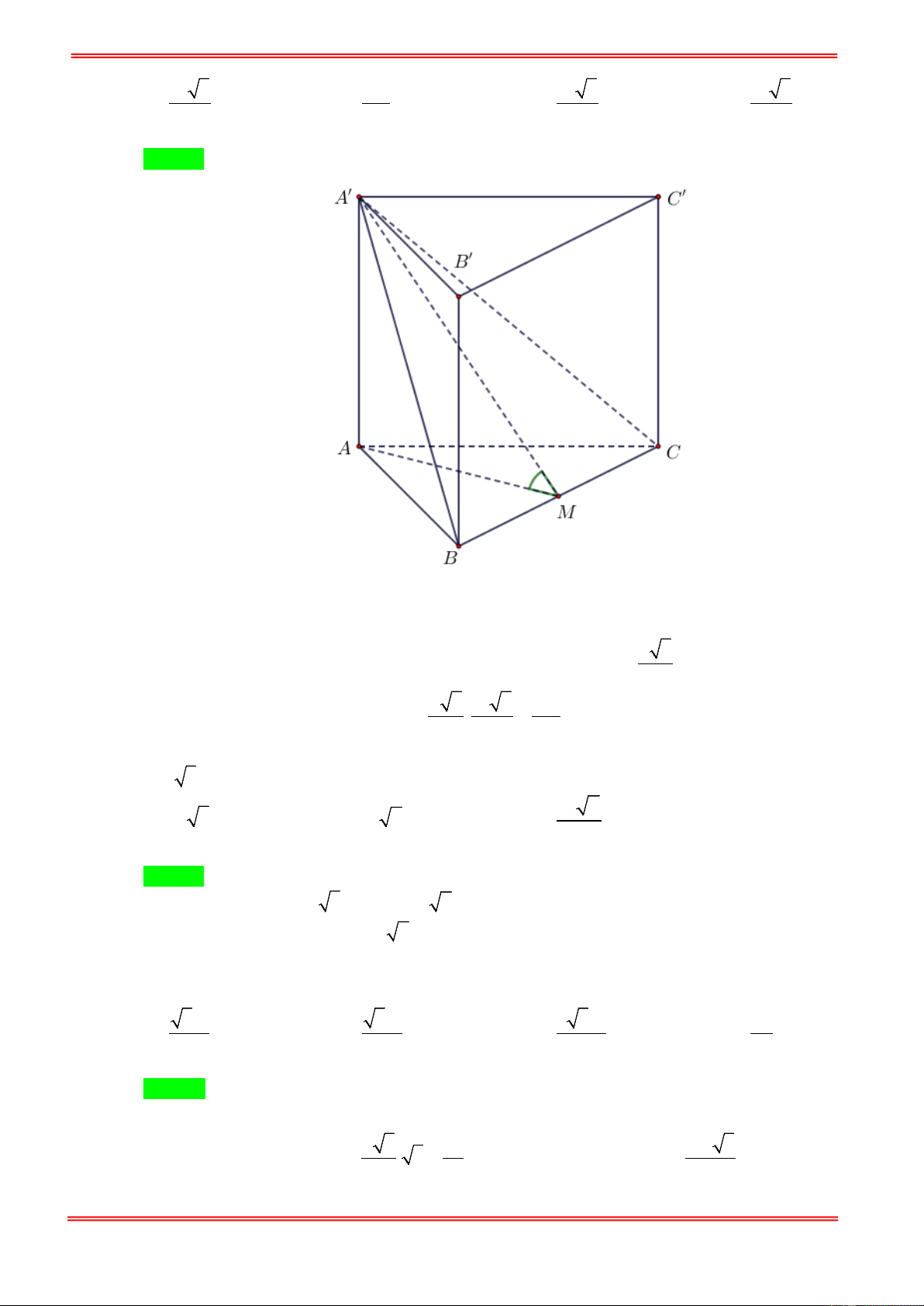
Câu 12. Cho khối lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng 2 , diện tích tam giác A′BC bằng
3 . Tính thể tích của khối lăng trụ. 2 5 A. 3 2 . B. . C. 2 5 . D. 2 . 3 Hướng dẫn giải Chọn A https://toanmath.com/ A′ B′ C′ A C M B .
Gọi M là trung điểm của BC . BC ⊥ AM Vì 
⇒ BC ⊥ A′M . BC ⊥ AA′ S = 1 ⇔ ′ = 1 ⇔ ′ = ⇔ ′ = ∆ ′ 3 A M .BC 3 A M .2 3 A M 3. A BC 2 2 2 2 AA′ =
AM − A′M = − ( )2 2 3 3 = 6 . 2 2 3 V = = = ′ ′ ′ S .A ' A . 6 3 2 . ABC. A B C ABC ∆ 4
Câu 13. Tính thể tích V của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a . 3 2a 3 3a 3 3a 3 2a A. V B. V C. V D. V 4 2 4 3 Hướng dẫn giải Chọn C a2 a3 3 3 V = .a = . 4 4
Câu 14. Cho lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng a và AB′ ⊥ BC′ . Tính thể tích của khối lăng trụ. 3 7a 3 6a 3 6a A. 3 V = 6a . B. V = . C. V = . D. V = . 8 8 4 Hướng dẫn giải Chọn C https://toanmath.com/ C' A' B' H C A I B .
Gọi I là trung điểm AB . Vì ABCA'B 'C ' là lăng trụ tam giác đều nên.
AI ⊥ ( BB 'C 'C ) => AI ⊥ BC ' .
Lại có: AC ' ⊥ BC ' nên suy ra BC ' ⊥ ( AIB') => BC ' ⊥ B'I .
Gọi H = B 'I ∩ BC '. HI BI 1 Ta có B
∆ HI đồng dạng C ∆ ' HB ' => =
= => B ' H = 2HI => B ' I = 3HI . B ' H B 'C ' 2 2 2 BI a a 3
Xét tam giác vuông B ' BI có 2 2
BI = HI.B ' I = 3HI => HI = = = . 3 12 2 2 2
a 3   a a 2 Suy ra 2 2 BB ' =
B ' I − BI =   − =     . 2    2  2 3 Vậy 3 a 2 a 6 2 V = S .BB' = a . = . ABC ∆ 4 2 8
Câu 15. Nếu khối lăng trụ đứng có đáy là hình vuông cạnh 2a và đường chéo mặt bên bằng 4a thì khối
lăng trụ đó có thể tích bằng. A. 3 4a . B. 3 8 3a . C. 3 12a . D. 3 6 3a . Hướng dẫn giải Chọn B Đườ 2 2
ng cao của lăng trụ bằng h = (4a) − (2a) = 2a 3 .
Thể tích khối lăng trụ bằng V = B h = ( a)2 3 . 2 .2a 3 = 8a 3 .
Câu 16. Cho hình lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng 2a , góc giữa hai đường thẳng AB′
và BC′ bằng 60° . Tính thể tích V của khối lăng trụ đó. 3 2 6a 3 2 3a A. 3
V = 2 6a . B. 3
V = 2 3a . C. V = . D. V = . 3 3 Hướng dẫn giải Chọn A https://toanmath.com/
Đặt AA′ = x (x > 0) .  
   
  
Ta có: AB′ BC′ = (BB′ − BA)(BC + BB′) 2 . = −B . A BC + BB′ . 2 2 2 2 = −B .
A BC.cos 60 + BB′ = x − 2a . 2 2 AB′ = BC′ = x + 4a .   2 2 AB .′BC′ x − 2a Theo đề: 1 0 cos 60 = ⇔ = 2 2 2 2 AB .′BC′ 2
x + 4a . x + 4a 2 2 2 2
⇔ x + 4a = 2 x − 2a 2 2 2 2
x + 4a = 2x − 4a ⇔  ⇔ x = 2a 2 . 2 2 2 2 x + 4a = 2 − x + 4a 2 Vậy AB 3 3 V = AA .′ = 2a 6 . 4
Câu 17. Một khối lăng trụ tam giác có đáy là tam giác đều cạnh 3, cạnh bên bằng 2 3 và tạo với mặt
phẳng đáy một góc 30 .° Khi đó thể tích khối lăng trụ là? 27 9 3 9 27 3 A. . B. . C. . D. . 4 4 4 4 Hướng dẫn giải Chọn A A′ C′ B′ C A B H Kẻ C H
′ ⊥ ( ABC) tại H ⇒ (CC′ ( ABC))  =  ; C C ′ H. C H ′
Bài ra (CC′ ( ABC ))  = ° ⇒  ; 30 C C ′ H = 30° 1 1 2 3 ⇒ sin 30° = = ⇒ C H ′ = CC′ = = 3. CC′ 2 2 2 https://toanmath.com/ Do đó 1 1 3 27 V = ′ = ′ ° = = ′ ′ ′ C H .S C H. A . B AC.sin 60 3. .3.3. . ABC. A B C ABC 2 2 2 4
Câu 18. Cho hình lăng trụ tứ giác đều ABC . D A′B C ′ D
′ ′ có cạnh đáy bằng a , khoảng cách từ A đến mặt phẳng ( a
A′BC ) bằng . Tính thể tích lăng trụ. 3 3 2a 3 3a 3 3a A. . B. 3 3 3a . C. . D. . 4 4 2 Hướng dẫn giải Chọn A A' D' B' C' a A H D a B C .
Ta có: BC ⊥ AA ,
′ BC ⊥ AB ⇒ BC ⊥ ( ABA′) ⇒ ( A′BC) ⊥ ( ABA′) . Kẻ a
AH ⊥ A′B ⇒ AH ⊥ ( A′BC ) AH = d ( ,
A ( A′BC )) = . 3 1 1 1 1 1 1 8 Xét A
∆ ′AB vuông tại A : = + ⇒ = − = 2 2 2 2 2 2 2 AH AB A′A A′ . A AH AB a a 2 3 ⇒ a 2 A′A = ⇒ V = ′ ′ ′ ′ . 4 ABCD. A B C D 4
Câu 19. Thể tích của khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng a bằng: 3 a 3 a 3 3 a 3 3 a 2 A. . B. . C. . D. . 3 4 6 3 Hướng dẫn giải Chọn B 2 3 a 3 a 3 Diện tích đáy là ⇒ V = . 4 4
Câu 20. Cho khối lăng trụ đều ABC.A′B C
′ ′ và M là trung điểm của cạnh AB . Mặt phẳng (B C ′ M ′ )
chia khối lăng trụ thành hai phần. Tính tỷ số thể tích của hai phần đó. 3 6 7 1 A. B. . C. . D. . 8 5 5 4 Hướng dẫn giải Chọn C https://toanmath.com/
Qua M kẻ đường thẳng song song với BC cắt AC tại N khi đó thiết diện tạo bởi mặt phẳng
(B'C 'M ) và khối chóp là tứ giác B'C 'NM
Khi đó thiết diện chia hình lăng trụ thành 2 phần là BCNMB'C ' và AMNA'B 'C '
Gọi S là giao điểm của C ' N với AA' V SA SM SN 1 1 1 1 1 Ta có SAMN = . . = . . = ⇒ V = V SAMN
SA ' B 'C ' V
SA' SB ' SC ' 2 2 2 8 8
SA ' B 'C " 7 7 1 7 1 ⇒ V = V = . .SA'.S = . .2AA'.S
AMNA ' B 'C '
SA ' B 'C '
A ' B 'C '
A ' B 'C ' 8 8 3 8 3 7 7 5 = AA'.S = V ⇒ V = V
A ' B 'C '
ABC. A ' B 'C ' BCNMB 'C '
ABC. A ' B 'C ' 12 12 12 Do đó tỉ 7 5 7
số thể tích hai phần là : = . 12 12 5
Câu 21. Cho hình lăng trụ tam giác đều ABC.A′B C
′ ′ có AB = a , đường thẳng AB′ tạo với mặt phẳng
(BCC B′′) một góc 30°. Tính thể tích V của khối lăng trụ đã cho. 3 a 2 3 a 6 3 a 6 3 3a A. V = . B. V = . C. V = . D. V = . 3 4 12 4 Hướng dẫn giải Chọn B
Gọi M là trung điểm của AB ⇒ AM ⊥ BC . Vì ABC. ′
A B′C′ là lăng trụ đứng ⇒ BB′ ⊥ ( ABC ) ⇒ BB′ ⊥ AM .
Suy ra AM ⊥ ( BCC′B′) ⇒ ( AB′ ( BCC′B′))  =  , AB′M = 30° .  AM
Tam giác AB′M vuông tại M, có sin AB ' M =
⇒ AB ' = a 3 . AB ' https://toanmath.com/ Tam giác ′
AA B′ vuông tại A' , có 2 2 ′ AA = AB′ − ′ A B′ = a 2 .
Thể tích khối lăng trụ ABC. ′ A B′C′ là 2 3 a 3 a 6 V = ′ AA S = a = . ABC ′ A B′C′ . 2. . ∆ABC 4 4
Câu 22. Cho lăng trụ đứng ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh a , góc tạo bởi hai mặt phẳng
( ABC), ( A′BC) bằng 60°. Tính thể tích khối lăng trụ ABC.A′B C ′ ′. 3 a 3 3 3a 3 3 a 3 3 3a 3 A. . B. . C. . D. . 24 4 6 8 Hướng dẫn giải Chọn D A' C' B' A C K B
Gọi K là trung điểm cạnh BC ′ ′
. Suy ra góc giữa mặt phẳng ( ABC ) và ( A BC ) là  A KA = 60° . a 3 AK =
(đường trung tuyến trong tam giác đều). 2 3a
AA′ = AK. tan 60° = . 2
Thể tích khối lăng trụ ABC.A′B C ′ ′ là: 1 3a 3 3 2 3 V = S .AA′ = a .sin 60 . ° = a . ABC ∆ 2 2 8
Câu 23. Khối lăng trụ tam giác đều có tất cả các cạnh bằng nhau và có thể tích là 9 thì độ dài mỗi cạnh 4 bằng. A. 3 . B. 3 . C. 6 243 . D. 3 3 . Hướng dẫn giải Chọn B Gọi độ dài cạnh là . a . 1 a 3 9 V = . h S = . h BH .AC = . a .a = ∆ 2 4 4 3
⇒ a = 3 3 ⇒ a = 3 . https://toanmath.com/ A' B' C' A H C B .
Câu 24. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng a là. 2 3 2 3 A. 3 V = a . B. 3 V = a . C. 3 V = a . D. 3 V = a . 4 4 3 2 Hướng dẫn giải Chọn B 2 2 3
Đáy là tam giác đều cạnh a 3 a 3 a 3 a nên B = ⇒ V = Bh = .a = . 4 4 4 .
Câu 25. Tính thể tích của khối lăng trụ đều ABC.A′B C
′ ′ có AB = AA′ = a . 3 3a 3 3a 3 3a A. . B. . C. . D. 3 a . 12 4 6 Hướng dẫn giải Chọn B 2 3 3a 3a V = S .AA′ = .a = . ABC 4 4
Câu 26. Cho lăng trụ đứng ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Mặt phẳng ( AB C ′ ′) tạo với mặt
đáy góc 60°. Tính theo a thể tích khối lăng trụ ABC.A′B C ′ ′ . 3 a 3 3 3a 3 3 a 3 3 3a 3 A. V = . B. V = . C. V = . D. V = . 8 8 2 4 Hướng dẫn giải Chọn B
A'M ⊥ B 'C '
Gọi M là trung điểm B 'C '. Ta có 
⇒ B 'C ' ⊥ AM nên góc giữa mặt phẳng
AA' ⊥ B 'C '
(AB'C ') tạo với đáy là góc  AMA ' = 60° . 3a
Tam giác AA ' M vuông tại A' nên 0
AA ' = A ' M . tan 60 = 2 3
Vậy thể tích khối lăng trụ 3a 3
ABC.A' B 'C ' là V = AA'.S = . A' B 'C ' 8
Câu 27. Tính thể tích V của khối lăng trụ đều ABC.A' B 'C ' biết AB = a và AB ' = 2a . https://toanmath.com/ 3 3a 3 a 3 3 a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . 4 2 12 4 Hướng dẫn giải Chọn A A’ C’ B’ A C B . Ta có: 2 2 2 2 BB′ =
AB′ − AB = 4a − a = a 3 . 2 3 Vậy a 3 3a V = S .BB′ = .a 3 = .
ABC. A' B 'C ' ABC 4 4
Câu 28. Cho hình lăng trụ tứ giác đều ABC . D A′B C ′ D
′ ′ có cạnh đáy 4 3 (m). Biết mặt phẳng (D B ′ C) hợp với đáy một góc ο
60 . Thể tích khối lăng trụ là. A. 3 325 m . B. 3 648 m . C. 3 478 m . D. 3 576 m . Hướng dẫn giải Chọn D A' D' B' C' A D B C .
Phân tích: ABC . D A′B C ′ D
′ ′ là một hình lăng trụ tứ giác đều, cũng có nghĩa rằng nó là một hình
hộp đứng có đáy là hình vuông cạnh 4 3 (m) .
Ta có BC ⊥ CD, BC ⊥ DD′ ⇒ BC ⊥ (CDD C
′ ′) ⇒ BC ⊥ CD′ . Suy ra ( ο D B ′ C) ( ABCD)  ( )=  (CD′ CD)=  , , D CD ′ = 60 .
Hướng dẫn giải: DD′ D ∆ CD ′ vuông tại D nên:  0 tan D C ′ D =
⇒ DD′ = 4 3.tan 60 = 12(m) . CD Vậy V = ′ = = ′ ′ ′ ′ DD .S
12.(4 3)2 576 m . ABCD A B C D ABCD ( 2 . )
Câu 29. Cho lăng trụ đứng ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh a , góc tạo bởi hai mặt phẳng
( ABC), (A′BC) bằng 60°. Tính thể tích khối lăng trụ ABC.A′B C ′ ′. 3 a 3 3 3a 3 3 3a 3 3 a 3 A. . B. . C. . D. . 6 4 8 24 Hướng dẫn giải https://toanmath.com/ Chọn C
Gọi K là trung điểm cạnh BC. Suy ra góc giữa mặt phẳng ( ABC) và ( A′BC) là  A′KA = 60° . a 3 AK =
(đường trung tuyến trong tam giác đều). 2 3a
AA′ = AK. tan 60° = . . 2
Thể tích khối lăng trụ ABC.A′B C ′ ′ là: 1 3a 3 3 2 3 V = S .AA′ = a .sin 60 . ° = a . ABC ∆ 2 2 8
Câu 30. Cho hình chóp S.ABC có SA ⊥ ( ABC ) , tam giác ABC vuông tại C , AC = a 2, 6 AB = a .
Tính thể tích khối chóp S.ABC biết SC = 3a 3 2a 42 3 a 6 3 a 14 A. . B. 3 14a . C. . D. . 3 3 3 Hướng dẫn giải Chọn D 1 1 3 1 a 14 2 2 2 2 V = .C . A C . B SA =
AC. AB − AC . SC − AC = a 2.2 . a a 7 = . S . ABC 6 6 6 3
Câu 31. Cho hình lăng trụ đều ABC.A′B C
′ ′. Biết khoảng cách từ điểm C đến mặt phẳng ( ABC′) bằng a ,
góc giữa hai mặt phẳng ( ABC′) và (BCC B ′ ′) bằng α với 1 cosα = (tham khảo hình vẽ 2 3
bên). Thể tích khối lăng trụ ABC.A′B C ′ ′ là A' C' B' A C B 3 a 2 3 3a 2 3 3a 2 3 3a 2 A. . B. . C. . D. 2 2 4 8 Hướng dẫn giải Chọn B https://toanmath.com/ A' C' B' H M A C G K J B
Gọi K, J lần lượt là trung điểm của AB, BC .
Gọi x là độ dài cạnh AB . x 3 AJ = CK = . 2
Ta có CH ⊥ ( ABC′) ⇒ d (C,( ABC′)) = CH = a .
Mặt khác AJ ⊥ (BCC B ′ ′) .
Nên ( ABC′),( BCC B ′ ′)  ( ) = 
(CH,AJ) =α = 
(CH,AG) (cosα =sinϕ). MG 1 AG AJ x x Ta có sin ϕ = = ⇔ MG = 2 = = 3 = . AG 2 3 2 3 3 3.2 2.3 3 6 HC x a x = ⇔ = ⇔ x = 2a . 3 6 3 6
Mà d (C,( ABC′)) = CH = a . 2a 3 a CH .CK ⇒ a 6 CC′ = 2 = = . 2 2 CK − CH ( 2 a 3 )2 2 − a 2 (2a)2 3 Vậy x 3 3 a 6 3a 2 V = .CC′ = . = . 4 4 2 2
Câu 32. Cho hình hộp đứng ABC . D A′B C ′ D
′ ′ có đáy là hình vuông cạnh a , góc giữa mặt phẳng (D A ′ B)
và mặt phẳng ( ABCD) bằng 30° . Thể tích khối hộp ABC . D A′B C ′ D ′ ′ bằng 3 a 3 3 a 3 3 a 3 A. 3 a 3 . B. . C. . D. . 3 9 18 Hướng dẫn giải Chọn A https://toanmath.com/ Ta có ( ADD A
′ ′) ⊥ ( AB) nên góc giữa mặt phẳng (D A
′ B) và mặt phẳng ( ABCD) là góc AD′ và A′D′ AA′ hay 
A′AD′ = 30° . Suy ra AA′ =
= a 3 . Vậy thể tích hộp 3 V = ′ ′ ′ ′ a 3 . tan 30° ABCD. A B C D
Câu 33. Cho hình lăng trụ tam giác đều ABCA′B C
′ ′ có AB = a , đường thẳng AB′ tạo với mặt phẳng
(BCC B′′) một góc 30°. Tính thể tích V của khối lăng trụ đã cho. 3 a 6 3 3a 3 a 6 3 a A. V = . B. V = .. C. V = . D. V = . . 12 4 4 4 Hướng dẫn giải Chọn C
Gọi M là trung điểm, do tam giác ABC đều nên AM ⊥ BC , mà AM ⊥ BB′nên AM ⊥ ( BCC B
′ ′). Suy ra hình chiếu vuông góc của AB′ trên (BCC B ′ ′) là B M ′ .
Vậy góc giữa đường thẳng AB′ và mặt phẳng (BCC B ′ ′) là góc  AB M ′ và  0 AB M ′ = 30 . a 3 2 2 AM =
⇒ AB′ = a 3 ⇒ AA′ = AB′ − A′B′ = a 2.. 2 3 a 6 V = . 4
Câu 34. Cho lăng trụ tam giác đều ABC.A′B C
′ ′ có chiều cao bằng 2 . Biết góc giữa đường thẳng AB′ và mặt phẳng ( 1 A′B C
′ ′) bằng α thỏa tanα =
. Tính thể tích khối lăng trụ ABC.A′B C ′ ′. 2 4 3 4 3 2 3 A. 4 3 . B. . C. . D. . 3 9 3 Hướng dẫn giải Chọn A https://toanmath.com/ A’ C’ α B’ A C B .
Góc tạo bởi AB′ và ( A′B C ′ ′) . là góc  AB A ′ ′ = α . AA′ AA′ Ta có: tan α = ⇒ A′B′ = = . A′B′ 2 2 tan α (2 2)2 3 Vậy V = ′ = = ′ ′ ′ S .AA .2 4 3 . ABC. A B C ABC 4
Câu 35. Cho lăng trụ tam giác đều ABC.A′B C
′ ′ cạnh đáy bằng a , chiều cao bằng 2a . Mặt phẳng (P) qua
B′ và vuông góc với A′C chia lăng trụ thành hai khối. Biết thể tích của hai khối là V và V với 1 2 V
V < V . Tỉ số 1 bằng 1 2 V2 1 1 1 1 A. B. C. D. 1 6 T 1 6 T 1 6 T 1 6 T 1 6 T 1 6 T 1 6 T 1 6 T 7 47 23 11 Hướng dẫn giải 1 6 T Chọn B
Gọi H là trung điểm của A′C′ , giác A ∆ ′B C ′ ′ đều nên B H
′ ⊥ A′C′ . Trong ( A′C CA ′
) , kẻ HE ⊥ A′C , HE ∩ A′A = I . B H ′ ⊥ A′C′ Ta có: 
⇒ A′C′ ⊥ (B H
′ I ) ⇒ (P) ≡ (B HI ′ ) .
HI ⊥ A′C′ https://toanmath.com/ A′E A′C′
A′C .′A′H a 5 A ∆ ′EH # A ∆ ′C C ′ ⇒ = ⇒ A′E = = . A′H A′C A′C 10 IH A′C
A′C.A′H a 5 A ∆ ′IH # A ∆ ′C C ′ ⇒ = ⇒ IH = = . A′H C C ′ C C ′ 4 1 2 a 15 S = ′ = ′ B H .HI . B HI 2 16 1 2 1 a 15 a 5 3 a 3 V = .S ′ = = ′ .A E . . . 1 3 B HI 3 16 10 96 2 a 3 3 a 3 V = ′ = = ′ ′ ′ S .A A .2a . ABC. A B C ABC 4 2 47 V 1 3 V = a 3 do đó 1 = . 2 96 V 47 2
Câu 36. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng 2a là. 3 a 3 3 a 3 A. . B. . 3 C. 2a 3 . D. 3 4a . 4 12 Hướng dẫn giải Chọn C
Giả sử khối lăng trụ đều là ABC.A′B C ′ ′ như hình bên. (2a)2 3
Tam giác ABC đều cạnh 2a có diện tích bằng 2 S = = a 3 . 4 .
Thể tích khối lăng trụ 2 3
V = AA .′S = 2 . a a 3 = 2a 3 .
Câu 37. Cho lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng a và AB′ ⊥ BC′ . Tính thể tích V của
khối lăng trụ đã cho. 3 a 6 3 7a 3 a 6 A. V = . B. V = . C. 3 V = a 6 . D. V = . 4 8 8 Hướng dẫn giải Chọn D
Gọi E là điểm đối xứng của C qua điểm B . Khi đó tam giác ACE vuông tại A . https://toanmath.com/ 2 2
⇒ AE = 4a − a = a 3 .
Mặt khác, ta có BC′ = B E
′ = AB′ nên tam giác AB E
′ vuông cân tại B′. AE ⇒ a a AB′ = 3 = 6 = . 2 2 2 2  a 6  a 2 Suy ra: 2 AA′ =   − a =   . 2 2   2 3 Vậy a 2 a 3 a 6 V = . = . 2 4 8
Câu 38. Cho lăng trụ ABCDA′B C ′ D
′ ′ có đáy ABCD là hình thoi cạnh a , tâm O và  ABC = 120° . Các
cạnh A′A ; A′B ; A′D cùng tạo với mặt đáy một góc bằng 45°. Tính theo a thể tích V của khối lăng trụ đã cho. 3 a 3 3 a 3 3a 3 3a A. B. C. D. 2 2 4 2 Hướng dẫn giải Chọn B A' B' D' C' B A H D C 2 a 3
ABCD là hình thoi cạnh a ,  ABC = 120° ⇒ A
∆ BD đều cạnh a , S = do đó ABD ∆ 4 2 a 3 S = . ABCD 2
Các cạnh A′A ; A′B ; A′D cùng tạo với mặt đáy một góc bằng 45°nên chóp A′ABD đều đỉnh a 3 A′ suy ra AH = . 3 3 a Suy ra V = = ′ ′ ′ ′ AH .S . ABCDA B C D ABCD 2
Câu 39. Cho hình lăng trụ đứng ABC.A′B C
′ ′, biết đáy ABC là tam giác đều cạnh a . Khoảng cách từ tâm a
O của tam giác ABC đến mặt phẳng ( A′BC ) bằng . Tính thể tích khối lăng trụ ABC.A′B C ′ ′. 6 3 3a 2 3 3a 2 3 3a 2 3 3a 2 A. . B. . C. . D. . 8 28 4 16 Hướng dẫn giải Chọn D 2 Diện tích đáy là a 3 B = S = . ABC ∆ 4
Chiều cao là h = d (( ABC);( A′B C ′ ′)) = AA′. https://toanmath.com/
Do tam giác ABC là tam giác đều nên O là trọng tâm của tam giác ABC . Gọi I là trung điểm
của BC , H là hình chiếu vuông góc của A lên A′I ta có AH ⊥ ( A′BC) ⇒ d ( ;
A ( A′BC )) = AH A' C' B' H K A C O I B d ( ;
O ( A′BC )) IO 1 d ( ; A A′BC ) = = ⇒ ( AH a a d ;
O ( A′BC )) ( ) = = = ⇒ AH = d ( ;
A ( A′BC )) IA 3 3 3 6 2
Xét tam giác A′AI vuông tại A ta có: 1 1 1 3 = + 1 1 1 ⇒ = − a 3 ⇒ a 3 3a 2 AA′ = ⇒ h = ⇒ V = . 2 2 2 ′ ′ ′ AH AA′ AI 2 2 2 AA′ AH AI ABC. A B C 2 2 2 2 16
Câu 40. Cho lăng trụ tam giác đều ABC.A′B C
′ ′ có độ dài cạnh đáy bằng 2a , cạnh bên bằng a 3 . Tính
thể tích V của lăng trụ. A. 3 V = 2a 3 . B. 3 V = 2a . C. 3 V = a 3 . D. 3 V = 3a . Hướng dẫn giải Chọn D (2a)2
Diện tích đáy tam giác đều 3 2 S = = a 3 . 4 Thể tích lăng trụ 2 3
V = S.h = a
3.a 3 = 3a .
Câu 41. Cho lăng trụ đều ABC.A′B C
′ ′ có cạnh đáy bằng 2a , diện tích xung quanh bằng 2 6 3a . Thể tích
V của khối lăng trụ. 3 1 A. 3 V = 3a . B. 3 V = a . C. 3 V = a . D. 3 V = a . 4 4 Hướng dẫn giải Chọn A
Do ABC.A′B C
′ ′ là lăng trụ đều nên S = = ′ ′ S ′ ′ S ABB A ACC A BCC B ′ ′ ⇒ 2 S = 3S = 3A . B AA' = 6 .
a AA' = 6 3a ⇔ AA' = a 3 xp ABB ' A' (2a)2 Do đó 3 3 V = AA'.S = a 3. = 3a ABC 4 https://toanmath.com/ A' C' B' A C B
Câu 42. Tính thể tích của khối lăng trụ tam giác đều có cạnh đáy bằng 2a và cạnh bên bằng a . 3 a 3 3 a 3 A. . B. 3 a 3 . C. 3 a . D. . 4 3 Hướng dẫn giải Chọn B
Vì lăng trụ đứng nên đường cao bằng a . (2a)2
Vì đáy là tam giác đều nên diện tích đáy: . 3 2 S = = a 3 . ABC 4 Thể tích: 2 3 V = S .a = a 3.a = a 3 . ABC
Câu 43. Cho hình lăng trụ đều ABC.A′B C
′ ′ có cạnh đáy bằng a , A′C hợp với mặt đáy ( ABC) một góc
60° . Thể tích của khối lăng trụ ABC.A′B C ′ ′ bằng: 3 3a 3 a 3 2a 3 3a A. . B. . C. . D. . 8 4 3 4 Hướng dẫn giải Chọn D A' C' B' a A C a B . 2 3 a 3 3a V = A ' . A S = a 3. = . ABC 4 4
Câu 44. Cho lăng trụ tam giác ABC.A′B C
′ ′ có đáy là tam giác vuông cân, cạnh huyền AC = 2a . Hình
chiếu của A lên mặt phẳng ( A′B C
′ ′) là trung điểm I của A′B′ , góc giữa cạnh bên và mặt đáy
bằng 60°. Thể tích khối lăng trụ ABC.A′B C ′ ′ là. 3 a 6 3 a 6 3 3a A. . B. 3 a 2 . C. . D. . 2 6 4 Hướng dẫn giải Chọn A https://toanmath.com/ .
Góc giữa cạnh bên AA′ và mặt đáy ( A′B C
′ ′) bằng 60° là góc  AA′I = 60° . AC A′B′ AB a
Ta có: AC = 2a nên AB = = 2
a 2 ⇒ A′I = = = . 2 2 2 2 2 3 Vậy AB a 6 V = = ′ ° = ′ ′ ′ AI.S A I. tan 60 . . ABC. A B C ABC 2 2
Câu 45..Cho lăng trụ tam giác ABC.A′B C
′ ′ có đáy là tam giác vuông cân, cạnh huyền AC = 2a . Hình
chiếu của A lên mặt phẳng ( A′B C
′ ′) là trung điểm I của A′B′ , góc giữa cạnh bên và mặt đáy
bằng 60°. Thể tích khối lăng trụ ABC.A′B C ′ ′ là. 3 a 6 3 a 6 3 3a A. . 3 C. a 2 . 2 B. 6 . D. 4 . Hướng dẫn giải Chọn A .
Góc giữa cạnh bên AA′ và mặt đáy ( A′B C
′ ′) bằng 60° là góc  AA′I = 60° . AC A′B′ AB a
Ta có: AC = 2a nên AB = = 2
a 2 ⇒ A′I = = = . 2 2 2 2 2 3 Vậy AB a 6 V = = ′ ° = ′ ′ ′ AI.S A I. tan 60 . . ABC. A B C ABC 2 2
Câu 46. Cho hình lăng trụ đứng ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a , cạnh bên AA′ = a 2 . Thể
tích của khối lăng trụ là 3 3a 3 a 3 3 a 6 3 a 6 A. . B. . C. . D. . 4 12 12 4 Hướng dẫn giải Chọn A https://toanmath.com/ A' C' B' A C B 2 3 a 3 a 6
Ta có V = Bh = S .AA′ = a 2. = . ABC 4 4
Câu 47. Cho lăng trụ tam giác đều ABC.A′B C
′ ′ có tất cả các cạnh đều bằng a 2 . Tính thể tích của khối lăng trụ. 3 a 3 3 a 6 3 a 6 3 a 3 A. . B. . C. . D. . 8 2 6 6 Hướng dẫn giải Chọn B (a )2 2 2 3
Đáy lăng trụ là tam giác đều cạnh a 3 a 2  → S = = day 4 4 2 3 a 3 a 6 ⇒ V = S . ′ AA = .a 2 = . day 2 2
Câu 48. Thể tích V của khối lăng trụ tam giác đều có cạnh đáy bằng 2a và cạnh bên bằng a là 4 2 T 4 2 T 4 2 T 4 2 T 4 2 T 4 2 T 4 2 T 3 a 3 3 a 3 3 a 3 A. V = . B. V = . C. 3 V = a 3 . D. V = . 3 2 4 Hướng dẫn giải Chọn C A' C' a B' A C 2a B ( a)2 2 3 Ta có V = S .AA′ = .a 3 = a 3 . ABC 4
Câu 49. Tính thể tích V của khối lăng trụ tam giác đều có tất cả các cạnh bằng a . 3 a 3 3 a 2 3 a 3 3 a 2 A. V = . B. V = . C. V = . D. V = . 2 4 4 3 Hướng dẫn giải Chọn C https://toanmath.com/ 2 3 a 3 a 3 Ta có: V = ′ = = ′ ′ ′ S .AA .a . ABC. A B C ABC ∆ 4 4
Câu 50. Cho hình lăng trụ tam giác ABC.A′B C
′ ′ có đáy ABC là tam giác vuông tại A , AB = a ,
AC = a 3 . Hình chiếu vuông góc của A′ lên ( ABC ) là trung điểm của BC . Góc giữa AA′ và
( ABC) bằng 60°. Tính thể tích V của khối lăng trụ đã cho. 3 a 3 3 3a 3 a 3 3a 3 A. V = . B. V = . C. V = . D. V = . 2 2 2 2 Hướng dẫn giải Chọn B B' C' A' B H C 60° a a 3 A .
Gọi H là trung điểm BC ⇒ A′H ⊥ ( ABC ) . 2 2 BC BC =
AB + AC = 2a ⇒ AH = = a . 2 2 1 a 3 2 3 a 3 3a
A′H = AH.tan 60° = a 3 ; S = A . B AC = Vậy, V = a 3. = . ABC ∆ 2 2 2 2
Câu 51. Cho hình lăng trụ đứng tam giác ABC.A′B C
′ ′ có đáy là ∆ABC đều cạnh a = 4 và biết S = ∆ ′ 8 . A BC
Tính thể tích khối lăng trụ. A. 2 3 . B. 4 3 . C. 6 3 . D. 8 3 . Hướng dẫn giải Chọn D https://toanmath.com/ Gọi 1 2S  2.8
M là trung điểm BC . Ta có SAM . A BC
BC AM    4 ABC 2 BC 4 4 3
Vì AM là đường trung tuyến của tam giác đều cạnh bằng 4 nên AM   2 3 . 2
Trong tam giác vuông AAM ta có 2 2 AA 
AM AM  1612  2 . 2
Thể tích khối lăng trụ 4 3 V S .AA  .2  8 3 . ABC  4
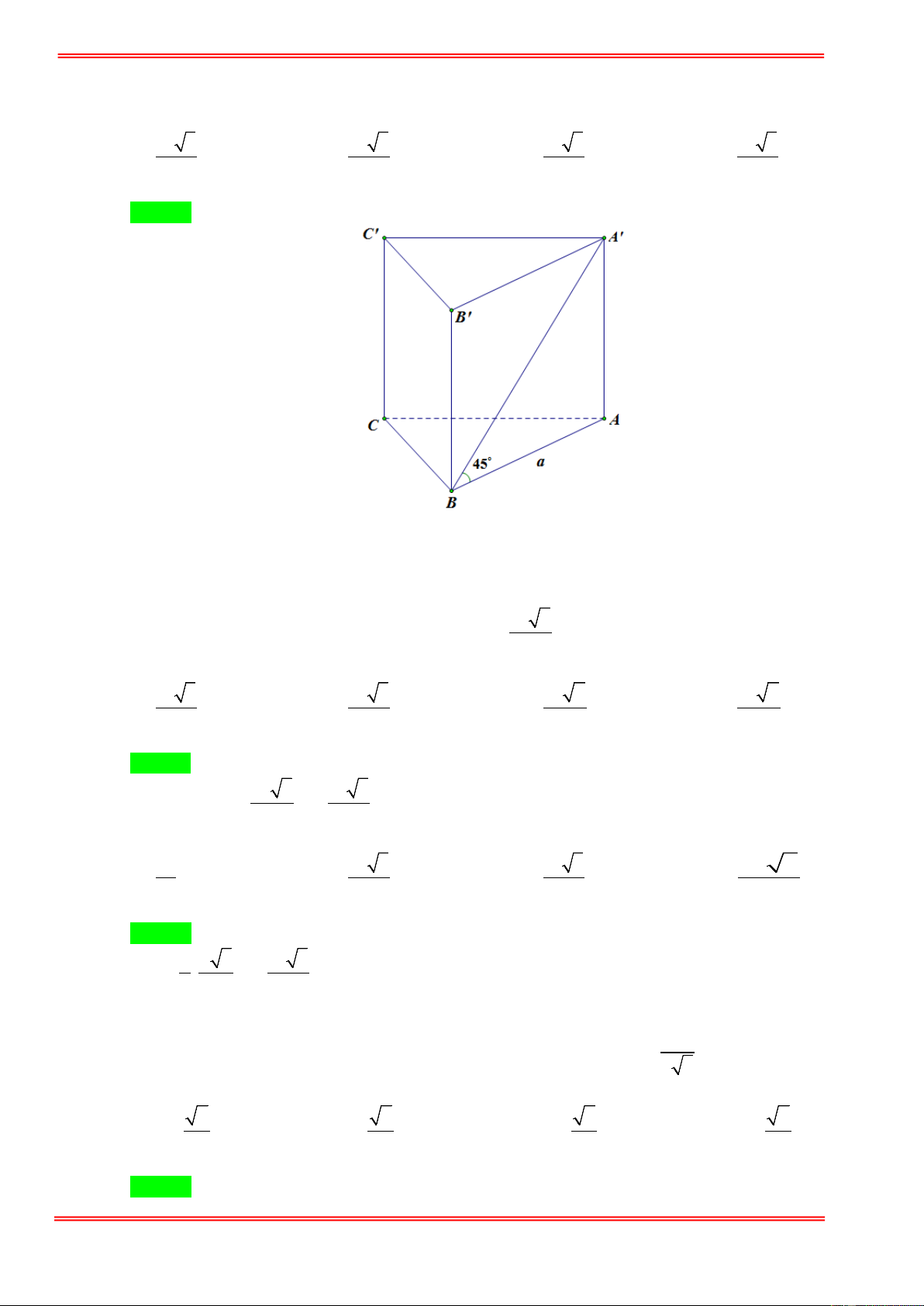
Câu 52. Cho lăng trụ đứng ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh a , cạnh bên A′B tạo với đáy
một góc 45° . Thể tích khối lăng trụ ABC.A′B C ′ ′là: 3 a 3 A. V = . B. 3 V = a 3 .
ABC. A' B 'C ' 4
ABC. A' B 'C ' 3 a 3 2a C. V = . D. V = .
ABC. A' B 'C ' 6
ABC. A' B 'C ' 3 Hướng dẫn giải Chọn A A' C' B' A C B . 2 a 3
Tam giác ABC đều ⇒ S = . ABC 4
Góc giữa A′B ( ABC)  ( )=  0 ,
A′BA = 45 ⇒ A
∆ ′AB vuông cân tại A .
⇒ A′A = AB = a . 2 3 a 3 a 3 V = S .AA ' = .a = (đvtt).
ABC. A' B 'C ' ABC 4 4
Câu 53. Cho hình lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng a , góc giữa mặt phẳng ( A′BC) và
mặt phẳng ( ABC) bằng 45°. Thể tích của khối lăng trụ ABC.A′B C ′ ′ bằng https://toanmath.com/ 3 a 3 3 3a 3 a 3 3 a 3 A. . B. . C. . D. . 2 8 8 4 Hướng dẫn giải Chọn B
Gọi M là trung điểm BC ⇒ AM ⊥ BC ⇒ BC ⊥ ( AMA′) ⇒ BC ⊥ MA′
Ta có ( ABC ) ∩ ( A′BC ) = BC , AM ⊥ BC , BC ⊥ MA′ ⇒ ( a
ABC ),( A′BC )  ( )= 
(AM,A′M) =  AMA′ = 45° 3 ⇒ AM = AA′ = . 2 2 3
Thể tích khối lăng trụ a 3 a 3 3a
V = AA .′S = . = . ABC 2 4 8
Câu 54. Cho hình lăng trụ tứ giác đều ABC . D A′B C ′ D
′ ′ có cạnh đáy bằng a . Biết đường chéo của mặt bên
là a 3 . Khi đó, thể tích khối lăng trụ bằng: 3 a 2 A. 3 a 3 . B. 3 a 2 . C. . D. 3 2a . 3 Hướng dẫn giải Chọn B
Ta có AB = a , A′B = a 3 ⇒ AA′ = a 2 . ⇒ V = ′ = ′ ′ ′ ′ AA . AB a . A B C D ( )2 3 2 ABCD.
Câu 55. Cho hình lăng trụ đứng ABC.A′B C
′ ′ có tam giác ABC là tam giác đều cạnh bằng a , góc giữa ( AB C
′ ′) và (A′B C ′ )′ bằng o
60 . Thể tích khối lăng trụ ABC.A′B C ′ ′ là. 3 3a 3 3a 3 3 3a 3 a A. . B. . C. . D. . 24 8 8 24 Hướng dẫn giải Chọn C
Gọi M là trung điểm của B 'C '. Khi đó dễ dàng xác định được  0 AMA' = 60 . a 3 3a 3 3a 3 Suy ra 0
AA ' = A ' M . tan 60 = . 3 = . Vậy V = AA′.S = . 2 2
ABC. A' B 'C ' ABC 8 https://toanmath.com/
Câu 56. Cho hình lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng a . Góc giữa đường thẳng A′B và
mặt phẳng ( ABC) bằng 45°. Tính thể tích của khối lăng trụ ABC.A′B C ′ ′. 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 12 24 4 Hướng dẫn giải Chọn D
Theo giả thiết, ta có AA′ ⊥ ( ABC) ⇒ BA là hình chiếu vuông góc của A′B trên ( ABC)
⇒ Góc giữa đường thẳng A′B và mặt phẳng ( ABC) là  ABA′ = 45° Do A
∆ BA′ vuông cân tại A ⇒ AA′ = AB = a 3
Vậy thể tích của khối lăng trụ a 3
ABC.A′B C ′ ′.là V = . 4
Câu 57. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a là: 3 a 3 3 a 3 3 a 2 3 a 2 A. . B. . C. . D. . 3 4 3 2 Hướng dẫn giải Chọn B 2 3 a 3 a 3 Ta có V = Bh = .a = . 4 4
Câu 58. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a là: 3 a 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 2 12 2 4 Hướng dẫn giải Chọn D 3 1 a 3 a 3 V = . a . .a = . 2 2 4
Câu 59. Cho hình lăng trụ đều ABC.A′B C
′ ′. Biết khoảng cách từ điểm C đến mặt phẳng ( ABC′) bằng a,
góc giữa hai mặt phẳng ( ABC′) và (BCC B ′ ′) bằng α với 1 cosα = (tham khảo hình vẽ 2 3
dưới đây). Thể tích khối lăng trụ ABC.A′B C ′ ′ bằng 2 2 2 2 A. 3 3a . B. 3 a . C. 3 3a . D. 3 3a . 4 2 2 8 Hướng dẫn giải Chọn C https://toanmath.com/
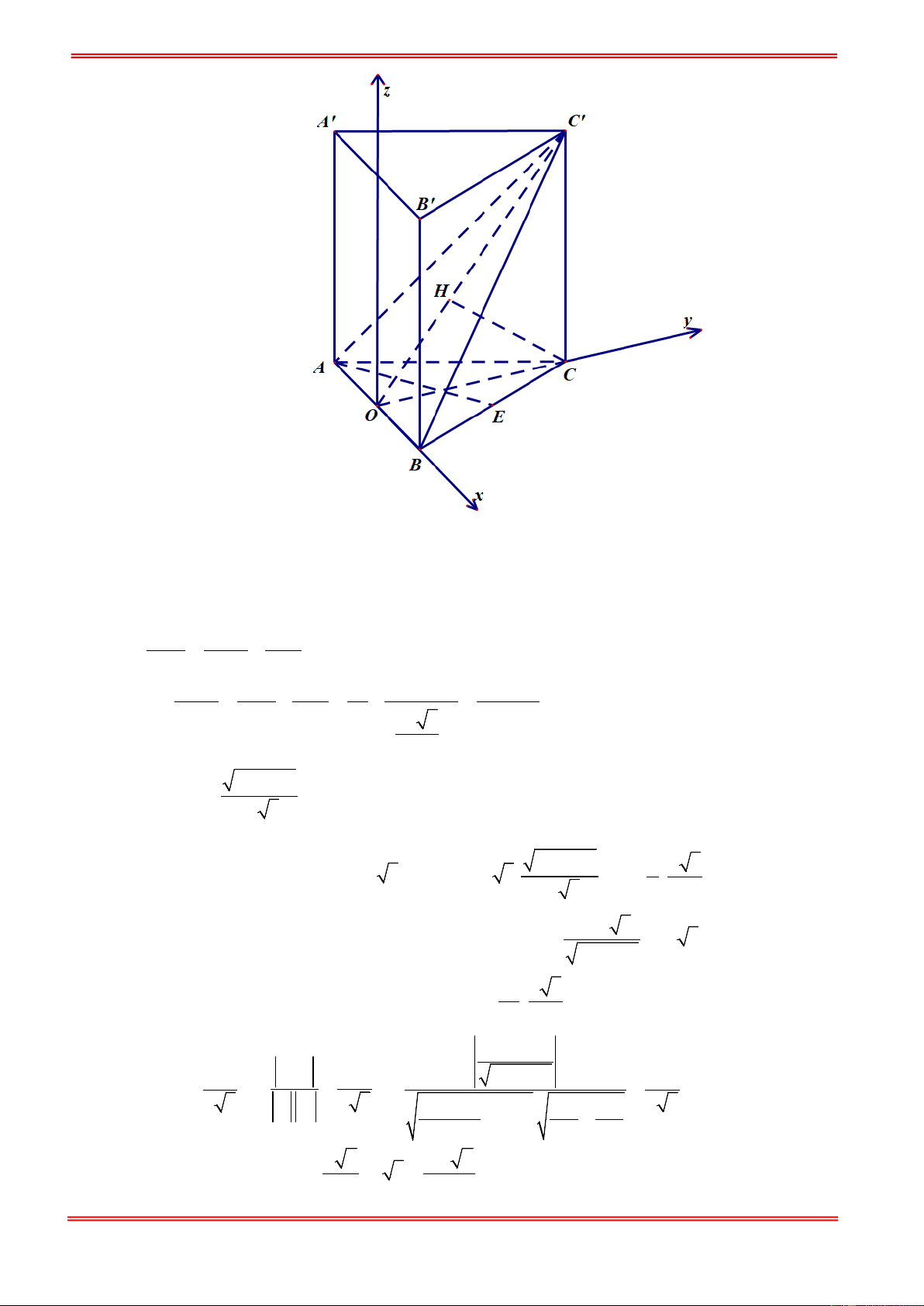
Gọi O là trung điểm của AB , E là trung điểm của BC Trong mp (C C
′ O) kẻ CH ⊥ C O ′ tại H
Khi đó d (C,( ABC′)) = CH = a
Chọn hệ trục tọa độ Oxyz như hình vẽ, gọi 2x là độ dài cạnh của tam giác ABC ta có 1 1 1 = + 2 2 2 CH C 'C CO 2 2 − ⇒ 1 1 1 1 1 3x a = − = − = 2 2 2 2 2 2 2 C 'C CH CO a   3 2 3 a x x   2   2 2 3x − a ⇒ C 'C = ax 3 Khi đó, 2 2  3x a  −  x x 3  A(− ; x 0; 0) C (0; x 3;0) , B ( ; x 0; 0) , , C ' 0; x 3;   , E  ; ; 0    ax 3    2 2      2   VTPT của mặt phẳng ( 2ax 3
ABC′) là n = OC ,′ AB = 2 0;− ; 2x 3  1     2 2  3x − a      VTPT của mặt phẳng ( 3x x 3 BCC B
′ ′) là n = AE =  ; ; 0  2   2 2     3 3ax 1 n .n 1 2 2 − cosα = ⇔ 1 2   = ⇔ 3x a 1 = ⇔ x = a 2 3 n n 2 3 2 4 2 2 12a x 9x 3x 2 3 1 2 4 +12x . + 2 2 3x − a 4 4 3 a 6 3a 2 2 V = ′ = = ′ ′ ′ C C.S .a 3 ABC. A B C ABC ∆ . 2 2 https://toanmath.com/
Câu 60. Cho hình lăng trụ đứng ABC.A' B 'C ' có đáy ABC đều cạnh bằng a và chu vi của mặt bên
ABB ' A ' bằng 6a . Thể tích của khối lăng trụ ABC.A' B 'C ' bằng 3 a 3 3 a 3 3 a 3 A. . B. 3 a 3 . C. . D. . 2 3 6 Hướng dẫn giải Chọn A A' C' B' A C B
Chu vi của hình chữ nhật 2( AB + AA') = 6a ⇒ AA' = 2a 2 3 a 3 a 3
Thể tích khối lăng trụ V = Bh = .2a = . 4 2
Câu 61. Cho lăng trụ đứng ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a và AB′ vuông góc với BC′ . Thể
tích của lăng trụ đã cho là. 3 a 6 3 a 6 3 a 6 3 a 6 A. . B. . C. . D. . 12 4 8 24 Hướng dẫn giải Chọn C .
Gọi I là trung điểm BC . Vì ABCA'B 'C ' là lăng trụ tam giác đều nên.
AI ⊥ ( BB 'C 'C ) => AI ⊥ BC ' .
Lại có giả thiết AC ' ⊥ BC ' nên suy ra BC ' ⊥ ( AIB') => BC ' ⊥ B'I .
Gọi H = B 'I ∩ BC '. HI BI 1 Ta có B
∆ HI đồng dạng C ∆ ' HB ' => =
= => B ' H = 2HI => B ' I = 3HI . B ' H B 'C ' 2 https://toanmath.com/ 2 2 BI a a 3
Xét tam giác vuông B ' BI có 2 2
BI = HI.B ' I = 3HI => HI = = = . 3 12 2 2 2
a 3   a a 2 Suy ra 2 2 BB ' =
B ' I − BI =   − =     . 2    2  2 3 Vậy 3 a 2 a 6 2 V = S .BB' = a . = . ABC ∆ 4 2 8
Câu 62. Cho hình lăng trụ tam giác đều ABC.A′B C
′ ′ có tất cả các cạnh bằng a . Gọi M , N lần lượt là
trung điểm của các cạnh AB và B C
′ ′. Mặt phẳng ( A′MN ) cắt cạnh BC tại .
P Thể tích khối đa diện MB . P A′B N ′ bằng. 3 7 3a 3 3a 3 7 3a 3 7 3a A. . B. . C. . D. . 68 32 96 32 Hướng dẫn giải Chọn C A' C' N B' A C M Q P B S .
Gọi Q là trung điểm của BC. Suy ra AQ A′N ⇒ MP AQ ⇒ P là trung điểm của BQ . Ta có BB ,
′ A′M , NP đồng quy tại S và B là trung điểm của B S
′ ⇒ SB′ = 2a . 2 3 a 3 a 3 S = ⇒ = ′ ′ V . A B N S . ′ ′ 8 A B N 12 1 3 7 7 3a V = V ⇒ V = = ′ ′ V . SMNP ′ ′ ′ ′ 8 SA B N MBPA B N 8 SA B N 96
Câu 63. Cho ( H ) là khối lăng trụ đứng tam giác đều có tất cả các cạnh đều bằng a . Thể tích của ( H ) bằng: 3 a 3 3 a 3 3 a 2 3 a A. . B. . C. . D. . 2 4 3 2 Hướng dẫn giải Chọn B https://toanmath.com/ a a 2
* Đáy lăng trụ là tam giác đều cạnh 3
a nên có diện tích là = a S
, đường cao h = a . 4 3 3
* Vậy thể tích khối lăng trụ = . = a V S h . 4
Câu 64. Cho khối lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng a 2 và mỗi mặt bên có diện tích bằng 2
4a . Thể tích khối lăng trụ đó là 3 2a 6 3 a 6 A. 3 2a 6 . B. . C. . D. 3 a 6 . 3 2 Hướng dẫn giải Chọn D C' A' B' A C B
Do ABC.A′B C
′ ′ là khối lăng trụ tam giác đều nên ABB A
′ ′ là hình chữ nhật. Mặt khác mỗi mặt bên có diện tích bằng 2 4a nên 2 4a 2 4a 2 A .
B AA′ = 4a ⇔ AA′ = ⇔ AA′ =
⇔ AA′ = 2 2a . AB a 2 Thể tích khối lăng trụ
ABC.A′B C ′ ′ là 1 1 V = ° ′ = ° 3 = ′ ′ ′ A . B A . B sin 60 .AA
a 2.a 2.sin 60 .2 2a a 6 . ABC. A B C 2 2
[DS11.C5.2.D0.d](THPT Quảng Xương 1 - Thanh Hóa- Lần 1- 2017 - 2018 - BTN) Gọi
k , k , k lần lượt là hệ số góc của tiếp tuyến của đồ thị các hàm số y = f ( x) , y = g ( x) , 1 2 3 ( ) = f x y
tại x = 2 và thỏa mãn k = k = 2k ≠ 0 khi đó g(x) 1 2 3 A. f ( ) 1 2 < . . 2 B. f ( ) 1 2 ≤ . . 2 https://toanmath.com/ C. f ( ) 1 2 ≥ . . 2 D. f ( ) 1 2 > . 2 Hướng dẫn giải Chọn. B.
f ′(2) g (2) − g′(2) f (2)
Theo đề bài ta có k = k = f ′(2) = g′(2) . k = . 1 2 3 2 g (2) Theo đề bài ta có
k = k = 2k ≠ 0 nên ta có phương trình 1 2 3
f ′(2) g (2) − f (2)   1 = f ′ 2 2
⇔ g (2) − 2g (2) + 2 f (2) = 0. 2 g (2) ( ) 2
Do g (2) là một giá trị thuộc tập giá trị của hàm số nên phương trình 2
g (2) − 2g (2) + 2 f (2) = 0
có nghiệm ⇔ ∆′ ≥ 0 ⇔ 1− 2 f (2) ≥ 0 ⇔ f ( ) 1 2 ≤ . 2
Câu 65. Cho hình lăng trụ tứ giác đều ABC . D A′B C ′ D
′ ′ có cạnh đáy bằng a . Biết đường chéo của mặt bên
là a 3 . Khi đó, thể tích khối lăng trụ bằng: 3 a 2 A. 3 a 3 . B. 3 a 2 . C. . D. 3 2a . 3 Hướng dẫn giải Chọn B .
Ta có AB = a , A′B = a 3 ⇒ AA′ = a 2 ⇒ V = ′ = ′ ′ ′ ′ AA . AB a . A B C D ( )2 3 2 ABCD.
Câu 66.Khối lăng trụ tam giác đều có tất cả các cạnh bằng a thì có thể tích bằng 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 12 4 8 Hướng dẫn giải Chọn C 2 3
Thể tích khối lăng trụ tam giác đều: a 3 a 3 V = . h S = . a = . 4 4
Câu 67. Từ một ảnh giấy hình vuông cạnh là 4cm , người ta gấp nó thành bốn phần đều nhau rồi dựng lên
thành bốn mặt xung quanh của hình hình lăng trụ tứ giác đều như hình vẽ. Hỏi thể tích của khối
lăng trụ này là bao nhiêu. 64 4 A. 3 cm B. 3 16cm . C. 3 cm D. 3 4cm . 3 3 Hướng dẫn giải Chọn D
Đáy là hình vuông có cạnh bằng 1 nên diện tích đáy: 2 S = 1cm . Thể tích lăng trụ là: 3 V = .
h S = 4cm https://toanmath.com/
Câu 68. Cho lăng trụ tứ giác đều ABC . D A′B C ′ D
′ ′ đáy hình có cạnh bằng a, đường chéo AC′ tạo với mặt bên ( BCC B ′ ′) một góc α ( 0
0 < α < 45 ). Tính thể tích của lăng trụ tứ giác đều ABC . D A′B C ′ D ′ ′ . A. 3 2 a cot α +1 . B. 3 2 a tan α −1 . C. 3 a cos 2α . D. 3 2 a cot α −1 . Hướng dẫn giải Chọn D . Ta có ngay  AC ' B = α . a
Tam giác ABC ' vuông tại B và 
AC ' B = α ⇒ BC ' = = a cotα.. tan α
Áp dụng định lý Pytago thì 2 2 2 CC ' =
BC ' − BC = a cot α −1. .
Thể tích khối lăng trụ 3 2 V = BC. . CD CC ' = a cot α −1. .
Câu 69. Cho khối lăng trụ ABC.A′B C
′ ′ có AB = BC = 5a , AC = 6a . Hình chiếu vuông góc của A′ trên mặt phẳng ( a 133
ABC ) là trung điểm của AB và A′C =
. Tính thể tích V của khối lăng trụ 2
ABC.A′B C ′ ′ theo . a . A. 3 V = 12 133a . 3 = = = B. V 4 133a . C. 3 V 12a . D. 3 V 36a . Hướng dẫn giải Chọn D A/ C/ B/ a 133 2 6a A C 5a 5a B .
Gọi H là trung điểm của AB . 2 2 2 2 AC + BC AB 97a  Tam giác A ∆ BC có 2 HC = − = . 2 4 4  Trong A ∆ ′HC ta có 2 2 A′H =
A′C − HC ⇒ A′H = 3a = h .  Diện tích đáy 2
S = 12a (dùng công thức Hê – rông).  6a
Thể tích khối lăng trụ ABC.A′B C ′ ′ là 2 3
V = S.h = 12a . = 36a . 2
Câu 70. Cho hình lăng trụ đều ABC.A′B 'C′ có cạnh đáy bằng a , cạnh bên a 3 . Thể tích của khối lăng trụ là. https://toanmath.com/ 3 a 3 3 a 3 3 a 7 3 3a A. . B. . C. . 7 4 5 D. 4 . Hướng dẫn giải Chọn D
Vì ABC.A′B 'C′ là hình lăng trụ đều nên đáy ABC là tam giác đều cạnh a . 2 1 a 3 S = A . B AC.sin 60° = . ABC ∆ 2 4 2 3 a 3 3a V = S .AA′ = .a 3 = . . ABC ∆ 4 4
Câu 71. Cho khối lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy là a và khoảng cách từ A đến mặt phẳng ( a
A′BC ) bằng . Tính thể tích của khối lăng trụ ABC.A′B C ′ ′. 2 3 3 2a 3 3a 2 3 3a 2 3 2a A. . B. . C. . D. . 12 16 48 16 Hướng dẫn giải Chọn B A' C' B' H A C M B
Gọi M là trung điểm BC , H là hình chiếu của A trên A′M . Nhận xét d ( ,
A ( A′BC )) = AH .
Tam giác AA′M vuông tại A nên có: 1 1 1 + = 1 4 4 ⇒ + = 1 8 a 3 ⇒ = ⇒ AA′ = 2 2 2 A′A AM AH 2 2 2 A′ A 3a a 2 2 A′ . A 3a 2 2 2 3 Thể tích của lăng trụ a 3 a 3 3a 2
ABC.A′B C ′ ′ là V = . = . 4 2 2 16
Câu 72. Cho lăng trụ tứ giác đều ABC . D A′B C ′ D
′ ′ có cạnh đáy bằng a 5 . Khoảng cách từ A đến mặt a 5
phẳng ( A' BC ) bằng
. Thể tích khối lăng trụ là: 2 3 5a 15 3 6a 3 3 a 5 A. . B. . C. 3 2a 2 . D. . 3 5 3 Hướng dẫn giải Chọn A https://toanmath.com/ AH ⊥ BC
Dựng AH ⊥ A' B . Do 
⇒ AH ⊥ ( A'BC)
AH ⊥ A'B
Do đó d ( A ( A BC)) a 5 , ' = AH = . 2 1 1 1 a 15 Mặt khác = + ⇒ AA' = . 2 2 2 AH AA' AB 3 3 5a 15 Suy ra V = AA'.S = .
ABCD. A ' B 'C ' D ' ABCD 3
Câu 73. Cho lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng 2a , khoảng cách từ A đến mặt phẳng ( a A′BC ) bằng
6 . Khi đó thể tích lăng trụ bằng. 2 4 3 4 A. 3 V = a . B. 3 V = a . C. 3 V = 3a . D. 3 V = a . 3 3 Hướng dẫn giải Chọn C .
Gọi I là trung điểm BC . H là hình chiếu của A lên A′I . AI ⊥ BC
 ⇒ BC ⊥ (AA′I) ⇒ ( A′BC) ⊥ (AA′I) theo giao tuyˆe n ′ A′I AA′ ⊥ BC
AH ⊥ A′I;
AH ⊂ ( AA′I ) .
⇒ AH ⊥ (A′BC) a 6 ⇒ d( ;
A ( A′BC)) = AH = 2 https://toanmath.com/ A
∆ ′AI vuông tại A : 1 1 1 1 1 1 = + 3. ⇒ = − ⇒ AA′ = a 3 2 2 2 2 2 AH AI AA′ AA′  a 6  (a 3)2   2   . (2a)2 3 3 V = S .AA′ = .a 3 = 3a . ABC 4 3a
Câu 74. Cho hình lăng trụ đều ABC.A′B 'C′ có AB = a , AA' =
. Gọi G là trọng tâm tam giác A′BC . 2
Tính thể tích tứ diện GABC theo a . 3 a 3 3 a 3 3 a 3 3 3a 3 A. . B. . D. . 16 12 C. 24 . 8 Hướng dẫn giải Chọn C 1 1 1 2 1 a 3 3a 3 a 3 V = .S .d G; ( ABC) = 1 1 .S . .d A′ ABC = .S . AA′ = . . = . ABC ∆ [ ;( )] G. ABC ABC ∆ [ ] ∆ 3 3 3 3 ABC 3 9 4 2 24
Câu 75. Tính thể tích V của khối lăng trụ tam giác đều ABC.A′B C
′ ′ có AA′ = BC = a . 3 a 3 3 a 2 3 a 3 3 a A. V = . B. V = . C. V = . D. V = . 4 6 12 3 Hướng dẫn giải Chọn A . 2 a 3 3 a 3 S = . Khi đó V = . ABC 4
ABC. A' B 'C ' 4 https://toanmath.com/
Câu 76. Cho lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh a , cạnh bên tạo với mặt phẳng bằng 0
45 . Hình chiếu của A trên mặt phẳng ( A′B C
′ ′) trùng với trung điểm của A′B′ . Tính thể
tích V của khối lăng trụ theo a . 3 a 3 3 a 3 3 a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . 2 24 8 16 Hướng dẫn giải Chọn C A C B A' C' H B' .
Gọi H là trung điểm của A'B , theo đề ta suy ra:
AH ⊥ ( A' B 'C ') . ⇒  0 a
AA' H = 45 khi đó 0
AH = A ' H . tan 45 = . 2 3 Vậy a 3 V = . 8
Câu 77. Cho lăng trụ ABC.A′B C
′ ′ có cạnh bên bằng 2a , đáy ABC là tam giác cân tại ; A AB =  2 ; a 0
BAC = 120 . Hình chiếu vuông góc của A′ trên mp ( ABC ) trùng với trung điểm của
cạnh BC . Tính thể tích khối chóp A .′BB C ′ C ′ ? 3 4a A. 3 3a . B. 3 2a . C. 3 4a . D. . 3 Hướng dẫn giải Chọn B
Gọi là H trung điểm của cạnh BC..
Xét tam giác ABC. có BH = 2 .
a sin60 = a 3; AH = 2 . a cos60 = ; a . Xét tam giác A′ .
HA vuông tại H có A′H = ( a)2 2 2 − a = a 3. .
Ta có: V = h ⋅ S . lt
Trong đó h = A′H = a 3 . 1 2 S
= AH ⋅ BC = 3a . ABC ∆ 2 Vậy 3 1 V = 3a . 3 3 ⇒ V = ⋅ = ′ 3a a . lt A . ABC 3 Mặt khác 3 3 3 V = − = − = ′ ′ ′ V V ′ 3a a 2a . A .BCB C lt A . ABC
Câu 78. Cho khối lăng trụ đứng có cạnh bên bằng 5 , đáy là hình vuông có cạnh bằng 4 . Hỏi thể tích khối lăng trụ là: A. 64 . B. 80 . C. 100 . D. 20 . Hướng dẫn giải Chọn B
Lăng trụ đứng có cạnh bên bằng 5 nên có chiều cao h = 5.
Thể tích khối lăng trụ là: 2 V = S
.h = 4 .5 = 80 . ABCD https://toanmath.com/
Câu 79. Cho hình lăng trụ tam giác đều ABC.A′B C
′ ′ có tất cả các cạnh bằng a . Gọi M , N lần lượt là
trung điểm của các cạnh AB và B C
′ ′. Mặt phẳng ( A′MN ) cắt cạnh BC tại P . Tính thể tích của khối đa diện MB . P A′B N ′ 3 3a 3 3a 3 7 3a 3 7 3a A. . B. . C. . D. . 24 12 96 32
Hướng dẫn giải Chọn C S A C M P B C' A' N B'
Gọi S là giao điểm của A′M và BB′ , khi đó P là giao điểm SN và BC . V SM SB SP 1 7 7 Ta có SMBP = . . = ⇒ V = = ′ ′ V ′ ′ . V ′ ′ MBP. A B N SA B N ′ ′ SA SB SN 8 8 8 SA B N 1 1 1 a 3 a 3 V = ′ = ′ ′ ′ ′ ° 1 = ° = ′ ′ SB .S SB . A B .B N sin 60 2 . a . a sin 60 . SA B N ∆ ′ ′ 3 A B N 3 2 6 2 12 3 7 7a 3 ⇒ V = = ′ ′ V . MBP. A B N ′ ′ 8 SA B N 96 °
Câu 80. Cho hình lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác vuông tại B , 
ACB = 60 , BC = a ,
AA′ = 2a . Cạnh bên tạo với mặt phẳng ( ABC ) một góc 30° .Thể tích khối lăng trụ ABC.A′B C ′ ′ bằng. 3 a 3 3 a 3 3 a 3 A. . B. . C. 3 a 3 . D. . 2 6 3 Hướng dẫn giải Chọn A
Trong tam giác ABC vuông tại B ta có: AB tan 60° =
⇒ AB = BC. 3 = a 3 . BC 2 Diện tích đáy: 1 a . 3 S = A . B BC = . ABC 2 2
Gọi H là hình chiếu của A′ lên mặt phẳng ( ABC). Góc giữa cạnh bên AA′ và đáy là  A′AH = 30° .
Trong tam giác vuông A′HA ta có: 1
A′H = AA .′sin 30° = 2 . a = a . 2 2 3 Thể tích lăng trụ là: a 3 a . 3
V = A′H . S = . a = . ABC 2 2 https://toanmath.com/
Câu 81. Cho hình lăng trụ tam giác ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh bằng a , hình chiếu vuông góc của a
A′ lên mặt phẳng ( ABC ) là trung điểm H của cạnh AB , cạnh 10 AA′ = . 2
Tính theo a tích của khối lăng trụ ABC.A′B C ′ ′. 3 a 3 3 3a 3 3 a 3 3 3a 3 A. . B. . C. V = . D. V = . 8 4 12 8 Hướng dẫn giải Chọn D a
H là trung điểm của AB và AB = a nên AH = . 2 Trong A ∆ A′H có 2 2 A′H = AA′ − AH 2 2 10a a 3a = − = . 4 4 2 2 3 a 3 3a 3a 3 Suy ra V = = ′ ′ ′ . . ABC. A B C 4 2 8
Câu 82. Cho hình lăng trụ tam giác đều có tất cả các cạnh đều bằng a . Tính theo a thể tích của khối lăng trụ. 3 2a 3 a 3 a 3 3 a 3 A. . B. . C. . D. . 3 3 4 12 Hướng dẫn giải Chọn C 2 3 a 3 a 3
V = AA .′S = . a = . ABC 4 4
Câu 83. Cho hình lăng trụ tam giác đều có các cạnh đều bằng 2a .Thể tích khối lăng trụ đều là: 3 2a 3 2a 3 3 a A. . B. . C. 3 2a 3 . D. . 3 3 3 Hướng dẫn giải Chọn C 2 (2a) 3 3 V = . B h =
.(2a) = 2 3a . 4
Câu 84. Một hình lăng trụ có đáy là tam giác đều cạnh bằng a , cạnh bên bằng b và tạo với mặt phẳng đáy
một góc α . Thể tích của khối lăng trụ đó là 3 3 3 3 A. 2 a b cosα . B. 2 a b cosα . C. 2 a b sin α . D. 2 a b sin α . 12 4 12 4 Hướng dẫn giải https://toanmath.com/ Chọn D A' C' B' A C H B
Gọi H là hình chiếu của A′ lên ( ABC ) .
Lúc đó góc giữa AA′ với ( ABC) là  A′AH = α . A′H Trong A ∆ ′AH có sinα =
⇒ A′H = bsinα AA′ . 2 2 a 3 a b 3 V = ′ = = ′ ′ ′ A H .S b sin α. sin α . ABC. A B C ABC ∆ 4 4
Câu 85.] Cho (H ) là khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng a Thể tích của (H ) bằng: 3 a 2 3 a 3 3 a 3 3 a A. . C. . D. . 3 B. 4 . 2 2 Hướng dẫn giải Chọn B A′ C′ B′ A a B C . 2 3 Thể tích của a 3 a 3
(H ) bằng V = . a = . 4 4
Câu 86. Cho hình lăng trụ ABC. ’ A ’
B C’ có đáy là tam giác đều cạnh a . Hình chiếu của A′ trên mặt phẳng
( ABC) là trung điểm H của cạnh BC . AA' = a 7 . Tính thể tích V của khối lăng trụ đã cho. 3 5 3a 3 3a 3 5 3a 3 5 3a A. . B. . C. . D. . 8 8 24 6 Hướng dẫn giải Chọn A 2 a 3
+ Diện tích đáy: S = . 4 + Chiều cao 5a 2 2 A ' H = AA ' − AH = . 2 2 3 a 3 5a 5 3a V = . = 4 2 8 .
Câu 87. Cho lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng a và AB′ ⊥ BC′ . Khi đó thể tích của
khối lăng trụ trên sẽ là: https://toanmath.com/ 3 6a 3 7a 3 6a A. V = . B. V = . C. 3 V = 6a . D. V = . 8 8 4 Hướng dẫn giải Chọn A A' C' B' x A C B  
    1 a
Ta có AB .′BC′ = ( AB + BB′).(BC + CC′) 2 2 = − a + x = 2
0 ⇔ x = A′A = . 2 2 2 3
Vậy thể tích lăng trụ là a 3 a 2 a 6 V = . = . 4 2 8
Câu 88. Cho hình lăng trụ đều ABC.A′B C
′ ′ có cạnh đáy bằng a . M , N là hai điểm thõa mãn 
   
MB + 2MB′ = 0 ; NB′ = 3NC′ . Biết hai mặt phẳng (MCA) và ( NAB) vuông góc với nhau. Tính
thể tích của hình lăng trụ. 3 3a 2 3 9a 2 3 9a 2 3 3a 2 A. B. C. D. 8 8 16 16 Hướng dẫn giải Chọn C https://toanmath.com/
Chọn hệ tọa độ Oxyz như hình vẽ  a   a 3   a   a 3 2h   a 3 a h  Ta có A 0; − ; 0  , B  ; 0; 0  , C 0; ;0   , M  ; 0;  , I  ; ;   2        2    2  2 3   4 4 3  
  a 3 a    a 3 a h  2   
ah ah 3 a 3  AB =  ; ; 0    , BI =  − ; ;  
 ⇒ n = AB, BI  =  ; ;      2 2   4 4 3   6 6 4   
  a 3 a 2h  2     2ah −a 3 
AC = (0; a;0) , AM =  ; ;  
 ⇒ n = AC, AM  =  ; 0;      2 2 3   2 3 2     2a h 3a 3a 6
Ta có ( NAB) ⊥ (MAC ) 2 2 4 ⇔ n .n = 0 ⇔ − = 0 ⇔ h = 1 2 6.3 8 4 3 3a 6 1 3 9a 2 V = = ′ ′ ′ . . . a . a . ABC. A B C 4 2 2 16
Câu 89. Cho ( H ) là hình lăng trụ xiên ABC.A′B C
′ ′ có đáy là tam giác đều cạch a , hình chiếu vuông góc
A′ lên đáy trùng với tâm đường tròn ngoại tiếp tam giác ABC và A′A hợp đáy bằng 60° . Thể
tích của (H ) bằng. 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 4 12 2 6 Hướng dẫn giải Chọn A 2 a 3 S = . ABC ∆ 4
Gọi O là hình chiếu của A′ lên mp( ABC) , I là trung điểm của BC .
Góc giữa AA′ và mp( ABC) là góc  A′AO = 60° . https://toanmath.com/ 2 a 3 AO = AI =
, A′O = A .
O tan 60° = a . 3 3 3 a 3 = ′ ( V S A O = . H ) . ABC ∆ 4 A' C' B' 60o A C O B .
Câu 90. Cho lăng trụ tam giác đều ABC.A′B C
′ ′ có độ dài cạnh đáy bằng 2a , cạnh bên bằng a 3 . Tính
thể tích V của lăng trụ. A. 3 V = 2a 3 . B. 3 V = 2a . C. 3 V = a 3 . D. 3 V = 3a . Hướng dẫn giải Chọn D (2a)2
Diện tích đáy tam giác đều 3 2 S = = a 3 . 4 Thể tích lăng trụ 2 3
V = S.h = a
3.a 3 = 3a .
Câu 91. Cho hình lăng trụ tam giác đều có các cạnh đều bằng .
a Thể tích khối lăng trụ đều là 3 2a 3 a 3 3 2a 2 3 a A. . B. . C. . D. . 3 4 3 3 Hướng dẫn giải Chọn B
Ta có hình lăng trụ tam giác đều là hình lăng trụ đứng có đáy là tam giác đều. Gọi hình lăng trụ
cần tính thể tích là ABCA’B’C’. 1 1 2 3a Ta có: S = A . B AC sinA = =  0 . a . a sin 60 ABC 2 2 4 2 3a 3 3a V = AA'.S = . a = ABCA'B'C'  ABC 4 4
Câu 92. Cho hình lăng trụ đứng ABC . D A′B C ′ D
′ ′ có đáy là hình vuông cạnh bằng 3, đường chéo AB′ của mặt bên ( ABB A
′ ′) có độ dài bằng 5. Tính thể tích V của khối lăng trụ ABC . D A′B C ′ D ′ ′ ?
A. V = 18 .
B. V = 48 .
C. V = 36 .
D. V = 45 . Hướng dẫn giải Chọn C https://toanmath.com/ D A C B 5 D' A' C' 3 B' .
Xét tam giác vuông AA′B′ có: 2 2 AA′ =
AB′ − A′B′ = 4 và có 2 S = 3 = 9. ABCD V = = ′ ′ ′ ′ 4.9 36 . ABCD. A B C D
Câu 93. Cho hình lăng trụ đều ABC.A′B C
′ ′ có cạnh đáy bằng a . Đường thẳng AB′ tạo với mặt phẳng
(BCC B′′) một góc 30°. Thể tích khối lăng trụ ABC.A′B C
′ ′ theo a . 3 a 6 3 a 3 a 6 3 3a A. . B. . C. . D. . 4 4 12 4 Hướng dẫn giải Chọn A A' B' A C M B
Gọi M là trung điểm của cạnh BC . Do ABC.A′B C
′ ′ là hình lăng trụ tam giác đều nên ta có AM ⊥ ( BCC B
′ ′) ⇒ ( AB′ (BCC B ′ ′)) =  , AB M ′ = 30°. AM AM 3a
Xét tam giác vuông AB M ′ ta có tan 30° = ⇔ AB′ = ⇔ AB′ = . AB′ tan 30° 2 2 2 9a a
Xét tam giác vuông B B ′ M ta có 2 2 BB′ = B M ′ − BM = − = a 2 . 4 4 3
Thể tích khối lăng trụ 1 a 6
ABC.A′B C ′ ′ là V = ° ′ = ′ ′ ′ A . B AC.sin 60 .BB . ABC. A B C 2 4
Câu 94. Cho khối lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng 2 , diện tích tam giác A′BC bằng
3 . Tính thể tích của khối lăng trụ. 2 5 A. 2 . B. . C. 3 2 . D. 2 5 . 3 Hướng dẫn giải Chọn C https://toanmath.com/ A′ B′ C′ A C M B .  ⊥ Gọi BC AM
M là trung điểm của BC .Vì 
⇒ BC ⊥ A′M . BC ⊥ AA′ 1 S = ⇔ ′ = 1 ⇔ ′ = ⇔ ′ = ∆ ′ 3 A M .BC 3 A M .2 3 A M 3 . A BC 2 2 2 2 AA′ =
AM − A′M = − ( )2 2 3 3 = 6 . 2 2 3 V = ′ = = ′ ′ ′ S .A A . 6 3 2 . ABC. A B C ABC ∆ 4
Câu 95. Cho hình lăng trụ đều ABC.A′B C
′ ′, biết khoảng cách từ điểm C đến mặt phẳng ( ABC′) bằng a ,
góc giữa hai mặt phẳng ( ABC′) và (BCC B ′ ′) bằng α với 1 cosα =
(tham khảo hình vẽ bên 3
dưới).Thể tích khối lăng trụ bằng C' B' A' C B A 3 9 15a 3 3 15a 3 3 15a 3 9 15a A. . B. . C. . D. . 20 20 10 10 Hướng dẫn giải Chọn A C' B' A' H C K B O A https://toanmath.com/
Gọi 2x là cạnh của tam giác đều, Gọi O, K lần lượt là trung điểm của AB, BC
Kẻ CK ⊥ C′O
Ta có CH ⊥ C O
′ và CH ⊥ AB nên CH ⊥ ( ABC′) và d (C,( ABC ')) = CH = a 1 1 1 1 1 1 Suy ra: = + = + 2 2 2 CH CC′ hay CO 2 2 2 a CC′ (1) 3x
Ta có hình chiếu vuông góc của tam giác ABC′ lên mặt phẳng (BCC B
′ ′) là tam giác KBC ' Do đó S 1 KBC ' = cosα = S 3 ABC ∆ ' 1 1 1 Ta có: S = . . x CC′ = ′ = ′ + = ′ +  và 2 2 2 2 S .A . B C O .A . B CC CO x CC 3x KBC ' ∆ 2 ABC ' 2 2 Do đó 1 1 2 2 2 2 2 2 . . x CC′ =
x CC′ + 3x ⇔ 3CC′ = 2 CC′ + 3x ⇔ 5CC′ = 12x (2) 2 3 Từ ( ) 1 1 4 3a 1 , (2) ta có 2 2 = +
⇔ 5CC′ = 9a ⇔ CC′ = 2 2 2 a CC′ 5CC′ 5 a 3 Suy ra x = 2 2 3
Vậy thể tích khối lăng trụ là 3 3a 3a 9 15a V = S .CC′ = . = . ABC 4 5 20
Câu 96.Cho hình chóp S.ABCD có đáy ABCD là hình vuông, các tam giác SAB và SAD là những tam
giác vuông tại A . Mặt phẳng (P) qua A vuông góc với cạnh bên SC cắt SB, SC, SD lần lượt
tại các điểm M , N, P . Biết SC = 8a ,  0
ASC = 60 . Tính thể tích khối cầu ngoại tiếp đa diện ABCDMNP ? A. 3
V = 6π a . B. 3
V = 24π a . C. 3
V = 32 3π a . D. 3
V = 18 3π a . Hướng dẫn giải Chọn C
Mặt phẳng ( AMNP) ⊥ ⇒  0 SC ANC = 90 ( ) 1 , SC ⊥ AM .
Do (SAB) ⊥ BC ⇒ BC ⊥ AM ⇒ AM ⊥ (SBC ) ⇒ ⊥ ⇒  0 AM MC AMC = 90 (2) Tương tự ta có  0 APC = 90 (3) https://toanmath.com/
Do ABCD là hình vuông nên từ ( )
1 , (2), (3) suy ra AC là đường kính mặt cầu ngoại tiếp đa diện ABCDMNP . AC 4
Xét tam giác SAC có sin 60 =
⇒ AC = 4 3a ⇒ R = 2 3a ⇒ V = π (2 3a)3 0 3 = 32 3π a . SC 3
Câu 97. Cho khối lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng 2 , diện tích tam giác A′BC bằng
3 . Tính thể tích của khối lăng trụ 2 5 A. 3 2 . B. 2 5 . C. 2 . D. . 3 Hướng dẫn giải Chọn A
Gọi M là trung điểm của BC . BC ⊥ AM Vì 
⇒ BC ⊥ A′M . BC ⊥ AA′ 1 S = ⇔ ′ = 1 ⇔ ′ = ⇔ ′ = ∆ ′ 3 A M .BC 3 A M .2 3 A M 3 . A BC 2 2 2 2 AA′ =
AM − A′M = − ( )2 2 3 3 = 6 . 2 2 3 V = = = ′ ′ ′ S .A ' A . 6 3 2 ABC. A B C ABC ∆ 4
Câu 98. Cho hình lăng trụ tứ giác ABC . D A′B C ′ D
′ ′ có đáy ABCD là hình vuông cạnh a và thể tích bằng 2
3a . Tính chiều cao h của hình lăng trụ đã cho. a A. h = .
B. h = 9a .
C. h = 3a .
D. h = a . 3 Hướng dẫn giải Chọn C Ta có 2 S = a . ABCD 2 V ′ ′ ′ ′ 3a Suy ra: ABCD. A B C D h = = = 3a . 2 S a ABCD
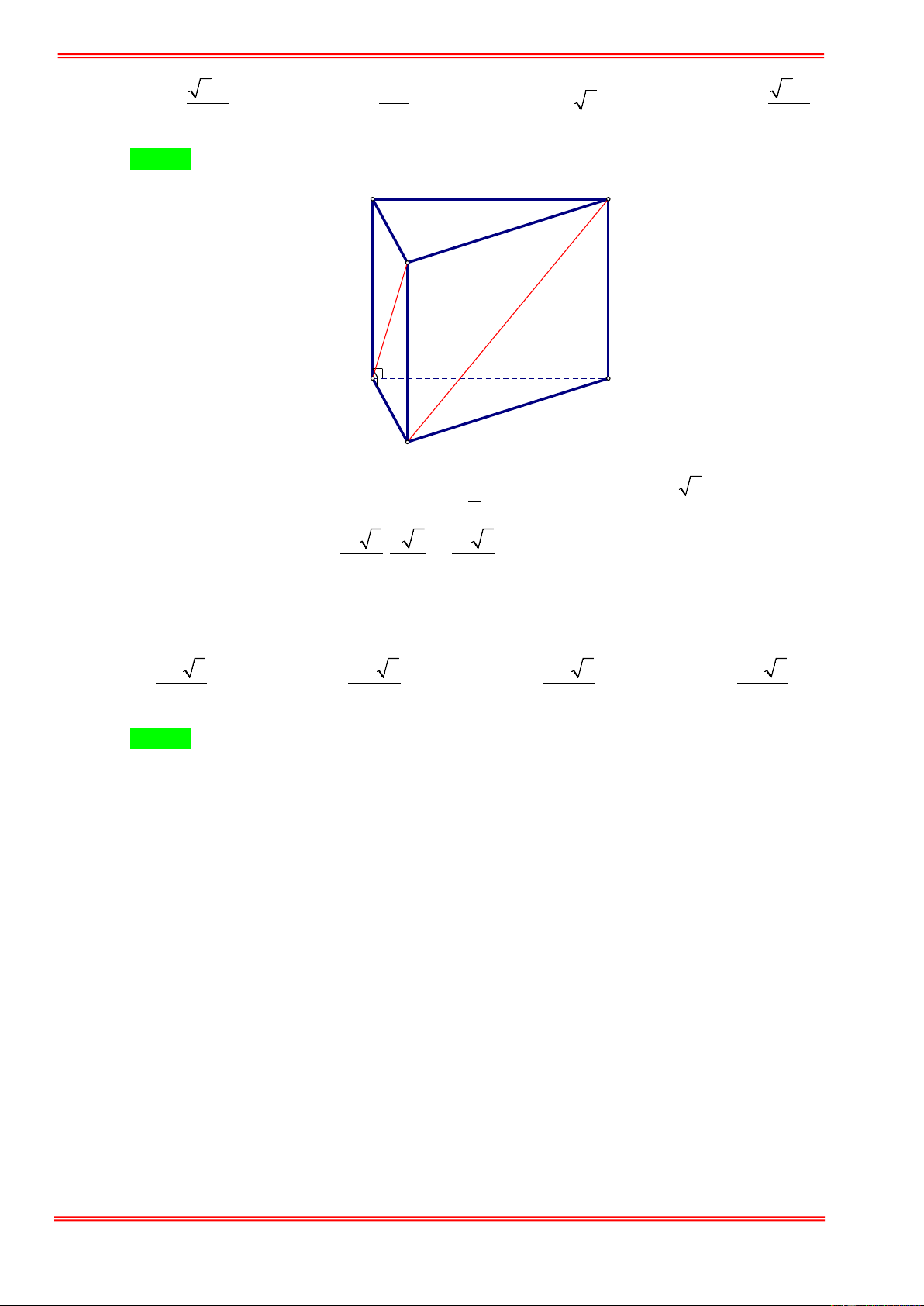
Câu 99. Cho lăng trụ đứng ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Góc tạo bởi cạnh BC′ và mặt đáy ( A′B C ′ ′) bằng o
30 . Tính thể tích khối lăng trụ. 3 3a 3 a 3 a 3 a A. . B. . C. . D. . 4 2 12 4 Hướng dẫn giải Chọn D https://toanmath.com/ . BC′  ( A′B C ′ ′) =  0 , BC B ′ ′ = 30  . 2 a 3 a 3 3 a S = ; 0
BB′ = tan 30 .B C ′ ′ = ⇒ V = . ABC 4 3 4
Câu 100.] Cho lăng trụ đứng ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh a , cạnh bên A′B tạo với đáy một góc 0
45 Thể tích khối lăng trụ ABC.A′B C ′ ′ là: 3 2a A. V = . B. 3 V = a 3 .
ABC. A' B 'C ' 3
ABC. A' B 'C ' 3 a 3 a 3 C. V = . D. V = .
ABC. A' B 'C ' 6
ABC. A' B 'C ' 4 Hướng dẫn giải Chọn D
Ta có AB là hình chiếu vuông góc của A′B lên mp( ABC) . A′ C′ B′ A C 45 0 B . ⇒ 
(A′B ABC )=  0 , ( ) ABA′ = 45 .
Khi đó tam giác ABA′ vuông cân tại A ⇒ AA′ = AB = a . 2 3 Vậy a 3 a 3 V = = ⇒ ′ ′ ′ .a chọn phương án. ABC.A B C 4 4 D.
Câu 101. Cho lăng trụ tam giác đều ABC.ABC có tất cả các cạnh bằng 2a . Tính thể tích khối lăng trụ
ABC.ABC . 3 a 3 3 a 3 A. 3 2a 3 . B. 3 a 3 . C. . D. . 4 2 Hướng dẫn giải Chọn D (2a)2 3 Ta có 3 V = S .AA′ = .2a = 2a 3 . ABC 4
------------- HẾT ------------- https://toanmath.com/
Document Outline

  • 3.2 BT KHỐI LĂNG TRỤ ĐỀU
    • THỂ TÍCH KHỐI LĂNG TRỤ ĐỀU
  • 3.2 HDG KHỐI LĂNG TRỤ ĐỀU
    • THỂ TÍCH KHỐI LĂNG TRỤ ĐỀU