Bài tập thể tích khối lăng trụ xiên có lời giải chi tiết Toán 12

Trong các bài toán liên quan đến việc tính thể tích khối lăng trụ thì bài toán về khối lăng trụ xiên thường có độ phức tạp nhiều hơn, vì việc xác định và tính độ dài đường cao của khối lăng trụ xiên là khó khăn hơn và các giả thiết đi kèm cũng có sự đa dạng nhiều hơn.Mời bạn đọc đón xem.

51 26 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

39 trang 8 tháng trước

Tác giả:

Profile Lan Tường
https://toanmath.com/
THỂ TÍCH KHỐI LĂNG TRỤ XIÊN
Câu 1. Cho lăng trụ tam giác
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Độ dài cạnh bên bằng
4a
. Mặt
phẳng
( )
BCC B
′′
vuông góc với đáy và
30B BC
′
= °
. Thể tích khối chóp
.ACC B
′′
là:
A.
3
3
6
a
. B.
3
3
12
a
. C.
3
3
18
a
. D.
3
3
2
a
.
Câu 2. Cho lăng trụ
có đáy
ABCD
là hình chữ nhật với
6
AB =
,
3
AD
=
,
3AC
′
=
và
mặt phẳng
(
)
AA C C
′′
vuông góc với mặt đáy. Biết hai mặt phẳng
( )
AA C C
′′
,
(
)
AABB
′′
tạo với
nhau góc
α
thỏa mãn
3
tan
4
α
=
. Thể tích khối lăng trụ
bằng?
A.
6
V =
. B.
8V
=
. C.
12
V =
. D.
10
V =
.
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi H là điểm trên cạnh SD sao cho
53SH SD
=
, mặt phẳng
( )
α
qua B, H và song song với đường thẳng AC cắt hai cạnh SA, SC lần
lượt tại E, F. Tính tỉ số thể tích
.
.
.
C BEHF
S ABCD
V
V
A.
1
.
7
B.
3
.
20
C.
6
.
35
D.
1
.
6
Câu 4. Cho lăng trụ tam giác
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Độ dài cạnh bên bằng
4a
. Mặt
phẳng
(
)
BCC B
′′
vuông góc với đáy và
30B BC
′
= °
. Thể tích khối chóp
.ACC B
′′
là:
A.
3
3
2
a
. B.
3
3
12
a
. C.
3
3
18
a
. D.
3
3
6
a
.
Câu 5. Cho hình lăng trụ
.
′′′
ABC A B C
có đáy
ABC
là tam giác vuông tại
A
. cạnh
2=BC a
và
60= °ABC
. Biết tứ giác
′′
BCC B
là hình thoi có
′
B BC
nhọn. Biết
( )
′′
BCC B
vuông góc với
( )
ABC
và
( )
′′
ABB A
tạo với
( )
ABC
góc
45°
. Thể tích của khối lăng trụ
.
′′′
ABC A B C
bằng
A.
3
37
a
. B.
3
7
a
. C.
3
3
7
a
. D.
3
6
7
a
.
Câu 6. Cho lăng trụ
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông tại
A
,
30ABC = °
. Điểm
M
là trung điểm
cạnh
AB
, tam giác
MA C
′
đều cạnh
23a
và nằm trong mặt phẳng vuông góc với đáy. Thể tích
khối lăng trụ
.ABC A B C
′′′
là
A.
3
72 2
7
a
. B.
3
24 3
7
a
. C.
3
72 3
7
a
. D.
3
24 2
7
a
.
Câu 7. Cho hình lăng trụ tứ giác
.ABCD A B C D
′′′′
có đáy
ABCD
là hình vuông cạnh
a
và thể tích bằng
3
3a
. Tính chiều cao
h
của lăng trụ đã cho.
A.
9ha=
. B.
3
a
h =
. C.
ha=
. D.
3ha=
.
Câu 8. Thể tích của khối lăng trụ có chiều cao bằng
h
và diện tích đáy bằng
B
là
A.
2
V Bh
=
. B.
V Bh
=
. C.
1
3
V Bh=
. D.
V Bh
π
=
.
Câu 9.Cho hình lăng trụ
.ABCD A B C D
′′′′
có đáy
ABCD
là hình vuông cạnh
a
. Các cạnh bên tạo với đáy
một góc
o
60
. Đỉnh
A
′
cách đều các đỉnh
,,,ABCD
. Trong các số dưới đây, số nào ghi giá trị thể
tích của hình lăng trụ nói trên?
https://toanmath.com/
A.
3
6
9
a
. B.
3
3
2
a
. C.
3
6
2
a
. D.
3
6
3
a
.
Câu 10.Tính thể tích
V
của khối lăng trụ có diện tích mặt đáy bằng
2
3 3 cm
và chiều cao bằng
6 cm
.
A.
(
)
3
9 2 cmV =
. B.
(
)
3
12 2 cmV
=
. C.
( )
3
92
cm
2
V =
. D.
(
)
3
3 2 cm
V
=
.
Câu 11.Cho lăng trụ đều
.ABC A B C
′′′
có
3cmAB
′
=
và đường thẳng
AB
′
vuông góc với đường thẳng
BC
′
. Thể tích khối lăng trụ
.ABC A B C
′′′
bằng
A.
3
27 6
cm
16
. B.
3
2 3cm
. C.
3
76
cm
4
. D.
3
9
cm
2
.
Câu 12. Cho hình lăng trụ
.ABC A B C

có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của
A
lên
mặt phẳng
ABC
trùng với trung điểm cạnh
BC
. Góc giữa
BB
và mặt phẳng
ABC
bằng
60
. Tính thể tích khối lăng trụ
.ABC A B C

.
A.
3
3
8
a
. B.
3
23
8
a
. C.
3
3
4
a
. D.
3
33
8
a
.
Câu 13. Cho lăng trụ
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh bằng
a
, biết
AA AB AC a
′′′
= = =
.
Tính thể tích khối lăng trụ
.ABC A B C
′′′
?
A.
3
3
4
a
. B.
3
2
4
a
. C.
3
3
4
a
. D.
3
4
a
.
Câu 14. Cho hình hộp
.ABCD A B C D
′′′′
có diện tích tứ giác
ABCD
bằng
12
, khoảng cách giữa hai mặt
phẳng
( )
ABCD
và
( )
ABCD
′′′′
bằng
2
. Tính thể tích
V
của khối hộp.
A.
12
V =
. B.
8V =
. C.
24
V =
. D.
72
V =
.
Câu 15. Cho lăng trụ tam giác
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh
22AB a
=
. Biết
8AC a
′
=
và
tạo với mặt đáy một góc
45°
. Thể tích khối đa diện
ABCC B
′′
bằng
A.
3
16 6
3
a
. B.
3
86
3
a
. C.
3
16 3
3
a
. D.
3
83
3
a
.
Câu 16. Cho khối lăng trụ
.ABC A B C
′′′
. Gọi
E
là trọng tâm tam giác
ABC
′′′
và
F
là trung điểm
BC
. Tính
tỉ số thể tích giữa khối
.B EAF
′
và khối lăng trụ
.ABC A B C
′′′
.
A.
1
8
. B.
1
5
. C.
1
6
. D.
1
4
.
Câu 17. Cho hình lăng trụ tam giác
.
′′′
ABC A B C
có đáy
ABC
là tam giác đều cạnh
2a
, hình chiếu của
′
A
trên mặt phẳng
( )
ABC
là trung điểm cạnh
BC
. Biết góc giữa hai mặt phẳng
(
)
′
ABA
và
( )
ABC
bằng
45°
. Tính thể tích
V
của khối chóp
.
′′
A BCC B
.
A.
3
3
2
a
. B.
3
=Va
. C.
3
3a
. D.
3
23
3
a
.
Câu 18. Cho khối lăng trụ có thể tích
,V
diện tích đáy là
B
và chiều cao
.h
Tìm khẳng định đúng?
A.
3V Bh=
. B.
1
3
V Bh=
. C.
V Bh=
. D.
V Bh=
.
Câu 19. Cho hình lăng trụ
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông tại
,
B
60 ,ACB =
,BC a=
2AA a
′
=
. Cạnh bên tạo với mặt phẳng
( )
ABC
một góc
30
. Thể tích khối lăng trụ
.ABC A B C
′′′
bằng
A.
3
3
6
a
. B.
3
3
3
a
. C.
3
3
2
a
. D.
3
3a
.
Câu 20.Cho
( )
H
là khối lăng trụ có chiều cao bằng
3,a
đáy là hình vuông cạnh
.a
Thể tích của
( )
H
bằng.
A.
3
4a
. B.
3
2a
. C.
3
3a
. D.
3
a
.
https://toanmath.com/
Câu 21.Cho hình lăng trụ
.ABCD A B C D
′′′′
có đáy là hình thoi cạnh bằng
a
và
120ABC = °
. Góc giữa cạnh
bên
AA
′
và mặt đáy bằng
60°
, điểm
'
A
cách đều các điểm
A
,
B
,
D
. Tính thể tích khối lăng trụ
đã cho theo
a
.
A.
3
3
6
a
. B.
3
3
3
a
. C.
3
3
2
a
. D.
3
3
12
a
.
Câu 22. Cho lăng trụ
.
ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của điểm
'A
lên mặt phẳng
(
)
ABC
trùng với trọng tâm tam giác
ABC
. Biết khoảng cách giữa hai đường thẳng
'AA
và
BC
bằng
3
4
a
. Khi đó thể tích của khối lăng trụ là
A.
3
3
3
a
. B.
3
3
6
a
. C.
3
3
24
a
. D.
3
3
12
a
.
Câu 23. Cho hình lăng trụ
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của điểm
A
′
lên mặt phẳng
(
)
ABC
trùng với trọng tâm tam giác
ABC
. Biết khoảng cách giữa hai đường thẳng
AA
′
và
BC
bằng
3
4
a
. Tính theo
a
thể tích
V
của khối lăng trụ
.ABC A B C
′′′
.
A.
3
3
12
a
V =
. B.
3
3
3
a
V =
. C.
3
3
24
a
V =
. D.
3
3
6
a
V =
.
Câu 24. Các đường chéo của các mặt của một hình hộp chữ nhật bằng
, , abc
. Thể tích của khối hộp đó là
A.
.
V abc=
B.
.V abc=++
C.
( )( )( )
22 2222 222
.
8
bcacababc
V
+− +− +−
=
D.
( )( )( )
22 2222 222
.
8
bcacababc
V
+− +− +−
=
Câu 25. Cho lăng trụ
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của điểm
A
′
lên
mặt phẳng
( )
ABC
trùng với trọng tâm của tam giác
ABC
. Biết khoảng cách giữa hai đường thẳng
AA
′
và
BC
bằng
3
4
a
. Khi đó thể tích của khối lăng trụ là
A.
3
3
24
a
. B.
3
3
12
a
. C.
3
3
36
a
. D.
3
3
6
a
.
Câu 26. Cho hình lăng trụ
.ABC A B C
′′′
, đáy
ABC
là tam giác đều cạnh
x
. Hình chiếu của đỉnh
A
′
lên
mặt phẳng
( )
ABC
trùng với tâm
ABC∆
, cạnh
2AA x
′
=
. Khi đó thể tích khối lăng trụ là:
A.
3
11
12
x
. B.
3
39
8
x
. C.
3
3
2
x
. D.
3
11
4
x
.
Câu 27. Cho hình hộp
có đáy là hình chữ nhật với
3, 7AB AD= =
và cạnh bên bằng
1
. Hai mặt bên
( )
ABB A
′′
và
( )
ADD A
′′
lần lượt tạo với đáy các góc
45°
và
60°
. Thể tích khối hộp
bằng
A.
33
B.
77
C.
7
D.
3
Câu 28. Thể tích của khối lăng trụ có chiều cao bằng
h
và diện tích đáy bằng
B
là
A.
1
6
V Bh=
. B.
1
3
V Bh=
. C.
1
2
V Bh=
. D.
V Bh=
.
https://toanmath.com/
Câu 29. Cho lăng trụ
111
.ABC A B C
có đáy
ABC
là tam giác vuông tại
C
, cạnh
5AC a=
. Hình chiếu vuông
góc của
1
A
lên mặt phẳng
ABC
là trung điểm của cạnh
AC
, góc giữa mặt phẳng
( )
11
AA B B
với
(
)
11
AAC C
bằng
o
30
, cạnh bên của lăng trụ tạo với đáy một góc
o
60
. Tính thể tích
V
của lăng trụ
111
.ABC A BC
?
A.
3
3.
8
a
V =
. B.
3
24
a
V =
. C.
3
8
a
V =
. D.
3
3.
24
a
V =
.
Câu 30.Cho hình lăng trụ có tất cả các cạnh đều bằng
a
, đáy là lục giác đều, góc tạo bởi cạnh bên và mặt
đáy là
60°
. Tính thể tích khối lăng trụ.
A.
3
9
4
Va=
. B.
3
3
4
Va
=
. C.
3
3
2
Va=
. D.
3
27
8
Va=
.
Câu 31. Khối lăng trụ
.
ABC A B C
′′′
có đáy là một tam giác đều cạnh
,a
góc giữa cạnh bên và mặt phẳng đáy
bằng
30°
Hình chiếu của đỉnh
A
′
trên mặt phẳng đáy
( )
ABC
trùng với trung điểm của cạnh
.BC
Tính thể tích của khối lăng trụ đã cho.
A.
3
3
4
a
. B.
3
3
12
a
. C.
3
3
8
a
. D.
3
3
3
a
.
Câu 32. Cho lăng trụ tam giác
.
′′′
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
, cạnh
22
=
AC
.
Biết
′
AC
tạo với mặt phẳng
( )
ABC
một góc
60°
và
4
′
=AC
. Tính thể tích
V
của khối đa diện
′′
ABCB C
.
A.
16 3
3
=V
. B.
16
3
=V
. C.
83
3
=V
. D.
8
3
=
V
.
Câu 33. Cho hình lăng trụ
.ABCABC
′′′
có thể tích bằng
30
. Gọi
I
,
J
,
K
lần lượt là trung điểm của
,
AA
′
,BB
′
CC
′
. Tính thể tích
V
của tứ diện
CIJK
.
A.
15
2
V =
. B.
12V =
. C.
6V =
. D.
5V =
.
Câu 34. Khối lăng trụ
.
′′′
ABC A B C
có đáy là tam giác đều,
a
là độ dài cạnh đáy. Góc giữa cạnh bên và
đáy là
30
°
. Hình chiếu vuông góc của
′
A
trên mặt
( )
ABC
trùng với trung điểm của
BC
. Thể
tích của khối lăng trụ đã cho là
A.
3
3
8
a
. B.
3
3
3
a
. C.
3
3
4
a
. D.
3
3
12
a
.
Câu 35. Cho lăng trụ
có đáy
ABCD
là hình thoi cạnh
a
, tâm
O
và
120ABC = °
. Góc giữa
cạnh bên
AA
′
và mặt đáy bằng
60°
. Đỉnh
A
′
cách đều các điểm
A
,
B
,
D
. Tính theo
a
thể tích
V
của khối lăng trụ đã cho.
A.
3
3
2
a
V =
. B.
3
3
6
a
V =
. C.
3
3
2
a
V =
. D.
3
3Va=
.
Câu 36. Cho hình hộp
.ABCD A B C D
′′′′
có đáy là hình chữ nhật với
3, 7AB AD= =
và cạnh bên bằng
1
. Hai mặt bên
( )
ABB A
′′
và
( )
ADD A
′′
lần lượt tạo với đáy các góc
45°
và
60°
. Thể tích khối hộp
bằng
A.
33
B.
77
C.
7
D.
3
Câu 37. Cho hình lăng trụ
ABCA B C
′′′
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của
A
′
lên
mặt phẳng
( )
ABC
trùng với trọng tâm tam giác
ABC
. Biết khoảng cách giữa hai đường thẳng
AA
′
và
BC
bằng
3
4
a
. Tính thể tích
V
của khối lăng trụ
.ABCA B C
′′′
https://toanmath.com/
A.
3
3
.
6
a
V
=
B.
3
3
.
24
a
V =
C.
3
3
.
12
a
V =
D.
3
3
.
3
a
V =
Câu 38. Cho khối lăng trụ
.
ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh bằng
a
, cạnh bên
AA a
′
=
, góc
giữa
AA
′
và mặt phẳng đáy bằng
30°
. Tính thể tích khối lăng trụ đã cho theo
a
.
A.
3
3
8
a
. B.
3
3
24
a
. C.
3
3
4
a
. D.
3
3
12
a
.
Câu 39. Cho hình lăng trụ
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của điểm
A
′
lên mặt phẳng
(
)
ABC
trùng với trọng tâm tam giác
ABC
. Biết khoảng cách giữa hai đường
AA
′
và
BC
bằng
3
4
a
. Tính thể tích
V
của khối lăng trụ
.ABC A B C
′′′
.
A.
3
3
24
a
V =
. B.
3
3
12
a
V =
. C.
3
3
3
a
V =
. D.
3
3
6
a
V =
.
Câu 46. Cho hình lăng trụ
.'' 'ABC A B C
có đáy là tam giác đều cạnh
3a
, hình chiếu của
'A
trên mặt phẳng
( )
ABC
trùng với tâm đường tròn ngoại tiếp tam giác
ABC
. Cạnh
'
AA
hợp với mặt phẳng đáy
một góc
45
°
. Thể tích của khối lăng trụ
.'' 'ABC A B C
tính theo
a
bằng.
A.
3
9
4
a
. B.
3
27
4
a
. C.
3
3
4
a
. D.
3
27
6
a
.
Câu 47. Khối lăng trụ có đáy là hình vuông cạnh
a
, đường cao bằng
3a
có thể tích bằng
A.
3
3
6
a
. B.
3
3
3
a
. C.
3
3a
. D.
3
23a
.
Câu 48. Cho lăng trụ
111
ABCA B C
có diện tích mặt bên
11
ABB A
bằng
4
; khoảng cách giữa cạnh
1
CC
và mặt
phẳng
(
)
11
ABB A
bằng 7. Tính thể tích khối lăng trụ
111
ABCA B C
.
A.
14
B.
28
3
C.
14
3
D.
28
Câu 49. Cho lăng trụ tam giác
.ABC A B C
′′′
. Các điểm
M
,
N
,
P
lần lượt thuộc các cạnh
AA
′
,
BB
′
,
CC
′
sao cho
1
2
AM
AA
=
′
,
2
3
BN
BB
=
′
và mặt phẳng
( )
MNP
chia lăng trụ thành hai phần có thể tích bằng
nhau. Khi đó tỉ số
CP
CC
′
là
A.
1
4
. B.
5
12
. C.
1
3
. D.
1
2
.
Câu 50. Cho hình lăng trụ
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh
a
,
3
2
a
AA
′
=
. Biết rằng hình chiếu
vuông góc của
A
′
lên
( )
ABC
là trung điểm
BC
. Tính thể tích
V
của khối lăng trụ đó.
A.
3
Va
=
. B.
3
2
3
a
V =
. C.
3
3
42
a
V =
. D.
3
3
2
Va=
.
Câu 51. Cho lăng trụ tam giác
.ABC A B C
′′′
có đáy là tam giác
ABC
đều cạnh bằng
a
. Hình chiếu vuông
góc của
A
′
trên mặt phẳng
( )
ABC
trùng với trung điểm
H
của cạnh
AB
. Góc giữa cạnh bên của
lăng trụ và mặt phẳng đáy bằng
o
30
. Tính thể tích của khối lăng trụ đã cho theo
a
.
A.
3
3
4
a
B.
3
4
a
C.
3
24
a
D.
3
8
a
Câu 52. Cho hình lăng trụ
.
′′′
ABC A B C
có đáy là tam giác vuông cân ở
C
. Cạnh
′
=
BB a
và tạo với đáy
một góc bằng
60°
. Hình chiếu vuông góc hạ từ
′
B
lên đáy trùng với trọng tâm của tam giác
ABC
. Thể tích khối lăng trụ
.
′′′
ABC A B C
là:
https://toanmath.com/
A.
3
93
80
a
. B.
3
9
80
a
. C.
3
33
80
a
. D.
3
3
80
a
.
Câu 53. Cho lăng trụ
.
ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của điểm
A
′
lên
mặt phẳng
( )
ABC
trùng với trọng tâm tam giác
ABC
. Biết khoảng cách giữa hai đường thẳng
AA
′
và
BC
bằng
3
4
a
. Khi đó thể tích của khối lăng trụ là
A.
3
3
6
a
. B.
3
3
3
a
. C.
3
3
24
a
. D.
3
3
12
a
.
Câu 54.Cho hình hộp
.ABCD A B C D
′′′′
có
60 , 7, 3,BCD AC a BD a AB AD=°= = >
,đường chéo
BD
′
hợp với mặt phẳng
(
)
ADD A
′′
góc
30
°
. Tính thể tích
V
của khối hộp
.ABCD A B C D
′′′′
.
A.
3
39
.
3
a
B.
3
23 .a
C.
3
33 .a
D.
3
39 .a
Câu 55. Cho hình lăng trụ
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của điểm
A
′
lên mặt phẳng
( )
ABC
trùng với trọng tâm tam giác
ABC
. Biết khoảng cách giữa hai đường thẳng
AA
′
và
BC
bằng
3
4
a
. Tính thể tích
V
của khối lăng trụ
.ABC A B C
′′′
.
A.
3
3
12
a
V =
. B.
3
3
3
a
V =
. C.
3
3
24
a
V =
. D.
3
3
6
a
V =
.
Câu 56. Cho lăng trụ
.ABC A B C
′′′
có đáy là tam giác đều cạnh
.
a
Hình chiếu vuông góc của mặt phẳng
( )
ABC
trùng với trọng tâm của tam giác
.ABC
Biết thể tích của khối lăng trụ là
3
3
4
a
. Khoảng
cách giữa hai đường thẳng
AB
′
và
BC
là:
A.
2
3
a
. B.
4
3
a
. C.
3
4
a
. D.
3
2
a
.
Câu 57. Một khối lăng trụ tam giác có các cạnh đáy bằng
13
,
14
,
15
cạnh bên tạo với mặt phẳng đáy một góc
30°
và có chiều dài bằng
8
. Khi đó thể tích khối lăng trụ là.
A.
340
. B.
336
. C.
274 3
. D.
124 3
.
Câu 58. Cho lăng trụ tam giác
.'' 'ABC A B C
có đáy
ABC
là đều cạnh
22
AB a=
. Biết
'8AC a=
và tạo với
mặt đáy một góc
0
45
. Thể tích khối đa diện
''ABCC B
bằng
A.
3
83
.
3
a
B.
3
86
.
3
a
C.
3
16 3
.
3
a
D.
3
16 6
.
3
a
Câu 59. Cho lăng trụ
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
,
AA b
′
=
và
AA
′
tạo với mặt đáy một góc
60°
. Tính thể tích khối lăng trụ.
A.
2
3
4
ab
. B.
2
3
8
ab
. C.
2
3
8
ab
. D.
2
1
8
ab
.
Câu 60. Cho khối lăng trụ tam giác
.'' 'ABC A B C
có thể tích bằng 30 (đơn vị thể tích). Thể tích của khối tứ
diện
AB C C
′′
là:
A. 5 (đơn vị thể tích). B. 10 (đơn vị thể tích).
C. 12,5 (đơn vị thể tích). D. 7,5 (đơn vị thể tích).
Câu 61.Cho lăng trụ
.ABCD A B C D
′′′′
với đáy
ABCD
là hình thoi,
2AC a=
,
0
120BAD =
. Hình chiếu vuông
góc của điểm
B
trên mặt phẳng
( )
ABCD
′′′′
là trung điểm cạnh
AB
′′
, góc giữa mặt phẳng
( )
AC D
′′
và mặt đáy lăng trụ bằng
o
60
. Tính thể tích
V
của khối lăng trụ
.
A.
3
3Va
=
. B.
3
63Va=
. C.
3
23Va=
. D.
3
33Va=
.
https://toanmath.com/
THỂ TÍCH KHỐI LĂNG TRỤ XIÊN
Câu 1.Cho lăng trụ tam giác
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Độ dài cạnh bên bằng
4a
. Mặt
phẳng
( )
BCC B
′′
vuông góc với đáy và
30B BC
′
= °
. Thể tích khối chóp
.ACC B
′′
là:
A.
3
3
6
a
. B.
3
3
12
a
. C.
3
3
18
a
. D.
3
3
2
a
.
Hướng dẫn giải
Chọn A
Gọi
H
là hình chiếu của
B
′
trên
BC
. Từ giả thiết suy ra:
(
)
B H ABC
′
⊥
.
1
. .sin
2
BB C
S BB BC B BC
′
′′
=
1
4 . .sin30
2
aa= °
2
a=
.
Mặt khác:
1
.
2
BB C
S B H BC
′
′
=
2
BB C
S
BH
BC
′
′
⇒=
2
2
2
a
a
a
= =
.
.
LT ABC
V BHS
′
=
2
3
2.
4
a
a=
3
3
2
a
=
.
..
1
2
A CC B A CC B B
VV
′′ ′′
=
12 1
.
23 3
LT LT
VV= =
3
13
.
32
a
=
3
3
6
a
=
.
Câu 2. Cho lăng trụ
có đáy
ABCD
là hình chữ nhật với
6AB =
,
3AD =
,
3AC
′
=
và
mặt phẳng
( )
AA C C
′′
vuông góc với mặt đáy. Biết hai mặt phẳng
( )
AA C C
′′
,
( )
AABB
′′
tạo với
nhau góc
α
thỏa mãn
3
tan
4
α
=
. Thể tích khối lăng trụ
bằng?
A.
6V =
. B.
8
V =
. C.
12V =
. D.
10V =
.
16THướng dẫn giải
16TChọn B
16TTừ 16T
B
16T kẻ 16T
BI AC⊥
( )
BI AA C C
′′
⇒⊥
16T.
M
C'
B'
D'
C
D
A
B
A'
I
H
K
https://toanmath.com/
Từ
I
kẻ
IH AA
′
⊥
( ) ( )
( )
, BAACC A BB IA H
′′ ′
=
′
⇒
.
Theo giải thiết ta có
3AC =
.
AB BC
BI
AC
⇒=
2=
.
Xét tam giác vuông
BIH
có
tan
BI
BHI
IH
=
tan
BI
IH
BHI
⇔=
42
3
IH⇔=
.
Xét tam giác vuông
ABC
có
2
.AI AC AB=
2
2
AB
AI
AC
⇒= =
.
Gọi
M
là trung điểm cả
AA
′
, do tam giác
AA C
′
cân tại
C
nên
CM AA
′
⊥
//CM IH⇒
.
Do
2
3
AI AH
AC AM
= =
2
3
AH
AM
⇒=
1
3
AH
AA
⇒=
′
.
Trong tam giác vuông
AHI
kẻ đường cao
HK
ta có
42
9
HK =
⇒
chiều cao của lăng trụ
là
3h HK=
42
3
=
.
Vậy thể tích khối lăng trụ
là
.
..
ABCD A B C D
V AB AD h
′′′′
=
42
63
3
=
8=
.
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi H là điểm trên cạnh SD sao cho
53SH SD=
, mặt phẳng
(
)
α
qua B, H và song song với đường thẳng AC cắt hai cạnh SA, SC lần
lượt tại E, F. Tính tỉ số thể tích
.
.
.
C BEHF
S ABCD
V
V
A.
1
.
7
B.
3
.
20
C.
6
.
35
D.
1
.
6
Hướng dẫn giải
Chọn B
- Đặt
.S ABCD
VV=
- Trong tam giác SOD ta có:
3
.. 1 3 .
4
IS BO HD IS SI SE SF
IO BD HS IO SO SA SC
=⇒=⇒ == =
- Ta có:
.
.
.
33
.
5 10
S HBC
S HBC
S DBC
V
SH V
V
V SD
==⇒=
- Mặt khác:
.
.
.
13
.
4 40
C FHB
C FHB
C SHB
V
CF V
V
V CS
==⇒=
https://toanmath.com/
- Mà:
.
..
.
63
2.
40 20
C BEHF
C BEHF C FHB
S ABCD
V
V
VV
V
==⇒=
Câu 4. Cho lăng trụ tam giác
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Độ dài cạnh bên bằng
4a
. Mặt
phẳng
( )
BCC B
′′
vuông góc với đáy và
30B BC
′
= °
. Thể tích khối chóp
.ACC B
′′
là:
A.
3
3
2
a
. B.
3
3
12
a
. C.
3
3
18
a
. D.
3
3
6
a
.
Hướng dẫn giải
Chọn D
Gọi
H
là hình chiếu của
B
′
trên
BC
. Từ giả thiết suy ra:
( )
B H ABC
′
⊥
.
1
. .sin
2
BB C
S BB BC B BC
′
′′
=
1
4 . .sin30
2
aa= °
2
a=
.
Mặt khác:
1
.
2
BB C
S B H BC
′
′
=
2
BB C
S
BH
BC
′
′
⇒=
2
2
2
a
a
a
= =
.
.
LT ABC
V BHS
′
=
2
3
2.
4
a
a=
3
3
2
a
=
.
..
1
2
A CC B A CC B B
VV
′′ ′′
=
12 1
.
23 3
LT LT
VV= =
3
13
.
32
a
=
3
3
6
a
=
.
Câu 5. Cho hình lăng trụ
.
′′′
ABC A B C
có đáy
ABC
là tam giác vuông tại
A
. cạnh
2=BC a
và
60= °
ABC
. Biết tứ giác
′′
BCC B
là hình thoi có
′
B BC
nhọn. Biết
( )
′′
BCC B
vuông góc với
( )
ABC
và
( )
′′
ABB A
tạo với
( )
ABC
góc
45°
. Thể tích của khối lăng trụ
.
′′′
ABC A B C
bằng
A.
3
37
a
. B.
3
7
a
. C.
3
3
7
a
. D.
3
6
7
a
.
Hướng dẫn giải
Chọn C
a
C'
A'
B'
C
B
A
H
4
a
https://toanmath.com/
Do
ABC
là tam giác vuông tại
,A
cạnh
2=BC a
và
60= °ABC
nên
=AB a
,
3
=AC a
.
Gọi
H
là hình chiếu vuông góc của
′
B
lên
BC
⇒
H
thuộc đoạn
BC
(do
′
B BC
nhọn)
( )
′
⇒⊥B H ABC
(do
( )
′′
BCC B
vuông góc với
( )
ABC
).
Kẻ
HK
song song
AC
( )
∈K AB
⇒⊥HK AB
(do
ABC
là tam giác vuông tại
A
).
( ) ( )
, 45 (1)

′′ ′ ′
⇒ = = °⇒ =

ABB A ABC B KH B H KH
Ta có
′
∆
BB H
vuông tại
H
22
4 (2)
′
⇒= −BH a B H
Mặt khác
HK
song song
AC
⇒=
BH HK
BC AC
.2
(3)
3
⇒=
HK a
BH
a
Từ (1), (2) và (3) suy ra
22
.2
4
3
′
′
−=
BH a
a BH
a
12
7
′
⇒=BH a
.
Vậy
3
.''
13
. ..
2
7
′
′′
= = =
ABC A B C ABC
a
V S B H AB AC B H
.
Câu 6. Cho lăng trụ
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông tại
A
,
30ABC = °
. Điểm
M
là trung
điểm cạnh
AB
, tam giác
MA C
′
đều cạnh
23a
và nằm trong mặt phẳng vuông góc với đáy.
Thể tích khối lăng trụ
.ABC A B C
′′′
là
A.
3
72 2
7
a
. B.
3
24 3
7
a
. C.
3
72 3
7
a
. D.
3
24 2
7
a
.
Hướng dẫn giải
Chọn A
60
°
2a
2a
K
H
C'
B'
A'
C
B
A
https://toanmath.com/
Gọi
H
là trung điểm của
MC
.
Ta có
( ) ( )
(
) ( )
( )
A H MC
A MC ABC A H ABC
A MC ABC MC
′
⊥
′′
⊥ ⇒⊥
′
∩=
.
Tam giác
MA C
′
đều cạnh
23a
Đặt
0AC x= >
, tam giác
ABC
vuông tại
A
có
30ABC = °
2
3
BC x
AB x
=
⇒
=
Áp dụng công thức tính độ dài trung tuyến ta có
2 2 2 222
22
4 3 43
12
2 4 24
7
CA CB AB x x x a
CM a x
++
= − ⇔ = − ⇔=
.
Suy ra
2
1 1 12 4 3 24 3
. ..
22 7
77
ABC
aa a
S AB AC= = =
.
Do đó
3
.
72 3
.
7
ABC A B C ABC
a
V AHS
′′′
′
= =
.
Câu 7. Cho hình lăng trụ tứ giác
.ABCD A B C D
′′′′
có đáy
ABCD
là hình vuông cạnh
a
và thể tích bằng
3
3a
. Tính chiều cao
h
của lăng trụ đã cho.
A.
9ha
=
. B.
3
a
h =
. C.
ha=
. D.
3ha=
.
Hướng dẫn giải
Chọn D
Ta có:
.
.
ABCD A B C D ABCD
V Sh
′′′′
=
.ABCD A B C D
ABCD
V
h
S
′′′′
⇔=
3
2
3a
a
=
3a=
.
Câu 8. Thể tích của khối lăng trụ có chiều cao bằng
h
và diện tích đáy bằng
B
là
A.
2
V Bh=
. B.
V Bh=
. C.
1
3
V Bh=
. D.
V Bh
π
=
.
H
C'
B'
A'
C
B
M
A
https://toanmath.com/
Hướng dẫn giải
Chọn B
Thể tích khối lăng trụ:
.V Bh
=
.
Câu 9.Cho hình lăng trụ
.ABCD A B C D
′′′′
có đáy
ABCD
là hình vuông cạnh
a
. Các cạnh bên tạo với đáy
một góc
o
60
. Đỉnh
A
′
cách đều các đỉnh
,,,ABCD
. Trong các số dưới đây, số nào ghi giá trị thể
tích của hình lăng trụ nói trên?
A.
3
6
9
a
. B.
3
3
2
a
. C.
3
6
2
a
. D.
3
6
3
a
.
Hướng dẫn giải
Chọn C
Gọi
O
là tâm hình vuông
ABCD
.Từ giả thiết
A
′
cách đều các đỉnh
A
,
B
,
C
ta suy ra hình chiếu
của
A
′
trên mặt phẳng
ABCD
là
O
hay
AO
′
là đường cao của khối lăng trụ.
Trong tam giác
A OA
′
vuông tại
A
và
60A OA
′
=
, ta có:
6
.tan60 . 3
2
2
aa
A O OA
′
= = =
.
Diện tích đáy
ABCD
là
2
ACDD
Sa=
.
Thể tích của khối lăng trụ là
3
6
..
2
ABCD
a
V Bh S AO
′
= = =
.
Vậy
3
6
2
a
V =
.
.
Câu 10.Tính thể tích
V
của khối lăng trụ có diện tích mặt đáy bằng
2
3 3cm
và chiều cao bằng
6 cm
.
A.
( )
3
9 2 cmV =
. B.
( )
3
12 2 cmV =
. C.
( )
3
92
cm
2
V
=
. D.
( )
3
3 2 cmV =
.
Hướng dẫn giải
ChọnA
Thể tích khối lăng trụ:
( )
3
. 33.6 92cmV Sh
= = =
.
Câu 11.Cho lăng trụ đều
.ABC A B C
′′′
có
3cmAB
′
=
và đường thẳng
AB
′
vuông góc với đường thẳng
BC
′
. Thể tích khối lăng trụ
.ABC A B C
′′′
bằng
A.
3
27 6
cm
16
. B.
3
2 3cm
. C.
3
76
cm
4
. D.
3
9
cm
2
.
Hướng dẫn giải
Chọn D
https://toanmath.com/
Gọi
M
là trung điểm của
BC
. Suy ra
( )
AM BCC B
′′
⊥
AM BC
′
⇒⊥
.
Mà
BC AB B M BC
′ ′′ ′
⊥⇒ ⊥
.
Đặt
AB a=
,
AA b
′
=
. Ta có
tan cotB BC BB M
′′ ′
=
2
2
ab a
b
ba
⇒ = ⇒=
.
Mà
22
33AB AB AA
′′
=⇒ +=
2
2
36
2
a
aa⇒ + =⇒=
.
Thể tích khối lăng trụ là
2
3
39
. 3. 6 . cm
42
ABC
V AA S
′
= = =
.
Câu 12. Cho hình lăng trụ
.ABC A B C

có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của
A
lên
mặt phẳng
ABC
trùng với trung điểm cạnh
BC
. Góc giữa
BB
và mặt phẳng
ABC
bằng
60
. Tính thể tích khối lăng trụ
.ABC A B C

.
A.
3
3
8
a
. B.
3
23
8
a
. C.
3
3
4
a
. D.
3
33
8
a
.
Hướng dẫn giải
Chọn D
.
Gọi
H
là trung điểm cạnh
BC
. Theo đề ra:
A H ABC
.
33
22
AB a
AH 
.
22
33
44
ABC
AB
vdt
a
S đ

.
Ta có:
', '
' 60
', ', 60
AA ABC A AH
A AH
AA ABC BB ABC


.
N
M
C'
B'
A
C
B
A'
60
°
C'
B'
A'
H
C
B
A
https://toanmath.com/
Xét
A AH
vuông tại
H
:
3
.tan60
2
A H AH a

.
Vậy
3
.
33
.
8
ABC
ABC A B C
a
V AHS đvtt


.
Câu 13. Cho lăng trụ
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh bằng
a
, biết
AA AB AC a
′′′
= = =
.
Tính thể tích khối lăng trụ
.ABC A B C
′′′
?
A.
3
3
4
a
. B.
3
2
4
a
. C.
3
3
4
a
. D.
3
4
a
.
Hướng dẫn giải
Chọn B
Gọi
H
là trọng tâm tam giác
ABC
. Theo giả thiết ta có
ABC
là tam giác đều cạnh bằng
a
và
AA AB AC a
′′′
= = =
nên
.
A ABC
′
là tứ diện đều cạnh
a
⇒
( )
A H ABC
′
⊥
hay
AH
′
là đường
cao của khối chóp
.A ABC
′
.
Xét tam giác vuông
A HA
′
ta có
22
AH AA AH
′′
= −
6
3
a
=
.
Diện tích tam giác
ABC
là
1
. .sin60
2
ABC
S aa= °
2
3
4
a
=
.
Thể tích khối lăng trụ
.ABC A B C
′′′
là
2
.
36
43
ABC A B C
aa
V
′′′
=
3
2
4
a
=
.
Câu 14. Cho hình hộp
.ABCD A B C D
′′′′
có diện tích tứ giác
ABCD
bằng
12
, khoảng cách giữa hai mặt
phẳng
( )
ABCD
và
(
)
ABCD
′′′′
bằng
2
. Tính thể tích
V
của khối hộp.
A.
12
V =
. B.
8V =
. C.
24V =
. D.
72V =
.
Hướng dẫn giải
Chọn B
Ta có
( )
( )
.,
ABCD
V S d A ABCD
′
=
(
) ( )
( )
.,
ABCD
S d A B C D ABCD
′′′′
=
12.2 24= =
.
Câu 15. Cho lăng trụ tam giác
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh
22AB a=
. Biết
8AC a
′
=
và
tạo với mặt đáy một góc
45°
. Thể tích khối đa diện
ABCC B
′′
bằng
A.
3
16 6
3
a
. B.
3
86
3
a
. C.
3
16 3
3
a
. D.
3
83
3
a
.
Hướng dẫn giải
Chọn A
B'
A
C
B
A'
H
https://toanmath.com/
Ta có
..ABC A B C A A B C ABCC B
V VV
′′′ ′′′ ′′
= +
..
ABCC B ABC A B C A A B C
VV V
′′ ′′′ ′′′
⇔= −
.
Mặt khác
..
1
3
AABC ABC ABC
VV
′′′ ′′′
=
nên
..ABCC B ABC A B C A A B C
VV V
′′ ′′′ ′′′
⇔= −
.
2
AABC
V
′′′
=
.
Gọi
H
là hình chiếu của
A
trên mặt phẳng
( )
ABC
′′′
khi đó góc giữa
AC
′
và mặt phẳng đáy
( )
ABC
′′′
là góc
45AC H
′
= °
.
Xét tam giác vuông
AHC
′
có
8AC a
′
=
và
45AC H
′
= °
nên
42AH a=
.
Thể tích khối chóp
.AABC
′′′
là
.
1
.
3
AABC ABC
V S AH
′′′ ′′′
=
( )
2
11
.22.sin60.42
32
aa
= °
3
86
3
a
=
Vậy thể tích khối đa diện
ABCC B
′′
là
.
2
ABCC B A A B C
VV
′′ ′′ ′
⇔=
3
16 6
3
a
=
.
Câu 16. Cho khối lăng trụ
.ABC A B C
′′′
. Gọi
E
là trọng tâm tam giác
ABC
′′′
và
F
là trung điểm
BC
.
Tính tỉ số thể tích giữa khối
.B EAF
′
và khối lăng trụ
.ABC A B C
′′′
.
A.
1
8
. B.
1
5
. C.
1
6
. D.
1
4
.
Hướng dẫn giải
Chọn C
Ta có
C'
B'
A
C
B
A'
H
E
M
F
A
A'
C
C'
B
B'
https://toanmath.com/
M
là trung điểm của
BC
′′
khi đó
1
2
EAF AA MF
SS
′
=
và
(
)
( )
(
)
( )
,,d B AA MF d B AEF
′′ ′
=
.
Vì
. ..B AA MF ABF A B M B ABF
VV V
′ ′ ′′ ′
= −
..
1
3
ABF A B M ABF A B M
VV
′′ ′′
= −
.
2
3
ABF A B M
V
′′
=
Suy ra
.
1
2
B EAF B AA MF
VV
′ ′′
=
.
12
..
23
ABF A B M
V
′′
=
.
11
..
32
ABC A B C
V
′′′
=
.
1
.
6
ABC A B C
V
′′′
=
.
Câu 17. Cho hình lăng trụ tam giác
.
′′′
ABC A B C
có đáy
ABC
là tam giác đều cạnh
2a
, hình chiếu của
′
A
trên mặt phẳng
( )
ABC
là trung điểm cạnh
BC
. Biết góc giữa hai mặt phẳng
( )
′
ABA
và
( )
ABC
bằng
45
°
. Tính thể tích
V
của khối chóp
.
′′
A BCC B
.
A.
3
3
2
a
. B.
3
=Va
. C.
3
3a
. D.
3
23
3
a
.
Hướng dẫn giải
Chọn B
Ta có :
. ..
′′′ ′′′ ′′
= +
ABC ABC AABC ABCCB
V VV
..
′ ′ ′′
= +
A ABC A BCC B
VV
.
Mà
..
′ ′′ ′′
=
A BCC B A BCC B
VV
..
′′′ ′
⇒=
A A B C A ABC
VV
.
Gọi
M
là trung điểm của
BC
,
I
là trung điểm của
AB
và
K
là trung điểm của
IB
. Khi đó :
( )
′
⊥A M ABC
.
Mặt khác :
//
⇒⊥
⊥
MK CI
MK AB
CI AB
.
⊥MK AB
,
′
⊥A M AB
′
⇒⊥A K AB
.
Góc giữa hai mặt phẳng
( )
′
ABA
và
(
)
ABC
chính là góc giữa
′
AK
và
KM
và bằng
′
A KM
45= °
nên tam giác
′
A KM
vuông cân tại
M
.
Trong tam giác
ABC
:
1 12 3 3
..
2 22 2
= = =
aa
MK CI
Trong tam giác vuông cân
′
A KM
:
3
2
′
= =
a
A M MK
.
..
1
.
3
′ ′′′
=
A ABC ABC A B C
VV
.
.. .
1
3
′ ′′ ′′′ ′′′
⇒= −
A BCC B ABC A B C ABC A B C
VV V
.
2
3
′′′
=
ABC A B C
V
2
..
3
∆
′
=
ABC
S AM
2
23
. 3.
32
=
a
a
3
= a
.
45
°
K
I
C
2a
M
B
A
C
'
B
'
A
'
https://toanmath.com/
Câu 18. Cho khối lăng trụ có thể tích
,V
diện tích đáy là
B
và chiều cao
.h
Tìm khẳng định đúng?
A.
3V Bh=
. B.
1
3
V Bh=
. C.
V Bh=
. D.
V Bh
=
.
Hướng dẫn giải
Chọn D
Theo công thức tính thể tích khối lăng trụ ta có
V Bh=
Câu 19. Cho hình lăng trụ
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông tại
,
B
60 ,ACB =
,BC a=
2AA a
′
=
. Cạnh bên tạo với mặt phẳng
( )
ABC
một góc
30
. Thể tích khối lăng trụ
.ABC A B C
′′′
bằng
A.
3
3
6
a
. B.
3
3
3
a
. C.
3
3
2
a
. D.
3
3a
.
Hướng dẫn giải
Chọn C
Trong tam giác
ABC
vuông tại
B
ta có:
tan 60 . 3 3
AB
AB BC a
BC
°= ⇒ = =
Diện tích đáy:
2
1 .3
.
22
ABC
a
S AB BC= =
.
Gọi
H
là hình chiếu của
A
′
lên mặt phẳng
( )
ABC
. Góc giữa cạnh bên
AA
′
và đáy là
30A AH
′
= °
.
Trong tam giác vuông
A HA
′
ta có:
1
.sin30 2 .
2
A H AA a a
′′
= °= =
Thể tích lăng trụ là:
23
3 .3
..
22
ABC
aa
V AH S a
′
= = =
Câu 20.Cho
( )
H
là khối lăng trụ có chiều cao bằng
3,a
đáy là hình vuông cạnh
.a
Thể tích của
( )
H
bằng.
A.
3
4a
. B.
3
2
a
. C.
3
3a
. D.
3
a
.
Hướng dẫn giải
Chọn C
23
. 3. 3V Bh aa a= = =
.
Câu 21.Cho hình lăng trụ
có đáy là hình thoi cạnh bằng
a
và
120ABC = °
. Góc giữa
cạnh bên
AA
′
và mặt đáy bằng
60°
, điểm
'
A
cách đều các điểm
A
,
B
,
D
. Tính thể tích khối
lăng trụ đã cho theo
a
.
A.
3
3
6
a
. B.
3
3
3
a
. C.
3
3
2
a
. D.
3
3
12
a
.
Hướng dẫn giải
2a
30
°
a
60
°
A
B
A'
B'
C'
H
C
https://toanmath.com/
Chọn C
Ta có điểm
A
′
cách đều các đỉnh
A
,
B
,
D
cho nên điểm
A
′
sẽ nằm trên trục đường tròn ngoại
tiếp của tam giác
ABD
.
Ta có
120ABC = °
nên
60ABD = °
⇒
tam giác
ABD
là tam giác đều
Vậy ta có
( )
A G ABD
′
⊥
với
G
là trọng tâm tâm tam giác
ABD
.
Dễ thấy
( )
( )
(
)
,,A A ABCD A A GA A AG
′ ′′
= =

60= °
.
Tam giác
ABD
đều,
AI
là trung tuyến (
I AC BD
= ∩
)
3
2
AI a⇒=
;
23
33
a
AG AI= =
.
Ta có
3
3
.
1
cot60
3
a
AG
AG a
′
= = =
°
.
Thể tích khối lăng trụ
1
.S .2S .2. . . .sin 60
2
ABCD ABD
V AG AG a aa
′′
= = = °
3
3
2
a=
.
Câu 22. Cho lăng trụ
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của điểm
'A
lên mặt phẳng
( )
ABC
trùng với trọng tâm tam giác
ABC
. Biết khoảng cách giữa hai đường
thẳng
'AA
và
BC
bằng
3
4
a
. Khi đó thể tích của khối lăng trụ là
A.
3
3
3
a
. B.
3
3
6
a
. C.
3
3
24
a
. D.
3
3
12
a
.
Hướng dẫn giải
Chọn D
I
D'
C'
B'
A'
G
D
C
B
A
https://toanmath.com/
Gọi H là trọng tâm của tam giác ABC
Suy ra
(
)
'A H ABC⊥
. Qua A kẻ đường thẳng Ax song song với BC. Ta có
//Ax BC
( ) (
)
(
)
', , 'd A A BC d BC A Ax⇒=
( )
( )
( )
( )
3
,' ,'
2
d M A Ax d H A Ax= =
Kẻ
'HK AA⊥
ta có
'
BC AM
BC A H
⊥
⊥
( )
'BC A AM BC HK⇒⊥ ⇒⊥
Mà
(
)
3
''
6
a
HK AA HK A Ax HK⊥⇒⊥ ⇒=
Ta có
22 2
111
'
'3
a
HA
HK HA HA
= + ⇒=
mà
23
33
'.
4 12
ABC ABC
aa
S V AHS= ⇒= =
.
Câu 23. Cho hình lăng trụ
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của điểm
A
′
lên mặt phẳng
( )
ABC
trùng với trọng tâm tam giác
ABC
. Biết khoảng cách giữa hai đường
thẳng
AA
′
và
BC
bằng
3
4
a
. Tính theo
a
thể tích
V
của khối lăng trụ
.ABC A B C
′′′
.
A.
3
3
12
a
V
=
. B.
3
3
3
a
V =
. C.
3
3
24
a
V =
. D.
3
3
6
a
V =
.
Hướng dẫn giải
Chọn A
Ta có
( )
A G ABC
′
⊥
nên
A G BC
′
⊥
;
BC AM⊥
( )
BC MAA
′
⇒⊥
https://toanmath.com/
Kẻ
MI AA
′
⊥
;
BC IM⊥
nên
( )
3
;
4
a
d AA BC IM
′
= =
Kẻ
GH AA
′
⊥
, ta có
2 23 3
.
3 34 6
AG GH a a
GH
AM IM
==⇔= =
2 22
2 2 22
33
.
111 .
36
3
3 12
aa
AG HG a
AG
HG A G AG
AG HG a a
′
= + ⇔= = =
′
−
−
22
.
33
..
3 4 12
ABC A B C ABC
aa a
V AGS
′′′
′
= = =
.
Câu 24. Các đường chéo của các mặt của một hình hộp chữ nhật bằng
, , abc
. Thể tích của khối hộp đó là
A.
.V abc=
B.
.
V abc=++
C.
(
)( )( )
22 2222 222
.
8
bcacababc
V
+− +− +−
=
D.
( )( )
(
)
22 2222 222
.
8
bcacababc
V
+− +− +−
=
Hướng dẫn giải
Chọn C
Giả sử hình hộp chữ nhật có ba kích thước:
,,xyz
.
Theo yêu cầu bài toán ta có
222 222 222
222 222 22222
222 222 222
xya yax yax
yzc yzc axbxc
xzb zbx zbx

+= =− =−

+=⇔ +=⇔ −+−=


+= =− =−

( )( )( )
222
2
222222222
222
2
222
2
2
28
2
abc
y
acbabcbca
abc
xV
bca
z
−+
=
+− +− +−
+−
⇔ = ⇒=
+−
=
Câu 25. Cho lăng trụ
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của điểm
A
′
lên
mặt phẳng
( )
ABC
trùng với trọng tâm của tam giác
ABC
. Biết khoảng cách giữa hai đường
thẳng
AA
′
và
BC
bằng
3
4
a
. Khi đó thể tích của khối lăng trụ là
z
c
b
a
x
y
A'
C'
D'
C
B
D
A
B'
https://toanmath.com/
A.
3
3
24
a
. B.
3
3
12
a
. C.
3
3
36
a
. D.
3
3
6
a
.
Hướng dẫn giải
Chọn B
Gọi
G
là trọng tâm của
ABC∆
,
M
là trung điểm của
BC
.
( )
A G ABC
′
⇒⊥
.
Trong
( )
AA M
′
dựng
MN AA
′
⊥
, ta có:
BC AM
BC A G
⊥
′
⊥
( )
BC AA G
′
⇒⊥
BC MN⇒⊥
.
( )
,d AA BC MN
′
⇒=
3
4
a
=
.
Gọi
H
là hình chiếu của
G
lên
AA
′
.
Ta có:
//GH MN
GH AG
MN AM
⇒=
2
3
=
2
3
GH MN⇒=
3
6
a
=
.
Xét tam giác
AA G
′
vuông tại
G
, ta có:
22 2
111
GH GA GA
= +
′
2 22
1 11
GA GH GA
⇒=−
′
22
11
33
63
aa
= −



2
27
3a
=
.
3
a
GA
′
⇒=
.
Vậy thể tích của khối lăng trụ là:
.
ABC
V S AG
′
=
2
3
.
43
aa
=
3
3
12
a
=
.
Câu 26.-2017]Cho hình lăng trụ
.ABC A B C
′′′
, đáy
ABC
là tam giác đều cạnh
x
. Hình chiếu của đỉnh
A
′
lên mặt phẳng
( )
ABC
trùng với tâm
ABC∆
, cạnh
2AA x
′
=
. Khi đó thể tích khối lăng trụ là:
A.
3
11
12
x
. B.
3
39
8
x
. C.
3
3
2
x
. D.
3
11
4
x
.
Hướng dẫn giải
ChọnA
Gọi
H
là hình chiếu vuông góc của
A
′
lên
( )
ABC
. Do
ABC∆
đều nên
H
là trọng tâm tam giác
ABC∆
.
Ta có
3
2
x
AM =
23
33
x
AH AM⇒= =
.
Xét tam giác vuông
AA H
′
∆
,
có
22
33
3
x
A H AA AH
′′
= −=
.
2
2
13 3
.
22 4
ABC
x
Sx
∆
= =
23
.
3 33 11
43 4
ABC A B C
xx x
V
′′′
=⋅=
.
N
H
B'
C'
M
A
C
B
A'
G
https://toanmath.com/
Câu 27. Cho hình hộp
có đáy là hình chữ nhật với
3, 7AB AD= =
và cạnh bên bằng
1
. Hai mặt bên
( )
ABB A
′′
và
( )
ADD A
′′
lần lượt tạo với đáy các góc
45°
và
60°
. Thể tích khối
hộp bằng
A.
33
B.
77
C.
7
D.
3
Hướng dẫn giải
Chọn D
Gọi
H
là hình chiếu của
A
′
trên
( )
ABCD
và
,KL
là hình chiếu của
H
trên
,
AB AD
.
Ta có các góc
45A KH
′
= °
và
60A LH
′
= °
.
Đặt
AH x
′
=
suy ra
3
;
3
x
HK x HL= =
.
Do đó
2
2 2 22 2
3
x
AA AH A H x x
′′
= + =++
2
73
1
37
x
x⇒ =⇒=
.
Thể tích khối hộp bằng
3
. . . 3 7. 3
7
V B h AB AD A H
′
= = = =
.
Câu 28. Thể tích của khối lăng trụ có chiều cao bằng
h
và diện tích đáy bằng
B
là
A.
1
6
V Bh=
. B.
1
3
V Bh
=
. C.
1
2
V Bh=
. D.
V Bh=
.
Hướng dẫn giải
Chọn D
Ta có thể tích khối lăng trụ
V Bh=
.
Câu 29. Cho lăng trụ
111
.ABC A BC
có đáy
ABC
là tam giác vuông tại
C
, cạnh
5AC a
=
. Hình chiếu
vuông góc của
1
A
lên mặt phẳng
ABC
là trung điểm của cạnh
AC
, góc giữa mặt phẳng
( )
11
AA B B
với
( )
11
AAC C
bằng
o
30
, cạnh bên của lăng trụ tạo với đáy một góc
o
60
. Tính thể tích
V
của lăng trụ
111
.
ABC A BC
?
A.
3
3.
8
a
V =
. B.
3
24
a
V =
. C.
3
8
a
V =
. D.
3
3.
24
a
V =
.
Hướng dẫn giải
Chọn A
O
D'
B'
C'
C
B
A'
D
A
H
K
L
https://toanmath.com/
.
Gọi
G
là trung điểm của
0
1 11
53
( ) A 60 .tan 60 .
2
O
AC AG ABC AG AG AG a
⇒⊥ ⇒ =⇒= =
Ta
có
( )
11
BC AAC C
⊥
.
Câu 30.Cho hình lăng trụ có tất cả các cạnh đều bằng
a
, đáy là lục giác đều, góc tạo bởi cạnh bên và mặt
đáy là
60°
. Tính thể tích khối lăng trụ.
A.
3
9
4
Va=
. B.
3
3
4
Va=
. C.
3
3
2
Va=
. D.
3
27
8
Va=
.
Hướng dẫn giải
ChọnA
.
Ta có
ABCDEF
là lục giác đều nên góc ở đỉnh bằng
120°
.
ABC
là tam giác cân tại
B
,
DEF
là tam giác cân tại
E
.
2
13
. .sin120
24
ABC DEF
a
S S aa= = °=
.
22
2. . .cosAC AB BC AB BC B= +−
22
1
2... 3
2
a a aa a

= +− − =


.
2
. 3. 3
ACDF
S AC AF a a a= = =
.
2 22
2
3 33 3
3
4 42
ABCDEF ABC ACDF DEF
a aa
S SS S a=+ += + + =
.
B
C
D
E
A
F
F'
A'
E'
D'
C'
B'
H
https://toanmath.com/
3
' 60 ' '.sin 60
2
a
B BH B H BB= °⇒ = °=
.
Suy ra
3
9
4
a
V =
.
Câu 31. Khối lăng trụ
.
ABC A B C
′′′
có đáy là một tam giác đều cạnh
,a
góc giữa cạnh bên và mặt phẳng
đáy bằng
30°
Hình chiếu của đỉnh
A
′
trên mặt phẳng đáy
( )
ABC
trùng với trung điểm của cạnh
.
BC
Tính thể tích của khối lăng trụ đã cho.
A.
3
3
4
a
. B.
3
3
12
a
. C.
3
3
8
a
. D.
3
3
3
a
.
Hướng dẫn giải
Chọn C
Gọi
H
là hình chiếu của
A
′
trên
( )
ABC
⇒
A H BC
′
⊥
.
Dễ thấy
AH BC⊥
(Vì
ABC∆
đều).
⇒
( )
(
)
( )
;;
A A ABC A A AH A AH
′ ′′
= =
(1).
Vì
ABC∆
đều
⇒
3
2
a
AH =
.
Trong
A AH
′
∆
vuông, ta có
31
.tan30
22
3
aa
A H AH
′
= °= ⋅ =
.
Vậy
23
.
33
.
24 8
ABC A B C ABC
aa a
V AHS
′′′
∆
′
= =⋅=
.
Câu 32. Cho lăng trụ tam giác
.
′′′
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
, cạnh
22=AC
.
Biết
′
AC
tạo với mặt phẳng
(
)
ABC
một góc
60°
và
4
′
=AC
. Tính thể tích
V
của khối đa diện
′′
ABCB C
.
A.
16 3
3
=
V
. B.
16
3
=V
. C.
83
3
=V
. D.
8
3
=V
.
Hướng dẫn giải
Chọn A
Phân tích: Tính thể tích của khối đa diện
′′
ABCB C
bằng thể tích khối của lăng trụ
.
′′′
ABC A B C
trừ đi thể tích của khối chóp
.
′′′
AABC
.
Giả sử đường cao của lăng trụ là
′
CH
.
Khi đó góc giữa
′
AC
mặt phẳng
( )
ABC
là góc
60
′
= °C AH
.
Ta có:
B
B
A
C
H
C
A
22
4
0
60
https://toanmath.com/
sin 60 2 3; 4
∆
′
′
°= ⇒ = =
′
ABC
CH
CH S
AC
( )
2
.
1
. 2 3. . 2 2 8 3
2
′′′
∆
′
= = =
ABC A B C ABC
V CHS
.
..
1 1 83
..
33 3
′′′ ′′′
∆
′
= = =
A A B C ABC ABC A B C
V CHS V
.
..
8 3 16 3
83
33
′′ ′′′ ′′′
= − =−=
ABBCC ABC ABC AABC
VV V
.
Câu 33. Cho hình lăng trụ
.ABCABC
′′′
có thể tích bằng
30
. Gọi
I
,
J
,
K
lần lượt là trung điểm của
,AA
′
,BB
′
CC
′
. Tính thể tích
V
của tứ diện
CIJK
.
A.
15
2
V =
. B.
12V =
. C.
6V =
. D.
5V =
.
Hướng dẫn giải
Chọn D
.
Nhận thấy:
( ) ( ) ( )
( )
(
)
( )
( )
C, IJ
1
IJ ABC A B C
2
C, A B C
dK
CK
K
CC
d
′′′
⇒==
′
′′′

.
( )
( )
( )
( )
IJ A B C
1 11 1
C, IJ . . . C, A B C . .30 5
3 32 6
CIJK K
V d KS d S
′′′
′′′
= = = =
.
Câu 34. Khối lăng trụ
.
′′′
ABC A B C
có đáy là tam giác đều,
a
là độ dài cạnh đáy. Góc giữa cạnh bên và
đáy là
30°
. Hình chiếu vuông góc của
′
A
trên mặt
(
)
ABC
trùng với trung điểm của
BC
. Thể
tích của khối lăng trụ đã cho là
A.
3
3
8
a
. B.
3
3
3
a
. C.
3
3
4
a
. D.
3
3
12
a
.
Hướng dẫn giải
Chọn A
Gọi
H
là trung điểm của cạnh
( )
′
⇒⊥BC A H ABC
1
30 tan30
3
′
′
⇒ = °⇒ °= =
AH
A AH
AH
.
https://toanmath.com/
Cạnh
33
22 2
′
= =⇒=
AB a a
AH A H
3
13 3
. .. .
22 2 8
′
⇒= = =
ABC
aa a
V AHS a
.
Câu 35. Cho lăng trụ
có đáy
ABCD
là hình thoi cạnh
a
, tâm
O
và
120
ABC = °
. Góc
giữa cạnh bên
AA
′
và mặt đáy bằng
60
°
. Đỉnh
A
′
cách đều các điểm
A
,
B
,
D
. Tính theo
a
thể tích
V
của khối lăng trụ đã cho.
A.
3
3
2
a
V
=
. B.
3
3
6
a
V
=
. C.
3
3
2
a
V =
. D.
3
3Va=
.
Hướng dẫn giải
Chọn A
Do
AB AD a= =
và
60BAD ABD= °⇒∆
đều cạnh
a
.
Mặt khác:
AA AB AD
′′′
= =
. Suy ra
.A ABD
′
là chóp đều nên
A
′
có hình chiếu vuông góc là tâm
H
của đường tròn ngoại tiếp tam giác
ABD
.
AH⇒
là hình chiếu vuông góc của
AA
′
lên đáy
( ) ( )
( )
, 60ABCD AA ABCD A AH
′′
⇒==°
.
22
33
2 2.
42
ABCD ABD
S S aa= = =
.
Tam giác
ABD
đều cạnh
a
nên
33
23
AO a AH a= ⇒=
.
Tam giác
A AH
′
vuông tại
H
nên:
3
tan 60 . 3
3
A H AH a a
′
= °= =
.
Vậy, thể tích khối lăng trụ là:
3
3
.
2
ABCD
V AHS a
′
= =
.
Câu 36. Cho hình hộp
có đáy là hình chữ nhật với
3, 7AB AD= =
và cạnh bên bằng
1
. Hai mặt bên
( )
ABB A
′′
và
( )
ADD A
′′
lần lượt tạo với đáy các góc
45°
và
60°
. Thể tích khối
hộp bằng
A.
33
B.
77
C.
7
D.
3
Hướng dẫn giải
Chọn D
https://toanmath.com/
Gọi
H
là hình chiếu của
A
′
trên
(
)
ABCD
và
,KL
là hình chiếu của
H
trên
,
AB AD
.
Ta có các góc
45A KH
′
= °
và
60A LH
′
= °
.
Đặt
AH x
′
=
suy ra
3
;
3
x
HK x HL= =
.
Do đó
2
2 2 22 2
3
x
AA AH A H x x
′′
= + =++
2
73
1
37
x
x⇒ =⇒=
.
Thể tích khối hộp bằng
3
. . . 3 7. 3
7
V B h AB AD A H
′
= = = =
.
Câu 37. Cho hình lăng trụ
ABCA B C
′′′
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của
A
′
lên
mặt phẳng
( )
ABC
trùng với trọng tâm tam giác
ABC
. Biết khoảng cách giữa hai đường thẳng
AA
′
và
BC
bằng
3
4
a
. Tính thể tích
V
của khối lăng trụ
.
ABCA B C
′′′
A.
3
3
.
6
a
V =
B.
3
3
.
24
a
V =
C.
3
3
.
12
a
V =
D.
3
3
.
3
a
V =
Hướng dẫn giải
Chọn C
M
là trung điểm của
BC
thì
( )
BC AA M
′
⊥
.
Gọi
MH
là đường cao của tam giác
A AM
′
thì
MH A A
′
⊥
và
HM BC⊥
nên
HM
là khoảng cách
AA
′
và
BC
.
Ta có
..A A HM A G AM
′′
= ⇔
2
2
33
.
42 3
aa a
AA AA
′′
= −
O
D'
B'
C'
C
B
A'
D
A
H
K
L
H
G
M
B
C
A
C'
B'
A'
https://toanmath.com/
2 22
22 2 2
4 42
43 .
3 3 93
a a aa
AA AA AA AA AA

′′ ′′′
⇔= −⇔ =⇔=⇔=



Đường cao của lăng trụ là
22
43
9 93
a aa
AG
′
= −=
.
Thể tích
23
33
.
3 4 12
LT
aaa
V = =
.
Câu 38. Cho khối lăng trụ
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh bằng
a
, cạnh bên
AA a
′
=
, góc
giữa
AA
′
và mặt phẳng đáy bằng
30°
. Tính thể tích khối lăng trụ đã cho theo
a
.
A.
3
3
8
a
. B.
3
3
24
a
. C.
3
3
4
a
. D.
3
3
12
a
.
Hướng dẫn giải
Chọn A
Kẻ
( )
A H ABC
′
⊥
,
( )
H ABC∈
. Khi đó góc giữa
AA
′
và mặt phẳng đáy bằng góc giữa
AA
′
và
AH
bằng
30A AH
′
= °
.
Trong
A AH
′
∆
vuông tại
H
, có
.sin .sin30AH AA AAH a
′′ ′
= = °
2
a
AH
′
⇔=
.
Ta có
2
.
3
..
42
ABC A B C ABC
aa
V S AH
′′′
′
= =
3
.
3
8
ABC A B C
a
V
′′′
⇔=
.
Câu 39. Cho hình lăng trụ
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của điểm
A
′
lên mặt phẳng
( )
ABC
trùng với trọng tâm tam giác
ABC
. Biết khoảng cách giữa hai đường
AA
′
và
BC
bằng
3
4
a
. Tính thể tích
V
của khối lăng trụ
.ABC A B C
′′′
.
A.
3
3
24
a
V =
. B.
3
3
12
a
V =
. C.
3
3
3
a
V =
. D.
3
3
6
a
V =
.
Hướng dẫn giải
Chọn B
https://toanmath.com/
Gọi
G
là trọng tâm tam giác
ABC
. Vì
( )
A G ABC
′
⊥
và tam giác
ABC
đều nên
A ABC
′
là
hình chóp đều. Kẻ
EF AA
′
⊥
và
(
)
BC AA E
′
⊥
nên
( )
3
,
4
a
d AA BC EF
′
= =
. Đặt
AG h
′
=
Ta có
2
2
3
3
a
AA h

′
= +



.
Tam giác
A AG
′
đồng dạng với tam giác
EAF
nên
AA AG AG
EA FA FE
′′
= =
2
2
3 33
. .. .
2 34 3
a aa a
A G EA A A FE h h h

′′
⇒ = ⇔ = + ⇔=



.
Thể tích
V
của khối lăng trụ
.ABC A B C
′′′
là
23
33
..
3 4 12
ABC
aa a
V AG S
= = =
.
Đặt
AH x HB x
′′
=⇒=
.
Ta có
K
là trọng tâm tam giác
AA B
′′
Suy ra
2
2
22
33 4
a
KB A B x
′
= = +
;
22
22
33
KA AH x a
′
= = +
.
KAB∆
vuông tại
K
nên
22 2
KB KA AB
+=
2
22
45
2
94
a
xa

⇔ +=


22 2
859xaa⇔+=
2
2
a
x⇔=
.
Vậy
.
ABC
V S AH
′
=
2
32
.
42
aa
=
3
6
8
a
=
.
Câu 46. Cho hình lăng trụ
.'' 'ABC A B C
có đáy là tam giác đều cạnh
3a
, hình chiếu của
'A
trên mặt
phẳng
(
)
ABC
trùng với tâm đường tròn ngoại tiếp tam giác
ABC
. Cạnh
'AA
hợp với mặt phẳng
đáy một góc
45°
. Thể tích của khối lăng trụ
.'' 'ABC A B C
tính theo
a
bằng.
A.
3
9
4
a
. B.
3
27
4
a
. C.
3
3
4
a
. D.
3
27
6
a
.
Hướng dẫn giải
Chọn B
Gọi
AI
là đường cao,
H
là tâm của tam giác
ABC
( )
A H ABC
′
⇒⊥
.
Vì
( )
( )
AA ABC A
A H ABC
′
∩=
⇒
′
⊥
góc giữa
AA
′
và
( )
ABC
là
45A AH A AH
′′
⇒=°
.
Ta có:
33 2
,3
23
a
AI AH AI a= = =
,
( )
2
2
33
93
44
ABC
a
a
S = =
.
.tan 45 3A H AH AH a
′
= °= =
.
Thể tích của lăng trụ là:
https://toanmath.com/
23
9 3 27
. 3.
44
ABC
aa
V AHS a
′
= = =
.
.
Câu 47. Khối lăng trụ có đáy là hình vuông cạnh
a
, đường cao bằng
3a
có thể tích bằng
A.
3
3
6
a
. B.
3
3
3
a
. C.
3
3
a
. D.
3
23a
.
Hướng dẫn giải
Chọn C
Áp dụng công thức tính thể tích khối lăng trụ ta có
2
.3V Bh a a= =
3
3a=
.
Câu 48. Cho lăng trụ
111
ABCA B C
có diện tích mặt bên
11
ABB A
bằng
4
; khoảng cách giữa cạnh
1
CC
và
mặt phẳng
( )
11
ABB A
bằng 7. Tính thể tích khối lăng trụ
111
ABCA B C
.
A.
14
B.
28
3
C.
14
3
D.
28
Hướng dẫn giải
Chọn A
Gọi thế tích lăng trụ
111
ABCA B C
là
V
.
Ta chia khối lăng trụ thành
111
ABCA B C
theo mặt phẳng
( )
1
ABC
được hai khối: khối chóp tam
giác
1
.C ABC
và khối chóp tứ giác
1 11
.C ABB A
Ta có
1
.
1
3
C ABC
VV=
1 11
.
2
3
C ABB A
VV⇒=
Mà
( )
( )
1 11 11
. 11
1 1 28
. .d ; .4.7
3 33
C ABB A ABB A
V S A ABB A= = =
. Vậy
V
=
28 3
. 14
32
=
I
B'
C'
A
B
C
H
A'
A
1
A
C
1
B
C
B
1
https://toanmath.com/
Câu 49. Cho lăng trụ tam giác
.ABC A B C
′′′
. Các điểm
M
,
N
,
P
lần lượt thuộc các cạnh
AA
′
,
BB
′
,
CC
′
sao cho
1
2
AM
AA
=
′
,
2
3
BN
BB
=
′
và mặt phẳng
( )
MNP
chia lăng trụ thành hai phần có thể
tích bằng nhau. Khi đó tỉ số
CP
CC
′
là
A.
1
4
. B.
5
12
. C.
1
3
. D.
1
2
.
Hướng dẫn giải
Chọn C
Áp dụng công thức :
.
.
1
3
ABC MNP
ABC A B C
V
AM BN CP
V AA BB CC
′′′

= ++

′′′

.
Ta có :
..ABC MNP ABC A B C
VV
′′′
=
nên
11
32
AM BN CP
AA BB CC

++ =

′′′

2
1
11
3
2
32
BB
AA
CP
AA BB CC

′
′

⇔ + +=

′ ′′


1
3
CP
CC
⇔=
′
.
Câu 50. Cho hình lăng trụ
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh
a
,
3
2
a
AA
′
=
. Biết rằng hình
chiếu vuông góc của
A
′
lên
( )
ABC
là trung điểm
BC
. Tính thể tích
V
của khối lăng trụ đó.
A.
3
Va=
. B.
3
2
3
a
V =
. C.
3
3
42
a
V =
. D.
3
3
2
Va=
.
Hướng dẫn giải
Chọn C
A
B
C
A
′
B
′
C
′
H
https://toanmath.com/
Gọi
H
là trung điểm
BC
.
Theo giả thiết,
AH
′
là đường cao hình lăng trụ và
22
6
.
2
a
A H AA AH
′
= −=
′
Vậy, thể tích khối lăng trụ là
23
Δ
3 63 2
..
42 8
ABC
aa a
V S AH= = =
′
.
Câu 51. Cho lăng trụ tam giác
.ABC A B C
′′′
có đáy là tam giác
ABC
đều cạnh bằng
a
. Hình chiếu vuông
góc của
A
′
trên mặt phẳng
( )
ABC
trùng với trung điểm
H
của cạnh
AB
. Góc giữa cạnh bên
của lăng trụ và mặt phẳng đáy bằng
o
30
. Tính thể tích của khối lăng trụ đã cho theo
a
.
A.
3
3
4
a
B.
3
4
a
C.
3
24
a
D.
3
8
a
Hướng dẫn giải
Chọn D
Ta có
AH
là hình chiếu của
AA
′
trên
( )
ABC
o
30A AH
′
⇒=
3
.
23
a
AH
′
⇒=
3
6
a
=
.
ABC
V AHS
′
=
2
33
.
64
aa
=
3
8
a
=
.
Câu 52. Cho hình lăng trụ
.
′′′
ABC A B C
có đáy là tam giác vuông cân ở
C
. Cạnh
′
=BB a
và tạo với
đáy một góc bằng
60°
. Hình chiếu vuông góc hạ từ
′
B
lên đáy trùng với trọng tâm của tam giác
ABC
. Thể tích khối lăng trụ
.
′′′
ABC A B C
là:
A.
3
93
80
a
. B.
3
9
80
a
. C.
3
33
80
a
. D.
3
3
80
a
.
Hướng dẫn giải
Chọn A
Gọi
P
là trọng tâm của
( )
′
∆ ⇒⊥ABC B P ABC
https://toanmath.com/
( )
( )
( )
, 60
′ ′′
⇒ = ⇒=°BB ABC B BP B BP
33
sin60
22
1
cos60
22

′
′
°= = =


′
⇒⇒


°= = =

′

BP a
BP
BB
BP a
BP
BB
Gọi
33
24
a
K BP AC BK BP
=∩⇒= =
22
2
1 3 35
2 4 10
aa
BC BC BC

⇒ + = ⇒=


2
3
31 3 5 9 3
. ..
2 2 10 80

′
⇒= = =


ABC
aaa
V BPS
.
Câu 53. Cho lăng trụ
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của điểm
A
′
lên
mặt phẳng
( )
ABC
trùng với trọng tâm tam giác
ABC
. Biết khoảng cách giữa hai đường thẳng
AA
′
và
BC
bằng
3
4
a
. Khi đó thể tích của khối lăng trụ là
A.
3
3
6
a
. B.
3
3
3
a
. C.
3
3
24
a
. D.
3
3
12
a
.
Hướng dẫn giải
Chọn D
Do
ABC
∆
đều trọng tâm
G
và
( )
A G ABC
′
⊥
nên
.A ABC
′
là hình chóp đều.
Gọi
M
là trung điểm của
BC
, khi đó
3
2
a
AM =
3
3
a
AG⇒=
.
Gọi
H
là hình chiếu của
M
trên
AA
′
. Khi đó do
( )
BC AA M
′
⊥
BC HM⇒⊥
nên
HM
là
đường vuông góc chung của hai đường thẳng
AA
′
và
BC
. Do đó
3
4
a
HM =
.
Đặt
AA AB AC x
′′ ′
= = =
, khi đó
2
2
3
a
AG x
′
= −
.
Do
2 ..
AA M
S A G AM MH AA
′
∆
′′
= =
2
2
33
..
2 34
a aa
xx⇒ −=
2
3
a
x⇒=
.
Do
2
3
4
ABC
a
S
∆
=
,
3
a
AG
′
=
3
.
3
.
12
ABC A B C ABC
a
V AGS
′′′
∆
′
⇒= =
.
G
M
B'
C'
A'
A
C
B
H
https://toanmath.com/
Câu 54.Cho hình hộp
.
ABCD A B C D
′′′′
có
60 , 7, 3,BCD AC a BD a AB AD=°= = >
,đường chéo
BD
′
hợp với mặt phẳng
(
)
ADD A
′′
góc
30°
. Tính thể tích
V
của khối hộp
.ABCD A B C D
′′′′
.
A.
3
39
.
3
a
B.
3
23 .a
C.
3
33 .a
D.
3
39 .a
Hướng dẫn giải
Chọn C
Đặt
Áp dụng định lý hàm cos và phân giác trong tam giác BCD
và
Với và
Vậy V hình hộp =
Câu 55. Cho hình lăng trụ
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của điểm
A
′
lên mặt phẳng
( )
ABC
trùng với trọng tâm tam giác
ABC
. Biết khoảng cách giữa hai đường
thẳng
AA
′
và
BC
bằng
3
4
a
. Tính thể tích
V
của khối lăng trụ
.ABC A B C
′′′
.
A.
3
3
12
a
V =
. B.
3
3
3
a
V =
. C.
3
3
24
a
V =
. D.
3
3
6
a
V =
.
Hướng dẫn giải
Chọn A
30
°
y
x
O
A
C
B
C'
A'
B'
D'
D
( )
;yx CD BC x y= = >
222
3a x y xy=+−
22 2
5xy a+=
2;x a ya
⇒= =
22xya= =
60C
=
BD AD→⊥
';(ADD'A') 30
BD→=
'3DD a→=
2
.sin 60 a 3
ABCD
S xy= =
3
33a
https://toanmath.com/
Gọi
M
là trung điểm của
BC
. Vẽ
MH AA
′
⊥
( )
H BC∈
.
Ta có
AM BC⊥
,
A G BC
′
⊥
( )
BC A AG
′
⇒⊥
BC MH
⇒⊥
( )
,d AA BC MH
′
⇒=
.
22
AH AM MH
= −
22
33
4 16
aa
= −
3
4
a
=
.
Ta có
tan
MH A G
GAH
AH AG
′
= =
.MH AG
AG
AH
′
⇒=
33
.
43
3
4
aa
a
=
3
a
=
.
Vậy
.
ABC
V S AG
′
=
2
3
.
43
aa
=
3
3
12
a
=
.
Câu 56. Cho lăng trụ
.ABC A B C
′′′
có đáy là tam giác đều cạnh
.a
Hình chiếu vuông góc của mặt phẳng
( )
ABC
trùng với trọng tâm của tam giác
.ABC
Biết thể tích của khối lăng trụ là
3
3
4
a
. Khoảng
cách giữa hai đường thẳng
AB
′
và
BC
là:
A.
2
3
a
. B.
4
3
a
. C.
3
4
a
. D.
3
2
a
.
Hướng dẫn giải
Chọn C
.
Phương pháp: Dựng hình vẽ như giả thiết bài toán.
+ phương pháp phổ biến nhất để tìm khoảng cách giữa 2 đường thẳng: tìm một mặt phẳng chứa 1
đường thẳng và song song với đường thẳng còn lại.
https://toanmath.com/
Cách giải: Gọi
F
là trọng tâm tam giác
.
ABC
Suy ra
AF
′
là đường cao của hình lăng trụ
02
13
. .sin 60
24
ABC
S aa a
∆
= =
.
Suy ra
AF a
′
=
.
AA
′
song song với mặt phẳng
( )
BCC B
′′
nên khoảng cách giữa
AA
′
và
BC
chính là khoảng
cách giữa
AA
′
và
( )
BCC B
′′
và cũng bằng khoảng cách từ
A
đến mặt phẳng này.
BC
vuông góc với
( )
.FOE
Dựng
FK
vuông góc với
OE
nên
(
)
( )
,'EF d F BCC=
.
Tính
( ) ( )
22
23
3
AA A F AF a OE
′′
= +==
.
Xét hình bình hành
:AOEA
′
(
)
( )
,d A ABCD
=
khoảng cách hình chiếu của
A
lên
OE
.
3
.' .
4
AOEA
S AO A F OE d a= = =
.
Câu 57. Một khối lăng trụ tam giác có các cạnh đáy bằng
13
,
14
,
15
cạnh bên tạo với mặt phẳng đáy một
góc
30°
và có chiều dài bằng
8
. Khi đó thể tích khối lăng trụ là.
A.
340
. B.
336
. C.
274 3
. D.
124 3
.
Hướng dẫn giải
Chọn B
.
Ta có:
S 21(21 13)(21 14)(21 15) 84
ABC∆
= − − −=
.
Gọi
O
là hình chiếu của
A
′
trên
( )
ABC
.
A AO
′
∆
vuông tại
O
cho ta:
.sin30 4A O AA
′′
= °=
.
Vậy:
.
84.4 336
ABC A B C
V
′′′
= =
.
Câu 58. Cho lăng trụ tam giác
.'' 'ABC A B C
có đáy
ABC
là đều cạnh
22AB a=
. Biết
'8AC a=
và tạo với
mặt đáy một góc
0
45
. Thể tích khối đa diện
''ABCC B
bằng
A.
3
83
.
3
a
B.
3
86
.
3
a
C.
3
16 3
.
3
a
D.
3
16 6
.
3
a
Hướng dẫn giải
Chọn D
a
O
H
C'
B'
A'
C
B
A
https://toanmath.com/
Gọi
H
là hình chiếu của
A
lên
( )
'''mp A B C
0
' 45
HC A⇒=
'AHC
⇒∆
vuông cân tại H.
'8
4 2.
22
AC a
AH a⇒= ==
NX:
( )
2
3
. '' .'''
2 2 .3
2 2 2 16 6
. .4 2. .
3 33 43
A BCC B ABC A B C ABC
a
a
V V AH S a= = = =
Gọi
H
là hình chiếu của
A
lên
( )
'''mp A B C
0
' 45HC A⇒=
'AHC⇒∆
vuông cân tại H.
'8
4 2.
22
AC a
AH a
⇒= ==
NX:
( )
2
3
. '' .'''
2 2 .3
2 2 2 16 6
. .4 2. .
3 33 43
A BCC B ABC A B C ABC
a
a
V V AH S a= = = =
Câu 59. Cho lăng trụ
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
,
AA b
′
=
và
AA
′
tạo với mặt đáy một
góc
60°
. Tính thể tích khối lăng trụ.
A.
2
3
4
ab
. B.
2
3
8
ab
. C.
2
3
8
ab
. D.
2
1
8
ab
.
Hướng dẫn giải
Chọn B
Kẻ
( )
A H ABC
′
⊥
tại
H
Suy ra góc giữa
AA
′
và đáy bằng
60A AH
′
= °
8a
2a
2
C'
B'
A
C
B
A'
H
A'
B'
C'
A
B
C
H
https://toanmath.com/
3
sin 60
2
AH
AA
′
⇒ °= =
′
33
22
b
AH AA
′′
⇒= =
.
Do đó
.
.
ABC A B C ABC
V AHS
′′′
′
=
2
31
. sin60
22
b
a= °
2
3
8
ab
=
.
Câu 60. Cho khối lăng trụ tam giác
.'' 'ABC A B C
có thể tích bằng 30 (đơn vị thể tích). Thể tích của khối tứ
diện
AB C C
′′
là:
A. 5 (đơn vị thể tích). B. 10 (đơn vị thể tích).
C. 12,5 (đơn vị thể tích). D. 7,5 (đơn vị thể tích).
Hướng dẫn giải
Chọn B
Ta có.
.
Khi đó ta có thể so sánh trực tiếp cũng được, tuy nhiên ở đây ta có thể suy luận nhanh như sau:
Khối
B ABC
′
có chung đường cao kẻ từ đỉnh B’ đến đáy
( )
ABC
và chung đáy
ABC
với hình
lăng trụ
.ABC A B C
′′′
. Do vậy
.
1
3
B ABC
ABC A B C
V
V
′
′′′
=
.
Tương tự ta có
.
.
1
3
AABC
ABC A B C
V
V
′′′
′′′
=
, khi đó
..
1
.
3
AABC ABC ABC
VV
′′′ ′′′
=
.
1
.30 10
3
AABC
V
′′′
⇒==
.
Câu 61.Cho lăng trụ
.
ABCD A B C D
′′′′
với đáy
ABCD
là hình thoi,
2AC a=
,
0
120BAD =
. Hình chiếu
vuông góc của điểm
B
trên mặt phẳng
( )
ABCD
′′′′
là trung điểm cạnh
AB
′′
, góc giữa mặt phẳng
( )
AC D
′′
và mặt đáy lăng trụ bằng
o
60
. Tính thể tích
V
của khối lăng trụ
.
A.
3
3
Va=
. B.
3
63Va=
. C.
3
23Va=
. D.
3
33Va=
.
Hướng dẫn giải
Chọn B
Gọi
H
là trung điểm
AB
′′
, suy ra
( )
BH ABCD
′′′′
⊥
.
Vì
ABCD
′′′′
là hình thoi và
o
120BAD ABC
′′ ′ ′′′
= ⇒∆
là tam giác đều cạnh
2a
.
A
C
B
A
C
https://toanmath.com/
Ta có:
( ) ( )
( ) ( )
( )
o
, 60
ACD ABCD CD
HC CD ACD ABCD BCH
BC C D
′′ ′′′′ ′′
∩=
′ ′′ ′′ ′′′′ ′
⊥⇒ ==
′ ′′
⊥
.
Có
ABC
′′′
∆
đều cạnh
2
a
nên
3
.2 3
2
CH a a
′
= =
.
Xét tam giác
BHC
′
vuông tại
H
có:
oo
tan 60 tan 60 3
BH
BH C H a
CH
′
= ⇒= =
′
.
(
)
2
2
3
2 2. . 2 2 3
4
ABCD ABC
S S aa
′′′′ ′′′
= = =
.
Vậy,
23
.
. 3.23 63
ABCD ABCD ABC
V BH S a a a
′′′′ ′′′
= = =
.
| 1/39
| | Tải xuống

Có thể bạn quan tâm:

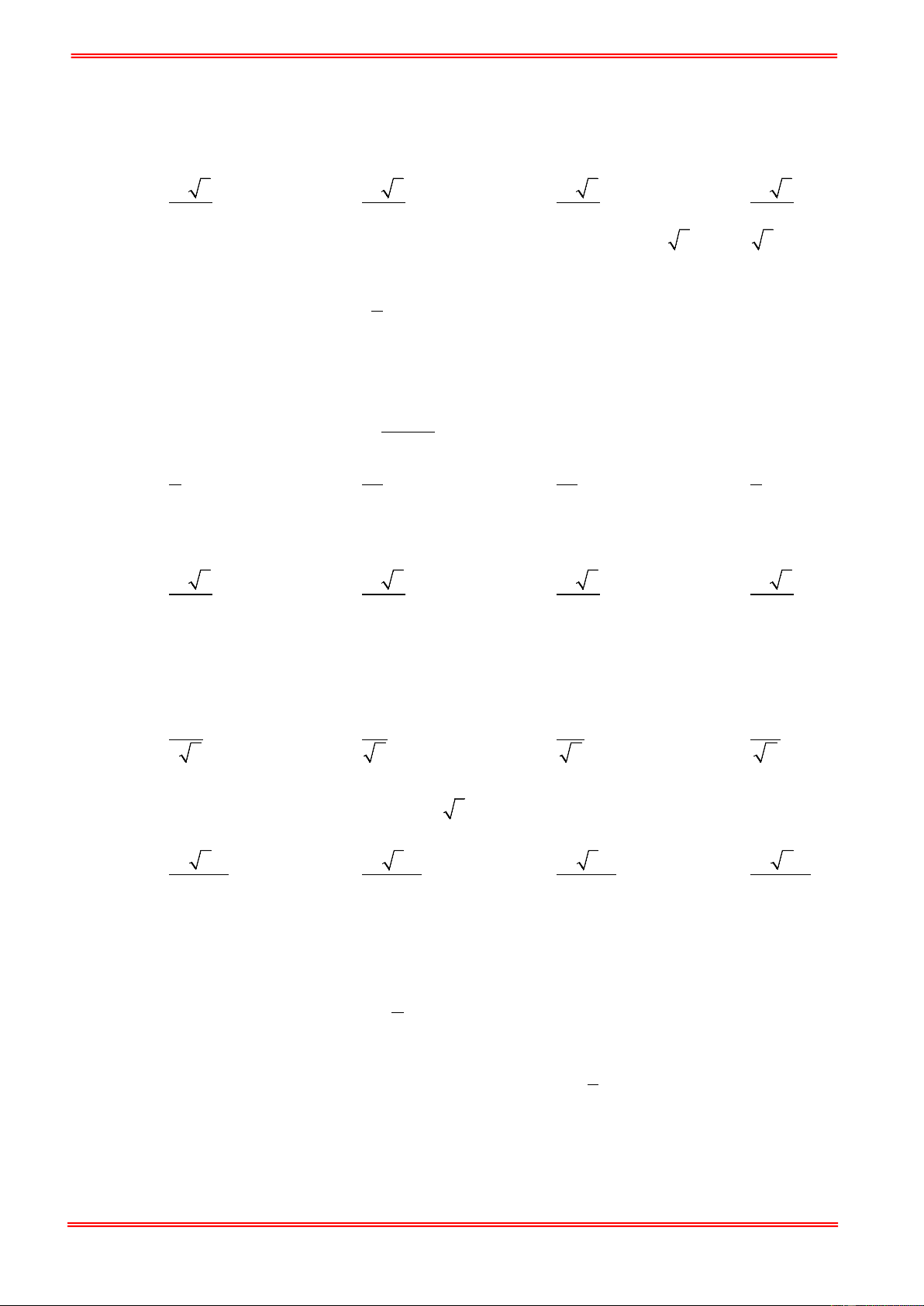
Preview text:


THỂ TÍCH KHỐI LĂNG TRỤ XIÊN
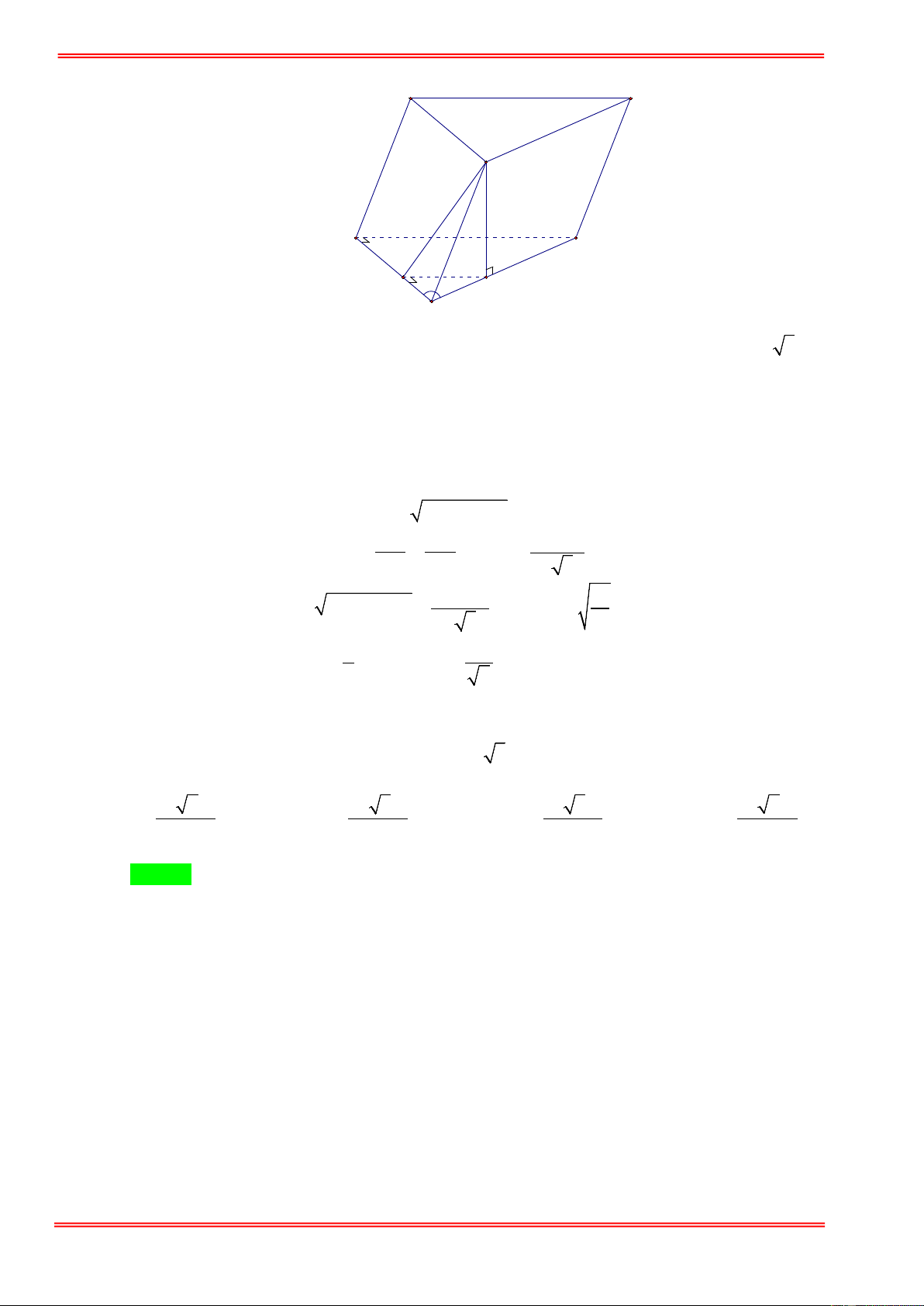
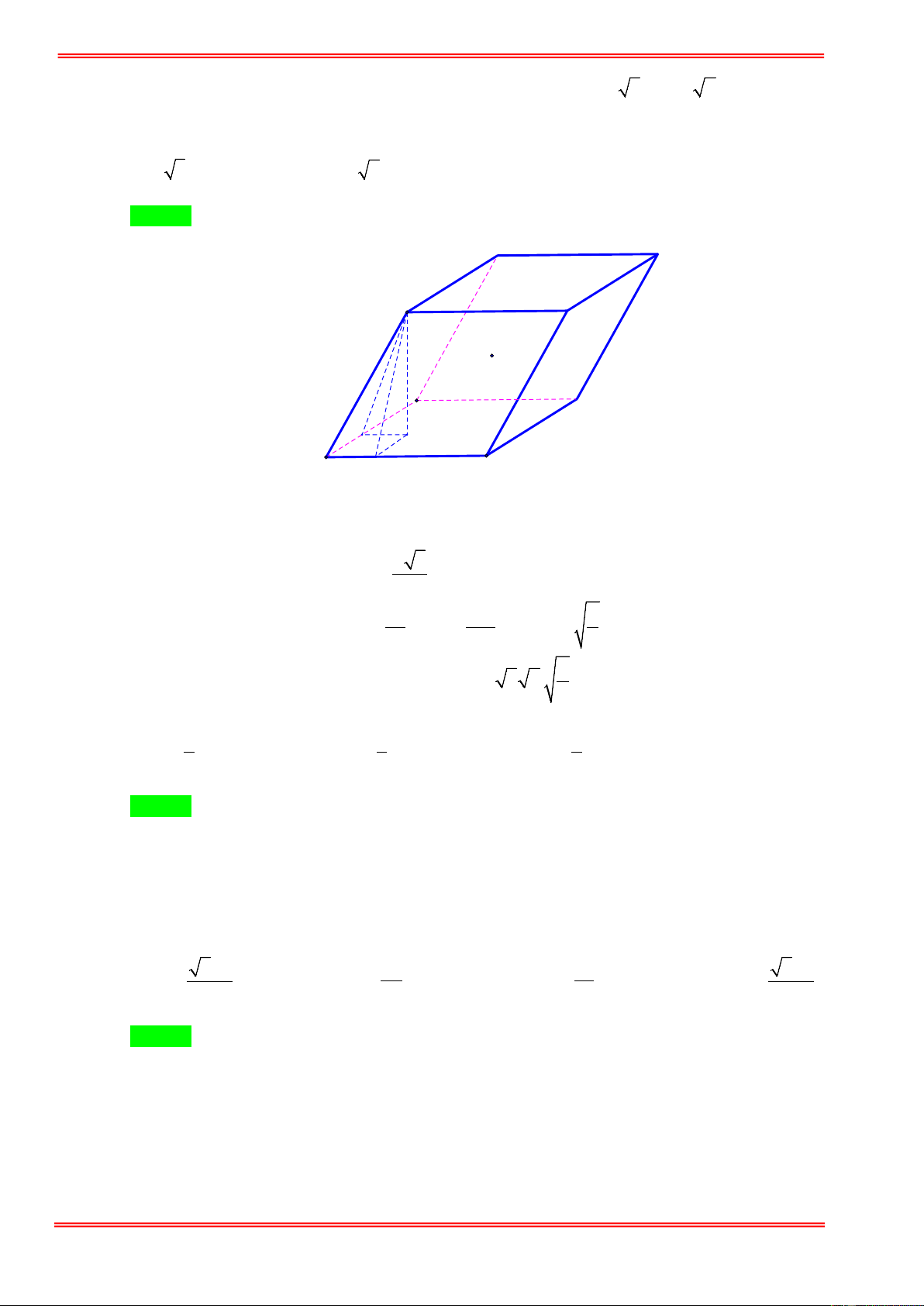
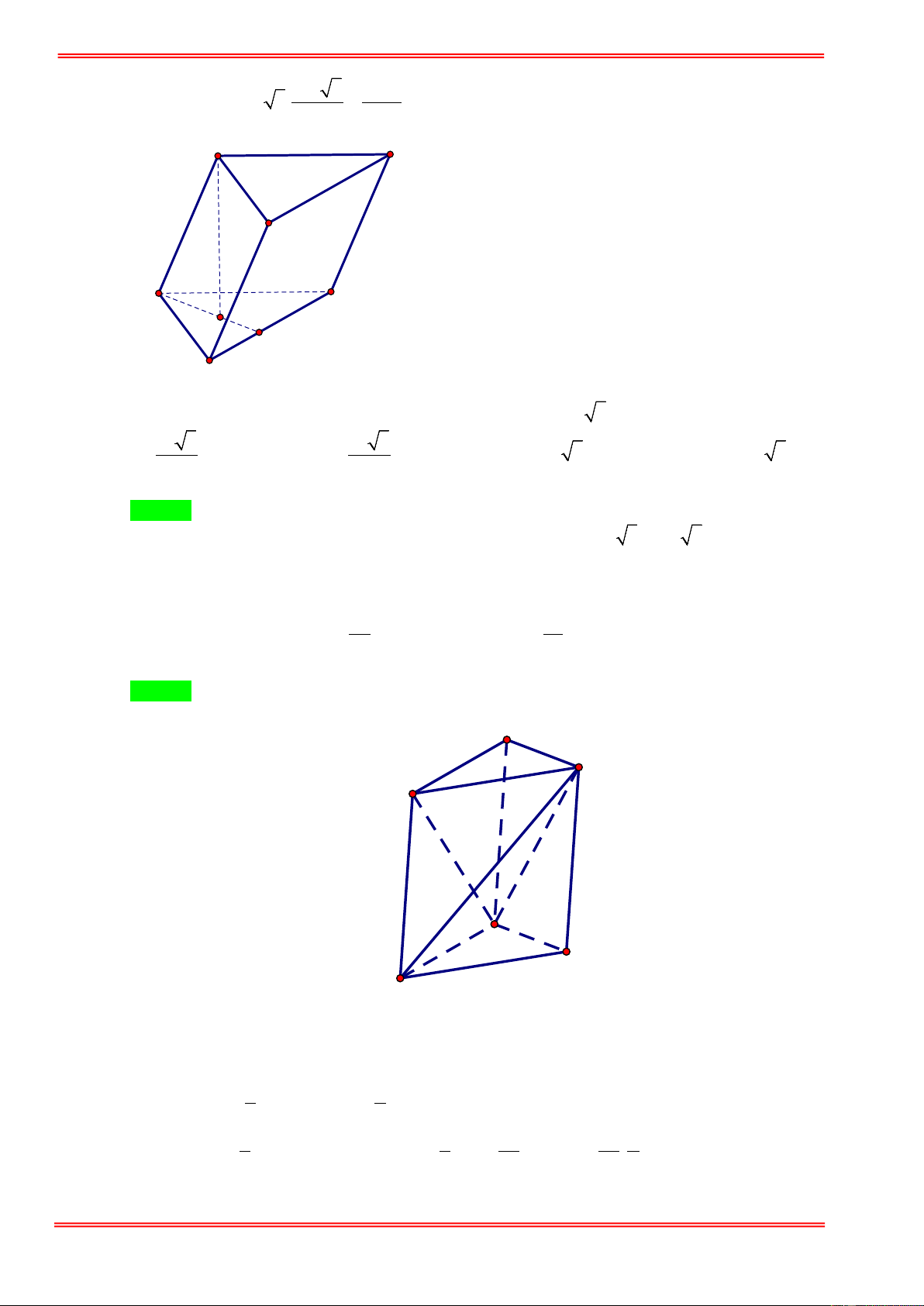
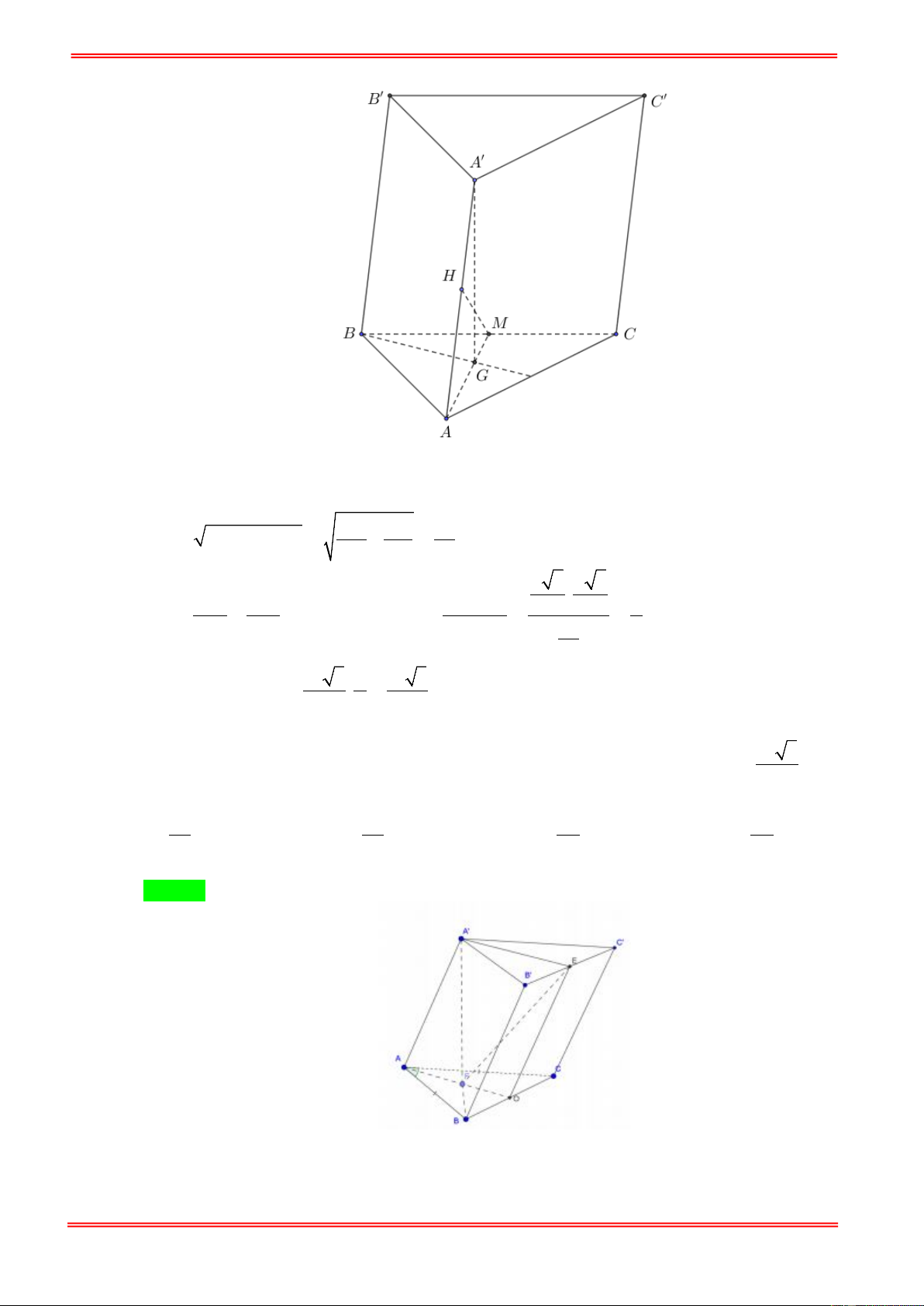
Câu 1. Cho lăng trụ tam giác ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Độ dài cạnh bên bằng 4a . Mặt phẳng (BCC B
′ ′) vuông góc với đáy và  B B
′ C = 30°. Thể tích khối chóp . A CC B ′ ′ là: 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 12 18 2
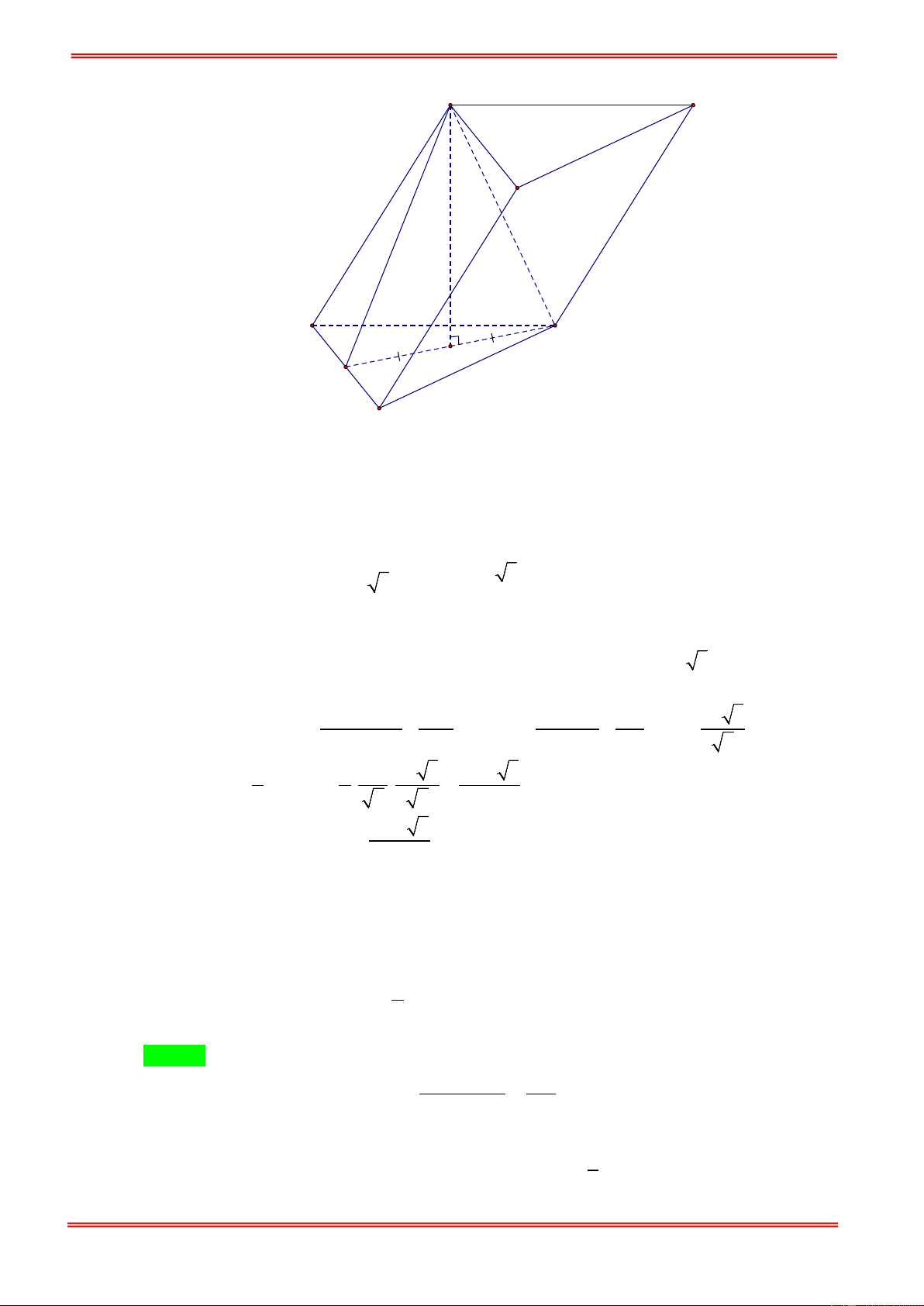
Câu 2. Cho lăng trụ ABC . D A′B C ′ D
′ ′ có đáy ABCD là hình chữ nhật với AB = 6 , AD = 3 , A′C = 3 và
mặt phẳng ( AA′C C
′ ) vuông góc với mặt đáy. Biết hai mặt phẳng ( AA′C C
′ ) , ( AA′B B ′ ) tạo với 3
nhau góc α thỏa mãn tanα =
. Thể tích khối lăng trụ ABC . D A′B C ′ D ′ ′ bằng? 4
A. V = 6 .
B. V = 8 .
C. V = 12 .
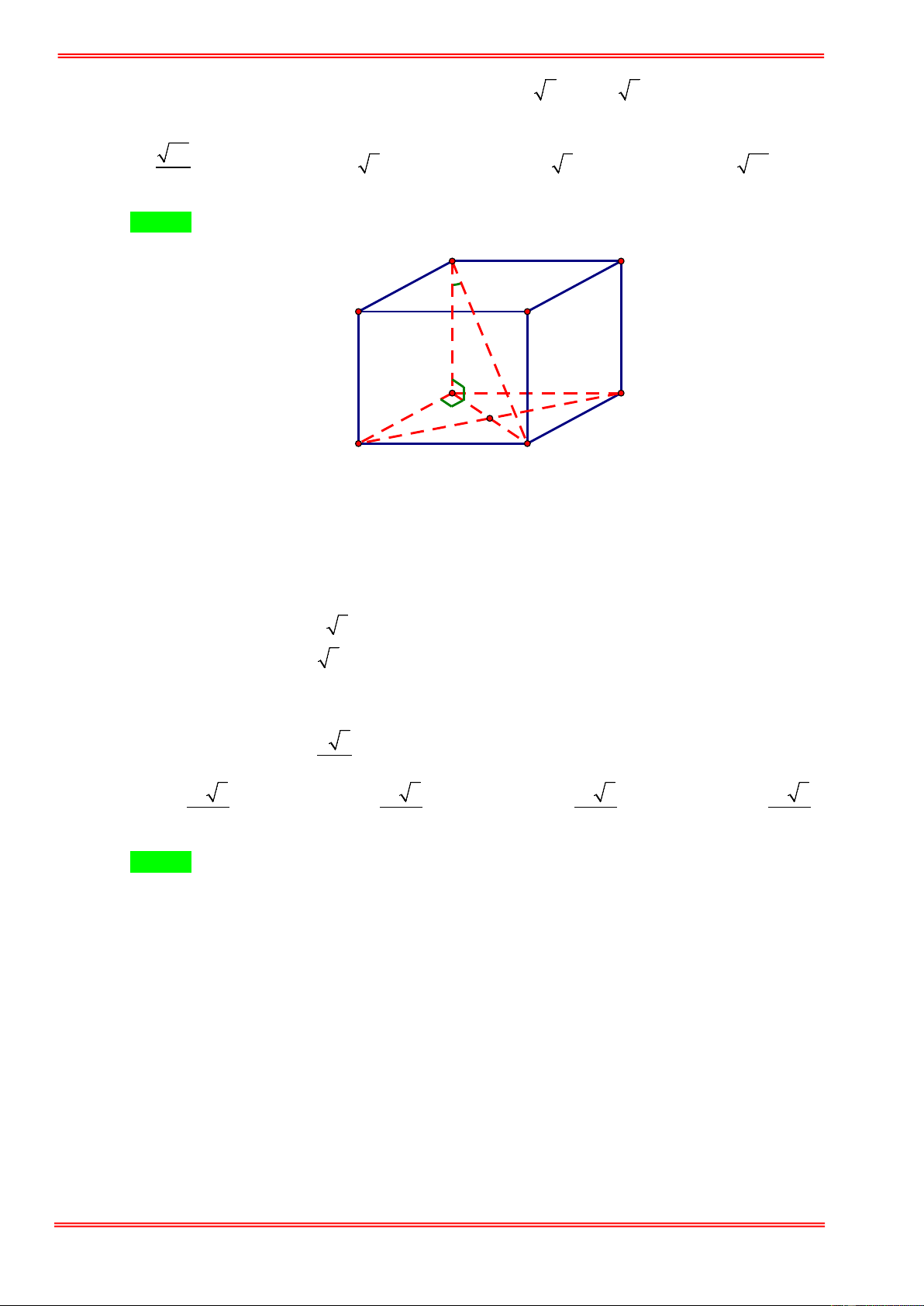
D. V = 10 .
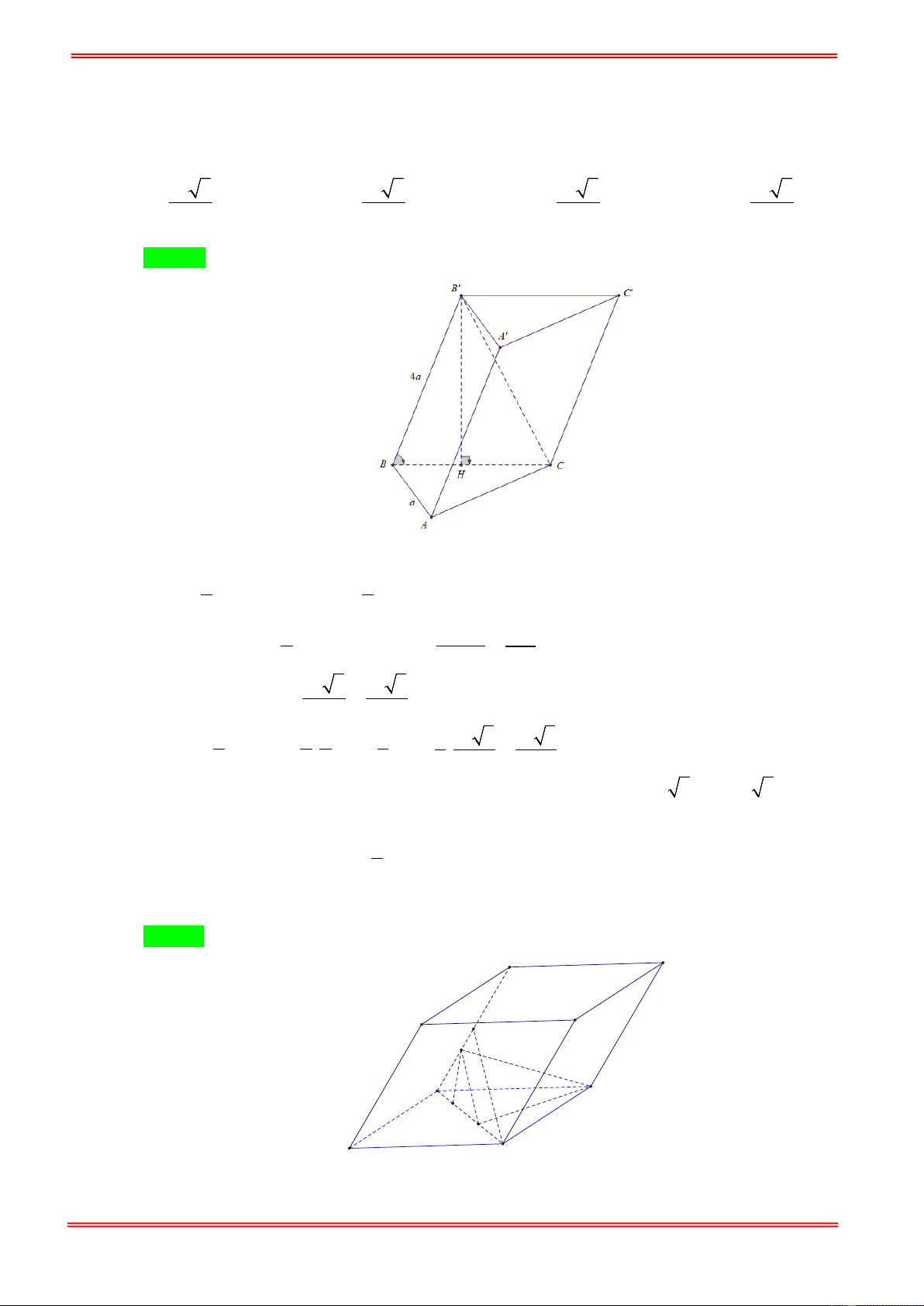
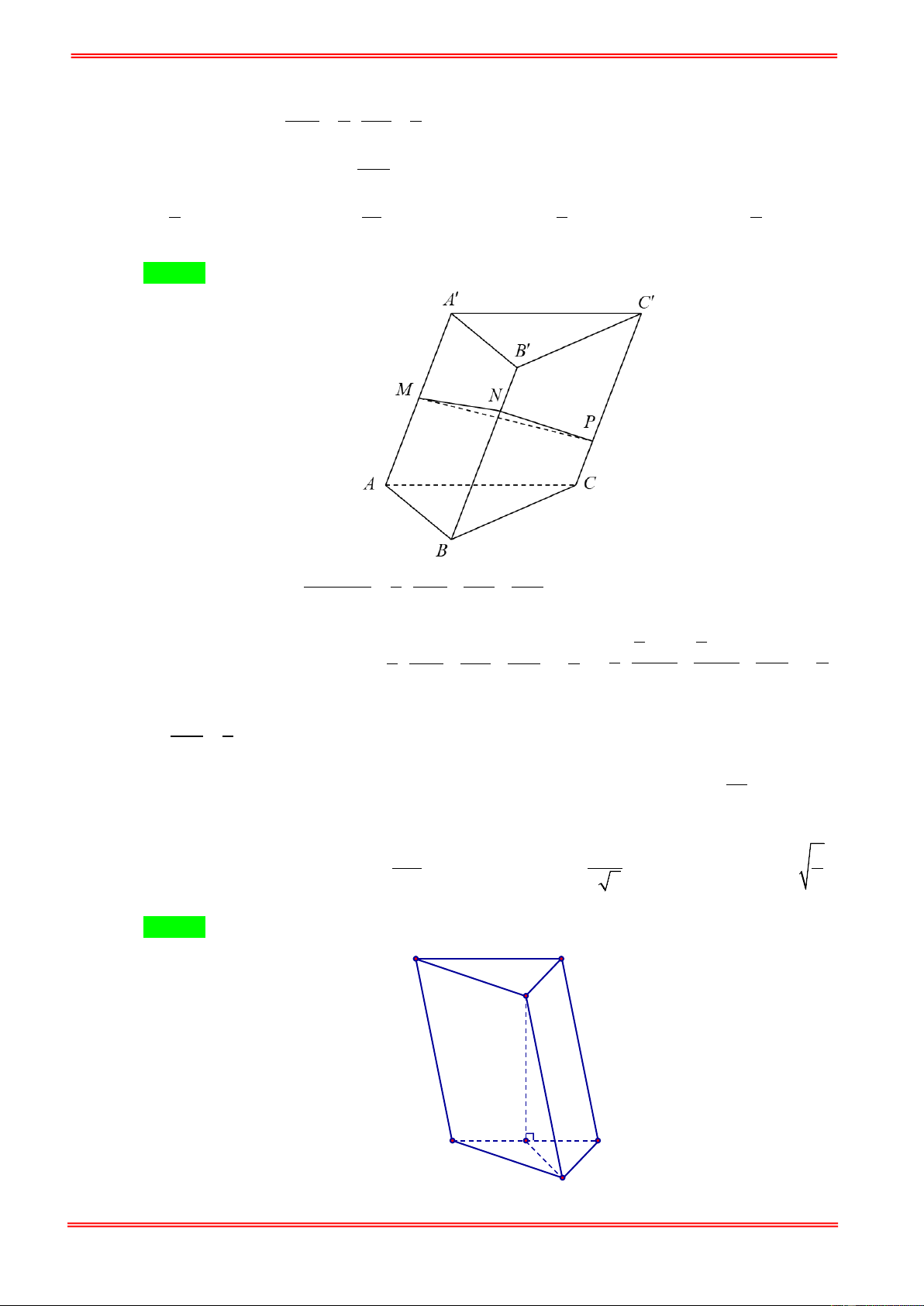
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi H là điểm trên cạnh SD sao cho
5SH = 3SD , mặt phẳng (α ) qua B, H và song song với đường thẳng AC cắt hai cạnh SA, SC lần lượt tại V
E, F. Tính tỉ số thể tích C.BEHF . VS.ABCD 1 3 6 1 A. . B. . C. . D. . 7 20 35 6
Câu 4. Cho lăng trụ tam giác ABC.A′B C
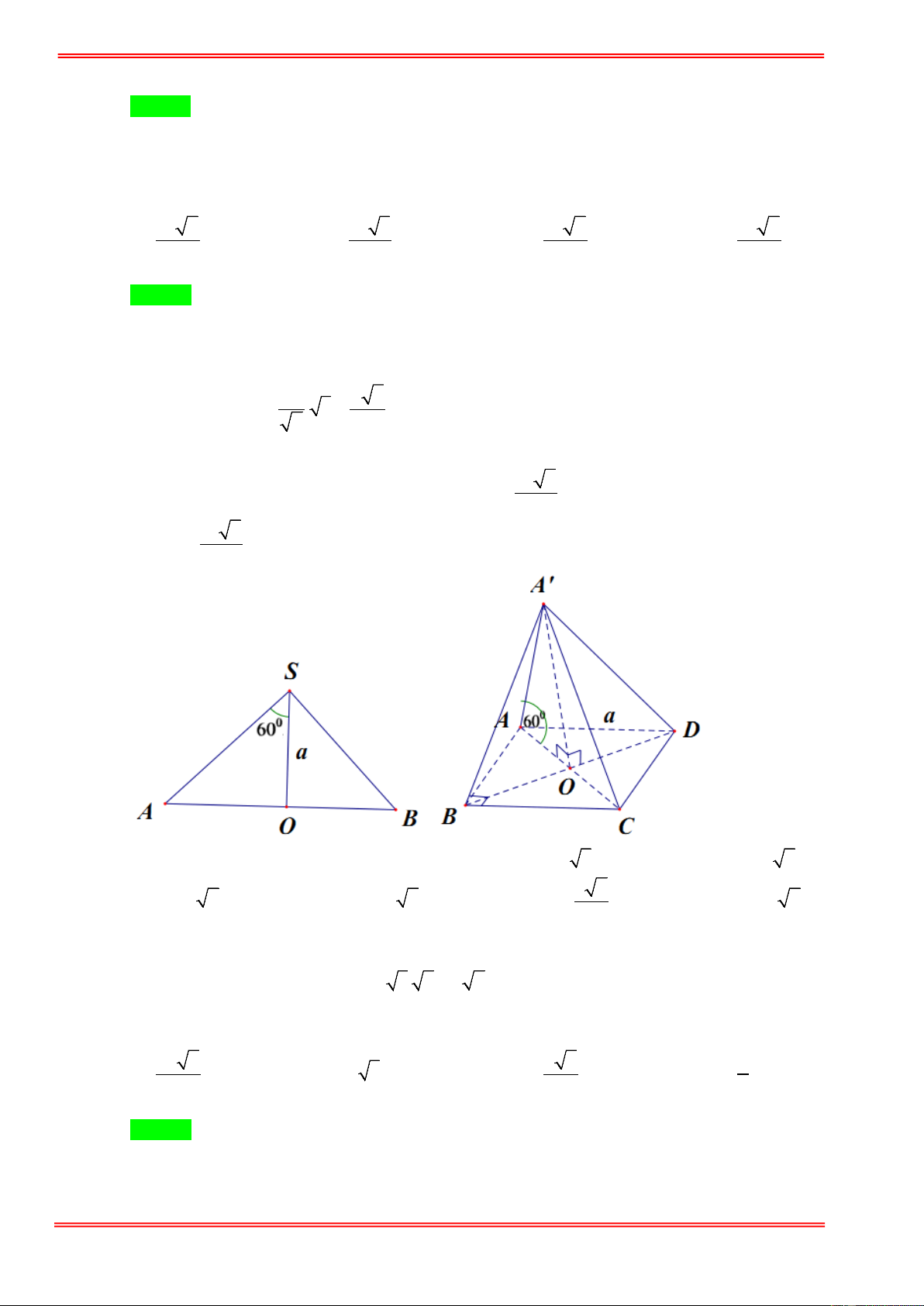
′ ′ có đáy là tam giác đều cạnh a . Độ dài cạnh bên bằng 4a . Mặt phẳng (BCC B
′ ′) vuông góc với đáy và  B B
′ C = 30°. Thể tích khối chóp . A CC B ′ ′ là: 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 2 12 18 6
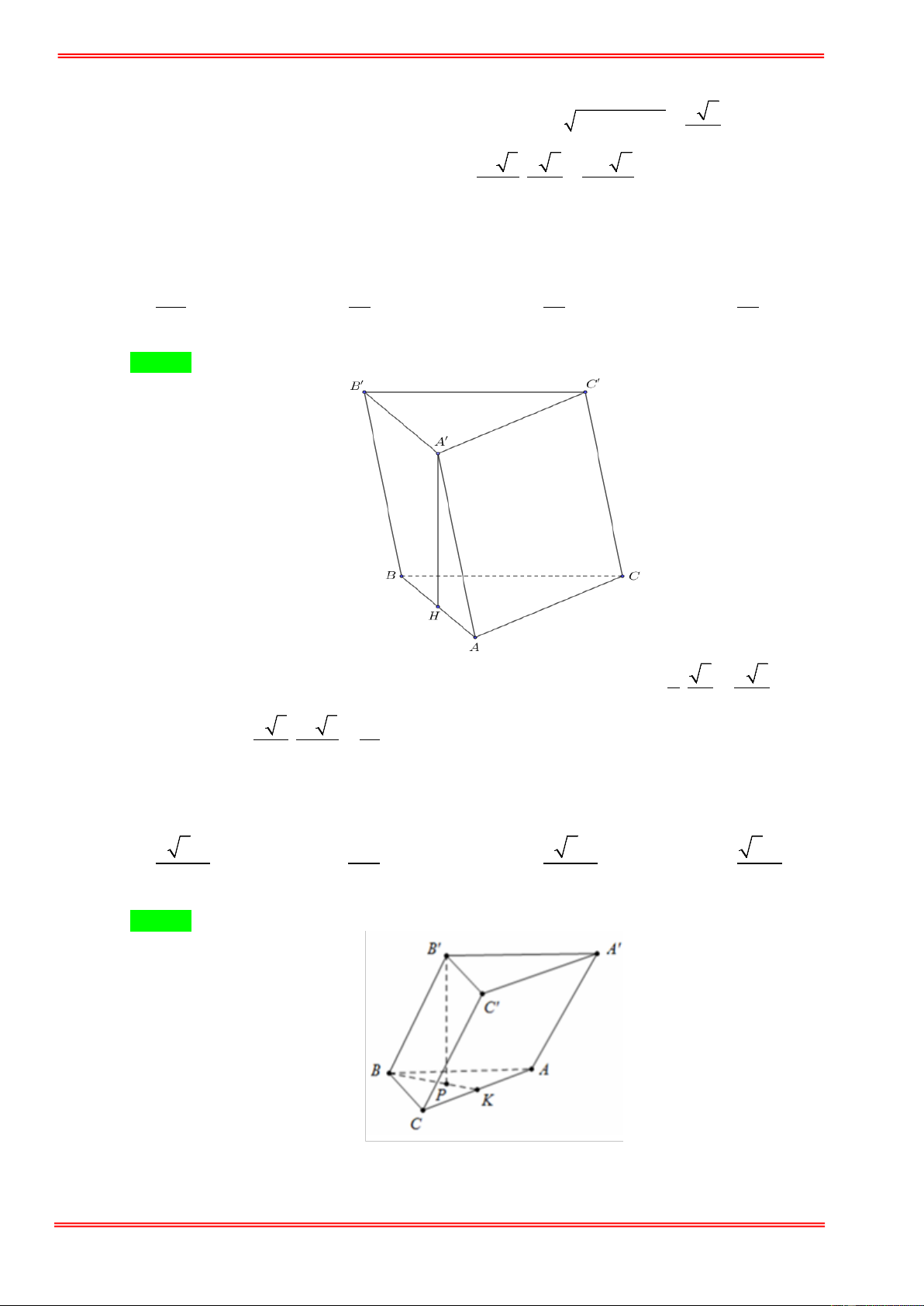
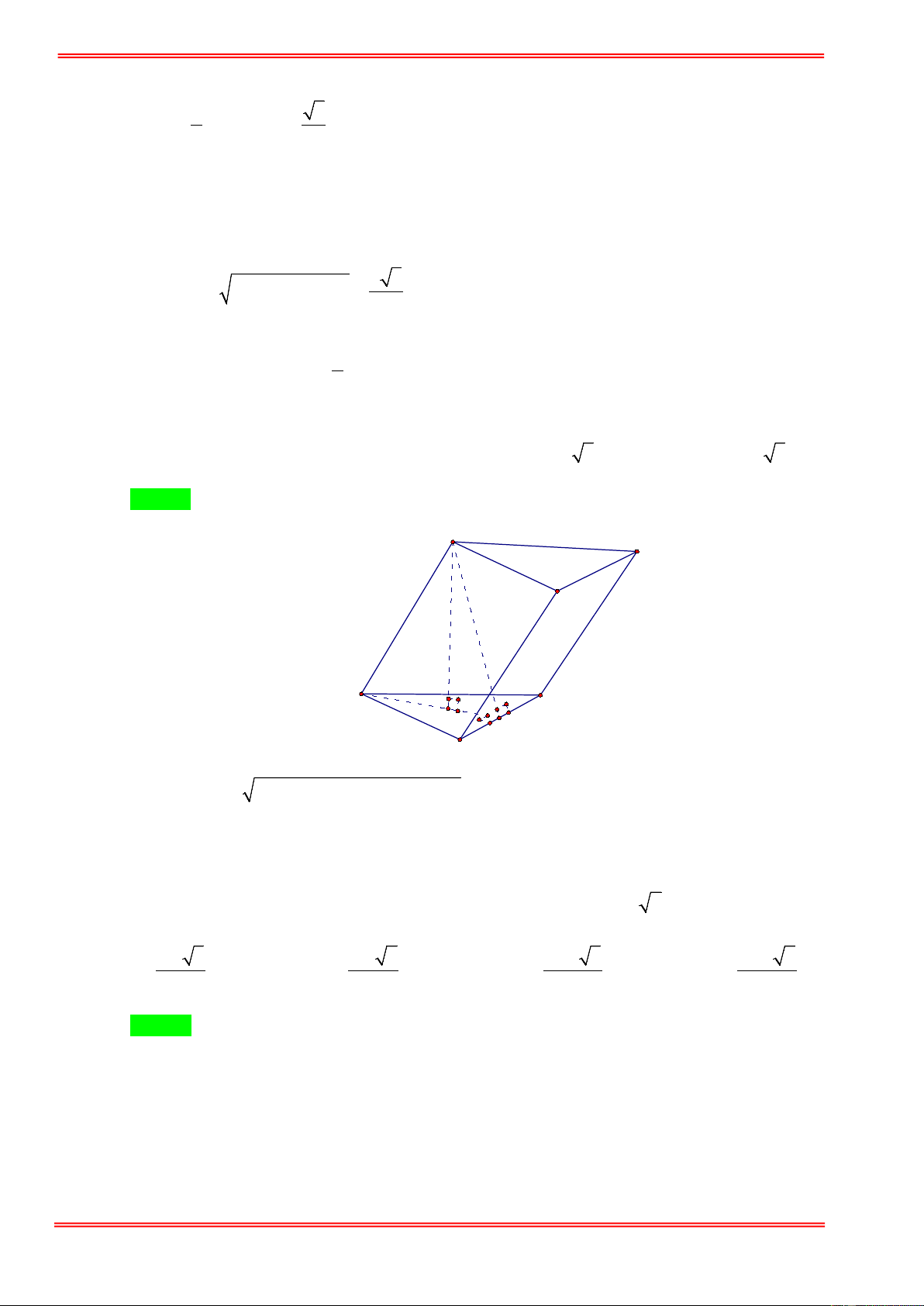
Câu 5. Cho hình lăng trụ ABC. ′
A B′C′ có đáy ABC là tam giác vuông tại A . cạnh BC = 2a và  ABC = 60°
. Biết tứ giác BCC′B′ là hình thoi có 
B′BC nhọn. Biết ( BCC′B′) vuông góc với ( ABC ) và ( ABB′ ′
A ) tạo với ( ABC ) góc 45° . Thể tích của khối lăng trụ ABC. ′
A B′C′ bằng 3 a 3 a 3 3a 3 6a A. . B. . C. . D. . 3 7 7 7 7
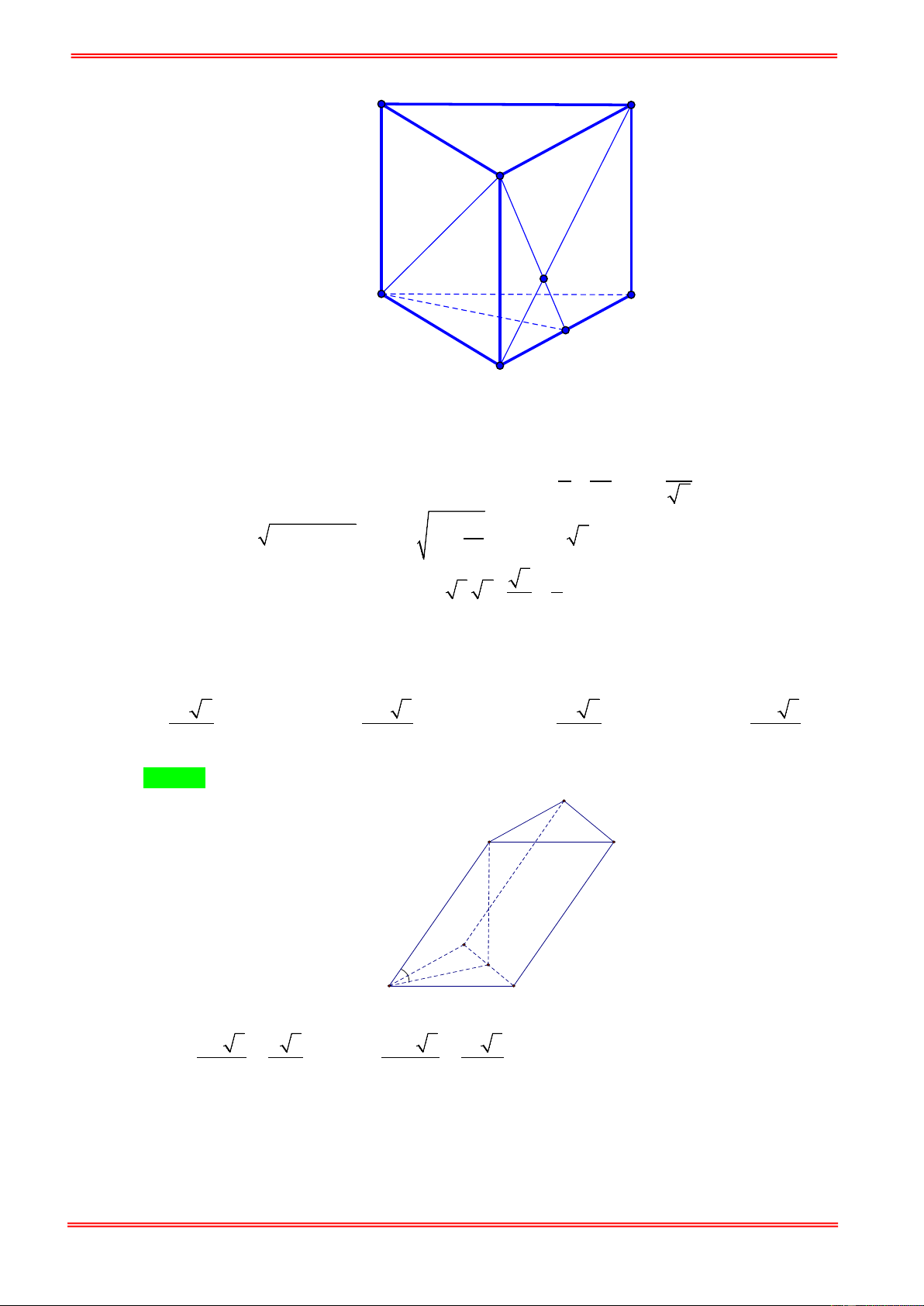
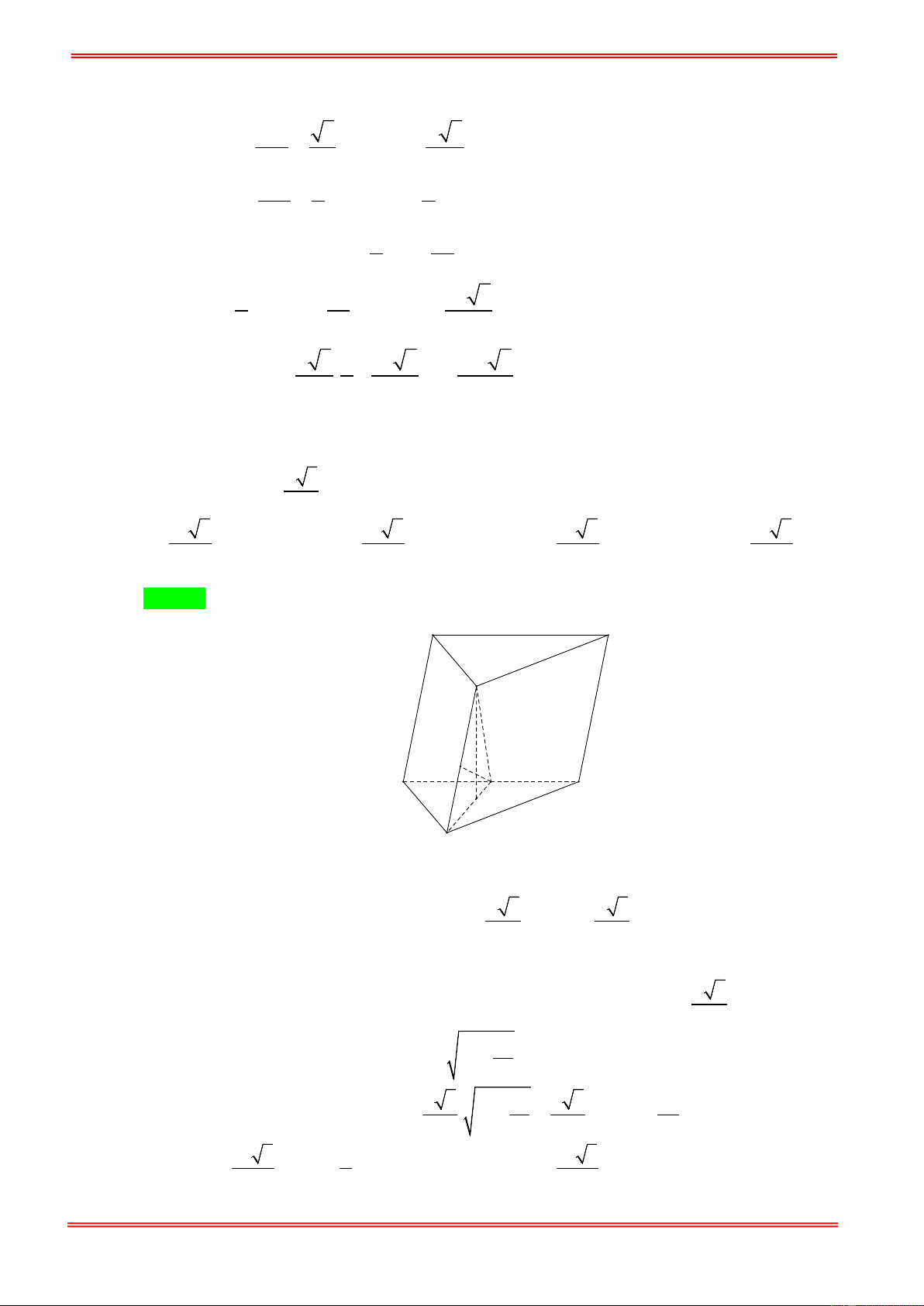
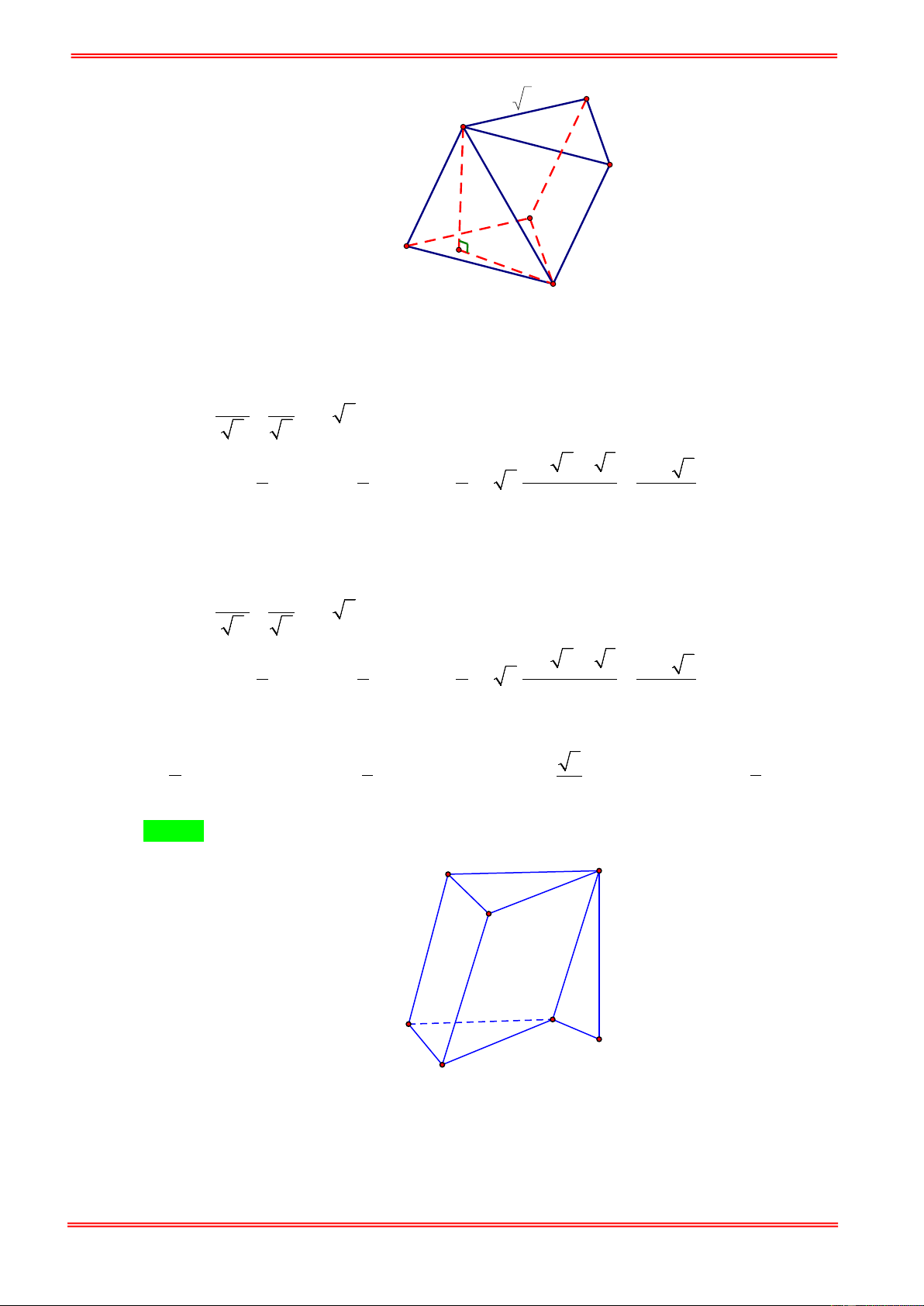
Câu 6. Cho lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác vuông tại A , 
ABC = 30° . Điểm M là trung điểm
cạnh AB , tam giác MA′C đều cạnh 2a 3 và nằm trong mặt phẳng vuông góc với đáy. Thể tích
khối lăng trụ ABC.A′B C ′ ′ là 3 72 2a 3 24 3a 3 72 3a 3 24 2a A. . B. . C. . D. . 7 7 7 7
Câu 7. Cho hình lăng trụ tứ giác ABC . D A′B C ′ D
′ ′ có đáy ABCD là hình vuông cạnh a và thể tích bằng 3 3a
. Tính chiều cao h của lăng trụ đã cho. a
A. h = 9a . B. h = .
C. h = a .
D. h = 3a . 3
Câu 8. Thể tích của khối lăng trụ có chiều cao bằng h và diện tích đáy bằng B là 1 A. 2
V = B h .
B. V = Bh . C. V = Bh .
D. V = π Bh . 3
Câu 9.Cho hình lăng trụ ABC . D A′B C ′ D
′ ′ có đáy ABCD là hình vuông cạnh a . Các cạnh bên tạo với đáy một góc o
60 . Đỉnh A′ cách đều các đỉnh ,
A B, C, D . Trong các số dưới đây, số nào ghi giá trị thể
tích của hình lăng trụ nói trên? https://toanmath.com/ 3 a 6 3 a 3 3 a 6 3 a 6 A. . B. . C. . D. . 9 2 2 3
Câu 10.Tính thể tích V của khối lăng trụ có diện tích mặt đáy bằng 2
3 3 cm và chiều cao bằng 6 cm . 9 2 A. V = ( 3 9 2 cm ) . B. V = ( 3 12 2 cm ) . C. V = ( 3 cm ) . D. V = ( 3 3 2 cm ) . 2
Câu 11.Cho lăng trụ đều ABC.A′B C
′ ′ có AB′ = 3cm và đường thẳng AB′ vuông góc với đường thẳng BC′
. Thể tích khối lăng trụ ABC.A′B C ′ ′ bằng 27 6 7 6 9 A. 3 cm . B. 3 2 3cm . C. 3 cm . D. 3 cm . 16 4 2
Câu 12. Cho hình lăng trụ ABC.AB C
  có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của A lên
mặt phẳng ABC trùng với trung điểm cạnh BC . Góc giữa BB và mặt phẳng ABC bằng 60
. Tính thể tích khối lăng trụ ABC.AB C   . 3 a 3 3 2a 3 3 a 3 3 3a 3 A. . B. . C. . D. . 8 8 4 8
Câu 13. Cho lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh bằng a , biết A′A = A′B = A′C = a .
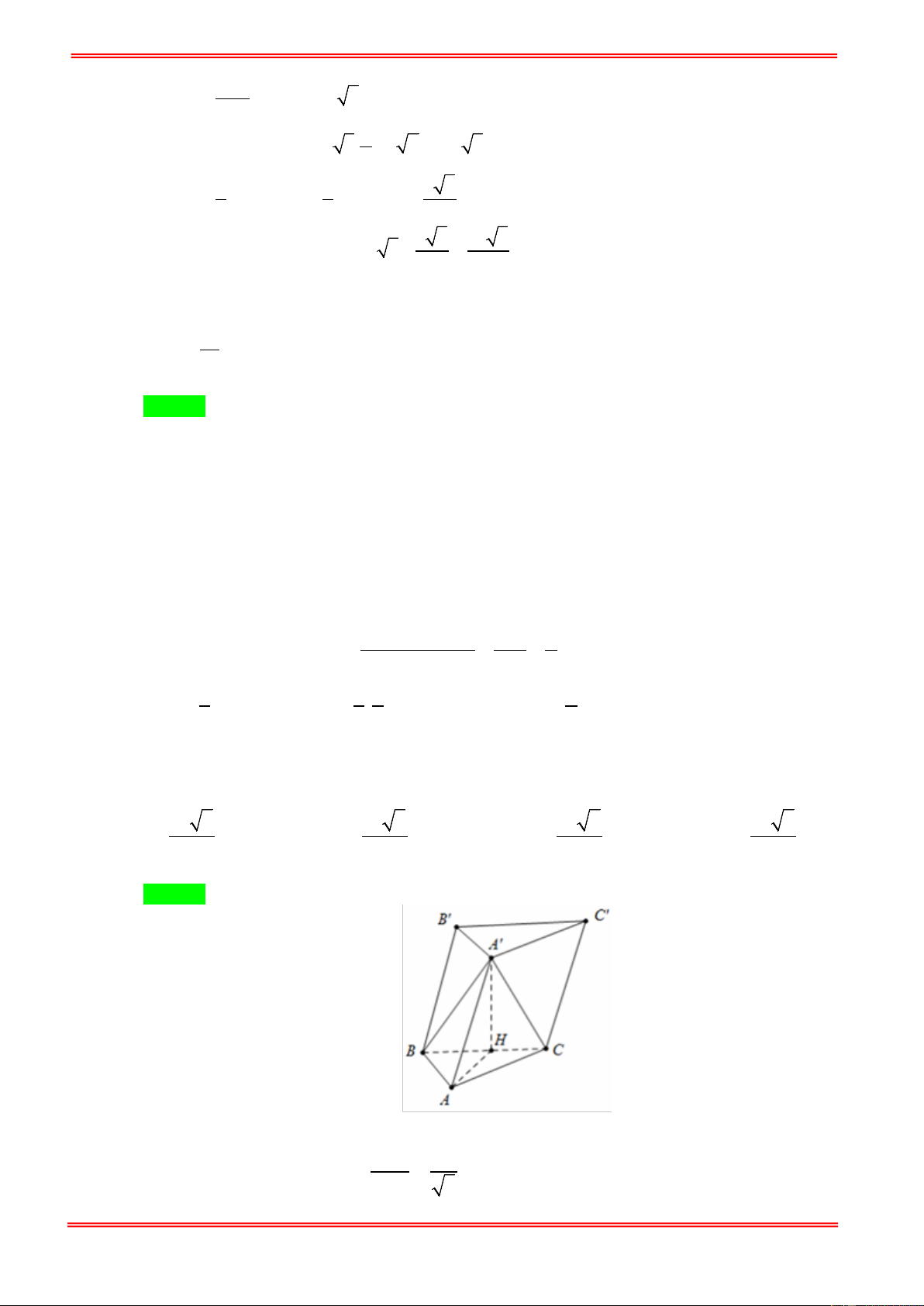
Tính thể tích khối lăng trụ ABC.A′B C ′ ′ ? 3 3a 3 a 2 3 a 3 3 a A. . B. . C. . D. . 4 4 4 4
Câu 14. Cho hình hộp ABC . D A′B C ′ D
′ ′ có diện tích tứ giác ABCD bằng 12, khoảng cách giữa hai mặt
phẳng ( ABCD) và ( A′B C ′ D
′ ′) bằng 2 . Tính thể tích V của khối hộp.
A. V = 12 .
B. V = 8 .
C. V = 24 .
D. V = 72 .
Câu 15. Cho lăng trụ tam giác ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh AB = 2a 2 . Biết AC′ = 8a và
tạo với mặt đáy một góc 45° . Thể tích khối đa diện ABCC B ′ ′ bằng 3 16a 6 3 8a 6 3 16a 3 3 8a 3 A. . B. . C. . D. . 3 3 3 3
Câu 16. Cho khối lăng trụ ABC.A′B C
′ ′. Gọi E là trọng tâm tam giác A′B C
′ ′ và F là trung điểm BC . Tính
tỉ số thể tích giữa khối B .′EAF và khối lăng trụ ABC.A′B C ′ ′. 1 1 1 1 A. . B. . C. . D. . 8 5 6 4
Câu 17. Cho hình lăng trụ tam giác ABC. ′
A B′C′ có đáy ABC là tam giác đều cạnh 2a , hình chiếu của ′ A
trên mặt phẳng ( ABC) là trung điểm cạnh BC . Biết góc giữa hai mặt phẳng ( AB ′ A ) và ( ABC )
bằng 45°. Tính thể tích V của khối chóp .
A BCC′B′ . 3 3 2 3a A. 3 a . B. 3 V = a . C. 3 a 3 . D. . 2 3
Câu 18. Cho khối lăng trụ có thể tích V , diện tích đáy là B và chiều cao .
h Tìm khẳng định đúng? 1
A. V = 3Bh . B. V = Bh . C. V = Bh .
D. V = Bh . 3
Câu 19. Cho hình lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác vuông tại B, 
ACB = 60 , BC = a, AA′ = 2a
. Cạnh bên tạo với mặt phẳng ( ABC ) một góc 30 . Thể tích khối lăng trụ ABC.A′B C ′ ′ bằng 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. 3 a 3 . 6 3 2
Câu 20.Cho ( H ) là khối lăng trụ có chiều cao bằng 3a, đáy là hình vuông cạnh .
a Thể tích của ( H ) bằng. A. 3 4a . B. 3 2a . C. 3 3a . D. 3 a . https://toanmath.com/
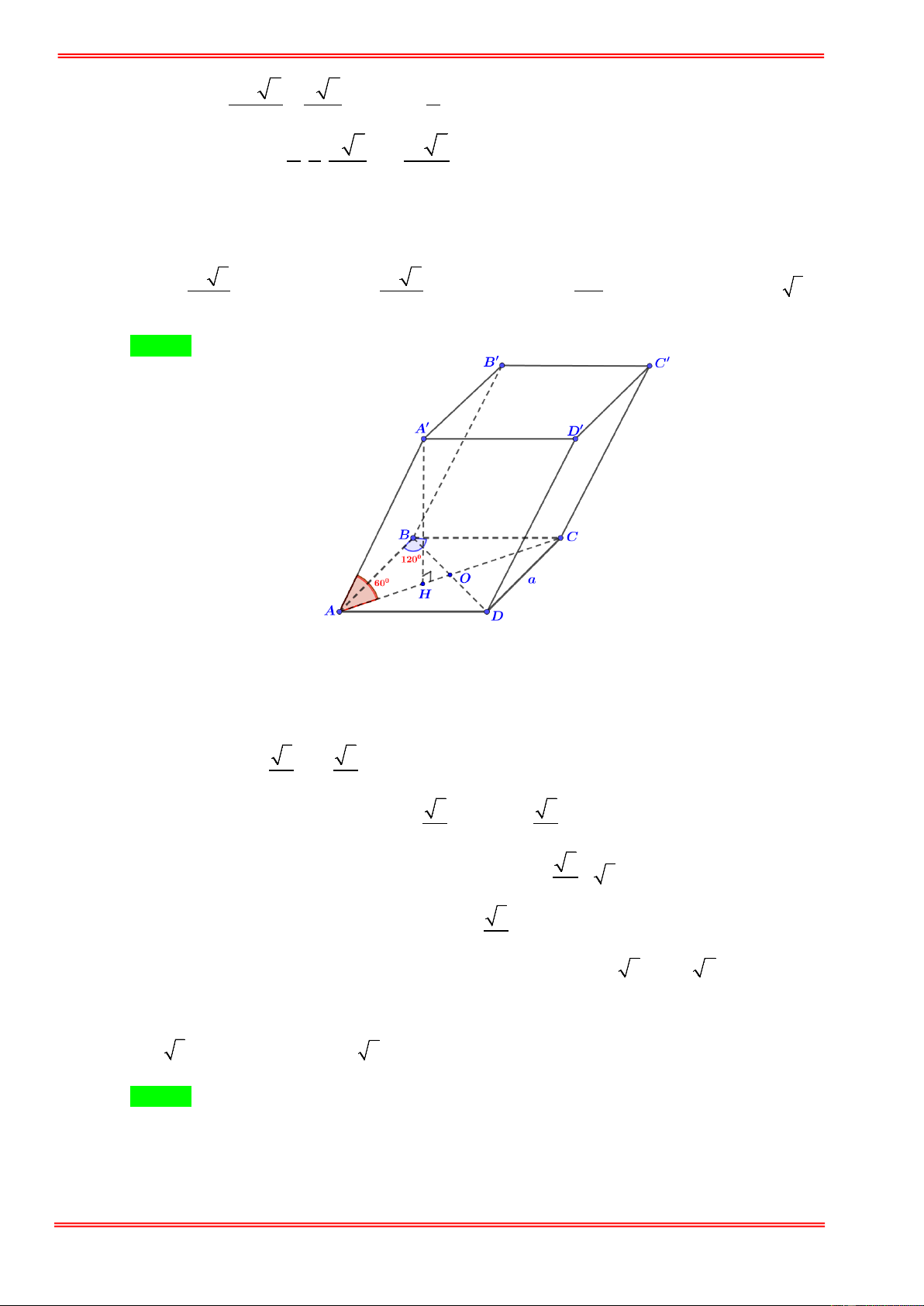
Câu 21.Cho hình lăng trụ ABC . D A′B C ′ D
′ ′ có đáy là hình thoi cạnh bằng a và 
ABC = 120° . Góc giữa cạnh
bên AA′ và mặt đáy bằng 60° , điểm A' cách đều các điểm A , B , D . Tính thể tích khối lăng trụ
đã cho theo a . 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 3 2 12
Câu 22. Cho lăng trụ ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của điểm A'
lên mặt phẳng ( ABC ) trùng với trọng tâm tam giác ABC . Biết khoảng cách giữa hai đường thẳng a 3
AA' và BC bằng
. Khi đó thể tích của khối lăng trụ là 4 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 3 6 24 12
Câu 23. Cho hình lăng trụ ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của điểm A′
lên mặt phẳng ( ABC) trùng với trọng tâm tam giác ABC . Biết khoảng cách giữa hai đường thẳng a 3
AA′ và BC bằng
. Tính theo a thể tích V của khối lăng trụ ABC.A′B C ′ ′. 4 3 a 3 3 a 3 3 a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . 12 3 24 6
Câu 24. Các đường chéo của các mặt của một hình hộp chữ nhật bằng a, b, c . Thể tích của khối hộp đó là A. V = . abc
B. V = a + b + . c ( 2 2 2
b + c − a )( 2 2 2
c + a − b )( 2 2 2
a + b − c ) C. V = . 8 ( 2 2 2
b + c − a )( 2 2 2
c + a − b )( 2 2 2
a + b − c ) D. V = . 8
Câu 25. Cho lăng trụ ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của điểm A′ lên
mặt phẳng ( ABC) trùng với trọng tâm của tam giác ABC . Biết khoảng cách giữa hai đường thẳng a
AA′ và BC bằng
3 . Khi đó thể tích của khối lăng trụ là 4 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 24 12 36 6
Câu 26. Cho hình lăng trụ ABC.A′B C
′ ′ , đáy ABC là tam giác đều cạnh x . Hình chiếu của đỉnh A′ lên
mặt phẳng ( ABC) trùng với tâm A
∆ BC , cạnh AA′ = 2x . Khi đó thể tích khối lăng trụ là: 3 x 11 3 x 39 3 x 3 3 x 11 A. . B. . C. . D. . 12 8 2 4
Câu 27. Cho hình hộp ABC . D A′B C ′ D
′ ′ có đáy là hình chữ nhật với AB = 3, AD = 7 và cạnh bên bằng 1
. Hai mặt bên ( ABB A ′ ′) và ( ADD A
′ ′) lần lượt tạo với đáy các góc 45° và 60°. Thể tích khối hộp bằng A. 3 3 B. 7 7 C. 7 D. 3
Câu 28. Thể tích của khối lăng trụ có chiều cao bằng h và diện tích đáy bằng B là 1 1 1 A. V = Bh .
B. V = Bh . C. V = Bh .
D. V = Bh . 6 3 2 https://toanmath.com/
Câu 29. Cho lăng trụ ABC.A B C có đáy ABC là tam giác vuông tại C , cạnh AC = 5a . Hình chiếu vuông 1 1 1
góc của A lên mặt phẳng ABC là trung điểm của cạnh AC , góc giữa mặt phẳng ( AA B B với 1 1 ) 1 (AAC C bằng o
30 , cạnh bên của lăng trụ tạo với đáy một góc o
60 . Tính thể tích V của lăng trụ 1 1 )
ABC.A B C ? 1 1 1 3 3.a 3 a 3 a 3 3.a A. V = . B. V = . C. V = . D. V = . 8 24 8 24
Câu 30.Cho hình lăng trụ có tất cả các cạnh đều bằng a , đáy là lục giác đều, góc tạo bởi cạnh bên và mặt
đáy là 60°. Tính thể tích khối lăng trụ. 9 3 3 27 A. 3 V = a . B. 3 V = a . C. 3 V = a . D. 3 V = a . 4 4 2 8
Câu 31. Khối lăng trụ ABC.A′B C
′ ′ có đáy là một tam giác đều cạnh a, góc giữa cạnh bên và mặt phẳng đáy
bằng 30° Hình chiếu của đỉnh A′ trên mặt phẳng đáy ( ABC) trùng với trung điểm của cạnh BC.
Tính thể tích của khối lăng trụ đã cho. 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 4 12 8 3
Câu 32. Cho lăng trụ tam giác ABC. ′
A B′C′ có đáy ABC là tam giác vuông cân tại A , cạnh AC = 2 2 .
Biết AC′ tạo với mặt phẳng ( ABC ) một góc 60° và AC′ = 4 . Tính thể tích V của khối đa diện
ABCB′C′ . 16 3 16 8 3 8 A. V = . B. V = . C. V = . D. V = . 3 3 3 3
Câu 33. Cho hình lăng trụ ABC.A B ′ C
′ ′ có thể tích bằng 30. Gọi I , J , K lần lượt là trung điểm của AA ,′ BB ,
′ CC′ . Tính thể tích V của tứ diện CIJK . 15 A. V = .
B. V = 12 .
C. V = 6 .
D. V = 5 . 2
Câu 34. Khối lăng trụ ABC. ′
A B′C′ có đáy là tam giác đều, a là độ dài cạnh đáy. Góc giữa cạnh bên và
đáy là 30° . Hình chiếu vuông góc của ′
A trên mặt ( ABC ) trùng với trung điểm của BC . Thể
tích của khối lăng trụ đã cho là 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 8 3 4 12
Câu 35. Cho lăng trụ ABC . D A′B C ′ D
′ ′ có đáy ABCD là hình thoi cạnh a , tâm O và 
ABC = 120° . Góc giữa
cạnh bên AA′ và mặt đáy bằng 60°. Đỉnh A′ cách đều các điểm A , B , D . Tính theo a thể tích
V của khối lăng trụ đã cho. 3 a 3 3 a 3 3 3a A. V = . B. V = . C. V = . D. 3 V = a 3 . 2 6 2
Câu 36. Cho hình hộp ABC . D A′B C ′ D
′ ′ có đáy là hình chữ nhật với AB = 3, AD = 7 và cạnh bên bằng 1
. Hai mặt bên ( ABB A ′ ′) và ( ADD A
′ ′) lần lượt tạo với đáy các góc 45° và 60°. Thể tích khối hộp bằng A. 3 3 B. 7 7 C. 7 D. 3
Câu 37. Cho hình lăng trụ ABCA′B C
′ ′ có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của A′ lên
mặt phẳng (ABC ) trùng với trọng tâm tam giác ABC . Biết khoảng cách giữa hai đường thẳng a
AA′ và BC bằng
3 . Tính thể tích V của khối lăng trụ ABCA′B C′ .′ 4 https://toanmath.com/ 3 a 3 3 a 3 3 a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . 6 24 12 3
Câu 38. Cho khối lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh bằng a , cạnh bên AA′ = a , góc
giữa AA′ và mặt phẳng đáy bằng 30° . Tính thể tích khối lăng trụ đã cho theo a . 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 8 24 4 12
Câu 39. Cho hình lăng trụ ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của điểm A′
lên mặt phẳng ( ABC ) trùng với trọng tâm tam giác ABC . Biết khoảng cách giữa hai đường AA′ a 3 và BC bằng
. Tính thể tích V của khối lăng trụ ABC.A′B C ′ ′ . 4 3 a 3 3 a 3 3 a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . 24 12 3 6
Câu 46. Cho hình lăng trụ ABC.A' B 'C ' có đáy là tam giác đều cạnh 3a , hình chiếu của A' trên mặt phẳng
(ABC) trùng với tâm đường tròn ngoại tiếp tam giác ABC . Cạnh AA' hợp với mặt phẳng đáy
một góc 45°. Thể tích của khối lăng trụ ABC.A'B 'C ' tính theo a bằng. 3 9a 3 27a 3 3a 3 27a A. . B. . C. . D. . 4 4 4 6
Câu 47. Khối lăng trụ có đáy là hình vuông cạnh a , đường cao bằng a 3 có thể tích bằng 3 a 3 3 a 3 A. . B. . C. 3 a 3 . D. 3 2a 3 . 6 3
Câu 48. Cho lăng trụ ABCA B C có diện tích mặt bên ABB A bằng 4 ; khoảng cách giữa cạnh CC và mặt 1 1 1 1 1 1
phẳng ( ABB A bằng 7. Tính thể tích khối lăng trụ ABCA B C . 1 1 ) 1 1 1 28 14 A. 14 B. C. D. 28 3 3
Câu 49. Cho lăng trụ tam giác ABC.A′B C
′ ′. Các điểm M , N , P lần lượt thuộc các cạnh AA′ , BB′ ,CC′ AM 1 BN 2 sao cho = =
MNP chia lăng trụ thành hai phần có thể tích bằng AA′ , 2 BB′ và mặt phẳng ( ) 3
nhau. Khi đó tỉ số CP CC′ là 1 5 1 1 A. . B. . C. . D. . 4 12 3 2 3a
Câu 50. Cho hình lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh a , AA′ = . Biết rằng hình chiếu 2
vuông góc của A′ lên ( ABC ) là trung điểm BC . Tính thể tích V của khối lăng trụ đó. 3 2a 3 3a 3 A. 3 V = a . B. V = . C. V = . D. 3 V = a . 3 4 2 2
Câu 51. Cho lăng trụ tam giác ABC.A′B C
′ ′ có đáy là tam giác ABC đều cạnh bằng a . Hình chiếu vuông
góc của A′ trên mặt phẳng ( ABC ) trùng với trung điểm H của cạnh AB . Góc giữa cạnh bên của
lăng trụ và mặt phẳng đáy bằng o
30 . Tính thể tích của khối lăng trụ đã cho theo a . 3 3a 3 a 3 a 3 a A. B. C. D. 4 4 24 8
Câu 52. Cho hình lăng trụ ABC. ′
A B′C′ có đáy là tam giác vuông cân ở C . Cạnh BB′ = a và tạo với đáy
một góc bằng 60° . Hình chiếu vuông góc hạ từ B′ lên đáy trùng với trọng tâm của tam giác ABC
. Thể tích khối lăng trụ ABC. ′
A B′C′ là: https://toanmath.com/ 3 9 3a 3 9a 3 3 3a 3 3a A. . B. . C. . D. . 80 80 80 80
Câu 53. Cho lăng trụ ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của điểm A′ lên
mặt phẳng ( ABC) trùng với trọng tâm tam giác ABC . Biết khoảng cách giữa hai đường thẳng a
AA′ và BC bằng
3 . Khi đó thể tích của khối lăng trụ là 4 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 3 24 12
Câu 54.Cho hình hộp ABC . D A′B C ′ D ′ ′ có  BCD = 60 ,
° AC = a 7, BD = a 3, AB > AD ,đường chéo BD′
hợp với mặt phẳng ( ADD A
′ ′) góc 30°. Tính thể tích V của khối hộp ABC . D A′B C ′ D ′ ′ . 39 A. 3 a . B. 3 2 3a . C. 3 3 3a . D. 3 39a . 3
Câu 55. Cho hình lăng trụ ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của điểm A′
lên mặt phẳng ( ABC) trùng với trọng tâm tam giác ABC . Biết khoảng cách giữa hai đường thẳng a
AA′ và BC bằng
3 . Tính thể tích V của khối lăng trụ ABC.A′B C ′ ′. 4 3 a 3 3 a 3 3 a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . 12 3 24 6
Câu 56. Cho lăng trụ ABC.A′B C
′ ′ có đáy là tam giác đều cạnh .
a Hình chiếu vuông góc của mặt phẳng ( 3 a 3
ABC ) trùng với trọng tâm của tam giác ABC. Biết thể tích của khối lăng trụ là . Khoảng 4
cách giữa hai đường thẳng AB′ và BC là: 2a 4a 3a 3a A. . B. . C. . D. . 3 3 4 2
Câu 57. Một khối lăng trụ tam giác có các cạnh đáy bằng 13 ,14 ,15 cạnh bên tạo với mặt phẳng đáy một góc
30° và có chiều dài bằng 8 . Khi đó thể tích khối lăng trụ là. A. 340 . B. 336 . C. 274 3 . D. 124 3 .
Câu 58. Cho lăng trụ tam giác ABC.A' B 'C ' có đáy ABC là đều cạnh AB = 2a 2 . Biết AC ' = 8a và tạo với mặt đáy một góc 0
45 . Thể tích khối đa diện ABCC ' B ' bằng 3 8a 3 3 8a 6 3 16a 3 3 16a 6 A. . B. . C. . D. . 3 3 3 3
Câu 59. Cho lăng trụ ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a , AA′ = b và AA′ tạo với mặt đáy một góc
60° . Tính thể tích khối lăng trụ. 3 3 3 1 A. 2 a b . B. 2 a b . C. 2 a b . D. 2 a b . 4 8 8 8
Câu 60. Cho khối lăng trụ tam giác ABC.A' B 'C ' có thể tích bằng 30 (đơn vị thể tích). Thể tích của khối tứ diện AB C ′ C ′ là:
A. 5 (đơn vị thể tích).
B. 10 (đơn vị thể tích).
C. 12,5 (đơn vị thể tích).
D. 7,5 (đơn vị thể tích).
Câu 61.Cho lăng trụ ABC . D A′B C ′ D
′ ′ với đáy ABCD là hình thoi, AC = 2a ,  0
BAD = 120 . Hình chiếu vuông
góc của điểm B trên mặt phẳng ( A′B C ′ D
′ ′) là trung điểm cạnh A′B′ , góc giữa mặt phẳng ( AC D ′ ′)
và mặt đáy lăng trụ bằng o
60 . Tính thể tích V của khối lăng trụ ABC . D A′B C ′ D ′ ′ . A. 3 V = 3a . B. 3
V = 6 3a . C. 3
V = 2 3a . D. 3
V = 3 3a . https://toanmath.com/
THỂ TÍCH KHỐI LĂNG TRỤ XIÊN
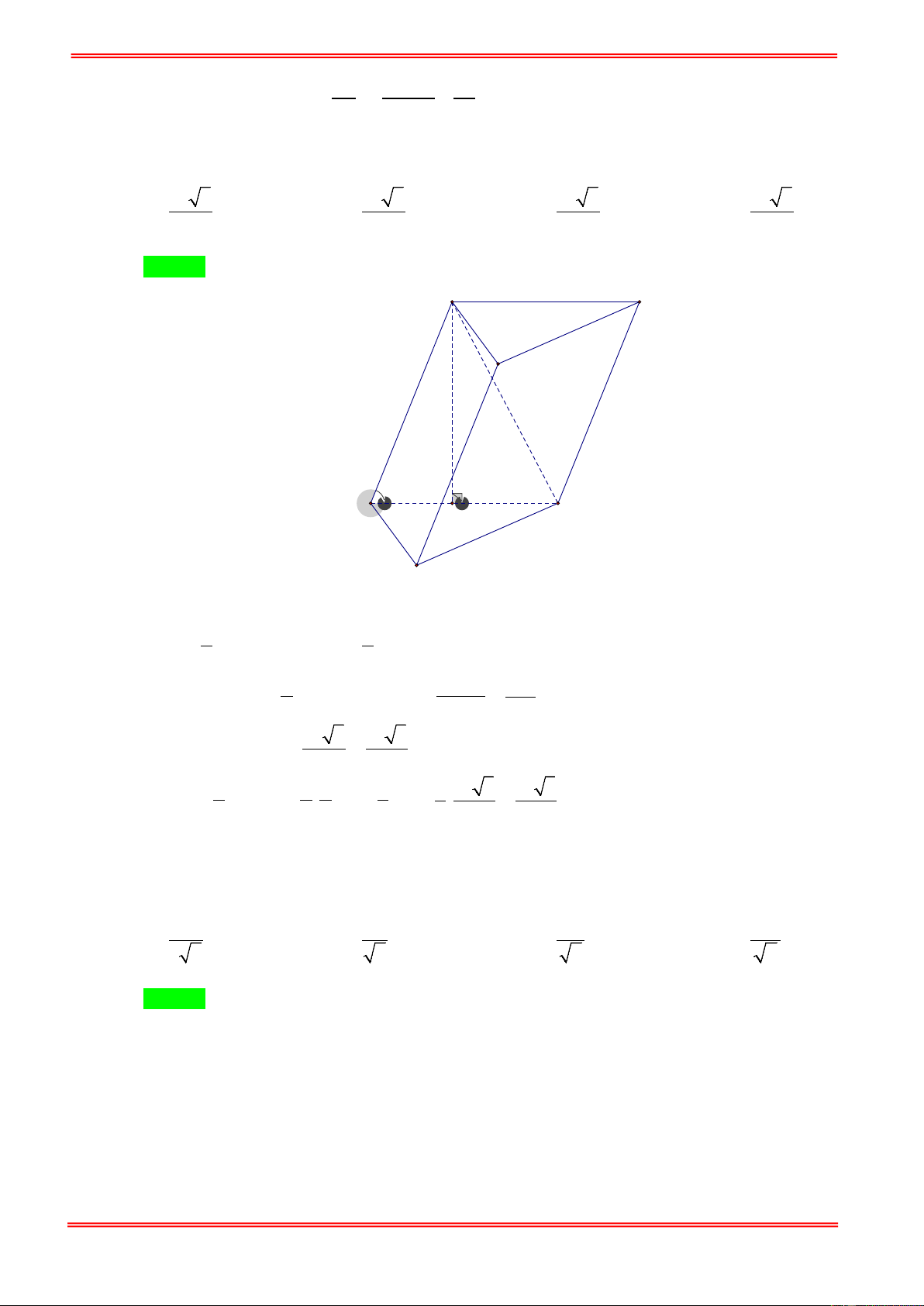
Câu 1.Cho lăng trụ tam giác ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Độ dài cạnh bên bằng 4a . Mặt phẳng (BCC B
′ ′) vuông góc với đáy và  B B
′ C = 30°. Thể tích khối chóp . A CC B ′ ′ là: 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 12 18 2 Hướng dẫn giải Chọn A
Gọi H là hình chiếu của B′ trên BC . Từ giả thiết suy ra: B H ′ ⊥ ( ABC). 1 = ′  1 S ′ = ° 2 = ′
BB .BC.sin B BC 4 . a . a sin 30 a . BB C 2 2 2 Mặt khác: 1 2S 2a S = ′ BB C ′ ⇒ ′ = = = ′ B H.BC B H 2a . BB C 2 BC a 2 a 3 3 a 3 V = B H ′ .S = 2 . a = . LT ABC 4 2 1 3 1 a 3 3 a 3 V = 1 2 1 = = ′ ′ V . V V = . = . . A CC B . ′ ′ 2 A CC B B 2 3 LT 3 LT 3 2 6
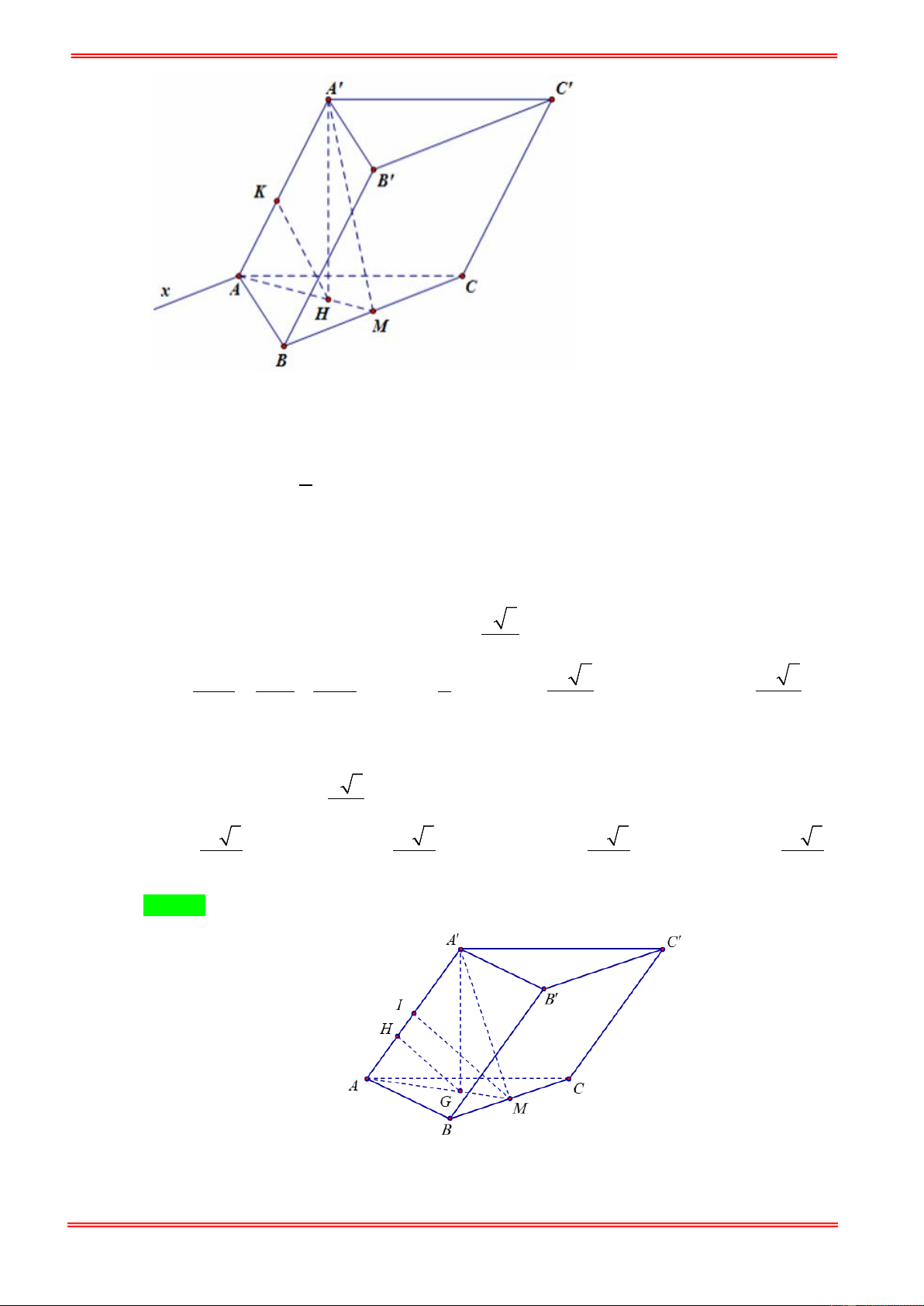
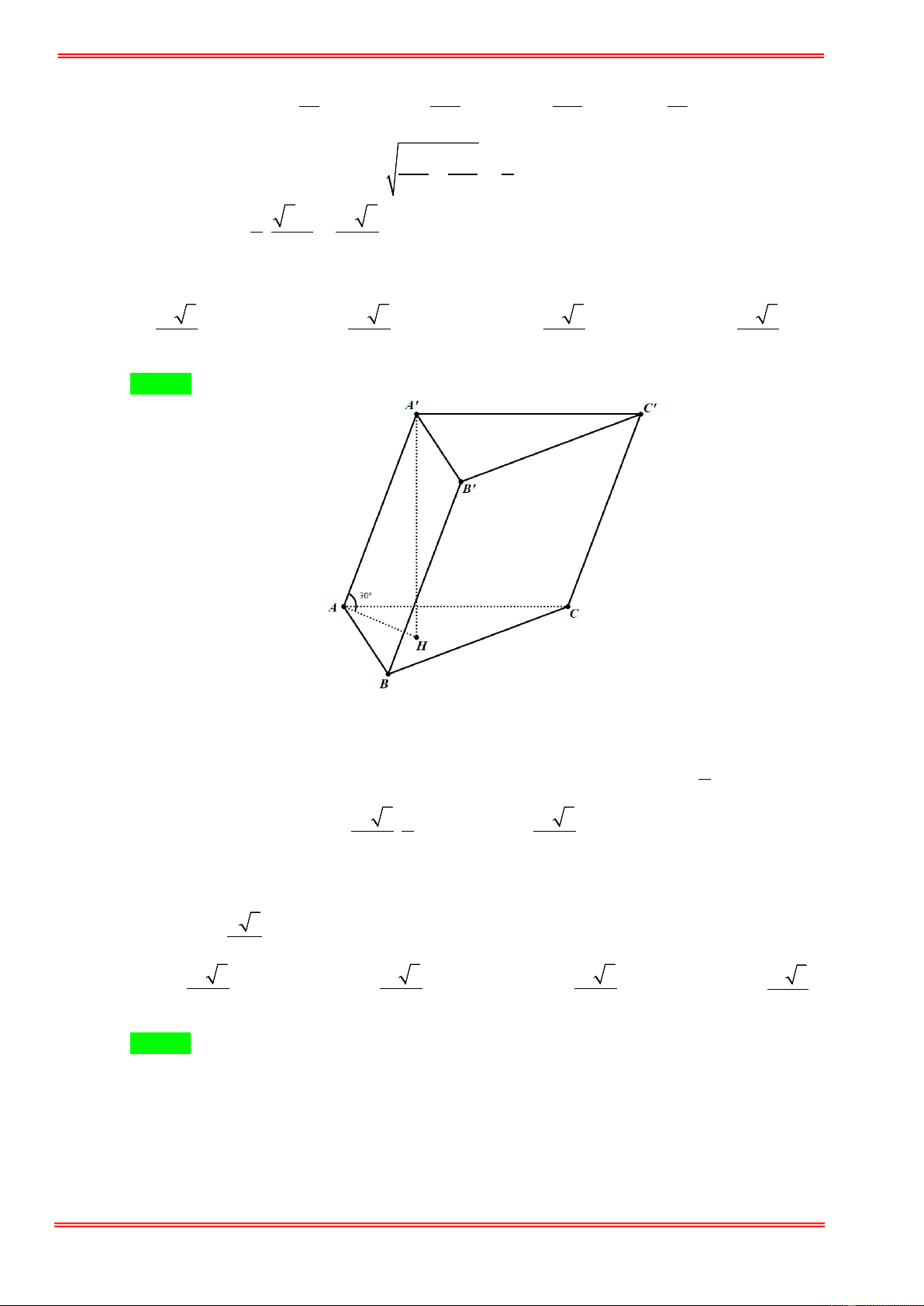
Câu 2. Cho lăng trụ ABC . D A′B C ′ D
′ ′ có đáy ABCD là hình chữ nhật với AB = 6 , AD = 3 , A′C = 3 và
mặt phẳng ( AA′C C
′ ) vuông góc với mặt đáy. Biết hai mặt phẳng ( AA′C C
′ ) , ( AA′B B ′ ) tạo với 3
nhau góc α thỏa mãn tanα =
. Thể tích khối lăng trụ ABC . D A′B C ′ D ′ ′ bằng? 4
A. V = 6 .
B. V = 8 .
C. V = 12 .
D. V = 10 . Hướng dẫn giải 1 6 T Chọn B 1 6 T A' B' D' M C' H A B K I D C
Từ B kẻ BI ⊥ AC ⇒ BI ⊥ ( AA′C C ′ ). 1 6 T 1 6 T 1 6 T 1 6 T 1 6 T https://toanmath.com/
Từ I kẻ IH ⊥ AA′ ⇒ (( AA′C C ′ ) ( AA′B B ′ ))  =  , B I H . AB BC
Theo giải thiết ta có AC = . 3 ⇒ BI = = 2 . AC BI BI
Xét tam giác vuông BIH có  tan BHI = ⇔ IH = 4 2 ⇔ IH = . IH  tan BHI 3 2 AB
Xét tam giác vuông ABC có 2
AI.AC = AB ⇒ AI = = 2 . AC
Gọi M là trung điểm cả AA′ , do tam giác AA′C cân tại C nên CM ⊥ AA′ ⇒ CM // IH . AI AH 2 AH AH Do = = 2 ⇒ = 1 ⇒ = AC AM 3 AM 3 AA′ . 3 4 2
Trong tam giác vuông AHI kẻ đường cao HK ta có HK =
⇒ chiều cao của lăng trụ 9 ABC . D A′B C ′ D ′ ′ là h = 4 2 3HK = . 3
Vậy thể tích khối lăng trụ ABC . D A′B C ′ D ′ ′ là V = 4 2 = ′ ′ ′ ′ A . B A . D h = 6 3 8 . ABCD. A B C D 3
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi H là điểm trên cạnh SD sao cho
5SH = 3SD , mặt phẳng (α ) qua B, H và song song với đường thẳng AC cắt hai cạnh SA, SC lần lượt tại V
E, F. Tính tỉ số thể tích C.BEHF . VS.ABCD 1 3 6 1 A. . B. . C. . D. . 7 20 35 6 Hướng dẫn giải Chọn B - Đặt V = V S . ABCD
- Trong tam giác SOD ta có: IS BO HD IS SI SE SF 3 . . = 1⇒ = 3 ⇒ = = = . IO BD HS IO SO SA SC 4 V SH 3 3V
- Ta có: S.HBC = = ⇒ V = . S . V SD 5 HBC 10 S .DBC V CF 1 3V
- Mặt khác: C.FHB = = ⇒ V = . C. V CS 4 FHB 40 C.SHB https://toanmath.com/ 6V V 3 - Mà: C. V = 2 BEHF V = ⇒ = . C.BEHF C.FHB 40 V 20 S . ABCD
Câu 4. Cho lăng trụ tam giác ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Độ dài cạnh bên bằng 4a . Mặt phẳng (BCC B
′ ′) vuông góc với đáy và  B B
′ C = 30°. Thể tích khối chóp . A CC B ′ ′ là: 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 2 12 18 6 Hướng dẫn giải Chọn D B' C' A' 4a B C H a A
Gọi H là hình chiếu của B′ trên BC . Từ giả thiết suy ra: B H ′ ⊥ ( ABC). 1 = ′  1 S ′ = ° 2 = ′
BB .BC.sin B BC 4 . a . a sin 30 a . BB C 2 2 2 Mặt khác: 1 2S 2a S = ′ BB C ′ ⇒ ′ = = = ′ B H.BC B H 2a . BB C 2 BC a 2 a 3 3 a 3 V = B H ′ .S = 2 . a = . LT ABC 4 2 1 3 1 a 3 3 a 3 V = 1 2 1 = = ′ ′ V . V V = . = . . A CC B . ′ ′ 2 A CC B B 2 3 LT 3 LT 3 2 6
Câu 5. Cho hình lăng trụ ABC. ′
A B′C′ có đáy ABC là tam giác vuông tại A . cạnh BC = 2a và 
ABC = 60° . Biết tứ giác BCC′B′ là hình thoi có 
B′BC nhọn. Biết ( BCC′B′) vuông góc với
( ABC) và ( ABB′ ′
A ) tạo với ( ABC ) góc 45° . Thể tích của khối lăng trụ ABC. ′
A B′C′ bằng 3 a 3 a 3 3a 3 6a A. . B. . C. . D. . 3 7 7 7 7 Hướng dẫn giải Chọn C https://toanmath.com/ A' C' B' A 2a C 2a K 60° H B
Do ABC là tam giác vuông tại ,
A cạnh BC = 2a và 
ABC = 60° nên AB = a , AC = a 3 .
Gọi H là hình chiếu vuông góc của B′ lên BC ⇒ H thuộc đoạn BC (do  B′BC nhọn)
⇒ B′H ⊥ ( ABC) (do (BCC′B′) vuông góc với ( ABC)).
Kẻ HK song song AC (K ∈ AB) ⇒ HK ⊥ AB (do ABC là tam giác vuông tại A ).  ⇒ ( ABB′ ′ A ) ( ABC )  =  ,
B′KH = 45° ⇒ B′H = KH (1)  
Ta có ∆BB′H vuông tại H 2 2
⇒ BH = 4a − B′H (2) Mặt khác BH HK .2
HK song song AC ⇒ = ⇒ = HK a BH (3) BC AC a 3 ′ Từ (1), (2) và (3) suy ra .2 12 2 2 4 − ′ = B H a a B H
⇒ B′H = a . a 3 7 3 Vậy 1 3 = ′ = ′ = a V S B H AB AC B H . ABC A B C′ . . . . ' ' ABC 2 7
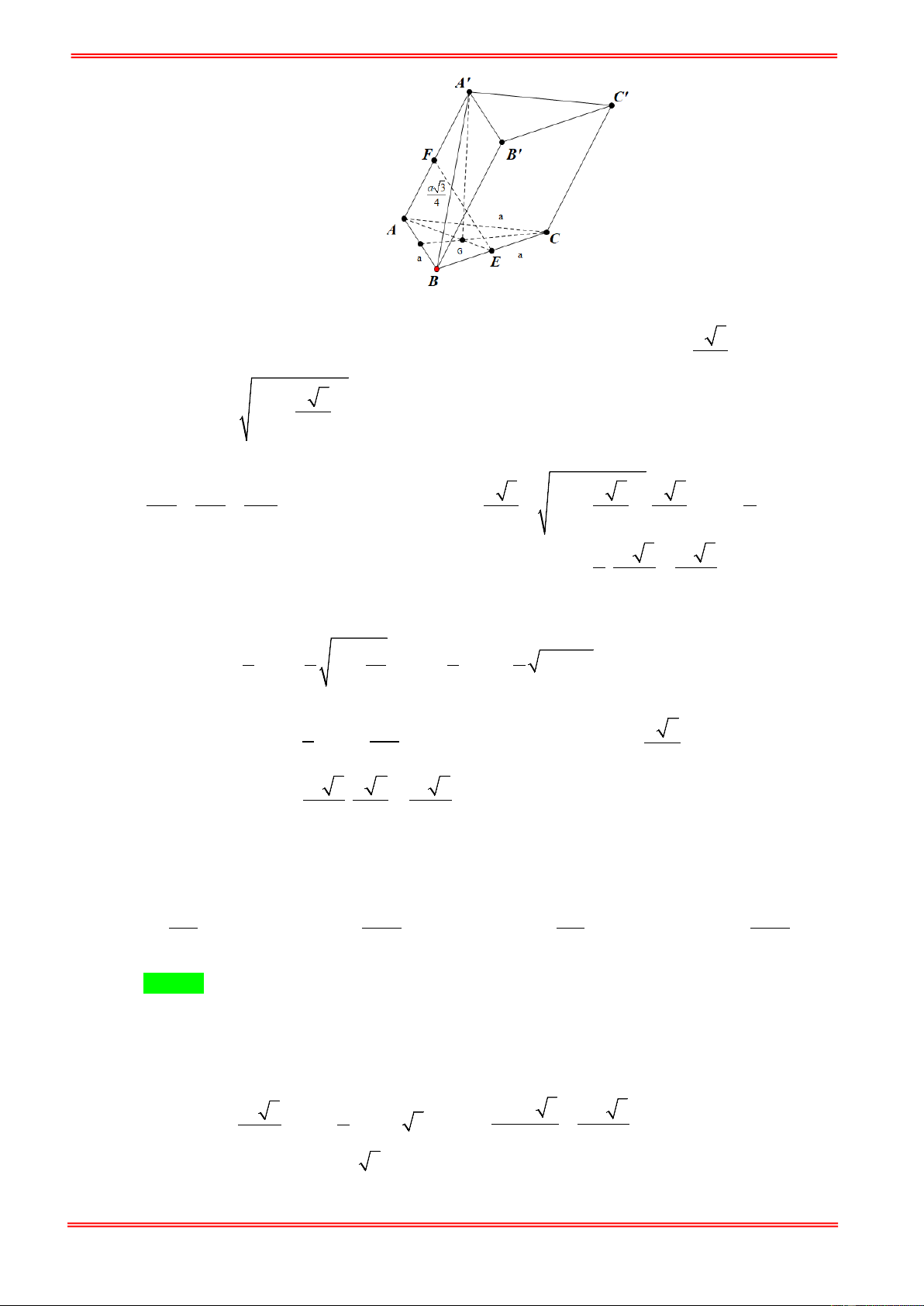
Câu 6. Cho lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác vuông tại A , 
ABC = 30° . Điểm M là trung
điểm cạnh AB , tam giác MA′C đều cạnh 2a 3 và nằm trong mặt phẳng vuông góc với đáy.
Thể tích khối lăng trụ ABC.A′B C ′ ′ là 3 72 2a 3 24 3a 3 72 3a 3 24 2a A. . B. . C. . D. . 7 7 7 7 Hướng dẫn giải Chọn A https://toanmath.com/ A' C' B' A C H M B
Gọi H là trung điểm của MC .
A′H ⊥ MC  Ta có (
A′MC) ⊥ ( ABC)
⇒ A′H ⊥ ( ABC) . (  A′MC  )∩( ABC) = MC MC = 2a 3
Tam giác MA′C đều cạnh 2a 3 ⇒ 
A′H = 3a  = Đặt BC 2x
AC = x > 0 , tam giác ABC vuông tại A có  ABC = 30° ⇒  AB = x 3
Áp dụng công thức tính độ dài trung tuyến ta có 2 2 2 2 2 2 CA + CB AB x + 4x 3x 4a 3 2 2 CM = − ⇔ 12a = − ⇔ x = . 2 4 2 4 7 2 1 1 12a 4a 3 24a 3 Suy ra S = A . B AC = . . = . ABC 2 2 7 7 7 3 Do đó 72a 3 V = ′ = ′ ′ ′ A H .S . ABC. A B C ABC 7
Câu 7. Cho hình lăng trụ tứ giác ABC . D A′B C ′ D
′ ′ có đáy ABCD là hình vuông cạnh a và thể tích bằng 3
3a . Tính chiều cao h của lăng trụ đã cho. a
A. h = 9a . B. h = .
C. h = a .
D. h = 3a . 3 Hướng dẫn giải Chọn D V 3 3a Ta có: V = ABCD A′B C ′ D ′ ′ ⇔ = = = ′ ′ ′ ′ S .h . h 3a . ABCD. A B C D ABCD S 2 a ABCD
Câu 8. Thể tích của khối lăng trụ có chiều cao bằng h và diện tích đáy bằng B là 1 A. 2
V = B h .
B. V = Bh . C. V = Bh .
D. V = π Bh . 3 https://toanmath.com/ Hướng dẫn giải Chọn B
Thể tích khối lăng trụ: V = . B h .
Câu 9.Cho hình lăng trụ ABC . D A′B C ′ D
′ ′ có đáy ABCD là hình vuông cạnh a . Các cạnh bên tạo với đáy một góc o
60 . Đỉnh A′ cách đều các đỉnh ,
A B, C, D . Trong các số dưới đây, số nào ghi giá trị thể
tích của hình lăng trụ nói trên? 3 a 6 3 a 3 3 a 6 3 a 6 A. . B. . C. . D. . 9 2 2 3 Hướng dẫn giải Chọn C
Gọi O là tâm hình vuông ABCD .Từ giả thiết A′cách đều các đỉnh A , B , C ta suy ra hình chiếu
của A′ trên mặt phẳng ABCD là O hay A′O là đường cao của khối lăng trụ.
Trong tam giác A′OA vuông tại A và 
A′OA = 60 , ta có: a a 6 A′O = . OA tan 60 = . 3 = . 2 2
Diện tích đáy ABCD là 2 S = a . ACDD 3
Thể tích của khối lăng trụ là a 6 V = . B h = S .A′O = . ABCD 2 3 Vậy a 6 V = . 2 .
Câu 10.Tính thể tích V của khối lăng trụ có diện tích mặt đáy bằng 2
3 3 cm và chiều cao bằng 6 cm . 9 2 A. V = ( 3 9 2 cm ) . B. V = ( 3 12 2 cm ) . C. V = ( 3 cm ) . D. V = ( 3 3 2 cm ) . 2 Hướng dẫn giải ChọnA
Thể tích khối lăng trụ: V = S h = = ( 3 . 3 3. 6 9 2 cm ) .
Câu 11.Cho lăng trụ đều ABC.A′B C
′ ′ có AB′ = 3cm và đường thẳng AB′ vuông góc với đường thẳng
BC′ . Thể tích khối lăng trụ ABC.A′B C ′ ′ bằng 27 6 7 6 9 A. 3 cm . B. 3 2 3cm . C. 3 cm . D. 3 cm . 16 4 2 Hướng dẫn giải Chọn D https://toanmath.com/ A' C' B' N A C M B
Gọi M là trung điểm của BC . Suy ra AM ⊥ ( BCC B
′ ′) ⇒ AM ⊥ BC′ .
Mà BC′ ⊥ AB′ ⇒ B M ′ ⊥ BC′. Đặ a 2b a
t AB = a , AA′ = b . Ta có  ′ ′ =  tan B BC cot BB M ′ ⇒ = ⇒ b = . b a 2 2 a Mà 2 2 AB′ = 3 ⇒ AB + AA′ = 3 2 ⇒ a + = 3 ⇒ a = 6 . 2
Thể tích khối lăng trụ là 2 3 9 3
V = AA .′S = 3. 6 . = cm . ABC 4 2
Câu 12. Cho hình lăng trụ ABC.AB C
  có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của A lên
mặt phẳng ABC trùng với trung điểm cạnh BC . Góc giữa BB và mặt phẳng ABC bằng
60 . Tính thể tích khối lăng trụ ABC.AB C   . 3 a 3 3 2a 3 3 a 3 3 3a 3 A. . B. . C. . D. . 8 8 4 8 Hướng dẫn giải Chọn D C' A' B' C H A 60° B .
Gọi H là trung điểm cạnh BC . Theo đề ra: AH ABC. AB 3 a 3 2 2 AB 3 a 3 AH   . S   vđ dt . ABC   2 2 4 4 
 AA',ABC    A' AH  Ta có:  
A' AH  60 . 
 AA',ABC
 BB',ABC   60  https://toanmath.com/ 3 Xét A
 AH vuông tại H : AH AH.tan 60  a . 2 3 Vậy 3a 3 V
AH.S      đvtt . ABC. A B C ABC   8
Câu 13. Cho lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh bằng a , biết A′A = A′B = A′C = a .
Tính thể tích khối lăng trụ ABC.A′B C ′ ′ ? 3 3a 3 a 2 3 a 3 3 a A. . B. . C. . D. . 4 4 4 4 Hướng dẫn giải Chọn B A' B' A C H B
Gọi H là trọng tâm tam giác ABC . Theo giả thiết ta có ABC là tam giác đều cạnh bằng a và
A′A = A′B = A′C = a nên A .′ABC là tứ diện đều cạnh a ⇒ A′H ⊥ ( ABC ) hay A′H là đường
cao của khối chóp A .′ABC . a
Xét tam giác vuông A′HA ta có 2 2 A′H = A′A − 6 AH = . 3 2 Diện tích tam giác 1 a 3 ABC là S = . a . a sin 60° = ABC . 2 4 2 3
Thể tích khối lăng trụ a 3 a 6 a 2
ABC.A′B C ′ ′ là V = .
ABC.A′B C ′ ′ = 4 3 4
Câu 14. Cho hình hộp ABC . D A′B C ′ D
′ ′ có diện tích tứ giác ABCD bằng 12, khoảng cách giữa hai mặt
phẳng ( ABCD) và ( A′B C ′ D
′ ′) bằng 2 . Tính thể tích V của khối hộp.
A. V = 12 .
B. V = 8 .
C. V = 24 .
D. V = 72 . Hướng dẫn giải Chọn B Ta có V = S
.d ( A ,′ ABCD = S
.d (( A′B C ′ D
′ ′), ABCD =12.2 = 24 . ABCD ( )) ABCD ( ))
Câu 15. Cho lăng trụ tam giác ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh AB = 2a 2 . Biết AC′ = 8a và
tạo với mặt đáy một góc 45° . Thể tích khối đa diện ABCC B ′ ′ bằng 3 16a 6 3 8a 6 3 16a 3 3 8a 3 A. . B. . C. . D. . 3 3 3 3 Hướng dẫn giải Chọn A https://toanmath.com/ C' A' H B' A C B Ta có V = + ⇔ = − ′ ′ ′ V ′ ′ ′ V V ′ ′ V ′ ′ ′ V . ABC. A B C . A A B C ABCC B ′ ′ ABCC B ABC. A B C . A A′B C ′ ′ 1 Mặt khác V = ⇔ = − = ′ ′ ′ V nên V ′ ′ V ′ ′ ′ V 2V . . A A B C ABC. ′ ′ ′ ′ ′ ′ ′ ′ ′ 3 A B C ABCC B ABC. A B C . A A B C . A A B C
Gọi H là hình chiếu của A trên mặt phẳng ( A′B C
′ ′) khi đó góc giữa AC′ và mặt phẳng đáy ( A′B C ′ ′) là góc  AC H ′ = 45° .
Xét tam giác vuông AHC′ có AC′ = 8a và  AC H
′ = 45° nên AH = 4a 2 . 1 3 8a 6 Thể tích khối chóp . A A′B C ′ ′ là V = = ° = ′ ′ ′
S ′ ′ ′.AH ( a )2 1 1 . 2 2 .sin 60 .4a 2 . A A B C 3 A B C 3 2 3 3 16a 6
Vậy thể tích khối đa diện ABCC B ′ ′ là ⇔ V = ′ ′ 2V = . ABCC B . A A′B C ′ ′ 3
Câu 16. Cho khối lăng trụ ABC.A′B C
′ ′. Gọi E là trọng tâm tam giác A′B C
′ ′ và F là trung điểm BC .
Tính tỉ số thể tích giữa khối B .′EAF và khối lăng trụ ABC.A′B C ′ ′. 1 1 1 1 A. . B. . C. . D. . 8 5 6 4 Hướng dẫn giải Chọn C B A F C B' A' E M C' Ta có https://toanmath.com/
M là trung điểm của B C ′ ′ khi đó 1 S = S
và d ( B ,′( AA′MF )) = d ( B ,′( AEF )) . EAF ′ 2 AA MF 1 2 Vì V = − = − = ′ ′ V ′ ′ V V ′ ′ V V B . AA MF ABF . A B M B . ′ ABF ABF . A B M ABF . ′ ′ ′ ′ 3 A B M . 3 ABF A B M 1 1 2 1 1 1 Suy ra V = = = = ′ V . .V . .V .V . B EAF B . ′ ′ ′ ′ ′ ′ ′ ′ ′ ′ 2 AA MF . 2 3 ABF A B M . 3 2 ABC A B C . 6 ABC A B C
Câu 17. Cho hình lăng trụ tam giác ABC. ′
A B′C′ có đáy ABC là tam giác đều cạnh 2a , hình chiếu của ′ A
trên mặt phẳng ( ABC) là trung điểm cạnh BC . Biết góc giữa hai mặt phẳng ( AB ′ A ) và ( ABC )
bằng 45°. Tính thể tích V của khối chóp .
A BCC′B′ . 3 3 2 3a A. 3 a . B. 3 V = a . C. 3 a 3 . D. . 2 3 Hướng dẫn giải Chọn B C' 2a B' A' B 45° C M K I A Ta có : V = V +V = V +V . ABC. ′ A B′C′ . A ′ A B′C′ . A BCC′B′ A . ′ ABC A . ′ BCC′B′ Mà V = V ⇒ V = V . A . ′ BCC′B′ . A BCC′B′ . A ′ A B′C′ A . ′ ABC
Gọi M là trung điểm của BC , I là trung điểm của AB và K là trung điểm của IB . Khi đó : ′
A M ⊥ ( ABC ) .
Mặt khác : MK // CI  ⇒ MK ⊥ ⊥ AB . CI AB MK ⊥ AB , ′ A M ⊥ AB ⇒ ′ A K ⊥ AB .
Góc giữa hai mặt phẳng ( AB ′
A ) và ( ABC ) chính là góc giữa ′
A K và KM và bằng  ′
A KM = 45° nên tam giác ′
A KM vuông cân tại M . 1 1 2a 3 a 3
Trong tam giác ABC : MK = CI = . = . 2 2 2 2 3
Trong tam giác vuông cân ′ A KM : ′ = = a A M MK . 2 1 V = ′ .V . A . ABC ABC. ′ A B′C′ 3 1 ⇒ 2 2 2 3 V = V − V = V = .S . ′ A M 2 = a .a 3. 3 = a . A . ′ BCC′B′ ABC. ′ A B′C′ ABC. ′ A B′C′ ABC ′ A B′C′ ∆ 3 . 3 3 ABC 3 2 https://toanmath.com/
Câu 18. Cho khối lăng trụ có thể tích V , diện tích đáy là B và chiều cao .
h Tìm khẳng định đúng? 1
A. V = 3Bh . B. V = Bh . C. V = Bh .
D. V = Bh . 3 Hướng dẫn giải Chọn D
Theo công thức tính thể tích khối lăng trụ ta có V = Bh
Câu 19. Cho hình lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác vuông tại B, 
ACB = 60 , BC = a,
AA′ = 2a . Cạnh bên tạo với mặt phẳng ( ABC ) một góc 30 . Thể tích khối lăng trụ ABC.A′B C ′ ′ bằng 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. 3 a 3 . 6 3 2 Hướng dẫn giải Chọn C A' C' 2a B' 30° A C 60° H a B AB
Trong tam giác ABC vuông tại B ta có: tan 60° =
⇒ AB = BC. 3 = a 3 BC 2 Diện tích đáy: 1 a . 3 S = A . B BC = . ABC 2 2
Gọi H là hình chiếu của A′ lên mặt phẳng ( ABC) . Góc giữa cạnh bên AA′ và đáy là  A′AH = 30° . 1
Trong tam giác vuông A′HA ta có: A′H = AA .′sin 30° = 2 . a = a 2 2 3 Thể tích lăng trụ là: a 3 a . 3
V = A′H . S = . a = ABC 2 2
Câu 20.Cho ( H ) là khối lăng trụ có chiều cao bằng 3a, đáy là hình vuông cạnh .
a Thể tích của ( H ) bằng. A. 3 4a . B. 3 2a . C. 3 3a . D. 3 a . Hướng dẫn giải Chọn C 2 3 V = . B h = 3 .
a a = 3a .
Câu 21.Cho hình lăng trụ ABC . D A′B C ′ D
′ ′ có đáy là hình thoi cạnh bằng a và 
ABC = 120° . Góc giữa
cạnh bên AA′ và mặt đáy bằng 60° , điểm A' cách đều các điểm A , B , D . Tính thể tích khối
lăng trụ đã cho theo a . 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 3 2 12 Hướng dẫn giải https://toanmath.com/ Chọn C B' C' A' D' D I C G A B
Ta có điểm A′ cách đều các đỉnh A , B , D cho nên điểm A′ sẽ nằm trên trục đường tròn ngoại
tiếp của tam giác ABD . Ta có  ABC = 120° nên 
ABD = 60° ⇒ tam giác ABD là tam giác đều
Vậy ta có A′G ⊥ ( ABD) với G là trọng tâm tâm tam giác ABD .
Dễ thấy ( A′A ( ABCD)) = ( A′A GA) =  , , A′AG = 60° . 3 2 a 3
Tam giác ABD đều, AI là trung tuyến ( I = AC ∩ BD ) ⇒ AI = a ; AG = AI = . 2 3 3 a 3 AG Ta có 3 A′G = = = . a . cot 60° 1 3 1 3
Thể tích khối lăng trụ V = A′ . G S = A′ .2 G S = .2. a . . a . a sin 60° 3 = a . ABCD ABD 2 2
Câu 22. Cho lăng trụ ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của điểm A'
lên mặt phẳng ( ABC ) trùng với trọng tâm tam giác ABC . Biết khoảng cách giữa hai đường a 3
thẳng AA' và BC bằng
. Khi đó thể tích của khối lăng trụ là 4 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 3 6 24 12 Hướng dẫn giải Chọn D https://toanmath.com/
Gọi H là trọng tâm của tam giác ABC
Suy ra A' H ⊥ ( ABC ) . Qua A kẻ đường thẳng Ax song song với BC. Ta có Ax / /BC ⇒ d ( A' ,
A BC ) = d ( BC,( A' Ax))
= d (M ( A Ax)) 3 , '
= d (H,( A' Ax)) 2 BC ⊥ AM
Kẻ HK ⊥ AA' ta có 
BC ⊥ A'H
⇒ BC ⊥ ( A' AM ) ⇒ BC ⊥ HK a
Mà HK ⊥ AA ⇒ HK ⊥ ( A Ax) 3 ' ' ⇒ HK = 6 1 1 1 a 2 3 a 3 a 3 Ta có = + ⇒ HA' = mà S =
⇒ V = A'H.S = . 2 2 2 HK HA HA' 3 ABC 4 ABC 12
Câu 23. Cho hình lăng trụ ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của điểm A′
lên mặt phẳng ( ABC) trùng với trọng tâm tam giác ABC . Biết khoảng cách giữa hai đường thẳng a
AA′ và BC bằng
3 . Tính theo a thể tích V của khối lăng trụ ABC.A′B C ′ ′. 4 3 a 3 3 a 3 3 a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . 12 3 24 6 Hướng dẫn giải Chọn A
Ta có A′G ⊥ ( ABC ) nên A′G ⊥ BC ; BC ⊥ AM ⇒ BC ⊥ (MAA′) https://toanmath.com/ a
Kẻ MI ⊥ AA′ ; BC ⊥ IM nên d ( AA′ BC ) 3 ; = IM = 4 AG GH 2 2 a 3 a 3
Kẻ GH ⊥ AA′ , ta có = = ⇔ GH = . = AM IM 3 3 4 6 a 3 a 3 . 1 1 1 A . G HG 3 6 a = + ⇔ A′G = = = 2 2 2 2 2 2 2 HG A′G AG − 3 AG HG a a − 3 12 2 2 a a 3 a 3 V = ′ = = ′ ′ ′ A . G S . . ABC. A B C ABC 3 4 12
Câu 24. Các đường chéo của các mặt của một hình hộp chữ nhật bằng a, b, c . Thể tích của khối hộp đó là A. V = . abc
B. V = a + b + . c ( 2 2 2
b + c − a )( 2 2 2
c + a − b )( 2 2 2
a + b − c ) C. V = . D. 8 ( 2 2 2
b + c − a )( 2 2 2
c + a − b )( 2 2 2
a + b − c ) V = . 8 Hướng dẫn giải Chọn C B C x a A y D b z c B' C' A' D'
Giả sử hình hộp chữ nhật có ba kích thước: x, y, z . 2 2 2 2 2 2 2 2 2
x + y = a
y = a − x
y = a − x   
Theo yêu cầu bài toán ta có 2 2 2 2 2 2 2 2 2 2 2
y + z = c ⇔ y + z = c ⇔ a − x + b − x = c    2 2 2 2 2 2 2 2 2 x + z = b
z = b − x
z = b − x    2 2 2 
a − b + c 2 y =  2   + − ( 2 2 2
a + c − b )( 2 2 2
a + b − c )( 2 2 2 2 2 2
b + c − a a b c 2 ) ⇔ x = ⇒ V = 2 8  2 2 2 
b + c − a 2 z =   2
Câu 25. Cho lăng trụ ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của điểm A′ lên
mặt phẳng ( ABC) trùng với trọng tâm của tam giác ABC . Biết khoảng cách giữa hai đường thẳng a
AA′ và BC bằng
3 . Khi đó thể tích của khối lăng trụ là 4 https://toanmath.com/ 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 24 12 36 6 Hướng dẫn giải Chọn B A' B' C' N H A B G M C
Gọi G là trọng tâm của A
∆ BC , M là trung điểm của BC .
⇒ A′G ⊥ ( ABC) . BC ⊥ AM
Trong ( AA′M ) dựng MN ⊥ AA′ , ta có: 
⇒ BC ⊥ ( AA′G) ⇒ BC ⊥ MN .
BC ⊥ A′G ⇒ a
d ( AA ,′ BC ) = 3 MN = . 4
Gọi H là hình chiếu của G lên AA′ . GH AG a
Ta có: GH / /MN ⇒ = 2 = 2 ⇒ GH = 3 MN = . MN AM 3 3 6
Xét tam giác AA′G vuông tại G , ta có: 1 1 1 = + 1 1 1 ⇒ = − 1 1 = − 27 = a . ⇒ GA′ = . 2 2 2 GH GA GA′ 2 2 2 GA′ GH GA 2 2  2 a 3   a 3  3a 3     6 3     2 3
Vậy thể tích của khối lăng trụ là: a 3 a a 3 V = S .A′G = . = . ABC 4 3 12
Câu 26.-2017]Cho hình lăng trụ ABC.A′B C
′ ′ , đáy ABC là tam giác đều cạnh x . Hình chiếu của đỉnh A′
lên mặt phẳng ( ABC) trùng với tâm A
∆ BC , cạnh AA′ = 2x . Khi đó thể tích khối lăng trụ là: 3 x 11 3 x 39 3 x 3 3 x 11 A. . B. . C. . D. . 12 8 2 4 Hướng dẫn giải ChọnA
Gọi H là hình chiếu vuông góc của A′lên ( ABC). Do A
∆ BC đều nên H là trọng tâm tam giác A ∆ BC . x 3 x Ta có AM = 2 3 ⇒ AH = AM = . 2 3 3 x 33 Xét tam giác vuông A ∆ A′H , có 2 2 A′H = AA′ − AH = . 3 2 1 3 x 3 2 3 x 3 x 33 x 11 2 S = x . = V = ⋅ = . ABC ∆ ′ ′ ′ 2 2 4 ABC. A B C 4 3 4 https://toanmath.com/
Câu 27. Cho hình hộp ABC . D A′B C ′ D
′ ′ có đáy là hình chữ nhật với AB = 3, AD = 7 và cạnh bên bằng
1. Hai mặt bên ( ABB A ′ ′) và ( ADD A
′ ′) lần lượt tạo với đáy các góc 45° và 60°. Thể tích khối hộp bằng A. 3 3 B. 7 7 C. 7 D. 3 Hướng dẫn giải Chọn D B' C' D' A' O C B K H A L D
Gọi H là hình chiếu của A′ trên ( ABCD) và K, L là hình chiếu của H trên AB, AD . Ta có các góc 
A′KH = 45° và  A′LH = 60° . Đặt x 3
A′H = x suy ra HK = ; x HL = . 3 2 2 Do đó x 7x 3 2 2 2 2 2
AA′ = AH + A′H = x + + x ⇒ =1⇒ x = . 3 3 7
Thể tích khối hộp bằng 3 V = . B h = A . B A . D A′H = 3 7. = 3. 7
Câu 28. Thể tích của khối lăng trụ có chiều cao bằng h và diện tích đáy bằng B là 1 1 1 A. V = Bh .
B. V = Bh . C. V = Bh .
D. V = Bh . 6 3 2 Hướng dẫn giải Chọn D
Ta có thể tích khối lăng trụ V = Bh .
Câu 29. Cho lăng trụ ABC.A B C có đáy ABC là tam giác vuông tại C , cạnh AC = 5a . Hình chiếu 1 1 1
vuông góc của A lên mặt phẳng ABC là trung điểm của cạnh AC , góc giữa mặt phẳng 1
(AA B B với (AAC C bằng o
30 , cạnh bên của lăng trụ tạo với đáy một góc o 60 . Tính thể tích 1 1 ) 1 1 )
V của lăng trụ ABC.A B C ? 1 1 1 3 3.a 3 a 3 a 3 3.a A. V = . B. V = . C. V = . D. V = . 8 24 8 24 Hướng dẫn giải Chọn A https://toanmath.com/ . Gọi O 5 3
G là trung điểm của ⇒ ⊥ ⇒  0 AC A G ( ABC)
A AG = 60 ⇒ A G = A . G tan 60 = . a Ta 1 1 1 2
có BC ⊥ ( AA C C . 1 1 )
Câu 30.Cho hình lăng trụ có tất cả các cạnh đều bằng a , đáy là lục giác đều, góc tạo bởi cạnh bên và mặt
đáy là 60°. Tính thể tích khối lăng trụ. 9 3 3 27 A. 3 V = a . B. 3 V = a . C. 3 V = a . D. 3 V = a . 4 4 2 8 Hướng dẫn giải ChọnA A' F' B' E' C' D' A F B E H C D .
Ta có ABCDEF là lục giác đều nên góc ở đỉnh bằng 120° .
ABC là tam giác cân tại B , DEF là tam giác cân tại E . 2 1 a 3 S = S = . a . a sin120° = . ABC DEF 2 4  1  2 2 AC =
AB + BC − 2.A . B BC.cos B 2 2 = a + a − 2. . a . a − = a 3   .  2  2 S
= AC.AF = a 3.a = a 3 . ACDF 2 2 2 a 3 a 3 3a 3 2 S = S + S + S = + a 3 + = . ABCDEF ABC ACDF DEF 4 4 2 https://toanmath.com/ a 3
B ' BH = 60° ⇒ B ' H = BB '.sin 60° = . 2 3 9a Suy raV = . 4
Câu 31. Khối lăng trụ ABC.A′B C
′ ′ có đáy là một tam giác đều cạnh a, góc giữa cạnh bên và mặt phẳng
đáy bằng 30° Hình chiếu của đỉnh A′ trên mặt phẳng đáy ( ABC) trùng với trung điểm của cạnh
BC. Tính thể tích của khối lăng trụ đã cho. 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 4 12 8 3 Hướng dẫn giải Chọn C
Gọi H là hình chiếu của A′ trên ( ABC) ⇒ A′H ⊥ BC .
Dễ thấy AH ⊥ BC (Vì A ∆ BC đều).
⇒ A′A ( ABC)  ( )=  (A′A AH)=  ; ; A′AH (1). a 3 Vì A
∆ BC đều ⇒ AH = . 2 a 3 1 a Trong A
∆ ′AH vuông, ta có A′H = AH.tan 30° = ⋅ = . 2 3 2 2 3 Vậy a a 3 a 3 V = ′ = ⋅ = ′ ′ ′ A H .S . ABC. A B C ABC ∆ 2 4 8
Câu 32. Cho lăng trụ tam giác ABC. ′
A B′C′ có đáy ABC là tam giác vuông cân tại A , cạnh AC = 2 2 .
Biết AC′ tạo với mặt phẳng ( ABC ) một góc 60° và AC′ = 4 . Tính thể tích V của khối đa diện
ABCB′C′ . 16 3 16 8 3 8 A. V = . B. V = . C. V = . D. V = . 3 3 3 3 Hướng dẫn giải Chọn A
Phân tích: Tính thể tích của khối đa diện ABCB′C′ bằng thể tích khối của lăng trụ ABC. ′ A B′C′
trừ đi thể tích của khối chóp . A ′ A B′C′ .
Giả sử đường cao của lăng trụ là C′H . B C A 4 B C 2 2 0 H 60 A
Khi đó góc giữa AC′mặt phẳng ( ABC) là góc  C′AH = 60° . Ta có: https://toanmath.com/ C′H sin 60° =
⇒ C′H = 2 3; S = 4 ∆ AC′ ABC 1 V = C′H S = = . ABC ′ A B′C′ . 2 3. . ∆ABC (2 2)2 8 3 . 2 1 1 8 3 V = C′H S = V = . A ′ A B′C′ . . . ∆ABC ABC. ′ A B′C′ 3 3 3 8 3 16 3 V = V −V = − = .
ABB′C′C ABC ′ A B′C′ A ′ A B′C′ 8 3 . . 3 3
Câu 33. Cho hình lăng trụ ABC.A B ′ C
′ ′ có thể tích bằng 30. Gọi I , J , K lần lượt là trung điểm của AA ,′ BB ,
′ CC′ . Tính thể tích V của tứ diện CIJK . 15 A. V = .
B. V = 12 .
C. V = 6 .
D. V = 5 . 2 Hướng dẫn giải Chọn D . Nhận thấy: d (C, IJK ) ( K )  ( )  ( ′ ′ ′) ( ) CK 1 IJ ABC A B C ⇒ = = . d (C,(A B ′ C ′ ′)) CC′ 2 1 V = d K S = d ′ ′ ′ S = = . CIJK ( ( )) 1 1 1 C, IJ . . . C, A B C . ′ ′ ′ .30 5 IJK ( ( )) ABC 3 3 2 6
Câu 34. Khối lăng trụ ABC. ′
A B′C′ có đáy là tam giác đều, a là độ dài cạnh đáy. Góc giữa cạnh bên và
đáy là 30° . Hình chiếu vuông góc của ′
A trên mặt ( ABC ) trùng với trung điểm của BC . Thể
tích của khối lăng trụ đã cho là 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 8 3 4 12 Hướng dẫn giải Chọn A
Gọi H là trung điểm của cạnh BC ⇒ ′ A H ⊥ ( ABC ) ⇒  ′ A H 1 ′
A AH = 30° ⇒ tan 30° = = . AH 3 https://toanmath.com/ Cạnh AB 3 a 3 = = ⇒ ′ = a AH A H 2 2 2 3 a 1 a 3 a 3 ⇒ V = ′ A H .S = . . .a = . ABC 2 2 2 8
Câu 35. Cho lăng trụ ABC . D A′B C ′ D
′ ′ có đáy ABCD là hình thoi cạnh a , tâm O và  ABC = 120° . Góc
giữa cạnh bên AA′ và mặt đáy bằng 60°. Đỉnh A′ cách đều các điểm A , B , D . Tính theo a
thể tích V của khối lăng trụ đã cho. 3 a 3 3 a 3 3 3a A. V = . B. V = . C. V = . D. 3 V = a 3 . 2 6 2 Hướng dẫn giải Chọn A
Do AB = AD = a và  BAD = 60° ⇒ A
∆ BD đều cạnh a .
Mặt khác: A′A = A′B = A′D . Suy ra A .′ABD là chóp đều nên A′ có hình chiếu vuông góc là tâm
H của đường tròn ngoại tiếp tam giác ABD .
⇒ AH là hình chiếu vuông góc của AA′ lên đáy ( ABCD) ⇒ ( AA′ ( ABCD))  =  , A′AH = 60° . 3 3 2 2 S = 2S = 2. a = a . ABCD ABD 4 2 3 3
Tam giác ABD đều cạnh a nên AO = a ⇒ AH = a . 2 3 3
Tam giác A′AH vuông tại H nên: A′H = AH tan 60° = . a 3 = a . 3
Vậy, thể tích khối lăng trụ là: 3 3
V = A′H.S = a . ABCD 2
Câu 36. Cho hình hộp ABC . D A′B C ′ D
′ ′ có đáy là hình chữ nhật với AB = 3, AD = 7 và cạnh bên bằng
1. Hai mặt bên ( ABB A ′ ′) và ( ADD A
′ ′) lần lượt tạo với đáy các góc 45° và 60°. Thể tích khối hộp bằng A. 3 3 B. 7 7 C. 7 D. 3 Hướng dẫn giải Chọn D https://toanmath.com/ B' C' D' A' O C B K H A L D
Gọi H là hình chiếu của A′ trên ( ABCD) và K, L là hình chiếu của H trên AB, AD . Ta có các góc 
A′KH = 45° và  A′LH = 60° . Đặt x 3
A′H = x suy ra HK = ; x HL = . 3 2 2 Do đó x 7x 3 2 2 2 2 2
AA′ = AH + A′H = x + + x ⇒ =1⇒ x = . 3 3 7
Thể tích khối hộp bằng 3 V = . B h = A . B A . D A′H = 3 7. = 3. 7
Câu 37. Cho hình lăng trụ ABCA′B C
′ ′ có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của A′ lên
mặt phẳng (ABC ) trùng với trọng tâm tam giác ABC . Biết khoảng cách giữa hai đường thẳng a
AA′ và BC bằng
3 . Tính thể tích V của khối lăng trụ ABCA′B C′ .′ 4 3 a 3 3 a 3 3 a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . 6 24 12 3 Hướng dẫn giải Chọn C A' C' H B' A C G M B
M là trung điểm của BC thì BC ⊥ (AA′M ).
Gọi MH là đường cao của tam giác A′AM thì
MH ⊥ A′A và HM ⊥ BC nên HM là khoảng cách AA′ và BC . 2 a 3 a 3 2 a Ta có A′ .
A HM = A′G.AM ⇔ .A′A = A′A − 4 2 3 https://toanmath.com/ 2 2 2   2 2 a 2 4a 2 4a 2a
⇔ A′A = 4 A′A −  ⇔ 3A′A = ⇔ A′A = ⇔ A′A = .  3  3 9 3   2 2
Đường cao của lăng trụ là 4a 3a a A′G = − = . 9 9 3 2 3 Thể tích a 3a a 3 V = . = . LT 3 4 12
Câu 38. Cho khối lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh bằng a , cạnh bên AA′ = a , góc
giữa AA′ và mặt phẳng đáy bằng 30° . Tính thể tích khối lăng trụ đã cho theo a . 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 8 24 4 12 Hướng dẫn giải Chọn A
Kẻ A′H ⊥ ( ABC) , H ∈( ABC). Khi đó góc giữa AA′ và mặt phẳng đáy bằng góc giữa AA′ và AH bằng  A′AH = 30° . a Trong A
∆ ′AH vuông tại H , có ′ = ′  A H A .
A sin A′AH = .
a sin 30° ⇔ A′H = . 2 2 a 3 a 3 a 3 Ta có V = ′ = ⇔ = ′ ′ ′ S .A H . V . ABC. A B C ABC ′ ′ ′ 4 2 ABC. A B C 8
Câu 39. Cho hình lăng trụ ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của điểm A′
lên mặt phẳng ( ABC ) trùng với trọng tâm tam giác ABC . Biết khoảng cách giữa hai đường AA′ a 3 và BC bằng
. Tính thể tích V của khối lăng trụ ABC.A′B C ′ ′ . 4 3 a 3 3 a 3 3 a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . 24 12 3 6 Hướng dẫn giải Chọn B https://toanmath.com/
Gọi G là trọng tâm tam giác ABC . Vì A′G ⊥ ( ABC ) và tam giác ABC đều nên A′ABC là hình chóp đề a
u. Kẻ EF ⊥ AA′ và BC ⊥ ( AA′E ) nên d ( AA′ BC ) 3 , = EF =
. Đặt A′G = h 4 2  a 3  Ta có 2 A′A = h +     . 3  
Tam giác A′AG đồng dạng với tam giác EAF nên 2 A′A AG A′G   = = a 3 a 3 a 3 a 2 ⇒ A′ . G EA = A′ . A FE ⇔ . h = h +   . ⇔ h =   . EA FA FE 2 3 4 3   2 3 a a 3 a 3
Thể tích V của khối lăng trụ ABC.A′B C
′ ′ là V = A . G S = . = . ABC 3 4 12
Đặt A′H = x ⇒ H B ′ = x .
Ta có K là trọng tâm tam giác AA′B′ 2 2 2 a 2 2 Suy ra 2 KB = A′B = x + ; 2 2 KA = AH ′ = x + a . 3 3 4 3 3 K ∆ AB vuông tại K nên 2 4  5a  2 2 2 a
KB + KA = AB 2 2 ⇔ 2x  +  = a 2 2 2 ⇔ 8x + 5a = 2 9a ⇔ x = . 9  4  2 2 3 Vậy a 3 a 2 a 6 V = S .A′H = . = . ABC 4 2 8
Câu 46. Cho hình lăng trụ ABC.A' B 'C ' có đáy là tam giác đều cạnh 3a , hình chiếu của A' trên mặt
phẳng ( ABC) trùng với tâm đường tròn ngoại tiếp tam giác ABC . Cạnh AA' hợp với mặt phẳng
đáy một góc 45°. Thể tích của khối lăng trụ ABC.A'B 'C ' tính theo a bằng. 3 9a 3 27a 3 3a 3 27a A. . B. . C. . D. . 4 4 4 6 Hướng dẫn giải Chọn B
Gọi AI là đường cao, H là tâm của tam giác ABC ⇒ A′H ⊥ ( ABC) . AA′ ∩  ( ABC) = A Vì 
⇒ góc giữa AA′ và ( ABC) là  ′ ⇒  A AH A′AH = 45° . A′H ⊥  ( ABC) 3a 3 2 ( a)2 2 3 3 9a 3 Ta có: AI = , AH =
AI = a 3 , S = = . ABC 2 3 4 4
A′H = AH. tan 45° = AH = a 3 .
Thể tích của lăng trụ là: https://toanmath.com/ 2 3 9a 3 27a
V = A′H .S = a 3. = . ABC 4 4 A' B' C' A B H I C .
Câu 47. Khối lăng trụ có đáy là hình vuông cạnh a , đường cao bằng a 3 có thể tích bằng 3 a 3 3 a 3 A. . B. . C. 3 a 3 . D. 3 2a 3 . 6 3 Hướng dẫn giải Chọn C
Áp dụng công thức tính thể tích khối lăng trụ ta có 2
V = Bh = a .a 3 3 = a 3 .
Câu 48. Cho lăng trụ ABCA B C có diện tích mặt bên ABB A bằng 4 ; khoảng cách giữa cạnh CC và 1 1 1 1 1 1
mặt phẳng ( ABB A bằng 7. Tính thể tích khối lăng trụ ABCA B C . 1 1 ) 1 1 1 28 14 A. 14 B. C. D. 28 3 3 Hướng dẫn giải Chọn A A 1 C 1 B 1 A B C
Gọi thế tích lăng trụ ABCA B C là V . 1 1 1
Ta chia khối lăng trụ thành ABCA B C theo mặt phẳng ( ABC được hai khối: khối chóp tam 1 ) 1 1 1
giác C .ABC và khối chóp tứ giác C .ABB A 1 1 1 1 1 2 Ta có V = V ⇒ V = V 1 C . ABC 3 1 C . 1 ABB 1 A 3 1 1 28 28 3 Mà V = .S .d ; A ABB A = .4.7 = . Vậy V = . = 14 1 C . 1 ABB 1 A 1 ABB 1 A ( ( 1 1 ) ) 3 3 3 3 2 https://toanmath.com/
Câu 49. Cho lăng trụ tam giác ABC.A′B C
′ ′. Các điểm M , N , P lần lượt thuộc các cạnh AA′ , AM 1 BN 2
BB′ , CC′ sao cho = =
MNP chia lăng trụ thành hai phần có thể AA′ , 2 BB′ và mặt phẳng ( ) 3
tích bằng nhau. Khi đó tỉ số CP CC′ là 1 5 1 1 A. . B. . C. . D. . 4 12 3 2 Hướng dẫn giải Chọn C
Áp dụng công thức V 1  AM BN CP  : ABC.MNP = + +   . V  ′ ′ ′ ′ ′ ′ 3 AA BB CC ABC. A B C  1 2  AA′ BB′ 1  AM BN CP  1 1  CP  1 Ta có : V = V nên + + = 2 3 ⇔  + +  = ABC.MNP
ABC. A′B C ′ ′   3  AA′ BB′ CC′  2 3 AA′ BB′ CC′ 2     CP 1 ⇔ = CC′ . 3 3a
Câu 50. Cho hình lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh a , AA′ = . Biết rằng hình 2
chiếu vuông góc của A′ lên ( ABC ) là trung điểm BC . Tính thể tích V của khối lăng trụ đó. 3 2a 3 3a 3 A. 3 V = a . B. V = . C. V = . D. 3 V = a . 3 4 2 2 Hướng dẫn giải Chọn C B′ C′ A′ H C B A https://toanmath.com/
Gọi H là trung điểm BC . a 6
Theo giả thiết, A′H là đường cao hình lăng trụ và 2 2 A′H = AA′ − AH = . 2 2 3 a 3 a 6 3a 2
Vậy, thể tích khối lăng trụ là V = S ′ = = Δ .A H . . ABC 4 2 8
Câu 51. Cho lăng trụ tam giác ABC.A′B C
′ ′ có đáy là tam giác ABC đều cạnh bằng a . Hình chiếu vuông
góc của A′ trên mặt phẳng ( ABC ) trùng với trung điểm H của cạnh AB . Góc giữa cạnh bên
của lăng trụ và mặt phẳng đáy bằng o
30 . Tính thể tích của khối lăng trụ đã cho theo a . 3 3a 3 a 3 a 3 a A. B. C. D. 4 4 24 8 Hướng dẫn giải Chọn D a a Ta có ⇒ 
AH là hình chiếu của A′A trên ( ABC ) o A′AH = 3 30 ⇒ A′H = 3 . = 2 3 6 2 a 3 a 3 3 a
V = A′H.S = . = . ABC 6 4 8
Câu 52. Cho hình lăng trụ ABC. ′
A B′C′ có đáy là tam giác vuông cân ở C . Cạnh BB′ = a và tạo với
đáy một góc bằng 60° . Hình chiếu vuông góc hạ từ B′ lên đáy trùng với trọng tâm của tam giác
ABC . Thể tích khối lăng trụ ABC. ′
A B′C′ là: 3 9 3a 3 9a 3 3 3a 3 3a A. . B. . C. . D. . 80 80 80 80 Hướng dẫn giải Chọn A
Gọi P là trọng tâm của ∆ABC ⇒ B′P ⊥ ( ABC) https://toanmath.com/
⇒ (BB′ ( ABC))  = (B′BP)  ⇒  , B′BP = 60°  B′P 3  a 3 si  n 60° = = B′  P =  BB′ 2  2 ⇒  ⇒  BP 1   a cos 60° = = BP =  BB′ 2  2 Gọi 3 3a
K = BP ∩ AC ⇒ BK = BP = 2 4 2 2  1   3a  3a 5 2 ⇒ BC + BC = ⇒ BC =      2   4  10 2 3
a 3 1  3a 5  9a 3 ⇒ V = B′ . P S = . . . ABC   = 2 2 10 80  
Câu 53. Cho lăng trụ ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của điểm A′ lên
mặt phẳng ( ABC) trùng với trọng tâm tam giác ABC . Biết khoảng cách giữa hai đường thẳng a
AA′ và BC bằng
3 . Khi đó thể tích của khối lăng trụ là 4 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 3 24 12 Hướng dẫn giải Chọn D B' C' A' H B M C G A Do A
∆ BC đều trọng tâm G và A′G ⊥ ( ABC) nên A .′ABC là hình chóp đều. Gọi a a
M là trung điểm của BC , khi đó 3 AM = 3 ⇒ AG = . 2 3
Gọi H là hình chiếu của M trên AA′ . Khi đó do BC ⊥ ( AA′M ) ⇒ BC ⊥ HM nên HM là
đường vuông góc chung của hai đường thẳng a
AA′ và BC . Do đó 3 HM = . 4 2 Đặt a
AA′ = A′B = A′C = x , khi đó 2 A′G = x − . 3 2 a 3 a a 3 a Do 2S = ′ = ′ 2 ⇒ − = 2 ⇒ = ∆ ′ A . G AM MH.AA . x .x x . AA M 2 3 4 3 2 a 3 a 3 a 3 Do S = , A′G = ⇒ V = ′ = ′ ′ ′ A . G S . ABC ∆ ∆ 4 3 ABC. A B C ABC 12 https://toanmath.com/
Câu 54.Cho hình hộp ABC . D A′B C ′ D ′ ′ có  BCD = 60 ,
° AC = a 7, BD = a 3, AB > AD ,đường chéo BD′
hợp với mặt phẳng ( ADD A
′ ′) góc 30°. Tính thể tích V của khối hộp ABC . D A′B C ′ D ′ ′ . 39 A. 3 a . B. 3 2 3a . C. 3 3 3a . D. 3 39a . 3 Hướng dẫn giải Chọn C D' C' 30° A' B' x D C O y A B
 Đặt x = C ; D y = BC (x > y)
 Áp dụng định lý hàm cos và phân giác trong tam giác BCD 2 2 2
3a = x + y − xy và 2 2 2
x + y = 5a ⇒ x = 2a; y = a
 Với x = 2y = 2a và C = 60 → BD ⊥ AD → 
BD '; (ADD'A') = 30 → DD ' = 3a  2 S = x . y sin 60 = a 3 ABCD  Vậy V hình hộp = 3 a 3 3
Câu 55. Cho hình lăng trụ ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của điểm A′
lên mặt phẳng ( ABC) trùng với trọng tâm tam giác ABC . Biết khoảng cách giữa hai đường thẳng a
AA′ và BC bằng
3 . Tính thể tích V của khối lăng trụ ABC.A′B C ′ ′. 4 3 a 3 3 a 3 3 a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . 12 3 24 6 Hướng dẫn giải Chọn A https://toanmath.com/
Gọi M là trung điểm của BC . Vẽ MH ⊥ AA′ (H ∈ BC).
Ta có AM ⊥ BC , A′G ⊥ BC ⇒ BC ⊥ ( A′AG) ⇒ BC ⊥ MH ⇒ d ( AA ,′ BC ) = MH . 2 2 3a 3a a 2 2 AH = AM − MH = − 3 = . 4 16 4 a 3 a 3 . MH A′G MH .AG a Ta có = = 
tan GAH ⇒ A′G = 4 3 = = . AH AG AH 3a 3 4 2 3 Vậy a 3 a a 3 V = S .A′G = . = . ABC 4 3 12
Câu 56. Cho lăng trụ ABC.A′B C
′ ′ có đáy là tam giác đều cạnh .
a Hình chiếu vuông góc của mặt phẳng ( 3 a 3
ABC ) trùng với trọng tâm của tam giác ABC. Biết thể tích của khối lăng trụ là . Khoảng 4
cách giữa hai đường thẳng AB′ và BC là: 2a 4a 3a 3a A. . B. . C. . D. . 3 3 4 2 Hướng dẫn giải Chọn C .
Phương pháp: Dựng hình vẽ như giả thiết bài toán.
+ phương pháp phổ biến nhất để tìm khoảng cách giữa 2 đường thẳng: tìm một mặt phẳng chứa 1
đường thẳng và song song với đường thẳng còn lại. https://toanmath.com/
Cách giải: Gọi F là trọng tâm tam giác ABC. Suy ra A′F là đường cao của hình lăng trụ 1 3 0 2 S = . a . a sin 60 = a . ABC ∆ 2 4
Suy ra A′F = a .
AA′ song song với mặt phẳng ( BCC B
′ ′) nên khoảng cách giữa AA′ và BC chính là khoảng
cách giữa AA′ và ( BCC B
′ ′) và cũng bằng khoảng cách từ A đến mặt phẳng này.
BC vuông góc với ( FOE ). Dựng FK vuông góc với OE nên EF = d ( F,( BCC ')) .
Tính AA′ = ( A′F )2 + ( AF )2 2 3 = a = OE . 3
Xét hình bình hành AOEA′ : d ( ,
A ( ABCD)) = khoảng cách hình chiếu của A lên OE . 3 S = A .
O A' F = OE.d = a . AOEA 4
Câu 57. Một khối lăng trụ tam giác có các cạnh đáy bằng 13 ,14 ,15 cạnh bên tạo với mặt phẳng đáy một
góc 30° và có chiều dài bằng 8 . Khi đó thể tích khối lăng trụ là. A. 340 . B. 336 . C. 274 3 . D. 124 3 . Hướng dẫn giải Chọn B A' C' B' C A O a H B . Ta có: S
= 21(21−13)(21−14)(21−15) = 84 . ABC ∆
Gọi O là hình chiếu của A′ trên ( ABC). A
∆ ′AO vuông tại O cho ta: A′O = AA .′sin 30° = 4 . Vậy: V = = ′ ′ ′ 84.4 336 . ABC. A B C
Câu 58. Cho lăng trụ tam giác ABC.A' B 'C ' có đáy ABC là đều cạnh AB = 2a 2 . Biết AC ' = 8a và tạo với mặt đáy một góc 0
45 . Thể tích khối đa diện ABCC ' B ' bằng 3 8a 3 3 8a 6 3 16a 3 3 16a 6 A. . B. . C. . D. . 3 3 3 3 Hướng dẫn giải Chọn D https://toanmath.com/ 2a 2 B A C 8a B' A' H C'
Gọi H là hình chiếu của A lên mp( A'B'C ') ⇒  0 HC ' A = 45 ⇒ A
∆ HC ' vuông cân tại H. AC ' 8a ⇒ AH = = = 4a 2. 2 2 (2a 2)2 3 . 3 2 2 2 16a 6 NX: V = V = AH.S = .4a 2. = . . A BCC ' B '
ABC. A' B 'C ' 3 3 ABC 3 4 3
Gọi H là hình chiếu của A lên mp( A'B'C ') ⇒  0 HC ' A = 45 ⇒ A
∆ HC ' vuông cân tại H. AC ' 8a ⇒ AH = = = 4a 2. 2 2 (2a 2)2 3 . 3 2 2 2 16a 6 NX: V = V = AH.S = .4a 2. = . . A BCC ' B '
ABC. A' B 'C ' 3 3 ABC 3 4 3
Câu 59. Cho lăng trụ ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a , AA′ = b và AA′ tạo với mặt đáy một
góc 60° . Tính thể tích khối lăng trụ. 3 3 3 1 A. 2 a b . B. 2 a b . C. 2 a b . D. 2 a b . 4 8 8 8 Hướng dẫn giải Chọn B C' A' B' A C H B
Kẻ A′H ⊥ ( ABC ) tại H
Suy ra góc giữa AA′ và đáy bằng  A′AH = 60° https://toanmath.com/ A′H 3 ⇒ 3 b 3 sin 60° = = ⇒ A′H = A′A = . A′A 2 2 2 2 Do đó b 3 1 3a b V = ′ 2 = ′ ′ ′ A H.S = . a sin 60° . ABC. A B C ABC 2 2 8
Câu 60. Cho khối lăng trụ tam giác ABC.A' B 'C ' có thể tích bằng 30 (đơn vị thể tích). Thể tích của khối tứ diện AB C ′ C ′ là:
A. 5 (đơn vị thể tích).
B. 10 (đơn vị thể tích).
C. 12,5 (đơn vị thể tích).
D. 7,5 (đơn vị thể tích). Hướng dẫn giải Chọn B Ta có. C B A C A .
Khi đó ta có thể so sánh trực tiếp cũng được, tuy nhiên ở đây ta có thể suy luận nhanh như sau: Khối B A
′ BC có chung đường cao kẻ từ đỉnh B’ đến đáy ( ABC) và chung đáy ABC với hình lăng trụ V ′ 1
ABC.A′B C
′ ′. Do vậy BABC = . V ′ ′ ′ 3 ABC. A B C
Tương tự ta có V ′ ′ ′ 1 1 1 . A A B C = , khi đó V = ⇒ = = ′ ′ ′ .V V ′ ′ ′ .30 10 . . A A B C
ABC.A′B C ′ ′ . A A B C V ′ ′ ′ 3 3 3 ABC. A B C
Câu 61.Cho lăng trụ ABC . D A′B C ′ D
′ ′ với đáy ABCD là hình thoi, AC = 2a ,  0
BAD = 120 . Hình chiếu
vuông góc của điểm B trên mặt phẳng ( A′B C ′ D
′ ′) là trung điểm cạnh A′B′ , góc giữa mặt phẳng ( AC D
′ ′) và mặt đáy lăng trụ bằng o
60 . Tính thể tích V của khối lăng trụ ABC . D A′B C ′ D ′ ′ . A. 3 V = 3a . B. 3
V = 6 3a . C. 3
V = 2 3a . D. 3
V = 3 3a . Hướng dẫn giải Chọn B
Gọi H là trung điểm A′B′ , suy ra BH ⊥ ( A′B C ′ D ′ ′). Vì A′B C ′ D ′ ′ là hình thoi và  o B A
′ ′D′ =120 ⇒ A ∆ ′B C
′ ′ là tam giác đều cạnh 2a . https://toanmath.com/ (  AC D
′ ′)∩( A′B C ′ D ′ ′) = C D ′ ′ 
Ta có: HC′ ⊥ C D ′ ′ ⇒ (( AC D
′ ′) ( A′B C ′ D ′ ′))  =  o , BC H ′ = 60 . BC′ ⊥ C D ′ ′  3 Có A ∆ ′B C
′ ′ đều cạnh 2a nên C H ′ = .2a = 3a . 2 BH
Xét tam giác BHC′ vuông tại H có: o o tan 60 = ⇒ BH = C H ′ tan 60 = 3a C H ′ . 3 S = = = ′ ′ ′ ′ 2S ′ ′ ′ 2. . a a . A B C D A B C (2 )2 2 2 3 4 Vậy, 2 3 V = = = ′ ′ ′ ′
BH .S ′ ′ ′ 3 . a 2 3a 6 3a . ABCD. A B C D A B C https://toanmath.com/
Document Outline

  • 3.3 BT KHỐI LĂNG TRỤ XIÊN
    • THỂ TÍCH KHỐI LĂNG TRỤ XIÊN
  • 3.3 HDG KHỐI LĂNG TRỤ XIÊN
    • THỂ TÍCH KHỐI LĂNG TRỤ XIÊN