Bài Tập Tích Phân Đường | Giải tích 3 | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Hà Nội
Trong kỳ nạp (từ 1 đến 2) một hỗn hợp không khí và xăng ở áp suất khí quyển bị kéo vàomột xi lanh qua van nạp như di chuyển piston đi xuống.sau đó piston nhanh chóng nén kết hợp với các van đóng cửa trong hành trình nén (từ 2 đến 3) trong đó tăng áp lực và khối lượng giảm. 3 tại các đốt cháy sparkplug nhiên liệu, tăng nhiệt độ và áp suất tại khối lượng gần như liên tục đến 4. Tài liệu được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Giải tích 3 (HUS) 10 tài liệu
Trường: Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Hà Nội 687 tài liệu
Tác giả:
Preview text:
BÀITẬPTÍCHPHÂNĐƯỜNG 2 Bàitập0.1.
1-4HãykiểmchứnglạirằngđịnhlýDivergencelàđúngchocáctrườngvectơF trênmiền E
1. Fpx,y,zq“3xi ` xyj ` 2xzk, E làhìnhốnggiớihạnbởicácmặtphẳngx “ 0,x “
1,y “ 0,y “ 1,z “ 0 vàz “ 1.
2. Fpx,y,zq“x2i ` xyj ` zk, E làhìnhkhốigiớihạnbởiparaboloidz “ 4 ´ x2 ´ y2 vàmặtphẳngxy.
3. Fpx,y,zq “ xz,y,xy, E làkhốicầux2 ` y2 ` z2 ď 16.
4. Fpx,y,zq “ xx2, ´y,zy, E làkhốitrụy2 ` z2 ď 9, 0 ď x ď 2 ¨ F ¨ dS,nghĩalà,tính
5-15HãyápdụngđịnhlýDivergenceđểtínhcáctíchphânmặt
cácthônglượngdòngcủaF quaS S
5. Fpx,y,zq“xyezi ` xy2z3j ´ yezk, S làmặtcủahìnhhộpgiớihạnbởicácmặtphẳng
tọađộvàcácmặtphẳngx “ 2,y “ 2 vàz “ 1.
6. Fpx,y,zq“x2yzi`xy2zj`xyz2k, S làmặtcủahìnhhộpgiớihạnbởicácmặtphẳng
x “ 0,x “ a,y “ 0,y “ b,z “ 0 vàz “ c,trongđóa,b vàc làcácsốdương.
7. Fpx,y,zq“3xy2i ` xezj ` z3k, S là khối giới hạn bởi mặt trụ y2 ` z2 “ 1 và các
mặtphẳngx “´1 vàx “ 2.
8. Fpx,y,zq “ px2 ` y3qi ` py3 ` z3qj ` pz3 ` x3qk, S làmặtcầucótâmtạigốctọađộ vàbánkính2.
9. Fpx,y,zq“x2 sin yi ` x cos yj ´ xzsin yk, S làmặt“cầuphẳng” x8 ` y8 ` z8 “ 8.
10. Fpx,y,zq“zi ` yj ` zxk, S là mặt tứ diện được cho bởi các mặt phẳng tọa độ và mặt x y z ` ` a b “ 1 c
11. Fpx,y,zq “ pcos z`xy2qi`xe´zj`psin y`x2zqk, S làmặtkhốigiớihạnbởiparaboloid
z “ x2 ` y2 vàmặtphẳngz “ 4. 3
12. Fpx,y,zq“x4i ´ x3z2j ` 4xy2zk, S làmặtkhốigiớihạnbởimặttrụx2 ` y2 “ 1 và
cácmặtphẳngz “ x ` 2 vàz “ 0. a
13. Fpx,y,zq “ |r|r,trongđór “ xi ` yj ` zk, S chứahìnhbáncầuz “ 1 ´ x2 ´ y2
vàđĩax2 ` y2 ď 1 trongmặtphẳngxy.
14. F “|r|2r,trongđór “ xi ` yj ` zk, S làmặtcầucóbánkínhR vàtâmtạigốctọa độ. a 15. Fp d x ư ,y ới ,zq mặ“tey z “tan 2 ´zi x ` 4 y ´ y 3 4, ´ x2 1 j ď `x x s ď in 1, y´k 1 , S ď y là ďkh
1 ối nằm trên mặt phẳng xyvà
16. HãysửdụngmộthệthốngmáytínhđềvẽratrườngvectơFpx,y,zq“sin x cos2 yi `
sin3 y cos4 zj ` sin5 z cos6 xk tronghìnhốngđượccắttừphầntámđườngtrònvàcác
mặt phẳng x “ π{2,y “ π{2 và z “ π{2. Sau đó hãy tính thông lượng dòng đi qua mặtốngnày. ¨
F ¨ dS, trong đó Fpx, y,zq“z2xi ` 17. Hãy
1 áp dụng định lý Devergence để tính p S
y3 ` tan zqj `px2z ` y2qk vàS lànửatrêncủamặtcầux2 ` y2 ` z2 “ 1.[Gợiý: 3
ChúýrằngS khônglàmặtkhépkín.Trướctiênhãytínhcáctíchphântrên S1 và S 2
2, trong đó S1 là đĩa x ` y2 ď 1, hướng xuống dưới và S2 “ S Y S1].
18. ChoFpx,y,zq“z tan´1py2qi ` z3lnpx2 ` 1qj ` zk.HãytìmthônglượngdòngcủaF
đi qua một phần paraboloid x2 ` y2 ` z2 “ 2 nằm trên mặt phẳng z “ 1 và hướng lêntrên.
19. Một trường vectơ F được chỉ ra trong hình. Hãy sử dụng giải thích của devergence
trongmụcnàyđểxácđịnhxemdivF làdươnghayâmtạiP1 vàP2. 4
20. (a) CácđiểmP1 vàP2 làcácđiểmnguồnhayđiểmlúnvới trườngvectơđượccho
tronghìnhvẽ?Hãychomộtlờigiảithíchtronghình.
(b) ChoFpx,yq “ xx,y2y,hãysửdụngđịnhnghĩacủadivergenceđểkiểmchứnglại câutrảlờitrongcâu(a).
21-22Hãyvẽtrườngvectơvàdựđoánrằngởđâuthìdiv F ą 0 vàdiv F ă 0.Sauđóhãy
tínhdivF đểkiểmtradựđoáncủabạn. 21. Fpx,yq “ xxy,x ` y2y 22. Fpx,yq“xx2,y2y εQ
23. HãykiểmchứngrằngdivE “ 0 vớiđiệntrườngEpxq“ x |x|3
24. HãyápdụngđịnhlýDivergenceđểtính ¨ p2x ` 2y ` z2qdS S
trongđóS làmặtcầux2 ` y2 ` z2 “ 1.
25-30Hãychứngminhcácmệnhđềsauđây,giảsửrằngS vàE thỏamãncácđiềukiện
củađịnhlýDivergencevàcáchàmvôhướngvàcácthànhphầncủatrườngvectơcócác đạo hàmriêngcấphailiêntục. ¨
a ¨ ndS“ 0,trongđóa làvectơhằng. 26. S 1 27. V pEq“ ¨
F ¨ dS,trongđóFpx,y,zq“xi ` yj ` zk 3 S 0.1Tómtắt 5 ¨ curlF ¨ dS“ 0 28. S ¨ ˚ ∇2f dV 29. DnfdS“ S E ¨ ˚ 30. pf∇gq¨ndS“ pf∇2g ` ∇f ¨ ∇gqdV S E ¨ ˚ 31. pf∇g ´ g∇fq¨ndS“ pf∇2g ´ g∇2fqdV S E
32. GiảsửrằngS vàE thỏamãncácđiềukiệncủađịnhlýDivergencevàf làmộthàm
vôhướngvớicácđạohàmriêngliêntục.Chứngminhrằng ¨ ˚ ∇f dV fndS“
Cáctíchphânmặtvàtíchphânbộib S E
acủacáchàmvectơlàcácvectơđượcxácđịnh
bởi tích phân của từng thành phần. [Gợi ý: Hãy áp dụng định lý Divergence cho
F “ fc,trongđóc làvectơhằngbấtkỳ.]
33. MộtkhốirắncómiềnxácđịnhE cómặtS vànóđượcnhúngvàomộtchấtlỏngcó
mậtđộρ.Talậpmộthệtrụctọađộsaochomặtphẳngxytrùngvớibềmặtcủachất
lỏngđó,vàcácgiátrịdươngcủaz đođộsâuvậtđónhúngxuốngchấtlỏng.Khiđó
ápsuấttạiđộsâuz làp “ ρgz,trongđóg làgiatốctrọnglực(xemMục8.3).Tổng
sốlựcđẩylênchấtrắnphụthuộcvàophânphốiápsuấtđượcchobởitíchphânmặt ¨ pndS F “´
trong đó n là vectơ pháp tuyến đơn vị ngoài. SHãy áp dụng kết quả của bài tập 31
đểchỉrarằngF “´W k,trongđóW làkhốilượngcủachấtlỏngbịchấtrắnchiếm
chỗ.(ChúýrằngF hướnglêntrênbởivìz hướngxuốngdưới).KếtquảcủaQuytắc
Archimedes: Tổng lực đẩy tác động lên một vật thể bằng với trọng lượng của chất lỏngbịchiếmchỗ. 0.1 Tómtắt
CáckếtquảchínhcủachươngnàylàcáckếtquảtrongnhiềuchiềucủaĐịnhlýCơbản
của Phép tính Vi tích phân. Để giúp cho đọc giả ghi nhớ được chúng, chúng tôi đã tổng 6 ˆ b F 1pxqdx“ F pbq´F paq ĐịnhlýCơbảncủaPTVP a ˆ
∇f ¨ dr “ f prpbqq´f prpaqq
ĐịnhlýCơbảncủaTíchPhânĐường C ¨ ˆ BP ˙ ˆ BQ ´ Pdx ` Qdy ĐịnhLýGreen Bx dA“ D By C ¨ ˆ F ¨ dr ĐịnhLýStokes curlF ¨ dS“ S C ˚ ¨ F ¨ dS ĐịnhLýDivergence divFdV“ E S
hợp lại trong mục này (không có các giả thiết) đề các đọc giả có thể hiểu được sự tương
tựgiữachúngmộtcáchdễdànghơn.Lưuýrằngtrongmỗitrườnghợpchúngtôicótích
phân của “đạo hàm” trên một miền ở bên trái, và bên phải chó các giá trị của hàm ban
đầutrênbiên củamiềnxácđịnh. Ôntập Kiểmtrađịnhnghĩa
1. Trườngvectơlàgì?Hãychobavídụvậtlývềtrườngvectơ.
2. (a) Thếnàolàtrườngvectơbảotoàn? (b) Hàmthếnănglàgì? 0.1Tómtắt 7
3. (a) Hãy viết định nghĩa của tích phân đường của một hàm vô hướng f trên một
đườngcongC ứngvớiđộdàicung.
(b) Làmthếnàođểtínhtíchphânđó?
(c) Hãyviếtbiểuthứctínhkhốilượngvàxácđịnhtâmkhốicủamộtsợidâymỏng
cóhìnhdạngnhưmộtđườngcongC nếusợidâycóhàmmậtđộρpx,yq.
(d) HãyviếtcácđịnhnghĩacủatíchphânđườngtrênC củamộthàmvôhướngf theobiếnx,y vàz.
(e) Làmthếnàođểtínhcáctíchphânnày?
4. (a) HãyđịnhnghĩatíchphânđườngcủamộttrườngvectơF trênmộtđườngcong
trơnC đượcchobởihàmvectơrptq.
(b) NếuF làmộttrườnglực,tíchphânđườngnàybiểudiễnchođạilượngnào?
(c) Nếu F “xP,Q,Ry, điều gì liên quan giữa tích phân đường của F và các tích
phânđườngcủacáchàmthànhphầnP,Q vàR.
5. HãyphátbiểuĐịnhlýCơbảncủatíchphânđường. ˆ
F ¨ dr độclậpvớiđườnglấytíchphân? 6. (a) Cóýnghĩagìkhinói C ˆ
F ¨ dr làđộclậpvớiđườnglấytíchphân,bạncóthểnói (b) Nếubạnbiếtrằng gìvềF? C
7. HãyphátbiểuđịnhlýGreen.
8. HãyviếtcácbiểuthứctínhdiệntíchgiớihạnbởiđườngcongC theotíchphânđường trênC.
9. GiảsửrằngF làmộttrườngvectơtrênR3. (a) HãyxácđịnhcurlF. (b) HãyxácđịnhdivF.
(c) NếuF làmộttrườngvậntốctrongdònglỏng,hãyđưaracácgiảithíchvậtlý
chocácđạilượngcurlF vàdivF.
10. NếuF “ P i ` Qj,làmthếnàođểkiểmtraxácđịnhxemF cóbảotoànhaykhông?
ĐiềugìxảyranếuF làmộttrườngvectơtrênR3. 8
11. (a) Mặtthamsốlàgì?Cácđườngconglướicủachúnglàgì?
(b) Hãyviếtmộtbiểuthứctínhdiệntíchcủamộtmặtthamsố.
(c) Diệntíchcủamộtmặtđượcchobởiphươngtrìnhz “ gpx,yq làgì?
12. (a) Hãyviếtrađịnhnghĩacủatíchphânmặtchomộthàmvôhướngf trênmặtS.
(b) Làm thế nào để tính tích phân nếu S là mặt tham số được cho bởi một hàm vectơrptq.
(c) TínhtươngtựvớiS đượcchobởiz “ gpx,yq.
(d) Nếu một miếng kim loại mỏng có hình dạng của một mặt S, và mật độ tại
px,y,zq làρpx,y,zq,viếtcácbiểuthứctínhkhốilượngvàtâmkhốicủamiếng kimloạiđó.
13. (a) Thếnàolàmặtcóhướng?Hãychomộtvídụcủamộtmặtkhôngcóhướng.
(b) Hãyđịnhnghĩatíchphânmăt(thôngluợngdòng)củamộttrườngvectơF trên
mặtcóhướngS cóvectơpháptuyếnn.
(c) LàmthếnàođểtínhtíchphânnếuS làmặtthamsốđượcchobởiphươngtrình vectơrpu,vq.
(d) TínhtươngtựnếuS đượcchobởiphươngtrìnhz “ gpx,yq.
14. HãyphátbiểuđịnhlýStokes.
15. HãyphátbiểuđịnhlýDivergence.
16. Các định lý sau đây tương tự như thế nào: Định lý Cơ bản của Phép tính Vi tích
phân,địnhlýGreen,địnhlýStokes,vàđịnhlýDivergence? CâuhỏiĐúng-Sai
Hãykiểmtraxemcácphátbiểudướiđâylàđúnghaysai,hãygiảithíchtạisao.Nếunó
sai,hãygiảithíchtạisaohoặcchomộtvídụphảnchứng.
1. NếuF làmộttrườngvectơ,thìdivF cũnglàmộttrườngvectơ.
2. NếuF làmộttrườngvectơ,thìcurlF cũnglàmộttrườngvectơ.
3. Nếuf cócácđạohàmriêngliêntụcmọicấptrênR3,thìdivpcurl∇fq“0. 0.1Tómtắt 9
4. Nếuf cócácđạohàmriêngliêntụcmọicấptrênR3 vàC làmộtđườngtrònbấtkỳ, ˆ ∇f ¨ dr “ 0. thì C
5. NếuF “ P i ` Qj vàPy “ Qx trênmộtmiềnmởD,thìF bảotoàn. ˆ ˆ fpx,yqds 6. fpx,yqds“´ ´C C
7. NếuF vàG làcáctrườngvectơvàdivF “ divG thìF “ G.
8. Côngthựchiệnbởimộttrườnglựcbảotoànkhimộtchấtđiểmdichuyểnquanhmột đườngcongkínbằngkhông.
9. NếuF vàG làcáctrườngvectơ,thì curlpF ` Gq“curlF ` curlG
10. NếuF vàG làcáctrườngvectơ,thì curlpF ¨ Gq“curlF ¨ curlG ¨ F ¨ dS“ 0.
11. NếuS làmộtmặtcầuvàF làmộttrườngvectơhằng,thì S
12. CómộttrườngvectơF thỏamãn curlF “ xi ` yj ` zk Bàitập0.2.
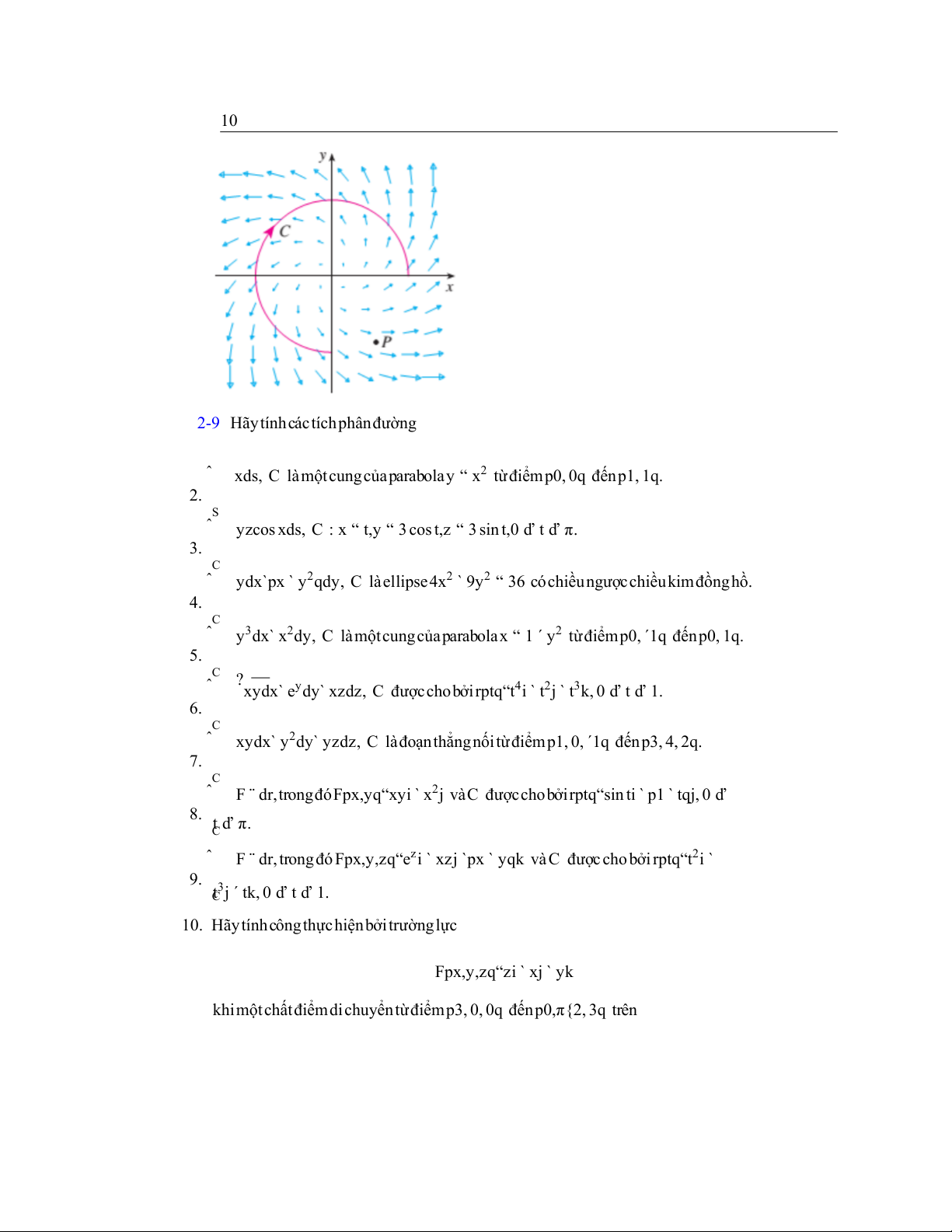
1. Một trường vectơ F, một đường cong C và một điểm P được chỉ ra tronghình. ˆ
F ¨ dr làdương,âmhaybằngkhông?Hãygiảithích. (a) Đạilượng C
(b) ĐạilượngdivFpP q làdương,âmhaybằngkhông?Hãygiảithích. 10
2-9 Hãytínhcáctíchphânđường ˆ
xds, C làmộtcungcủaparabolay “ x2 từđiểmp0, 0q đếnp1, 1q. 2. S ˆ
yzcos xds, C : x “ t,y “ 3 cos t,z “ 3 sin t,0 ď t ď π. 3. C ˆ
ydx`px ` y2qdy, C làellipse4x2 ` 9y2 “ 36 cóchiềungượcchiềukimđồnghồ. 4. C ˆ
y3dx` x2dy, C làmộtcungcủaparabolax “ 1 ´ y2 từđiểmp0, ´1q đếnp0, 1q. 5. C ˆ
?xydx` eydy` xzdz, C đượcchobởirptq“t4i ` t2j ` t3k,0 ď t ď 1. 6. C ˆ
xydx` y2dy` yzdz, C làđoạnthẳngnốitừđiểmp1, 0, ´1q đếnp3, 4, 2q. 7. C ˆ
F ¨ dr,trongđóFpx,yq“xyi ` x2j vàC đượcchobởirptq“sin ti ` p1 ` tqj, 0 ď 8. t ď π. C ˆ
F ¨ dr, trong đó Fpx,y,zq“ezi ` xzj `px ` yqk và C được cho bởi rptq“t2i ` 9. C t3j ´ tk, 0 ď t ď 1.
10. Hãytínhcôngthựchiệnbởitrườnglực Fpx,y,zq“zi ` xj ` yk
khimộtchấtđiểmdichuyểntừđiểmp3, 0, 0q đếnp0,π{2, 3q trên 0.1Tómtắt 11 (a) mộtđườngthẳng.
(b) mộtđườngđinhốcx “ 3 cos t,y “ t,z “ 3 sin t.
11-12 Hãy chỉ ra rằng F là trường vectơ bảo toàn. Sau đó hãy tìm một hàm f thỏa mãn F “ ∇f.
11. Fpx,yq “ p1 ` xyqexyi `pey ` x2exyqj
12. Fpx,y,zq“sin yi ` x cos yj ´ sin zk ˆ F ¨ dr
13-14 HãychỉrarằngF làtrườngvectơbảotoànvàápdụnggiảthiếtnàyđểtính trênđườngcongchotrước. C
13. Fpx,yq “ p4x3y2 ´ 2xy3qi `p2x4y ´ 3x2y2 ` 4y3qj, C : rptq “ pt ` sin πtqi `p2t ` cos πtqj, 0 ď t ď 1
14. Fpx,y,zq“eyi`pxey `ezqj`yezk, C làđoạnthẳngnốitừđiểmp0, 2, 0q đếnp4, 0, 3q. ˆ xy2dx´ x2ydy,
15. Hãy chứng tỏ rằng định lý Green là đúng với tích phân đường
trong đó C chứa parabola y “ x2 từ điểm p´1, 1q đến p1, 1q C và đoạn thẳng nối từ điểmp1, 1q đếnp´1, 1q.
16. HãyápdụngđịnhlýGreenđểtính ˆ a1`x3dx`2xydy C
trongđóC làmiềntamgiáccócácđỉnhp0, 0q, p1, 0q vàp1, 3q. ˆ
x2ydx´ xy2dy, trong đó C là đường tròn
17. Hãy áp dụng định lý Green để tính
x2 ` y2 “ 4 cóchiềungượcchiềuki C mđồnghồ.
18. HãytínhcurlF vàdivF nếu
Fpx,y,zq“e´x sin yi ` e´y sin zj ` e´z sin xk
19. HãychỉrarằngkhôngcótrườngvectơG thỏamãn curlG “ 2xi ` 3yzj ´ xz2k 12
20. Hãychỉrarằng,vớicácđiềukiệnscủacáctrườngvectơF vàG thì
curlpF ˆ Gq“FdivG ´ GdivF `pG ¨ ∇qF ´pF ¨ ∇qG
21. NếuC làmộtđườngcongđơntrơnbấtkỳkhéokínvàf vàg làcáchàmkhảvi,hãy ˆ fpxqdx` gpyqdy“ 0. chỉrarằng C
22. Nêúf vàg làhaihàmkhảvi,hãychỉrarằng
∇2pf gq“f ∇2g ` g∇2f ` 2∇f ¨ ∇g
23. Nếu f là một hàm điều hoà, nghĩa là, ∇2f “ 0, hãy chi ra rằng tích phân đường
intfydx´ fxdylàđộclậpvớimọimiềnđơnliênD.
24. (a) HãypháchọađườngcongC vớicácphươngtrìnhthamsố
x “ cos t y“ sin t z“ sin t 0 ď t ď 2π ˆ
2xe2ydx`p2x2e2y ` 2y cot zqdy´ y2 csc2 zdz. (b) Hãytính C
25. Hãytínhdiệntíchcủamộtphầncủamặtz “ x2 ` 2y trênmiềntamgiáccócácđỉnh làp0, 0q, p1, 0q vàp1, 2q.
26. (a) Hãytìmphươngtrìnhcủamặtphẳngtiếptuyếntạiđiểmp4, ´2, 1q vớimặttham sốS đượcchobởi
rpu,vq“v2i ´ uvj ` u2k 0 ď u ď 3, ´3 ď v ď 3
(b) Hãy sử dụng một máy tính để vẽ mặt S và mặt phẳng tiếp tuyến đã tìm trong câu(a).
(c) Thiếtlập,nhưngkhôngtính,tíchphânđểtínhdiệntíchmặtS. (d) Nếu z2 x2 y2 Fpx,y,zq“ i ` j ` 1 ` x2 1 ` y2 k 1 ` z2 ¨
F ¨ dSchínhxácđếnbốnchữsốthậpphân. hãytính S
27-30 Hãytínhcáctíchphânmặt 0.1Tómtắt 13 ¨
zdStrong đó S là một phần của paraboloid z “ x2 ` y2 nằm dưới mặt phẳng 27. z “ 4. S ¨ 28.
px2z ` y2zqdS, trong đó S là một phần của mặt phẳng z “ 4 ` x ` y nằm bên
Strong mặt trụ x2 ` y2 “ 4. ¨
F ¨ dS, trong đó Fpx,y,zq“xzi2yj ` 3xk và S là mặt cầu x2 ` y2 ` z2 “ 4 và 29. hướngrangoài. S ¨
F ¨ dS, trong đó Fpx,y,zq“x2i ` xyj ` zk và S là một phần của paraboloid 30.
Sz “ x2 ` y2 bên dưới mặt phẳng z “ 1 và hướng lên trên.
31. HãychứngtỏrằngđịnhlýStokeslàđúngvớitrườngvectơFpx,y,zq“x2i`y2j`z2k,
trongđóS làmộtphầncủaparaboloidz “ 1 ´ x2 ´ y2 nằmtrênmặtphẳngxyvàS hướnglêntrên. ¨
curlF ¨ dS, trong đó Fpx,y,zq“x2yzi `
32. Hãy áp dụng định lý Stokes để tính
yz2j ` z3exyk, S làmộtphầncủamặt S
cầux2 ` y2 ` z2 “ 5 nằmtrênmặtphẳngz “ 1 vàS hướnglêntrên. ¨
F ¨ dr,trongđóFpx,y,zq“xyi ` yzj ` zxk,
33. HãyápdụngđịnhlýStokesđểtính
C là tam giác có các đỉnh p1, 0, 0 C
q, p0, 1, 0q và p0, 0, 1q hướng ngược chiều kim đồng hồnhìntừbêntrên. ¨ F ¨ dS,trongđóFpx,y,zq“
34. HãyápdụngđịnhlýDivergenceđểtínhtíchphânmặt
x3i ` y3j ` z3k vàS làmặtcủahìnhkhốiđượcgiới Shạnbởimặttrụx2 ` y2 “ 1 và
cácmặtphẳngz “ 0 vàz “ 2.
35. HãychứngtỏrằngđịnhlýDivergencelàđúngvớitrườngvectơFpx,y,zq“xi`yj`zk,
trongđóE làquảcầuđơnvịx2 ` y2 ` z2 ď 1.
36. Hãytínhthônglượngdòngbênngoàicủa xi ` yj ` zk Fpx,y,zq“ px2 ` y2 ` z2q3{2
quaellipsoid4x2 ` 9y2 ` 6z2 “ 36. 14 37. Cho
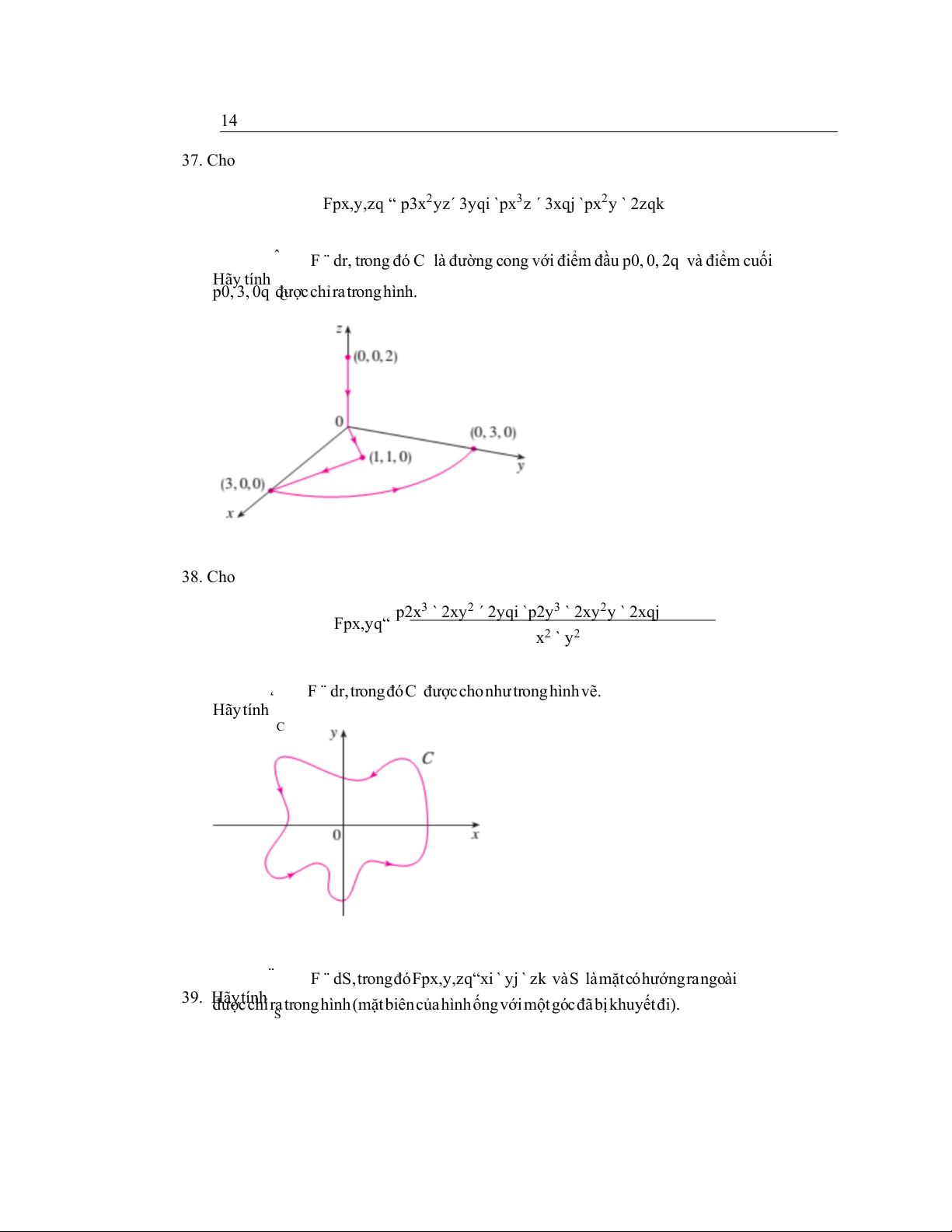
Fpx,y,zq “ p3x2yz´ 3yqi `px3z ´ 3xqj `px2y ` 2zqk ˆ
F ¨ dr, trong đó C là đường cong với điểm đầu p0, 0, 2q và điểm cuối Hãy tính p0, 3, 0q C đượcchỉratronghình. 38. Cho
p2x3 ` 2xy2 ´ 2yqi `p2y3 ` 2xy2y ` 2xqj Fpx,yq“ x2 ` y2 ˛
F ¨ dr,trongđóC đượcchonhưtronghìnhvẽ. Hãytính C ¨
F ¨ dS,trongđóFpx,y,zq“xi ` yj ` zk vàS làmặtcóhướngrangoài 39. Hãytính
đượcchỉratronghình(mặtbiêncủahìnhốngvớimộtgócđãbịkhuyếtđi). S 0.1Tómtắt 15
40. NếucácthànhphầncủaF cócácđạohàmriêngcấphai liêntụcvàS làmặtphẳng ¨ curlF ¨ dS“ 0.
biêncủamiềnđơnliên,hãychỉrarằng S
41. Nếua làmộtvectơhằng,r “ xi ` yj ` zk vàS làmặtcóhướng,trơnvớiđườngbiên
C đơn,đóngtrơnvàhướngtheochiềudương,hãychỉrarằng ¨ ˆ 2a ¨ dS“ pa ˆ rq¨dr S C Bàitoánmởrộng
1. Cho S là một mặt tham số trơn và cho P là một điểm sao cho mỗi đường bắt đầu
từ P giao với S cùng một lúc. Góc khốiΩpSq đối diện bởi S tại P là tập hợp các
đườngthẳngbắtđầutừP vàđiquaS.ChoSpaq làgiaotuyếncủaΩpSq vớibềmặt
củamặtcầutâmP vàbánkínha.Khiđósốđocủagóckhối(đơnvịsteradian)được xácđịnhbởi diệntíchSpaq |ΩpSq|“ a2
HãyápdụngđịnhlýDivergencechophầncủaΩpSq giữaSpaq vàS đểchỉrarằng ¨ r ¨ n dS r3 |ΩpSq|“ S
trong đó r là bán kính vectơ từ điểm P đến một điểm bất kỳ trên S, r “|r|, và
vectơpháptuyếnđơnvịn lấytừđiểmP . 16
Điềunàychỉrarằngđịnhnghĩacủasốđocủagóckhốikhôngphụthuộcvàbánkính
a của mặt cầu. Do đó số đo của góc khối bằng diện tích lấy trên một mặt cầu đơn
vị.(Chúýsựtươngtựvớiđịnhnghĩacủasốđoradian).Tổnggóckhốichobởihình
cầutạitâmcủanóvìvậybằng4π steradian.
2. HãytìmmộtđườngcongC đóng,đơn,cóchiềudươngcótíchphânđường ˆ py3 ´ yqdx´ 2x3dy C đạtgiátrịcựcđại.
3. ChoC làmộtđườngcongtrongkhônggianđơn,đóng,trơntừngkhúcnằmtrênmặt
phẳngcóvectơpháptuyếnđơnvịn “xa,b,cy vàcóchiềudươngứngvớin.Hãychỉ
rarằngdiệntíchhìnhphẳnggiớihạnbởiC là 1 ˆ
pbz´ cyqdx`pcx´ azqdy`pay´ bxqdz 2 C
4. Xem xét hình dạng của một mặt có phương trình tham số x “ sin u,y “ sin v,z “
sinpu ` vq. Trước hết hãy vẽ đồ thị mặt đó theo nhiều hướng nhìn khác nhau. Hãy
giảithíchtạisaosựxuấthiệncủacácđồthịnàybằngcáchxácđịnhvếtcủacácmặt 1
nằmngangz “ 0,z “˘1 vàz “˘ . 2
5. Hãychứngminhmệnhđềsauđây
∇pF ¨ Gq “ pF ¨ ∇qG `pG ¨ ∇qF ` F ˆ curlG ` G ˆ curlF 0.1Tómtắt 17
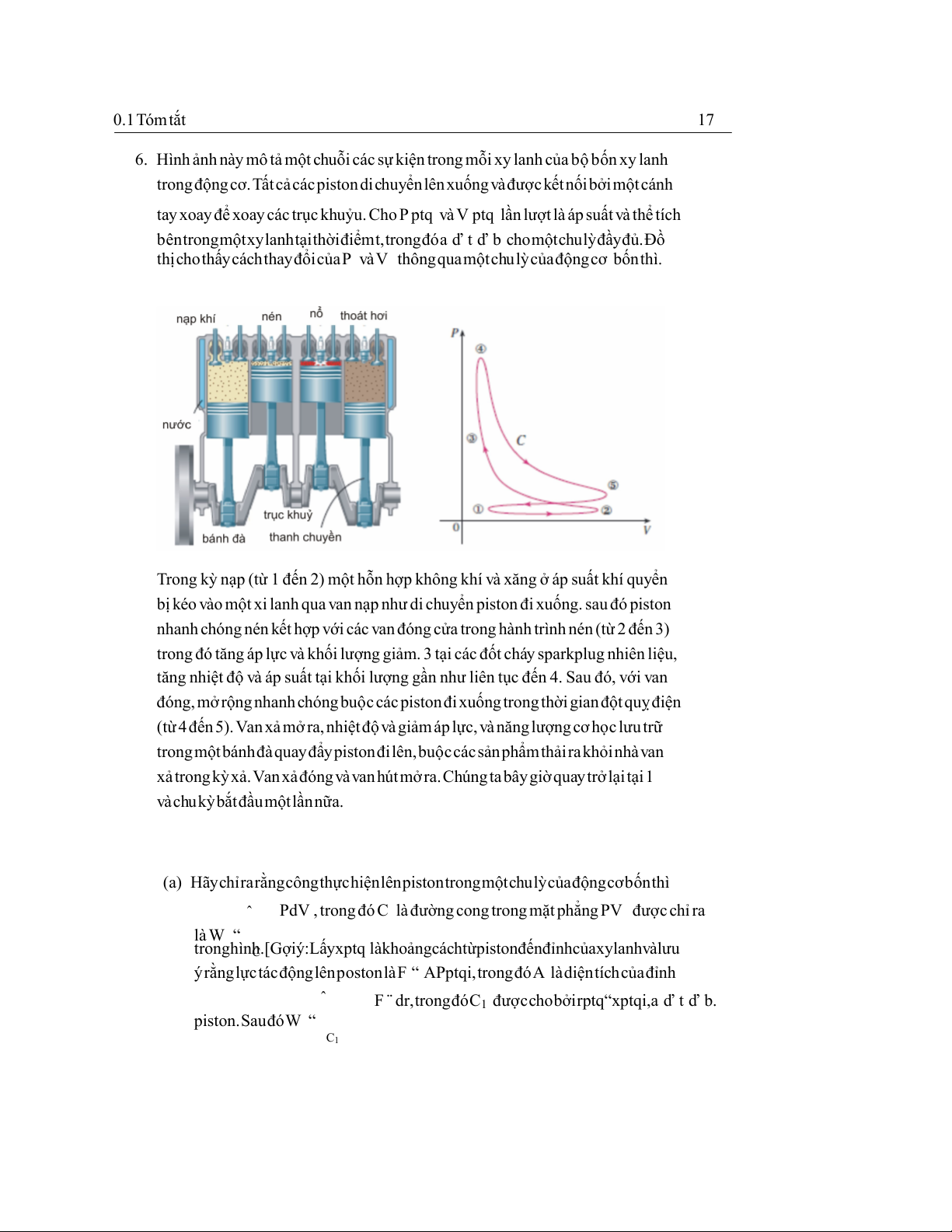
6. Hình ảnh này mô tả một chuỗi các sự kiện trong mỗi xy lanh của bộ bốn xy lanh
trongđộngcơ.Tấtcảcácpistondichuyểnlênxuốngvàđượckếtnốibởimộtcánh
tay xoay để xoay các trục khuỷu. Cho P ptq và V ptq lần lượt là áp suất và thể tích
bêntrongmộtxylanhtạithờiđiểmt,trongđóa ď t ď b chomộtchulỳđầyđủ.Đồ
thịchothấycáchthayđổicủaP vàV thôngquamộtchulỳcủađộngcơ bốnthì.
Trong kỳ nạp (từ 1 đến 2) một hỗn hợp không khí và xăng ở áp suất khí quyển
bị kéo vào một xi lanh qua van nạp như di chuyển piston đi xuống. sau đó piston
nhanh chóng nén kết hợp với các van đóng cửa trong hành trình nén (từ 2 đến 3)
trong đó tăng áp lực và khối lượng giảm. 3 tại các đốt cháy sparkplug nhiên liệu,
tăng nhiệt độ và áp suất tại khối lượng gần như liên tục đến 4. Sau đó, với van
đóng, mở rộng nhanh chóng buộc các piston đi xuống trong thời gian đột quỵ điện
(từ 4 đến 5). Van xả mở ra, nhiệt độ và giảm áp lực, và năng lượng cơ học lưu trữ
trongmộtbánhđàquayđẩypistonđilên,buộccácsảnphẩmthảirakhỏinhàvan
xảtrongkỳxả.Vanxảđóngvàvanhútmởra.Chúngtabâygiờquaytrởlạitại1
vàchukỳbắtđầumộtlầnnữa.
(a) Hãychỉrarằngcôngthựchiệnlênpistontrongmộtchulỳcủađộngcơbốnthì ˆ
PdV , trong đó C là đường cong trong mặt phẳng PV được chỉ ra là W “
tronghìnCh.[Gợiý:Lấyxptq làkhoảngcáchtừpistonđếnđỉnhcủaxylanhvàlưu
ýrằnglựctácđộnglênpostonlàF “ APptqi,trongđóA làdiệntíchcủađỉnh ˆ
F ¨ dr,trongđóC1 đượcchobởirptq“xptqi,a ď t ď b. piston.SauđóW “ C1 18
MộtphươngphápkháclàtínhtổngRiemanntrựctiếp].
(b) Hãyápdụngcôngthức(??)đểchỉrarằngcôngthựchiệnlàchênhlệchbởicác
diệntíchhìnhphẳnggiớihạnbởihaivònglặpcủaC.