Bài tập Tích phân suy rộng | Giải tích 1 | Đại học Bách Khoa Hà Nội

Bài tập Tích phân suy rộng | Giải tích 1 | Đại học Bách Khoa Hà Nội. Tài liệu được biên soạn giúp các bạn tham khảo, củng cố kiến thức, ôn tập và đạt kết quả cao kết thúc học phần. Mời các bạn đọc đón xem!

10 5 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Giải tích 1

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

26 trang 2 tháng trước

Tác giả:

Profile Thùy Dương
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
TÍCH PHÂN SUY R ỘNG
Câu 1: Khảo sát s h i t c a tích phân suy r ng: ự ộ ụ ủ ộ
2
6
2
1
x
dx
x

Giải
Đặt
2
6
2 2
1
x
dx f x dx
x
 
2 2 3
6 6 6
1
~ 0, 1.
1 1
x x
f x
x x x
f x g x lim lim
x g x
x x x
 
Vì
2
1
dx
x

phân k ỳ
1 ,
nên
2
6
2
1
x
dx
x

phân k theo tiêu chu n so sánh 2 ỳ ẩ
Câu 2: Khả ự ộ ụ ủ ộo sát s h i t c a tích phân suy r ng:
1
2
0
1
2 1
x
dx
x x
Giải:
Tích phân
suy r ng lo i 2 t i cộ ạ ạ ận dưới
0x
; Đặt
2
1
2 1
x
f x
x x
Xét
1
g x
x
có
2
0 0
1
1.
2 1
x x
f x
x
lim lim
g x x
Mặt khác
1
0
dx
x
h i t nên tích phân ộ ụ
1
2
0
1
2 1
x
dx
x x
cũng hội tụ
Câu 3: Khả ự ộ ụ ủ ộo sát s h i t c a tích phân suy r ng:
3
1
1
1
sinx
dx
x x

Giải
Ta có:
2
3
1 2
0 , 1.
1
sinx
x
x
x x
Vì
2
1
2
dx
x

nên
3
1
1
1
sinx
dx
x x

- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
Vậy
3
1
1
1
sinx
dx
x x

hội tụ tuy i theo tiêu chuệt đố ẩn so sánh 1.
Câu 4: Khả ự ộ ụ ủ ộo sát s h i t c a tích phân suy r ng:
2
7
1
1
.
1 2
x arctan x
J dx
x x

Giải:
2 2 22
1 2
7 7 7
1 1 2
1 1 1
1 2 1 2 1 2
x arctan x x arctan x x arctan x
J dx dx dx J J
x x x x x x
 
Khi
2
1
7
2
1
4
1 : ~
1 2
3 1
x arctanx
x f x g x
x x
x
Mà
2
1
g x
h i t nên ộ ụ
1
J
h i t ộ ụ
Khi
2 2
8 2
7
2
1 1
: ~
1 2
x arctanx x
x f x g x
x
x x
x

Mà
2
g x dx

h i t nên ộ ụ
2
J
h i t ộ ụ
Vậy
1 2
J J J
h i t ộ ụ
Câu 5: Khả ự ộ ụ ủ ộo sát s h i t c a tích phân suy r ng:
3
8
1
1
x x
dx
x

Giải:
Đặt
3
8
1 1
1
x x
dx f x dx
x
 
Khi
3 3
8 8
1
: ~
1 1
x x x
x f x
x
x x

Chọn
1
,g x
x
ta có
3
8
. 1
1
x x
f x
x x
lim lim x
g x
x
 
- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
Mặt khác ta có
1
g x dx

phân k ỳ
1 .p
Vậy theo tiêu chu n so sánh 2, tích phân ẩ
3
8
1
1
x x
dx
x

phân k ỳ
Câu 6: Khả ự ộ ụ ủ ộo sát s h i t c a tích phân suy r ng:
5
1
4 1
x
dx
x

Giải:
Đặt
5
1 1
4 1
x
dx f x dx
x
 
Khi
2
5
1
: ~
2
4
x
x f x
x
x

Chọn
2
1
,
2
g x
x
ta có
2
5
.2 1.
1
x x
f x
x
lim lim x
g x
x
 
Mặt khác ta có
1
g x dx

hội tụ
2 1 .p
Vậy theo tiêu chu n so sánh 2, tích phân ẩ
5
1
4 1
x
dx
x

h i t ộ ụ
Câu 7: Khả ự ộ ụ ủ ộo sát s h i t c a tích phân suy r ng:
2
4
1
7 3
3
x x
dx
x x x

Giải:
Với
[1; ),x
xét
2 2
4 2
4
7 3 1
0, 0
3 3
3
x x x
f x g x
x x
x x x
2
2
4
7 3
.3 1
3
x x
f x
x x
lim lim x
g x
x x x
 
Suy ra
2
4
1
7 3
3
x x
K dx
x x x
và
2
1
1
3
dx
x
cùng tính ch t h i t ấ ộ ụ
- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
Mà
2
1
1
3
dx
x
h i t , vì ộ ụ
2 1p
. V y K h i t ậ ộ ụ
Câu 8: Tích phân suy r ng ộ
1,01
2 2
2
2 4
x dx
x x
h i t hay phân kộ ụ ỳ?
Giải:
Với
[2; ),x
xét
1,01
0,99
2 2
1
0, 0
2 4
x
f x g x
x
x x
1,01
0,99
2 2
1
.
2
2 4
x x
f x
x
lim lim x
g x
x x
 
Mà
3
0,99
2
dx
x
phân k nên ỳ
1,01
2 2
2
2 4
x dx
x x
phân k theo tiêu chu n so sánh gi i h n ỳ ẩ ớ ạ
Câu 9: Khả ự ộ ụ ủo sát s h i t c a tích phân:
3
6
1
5 1x x
dx
x sinx

Giải
Đặt
3
6
1 1
5 1x x
dx f x dx
x sinx
 
Khi
3
6 3
1
: ~
x
x f x
x x

Xét
3
1
,g x
x
ta có
3 3
6
5 1
1.
x x
x x x
f x
lim lim
g x x sinx
 
Mặt khác ta có
3
1
1
dx
x

hội t nên ụ
3
6
1
5 1x x
dx
x sinx

hội t ụ
Câu 10: Khả ự ộ ụ ủo sát s h i t c a tích phân:
2
1
1
.
1
x
dx
x x
Giải
Tích phân
2 2
1 1
1
1
x
dx f x dx
x x
là tích phân suy r ng lo i 2 t i c ộ ạ ạ ận dưới.
- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
Xét hàm
1 1 1
1 1
1 1
1
; 4
1
1
x x x
x x
f x x x
g x lim lim lim
x g x x
x x
mà
2
1
1
1
dx
x
phân kì nên tích phân
2
1
1
1
x
dx
x x
phân kì
Câu 11: Xét s h i t c a tích phân suy r ng: ự ộ ụ ủ ộ
34 2
0
3 . 2
.
2.
si n x
I dx
x x

Giải:
2
1 2
3 3 34 2 4 2 4 2
0 0 2
3 2 3 2 3 . 2
2. 2. 2.
sin x sin x si n x
I dx dx dx I I
x x x x x x
 
Xét
2
1
3
4 2
0
3 2
2.
sin x
I dx
x x
Hàm dưới dấu tích phân là hàm không âm.
Ta có:
3 34 2 2
3 2 3 0
0 : ~
2. 2.
sin x
x VCB
x x x
Mà
2
3 2
0
3
2.
dx
x
h i t do ộ ụ
2
1
3
nên
1
I
h i t (TCSS2) ộ ụ
Xét
2
3
4 2
2
3 . 2
.
2.
si n x
I dx
x x

Ta có :
4
34 2
3 2 4
0 ; [2; )
2.
sin x
x
x
x x

Mà
4
2
3
dx
x

h i t do ộ ụ
4 1
nên
2
I
h i t (TCSS1) K t lu n: I h i t ộ ụ ế ậ ộ ụ
Câu 12: Khả ự ộ ụ ủo sát s h i t c a tích phân sau:
3 2
5 3 2
1
5 1
2 5 1
x x
dx
x x x

Giải:
Đặt
3 2
5 3 2
5 1
2 5 1
x x
f x
x x x
. Xét hàm
2
1 1
;
2
x
f x
g x lim
x g x

Mà
2
1
1
dx
x

h i t nên ộ ụ
3 2
5 3 2
1
5 1
2 5 1
x x
dx
x x x

h i t ộ ụ
- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
Câu 13: Khả ự ộ ụ ủo sát s h i t c a tích phân sau:
2
3 2
1
. 1
1
x ln x
dx
x
Giải
Đặt
3 2
. 1
1
x ln x
h x
x
. Xét hàm
3
3 3
1 1
1
1 2
;
1 1 2
x x
h x xln x
ln
k x lim lim
k x
x x
Mà
2
3
1
1
1
dx
x
h i t nên ộ ụ
2
3 2
1
. 1
1
x ln x
dx
x
h i t ộ ụ
Câu 14: Khả ự ộ ụ ủ ộo sát s h i t c a tích phân suy r ng:
1
3
0
1
x
dx
x
Giải
Ta có:
1
3
2
1
0 ~
1
3 1
x
x
x
khi
1
x
Mà
1
1
2
0
1 x dx
h i t ộ ụ
1
3
0
1
x
dx
x
h i t ộ ụ
Câu 15: Tích phân suy r i t hay phân kì? Tính giá tr tích phân n u có: ộng sau đây hộ ụ ị ế
0
1
.
1
dx
x x
Giải
1 1
0
0 0 1 1
1 1 1 1 1
1 1 1 1 1
t
t
t
t
dx dx dx lim dx lim dx
x x x x x x x x x x

2
1 1
2 2
1
1
dx du arctan x C
u
x x
(Đặt
u x
)
0
0
1
1
2 2
1
1
t
t
t
dx lim arctan x lim arctan x
t
x x

0
2. 2 2 2.
4 4
t
t
x lim arctan t lim arctan t

Câu 16: Khả ự ộ ụ ủ ộo sát s h i t c a tích phân suy r ng:
5
3
2
7 3
2 2
sinx
dx
x x

- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
Giải:
3
1 2
5 5 5
3 3 3
2 2 3
7 3 7 3 7 3
2 2 2 2 2 2
sinx sinx sinx
dx dx dx I I
x x x x x x
 
Xét
1
I
Khi
5
3
3
7 3 7 3 2
2 : ~
2 .34
2 2
sinx sin
x
x
x x
Do
3
3
2
7 3 2 1
, 1
3
2 .34
sin
dx
x
h i t nên ộ ụ
1
I
h i t ( TCSS2) ộ ụ
Xét
2
I
Khi
2
5 5
3 3
7 3 10 10
: ~ .
2 2 2 2
sinx
x
x
x x x x

Do
2
3
10
; 2 1dx
x

h i t nên ộ ụ
5
3
3
10
2 2
dx
x x

h i t (TCSS2) nên ộ ụ
1
I
h i t ( TCSS1) ộ ụ
Vậy
1 2
I I I
h i t . ộ ụ
Câu 17: Khả ự ộ ụ ủ ộo sát s h i t c a tích phân suy r ng:
2
3
5
2
3 1
2 3
x x
J dx
x x
Giải
Khi
2
5 5
3 1 9
2 : ~ 0 1
2 3 5 2
x x
x
x x x
Mà
3 3
5
5 5
2 2
9 9
5
5 2 2
dx
dx
x x
h i t vì ộ ụ
1
1 2
5
Từ
1
và
2
J
hội t (theo tiêu chuụ ẩn so sánh 2)
Câu 18: Khả ự ộ ụ ủ ộo sát s h i t c a tích phân suy r ng:
3 4
1
1
1
x
dx
x x

Giải:
- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
Ta có:
5
3 4
2
1 1
0 ~
1
x
x x
x
khi
x 
5
2
1
x dx

h i t ộ ụ
3 4
1
1
1
x
dx
x x

h i t ộ ụ
Câu 19: Khả ự ộ ụ ủ ộo sát s h i t c a tích phân suy r ng:
2
3 2
1
1
4 4
sinx
dx
x x x
Giải
Đặt
2 2
3 2
1 1
1
4 4
sinx
dx f x dx
x x x
là tích phân suy r ng lo i 2 t i c n trên 𝑥 ộ ạ ạ ậ
2x
Xét hàm
2
2 3 2
2 2 2
1 2
1 1 1 2
;
4 4 2
2
x x x
f x sinx x
sinx sin
g x lim lim lim
g x x x x x
x
h u h n ữ ạ
Mà
2
2
1
1
2
dx
x
phân k nên ỳ
2
3 2
1
1
4 4
sinx
dx
x x x
phân k ỳ
Câu 20: Khả ự ộ ụ ủ ộo sát s h i t c a tích phân suy r ng:
3 2
0
1
1
x x x
dx
x x

Giải
Khi
33 2
2
1 1 1
, ~
1
x x
x
x x
x

Mà
3
1
2
1
dx
x

h i t ộ ụ
Vậy
3 2
0
1
1
x x x
dx
x x

h i t theo tiêu chu n so sánh 2 ộ ụ ẩ
Câu 21: Khả ự ộ ụ ủ ộo sát s h i t c a tích phân suy r ng:
2
4
1
1
.
1
dx
x
Giải:
Khi
4
1 1
1 : ~
2 1
1
x
x
x
- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
Mặt khác:
2
1
1
2 1
dx
x
h i t do ộ ụ
1
1
2
Vậy
2
2
1
.
5 6
x lnx
dx
x x
h i t theo tiêu chu n so sánh 2 ộ ụ ẩ
Câu 22: Khả ự ộ ụ ủ ộo sát s h i t c a tích phân suy r ng:
2
1
1
sinx
dx
x

Giải
Ta có:
2 2
1
, 1
1
sinx
x
x x
Mà
2
1
dx
x

h i t nên ộ ụ
2
1
1
sinx
dx
x

h i t ộ ụ
Câu 23: Tính tích phân suy r ng: ộ
2
2
. 1
dx
x x x

Giải:
Đặt
2
2
2
2
2 1
1
1
1 2
2 1
t t
t
x x t x x dx dt
t
t
Đổ ậi c n:
2 2
1
1 ; 2 5 2; 1
2
x
t x x x x t x t lim x x x


1
2
2
5 2
2 1
1 2
dt
I arctan
t
Câu 24: Tính tích phân suy r ng: ộ
19
3 2
1
3
. 1
dx
x x

Giải:
19
3 19 21
3 2
7
1 1 13
3
2
1
. 1
1
dx dx dx
x x
x x
x
x
  
Đặt
3
3
2 2
1 1
1 1t t
x x
- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
3
1
2
3
3
2
3 3 27
1 . 4
2 10 80
I t t dt
Câu 25: Khả ự ộ ụ ủo sát s h i t c a tích phân:
3 2
0
1
m
x
I dx
cos x
Giải:
2
3 3 32 2 2
0 0
2
1 1 1
m m m
x x x
I dx dx dx
cos x cos x cos x
Khi
2
2
3
3
1
0 : ~
2.
2
m
m
x
x f x
x
x
. Tp HT khi và ch khi ỉ
2 1
1
3 3
m m
Khi
2
2
3 3
3
3
: ~
1 1
2.
2
m m m
x
x f x
cos x cos x
x
x
. TP h i t ộ ụ
m
Vậy tp đã cho HT với
1
3
m
Câu 26: Tính tích phân suy r ng: ộ
3 2
e
dx
I
x ln x ln x lnx

Giải:
Đặt
dx
t lnx dt
x
. Ta được tpsr loại 1 của hàm hữu tỉ:
2 3
1
3
3
8
dt
I ln
t t t

Câu 27: o sát s h i t c a tích phân: Khả ự ộ ụ ủ
1
0
1
lnx
I dx
x x
Giải
1
1 1
2
1
0 0
2
1 1 1
lnx lnx lnx
I dx dx dx
x x x x x x
- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
Khi
1
0 : ~ .x f x
x
TPHT
Khi
1
1 : ~
1
x f x
x
. TP h i t khi và ch khi ộ ụ ỉ
2
Vậy tp đã cho HT khi và chỉ khi
2
Câu 28: Tính tích phân suy r ng: ộ
1
0
1
n
I ln x dx
Giải:
Đặt
1 1
t t
t ln x x e dx e dt
. Ta được tích phân
0
1
1 2
0
1 ... 1 . !. . 1 . !.
n n
n t n t n t n t t t
I t e dt t e nt e n n t e n t e n e


Câu 29: Tìm t t c các giá tr ấ ả ị
0m
tích phân: để
2
1
3
3
2
0
m
x x
I
x arctanx
h i t ộ ụ
Giải
Hàm
0, (0; 2].f x x
Ta s so sánh khi ẽ
0
x
.Lưu ý: Không nhận xét f dương thì trừ
điểm
2
3
42
3
1
2 : ~
x
f x
x
x
TP phân k ỳ
2
3
2
2 : ~
2
x
f x
x
TP phân k ỳ
2
3
1
2 : ~
2
3
x
f x
x
x
h i t khi và ch khi TP ộ ụ ỉ
2 5
1
3 3
Vậy
I
h i t khi và ch khi ộ ụ ỉ
5
0
3
Câu 30: Tìm s ố thực
0m
tích phân sau h i t để ộ ụ
2
1
0
1
.
1
m m
x
I dx
x x

- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
Giải:
Ta có:
1
2 2 2
1 2
1 1 1
0 0 1
1 1 1
1 1 1
m m m m m m
x x x
I dx dx dx I I
x x x x x x
 
Hàm
0, 0f x x
1
1
0 : ~
m
x f x I
x
h i t khi và ch khi ộ ụ ỉ
1m
2
2
1
: ~
m
x f x I
x

h i t khi và ch khi ộ ụ ỉ
1
2
m
Vậy
I
h i t khi và ch khi ộ ụ ỉ
1
1
2
m
Câu 31: Tìm
tích phân sau h i t để ộ ụ
1
2
2
0
1 4
dx
I
x x
. Tính tích phân khi
2
Giải
Ta th y 2 c n c a tích phân làm cho bi u th i d nh. Nên ta tách ra ấ ậ ủ ể ức dướ ấu tích phân không xác đị
thành 2 tích phân suy r ng loộ ại 2 như sau:
1 1 1
2 4 2
1 2
2 2 2
1
0 0
4
1 4 1 4 1 4
dx dx dx
I I I
x x x x x x
Xét tích phân
1
I
:
1
4
1
2
0
1 4
dx
I
x x
Xét khi
0
x
:
+ Khi
1
2
1
0 : ~ 0
1 4
I
x x
h i t ộ ụ
+ Khi
1
2 2
1 1
0 : ~ ~ 1
1 4 1 4
I
x x x
h i t ộ ụ
+ Khi
2
1 1
0 : ~
1 4
x
x x
Như vậy thì để
1
I
h i t ng h p này ộ ụ thì trong trườ ợ
ph i thả ỏa
0 1
- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
Tổng h p lợ ại thì với
1
thì
1
I
h i t ! ộ ụ
Xét tích phân
1
2
2 2
2
1
4
:
1 4
dx
I I
x x
Xét khi
1
2
x
:
+ Khi
1
2
2
1
1 1 1 1 1
0 : ~
1
1 2 1 2 1 11 4
2 1 2
1
2 2
2
2
2 2
2
x x xx x
x
x
x
ng lo i 2 và do đây là tích phân suy rộ ạ
1
1
2
nên
2
I
h i t . ộ ụ
+ Khi
2
1
2
2
1 1
0 : ~
1 4
1
2
2
I
x x
x
h i t . ộ ụ
+ Khi
2
1
2
2
1
1 1
0 : ~
1 4
1
2
2
I
x x
x
h i t ộ ụ
KẾT LUẬN: Do
2
I
i t cho đã hộ ụ nên để
I
h i t thì ộ ụ
1
I
ph i h i t . Vả ộ ụ ậy
1
a mãn. thỏ
* Tính tích phân khi
2
Khi
2
thì ta có tích phân sau:
1 1
2 22 2
2
2
0 0
1
2
1
1 4
4
x x
I dx dx
x
x
Đặt:
1
2
x sint
với
2 2
t
1
2
dx costdt
Đổ ậi c n:
1
0 0;
2 2
x t x t
Tích phân tr thành: ở
2 2
2
0 0
1 1 1 2
8 8 2 2 32
cos t
sin tdt dt
- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
Câu 32: Tìm
tích phân sau h i tđể ộ ụ
2 2
2 3
1
x x
I x e e dx

. Tính tích phân khi
5
Giải:
Đây là tích phân suy rộng loại 1.
Khi
x 
, ta có:
2 2 2 2
2 3 2 3
2 2 2 2
2 3 5 5
1 1 ~
x x x x
x
x e e x e e x
x x x x
Để ộ ụ tích phân h i t thì:
2 1 1
Khi
5
, tích phân tr thành: ở
2 2
2 3
5
1
x x
e e
I dx
x

Đặt:
2 3
1 2
u du dx
x x
. i c n: Đổ ậ
1 1; 0x u x u 
Tích phân tr thành: ở
1 1 1
2 3 2 3
1 2
0 0 0
1 1 1
2 2 2
u u u u
I u e e du ue du ue du I I
Đến đây dễ dàng tính đượ c
1 2
,I I
b ng tích phân t ng phân ằ ừ
Vậy
2
3
2 5
8 9 72
e
I
e
Câu 33: Cho tích phân
2
1
2 1
m
dx
I
x x

.Tìm
m
tích phân I h i t và tính tích phân khi để ộ ụ
2m
Giải:
Do
1x
làm cho bi u th c trong d ng ể ứ ấu tích phân không xác định. Nên đây là tích phân suy rộ
loại 1 và 2.
Tách ra thành 2 tích phân sau:
2
1 2
2 2 2
1 1 2
2 1 2 1 2 1
m m m
dx dx dx
I I I
x x x x x x
 
Xét tích phân
1
I
sau:
2 2
1
2
1 1
2 1 1
2 1
m
m
dx dx
I
x x xx x
- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
Khi
1
2
1
1 : ~
2 1 1
3 2 1
m
dx
x
x x x
x
+ Đây là tích phân suy rộng loại 2, thấy
1
1
1
2
I
hội tụ.
Xét tích phân
2
2
2
2 1
m
dx
I
x x

Khi
x 
ng h p cta xét các trườ ợ ủa
m
như sau:
Khi
0,m
xét
2
2
1 1
~ 1
2
2 1
m
I
x
x x
phân k ỳ
I
phân k ỳ
Khi
0,m
xét:
2
2
1 1
~ 1
3
2 1
m
I
x
x x
phân k ỳ
I
phân k ỳ
Khi
0,m
xét:
1
2
1 1
~
2 1
m
m
x
x x
Như vậy khi
0m
thì ta thấy
2
1 1m I
hội tụ ng lo(do đây là tích phân suy rộ ại 1).
Kết luận: + Do
1
I
h i t ộ ụ nên để
I
h i t thì ch ph thu c vào ộ ụ ỉ ụ ộ
2
I
. Suy ra,
I
h i t khi ộ ụ
0m
.
Tính tích phân khi
2 :m
Khi
2,m
thành: tích phân đã cho trở
2 2
2
1 1
2
1
2 1
2 1
dx dx
I
x x
x x
x
 
Đặt:
2 2
22 2 2
2
1 1 1
1 1
1
1
t
t t x xdx dt
x x t
t
Tích phân đã tương đương với:
2
2
1 1 1
2
2
2 2
1 0 0 0
2
2 2
2
1
1
1 1
1
3
1 1
2
1
2
2
2 1
1 2
1 1
t
t
xdx
t
dt dt dt
t
t t
t
x x
t
t t
x

- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
1 1 1
0 0 0
6 6
1 1 1 1 1 1
2 2
2
2 6 2 6
6 6 6 6 6 6
2 2 2 2 2 2
t t
dt dt
t t t t t t
1
1 6 6 1
5 2 6
0
2 2
2 6 2 6
ln t ln t ln
Câu 34: Cho tích phân
2
2
1 2 5 2
m
dx
I
x x x

.Tìm
m
tích phân I h i t và tính tích để ộ ụ
phân khi
1m
Giải:
- Do
2x
làm cho bi u th c trong d nh ể ứ ấu tích phân không xác định. Nên đây là tích phân bất đị
loại 1 và 2.
Tách ra thành 2 tích phân sau:
3
1 2
2 2 2
2 2 3
1 2 5 2 1 2 5 2 1 2 5 2
m m m
dx dx dx
I I I
x x x x x x x x x
 
Xét tích phân
1
I
sau:
3 3
1
2
2 2
1
1 2 5 2
1 2 2
2
m
m
dx dx
I
x x x
x x x
Khi
1
2
1 1
2 : ~
1
3 2 1 2
1 2 2
2
m
m
x
x
x x x
Nhậ ọn thấy với m i
0m
(lưu ý vì hàm số xác đị chỉ nh khi
0m
). Thì
3 2 1
m
luôn là h ng. ằ
Do đó thấy
1
1
1
2
I
h i t ng lo i 2). ộ ụ (đây là tích phân suy rộ ạ
Xét tích phân
2
2
3
1 2 5 2
m
dx
I
x x x

Khi
x 
ng h p cta xét các trườ ợ ủa
x 
như sau:
Khi
0,m
ta xét hàm dương sau:
2
2
1 1
~ 1
2
1 2 5 2
m
I
x
x x x
phân k ỳ
I
phân
kỳ
- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
Khi
0 :m
không xét vì làm hàm s nh ố không xác đị
I
không có tích phân.
* Khi
0,m
ta có:
1
2
1 1
~
2
1 2 5 2
m
m
x
x x x
Như vậy khi
0m
thì ta thấy
2
1 1m I
hội tụ.
Kết luận: + Do
1
I
h i t ộ ụ nên để
I
h i t thì ch ph thu c vào ộ ụ ỉ ụ ộ
1
I
Suy ra,
I
h i t khi m > 0. ộ ụ
Tính tích phân khi
2
2
1:
1 2 5 2
dx
m
x x x

Đặt:
2
1 1
1x dx dt
t t
Tích phân đã tương đương với:
0
2
2 2
2 1
1
1 2 5 2
1 1 1
2 1 5 1 2
dx
t
dt
x x x
t t t

1 1 1
2 2
0 0 0
2
2 1
2
9 1
1
4 2
dt dt dt
t t
t
t
t t
Đặt
1 3 3
cos
2 2 2
t sinu dt udu
Tích phân tr thành: ở
2
1
3
3
1
2
3
2 3
2
arcsin
cosudu
arcsin
cosu
Câu 35: Tính tích phân
2
1
1
4
I dx
x x

Giải
Xét:
2
4 0 2x x
x
1
2
2
4 x
2
4 x
0
2
4x
- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
Vậy, ta có:
2
1 2
2 2
2
1 1 2
1 1 1
4 4
4
I dx dx dx I I
x x x x
x x
 
Xét
1
:I
Đặt
2
1 1 1
t x dx dt
x t t
Với
1
1
1
2
2
t
x
x
t
1 1
2 1
2 2
2
2
1
2 2 2
1
1 1 1
2
2
1
1
1 1 1
2 4 1 2 3
1
2 2
1 1
4 4 1 4 1
4
2
dt
dt dt
t
I dx ln t t ln
x x t t
t t
Tương tự với
2
4
I
Vậy
1 2
1
2 3
2 4
I I I ln
Câu 36: Tìm t t c s ấ ả ố thực
0
tích phân để
3 2
0
1x ln x
I dx
x arctanx

h i t ộ ụ
Giải:
2
1 2
3 2 3 2 3 2
0 0 2
1 1 1x ln x x ln x x ln x
I dx dx dx I I
x arctanx x arctanx x arctanx
 
Đặt
3 2
1x ln x
f x
x arctanx
Xét
1
:I
Khi
2
1
2 2 1
3 2 3 2
1 1
2
1
2 2
0 : ~ ~ ~
x
x
x x
x x x x x
x
x f x
x x x
x x x x
Suy ra
1
I
cùng b n ch t vả ấ ới
2
1
0
1
dx
x
- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
Vậy để
1
I
h i t thì: ộ ụ
1 1 2 1
Xét
2
:I
Khi
3 2
1
: ~
x
x f x
x x

Suy ra
2
I
cùng b n ch t vả ấ ới
2
2
1
dx
x

Vậy để
2
I
h i t thì: ộ ụ
1
2 1 2
2
Từ
1
và
2
: Để I HỘI T Ụ thì
1
2
2
Câu 37: Tìm t t c các s ấ ả ố thực
tích phân sau h i t để ộ ụ
1
0
1
1
I dx
x xarctanx
. Tính giá
trị c a tích phân khi ủ
1
2
Giải
0x
m kì d . là điể ị
Khi
0 :
x
TH1:
0 0
1
0 :
x x
lim x lim
x

1
2
1 1 1
~ ~
1 .
.
2 2
x x arctanx
x x
Suy ra cùng b n ch t v𝐼 ả ấ ới
1 1
1
0 0
2
2
2
1
2
dx dx
x
x
Dễ thấy
1
0
2
2
1
dx
x
h i t ộ ụ
I
h i t ộ ụ
1
TH2:
1
2
1 1 1
0 : ~ ~
1 . .x x arctanx x x
x
- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
Suy ra cùng b n ch t v𝐼 ả ấ ới
1
1
0
2
dx
x
Vậy để I hội tụ
1
1 1 2
2
Từ
1
và
2
suy ra
1
Khi
1
,
2
tích phân tr thành: ở
1
0
1
1 .
I dx
x x arctan x
Đặt
4
0
2
4 2
4
2 1
0
dx dt
t arctan x dt I t
x x t
Câu 38: Xét tính h i t c a tích phân: ộ ụ ủ
2 2
0
.
0, 0
x sin ax
dx k a
k x

Giải
Xét hàm
2 2
,
x
g x
k x
ta có:
2 2
2
2 2
'
k x
g x
k x
. Như vậy
x k
thì
' 0g x
khi đó hàm
g x
u gi m và đơn điệ ả
2 2
0
x x
x
lim g x lim
k x
 
Mặt khác, v i mớ ọi
0
1 2
: sin
A
cosAa
A a axdx M
a a
Theo d u hiấ ệu tích phân Dirichle tích phân đã cho hội tụ
Câu 39: Xét s h i t c a tích phân: ự ộ ụ ủ
a
sinx
dx
x
với
0a
Trước h nh lý Dirichlet tích phân ết theo đị
a
sinx
dx
x
h i t . Tuy nhiên, tích phân ộ ụ
a
sinx
dx
x
không
hội tụ.
Do
2
0, [ , )
sinx
sin x
x a
x x

Mặt khác:
2
1 2
2
sin x cos x
x x
nên
2
1 1 2
2 2
a a a
sin x dx cos x
dx dx
x x x
- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
Tích phân th nh t phân kì, tích phân th hai h i t . V y tích phân ứ ấ ứ ộ ụ ậ
2
a
sin x
dx
x
phân kỳ,
a
sinx
dx
x
phân k ỳ
Câu 40: Tính tích phân suy r ng ộ
2
2
0
2
1
2
x
e
dx
x
Đặt:
2
2
0
x
e
I dx
x
Khi đó, ta có:
2
2
2
2
1
2
0 0 0 0 0 0
.
2
1
x t
x t
t x
x t
e e
dx e e dtdx e e dtdx dt
x
t
Ta th y y: ấ
2
2
2
0 02
1
'
2 2
11
2
t
x
e t
dt I e dt
t
x
Nhưng
2 2 2 2 2 2
0 0 0 0 0
1 1 1
1 2 1 2
0
1 1 1 1
t t t t t t
t
e dt te dt e dt te e dt e dt
t t t t
Vậy
2
2
0
2
1
2
x
e
dx
x
Câu 41: Tìm
tích phân sau h i tđể ộ ụ:
52 4
0 1 1
x dx
I
x x cosx

Giải:
1
1 2
5 5 52 4 2 4 2 4
0 0 1
1 1 1 1 1 1
x dx x dx x dx
I I I
x x cosx x x cosx x x cosx
 
Xét
1
2
2
, 0 : ~I x f x
x
1
I
cùng b n ch t vả ấ ới
1
2
0
2
dx
x
- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
Vậy
1
I
h i t ộ ụ
2 1 1
Xét
2
14
5
2
, : ~I x f x
x

2
I
cùng b n ch t vả ấ ới
14
1
5
2
dx
x

Vậy
2
I
h i t ộ ụ
2 1 1
Câu 42: Tìm
tích phân sau h i t : để ộ ụ
2
1
0
1
1
x
I dx
x x

Giải:
12 2 2
1 2
1 1 1
0 0 1
1 1 1
1 1 1
x x x
I dx dx dx I I
x x x x x x
 
Khi
1
Xét
1
1
, 0 : ~I x f x
x
1
I
cùng b n ch t vả ấ ới
1
0
1
dx
x
Vậy
1
I
h i t ộ ụ
1
Xét
2
2
1
, : ~I x f x
x

2
I
cùng b n ch t vả ấ ới
2
1
1
dx
x

Vậy
2
I
h i t ộ ụ
1
2 1
2
Khi
1
làm tương tự
Câu 43: Xét s h i t c a tích phân sau: ự ộ ụ ủ
2
0
dx
I
sinxcosx
Giải:
- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
0,f x
k d tỳ ị ại
2
và
0
tách c n ậ
32 2
1 2
0 0
3
dx dx dx
I I I
sinxcosx sinxcosx sinxcosx
Xét
1
:I f x
k d t i 0 ỳ ị ạ
1
0 : ~ .x f x
x
Vì
3
1
0
2
1
x
h i t nên ộ ụ
1
I
h i t ộ ụ
Xét
2
:I f x
k d tỳ ị ại
2
1 1
: ~
2
.
2
2
x f x
sinx sin x
x
Vì
2
1
2
3
1
2
x
h i t nên ộ ụ
2
I
h i t ộ ụ
Vậy
1 2
I I I
h i t ộ ụ
Câu 44: Tính tích phân suy r ng: ộ
2
1
1
dx
I
x x x

Giải:
1x
l m k d à điể ỳ ị
Tích phân suy r ng k t h p. Ta tách thành 2 tích phân: ộ ế ợ
2
2 2 2
1 1 2
1 1 1
dx dx dx
I
x x x x x x x x x
 
Xét
2 2 2
1
2 2
1 1
2
1
2
3 2
1 1
1 1
1
1
k k
k k
dx dx dx
I lim lim
x x x x x x
x
x
x
Đặt:
2
1
1
1
dx
t dt
x
x
- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
Đổ ậi c n:
x
1
2
t
1
2
1
3
Ta có:
2 2
1
2
1 1 1
1
2 2 2
3
2 3 3 1 2 3 3 1 2 2
2 2 12
1
2 4 2 2 2 4 2 2 2 2
2 3 1
3
k
k k k
k
dt
I lim lim ln t t t lim ln k k k ln ln
t t
2
2 2
2
2 2 2
2
3 2
1 1
1 1
1
1
k
k k
dx dx dx
I lim lim
x x x x x x
x
x
x
 
 
Giải tương tự:
2
2 1 2 3 2
2 12 2 4 2
I ln ln
Vậy
1 2
2 3 2
2 2
2 4 2
I I I ln ln
Câu 45: Xét s h i t c a tích phân: ự ộ ụ ủ
54
0
2 1
3 1
x
dx
x x

Giải:
Khi
x 
ta so sánh:
5 1
54
4 4
2 1 ~ 2 ; 3 1 ~x x x x x x x
Nên b t bu c ph u thành t ắ ộ ải chia tp ban đầ ổng 2 tp như sau:
1
1 2
5 5 54 4 4
0 0 1
2 1 2 1 2 1
3 1 3 1 3 1
x x x
I dx dx dx I I
x x x x x x
 
1
I
là tp c a hàm liên t n l nh (tp HT) ủ ục trong đoạ ấy tp nên là tp xác đị
Tp
2
I
là tp HT khi và ch khi ỉ
1
1
4
1
dx
x

HT (theo so sánh trên)
Do v khi ậy, tp đã cho HT khi và chỉ
3
4
- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
BÀI T LUY N ẬP TỰ Ệ
Câu 1: Khả ự ộ ụ ủ ộo sát s h i t c a tích phân suy r ng:
2
5
1
1
4
x arctan
x
J dx
x x x

Câu 2: Khả ự ộ ụ ủo sát s h i t c a tích phân
1
3
0
1 1x x
I dx
sin x
Câu 3: Khả ự ộ ụ ủo sát s h i t c a tích phân
2
2
1
3 2
1
x x
I x ln dx
x x

Câu 4: Cho tích phân
2
0
1
arctanx
dx
x

. Tìm
tích phân h i t và tính tích phân khi để ộ ụ
3
2
Câu 5: Cho tích phân
1
0
1
arcsin xdx
I
x x
. Tìm
tích phân h i t và tính tích phân khi để ộ ụ
1
Câu 7: Xét tích phân suy r ng ộ
3
0
,
1 1
dx
x x
là tham s . Tìm giá tr ố ị
nguyên dương bé
nh iất để tích phân suy rộng này hội tụ. Vớ
c, tính tích phân này. tìm đượ
Câu 9: Xét tích phân suy r ngộ
3 2
1
1
.
. 1
m
dx
x x
Tìm
m
u ki n v tích phân suy r ng này điề ệ ề m để ộ
hội tụ. Tính giá tr tích phân này khi ị
7
3
m
x
g
ậ ị ữ ạ
ớ ừa tìm đượ ị ớ ạ
Câu 11: Khả ự ộ ụ ủo sát s h i t c a
2
0
x
sinhx
I dx
e cosx
khai triển maclaurin nhé
f(x) = bthuc dưới dấu tphan
g(x) = x/x^2
=> lim f(x)/g(x)= 2/3
-> tphan của g(X) phân kỳ
b1: h i t - ph ng pháp làm: arctan(1/x) ~ ộ ụ ươ
1/x
b2: dùng tg gđ
alpha > -1/2
cách làm:
cho cái trên t ng ng v i x^(alpha)/c n xở ươ đươ ớ ă
Xét:
limx->0+ c a bi u th c trong tp ban u v i tphan ãủ ể ứ đầ ớ đ
ch nọ
xét v i hàm g(x) = x^alphaớ
nhận th y hàm dấ ưới dấu tphan nhỏ h n rơ ất nhi u so ề
với hàm g(x)
-> g(X) h i t thì f(x) h i tộ ụ ộ ụ
mà g(x) h i t (=) alpha < -1ộ ụ
dễ ch ng minh alpha > 1/2 bứ ằng cách cho bthuc dưới tphan nhỏ h n (pi/2)/(x^2+1)ơ
^alpha
tính thì cách làm là chúng ta t x=tant r i xong tphan t ng ph n là ra r i nhéđặ ồ ừ ầ ồ
alpha<3 cái này h i t (t làm nhé l i nói cách gi i)để ộ ụ ự ườ ả
tính tích phân: i bi n: t = arcsin (c n x) -> t gi i n tđổ ế ă ự ả ố
- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
không hi u alpha t âuể đặ ở đ
alpha > -2
=> alpha = 1 (s nguyên dg u tiên)ố đầ
tách theo hàm phân th c h u t tínhứ ữ ỉ để
m > 1/3 (r t d chminh)ấ ễ để
cách tính: cho c n b c 3 x m 7 nhân cái x^7 vào bthuc (1+x^2) r i sau ó rút ă ậ ũ ồ đ
x^9 (bi n thành x^3) * (c n (x^2 + 1/x^2)) ra ngoài, và t cái c n là cế ă đặ ă đ
b loz gì y ? l i nhéđấ ỗ đề
Lời giải thực hi n: HOÀNG HUY QUÂN ệ – L p: Kớ ỹ thuật nhi K64 và NGUYệt – ỄN TH MAI Ị
HƯƠNG – ớp: TĐH 09 – L K64
Câu 12: Tìm
tích phân sau h i t để ộ ụ
2 2
1
1
1
x sin x
I
x lnx

Câu 13: Tìm
tích phân sau h i t để ộ ụ
54
1
2 1
3 1
x
I
x x

Câu 14: Tìm
tích phân sau h i t để ộ ụ
2
2
3
0
1
1
x arcsin
x
dx
x x

chia TH ra:
+ TH1: a<=0 -> phân kỳ
+ TH2: a > 0 thì bđầu xét:
cái bthuc dưới căn tg đg x^2/x^a
=> hội tụ khi alpha >2
chia TH ra:
TH1: a<=0 -> pky
TH2: a>0 -> a>3/4 thì hội tụ
chia th nốt, làm y hệt :))
- Nguy n Th Thi n - L p: HTTTQL - K67ễ ế ệ ớ
| 1/26
| | Tải xuống

Có thể bạn quan tâm:

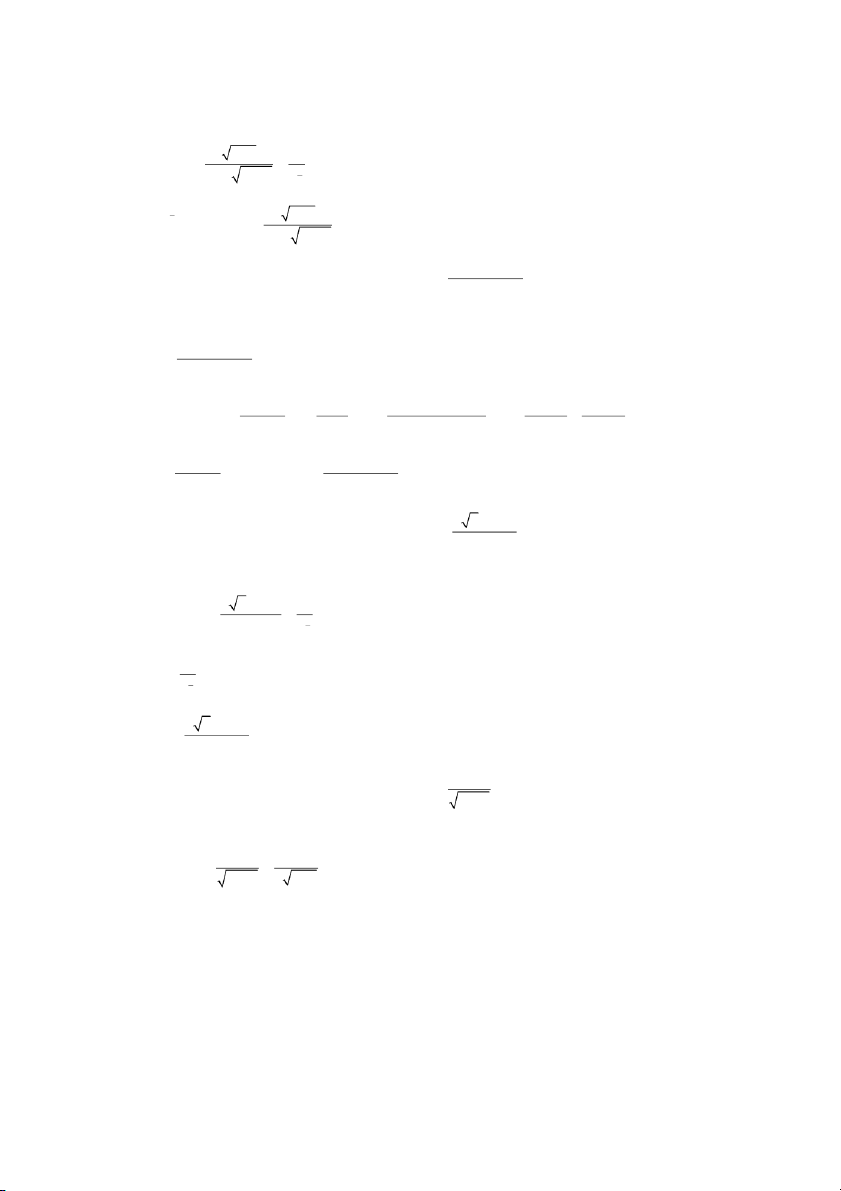
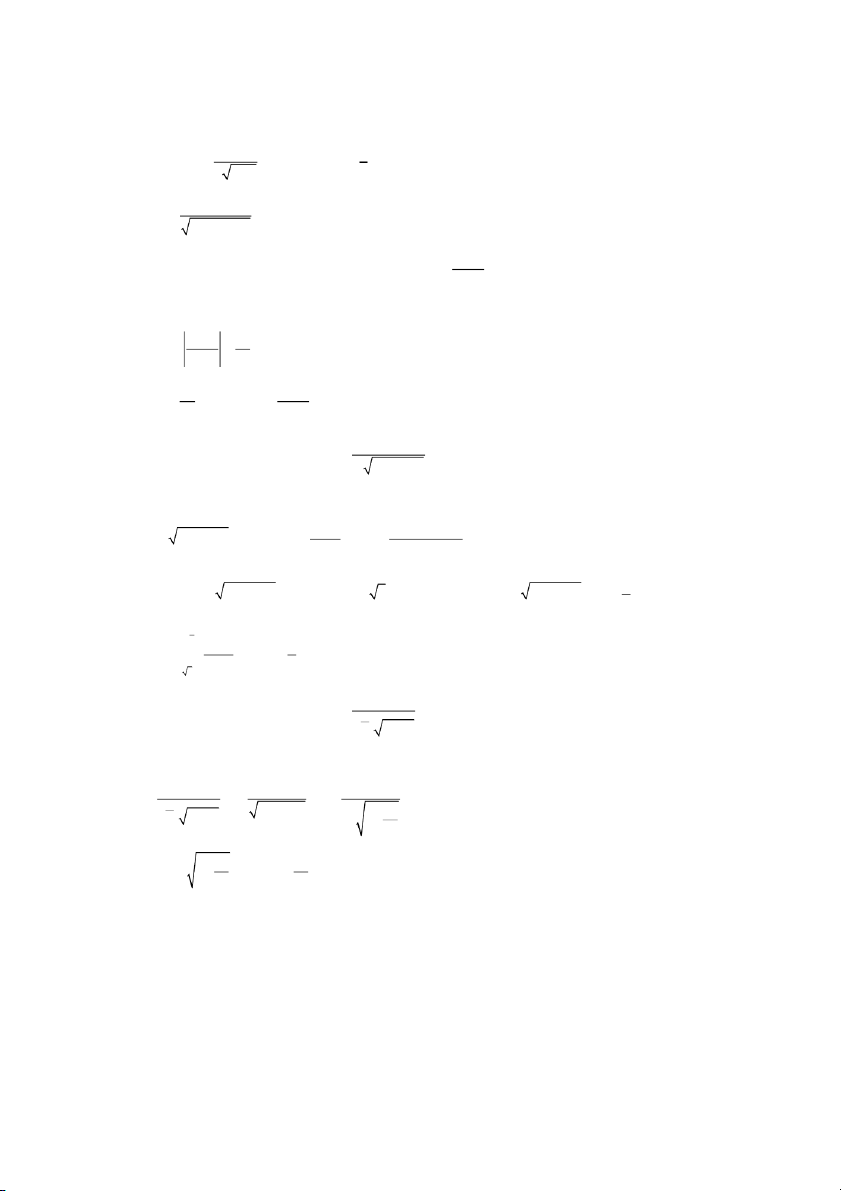
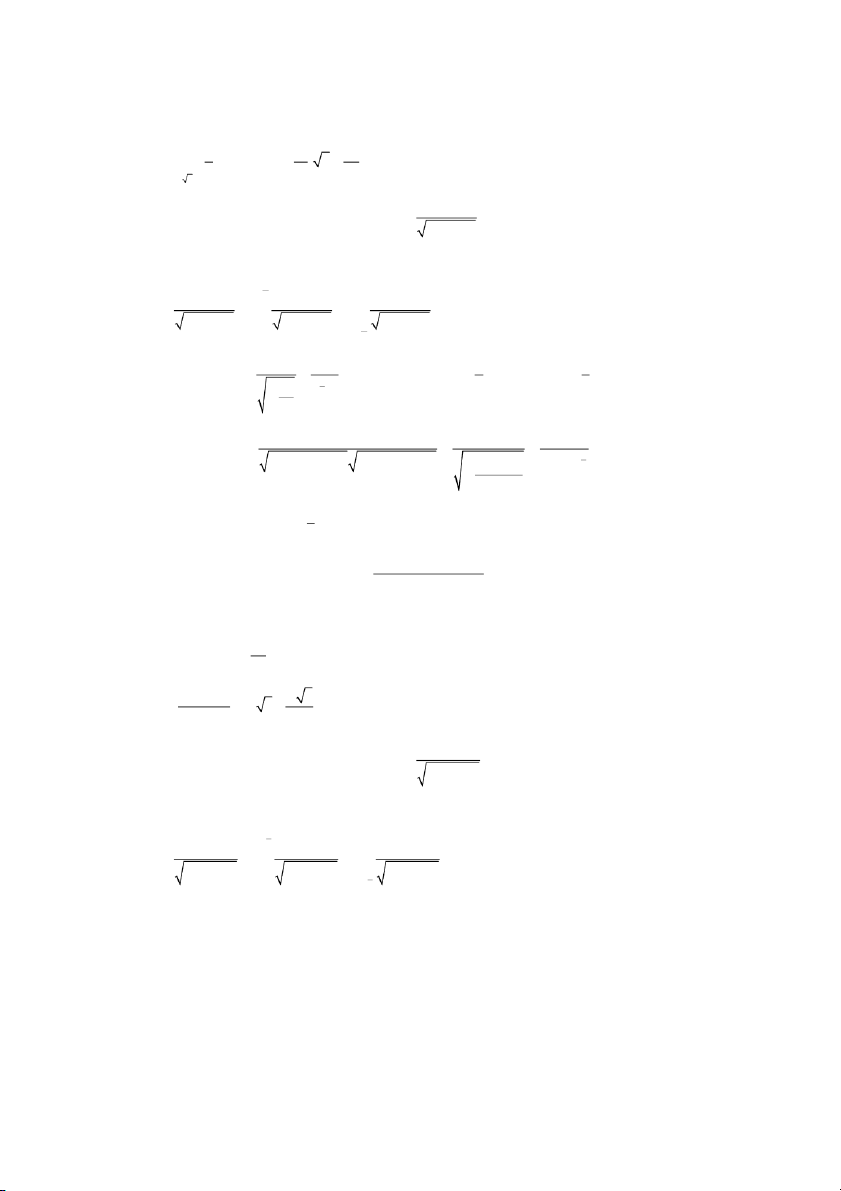
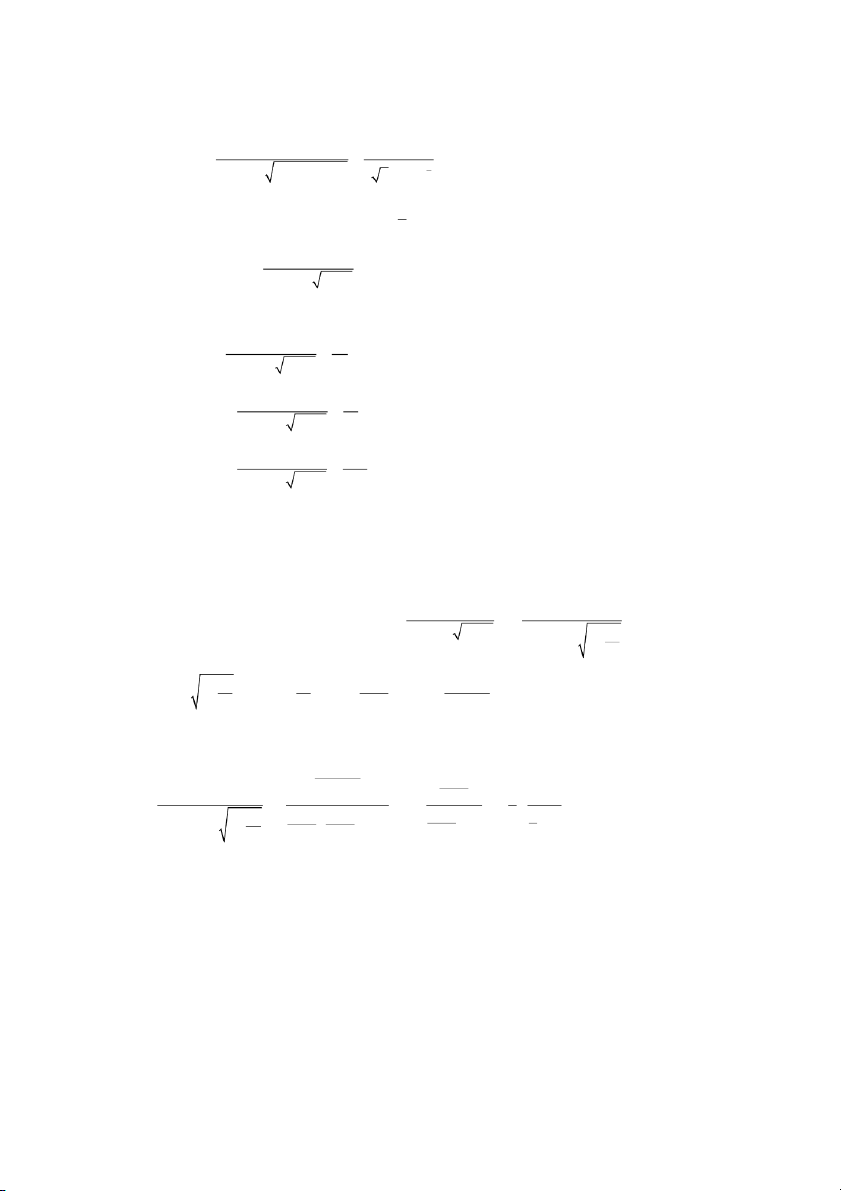
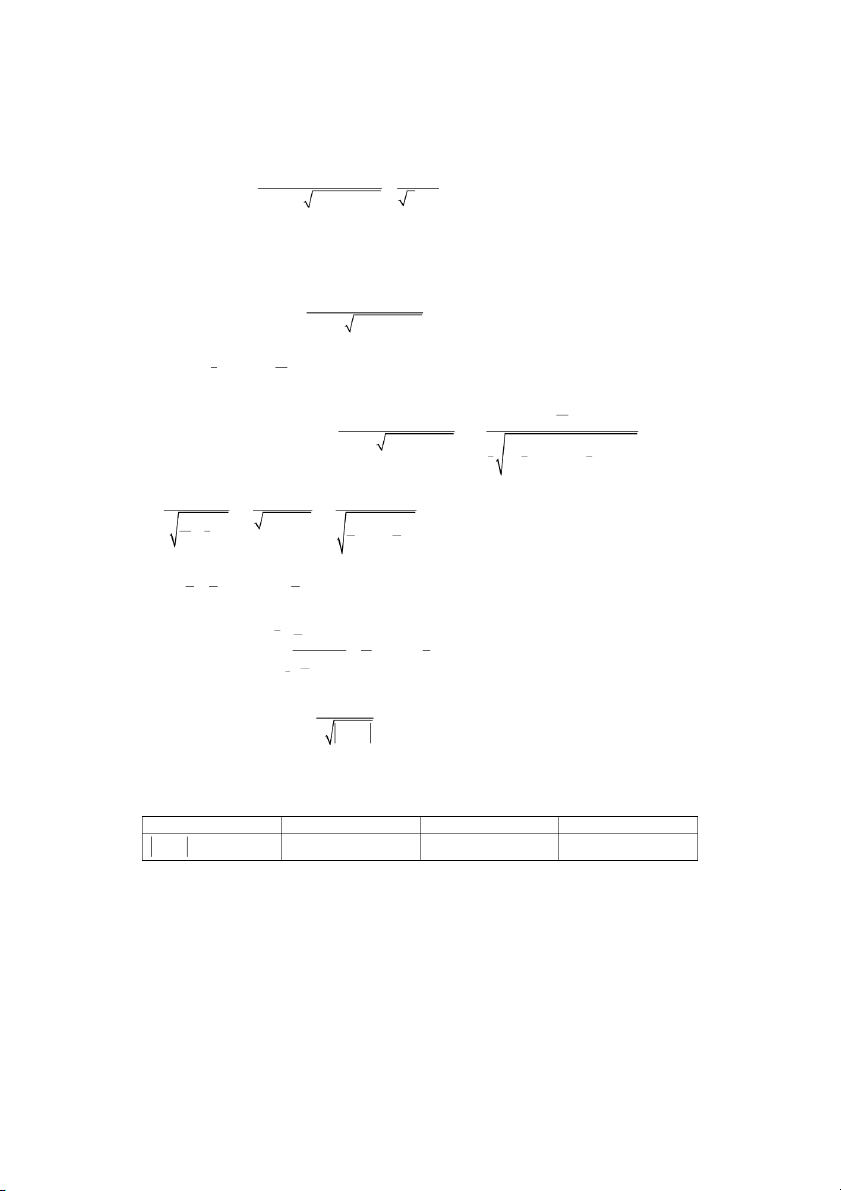
Preview text:

Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67
TÍCH PHÂN SUY RỘN G  2 Câu 1: x Khảo sát s h ự i ộ t c ụ a ủ tích phân suy r ng: ộ dx  6  2 x 1 Giải  2  x Đặt dx f   xdx 6  2 x 1 2 2 2 3   x x 1 f x x f x  ~   g    x  0, limlim 1. 6 6 x  1 x x x
 g xx 6 x  1  1  2 x Vì dx  phân k ỳ    1 , nên dx  phân k t
ỳ heo tiêu chuẩn so sánh 2 x 6  2 2 x 1 1 2  Câu 2: x 1 Khảo sát sự ộ
h i tụ của tích phân suy rộng: dx  2 x 1 x 0   Giải: 1 2 x 1 2 x 1 Tích phân dx  suy r ng l ộ
oại 2 tại cận dưới x  0 ; Đặt f x  2 x 1 x 2x   1 x 0   f   2 x x  1 Xét   1 g x  có limlim 1. x x   0 g  x
x 0  2x   1 1 dx 1 2 x 1 Mặt khác  h i ộ t nê ụ n tích phân dx  cũng hội tụ x 2x 1 x 0   0   Câu 3: 1 sinx Khảo sát sự ộ
h i tụ của tích phân suy rộng: dx   x x  3 1 1 Giải 1 sinx 2 Ta có: 0   , x   1.    2 3 1 x x x  2  1  sinx Vì dx  nên dx  2 x 1 x x 13 1
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67  1  sinx Vậy dx
hội tụ tuyệt đối theo tiêu chuẩn so sánh 1. xx  3 1 1  2
x arctan x 1 
Câu 4: Khảo sát sự ộ
h i tụ của tích phân suy rộng: J dx.   x   1  7 1 x  2 Giải:  2
x arctan  2 2 x  1
x arctanx  2  1
x arctan  x  1 J dx dx
dx J J     x 1   x 2  x 1  x 2  x 1   x 2 1 2 7 7 7 1 1 2   2    x arctanx 1 Khi x f x 4 1 :  ~ g x
x  1 x  2 3 x  1 7 2 1 2 Mà g x   h i ộ t nê ụ n J h i ộ t ụ 1 1 2 2
x arctanx 1 x 1
Khi x  : f x   ~   g x 8 2    1 7 2 x x x 2 x  Mà g
 xdx h iộ t nê ụ n J h i ộ t ụ 2 2
Vậy J J J h i ộ t ụ 1 2  3  Câu 5: x x Khảo sát sự ộ
h i tụ của tích phân suy rộng: dx  x 8 1 1 Giải:  3  x x Đặt dx f   x dx x 8 1 1 1 3 3 x x x 1
Khi x  : f x   ~    8 1   8 1 x x x f x 3 x x
Chọn g x 1  , ta có limlim  .x  1 x
x  g xx  x 8 1
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67  Mặt khác ta có g
 xdx phân k ỳ p  1. 1  3 x x
Vậy theo tiêu chuẩn so sánh 2, tích phân dx  phân k ỳ x 8 1 1  Câu 6: x Khảo sát sự ộ
h i tụ của tích phân suy rộng: dx   x  5 1 4 1 Giải:   Đặ x t dx f    x dxx  5 1 1 4 1 x 1
Khi x   : f x  ~  2 5 2 4 x x 1 f x x
Chọn g x  , ta có 2 limlim  .2x  1. 2 2x
x  g xx  x15  Mặt khác ta có g
 xdx hội tụ p  2 1. 1  x
Vậy theo tiêu chuẩn so sánh 2, tích phân dx  h i ộ t ụ  x  5 1 4 1  2   Câu 7: x 7 x 3 Khảo sát sự ộ
h i tụ của tích phân suy rộng: dx  4 3x x x 1 Giải: 2 2 x  7x 3 x 1
Với x [1; ), xét f x  
 0,g x    0 4 4 2 3x x x 3x 3x f x  2  x 7x 3  2 limlim x   
x  g x .3 1 4
x   3x x x   2  x  7x  3 1 Suy ra K dx  và dx
cùng tính chất hội tụ 4 2 3x x x 3x 1 1
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67  1 Mà dx  h i ộ t , vì ụ
p  2  1. Vậy K hội t ụ 2 3x 1  1,01 Câu 8: x dx Tích phân suy rộng  h i ộ t ha ụ y phân kỳ? 2 2 x   x 2 2 4 Giải: 1,01 x 1
Với x [2;), xét f x 
 0, g x   0 0,99 2 2 2  4 x x x f x  1,01  x  1 0,99 limlim x   
x  g x . x  2 2 2
 2 x  4  x  3  dx 1,01 x dx Mà  phân k nê ỳ n  phân k t
ỳ heo tiêu chuẩn so sánh giới hạn 0,99 x 2 2   2 x x 2 2 4  3   Câu 9: x 5x 1 Khảo sát sự ộ h i tụ của tích phân: dx  6 x sinx 1 Giải  3    Đặ x 5x 1 t dx f x dx   6   x sinx 1 1 3 x 1
Khi x  : f x  ~  6 3 x x 3 3 1 f x
x x  5x  1
Xét g x , ta có limlim   1. 3 x
x  g x 6 x  x sinx   1 3 x  5x 1 Mặt khác ta có dx  hội t nên ụ dx  hội t ụ 3 x 6 x sinx 1 1 2  Câu 10: 1 x Khảo sát sự ộ h i tụ của tích phân: dx.   1 x x 1 Giải 2 2 1 x Tích phân dx f x dx   là tích phân suy r ng l ộ oại 2 tại cận dưới. x x  1  1   1
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67   1 f x
  xx 
1 x  x 1 1 1 
Xét hàm g x     ; limlimlim  4 1     x 1 xg xx 1  x x 1 x 1  x 2 1 2 1 x mà dx  phân kì nên tích phân dx  phân kì x  1  1 x x 1 1   Câu 11: 3 si.n2x Xét s h ự i ộ t c ụ ủa tích phân suy r ng: ộ I d . x  4 3 2  0 x 2. x Giải:  2  3 sin2x 3 sin2x
3 si.n2x I dx dx
dx I I    1 2 4 3 2 4 3 2 4 3 2    0 x 2. x 0 x 2. x 2 x 2. x 2 3  sin2x Xét I dx  1 4 3 2  0 x 2. x
Hàm dưới dấu tích phân là hàm không âm. 3 si 2 n x 3 0 Ta có: x 0  : ~ VCB  4 3 2 3 2 x  2. x 2. x 2 3   Mà dx  h i ộ t do ụ 2   1   nên I h i ộ tụ (TCSS2) 1 3 2  3  0 2. x
 3 si.n2x 3  si 2 n x 4 Xét I d . x  Ta có : 0   ;x[2;) 2 4 3 2  4 4 3 2 x x x 2 x 2. x 2.  3 Mà dx  h i ộ t do ụ
  4 1 nên I h i ộ t ( ụ TCSS1) Kết luận: I h i ộ tụ 4 x 2 2  3 2   Câu 12: x 5 x 1 Khảo sát sự ộ
h i tụ của tích phân sau: dx  5 3 2
2x x  5x 1 1 Giải: 3 2 x  5x  1 f x Đặ 1 1 t f x  . Xét hàm g    x  ; lim  5 3 2
2x x  5x  1 2 x x
 g x 2   1 3 2 x  5x 1 Mà dx  h i ộ t nê ụ n dx  h i ộ tụ 2 x 5 3 2
2x x  5x 1 1 1
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67
2 x .ln 1x
Câu 13: Khảo sát sự ộ
h i tụ của tích phân sau: dx  3 2  1 x 1 Giải x lnx 1 h x
xln 1 x  Đặ . 1 l 2 n t h x    
. Xét hàm k x     ; limlim  3 2   x  3   3 3 1 x 1 x  1 k xx 1 x  1 2 2 1
2 x .ln 1x  Mà dx  h i ộ t nê ụ n dx  h i ộ t ụ 3 x 1 3 2  1 1 x 1 1 Câu 14: x Khảo sát sự ộ
h i tụ của tích phân suy rộng: dx  3 0 1  x Giải x 1 Ta có: 0  ~ khi x 1  1  x 3  x  1 3 2 1 1 1 1  x
Mà 1 x  2dx  h i ộ t ụ  dx  h i ộ t ụ 3  0 x 0 1
Câu 15: Tích phân suy rộng sau đây hội t ha ụ
y phân kì? Tính giá trị tích phân nếu có:  1 d . xx 1 x 0   Giải  1  1 1 1 1 1 t 1       dx dx dx lim dx lim dx     x 1 xx 1 xx 1 x  t 0 x 1 tx  x 1 x 0 0 1 t   1   1 1     
(Đặt u x ) x dx du arctan x C 1 x 2 2 2 1  u  1       t dx
lim 2arctan x 1 lim arctan x t t 2  x 1 x 0 t  1 0      
x lim 2. 2arctan t lim 2arctan t 2.       t 0  4 t    4    Câu 16: 7 3sinx Khảo sát sự ộ
h i tụ của tích phân suy rộng: dx   x  2  5 3 2 x   2
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67 Giải:  3 7 3   sinx 7 3sinx 7 3sinx dx dx
dx I I   
x2 x 2 
x 2 x 2
x2 x 2 1 2 5 5 5 3 3 3 2 2 3 Xét I 1    7 3sinx 7 3sin2 Khi x  2 : ~ x  2 5 x  2 3 3  x 2.34 3 7  3si 2 n 1 Do d , x    1  h i ộ t nê ụ n I ộ ụ 1 h i t ( TCSS2) 3 x  2 .34 3 2   Xét I 2 7  3sinx 10 10 Khi x   :  ~ .   2  2    2   2 2 5 5 3 3 x x x x x   10 10 Do d ; x   2  1  hội t nê ụ n dx  h i ộ t ( ụ TCSS2) nên I h i ộ t ( ụ TCSS1) 2 x  1 x 2 5 3 3 x   3 2
Vậy I I I h i ộ t . ụ 1 2  2 3 x  3x   1
Câu 17: Khảo sát sự ộ
h i tụ của tích phân suy rộng: J dx  5   2
x 23 x Giải 2 x  3  x 1  9 Khi x  2 : ~  0  1
5 x  2x  3 5 5 x  2 3 3 9 9 dx 1 Mà dx    h i ộ t vì ụ    12 5 x 2 5 5 5 5 x 2 5 2 2  
Từ 1 và 2  J hội tụ (theo tiêu chuẩn so sánh 2)   Câu 18: x 1 Khảo sát sự ộ
h i tụ của tích phân suy rộng: dx  3 4   1 x x 1 Giải:
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67 x 1 1 Ta có: 0  ~ khi x   5 3 4 x x  1 2 x  5   x 1 2 x dx  h i ộ t ụ  dx  h i ộ t ụ 3 4   1 1 x x 1 2  Câu 19: 1 sinx Khảo sát sự ộ
h i tụ của tích phân suy rộng: dx  3 2
x  4x  4x 1 Giải 2 2  Đặ 1 sinx t dx f x dx  
𝑥 là tích phân suy rộng loại 2 tại cận trên x  2 3 2  
x  4x  4x 1 1 1 f x
1 sinx x  22 1 sinx 1 sin 2
Xét hàm g x  ;    h u h ữ ạn  lim lim lim    x  22 xg  3 2 2 x2   x2 x x 4 x 4 x x 2 2 1 2 1 sinx Mà  ỳ dxdx phân k nên  phân k ỳ 3 2 x  22
x  4x  4x 1 1    Câu 20: x x x 1 Khảo sát sự ộ
h i tụ của tích phân suy rộng: dx  3 2 x x 1 0 Giải x x 1 1 1 Khi x   ,  ~ 3 2 3 x x 1 2 x  1 Mà dx  h i ộ t ụ 3 1 2 x
 x x x 1 Vậy dx  hội t t
ụ heo tiêu chuẩn so sánh 2 3 2 x x 1  0 2 Câu 21: 1 Khảo sát sự ộ
h i tụ của tích phân suy rộng: dx.  4 x 1  1 Giải: 1 1 Khi x 1  : ~ 4 x 1 2 x 1 
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67 2 1 Mặt khác: dx  h i ộ t do ụ 1   1 2 x  1 2 1 2 x lnx Vậy d . x  hội t t
ụ heo tiêu chuẩn so sánh 2 2   1 x 5 x 6  Câu 22: sinx Khảo sát sự ộ
h i tụ của tích phân suy rộng: dx  2 x  1 1 Giải sinx 1 Ta có:  , x  1  2 2 x  1 x   dx sinx Mà  h i ộ t nê ụ n dx  h i ộ t ụ 2 x 2 x  1 1 1  Câu 23: dx Tính tích phân suy r ng: ộ  2   2 x. x x 1 Giải: 2 t 1   2 2 t t 1   2 
Đặt x x 1  t x x   dx dt 1 2t 2t  2 1 Đổ 1 i cận: 2 t
x x 1  ;
x x  2  t  5  2; x    t lim
x x   x x  2 1  2 1 2 2dt 1  I   arctan  2 t 1  2 5 2  Câu 24: dx Tính tích phân suy r ng: ộ  19 1 3 2 3 x . 1 x Giải:    dx dx dx      19 3 19 21 x x 1 1 3 3 2 1 1 7 3 x . 1 x x 1 2 x Đặ 1 1 t 3  3 t 1  t 1 2 2 x x
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67 1 3
I   t t  2 3 27 3 3 1 dt  . 4   2 10 80 3 2  m Câu 25: x Khảo sát sự ộ
h i tụ của tích phân: I dx  3 2  0 1 cos x Giải:   m 2 mm x x x I dx dxdx    3 2 3 2 3 2    0 1 cos x 0 1 cos x  1 cos x 2 m x 1
Khi x 0 : f x ~  . Tp HT khi và chỉ 2 1 khi
m 1  m   2 2  m x 3 3 3 3 2. x 2 m m m x  
Khi x  : f x   ~  . TP h i ộ t ụ m  1 cos   x 1 cos   x    x    2 2 3 3 3 x 3 2. 2 1
Vậy tp đã cho HT với m   3  Câu 26: dx Tính tích phân suy r ng: ộ I   x 3 2
ln xln xlnx e  Giải: dx
Đặt t lnx dt
. Ta được tpsr loại 1 của hàm hữu tỉ: x  dt  3 I   ln 3  2 3
tt t 8 1 1 Câu 27: lnx Khảo sát s h ự i ộ t c ụ a ủ tích phân: I dx   0 x 1 x  Giải 1 1 2 1 lnx lnx lnx I dx dx dx       0 x 1 x  0 x 1 x  1 x 1 x  2
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67 Khi x   f   1 0 : x ~ . TPHT x  1
Khi x  1 : f x ~ . TP h i ộ t khi ụ và chỉ khi   2   1   x
Vậy tp đã cho HT khi và chỉ khi   2 1
Câu 28: Tính tích phân suy r ng: ộ n
I ln 1 xdx  0 Giải: Đặt  1  t   1 t t ln x x e
dx e dt . Ta được tích phân 0 n t n t n tI
t e dt t e nt e n   n t n t n n1 t e  ...   1   1 t 0 1 2 . !
n . .te   1   . ! n .e   2 1 3 3 x x
Câu 29: Tìm tất cả các giá trị m  0 để tích phân: I   h i ộ t ụ 2 m x arctanx 0 Giải
Hàm f x   0, x
  (0; 2]. Ta sẽ so sánh khi x 0
 .Lưu ý: Không nhận xét f dương thì trừ điểm 2   f x  3 x 1 2 : ~   TP phân k ỳ 2 4 x 3 x 2 x
  2 : f x  3 ~  TP phân k ỳ 2 2x 2   f x  3 x 1 2 : ~   T h P i ộ t khi ụ và chỉ 2 5 khi   1   x  2 x  3 3 3 Vậy I h i ộ t khi ụ và chỉ 5 khi 0   3  2  Câu 30: 1 x Tìm s
ố thực m  0 để tích phân sau h i ộ t ụ I dxmx  . m 1 1 x 0 
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67 Giải:  2 1 2  2 1  x 1  x 1  x Ta có: I dx dx
dx I I    m x 1 mx   m x 1 mx   m x 1 mx   1 2 1 1 1 0 0 1
Hàm f x   0, x   0 x   f x 1 0 : ~  I h i ộ t khi ụ và chỉ khi m  1 m 1 x
x   f x  1 : ~  I h i ộ t khi ụ và chỉ 1 khi m  2 m 2 x 2 Vậy I h i ộ t khi ụ và chỉ 1 khi  m  1 2 1 2 Câu 31: dx
Tìm  để tích phân sau h i ộ t ụ I  
. Tính tích phân khi   2   2  0 x 1 4 x Giải Ta thấy 2 cận c a
ủ tích phân làm cho biểu th i ức dướ d nh. N
ấu tích phân không xác đị ên ta tách ra
thành 2 tích phân suy r ng l ộ oại 2 như sau: 1 1 1 2 4 2 dx dx dx I     I I    1 2  2  2  2    0 x 1 4x 0 x 1 4x 1 x 1 4x 4 1 4 dx
Xét tích phân I : I  1  1  2  0 x 1 4 x Xét khi x 0  : 1 + Khi   0 : ~ 0  I h i ộ t ụ 1  2 x 1 4 x 1 1 + Khi   0 : ~ ~ 1  I h i ộ tụ 1  2 2 x 1 4 x 1 4 x 1 1 + Khi   0 : ~ 2   1  4 x x x
Như vậy thì để I h i
ộ tụ thì trong trường hợp này  phải thỏa 0   1 1
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67
Tổng hợp lại thì với   1 thì I h i ộ t ! ụ 1 1 2 dx
Xét tích phân I : I   2 2  2 1 x 1 4x 4  1 Xét khi x  : 2 + Khi 1 1 1 1 1   0 :  ~   x  1 4x x   x   1 2 1 1 2 1 2 x 1   1 x  2 2 1 2       1 2 2 x 1 2    2  x 2 2      2 
 do đây là tích phân suy rộng loạ 1 i 2 và   1 nên I h i ộ t . ụ 2 2 1 1 + Khi   0 : ~  I h i ộ tụ. 1 2  2 x 1 4 x 2  1  2  x    2  1 1 + Khi   0 : ~  I h i ộ t ụ 1 2  2 x 1 4 x 2 1    1  2  x    2 
KẾT LUẬN: Do I đã hội tụ c nên để ho I h i ộ t t ụ hì I phải h i ộ t . V ụ ậy   1 th a ỏ mãn. 2 1
* Tính tích phân khi   2 1 1 2 2 2 2 x 1 x Khi   2
 thì ta có tích phân sau: I dx dx   2 1 4 2 x 1 0 0 2  x 4   Đặ 1 1 t: x sint với   t   dx costdt 2 2 2 2  Đổ 1
i cận: x  0 t  0; x  t  2 2   2 2 1
1  1 cos2t   Tích phân trở thành: 2 sin tdt   dt     8 8  2 2  32 0 0
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67  2 3   
Câu 32: Tìm  để tích phân sau h i ộ tụ 2 2  x x I
x e edx    
. Tính tích phân khi  5 1   Giải:
Đây là tích phân suy rộng loại 1. 2 3 2 3            x 2 2 2 2    2 3 5 5
Khi x   , ta có: x x x
x e e
  x e  1 x  e  1 ~ x     2 2 2 2              x x x x  
Để tích phân hội tụ thì: 2   1   1 2 3   2 2 x x ee
Khi  5 , tích phân trở thành: I dx  5 x 1 Đặ 1 2 t: u   du  
dx . Đổi cận: x  1  u  1; x    u  0 2 3 x x 1 1 1 1 uu 1 u 1 Tích phân trở thành:    2 3   2 3  u I u e e du ue du ue
du I I   1 2 2 2 2 0 0 0
Đến đây dễ dàng tính đượ
c I , I bằng tích phân từng phân 1 2 2 e 2 5 Vậy I    3 8 9e 72  Câu 33: dx
Cho tích phân I   để ộ ụ  .Tìm m
tích phân I h i t và tính tích phân khi m x   2 x  1 2 1 m  2 Giải:
Do x  1 làm cho biểu th c ứ trong d ng
ấu tích phân không xác định. Nên đây là tích phân suy rộ loại 1 và 2.
Tách ra thành 2 tích phân sau:  2  dx dx dx I       I I   m
x  2  x 1  m
x  2  x 1  m x  2  1 2 2 2 2  1 1 2 x 1 2 2 dx dx
Xét tích phân I sau: I     1 1  m x  2 2     1 x 1 m 1  x 2 x  1  x  1
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67  dx 1 Khi x 1 :  m x   ~ 2
x  1 x   1 3 2  x  12 1
+ Đây là tích phân suy rộ 1 ng loại 2, thấy   1  I hội tụ. 1 2  dx
Xét tích phân I   2  m x   2 x  2 2 1
Khi x   ta xét các trường hợp của m như sau: 1 1 Khi m  0, xét     I phân k ỳ I phân k ỳ m  2 ~ 1 2 2 1 2x x x 1 1 Khi m  0, xét:     I phân k ỳ  I phân k ỳ m x   ~ 1 2 2 3 2 x  1 x 1 1 Khi m  0, xét:   m   ~ m 1 2 2  1 x x x
Như vậy khi m  0 thì ta thấy m 1  1 I hội tụ (do đây là tích phân suy rộng loại 1). 2 Kết luận: + Do I
ộ ụ nên để I ộ ụ ỉ ụ ộ I . Suy ra, I ộ ụ m  0 . 1 h i t h i t thì ch ph thu c vào 2 h i t khi
Tính tích phân khi m  2 :   dx dx Khi m  2, t
tích phân đã cho trở hành: I     x  2 x 1 1 1  2  2 1 x  2 x  2  1 2 x Đặ 1 1 1 t t: 2 2 t  1   t  1  x   xdx dt 2 2 2 x x 1  t  2 1  t 2
Tích phân đã tương đương với: t 1  1 1t xdx 2 2 1 1 2  1 1 1 tdt dt dt     1 1  1  t 2 3
1 x x 2  2 2 2 0 0 0 1    2 t  2tt  2 2 2 2 x
1 t  1 t  1 t 2
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67 6 6 1 1  t   t 1 1 1 1 1 1 1 2 2  dt    dt    2  6  6  2 6  6  6  2 6  6   6  0 0 0   t   t    t   t    t    t  2 2 2 2 2 2           1  6 6  1 1   lnt lnt   ln 5  2 6  2 6  2 2  0 2 6    Câu 34: dx
Cho tích phân I   để ộ ụ  .Tìm m
tích phân I h i t và tính tích m x   2 x x  2 1 2 5 2 phân khi m  1 Giải:
- Do x  2 làm cho biểu th c ứ trong d nh
ấu tích phân không xác định. Nên đây là tích phân bất đị loại 1 và 2.
Tách ra thành 2 tích phân sau:  3  dx dx dx I        I I   m
x  1 2x  5x  2  m
x  1 2x  5x  2  m x  1 1 2 2 2 2   2 2 3 2x 5x 2 3 3 dx dx
Xét tích phân I sau: I   1   1  m x   2 1 2x  5x  2   m 1 2 2 x   1 2 x  x    2   2   1 1 Khi x  2 : ~      x   1 x  x     3 2m m 1  x 2 1 2 2 12  2
Nhận thấy với mọi m  0 (lưu ý vì hàm số chỉ x
ác định khim  0 ). Thì 3 2m   1 luôn là hằng. Do đó thấ 1 y   1 I h i ộ t
ụ (đây là tích phân suy rộng loại 2). 1 2  dx
Xét tích phân I   2  m x   2 x x  3 1 2 5 2
Khi x   ta xét các trường hợp của x   như sau: 1 1
Khi m  0, ta xét hàm dương sau:      I phân k ỳ I phân m x   ~ 1 2 2 1 2x  5x  2 2 x kỳ
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67
Khi m  0 : không xét vì làm hàm s
ố không xác định  I không có tích phân. 1 1
* Khi m  0, ta có:  mx   ~ m 1 2 1 2x  5x  2 2x
Như vậy khi m  0 thì ta thấy m 1  1 I hội tụ. 2
Kết luận: + Do I h i ộ t ụ nên để I h i ộ t t ụ hì chỉ phụ thu c
ộ vào I Suy ra, I hội t khi ụ m > 0. 1 1  dx
Tính tích phân khi m  1:  x   2   2 1 2x 5x 2 Đặ 1 1
t: x 1   dx   dt 2 t t 1  0 2
Tích phân đã tương đương vớ dx i: t   dt    x   2 2   2 1 2 x 5x 2 1 1 1  1  2 1  5 1  2     tt   t  1 1 1 dt dt dt       2 2 2 1   0 0 2 t t 0 9  1 t 1    2  t t t   4  2  Đặ 1 3 3 t t
sinu dt  cos udu 2 2 2  3 2 cosudu  1 Tích phân trở thành: 2   arcsin  3 2 3 1 arcsin cosu 3 2  Câu 35: 1
Tính tích phân I dx  2 1 x 4 x Giải Xét: 2
4  x  0  x  2 x 1 2  2 4  2 x 4  x 0 2 x  4
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67  2  1 1 1 Vậy, ta có: I dx dx
dx I I    1 2 2 2 2    1 x 4 x 1 x 4 x 2 x x 4 Xét I : 1 1 1 1 Đặt t
x   dx   dt 2 x t tt  1 x  1  Với    1 x  2  t   2 1 1 1 2  dt 1 2 2 1 2 1 dt dt 1 t 2 1 I dx   
ln 2t  4t 1     1  ln 2 3 1 2 2 2 x 4 x 1 1 4t  1 4t  1 2 2 1 1 1 1 4  2 2 2 t t
Tương tự với I  2 4 1 
Vậy I I I ln 2  3  1 2   2 4 
x  ln 1 x
Câu 36: Tìm tất cả s
ố thực   0 để tích phân I   ộ ụ  dx  h i t 3 2 0
x arctanx  Giải:        
x ln 1 x  2
x ln 1 x
x ln 1 x I            
x arctanx dx
x arctanx dx
x arctanx dx I I 1 2 3 2 3 2 3 2 0 0 2   x ln 1  x
Đặt f x       3 2
x arctanx  Xét I : 1  2  x          xx x    x x 1
x  x 1 x      1 2      2   2 x  1
Khi x 0 : f x  ~         ~ ~  2 2  1  3 2 3 2 x x x x x x x 2 1
Suy ra I cùng bản chất với dx  1 1 x 0
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67 Vậy để I h i ộ t t
ụ hì:  1 1   2  1 1 Xét I : 2 x 1
Khi x  : f x  ~  3 2 x x   1 Suy ra I ả ấ ớ dx 2 cùng b n ch t v i  2 x  2 1 Vậy để I ộ ụ 2  1      2 2 h i t thì: 2 1
Từ 1 và 2  : Để I HỘI TỤ thì    2 2 1 Câu 37: 1 Tìm tất cả các s
ố thực  để tích phân sau h i ộ t ụ I dx  . Tính giá x  1 0   xarctanx trị c a ủ 1 tích phân khi   2 Giải x  0 m là điể kì dị. Khi x 0  :  1
TH1:   0 : lim x lim       x0 x0 x 1 1 1  ~ ~  x  1   1 . x arctanx   2 . x x 2 2 1 1 dx 2 dx
Suy ra 𝐼 cùng bản chất với    1   1 0 2 0 x 2 2 x 1 2 dx Dễ thấy
ộ ụ  I ộ ụ 1   h i t h i t 1 0 2 x 1 1 1 TH2:   0 : ~ ~   x   1 1 . x arctanx . x x 2 x
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67 1 dx
Suy ra 𝐼 cùng bản chất với  1  0 2 x 1  Vậy để I hội tụ  1    1  2 2
Từ 1 và 2  suy ra   1 1 1 1
Khi   , tích phân trở thành: I dx  2 0  x  1 . x arctan x   4 dx dt Đặ 2
t t arctan x dt   I   t   
2 x 1  x  4 4 2 t 0 0  . x sinaxCâu 38: Xét tính h i ộ t c ụ a ủ tích phân: dx
k  0,a  0 2 2 k x 0 Giải x 2 2 k x
Xét hàm g x  
, ta có: g ' x 
. Như vậy x k thì g '  x  0 khi đó hàm 2 2 2 k x  2 2 k x x g 
x đơn điệu giảm và lim g x  lim  0 2 2 x
x k x A 1 cosAa 2
Mặt khác, với mọi A a : sinaxdx    Ma a 0
Theo dấu hiệu tích phân Dirichle tích phân đã cho hội tụ  Câu 39: sinx Xét s h ự i ộ t c ụ ủa tích phân: dx  với a  0 x a   sinx sinx
Trước hết theo định lý Dirichlet tích phân dx  h i ộ t . T ụ uy nhiên, tích phân dx  không x x a a hội tụ. 2 sinx sin x Do   0, x  [  , a  )  x x 2    sin x 1  cos2 x 2 sin x 1 dx 1 co 2 s x Mặt khác:  nên dx   dx    x 2x x 2 x 2 x a a a
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67  2 sin x Tích phân th nh ứ
ất phân kì, tích phân thứ hai h i ộ tụ. Vậy tích phân dx  phân kỳ, x asinxdx  phân k ỳ x a 2  xCâu 40: e Tính tích phân suy r ng ộ dx  2  1  0 2 x     2  2   x Đặ e t: I     dx  2 x   0 2   x      t 2 e         e x  2x  Khi đó, ta có t t 1 t 2 : x dx e e dtdx e e dtdx  . dt       2 x   2 1  t 0 0 0 0 0 0 2  xe 1 tt    Ta thấy y: 2 dt I '  e dt     2  1   2  2 1 t 0 2 0 x     2  Nhưng  tt      1 t t      1 t  1 t t  2 2 2 2 2 2 e dt  1 te dt e dt  2      1 te   e dt e dt  2   1  t 1  t 0 1 t 1 t 0 0 0   0 0 2  x e Vậy dx    2  1  0 2 x     2    Câu 41: x dx
Tìm  để tích phân sau h i ộ tụ: I    2  x  5 4   0 1 1 x cosx  Giải:   1  x dx xdx xdx I        I I   2 1 x  4
1  x cosx   2 1 x   4
1 x cosx   2 1 x   4 0 0 1
1 x cosx  1 2 5 5 5  2
Xét I , x 0 : f x ~ 1   2   x 1  2
I cùng bản chất với dx 1  2 x   0
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67 Vậy I h i ộ t
ụ  2   1   1 1 2
Xét I , x   : f x ~ 2   14   5 x   2
I cùng bản chất với dx  2 14  1 5 x Vậy I h i ộ t
ụ  2  1  1 2  2  Câu 42: 1 x
Tìm  để tích phân sau h i ộ t : ụ I    x  dx  1  x 0 1  Giải:  2 1 2  2 1 x 1 x 1 x I           dx dx dx I I    x      1 xx 1 xx 1 x  1 2 1 1 1 0 0 1 Khi   1   1
Xét I , x  0 : f x ~ 1    x 1  1
I cùng bản chất với dx 1  x  0 Vậy I h i ộ t ụ    1 1 1
Xét I , x   : f x ~ 2   2 x   1
I cùng bản chất với dx 2  2 x  1 Vậy I h i ộ t ụ 1  2 1    2 2 Khi   1  làm tương tự  2 Câu 43: dx Xét s h ự i ộ t c
ụ ủa tích phân sau: I   sinxcosx 0 Giải:
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67 
f x  0, k d ỳ ị tại và 0  tách cận 2    2 3 2 dx dx dx I     I I    1 2 sinxcosx sinxcosxsinxcosx 0 0 3
Xét I : f x k d ỳ ị tại 0 1    3 1 x   f   1 0 : x ~ . Vì  h i ộ t nê ụ n I h i ộ t ụ 1 x 1 0 2 x
Xét I : f x k d ỳ ị tại 2   2   x f x 1 1 :  ~ 2     sinx.sinx    x  2  2  2 1 Vì  h i ộ t nê ụ n I h i ộ t ụ 1 2  2    3  x    2 
Vậy I I I h i ộ t ụ 1 2  Câu 44: dx Tính tích phân suy r ng: ộ I   x  2  1 1 x x Giải: x  1 là m điể k d
ỳ ị  Tích phân suy r ng k ộ
ết hợp. Ta tách thành 2 tích phân:  2  dx dx dx I       x 1 2 x xx 1 2 x xx 1 2  1 1 2 x x 2 2 2 dx dx dx Xét I   limlim    1    x 1   2 k x x     k x 1 2 1 k 1 x x k x 1  2 3 2 1 1   x 1  x 1  2 dx Đặ 1 t: t   dt x  1  x 2 1
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67 Đổi cận: x 1 2 t 1 1 2 3 Ta có: k k dt 2 3 2 3 1 2 3 2 3 1 2 2 I limlim ln t   t t   lim ln k   k k     2ln2  l 1 n 2  1   1 2  1 1 1 k 1 2t 3t 1 k 2 4 2 2 k 2 4 2 2 2 2 2 2 3 2 3  k  dx dx dx I   limlim    2 x 1 2 k x x  x 1 2 k x x  x 12 3 2 2 2 2 1   x  1 x12 2 1 2  3 2 
Giải tương tự: I lnln   2  2 12 2  4 2    2  3 2 
Vậy I I I   2ln2  ln   1 2   2  4 2    Câu 45: 2 x 1 Xét s h ự i ộ t c ụ ủa tích phân: dx     0  3 x  4 5 x 1 Giải:    
Khi x   ta so sánh: x x   x  5 1 4 5 4 4 2 1 ~ 2 ; 3
x 1 ~ x x x Nên bắt bu c ộ ph u t ải chia tp ban đầ hành t ổng 2 tp như sau:  1  2x 1 2x 1 2x  1 I dx dx
dx I I             0 3 x 4 x 1 0 3 x 4 x 1 1 3 x  1 2 5 5 4 5 x 1 I là tp c a
ủ hàm liên tục trong đoạn lấy tp nên là tp xác định (tp HT) 1  1
Tp I là tp HT khi và chỉ khi dx  HT (theo so sánh trên) 2 1   1 4 x
Do vậy, tp đã cho HT khi và chỉ 3 khi   4
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67
BÀI TẬP TỰ LUYỆN 1 2  x arctan
b1: hội tụ - phương pháp làm: arctan(1/x) ~
Câu 1: Khảo sát sự ộ
h i tụ của tích phân suy rộng: x J dx  1/x 5 x x x  4 b2: dùng tg đg 1 alpha > -1/2 cách làm: 1  3    Câu 2: 1 x 1 x
cho cái ở trên tương đương với x^(alpha)/căn x Khảo sát sự ộ
h i tụ của tích phân I dx  Xét: sin x 0
limx->0+ của biểu thức trong tp ban đầu với tphan đã chọn  2     xét với hàm g(x) = x^alpha Câu 3:x 3x 2 Khảo sát sự ộ
h i tụ của tích phân I x ln dx   
nhận thấy hàm dưới dấu tphan nhỏ hơn rất nhiều so 2 x  x 1   với hàm g(x) 1
-> g(X) hội tụ thì f(x) hội tụ ộ ụ 
mà g(x) h i t (=) alpha < -1 Câu 4: arctanx Cho tích phân dx  để ộ ụ 3     . Tìm 
tích phân h i t và tính tích phân khi 2 
dễ chứng minh alpha > 1/2 bằng cách cho bthuc dưới tphan nhỏ hơ2 n (pi/2)/(x^2+1) 0 1 x  ^alpha
tính thì cách làm là chúng ta đặt x=tant rồi xong tphan từng phần là ra rồi nhé 1 Câu 5: arcsin xdx
Cho tích phân I  
. Tìm  để tích phân h i ộ t và ụ
tính tích phân khi   1   0
x 1 x alpha<3 để cái này hội tụ (tự làm nhé lười nói cách giải)
tính tích phân: đổi biến: t = arcsin (căn x) -> tự giải nốt   
không hiểu alpha đặt ở đâu      Câu 7: dx Xét tích phân suy r ng ộ  , là tham s . T ố
ìm giá trị  nguyên dương bé 3 1  x 1  x 0  
nhất để tích phân suy rộng này hội tụ. Với tìm được, tính tích phân này. alpha > -2
=> alpha = 1 (số nguyên dg đầu tiên) 
tách theo hàm phân thức hữu tỉ để tính Câu 9: 1 Xét tích phân suy r ng ộ d . x  Tìm m u ki điề ện về t
m để ích phân suy r ng nà ộ y m 3 2  1 x . 1 x
m > 1/3 (rất dễ để chminh) hội tụ. Tính giá trị 7
tích phân này khi m
cách tính: cho căn bậc 3 x mũ 7 nhân cái x^7 vào bthuc (1+x^2) rồi sau đó rút
3 x^9 (biến thành x^3) * (căn (x^2 + 1/x^2)) ra ngoài, và đặt cái căn là đc ậ ị ữ ạ  g x ớ ừa tìm đượ ị ớ ạ
b loz gì đấy ? lỗi đề nhé  khai triển maclaurin nhé Câu 11: sinhx Khảo sát sự ộ h i tụ của I dx
f(x) = bthuc dưới dấu tphan 2 x e cosx 0 g(x) = x/x^2 => lim f(x)/g(x)= 2/3
-> tphan của g(X) phân kỳ
Lời giải thực hiện: HOÀNG HUY QUÂN – Lớp: Kỹ thuật nhiệt – K64 và NGUYỄN THỊ MAI
HƯƠNG – Lớp: TĐH 09 – K64 - Nguyễn Thế Thiện - Lớp: HTTTQL - K67 chia TH ra:  2 x sin  2
x 1 + TH1: a<=0 -> phân kỳ
Câu 12: Tìm  để tích phân sau h i ộ t ụ I  
 + TH2: a > 0 thì bđầu xét: x  lnx  1   1
cái bthuc dưới căn tg đg x^2/x^a
=> hội tụ khi alpha >2   Câu 13: 2x 1
Tìm  để tích phân sau h i ộ t ụ I      chia TH ra: 1 3 x 4 5x 1 TH1: a<=0 -> pky
TH2: a>0 -> a>3/4 thì hội tụ 1 2
 x arcsin 2
Câu 14: Tìm  để tích phân sau h i ộ t ụ x dx
chia th nốt, làm y hệt :))  3 1  x x 0