Bài Tập Toán 9 Tuần 2 Có Lời Giải Chi Tiết

BÀI TẬP TOÁN 9 TUẦN 2
I. ĐẠI SỐ: PHÉP NHÂN CĂN THỨC BẬC HAI.
Bài 1. Thực hiện các phép tính sau: a) 30. 30 ; b) 5. 720 ; c) 3. 48 ; d) 3. 147 ; e) 16. 25 ; g) 320.45 ; h) 2 2 5,5 − 4,5 ; i) 2 2 25,4 − 23,6 ; k) 196.0,81.0,36 ;
Bài 2. a) (2 2 − 2 5 + 3 2).( 18 − 20 + 2 2); b) (1+ 2 − 5).(1+ 2 + 5).
Bài 3. Với giá trị nào của a thì biểu thức sau có nghĩa: a) a −1 ; b) (a − 3).(a + 5) ; c) 1− 3a ; 3 a − 3 d) 1− 2 a + a ; e) ; f) . a + 5 2a − 5 Bài 4. Tính:
a) A = 5 − 3 − 29 − 6 20 ; b) B = 2 3 + 5 − 13 + 48 ;
c) C = 4 − 2 3 + 3 − 2 2 ;
d) A = 9 − 2 20 + 12 − 2 35 .
II. HÌNH HỌC: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG.
Bài 1. Cho tam giác ABC , biết BC = 7,5cm ; CA = 4,5cm ; AB = 6cm .
a) Tam giác ABC là tam giác gì? Tính đường cao AH của tam giác ABC .
b) Tính độ dài các đoạn BH,CH .
Bài 2. Cho tam giác ABC vuông ở A , đường cao AH . Biết BH = 9cm , CH = 16cm
a) Tính độ dài các cạnh AB , AC . b) Tính chiều cao AH . 3
Bài 3. Cho tam giác vuông có tỉ số giữa một cạnh góc vuông và cạnh huyền bằng . Cạnh góc 5
vuông còn lại dài 12cm . Tính độ dài đường cao, độ dài hai hình chiếu của cạnh góc vuông lên cạnh huyền.
…………..………………………Hết………………………………… Trang 1
BÀI TẬP TĂNG CƯỜNG TOÁN 9 TUẦN 2
HƯỚNG DẪN GIẢI CHI TIẾT
I. ĐẠI SỐ: PHÉP NHÂN CĂN THỨC BẬC HAI.
Bài 1. Thực hiện các phép tính sau: a) 30. 30 b) 5. 720 c) 3. 48 d) 3. 147 e) 16. 25 g) 320.45 h) 2 2 5,5 − 4,5 i) 2 2 25, 4 − 23, 6 k) 196.0,81.0,36 Lời giải a) 2 30. 30 = 30 = 30 .
b) 5. 720 = 5. 5. 144 = 5.5. 144 2 2 = 5 . 12 = 5.12 = 60 .
c) 3. 48 = 3. 16.3 = 3. 3. 16 = 3.3. 16 2 2 = 3 . 4 = 3.4 = 12 .
d) 3. 147 = 3. 49.3 = 3. 3. 49 = 3.3. 49 2 2 = 3 . 7 = 3.7 = 21. e) 2 2 16. 25 = 4 . 5 = 4.5 = 20 .
g) 320.45 = 64.5.5.9 = 64. 25. 9 2 2 2 = 8 . 5 . 3 = 8.5.3 = 120 . h) 2 2
5,5 − 4,5 = (5,5 − 4,5).(5,5 + 4,5) = 10 . i) 2 2
25, 4 − 23,6 = (25,4 + 23,6).(25,4 − 23,6) = 49.1,8 = 49.0,9.2 = 49. 0,9. 2 2 2
= 7 . 0,3 . 2 = 7.0,3. 2 = 2,1 2 .
k) 196.0,81.0,36 = 196. 0,81. 0,36 2 2 2
= 13 . 0,9 . 0,6 = 13.0,9.0,6 = 7,02 . Bài 2. Tính
a) (2 2 − 2 5 +3 2).( 18 − 20 + 2 2)
= (5 2 − 2 5).(3 2 − 2 5 + 2 2)
= (5 2 − 2 5).(5 2 − 2 5) = ( − )2 5 2 2 5 Trang 2 = 50 − 20 10 + 20 = 70 − 20 10 b) (1+ 2 − 5).(1+ 2 + 5) 2 2 = (1+ 2) −( 5) = 1+ 2 2 + 2 − 5 2 = 2 − + 2 2
Bài 3. Với giá trị nào của a thì biểu thức sau có nghĩa: a) a −1
Ta có: a −1 có nghĩa  a −1  0  a  1
b) (a − 3)(a + 5)
Ta có: (a − 3)(a + 5) có nghĩa  (a − 3)(a + 5)  0 a − 3  0 a  3   a + 5  0 a  −5 a  3       a − 3  0   a  5 −  a 3   a + 5  0 a  −5 c) 1− 3a
Ta có: 1− 3a có nghĩa  1− 3a  0  3a  1 1  a  3
d) 1− 2 a + a
Ta có: 1− 2 a + a = ( a − )2 1 ( a − )2
1  0 (luôn đúng )
Do đó: 1− 2 a + a có nghĩa    a  0 a  0 3 e) a + 5 3 Ta có: có nghĩa 3 
 0  a + 5  0  a  5 − a + 5 a + 5 Trang 3 a − 3 f) 2a − 5 a  3 a − 3  0  5   a  a  3 a − 3  2a − 5  0  Ta có: có nghĩa 2     5 . 2a − 5   a − 3  0 a  3 a     2 2a − 5  0  5 a    2 Bài 4. Tính: a) 5 − 3− 29− 6 20 ; b) 2 3+ 5− 13+ 48 ; c) 4− 2 3 + 3− 2 2 ; d) 9− 2 20 + 12− 2 35 . Lời giải a) Ta có 2 5 − 3− 29− 6 20 = 5 − 3− 9− . 2 . 3 20 + 20 = 5 − 3− (3− 20) = 5 − 3− 3− 20 = 5 − 3− ( 20 − ) 3 = 5 − 6− 20 = 5 − 6− 2 5 2 = 5 − 1− . 2 . 1 5 + 5 = 5 − (1− 5) = 5 − 1− 5 = 5 − ( 5 − ) 1 = 1 = 1. b) Ta có
2 3+ 5− 13+ 48 = 2 3+ 5− 13+ 2 12 = 2 3+ 5− 1+ . 2 . 1 12 +12 2 = 2
2 3+ 5− (1+ 12) = 2 3+ 4− 12 = 2 3+ 4−2 3 = 2 3+ ( 3 − ) 1 2 = 2 2+ 3 = . 2 4+ 2 3 = . 2 (1+ 3) = . 2 (1+ 3) = 2 + 6 . c) Ta có 2 2
4− 2 3 + 3− 2 2 = ( 3 − ) 1 + ( 2 − ) 1
= 3 −1 + 2 −1 = 3 −1+ 2 −1= 3 + 2 − 2 d) Ta có
9 − 2 20 + 12 − 2 35 = 5− . 2 . 5 4 + 4 + 7− 2 . 7 5 + 5 Trang 4 2 2
= ( 5−2) + ( 7 − 5) = 5−2 + 7 − 5 = 5−2+ 7 − 5 = 7 −2.
II. HÌNH HỌC: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG.
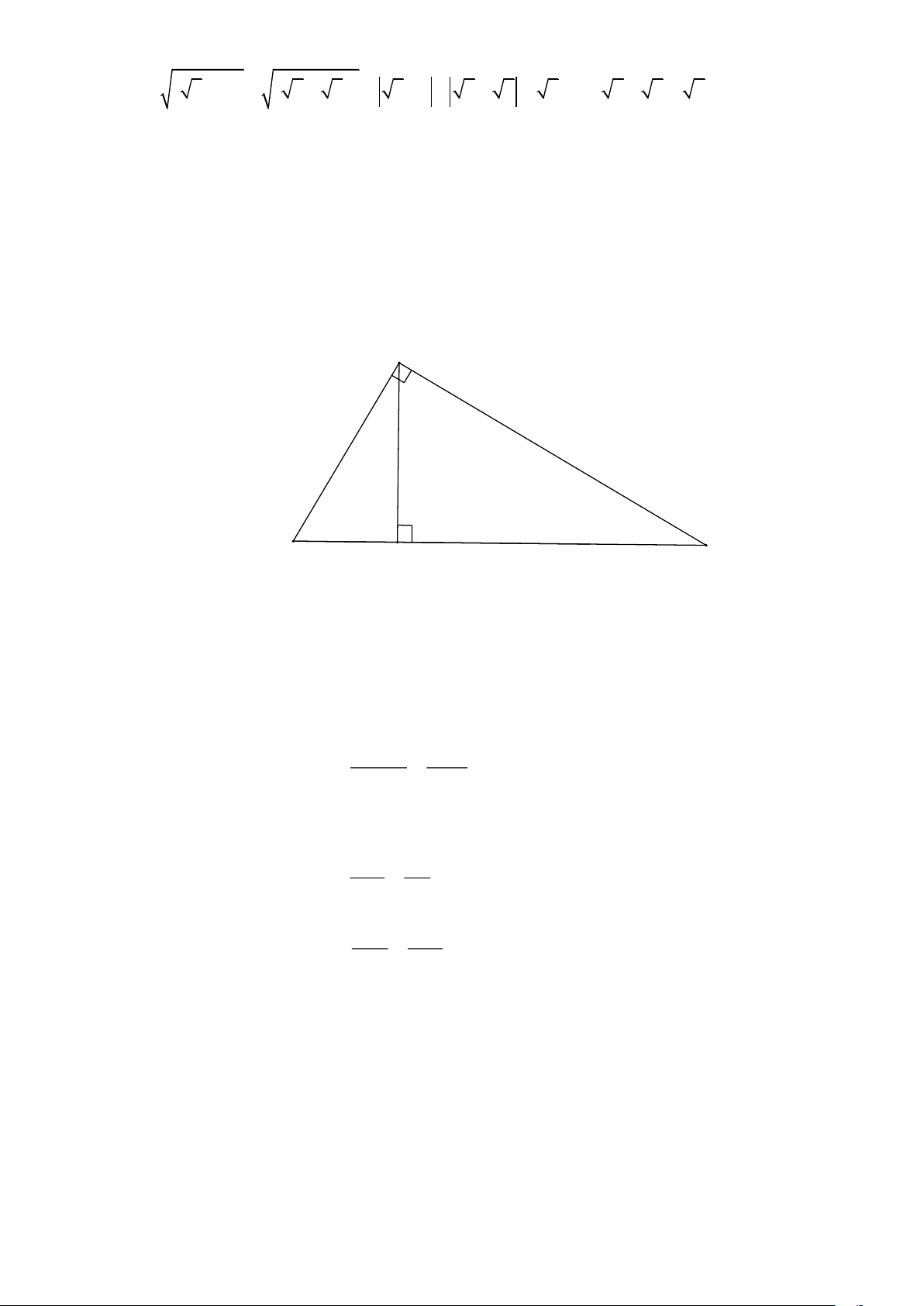
Bài 1. Cho tam giác ABC , biết BC = , 7 5cm ; CA = , 4 5cm ; AB = 6cm .
a) Tam giác ABC là tam giác gì? Tính đường cao AH của tam giác ABC .
b) Tính độ dài các đoạn BH ,CH . Lời giải A C H B a) Ta thấy BC2 = , 2 7 5 = 5 ,
6 25 và AB2 + AC2 = 2 + , 2 6 4 5 = 5 ,
6 25  BC2 = AB2 + AC2
nên theo định lí Pytago đảo suy ra ABC vuông tại A .
Tam giác ABC vuông tại A , đường cao AH nên theo hệ thức lượng trong tam giác vuông ta có A . B AC . 6 , 4 5 A .
B AC = BC.AH  AH = = = , 3 6(cm). BC , 7 5
b) Áp dụng hệ thức lượng trong tam giác vuông ABC tại A , đường cao AH ta có 6 2 AB2 2
+) AB = BC.BH  BH = = = , 4 8(cm). BC , 7 5 4 5 2 AC2 , 2
+) AC = BC.CH  CH = = = , 2 7(cm). BC , 7 5
Bài 2. Cho tam giác ABC vuông ở A , đường cao AH . Biết BH = 9cm , CH = 16cm
a) Tính độ dài các cạnh AB , AC .
b) Tính chiều cao AH . Lời giải Trang 5 A B 9 H 16 C
a) Tính độ dài các cạnh AB, AC .
Ta có: BC = BH + HC = 9 +16 = 25(cm) .
Áp dụng hệ thức lượng trong tam giác ABC vuông ở A , đường cao AH , ta có: 2
AB = BH.BC = 9.25 = 225(cm)  AB = 225 =15(cm) . 2
AC = CH.BC = 16.25 = 400(cm)  AC = 400 = 20(cm) .
b) Tính chiều cao AH .
Cách 1: Áp dụng hệ thức lượng trong tam giác ABC vuông ở A , đường cao AH , ta có: .
AB AC = AH.BC  15.20 = AH.25 15.20  AH = 25  AH =12(cm) .
Cách 2: Áp dụng hệ thức lượng trong tam giác ABC vuông ở A , đường cao AH , ta có: 2
AH = BH.HC = 9.16 = 144 .  AH = 144 =12(cm) .
Bài 3. Cho tam giác vuông có tỉ số giữa một cạnh góc vuông và cạnh huyền bằng 3 . Cạnh góc 5
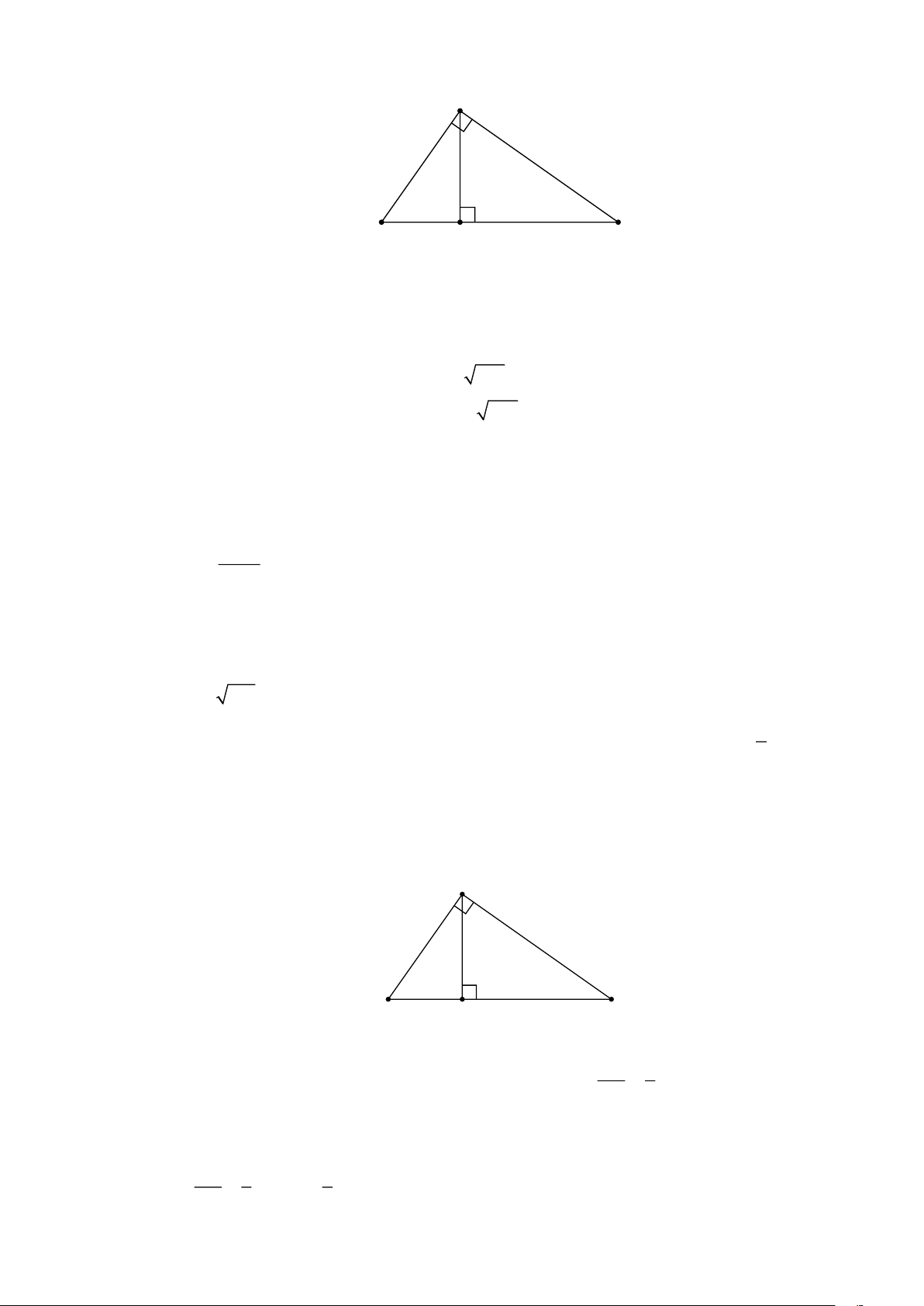
vuông còn lại dài 12cm . Tính độ dài đường cao, độ dài hai hình chiếu của cạnh góc vuông lên cạnh huyền. Lời giải A 12 B H C Giả sử tam giác AB
ABC vuông ở A có đường cao AH và 3 = , AC = 12(cm) . BC 5
Ta cần tính AH , BH ,CH . +) Vì AB 3 3
=  AB = .BC ( ) 1 BC 5 5 Trang 6
Xét ABC vuông ở A , ta có: 2 2 2
BC = AB + AC (Định lý Pi-ta-go) 2  3 2  2  BC = .BC + AC    5  9 2 2 2  BC − .BC = 12 25 16 2  .BC = 144 25 2  BC = 225  BC =15(cm) . Thay vào ( ) 3
1 ta có: Vì AB = .15  AB = 9(cm) . 5
+) Áp dụng hệ thức lượng trong ABC vuông ở A , đường cao AH , ta có: 2
AB = BH.BC 2  9 = BH.15  81 = BH.15 81  BH = 15  BH = 5, 4(cm).
CH = BC − BH = 15 − 5, 4 = 9,6(cm) . Lại có: .
AB AC = AH.BC  9.12 = AH.15 9.12  AH = 15  AH = 7,2(cm).
Vậy AH = 7,5(cm); BH = 5,4(cm) ;CH = 9,6(cm) .  HẾT  Trang 7