

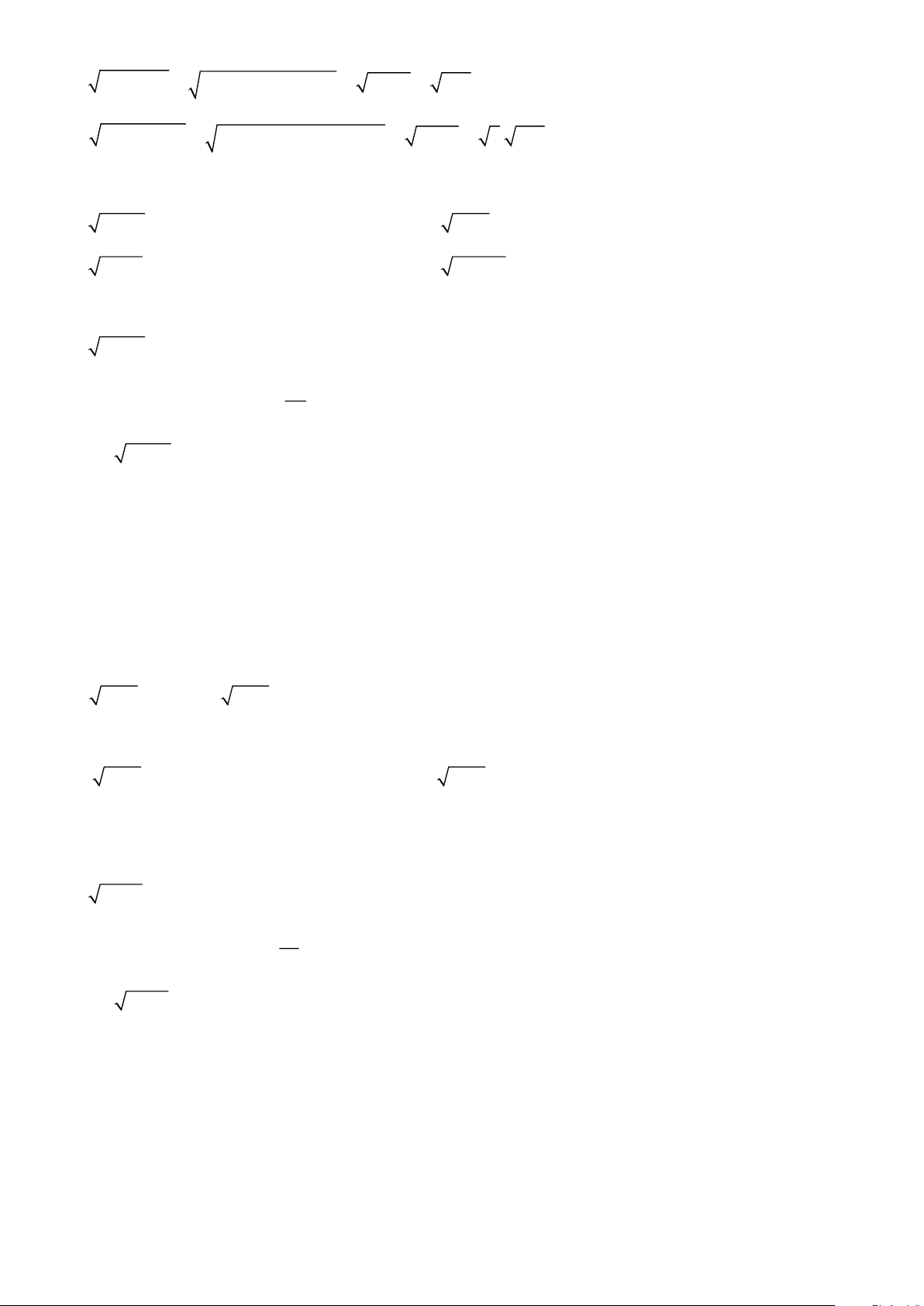
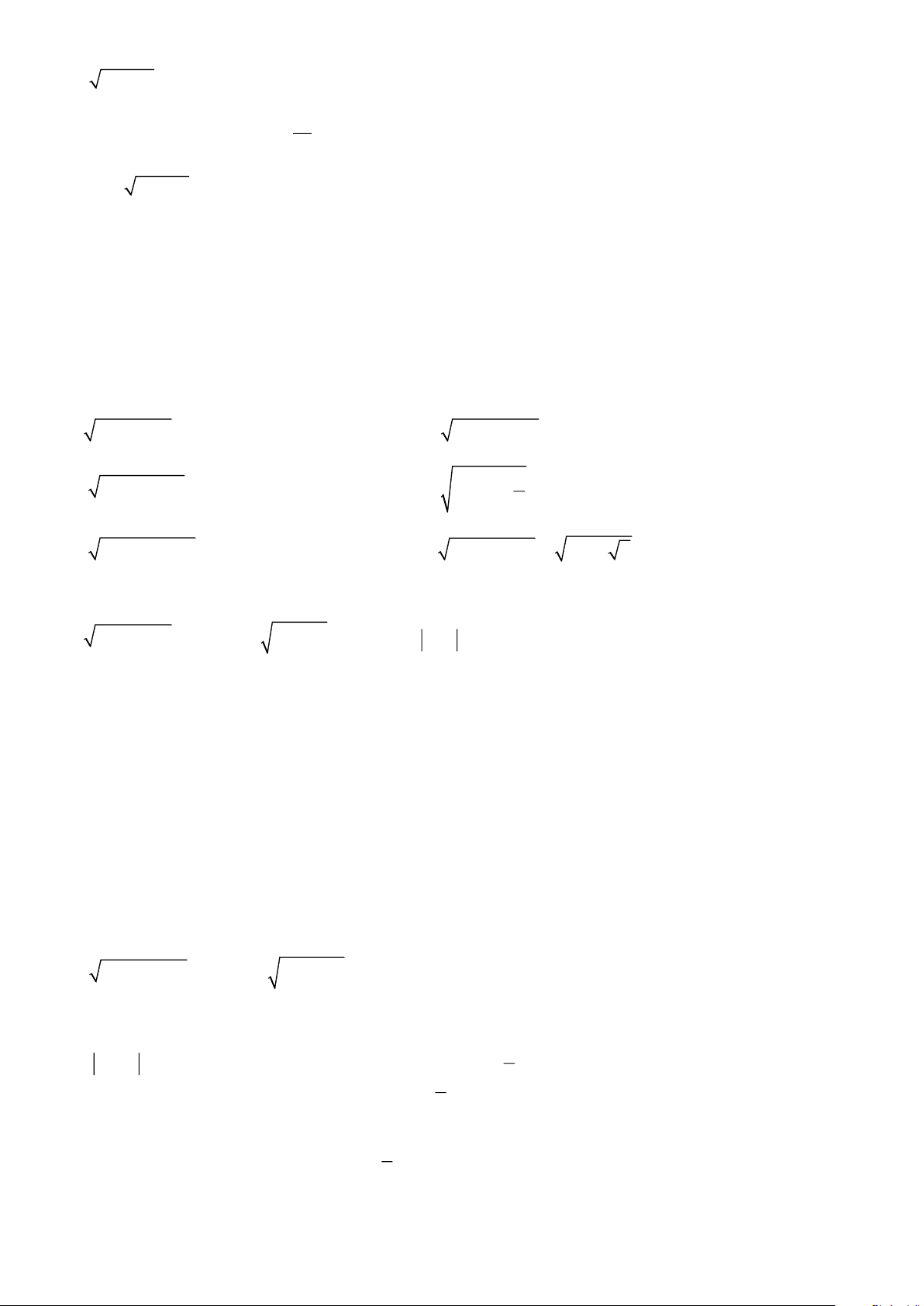
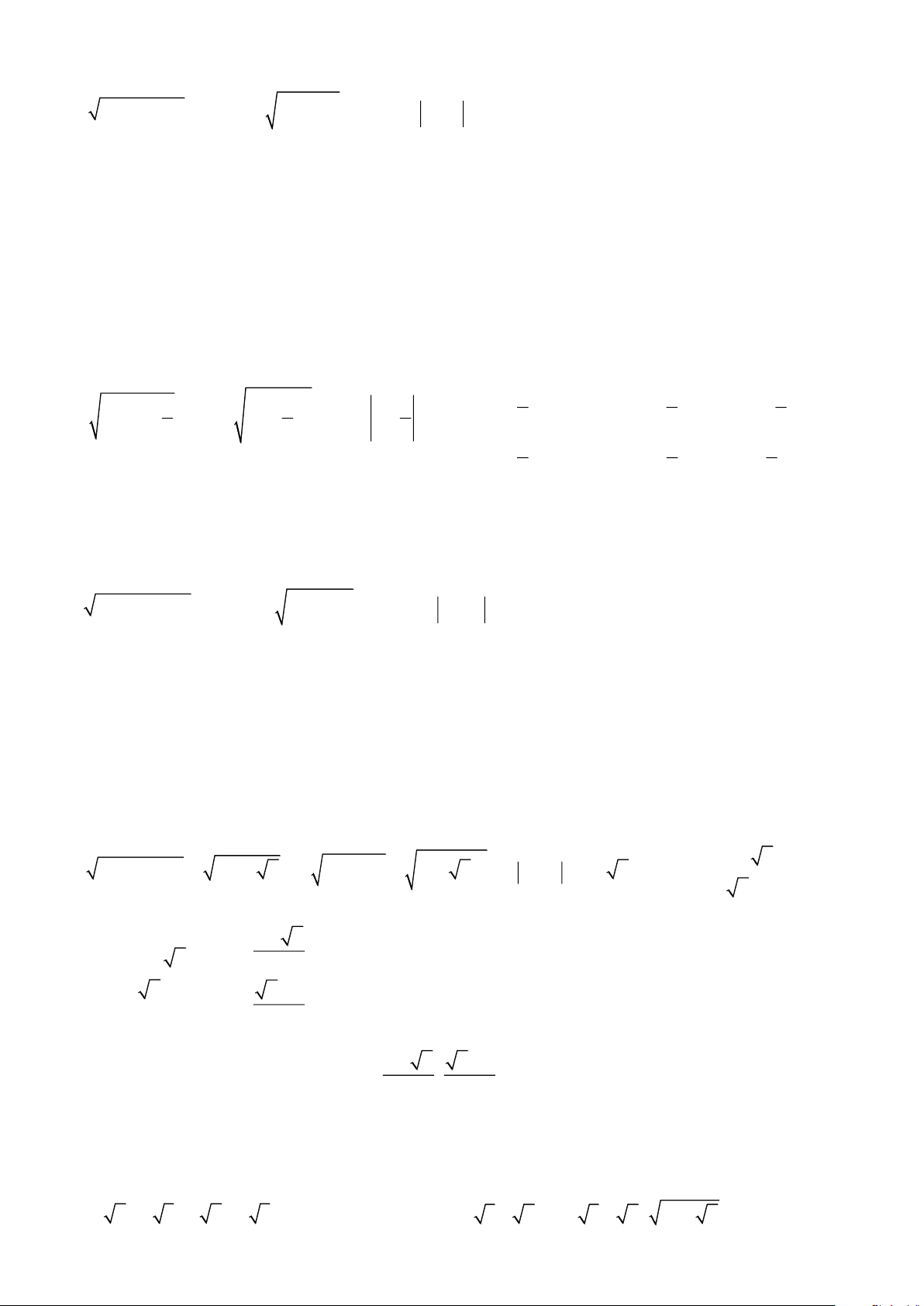
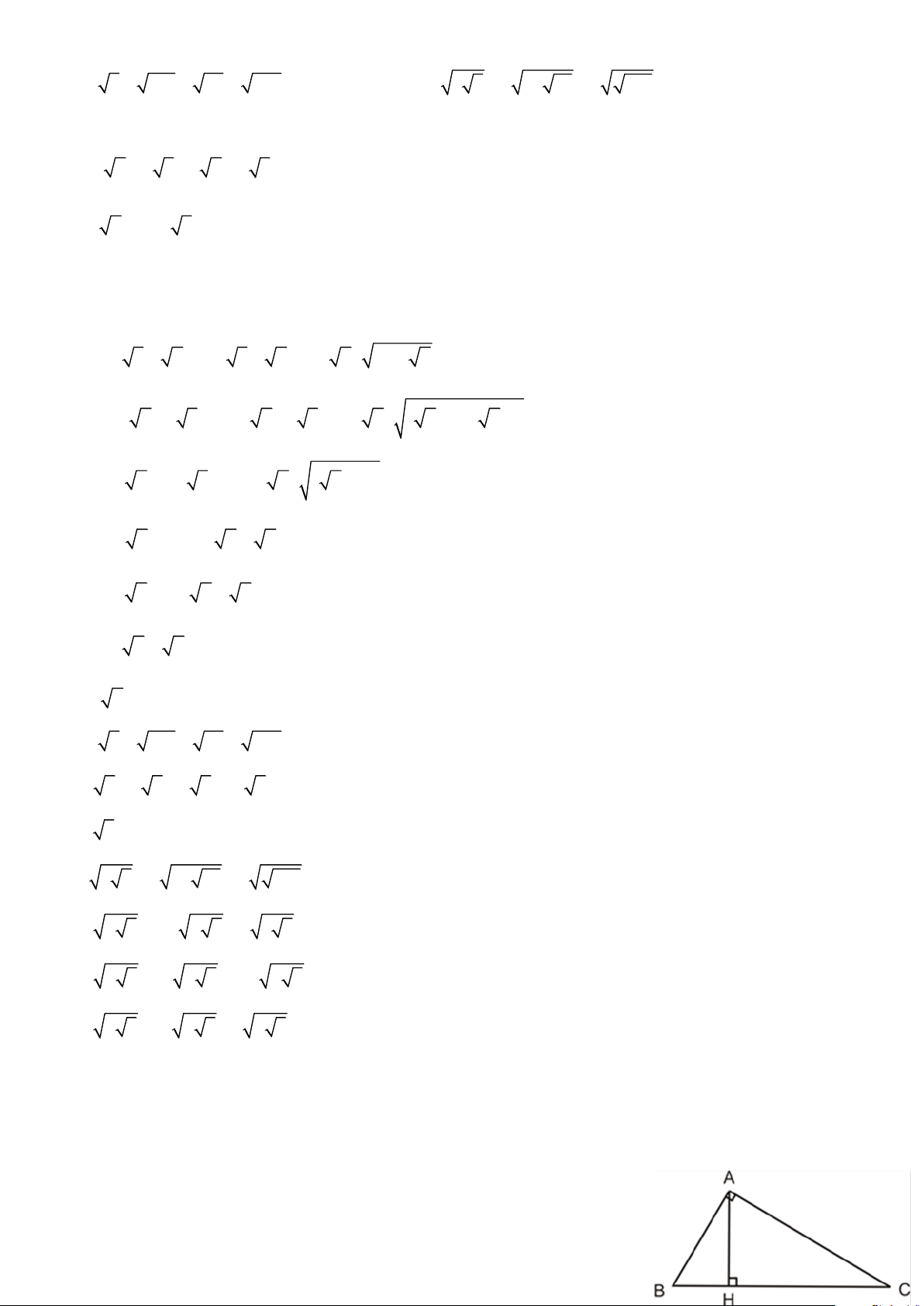

Preview text:
BÀI TẬP TOÁN 9 TUẦN 3
I. ĐẠI SỐ: QUY TẮC KHAI PHƯƠNG MỘT THƯƠNG Bài 1. Tính: 3 36 288 8 a) 45 : 80 b) 13 : 468 c) : d) : 15 45 169 225 72 e) : 8 g) (7 48 + 3 27 − 2 12): 3 h) ( 125 + 245 − 5): 5 9 Bài 2. Tính: a) 2 2 37 − 35 b) 2 2 221 − 220 c) 2 2 65 − 63 d) 2 2 117 −108
Bài 3. Giải các phương trình sau: a) 2x + 5 = 5 b) x − 7 + 3 = 0 c) 3x +1 = 10 d) 16 − 7x = 11
Bài 4. Giải các phương trình sau: a) 2 2
x − 2x +1 = x −1 b) 2
4x − 4x +1 = x −1 1 c) 4 2
x − 2x +1 = x −1 d) 2 x + x + = x 4 e) 4 2
x − 8x +16 = 2 − x f) 2
9x + 6x +1 = 11− 6 2 Bài 5. Tính: a) (3 2 − 2 3)(3 2 + 2 3)
b) (2 + 3 − 2)(2 − 3 − 2) 3− 2 2 c) 2 5 − 125 − 80 + 605 d) 8 3 − 2 25 12 + 4 192
II.HÌNH HỌC : LUYÊN TẬP HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Bài 1. Cho ABC vuông ở A , đường cao AH .Tính diện tích tam giác ABC biết AH = 12cm ,
BH = 9cm 5
Bài 2. Cho một tam giác vuông biết tỉ số hai cạnh góc vuông là
, cạnh huyền là 26cm .Tính độ dài 12
cạnh góc vuông và hình chiếu của hai cạnh góc vuông trên cạnh huyền.
Bài 3. Tính diện tích của hình thang ABCD có đường cao bằng 12cm hai đường chéo AC và BD
vuông góc nhau, BD = 15cm
…………………………………….HẾT……………………………………. Trang 1
HƯỚNG DẪN GIẢI CHI TIẾT
I. ĐẠI SỐ: QUY TẮC KHAI PHƯƠNG MỘT THƯƠNG Bài 1. Tính: 3 36 288 8 a) 45 : 80 b) 13 : 468 c) : d) : 15 45 169 225 72 e) : 8 g) (7 48 + 3 27 − 2 12): 3 h) ( 125 + 245 − 5): 5 9 Lời giải 45 9 3 a) 45 : 80 = = = 80 16 4 13 1 1 b) 13 : 468 = = = 468 36 6 3 36 3 36 1 1 c) : = : = = 15 45 15 45 4 2 288 8 288 8 8100 90 d) : = : = = 169 225 169 225 169 13 72 72 e) : 8 = :8 = 1 = 1 9 9 g) ( + − ) 7 48 3 27 2 12 48 27 12 7 48 3 27 2 12 : 3 = + − = 7 + 3 − 2 3 3 3 3 3 3
= 7 16 + 3 9 − 2 4 = 7.4 + 3.3 − 2.2 = 33 h) ( + − ) 125 245 5 125 245 125 245 5 : 5 = + − = + −1 5 5 5 5 5
= 25 + 49 −1 = 5 + 7 −1 = 11 Bài 2. Tính: a) 2 2 37 − 35 b) 2 2 221 − 220 c) 2 2 65 − 63 d) 2 2 117 −108 Lời giải a) 2 2
37 − 35 = (37 − 35)(37 + 35) = 2.72 = 144 =12 b) 2 2
221 − 220 = (221− 220)(221+ 220) = 1.441 = 441 = 21 Trang 2 c) 2 2
65 − 63 = (65 − 63)(65 + 63) = 2.128 = 256 =16 d) 2 2
117 −108 = (117 −108)(117 +108) = 9.225 = 9. 225 = 3.15 = 45
Bài 3. Giải các phương trình sau: a) 2x + 5 = 5 b) x − 7 + 3 = 0 c) 3x +1 = 10 d) 16 − 7x = 11 Lời giải a) 2x + 5 = 5 5 −
Điều kiện : 2x + 5 0 x 2 Ta có 2x + 5 = 5 2x + 5 = 25 2x = 20
x = 10 (thỏa mãn điều kiện)
Vậy phương trình có tập nghiệm S = 10 .
b) x − 7 + 3 = 0 x − 7 = −3
Điều kiện : x − 7 0 x 7
Vì x − 7 0 nên không có giá trị nào của x để x − 7 = −3 .
Vậy phương trình vô nghiệm. c) 3x +1 = 10 1 −
Điều kiện : 3x +1 0 x 3 Ta có 3x +1 = 10 3x +1 = 100 3x = 99
x = 33 (thỏa mãn điều kiện)
Vậy phương trình có tập nghiệm S = 33 . Trang 3 d) 16 − 7x = 11 16
Điều kiện : 16 − 7x 0 x 7
Ta có : 16 − 7x = 11 16 − 7x = 121 7x = −105
x = −15 (thỏa mãn điều kiện)
Vậy phương trình có tập nghiệm S = − 15 .
Bài 4. Giải các phương trình sau: a) 2 2
x − 2x +1 = x −1 b) 2
4x − 4x +1 = x −1 1 c) 4 2
x − 2x +1 = x −1 d) 2 x + x + = x 4 e) 4 2
x − 8x +16 = 2 − x f) 2
9x + 6x +1 = 11− 6 2 Lời giải a) 2 2
x − 2x +1 = x −1 (x − )2 2 1 = x −1 2
x −1 = x −1 2 x −1 0 2 x −1 0 2 x −1 0 2 x 1 2 x 1 2
x −1= x −1 2
x − x = 0 2
x − x = 0 x(x − ) 1 = 0
x(x − ) 1 = 0 2
x −1 = −x +1 2
x + x − 2 = 0 2
x + x − 2 = 0 2
x + 2x − x − 2 = 0 (x + 2)(x − ) 1 = 0 2 x 1 2 x 1 x = 0 x = 0 x =1 x −1 = 0 x = 1 x = 2 − x + 2 = 0 x = −2
Vậy tập nghiệm của phương trình là S = 2 − ;1 . b) 2
4x − 4x +1 = x −1 ( x − )2 2 1 = x −1 x −1 0 x 1 x = 0 2
2x −1 = x −1 2x −1 = x −1 x = 2 3
2x −1 = −( x − )1 x = 3 2
Vậy tập nghiệm của phương trình là S = . 3 Trang 4 x −1 0 x 1 c) 4 2
x − 2x +1 = x −1 (x − )2 2 1 = x −1 2
x −1 = x −1 2
x −1= x −1 2
x − x = 0 2
x −1 =1− x 2
x + x − 2 = 0 x 1 x 1 x 1 x = 0 x = 0 x( x − ) 1 = 0 x = 1 x + 2 = 0 x = −2 ( x − ) 1 ( x + 2) = 0 ( x − ) 1 = 0 x =1
Vậy tập nghiệm của phương trình là S = 1 . x 0 x 0 x 0 1 1 1 1 2 1 1 x + = x 0x = − 0x = − d) 2 x + x + = x x + = x
x + = x 2 2 2 4 2 2 1 1 1 x + = −x 2x = − x = − 2 2 4 x
Vậy tập nghiệm của phương trình là S = . 2 − x 0 2 − x 0 e) 4 2
x − 8x +16 = 2 − x (x − )2 2 4 = 2 − x 2
x − 4 = 2 − x 2
x − 4 = 2 − x 2
x + x − 6 = 0 2
x − 4 = x − 2 2
x − x − 2 = 0 − − 2 x 0 2 x 0 2 − x 0 x = 3 − x + 3 = 0 x = −3
( x − 2)( x + 3) = 0 x = 2 x − 2 = 0 x = 2 ( x + ) 1 ( x − 2) = 0 x = 1 − x +1 = 0 x = −1
Vậy tập nghiệm của phương trình là S = 1 − ;2;− 3 . 3x +1 = 3− 2 f) 2
9x + 6x +1 = 11− 6 2 ( x + ) = ( − )2 2 3 1 3 2
3x +1 = 3− 2 3x +1 = 2 −3 2 − 2 = 3x = 2 − 2 x 3 . 3x = 2 − 4 2 − 4 x = 3 2 − 2 2 − 4
Vậy tập nghiệm của phương trình là S = ; . 3 3 Bài 5. Tính: a) (3 2 − 2 3)(3 2 + 2 3)
b) (2 + 3 − 2)(2 − 3 − 2) 3− 2 2 Trang 5 c) 2 5 − 125 − 80 + 605 d) 8 3 − 2 25 12 + 4 192 Lời giải a) (3 2 − 2 3)(3 2 + 2 3) = ( )2 −( )2 3 2 2 3 = 18 −12 = 6 .
b) (2 + 3 − 2)(2 − 3 − 2)(3+ 2) 3− 2 2 = ( − )+ ( − )− ( + ) ( )2 2 2 3 2 2 3 3 2 2 − 2 2 +1 ( )2 ( )2 = − − ( + ) ( − )2 2 2 3 3 2 2 1
= (6− 4 2 −3)(3+ 2)( 2 − ) 1 = (3− 4 2)(3+ 2)( 2 − ) 1 = (1−9 2)( 2 − ) 1 =10 2 −19 . c) 2 5 − 125 − 80 + 605 = 2 5 − 5 5 − 4 5 +11 5 = 4 5 . d) 8 3 − 2 25 12 + 4 192 = 2 2 3 − 2.5 2 3 + 4 8 3 = 2 2 3 −10 2 3 + 4.2 2 3 = 2 2 3 −10 2 3 + 8 2 3 = 0 .
II.HÌNH HỌC : LUYÊN TẬP HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Bài 1. Cho ABC vuông ở A , đường cao AH .Tính diện tích tam giác ABC biết AH = 12cm , BH = 9cm . Lời giải Trang 6
Tam giác AHB vuông ở H , ta có theo định lí pitago: 2 2 2 2 2
AB = AB + HB = 12 + 9 = 144 + 81 = 225
Tam giác ABC vuông ở A , AH là đường cao thuộc cạnh huyền BC nên 2
AB = BC.BH suy ra : 2 AB 225 BC = = = 25(cm) BH 9 1 1 2 S
= BC.AH = .25.12 =150(cm ) ABC 2 2 5
Bài 2. Cho một tam giác vuông biết tỉ số hai cạnh góc vuông là
, cạnh huyền là 26cm .Tính độ dài 12
cạnh góc vuông và hình chiếu của hai cạnh góc vuông trên cạnh huyền. Lời giải AB 5
Giả sử ABC vuông ở A có : = và BC = 26(cm) AC 12 AB 5 AB AC Vì = nên = = k ( k >0) AC 12 5 12
Suy ra AB = 5k, AC = 12k
ABC vuông ở A ta có: 2 2 2
AB + AC = BC hay 2 2 2
(5k) + (12k) = 26 Suy ra 2 169k = 676 do đó 2
k = 4 ,suy ra k = 2
Vậy AB = 5.2 = 10(cm), AC = 12.2 = 24(cm)
ABC vuông ở A ta có AH là đường cao nên: 2 2 2 AB 10
AB = BC.BH do đó BH = = 3,85(cm) BC 26 2 2 2 AC 24
AC = BC.CH do đó CH = = 22,15(cm) BC 26
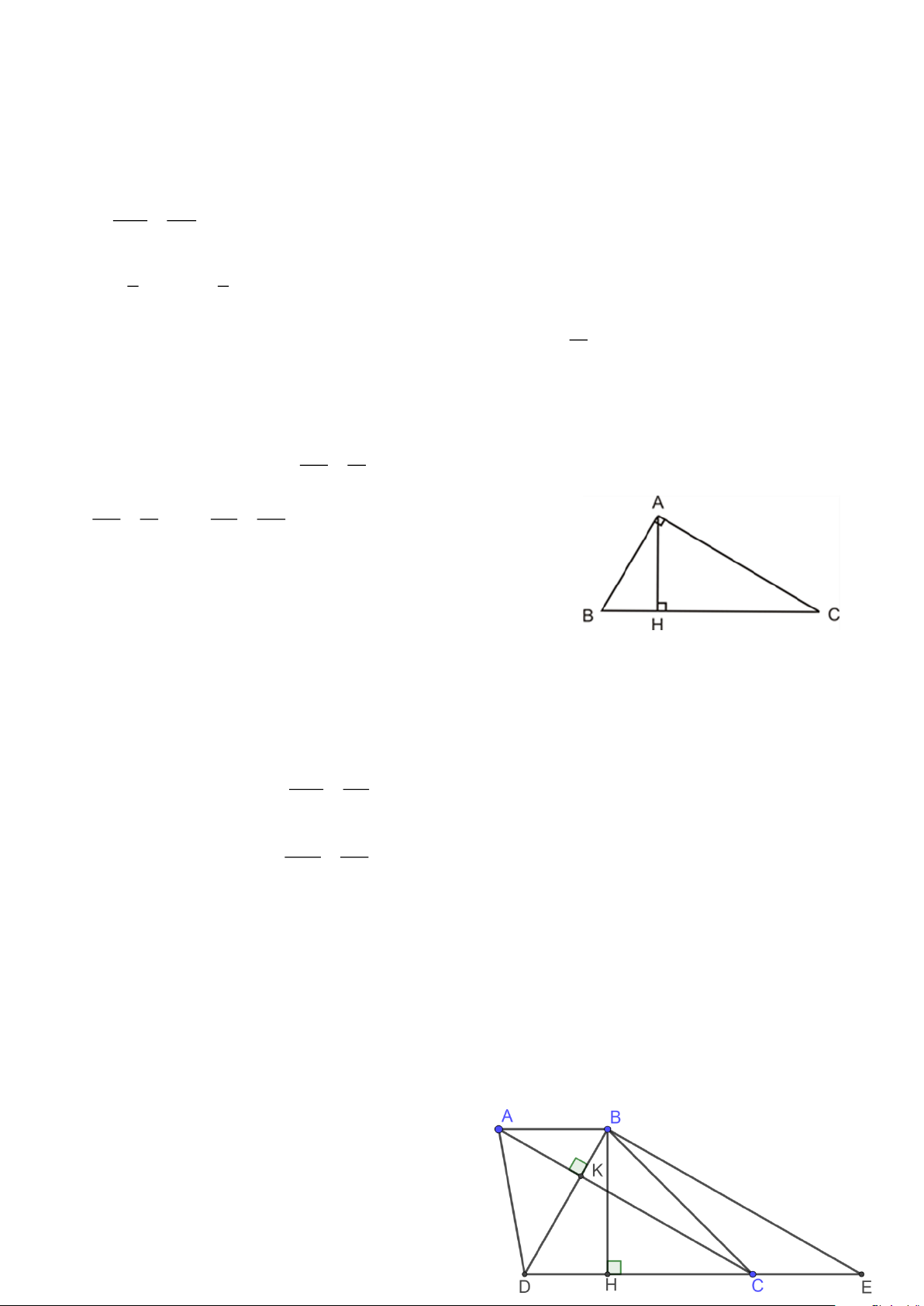
Bài 3. Tính diện tích của hình thang ABCD có đường cao bằng 12cm hai đường chéo AC và BD
vuông góc nhau, BD = 15cm . Lời giải
Qua B vẽ đường thẳng song song với AC , cắt DC ở E . Gọi BH là đường cao của hình thang.
Ta có BE//AC , CA ⊥ DB nên BE ⊥ BD
Áp dụng định lí pi ta go vào tam giác vuông BDH ,ta có: 2 2 2
BH + HD = BD 2 2 2 12 + HD = 15 2
HD = 225 −144 = 81 HD = 9(cm)
BDE vuông ở B nên ta có: Trang 7 2
BD = DE.DH 2
15 = DE.9 DE = 225 : 9 = 25(cm)
vì AB = CE nên AB + CD = DE = 2 ( 5 cm) Do đó 2 S = 25.12 : 2 =150(cm ) . ABCD HẾT Trang 8




