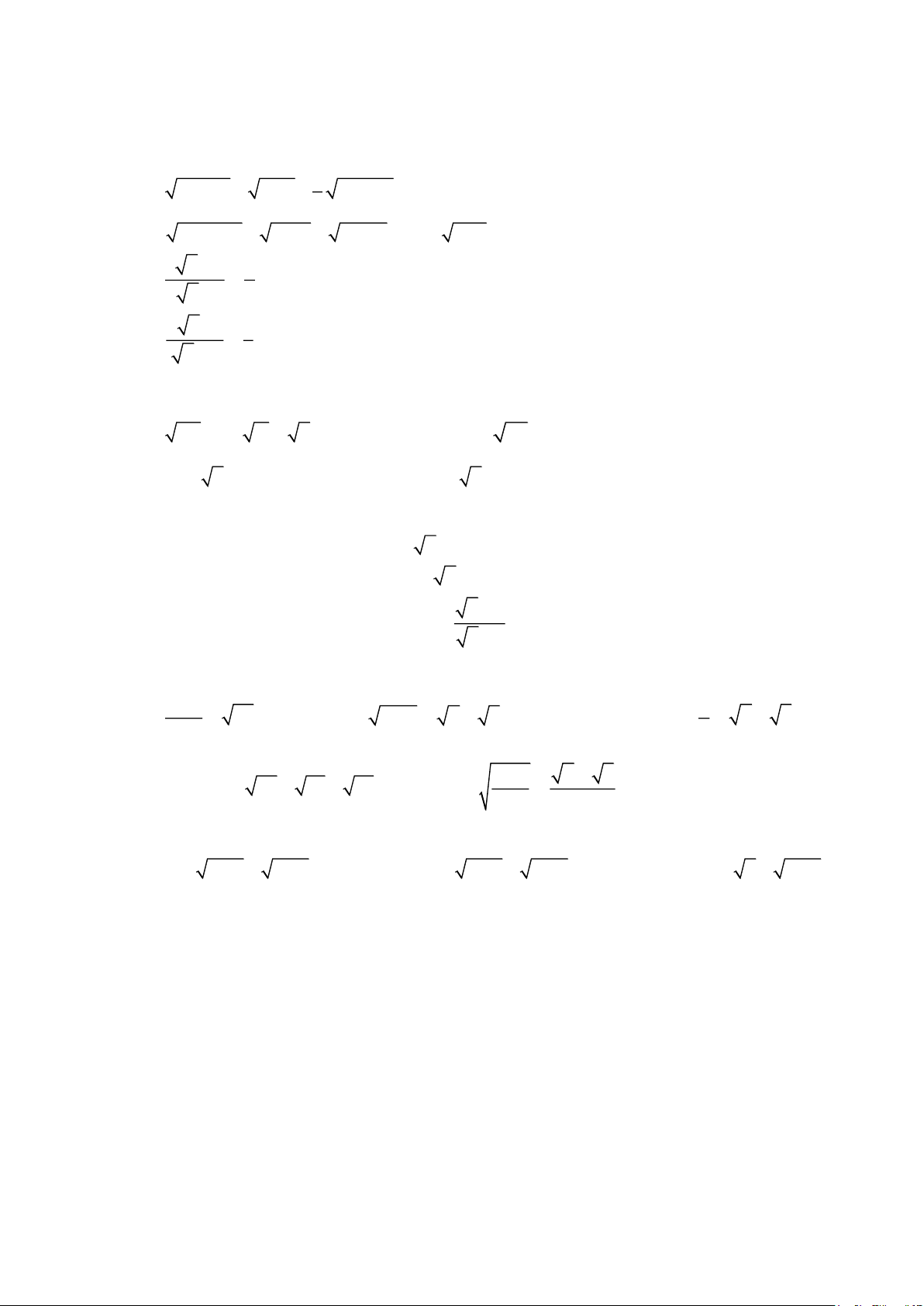
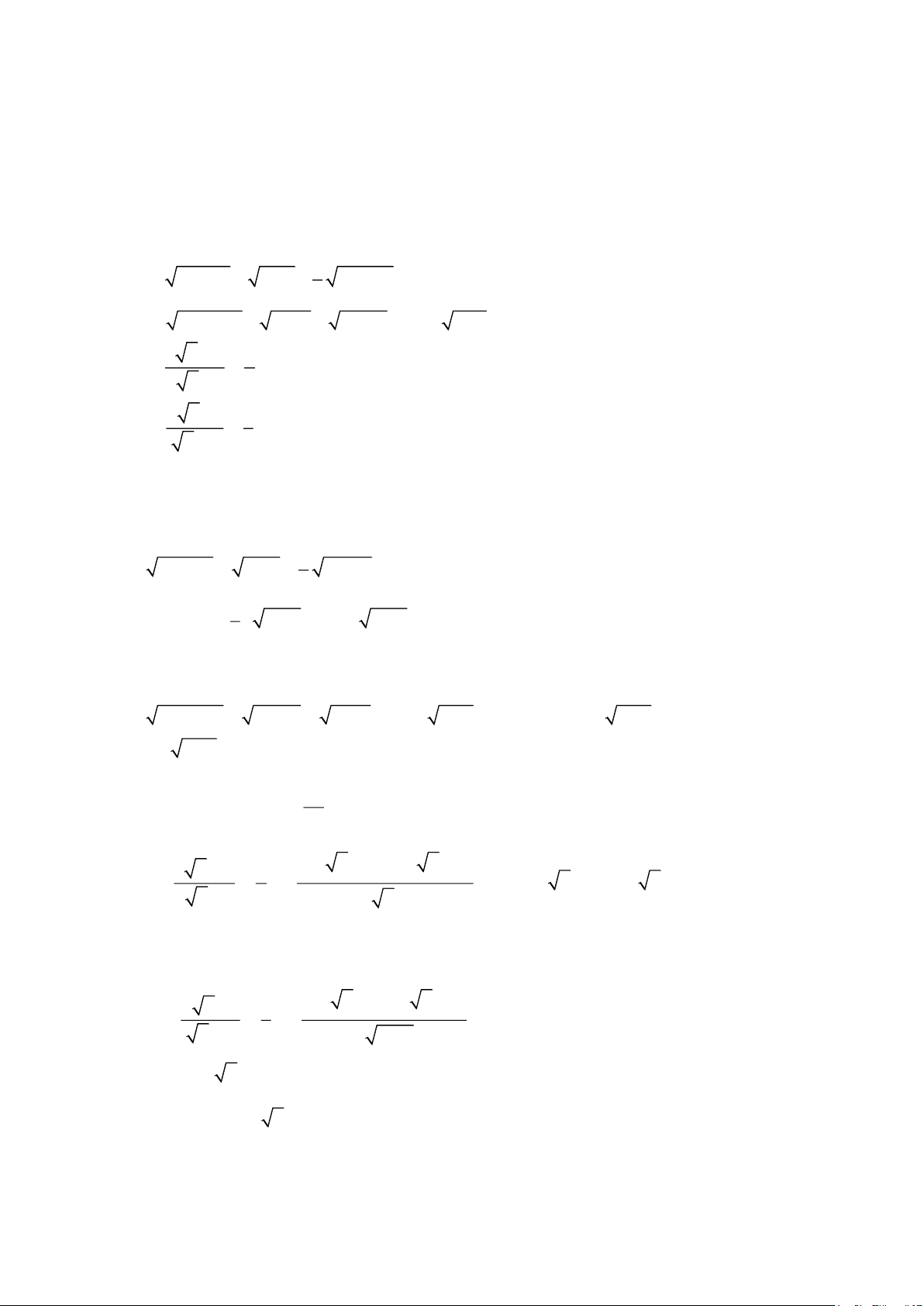


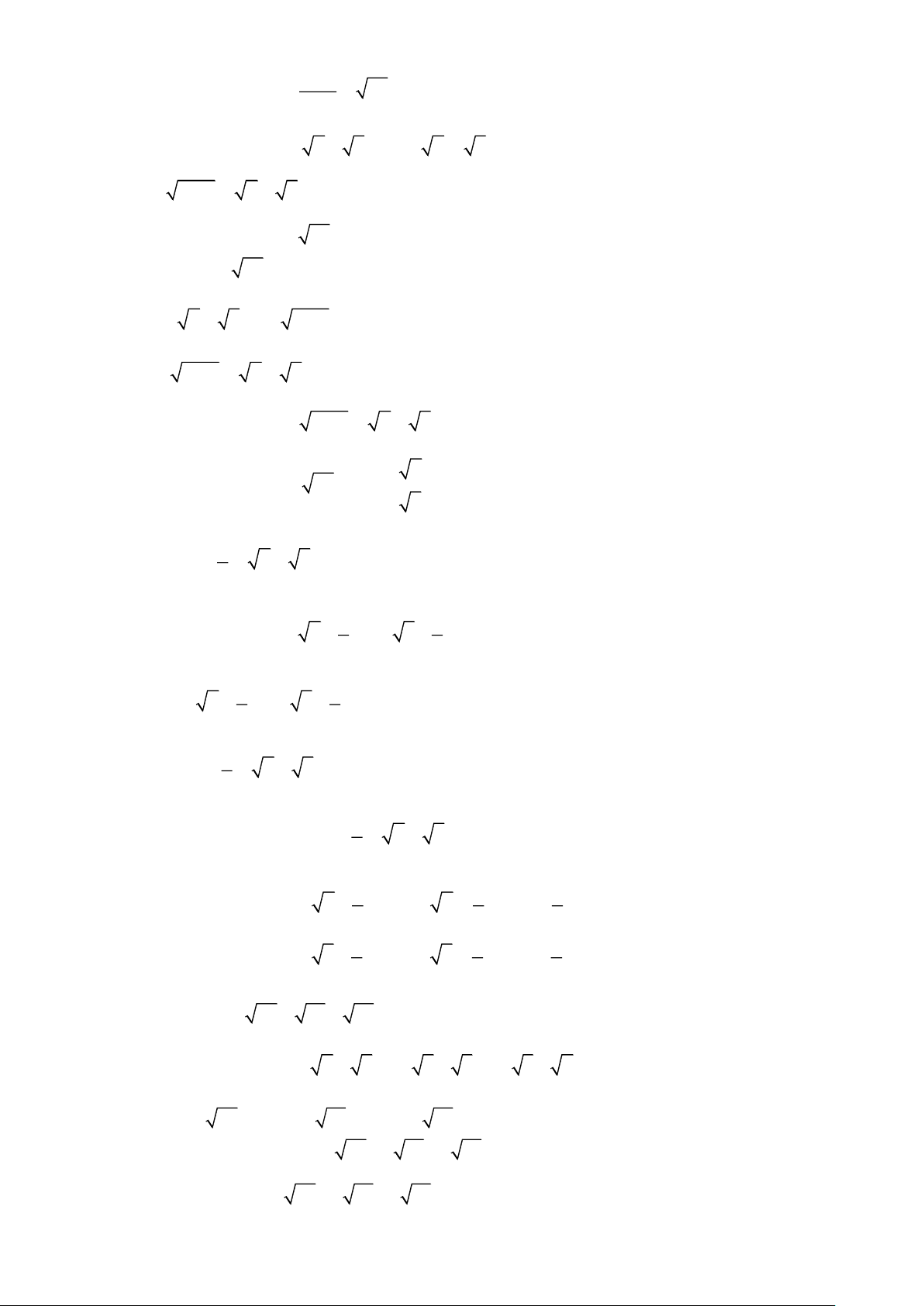
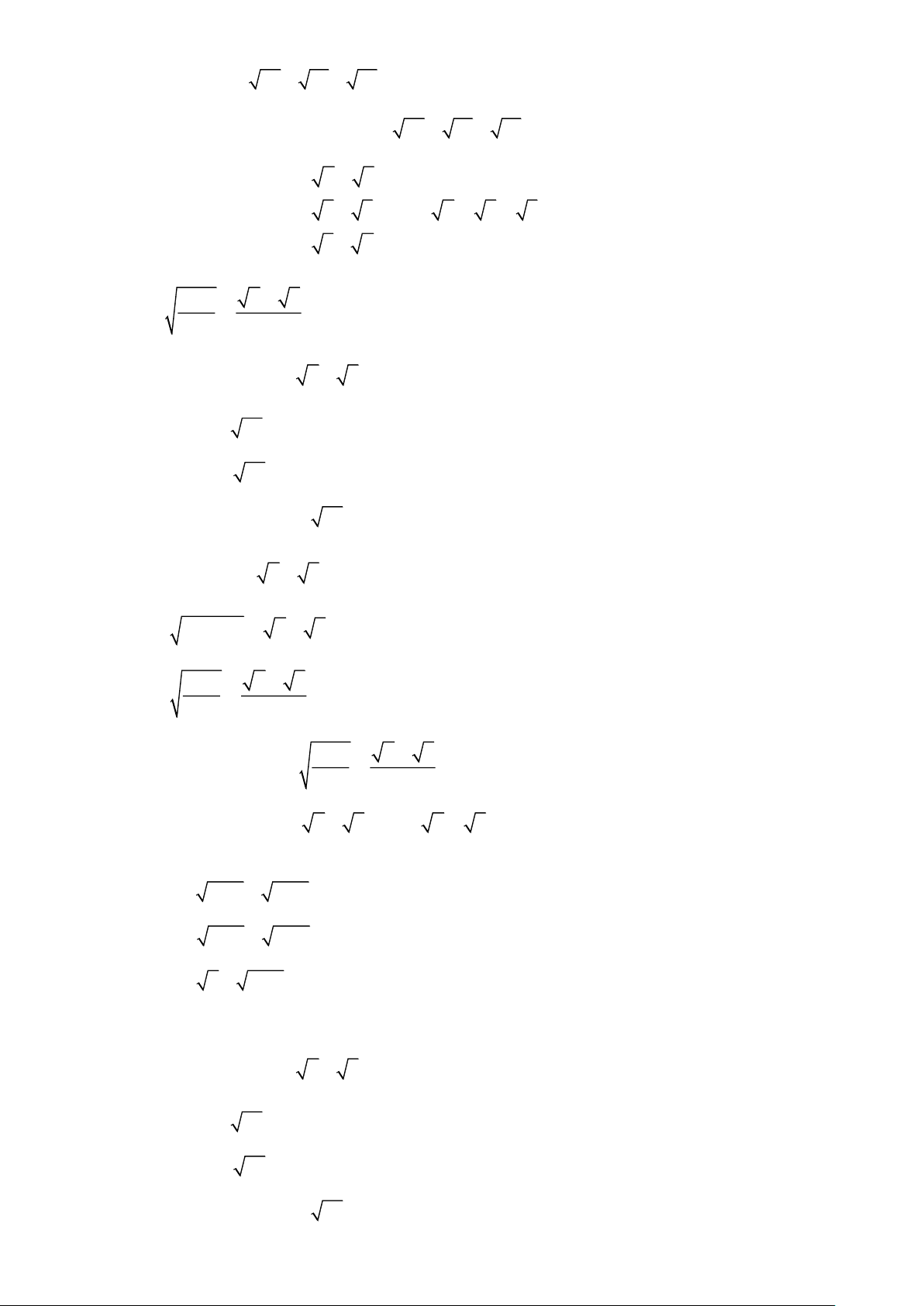


Preview text:
BÀI TẬP TOÁN 9 TUẦN 5
I. ĐẠI SỐ: BIẾN ĐỔI ĐƠN GIẢN BIỂU THỨC CHỨA CĂN BẬC HAI. Bài 1.
Giải phương trình: 1
a) 4x −12 + x − 3 − 9x − 27 = 8 3
b) 36x + 36 − 9x+9 + 4x + 4 = 42 − x +1 3 x − 6 1 c) = 7 x − 3 6 2 x +1 1 d) = x − 3 3 Bài 2.
Phân tích đa thức thành nhân tử ( ,
m n, a,b 0) .
a) mn +1+ m + n
b) a + b − 2 ab − 25
c) a − 4 a − 5
d) a − 5 a + 6 Bài 3. Tính giá trị
a) Lớn nhất của biểu thức A = 14 x − x
b) Nhỏ nhất của biểu thức B = x − 4 x +12 x + 2 Bài 4.
Tìm giá trị x nguyên để biểu thức A =
nhận giá trị nguyên. x − 5 Bài 5.
Cho các số không âm a , b , c . Chứng minh: a + b 1 a) ab .
b) a + b a + b .
c) a + b + a + b . 2 2 a + b a + b
d) a + b + c ab + bc + ca . e) . 2 2 Bài 6.
Tìm giá trị lớn nhất của các biểu thức sau:
a) A = x − 2 + 4 − x .
b) B = 6 − x + x + 2 .
c) C = x + 2 − x . II. HÌNH HỌC: Bài 1.
Cho tam giác ABC vuông ở A , AB = 6cm ; AC = 8cm . a) Tính BC , ˆ ˆ B,C .
b) Phân giác của  cắt BC tại D . Tính BD , CD .
c) Từ D kẻ DE và DF lần lượt vuông góc với AB , AC . Tứ giác AEDF là hình gì?
d) Tính chu vi và diện tích tứ giác AEDF . Bài 2.
Cho tam giác ABC cạnh AB = 6c ;
m AC = 4,5c ;
m BC = 7,5cm .
a) Chứng minh rằng tam giác ABC vuông. Tính góc B , góc C và đường cao AH của tam giác.
b) Tìm tập hợp các điểm M sao cho diện tích tam giác ABC bằng diện tích tam giác BMC . Bài 3.
Cho tam giác ABC vuông tại A , đường cao AH chia BC thành hai đoạn BH = 5c ,
m CH = 20cm . Chứng minh ˆ ˆ tgB = 4tgC . Trang 1
…………………………………….HẾT…………………………………….
HƯỚNG DẪN GIẢI CHI TIẾT I.
ĐẠI SỐ: BIẾN ĐỔI ĐƠN GIẢN BIỂU THỨC CHỨA CĂN BẬC HAI.
Bài 1: Giải phương trình: 1
a) 4x −12 + x − 3 − 9x − 27 = 8 3
b) 36x + 36 − 9x+9 + 4x + 4 = 42 − x +1 3 x − 6 1 c) = 7 x − 3 6 2 x +1 1 d) = x − 3 3 Lời giải a) ĐKXĐ: x 3 1 4x −12 + x − 3 − x − 27 = 8 3 1 2 +1−
x − 3 = 8 x − 3 = 3 x − 3 = 9 x = 12(TM ) 3 b) ĐKXĐ: x −1
36x + 36 − 9x + 9 + 4x+4 = 42 − x + 1 (6 − 3 + 2 + ) 1 x + 1 = 42
x +1 = 7 x +1 = 49 x = 48(TM ) 9
c) ĐKXĐ: x 0; x 49 6 x −
(3 x −6)−(7 x −3 3 6 1 ) = = x =
x = x = TM 7 x − 3 6 6(7 x − 3) 0 11 33 3 9( )
d) ĐKXĐ: x 0; x 9 3 x +
(2 x + )1−( x −3 2 1 1 ) = = x − 3 3( x − 3) 0 3 5 x = −6 (Vô lý vì 5 x 0 x 0; x 9 )
Vậy phương trình đãch o vô nghiệm.
Bài 2: Phân tích đa thức thành nhân tử ( ,
m n, a,b 0) . Trang 2
a) mn +1+ m + n .
b) a + b − 2 ab − 25
c) a − 4 a − 5 .
d) a − 5 a + 6 . Lời giải a)
mn +1+ m + n = ( mn + m) + ( n + ) 1 = ( n + ) 1 ( m + ) 1 b) Ta có:
a + b − 2 ab − 25 = (a + b − 2 ab ) − 25 = ( a − b)2 2
− 5 = ( a − b − 5)( a − b + 5)
c) a − 4 a − 5 = (a + a ) − (5 a + 5) = ( a + ) 1 ( a − 5)
d) a − 5 a + 6 = (a − 2 a ) − (3 a − 6) = ( a − 2)( a − 3)
Bài 3: Tính giá trị
a) Lớn nhất của biểu thức A = 14 x − x
b) Nhỏ nhất của biểu thức B = x − 4 x +12 . Lời giải
a) Ta có: A = −(x − x + )+ = −( x − )2 14 49 49 7 + 49 0 + 49 Do −( x − )2 7 0 x 0
Vậy GTLN của A = 49 dấu bằng xảy ra khi và chỉ khi x − 7 = 0 x = 49
b) Ta có: B = x − x +
= (x − x + ) + = ( x − )2 4 12 4 4 8 2 + 8 8 Vì ( x − )2 2 0 x 0
Vậy GTNN của B = 8 dấu bằng xảy ra khi và chỉ khi x − 2 = 0 x = 2 x = 4 . x + 2 Bài 4.
Tìm giá trị x nguyên để biểu thức A =
nhận giá trị nguyên. x − 5 Lời giải x 0 x 0 x 0
+) Điều kiện xác định: x −5 0 x 5 x 25 Trang 3 x + 2 x − 5 + 7 7 +) A = = =1+ x − 5 x − 5 x − 5
+) Trường hợp 1: Nếu x không là số chính phương
x − 5 là số vô tỉ 7 A = 1+ là số vô tỉ x − 5
A Z (loaïi)
+) Trường hợp 2: Nếu x là số chính phương 7 7 A = 1+ là số nguyên
là số nguyên x − 5Ö (7) x − 5 x − 5 x − 5 7 − 1 − 1 7 x −2 4 6 12 x loaïi 16 (thoûa maõn)
36 (thoûa maõn) 144 (thoûa maõn)
Vậy x = 16 , x = 36 , x = 144 là các giá trị cần tìm. Bài 5.
Cho các số không âm a , b , c . Chứng minh: a + b a) ab . 2
b) a + b a + b . 1
c) a + b + a + b . 2
d) a + b + c ab + bc + ca . a + b a + b e) . 2 2 Lời giải a + b a) ab . 2
Với a,b 0 ta có: ( a − b )2 0
a + b − 2 ab 0
a + b 2 ab a + b ab (ñpcm) 2 Trang 4 a + b
Vậy với a,b 0 thì ab . 2
Dấu " = " xảy ra khi a − b = 0 a = b a = b 0 .
b) a + b a + b .
Với a,b 0 ta có: 2 ab 0
a + b + 2 ab a + b ( + )2 ( + )2 a b a b
a + b a + b (ñpcm)
Vậy với a,b 0 thì a + b a + b . a = 0 a = 0
Dấu " = " xảy ra khi ab = 0 . b = 0 b = 0 1
c) a + b + a + b . 2 2 2 1 1
Với a,b 0 ta có: a − + b − 0 2 2 1 1
a − a + + b − b + 0 4 4 1
a + b + a + b (ñpcm) 2 1
Vậy với a,b 0 thì a + b + a + b . 2 1 1 1 a − = 0 a = a = 2 2 4 Dấu " = " xảy ra khi 1 1 1 b 0 b b − = = = 2 2 4
d) a + b + c ab + bc + ca . 2 2 2 Với a, ,
b c 0 ta có: ( a − b) +( b − c ) +( c − a ) 0
a − 2 ab + b + b − 2 bc + c + c − 2 ca + a 0
a + b + b + c + c + a 2 ab + 2 bc + 2 ca
2(a + b + c) 2 ab + 2 bc + 2 ca Trang 5
a + b + c ab + bc + ca (ñpcm) Vậy với a, ,
b c 0 thì a + b + c ab + bc + ca . a − b = 0
Dấu " = " xảy ra khi b − c = 0 a = b = c a = b = c c − a = 0 a + b a + b e) . 2 2
Với a,b 0 ta có: ( a − b )2 0
a + b − 2 ab 0
a + b 2 ab
2(a + b) a + b + 2 ab ( + ) ( + )2 2 a b a b
2(a + b) a + b a + b a + b (ñpcm) 2 2 a + b a + b
Vậy với a,b 0 thì . 2 2
Dấu " = " xảy ra khi a − b = 0 a = b a = b 0 . Bài 6.
Tìm giá trị lớn nhất của các biểu thức sau:
a) A = x − 2 + 4 − x .
b) B = 6 − x + x + 2 .
c) C = x + 2 − x . Lời giải
Với a,b 0 ta có: ( a − b )2 0
a + b − 2 ab 0
a + b 2 ab
2(a + b) a + b + 2 ab Trang 6 ( + ) ( + )2 2 a b a b
2(a + b) a + b
Vậy với a,b 0 thì 2(a + b) a + b . Dấu " = " xảy ra khi a = b 0 . ( ) 1
a) A = x − 2 + 4 − x . x − 2 0 x 2
+) Điều kiện xác định: 2 x 4 4 − x 0 x 4 +) Áp dụng ( )
1 ta có: A = x − 2 + 4 − x 2( x − 2 + 4 − x) A 2 2 x 4
Vậy giá trị lớn nhất của A là 2 , dấu bằng xảy ra khi và chỉ khi x = 3.
x − 2 = 4 − x
b) B = 6 − x + x + 2 . 6 − x 0 x 6
+) Điều kiện xác định: 2 − x 6 x + 2 0 x 2 − +) Áp dụng ( )
1 ta có: B = 6 − x + x + 2 2(6 − x + x + 2) B 4 2 − x 6
Vậy giá trị lớn nhất của B là 4 , dấu bằng xảy ra khi và chỉ khi x = 2
6 − x = x + 2
c) C = x + 2 − x . x 0 x 0
+) Điều kiện xác định: 0 x 2 2 − x 0 x 2 +) Áp dụng ( )
1 ta có: C = x + 2 − x 2( x + 2 − x) C 2 0 x 2
Vậy giá trị lớn nhất của C là 2 , dấu bằng xảy ra khi và chỉ khi x =1. x = 2 − x II. HÌNH HỌC: Bài 1.
Cho tam giác ABC vuông ở A , AB = 6cm ; AC = 8cm . a) Tính BC , ˆ ˆ B,C .
b) Phân giác của  cắt BC tại D . Tính BD , CD .
c) Từ D kẻ DE và DF lần lượt vuông góc với AB , AC . Tứ giác AEDF là hình gì? Trang 7
d) Tính chu vi và diện tích tứ giác AEDF . Lời giải A F E C B D
a) Theo định lý Py-ta-go ta có 2 2 2 2 2 2 2
BC = AB + AC BC = AB + AC = 6 + 8 = 10cm . AB 6 3 ' ' ' ˆ ˆ ˆ sinC = = = C 36 5
2 B 90 − 36 5 2 = 53 8 . BC 10 5
b) Theo tính chất của đường phân giác ta có: BD AB 6 3 BD 3 BD 3 30 = = = = = BD = cm . CD AC 8 4 CD + BD 4 + 3 BC 7 7 30 40
CD = BC − BD = 10 − = cm . 7 7
c) Tứ giác AEDF có ˆ ˆ ˆ
A = E = F = 90 nên AEDF là hình chữ nhật. Lại có đường chéo AD
đồng thời là tia phân giác nên AEDF là hình vuông. d) Ta có
DE ⊥ AB DE// AC . AC ⊥ AC Theo định lý Talet : BD ED BD 30 / 7 24 = ED = .AC = .8 = cm . BC AC BC 10 7 24 96
Chu vi hình vuông AEDF : P = .4 = cm . 7 7 2 24 576
Diện tích hình vuông AEDF : 2 S = = cm . 7 49 Bài 2.
Cho tam giác ABC cạnh AB = 6c ;
m AC = 4,5c ;
m BC = 7,5cm .
a) Chứng minh rằng tam giác ABC vuông. Tính góc B , góc C và đường cao AH của tam giác.
b) Tìm tập hợp các điểm M sao cho diện tích tam giác ABC bằng diện tích tam giác BMC . Lời giải Trang 8 A M C K B H a) Ta có: 2 2 2 2
AB + AC = 6 + 4,5 = 56, 25 2 2 BC = 7,5 = 56, 25 2 2 2
BC = AB + AC ABC vuông tại A. AC 4,5 3 ' ' ˆ ˆ ˆ sin B = = = B 36 5 2 C 53 8 . BC 7,5 5 A . B AC 6.4,5 AH.BC = AB.AC AH = = = 3,6cm . BC 7,5 b) Phần thuận:
Kẻ MK vuông góc với BC tại K . Ta có 1 S = AH.BC ABC 2 1 S = MK.BC M BC 2 = = = S S AH MK 3,6cm . A BC A BC
Vậy M di chuyển trên đường thẳng d song song với BC , cách BC một khoảng bằng AH hay 3,6 cm. Phần đảo
Lấy điểm M d . Kẻ M K
⊥ BC . Vì d cách BC một khoảng bằng AH nên M K = AH . 1 1 Do đó S = = = . M K .BC AH.BC S M BC 2 2 A BC Kết luận:
Tập hợp các điểm M sao cho diện tích tam giác ABC bằng diện tích tam giác BMC là đường thẳng
song song với BC , cách BC một khoảng bằng AH hay 3,6 cm. Có 2 đường thẳng như thế. Bài 3.
Cho tam giác ABC vuông tại A , đường cao AH chia BC thành hai đoạn BH = 5c ,
m CH = 20cm . Chứng minh ˆ ˆ tgB = 4tgC . Lời giải Trang 9 A B 5 20 H C AH AH
Trong tam giác vuông HAB ta có ˆ tgB = = BH 5 AH AH
Trong tam giác vuông HAC ta có ˆ tgC = = CH 20 Do đó ˆ ˆ tgB = 4tgC . HẾT Trang 10




