Bài tập trắc nghiệm cực trị hình học trong số phức Toán 12

Bài tập trắc nghiệm cực trị hình học trong số phức Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Số phức

Môn: Toán 12

Thông tin:

56 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
Vấn đề 1. Điểm và đường thẳng
Câu 1. Xét các số phức
, zw
thỏa mãn
22 4z izi
và
1.w iz
Giá trị nhỏ nhất của
w
bằng
A.
2
.
2
B.
32
.
2
C.
2.
D.
2 2.
Câu 2. Xét các số phức
thỏa mãn
1 2.zz i 
Giá trị nhỏ nhất của biểu thức
12 112P iz i 
bằng
A.
5
.
2
B.
5
.
2
C.
2
.
5
D.
5
.
2
Câu 3. Xét các số phức
thỏa mãn
1 3.z i zi
Môđun lớn nhất của số phức
1
w
z
là
A.
25
.
7
B.
45
.
7
C.
95
.
10
D.
75
.
10
Câu 4. Xét các số phức
thỏa mãn

2
2 5 1 2 3 1.z z z iz i 
Giá trị nhỏ nhất của
biểu thức
22Pz i 
bằng
A.
1.
B.
3
.
2
C.
5
.
2
D.
5.
Câu 5. Xét các số phức
thoã mãn
2 1 2.
ziz i 
Gọi
w
là số phức thoã mãn điều kiện
1 2.
w iz

Giá trị nhỏ nhất của biểu thức
Pw
bằng
A.
1
.
3
B.
1
.
5
C.
5
.
34
D.
5
.
41
Câu 6. Xét các số phức
, zw
thỏa mãn
13 2z izi
và
1 3 2.w i wi
Giá trị nhỏ
nhất của biểu thức
P zw
là
A.
13 1
.
2
B.
26
.
4
C.
3
.
13
D.
3 26
.
13
Vấn đề 2. Điểm và đường tròn
Câu 1. Xét các số phức
thỏa mãn
11iz
. Gọi
, mM
lần lượt là giá trị nhỏ nhất và giá
trị lớn nhất của biểu thức
.Pz
Tính
2020 .S Mm 
A.
2014.S
B.
2016.
S
C.
2018.S
D.
2022.S
Câu 2. Xét các số phức
thỏa mãn
23 1zi
. Giá trị lớn nhất và giá trị nhỏ nhất của
biểu thức
1Pz i

lần lượt là
A.
13 2
và
13 2
. B.
13 1
và
13 1
.
C.
và
. D.
13 4
và
13 4
.
Câu 3. Xét các số phức
thỏa mãn
1 1 7 2.iz i

Gọi
, mM
lần lượt là giá trị nhỏ
nhất và giá trị lớn nhất của
.
Pz
Tính
.S Mm
A.
2.S
B.
4.S
C.
10.S
D.
24.S
Câu 4. Xét các số phức
, zw
thỏa mãn
1
21
1
iz
i

và
.w iz
Giá trị lớn nhất của biểu
thức
P zw
bằng
A.
B.
23
C.
32
D.
33
Câu 5. Xét các số phức
12
, zz
thỏa mãn
1
11zi
và
21
2.z iz
Giá trị nhỏ nhất của biểu
thức
12
2P zz
bằng
A.
2 2.
B.
2 2 2.
C.
4 2 2.
D.
8 2.
Câu 6. Xét các số phức
thỏa mãn
không phải là số thực và
2
2
z
w
z
là số thực. Tìm
giá trị lớn nhất
max
P
của biểu thức
1.Pz i 
A.
max
2.
P
B.
max
2.P
C.
max
2 2.P
D.
max
8.
P
Câu 7. Xét các số phức
thỏa mãn
2z
. Biểu thức
zi
P
z
đạt giá trị nhỏ nhất và giá
trị lớn nhất lần lượt tại
1
z
và
2
z
. Tìm phần ảo
của số phức
12
.wz z
A.
4.a 
B.
0.a
C.
1.a
D.
4.a
Câu 8. Xét các số phức
thỏa mãn
1.z
Gọi
, Mm
lần lượt là giá trị lớn nhất và nhỏ nhất
của
2
.
2
zi
P
z
Tỉ số
M
m
bằng
A.
5 32
.
4
B.
9 42
.
7
C.
10 6 34
.
9
D.
25 4 34
.
9
Câu 9. Xét hai số phức
12
, zz
thay đổi thỏa mãn
12 12
4 2 2.
zz zz i 
Gọi
,
AB
lần
lượt là giá trị nhỏ nhất và giá trị lớn nhất của biểu thức
22
12
.zz
Giá trị của
AB
là
A.
20.
B.
24.
C.
28.
D.
32.
Câu 10. Xét các số phức
, z
thỏa mãn
|| 5z
và
4 3 1 2.
iz i

Giá trị nhỏ nhất của
||
bằng
A.
3 5.
B.
4 5.
C.
5 5.
D.
6 5.
Câu 11. Cho số phức
thỏa mãn đồng thời
12 5zi
và
1zi 
có môđun lớn
nhất. Số phức
z
có môđun bằng
A.
6.
B.
2 5.
C.
3 2.
D.
5 2.
Câu 12. Xét các số phức
thỏa mãn
2 4 2 2.zi
Trong các số phức
w
thỏa mãn
1,wz i
gọi
1
w
và
2
w
lần lượt là số phức có môđun nhỏ nhất và môđun lớn nhất. Khi đó
12
ww
bằng
A.
2 6.i
B.
2 4.
i
C.
4 12 .i
D.
4 8.i
Câu 13. Xét các số phức
thỏa
1 2 25zi

và số phức
thỏa
5 10 3 4 25 .i iz i 
Tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
P
bằng
A.
2 10.
B.
4.
C.
4 5.
D.
6.
Câu 14. Xét các số phức
thỏa mãn
2
.
zz zz z
Giá trị lớn nhất của biểu thức
52Pz i 
bằng
A.
2 3 5.
B.
2 5 3.
C.
5 2 3.
D.
5 3 2.
Vấn đề 3. Đường thẳng và đường tròn
Câu 1. Xét các số phức
1
z
thỏa mãn
22
11
21z zi
và các số phức
2
z
thỏa mãn
2
45zi
. Giá trị nhỏ nhất của
12
Pzz
bằng
A.
5.
B.
2 5.
C.
25
.
5
D.
35
.
5
Câu 2. Gọi
1
C
là tập hợp các số phức
w
thỏa mãn
2 3 3 2.wiwi 
Gọi
2
C
là tập
hợp các số phức
thỏa mãn
2 4 1.zi
Giá trị nhỏ nhất của biểu thức
P wz
bằng
A.
23 1
. B.
23 1
. C.
32 1
. D.
32 1
.
Câu 3. Xét các số thức
thỏa mãn
24zizi

và
3 3 1.zi
Giá trị lớn nhất của biểu
thức
21Pz
bằng
A.
5 2.
B.
10
C.
10 1.
D.
13 1.
Câu 4. Xét các số phức
, zw
thỏa mãn
22 1iz i z

và
max 2 2 , 2.w iw
Giá trị
nhỏ nhất của biểu thức
P zw

bằng
A.
1
.
25
B.
5
.
2
C.
9
.
25
D.
13
.
25
Câu 5. Xét các số phức
, zw
thỏa mãn
max ; 1 1
.
12 2
zz i
w iw i


Giá trị nhỏ nhất của biểu thức
P zw

bằng
A.
0.
B.
1
.
6
C.
2 1.
D.
2 2 1.
Câu 6. Kí hiệu
S
là tập hợp các số phức
thỏa mãn
1 34z 
và
12z mi z m i
(trong đó
m
). Gọi
12
, zz
là hai số phức thuộc tập hợp
S
sao cho
12
zz
là lớn nhất. Khi
đó, hãy tính giá trị của biểu thức
12
.zz
A.
12
2.
zz
B.
12
2.
zz
C.
12
10.
zz
D.
12
130.zz

Câu 7. Biết số phức
;z x yi x y
thỏa mãn đồng thời
34 5zi
và biểu thức
22
2P z zi 
đạt giá trị lớn nhất. Tính
z
.
A.
33z
. B.
50z
. C.
10z
. D.
52
z
.
Câu 8. Xét các số phức
thỏa mãn
1 3 13.zi

Gọi
, mM
lần lượt là giá trị nhỏ nhất và
lớn nhất của biểu thức
22
2 3.
Pz zi 
Tổng
mM
bằng
A.
10.
B.
25.
C.
34.
D.
40.
Câu 9. Xét các số phức
;z x yi x y
thỏa mãn
1 2 4.iz i 
Giá trị lớn nhất của
biểu thức
3T xy 
bằng
A.
4.
B.
4 2.
C.
4 2 2.
D.
8.
Câu 10. Xét các số phức
thỏa mãn
| 2 1 2.zi 
Giá trị nhỏ nhất của biểu thức
| 1 2| | 3 4| | 5 6|Pz iz iz i  
được viết dưới dạng
,ab
với
a
b
là phân số tối giản.
Giá trị của
ab
bằng
A.
10.
B.
11.
C.
12.
D.
17.
Câu 11. Xét các số phức
12
,
zz
thoả mãn
1 22
3 4 1, 1z i z zi
và
12
2
zz
i
là số thực.
Gọi
, Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
12
.zz
Tính
P Mm
.
A.
14 5.P
B.
16 5.P
C.
18 5.P
D.
20 5.P
Câu 12. Cho
1
z
là số phức,
2
z
là số thực thoả mãn
1
21zi
và
21
1
zz
i
là số thực. Tổng giá
trị lớn nhất và giá trị nhỏ nhất của biểu thức
12
Pzz
là
A.
2.
B.
2 2.
C.
32
D.
4 2.
Câu 13. Cho
z x yi

,xy
là số phức thỏa mãn
2 3 2 5.z i zi 
Gọi
, Mm
lần lượt là giá trị lớn nhất và nhỏ nhất của
22
8 6.Px y x y
Giá trị
Mm
bằng
A.
156
2 10.
5
B.
156
2 10.
5
C.
60 20 10.
D.
60 20 10.
Vấn đề 4. Đường tròn và đường tròn
Câu 1. Xét các số phức
12
, zz
thỏa mãn
1
41z 
và
2
2 1.iz 
Giá trị nhỏ nhất của biểu
thức
12
2Pz z
bằng
A.
2 5 2.
B.
4 2.
C.
4 2 3.
D.
4 2 3.
Câu 2. Xét các số phức
12
,
zz
thỏa mãn
1
352zi
và
2
1 2 4.
iz i

Giá trị lớn nhất của
biểu thức
12
23P iz z
bằng
A.
313 16.
B.
313.
C.
313 8.
D.
313 2 5.
Câu 3. Xét các số phức
12
, zz
thỏa mãn
1
12z
và
2
3 4 5.zi
Giá trị nhỏ nhất của biểu
thức
12
Pzz
bằng
A.
0.
B.
2.
C.
7.
D.
17.
Câu 4. Có bao nhiêu giá trị của tham số
m
để tồn tại duy nhất số phức
thỏa mãn
.1zz
và
3z im 
?
A.
0.
B.
1.
C.
2.
D.
3.
Câu 5. Gọi
S
là tập hợp các số phức
thỏa mãn
3zi
và
15z 
. Gọi
12
, zz S
lần
lượt là các số phức có mođun nhỏ nhất và lớn nhất. Khẳng định nào sau đây đúng ?
A.
12
2 12 2 .

zz i
B.
12
2 2 12 .  zz i
C.
12
2 6 4. zz i
D.
12
2 12 4 . zz i
Câu 6. Xét các số phức
thỏa mãn
1 2 4.zi 
Gọi
M
là giá trị lớn nhất của
23zi
,
m
là giá trị nhỏ nhất của
22zi
. Tính
.
Mm
A.
3.Mm

B.
5.
Mm

C.
6.Mm
D.
7.Mm
Câu 7. Xét các số phức
thỏa mãn
2 25
.
4 22
zi
zi


Giá trị lớn nhất của
14Tz i 
bằng
A.
3 2.
B.
3 5.
C.
5 2.
D.
6.
Câu 8. Xét các số phức
,z x yi x y
thỏa mãn
11
.
33 5
zi
zi


Gọi
, mM
lần lượt là
giá trị nhỏ nhất và giá trị lớn nhất của biểu thức
2.Px y
Tỉ số
M
m
bằng
A.
5
.
4
B.
7
.
2
C.
9
.
4
D.
14
.
5
Câu 9. Xét các số phức
;z x yi x y
thỏa mãn
13
.
3 4 10
zi
zi


Giá trị nhỏ nhất của
biểu thức
3
Px y
bằng
A.
5.
B.
7.
C.
13.
D.
4 3 10.
Vấn đề 5. Parabol
Câu 1. Xét các số phức
,z a bi a b
thỏa
2
4 15 1 .z z i iz z 
Tính
4P ab
khi
1
3
2
zi
đạt giá trị nhỏ nhất.
A.
4.
P
B.
5.P
C.
6.
P
D.
7.P
Câu 2. Xét hai số phức
12
, zz
thỏa mãn
1 11
22
zi zz i
và
2
10 1.zi
Giá trị nhỏ
nhất của biểu thức
12
zz
bằng
A.
10 1.
B.
3 5 1.
C.
101 1.
D.
101 1.
Vấn đề 6. Đoạn thẳng – tia
Câu 1. Xét các số phức
thỏa mãn
2 4 7 6 2.z iz i 
Gọi
, mM
lần lượt là giá trị
nhỏ nhất và giá trị lớn nhất của
1zi
. Tính
.P mM

A.
13 73P 
. B.
52 273
2
P
. C.
52 273P 
. D.
5 2 73
2
P
.
Câu 2. Xét các số phức
thỏa mãn
1 8 3 53.
z iz i

Giá trị lớn nhất của biểu thức
12Pz i 
bằng
A.
53.
B.
53.
C.
185
.
2
D.
106.
Câu 3. Xét các số phức
thỏa mãn
2 3 6 2 17.z iz i 
Gọi
,
Mm
lần lượt là giá trị
lớn nhất và giá trị nhỏ nhất của biểu thức
12 2P z iz i 
.
A.
3 2, 0.Mm
B.
3 2, 2.Mm
C.
32, 52 25.Mm 
D.
2, 5 2 2 5.Mm 
Câu 4. Xét các số phức
thỏa mãn
3 2 3 3 5.
z iz i 
Gọi
,
Mm
lần lượt là giá trị
lớn nhất và giá trị nhỏ nhất của biểu thức
2 13Pz z i 
.
A.
17 5, 3 2.Mm
B.
26 2 5, 3 2.Mm

C.
26 2 5, 2.Mm
D.
17 5, 2.
Mm

Câu 5. Xét các số phức
12
,
zz
thỏa
11 2
5
1 2 3 3 2 1 17.
2
ziziz i 
Giá trị lớn
nhất của
12 1
2Pzz z i 
bằng
A.
2 17.
B.
3 29.
C.
17 29.
D.
17 2 29.
Câu 6. Xét các số phức
thỏa mãn
2 2 1 3 34.
iz i z i 
Giá trị nhỏ nhất của biểu
thức
12
P iz i

bằng
A.
9
.
17
B.
3 2.
C.
4 2.
D.
26.
Câu 7. Xét các số phức
đồng thời thỏa mãn
43 43 10z iz i
 
và
34zi
nhỏ
nhất. Môđun của số phức
bằng
A.
5.
B.
5 2.
C.
6 2.
D.
10.
Câu 8. Xét các số phức
z a bi
,ab
thỏa mãn
1 2 3.z izi
Tính
P ab
khi
34 1T z iz i 
đạt giá trị lớn nhất.
A.
2.
P
B.
6.
P
C.
26
.
3
P
D.
28
.
3
P
Câu 9. Xét các số phức
thỏa mãn
2 2.z zi
Giá trị nhỏ nhất của biểu thức
12 34 56Pz iz iz i  
được viết dưới dạng
17
2
ab
với
, .ab
Tính
.ab
A.
2.ab

B.
3.ab
C.
4.ab

D.
7.ab
Câu 10. Xét các số phức
12
, zz
đồng thời thỏa mãn
12 3 2z iz i
và
12
5.zz
Giá
trị nhỏ nhất của biểu thức
12
13 13
z iz i 
bằng
A.
14 5
.
5
B.
3 85
.
5
C.
1105
.
5
D.
1165
.
5
Vấn đề 7. Phương pháp lấy đối xứng
Câu 1. Xét các số phức
;
z a bi a b

thỏa mãn
5 3 1 5.z iz i 
Tính
ab
khi
biểu thức
22 37Pz iz i 
đạt giá trị nhỏ nhất.
A.
1.
ab 
B.
0.ab
C.
1.
ab
D.
2.
ab
Câu 2. Xét các số phức
12
, , zz z
thỏa mãn
12
45 1 1
z iz
và
4 8 4.ziz i 
Tính
12
M zz
khi
12
P zz zz

đạt giá trị nhỏ nhất.
A.
2 5.M
B.
6.
M
C.
41.M
D.
8.M
Câu 3. Xét các số phức
12
, zz
thỏa mãn
1
32 1zi
và
2
2 1.
zi
Số phức
có phần
thực bằng
, phần ảo bằng
thỏa mãn
2 0.ab

Tính
Pab
khi
12
2zz z z 
đạt
giá trị nhỏ nhất.
A.
1.P
B.
3.
P
C.
4.P
D.
7.P
Câu 4. Xét các số phức
12
, zz
thỏa mãn
11
53 13z iz i

và
22
4 3 2 3.z iz i 
Giá trị nhỏ nhất của biểu thức
12 1 2
66Pzz z i z i
bằng
A.
2 10.
B.
7
.
2
C.
4 130
.
13
D.
18
.
13
Vấn đề 8. Tâm tỉ cự
Câu 1. Xét các số phức
thỏa mãn
| 5 | |2 3 |.
zi i
Đặt
22
39 15.
Pz i z i 
Biết
P
đạt giá trị nhỏ nhất tại
1
z
và
P
đạt giá trị lớn nhất tại
2
.z
Giá trị của biểu thức
12
zz
bằng
A.
2 13.
B.
2 15.
C.
4 3.
D.
52.
Câu 2. Xét các số phức
thỏa mãn
1 2 3 2.zi
Gọi
, mM
lần lượt là giá trị nhỏ nhất và
lớn nhất của biểu thức
22
32 2 2 .Pz i z i 
Tổng
mM
bằng
A.
30.
B.
12.
C.
14.
D.
68.
Câu 3. Xét các số phức
z ai
,ab
thỏa mãn
4 3 5.zi
Tính
ab
khi biểu thức
2 22
22 2 4 3 2Qz i z i z i  
đạt giá trị lớn nhất.
A.
11.ab
B.
12.
ab
C.
13.ab
D.
14.ab
Câu 4. Xét các số phức
12
, zz
thỏa mãn
34 2zi
và
12
1.zz
Giá trị nhỏ nhất của
biểu thức
22
12
Pz z
bằng
A.
4 3 5.
B.
6 2 5.
C.
5.
D.
10.
Vấn đề 9. Phương pháp cân bằng hệ số
Câu 1. Xét các số phức
thỏa mãn
1.z
Giá trị lớn nhất của
12 1Tz z 
bằng
A.
2 5.
B.
2 10.
C.
3 2.
D.
3 5.
Câu 2. Xét các số phức
thỏa
1 2.z 
Giá trị lớn nhất của
2T zi z i 
bằng
A.
4.
B.
4 2.
C.
8.
D.
8 2.
Câu 3. Xét các số phức
z a bi
;ab
có môđun bằng
và phần ảo dương. Tính giá trị
biểu thức
2018
52S ab



khi biểu thức
2 32Pz z
đạt giá trị lớn nhất.
A.
0.S
B.
1.S
C.
2018
2.S
D.
1009
2.S
Câu 4. Xét các số phức
thỏa mãn
11
.
3
2
z
zi
Gọi
,
Mm
lần lượt là giá trị lớn nhất và
nhỏ nhất của
2 4 7.P zi z i  
Giá trị
Mm
bằng
A.
10 2 5.
B.
10 4 5.
C.
20 2 5.
D.
20 4 5.
Câu 5. Xét số phức
thỏa mãn
1 2 2 2.zi
Với
, ab
là số thực dương cho trước, giá trị
lớn nhất của biểu thức
1 34
P az bz i 
bằng
A.
22
.ab
B.
22
2 2.ab
C.
22
42 2 .ab
D.
22
.
ab
Câu 6. Xét các số phức
,z a bi a b
thỏa mãn
4 3 5.zi
Tính
ab
khi biểu
thức
13 1Pz iz i
 
đạt giá trị lớn nhất.
A.
4.ab
B.
6.ab
C.
8.ab
D.
10.ab
Câu 7. Xét các số phức
,z a bi a b
thỏa mãn
4 3 2 2.
zi
Tính
2ab
khi biểu
thức
12 96
Pz iz i

đạt giá trị lớn nhất.
A.
2 7.ab
B.
2 9.ab

C.
2 12.ab
D.
2 13.ab
Câu 8. Xét các số phức
thỏa mãn
2 2 1.zi
Giá trị lớn nhất của biểu thức
32 2 2 4Pz i z i 
bằng
A.
5.
B.
2 5.
C.
3 15.
D.
10.
Câu 9. Xét các số phức
thoả mãn
2 2 2.zi
Gọi
,
Mm
lần lượt là giá trị lớn nhất, giá
trị nhỏ nhất của biểu thức
3 2 3 4.
Pz iz i  
Tính
.
Mm
A.
226 62.
Mm
B.
2 26 8 2.
Mm
C.
11 2.Mm
D.
16 2.Mm
Câu 10. Xét các số phức
,
z a bi a b
thỏa mãn
3 2 2.zi
Tính
ab
khi biểu thức
12 2 25Tz i z i 
đạt giá trị nhỏ nhất.
A.
3.ab
B.
2 3.ab
C.
4 3.ab
D.
4 3.ab
Câu 11. Xét các số phức
,z a bi a b
thỏa mãn
2.z
Tính
ab
khi biểu thức
4 2 14Pz z i 
đạt giá trị nhỏ nhất.
A.
2.ab

B.
2.
ab
C.
2 5.ab
D.
4 5.ab
Câu 12. Xét các số phức
thỏa mãn điều kiện
1.zi
Giá trị nhỏ nhất của biểu thức
2 2 23
Pz i z i 
bằng
A.
43
.
3
B.
2.
C.
3.
D.
3.
Câu 13. Xét các số phức
thỏa mãn điều kiện
1 5.zi
Giá trị lớn nhất của biểu thức
2 8 79P ziz i 
bằng
A.
5
.
2
B.
53
.
2
C.
55
.
2
D.
5 5.
Câu 14. Xét các số phức
thỏa
1.z
Giá trị lớn nhất của biểu thức
22 2Tz z
bằng
A.
2.
B.
2 5.
C.
5.
D.
5 2.
Câu 15. Xét các số phức
thỏa mãn
2 1 3 2.zi
Giá trị lớn nhất của biểu thức
1 3 12Pz z i 
bằng
A.
2 2.
B.
4.
C.
4 2.
D.
4 3.
Câu 16. Cho số phức
z a bi

,ab
thỏa mãn
3 3 6.zi
Tính
ab
khi biểu thức
2 63 3 15Pz iz i 
đạt giá trị nhỏ nhất.
A.
2 2 5.ab
B.
2 5 2.ab
C.
2 5 4.ab
D.
4 2 5.ab
Vấn đề 10. Elip
Câu 1. Xét các số phức
thỏa mãn
4 4 10zz
. Giá trị lớn nhất và nhỏ nhất của
z
lần lượt là
A.
10
và
4.
B.
và
4.
C.
và
3.
D.
và
3.
Câu 2. Xét các số phức
thỏa mãn
22
4.
11
iz iz
ii


Gọi
M
và
lần lượt là giá trị
lớn nhất và giá trị nhỏ nhất của
.z
Tính
..Mn
A.
. 1.Mn
B.
. 2.
Mn
C.
. 2 2.Mn
D.
. 2 3.Mn
Câu 3. Xét số phức
thỏa mãn
2 1 2 1 10.zi zi  
Gọi
M
và
m
là giá trị lớn
nhất và giá trị nhỏ nhất của
.
z
Tính tổng
.SMm

A.
17.S
B.
2 21.S
C.
8.
S
D.
9.
S
Câu 4. Xét các số phức
thoả mãn
1 3 6.z iz i
Tìm giá trị nhỏ nhất
min
P
của
biểu thức
1 4.Pz i 
A.
min
2 5 2.P 
B.
min
2 5 2.
P

C.
min
5 2.P 
D.
min
5 2.P 
Câu 5. Xét các số phức
thỏa
1 1 3 6 5.z iz i
Giá trị lớn nhất của
23Pz i 
bằng
A.
2 5.
B.
4 5.
C.
5 5.
D.
6 5.
---------- HẾT ----------
Cực trị Hình học trong
SOÁ PHÖÙC
1) Điểm và đường thẳng…………………………………………………………....…………… 00
2) Điểm và đường tròn ……………………………………………………………………………. 00
3) Đường thẳng và đường tròn ………………………………………….…………..……. 00
4) Đường tròn và đường tròn ……………………………………………….………….….. 00
5) Parabol………………………………………………………………………………….…………….….… 00
6) Đoạn thẳng – tia ……………………………………………………………….………………..… 00
7) Phương pháp lấy đối xứng …………………………………………….………………… 00
8) Tâm tỉ cự ………………………………………………………………………………….…………..…. 00
9) Phương pháp cân bằng hệ số ……………………………………….…………….….. 00
10) Elip ………………………………………………………………………………………….………………. 00
Vấn đề 1. Điểm và đường thẳng
Câu 1. Xét các số phức
, zw
thỏa mãn
22 4z izi
và
1.w iz
Giá trị nhỏ nhất của
w
bằng
A.
2
.
2
B.
32
.
2
C.
2.
D.
2 2.
Lời giải. Đặt
z x yi
,xy
và
;M xy
là điểm biểu diễn số phức
.z
Từ
22 2
2
22 4 2 2 4 2
z i z i x y x y xy  
tập hợp điểm
M
là đường thẳng
: 2.xy 
Ta có
1P w iz i z i z i MN 
với
0;1 .N
Dựa vào hình vẽ ta thấy
min min
012
2
,.
2
2
P MN d N


Chọn A.
Cách 2. Đặt
; .z x yi x y
Từ
22 4 2 .z izi y x 
Khi đó
1 1 1 2 1 1.w iz i x yi ix y ix x x xi    
Suy ra
2
2
2
112
12 .
2 22
wx x x



Câu 2. Xét các số phức
thỏa mãn
1 2.zz i 
Giá trị nhỏ nhất của biểu thức
12 112
P iz i 
bằng
A.
5
.
2
B.
5
.
2
C.
2
.
5
D.
5
.
2
Lời giải. Đặt
z x yi
,xy
và
;M xy
là điểm biểu diễn số phức
.z
Từ
22
22
12 1 2 2 4 5zz i xy x y x y
 
tập hợp điểm
M
là
đường thẳng
: 2 4 5.
xy

Ta có
11 2
12 112 12 5 34 5
12
i
P i z i i z z i MN
i
 
với
3; 4 .N
Dựa vào hình vẽ ta thấy
min min min
2. 3 4.4 5
5
5. , 5 .
2
20
P MN P d N


Chọn D.
Câu 3. Xét các số phức
thỏa mãn
1 3.z i zi
Môđun lớn nhất của số phức
1
w
z
là
A.
25
.
7
B.
45
.
7
C.
95
.
10
D.
75
.
10
Lời giải. Đặt
z x yi
,xy
và
;M xy
là điểm biểu diễn số phức
.
z
Từ
22 2
2
1 3 1 1 3 24 7z i zi x y x y x y
 
t ập hợp điểm
M
là đường thẳng
: 2 4 7.xy 
Ta có
11 1
w
z z OM

với
0;0 .O
Dựa vào hình vẽ ta thấy
min
max max
1 20 2 5
.
, 2.0 4.0 7 7
w OM w
dO


Chọn A.
Câu 4. Xét các số phức
thỏa mãn

2
2 5 1 2 3 1.z z z iz i

Giá trị nhỏ nhất của
biểu thức
22Pz i 
bằng
A.
1.
B.
3
.
2
C.
5
.
2
D.
5.
Lời giải. Ta có

2
2 5 12 3 1z z z iz i 
 
12
12 12 12 3 1 .
12 3 1
zi
z iz i z iz i
z izi

 

TH 1. Với
1 2.zi
Khi đó
22 12 22 1.
Pz i i i  
TH 2. Với
1 2 3 1.z izi
Đặt
z x yi

,xy
và
;M xy
là điểm biểu diễn số phức
.z
Từ
2222
12 3 1 1 2 1 3 2 1 0zizi xy xy y  
tập hợp
điểm
M
là đường thẳng
: 2 1 0.y 
Ta có
22P z i MA 
với
2; 2 .A
Dựa vào hình vẽ ta thấy
min min min
2. 2 1
3
,.
22
P MA P d A


So sánh hai trường hợp ta thấy
min
1.P
Chọn A.
Câu 5. Xét các số phức
thoã mãn
2 1 2.ziz i 
Gọi
w
là số phức thoã mãn điều kiện
1 2.w iz
Giá trị nhỏ nhất của biểu thức
Pw
bằng
A.
1
.
3
B.
1
.
5
C.
5
.
34
D.
5
.
41
Lời giải. Đặt
z x yi
,xy
và
;M xy
là điểm biểu diễn số phức
.z
Từ
222
2
2 12 2 1 2 2 8 1ziz i x y x y x y  
tập hợp điểm
M
là đường thẳng
: 2 8 1.
xy 
Ta có
2
21 2
1Pw i iz z MN


với
1;1 .N
Dựa vào hình vẽ ta thấy
min min min
2. 1 8.1 1
5
2, 2 .
68 34
P MN P d N


Chọn C.
Câu 6. Xét các số phức
, zw
thỏa mãn
13 2z izi
và
1 3 2.w i wi
Giá trị nhỏ
nhất của biểu thức
P zw
là
A.
13 1
.
2
B.
26
.
4
C.
3
.
13
D.
3 26
.
13
Lời giải. Gọi
z a bi
và
w c di
, , , .abcd
22 2
2
13 2 1 3 2 5 3z izi a b a b ab
 
tập hợp điểm
M
biểu diễn số phức
là phần tô đậm như trên đồ thị có tính biên
:53xy
.
22 2
2
13 2 1 3 2 5 3
w i wi c d c d cd  
tập hợp điểm
N
biểu diễn số phức
w
là phần gạch chéo như trên đồ thị có tính biên
:5 3xy

.
Dựa vào hình vẽ ta thấy
3 26
;.
13
P z w MN d

Dấu
""
xảy ra khi và chỉ khi
M 
,
NM
và
MN

. Chọn D.
Vấn đề 2. Điểm và đường tròn
Câu 1. Xét các số phức
thỏa mãn
11iz
. Gọi
, mM
lần lượt là giá trị nhỏ nhất và giá
trị lớn nhất của biểu thức
.Pz
Tính
2020 .
S Mm 
A.
2014.
S
B.
2016.
S
C.
2018.S
D.
2022.S
Lời giải. Ta có
11 . 1 1iz izi zi  
tập hợp các điểm biểu diễn số
phức
thuộc đường tròn có tâm
0; 1I
, bán kính
1R
.
Khi đó
min
max
11 0
0
2018.
2
11 2
P OI R
m
S
M
P OI R


 




Chọn C.
Câu 2. Xét các số phức
thỏa mãn
23 1zi
. Giá trị lớn nhất và giá trị nhỏ nhất của
biểu thức
1
Pz i 
lần lượt là
A.
13 2
và
13 2
. B.
13 1
và
13 1
.
C.
và
. D.
13 4
và
13 4
.
Lời giải. Ta có
23 1
zi 
tập hợp các điểm
M
biểu diễn số phức
thuộc đường tròn
có tâm
2;3I
, bán kính
1.R
Ta có
11P z i z i MA 
với
1;1 .A
Vậy
min 1
max 2
13 1
.
13 1
P AM AI R
P AM AI R


Chọn B.
Cách 2. Ta có
1 1.Pz i z i 
Theo giả thiết:
1 23 1 32 1 32 13z izi izi iP  
Suy ra
13 1 1 13 1 13 1 13 1.PP P  
Câu 3. Xét các số phức
thỏa mãn
1 1 7 2.iz i 
Gọi
, mM
lần lượt là giá trị nhỏ
nhất và giá trị lớn nhất của
.Pz
Tính
.S Mm
A.
2.S
B.
4.S
C.
10.S
D.
24.S
Lòi giải. Ta có
17 2
1 17 2 3 4 1
11
i
iz i z z i
ii


tập hợp các
điểm
M
biểu diễn số phức
thuộc đường tròn có tâm
3; 4I
, bán kính
1R
.
Khi đó
min 1
max 2
51 4
4
2.
6
51 6
P OM OI R
m
S
M
P OM OI R


 




Chọn A.
Câu 4. Xét các số phức
, zw
thỏa mãn
1
21
1
iz
i

và
.w iz
Giá trị lớn nhất của biểu
thức
P zw
bằng
A.
B.
23
C.
32
D.
33
Lời giải. Từ
1 21
1
21 2 1
1 11
iz i
i
z zi
i ii



tập hợp các điểm
M
biểu diễn số phức
thuộc đường tròn có tâm
0;2 ,I
bán kính
1.R
Theo giả thiết
1 22
w iz
P z w z iz z i z OM

với
0;0 .
O
Dựa vào hình vẽ ta thấy
max 2
2 2 2 2 1 3 2.P OM OI R 
Chọn C.
Câu 5. Xét các số phức
12
,
zz
thỏa mãn
1
11zi
và
21
2.
z iz
Giá trị nhỏ nhất của biểu
thức
12
2P zz

bằng
A.
2 2.
B.
2 2 2.
C.
4 2 2.
D.
8 2.
Lời giải. Từ
1
11zi 
tập hợp các điểm
M
biểu diễn số phức
1
z
thuộc đường tròn
có tâm
1; 1 ,I
bán kính
1.R
Theo giả thiết ta có
21
2
12 1 1 1
2 2 2 21 2 2
z iz
P z z z iz i z OM

với
0;0 .O
Dựa vào hình vẽ ta thấy
min 1
22 22 22 2 1 4 22.
P OM OI R

Chọn C.
Câu 6. Xét các số phức
thỏa mãn
không phải là số thực và
2
2
z
w
z
là số thực. Tìm
giá trị lớn nhất
max
P
của biểu thức
1.Pz i 
A.
max
2.P
B.
max
2.P
C.
max
2 2.P
D.
max
8.P
Lời giải. Vì
không phải là số thực nên
0
zz
.
Ta có
22
.
22
zz
ww
zz


Vì
w
là số thực nên
22
22
zz
ww
zz


2
22
0
2 2 2 . 2 2.
.2
zz
z z z z zz zzzz z z
zz


loaïi
Suy ra tập hợp các điểm
M
biểu diễn số phức
là đường tròn có tâm
0;0O
, bán kính
2R
.
Ta có
1P z i MA

với
1;1 .A
Vậy
max
2 2 2 2.P AO R 
Chọn C.
Câu 7. Xét các số phức
thỏa mãn
2z
. Biểu thức
zi
P
z
đạt giá trị nhỏ nhất và giá
trị lớn nhất lần lượt tại
1
z
và
2
z
. Tìm phần ảo
của số phức
12
.wz z
A.
4.
a 
B.
0.
a
C.
1.a
D.
4.
a
Lời giải. Biến đổi
11
1
zi i
P ii
z z zz

.
Đặt
1
'z
z
, khi đó
1
'1
2
'2
.
z
P zi

1 
tập hợp các số phức
'z
là hình tròn tâm
0;0O
, bán kính
1
2
R
(trừ tâm
O
).
Xét
2.
Đặt
0;1A P MA 
với
M
là điểm biểu diễn của số phức
'z
.
Dựa vào hình vẽ, ta thấy
min 1
max 2
11 1
khi ' 2
22
3 11
khi ' 2
22
P AM z i z i
z
P AM z i z i
z


1
2
2
0 0.
2
zi
wi
zi

 
Chọn B.
Câu 8. Xét các số phức
thỏa mãn
1.
z
Gọi
, Mm
lần lượt là giá trị lớn nhất và nhỏ nhất
của
2
.
2
zi
P
z
Tỉ số
M
m
bằng
A.
5 32
.
4
B.
9 42
.
7
C.
10 6 34
.
9
D.
25 4 34
.
9
Lời giải. Đặt
22
22 22 .
22
zi wi
w wz z i zw w i z
zw

 

Theo giả thiết
2
1 1 2 2.
2
wi
z wi w
w

Gọi
,.w x yi x y
Khi đó từ
22wi w
22
2 22
2
2 2 17
2 21 2
3 39
x y x yx y










tập hợp các điểm
M
biểu diễn số phức
thuộc đường tròn có tâm
22
;,
33
I



bán
kính
17
.
3
R
Do đó
min
2 2 17
2 25 4 34
33
.
29
2 2 17
33
max
P OI R
zi M
Pw
zm
P OI R


 

Chọn D.
Câu 9. Xét hai số phức
12
, zz
thay đổi thỏa mãn
12 1 2
4 2 2.zz zz i

Gọi
, AB
lần
lượt là giá trị nhỏ nhất và giá trị lớn nhất của biểu thức
22
12
.zz
Giá trị của
AB
là
A.
20.
B.
24.
C.
28.
D.
32.
Lời giải. Gọi
, MN
lần lượt là điểm biểu diễn của hai số phức
12
, .zz
Gọi
K
là trung điểm của
MN
K 
là điểm biểu diễn của số phức
12
.
2
zz
12
2 2.z z MN 
12
12
42 2 2 1
2
zz
zz i i
 
tập hợp các điểm
K
thuộc đường tròn có tâm
2;1 ,I
bán kính
1.R
Ta có
2
2
22
22 2 2
12
2 2 2.
2
MN
MN
T z z OM ON OK OK

Suy ra
max max
T OK
, mà
2
max max
15 215 21445;OK OI R T 
min min
T OK
, mà
2
min min
1 5 2 1 5 2 14 4 5.OK OI R T 
Vậy
14 4 5
28.
14 4 5
A
AB
B



Chọn C.
Cách 2. Ta có
22 2 2 2
1 2 12 12 12
22 2 4 .T z z zz zz zz  
Từ
12 12
12
12
12
2 4 2 25 2
42 2 .
2 42
25 2
zz i zz
zz i
zz i
zz







Vậy
14 4 5 14 4 5.T 
Câu 10. Xét các số phức
, z
thỏa mãn
|| 5z
và
4 3 1 2.iz i 
Giá trị nhỏ nhất của
||
bằng
A.
3 5.
B.
4 5.
C.
5 5.
D.
6 5.
Lời giải. Ta có
43 12 12 43 .iz i i iz
 
Suy ra
12 43 43. 5.5i iz i z 
tập hợp các điểm
M
biểu diễn số phức
thuộc đường tròn có tâm
1; 2 ,I
bán kính
5 5.
R
Vậy
min
5 5 5 4 5.OI R 
Chọn B.
Câu 11. Cho số phức
thỏa mãn đồng thời
12 5zi
và
1zi 
có môđun lớn
nhất. Số phức
z
có môđun bằng
A.
6.
B.
2 5.
C.
3 2.
D.
5 2.
Lời giải. Ta có
1 12 2 2 12.zi zii izi

 
Suy ra
2 12 5iz i

tập hợp các điểm
M
biểu diễn số phức
thuộc đường
tròn có tâm
2; 1 ,I
bán kính
5.R
Dựa vào hình vẽ ta thấy số phức
có môđun lớn nhất có điểm biểu diễn là
1
4; 2 .M
Với
1
1
4; 2 4 2 3 3 3 2.
zi
M i z iz


Chọn C.
Câu 12. Xét các số phức
thỏa mãn
2 4 2 2.zi
Trong các số phức
w
thỏa mãn
1,wz i
gọi
1
w
và
2
w
lần lượt là số phức có môđun nhỏ nhất và môđun lớn nhất. Khi đó
12
ww
bằng
A.
2 6.i
B.
2 4.i
C.
4 12 .i
D.
4 8.i
Lời giải. Từ
2 4 22zi 
tập hợp các điểm
M
biểu diễn số phức
thuộc đường
tròn có tâm
2;4 ,I
bán kính
2 2.R
Ta có
1 .1 2 2P w z i z i z OM 
với
0;0 .O
Dựa vào hình vẽ ta thấy
min 1
2.P OM
Dấu
'' ''
xảy ra
11
12 121 13.MM z i w i i i 
max 2
2.P OM
Dấu
'' ''
xảy ra

22
36 361 39.MM z i w i i i 
Vậy
12
4 12 .ww i 
Chọn C.
Cách 2. Ta có
 
1 1 24 26 26 1 24.w z i w iz i i w i iz i  
Suy ra

26 1 24 1 . 24 2.22 4wi izi izi
 
tập hợp các điểm
N
biểu diễn số phức
w
thuộc đường tròn có tâm
2;6 ,J
bán kính
4.r
Dựa vào hình vẽ ra thấy số phức
w
có môđun nhỏ nhất có điểm biểu diễn là
1
;N
phức
w
có
môđun lớn nhất có điểm biểu diễn là
2
.N
Khi đó
12 1 2 12
2 2 2 6 4 12 .w w ON ON OJ w w i i 
  
Câu 13. Xét các số phức
thỏa
1 2 25zi
và số phức
thỏa
5 10 3 4 25 .i iz i

Tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
P
bằng
A.
2 10.
B.
4.
C.
4 5.
D.
6.
Lời giải. Ta có
5 10 3 4 25i iz i 

5 10 3 4 1 2 5 35i iz i i 
(mục đích để tạo ra
12zi
)

5 10 5 35 3 4 1 2i i iz i 
(chuyển vế).
Suy ra

5 10 5 35 3 4 1 2 5.2 5 10 5.i i iz i

5 35 10 5
32 32
5 10 5 10
i
ii
ii

 

tập hợp các điểm
M
biểu
diễn số phức
thuộc đường tròn có tâm
3;1 ,I
bán kính
2.R
Dựa vào hình vẽ ta thấy
min 1
min max
max 2
10 2
2 10.
10 2
P OM OI R
PP
P OM OI R



Chọn A.
Câu 14. Xét các số phức
thỏa mãn
2
.zz zz z 
Giá trị lớn nhất của biểu thức
52
Pz i 
bằng
A.
2 3 5.
B.
2 5 3.
C.
5 2 3.
D.
5 3 2.
Lời giải. Đặt
,,z x yi x y
suy ra
2
2 22
2
2.
zz x
z x yi z z yi
z z xy



Từ giả thiết
2 22
22 .zz zz z x y x y 
*
TH 1.
0
,
0
x
y
khi đó
*
trở thành
22
1 12xy 
có hình biểu diễn là cung tròn nét
liền ở góc phần tư thứ
I.
Tương tự cho các trường hợp còn lại (tham khảo hình vẽ)
Gọi
5; 2A
và
;M xy
là điểm biểu diễn số phức
,
z
khi đó
52 .P z i MA 
Vì
A
nằm ở góc phần tư thứ
I
nên
MA
lớn nhất khi
M
phải nằm ở góc phần tư thứ
III .
Suy ra
max 3 3
3 5 2.MA AI R 
Vậy
max 3 5 2.P 
Chọn A.
Vấn đề 3. Đường thẳng và đường tròn
Câu 1. Xét các số phức
1
z
thỏa mãn
22
11
21z zi
và các số phức
2
z
thỏa mãn
2
45zi
. Giá trị nhỏ nhất của
12
Pzz
bằng
A.
5.
B.
2 5.
C.
25
.
5
D.
35
.
5
Lời giải. Gọi
; z x yi x y
. Ta có
22 2 2
22
2 1 2 1 1 2 10z zi x y x y x y  
tập hợp các số
phức
1
z
là đường thẳng
: 2 1 0.xy 
22
4 5 4 1 5 4 15z i x yi x y
 
tập hợp các số phức
2
z
là đường tròn
C
có tâm
4;1 ,I
bán kính
5.R
Khi đó biểu thức
12
Pzz

là khoảng cách từ một điểm thuộc
đến một điểm thuộc
C
.
Từ đó suy ra
min
8 35
, 5.
5
5
P MN d I R

Chọn D.
Câu 2. Gọi
1
C
là tập hợp các số phức
w
thỏa mãn
2 3 3 2.wiwi 
Gọi
2
C
là tập
hợp các số phức
thỏa mãn
2 4 1.zi
Giá trị nhỏ nhất của biểu thức
P wz
bằng
A.
23 1
. B.
23 1
. C.
32 1
. D.
32 1
.
Lời giải. Đặt
; , , , .z x yi w a bi x y a b 
Ta có
23 32wiwi 
2222
2332 0a y a b ab  
tập hợp
điểm
M
biểu diễn số phức
w
thuộc nửa mặt phẳng bờ
:0xy 
và kể cả bờ (miền tô đậm
như hình vẽ). Gọi miền này là
1
.C
22
24 1 2 4 1 2 4 1z i x yi x y
 
tập hợp điểm
N
biểu
diễn số phức
là hình tròn
2
C
có tâm
2; 4 ,I
bán kính
1.R
Khi đó biểu thức
P z w MN

là khoảng cách từ một điểm thuộc
1
C
đến một điểm
thuộc
2
C
.
Từ đó suy ra
min
, 3 2 1.
P dI R 
Chọn C.
Câu 3. Xét các số thức
thỏa mãn
24zizi 
và
3 3 1.zi
Giá trị lớn nhất của biểu
thức
21Pz
bằng
A.
5 2.
B.
10
C.
10 1.
D.
13 1.
Lời giải. Gọi
,z x yi x y
. Ta có
22
22
24 2 4 3zizi xy xy y  
tập hợp điểm biểu diễn số
phức
thuộc nửa mặt phẳng bờ
:3y
, kể cả bờ (miền tô đậm). Gọi miền này là
1
.C
22
33 1 3 3 1 3 3 1z i x yi x y  
tập hợp điểm biểu diễn
số phức
là đường tròn
2
C
có tâm
3;3 ,I
bán kính
1.R
Như vậy tập hợp điểm
M
biểu diễn số phức
là giao của
1
C
và
2
C
. Đó chính là phần
cung tròn nét liền như trên hình vẽ (có tính 2 điểm đầu mút
2;3 , 4;3DC
của cung).
Khi đó
21 1P z MB 
với
2;0
B
và
MB
là khoảng cách từ điểm
B
đến một điểm
thuộc cung tròn
CD
.
Từ đó suy ra
max
1 13 1.P BC 
Chọn D.
Câu 4. Xét các số phức
, zw
thỏa mãn
22 1iz i z
và
max 2 2 , 2.
w iw
Giá trị
nhỏ nhất của biểu thức
P zw
bằng
A.
1
.
25
B.
5
.
2
C.
9
.
25
D.
13
.
25
Lời giải. Gọi
;,Mxy N
lần lượt là điểm biểu diễn của hai số phức
,.zw
221221iz i z z i z 
2 22
2
2 2 1 2 4 70x y x y xy

tập hợp điểm
M
biểu diễn số phức
thuộc nửa mặt phẳng bờ
:2 4 7 0xy
không chứa
O
(kể cả bờ).
max 2 2 , 2,w iw
suy ra
2 2 2 2 , 2; 2
2 2, 0;0
w i NI I
w NO O











N

thuộc phần chung của hai hình tròn
;2
I
và
;2O
. Mà hai hình tròn này tiếp
xúc ngoài tại điểm
1; 1 .E
Do đó
1; 1 .
NE
Ta có
P z w MN
nên
P
nhỏ nhất khi
MN
ngắn nhất, khi đó
M
là hình chiếu của
N
trên
và
min
2
2
2 1 4.1 7
13
,.
25
24
P dN



Chọn D.
Câu 5. Xét các số phức
, zw
thỏa mãn
max ; 1 1
.
12 2
zz i
w iw i


Giá trị nhỏ nhất của biểu thức
P zw
bằng
A.
0.
B.
1
.
6
C.
2 1.
D.
2 2 1.
Lời giải. Gọi
,;
MNxy
lần lượt là điểm biểu diễn của hai số phức
,.zw
2 2 22
12 2 1 2 2 1 0
w i w i x y x y xy
 
tập hợp
điểm
N
biểu diễn số phức
w
thuộc nửa mặt phẳng bờ
:0xy 
và kể cả bờ (miền tô đậm
như hình vẽ).
max ; 1 1,
zz i
suy ra
1 1 1, 1;1
1 1, 0; 0
z i MI I
z MO O









M 
thuộc phần chung của hai hình tròn
;1I
và
;1O
(phần gạch sọc như hình vẽ).
Ta có
P z w MN
nên
P
nhỏ nhất khi
MN
ngắn nhất. Dựa vào hình vẽ ta thấy
MN
ngắn nhất khi
NO
và
min
1 2 1.MN OI

Chọn C.
Câu 6. Kí hiệu
S
là tập hợp các số phức
thỏa mãn
1 34z 
và
12z mi z m i
(trong đó
m
). Gọi
12
,
zz
là hai số phức thuộc tập hợp
S
sao cho
12
zz
là lớn nhất. Khi
đó, hãy tính giá trị của biểu thức
12
.zz
A.
12
2.zz

B.
12
2.zz
C.
12
10.
zz

D.
12
130.zz
Lời giải. Đặt
,.z x yi x y
Khi đó
1 34
z 
tập hợp điểm biểu diễn số phức
thuộc đường tròn
C
có tâm
1; 0 ,I
bán kính
34.R
1
1 2 2 2 42 3 0z mi z m i m x m y

tập hợp điểm biểu diễn số phức
thuộc đường thẳng
: 2 2 4 2 3 0.m x my 
2
Từ
1
và
2,
suy ra tập các điểm biểu diễn số phức
của tập
S
là giao điểm của
và
.C
Gọi
, AB
lần lượt là các điểm biểu diễn của hai số phức
12
, .zz
Suy ra
12
.z z AB
Để
AB
lớn nhất
,dI
nhỏ nhất

đi qua điểm
.I
Khi đó
là trung điểm của
AB
nên
12
2 2 2.z z OA OB OI OI
  
Chọn B.
Câu 7. Biết số phức
;z x yi x y
thỏa mãn đồng thời
34 5zi
và biểu thức
22
2P z zi 
đạt giá trị lớn nhất. Tính
z
.
A.
33z
. B.
50z
. C.
10z
. D.
52z
.
Lời giải. Vì
34 5zi 
tập hợp các điểm biểu diễn số phức
là đường tròn
C
có tâm
3; 4I
và bán kính
5
R
.
Ta có
22
22
22
2 1 2 1 423P x yi x y i x y x y x y

 


4 2 3 0.
xy P

Ta tìm
P
sao cho đường thẳng
:4 2 3 0xy P 
và đường tròn
C
có điểm chung
12 8 3
, 5 23 10 13 33.
20
P
dI R P P


Do đó
max
33P
. Dấu
""
xảy ra
22
4 2 30 0
5
5
3 45
xy
x
y
xy






.
Vậy
22
5 5 52z 
. Chọn D.
Câu 8. Xét các số phức
thỏa mãn
1 3 13.zi
Gọi
, mM
lần lượt là giá trị nhỏ nhất và
lớn nhất của biểu thức
22
2 3.Pz zi 
Tổng
mM
bằng
A.
10.
B.
25.
C.
34.
D.
40.
Lời giải. Đặt
;.z x yi x y
Từ giả thiết
22
1 3 13 1 3 13.zi x y

Suy ra tập hợp các điểm biểu diễn
số phức
là đường tròn
C
có tâm
1; 3 ,I
bán kính
13.
R
Lại có
22
2 3 465 465 0.Pz zi xy xy P 
Suy ra tập hợp các số phức
thuộc đường thẳng
: 4 6 5 0.
xy P

Để tồn tại
thì
và
C
phải có điểm chung
4.1 6.3 5
, 13
16 36
P
dI R


9
9 43 31 46
43
72 .
m
PmP M
M



Chọn C.
Dấu
'' ''
xảy ra khi
thay 43
max
:4 6 4 .4 03 8
P
P xy
 
Tọa độ điểm
thỏa
22
3
1 3 13
3 6.
6
4 6 48 0
x
xy
zi
y
xy






thay 9
min
.9 :4 6 4 0
P
P xy

  
Tọa độ điểm
thỏa
22
1
1 3 13
1.
0
4 6 40
x
xy
z
y
xy







Cách 2. Ta có
22
2 3 465Pz zi x y 
22
22 22
17 4 1 6 3 4 6 1 3 4 6 .13 26P x y xy




Câu 9. Xét các số phức
;z x yi x y
thỏa mãn
1 2 4.iz i 
Giá trị lớn nhất của
biểu thức
3T xy 
bằng
A.
4.
B.
4 2.
C.
4 2 2.
D.
8.
Lời giải. Ta có
2 4 13
1 2 4 22
1 1 22
i
iz i z z i
ii
 

tập hợp các số
phức
là đường tròn
C
có tâm
13
;,
22
I


bán kính
2 2.
R
Ta có
30
3.
30
xy T
T xy
xy T



Với
: 3 0.xy T 
Để tồn tại số phức
tức là
và
C
phải có điểm chung
13
3
22
, 2 2 0 8.
2
T
dI R T


Với
: 3 0.
xy T 
Để tồn tại số phức
tức là
và
C
phải có điểm chung
13
3
22
, 2 2 8 0.
2
T
dI R T


So sánh hai trường hợp, ta có
max
8.
T
Chọn D.
Câu 10. Xét các số phức
thỏa mãn
| 2 1 2.zi 
Giá trị nhỏ nhất của biểu thức
| 1 2| | 3 4| | 5 6|Pz iz iz i  
được viết dưới dạng
,
ab
với
a
b
là phân số tối giản.
Giá trị của
ab
bằng
A.
10.
B.
11.
C.
12.
D.
17.
Lời giải. Đặt
,.z x yi x y
Khi đó
2
2
2 12 2 5z ix y  
tập hợp điểm
M
biểu diễn số phức
thuộc
đường tròn
C
có tâm
2;0 ,I
bán kính
5.R
Ta có
12 34 56P z i z i z i MA MB MC  
với
1;2 , 3;4 , 5;6 .AB C
Nhận thấy các điểm
, , ABC
cùng thuộc đường thẳng
: 1.dy x
Đường thẳng
d
cắt
đường tròn
C
tại hai điểm
0;1
P
và
3; 2 .
Q

Vậy
min
P MP
và
min
9
9 2 11.
2
a
P PA PB PC a b
b

Chọn B.
Câu 11. Xét các số phức
12
, zz
thoả mãn
1 22
3 4 1, 1z i z zi
và
12
2
zz
i
là số thực.
Gọi
, Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
12
.zz
Tính
P Mm
.
A.
14 5.P
B.
16 5.
P
C.
18 5.P
D.
20 5.P
Lời giải. Đặt
12
, , , , .z a bi z c di a b c d 
Gọi
; , ;Aab B cd
lần lượt là hai điểm biểu diễn số phức
12
, .zz
Suy ra
12 12
.z z OA OB BA z z AB 
  
Do đó từ
12
2; 1 .
2
zz
k k BA k
i


Suy ra đường thẳng
AB
có VTPT
1; 2 .
AB
n

1
34 1zi 
tập hợp các điểm
A
là đường tròn
C
có tâm
3; 4 ,I
bán kính
1.R
22
22
22
1 1 10z z i c d c d cd  
tập hợp các điểm
B
là đường
thẳng
: 0.xy 
Gọi
là góc giữa
và
AB
, ta có
.
3 10 1
cos sin .
10
10
.
AB
AB
nn
nn


 
 
Theo yêu cầu bài toán ta cần tìm GTLN và GTNN của
.AB
Do
,dI R
nên suy ra
không cắt
.C
Gọi
H
là hình chiếu của
A
trên
, ta có
,
max
max 7 5 10
sin sin
14 5.
sin
,
min
min 7 5 10
sin sin
dI R
AH
AB
AH
AB P
dI R
AH
AB







Chọn A.
Câu 12. Cho
1
z
là số phức,
2
z
là số thực thoả mãn
1
21zi
và
21
1
zz
i
là số thực. Tổng giá
trị lớn nhất và giá trị nhỏ nhất của biểu thức
12
Pzz
là
A.
2.
B.
2 2.
C.
32
D.
4 2.
Lời giải. Gọi
, MN
lần lượt là hai điểm biểu diễn số phức
12
, .
zz
Suy ra
21 12
.z z ON OM MN z z MN 
  
Do đó từ
21
1;1 .
1
zz
k k MN k
i


Suy ra đường thẳng
MN
có VTPT
1; 1 .
MN
n 

1
21
zi 
tập hợp các điểm
M
là đường tròn
C
có tâm
0;2 ,I
bán kính
1.R
2
z
là số thực

tập hợp các điểm
N
là đường thẳng
: 0.y
Gọi
là góc giữa
và
MN
, ta có
.
22
cos sin .
22
.
MN
MN
nn
nn


 
 
Theo yêu cầu bài toán ta cần tìm GTLN và GTNN của
.MN
Do
,dI R
nên suy ra
không cắt
.
C
Vì
IO 
nên
O
là hình chiếu của
M
trên
, ta có
sin
MO
MN
,
max
max 3 2
sin sin
.
,
min
min 2
sin sin
dI R
MO
MN
dI R
MO
MN







Chọn D.
Câu 13. Cho
z x yi

,xy
là số phức thỏa mãn
2 3 2 5.z i zi 
Gọi
, Mm
lần lượt là giá trị lớn nhất và nhỏ nhất của
22
8 6.Px y x y
Giá trị
Mm
bằng
A.
156
2 10.
5
B.
156
2 10.
5
C.
60 20 10.
D.
60 20 10.
Lời giải. Ta có
22
23 2 2 2 0
.
2 5 2 1 25
z i zi x y
zi x y


Suy ra tập hợp các điểm
;
M xy
thỏa
yêu cầu bài toán nằm trên miền
H
tô đậm được giới hạn bởi đường thẳng
:2 2dxy 
và
đường tròn
C
có tâm
2; 1 ,I
bán kính
5R
(kể cả biên) như hình vẽ.
Ta có
22
22 2
8 6 4 3 25 25P x y x y x y JM 
với
4; 3 .J 
Gọi giao điểm của
d
và
C
là
2; 6 , 2;2 ;AB
C
là giao điểm của đoạn
IJ
với
.C
Dựa vào hình vẽ ta thấy
min , , 2 10 5.JM JA JB JC JC IJ IC IJ R
 
max , , 3 5.JM JA JB JC JA

Vậy
2
2
3 5 25 20
60 20 10.
2 10 5 25 40 20 10
M
Mm
m



Chọn C.
Vấn đề 4. Đường tròn và đường tròn
Câu 1. Xét các số phức
12
, zz
thỏa mãn
1
41z 
và
2
2 1.iz 
Giá trị nhỏ nhất của biểu
thức
12
2
Pz z
bằng
A.
2 5 2.
B.
4 2.
C.
4 2 3.
D.
4 2 3.
Lời giải. Đặt
3 2 1 2 1 2 13
2 22 .
z z Pz z z z zz  
Từ
3 22 3
1
2
2
z zz z 
, thay vào
2
21
iz 
ta được
33
1
2 1 4 2.
2
iz z i 
Gọi
,
AB
là hai điểm biểu diễn cho hai số phức
31
, .zz
3
42zi A 
đường tròn tâm
0;4 ,I
bán kính
3
1.R
1
41zB 
đường tròn tâm
4;0 ,J
bán kính
1
1.R
Khi đó
min 1 2
13
max 1 2
42 3
.
42 3
P IJ R R
P z z AB
P IJ R R



Chọn C.
Cách 2. Biến đổi
2
2 22 2
2
2
21 1 1 2 1 2 4 2
iz
iz z z i z i
ii
   
.
Ta có
12 1 2
2 4 2 4 44Pz z z z i i
 
21
21
2 4 44 4
4 4 2 4 4 4 2 3.
z i iz
i z iz

 
Câu 2. Xét các số phức
12
, zz
thỏa mãn
1
352zi
và
2
1 2 4.iz i
Giá trị lớn nhất của
biểu thức
12
23P iz z
bằng
A.
313 16.
B.
313.
C.
313 8.
D.
313 2 5.
Lời giải. Đặt
3 2 1 2 1 3 13
2 3 23 22 2 .iz z P iz z iz iz z z 
Từ
3 22 3
2
23
3
iz z iz z
, thay vào
2
12 4iz i
ta được
33
23
1 2 4 3 6.
32
zi z i
Gọi
, AB
là hai điểm biểu diễn cho hai số phức
13
, .zz
1
352zi
A 
đường tròn tâm
5;3 ,I
bán kính
1
2.R
3
3
36
2
zi B 
đường tròn tâm
3
; 3,
2
J


bán kính
2
6.R
Khi đó
min 1 2
13
max 1 2
2 313 16
22 .
2 313 16
P IJ R R
P z z AB
P IJ R R



Chọn A.
Câu 3. Xét các số phức
12
, zz
thỏa mãn
1
12z
và
2
3 4 5.zi
Giá trị nhỏ nhất của biểu
thức
12
Pzz
bằng
A.
0.
B.
2.
C.
7.
D.
17.
Lời giải. Gọi
,
AB
là hai điểm biểu diễn cho hai số phức
12
, .zz
1
12z
A 
đường tròn tâm
0;0 ,
O
bán kính
1
12.R
2
34 5zi B 
đường tròn tâm
3; 4 ,I
bán kính
2
5.R
Khi đó
min 1
12
max 1
22
.
2 22
P OI R
P z z AB
P OI R



Chọn B.
Câu 4. Có bao nhiêu giá trị của tham số
m
để tồn tại duy nhất số phức
thỏa mãn
.1
zz
và
3
z im 
?
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải. Gọi
A
là điểm biểu diễn cho số phức
.z
2
.1 1 1zz z z 
A

đường tròn
1
C
có tâm
0;0 ,O
bán kính
1
1.R
Ta thấy
03m zi 
không thỏa mãn
.1zz
nên suy ra
0.m
3z im

A 
đường tròn
2
C
có tâm
3; 1 ,I
bán kính
2
.Rm
Nhận thấy
1
2
OI R
suy ra
nằm ngoài
1
.C
Để có duy nhất số phức
thì
1
C
và
2
C
tiếp xúc ngoài hoặc tiếp xúc trong, điều điều này
xảy ra khi
12
21
12 1
.
12 3
OI R R
mm
R R OI m m








Vậy có
giá trị của
m
thỏa mãn. Chọn C.
Câu 5. Gọi
S
là tập hợp các số phức
thỏa mãn
3zi
và
15z 
. Gọi
12
, zz S
lần
lượt là các số phức có mođun nhỏ nhất và lớn nhất. Khẳng định nào sau đây đúng ?
A.
12
2 12 2 . zz i
B.
12
2 2 12 .

zz i
C.
12
2 6 4. zz i
D.
12
2 12 4 . zz i
Lời giải. Giả sử
,z a bi a b
. Ta có
22
2 22
1 1 51 5z ab ab


tập hợp các số phức
nằm trong hoặc trên đường tròn tâm
1; 0 ,A
bán kính
5
R
.
22
2 22
13 13zi ab ab  

tập hợp các số phức
nằm ngoài hoặc trên đường tròn tâm
0;1 ,B
bán kính
'3R
.
Dựa vào hình vẽ ta thấy
min 1
12
max 2
02
2 12 2 .
60
zz i
zz i
zz i



Chọn A.
Cách 2. Áp dụng bất đẳng thức
1 2 12 1 2
z z zz z z 
.
Ta có
12
3 2
2 6.
1 1 5 6
zi z i z
z
zz z










Dấu
'' ''
thứ nhất xảy ra khi
1
3zi
, kết hợp với
15z 
ta được
1
11
1
3
1 5 2.
2
zi
z zi
z


Tương tự cho dấu
'' ''
thứ hai, ta được
2
2 2 12
2
15
6 6 2 12 2
3
z
z z zz i
zi

 

.
Câu 6. Xét các số phức
thỏa mãn
1 2 4.zi 
Gọi
M
là giá trị lớn nhất của
23zi
,
m
là giá trị nhỏ nhất của
22zi
. Tính
.Mm
A.
3.Mm
B.
5.Mm

C.
6.Mm
D.
7.Mm
Lời giải. Giả sử
,
z a bi a b
. Ta có
22 22
2 2142116
ziab ab
 

tập hợp điểm
M
biểu diễn
số phức
nằm trong hoặc trên đường tròn tâm
2; 1 ,A
bán kính
4.R
22 22
2 211211
ziab ab  

tập hợp điểm
M
biểu diễn số
phức
nằm ngoài hoặc trên đường tròn tâm
2; 1 ,A
bán kính
1.R
Khi đó
23
T z i MC 
với
2; 3C
min
max 3
0
;
6
T
T CM AC R


22P z i MB 
với
2;2B
min 1
max 2
1
.
9
P BM AB R
P BM AB R



Vậy
max min
7.TP
Chọn D.
Câu 7. Xét các số phức
thỏa mãn
2 25
.
4 22
zi
zi


Giá trị lớn nhất của
14Tz i 
bằng
A.
3 2.
B.
3 5.
C.
5 2.
D.
6.
Lời giải. Giả sử
,.z a bi a b
Ta có
22
22
2 2 2 5 2 20zi ab ab  

tập hợp điểm
M
biểu diễn số phức
nằm trong hoặc trên đường tròn
1
C
có tâm
0; 2 ,A
bán kính
2 5.R
1
22
22
4 4 22 4 8zi ab ab  

tập hợp điểm
M
biểu diễn số phức
nằm trong hoặc trên đường tròn
2
C
có tâm
0;4 ,B
bán kính
2 2.
R
2
Từ
1
và
2
suy ra tập hợp điểm
M
biểu diễn số phức
nằm trên phần giao của hai hình
tròn
1
C
và
2
C
(phần tô đậm trong hình vẽ).
Khi đó
14 14T z i z i MC 
với
1; 4 .
C

Dựa vào hình vẽ ta thấy
max
T
khi
M
sẽ rơi vào các vị trí
1
M
hoặc
2
M
hoặc
3
.M
Ta có
1
2
2
2 max 1
31
35
1 2 2 5 3 5.
CM
CM T CM
CM CM

Chọn B.
Câu 8. Xét các số phức
,z x yi x y
thỏa mãn
11
.
33 5
zi
zi


Gọi
, mM
lần lượt là
giá trị nhỏ nhất và giá trị lớn nhất của biểu thức
2.Px y
Tỉ số
M
m
bằng
A.
5
.
4
B.
7
.
2
C.
9
.
4
D.
14
.
5
Lời giải. Ta có
11zi

tập hợp điểm
M
biểu diễn số phức
nằm ngoài hoặc trên đường tròn
1
C
có tâm
1;1 ,I
bán kính
1.R
1
33 5zi

tập hợp điểm
M
biểu diễn số phức
nằm trong hoặc trên đường
tròn
2
C
có tâm
3;3 ,J
bán kính
5.R
2
Từ
1
và
2
suy ra tập hợp điểm
M
biểu diễn số phức
là phần tô đậm trong hình vẽ (có
tính biên)
Gọi
là đường thẳng có phương trình
2 0.x yP 
Khi đó để bài toán có nghiệm (tồn tại
số phức thỏa mãn yêu cầu bài toán) thì đường thẳng
và miền tô đậm phải có điểm chung
9
14
7
, 5 5 4 14 .
4
2
5
P
M
M
dJ P
m
m
 
Chọn B.
Dấu
""
xảy ra khi
14M
đạt được khi
22
2 14 0
4
.
5
3 35
xy
x
y
xy





4m
đạt được khi
22
2 40
2
.
1
3 35
xy
x
y
xy





Câu 9. Xét các số phức
;z x yi x y

thỏa mãn
13
.
3 4 10
zi
zi


Giá trị nhỏ nhất của
biểu thức
3Px y
bằng
A.
5.
B.
7.
C.
13.
D.
4 3 10.
Lời giải. Ta có
13
zi


tập hợp điểm
M
biểu diễn số phức
nằm ngoài hoặc trên đường tròn
1
C
có tâm
1;1 ,I
bán kính
3.R
1
3 4 10zi

tập hợp điểm
M
biểu diễn số phức
nằm trong hoặc trên đường
tròn
2
C
có tâm
3; 4 ,J
bán kính
10.R
2
Từ
1
và
2
suy ra tập hợp điểm
M
biểu diễn số phức
là phần tô đậm trong hình vẽ (có
tính biên)
Gọi
là đường thẳng có phương trình
3 0.x yP 
Khi đó để bài toán có nghiệm (tồn tại
số phức thỏa mãn yêu cầu bài toán) thì đường thẳng
và miền tô đậm phải có điểm chung.
Bằng cách tịnh tiến các đường thẳng song song với nhau (cùng có VTPT là
1; 3n
) ta thấy
P
đạt giá trị nhỏ nhất bằng
khi
đi qua điểm
4;1 .
A
Chọn B.
Vấn đề 5. Parabol
Câu 1. Xét các số phức
,z a bi a b
thỏa
2
4 15 1 .z z i iz z 
Tính
4P ab
khi
1
3
2
zi

đạt giá trị nhỏ nhất.
A.
4.P
B.
5.P
C.
6.P
D.
7.P
Lời giải. Từ
2
22
4 15 1 4.2 15 2 1 2
22
aa
zz iizz bi iia b  
tập
hợp điểm
M
biểu diễn số phức
là Parabol
2
:2
22
xx
Py 
(như hình vẽ).
Ta có
1
3
2
T z i MA
với
1
; 3.
2
A


Ta thấy
39
8
MA BA
với
1 15
;
28
B


là đỉnh của của
.P
Vậy
min min
.T MA AB

Dấu
""
xảy ra khi
1 15
, 4 7.
28
MBa b a b

Chọn D.
Cách 2. Ta có
22
2
4 15 1 4.2 15 2 1 2 4.zz iizz bi iia ba a 
1
Suy ra
2
1 15 15
2.
24 8
ba b



Khi đó
2
2
22
11 1
3 3 69
22 4
Tz i a b aa b b



1
2
21 39
8.
48
Tbb

Dấu
""
xảy ra khi
15 1
.
82
ba 
Câu 2. Xét hai số phức
12
, zz
thỏa mãn
1 11
22zi zz i
và
2
10 1.zi
Giá trị nhỏ
nhất của biểu thức
12
zz
bằng
A.
10 1.
B.
3 5 1.
C.
101 1.
D.
101 1.
Lời giải. Đặt
1
,.z a bi a b
2
22
2
1 11
2 2 2. 1 2 2
4
a
zi zz i a b b b  
tập hợp điểm
M
biểu diễn số phức
1
z
là một Parabol
2
:
4
x
Py
có đỉnh
0;0 .O
2
10 1zi 
tập hợp điểm
N
biểu diễn số phức
2
z
là đường tròn
C
có tâm
10;1 ,I
bán kính
1.
R
Khi đó biểu thức
12
P z z MN
là khoảng cách từ một điểm thuộc
P
đến một điểm
thuộc
C
.
Ta có
1.MN NI MI MN MI NI MI 
Suy ra
min min
.MN IM
Ta có
22
22
22
2
5
10 1 4 4 45 45
4 42
xx
IM x x




 






45 3 5.IM 
Do đó
min
3 5 1.MN 
Dấu
""
xảy ra khi
2
2
2
5
4 4 0 4.
42
x
xx



Vậy
12
min
3 5 1.zz 
Chọn B.
Cách 2. Xét điểm
2
;.
4
a
Ma


Tiếp tuyến của
P
tại
M
có phương trình
2
:.
24
aa
y xa 
Gọi
;1
2
a
n



là một VTPT của đường thẳng
;
2
10; 1 .
4
a
IM a




Khi đó
min
IM IM

cùng phương với
, suy ra
4.a
Với
min min
4 6;3 35 35 1.
a IM IM MN   

Vấn đề 6. Đoạn thẳng – tia
Câu 1. Xét các số phức
thỏa mãn
2 4 7 6 2.z iz i 
Gọi
, mM
lần lượt là giá trị
nhỏ nhất và giá trị lớn nhất của
1zi
. Tính
.P mM
A.
13 73P 
. B.
52 273
2
P
. C.
52 273P 
. D.
5 2 73
2
P
.
Lời giải. Gọi
; , 2;1 , 4;7 , 1; 1Mxy A B C
lần lượt là điểm biểu diễn các số phức
,
z
2 ,4 7 ,1i ii
trong mặt phẳng tọa độ.
Từ
2 4 7 62 62z i z i MA MB AB 
M
thuộc đoạn thẳng
.AB
Ta có
1.T z i CM 
Dựa vào hình vẽ, ta thấy
min min
5
,.
2
T CM d C AB
max
73 ; 13 73.CB CA CM CB 
Vậy
5 273 52
73
2
2
P

. Chọn B.
Cách 2. Phương trình đường thẳng
: 3.AB y x
Gọi
;3M x x AB
với
2;4x 
(do
M
nằm trong đoạn
AB
).
Ta có
3
22
2
1 1 1 1 1 2 6 17.
yx
Tz i x y i x y x x

 
Khảo sát hàm
2
2 6 17fx x x 
trên đoạn
2;4 .
Câu 2. Xét các số phức
thỏa mãn
1 8 3 53.z iz i

Giá trị lớn nhất của biểu thức
12Pz i 
bằng
A.
53.
B.
53.
C.
185
.
2
D.
106.
Lời giải. Gọi
; , 1;1 , 8;3 , 1; 2
Mxy A B C
lần lượt là điểm biểu diễn các số phức
,
z
1 ,8 3, 1 2
ii i 
trong mặt phẳng tọa độ.
Từ
1 8 3 53 53z i z i MA MB AB M 
thuộc đoạn thẳng
.AB
Ta có
12P z i MC

. Vì
13 , 106CA CB
CA CM CB


, kết hợp với hình vẽ ta suy ra
max
106.
P
Dấu
'' ''
xảy ra khi
M
trùng
.B
Chọn D.
Câu 3. Xét các số phức
thỏa mãn
2 3 6 2 17.z iz i 
Gọi
, Mm
lần lượt là giá trị
lớn nhất và giá trị nhỏ nhất của biểu thức
12 2P z iz i 
.
A.
3 2, 0.Mm

B.
3 2, 2.
Mm
C.
32, 52 25.Mm 
D.
2, 5 2 2 5.
Mm 
Lời giải. Gọi
, 2;3 , 6;1CA B
lần lượt là điểm biểu diễn các số phức
,z
2 3 ,6ii
trong mặt phẳng tọa độ.
Từ
2 3 6 2 17 2 17z i z i CA CB AB C 
thuộc đoạn thẳng
.AB
Ta có
12 2P z i z i CD CE 
với
1;2 , 2; 1 .
DE
Nhận thấy
,DE
nằm về một phía của đường thẳng
.AB
3 2.CD CE DE
Dấu
""
xảy ra khi
.C DE AB
0.CD CE
Dấu
""
xảy ra khi
C AB
và
C
thuộc đường trung trực của đoạn
.DE
Vậy
3 2 , 0.Mm

Chọn A.
Cách 2. Phương trình đường thẳng
: 4 10 0.AB x y 
Gọi
10 4 ;M y y AB
với
1; 3y
(do
M
nằm trong đoạn
AB
).
Ta có
22 22
22 22
1 2 1 2 1 2 11 4 2
.
2 2 1 2 1 84 1
z ix y i x y y y
z ix y i x y y y
  
  
Khi đó
22
1 2 2 17 92 125 17 62 65 .Pz izi yy yy  
Khảo sát hàm
22
17 92 125 17 62 65
fy yy yy  
trên đoạn
1; 3 .
Câu 4. Xét các số phức
thỏa mãn
3 2 3 3 5.z iz i 
Gọi
, Mm
lần lượt là giá trị
lớn nhất và giá trị nhỏ nhất của biểu thức
2 13Pz z i 
.
A.
17 5, 3 2.Mm
B.
26 2 5, 3 2.Mm
C.
26 2 5, 2.Mm
D.
17 5, 2.Mm
Lời giải. Gọi
, 3;2 , 3; 1CA B
lần lượt là điểm biểu diễn các số phức
,z
3 2 , 3ii
trong mặt phẳng tọa độ.
Từ
3 2 3 35 35
z i z i CA CB AB C
 
thuộc đoạn thẳng
.AB
Ta có
2 13P z z i CD CE 
với
2;0 , 1;3 .DE
Nhận thấy
,
DE
nằm về hai phía so với đường thẳng
.AB
3 2.
CD CE DE
Dấu
""
xảy ra khi
, , DCE
theo thứ tự đó thẳng hàng.
max ; 26 2 5.CD CE BD BE AD AE BD BE
Dấu
""
xảy ra khi
.CB
Vậy
26 2 5, 3 2.Mm
Chọn B.
Cách 2. Phương trình đường thẳng
: 2 1 0.
AB x y 
Gọi
1 2;M y y AB
với
1; 2y 
(do
M
nằm trong đoạn
AB
).
Ta có
22
22
22 2
2
2 2 2 32
13 1 3 1 3 4 3
z x yi x y y y
z ix y i x y y y
 
  
.
Khi đó
22
2 13 5 129 5 69Pz z i y y y y 
.
Khảo sát hàm
22
5 129 5 69fy y y y y 
trên đoạn
1; 2 .
Câu 5. Xét các số phức
12
, zz
thỏa
11 2
5
1 2 3 3 2 1 17.
2
ziziz i 
Giá trị lớn
nhất của
12 1
2Pzz z i 
bằng
A.
2 17.
B.
3 29.
C.
17 29.
D.
17 2 29.
Lời giải. Đặt
12
, z a bi z c di 
,,, ;
abcd
Gọi
; , ; , 1;2 , 3;3M ab N cd A B
lần
lượt là điểm biểu diễn các số phức
12
, , 1 2 , 3 3izz i
trong mặt phẳng tọa độ.
11
1 2 3 3 17 17z i z i MA MB AB M 
thuộc đoạn thẳng
.AB
2
5 17
2 1 17
2 22
AB
z i NI
với
5
1; .
2
I


Ta thấy
là trung điểm của
.AB
Suy ra
N
thuộc đường tròn
C
có tâm
,I
đường kính
AB
(như hình bên dưới).
Ta có
12 1
2P z z z i MN MD 
với
2;1 .D
Nhận thấy
M
nằm trên đoạn thẳng
AB
và
NC
17MN AB 
và
max , 29.MD AD BD BD 
Suy ra
12 1
2 17 29.P z z z i MN MD 
Dấu
""
xảy ra khi
.
MB
NA
Vậy
max
17 29.P 
Chọn C.
Câu 6. Xét các số phức
thỏa mãn
2 2 1 3 34.iz i z i 
Giá trị nhỏ nhất của biểu
thức
12P iz i
bằng
A.
9
.
17
B.
3 2.
C.
4 2.
D.
26.
Lời giải. Gọi
; , 2; 2 , 1;3M xy A B
lần lượt là điểm biểu diễn các số phức
,
z
2 2,i
13i
trong mặt phẳng tọa độ
Từ
2 2 1 3 34 2 2 1 3 34 34iz i z i z i z i MA MB AB
 
M 
nằm trên tia đối của tia
.BA
Ta có
1 2 21 2P i z i z i MC 
với
1; 1 .C 
Ta thấy
min min min
4 4 2.MC M B MC CB P  
Chọn C.
Cách 2. Phương trình đường thẳng
: 5 3 4 0.AB x y 
Suy ra
45
;
3
x
Mx


với
1x 
.
Khi đó
2
22 2
45
1 221 21 121 1.
3
x
P iz i z i x y x

 

Khảo sát hàm
2
2
45
11
3
x
fx x



trên
; 1.
Câu 7. Xét các số phức
đồng thời thỏa mãn
43 43 10z iz i
và
34
zi
nhỏ
nhất. Môđun của số phức
bằng
A.
5.
B.
5 2.
C.
6 2.
D.
10.
Lời giải. Gọi
; , 4; 3 , 4;3M xy A B
lần lượt là điểm biểu diễn các số phức
,z
4 3,i
43i
trong mặt phẳng tọa độ.
Từ
4 3 4 3 10 4 3 4 3 10 10ziz i zizi MAMB AB   
M 
nằm trên tia đối của tia
.BA
Ta có
34
z i MC
với
3; 4 .C
Ta thấy
min
5 2.MC CB
Dấu
'' ''
xảy ra
5.MB z 
Chọn A.
Cách 2. Phương trình đường thẳng
44
: 4 4 ;3 3
33
xt
AB M m m
yt



với
0.m
Gọi
3; 4 ,C
ta có
2
3 4 25 50 50 50 5 2.z i MC m m
Dấu
""
xảy ra khi và chỉ khi
0 4;3 .
mM 
Câu 8. Xét các số phức
z a bi
,ab
thỏa mãn
1 2 3.z izi

Tính
P ab
khi
34 1T z iz i 
đạt giá trị lớn nhất.
A.
2.P
B.
6.P
C.
26
.
3
P
D.
28
.
3
P
Lời giải. Ta có
22 2
2
12 3 1 2 3 2 0z i z i a b a b ab  
tập hợp điểm
M
biểu diễn số phức
thuộc đường thẳng
: 2 0.dx y
Gọi
3; 4 , 1; 1 .AB
Ta thấy
,
AB
nằm về cùng phía so với
.d
Khi đó
34 1 .T z i z i MA MB AB 
Dấu
""
xảy ra
11 17 28
;.
33 3
M AB d M P a b

 

Chọn D.
Câu 9. Xét các số phức
thỏa mãn
2 2.z zi
Giá trị nhỏ nhất của biểu thức
12 34 56Pz iz iz i  
được viết dưới dạng
17
2
ab
với
, .ab
Tính
.ab
A.
2.ab
B.
3.ab
C.
4.ab
D.
7.ab
Lời giải. Đặt
,.z x yi x y
Khi đó
22
22
22 2 2z z i x y x y yx  
tập hợp điểm
M
biểu
diễn số phức
thuộc đường thẳng
:.dy x
Ta có
12 34 56P z i z i z i MA MB MC  
với
1;2 , 3;4 , 5;6 .
AB C
Nhận thấy
B
là trung điểm của
AC
nên suy ra
2 22
.
24
MA MC AC
MB

Do đó
2
2 22 2
.
24 4 4
MA MC
MA MC AC AC
P MA MC MA MC
 
Lấy điểm
2;1A
đối xứng với
A
qua
,d
ta có
2
2 22
.
4 4 44
MA MC
AC A C AC
MA MC A C

Suy ra
22
1
1 2 17
3.
2
44
2
a
A C AC
P AC a b
b

Chọn B.
Cách 2. Ta có
12 34 56Pz iz iz i  
22 2
2 6 5 2 14 25 2 22 61.
xx x x x x
 
Suy ra
2 22 2
3 1 11 1 7 1 3 11 1 1
1 17.
24 2 4 24 2 2 22
2
P
x x x xx
 

 
  

 


 
 
Dấu
""
xảy ra
3 11
7
22
.
7
2
2
xx
x
x


Câu 10. Xét các số phức
12
, zz
đồng thời thỏa mãn
12 3 2z iz i
và
12
5.zz
Giá
trị nhỏ nhất của biểu thức
12
13 13z iz i 
bằng
A.
14 5
.
5
B.
3 85
.
5
C.
1105
.
5
D.
1165
.
5
Lời giải. Với
,z x yi
theo giả thiết có
22 2 2
1 2 3 2 2 2 0.x y x y xy

Xét
12
, , 1 3Mz Nz P i
theo giả thiết có
, : 2 20MN x y
và
5.MN
Ta cần tìm giá trị nhỏ nhất của
.PM PN
Gọi
H
là hình chiếu vuông góc của
P
lên
7
,.
5
PH d P

Ta có
22
2 2 22
PM PN PH HM PH HN PH PH HM HN
22
49 1105
4 4. 5 .
55
PH MN



Dấu
""
xảy ra
PH HM
H
PH HN
HM HN MN


là trung điểm đoạn thẳng
.MN
Chọn C.
Vấn đề 7. Phương pháp lấy đối xứng
Câu 1. Xét các số phức
;z a bi a b
thỏa mãn
5 3 1 5.z iz i 
Tính
ab
khi
biểu thức
22 37Pz iz i

đạt giá trị nhỏ nhất.
A.
1.ab 
B.
0.ab
C.
1.ab
D.
2.ab
Lời giải. Đặt
z x yi
,.xy
Từ
222 2
53 15 5 3 1 5 2 1z iz i x y x y x y


tập hợp
điểm
;M xy
biểu diễn số phức
là đường thẳng
: 2 1.xy
Khi đó
22 37P z i z i MA MB 
với
2; 2 , 3;7 .AB
Gọi
C
là điểm đối xứng của
A
qua đường thẳng
,
khi đó ta tìm được
0; 2C 
phương
trình đường thẳng
: 3 2 0.BC x y
Ta có
.P MA MB MC MB BC 
Dấu
'' ''
xảy ra khi khi
1;1M BC M 
1
0.
1
a
ab
b


Chọn B.
Câu 2. Xét các số phức
12
, , zz z
thỏa mãn
12
45 1 1z iz
và
4 8 4.ziz i 
Tính
12
M zz
khi
12
P zz zz 
đạt giá trị nhỏ nhất.
A.
2 5.M
B.
6.M
C.
41.M
D.
8.M
Lời giải.
1
45 1zi 
tập hợp điểm
A
biểu diễn số phức
1
z
là đường tròn
1
C
có
tâm
4;5 ,I
bán kính
1
1.R
2
11z 
tập hợp điểm
B
biểu diễn số phức
2
z
là đường tròn
2
C
có tâm
1; 0 ,J
bán kính
2
1.R
Đặt
z a bi
, .
ab
Ta có
222
2
4 84 4 8 4ziz i a b a b

4
ab

tập hợp điểm
C
biểu diễn số phức
nằm trên đường thẳng
: 4.xy 
Khi đó
12
.P z z z z CA CB 
Gọi
K
là điểm đối xứng của
J
qua đường thẳng
,
khi đó ta tìm được
4; 3
K 
phương
trình đường thẳng
: 4.
IK x
Do đó
min
P
khi và chỉ khi
C IK 
và
1
2
o giua
o giua
A CI C A CI
B CJ C B CJ


12
4;4 , 2;0 2 5.A B M z z AB  
Chọn A.
Câu 3. Xét các số phức
12
, zz
thỏa mãn
1
32 1zi
và
2
2 1.
zi
Số phức
có phần
thực bằng
, phần ảo bằng
thỏa mãn
2 0.ab
Tính
Pab
khi
12
2zz z z 
đạt
giá trị nhỏ nhất.
A.
1.P
B.
3.P
C.
4.P
D.
7.P
Lời giải. Ta có
Số phức
có phần thực bằng
, phần ảo bằng
thỏa mãn
20ab

nên tập hợp điểm
A
biểu diễn số phức
là đường thẳng
: 2.dy x
1
32 1zi 
tập hợp điểm
B
biểu diễn số phức
1
z
là đường tròn có tâm
3; 2 ,D 
bán kính bằng
1.
22
2 1 2 4 2 2.zi z i 
Đặt
32
2zz
khi đó
3
42 2zi

tập hợp điểm
C
biểu diễn số phức
3
z
là đường tròn có tâm
4;2 ,E
bán kính bằng
2.
Khi đó
1 2 13
2.T zz z z zz zz ABAC  
Gọi
H
là điểm đối xứng của
E
qua đường thẳng
,d
khi đó ta tìm được
4; 2H

phương
trình đường thẳng
: 2.DH y 
Do đó
min
T
khi và chỉ khi
A DH d

tọa độ điểm
A
là nghiệm của hệ
2
2
yx
y

1
1; 2 3 .
2
a
A Pab
b

 

Chọn B.
Cách 2. Ta có
12 1 2
2 32 32 42 2 2zz z z z i z i z i z i
 
12
22 22
22 22
32 32 42 2 2
32 42 3
3 2 4 23
3 2 2 4 2 2 3.
z iz iz i z i
z iz i
ab ab
aa aa
 



Xét hàm
22 22
3 22 4 22 3ya a a a 
trên
,
ta được
min 4fa
.
Dấu
'' ''
xảy ra khi
1 2.ab 
Suy ra
3.P
Câu 4. Xét các số phức
12
, zz
thỏa mãn
11
53 13z iz i 
và
22
4 3 2 3.z iz i 
Giá trị nhỏ nhất của biểu thức
12 1 2
66Pzz z iz i
bằng
A.
2 10.
B.
7
.
2
C.
4 130
.
13
D.
18
.
13
Lời giải. Goi
12
, z a bi z c di 
, , , .abcd
Khi đó ta có
2222
11
222 2
22
53 13 5 3 1 3
23 6
33
43 23
4323
z iz i a b a b
ab
cd
z iz i
cdcd







 



tập hợp
M
biểu diễn số phức
1
z
nằm trên đướng thẳng
: 2 3 6,dx y

tập hợp
N
biểu diễn số phức
2
z
nằm trên đướng thẳng
: 3 3.xy

Gọi
6;1 , 6; 1 .AB
Khi đó
12 1 2 12 1 2
66 66Pzz z iz i zz z iz i
MN MA NB MN NB MA MB MA BC 
với
C
là điểm đối xứng của
A
qua
.d
Ta tìm được
66 31
;
13 13
C


4 130
.
13
BC

Chọn C.
Dấu
""
xảy ra khi
M BC d

và
.
NB
Vấn đề 8. Tâm tỉ cự
Câu 1. Xét các số phức
thỏa mãn
| 5 | |2 3 |.zi i
Đặt
22
39 15.Pz i z i 
Biết
P
đạt giá trị nhỏ nhất tại
1
z
và
P
đạt giá trị lớn nhất tại
2
.z
Giá trị của biểu thức
12
zz
bằng
A.
2 13.
B.
2 15.
C.
4 3.
D.
52.
Lời giải. Từ
5 2 3 5 13zi izi 
tập hợp điểm
M
biểu diễn số phức
thuộc trên đường tròn
C
có tâm
5;1 ,C
bán kính
13.
R
Ta có
22
22
39 15
P z i z i MA MB 
với
3; 9 , 1; 5 .AB
Trong mặt phẳng
Oxy
chọn điểm
thỏa
22
0 1; 7 .
22
IA
IA IB I
IB

 
Có
22
2 2 2 22 2
2 2 16 2 .MA MB MI IA MI IB MI MI IA IB IA IB MI 
      
Do đó
min min 1
1
12
2
max max 2
3; 4
34
2 13.
72
7; 2
P MI M M
zi
zz
zi
P MI M M


 





Chọn A.
Câu 2. Xét các số phức
thỏa mãn
1 2 3 2.zi
Gọi
, mM
lần lượt là giá trị nhỏ nhất và
lớn nhất của biểu thức
22
32 2 2 .Pz i z i 
Tổng
mM
bằng
A.
30.
B.
12.
C.
14.
D.
68.
Lời giải. Từ
1 2 32zi 
tập hợp điểm
M
biểu diễn số phức
nằm trên đường
tròn
C
có tâm
1; 2 ,C
bán kính
3 2.R
Ta có
22
22
32 2 2 2P z i z i MA MB 
với
3; 2 , 2;1 .AB
Trong mặt phẳng
Oxy
chọn điểm
thỏa
2 10
2 0 1; 4 .
10
IA
IA IB I
IB

 
Có
22
2 2 2 22 2
2 2 2 2 2 20 .MA MB MI IA MI IB MI MI IA IB IA IB MI 
      
Do đó
2
2
min 2
min max
2
2
max min
max 1
20 20 30
30
12.
18
20 20 18
P IM CI R
P MI
m
S
P MI M
P IM CI R
 


  



 

Chọn B.
Câu 3. Xét các số phức
z ai
,
ab
thỏa mãn
4 3 5.zi
Tính
ab
khi biểu thức
2 22
22 2 4 3 2Qz i z i z i 
đạt giá trị lớn nhất.
A.
11.ab
B.
12.ab
C.
13.ab
D.
14.ab
Lời giải. Ta có
43 5zi 
tập hợp điểm
M
biểu diễn số phức
nằm trên đường
tròn
4;3 ,I
bán kính
5.r
Ta có
2 22
222
22 2 4 3 2 2 3
Q z i z i z i MA MB MC 
với
2;2 , 4; 1 , 0; 2 .ABC 
Trong mặt phẳng
Oxy
chọn điểm
N
thỏa mãn
2 3 0 1; 1 .NA NB NC N 
  
Có
222
222
23 2 3Q MA MB MC MN NA MN NB MN NC
     
22 2 2
22 2 2
6 2 3 2 2. 3.
6 2 3.
MN NA NB NC MN NA NB NC
MN NA NB NC


   
Suy ra
max
Q
khi
max
MN
M 
đối xứng với
N
qua
(vì
N
thuộc đường tròn tâm
bán
kính
5r
)
7;7 .
M 
Vậy
7 7 14.ab
Chọn D.
Câu 4. Xét các số phức
12
, zz
thỏa mãn
34 2zi
và
12
1.zz
Giá trị nhỏ nhất của
biểu thức
22
12
Pz z
bằng
A.
4 3 5.
B.
6 2 5.
C.
5.
D.
10.
Lời giải. Ta có
34 2zi 
tập hợp điểm
M
biểu diễn số phức
nằm trên đường
tròn
C
có tâm
3; 4 ,I
bán kính
2.R
Gọi
, AB C
lần lượt là điểm biểu diễn của
12
, .
zz
Suy ra
12
.z z AB
Khi đó
22
22
22
12
P z z OA OB OI IA OI IB 
   
2. 2. 2. .cos , 2 10.OI IA IB OI BA OI AB OI BA OI

      
Dấu
""
xảy ra khi
0.OI k BA k
 
Chọn D.
Vấn đề 9. Phương pháp cân bằng hệ số
Câu 1. Xét các số phức
thỏa mãn
1.z
Giá trị lớn nhất của
12 1
Tz z 
bằng
A.
2 5.
B.
2 10.
C.
3 2.
D.
3 5.
Lời giải. Từ
1
z 
tập hợp điểm
M
biểu diễn số phức
thuộc đường tròn
C
có tâm
0;0O
, bán kính
1.
R
Gọi
1; 0 , 1; 0 .AB
Nhận thấy
AB
là đường kính của
C
nên
2 22
4.MA MB AB 
Khi đó
22 2 2
2 1 2 5.4 2 5.
T MA MB MA MB
Chọn A.
Nhận xét. Bài này rơi vào trường hợp đặc biệt là
AB
là đường kính của đường tròn.
Nếu bài toán hỏi giá trị nhỏ nhất thì ta có đánh giá
2.
MA MB MA
Dấu
'' ''
xảy ra khi và
chỉ khi
.MB
Khi đó
min 2 .MA MB AB
Câu 2. Xét các số phức
thỏa
1 2.z 
Giá trị lớn nhất của
2T zi z i 
bằng
A.
4.
B.
4 2.
C.
8.
D.
8 2.
Lời giải. Từ
12z 
tập hợp điểm
M
biểu diễn số phức
thuộc đường tròn
C
có
tâm
1; 0I
, bán kính
2.R
Gọi
0; 1 , 2;1 .AB
Nhận thấy
AB
là đường kính của
C
nên
2 22
8.MA MB AB 
Khi đó

22 2 2
1 1 2.8 4.T MA MB MA MB

Chọn A.
Câu 3. Xét các số phức
z a bi
;ab
có môđun bằng
và phần ảo dương. Tính giá trị
biểu thức
2018
52S ab



khi biểu thức
2 32Pz z
đạt giá trị lớn nhất.
A.
0.S
B.
1.S
C.
2018
2.
S
D.
1009
2.
S
Lời giải. Gọi
;M ab
với
0
b
là điểm biểu diễn số phức
.z
Gọi
2;0 , 2;0 .
AB
Ta có
22
2 2 4.z a bi a b 
Suy ra
M
thuộc đường tròn
C
đường kính
AB
nên
2 22
16.MA MB AB 
Khi đó

22 2 2
2 3 2 3 1 3 4 10.P z z MA MB MA MB
Dấu
""
xảy ra khi
2018
0
86 8 6
; 5 2 0.
55 5 5
3
b
MC
MS
MB
MA





 







Chọn A.
Câu 4. Xét các số phức
thỏa mãn
11
.
3
2
z
zi
Gọi
,
Mm
lần lượt là giá trị lớn nhất và
nhỏ nhất của
2 4 7.
P zi z i 
Giá trị
Mm
bằng
A.
10 2 5.
B.
10 4 5.
C.
20 2 5.
D.
20 4 5.
Lời giải. Gọi
;z a bi x y z a bi

và
;M ab
là điểm biểu diễn số phức
.
z
Ta có
22
22
11
21 3 2 1 3
3
2
z
z zi a b a b
zi




22
2 3 20.
ab 
Suy ra
M
thuộc đường tròn
C
có tâm
2;3 ,I
bán kính
2 5.R
Vì
47 47 2 47 2z i z i P z i z i MA MB   
với
0; 1 , 4;7 .AB
Nhận thấy
AB
là đường kính của đường tròn
C
nên
2 22
80.MA MB AB

2.MA MB MA

Dấu
""
xảy ra khi
.
MB
Khi đó
min 2 4 5.m MA MB AB


22 2 2
2 1 2 5.80 20.
MA MB MA MB 
Vậy
20 4 5.
Mm
Chọn D.
Câu 5. Xét số phức
thỏa mãn
1 2 2 2.zi
Với
, ab
là số thực dương cho trước, giá trị
lớn nhất của biểu thức
1 34
P az bz i 
bằng
A.
22
.
ab
B.
22
2 2.ab
C.
22
42 2 .ab
D.
22
.ab
Lời giải. Từ
1 2 22zi 
tập hợp điểm
M
biểu diễn số phức
thuộc đường tròn
C
có tâm
1; 2 ,I
bán kính
2 2.R
Vì
34 34 1 34 . .
z i z i P a z b z i a MA b MB
 
với
1;0, 3;4.AB
Nhận thấy
AB
là đường kính của đường tròn
C
nên
2 22
32.MA MB AB

Ta có

22 2 2 22 2 2
. . 32 4 2 2 .
P a MA b MB a b MA MB a b a b 
Dấu
'' ''
xảy ra
MA MB
ab

MA a
MB b

tan .
a
MBA
b

Vì
, 0ab
nên phương trình
tan
a
x
b
luôn có nghiệm. Tức là, luôn có điểm
M
thuộc đường tròn để đẳng thức xảy ra.
Vậy giá trị lớn nhất của
P
là
22
42 2 .
ab
Chọn C.
Câu 6. Xét các số phức
,z a bi a b

thỏa mãn
4 3 5.
zi
Tính
ab
khi biểu
thức
13 1Pz iz i  
đạt giá trị lớn nhất.
A.
4.ab
B.
6.ab
C.
8.ab
D.
10.ab
Lời giải. Từ
43 5zi

tập hợp điểm
M
biểu diễn số phức
thuộc đường tròn
tâm
4;3I
, bán kính
5.
R
Gọi
1; 3 , 1; 1AB
và
0;1N
là trung điểm của
.AB
Khi đó
22
13 1 2 .P z i z i MA MB MA MB  
Mà
2
22 2
2.
2
AB
MA MB MN

Do đó để
max max
, , P MN M I N 
theo thứ tự đó thẳng
hàng, suy ra
6; 4 10.  M ab
Chọn D.
Nhận xét.
min
, , P NMI 
theo thứ tự đó thẳng hàng, suy ra
2;2 .M
Bài toán rơi vào trường hợp đặc biệt là đường trung trực của đoạn
AB
đi qua tâm của
đường tròn, nếu không rơi vào trường hợp đặc biệt thì trở thành bài toán vô cùng khó.
Câu 7. Xét các số phức
,z a bi a b
thỏa mãn
4 3 2 2.
zi

Tính
2ab
khi biểu
thức
12 96Pz iz i 
đạt giá trị lớn nhất.
A.
2 7.
ab
B.
2 9.ab
C.
2 12.ab
D.
2 13.ab
Lời giải. Từ
4 3 22zi 
tập hợp điểm
M
biểu diễn số phức
thuộc đường tròn
C
có tâm
4;3 ,I
bán kính
2 2.R
Gọi
1; 2 , 9; 6AB
và
5; 2N
là trung điểm của
.AB
Khi đó
22
12 96 2 .P z i z i MA MB MA MB 
Mà
2
22 2
2.
2
AB
MA MB MN
Do đó để
max max
, , P MN M I N 
theo thứ tự đó thẳng
hàng, suy ra
2;5 2 9.M ab 
Chọn B.
Câu 8. Xét các số phức
thỏa mãn
2 2 1.zi
Giá trị lớn nhất của biểu thức
32 2 2 4Pz i z i 
bằng
A.
5.
B.
2 5.
C.
3 15.
D.
10.
Lời giải. Từ
22 1zi 
tập hợp điểm
M
biểu diễn số phức
thuộc đường tròn
C
có tâm
2;2 ,
I
bán kính
1.R
Ta có
32 2 12 32 2 12.Pz iz iz iz i
 
Gọi
3;2 , 1;2
AB
. Nhận thấy
I
là trung điểm của
.AB
Khi đó
22 2 2
32 2 12 2 1 2
P z i z i MA MB MA MB 
2
22 2
5 5 2 5.4 2 5.
2
AB
MA MB MI



Dấu
""
xảy ra
2.
12
MA MB
MB MA 
Chọn B.
Câu 9. Xét các số phức
thoả mãn
2 2 2.zi

Gọi
, Mm
lần lượt là giá trị lớn nhất, giá
trị nhỏ nhất của biểu thức
3 2 3 4.Pz iz i  
Tính
.Mm
A.
226 62.Mm
B.
2 26 8 2.
Mm
C.
11 2.Mm
D.
16 2.Mm
Lời giải. Từ
2 22zi 
tập hợp các điểm
K
biểu diễn số phức
thuộc đường tròn
C
có tâm
2;1 ,I
bán kính
2 2.R
Gọi
3; 2 , 3; 4AB

và
0; 1
N
là trung điểm của
.AB
Nhận thấy
.
NC
Khi đó
22
32 34 2 .
P z i z i KA KB KA KB  
Mà
2
22 2
2.
2
AB
KA KB KN
Do đó để
max max
.P KN
Dấu
""
xảy ra khi
K
đối xứng
N
qua
nên
4;3K
10 2M KA KB 
.
min min
6 2.P KN K N m KA KB AN NB AB  
Vậy
16 2.Mm
Chọn D.
Câu 10. Xét các số phức
,z a bi a b
thỏa mãn
3 2 2.zi
Tính
ab
khi biểu thức
12 2 25Tz i z i 
đạt giá trị nhỏ nhất.
A.
3.ab
B.
2 3.
ab
C.
4 3.
ab
D.
4 3.
ab
Lời giải. Từ
32 2zi 
tập hợp điểm
M
biểu diễn số phức
thuộc đường tròn tâm
3; 2 ,I
bán kính
2.
R
Khi đó
12 2 25 2T z i z i MA MB

với
1; 2 , 2; 5 .AB
Gọi điểm
2;2 .C IA
Ta có
2.
IC IM
IM IA
MIC AIM MA CM
MIC AIM

∽
Suy ra
2 2.T MB MC BC 
Dấu
""
xảy ra khi
, , MBC
theo thứ tự thẳng hàng. Khi
đó ta tìm được
2
2;2 3 4 3.
23
a
M ab
b


Chọn D.
Nhận xét.
Kỹ thuật chọn điểm
:
C
Chọn điểm
C
thỏa mãn hệ thức
2MA MC
 
với vị trí của
M
như hình vẽ bên dưới.
Mục đích chọn điểm
C
như thế để tạo ra
22T MC MB

gọi là phương pháp cân bằng hệ
số. Dĩ nhiên không phải bài nào cũng cân bằng được, hệ số được cho trong dữ kiện đề bài phải
được tác giả xử lý ngon lành trước rồi.
Câu 11. Xét các số phức
,z a bi a b
thỏa mãn
2.z
Tính
ab
khi biểu thức
4 2 14Pz z i 
đạt giá trị nhỏ nhất.
A.
2.ab 
B.
2.
ab

C.
2 5.
ab
D.
4 5.
ab

Lời giải. Từ
2z

tập hợp điểm
M
biểu diễn số phức
thuộc đường tròn tâm
0;0 ,O
bán kính
2.R
Khi đó
4 2 14 2P z z i MA MB 
với
4;0, 1; 4.
AB

Gọi điểm
1; 0 .H OA
Chứng minh được
2.
MA MH
Suy ra
2 2.P MH MB BH 
Dấu
""
xảy ra khi
, ,
HMB
theo thứ tự thẳng hàng. Khi
đó ta tìm được
0
0; 2 2.
2
a
M ab
b


Chọn A.
Câu 12. Xét các số phức
thỏa mãn điều kiện
1.zi
Giá trị nhỏ nhất của biểu thức
2 2 23Pz i z i 
bằng
A.
43
.
3
B.
2.
C.
3.
D.
3.
Lời giải. Từ
1zi 
tập hợp điểm
M
biểu diễn số phức
thuộc đường tròn tâm
0; 1 ,I
bán kính
1.R
Khi đó
2 2 23 2 2 23 2P z i z i z i z i MA MB  
với
2; 1 , 2; 3 .AB
Gọi điểm
2
;1 .
2
C IA



Chứng minh được
2.MA MC
Suy ra
2 2.
P MC MB BC 
Dấu
""
xảy ra khi
, , BM C
theo thứ tự đó thẳng hàng.
Vậy
min
2 3.P BC

Chọn D.
Câu 13. Xét các số phức
thỏa mãn điều kiện
1 5.zi
Giá trị lớn nhất của biểu thức
2 8 79
P ziz i

bằng
A.
5
.
2
B.
53
.
2
C.
55
.
2
D.
5 5.
Lời giải. Từ
15zi

tập hợp điểm
M
biểu diễn số phức
thuộc đường tròn tâm
1;1 ,I
bán kính
5.R
Khi đó
2 8 79 2P z i z i MA MB 
với
0;8 , 7;9 .AB
Gọi điểm
5
;3 .
2
C IB


Chứng minh được
2.MB MC
Suy ra
2 2.
P MA MC AC 
Dấu
""
xảy ra khi
, , AC M
theo thứ tự đó thẳng hàng.
Vậy
max
2 5 5.P AC
Chọn D.
Câu 14. Xét các số phức
thỏa
1.z
Giá trị lớn nhất của biểu thức
22 2
Tz z
bằng
A.
2.
B.
2 5.
C.
5.
D.
5 2.
Lời giải. Từ
1z 
tập hợp điểm
M
biểu diễn số phức
thuộc đường tròn tâm
0;0 ,O
bán kính
1.R
Gọi
2;0 , 2;0 .AB
Khi đó ta có
22 2 2T z z MA MB 
2
22 2 2 2
1 2 5 2 5 2.
2
AB
MA MB MO



max
5 2.T 
Dấu bằng xảy ra khi
.
2
MC
MB MA
Chọn D.
Cách 2. Đặt
,.z a bi a b

Từ
22
1 1.z ab
Ta có
22
22
22 2 2 2 2Tz z a b a b 
22
22 2 2 22
1 2 2 2 10 4 5 2.a b a b ab

 


Dấu
""
xảy ra khi
22
22
22
22
3
1
1
4
.
7
24 5 5 4
22 2
4
a
ab
ab
aa
a ba b
b











Câu 15. Xét các số phức
thỏa mãn
2 1 3 2.zi
Giá trị lớn nhất của biểu thức
1 3 12Pz z i 
bằng
A.
2 2.
B.
4.
C.
4 2.
D.
4 3.
Lời giải. Từ
13 2
2 13 2
22 2
zi z i 
tập hợp điểm
M
biểu diễn số phức
thuộc đường tròn
C
có tâm
13
;,
22
I


bán kính
2
.
2
R
Gọi
1; 0 , 1; 2 .AB
Nhận thấy
BC
và
3 0.IA IB
 
Khi đó
22
1 3 1 2 3 1. 3. 3 1 3 3 .P z z i MA MB MA MB MA MB 
Ta có
22
22
33MA MB MI IA MI IB 
   
22 2 22 2
4323438.MI IA IB MI IA IB MI IA IB  
  
Vậy
1 3 .8 4 2.P 
Dấu
'' ''
xảy ra
3
0;1 .
1
3
MA MB
MA MB M N 
Chọn C.
Câu 16. Cho số phức
z a bi

,ab
thỏa mãn
3 3 6.zi
Tính
ab
khi biểu thức
2 63 3 15Pz iz i 
đạt giá trị nhỏ nhất.
A.
2 2 5.ab
B.
2 5 2.ab
C.
2 5 4.ab
D.
4 2 5.ab
Lời giải. Từ
33 6
zi 
tập hợp điểm
M
biểu diễn số phức
thuộc đường tròn tâm
3;3 ,I
bán kính
6.R
Khi đó
2 63 3 15 2 3P z i z i MA MB 
với
6; 3 , 1; 5 .AB 
Xét điểm
1; 3 ,
C
ta thấy
C IA
và
23
.
32
IC IM
IMC IAM MA MC
IM IA
 
∽
Suy ra
min
33 3P MC MB BC P BC 
khi
, ,
BMC
theo thứ tự đó thẳng hàng
1; 3 5 .M 
Vậy
2 2 5.ab
Chọn A.
Vấn đề 10. Elip
Câu 1. Xét các số phức
thỏa mãn
4 4 10zz

. Giá trị lớn nhất và nhỏ nhất của
z
lần lượt là
A.
10
và
4.
B.
và
4.
C.
và
3.
D.
và
3.
Lời giải. Đặt
;.z x yi x y
Gọi
;M xy
là điểm biểu diễn của số phức
.z
Trong mặt phẳng với hệ tọa độ
Oxy
, gọi
1
4;0F
và
2
4;0F
thì giả thiết bài toán đã cho có
dạng
12
10.MF MF
Mà
12
8 10FF 
quỹ tích điểm
M
là đường Elip có hai tiêu điểm là
12
, ;FF
độ dài trục
lớn
2 10,a
tiêu cự
2 8,c
độ dài trục nhỏ
22
22 6b ac 
(tham khảo hình vẽ).
Dựa vào hình vẽ, ta thấy
12
max
12
min
5
.
3
z OA OA
z OB OB


Chọn D.
Cách 2. Ta có
10 4 4 4 4 2 5z z zz z z 
.
Áp dụng bất đẳng thức Bunhiacopxki, ta có
2 22
100 4 .1 4 .1 4 4 .2zz z z




22
4 4 50zz




22
2 2 22
4 4 50 9 3.
a b a b ab z  
Câu 2. Xét các số phức
thỏa mãn
22
4.
11
iz iz
ii


Gọi
M
và
lần lượt là giá trị
lớn nhất và giá trị nhỏ nhất của
.z
Tính
..
Mn
A.
. 1.
Mn
B.
. 2.Mn
C.
. 2 2.
Mn
D.
. 2 3.
Mn
Lời giải. Đặt
;.z x yi x y
Gọi
;M xy
là điểm biểu diễn của số phức
.
z
Ta có
22
4 1 1 4.
11
iz iz z i z i
ii
 

1
Gọi
1
1;1F
là điểm biểu diễn số phức
1;
i
2
1; 1F
là điểm biểu diễn số phức
1.i
Phương trình
1
được viết lại:
12
4.MF MF
Mà
12
22 4FF 
quỹ tích điểm
M
là đường Elip có hai tiêu điểm là
12
, ;
FF
độ dài
trục lớn
2 4,a
tiêu cự
2 2 2,c
độ dài trục nhỏ
22
2 2 22b ac 
(tham khảo hình vẽ).
Dựa vào hình vẽ, ta thấy
12
max
12
min
2
2
. 2 2.
2
2
z OA OA
M
Mn
n
z OB OB







Chọn C.
Cách 2. Ta có
22
4 2 2 2 2.
11
iz iz iz z z M
ii


Lại có
2
22 2
22
2 22
22 2 2 2
4 1 1 2.2 4 2
1 1 11 1
iz iz iz iz iz z
ii i i i






 









2
2 2 2.zz n 
Câu 3. Xét số phức
thỏa mãn
2 1 2 1 10.zi zi 
Gọi
M
và
m
là giá trị lớn
nhất và giá trị nhỏ nhất của
.z
Tính tổng
.
SMm
A.
17.S
B.
2 21.S
C.
8.S
D.
9.S
Lời giải. Đặt
;.z x yi x y
Gọi
;M xy
là điểm biểu diễn của số phức
.z
Ta có
2 1 2 1 10 2 2 10.z i z i z iz i 
1
Gọi
1
2;1F
là điểm biểu diễn số phức
2;i
2
2;1F
là điểm biểu diễn số phức
2.i
Phương trình
1
được viết lại:
12
10.MF MF
Mà
12
4 10FF 
quỹ tích điểm
M
là đường Elip có hai tiêu điểm là
12
, ;FF
độ dài trục
lớn
2 10,a
tiêu cự
2 4,c
độ dài trục nhỏ
22
2 2 2 21b ac 
(tham khảo hình vẽ).
Dựa vào hình vẽ, ta thấy
min
21 1.z OC

Ta có
5;1A
là điểm nằm trên trục lớn ;
0; 21 1B
là điểm nằm trên trục nhỏ. Vì
OB OA
suy ra
B
là điểm nằm trên Elip cách xa gốc
O
nhất. Suy ra
max
21 1.
z OB

Vậy
2 21.Mm
Chọn B.
Cách 2. Tập hợp điểm
M
biểu diễn số phức
nằm trên elip
2
2
1
: 1.
25 21
y
x
E

Đặt
5sin
1 21 cos
at
bt

với
0;2 .t
Khi đó
2
2
2 22 2 2
25sin 1 21 cos 26 4 cos 2 21 cos
z OM a b t t t t 
1 21 1 21.z 
Suy ra
max
min
0
1 21 khi cos 1
1 21
.
0
1 21 khi cos 1
1 21
a
zt
b
a
zt
b


 

Câu 4. Xét các số phức
thoả mãn
1 3 6.z iz i
Tìm giá trị nhỏ nhất
min
P
của
biểu thức
1 4.Pz i 
A.
min
2 5 2.P 
B.
min
2 5 2.P 
C.
min
5 2.P 
D.
min
5 2.P 
Lời giải. Đặt
;.z x yi x y
Gọi
;
M xy
là điểm biểu diễn của số phức
.
z
Trong mặt phẳng với hệ tọa độ
Oxy
, gọi
1
1;1
F
và
2
3; 1F
thì giả thiết bài toán đã cho có
dạng
12
6.
MF MF

Mà
12
25 6FF 
quỹ tích điểm
M
là đường Elip có hai tiêu điểm là
12
, ;
FF
độ dài
trục lớn
2 6,a
tiêu cự
2 2 5,c
độ dài trục nhỏ
22
22 4b ac 
(tham khảo hình vẽ).
Dựa vào hình vẽ, ta thấy
14Pz i 
nhỏ nhất
MN
nhỏ nhất (với
1; 4N 
là điểm
biểu diễn số phức
14i
)
1
.MB
Khi đó
min 1 1
2 5 2.MN B N IN IB 
Chọn A.
Nhận xét. Bài này đặc biệt ở chỗ điểm
N
thuộc đường thẳng
12
.BB
Câu 5. Xét các số phức
thỏa
1 1 3 6 5.z iz i

Giá trị lớn nhất của
23
Pz i 
bằng
A.
2 5.
B.
4 5.
C.
5 5.
D.
6 5.
Lời giải. Đặt
;.z x yi x y
Gọi
;M xy
là điểm biểu diễn của số phức
.
z
Trong mặt phẳng với hệ tọa độ
Oxy
, gọi
1
1;1F
và
2
1; 3
F

thì giả thiết bài toán đã cho có
dạng
12
6 5.
MF MF

Mà
12
25 65FF

quỹ tích điểm
M
là đường Elip có hai tiêu điểm là
12
, ;
FF
độ dài
trục lớn
2 6 5,a
tiêu cự
2 2 5,c
độ dài trục nhỏ
22
2 2 4 10
b ac

(hình vẽ).
Dựa vào hình vẽ, ta thấy
max 2
min 1
55
5
P CA
P CA


với
2;3 .C
Chọn C.
Nhận xét. Bài này đặc biệt ở chỗ điểm
C
thuộc đường thẳng
12
.
AA
Những bài Elip trên thuộc dạng Elip không chính tắc (Elip xiên), nó không nằm trong chương
trình SGK hiện hành nên bạn đọc chỉ tham khảo thêm, tuy nhiên cũng có cách đặt ẩn phụ
(tịnh tiến + quay) để đưa về Elip cơ bản như chương trình SGK hiện hành nhưng công thức
cồng kềnh và khó nhớ. Vì thế ở đây ta chỉ khai thác những bài đặc biệt là tìm GTLN-GTNN
của khoảng cách từ một điểm thuộc Elip đến một điểm cố định mà điểm cố định này phải
thuộc các đường thẳng chứa các trục của Elip.
---------- HẾT ----------
| 1/56
| | Tải xuống

Có thể bạn quan tâm:

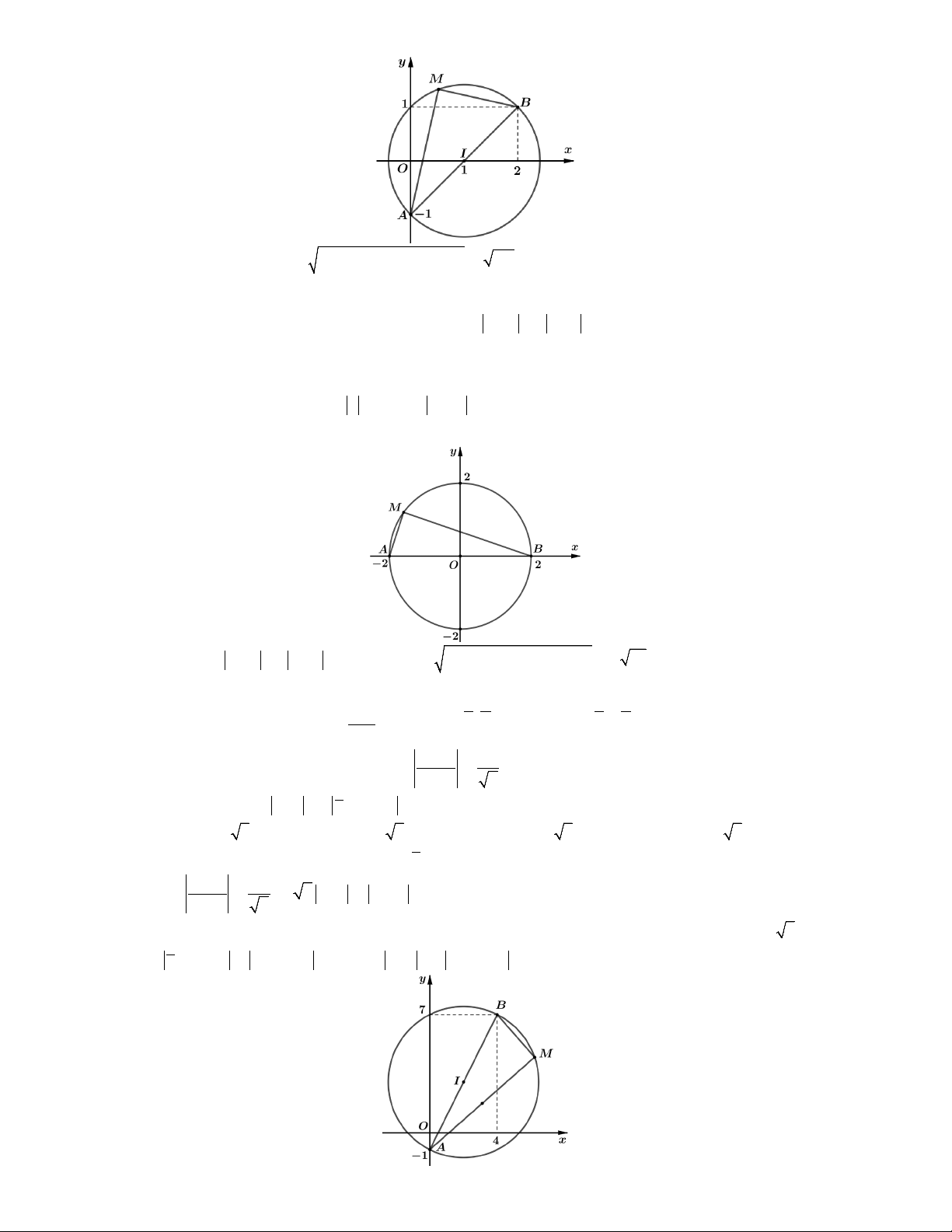
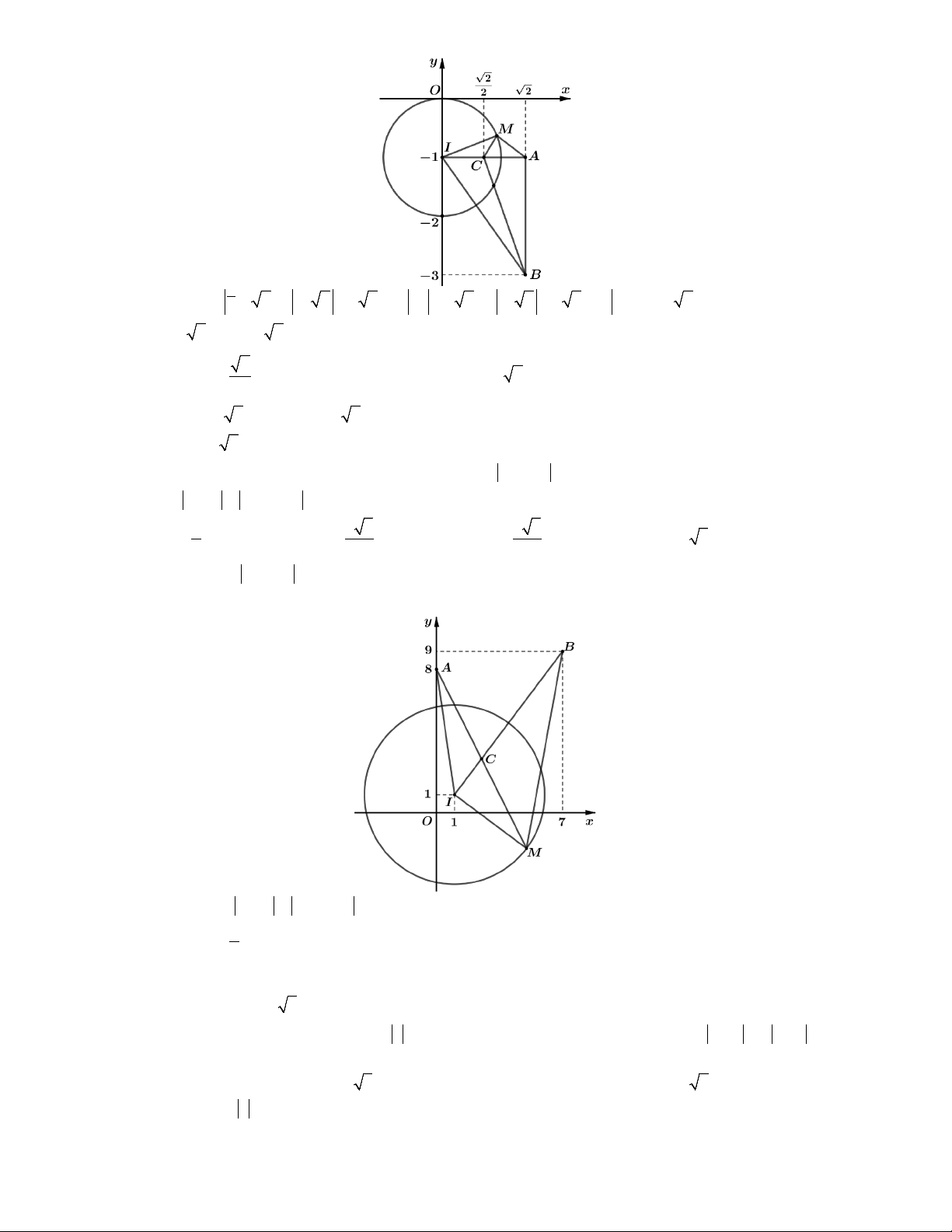
Preview text:

Vấn đề 1. Điểm và đường thẳng
Câu 1. Xét các số phức z, w thỏa mãn z  22i z 4i và w iz 1. Giá trị nhỏ nhất của w bằng A. 2 . B. 3 2 . C. 2. D. 2 2. 2 2
Câu 2. Xét các số phức z thỏa mãn z z 1 2i . Giá trị nhỏ nhất của biểu thức
P  1 2iz 11 2i bằng A. 5 . B. 5. C. 2 . D. 5 . 2 2 5 2
Câu 3. Xét các số phức z thỏa mãn z 1i z 3i . Môđun lớn nhất của số phức 1 w  là z A. 2 5 . B. 4 5 . C. 9 5 . D. 7 5 . 7 7 10 10
Câu 4. Xét các số phức z thỏa mãn 2
z 2z  5  z 1 2iz 3i  
1 . Giá trị nhỏ nhất của
biểu thức P z 2  2i bằng A. 1. B. 3 . C. 5 . D. 5. 2 2
Câu 5. Xét các số phức z thoã mãn z  2i z 12i . Gọi w là số phức thoã mãn điều kiện
w  1iz  2. Giá trị nhỏ nhất của biểu thức P w bằng A. 1. B. 1. C. 5 . D. 5 . 3 5 34 41
Câu 6. Xét các số phức z, w thỏa mãn z 13i z  2i và w 13i w 2i . Giá trị nhỏ
nhất của biểu thức P z w là A. 13 1. B. 26 . C. 3 . D. 3 26 . 2 4 13 13
Vấn đề 2. Điểm và đường tròn
Câu 1. Xét các số phức z thỏa mãn iz 1  1 . Gọi ,
m M lần lượt là giá trị nhỏ nhất và giá
trị lớn nhất của biểu thức P z . Tính S  2020 M  . m A. S  2014. B. S  2016. C. S  2018. D. S  2022.
Câu 2. Xét các số phức z thỏa mãn z 23i  1 . Giá trị lớn nhất và giá trị nhỏ nhất của
biểu thức P z 1i lần lượt là
A. 13  2 và 13 2 .
B. 13 1 và 13 1. C. 6 và 4 .
D. 13  4 và 13 4 .
Câu 3. Xét các số phức z thỏa mãn 1iz 17i  2. Gọi ,
m M lần lượt là giá trị nhỏ
nhất và giá trị lớn nhất của P z . Tính S M  . m A. S  2.
B. S  4. C. S  10. D. S  24. 1iz
Câu 4. Xét các số phức z, w thỏa mãn
 2  1 và w iz. Giá trị lớn nhất của biểu 1i
thức P z w bằng A. 3 B. 2 3 C. 3 2 D. 3 3
Câu 5. Xét các số phức z , z thỏa mãn z 1i  1 và z  2iz . Giá trị nhỏ nhất của biểu 1 2 1 2 1
thức P  2z z bằng 1 2 A. 2 2. B. 22 2. C. 4 2 2. D. 8 2.
Câu 6. Xét các số phức z
z thỏa mãn z không phải là số thực và w  là số thực. Tìm 2 2  z
giá trị lớn nhất P của biểu thức P z 1i . max A. P  2. B. P  2. C. P  2 2. D. P  8. max max max max
Câu 7. Xét các số phức 
z thỏa mãn z  2 . Biểu thức z i P
đạt giá trị nhỏ nhất và giá z
trị lớn nhất lần lượt tại z và z . Tìm phần ảo a của số phức w z z . 1 2 1 2 A. a  4. B. a  0. C. a  1. D. a  4.
Câu 8. Xét các số phức z thỏa mãn z  1. Gọi M , m lần lượt là giá trị lớn nhất và nhỏ nhất của 2z i P
. Tỉ số M bằng z 2 m A. 53 2    . B. 9 4 2 . C. 10 6 34 . D. 25 4 34 . 4 7 9 9
Câu 9. Xét hai số phức z , z thay đổi thỏa mãn z z z z  4 2i  2. Gọi , A B lần 1 2 1 2 1 2
lượt là giá trị nhỏ nhất và giá trị lớn nhất của biểu thức 2 2 z z
. Giá trị của A B là 1 2 A. 20. B. 24. C. 28. D. 32.
Câu 10. Xét các số phức z, thỏa mãn |z| 5 và  43iz 12i. Giá trị nhỏ nhất của || bằng A. 3 5. B. 4 5. C. 5 5. D. 6 5.
Câu 11. Cho số phức z thỏa mãn đồng thời z 1 2i  5 và z 1i có môđun lớn
nhất. Số phức z có môđun bằng A. 6. B. 2 5. C. 3 2. D. 5 2.
Câu 12. Xét các số phức z thỏa mãn z 24i  2 2. Trong các số phức w thỏa mãn
w z 1i, gọi w và w lần lượt là số phức có môđun nhỏ nhất và môđun lớn nhất. Khi đó 1 2 w w bằng 1 2
A. 2  6i.
B. 2  4i.
C. 4 12i.
D. 4 8i.
Câu 13. Xét các số phức z thỏa z 1 2i  2 5 và số phức thỏa 510i 34iz 25i.
Tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P bằng A. 2 10. B. 4. C. 4 5. D. 6.
Câu 14. Xét các số phức z thỏa mãn 2
z z z z z . Giá trị lớn nhất của biểu thức
P z 52i bằng A. 2 3 5. B. 2 5 3. C. 5  2 3. D. 5 3 2.
Vấn đề 3. Đường thẳng và đường tròn
Câu 1. Xét các số phức z thỏa mãn 2 2
z 2  z i  1 và các số phức z thỏa mãn 1 1 1 2
z  4 i  5 . Giá trị nhỏ nhất của P z z bằng 2 1 2 A. 5. B. 2 5. C. 2 5 . D. 3 5 . 5 5
Câu 2. Gọi C là tập hợp các số phức w thỏa mãn w 23i w 32i . Gọi C là tập 2  1 
hợp các số phức z thỏa mãn z 2  4i 1. Giá trị nhỏ nhất của biểu thức P w z bằng A. 2 3 1 . B. 2 3 1 . C. 3 2 1 . D. 3 2 1 .
Câu 3. Xét các số thức z thỏa mãn z 2i z 4i và z 33i 1. Giá trị lớn nhất của biểu
thức P z 2 1 bằng A. 5  2. B. 10 C. 10 1. D. 13 1.
Câu 4. Xét các số phức z, w thỏa mãn iz 2i 2  z 1 và max w 22i , w  2. Giá trị
nhỏ nhất của biểu thức P z w bằng A. 1 . B. 5 . C. 9 . D. 13 . 2 5 2 2 5 2 5 m  ax 
z ; z 1i 1
Câu 5. Xét các số phức z, w thỏa mãn 
. Giá trị nhỏ nhất của biểu thức
w 12i w 2i 
P z w bằng A. 0. B. 1 . C. 2 1. D. 2 2 1. 6
Câu 6. Kí hiệu S là tập hợp các số phức z thỏa mãn z 1  34 và z 1 mi z m  2i
(trong đó m   ). Gọi z , z là hai số phức thuộc tập hợp S sao cho z z là lớn nhất. Khi 1 2 1 2
đó, hãy tính giá trị của biểu thức z z . 1 2
A. z z  2.
B. z z  2.
C. z z  10.
D. z z  130. 1 2 1 2 1 2 1 2
Câu 7. Biết số phức z x yi  ;
x y   thỏa mãn đồng thời z 3 4i  5 và biểu thức 2 2
P z  2  z i đạt giá trị lớn nhất. Tính z . A. z  33 . B. z  50 . C. z  10 . D. z  5 2 .
Câu 8. Xét các số phức z thỏa mãn z 13i  13. Gọi ,
m M lần lượt là giá trị nhỏ nhất và
lớn nhất của biểu thức 2 2
P z  2  z 3i . Tổng m M bằng A. 10. B. 25. C. 34. D. 40.
Câu 9. Xét các số phức z x yi  ;
x y   thỏa mãn 1iz  2i  4. Giá trị lớn nhất của
biểu thức T x y 3 bằng A. 4. B. 4 2. C. 4  2 2. D. 8.
Câu 10. Xét các số phức z thỏa mãn | z  2  1 2i . Giá trị nhỏ nhất của biểu thức P |
z 12i||z 34i||z 56i| được viết dưới dạng a b, với a là phân số tối giản. b
Giá trị của a b bằng A. 10. B. 11. C. 12. D. 17.
Câu 11. Xét các số phức z z
z , z thoả mãn z 3 4i  1, z 1  z i và 1 2 là số thực. 1 2 1 2 2 2 i
Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của z z . Tính P M m . 1 2 A. P  14 5. B. P  16 5. C. P  18 5. D. P  20 5. Câu 12. Cho z z
z là số phức, z là số thực thoả mãn z 2i  1 và 2
1 là số thực. Tổng giá 1 2 1 1i
trị lớn nhất và giá trị nhỏ nhất của biểu thức P z z là 1 2 A. 2. B. 2 2. C. 3 2 D. 4 2.
Câu 13. Cho z x yi x, y   là số phức thỏa mãn z 23i z i 2  5. Gọi M, m
lần lượt là giá trị lớn nhất và nhỏ nhất của 2 2
P x y  8x  6 .
y Giá trị M m bằng A. 156 2 10. B. 156  2 10. C. 6020 10. D. 60  20 10. 5 5
Vấn đề 4. Đường tròn và đường tròn
Câu 1. Xét các số phức z ,
z  4  1 và iz 2  1. Giá trị nhỏ nhất của biểu 1 z thỏa mãn 2 1 2
thức P z  2 bằng 1 z2 A. 2 5 2. B. 4  2. C. 4 2 3. D. 4 2 3.
Câu 2. Xét các số phức z , z thỏa mãn z 3i 5  2 và iz 1 2i  4. Giá trị lớn nhất của 1 2 1 2
biểu thức P  2iz 3z bằng 1 2 A. 313 16. B. 313. C. 313 8. D. 313  2 5.
Câu 3. Xét các số phức z , z thỏa mãn z  12 và z 34i  5. Giá trị nhỏ nhất của biểu 1 2 1 2
thức P z z bằng 1 2 A. 0. B. 2. C. 7. D. 17.
Câu 4. Có bao nhiêu giá trị của tham số m để tồn tại duy nhất số phức z thỏa mãn z.z  1
và z  3 i m ? A. 0. B. 1. C. 2. D. 3.
Câu 5. Gọi S là tập hợp các số phức z thỏa mãn z i  3 và z 1  5 . Gọi z , z S lần 1 2
lượt là các số phức có mođun nhỏ nhất và lớn nhất. Khẳng định nào sau đây đúng ?
A. z  2z 122 .i B. z  2z  212 .i C. z  2z  64 .i
D. z  2z 12 4 .i 1 2 1 2 1 2 1 2
Câu 6. Xét các số phức z thỏa mãn 1 z 2 i  4. Gọi M là giá trị lớn nhất của
z 2  3i , m là giá trị nhỏ nhất của z  2 2i . Tính M  . m
A. M m  3.
B. M m  5.
C. M m  6.
D. M m  7.
 z 2i  2 5
Câu 7. Xét các số phức  z thỏa mãn 
. Giá trị lớn nhất của T z 1 4i bằng
 z 4i  2 2  A. 3 2. B. 3 5. C. 5  2. D. 6.
 z 1i 1
Câu 8. Xét các số phức z x yi
x, y   thỏa mãn  . Gọi ,
m M lần lượt là
 z 33i  5 
giá trị nhỏ nhất và giá trị lớn nhất của biểu thức P x  2 .
y Tỉ số M bằng m A. 5 . B. 7 . C. 9 . D. 14 . 4 2 4 5
 z 1i  3
Câu 9. Xét các số phức z x yi  ;
x y   thỏa mãn 
. Giá trị nhỏ nhất của
 z 34i  10 
biểu thức P x 3y bằng A. 5. B. 7. C. 13. D. 4 3 10. Vấn đề 5. Parabol
Câu 1. Xét các số phức z a bi  ,
a b   thỏa z z  i i z z  2 4 15
1 . Tính P a   4b khi 1
z   3i đạt giá trị nhỏ nhất. 2 A. P  4. B. P  5. C. P  6. D. P  7.
Câu 2. Xét hai số phức z , z thỏa mãn 2 z i z z 2i và z i 10  1. Giá trị nhỏ 1 2 1 1 1 2
nhất của biểu thức z z bằng 1 2 A. 10 1. B. 3 5 1. C. 101 1. D. 101 1.
Vấn đề 6. Đoạn thẳng – tia
Câu 1. Xét các số phức z thỏa mãn z  2i z 4 7i  6 2. Gọi ,
m M lần lượt là giá trị
nhỏ nhất và giá trị lớn nhất của z 1i . Tính P m M. A.   P  13  73 . B. 5 2 2 73 P  .
C. P  5 2  2 73 . D. 5 2 73 P  . 2 2
Câu 2. Xét các số phức z thỏa mãn z 1i z 83i  53. Giá trị lớn nhất của biểu thức
P z 1 2i bằng A. 53. B. 53. C. 185 . D. 106. 2
Câu 3. Xét các số phức z thỏa mãn z  23i z 6i  2 17. Gọi M , m lần lượt là giá trị
lớn nhất và giá trị nhỏ nhất của biểu thức P z 12i z 2 i . A. M  3 2, 0. m B. M  3 2, 2. m C. M  3 2, m  5 2 2 5. D. M  2, m  5 2 2 5.
Câu 4. Xét các số phức z thỏa mãn z 32i z 3i  3 5. Gọi M , m lần lượt là giá trị
lớn nhất và giá trị nhỏ nhất của biểu thức P z  2  z 13i .
A. M  17  5, m  3 2.
B. M  26  2 5, m  3 2.
C. M  26  2 5, 2 m  .
D. M  17  5, 2 m  .
Câu 5. Xét các số phức 5
z , z thỏa z 12i z 33i  2 z 1 i  17. Giá trị lớn 1 2 1 1 2 2
nhất của P z z z  2i bằng 1 2 1 A. 2 17. B. 3 29. C. 17  29. D. 17  2 29.
Câu 6. Xét các số phức z thỏa mãn iz 2i 2  z 13i  34. Giá trị nhỏ nhất của biểu
thức P  1iz 2i bằng A. 9 . B. 3 2. C. 4 2. D. 26. 17
Câu 7. Xét các số phức z đồng thời thỏa mãn z 4 3i z  4 3i  10 và z 34i nhỏ
nhất. Môđun của số phức z bằng A. 5. B. 5 2. C. 6 2. D. 10.
Câu 8. Xét các số phức z a bi  ,
a b   thỏa mãn z 12i z 3i . Tính P a b khi
T z 3 4i z 1i đạt giá trị lớn nhất. A. P  2. B. P  6. C. 26 P  . D. 28 P  . 3 3
Câu 9. Xét các số phức z thỏa mãn z  2  z  2i . Giá trị nhỏ nhất của biểu thức a b
P z 12i z 3 4i z 56i được viết dưới dạng 17 với ,a b  .  Tính a  . b 2
A. a b  2.
B. a b  3.
C. a b  4.
D. a b  7.
Câu 10. Xét các số phức z , z đồng thời thỏa mãn z 12i z 3 2i và z z  5. Giá 1 2 1 2
trị nhỏ nhất của biểu thức z 13i z 13i bằng 1 2 A. 14 5 . B. 3 85 . C. 1105 . D. 1165 . 5 5 5 5
Vấn đề 7. Phương pháp lấy đối xứng
Câu 1. Xét các số phức z a bi  ;
a b   thỏa mãn z 53i z 15i . Tính a b khi
biểu thức P z 22i z 37i đạt giá trị nhỏ nhất.
A. a b  1.
B. a b  0.
C. a b  1.
D. a b  2.
Câu 2. Xét các số phức z, z, z thỏa mãn z 4 5i z 1  1 và z  4i z 8  4i . Tính 1 2 1 2
M z z khi P z z z z đạt giá trị nhỏ nhất. 1 2 1 2 A. M  2 5.
B. M  6. C. M  41. D. M  8.
Câu 3. Xét các số phức z , z thỏa mãn z 3 2i  1 và z  2i  1. Số phức z có phần 1 2 1 2
thực bằng a , phần ảo bằng b thỏa mãn 2a b  0. Tính P a b khi z z z 2z đạt 1 2 giá trị nhỏ nhất. A. P  1. B. P  3. C. P  4. D. P  7.
Câu 4. Xét các số phức z , z thỏa mãn z 53i z 13i và z 4 3i z 2 3i . 1 2 1 1 2 2
Giá trị nhỏ nhất của biểu thức P z z z 6 i z 6i bằng 1 2 1 2 A. 2 10. B. 7 . C. 4 130 . D. 18 . 2 13 13
Vấn đề 8. Tâm tỉ cự
Câu 1. Xét các số phức z thỏa mãn |z 5i| |  2 3i|. Đặt 2 2
P z  39i z 15i . Biết
P đạt giá trị nhỏ nhất tại z và P đạt giá trị lớn nhất tại z . Giá trị của biểu thức z z 1 2 1 2 bằng A. 2 13. B. 2 15. C. 4 3. D. 52.
Câu 2. Xét các số phức z thỏa mãn z 12i  3 2. Gọi ,
m M lần lượt là giá trị nhỏ nhất và
lớn nhất của biểu thức 2 2
P z 3  2i 2 z 2 i . Tổng m M bằng A. 30. B. 12. C. 14. D. 68.
Câu 3. Xét các số phức z a i  ,
a b   thỏa mãn z 4 3i  5. Tính a b khi biểu thức 2 2 2
Q z  2 2i  2 z  4 i  3 z  2i đạt giá trị lớn nhất.
A. a b  11.
B. a b  12.
C. a b  13.
D. a b  14.
Câu 4. Xét các số phức z , z thỏa mãn z 34i  2 và z z  1. Giá trị nhỏ nhất của 1 2 1 2 biểu thức 2 2
P z z bằng 1 2 A. 4 3 5. B. 62 5. C. 5. D. 10.
Vấn đề 9. Phương pháp cân bằng hệ số
Câu 1. Xét các số phức z thỏa mãn z  1. Giá trị lớn nhất của T z 1  2 z 1 bằng A. 2 5. B. 2 10. C. 3 2. D. 3 5.
Câu 2. Xét các số phức z thỏa z 1  2. Giá trị lớn nhất của T z i z 2i bằng A. 4. B. 4 2. C. 8. D. 8 2.
Câu 3. Xét các số phức z a bi a;b   có môđun bằng 2 và phần ảo dương. Tính giá trị
biểu thức S   a b 2018 5  2  
khi biểu thức P  2  z 3 2 z đạt giá trị lớn nhất. A. S  0. B. S  1. C. 2018 S  2 . D. 1009 S  2 .
Câu 4. Xét các số phức z z thỏa mãn 1 1 
. Gọi M , m lần lượt là giá trị lớn nhất và z  3i 2
nhỏ nhất của P z i  2 z 4 7i . Giá trị M m bằng A. 10  2 5. B. 10  4 5. C. 20  2 5. D. 20  4 5.
Câu 5. Xét số phức z thỏa mãn z 12i  2 2. Với ,
a b là số thực dương cho trước, giá trị
lớn nhất của biểu thức P a z 1 b z 3 4i bằng A. 2 2
a b . B. 2 2 2a  2b . C. 2 2
4 2a  2b . D. 2 2
a b .
Câu 6. Xét các số phức z a bi  ,
a b   thỏa mãn z 4 3i  5. Tính a b khi biểu
thức P z 13i z 1i đạt giá trị lớn nhất.
A. a b  4.
B. a b  6.
C. a b  8.
D. a b  10.
Câu 7. Xét các số phức z a bi  ,
a b   thỏa mãn z 4 3i  2 2. Tính 2a b khi biểu
thức P z 1 2i z 96i đạt giá trị lớn nhất.
A. 2a b  7.
B. 2a b  9.
C. 2a b  12.
D. 2a b  13.
Câu 8. Xét các số phức z thỏa mãn z 22i  1. Giá trị lớn nhất của biểu thức
P z 32i  2z 2  4i bằng A. 5. B. 2 5. C. 3 15. D. 10.
Câu 9. Xét các số phức z thoả mãn z 2i  2 2. Gọi M , m lần lượt là giá trị lớn nhất, giá
trị nhỏ nhất của biểu thức P z 32i z 3 4i . Tính M  . m
A. M m  2 26  6 2.
B. M m  2 26 8 2.
C. M m  11 2.
D. M m  16 2.
Câu 10. Xét các số phức z a bi  ,
a b   thỏa mãn z 32i  2. Tính a b khi biểu thức
T z 12i  2 z 2 5i đạt giá trị nhỏ nhất.
A. a b  3.
B. a b  2  3.
C. a b  4  3.
D. a b  4  3.
Câu 11. Xét các số phức z a bi  ,
a b   thỏa mãn z  2. Tính a b khi biểu thức
P z  4  2 z 1 4i đạt giá trị nhỏ nhất.
A. a b  2.
B. a b  2.
C. a b  2 5.
D. a b  4 5.
Câu 12. Xét các số phức z thỏa mãn điều kiện z i  1. Giá trị nhỏ nhất của biểu thức
P z  2 i  2 z  2  3i bằng A. 4 3 . B. 2. C. 3. D. 3. 3
Câu 13. Xét các số phức z thỏa mãn điều kiện z 1i  5. Giá trị lớn nhất của biểu thức
P  2 z 8i z 7 9i bằng A. 5 . B. 5 3 . C. 5 5 . D. 5 5. 2 2 2
Câu 14. Xét các số phức z thỏa z  1. Giá trị lớn nhất của biểu thức T z  2  2 z 2 bằng A. 2. B. 2 5. C. 5. D. 5 2.
Câu 15. Xét các số phức z thỏa mãn 2z 13i  2. Giá trị lớn nhất của biểu thức
P z 1  3 z 12i bằng A. 2 2. B. 4. C. 4 2. D. 4 3.
Câu 16. Cho số phức z a bi  ,
a b   thỏa mãn z 33i  6. Tính a b khi biểu thức
P  2 z  6 3i  3 z 1 5i đạt giá trị nhỏ nhất.
A. a b  22 5. B. a b  2 5 2.
C. a b  2 5 4.
D. a b  4 2 5. Vấn đề 10. Elip
Câu 1. Xét các số phức z thỏa mãn z  4  z 4  10 . Giá trị lớn nhất và nhỏ nhất của z lần lượt là A. 10 và 4. B. 5 và 4. C. 4 và 3. D. 5 và 3.
Câu 2. Xét các số phức z thỏa mãn 2 2 iz   iz
 4. Gọi M và n lần lượt là giá trị 1i i 1
lớn nhất và giá trị nhỏ nhất của z . Tính M. . n
A. M.n  1.
B. M.n  2.
C. M.n  2 2.
D. M.n  2 3.
Câu 3. Xét số phức z thỏa mãn z 2i 1  z 2i 1 10. Gọi M và m là giá trị lớn
nhất và giá trị nhỏ nhất của z . Tính tổng S M  . m
A. S  17.
B. S  2 21.
C. S  8. D. S  9.
Câu 4. Xét các số phức z thoả mãn z 1i z 3i  6. Tìm giá trị nhỏ nhất P của min
biểu thức P z 1 4i .
A. P  2 5 2.
B. P  2 5  2.
C. P  5 2.
D. P  5 2. min min min min
Câu 5. Xét các số phức z thỏa z 1i z 13i  6 5. Giá trị lớn nhất của P z 23i bằng A. 2 5. B. 4 5. C. 5 5. D. 6 5.
---------- HẾT ----------
Cực trị Hình học trong SOÁ PHÖÙC
1) Điểm và đường thẳng…………………………………………………………....…………… 00
2) Điểm và đường tròn ……………………………………………………………………………. 00
3) Đường thẳng và đường tròn ………………………………………….…………..……. 00
4) Đường tròn và đường tròn ……………………………………………….………….….. 00
5) Parabol………………………………………………………………………………….…………….….… 00
6) Đoạn thẳng – tia ……………………………………………………………….………………..… 00
7) Phương pháp lấy đối xứng …………………………………………….………………… 00
8) Tâm tỉ cự ………………………………………………………………………………….…………..…. 00
9) Phương pháp cân bằng hệ số ……………………………………….…………….….. 00
10) Elip ………………………………………………………………………………………….………………. 00
Vấn đề 1. Điểm và đường thẳng
Câu 1. Xét các số phức z, w thỏa mãn z  22i z 4i và w iz 1. Giá trị nhỏ nhất của w bằng A. 2 . B. 3 2 . C. 2. D. 2 2. 2 2
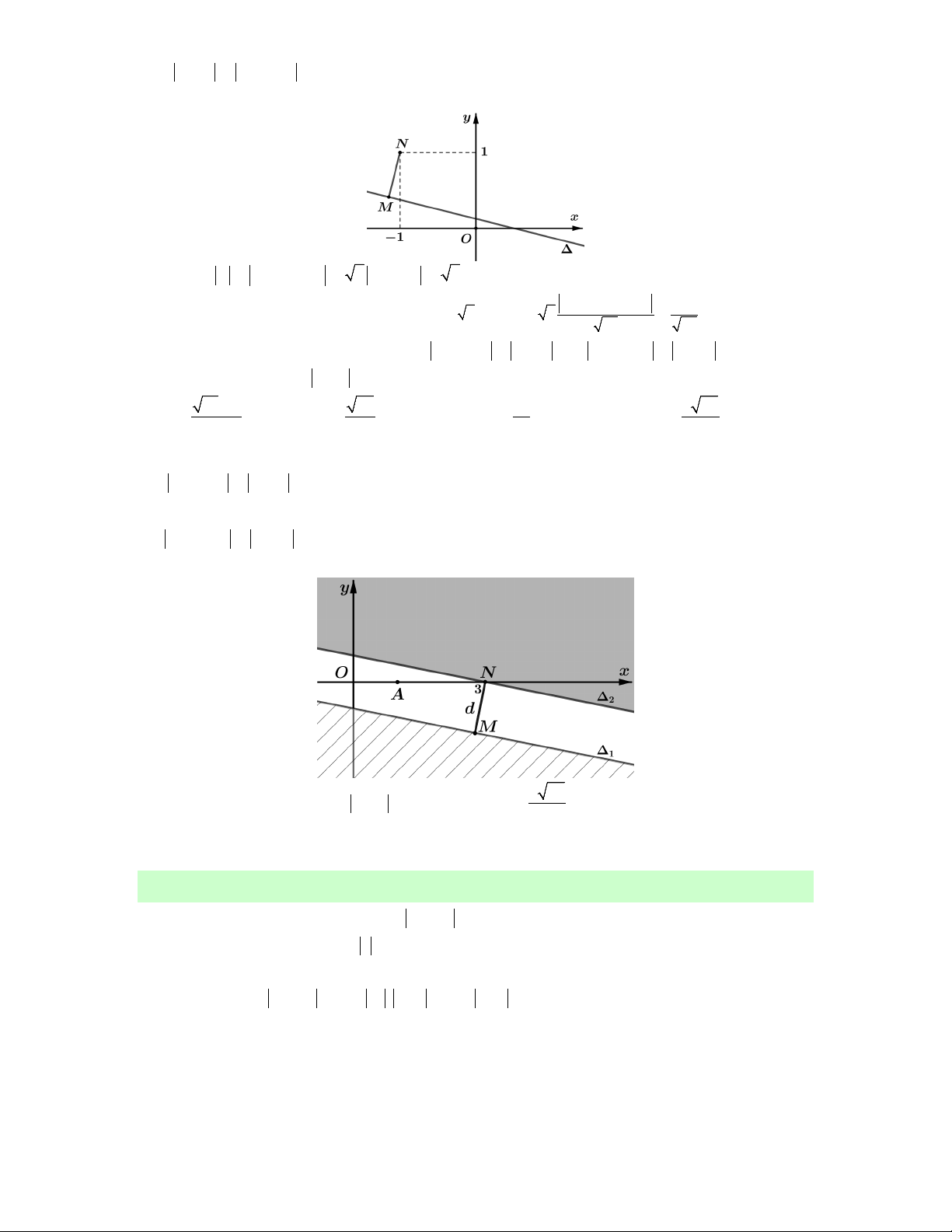
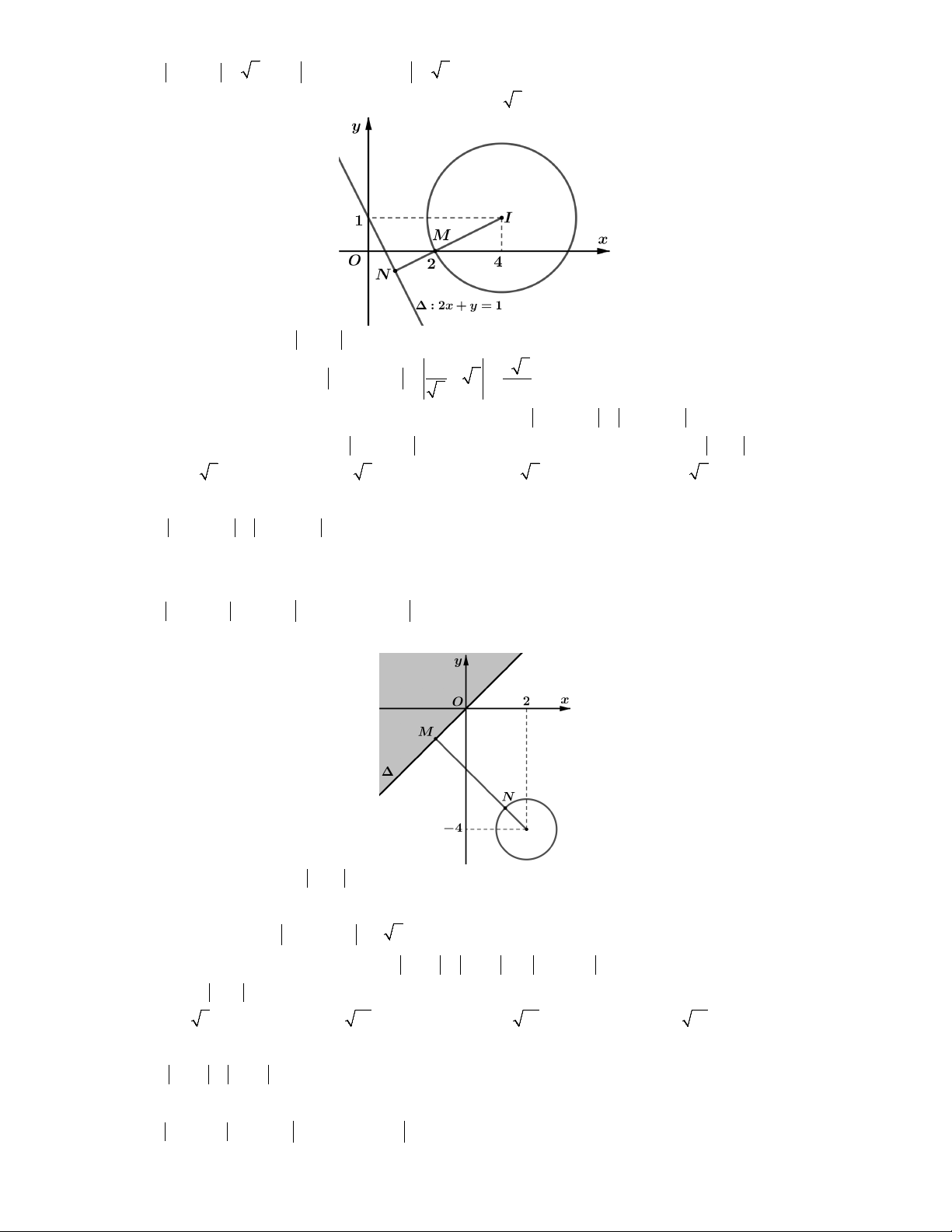
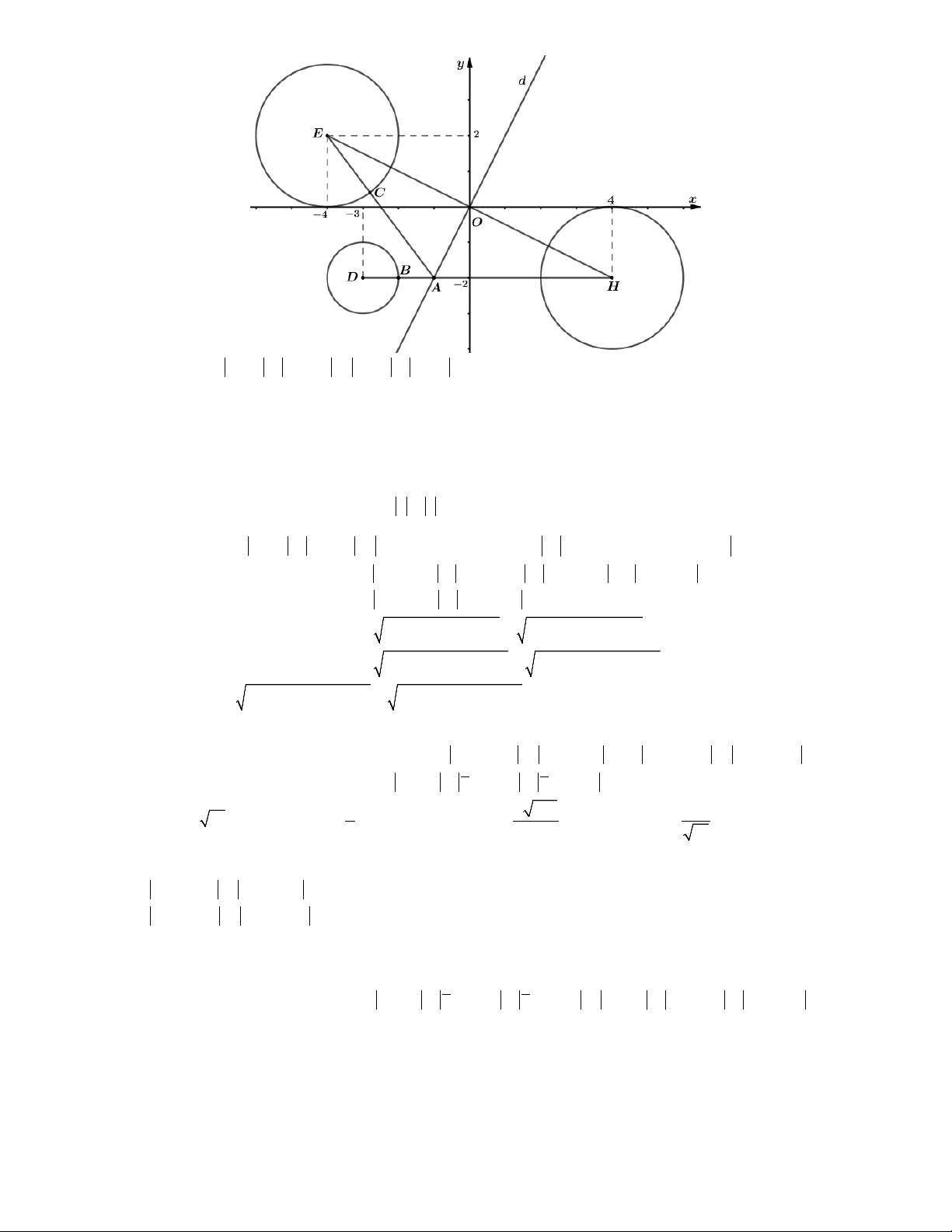
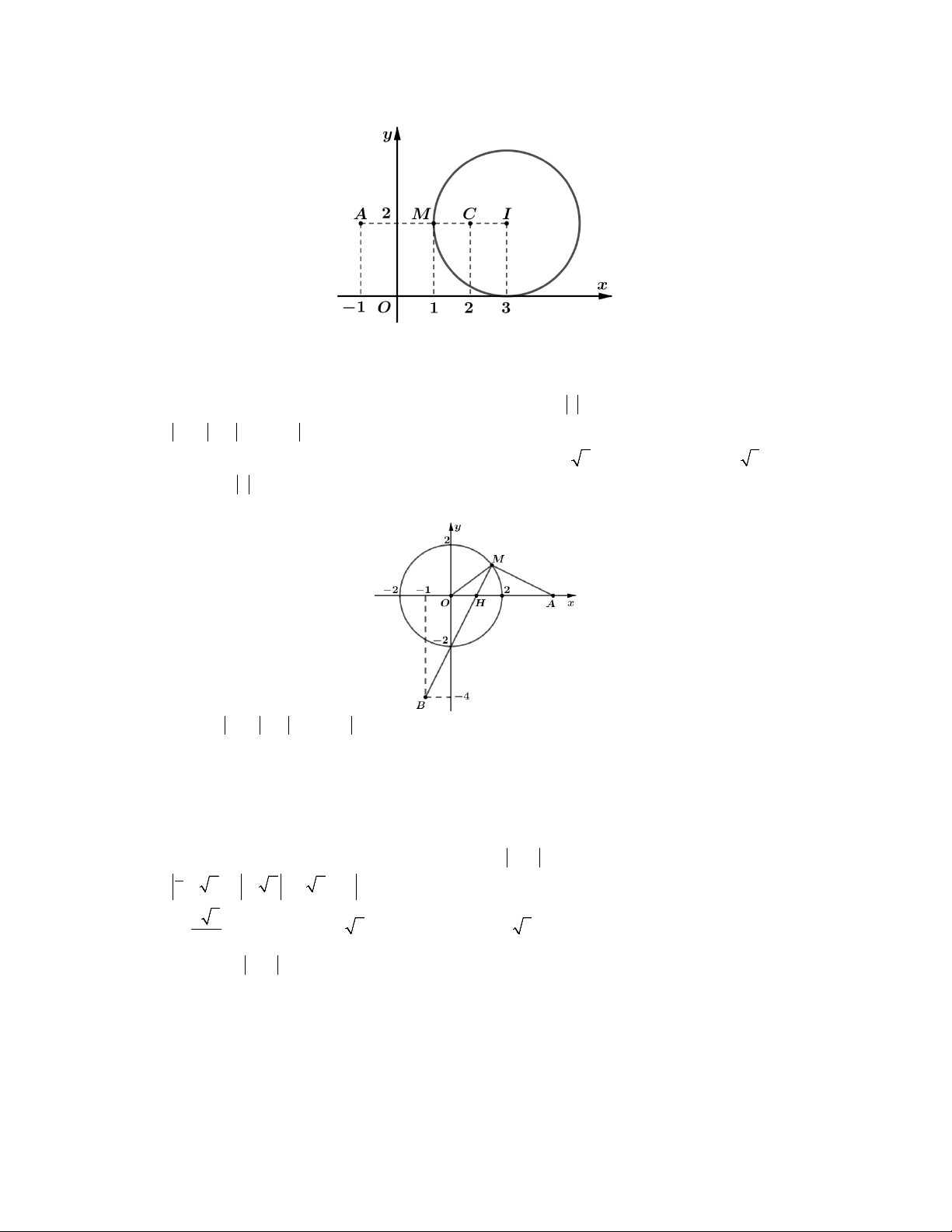
Lời giải. Đặt z x yi x, y   và M x; y là điểm biểu diễn số phức z.
Từ z   i z i 
x  2 y  2  x y  2 2 2 2 4 2 2
4  x y  2 
 tập hợp điểm M
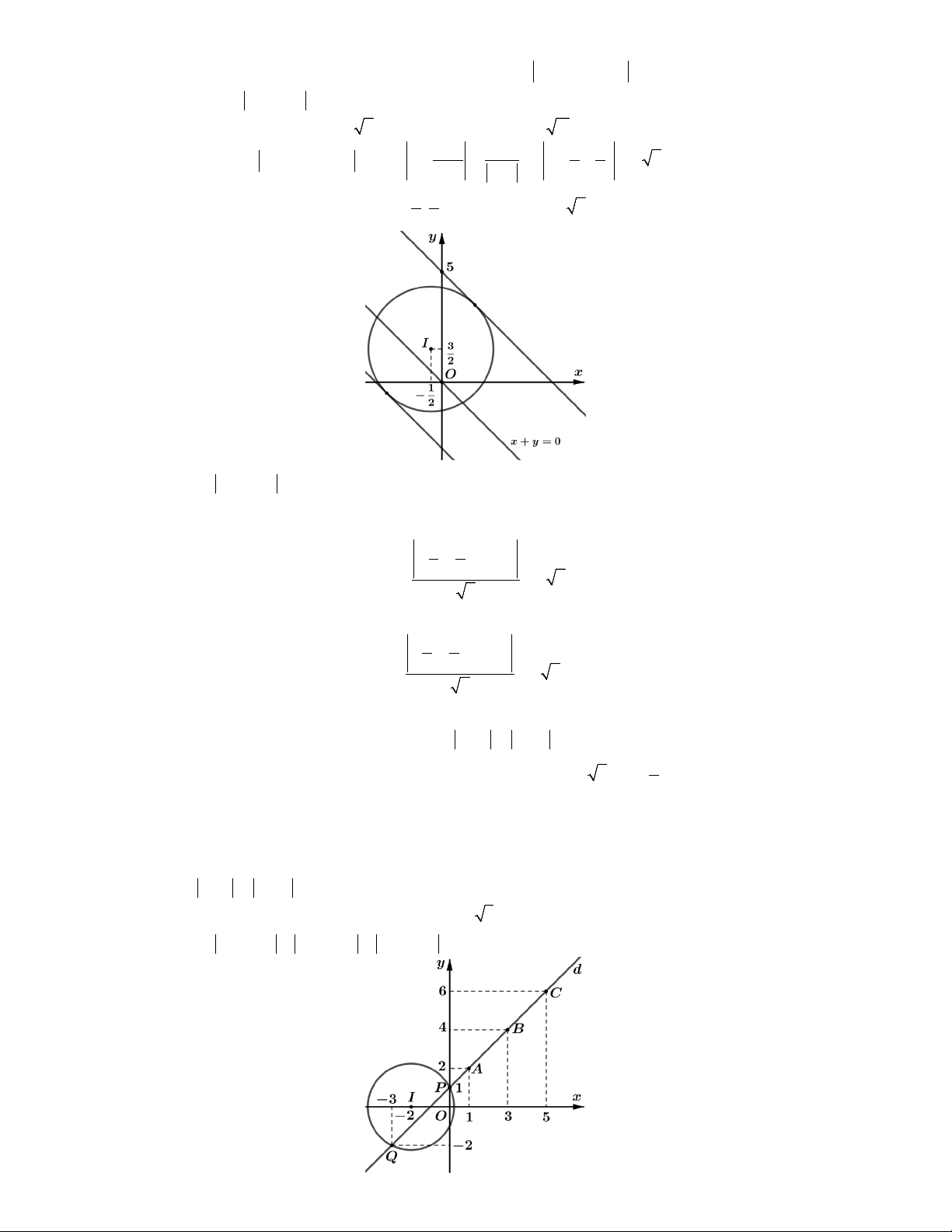
là đường thẳng  : x y  2.
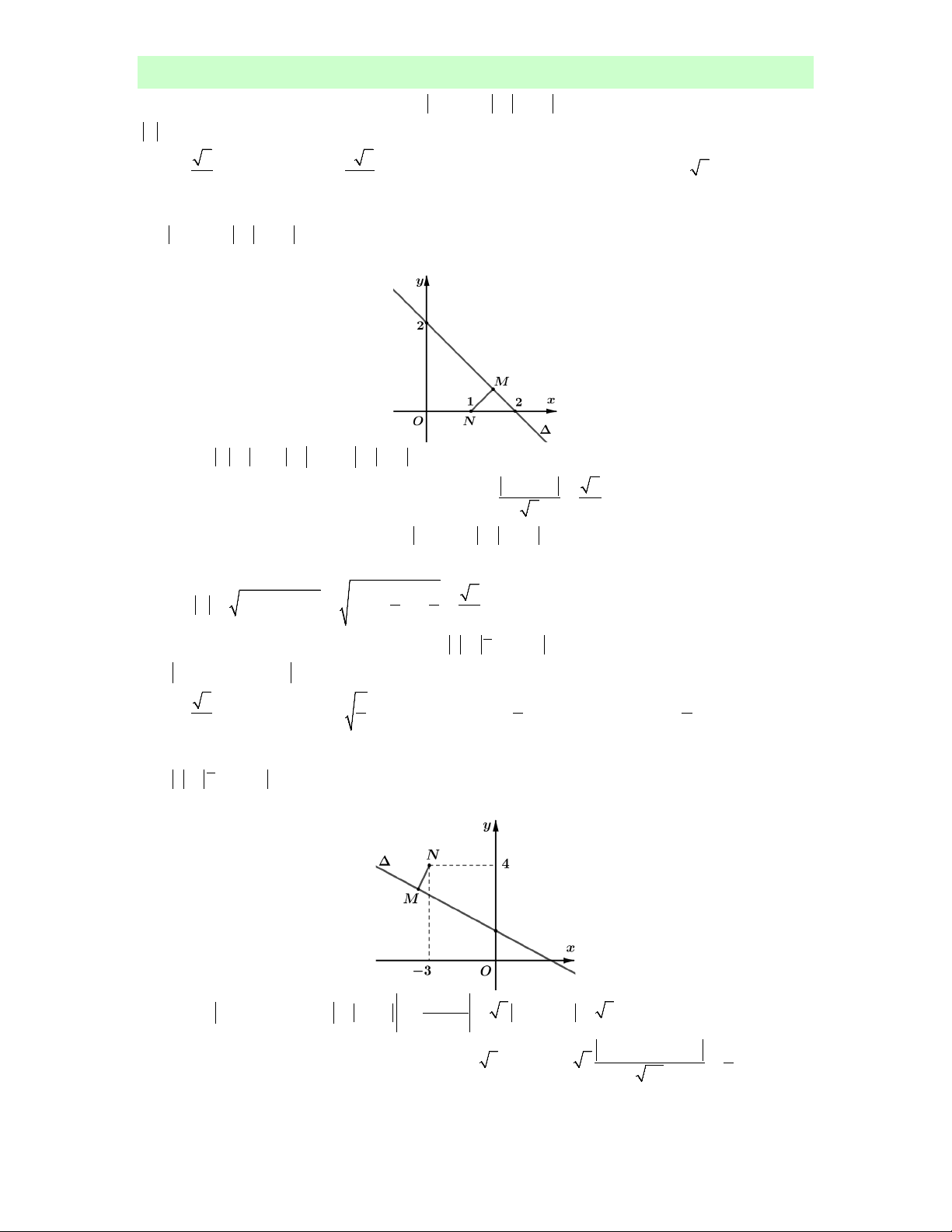
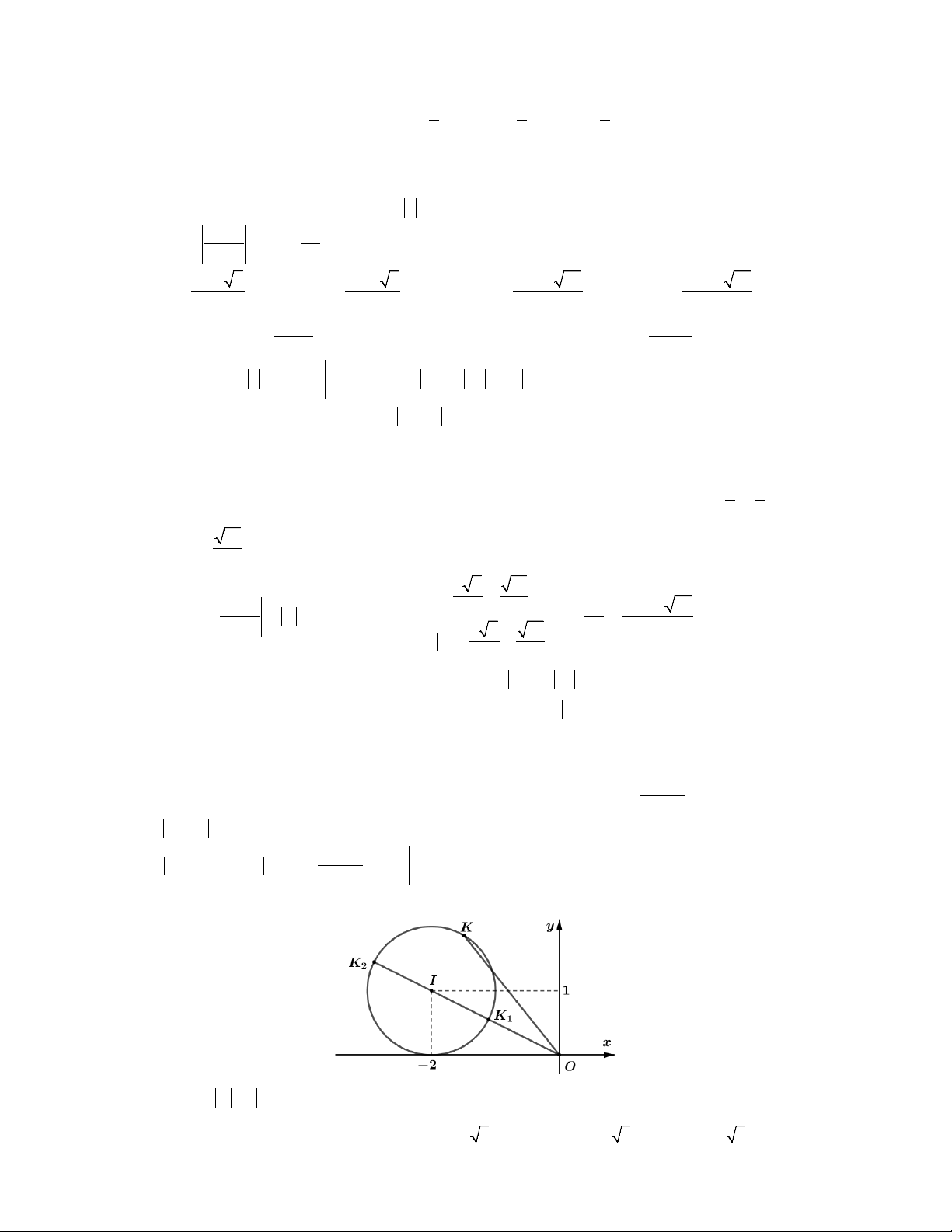
Ta có P w iz 1  i z i  z i MN với N 0;  1 . 0 12
Dựa vào hình vẽ ta thấy 2 PMNd N,   . Chọn A. min min   2 2
Cách 2. Đặt z x yi  ;
x y  . Từ z  22i z 4i 
y  2  x.
Khi đó w iz 1  i x yi1 ix y 1 ix 2 x1 x   1  xi. 2  
Suy ra w  x  2 1 1 2 2
1  x  2x      .   2 2 2
Câu 2. Xét các số phức z thỏa mãn z z 1 2i . Giá trị nhỏ nhất của biểu thức
P  1 2iz 11 2i bằng A. 5 . B. 5. C. 2 . D. 5 . 2 2 5 2
Lời giải. Đặt z x yi x, y   và M x; y là điểm biểu diễn số phức z.
Từ z z   i 
x y  x  2 y  2 2 2 1 2 1
2  2x  4 y  5 
 tập hợp điểm M là
đường thẳng  : 2x  4y  5. Ta có     i 11 2i P
1 2 z 11 2i  1 2i z
 5 z 34i  5MN với N 3;4. 1 2i 2.  3  4.4 5
Dựa vào hình vẽ ta thấy 5 PMNP  5.d N,  5  . Chọn D. min min min   20 2
Câu 3. Xét các số phức z thỏa mãn z 1i z 3i . Môđun lớn nhất của số phức 1 w  là z A. 2 5 . B. 4 5 . C. 9 5 . D. 7 5 . 7 7 10 10
Lời giải. Đặt z x yi x, y   và M x; y là điểm biểu diễn số phức z.
Từ z  i z i 
x  2 y  2  x y  2 2 1 3 1 1
3  2x  4 y  7 
 t ập hợp điểm M
là đường thẳng  : 2x  4y  7. Ta có 1 1 1 w    với O0;0. z z OM
Dựa vào hình vẽ ta thấy 1 20 2 5 wOMw    . Chọn A. max min max d O, 2.0  4.0 7 7
Câu 4. Xét các số phức z thỏa mãn 2
z 2z  5  z 1 2iz 3i  
1 . Giá trị nhỏ nhất của
biểu thức P z 2  2i bằng A. 1. B. 3 . C. 5 . D. 5. 2 2 Lời giải. Ta có 2
z 2z  5  z 1 2iz 3i   1 z  12i
 z 12iz 12i  z 12iz 3i   1   . 
z 12i z  3i 1 
TH 1. Với z  12i. Khi đó P z 2  2i  12i 2  2i  1.
TH 2. Với z 12i z  3i 1 .
Đặt z x yi x, y   và M x; y là điểm biểu diễn số phức z.
Từ z   i z i  
x  2 y  2  x  2 y  2 1 2 3 1 1 2 1
3  2y 1  0   tập hợp
điểm M là đường thẳng  : 2y 1  0.
Ta có P z 2  2i MA với A2;2. 2.21
Dựa vào hình vẽ ta thấy 3 PMAPd , A    . min min min   2 2
So sánh hai trường hợp ta thấy P  1. Chọn A. min
Câu 5. Xét các số phức z thoã mãn z  2i z 12i . Gọi w là số phức thoã mãn điều kiện
w  1iz  2. Giá trị nhỏ nhất của biểu thức P w bằng A. 1. B. 1. C. 5 . D. 5 . 3 5 34 41
Lời giải. Đặt z x yi x, y   và M x; y là điểm biểu diễn số phức z.
Từ z i z   i 
x y  2  x  2 y  2 2 2 1 2 2 1
2  2x  8y  1   tập hợp điểm
M là đường thẳng  : 2x  8y  1.
Ta có P w  1iz 2  2 z 1i  2MN với N 1;  1 .  2.  
Dựa vào hình vẽ ta thấy 1  8.11 5 PMN
P  2d N,  2  . Chọn C. min min min   68 34
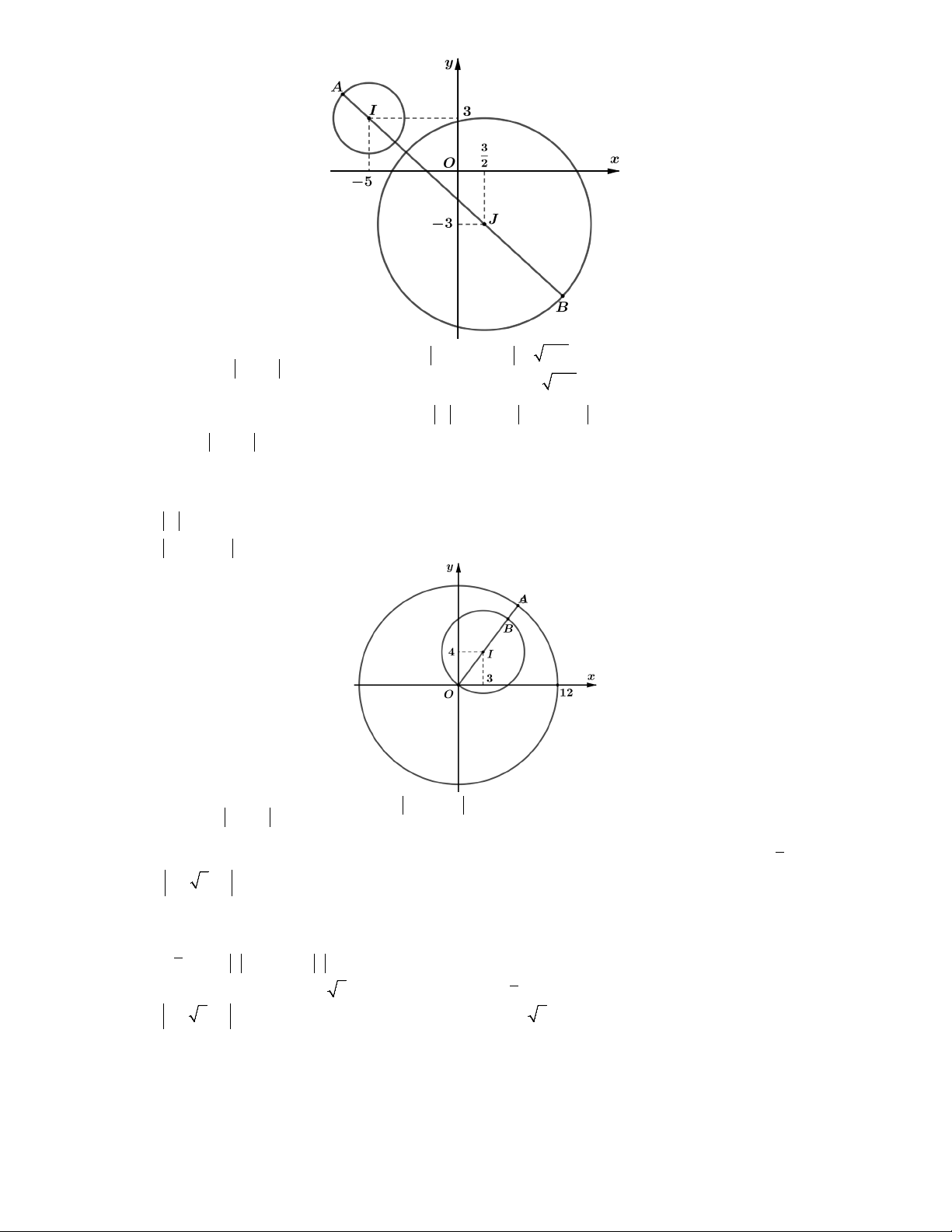
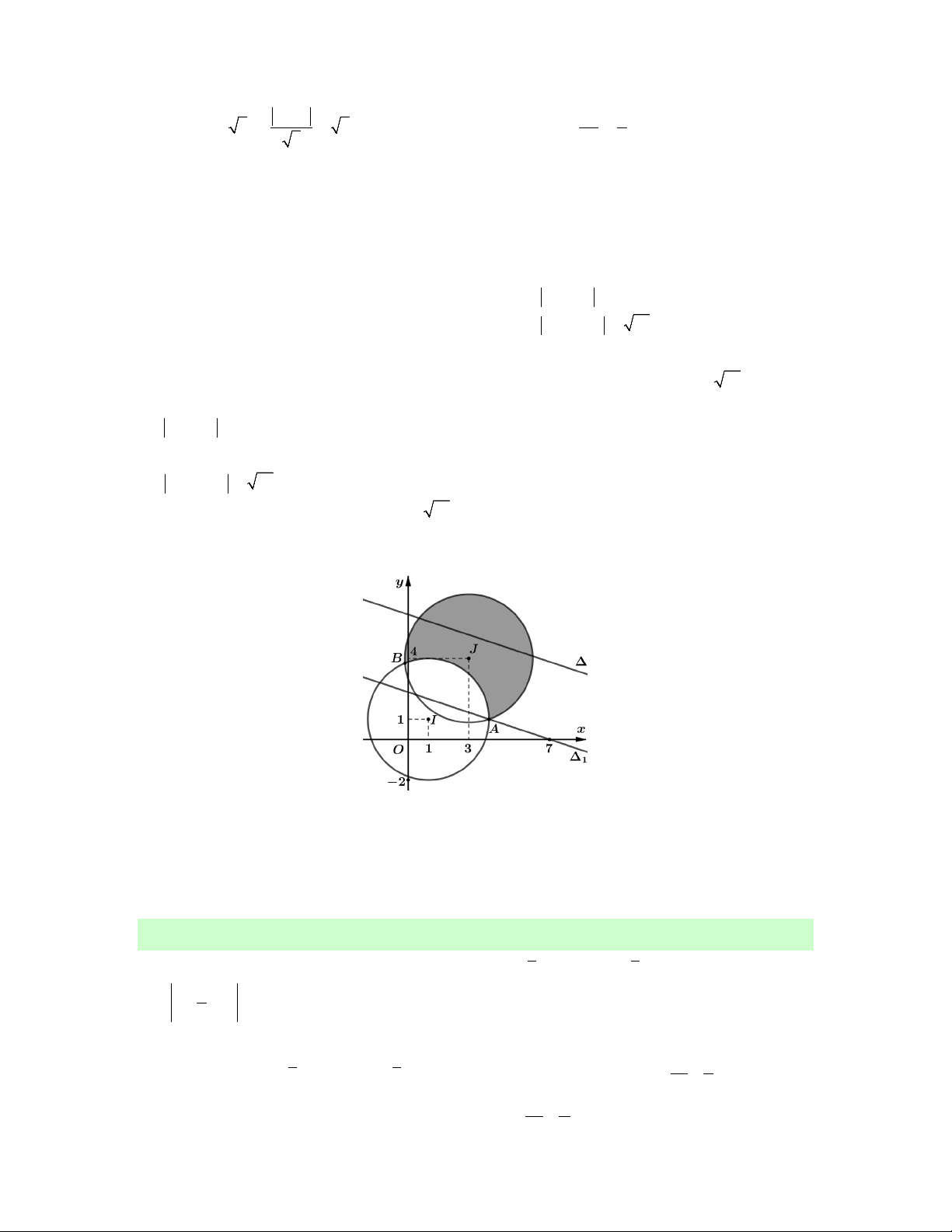
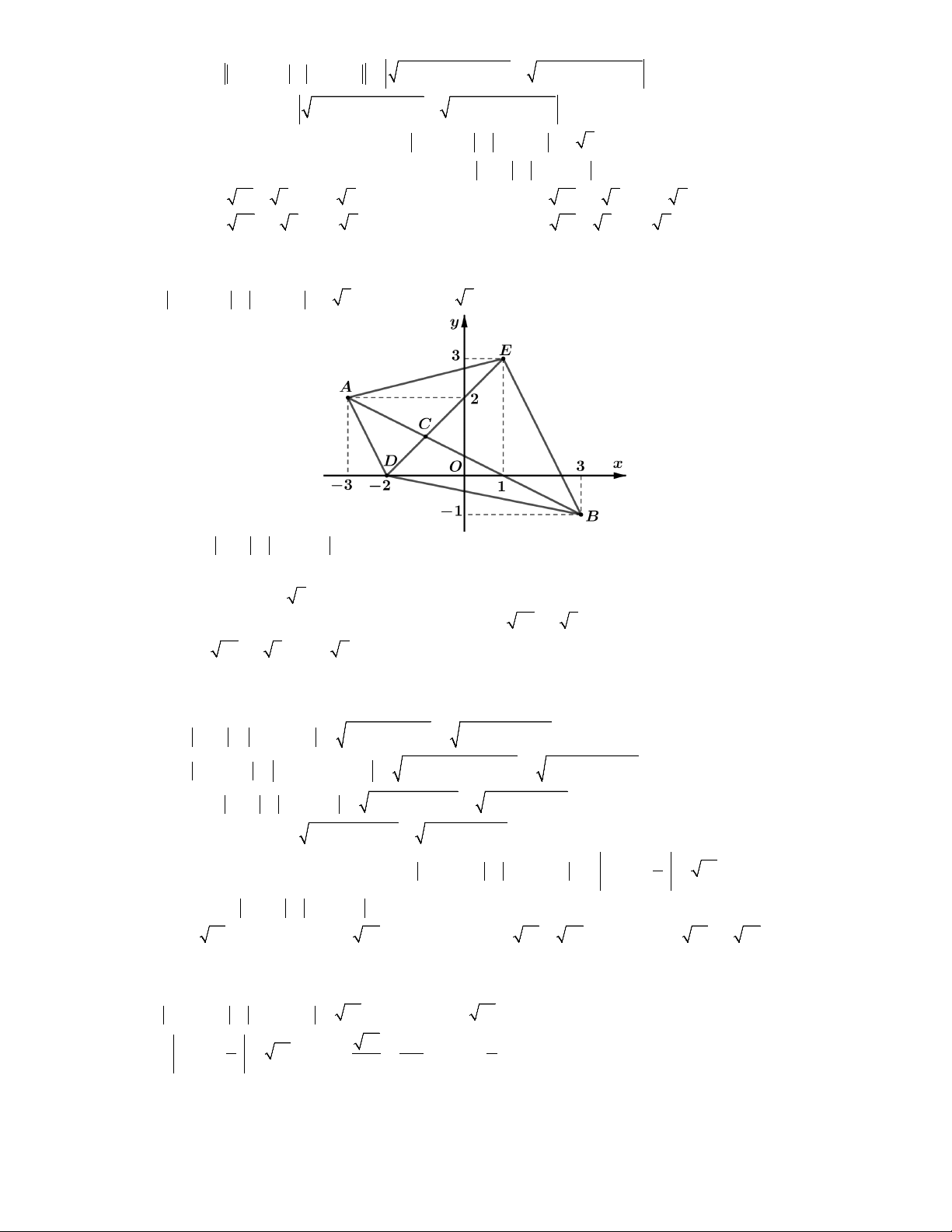
Câu 6. Xét các số phức z, w thỏa mãn z 13i z  2i và w 13i w 2i . Giá trị nhỏ
nhất của biểu thức P z w là A. 13 1. B. 26 . C. 3 . D. 3 26 . 2 4 13 13
Lời giải. Gọi z a bi và w c di  ,
a b, c, d  .
z   i z i 
a  2 b  2  a b  2 2 1 3 2 1 3
2  a  5b  3 
 tập hợp điểm M
biểu diễn số phức z là phần tô đậm như trên đồ thị có tính biên  : x 5y  3 .
w   i w i 
  c  2 d  2  c d  2 2 1 3 2 1 3
2  c  5d  3   tập hợp điểm
N biểu diễn số phức w là phần gạch chéo như trên đồ thị có tính biên  : x  5y  3 .
Dựa vào hình vẽ ta thấy P z w MN d   3 26 ;  . 13
Dấu "  " xảy ra khi và chỉ khi M   , N M và MN   . Chọn D.
Vấn đề 2. Điểm và đường tròn
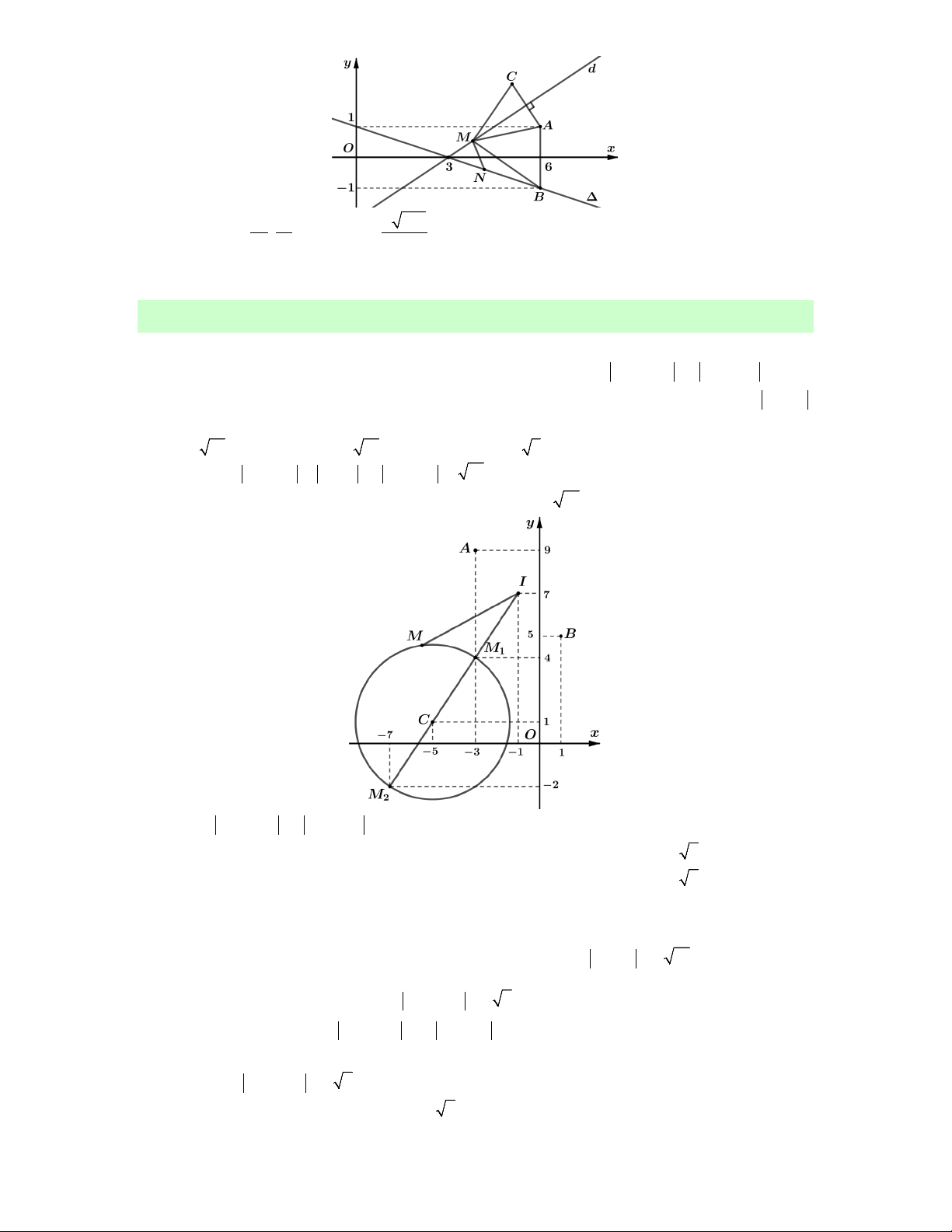
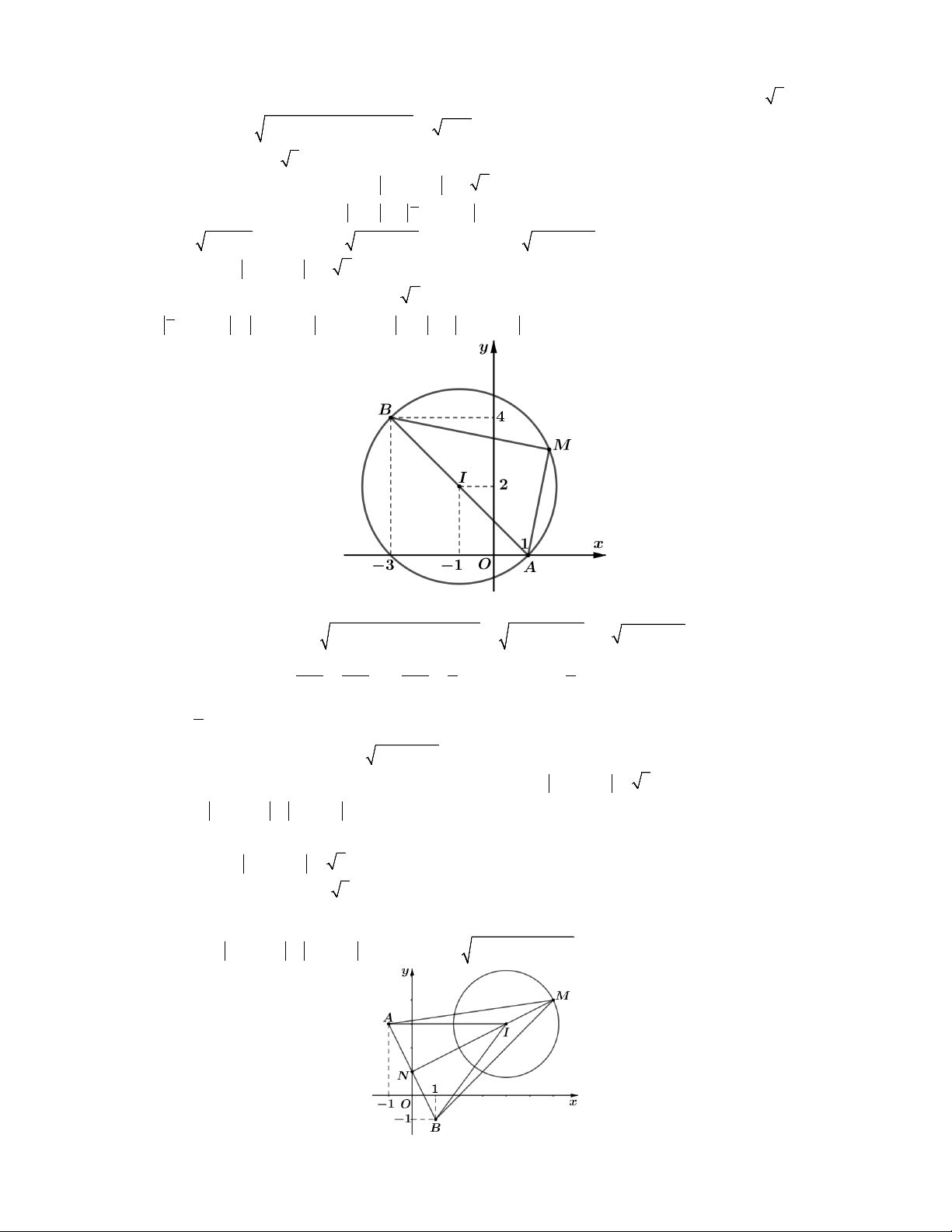
Câu 1. Xét các số phức z thỏa mãn iz 1 1 . Gọi ,
m M lần lượt là giá trị nhỏ nhất và giá
trị lớn nhất của biểu thức P z . Tính S  2020 M  . m A. S  2014. B. S  2016. C. S  2018. D. S  2022.
Lời giải. Ta có iz 1  1  i
 . z i  1  z i  1 
 tập hợp các điểm biểu diễn số
phức z thuộc đường tròn có tâm I 0; 
1 , bán kính R  1 .
P OI R  11  0 m   0 Khi đó min      
S  2018. Chọn C.
P OI R 11 2 M  2  max 
Câu 2. Xét các số phức z thỏa mãn z 23i  1 . Giá trị lớn nhất và giá trị nhỏ nhất của
biểu thức P z 1i lần lượt là
A. 13  2 và 13 2 .
B. 13 1 và 13 1. C. 6 và 4 .
D. 13  4 và 13 4 .
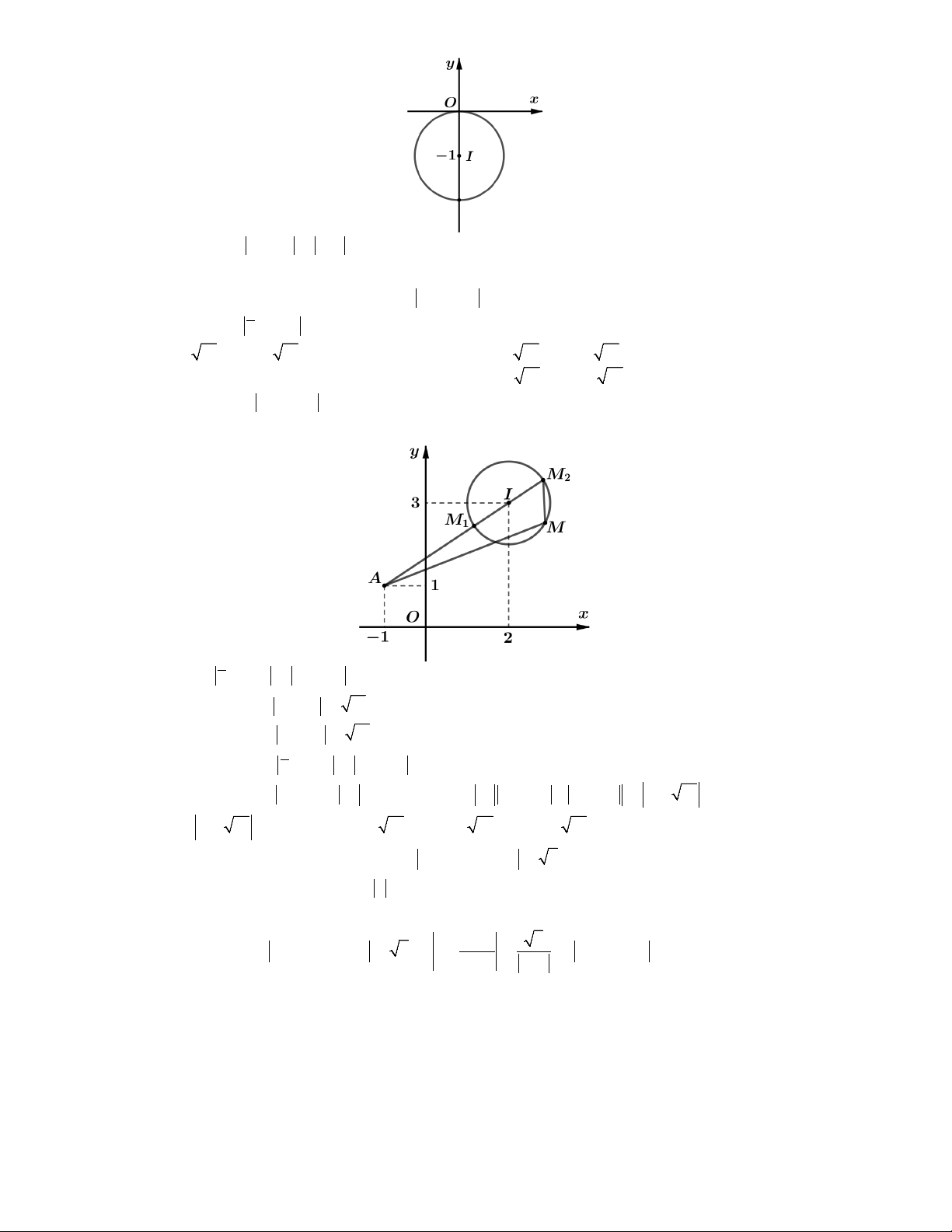
Lời giải. Ta có z 23i  1 
 tập hợp các điểm M biểu diễn số phức z thuộc đường tròn có tâm I 2; 
3 , bán kính R  1.
Ta có P z 1i z 1i MA với A1;  1 .
P AM AI R  13  1 Vậy min 1  . Chọn B.
P AM AI R  13 1  max 2
Cách 2. Ta có P z 1i z 1i .
Theo giả thiết: 1  z 23i  z 1i32i z 1i  32i P  13
Suy ra P  13 1 
1 P  13 1 13 1 P  13 1.
Câu 3. Xét các số phức z thỏa mãn 1iz 17i  2. Gọi ,
m M lần lượt là giá trị nhỏ
nhất và giá trị lớn nhất của P z . Tính S M  . m A. S  2.
B. S  4. C. S  10. D. S  24. Lòi giải. Ta có   i 1 7i 2 1
z 17i  2  z  
z 3 4i  1   tập hợp các 1i 1i
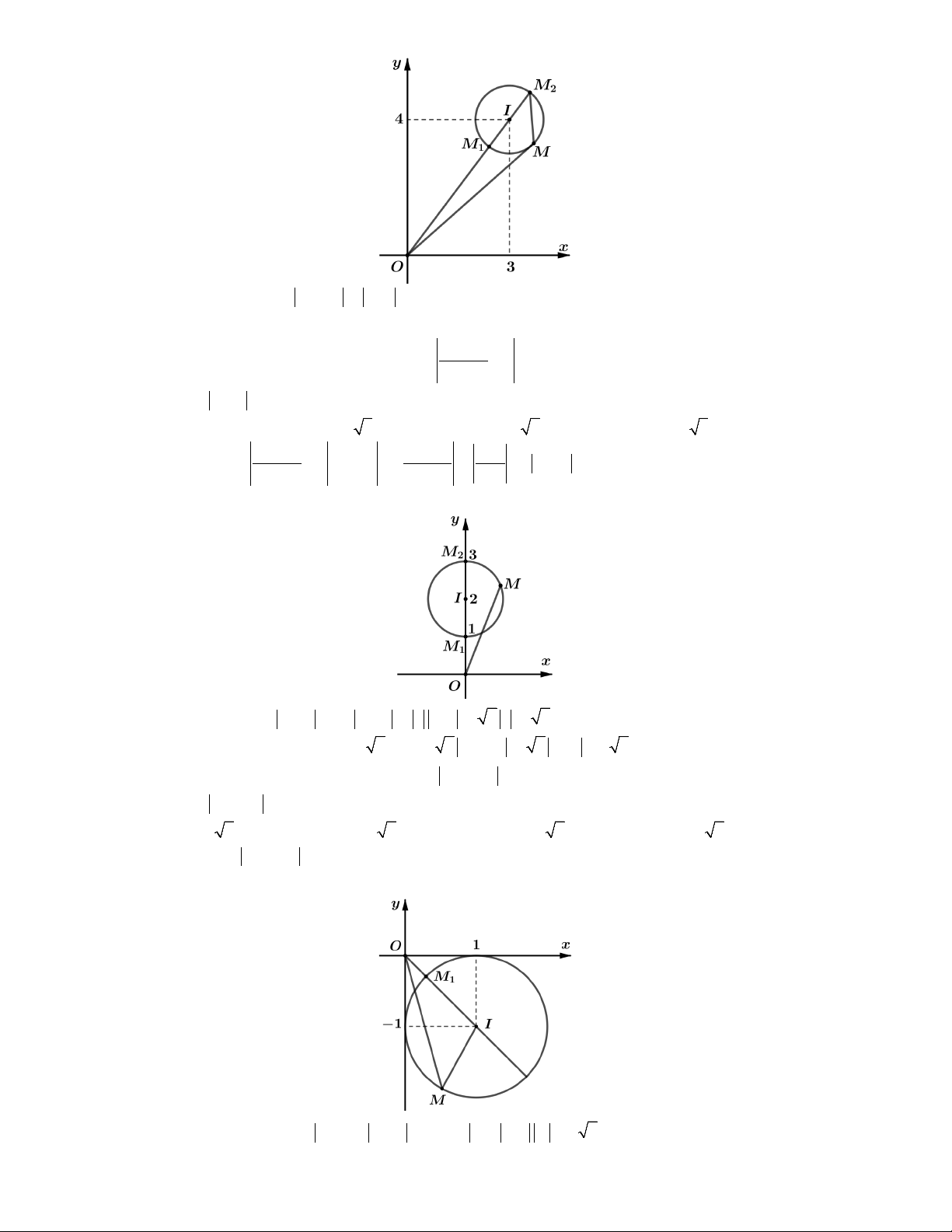
điểm M biểu diễn số phức z thuộc đường tròn có tâm I 3;4 , bán kính R 1 .
P OM OI R  51  4 m   4 Khi đó min 1      
S  2. Chọn A.
P OM OI R  51 6 M  6  max 2  1iz
Câu 4. Xét các số phức z, w thỏa mãn
 2  1 và w iz. Giá trị lớn nhất của biểu 1i
thức P z w bằng A. 3 B. 2 3 C. 3 2 D. 3 3 1iz 21iLời giải. Từ 1i  2  1  z  
z 2i  1 
 tập hợp các điểm M 1i 1i 1i
biểu diễn số phức z thuộc đường tròn có tâm I 0;2, bán kính R 1. wiz
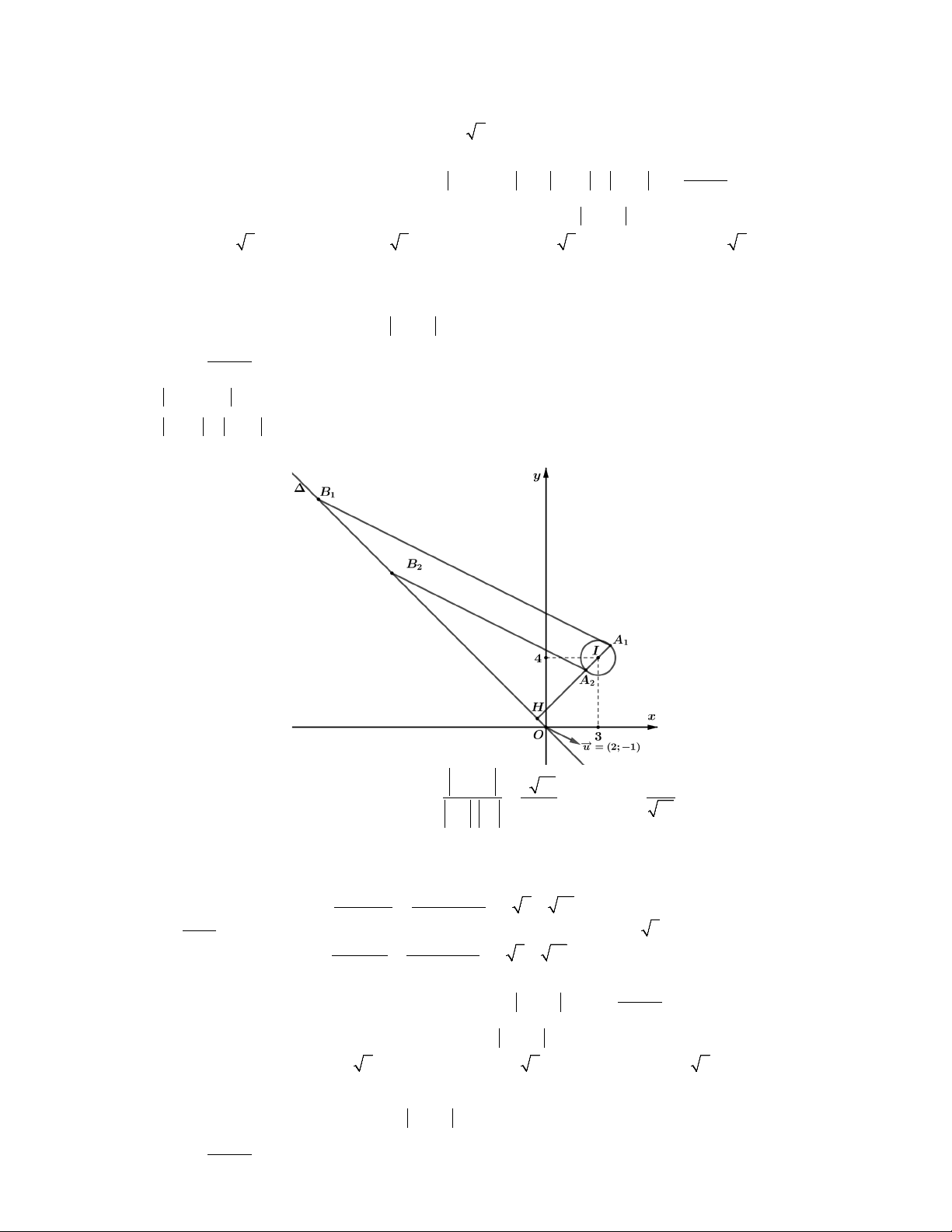
Theo giả thiết P z w z iz z 1i  2 z  2OM với O0;0.
Dựa vào hình vẽ ta thấy P
 2OM  2 OI R  2 2 1  3 2. Chọn C. max 2
Câu 5. Xét các số phức z , z thỏa mãn z 1i  1 và z  2iz . Giá trị nhỏ nhất của biểu 1 2 1 2 1
thức P  2z z bằng 1 2 A. 2 2. B. 22 2. C. 4 2 2. D. 8 2.
Lời giải. Từ z 1i  1 
 tập hợp các điểm M biểu diễn số phức z thuộc đường tròn 1 1 có tâm I 1; 
1 , bán kính R  1. z 2iz Theo giả thiết ta có 2 1
P  2z z
 2z 2iz  2 1i z  2 2OM với O 0;0. 1 2 1 1 1
Dựa vào hình vẽ ta thấy P  2 2OM  2 2 OI R  2 2 2 1  4 2 2. Chọn C. min 1
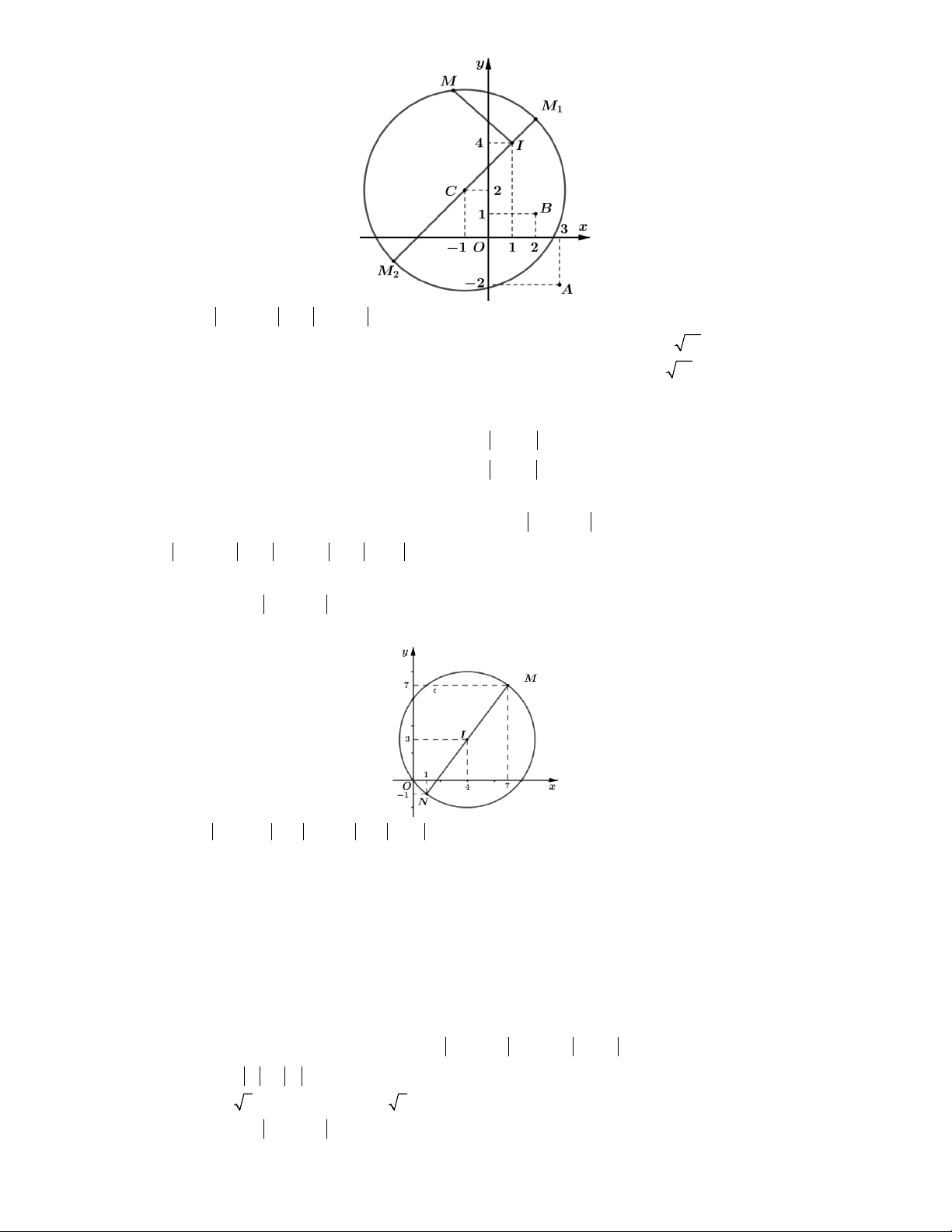
Câu 6. Xét các số phức z
z thỏa mãn z không phải là số thực và w  là số thực. Tìm 2 2  z
giá trị lớn nhất P của biểu thức P z 1i . max A. P  2. B. P  2. C. P  2 2. D. P  8. max max max max
Lời giải. Vì z không phải là số thực nên z z  0 . Ta có z z z z w   w
. Vì w là số thực nên w w   2 2 2  z 2  z 2 2 2  z 2  z  loaïi   z z
z 2  z  z 2  z  0  
 2z z   z.z z z  2 2 2  
z  2  z  2.  z.z  2 
Suy ra tập hợp các điểm M biểu diễn số phức z là đường tròn có tâm O0;0, bán kính R  2 .
Ta có P z 1i MA với A1;  1 . Vậy P
AO R  2  2  2 2. Chọn C. max
Câu 7. Xét các số phức 
z thỏa mãn z  2 . Biểu thức z i P
đạt giá trị nhỏ nhất và giá z
trị lớn nhất lần lượt tại z và z . Tìm phần ảo a của số phức w z z . 1 2 1 2 A. a  4. B. a  0. C. a  1. D. a  4.
Lời giải. Biến đổi z i i 1 1 P
 1  i   i . z z z z  1  z '     1 Đặt 1
z '  , khi đó  2 . z
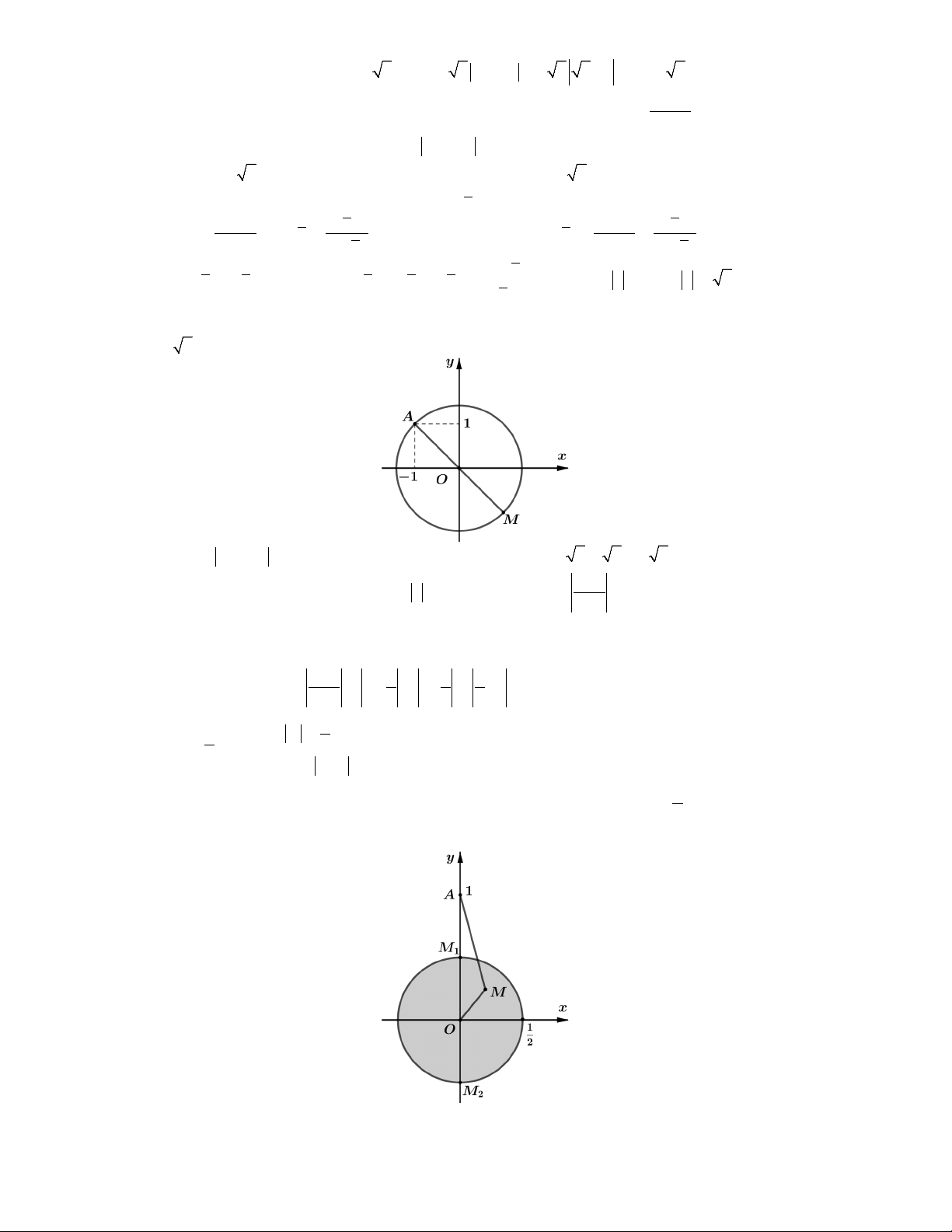
P z'i 2     1 
 tập hợp các số phức z ' là hình tròn tâm O 0;0, bán kính 1
R  (trừ tâm O ). 2
 Xét 2. Đặt A0;  1 
P MA với M là điểm biểu diễn của số phức z ' .  1 1 1
P AM  khi z '  i 
z   2i  min 1
Dựa vào hình vẽ, ta thấy  2 2 z   3 1 1
P AM  khi z '   i z   2i max 2  2 2 z
z  2i 1    
w  0  0i. Chọn B.z  2i  2
Câu 8. Xét các số phức z thỏa mãn z  1. Gọi M , m lần lượt là giá trị lớn nhất và nhỏ nhất của 2z i P
. Tỉ số M bằng z 2 m A. 53 2    . B. 9 4 2 . C. 10 6 34 . D. 25 4 34 . 4 7 9 9 Lời giải. Đặt 2z i     
  z i z w   2w i w w z 2 2
2  2w i   z  . z 2 w 2 Theo giả thiết 2w i z  1  
 1  2w i w 2 . w 2
Gọi w x yi x, y  . Khi đó từ 2w i w 2 2 2     
 2x2 2y  2 1  x 22 2 2 17 2
y  x       y      3  3 9   
 tập hợp các điểm M biểu diễn số phức z thuộc đường tròn có tâm 2 2 I   ;   ,  bán  3 3 kính 17 R  . 3  2 2 17
P OI R   max   Do đó 2z i  3 3 M 25  4 34 P   w      . Chọn D. z 2  2 2 17 m 9
P OI R     min  3 3
Câu 9. Xét hai số phức z , z thay đổi thỏa mãn z z z z  4 2i  2. Gọi , A B lần 1 2 1 2 1 2
lượt là giá trị nhỏ nhất và giá trị lớn nhất của biểu thức 2 2 z z
. Giá trị của A B là 1 2 A. 20. B. 24. C. 28. D. 32.
Lời giải. Gọi M , N lần lượt là điểm biểu diễn của hai số phức z , z . 1 2 Gọi z z
K là trung điểm của MN 
K là điểm biểu diễn của số phức 1 2 . 2
z z  2   MN  2. 1 2 z z  1 2
z z  4 2i  2   2 i  1 
 tập hợp các điểm K thuộc đường tròn có tâm 1 2 2 I 2; 
1 , bán kính R  1. 2 MN 2 Ta có 2 2 2 2 2 MN 2
T z z
OM ON  2OK   2OK  2. 1 2 2 Suy ra TOK , mà OK
OI R  1 5  T
 2 1 5  2  14  4 5; max max  2 max max TOK , mà OK
OI R  1 5  T
 2 1 5  2  14 4 5. min min  2 min min A 144 5 Vậy  
A B  28. Chọn C. B 14 4 5  Cách 2. Ta có 2 2 2 2 2
2T  2 z  2 zz zz z
 4  z z . 1 2 1 2 1 2 1 2 2
  z z  42i
 z z  2 5 2 Từ 1 2   1 2 z z 4 2i 2          . 1 2 2
  z z  42i  1 2 
z z  2 5 2 1 2 
Vậy 14 4 5 T 14  4 5.
Câu 10. Xét các số phức z, thỏa mãn |z| 5 và  43iz 12i. Giá trị nhỏ nhất của || bằng A. 3 5. B. 4 5. C. 5 5. D. 6 5.
Lời giải. Ta có  43iz 12i 12i  43iz.
Suy ra 1 2i  43iz  43i . z  5. 5 
 tập hợp các điểm M biểu diễn số phức
thuộc đường tròn có tâm I 1;2, bán kính R  5 5. Vậy
OI R  5 5 5  4 5. Chọn B. min
Câu 11. Cho số phức z thỏa mãn đồng thời z 1 2i  5 và z 1i có môđun lớn
nhất. Số phức z có môđun bằng A. 6. B. 2 5. C. 3 2. D. 5 2.
Lời giải. Ta có z 1i  z 12i2i 2 i  z 12i.
Suy ra 2 i z 1 2i  5 
 tập hợp các điểm M biểu diễn số phức thuộc đường
tròn có tâm I 2; 
1 , bán kính R  5.
Dựa vào hình vẽ ta thấy số phức có môđun lớn nhất có điểm biểu diễn là M 4;2 . 1   Với 4;2 z 1   4 2  i M i 
z  33i z  3 2. Chọn C. 1
Câu 12. Xét các số phức z thỏa mãn z 24i  2 2. Trong các số phức w thỏa mãn
w z 1i, gọi w và w lần lượt là số phức có môđun nhỏ nhất và môđun lớn nhất. Khi đó 1 2 w w bằng 1 2
A. 2  6i.
B. 2  4i.
C. 4 12i.
D. 4 8i.
Lời giải. Từ z 24i  2 2 
 tập hợp các điểm M biểu diễn số phức z thuộc đường
tròn có tâm I 2;4, bán kính R  2 2.
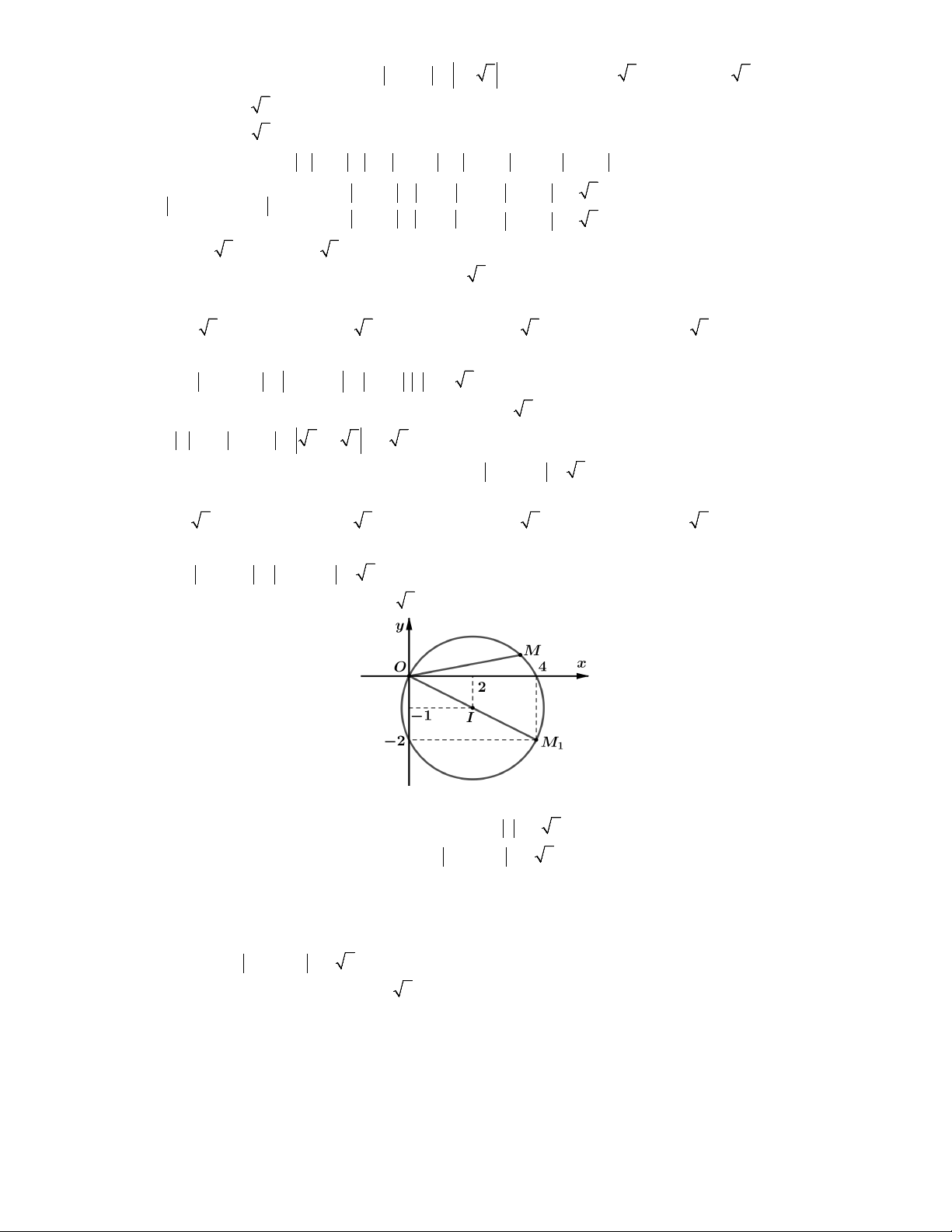
Ta có P w z 1i  z . 1i  2 z  2OM với O0;0.
Dựa vào hình vẽ ta thấy  P
 2OM . Dấu ''  '' xảy ra  M M z  1 2i 
w  1 2i 1i  13i. 1 1    min 1  P
 2OM . Dấu ''  '' xảy ra  M M z  3  6i 
w  3  6i 1i  3 9i. 2 2    max 2
Vậy w w  4 12i. Chọn C. 1 2
Cách 2. Ta có w z 1i  w  1iz 24i2 6i w 26i  1iz 24i.
Suy ra w  26i  1iz 24i  1i . z 24i  2.2 2  4 
 tập hợp các điểm N
biểu diễn số phức w thuộc đường tròn có tâm J 2;6, bán kính r  4.
Dựa vào hình vẽ ra thấy số phức w có môđun nhỏ nhất có điểm biểu diễn là N ; phức w có 1
môđun lớn nhất có điểm biểu diễn là N . 2
  
Khi đó w w ON ON  2OJ 
w w  2 2  6i  4 12i. 1 2 1 2 1 2  
Câu 13. Xét các số phức z thỏa z 1 2i  2 5 và số phức thỏa 510i 34iz 25i.
Tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P bằng A. 2 10. B. 4. C. 4 5. D. 6.
Lời giải. Ta có 510i 34iz 25i
 510i 34iz 12i535i (mục đích để tạo ra z 12i )
 510i535i  34iz 12i (chuyển vế).
Suy ra 510i535i  34iz 12i  5.2 5 10 5. 5  35i 10 5   
3i  2  3i  2 
 tập hợp các điểm M biểu 5 10i 5 10i
diễn số phức thuộc đường tròn có tâm I 3; 
1 , bán kính R  2.
P OM OI R  10 2
Dựa vào hình vẽ ta thấy  min 1    P P  2 10. Chọn A. min max
P OM OI R  10 2  max 2
Câu 14. Xét các số phức z thỏa mãn 2
z z z z z . Giá trị lớn nhất của biểu thức
P z 52i bằng A. 2 3 5. B. 2 5 3. C. 5  2 3. D. 5 3 2.
z z  2xLời giải. Đặt 
z x yi x, y  , suy ra z x yi    
z z  2yi .  2 2 2 2
 z z x y  Từ giả thiết 2 2 2
z z z z z 
2 x  2 y x y . * x  0  TH 1. 
, khi đó * trở thành x  2 y  2 1
1  2 có hình biểu diễn là cung tròn nét y  0 
liền ở góc phần tư thứ I.
Tương tự cho các trường hợp còn lại (tham khảo hình vẽ)
Gọi A5;2 và M x; y là điểm biểu diễn số phức z, khi đó P z 52i  . MA
Vì A nằm ở góc phần tư thứ I nên MA lớn nhất khi M phải nằm ở góc phần tư thứ III. Suy ra MA
AI R  3 5  2. Vậy max P  3 5  2. Chọn A. max 3 3
Vấn đề 3. Đường thẳng và đường tròn
Câu 1. Xét các số phức z thỏa mãn 2 2
z 2  z i  1 và các số phức z thỏa mãn 1 1 1 2
z  4 i  5 . Giá trị nhỏ nhất của P z z bằng 2 1 2 A. 5. B. 2 5. C. 2 5 . D. 3 5 . 5 5
Lời giải. Gọi z x yi  ;
x y   . Ta có  2 2 z
z i  
x  2  y x y  2 2 2 2 1 2
1  1  2x y 1  0   tập hợp các số
phức z là đường thẳng  : 2x y 1  0. 1 2 2
z  4 i  5 
 x 4y  
1 i  5  x 4 y   1  5 
 tập hợp các số phức
z là đường tròn C  có tâm I 4; 
1 , bán kính R  5. 2
Khi đó biểu thức P z z là khoảng cách từ một điểm thuộc  đến một điểm thuộc C. 1 2 Từ đó suy ra 8 3 5 P
MN d I,  R   5  . Chọn D. min   5 5
Câu 2. Gọi C là tập hợp các số phức w thỏa mãn w 23i w 32i . Gọi C là tập 2  1 
hợp các số phức z thỏa mãn z 2  4i 1. Giá trị nhỏ nhất của biểu thức P w z bằng A. 2 3 1 . B. 2 3 1 . C. 3 2 1 . D. 3 2 1 .
Lời giải. Đặt z x yi;
w a bi
x, y,a,b  . Ta có
w  2 3i w 3  2i 
a  2 y  2 a  2 b  2 2 3 3
2  a b  0   tập hợp
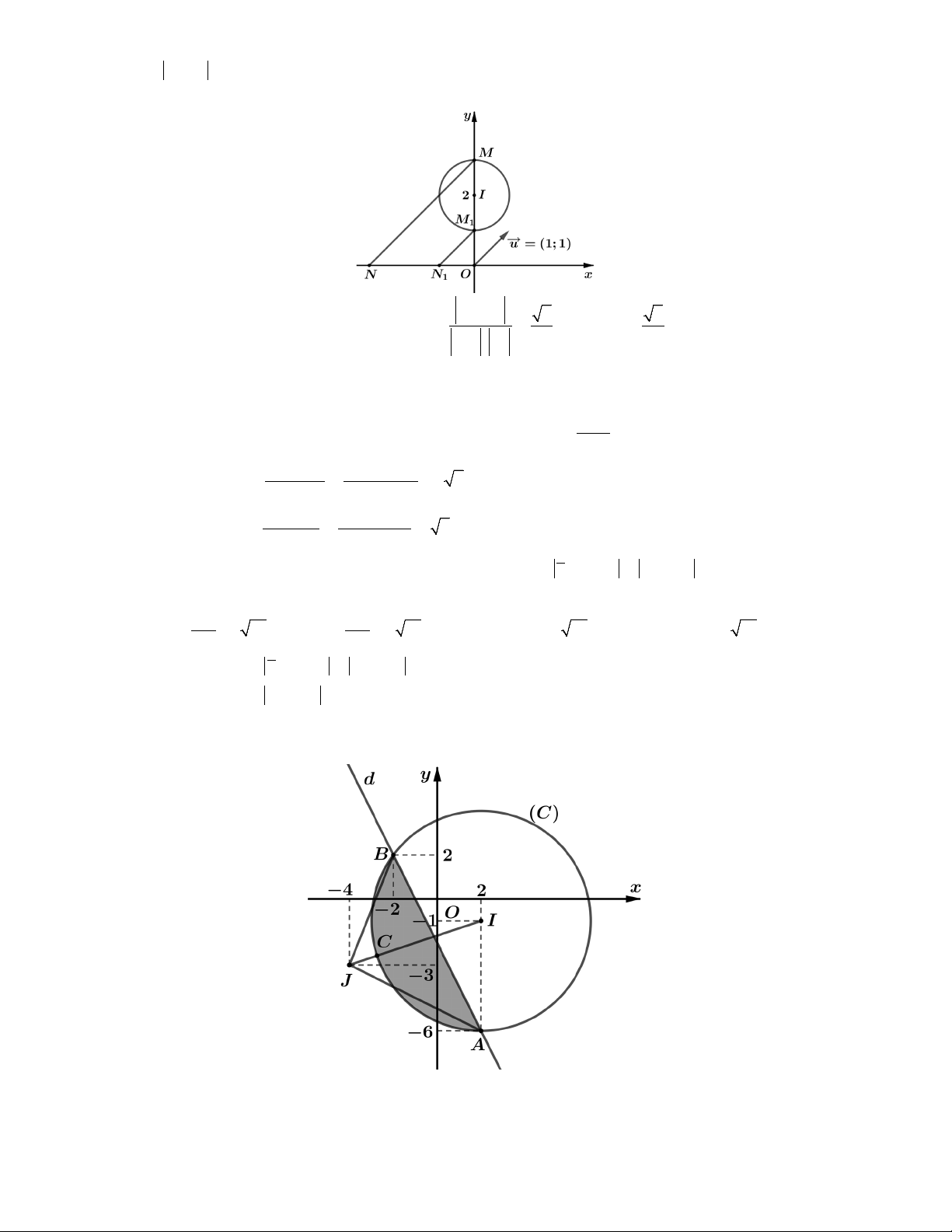
điểm M biểu diễn số phức w thuộc nửa mặt phẳng bờ  : x y  0 và kể cả bờ (miền tô đậm
như hình vẽ). Gọi miền này là C . 1  2 2
z 2  4i 1 
 x 2y  4i 1  x 2 y  4 1 
 tập hợp điểm N biểu
diễn số phức z là hình tròn C có tâm I 2;4, bán kính R 1. 2 
Khi đó biểu thức P z w MN là khoảng cách từ một điểm thuộc C đến một điểm 1  thuộc C . 2 
Từ đó suy ra P d I,  R  3 2 1. Chọn C. min  
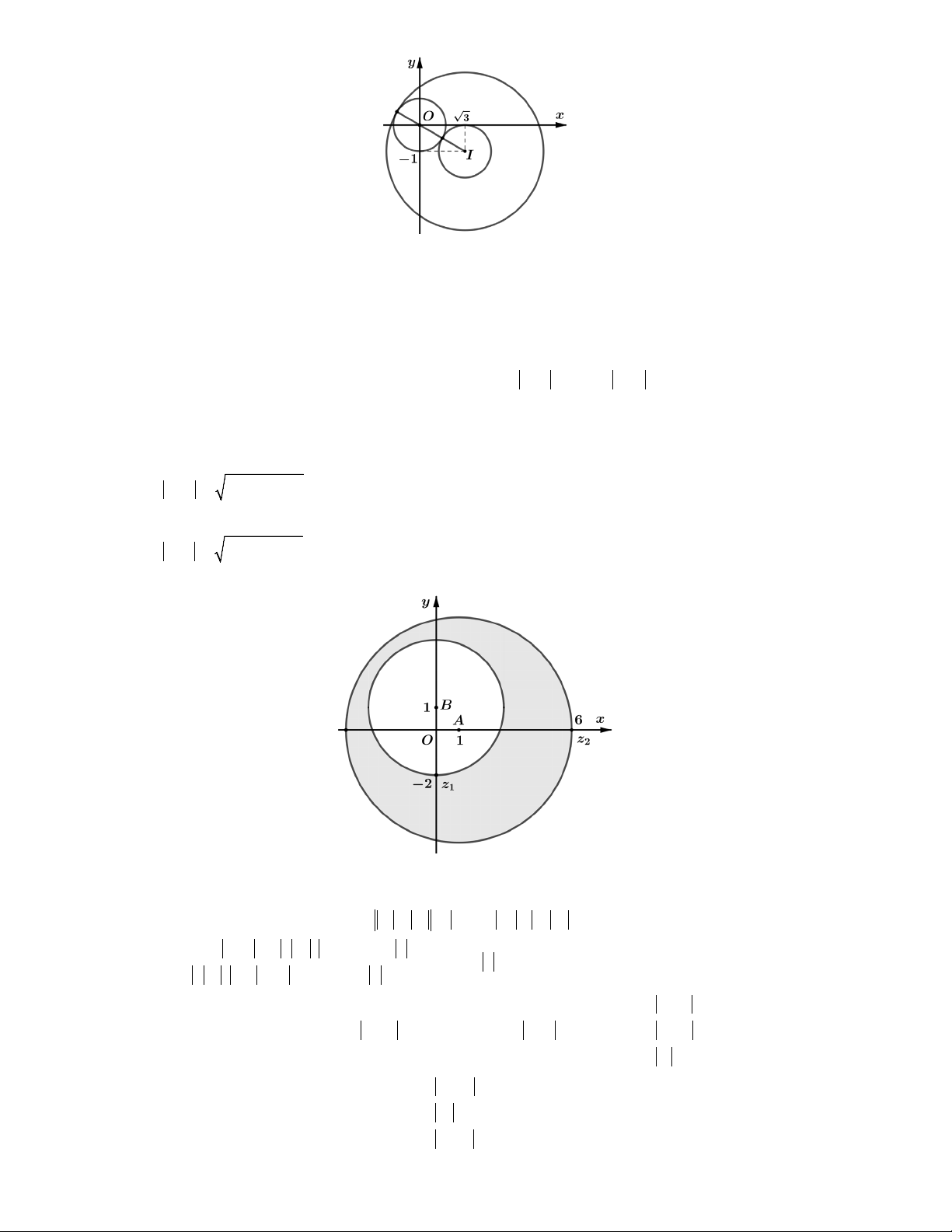
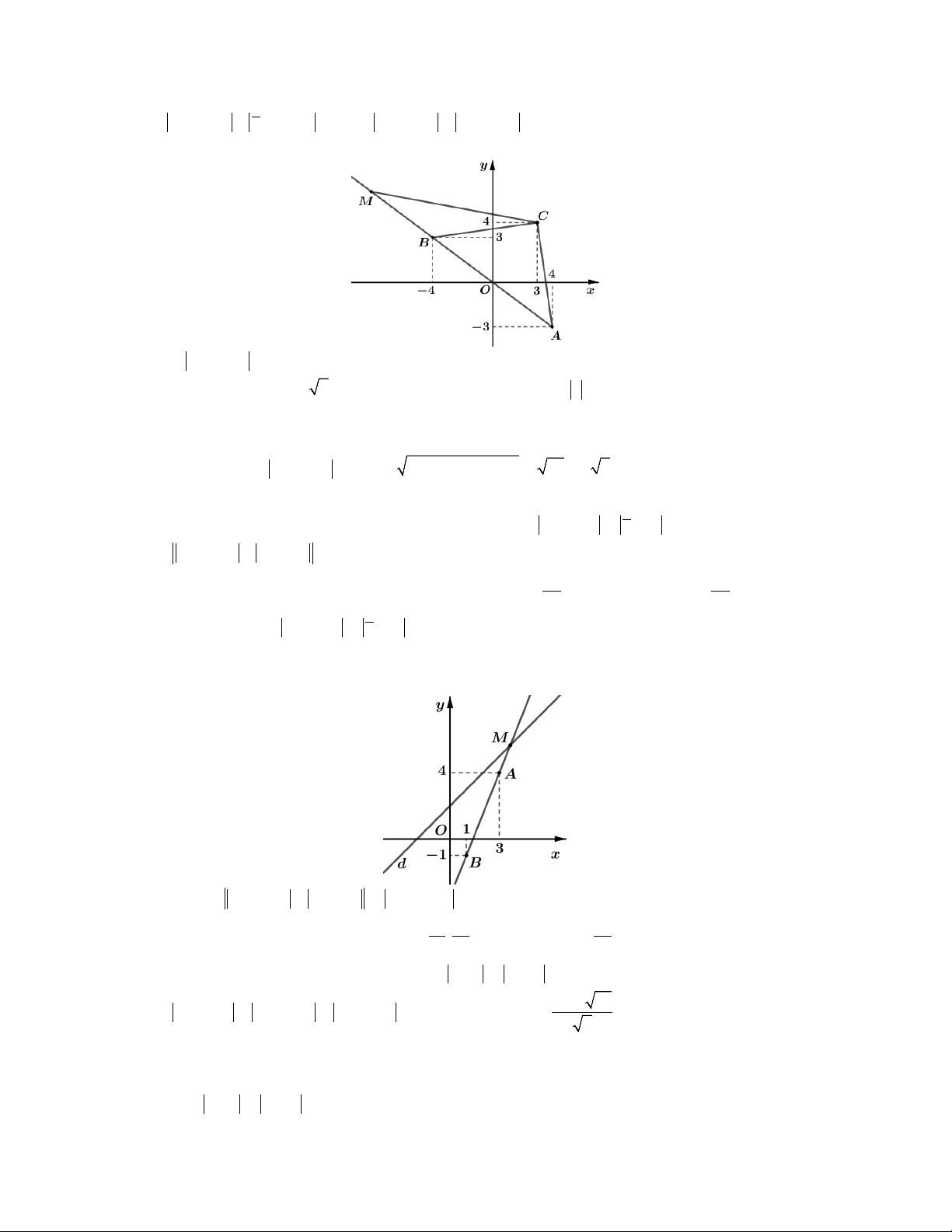
Câu 3. Xét các số thức z thỏa mãn z 2i z 4i và z 33i  1. Giá trị lớn nhất của biểu
thức P z 2 1 bằng A. 5  2. B. 10 C. 10 1. D. 13 1.
Lời giải. Gọi z x yi
x, y   . Ta có
z i z i 
x y  2  x y  2 2 2 2 4 2 4  y  3 
 tập hợp điểm biểu diễn số
phức z thuộc nửa mặt phẳng bờ  : y  3 , kể cả bờ (miền tô đậm). Gọi miền này là C . 1  2 2
z 33i  1   x   3 y  
3 i  1  x   3 y   3  1 
 tập hợp điểm biểu diễn
số phức z là đường tròn C có tâm I 3; 
3 , bán kính R  1. 2 
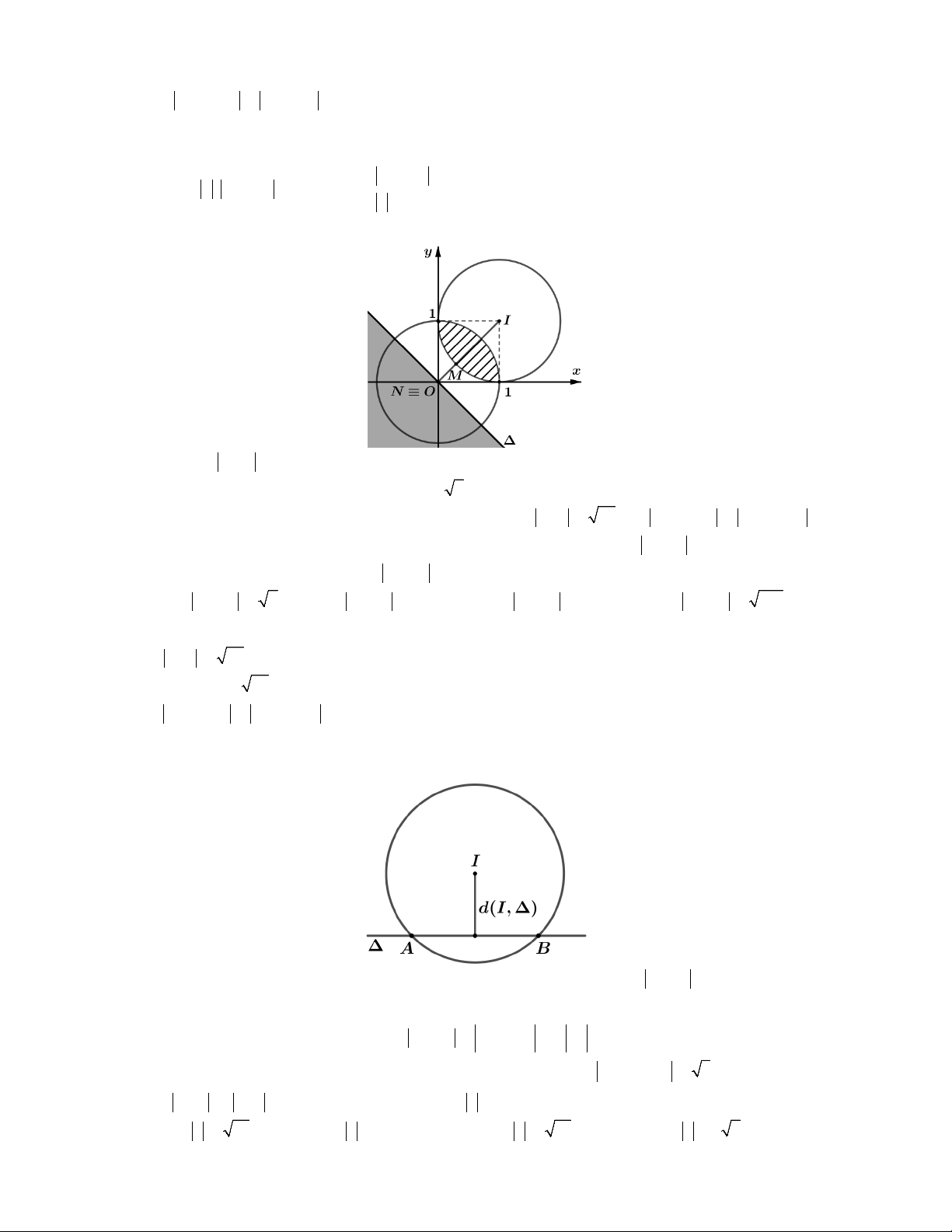
Như vậy tập hợp điểm M biểu diễn số phức z là giao của C và C . Đó chính là phần 2  1 
cung tròn nét liền như trên hình vẽ (có tính 2 điểm đầu mút D2  ;3 , C  4  ;3 của cung).
Khi đó P z 2 1  MB 1 với B2;0 và MB là khoảng cách từ điểm B đến một điểm
thuộc cung tròn CD . Từ đó suy ra P
BC 1  13 1. Chọn D. max
Câu 4. Xét các số phức z, w thỏa mãn iz 2i 2  z 1 và max w 22i , w  2. Giá trị
nhỏ nhất của biểu thức P z w bằng A. 1 . B. 5 . C. 9 . D. 13 . 2 5 2 2 5 2 5
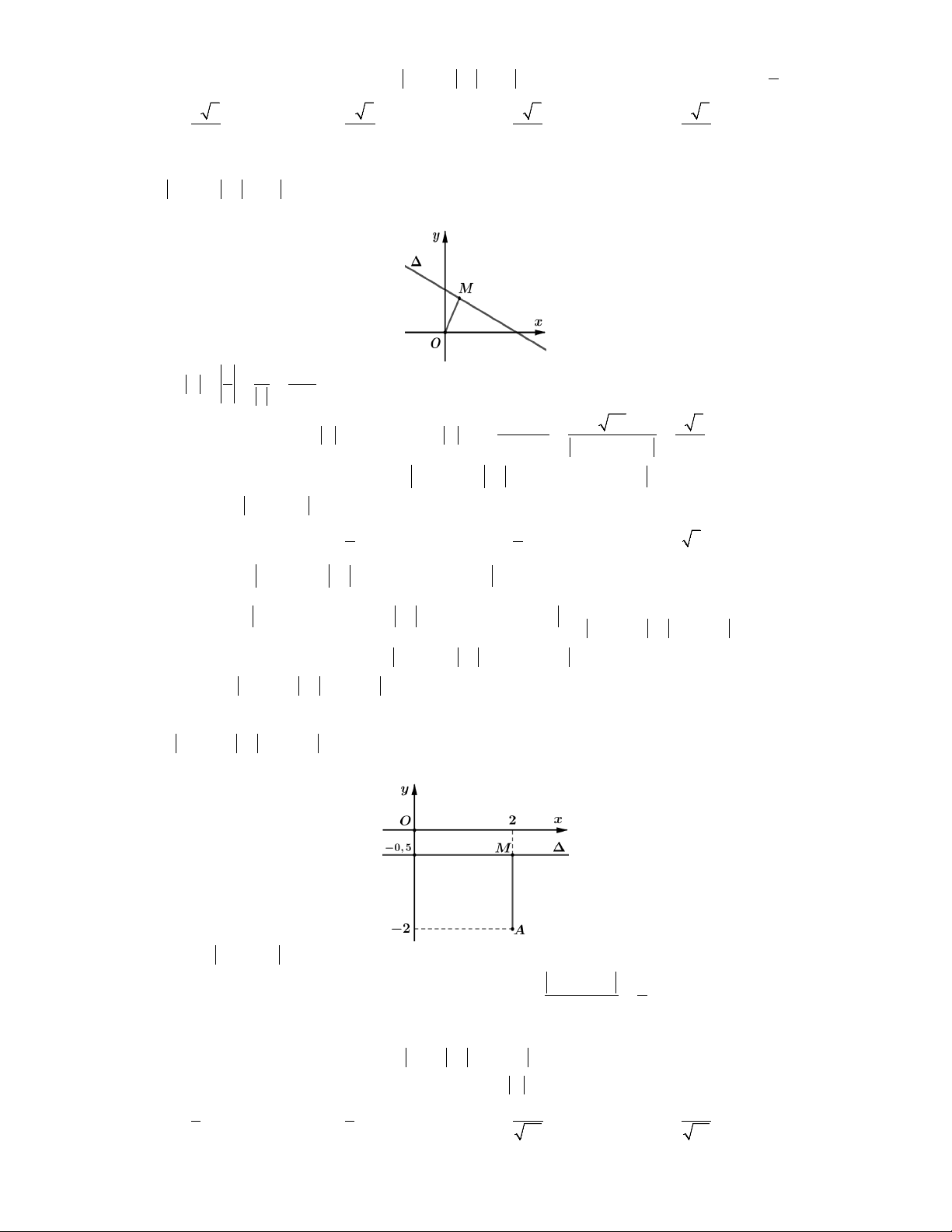
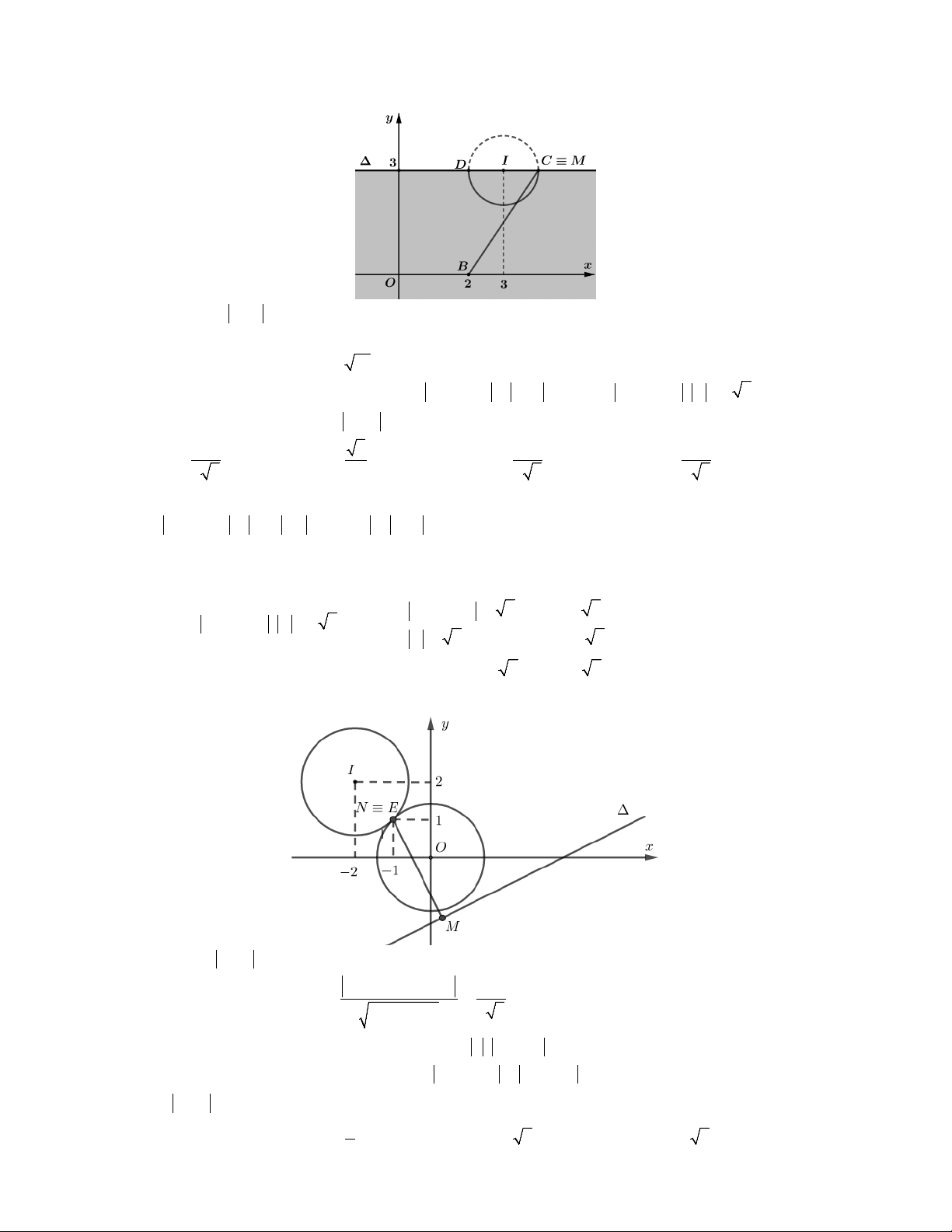
Lời giải. Gọi M x; y, N lần lượt là điểm biểu diễn của hai số phức z, w.
iz 2i 2  z 1  z 2  2i z 1
 x  2 y  2 x  2 2 2 2
1  y  2x  4 y 7  0 
 tập hợp điểm M biểu diễn số phức
z thuộc nửa mặt phẳng bờ  : 2x  4 y 7  0 không chứa O (kể cả bờ).
 w 22i  2 NI  2 , I   2; 2
 max  w  22i , w   2, suy ra     w 2  
NO  2, O 0;0   
N thuộc phần chung của hai hình tròn I; 2 và O; 2. Mà hai hình tròn này tiếp
xúc ngoài tại điểm E 1; 
1 . Do đó N E 1;  1 .
Ta có P z w MN nên P nhỏ nhất khi MN ngắn nhất, khi đó M là hình chiếu của N 2  1  4.17 trên 13  và Pd N,    . Chọn D. min    2 2 2 5 2  4 m  ax 
z ; z 1i 1
Câu 5. Xét các số phức z, w thỏa mãn 
. Giá trị nhỏ nhất của biểu thức
w 12i w 2i 
P z w bằng A. 0. B. 1 . C. 2 1. D. 2 2 1. 6
Lời giải. Gọi M , N x; y lần lượt là điểm biểu diễn của hai số phức z, w. 
w   i w  i 
x  2 y  2 x  2 y  2 1 2 2 1 2 2
1  x y  0   tập hợp
điểm N biểu diễn số phức w thuộc nửa mặt phẳng bờ  : x y  0 và kể cả bờ (miền tô đậm như hình vẽ).
 z 1i 1 MI 1, I 1;  1
 max  z ; z 1i  1, suy ra       z 1  
MO 1, O  0;0  
M thuộc phần chung của hai hình tròn I ;  1 và O; 
1 (phần gạch sọc như hình vẽ).
Ta có P z w MN nên P nhỏ nhất khi MN ngắn nhất. Dựa vào hình vẽ ta thấy MN
ngắn nhất khi N O và MN
OI 1  2 1. Chọn C. min
Câu 6. Kí hiệu S là tập hợp các số phức z thỏa mãn z 1  34 và z 1 mi z m  2i
(trong đó m   ). Gọi z , z là hai số phức thuộc tập hợp S sao cho z z là lớn nhất. Khi 1 2 1 2
đó, hãy tính giá trị của biểu thức z z . 1 2
A. z z  2.
B. z z  2.
C. z z  10.
D. z z  130. 1 2 1 2 1 2 1 2
Lời giải. Đặt z x yix, y  . Khi đó
z 1  34 
 tập hợp điểm biểu diễn số phức z thuộc đường tròn C  có tâm I 1;0, bán kính R  34.   1
z 1 mi z m  2i  2m 2x 4 2my  3  0 
 tập hợp điểm biểu diễn số phức
z thuộc đường thẳng  : 2m 2x 4 2my 3  0. 2 Từ  
1 và 2, suy ra tập các điểm biểu diễn số phức z của tập S là giao điểm của  và C . Gọi ,
A B lần lượt là các điểm biểu diễn của hai số phức z ,
z . Suy ra z z AB. 1 2 1 2
Để AB lớn nhất  d I, nhỏ nhất   đi qua điểm I.   
Khi đó I là trung điểm của AB nên z z OA OB  2 OI  2OI  2. Chọn B. 1 2
Câu 7. Biết số phức z x yi  ;
x y   thỏa mãn đồng thời z 3 4i  5 và biểu thức 2 2
P z  2  z i đạt giá trị lớn nhất. Tính z . A. z  33 . B. z  50 . C. z  10 . D. z  5 2 .
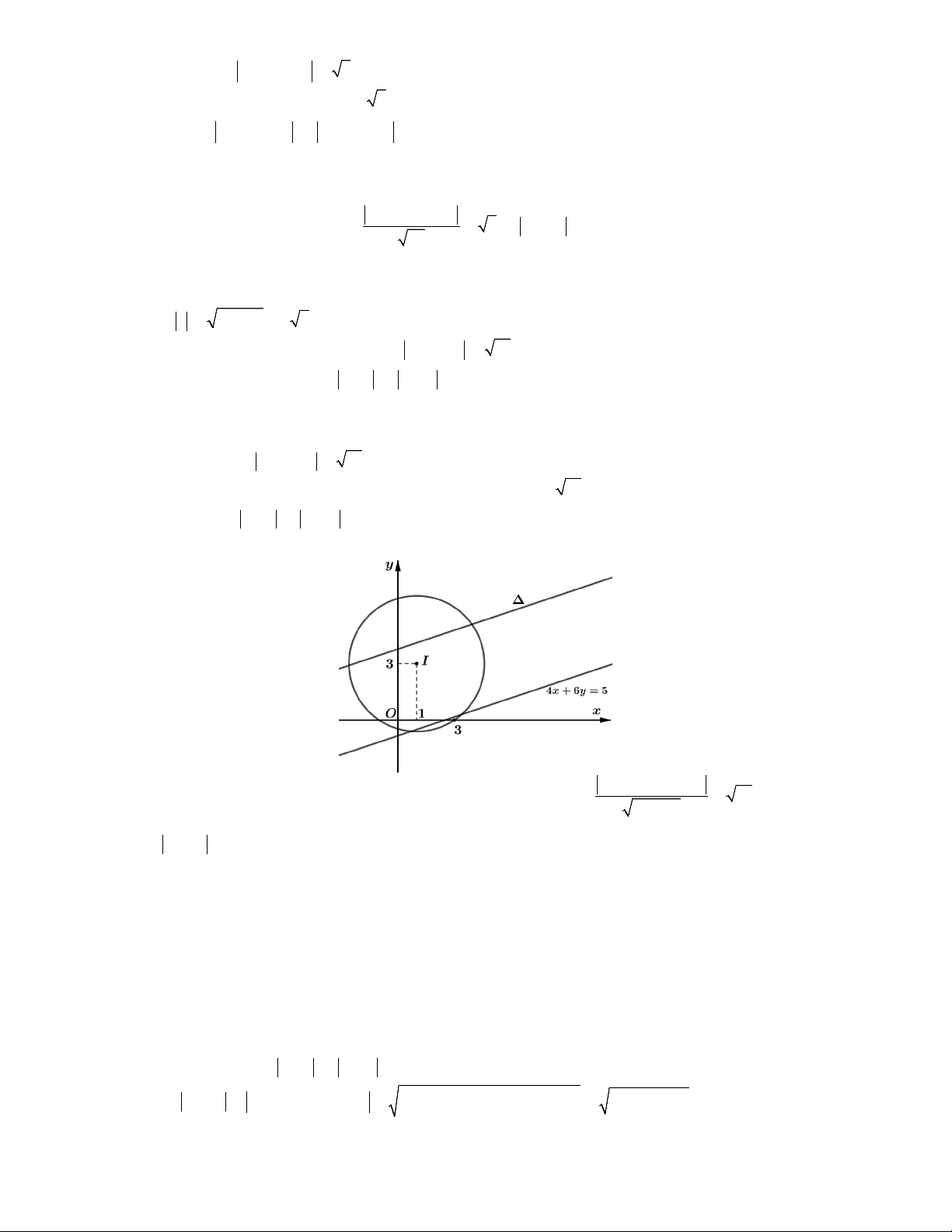
Lời giải. Vì z 3 4i  5 
 tập hợp các điểm biểu diễn số phức z là đường tròn C
có tâm I 3;4 và bán kính R  5 . Ta có Px  2 yi x y  2 ix 2 y
x y 2 2 2 2 1 2 1             
 4x  2y 3    
 4x  2y 3 P  0.
Ta tìm P sao cho đường thẳng  : 4x  2y 3 P  0 và đường tròn C có điểm chung 12  8  3   P
d I, R
 5  23 P 10  13  P  33. 20
4x 2y 30  0   x  5 Do đó P
 33 . Dấu "  " xảy ra     . max    x  2
3 y 42  5 y 5   Vậy 2 2
z  5  5  5 2 . Chọn D.
Câu 8. Xét các số phức z thỏa mãn z 13i  13. Gọi ,
m M lần lượt là giá trị nhỏ nhất và
lớn nhất của biểu thức 2 2
P z  2  z 3i . Tổng m M bằng A. 10. B. 25. C. 34. D. 40.
Lời giải. Đặt z x yix; y  .
 Từ giả thiết z   i  
x  2 y  2 1 3 13 1
3  13. Suy ra tập hợp các điểm biểu diễn
số phức z là đường tròn C có tâm I 1; 
3 , bán kính R  13.  Lại có 2 2
P z  2  z 3i  4x  6y 5 
 4x  6y 5 P  0. Suy ra tập hợp các số phức
z thuộc đường thẳng  : 4x  6y 5 P  0. 4.1 6.35 P
Để tồn tại z thì  và C phải có điểm chung  d I, R   13 16  36 m   9
 17  P  26  9 P 43      
m M  34. Chọn C.M  43  Dấu ''  '' xảy ra khi  thay 43 43 P P  
 : 4x  6y 48  0. Tọa độ điểm z thỏa max   x  2 1 y  2 3  13 x  3     
z  3 6i.
4x 6y48  0 y  6    thay 9 9 P P 
   : 4x  6y  4  0. Tọa độ điểm z thỏa min   x  2 1 y  2 3  13 x  1       z  1.
4x 6y 4  0 y  0   Cách 2. Ta có 2 2
P z  2  z 3i  4x  6y 5 Px  y    x  2 y 2 2 2                 2 2 17 4 1 6 3 4 6 1 3 4  6 .13  26  
Câu 9. Xét các số phức z x yi  ;
x y   thỏa mãn 1iz  2i  4. Giá trị lớn nhất của
biểu thức T x y 3 bằng A. 4. B. 4 2. C. 4  2 2. D. 8.
Lời giải. Ta có   i 2 i 4 1 3 1
z  2 i  4  z  
z   i  2 2   tập hợp các số 1i 1i 2 2  
phức z là đường tròn C có tâm 1 3 I   ; , 
bán kính R  2 2.  2 2
x y 3 T   0
Ta có T x y 3   .
x y 3T  0 
 Với  : x y  3 T
  0. Để tồn tại số phức z tức là  và C  phải có điểm chung 1 3   3 T
d I  2 2 ,  R
 2 2  0 T  8. 2
 Với  : x y 3T  0. Để tồn tại số phức z tức là  và C phải có điểm chung 1 3   3 T
d I  2 2 ,  R
 2 2  8 T  0. 2
So sánh hai trường hợp, ta có T  8. Chọn D. max
Câu 10. Xét các số phức z thỏa mãn | z  2  1 2i . Giá trị nhỏ nhất của biểu thức P |
z 12i||z 34i||z 56i| được viết dưới dạng a b, với a là phân số tối giản. b
Giá trị của a b bằng A. 10. B. 11. C. 12. D. 17.
Lời giải. Đặt z x yi x, y  .
Khi đó z    i  x  2 2 2 1 2 2  y  5 
 tập hợp điểm M biểu diễn số phức z thuộc
đường tròn C có tâm I 2;0, bán kính R  5.
Ta có P z 12i z 34i z 56i MA MB MC với A1;2, B 3;4, C  5;6. Nhận thấy các điểm ,
A B, C cùng thuộc đường thẳng d : y x 1. Đường thẳng d cắt
đường tròn C tại hai điểm P 0; 
1 và Q 3;2. a   9
Vậy P M P và P PA PB PC 9 2        
a b  11. Chọn B. min min b   2 
Câu 11. Xét các số phức z z
z , z thoả mãn z 3 4i  1, z 1  z i và 1 2 là số thực. 1 2 1 2 2 2 i
Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của z z . Tính P M m . 1 2 A. P  14 5. B. P  16 5. C. P  18 5. D. P  20 5.
Lời giải. Đặt z a bi, z c di a,b,c,d   . 1 2  
Gọi Aa;b, B
c;d  lần lượt là hai điểm biểu diễn số phức z , z . 1 2
  
Suy ra z z OAOB BA 
z z AB. 1 2 1 2  
Do đó từ z z 1
2  k k   
BA k 2; 
1 . Suy ra đường thẳng AB có VTPT n AB 1;2. 2 i
z 3 4i  1 
 tập hợp các điểm A là đường tròn C  có tâm I 3;4, bán kính R  1. 1
z 1  z i  c  2
1  d c d  2 2 2
1  c d  0 
 tập hợp các điểm B là đường 2 2
thẳng  : x y  0.   n .n Gọi AB  3 10 1
là góc giữa  và AB , ta có cos     sin . 10 n . n 10 AB
Theo yêu cầu bài toán ta cần tìm GTLN và GTNN của AB.
Do d I, R nên suy ra  không cắt C. Gọi H là hình chiếu của A trên  , ta có  max AH
d I, R m  ax AB    7 5  10 AH  sin sin AB    
P  14 5. Chọn A. sin  min AH
d I, R min  AB    7 5  10  sin  sinCâu 12. Cho z z
z là số phức, z là số thực thoả mãn z 2i  1 và 2
1 là số thực. Tổng giá 1 2 1 1i
trị lớn nhất và giá trị nhỏ nhất của biểu thức P z z là 1 2 A. 2. B. 2 2. C. 3 2 D. 4 2.
Lời giải. Gọi M , N lần lượt là hai điểm biểu diễn số phức z , z . 1 2
  
Suy ra z z ON OM MN 
z z MN. 2 1 1 2  
Do đó từ z z 2
1  k k   
MN k1; 
1 . Suy ra đường thẳng MN có VTPT n   MN 1;  1 . 1i
z 2i  1 
 tập hợp các điểm M là đường tròn C  có tâm I 0;2, bán kính R  1. 1
z là số thực 
 tập hợp các điểm N là đường thẳng  : y  0. 2   n .n Gọi MN  2 2
là góc giữa  và MN , ta có cos     sin . 2 2 n . n MN
Theo yêu cầu bài toán ta cần tìm GTLN và GTNN của MN.
Do d I, R nên suy ra  không cắt C. Vì MO
IO   nên O là hình chiếu của M trên  , ta có MN  sin  max MO
d I, R m  ax MN    3 2  sin sin    . Chọn D.  min MO
d I, R min  MN    2  sin  sin
Câu 13. Cho z x yi x, y   là số phức thỏa mãn z 23i z i 2  5. Gọi M, m
lần lượt là giá trị lớn nhất và nhỏ nhất của 2 2
P x y  8x  6 .
y Giá trị M m bằng A. 156 2 10. B. 156  2 10. C. 6020 10. D. 60  20 10. 5 5
 z 23i z i 2  2x y 2  0
Lời giải. Ta có 
. Suy ra tập hợp các điểm M x; y thỏa
 z i 2  5  x 22 y  2 1  25 
yêu cầu bài toán nằm trên miền H  tô đậm được giới hạn bởi đường thẳng d : 2x y  2 và
đường tròn C có tâm I 2; 
1 , bán kính R  5 (kể cả biên) như hình vẽ.
Ta có P x y x y  x  2 y  2 2 2 2 8 6 4
3 25  JM 25 với J 4;  3 .
Gọi giao điểm của d và C là A2;6, B 2;
 2; C là giao điểm của đoạn IJ với C .
Dựa vào hình vẽ ta thấy  JM  min  ,
JA JB, JC  JC IJ IC IJ R  2 10 5.  JM  max  ,
JA JB, JC  JA  3 5. M   3 52 25 20 Vậy  
M m  60 20 10. Chọn C.m  2 10  2 5 25  40 20 10 
Vấn đề 4. Đường tròn và đường tròn
Câu 1. Xét các số phức z ,
z  4  1 và iz 2  1. Giá trị nhỏ nhất của biểu 1 z thỏa mãn 2 1 2
thức P z  2 bằng 1 z2 A. 2 5 2. B. 4  2. C. 4 2 3. D. 4 2 3.
Lời giải. Đặt z  2z 
P z  2z z  2z z z . 3 2 1 2 1  2  1 3 Từ 1 1
z  2z z   z , thay vào iz 2  1 ta được  iz 2  1  z  4i  2. 3 2 2 3 2 2 3 3 2 Gọi ,
A B là hai điểm biểu diễn cho hai số phức z , z . 3 1
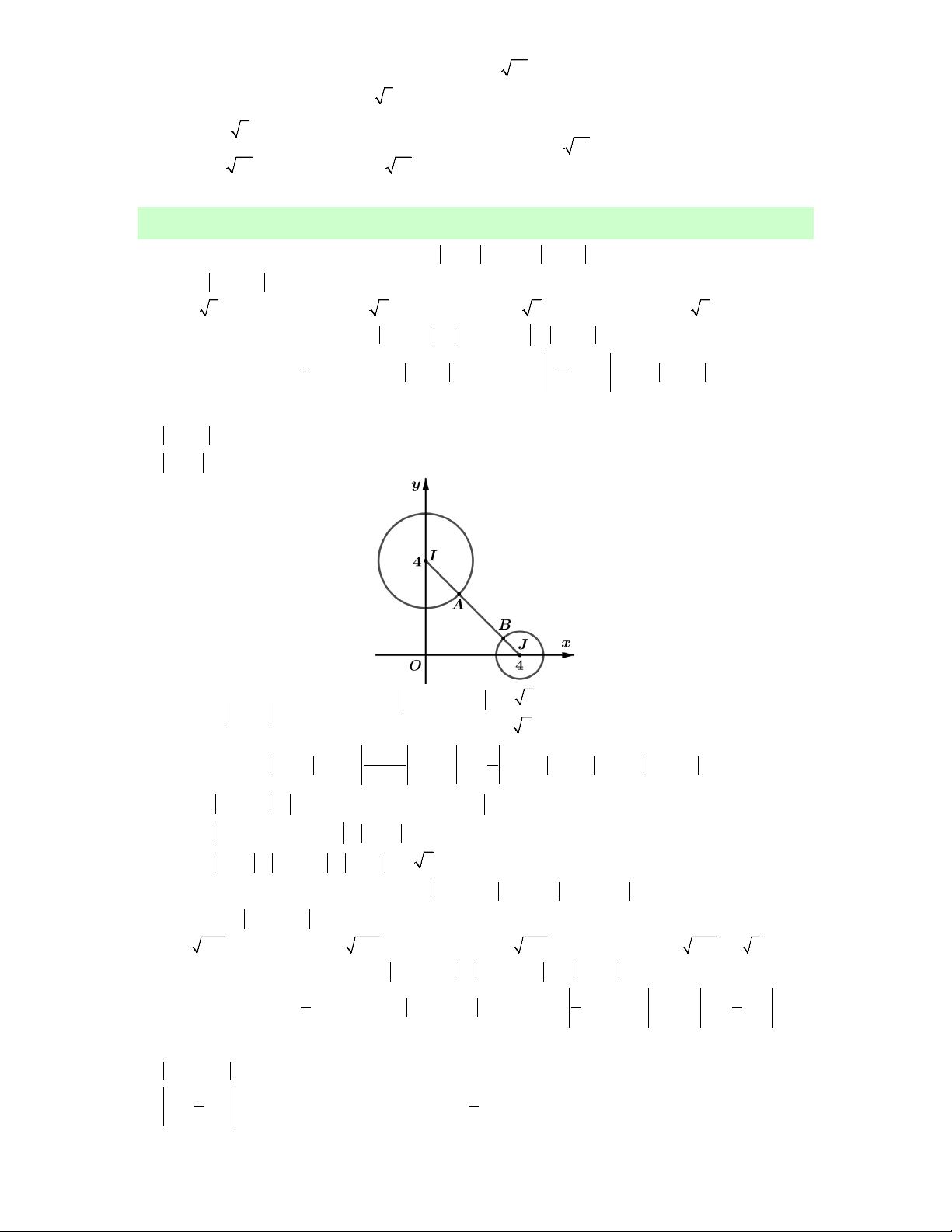
z  4i  2 
A  đường tròn tâm I 0;4, bán kính R  1. 3 3
z  4  1 
B  đường tròn tâm J 4;0, bán kính R  1. 1 1
P IJ R R  4 2 3 Khi đó  min 1 2 P z z AB       . Chọn C. 1 3
P IJ R R  4 2 3  max 1 2 Cách 2. Biến đổi iz 2 2 2 iz 2  1 
 1  z   1  z  2i  1  2z  4i  2 . 2 2 2 2 i i
Ta có P z  2z z 4  2z  4i  4 4i 1 2  1   2   
 2z  4i  4 4i z 4 2    1
 4 4i  2z  4i z 4  4 2 3. 2 1
Câu 2. Xét các số phức z , z thỏa mãn z 3i 5  2 và iz 1 2i  4. Giá trị lớn nhất của 1 2 1 2
biểu thức P  2iz 3z bằng 1 2 A. 313 16. B. 313. C. 313 8. D. 313  2 5.
Lời giải. Đặt 2iz  3z 
P  2iz 3z  2iz 2iz  2 z z . 3 2 1 2 1 3 1 3 Từ 2 2 3
2iz  3z iz z , thay vào iz 1 2i  4 ta được
z 1 2i  4  z   3i  6. 3 2 2 3 3 2 3 3 3 2 Gọi ,
A B là hai điểm biểu diễn cho hai số phức z , z . 1 3
z 3i  5  2 
A  đường tròn tâm I 5; 
3 , bán kính R  2. 1 1 3  
z   3i  6 
B  đường tròn tâm 3
J  ;3, bán kính R  6. 3 2 2  2
P  2 IJ R R  313 16 Khi đó  min 1 2 P 2 z z 2AB       . Chọn A. 1 3
P  2 IJ R R  313 16 max  1 2  
Câu 3. Xét các số phức z , z thỏa mãn z  12 và z 34i  5. Giá trị nhỏ nhất của biểu 1 2 1 2
thức P z z bằng 1 2 A. 0. B. 2. C. 7. D. 17. Lời giải. Gọi ,
A B là hai điểm biểu diễn cho hai số phức z , z . 1 2  z  12 
A  đường tròn tâm O 0;0, bán kính R  12. 1 1
z 3 4i  5 
B  đường tròn tâm I 3;4, bán kính R  5. 2 2
P  2OI R  2 Khi đó min 1 P z z AB       . Chọn B. 1 2
P  2OI R  22  max 1
Câu 4. Có bao nhiêu giá trị của tham số m để tồn tại duy nhất số phức z thỏa mãn z.z  1
và z  3 i m ? A. 0. B. 1. C. 2. D. 3.
Lời giải. Gọi A là điểm biểu diễn cho số phức z.  2
z.z  1  z  1   z  1 
A  đường tròn C có tâm O0;0, bán kính R  1. 1  1
 Ta thấy m  0 
z  3 i không thỏa mãn z.z  1 nên suy ra m  0.
z  3 i m 
A  đường tròn C có tâm I  3;  1 , bán kính R  . m 2  2
Nhận thấy OI  2  R suy ra I nằm ngoài C . 1  1
Để có duy nhất số phức z thì C và C tiếp xúc ngoài hoặc tiếp xúc trong, điều điều này 2  1  O
I R Rm 1  2 m  1 xảy ra khi 1 2       .
R R OIm 12 m  3  2 1  
Vậy có 2 giá trị của m thỏa mãn. Chọn C.
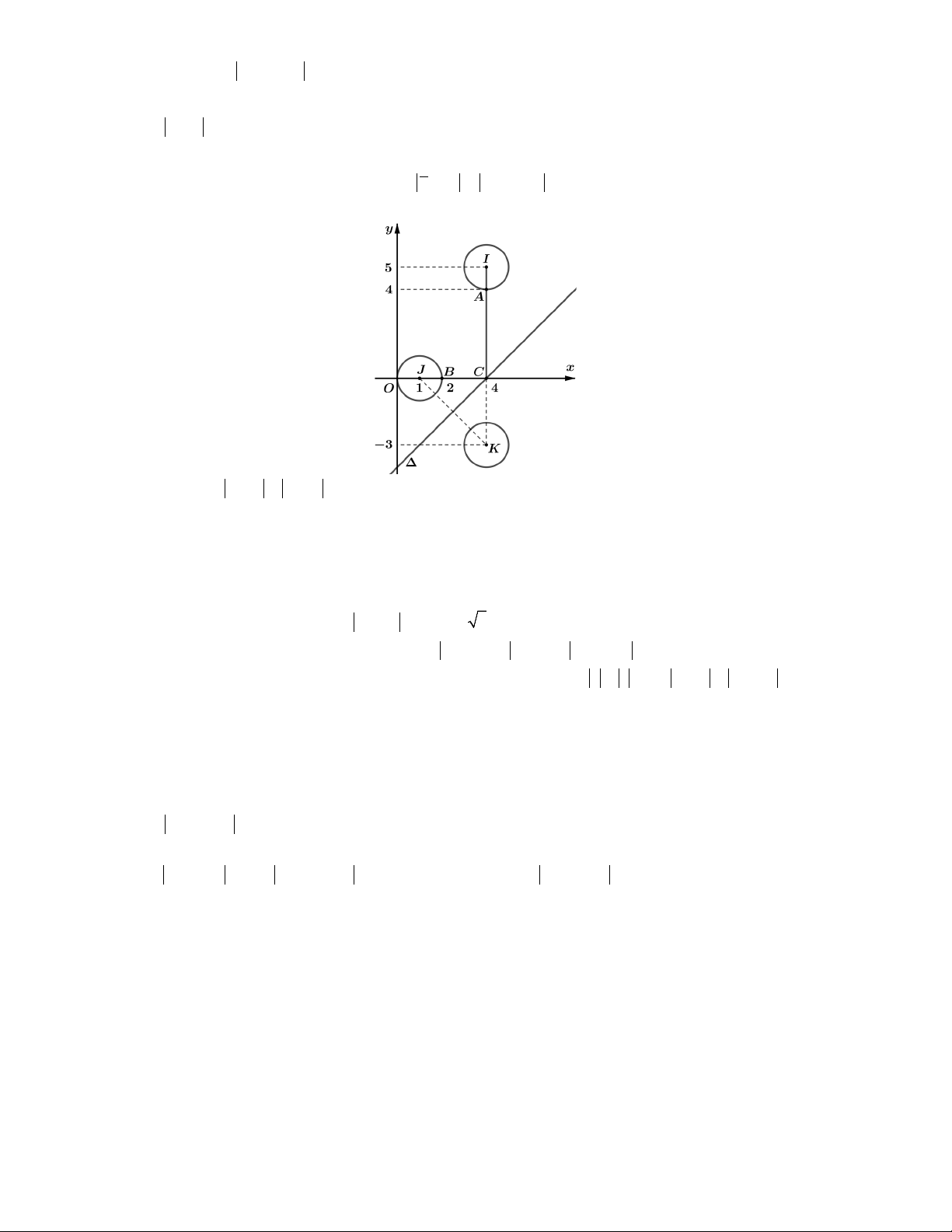
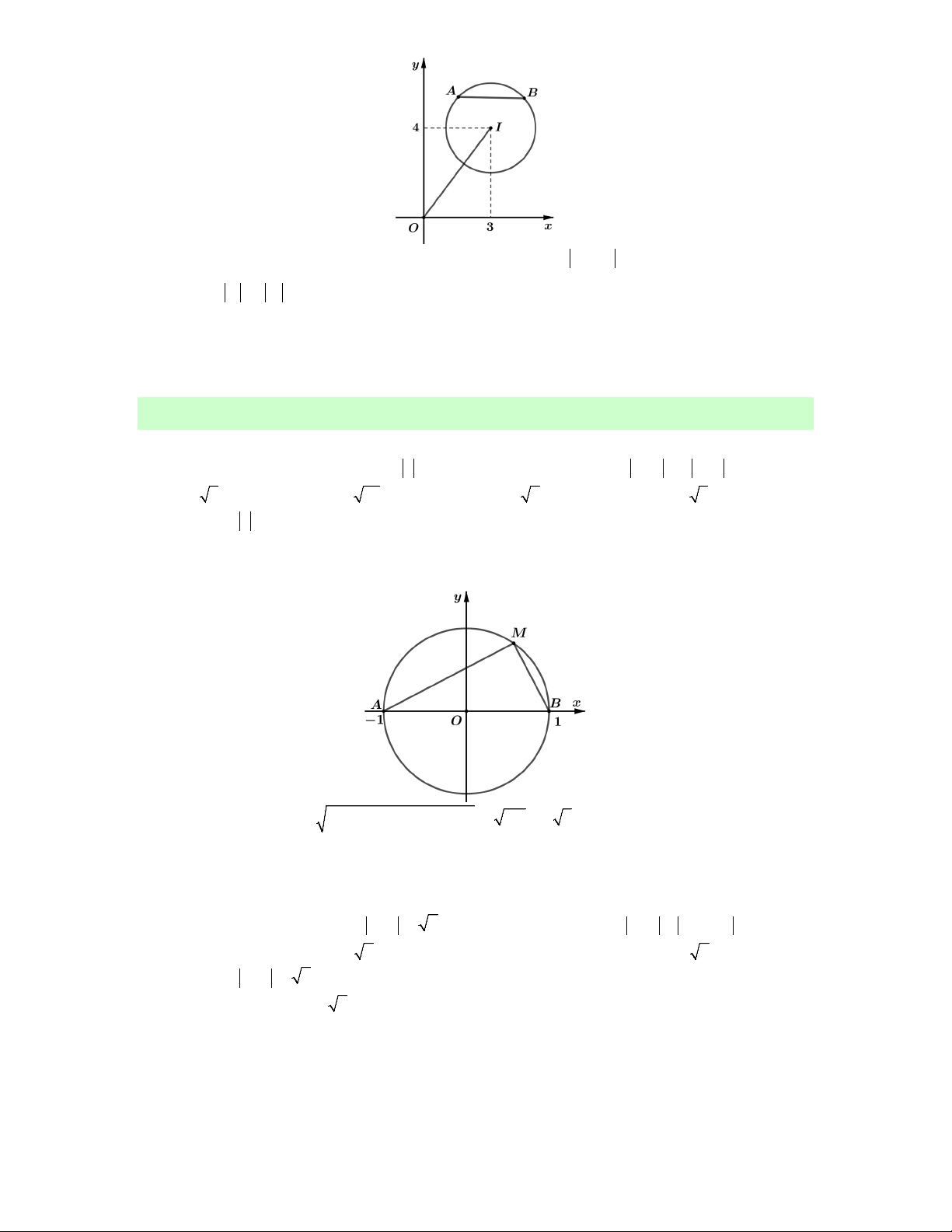
Câu 5. Gọi S là tập hợp các số phức z thỏa mãn z i  3 và z 1  5 . Gọi z , z S lần 1 2
lượt là các số phức có mođun nhỏ nhất và lớn nhất. Khẳng định nào sau đây đúng ?
A. z  2z 122 .i B. z  2z  212 .i C. z  2z  64 .i
D. z  2z 12 4 .i 1 2 1 2 1 2 1 2
Lời giải. Giả sử z a bi  ,
a b   . Ta có 2 2
z   a   2
b   a   2 2 1 1 5 1  b  5 
 tập hợp các số phức z nằm trong hoặc trên đường tròn tâm A1;0, bán kính R  5 . 2 2  2
z i a b   2
  a b   2 1 3 1  3 
 tập hợp các số phức z nằm ngoài hoặc trên đường tròn tâm B0; 
1 , bán kính R '  3 . z
z  0 2i
Dựa vào hình vẽ ta thấy min 1  
z  2z  12 2i. Chọn A. 1 2 z
z  6  0i  max 2
Cách 2. Áp dụng bất đẳng thức z z z z z z . 1 2 1 2 1 2         1 2 3 z i z i 2    z Ta có     
2  z  6.
 z  1  z 1  5    z  6 
 z i  3 1 
Dấu ''  '' thứ nhất xảy ra khi z i  3 , kết hợp với z 1  5 ta được  z 1  5  z  2i. 1 1 1 z 2 1   z 1  5 2 
Tương tự cho dấu ''  '' thứ hai, ta được  z  6   z  6 
z  2z  12 2i . 2 2 1 2
z i 3 2 
Câu 6. Xét các số phức z thỏa mãn 1 z 2 i  4. Gọi M là giá trị lớn nhất của
z 2  3i , m là giá trị nhỏ nhất của z  2 2i . Tính M  . m
A. M m  3.
B. M m  5.
C. M m  6.
D. M m  7.
Lời giải. Giả sử z a bi  ,
a b   . Ta có 2 2 2 2
z 2 i  a 2 b  
1  4  a 2 b   1 16 
 tập hợp điểm M biểu diễn
số phức z nằm trong hoặc trên đường tròn tâm A2; 
1 , bán kính R  4. 2 2 2 2
z 2 i  a 2 b  
1 1  a 2 b   1 1 
 tập hợp điểm M biểu diễn số
phức z nằm ngoài hoặc trên đường tròn tâm A2; 
1 , bán kính R  1. T   0
Khi đó T z 2 3i MC với C 2;  3 min    ; T
CM AC R  6  max 3
P BM AB R 1
P z  22i MB với B2;2 min 1    .
P BM AB R  9  max 2 Vậy TP  7. Chọn D. max min
 z 2i  2 5
Câu 7. Xét các số phức  z thỏa mãn 
. Giá trị lớn nhất của T z 1 4i bằng
 z 4i  2 2  A. 3 2. B. 3 5. C. 5  2. D. 6.
Lời giải. Giả sử z a bi  , a b  . Ta có 2 2  2
z i a b   2 2
2  2 5  a b  2  20 
 tập hợp điểm M biểu diễn số phức
z nằm trong hoặc trên đường tròn C có tâm A0;2, bán kính R  2 5.   1 1  2 2  2
z i a b   2 4
4  2 2  a b 4  8 
 tập hợp điểm M biểu diễn số phức z
nằm trong hoặc trên đường tròn C có tâm B0;4, bán kính R  2 2. 2 2  Từ  
1 và 2 suy ra tập hợp điểm M biểu diễn số phức z nằm trên phần giao của hai hình
tròn C và C (phần tô đậm trong hình vẽ). 2  1 
Khi đó T z 14i z 1 4i MC với C 1;4. Dựa vào hình vẽ ta thấy T khi M max
sẽ rơi vào các vị trí M hoặc M hoặc M . 1 2 3 CM   3 5  1  Ta có CM   1 2 2 52 2  T
CM  3 5. Chọn B. 2 max 1 CM  CM 3 1 
 z 1i 1
Câu 8. Xét các số phức z x yi
x, y   thỏa mãn  . Gọi ,
m M lần lượt là
 z 33i  5 
giá trị nhỏ nhất và giá trị lớn nhất của biểu thức P x  2 .
y Tỉ số M bằng m A. 5 . B. 7 . C. 9 . D. 14 . 4 2 4 5
Lời giải. Ta có
z 1i 1 
 tập hợp điểm M biểu diễn số phức z nằm ngoài hoặc trên đường tròn
C có tâm I 1; 
1 , bán kính R  1.   1 1 
z 33i  5 
 tập hợp điểm M biểu diễn số phức z nằm trong hoặc trên đường
tròn C có tâm J 3; 
3 , bán kính R  5. 2 2  Từ  
1 và 2 suy ra tập hợp điểm M biểu diễn số phức z là phần tô đậm trong hình vẽ (có tính biên)
Gọi  là đường thẳng có phương trình x  2y P  0. Khi đó để bài toán có nghiệm (tồn tại
số phức thỏa mãn yêu cầu bài toán) thì đường thẳng  và miền tô đậm phải có điểm chung 9  P M 14 d JM 7 , 5 5 4 P 14                . Chọn B. 5 m   4 m 2  Dấu "  " xảy ra khi
x 2y 14  0   x  4
M  14 đạt được khi     .   x  2 3 y  2 3  5 y  5  
x 2y 4  0   x  2
m  4 đạt được khi     .   x  2 3 y  2 3  5 y  1  
 z 1i  3
Câu 9. Xét các số phức z x yi  ;
x y   thỏa mãn 
. Giá trị nhỏ nhất của
 z 34i  10 
biểu thức P x 3y bằng A. 5. B. 7. C. 13. D. 4 3 10.
Lời giải. Ta có
z 1i  3 
 tập hợp điểm M biểu diễn số phức z nằm ngoài hoặc trên đường tròn
C có tâm I 1; 
1 , bán kính R  3.   1 1 
z 3 4i  10 
 tập hợp điểm M biểu diễn số phức z nằm trong hoặc trên đường
tròn C có tâm J 3;4, bán kính R  10. 2 2  Từ  
1 và 2 suy ra tập hợp điểm M biểu diễn số phức z là phần tô đậm trong hình vẽ (có tính biên)
Gọi  là đường thẳng có phương trình x 3y P  0. Khi đó để bài toán có nghiệm (tồn tại
số phức thỏa mãn yêu cầu bài toán) thì đường thẳng  và miền tô đậm phải có điểm chung. 
Bằng cách tịnh tiến các đường thẳng song song với nhau (cùng có VTPT là n  1;  3 ) ta thấy
P đạt giá trị nhỏ nhất bằng 7 khi  đi qua điểm A4;  1 . Chọn B. Vấn đề 5. Parabol
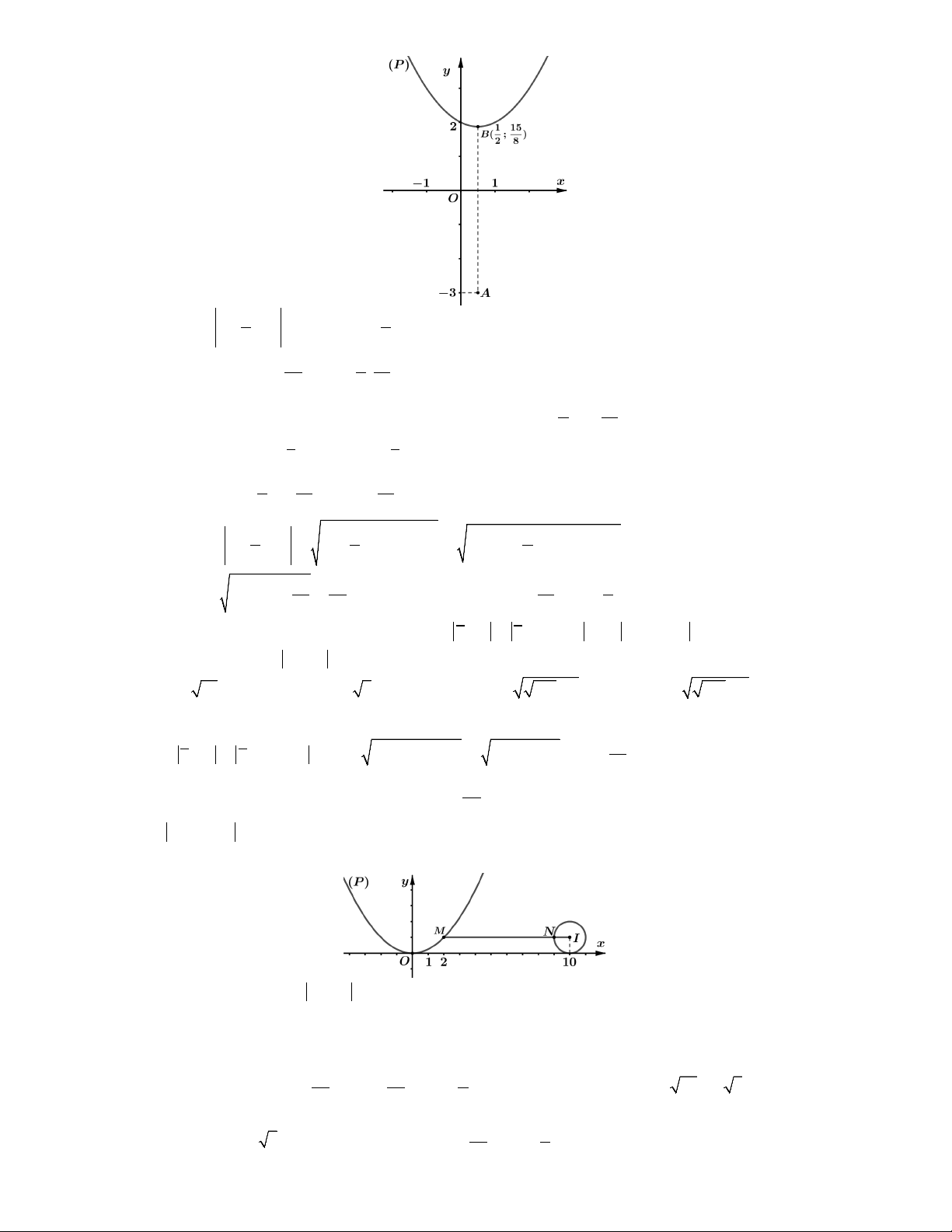
Câu 1. Xét các số phức z a bi  ,
a b   thỏa z z  i i z z  2 4 15
1 . Tính P a   4b khi 1
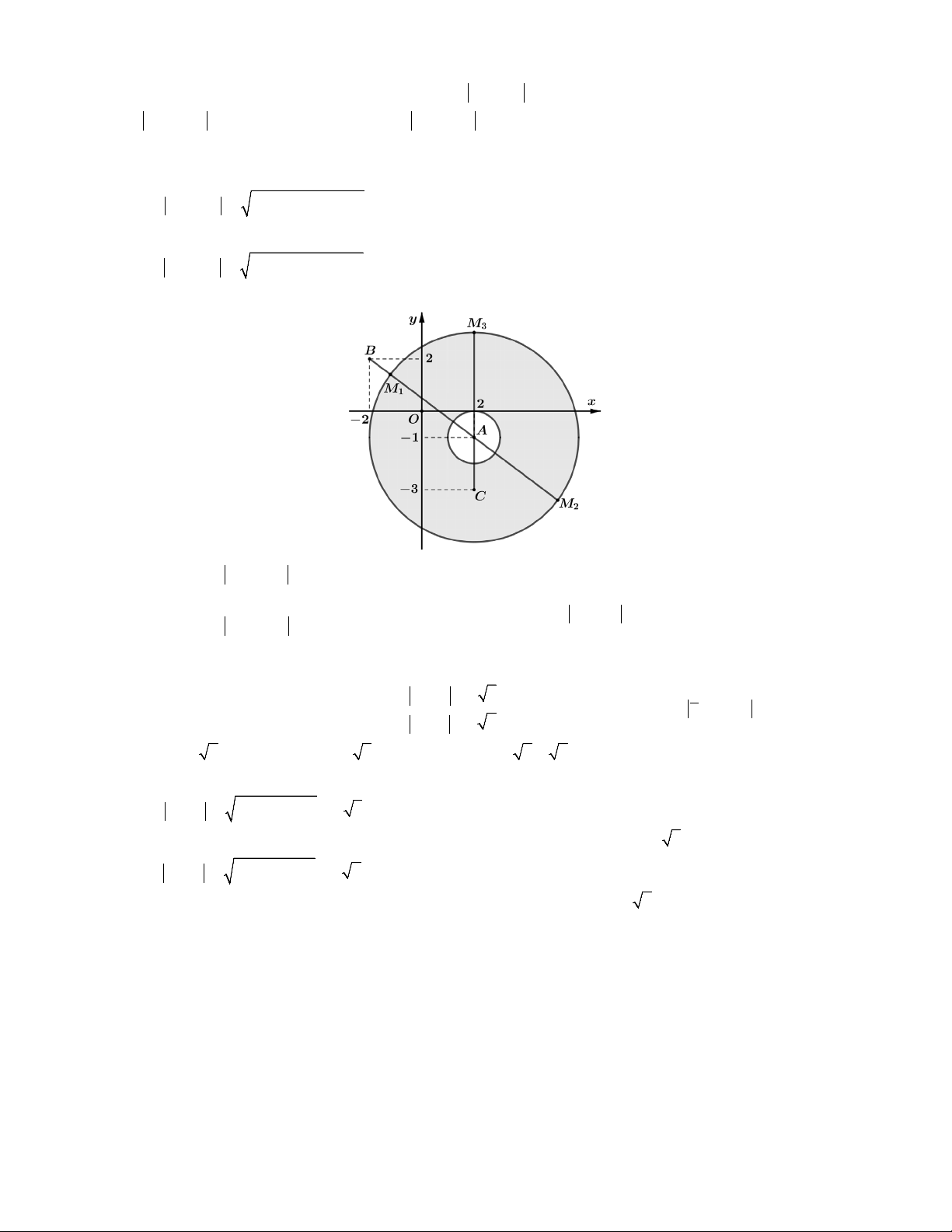
z   3i đạt giá trị nhỏ nhất. 2 A. P  4. B. P  5. C. P  6. D. P  7. 2
Lời giải. Từ z z  i iz z  2  
bi i i a  2 a a 4 15 1 4.2 15 2 1  b    2   tập 2 2 2 hợp điểm x x
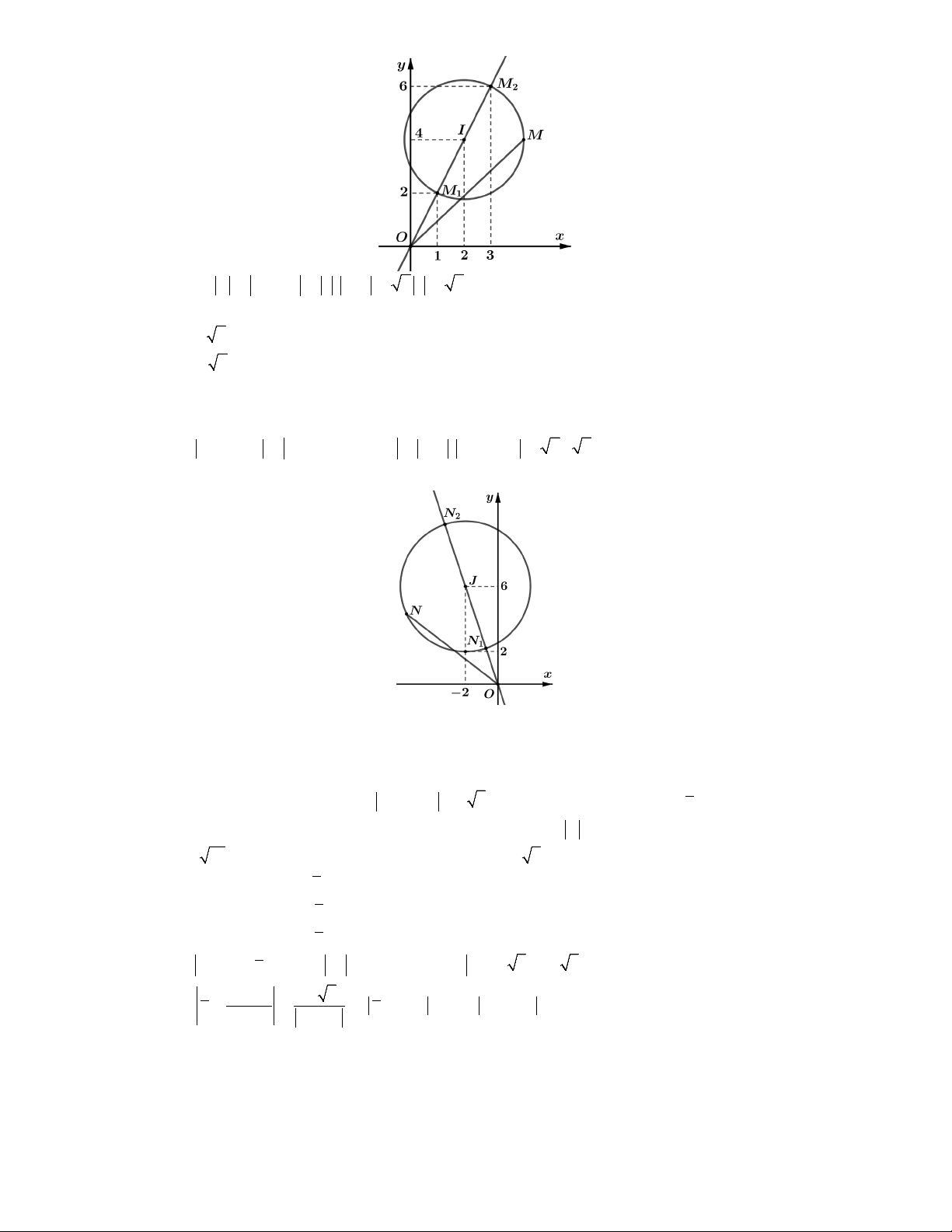
M biểu diễn số phức z là Parabol P: y    2 (như hình vẽ). 2 2   Ta có 1
T z   3i MA với 1 A ;3. 2 2    Ta thấy 39 MA BA  với 1 15
B ;  là đỉnh của của P. 8 2 8 
Vậy T MA AB. Dấu "  " xảy ra khi 1 15
M B a  ,b    a
  4b  7. Chọn D. min min 2 8
Cách 2. Ta có z z  i iz z  2  
bi i i a  2 2 4 15 1 4.2 15 2
1  2b a a  4.   1 2   Suy ra 1 15 15 2b  a      b  .   2 4 8 2   Khi đó 1 1
T z   3i  a
  b  2 1 2 2
3  a a   b  6b  9 2  2 4  1 21 39 2
T b 8b   . Dấu "  " xảy ra khi 15 1 b   a  . 4 8 8 2
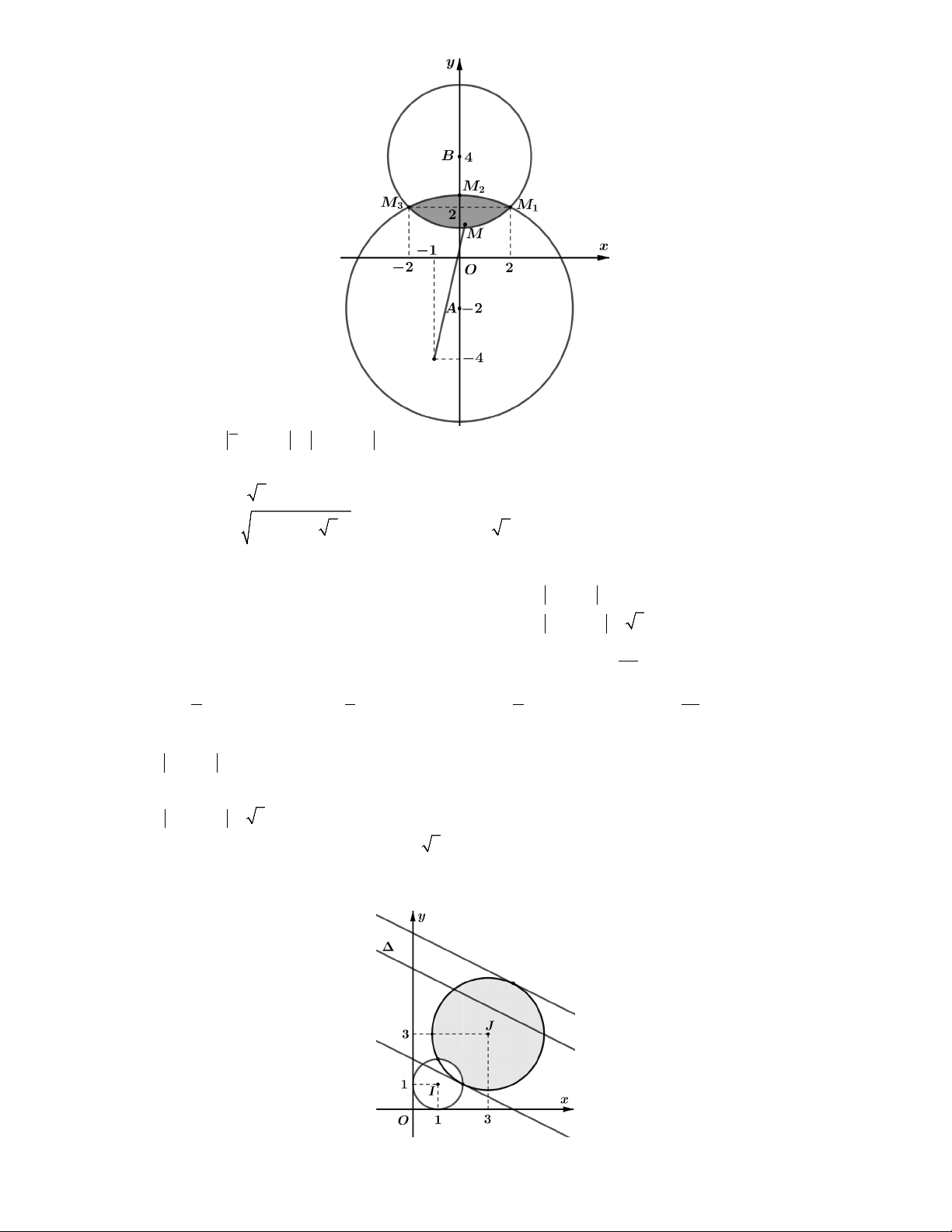
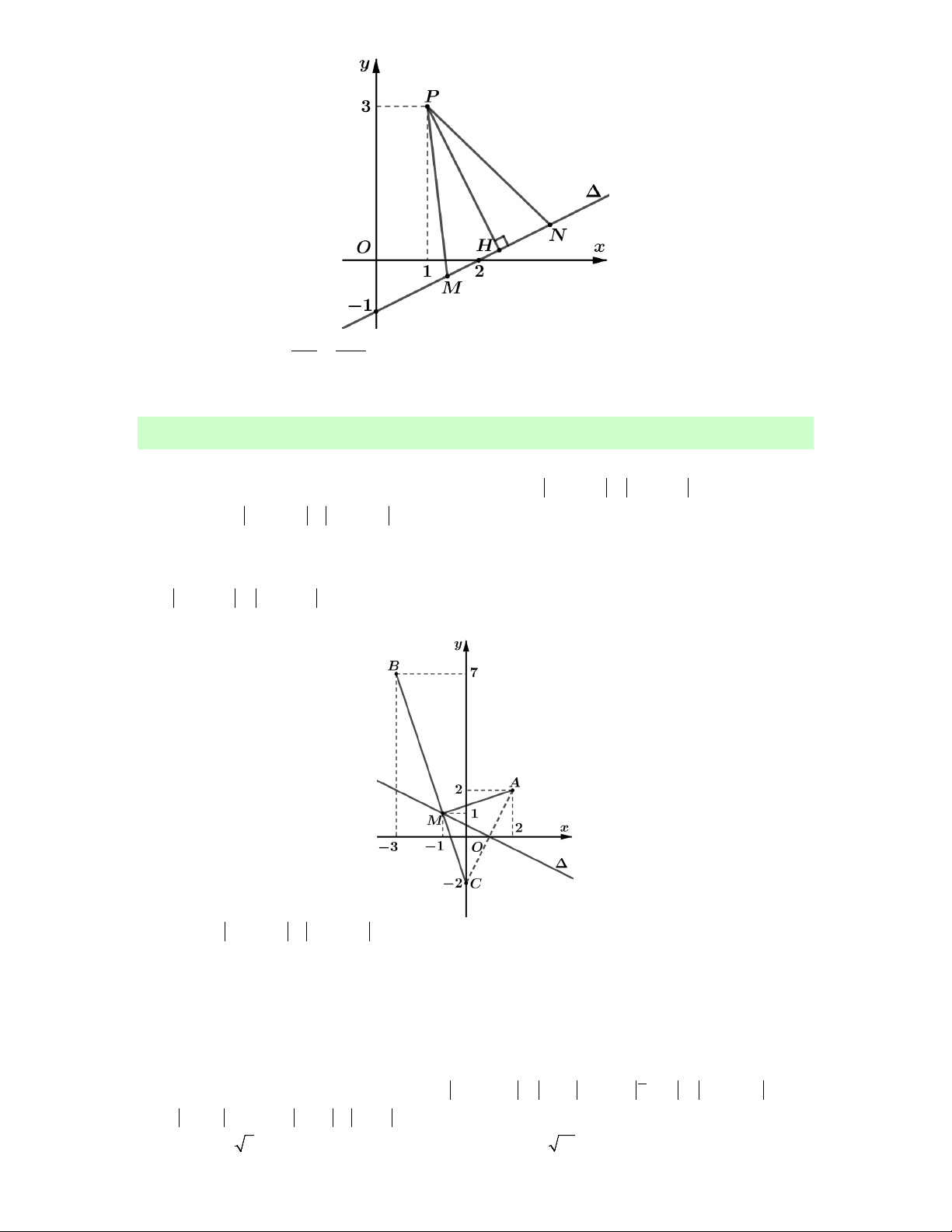
Câu 2. Xét hai số phức z , z thỏa mãn 2 z i z z 2i và z i 10  1. Giá trị nhỏ 1 2 1 1 1 2
nhất của biểu thức z z bằng 1 2 A. 10 1. B. 3 5 1. C. 101 1. D. 101 1.
Lời giải. Đặt z a bi a,b   . 1   2 2 2 a  2
2 z i z z 2i  2. a b
 1  2b 2  b  
 tập hợp điểm M 1 1 1     4 2 biểu diễn số phức x
z là một Parabol P: y
có đỉnh O0;0. 1 4
z i 10  1 
 tập hợp điểm N biểu diễn số phức z là đường tròn C  có tâm 2 2 I 10; 
1 , bán kính R  1.
Khi đó biểu thức P z z MN là khoảng cách từ một điểm thuộc P đến một điểm 1 2 thuộc C.
Ta có MN NI MI 
MN MI NI MI 1. Suy ra MNIM . min min 2 2 2 2    
Ta có IM  x  2 x   x 5 10  1       4    IM  45  3 5.     x 42 2  45  45 4   4  2 2 2   Do đó x 5 MN
 3 5 1. Dấu "  " xảy ra khi  4   
x 42  0   x  4. min  4  2 Vậy z z
 3 5 1. Chọn B. 1 2 min 2   2 Cách 2. Xét điểm a a a
M a; . 
Tiếp tuyến của P tại M có phương trình  : y  x a .  4  2 4    2    Gọi a a
n   ;1   
là một VTPT của đường thẳng ;
IM  a 10; 1. 2   4    Khi đó IM
IM cùng phương với n , suy ra a  4. min  Với a  4   IM  6;  3   IM  3 5   MN  3 5 1. min min
Vấn đề 6. Đoạn thẳng – tia
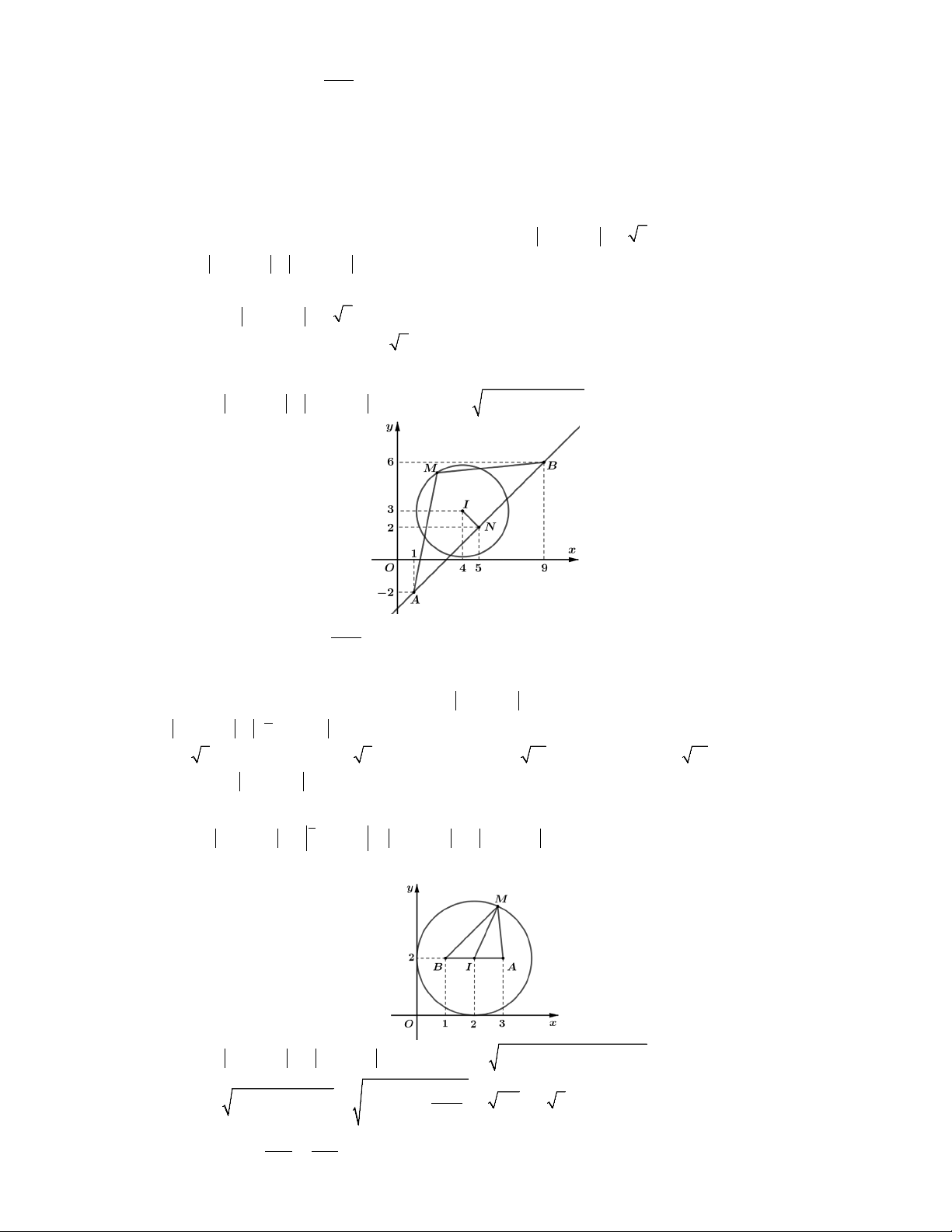
Câu 1. Xét các số phức z thỏa mãn z  2i z 4 7i  6 2. Gọi ,
m M lần lượt là giá trị
nhỏ nhất và giá trị lớn nhất của z 1i . Tính P m M. A.   P  13  73 . B. 5 2 2 73 P  .
C. P  5 2  2 73 . D. 5 2 73 P  . 2 2
Lời giải. Gọi M x ; y, A2;  1 , B 4 ;7, C  1; 
1 lần lượt là điểm biểu diễn các số phức z,
2 i , 4 7i , 1i trong mặt phẳng tọa độ.
Từ z  2i z 4 7i  6 2  MA MB  6 2  AB 
M thuộc đoạn thẳng AB.
Ta có T z 1i CM. Dựa vào hình vẽ, ta thấy 5  TCMd C, AB  . min min   2  CB  73 ; 13 CA   CMCB  73. max Vậy 5 2 73  5 2 P  73   . Chọn B. 2 2
Cách 2. Phương trình đường thẳng AB : y x 3.
Gọi M x;x  
3  AB với x 2;4 (do M nằm trong đoạn AB ). yx 3
Ta có T z  i  x  y  i  x  2 y  2 2 1 1 1 1 1 
2x  6x 17.
Khảo sát hàm f x 2
 2x  6x 17 trên đoạn 2;4.
Câu 2. Xét các số phức z thỏa mãn z 1i z 83i  53. Giá trị lớn nhất của biểu thức
P z 1 2i bằng A. 53. B. 53. C. 185 . D. 106. 2
Lời giải. Gọi M x ; y, A1;  1 , B8; 
3 , C 1;2 lần lượt là điểm biểu diễn các số phức z,
1i , 8  3i , 12i trong mặt phẳng tọa độ.
Từ z 1i z 83i  53  MA MB  53  AB 
M thuộc đoạn thẳng AB.  Ta có CA CB
P z 1 2i MC . Vì 13 , 106 
, kết hợp với hình vẽ ta suy ra CA
 CM CBP
 106. Dấu ''  '' xảy ra khi M trùng B. Chọn D. max
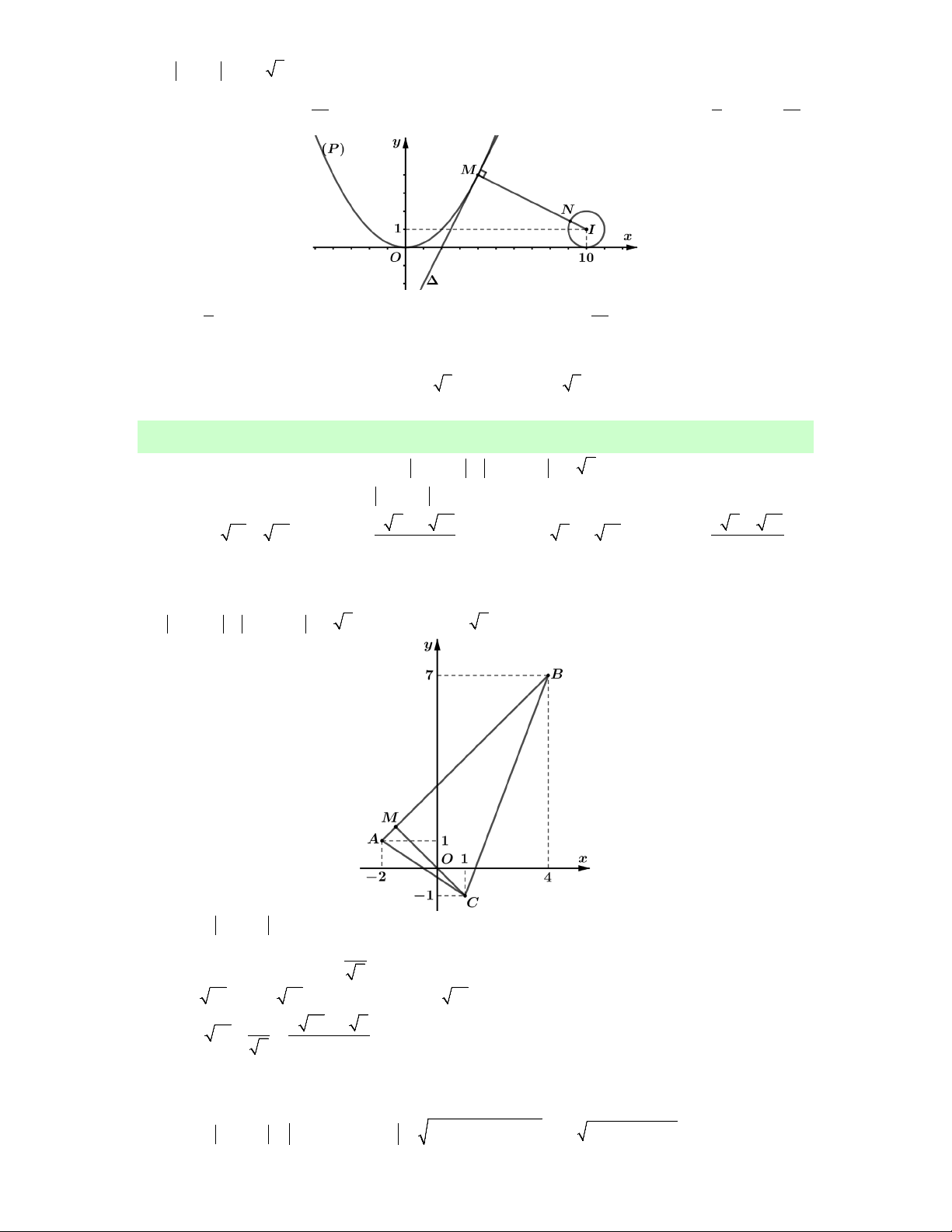
Câu 3. Xét các số phức z thỏa mãn z  23i z 6i  2 17. Gọi M , m lần lượt là giá trị
lớn nhất và giá trị nhỏ nhất của biểu thức P z 12i z 2 i . A. M  3 2, 0. m B. M  3 2, 2. m C. M  3 2, m  5 2 2 5. D. M  2, m  5 2 2 5.
Lời giải. Gọi C , A2;  3 , B6; 
1 lần lượt là điểm biểu diễn các số phức z, 2  3i , 6 i
trong mặt phẳng tọa độ.
Từ z  23i z 6i  2 17  CA CB  2 17  AB 
C thuộc đoạn thẳng AB.
Ta có P z 12i z 2 i CD CE với D1;2, E 2;  1 .
Nhận thấy D,E nằm về một phía của đường thẳng AB.
CD CE DE  3 2. Dấu "  " xảy ra khi C DE AB.
CD CE  0. Dấu "  " xảy ra khi C AB và C thuộc đường trung trực của đoạn DE.
Vậy M  3 2 , m  0. Chọn A.
Cách 2. Phương trình đường thẳng AB : x  4 y 10  0.
Gọi M 104y; y AB với y 1;3 (do M nằm trong đoạn AB ).
 z 12i x 1y2i  x  2
1 y 22  114 y2 y 22 Ta có  .
 z2i x2y 1i  x22 y 2
1  84 y2 y  2 1  Khi đó 2 2
P z 12i z 2 i  17y 92y 125  17y 62y  65 .
Khảo sát hàm f y 2 2
 17y 92y 125  17y 62y  65 trên đoạn 1;3.
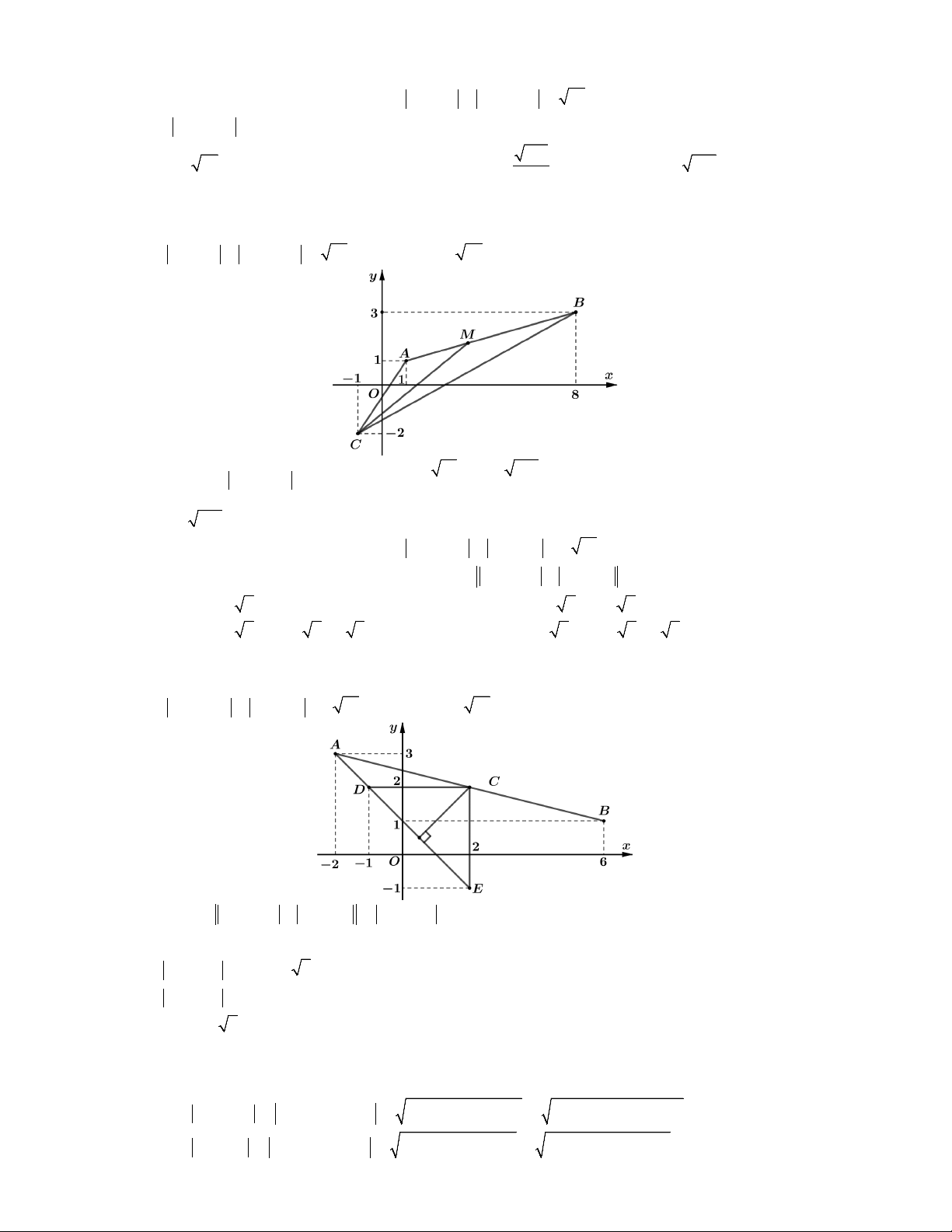
Câu 4. Xét các số phức z thỏa mãn z 32i z 3i  3 5. Gọi M , m lần lượt là giá trị
lớn nhất và giá trị nhỏ nhất của biểu thức P z  2  z 13i .
A. M  17  5, m  3 2.
B. M  26  2 5, m  3 2.
C. M  26  2 5, 2 m  .
D. M  17  5, 2 m  .
Lời giải. Gọi C , A3;2, B3; 
1 lần lượt là điểm biểu diễn các số phức z, 3  2i , 3i
trong mặt phẳng tọa độ.
Từ z 32i z 3i  3 5  CA CB  3 5  AB 
C thuộc đoạn thẳng AB.
Ta có P z  2  z 13i CD CE với D2;0, E 1;  3 .
Nhận thấy D, E nằm về hai phía so với đường thẳng AB.
CD CE DE  3 2. Dấu "  " xảy ra khi D,
C, E theo thứ tự đó thẳng hàng.
CD CE  max BD BE; AD AE  BD BE  26  2 5. Dấu "  " xảy ra khi C B.
Vậy M  26  2 5,
m  3 2. Chọn B.
Cách 2. Phương trình đường thẳng AB : x  2y 1  0.
Gọi M 12y; y AB với y 1;2 (do M nằm trong đoạn AB ).
 z 2  x 2 yi  x 22  y  32y2 2 2  y Ta có  .
 z13i x1y 3i  x 2 1 y  2
3  4 y y  2 2 3  Khi đó 2 2
P z  2  z 13i  5y 12y  9  5y 6y  9 .
Khảo sát hàm f y 2 2
 5y 12y  9  5y 6y  9 trên đoạn  1;  2.
Câu 5. Xét các số phức 5
z , z thỏa z 12i z 33i  2 z 1 i  17. Giá trị lớn 1 2 1 1 2 2
nhất của P z z z  2i bằng 1 2 1 A. 2 17. B. 3 29. C. 17  29. D. 17  2 29.
Lời giải. Đặt z a bi, z c di  ,
a b,c,d  ; Gọi M a;b, N
c;d , A 1;2, B 3;  3 lần 1 2
lượt là điểm biểu diễn các số phức z , z , 1 2i, 33i trong mặt phẳng tọa độ. 1 2
z 12i z 33i  17  MA MB  17  AB 
M thuộc đoạn thẳng AB. 1 1 5 17 AB  
 2 z 1 i  17  NI   với 5 I 1;   
. Ta thấy I là trung điểm của AB. Suy ra 2 2 2 2  2
N thuộc đường tròn C  có tâm I, đường kính AB (như hình bên dưới).
Ta có P z z z  2i MN MD với D2;  1 . 1 2 1
Nhận thấy M nằm trên đoạn thẳng AB và N C 
MN AB  17 và MD  maxAD,BD  BD  29. M B
Suy ra P z z z  2i MN MD  17  29. Dấu "  " xảy ra khi  . 1 2 1 N A  Vậy P
 17  29. Chọn C. max
Câu 6. Xét các số phức z thỏa mãn iz 2i 2  z 13i  34. Giá trị nhỏ nhất của biểu
thức P  1iz 2i bằng A. 9 . B. 3 2. C. 4 2. D. 26. 17
Lời giải. Gọi M x; y, A 2;2, B 1; 
3 lần lượt là điểm biểu diễn các số phức z, 2 2i,
13i trong mặt phẳng tọa độ
Từ iz 2i 2  z 13i  34  z 2  2i z 13i  34  MAMB  34  AB 
M nằm trên tia đối của tia . BA
Ta có P  1iz 2i  2 z 1i  2MC với C 1;  1 . Ta thấy MC
M B   MCCB  4   P  4 2. Chọn C. min min min   
Cách 2. Phương trình đường thẳng x
AB : 5x  3y  4  0. Suy ra 4 5 M x;   với x  1 .  3  2   
Khi đó   iz i z  i
x  2 y  2  x  2 4 5x P 1 2 2 1 2 1 1 2 1  1 .   3  2   
Khảo sát hàm     2 4 5x f x x 1  1  trên  ;    1 .  3 
Câu 7. Xét các số phức z đồng thời thỏa mãn z 4 3i z  4 3i  10 và z 34i nhỏ
nhất. Môđun của số phức z bằng A. 5. B. 5 2. C. 6 2. D. 10.
Lời giải. Gọi M x; y, A 4;  3 , B 4; 
3 lần lượt là điểm biểu diễn các số phức z, 4 3i,
4 3i trong mặt phẳng tọa độ.
Từ z 4 3i z  4 3i  10  z 4 3i z  4 3i  10  MAMB  10  AB 
M nằm trên tia đối của tia . BA
Ta có z 34i MC với C 3;4. Ta thấy MC
CB  5 2. Dấu ''  '' xảy ra  M B 
z  5. Chọn A. min
x  4  4t
Cách 2. Phương trình đường thẳng AB :  
M 4  4m;33m với m  0. y  33t 
Gọi C 3;4, ta có 2
z 3 4i MC  25m 50m  50  50  5 2.
Dấu "  " xảy ra khi và chỉ khi m  0   M 4;  3 .
Câu 8. Xét các số phức z a bi  ,
a b   thỏa mãn z 12i z 3i . Tính P a b khi
T z 3 4i z 1i đạt giá trị lớn nhất. A. P  2. B. P  6. C. 26 P  . D. 28 P  . 3 3
Lời giải. Ta có z   i z i 
a  2 b  2  a  b   2 2 1 2 3 1 2
3  a b  2  0  
tập hợp điểm M biểu diễn số phức z thuộc đường thẳng d : x y  2  0.
Gọi A3;4,B1;  1 . Ta thấy ,
A B nằm về cùng phía so với d.
Khi đó T z 34i z 1i MAMB AB.   Dấu "  " xảy ra 11 17 28
M AB d 
M  ;  
P a b  .  Chọn D.  3 3  3
Câu 9. Xét các số phức z thỏa mãn z  2  z  2i . Giá trị nhỏ nhất của biểu thức a b
P z 12i z 3 4i z 56i được viết dưới dạng 17 với ,a b  .  Tính a  . b 2
A. a b  2.
B. a b  3.
C. a b  4.
D. a b  7.
Lời giải. Đặt z x yi x, y  .
Khi đó z   z i 
x  2  y x y  2 2 2 2 2 2
2  y x 
 tập hợp điểm M biểu
diễn số phức z thuộc đường thẳng d : y x.
Ta có P z 12i z 34i z 56i MA MB MC với A1;2, B 3;4, C  5;6. 2 2 2 Nhận thấy MA MC AC
B là trung điểm của AC nên suy ra MB   . 2 4 Do đó MA MC ACMA MC2 2 2 2 2         AC P MA MC MA MC   . 2 4 4 4
Lấy điểm A2; 
1 đối xứng với A qua d, ta có MA MC2 2 2 2    AC AC AC MA MC    AC   . 4 4 4 4 2 2 AC AC 1 2 17 a  1 Suy ra P A C       
a b  3. Chọn B. 4 4 2 b   2 
Cách 2. Ta có P z 12i z 34i z 56i 2 2 2
 2x 6x 5  2x 14x  25  2x 22x  61. 2 2 2 2 Suy ra P  3 1  11 1  7 1  3 11 1 1  x         x           x           x   x    1    17. 2 2 4 2 4  2 4  2 2  2 2  3 11
x   x   Dấu  2 2 7 "  " xảy ra    x  .  7 2 x   2
Câu 10. Xét các số phức z , z đồng thời thỏa mãn z 12i z 3 2i và z z  5. Giá 1 2 1 2
trị nhỏ nhất của biểu thức z 13i z 13i bằng 1 2 A. 14 5 . B. 3 85 . C. 1105 . D. 1165 . 5 5 5 5
Lời giải. Với z x yi, theo giả thiết có x  2 y  2  x  2 y  2 1 2 3
2  x 2y 2  0. Xét M z , N z ,
P 1 3i theo giả thiết có M , N   : x 2y 2  0 và MN  5. 1   2   
Ta cần tìm giá trị nhỏ nhất của PM PN.
Gọi H là hình chiếu vuông góc của P lên  
PH d P  7 ,  . 5 Ta có         2   2 2 2 2 2 PM PN PH HM PH HN PH PH HM HN   49 1105 2 2
 4PH MN  4.   5  .   5  5 PH HM  Dấu  "  " xảy ra   PH HN
H là trung điểm đoạn thẳng MN. Chọn C.
HM HN MN
Vấn đề 7. Phương pháp lấy đối xứng
Câu 1. Xét các số phức z a bi  ;
a b   thỏa mãn z 53i z 15i . Tính a b khi
biểu thức P z 22i z 37i đạt giá trị nhỏ nhất.
A. a b  1.
B. a b  0.
C. a b  1.
D. a b  2.
Lời giải. Đặt z x yi x, y  .
Từ z   i z   i 
x  2 y  2  x  2 y  2 5 3 1 5 5 3 1
5  x  2y  1   tập hợp
điểm M x; y biểu diễn số phức z là đường thẳng  : x 2y 1.
Khi đó P z 22i z 37i MA MB với A2;2, B 3;  7.
Gọi C là điểm đối xứng của A qua đường thẳng ,
 khi đó ta tìm được C 0;2   phương
trình đường thẳng BC : 3x y  2  0.
Ta có P MA MB MC MB BC. Dấu ''  '' xảy ra khi khi M BC    M 1;  1 a   1   
a b  0. Chọn B. b   1 
Câu 2. Xét các số phức z, z, z thỏa mãn z 4 5i z 1  1 và z  4i z 8  4i . Tính 1 2 1 2
M z z khi P z z z z đạt giá trị nhỏ nhất. 1 2 1 2 A. M  2 5.
B. M  6. C. M  41. D. M  8.
Lời giải.z 4 5i  1 
 tập hợp điểm A biểu diễn số phức z là đường tròn C có 1  1 1 tâm I 4; 
5 , bán kính R  1. 1  z 1  1 
 tập hợp điểm B biểu diễn số phức z là đường tròn C có tâm J 1;0, 2  2 2 bán kính R  1. 2
 Đặt z a bi  , a b  
. Ta có z i z   i  a  b
  2  a  2 b  2 2 4 8 4 4 8 4
a b  4 
 tập hợp điểm C biểu diễn số phức z nằm trên đường thẳng  : x y  4.
Khi đó P z z z z CA CB. 1 2
Gọi K là điểm đối xứng của J qua đường thẳng ,
 khi đó ta tìm được K 4;  3   phương
trình đường thẳng IK : x  4.
A CI C A o giua CI 1   
Do đó P khi và chỉ khi C IK  và  min
B CJ C B o giua CJ 2     
A4;4,B2;0 
M z z AB  2 5. Chọn A. 1 2
Câu 3. Xét các số phức z , z thỏa mãn z 3 2i  1 và z  2i  1. Số phức z có phần 1 2 1 2
thực bằng a , phần ảo bằng b thỏa mãn 2a b  0. Tính P a b khi z z z 2z đạt 1 2 giá trị nhỏ nhất. A. P  1. B. P  3. C. P  4. D. P  7. Lời giải. Ta có
 Số phức z có phần thực bằng a , phần ảo bằng b thỏa mãn 2a b  0 nên tập hợp điểm
A biểu diễn số phức z là đường thẳng d : y  2x.
z  3  2i  1  tập hợp điểm B biểu diễn số phức z là đường tròn có tâm D 3;2, 1 1 bán kính bằng 1.
z  2 i  1  2z  4 2i  2. Đặt z  2z khi đó z  4 2i  2 2 2 3 2 3
 tập hợp điểm C biểu diễn số phức z là đường tròn có tâm E 4;2, bán kính bằng 2. 3
Khi đó T z z z 2z z z z z AB AC. 1 2 1 3
Gọi H là điểm đối xứng của E qua đường thẳng d, khi đó ta tìm được H 4;2   phương
trình đường thẳng DH : y  2. y  2x
Do đó T khi và chỉ khi A DH d 
 tọa độ điểm A là nghiệm của hệ  min y 2  a   1 A 1; 2        
P a b  3. Chọn B. b   2 
Cách 2. Ta có z z z 2z z 3 2i z 3 2i z  4 2i 2 z  2i 1 2    1     2 
z 3  2i z 3  2i z  4 2i 2 z  2i 1 2
z 3  2i z  4 2i 3  a  2
3 b  22  a  42 b 22 3  a  2
3 2a  22  a  42 2a 22 3.
Xét hàm y  a  2  a  2  a  2  a  2 3 2 2 4 2 2 3 trên ,
 ta được min f a  4 . 
Dấu ''  '' xảy ra khi a  1 
b  2. Suy ra P  3.
Câu 4. Xét các số phức z , z thỏa mãn z 53i z 13i và z 4 3i z 2 3i . 1 2 1 1 2 2
Giá trị nhỏ nhất của biểu thức P z z z 6 i z 6i bằng 1 2 1 2 A. 2 10. B. 7 . C. 4 130 . D. 18 . 2 13 13
Lời giải. Goi z a bi, z c di a, b, c, d  . Khi đó ta có 1 2
 z 53i z 13i     a  2 5 b  2 3  a  2 1 b  2 3  1 1 2
a 3b  6       
 z 43i z 23i  
 c 42 d  2
3  c 22 d  2 c  3d  3 2 2 3   
 tập hợp M biểu diễn số phức z nằm trên đướng thẳng d : 2x 3y  6, tập hợp N 1
biểu diễn số phức z nằm trên đướng thẳng  : x 3y  3. 2 Gọi A6;  1 , B 6; 
1 . Khi đó P z z z 6 i z 6 i z z z 6 i z 6 i 1 2 1 2 1 2 1 2
MN MA NB  MN NB MA MB MA BC với C là điểm đối xứng của A qua d.   Ta tìm được 66 31 4 130 C  ;     BC  . Chọn C. 13 13 13
Dấu "  " xảy ra khi M BC d và N B.
Vấn đề 8. Tâm tỉ cự
Câu 1. Xét các số phức z thỏa mãn |z 5i| |  2 3i|. Đặt 2 2
P z  39i z 15i . Biết
P đạt giá trị nhỏ nhất tại z và P đạt giá trị lớn nhất tại z . Giá trị của biểu thức z z 1 2 1 2 bằng A. 2 13. B. 2 15. C. 4 3. D. 52.
Lời giải. Từ z 5i  2 3i z 5i  13 
 tập hợp điểm M biểu diễn số phức z
thuộc trên đường tròn C có tâm C 5; 
1 , bán kính R  13. Ta có 2 2 2 2
P z  39i z 15i MA MB với A3;9, B 1;  5 .    IA  2 2
Trong mặt phẳng Oxy chọn điểm I thỏa IA IB 0 I  1;7         . IB  2 2    2   2
   Có 2 2
MA MB  MI IA MI IB 2
MI MI IAIB 2 2 2 2 2
IA IB  16  2MI . P MI
M M 3;4  min min 1  
z  3  4i Do đó  1     
z z  2 13. Chọn A.
P MI M M 7;2
z  72i max max 2   1 2   2
Câu 2. Xét các số phức z thỏa mãn z 12i  3 2. Gọi ,
m M lần lượt là giá trị nhỏ nhất và
lớn nhất của biểu thức 2 2
P z 3  2i 2 z 2 i . Tổng m M bằng A. 30. B. 12. C. 14. D. 68.
Lời giải. Từ z 12i  3 2 
 tập hợp điểm M biểu diễn số phức z nằm trên đường
tròn C có tâm C 1;2, bán kính R  3 2. Ta có 2 2 2 2
P z 3  2i 2 z 2 i MA 2MB với A3;2, B 2;  1 .    IA  2 10
Trong mặt phẳng Oxy chọn điểm I thỏa IA 2IB 0 I 1;4        . IB  10    2   2    Có 2 2
MA MB  MI IA  MI IB 2
 MI MI IAIB 2 2 2 2 2 2 2
IA 2IB  20  MI . 2  2 P MI
P  20IM  20 CI R  30 m   30 Do đó min max min 2          S  12. 2    2 P MIM  18  max min P
 20  IM  20 CI R  18  max 1  Chọn B.
Câu 3. Xét các số phức z a i  ,
a b   thỏa mãn z 4 3i  5. Tính a b khi biểu thức 2 2 2
Q z  2 2i  2 z  4 i  3 z  2i đạt giá trị lớn nhất.
A. a b  11.
B. a b  12.
C. a b  13.
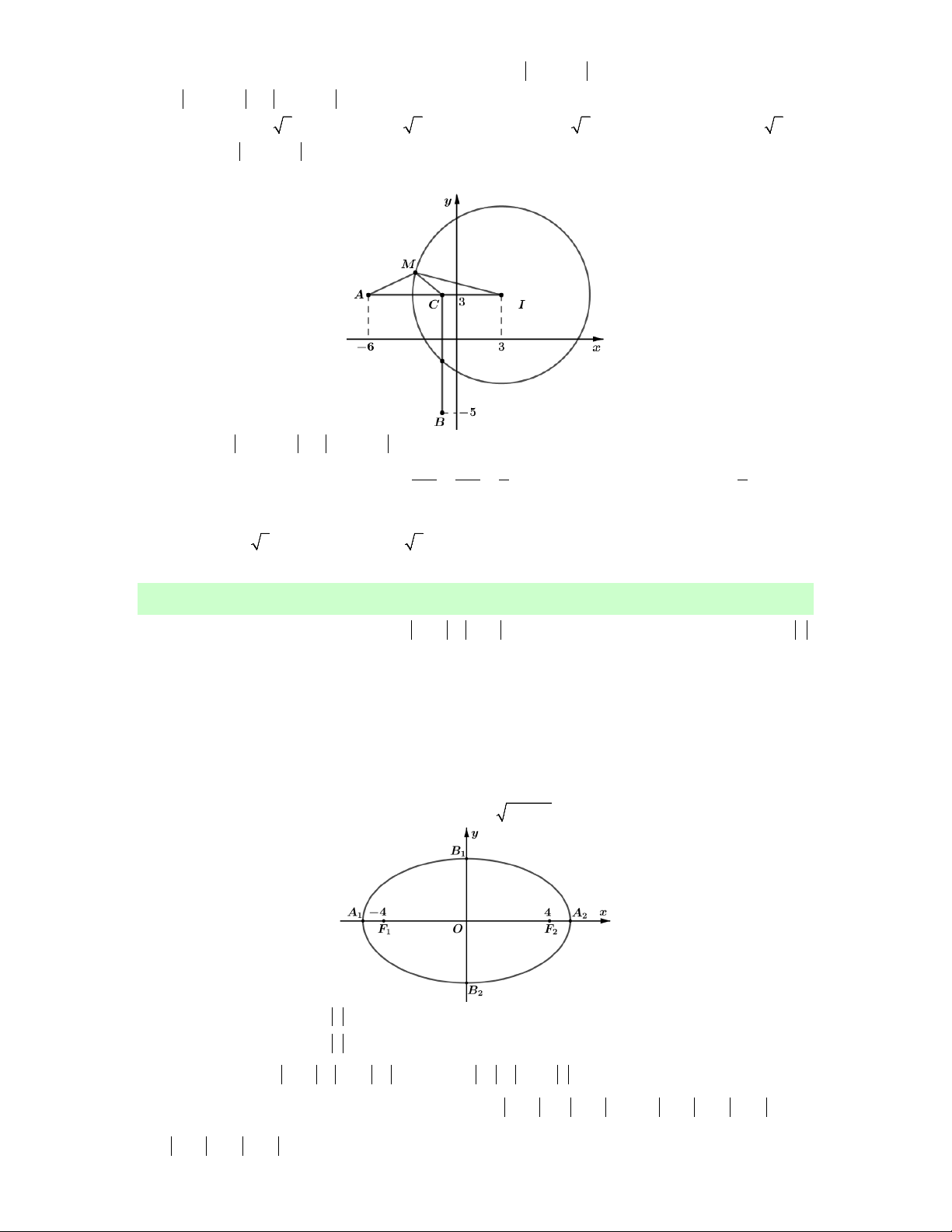
D. a b  14.
Lời giải. Ta có z 4 3i  5 
 tập hợp điểm M biểu diễn số phức z nằm trên đường tròn I 4; 
3 , bán kính r  5. Ta có 2 2 2 2 2 2
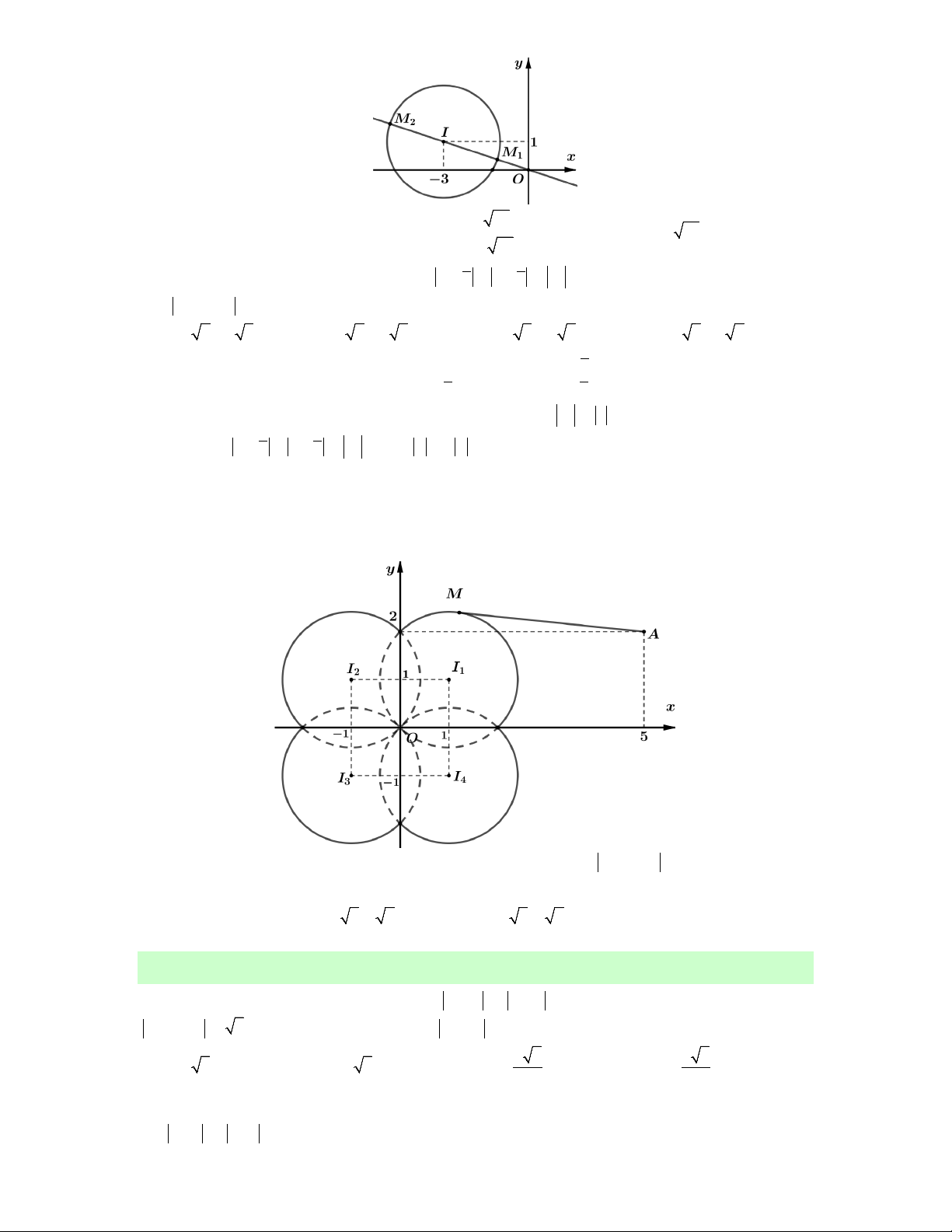
Q z  2  2i  2 z  4  i  3 z  2i MA  2MB  3MC với A2;2, B 4;  1 , C  0;2.    
Trong mặt phẳng Oxy chọn điểm N thỏa mãn NA  2NB 3NC  0   N 1;  1 .   2   2   2 Có 2 2 2
Q MA  2MB  3MC  MN NA 2MN NB 3MN NC     2  6MN  2 2 2
NA  2NB  3NC 2MN NA2.NB 3.NC 2  6MN  2 2 2
NA  2NB  3NC . Suy ra Q khi MN 
M đối xứng với N qua I (vì N thuộc đường tròn tâm I bán max max kính r  5 ) 
M 7;7. Vậy a b  7 7  14. Chọn D.
Câu 4. Xét các số phức z , z thỏa mãn z 34i  2 và z z  1. Giá trị nhỏ nhất của 1 2 1 2 biểu thức 2 2
P z z bằng 1 2 A. 4 3 5. B. 62 5. C. 5. D. 10.
Lời giải. Ta có z 34i  2 
 tập hợp điểm M biểu diễn số phức z nằm trên đường
tròn C có tâm I 3;4, bán kính R  2. Gọi ,
A B  C  lần lượt là điểm biểu diễn của z ,
z . Suy ra z z AB. 1 2 1 2   2   2 Khi đó 2 2 2 2
P z z
OA OB OI IA OI IB 1 2           
 2OI.IAIB 2OI.BA  2OI.AB.cosOI,BA2OI 10.  
Dấu "  " xảy ra khi OI kBA k  0. Chọn D.
Vấn đề 9. Phương pháp cân bằng hệ số
Câu 1. Xét các số phức z thỏa mãn z  1. Giá trị lớn nhất của T z 1  2 z 1 bằng A. 2 5. B. 2 10. C. 3 2. D. 3 5.
Lời giải. Từ z  1 
 tập hợp điểm M biểu diễn số phức z thuộc đường tròn C  có tâm
O 0;0, bán kính R  1. Gọi A 1;  0, B
1;0. Nhận thấy AB là đường kính của C  nên 2 2 2
MA MB AB  4.
Khi đó T MA MB   2 2   2 2 2 1 2
MA MB   5.4  2 5. Chọn A.
Nhận xét. Bài này rơi vào trường hợp đặc biệt là AB là đường kính của đường tròn.
Nếu bài toán hỏi giá trị nhỏ nhất thì ta có đánh giá MA  2MB  .
MA Dấu ''  '' xảy ra khi và
chỉ khi M B. Khi đó minMA 2MB AB.
Câu 2. Xét các số phức z thỏa z 1  2. Giá trị lớn nhất của T z i z 2i bằng A. 4. B. 4 2. C. 8. D. 8 2.
Lời giải. Từ z 1  2 
 tập hợp điểm M biểu diễn số phức z thuộc đường tròn C  có
tâm I 1;0, bán kính R  2. Gọi A0;  1 , B 2; 
1 . Nhận thấy AB là đường kính của C  nên 2 2 2
MA MB AB  8.
Khi đó T MA MB   2 2   2 2 1 1
MA MB   2.8  4. Chọn A.
Câu 3. Xét các số phức z a bi a;b   có môđun bằng 2 và phần ảo dương. Tính giá trị
biểu thức S   a b 2018 5  2  
khi biểu thức P  2  z 3 2 z đạt giá trị lớn nhất. A. S  0. B. S  1. C. 2018 S  2 . D. 1009 S  2 .
Lời giải. Gọi M a;b với b  0 là điểm biểu diễn số phức z.
Gọi A2;0, B 2;0. Ta có 2 2 z  2 
a bi  2  a b  4. Suy ra M thuộc đường tròn
C đường kính AB nên 2 2 2
MA MB AB  16.
Khi đó P   z
z MA MB   2 2   2 2 2 3 2 3 1 3
MA MB   4 10.
M C 2018        Dấu  b 8 6 8 6 "  " xảy ra khi 0    M   ;   S  5   Chọn A.       2  0. MBMA   5 5   5 5     3
Câu 4. Xét các số phức z z thỏa mãn 1 1 
. Gọi M , m lần lượt là giá trị lớn nhất và z  3i 2
nhỏ nhất của P z i  2 z 4 7i . Giá trị M m bằng A. 10  2 5. B. 10  4 5. C. 20  2 5. D. 20  4 5.
Lời giải. Gọi z a bi x; y   
z a bi và M a;b là điểm biểu diễn số phức z. Ta có z 1 1 2 z 1 z 3i 2 a 2 1 b          
a b    2 2 2 3 z  3i 2  
 a  2 b  2 2
3  20. Suy ra M thuộc đường tròn C  có tâm I 2; 
3 , bán kính R  2 5.
Vì z 4 7i z 4 7i 
P z i  2 z 4 7i MA  2MB với A0;  1 , B 4;7.
Nhận thấy AB là đường kính của đường tròn C nên 2 2 2
MA MB AB  80.
MA  2MB  .
MA Dấu "  " xảy ra khi M B. Khi đó m  minMA  2MB  AB  4 5.
MA MB   2 2   2 2 2 1 2
MA MB   5.80  20.
Vậy M m  20  4 5. Chọn D.
Câu 5. Xét số phức z thỏa mãn z 12i  2 2. Với ,
a b là số thực dương cho trước, giá trị
lớn nhất của biểu thức P a z 1 b z 3 4i bằng A. 2 2
a b . B. 2 2 2a  2b . C. 2 2
4 2a  2b . D. 2 2
a b .
Lời giải. Từ z 12i  2 2 
 tập hợp điểm M biểu diễn số phức z thuộc đường tròn
C có tâm I 1;2, bán kính R  2 2.
Vì z 3 4i z 34i 
P a z 1 b z 34i  . a MA  .
b MB với A1;0, B 3;4.
Nhận thấy AB là đường kính của đường tròn C nên 2 2 2
MA MB AB  32.
Ta có P a MA b MB   2 2 a b  2 2
MA MB    2 2 a b  2 2 . .
32  4 2a  2b . Dấu a ''  '' xảy ra MA MB   MA a     tan MBA  . Vì , a
b  0 nên phương trình a b MB b b a
tan x  luôn có nghiệm. Tức là, luôn có điểm M thuộc đường tròn để đẳng thức xảy ra. b
Vậy giá trị lớn nhất của P là 2 2
4 2a  2b . Chọn C.
Câu 6. Xét các số phức z a bi  ,
a b   thỏa mãn z 4 3i  5. Tính a b khi biểu
thức P z 13i z 1i đạt giá trị lớn nhất.
A. a b  4.
B. a b  6.
C. a b  8.
D. a b  10.
Lời giải. Từ z 4 3i  5 
 tập hợp điểm M biểu diễn số phức z thuộc đường tròn tâm I 4; 
3 , bán kính R  5. Gọi A1;  3 , B 1;  1 và N 0; 
1 là trung điểm của AB.
Khi đó P z   i z  i MA MB   2 2 1 3 1
2 MA MB . 2 Mà 2 2 2   2 AB MA MB MN  . Do đó để PMN 
M , I, N theo thứ tự đó thẳng 2 max max
hàng, suy ra M 6;4 
a b 10. Chọn D. Nhận xét.  P   N, M ,
I theo thứ tự đó thẳng hàng, suy ra M 2;2. min
 Bài toán rơi vào trường hợp đặc biệt là đường trung trực của đoạn AB đi qua tâm của
đường tròn, nếu không rơi vào trường hợp đặc biệt thì trở thành bài toán vô cùng khó.
Câu 7. Xét các số phức z a bi  ,
a b   thỏa mãn z 4 3i  2 2. Tính 2a b khi biểu
thức P z 1 2i z 96i đạt giá trị lớn nhất.
A. 2a b  7.
B. 2a b  9.
C. 2a b  12.
D. 2a b  13.
Lời giải. Từ z 4 3i  2 2 
 tập hợp điểm M biểu diễn số phức z thuộc đường tròn
C có tâm I 4; 
3 , bán kính R  2 2.
Gọi A1;2, B
9;6 và N 5;2 là trung điểm của AB.
Khi đó P z   i z   i MA MB   2 2 1 2 9 6
2 MA MB . 2 Mà 2 2 2 AB
MA MB  2MN  . Do đó để PMN 
M , I, N theo thứ tự đó thẳng 2 max max
hàng, suy ra M 2;  5 
2a b  9. Chọn B.
Câu 8. Xét các số phức z thỏa mãn z 22i  1. Giá trị lớn nhất của biểu thức
P z 32i  2z 2  4i bằng A. 5. B. 2 5. C. 3 15. D. 10.
Lời giải. Từ z 22i  1 
 tập hợp điểm M biểu diễn số phức z thuộc đường tròn C
có tâm I 2;2, bán kính R 1.
Ta có P z 32i  2 z 1 2i z 32i  2 z 12i .
Gọi A3;2, B
1;2 . Nhận thấy I là trung điểm của AB.
Khi đó P z   i z   i MA MB   2 2   2 2 3 2 2 1 2 2 1 2 MA MB  2     2 2 MA MB  2 AB 5  52MI     5.4  2 5.   2  Dấu MA MB "  " xảy ra   MB  2 . MA Chọn B. 1 2
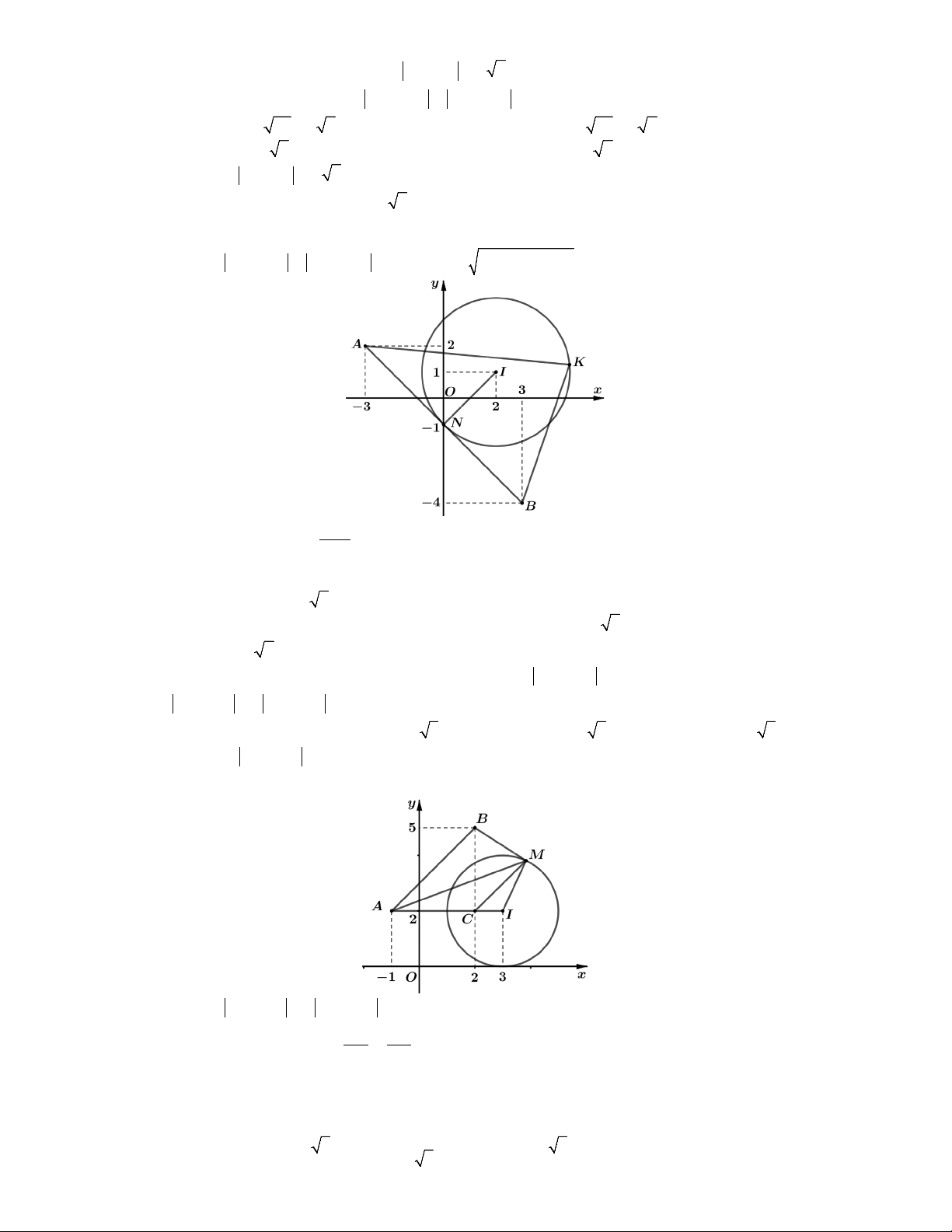
Câu 9. Xét các số phức z thoả mãn z 2i  2 2. Gọi M , m lần lượt là giá trị lớn nhất, giá
trị nhỏ nhất của biểu thức P z 32i z 3 4i . Tính M  . m
A. M m  2 26  6 2.
B. M m  2 26 8 2.
C. M m  11 2.
D. M m  16 2.
Lời giải. Từ z 2i  2 2 
 tập hợp các điểm K biểu diễn số phức z thuộc đường tròn
C có tâm I 2; 
1 , bán kính R  2 2.
Gọi A3;2, B
3; 4 và N 0; 
1 là trung điểm của AB. Nhận thấy N  C .
Khi đó P z   i z   i KA KB   2 2 3 2 3 4
2 KA KB . 2 Mà 2 2 2 AB
KA KB  2KN  . Do đó để 2  PKN
. Dấu "  " xảy ra khi K đối xứng N qua I nên K 4;  3 max max 
M KA KB  10 2 .  PKN
K N 
m KA KB AN NB AB  6 2. min min
Vậy M m  16 2. Chọn D.
Câu 10. Xét các số phức z a bi  ,
a b   thỏa mãn z 32i  2. Tính a b khi biểu thức
T z 12i  2 z 2 5i đạt giá trị nhỏ nhất.
A. a b  3.
B. a b  2  3.
C. a b  4  3.
D. a b  4  3.
Lời giải. Từ z 32i  2 
 tập hợp điểm M biểu diễn số phức z thuộc đường tròn tâm
I 3;2, bán kính R  2.
Khi đó T z 12i  2 z 25i MA  2MB với A1;2, B 2;  5 . IC IM   
Gọi điểm C 2;2 . IA Ta có IM IA    MIC ∽ AIM    MA  2CM.   MIC AIM   
Suy ra T  2MB MC 2BC. Dấu "  " xảy ra khi M, B, C theo thứ tự thẳng hàng. Khi a  
đó ta tìm được M   2 2;2 3     
a b  4  3. Chọn D. b   2 3  Nhận xét.  
 Kỹ thuật chọn điểm C : Chọn điểm C thỏa mãn hệ thức MA  2MC với vị trí của M như hình vẽ bên dưới.
 Mục đích chọn điểm C như thế để tạo ra T  2MC  2MB gọi là phương pháp cân bằng hệ
số. Dĩ nhiên không phải bài nào cũng cân bằng được, hệ số được cho trong dữ kiện đề bài phải
được tác giả xử lý ngon lành trước rồi.
Câu 11. Xét các số phức z a bi  ,
a b   thỏa mãn z  2. Tính a b khi biểu thức
P z  4  2 z 1 4i đạt giá trị nhỏ nhất.
A. a b  2.
B. a b  2.
C. a b  2 5.
D. a b  4 5.
Lời giải. Từ z  2 
 tập hợp điểm M biểu diễn số phức z thuộc đường tròn tâm O 0;0, bán kính R  2.
Khi đó P z 4  2 z 1 4i MA  2MB với A4;0, B 1;4.
Gọi điểm H 1;0O .
A Chứng minh được MA  2MH.
Suy ra P  2MH MB 2BH. Dấu "  " xảy ra khi H, M ,
B theo thứ tự thẳng hàng. Khi a   0
đó ta tìm được M 0; 2     
a b  2. Chọn A. b   2 
Câu 12. Xét các số phức z thỏa mãn điều kiện z i  1. Giá trị nhỏ nhất của biểu thức
P z  2 i  2 z  2  3i bằng A. 4 3 . B. 2. C. 3. D. 3. 3
Lời giải. Từ z i  1 
 tập hợp điểm M biểu diễn số phức z thuộc đường tròn tâm I 0; 
1 , bán kính R  1.
Khi đó P z  2 i  2 z  2 3i z  2 i  2 z  2 3i MA  2MB với A 2;  1 , B 2;  3 .   Gọi điểm 2 C  ;1    .
IA Chứng minh được MA  2MC.  2 
Suy ra P  2 MC MB 2BC. Dấu "  " xảy ra khi B, M ,
C theo thứ tự đó thẳng hàng.
Vậy P  2BC  3. Chọn D. min
Câu 13. Xét các số phức z thỏa mãn điều kiện z 1i  5. Giá trị lớn nhất của biểu thức
P  2 z 8i z 7 9i bằng A. 5 . B. 5 3 . C. 5 5 . D. 5 5. 2 2 2
Lời giải. Từ z 1i  5 
 tập hợp điểm M biểu diễn số phức z thuộc đường tròn tâm I 1; 
1 , bán kính R  5.
Khi đó P  2 z 8i z 79i  2MAMB với A0;8, B 7;9.   Gọi điểm 5
C  ;3 IB. 
Chứng minh được MB  2MC. 2 
Suy ra P  2MAMC 2AC. Dấu "  " xảy ra khi ,
A C, M theo thứ tự đó thẳng hàng. Vậy P
 2AC  5 5. Chọn D. max
Câu 14. Xét các số phức z thỏa z  1. Giá trị lớn nhất của biểu thức T z  2  2 z 2 bằng A. 2. B. 2 5. C. 5. D. 5 2.
Lời giải. Từ z  1 
 tập hợp điểm M biểu diễn số phức z thuộc đường tròn tâm O 0;0, bán kính R  1.
Gọi A2;0, B
2;0. Khi đó ta có T z  2  2 z 2  MA  2MB 2     2 2   2 2 MA MB  2 AB 1 2  52MO     5 2.   2 
M C  T
 5 2. Dấu bằng xảy ra khi  . Chọn D. max MB  2MA
Cách 2. Đặt z a bi  , a b  . Từ 2 2
z  1  a b  1.
Ta có T z   z   a  2 b  a  2 2 2 2 2 2 2 2 2  b  a  2 ba 2 2 2 2 2 b              2 2 1 2 2 2
10 a b  4  5 2.  3 2 2   2 2    1 a a b    a  b 1  Dấu    4 "  " xảy ra khi       . 2
 a 22 b  a22 2 2 b 2  4a 5 5 4a        7 b     4
Câu 15. Xét các số phức z thỏa mãn 2z 13i  2. Giá trị lớn nhất của biểu thức
P z 1  3 z 12i bằng A. 2 2. B. 4. C. 4 2. D. 4 3. Lời giải. Từ 1 3 2
2z 13i  2  z   i  
 tập hợp điểm M biểu diễn số phức z 2 2 2  
thuộc đường tròn C có tâm 1 3 I   ; ,  bán kính 2 R  .  2 2 2   
Gọi A1;0, B 1;
 2. Nhận thấy B C  và IA 3IB  0.
Khi đó P z   z   i MA MB MA MB     2 2 1 3 1 2 3 1. 3. 3
1 3 MA  3MB .   2   2 Ta có 2 2
MA  3MB  MI IA 3MI IB    2 2 2
MI IA IB MI IAIB 2 2 2 4 3 2 3
 4MI IA 3IB  8. Vậy MA 3MB P  1 
3 .8  4 2. Dấu ''  '' xảy ra  
MA MB 
M N 0;  1 . 1 3 Chọn C.
Câu 16. Cho số phức z a bi  ,
a b   thỏa mãn z 33i  6. Tính a b khi biểu thức
P  2 z  6 3i  3 z 1 5i đạt giá trị nhỏ nhất.
A. a b  22 5. B. a b  2 5 2.
C. a b  2 5 4.
D. a b  4 2 5.
Lời giải. Từ z 33i  6 
tập hợp điểm M biểu diễn số phức z thuộc đường tròn tâm I 3; 
3 , bán kính R  6.
Khi đó P  2 z  63i 3 z 15i  2MA 3MB với A6;  3 , B 1;    5 . Xét điểm IC IM C 1; 
3 , ta thấy C IA và 2 3     IMC ∽ IAM    MA MC. IM IA 3 2
Suy ra P  3MC MB 3BC   P  3BC khi B, M ,
C theo thứ tự đó thẳng hàng min 
M 1;3 5. Vậy a b  22 5. Chọn A. Vấn đề 10. Elip
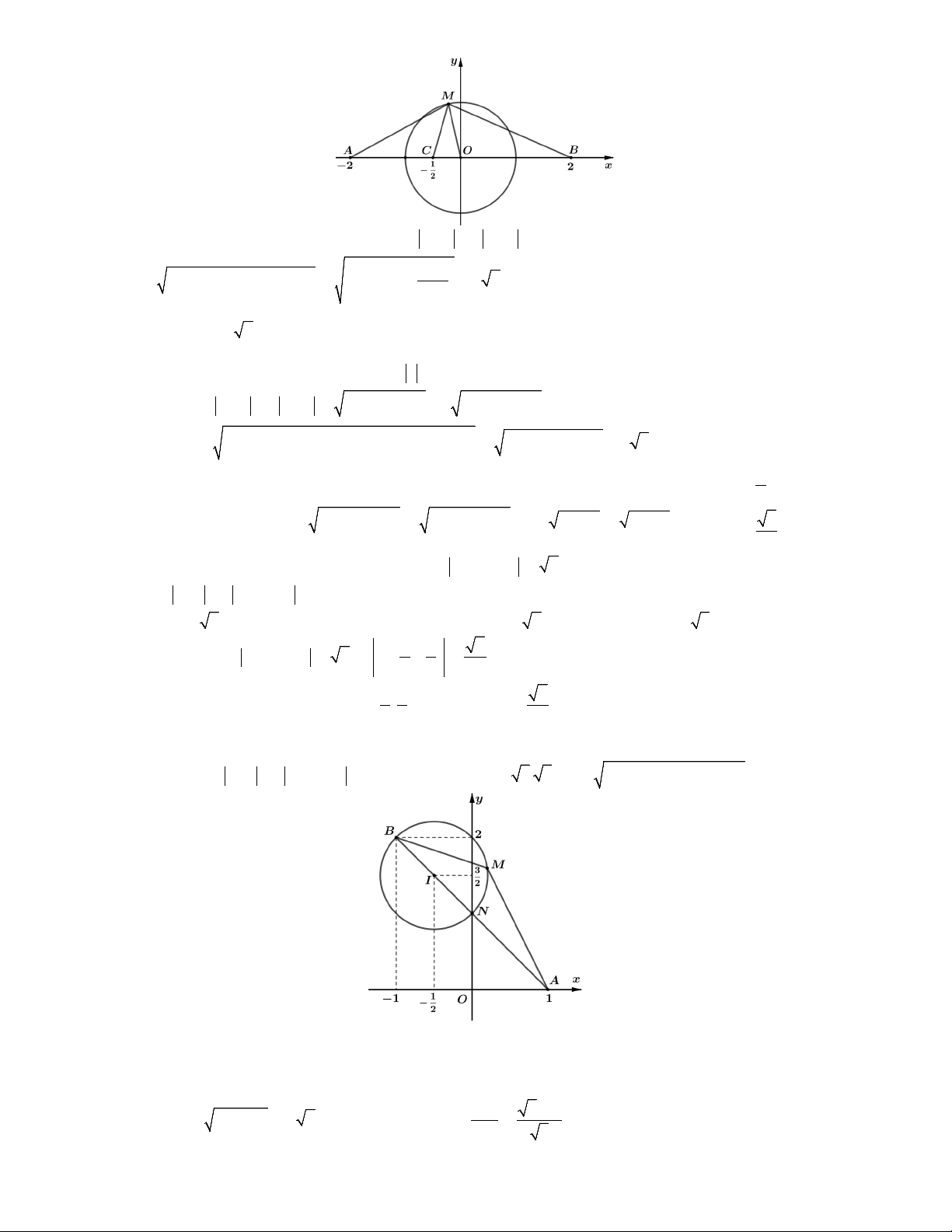
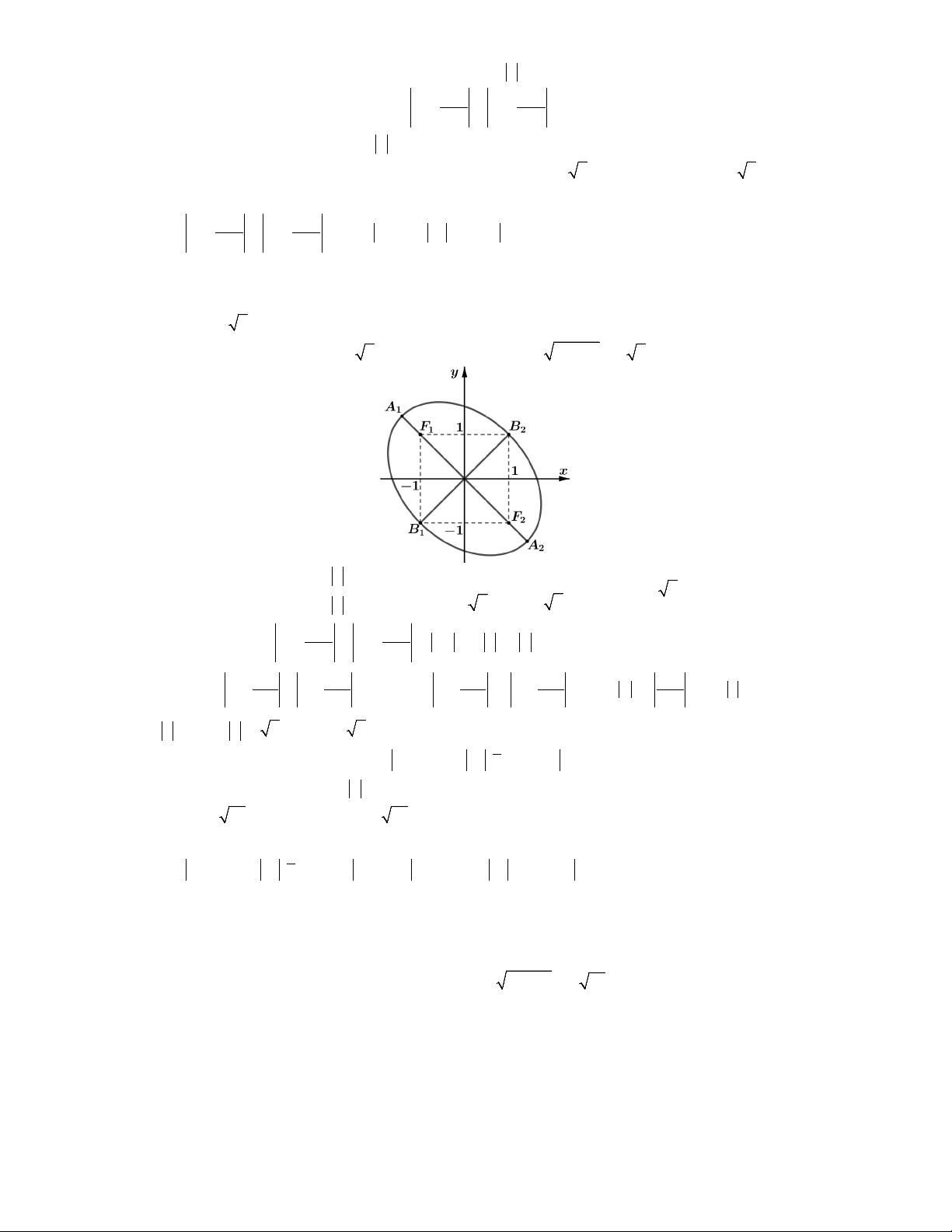
Câu 1. Xét các số phức z thỏa mãn z  4  z 4  10 . Giá trị lớn nhất và nhỏ nhất của z lần lượt là A. 10 và 4. B. 5 và 4. C. 4 và 3. D. 5 và 3.
Lời giải. Đặt z x yix; y  . Gọi M x; y là điểm biểu diễn của số phức z.
Trong mặt phẳng với hệ tọa độ Oxy , gọi F 4;0 và F 4;0 thì giả thiết bài toán đã cho có 2   1  
dạng MF MF  10. 1 2
Mà F F  8 10 
 quỹ tích điểm M là đường Elip có hai tiêu điểm là F , F ; độ dài trục 1 2 1 2
lớn 2a  10, tiêu cự 2c  8, độ dài trục nhỏ 2 2
2b  2 a c  6 (tham khảo hình vẽ).  z
OA OA  5
Dựa vào hình vẽ, ta thấy  max 1 2  . Chọn D.
 z OB OB  3  min 1 2
Cách 2. Ta có 10  z 4  z  4  z 4  z  4  2z   z  5 .
Áp dụng bất đẳng thức Bunhiacopxki, ta có  z z 2  z  2  z 2 100 4 .1 4 .1 4 4          .2     z  2  z 2 4 4       50   
 a  2 b a  2 2 2 2 2 4
4  b  50  a b  9   z  3.
Câu 2. Xét các số phức z thỏa mãn 2 2 iz   iz
 4. Gọi M và n lần lượt là giá trị 1i i 1
lớn nhất và giá trị nhỏ nhất của z . Tính M. . n
A. M.n  1.
B. M.n  2.
C. M.n  2 2.
D. M.n  2 3.
Lời giải. Đặt z x yix; y  . Gọi M x; y là điểm biểu diễn của số phức z. Ta có 2 2 iz   iz
 4  z 1i z 1i  4.   1 1i i 1
Gọi F 1;1 là điểm biểu diễn số phức 1i; F 1;1 là điểm biểu diễn số phức 1i. 2   1   Phương trình  
1 được viết lại: MF MF  4. 1 2
Mà F F  2 2  4 
 quỹ tích điểm M là đường Elip có hai tiêu điểm là F , F ; độ dài 1 2 1 2
trục lớn 2a  4, tiêu cự 2c  2 2, độ dài trục nhỏ 2 2
2b  2 a c  2 2 (tham khảo hình vẽ).  z
OA OA  2   M  2
Dựa vào hình vẽ, ta thấy max 1 2      
M.n  2 2. Chọn C.
 z OB OB  2 n   2  min 1 2  Cách 2. Ta có 2 2 4  iz   iz
 2iz  2 z z  2   M  2. 1i i 1 2 2 2 2       Lại có 2 2         iz   iz         2 2 2 2 4 1 1  iz   iz      2.2 iz            4        2 2 2 2 z  2 1 i i 1 1 i 1 i   1   i  2
z  2  z  2  n  2.
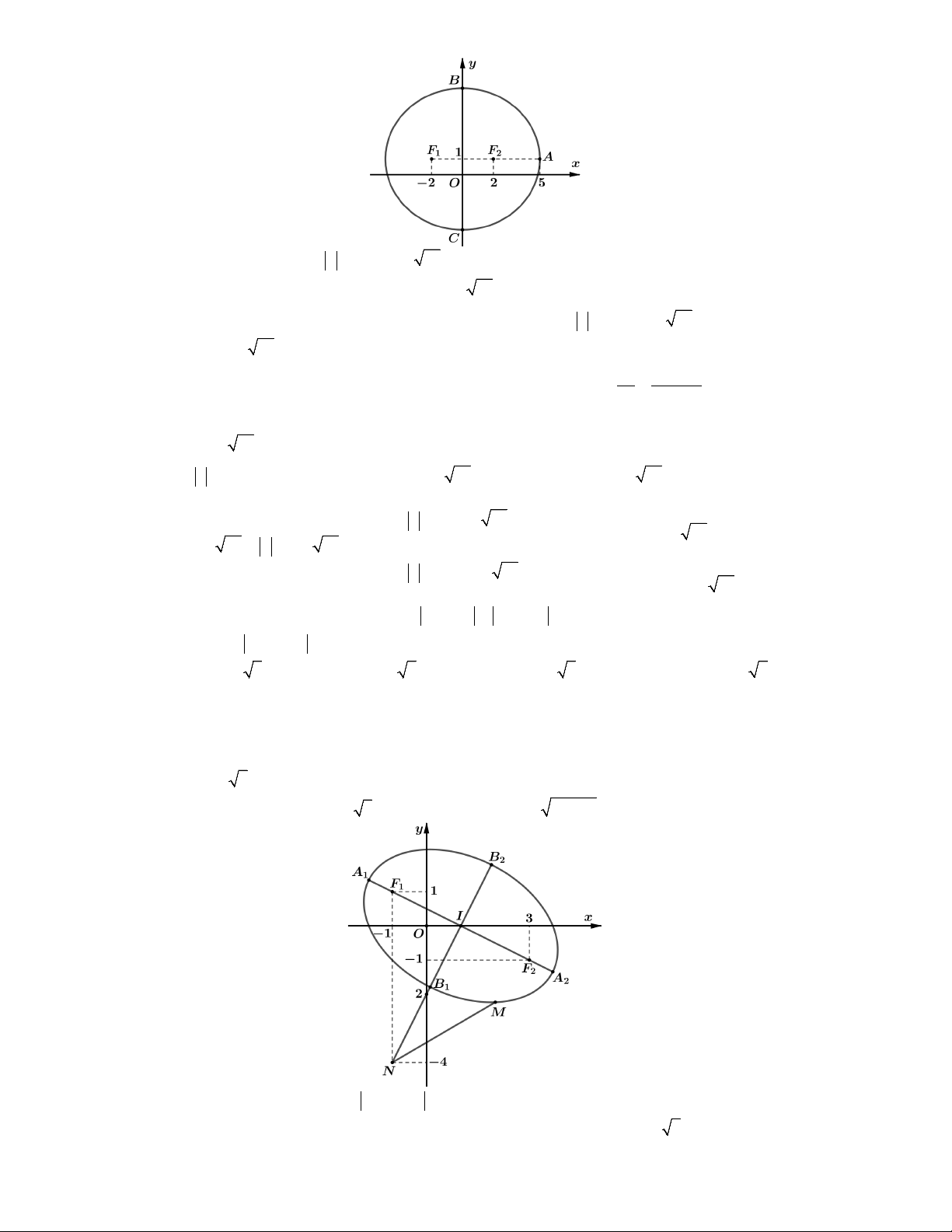
Câu 3. Xét số phức z thỏa mãn z 2i 1  z 2i 1 10. Gọi M và m là giá trị lớn
nhất và giá trị nhỏ nhất của z . Tính tổng S M  . m
A. S  17.
B. S  2 21.
C. S  8. D. S  9.
Lời giải. Đặt z x yix; y  . Gọi M x; y là điểm biểu diễn của số phức z.
Ta có z 2i 1  z 2i 1 10  z 2 i  z 2 i 10.   1
Gọi F 2;1 là điểm biểu diễn số phức 2 i; F 2;1 là điểm biểu diễn số phức 2 i. 2   1   Phương trình  
1 được viết lại: MF MF  10. 1 2
Mà F F  4 10 
 quỹ tích điểm M là đường Elip có hai tiêu điểm là F , F ; độ dài trục 1 2 1 2
lớn 2a  10, tiêu cự 2c  4, độ dài trục nhỏ 2 2
2b  2 a c  2 21 (tham khảo hình vẽ).
Dựa vào hình vẽ, ta thấy zOC  21 1. min Ta có A5; 
1 là điểm nằm trên trục lớn ; B0; 21  
1 là điểm nằm trên trục nhỏ. Vì OB OA
suy ra B là điểm nằm trên Elip cách xa gốc O nhất. Suy ra zOB  21 1. max
Vậy M m  2 21. Chọn B. xy  2 2 1
Cách 2. Tập hợp điểm M biểu diễn số phức z nằm trên elip E:   1. 25 21 a   5sin t Đặt 
với t 0;2. b  1 21cost
Khi đó z OM a b t   t2 2 2 2 2 2 2 25sin 1 21 cos
 26 4 cos t  2 21 cos t a   0  z
 1 21 khi cos t  1     max  b  1 21 
1 21  z 1 21. Suy ra   .  a   0  z
 1 21 khi cos t  1    min  b     1 21 
Câu 4. Xét các số phức z thoả mãn z 1i z 3i  6. Tìm giá trị nhỏ nhất P của min
biểu thức P z 1 4i .
A. P  2 5 2.
B. P  2 5  2.
C. P  5 2.
D. P  5 2. min min min min
Lời giải. Đặt z x yix; y  . Gọi M x; y là điểm biểu diễn của số phức z.
Trong mặt phẳng với hệ tọa độ Oxy , gọi F 1;1 và F 3;1 thì giả thiết bài toán đã cho có 2   1  
dạng MF MF  6. 1 2
Mà F F  2 5  6 
 quỹ tích điểm M là đường Elip có hai tiêu điểm là F , F ; độ dài 1 2 1 2
trục lớn 2a  6, tiêu cự 2c  2 5, độ dài trục nhỏ 2 2
2b  2 a c  4 (tham khảo hình vẽ).
Dựa vào hình vẽ, ta thấy P z 1 4i nhỏ nhất  MN nhỏ nhất (với N 1;4 là điểm
biểu diễn số phức 14i )  M B . Khi đó MN
B N IN IB  2 5 2. Chọn A. 1 min 1 1
Nhận xét. Bài này đặc biệt ở chỗ điểm N thuộc đường thẳng B B . 1 2
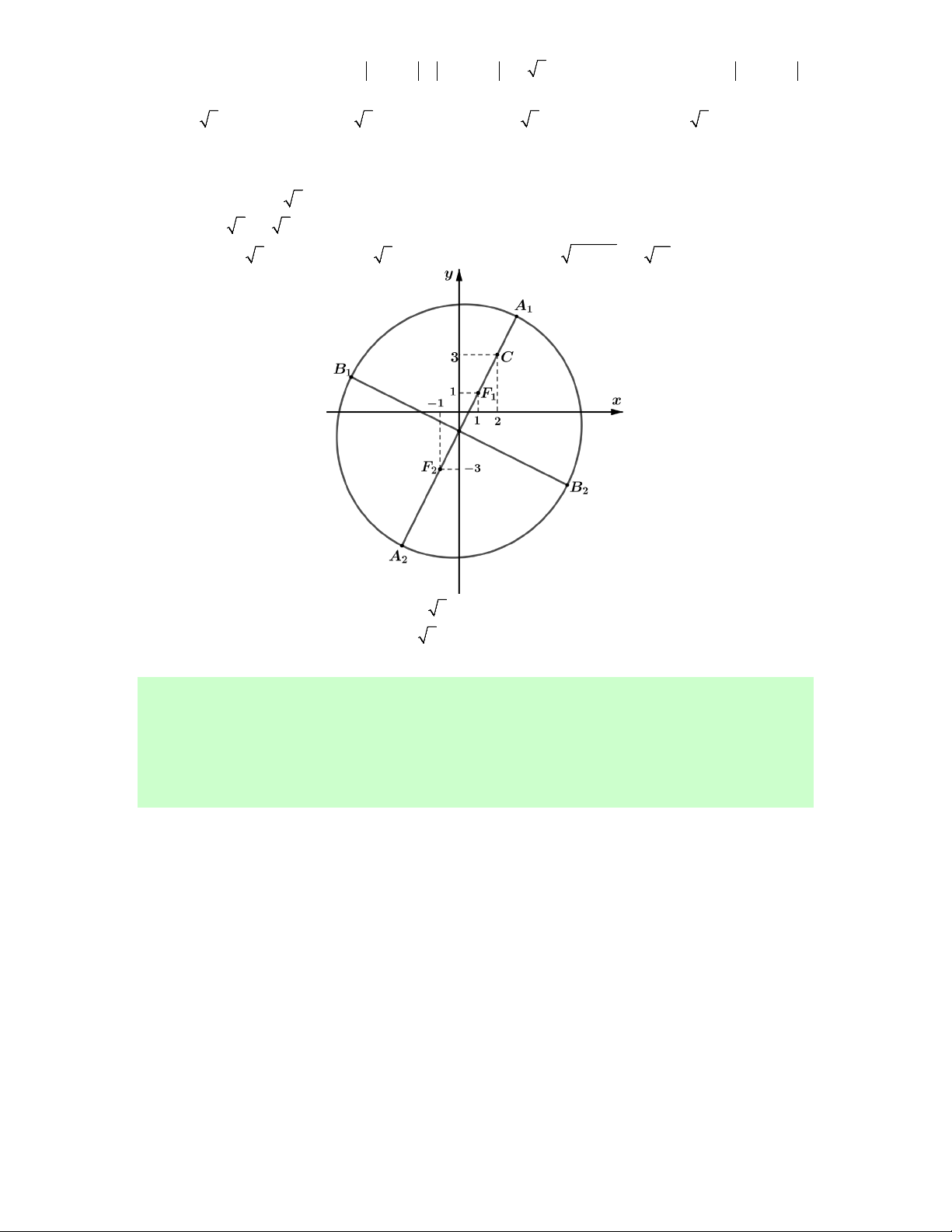
Câu 5. Xét các số phức z thỏa z 1i z 13i  6 5. Giá trị lớn nhất của P z 23i bằng A. 2 5. B. 4 5. C. 5 5. D. 6 5.
Lời giải. Đặt z x yix; y  . Gọi M x; y là điểm biểu diễn của số phức z.
Trong mặt phẳng với hệ tọa độ Oxy , gọi F 1;1 và F 1;3 thì giả thiết bài toán đã cho có 2   1  
dạng MF MF  6 5. 1 2
Mà F F  2 5  6 5 
 quỹ tích điểm M là đường Elip có hai tiêu điểm là F , F ; độ dài 1 2 1 2
trục lớn 2a  6 5, tiêu cự 2c  2 5, độ dài trục nhỏ 2 2
2b  2 a c  4 10 (hình vẽ).
P CA  5 5
Dựa vào hình vẽ, ta thấy  max 2  với C 2;  3 . Chọn C.
P CA  5  min 1
Nhận xét. Bài này đặc biệt ở chỗ điểm C thuộc đường thẳng A A . 1 2
Những bài Elip trên thuộc dạng Elip không chính tắc (Elip xiên), nó không nằm trong chương
trình SGK hiện hành nên bạn đọc chỉ tham khảo thêm, tuy nhiên cũng có cách đặt ẩn phụ
(tịnh tiến + quay) để đưa về Elip cơ bản như chương trình SGK hiện hành nhưng công thức
cồng kềnh và khó nhớ. Vì thế ở đây ta chỉ khai thác những bài đặc biệt là tìm GTLN-GTNN
của khoảng cách từ một điểm thuộc Elip đến một điểm cố định mà điểm cố định này phải
thuộc các đường thẳng chứa các trục của Elip.
---------- HẾT ----------
Document Outline

  • DE
  • DAPAN