






















































Preview text:
BÀI TẬP TRẮC NGHIỆM ĐẠO HÀM
KHÁI NIỆM ĐẠO HÀM A. LÝ THUYẾT
1. Định nghĩa đạo hàm tại một điểm.
Cho hàm số y = f (x) xác định trên ( ; a b) và x Î ; a b 0
( ). Nếu tồn tại giới hạn (hữu hạn)
f ( x) - f (x0 ) lim
thì giới hạn đó được gọi là đạo hàm của hàm số y = f (x) tại điểm x . 0 x® 0 x x - x0 f x - f x
Kí hiệu: f ¢(x y¢(x f ¢( x = lim 0 ) ( ) ( 0) 0 ) 0 ) hoặc . Vậy . x® 0 x x - x0 STUDY TIP y D Nếu x
D = x - x và y
D = f (x)- f (x = f x + x D - f x f ¢(x = lim 0 ) 0 ) ( 0 ) ( 0) thì . 0 x D ®0 x D ü x
D gọi là số gia của đối số tại điểm x . 0 ü
Dy gọi là số gia của hàm số tương ứng.
2. Đạo hàm bên trái, bên phải.
a) Đạo hàm bên trái. ¢( f x - f x - y D f x = lim = lim x x- ® x ® x x < x 0 ) ( ) ( 0) trong đó được hiểu là và . 0 0 x - - ® - D ® D 0 0 x x 0 x x x 0
b) Đạo hàm bên phải. ¢( f x - f x + y D f x = lim = lim x x+ ® x ® x x > x 0 ) ( ) ( 0) trong đó được hiểu là và . 0 0 x + + ® - D ® D 0 0 x x 0 x x x 0
Nhận xét: Hàm số f (x) có đạo hàm tại điểm x Û f (x+ ¢ f (x- ¢ 0 ) 0 ) và
tồn tại và bằng nhau. Khi đó 0
f (x+ = f x- ¢ ¢ = f ¢ x 0 ) ( 0 ) ( 0).
3. Đạo hàm trên khoảng, trên đoạn.
a) Hàm số y = f (x) được gọi là có đạo hàm trên khoảng ( ;
a b) nếu có đạo hàm tại mọi điểm trên khoảng đó.
b) Hàm số y = f (x) được gọi là có đạo hàm trên đoạn [ ;
a b] nếu có đạo hàm trên khoảng ( ; a b) và có
đạo hàm phải tại a và đạo hàm trái tại b .
4. Quan hệ giữa sự tồn tại của đạo hàm và tính liện tục của hàm số.
- Nếu hàm số y = f (x) có đạo hàm tại điểm x thì nó liên tục tại điểm đó. 0 STUDY TIP ü
Hàm số liên tục tại điểm x có thể không có đạo hàm tại điểm đó. 0 Trang 1 ü
Hàm số không liên tục tại x thì không có đạo hàm tại điểm đó. 0
B. CÁC DẠNG TOÁN TÍNH ĐẠO HÀM BẰNG ĐỊNH NGHĨA Phương pháp:
1. Tính đạo hàm của hàm số y = f (x) tại điểm x bằng định nghĩa. 0 Cách 1:
f ( x) - f (x0 ) - Tính lim (1). x® 0 x x - x0 -
Nếu tồn tại giới hạn (1) thì hàm số có đạo hàm tại x và ngược lại thì hàm số không có đạo 0 hàm tại x . 0
Cách 2: Tính theo số gia. -
Cho x một số gia x D : x
D = x - x Þ y D = f x + x D - f x 0 ( 0 ) ( 0). 0 y D - Lập tỉ số . x D y D - Tính giới hạn lim . x D ®0 x D
2. Mối quan hệ giữa tính liên tục vào đạo hàm. -
Hàm số y = f (x) liên tục tại điểm x Û lim f (x) = f ( x Û lim = 0 0 ) . 0 x® D ® 0 x x 0 -
Hàm số y = f (x) có đạo hàm tại điểm x Þ y = f (x) liên tục tại điểm x . 0 0 -
Hàm số y = f (x) liên tục tại điểm x chưa chắc có đạo hàm tại điểm x . 0 0
Ví dụ 1. Cho hàm số f ( x) = x +1. Tính đạo hàm của hàm số tại điểm x = . 1 0 2 2 2 A. . B. . C. 2 2 . D. . 4 2 3 Lời giải Đáp án A.
f ( x) - f ( ) 1 x +1 - 2 Cách 1: Xét lim = lim x 1 ® x 1 x -1 ® x -1 x -1 = 1 1 2 lim = lim = = . x 1 ® (x - ) 1 ( x +1+ 2) x 1 ® x +1 + 2 2 2 4 Cách 2: y D = f ( x D + ) 1 - f ( ) 1 = x D + 2 - 2 . y D x D + 2 - 2 = . x D x D y D x D + 2 - 2 x D 1 2 lim = lim = lim = lim = . x D ®0 x D ®0 x D ®0 x D x D x D ( 2+ x
D + 2) xD®0 2+ x D + 2 4 STUDY TIP Trang 2 - 2 a - b Nhân lượng liên hợp: a b a - b = và a - b = . a + b a + b
Giải theo cách 1 tỏ ra đơn giản và nhanh hơn cách 2.
Ví dụ 2. Khi tính đạo hàm của hàm số f (x) 2
= x + 5x -3 tại điểm x = 2, một học sinh đã tính theo các 0 bước sau:
Bước 1: f (x) - f (2) = f (x) -1 . 1
f (x) - f ( ) 2 2
x + 5x - 3-11 ( x - 2)( x + 7) Bước 2: = = = x + 7. x - 2 x - 2 x - 2
f (x) - f (2) Bước 3: lim
= lim(x + 7) = 9. Vậy f ¢(2) = 9. x®2 x®2 x - 2
Tính toán trên nếu sai thì sai ở bước nào. A. Bước 1. B. Bước 2. C. Bước 3 . D. Tính toán đúng. Lời giải
Học sinh tính đạo hàm bằng định nghĩa theo cách 1 các bước đều đúng. STUDY TIP Phương trình bậc hai 2
ax + bx + c = 0 có hai nghiệm x , x Û a(x - x x - x = 0 1 ) ( 2 ) . 1 2
Ví dụ 3. Số gia của hàm số ( ) 2
f x = x ứng với số gia x
D của đối số x tại x = - 1 là: 0 A. ( x D )2 -2 x D -1. B. ( x D )2 + 2 x D + 2. C. ( x D )2 + 2 x D . D. ( x D )2 - 2 x D . Lời giải Đáp án D. Với số gia x
D của đối số x tại điểm x = - , t 1 a có: y D = (- + x D )2 - = ( x D )2 1 1 - 2D . x 0
Ví dụ 4. Cho hàm số ( ) 2
f x = x - x, đạo hàm của hàm số ứng với số gia x
D của đối số x tại x là: 0 A. lim x D - x x D - x D lim ( x D + 2x -1 0 ) x D ® ( )2 2 .0 0 ). B. . x D ®0 C. lim ( x D + 2x +1 lim x D + x x D + x D x D ® ( )2 2 .0 0 ) 0 ) . D. . x D ®0 Lời giải Đáp án B. Ta có: y D = (x + x D - x + x
D - x - x = x D + 2x . x D - x D 0 )2 ( 0 ) ( 0 0) ( )2 2 0 Þ ¢( y D f x = lim = lim x D + 2x -1 0 ) ( 0 ). x D ®0 x D ®0 x D
Ví dụ 5. Cho hàm số y = f (x) có đao hàm tại điểm x là f ¢(x0 ). Khẳng định nào sau đây là sai. 0 f x - f x f x + x D - f x
A. f ¢( x = lim f ¢( x = lim 0 ) ( 0 ) ( 0) 0 ) ( ) ( 0) . B. . x® 0 x x - x x D 0 ® x D 0
f x + h - f x
f x + x - f x
C. f ¢(x = lim f ¢( x = lim 0 ) ( 0 ) ( 0) 0 ) ( ) ( 0) . D. . h®0 h x® 0 x x - x0 Lời giải Trang 3 Đáp án D.
- A đúng theo định nghĩa. - B đúng vì x
D = x - x nên x ® x Þ x D ® 0. 0 0
- C đúng. Đặt h = x
D = x - x Þ x = h + x , h ® 0 khi x ® x . 0 0 0
f ( x + h) - f (x
f (x + h - f x 0 ) ( 0) 0 ) ¢( f x - f x f x = lim = lim = 0 ) ( ) ( 0) lim . x® 0 x x - x h®0 h + x - x h®0 h 0 0 0 - Vậy D sai.
Ví dụ 6. Xét ba mệnh đề sau:
(1) Nếu hàm số f (x) có đạo hàm tại điểm x = x thì f (x) liên tục tại điểm đó. 0
(2) Nếu hàm số f (x) liên tục tại điểm x = x thì f (x) có đạo hàm tại điểm đó . 0
(3) Nếu hàm số f (x) gián đoạn tại điểm x = x thì chắc chắn f (x) không có đạo hàm tại 0 điểm đó . Trong ba mệnh trên: A. (1) và (3) đúng. B. (2) đúng.
C. (1) và (2) đúng . D. (2) và (3) đúng. Lời giải Đáp án A.
Mệnh đề (2) sai vì: Xét hàm số f (x) = x có tập xác định D = ! nên hàm số liên tục trên ! ,
f ( x) - f (0)
f ( x) - f (0) nhưng ta có: lim = 1 và lim = -
1 nên hàm số không có đạo hàm tại x 0+ ® x - 0 x 0- ® x - 0 x = 0 . STUDY TIP - Khi x 0+ ®
Þ x > 0 nên x = x. - Khi x 0- ®
Þ x < 0 nên x = -x. 2 x + x +1
Ví dụ 7. Cho hàm số y = f ( x) =
. Tính đạo hàm của hàm số tại điểm x = 1 - . x 0 A. 2 . B. 1. C. 0 . D. Không tồn tại. Lời giải Đáp án D.
Hàm số liên tục tại x = 1 - . 0
f ( x) - f (- ) 2 1 x + 2x +1 Ta có lim = lim = 0 (1). x 1+ + x 1 x 1 + ®- ®- x ( x + ) 1
f ( x) - f (- ) 2 1 x -1 lim = lim = 2 (2). x 1- + x 1 x 1 - ®- ®- x ( x + ) 1
Từ (1) và (2) Þ hàm số không có đạo hàm tại điểm x = - . 1 0 STUDY TIP
Hàm số f (x) có đạo hàm tại x Û f x+ = f x- ¢ ¢ = f ¢ x 0 ( 0 ) ( 0 ) ( 0) Trang 4 ìï - - x khi x ¹
Ví dụ 8. Cho hàm số f (x) 3 4 0 = í
. Khi đó f ¢(0) là kết quả nào sau đây? 1 ïî khi x = 0 1 1 1 A. . B. . C. . D. 2 . 4 16 2 Lời giải Đáp án A.
f (x) - f (0) 2 - 4 - x 1 1 Ta có: lim = lim = lim = . x®0 x®0 x®0 x - 0 x 2 + 4 - x 4 ìï x khi x >1
Ví dụ 9. Cho hàm số f (x) = í . Khi đó f ¢( )
1 là kết quả nào sau đây. 2 ïîx khi x £1 1 A. . B. 1. C. 2 . D. f ¢( ) 1 không tồn tại. 2 Lời giải Đáp án D. Ta có: f ( ) 2 1 =1 = . 1 - 2 - x -1 f ¢( + ) x 1 1 1 1 = lim = lim = và f ¢(1 ) = lim = lim (x + ) 1 = . 2 x 1+ ® - x 1 x 1 + ® x +1 2 x 1- ® - x 1 x 1 + ®
Vì f '(1+ ) f '(1- ¹
) nên hàm số f (x) không tồn tại đạo hàm tại x = .1 0
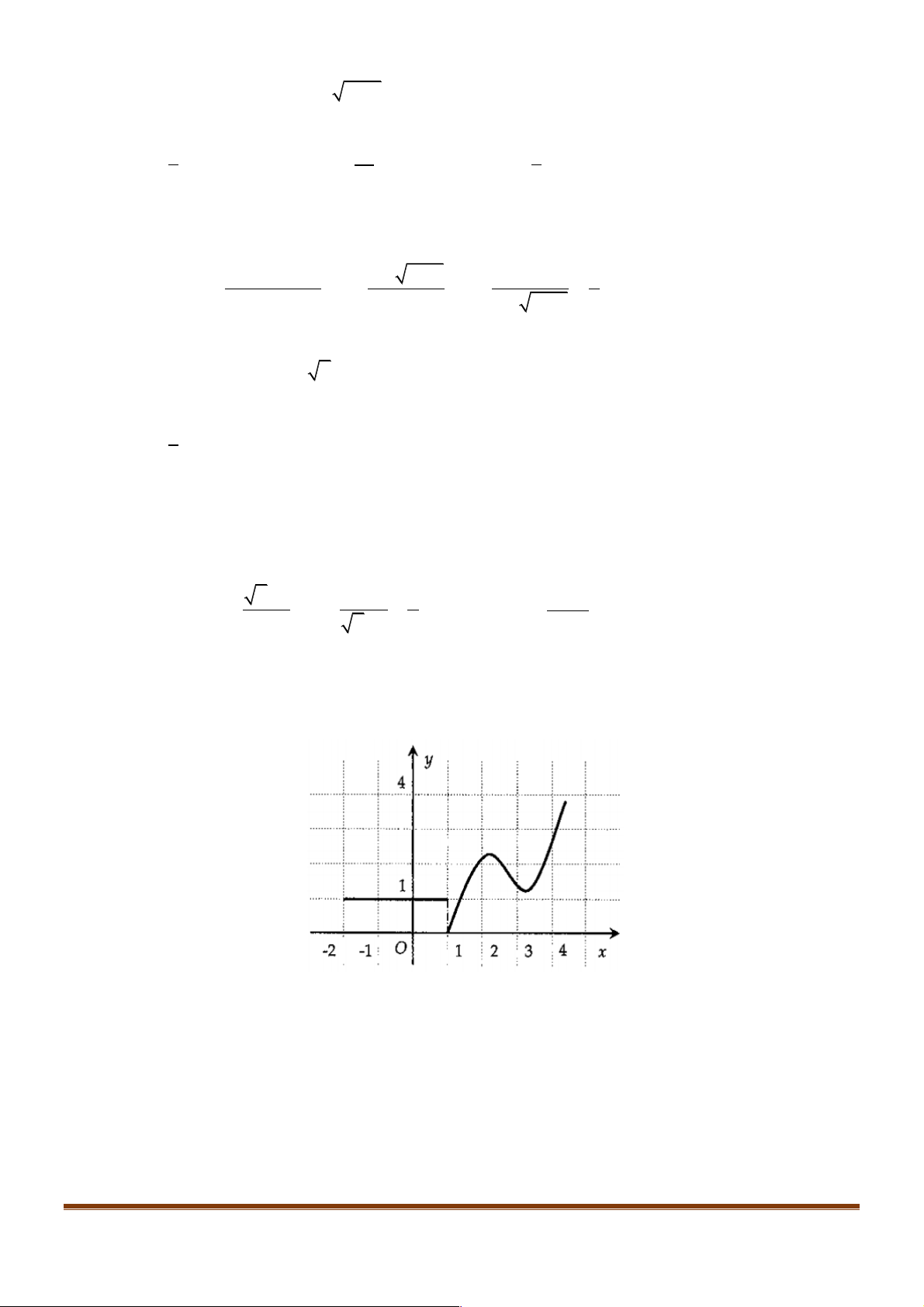
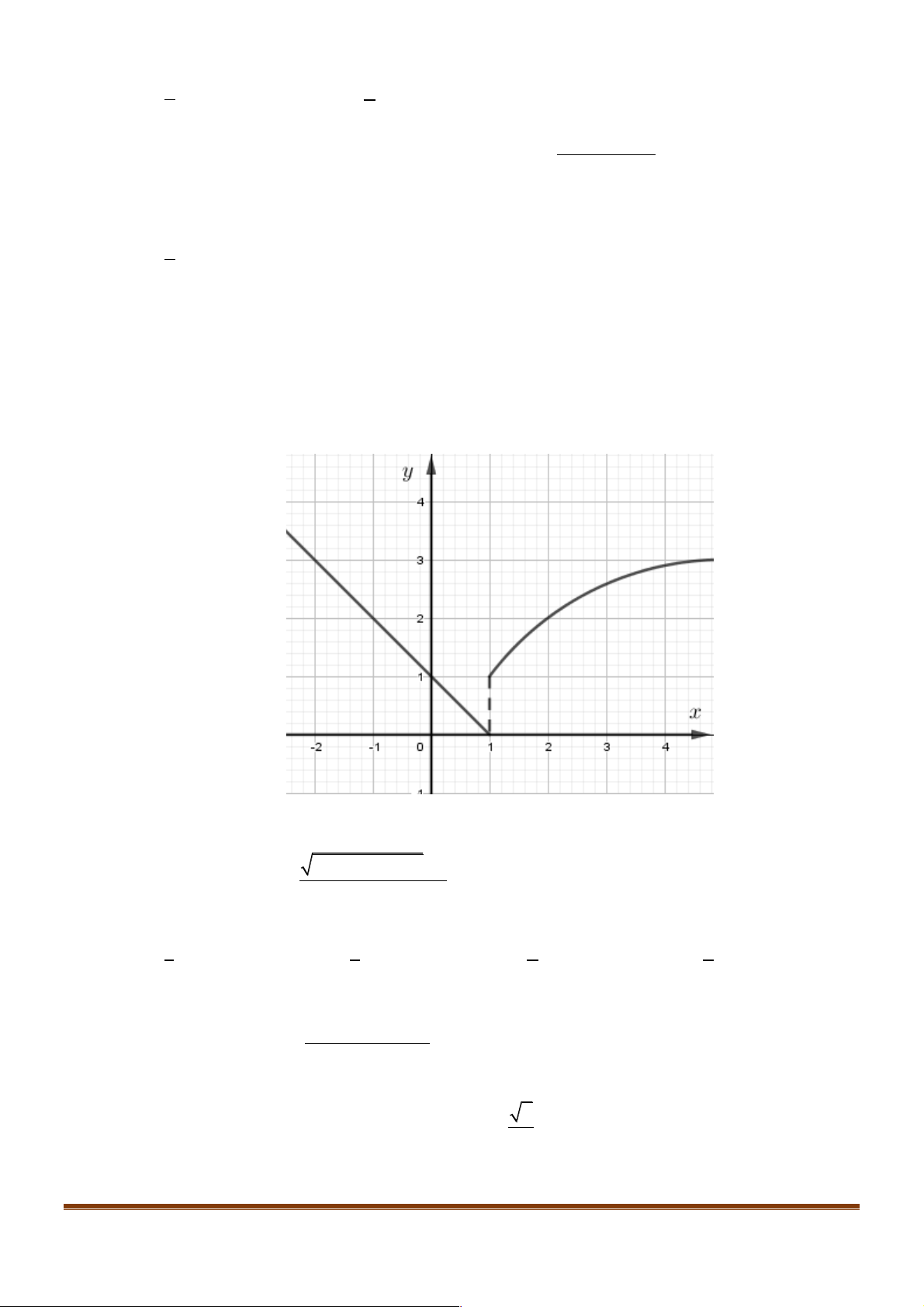
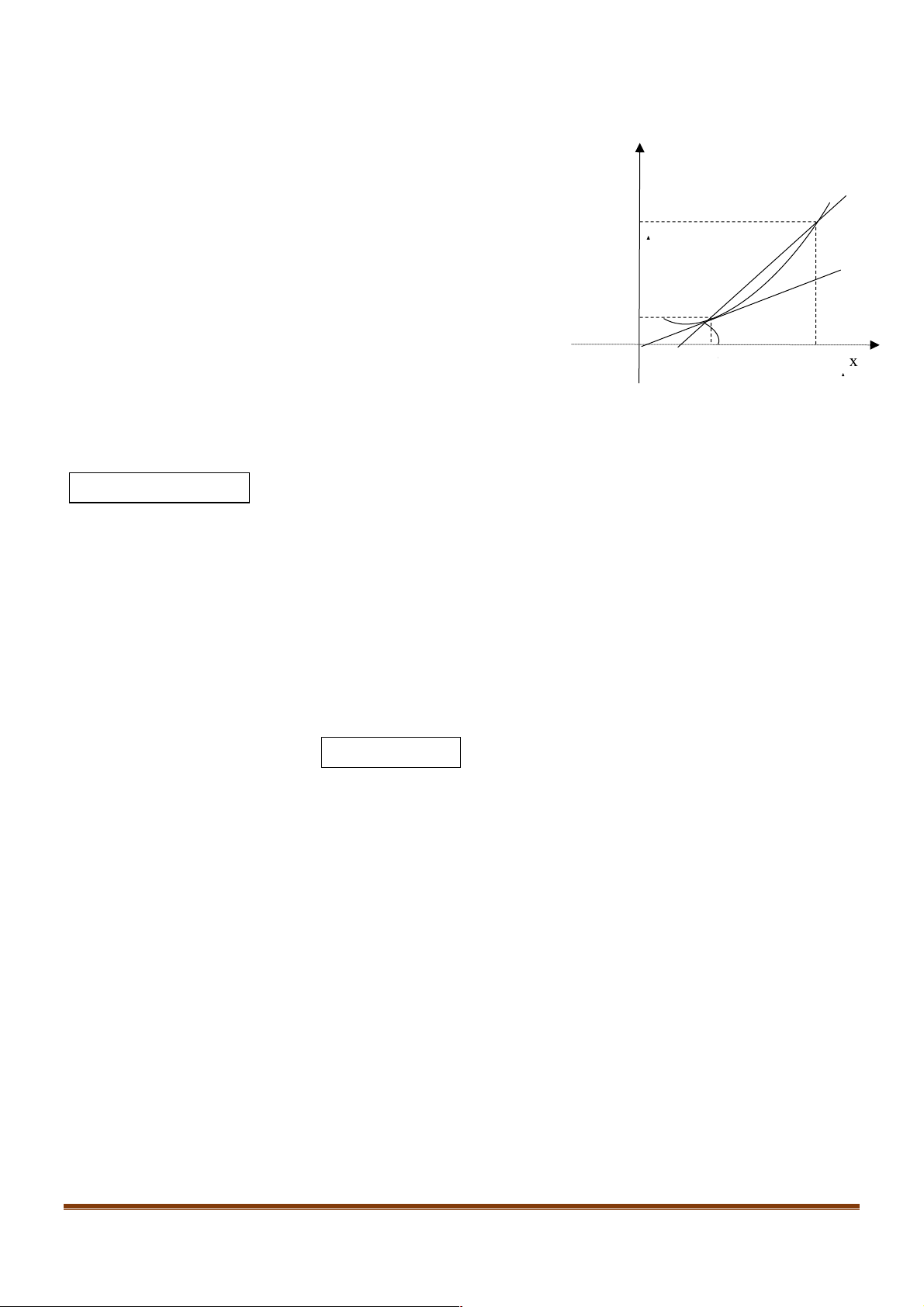
Ví dụ 10. Cho đồ thị hàm số y = f (x) như hình vẽ. Mệnh đề nào sau đây sai.
A. Hàm số có đạo hàm tại x = 0 .
B. Hàm số có đạo hàm tại x = 1.
C. Hàm số có đạo hàm tại x = 2 .
D. Hàm số có đạo hàm tại x = 3. Lời giải Đáp án B.
Tại x = 1 đồ thị hàm số bị ngắt nên hàm số không liên tục. Vậy hàm số không có đạo hàm tại x = 1. STUDY TIP Trang 5
- Đồ thị của hàm số liên tục trên khoảng là một đường liền trên khoảng đó.
- Hàm số không liên tục tại điểm x thì không có đạo hàm tại x . 0 0 2 ì x -1 ï khi x ¹ 1
Ví dụ 11. Tìm a để hàm số f ( x) = í x -1
có đạo hàm tại điểm x = 1. ïîa khi x = 1 A. a = 2 - . B. a = 2 . C. a = 1 1 . D. a = . 2 Lời giải Đáp án B.
Để hàm số có đạo hàm tại x = 1 thì trước hết f (x) phải liên tục tại x =1. 2 x -1 - 2 2 x -1 f x - f 1 lim = 2 = f ( )
1 = a . Khi đó f ¢( ) ( ) ( ) x -1 1 = lim = lim = . 1 x 1 ® x -1 x 1 ® x 1 x -1 ® x -1 Vậy a = 2 . STUDY TIP
Hàm số f (x) liên tục tại x Û lim f x = f x 0 ( ) ( 0). x® 0 x 2 ì x -1 ï khi x ³ 0
Ví dụ 12. Tìm a,b để hàm số f ( x) = í x -1
có đạo hàm tại điểm x = 0 .
ïîax +b khi x < 0 ìa = 11 - ìa = 10 - ìa = 12 - ìa = -1 A. í . B. í . C. í . D. í . b î =11 b î =10 b î =12 îb = 1 Lời giải Đáp án D.
Trước tiên hàm số phải liên tục tại x = 0 lim f ( )
x =1= f (0), lim f ( )
x = b Þ b =1 x 0+ x 0- ® ®
f (x) - f (0) x -1 Xét lim = lim = 1 - x 0+ x 0 x + ® ® x +1
f (x) - f (0) lim = lim a = a x 0- x 0 x - ® ®
Hàm số có đạo hàm tại x = 0 Û a = 1 - STUDY TIP
Hàm số f (x) liên tục tại x Û lim f (x) = lim f (x) = f (x ) 0 + - 0 x® ® 0 x x 0 x 2 ìax + bx +1 khi x ³ 0
Ví dụ 13. Tìm a,b để hàm số f (x) = í
có đạo hàm tại điểm x = 0
îasin x + bcos x khi x < 0 0
A. a = 1;b =1. B. a = 1 - ;b =1. C. a = 1 - ;b = - . 1
D. a = 0;b = 1. Trang 6 Lời giải Đáp án A Ta có: f (0) =1 2
lim f (x) = lim(ax + bx +1) =1 x®0+ x®0+
lim f (x) = lim(asin x + bcos x) = b x®0- x®0-
Để hàm số liên tục thì b = 1 2 + ax + x +1-1 f ( ¢ 0 ) = lim =1 x®0+ x x x 2 x 2a sin cos - 2sin -
a sinx + b cos x -1 2 2 2 f ( ¢ 0 ) = lim = lim x®0- x®0 x - x x x sin sin 2 æ x ö 2 x = lim . lim a cos - lim . lim sin = a ç ÷ x®0- x x®0- x®0- x x®0 è 2 - ø 2 2 2
Để tồn tại f (0) Þ f (0+ ) = f (0- ¢ ¢ ¢ ) Û a = 1 STUDY TIP sinx sinf(x)
Giới hạn lượng giác lim =1Þ lim =1 x 0 ® f ( x) 0 x ® f (x)
Ví dụ 14. Cho hàm số f (x) = x(x -1)(x - 2)...(x -1000). Tính f (0 ¢ ). A.10000!. B.1000!. C.1100!. D.1110!. Lời giải Đáp án B.
f (x) - f (0)
x(x -1)(x - 2)...(x -1000) - 0 f ( ¢ x) = lim = lim
= lim(x -1)(x - 2)...(x -1000) x®0 x®0 x®0 x - 0 x = ( 1 - )( 2) - ...( 1000) - = 1000! STUDY TIP
Hoán vị n phần tử: P = n!=1.2...(n -1)n n
C. BÀI TẬP RÈN LUYỆN KỸ NĂNG
Câu 1. Số gia của hàm số 3
f (x) = x ứng với x = 2 và x D =1 bằng bao nhiêu? 0 A. 19 - . B. 7 . C.19. D. 7 - . y D Câu 2. Tỉ số
của hàm số f (x) = 2x(x -1) theo x và x D là: x D
A. 4x + 2 x D + 2 . B. 2 4x + 2( x D ) - 2.
C. 4x + 2 x D - 2. D. 2 4 . x x D + 2( x D ) + 2 x D .
Câu 3. Số gia của hàm số 2
f (x) = x - 4x +
1 ứng với x và x D là: A. x D ( x D + 2x - 4) . B. 2x + x D . C. x D (2x - 4 x D ).
D. 2x - 4 x D . 2 ì x +1-1 ï khi x ¹ 0
Câu 4. Cho hàm số f (x) xác định: f (x) = .Giá trị f (0 ¢ ) bằng: í x ï î0 khi x = 0 Trang 7 1 1 A. . B. - . C. 2 - . D. Không tồn tại. 2 2 3 2
ì x - 4x + 3x ï khi x ¹ 1
Câu 5. Cho hàm số f (x) xác định trên ! \{ } 2 bởi 2
f (x) = í x - 3x + 2 .Giá trị f (1 ¢ ) ïî0 khi x = 1 bằng: 3 A. . B.1. C. 0 . D. Không tồn tại. 2
Câu 6. Xét hai mệnh đề:
(I ) f (x) có đạo hàm tại x thì f (x) liên tục tại x . 0 0
(II ) f (x) có liên tục tại x thì f (x) đạo hàm tại x . 0 0 Mệnh đề nào đúng? A. Chỉ (I ) . B. Chỉ (II ).
C. Cả hai đều sai.
D. Cả hai đều đúng.
Câu 7. Cho đồ thị hàm số y = f (x) như hình vẽ:
Hàm số không có đạo hàm tại các điểm nào sau đây? A. x = 0 . B. x = 1. C. x = 2 . D. x = 3. 3 2
ì x - 2x + x +1-1 ï khi x ¹ 1
Câu 8. Cho hàm số f (x) = .Giá trị f (1 ¢ ) bằng: í x -1 ï î0 khi x = 1 1 1 1 1 A. . B. . C. . D. . 3 5 2 4 ì2x + 3 khi x ³ 1 ï Câu 9. Cho hàm số 3 2 f (x) = í .Giá trị f (1 ¢ ) bằng:
x + 2x - 7x + 4 ï khi x < 1 î x -1 A. 0 . B. 4 . C. 5 . D. Không tồn tại. ì x ï khi x ¹ 0
Câu 10. Cho hàm số f (x) xác định trên +
! bởi f (x) = í x Xét hai mệnh đề sau: ïî0 khi x = 0 Trang 8 (I ) f (0 ¢ ) =1 .
(II ) Hàm số không có đạo hàm tại x = 0. 0 Mệnh đề nào đúng? A. Chỉ (I ) . B. Chỉ (II ).
C. Cả hai đều đúng.
D. Cả hai đều sai.
Câu 11. Xét hai câu sau: x (1) Hàm số y =
liên tục tại x = 0 . x +1 x (2) Hàm số y =
có đạo hàm tại x = 0 . x +1 Trong 2 câu trên: A. (2) đúng. B. (1) đúng.
C.Cả (1) , (2)đều đúng. D. Cả (1) , (2)đều sai. 3 2 2
ì 4x +8 - 8x + 4 khi x ¹ 0 Câu 12. Cho hàm số ï f (x) = .Giá trị của f (0 ¢ ) bằng: í x ï î0 khi x = 0 1 5 A. . B. - 4 . C. . D.Không tồn tại. 3 3 3 ì p ïxsin khi x ¹ 0
Câu 13. Với hàm số f (x) = í x
.Để tìm đạo hàm f '(x) = 0 một học sinh lập luận qua ïî0 khi x = 0 các bước như sau: p
1. f (x) = x . sin £ x . x
2.Khi x ® 0 thì x ® 0 nên f (x) ® 0 Þ f (x) ® 0. 3.Do lim f ( ) x = lim f ( )
x = f (0) = 0 nên hàm số liên tục tại x = 0 . x 0+ x 0- ® ®
4.Từ f (x) liên tục tại x = 0 Þ f (x) có đạo hàm tại x = 0 .
Lập luận trên nếu sai thì bắt đầu từ bước: A.Bước 1. B.Bước 2. C.Bước 3. D.Bước 4. ì 1 ïxsin khi x ¹ 0 Câu 14. Cho hàm số 2 f (x) = í x . ïî0 khi x = 0
(1) Hàm số f (x) liên tục tại điểm x = 0 .
(2) Hàm số f (x) không có đạo hàm tại điểm x = 0 .
Trong các mệnh đề trên: A.Chỉ (1) đúng. B. Chỉ (2) đúng.
C.Cả (1),(2) đều đúng. D. Cả (1),(2) đều sai. 2
ìax + bx khi x ³1
Câu 15. Cho hàm số f (x) = í
.Tìm a,b để hàm số có đạo hàm tại x = 1 î2x -1 khi x < 1 A. a = 1, - b = 0. B. a = 1, - b =1.
C. a = 1,b = 0.
D. a = 1,b = 1. 2 ìsin x ï khi x > 0
Câu 16. Cho hàm số f (x) = í x .Giá trị của f (0 ¢ ) bằng: ï 2
îx + x khi x £ 0 Trang 9 A.1. B. 2 . C. 3 . D. 5 .
Câu 17. Xét hàm số y = f (x) có tập xác định là đoạn [ ;
a b] đồng thời nếu x ® x Î ; a b f (x) ®1 0 [ ] thì với 3 điều kiện:
I. f (x) là hàm số liên tục trái và liên tục phải của x . 0 II. f (x ) =1. 0
III. f (x) có đạo hàm tại x . 0
Trong ba điều kiện trên, điều kiện cần và đủ để f (x) liên tục tại x là: 0 A. Chỉ I. B. Chỉ II. C. Chỉ I và II. D. Chỉ II và III.
Câu 18. Xét ba hàm số:
I. f (x) = x .x
II. g(x) = x III. (
h x) = x +1 x
Hàm số không có đạo hàm tại x = 0 là: A. Chỉ I. B. Chỉ II. C. Chỉ I và II. D. Chỉ I và III.
D. HƯỚNG DẪN GIẢI Câu 1. Đáp án C. y
D = f (x + x
D - f x = x + x D - x 0 ) ( 0) ( 0 )3 3 0 Với x = 2, x D =1Þ y D =19 0 Câu 2. Đáp án C. y D
f (x) - f (x 2 x - x
x + x - 2 x - x 0 ) ( 0 ) ( 0 ) ( 0 ) = =
= 2x + 2x - 2 0 x D x - x x - x 0 0
(Với x = x - x D ) 0 Câu 3. Đáp án A. y D = f ( x
D + x) - f (x) = ( x D + x)2 - ( x D + x) + -( 2 4 1 x - 4x + ) 1 = x D ( x D + 2x - 4) Câu 4. Đáp án A.
f (x) - f (0) 2 x +1 -1 1 1 Xét lim = lim = lim = 2 x®0 x®0 x®0 2 x x x +1 +1 2 Vậy f ¢( ) 1 0 = 2 Câu 5. Đáp án D.
f ( x) - f ( ) 3 2 1
x - 4x + 3x x (x - 3) Xét lim = lim = lim = ¥ x® x -1 x® ( x - ) 1 ( 2 1 1
x - 3x + 2) x 1 ® ( x - ) 1 ( x - 2) Câu 6. Đáp án A.
(II) Sai : ví dụ: f (x) = x thì f (x) liên tục tại x = 0 nhưng f (x)không có đạo hàm tại x = 0
(I) Đúng theo đáp án đã trình bày Câu 7. Đáp án B.
Tại x = 1, đồ thị hàm số bị gián đoạn nên hàm số không liên tục tại đó
Þ hàm số không có đạo hàm Câu 8. Đáp án C. Trang 10
f (x)- f ( ) 1 3 x - 2 2 x + x +1 x 1 lim = lim = lim = x 1 ® x -1 x 1 ® (x - )12 x 1 ® 3 2
x - x + x + + 2 2 1 1 Câu 9. Đáp án D.
lim f (x) = lim(2x + ) 3 = 5 x 1+ ® x 1+ ® 3 2
x + x - x + lim f (x) 2 7 4 = lim = lim( 2 x + 3x - 4) = 0 x 1- ® x 1- ® x -1 x 1- ®
Vậy không tồn tại f ¢( ) 1 Câu 10. Đáp án B. x -0 ¢( ) 1 0 = lim x f = lim = +¥ x®0 x®0 x - 0 x x Vậy (I) sai, (II) đúng Câu 11. Đáp án B. x Ta có: lim
= 0 = f (0) ÞHàm số liên tục tại x = 0 x®0 x + 1
f (x) - f (0) x 1 lim = lim = lim =1 x®0+ - x®0 x 0
+ x ( x + ) x®0 1 + ( x + ) 1
f (x) - f (0) x 1 - lim = lim = lim = 1 - x®0- - x®0 x 0
- x ( x + ) x®0 1 - ( x + ) 1
Vậy hàm số không có đạo hàm tại x = 0 Câu 12. Đáp án B.
f (x) - f (0) 3 4 2 x + 8 - 8 2 x + 4 3 4 2 x + 8 - 2 + 2 - 8 2 x + 4 lim = lim = lim 2 2 x®0 x®0 x®0 x x x Ta có: æ ö 1 ç 4 2 x 8 2 x ÷ 1 5 = lim - = - = - 2 x®0 x çç 3 è (4 2 x + 8) 2 2 2 3 2 + x + + + x + ÷÷ 3 3 2 4 8 4 2 8 4 ø Câu 13. Đáp án D.
f (x)- f (0) p
Một hàm số liên tục tại x0 chưa chắc có đạo hàm tại điểm đó, hơn nữa = sin x - 0 x
không có giới hạn khi x ® 0 Câu 14. Đáp án C. 1
Ta có: - x £ x.sin £ x x2 Þ lim(- x ) 1 1 £ lim . x sin £ lim x = 0 Þ lim . x sin = 0 = f (0 ) 2 2 x®0 x®0 x®0 x®0 x x
Vậy hàm số liên tục tại x = 0
f (x)- f (0) æ 1 ö Xét lim = limçsin ÷ x® x - 0 è 2 0 x ø 1 Lấy dãy (xn): x = có: n p + 2np 2 Trang 11 1 æ p ö lim x = lim = 0 Þ lim f x = + np = n ( n ) lim sin 2 1 ç ÷ n®+¥ n®+¥ n p ®+¥ è 2 ø + 2np 2
Lấy dãy x ¢ x ¢ =
= , tương tự ta cũng có: ( n ) 1 1 : n p 2 + 2p n 6 æ p ö 1 f x - f 0 1
lim x ¢ = 0 Þ lim f x ¢ = 0 Þ lim sin + 2np = Þ lim = limsin không n ç ÷ ®+¥ ®+¥ ( n n n ) ( ) ( ) 2 n®+¥ x®0 x®0 è 6 ø 2 x - 0 x tồn tại Câu 15. Đáp án C.
ìlim f (x) = a + b = f ( ) 1 ï + Ta có: x 1 í ® Þ a + b =
lim f (x) = lim(2x - ) 1 1 = 1 ïîx 1- ® x 1- ®
f (x)- f ( ) 1
ax2 + bx - (a + b) lim = lim = lim[a(x + ) 1 + b] = a 2 + b x + ®1 x - x + ® 1 1 x - x + ® 1 1
f (x)- f ( ) 1 2 2
x -1- (a + b) 2x -1-1 lim = lim = lim = 2 x 1- ® x -1 x 1- ® x -1 x 1- ® x -1 ìa + b = 1 ìa = 1 Ta có hệ: í Û í î2a + b = 2 îb = 0 Câu 16. Đáp án A. 2 x æ x ö lim f (x) sin sin = lim = limç .sin x÷ = 0 x 0+ ® x 0+ ® x 0+ ® x è x ø
lim f (x) = lim( 2 x + x) = 0 x 0- ® x 0- ®
Suy ra hàm số liên tục tại x = 0
f (x)- f (0) sin 2 x
f (x)- f (0) 2 x + x lim = lim = ; 1 lim = lim = 1 x 0+ ® x - 0 x 0+ ® x 0- ® x x - 0 x 0- ® x
Vậy: f (0) = f (0- ) = f (0+ ¢ ¢ ¢ )= 1 Câu 17. Đáp án C.
- f(x) liên tục tại x0 tức là x ® x thì f (x) ® f (x 0 ) nên (I) và (II) đúng. 0
- f(x) có đạo hàm tại x0 là điều điện đủ để f(x) liên tục tại x0. f(x) liên tục tại x0 nhưng có
thể f(x) không có đạo hàm tại điểm đó. Câu 18. Đáp án B.
g(x)- g(0) 1 Ta có: lim = lim
= +¥. Vậy g (x) không có đạo hàm tại x = 0 . + x®0 x - + x® 0 0 x Trang 12
CÁC QUY TẮC TÍNH ĐẠO HÀM A. LÝ THUYẾT
1. Đạo hàm của tổng, hiệu, tích, thương
Cho các hàm số u = u (x); v = v(x)có đạo hàm tại điểm x thuộc khoảng xác định. Ta có:
1. (u + v)¢ = u¢+ v¢ 2. (u -v)¢ = u¢ - v¢
æ u ¢ö u v - v u æ 1 ¢ ¢ ¢ ö v¢ 3. ( . u v)¢ = u v ¢ + v u ¢ 4. = Þ = - ç ÷ 2 ç ÷ 2 è v ø v è v ø v STUDY TIP Mở rộng:
1. (u ±u ±...±u ¢ = u ¢ ±u ¢ ±...±u ¢ 1 2 n ) 1 2 n 2. ( . u . v w)¢ = u .¢ . v w + . u v .¢w + . u . v w¢
2. Đạo hàm của hàm số hợp
Cho hàm số y = f (u(x) = f (u )với u = u(x . K
) hi đó: y ¢ = y ¢.u ¢ x u x
3. Bảng công thức đạo hàm của các hàm số sơ cấp cơ bản
Đạo hàm các hàm số sơ cấp cơ bản
Đạo hàm các hàm hợp u = u(x)
(c)¢ = 0, c là hằng số (x)¢ =1 ¢ 1 ¢ æ ö 1 æ 1 ö u¢ = - = - ç ÷ ç ÷ 2 2 è x ø x è u ø u ( ¢ ( ¢ ¢ u ) u x ) 1 = = 2 x 2 u ( (ua )¢ a 1 - xa )¢ a 1 = a.x - = a.u .¢u ( ¢ sin x)¢ = cos x
(sinu) = u .¢cosu ( ¢
cos x)¢ = -sin x (cosu) = u - .¢sin u u¢ ( ¢ 2 tan x) 1 ¢ 2 = =1+ tan x (tanu) = = u .¢ 1+ tan x 2 ( ) 2 cos x cos u 1 ( ¢ 2 x) 1 cot ¢ = - = -( 2 1+ cot x (cotu) = -
= -u .¢ 1+ cot u 2 ( ) 2 ) sin x sin u STUDY TIP
Với các hàm số đã cho trong bảng được xác định với điều kiện đầy đủ. Trang 13
B. Các dạng toán về quy tắc tính đạo hàm
Đạo hàm của hàm đa thức - hữu tỉ - căn thức và hàm hợp Phương pháp:
- Sử dụng các quy tắc, công thức tính đạo hàm trong phần lý thuyết.
- Nhận biết và tính đạo hàm của hàm số hợp, hàm số có nhiều biểu thức.
- Sử dụng đạo hàm để giải phương trình, bất phương trình, chứng minh đẳng thức, bất đẳng thức..
Ví dụ 15. Đạo hàm của hàm số y = 2
- x5 + 4 x bằng biểu thức nào dưới đây? 4 2 4 4 4 1 4 1 A. -10x + B. -10x + C. -10x + D. -10x - x x x x Lời giải Đáp án C. Trang 14 Trang 15 Lời giải 2 4 y¢ = 10 - x + . x 2x +1 a
Ví dụ 2. Đạo hàm của hàm số y =
bằng biểu thức có dạng
. Khi đó a nhận giá trị nào x + 2 (x + 2)2 sau đây: A. a = 3 - . B. a = 5 . C. a = 3. D. a = 5 - . Lời giải Đáp án C.
(2x )1¢ (x 2) (2x )1(x 2)¢ + + - + + 3 y¢ = = Þ a = 3. (x + 2)2 (x + 2)2 STUDY TIP æ ax b ¢ + ö ad - bc =
với c ¹ 0 và ad - bc ¹ 0 ç ÷ è cx + d ø (cx + d)2 2 x - x +1 2 ax + bx
Ví dụ 3. Đạo hàm của hàm số y =
bằng biểu thức có dạng . Khi đó . a b bằng: x -1 (x - )2 1 A. . a b = 2 - . B. . a b = 1 - . C. . a b = 3. D. . a b = 4 . Lời giải Đáp án A.
(2x - )1(x - )1-( 2x - x+ ) 2 1 x - 2x
Cách 1: y¢ = = Þ . a b = 2. - (x - )2 1 (x - )2 1 2 1 1 x - 2x
Cách 2: y = x + Þ y¢ =1- = x -1 (x - )2 1 (x - )2 1 STUDY TIP Trang 16 2 ¢ 2
æ ax + bx + c ö aa x ¢ + 2ab x ¢ + bb¢ - ac¢ Với . a a¢ ¹ 0 ta có ç ÷ = è a x ¢ + b¢ ø (a x¢ +b¢)2 2 x + x + 3 ax + b
Ví dụ 4. Đạo hàm của hàm số y =
bằng biểu thức có dạng
.Khi đó a + b bằng: 2 x + x -1 (x + x- )2 2 1
A. a + b = 4 .
B. a + b = 5 .
C. a + b = 10 - .
D. a + b = 12 - . Lời giải Đáp án D. 2 x + x -1+ 4 4 4 - (2x + ) 1 8x + 4
Cách 1: y = =1+ Þ y¢ = = - 2 2 x + x -1 x + x -1 ( 2x + x- )2 1 ( 2x + x- )2 1 æ u ¢ö u v ¢ - uv¢
Cách 2: Áp dụng = ç ÷ 2 è v ø v
(2x+ )1( 2x + x- )1-( 2x + x+3)(2x+ )1 8 - x - 4 y¢ = = Þ a + b = 12 - (x + x- )2 1 (x + x- )2 2 2 1 STUDY TIP a b a c b c 2 x + 2 x + 2
ax + bx + c ¢ æ ö a b a c b c 1 1 1 1 1 1 ç ÷ = 2
a x + b x + c è ø ( 2 1 1 1
a x + b x + c 1 1 1 )2
Ví dụ 5. Đạo hàm của hàm số 2
y = ax + (a - ) 3 2
1 x + a - a (với a là hằng số) tại mọi x Î ! là:
A. 2x + a -1.
B. 2ax +1- a . C. 2
2ax + 3a - 2a +1. D. 2ax + a -1. Lời giải Đáp án D.
y¢ = 2ax + a - 1 STUDY TIP
Với c là hằng số thì (c)¢ = 0 ( .cu)¢ = .cu¢ ( nx)¢ n 1 - * = nx ,n Î • ax + b
Ví dụ 6. Đạo hàm của hàm số 2
y = x + x +1 bằng biểu thức có dạng
. Khi đó a - b bằng: 2 2 x + x +1
A. a - b = 2.
B. a - b = 1 - .
C. a - b = 1.
D. a - b = 2 - . Lời giải ( 2x x )1¢ + + 2x +1 Đáp án C. y¢ = = Þ a - b =1 2 2 2 x + x +1 2 x + x +1
Ví dụ 7. Đạo hàm của hàm số y = (x - x + )5 2 1 là: 4 A. ( 2 4 x - x + ) 1 (2x - ) 1 .
B. (x - x + )4 2 5 1 . Trang 17 4 4 C. ( 2 5 x - x + ) 1 (2x - ) 1 . D. ( 2 x - x + ) 1 (2x - ) 1 . Lời giải Đáp án C. y (x x )4(x x )¢ ¢ = - + - + = (x - x + )4 2 2 2 5 1 1 5 1 (2x - ) 1 STUDY TIP ( nu)¢ n 1 - * = . n u u ¢ , n Î •
Với u = u (x): ( )¢ u¢ u = 2 u
Ví dụ 8. Đạo hàm của hàm số y = ( 2 x + )( 2
1 5-3x ) bằng biểu thức có dạng 3 ax + a
bx. Khi đó T = b bằng: A. 1 - . B. 2 - . C. 3 . D. 3 - . Lời giải Đáp án D. y ( 2x )¢( 2 x ) ( 2 x )( 2 x )¢ ¢ = + - + + - = x( 2 - x )+( 2 x + )(- x) 3 1 5 3 1 5 3 2 5 3 1 6 = 1 - 2x + 4x STUDY TIP
Với u = u (x),v = v(x): (uv)¢ = u v¢ + uv¢
Ví dụ 9. Đạo hàm của hàm số 2
y = x (2x + )
1 (5x -3) bằng biểu thức có dạng 3 2
ax + bx + cx. Khi đó
a + b + c bằng: A. 31. B. 24 . C. 51. D. 34. Lời giải Đáp án A.
Cách 1: y¢ = x( x + )( x - ) 2 + x ( x - ) 2 + x ( x + ) 3 2 2 2 1 5 3 .2 5 3 2
1 .5 = 40x -3x - 6x
Cách 2: Nhân vào rút gọn ta được 4 3 2 3 2
y =10x - x -3x Þ y¢ = 40x - 3x - 6x nên a + b + c = 31 STUDY TIP
u = u (x),v = v(x),w = w(x) Þ (uvw)¢ = u v¢w + uv w ¢ +uvw¢ x Ví dụ 10.
Đạo hàm của hàm số y =
( a là hằng số) là: 2 2 a - x 2 a 2 a 2 2a 2 a A. - . B. . C. . D. . (a - x )3 2 2 ( 3 3 a + x )3 2 2 ( 2 2 a - x ) ( 2 2 a - x ) Lời giải Đáp án D. 2 2 2 x a - x + 2 2 2 a - x a y¢ = = 2 2 a - x (a - x )3 2 2 Trang 18 1 ax
Ví dụ 11. Đạo hàm của hàm số y =
bằng biểu thức có dạng
. Khi đó a nhận giá trị 2 x +1 (x + )3 2 1 nào sau đây: A. a = 4 - . B. a = 1 - . C. a = 2 . D. a = 3 - . Lời giải Đáp án B. ( ¢ 2 x 1) ( 2x )1¢ + - + -x y¢ = - = = Þ a = -1 2 2 x +1 2 x +1.( 2 x + ) 2 1 x +1.( 2 x + ) 1 STUDY TIP ¢ u¢
u = u (x) :( u ) = 2 u 2
ìïx + x +1 khi x £1
Ví dụ 12. Đạo hàm của hàm số f (x) = í là:
ïî x -1+3 khi x >1 ì2x khi x < 1
ì2x +1 khi x <1 ï ï
A. f ¢( x) = í 1 .
B. f ¢( x) = í 1 . khi x > 1 ï khi x > 1 î2 x -1 ïî x-1 ì2x +1 khi x £1 ì2x +1 khi x <1 ï ï
C. f ¢( x) = í 1 .
D. f ¢( x) = í 1 . khi x > 1 ï khi x > 1 î2 x -1 ïî2 x-1 Lời giải Đáp án D.
Với x <1: f ¢(x) = 2x + 1 Với x > f ¢(x) 1 1: = 2 x -1
f (x) - f ( ) 1 x -1 Với x = 1, ta có lim = lim
= +¥ nên không có đạo hàm tại x =1. x 1+ - x 1 x 1 + ® ® x -1 ì2x +1 khi x <1 ï
Vậy f ¢( x) = í 1 khi x > 1 ïî2 x-1 STUDY TIP
Loại bài toán kết hợp giữa tính đạo hàm bằng công thức và tính đạo hàm bằng định nghĩa tại 1 điểm x . 0 2 ì3- x khi x <1 ïï
Ví dụ 13. Tính đạo hàm của hàm số f ( x) 2 = í . 1 ï khi x ³ 1 ïî x Trang 19 ì ì-x khi x < 1 ï-x khi x <1 ï ï
A. f ¢( x) = í 1 .
B. f ¢( x) = í 1 - khi x = 1. - khi x > 1 ï 2 î x ï 1 ï- khi x > 1 2 î x ì ì-x khi x <1 ï-x khi x <1 ï ï
C. f ¢( x) = í 1 .
D. f ¢( x) = 1 í khi x = 1. khi x > 1 ï 2 î x ï 1 ï- khi x > 1 2 î x Lời giải Đáp án B.
Với x <1: f ¢(x) = -x 1
Với x > 1: f ¢( x) = - 2 x ì f ( x) 1 lim = lim =1 ïïx 1+ ® x 1+ ® x Với x = 1, ta có í
Þ lim f (x) = lim f (x) =1= f ( ) 1 2 + - f ( x) x 1 ® x 1 3 ® - ï x lim = lim =1 ïîx 1- ® x 1- ® 2
Þ Hàm số liên tục tại x =1. ì 1 ï
f ( x) - f ( ) -1 1 ïlim = lim x = 1 - + + ï ® - ® - Xét x 1 x 1 x 1 x 1 í Þ f ¢( ) 1 = 1 - 2 3 - x ï ï
f ( x) - f ( ) -1 1 2 lim = lim = 1 - ïx 1- ® î - x 1 x 1 - ® x -1 ì ï-x khi x <1 ï
Vậy f ¢( x) = í 1 - khi x = 1 ï 1 ï- khi x > 1 2 î x STUDY TIP
- Trên các khoảng xác định ta tính đạo hàm bằng quy tắc.
- Tại điểm x = x ta xét đạo hàm bằng định nghĩa. 0
Ví dụ 14. Cho hàm số f ( x) = ( x - )2 2 3 1 . Giá trị f ¢( ) 1 là: A. 4 . B. 8 . C. 4 - . D. 24 . Lời giải Đáp án D. ¢
Cách 1: f ¢(x) = ( 2 x - )( 2 x - ) = x( 2 2 3 1 3 1 12 3x - ) 1 Þ f ¢( ) 1 = 24 Trang 20
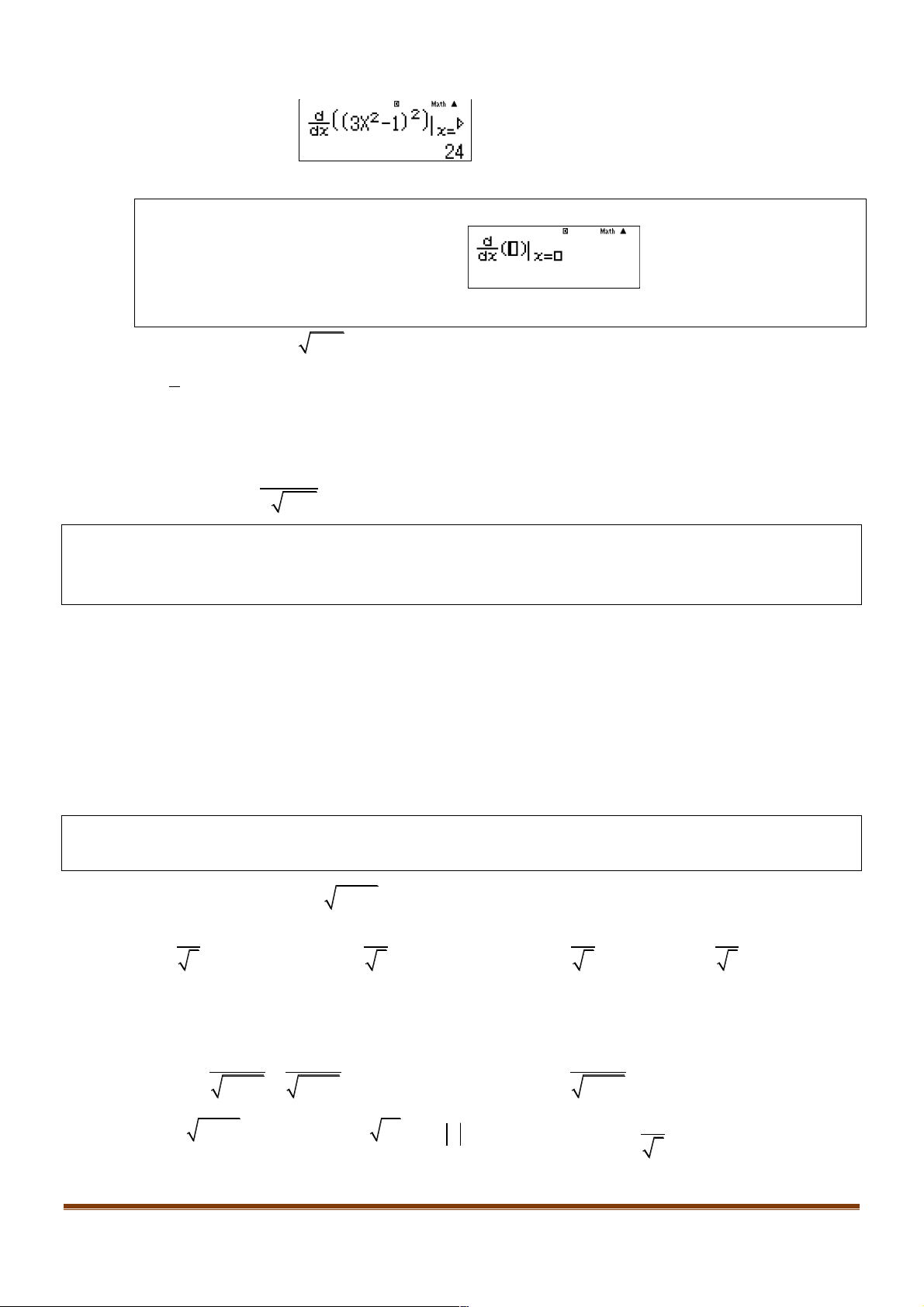
Cách 2: Sử dụng MTCT Nhập vào màn hình:
Nhận xét: Bằng cách 2 ta có thể tính nhanh chóng đạo hàm tại một điểm xác định x = x . 0 STUDY TIP Dùng MTCT:
Tính đạo hàm của hàm số tại một điểm chỉ ra x = x . 0
Ví dụ 15. Cho hàm số f ( x) = x -1. Đạo hàm của hàm số tại x =1là: 1 A. . B. 1. C. 0 . D. Không tồn tại. 2 Lời giải Đáp án D. Ta có: f ¢(x) 1 =
Þ Không tồn tại f ¢( )
1 vì f ¢(x) xác định với x >1. 2 x -1 STUDY TIP
Với bài toán này nếu sử dụng MTCT thì kết quả là màn hình hiển thị thông báo “Math ERROR” và không tính được.
Ví dụ 16. Cho hàm số f (x) 4 2 = 2
- x + 4x +1. Tập các giá trị của x để f ¢(x) < 0 là: A. ( 1 - ;0)È(1;+¥). B. ( 1 - ;0). C. (1;+¥). D. ( ;0 -¥ ). Lời giải Đáp án A. é 1 - < x < 0 f ¢(x) 3 = 8
- x + 8x Þ f ¢(x) < 0 Û ê ëx >1 STUDY TIP
Nhận biết được loại bài toán kết hợp việc tính đạo hàm và giải bất phương trình.
Ví dụ 17. Cho hàm số f (x) 2
= x + x +1. Tập các giá trị của x để 2 .
x f ¢(x) - f (x) ³ 0 là: é 1 ö æ 1 ö æ 1 ö é 2 ö A. ;+¥ . B. ;+¥ . C. ; -¥ . D. ;+¥ . ê ÷ ç ÷ ç ÷ ê ÷ ë 3 ø è 3 ø è 3 ø ë 3 ø Lời giải Đáp án A. f ¢(x) x f (x) f x =1+ = Þ 2 .
x f ¢(x) - f (x) ( ) ³ 0 Û 2 . x - f (x) ³ 0 2 2 2 x +1 x +1 x +1 ìx ³ 0 1 2
Û 2x ³ x +1 (do f (x) 2
> x + x = x + x ³ 0) Û í Û x ³ 2 3 î x ³1 3 Trang 21 é 1 ö Vậy x Î ;+¥ ê ÷ ë 3 ø STUDY TIP
• x ³ x Þ x + x ³ 0 ì f
ï ( x) ³ 0, g ( x) ³ 0
• f (x) £ g (x) Û íïfî (x)£ g(x) 1
Ví dụ 18. Cho hàm số f (x) 3 2
= x - 2 2x + 8x - .
1 Tập các giá trị của x để f ¢(x) = 0 là: 3 A. {-2 2}. B. {2; 2}. C. {-4 2}. D. {2 2}. Lời giải Đáp án D. f ¢( x) 2 = x - 4 2x + 8
f ¢( x) = 0 Û x = 2 2 STUDY TIP
- Nhận biết được loại bài toán kết hợp giữa việc tính đạo hàm và giải phương trình.
- Sau khi tính được đạo hàm ta có thể thử các đáp án vào phương trình để tìm ra kết quả. 3 x
Ví dụ 19. Cho hàm số f ( x) =
. Tập nghiệm của phương trình f ¢(x) = 0 là: x -1 ì 2ü ì 2ü ì 3ü ì 3ü A. í0; ý. B. í0;- ý. C. í0; ý. D. í0;- ý. î 3þ î 3þ î 2þ î 2þ Lời giải Đáp án C. 2 3 3 2 3x x -1 - x 2x - 3x f ¢( x) ( ) = = (x- )2 1 (x- )2 1 éx = 0 f ¢( x) 3 2
= 0 Û 2x - 3x = 0 ê Û 3 (thỏa mãn) êx = ë 2 3 mx
Ví dụ 20. Cho hàm số f (x) 2 = - mx + (3m - ) 1 x + .
1 Tập các giá trị của tham số m để y¢ £ 0 với 3 x " Î ! là: A. ( ; -¥ 2ù . B. ;2 -¥ . C. ( ;0 -¥ ]. D. ( ;0 -¥ ). û ( ] Lời giải Đáp án C. 2
y¢ = mx - 2mx + 3m -1 2
y¢ £ 0 Û mx - 2mx + 3m -1£ 0 ( ) 1 Trang 22
+ Với m = 0 thì (1) trở thành 1
- £ 0 nên đúng với x " Î ! . ìa < 0 ìm < 0
+ Với m ¹ 0 khi đó (1) đúng với x " Î! Û í Û í Û m < 0 îD¢ £ 0 1 î - 2m ³ 0 Vậy m £ 0 STUDY TIP f ( x) ìa > 0 ³ 0,"x Û íîD £0 Cho f (x) 2 = ax +bx + , c a ¹ 0 f ( x) ìa < 0 £ 0,"x Û íîD £0
Ví dụ 21. Cho hàm số f (x) 3
= 2mx - mx . Số x =1 là nghiệm của bất phương trình f ¢(x) £ 1 khi và chỉ khi: A. m £ 1 - . B. m > 1 - . C. 1 - £ m £1. D. m ³ 1 - . Lời giải Đáp án D. f ¢(x) 2 = 2m -3mx
Số x = 1 là nghiệm của bất phương trình f ¢(x) £1Û 2m -3m £1Û m ³ 1 - .
DẠNG 2. ĐẠO HÀM CÁC HÀM SỐ LƯỢNG GIÁC Phương pháp chung:
- Vận dụng các công thức đạo hàm bốn hàm số y = sin x , y = cos x , y = tan x, y = cot x và hàm hợp của nó.
- Vận dụng phối hợp các quy tắc đạo hàm của tổng, hiệu, tích, thương và hàm số hợp
- Vận dụng các phương trình lượng giác cơ bản, phương trình bậc nhất với sinx và cosx, phương trình
tích số…để giải phương trình y ' = 0
Chú ý: Biến đổi lượng giác để thu gọn các hàm số, biểu thức lượng giác STUDY TIP n n 1 (sin u)' nsin - = . u (sin u)' n n 1 (cos u)' ncos - = . u (cosu)' n n 1 (tan u)' n tan - = . u (tan u)' n n 1 (cot u)' ncot - = . u (cot u)'
Ví dụ 16. Đạo hàm của hàm số y = 2sin 3 .
x cos5x có biểu thức nào sau đây? A. 30cos3 . x sin 5x . B. 8
- cos8x + 2cos 2x . Trang 23
C. 8cos8x - 2cos 2x . D. 30
- cos3x + 30sin 5x . Đáp án C Lời giải
Cách 1: Ta có y = sin8x - sin 2x Þ y ' = 8cos8x - 2cos 2x Cách 2: y ' = 6cos3 .
x cos5x -10sin 3 . x sin 5x
= 3cos8x + 3cos 2x - 5cos 2x + 5cos8x
= 8cos8x - 2cos 2x
Nhận xét: Nếu dùng cách 1 sử dụng công thức biến đổi từ tích sang tổng rút gọn rồi sau đó việc
tính đạo hàm y ' sẽ đơn giản hơn. STUDY TIP 1
sin a cosb = [sin(a - b) + sin(a + b)] 2 1
cos a cosb = [cos(a - b) + cos(a + b)] 2 sin x + cos x a
Ví dụ 17. Đạo hàm của hàm số y = có biểu thức dạng
. Vậy giá trị a là: sin x - cos x 2 (sin x - cos x) A. a = 1. B. a = 2 - . C. a = 3. D. a = 2 . Đáp án B Lời giải
(cos x - sin x)(sin x - cos x) - (sin x + cos x)(cos x + sin x) 2 - y ' = = . 2 2 (sin x - cos x) (sin x - cos x) Þ a = 2 - STUDY TIP u
u 'v - uv ' Áp dụng quy tắc: ( )' = và 2 2
sin x + cos x =1 2 v v
Ví dụ 18. Đạo hàm của hàm số y = cot x là: 1 - 1 - 1 -sin x A. . B. . C. . D. . 2 sin x cot x 2 2sin x cot x 2 cot x 2 cot x Đáp án B Lời giải (cot x)' 1 - Cách 1: y ' = = 2 2 cot x 2sin x cot x
Cách 2: Học sin có thể sử dụng MTCT tính đạo hàm của hàm số y = cot x tại một điểm p
x = ta được kết quả 1 - 4 p
Với x = thay vào từng đáp án ta được đáp án B 4 STUDY TIP
Ví dụ 19. Đạo hàm của hàm số 2 3
y = cos (sin x) là biểu thức nào sau đây? A. 3 2 -sin(2sin x).sin . x cos x. B. 3 2 6s - in(2sin x).sin . x cos x . 3 2 C. 7s - in(2sin x).sin . x cos x . D. 3 2 3s - in(2sin x).sin . x cos x. Đáp án D Trang 24 Lời giải Cách 1: 2
y = cos u, với 3 u = sin x 3 2 Þ y ' = 3 - sin(2sin x).sin . x cos x Cách 2: Sử dụng MTCT
- Nhập biểu thức của hàm số 2 3
y = cos (sin x) ở đơn vị radian p
- Thay x = vào từng đáp án ta được đáp án D 4
Nhận xét: Với bài toán này việc sử dụng MTCT trở nên phức tạp hơn nhiều với việc giải tự luận thuần túy STUDY TIP cos x 4
Ví dụ 20. Đạo hàm của hàm số y = -
+ cot x là biểu thức nào sau đây? 3 3sin x 3 A. 3 cot x - . 1 B. 4 3cot x -1. C. 4 cot x -1. D. 4 cot x . Đáp án C Lời giải 1 4 1
Ta rút gọn hàm số đã cho 2 3
y = - cot x(1+ cot x) + cot x = - cot x + cot x 3 3 3 2 2 2 4
Þ y ' = cot x(1+ cot x) -1- cot x = cot x - 1 STUDY TIP
Học sinh cần biến đổi hàm số đã cho về dạng đơn giản hơn thì việc tính toán đạo hàm sẽ nhanh hơn.
Ví dụ 21. Đạo hàm của hàm số 2 2
y = tan x - cot x là: tan x cot x tan x cot x tan x cot x A. 2 + 2 . B. 2 - 2 . C. 2 + 2
. D. 2 tan x - 2cot x . 2 2 cos x sin x 2 2 cos x sin x 2 2 sin x cos x Đáp án A Lời giải 1 æ
1 ö 2 tan x 2cot x y ' = 2 tan . x - 2cot x - = + 2 ç 2 ÷ 2 2 cos x
è sin x ø cos x sin x ì 1 3
ïx .sin khi x ¹ 0
Ví dụ 22. Cho hàm số f (x) = í x
. Đạo hàm f '(x) là biểu thức nào sau đây? ïî0 khi x = 0 ì 1 1 ì 1 1 2
ïx .sin - x cos khi x ¹ 0 2 3
ï x .sin - x cos khi x ¹ 0
A. f '(x) = í x x .
B. f '(x) = í x x . ïî 1 - khi x = 0 1 ïî khi x = 0 ì 1 1 ì 1 1 2 3
ï x .sin + x cos khi x ¹ 0 2 3
ï x .sin - x cos khi x ¹ 0
C. f '(x) = í x x .
D. f '(x) = í x x . ïî0 khi x = 0 ïî0 khi x = 0 Đáp án D Lời giải 1 1 Với 2
x ¹ 0 Þ f '(x) = 3x sin - x cos x x
f (x) - f (0)
Với x = 0 Þ f '(x) = lim = 0 x®0 x Trang 25 ì 1 1 2 3
ï x .sin - x cos khi x ¹ 0 Þ f '(x) = í x x ïî0 khi x = 0 STUDY TIP
Bạn đọc nhận biết loại bài toán tính đạo hàm của hàm số có nhiều biểu thức:
- Với x ¹ x tính đạo hàm bằng công thức 0
- Với x = x tính đạo hàm bằng định nghĩa 0
Ví dụ 23. Đạo hàm của hàm số 2
y = 3tan x + cot 2x là: 2 2
3tan x(1+ tan x) - (1+ cot 2x) 2 2
3tan x(1+ tan x) - (1+ cot 2x) A. . B. . 2
3 3tan x + cot 2x 2
2 3tan x + cot 2x 2 2
3tan x(1+ tan x) + (1+ cot 2x) 2 2
3tan x(1+ tan x) - (1+ cot 2x) C. . D. . 2 3tan x + cot 2x 2 3tan x + cot 2x Đáp án D Lời giải 2 2
3tan x(1+ tan x) - (1+ cot 2x)
Ta có: y = u với 2
u = 3tan x + cot 2x Þ y ' = 2 3tan x + cot 2x STUDY TIP u '
Vận dụng giữa các quy tắc tính đạo hàm và đạo hàm của hàm số hợp ( u ) ' = 2 u cos x
Ví dụ 24. Cho hàm số f (x) = , chọn kết quả sai? 1+ 2sin x p 5 p A. f '( ) = - . B. f '(0) = 2 - 1 . C. f '( ) = - . D. f '(p ) = 2 - . 6 4 2 3 Đáp án A Lời giải -sin x - 2 p 5
Cách 1: Ta có f '(x) = Þ f '( ) = - 2 (1+ 2sin x) 6 8
Cách 2: Sử dụng MTCT tính đạo hàm của hàm số tại một điểm STUDY TIP
Ví dụ 25. Cho hàm số 2
y = f (x) - cos x với f (x) là hàm số liên tục trên ! . Trong 4 biểu thức dưới đây,
biểu thức nào xác định f (x) thỏa mãn y ' = 1 x " Î! ? 1 A. x + 1 cos 2x .
B. x - cos 2x .
C. x - sin 2x .
D. x + sin 2x . 2 2 Đáp án A Lời giải
Ta có: y ' = f '(x) + 2cos xsin x = f '(x) + sin 2x 1
y '(x) =1 Û f '(x) + sin 2x =1 Û f '(x) =1- sin 2x Þ f (x) = x + cos 2x 2 STUDY TIP
Bài toán ngược xác định hàm số f (x) khi biết được f '(x)
Ví dụ 26. Cho hàm số 6 6 2 2
f (x) = sin x + cos x + 3sin x cos x . Khi đó f '(x) có giá trị bằng bao nhiêu? A. 1. B. 2 . C. 0 . D. 1 - . Trang 26 Đáp án C Lời giải Cách 1: 5 5 3 3
f '(x) = 6sin xcos x - 6cos xsin x + 3(2sin xcos x - 2cos xsin ) x 4 4 2 2
= 6sin xcos x(sin x - cos x + cos x -sin x) 2 2 2 2
= 6sin xcos x(sin x - cos x + cos x -sin x) = 0.
Cách 2: Sử dụng MTCT tính đạo hàm tại điểm x bất kì ta được kết quả f '(x) = 0 STUDY TIP
Ta có thể rút gọn biểu thức rồi tính đạo hàm sau 1
Ví dụ 27. Cho hàm số 4 4
f (x) = sin x + cos ;
x g(x) = cos 4x . Mệnh đề nào sau đây là đúng? 4
A. f '(x) - g '(x) = 1 0.
B. f (x) = g(x) + . 4
C. 2 f '(x) - 3g '(x) =1.
D. 3 f '(x) + 2g '(x) = 1 - . Đáp án A Lời giải Ta có: 3 3 2 2
f '(x) = 4sin xcos x + 4cos x(-sin ) x = 4sin xcos ( x sin x - cos ) x = -sin 4x .
g '(x) = -sin 4x.
Vậy f '(x) - g '(x) = 0 STUDY TIP 3
Dùng biến đổi lượng giác thì ta được f (x) = g(x) + do 2 hàm số khác nhau một hằng số nên cùng 4 đạo hàm.
Ví dụ 28. Cho hàm số 2
y = cos x + sin x. Phương trình y ' = 0 có bao nhiêu nghiệm thuộc khoảng (0;p ) A. 1 nghiệm. B. 2 nghiệm. C. 3 nghiệm. D. 4 nghiệm. Đáp án C Lời giải y ' = 2
- cos xsin x + cos x = cos x(1- 2sin x) é p x = + kp ê 2 écos x = 0 ê p y ' = 0 ê ê Û 1 Û x = + k2p ;(k Î!) êsin x = ê 6 ë 2 ê 5p êx = + k2p êë 6 p p 5p Vì x (0;p ì ü Î ) Þ x Î í ; ;
ý. Vậy có 3 nghiệm thuộc khoảng (0;p ) î 6 2 6 þ STUDY TIP
Loại bài toán kết hợp giữa tính đạo hàm và giải phương trình lượng giác
Ví dụ 29. Cho hàm số y = (m +1)sin x + mcos x - (m + 2)x + . T
1 ìm giá trị của m để y ' = 0 có nghiệm? ém £ 1 - A. . B. m ³ 2 . C. 1 - £ m £ 3. D. m £ 2 - . ê ëm ³ 3 Trang 27 Đáp án A Lời giải
y ' = (m +1)cos x - msin x - (m + 2)
Phương trình y ' = 0 Û (m +1)cos x - msin x = (m + 2)
Điều kiện phương trình có nghiệm là 2 2 2
a + b ³ c ém £ 1 - 2 2 2 2
Û (m +1) + m ³ (m + 2) Û m - 2m - 3 ³ 0 Û ê ëm ³ 3 STUDY TIP
Phương trình bậc nhất với sin x và cos x a sin x + b cos x = c có nghiệm 2 2 2
Û a + b ³ c
C. BÀI TẬP RÈN LUYỆN KỸ NĂNG
Dạng 1: Đạo hàm của hàm đa thức – hữu tỷ - căn thức và hàm hợp
Câu 19. Đạo hàm của hàm số 3 2
y = 2x - 9x +12x - 4 là: A. 2 5x -11x - 4. B. 2 6x -18x +12. C. 2 6x +18x -12. D. 2 6x - 9x -12.
Câu 20. Đạo hàm của hàm số 3 2 2 3 2
y = -x + 3mx + 3(1- m )x + m - m (với m là tham số) bằng: A. 2 2 3
- x + 6mx +1- m . B. 2
-x + 3mx -1- 3m. C. 2 2
3x - 6mx - 3+ 3m . D. 2 2 3
- x + 6mx + 3- 3m .
Câu 21. Đạo hàm của hàm số 2 2 2
y = (x +1) (3+ 5x ) bằng biểu thức có dạng 5 3
ax + bx + cx . Khi đó
a - b + c bằng: A. 0. B. 1. C. 2. D. 5.
Câu 22. Đạo hàm của hàm số 2 3 4
y = (x +1)(x + 2)(x + 3) bằng biểu thức có dạng 8 6 5 4 3 2
ax + bx + cx +15x + dx + ex + gx. Khi đó a - b + c - d + e - g bằng: A. 0. B. 2. C. 3. D. 5. 2x +1 a
Câu 23. Đạo hàm của hàm số y =
bằng biểu thức có dạng
. Khi đó a nhận giá trị nào sau x -1 2 (x -1) đây? A. a = 2 - . B. a = 1 - . C. a = 3 - . D. a = 3 . 2 -x + 3x -3 2 ax + bx
Câu 24. Đạo hàm của hàm số y =
bằng biểu thức có dạng . Khi đó . a b bằng: 2(x -1) 2 2(x -1) A. 2 - . B. 1 - . C. 4 . D. 6 . 2 2x + 3x -1 2
ax + bx + c
Câu 25. Đạo hàm của hàm số y =
bằng biểu thức có dạng
. Khi đó a + b + c 2 x - 5x + 2 2 (x - 5x + 2) bằng: A. 1 - . B. 2 . C. 3 . D. 2 - . 2 -x + 2x + 3 4 3 2
ax + bx + cx + dx + e
Câu 26. Đạo hàm của hàm số y =
bằng biểu thức có dạng . Khi đó 3 x - 2 3 2 (x - 2)
a + b + c + d + e bằng: A. 12 - . B. 10 - . C. 8. D. 5. Trang 28 2
ax + bx + c
Câu 27. Đạo hàm của hàm số 2
y = (x - 2) x +1 biểu thức có dạng . Khi đó . a . b c bằng: 2 x +1 A. 2 - . B. 4 - . C. 6 - . D. 8 - .
Câu 28. Đạo hàm của hàm số 6 4 2
y = (x - 3x ) bằng biểu thức nào sau đây? A. 11 9 7
12x - 52x + 64x . B. 11 9 7
12x - 73x + 49x . C. 11 9 7
12x - 62x + 70x . D. 11 9 7
12x - 60x + 72x . ax + b a
Câu 29. Đạo hàm của hàm số 2
y = 5x - 2x +1 biểu thức có dạng . Khi đó T = bằng: 2 5x - 2x +1 b A. T = 5 - . B. T = 5 . C. T = 10 - . D. T = 10 . 1
Câu 30. Đạo hàm của hàm số y =
bằng biểu thức nào sau đây? x +1 - x -1 1 1 A. - . B. . 2 ( x +1 + x -1) 2 x +1 + 2 x -1 1 1 1 1 C. - . D. + . 4 x +1 4 x -1 2 x +1 2 x -1 x -1 ax + b
Câu 31. Đạo hàm của hàm số y = biểu thức có dạng . Khi đó P = . a b bằng: 2 x +1 2 3 (x +1) A. P = 1 . B. P = 1 - . C. P = 2 . D. P = 2 - . 1 x + x -
Câu 32. Đạo hàm của hàm số x y =
bằng biểu thức nào sau đây?. x - x 2 4 x - 2x - 3 2 4 x + 2x - 3 2 x - 2x - 2 2 x + 2x +1 A. . B. . C. . D. . 3 2
2 x (x - x) 2
x x(x - x) 2
2x x(x - x) 2
2x x(x - x) 2 3x + 2x +1
Câu 33. Cho hàm số f (x) =
. Giá trị f '(0) là: 2 2 3x + 2x +1 1 A. 0 . B. 1. C. . D. Không tồn tại. 2 1- x 1
Câu 34. Cho hàm số f (x) =
thì f '(- ) có giá trị là: 2x +1 2 A. 0 . B. 3 . C. 3 - . D. Không tồn tại. x
Câu 17: Cho f (x) = thì f ¢(0)
(x - )1(x -2)!(x -2017) 1 A. . B. 2017! 1 . C. - . D. 2017 - !. 2017! 2017! 2 ìx khi x ³1
Câu 18: Cho hàm số f (x) = í . Hãy chọn đáp án sai:
î2x -1 khi x <1 A. f ¢( ) 1 =1.
B. Hàm số có đạo hàm tại x = . 1 0 Trang 29 ì x khi x ³
C. Hàm số liên tục tại x = . 1
D. f ¢( x) 2 1 = í . 0 îx khi x <1
Câu 19: Cho hàm số f (x) 2
= x + 4 - x . Tập các giá trị của x để f ¢(x) > 0 là: A. ( ;0 -¥ ). B. é-2; 2 ( 2; - 2 ) ë ). C. ( 2; - 2]. D. x
Câu 20: Cho hàm số f (x) =
. Tập nghiệm của bất phương trình f ¢(x) £ 0 là: 3 x +1 æ 1 ö é 1 ö æ 1 ù é 1 ö A. ç ; -¥ ÷. B. ; +¥ . C. ; -¥ . D. ; +¥ . ç 2 ÷ ê ÷ ç ú ê ÷ è ø ë 2 ø 3 è 2 û 3 ë 2 ø
Câu 21: Đạo hàm của hàm số y = x + x + x là biểu thức nào sau đây? 1 é 1 1 ù æ ö A. 1 ê + . 1+ ú. ç ÷
2 x + x + x êë 2 x + x è 2 x øúû 1 é 1 1 ù æ ö B. 1 ê + . 1+ ú . ç ÷
x + x + x êë x + x è x øúû 1 é 1 1 ù æ ö C. 1 ê + . 1+ ú. ç ÷
x + x + x êë 2 x + x è 2 x øúû 1 é 1 1 ù æ ö D. 1 ê - . 1+ ú . ç ÷
2 x + x + x êë 2 x + x è 2 x øúû
Câu 22: Cho f (x) 5 3
= x + x - 2x - . T 3 ính f ¢( ) 1 + f ¢(- ) 1 + 4 f ¢(0). A. 4 . B. 5 . C. 6 . D. 7 . 1 1
Câu 23: Cho hàm số f (x) 2 = +
+ x . Tính f ¢( ) 1 . x x 1 A. . B. 1. C. 2 . D. 3 . 2 3 æ 1 ö
Câu 24: Cho hàm số y = x -
. Hàm số có đạo hàm f ¢(x) bằng: ç ÷ è x ø 3 æ 1 1 1 ö 3 1 A. x + + + .
B. x x - 3 x + - . ç 2 2 ÷ è x x x x x ø x x x 3 æ 1 1 1 ö 3 æ 1 1 1 ö C. - x + + - . D. x - - + . ç 2 2 ÷ ç ÷ è x x x x x ø 2 2 è x x x x x ø 2 æ1- x ö
Câu 25: Đạo hàm của hàm số y = ç
÷ bằng biểu thức nào sau đây? ç1 x ÷ + è ø Trang 30 1- x 1 1- x 1 - A. 2 . . B. 2 . . 1+ x (1+ x)2 1+ x x (1+ x)2 æ1- x ö 1 - æ1- x ö 1 C. ç ÷. . D. 2ç ÷. . ç1 x ÷ + ç ÷ è ø x (1+ x)2 1+ x è ø x (1+ x)2 3 æ 2x +1ö
Câu 26: Cho hàm số y =
. Đạo hàm y¢ bằng biểu thức nào sau đây? ç ÷ è x -1 ø 3(2x + )2 1 (2x + )2 1 -(2x + )2 1 -9(2x + )2 1 A. . B. . C. . D. . (x - )4 1 (x - )4 1 (x - )4 1 (x - )4 1
Câu 27: Cho hàm số y = (m - ) 3 x - (m + ) 2 1 3
2 x - 6(m + 2) x + . T
1 ập giá trị của m để y¢ ³ 0 x " Î ! là A. [3;+¥). B. [1;+¥). C. Æ . D. é4 2; +¥ ë ). 2 ì x + x +1 ï khi x ³ 0
Câu 28: Cho hàm số f ( x) = í x +1
. Tìm a , b để hàm số f (x) có đạo hàm trên ! . ï 2
îx + ax + b khi x < 0
A. a = 0 , b = 11.
B. a = 10 , b = 11.
C. a = 20 , b = 21.
D. a = 0 , b = 1. 2 2 mx mx
Câu 29: Cho hàm số f (x) = - +
- (3- m) x + 2. Tìm m để f ¢(x) = 0 có hai nghiệm phân biệt 3 2 cùng dấu. é 3 ù æ12 ö é 3 ö A. m Î ; 2 . B. mÎ(- ;3 ¥ ). C. m Î ;3 . D. m Î ; +¥ . ê ç ÷ ê ÷ 2 ú ë û è 5 ø ë 2 ø + x - - x
Câu 30: Cho hàm số f ( x) 1 1 =
. Đạo hàm f ¢(x) là biểu thức nào sau đây? 1+ x + 1- x ì 1 ì 2 ï-
khi x < -1, x > 1 ï
khi x < -1, x > 1 A. 2 í x . B. 2 í x . 1 ïî
khi -1 < x < 1 1 ïî khi -1 £ x £ 1 ì 1 ì 3 ï khi x < 1, - x > 1 ï-
khi x < -1, x > 1 C. 2 í x . D. 2 í x . ïî 1 - khi -1 £ x £ 1 ïî2
khi -1 < x < 1
Dạng 2: Đạo hàm các hàm số lượng giác Câu 31: Hàm số 2 y = cos .
x sin x có đạo hàm là biểu thức nào sau đây? A. x( 2 sin 3cos x + ) 1 . B. x( 2 sin 3cos x - ) 1 . C. x( 2 sin cos x - ) 1 . D. x( 2 sin cos x + ) 1 . 1
Câu 32: Hàm số y = (1+ tan x)2 có đạo hàm là biểu thức nào sau đây? 2 Trang 31 A. ( + )2 1 tan x . B. 2 1+ tan x. C. ( + x)( 2 1 tan
1+ tan x). D. 1+ tan x. cos x
Câu 33: Đạo hàm của hàm số y =
là biểu thức nào sau đây? 2 2sin x 2 1+ sin x 2 1+ cos x 2 1+ sin x 2 1+ cos x A. - . B. - . C. . D. . 3 2sin x 3 2sin x 3 2sin x 3 2sin x x æ p ö æ p ö
Câu 34: Cho hàm số f ( x) cos = . Giá trị của f ¢ - f ¢ - là ç ÷ ç ÷ 1- sin x è 6 ø è 6 ø 4 4 8 8 A. . B. . C. . D. . 3 9 9 3
sin x - x cos x 2
ax + bx + c
Câu 35: Hàm số y = có y¢ =
. Hỏi T = a + b + c bằng:
cos x + xsin x ( x + x x)2 cos sin A. 1. B. 2 . C. 0 . D. 1 - . x Câu 36: Cho hàm số 2 y = cos 2 . x sin . Xét hai kết quả: 2 x x 1 (I) 2 y¢ = 2 - sin 2 . x sin + sin . x cos 2x (II) 2 y¢ = 2sin 2 . x sin + sin . x cos 2x. 2 2 2 Cách nào đúng? A. Chỉ (I). B. Chỉ (II).
C. Cả 2 đều đúng.
D. Không có cách nào. p
Câu 37: Đạo hàm của hàm số 2
y = cot (cos x) + sin x - là biểu thức nào sau đây? 2 1 cos x 1 cos x A. 2c - ot (cos x) + . B. 2cot (cos x) sinx + . 2 sin (cos x) p 2 sin (cos x) p 2 sin x - 2 sin x - 2 2 1 cos x 1 cos x C. 2c - ot (cos x) + . D. 2cot (cos x) sinx + . 2 sin (cos x) p 2 sin (cos x) p sin x - sin x - 2 2 sin x x
Câu 38: Đạo hàm của hàm số y = +
là biểu thức nào sau đây? x sin x æ 1 1 ö æ 1 1 ö
A. ( x cos x - sin x) - .
B. ( x cos x + sin x) + . ç 2 2 ÷ ç ÷ è x sin x ø 2 2 è x sin x ø æ 1 1 ö æ 1 1 ö
C. ( xsin x - cos x) - .
D. ( xsin x + cos x) - . ç 2 2 ÷ ç ÷ è x sin x ø 2 2 è x sin x ø 1
Câu 39: Đạo hàm của hàm số y =
là biểu thức nào sau đây? sin x Trang 32 -cot x cot x cot x -cot x A. . B. . C. . D. . sin x sin x sin x sin x
Câu 40: Cho hàm số y = ( 2 x) ( 2 sin cos
.cos sin x). Đạo hàm y¢ = .s a in 2 .
x cos(cos2x). Giá trị của a là
số nguyên thuộc khoảng nào sau đây? A. (0;2). B. ( 1 - ;5). C. ( 3; - 2). D. (4;7).
Câu 41: Cho hàm số f (x) có đạo hàm với mọi x và thỏa mãn f (2x) = 4cos .
x f (x) - 2x. Tính f ¢(0). A. f ¢(0) = 0. B. f ¢(0) = . 1 C. f ¢(0) = 2 - . D. f ¢(0) = 3. x
Câu 42: Cho hàm số f (x) cos =
. Biểu diễn nghiệm của phương trình lượng giác f ¢(x) = 0 trên cos 2x
đường tròn lượng giác ta được mấy điểm phân biệt? A. 1 điểm. B. 2 điểm. C. 4 điểm. D. 6 điểm.
Câu 43: Cho hàm số y = cot 2x . Hệ thức nào sau đây là đúng? A. 2
y¢ + 2y + 2 = 0. B. 2
y¢ - 2y - 2 = 0. C. 2
y¢ + 3y + 5 = 0. D. 2
y¢ + 3y + 7 = 0. ì n 1 ïx .sin khi x ¹ 0
Câu 44: Tìm số nguyên dương n sao cho hàm số f ( x) = í x có đạo hàm trên ! . ïî0 khi x = 0 A. n = 1. B. n = 2 . C. n ³ 2 . D. n = 3.
Câu 45: Cho hàm số f (x) 2
= sin x + sin 2x. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của f ¢(x) trên ! .
A. m = - 2 , M = 2 . B. m = 1 - , M =1. C. m = 2 - , M = 2 .
D. m = - 5 , M = 5 .
Câu 46: Cho hàm số f (x) = -cos x +sin x -cos2x. Phương trình f ¢(x) =
1 tương đương với phương trình nào sau đây? A. sin x = 0 .
B. sin x -1 = 0 . C. (sin x - ) 1 (cos x - ) 1 = 0. D. cos x = 0 .
Câu 47: Cho hàm số f (x) 2 2
= sin x +3cos x. Tập giá trị của hàm số f ¢(x) trên ! là: A. [ 4; - 4]. B. [ 2; - 2]. C. [ 1 - ; ] 1 . D. [ 3; - ]3. 3 cos x
Câu 48: Cho hàm số f (x) 3 = 2
+ sin x - 2cos x - 3sin x. Biểu diễn nghiệm của phương trình 3
lượng giác f ¢(x) trên đường tròn ta được mấy điểm phân biệt? A. 1 điểm. B. 2 điểm. C. 4 điểm. D. 6 điểm.
Câu 49: Trong các hàm số dưới đây, hàm số nào có đạo hàm là 2 sin x ? 3 sin x x 3 sin x x A. y = 1 .
B. y = + sin 2x.
C. y = x - 1 .
D. y = - sin 2x . 3 2 4 3 2 4 Trang 33
Câu 50: Hàm số nào sau đây có đạo hàm luôn bằng 0 ? A. 2 y =1- sin x. B. 2 2
y = sin x - cos x. C. 2 2
y = sin x + cos x. D. y = cos 2x.
Câu 51: Hàm số nào sau đây có đạo hàm y¢ = . x sin x ?
A. y = x cos x .
B. y = x cos x - sin x. 1
C. y = sin x - x cos x. D. 2
y = x .sin x . 2
Câu 52: Xét hàm số f (x) 3
= cos 2x . Chọn câu sai: æ p ö 2 - sin 2x A. f = 1 - .
B. f ¢( x) = . ç ÷ è 2 ø 3 2 3 cos 2x æ p ö C. f ¢ = . 1 D. 2
3y .y¢ + 2sin 2x = 0. ç ÷ è 2 ø 1 1 1 1 1 1 x
Câu 53: Cho hàm số y = + +
+ cos x với xÎ(0;p ) có y¢ là biểu thức có dạng . a sin . 2 2 2 2 2 2 8
Khi đó a nhận giá trị nào sau đây: 1 1 1 A. . B. - 1 . C. . D. - . 4 4 8 8 æ p ö æ p ö æ 2p ö æ 2p ö
Câu 54: Cho hàm số f (x) 2 2 2 2 2 = cos - x + cos + x + cos - x + cos + x - 2sin x . ç ÷ ç ÷ ç ÷ ç ÷ è 3 ø è 3 ø è 3 ø è 3 ø
Hàm số có f ¢(x) bằng: A. 6 . B. 2sin 2x . C. 0 . D. 2 cos 2x .
Hướng dẫn giải chi tiết
Dạng 1: Đạo hàm của hàm đa thức Câu 1: Đáp án B. 2
y¢ = 6x -18x +12. Câu 2: Đáp án D. 2
y¢ = - x + mx + ( 2 3 6 3 1- m ). Câu 3: Đáp án A.
y¢ = (x + ) + x ( + x ) + (x + )2 2 2 2 2 1 2 . 3 5 1 .10x = ( 3x + x)( 2 + x ) 5 3 4 4 3 5
+10x + 20x +10x 5 3
= 30x + 52x + 22 . x
Þ a - b + c = 0 . Câu 4: Đáp án C. Trang 34 y¢ = x( 3 x + )( 4 x + ) 2
+ x ( 2x + )( 4x + ) 3 + x ( 2x + )( 3 2 2 3 3 1 3 4 1 x + 2) = x( 7 4 3
x + x + x + ) 2 + x ( 6 4 2
x + x + x + ) 3 + x ( 5 3 2 2 2 3 6 3 3 3 4
x + x + 2x + 2) 8 6 5 4 3 2
= 9x + 7x +12x +15x +8x + 9x +12x .
Þ a - b + c - d + e - g = 3. Câu 5: Đáp án C. Câu 6: Đáp án A. ( 2 - x + 3)(x - ) 1 - ( 2 -x + 3x - 3) 2 -x + 2x y¢ = = 2( x - )2 1 2( x - )2 1 . Câu 7: Đáp án D. ( 2 6x + 3)( 2 x - 5x + 2) -( 3 2x + 3x - ) 1 (2x -5) 2 13 - x +10x +1 y¢ = ( = x - 5x + 2)2 (x -5x+2)2 2 2 .
Þ a + b + c = -2 . Câu 8: Đáp án A. ( 2 - x + 2)( 3 x - 2) 2 -3x ( 2 -x + 2x + 3) 4 3 2
x - 4x - 9x + 4x - 4 y¢ = ( = x - 2)2 (x -2)2 3 3
Þ a + b + c + d + e = -12 Câu 9: Đáp án B. 2 2x 2x - 2x +1 2
y¢ = x +1 + (x - 2). = 2 2 2 x +1 x +1 . Câu 10: Đáp án D. y¢ = ( 6 4 x - x )( 5 3 x - x ) 11 9 7 2 3 6 12
=12x -60x + 72x . Câu 11: Đáp án A. 10x - 2 5x -1 a y¢ = = Þ T = = 5 - 2 2 2 5x - 2x +1 5x - 2x +1 b . Câu 12: Đáp án C. 1
Nhân liên hợp ta có: y = ( x +1 - x -1) Þ 1 1 y¢ = - . 2 4 x +1 4 x -1 Câu 13: Đáp án A. 2 x x +1 - ( x - ) 1 . 2 2 2 x +1
x +1- x + x x +1 y¢ = = = 2 x +1 (x + )3 1 (x + )3 2 2 1 . Þ P = . a b = 1. Câu 14: Đáp án A. Trang 35 æ 1 1 ö æ 1 öæ 1 ö 1+ +
x - x - x + x - 1- ç 2 ÷ ( ) ç ÷ç ÷ è 2 x x ø è x øè 2 x y ø ¢ = (x- x)2 2 3 - - x 2 x 2x x 4 x - 2x - 3 = = . (x- x)2
2x x (x - x)2 Câu 15: Đáp án C. 4 3 2
9x + 6x - 9x + 8x + 4
Cách 1: Tính f ¢( x) = Þ f ¢ 0 =1. 4( 3 2 3x + 2x + ) ( ) 3 2 1 3x + 2x +1
Cách 2: Dùng MTCT ta được kết quả. Câu 16: Đáp án D. Câu 17: Đáp án C.
x 1 x 2 ! x 2017
x é x 1 x 2 ! x 2017 ¢ - - - - - - - ù Ta có: f ( x) ( )( ) ( ) ë( )( ) ( )û ¢ = é(x - )
1 ( x - 2)!( x - 2017) 2 ù ë û - - ! - Þ f ¢( ) ( )1( 2) ( 2017) 1 0 = = - . éë(- ) 1 ( 2 - )!( 2 - 017) 2 ù 2017! û Câu 18: Đáp án A. Ta có: f ( ) 1 = ,
1 lim f (x) =1 = lim f (x) Þ Hàm số liên tục tại x =1. x 1+ x 1- ® ®
Khi x > 1: f ¢(x) = 2x.
x < 1: f ¢(x) = 2.
f (x) - f ( ) 2 1 x -1
f (x) - f ( ) 1 2(x - ) 1
Với x = 1, ta xét: lim = lim = 2; lim = lim = 2. x 1+ - x 1 x 1 + ® ® x -1 x 1- - x 1 x 1 - ® ® x -1 Vậy f ¢( ) 1 = 2. Câu 19: Đáp án B.
Điều kiện: x Î[ 2; - 2]. é 2 - £ x < 0 ¢( ) x f x = 1- ; f ¢(x) 2
> 0 Û 4 - x > x Û ê Û 2 - £ x < 2 . 2 4 - x ë0 £ x < 2 Câu 20: Đáp án D. 3 3 - + ì- + £ f ¢(x) 2x 1 2x 1 0 1 =
Þ f ¢ x £ 0 Û í Û x ³ 2 ( ) . (x + ) 3 3 1 îx ¹ 1 - 2 Câu 21: Đáp án A.
Ta có: y = u với u = x + x + x . Trang 36 1 é 1 ù é ù ¢ æ ö Þ y¢ = ê + (x+ x) 1 1 1 1 ú = 1 ê + 1+ ú . ç ÷
2 x + x + x êë 2 x + x
úû 2 x + x + x êë 2 x + x è 2 x øúû Câu 22: Đáp án A. Ta có: f ¢(x) 4 2
= 5x +3x - 2 Þ f ¢( ) 1 + f ¢(- ) 1 + 4 f ¢(0) = 4. Câu 23: Đáp án A. 1 1 1
Ta có: f ¢(x) = - - + 2x Þ f ¢ 1 = 2 ( ) . x 2x x 2 Câu 24: Đáp án D. 2 æ 1 ö æ 1 1 ö 3 æ 1 1 1 ö
Ta có: f ¢( x) = 3 x - + = x - - + . ç ÷ ç ÷ ç 2 ÷ è
x ø è 2 x 2x x ø 2 è x x x x x ø Câu 25: Đáp án B. - x Ta có: 2 y = 1 u với u = . 1+ x 1 - ¢ æ - ö æ - ö æ - ö ( + x) 1 1 - (1- x) 1 x 1 x 1 x 2 x 2 x æ1- x ö 1 - y¢ = 2.ç ÷.ç ÷ = 2.ç ÷. = ç ÷
ç1 x ÷ ç1 x ÷ ç1 x ÷ è ø è ø è ø ( + ) 2. . 2 ç1 ÷ + + + 1 + x x è ø x (1+ x)2 . Câu 26: Đáp án D. x + 3 - 9 - (2x + )2 1 Ta có: 3 y = 2 1 u , u = , u¢ = Þ y¢ = . x -1 (x - )2 1 (x - )4 1 Câu 27: Đáp án C. y¢ = é(m - ) 2 3
1 x - 2(m + 2) x - 2(m + 2)ù. ë û
y¢ ³ Û (m- ) 2 0
1 x - 2(m+ 2) x - 2(m+ 2) ³ 0 (1) Với m = 1 thì ( ) 1 Û 6
- x - 6 ³ 0 Û x £ 1 - Þ m = 1 (loại). ìa > 0 ìm >1 ï Với m ¹ 1Þ ( ) 1 đúng x " Î! Û í Û í Û m vô nghiệm. îD £ 0 ( ï m + 2 î )3m £ 0 Câu 28: Đáp án D.
Với x ¹ 0 hàm số luôn có đạo hàm.
Để hàm số có đạo hàm trên ! thì hàm số phải có đạo hàm tại x = 0 . lim f (x) = ,
1 lim f (x) = b Þ b = . 1 x 0+ ® x 0- ®
Để hàm số liên tục tại x = 0 Þ b = 1. 2 x + x +1
f (x) - f ( ) -1 0
f (x) - f (0) 2
x + ax + b -1 Xét x +1 lim = lim = 0; lim = lim = a. x 0+ x - 0 x 0+ ® ® x x 0- x - 0 x 0- ® ® x Trang 37
Þ a = 0 . Vậy a = 0 , b =1. Câu 29: Đáp án C. f ¢(x) 2 = m
- x + mx -(3-m); f ¢(x) 2 = 0 Û m
- x + mx -(3-m) = 0 ( ) 1 . ì ì ¹ ïm ¹ 0 a 0 ï ï 12 Theo bài ra ta có: 2 íD > 0 Û 5
í m -12m > 0 Û < m < 3. 5 ïP 0 ï > 3 - m î ï > 0 î m Câu 30: Đáp án A. ì1 ï khi x < 1, - x >1
Lập bảng dấu ta được: f ( x) = í x .
ïîx khi-1£ x £1 1 - Với x < 1
- hoặc x >1 Þ f ¢(x) = - . 2 x - Với 1
- < x <1Þ f ¢(x) = . 1
Ta có lim f (x) = lim f (x) = -
1 nên hàm số liên tục tại x = 1 - . x 1- x 1+ ®- ®-
f (x) - f (- ) 1
f (x) - f (- ) 1 Xét lim = - , 1 lim =
1 nên hàm số không có đạo hàm tại x = 1 - . x 1- ®- x +1 x 1+ ®- x +1
Bằng cách tương tự ta cũng chỉ ra được hàm số không có đạo hàm tại x = 1. ì1 ï khi x < 1, - x >1
Vậy f ( x) = í x .
ïîx khi-1< x <1
Dạng 2: Đạo hàm các hàm số lượng giác Câu 31: Đáp án B. 2 3 y¢ = x x - x = x ( 2 2sin .cos sin sin 3cos x - ) 1 . Câu 32: Đáp án C. y ( x)( x)¢ ¢ = + + = ( + x) 2 1 tan 1 tan 1 tan 1+ tan x . ( ) Câu 33: Đáp án B. 3 2 2 2 -sin x - 2sin . x cos . x cos x sin x + 2cos x 1+ cos x y¢ = = - = - . 4 3 3 2sin x 2sin x 2sin x Câu 34: Đáp án A. æ p ö æ p ö Ta có: f ¢( x) 1 4 = Þ f ¢ - f ¢ - = . ç ÷ ç ÷ 1- sin x è 6 ø è 6 ø 3 Câu 35: Đáp án A. Trang 38
xsin x (cos x + xsin x) - xcos x(sin x - xcos x) 2 x y¢ = =
Þ a = 1, b = 0, c = 0.
(cos x + xsin x)2
(cos x + xsin x)2
Vậy T = a + b + c = 1. Câu 36: Đáp án D. 2 x 1 y¢ = 2 - sin 2 . x sin + sin . x cos 2x . 2 2 Câu 37: Đáp án B. p ¢ æ ö sin x - ç ÷ ¢ =
( x)éë ( x) ¢ è 2 ø x y 2cot cos cot cos ù + = 2cot û (cos x) 1 cos + . 2 p sin (cos x) p 2 sin x - 2 sin x - 2 2 Câu 38: Đáp án A. .
x cos x - sin x sin x - x cos x æ ö y¢ = + = (x x - x) 1 1 .cos sin - . 2 2 ç 2 2 ÷ x sin x è x sin x ø Câu 39: Đáp án A. 1 2 - sin . x cos x cot x Ta có: y = nên y¢ = = - . 2 sin x 2 2 sin sin . sin x x x Câu 40: Đáp án C
𝑦! = −2 sin 𝑥 . cos 𝑥. cos(cos"𝑥) .cos(sin"𝑥) − 2 sin 𝑥 . cos 𝑥.sin(cos"𝑥).sin(sin"𝑥)
= −sin(2𝑥).cos(cos"𝑥 − sin"𝑥) = −sin(2𝑥).cos(cos 2𝑥) Þ a = 1 - . Câu 41. Đáp án B.
Lấy đạo hàm 2 vế ta có: 2 f ¢(2x) - 4sin . x f (x) + 4cos . x f ¢(x) - 2
Thay 𝑥 = 0 ⇒ 2 ∙ 𝑓!(0) = 4 ∙ 𝑓!(0) − 2 ⇔ 𝑓!(0) = 1. Câu 42. Đáp án B. 1 -sin .
x cos 2x - cos x (-sin 2x) f ¢( x) 2 cos 2x sin x = = 3 cos 2x cos 2x
𝑓!(𝑥) = 0 ⇒ sin𝑥 = 0 ⇔ 𝑥 = 𝑘𝜋, 𝑘 ∈ 𝑍.
Ta biểu diễn được 2 điểm phân biệt trên đường tròn lượng giác. Câu 43. Đáp án A. y¢ = - ( 2 2 1+ cot 2x). Do đó: 2 y¢ + y + = - ( 2 + x) 2 2 2
2 1 cot 2 + 2cot 2x + 2 = 0 Câu 44. Đáp án C.
Ta có: lim 𝑓(𝑥) = lim =𝑥& ∙ sin '> = 𝑓(0) = 0 #→% #→% #
lim ((#)+((%) = lim =𝑥&+' ∙ sin '> = 𝑓(0) = 0 (1) #→% #+% #→% # Trang 39
Với n = 1 thì giới hạn ( )
1 không tồn tại và 𝑛 ≥ 2 thì: lim =𝑥&+' ∙ sin '> = 0 . #→% #
Vậy hàm số có đạo hàm trên R khi 𝑛 ≥ 2. Câu 45. Đáp án D. f ¢(x) = 2sin .
x cos x + 2cos 2x = sin 2x + 2cos 2x
Đặt t = sin 2x + 2cos x.
Điều kiện phương trình có nghiệm là: 1" + 2" ≥ 𝑡" ⟺ −√5 ≤ 𝑡 ≤ √5.
Vậy M = 5,m = - 5 . Câu 46. Đáp án C.
𝑓!(𝑥) = sin𝑥 + cos𝑥 + 2sin2𝑥
f ¢(x) =1Û sin x + cos x + 2sin 2x = 1 Đặt t = x + x ( t £ ) 2 sin cos
2 Þ sin 2x = t -1 é t = 1 Khi đó phương trình 2 2t t 3 0 ê Û + - = Û 3 êt = - (l) ë 2 𝑥 = 𝑘2𝜋
Với 𝑡 = 1 ⇔ sin𝑥 + cos𝑥 = 1 ⇔ √2 sin =𝑥 + ,> = 1 ⇔ G -
𝑥 = , + 𝑘2𝜋 (𝑘 ∈ 𝑍) . "
Nghiệm trên cũng là nghiệm của phương trình (sin x- ) 1 (cos x- ) 1 = 0. Câu 47. Đáp án B. f ¢(x) = 2s - in 2x Þ 2 - £ f (x) £ 2
Vậy tập giá trị của hàm số f ¢(x) là [ 2; - 2]. Câu 48. Đáp án B. f ¢(x) 3 3
= 2sin x -3cos x f ¢(x) 3 3 3 3
= 0 Û tan x = Û tan x = . 2 2
Vậy có hai điểm biểu diễn nghiệm trên đường tròn lượng giác. Câu 49. Đáp án D. 𝑥 1 1 1
𝑦 = − sin2𝑥 ⇒ 𝑦! = − cos2𝑥 = sin"𝑥 2 4 2 2 Câu 50. Đáp án C. 2 2
y = sin x + cos x =1Þ y¢ = 0 x " . Câu 51. Đáp án C.
y = sin x - cos x Þ y¢ = cos x -(cos x - xsin x) = xsin x Câu 52. Đáp án C. - f (x) 2sin 2x 3 3
= cos 2x Þ f (x) 2
= cos 2x Þ 3. f (x). f (x) = (cos2x)¢ ¢ Þ f ¢(x) = 3 2 3 cos 2x æ p ö Nên B đúng. Vì 3 f = cosp = 1 - nên C sai. ç ÷ è 2 ø Câu 53. Đáp án D. Trang 40 1 1 x x Ta có: 2 + cos x = cos = cos 2 2 2 2 x x 1 x
Tương tự ta có biểu thức tiếp theo: 2 y = cos = cos Þ y¢ = - sin 8 8 8 8 Câu 54. Đáp án C. æ p ö æ p ö æ p ö æ p ö f ¢(x) 2 2 4 4 = sin - 2x - sin + 2x + sin - 2x - sin + 2x - 2sin 2x ç ÷ ç ÷ ç ÷ ç ÷ è 3 ø è 3 ø è 3 ø è 3 ø 2p 4p æ 1 1 ö = 2 - cos .sin 2x - 2cos
.sin 2x - 2sin 2x = + -1 2sin 2x = 0 ç ÷ 3 3 è 2 2 ø
VI PHÂN. ĐẠO HÀM CẤP CAO A. LÝ THUYẾT
1. Vi phân của hàm số a) Định nghĩa
Cho hàm số y = f (x) xác định trên ( ;
a b) và có đạo hàm tại xÎ( ;
a b). Ta gọi tích f ¢(x). x D
(hoặc y .¢Dx ) là vi phân của hàm số y = f (x) tại x ứng với số gia x D .
Kí hiệu: df (x) hoặc dy.
Vậy ta có: dy = y .¢ x
D hoặc df (x) = f ¢(x). x D .
b) Ứng dụng của vi phân vào phép tính gần đúng y D Do f ¢(x = lim 0 ) x D ®0 x D y D Với x
D đủ nhỏ thì f ¢(x » Û y
D = f ¢ x . x
D Û f (x + x
D » f x + f ¢ x . x D 0 ) ( 0) ( 0) 0 ) ( 0) . x D STUDY TIP
Với y = x ta có: dy (x)¢ = . x D Û dx = x
D . Vậy df (x) = f ¢(x)dx.
2. Đạo hàm cấp cao
a) Đạo hàm cấp hai
Giả sử hàm số y = f (x) có đạo hàm f ¢(x) . Khi đó đạo hàm của hàm số f ¢(x) nếu có, được gọi là
đạo hàm cấp hai của hàm số f (x).
Kí hiệu: y¢¢ hay f ¢ (x). Viết: f (x) = é f ë (x) ¢ ¢ ¢ ù . û
b) Đạo hàm cấp n . Trang 41
Cho hàm số y = f (x) có đạo hàm cấp 𝑛 − 1 (𝑛 ∈ 𝑁, 𝑛 ≥ 4). Kí hiệu (n- )1 f
(x). Nếu (n- )1 f (x) có
đạo hàm thì đạo hàm của nó được gọi là đạo hàm cấp n của f (x). ¢ Kí hiệu: (n) f (x) hoặc (n) y . Viết: (n) f (x) (n- )1 = é f (x)ù . ë û STUDY TIP
Đạo hàm cấp 3 của hàm số y = f (x) là f ¢¢(x) hoặc (3) f
(x) hay y¢¢¢.
c) Ý nghĩa cơ học của đạo hàm cấp hai
Xét một vật chuyển động xác định bởi phương trình s = f (t) với f (t) là hàm số có đạo hàm.
Khi đó gia tốc tức thời (g ) của chuyển động tại thời điểm t là đạo hàm cấp hai của hàm số f (t) là
g (t) = f ¢ (t). STUDY TIP
Vận tốc tức thời tại thời điểm t là v(t) = f ¢(t).
B. CÁC DẠNG TOÁN VỀ VI PHÂN VÀ ĐẠO HÀM CẤP CAO.
Dạng 1. Vi phân hàm số. Phương pháp:
- Tính vi phân của hàm số f (x) tại x cho trước: df (x = f ¢ x . x D 0 ) ( 0) . 0
- Tính vi phân của hàm số f (x): df (x) = f ¢(x).dx.
- Dùng vi phân tính gần đúng.
Ví dụ 30. Vi phân của hàm số f (x) 2
= 3x - x tại điểm x = 2 ứng với x D = 0,1 là: A. -0,07 . B. 10. C. 1,1 . D. 0, - 4 . Lời giải Đáp án C.
Ta có: f ¢(x) = 6x -1Þ f ¢(2) =11Þ df (2) = f ¢(2). x D =11.0,1=1,1. p
Ví dụ 31. Vi phân của hàm số f (x) = sin 2x tại điểm x = ứng với x D = 0,01 là: 3 A. -1, . 1 B. 10. C. 0,1 . D. 0 - , . 01 Lời giải Đáp án D. æ p ö æ p ö æ p ö
f ¢( x) = 2cos 2x Þ f ¢ = 1 - Þ df = f ¢ . x D = 0 - ,01. ç ÷ ç ÷ ç ÷ è 3 ø è 3 ø è 3 ø STUDY TIP
Việc tính vi phân của hàm số tại một điểm x chính là tích của đạo hàm tại một điểm x và số 0 0 gia x D tương ứng. Trang 42 ( x - )2 1
Ví dụ 32. Cho hàm số f (x) =
. Biểu thức 0,01. f ¢(0,0 ) 1 là số nào? x A. 9 . B. 9 - . C. 90 . D. 90 - . Lời giải Đáp án D. f ¢(x) 1 1 = - Þ f ¢ 0,01 = 9 - 000 Þ 0,01f 0,01 = 9 - 0 2 ( ) ( ) . x x x
Ví dụ 33. Vi phân của hàm số y = x x là: 5 A. 3 1 dy = 3 dx . B. dy = dx . C. dy = dx . D. dy = dx. 4 x 2 x 4 x 2 x Lời giải Đáp án A. √#/#∙ ! . 𝑦! =
"√$ = 2√# = 2 ⇒ d𝑦 = 2 d𝑥 "1#√# -1#√# -1√# -1√# STUDY TIP
Việc tính vi phân của hàm số f (x) chính là tích của đạo hàm với dx tương ứng. 1
Ví dụ 34. Vi phân của hàm số y = là: (1+ tan x)2 2 2 - A. dy = dx . B. dy = dx .
cos x (1+ tan x)3 2
cos x (1+ tan x)3 2 C. . d𝑦 = ' d𝑥. D. d𝑦 = +' d𝑥. cos#('/678 #)% cos"#('/678 #)" Lời giải Đáp án B. - ( + x) 1 2 1 tan 2 2 - Ta có: cos x dy = dx = dx (1+ tan x)4 cos x(1+ tan x)3 2
Ví dụ 35. Cho hàm số 2
y = 1+ cos 2x . Chọn kết quả đúng: -sin 4x -sin 4x
A. df (x) = dx.
B. df ( x) = dx. 2 2 1+ cos 2x 2 1+ cos 2x cos 2x -sin 2x
C. df ( x) = dx .
D. df ( x) = dx. 2 1+ cos 2x 2 1+ cos 2x Lời giải Đáp án B. ( 2 1 cos 2x)¢ + -sin 4x
Ta có: df ( x) = dx = dx 2 2 2 1+ cos 2x 1+ cos 2x STUDY TIP Trang 43
Có thể sử dụng MTCT để tìm đạo hàm của hàm số sau đó ta cũng được kết quả của tính vi phân. 2
ìx + x khi x ³ 0
Ví dụ 36. Cho hàm số f (x) = í
. Khẳng định nào sau đây là sai:
îx khi x < 0 A. f (0+ ¢ ) = .1 B. f (0- ¢ ) = .1
C. df (0) = dx .
D. Hàm số không có vi phân tại x = 0 . Lời giải Đáp án D. 2 + x + x - x Ta có: f ¢(0 ) = lim =1; f ¢ = = df (0) = dx + (0 ) lim 1 và . x®0 x®0 x - x STUDY TIP
Với hàm số có nhiều biểu thức việc tính đạo hàm của hàm ta dùng định nghĩa.
Ví dụ 37. Cho hàm số 2
y = x + x +1. Mệnh đề nào sau đây đúng: A. 2
1+ x .dy - ydx = 0 . B. 2
1+ x .dx - dy = 0. C. 2
xdx + 1+ x .dy = 0 . D. 2
1+ x .dy + xy = 0 . Lời giải Đáp án A. dy
Ta có: dy = y dx ¢ Þ y¢ = mà dx 𝑦! = 1 + # = 9 ⇒ d9 = 9
⇒ √𝑥" + 1 ∙ d𝑦 − 𝑦d𝑥 = 0. √#"/' √#"/' d# √#"/'
Ví dụ 38. Dùng vi phân tính gần đúng 3 26, 7 có giá trị là: A. 2,999 . B. 2,98. C. 2,97 . D. 2,89. Lời giải Đáp án A. 1 Xét ( ) 3
f x = x thì f ¢( x) = . Cho x = 27, x D = 0 - ,3. 3 2 0 3. x
Theo công thức gần đúng f (x + x
D » f ¢ x . x D + f x 0 ) ( 0) ( 0) 1 3 3 Þ 27,3 » 27 + ( 0 - ,3) » 2,999. 27 STUDY TIP
Sử dụng vi phân để tính gần đúng ta xét hàm số f (x) và chọn x , x D sao cho phù hợp. 0
Ví dụ 39. Dùng vi phân tính gần đúng sin 29° có giá trị là: A. 0, 4849. B. 0,5464. C. 0, 4989. D. 0, 4949. Đáp án A. Lời giải Trang 44 p p
Xét f (x) = sin x với 29° = - (rad) . 6 180
Có f ¢(x) = cos x. p p æ p p ö p æ p ö æ p ö Chọn x = , x D = - Þ sin - » sin + cos . - » 0,4849. 0 ç ÷ ç ÷ ç ÷ 6 180 è 6 180 ø 6 è 6 ø è 180 ø
DẠNG 2. Tính đạo hàm cấp cao và ý nghĩa cơ học của đạo hàm cấp hai. Phương pháp:
- Tính đạo hàm cấp cao: Áp dụng trực tiếp định nghĩa: ¢ y = ( y )¢ ¢ ¢ , y = ( y )¢ ¢¢ ¢ ,…, (n) (n ) y = ( 1 y - ) .
- Tính đạo hàm cấp n: Trước tiên ta tính đạo hàm cấp 1, cấp 2, … sau đó dự đoán công thức tổng quát của (n) f (x).
- Chứng minh đẳng thức có chứa đạo hàm: Tính đến đạo hàm cấp cao nhất có trong đẳng thức rồi
thay thế vào vị trí tương ứng và biến đổi cho ta được kết quả.
- Ý nghĩa của đạo hàm cấp hai: Gia tốc tức thời (g ) tại thời điểm t là đạo hàm cấp 2 của hàm số
s = f (t).
Ví dụ 40. Tính y¢¢, biết 2
y = x 1+ x . x ( 2 3 + 2x ) 2x( 2 3 + 2x ) A. y¢¢ = . B. y¢ = . ( 2 1+ x ) 2 1+ x (1+ x )3 2 x ( 2 3 - 2x ) x( 2 1+ x ) C. y¢ = . D. y¢ = . ( 3 1+ x )2 2 2 ( 2 1+ x ) Đáp án A Lời giải 1+ 2x 4x ¢ ( 2 1+ x ) - x( 2 1+ 2x ) x ( 2 2 3 + 2x ) y¢ =
Þ y¢ = ( y¢) = = 2 1+ x ( 2 1+ x ) 2 1+ x ( 2 1+ x ) 2 1+ x STUDY TIP æ d ö
Sau khi tính được đạo hàm bậc nhất y¢ ta có thể sử dụng MTCT với chức năng: ç ( ) ! để kiểm ÷ dx è x ø
tra và tính được kết quả.
Ví dụ 41. Cho f (x) = ( x - )5 2 3 . Tính f ¢ (3). A. 4230 . B. 4320 . C. 4204 . D. 4132 . Đáp án B. Lời giải
Ta có: f ¢(x) = ( x - )4 10 2
3 , f ¢ (x) = ( x - )3 80 2 3 , f ¢ (x) = ( x- )2 480 2 3 . Þ f ¢ (3) = 4320 STUDY TIP Trang 45
f (x) = é f ë (x) ¢ ¢ ¢ ù ; f x = é f x ¢ ¢¢ ¢ ù û ( ) ë ( )û f ¢ (x) 2
= 480(2x -3) Þ f ¢ (3) = 4320 dy
Cách khác sử dụng chức năng
( ) nhập biểu thức đạo hàm của f ''(x) tại điểm dx x =!
x = 2 rồi so sánh kết quả ta được đáp án B 1
Ví dụ 3. Cho hàm số y = .Tính (4) y x -4 1.2.3.4 4! - 1. - 2.3.4 A. (4) y = . B. (4) y = . C. (4) y = . D. (4) y = . 5 x 5 x 5 x 6 x Đáp án B Lời giải: 1 1.2 ( ) 1.2.3 ( ) (- )4 1 .4! 3 4 4! y¢ = - , y¢ = , y = Þ y = = 2 3 4 4 1 + 5 x x x x x STUDY TIP (n) æ 1 ö ( 1 - )n.n! Tổng quát: = ç ÷ n 1 è x ø x + 1
Ví dụ 4. Đạo hàm cấp n của hàm số y = , a ¹ 0 là: ax + b 2 .n n a n 1 n - . n a .n! 1 n - .n! 1 n - . n a .n! (n) ( ) (n) ( ) (n) ( ) n . ! A. ( ) y = . B. y = . C. y = . D. y = . n 1 (ax + b) + n 1 (x +1) + n 1 (ax + b) + n 1 (ax + b) + Đáp án D Lời giải: 2 3 a 2a -a .2.3 y¢ = - , y¢¢ = , y¢¢ = (ax +b)2 (ax +b)3 (ax +b)4 ( 1 - )n. n a n n . ! Dự đoán công thức ( ) y = n 1 (ax + ) b +
Nhận xét: Việc dự đoán công thức ta đã được ngay kết quả của bài toán. Tuy nhiên để hiểu rõ
và chính xác hơn ta có thể chứng minh công thức tổng quát bằng phương phức quy nạp toán
học ( bạn đọc tự làm) STUDY TIP
Phương pháp quy nạp: ta cần chứng minh mệnh đề P(n) * ,nÎ N
+ Kiểm tra với n =1, 2 … Trang 46
+ Giả sử mệnh đề đúng với n = k ³1, ta chứng minh mệnh đề cũng đúng với n = k +1 . 2 x + x +1
Ví dụ 5. Đạo hàm cấp ba của hàm số y = là: x +1 6 - 4 - 6 12 - A. . B. . C. . D. . 4 (x +1) 3 (x +1) 3 (x +1) 4 (x +1) Đáp án A Lời giải : 1
Ta phân tích y = x + x +1 ' 1 2 6 y 1 , y¢¢ = , y¢ - Þ = - ¢ = . (x + )2 1 (x + )3 1 (x + )4 1
Nhận xét: Với hàm phân thức bậc của tử cao hơn hoặc bằng bậc của mẫu thì ta chia tách phân A
số và đưa về các phân số dạng ax + b 2x +1
Ví dụ 6. Đạo hàm cấp 4 của hàm số y = là : 2 x - 5x + 6 7.4! 5.4! 5.4! 2.4! A. (4) y = - . B. (4) y = - . 5 5 (x - 3) (x - 2) 5 5 (x - 3) (x - 2) 5.4! 7.4! 7 5 C. (4) y = - . D. (4) y = - . 5 5 (x - 2) (x - 3) 5 5 (x - 3) (x - 2) Đáp án A Lời giải : 2x +1 7 5 (4) 4 æ 1 ö ( 1 - ) .4! 4! y = = - . Mà = = ç ÷ (x - 2)(x - 3) x - 3 x - 2 5 5 è x - 2 ø (x - 2) (x - 2) (4) 4 æ 1 ö ( 1 - ) .4! 4! = = ç ÷ 5 5 è x - 3 ø (x - 3) (x - 3) 7.4! 5.4! (4) Þ y = - 5 5 (x - 3) (x - 2)
Nhận xét: Với các hàm phân thức có bậc của tử nhỏ hơn bậc của mẫu thì ta cố gắng đưa mẫu A
số về dạng tích và phân tích phân số thành tổng, hiệu các phân số dạng ax + b STUDY TIP 2x +1 A B = + (x - 2)(x - 3) x - 2 x - 3 Các hằng số ,
A B tìm được bằng cách quy đồng và đồng nhất hệ số 2 vế
Ví dụ 7. Đạo hàm cấp 3 của hàm số y = sin x là: Trang 47 æ 5p ö æ p ö æ 3p ö A. (3) y = sin x + . B. (3) y = sin x + . C. (3)
y = sin (x +p ). D. (3) y = sin x + . ç ÷ ç ÷ ç ÷ è 2 ø è 2 ø è 2 ø Đáp án D Lời giải: æ p ö
Ta có: y¢ = cos x = sin x + ç ÷ è 2 ø æ p ö æ p ö y ¢ = cos x + = sin ç ÷
(x +p ) = sin x + 2 ç ÷ è 2 ø è 2 ø æ p ö y¢¢¢ = (x +p ) 3 cos = sin x + ç ÷ è 2 ø STUDY TIP Tổng quát: np np (n)
(sin x) = sin(x + ) ; (n) (cos x) = cos(x + ) (với *
n ³1, n Î N ) 2 2 [ æ p ö
ax + b ](n) n sin( ) n
= a .sin ax + b + ç ÷ è 2 ø [ é p ù
ax + b ](n) n cos( ) n
= a .cos ax + b + ê 2 ú ë û
Ví dụ 8. Đạo hàm cấp 4 của hàm số 4
y = sin x là : A. 8
- cos 2x + 32cos 4x . B. 4cos 2x +16cos 4x . C. 8cos 2x -12cos 2x . D. 6cos 2x - 32cos 4x . Đáp án A Lời giải : 1 3 1 1 Ta có: 4 y = sin x = ( 2
1- 2cos 2x + cos 2x) = - cos2x + cos4x 4 8 2 8 1
Þ y¢ = sin 2x - sin 4x , 2
y¢ = 2cos 2x - 2cos 4x, y¢ = 4
- sin 2x +8sin 4x, (4) y = 8
- cos 2x + 32cos 4x. STUDY TIP
Đối với hàm lượng giác, khi tính đạo hàm bậc cao thì ta biến đổi hạ bậc hoặc biến đổi từ tích
thành tổng để đưa về bậc nhất, sin(ax + )
b , cos(ax + b).
Ví dụ 9. Đạo hàm cấp 4 của hàm số y = sin 5 .
x sin 3x là: A. (4) y = 2048 - cos8x +8cos 2x . (4)
B. y = 2048cos8x -8cos 2x. Trang 48 C. (4)
y =1024cos16x + 4cos 4x . D. (4)
y = 2048cos8x - 4cos 4x . Đáp án. A. Lời giải : 1
Ta có y = (cos 2x - cos8x) (4) Þ y = 2
- 048cos8x +8cos 2x. 2 STUDY TIP 1+ cos 2x 2 cos x = 2 1 sin . x sin y = écos ë
(x - y)-cos(x + y)ù 2 û 1 1
Ví dụ 10. Cho hàm số 3 2
f (x) = x + x -12x - .
1 Tập hợp các giá trị x để đạo hàm cấp 2 của f (x) 3 2 không âm là : æ 1 ù æ 1 ö é1 ö é 1 ö A. ; -¥ - . B. ; +¥ . C. ; +¥ . D. - ;+¥ . ç ç ÷ ê ÷ ê ÷ 2 ú è û è 2 ø ë2 ø ë 2 ø Đáp án. D. Lời giải: f ¢(x) 2
= x + x -12, f ¢ (x) = 2x +
1 Do đó: f ¢ ( x) 1 ³ 0 Û x ³ - . 2
Ví dụ 11. Một chất điểm chuyển động thẳng được xác định bởi phương trình : 3 2
s = t - 3t + 5t + 2, trong
đó t tính bằng giây và s tính bằng mét. Gia tốc của chuyển động khi t = 3 là: A. 2 24m / s . B. 2 17m / s . C. 2 14m / s . D. 2 12m / s . Đáp án D Lời giải:
Gia tốc chuyển động tại t = 3s là s ''(3) Ta có: s¢(t) 2 = 3t - 6t + 5
s¢ (t) = t - Þ s¢ ( ) 2 6 6 3 =12m / s . STUDY TIP
Bài toán vận dụng ý nghĩa cơ học của đạo hàm bậc 2. Gia tốc tức thời (g ) tại thời điểm
t : g t = s ' t 0 ( 0) ( 0)
Ví dụ 12. Cho hàm số 2
y = 2x - x . Mệnh đề nào sau đây là đúng ? A. 3 y .y ¢ +1 = 0. B. 2 y .y ¢ -1 = 0. C. 2
3y .y¢ +1 = 0.. D. 3
2y .y¢ + 3 = 0. Đáp án A Lời giải : Trang 49 1- x 1 Ta có: y¢ = , y¢ = - 2 2x - x (2x- x )3 2 3 1 - Thay vào: 3 y .y¢ +1 = ( 2 2x - x ) ( ) . +1 = 1 - +1 = 0. (2x- x )3 2 3 3 sin x + cos x
Ví dụ 13. Cho hàm số y =
. Mệnh đề nào sau đây đúng ? 1- sin x!cos x
A. 2y¢ + y = 0.
B. y¢¢ + y = 0.
C. y¢ - y = 0.
D. 2y ¢ - 3y = 0. Lời giải : ( x + x)( 2 2 sin cos
sin x + cos x - sin x cos x) Ta có : y = = sin x + cos x 1- sin x cos x
Þ y¢ = cos x - sin x, y¢ = -sin x - cos x Þ y¢ + y = 0. STUDY TIP
Với các biểu thức lượng giác phức tạp ta cần biến đổi rút gọn rồi sau đó tính đạo hàm cấp cao
Ví dụ 14. Phương trình chuyển động của một chất điểm 3 2
s = t - 3t - 9t + 2 (s tính bằng mét, t tính bằng
giây). Tìm gia tốc tức thời tại thời điểm vận tốc bằng 0. A. 2 10 m / s . B. 2 12 m / s . C. 2 8 m / s . D. 2 16 m / s . Đáp án. B. Lời giải: é = -
v(t) = s¢(t) t 1 l 2 ( )
= 0 Û 3t - 6t - 9 = 0 Û ê ët = 3 2
Þ g (3) =12m / s .
Dạng 3 :Dùng đạo hàm để giải toán tổ hợp k C n Phương pháp:
Cách 1: Từ khai triển (1+ )n x = 0 1 1 2 2 1 - 1
C + C x + C x + ... n n- n n + C x + C x n n n n n
Lấy đạo hàm cấp 1, cấp 2 ở hai vế khai triển của nhị thức
-Chọn x = x và chọn n thích hợp. 0
Cách 2: Sử dụng MTCT tính thay với một vài giá trị n = 1, 2,
… và kiểm tra tính đúng sai ta đi
đến việc lựa chọn đáp án
Ví dụ 15. Đẳng thức nào sau đây đúng? A. 1 2 3 n n 1 C 2C 3C nC .2 n - + + +…+ = , n Î N. n n n n Trang 50 B. 1 2 3 C + 2C + 3 n
C +…+ nC = n + nÎ N n n n n ( )1.2n, . C. 1 2 3 n C C C nC n - + + +…+ = - nÎ N n n n n ( ) n 1 2 3 1 .2 , . D. 1 2 3 n C C C nC n + + + +…+ = + nÎ N n n n n ( ) n 1 2 3 1 .2 , . Đáp án A Lời giải:
Cách 1: Xét f (x) = ( + x)n 0 1 1 n n 1 1 - n n
= C +C x +…+C x +C x "xÎR n n n n
f (x) n( x)n 1- 1 2 C xC n x - C - n x - = + = + +…+ - + C n n ( ) n 2 n 1 n 1 ' 1 2 1 . . . n n n (' )1 1 2 f C C n C - n C n - = + +…+ - + = n n ( ) n 1 n n 1 2 1 . . .2 . n n
Cách 2: Sử dụng MTCT -Chọn với n = 1: 1 C 0 = 2 = 1 (đúng) 1 -Chọn với n = 2 : 1 2
C + 2C = 2.2 = 4 (đúng) 2 2 ….
Từ việc thử đáp án ta được kết quả
Ví dụ 16. Tính tổng với n Î N, n ³ 2 : 2 3 n 1 S 1.2.C 2.3.C
... (n 2).(n 1).C - = + + + - - + (n -1). . n n C n n n n A. 2 ( 1).( 2).2n n n - - - . B. 2 .( 1).2n n n - - . C. 1 .( 1).2n n n - - .
D. ( -1).( - 2).2n n n . Đáp án B Lời giải:
Cách 1: Xét hàm số n 0 1 1 2 2 n 1 - n 1
f (x) = (1+ x) = C + C x + C x + ... - n n + C x + C x n n n n n Suy ra:
f (x) n( x)n 1- 1 2 C xC n x - C - n x - = + = + +…+ - + C n n ( ) n 2 n 1 n 1 ' 1 2 1 . . . n n n ¢ ( ) ( ) ( ) 2 1 . . 1 n f x n n x - = - + 2 3 n-3 n 1 - n-2 =1.2.C + 2.3. .
x C + ...+ (n - 2).(n -1)x .C + (n -1). . n x . n C n n n n f ¢ ( ) 2 3 C C n
n - C - + n - n C n n - = + +…+ - = - n n ( ) ( ) n 1 n ( ) nn ( ) n 2 1 1.2. 2.3. 2 . 1 . 1 . . 1 2 .
Cách 2: Sử dụng MTCT ta thử với một vài giá trị n ³ 2. -Với n = 2 Þ 2 1
S = 1.2.C = 2.1.2 = 2 (đúng) 2 -Với n = 3 Þ 2 3
S = 1.2.C + 2.3.C = 3.2.2 = 12 (đúng) 3 3 …
So sánh, đối chiếu các đáp án ta được kết quả. Trang 51 STUDY TIP
Nếu trong biểu thức thiếu 2 số hạng đầu tiên hoặc 2 số hạng cuối cùng của khai triển nhị thức
đồng thời các hệ số là tích của 2 số tự nhiên lien tiếp ta dung đạo hàm cấp 2.
Ví dụ 17. Tính tổng 0 1 2
S = C + 2C + 3C + ...+ (n +1) n C bằng n n n n A. 1 .2n n - . B. 1 ( 1).2n n - + . C. 1 ( 2).2n n - + . D. ( 1).2n n + . Đáp án C Lời giải:
Cách 1: Ta có: n 0 1 1 2 2 n 1 - n 1
(1+ x) = C + C x + C x + ... - n n
+ C x + C x " x Î R n n n n n
Nhân 2 vế với x ta được: n 0 2 1 3 2 n n 1 - n 1 x(1 x) . x C x .C x .C ... x .C x + + = + + + + + . n C n n n n n
Lấy đạo hàm 2 vế ta được : n n 1 - 0 1 2 2
(1+ x) + nx(1+ x) = C + 2 .
x C + 3x .C + ...+ (n +1) n x . n C n n n n
Thay x = 1 ta được: 0 1 2 n n n 1 - n 1 S C 2C 3C ... (n 1)C 2 .2 n (n 2).2 - = + + + + + = + = + . n n n n
Cách 2: Sử dụng MTCT (bạn đọc tự thử lại) STUDY TIP
Nếu trong khai triển nhị thức vẫn có số hạng đầu hoặc số hạng cuối và hệ số tăng thêm 1 đơn vị
thì ta nhân 2 vế với x và sau đó dùng đạo hàm cấp 1.
Ví dụ 18. Tìm số nguyên dương n sao cho: 1 2 2 3 3 4 2n 2n 1 C - 2.2.C + 3.2 .C - 4.2 .C
+...+ (2n +1).2 .C + = 2017 2n 1 + 2n 1 + 2n 1 + 2n 1 + 2n 1 + A. n = 1005. B. n = 1006 . C. n = 1007 . D. n = 1008. Đáp án D Lời giải: Với x
" Î ! ta có: (1+ x)2n 1+ 0 1 1 2 2 3 3 2n 1 + 2n 1 = C
+C .x +C .x +C .x +...+C .x + 2n 1 + 2n 1 + 2n 1 + 2n 1 + 2n 1 +
Lấy đạo hàm hai vế theo x ta được:
(2n+ )1(1+ x)2n 1 2 2 3 = C + 2 . x C +3x .C +...+ 2n +1 . n x . n C + ( )1 2n 1 + 2n 1 + 2n 1 + ( ) 2 2 1 2n 1 + Thay x = 2 - vào ( ) 1 ta được: 1 2 2 3 4 2n +1 = C - 2.2.C +3.2 .C - 4.2.C +...+ 2n +1 . n x . n C + 2n 1 + 2n 1 + 2n 1 + 2n 1 + ( ) 2 2 1 2n 1 +
Từ yêu cầu bài toán ta có : 2n +1 = 2017 Û n = 2018 .
STUDY TIP : Nhận biết được cần sử dụng đạo hàm cấp 1 và chọn giá trị x = x dựa vào cơ 0 số n
a với chỉ số n tăng dần. 99 100 198 199 æ 1 ö æ 1 ö æ 1 ö æ 1 ö
Ví dụ 5: Tính tổng: 0 1 0 100 S = 100.C -101.C +...+199.C + 200.C 100 ç ÷ 100 ç ÷ 100 ç ÷ 100 ç ÷ è 2 ø è 2 ø è 2 ø è 2 ø A.10. B. 0 . C.1. D.100. Đáp án B.
Lời giải: 100
Xét f (x) = (x + x) = x ( + x)100 2 100 1 100 = x ( 0 1 2 2 100 100
C + C x + C x + C x 100 100 100 100 ) Trang 52 0 100 1 101 2 102 100 200
= C .x + C .x + C x +...+ C x 100 100 100 100 Þ f (x) =
( x+ ) (x + x)99 2 ' 100 2 1 . 99 0 100 1 101 2 199 100
=100x .C +101x .C +102x .C +...+ 200x C 100 100 100 100 1
Lấy x = - ta được: 2 99 100 199 æ 1 ö æ 1 ö æ 1 0 1 ö 100 0 = 100 - C +101 C -...- 200 C Û S = 0. ç ÷ 100 ç ÷ 100 ç ÷ 100 è 2 ø è 2 ø è 2 ø 1
STUDY TYP : Xuất phát từ nhị thức ( + )100 2 x x
, sau khi dùng đạo hàm cấp 1, chọn x = - . 0 2
C. BÀI TẬP RÈN LUYỆN KĨ NĂNG
DẠNG 1: VI PHÂN CỦA HÀM SỐ Câu 1. Cho hàm số 3
y = x . Tính vi phân của hàm số tại x = 1 với số gia x D = 0,01. 0 A. 0, 01. B. ( )2 3. 0,01 . C. ( )3 0,01 . D. 0, 03. x + 3
Câu 2. Cho hàm số y =
.Vi phân của hàm số tại x = 3 - là: 1- 2x 1
A. dy = dx . B. dy = 1 7dx.
C. dy = - dx . D. dy = 7 - dx. 7 7 æ p ö
Câu 3. Xét hàm số x = sin y 0 < y <
cùng với ba đẳng thức: ç ÷ è 2 ø ( ) dx dy 1 1 dy I = cos y ; (II) = = ; (III ) = cos x; dy 2 dx cos y 1- x dx
Số đẳng thức đúng là: A. Chỉ (I ).
B. Chỉ (III ) .
C.Chỉ (I ) và (II ).
D. Chỉ (I ) và (III ) .
Câu 4. Vi phân của hàm số 2 y = cos 3x là: A. 2
dy = 3sin 3xdx .
B. dy = sin 6xdx . C. dy = 3 - sin 6xdx.
D. dy = 6sin 6xdx.
Câu 5. Với hàm số 2 3
x y + y = 2 thì đạo hàm y¢ tại điểm (1 ) ;1 bằng: 3 A. - . B. 1 - 1 . C. - . D. 0 . 2 2
Câu 6. Cho hàm số y = sin (sin x). Vi phân của hàm số là:
A. dy = cos(sin x).sin xdx .
B. dy = sin.(cos x).dx.
C. dy = cos(sin x),cos xdx .
D. dy = cos(sin x)dx.
x sin x + cos x
Câu 7. Vi phân của hàm số y = bằng:
x cos x - sin x dx 2 x dx A. dy = . B. dy = . (x x - x)2 cos sin (x x - x)2 cos sin cos xdx 2 x sin xdx C. dy = . D. dy = .
(xcos x -sin x)2
(xcos x -sin x)2 dy
Câu 8. Xét hàm số f ¢(x) 2 = x - . N 1 ếu đặt = ( 2 y f x ) thì
nhận kết quả nào sau đây? dx A. x( 4 2 x - ) 1 . B. x( 2 2 x - ) 1 . C. 4 x - . 1 D. 2 x - . 1 Trang 53 Câu 9. Xét hàm số 2
y = x . Gọi Dx, dy theo thứ tự là số gia và vi phân của hàm số y tại x = 1 và 0 dx = 0, 01 . Hiệu của y D - dy bằng: A. 0,001. B. 0,002 . C. 0,0001. D. 0,00001. æ p p ö p Câu 10. Xét 2
cos y = sin x 0 < y < ,0 < x <
. Đạo hàm của y tại x = là: ç ÷ è 2 2 ø 4 p p -2 - 3 A. . B. . C. . D. . 6 3 3 2 2 2 - x - 2x +1
Câu 11. Vi phân của hàm số y = là: (x + x+ )2 2 1 2(2x + ) 1 ( 2 x + x - 2)
(2x + )1( 2x - x+ )1 A. dy = dx. B. dy = dx . ( 3 x + x + )3 2 1 ( 2x + x+ )1
(3x - )1( 2x -2x+5)
(x + )1( 2x + x-2) C. dy = dx . D. dy = dx. ( 3 x + x + )3 2 1 ( 2x + x+ )1
Câu 12. Cho hàm số: y = 2
- 1- x . Kết luận nào sau đây là đúng?
A. 1- x dy - dx = 0 . B. - 1- x dx - dy = 0.
C. 2 1- x dy + dx = 0. D. 1- x dy + dx = 0.
DẠNG 2: TÍNH ĐẠO HÀM CẤP CAO VÀ Ý NGHĨA CƠ HỌC CỦA ĐẠO HÀM CẤP HAI:
Câu 13. Hàm số nào dưới đây có đạo hàm câp hai là 6x ? A. 2 y = 3x . B. 3 y = 2x . C. 3 y = x . D. 2 y = x . æ p ö Câu 14. Cho hàm số 2
y = cos x. Khi đó (3) y bằng: ç ÷ è 3 ø A. 2 . B. 2 3 . C. 2 - 3 . D. 2 - . Câu 15. Cho hàm số 2
y = x +1 . Xét hai đẳng thức:
(I) .yy¢ = 2x;
(II) 2y.y¢ = y¢ . Đẳng thức nào đúng? A.Chỉ (I ). B.Chỉ (II ).
C. Cả hai đều sai.
D. Cả hai đều đúng. 2 5x - 3x - 20
Câu 16. Đạo hàm cấp 2 của hàm số y = bằng: 2 x - 2x - 3 2( 3 2
7x +15x - 93x + 77) 2( 3 2
7x -15x + 93x - 77) A. y = . B. y = . ( 3 x - 2x + 3)3 2 ( 2x -2x+3) 2( 3 2
7x +15x + 93x - 77) 2( 3 2
7x -15x - 93x + 77) C. y = . D. y = . ( 3 x - 2x - 3)3 2 ( 2x -2x-3) Câu 17. Hàm số 2
y = sin x có đạo hàm cấp 4 là: A. 2 cos 2x . B. 2 -cos 2x . C.8cos 2x . D. 8 - cos 2x .
Câu 18. Cho hàm số y = cos x . Khi đó (2016) y (x) bằng: A. - cos x . B. sin x . C. -sin x . D. cos x . 1
Câu 19. Đạo hàm cấp n của hàm số y = là: x -1 Trang 54 (- )1n n n n! (- )1 .n! (- )1 .n! A. . B. . C. . D. . (x - )n 1 1 + (x ) 1 1 n+ - (x - )n 1 1 + (x - )1n
Câu 20. Đạo hàm cấp 2 của hàm số : y = tan x + cot x + sin x + cos x là: 2 tan x 2cot x A. -
- sin x + cos x. B. 0 . 2 2 cos x sin x 2 tan x 2cot x C. 2 2
tan x - cot x + cos x - sin x . D. +
- sin x - cos x. 2 2 cos x sin x
Câu 21. Cho hàm số y = sin 2x. Đẳng thức nào sau đây là đúng với mọi x ?
A. y + ( y¢)2 2 = 4.
B. 4y + y¢¢ = 0.
C. 4y - y¢¢ = 0 .
D. y = y .¢tan 2x . Câu 22. Cho hàm số 2
y = cos 2x. Giá trị của biểu thức m n
y + y +16y¢ +16y -8 là kết quả nảo? A. 0 . B.8 . C. 8 - . D.16cos 4x . æ p ö
Câu 23. Cho hàm số y = f (x) = cos 2x - . Phương trình (4) f (x) = 8
- có số nghiệm thuộc đoạn ç ÷ è 3 ø [0;p] là: A.1 . B. 2 . C. 3 . D. 0 .
Câu 24. Cho hàm số f (x) = (x + )3 5 1 + 4(x + )
1 .Tập nghiệm của phương trình f ¢ (x) = 0là: A.[ 1 - ;2] . B. ( ;0 -¥ ]. C. Æ . D.{ } 1 - . 2 2 - x + 3x
Câu 25. Cho hàm số y =
. Đạo hàm cấp 4 của hàm số này là: 1- x 16 32 24 - 24 A. (4) y = . B. (4) y = . C. (4) y = . D. (4) y = . (x - )5 1 (x - )5 1 (x - )5 1 (x - )5 1
Câu 26. Cho hàm số y = .
x sin x. Tìm hệ thức đúng:
A. y¢ + y = 2c - os x.
B. y¢ - y¢ = 2cos x .
C. y¢ + y¢ = 2cos x.
D. y¢ + y = 2cos x .
Câu 27. Phương trình chuyển động của một chất điểm 2 3
s =15 + 20t -8t ( s tính bằng mét, t tính bằng
giây). Vận tốc tức thời của chất điểm tại thời điểm gia tốc bằng 0 là: 50 10 A. m / s . B. m / s.
C.15m / s .
D. 20m / s . 3 3
Câu 28. Một chất điểm chuyển động thẳng xác định bởi phương trình 3 2 s = t
- + 9t + t +10 trong đó t
tính bằng giây, s tính bằng mét. Thời gian vận tốc của chất điểm đạt giá trị lớn nhất là:
A. t = 5 s .
B. t = 6 s .
C. t = 2 s .
D. t = 3s.
Câu 29. Một chất điểm chuyển động thẳng xác định bởi phương trình 3 2
s = t - 2t + 4t +1 trong đó t là
giây, s là mét. Gia tốc của chuyển động khi t = 2 là:
A.12 m / s .
B. 8m / s.
C. 7 m / s.
D. 6 m / s.
Câu 30. Cho chuyển động thẳng xác định bởi phương trình 3 2
s = t - 3t ( t tính bằng giây, s tính bằng
mét). Mệnh đề nào sau đây là đúng?
A. Gia tốc của chuyển động khi t = 4 s là 2 g =18m / s .
B. Gia tốc của chuyển động khi t = 4 s là 2 g = 9m / s .
C. Gia tốc của chuyển động khi t = 3s là 2 g =12m / s .
D. Gia tốc của chuyển động khi t = 3s là 2 g = 24m / s .
DẠNG 3: DÙNG ĐẠO HÀM ĐỂ GIẢI TOÁN TỔ HỢP Trang 55
Câu 31. Tính tổng S C C C - = - + - + - n C n n n ( )n 1 1 2 3 2 3 ... 1 . . n . n A. 0 . B.1 . C.10. D.100. Câu 32. Tính tổng: 999 1 998 2 0 1000 S = 1.2 C + 2.2 C +...+1000.2 C . 1000 1000 1000 A. 999 1000.2 . B. 1000 999.3 . C. 999 1000.3 . D. 999 999.3 .
Câu 33. Tìm số nguyên dương n thỏa mãn: 1 2 3
1.C + 2.C + 3.C + ...+ . n n C = 11264. n n n n A. n = 9 . B. n = 10 . C. n = 11. D. n = 12 . Câu 34. 2 1 2 2 2 3 2 2000 S = 1 .C + 2 .C + 3 .C +...+ 2000 .C . 2000 2000 2000 2000 A. 1998 2000.2001.2 . B. 1999 1999.2000.2 . C. 1999 2000.2001.2 . D. 2000 2000.2001.2 . Câu 35. Tính tổng: 0 2 1 3 2 4 198 200 S = 2.1.3 .C
- 3.2.3 .C + 4.3.3 .C -...+ 200.199.3 .C . 200 200 200 200 A. 199 200.199.2 . B. 200 199.198.2 . C. 198 200.199.2 . D. 199 199.198.2 .
Câu 36. Tìm số tự nhiên n thỏa mãn: 0 1 2 n 1 1.C 2.C 3.C ... . n C - + + + + + n + C £ n + n n n n ( )1. n 1024 n ( 2).
A. nÎ{0;1;2;3;4;5;6;7;8;9;10;1 } 1 .
B. nÎ{0;1;2;3;4;5;6;7;8;9;1 } 0 .
C. nÎ{0;1;2;3;4;5;6;7;8; } 9 .
D. nÎ{0;1;2;3;4;5;6;7; } 8 . Câu 37. Tính tổng: 1 2 3 4 5 6 99 100
S = 2.2 .C + 4.2 .C + 6.2 .C +...+100.2 .C . 100 100 100 100 A. ( 99 50 3 + ) 1 . B. ( 98 100 3 + ) 1 . C. ( 99 200 3 + ) 1 . D. ( 200 25 3 + ) 1 .
Câu 38. Đẳng thức nào sau đây đúng? 1 2 3 n n æ 3 n ö A. 1 2 3 C + C + C + ...+ C = n -1 0 n 1 n 2 n n 1 - n ( ) . ç ÷ 2 2 2 2 è 2 ø B. 0 n n C n C - n C - - C n - + - + - + + = + n ( ) 1 n 1 n ( ) 2 n 2 n 1 1 n n ( ) n 1 .3 . 1 3 . 2 3 . ... 1.3 . 1 .4 . C. 2 4 6 2 2.C + 4.C + 6.C +...+ 2 . n n C = 2n +1 2 n- 2n 1 + 2n 1 + 2n 1 + 2n 1 + ( ) 2 1. D. 1 3 5 1.C 3.C 5.C ... 2n 1 . n C - 2 . n 2 n+ + + + + - = 2n 2n 2n ( ) 2 1 2 1. 2n
D. HƯỚNG DẪN GIẢI CHI TIẾT
DẠNG 1: VI PHÂN CỦA HÀM SỐ
Câu 1. Đáp án D. 2, dy = 3.1 .0,01 = 0,03
Câu 2. Đáp án A. 7 1 1 Ta có: y¢ =
Þ y¢ 3 = Þ dy = dx 2 ( ) . (1- 2x) 7 7
Câu 3. Đáp án C. æ p ö dx dy 1 1
Ta có: x = sin y 0 < y < Þ dx = cos d y y Þ = cos y và = = đúng. ç ÷ è 2 ø dy 2 dx cos y 1- x
Câu 4. Đáp án C. y¢ = 2cos3x( 3 - sin3x) = 3 - sin 6x Þ dy = 3 - sin 6 d x x .
Câu 5. Đáp án C. 2 3
x y + y = Þ d ( 2 x y)+ d ( 3 y ) 2 2 2 = 0 Û 2x d
y x + x dy + 3y dy = 0 tại điểm (1 ) ;1 ta có: dy 1
2dx + dy + 3dy = 0 Þ 4dy = 2 - dx Þ = - = y¢( ) 1 . dx 2
Câu 6. Đáp án C.
y¢ = cosx.cos(sin x) Þ dy = cos .
x cos(sin x)dx .
Câu 7. Đáp án B. Trang 56
(xcos x)(xcos x -sin x)-(xsin x + cos x)(-xsin x) 2 x Ta có : y¢ = = .
(xcos x -sin x)2
(xcos x -sin x)2
Câu 8. Đáp án A. Đặt 2
u = x Þ y = f (u) Từ f ¢(x) 2
= x - Þ f ¢(u) 2 1 = u - 1 dy dy du Þ = = ¢( ) du f u = ( 2
u - ) x = x( 4 . . 1 2 2 x - ) 1 . dx du dx dx
Câu 9. Đáp án C. Chọn x
D = dx = 0,01; x =1Þ y = 1 0 0
dy = 2.0,01 = 0,02 Þ y D - dy = 0, 0001 .
Câu 10. Đáp án C. 2
cos y = sin x Þ -sin d y y = sin 2 d x x . p dy sin 2x sin 2x -sin Þ = = dy 2
(vì sin y > 0 ) 2 Þ = y¢ = = - . 2 dx
-sin y - 1- cos y dx p 4 3 1- sin 4
Câu 11. Đáp án A. ( 4
- x - 2)(x + x + )2 2 1 - ( 2 2 - x - 2x)2( 2 x + x + ) 1 (2x + ) 1 2(2x + ) 1 ( 2 x + x - 2) y¢ = = . ( 3 x + x + )4 2 1 ( 2x + x+ )1
Lưu ý: có thể sử dụng MTCT tính đạo hàm tại một điểm x = 0 và thử lại x = 0 vào các Đáp án
ta được kết quả là A.
Câu 12. Đáp án A. 1 dx Ta có: y¢ = , dy =
Þ 1- xdy - dx = 0. 1- x 1- x
DẠNG 2: TÍNH ĐẠO HÀM CẤP CAO VÀ Ý NGHĨA CƠ HỌC CỦA ĐẠO HÀM CẤP HAI.
Câu 13. Đáp án C. 3 2
y = x , y¢ = 3x , y¢ = 6x
Câu 14. Đáp án B. ( æ p 3) (3) ö
y¢ = -sin 2x, y¢ = 2
- cos 2x Þ y = 4sin 2x Þ y = 2 3 . ç ÷ è 3 ø
Câu 15. Đáp án C. 2 . x x x +1 - 2 x x +1 1 Ta có: y¢ = , y¢ = = 2 2 x +1 x +1 (x + )3 2 1 Þ 1 . y y¢ = x và 2 y .y¢ =
nên (I ) và (II ) sai. 2 x +1
Câu 16. Đáp án B. - + - 2 x x ( 3 2 2
7x -15x + 93 x - 77 7 10 31 ) Ta có y¢ = Þ y¢ = . (x -2x-3)2 (x -2x-3)3 2 2
Kết luận: Ta có thể sử dụng MTCT tính đạo hàm tại 1 điểm x = 0 của y¢ và thử với x = 0 vào
các Đáp án ta được kết quả.
Câu 17. Đáp án D. Trang 57 Ta có: (4)
y¢ = sin 2x, y¢ = 2cos x, y¢ = 4
- sin 2x Þ y (x) = 8 - cos 2x.
Câu 18. Đáp án D. æ np ö Áp dụng (n) cos (x) (2016) = cos x + Þ y ç ÷
(x) = cos(x +1008p ) = cos x. è 2 ø
Câu 19. Đáp án C. n n æ n 1 ö (- )1 . n a .n! -1 .n! Áp dụng =
ta được: (n) ( ) y = . ç ÷ è ax + b ø
(ax +b)n 1+ (x - )n 1 1 +
Câu 20. Đáp án D. 2 tan x 2cot x 2 2
y¢ = tan x - cot x + cos x - sin x Þ y¢ = +
- sin x - cos x . 2 2 cos x sin x
Câu 21. Đáp án B. y¢ = 2cos 2 , x y¢ = 4
- sin 2x Þ 4y + y¢ = 0
Câu 22. Đáp án A. y¢ = 2s - in 4 , x y¢ = 8c - os 4 ,
x y¢ = 32sin 4x Þ y¢ + y¢ +16y¢ +16y -8 = 0.
Câu 23. Đáp án B. æ np ö Áp dụng écos ë (ax +b) n n
ù = a .cos ax + b + û ç ÷ è 2 ø ( æ p 4) ö Þ f (x) (4)
=16.cos 2x - + 2p Þ f ç ÷ (x) = -8 è 3 ø é p x = + kp p 1 ê æ ö 2 Û cos 2x - = - Û ç ÷ ê (k Î!) . è 3 ø 2 p - êx = + kp êë 6 p p Với x Î[ p ] 5 0; Þ x = , x = . 2 6
Câu 24. Đáp án D.
f ¢(x) = (x + )2 15
1 + 4, f ¢ (x) = 30(x + )
1 Þ f ¢ (x) = 0 Û x = - . 1
Câu 25. Đáp án C. 1 1 2 - 2.3 ( - - 4) 2.3.4 24 y = 2x -1- Þ y¢ = 2 + , y¢ = , y¢¢ = , y = = . x -1 (x - )2 1 (x - )3 1 (x - )4 1 (x - )5 1 (x - )5 1
Câu 26. Đáp án D.
Ta có: y¢ = sin x + x cos x, y¢ = 2cos x - xsin x Þ y¢ + y = 2cos x .
Câu 27. Đáp án A.
Ta có : g (t) = s¢ (t) = 40 - 48t 5
Gia tốc: g (t) = 0 Û t = Þ v(t) = s¢(t) 2 = 40 - 24t . 6 2 æ 5 ö 5 æ 5 ö 50 v = 40. - 24. = ç ÷ ç ÷ (m / s) è 6 ø 6 è 6 ø 3
Câu 28. Đáp án D.
v(t) = s¢(t) = - t + t + = - (t - t + )+ = - (t - )2 2 2 3 18 1 3 6 9 28 28 3 3 ³ 28
Vậy vận tốc đạt giá trị lớn nhất khi t = 3s .
Câu 29. Đáp án B. s¢(t) 2
= 3t - 4t + 4,s¢ (t) = 6t - 4 Trang 58
Vậy gia tốc g ( ) = s¢¢( ) = ( 2 2 2 8 m / s )
Câu 30. Đáp án A. s¢(t) 2
= t - t s¢ (t) = t - Þ s¢ ( ) = ( 2 3 6 , 6 6 4 18 m / s )
DẠNG 3: DÙNG ĐẠO HÀM ĐỂ GIẢI TOÁN TỔ HỢP k C n
Câu 28. Đáp án A.
Từ nhị thức ( + x)n 0 1 1 2 2 1
= C +C x +C x +... n n +C x n n n n ( ) * lấy đạo hàm hai vế:
n( + x)n 1- 1 2 2 3 n 1 1
= C + 2xC +3x C +... - n + nx C n n n n (* ) * . Thay x = 1 - ta được S C C C - = - + - - - C = n n n ( )n 1 1 2 3 2 3 ... 1 n 0. n
Câu 29. Đáp án C.
Xét khai triển nhị thức (1+ )n
x . Lấy đạo hàm bậc nhất hai vế ta được
n( + x)n 1- 1 2 2 3 n 1 1
= C + 2xC +3x C +... - n + nx C n n n n Cho x = 2 ta được 1 3n S n - = .
Với n = 1000 ta được 999 S =1000.3
Câu 30. Đáp án C.
Xét khai triển nhị thức (1+ )n
x . Lấy đạo hàm bậc nhất hai vế ta được
n( + x)n 1- 1 2 2 3 n 1 1
= C + 2xC +3x C +... - n + nx C n n n n Cho x = 1 ta được 1 2 3 n n 1 1C 2C 3C ... nC .2 n - + + + + = =11264 Þ n = 11 n n n n
Câu 31. Đáp án A. Xét 2 1 2 2 2 3 2
S = 1 C + 2 C + 3 C + ... n + n C = ( - ) 1 C +
- C + + n n + - C n ( ) 2 1 2 1 2 3 1 ... n ( 1 )1 n n n n n n 1 2 3 = é C + C +
C + + n(n + ) n 1 2 3 1.2. 2.3 3.4 ... 1 C ù - 1
é C + 2C + 3C +... n + nC ù ë n n n n û ë n n n n û = A- B Từ câu 3 thì 1 2n B n - =
Xét khai triển x( x)n 0 2 1 3 2 n 1 1 . x C x .C x .C ... x + + = + + + + . n C n n n n
Lấy đạo hàm hai vế: ( + x)n + nx( + x)n 1- 0 1 2 2 1 1 = C + 2 .
x C + 3x .C +...+ n + x C n n n ( )1 n. n n
Tiếp tục lấy đạo hàm ta có: n( x)n 1- n(
x)n 1- n(n ) x( x)n-2 1 1 2 C x C n n x - + + + + - + = + + + + C n n ( ) n 1 1 1 1 1 1.2. 2.3 . ... 1 . n n Cho n 1
x = Þ A = n - + n(n - ) n-2 Þ S = n(n + ) n-2 1 2 .2 1 .2 1 .2 Với 1998
n = 2000 Þ S = 2000.2001.2 .
Câu 32. Đáp án C. Từ khai triển ( - )200 1 x
lấy đạo hàm đến cấp 2 hai vế, sau đó thay x = 3 ta được 198 S = 200.199.2 . Câu 33. Đáp án A.
Từ ví dụ 3 - Dạng 3. Phần lý thuyết ta có: 0 1 2 C C C n C n - + + + + + = + n n n ( ) nn ( ) n 1 1. 2. 3. ... 1 . 2 2 .
Theo yêu cầu của bài toán Þ (n + ) n 1- £ (n+ ) n 1 - 10 2 .2 1024. 2 Û 2
£1024 = 2 Û n £11, nΕ . Vậy chọn A. Câu 34. Đáp án A. Khai triển ( + )100 1 x
và lấy đạo hàm cấp 1. Khai triển ( - )100 1 x
và lấy đạo hàm cấp 1. Trang 59
Cộng vế với vế và thay x = 2 ta được S = ( 99 50 3 + ) 1 Câu 35. Đáp án C.
Cách 1: Khai triển ( )2 1 1 n x + +
và lấy đạo hàm cấp 1. Khai triển ( )2 1 1 n x + -
và lấy đạo hàm cấp 1.
Cộng vế với vế và thay x = 1 ta được kết quả đáp án C.
Cách 2: Thử với n = 1, 2và các đáp án thì ta được kết quả đáp án C đúng Trang 60
TIẾP TUYẾN VỚI ĐỒ THỊ HÀM SỐ A. LÝ THUYẾT
1. Tiếp tuyến của đường cong phẳng. Định nghĩa: y
Nếu cát tuyến M M có vị trí giới hạn M T . Khi điểm 0 0
M di chuyển trên (C) và dần đến M thì đường thẳng 0 (C) M T f(x
gọi là tiếp tuyến của đường cong (C) tại điểm M . 0)+ M 0 0
Điểm M (x ; f (x ))được gọi là tiếp điểm. 0 0 0 Định lý: T M0
Cho hàm số y = f ( x) xác định và có đạo hàm trên ( ; a b) và (C) f(x0)
là đồ thị hàm số. Đạo hàm của hàm số f (x) tại điểm x0 là hệ số góc x0 x0+ x
của tiếp tuyến M T của (C) tại M (x ; f (x )). 0 0 0 0
2. Phương trình tiếp tuyến
a. Tiếp tuyến tại một điểm
Phương trình tiếp tuyến của đồ thị hàm số (C): y = f (x) tại điểm M (x ; y )Î C 0 0 0 ( ):
y = f ¢( x x - x + y 0 ) ( 0 ) 0 STUDY TIP
- Hệ số góc k = f ¢(x0 ).
- Nếu cho x thì thế vào y = f (x) tìm y . 0 0
- Nếu cho y thì thế vào y = f (x) giải phương trình tìm x . 0 0
b. Tiếp tuyến biết hệ số góc
- Hệ số góc k của tiếp tuyến: k = f ¢(x * 0 ) ( ) Giải phương trình ( )
* ta tìm được hoành độ của tiếp điểm x thế và phương trình y = f (x) tìm tung độ 0 y . 0
- Khi đó phương trình tiếp tuyến: y = k ( x - x + y d 0 ) 0 ( ) STUDY TIP
* Tiếp tuyến d // : D y = a x +
b Þ k = a . * Tiếp tuyến d ^ : D y = a x +
b Þ k.a = 1 - .
* k = tana , với a là góc giữa d và tia Ox .
c. Tiếp tuyến đi qua một điểm
Lập phương trình tiếp tuyến d với (C) biết d đi qua điểm M (x ; y M M ) Phương pháp:
- Gọi M x ; y Î C 0 ( 0 0 ) ( ) là tiếp điểm.
- Phương trình tiếp tuyến tại M : y = f ¢ x x - x + y d 0 ( 0)( 0 ) 0 ( ).
- Vì đường thẳng d đi qua M nên y - y = f ¢ x x - x x M 0
( 0)( M 0). Giải phương trình ta tìm được rồi suy 0 ra y . 0 STUDY TIP
Điểm M (x ; y (C) 0
0 ) có thể thuộc hoặc không thuộc đường cong
B. CÁC DẠNG TOÁN VỀ TIẾP TUYẾN VỚI ĐỒ THỊ HÀM SỐ. Trang 61
Ví dụ 1. Cho hàm số 3 2
y = x + 3x +
1 có đồ thị (C). Phương trình tiếp tuyến của (C) tại điểm M ( 1 - ;3) là: A. y = 3 - . x
B. y = -x + 3. C. y = 9 - x + 6. D. y = 9 - x - 6. Đáp án A.
Lời giải:
Tập xác định: D = ! 2
y¢ = 3x + 6x
Phương trình tiếp tuyến tại M ( 1
- ;3) là: y = y¢(- ) 1 (x + ) 1 + 3 Û y = 3 - x 4
Ví dụ 2. Cho hàm số y =
có đồ thị (C). Phương trình tiếp tuyến của (C) tại điểm có hoành độ x -1 x = 1 - là: 0
A. y = -x + 2.
B. y = x + 2.
C. y = x - 1.
D. y = -x - 3. Đáp án D.
Lời giải:
Tập xác định: D = ! \{ } 1 4 y¢ = -
; y¢ -1 = -1; y -1 = -2 2 ( ) ( ) (x - )1
Phương trình tiếp tuyến tại M 1 - ;- 2 y = y¢(- ) 1 (x + ) 1 - y (- ) 1 = -x - 3 0 ( ) là: STUDY TIP
Học sinh nhận biết các bài toán về viết phương trình tiếp tuyến tại 1 điểm
- Cho M (x ; y Î C 0 0 ) ( ). - Cho x tìm y . 0 0 - Cho y tìm x . 0 0 -
Ví dụ 3. Cho hàm số 4 2
y = x + 2x -1 (C). Phương trình tiếp tuyến tại điểm có tung độ y = 2 là: 0
A. y = 8x - 6; y = 8 - x - 6.
B. y = 8x - 6; y = 8 - x + 6.
C. y = 8x -8; y = 8 - x + 8.
D. y = 41x -17. Đáp án A.
Lời giải:
Tập xác định: D = ! 3
y¢ = 4x + 4x 4 2
y = 2 Û x + 2x -1 = 2 Þ x = 1 - ; x =1 0
Phương trình tiếp tuyến tại M (1;2): y = 8x -6.
Phương trình tiếp tuyến tại M ( 1 - ;2): y = 8 - x - 6. STUDY TIP
Giải phương trình 4 2
ax + bx + c = 0,(a ¹ 0). Đặt 2
t = x ,t ³ 0 suy ra giải phương trình bậc hai 2 .
a t + bt + c = 0 4x + 2
Ví dụ 4. Tiếp tuyến của đồ thị hàm số y =
tại điểm x = 3có hệ số góc bằng: x - 2 0 A. 3. B. 7. - C. 10. - D. 3. - Đáp án C.
Lời giải:
Tập xác định: D = ! \{ } 2 Trang 62 10 y¢ = - ; k = y¢ 3 - = -10. 2 ( ) (x - 2) 3 x
Ví dụ 5. Tiếp tuyến của đồ thị hàm số 2 y =
+ 3x - 2 có hệ số góc k = 9 - có phương trình là: 3 A. y = 9 - x -11. B. y = 9 - x - 27. C. y = 9 - x + 43. D. y = 9 - x +11. Đáp án A.
Lời giải:
Tập xác định: D = ! 2
y¢ = x + 6x k = 9 - Û y¢(x = 9 - Û x = 3 - Þ y =16. 0 ) 0 0
Phương trình tiếp tuyến tại M ( 3; - 16): y = 9 - x -1 1 STUDY TIP
Học sinh nhận biết được loại bài toán viết phương trình tiếp tuyến khi biết hệ số góc
k :k = f ¢(x . 0 ) 2x + 2
Ví dụ 6. Cho hàm số y =
(C). Phương trình tiếp tuyến biết tiếp tuyến song song với đường thẳng x -1 d : y = 4 - x + 1 là: A. y = 4 - x - 2; y = 4 - x +14. B. y = 4 - x + 21; y = 4 - x +14. C. y = 4 - x + 2; y = 4 - x +1 . D. y = 4 - x +12; y = 4 - x +14. Đáp án A.
Lời giải: 4 -
Tập xác định: D = ! \{ } 1 . y¢ = (x - )2 1 4 - éx = 0
Gọi M (x ; y Þ y¢(x = 4 - Û 4 - = Þ 0 ) 0 0 0 ) là tiếp điểm ( ê x - )2 1 x = 2 ë 0
Phương trình tiếp tuyến tại M (0;-2): y = 4 - x - 2.
Phương trình tiếp tuyến tại M (2;6): y = 4 - x +14. STUDY TIP
Hai đường thẳng song song thì cùng hệ số góc.
Hai đường thẳng vuông góc thì tích hai hệ số góc của hai đường thẳng bằng 1. -
Ví dụ 7. Cho hàm số 3 2
y = x - 2x + 2x (C). Gọi x , x là hoành độ các điểm M , N trên (C) mà 1 2
tiếptuyến tại đó vuông góc với đường thẳng y = -x + 2017. Khi đó x + x bằng: 1 2 8 2 4 5 A. . B. . C. . D. . 3 3 3 3 Đáp án C.
Lời giải:
Tập xác định: D = ! . 2
y¢ = 3x - 4x + 2. Từ giả thiết suy ra x + x là nghiệm của phương trình 1 2 4 2 2
1 = 3x - 4x + 2 Û 3x - 4x +1 = 0 Þ x + x = 1 2 3 2x +1
Ví dụ 8. Cho hàm số y =
(C). Viết phương trình tiếp tuyến của (C) biết tiếp tuyến đi quađiểm x -1 M ( 7; - 5). Trang 63 3 1 3 29
A. y = - x + ; y = - x + 3 1 3 2 .
B. y = - x - ; y = - x + . 4 4 16 16 4 2 16 16 3 1 3 9
C. y = - x - ; y = - x + 3 1 3 29 .
D. y = - x - ; y = - x + . 4 4 16 16 4 4 16 16 Đáp án D.
Lời giải: 3 -
Tập xác định: D = ! \{ } 1 . y¢ = . (x - )2 1
Gọi M (x ; y M ( 7; - 5) 0
0 ) là tiếp điểm. Do tiếp tuyến qua nên: 3 - 2x +1 5 = 7 - - x +
Þ x - 4x - 5 = 0 Þ x = -1; x = 5. 2 ( 0 ) 0 2 (x - ) 0 0 0 0 1 x -1 0 0 3 1
Ta tìm được hai phương trình tiếp tuyến là: y = - x - 3 29 và y = - x + . 4 4 16 16 STUDY TIP
Học sinh cần phân biệt loại bài toán viết phương trình tiếp tuyến tại một điểm M x ; y 0 ( 0 0 ) và
viết phương trình tiếp tuyến đi qua điểm M (x ; y M (x ; y M M ) M
M ) . Dấu hiệu ban đầu là điểm
có thể thuộc đường cong (C) hay có thể không thuộc đường cong (C)
Ví dụ 9. Cho hàm số 3
y = x -1- m(x + ) 1 (C m (Cm)
m ) . Có bao nhiêu giá trị của để tiếp tuyến tại tạo
với hai trục tọa độ một tam giác có diện tích bằng 8? A. 1. B. 2. C. 3. D. 4. Đáp án D.
Lời giải: (C
Oy :M (0;1- m) m ) giao với 2 y¢ = 3x - , m y(0) = m -
Phương trình tiếp tuyến của (C
M : y = -mx +1- m m ) tại
Nếu m = 0 tiếp tuyến song song với Ox (loại)
Xét m ¹ 0.Gọi A , B lần lượt là giao điểm tiếp tuyến và hai trục tọa độ æ1- m ö Þ A ;0 ; B ç ÷ (0;1- m) . è m ø 1 1 1- m (1- m)2 ém = 9 ± 4 5 Ta có S = 8 Û O . A OB = 8 Û 1- m = 8 Û =16 Û ê . OAB 2 2 m m êëm = 7 - ± 4 3
Vậy có bốn giá trị của m thỏa mãn.
Ví dụ 10. Cho hàm số 3 2
y = x - 2x + (m - )
1 x + 2m (C m m ). Tìm
để tiếp tuyến có hệ số góc nhỏ nhất của đồ thị (C D : y = 2x +1
m ) vuông góc với đường thẳng
A. m = 1. B. m = 11 2. C. m = 6 . D. m = . 6 11 Đáp án C.
Lời giải: 2
y¢ = 3x - 4x + m - 1 2 æ 2 ö 7 7
Ta có y¢ = 3 x - + m - ³ m - ç ÷ è 3 ø 3 3 Trang 64
Tiếp tuyến tại điểm có hoành độ 2
x = có hệ số góc nhỏ nhất và hệ số góc đó có giá trị 3 7 k = m - . 3 æ 7 ö 11 Theo bài ra: 2.k = 1 - Û 2 m - = 1 - Þ m = . ç ÷ è 3 ø 6 Trang 65
C. BÀI TẬP RÈN LUYỆN KỸ NĂNG x -1
Câu 35. Viết phương trình tiếp tuyến của đồ thị hàm số y =
tại điểm có hoành độ x = 0 x +1 0
A. y = 2x + . 1
B. y = 2x - . 1
C. y = x - 2.
D. y = x + 2 .
Câu 36. Viết phương trình tiếp tuyến của đồ thị hàm số y = x + 2 tại điểm có tung độ y = 2 0 1 3
A. y = x + 1 3 .
B. y = x - 3 3 .
C. y = x - 3 1 .
D. y = x + . 4 2 4 2 2 2 2 4
Câu 37. Số tiếp tuyến của đồ thị hàm số f (x) = sin x , x Î[0;2p ] song song với đường thẳng 1 y = x + 3 là : 2 A. 0. B. 1. C. 2. D. 3.
Câu 38. Tiếp tuyến của đồ thị hàm số 3 2
y = x - x +1 tại điểm x = - 1 có hệ số góc bằng : 0 A. 7. B. 5. C. 1. D. -1. 2x - 4
Câu 39. Cho hàm số y =
có đồ thị là (C). Phương trình tiếp tuyến tại giao điểm của (C) với x - 3 trục hoành là:
A. y = 2x - 4.
B. y = 3x +1. C. y = 2 - x + 4.
D. y = 2x.
Câu 40. Tiếp tuyến của đồ thị hàm số 3
y = x - 2x + 2 vuông góc với đường phân giác của góc phần tư
thứ nhất trên hệ trục Oxy là:
A. y = -x - 2 và y = -x + . 4 1 5 3
B. y = -x + + 1 5 3 và y = -x + - . 3 9 3 9 1 18 - 5 3 +
C. y = -x + + 1 18 5 3 và y = -x - + . 3 9 3 9 1 18 - 5 3 +
D. . y = -x - - 1 18 5 3 và y = -x + - 3 9 3 9 x -1
Câu 41. Phương trình tiếp tuyến của đồ thị hàm số y =
(C) tại các giao điểm của (C) với các x trục tọa độ là :
A. y = x - . 1
B. y = x - 1 và y = x + . 1
C. y = -x + . 1
D. y = x + . 1 Câu 42. Cho hàm số 2
y = x - 6x + 5 có tiếp tuyến song song trục hoành. Phương trình tiếp tuyến đó là : A. x = 3 - . B. y = -4. C. y = 4. D. y = 3. 4
Câu 43. Cho hàm số y = 2 - có đồ thị là (C). Phương trình tiếp tuyến với (C) vuông góc với đường x
thẳng y = -x + 2 là:
A. y = x + 4 .
B. y = x - 2 và y = x + 4.
C. y = x - 2 và y = x + 6.
D. y = x + 3 và y = x - . 1 x +1
Câu 44. Cho hàm số y =
có đồ thị là (C). Có bao nhiêu nhiêu cặp điểm thuộc (C) mà tiếp tuyến x -1
tại đó song song với nhau? A. 0. B. 1. C. 2. D. Vô số. Trang 66 1
Câu 45. Trên đồ thị hàm số y =
có điểm M (x ; y ) sao cho tiếp tuyến tại đó cùng vói các trục tọa x -1 0 0
độ tạo thành một tam giác có diện tích bằng 2. Khi đó x + y bằng : 0 0 13 1 A. 3 . B. . C. - 13 . D. - . 3 7 4 1
Câu 46. Cho hàm số (C) 3 2
: y = x + x - 2 . Phương trình tiếp tuyến của (C) tại điểm có hoành độ là 3
nghiệm của phương trình y¢ = 0 là 7
A. y = -x - 7 .
B. y = -x + 7 .
C. y = x - 7 .
D. y = x . 3 3 3 3
Câu 47. Số cặp điểm A, B trên đồ thị hàm số 3 2
y = x + 3x + 3x + 5 mà tiếp tuyến tại , A B vuông góc với nhau là: A. 1. B. 2 . C. 0 . D. Vô số. Câu 48. Qua điểm (
A 0;2) có thể ké được bao nhiêu tiếp tuyến với đồ thị hàm số 4 2
y = x - 2x + 2 (C)? A. 0. B. 1. C. 2. D. 3. Câu 49. Cho hàm số 3 3
y = x - 3x + 2 có đồ thị (C). Đường thẳng nào sau đây là tiếp tuyến với (C) và
có hệ số góc nhỏ nhất? A. y = 3 - x + 3. B. y = 1. C. y = 5 - x + 7. D. y = 3 - x - . 3 2 x
Câu 50. Cho hai hàm số f ( x) 1 = và g (x) =
. Góc giữa hai tiếp tuyến của mỗi đồ thị hàm số đă x 2 2
cho tại giao điểm của chúng là: A. 0 60 . B. 0 90 . C. 0 45 . D. 0 30 . 1
Câu 51. Tìm m để đồ thị: (C
y = mx + m - x + - m x + m ) 3 : ( ) 2 1
(4 3 ) 1 tồn tại đúng 2 điểm có hoành độ 3
dương mà tiếp tuyến tại đó vuông góc với đường thẳng x + 2y - 3 = 0. æ 1 ö æ 1 2 ö æ 1 ö æ 1 7 ö A. m Î 0; È ; . B. m Î 0; È ; . ç ÷ ç ÷ ç ÷ ç ÷ è 4 ø è 2 3 ø è 4 ø è 2 3 ø æ 1 ö æ 1 8 ö æ 1 ö æ 1 2 ö C. m Î 0; È ; . D. m Î 0; È ; . ç ÷ ç ÷ ç ÷ ç ÷ è 2 ø è 2 3 ø è 2 ø è 2 3 ø 2x -1
Câu 52. Cho hàm số y =
có đồ thị (C). Viết phương trình tiếp tuyến với (C) biết tiếp tuyến này x -1
cắt Ox,Oy lần lượt tại A, B sao cho OA = 4OB . 1 5
A. y = - x + 1 13 và y = - x + 1 5 .
B. y = - x - 1 13 và y = - x - . 4 4 4 4 4 4 4 4 1 5 1
C. y = - x + 1 3 và y = - x + 1 1 .
D. y = - x + 5 và y = x - . 4 4 4 4 4 2 4 2 Câu 53. Cho hàm số 3 2
y = x - 3x + m. Tiếp tuyến tại điểm có hoành độ x =
1 cắt các trục Ox,Oy lần 0 luợt tại ,
A B sao cho diện tích AO D 3
B bằng . Hỏi m là giá trị nguyên nằm trong khoảng nào 2 sau đây? A. ( ; -¥ 1 - ) È (0;+ ) ¥ . B. ( ; -¥ 5 - ) È (1;+¥). C. ( 4 - ;0). D. (-2;2).
Câu 54. Tìm m để tiếp tuyến của đồ thị hàm số 3
y = x - mx + m - l tại điểm x = 1 cắt đường tròn 0
(x - )2 + ( y - )2 1 2
3 = theo cung có độ dài nhỏ nhất. 5 Trang 67
A. m = 1 hoặc m = 2 . B. m = 5 1 hoặc m = - . 2 C. m = 3 - hoặc m = 1 - D. m = 1 - hoặc m = 3 . Câu 55. Cho hàm số 3 2
y = x + ax + bx + ,
c c < 0 có đồ thị (C) cắt Oy tại A và có hai điểm chung với
Ox là M , N . Tiếp tuyến với đồ thị tại M đi qua A . Tìm T = a + b + c biết S =1. AMN A. T = 1 - . B. T = 2. C. T = 5 . D. T = 3 - . HƯỚNG DẪN GIẢI Câu 19. Đáp án B. 2 y¢ =
; x = 0 Þ y = - 1 0 0 x +1
Phương trình tiếp tuyến tại M (0; 1
- ) là: y = y (0 ¢ )(x - 0) - 1 Û y = 2x - . 1 Câu 20. Đáp án A. 1 y¢ =
; y = 2 Þ x + 2 = 2 Û x = 2 0 0 0 2 x + 2
Phương trình tiếp tuyến tại M (2;2) là y = y (2 ¢ )(x - 1 3 2) Û y = x + . 4 2 Câu 21. Đáp án C. 1 1 p
f (¢x) = cos x. Theo giả thiết Þ f (¢x ) = Û cos x = Û x = ± + k2p ,k Î Z 0 2 0 0 2 3 p 5p
Do x Î[0;2p ] Þ x = ; x = . 0 0 0 3 3
Vậy có 2 tiếp tuyến thỏa mãn. Câu 22. Đáp án B. 2
y¢ = 3x - 2x Þ y¢( ) 1 = 5 Câu 23. Đáp án C.
Giao điểm của (C) với Ox là ( A 2;0). -2 y¢ = (x -3)2
Phương trình tiếp tuyến tại ( A 2;0) là :
y = y¢(2)(x - 2) + 0 Û y = 2 - x + 4 Câu 24. Đáp án C. 2 y = 3x - 2
Đường phân giác của góc phần tư thứ nhất D : y = x Þ y¢( 1 x .1 = 1 - Û 3x - 2 = 2 - Û x = ± 0 ) 2 0 0 3 1 18 - 5 3 +
Vậy phương trình tiếp tuyến cần tìm là : y = -x + + 1 18 5 3 và y = -x - + 3 9 3 9 Câu 25. Đáp án A. TXĐ: D = R \{0
} nên (C) không giao với Oy.
(C) giao với Ox tại M (1;0) nên phương trình tiếp tuyến là: y = y (1
¢ )(x -1) = x - . 1 Câu 26. Đáp án B.
Ta có: y¢ = 2x - 6 .
Phương trình tiếp tuyến song song với trục hoành Trang 68
Þ y (¢x ) = 0 Û x = 3 Þ y = 4 0 0 0
Phương trình tiếp tuyến là: y = -4. Câu 27. Đáp án C. 4
TXĐ: D = R \ { } 0 ; y¢ = . 2 x 4 éx = 2
Theo giả thiết y¢(x 1 - = 1 - Û y¢ x =1 Û =1 Û 0 ) ( ) ( 0) 0 2 ê x x = 2 - 0 ë 0
Vậy phương trình tiếp tuyến là y = x - 2 và y = x + 6 Câu 28. Đáp án D. 2 - y¢ =
.Đồ thị hàm số có tâm đối xứng I(1;1) . (x - )2 1 Lấy điểm (
A x ; y ) Î(C), gọi B là điểm đối xứng với A qua I Þ B(2 - x ;2 - y )Î(C) . Ta có: 0 0 0 0 2 -
+ Hệ số góc của phưong trình tại A là: k = y¢ x = A ( 0) (x - )2 1 0 2 -
+ Hệ số góc của phương trình tại B là: k = y¢ - x = B (2 0 ) (x - )2 1 0
Ta thấy k = k nên có vô số cặp điểm ,
A B Î(C) mà tiếp tuyến tại đó song song với nhau. A B Câu 29. Đáp án D. 1 Ta có y¢ = - . (x - )2 1 1 1
Phương trình tiếp tuyến tại M(x ; y ) Î(C) là : y = - x - x + (D) 2 ( 0 ) 0 0 (x - )1 x -1 0 0
(D) giao với Ox : A(2x -1;0 0 ). æ 2x 1 ö - (D) giao với 0 Oy : Bç 0; ÷. ç (x )2 1 ÷ - è 0 ø 2 1 æ 2x -1ö 3 0 S = O . AOB Û ç
÷ = 4 Û x = Þ y = 4 - OAB 0 0 2 x -1 4 è 0 ø 3 13
Vậy x + y = - 4 = - . 0 0 4 4 Câu 30. Đáp án A. 2 y' = x + 2 , x y" = 2x + 2 y ( 4
" x = 0 Û 2x + 2 = 0 Û x = 1 - Þ y = - 0 ) 0 0 0 3 æ 4 ö 7
Phương trình tiếp tuyến tại M -1;-
là : y = -x - . ç ÷ è 3 ø 3 Câu 31. Đáp án C. 2
y¢ = 3x + 6x + 3. Gọi A(x ; y ), B(x ; y A A B B ) .
Tiếp tuyến tại A, B lần lượt có hệ số góc là: 2 2
k = 3x + 6x + 3, k = 3x + 6x + 3 A A A B B B
Theo giả thiết: k .k = 1 - A B Trang 69 Û ( 2 x + x + x + x + = - A A )( 2 3 6 3 3 6 B B )3 1 Û ( 2 x + x + x + x + = - A A )( 2 9 2 1 2 B B )1 1 Û (x + x + = - A )2 ( B )2 9 1 1 1 (Vô lý).
Vậy không tồn tại cặp điểm , A B thỏa mãn. Câu 32. Đáp án D. 3
y¢ = 4x - 4x . Gọi M x ; y Î C 0 ( 0 0 ) ( ) .
Phương trình tiếp tuyến tại M là: 0 y = ( 3
4x - 4x )(x - x ) 4 2 + x - 2x + 2 D 0 0 0 0 0 ( )
Vì D đi qua A(0;2) nên: 2 = ( 3 4x - 4x
-x + x - 2x + 2 0 0 )( 0 ) 4 2 0 0 éx = 0 0 4 2 3x 2x 0 ê Û - + = Û 0 0 2 êx = ± 0 êë 3
Ứng với 3 hoành độ x ta viết được 3 phương trình tiếp tuyến với (C) . 0 Câu 33. Đáp án A. 2
y¢ = 3x - 6x . Gọi M x ; y Î C 0 ( 0 0 ) ( ) .
Phương trình tiếp tuyến tại M là: y = y¢(x x - x + y 0 ) ( 0 ) 0 0
Hệ số góc của tiếp tuyến tại M :
y¢(x ) = 3x -6x = 3(x - )2 2
1 -3 Û y¢ x ³ 3 - 0 0 0 0 ( 0)
Do đó, hệ số góc nhỏ nhất là 3 - khi x = 1 0 Þ y = 0 . 0
Phương trình tiếp tuyến tại M 0;1 y = 3 - x + 3 0 ( ) là: Câu 34. Đáp án B.
Phương trình hoành độ giao điểm: 2 1 x 1 2 =
Û = x Þ x =1, x ¹ 0 x 2 2 x Þ æ 1 ö giao điểm M 1; . ç ÷ è 2 ø Ta có f ¢( ) 1 1 1 = - ; g ( ¢ 1) = Þ f ¢( ) 1 .g¢( ) 1 = - 1 2 2
Vậy góc giữa 2 tiếp tuyến đó là 0 90 . Câu 35. Đáp án D. 2
y¢ = mx + 2(m - ) 1 x + 4 -3m æ 1 ö Theo bài ra y .¢ - = 1 - Û y¢ = 2 ç ÷ è 2 ø 2 Û mx + 2(m- )
1 x + 2 -3m = 0 có 2 nghiệm dương phân biệt Trang 70 ìm ¹ 0 ìm ¹ 0 ï 1 ï ïm ¹ ïD¢ > 0 ï 2 æ 1 ö æ 1 2 ö Û í Û í hay m Î 0; È ; . S > 0 0 m 1 ç ÷ ç ÷ < < ï ï è 2 ø è 2 3 ø ïîP > 0 ï 2 ï0 < m < î 3 Câu 36. Đáp án A.
Phương trình tiếp tuyến tại M x ; y Î C 0 ( 0 0 ) ( ) là: 2 -x 2x - 2x +1 0 0 y = + D 2 2 ( ) (x -1 x -1 0 ) ( 0 )
(D) giao với Ox tại A( 2 2x - 2x +1;0 . 0 0 ) 2 æ ö ( - + D) 2x 2x 1 0 0
giao với Oy tại B ç 0; ÷. ç (x )2 1 ÷ - è 0 ø é = OA = OB Û ( x 3 4 x -1 = 4 Û 0 )2 0 êx = 1 - ë 0
Từ đó ta được 2 phương trình tiếp tuyến là: 1 5 y = - x + 1 13 và y = - x + . 4 4 4 4 Câu 37. Đáp án A.
Với x =1Þ y = m - 2 Þ M 1;m - 2 0 0 ( )
Phương trình tiếp tuyến tại M là (D): y = 3 - x + m+1 ( æ + D) m 1 ö
giao với Ox tại A ;0 . ç ÷ è 3 ø
(D) giao với Oy tại B(0;m+ )1. 3 1 3 m +1 S = Û O . AOB = Û . m +1 = 3 OAB 2 2 2 3 Û ( é = - m + )2 m 4 1 = 9 Û . ê ëm = 2 Câu 38. Đáp án B.
Với x =1Þ y = 0 Þ M 1;0 , y¢ = 3x - m 0 0 ( ) 2
Phương trình tiếp tuyến tại M (1;0) là:
(3-m)x- y -3+m = 0 (D) 1
Đường tròn tâm I (2;3) và bán kính R = . 5
Vì IM > R nên độ dài cung nhỏ nhất khi (D) tiếp xúc với đường tròn tức là: - - - + d (I D) (3 m).2 3 3 m 1 ; = R Û = ( - m)2 5 3 +1 ém = 1 2 2m 3m 5 0 ê Û + - = Û 5 . êm = - ë 2 Trang 71 Câu 39. Đáp án A.
Giả sử (C) cắt Ox tại M ( ;0 m ), N ( ;0
n ), cắt Oy tại A(0;c).
Tiếp tuyến tại M có phương trình: y = ( 2
3m + 2am + b)(x -m) (D)
Tiếp tuyến (D) đi qua A nên 3 2
3m + 2am + bm + c = 0 3 2 Û m + am = ( 3 2 2
0 do m + am + bm + c = 0) a Û m = - . 2
Vì (C) cắt Ox tại 2 điểm nên (C) tiếp xúc với Ox (do tính chất đồ thị hàm bậc 3 học sinh sẽ
được học rõ hơn lớp 12).
Nếu M là tiếp điểm Þ Ox đi qua A (vô lý)
Þ (C) tiếp xúc với Ox tại N. Do đó = + + + = ( - )2 3 2 y x ax bx c
x n (x - m) ì a a m = - , n = -
ìm + 2n = -a ï 2 4 ï ï 2 3 Þ í2 .
m n + n = b Û ía = 32c (I ) ï 2 ï 2 . m n = -c 5a = 16b î ï ïî Mặt khác S =1Û - .
c n - m = 2 Û - . c a = 8 AM D N 3 ìa = 32c ï
- Với a > 0 Þ íac = 8 - (vô nghiệm) ï 2 5a = 16b î 3 ìa = 32c ìa = 4 - ï ï
- Với a < 0 Þ íac = 8 Û b í = 5 ï 2 5a =16b ïc = 2 - î î
Þ T = a + b + c = -1. Trang 72




