Bài tập trắc nghiệm hình học Oxyz – Huỳnh Văn Lượng Toán 12

Bài tập trắc nghiệm hình học Oxyz – Huỳnh Văn Lượng Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

85 43 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Phương pháp tọa độ trong không gian

Môn: Toán 12

Thông tin:

28 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
A.
H
H
U
U
Ỳ
Ỳ
N
N
H
H
V
V
Ă
Ă
N
N
L
L
Ư
Ư
Ợ
Ợ
N
N
G
G
0
0
9
9
1
1
8
8
.
.
8
8
5
5
9
9
.
.
3
3
0
0
5
5
–
–
0
0
1
1
2
2
3
3
4
4
.
.
4
4
4
4
4
4
.
.
3
3
0
0
5
5
–
–
0
0
9
9
3
3
3
3
.
.
4
4
4
4
4
4
.
.
3
3
0
0
5
5
0
0
9
9
6
6
3
3
.
.
1
1
0
0
5
5
.
.
3
3
0
0
5
5
–
–
0
0
9
9
2
2
9
9
.
.
1
1
0
0
5
5
.
.
3
3
0
0
5
5
–
–
0
0
6
6
6
6
6
6
.
.
5
5
1
1
3
3
.
.
3
3
0
0
5
5
--

----
www.huynhvanluong.com
Chúc các em đạt kết quả cao trong kỳ thi sắp tới
Huỳnh Văn Lượng
(đồng hành cùng hs trong suốt chặn đường THPT)
LƯU HÀNH NỘI BỘ
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 2 0918.859.305-01234.444.305
HỆ THỐNG KIẾN THỨC HÌNH Oxyz
Download miễn phí tại Website: www.huynhvanluong.com
Biên soạn: Huỳnh Văn Lượng (email: hvluong@hcm.vnn.vn)
0918.859.305 – 01234.444.305 – 0933.444.305-0929.105.305 -0963.105.305-0666.513.305-0996.113.305
------------------------------------------------------
1. Tọa độ điểm và véctơ :
• Hệ toạ độ trong không gian gồm ba trục
, ,
Ox Oy Oz
đôi một vuông góc, các véc tơ đơn vị tương ứng
trên ba trục lần lượt là:
),0;0;1(=i
)0;1;0(=j
,
)1;0;0(=k
•
(
)
; ;
u x y z u xi y j z k
⇔ = + +
.
•
222
zyxuz)y; (x;u ++=⇒=
•
)
; ;
B A B A B A
AB x x y y z z
= − − −
•
( ) ( ) ( )
= = = − + − + −
2 2 2
B A B A B A
AB BA AB x x y y z z
.
• Neáu I laø trung ñieåm cuûa AB thì I ; ;
2 2 2
A B A B A B
x x y y z z
+ + +
• Neáu G laø troïng taâm cuûa ∆ABC thì
; ;
3 3 3
A B C A B C A B C
x x x y y y z z z
G
+ + + + + +
• Neáu G laø troïng taâm tứ diện ABCD thì
4 4 4
A B C D A B C D A B C C
x x x x y y y y z z z z
G ; ;
+ + + + + + + + +
• ABCD laø hình bình haønh ⇔
AB=DC
• D là chân đường phân giác trong của góc A thì
DB AB
AC
DC
= −
⇒
tọa độ D
• I là tâm
ñöôøng troøn noäi tieáp ∆ABC thì
IA BA
BD
ID
= −
⇒
tọa độ K
2. Tích các hai vectơ và ứng dụng:
a) Tích vô hướng: Cho
(
)
(
)
1 1 1 2 2 2
; ; & ; ;
u x y z v x y z
. Ta có:
•
(
)
=
. . .cos ,
u v u v u v
•
= + +
1 2 1 2 1 2
.
uv x x y y z z
.
•
0...0.
212121
=++⇔=⇔⊥ zzyyxxvuvu
b) Tích höõu höôùng: cho hai vectơ
(
)
1 1 1
; ;
u x y z
và
(
)
2 2 2
; ;
v x y z
. Ta có:
•
(
)
, . .sin ,
u v u v u v
=
.
•
1 1 1 1 1 1
2 2 2 2 2 2
, ; ;
y z z x x y
u v
y z z x x y
=
.
•
&
u v
cùng phương
⇔
, 0
u v
=
⇔
2 2 2
1 1 1
x y z
x y z
= =
• A,B,C thẳng hàng ⇔
AB, AC
cùng phương
• A,B,C,D là ba đỉnh của tam giác ⇔
AB, AC
không cùng phương
• Diện tích tam giác:
1
,
2
ABC
S AB AC
=
• Diện tích hình bình hành: ,
ABCD
S AB AD
=
Luy
ệ
n thi THPT Qu
ố
c gia (Hình Oxyz) www.huynhvanluong.com
Hu
ỳ
nh v
ă
n L
ượ
ng Trang 3 0918.859.305-01234.444.305
c) Tích hoãn hôïp (hỗn tạp):
•
, ,w
u v
đồ
ng ph
ẳ
ng
, . 0
u v w
⇔ =
•
A,B,C,D là b
ố
n
đỉ
nh c
ủ
a t
ứ
di
ệ
n
⇔
AB, AC, AD
không
đồ
ng ph
ẳ
ng.
•
Th
ể
tích kh
ố
i h
ộ
p:
. ' ' ' '
, . '
ABCD A B C D
V AB AD AA
=
.
•
Th
ể
tích t
ứ
di
ệ
n:
1
, .
6
ABCD
V AB AC AD
=

.
--------------------------------------
3. Mặt phẳng
:
a) Phương trình mặt phẳng:
•
M
ặ
t ph
ẳ
ng qua
đ
i
ể
m
(
)
0 0 0
; ;
M x y x
và có vect
ơ
pháp tuy
ế
n
(
)
; ;
n A B C
:
(
)
(
)
(
)
0 0 0
0
A x x B y y C z z
− + − + − =
.
•
M
ặ
t ph
ẳ
ng
(
)
α
c
ắ
t tr
ụ
c
, ,
Ox Oy Oz
l
ầ
n l
ượ
t t
ạ
i
(
)
(
)
(
)
;0;0 , 0; ;0 , 0;0;
A a B b C c
, có ph
ươ
ng trình
theo
đ
o
ạ
n ch
ắ
n là:
( )
1 0
x y z
abc
a b c
+ + = ≠
b) Vị trí tương đối của hai mặt phẳng
.
Cho hai m
ặ
t ph
ẳ
ng
(
)
: 0
Ax By Cz Dα
+ + + =
và
(
)
' : ' ' ' ' 0
A x B y C z Dα
+ + + =
, ta có:
o
( ) ( )
α α
≡ ⇔ = = ='
' ' ' '
A B C D
A B C D
.
o
( ) ( )
α α
⇔ = = ≠/ / '
' ' ' '
A B C D
A B C D
.
o
(
)
α
c
ắ
t
(
)
'
α
' '
A B
A B
⇔ ≠ ho
ặ
c
' '
B C
B C
≠ ho
ặ
c
' '
A C
A C
≠ (t
ứ
c là ngoài 2 t/h trên)
o
(
)
(
)
α α
⊥ ⇔ + + =
' ' ' ' 0
AA BB CC
.
c) Khoảng cách từ một điểm tới một mặt phẳng
.
Cho
(
)
: 0
Ax By Cz D
α
+ + + =
⇒
( )
( )
α
+ + +
=
+ +
2 2 2
,
M M M
Ax By Cz D
d M
A B C
.
5. Đường thẳng
:
a) Phương trình của đường thẳng: Đườ
ng th
ẳ
ng
đ
i qua
(
)
0 0 0
; ;
M x y z
và có VTCP
(
)
; ;
u a b c
=
PT tham s
ố
:
0
0
0
x x at
y y bt
z z ct
= +
= +
= +
(t
∈
R
) PT chính t
ắ
c:
c
zz
b
yy
a
xx
000
−
=
−
=
−
( a.b.c
0
≠
)
b) Vị trí tương đối giữa hai đường thẳng:
Đườ
ng th
ẳ
ng d
đ
i qua
0
M
và có VTCP
u
, d’
đ
i qua
0
'
M
và có
VTCP
u
'
, ta có
:
•
(d) và (d
’
)
đồ
ng ph
ẳ
ng ⇔
'
0 0
u,u ' .M M 0
=
•
d chéo d’
⇔
[
]
0 0
, ' . ' 0
u u M M
≠
•
d và d’ c
ắ
t nhau
⇔
[
]
[ ]
0 0
, ' 0
, ' . ' 0
u u
u u M M
≠
=

•
// '
d d
⇔
[
]
0 0
, ' 0
, ' 0
u u
u M M
=
≠
c) Khoảng cách:
Luy
ệ
n thi THPT Qu
ố
c gia (Hình Oxyz) www.huynhvanluong.com
Hu
ỳ
nh v
ă
n L
ượ
ng Trang 4 0918.859.305-01234.444.305
•
o
MM ,u
d(M,
∆
)=
u
•
o o
u,u' .M M'
d(∆, ∆') =
u,u'

4.
Phương trình mặt cầu:
•
Dạng 1:
Phương trình mặt cầu (S) có tâm I(a; b; c) và bán kính R:
2222
)()()(
Rczbyax =−+−+−
•
Dạng 2:
0222
222
=+−−−++ dczbyaxzyx
(với
0
222
>−++
dcba
) là phương trình mặt cầu
có tâm I(a; b; c) và bán kính R =
dcba −++
222
* V
ị
trí t
ươ
ng
đố
i gi
ữ
a m
ặ
t c
ầ
u và m
ặ
t ph
ẳ
ng: Cho m
ặ
t c
ầ
u (S) có
tâm I(a;b;c) bán kính R và
m
ặ
t ph
ẳ
ng (P): Ax+By+Cz+D=0.
•
N
ế
u d(I,(P)) > R thì m
ặ
t ph
ẳ
ng (P) và m
ặ
t c
ầ
u (S) không có
đ
i
ể
m chung.
•
N
ế
u d(I,(P)) = R thì m
ặ
t ph
ẳ
ng (P) và m
ặ
t c
ầ
u (S) ti
ế
p xúc nhau.
•
N
ế
u d(I,(P)) < R thì m
ặ
t ph
ẳ
ng (P) và m
ặ
t c
ầ
u (S) c
ắ
t nhau theo giao tuy
ế
n là
đườ
ng tròn có
bán kính
2 2
r R d
= −
và tâm H c
ủ
a là hình chi
ế
u c
ủ
a I lên m
ặ
t ph
ẳ
ng (P).
5.
Hình chiếu vuông góc của điểm M:
a) Tìm hình chiếu vuông góc của 1 điểm M trên một mặt phẳng
)(
α
•
Viết phương trình đường thẳng d đi qua M và vuông góc với
)(
α
•
Gọi H là hình chiếu của M trên
)(
α
)(
α
∩
=
⇒
dH
b) Tìm hình chiếu vuông góc của một điểm M trên 1 đường thẳng d
Cách 1: _ Viết phương trình mặt phẳng
)(
α
đi qua M và vuông góc với d
_ Gọi H là hình chiếu của M trên d
)(
α
∩
=
⇒
dH
Cách 2: _ Chuyển phương trình đường thẳng d về dạng tham số
_ Gọi I là một điểm bất kì thuộc d
⇒
tọa độ điểm I theo tham số t
_ I là hình chiếu của M trên d
⇔
0. =⇔⊥
d
uMIdMI
⇒
t
⇒
Tọa độ I.
6.
Hình chiếu vuông góc của đường thẳng lên mặt phẳng:
Cách 1:Cho đường thẳng d và mặt phẳng
(
)
α
. Tìm phương trình hình chiếu của d trên
(
)
α
- Viết phương trình mặt phẳng
(
)
β
chứa d và
(
)
(
)
β α
⊥
- Gọi d’ là hình chiếu vuông góc của d trên
(
)
α
. Suy ra
(
)
(
)
'd
β α
= ∩
Cách 2:Cho đường thẳng d và mặt phẳng
(
)
α
. Tìm phương trình hình chiếu của d trên
(
)
α
- Tìm giao điểm A của d và
(
)
α
- Lấy
B d
∈
rồi tìm toạ độ của H là hình chiếu vuông góc của B trên
(
)
α
- Viết phương trình của đường thẳng AH đi qua A và H.
Chú ý : Nếu
(
)
//d
α
thì làm như sau :
- Lấy
A d
∈
rồi tìm toạ độ của H là hình chiếu vuông góc của A trên
(
)
α
- Gọi d’ là hình chiếu vuông góc của d trên d. Suy ra d’ song song với d và d’ đi qua H
7.
Các dạng viết phương trình đường thẳng:
Loại 1: Viết phương trình đường thẳng d khi biết điểm đi qua và véctơ chỉ phương
(áp d
ụ
ng công th
ứ
c)
Loại 2: Viết phương trình đường thẳng (d) qua A và cắt cả hai đt
)(
1
d
,
)(
2
d
cho trước.
Cách 1:
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 5 0918.859.305-01234.444.305
• Viết phương trình mặt phẳng (P) đi qua A và chứa
)(
1
d
• Viết phương trình mặt phẳng (Q) đi qua A và chứa
)(
2
d
•
)()( QPd
∩
=
Cách 2:
• Viết phương trình mặt phẳng (P) đi qua A và chứa
)(
1
d
.
• Xác định giao điểm B của
)(
2
d
và (P).
• Viết phương trình đường thẳng (d): đi qua A và có vecto chỉ phương là
AB
.
Loại 3: Viết phương trình đường thẳng (d) qua A và vuông góc với hai đường thẳng
)(
1
d
,
)(
2
d
Cách 1:
• Viết phương trình mặt phẳng (P) đi qua A và vuông góc với
)(
1
d
• Viết phương trình mặt phẳng (Q) đi qua A và vuông góc với
)(
2
d
•
)()( QPd
∩
=
Cách 2:
• Xác định các vecto chỉ phương của
)(
1
d
,
)(
2
d
lần lượt là
1
d
u và
2
d
u
• Gọi
w
là vecto chỉ phương của đường thẳng (d), ta có:
⊥
⊥
2
1
d
d
uw
uw
];[
21
dd
uuw =⇔
• Viết phương trình đường thẳng (d): đi qua A và có vecto chỉ phương là
w
.
Loại 4: Viết phương trình đường thẳng (d) đi qua A, vuông góc với
)(
1
d
và cắt
)(
2
d
cho trước.
Cách 1:
• Viết phương trình mặt phẳng (P) đi qua A và vuông góc với
)(
1
d
• Viết phương trình mặt phẳng (Q) đi qua A và chứa )(
2
d
•
)()( QPd
∩
=
Cách 2:
• Viết phương trình mặt phẳng (P) đi qua A và vuông góc với )(
1
d
• Xác định giao điểm B của
)(
2
d
và (P):
• Viết phương trình đường thẳng (d): đi qua A và có vecto chỉ phương là
AB
.
Loại 5: Viết phương trình đường vuông góc chung (
∆
) của 2 đường thẳng chéo nhau.
Cho 2 đường thẳng chéo nhau: d có vtcp
u
và đường thẳng d’ có vtcp
v
. Gọi
];[ vuw =
Cách 1:
• Viết phương trình mặt phẳng
)(
α
chứa d và song song với
w
.
• Viết phương trình mặt phẳng
)(
β
chứa d’ và song song với
w
• Phương trình đường vuông góc chung của d và d’ là
)()(
β
α
∩
=
∆
Cách 2:
• Chuyển d và d’ về Loại phương trình tham số theo “t” và “u”. Gọi
';
)()(
dNdM
ut
∈∈
.
• MN là đoạn vuông góc chung của d và d’ ⇒
=
=
⇔
0.
0.
'd
d
uMN
uMN
t, u
⇒
tọa độ
NM ,
• Viết phương trình đường thẳng (
∆
): đi qua M và có vecto chỉ phương là
MN
.
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 6 0918.859.305-01234.444.305
Bài 1. TOẠ ĐỘ CỦA ĐIỂM VÀ VECTƠ TRONG KHÔNG GIAN
1. Cho 3 vectơ
(1; 2; 3), ( 2;3;4), ( 3;2;1)
a b c
= − = − = −
. Toạ độ của vectơ
2 3 4
n a b b
= − +
là:
A.
( 4; 5; 2)
n
= − − −
B.
( 4;5;2)
n
= −
C.
(4; 5;2)
n
= −
D.
(4; 5; 2)
n
= − −
2. cho vecto
(
)
AO 3 i 4j 2k 5j
= + − +
. Tọa độ của điểm A là
A.
(
)
3, 2,5
−
B.
(
)
3, 17,2
− −
C.
(
)
3,17, 2
−
D.
(
)
3,5, 2
−
3. Cho 3 điểm
A(-3 ; 4 ; -2), B(-5 ; 6 ; 2), C(-4 ; 7
; -1)
. Tìm toạ độ của điểm
M
thoả mãn hệ thức
2 3
AM AB BC
= +
 

?
A.
(4; 11; 3)
M
−
B.
( 4;11; 3)
M
− −
C.
(4;11; 3)
M
−
D.
( 4; 11;3)
M
− −
4
. Cho tam giác
ABC
:
A(1; 2 ; 3), B(3 ; 2 ; 1), C(1 ; 4 ; 1)
. Tam giác
ABC
là tam giác gì?
A. Tam giác cân B. Tam giác vuông
C. Tam giác đều D. Tam giác thường
5. Cho tam giác
ABC
:
A(1; 2 ; 3), B(7 ; 10 ; 3), C(-1 ; 3 ; 1
)
. Tam giác
ABC
có đặc điểm nào dưới
đây?
A. Tam giác cân B. Tam giác nhọn
C. Tam giác vuông D. Tam giác tù
6. Cho tam giác
ABC
biết
A(2; 4 ; -3)
và
(-3; -1 ; 1), (2; -6 ; 6)
AB AC
= =
 
. Khi đó trọng tâm
G
của
tam giác có toạ độ là:
A.
5 5 2
( ; ; )
3 3 3
G B.
5 5 2
( ; ; )
3 3 3
G − C.
5 5 2
( ; ; )
3 3 3
G − D.
5 5 2
( ; ; )
3 3 3
G −
7. Cho 3 điểm A(2; 1; 4), B(–2; 2; –6), C(6; 0; –1). Tích
AB AC
.

bằng:
A.
–67
B.
65
C.
67
D.
33
8. Cho tam giác
ABC
:
(-3; 0; 4), (-1; 0 ; -2)
AB BC
= =


. Độ dài đường trung tuyến
AM
bằng bao
nhiêu?
A.
9
2
B.
95
2
C.
85
2
D.
105
2
9. Với 2 vectơ
(4; 2; 4), (6; 3;2)
a b
= − − = −
. Hãy tính giá trị của biểu thức
(2 3 )( 2 )
a b a b
− +
?
A.
-100
B.
200
−
C.
150
−
D.
250
−
10. Xét 3 điểm
(2;4; 3), ( 1; 3; 2), (4; 2;3)
A B C
− − − −
. Tìm toạ độ đỉnh
D
của hình bình hành
ABCD
?
A.
(7; 1;2)
D
−
B.
(7;1; 2)
D
−
C.
( 7;1;2)
D
−
D.
( 7; 1; 2)
D
− − −
11. Cho 4 điểm
(2; 1;4), (5;2;1), (3; 1;0), ( 3; 7;6)
A B C D
− − − −
. Tứ giác
ABCD
là hình gì?
A. Hình bình hành B. Hình thoi
C. Hình thang D. Hình chữ nhật
12. Cho 2 vectơ
(3; 2;1), (2;1; 1)
a b
= − = −
. Với giá trị nào của
m
để 2 vectơ
3
u ma b
= −
và
3
v a mb
= +
vuông góc với nhau?
A.
m=-1
m=-9
B.
m=1
m=-9
C.
m=1
m=9
D.
m=-1
m=9
13. Cho 3 vectơ
(2;3;1), (1; 2; 1), ( 2;4; 3)
a b c
= = − − = −
. Hãy tìm vectơ
x
sao cho
. 3, . 4, . 2
x a b x c x
= = =
?
A.
(4;5;10)
x
=
B.
( 4; 5; 10)
x
= − − −
C.
(4; 5;10)
x
= −
D.
( 4;5; 10)
x
= − −
14. Góc tạo bởi 2 vectơ
( 4;2;4)
a
= −
và
(2 2; 2 2; 0)
b
= −
bằng:
A.
0
30
B.
0
45
C.
0
90
D.
0
135
15. Cho ba vectơ
(
)
(
)
1,1,0 ; (1,1,0); 1,1,1
a b c= − = =
. Tìm mệnh đề nào đúng?
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 7 0918.859.305-01234.444.305
A.
0
a b c
+ + =
B.
, ,
a b c
đồng
phẳng.
C.
( )
6
cos ,
3
b c =
D.
. 1
a b
=
16. Cho tam giác
ABC
:
(2;2;2), (4;0;3), (0;1;0)
A B C
. Diện tích của tam giác này bằng bao nhiêu?
A.
65
2
đvdt
B.
55
2
đvdt
C.
75
2
đvdt D.
95
2
đvdt
17. Cho hình bình hành
ABCD
:
(2; 4; 4), (1;1; 3), ( 2; 0;5), ( 1; 3; 4)
A B C D
− − − −
. Diện tích của hình này
bằng:
A.
245
đvdt B.
345
đvdt C.
615
đvdt D.
618
đvdt
18. Cho tứ diện
ABCD
:
(0;0;1), (2;3;5), (6;2; 3), (3;7;2)
A B C D
. Hãy tính thể tích của tứ diện?
A. 10 đvdt B. 20 đvdt C. 30 đvdt D. 40 đvdt
19. Xét 3 vectơ
( 1;1; 0), (1;1;0), (1;1;1)
a b c
= − = =
. Trong các mệnh đề sau, mệnh đề nào đúng?
A.
a b c o
+ + =
B.
2
( , )
6
cos b c =
C.
, ,
a b c
đồng phẳng
D.
. 1
c a
=
20. Trên hệ trục toạ độ Oxyz cho 3 vectơ
( 1;1;0), (1;1; 0), (1;1;1)
a b c
= − = =
, hình hộp
. ' ' ' '
OACB O A C B
thoả mãn điều kiện
, ,
OA a OB b OC c
= = =

 
. Hãy tính thể tích của hình hộp trên?
A.
1
3
đvtt B.
2
3
đvtt
C.
2
đvtt D.
6
đvtt
21. Trong không gian với hệ trục toạ độ Oxyz cho bốn điểm
(1;0;0), (0;1;0), (0;0;1), (1;1;1)
A B C D
. Mặt cầu
ngoại tiếp tứ diện
ABCD
có bán kính bằng bao nhiêu?
A.
3
4
B.
3
C.
2
D.
3
2
22. Với 2 vectơ
2 1
(3;2; 1), (1; ; )
3 3
u v
= − = −
. Tập hợp các điểm
M
thoả mãn
,( , )
OM au bv a b
= + ∈

là đường thẳng đi qua điểm nào dưới đây?
A.
3 1 1
( ; ; )
2 2 2
N − − B.
3 1
( ;1; )
2 2
N
− −
C.
3 1
( ; 1; )
2 2
N
− −
D.
3 1
( ;1; )
2 2
N
−
23. Cho 3 điểm
(1;1;1), (1;1;0), (1; 0;1)
A B C
. Tìm mệnh đề đúng trong các mệnh đề sau:
A.
OABC
là tứ diện
B.
2
OA OB i j k
+ = + +


C.
, ,
A B C
thẳng hàng
D.
2
OA OB OC
= +

 
24. Hình chóp
.
S ABC
có thể tích bằng 6 và toạ độ 3 đỉnh
(1;2; 3), (0;2; 4), (5;3;2)
A B C
− −
. Hãy tính độ dài
đường cao của hình chóp xuất phát từ đỉnh
S
?
A.
8
B.
4
C.
12 3
D.
6 3
25. Xét các bộ 3 điểm sau:
I.
(2;2;1), (2; 1;3), (1; 1;2)
A B C
− −
.
II.
(1;2;3), ( 2; 4; 0), (4; 0;6)
A B C
−
.
III.
(1;2;3), (1;1;1), (0; 0;1)
A B C
Trong các bộ 3 điểm trên, bộ nào là 3 điểm thẳng hàng?
A. III B. I và II C. II D. I
26. Xét tam giác
ABC
:
(2; 1; 2), ( 1;1;2), ( 1;1;0)
A B C
− − − −
. Tính độ dài đường cao xuất phát từ
A
?
A.
13
2
B.
2 13
C.
13
2
D.
13
2
4. Tính giá trị của góc
A
của tam giác
ABC
biết
A(2; 1 ; 1), B(1 ; 2 ; 1), C(1 ; 1 ; 2)
?
A.
3
4
π
B.
3
π
C.
2
π
D.
4
π
25. Tính giá trị của góc giữa 2 vectơ
(2;5;0), (3; 7; 0)
a b
−
?
A.
0
135
B.
0
30
C.
0
45
D.
0
60
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 8 0918.859.305-01234.444.305
26.
Cho A(1; 2; –3) và B(6; 5; –1). Nếu OABC là hình bình hành thì toạ độ điểm C là:
A.
(–5;–3;–2)
B.
(–3;–5;–2)
C.
(3;5;–2)
D.
(5; 3; 2)
27.
Trong mặt phẳng Oxyz Cho tứ diện ABCD có A(2;3;1), B(4;1;-2), C(6;3;7), D-5;-4;-8).
Độ dài đường cao kẻ từ D của tứ diện là
A.
11
B.
6 5
5
C.
5
5
D.
4 3
3
28.
Cho A(1;0;0), B(0;1;0), C(0;0;1) và D(-2;1;-1).Thể tích của tứ diện ABCD là
A.
1
B.
2
C.
1
2
D.
1
3
29.
Cho tam giác ABC có A = (1;0;1), B = (0;2;3), C = (2;1;0). Độ dài đường cao của tam
giác kẻ từ C là
A.
26
B.
26
2
C.
26
3
D.
26
30.
Trong không gian Oxyz, cho bốn điểm
(
)
(
)
(
)
(
)
1,0,0 ; 0,1,0 ; 0,0,1 ; 1,1,1
A B C D
. Xác
định tọa độ trọng tâm G của tứ diện ABCD
A.
1 1 1
, ,
2 2 2
B.
1 1 1
, ,
3 3 3
C.
2 2 2
, ,
3 3 3
D.
1 1 1
, ,
4 4 4
1. Mặt cầu
2 2 2
( ) : 2 4 4 16 0
S x y z x y z
+ + − + − − =
có tâm và bán kính là:
A.
(1;2;2); 2
I R
=
B.
( 1;2; 2); 3
I R
− − =
C.
( 1; 2; 2); 4
I R
− − − =
D.
(1; 2;2); 5
I R
− =
2. Để phương trình
2 2 2 2
2( 2) 4 2 5 9 0
x y z m x my mz m
+ + − + + − + + =
là phương trình mặt cầu thì
điều kiện của
m
là:
A.
( ; 5) (1; )
m
∈ −∞ − ∪ +∞
B.
( ;1) (5; )
m
∈ −∞ ∪ +∞
C.
( ; 1) (5; )
m
∈ −∞ − ∪ +∞
D.
( ; 5) ( 1; )
m
∈ −∞ − ∪ − +∞
3. Lập phương trình mặt cầu tâm
(2; 4; 1)
I
−
và đi qua điểm
(5;2;3)
A
?
A.
2 2 2
4 8 2 8 0
x y z x y z
+ + − + − − =
B.
2 2 2
4 8 2 8 0
x y z x y z
+ + − − + − =
C.
2 2 2
4 8 2 8 0
x y z x y z
+ + + + + − =
D.
2 2 2
4 8 2 8 0
x y z x y z
+ + + − + − =
4. Mặt cầu (S) có tâm I(1;2;-3) và đi qua A(1;0;4) có phương trình
A.
+ + + + − =
2 2 2
(x 1) (y 2) (z 3) 53
B.
+ + + + + =
2 2 2
(x 1) (y 2) (z 3) 53
C.
− + − + − =
2 2 2
(x 1) (y 2) (z 3) 53
D.
− + − + + =
2 2 2
(x 1) (y 2) (z 3) 53
5. Viết phương trình mặt cầu đường kính
AB
biết:
(1; 2; 4), (3; 4; 2)
A B
− − −
?
A.
2 2 2
4 6 2 3 0
x y z x y z
+ + + + + + =
B.
2 2 2
4 6 2 3 0
x y z x y z
+ + + − + + =
C.
2 2 2
4 6 2 3 0
x y z x y z
+ + − + − + =
D.
2 2 2
4 6 2 3 0
x y z x y z
+ + + − + − =
6. Hãy lập phương trình mặt cầu tâm
(2;1; 4)
I
−
và tiếp xúc với mặt phẳng
( ) : 2 2 7 0
P x y z
− + − =
?
A.
2 2 2
4 2 8 4 0
x y z x y z
+ + + + + − =
B.
2 2 2
4 2 8 4 0
x y z x y z
+ + + − + − =
C.
2 2 2
4 2 8 4 0
x y z x y z
+ + + + − − =
D.
2 2 2
4 2 8 4 0
x y z x y z
+ + − − + − =
Bài 2. MẶT CẦU
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 9 0918.859.305-01234.444.305
7. Hãy lập phương trình mặt cầu tâm
( 5;1;1)
I
−
và tiếp xúc ngoài với mặt cầu
2 2 2
( ) : ( 1) ( 2) ( 3) 9
x y z
ω
− + + + − =
?
A.
2 2 2
10 2 2 11 0
x y z x y z
+ + + + + + =
B.
2 2 2
10 2 2 11 0
x y z x y z
+ + + − + + =
C.
2 2 2
10 2 2 11 0
x y z x y z
+ + + − − + =
D.
2 2 2
10 2 2 11 0
x y z x y z
+ + − + + + =
7.Phương trình mặt cầu (S) có tâm
I( 1; 2 ; 3)
−
và đi qua điểm
M(1; 0 ;1)
là :
A.
(
)
2 2 2
S :(x 1) (y 2) (z 3) 12
+ + + + − =
B.
(
)
2 2 2
S : (x 1) (y 2) (z 3) 81
+ + − + − =
C.
(
)
2 2 2
S : (x 1) (y 2) (z 3) 21
+ + − + + =
D.
(
)
2 2 2
S : (x 1) (y 2) (z 3) 12
+ + − + − =
8.Phương trình mặt cầu (S) có đường kính AB với
A(4 ; 3; 7)
−
,
B(2 ;1; 3)
là :
A.
(
)
2 2 2
S :(x 3) (y 1) (z 5) 49
− + + + − =
B.
(
)
2 2 2
S :(x 3) (y 1) (z 5) 9
− + + + − =
C.
(
)
2 2 2
S : (x 3) (y 1) (z 5) 9
− + − + − =
D.
(
)
2 2 2
S : (x 3) (y 1) (z 5) 9
− + + + + =
9. Mặt cầu (S) có tâm
I(1; 4 ; 7)
−
và tiếp xúc với mặt phẳng
(
)
: 6x 6y 7z 42 0
α + − + =
là :
A.
(
)
2 2 2
S :(x 1) (y 4) (z 7) 121
+ + − + + = B.
(
)
2 2 2
S :(x 1) (y 4) (z 7) 121
− + − + − =
C.
(
)
2 2 2
S : (x 1) (y 4) (z 7) 121
− + − + + = D.
(
)
2 2 2
S : (x 1) (y 4) (z 7) 121
− + + + + =
10. Cho
( )
2 2 2
: x + y + z 4x + 2y z = 0
S
− − 4
. Tìm tâm và bán kính của mặt cầu (S).
A. Tâm
(
)
I
2 ;1;2
, bán kính
R 3
=
. B. Tâm
(
)
I
2 ; 1;2
−
, bán kính
R 3
=
C. Tâm
(
)
I
2 ; 1;2
−
, bán kính
R 4
=
D. Tâm
(
)
I
2 ;1; 2
−
, bán kính
R 3
=
11. Phương trình mặt cầu (S) có tâm
(1; 2 ;3)
I bán kính R = 2 là.
A.
(
)
2 2 2
S : (x 1) (y 2) (z 3) 4
− + + + − =
B.
(
)
2 2 2
S : (x 1) (y 2) (z 3) 4
− + − + + =
C.
(
)
2 2 2
S : (x 1) (y 2) (z 3) 4
− + − + − =
D.
(
)
2 2 2
S : (x 1) (y 2) (z 3) 4
+ + − + − =
12. Viết phương trình mặt cầu đi qua 3 điểm
(1;2; 0), ( 1;1;3), (2;0; 1)
A B C
− −
và có tâm thuộc mặt phẳng
(Oxz)?
A.
2 2 2
6 6 1 0
x y z x z
+ + + + + =
B.
2 2 2
6 6 1 0
x y z x z
+ + + − + =
C.
2 2 2
6 6 1 0
x y z x z
+ + − + + =
D.
2 2 2
6 6 1 0
x y z x z
+ + − − + =
13. Hãy xét vị trí tương đối giữa mặt phẳng
( ) : 2 3 6 9 0
P x y z
− + − =
và mặt cầu
2 2 2
( ) : ( 1) ( 3) ( 2) 16
S x y z
− + − + + =
?
A. Không cắt nhau B. Cắt nhau
C. Tiếp xúc nhau
D.
( )
P
đi qua tâm của mặt cầu
( )
S
14. Hãy xét vị trí tương đối giữa 2 mặt cầu
2 2 2
( ) : 8 4 2 4 0
S x y z x y z
+ + − + − − =
và
2 2 2
( ') : 4 2 4 5 0
S x y z x y z
+ + + − − + =
?
A. Không cắt nhau B. Cắt nhau
C. Tiếp xúc ngoài D. Tiếp xúc trong
15. Cho mặt cầu
2 2 2
( ) : ( 2) ( 1) ( 1) 36
S x y z
− + − + + =
và điểm
( 2; 1;3)
M
− −
. Hãy lập phương trình mặt
phẳng tiếp diện của
( )
S
tại điểm
M
?
A.
2x+y+2z+11=0
B.
2x-y+2z+11=0
C.
2x-y-2z+11=0
D.
2x+y-2z+11=0
16. Tìm điều kiện của
m
để mặt phẳng
( ) : 3 2 6 7 0
P x y z
+ − + =
cắt mặt cầu
2 2 2 2
( ) : ( 2) ( 1) ( 1) ( 2)
S x y z m
− + − + + = +
?
A.
( ;1) (5; )
m
∈ −∞ ∪ +∞
B.
( ; 1) (5; )
m
∈ −∞ − ∪ +∞
C.
( ; 5) (1; )
m
∈ −∞ − ∪ +∞
D.
( ; 5) ( 1; )
m
∈ −∞ − ∪ − +∞
1
7. L
ập phương trình mặt phẳng tiếp diện của mặt cầu
2 2 2
( ) : 6 4 2 11 0
S x y z x y z
+ + − + − − =
, biết mặt
phẳng đó song song với mặt phẳng
( ) : 4 3 17 0
x z
α
+ − =
?
A.
4 3 10 0
x z
+ + =
và
4 3 40 0
x z
+ − =
B.
4 3 10 0
x z
+ + =
và
4 3 40 0
x z
+ − =
C.
4 3 10 0
x z
+ + =
và
4 3 40 0
x z
+ + =
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 10 0918.859.305-01234.444.305
D.
4 3 10 0
x z
+ − =
và
4 3 40 0
x z
+ − =
18. Cho 2 điểm
(1;2;1), (3;1; 2)
A B
−
. Tập hợp các điểm
( ; ; )
M x y z
sao cho
2 2
30
MA MB
+ =
là một mặt
cầu có phương trình là:
A.
2 2 2
4 3 5 0
x y z x y z
+ + − − + − =
B.
2 2 2
4 3 5 0
x y z x y z
+ + + + + + =
C.
2 2 2
4 3 5 0
x y z x y z
+ + + − + − =
D.
2 2 2
4 3 5 0
x y z x y z
+ + − + − + =
19. Lập phương trình mặt cầu tâm
( 5;1;1)
I
−
và tiếp xúc với đường thẳng
2 1 3
:
2 1 1
x y z
d
− − +
= =
−
?
A.
2 2 2
2 4 12 36 0
x y z x y z
+ + + + + + =
B.
2 2 2
2 4 12 36 0
x y z x y z
+ + + − + − =
C.
2 2 2
2 4 12 36 0
x y z x y z
+ + + + − − =
D.
2 2 2
2 4 12 36 0
x y z x y z
+ + − − + + =
20. M
ặt cầu
( )
S
tâm
(4;2; 2)
I
−
tiếp xúc với mặt phẳng
( ) : 12 5 5 0
P x z
− + =
. Hãy tính bán kính
R
của
mặt cầu đó?
A.
39
13
R =
B.
13
R
=
C.
3
R
=
D.
39
R
=
21. Bán kính của mặt cầu tâm
(1; 3;5)
I
và tiếp xúc với đường thẳng
: 1
2
x t
d y t
z t
=
= −
= −
bằng bao nhiêu?
A.
7
R
=
B.
7
R
=
C.
14
R
=
D.
14
R
=
22. Cho mặt cầu
2 2 2
( ) : ( 1) ( 2) ( 3) 12
S x y z
+ + − + − =
. Trong các mệnh đề sau, mệnh đề nào đúng?
A.
( )
S
đi qua điểm
( 3;4;2)
N
−
B.
( )
S
đi qua điểm
(1; 0;1)
M
C.
( )
S
có bán kính
2 3
R
=
D.
( )
S
có tâm
( 1;2;3)
I
−
23. Tìm bán kính mặt cầu ngoại tiếp tứ diện
OABC
biết
(1;0; 0), (0;1; 0), (0;0;1)
A B C
?
A.
2
2
R = B.
3
2
R =
C.
3
R
=
D.
2
R
=
24. Cho mặt cầu
2 2 2
( ) : 2 2 0
S x y z x z
+ + − − =
và mặt phẳng
( ) : 4 3 1 0
x y
α
+ + =
. Trong các mệnh đề
s
au, m
ệnh đề nào đúng?
A.
( )
α
cắt mặt cầu
( )
S
theo một đường tròn có bán kính nhỏ hơn bán kính mặt cầu.
B.
( )
α
đi qua tâm của mặt cầu
( )
S
C.
( )
α
tiếp xúc với mặt cầu
( )
S
D.
( ) ( )
S
α
∩ = ∅
25. Lập phương trình mặt cầu có tâm I nằm trên đường thẳng
9
( ) : 7 / 3 6
7 / 3 6
x t
d y t
z t
=
= −
= −
và tiếp xúc với hai mặt
phẳng
1
( ) : 2 2 2 0
P x y z
+ − − =
và
2
( ) : 2 2 4 0
P x y z
+ − + =
?
A.
2 2 2
( ) : ( 11) ( 2) ( 4) 25
S x y z
+ + − + − =
B.
2 2 2
( ) : ( 2) ( 3) 16
S x y z
+ + + − =
C.
2 2 2
( ) : ( 1) ( 3) ( 3) 1
S x y z
+ + − + − =
D.
2 2 2
( ) : ( 1) ( 2) ( 3) 1
S x y z
+ + − + − =
26. Lập phương trình mặt cầu có tâm I nằm trên đường thẳng
( ) : 2
1
x t
d y
z
=
=
= −
và cắt mặt phẳng
( ) : 0
P y z
− =
theo thiết diện là đường tròn lớn có bán kính bằng 4?
A.
2 2 2
( ) : ( 1) ( 2) ( 2) 16
S x y z
+ + − + − =
B.
2 2 2
( ) : ( 1) ( 2) 16
S x y z
+ + − + =
C.
2 2 2
( ) : ( 1) ( 2) 16
S x y z
+ + + − =
D.
2 2 2
( ) : ( 2) ( 2) 16
S x y z
+ − + − =
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 11 0918.859.305-01234.444.305
27. Cho đường thẳng
1
( ) : 3
2
x t
d y t
z t
= − +
= −
= − +
và 2 mặt phẳng
( ) : 2 3 0
P x y z
− − + =
và
( ) : 2 2 1 0
Q x y z
+ − − =
. Lập phương trình mặt cầu có tâm I là giao điểm của
( )
d
và
( )
P
, sao cho mặt
phẳng
( )
Q
cắt mặt cầu theo giao tuyến là một đường tròn
( )
C
có chu vi bằng
2
π
?
A.
2 2 2
( ) : ( 1) 11
S x y z
+ + + =
B.
2 2 2
( ) : ( 1) ( 1) 2
S x y z
+ − + + =
C.
2 2 2
( ) : ( 2) 11
S x y z
+ − + =
D.
2 2 2
( ) : ( 1) ( 2) 16
S x y z
+ − + + =
2
8. L
ập phương trình mặt cầu tâm
(2; 3; 1)
I
−
cắt đường thẳng
( ) : 11/2 1/2
14
x t
d y t
z t
=
= − +
= − −
tại 2 điểm
,
A B
sao cho
16
AB
=
?
A.
2 2 2
( ) : ( 3) ( 4) ( 5) 625
S x y z
− + − + + =
B.
2 2 2
( ) : ( 2) ( 3) ( 4) 256
S x y z
− + − + + =
C.
2 2 2
( ) : ( 2) ( 3) ( 1) 289
S x y z
− + − + + =
D.
2 2 2
( ) : ( 1) ( 1) ( 1) 9
S x y z
− + − + + =
29. Cho mặt cầu
2 2 2
( ) : 4 2 2 3 0
S x y z x y z
+ + − − − + =
. Hãy lập phương trình mặt cầu
1
( )
S
đối xứng
với mặt cầu
( )
S
qua điểm
(1;2; 3)
E
?
A.
2 2 2
1
( ) : ( 3) ( 5) 3
S x y z
+ − + − =
B.
2 2 2
1
( ) : ( 5) 9
S x y z
+ + − =
C.
2 2 2
1
( ) : ( 3) 1
S x y z
+ − + =
D.
2 2 2
1
( ) : 1
S x y z
+ + =
30.Trong không gian Oxyz cho mặt cầu (S): x
2
+ y
2
+ z
2
+ 6x – 4y + 4z + 1 = 0. Viết phương trình
mặt phẳng (P) song song với mặt phẳng (Q): 2x + y + 2z - 4 = 0 và tiếp xúc với mặt cầu (S).
A.2x+y+2z-20=0 B.2x+y+2z+20=0 C.2x+y-2z+20=0 D.2x-y+2z+20=0
31. Cho (S) là mặt cầu tâm I(2,1,-1) và tiếp xúc với mặt phẳng (P): 2x-2y-z+3=0. bán kính (S) là
A: 2; B: 2/3; C: 4/3; D:2/9
32.
Cho bốn điểm A(1;1;1), B(1;2;1), C(1;1;2) và D(2;2;1). Tâm I của mặt cầu ngoại tiếp tứ
diện ABCD có tọa độ :
A.
(
)
3;3; 3
−
B.
3 3 3
; ;
2 2 2
−
C.
3 3 3
; ;
2 2 2
D.
(
)
3;3;3
33.
Cho mặt cầu (S):
x y z x y z
2 2 2
8 4 2 4 0
+ + − + + − =
. Bán kính R của mặt cầu (S) là:
A. R =
17
B.
R =
88
C.
R = 2 D. R = 5
34.
Cho 2 điểm A(2; 4; 1), B(–2; 2; –3). Phương trình mặt cầu đường kính AB là:
A.
x y z
2 2 2
( 3) ( 1) 9
+ − + − =
B.
x y z
2 2 2
( 3) ( 1) 9
+ + + − =
c.
x y z
2 2 2
( 3) ( 1) 3
+ − + + =
D.
x y z
2 2 2
( 3) ( 1) 9
+ − + + =
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 12 0918.859.305-01234.444.305
Bài 3 MẶT PHẲNG
1. Phương trình tổng quát của mặt phẳng (P) đi qua điểm M(2 ; 3 ; 5) và vuông góc với vectơ
(4;3;2)
n
=
:
A.
4x+3y+2z+27=0
B.
4x-3y+2z-27=0
C.
4x+3y+2z-27=0
D.
4x+3y-2z+27=0
2. Phương trình tổng quát của mặt phẳng (P) đi qua điểm M(2 ; 3 ; -1) và song song với mặt phẳng
( ) : 5 3 2 10 0
Q x y z
− + − =
là:
A.
5x-3y+2z+1=0
B.
5x+5y-2z+1=0
C.
5x-3y+2z-1=0
D.
5x+3y-2z-1=0
3. Phương trình tổng quát của mặt phẳng
( )
ABC
với
(2; 0;3), (4; 3;2), (0;2;5)
A B C
−
là:
A.
2x+y+z+7=0
B.
2x+y+z-7=0
C.
2x-y+z-7=0
D.
2x-y+z+7=0
4. Phương trình tổng quát của mặt phẳng trung trực của AB với
(2; 0;3), (4; 4;1)
A B
−
là:
A.
2x+3z-11=0
B.
x-2y-z-5=0
C.
4x-4y+z-11=0
D.
x-2y-z=0
5. Lập phương trình tổng quát của mặt phẳng chứa điểm M(1 ; -2 ; 3) và có cặp vectơ chỉ phương
(0; 3; 4), (3; 1; 2)
v u
= = − −
?
A.
2x+12y+9z+53=0
B.
2x+12y+9z-53=0
C.
2x-12y+9z-53=0
D.
2x-12y+9z+53=0
6. Viết phương trình mặt phẳng đi qua 2 điểm
(4; 0;2), (1; 3; 2)
A B
−
và song với đường thẳng
1 3
( ) :
4 5 3
x y z
d
− +
= = ?
A.
29x+7y+27z+62=0
B.
29x+7y+27z-62=0
C.
29x-7y+27z+62=0
D.
29x-7y-27z-62=0
7. Mặt phẳng trung trực của đoạn thẳng AB có phương trình là ,với A(1;2;-3),B(-3;2;9)
A.
-x-3z-10=0
B.
-4x+12z-10=0
C.
-x-3z-10=0
D.
-x+3z-10=0
8. Phương trình nào dưới đây là phương trình của mặt phẳng đi qua 3 điểm không thẳng hàng
( 3;0;0), (0;4; 0), (0;0; 2)
A B C
− −
?
A.
x
1
-3 4 2
y z
+ + =
−
B.
x
1
-3 4 2
y z
− + =
−
C.
x
1
3 4 2
y z
+ + =
−
D.
x
1
-3 4 2
y z
+ + =
−
9. Hãy lập phương trình mặt phẳng đi qua điểm M(5 ; 4 ; 3) và chắn trên các trục toạ độ dương những đoạn
thẳng bằng nhau?
A.
x
1
12 12 12
y z
− − =
B.
x
1
-12 12 12
y z
+ + =
C.
x
1
12 12 12
y z
+ + =
D.
x
1
12 12 12
y z
− + =
10. Mặt phẳng nào dưới đây đi qua điểm M(3 ; -1 ; -5) và vuông góc với 2 mặt phẳng
( ) : 3 2 2 7 0,( ) : 5 4 3 1 0
x y z x y z
α β
− + + = − + + =
?
A.
2x+y+2z+15=0
B.
2x+y-2z-15=0
C.
2x-y+2z-15=0
D.
2x-y-2z-15=0
11. Viết phương trình tổng quát của mặt phẳng chứa hai điểm
(2; 1;4), (3;2; 1)
A B
− −
và vuông góc với mặt
phẳng
( ) : 2 3 0
x y z
α
+ + − =
?
A.
11x+7y+2z+21=0
B.
11x-7y+2z+21=0
C.
11x+7y-2z-21=0
D.
11x-7y-2z-21=0
12. Phương trình của mp(P) đi qua điểm A(1;-1;-1) và vuông góc với đường thẳng
2
: 1
1 2
x t
d y t
z t
= −
= +
= − +
là:
A. x - y - 2z + 4=0 B. x - y + 2z - 4=0 C. x - y + 2z + 4=0 D.x – y – 2z – 4 = 0
13. Lập phương trình của mặt phẳng (P) đi qua điểm A(1;-1;-1) và vuông góc với đường thẳng
d :
x+3 1-y z+2
= =
2 3 4
là : A. 2x-3y +4z -1=0 B. 2x-3y +4z +1=0
C. 2x-3y -4z -1=0 D. 2x-3y -4z +1=0
14. Lập phương trình của mặt phẳng (P) chứa hai đường thẳng :
:
x=7+3t
y=2+2t
z=1-2t
∆
và
∆
x-1 y+2 z-5
': = =
2 -3 4
A. 2x – 16y – 13z – 31 = 0 B. 2x – 16y +13z + 31 = 0
C. 2x + 16y – 13z + 31 = 0 D. 2x – 16y – 13z + 31 = 0
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 13 0918.859.305-01234.444.305
15. Phương trình của mặt phẳng
( )
P
chứa đường thẳng là giao tuyến của hai mặt phẳng
5 9 13 0, 3 5 1 0
x y z x y z
+ + − = − − + =
và đi qua điểm
(0;2;1)
M
?
A.
x
1
3 3 3
y z
+ + =
B.
x
1
3 3 3
y z
− + + =
C.
x-y-z+3=0
D.
x-y+z+3=0
16. Lập phương trình của mặt phẳng
( )
α
chứa giao tuyến của 2 mặt phẳng
( ) : 2 12 3 0
P x y z
− − − =
và
( ) : 1 0
Q x z
− − =
, và vuông góc với mặt phẳng
( ) : 2 5 1 0
R x y z
+ + − =
?
A.
5x-z+1=0
B.
3x+y-z-1=0
C.
4x+3y-2z-1=0
D.
4x+3y-2z+1=0
17. Tìm giá trị của
,
m n
để 2 mặt phẳng
( ) : ( 3) 3 ( 1) 6 0
m x y m z
α
+ + + − + =
và
( ) : ( 1) 2 (2 1) 2 0
n x y n z
β
+ + + − − =
song song với nhau?
A.
5 2
m= ,
2 3
n
=
B.
5 2
m= ,
2 3
n
= −
C.
5 2
m=- ,
2 3
n
=
D.
5 2
m=- ,
2 3
n
= −
18. gọi (P) là mặt phẳng cắt ba trục tọa độ tại ba điểm
(
)
(
)
(
)
8,0,0 ; 0, 2,0 ; 0,0,4
A B C
−
.
Phương trình của mặt phẳng (P) là:
A.
1
4 1 2
x y z
+ + =
−
B.
0
8 2 4
x y z
+ + =
−
C.
4 2 8 0
x y z
− + − =
D.
4 2 0
x y z
− + =
19. Tìm giá trị của
m
để 2 mặt phẳng
( ) : (2 1) 3 2 3 0
m x my z
α
− − + + =
và
( ) : ( 1) 4 5 0
mx m y z
β
+ − + − =
vuông góc với nhau?
A.
m=4
m=-2
B.
m=4
m=2
C.
m=-4
m=-2
D.
m=-4
m=2
20. Phương trình các mặt phẳng song song với mặt phẳng
( ) : 2 2 5 0
P x y z
+ − + =
và cách điểm
(2; 1; 4)
B
−
một khoảng bằng 4 là:
A.
2 2 4 0
x y z
+ − + =
và
2 2 20 0
x y z
+ + + =
B.
2 2 20 0
x y z
+ − + =
và
2 2 4 0
x y z
+ − − =
C
.
2 2 20 0
x y z
− + + =
và
2 2 4 0
x y z
− + + =
D.
2 2 20 0
x y z
− + + =
và
2 2 4 0
x y z
− + − =
21. Tìm điểm
M
trên trục Oy cách đều 2 mặt phẳng
( ) : 1 0
x y z
α
+ − + =
và
( ) : 5 0
x y z
β
+ − − =
?
A.
(0;1;0)
M
B.
(0;2;0)
M
C.
(0; 3;0)
M
D.
(0; 3; 0)
M
−
22. Gọi
, ,
A B C
lần lượt là hình chiếu của điểm
(2;3; 5)
M
−
lên các trục Ox, Oy, Oz. Khi đó phương trình
mặt phẳng
( )
ABC
là:
A.
15 10 6 30 0
x y z
+ + + =
B.
15 10 6 30 0
x y z
− + − =
C.
x
1
2 3 5
y z
+ − =
D.
x
1
2 3 5
y z
+ + =
−
23. Cho tam giác
ABC
có:
(1;0;0), (0;2; 0), (3; 0; 4)
A B C
. Tìm toạ độ điểm
M
thuộc mặt phẳng Oxy sao
cho
( )
MC ABC
⊥
?
A.
3 11
(0; ; )
2 2
M −
B.
3 11
(0; ; )
2 2
M − −
C.
3 11
(0; ; )
2 2
M −
D.
3 11
(0; ; )
2 2
M
24. Cho điểm
(2;6; 3)
I
−
và các mặt phẳng
( ) : 2 0,( ) : 6 0,( ) : 3 0
x y z
α β γ
− = − = + =
. Trong các mệnh
đề sau, hãy tìm mệnh đề sai?
A.
( ) ( )
α β
⊥
B.
( )
Oz
γ
C.
( ) ( )
Oxz
β
D.
( )
I
α
∈
2
5. Trong không gian với hệ trục toạ độ Oxyz cho các điểm
(1;0;0), (0;2; 0), (0;0; 3), (1;2; 0)
A B C D
. Viết
phương trình mặt phẳng
( ' ')
DA B
với
', '
A B
là 2 đỉnh của hình hộp chữ nhật
. ' ' '
OADB CA D B
?
A.
6x+3y+z-12=0
B.
6x+3y-z-12=0
C.
6x-3y+z-12=0
D.
6x-3y-z+12=0
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 14 0918.859.305-01234.444.305
Bài4. ĐƯỜNG THẲNG
1. Lập phương trình tham số của đường thẳng
d
đi qua điểm
(1; 0;3)
A
và
(4;2; 1)
B
−
?
A.
1 3
2
3 4
x t
y t
z t
= +
=
= −
B.
1 4
2
3
x t
y t
z t
= +
=
= −
C.
4
2
1 3
x t
y
z t
= +
=
= − +
D.
1 5
2
3 2
x t
y t
z t
= +
=
= +
2
. Phương trình chính tắc của d đi qua hai điểm A(1;2;-3) và B(3;-1;1) là:
A.
− − +
= =
−
1 2 3
3 1 1
x y z
B.
3 1 1
1 2 3
x y z
− + −
= =
−
C.
− − +
= =
−
1 2 3
2 3 4
x y z
D.
1 2 3
2 3 4
x y z
+ + −
= =
−
3. Phương trình chính tắc của đường thẳng
d
đi qua điểm
(1; 2;5)
M
−
và vuông góc với mặt phẳng
( ) : 4 3 2 5 0
x y z
α
− + + =
là:
A.
1 2 5
4 3 2
x y z
− + −
= =
−
B.
1 2 5
4 3 2
x y z
− + −
= =
− −
C.
1 2 5
4 3 2
x y z
− + −
= = D.
1 2 5
4 3 2
x y z
− + −
= =
− − −
4. Phương trình nào dưới đây không phải là phương trình chính tắc của đường thẳng
3 2
: 2 3
2 5
x t
d y t
z t
= −
= +
= − +
?
A.
3 2 2
2 3 5
x y z
− − +
= =
−
B.
3 2 2
2 3 5
x y z
− − +
= =
− −
C.
3 2 2
4 6 10
x y z
− − +
= =
− −
D.
2 3 5
3 2 2
x y z
+ − −
= =
−
5. Hãy tìm một vectơ chỉ phương của đường thẳng là giao tuyến của hai mặt phẳng
2 3 5 8 0, 2 1 0
x y z x y z
− − + = + − − =
?
A.
(11; 1; 5)
u
= − −
B.
( 11;1;5)
u
= −
C.
(11; 1;5)
u
= −
D.
(11;1;5)
u
=
6. Phương trình tham số của đường thẳng đi qua điểm A(1; 2;3) và có VTCP
( 2;0;1)
u = −
là:
A.
1 2
: 2
3
x t
d y
z t
= −
=
= +
B.
1 2
: 2
3
x t
d y
z t
= +
=
= +
C.
1
: 2
3
x t
d y
z t
= −
=
= +
D.
1
: 2
3
x t
d y
z t
= +
=
= −
7. Lập phương trình tham số của đường thẳng d đi qua hai điểm A(1;2;3) và B(2;1;1)
A.
1
: 2
3 2
x t
d y t
z t
= +
= −
= −
B.
= −
= +
= −
1
: 2
3 2
x t
d y t
z t
C.
1
: 2
3
x t
d y t
z t
= −
= +
= +
D.
1
: 2
3
x t
d y t
z t
= +
= −
= −
8
. L
ập phương trình tham số của đường thẳng d đi qua điểm M(1;-2;3) và song song với đường thẳng
∆
1 2
: 2
3
x t
y t
z t
= − +
= +
= − −
A.
1 2
: 2
3
x t
d y t
z t
= +
= − −
= −
B.
1 2
: 2
3
x t
d y t
z t
= +
= − +
= +
C.
1 2
: 2
3
x t
d y t
z t
= +
= − +
= −
D.
1 2
: 2
3
x t
d y t
z t
= +
= − −
= − +
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 15 0918.859.305-01234.444.305
9. Phương trình tham số của đường thẳng d đi qua điểm N(-1;2;-3) và song song với đường thẳng
∆:
x y+1 1-z
= =
2 2 3
là: A. d :
x=-1+2t
y=2+2t
z=-3 +3t
B. d :
x=-1+2t
y=2+2t
z=3 +3t
C. d :
x=-1+2t
y=2-2t
z=-3 -3t
D. d :
x=-1+2t
y=2+2t
z=-3 -3t
1
0. L
ập phương trình chính tắc của đường thẳng d đi qua điểm A(2;3;-5) và có vecto chỉ phương
( 4;8;10)
u = −
A.
x-2 y-3 z+5
= =
3 -1 2
B.
x-2 y-3 z+5
= =
-2 4 5
C.
x-2 y-3 z+5
= =
1 3 -2
D.
x-2 y-3 z+5
= =
2 4 5
11. Cho đường thẳng d :
2 2
3
3 5
x t
y t
z t
= +
= −
= − +
. Phương trình chính tắc của d là:
A.
2 3
2 3 5
x y z
− +
= =
−
B.
2 3
2 3 5
x y z
+ −
= =
−
C. x -2 = y = z+3 D. x+2 = y = z - 3
12. Cho đường thẳng d :
2 2
3
3 5
x t
y t
z t
= +
= −
= − +
. Một véc tơ chỉ phương của d là :
A.
= −
(2;0; 3)
u
B.
(2; 3; 5)
u = −
C.
(2;3; 5)
u
= −
D.
(
)
=
2;0;5
u
13. Tìm
m
để 2 đường thẳng
1
:
2 3
x y z
d
m
= =
−
và
2
1 5
:
3 2 1
x y z
d
+ +
= =
cắt nhau?
A.
m=1
B.
m=2
C.
m=3
D.
m=4
14. Cho 2 điểm
( 1;3; 5), ( 1; ;1 )
A B m m m
− − − −
. Giá trị của
m
để đường thẳng
AB
song song với mặt
phẳng
( ) : 4 0
x y z
α
+ − + =
là:
A.
m=1
B.
m=2
C.
m=3
D.
m=4
15. Giá trị nào của
m
để đường thẳng
1 2 3
:
2 1 2
x y z
d
m m
− + +
= =
−
vuông góc với mặt phẳng
( ) : 3 2 5 0
P x y z
+ − − =
là:
A.
m=1
B.
m=-1
C.
m=2
D.
m=-2
16. Khoảng cách từ điểm
(2;3;1)
A
đến đường thẳng
1 4
: 2 2
1 4
x t
d y t
z t
= −
= +
= − +
bằng :
A.
3
B.
5
C.
6
D.
7
17. Khoảng cách từ điểm
(2; 3;1)
A
đến mặt phẳng (P): 2x + y -2z +1 = 0 bằng :
A.
3
B.
5
C. 2
D.
7
18. Tìm tất cả các giá trị của
m
để đường thẳng
1 3 1
:
2 2
x y z
d
m m
+ − −
= =
−
cắt mặt phẳng
( ) : 3 2 5 0
P x y z
+ + − =
?
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 16 0918.859.305-01234.444.305
A.
1
m
5
≠
B.
3
m
5
≠
C.
2
m
5
≠
D.
4
m
5
≠
19. Tìm tất cả các giá trị của
m
để đường thẳng là giao tuyến của hai mặt phẳng
3 2 3 0, 4 3 4 2 0
x y z x y z
− + + = − + + =
song song với mặt phẳng
( ) : 2 ( 3) 2 0
P x y m z
− + + − =
?
A.
m=5
B.
m=-5
C.
m=3
D.
m=-3
20. Khoảng cách giữa 2 đường thẳng song song
1
3 2
:
1 2 1
x y z
d
− −
= = và
2
3 1 2
:
1 2 1
x y z
d
− + −
= =
bằng:
A.
5 6
6
B.
5 3
6
C.
5 30
6
D.
5 5
6
21. Phương trình mặt phẳng
( )
α
chứa đường thẳng là giao tuyến của hai mặt phẳng
0, 0
x y z x y z
− + = + − =
và song song với đường thẳng
1
1 3 4
:
3 2 4
x y z
d
− − +
= =
−
:
A.
2x+y+z+1=0
B.
2x-y+z-1=0
C.
2x-y+z=0
D.
2x+y-z=0
22. Xét vị trí tương đối giữa 2 đường thẳng
1 2
1 3 2 2 1 4
: , :
2 2 3 3 2 4
x y z x y z
d d
− + − − − +
= = = =
ta
được kết quả nào?
A. Cắt nhau B. Song song C. Chéo nhau D. Trùng nhau
23. Cho mặt phẳng
( ) : 2 3 1 0
x y z
α
+ + + =
và đường thẳng
3
: 2 2
1
x t
d y t
z
= − +
= −
=
. Tìm mệnh đề đúng trong
các mệnh đề sau?
A.
d ( )
α
⊂
B.
d ( )
α
C.
d ( )=M
α
∩
D.
d ( )
α
⊥
24. Trong không gian với hệ trục toạ độ Oxyz cho đường thẳng là giao tuyến của hai mặt phẳng
2 2 0
2 5 0
x y z
x z
− − − =
+ − =
. Gọi
M d
∈
và
u
là vectơ chỉ phương của đường thẳng . Tìm nhận định đúng?
A.
(3; 1;1)
M
−
và
(1; 1;2)
u
−
B.
(3;1; 1)
M
−
và
(1;1; 2)
u
−
C.
(3;1; 1)
M
−
và
(1;1;2)
u
D. Cả 3 đáp án trên đều sai
25. Xét vị trí tương đối của 2 đường thẳng
1
: 2
3
x t
d y t
z t
= +
= +
= −
và
1 2
' : 1 2
2 2
x u
d y u
z u
= +
= − +
= −
?
A.
d
và
'
d
chéo nhau
B.
d '
d
C.
d ' =M
d
∩
D.
d '
d
≡
26. Cho 4 điểm
A(1; 1 ; 1), B(1 ; 3 ; 5), C(1 ; 1 ; 4),
D(2;3;2)
. Gọi
I,J
lần lượt là trung điểm của
,
AB CD
. Khẳng định nào sau đây đúng?
A.
I J
≡
B.
( )
IJ ABC
⊥
C.
AB IJ
⊥
D.
CD IJ
⊥
27. Khoảng cách từ điểm
( 2; 4; 3)
M
− −
đến mặt phẳng
( ) : 2 2 3 0
x y z
α
− + − =
bằng bao nhiêu?
A. 11 B. 1 C. 2 D. 3
28. Cho t
ứ diện
ABCD
với
A(4; 1 ; 5), B(1 ; 1 ; 1), C(4 ; 6 ; 5),
D(4;0;3)
. Tính chiều cao của tứ diện
xuất phát từ đỉnh
A
?
A.
5 2
3
B.
5 3
3
C.
5 3
2
D.
15 139
139
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 17 0918.859.305-01234.444.305
29. Trong không gian với hệ trục toạ độ Oxyz cho hình lập phương
. ' ' ' '
ABCD A B C D
cạnh
a
. Hãy tính
khoảng cách giữa 2 đường thẳng
AC
và
'
BD
?
A.
5
6
a
B.
6
3
a
C.
6
6
a
D.
6
5
a
30. Cho 2 điểm
0 1
(2; 3;1), (1; 1;1)
M M
−
và đường thẳng là giao tuyến của hai mặt phẳng
2 5 0,2 5 0
x y x z
− + = + + =
, gọi
0 0
( , )
d d M
= ∆
và
1 1
( , )
d d M
= ∆
. Hãy tìm mệnh đề đúng trong
các mệnh đề sau?
A.
0 1
d d
>
B.
0 1
2 2
3
d d− =
C.
0 1
6 3
d d
+ =
D.
0 1
d d
<
31. Cho mặt phẳng
( ) : 3 2 5 0
x y z
α
− − + =
và đường thẳng
1 7 3
:
2 1 4
x y z
− − −
∆ = = . Gọi
( )
β
là mặt
phẳng chứa đường thẳng
∆
và song song với
( )
α
. Tính khoảng cách giữa 2 mặt phẳng
( )
α
và
( )
β
?
A.
3
14
B.
3
14
C.
9
14
D.
9
14
32. Nếu điểm
(0;0; )
M t
cách đều điểm
1
(2; 3;4)
M
và mặt phẳng
( ) : 2 3 17 0
P x y z
+ + − =
thì
t
có giá trị
bằng bao nhiêu?
A.
3
t
=
B.
3
t
= −
C.
3
t
=
D.
3
t
= −
33. Khoảng cách gữa 2 mặt phẳng song song
( ) : 5 0,( ) : 2 2 2 3 0
P x y z Q x y z
+ − + = + − + =
sau đây
bằng bao nhiêu?
A.
7
2
B.
7
2 3
C.
2
3
D.
2
34. Cho điểm A(0;-1;3) và đường thẳng d
1 2
2
1
x t
y
z
= +
=
= −
.
Khoảng cách từ A đến d bằng
A.
8
B.
3
C.
14
D.
6
35. Cho 2 đường thẳng chéo nhau
1
1
: 1
1
x t
d y t
z t
= +
= − −
= +
và
2
3 2
:
3 3 3
x y z
d
− +
= =
−
. Độ dài đường vuông góc
chung của 2 đường thẳng trên bằng bao nhiêu?
A.
112
3
B.
104
3
C.
114
3
D. Đáp số A, B, C sai
36.
Mặt phẳng (Q) song song với mp(P): x+2y+z-4=0 và cách D(1;0;3) một khoảng bằng
6
có phương trình là
A.
x+2y+z+2=0 B. x+2y-z-10=0
C.
x+2y+z-10=0 D.
x+2y+z+2=0 và
x+2y+z-10=0
37.
Cho hai điểm A(1;-1;5) và B(0;0;1). Mặt phẳng (P) chứa A, B và song song với Oy có
phương trình là
A.
4 1 0
x y z
+ − + =
B.
2 5 0
x z
+ − =
C.
4 1 0
x z
− + =
D.
4 1 0
y z
+ − =
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 18 0918.859.305-01234.444.305
BÀI TẬP VỀ GIAO ĐIỂM – HÌNH CHIẾU - ĐỐI XỨNG
1. Tìm toạ độ giao điểm
M
của đường thẳng
1 2
: 2
1
x t
d y t
z t
= +
= − −
= −
và mặt phẳng
( ) : 4 5 0
P x y z
− − + =
?
A.
(1;1;2)
M
B.
(1; 1;2)
M
−
C.
(1;1; 2)
M
−
D.
( 1; 1;2)
M
− −
2
. Toạ độ giao điểm
M
của 2 đường thẳng
1
1 8
: 1 3
2 5
x t
d y t
z t
= −
= +
= −
và
2
7 3 5
:
2 5 2
x y z
d
− − −
= =
−
là:
A.
(9;2;7)
M
B.
(9;2; 7)
M
−
C.
(9; 2; 7)
M
− −
D.
(9; 2;7)
M
−
3. Cho điểm
(1;2; 1)
A
−
và đường thẳng
3 0
( ) :
1 0
x y z
d
y z
+ + − =
+ − =
. Xác định toạ độ hình chiếu vuông góc
H
của
A
lên đường thẳng
( )
d
?
A.
(2;1;1)
H
B.
(2;2; 1)
H
−
C.
(2;2;1)
H
D.
(2;1; 1)
H
−
4. Cho mặt phẳng (P): 3x -8y +7z -1=0 và hai điểm A(0;0;-3), A(2;0;-1). Tìm giao điểm M của mp(P) và
đường thẳng AB. (Theo đề thi Đại học Quốc gia Hà Nội, khối A- 2000)
A. M(2;3;-1) B. M(11;0;-4) C. M(11/5;0;4/5) D. Một điểm khác.
5. Trong không gian cho điểm A(1;1;1) và đường thẳng
14 4
:
5 2
= +
=
= − −
x t
d y t
z t
.Xác định điểm H là hình chiếu
vuông góc của A lên d A. H(2;3;-1) B H(2;-3;-1) C. H(2;-3;1) D. H(2;-3;-1)
6. 6. Trong không gian Oxyz, cho mp(P) :x+ y +z -1 =0 và đường thẳng d có phương trình:
1
:
1
=
=
= −
x
d y t
z
.Tìm
giao điểm A của d và mp(P) (Đại học Hàng Hải-2000)
A. A(1;1;-1) B. A(1;1;1) C. A(1;-1;-1) D. A(1;-1;1)
7. Cho mặt phẳng
( ) : 5 14 0
P x y z
+ + − =
và điểm
(1; 4; 2)
M
− −
. Tìm toạ độ hình chiếu
H
của điểm
M
lên mặt phẳng
( )
P
?
A.
(2; 3; 3)
H
B.
(2; 3; 3)
H
−
C.
(2; 3; 3)
H
−
D.
( 2; 3; 3)
H
− −
8. Tìm giao điểm của
− +
= =
−
3 1
:
1 1 2
x y z
d và
(
)
P : 2x y z 7 0
− − − =
A. M(3;-1;0) B. M(0;2;-4) C. M(6;-4;3) D. M(1;4;-2)
9. Tìm giao điểm của
3 1
:
1 1 2
x y z
d
− +
= =
−
và
(
)
: 2 7 0
P x y z
− − − =
A, M(1;4;-2) B, M(0;2;-4) C, M(6;-4;3) D, M(5;-1;2)
Cho điểm
(2; 3; 1)
A
−
. Hãy tìm toạ độ điểm
'
A
đối xứng với
A
qua mặt phẳng
( ) : 2 5 0
P x y z
− − − =
?
A.
'(4;2;2)
A
B.
'(4;2; 2)
A
−
C.
'( 4;2; 2)
A
− −
D.
'( 4;2;2)
A
−
10. Cho điểm A(2;3;5) và mp (P): 2x +3y+z -17=0 , gọi d là đường thẳng đi qua A và vuông góc với mp(P) .
Xác định giao điểm M của d và trục Oz.
A. M(0;0;2) B. M(0;0;3) C. M(0;0;4) D. M(0;0;-4)
11. Xác định giao điểm B của đường thẳng:(L) : x+1 =(y-1)/2 =(z-3)/-2 và
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 19 0918.859.305-01234.444.305
mặt phẳng (P): 2x -2y +z -3 =0.
A. B(-2;1;5) B. B(-2;-1;5) C. B(-2;-1;-5) D. B(2;-1;5)
12. Xác định giao điểm C của mặt phẳng (P) : x+ y +z -3 =0 và đường thẳng :
x=3-2t
y=-1 +2t
z=2 -t
∆
A. C(0;1;1) B. C(1;0;1) C. C(1;1;0) D. C(1;1;1)
13. Tìm giao điểm M của đường thẳng :
x=4+3t
y=-6-3t
z=t
∆
và mặt phẳng (P) : 2x+ 4y - 3z - 1 =0
A. M(-1;1;-1) B. M(-1;-1;1)
C. M(1;-1;-1) D.M(1;1;1)
14: Tìm giao điểm M của đường thẳng d :
x=3-4t
y=-1 +t
z=2 +3t
và mặt phẳng (P): 3x – 8y – 2z – 36 = 0
A. M(1;1;1) B. M(3;-2;1) C.
85 49 17
; ;
11 22 22
M
− −
D.
85 49 17
; ;
13 26 26
M
− −
15. Tìm hình chiếu H của điểm A(2;-1;3) trên đường thẳng (D):
x=3t
y=-7 +5t
z=2 +2t
A. H(3;-2;-4) B. H(3;2;4) C. H(-3;-2;4) D. Một điểm khác.
16. Xác định điểm A' đối xứng của điểm A(2;-1;3) qua đường thẳng d:
x=3t
y=-7 +5t
z=2 +2t
A. A'(4;3;5) B. A'(4;3;-5) C. A'(4;-3;5) D. A'(4;-3;-5)
17. Giao điểm của hai đường thẳng d :
3 2
2 3
6 4
x t
y t
z t
= − +
= − +
= +
và d’ :
5 '
1 4 '
20 '
x t
y t
z t
= +
= − −
= +
là :
A. (-3;-2;6) B. (5;-1;20) C. (3;7;18) D.(3;-2;1)
18. Cho 3 mp (P):x + 2y – z – 6 = 0 ; (Q): 2x – y + 3z +13 = 0; (R): 3x – 2y + 3z +16 = 0 cắt nhau tại điểm
A.Tọa độ điểm A là: A. A(1;2;3) B. A(1;-2;3) C. A(-1;-2;3) D. A(-1;2;-3)
19. Hình chiếu vuông góc của A(-2;4;3) trên mặt phẳng
2 3 6 19 0
x y z
− + + =
có tọa độ là:
A. (1;-1;2) B. −
20 37 3
( ; ; )
7 7 7
C.
2 37 31
( ; ; )
5 5 5
−
D. Kết quả khác
20: Trong không gian với hệ trục toạ độ Oxyz, cho điểm M(1;1;1) và mặt phẳng (P) có phương trình x + 2y
– 3z + 14 = 0 . Toạ độ hình chiếu vuông góc của điểm M trên mặt phẳng (P) là:
A. (-9;-11;-1) B. (3;5;-5) C. (0;-1;4) D.(-1;-3;7)
21. Tìm tọa độ điểm H là hình chiếu của điểm M(2;0;1) lên đường thẳng d :
1 2
1 2 1
x y z
− −
= = :
A.H (1;0;2) B. H(2;2;3) C.H(0;-2;1) D. H(-1;-4;0)
22: Xác định điểm đối xứng A' của điểm A(4;1;6) qua đường thẳng :
5 2
: 7 2
x t
d y t
z t
− +
= −
=
A. A’(27;26;14) B. A’(27;-26;14) C. A’(27;26;-14) D. A’(27;-26;-14)
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 20 0918.859.305-01234.444.305
23. Xác định toạ độ hình chiếu
'
M
của điểm
(1;2;6)
M
lên đường thẳng
2 1 3
:
2 1 1
x y z
d
− − +
= =
−
?
A.
'(0;2;4)
M
B.
'(0; 2; 4)
M
− −
C.
'(0; 2;4)
M
−
D.
(0;2; 4)
M
−
24. Xác định điểm đối xứng A' của điểm A(1;1;1) qua đường thẳng: d: (x-1)/2=y/3=(z+1)/-2
A. A'(1;2;3) B. A'(13/17; 23/17; -47/17)
C. A'(13/17; -23/17; -47/17) D. A'(-1;-2;-3)
25. Xác định điểm đối xứng A' của điểm A(2;-1;1) qua đường thẳng :
1 2
: 1
2
x t
d y t
z t
= +
= − −
=
A
.
16 -17 7
A'( ; ; )
9 9 9
B.
16 17 7
A'( ; ; )
9 9 9
C. A’(16;-17;-7) D. A’(16;-17;7)
26. Cho mp(P):x+y-z-4=0 và điểm A(1;-2;-2). Dựng AH ⊥ (P) tại H.Tìm tọa độ của H.
A. H(2;-1;3) B. H(2;-1;-3) C. H(2;1;3) D. H(2;1;-3)
27.Cho mặt phẳng (P): x+y-z-4=0 và điểm A(1;-2;-2). Gọi A' là điểm đối xứng của A qua (P). Hãy xác định
A'. A. A'(3;0;-4) B. A'(3;0;8) C. A'(3;4;8) D. A'(3;4;-4)
28. Cho mặt phẳng (P): 2x – y + 3z + 17 = 0 và điểm A(5;2;-1). Gọi A' là điểm đối xứng của A qua (P). Hãy
xác định A'.
A. A'(-3;-6;-13) B. A'(-3;-6;13) C. A'(-3;6;-13) D. A'(3;4;8)
29. Hình chiếu vuông góc của điểm A(0;1;2) trên mp (P) : x + y + z = 0 có tọa độ là:
A. (–2;2;0) B. (–2;0;2) C. (–1;1;0) D. (–1;0;1)
30. Hình chiếu của
1 1 2
( ) :
2 1 1
x y z
d
− + −
= =
trên mặt phẳng Oxy có phương trình là:
A.
1 2
1
0
x t
y t
z
= +
= − +
=
B.
1 5
2 3
0
x t
y t
z
= − +
= −
=
C.
1 2
1
0
x t
y t
z
= − −
= − +
=
D. Đáp án khác
31. Hình chi
ếu vuông góc của điểm A(0;1;2) trên mp (P) : x + y + z = 0 có tọa độ là:
A. (–2;2;0) B. (–2;0;2) C. (–1;1;0) D. (–1;0;1)
32. Hình chiếu của
1 1 2
( ) :
2 1 1
x y z
d
− + −
= =
trên mặt phẳng Oxy có phương trình là:
A.
1 2
1
0
x t
y t
z
= +
= − +
=
B.
1 5
2 3
0
x t
y t
z
= − +
= −
=
C.
1 2
1
0
x t
y t
z
= − −
= − +
=
D. Đáp án khác
33. Cho điểm M (1;0;0) và
2 1
( ) :
1 2 1
x y z
− −
∆ = =
. Gọi M’ (a,b,c) là điểm đối xứng của M qua
( )
∆
. Giá trị a
– b + c là : A.1 B.-1 C.3 D.-2
34. Cho A(-1;1;2), B(0;1;1), C(1;0;4) và đường thẳng
( ) : 2
3
x t
d y t
z t
= −
= +
= −
. Cao độ giao điểm của (d) và mặt
ph
ẳng (ABC) là: A. 3 B. -1 C. 0 D. 6
35. Cho (d):
1 2 1
1 2 1
x y z
− + −
= =
−
và (P):
2 2 0
x y z
+ + + =
. Giao điểm A của (D) và (P) có tung độ là :
A.0 B. 2 C. 4 D. -4
36. Cho 2 điểm
( 1;3; 2), ( 9;4;9)
A B
− − −
và mặt phẳng
( ) : 2 1 0
P x y z
− + + =
. Tìm điểm
M
thuộc mặt
phẳng
( )
P
sao cho biểu thức
MA MB
+
nhỏ nhất?
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 21 0918.859.305-01234.444.305
A.
( 1;2; 3)
M
−
B.
(1;2;3)
M
C.
(1; 2;3)
M
−
D.
(1;2; 3)
M
−
37. Cho đường thẳng
2 1 2
( ) :
1 2 1
x y z
d
− − +
= = . Tìm trên đường thẳng
( )
d
điểm
( ; ; )
M x y z
sao cho
2 2 2
x y z
+ +
nhỏ nhất?
A.
(1;1; 1)
M
−
B.
(1; 1;1)
M
−
C.
( 1;1;1)
M
−
D.
(1; 1; 3)
M
− −
38. Cho 2 điểm
(1;1; 0), (3; 1; 4)
A B
−
và đường thẳng
1 1 2
( ) :
1 1 2
x y z
d
+ − +
= =
−
. Tìm điểm
M
thuộc
đường thẳng
( )
d
sao cho tổng độ dài
MA MB
+
nhỏ nhất?
A.
(1;1;2)
M
B.
(1;1; 2)
M
−
C.
(1; 1;2)
M
−
D.
( 1;1;2)
M
−
A
.
(1;1;9)
M
B.
(0; 0;9)
M
C.
(0;1; 9)
M
D.
(1; 0;9)
M
39. Hình chiếu của đường thằng (d):
1 2 2
2 1 1
x y z
− + −
= =
trên mặt phẳng Oxy có phương trình là :
A.
1 2
1
0
x t
y t
z
= +
= − +
=
B.
1 5
2 3
0
x t
y t
z
= − +
= −
=
C.
1 2
1
0
x t
y t
z
= − −
= − +
=
D. Đáp án khác
40.
Tọa độ hình chiếu vuông góc của M(2; 0; 1) trên đường thằng
1
: 2
1 2
x y
z
−
= = −
là:
A.
(2; 2; 3)
B.
(1; 0; 2)
C.
(0; -2; 1)
D.
(-1; -4; 0)
41. Hình chiếu của đường thằng (d):
1 2
1
3 6
x t
y t
z t
= +
= − +
= −
trên mặt phẳng Oxy có phương trình là :
A.
1 2
1
0
x t
y t
z
= +
= − +
=
B.
1 5
2 3
0
x t
y t
z
= − +
= −
=
C.
1 2
1
0
x t
y t
z
= − −
= − +
=
D. Đáp án khác
42 .
Cho mặt phẳng
(
)
:3x 2y z 6 0
α − + + =
và điểm
(
)
A 2, 1,0
− . Hình chiếu vuông góc của A
lên mặt phẳng
(
)
α
là:
A.
(
)
1, 1,1
−
B.
(
)
1,1, 1
− −
C.
(
)
3, 2,1
−
D.
(
)
5, 3,1
−
43 .
Cho điểm A(1;1;1) và đường thẳng
6 4
: 2
1 2
x t
d y t
z t
= −
= − −
= − +
.
Hình chiếu của A trên d có tọa độ là
A.
(
)
2; 3; 1
− −
B.
(
)
2;3;1
C.
(
)
2; 3;1
−
D.
(
)
2;3;1
−
44.
Trong hệ trục Oxyz , M’ là hình chiếu vuông góc của
(
)
M 3,2,1
trên Ox . M’ có toạ độ
là:
A.
(
)
0,0,1
B.
(
)
3,0,0
C.
(
)
3,0,0
−
D.
(
)
0,2,0
45. Cho mặt cầu
2 2 2
( ) : 2 4 2 3 0
S x y z x y z
+ + − − + − =
. Hãy lập phương trình mặt cầu
1
( )
S
đối xứng
với mặt cầu
( )
S
qua mặt phẳng
( ) : 5 0
P x y z
+ − − =
?
A.
2 2 2
1
( ) : 2 12 0
S x y z x y z
+ + − − + + =
B.
2 2 2
1
( ) : 6 8 2 20 0
S x y z x y z
+ + − − + + =
C.
2 2 2
( ) : 100
S x y z
+ + =
D.
2 2 2
( ) : 6 8 12 10 0
S x y z x y z
+ + − − + + =
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 22 0918.859.305-01234.444.305
BÀI TẬP TỔNG HỢP
Câu 1: Định giá trị của m để đường thẳng d:
x+1 y-2 z+3
= =
3 m -2
song song với mp(P): x-3y +6z =0
A. m=-4 B. m=-3 C. m=-2 D. m=-1
Câu 2: Tìm các giá trị của m và n để cho mặt phẳng (P): mx +ny +3z -5=0 vuông góc với đường thẳng d:
x=3 +2t; y=5- 3t; z= -2-2t
A. m=-3; n=-9/2 B. m=3; n=-9/2 C. m=-3; n=9/2 D. m=-3; n=9/2
Câu 3: Tìm các giá trị
của m và n để cho mặt phẳng (P) vuông góc với đường thẳng d :
(P): 3x -2y +mx +1=0 d:
2 1 5
4 3
x y z
n
− + −
= =
−
A. m=3/2; n=-6 B. m=3/2; n=6
C. m=-3/2; n=-6 D. m=-3/2; n=6
Câu 4: Tính khoảng cách d từ A (2;-1;3) đến đường thẳng (D):
x=3t
y=-7 +5t
z=2 +2t
A. d=
2
B. d=
3
C. d=
2 3
D. d=
3 2
Câu 5: Tính khoảng cách d từ A (1;-2;1) đến đường thẳng d :
+
=
+
1 1
x=
2 2
5 3
z=
2 2
t
y t
t
A. d=
3 14
14
B. d=
14
14
C. d=2 D. Một đáp số khác
Câu 6: Cho mặt phẳng (P) 2x+y+3z+1=0 và đuờng thẳng d có phương trình tham số:
3
2 2
1
x t
y t
z
= − +
= −
=
, trong các mệnh đề sau, mệnh đề nào đúng:
A. d vuông góc với (P); B. d cắt (P);
C. d song song với (P); D. d thuộc (P)
C©u 7 :
Cho điểm M(2; 1; 0) và đường thẳng ∆:
x y z
1 1
2 1 1
− +
= =
−
. Đường thẳng d đi qua điểm M,
cắt và vuông góc với ∆ có vec tơ chỉ phương là :
A.
− −
(2; 1; 1)
B.
−
(2;1; 1)
C.
−
(1; 4;2)
D.
− −
(1; 4; 2)
Câu 8:
Tìm m để hai đường thẳng cắt nhau biết d :
= +
=
= − +
1
1 2
x mt
y t
z t
và d’ :
1 '
2 2 '
3 '
x t
y t
z t
= −
= +
= −
:
A
. 0 B. 1 C. -1 D. 2
Câu 9: Khoảng cách giữa hai đường thẳng d:
= +
= − −
=
1 2
1
1
x t
y t
z
và d’ :
2 2 3
1 1 1
x y z
− + −
= =
−
là :
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 23 0918.859.305-01234.444.305
A.
6
B.
6
2
C.
1
6
D.
2
Câu 10: Cho hai đường thẳng d1:
2 1
4 6 8
x y z
− +
= =
− −
và d2:
7 2
6 9 12
x y z
− −
= =
−
. Vị trí tương đối giữa d1 và
d2 là: A. Trùng nhau B. Song song C. Cắt nhau D. Chéo nhau
Câu 11: Khoảng cách giữa hai đường thẳng d1:
2 1
4 6 8
x y z
− +
= =
− −
và d2:
7 2
6 9 12
x y z
− −
= =
−
là:
A.
35
17
B.
35
17
C.
854
29
D.
854
29
Câu 12: Phương trình mặt phẳng chứa d1:
1 2 4
2 1 3
x y z
− + −
= =
−
và d2:
1 2
1 1 3
x y z
+ +
= =
−
là :
A.
3 2 5 0
x y
+ − =
B.
6 9 8 0
x y z
+ + + =
C.
8 19 4 0
x y z
− + + + =
D. Tất cả đều sai
Câu 13: Trong không gian với hệ toạ độ Oxyz, cho đường thẳng (d):
. Véc tơ nào sau đây là véc tơ chỉ phương của (d)?
A. B. C. D.
Câu 14: Trong không gian với hệ toạ độ Oxyz, cho điểm M(-2;1;1) và đường thẳng (d) có phương trình
. PT mặt phẳng (P) qua M vàvuông góc với đường thẳng (d) là:
A. 2x + y - z + 4 = 0 B. 2x -y + z + 4 = 0
C. 4x -2y + 2z + 7 = 0 D. x + y -z + 2 = 0
Câu 15 Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (P): x + 2y -2z + 5 = 0. Khoảng cách từ M(
t; 2; -1) đến mặt phẳng (P) bằng 1 khi và chỉ khi :
A. B. C. D.
Câu 16: Cho hai đường thẳng d :
1
2
3
x t
y t
z t
= +
= +
= −
và d’ :
1 2 '
1 2 '
2 2 '
x t
y t
z t
= +
= − +
= −
.Tìm mệnh đề đúng:
A. d c
ắt d’ B. d ≅ d’ C. d chéo với d’ D. d // d’
Câu 17: Khoảng cách từ điểm M(2;0;1) đến đường thẳng d :
1 2
1 2 1
x y z
− −
= =
là :
A.
12
B.
3
C.
2
D.
12
6
Câu 18: Mặt phẳng chứa 2 điểm A(1;0;1) và B(-1;2;2) và song song với trục 0x có phương trình là:
A. x + 2z – 3 = 0; B. y – 2z + 2 = 0; C. 2y – z + 1 = 0; D. x + y – z = 0
Câu 19: Cho hai đường thẳng d
1
:
2 1
4 6 8
x y z
− +
= =
− −
và d
2
:
7 2
6 9 12
x y z
− −
= =
−
. Vị trí tương đối giữa d
1
và d
2
là: A. Trùng nhau B. Song song C. Cắt nhau D. Chéo nhau
Câu 20: Khoảng cách giữa hai đường thẳng d
1
:
2 1
4 6 8
x y z
− +
= =
− −
và d
2
:
− −
= =
−
7 2
6 9 12
x y z
là:
A.
35
17
B.
35
17
C.
854
29
D.
854
29
Câu 21: Phương trình mặt phẳng chứa d
1
:
− + −
= =
−
1 2 4
2 1 3
x y z
và d
2
:
1 2
1 1 3
x y z
+ +
= =
−
là :
A.
3 2 5 0
x y
+ − =
B.
6 9 8 0
x y z
+ + + =
C.
8 19 4 0
x y z
− + + + =
D. Tất cả đều sai
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 24 0918.859.305-01234.444.305
Câu 22 Mặt cầu tâm I(1;3;5) tiếp xúc với đường thẳng d:
1
2
x t
y t
z t
=
= − −
= −
có bán kính là:
A.
14
B. 14 C.
7
D. 7
Câu 23: Cho (S) là mặt cầu tâm I(2,1,-1) và tiếp xúc với mặt phẳng (P): 2x-2y-z+3=0. bán kính (S) là
A: 2; B: 2/3; C: 4/3; D:2/9
Câu 24:
Cho m
ặt phẳng (P) : x +y -z +1 =0 và đường thẳng
2
:
1 2
x t
d y t
z t
= −
=
= +
.Viết phương trình mp(Q) chứa đường
thẳng d và vuông góc với (P)
A. (Q): 2x+3z -2=0 B. (Q): 2x - z + 1= 0
C. (Q): x - z + 1 =0 D (Q): x + z – 1 = 0
Câu 25. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm
(
)
(
)
(
)
A ; – ; , B ; – ; ,C ; ; –
1 2 0 0 1 1 2 1 1
và
(
)
D ; ;
3 1 4
. Hỏi có tất cả bao nhiêu mặt phẳng cách đều bốn điểm đó ?
Câu 26: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
P : x
(
y z
)
+ + + =
3 4 2 4 0
và điểm
(
)
A ; – ;
1 2 3
. Tính khoảng cách d từ A đến (P).
A.
d
=
5
9
B.
d =
5
29
C.
d =
5
29
D.
d =
5
3
Câu 27:Cho điểm A(2;-1;3) và đường thẳng :
=
= − +
= +
3
: 7 5
2 2
x t
d y t
z t
.Lập phương trình chính tắc của đường thẳng
d’ đi qua A ,vuông góc với d và cắt d
A.
2 1 3
1 1 1
x y z
+ + −
= = B.
C.
2 1 3
1 1 1
x y z
+ + −
= =
−
D.
2 1 3
1 1 1
x y z
− + −
= =
−
Câu 28: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình :
y
x z
−
− +
= =
2
10 2
5 1 1
.
Xét mặt phẳng
+ + + =
: 10 2
( )
11 0
P x y mz
, m là tham số thực. Tìm tất cả các giá trị của m để mặt
phẳng (P) vuông góc với đường thẳng d.
A.
m –
=
2
B.
m
=
2
C.
m –
=
52
D.
m
=
52
Câu 29: Trong không gian với hệ tọa độ Oxyz, cho hai điểm
(
)
(
)
A ; ; và B ; ;
0 1 1 1 2 3
. Viết phương trình
của mặt phẳng (P) đi qua A và vuông góc với đường thẳng AB.
A.
x y z –
+ + =
2 3 0
B.
x y z –
+ + =
2 6 0
C.
x y z –
+ + =
3 4 7 0
D.
x y z –
+ + =
3 4 26 0
Câu 30: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
x y 1 z 2
d :
1 2 3
+ +
= =
và mặt phẳng
(
)
P : x 2y 2z 3 0
+ − + =
. Tìm điểm M có các tọa độ âm thuộc d sao cho khoảng cách từ M đến (P) bằng 2.
A.
(
)
− − −
2; 3; 1
M B.
(
)
M 1; 3; 5
− − −
C.
(
)
M 2; 5; 8
− − −
D.
(
)
M 1; 5; 7
− − −
A
. 1 m
ặt phẳng. B. 4 mặt phẳng C. 7 mặt phẳng D. Có vô số mặt phẳng
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 25 0918.859.305-01234.444.305
Câu 31: Trong không gian với hệ tọa độ Oxyz, cho điểm
(
)
A ; ;
1 0 2
và đường thẳng d có phương trình
:
y
x z
− +
= =
1 1
1 1 2
. Viết ptrình đường thẳng ∆ đi qua A, vuông góc và cắt d.
A.
( )
y
x z
:
− −
∆ = =
1 2
1 1 1
B.
( )
y
x z
:
− −
∆ = =
−
1 2
1 1 1
C.
( )
y
x z
:
− −
∆ = =
1 2
2 2 1
D.
( )
y
x z
:
− −
∆ = =
−
1 2
1 3 1
Câu 32:Trong không gian
,
Oxyz
cho điểm
(
)
1; 1;0
A − và mặt phẳng
(
)
: 2 2 1 0
P x y z
− + − =
. Tìm
(
)
M P
∈ sao
cho
AM OA
⊥
và độ dài AM bằng ba lần khoảng cách từ A đến
(
)
P
.
(
)
. 1; 1;3
A M −
(
)
. 1; 1; 3
B M
− − −
(
)
. 1; 1; 3
C M −
D.
(
)
− −
M
1; 1; 3
Câu 33:
Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
y
x z
d
1
2
:
1 2 3
+
+
= =
và mặt phẳng
(
)
P x y z
: 2 2 3 0
+ − + =
. Tìm tọa độ điểm M có tọa độ âm thuộc
d
sao cho khoảng cách từ M đến
(
)
P
bằng 2.
(
)
. 2; 3; 1
A M
− − −
B.
(
)
− − −
1; 3; 5
M
(
)
. 2; 5; 8
C M
− − −
D.
(
)
− − −
M
1; 5; 7
Câu 34:Trong không gian Oxyz cho mặt phẳng
(
)
P
và đường thẳng d có phương trình lần lượt là
(
)
P : x 2y 3z 4 0
+ − + =
và
y 2
x 2 z
d :
1 1 1
−
+
= =
−
. Viết phương trình đường thẳng
∆
nằm trong mặt phẳng (P),
vuông góc và cắt đường thẳng d.
1
. : 2
2
x t
A y t
z t
= − −
∆ = −
= −
= − −
∆ = −
= −
3
. : 1
1 2
x t
B y t
z t
C.
= − +
∆ = −
= −
x t
y t
z t
3
: 1 2
1
1
. : 2 2
2
x t
D y t
z t
= − +
∆ = −
= −
Câu 35: Trong không gian với hệ trục tọa độ
,
Oxyz
cho đường thẳng có phương trình
1
1
:
2 2 1
y
x z
+
−
∆ = =
−
Tính khoảng cách từ O đến đường thẳng
∆
.
. 2
A
. 2
B C. 1
1
.
2
D
Câu 36:Cho đường thẳng
y 5
x 8 z 8
d :
1 2 1
−
− −
= =
−
và mặt phẳng (P):
x 2y 5z 1 0
+ + + =
. Tính khoảng cách giữa d
và (P). A.
59
30
29
.
30
B
29
.
20
C
29
.
50
D
Câu 37: Mặt phẳng (P) chứa đường thẳng
1 1
( ) :
2 1 3
x y z
d
− +
= =
và vuông góc với
( ) : 2 0
Q x y z
+ − =
có
phương trình là:
A.
2 1 0
x y
− − =
B.
2 0
x y z
− + =
C.
2 0
x y z
+ + =
D.
2 1 0
x y
+ − =
Câu 38: Cho (P):
3 1
2 2 1 0, (1;2; 3),( ) :
1 2 2
− +
+ − + = − = =
−
x y z
x y z A d
. Đường thẳng
( )
∆
qua A vuông góc
với (d) và song song với (P) có véc tơ chỉ phương có cao độ là:
A.1 B. 2 C. 3 D. 4
Câu 39: Cho A(1;5;0), B(3;3;6) và:
1 1
2 1 2
x y z
+ −
= =
−
. Điểm M thuộc
( )
∆
để tam giác MAB có diện tích nhỏ
nhất có tung độ là: A.1 B. 2 C. 3 D. 0
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 26 0918.859.305-01234.444.305
Câu 40: Cho A(1;5;0), B(3;3;6) và
( )
1 1
:
2 1 2
x y z
+ −
∆ = =
−
. Điểm M thuộc
(
)
∆
để tam giác MAB có diện tích
nhỏ nhất có tung độ là: A.1 B. 2 C. 3 D. 0
Câu 41: Cho
(
)
2,1, 1 ,( ) : 2 2 3 0
A P x y z
− + − + =
. (d) là đường thẳng đi qua A và vuông góc với (P). Tìm tọa
độ M thuộc (d) sao cho
3
OM =
.
A.
(
)
1, 1, 2
−
hoặc
5 1 1
, ,
2 3 3
−
B.
(
)
1, 1,1
−
hoặc
5 1 1
, ,
3 3 3
−
C.
(
)
3,3, 3
−
hoặc
7 5 5
, ,
3 3 3
−
D.
(
)
0,1, 1
−
hoặc
2 1 1
, ,
3 3 3
−
Câu 42: Cho A(2;0;-3), B(4;-2;-1),
( ) : 2 4 0
P x y z
+ + + =
. Phương trình đường thẳng (d) thuộc (P) sao cho
mọi điểm thuộc (d) cách đều A và B có vectơ chỉ phương là: A. (1;-1;1) B. (3;1;-2) C.
(1;1;2) D. (-1;0;-2)
Câu 43 Cho
( )
1 2
1 2 '
: 2 ;( ) : 1 '
2 2 1
x t x t
y t y t
z t z
= + = +
∆ = − ∆ = −
= − − =
. Vị trí tương đối của hai đường thẳng là:
A. Song song B. Chéo nhau C. Cắt nhau D. Trùng nhau
Câu 44: Cho A(-1,-2,2), B(-3,-2,0),
( ) : 3 2 0
P x y z
+ − + =
. Vectơ chỉ phương của đường thẳng giao tuyến
của (P) và mặt phẳng trung trực của AB là:
A. (1,-1,0) B. (2,3,-2) C. (1,-2,0) D. (3,-2,-3
Câu 45: PT tham số của đường thẳng
∆
đi qua điểm M(2;0;-1) và có vecto chỉ phương
(4; 6;2)
a = −
A,
= − +
= −
= +
2 4
6
1 2
x t
y t
z t
; B,
2 2
3
1
x t
y t
z t
= − +
= −
= +
; C,
2 2
3
1
x t
y t
z t
= +
= −
= − +
; D,
4 2
3
2
x t
y t
z t
= +
= −
= +
Câu 46: Cho d là đường thẳng đi qua điểm A(1;2;3) và vuông góc với mặt phẳng
(
)
: 4 3 7 1 0
x y z
α
+ − + =
.
Phương trình tham số của d là:
A,
1 4
2 3
3 7
x t
y t
z t
= − +
= − +
= − −
; B
1 4
2 3
3 7
x t
y t
z t
= +
= +
= −
; C,
= +
= −
= −
1 3
2 4
3 7
x t
y t
z t
; D,
1 8
2 6
3 14
x t
y t
z t
= − +
= − +
= − −
Câu 47: Cho 2 đường thẳng:
1
1 2
: 2 3
3 4
x t
d y t
z t
= +
= +
= +
và
2
3 4 '
: 5 6 '
7 8 '
x t
d y t
z t
= +
= +
= +
. Trong các mệnh đề sau, mệnh đề nào
đúng? A,
1 2
d d
⊥
; B,
1 2
/ /
d d
; C,
=
1 2
d d
; D,
1
d
và
2
d
chéo nhau
Câu 48 : Cho mặt phẳng
(
)
: 2 3 1 0
x y z
α
+ + + =
và đường thẳng d có phương trình tham số :
3
2 2
1
x t
y t
z
= − +
= −
=
.
Trong các mệnh đề sau, mệnh đề nào đúng?
A,
(
)
d
α
⊥ ; B,
d
cắt
(
)
α
; C,
(
)
/ /d
α
; D,
(
)
d
α
⊂
Câu 49: Mặt phẳng (P) đi qua điểm A(1;2;0) và vuông góc với đường thẳng d:
x 1 y z 1
2 1 1
− +
= =
−
có phương
trình là:
A. 2x + y – z + 4 = 0 B.
–2x – y + z + 4 = 0
C. –2x – y + z – 4 = 0 D. x + 2y – 5 = 0
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 27 0918.859.305-01234.444.305
Câu 50: Mặt phẳng (P) chứa đường thẳng d:
x 1 y z 1
2 1 3
− +
= =
và vuông góc với mặt phẳng
(Q) : 2x y z 0
+ − =
có phương trình là:
A. x + 2y – 1 = 0 B. x − 2y + z = 0 C. x − 2y – 1 = 0 D. x + 2y + z = 0
Câu 51: Hai mặt phẳng (P) và (Q) có giao tuyến cắt trục Ox là:
A. (P): 4x – 2y + 5z – 1 = 0 và (Q): 2x – y + 3z – 2 = 0
B. (P): 3x – y + z – 2 = 0 và (Q): x + y + z + 1 = 0
C. (P): x – y – 3z + 3 = 0 và (Q): 4x – y + 2z – 3 = 0
D.
(P): 5x + 7y – 4z + 5 = 0 và (Q): x – 3y + 2z + 1 = 0
Câu 52 Trong không gian với hệ toạ độ 0xyz cho A(2;0;0); B(0;3;1); C(-3;6;4). Gọi M là điểm nằm trên
cạnh BC sao cho MC = 2MB. Độ dài đoạn AM là:
A.
3 3
B.
2 7
C.
29
D.
30
Câu 53: Cho điểm M(–3; 2; 4), gọi A, B, C lần lượt là hình chiếu của M trên Ox, Oy, Oz. Mặt phẳng song
song với mp(ABC) có phương trình là:
A. 4x – 6y –3z + 12 = 0 B. 3x – 6y –4z + 12 = 0
C. 6x – 4y –3z – 12 = 0 D. 4x – 6y –3z – 12 = 0
câu 54. Trong không gian với hệ trục toạ độ Oxyz cho 2 đường thẳng
1
7 3 9
( ) :
1 2 1
x y z
d
− − −
= =
−
;
2
3 1 1
( ) :
7 2 3
x y z
d
− − −
= =
−
. Viết phương trình đường vuông góc chung
( )
∆
của 2 đường thẳng trên?
A.
3 2 6 0
( :
5 34 11 38 0
x y z
x y z
− − − =
∆
+ − + =
B.
3 2 6 0
( ) :
5 34 11 38 0
x y z
x y z
− − − =
∆
+ + − =
C.
3 2 6 0
( ) :
5 34 11 38 0
x y z
x y z
− − − =
∆
+ − − =
D.
3 2 6 0
( ) :
5 34 11 38 0
x y z
x y z
− − − =
∆
− − + =
câu 55. Xác định toạ độ điểm
'
A
đối xứng với điểm
(2; 1;3)
A
−
qua đường thẳng
3
( ) : 7 5
2 2
x t
d y t
z t
=
= − +
= +
?
A.
'(4;3;5)
A
B.
'(4; 3; 5)
A
−
C.
(4; 3;5)
A
−
D.
(4; 3; 5)
M
− −
câu 56. Xác định tham số
,
m n
để mặt phẳng
( ) : 5 4 0
P x ny z m
+ + + =
thuộc chùm mặt phẳng :
,
( ) : (3 7 3) ( 9 2 5) 0
Q x y z x y z
α β
α β
− + − + − − + =
?
A.
11, 5
m n
= =
B.
11, 5
m n
= − = −
C.
11, 5
m n
= − =
D.
11, 5
m n
= = −
Câu 57. Lập phương trình đường thẳng
( )
∆
đi qua điểm
( 1;2; 3)
M
− −
vuông góc với đường thẳng
2 1 1
( ) :
6 2 3
x y z
d
− − −
= =
− −
và cắt đường thẳng
1 1 3
( ') :
3 2 5
x y z
d
− + −
= =
−
?
A.
1 1 3
( ) :
2 3 6
x y z
− + +
∆ = =
−
B.
1 1 3
( ) :
2 3 6
x y z
− − −
∆ = =
−
C.
1 1 3
( ) :
2 3 6
x y z
+ + −
∆ = =
−
D.
1 1 3
( ) :
2 3 6
x y z
− + −
∆ = =
−
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Huỳnh văn Lượng Trang 28 0918.859.305-01234.444.305
C©u 58 :
Bán kính của mặt cầu tâm I(3;3;-4), tiếp xúc với trục Oy bằng
A.
5
B.
4
C.
5
D.
5
2
C©u 59 :
Trong không gian toạ độ Oxyz, cho mặt phẳng
(
)
: 2x y z 5 0
α + + + =
và đường thẳng
x 1 y 3 z 2
d :
3 1 3
− − −
= =
− −
. Toạ độ giao điểm của d và
(
)
α
là
A.
(
)
4,2, 1
−
B.
(
)
17,9,20
−
C.
(
)
17,20,9
−
D.
(
)
2,1,0
−
C©u 60 :
Cho mặt phẳng
(
)
: 4x 2y 3z 1 0
α − + + =
và mặt cầu
(
)
2 2 2
S : x y z 2x 4y 6z 0
+ + − + + =
. Khi
đó, mệnh đề nào sau đây là một mệnh đề sai:
A
.
(
)
α
cắt
(
)
S
theo một đường tròn
B.
(
)
α
tiếp xúc với
(
)
S
C.
(
)
α
có điểm chung với
(
)
S
D.
(
)
α
đi qua tâm của
(
)
S
C©u 61 :
Trong không gian Oxyz, tam giác ABC có
(
)
(
)
(
)
1,0,0 ; 0,2,0 ; 3,0,4
A B C . Tọa độ
điểm M trên mặt phẳng Oyz sao cho MC vuông góc với (ABC) là:
A.
3 11
0, ,
2 2
B.
3 11
0, ,
2 2
−
C.
3 11
0, ,
2 2
−
D.
3 11
0, ,
2 2
− −
C©u 62 :
Cho 3 điểm A(1; –2; 1), B(–1; 3; 3), C(2; –4; 2). Một VTPT
n
của mặt phẳng (ABC) là:
A.
n
( 1;9;4)
= −
B.
n
(9;4;1)
=
C.
n
(4;9; 1)
= −
D.
n
(9;4; 1)
= −
C©u 63 :
Trong không gian Oxyz, xác định các cặp giá trị (l, m) để các cặp mặt phẳng sau đây
song song với nhau:
2 3 5 0; 6 6 2 0
x ly z mx y z
+ + − = − − − =
A.
(
)
3,4
B.
(
)
4; 3
−
C.
(
)
4,3
−
D.
(
)
4,3
C©u 64 :
Cho hai mặt phẳng song song (P):
nx y z
7 6 4 0
+ − + =
và (Q):
x my z
3 2 7 0
+ − − =
. Khi đó
giá trị của m và n là:
A.
m n
7
; 1
3
= =
B.
n m
7
; 9
3
= =
C.
m n
3
; 9
7
= =
D.
m n
7
; 9
3
= =
C©u 65 :
Vị trí tương đối của hai đường thẳng
= + = +
= − − = +
= + = −
x t x ts
d y t d y t
z t z t
1 2
1 2 7 3
: 2 3 ; : 2 2
5 4 1 2
là:
A.
Chéo nhau
B.
Trùng nhau
C.
Song song
D.
Cắt nhau
| 1/28
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

A.
HUỲNH VĂN LƯỢNG
0918.859.305 – 01234.444.305 – 0933.444.305
0963.105.305 – 0929.105.305 – 0666.513.305 ------ LƯU HÀNH NỘI BỘ
www.huynhvanluong.com Chúc các em
đạt kết quả cao trong kỳ thi sắp tới
Huỳnh Văn Lượng
(đồng hành cùng hs trong suốt chặn đường THPT)
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
HỆ THỐNG KIẾN THỨC HÌNH Oxyz
Download miễn phí tại Website: www.huynhvanluong.com
Biên soạn: Huỳnh Văn Lượng (email: hvluong@hcm.vnn.vn)
0918.859.305 – 01234.444.305 – 0933.444.305-0929.105.305 -0963.105.305-0666.513.305-0996.113.305
------------------------------------------------------
1. Tọa độ điểm và véctơ :
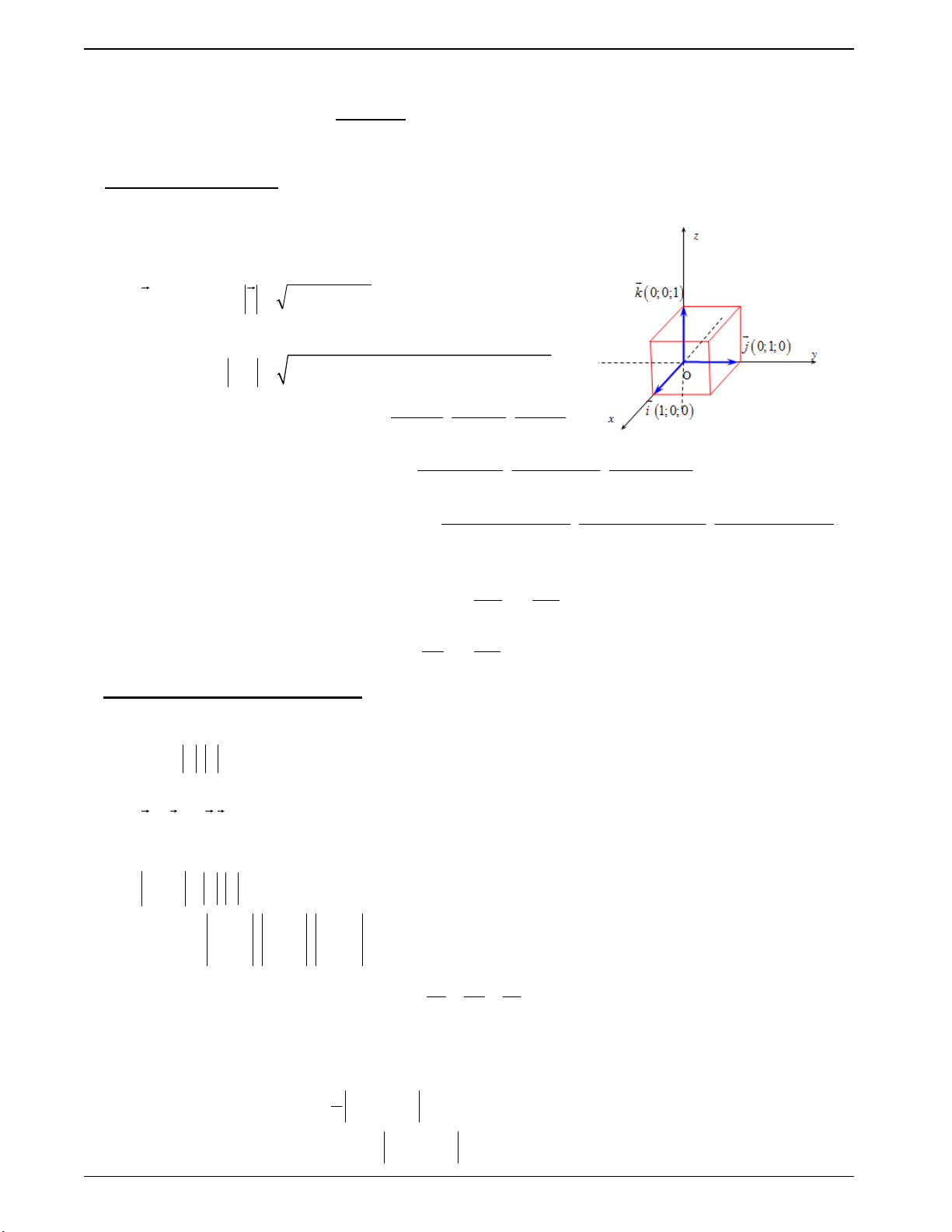
• Hệ toạ độ trong không gian gồm ba trục Ox ,Oy ,Oz đôi một vuông góc, các véc tơ đơn vị tương ứng
trên ba trục lần lượt là: i = ) 0 ; 0 ; 1 ( , j = ( 0 ; 1 ; 0 ) , k = ( ) 1 ; 0 ; 0 •
u (x;y;z )⇔u = xi + y j + z k . • 2 2 2 u = y; (x; z) ⇒ u = x + y + z • AB = (x − x ;y − y ;z −z B A B A B A ) 2 2 2 • AB = BA = AB = (x − x y y z z B A ) + ( − B A ) + ( − B A ) . x + x y + y z + z  •
Neáu I laø trung ñieåm cuûa AB thì I A B  ; A B ; A B   2 2 2 
x + x + x y + y + y
z + z + z  •
Neáu G laø troïng taâm cuûa ∆ABC thì A B C G  ; A B C ; A B C   3 3 3   x + x + x + x y + y + y + y z + z + z + z  •
Neáu G laø troïng taâm tứ diện ABCD thì A B C D A B C D A B C C G  ; ;   4 4 4  •
ABCD laø hình bình haønh ⇔ AB=DC •
D là chân đường phân giác trong của góc A thì DB AB = − ⇒ tọa độ D DC AC •
I là tâm ñöôøng troøn noäi tieáp ∆ABC thì IA BA = − ⇒ tọa độ K ID BD
2. Tích các hai vectơ và ứng dụng:
a) Tích vô hướng: Cho u (x ; y ;z & v x ; y ;z 1 1 1 ) ( 2 2 2 ) . Ta có: • u.v = u .v .cos(u,v ) • u.v = x x + y y + z z 1 2 1 2 1 2 . • u ⊥ v ⇔ .
u v = 0 ⇔ x .x + y .y + z .z = 0 1 2 1 2 1 2
b) Tích höõu höôùng: cho hai vectơ u (x ; y ;z v x ;y ;z 1 1 1 ) và ( 2 2 2 ) . Ta có: • u  ,v  = u .v .sin   (u,v ).  y z z x x y  •   1 1 1 1 1 1 u,v =  ; ;  
  y z z x x y .  2 2 2 2 2 2  x y z •
u &v cùng phương ⇔ u  ,v  = 0   ⇔ 2 2 2 x = y = z 1 1 1
• A,B,C thẳng hàng ⇔ AB, AC cùng phương •
A,B,C,D là ba đỉnh của tam giác ⇔ AB, AC không cùng phương 1 •
Diện tích tam giác: SAB, AC = ABC 2   •
Diện tích hình bình hành: SAB, AD = ABCD  
Huỳnh văn Lượng Trang 2
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
c) Tích hoãn hôïp (hỗn tạp):
• u,v ,w đồng phẳng u  ,v  ⇔ .w = 0  
• A,B,C,D là bốn đỉnh của tứ diện ⇔ AB, AC, AD không đồng phẳng.
• Thể tích khối hộp: VAB, AD = .AA' .
ABCD. A' B 'C ' D '   1
• Thể tích tứ diện: V AB,AC  = .AD ABCD 6   .
--------------------------------------
3. Mặt phẳng:
a) Phương trình mặt phẳng:
• Mặt phẳng qua điểm M (x ; y ;x n ; A B;C 0 0
0 ) và có vectơ pháp tuyến ( ) :
A(x − x + B y − y +C z −z = 0 0 ) ( 0 ) ( 0 ) .
• Mặt phẳng (α ) cắt trục Ox, Oy , Oz lần lượt tại A( ;
a 0;0), B (0;b;0),C (0;0;c ) , có phương trình x y z
theo đoạn chắn là: + + = 1 (abc ≠ 0) a b c
b) Vị trí tương đối của hai mặt phẳng.
Cho hai mặt phẳng (α ) : Ax + By +Cz + D = 0 và (α ') :A'x + B ' y +C 'z + D ' = 0 , ta có: A B C D o (α ) ≡ (α ') ⇔ = = = A' B ' C ' D ' . A B C D o (α ) / /(α ') ⇔ = = ≠ A' B ' C ' D ' . A B B C A C o
(α ) cắt (α ') ⇔ ≠ hoặc ≠ hoặc ≠
(tức là ngoài 2 t/h trên) A ' B ' B ' C ' A ' C ' AA BB CC o (α ) ⊥ (α ') ⇔ '+ + ' ' = 0 .
c) Khoảng cách từ một điểm tới một mặt phẳng. Ax + By +Cz + D M M M
Cho (α ) : Ax + By +Cz + D = 0 ⇒d (M ,(α )) = . 2 A + 2 B + 2 C
5. Đường thẳng:
a) Phương trình của đường thẳng:
Đường thẳng đi qua M ( x ; y ; u = ; a ; 0
0 z0 ) và có VTCP ( b c) x = 0 x + at  PT tham s x − x y − y z − z ố:  y = (t∈R) PT chính tắc: 0 0 0 ( a.b.c ≠ 0 ) 0 y + bt = =  a b c
z = z0 + ct
b) Vị trí tương đối giữa hai đường thẳng: Đường thẳng d đi qua M M '
0 và có VTCP u , d’ đi qua 0 và có
VTCP u ', ta có:
• (d) và (d’) đồng phẳng ⇔ ' u,u '.M M = 0   0 0
• d chéo d’ ⇔ [u,u '].M M ' ≠ 0 0 0 [   u,u '] ≠ 0
• d và d’ cắt nhau ⇔  [  u,u '  ].M M ' = 0 0 0 [  u, u '  ] = 0
• d // d ' ⇔  
u, M M ' ≠ 0  0 0 
c) Khoảng cách:
Huỳnh văn Lượng Trang 3
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com MM ,u  o  • d(M, ∆)= u  u, u'.M M'   • o o d(∆, ∆') = u,u'  
4. Phương trình mặt cầu:
• Dạng 1: Phương trình mặt cầu (S) có tâm I(a; b; c) và bán kính R: 2 2 2 2
(x − a) + ( y − b) + (z − c) = R
• Dạng 2: 2 2 2
x + y + z − 2ax − 2by − 2cz + d = 0 (với 2 2 2
a + b + c − d > 0 ) là phương trình mặt cầu
có tâm I(a; b; c) và bán kính R = a2 + b2 + c2 − d
* Vị trí tương đối giữa mặt cầu và mặt phẳng: Cho mặt cầu (S) có tâm I(a;b;c) bán kính R và
mặt phẳng (P): Ax+By+Cz+D=0.
• Nếu d(I,(P)) > R thì mặt phẳng (P) và mặt cầu (S) không có điểm chung.
• Nếu d(I,(P)) = R thì mặt phẳng (P) và mặt cầu (S) tiếp xúc nhau.
• Nếu d(I,(P)) < R thì mặt phẳng (P) và mặt cầu (S) cắt nhau theo giao tuyến là đường tròn có bán kính 2 2
r = R − d và tâm H của là hình chiếu của I lên mặt phẳng (P).
5.Hình chiếu vuông góc của điểm M:
a) Tìm hình chiếu vuông góc của 1 điểm M trên một mặt phẳng (α )
• Viết phương trình đường thẳng d đi qua M và vuông góc với (α )
• Gọi H là hình chiếu của M trên (α ) ⇒ H = d ∩ (α )
b) Tìm hình chiếu vuông góc của một điểm M trên 1 đường thẳng d
Cách 1: _ Viết phương trình mặt phẳng (α ) đi qua M và vuông góc với d
_ Gọi H là hình chiếu của M trên d ⇒ H = d ∩ (α )
Cách 2: _ Chuyển phương trình đường thẳng d về dạng tham số
_ Gọi I là một điểm bất kì thuộc d ⇒ tọa độ điểm I theo tham số t
_ I là hình chiếu của M trên d ⇔ MI ⊥ d ⇔ MI.u = 0 ⇒ t ⇒ Tọa độ I. d
6.Hình chiếu vuông góc của đường thẳng lên mặt phẳng:
Cách 1:Cho đường thẳng d và mặt phẳng (α ) . Tìm phương trình hình chiếu của d trên (α )
- Viết phương trình mặt phẳng (β ) chứa d và (β ) ⊥ (α )
- Gọi d’ là hình chiếu vuông góc của d trên (α ) . Suy ra d ' = (β ) ∩(α )
Cách 2:Cho đường thẳng d và mặt phẳng (α ) . Tìm phương trình hình chiếu của d trên (α )
- Tìm giao điểm A của d và (α )
- Lấy B ∈ d rồi tìm toạ độ của H là hình chiếu vuông góc của B trên (α )
- Viết phương trình của đường thẳng AH đi qua A và H.
Chú ý : Nếu d // (α ) thì làm như sau :
- Lấy A∈ d rồi tìm toạ độ của H là hình chiếu vuông góc của A trên (α )
- Gọi d’ là hình chiếu vuông góc của d trên d. Suy ra d’ song song với d và d’ đi qua H
7.Các dạng viết phương trình đường thẳng:
Loại 1: Viết phương trình đường thẳng d khi biết điểm đi qua và véctơ chỉ phương
(áp dụng công thức)
Loại 2: Viết phương trình đường thẳng (d) qua A và cắt cả hai đt (d ) ( 1 , d ) 2
cho trước. Cách 1:
Huỳnh văn Lượng Trang 4
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com •
Viết phương trình mặt phẳng (P) đi qua A và chứa ( ) 1 d •
Viết phương trình mặt phẳng (Q) đi qua A và chứa (d ) 2 •
d = (P) ∩ (Q) Cách 2: •
Viết phương trình mặt phẳng (P) đi qua A và chứa (d ) . 1 •
Xác định giao điểm B của (d ) và (P). 2 •
Viết phương trình đường thẳng (d): đi qua A và có vecto chỉ phương là AB .
Loại 3: Viết phương trình đường thẳng (d) qua A và vuông góc với hai đường thẳng (d ) ( 1 , d ) 2 Cách 1: •
Viết phương trình mặt phẳng (P) đi qua A và vuông góc với ( ) 1 d •
Viết phương trình mặt phẳng (Q) đi qua A và vuông góc với (d ) 2 •
d = (P) ∩ (Q) Cách 2: •
Xác định các vecto chỉ phương của ( ) ( lần lượt là 1 d , d ) 2 u và u 1 d d2 w ⊥ ud •
Gọi w là vecto chỉ phương của đường thẳng (d), ta có:  1
⇔ w = [u ;u ] d  1 d2 w ⊥ ud2 •
Viết phương trình đường thẳng (d): đi qua A và có vecto chỉ phương là w .
Loại 4: Viết phương trình đường thẳng (d) đi qua A, vuông góc với (d ) (
1 và cắt d ) 2
cho trước. Cách 1: •
Viết phương trình mặt phẳng (P) đi qua A và vuông góc với ( ) 1 d •
Viết phương trình mặt phẳng (Q) đi qua A và chứa (d ) 2 •
d = (P) ∩ (Q) Cách 2: •
Viết phương trình mặt phẳng (P) đi qua A và vuông góc với (d ) 1 •
Xác định giao điểm B của (d ) và (P): 2 •
Viết phương trình đường thẳng (d): đi qua A và có vecto chỉ phương là AB .
Loại 5: Viết phương trình đường vuông góc chung ( ∆ ) của 2 đường thẳng chéo nhau.
Cho 2 đường thẳng chéo nhau: d có vtcp u và đường thẳng d’ có vtcp v . Gọi w = [u;v] Cách 1: •
Viết phương trình mặt phẳng (α ) chứa d và song song với w . •
Viết phương trình mặt phẳng (β ) chứa d’ và song song với w •
Phương trình đường vuông góc chung của d và d’ là ∆ = (α) ∩ (β ) Cách 2: •
Chuyển d và d’ về Loại phương trình tham số theo “t” và “u”. Gọi M ∈ d; N ∈ d' . (t ) (u) MN.u = 0 •
MN là đoạn vuông góc chung của d và d’ ⇔  d
⇒ t, u⇒ tọa độ M , N MN.u = 0 d ' •
Viết phương trình đường thẳng ( ∆ ): đi qua M và có vecto chỉ phương là MN .
Huỳnh văn Lượng Trang 5
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Bài 1. TOẠ ĐỘ CỦA ĐIỂM VÀ VECTƠ TRONG KHÔNG GIAN 1. Cho 3 vect
ơ a = (1;−2; 3),b = (−2; 3; 4),c = (−3;2;1). Toạ độ của vectơ n = 2a − 3b + 4b là: A. n = (−4;−5;−2) B.n = ( 4 − ;5;2) C.n = (4;−5;2) D.n = (4; 5 − ; 2 − )
2. cho vecto AO = 3(i + 4j) − 2k + 5j . Tọa độ của điểm A là A. (3, 2 − ,5) B. ( 3 − , 1 − 7, 2) C. (3,17, 2 − ) D. (3,5, −2)
3. Cho 3 điểm A(-3 ; 4 ; -2), B(-5 ; 6 ; 2), C(-4 ; 7 ; -1). Tìm toạ độ của điểm M thoả mãn hệ thức AM = 2AB + 3BC ? A.M(4;−11;3) B.M(−4;11;−3) C.M(4;11;−3) D.M(−4;−11;3)
4. Cho tam giác ABC : A(1; 2 ; 3), B(3 ; 2 ; 1), C(1 ; 4 ; 1). Tam giác ABC là tam giác gì? A. Tam giác cân B. Tam giác vuông C. Tam giác đều D. Tam giác thường
5. Cho tam giác ABC : A(1; 2 ; 3), B(7 ; 10 ; 3), C(-1 ; 3 ; 1). Tam giác ABC có đặc điểm nào dưới đây? A. Tam giác cân B. Tam giác nhọn C. Tam giác vuông D. Tam giác tù
6. Cho tam giác ABC biết A(2; 4 ; -3) và AB = (-3; -1 ; 1),AC = (2; -6 ; 6). Khi đó trọng tâm G của tam giác có toạ độ là: A. 5 5 2 G( ; ; ) B. 5 5 2 G( ;− ; ) C. 5 5 2 G(− ; ; ) D. 5 5 2 G( ; ;− ) 3 3 3 3 3 3 3 3 3 3 3 3
7. Cho 3 điểm A(2; 1; 4), B(–2; 2; –6), C(6; 0; –1). Tích AB.AC bằng: A. –67 B. 65 C. 67 D. 33
8. Cho tam giác ABC : AB = (-3; 0; 4),BC = (-1; 0 ; -2) . Độ dài đường trung tuyến AM bằng bao nhiêu? A. 9 B. 95 C. 85 D. 105 2 2 2 2 9. V
ới 2 vectơ a = (4;−2;−4),b = (6;−3;2) . Hãy tính giá trị của biểu thức (2a − 3b)(a + 2b)? A. -100 B.−200 C.−150 D.−250 10. Xét 3 điểm (
A 2; 4;−3), B(−1; 3;−2),C (4;−2; 3). Tìm toạ độ đỉnh D của hình bình hành ABCD ? A.D(7;−1;2) B.D(7;1;−2) C.D(−7;1;2) D.D(−7;−1;−2) 11. Cho 4 điểm (
A 2;−1; 4), B(5;2;1),C (3;−1; 0), D(−3;−7; 6). Tứ giác ABCD là hình gì? A. Hình bình hành B. Hình thoi C. Hình thang D. Hình chữ nhật 12. Cho 2 vect ơ a = (3; 2 − ;1),b = (2;1; 1
− ) . Với giá trị nào của m để 2 vectơ u = ma − 3b và
v = 3a + mb vuông góc với nhau? m=-1 m=1 m=1 m=-1 A. B. C. D.  m=-9     m=-9 m=9 m=9     13. Cho 3 vect ơ a = (2; 3;1),b = (1; 2 − ; 1 − ),c = (−2; 4; 3) . Hãy tìm vectơ x sao cho x.a = 3, . b x = 4,c.x = 2 ? A. x = (4;5;10) B.x = (−4;−5;−10) C.x = (4;−5;10) D.x = ( 4 − ;5; 1 − 0) 14. Góc t
ạo bởi 2 vectơ a = (−4;2; 4) và b = (2 2;−2 2; 0) bằng: A. 0 30 B. 0 45 C. 0 90 D. 0 135
15. Cho ba vectơ a = (−1,1,0);b = (1,1,0);c = (1,1, )
1 . Tìm mệnh đề nào đúng?
Huỳnh văn Lượng Trang 6
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com a,b, A. c đồng
a + b + c = 0 B. C. (b c) 6 cos , = D. . a b = 1 phẳng. 3 16. Cho tam giác ABC : (
A 2;2;2), B(4; 0; 3),C (0;1; 0) . Diện tích của tam giác này bằng bao nhiêu? A. 65 đvdt
B. 55 đvdt
C. 75 đvdt
D. 95 đvdt 2 2 2 2
17. Cho hình bình hành ABCD : (
A 2; 4;−4), B(1;1;−3),C (−2; 0;5),D(−1; 3; 4). Diện tích của hình này bằng: A. 245 đvdt B. 345 đvdt C. 615 đvdt D. 618 đvdt 18. Cho tứ diện ABCD : (
A 0; 0;1),B(2; 3;5),C (6;2; 3), D(3;7;2) . Hãy tính thể tích của tứ diện? A. 10 đvdt B. 20 đvdt
C. 30 đvdt D. 40 đvdt 19. Xét 3 vect
ơ a = (−1;1; 0),b = (1;1; 0),c = (1;1;1). Trong các mệnh đề sau, mệnh đề nào đúng? A. a + b + c = o B. 2 cos( , b c) = 6 C. a, ,
b c đồng phẳng D. . c a = 1 20. Trên h
ệ trục toạ độ Oxyz cho 3 vectơ a = (−1;1; 0),b = (1;1; 0),c = (1;1;1), hình hộp
OACB.O ' A 'C ' B ' thoả mãn điều kiện OA = a,OB = ,
b OC = c . Hãy tính thể tích của hình hộp trên? A. 1 đvtt
B. 2 đvtt C.2 đvtt D. 6 đvtt 3 3
21. Trong không gian với hệ trục toạ độ Oxyz cho bốn điểm (
A 1; 0; 0),B(0;1; 0),C (0; 0;1),D(1;1;1). Mặt cầu
ngoại tiếp tứ diện ABCD có bán kính bằng bao nhiêu? A. 3 B. 3 C. 2 D. 3 4 2 22. V ới 2 vectơ 2 1
u = (3;2;−1),v = (1; ;− ) . Tập hợp các điểm M thoả mãn OM = au + bv ,(a,b ∈ ) 3 3
là đường thẳng đi qua điểm nào dưới đây? A. 3 1 1 N (− ;− ; ) B. 3 1 N (− ;1;− ) C. 3 1 N ( ;−1;− ) D. 3 1 N ( ;1;− ) 2 2 2 2 2 2 2 2 2 23. Cho 3 điểm (
A 1;1;1), B(1;1; 0),C (1; 0;1) . Tìm mệnh đề đúng trong các mệnh đề sau:
A.OABC là tứ diện B.OA +OB = 2i + j + k C. , A B,C thẳng hàng D.OA = OB + 2OC
24. Hình chóp S.ABC có thể tích bằng 6 và toạ độ 3 đỉnh (
A 1;2;−3),B(0;2;−4),C (5; 3;2) . Hãy tính độ dài
đường cao của hình chóp xuất phát từ đỉnh S ? A. 8 B. 4 C.12 3 D. 6 3
25. Xét các bộ 3 điểm sau: I. (
A 2;2;1),B(2;−1; 3),C (1;−1;2) . II. (
A 1;2; 3),B(−2; 4; 0),C (4; 0;6) . III. ( A 1;2; 3),B(1;1;1),C (0; 0;1)
Trong các bộ 3 điểm trên, bộ nào là 3 điểm thẳng hàng? A. III B. I và II C. II D. I 26. Xét tam giác ABC : (
A 2;−1;−2),B(−1;1;2),C (−1;1; 0) . Tính độ dài đường cao xuất phát từ A ? A. 13 B.2 13 C. 13 D. 13 2 2
24. Tính giá trị của góc A của tam giác ABC biết A(2; 1 ; 1), B(1 ; 2 ; 1), C(1 ; 1 ; 2)? π π π A. 3π B. C. D. 4 3 2 4 25. Tính giá tr
ị của góc giữa 2 vectơ a(2;5; 0), ( b 3;−7; 0) ? A. 0 135 B. 0 30 C. 0 45 D. 0 60
Huỳnh văn Lượng Trang 7
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com 26.
Cho A(1; 2; –3) và B(6; 5; –1). Nếu OABC là hình bình hành thì toạ độ điểm C là: A. (–5;–3;–2) B. (–3;–5;–2) C. (3;5;–2) D. (5; 3; 2) 27.
Trong mặt phẳng Oxyz Cho tứ diện ABCD có A(2;3;1), B(4;1;-2), C(6;3;7), D-5;-4;-8).
Độ dài đường cao kẻ từ D của tứ diện là A. 6 5 4 3 11 B. C. 5 D. 5 5 3 28.
Cho A(1;0;0), B(0;1;0), C(0;0;1) và D(-2;1;-1).Thể tích của tứ diện ABCD là 1 1 A. 1 B. 2 C. D. 2 3 29.
Cho tam giác ABC có A = (1;0;1), B = (0;2;3), C = (2;1;0). Độ dài đường cao của tam giác kẻ từ C là A. 26 26 B. C. 26 D. 26 2 3 30.
Trong không gian Oxyz, cho bốn điểm A(1,0,0); B(0,1,0);C (0,0, ) 1 ; D(1,1, ) 1 . Xác
định tọa độ trọng tâm G của tứ diện ABCD  1 1 1   1 1 1   2 2 2   1 1 1  A.  , ,  B.  , ,  C.  , ,  D.  , ,   2 2 2   3 3 3   3 3 3   4 4 4  Bài 2. MẶT CẦU 1. Mặt cầu 2 2 2
(S) : x + y + z − 2x + 4y − 4z − 16 = 0 có tâm và bán kính là: A.I(1;2;2); R = 2 B.I(−1;2;−2); R = 3
C.I(−1;−2;−2); R = 4 D.I(1;−2;2); R = 5 2. Để phương trình 2 2 2 2
x + y + z − 2(m + 2)x + 4my − 2mz + 5m + 9 = 0 là phương trình mặt cầu thì điều kiện của m là: A.m ∈ (− ; ∞ −5) ∪ (1;+ ) ∞ B.m ∈ (− ; ∞ 1) ∪ (5;+ ) ∞ C.m ∈ (− ; ∞ −1) ∪ (5;+ ) ∞ D.m ∈ (− ; ∞ −5) ∪ (−1;+ ) ∞
3. Lập phương trình mặt cầu tâm I(2; 4;−1) và đi qua điểm ( A 5;2; 3) ? A. 2 2 2
x + y + z − 4x + 8y − 2z − 8 = 0 B. 2 2 2
x + y + z − 4x − 8y + 2z − 8 = 0 C. 2 2 2
x + y + z + 4x + 8y + 2z − 8 = 0 D. 2 2 2
x + y + z + 4x − 8y + 2z − 8 = 0
4. Mặt cầu (S) có tâm I(1;2;-3) và đi qua A(1;0;4) có phương trình A. 2 2 2 ( 2 2 2 + x 1) +( + y 2) +( − z 3) =53 B. ( + x 1) +( + y 2) +( + z 3) =53 C. 2 2 2 ( 2 2 2 − x 1) +( − y 2) +( − z 3) =53 D. ( − x 1) +( − y 2) +( + z 3) =53
5. Viết phương trình mặt cầu đường kính AB biết: ( A 1;−2; 4), B(3;−4;−2)? A. 2 2 2
x + y + z + 4x + 6y + 2z + 3 = 0 B. 2 2 2
x + y + z + 4x − 6y + 2z + 3 = 0 C. 2 2 2
x + y + z − 4x + 6y − 2z + 3 = 0 D. 2 2 2
x + y + z + 4x − 6y + 2z − 3 = 0
6. Hãy lập phương trình mặt cầu tâm I(2;1;−4) và tiếp xúc với mặt phẳng (P) : x − 2y + 2z − 7 = 0 ? A. 2 2 2
x + y + z + 4x + 2y + 8z − 4 = 0 B. 2 2 2
x + y + z + 4x − 2y + 8z − 4 = 0 C. 2 2 2
x + y + z + 4x + 2y − 8z − 4 = 0 D. 2 2 2
x + y + z − 4x − 2y + 8z − 4 = 0
Huỳnh văn Lượng Trang 8
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
7. Hãy lập phương trình mặt cầu tâm I(−5;1;1) và tiếp xúc ngoài với mặt cầu 2 2 2
(ω) : (x − 1) + (y + 2) + (z − 3) = 9 ? A. 2 2 2
x + y + z + 10x + 2y + 2z + 11 = 0 B. 2 2 2
x + y + z + 10x − 2y + 2z + 11 = 0 C. 2 2 2
x + y + z + 10x − 2y − 2z + 11 = 0 D. 2 2 2
x + y + z − 10x + 2y + 2z + 11 = 0
7.Phương trình mặt cầu (S) có tâm I( 1
− ; 2 ; 3) và đi qua điểm M(1 ; 0 ; 1) là : A. ( ) 2 2 2
S : (x +1) + (y + 2) + (z − 3) = 12 B. ( ) 2 2 2
S : (x +1) + (y − 2) + (z − 3) = 81 C. ( ) 2 2 2
S : (x +1) + (y − 2) + (z + 3) = 21 D. ( ) 2 2 2
S : (x +1) + (y − 2) + (z − 3) = 12
8.Phương trình mặt cầu (S) có đường kính AB với A(4 ; − 3 ; 7) , B(2 ;1; 3) là : A. ( ) 2 2 2
S : (x − 3) + (y +1) + (z − 5) = 49 B. ( ) 2 2 2
S : (x − 3) + (y +1) + (z − 5) = 9 C. ( ) 2 2 2
S : (x − 3) + (y −1) + (z − 5) = 9 D. ( ) 2 2 2
S : (x − 3) + (y +1) + (z + 5) = 9
9. Mặt cầu (S) có tâm I(1; 4 ; − 7) và tiếp xúc với mặt phẳng (α) : 6x + 6y − 7z + 42 = 0 là : A. ( ) 2 2 2
S : (x +1) + (y − 4) + (z + 7) = 121 B. ( ) 2 2 2
S : (x −1) + (y − 4) + (z − 7) = 121 C. ( ) 2 2 2
S : (x −1) + (y − 4) + (z + 7) = 121 D. ( ) 2 2 2
S : (x −1) + (y + 4) + (z + 7) = 121 10. Cho (S) 2 2 2
: x + y + z − 4x + 2y − 4z = 0 . Tìm tâm và bán kính của mặt cầu (S).
A. Tâm I(2 ;1;2) , bán kính R = 3 . B. Tâm I(2 ; 1 − ; 2) , bán kính R = 3 C. Tâm I(2 ; 1
− ; 2) , bán kính R = 4 D. Tâm I(2 ;1; 2 − ) , bán kính R = 3
11. Phương trình mặt cầu (S) có tâm I (1; 2 ;3) bán kính R = 2 là. A. ( ) 2 2 2
S : (x −1) + (y + 2) + (z − 3) = 4 B. ( ) 2 2 2
S : (x −1) + (y − 2) + (z + 3) = 4 C. ( ) 2 2 2
S : (x −1) + (y − 2) + (z − 3) = 4 D. ( ) 2 2 2
S : (x +1) + (y − 2) + (z − 3) = 4
12. Viết phương trình mặt cầu đi qua 3 điểm ( A 1;2; 0),B( 1 − ;1; 3),C(2; 0; 1
− ) và có tâm thuộc mặt phẳng (Oxz)? A. 2 2 2 x + y + z + 6x + 6z + 1 = 0 B. 2 2 2
x + y + z + 6x − 6z + 1 = 0 C. 2 2 2 x + y + z − 6x + 6z + 1 = 0 D. 2 2 2
x + y + z − 6x − 6z + 1 = 0
13. Hãy xét vị trí tương đối giữa mặt phẳng (P) : 2x − 3y + 6z − 9 = 0 và mặt cầu 2 2 2
(S) : (x − 1) + (y − 3) + (z + 2) = 16 ? A. Không cắt nhau B. Cắt nhau C. Tiếp xúc nhau
D.(P) đi qua tâm của mặt cầu (S)
14. Hãy xét vị trí tương đối giữa 2 mặt cầu 2 2 2
(S) : x + y + z − 8x + 4y − 2z − 4 = 0 và 2 2 2
(S ') : x + y + z + 4x − 2y − 4z + 5 = 0 ? A. Không cắt nhau B. Cắt nhau C. Tiếp xúc ngoài D. Tiếp xúc trong 15. Cho mặt cầu 2 2 2
(S) : (x − 2) + (y − 1) + (z + 1) = 36 và điểm M(−2;−1; 3). Hãy lập phương trình mặt
phẳng tiếp diện của (S) tại điểm M ? A.2x+y+2z+11=0 B.2x-y+2z+11=0 C.2x-y-2z+11=0 D.2x+y-2z+11=0 16. Tìm điều kiện của m để mặt phẳng (P) : 3x + 2y − 6z + 7 = 0 cắt mặt cầu 2 2 2 2
(S) : (x − 2) + (y − 1) + (z + 1) = (m + 2) ? A.m ∈ (− ; ∞ 1) ∪ (5;+ ) ∞ B.m ∈ (− ; ∞ −1) ∪ (5;+ ) ∞ C.m ∈ (− ; ∞ −5) ∪ (1;+ ) ∞ D.m ∈ (− ; ∞ −5) ∪ (−1;+ ) ∞
17. Lập phương trình mặt phẳng tiếp diện của mặt cầu 2 2 2
(S) : x + y + z − 6x + 4y − 2z − 11 = 0 , biết mặt
phẳng đó song song với mặt phẳng (α) : 4x + 3z − 17 = 0 ?
A. 4x + 3z + 10 = 0 và 4x + 3z − 40 = 0
B. 4x + 3z + 10 = 0 và 4x + 3z − 40 = 0
C. 4x + 3z + 10 = 0 và 4x + 3z + 40 = 0
Huỳnh văn Lượng Trang 9
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
D. 4x + 3z − 10 = 0 và 4x + 3z − 40 = 0 18. Cho 2 điểm (
A 1;2;1), B(3;1;−2). Tập hợp các điểm M(x;y;z) sao cho 2 2 MA + MB = 30 là một mặt cầu có phương trình là: A. 2 2 2
x + y + z − 4x − 3y + z − 5 = 0 B. 2 2 2
x + y + z + 4x + 3y + z + 5 = 0 C. 2 2 2
x + y + z + 4x − 3y + z − 5 = 0 D. 2 2 2
x + y + z − 4x + 3y − z + 5 = 0 − − + 19. L x y z
ập phương trình mặt cầu tâm I(−5;1;1) và tiếp xúc với đường thẳng 2 1 3 d : = = ? 2 −1 1 A. 2 2 2
x + y + z + 2x + 4y + 12z + 36 = 0 B. 2 2 2
x + y + z + 2x − 4y + 12z − 36 = 0 C. 2 2 2
x + y + z + 2x + 4y − 12z − 36 = 0 D. 2 2 2
x + y + z − 2x − 4y + 12z + 36 = 0
20. Mặt cầu (S) tâm I(4;2;−2) tiếp xúc với mặt phẳng (P) : 12x − 5z + 5 = 0 . Hãy tính bán kính R của mặt cầu đó? A. 39 R = B.R = 13 C.R = 3 D.R = 39 13 x   =  t  
21. Bán kính của mặt cầu tâm I(1; 3;5) và tiếp xúc với đường thẳng d : y 
 = 1 − t bằng bao nhiêu?  z  = 2 −  t   A.R = 7 B.R = 7 C.R = 14 D.R = 14 22. Cho mặt cầu 2 2 2
(S) : (x + 1) + (y − 2) + (z − 3) = 12 . Trong các mệnh đề sau, mệnh đề nào đúng?
A.(S) đi qua điểm N(−3;4;2)
B.(S) đi qua điểm M(1;0;1)
C.(S) có bán kính R = 2 3
D.(S) có tâm I(−1;2;3)
23. Tìm bán kính mặt cầu ngoại tiếp tứ diện OABC biết (
A 1; 0; 0),B(0;1; 0),C (0; 0;1) ? A. 2 R = B. 3 R = C.R = 3 D.R = 2 2 2 24. Cho mặt cầu 2 2 2
(S) : x + y + z − 2x − 2z = 0 và mặt phẳng (α) : 4x + 3y + 1 = 0 . Trong các mệnh đề
sau, mệnh đề nào đúng?
A.(α) cắt mặt cầu (S) theo một đường tròn có bán kính nhỏ hơn bán kính mặt cầu.
B.(α) đi qua tâm của mặt cầu (S)
C.(α) tiếp xúc với mặt cầu (S)
D.(α) ∩ (S) = ∅ x   =  9t  
25. Lập phương trình mặt cầu có tâm I nằm trên đường thẳng (  d) : y
 = 7 / 3 − 6t và tiếp xúc với hai mặt  z  = 7 / 3 −  6t  
phẳng (P ) : x + 2y − 2z − 2 = 0 và (P ) : x + 2y − 2z + 4 = 0 ? 1 2 A. 2 2 2
(S) : (x + 11) + (y − 2) + (z − 4) = 25 B. 2 2 2
(S) : (x + 2) + y + (z − 3) = 16 C. 2 2 2
(S) : (x + 1) + (y − 3) + (z − 3) = 1 D. 2 2 2
(S) : (x + 1) + (y − 2) + (z − 3) = 1 x   =  t  
26. Lập phương trình mặt cầu có tâm I nằm trên đường thẳng (d) : y   = 2 và cắt mặt phẳng  z  = −  1  
(P) : y − z = 0 theo thiết diện là đường tròn lớn có bán kính bằng 4? A. 2 2 2
(S) : (x + 1) + (y − 2) + (z − 2) = 16 B. 2 2 2
(S) : (x + 1) + (y − 2) + z = 16 C. 2 2 2
(S) : (x + 1) + y + (z − 2) = 16 D. 2 2 2
(S) : x + (y − 2) + (z − 2) = 16
Huỳnh văn Lượng Trang 10
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com x   = −1 +  t   27. Cho đường thẳng (d) : y   = 3 − t và 2 mặt phẳng (P) : x − 2y − z + 3 = 0 và  z  = −2 +  t  
(Q) : 2x + y − 2z − 1 = 0 . Lập phương trình mặt cầu có tâm I là giao điểm của (d) và (P) , sao cho mặt
phẳng (Q) cắt mặt cầu theo giao tuyến là một đường tròn (C ) có chu vi bằng 2π ? A. 2 2 2 (S) : x + y + (z + 1) = 11 B. 2 2 2
(S) : x + (y − 1) + (z + 1) = 2 C. 2 2 2 (S) : x + (y − 2) + z = 11 D. 2 2 2
(S) : x + (y − 1) + (z + 2) = 16 x   = t   
28. Lập phương trình mặt cầu tâm 
I (2; 3;−1) cắt đường thẳng (d) : y
 = −11/ 2 + 1/ 2t tại 2 điểm , A B  z  = −14 −  t   sao cho AB = 16 ? A. 2 2 2
(S) : (x − 3) + (y − 4) + (z + 5) = 625 B. 2 2 2
(S) : (x − 2) + (y − 3) + (z + 4) = 256 C. 2 2 2
(S) : (x − 2) + (y − 3) + (z + 1) = 289 D. 2 2 2
(S) : (x − 1) + (y − 1) + (z + 1) = 9 29. Cho mặt cầu 2 2 2
(S) : x + y + z − 4x − 2y − 2z + 3 = 0 . Hãy lập phương trình mặt cầu (S ) đối xứng 1
với mặt cầu (S) qua điểm E(1;2; 3)? A. 2 2 2
(S ) : x + (y − 3) + (z − 5) = 3 B. 2 2 2
(S ) : x + y + (z − 5) = 9 1 1 C. 2 2 2 (S ) : x + (y − 3) + z = 1 D. 2 2 2 (S ) : x + y + z = 1 1 1
30.Trong không gian Oxyz cho mặt cầu (S): x2 + y2 + z2 + 6x – 4y + 4z + 1 = 0. Viết phương trình
mặt phẳng (P) song song với mặt phẳng (Q): 2x + y + 2z - 4 = 0 và tiếp xúc với mặt cầu (S). A.2x+y+2z-20=0 B.2x+y+2z+20=0 C.2x+y-2z+20=0 D.2x-y+2z+20=0
31. Cho (S) là mặt cầu tâm I(2,1,-1) và tiếp xúc với mặt phẳng (P): 2x-2y-z+3=0. bán kính (S) là A: 2; B: 2/3; C: 4/3; D:2/9 32.
Cho bốn điểm A(1;1;1), B(1;2;1), C(1;1;2) và D(2;2;1). Tâm I của mặt cầu ngoại tiếp tứ diện ABCD có tọa độ : (3;3;  3 3 3   3 3 3  −3) A. B.  ; − ;  C.  ; ;  D. (3;3;3)  2 2 2   2 2 2  33.
Cho mặt cầu (S): x2 + y2 + z2 − 8x + 4y + 2z − 4 = 0 . Bán kính R của mặt cầu (S) là: A. R = 17 B. R = 88 C. R = 2 D. R = 5 34.
Cho 2 điểm A(2; 4; 1), B(–2; 2; –3). Phương trình mặt cầu đường kính AB là: A. x2 2 2 2 + y 2 − + z 2 ( 3) ( −1) = 9 B. x + (y + 3) + (z −1) = 9 c. x2 2 2 2 + y 2 − + z 2 ( 3) ( +1) = 3 D. x + (y − 3) + (z +1) = 9
Huỳnh văn Lượng Trang 11
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Bài 3 MẶT PHẲNG 1. Ph
ương trình tổng quát của mặt phẳng (P) đi qua điểm M(2 ; 3 ; 5) và vuông góc với vectơ n = (4; 3;2) : A. 4x+3y+2z+27=0 B. 4x-3y+2z-27=0 C. 4x+3y+2z-27=0 D. 4x+3y-2z+27=0
2. Phương trình tổng quát của mặt phẳng (P) đi qua điểm M(2 ; 3 ; -1) và song song với mặt phẳng
(Q) : 5x − 3y + 2z − 10 = 0 là: A. 5x-3y+2z+1=0 B. 5x+5y-2z+1=0 C. 5x-3y+2z-1=0 D. 5x+3y-2z-1=0
3. Phương trình tổng quát của mặt phẳng (ABC ) với (
A 2; 0; 3),B(4;−3;2),C (0;2;5) là: A.2x+y+z+7=0 B.2x+y+z-7=0 C.2x-y+z-7=0 D.2x-y+z+7=0
4. Phương trình tổng quát của mặt phẳng trung trực của AB với ( A 2; 0; 3),B(4;−4;1) là: A.2x+3z-11=0 B. x-2y-z-5=0 C. 4x-4y+z-11=0 D. x-2y-z=0
5. Lập phương trình tổng quát của mặt phẳng chứa điểm M(1 ; -2 ; 3) và có cặp vectơ chỉ phương v = (0; 3; 4),u = (3; 1 − ;−2) ?
A.2x+12y+9z+53=0 B.2x+12y+9z-53=0 C.2x-12y+9z-53=0 D.2x-12y+9z+53=0
6. Viết phương trình mặt phẳng đi qua 2 điểm (
A 4; 0;2),B(1; 3;−2) và song với đường thẳng x − 1 y z + 3 (d) : = = ? 4 5 3 B. A.29x+7y+27z+62=0 29x+7y+27z-62=0
C.29x-7y+27z+62=0 D.29x-7y-27z-62=0
7. Mặt phẳng trung trực của đoạn thẳng AB có phương trình là ,với A(1;2;-3),B(-3;2;9) A. -x-3z-10=0 B. -4x+12z-10=0 C. -x-3z-10=0 D. -x+3z-10=0
8. Phương trình nào dưới đây là phương trình của mặt phẳng đi qua 3 điểm không thẳng hàng (
A −3; 0; 0),B(0; 4; 0),C (0; 0;−2) ? A. x y z y z y z y z + + = 1 B. x − + = 1 C. x + + = 1 D. x + + = 1 -3 4 −2 -3 4 −2 3 −4 2 -3 −4 2
9. Hãy lập phương trình mặt phẳng đi qua điểm M(5 ; 4 ; 3) và chắn trên các trục toạ độ dương những đoạn thẳng bằng nhau? A. x y z y z y z y z − − = 1 B. x + + = 1 C. x + + = 1 D. x − + = 1 12 12 12 -12 12 12 12 12 12 12 12 12
10. Mặt phẳng nào dưới đây đi qua điểm M(3 ; -1 ; -5) và vuông góc với 2 mặt phẳng
(α) : 3x − 2y + 2z + 7 = 0,(β) : 5x − 4y + 3z + 1 = 0 ? A.2x+y+2z+15=0 B.2x+y-2z-15=0 C.2x-y+2z-15=0 D.2x-y-2z-15=0
11. Viết phương trình tổng quát của mặt phẳng chứa hai điểm (
A 2;−1; 4), B(3;2;−1) và vuông góc với mặt
phẳng (α) : x + y + 2z − 3 = 0 ?
A.11x+7y+2z+21=0 B.11x-7y+2z+21=0 C.11x+7y-2z-21=0 D.11x-7y-2z-21=0 x = 2 − t
12. Phương trình của mp(P) đi qua điểm A(1;-1;-1) và vuông góc với đường thẳng d :  y = 1+ t là:  z = 1 − + 2t A. x - y - 2z + 4=0
B. x - y + 2z - 4=0 C. x - y + 2z + 4=0 D.x – y – 2z – 4 = 0
13. Lập phương trình của mặt phẳng (P) đi qua điểm A(1;-1;-1) và vuông góc với đường thẳng x+3 1-y z+2 d : = = là : A. 2x-3y +4z -1=0 B. 2x-3y +4z +1=0 2 3 4 C. 2x-3y -4z -1=0 D. 2x-3y -4z +1=0 x=7+3t  x-1 y+2 z-5
14. Lập phương trình của mặt phẳng (P) chứa hai đường thẳng : ∆ : y=2+2t và ∆ ' : = =  2 -3 4 z=1-2t
A. 2x – 16y – 13z – 31 = 0 B. 2x – 16y +13z + 31 = 0 C. 2x + 16y – 13z + 31 = 0 D. 2x – 16y – 13z + 31 = 0
Huỳnh văn Lượng Trang 12
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
15. Phương trình của mặt phẳng (P) chứa đường thẳng là giao tuyến của hai mặt phẳng
x + 5y + 9z − 13 = 0, 3x − y − 5z + 1 = 0 và đi qua điểm M(0;2;1)? A. x y z y z + + = 1 B. x − + + = 1 C. x-y-z+3=0 D. x-y+z+3=0 3 3 3 3 3 3
16. Lập phương trình của mặt phẳng (α) chứa giao tuyến của 2 mặt phẳng (P) : 2x − y − 12z − 3 = 0 và
(Q) : x − z − 1 = 0 , và vuông góc với mặt phẳng (R) : x + 2y + 5z − 1 = 0 ? A. 5x-z+1=0 B. 3x+y-z-1=0 C. 4x+3y-2z-1=0 D. 4x+3y-2z+1=0 17. Tìm giá trị của , m n để 2 mặt phẳng
(α) : (m + 3)x + 3y + (m − 1)z + 6 = 0 và
(β) : (n + 1)x + 2y + (2n − 1)z − 2 = 0 song song với nhau? A. 5 2 m= , n = B. 5 2 m= , n = − C. 5 2 m=- , n = D. 5 2 m=- , n = − 2 3 2 3 2 3 2 3
18. gọi (P) là mặt phẳng cắt ba trục tọa độ tại ba điểm A(8,0,0); B(0,−2,0);C (0,0,4) .
Phương trình của mặt phẳng (P) là: x y z x y z A. + + = 1 B. + + = 0 4 1 − 2 8 2 − 4
C. x − 4y + 2z − 8 = 0
D. x − 4y + 2z = 0 19. Tìm giá trị của m để 2 mặt phẳng
(α) : (2m − 1)x − 3my + 2z + 3 = 0 và
(β) : mx + (m − 1)y + 4z − 5 = 0 vuông góc với nhau? m=4 m=4 m=-4 m=-4 A. B. C. D.  m=-2     m=2 m=-2 m=2    
20. Phương trình các mặt phẳng song song với mặt phẳng (P) : x + 2y − 2z + 5 = 0 và cách điểm
B(2;−1; 4) một khoảng bằng 4 là:
A.x + 2y − 2z + 4 = 0 và x + 2y + 2z + 20 = 0
B.x + 2y − 2z + 20 = 0 và x + 2y − 2z − 4 = 0
C.x − 2y + 2z + 20 = 0 và x − 2y + 2z + 4 = 0
D.x − 2y + 2z + 20 = 0 và x − 2y + 2z − 4 = 0
21. Tìm điểm M trên trục Oy cách đều 2 mặt phẳng (α) : x + y − z + 1 = 0 và (β) : x + y − z − 5 = 0 ? A.M(0;1;0) B.M(0;2;0) C.M(0;3;0) D.M(0;−3;0) 22. Gọi ,
A B,C lần lượt là hình chiếu của điểm M(2; 3;−5) lên các trục Ox, Oy, Oz. Khi đó phương trình mặt phẳng (ABC ) là:
A.15x + 10y + 6z + 30 = 0
B.15x − 10y + 6z − 30 = 0 C. x y z y z + − = 1 D. x + + = 1 2 3 5 2 −3 5 23. Cho tam giác ABC có: (
A 1; 0; 0),B(0;2; 0),C (3; 0; 4). Tìm toạ độ điểm M thuộc mặt phẳng Oxy sao cho MC ⊥ (ABC ) ? A. 3 11 M (0;− ; ) B. 3 11 M (0;− ;− ) C. 3 11 M (0; ;− ) D. 3 11 M (0; ; ) 2 2 2 2 2 2 2 2
24. Cho điểm I(2;6;−3) và các mặt phẳng (α) : x − 2 = 0,(β) : y − 6 = 0,(γ) : z + 3 = 0 . Trong các mệnh
đề sau, hãy tìm mệnh đề sai? A.(α) ⊥ (β) B.(γ) Oz C.(β) (Oxz) D.I ∈ (α)
25. Trong không gian với hệ trục toạ độ Oxyz cho các điểm (
A 1; 0; 0),B(0;2; 0),C (0; 0; 3),D(1;2; 0) . Viết
phương trình mặt phẳng (DA' B ') với A',B ' là 2 đỉnh của hình hộp chữ nhật OADB.CA' D ' B ' ? A. 6x+3y+z-12=0 B. 6x+3y-z-12=0 C. 6x-3y+z-12=0 D. 6x-3y-z+12=0
Huỳnh văn Lượng Trang 13
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Bài4. ĐƯỜNG THẲNG
1. Lập phương trình tham số của đường thẳng d đi qua điểm ( A 1; 0; 3) và B(4;2;−1) ? x   = 1 +    3t x = 1 +  4t   A.  y    = 2t B. y  = 2t     z  = 3 −   4t z = 3 −  t     x   = 4 +    t x = 1 +  5t   C.  y    = 2 D. y  = 2t     z  = −1 +   3t z = 3 +  2t    
2. Phương trình chính tắc của d đi qua hai điểm A(1;2;-3) và B(3;-1;1) là: x −1 y − 2 z + 3 x − 3 y +1 z −1 A. = = B. 3 = = −1 1 1 2 −3 x −1 y − 2 z + 3 x +1 y + 2 z − 3 C. = = D. 2 = = −3 4 2 −3 4
3. Phương trình chính tắc của đường thẳng d đi qua điểm M(1;−2;5) và vuông góc với mặt phẳng
(α) : 4x − 3y + 2z + 5 = 0 là: − + − − + − A. x 1 y 2 z 5 x y z = = B. 1 2 5 = = 4 −3 2 −4 −3 2 − + − − + − C. x 1 y 2 z 5 x y z = = D. 1 2 5 = = 4 3 2 −4 −3 −2 x   = 3 −  2t  
4. Phương trình nào dưới đây không phải là phương trình chính tắc của đường thẳng d : y   = 2 + 3t ?  z  = −2 +  5t   − − + − − + A. x 3 y 2 z 2 x y z = = B. 3 2 2 = = −2 3 5 2 −3 −5 − − + + − − C. x 3 y 2 z 2 x y z = = D. 2 3 5 = = 4 −6 −10 3 2 −2
5. Hãy tìm một vectơ chỉ phương của đường thẳng là giao tuyến của hai mặt phẳng
2x − 3y − 5z + 8 = 0, x + y − 2z − 1 = 0 ? A. u = (11; 1 − ; 5 − ) B.u = (−11;1;5) C.u = (11; 1 − ;5) D.u = (11;1;5)
6. Phương trình tham số của đường thẳng đi qua điểm A(1; 2;3) và có VTCP u = (−2; 0;1) là: x = 1− 2tx = 1+ 2tx = 1− tx = 1+ t     A. d : y = 2
B. d :  y = 2
C. d :  y = 2 D. d : y = 2     z = 3 + tz = 3 + tz = 3 + tz = 3 − t
7. Lập phương trình tham số của đường thẳng d
đi qua hai điểm A(1;2;3) và B(2;1;1) x = 1+ t x = 1− t x = 1− tx = 1+ t    
A. d : y = 2 − t B. d : y = 2 + t
C. d :  y = 2 + t
D. d :  y = 2 − t     z = 3 − 2t z = 3 −  2t z = 3 + tz = 3 − t
8. Lập phương trình tham số của đường thẳng d đi qua điểm M(1;-2;3) và song song với đường thẳng x = −1+ 2tx = 1+ 2tx = 1+ 2tx = 1+ 2tx = 1+ 2t     
∆:  y = 2 + t
A. d :  y = 2 − − t
B. d :  y = 2 − + t
C. d :  y = 2 − + t
D. d :  y = 2 − − t     
z = −3 − tz = 3 − tz = 3 + tz = 3 − tz = −3 + t
Huỳnh văn Lượng Trang 14
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
9. Phương trình tham số của đường thẳng d đi qua điểm N(-1;2;-3) và song song với đường thẳng x=-1+2t x=-1+2t x y+1 1-z   ∆: = = là: A. d : y=2+2t B. d : y=2+2t 2 2 3   z=-3 +3t z=3 +3t x=-1+2t x=-1+2t   C. d : y=2-2t D. d : y=2+2t  z=-3 -3t  z=-3 -3t
10. Lập phương trình chính tắc của đường thẳng d đi qua điểm A(2;3;-5) và có vecto chỉ phương x-2 y-3 z+5 x-2 y-3 z+5 u = ( 4 − ;8;10) A. = = B. = = 3 -1 2 -2 4 5 x-2 y-3 z+5 x-2 y-3 z+5 C. = = D. = = 1 3 -2 2 4 5 x = 2 + 2t
11. Cho đường thẳng d :  y = 3 − t
. Phương trình chính tắc của d là:  z = 3 − + 5t x − 2 y z + 3 x + 2 y z − 3 A. = = B. = = 2 3 − 5 2 −3 5 C. x -2 = y = z+3 D. x+2 = y = z - 3 x = 2 + 2t
12. Cho đường thẳng d :  y = 3 − t
. Một véc tơ chỉ phương của d là :  z = 3 − + 5t A. u = (2;0;−3) B. u = (2; −3; 5) C. u = (2;3; 5 − ) D. u = (2;0;5) + + 13. Tìm x y z x 1 y 5 z
m để 2 đường thẳng d : = = và d : = = cắt nhau? 1 2 −3 m 2 3 2 1 A. m=1 B. m=2 C. m=3 D. m=4 14. Cho 2 điểm (
A −1; 3;−5), B(m − 1;m;1 − m) . Giá trị của m để đường thẳng AB song song với mặt
phẳng (α) : x + y − z + 4 = 0 là: A. m=1 B. m=2 C. m=3 D. m=4 − + + 15. Giá tr x y z
ị nào của m để đường thẳng 1 2 3 d : = =
vuông góc với mặt phẳng m 2m − 1 2
(P) : x + 3y − 2z − 5 = 0 là: A. m=1 B. m=-1 C. m=2 D. m=-2 x   = 1 −  4t  
16. Khoảng cách từ điểm (
A 2; 3;1) đến đường thẳng d : y   = 2 + 2t bằng :  z  = −1 +  4t   A. 3 B. 5 C. 6 D. 7
17. Khoảng cách từ điểm (
A 2; 3;1) đến mặt phẳng (P): 2x + y -2z +1 = 0 bằng : A. 3 B. 5 C. 2 D. 7 + − − 18. Tìm t x y z
ất cả các giá trị của m để đường thẳng 1 3 1 d : = = cắt mặt phẳng 2 m m − 2 (P) : x + 3y + 2z − 5 = 0 ?
Huỳnh văn Lượng Trang 15
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com A. 1 m ≠ B. 3 m ≠ C. 2 m ≠ D. 4 m ≠ 5 5 5 5
19. Tìm tất cả các giá trị của m để đường thẳng là giao tuyến của hai mặt phẳng
3x − 2y + z + 3 = 0, 4x − 3y + 4z + 2 = 0 song song với mặt phẳng
(P) : 2x − y + (m + 3)z − 2 = 0 ? A. m=5 B. m=-5 C. m=3 D. m=-3 − − − + − 20. Kho x y 3 z 2 x 3 y 1 z 2
ảng cách giữa 2 đường thẳng song song d : = = và d : = = 1 1 2 1 2 1 2 1 bằng: A. 5 6 B. 5 3 C. 5 30 D. 5 5 6 6 6 6
21. Phương trình mặt phẳng (α) chứa đường thẳng là giao tuyến của hai mặt phẳng x − 1 y − 3 z + 4
x − y + z = 0,x + y − z = 0 và song song với đường thẳng d : = = : 1 3 −2 4 A.2x+y+z+1=0 B.2x-y+z-1=0 C.2x-y+z=0 D.2x+y-z=0 − + − − − + 22. Xét v x 1 y 3 z 2 x 2 y 1 z 4
ị trí tương đối giữa 2 đường thẳng d : = = ,d : = = ta 1 2 2 2 3 3 2 4 được kết quả nào? A. Cắt nhau B. Song song C. Chéo nhau D. Trùng nhau x   = −3 +  t   23. Cho mặt phẳng ( 
α) : 2x + y + 3z + 1 = 0 và đường thẳng d : y
 = 2 − 2t . Tìm mệnh đề đúng trong  z  =  1   các mệnh đề sau? A. d ⊂ (α) B. d (α) C. d ∩ (α)=M D. d ⊥ (α)
24. Trong không gian với hệ trục toạ độ Oxyz cho đường thẳng là giao tuyến của hai mặt phẳng x  − 2y − z − 2 =  0  
. Gọi M ∈ d và u là vectơ chỉ phương của đường thẳng . Tìm nhận định đúng? 2  x + z − 5 = 0   A.
M(3;−1;1) và u(1;−1;2) B.
M(3;1;−1) và u(1;1;−2) C.
M(3;1;−1) và u(1;1;2)
D. Cả 3 đáp án trên đều sai x   = 1 +    t x = 1 +  2u    
25. Xét vị trí tương đối của 2 đường thẳng d : y    = 2 + t và d ' : y  = −1 + 2u ?     z  = 3 −   t z = 2 −  2u    
A. d và d ' chéo nhau B. d d ' C. d ∩ d ' =M D. d ≡ d '
26. Cho 4 điểm A(1; 1 ; 1), B(1 ; 3 ; 5), C(1 ; 1 ; 4), D(2;3;2) . Gọi I,J lần lượt là trung điểm của
AB,CD . Khẳng định nào sau đây đúng? A. I ≡ J B.IJ ⊥ (ABC ) C.AB ⊥ IJ D.CD ⊥ IJ
27. Khoảng cách từ điểm M(−2;−4;3) đến mặt phẳng (α) : 2x − y + 2z − 3 = 0 bằng bao nhiêu? A. 11 B. 1 C. 2 D. 3
28. Cho tứ diện ABCD với A(4; 1 ; 5), B(1 ; 1 ; 1), C(4 ; 6 ; 5), D(4;0;3) . Tính chiều cao của tứ diện xuất phát từ đỉnh A ? A. 5 2 B. 5 3 C. 5 3 D. 15 139 3 3 2 139
Huỳnh văn Lượng Trang 16
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
29. Trong không gian với hệ trục toạ độ Oxyz cho hình lập phương ABCD.A' B 'C ' D ' cạnh a . Hãy tính
khoảng cách giữa 2 đường thẳng AC và BD ' ? A. a 5 B. a 6 C. a 6 D. a 6 6 3 6 5
30. Cho 2 điểm M (2; 3;1),M (1;−1;1) và đường thẳng là giao tuyến của hai mặt phẳng 0 1
2x − y + 5 = 0,2x + z + 5 = 0 , gọi d = d(M , ) ∆ và d = d(M , )
∆ . Hãy tìm mệnh đề đúng trong 0 0 1 1 các mệnh đề sau? A. 2 2 d > d B. − = C.d + d = D.d < d 0 1 d d 6 3 0 1 0 1 3 0 1 − − − 31. Cho m x y z
ặt phẳng (α) : 3x − 2y − z + 5 = 0 và đường thẳng 1 7 3 ∆ : = = . Gọi (β) là mặt 2 1 4
phẳng chứa đường thẳng ∆ và song song với (α) . Tính khoảng cách giữa 2 mặt phẳng (α) và (β) ? A. 3 B. 3 C. 9 D. 9 14 14 14 14
32. Nếu điểm M(0;0;t) cách đều điểm M (2; 3;4) và mặt phẳng (P) : 2x + 3y + z − 17 = 0 thì t có giá trị 1 bằng bao nhiêu? A.t = 3 B.t = −3 C.t = 3 D.t = − 3
33. Khoảng cách gữa 2 mặt phẳng song song (P) : x + y − z + 5 = 0,(Q) : 2x + 2y − 2z + 3 = 0 sau đây bằng bao nhiêu? A. 7 B. 7 C. 2 D.2 2 2 3 3  x = 1+ 2t 34. 
Cho điểm A(0;-1;3) và đường thẳng d  y = 2
.Khoảng cách từ A đến d bằng   z = −1 A. 8 B. 3 C. 14 D. 6 x   = 1 +  t   − + 35. Cho 2 x 3 y z 2
đường thẳng chéo nhau d : y   = −1 − t và d : = =
. Độ dài đường vuông góc 1  2  3 −3 3 z  = 1 +  t  
chung của 2 đường thẳng trên bằng bao nhiêu? A. 112 B. 104 C. 114
D. Đáp số A, B, C sai 3 3 3 36.
Mặt phẳng (Q) song song với mp(P): x+2y+z-4=0 và cách D(1;0;3) một khoảng bằng 6 có phương trình là A. x+2y+z+2=0 và x+2y+z+2=0 B. x+2y-z-10=0 C. x+2y+z-10=0 D. x+2y+z-10=0 37.
Cho hai điểm A(1;-1;5) và B(0;0;1). Mặt phẳng (P) chứa A, B và song song với Oy có phương trình là
A. 4x + y − z +1 = 0
B. 2x + z − 5 = 0
C. 4x − z +1 = 0 D. y + 4z −1 = 0
Huỳnh văn Lượng Trang 17
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
BÀI TẬP VỀ GIAO ĐIỂM – HÌNH CHIẾU - ĐỐI XỨNG x   = 1 +  2t  
1. Tìm toạ độ giao điểm M của đường thẳng d : y 
 = −2 − t và mặt phẳng (P) : 4x − y − z + 5 = 0 ?  z  = 1 −  t   A.M(1;1;2) B.M(1;−1;2) C.M(1;1;−2) D.M(−1;−1;2) x   = 1 −  8t   − − − 2. To x 7 y 3 z 5
ạ độ giao điểm M của 2 đường thẳng d : y   = 1 + 3t và d : = = là: 1  2  2 −5 2 z  = 2 −  5t   A.M(9;2;7) B.M(9;2;−7) C.M(9;−2;−7) D.M(9;−2;7) x  + y + z − 3 =  0 3. Cho điểm ( 
A 1;2;−1) và đường thẳng (d) : 
. Xác định toạ độ hình chiếu vuông góc y  + z − 1 = 0  
H của A lên đường thẳng (d)? A.H(2;1;1) B.H(2;2;−1) C.H(2;2;1) D.H(2;1;−1)
4. Cho mặt phẳng (P): 3x -8y +7z -1=0 và hai điểm A(0;0;-3), A(2;0;-1). Tìm giao điểm M của mp(P) và đường thẳng AB.
(Theo đề thi Đại học Quốc gia Hà Nội, khối A- 2000) A. M(2;3;-1) B. M(11;0;-4) C. M(11/5;0;4/5) D. Một điểm khác. x = 14 + 4t
5. Trong không gian cho điểm A(1;1;1) và đường thẳng d : y = t
.Xác định điểm H là hình chiếu  z = 5 − − 2t
vuông góc của A lên d A. H(2;3;-1) B H(2;-3;-1) C. H(2;-3;1) D. H(2;-3;-1) x = 1 
6. 6. Trong không gian Oxyz, cho mp(P) :x+ y +z -1 =0 và đường thẳng d có phương trình: d :  y = t .Tìm  z = −1
giao điểm A của d và mp(P) (Đại học Hàng Hải-2000) A. A(1;1;-1) B. A(1;1;1) C. A(1;-1;-1) D. A(1;-1;1)
7. Cho mặt phẳng (P) : x + y + 5z − 14 = 0 và điểm M(1;−4;−2) . Tìm toạ độ hình chiếu H của điểm M lên mặt phẳng (P) ? A.H(2;3;3) B.H(2;3;−3) C.H(2;−3;3) D.H(−2;−3;3) x − 3 y + 1 z 8. Tìm giao điểm của d : = =
và P : 2x − y − z − 7 = 0 1 ( ) −1 2 A. M(3;-1;0) B. M(0;2;-4) C. M(6;-4;3) D. M(1;4;-2) x − 3 y + 1 9. Tìm giao z điểm của d : = =
và (P) : 2x − y − z − 7 = 0 1 1 − 2 A, M(1;4;-2) B, M(0;2;-4) C, M(6;-4;3) D, M(5;-1;2) Cho điểm (
A 2; 3;−1) . Hãy tìm toạ độ điểm A ' đối xứng với A qua mặt phẳng (P) : 2x − y − z − 5 = 0 ? A.A'(4;2;2) B.A'(4;2;−2) C.A'(−4;2;−2) D.A'(−4;2;2)
10. Cho điểm A(2;3;5) và mp (P): 2x +3y+z -17=0 , gọi d là đường thẳng đi qua A và vuông góc với mp(P) .
Xác định giao điểm M của d và trục Oz. A. M(0;0;2) B. M(0;0;3) C. M(0;0;4) D. M(0;0;-4)
11. Xác định giao điểm B của đường thẳng:(L) : x+1 =(y-1)/2 =(z-3)/-2 và
Huỳnh văn Lượng Trang 18
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
mặt phẳng (P): 2x -2y +z -3 =0. A. B(-2;1;5) B. B(-2;-1;5) C. B(-2;-1;-5) D. B(2;-1;5) x=3-2t 
12. Xác định giao điểm C của mặt phẳng (P) : x+ y +z -3 =0 và đường thẳng ∆ : y=-1 +2t  z=2 -t A. C(0;1;1) B. C(1;0;1) C. C(1;1;0) D. C(1;1;1) x=4+3t 
13. Tìm giao điểm M của đường thẳng ∆ : y=-6-3t và mặt phẳng (P) : 2x+ 4y - 3z - 1 =0  z=t A. M(-1;1;-1) B. M(-1;-1;1) C. M(1;-1;-1) D.M(1;1;1) x=3-4t 
14: Tìm giao điểm M của đường thẳng d : y=-1 +t và mặt phẳng (P): 3x – 8y – 2z – 36 = 0  z=2 +3t  85 4 − 9 1 − 7   85 −49 −17  A. M(1;1;1) B. M(3;-2;1) C. M  ; ;  D. M  ; ;   11 22 22   13 26 26  x=3t 
15. Tìm hình chiếu H của điểm A(2;-1;3) trên đường thẳng (D): y=-7 +5t  z=2 +2t A. H(3;-2;-4) B. H(3;2;4) C. H(-3;-2;4) D. Một điểm khác. x=3t 
16. Xác định điểm A' đối xứng của điểm A(2;-1;3) qua đường thẳng d: y=-7 +5t  z=2 +2t A. A'(4;3;5) B. A'(4;3;-5) C. A'(4;-3;5) D. A'(4;-3;-5) x = −3 + 2tx = 5 + t '  
17. Giao điểm của hai đường thẳng d :  y = 2 − + 3t và
d’ :  y = −1− 4t ' là :   z = 6 + 4tz = 20 + t ' A. (-3;-2;6) B. (5;-1;20) C. (3;7;18) D.(3;-2;1)
18. Cho 3 mp (P):x + 2y – z – 6 = 0 ; (Q): 2x – y + 3z +13 = 0; (R): 3x – 2y + 3z +16 = 0 cắt nhau tại điểm
A.Tọa độ điểm A là: A. A(1;2;3) B. A(1;-2;3) C. A(-1;-2;3) D. A(-1;2;-3)
19. Hình chiếu vuông góc của A(-2;4;3) trên mặt phẳng 2x − 3y + 6z +19 = 0 có tọa độ là: 20 37 3 2 37 31 A. (1;-1;2) B. (− ; ; ) C. (− ; ; ) D. K 7 7 7 ết quả khác 5 5 5
20: Trong không gian với hệ trục toạ độ Oxyz, cho điểm M(1;1;1) và mặt phẳng (P) có phương trình x + 2y
– 3z + 14 = 0 . Toạ độ hình chiếu vuông góc của điểm M trên mặt phẳng (P) là: A. (-9;-11;-1) B. (3;5;-5) C. (0;-1;4) D.(-1;-3;7) x −1 y z − 2
21. Tìm tọa độ điểm H là hình chiếu của điểm M(2;0;1) lên đường thẳng d : = = : 1 2 1 A.H (1;0;2) B. H(2;2;3) C.H(0;-2;1) D. H(-1;-4;0) x − 5 + 2t
22: Xác định điểm đối xứng A' của điểm A(4;1;6) qua đường thẳng : d :  y = 7 − 2t  z = t A. A’(27;26;14) B. A’(27;-26;14) C. A’(27;26;-14) D. A’(27;-26;-14)
Huỳnh văn Lượng Trang 19
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com − − + 23. Xác x y z
định toạ độ hình chiếu M ' của điểm M (1;2;6) lên đường thẳng 2 1 3 d : = = ? 2 −1 1 A.M '(0;2;4) B.M '(0;−2;−4) C.M '(0;−2; 4) D.M(0;2;−4)
24. Xác định điểm đối xứng A' của điểm A(1;1;1) qua đường thẳng: d: (x-1)/2=y/3=(z+1)/-2 A. A'(1;2;3) B. A'(13/17; 23/17; -47/17) C. A'(13/17; -23/17; -47/17) D. A'(-1;-2;-3) x = 1+ 2t
25. Xác định điểm đối xứng A' của điểm A(2;-1;1) qua đường thẳng : d : y = 1 − − t  z = 2t 16 -17 7 16 17 7 A. A'( ; ; ) B. A'( ; ; ) C. A’(16;-17;-7) D. A’(16;-17;7) 9 9 9 9 9 9
26. Cho mp(P):x+y-z-4=0 và điểm A(1;-2;-2). Dựng AH ⊥ (P) tại H.Tìm tọa độ của H. A. H(2;-1;3) B. H(2;-1;-3) C. H(2;1;3) D. H(2;1;-3)
27.Cho mặt phẳng (P): x+y-z-4=0 và điểm A(1;-2;-2). Gọi A' là điểm đối xứng của A qua (P). Hãy xác định
A'. A. A'(3;0;-4) B. A'(3;0;8) C. A'(3;4;8) D. A'(3;4;-4)
28. Cho mặt phẳng (P): 2x – y + 3z + 17 = 0 và điểm A(5;2;-1). Gọi A' là điểm đối xứng của A qua (P). Hãy xác định A'. A. A'(-3;-6;-13) B. A'(-3;-6;13) C. A'(-3;6;-13) D. A'(3;4;8)
29. Hình chiếu vuông góc của điểm A(0;1;2) trên mp (P) : x + y + z = 0 có tọa độ là: A. (–2;2;0) B. (–2;0;2) C. (–1;1;0) D. (–1;0;1) 30. Hình chiếu của x − 1 y + 1 z − 2 (d ) : = =
trên mặt phẳng Oxy có phương trình là: 2 1 1  x = 1 + 2t
x = −1 + 5t
x = −1 − 2t A.     y = −1 + t
B.  y = 2 − 3t
C.  y = −1 + t D. Đáp án khác     z = 0  z = 0  z = 0
31. Hình chiếu vuông góc của điểm A(0;1;2) trên mp (P) : x + y + z = 0 có tọa độ là: A. (–2;2;0) B. (–2;0;2) C. (–1;1;0) D. (–1;0;1) 32. Hình chiếu của x − 1 y + 1 z − 2 (d ) : = =
trên mặt phẳng Oxy có phương trình là: 2 1 1  x = 1 + 2t
x = −1 + 5t
x = −1 − 2t A.     y = −1 + t
B.  y = 2 − 3t
C.  y = −1 + t D. Đáp án khác     z = 0  z = 0  z = 0 x − 2 y − 1 33. Cho z điểm M (1;0;0) và (∆) : = =
. Gọi M’ (a,b,c) là điểm đối xứng của M qua (∆) . Giá trị a 1 2 1 – b + c là : A.1 B.-1 C.3 D.-2 x = −t
34. Cho A(-1;1;2), B(0;1;1), C(1;0;4) và đường thẳng (d ) :  y = 2 + t . Cao độ giao điểm của (d) và mặt  z = 3 − t phẳng (ABC) là: A. 3 B. -1 C. 0 D. 6 x − 1 y + 2 z − 1 35. Cho (d): = =
và (P): 2x + y + z + 2 = 0 . Giao điểm A của (D) và (P) có tung độ là : 1 2 −1 A.0 B. 2 C. 4 D. -4 36. Cho 2 điểm (
A −1; 3;−2), B(−9; 4; 9) và mặt phẳng (P) : 2x − y + z + 1 = 0 . Tìm điểm M thuộc mặt
phẳng (P) sao cho biểu thức MA + MB nhỏ nhất?
Huỳnh văn Lượng Trang 20
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com A.M(−1;2; 3) B.M(1;2; 3) C.M(1;−2; 3) D.M(1;2;−3) − − + 37. Cho x y z đường thẳng 2 1 2 (d) : = =
. Tìm trên đường thẳng (d) điểm M(x;y;z) sao cho 1 2 1 2 2 2 x + y + z nhỏ nhất? A.M(1;1;−1) B.M(1;−1;1) C.M(−1;1;1) D.M(1;−1;−3) + − + 38. Cho 2 x y z điểm (
A 1;1; 0), B(3;−1; 4) và đường thẳng 1 1 2 (d) : = = . Tìm điểm M thuộc 1 −1 2
đường thẳng (d) sao cho tổng độ dài MA + MB nhỏ nhất? A.M(1;1;2) B.M(1;1;−2) C.M(1;−1;2) D.M(−1;1;2) A.M(1;1;9) B.M(0; 0;9) C.M(0;1;9) D.M(1; 0;9) x − 1 y + 2 z − 2
39. Hình chiếu của đường thằng (d): = =
trên mặt phẳng Oxy có phương trình là : 2 1 1 x = 1 + 2tx = −1 + 5t
x = −1 − 2t A.     y = −1 + t
B.  y = 2 − 3t
C.  y = −1 + t D. Đáp án khác    z = 0 z = 0 z = 0 40. x −1 y
Tọa độ hình chiếu vuông góc của M(2; 0; 1) trên đường thằng : = = z − 2 là: 1 2 A. (2; 2; 3) B. (1; 0; 2) C. (0; -2; 1) D. (-1; -4; 0) x = 1+ 2t 41. Hình chi 
ếu của đường thằng (d):  y = −1+ t trên mặt phẳng Oxy có phương trình là :  z = 3 − 6tx = 1 + 2tx = −1 + 5t
x = −1 − 2t A.     y = −1 + t
B.  y = 2 − 3t
C.  y = −1 + t D. Đáp án khác    z = 0 z = 0 z = 0 42 .
Cho mặt phẳng (α) : 3x − 2y + z + 6 = 0 và điểm A(2, 1
− , 0). Hình chiếu vuông góc của A lên mặt phẳng (α) là: A. (1,−1, ) 1 B. ( 1 − ,1, − ) 1 C. (3, 2 − , ) 1 D. (5, 3 − , ) 1 43 . x = 6 − 4t
Cho điểm A(1;1;1) và đường thẳng d : y = −2 − t .  z = −1+ 2t
Hình chiếu của A trên d có tọa độ là A. (2; 3 − ; − ) 1 B. (2;3; ) 1 C. (2;−3; ) 1 D. (−2;3; ) 1 44.
Trong hệ trục Oxyz , M’ là hình chiếu vuông góc của M(3, 2, )
1 trên Ox . M’ có toạ độ là: A. (0,0, ) 1 B. (3, 0, 0) C. ( 3 − , 0, 0) D. (0, 2,0) 45. Cho mặt cầu 2 2 2
(S) : x + y + z − 2x − 4y + 2z − 3 = 0 . Hãy lập phương trình mặt cầu (S ) đối xứng 1
với mặt cầu (S) qua mặt phẳng (P) : x + y − z − 5 = 0 ? A. 2 2 2
(S ) : x + y + z − x − y + 2z + 12 = 0 B. 2 2 2
(S ) : x + y + z − 6x − 8y + 2z + 20 = 0 1 1 C. 2 2 2 (S) : x + y + z = 100 D. 2 2 2
(S) : x + y + z − 6x − 8y + 12z + 10 = 0
Huỳnh văn Lượng Trang 21
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
BÀI TẬP TỔNG HỢP x+1 y-2 z+3
Câu 1: Định giá trị của m để đường thẳng d: = =
song song với mp(P): x-3y +6z =0 3 m -2 A. m=-4 B. m=-3 C. m=-2 D. m=-1
Câu 2: Tìm các giá trị của m và n để cho mặt phẳng (P): mx +ny +3z -5=0 vuông góc với đường thẳng d: x=3 +2t; y=5- 3t; z= -2-2t A. m=-3; n=-9/2 B. m=3; n=-9/2 C. m=-3; n=9/2 D. m=-3; n=9/2
Câu 3: Tìm các giá trị của m và n để cho mặt phẳng (P) vuông góc với đường thẳng d : x − 2 y +1 z − 5 (P): 3x -2y +mx +1=0 d: = = n 4 3 − A. m=3/2; n=-6 B. m=3/2; n=6 C. m=-3/2; n=-6 D. m=-3/2; n=6 x=3t 
Câu 4: Tính khoảng cách d từ A (2;-1;3) đến đường thẳng (D): y=-7 +5t  z=2 +2t A. d= 2 B. d= 3 C. d= 2 3 D. d= 3 2  1 1 x= + t  2 2 
Câu 5: Tính khoảng cách d từ A (1;-2;1) đến đường thẳng d : y = t  5 3 z= + t  2 2 3 14 14 A. d= B. d= C. d=2 D. Một đáp số khác 14 14
Câu 6: Cho mặt phẳng (P) 2x+y+3z+1=0 và đuờng thẳng d có phương trình tham số: x = −3 + t
y = 2 − 2t , trong các mệnh đề sau, mệnh đề nào đúng:  z = 1 A. d vuông góc với (P); B. d cắt (P); C. d song song với (P); D. d thuộc (P) x −1 y +1 z C©u 7 :
Cho điểm M(2; 1; 0) và đường thẳng ∆: 2 = 1 = 1. Đường thẳng d đi qua điểm M, −
cắt và vuông góc với ∆ có vec tơ chỉ phương là : A. (2;−1;−1) B. (2;1;−1) C. (1; −4;2) D. (1;−4;−2) Câu 8: x = 1+ mt x = 1− t '  
Tìm m để hai đường thẳng cắt nhau biết d : y = t và
d’ :  y = 2 + 2t ' :   z = −1+  2t z = 3 − t ' A. 0 B. 1 C. -1 D. 2 x = 1+ 2t  x − 2 y + 2 z − 3
Câu 9: Khoảng cách giữa hai đường thẳng d: y = −1− t và d’ : = = là :  1 − 1 1 z =  1
Huỳnh văn Lượng Trang 22
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com 6 1 A. 6 B. C. D. 2 2 6 x − 2 y z +1 x − 7 y − 2 Câu 10: Cho hai z đường thẳng d1: = = và d2: = =
. Vị trí tương đối giữa d1 và 4 6 − 8 − −6 9 12 d2 là: A. Trùng nhau B. Song song C. Cắt nhau D. Chéo nhau x − 2 y z +1 x − 7 y − 2 Câu 11: Kho z
ảng cách giữa hai đường thẳng d1: = = và d2: = = là: 4 −6 8 − 6 − 9 12 35 35 854 854 A. B. C. D. 17 17 29 29 x −1 y + 2 z − 4 x +1 y z + 2
Câu 12: Phương trình mặt phẳng chứa d1: = = và d2: = = là : 2 − 1 3 1 −1 3
A. 3x + 2 y − 5 = 0
B. 6x + 9 y + z + 8 = 0
C. −8x +19 y + z + 4 = 0 D. Tất cả đều sai
Câu 13: Trong không gian với hệ toạ độ Oxyz, cho đường thẳng (d):
. Véc tơ nào sau đây là véc tơ chỉ phương của (d)? A. B. C. D.
Câu 14: Trong không gian với hệ toạ độ Oxyz, cho điểm M(-2;1;1) và đường thẳng (d) có phương trình
. PT mặt phẳng (P) qua M vàvuông góc với đường thẳng (d) là: A. 2x + y - z + 4 = 0 B. 2x -y + z + 4 = 0 C. 4x -2y + 2z + 7 = 0 D. x + y -z + 2 = 0
Câu 15 Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (P): x + 2y -2z + 5 = 0. Khoảng cách từ M(
t; 2; -1) đến mặt phẳng (P) bằng 1 khi và chỉ khi : A. B. C. D. x = 1+ tx = 1+ 2t '  
Câu 16: Cho hai đường thẳng d :  y = 2 + t và d’ :  y = −1+ 2t ' .Tìm mệnh đề đúng:   z = 3 − t
z = 2 − 2t ' A. d cắt d’ B. d ≅ d’ C. d chéo với d’ D. d // d’ x −1 y z − 2
Câu 17: Khoảng cách từ điểm M(2;0;1) đến đường thẳng d : = = là : 1 2 1 12 A. 12 B. 3 C. 2 D. 6
Câu 18: Mặt phẳng chứa 2 điểm A(1;0;1) và B(-1;2;2) và song song với trục 0x có phương trình là: A. x + 2z – 3 = 0; B. y – 2z + 2 = 0; C. 2y – z + 1 = 0; D. x + y – z = 0 x − 2 y z +1 x − 7 y − 2 Câu 19: Cho hai z đường thẳng d1: = = và d2: = =
. Vị trí tương đối giữa d1 và d2 4 −6 −8 −6 9 12 là: A. Trùng nhau B. Song song C. Cắt nhau D. Chéo nhau x − 2 y z +1 x − 7 y − 2 z
Câu 20: Khoảng cách giữa hai đường thẳng d1: = = và d = = là: 4 2: −6 −8 −6 9 12 35 35 854 854 A. B. C. D. 17 17 29 29 x −1 y + 2 z − 4 x +1 y z + 2
Câu 21: Phương trình mặt phẳng chứa d1: = = và d2: = = là : −2 1 3 1 −1 3
A. 3x + 2 y − 5 = 0
B. 6x + 9 y + z + 8 = 0
C. −8x +19 y + z + 4 = 0 D. Tất cả đều sai
Huỳnh văn Lượng Trang 23
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com x = t
Câu 22 Mặt cầu tâm I(1;3;5) tiếp xúc với đường thẳng d:  y = 1
− − t có bán kính là:  z = 2 − t A. 14 B. 14 C. 7 D. 7
Câu 23: Cho (S) là mặt cầu tâm I(2,1,-1) và tiếp xúc với mặt phẳng (P): 2x-2y-z+3=0. bán kính (S) là A: 2; B: 2/3; C: 4/3; D:2/9 Câu 24: x = −2t
Cho mặt phẳng (P) : x +y -z +1 =0 và đường thẳng d :  y = t
.Viết phương trình mp(Q) chứa đường  z = 1+ 2t
thẳng d và vuông góc với (P) A. (Q): 2x+3z -2=0 B. (Q): 2x - z + 1= 0 C. (Q): x - z + 1 =0 D (Q): x + z – 1 = 0
Câu 25. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A( ; 1 –2; 0) ,B(0; – ; 1 ) 1 ,C (2; ; 1 – ) 1 và D (3; ;
1 4) . Hỏi có tất cả bao nhiêu mặt phẳng cách đều bốn điểm đó ? A. 1 mặt phẳng. B. 4 mặt phẳng C. 7 mặt phẳng D. Có vô số mặt phẳng
Câu 26: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) : 3x + 4y + 2z + 4 = 0 và điểm A ( ;
1 –2; 3) . Tính khoảng cách d từ A đến (P). 5 5 5 5 A. d = B. d = C. d = D. d = 9 29 29 3 x = 3t 
Câu 27:Cho điểm A(2;-1;3) và đường thẳng : d : y = −7 + 5t .Lập phương trình chính tắc của đường thẳng z = 2 +  2t
d’ đi qua A ,vuông góc với d và cắt d x + 2 y +1 z − 3 A. = = B. 1 1 1 x + 2 y +1 z − 3 x − 2 y +1 z − 3 C. = = D. = = 1 −1 1 1 1 − 1 10 2 2 Câu 28: − − + Trong không gian v x z
ới hệ tọa độ Oxyz, cho đường thẳng d có phương trình : y = = . 5 1 1
Xét mặt phẳng (P) : 10x + 2y + mz + 11 = 0 , m là tham số thực. Tìm tất cả các giá trị của m để mặt
phẳng (P) vuông góc với đường thẳng d. A. m = –2 B. m = 2 C. m = –52 D. m = 52
Câu 29: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(0; ; 1 ) 1 và B( ;
1 2; 3) . Viết phương trình
của mặt phẳng (P) đi qua A và vuông góc với đường thẳng AB. A. x + y + 2z – 3 = 0 B. x + y + 2z – 6 = 0 C. x + 3y + 4z – 7 = 0 D. x + 3y + 4z – 26 = 0 x y +1 z + 2
Câu 30: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : = = và mặt phẳng 1 2 3
(P) : x + 2y − 2z + 3 = 0 . Tìm điểm M có các tọa độ âm thuộc d sao cho khoảng cách từ M đến (P) bằng 2. A. M (−2;−3;− ) 1 B. M( 1 − ; 3 − ; 5 − ) C. M (−2;−5; 8 − ) D. M ( 1 − ; −5; 7 − )
Huỳnh văn Lượng Trang 24
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
Câu 31: Trong không gian với hệ tọa độ Oxyz, cho điểm A( ;
1 0; 2) và đường thẳng d có phương trình x −1 y +1 : z = =
. Viết ptrình đường thẳng ∆ đi qua A, vuông góc và cắt d. 1 1 2 −1 − 2 −1 − 2 A. ( x z ∆) x y z : = = B. (∆) y : = = 1 1 1 1 1 −1 −1 − 2 −1 − 2 C. ( x z ∆) x y z : = = D. (∆) y : = = 2 2 1 1 −3 1
Câu 32:Trong không gian Oxyz, cho điểm A(1; 1
− ; 0) và mặt phẳng (P) : 2x − 2y + z − 1 = 0 . Tìm M ∈(P) sao
cho AM ⊥ OA và độ dài AM bằng ba lần khoảng cách từ A đến (P) . . A M (1; −1; 3) . B M (−1; −1; −3) C. M (1; −1; 3) D. M (1;−1;−3) Câu 33: Trong không x + 1 z + 2
gian với hệ tọa độ Oxyz , cho đường thẳng y d : = = và mặt phẳng 1 2 3
(P) : x + 2y − 2z + 3 = 0 . Tìm tọa độ điểm M có tọa độ âm thuộc d sao cho khoảng cách từ M đến (P) bằng 2. . A M (−2; −3; −1) B. M (−1;−3;−5) C. M (−2; −5; −8) D. M (−1;−5;−7)
Câu 34:Trong không gian Oxyz cho mặt phẳng (P) và đường thẳng d có phương trình lần lượt là + − ( x 2 z
P) : x + 2y − 3z + 4 = 0 và y 2 d : = =
. Viết phương trình đường thẳng ∆ nằm trong mặt phẳng (P), 1 1 1 −
vuông góc và cắt đường thẳng d. x 3  = − − t x = −1 − t x = −3 + t x = 1 − + t     . A ∆ : y = 2 − t . B ∆ : y = 1− t C. ∆ : y = 1 − t 2 . D ∆ : y = 2 − 2t    z = −   2t z = 1−  2t z = 1 − t z = 2 − t
Câu 35: Trong không gian v + ới hệ trục tọa độ x y z −
Oxyz, cho đường thẳng có phương trình 1 1 ∆ : = = 2 −2 1
Tính khoảng cách từ O đến đường thẳng ∆ . A. 2 . B 2 C. 1 1 . D 2 Câu 36:Cho − − đường thẳng x 8 y 5 z − 8 d : = =
và mặt phẳng (P): x + 2y + 5z +1 = 0 . Tính khoảng cách giữa d 1 2 −1 và (P). A. 59 29 29 29 . B C. D. 30 30 20 50 Câu 37: x − 1 y z + 1
Mặt phẳng (P) chứa đường thẳng (d ) : = =
và vuông góc với (Q) : 2x + y − z = 0 có 2 1 3 phương trình là:
A. 2x − y −1 = 0
B. x − 2 y + z = 0
C. x + 2 y + z = 0
D. x + 2 y −1 = 0 x − 3 y z +1
Câu 38: Cho (P): 2x + y − 2z +1 = 0, (
A 1; 2; −3), (d ) : = =
. Đường thẳng (∆) qua A vuông góc 1 2 −2
với (d) và song song với (P) có véc tơ chỉ phương có cao độ là: A.1 B. 2 C. 3 D. 4 x + 1 y − 1
Câu 39: Cho A(1;5;0), B(3;3;6) và: z = =
. Điểm M thuộc (∆) để tam giác MAB có diện tích nhỏ 2 1 − 2
nhất có tung độ là: A.1 B. 2 C. 3 D. 0
Huỳnh văn Lượng Trang 25
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com x + 1 y − 1
Câu 40: Cho A(1;5;0), B(3;3;6) và (∆) : z = =
. Điểm M thuộc (∆) để tam giác MAB có diện tích 2 −1 2
nhỏ nhất có tung độ là: A.1 B. 2 C. 3 D. 0
Câu 41: Cho A(2,1,− )
1 , (P) : x + 2 y − 2z + 3 = 0 . (d) là đường thẳng đi qua A và vuông góc với (P). Tìm tọa
độ M thuộc (d) sao cho OM = 3 . A.     (1, − − −1, 2) hoặc 5 1 1  , ,  B. (1,−1, ) 1 hoặc 5 1 1  , ,   2 3 3   3 3 3  C.     (3,3, − − −3) hoặc 7 5 5  , ,  D. (0,1,− ) 1 hoặc 2 1 1  , ,   3 3 3   3 3 3 
Câu 42: Cho A(2;0;-3), B(4;-2;-1), (P) : x + y + 2z + 4 = 0 . Phương trình đường thẳng (d) thuộc (P) sao cho
mọi điểm thuộc (d) cách đều A và B có vectơ chỉ phương là: A. (1;-1;1) B. (3;1;-2) C. (1;1;2) D. (-1;0;-2)  x = 1 + tx = 2 + t ' Câu 43 Cho  
(∆ :  y = 2 − t ;(∆ ) :  y = 1 − t ' . Vị trí tương đối của hai đường thẳng là: 1 ) 2  
z = −2 − 2tz = 1 A. Song song B. Chéo nhau C. Cắt nhau D. Trùng nhau
Câu 44: Cho A(-1,-2,2), B(-3,-2,0), (P) : x + 3y − z + 2 = 0 . Vectơ chỉ phương của đường thẳng giao tuyến
của (P) và mặt phẳng trung trực của AB là: A. (1,-1,0) B. (2,3,-2) C. (1,-2,0) D. (3,-2,-3
Câu 45: PT tham số của đường thẳng ∆ đi qua điểm M(2;0;-1) và có vecto chỉ phương a = (4;−6;2) x = −2 + 4t x = −2 + 2tx = 2 + 2tx = 4 + 2t     A,  y = −6t ; B,  y = 3 − t ; C,  y = 3 − t ;
D,  y = −3t     z = 1+  2t  z = 1 + tz = −1 + tz = 2 + t
Câu 46: Cho d là đường thẳng đi qua điểm A(1;2;3) và vuông góc với mặt phẳng (α ) : 4x + 3y − 7z +1 = 0 .
Phương trình tham số của d là:  x = −1+ 4tx = 1 + 4t  x = 1+ 3t  x = −1+ 8t     A,  y = 2 − + 3t ;
B  y = 2 + 3t ; C, y = 2 − 4t ; D,  y = 2 − + 6t    
z = −3 − 7tz = 3 − 7t z = 3 −  7t
z = −3 −14tx = 1+ 2tx = 3 + 4t '  
Câu 47: Cho 2 đường thẳng: d :  y = 2 + 3 và d :  y = 5 + 6t ' . Trong các mệnh đề sau, mệnh đề nào 1 t 2    z = 3 + 4tz = 7 + 8t ' đúng? A, d ; B, d / / d d ; D, d chéo nhau 1 ⊥ d2 1 d ; C, = 2 1 2 d và 1 2  x = −3 + t
Câu 48 : Cho mặt phẳng (α ) : 2x + y + 3z +1 = 0 và đường thẳng d có phương trình tham số :  y = 2 − 2t .   z = 1
Trong các mệnh đề sau, mệnh đề nào đúng? A, d ⊥ (α ) ; B, d cắt (α ) ; C, d / / (α ) ; D, d ⊂ (α ) Câu 49: − +
Mặt phẳng (P) đi qua điểm A(1;2;0) và vuông góc với đường thẳng d: x 1 y z 1 = = có phương 2 1 1 − trình là: A. 2x + y – z + 4 = 0 B. –2x – y + z + 4 = 0 C. –2x – y + z – 4 = 0 D. x + 2y – 5 = 0
Huỳnh văn Lượng Trang 26
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com Câu 50: M − +
ặt phẳng (P) chứa đường thẳng d: x 1 y z 1 = =
và vuông góc với mặt phẳng 2 1 3
(Q) : 2x + y − z = 0 có phương trình là: A. x + 2y – 1 = 0 B. x − 2y + z = 0 C. x − 2y – 1 = 0 D. x + 2y + z = 0
Câu 51: Hai mặt phẳng (P) và (Q) có giao tuyến cắt trục Ox là:
A. (P): 4x – 2y + 5z – 1 = 0 và (Q): 2x – y + 3z – 2 = 0
B. (P): 3x – y + z – 2 = 0 và (Q): x + y + z + 1 = 0
C. (P): x – y – 3z + 3 = 0 và (Q): 4x – y + 2z – 3 = 0
D. (P): 5x + 7y – 4z + 5 = 0 và (Q): x – 3y + 2z + 1 = 0
Câu 52 Trong không gian với hệ toạ độ 0xyz cho A(2;0;0); B(0;3;1); C(-3;6;4). Gọi M là điểm nằm trên
cạnh BC sao cho MC = 2MB. Độ dài đoạn AM là: A. 3 3 B. 2 7 C. 29 D. 30
Câu 53: Cho điểm M(–3; 2; 4), gọi A, B, C lần lượt là hình chiếu của M trên Ox, Oy, Oz. Mặt phẳng song
song với mp(ABC) có phương trình là: A. 4x – 6y –3z + 12 = 0 B. 3x – 6y –4z + 12 = 0 C. 6x – 4y –3z – 12 = 0 D. 4x – 6y –3z – 12 = 0 − − − câu 54. Trong không gian v x 7 y 3 z 9
ới hệ trục toạ độ Oxyz cho 2 đường thẳng (d ) : = = ; 1 1 2 −1 x − 3 y − 1 z − 1 (d ) : = =
. Viết phương trình đường vuông góc chung ( )
∆ của 2 đường thẳng trên? 2 −7 2 3 3  x − 2y − z − 6 =  0 3  x − 2y − z − 6 =  0 A.( :  ∆   B.( ) ∆ :  5  x + 34y − 11z + 38 = 0  + + − =  5x 34y 11z 38 0    3  x − 2y − z − 6 =  0 3  x − 2y − z − 6 =  0 C.( ) :  ∆   D.( ) ∆ :  5  x + 34y − 11z − 38 = 0  − − + =  5x 34y 11z 38 0    câu 55.
Xác định toạ độ điểm A' đối xứng với điểm (
A 2;−1; 3) qua đường thẳng x   =  3t   (d) : y   = −7 + 5t ?  z  = 2 +  2t   A.A'(4; 3;5) B.A'(4; 3;−5) C. ( A 4;−3; 5) D.M(4;−3;−5)
câu 56. Xác định tham số m,n để mặt phẳng (P) : 5x + ny + 4z + m = 0 thuộc chùm mặt phẳng : (Q ) : (
α 3x − 7y + z − 3) + β(x − 9y − 2z + 5) = 0 ? α,β A.m = 11, n = 5 B.m = −11, n = −5 C.m = −11, n = 5 D.m = 11, n = −5
Câu 57. Lập phương trình đường thẳng ( )
∆ đi qua điểm M(−1;2;−3) vuông góc với đường thẳng x − 2 y − 1 z − 1 x − y + z − (d) : = = và cắt đường thẳng 1 1 3 (d ') : = = ? 6 −2 −3 3 2 −5 − + + − − − A. x 1 y 1 z 3 x y z ( ) ∆ : = = B. 1 1 3 ( ) ∆ : = = 2 −3 6 2 −3 6 + + − − + − C. x 1 y 1 z 3 x y z ( ) ∆ : = = D. 1 1 3 ( ) ∆ : = = 2 −3 6 2 −3 6
Huỳnh văn Lượng Trang 27
0918.859.305-01234.444.305
Luyện thi THPT Quốc gia (Hình Oxyz) www.huynhvanluong.com
C©u 58 : Bán kính của mặt cầu tâm I(3;3;-4), tiếp xúc với trục Oy bằng 5 A. 5 B. 4 C. 5 D. 2
C©u 59 : Trong không gian toạ độ Oxyz, cho mặt phẳng (α) : 2x + y + z + 5 = 0 và đường thẳng x −1 y − 3 z − 2 d : = =
. Toạ độ giao điểm của d và (α) là 3 1 − 3 − A. (4,2,− ) 1 B. ( 1 − 7,9, 20) C. ( 1 − 7, 20,9) D. (−2,1,0)
C©u 60 : Cho mặt phẳng (α) : 4x − 2y + 3z +1 = 0 và mặt cầu ( ) 2 2 2
S : x + y + z − 2x + 4y + 6z = 0 . Khi
đó, mệnh đề nào sau đây là một mệnh đề sai:
A. (α) cắt (S) theo một đường tròn
B. (α) tiếp xúc với (S)
C. (α) có điểm chung với (S)
D. (α) đi qua tâm của (S)
C©u 61 : Trong không gian Oxyz, tam giác ABC có A(1,0,0);B(0,2,0);C (3,0,4). Tọa độ
điểm M trên mặt phẳng Oyz sao cho MC vuông góc với (ABC) là:  3 11  3 11  3 11  3 11 A.  0, ,  B.  0, , −  C.  0,− ,  D.  0,− ,−   2 2   2 2   2 2   2 2 
C©u 62 : Cho 3 điểm A(1; –2; 1), B(–1; 3; 3), C(2; –4; 2). Một VTPT n của mặt phẳng (ABC) là: A. n = (−1; 9; 4) B. n = (9; 4;1) C. n = (4;9; −1) D. n = (9; 4; −1)
C©u 63 : Trong không gian Oxyz, xác định các cặp giá trị (l, m) để các cặp mặt phẳng sau đây
song song với nhau: 2x + ly + 3z − 5 = 0;mx − 6 y − 6z − 2 = 0 A. (3,4) B. (4; 3 − ) C. (−4,3) D. (4,3)
C©u 64 : Cho hai mặt phẳng song song (P): nx + 7y − 6z + 4 = 0 và (Q): 3x + my − 2z − 7 = 0 . Khi đó giá trị của m và n là: 7 7 3 7 A. m = ; n = 1 = ; = 9 C. m = ; n = 9 = ; = 9 3 B. n m 3 7 D. m n 3 C©u 65 : x = 1+ 2t x = 7 + 3   ts
Vị trí tương đối của hai đường thẳng d : y = −2 − t 3 ;d : y = 2 + 2t 1 2 là: z 5 4t  = + z = 1−   2t A. Chéo nhau B. Trùng nhau C. Song song D. Cắt nhau
Huỳnh văn Lượng Trang 28
0918.859.305-01234.444.305