





































Preview text:
HÌNH HOÏC Oxyz Vận dụng cao
Phần 1. Các bài toán cơ bản ở mức vận dụng
Phần 2. Cực trị trong hình học Oxyz
Phần 3. Các bài toán về mặt cầu
Phần 4. Bài toán cực trị sử dụng tâm tỷ cự
Phần 5. Bài toán hỏi số mặt phẳng, số mặt cầu
Phần 6. Bài toán quỹ tích
Phần 1. Các bài toán cơ bản ở mức vận dụng
Câu 1. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P: x 2y 3z 4 0 và hai đường thẳng x 1 y z 1 x 1 y 3 z 1 d : , d :
. Mặt phẳng song song với 1 1 1 2 2 2 1 1
P và cắt d , d theo thứ tự tại M, N sao cho MN 3. Điểm nào sau đây thuộc ? 1 2 A. A1;2; 3 .
B. B0;1; 3 .
C. C 0;1; 3 . D. D0;1; 3 .
Câu 2. Trong không gian với hệ tọa độ Oxyz, cho điểm A1;2; 3 và mặt phẳng
P: x y z 1 0. Gọi là mặt phẳng đi qua A và có vectơ pháp tuyến n 1;b;c biết ,
rằng vuông góc với P và cắt các tia Ox , Oz lần lượt tại M và N thỏa OM 3ON.
Khẳng định nào sau đây đúng ?
A. b c 84.
B. b c 7.
C. b c 7.
D. b c 84.
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho hai điểm M 1;2; 3 , N 3;1; 3 và hai đường thẳng x y 2 z x 4 y 1 z 5 d : , d :
. Gọi là mặt phẳng đi qua M ; cắt d 1 1 2 1 2 2 1 3 1
tại A và cắt d tại B sao cho A , B , N thẳng hàng. Điểm nào sau đây không thuộc ? 2
A. A0;2;0.
B. A4;0;0.
C. C 0;0; 3 .
D. D1;1; 1 .
Câu 4. Trong không gian với hệ tọa độ Oxyz, gọi là đường thẳng đi qua A1;2; 3 và có vectơ chỉ phương x 3 y 7 z 3
u a;b;
1 , biết đồng thời cắt cả hai đường thẳng d : 1 1 3 1
x 2 2t và
d : y t
. Khẳng định nào sau đây là đúng ? 2 z 2
A. a b 3.
B. a b 4.
C. a b 5.
D. a b 6.
Câu 5. Trong không gian với hệ tọa độ Oxyz, cho điểm A1;0;2 và đường thẳng x 1 y z 1 d :
. Viết phương trình đường thẳng đi qua ,
A vuông góc và cắt d . 1 1 2 A. x 1 y z 2 x y z : . B. 1 2 : . 1 1 1 1 1 1 C. x 1 y z 2 x y z : . D. 1 2 : . 2 2 1 1 3 1
Câu 6. Trong không gian với hệ tọa độ x y z
Oxyz , cho đường thẳng 1 1 2 d : và mặt 2 2 1
phẳng P: x 2y 2z 7 0 . Gọi I là giao điểm của d và P . Tính khoảng cách từ điểm
M thuộc d đến P , biết IM 9. A. 3 2. B. 2 5. C. 15. D. 8.
Câu 7. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A3;3; 1 , B0;2; 1 và mặt phẳng
P: x y z 7 0 . Đường thẳng d nằm trong P sao cho mọi điểm của d cách đều hai điểm ,
A B có phương trình là x t x 2t x t x t A.
y 7 3t .
B. y 73t .
C. y 73t .
D. y 73t . z 2t z t z 2t z 2t
Câu 8. Trong không gian với hệ tọa độ Oxyz , cho điểm A0;0;2 và hai đường thẳng x 1t
d : 2x y z , d ' : y 2t . Tìm tọa độ của điểm N thuộc đường thẳng d ' sao cho đường z 0
thẳng AN cắt đường thẳng d tại một điểm.
A. N 0;3;0.
B. N 2;1;0.
C. N 1;2;0. D. N 0;0; 3 .
Câu 9. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P: x 3y 2z 2 0 và đường thẳng x 1 y 1 z 4 d :
. Đường thẳng qua A1;2;
1 và cắt P, d lần lượt tại 2 1 1 B, C
a;b;c sao cho C là trung điểm của AB. Giá trị của biểu thức a b c bằng A. 15. B. 12. C. 5. D. 11.
Câu 10. Trong không gian với hệ tọa độ Oxyz, cho điểm A1;2; 3 và mặt phẳng
P: 2x y 4z 1 0. Đường thẳng d đi qua điểm ,
A song song với mặt phẳng P, đồng
thởi cắt trục Oz. Phương trình tham số của đường thẳng d là
x 15t x t
x 13t x 1t A.
y 2 6t .
B. y 2t .
C. y 2 2t.
D. y 2 6t. z 3 t z 2 t z 3 t z 3 t
Câu 11. Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A2;4;
1 , B1;2;0,C4;1; 3 và
mặt phẳng : x2y z 7 0. Gọi P là mặt phẳng qua C và vuông góc với sao cho d ;
A P 2d ; B P.
Giả sử phương trình của P: ax by cz d 0. Tính 2 2 2 2
a b c d . A. 4. B. 3. C. 2. D. 1.
Câu 12. Trong không gian với hệ tọa độ Oxyz, cho mp P đi qua M 1;2; 1 , N 1;0; 1 đồng
thời cắt Ox,Oy theo thứ tự tại ,
A B (khác O ) sao cho AM 3 . Khi đó P có một véc tơ BN
pháp tuyến n 1; ;
m n thì tổng m n bằng A. 2. B. 1. C. 1. D. 0.
Câu 13. Trong không gian với hệ tọa độ Oxyz, cho A2;5; 3 , B2;1; 1 ,C2;0; 1 và mặt phẳng
: 3x 4y 5z 1 0. Gọi D ; a ;
b c (với c 0 ) thuộc sao cho có vô số mặt phẳng P
chứa C, D và khoảng cách từ A đến P gấp 3 lần khoảng cách từ B đến P. Tính giá trị biểu thức 2 2 2
S a b c . A. S 24. B. S 25. C. S 27. D. S 26.
Câu 14. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng : x z 3 0 và điểm M 1;1;
1 . Gọi A là điểm thuộc trục Oz, B là hình chiếu của A lên . Biết rằng tam giác
MAB cân tại M. Đoạn thẳng MA có độ dài bằng A. 6 hoặc 18. B. 6 hoặc 102. C. 18. D. 6.
Câu 15. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A0;0; 3 , B2;0; 1 và mặt
phẳng P: 3x8y 7z 1 0. Điểm Ca; ;
b c là điểm nằm trên mặt phẳng P, có hoành độ
dương để tam giác ABC đều. Tính ab 3 .c A. 7. B. 9. C. 5. D. 3.
Câu 16. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A2;0;
1 , B1;0;0,C1;1; 1 và mặt
phẳng P: x y z 2 0. Điểm M ; a ;
b c nằm trên mặt phẳng P thỏa mãn
MA MB MC. Tính T a 2b 3 . c A. T 5. B. T 3. C. T 2. D. T 4.
Câu 17. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A2;1 ;1 , M 5;3 ;1 , N 4;1;2 và
mặt phẳng P: y z 27. Biết rằng tồn tại điểm B trên tia AM , điểm C trên P và điểm
D trên tia AN sao cho tứ giác ABCD là hình thoi. Tọa độ của điểm C là
A. 15;21;6.
B. 21;21;6.
C. 15;7;20. D. 21;19; 8 .
Câu 18. Trong không gian với hệ tọa độ Oxyz, cho các điểm A1;0;0, B0;2;0,C0;0;4. Viết
phương trình đường thẳng đi qua trực tâm H của A
BC và vuông góc với mặt phẳng ABC. A. x1 x y z : y z . B. 1 1 : . 4 2 1 4 2 1 C. : x y z x y z . D. 1 1 : . 4 2 1 4 2 1
Câu 19. Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A1;2; 1 , B 2;2; 1 , C
1;2;2. Hỏi đường phân giác trong góc A của tam giác ABC cắt
mặt phẳng Oyz tại điểm nào sau đây ? A. 4 8 0; ; . B. 2 4 0; ; . C. 2 8 0; ; . D. 2 8 0; ; . 3 3 3 3 3 3 3 3
Câu 20. Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC nhọn có H 2;2; 1 , 8 4 8 K ; ; ,
O lần lượt là hình chiếu vuông góc của A , B , C trên các cạnh BC , AC , AB . 3 3 3
Đường thẳng d đi qua A và vuông góc với mặt phẳng ABC có phương trình là 8 2 2 x y z A. x 4 y 1 z 1 d : . B. 3 3 3 d : . 1 2 2 1 2 2 4 17 1 x y z C. 9 9 9 x y z d : . D. 6 d : . 1 2 2 1 2 2
Câu 21. Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A2;3; 3 , phương trình
đường trung tuyến d kẻ từ B là x3 y 3 z 2
, phương trình đường phân giác trong 1 1 2 1
d của góc C là x2 y 4 z 2
. Đường thẳng BC có một vectơ chỉ phương là 2 2 1 1
A. u 2;1; 1 .
B. u 1;1;0.
C. u 1;1;0.
D. u 1;2; 1 .
Câu 22. Trong không gian với hệ tọa độ Oxyz , cho ba điểm A0;0;0, B 0;1; 1 , C 1;0; 1 . Xét
điểm D thuộc mặt phẳng Oxy sao cho tứ diện ABCD là một tứ diện đều. Kí hiệu
Dx ; y ;z là tọa độ của điểm D . Tổng x y bằng 0 0 0 0 0 A. 0 . B. 1. C. 2 . D. 3 .
Câu 23. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S x 2 y z 2 2 : 1 2 4 và
x 2t đường thẳng
d : y t
. Tìm các giá trị của m để d cắt S tại hai điểm phân biệt , A B
z mt
sao cho các mặt phẳng tiếp diện của S tại A và B vuông góc với nhau. m 1 m 1 m 0 A. . B. C. D. Đáp án khác. . . m 4 m 0 m 4
Câu 24. Trong không gian với hệ tọa độ Oxyz, cho bốn đường thẳng x 1 y 2 : z d , 1 1 2 2 x 2 y 2 : z d x y z 1 x2 y z 1 , d : , d : . Gọi 2
là đường thẳng cắt cả 2 4 4 3 2 1 1 4 2 2 1
bốn đường thẳng đã cho. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng .
A. u 2;0;1 .
B. u 2;1;1 .
C. u 2;1;1 .
D. u 1;2;2 . 4 1 2 3
Câu 25. Trong không gian với hệ tọa độ Oxyz, cho bốn đường thẳng x2 y 2 z 1 : , 1 1 1 1 x1 y 1 z x y 2 z 1 x5 y a z b : , : và : . Biết không tồn tại 2 3 1 2 1 1 1 1 4 1 3 1
đường thẳng nào trong không gian mà cắt được đồng thời cả bốn đường thẳng trên. Tính giá
trị của T a2 . b A. T 2. B. T 3. C. T 2.
D. T 3.
Câu 26. Trong không gian với hệ tọa độ Oxyz, cho S 1;2; 3 và các điểm ,
A B,C thuộc các trục
Ox,Oy,Oz sao cho hình chóp S.ABC có các cạnh ,
SA SB, SC đôi một vuông góc với nhau. Tính
thể tích khối chóp S.ABC. A. 343. B. 343. C. 343. D. 343. 6 18 12 36
Câu 27. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng đi qua điểm M 1;2; 1 và
cắt các tia Ox,Oy,Oz lần lượt tại ,
A B,C sao cho độ dài ,
OA OB,OC theo thứ tự tạo thành cấp
số nhân có công bội bằng 2. Tính khoảng cách từ gốc tọa độ tới mặt phẳng . A. 4 . B. 21 . C. 3 21 . D. 9 21. 21 21 7
Câu 28. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S 2 2 2
: x y z 3 . Một mặt
phẳng tiếp xúc với mặt cầu S và cắt các tia Ox, Oy,
Oz tương ứng tại ,
A B, C . Tính giá trị của biểu thức 1 1 1 T . 2 2 2 OA OB OC A. 1 T . B. 1 T . C. 1 T .
D. T 3 . 3 3 9
Câu 29. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A6;3;4, Ba;b;c. Gọi M , N,
P lần lượt là giao điểm của đường thẳng AB với các mặt phẳng tọa độ
Oxy, Oyz , Ozx sao cho M , N,
P nằm giữa A và B thỏa mãn AM MN NP PB. Giá
trị của biểu thức a b c bằng A. 40. B. 32. C. 24. D. 17.
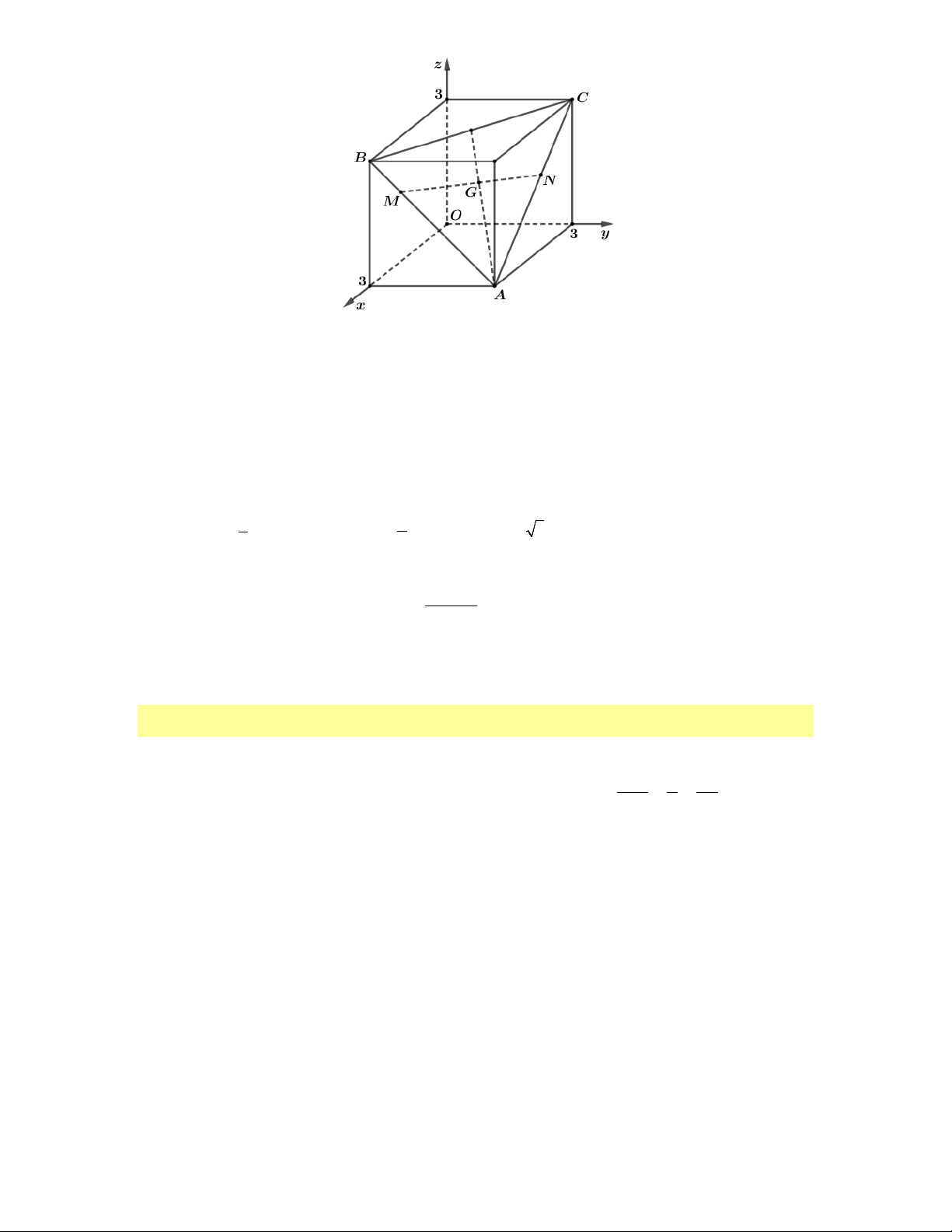
Câu 30. Trong không gian với hệ tọa độ Oxyz, cho hình lăng trụ tam giác đều ABC.A B C có 1 1 1 A
3;1;1 , hai đỉnh B,C thuộc trục Oz và AA 1, ( C không trùng O ). Biết u a;b;2 là 1 1
một véc tơ chỉ phương của đường thẳng A C. Tính 2 2
T a b . 1 A. T 4.
B. T 5. C. T 9. D. T 16.
Phần 2. Cực trị trong hình học Oxyz x t
Câu 1. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d :y 1t và điểm z 4
A1;1;2. Đường thẳng nằm trong mặt phẳng tọa độ Oxy sao cho A cách đều d và .
Tìm giá trị lớn nhất của khoảng cách giữa d và . A. d 1. B. d 3 2. C. d 2. D. Không tồn tại. max max max
Câu 2. Trong không gian với hệ tọa độ x1 y z 2
Oxyz, cho hai đường thẳng d : và 1 2 1 1 x1 y 2 z 2 d :
. Gọi là đường thẳng song song với P: x y z 7 0 và cắt 2 1 3 2
d ,d lần lượt tại hai điểm ,
A B sao cho AB ngắn nhất. Phương trình của đường thẳng là 1 2 x 6 t x 6 x 6 2t x 12t A. 5 5 5 y 5 . B. y .
C. y t .
D. y t . 2 2 2
z 9 t 9 9 9
z t
z t
z t 2 2 2 Câu 3. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A4;1;
3 , B1;2; 1 ,C3;2;
3 và D0;3;
5 . Mặt phẳng qua D và tổng khoảng cách ,
A B,C đến lớn nhất, đồng thời ba điểm ,
A B,C nằm về cùng một phía so với mặt
phẳng . Điểm nào dưới đây thuộc mặt phẳng .
A. M 7;3;4.
B. M 2;0;7.
C. M 1;1;6.
D. M 36;1; 1 .
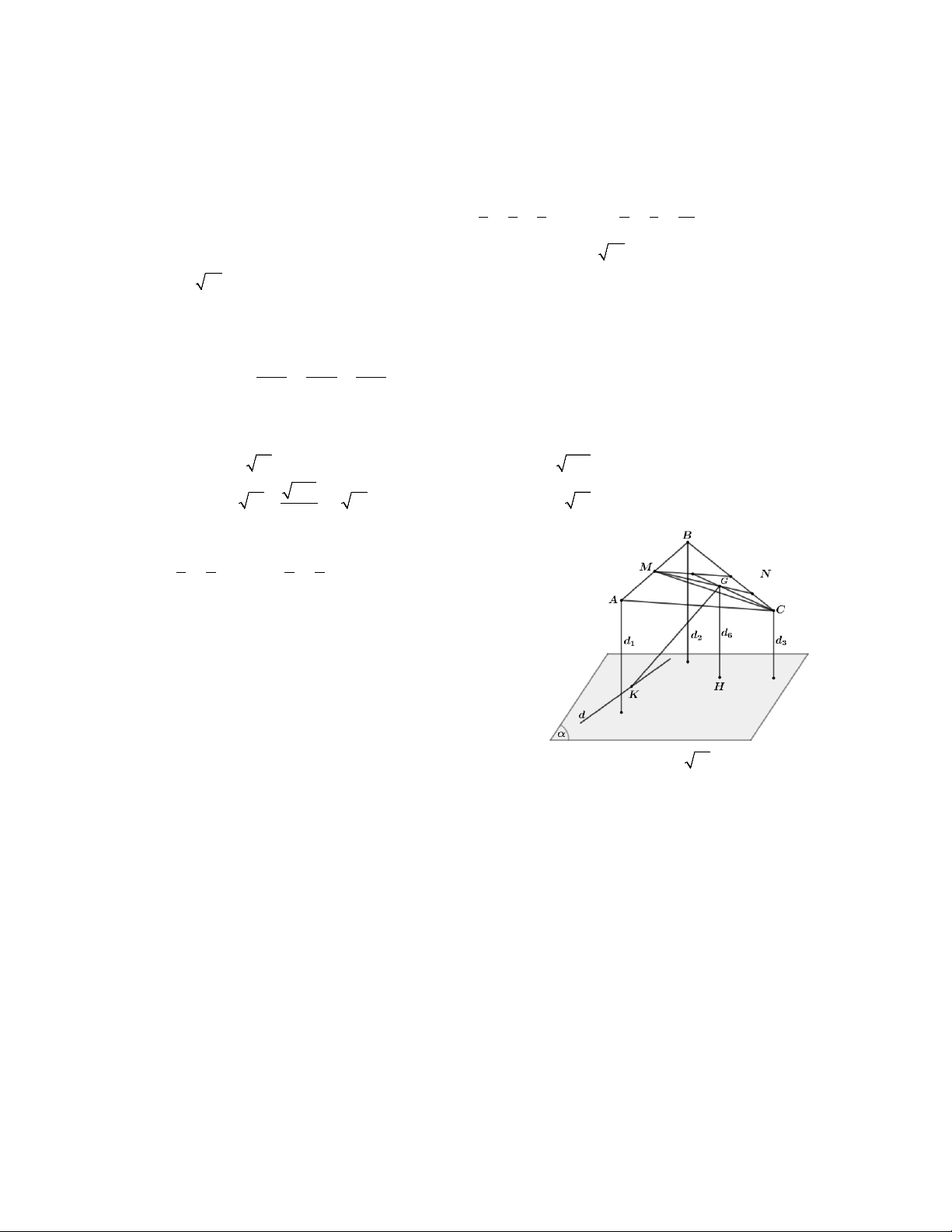
Câu 4. Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A2;1;0, B4;4; 3 ,C2;3;2 và đường thẳng x1 y 1 z 1 d :
. Gọi là mặt phẳng chứa d sao cho ,
A B,C ở cùng phía 1 2 1
đối với mặt phẳng . Gọi d ,d ,d lần lượt là khoảng cách từ ,
A B,C đến . Tìm giá trị 1 2 3
lớn nhất của T d 2d 3d . 1 2 3 A. T 6 14. B. T 203. max max C. 203 T 14 3 21. D. T 2 21. max 3 max
Câu 5. Trong không gian với hệ trục tọa độ Oxyz, gọi d là đường thẳng đi qua A2;1;0 song
song với mặt phẳng P: x y z 0 và tổng khoảng cách từ M 0;2;0, N 4;0;0 tới đường
thẳng d có giá trị nhỏ nhất. Véc-tơ chỉ phương u của d có tọa độ là: A. 1;0; 1 . B. 2;1 ;1 . C. 3;2; 1 . D. 0;1; 1 .
Câu 6. Trong không gian với hệ tọa độ Oxyz, gọi là đường thẳng đi qua điểm A2;1;0,
song song với mặt phẳng P: x y z 0 và có tổng khoảng cách từ các điểm
M 0;2;0, N 4;0;0 tới đường thẳng đó đạt giá trị nhỏ nhất? Vectơ chỉ phương của là vectơ nào sau đây? A. u B. u C. u D. u 2;1 ;1 3;2; 1 1;0; 1 0;1; 1
Câu 7. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng x 1 y 2 : z d và điểm 1 2 1 A2;1
;1 . Gọi là đường thẳng đi qua A sao cho tổng khoảng cách từ O đến và khoảng
cách từ d đến lớn nhất. Biết u 2; ;
b c là một vectơ chỉ phương của .
Tính tổng b . c A. 3. B. 3. C. 4. D. 4.
Câu 8. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A1;4;4, B1;7;2, C1;4;2.
Mặt phẳng P: 2x by cz d 0 qua A và thỏa mãn T d B,P 2d C,P đạt giá trị
lớn nhất. Tính b c d . A. 77. B. 52. C. 45. D. 65.
Câu 9. Cho hình hộp chữ nhật ABCD.A' B 'C ' D ' có điểm A trùng gốc tọa độ O, các điểm
Bm;0;0, D0;m;0, A'0;0;n với , m
n 0 và m n 4. Gọi M là trung điểm của CC '.
Thể tích tứ diện BDA' M lớn nhất bằng bao nhiêu? A. 64 . B. 9 . C. 4 . D. 16 . 27 4 3 27
Câu 10. Trong không gian với hệ tọa độ Oxyz, cho A3;3;0, B3;0; 3 ,C0;3;
3 . Mặt phẳng P
đi qua O, vuông góc với mặt phẳng ABC sao cho mặt phẳng P cắt các cạnh AB, AC tại
các điểm M , N thỏa mãn thể tích tứ diện OAMN nhỏ nhất. Mặt phẳng P có phương trình:
A. x y 2z 0.
B. x y 2z 0.
C. x z 0.
D. y z 0.
Phần 3. Các bài toán về mặt cầu
Câu 1. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng x 1 : y z d và hai điểm 2 1 2
A2;1;0, B2;3;2. Gọi S là mặt cầu đi qua hai điểm ,
A B và có tâm thuộc đường thẳng d.
Diện tích của mặt cầu S bằng A. 68 . B. 25 . C. 74 . D. 26 .
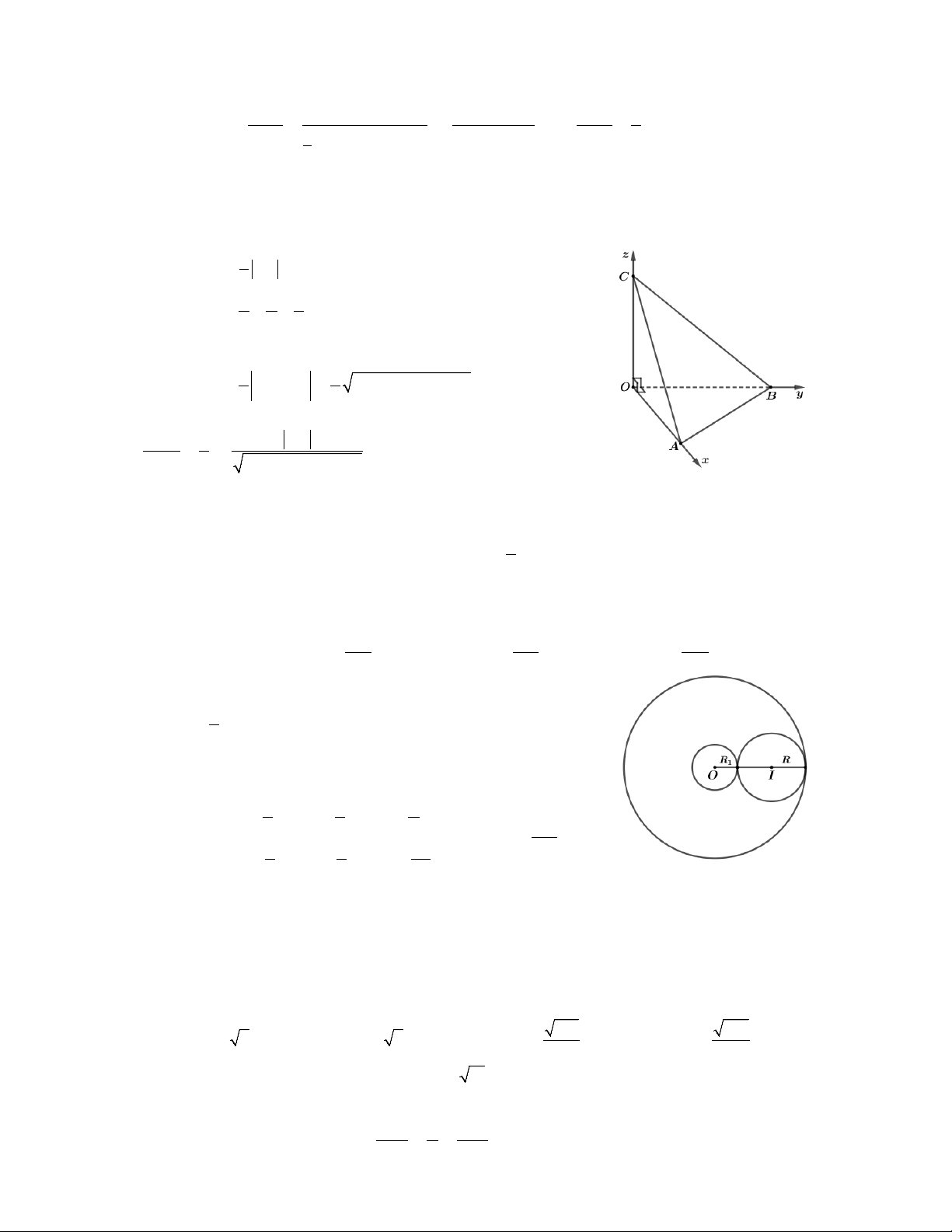
Câu 2. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S có tâm I 3;2;2 bán kính 1 1
R 2, mặt cầu S có tâm I 1;0;1 bán kính R 1. Mặt phẳng P đồng thời tiếp xúc với 2 2 1 2
S và S cắt đoạn I I có dạng 2x by cz d 0. Tính T b c d. 2 1 1 2 A. 5. B. 3. C. 1. D. 2.
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S 2 2 2
: x y z 9 và mặt phẳng
P: x y z 3 0. Gọi S là mặt cầu chứa đường tròn giao tuyến của S và P đồng
thời S tiếp xúc với mặt phẳng Q: x y z 5 0. Gọi I ; a ;
b c là tâm của mặt cầu S. Tính T . abc A. T 1. B. 1 T . C. T 1. D. 1 T . 8 8
Câu 4. Trong không gian với hệ tọa độ Oxyz, cho các mặt phẳng P: x y 2z 1 0,
Q: 2x y z 1 0. Gọi S là mặt cầu có tâm thuộc trục hoành, đồng thời S cắt mặt
phẳng P theo giao tuyến là một đường tròn có bán kính bằng 2 và S cắt mặt phẳng Q
theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ có đúng một
mặt cầu S thỏa yêu cầu. A. r 3. B. 3 r . C. r 2. D. 3 2 r . 2 2
Câu 5. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A3;1;2, B5;7;0. Có tất cả bao nhiêu giá trị của tham số m để phương trình 2 2 2
x y z x my m 2 4 2 2
1 z m 2m 8 0 là phương trình của một mặt cầu S sao cho qua hai điểm ,
A B có duy nhất một mặt phẳng cắt mặt cầu S đó theo giao tuyến là một
đường tròn có bán kính bằng 1. A. 1. B. 4. C. 3. D. 2.
Câu 6. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P: x 2y 2z 3 0 và mặt
cầu S có tâm I 5;3;
5 , bán kính R 2 5 . Từ một điểm A thuộc mặt phẳng P kẻ một
đường thẳng tiếp xúc với mặt cầu S tại điểm B . Tính OA biết rằng AB 4 . A. OA 3. B. OA 11. C. OA 6. D. OA 5.
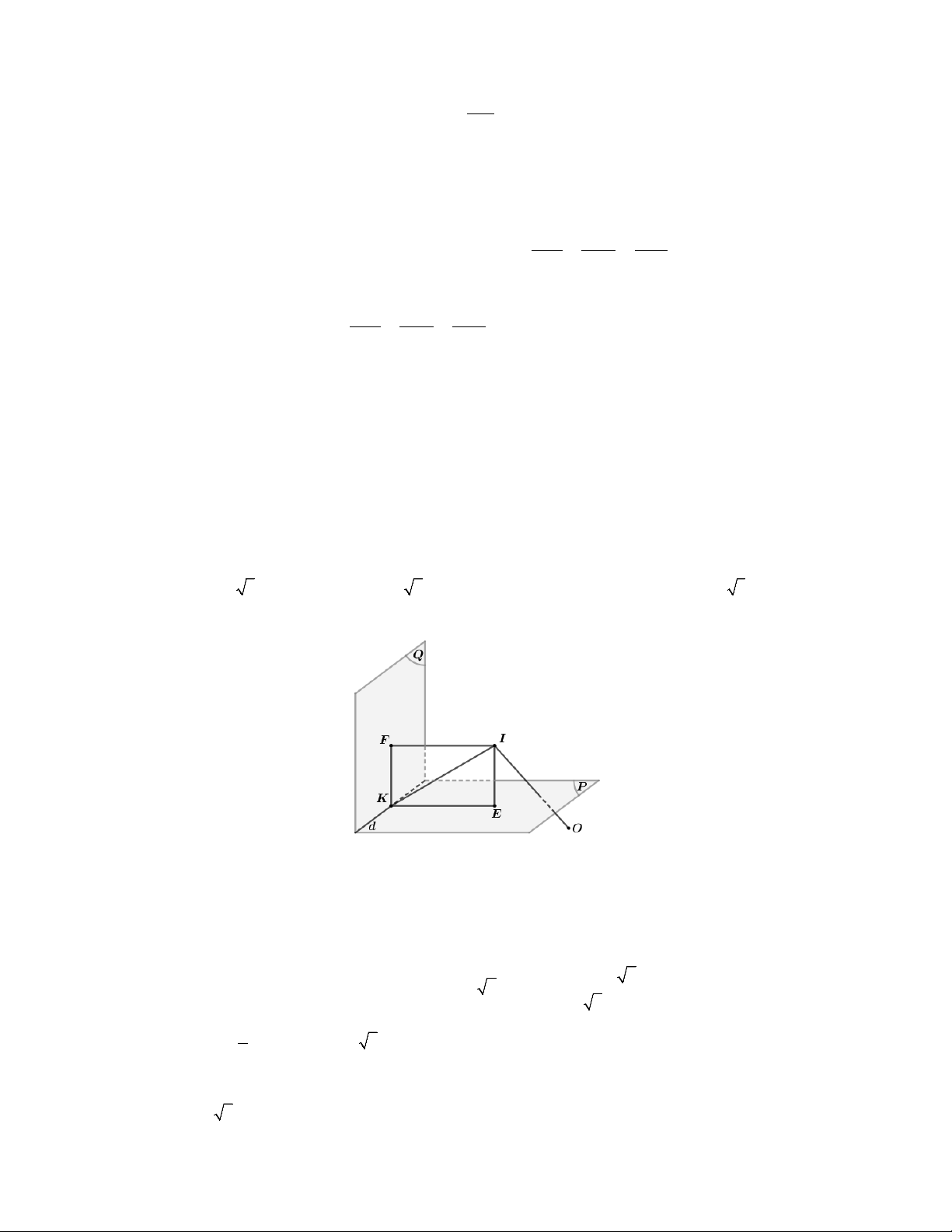
Câu 7. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S 2 2 2
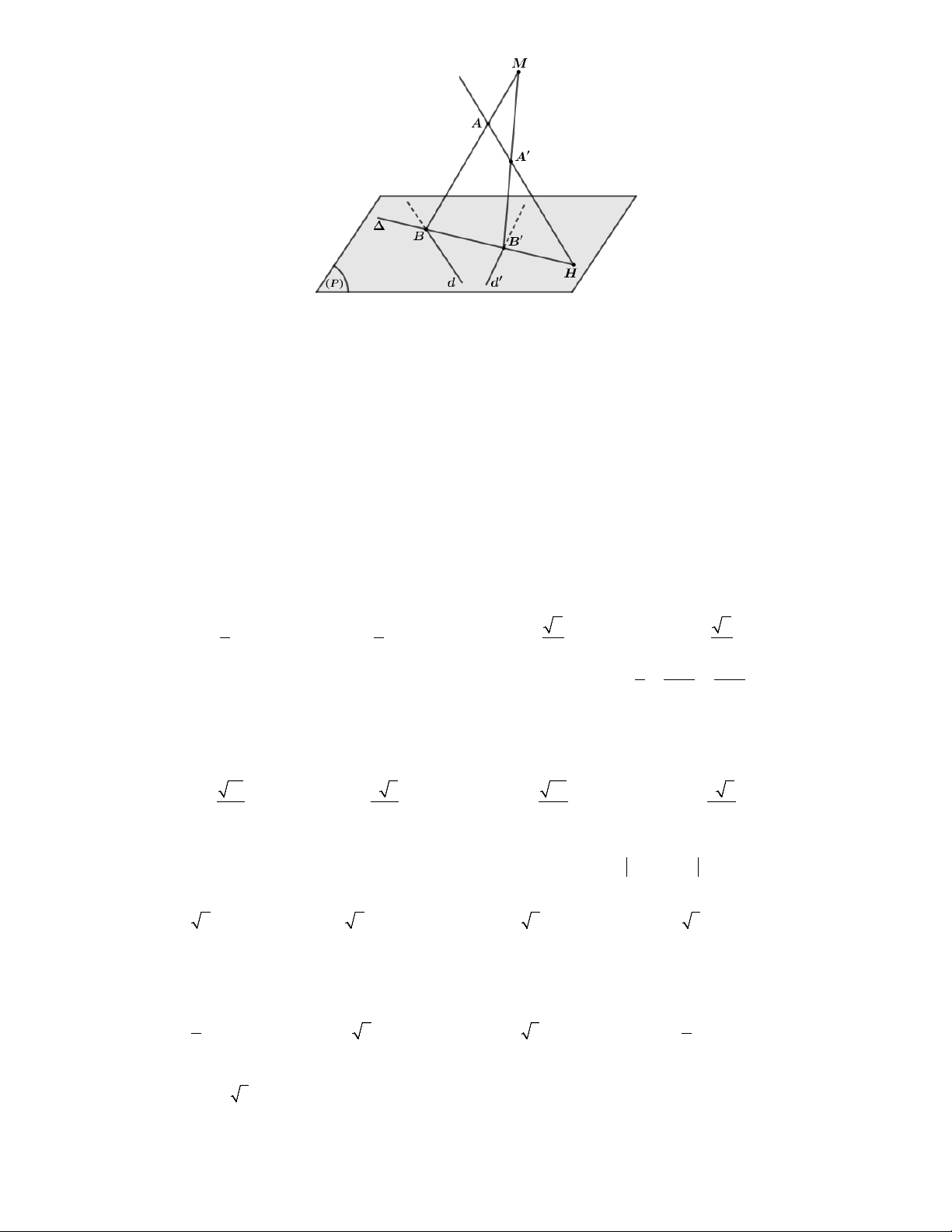
: x y z 2x 2z 1 0 và đường thẳng x y 2 z d :
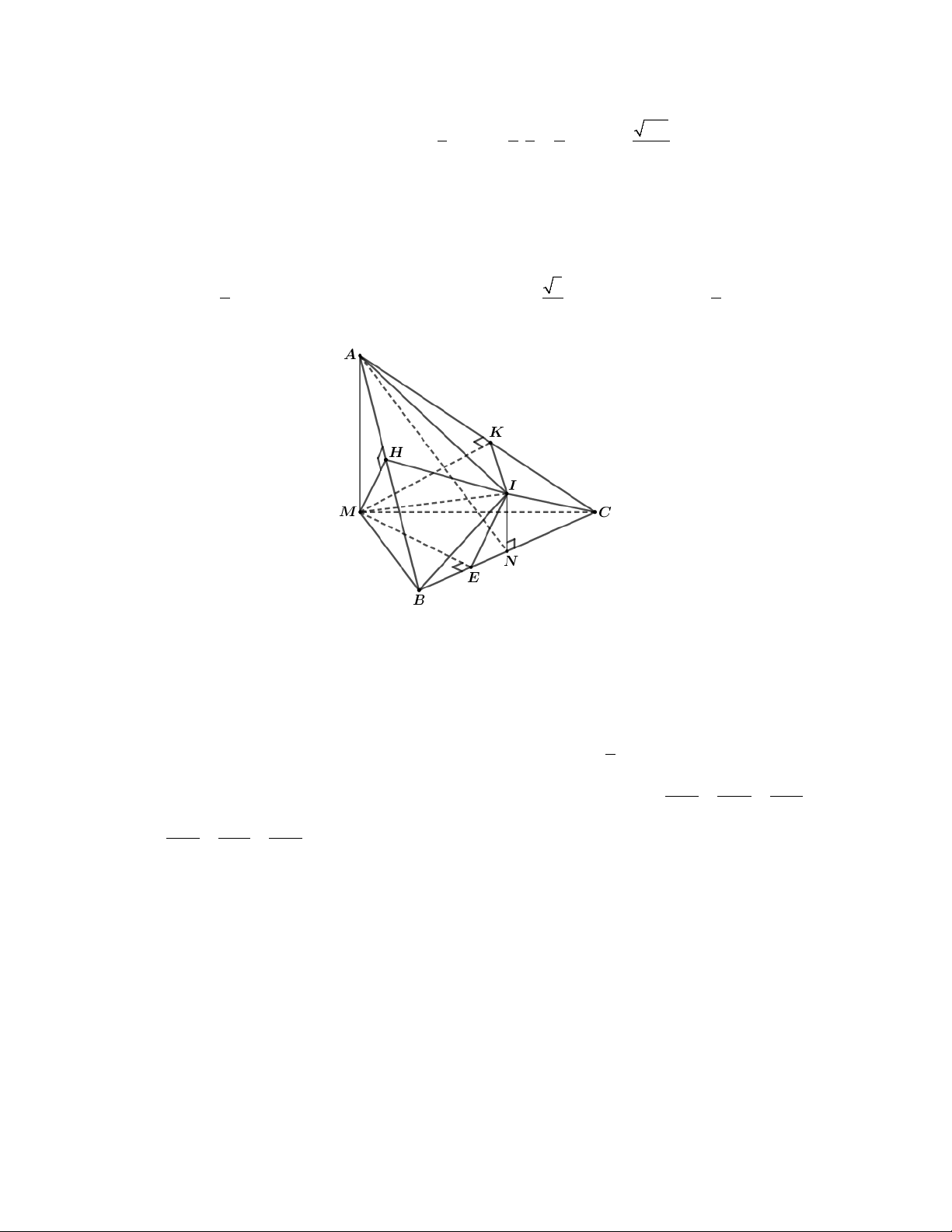
. Hai mặt phẳng P , P chứa d và tiếp xúc với S tại T 1 1 1
và T (tham khảo hình vẽ). Tìm tọa độ trung điểm H của TT . P T I H K T P d A. 5 1 5 H ; ; . B. 5 2 7 H ; ; . C. 5 1 5 H ; ; . D. 7 1 7 H ; ; . 6 3 6 6 3 6 6 3 6 6 3 6
Câu 8. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S x 2 y 2 z 2 : 1 2 1 3,
và hai điểm A1;0;4, B0;1;4. Các mặt phẳng P , P cùng chứa đường thẳng AB và hai 1 2
mặt phẳng này lần lượt tiếp xúc với mặt cầu S tại các điểm H , H . Điểm K nào trong số 1 2
các điểm sau đây nằm trên đường thẳng H H . 1 2
A. K 1;4;2.
B. K 1;3;2. C. K 1;5; 3 .
D. K 1;32.
Câu 9. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S x 2 y 2 z 2 : 1 1 2 4
và điểm A1;1;
1 . Ba mặt phẳng thay đổi đi qua A và đôi một vuông góc nhau, cắt mặt cầu
theo thiết diện là ba hình tròn. Tổng diện tích của ba hình tròn này bằng A. 3 . B. 4 . C. 11 . D. 12 . Câu 10. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S 2 2 2
: x y z 2ax2by 2cz d 0, với a,b,c 0. Biết mặt cầu S cắt 3 mặt phẳng toạ
độ theo 3 đường tròn có bán kính r 5 và mặt cầu S đi qua điểm M 0;1;2. Tính tổng
a b c d. A. 25. B. 75. C. 40. D. 10. Câu 11. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu
S x 2 y 2 z 2 : 3 2
4 12 và M x ; y ;z là điểm thay đổi thuộc S. Giá trị lớn o o o
nhất của biểu thức P x y z bằng? o o o A. 10. B. 11. C. 12. D. 14. Câu 12. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu 2 m S x y z m
(với m 0 là tham số thực) và hai điểm m 2 2 2 : 1 1 4 A2;3;
5 , B1;2;4. Tìm giá trị nhỏ nhất của m để trên S tồn tại điểm M sao cho m 2 2
MA MB 9. A. m 1.
B. m 3 3.
C. m 84 3. D. 4 3 m . 2
Câu 13. Trong không gian với hệ tọa độ Oxyz, cho điểm A0;1;2, mặt phẳng
: x y z 4 0 và S x 2 y 2 z 2 : 3 1
2 16. Gọi P là mặt phẳng đi qua , A
vuông góc với và đồng thời P cắt mặt cầu S theo giao tuyến là một đường tròn có bán
kính nhỏ nhất. Tọa độ giao điểm M của P và trục xOx là A. 1 M ;0;0.
B. M 1;0;0. C. 1 M ;0;0. D. 1 M ;0;0. 3 2 3
Câu 14. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S x 2 y 2 2 : 3 1 z 4 và
x 1 2t
đường thẳng d :y 1t ,t . Mặt phẳng chứa d và cắt S theo một đường tròn có bán
z t
kính nhỏ nhất có phương trình là
A. 3x2y 4z 8 0.
B. y z 1 0.
C. x2y 3 0.
D. x 3y 5z 2 0.
Câu 15. Trong không gian với hệ tọa độ Oxyz, cho hai mặt cầu
S :x 2
3 y 22 z 22 4, S :x 2 2
1 y z 1 1. Gọi d là đường thẳng đồng 2 2 1
thời tiếp xúc với hai mặt cầu trên, cắt đoạn thẳng nối tâm hai mặt cầu và cách gốc tọa độ O
một khoảng lớn nhất. Nếu u ;
a 1;b là một vectơ chỉ phương của d thì tổng S 2a 3b bằng bao nhiêu? A. S 2. B. S 1. C. S 0. D. S 4.
Câu 16. Trong không gian với hệ tọa độ Oxyz, cho các điểm A(2;3;3), B( 2; − 1 − ; ) 1 . Gọi (S ) và
(S′) là hai mặt cầu thay đổi nhưng luôn tiếp xúc với đường thẳng AB lần lượt tại các điểm ,
A B đồng thời tiếp xúc ngoài với nhau tại điểm M (a,b,c). Tính giá trị của a + b + c biết rằng
khoảng cách từ điểm M tới mặt phẳng (P) : x + 2y − 2z + 2018 = 0 đạt giá trị lớn nhất?
A. a + b + c = 4.
B. a + b + c = 5.
C. a + b + c = 3.
D. a + b + c = 2.
Câu 17. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S có tâm I và bán kính bằng 3
sao cho luôn tiếp xúc với mặt phẳng Ox .
y Khi các đường tròn giao tuyến của S với hai mặt
phẳng tọa độ còn lại có diện tích lớn nhất thì tâm I của mặt cầu thuộc mặt phẳng nào?
A. x y z 1 0. B. x y z 0.
C. x2y 1 0.
D. x y 0.
Câu 18. Trong không gian với hệ tọa độ Oxyz , cho ba mặt phẳng
P : 2x y 2z 5 0, P : 2x y 2z 13 0, Q: 2x2y z 5 0, và điểm A2;0;0 2 1
nằm giữa hai mặt phẳng P , P . Mặt cầu S di động có tâm I a; ;
b c luôn đi qua A và 1 2
luôn tiếp xúc với hai mặt phẳng P , P . Khi khối cầu S cắt mặt phẳng Q theo thiết 1 2
diện là hình tròn có diện tích lớn nhất thì a b2c bằng A. 0. B. 3. C. 3. D. 2.
Câu 19. Trong không gian với hệ tọa độ Oxyz, cho S :x 2 2
1 y z 2 1, 1 2
x 3t
S :x 2 3 y 22 2
z 4 và đường thẳng d :y 1t. Gọi ,
A B là 2 điểm tùy ý thuộc 2
z 52t
S , S và M thuộc đường thẳng d. Khi đó giá trị nhỏ nhất của biểu thức P MA MB 1 2 bằng bao nhiêu?
A. P 2 6 3.
B. P 2 6 3.
C. P 2 3 3.
D. P 2 3 3. min min min min
Câu 20. Trong không gian với hệ tọa độ Oxyz, cho S :x 2 2 2
1 y z 4, 1
x 2t
S :x22 y 2 3 z 2
1 1 và đường thẳng d :y 3t . Gọi ,
A B là 2 điểm tùy ý 2
z 2t
thuộc S , S và M thuộc đường thẳng d. Khi đó giá trị nhỏ nhất của biểu thức 1 2
P MA MB bằng A. 2211 . B. 3707 3. C. 1771 2 110 . D. 3707 . 11 11 11 11 Câu 21. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu
S x 2 y 2 z 2 : 2 2
2 12 và điểm A4;4;0. Gọi B là điểm thuộc mặt cầu S.
Diện tích tam giác OAB có giá trị lớn nhất bằng: A. 6. B. 8 3. C. 4 6 2. D. 8 3 2.
Câu 22. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S x 2 2 :
1 y z 22 25. Gọi
Ax y z và Bx y z là hai điểm thuộc mặt cầu thỏa mãn biểu thức
B ; B , B
A ; A ; A
T 2x x y y z z đạt giá trị lớn nhất. Trung điểm của đoạn thẳng AB thuộc A B A B A B mặt phẳng nào sau đây?
A. y 4z 5 0.
B. x 5y 6z 10 0.
C. x 3y 2z 3 0.
D. x 3y 7z 10 0.
Câu 23. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S x 2 y 2 2 : 1 4 z 8 và
các điểm A3;0;0, B4;2;
1 . Gọi M là điểm thuộc mặt cầu S. Giá trị nhỏ nhất của
MA 2MB bằng A. 2 2. B. 6 2. C. 2 3. D. 6 3.
Câu 24. Trong không gian với hệ tọa độ Oxyz, cho 3 đường thẳng x1 y 1 z 1 d : , 1 2 1 2 x3 y 1 z 2 d : x4 y 4 z 1 , d :
. Mặt cầu bán kính nhỏ nhất tâm I a; ; b c tiếp 2 1 2 2 3 2 2 1
xúc với 3 đường thẳng d ,d ,d . Tính S a 2b 3 .c 1 2 3
A. S 10. B. S 11. C. S 12. D. S 13.
Câu 25. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S x 2 y 2 z 2 : 1 2 3 4. x 1t
Xét đường thẳng d : y mt
với m là tham số thực. Giả sử P và P ' là hai mặt phẳng
z m 1t
chứa d, tiếp xúc với S lần lượt tại T và T '. Khi m thay đổi, tính giá trị nhỏ nhất của độ
dài đoạn thẳng TT '. A. 4 13 . B. 2 2. C. 2. D. 2 11 . 5 3
Câu 26. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S có phương trình 2 2 2
x y z 4x 2y 2z 3 0 và điểm A5;3;2. Một đường thẳng d thay đổi luôn đi qua
A và luôn cắt mặt cầu tại hai điểm phân biệt M , N. Tính giá trị nhỏ nhất của biểu thức
S AM 4AN. A. S 50.
B. S 5 34 9.
C. S S 5 34 9.
D. S 20. min min min min min
Câu 27. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S x 2 y 2 z 2 : 1 2 2 9
và hai điểm M 4;4;2, N 6;0;6. Gọi E là điểm thuộc mặt cầu S sao cho EM EN đạt giá
trị lớn nhất. Viết phương trình tiếp diện của mặt cầu S tại E.
A. x2y 2z 8 0.
B. 2x y 2z 9 0.
C. 2x 2y z 1 0.
D. 2x2y z 9 0. Câu 28. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S 2 2 2
: x y z 2x 4y 2z 4 0. Gọi P,Q là hai mặt phẳng vuông góc với nhau theo
giao tuyến d và đồng thời tiếp xúc với S, K là hình chiếu vuông góc của tâm I của mặt
cầu S lên d và M là giá trị lớn nhất của diện tích tam giác OIK ( O là gốc tọa độ). Hãy
chọn khẳng định đúng về M.
A. M 2 3; 4 .
B. M 2;2 2.
C. Không tồn tại M. D. M 2 3; 4 .
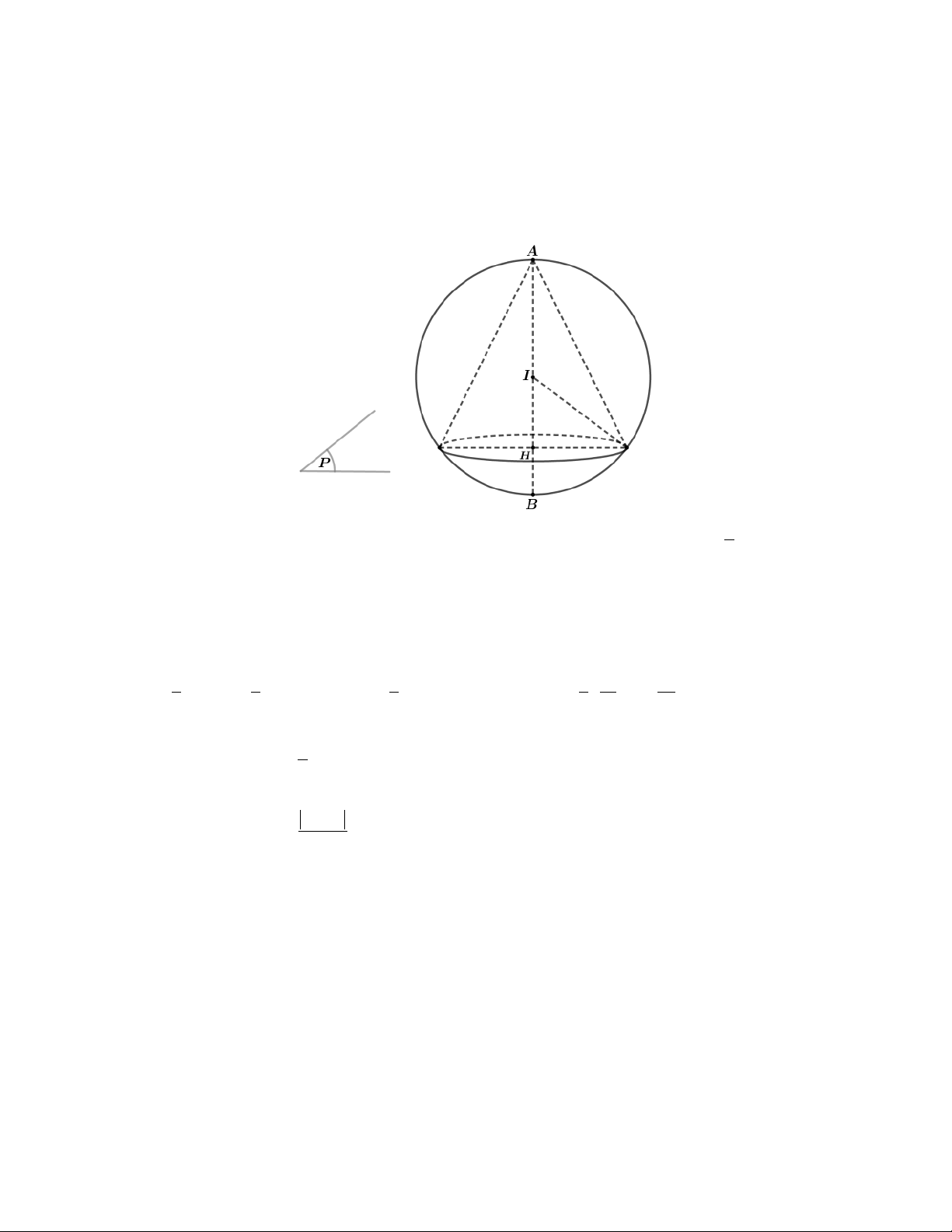
Câu 29. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A2;1; 3 , B6;5;
5 . Gọi S là mặt
cầu có đường kính A .
B Mặt phẳng P vuông góc với đoạn AB tại H sao cho khối nón đỉnh
A và đáy là hình tròn tâm H (giao của măt cầu S và mặt phẳng P) có thể tích lớn nhất,
biết rằng P: 2x by cz d 0 với , b c,d .
Tính S b c d. A. S 18. B. S 11. C. S 24. D. S 14.
Câu 30. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S x 2 y 2 z 2 : 1 1 3 25
và mặt phẳng P: 2x y 2z 4 0. Mặt phẳng P cắt mặt cầu S theo giao tuyến là
đường tròn T,CD là một đường kính cố định của T, A là điểm thay đổi trên T ( A khác
C và D ). Đường thẳng đi qua A và vuông góc với P cắt S tại .
B Giá trị lớn nhất của
khoảng cách từ A đến mặt phẳng BCD bằng A. 12 . B. 13. C. 15. D. 11. 13 4
Phần 4. Bài toán cực trị sử dụng tâm tỷ cự
Câu 1. Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A1;3; 5 , B2;6; 1 ,C4;12; 5 và
mặt phẳng P: x 2y 2z 5 0. Gọi M là điểm thuộc mặt phẳng P sao cho biểu thức
T MA4MB MA MB MC đạt giá trị nhỏ nhất. Biết rằng M x ; y ; z , hỏi x thuộc 0 0 0 0
khoảng nào trong các khoảng sau. A. 0;2. B. 2;4. C. 4; 1 . D. 5;4.
Câu 2. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A1;0; 3 , B3;1; 3 , C 1;5; 1 và
M x; y;0. Tìm giá trị nhỏ nhất T của biểu thức T 2 MA MB MC . min A. T 2 35. B. T 2 37.
C. T 2 38. D. T 12. min min min min
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A1;1;0, B2;0;
1 ,C0;0;2 và mặt
phẳng P: x 2y z 4 0. Gọi M ; a ;
b c là điểm thuộc mặt phẳng P sao cho
S . MA MB .
MB MC MC.MA đạt giá trị nhỏ nhất. Tính Q a b 6 . c A. Q 2. B. Q 2. C. Q 0. D. Q 1.
Câu 4. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A0;1; 1 , B 3;0; 1 , C 0;21;19 và
mặt cầu S x 2 y 2 z 2 : 1 1
1 1. Gọi M a;b;c là điểm thuộc mặt cầu S sao cho biểu thức 2 2 2
T 3MA 2MB MC đạt giá trị nhỏ nhất. Tính tổng S a b c. A. S 0. B. 12 S . C. 14 S . D. 16 S . 5 5 5
Câu 5. Trong không gian với hệ tọa độ Oxyz, cho A1;1;
1 , B1;2;0,C3;1;2. Giả sử M ; a ;
b c thuộc mặt cầu S x 2 2 :
1 y z 2 1 861 sao cho 2 2 2
P 2MA 7MB 4MC đạt
giá trị nhỏ nhất. Giá trị T a b c bằng A. T 49. B. T 51. C. T 55. D. T 47.
Phần 5. Bài toán hỏi số mặt phẳng, số mặt cầu
Câu 1. Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng P: 2x z 2 0,
Q: 4y 5z 8 0. Có bao nhiêu mặt phẳng chứa giao tuyến của P và Q, đồng thời cắt x O x, z O
z lần lượt tại ,
A B (khác O ) thỏa mãn OA OB ? A. 1. B. 2. C. 3. D. 4.
Câu 2. Trong không gian với hệ tọa độ Oxyz, cho điểm M 1;2;
3 . Hỏi có bao nhiêu mặt phẳng
P đi qua M và cắt các trục x O x, y Oy , z Oz
lần lượt tại các điểm , A B,C sao cho
OA 2OB 3OC 0? A. 4. B. 3. C. 1. D. 8.
Câu 3. Trong không gian với hệ tọa độ Oxyz , cho các mặt phẳng P: 2x y z 2 0 ,
Q: x 2y z 2 0 , R: x y 2z 2 0 và T : x y z 0 . Hỏi có nhiêu mặt cầu có
tâm thuộc T và tiếp xúc với P, Q , R ? A. 1. B. 2. C. 3. D. 4.
Câu 4. Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A3;7; 1 , B8;3;
8 và C3;3;0. Gọi
S là mặt cầu tâm A bán kính bằng 3 và S là mặt cầu tâm B bán kính bằng 6. Hỏi có 2 1
tất cả bao nhiêu mặt phẳng đi qua C và tiếp xúc đồng thời với cả hai mặt cầu S , S . 1 2 A. 1. B. 2. C. 3. D. 4. Câu 5. Trong không gian với hệ tọa độ Oxyz, cho điểm A 3 3 1 1;2; 3 , B ; ;
,C1;1;4, D5;3;0.
Gọi S là mặt cầu tâm A bán kính bằng 3,S là 2 1 2 2 2
mặt cầu tâm B bán kính bằng 3 . Có bao nhiêu mặt phẳng tiếp xúc với 2 mặt cầu S , S 1 2 2
đồng thời song song với đường thẳng đi qua C và . D A. 1. B. 2. C. 4. D. Vô số.
Phần 6. Bài toán quỹ tích
Câu 1. Trong không gian với hệ tọa độ Oxyz, cho điểm A2;1;0 và mặt cầu
S x y 2 z 2 2 : 1
2 8. Đường thẳng thay đổi qua A và tiếp xúc với S tại B.
Biết khi thay đổi thì B thuộc một đường cong cố định. Diện tích của hình phẳng giới
hạn bởi đường cong bằng A. 2 . B. 8 . C. 3 . D. 4 . 3
Câu 2. Trong không gian với hệ tọa độ Oxyz, cho điểm A1;2;
3 và mặt phẳng P có
phương trình 2x 2y z 9 0. Đường thẳng đi qua A và vuông góc với mặt phẳng
Q: 3x 4y4z 5 0 cắt P tại điểm .
B Điểm M nằm trong mặt phẳng P sao cho M
luôn nhìn đoạn AB dưới một góc vuông và độ dài MB lớn nhất. Tính độ dài . MB A. 5 . B. 5. C. 41 . D. 41. 2 2
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho điểm M thuộc mặt cầu
S x 2 y 2 z 2 : 3 3
2 9 và ba điểm A1;0;0; B2;1; 3 ;C0;2; 3 . Biết rằng quỹ tích
các điểm M thỏa mãn 2 MA 2 .
MB MC 8 là đường tròn cố định, tính bán kính r đường tròn này.
A. r 3.
B. r 6.
C. r 3. D. r 6.
Câu 4. Trong không gian với hệ tọa độ Oxyz, cho các điểm Aa;0;0, B0;b;0, C 0;0;c với
a, b, c dương. Biết ,
A B, C di động trên các tia Ox, Oy, Oz sao cho a b c 2 . Biết rằng khi ,
a b, c thay đổi thì quỹ tích tâm hình cầu ngoại tiếp tứ diện OABC thuộc mặt phẳng P cố
định. Khoảng cách từ M 2019;0;0 tới mặt phẳng P bằng A. 2018. B. 2018 . D. 2019 . C. 2020 . 3 3 3
Câu 5. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S x 2 y 2 z 2 : 1 1 2 9
và điểm M 1;3;
1 . Biết rằng các tiếp điểm của các tiếp tuyến kẻ từ M tới mặt cầu đã cho
luôn thuộc vào đường tròn C. Tìm tâm J và bán kính r của đường tròn C. A. 11 23 J 1; ; và 12 r . B. 41 11 23 J ; ; và 12 r . 25 25 25 25 25 25 5 C. 11 23 J 1; ; và 12 r . D. 11 73 J 1; ; và 12 r . 25 25 5 25 25 25
Câu 6. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P: x y z 3 0 và hai điểm A1;1;
1 , B3;3;
3 . Mặt cầu S đi qua hai điểm ,
A B và tiếp xúc với P tại điểm C.
Biết rằng C luôn thuộc một đường tròn cố định. Tính bán kính R của đường tròn đó. A. 2 11 R . B. 2 33 R . C. R 4. D. R 6. 3 3 Câu 7. Trong không gian với hệ tọa độ
Oxyz, cho mặt phẳng P
m x m y mz m thay đổi. Hình chiếu vuông góc của điểm A1;0; 3 lên m : 1 2 2 1 0
mặt phẳng P luôn thuộc một đường tròn cố định có bán kính là m A. R 1. B. 1 R . C. 2 R . D. 3 R . 2 2 2
Câu 8. Trong không gian với hệ tọa độ Oxyz, cho điểm A2;11; 5 và mặt phẳng
P mx 2
m y 2 : 2 1 m
1 z 10 0. Biết khi m thay đổi thì tồn tại hai mặt cầu cố định
tiếp xúc với P và cùng đi qua .
A Tổng bán kính của hai mặt cầu đó là A. 4 2. B. 5 3. C. 6 3. D. 12 2.
Câu 9. Trong không gian với hệ tọa độ Oxyz, cho các điểm ,
A B,C (không trùng O) lần lượt
thay đổi trên các trục Ox,Oy,Oz và luôn thỏa mãn điều kiện: tỉ số giữa diện tích của tam giác
ABC và thể tích khối tứ diện OABC bằng 3 . Biết rằng mặt phẳng ABC luôn tiếp xúc với 2
một mặt cầu cố định, bán kính của mặt cầu đó bằng A. 3. B. 2. C. 4. D. 1. Câu 10. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S x
2 y
2 z 2 1 : cos sin sin sin cos
, với , là các góc thay đổi nhưng luôn 4
thỏa mãn , 0;2. Khi đó mặt cầu S thay đổi nhưng luôn tiếp xúc với hai mặt cầu cố
định S , S . Tính tổng thể thích của hai khối cầu S và S đó. 2 1 1 2 A. 16 . B. 21 . C. 14 . D. 67 . 8 3 3
Câu 11. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A0;2;2 và B2;2;0. Gọi I 1;1; 1 và J 3;1;
1 là tâm của hai đường tròn nằm trên hai mặt phẳng khác nhau và có
chung một dây cung AB. Biết rằng luôn có một mặt cầu S đi qua cả hai đường tròn ấy.
Tính bán kính R của S. A. R 2 2.
B. R 2 6. C. 129 R . D. 219 R . 3 3
Câu 12. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S x 2 y 2 z 2 : 1 1 3 9
và điểm M 2;3;
5 . Ba tia Mx, My, Mz thay đổi, đôi một vuông góc với nhau và cắt mặt cầu
S tại 3 điểm ,
A B,C. Biết rằng hình chiếu của M lên mỗi đường thẳng AB, BC,CA cùng
thuộc một mặt cầu bán kính .
R Khẳng định nào sau đây đúng? A. 3 R .
B. R 3. C. 5 R . D. 3 R . 2 2 4
Câu 13. Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng x2 y 5 z 2 d : , 1 2 1 x2 y 1 z 2 d : và hai điểm A ;
a 0;0, A0;0;b. Gọi P là mặt phẳng chứa d và d , 1 2 1
H là giao điểm của đường thẳng AA và mặt phẳng P. Một đường thẳng thay đổi trên
P nhưng luôn đi qua H đồng thời cắt d và d lần lượt tại B, B . Hai đường thẳng
AB, AB cắt nhau tại điểm M. Biết điểm M luôn luôn thuộc một đường thẳng cố định có vé-
tơ chỉ phương u 15;10;
1 (tham khảo hình vẽ). Tính T a . b A. T 8. B. T 9. C. T 9. D. T 6.
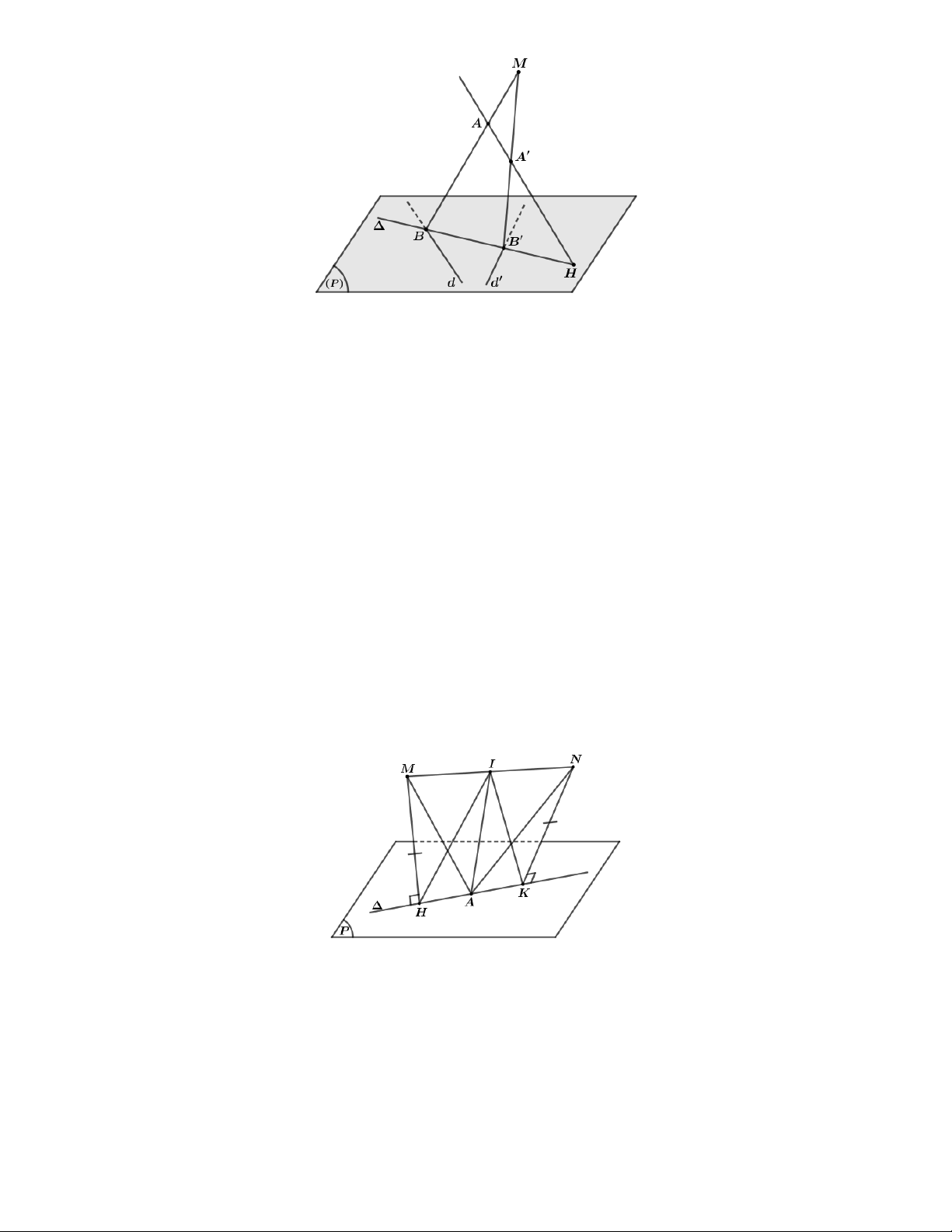
Câu 14. Trong không gian với hệ tọa độ Oxyz, cho hai điểm M 1;2; 3 , N 3;4; 5 và mặt phẳng
P: x 2y 3z 14 0. Gọi là đường thẳng thay đổi nằm trong mặt phẳng P, các điểm
H, K lần lượt là hình chiếu vuông góc của M , N trên .
Biết rằng khi MH NK thì trung
điểm của HK luôn thuộc một đường thẳng d cố định, phương trình của d là x 1 x t x t x t A.
y 132t .
B. y 132t.
C. y 13 2t.
D. y 132t.
z 4 t
z 4 t
z 4 t
z 4t
Câu 15. Trong không gian với hệ tọa độ Oxyz, cho điểm A1;1;0. Giả sử B,C là các điểm thay
đổi nằm trên các trục Ox và Oz. Gọi M là trung điểm của AC. Biết rằng khi B và C thay
đổi nhưng nằm trên các trục Ox và Oz thì hình chiếu vuông góc H của M trên đường thẳng
AB luôn nằm trên một đường tròn cố định. Tính bán kính của đường tròn đó? A. 1 R . B. 1 R . C. 2 R . D. 2 R . 4 2 2 4
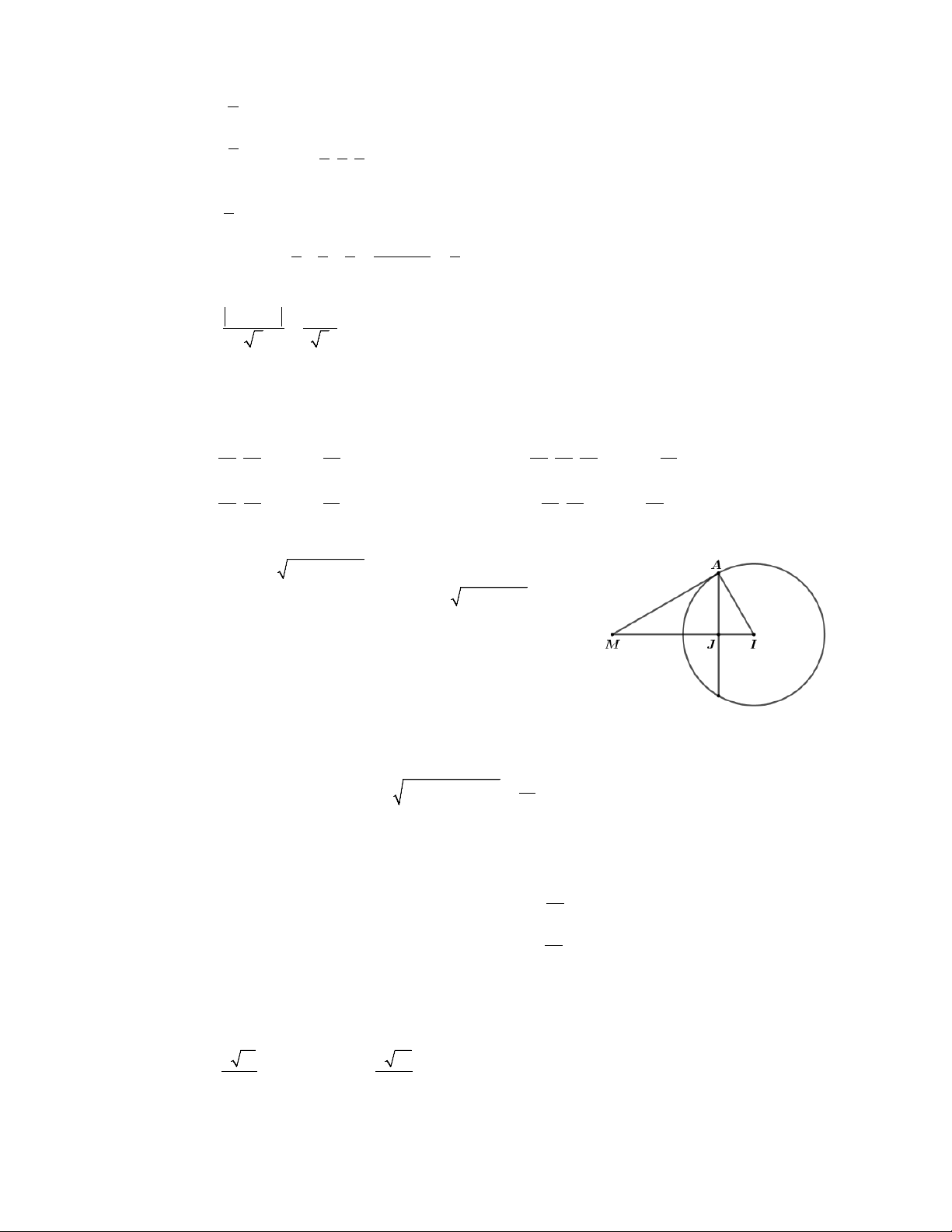
Câu 16. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng x y 1 z 1 d : và điểm 2 1 1 A1;1;
1 . Hai điểm B,C di động trên đường thẳng d sao cho mặt phẳng OAB vuông góc với
mặt phẳng OAC. Gọi điểm B là hình chiếu vuông góc của điểm B lên đường thẳng AC.
Biết rằng quỹ tích các điểm B là đường tròn cố định, tính bán kính r đường tròn này. A. 15 r . B. 3 5 r . C. 70 r . D. 3 5 r . 5 5 10 10
Câu 17. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S 2 2
: x y z 2 3 8 và hai điểm A4;4; 3 , B1;1;
1 . Gọi C là tập hợp các điểm M S để cho MA2MB đạt giá trị nhỏ
nhất. Biết rằng C là một đường tròn bán kính . R Tính . R A. 7. B. 6. C. 2 2. D. 3.
Câu 18. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A2;0;0, B0;4;0,C0;0;6, điểm
M thay đổi trên mặt phẳng ABC, N là điểm trên tia OM sao cho OM.ON 12. Biết khi
M thay đổi thì điểm N luôn nằm trên mặt cầu cố định. Tính bán kính mặt cầu đó A. 7 . B. 3 2. C. 2 3. D. 5 . 2 2
Câu 19. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S có tâm O ( O là gốc tọa độ) 1
bán kính là 3 và mặt cầu S có tâm O2;3;6 và bán kính bằng 4. Biết tập hợp các điểm 2
A trong không gian mà độ dài tiếp tuyến kẻ từ A tới S và S bằng nhau là một mặt 2 1
phẳng (còn gọi là mặt phẳng đẳng phương) .Viết phương trình mặt mặt phẳng đó . A. x y z x y z x y z x y z 1. B. 1. C. 1. D. 1. 2 3 6 9 2 3 9 6 3 3 6 9
Câu 20. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P: 2x 2y z 4 0 và các
điểm A2;1;2; B3;2;2. Điểm M thuộc mặt phẳng P sao cho các đường thẳng , MA MB
luôn tạo với mặt phẳng P các góc bằng nhau. Biết rằng điểm M luôn thuộc đường tròn C
cố định. Tìm tọa độ tâm của đường tròn C. A. 10 14 ;3; . B. 17 17 17 ; ; . C. 74 97 62 ; ; . D. 32 49 2 ; ; . 3 3 21 21 21 27 27 27 9 9 9
---------- HẾT ----------
HÌNH HOÏC Oxyz Vận dụng cao
Phần 1. Các bài toán cơ bản ở mức vận dụng
Câu 1. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P: x 2y 3z 4 0 và hai đường thẳng x 1 y z 1 x 1 y 3 z 1 d : , d :
. Mặt phẳng song song với 1 1 1 2 2 2 1 1
P và cắt d , d theo thứ tự tại M, N sao cho MN 3. Điểm nào sau đây thuộc ? 1 2 A. A1;2; 3 .
B. B0;1; 3 .
C. C 0;1; 3 . D. D0;1; 3 .
Lời giải. Mặt phẳng P có VTPT n 1;2; 3 . P
M d M 1m; m ;1 2m 1 Điểm
MN 2n m;n m 3;n 2m là VTCP của .
N d N 12n;3n;1n 2
● P n MN n .MN 0 2nm1n m
3 2n 2m3 0 n 2 3 . m P P ● Ta có
2 2 2 n23 3 2 3 2 3 m MN n m n m n m
m 1 M 0;1; 3 . qua M 0;1; 3
Khi đó :
: x 2y 3z 11 0. Chọn B. VTPT n 1; 2; 3
Câu 2. Trong không gian với hệ tọa độ Oxyz, cho điểm A1;2; 3 và mặt phẳng
P: x y z 1 0. Gọi là mặt phẳng đi qua A và có vectơ pháp tuyến n 1;b;c biết ,
rằng vuông góc với P và cắt các tia Ox , Oz lần lượt tại M và N thỏa OM 3ON.
Khẳng định nào sau đây đúng ?
A. b c 84.
B. b c 7.
C. b c 7.
D. b c 84.
Lời giải. Mặt phẳng P có VPPT n 1;1; 1 . P
Ox M m;0;0 m 0 Ta có với
. Vì OM 3ON m 3 . n
Oz N0;0;n n 0
AM 3n1;2; 3
Suy ra M 3n;0;0 AM , AN 2
2n;3n 10n;6n.
AN 1;2;n 3
n 0 loai 2
Do P nên AM, AN .n 0 n n n n P 2 .1 3 10 . 1 6 .1 0 . n 6
Với n 6, suy ra AM , AN 12;48;36. qua A 1;2; 3
Khi đó :
: x 4 y 3z 18 0. Chọn C. VTPT , AM AN 12;48;36
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho hai điểm M 1;2; 3 , N 3;1; 3 và hai đường thẳng x y 2 z x 4 y 1 z 5 d : , d :
. Gọi là mặt phẳng đi qua M ; cắt d 1 1 2 1 2 2 1 3 1
tại A và cắt d tại B sao cho A , B , N thẳng hàng. Điểm nào sau đây không thuộc ? 2
A. A0;2;0.
B. A4;0;0.
C. C 0;0; 3 .
D. D1;1; 1 .
d A A d A a;22a; a 1 1
Lời giải. Vì .
d B B d B 4 2b;1b;53b 2 2
NA a3;2a3; a 3 Suy ra
NB 2b 1; b 2;3b 2
N , A NB
6a 12b 7ab 12;3a 3b 5ab 3;9b 3ab 9.
6a 12b 7ab 12 0 a 0
Do A , B , N thẳng hàng , NA NB 0
3a 3b 5ab 3 0 . b 1 9 b 3ab 9 0 A0;2;0
MA 1;4; 3 Suy ra , MA MB 2;4;6. B2;0;2
MB 1;2; 1 qua M 1;2; 3
Khi đó :
: x 2y 3z 4 0. Chọn C. VTPT , MA MB 2;4;6
Câu 4. Trong không gian với hệ tọa độ Oxyz, gọi là đường thẳng đi qua A1;2; 3 và có vectơ chỉ phương x 3 y 7 z 3
u a;b;
1 , biết đồng thời cắt cả hai đường thẳng d : 1 1 3 1
x 2 2t và
d : y t
. Khẳng định nào sau đây là đúng ? 2 z 2
A. a b 3.
B. a b 4.
C. a b 5.
D. a b 6.
M d M d M 3m;73m;3m 1 1
Lời giải. Gọi
N d N d N 22n; n ;2 2 2
AM m 2;3m 5;m Suy ra
AN 2n 3; n 2; 1
AM,AN
5m mn 5;2m 2mn 2;11m 12n 5mn 11 . Do , A M ,
N cùng thuộc nên 5
m mn5 0 m
1 M 4;4;4 AM , AN 0
2m 2mn 2 0 . n 0 N 2;0;2
11m 12n 5mn 11 0
Khi đó có VTCP là MN 6;4;2
chọn u 3;2; 1 . Chọn C.
Câu 5. Trong không gian với hệ tọa độ Oxyz, cho điểm A1;0;2 và đường thẳng x 1 y z 1 d :
. Viết phương trình đường thẳng đi qua ,
A vuông góc và cắt d . 1 1 2 A. x 1 y z 2 x y z : . B. 1 2 : . 1 1 1 1 1 1 C. x 1 y z 2 x y z : . D. 1 2 : . 2 2 1 1 3 1
Lời giải. Gọi B d , suy ra B d nên B1t;t;12t.
Khi đó có VTCP là AB t;t;2t
3 . Đường thẳng d có VTCP u 1;1;2 . d
Theo đề bài: d AB.u t t 4t 6 0 t 1 B2;1; 1 . d Đường thẳng x y z
cần tìm đi qua hai điểm , A B nên 1 2 : . Chọn B. 1 1 1
Câu 6. Trong không gian với hệ tọa độ x y z
Oxyz , cho đường thẳng 1 1 2 d : và mặt 2 2 1
phẳng P: x 2y 2z 7 0 . Gọi I là giao điểm của d và P . Tính khoảng cách từ điểm
M thuộc d đến P , biết IM 9. A. 3 2. B. 2 5. C. 15. D. 8.
Lời giải. Đường thẳng d có VTCP u 2;2;
1 . Mặt phẳng P có VTPT n P 1;2;2. d d u .n Suy ra sin của góc d P 8
tạo bởi d và P bằng M . 9 u . n d P
Khi đó d M ,P IM.sin 8. Chọn D. I
P
Câu 7. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A3;3; 1 , B0;2; 1 và mặt phẳng
P: x y z 7 0 . Đường thẳng d nằm trong P sao cho mọi điểm của d cách đều hai điểm ,
A B có phương trình là x t x 2t x t x t A.
y 7 3t .
B. y 73t .
C. y 73t .
D. y 73t . z 2t z t z 2t z 2t
Lời giải. Phương trình mặt phẳng trung trực của AB là : 3x y 7 0 .
Đường thẳng cần tìm d cách đều hai điểm ,
A B nên sẽ thuộc mặt phẳng .
x y z 7 0 z 2t
Lại có d P , suy ra d P hay d :
. Chọn x t , ta được . 3
x y 7 0 y 73t Chọn C.
Câu 8. Trong không gian với hệ tọa độ Oxyz , cho điểm A0;0;2 và hai đường thẳng x 1t
d : 2x y z , d ' : y 2t . Tìm tọa độ của điểm N thuộc đường thẳng d ' sao cho đường z 0
thẳng AN cắt đường thẳng d tại một điểm.
A. N 0;3;0.
B. N 2;1;0.
C. N 1;2;0. D. N 0;0; 3 . x t '
M m;2m;2m d
Lời giải. Viết lại x y z d : d :
y 2t '. Gọi . 1 2 2
N 1n;2n;0 d ' z 2t '
AM m;2m;2m2 Suy ra AM , AN
2mn 8m 2n 4;2mn 4m 2n 2;3mn .
AN 1n;2n;2
Để AN cắt d tại M ba điểm , A M , N thẳng hàng AM,AN 0 2
mn8m2n 4 0 1 m 2
mn 4m 2n 2 0 2
N 1;2;0. Chọn C. 3mn 0 n 0
Câu 9. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P: x 3y 2z 2 0 và đường thẳng x 1 y 1 z 4 d :
. Đường thẳng qua A1;2;
1 và cắt P, d lần lượt tại 2 1 1 B, C
a;b;c sao cho C là trung điểm của AB. Giá trị của biểu thức a b c bằng A. 15. B. 12. C. 5. D. 11.
Lời giải. Ta có C d
C 1 2t;1t;4 t. Do C là trung điểm của AB
B4t 1;2t 4;2t 9.
Mà B P
t t t 9 7 1 4 1 3 2 4 2 2
9 2 0 t C 8; ; . 2 2 2 Suy ra 7 1
a b c 8 5. Chọn C. 2 2
Câu 10. Trong không gian với hệ tọa độ Oxyz, cho điểm A1;2; 3 và mặt phẳng
P: 2x y 4z 1 0. Đường thẳng d đi qua điểm ,
A song song với mặt phẳng P, đồng
thởi cắt trục Oz. Phương trình tham số của đường thẳng d là
x 15t x t
x 13t x 1t A.
y 2 6t .
B. y 2t .
C. y 2 2t.
D. y 2 6t. z 3 t z 2 t z 3 t z 3 t
Lời giải. Gọi d Oz B0;0;z
d có VTCP là AB 1;2;z 3 . 0 0
Mặt phẳng P có VTPT n 2;1;4.
Theo giả thiết d P
AB.n 0 2 2 4z 12 0 z 2 AB 1;2; 1 . 0 0
Vậy đường thẳng d có VTCP u 1;2;
1 nên loại các phương án A, C, D. Chọn B.
Câu 11. Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A2;4;
1 , B1;2;0,C4;1; 3 và
mặt phẳng : x2y z 7 0. Gọi P là mặt phẳng qua C và vuông góc với sao cho d ;
A P 2d ; B P.
Giả sử phương trình của P: ax by cz d 0. Tính 2 2 2 2
a b c d . A. 4. B. 3. C. 2. D. 1. IA 2IB
Lời giải. Gọi I P A .
B Lại có d ;
A P 2d ; B P .
IA2IB
Trường hợp 1. I nằm ngoài AB mà IA 2IB I 0;0; 1 . Ta có n IC,n
P x z P 7;0; 7//1;0; 1 1 0.
Trường hợp 2. I nằm trong đoạn AB mà 4 8 1
IA 2IB I ; ; . 3 3 3 Ta có n IC,n
P x z P 21;0; 21 //1;0; 1 : 1 0.
Qua hai trường hợp suy ra 2 2 2 2
a 1,b 0,c 1,d 1
a b c d 3. Chọn B.
Câu 12. Trong không gian với hệ tọa độ Oxyz, cho mp P đi qua M 1;2; 1 , N 1;0; 1 đồng
thời cắt Ox,Oy theo thứ tự tại ,
A B (khác O ) sao cho AM 3 . Khi đó P có một véc tơ BN
pháp tuyến n 1; ;
m n thì tổng m n bằng A. 2. B. 1. C. 1. D. 0.
Lời giải. Giả sử P cắt ba trục tọa độ tại các điểm Aa;0;0, B0; ;
b 0,C0;0;c với abc 0.
Phương trình đoạn chắn của mặt phẳng : x y z P 1. a b c 1 2 1 1 a b c b 1
Vì P qua M , N nên ta có hệ phương trình . 1 1 1
a c ac a c a 3
Từ AM 3BN a 2 1 5 3 2 2b . a 1 Với 3
a 3 c P: x 3y 4z 3 0
m n 1. 4
Với a 1 1c c không có giá trị thỏa mãn. Chọn B.
Câu 13. Trong không gian với hệ tọa độ Oxyz, cho A2;5; 3 , B2;1; 1 ,C2;0; 1 và mặt phẳng
: 3x 4y 5z 1 0. Gọi D ; a ;
b c (với c 0 ) thuộc sao cho có vô số mặt phẳng P
chứa C, D và khoảng cách từ A đến P gấp 3 lần khoảng cách từ B đến P. Tính giá trị biểu thức 2 2 2
S a b c . A. S 24. B. S 25. C. S 27. D. S 26.
Lời giải. Vì khoảng cách từ A đến P gấp 3 lần khoảng cách từ B đến P P đi qua
giao điểm I của AB và P và có thể xảy ra hai trường hợp sau:
Trường hợp 1. IA 3IB
I 1;2;0. Ta tìm được giao điểm D đường thẳng JC và là D4;4; 1 (loại).
Trường hợp 2. IA 3IB I 4;1;
3 . Ta tìm được giao điểm D đường thẳng IC và là D4;1; 3 (thỏa). a 4 Vậy 2 2 2 b 1
S a b c 26. Chọn D. c 3
Câu 14. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng : x z 3 0 và điểm M 1;1;
1 . Gọi A là điểm thuộc trục Oz, B là hình chiếu của A lên . Biết rằng tam giác
MAB cân tại M. Đoạn thẳng MA có độ dài bằng A. 6 hoặc 18. B. 6 hoặc 102. C. 18. D. 6.
Lời giải. Vì A là điểm thuộc trục Oz, nên A0;0;a. B là hình chiếu của A lên , ta tìm được a 3 a 3 B ;0;
trung điểm của AB là 2 2 a 3 3a3 I a 1 3a 7 ;0; MI ;1; . 4 4 4 4
Ta có AB nên AB có một véc-tơ chỉ phương là u 1;0; 1 .
Lại có tam giác MAB cân tại M a 1
MI AB MI u 3a7 . 0 .1 1 .0 . 1 0 4 4 a 3. Vậy A0;0;
3 MA 1;1;2
MA 6. Chọn D.
Câu 15. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A0;0; 3 , B2;0; 1 và mặt
phẳng P: 3x8y 7z 1 0. Điểm Ca; ;
b c là điểm nằm trên mặt phẳng P, có hoành độ
dương để tam giác ABC đều. Tính ab 3 .c A. 7. B. 9. C. 5. D. 3.
Lời giải. Trung điểm của AB là I 1;0;2 và tính được AB 1;0; 1 .
Phương trình mặt phẳng trung trực của đoạn AB là Q: x z 1 0.
x z 1 0
Giao tuyến d của P và Q là x y 1 z 1 d : d : . 3
x8y 7z 1 0 2 1 2 Chọn C2 ; c 1 ;
c 12c d. Tam giác ABC đều khi và chỉ khi AB AC t 1
2t2 1t2 22t2 2
2 2 9t 6t 3 0 1 C2;2; 3 . t 3
Vậy ab 3c 5. Chọn C.
Câu 16. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A2;0;
1 , B1;0;0,C1;1; 1 và mặt
phẳng P: x y z 2 0. Điểm M ; a ;
b c nằm trên mặt phẳng P thỏa mãn
MA MB MC. Tính T a 2b 3 . c A. T 5. B. T 3. C. T 2. D. T 4.
Lời giải. Ta có AB1;0; 1 , BC0;1;
1 và trung điểm của AB, BC lần lượt là 3 1 1 1
I ;0; , J 1; ; . 2 2 2 2
Mặt phẳng trung trực của đoạn thẳng AB là : x z 2 0.
Mặt phẳng trung trực của đoạn thẳng BC là : y z 2 0.
Do MA MB MC nên M và M , lại có M P
tọa độ M là nghiệm của hệ
x z 2 0
yz10 M1;0; 1T a2b3c4. Chọn D.
x yz20
Câu 17. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A2;1 ;1 , M 5;3 ;1 , N 4;1;2 và
mặt phẳng P: y z 27. Biết rằng tồn tại điểm B trên tia AM , điểm C trên P và điểm
D trên tia AN sao cho tứ giác ABCD là hình thoi. Tọa độ của điểm C là
A. 15;21;6.
B. 21;21;6.
C. 15;7;20. D. 21;19; 8 .
x 23t
x 2 2u
Lời giải. Ta có AM :
y 1 4t và AN :y 1 2u. z 1 z 1u
Gọi B23t;1 4t
;1 AM , D2 2u;1 2u;1u AN.
Vì tứ giác ABCD là hình thoi AD BC
C3t 2u 2;4t 2u 1;u 1 .
Mà C P 4t 3u 27 1 .
Vì tứ giác ABCD là hình thoi nên suy ra 2 2 2 2 AB AD
25t 9u 2. t 3 Từ
1 và 2 tìm được
C21;21;6. Chọn B. u 5
Câu 18. Trong không gian với hệ tọa độ Oxyz, cho các điểm A1;0;0, B0;2;0,C0;0;4. Viết
phương trình đường thẳng đi qua trực tâm H của A
BC và vuông góc với mặt phẳng ABC. A. x1 x y z : y z . B. 1 1 : . 4 2 1 4 2 1 C. : x y z x y z . D. 1 1 : . 4 2 1 4 2 1
Lời giải. Phương trình đoạn chắn của mặt phẳng : x y z ABC 1 hay 1 2 4
ABC: 4x 2y z 4 0. Suy ra mặt phẳng ABC có một VTPT là n 4;2; 1 . Vì ,
OA OB,OC đôi một vuông góc nên suy ra OH x y z ABC
: . Chọn C. 4 2 1
Câu 19. Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A1;2; 1 , B 2;2; 1 , C
1;2;2. Hỏi đường phân giác trong góc A của tam giác ABC cắt
mặt phẳng Oyz tại điểm nào sau đây ? A. 4 8 0; ; . B. 2 4 0; ; . C. 2 8 0; ; . D. 2 8 0; ; . 3 3 3 3 3 3 3 3
AB 3;4;0 AB 5
Lời giải. Ta có AC 0;0; 1 AC 1
VTCP của đường phân giác trong góc A của tam giác ABC là 1 1 3 4 u AB AC ; ;1. AB AC 5 5 3 x 1 t 5
Phương trình đường phân giác góc 4
A là d : y 2 t 5
z 1t
Đường thẳng d cắt mặt phẳng Oyz tại 2 8 M 0; ; . Chọn C. 3 3
Câu 20. Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC nhọn có H 2;2; 1 , 8 4 8 K ; ; ,
O lần lượt là hình chiếu vuông góc của A , B , C trên các cạnh BC , AC , AB . 3 3 3
Đường thẳng d đi qua A và vuông góc với mặt phẳng ABC có phương trình là 8 2 2 x y z A. x 4 y 1 z 1 d : . B. 3 3 3 d : . 1 2 2 1 2 2 4 17 1 x y z C. 9 9 9 x y z d : . D. 6 d : . 1 2 2 1 2 2
Lời giải. Để giải quyết bài này ta sử dụng hai tính chất sau:
Tâm đường tròn nội tiếp tam giác OHK là trực tâm của tam giác ABC.
Công thức tâm tỷ cự của tâm đường tròn nội tiếp tam giác OHK là
HK.IO OH.IK OK.IH 0. A K O I B H C
Mặt phẳng ABC có VTPT n O H,OK 4; ;8 ;8. Ta có OH 3, OK 4, HK 5.
Gọi I là trực tâm của tam giác ABC , suy ra I là tâm đường tròn nội tiếp tam giác OHK .
HK.x OH.x OK.x O K H x I
HK OH OK x 0 I Khi đó tọa độ điểm
HK.y OH.y OK.y
I được xác định: O K H y y 1 , suy ra I I
HK OH OK z 1
HK.z OH.z OK. I z O K H z I
HK OH OK I 0;1; 1 . x 2t Đường thẳng
AH : y 1 t . Điểm A AH
A2t;1 t; 1 . z 1 Ta có O . A OI 0 A4;1; 1 . Chọn A.
Câu 21. Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A2;3; 3 , phương trình
đường trung tuyến d kẻ từ B là x3 y 3 z 2
, phương trình đường phân giác trong 1 1 2 1
d của góc C là x2 y 4 z 2
. Đường thẳng BC có một vectơ chỉ phương là 2 2 1 1
A. u 2;1; 1 .
B. u 1;1;0.
C. u 1;1;0.
D. u 1;2; 1 . Lời giải.
Gọi M là trung điểm của AC. Vì M d nên M 3 ; p 3 2 ; p 2 p. 1
Mặt khác M là trung điểm của AC nên C42 p;3 4 p;12 p. Mà C p p p
d nên ta có phương trình 4 2 2 3 4 4 1 2 2 p 0 C4;3; 1 . 2 2 1 1
Gọi A là điểm đối xứng với A qua CD , suy ra AA d và A BC . 2
Gọi K AA d K là trung điểm của AA, khi đó ta có AA d tại K. 2 2
Do vậy điểm K d K 2 2q;4q;2q . 2
Kết hợp với AK d nên ta có AI.u q 0 K 2;4;2 A2;5; 1 . d 0 2 2
AC 2;2;0 chọn VTCP của đường thẳng BC là u 1;1;0. Chọn C.
Câu 22. Trong không gian với hệ tọa độ Oxyz , cho ba điểm A0;0;0, B 0;1; 1 , C 1;0; 1 . Xét
điểm D thuộc mặt phẳng Oxy sao cho tứ diện ABCD là một tứ diện đều. Kí hiệu
Dx ; y ;z là tọa độ của điểm D . Tổng x y bằng 0 0 0 0 0 A. 0 . B. 1. C. 2 . D. 3 .
Lời giải. Tính được AB BC CA 2 . DA 2 Do
D Oxy
Dx ; y ;0 . Yêu cầu bài toán DA DB DC 2 DB 2 0 0 DC 2 2 2 2 2
x y 2 0 0 x y 2 0 0 x 1 2 x y 2 2 1 1 2 x y 1 1
x y 2. Chọn C. 0 0 0 0 2 0 0 0 y 1 0 2
x y x 2 2 2 1 y 1 1 1 2 0 0 0 0
Câu 23. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S x 2 y z 2 2 : 1 2 4 và
x 2t đường thẳng
d : y t
. Tìm các giá trị của m để d cắt S tại hai điểm phân biệt , A B
z mt
sao cho các mặt phẳng tiếp diện của S tại A và B vuông góc với nhau. m 1 m 1 m 0 A. . B. C. D. Đáp án khác. . . m 4 m 0 m 4
Lời giải. Mặt cầu S có tâm I 1;0;2 và bán kính R 2. d A I B
Hai mặt phẳng tiếp diện của S tại A và B vuông góc với nhau IAB vuông cân IA R d I, AB 2
d I,d 2. 2 2
Đường thẳng d đi qua M 2;0;m và có VTCP u 1;1; 1 . Suy ra IM 1;0;m 2 IM.u m 2; m 3; 1 . IM.u 2 2m 10m 14 m 1
Vậy d I,d 2
2 2m 10m 8 0 . Chọn A. u 3 m 4
Câu 24. Trong không gian với hệ tọa độ x 1 y 2
Oxyz, cho bốn đường thẳng : z d , 1 1 2 2 x 2 y 2 : z d x y z 1 x2 y z 1 , d : , d : . Gọi 2
là đường thẳng cắt cả 2 4 4 3 2 1 1 4 2 2 1
bốn đường thẳng đã cho. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng .
A. u 2;0;1 .
B. u 2;1;1 .
C. u 2;1;1 .
D. u 1;2;2 . 4 1 2 3
Lời giải. Ta có d //d . Phương trình mặt phẳng d , d : y z 2 0. 1 2 1 2. Gọi 1 3
A d d , d A 1;
; , B d d ,d B 4;2;0 . 4 1 2 3 1 2 2 2
Khi đó AB là đường thẳng . 3 3 AB 3 ; ;
u 2;1; 1 là vectơ chỉ phương của đường 2 2 2 thẳng . Chọn B.
Câu 25. Trong không gian với hệ tọa độ Oxyz, cho bốn đường thẳng x2 y 2 z 1 : , 1 1 1 1 x1 y 1 z x y 2 z 1 x5 y a z b : , : và : . Biết không tồn tại 2 3 1 2 1 1 1 1 4 1 3 1
đường thẳng nào trong không gian mà cắt được đồng thời cả bốn đường thẳng trên. Tính giá
trị của T a2 . b A. T 2. B. T 3. C. T 2.
D. T 3.
Lời giải. Ta thấy // . Gọi P là mặt phẳng chứa và . 1 3 1 3
Phương trình mặt phẳng P: x 2y z 3 0. Gọi I
2a b 22 3b 24 2a 7b 8 P
I 0;1;1 và J P J ; ; 4 2 6 6 6
2a b22 3b18 2a 7b14 IJ ; ; . 6 6 6
Theo yêu cầu bài toán suy ra IJ cùng phương với u 1,1,1 . 1
2a b 22
3b18 2a 7b14
a 2b 2. Chọn C. 6 6 6
Câu 26. Trong không gian với hệ tọa độ Oxyz, cho S 1;2; 3 và các điểm ,
A B,C thuộc các trục
Ox,Oy,Oz sao cho hình chóp S.ABC có các cạnh ,
SA SB, SC đôi một vuông góc với nhau. Tính
thể tích khối chóp S.ABC. A. 343. B. 343. C. 343. D. 343. 6 18 12 36
SA a1;2; 3
Lời giải. Gọi Aa;0;0, B0; ;
b 0,C0;0;c
SB 1;b2; 3 .
SC 1;2;c 3 a 7 SA SB . SA SB 0
a 2b 14 Vì ,
SA SB, SC đôi một vuông góc 7
SB SC .
SB SC 0 2b 3c 14 b . 2 a 3c 14 SA SC . SA SC 0 7 c 3 Do ,
SA SB, SC đôi một vuông góc, nên 1 1 7 7 343 V SA SB SC Chọn D. SABC . . .7. . . 6 6 2 3 36
Câu 27. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng đi qua điểm M 1;2; 1 và
cắt các tia Ox,Oy,Oz lần lượt tại ,
A B,C sao cho độ dài ,
OA OB,OC theo thứ tự tạo thành cấp
số nhân có công bội bằng 2. Tính khoảng cách từ gốc tọa độ tới mặt phẳng . A. 4 . B. 21 . C. 3 21 . D. 9 21. 21 21 7
Lời giải. Gọi Aa,0,0, B0, ,
b 0,C0,0,c theo đề ra ta có a,b,c dương.
Phương trình đoạn chắn của mặt phẳng Vì mặt phẳng 1 2 1
đi qua điểm M 1;2;
1 nên ta có 1 1 . a b c Do ,
OA OB,OC theo thứ tự tạo thành cấp số nhân có công bội bằng 2 c 2b 4a 2. Từ 1 và 2 , suy ra 9 9 9
a OA ,OB ,OC 9. 4 4 2 Đặt d ; O 1 1 1 1 7 3 21
h suy ra h . Chọn C. 2 2 2 2 h OA OB OC 27 7
Câu 28. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S 2 2 2
: x y z 3 . Một mặt
phẳng tiếp xúc với mặt cầu S và cắt các tia Ox, Oy,
Oz tương ứng tại ,
A B, C . Tính giá trị của biểu thức 1 1 1 T . 2 2 2 OA OB OC A. 1 T . B. 1 T . C. 1 T .
D. T 3 . 3 3 9
Ox Aa;0;0 Lời giải. Gọi x y z x y z Oy
B 0;b;0
: 1 hay : 1 0. a b c a b c
Oz C0;0;c
Mặt cầu S có tâm I 0;0;0, bán kính R 3 . 1 Do 1 1 1 1
tiếp xúc với S nên d I, R 3 . 2 2 2 1 1 1 a b c 3 2 2 2 a b c Suy ra 1 1 1 1 1 1 1 T . Chọn B. 2 2 2 2 2 2 OA OB OC a b c 3
Cách trắc nghiệm. Do bài toán đúng với mọi nên ta chọn một trường hợp đặc biệt. Chọn điểm M 1;1; 1 thuộc S.
Khi đó mặt phẳng thỏa mãn bài toán sẽ đi qua M và nhận OM làm một VTPT nên có
phương trình : x y z 3 0 .
Ox A3a;0;0 Suy ra
Oy B 1 1 1 1 1 1 1 0;3;0 T . 2 2 2 OA OB OC 9 9 9 3
Oz C0;0; 3
Câu 29. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A6;3;4, Ba;b;c. Gọi M , N,
P lần lượt là giao điểm của đường thẳng AB với các mặt phẳng tọa độ
Oxy, Oyz , Ozx sao cho M , N,
P nằm giữa A và B thỏa mãn AM MN NP PB. Giá
trị của biểu thức a b c bằng A. 40. B. 32. C. 24. D. 17. Lời giải. Vì
a 6 b 3 c 4
AM MN NP PB
N là trung điểm của AB N ; ; . 2 2 2 Mà a b c
N Oyz suy ra
6 0 a 6. Suy ra 3 4 N 0; ;
và B6;b;c. 2 2 2 Vì b 9 c 12
AM MN M là trung điểm của AN M 3; ; . 4 4 Mà c
M Oxy suy ra
12 0 c 12. 4 Vì 3b 3 3c 4
NP PB P là trung điểm của NB P 3; ; . 4 4 Mà b
P Oxz suy ra 3
3 0 b 1. 4
Vậy a b c 17 . Chọn D.
Câu 30. Trong không gian với hệ tọa độ Oxyz, cho hình lăng trụ tam giác đều ABC.A B C có 1 1 1 A
3;1;1 , hai đỉnh B,C thuộc trục Oz và AA 1, ( C không trùng O ). Biết u a;b;2 là 1 1
một véc tơ chỉ phương của đường thẳng A C. Tính 2 2
T a b . 1 A. T 4.
B. T 5. C. T 9. D. T 16.
Lời giải. Gọi I là trung điểm của BC I 0;0; 1 . Do ABC
đều AI BC , mà BC AA BC AA I BC A I 1 1 1
I là hình chiếu vuông góc của A trên Oz. 1
Ta có d A ,Oz 2 2 A I 2
AI A I AA 3. 1 1 1 1 2AI Suy ra BC 3 CI
1 (do tam giác ABC đều) 2 2
Vì C Oz nên gọi C 0;0;c với c 0 . loaïi 2 c 0
Từ IC 1 c 1 1
C 0;0;2
A C 3;1;1 . 1 c 2
Chọn VTCP của A C là u2 3;2;2 2 2
T a b 16. Chọn D. 1
Phần 2. Cực trị trong hình học Oxyz x t
Câu 1. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d :y 1t và điểm z 4
A1;1;2. Đường thẳng nằm trong mặt phẳng tọa độ Oxy sao cho A cách đều d và .
Tìm giá trị lớn nhất của khoảng cách giữa d và . A. d 1. B. d 3 2. C. d 2. D. Không tồn tại. max max max
Lời giải. Lấy M 0;1;4 d, MA 1; 2; 2,u MA u d 1; 1;0 , d 2; 2; 1 . 22 22 2 1 Kẻ AH 3 3 2
d H d
AH d , A d . 2 1 2 2 2 2 1 0
Lấy K đối xứng với H qua .
A Suy ra HK 2AH 3 2 là giá trị lớn nhất của d , d.
Thật vậy, lấy thỏa d ,
A AH AH AH ' AH AK HH ' H 'K
HH ' HK. Chọn C.
Câu 2. Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng x1 y z 2 d : và 1 2 1 1 x1 y 2 z 2 d :
. Gọi là đường thẳng song song với P: x y z 7 0 và cắt 2 1 3 2
d ,d lần lượt tại hai điểm ,
A B sao cho AB ngắn nhất. Phương trình của đường thẳng là 1 2 x 6 t x 6 x 6 2t x 12t A. 5 5 5 y 5 . B. y .
C. y t .
D. y t . 2 2 2
z 9 t 9 9 9
z t
z t
z t 2 2 2
Lời giải. Gọi A1 2a; a; 2a d , B1 ; b 23 ;
b 22b d . 1 2
VTCP của là AB b2 ;
a 3ba2; 2b a 4, VTPT của P là n P 1; 1; 1 .
Vì //P nên AB n AB n b a Khi đó AB a
1; 2a 5; 6a P . P 0 1. 2 AB 5 49 7 2 a
2 a 2 a2 1 2 5 6 2
6a 30a 62 6a , a . 2 2 2 Dấu " 5 9 7 7 " xảy ra khi 5 a A6; ; , AB ; 0; . 2 2 2 2 2
Đường thẳng đi qua điểm 5 9 A6; ;
và vec tơ chỉ phương u d 1; 0; 1 2 2 x6 t
Vậy phương trình đường thẳng 5 :y . Chọn B. 2 9
z t 2
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A4;1;
3 , B1;2; 1 ,C3;2;
3 và D0;3;
5 . Mặt phẳng qua D và tổng khoảng cách ,
A B,C đến lớn nhất, đồng thời ba điểm ,
A B,C nằm về cùng một phía so với mặt
phẳng . Điểm nào dưới đây thuộc mặt phẳng .
A. M 7;3;4.
B. M 2;0;7.
C. M 1;1;6.
D. M 36;1; 1 .
Lời giải. Trọng tâm của tam giác ABC là 2 1 1 2 8 14 G ; ; GD ; ; . 3 3 3 3 3 5
Theo đề S d ,
A d B, d C, 3d G, 3GD 2 66 S
2 66 khi GD và D max
Phương trình mặt phẳng : x4y 7z 47 0. Đối chiếu đáp án chọn A.
Câu 4. Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A2;1;0, B4;4; 3 ,C2;3;2 và đường thẳng x1 y 1 z 1 d :
. Gọi là mặt phẳng chứa d sao cho ,
A B,C ở cùng phía 1 2 1
đối với mặt phẳng . Gọi d ,d ,d lần lượt là khoảng cách từ ,
A B,C đến . Tìm giá trị 1 2 3
lớn nhất của T d 2d 3d . 1 2 3 A. T 6 14. B. T 203. max max C. 203 T 14 3 21. D. T 2 21. max 3 max
Lời giải. Trung điểm của AB, BC lần lượt là 5 3 M 1; ; và 7 5 N 3
; ; . Trọng tâm của tam giác 2 2 2 2
MNC là G2;3;2.
Gọi d ,d ,d lần lượt là khoảng cách từ M , N,G đến 4 5 6 . Ta có
T d 2d 3d d d d d 2d 1 2 3 1 2 2 3 3
2d 2d 2d 6d . 4 5 3 6
Kẻ GH ,GK d H , K d. Ta chứng minh được IH IK d 6 14. 6
Dấu " " xảy ra khi H K hay IK . Chọn A.
Câu 5. Trong không gian với hệ trục tọa độ Oxyz, gọi d là đường thẳng đi qua A2;1;0 song
song với mặt phẳng P: x y z 0 và tổng khoảng cách từ M 0;2;0, N 4;0;0 tới đường
thẳng d có giá trị nhỏ nhất. Véc-tơ chỉ phương u của d có tọa độ là: A. 1;0; 1 . B. 2;1 ;1 . C. 3;2; 1 . D. 0;1; 1 .
Lời giải. Mặt phẳng đi qua A2;1;0 và song song với mặt phẳng P là:
: x y z 1 0.
Ta có MN 4;2;0 , n MN,n a P 2;4; 2 . P 1; 1; 1
Ta thấy A là trung điểm của MN nên dường thẳng d là hình chiếu vuông góc của đường
thẳng MN trên mặt phẳng , khi đó véc tơ chỉ phương của đường thẳng d là u n a Chọn A. P , 6;0; 6.
Câu 6. Trong không gian với hệ tọa độ Oxyz, gọi là đường thẳng đi qua điểm A2;1;0,
song song với mặt phẳng P: x y z 0 và có tổng khoảng cách từ các điểm
M 0;2;0, N 4;0;0 tới đường thẳng đó đạt giá trị nhỏ nhất? Vectơ chỉ phương của là vectơ nào sau đây? A. u B. u C. u D. u 2;1 ;1 3;2; 1 1;0; 1 0;1; 1
Lời giải. Vì là đường thẳng đi qua điểm ,
A song song với mặt phẳng P nằm
trong mặt phẳng qua A và song song với mặt phẳng P.
Nhận thấy A là trung điểm của MN nên d M , d N,.
Ta có d M , d N, d M ,. Dấu " " xảy ra khi nằm trong mặt phẳng chứa
MN và vuông góc với .
Mặt phẳng có véc-tơ pháp tuyến là n n AM P , 1;2; 1 .
Đường thẳng là giao tuyến của Q và R nên nhận u làm một véc- n ,n 3;0; 3
tơ chỉ phương. Đối chiếu đáp án, chọn B.
Câu 7. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng x 1 y 2 : z d và điểm 1 2 1 A2;1
;1 . Gọi là đường thẳng đi qua A sao cho tổng khoảng cách từ O đến và khoảng
cách từ d đến lớn nhất. Biết u 2; ;
b c là một vectơ chỉ phương của .
Tính tổng b . c A. 3. B. 3. C. 4. D. 4.
Lời giải. Do O, ,
A d cố định, gọi H là hình chiếu của A lên d, khi đó: d OA O; d d OA AH. O; d; d HA d; OA OA u Dấu " " xảy ra
. Vậy ta có thể chọn u ; OA HA . HA HA u
Khi đó ta tìm được H 1;2;0 HA 1;1; 1 ,OA 2;1; 1 . b 1 Vậy u ; OA HA 2;1; 3
b c 4. Chọn D. c 3
Câu 8. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A1;4;4, B1;7;2, C1;4;2.
Mặt phẳng P: 2x by cz d 0 qua A và thỏa mãn T d B,P 2d C,P đạt giá trị
lớn nhất. Tính b c d . A. 77. B. 52. C. 45. D. 65. Lời giải.
Trường hợp 1. B, C cùng phía so với P.
Gọi I thõa mãn IB 2IC 0
I 1;5;2. Gọi H là hình chiếu
vuông góc của I trên P IH . IA
Có T d B,P 2d C,P 3d I,P 3IH 3IA . Vậy maxT 3 .
IA Dấu " = " xảy ra khi và chỉ khi H A hay IA P. b 9
Suy ra P: 2x 9y 6z 62 0 c 6
b c d 65. d 62
Trường hợp 2. B, C hai phía so với P. Gọi B là điểm đối
xứng của B qua A
B3;15;10. Gọi D thõa mãn 1 7
DB 2DC 0 D ; ;2. Gọi K là 3 3
hình chiếu vuông góc của D trên P DK . DA
Có T d B,P 2d C,P d B,P 2d C,P 3d I,P 3DK 3 . DA Vậy maxT 3 .
DA Dấu " = " xảy ra khi và chỉ khi K A hay DA P. b 5
Suy ra P: 2x 5y 6z 46 0 c 6
b c d 45. d 46
Từ hai trường hợp
→ maxT = 65. Chọn D.
Câu 9. Cho hình hộp chữ nhật ABCD.A' B 'C ' D ' có điểm A trùng gốc tọa độ O, các điểm
Bm;0;0, D0;m;0, A'0;0;n với , m
n 0 và m n 4. Gọi M là trung điểm của CC '.
Thể tích tứ diện BDA' M lớn nhất bằng bao nhiêu? A. 64 . B. 9 . C. 4 . D. 16 . 27 4 3 27
Lời giải. Từ giả thiết, ta suy ra n
C m;m;0, C m;m;n và M m;m;
là trung điểm CC . 2
BA m;0;n Ta có n BA';BD 2
mn;mn;m và BM 0;m; .
BD m;m;0 2 2 2
1 m .n m m 3 2 4 Thể tích khối chóp m 4m
BDAM là V .
BA';BD .BM . BDA M 6 4 4 4 3 2 Xét hàm m 4m 8 64 f m
trên khoảng 0;4 , ta được max f m f . Chọn A. 4 0;4 3 27 2
Cách khác. Áp dụng BĐT Côsi, ta có 1 1 1 m n 64 2 3
4 m n m m n 3 m n . 2 2 4 4 27
Câu 10. Trong không gian với hệ tọa độ Oxyz, cho A3;3;0, B3;0; 3 ,C0;3;
3 . Mặt phẳng P
đi qua O, vuông góc với mặt phẳng ABC sao cho mặt phẳng P cắt các cạnh AB, AC tại
các điểm M , N thỏa mãn thể tích tứ diện OAMN nhỏ nhất. Mặt phẳng P có phương trình:
A. x y 2z 0.
B. x y 2z 0.
C. x z 0.
D. y z 0. Lời giải x 3
Đường thẳng AB có phương trình y 3t. Mà M AB M 3;3 ;
a a với 0 a 3. z t
x 3t
Đường thẳng AC có phương trình y 3
. Mà N AC N 3 ;
b 3;bvới 0 b 3.
z t
Gọi G là trọng tâm ABC
G2;2;2 và OG ABC M ,G, N thẳng hàng
ab a . b Ta có 1 V OG S với 1 S AM AN a b AMN . .sin 60 3. . . OAMN . . 3 AMN 2 Do đó V nhỏ nhất khi S nhỏ nhất OAMN AMN a b2
Áp dụng bất đẳng thức côsi, ta có: a b a b2 . . 4 . a b 0 . a b 4. 4
Dấu bẳng xảy ra khi a b hay MN //BC
M 3;1;2, N 1;3;2.
Vậy phương trình mặt phẳng P: x y2z 0. Chọn A.
Phần 3. Các bài toán về mặt cầu
Một số bài tập cơ bản ở mức độ vận dụng
Câu 1. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng x 1 : y z d và hai điểm 2 1 2
A2;1;0, B2;3;2. Gọi S là mặt cầu đi qua hai điểm ,
A B và có tâm thuộc đường thẳng d.
Diện tích của mặt cầu S bằng A. 68 . B. 25 . C. 74 . D. 26 .
Lời giải. Gọi I là tâm và R là bán kính của mặt cầu S. Vì I d
I 1 2t;t;2t. Theo đề ta có 2 2 2 IA
IB R t 2 t 2 t2 t2 t 2 t 2 2 1 1 2 3 2 3 2 2 2 2
t 1 R IA 17. Vậy 2
S 4R 68 . Chọn A
Câu 2. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S có tâm I 3;2;2 bán kính 1 1
R 2, mặt cầu S có tâm I 1;0;1 bán kính R 1. Mặt phẳng P đồng thời tiếp xúc với 2 2 1 2
S và S cắt đoạn I I có dạng 2x by cz d 0. Tính T b c d. 2 1 1 2 A. 5. B. 3. C. 1. D. 2. Lời giải.
Tính được I I 2;2;1
I I 3 R R S tiếp xúc với S . Gọi A là tiếp điểm của 2 1 2 1 1 2 1 2 hai mặt cầu 5 2 4 A ; ; . 3 3 3
Mặt phẳng P đồng thời tiếp xúc với S và S cắt đoạn I I là mặt phẳng vuông góc với 2 1 1 2 b 2
I I tại A là: 2x 2y z 6 0 c
1
T b c d 3. Chọn B. 2 1 d 6
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S 2 2 2
: x y z 9 và mặt phẳng
P: x y z 3 0. Gọi S là mặt cầu chứa đường tròn giao tuyến của S và P đồng
thời S tiếp xúc với mặt phẳng Q: x y z 5 0. Gọi I a; ;
b c là tâm của mặt cầu S. Tính T . abc A. T 1. B. 1 T . C. T 1. D. 1 T . 8 8
Lời giải .Mặt cầu S có dạng: 2 2 2
x y z 9 mx y z
3 0 S 2 2 2
: x y z mx my mz 93m 0. 2
Như vây mặt cầu S có tâm m 3m ; m ; m I và bán kính R 3m 9. 2 2 2 4 m 5 2
Vì S tiếp xúc với mặt phẳng Q nên , 2 3m
d I Q R 3m 9 3 4 2
m 10 9m 36m 108
m 1 suy ra 1 1 1 I ; ; . Vậy 1
T abc . Chọn D. 2 2 2 8
Câu 4. Trong không gian với hệ tọa độ Oxyz, cho các mặt phẳng P: x y 2z 1 0,
Q: 2x y z 1 0. Gọi S là mặt cầu có tâm thuộc trục hoành, đồng thời S cắt mặt
phẳng P theo giao tuyến là một đường tròn có bán kính bằng 2 và S cắt mặt phẳng Q
theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ có đúng một
mặt cầu S thỏa yêu cầu. A. r 3. B. 3 r . C. r 2. D. 3 2 r . 2 2
Lời giải. Gọi I ;0
m ;0 là tâm mặt cầu có bán kính R , d , d là các khoảng cách từ I đến 1 2
P và Q . m 1 2m1 Ta có d và d . 1 6 2 6 Theo đề ta có 2 2 2 2 2 m 2m 1 4m 4m 1 2 2 2
d 4 d r 4
r m 2m 2r 8 0 1 . 1 2 6 6
Yêu cầu bài toán tương đương phương trình
1 có đúng một nghiệm m 2 r 2 9 3 2 1 2
8 0 r r . Chọn D. 2 2
Câu 5. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A3;1;2, B5;7;0. Có tất cả bao nhiêu giá trị của tham số m để phương trình 2 2 2
x y z x my m 2 4 2 2
1 z m 2m 8 0 là phương trình của một mặt cầu S sao cho qua hai điểm ,
A B có duy nhất một mặt phẳng cắt mặt cầu S đó theo giao tuyến là một
đường tròn có bán kính bằng 1. A. 1. B. 4. C. 3. D. 2.
Lời giải. S là một mặt cầu, khi đó mặt cầu S có tâm I 2; ; m m 1 bán kính m 2 6 2 2
R m 3
m 3 m 3. Ngoài ra ta có d I; AB . 11 - Nếu R 1
không tồn tại mặt phẳng nào để thỏa yêu cầu bài toán. - Nếu R 1
có duy nhất một mặt phẳng qua tâm và chứa AB khi đó 2
R m 3 1 m 2 . Loại vì
nên có vô số mặt phẳng cắt mặt cầu đó theo giao tuyến m 2 I AB S m 2
là một đường tròn có bán kính bằng 1. Suy ra có 1 giá trị . m - R 1, + nếu 2 2 2
R 1 d I; AB
có hai mặt phẳng thỏa yêu cầu. + nếu 2 2 2
R 1 d I; AB
không có mặt phẳng nào thỏa yêu cầu. m 2 6 m2 2 2 2 2 2
+ nếu R 1 d I; AB m 31
34 (loại m 2 vì R 1). 11 m 2
Khi đó có duy nhất 1 mặt phẳng qua AB và cắt S theo một đường tròn có bán kính 1 Vậy có 2 giá trị .
m Chọn D.
Câu 6. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P: x 2y 2z 3 0 và mặt
cầu S có tâm I 5;3;
5 , bán kính R 2 5 . Từ một điểm A thuộc mặt phẳng P kẻ một
đường thẳng tiếp xúc với mặt cầu S tại điểm B . Tính OA biết rằng AB 4 . A. OA 3. B. OA 11. C. OA 6. D. OA 5.
Lời giải. Gọi Aa;b;c. Do A P
a 2b 2c 3 0. 1 52. 3 2.53 d
I,P 6 Ta có 1 22 2 2 2
IA d I,P
IA P hay A là hình chiếu 2 2 2 2
IA AB IB AB R 6
vuông góc của I trên mặt phẳng P .
Do đó ta dễ dàng tìm được A3;1; 1
OA 11 . Chọn B.
Câu 7. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S 2 2 2
: x y z 2x 2z 1 0 và đường thẳng x y 2 z d :
. Hai mặt phẳng P , P chứa d và tiếp xúc với S tại T 1 1 1
và T (tham khảo hình vẽ). Tìm tọa độ trung điểm H của TT . P T I H K T P d A. 5 1 5 H ; ; . B. 5 2 7 H ; ; . C. 5 1 5 H ; ; . D. 7 1 7 H ; ; . 6 3 6 6 3 6 6 3 6 6 3 6
Lời giải. Mặt cầu S có tâm mặt cầu I 1; 0;
1 , bán kính R 1 . d IT
Gọi K d ITT . Ta có
d ITT nên K là hình chiếu vuông góc của I trên d IT
d K 0; 2; 0. 2 2 Ta có IH IH.IK R 1 1 1 5 1 5
IH IK H ; ; . Chọn A. 2 2 IK IK IK 6 6 6 6 3 6
Câu 8. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S x 2 y 2 z 2 : 1 2 1 3,
và hai điểm A1;0;4, B0;1;4. Các mặt phẳng P , P cùng chứa đường thẳng AB và hai 1 2
mặt phẳng này lần lượt tiếp xúc với mặt cầu S tại các điểm H , H . Điểm K nào trong số 1 2
các điểm sau đây nằm trên đường thẳng H H . 1 2
A. K 1;4;2.
B. K 1;3;2. C. K 1;5; 3 .
D. K 1;32.
Lời giải. Mặt cầu S có tâm I 1;2; 1 và bán kính R 3. x 1t
Phương trình đường thẳng AB :y t t . z 4
Vì mặt phẳng P , P cùng chứa đường thẳng AB và hai 1 2
mặt phẳng này lần lượt tiếp xúc với mặt cầu S tại các IH AB điểm 1 H , H IH H A .
B AB 1;1;0. 1 2 1 2 IH AB 2
Phương trình mặt phẳng IH H :x y 3 0. 1 2
Gọi H là giao điểm của AB và IH H . Khi đó H 1;2;4. 1 2
Gọi M là giao điểm của H H và IH. Khi đó H M IH 1 2 1 2 Ta có IM IM.IH R 1 nên 1
IM IH, từ đó ta tìm được M 1;2;2. 2 2 IH IH IH 3 3
H H vuông góc với IH và AB nên đường H H có vectơ chỉ phương 1 2 1 2 1 u IH, AB 1;1;0. 3
x 1t
Phương trình H H : y 2t . Đối chiếu đáp án Chọn A. 1 2 z 2
Câu 9. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S x 2 y 2 z 2 : 1 1 2 4
và điểm A1;1;
1 . Ba mặt phẳng thay đổi đi qua A và đôi một vuông góc nhau, cắt mặt cầu
theo thiết diện là ba hình tròn. Tổng diện tích của ba hình tròn này bằng A. 3 . B. 4 . C. 11 . D. 12 .
Lời giải. Mặt cầu S có tâm I 1;1;2 , bán kính R 2 .
Gọi ba mặt phẳng đôi một vuông góc thỏa mãn bài toán là ,, . Gọi M , N,
P lần lượt là hình chiếu vuông góc của I trên ,, . Suy ra M , N, P là
tâm của các đường tròn giao tuyến. N M R M I R I A P
Xét đường tròn giao tuyến nằm trong mặt phẳng có: 2 2 2
R R IM . Tương tự, ta có 2 2 2
R R IN và 2 2 2
R R IP . Suy ra 2 2 2 2 2 2 2 2 2
R R R 3R IM IN IP 3R IA 11 .
Vậy tổng diện tích ba hình tròn: 2 2 2
S R R R 2 2 2
R R R . Chọn C. 11 Câu 10. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S 2 2 2
: x y z 2ax2by 2cz d 0, với a,b,c 0. Biết mặt cầu S cắt 3 mặt phẳng toạ
độ theo 3 đường tròn có bán kính r 5 và mặt cầu S đi qua điểm M 0;1;2. Tính tổng
a b c d. A. 25. B. 75. C. 40. D. 10.
Lời giải. Mặt cầu S có tâm I a,b,c.
Vì S cắt 3 mặt phẳng toạ độ theo 3 đường tròn có bán
kính bằng nhau a b c I ; a ;
a a với a 0. Suy ra 2
R a 25.
Mặt khác S đi qua điểm M 0;1;2 a 5 2 2
IM R a 25 3a 6a 5 .
a 2 l Với a 5 R 50, khi đó
a b c 5
a b c d 40. Chọn C d 25 Bài toán cực trị
Câu 11. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu
S x 2 y 2 z 2 : 3 2
4 12 và M x ; y ;z là điểm thay đổi thuộc S. Giá trị lớn o o o
nhất của biểu thức P x y z bằng? o o o A. 10. B. 11. C. 12. D. 14.
Lời giải. Ta có P x
3 y 2z 45
P 5 x
3 y 2z 4. o o o o o o
Áp dụng BĐT Bunhiacopxki, ta có P 2 5 x
3 y 2z 4 o o o 2 1 1 1 . x 2 3 y 22 z 42 3.12 36. 0 0 0
Suy ra 6 P 5 61 P 11. Chọn B.
Câu 12. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu 2 m S x y z m
(với m 0 là tham số thực) và hai điểm m 2 2 2 : 1 1 4 A2;3;
5 , B1;2;4. Tìm giá trị nhỏ nhất của m để trên S tồn tại điểm M sao cho m 2 2
MA MB 9. A. m 1.
B. m 3 3.
C. m 84 3. D. 4 3 m . 2 2
Lời giải. Mặt cầu m S x m y z m
có tâm I 1;1;m và bán kính R . m 2 2 2 : 1 1 4 2 Gọi M ; a ; b c, theo đề 2 2
MA MB 9 a22 b 2 3 x 2 5 a 2
1 b22 x42 9
a b c4 0
điểm M nằm trên mặt phẳng : x y z 4 0.
Suy ra M S
d M R m Chọn C. m ; 8 4 3 8 4 3.
Câu 13. Trong không gian với hệ tọa độ Oxyz, cho điểm A0;1;2, mặt phẳng
: x y z 4 0 và S x 2 y 2 z 2 : 3 1
2 16. Gọi P là mặt phẳng đi qua , A
vuông góc với và đồng thời P cắt mặt cầu S theo giao tuyến là một đường tròn có bán
kính nhỏ nhất. Tọa độ giao điểm M của P và trục xOx là A. 1 M ;0;0.
B. M 1;0;0. C. 1 M ;0;0. D. 1 M ;0;0. 3 2 3
Lời giải. Mặt phẳng P là mặt phẳng đi qua A có dạng:
ax by cz b c 2 2 2 2
0 a b c 0.
Vì P vuông góc với và đồng thời P cắt mặt cầu S
theo giao tuyến là một đường tròn có tâm là H .
Khi đó ta có hệ phương trình
ab c 0 3a d I P * . ; IH 2 2 2
a b c
Đường tròn giao tuyến có bán kính r nhỏ nhất khi và chỉ khi IH lớn nhất a 0. Khi đó từ * , suy ra 3 IH 6 max IH 6. 2 2 1 1 c c a a Dấu " c
" xảy ra khi và chỉ khi 1
a 2c b . c a 2
Chọn c 1 suy ra P2x y z 1 0. suy ra giao điểm M của P và trục xOx là 1 M ;0;0. 2 Chọn C.
Câu 14. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S x 2 y 2 2 : 3 1 z 4 và
x 1 2t
đường thẳng d :y 1t ,t . Mặt phẳng chứa d và cắt S theo một đường tròn có bán
z t
kính nhỏ nhất có phương trình là
A. 3x2y 4z 8 0.
B. y z 1 0.
C. x2y 3 0.
D. x 3y 5z 2 0.
Lời giải. Mặt cầu S x 2 y 2 2 : 3 1 z 4 có tâm
I 3;1;0 bán kính R 2.
Gọi r là bán kính đường tròn giao tuyến của mặt phẳng
chứa d và cắt S, gọi H là hình chiếu vuông góc của I trên
đường thẳng . Ta có 2 2
r R IH r IH , IH khi H là hình chiếu min max max
vuông góc của của I trên đường thẳng d.
Ta tìm được H 3;0;
1 IM 0;1; 1 .
Phương trình mặt phẳng : y x 1 0. Chọn B.
Câu 15. Trong không gian với hệ tọa độ Oxyz, cho hai mặt cầu
S :x 2
3 y 22 z 22 4, S :x 2 2
1 y z 1 1. Gọi d là đường thẳng đồng 2 2 1
thời tiếp xúc với hai mặt cầu trên, cắt đoạn thẳng nối tâm hai mặt cầu và cách gốc tọa độ O
một khoảng lớn nhất. Nếu u ;
a 1;b là một vectơ chỉ phương của d thì tổng S 2a 3b bằng bao nhiêu? A. S 2. B. S 1. C. S 0. D. S 4.
Lời giải. Mặt cầu S , S có tâm và bán kính lần lượt là I 3;2;2 , I 1;0;1 và R 2, R 1. 1 2 1 2 1 2
Suy ra I I 3 R R
S , S tiếp xúc ngoài với nhau tại điểm 5 2 4 A ; ; . 1 2 1 2 1 2 3 3 3
Vì d là đường thẳng đồng thời tiếp xúc với hai mặt cầu S , S suy ra d đi qua A và 1 2 d I I . 1 2
d O,d lớn nhất khi và chỉ khi d .
OA Khi đó d có 1 VTCP là I I ,OA 6;3;6 . 1 2 a 2
Chọn VTCP của đường thẳng d là u 2;1;2 b 1
S 2a 3b 2. Chọn A. c 2
Câu 16. Trong không gian với hệ tọa độ Oxyz, cho các điểm A(2;3;3), B( 2; − 1 − ; ) 1 . Gọi (S ) và
(S′) là hai mặt cầu thay đổi nhưng luôn tiếp xúc với đường thẳng AB lần lượt tại các điểm ,
A B đồng thời tiếp xúc ngoài với nhau tại điểm M (a,b,c). Tính giá trị của a + b + c biết rằng
khoảng cách từ điểm M tới mặt phẳng (P) : x + 2y − 2z + 2018 = 0 đạt giá trị lớn nhất?
A. a + b + c = 4.
B. a + b + c = 5.
C. a + b + c = 3.
D. a + b + c = 2.
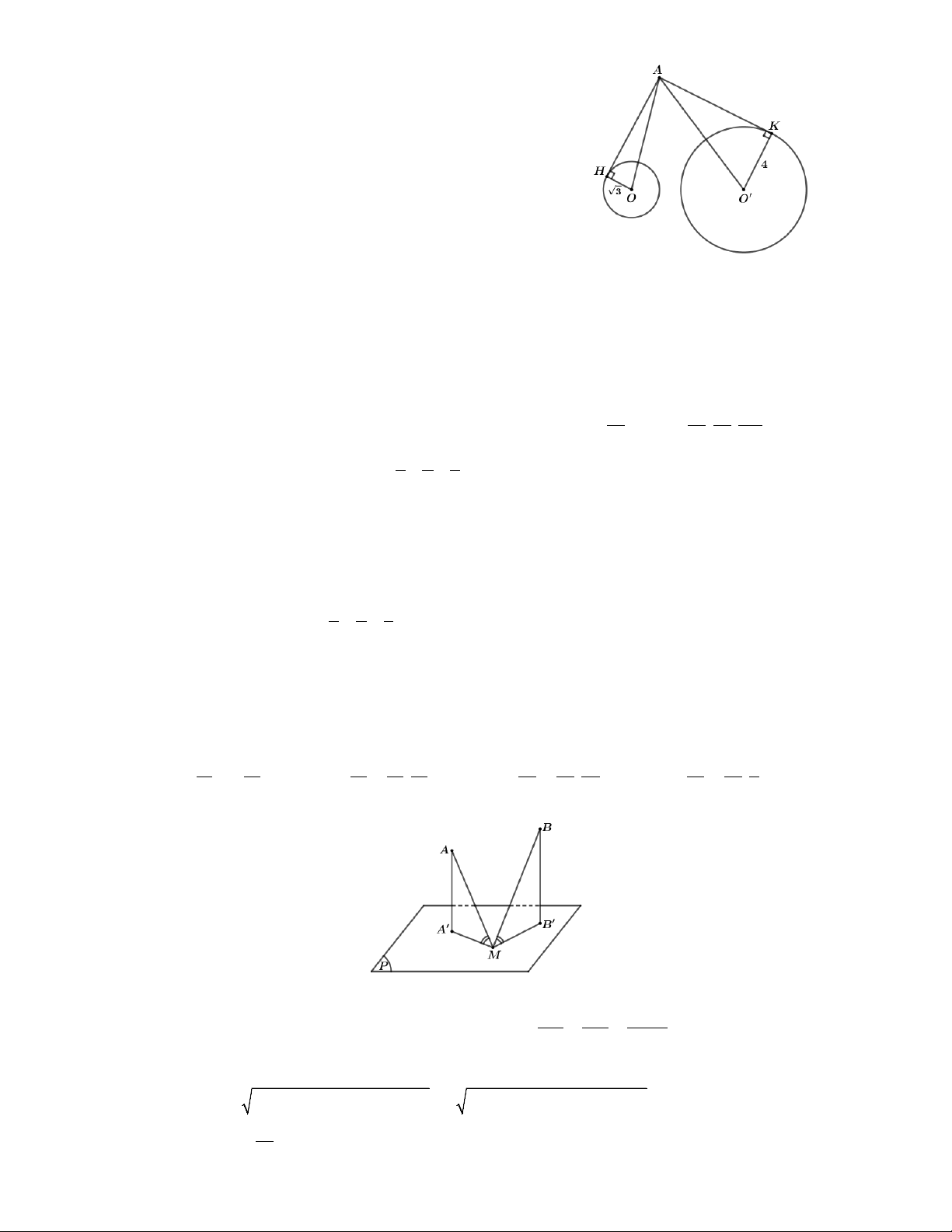
Lời giải. Gọi tâm của hai mặt cầu (S ) và (S′) lần lượt là I , I 1 2 IM = IA
Kẻ tiếp tuyến d chung của (S ) và (S′) tại M , d cắt AB tại I → → I là IM = IB
trung điểm của AB và MA ∆
B vuông tại M
→ M thuộc mặt cầu (S tâm I (0;1;2) bán 1 ) kính IA = 3. + − +
→d (M (P)) = d (I (P)) 0 2.1 2.2 2018 ; ; + IA = + 3 = 675. max 2 2 1 + 2 + ( 2 − )2
Dấu " = " xảy ra khi và chỉ khi IM ⊥ (P).
Phương trình đường thẳng x y −1 z − 2 IM : = = . Mặt cầu (S ) 2
: x + y −1 + z − 2 = 9. 1 ( )2 ( )2 1 2 2 −
Tìm được giao điểm IM và (S là M 1;3;0 ,M 1; − 1; − 4 . 1 ( ) 2 ( ) 1 ) a = 1
Ta thấy d (M ; P = 675,d M ; P = 669 M (1;3;0) b ⇒ ⇒ = 3
→a + b + c = 4. Chọn A. 1 ( )) ( 2 ( )) c = 0
Câu 17. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S có tâm I và bán kính bằng 3
sao cho luôn tiếp xúc với mặt phẳng Ox .
y Khi các đường tròn giao tuyến của S với hai mặt
phẳng tọa độ còn lại có diện tích lớn nhất thì tâm I của mặt cầu thuộc mặt phẳng nào?
A. x y z 1 0. B. x y z 0.
C. x2y 1 0.
D. x y 0.
Lời giải. Gọi I ;
x y; z. Vì mặt cầu S luôn tiếp xúc với mặt phẳng Oxy d
3 z 3 1 .
I ,Oxy
Các đường tròn giao tuyến của S với các mặt phẳng tọa độ Oyz,Ozx có diện tích lớn nhất I Oyz
I Oz 2. I Ozx I 0;0; 3 Từ 1 và 2, suy ra
I mp : x y 0. Chọn D. I 0;0; 3
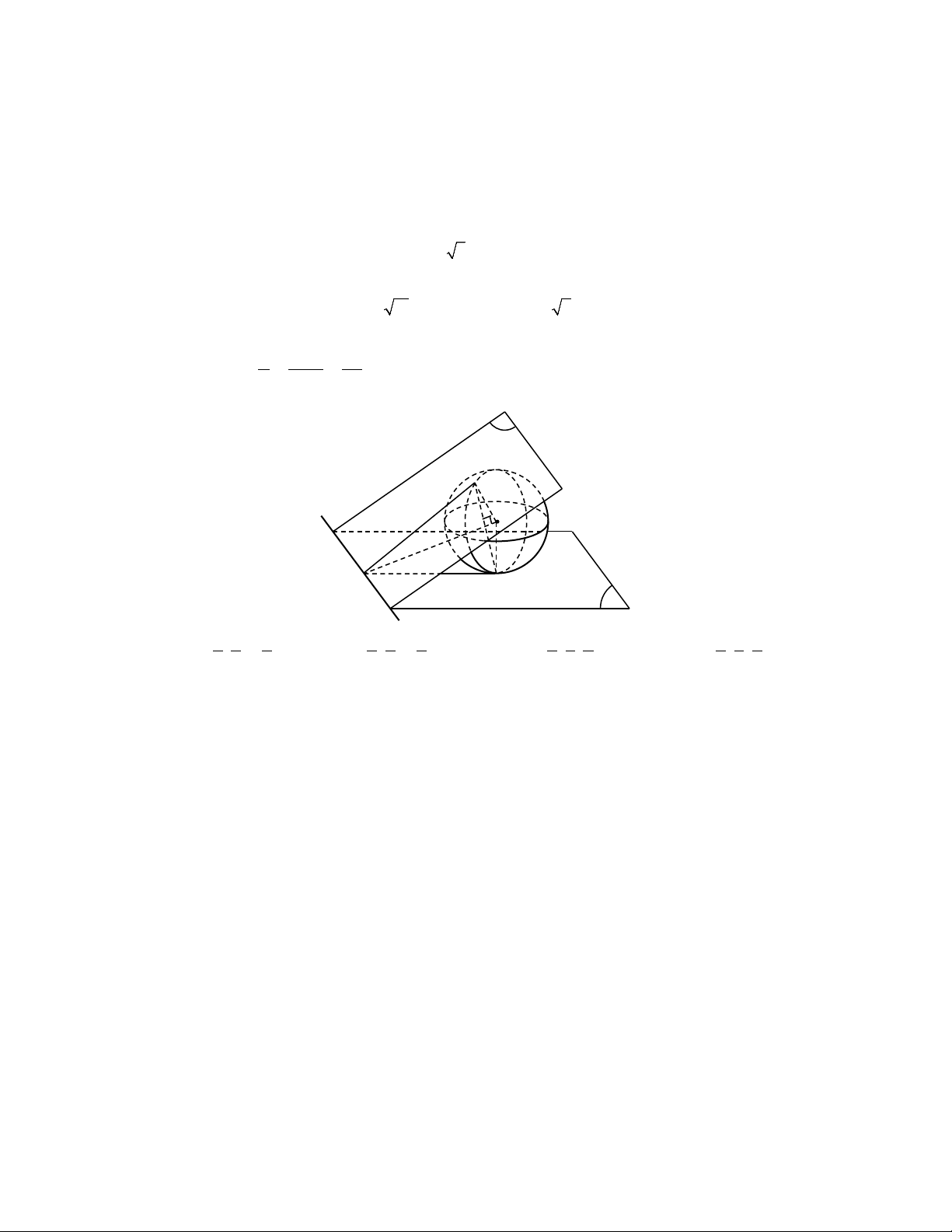
Câu 18. Trong không gian với hệ tọa độ Oxyz , cho ba mặt phẳng
P : 2x y 2z 5 0, P : 2x y 2z 13 0, Q: 2x2y z 5 0, và điểm A2;0;0 2 1
nằm giữa hai mặt phẳng P , P . Mặt cầu S di động có tâm I ; a ;
b c luôn đi qua A và 1 2
luôn tiếp xúc với hai mặt phẳng P , P . Khi khối cầu S cắt mặt phẳng Q theo thiết 1 2
diện là hình tròn có diện tích lớn nhất thì a b2c bằng A. 0. B. 3. C. 3. D. 2.
Lời giải. Ta tính được d
P , P 6. Ta tìm được mặt phẳng cách đều cả hai mặt phẳng 1 2
P , P là : 2a b 2c 4 0. 1 2
Gọi bán kính của mặt cầu S là .
R Vì mặt cầu S luôn tiếp xúc với hai mặt phẳng P , P 1 2
I 2a b 2c 4 0 . R 3 R 3
Theo đề, ta có A S
IA R 3. Suy ra I thuộc mặt cầu S có tâm A và bán kính 3. Ta có d ,
A Q 3
mặt cầu S tiếp xúc với mặt phẳng Q.
Khối cầu S cắt mặt phẳng Q theo thiết diện là hình tròn có diện tích lớn nhất khi I là
tiếp điểm của mặt cầu S với mặt phẳng Q. Khi đó
2ab2c4 0 a 0
I Q 2a 2b c 5 0 b 2
a b2c 0. Chọn A. a 2 2 2 c 1 2 b c 9
Câu 19. Trong không gian với hệ tọa độ Oxyz, cho S :x 2 2
1 y z 2 1, 1 2
x 3t
S :x 2 3 y 22 2
z 4 và đường thẳng d :y 1t. Gọi ,
A B là 2 điểm tùy ý thuộc 2
z 52t
S , S và M thuộc đường thẳng d. Khi đó giá trị nhỏ nhất của biểu thức P MA MB 1 2 bằng bao nhiêu?
A. P 2 6 3.
B. P 2 6 3.
C. P 2 3 3.
D. P 2 3 3. min min min min Lời giải.
Mặt cầu S lần lượt có tâm I 1;0;2 và bán kính R 1, mặt 1 1
cầu S lần lượt có tâm J 3;2;0 và bán kính R 2. Gọi 2 2
E IJ d E1;1; 1 .
Để MA MB M , ,
A B nằm trên mặt phẳng IJ,d. min
Gọi H, K lần lượt là giao của các tia IM , JM với S , S . 1 2 Ta có:
MA MB MH MK MI MJ 3 MA MB MI MJ min min
Lại có EI EJ I, J nằm khác phía so với d
MI MJ IJ MI MJ IJ 2 6
MA MB 2 6 3. Chọn A. min min
Câu 20. Trong không gian với hệ tọa độ Oxyz, cho S :x 2 2 2
1 y z 4, 1
x 2t
S :x22 y 2 3 z 2
1 1 và đường thẳng d :y 3t . Gọi ,
A B là 2 điểm tùy ý 2
z 2t
thuộc S , S và M thuộc đường thẳng d. Khi đó giá trị nhỏ nhất của biểu thức 1 2
P MA MB bằng A. 2211 . B. 3707 3. C. 1771 2 110 . D. 3707 . 11 11 11 11
Lời giải. Mặt cầu S lần lượt có tâm I 1;0;0 và bán kính R 2, 1 1
mặt cầu S lần lượt có tâm J 2;3; 1 và bán kính 2 R 1 IJ //d. 2
Để MA MB M , ,
A B nằm trên mặt phẳng IJ,d. min
Gọi H, K lần lượt là giao của các tia IM , JM với S , S . 1 2 Ta có:
MA MB MH MK MI MJ 3 MA MB MI MJ min min
Gọi I là điểm đối xứng của I qua d MI MJ MI MJ I J
MI MJ M I J d
MA MB I J 3. min min Dễ dàng tìm được: 35 6 42 3707 I I J
MA MB 3707 ; ; = 3. Chọn B. min 11 11 11 11 11
Câu 21. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu
S x 2 y 2 z 2 : 2 2
2 12 và điểm A4;4;0. Gọi B là điểm thuộc mặt cầu S.
Diện tích tam giác OAB có giá trị lớn nhất bằng: A. 6. B. 8 3. C. 4 6 2. D. 8 3 2.
Lời giải. Ta có O0;0;0S và OA 4 2 không đổi. Do đó để S
lớn nhất d B,OA lớn nhất. O AB
Gọi M là trung điểm O ,
A I là tâm mặt cầu S. Ta có 2 2 2
IM IA AM 4 IM 2.
Ta có d B,OA MB MI IB MI R 2 2 3 .
Dấu '' '' xảy ra khi M, I, B thẳng hàng. Khi đó 1 S
4 2. 2 2 3 4 6 2 . Chọn C. O AB max 2
Câu 22. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S x 2 2 :
1 y z 22 25. Gọi
Ax y z và Bx y z là hai điểm thuộc mặt cầu thỏa mãn biểu thức
B ; B , B
A ; A ; A
T 2x x y y z z đạt giá trị lớn nhất. Trung điểm của đoạn thẳng AB thuộc A B A B A B mặt phẳng nào sau đây?
A. y 4z 5 0.
B. x 5y 6z 10 0.
C. x 3y 2z 3 0.
D. x 3y 7z 10 0.
Lời giải. Mặt cầu S có bán kính R 5.
Gọi u 2;1; 1 thì T .
u BA u . BA .cosu,B A 6.2 . R
Vậy T đạt giá trị lớn nhất bằng 10 6 khi u, BA cùng hướng và AB 2R nên trung điểm của
đoạn AB là tâm I 1;0;2 của mặt cầu. Đối chiếu đáp án Chọn C.
Câu 23. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S x 2 y 2 2 : 1 4 z 8 và
các điểm A3;0;0, B4;2;
1 . Gọi M là điểm thuộc mặt cầu S. Giá trị nhỏ nhất của
MA 2MB bằng A. 2 2. B. 6 2. C. 2 3. D. 6 3.
Lời giải. Ta thấy IA 4 2 2 . R
MA MB x 2 2 2 2
3 y z 2 x42 y 22 z 2 1 .
Vì M S nên ta có phương trình 2 2 2
x y z x y 2 2 2 2 8 9
3 x y z 2x8y 27. Ta có x 2 2 2 2 2 2
3 y z x y z 6x 9 2 2 2
x y z 6x27 36 2 2 2
x y z x 2 2 2 6
3 x y z 2x8y36 2 2 2 x y z y 2 x y 2 2 4 6 9 4 3 z Vậy 2 MA MB
x y 2 2 z
x 2 y 2 z 2 2 2 2 2 2 3 2 4 2 1 2 4 1 1 6 2. Chọn B.
Câu 24. Trong không gian với hệ tọa độ Oxyz, cho 3 đường thẳng x1 y 1 z 1 d : , 1 2 1 2 x3 y 1 z 2 d : x4 y 4 z 1 , d :
. Mặt cầu bán kính nhỏ nhất tâm I ; a ; b c tiếp 2 1 2 2 3 2 2 1
xúc với 3 đường thẳng d ,d ,d . Tính S a 2b 3 .c 1 2 3
A. S 10. B. S 11. C. S 12. D. S 13.
d d ,d d ,d d
Lời giải. Ta chứng minh được 1 2 1 3 2 3 . d
d ;d d d ;d d d ;d 3 1 2 1 3 2 3
Dựng hình lập phương sao cho d ,d ,d chứa 3 cạnh của hình lập phương có cạnh hình lập 1 2 3 phương là 3.
d ,d ,d lần lượt đi qua các điểm 1;1; 1 ,3;1;2,4;4; 1 mà 1 2 3
khoảng cách giữa hai điểm 1;1;
1 và 3;1;2 bằng 3 (đúng
bằng cạnh hình lập phương), khoảng cách giữa hai điểm 1;1; 1 và 4;4;
1 bằng 3 2 (bằng đường chéo của các mặt
hình lập phương) còn khoảng cách giữa hai điểm 3;2; 1 và 4;4;
1 bằng 3 3 . Do đó ta có thể chọn d ,d ,d lần lượt chứa 1 2 3
AB, AD,CC và A1;1;
1 , A3;1;2,C4;4; 1 (như hình vẽ).
Suy ra mặt cầu có bán kính nhỏ nhất tiếp xúc với 3 đường
thẳng d ,d ,d có tâm là tâm hình lập phương
I là trung điểm của 1 2 3 7 a 2 7 3 3 3 A C
I ; ; b
S a 2b 3c 11. Chọn B. 2 2 2 2 3 c 2
Câu 25. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S x 2 y 2 z 2 : 1 2 3 4. x 1t
Xét đường thẳng d : y mt
với m là tham số thực. Giả sử P và P ' là hai mặt phẳng
z m 1t
chứa d, tiếp xúc với S lần lượt tại T và T '. Khi m thay đổi, tính giá trị nhỏ nhất của độ
dài đoạn thẳng TT '. A. 4 13 . B. 2 2. C. 2. D. 2 11 . 5 3
Lời giải. Mặt cầu S có tâm I 1;2;
3 và bán kính R IT IT ' 2. T H M I T' Ta có 1 1 1 1 1 1 1
TT ' 2TH mà . * 2 2 2 2 2 TH TI TM 4 TM 4 IM 4
Ta đi tìm GTNN của độ dài cạnh IM.
Do M d M 1t; mt ;m 1 t
IM t; m
t 2;m 1 t 3
IM t mt 22 m 2 1 t 3 1 m m 2 2 2 2 2
1 t 4m 6 m 1 t 13 2
2m 2m 2 2t 62m 2
t 13 IM 0.
Để phương trình có nghiệm t thì m2 2
m m 2 ' 3 2 2 2 13 IM 0 m 2 3 m 2 3 2 2 13 IM IM 13 f m . 2 2 2m 2m 2 2m 2m 2 Khảo sát hàm 1 25 25
f m ta được f m 2 f IM . 5 3 3 Khi đó 1 1 1 25 52 4 13 * T H T
T ' 2TH . Chọn A. 2 TH 4 25 52 25 5 4 3
Câu 26. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S có phương trình 2 2 2
x y z 4x 2y 2z 3 0 và điểm A5;3;2. Một đường thẳng d thay đổi luôn đi qua
A và luôn cắt mặt cầu tại hai điểm phân biệt M , N. Tính giá trị nhỏ nhất của biểu thức
S AM 4AN. A. S 50.
B. S 5 34 9.
C. S S 5 34 9.
D. S 20. min min min min min
Lời giải. Mặt cầu S có tâm I 2;1; 1 và bán kính
R 3. Kẻ tiếp tuyến AH (với H là tiếp điểm).
Ta có IA 3;4;
3 IA 34 AH 5. Ta có 2
AM.AN AH AM.AN 25.
Đặt AN x 34 3 x 34 3. 25 AM . Khi đó ta có x 25
S 4AN AM 4x f x x Xét f x 25 4x trên 34 3; 34 3 . x 2 f x 25 4x 25 4 0 x 34 3; 34 3 S f
34 3 5 34 9. Chọn B. min 2 2 x x
Sai lầm. Mặt cầu S có tâm I 2;1;
1 và bán kính R 3. Kẻ tiếp tuyến AH (với H là tiếp điểm).
Ta có IA 3;4;
3 IA 34 AH 5. Ta có 2
AM.AN AH AM.AN 25.
S AM 4AN 2 AM.4AN 20. Chọn D.
Câu 27. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S x 2 y 2 z 2 : 1 2 2 9
và hai điểm M 4;4;2, N 6;0;6. Gọi E là điểm thuộc mặt cầu S sao cho EM EN đạt giá
trị lớn nhất. Viết phương trình tiếp diện của mặt cầu S tại E.
A. x2y 2z 8 0.
B. 2x y 2z 9 0.
C. 2x 2y z 1 0.
D. 2x2y z 9 0. Lời giải
Ta có I 1;2;2 là tâm của mặt cầu S. Gọi P là trung điểm của MN P5;2;4. 2 Ta có 2 2 2 2 2 22 MN EM EN EM EN EP . 2 EM EN
Suy ra EM EN lớn nhất khi . EP max
Khi đó E là giao điểm của đường thẳng IP với mặt cầu S (với I nằm giữa E, P ). Có IP x y z
4;4;2 , do đó phương trình đường thẳng 1 2 2 IP : . 2 2 1
x 2 y 2 z 2 1 2 2 9 E3;0; 3
Tọa độ E là nghiệm của hệ x1 y 2 z 2 . E 1;4; 1 2 2 1
Do EP lớn nhất nên E1;4; 1 .
Suy ra EI 2;2;
1 , phương trình mặt phẳng tiếp diện tại E là: 2x2y z 9 0. Chọn D.
Câu 28. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S 2 2 2
: x y z 2x 4y 2z 4 0. Gọi P,Q là hai mặt phẳng vuông góc với nhau theo
giao tuyến d và đồng thời tiếp xúc với S, K là hình chiếu vuông góc của tâm I của mặt
cầu S lên d và M là giá trị lớn nhất của diện tích tam giác OIK ( O là gốc tọa độ). Hãy
chọn khẳng định đúng về M.
A. M 2 3; 4 .
B. M 2;2 2.
C. Không tồn tại M. D. M 2 3; 4 . Lời giải.
Giả sử S tiếp xúc với P,Q lần lượt tại E và F
K d IEF.
Ta chứng minh được d IEF
K IEF. Theo đề, P,Q là hai mặt phẳng vuông góc
với nhau theo giao tuyến d và đồng thời tiếp xúc với S, từ đó ta chứng minh được tứ giác
IEKF là hình vuông.
IE IF 2 IK 2
Mặt cầu S có tâm I 1;2;
1 và bán kính R 2 . OI 6 Ta có 1 S IK IO OIK OIK OIK . .sin 6.sin . 2 S
đạt giá trị lớn nhất khi sin OIK lớn nhất OIK 90. OIK
Vậy M 6. Dấu " " xảy ra khi OI IK. Chọn B.
Câu 29. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A2;1; 3 , B6;5;
5 . Gọi S là mặt
cầu có đường kính A .
B Mặt phẳng P vuông góc với đoạn AB tại H sao cho khối nón đỉnh
A và đáy là hình tròn tâm H (giao của măt cầu S và mặt phẳng P) có thể tích lớn nhất,
biết rằng P: 2x by cz d 0 với , b c,d .
Tính S b c d. A. S 18. B. S 11. C. S 24. D. S 14. Lời giải.
Ta có AB 4;4;2. Mặt cầu S đường kính AB có tâm I 4;3;4 và bán kính 1 R AB 3. 2
Gọi r là bán kính của đường tròn tâm H. Vì thể tích khối nón lớn nhất nên ta chỉ cần xét
trường hợp H thuộc đoạn IB, tức là AH 3. Đặt 2 2 2 2
IH x,0 x 3 r R x 9 x . .
Khi đó thể tích khối nón đỉnh A và đáy là hình tròn tâm H là: 1 3 COSI 2 1 V 1 1 12 32
AH.r 3 x. 2
9 x 3 x .3 x62x . . 3 3 6 6 3 3
Dấu " " xảy ra khi 3 x 62x x 1.
Mặt phẳng P nhận 1 AB 2;2; 1 làm véc tơ pháp tuyến 2
Phương trình mặt phẳng P: 2x 2y z m 0. m m
Lại có d H P 18 15 ; 1 1 . 3 m 21
Với m 15
mặt phẳng P: 2x 2y z 15 0. Khi đó I và B nằm cùng phía so với
mặt phẳng P ( AH d ;
A P 3 ) nên loại.
Với m 21
mặt phẳng P: 2x 2y z 21 0. Khi đó I và B nằm khác phía so với
mặt phẳng P ( AH d ;
A P 3 ) nên nhận.
Vậy b 2,c 1,d 21
S 18. Chọn A.
Câu 30. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S x 2 y 2 z 2 : 1 1 3 25
và mặt phẳng P: 2x y 2z 4 0. Mặt phẳng P cắt mặt cầu S theo giao tuyến là
đường tròn T,CD là một đường kính cố định của T, A là điểm thay đổi trên T ( A khác
C và D ). Đường thẳng đi qua A và vuông góc với P cắt S tại .
B Giá trị lớn nhất của
khoảng cách từ A đến mặt phẳng BCD bằng A. 12 . B. 13. C. 15. D. 11. 13 4
Lời giải. Mặt cầu S có tâm I 1;1;
3 và bán kính R 5.
Gọi J là trung điểm của CD, vì A CD vuông tại A
IJ ACD
IJ //AB 1 .
Vì I là tâm của mặt cầu S
I nằm trên mặt phẳng
trung trực của AB 2. Từ 1 và 2
AB 2.JI 2.d I;P 6. Ta có 2 2
CD 2.CJ 2 R IJ 8.
Dựng AH BCD
AH d ; A BCD.
Vì AB, AC, AD đôi một vuông góc nên 1 1 1 1 1 4 1 4 1 1 13 . 2 2 2 2 2 2 2 2 2 AH AB AC AD AB AC AD AB CD 36 16 144 2 144 12 AH AH
. Dấu " " xảy ra AC AD 4 2. 13 13 Vậy 12 AH . Chọn A. max 13
Phần 4. Bài toán cực trị sử sụng tâm tỷ cự
Câu 1. Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A1;3; 5 , B2;6; 1 ,C4;12; 5 và
mặt phẳng P: x 2y 2z 5 0. Gọi M là điểm thuộc mặt phẳng P sao cho biểu thức
T MA4MB MA MB MC đạt giá trị nhỏ nhất. Biết rằng M x ; y ; z , hỏi x thuộc 0 0 0 0
khoảng nào trong các khoảng sau. A. 0;2. B. 2;4. C. 4; 1 . D. 5;4.
Lời giải. Gọi điểm I sao cho IA IB IC 0 I 1;1; 3
và điểm JA4JB 0 J 3;7; 3 .
Ta có T MA4MB MA MB MC 3MJ JA4JB 3MI IA IB IC 3MJ MI. Ta có 1 2.
1 2.3 3 2.72 3 9.23 0 I, J
nằm về hai phía của P.
Suy ra T khi và chỉ khi M , I, J thẳng hàng hay M IJ P. max IJ x y z
4;8;6, phương trình đường thẳng 1 1 3 IJ : . 2 4 3 Từ đó ta tìm được 3 5 3 M ; ; . Chọn A. 4 2 8
Câu 2. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A1;0; 3 , B3;1; 3 , C 1;5; 1 và
M x; y;0. Tìm giá trị nhỏ nhất T của biểu thức T 2 MA MB MC . min A. T 2 35. B. T 2 37.
C. T 2 38. D. T 12. min min min min
Lời giải. Phải nhận thấy được
M x; y;0 mặt phẳng Oxy. I A
Gọi I là trung điểm của BC, suy ra I 1;3;2 .
Khi đó MB MC 2MI. M
Ta có T 2 MA MB MC 2MA MI . J
Vì z 3 0 và z 2 0 A và I nằm về cùng phía đối với mp Oxy. A I
Lấy đối xứng điểm I 1;3;2 qua mpOxy, ta được điểm J 1;3;2.
Khi đó MI MJ , suy ra T 2MA MJ 2AJ 2 38.
Dấu " " xảy ra khi M MJ Oxy 1 9 M ; ;0.
Vậy T 2 38. Chọn C. 9 5 min
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A1;1;0, B2;0;
1 ,C0;0;2 và mặt
phẳng P: x 2y z 4 0. Gọi M ; a ;
b c là điểm thuộc mặt phẳng P sao cho
S . MA MB .
MB MC MC.MA đạt giá trị nhỏ nhất. Tính Q a b 6 . c A. Q 2. B. Q 2. C. Q 0. D. Q 1. 1 1 G ; ;1
Lời giải. Gọi G là trọng tâm tam giác ABC, ta có 3 3 .
GA
GBGC 0 Theo đề bài, ta có
S . MA MB .
MB MC MC.MA
MG G
A .MG GBMG GB.MG GCMG GC.MG G A
2 3MG 2M .
G GAGBGC . GAGB .
GB GC GC.GA
2
3MG 2M .0 G . GAGB .
GB GC GC.GA
2 3MG 0 . GAGB .
GB GC GC.GA
2 3MG . GAGB .
GB GC GC.GA .
Vì . GAGB .
GB GC GC.GA là một hằng số nên ta có S đạt giá trị nhỏ nhất khi MG đạt giá
trị nhỏ nhất hay M là hình chiếu của G trên mặt phẳng P.
Gọi là đường thẳng đi qua điểm G và vuông góc với mặt phẳng P, ta có M P. 1 x t 3
Phương trình đường thẳng 1
là y 2t t . 3 z 1 t
Giải hệ phương trình 11 13 1 11 13 6 M ; ;
Q a b 6c 2. P 9 9 9 9 9 9 Chọn B.
Câu 4. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A0;1; 1 , B 3;0; 1 , C 0;21;19 và
mặt cầu S x 2 y 2 z 2 : 1 1
1 1. Gọi M a;b;c là điểm thuộc mặt cầu S sao cho biểu thức 2 2 2
T 3MA 2MB MC đạt giá trị nhỏ nhất. Tính tổng S a b c. A. S 0. B. 12 S . C. 14 S . D. 16 S . 5 5 5
Lời giải. Gọi M a b cS a 2 b 2 c 2 ; ; 1 1
1 1 và I là điểm thỏa
3IA 2IB IC 0 I 1;4; 3 . 2 2 2 Ta có 2 2 2
T 3MA 2MB MC 3MI IA 2MI IB MI IC 2
MI MI IA IB IC 2 2 2 2 2 2 2 6 2 3 2
3IA 2IB IC 6MI 3IA 2IB IC .
Do đó để T đạt giá trị nhỏ nhất thì MI đạt giá trị nhỏ nhất (do 2 2 2
3IA 2IB IC không đổi).
Cách tìm điểm M như sau:
Viết phương trường đường thẳng d qua I và tâm J 1;1;
1 của mặt cầu S.
Tìm giao điểm của d với S ta được hai điểm M và M . 1 2
So sánh IM và IM giá trị nào nhỏ hơn thì thỏa mãn (giá trị còn lại là đáp án của bài 1 2
toán hỏi biểu thức T đạt giá trị lớn nhất.
Làm theo các bước trên ta được điểm 8 1 M 1; ; thỏa mãn. Suy ra 14
a b c . Chọn C. 5 5 5
Câu 5. Trong không gian với hệ tọa độ Oxyz, cho A1;1;
1 , B1;2;0,C3;1;2. Giả sử M ; a ;
b c thuộc mặt cầu S x 2 2 :
1 y z 2 1 861 sao cho 2 2 2
P 2MA 7MB 4MC đạt
giá trị nhỏ nhất. Giá trị T a b c bằng A. T 49. B. T 51. C. T 55. D. T 47.
Lời giải. Chọn điểm I sao cho 2IA7IB 4IC 0
I 21;16;10. Ta thấy I S. 2 2 2 Ta có 2 2 2
P 2MA 7MB 4MC 2MI
IA 7MI IB 4MI IC 2 2 2
IA IB IC 2
MI MI IA IB IC 2 2 2
IA IB IC 2 2 7 4 2 2. 7. 4. 2 7 4 MI 2 2 2
2IA 7IB 4IC . a 21
Dấu " " xảy ra khi MI 0 M I M 21;16;10 b 16
T a b c 47. c 10 Chọn D.
Phần 5. Bài toán hỏi số mặt phẳng, số mặt cầu
Câu 1. Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng P: 2x z 2 0,
Q: 4y 5z 8 0. Có bao nhiêu mặt phẳng chứa giao tuyến của P và Q, đồng thời cắt x O x, z O
z lần lượt tại ,
A B (khác O ) thỏa mãn OA OB ? A. 1. B. 2. C. 3. D. 4.
Aa;0;0 x O x Lời giải. Gọi a b
với ab 0 , vì OA OB .
B0;0;b z O z a b
Chọn M 1;2;0 và N 3;7;4 thuộc giao tuyến của hai mặt phẳng P và Q.
Suy ra MA a 1;2;0, MB 1;2;b, MN 2;5;4.
Vì M , N, ,
A B cùng thuộc một mặt phẳng , MA MB .MN 0
8a 4b 5b1a 0. 1 a 0 9
Trường hợp 1. a b khi đó 1 trở thành 2
5a 9a 0 9
a b . a 5 5
Suy ra có một mặt phẳng thảo mãn yêu cầu bài toán. a 0 7
Trường hợp 2. a b khi đó 1 trở thành 2
5a 7a 0 7 a b . a 5 5
Suy ra có một mặt phẳng thảo mãn yêu cầu bài toán.
Vậy có 2 mặt phẳng thảo mãn yêu cầu bài toán. Chọn B.
Câu 2. Trong không gian với hệ tọa độ Oxyz, cho điểm M 1;2;
3 . Hỏi có bao nhiêu mặt phẳng
P đi qua M và cắt các trục x O x, y Oy , z Oz
lần lượt tại các điểm , A B,C sao cho
OA 2OB 3OC 0? A. 4. B. 3. C. 1. D. 8.
Lời giải. Gọi tọa độ các điểm Aa;0;0, B0; ;
b 0,C0;0;c với abc 0 lần lượt là tọa độ các
giao điểm của mặt phẳng P cắt các trục x O x, y Oy , z Oz .
Suy ra phương trình mặt phẳng : x y z ABC 1. a b c
Vì mặt phẳng P đi qua điểm M 1;2;
3 nên ta có phương trình 1 2 3 1 1 . a b c
a 2b 3c
a 2b 3c
Mặt khác OA 2OB 3OC
a 2 b 3 c 2.
a 2b 3c
a 2b 3c Từ
1 và 2 ta tìm được 4 bộ nghiệm a; ; b c
có 4 mặt phẳng thỏa. Chọn A.
Câu 3. Trong không gian với hệ tọa độ Oxyz , cho các mặt phẳng P: 2x y z 2 0 ,
Q: x 2y z 2 0 , R: x y 2z 2 0 và T : x y z 0 . Hỏi có nhiêu mặt cầu có
tâm thuộc T và tiếp xúc với P, Q , R ? A. 1. B. 2. C. 3. D. 4.
Lời giải. Giả sử mặt cầu S có tâm I a;b;cT
a b c 0 .
Theo đề bài, ta có d I,P d I,Q d I,R
2a b c 2
a 2b c 2
a b 2c 2 6 6 6 a b
2a b c 2 a 2b c 2
3a 2 3b 2
3a 3b 4
abc 0 . 2
a b c 2 a b 2c 2 3
a 2 3c 2 a c
3a 3c 4 a
b c 0 Trường hợp 1. a b I 0;0;0 . a c
Tương tự cho ba trường hợp còn lại. Chọn D.
Câu 4. Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A3;7; 1 , B8;3;
8 và C3;3;0. Gọi
S là mặt cầu tâm A bán kính bằng 3 và S là mặt cầu tâm B bán kính bằng 6. Hỏi có 2 1
tất cả bao nhiêu mặt phẳng đi qua C và tiếp xúc đồng thời với cả hai mặt cầu S , S . 1 2 A. 1. B. 2. C. 3. D. 4.
Lời giải. Phương trình mặt phẳng đi qua C là P ax by cz 2 2 2 : 3 3
0 a b c 0.
Theo yêu cầu bài toán (P) tiếp xúc với cả hai mặt cầu S , S , suy ra 1 2 2 2 2
4b + c = 3 a + b + c d ( ( ) 1 ; A (P)) = 2 2 2 3
4b + c = 3 a + b + c 5
a = 8b − 6c ⇔ ⇔ d ( . ; B (P)) 2 2 2 = + = + + 2 2 2 6 5a 8c 6 a b c
4b + c = 3 a + b + c (2) 5 a = 8 − b −10c b = 2c
(P) : 2x + 2y + z −12 = 0 Hệ ( ) 1 ⇔ 262
→ có hai mặt phẳng thỏa là 1 . b = c
(P : 62x − 262y − 401z + 600 = 0 2 ) 401 Hệ ( )
1 ⇔ b = c = 0
→ không có mặt phẳng nào thỏa yêu cầu.
Vậy có 2 mặt phẳng thỏa yêu cầu. Chọn B.
Câu 5. Trong không gian với hệ tọa độ Oxyz, cho điểm A 3 3 1 1;2; 3 , B ; ;
,C1;1;4, D5;3;0.
Gọi S là mặt cầu tâm A bán kính bằng 3,S là 2 1 2 2 2
mặt cầu tâm B bán kính bằng 3 . Có bao nhiêu mặt phẳng tiếp xúc với 2 mặt cầu S , S 1 2 2
đồng thời song song với đường thẳng đi qua C và . D A. 1. B. 2. C. 4. D. Vô số. Lời giải. Ta tính được 3 3 AB 3 9
, lại có R R 3 nên giao tuyến hai mặt cầu là một đường 2 1 2 2 2 tròn.
Gọi I AB với là mặt phẳng thỏa mãn bài toán. Hạ BK, AH vuông góc với mặt
phẳng . Khi đó ta có I nằm ngoài AB và B là trung điểm AI vì 3 1 1
R R BK AH. 2 1 2 2 2
Suy ra I 2;1;2. Gọi phương trình mặt phẳng
ax by cz 2 2 2 : 2 1 2
0, a b c 0.
Vì //CD mà CD 4;2;4 nên ta có 2a b2c 0 b 2c2 . a
a 2c b 2 5 c a b c Khi đó d ,
A 3
3 c a2 2
a 2c2a2 2 c 1 . 2 2 2
a b c
a c b c 2 Khi đó ta có
Trường hợp 1. b 2 ;
c a 2c : 2cx22cy
1 cz 2 0 2x2y z 4 0.
Vì C
mặt phẳng 2x 2y z 4 0 không thỏa. Trường hợp 2. 1
b c a c 1 ;
: cx2cy
1 cz 2 0 x 2y 2z 8 0. 2 2
Ta thấy C, D
x 2y 2z 8 0 thỏa.
Vậy x 2y 2z 8 0. Chọn A.
Phần 6. Bài toán quỹ tích
Câu 1. Trong không gian với hệ tọa độ Oxyz, cho điểm A2;1;0 và mặt cầu
S x y 2 z 2 2 : 1
2 8. Đường thẳng thay đổi qua A và tiếp xúc với S tại B.
Biết khi thay đổi thì B thuộc một đường cong cố định. Diện tích của hình phẳng giới
hạn bởi đường cong bằng A. 2 . B. 8 . C. 3 . D. 4 . 3
Lời giải. Mặt cầu S có tâm là I 0;1;2 và bán kính
R 2 2 IB.
Theo đề ta suy ra IB AB và B nằm trên đường tròn có
tâm H bán kính HB như hình vẽ. Ta tính được 2 2
IA 2 3 AB IA IB 2. Từ đó tính được IB.AB 2 6 HB . AI 3
Vậy diện tích hình phẳng được giới hạn bởi đường cong là 8 2 S HB . Chọn B. 3
Câu 2. Trong không gian với hệ tọa độ Oxyz, cho điểm A1;2;
3 và mặt phẳng P có
phương trình 2x 2y z 9 0. Đường thẳng đi qua A và vuông góc với mặt phẳng
Q: 3x 4y4z 5 0 cắt P tại điểm .
B Điểm M nằm trong mặt phẳng P sao cho M
luôn nhìn đoạn AB dưới một góc vuông và độ dài MB lớn nhất. Tính độ dài . MB A. 5 . B. 5. C. 41 . D. 41. 2 2 Lời giải.
Đường thẳng đi qua A và vuông góc với mặt phẳng Q là x1 y 2 z 3 d : . 3 4 4
Giao điểm của đường thẳng d và mặt phẳng P là B2;2; 1 .
Điểm M nằm trong mặt phẳng P sao cho M luôn nhìn AB dưới một góc vuông nên M
nằm trên đường tròn C là giao của mặt cầu đường kính AB với mặt phẳng P. Khi đó độ
dài MB lớn nhất khi và chỉ khi độ dài MB bằng đường kính của C. Gọi bán kính của đường
tròn C là r , trung điểm của AB là 1 I I ;0;1,d 3. ( ,( ) 2 I P 2 2 Ta có 2 2 AB 2 2 AB 5 IH r d r r
. Vậy độ dài MB lớn nhất là 5. I ,(P) 4 4 2
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho điểm M thuộc mặt cầu
S x 2 y 2 z 2 : 3 3
2 9 và ba điểm A1;0;0; B2;1; 3 ;C0;2; 3 . Biết rằng quỹ tích
các điểm M thỏa mãn 2 MA 2 .
MB MC 8 là đường tròn cố định, tính bán kính r đường tròn này.
A. r 3.
B. r 6.
C. r 3. D. r 6.
Lời giải. Mặt cầu S có tâm I 3;3;2, bán kính R 3. Gọi M x, y, z, khi đó 2 MA 2 .
MB MC 8 x 2 2 2
y z x
x y y 2 1 2 2 1 2 z 9 8
x 2 y 2 2 1
1 z 9 S.
Vậy M cũng thuộc mặt cầu S có tâm I 1;1;0, bán kính R 3.
Do đó M thuộc đường tròn giao tuyến của hai mặt cầu S và S có bán kính 2 2 II r R 6. Chọn B. 2
Câu 4. Trong không gian với hệ tọa độ Oxyz, cho các điểm Aa;0;0, B0;b;0, C 0;0;c với
a, b, c dương. Biết ,
A B, C di động trên các tia Ox, Oy, Oz sao cho a b c 2 . Biết rằng khi
a, b, c thay đổi thì quỹ tích tâm hình cầu ngoại tiếp tứ diện OABC thuộc mặt phẳng P cố
định. Khoảng cách từ M 2019;0;0 tới mặt phẳng P bằng A. 2018. B. 2018 . D. 2019 . C. 2020 . 3 3 3 Lời giải. Gọi a b
M là trung điểm AB M ; ;0
là tâm đường tròn ngoại tiếp O AB. 2 2 a x 2 Gọi b
d là đường thẳng qua M và vuông góc với mặt phẳng OAB Oxy d : y . 2 z t Gọi c
là mặt phẳng trung trực của đoạn OC
: z 0. 2
Khi đó tâm mặt cầu ngoại tiếp tứ diện OABC là giao điểm của d và có tọa độ là nghiệm a x 2 b của hệ y a b c 2
I ; ; . 2 2 2 z t c z 0. 2 Ta có a b c
a b c 2
x y z 1
x y z 1 0 . Điều này chứng tỏ I I I 2 2 2 2 2 I I I
tâm I của mặt cầu luôn thuộc mặt phẳng P: x y z 1 0. Khi đó 2019 1
d M P 2018 , . Chọn B. 3 3
Câu 5. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S x 2 y 2 z 2 : 1 1 2 9
và điểm M 1;3;
1 . Biết rằng các tiếp điểm của các tiếp tuyến kẻ từ M tới mặt cầu đã cho
luôn thuộc vào đường tròn C. Tìm tâm J và bán kính r của đường tròn C. A. 11 23 J 1; ; và 12 r . B. 41 11 23 J ; ; và 12 r . 25 25 25 25 25 25 5 C. 11 23 J 1; ; và 12 r . D. 11 73 J 1; ; và 12 r . 25 25 5 25 25 25
Lời giải. Mặt cầu S có tâm I 1;1;2 và bán kính R 3. Ta tính được 2 2 2
IM 0 4 3 5.
Gọi A là một tiếp điểm, ta tính được 2 2
MA IM IA 4. Gọi A ;
x y;z là một tiếp điểm.
Vì MA x 2 y 2 z 2 4 1 3 1 16.
Tọa độ của A là nghiệm của hệ x 2 1 y 2 3 z 2 1 16
4y 3z 1 0. x 2 1 y 2
1 z 22 9
Vậy A P 2 2
y z
r R d I P 12 : 4 3 1 0 ,
, J là hình chiếu vuông góc của I lên 5 P.
4y 3z 1 0 x 1 x 1
Tọa độ của J là nghiệm của hệ 11 y . Chọn C.
y 1 4t 25 z 2 3t 23 z 25
Câu 6. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P: x y z 3 0 và hai điểm A1;1;
1 , B3;3;
3 . Mặt cầu S đi qua hai điểm ,
A B và tiếp xúc với P tại điểm C.
Biết rằng C luôn thuộc một đường tròn cố định. Tính bán kính R của đường tròn đó. A. 2 11 R . B. 2 33 R . C. R 4. D. R 6. 3 3 x 1 t Lời giải. Ta có
AB 4;4;4, phương trình đường thẳng AB : y 1 t .
z 1t x 1t x 3 y 1t Gọi
I AB P
tọa độ I thỏa mãn t2
y 3, suy ra I 3,3, 3 . z 1 t z 3
x yz 3 0
Suy ra IA 2 3 và IB 6 3.
Theo đề IC tiếp xúc với mặt cầu S nên 2 IC . IA IB 36
IC 6. Điều này chứng tỏ
điểm C luôn cách điểm I một khoảng bằng 6 (không đổi). Chọn D. Câu 7. Trong không gian với hệ tọa độ
Oxyz, cho mặt phẳng P
m x m y mz m thay đổi. Hình chiếu vuông góc của điểm A1;0; 3 lên m : 1 2 2 1 0
mặt phẳng P luôn thuộc một đường tròn cố định có bán kính là m A. R 1. B. 1 R . C. 2 R . D. 3 R . 2 2 2
Lời giải. Ta có P
m x m y mz m m x y z x y m : 1 2 2 1 0 2 2 1 0.
Suy ra mặt phẳng P chứa giao tuyến của hai mặt phẳng : x y z 2 0 và m
: x2y 1 0.
x 2t 1
Suy ra d :y t P m .
z t1
Gọi H là hình chiếu của A trên đường thẳng d, ta tìm được H 1;1;2.
Gọi K là hình chiếu của A trên mặt phẳng P suy ra AK P AK KH A KH m m , vuông tại K
K nằm trên đường tròn đường kính AH.
Ta tính được AH 2
hình chiếu vuông góc của điểm A lên mặt phẳng P luôn thuộc m
một đường tròn cố định có bán kính 2 . Chọn C. 2
Câu 8. Trong không gian với hệ tọa độ Oxyz, cho điểm A2;11; 5 và mặt phẳng
P mx 2
m y 2 : 2 1 m
1 z 10 0. Biết khi m thay đổi thì tồn tại hai mặt cầu cố định
tiếp xúc với P và cùng đi qua .
A Tổng bán kính của hai mặt cầu đó là A. 4 2. B. 5 3. C. 6 3. D. 12 2.
Lời giải. Gọi I a,b,c, R lần lượt là tâm và bán kính của mặt cầu S tiếp xúc với P và đi qua . A 2ma 2 m 1 b 2 m 1 c10
Suy ra R d I P 1 2ma2c10 , . b c . 2 2 4 2 4 2
4m m 2m 1 m 2m 1 2 m 1 a 0 a 0
Vì S là mặt cầu cố định nên R không đổi I 0; ; b 5 . 2c10 0 c 5 1 b 25
Ta có d I,P IA
b5 4b 2 2
1 b 34b 225 0 2 b 9 I 0;25; 5 R 10 2
. Vậy tổng bán kính hai mặt cầu đó là 12 2. Chọn D. I 0;9; 5 R 2 2
Câu 9. Trong không gian với hệ tọa độ Oxyz, cho các điểm ,
A B,C (không trùng O) lần lượt
thay đổi trên các trục Ox,Oy,Oz và luôn thỏa mãn điều kiện: tỉ số giữa diện tích của tam giác
ABC và thể tích khối tứ diện OABC bằng 3 . Biết rằng mặt phẳng ABC luôn tiếp xúc với 2
một mặt cầu cố định, bán kính của mặt cầu đó bằng A. 3. B. 2. C. 4. D. 1. Lời giải.
Cách 1. Ta có S S 3 S ABC ABC , mà ABC 3 V 1
d O, ABC VOABC 2 OABC S d O ABC ABC . , 3
d O,ABC 2. Vậy mặt phẳng ABC luôn tiếp xúc mặt cầu tâm O có bán kính R 2 . Chọn B.
Cách 2. Giả sử Aa;0;0, B0; ;
b 0,C0;0;c (với abc 0 ). 1 V abc OABC 6 . : x y z ABC
1 ABC: bcx cay abz abc 0 a b c
Lại có AB a; ;0
b , AC a;0;c, AB, AC
bc,ca, ab
1 1 2 2 2 2 2 2 S AB AC b c c a a b ABC , . 2 2 Theo đề, ta có S abc A BC 3 2
d O,ABC 2. 2 2 2 2 2 2 VOABC 2
b c c a a b
Vậy mặt phẳng ABC luôn tiếp xúc với mặt cầu tâm O bán kính R 2. Chọn B. Câu 10. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S x
2 y
2 z 2 1 : cos sin sin sin cos
, với , là các góc thay đổi nhưng luôn 4
thỏa mãn , 0;2. Khi đó mặt cầu S thay đổi nhưng luôn tiếp xúc với hai mặt cầu cố
định S , S . Tính tổng thể thích của hai khối cầu S và S đó. 2 1 1 2 A. 16 . B. 21 . C. 14 . D. 67 . 8 3 3
Lời giải. Mặt cầu S có tâm I cossin ;sin sin ;cos và bán kính 1 R . 2 Ta thấy 2 2 2 2 2 2
OI cos sin sin sin cos 1 S , S có 1 2 cùng tâm . O 1 4
R IOR V R 1 3 1 1 2 3 6 14 V V . 1 2 3 4 R IO R V
R 3 9 3 2 2 2 2 3 2 Chọn C.
Câu 11. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A0;2;2 và B2;2;0. Gọi I 1;1; 1 và J 3;1;
1 là tâm của hai đường tròn nằm trên hai mặt phẳng khác nhau và có
chung một dây cung AB. Biết rằng luôn có một mặt cầu S đi qua cả hai đường tròn ấy.
Tính bán kính R của S. A. R 2 2.
B. R 2 6. C. 129 R . D. 219 R . 3 3
Lời giải. Ta tính được IA IB JA JB 11. Suy ra tâm H của mặt cầu S nằm trên
đường thẳng đi qua trung điểm M 1;0;
1 của AB và trung điểm N 2;1;0 của IJ.
Phương trình đường thằng x 1 y z 1 MN :
. Suy ra H 1 h;h;1h. 1 1 1
Ta tính được IA 1;1;
3 , IH h;h 1;2h
Vì mặt cầu S đi qua đường tròn tâm I và cung AB nên IH IA IH.IA 0
h h h 5 8 5 2 129 . 1 1 .1 2
.3 0 h H ; ; HA . R Chọn C. 3 3 3 3 3
Câu 12. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S x 2 y 2 z 2 : 1 1 3 9
và điểm M 2;3;
5 . Ba tia Mx, My, Mz thay đổi, đôi một vuông góc với nhau và cắt mặt cầu
S tại 3 điểm ,
A B,C. Biết rằng hình chiếu của M lên mỗi đường thẳng AB, BC,CA cùng
thuộc một mặt cầu bán kính .
R Khẳng định nào sau đây đúng? A. 3 R .
B. R 3. C. 5 R . D. 3 R . 2 2 4
Lời giải. Mặt cầu S có tâm I 1;1;
3 và bán kính r 3.
Gọi N là trung điểm của BC và ba điểm H, K, E lần lượt là hình chiếu của M trên
AB, AC, BC. Ta có M 2;3; 5 S.
Suy ra IN MBC
IN ME ME IE.
Chứng minh tương tự ta có MH IH và MK IK.
Suy ra H, K, E cùng thuộc mặt cầu đường kính IM 3. Vậy 3
R . Chọn A. 2
Câu 13. Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng x2 y 5 z 2 d : , 1 2 1 x2 y 1 z 2 d : và hai điểm A ;
a 0;0, A0;0;b. Gọi P là mặt phẳng chứa d và d , 1 2 1
H là giao điểm của đường thẳng AA và mặt phẳng P. Một đường thẳng thay đổi trên
P nhưng luôn đi qua H đồng thời cắt d và d lần lượt tại B, B . Hai đường thẳng
AB, AB cắt nhau tại điểm M. Biết điểm M luôn luôn thuộc một đường thẳng cố định có vé-
tơ chỉ phương u 15;10;
1 (tham khảo hình vẽ). Tính T a . b A. T 8. B. T 9. C. T 9. D. T 6.
Lời giải. Gọi I d d , ta tìm được I 1;3; 1 .
Gọi mp mpd,
A ,mp mpd , A. Ta thấy IM. Vì điểm M luôn luôn thuộc
một đường thẳng cố định có vé-tơ chỉ phương u 15;10;
1 nên u là một véc-tơ chỉ phương IM.
mp chứa d và IM nên ta viết được phương trình : x 2y 5z 10 0.
mp chứa d và IM nên ta viết được phương trình : 3x 4y 5z 20 0.
Vì A A2;0;0
a 2, A A0;0;4 b 4.
Vậy T a b 6. Chọn D.
Câu 14. Trong không gian với hệ tọa độ Oxyz, cho hai điểm M 1;2; 3 , N 3;4; 5 và mặt phẳng
P: x 2y 3z 14 0. Gọi là đường thẳng thay đổi nằm trong mặt phẳng P, các điểm
H, K lần lượt là hình chiếu vuông góc của M , N trên .
Biết rằng khi MH NK thì trung
điểm của HK luôn thuộc một đường thẳng d cố định, phương trình của d là x 1 x t x t x t A.
y 132t .
B. y 132t.
C. y 13 2t.
D. y 132t.
z 4 t
z 4 t
z 4 t
z 4t Lời giải.
Gọi I, A lần lượt là trung điểm của MN và HK. Ta chứng minh được AI MN AI luôn
thuộc mặt phẳng trung trực của đoạn thẳng MN
d là giao tuyến của hai mặt
phẳng P và .
MN 2;2;2, I 2;3;4. Phương trình mặt phẳng : x y z 9 0.
: 9 0 x t x y z d :
y 132t t . Chọn B.
P: x2y 3z14 0
z 4t
Câu 15. Trong không gian với hệ tọa độ Oxyz, cho điểm A1;1;0. Giả sử B,C là các điểm thay
đổi nằm trên các trục Ox và Oz. Gọi M là trung điểm của AC. Biết rằng khi B và C thay
đổi nhưng nằm trên các trục Ox và Oz thì hình chiếu vuông góc H của M trên đường thẳng
AB luôn nằm trên một đường tròn cố định. Tính bán kính của đường tròn đó? A. 1 R . B. 1 R . C. 2 R . D. 2 R . 4 2 2 4 Lời giải.
Gọi N là trung điểm của OA 2 NA . 2
MN ABC Ta có
NH A .B Suy ra H nằm trên đường tròn C đường kính NA
MH AB
bán kính đường tròn C là 2 R . Chọn D. 4
Câu 16. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng x y 1 z 1 d : và điểm 2 1 1 A1;1;
1 . Hai điểm B,C di động trên đường thẳng d sao cho mặt phẳng OAB vuông góc với
mặt phẳng OAC. Gọi điểm B là hình chiếu vuông góc của điểm B lên đường thẳng AC.
Biết rằng quỹ tích các điểm B là đường tròn cố định, tính bán kính r đường tròn này. A. 15 r . B. 3 5 r . C. 70 r . D. 3 5 r . 5 5 10 10 Lời giải.
Ta có u là véc tơ chỉ phương của đường thẳng d. Ta thấy . OA u OAd d 0 . d 2; 1; 1
Lại có H 0;1;
1 d và OH.u 0 nên H là hình chiếu của O lên đường thẳng d. d
OH.OA 0
OH OA
OA OBC
OB OA
OB OAC 1 .
Vì B là hình chiếu vuông góc của B lên AC
AB BB 2. Từ 1 ,2
OB AB
B nằm trên mặt cầu S đường kính . OA 2 2 2
Phương trình mặt cầu S : 1 1 1 3 x y . z 2 2 2 4 Mà B ,
A d:2x 5y z 6 0 nên B ' thuộc đường tròn C , với CS , A d . Từ đó tính được 3 5 r . Chọn D. 10
Câu 17. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S 2 2
: x y z 2 3 8 và hai điểm A4;4; 3 , B1;1;
1 . Gọi C là tập hợp các điểm M S để cho MA2MB đạt giá trị nhỏ
nhất. Biết rằng C là một đường tròn bán kính . R Tính . R A. 7. B. 6. C. 2 2. D. 3.
Lời giải. Mặt cầu S có tâm I 0;0;
3 và bán kính R 4 2.
Gọi C trên đoạn IA thỏa mãn 1 IC IA C1;1; 3 . 4 Xét IA M và IMC , ta có I chung IA M ∽ IMC MA 2MC. IA IM 2 IM IC
Từ đó P MA2MB 2 MC MB 0.
Dấu " " xảy ra khi M nằm trên mặt phẳng trung trực của BC.
Mặt phẳng trung trực P của BC là P: z 2.
Khi đó M nằm trên đường tròn có bán kính R2 2
R d I,P2 81 7. ChọnA.
Câu 18. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A2;0;0, B0;4;0,C0;0;6, điểm
M thay đổi trên mặt phẳng ABC, N là điểm trên tia OM sao cho OM.ON 12. Biết khi
M thay đổi thì điểm N luôn nằm trên mặt cầu cố định. Tính bán kính mặt cầu đó A. 7 . B. 3 2. C. 2 3. D. 5 . 2 2
Lời giải. Phương trình mặt phẳng ABC: 6x 3y 2z 12.
Giả sử N x y z 2 2 2
; ; ON x y z . Vì N là điểm trên tia OM và thỏa OM.ON 12, suy ra 12 12 12
OM OM ONOM .ON 2 2 2 2 ON ON
x y z 12x 12y 12 ; ; z N . 2 2 2 2 2 2 2 2 2
x y z x y z x y z 2 Vì 6.12x 3.12y 2.12z N ABC x 2 3 y
z 2 49 12 3 1 . 2 2 2 2 2 2 2 2 2
x y z
x y z
x y z 2 4
Vậy N thuộc mặt cầu cố định bán kính 7
R . Chọn A. 2
Câu 19. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S có tâm O ( O là gốc tọa độ) 1
bán kính là 3 và mặt cầu S có tâm O2;3;6 và bán kính bằng 4. Biết tập hợp các điểm 2
A trong không gian mà độ dài tiếp tuyến kẻ từ A tới S và S bằng nhau là một mặt 2 1
phẳng (còn gọi là mặt phẳng đẳng phương) .Viết phương trình mặt mặt phẳng đó . A. x y z x y z x y z x y z 1. B. 1. C. 1. D. 1. 2 3 6 9 2 3 9 6 3 3 6 9 Lời giải.
Cách 1. Mặt phẳng đẳng phương là mặt phẳng tập hợp tất
cả các điểm có cùng phương tích với hai mặt cầu không đồng
tâm. Và mặt đẳng phương vuông góc với trục nối hai tâm của mặt cầu .
Gọi P là mặt phẳng đẳng phương của S và S P 2 1
nhận OO2,3,6 là vectơ pháp tuyến n OO . P 2,3,6
Mặt khác mặt phẳng đẳng phương P của S và S đi 2 1
qua một điểm M thuộc OO có cùng phương tích với hai mặt cầu. x 2t
Phương trình đường thẳng OO
y 3t
M 2t;3t;6t. z 6t Mà 2 2 2 2 P P MO R MO R
M /O,R
M /O ,R
t2 t2 t2 t 2 t 2 t 2 18 36 54 108 2 3 6 3 2 2 3 3 6 6 16 t M ; ; . 49 49 49 49
Vậy : : 2 3 6 18 0 x y z P x y z 1. 9 6 3
Cách 2. Gọi A ;
x y; z thỏa mãn yêu cầu bài toán.
Gọi H, K lần lượt là tiếp điểm các tiếp tuyến kẻ từ A tới mặt cầu tâm O,O . Khi đó ta có 2 2
AH AK AO 3 AO 16 . 2 2 2 2 2
AO AO 13 0 x y z x22 x 2
3 x62 13 0 4 6 12 36 0 x y z x y z
1. Chọn C. 9 6 3
Câu 20. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P: 2x 2y z 4 0 và các
điểm A2;1;2; B3;2;2. Điểm M thuộc mặt phẳng P sao cho các đường thẳng , MA MB
luôn tạo với mặt phẳng P các góc bằng nhau. Biết rằng điểm M luôn thuộc đường tròn C
cố định. Tìm tọa độ tâm của đường tròn C. A. 10 14 ;3; . B. 17 17 17 ; ; . C. 74 97 62 ; ; . D. 32 49 2 ; ; . 3 3 21 21 21 27 27 27 9 9 9 Lời giải.
Gọi A, B lần lượt là hình chiếu vuông góc của ,
A B trên P. d Khi đó ta có AMA MA AA
BMB . Suy ra A MA ∽ B MB A ;P 2 MA 2 . MB MB BB
dB ;P Gọi M ;
x y; z. Khi đó ta có
MA MB x 2 y 2 z 2 x 2 y 2 z 2 2 2 1 2 2 3 2 2 . 2 2 2 20
x y z
x 6y 4z 59 0 S. 3
Suy ra M thuộc đường tròn giao tuyến của P với mặt cầu S.Mặt cầu S có tâm 10 I ;3;2. 3
Tâm H của đường tròn C là hình chiếu vuông góc của I trên P. Từ đó ta tìm được 74 97 62 H ; ; . Chọn C. 27 27 27
---------- HẾT ----------
Document Outline
- DE
- DAP AN 1
- DAP AN 2




