












































Preview text:
MẠC LÊ CHÍ ĐẠO KẾT NỐI TRI THỨC VỚI CUỘC SỐNG TO T ÁN O 9
BÀI TẬP TRẮC NGHIỆM TẬP MỘT B C y x = − b 2a O A D x ∆ − 4a a > 0 H
TÀI LIỆU LƯU HÀNH NỘI BỘ Muåc luåc Phần I ĐẠI SỐ Chương 1.
CĂN BẬC HAI – CĂN BẬC BA 2 Bài 1. CĂN BẬC HAI 2 B
BÀI TẬP TRẮC NGHIỆM. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Bài 2. CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC 4 B
BÀI TẬP TRẮC NGHIỆM. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Bài 3. LIÊN HỆ GIỮA PHÉP NHÂN – CHIA VÀ PHÉP KHAI PHƯƠNG 6 B
BÀI TẬP TRẮC NGHIỆM. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .6
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
Bài 4. BIẾN ĐỔI ĐƠN GIẢN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI 10 B
BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
Bài 5. RÚT GỌN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI 14 B
BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 Bài 6. CĂN BẬC BA 18 B
BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20 Chương 2. HÀM SỐ BẬC NHẤT 21
Bài 1. NHẮC LẠI VÀ BỔ SUNG CÁC KHÁI NIỆM VỀ HÀM SỐ 21 B
BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 Bài 2. HÀM SỐ BẬC NHẤT 24 B
BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25 Mục lục
Bài 3. ĐỒ THỊ HÀM SỐ BẬC NHẤT 27 B
BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
Bài 4. ĐƯỜNG THẲNG SONG SONG VÀ ĐƯỜNG THẲNG CẮT NHAU 31 B
BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
Bài 5. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG 35 B
BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37 Phần II HÌNH HỌC Chương 1.
HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG 39
Bài 1. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG 39 B
BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
Bài 2. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN 46 B
BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
Bài 3. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG 49 B
BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
Bài 4. ỨNG DỤNG THỰC TẾ CÁC TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN 52 B
BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54 Chương 2. ĐƯỜNG TRÒN 55
Bài 1. SỰ XÁC ĐỊNH ĐƯỜNG TRÒN. TÍNH CHẤT ĐỐI XỨNG CỦA ĐƯỜNG TRÒN 55 B
BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59 ii
BÀI TẬP TRẮC NGHIỆM TOÁN 9 Mục lục
Bài 2. ĐƯỜNG KÍNH VÀ DÂY CỦA ĐƯỜNG TRÒN 60 B
BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
Bài 3. DẤU HIỆU NHẬN BIẾT TIẾP TUYẾN CỦA ĐƯỜNG TRÒN 63 B
BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
Bài 4. VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN 67 B
BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
Bài 5. TÍNH CHẤT CỦA HAI TIẾP TUYẾN CẮT NHAU 70 B
BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
Bài 6. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG TRÒN 73 B
BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75 GV: Mạc Lê Chí Đạo – 0946820895 iii Mục lục iv
BÀI TẬP TRẮC NGHIỆM TOÁN 9 I PHẦN ĐẠI SỐ Chûúng 1
CĂN BẬC HAI – CĂN BẬC BA
CĂN BẬC HAI – CĂN BẬC BA §1. CĂN BẬC HAI A B
BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho số thực a > 0. Số nào sau đây là căn bậc hai số học của a? √ √ √ √ A. a. B. − a. C. 2a. D. 2 a.
Câu 2. Cho số thực a > 0. Căn bậc hai số học của a là x khi và chỉ khi √ √ A. x = a. B. x = a. C. a2 = x và x ≥ 0. D. x2 = a và x ≥ 0.
Câu 3. Số nào sau đây là căn bậc hai số học của số a = 0,36? A. −0,6. B. 0,6. C. 0,9. D. 0,18.
Câu 4. Số nào sau đây là căn bậc hai số học của số a = 2,25? A. −1,5 và 1,5. B. 1,25. C. 1,5. D. −1,5.
Câu 5. Khẳng định nào sau đây đúng? √ √ A. A2 = A khi A < 0. B. A2 = −A khi A ≥ 0. √ √ √ √ C. A < B ⇔ 0 ≤ A < B. D. A > B ⇔ A < B.
Câu 6. Khẳng định nào sau đây sai? √ √ A. A2 = −A khi A < 0. B. A2 = A khi A ≥ 0. √ √ C. A < B ⇔ 0 ≤ A < B.
D. A > B ⇔ 0 ≤ A < B. √
Câu 7. So sánh hai số 2 và 1 + 2. √ √ √ A. 2 ≥ 1 + 2. B. 2 = 1 + 2. C. 2 < 1 + 2. D. Không thể so sánh. √
Câu 8. So sánh hai số 5 và 50 − 2. √ √ A. 5 > 50 − 2. B. 5 = 50 − 2. √ C. 5 < 50 − 2.
D. Chưa đủ điều kiện để so sánh. √ Câu 9. Biểu thức x − 3 có nghĩa khi A. x < 3. B. x < 0. C. x ≥ 0. D. x ≥ 3. √ Câu 10. Biểu thức x − 3 có nghĩa khi A. x < 3. B. x < 0. C. x ≥ 0. D. x ≥ 3. √ Câu 11. Biểu thức 10 + 100x có nghĩa khi 1 1 A. x < 10. B. x ≥ − . C. x ≥ . D. x ≥ 10. 10 10 2 √ 9 … 16 √
Câu 12. Giá trị của biểu thức 25 − + 169 bằng 5 2 81 A. 12. B. 13. C. 14. D. 15. 2
BÀI TẬP TRẮC NGHIỆM TOÁN 9 1. CĂN BẬC HAI 2 √ 26 … 81 √
Câu 13. Giá trị của biểu thức 49 + − 625 bằng 7 3 169 A. −17. B. 15. C. 18. D. 17. √
Câu 14. Tìm các số không âm thỏa mãn x ≥ 3. A. x ≥ 9. B. x < 9. C. x > 9. D. x ≤ 9. √
Câu 15. Tìm các số không âm thỏa mãn 5x < 10. A. 0 ≤ x < 20. B. x < 20. C. x > 0. D. x < 2. √
Câu 16. Tìm giá trị của x không âm biết 2 x − 30 = 0. A. x = −15. B. x = 225. C. x = 25. D. x = 15. √
Câu 17. Tìm giá trị của x không âm biết 5 2x − 125 = 0. 25 625 A. x = . B. x = 125. C. x = . D. x = 25. 2 2 … √ … √ Ä ä2 Ä ä2
Câu 18. Giá trị của biểu thức 2 − 3 + 1 − 3 bằng √ A. 3. B. 1. C. 2 3. D. 2. … √ … √ Ä ä2 Ä ä2
Câu 19. Rút gọn biểu thức sau 5 − 11 + 3 − 11 . √ √ A. 2 + 2 11. B. 8. C. 2. D. 2 11. » »
Câu 20. Giá trị của biểu thức 6 (−2,5)2 − 8 (−0,5)2 bằng A. 15. B. −11. C. 11. D. −13. Å 8 ã2 »
Câu 21. Giá trị của biểu thức 9 − + (−0,8)2 bằng 3 A. 24,64. B. 32. C. −24,8. D. 24,8. BẢNG ĐÁP ÁN 1. A 2. D 3. B 4. C 5. C 6. D 7. C 8. C 9. D 10. D 11. B 12. B 13. A 14. A 15. A 16. B 17. C 18. B 19. C 20. C 21. D GV: Mạc Lê Chí Đạo – 0946820895 3
Chương 1. CĂN BẬC HAI – CĂN BẬC BA
§2. CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC A B
BÀI TẬP TRẮC NGHIỆM √ √ p p
Câu 1. Giá trị của biểu thức 15 + 6 6 − 15 − 6 6 bằng √ √ A. 2 6. B. 6. C. 6. D. 12. √ √ p p
Câu 2. Giá trị của biểu thức 19 + 8 3 + 19 − 8 3 bằng √ √ A. 2 3. B. 8 + 2 3. C. 6. D. 8. √
Câu 3. Điều kiện xác định của 5 − 3x là 5 5 3 3 A. x ≤ . B. x ≥ . C. x ≥ . D. x ≤ . 3 3 5 5 √
Câu 4. Điều kiện xác định của 125 − 5x là A. x ≤ 15. B. x ≥ 25. C. x ≤ 25. D. x ≥ 0. √
Câu 5. Rút gọn biểu thức A = 36a2 + 3a với a > 0. A. −9a. B. −3a. C. 3a. D. 9a. √
Câu 6. Rút gọn biểu thức A = 144a2 − 9a với a > 0. A. −9a. B. −3a. C. 3a. D. 9a. … −2 Câu 7. Biểu thức có nghĩa khi 3x − 1 1 1 1 1 A. x < . B. x ≤ . C. x ≥ . D. x > . 3 3 3 3 (−5)2 Câu 8. Biểu thức có nghĩa khi 6 − 3x A. x < 2. B. x > 2. C. x ≤ 2. D. x ≥ 2. √ √
Câu 9. Rút gọn biểu thức a2 + 8a + 16 +
a2 − 8a + 16 với −4 ≤ a ≤ 4. A. 2a. B. 8. C. −8. D. −2a. √ √ 3 3
Câu 10. Rút gọn biểu thức 4a2 + 12a + 9 + 4a2 − 12a + 9 với − ≤ x ≤ . 2 2 A. −4a. B. 4a. C. −6. D. 6. √ √
Câu 11. Tìm x thỏa mãn phương trình x2 − x − 6 = x − 3 A. x = 2. B. x = 4. C. x = 1. D. x = 3. √ √
Câu 12. Tìm x thỏa mãn phương trình 2x2 − 3x = 3x − 4 A. x = 2. B. x = 4. C. x = 1. D. x = 1; x = 2. √
Câu 13. Nghiệm của phương trình 2x2 + 2 = 3x − 1 là A. x = 2. B. x = 5. C. x = 1. D. x = 3. √
Câu 14. Nghiệm của phương trình 2x2 + 31 = x + 4 là A. x = 2. B. x = 5. C. x = 3. D. x = 3; x = 5. √
Câu 15. Nghiệm của phương trình x2 + 6x + 9 = 4 − x là 1 1 A. x = 2. B. x = . C. x = . D. x = 3. 4 2 4
BÀI TẬP TRẮC NGHIỆM TOÁN 9
2. CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC √
Câu 16. Số nghiệm của phương trình 4x2 + 4x + 1 = 3 − 4x là A. 0. B. 4. C. 1. D. 2. √x2 −6x+9
Câu 17. Rút gọn biểu thức với x < 3. x − 3 A. −1. B. 1. C. 2. D. −2. √x2 +10x+25
Câu 18. Rút gọn biểu thức với x < −5. −5 − x A. −1. B. 1. C. 2. D. −2. √ √
Câu 19. Giá trị nhỏ nhất của biểu thức A = m2 + 2m + 1 + m2 − 8m + 16 là A. 2. B. 9. C. 5. D. 10. √ √
Câu 20. Giá trị nhỏ nhất của biểu thức B = 4a2 − 4a + 1 + 4a2 − 12a + 9 là A. 2. B. 1. C. 4. D. 10. BẢNG ĐÁP ÁN 1. A 2. D 3. A 4. C 5. D 6. C 7. A 8. A 9. B 10. D 11. D 12. A 13. C 14. D 15. C 16. C 17. A 18. B 19. C 20. A GV: Mạc Lê Chí Đạo – 0946820895 5
Chương 1. CĂN BẬC HAI – CĂN BẬC BA
§3. LIÊN HỆ GIỮA PHÉP NHÂN – CHIA VÀ PHÉP KHAI PHƯƠNG A B
BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho a là số không âm, b là số dương. Khẳng định nào sau đây là đúng? √ √ √ … a a … a a … a − a … a a A. = . B. = √ . C. = √ . D. = √ . b b b b b b b b
Câu 2. Cho a là số không âm, b, c là số dương. Khẳng định nào sau đây là đúng? √ √ √ √ … a a ab … ab a ab A. = √ . B. √ = . C. √ = √ . D. Cả A, B đều đúng. b b c c bc c
Câu 3. Cho a, b là hai số không âm. Khẳng định nào sau đây là đúng? √ √ √ √ √ √ √ √ √ √ a A. ab = a · b. B. a · b = b · a. C. a · b = ab. D. ab = √ . b
Câu 4. Khẳng định nào sau đây là đúng? √ √ √ √ √ 2018 A. 2018 + 2019 = 2018 + 2019. B. 2018 · 2019 = √ . 2019 √ √ √ √ 2018 C. 2018 · 2019 = 2018 · 2019. D. 2018 · 2019 = √ . 2019 √ √
Câu 5. Kết quả của phép tính 2,5 · 14,4 bằng A. 36. B. 6. C. 18. D. 9. √ √
Câu 6. Kết quả của phép tính 1,25 · 51,2 bằng A. 32. B. 16. C. 64. D. 8. … 81
Câu 7. Kết quả của phép tính bằng 169 9 9 3 13 A. . B. . C. . D. . 13 169 13 9 … 1, 21
Câu 8. Kết quả của phép tính bằng 576 1, 1 11 11 240 A. . B. . C. . D. . 240 24 240 11 … −999
Câu 9. Kết quả của phép tính là 111 A. 9. B. −9. C. −3. D. Không tồn tại. … 625
Câu 10. Kết quả của phép tính là −729 25 25 5 A. . B. − . C. − . D. Không tồn tại. 27 27 7 » Câu 11. Phép tính
(−5)2 · 72 có kết quả là A. 35. B. 5. C. −35. D. Không tồn tại. » Câu 12. Phép tính
122 · (−11)2 có kết quả là A. −33. B. −132. C. 132. D. Không tồn tại. 6
BÀI TẬP TRẮC NGHIỆM TOÁN 9
3. LIÊN HỆ GIỮA PHÉP NHÂN – CHIA VÀ PHÉP KHAI PHƯƠNG » 1
Câu 13. Rút gọn biểu thức a4 (2a − 1)2 với a ≥ ta được 2 A. a · (2a − 1). B. (1 − 2a) · a2. C. (2a − 1) · a2. D. (1 − 2a) · a. » 3
Câu 14. Rút gọn biểu thức
9 (−a)2 · (3 − 4a)6 với a ≥ ta được 4 A. 3a · (4a − 3)3. B. −3a · (4a − 3)3. C. 3a · (4a − 3). D. 3a · (3 − 4a)3. » 3
Câu 15. Rút gọn biểu thức
a2 · (2a − 3)2 với 0 ≤ a < ta được 2 A. a · (2a − 3). B. a2 · (3 − 2a). C. a2 · (2a − 3). D. a · (3 − 2a). »
Câu 16. Rút gọn biểu thức
0,9 · 0,1 · (3 − x)2 với x > 3 ta được A. 0,3 · (x − 3). B. 0,3 · (3 − x). C. 0,9 · (x − 3). D. 0,1 · (x − 3). √ √ √
Câu 17. Giá trị của biểu thức x − 2 · x + 2 khi x = 29 là A. 29. B. 5. C. 10. D. 25. √ √ √
Câu 18. Giá trị của biểu thức 5x + 3 · 5x − 3 khi x = 3,6 là A. 3, 6. B. 3. C. 81. D. 9. a − b ab
Câu 19. Rút gọn biểu thức E = √ ·
với 0 < a < b ta được 2 a (a − b)2 √ √ √ a b b √ A. . B. . C. − . D. a b. 2 2 2 2 (a + b) … b
Câu 20. Rút gọn biểu thức D = √ · với a, b > 0 ta được b a2 + 2ab + b2 √b √ A. a + b. B. 2. C. . D. 2 b. 2 a4
Câu 21. Rút gọn biểu thức với b ̸= 0 ta được b2 a2 a a2 a2 A. . B. . C. − . D. . b b b |b| 3m 64n2
Câu 22. Rút gọn biểu thức ·
với m > 0; n < 0 ta được 8n 9m2 m m A. −1. B. 1. C. . D. − . n n … 9
Câu 23. Rút gọn biểu thức 4a4b2 · với a · b ̸= 0 ta được a8b4 a2 A. . B. 12. C. 6. D. 36. b a2 … 121
Câu 24. Rút gọn biểu thức · với a · b ̸= 0 ta được 11 a4b10 1 1 11 A. . B. . C. . D. b5. b5 b5 b5 √x3 +2x2
Câu 25. Rút gọn biểu thức √ với x > 0 ta được x + 2 √ √ A. x. B. −x. C. x. D. x + 2. GV: Mạc Lê Chí Đạo – 0946820895 7
Chương 1. CĂN BẬC HAI – CĂN BẬC BA √9x5+33x4
Câu 26. Rút gọn biểu thức √ với x > 0 ta được 3x + 11 √ √ A. x2. B. x4. C. 3x2. D. 3x + 11. √x2 −5x
Câu 27. Với x > 5, cho biểu thức A = √
và B = x. Có bao nhiêu giá trị của x để A = B? x − 5 A. 1. B. 2. C. 0. D. Vô số. √x2 +6x
Câu 28. Với x > 0, cho biểu thức A = √
và B = 2x. Có bao nhiêu giá trị của x để A = B? x + 6 A. 1. B. 2. C. 0. D. Vô số. √ x − xy
Câu 29. Với x, y ≥ 0; x ̸= y, rút gọn biểu thức A = ta được x − y √ √ √ x 1 y x A. √ √ . B. √ √ . C. √ √ . D. √ √ . x − y x − y x − y x + y √ 3x − 3xy
Câu 30. Với x, y ≥ 0; 3x ̸= y, rút gọn biểu thức B = ta được 3x − y √ √ √ 3x 1 3x 3 x A. √ √ . B. √ √ . C. √ √ . D. √ √ . 3x − y 3 x − y 3x + y 3 x + y √ √ √ √ Ä ä 3
Câu 31. Giá trị của biểu thức 12 + 2 27 · − 150 bằng 2 √ √ √ √ A. 12 − 5 6. B. 12 + 5 6. C. 12 + 6. D. 12 − 6. √ √ √ √
Câu 32. Giá trị của biểu thức 252 − 700 + 1008 − 448 bằng √ √ √ A. 7. B. 0. C. 4 7. D. 5 7. √ √ a − b a3 + b3
Câu 33. Với a ≥ 0, b ≥ 0, a ̸= b, rút gọn biểu thức √ √ − ta được a − b a − b √ √ √ ab ab − 2b 2b ab − 2a A. √ √ . B. √ √ . C. √ √ . D. √ √ . a − b a − b a − b a − b √ √ 2a + 3b 8a3 − 27b3
Câu 34. Với a ≥ 0, b ≥ 0, 2a ̸= 3b, rút gọn biểu thức √ √ + ta được 2a + 3b 3b − 2a √ √ √ √ − 6ab 6ab − 6ab 6ab A. √ √ . B. √ √ . C. √ √ . D. √ √ . 2a + 3b 2a + 3b 2a − 3b 2a − 3b x − y √ √
Câu 35. Kết quả thu gọn của P = √ √ + x −
y với x, y > 0; x ̸= y là x − y √ √ √ √ A. −2 x. B. 2 y. C. 2 x. D. −2 y. 9x − 7 √
Câu 36. Khẳng định nào sau đây đúng về nghiệm x0 của phương trình √ = 7x + 5? 7x + 5 A. x0 < 5. B. x0 > 8. C. x0 > 9. D. 5 < x0 < 7. 8 + 3x √
Câu 37. Khẳng định nào sau đây đúng về nghiệm x0 (nếu có) của phương trình √ = 2x − 5? 2x − 5 A. x0 > 3. B. x0 = −13. C. x0 ∈ ∅. D. x0 = 13. √ √ 1 √
Câu 38. Nghiệm của phương trình 4x − 20 + x − 5 − 9x − 45 = 4 là 3 A. x = −9. B. x = 5. C. x = 8. D. x = 9. 8
BÀI TẬP TRẮC NGHIỆM TOÁN 9
3. LIÊN HỆ GIỮA PHÉP NHÂN – CHIA VÀ PHÉP KHAI PHƯƠNG 3 √ 1 √ … x − 1
Câu 39. Nghiệm của phương trình x − 1 − 9x − 9 + 16 = 12 là 2 2 64 A. x = 37. B. x = 7. C. x = 35. D. x = 5. √ √
Câu 40. Giá trị của x thỏa mãn 4x2 − 9 − 2x − 3 = 0 là 2 5 1 3 A. . B. . C. . D. . 3 2 2 2 BẢNG ĐÁP ÁN 1. B 2. D 3. C 4. C 5. B 6. D 7. A 8. C 9. D 10. D 11. A 12. C 13. C 14. A 15. D 16. A 17. B 18. D 19. C 20. B 21. D 22. A 23. B 24. A 25. A 26. C 27. C 28. A 29. D 30. C 31. A 32. B 33. B 34. A 35. C 36. D 37. C 38. D 39. A 40. D GV: Mạc Lê Chí Đạo – 0946820895 9
Chương 1. CĂN BẬC HAI – CĂN BẬC BA
§4. BIẾN ĐỔI ĐƠN GIẢN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI A B
BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho các biểu thức A, B mà A · B ≥ 0; B ̸= 0, khẳng định nào sau đây đúng? √ √ √ … A AB … A AB … A A … A AB A. = . B. = − . C. = . D. = √ . B B B B B B B B
Câu 2. Cho các biểu thức A, B,C với A, B,C > 0, khẳng định nào sau đây đúng? √ √ √ … A ABC … A ABC … A ABC … A ABC A. = . B. = − . C. = . D. = √ . BC B BC BC BC BC BC BC
Câu 3. Cho các biểu thức A < 0; B ≥ 0, khẳng định nào sau đây là đúng? √ √ √ √ √ √ √ √ A. A2B = A B. B. A2B = −A B. C. A2B = −B A. D. A2B = B A.
Câu 4. Cho các biểu thức A, B ≥ 0, khẳng định nào sau đây là đúng? √ √ √ √ √ √ √ √ A. A2B = A B. B. B2A = A B. C. A2B = B A. D. B2A = −B A. » Câu 5. Đưa thừa số
81 (2 − y)4 ra ngoài dấu căn ta được A. 9 (2 − y). B. 81 (2 − y)2. C. 9 (2 − y)2. D. −9 (2 − y)2. » Câu 6. Đưa thừa số
144 (3 + 2a)4 ra ngoài dấu căn ta được A. 12 (3 + 2a)4. B. 144 (3 + 2a)2. C. −12 (3 + 2a)2. D. 12 (3 + 2a)2. √
Câu 7. Đưa thừa số 5y y (y ≥ 0) vào trong dấu căn ta được √ A. p5y2. B. p25y3. C. p5y3. D. p25y y. √
Câu 8. Đưa thừa số −7x 2xy (x, y ≥ 0) vào trong dấu căn ta được A. p98x3y. B. −p98x3y. C. −p14x3y. D. p49x3y. … 35 Câu 9. Đưa thừa số x −
(x < 0) vào trong dấu căn ta được x √ √ √ √ A. −35x. B. − −35x. C. 35x. D. 35x2. … 12 Câu 10. Đưa thừa số 5x −
(x < 0) vào trong dấu căn ta được x3 … 300 … 300 … 300 … 60 A. . B. − . C. − − . D. − − . x x x x √ √
Câu 11. So sánh hai số 5 3 và 4 5. √ √ √ √ √ √ √ √ A. 5 3 > 4 5. B. 5 3 = 4 5. C. 5 3 ≥ 4 5. D. 5 3 < 4 5. √ √
Câu 12. So sánh hai số 9 7 và 8 8. √ √ √ √ √ √ √ √ A. 9 7 < 8 8. B. 9 7 = 8 8. C. 9 7 ≥ 8 8. D. 9 7 > 8 8. 4
Câu 13. Khử mẫu biểu thức sau xy với x, y > 0 ta được x2y2 √ √ A. 4. B. −xy. C. 2. D. 2. −9
Câu 14. Khử mẫu biểu thức sau −2xy
với x < 0; y > 0 ta được x3y2 10
BÀI TẬP TRẮC NGHIỆM TOÁN 9
4. BIẾN ĐỔI ĐƠN GIẢN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI √ √ √ √ A. −6 x. B. −6 −x. C. 6 x. D. −6 x. 3
Câu 15. Khử mẫu biểu thức sau −xy
với x < 0; y < 0 ta được xy √ √ √ √ A. xy. B. −xy. C. 3xy. D. − 3xy. 1 1 a
Câu 16. Sau khi rút gọn biểu thức √ +
√ ta được phân số tối giản (a, b ∈ Z). Khi đó 5 + 3 2 5 − 3 2 b giá trị 2a bằng A. 20. B. 10. C. 7. D. 14. 2 2 a
Câu 17. Sau khi rút gọn biểu thức √ +
√ ta được phân số tối giản (a, b ∈ Z). Khi đó 7 + 3 5 7 − 3 5 b giá trị a + b bằng A. 28. B. 7. C. 8. D. 14. √ √ √ √
Câu 18. Rút gọn biểu thức 32x + 50x − 2 8x +
18x với x ≥ 0 ta được kết quả là √ √ √ √ A. 8 2x. B. 10 2x. C. 20 x. D. 2 10x. √ √ √ √
Câu 19. Rút gọn biểu thức 27x − 48x + 4 75x +
243x với x ≥ 0 ta được kết quả là √ √ √ A. 403x. B. 28 3x. C. 39 x. D. 28 x. √ √ √ √
Câu 20. Rút gọn biểu thức 5 a − 4b 25a3 + 5a 16ab2 − 9a với a, b ≥ 0 ta được kết quả là √ √ √ √ A. 2 2a. B. 4 a. C. 8 a. D. 2 a. √ √ √
Câu 21. Rút gọn biểu thức 7 x + 11y 36x5 − 2x2p16xy2 − 25x với x, y ≥ 0 ta được kết quả là √ √ √ √ √ √ √ √ A. 2 x + 58x2y x. B. 2 x − 58x2y x. C. 2 x + 56x2y x. D. 12 x + 58x2y x. … 16a … a … 4a
Câu 22. Giá trị của biểu thức 2 − 3 − 6 bằng 3 27 75 √ √ √ √ 23 3a 3a 23 a 3 3a A. . B. . C. . D. . 15 15 15 15 √ … a … 4 … 4a
Câu 23. Rút gọn biểu thức 5 a + 6 − a + 5
với a > 0 ta được kết quả là 4 a 25 √ √ √ √ A. 12 a. B. 8 a. C. 6 a. D. 10 a. 2a
Câu 24. Trục căn thức ở mẫu biểu thức
√ với a ≥ 0; a ̸= 4 ta được 2 − a √ √ √ √ −2a a + 4a 2a a − 4a 2a a + 4a 2a a + 4a A. . B. . C. . D. − . 4 − a 4 − a 4 − a 4 − a 3
Câu 25. Trục căn thức ở mẫu biểu thức √
với a ≥ 0; a ̸= 12 ta được 6 + 3a √ √ √ √ 6 + 3a 6 − 3a 6 + 3a 6 − 3a A. . B. . C. . D. . 12 + a 12 + a 12 − a 12 − a 6
Câu 26. Trục căn thức ở mẫu biểu thức √ √ với x, y ≥ 0 ta được x + 2y √ √ √ √ √ √ √ √ 6 x − 2y 6 x + 2y 6 x − 2y 6 x + 2y A. . B. . C. . D. . x − 4y x − 2y x − 2y x + 2y 4 4
Câu 27. Trục căn thức ở mẫu biểu thức √
√ với x, y ≥ 0; x ̸= y ta được 3 x + 2 y 9 √ √ √ √ √ √ √ √ 3 x − 2 y 12 x − 8 y 12 x + 8 y 12 x − 8 y A. . B. . C. . D. . 9x − 4y 3x + 2y 9x + 4y 9x − 4y GV: Mạc Lê Chí Đạo – 0946820895 11
Chương 1. CĂN BẬC HAI – CĂN BẬC BA √ √ √ √ Ç å 14 − 7 15 − 5 1
Câu 28. Giá trị của biểu thức √ + √ : √ √ bằng 1 − 2 1 − 3 7 − 5 A. −3. B. −2. C. 2. D. 3. √ √ √ Ç å 10 + 2 10 30 − 6 1
Câu 29. Giá trị của biểu thức √ √ + √ √ : √ √ bằng 5 + 2 5 − 1 2 5 − 6 A. 28. B. 14. C. −14. D. 15. 3 √ … 2 … 3
Câu 30. Giá trị của biểu thức 6 + 2 − 4 bằng 2 3 2 √ √ √ 6 √ 6 6 A. . B. 6. C. . D. . 6 2 3 √ √ √ √
Câu 31. Cho ba biểu thức P = x y + y x; Q = x x + y y; R = x − y. Biểu thức nào bằng với biểu √ √ √ √ thức x − y · x + y với x, y không âm? A. P. B. Q. C. R. D. P − Q. √ √ √ √ x x − y y √ √ √ √
Câu 32. Cho ba biểu thức M = x + y2 ; N = √ √ ; P = x − y · x + y. Biểu x − y √
thức nào bằng với biểu thức x +
xy + y với x, y không âm và x ̸= y? A. M. B. N. C. P. D. M · N. √ √
Câu 33. Số nghiệm của phương trình 4x2 − 9 = 2 2x + 3 là A. 1. B. 0. C. 3. D. 2. √ √
Câu 34. Số nghiệm của phương trình 9x2 − 16 = 3 3x − 4 là A. 1. B. 0. C. 3. D. 2. 2 √ 1 √ … x − 1 Câu 35. Phương trình 9x − 9 − 16x − 16 + 27 = 4 có bao nhiêu nghiệm? 3 4 81 A. 1. B. 0. C. 3. D. 2. √ … x − 2 √ Câu 36. Phương trình 4x − 8 − 2 + 9x − 18 = 8 có nghiệm 4 A. x = 8. B. x = 4. C. x = 2. D. x = 6. … 3 … 1 … 1
Câu 37. Giá trị của biểu thức + − 2 bằng 20 60 15 A. 1. B. 0. C. 3. D. 2. a a a √
Câu 38. Rút gọn biểu thức √ + √ − √ − 5a ta được 5 + 1 5 − 2 3 − 5 A. 2a. B. a. C. 3a. D. 12a. 4a 2a a
Câu 39. Rút gọn biểu thức √ √ − √ − √ √ ta được 7 − 3 2 − 2 3 + 2 √ √ √ Ä ä Ä ä A. 2a. B. 2 7a. C. a 7 + 2 . D. a 7 − 2 . √ √ p p 6 + 2 5 5 − 2 6
Câu 40. Rút gọn biểu thức √ + √ √ ta được 5 + 1 3 − 2 A. 2. B. −2. C. 1. D. 0. BẢNG ĐÁP ÁN 12
BÀI TẬP TRẮC NGHIỆM TOÁN 9
4. BIẾN ĐỔI ĐƠN GIẢN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI 1. A 2. C 3. B 4. A 5. C 6. D 7. B 8. B 9. B 10. C 11. D 12. D 13. D 14. B 15. D 16. A 17. C 18. A 19. B 20. D 21. A 22. A 23. B 24. C 25. D 26. C 27. D 28. B 29. B 30. A 31. C 32. B 33. D 34. D 35. A 36. D 37. B 38. B 39. D 40. A GV: Mạc Lê Chí Đạo – 0946820895 13
Chương 1. CĂN BẬC HAI – CĂN BẬC BA
§5. RÚT GỌN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI A B
BÀI TẬP TRẮC NGHIỆM … √ √ Ä ä2 p
Câu 1. Giá trị của biểu thức 4 − 5 − 6 − 2 5 bằng √ √ A. 5 − 2 5. B. 4. C. 5 + 2 5. D. 1. … √ √ √ Ä ä2 p
Câu 2. Giá trị của biểu thức 2 + 5 − 7 − 2 10 bằng √ √ √ A. 2 2. B. 0. C. 2 5. D. 2. √ √ p p
Câu 3. Giá trị của biểu thức 17 − 12 2 + 9 + 4 2 bằng √ √ A. 3 + 4 2. B. 4. C. 2. D. 4 2. √ √ √ √
Câu 4. Giá trị của biểu thức 32 + 50 − 3 8 − 18 bằng A. 1. B. 0. C. 2. D. 3. √ √ √ √
Câu 5. Giá trị của biểu thức 2 32 − 27 − 4 8 + 3 75 bằng √ √ √ √ √ A. 16 2 + 12 3. B. 15 3. C. 12 3. D. 16 2. √ √ √ √
Câu 6. Giá trị của biểu thức 125 − 4 45 + 3 20 − 80 bằng √ √ √ √ A. 5. B. −5 5. C. 10 5. D. 5 5. √ … a … 4 √
Câu 7. Rút gọn biểu thức 5 a + 2 − a − 25a với a > 0 ta được 4 a √ √ √ √ A. a. B. 4 a. C. 2 a. D. − a. √ 1 … 32a a … 3 √
Câu 8. Rút gọn biểu thức 3 8a + − √ − 2a với a > 0 ta được 4 25 3 2a 47 √ 21 √ 47 √ 47 √ A. a. B. a. C. 2a. D. 2a. 10 5 10 5 √ √ √ Ä ä p
Câu 9. Giá trị của biểu thức 5 + 2 7 − 2 10 bằng A. 4. B. 5. C. 2. D. 3. √ √ √ Ä ä p
Câu 10. Giá trị của biểu thức 3 2 + 6 6 − 3 3 bằng A. 6. B. 5. C. 2. D. 3. √ √ Ä ä p
Câu 11. Giá trị của biểu thức 5 − 1 6 + 2 5 bằng A. 6. B. 4. C. 2. D. 3. √ √ … 16 2 √
Câu 12. Rút gọn biểu thức 2 a − 9a3 + a2 +
36a5 với a > 0 ta được a a2 √ √ √ √ √ √ √ √ A. 14 a + a a. B. 14 a − a a. C. 14 a + 2a a. D. 20 a − 2a a. Å 1 … a 3 √ 4 √ ã 1
Câu 13. Rút gọn biểu thức − 2a + 200a : ta được 2 2 2 5 8 √ √ √ √ A. 66 2a. B. 52 2a. C. 54 a. D. 54 2a.
Câu 14. Đẳng thức nào dưới đây đúng? a − b a2b4 A.
= a với a − b > 0, b ̸= 0. b2 a2 − 2ab + b2 14
BÀI TẬP TRẮC NGHIỆM TOÁN 9
5. RÚT GỌN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI a − b a2b4 B.
= |a| với a − b > 0, b ̸= 0. b2 a2 − 2ab + b2 a − b a2b4 C.
= ab với a − b > 0, b ̸= 0. b2 a2 − 2ab + b2 a − b a2b4 D.
= a − b với a − b > 0, b ̸= 0. b2 a2 − 2ab + b2
Câu 15. Với a, b > 0 đẳng thức nào dưới đây đúng? √ √ √ √ a b + b a a − b √ a b + b a a − b √ A. √ + √ √ = 2 a. B. √ + √ √ = a. ab a + b ab a + b √ √ √ √ a b + b a a − b a b + b a a − b √ C. √ + √ √ = 2. D. √ + √ √ = 2 b. ab a + b ab a + b
Câu 16. Chọn khẳng định đúng. √ √ √ √ √ √ Ç å Ç å 2 3 − 6 216 Å −a ã 3a 2 3 − 6 216 Å −a ã 3a A. √ − · √ = − . B. √ − · √ = . 8 − 2 3 6 2 8 − 2 3 6 2 √ √ √ √ √ √ Ç å Ç å 2 3 − 6 216 Å −a ã a 2 3 − 6 216 Å −a ã a C. √ − · √ = − . D. √ − · √ = . 8 − 2 3 6 2 8 − 2 3 6 2
Câu 17. Chọn khẳng định đúng. √ √ √ √ Ç å 14 − 7 15 − 5 1 A. √ + √ : √ √ = 2a. Ä ä 1 − 2 1 − 3 a 7 − 5 √ √ √ √ Ç å 14 − 7 15 − 5 1 2 B. √ + √ : √ √ = . Ä ä 1 − 2 1 − 3 a 7 − 5 a √ √ √ √ Ç å 14 − 7 15 − 5 1 C. √ + √ : √ √ = −2a. Ä ä 1 − 2 1 − 3 a 7 − 5 √ √ √ √ Ç å 14 − 7 15 − 5 1 a D. √ + √ : √ √ = − . Ä ä 1 − 2 1 − 3 a 7 − 5 2 2x
Câu 18. Cho biểu thức P = √
. Giá trị của P khi x = 9 là x + 1 9 9 A. . B. . C. 9. D. 18. 2 4 √x
Câu 19. Cho biểu thức P = √
với x ≥ 0, x ̸= 1. Giá trị của P khi x = 4 là x − 1 2 A. 4. B. 2. C. −2. D. . 3 x 2
Câu 20. Cho biểu thức P = √ . Giá trị của P khi x = √ là x + 1 2 − 3 A. 4. B. 2. C. 3. D. 1. √x 8
Câu 21. Cho biểu thức P = √ . Giá trị của P khi x = √ là x − 1 3 − 5 √ √ 5 + 5 √ A. 5 + 5. B. 5. C. . D. 5. 5 √x+1 √
Câu 22. Cho biểu thức P = √
. Giá trị của P khi x = 3 + 2 2 là x − 2 √ √ √ A. 4 + 3 2. B. 4 − 3 2. C. 3. D. 3 2. GV: Mạc Lê Chí Đạo – 0946820895 15
Chương 1. CĂN BẬC HAI – CĂN BẬC BA √x
Câu 23. Cho biểu thức P = √
với x ≥ 0, x ̸= 4. Giá trị của P khi x thỏa mãn phương trình x − 2 x2 − 5x + 4 = 0 bằng 1 √ A. − . B. 2. 2 C. −1.
D. Không tồn tại giá trị P. √ x + 2 x + 2 Câu 24. Cho biểu thức P = √
với x > 0. So sánh P với 4. x A. P > 4. B. P < 4. C. P = 4. D. P ≤ 4. √ 2 x + 1
Câu 25. Cho biểu thức A = √
với x ≥ 0. So sánh A với 2. x + 1 A. A > 2. B. A < 2. C. A = 2. D. A ≥ 2. √x+3
Câu 26. Cho biểu thức P = √
với x ≥ 0. So sánh P với 1. x + 2 A. P > 1. B. P < 1. C. P = 1. D. P ≤ 1. √ 3 x − 1 √
Câu 27. Cho biểu thức P = √
với x ≥ 0. Tìm x biết P = x. x + 1 A. 1. B. 2. C. 4. D. 3. √ √ x + 1 x − 1
Câu 28. Cho biểu thức A = √
với x ≥ 0, x ̸= 4. Tìm các giá trị của x biết A = . x − 2 2 A. x = 0, x = 5. B. x = 0. C. x = 0, x = 25. D. x = 5, x = 1. 2 Câu 29. Cho P = √
. Có bao nhiêu giá trị của x ∈ Z để P nhận giá trị nguyên. x + 1 A. 1. B. 2. C. 0. D. 4. √x+3 Câu 30. Cho P = √
. Có bao nhiêu giá trị của x ∈ Z để P nhận giá trị nguyên. x − 2 A. 3. B. 2. C. 0. D. 4. √ √ √ x + 1 2 x 2 + 5 x
Câu 31. Rút gọn biểu thức A = √ + √ +
với x ≥ 0, x ̸= 4 ta được x − 2 x + 2 4 − x √ √ √ 3 x x 2 x 3 A. A = √ . B. A = √ . C. A = √ . D. A = √ . x + 2 x + 2 x + 2 x + 2 √ √ Å x − 2 x + 2 ã (1 − x)2
Câu 32. Rút gọn biểu thức B = − √ ·
với x ≥ 0, x ̸= 1 ta được x − 1 x + 2 x + 1 2 √ √ √ √ A. B = x − x. B. B = x − x. C. B = x + x. D. B = x + 2 x. √ √ Å 4 x 8x ã Å x − 1 2 ã
Câu 33. Rút gọn biểu thức P = √ + : √ − √
với x ≥ 0, x ̸= 4, x ̸= 9 ta 2 + x 4 − x x − 2 x x được 4x 4x x 4x A. P = √ . B. P = √ . C. P = √ . D. P = − √ . x − 3 x + 3 x − 3 x − 3 √ √ √ 2 x − 9 x + 3 2 x + 1
Câu 34. Rút gọn biểu thức C = √ − √ − √
với x ≥ 0, x ̸= 4, x ̸= 9 ta được x − 5 x + 6 x − 2 3 − x √ √ √ √ x − 1 x − 1 x + 1 x + 1 A. C = √ . B. C = √ . C. C = √ . D. C = √ . x − 3 x + 3 x − 3 x + 3 √ Å x 2 ã 1
Câu 35. Rút gọn biểu thức C = √ + √ : √
với x ≥ 0, x ̸= 1 ta được x − 1 x − x x − 1 16
BÀI TẬP TRẮC NGHIỆM TOÁN 9
5. RÚT GỌN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI √ √ x − 2 x + 2 x + 2 x A. C = √ . B. C = √ . C. C = √ . D. C = . x x x x + 2 Å 2x + 1 1 ã Å x + 4 ã
Câu 36. Rút gọn biểu thức P = √ − √ : 1 − √ ta được x3 − 1 x − 1 x + x + 1 √ √ √ √ x x 3 + x x A. P = √ . B. P = √ . C. P = √ . D. P = − √ . x − 3 x + 3 x − 3 x − 3 √ 2 x − 1
Câu 37. Cho biểu thức A = √
với x ≥ 0. Có bao nhiêu giá trị của x để A nhận giá trị nguyên? x + 2 A. 2. B. 1. C. 0. D. 3. √ √ √ 1 √ 3 5 + 5 5 3 5
Câu 38. Cho các biểu thức A = √ − 27 + √ ; B = √ + √ − √ . Khẳng định 3 − 1 3 5 + 2 5 − 1 3 + 5 đúng là A. B > A > 0. B. A < B < 0. C. A < 0 < B. D. B < 0 < A. 3 4 1
Câu 39. Rút gọn biểu thức A = √ √ + √ √ + √ √ ta được 5 − 2 6 + 2 6 + 5 √ √ A. A = 1. B. A = 4. C. A = 6. D. A = 2 6. √ 1 2 2
Câu 40. Rút gọn biểu thức E = √ + √ − √ ta được 2 + 3 6 3 + 3 √ √ √ √ 3 + 3 3 − 3 3 + 3 3 − 3 A. E = . B. E = . C. E = . D. E = . 2 2 3 3 BẢNG ĐÁP ÁN 1. A 2. A 3. B 4. B 5. C 6. B 7. D 8. C 9. D 10. A 11. B 12. A 13. D 14. B 15. A 16. B 17. C 18. A 19. B 20. B 21. C 22. A 23. C 24. A 25. B 26. A 27. A 28. C 29. B 30. A 31. A 32. B 33. A 34. C 35. B 36. A 37. B 38. C 39. D 40. D GV: Mạc Lê Chí Đạo – 0946820895 17
Chương 1. CĂN BẬC HAI – CĂN BẬC BA §6. CĂN BẬC BA A B
BÀI TẬP TRẮC NGHIỆM
Câu 1. Khẳng định nào sau đây đúng? √ √ A. 3 a3 = x ⇔ a3 = x. B. 3 a3 = −x ⇔ a3 = −x. √ √ C. 3 a3 = x ⇔ a = x3. D. 3 a3 = −x ⇔ a = x3.
Câu 2. Khẳng định nào sau đây đúng? √ √ A. 3 a3 = 2x ⇔ a3 = 2x. B. 3 a3 = 2x ⇔ 2a = x3. √ √ C. 3 a3 = 2x ⇔ a = 2x3. D. 3 a3 = 2x ⇔ a = 8x3.
Câu 3. Khẳng định nào sau đây đúng? √ √ √ √ A. 3 a > 3 b ⇔ a > b. B. 3 a > 3 b ⇔ a < b. √ √ √ √ C. 3 a ≥ 3 b ⇔ a = b. D. 3 a < 3 b ⇔ a > b.
Câu 4. Khẳng định nào sau đây sai? √ √ √ √ A. a > b ⇔ 3 a > 3 b. B. a < b ⇔ 3 a < 3 b. √ √ √ √ C. a ≥ b ⇔ 3 a ≥ 3 b. D. a < b ⇔ 3 a > 3 b.
Câu 5. Khẳng định nào sau đây sai? √ √ √ √ … a 3 a A. 3 a · 3 b = 3 ab. B. 3 = √ với b ̸= 0. b 3 b √ √ C. ( 3 a)3 = a. D. 3 a3 = |a|.
Câu 6. Khẳng định nào sau đây đúng? √ √ √ √ 3 a a A. 3 ab = a · b. B. √ = với b ̸= 0. 3 b b √ √ 3 a … a C. 3 a = −a khi a < 0. D. √ = 3 với b ̸= 0. 3 b b
Câu 7. Căn bậc 3 của 9 kí hiệu là gì? √ √ √ A. 3 9. B. 9. C. 9 3. D. 2 9.
Câu 8. Chọn khẳng định đúng. √ √ √ √ A. 3 27 = 9. B. 3 27 = 3. C. 3 27 = −3. D. 3 27 = −9.
Câu 9. Chọn khẳng định đúng. √ √ √ √ A. 3 −125 = −25. B. 3 −125 = −5. C. 3 −125 = 25. D. 3 −125 = 5.
Câu 10. Chọn khẳng định đúng với a ̸= 0. … 1 1 … 1 1 … 1 1 … 1 1 A. 3 − = − . B. 3 − = . C. 3 − = . D. 3 − = − . 8a3 2a 8a3 2a 8a3 4a 8a3 2a2 √ √
Câu 11. Kết quả của phép tính 3 27 − 3 125 là √ √ A. 2. B. −2. C. 3 98. D. − 3 98. √ √ √
Câu 12. Kết quả của phép tính 3 8 − 3 −216 + 3 512 là A. 14. B. 16. C. 18. D. 12. √
Câu 13. Tìm giá trị của x để 3 16x − 5 có nghĩa. Chọn câu đúng nhất. A. x = 4. B. x = 5. C. x = 8. D. x là số thực. 18
BÀI TẬP TRẮC NGHIỆM TOÁN 9 6. CĂN BẬC BA √
Câu 14. Thu gọn 3 125a3 ta được A. 25a. B. 5a. C. −25a3. D. −5a. … 1 Câu 15. Thu gọn 3 − với a ̸= 0 ta được 27a3 1 1 1 1 A. . B. . C. − . D. − . 3a 4a 3a 8a √ √ √ √ Ä Ä√ ä
Câu 16. Rút gọn biểu thức
3 a2 + 3 ab + 3 b2ä · 3 a − 3 b ta được a A. a + b. B. a − b. C. ab. D. . b … 27 √ 1 √
Câu 17. Rút gọn biểu thức 3 − 3 a3 + 3 64a3 − 1000a3 ta được 512 3 7a 5a 7a 5a A. . B. . C. . D. . 24 24 8 8 √ √ √
Câu 18. Rút gọn biểu thức 3
2 27a3 − 3 3 8a3 + 4 3 125a3 ta được A. 14a. B. 20a. C. 9a. D. −8a. √ √
Câu 19. Rút gọn biểu thức B = 3
p17 5 + 38 − 3p17 5 − 38 ta được √ √ A. B = 4. B. B = 5. C. B = 2 5. D. B = 2. √ √
Câu 20. Rút gọn biểu thức A = 3
p9 + 4 5 + 3p9 − 4 5 ta được √ A. A = 3. B. A = 3. C. A = 6. D. A = 27. √ √
Câu 21. Cho A = 2 3 3 và B = 3 25. Chọn khẳng định đúng. A. A < B. B. A > B. C. A ≥ B. D. A + B = 0. √ √
Câu 22. Cho M = 5 3 6 và N = 6 3 5. Chọn khẳng định đúng. A. M > N. B. M < N. C. M ≥ N. D. M + N = 0. √ √
Câu 23. Cho A = 3 3 2 và B = 3 42. Chọn khẳng định đúng. A. A < B. B. A > B. C. A ≥ B. D. A + B = 0. √
Câu 24. Tìm x biết 3 2x + 1 > −3. A. x = −14. B. x < −14. C. x > −14. D. x > −12. √
Câu 25. Tìm x biết 3 4 − 2x > 4. A. x < 30. B. x > −30. C. x < −30. D. x > 30. √
Câu 26. Tìm số nguyên x nhỏ nhất thỏa mãn bất phương trình 3 3 − 2x ≤ 4. A. x = −31. B. x = −30. C. x = −32. D. x = −29. √
Câu 27. Tìm số nguyên x lớn nhất thỏa mãn bất phương trình 3 7 + 4x ≤ 5. A. x = 31. B. x = 28. C. x = 30. D. x = 29. 343a3b6
Câu 28. Rút gọn biểu thức 3 ta được −125 −7ab2 7ab2 −ab2 ab2 A. . B. . C. . D. . 5 5 5 5 √ 3 −64a5b5
Câu 29. Rút gọn biểu thức √ ta được 3 a2b2 A. 4ab. B. −8ab. C. 16ab. D. −4ab. GV: Mạc Lê Chí Đạo – 0946820895 19
Chương 1. CĂN BẬC HAI – CĂN BẬC BA √ √
Câu 30. Nghiệm của phương trình 2 3 x + 3 2 3 x − 3 = −8 là A. x = −1. B. x = 3.
C. x = −1 hoặc x = 1. D. x = 3 hoặc x = −3. √
Câu 31. Số nghiệm của phương trình 3 2x + 1 = 3 là A. 2. B. 0. C. 1. D. 3. √
Câu 32. Nghiệm của phương trình 3 2 − 3x = −3 là 29 A. x = . B. x = 9. 3 25 C. x = .
D. Phương trình vô nghiệm. 3 √
Câu 33. Khẳng định nào đúng khi nói về nghiệm của phương trình 3 3x − 2 = −2? A. Là số nguyên âm. B. Là phân số. C. Là số vô tỉ. D. Là số nguyên dương. √
Câu 34. Khẳng định nào đúng khi nói về nghiệm của phương trình 3 x3 + 6x2 = x + 2? A. Là số nguyên âm. B. Là phân số. C. Là số vô tỉ. D. Là số nguyên dương. √
Câu 35. Số nghiệm của phương trình 3 5 + x − x = 5 là A. 2. B. 0. C. 1. D. 3. √
Câu 36. Tổng các nghiệm của phương trình 3 x − 2 + 2 = x là A. 6. B. 5. C. 2. D. 3. √ √
Câu 37. Tổng các nghiệm của phương trình 3 12 − 2x + 3 23 + 2x = 5 là 1 11 19 A. 2. B. . C. − . D. . 2 2 2 √ √
Câu 38. Tập nghiệm của phương trình 3 x + 1 + 3 7 − x = 2 là A. S = {1; −7}. B. S = {−1; 7}. C. S = {7}. D. S = {−1}. √ √
Câu 39. Rút gọn biểu thức 3 x3 + 3x2 + 3x + 1 − 3 8x3 + 12x2 + 6x + 1 ta được A. x. B. −x. C. 2x. D. −2x. √ √
Câu 40. Rút gọn biểu thức 3 x3 + 3x2 + 3x + 1 − 3 125x3 + 75x2 + 15x + 1 ta được A. −4x. B. −6x. C. 4x. D. 6x. BẢNG ĐÁP ÁN 1. C 2. D 3. A 4. D 5. D 6. D 7. A 8. B 9. B 10. A 11. B 12. B 13. D 14. B 15. C 16. B 17. A 18. B 19. A 20. A 21. A 22. B 23. B 24. C 25. C 26. B 27. D 28. A 29. D 30. C 31. C 32. A 33. A 34. B 35. D 36. A 37. C 38. B 39. B 40. A 20
BÀI TẬP TRẮC NGHIỆM TOÁN 9 Chûúng 2 HÀM SỐ BẬC NHẤT HÀM SỐ BẬC NHẤT
§1. NHẮC LẠI VÀ BỔ SUNG CÁC KHÁI NIỆM VỀ HÀM SỐ A B
BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho hàm số y = f (x) xác định trên D. Với x1, x2 ∈ D, x1 < x2. Khẳng định nào sau đây đúng?
A. f (x1) < f (x2) thì hàm số đồng biến trên D.
B. f (x1) < f (x2) thì hàm số nghịch biến trên D.
C. f (x1) > f (x2) thì hàm số đồng biến trên D.
D. f (x1) = f (x2) thì hàm số đồng biến trên D.
Câu 2. Cho hàm số y = f (x) xác định trên D. Với x1, x2 ∈ D, x1 > x2. Khẳng định nào sau đây đúng?
A. f (x1) < f (x2) thì hàm số đồng biến trên D.
B. f (x1) > f (x2) thì hàm số nghịch biến trên D.
C. f (x1) > f (x2) thì hàm số đồng biến trên D.
D. f (x1) = f (x2) thì hàm số đồng biến trên D.
Câu 3. Cho hàm số f (x) = 3 − x2. Khi đó f (−1) bằng A. −2. B. 2. C. 1. D. 0.
Câu 4. Cho hàm số f (x) = x3 + x. Khi đó f (2) bằng A. 4. B. 6. C. 8. D. 10.
Câu 5. Cho hàm số f (x) = x3 − 3x − 2. Khi đó 2 f (3) bằng A. 16. B. 8. C. 32. D. 64.
Câu 6. Cho hàm số f (x) = 3x2 + 2x + 1. Khi đó f (3) − 2 f (2) bằng A. 34. B. 17. C. 20. D. 0.
Câu 7. Cho hai hàm số f (x) = −2x3 và g (x) = 10 − 3x. So sánh f (−2) và g (−1). A. f (−2) < g (−1).
B. Không đủ điều kiện so sánh. C. f (−2) = g (−1). D. f (−2) > g (−1). 3x Å 2 ã
Câu 8. Cho hai hàm số f (x) = −6x4 và g (x) = 7 − . So sánh f (−1) và g . 2 3 Å 2 ã Å 2 ã A. f (−1) = g . B. f (−1) > g . 3 3 Å 2 ã C. f (−1) < g .
D. Không đủ điều kiện so sánh. 3 GV: Mạc Lê Chí Đạo – 0946820895 21
Chương 2. HÀM SỐ BẬC NHẤT
Câu 9. Cho hai hàm số f (x) = x2 và g (x) = 5x − 4. Có bao nhiêu giá trị của a để f (a) = g (a)? A. 0. B. 1. C. 2. D. 3. 1
Câu 10. Cho hai hàm số f (x) = −2x2 và g (x) = 3x + 5. Giá trị nào của a để f (a) = g (a). 2 A. a = 0. B. a = 1. C. a = 2. D. Không tồn tại.
Câu 11. Cho hai hàm số f (x) = 2x2 và g (x) = 4x − 2. Có bao nhiêu giá trị của a để f (a) = g (a)? A. 0. B. 1. C. 2. D. 3.
Câu 12. Cho hàm số f (x) = 5,5x có đồ thị (C). Điểm nào sau đây thuộc đồ thị hàm số (C)? A. M (0; 1). B. N (2; 11). C. P (−2; 11). D. Q (−2; 12).
Câu 13. Cho hàm số f (x) = 3x − 2 có đồ thị (C). Điểm nào sau đây thuộc đồ thị hàm số (C)? A. M (0; 1). B. N (2; 3). C. P (−2; −8). D. Q (−2; 0). 1
Câu 14. Cho hàm số f (x) = − x có đồ thị (C) và các điểm M (0; 4), P (4; −1), Q (−4; 1), A (8; −2), 4
O (0; 0). Có bao nhiêu điểm trong số các điểm trên thuộc đồ thị hàm số (C)? A. 4. B. 3. C. 2. D. 1.
Câu 15. Cho hàm số f (x) = 3x có đồ thị (C) và các điểm M (1; 1), P (−1; −3), Q (3; 9), A (−2; 6),
O (0; 0). Có bao nhiêu điểm trong số các điểm trên thuộc đồ thị hàm số (C)? A. 4. B. 3. C. 2. D. 1.
Câu 16. Đường thẳng nào sau đây đi qua điểm M (1; 4)? A. 2x + y − 3 = 0. B. y − 5 = 0. C. 4x − y = 0. D. 5x + 3y − 1 = 0.
Câu 17. Đường thẳng nào sau đây đi qua điểm N (1; 1)? A. 2x + y − 3 = 0. B. y − 3 = 0. C. 4x + 2y = 0. D. 5x + 3y − 1 = 0.
Câu 18. Hàm số y = 1 − 4x là hàm số A. đồng biến. B. hàm hằng. C. nghịch biến.
D. đồng biến với x > 0.
Câu 19. Hàm số y = 5 − 3x là hàm số A. nghịch biến. B. hàm hằng. C. đồng biến.
D. đồng biến với x > 0.
Câu 20. Hàm số y = 5x − 16 là hàm số A. đồng biến. B. hàm hằng. C. nghịch biến.
D. nghịch biến với x > 0. 1
Câu 21. Hàm số y = x + 3 là hàm số 2 A. hàm hằng. B. đồng biến. C. nghịch biến.
D. nghịch biến với x < 0.
Câu 22. Cho hàm số y = (3m − 2) x + 5m. Tìm m để hàm số nhận giá trị là 2 khi x = −1. A. m = 0. B. m = 1. C. m = 2. D. m = −1. 5 − m Câu 23. Cho hàm số y =
x − 2m − 1. Tìm m để hàm số nhận giá trị là −5 khi x = 2. 2 A. m = 5. B. m = 3. C. m = 2. D. m = −3.
Câu 24. Cho hàm số y = mx − 3m + 2. Tìm m để đồ thị hàm số đi qua điểm A (2; −3). A. m = 3. B. m = 4. C. m = 5. D. m = 6. 22
BÀI TẬP TRẮC NGHIỆM TOÁN 9
1. NHẮC LẠI VÀ BỔ SUNG CÁC KHÁI NIỆM VỀ HÀM SỐ
Câu 25. Cho hàm số y = (2 − 3m) x − 6. Tìm m để đồ thị hàm số đi qua điểm A (−3; 6). A. m = 3. B. m = 4. C. m = 9. D. m = 2. √x+1
Câu 26. Cho hàm số f (x) = √ . Tính f a2 với a < 0. 2 x + 3 a + 1 2a + 1 2a − 1 1 − a A. f a2 = . B. f a2 = . C. f a2 = . D. f a2 = . 3 + 2a 3 − 2a 3 + 2a 3 − 2a √ 2 x − 2
Câu 27. Cho hàm số f (x) = √ . Tính f 4a2 với a ≤ 0. x + 4 2a − 1 2a + 1 a − 2 2a + 1 A. f 4a2 = . B. f 4a2 = . C. f 4a2 = . D. f 4a2 = . a + 2 a − 2 2a + 1 a + 2 √ √ Ä ä
Câu 28. Cho hàm số y = 3 + 2 2 x − 2 − 1. Tìm x để y = 0. √ √ √ A. x = 1. B. x = 2 + 1. C. x = 2. D. x = 2 − 1. √ √ Ä ä Câu 29. Cho hàm số y =
3 + 2 x − 4 − 4 3. Tìm x để y = 3. √ √ √ √ A. x = 2 + 3. B. x = 3. C. x = 3 + 2. D. x = 3 − 2. BẢNG ĐÁP ÁN 1. A 2. C 3. B 4. D 5. C 6. D 7. D 8. A 9. C 10. D 12. B 13. C 14. A 15. B 16. C 17. A 18. C 19. C 20. A 21. B 22. A 23. B 24. C 25. D 26. D 27. A 29. C GV: Mạc Lê Chí Đạo – 0946820895 23
Chương 2. HÀM SỐ BẬC NHẤT
§2. HÀM SỐ BẬC NHẤT A B
BÀI TẬP TRẮC NGHIỆM
Câu 1. Chọn đáp án đúng nhất. Hàm số y = ax + b là hàm số bậc nhất khi A. a = 0. B. a < 0. C. a > 0. D. a ̸= 0.
Câu 2. Chọn đáp án đúng nhất. Với a ̸= 0 hàm số y = ax + b là hàm số A. bậc nhất. B. hàm hằng. C. đồng biến. D. nghịch biến.
Câu 3. Chọn đáp án đúng nhất. Hàm số y = ax + b là hàm số đồng biến khi A. a = 0. B. a < 0. C. a > 0. D. a ̸= 0.
Câu 4. Chọn đáp án đúng nhất. Hàm số y = ax + b là hàm số nghịch biến khi A. a = 0. B. a < 0. C. a > 0. D. a ̸= 0.
Câu 5. Hàm số nào dưới đây là hàm số bậc nhất? √ A. y = 2x + 1. B. y = 0x + 3. C. y = 2x2 + x + 1. D. y = x + 2 + 4.
Câu 6. Hàm số nào dưới đây không phải là hàm số bậc nhất? x 2 A. y = x. B. y = 3 − . C. y = . D. y = 7 − 5x. 2 x x 1
Câu 7. Trong các hàm số y = 5, y = + 1, y = x3 + 2x + 1, y =
+ 2, y = 3x có bao nhiêu hàm số là 2 x hàm số bậc nhất? A. 3. B. 2. C. 4. D. 1. √
Câu 8. Tìm m để hàm số y =
2 − mx + 1 là hàm số bậc nhất. A. m < 2. B. m > 2. C. m = 2. D. m ̸= 2. 1
Câu 9. Tìm m để hàm số y = √
x + m là hàm số bậc nhất. 2m − 3 3 3 3 3 A. m < . B. m ̸= . C. m = . D. m > . 2 2 2 2 m + 1
Câu 10. Tìm m để hàm số y =
x + 2m − 3 là hàm số bậc nhất. m − 2 A. m ̸= −1. B. m > −1. C. m ̸= {−1; 2}. D. m ̸= 2. 3m Câu 11. Hàm số y =
x − 5 là hàm số bậc nhất khi 1 − 2m ß 1 ™ 1 A. m ̸= 0; . B. m > 0. C. m ̸= . D. m ̸= 0. 2 2
Câu 12. Hàm số nào sau đây là hàm số nghịch biến trên R? A. y = 2x − 1. B. y = − (1 − 3x). C. y = − (2x − 1). D. y = x. 1 x
Câu 13. Trong các hàm số y = −3x + 2, y = − (−x + 1), y = 6 − , y = − (1 − 2x) có bao nhiêu 3 2 hàm số nghịch biến? A. 1. B. 3. C. 4. D. 2.
Câu 14. Hàm số nào sau đây là hàm số bậc nhất và đồng biến? √ A. y = 2 (4 − x) + 5. B. y = 3 − (2x + 2). C. y = x3 − x. D. y = − (9 − x). 24
BÀI TẬP TRẮC NGHIỆM TOÁN 9 2. HÀM SỐ BẬC NHẤT
Câu 15. Hàm số nào sau đây là hàm số đồng biến trên R? √ x 3 A. y = − − 3 . B. y = (x + 1). C. y = −5 − 3x. D. y = − (9 + 3x). 2 2
Câu 16. Tìm m để hàm số y = (8 − 4m) x + 5 nghịch biến trên R. A. m > 2. B. m < 2. C. m = 2. D. m ̸= 2. m − 1
Câu 17. Với giá trị nào của m thì hàm số y =
x − 5 là hàm số nghịch biến? m2 + 2m + 2 A. m < 1. B. m > 1. C. m = 1. D. Với mọi m. m Câu 18. Cho hàm số y =
− 3 x + m + 1. Tìm m để hàm số đã cho nghịch biến. 2 A. m > 6. B. m = 6. C. m < 6. D. m ̸= 6.
Câu 19. Cho hàm số y = 5mx − 2x + m. Tìm m để hàm số đã cho đồng biến. 2 5 2 5 A. m < . B. m > . C. m > . D. m < . 5 2 5 2
Câu 20. Hàm số y = −2m2 + 4m − 5 x − 7m + 5 đồng biến khi 5 A. m < 3. B. m > . 2 C. Không có m thỏa mãn. D. Với mọi m.
Câu 21. Cho hàm số y = m2 − 1 x + 5m. Tìm m để hàm số đã cho đồng biến trên R. A. m < −1. B. m > 1. C. m > −1.
D. m > 1 hoặc m < −1. √ Câu 22. Cho hàm số y =
m2 + 3x + 1. Kết luận nào sau đây là đúng? √
A. Hàm số đã cho nghịch biến với mọi m.
B. Hàm số đã cho nghịch biến với m > 3.
C. Hàm số đã cho là hàm hằng.
D. Hàm số đã cho đồng biến với mọi m. √ √ Ç å 2 + 3 2 − 3 Câu 23. Cho hàm số y = √ + √
x − 5. Kết luận nào sau đây là đúng? 2 − 3 2 + 3
A. Hàm số đã cho nghịch biến.
B. Hàm số đã cho đồng biến.
C. Hàm số đã cho là hàm hằng.
D. Hàm số đã cho đồng biến với x > 0. √ Câu 24. Cho hàm số y =
m − 3 − 2 x − m. Giá trị nguyên nhỏ nhất của m để hàm số đồng biến là A. m = 8. B. m = 9. C. m = 3. D. m = 7. √
Câu 25. Cho hàm số y = 5 − 5 − m x + m + 2. Với giá trị nguyên lớn nhất nào của m thì hàm số đã cho nghịch biến? A. m = 5. B. m = −20. C. m = −19. D. m = −21.
Câu 26. Với giá trị nào của m thì hàm số y = (3m − 1) mx + 6m là hàm số bậc nhất? 1 ß 1 ™ A. m ̸= 0. B. m ̸= . C. m ̸= 0; . D. Với mọi m. 3 3
Câu 27. Với giá trị nào của m thì hàm số y = m2 − 9m + 8 x + 10 là hàm số bậc nhất? A. m ̸= {1; 8}. B. m ̸= 1. C. m ̸= 8. D. Với mọi m.
Câu 28. Hàm số y = a2 − 4 x2 + (b − 3a) (b + 2a) x − 2 là hàm số bậc nhất khi A. a = 2, b ̸= {6; −4}. B. a = −2, b ̸= {−6; 4}. C. a = 2, a = −2. D. Cả A, B đều đúng. GV: Mạc Lê Chí Đạo – 0946820895 25
Chương 2. HÀM SỐ BẬC NHẤT BẢNG ĐÁP ÁN 1. D 2. A 3. C 4. B 5. A 6. C 7. B 8. A 9. D 10. C 11. A 12. C 13. D 14. D 15. B 16. A 17. A 18. C 19. C 20. C 21. D 22. D 23. B 25. D 26. C 27. A 28. D 26
BÀI TẬP TRẮC NGHIỆM TOÁN 9
3. ĐỒ THỊ HÀM SỐ BẬC NHẤT
§3. ĐỒ THỊ HÀM SỐ BẬC NHẤT A B
BÀI TẬP TRẮC NGHIỆM
Câu 1. Chọn khẳng định đúng về đồ thị hàm số y = ax + b (a ̸= 0).
A. Là đường thẳng đi qua gốc tọa độ.
B. Là đường thẳng song song với trục hoành. Å b ã
C. Là đường thẳng đi qua hai điểm A (0; b), B − ; 0 với b ̸= 0. a
D. Là đường cong đi qua gốc tọa độ.
Câu 2. Chọn khẳng định đúng về đồ thị hàm số y = ax + b (a ̸= 0) với b = 0.
A. Là đường thẳng đi qua gốc tọa độ.
B. Là đường thẳng song song với trục hoành. Å b ã
C. Là đường thẳng đi qua hai điểm A (1; b), B − ; 0 với b ̸= 0. a
D. Là đường cong đi qua gốc tọa độ. 4
Câu 3. Đồ thị hàm số y = 3 (x − 1) +
đi qua điểm nào dưới đây? 3 Å 5 ã Å 3 ã Å 2 1 ã Å 4 ã A. A − ; 0 . B. B 1; . C. C ; . D. D 4; . 3 4 3 3 3 2
Câu 4. Đồ thị hàm số y = 5x −
đi qua điểm nào dưới đây? 5 Å 22 ã Å 1 3 ã Å 2 3 ã A. A 1; . B. B ; . C. C − ; − . D. D (2; 10). 5 5 5 25 5
Câu 5. Cho hai đường thẳng d1 : y = 2x − 2 và d2 : y = 3 − 4x. Tung độ giao điểm của d1 và d2 có tọa độ là 1 2 A. y = − . B. y = . C. y = 1. D. y = −1. 3 3
Câu 6. Cho hai đường thẳng d1 : y = x − 1 và d2 : y = 2 − 3x. Tung độ giao điểm của d1 và d2 có tọa độ là 7 1 1 A. y = −4. B. y = . C. y = . D. y = − . 4 4 4 1
Câu 7. Cho đường thẳng d : y = 3x − . Giao điểm của d với trục tung là 2 Å 1 ã Å 1 ã Å 1 ã Å 1 ã A. A ; 0 . B. B 0; . C. C 0; − . D. D 0; − . 6 2 6 2
Câu 8. Cho đường thẳng d : y = 2x + 6. Giao điểm của d với trục tung là Å 1 ã A. P 0; . B. N (6; 0). C. M (0; 6). D. D (0; −6). 6
Câu 9. Cho hàm số y = (1 − m) x + m. Xác định m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ x = −3. 1 3 3 4 A. m = . B. m = . C. m = − . D. m = . 2 4 4 5 m + 2 Câu 10. Cho hàm số y =
x − 2m + 1. Xác định m để đồ thị hàm số cắt trục hoành tại điểm có 3 hoành độ x = 9. GV: Mạc Lê Chí Đạo – 0946820895 27
Chương 2. HÀM SỐ BẬC NHẤT A. m = −7. B. m = 7. C. m = −2. D. m = −3.
Câu 11. Cho hàm số y = (3 − 2m) x + m − 2. Xác định m để đồ thị hàm số cắt trục tung tại điểm có tung độ y = −4. A. m = 1. B. m = −1. C. m = −2. D. m = 2. 5 + m
Câu 12. Cho hàm số y = (2 − m) x −
. Xác định m để đồ thị hàm số cắt trục tung tại điểm có 2 tung độ y = 3. A. m = 11. B. m = −11. C. m = −12. D. m = 1. 1
Câu 13. Cho hàm số y = mx − 2 có đồ thị là đường thẳng d1 và cắt hàm số y = x + 1 có đồ thị là 2
đường thẳng d2. Xác định m để hai đường thẳng d1 và d2 cắt nhau tại một điểm có hoành độ x = −4. 1 1 1 1 A. m = − . B. m = . C. m = . D. m = − . 4 4 2 2 m Câu 14. Cho hàm số y =
x = 1 có đồ thị là đường thẳng d1 và cắt hàm số y = 3x − 2 có đồ thị là 2
đường thẳng d2. Xác định m để hai đường thẳng d1 và d2 cắt nhau tại một điểm có hoành độ x = −1. A. m = 3. B. m = 12. C. m = −12. D. m = −3.
Câu 15. Cho hàm số y = (m + 1) x − 1 có đồ thị là đường thẳng d1 và cắt hàm số y = x + 1 có đồ thị là
đường thẳng d2. Xác định m để hai đường thẳng d1 và d2 cắt nhau tại một điểm có tung độ y = 4. 3 3 2 2 A. m = . B. m = − . C. m = . D. m = − . 2 2 3 3
Câu 16. Cho hàm số y = 2 (m − 2) x + m có đồ thị là đường thẳng d1 và cắt hàm số y = −x − 1 có
đồ thị là đường thẳng d2. Xác định m để hai đường thẳng d1 và d2 cắt nhau tại một điểm có tung độ y = 3. 7 7 13 13 A. m = . B. m = − . C. m = − . D. m = . 13 13 7 7
Câu 17. Với giá trị nào của m thì đồ thị hàm số y = −2x + m + 2 và y = 5x + 5 − 2m cắt nhau tại một điểm trên trục tung? A. m = 1. B. m = 0. C. m = −1. D. m = 2.
Câu 18. Với giá trị nào của m thì đồ thị hàm số y = 3x − 2m và y = −x + 1 − m cắt nhau tại một điểm trên trục tung? A. m = 1. B. m = 0. C. m = −1. D. m = 2.
Câu 19. Cho ba đường thẳng d1 : y = −2x, d2 : y = −3x − 1, d3 : y = x + 3. Khẳng định nào sau đây đúng?
A. Giao điểm của d1 và d3 là A (2; 1).
B. Ba đường thẳng trên không đồng quy.
C. Đường thẳng d2 đi qua điểm B (1; 4).
D. Ba đường thẳng trên đồng quy tại điểm M (−1; 2).
Câu 20. Cho ba đường thẳng d1 : y = −x + 5, d2 : y = 3x − 1, d3 : y = −2x + 6. Khẳng định nào sau đây đúng?
A. Giao điểm của d1 và d2 là M (0; 5).
B. Ba đường thẳng trên không đồng quy.
C. Ba đường thẳng trên đồng quy tại điểm P (1; 4).
D. Ba đường thẳng trên đồng quy tại điểm N (0; 5).
Câu 21. Tìm m để ba đường thẳng d1 : y = x, d2 : y = 4 − 3x và d3 : y = mx − 3 đồng quy. A. m = 1. B. m = 0. C. m = −1. D. m = 4. 28
BÀI TẬP TRẮC NGHIỆM TOÁN 9
3. ĐỒ THỊ HÀM SỐ BẬC NHẤT
Câu 22. Tìm m để ba đường thẳng d1 : y = 6 − 5x, d2 : y = (m + 2) x + m và d3 : y = 3x + 2 đồng quy. 5 3 5 A. m = . B. m = . C. m = − . D. m = −2. 3 5 3
Câu 23. Cho đường thẳng d : y = −2x − 4. Gọi A, B lần lượt là giao điểm của d với trục hoành và
trục tung. Tính diện tích tam giác OAB. A. 2. B. 4. C. 3. D. 8.
Câu 24. Cho đường thẳng d : y = −3x + 2. Gọi A, B lần lượt là giao điểm của d với trục hoành và
trục tung. Tính diện tích tam giác OAB. 4 2 3 2 A. . B. − . C. . D. . 3 3 2 3
Câu 25. Cho đường thẳng d1 : y = −x + 2 và d2 : y = 5 − 4x. Gọi A, B lần lượt là giao điểm của d1
với d2 và d1 với trục hoành. Tổng hoành độ giao điểm của A và B là A. 2. B. 5. C. 3. D. 8. 4 − x
Câu 26. Cho đường thẳng d1 : y =
và d2 : y = 8 − 2x. Gọi A, B lần lượt là giao điểm của d1 với 3
d2 và d1 với trục tung. Tổng tung độ giao điểm của A và B là 4 2 A. . B. . C. 9. D. 8. 3 3 1
Câu 27. Gọi d1 là đồ thị hàm số y = mx + 1 và d2 là đồ thị hàm số y = x − 2. Xác định giá trị của m 2
để M (2; −1) là giao điểm của d1 và d2. A. m = 1. B. m = 2. C. m = −1. D. m = −2.
Câu 28. Gọi d1 là đồ thị hàm số y = − (2m − 2) x + 4m và d2 là đồ thị hàm số y = 4x − 1. Xác định
giá trị của m để M (1; 3) là giao điểm của d1 và d2. 1 1 A. m = . B. m = − . C. m = 2. D. m = −2. 2 2
Câu 29. Tìm m để ba đường thẳng d1 : y = (m + 2) x − 3, d2 : y = 3x + 1 và d3 : y = 2x − 5 cắt nhau tại một điểm. 1 1 A. m = . B. m = − . C. m = −1. D. m = 1. 3 3
Câu 30. Tìm m để ba đường thẳng d1 : y = (m + 2) x − 3m − 3, d2 : y = x + 2 và d3 : y = mx + 2 cắt nhau tại một điểm. 1 1 A. m = . B. m = − . C. m = −1. D. m = 1. 3 3
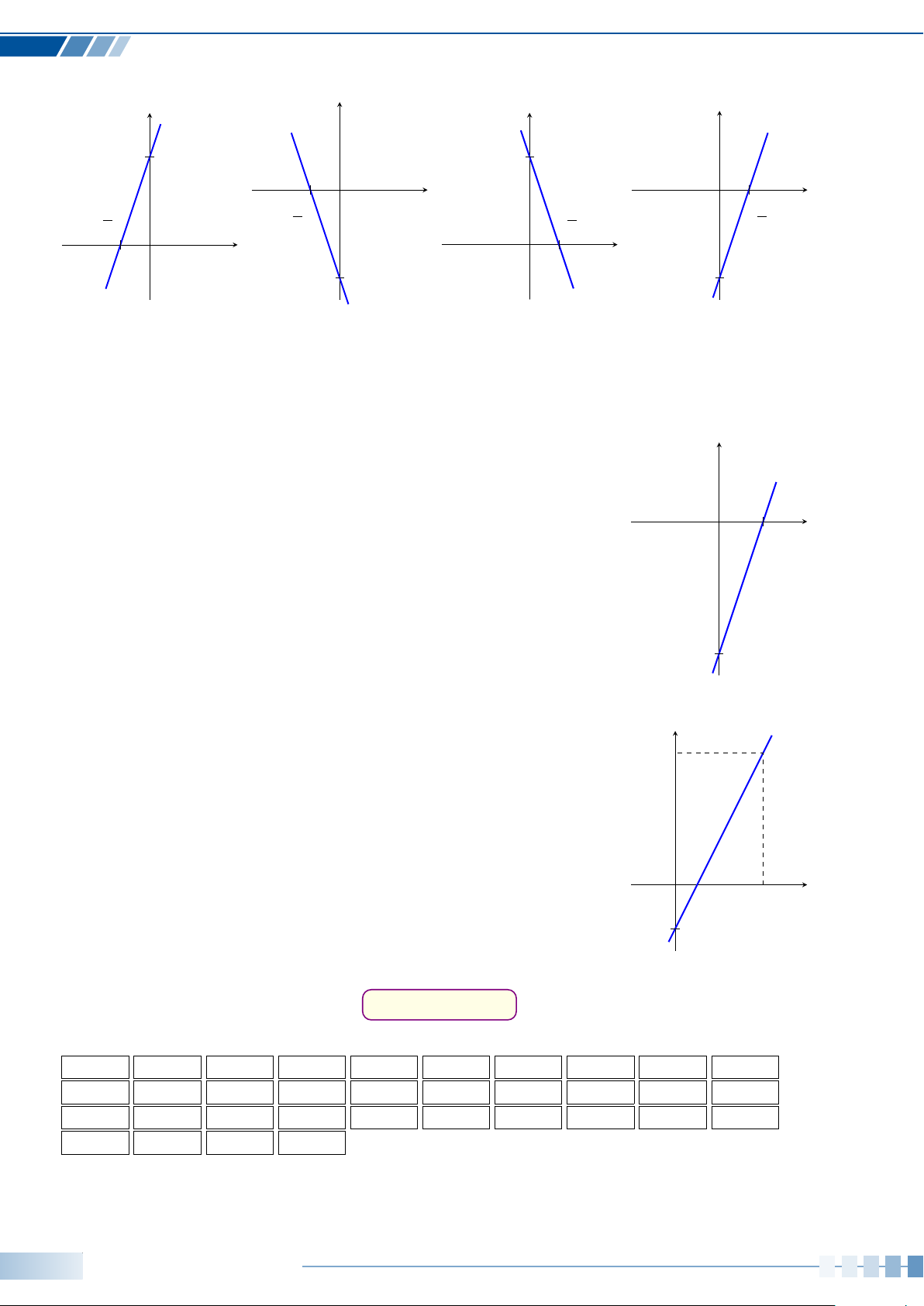
Câu 31. Trong các hình vẽ sau, hình vẽ nào là đồ thị hàm số y = 2x + 1? y y y y 2 2 1 1 1 1 − −1 x 2 x 2 x 1 x O O O O Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4. GV: Mạc Lê Chí Đạo – 0946820895 29
Chương 2. HÀM SỐ BẬC NHẤT
Câu 32. Trong các hình vẽ sau, hình vẽ nào là đồ thị hàm số y = 3x − 2? y y y y 2 2 x x 2 2 O 2 O 2 − − 3 x 3 3 x 3 O O −2 −2 Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4. Câu 33.
Hình vẽ bên là đồ thị của hàm số nào dưới đây? y A. y = 2x − 2. B. y = 3x − 3. C. y = x − 1. D. y = x + 1. x O 1 −3 Câu 34.
Hình vẽ bên là đồ thị của hàm số nào dưới đây? y 3 A. y = 2x − 1. B. y = x − 1. C. y = x − 2. D. y = −2x − 1. x O 2 −1 BẢNG ĐÁP ÁN 1. C 2. A 3. C 4. B 5. A 6. D 7. D 8. C 9. B 10. A 11. C 12. B 13. A 14. B 15. C 16. D 17. A 18. C 19. D 20. C 21. D 22. A 23. B 24. D 25. C 26. A 27. C 28. A 29. A 30. B 31. B 32. D 33. B 34. A 30
BÀI TẬP TRẮC NGHIỆM TOÁN 9
4. ĐƯỜNG THẲNG SONG SONG VÀ ĐƯỜNG THẲNG CẮT NHAU
§4. ĐƯỜNG THẲNG SONG SONG VÀ ĐƯỜNG THẲNG CẮT NHAU A B
BÀI TẬP TRẮC NGHIỆM
Câu 1. Hai đường thẳng d : y = ax + b (a ̸= 0) và d′ : y = ax + b (a ̸= 0) (a′ ̸= 0) cắt nhau khi ®a ̸= a′ ®a = a′ ®a ̸= a′ A. a ̸= a′. B. b ̸= b′ . C. b ̸= b′ . D. b = b′ .
Câu 2. Hai đường thẳng d : y = ax + b (a ̸= 0) và d′ : y = ax + b (a ̸= 0) (a′ ̸= 0) trùng nhau khi ®a ̸= a′ ®a = a′ ®a = a′ A. a ̸= a′. B. b ̸= b′ . C. b ̸= b′ . D. b = b′ .
Câu 3. Hai đường thẳng d : y = ax + b (a ̸= 0) và d′ : y = ax + b (a ̸= 0) (a′ ̸= 0) có a = a′ và b ̸= b′. Khi đó A. d//d′. B. d ≡ d′. C. d cắt d′. D. d ⊥ d′.
Câu 4. Hai đường thẳng d : y = ax + b (a ̸= 0) và d′ : y = ax + b (a ̸= 0) (a′ ̸= 0) có a ̸= a′. Khi đó A. d//d′. B. d ≡ d′. C. d cắt d′. D. d ⊥ d′.
Câu 5. Cho hai đường thẳng d : y = x + 3 và d′ : y = −2x. Khi đó A. d//d′. B. d ≡ d′. C. d cắt d′. D. d ⊥ d′. 1 1
Câu 6. Cho hai đường thẳng d : y = − x + 1 và d′ : y = − x + 2. Khi đó 2 2 A. d//d′. B. d ≡ d′. C. d cắt d′. D. d ⊥ d′.
Câu 7. Với giá trị nào của m thì hai đường thẳng d : y = (m + 2) x − m và d′ : y = 2x − 2m + 1 cắt nhau? A. m ̸= −2. B. m ̸= −4. C. m ̸= {−2; −4}. D. m ̸= {2; −4}.
Câu 8. Với giá trị nào của m thì hai đường thẳng d : y = (3 − 2m) x − 2 và d′ : y = 4x − m + 2 cắt nhau? ß 3 1 ™ ß 3 1 ™ 1 A. m ̸= ; − . B. m ̸= −4. C. m ̸= − ; . D. m ̸= − . 2 2 2 2 2
Câu 9. Với giá trị nào của m thì hai đường thẳng d : y = (m + 2) x − m và d′ : y = −2x − 2m + 1 song song với nhau? A. m = −2. B. m = −4. C. m = 2. D. m ̸= {2; −4}.
Câu 10. Với giá trị nào của m thì hai đường thẳng d : y = (2m − 3) x + 7 và d′ : y = 3x + 2 song song với nhau? A. m = 2. B. m = −4. C. m = 2. D. m = 3.
Câu 11. Với giá trị nào của m thì hai đường thẳng d : y = (2m − 2) x + m − 2 và d′ : y = 3x − 3m song song với nhau? 2 2 5 5 A. m = − . B. m = . C. m = . D. m = − . 5 5 2 2
Câu 12. Với giá trị nào của m thì hai đường thẳng d : y = (2m − 3) x − 2 và d′ : y = −x + m + 1 song song với nhau? GV: Mạc Lê Chí Đạo – 0946820895 31
Chương 2. HÀM SỐ BẬC NHẤT 3 3 A. m = 1. B. m = −1. C. m = . D. m ̸= . 2 2
Câu 13. Với giá trị nào của m thì hai đường thẳng d : y = (m + 2) x − m và d′ : y = −2x − 2m + 1
trùng nhau? m = −2 m = −4 m = 2 Không tồn tại m thỏa mãn m
Câu 14. Với giá trị nào của m thì hai đường thẳng d : y = (1 − m) x + và d′ : y = −x + 1 trùng 2
nhau? m = −2 m = −4 m = 2 Không tồn tại m thỏa mãn
Câu 15. Cho hàm số y = (m − 5) x − 4. Tìm m để hàm số nhận giá trị là 5 khi x = 3. A. m = 6. B. m = 7. C. m = 8. D. m = −3.
Câu 16. Cho hàm số y = 7mx − 3m + 2. Tìm m để hàm số nhận giá trị là 11 khi x = 1. 9 4 9 A. m = . B. m = . C. m = 9. D. m = − . 4 9 4
Câu 17. Viết phương trình đường thẳng d biết d cắt trục tung tại điểm có tung độ bằng −2 và cắt trục
hoành tại điểm có hoành độ bằng 1. A. y = 2x + 2. B. y = −2x − 2. C. y = 3x − 2. D. y = 2x − 2.
Câu 18. Viết phương trình đường thẳng d biết d cắt trục tung tại điểm có tung độ bằng 3 và cắt trục
hoành tại điểm có hoành độ bằng −4. 3 3 3 3 A. y = − x + 3. B. y = x + 3. C. y = − x − 3. D. y = x − 3. 4 4 4 4
Câu 19. Viết phương trình đường thẳng d biết d song song với đường thẳng d′ : y = 3x + 1 và đi qua điểm M (−2; 2). A. y = 2x + 8. B. y = 3x + 8. C. y = 3x − 8. D. y = 3x.
Câu 20. Viết phương trình đường thẳng d biết d song song với đường thẳng d′ : y = −2x − 5 và đi qua điểm M (−1; 4). A. y = 2x − 2. B. y = −2x + 3. C. y = −2x + 2. D. y = −2x. 1
Câu 21. Viết phương trình đường thẳng d biết d vuông góc với đường thẳng d′ : y = − x + 3 và đi 2 qua điểm M (2; −1). 1 A. y = 2x + 5. B. y = −x + 4. C. y = 2x − 5. D. y = − x. 2 1
Câu 22. Viết phương trình đường thẳng d biết d vuông góc với đường thẳng d′ : y = x + 2 và đi qua 5 điểm M (−4; 2). A. y = −5x + 18. B. y = 5x + 18. C. y = 5x − 18. D. y = −5x − 18. 1
Câu 23. Viết phương trình đường thẳng d biết d vuông góc với đường thẳng y = x + 3 và cắt đường 3
thẳng y = 2x + 1 tại điểm có tung độ bằng 5. A. y = −3x + 11. B. y = −3x + 4. C. y = −3x. D. y = 3x + 11.
Câu 24. Viết phương trình đường thẳng d biết d vuông góc với đường thẳng y = 4x + 1 và cắt đường
thẳng y = x − 1 tại điểm có tung độ bằng 3. 1 1 1 1 A. y = − x − 4. B. y = − x + 4. C. y = − x + 2. D. y = − x. 4 4 4 4
Câu 25. Viết phương trình đường thẳng d biết d song song với đường thẳng y = −2x + 1 và cắt trục
hoành tại điểm có hoành độ bằng 3. A. y = −2x + 6. B. y = −3x + 6. C. y = −2x − 4. D. y = −2x + 1. 32
BÀI TẬP TRẮC NGHIỆM TOÁN 9
4. ĐƯỜNG THẲNG SONG SONG VÀ ĐƯỜNG THẲNG CẮT NHAU
Câu 26. Viết phương trình đường thẳng d biết d song song với đường thẳng y = −5x − 3 và cắt trục
hoành tại điểm có hoành độ bằng 5. 1 A. y = x − 25. B. y = 5x + 25. C. y = −5x + 25. D. y = −5x − 25. 5
Câu 27. Viết phương trình đường thẳng d biết d đi qua hai điểm A (1; 2) và B (−2; 0). 2 4 2 4 2 4 2 4 A. y = − x − . B. y = − x + . C. y = x − . D. y = x + . 3 3 3 3 3 3 3 3
Câu 28. Viết phương trình đường thẳng d biết d đi qua hai điểm A (3; 3) và B (−1; 4). 1 15 1 15 1 15 1 15 A. y = x − . B. y = − x + . C. y = − x − . D. y = x + . 4 4 4 4 4 4 4 4
Câu 29. Tìm điểm cố định mà đường thẳng d : y = 3mx − (m + 3) đi qua với mọi m. Å 1 ã Å 1 ã Å 1 ã Å 1 ã A. M ; 3 . B. M ; −3 . C. M − ; −3 . D. M − ; 3 . 3 3 3 3
Câu 30. Tìm điểm cố định mà đường thẳng d : y = (5m − 2) x + m + 1 đi qua với mọi m. Å 7 1 ã Å 1 7 ã Å 1 7 ã A. M ; . B. M (1; 7). C. M − ; . D. M ; . 2 2 2 2 2 2 1
Câu 31. Cho tam giác ABC có đường thẳng BC : y = − x + 1 và A (1; 2). Viết phương trình đường 3 2 2
cao AH của tam giác ABC. y = 3x − y = 3x + y = 3x + 2 y = 3x − 1 3 3
Câu 32. Cho đường thẳng d : y = m2 − 2m + 2 x + 4. Tìm m để d cắt Ox tại A và cắt Oy tại B sao
cho diện tích tam giác OAB lớn nhất. A. m = 1. B. m = 0. C. m = −1. D. m = 2. √k+1 √
Câu 33. Điểm cố định mà đường thẳng d : y = √ x +
k + 3 (k ≥ 0) luôn đi qua là 3 − 1 √ √ √ √ Ä ä Ä ä A. M 1 − 3; 3 − 1 . B. M 3; 3 . √ √ Ä ä C. M 3; 3 − 1 . D. Cả A, B, C đều sai.
Câu 34. Cho đường thẳng d : y = (2m + 1) x − 1. Tìm m để d cắt hai trục tọa độ tạo thành tam giác 1 có diện tích bằng . 2 A. m = 0. B. m = 1. C. m = −1. D. Cả A và C đều đúng.
Câu 35. Biết đường thẳng d : y = mx + 4 cắt Ox tại A và cắt Oy tại B sao cho diện tích tam giác OAB
bằng 6. Khi đó giá trị của m là 4 4 4 4 A. m = ± . B. m < . C. m > . D. m = . 3 3 3 3
Câu 36. Cho đường thẳng d : y = (k − 2) x − 1. Tìm k để d cắt hai trục tọa độ tạo thành tam giác có diện tích bằng 1. 5 3 A. k = . B. k = . 2 2 C. k = 1. D. Cả A và B đều đúng.
Câu 37. Cho đường thẳng d : y = mx + m − 1. Tìm m để d cắt Ox tại A và cắt Oy tại B sao cho tam giác AOB vuông cân. A. m < 1. B. m = 1. C. m > 1. D. m = 1 hoặc m = −1. GV: Mạc Lê Chí Đạo – 0946820895 33
Chương 2. HÀM SỐ BẬC NHẤT BẢNG ĐÁP ÁN 1. A 2. D 3. A 4. C 5. C 6. A 7. C 8. A 9. B 10. A 11. A 12. A 13. D 14. D 15. C 16. A 17. D 18. B 19. B 20. C 21. C 22. D 23. A 24. A 25. A 26. C 27. D 28. B 29. B 30. D 31. D 32. A 33. A 34. D 35. A 36. D 37. D 34
BÀI TẬP TRẮC NGHIỆM TOÁN 9
5. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
§5. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG A B
BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho đường thẳng d : y = ax + b (a ̸= 0). Hệ số góc của đường thẳng d là 1 A. −a. B. a. C. . D. b. a
Câu 2. Cho đường thẳng d : y = −kx + b (k ̸= 0). Hệ số góc của đường thẳng d là 1 A. −k. B. k. C. . D. b. k
Câu 3. Cho đường thẳng d : y = ax + b (a > 0). Gọi α là góc tạo bởi tia Ox và d. Khẳng định nào dưới đây đúng? A. a = − tan α. B. a = tan (180◦ − α). C. a = tan α.
D. a = − tan (180◦ − α).
Câu 4. Cho đường thẳng d : y = ax + b (a < 0). Gọi α là góc tạo bởi tia Ox và d. Khẳng định nào dưới đây đúng? A. tan α < 0. B. tan α > 0. C. tan α = 0. D. tan α = 1.
Câu 5. Hệ số góc của đường thẳng d : y = 2x + 1 là 1 A. −2. B. . C. 1. D. 2. 2 1
Câu 6. Hệ số góc của đường thẳng d : y = x − 10 là 3 1 1 A. 3. B. . C. − . D. −3. 3 3
Câu 7. Cho đường thẳng d : y = (m + 2) x − 5 đi qua điểm A (−1; 2). Hệ số góc của đường thẳng d là A. 1. B. 11. C. −7. D. 7.
Câu 8. Cho đường thẳng d : y = (2m − 3) x + m đi qua điểm A (3; −1). Hệ số góc của đường thẳng d là 5 5 7 7 A. − . B. . C. − . D. . 7 7 5 5
Câu 9. Tìm hệ số góc của đường thẳng d : y = (2m − 4) x + 5 biết đường thẳng d song song với đường
thẳng d′ : 2x − y − 3 = 0. A. 1. B. −2. C. 3. D. 2.
Câu 10. Tìm hệ số góc của đường thẳng d : y = 5mx + 4m − 1 biết đường thẳng d song song với
đường thẳng d′ : x − 3y + 1 = 0. 1 2 A. . B. . C. 1. D. 3. 3 3
Câu 11. Tìm hệ số góc của đường thẳng d biết d đi qua gốc tọa độ O và điểm M (1; 3). A. −2. B. 3. C. 1. D. 2.
Câu 12. Tìm hệ số góc của đường thẳng d biết d đi qua điểm A (1; 1) và điểm M (−1; 2). 1 1 A. − . B. . C. 1. D. 2. 2 2 GV: Mạc Lê Chí Đạo – 0946820895 35
Chương 2. HÀM SỐ BẬC NHẤT
Câu 13. Tìm hệ số góc của đường thẳng d biết d đi qua điểm M (−3; 2) và điểm N (1; −1). 4 4 3 3 A. − . B. . C. . D. − . 3 3 4 4
Câu 14. Tìm m biết đường thẳng d : y = (m + 2) x − 5 có hệ số góc k = −4. m = −4 m = −6 m = −5 m = −3 m + 1
Câu 15. Tìm m biết đường thẳng d : y =
x + 2m có hệ số góc k = −2. m = 5 m = −6 m = −7 3 m = −3
Câu 16. Tìm hệ số góc của đường thẳng d : y = (3 − m) x + 2 biết đường thẳng d vuông góc với đường
thẳng d′ : x − 2y − 6 = 0. A. −2. B. 3. C. 1. D. 2.
Câu 17. Tìm hệ số góc của đường thẳng d : y = (2m + 5) x + 1 biết đường thẳng d vuông góc với
đường thẳng d′ : y − 2x = 0. 1 1 A. −2. B. − . C. . D. 2. 2 2 √
Câu 18. Tính góc tạo bởi tia Ox và đường thẳng y = 3x − 6. A. 45◦. B. 30◦. C. 60◦. D. 90◦. 1
Câu 19. Tính góc tạo bởi tia Ox và đường thẳng y = √ x + 2. 3 A. 45◦. B. 30◦. C. 60◦. D. 90◦. √
Câu 20. Cho đường thẳng d : y = mx +
3. Tính góc tạo bởi tia Ox và đường thẳng d biết d đi qua điểm A (3; 0). A. 120◦. B. 150◦. C. 60◦. D. 90◦. √
Câu 21. Cho đường thẳng d : y = (2m − 1) x + 2 5. Tính tan α với α là góc tạo bởi tia Ox và đường √ √ Ä ä
thẳng d biết d đi qua điểm A 1; 2 5 − 2 . √ √ 2 √ √ A. tan α = 2 − 1. B. tan α = . C. tan α = 2. D. tan α = − 2. 2
Câu 22. Viết phương trình đường thẳng d biết d có hệ số góc bằng −4 và đi qua điểm A (3; −2). A. y = −4x + 10. B. y = 4x + 10. C. y = −4x − 10. D. y = −4x.
Câu 23. Viết phương trình đường thẳng d biết d có hệ số góc bằng 2 và đi qua điểm A (2; 1). A. y = −2x + 3. B. y = 2x − 3. C. y = −2x − 3. D. y = 2x + 5.
Câu 24. Viết phương trình đường thẳng d biết d đi qua B (−1; 1) và tạo với trục Ox một góc bằng 45◦. A. y = x − 2. B. y = x + 2. C. y = −x − 2. D. y = x + 1. √ Ä ä
Câu 25. Viết phương trình đường thẳng d biết d đi qua B
3; 5 và tạo với trục Ox một góc bằng 60◦. √ √ √ √ √ √ A. y = 3x − 5 3. B. y = 3x + 3. C. y = 3x + 8. D. y = 3x − 8.
Câu 26. Viết phương trình đường thẳng d biết d tạo với trục Ox một góc bằng 60◦ và cắt trục hoành
tại điểm có hoành độ bằng −2. √ √ √ √ √ √ √ A. y = 3x − 3. B. y = − 3x + 2 3. C. y = 3x. D. y = 3x + 2 3.
Câu 27. Viết phương trình đường thẳng d biết d tạo với trục Ox một góc bằng 30◦ và cắt trục hoành
tại điểm có hoành độ bằng 6. √ √ √ 3 3 √ 3 √ √ √ A. y = x. B. y = x + 2 3. C. y = x − 2 3. D. y = 3x − 2 3. 3 3 3 36
BÀI TẬP TRẮC NGHIỆM TOÁN 9
5. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
Câu 28. Đường thẳng y = 2 (m + 1) x − 5m − 8 đi qua A (3; −5) có hệ số góc bằng A. −4. B. 4. C. 3. D. 2. m
Câu 29. Đường thẳng y = 6 −
x − 2m + 3 đi qua A (−2; 4) có hệ số góc bằng 2 25 25 1 A. −13. B. . C. − . D. − . 2 2 2
Câu 30. Viết phương trình đường thẳng d biết d tạo với đường thẳng y = 1 một góc bằng 120◦ và cắt
trục tung tại điểm có tung độ bằng −2. √ √ √ √ A. y = − 3x − 2. B. y = − 3x + 2. C. y = 3x − 2. D. y = 3x + 2.
Câu 31. Viết phương trình đường thẳng d biết d tạo với đường thẳng y = 2 (theo chiều dương) một
góc bằng 135◦ và cắt trục tung tại điểm có tung độ bằng 4. A. y = x − 4. B. y = −x − 4. C. y = x + 4. D. y = −x + 4. BẢNG ĐÁP ÁN 1. B 2. A 3. C 4. A 5. D 6. B 7. C 8. A 9. D 10. A 11. B 12. A 13. D 14. D 15. D 16. A 17. B 18. C 19. B 20. B 21. D 22. A 23. B 24. B 25. D 26. D 27. C 28. A 29. B 30. A 31. D GV: Mạc Lê Chí Đạo – 0946820895 37 II PHẦNHÌNH HỌC
HỆ THỨC LƯỢNG TRONG TAM GIÁC Chûúng 1 HỆ THỨC LƯỢNG VUÔNG TRONG TAM GIÁC VUÔNG
§1. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG A B
BÀI TẬP TRẮC NGHIỆM Câu 1.
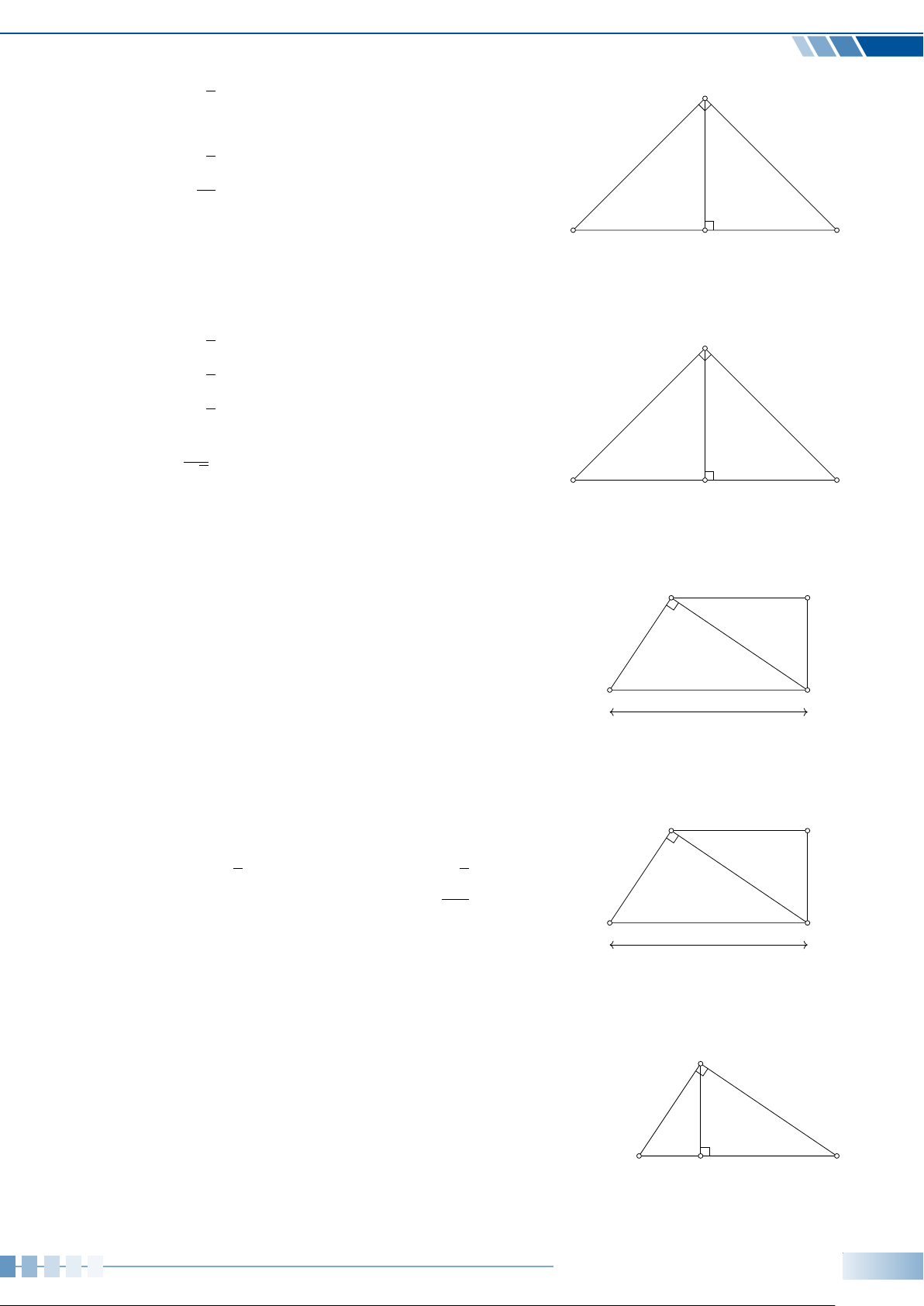
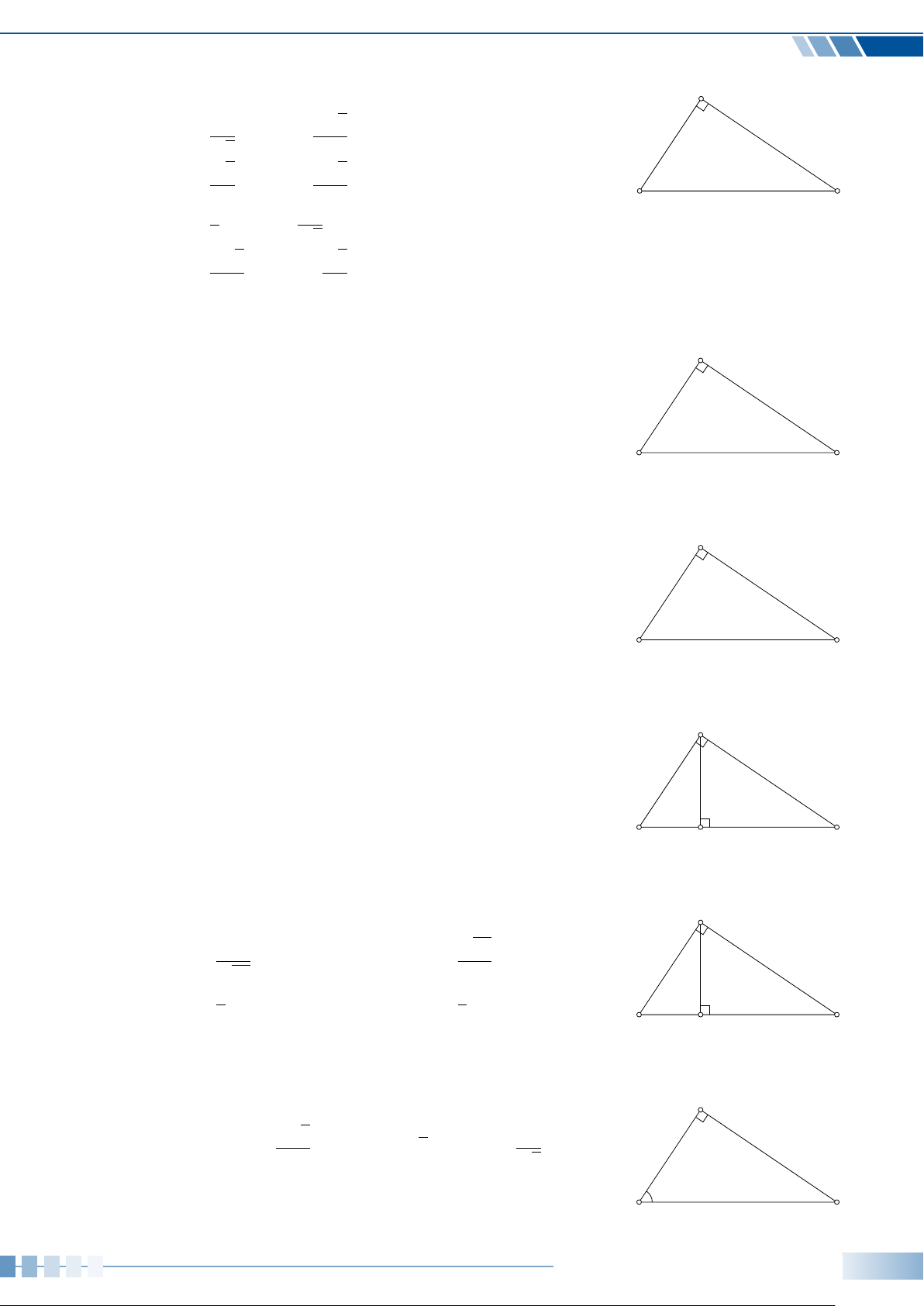
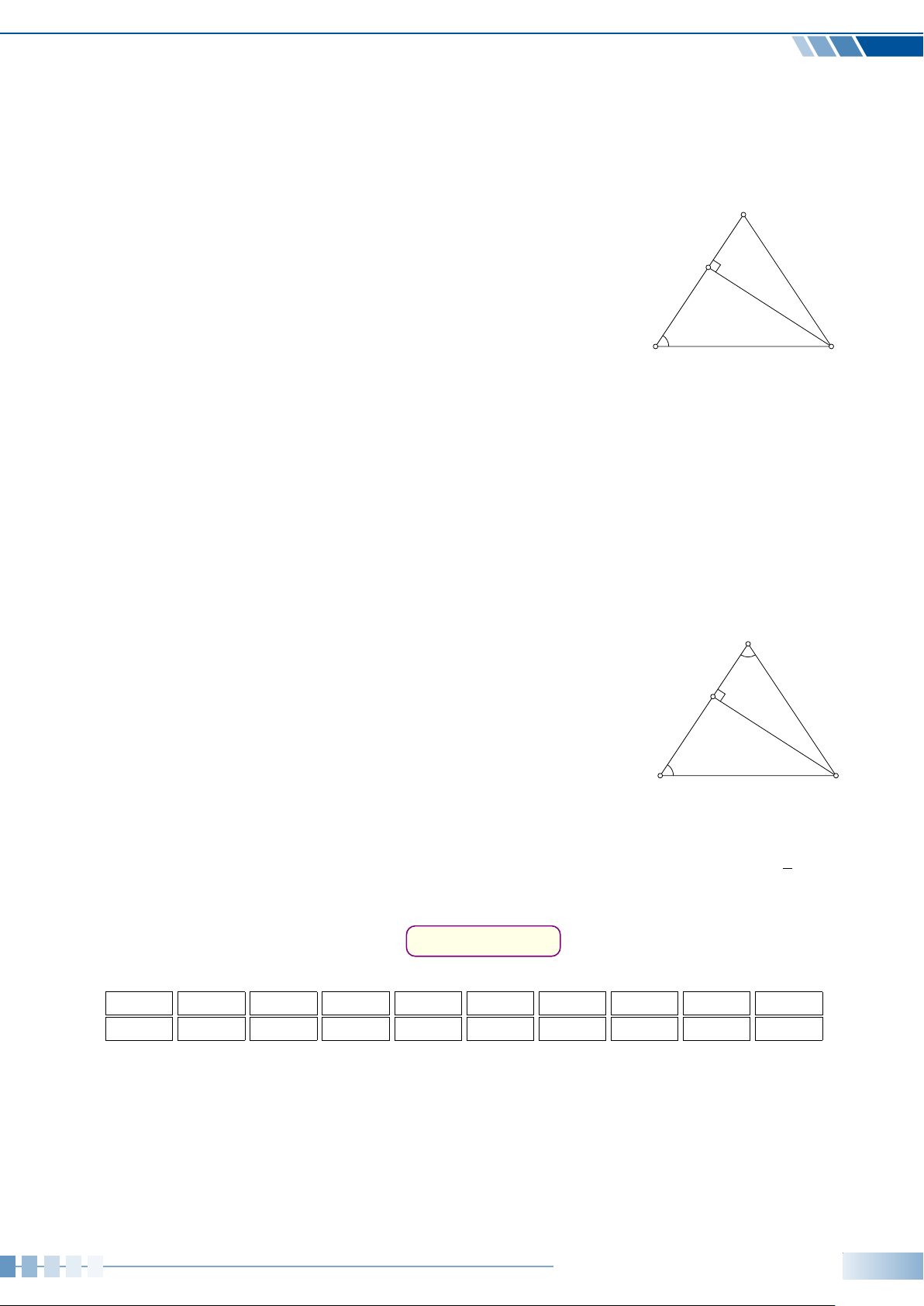
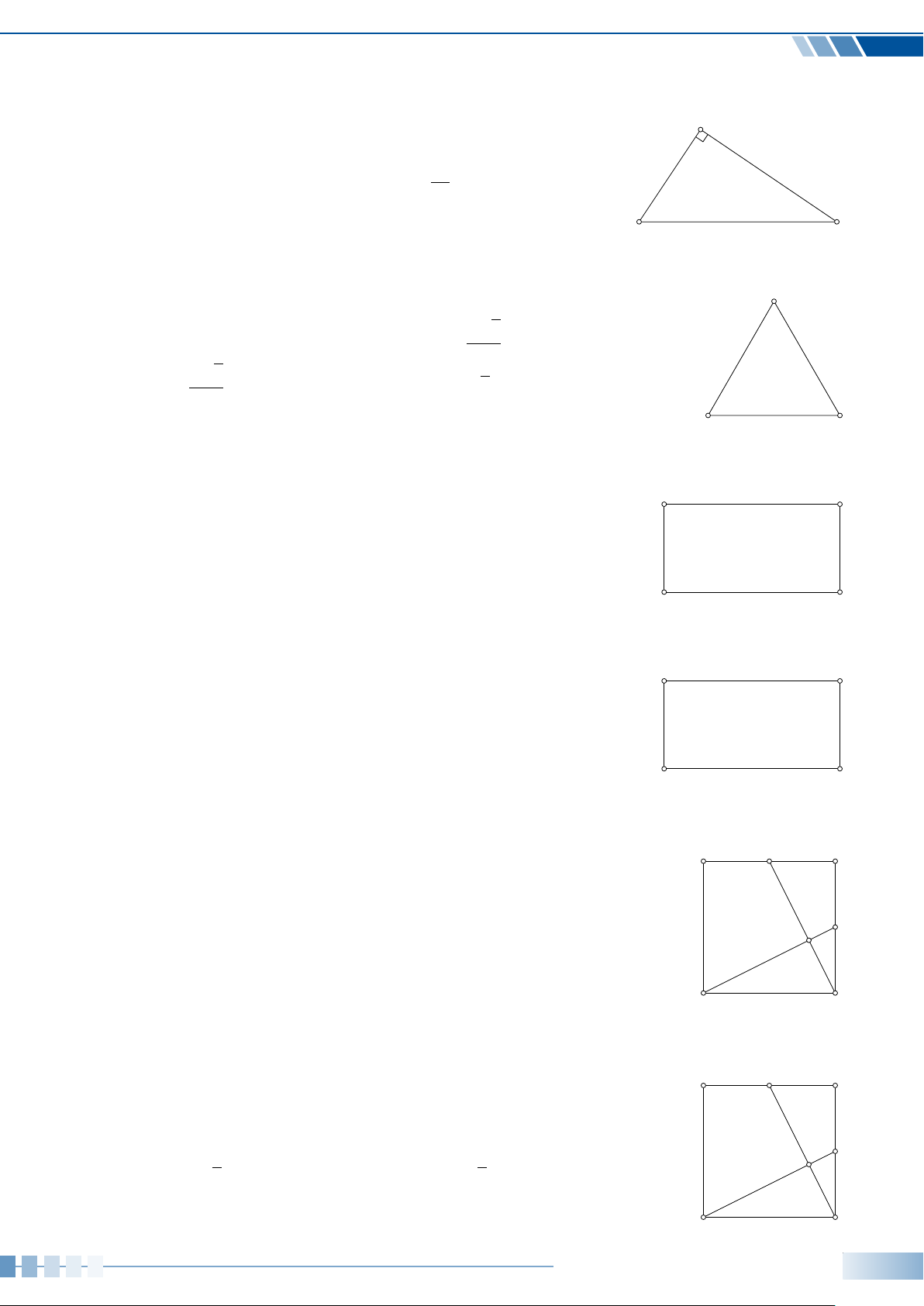
Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Hệ A
thức nào sau đây là đúng? A. AH2 = AB · AC. B. AH2 = BH ·CH. C. AH2 = AB · BH. D. AH2 = CH · BC. B C H
Câu 2. “Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng · · · ”. Cụm từ thích
hợp điền vào chỗ trống là
A. Tích hai cạnh góc vuông.
B. Tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
C. Tích cạnh huyền và 1 cạnh góc vuông.
D. Tổng nghịch đảo các bình phương của hai cạnh góc vuông. Câu 3.
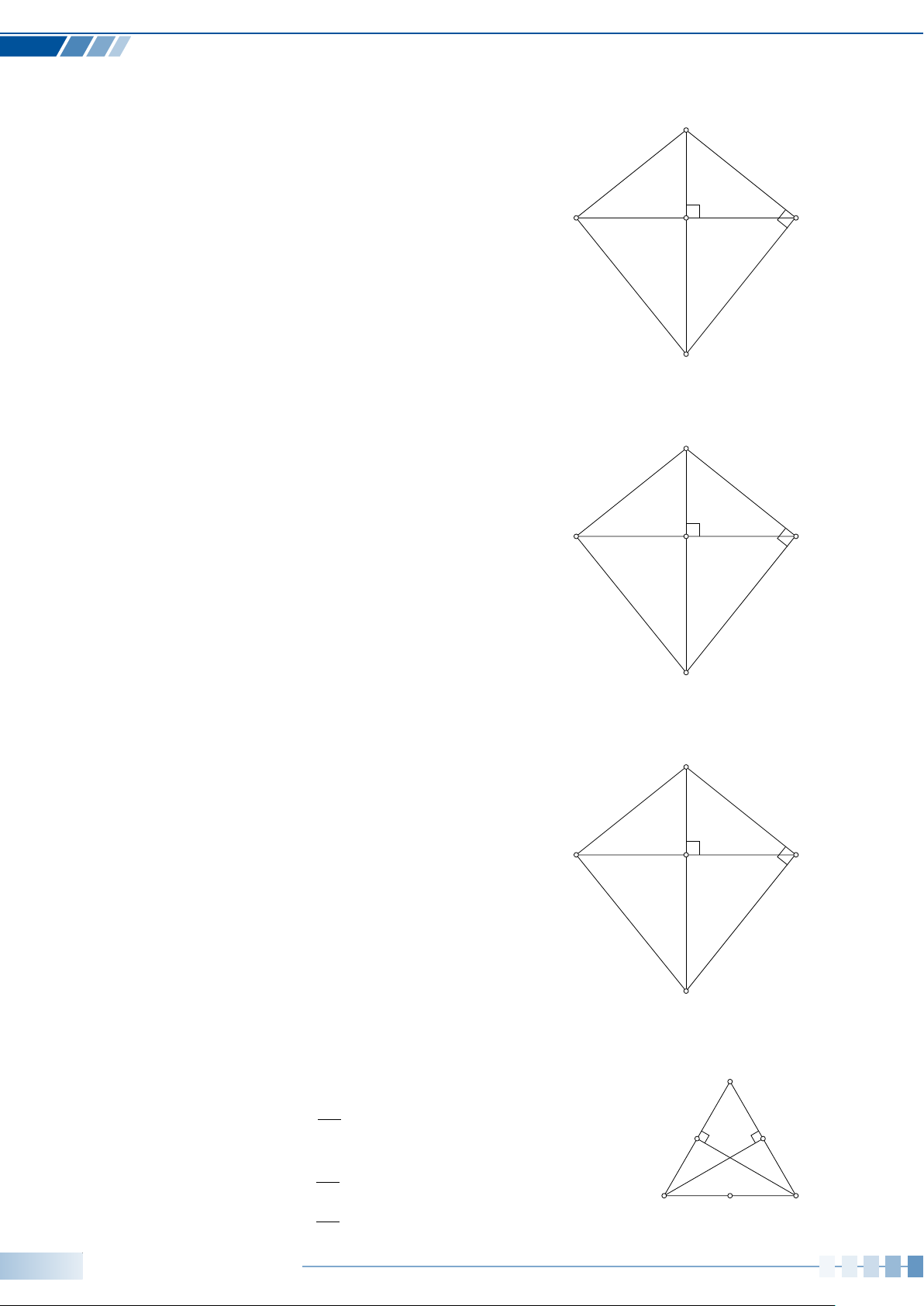
Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Hệ A
thức nào sau đây là sai? A. AB2 = BH · BC. B. AC2 = CH · BC. AB2 + AC2 C. AB · AC = AH · BC. D. AH2 = . AB2 · AC2 B C H Câu 4.
Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Hệ A
thức nào sau đây là sai? 1 1 1 A. AC2 = CH · BC. B. = + . AH2 AB2 AC2 C. AH · BC = BH ·CH. D. AH2 = BH ·CH. B C H Câu 5. GV: Mạc Lê Chí Đạo – 0946820895 39
Chương 1. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Tính x, y trong hình vẽ bên. A A. x = 3,6; y = 6,4. B. y = 3,6; x = 6,4. C. x = 4; y = 6. D. x = 2,8; y = 7,2. 6 8 B C x H y Câu 6.
Tính x, y trong hình vẽ bên. A A. x = 3,2; y = 1,8. B. y = 1,8; x = 3,2. C. x = 2; y = 3. D. x = 3; y = 2. 3 4 B C x H y Câu 7.
Tính x, y trong hình vẽ bên. √ √ A 35 74 √ 35 74 √ A. x = ; y = 74. B. y = ; x = 74. 74 74 5 7 C. x = 4; y = 6. D. x = 2,8; y = 7,2. x B C H y Câu 8.
Tính x, y trong hình vẽ bên. √ A 60 A. x = 4; y = 19. B. y = ; x = 13. 13 60 5 x 12 C. x = 4; y = 13. D. x = ; y = 13. 13 B C H y Câu 9.
Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). A
Cho biết AB : AC = 3 : 4 và BC = 15cm. Tính độ dài đoạn thẳng BH. A. BH = 5,4cm. B. BH = 4,4cm. C. BH = 5,2cm. D. BH = 5cm. B C H 15cm Câu 10.
Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Cho √ A
biết AB : AC = 4 : 5 và BC =
41cm. Tính độ dài đoạn thẳng CH
(làm tròn đến chữ số thập phân thứ nhất). A. CH ≈ 2,5cm. B. CH ≈ 4cm. C. CH ≈ 3,8cm. D. CH ≈ 3,9cm. B C H √41cm 40
BÀI TẬP TRẮC NGHIỆM TOÁN 9
1. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG Câu 11.
Tính x, y trong hình vẽ bên. A A. x = 7,2; y = 11,8. B. x = 7; y = 12. C. x = 7,2; y = 12,8. D. x = 7,2; y = 12. 12 B C x H y 20 Câu 12.
Tính x, y trong hình vẽ bên. A A. x = 6,5; y = 9,5. B. x = 6,25; y = 9,75. C. x = 9,25; y = 6,75. D. x = 6; y = 10. 10 B C x H y 16 Câu 13.
Tìm x trong hình vẽ bên (làm tròn đến chữ số thập phân thứ A hai). A. x ≈ 8,81. B. x ≈ 8,82. 12 x 13 C. x ≈ 8,83. D. x ≈ 8,80. B C H Câu 14. Tìm x trong hình vẽ bên. A A. x = 14. B. x = 13. √ C. x = 12. D. x = 145. 15 x 20 B C H Câu 15.
Cho tam giác ABC vuông tại A, có đường cao AH. Biết BC = 7,5 A
cm, CH = 5 cm. Độ dài đường cao AH bằng √2 5 A. AH = cm. B. AH = √ cm. 5 2 √ √ C. AH = 39,5 cm. D. AH = 5 2 cm. 5cm B C H 7,5cm Câu 16.
Cho tam giác ABC vuông tại A, có đường cao AH (hình vẽ bên). A Độ dài AH bằng √ A. 3. B. 1,5. C. 18. D. 9. B C 2cm H 4,5cm GV: Mạc Lê Chí Đạo – 0946820895 41
Chương 1. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG Câu 17.
Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Cho A
biết AB : AC = 3 : 4 và AH = 6cm. Tính độ dài đoạn thẳng CH. A. CH = 8cm. B. CH = 6cm. C. CH = 10cm. D. CH = 12cm. 6cm B C H Câu 18.
Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). A
Cho biết AB : AC = 3 : 7 và AH = 42cm. Tính độ dài đoạn thẳng CH. A. CH = 96cm. B. CH = 49cm. 42cm C. CH = 98cm. D. CH = 89cm. B C H Câu 19.
Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Cho A HB 1 biết =
và AH = 4cm. Tính chu vi tam giác ABC. HC√ 4 √ A. 5 5 + 8cm. B. 5 5 + 12cm. √ √ 4cm C. 4 5 + 8cm. D. 6 5 + 10cm. B C H Câu 20.
Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Cho A AB 3 biết =
và AH = 42cm. Tính độ dài đoạn thẳng BH, CH. AC 7 A. BH = 18cm; CH = 98cm. B. BH = 24cm; CH = 72cm. 42cm C. BH = 20cm; CH = 78cm. D. BH = 28cm; CH = 82cm. B C H Câu 21.
Tính x, y trong hình vẽ bên. √ √ √ √ A A. x = 2 5; y = 5. B. x = 5; y = 3 5. √ √ √ √ C. x = 5; y = 2 5. D. x = 2 5; y = 2 5. x y B C 1 H 4 Câu 22.
Tính x, y trong hình vẽ bên. √ √ √ √ A A. x = 14; y = 35. B. x = 35; y = 3 14. √ √ √ √ C. x = 24; y = 3 5. D. x = 6; y = 2 15. x y B C 2 H 5 Câu 23. 42
BÀI TẬP TRẮC NGHIỆM TOÁN 9
1. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG Tìm x trong hình vẽ bên. √ A A. x = 6 2. B. x = 6. √ C. x = 6 3. x 6 x √ D. x = 82. B C H Câu 24. Tìm x trong hình vẽ bên. √ A A. x = 6 2. √ B. x = 8 2. √ C. x = 8 3. x 8 x 8 D. x = √ . 2 B C H Câu 25.
Cho ABCD là hình thang vuông tại A và D. Đường chéo BD B
vuông góc với BC. Biết AD = 12cm, CD = 25cm. Tính độ dài A BC, biết BC < 20cm. A. BC = 15cm. B. BC = 16cm. 12cm C. BC = 14cm. D. BC = 17cm. C D 25cm Câu 26.
Cho ABCD là hình thang vuông tại A và D. Đường chéo BD B
vuông góc với BC. Biết AD = 10cm, CD = 20cm. Tính độ dài A BC, biết BC < 20cm. √ √ A. BC = 10 3cm. B. BC = 10 2cm. 10cm √ C. BC = 10cm. D. BC = 110cm. C D 20cm Câu 27.
Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Cho A
biết AB : AC = 3 : 4 và AB + AC = 21. Tính độ dài các cạnh của tam giác ABC. A. AB = 9; AC = 10; BC = 15. B. AB = 9; AC = 12; BC = 15. C. AB = 8; AC = 10; BC = 15. B C H D. AB = 8; AC = 12; BC = 15. Câu 28. GV: Mạc Lê Chí Đạo – 0946820895 43
Chương 1. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Cho A
biết AB : AC = 5 : 12 và AB + AC = 34. Tính độ dài các cạnh của tam giác ABC. A. AB = 5; AC = 12; BC = 13. B. AB = 24; AC = 10; BC = 26. C. AB = 10; AC = 24; BC = 26. B C H D. AB = 26; AC = 12; BC = 24. Câu 29.
Cho tam giác ABC vuông tại A, đường cao AH. A
Cho biết BH = 4cm, CH = 9cm. Gọi D, E lần lượt là hình chiếu E
vuông góc của H trên các cạnh AB và AC. Các đường thẳng vuông
góc với DE tại D và E lần lượt cắt BC tại M, N (như hình vẽ). Tính D độ dài đoạn thẳng DE. A. DE = 5cm. B. DE = 8cm. B C M H N C. DE = 7cm. D. DE = 6cm. Câu 30.
Cho tam giác ABC vuông tại A, đường cao AH. A
Cho biết BH = 9cm, CH = 16cm. Gọi D, E lần lượt là hình chiếu E
vuông góc của H trên các cạnh AB và AC. Các đường thẳng vuông
góc với DE tại D và E lần lượt cắt BC tại M, N (như hình vẽ). Tính D độ dài đoạn thẳng DE. A. DE = 12cm. B. DE = 8cm. B C M H N C. DE = 15cm. D. DE = 6cm.
Câu 31. Tính diện tích hình thang ABCD có đường cao bằng 12cm, hai đường chéo AC và BD vuông góc với nhau, BD = 15cm. A. 150cm2. B. 300cm2. C. 125cm2. D. 200cm2. Ä
Câu 32. Cho hình thang vuông ABCD b A = b
D = 90◦ä có hai đường chéo AC và BD vuông góc với
nhau tại H. Biết HD = 18cm, HB = 8cm. Tính diện tích hình thang ABCD. A. 504cm2. B. 505cm2. C. 506cm2. D. 507cm2.
Câu 33. Cho tam giác ABC cân tại A, kẻ đường cao AH và CK. Biết AH = 7,5cm, CK = 12cm. Tính độ dài BC, AB. A. AB = 10,5cm; BC = 18cm. B. AB = 12cm; BC = 22cm. C. AB = 12, 5cm; BC = 20cm. D. AB = 15cm; BC = 24cm.
Câu 34. Cho tam giác ABC vuông tại A, đường cao AH. Gọi M, N theo thứ tự là trung điểm của AB
và AC. Biết HM = 15cm, HN = 20cm. Tính độ dài HB, HC, AH.
A. HB = 12cm; HC = 28cm; AH = 20cm.
B. HB = 15cm; HC = 30cm; AH = 20cm.
C. HB = 16cm; HC = 30cm; AH = 22cm.
D. HB = 18cm; HC = 32cm; AH = 24cm.
Câu 35. Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. Các phân giác trong và ngoài của
góc B cắt đường thẳng AC lần lượt tại M, N. Tính độ dài AM, AN. A. AM = 3cm; AN = 9cm. B. AM = 2cm; AN = 18cm. C. AM = 4cm; AN = 9cm. D. AM = 3cm; AN = 12cm.
Câu 36. Cho tam giác ABC vuông tại A có cạnh AB = 30cm, AC = 40cm, đường cao AH và đường
trung tuyến AM. Tính độ dài BH, HM, MC.
A. BH = 18cm; HM = 7cm; MC = 25cm.
B. BH = 12cm; HM = 8cm; MC = 20cm.
C. BH = 16cm; HM = 8cm; MC = 24cm.
D. BH = 16cm; HM = 6cm; MC = 22cm.
Câu 37. Một tam giác vuông có cạnh huyền bằng 5, đường cao ứng với cạnh huyền bằng 2. Hãy tính
cạnh nhỏ nhất của tam giác vuông này. 44
BÀI TẬP TRẮC NGHIỆM TOÁN 9
1. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG √ √ A. 5. B. 3. C. 1. D. 2.
Câu 38. Cho △ABC vuông tại A, các cạnh AB, AC tương ứng tỉ lệ với 3 và 4. Biết đường cao AH = 18cm. Tính chu vi △ABC. A. 90cm. B. 91cm. C. 89cm. D. 88cm.
Câu 39. Cho △ABC vuông tại A có AB = 3cm, AC = 4cm, đường cao AH và đường trung tuyến AM.
Độ dài đoạn thẳng HM bằng 7 9 43 5 A. cm. B. cm. C. cm. D. cm. 10 5 10 2 Câu 40.
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 10cm, A
AH = 6cm. Tính độ dài các cạnh AC, BC của tam giác ABC. A. AC = 6,5cm; BC = 12cm. B. AC = 7,5cm; BC = 12,5cm. 13cm C. AC = 8cm; BC = 13cm. D. AC = 8,5cm; BC = 14,5cm. B C 5cm H BẢNG ĐÁP ÁN 1. B 2. B 3. D 4. C 5. A 6. B 7. A 8. D 9. A 10. D 11. C 12. B 13. B 14. C 15. B 16. A 17. A 18. C 19. D 20. A 21. C 22. A 23. A 24. B 25. A 26. B 27. B 28. C 29. D 30. A 31. A 32. D 33. C 34. D 35. D 36. A 37. A 38. A 39. A 40. B GV: Mạc Lê Chí Đạo – 0946820895 45
Chương 1. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
§2. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN A B
BÀI TẬP TRẮC NGHIỆM Câu 1.
Cho tam giác MNP vuông tại M. Khi đó cos ’ MNP bằng M MN MP MN MP A. . B. . C. . D. . NP NP MP MN N P Câu 2.
Cho tam giác MNP vuông tại M. Khi đó tan ’ MNP bằng M MN MP MN MP A. . B. . C. . D. . NP NP MP MN N P
Câu 3. Cho α là góc nhọn bất kỳ. Khẳng định đúng là A. sin α + cos α = 1. B. sin2 α + cos2 α = 1. C. sin3 α + cos3 α = 1. D. sin α − cos α = 1.
Câu 4. Cho α là góc nhọn bất kỳ. Khẳng định sai là sin α cos α A. tan α = . B. cot α = . cos α sin α C. tan α · cot α = 1. D. tan2 α − 1 = cos2 α.
Câu 5. Cho α và β là hai góc nhọn bất kì thỏa mãn α + β = 90◦. Khẳng định đúng là A. tan α = sin β . B. tan α = cot β . C. tan α = cos α. D. tan α = tan β .
Câu 6. Khẳng định nào sau đây là đúng? Cho hai góc phụ nhau thì
A. sin góc này bằng cos góc kia. B. sin hai góc bằng nhau.
C. tan góc này bằng cot góc kia. D. Cả A và C đều đúng. Câu 7.
Cho tam giác ABC vuông tại C có BC = 1,2cm, AC = 0,9cm. Tính C
các tỉ số lượng giác sin B và cos B. A. 1,2cm 0,9cm sin B = 0,6; cos B = 0,8. B. sin B = 0,8; cos B = 0,6. C. sin B = 0,4; cos B = 0,8. D. sin B = 0,6; cos B = 0,4. A B Câu 8.
Cho △ABC vuông tại A có AC = 3, AB = 4. Khi đó cos B bằng A 3 3 4 4 A. . B. . C. . D. . 4 5 3 5 3 4 B C Câu 9. 46
BÀI TẬP TRẮC NGHIỆM TOÁN 9
2. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
Cho tam giác ABC vuông tại C có AC = 1cm, BC = 2cm. Tính các C
tỉ số lượng giác sin B và cos B.√ 1 2 3 A. sin B = √ ; cos B = . 1cm 3 3 √ √ 5 2 5 B. sin B = ; cos B = . 5 5 A B 1 2 2cm C. sin B = ; cos B = √ . 2 5 √ √ 2 5 5 D. sin B = ; cos B = . 5 5 Câu 10.
Cho tam giác ABC vuông tại A có BC = 8cm, AC = 6cm. Tính tỉ A
số lượng giác tanC (làm tròn đến chữ số thập phân thứ hai). A. tanC ≈ 0, 87. B. tanC ≈ 0, 86. 6cm C. tanC ≈ 0, 88. D. tanC ≈ 0, 89. B C 8cm Câu 11.
Cho tam giác ABC vuông tại A có BC = 9cm, AC = 5cm. Tính tỉ A
số lượng giác tanC (làm tròn đến chữ số thập phân thứ nhất). A. tanC ≈ 0,67. B. tanC ≈ 0,5. 5cm C. tanC ≈ 1,4. D. tanC ≈ 1,5. B C 9cm Câu 12.
Cho tam giác ABC vuông tại A, đường cao AH có AB = 13cm, A
BH = 5cm. Tính tỉ số lượng giác sinC (làm tròn đến chữ số thập phân thứ hai). 13cm A. sinC ≈ 0,35. B. sinC ≈ 0,37. C. sinC ≈ 0,39. D. sinC ≈ 0,38. B C 5cm H Câu 13.
Cho tam giác ABC vuông tại A, đường cao AH có AC = 15cm, A
CH = 6cm. Tính tỉ số lượng giác cos B. √ 5 21 A. cos B = √ . B. cos B = . 15cm 21 5 3 2 C. cos B = . D. cos B = . 5 5 B C H 6cm Câu 14.
Cho tam giác ABC vuông tại A, ‘
ABC = 60◦, AB = 5cm. Độ dài A cạnh AC bằng √ 5 3 √ 5 A. 10cm. B. cm. C. 5 3cm. D. √ cm. 5cm 2 3 60◦ B C Câu 15. GV: Mạc Lê Chí Đạo – 0946820895 47
Chương 1. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Cho tam giác ABC vuông tại A, đường cao AH có CH = 4cm, A
BH = 3cm. Tính tỉ số lượng giác cosC (làm tròn đến chữ số thập phân thứ hai). A. cosC ≈ 0,76. B. cosC ≈ 0,77. C. cosC ≈ 0,75. D. cosC ≈ 0,78. B C 3cm H 4cm Câu 16.
Cho tam giác ABC vuông tại A, đường cao AH có CH = 11cm, A
BH = 12cm. Tính tỉ số lượng giác cosC (làm tròn đến chữ số thập phân thứ hai). A. cosC ≈ 0,79. B. cosC ≈ 0,69. C. cosC ≈ 0,96. D. cosC ≈ 0,66. B C 12cm H 11cm Câu 17.
Cho △ABC vuông tại A. Hãy tính tanC biết rằng cot B = 2. A 1 1 A. tanC = . B. tanC = 4. C. tanC = 2. D. tanC = . 4 2 B C Câu 18.
Cho △ABC vuông tại A. Hãy tính tanC biết rằng tan B = 4. A 1 1 A. tanC = . B. tanC = 4. C. tanC = 2. D. tanC = . 4 2 B C Câu 19. 7
Cho △ABC vuông tại A có AB = 5cm, cotC = . Tính độ dài các 8 A
đoạn thẳng AC và BC (làm tròn đến chữ số thập phân thứ hai).
A. AC ≈ 4,39cm; BC ≈ 6,66cm. 5cm
B. AC ≈ 4,38cm; BC ≈ 6,65cm.
C. AC ≈ 4,38cm; BC ≈ 6,64cm. D. B AC ≈ 4,37cm; BC ≈ 6,67cm. C Câu 20. 5
Cho △ABC vuông tại A có AB = 9cm, tanC = . Tính độ dài các 4 A
đoạn thẳng AC và BC (làm tròn đến chữ số thập phân thứ hai). A. AC = 7cm; BC ≈ 7,2cm. 9cm B. AC = 7cm; BC ≈ 11,53cm. C. AC ≈ 5,2cm; BC = 11cm.
D. AC ≈ 7,2cm; BC ≈ 11,53cm. B C BẢNG ĐÁP ÁN 1. A 2. D 3. B 4. D 5. B 6. D 7. A 8. D 9. B 10. C 11. D 12. D 13. B 14. C 15. A 16. B 17. C 18. A 19. B 20. D 48
BÀI TẬP TRẮC NGHIỆM TOÁN 9
3. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG
§3. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG A B
BÀI TẬP TRẮC NGHIỆM Câu 1.
Cho tam giác MNP vuông tại N. Hệ thức nào sau đây là đúng? N A. MN = MP · sin P. B. MN = MP · cos P. C. MN = MP · tan P. D. MN = MP · cot P. M P Câu 2.
Cho tam giác MNP vuông tại N. Hệ thức nào sau đây là đúng? N A. NP = MP · sin P. B. NP = MN · cot P. C. NP = MN · tan P. D. NP = MP · cos P. M P
Câu 3. Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Chọn khẳng định sai? A. b = a · sin B = a · cosC. B. a = c · tan B = c · cotC. C. a2 = b2 + c2. D. c = a · sinC = a · cos B. Câu 4.
Cho tam giác ABC vuông tại A có BC = a, AC = b, ‘ ABC = 50◦. A Chọn khẳng định đúng? A. b = c · sin 50◦. B. b = c · tan 50◦. b C. b = c · cos 50◦. D. b = c · cot 50◦. 50◦ B C a Câu 5.
Cho △ABC vuông tại A có AC = 10 cm, b C = 30◦. Tính AB, BC. √ √ A 5 3 20 3 A. AB = cm; BC = cm. 3√ 3√ 10 3 14 3 10 cm B. AB = cm; BC = cm. 3√ 3 10 3 √ 30◦ B C C. AB = cm; BC = 20 3 cm. 3√ √ 10 3 20 3 D. AB = cm; BC = cm. 3 3 Câu 6.
Cho △ABC vuông tại A có AC = 20cm, b C = 60◦. Tính AB, BC. √ A A. AB = 20 3cm; BC = 40cm. √ √ B. AB = 20 3cm; BC = 40 3cm. 20cm C. AB = 20cm; BC = 40cm. √ D. AB = 20cm; BC = 20 3cm. 60◦ B C GV: Mạc Lê Chí Đạo – 0946820895 49
Chương 1. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG Câu 7.
Cho △ABC vuông tại A có BC = 12cm, b B = 40◦. Tính AC, b C (làm A
tròn đến chữ số thập phân thứ hai). A. AC ≈ 7,71cm; b C = 40◦. B. AC ≈ 7,72cm; b C = 50◦. C. AC ≈ 7,71cm; b C = 50◦. D. AC ≈ 7,73cm; b C = 50◦. 40◦ B C 12cm Câu 8.
Cho △ABC vuông tại A có BC = 15cm, b B = 55◦. Tính AC, b C (làm A
tròn đến chữ số thập phân thứ hai). A. AC ≈ 12,29cm; b C = 45◦. B. AC ≈ 12,29cm; b C = 35◦. C. AC ≈ 12,2cm; b C = 35◦. D. AC ≈ 12,92cm; b C = 40◦. 55◦ B C 15cm Câu 9.
Cho △ABC vuông tại A có BC = 15cm, AB = 12cm. Tính AC, b B A (làm tròn đến phút). A. AC = 8cm; 12cm b B ≈ 36◦52′. B. AC = 9cm; b B ≈ 36◦52′. C. AC = 9cm; b B ≈ 37◦52′. D. AC = 9cm; b B ≈ 36◦55′. B C 15cm Câu 10.
Cho △ABC vuông tại A có AC = 7cm, AB = 5cm. Tính BC, b C (làm A tròn đến phút). √ A. BC = 74cm; b B ≈ 35◦32′. √ 5cm 7cm B. BC = 74cm; b B ≈ 36◦32′. √ C. BC = 74cm; b B ≈ 35◦33′. √ B C D. BC = 75cm; b B ≈ 35◦32′. Câu 11.
Cho tam giác ABC vuông tại A có BC = 26cm, AB = 10cm. Tính A AC, b C (làm tròn đến độ). A. AC = 22cm; 10cm b C ≈ 67◦. B. AC = 24cm; b C ≈ 66◦. C. AC = 24cm; b C ≈ 67◦. D. AC = 24cm; b C ≈ 68◦. B C 26cm
Câu 12. Cho tam giác ABC có AB = 16cm, AC = 14cm và b
B = 60◦. Tính độ dài cạnh BC. A. BC = 10cm. B. BC = 11cm. C. BC = 9cm. D. BC = 12cm.
Câu 13. Cho tam giác ABC có AB = 12cm, AC = 15cm và b
B = 60◦. Tính độ dài cạnh BC. √ √ A. BC = 3 3 + 6cm. B. BC = 3 13 + 6cm. C. BC = 9cm. D. BC = 6cm.
Câu 14. Cho tam giác ABC có b B = 60◦, b
C = 55◦, AC = 3,5cm. Diện tích tam giác ABC gần nhất với giá trị nào dưới đây? A. 4. B. 5. C. 7. D. 8. 50
BÀI TẬP TRẮC NGHIỆM TOÁN 9
3. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG
Câu 15. Cho tam giác ABC có b B = 70◦, b
C = 35◦, AC = 4,5cm. Diện tích tam giác ABC gần nhất với giá trị nào dưới đây? A. 4. B. 5. C. 6. D. 8. Câu 16. Cho △ABC cân tại A, b
B = 65◦, đường cao CH = 3,6. Giải A △ABC. A. b A = 50◦; b
C = 65◦; AB = AC = 5,6; BC = 8,52. B. b A = 50◦; b
C = 65◦; AB = AC = 5,6; BC = 4,42. H 3,6 C. b A = 50◦; b
C = 65◦; AB = AC = 4,7; BC = 4,24. D. b A = 50◦; b
C = 65◦; AB = AC = 4,7; BC = 3,97. 65◦ B C
Câu 17. Một tam giác cân có đường cao ứng với đáy đúng bằng độ dài đáy. Tính các góc của tam giác đó. A. b A = 45◦; b B = b C = 67◦30′. B. b A = 30◦; b B = b C = 75◦. C. b A = 48◦6′; b B = b C = 65◦57′. D. b A = 53◦8′; b B = b C = 63◦26′.
Câu 18. Cho tam giác ABC vuông cân tại A (AB = AC = a). Phân giác của góc B cắt cạnh AC tại D.
Tính độ dài AD, CD theo a.
A. AD = a · cos 22,5◦; CD = a − a · cos 22,5◦.
B. AD = a · sin 22,5◦; CD = a − a · sin 22,5◦.
C. AD = a · tan 22,5◦; CD = a − a · tan 22,5◦.
D. AD = a · cot 22,5◦; CD = a − a · cot 22,5◦. Câu 19. Cho △DEF có DE = 7cm, b D = 40◦, b
F = 58◦. Tính độ dài đường D
cao EI của tam giác đó (làm tròn đến chữ số thập phân thứ nhất). 40◦ A. EI = 4,5cm. B. EI = 5,4cm. I C. EI = 5,9cm. D. EI = 5,6cm. 7cm 58◦ F E
Câu 20. Cho hình thang vuông tại A và D, b
C = 50◦. Biết AB = 2, AD = 1,2. Tính diện tích hình thang ABCD. 5 A. SABCD = 2 (đvdt). B. SABCD = 3 (đvdt). C. SABCD = 4 (đvdt). D. SABCD = (đvdt). 2 BẢNG ĐÁP ÁN 1. A 2. B 3. B 4. D 5. D 6. A 7. C 8. B 9. B 10. A 11. C 12. A 13. B 14. B 15. C 16. D 17. D 18. C 19. A 20. B GV: Mạc Lê Chí Đạo – 0946820895 51
Chương 1. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
§4. ỨNG DỤNG THỰC TẾ CÁC TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN A B
BÀI TẬP TRẮC NGHIỆM Câu 1.
Một cột đèn có bóng trên mặt đất dài 7,5m. Các tia nắng mặt trời tạo
với mặt đất một góc xấp xỉ bằng 42◦. Tính chiều cao của cột đèn. (làm
tròn đến chữ số thập phân thứ ba) A. 6,753m. B. 6,75m. C. 6,751m. D. 6,755m. 7,5m 42◦ Câu 2.
Một cột đèn AB cao 6m có bóng in trên mặt đất là AC dài 3,5m. B Tính góc ‘
BCA (làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất. A. 58◦45′. B. 59◦50′. C. 59◦45′. D. 59◦4′. 6m 3,5m A C Câu 3.
Một cột đèn AB cao 7m có bóng in trên mặt đất là AC dài 4m. B Tính góc ‘
BCA (làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất. A. 59◦45′. B. 62◦. C. 61◦15′. D. 60◦15′. 7m 4m A C Câu 4. 52
BÀI TẬP TRẮC NGHIỆM TOÁN 9
4. ỨNG DỤNG THỰC TẾ CÁC TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
Một cầu trượt trong công viên có độ dốc là 28◦ và
có độ cao là 2,1m. Tính độ dài của mặt cầu trượt.
(làm tròn đến chữ số thập phân thứ hai) A. 3,95m. B. 3,8m. C. 4,5m. D. 4,47m. C 2,1m 28◦ A B Câu 5.
Một cầu trượt trong công viên có độ dốc là 25◦ và
có độ cao là 2,4m. Tính độ dài của mặt cầu trượt.
(làm tròn đến chữ số thập phân thứ hai) A. 5,86m. B. 5m. C. 5,68m. D. 5,9m. C 2,4m 25◦ A B Câu 6.
Tính chiều cao của cây trong bình bên (làm tròn đến chữ số thập C phân thứ nhất). A. 14,3m. B. 15,7m. C. 16,8m. D. 17,2m. 35◦ 1, 7m A 20m B Câu 7.
Một cái cây cao 9m bị gió bão làm gãy ngang thân cây, ngọn cây chạm đất
cách gốc 3m. Hỏi điểm gãy cách gốc bao nhiêu? A. 6m. B. 5m. C. 4m. D. 3m. 3m Câu 8.
Một cái cây cao 8m bị gió bão làm gãy ngang thân cây, ngọn cây chạm đất
cách gốc 3,5m. Hỏi điểm gãy cách gốc bao nhiêu? (làm tròn đến chữ số thập phân thứ hai). A. 3,32m. B. 3,23m. C. 4m. D. 3m. 3,5m GV: Mạc Lê Chí Đạo – 0946820895 53
Chương 1. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG Câu 9.
Nhà bạn Vũ có một chiếc thang dài 3,5m. Cần đặt chân thang cách chân
tường một khoảng bằng bao nhiêu để nó tạo được với mặt đất một góc
“an toàn” là 62◦ (tức là đảm bảo thang không bị đổ khi sử dụng). (làm 3,5m
tròn đến chữ số thập phân thứ hai) A. 1,65m. B. 1,64m. C. 1,68m. D. 1,69m. 62◦ BẢNG ĐÁP ÁN 1. A 2. C 3. D 4. D 5. C 6. B 7. C 8. B 9. B 54
BÀI TẬP TRẮC NGHIỆM TOÁN 9 Chûúng 2 ĐƯỜNG TRÒN ĐƯỜNG TRÒN
§1. SỰ XÁC ĐỊNH ĐƯỜNG TRÒN. TÍNH CHẤT ĐỐI
XỨNG CỦA ĐƯỜNG TRÒN A B
BÀI TẬP TRẮC NGHIỆM
Câu 1. Số tâm đối xứng của đường tròn là A. 1. B. 2. C. 3. D. 4.
Câu 2. Tâm đối xứng của đường tròn là
A. Điểm bất kì bên trong đường tròn.
B. Điểm bất kì bên ngoài đường tròn.
C. Điểm bất kì trên đường tròn. D. Tâm của đường tròn.
Câu 3. Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn?
A. Đường tròn không có trục đối xứng.
B. Đường tròn có duy nhất một trục đối xứng là đường kính.
C. Đường tròn có hai trục đối xứng là hai đường kính vuông góc với nhau.
D. Đường tròn có vô số trục đối xứng là đường kính.
Câu 4. Điền từ thích hợp vào chỗ trống: “Đường tròn có · · · trục đối xứng”. A. 1. B. 2. C. Vô số. D. 3.
Câu 5. Tâm đường tròn ngoại tiếp tam giác là
A. Giao của ba đường phân giác.
B. Giao của ba đường trung trực.
C. Giao của ba đường cao.
D. Giao của ba đường trung tuyến.
Câu 6. Giao của ba đường trung trực của tam giác là
A. Tâm đường tròn ngoại tiếp tam giác (đường tròn đi qua ba đỉnh của tam giác).
B. Tâm đường tròn nội tiếp tam giác (đường tròn tiếp xúc với ba cạnh của tam giác).
C. Tâm đường tròn cắt ba cạnh của tam giác.
D. Tâm đường tròn đi qua 1 đỉnh và cắt hai cạnh của tam giác.
Câu 7. Cho đường tròn (O; R) và điểm M bất kỳ, biết rằng OM = R. Chọn khẳng định đúng.
A. Điểm M nằm ngoài đường tròn.
B. Điểm M nằm trên đường tròn.
C. Điểm M nằm trong đường tròn.
D. Điểm M không thuộc đường tròn.
Câu 8. Cho đường tròn (O; R) và điểm M bất kỳ, biết rằng OM > R. Chọn khẳng định đúng.
A. Điểm M nằm ngoài đường tròn.
B. Điểm M nằm trên đường tròn.
C. Điểm M nằm trong đường tròn.
D. Điểm M không thuộc đường tròn.
Câu 9. Cho đường tròn (O; R) và điểm M bất kỳ, biết rằng OM < R. Chọn khẳng định đúng.
A. Điểm M nằm ngoài đường tròn.
B. Điểm M nằm trên đường tròn.
C. Điểm M nằm trong đường tròn.
D. Điểm M không thuộc đường tròn. GV: Mạc Lê Chí Đạo – 0946820895 55 Chương 2. ĐƯỜNG TRÒN
Câu 10. Xác định tâm và bán kính của đường tròn đi qua bốn đỉnh của hình vuông ABCD cạnh a. √
A. Tâm là điểm A và bán kính R = a 2. √
B. Tâm là giao điểm hai đường chéo và bán kính R = a 2. √ a 2
C. Tâm là giao điểm hai đường chéo và bán kính R = . √ 2 a 2
D. Tâm là điểm B và bán kính R = . 2
Câu 11. Tính bán kính R của đường tròn đi qua bốn đỉnh của hình vuông ABCD cạnh 3cm. √ √ √ 3 2 3 3 A. R = 3 2cm. B. R = cm. C. R = 3cm. D. R = cm. 2 2
Câu 12. Tâm của đường tròn ngoại tiếp tam giác vuông là
A. Trung điểm cạnh huyền.
B. Trung điểm cạnh góc vuông lớn hơn. C. Giao ba đường cao.
D. Giao ba đường trung tuyến.
Câu 13. Chọn câu đúng. Bán kính của đường tròn ngoại tiếp tam giác vuông bằng
A. cạnh nhỏ nhất của tam giác vuông.
B. nửa cạnh góc vuông lớn hơn. C. nửa cạnh huyền. D. 4cm.
Câu 14. Cho tam giác ABC có các đường cao BD, CE. Biết rằng bốn điểm B, E, D, C cùng nằm trên
một đường tròn. Chỉ rõ tâm và bán kính của đường tròn đó. 2
A. Tâm là trọng tâm tam giác ABC và bán kính R = AI với I là trung điểm BC. 3 AB
B. Tâm là trung điểm AB và bán kính R = . 2 BD
C. Tâm là giao điểm của BD và EC, bán kính R = . 2 BC
D. Tâm là trung điểm BC và bán kính R = . 2
Câu 15. Cho tam giác ABC có các đường cao BD, CE. Chọn khẳng định đúng.
A. Bốn điểm B, E, D, C cùng nằm trên một đường tròn.
B. Năm điểm A, B, E, D, C cùng nằm trên một đường tròn. C. Cả A, B đều đúng. D. Cả A, B đều sai.
Câu 16. Trên mặt phẳng tọa độ Oxy, xác định vị trí tương đối của điểm A (−1; −1) và đường tròn
tâm là gốc tọa độ O, bán kính R = 2.
A. Điểm A nằm ngoài đường tròn.
B. Điểm A nằm trên đường tròn.
C. Điểm A nằm trong đường tròn.
D. Không kết luận được.
Câu 17. Trên mặt phẳng tọa độ Oxy, xác định vị trí tương đối của điểm A (−3; −4) và đường tròn
tâm là gốc tọa độ O, bán kính R = 3.
A. Điểm A nằm ngoài đường tròn.
B. Điểm A nằm trên đường tròn.
C. Điểm A nằm trong đường tròn.
D. Không kết luận được. Câu 18.
Cho tam giác ABC vuông tại A, có AB = 15cm, AC = 20cm. Tính A
bán kính đường tròn ngoại tiếp tam giác ABC. 25 15cm 20cm A. R = 25cm. B. R = cm. 2 C. R = 15cm. D. R = 20cm. B C 56
BÀI TẬP TRẮC NGHIỆM TOÁN 9
1. SỰ XÁC ĐỊNH ĐƯỜNG TRÒN. TÍNH CHẤT ĐỐI XỨNG CỦA ĐƯỜNG TRÒN Câu 19.
Cho tam giác ABC vuông tại A, có AB = 5cm, AC = 12cm. Tính A
bán kính đường tròn ngoại tiếp tam giác ABC. 13 5cm 12cm A. R = 26cm. B. R = cm. 2 C. R = 13cm. D. R = 6cm. B C Câu 20.
Cho tam giác đều ABC cạnh bằng 2cm. Tính bán kính của đường tròn ngoại A tiếp tam giác ABC. √ 2 5 A. R = 3cm. B. R = cm. √ 5 2 3 √ C. R = cm. D. R = 3cm. 3 B C Câu 21.
Cho hình chữ nhật ABCD có AB = 12cm, BC = 5cm. Tính bán kính A B
đường tròn đi qua bốn đỉnh A, B, C, D. A. R = 7,5cm. B. R = 12cm. C. R = 6cm. D. R = 6,5cm. D C Câu 22.
Cho hình chữ nhật ABCD có AB = 8cm, BC = 6cm. Tính bán kính A B
đường tròn đi qua bốn đỉnh A, B, C, D. A. R = 5cm. B. R = 10cm. C. R = 6cm. D. R = 2,5cm. D C Câu 23.
Cho hình vuông ABCD. Gọi M, N lần lượt là trung điểm của AB, AC. Gọi A M B
E là giao điểm của CM và DN. Tâm của đường tròn đi qua bốn điểm A, D, E, M là A. Trung điểm của DM. B. Trung điểm của DB. N C. Trung điểm của DE. D. Trung điểm của DA. E D C Câu 24.
Cho hình vuông ABCD. Gọi M, N lần lượt là trung điểm của AB, AC. Gọi A M B
E là giao điểm của CM và DN. Bán kính của đường tròn đi qua bốn điểm A, D, E, M là A. R = 5cm. B. R = 10cm. N √ √ C. R = 2 5cm. D. R = 5cm. E D C GV: Mạc Lê Chí Đạo – 0946820895 57 Chương 2. ĐƯỜNG TRÒN Câu 25.
Cho △ABC cân tại A, đường cao AH = 2cm, BC = 8cm. Đường A
vuông góc với AC tại C cắt đường thẳng AH ở D. Các điểm nào
sau đây cùng thuộc một đường tròn? A. D, H, B, C. B. A, B, H, C. C. A, B, D, H. D. A, B, D, C. B H C D Câu 26.
Cho △ABC cân tại A, đường cao AH = 2cm, BC = 8cm. Đường A
vuông góc với AC tại C cắt đường thẳng AH ở D. Tính đường
kính của đường tròn đi qua các điểm A, B, D, C. A. d = 8cm. B. d = 12cm. C. d = 10cm. D. d = 5cm. B H C D Câu 27.
Cho △ABC cân tại A, đường cao AH = 4cm, BC = 6cm. Đường A
vuông góc với AC tại C cắt đường thẳng AH ở D. Khẳng định đúng là A. ‘ ABC = 90◦. B. DB = DC. B H C
C. Bốn điểm A, B, D, C cùng thuộc một đường tròn. D. Cả A, B, C đều đúng. D Câu 28.
Cho tam giác đều ABC cạnh bằng a, các đường cao BM và CN. Gọi D là A
trung điểm cạnh BC. Đường tròn đi qua bốn điểm B, N, M, C là BC
A. Đường tròn tâm D bán kính . 2 N M
B. Đường tròn tâm D bán kính BC. BC
C. Đường tròn tâm B bán kính . 2 BC B C D
D. Đường tròn tâm C bán kính . 2 58
BÀI TẬP TRẮC NGHIỆM TOÁN 9
1. SỰ XÁC ĐỊNH ĐƯỜNG TRÒN. TÍNH CHẤT ĐỐI XỨNG CỦA ĐƯỜNG TRÒN Câu 29.
Cho tam giác đều ABC cạnh bằng a, các đường cao BM, CN. Gọi D là trung A
điểm cạnh BC. Gọi G là giao điểm của BM và CN. Xác định vị trí tương đối
của điểm G và điểm A với đường tròn đi qua bốn điểm B, N, M, C.
A. Điểm G nằm ngoài đường tròn, điểm A nằm trong đường tròn. N M
B. Điểm G nằm trong đường tròn, điểm A nằm ngoài đường tròn. G
C. Điểm G và điểm A cùng nằm trên đường tròn.
D. Điểm G và điểm A cùng nằm ngoài đường tròn. B C D Câu 30. A
Cho tam giác đều ABC cạnh bằng 3cm, các đường cao BM và CN. Gọi O là
trung điểm cạnh BC. Bốn điểm nào sau đây cùng thuộc một đường tròn? A. B, N, M, C. B. A, B, M, N. N M C. A, C, M, N. D. Cả A, B, C đều sai. B C O Câu 31. A
Cho tam giác đều ABC cạnh bằng 3cm, các đường cao BM và CN. Gọi G là
giao điểm của BM và CN. Tính bán kính đường tròn đi qua bốn điểm A, N, G, M. √ √ N M √ 6 √ 3 A. 2 3. B. . C. 3. D. . 2 2 G B C BẢNG ĐÁP ÁN 1. A 2. D 3. D 4. C 5. B 6. A 7. B 8. A 9. C 10. C 11. B 12. A 13. C 14. D 15. A 16. C 17. A 18. B 19. B 20. C 21. D 22. A 23. A 24. D 25. D 26. C 27. D 28. A 29. B 30. A 31. D GV: Mạc Lê Chí Đạo – 0946820895 59 Chương 2. ĐƯỜNG TRÒN
§2. ĐƯỜNG KÍNH VÀ DÂY CỦA ĐƯỜNG TRÒN A B
BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho đường tròn (O) đường kính AB và dây CD không đi qua tâm. Khẳng định nào sau đây là đúng? A. AB > CD. B. AB = CD. C. AB < CD. D. AB ≤ CD.
Câu 2. “Trong các dây của một đường tròn, đường kính là dây có độ dài · · · ”. Cụm từ thích hợp điền vào chỗ trống là A. nhỏ nhất. B. lớn nhất. C. bằng 10cm.
D. bằng tổng hai dây bất kì.
Câu 3. Cho đường tròn (O) có hai dây AB, CD không đi qua tâm. Biết khoảng cách từ tâm đến hai
dây là bằng nhau. Kết luận nào sau đây là đúng? A. AB > CD. B. AB = CD. C. AB < CD. D. AB//CD.
Câu 4. Cho đường tròn (O) có hai dây AB, CD không đi qua tâm. Biết khoảng cách từ tâm O đến dây
AB lớn hơn khoảng cách từ tâm O đến dây CD. Kết luận nào sau đây là đúng? A. AB > CD. B. AB = CD. C. AB < CD. D. AB//CD.
Câu 5. “Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì · · ·
với dây ấy”. Điền vào dấu · · · cụm từ thích hợp. A. nhỏ hơn. B. bằng. C. song song. D. vuông góc.
Câu 6. “Trong một đường tròn, đường kính vuông góc với dây thì · · · của dây ấy ”. Điền vào dấu · · · cụm từ thích hợp. A. đi qua trung điểm.
B. đi qua giao điểm của dây ấy với đường tròn. C. đi qua điểm bất kì.
D. đi qua điểm chia dây thành hai phần có tỉ lệ 2 : 3.
Câu 7. Chọn khẳng định sai trong các khẳng định sau. Trong hai dây của một đường tròn
A. Dây nào lớn hơn thì dây đó xa tâm hơn.
B. Dây nào nhỏ hơn thì dây đó xa tâm hơn.
C. Dây nào gần tâm hơn thì dây đó lớn hơn.
D. Hai dây bằng nhau thì cách đều tâm.
Câu 8. Chọn khẳng định đúng trong các khẳng định sau. Trong hai dây của một đường tròn.
A. Dây nào lớn hơn thì dây đó xa tâm hơn.
B. Hai dây đi qua tâm thì vuông góc với nhau.
C. Dây nào gần tâm hơn thì dây đó nhỏ hơn.
D. Hai dây cách đều tâm thì bằng nhau.
Câu 9. Cho đường tròn (O) có bán kính R = 5cm. Khoảng cách từ tâm đến dây AB là 3cm. Tính độ dài dây AB. A. AB = 4cm. B. AB = 8cm. C. AB = 16cm. D. AB = 12cm.
Câu 10. Cho đường tròn (O) có bán kính R = 6,5cm. Khoảng cách từ tâm đến dây AB là 2,5cm. Tính độ dài dây AB. A. AB = 3cm. B. AB = 8cm. C. AB = 6cm. D. AB = 12cm.
Câu 11. Cho đường thẳng d cắt đường tròn (O) tại hai điểm phân biệt A, B. Biết khoảng cách từ điểm
O đến đường thẳng d bằng 3cm và độ dài đoạn thẳng AB bằng 8cm. Bán kính đường tròn (O) bằng A. 7cm. B. 11cm. C. 3cm. D. 5cm.
Câu 12. Cho đường tròn (O; R) có hai dây AB, CD bằng nhau và vuông góc với nhau tại I. Giả sử
IA = 2cm, IB = 4cm. Tổng khoảng cách từ tâm O đến dây AB, CD bằng 60
BÀI TẬP TRẮC NGHIỆM TOÁN 9
2. ĐƯỜNG KÍNH VÀ DÂY CỦA ĐƯỜNG TRÒN A. 4cm. B. 1cm. C. 3cm. D. 2cm.
Câu 13. Cho đường tròn (O; R) có hai dây AB, CD bằng nhau và vuông góc với nhau tại I. Giả sử
IA = 6cm, IB = 3cm. Tổng khoảng cách từ tâm O đến dây AB, CD bằng A. 4cm. B. 1cm. C. 3cm. D. 2cm.
Câu 14. Cho đường tròn (O; R) có hai dây AB, CD vuông góc với nhau tại M. Biết AB = 12cm,
CD = 12cm, MC = 2cm. Khoảng cách từ tâm O đến dây AB bằng A. 4cm. B. 5cm. C. 3cm. D. 2cm.
Câu 15. Cho đường tròn (O; R) có hai dây AB, CD vuông góc với nhau tại M. Biết CD = 8cm,
MC = 1cm. Khoảng cách từ tâm O đến dây AB bằng A. 4cm. B. 5cm. C. 3cm. D. 2cm.
Câu 16. Cho đường tròn (O; R) có hai dây AB, CD vuông góc với nhau tại M. Biết AB = 14cm,
CD = 12cm, MC = 2cm. Bán kính R và khoảng cách từ tâm O đến dây CD lần lượt là √ √ √ √ √ √ A. 8cm; 29cm. B. 65cm; 29cm. C. 29cm; 65cm. D. 29cm; 8cm.
Câu 17. Cho đường tròn (O; R) có hai dây AB, CD vuông góc với nhau tại M. Biết AB = 10cm,
CD = 8cm, MC = 1cm. Bán kính R và khoảng cách từ tâm O đến dây CD lần lượt là √ √ √ √ √ A. 34cm; 9cm. B. 6cm; 3cm. C. 34cm; 3 2cm. D. 3 2cm; 34cm.
Câu 18. Cho nửa đường tròn (O), đường kính AB và một dây CD. Kẻ AE và BF vuông góc với CD
lần lượt tại E và F. So sánh độ dài CE và DF. A. CE > DF. B. CE = 2DF. C. CE < DF. D. CE = DF.
Câu 19. Cho nửa đường tròn (O), đường kính AB và một dây MN. Kẻ AE và BF vuông góc với MN
lần lượt tại E và F. So sánh độ dài OE và OF. 3 A. OE = OF. B. OE = OF. C. OE < OF. D. OE > OF. 2
Câu 20. Cho đường tròn (O), đường kính AB. Kẻ hai dây AC và BD song song. So sánh độ dài AC và BD. A. AC > BD. B. AC < BD. C. AC = BD. D. AC = 3BD.
Câu 21. Cho đường tròn (O), đường kính AB. Lấy điểm C là trung điểm của đoạn OB. Kẻ dây MN
qua C và dây AD//MN. So sánh độ dài AD và MN. A. AD = 2 · MN. B. AD = MN. C. AD > MN. D. AD < MN.
Câu 22. Cho đường tròn (O), dây cung AB và CD với CD < AB. Giao điểm K của các đường thẳng
AB và CD nằm ngoài đường tròn. Vẽ đường tròn (O; OK), đường tròn này cắt KA và KC lần lượt tại M và N. So sánh KM và KN. 4 A. KN > KM. B. KN < KM. C. KN = KM. D. KN = KM. 3
Câu 23. Cho đường tròn (O), dây cung AB và CD với CD = AB. Giao điểm K của các đường thẳng
AB và CD nằm ngoài đường tròn. Vẽ đường tròn (O; OK), đường tròn này cắt KA và KC lần lượt tại M và N. So sánh KM và KN. 4 A. KN > KM. B. KN < KM. C. KN = KM. D. KN = KM. 3
Câu 24. Cho đường tròn (O; 10cm). Dây AB và CD song song, có độ dài lần lượt là 16cm và 12cm.
Tính khoảng cách giữa hai dây. A. 14cm. B. 10cm. C. 12cm. D. 16cm.
Câu 25. Cho đường tròn (O; 8cm). Dây AB và CD song song, có độ dài lần lượt là 14cm và 10cm.
Tính khoảng cách giữa hai dây. GV: Mạc Lê Chí Đạo – 0946820895 61 Chương 2. ĐƯỜNG TRÒN √ √ √ √ 38 + 15 √ √ A. 2 15cm. B. 2 39cm. C. cm. D. 39 + 15cm. 2
Câu 26. Cho đường tròn (O; R). Hai dây AB, CD song song với nhau sao cho tâm O nằm trong dải √
song song tạo bởi AB, CD. Biết khoảng cách giữa hai dây đó bằng 11cm và AB = 10 3cm, CD = 16cm. Tính bán kính R. √ √ √ A. R = 5 2cm. B. R = 10 2cm. C. R = 10cm. D. R = 5 3cm.
Câu 27. Cho tam giác ABC nhọn và có các đường cao BD, CE. So sánh BC và DE. 2 A. BC = DE. B. BC < DE. C. BC > DE. D. BC = DE. 3
Câu 28. Cho hình vuông ABCD. Gọi M, N lần lượt là trung điểm của AB, BC. Gọi E là giao điểm
của CM và DN. So sánh AE và DM. 2 A. DM = AE. B. DM < AE. C. DM = AE. D. DM > AE. 3
Câu 29. Cho đường tròn (O), đường kính AB = 14cm, dây CD có độ dài 12cm vuông góc với AB tại
H với H nằm giữa O và B. Độ dài AH bằng √ √ √ A. 7 + 13cm. B. 7 − 13cm. C. 7cm. D. 7 − 2 13cm.
Câu 30. Cho đường tròn (O), đường kính AB = 20cm, dây CD có độ dài 16cm vuông góc với AB tại
H với H nằm giữa O và B. Độ dài AH bằng A. 12cm. B. 18cm. C. 16cm. D. 15cm.
Câu 31. Cho đường tròn (O; R) và một dây CD. Từ O kẻ tia vuông góc với CD tại M, cắt (O; R) tại
H. Biết CD = 16cm, MH = 4cm. Bán kính R bằng √ √ A. 12 2cm. B. 10 2cm. C. 12cm. D. 10cm. BẢNG ĐÁP ÁN 1. A 2. B 3. B 4. C 5. D 6. A 7. A 8. D 9. B 10. D 11. D 12. D 13. C 14. A 15. C 16. B 17. C 18. D 19. A 20. C 21. D 22. B 23. C 24. A 25. D 26. C 27. C 28. D 29. A 30. C 31. D 62
BÀI TẬP TRẮC NGHIỆM TOÁN 9
3. DẤU HIỆU NHẬN BIẾT TIẾP TUYẾN CỦA ĐƯỜNG TRÒN
§3. DẤU HIỆU NHẬN BIẾT TIẾP TUYẾN CỦA ĐƯỜNG TRÒN A B
BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho (O; R). Đường thẳng d là tiếp tuyến của đường tròn (O; R) tại tiếp điểm A khi
A. d ⊥ OA tại A và A ∈ (O). B. d ⊥ OA. C. A ∈ (O). D. d//OA.
Câu 2. “Nếu một đường thẳng đi qua một điểm của đường tròn và · · · thì đường thẳng đó là một tiếp
tuyến của đường tròn”. Cụm từ thích hợp điền vào chỗ trống là
A. song song với bán kính đi qua tiếp điểm đó.
B. vuông góc với bán kính đi qua tiếp điểm đó.
C. song song với bán kính đường tròn.
D. vuông góc với bán kính bất kì.
Câu 3. Cho (O; 5cm). Đường thẳng d là tiếp tuyến của đường tròn (O; 5cm), khi đó
A. khoảng cách từ O đến đường thẳng d nhỏ hơn 5.
B. khoảng cách từ O đến đường thẳng d lớn hơn 5.
C. khoảng cách từ O đến đường thẳng d bằng hơn 5. √
D. khoảng cách từ O đến đường thẳng d bằng hơn 5.
Câu 4. Cho (O; 4cm). Đường thẳng d là tiếp tuyến của đường tròn (O; 4cm), khi đó
A. khoảng cách từ O đến đường thẳng d nhỏ hơn 4.
B. khoảng cách từ O đến đường thẳng d bằng hơn 4.
C. khoảng cách từ O đến đường thẳng d lớn hơn 4.
D. khoảng cách từ O đến đường thẳng d bằng hơn 2.
Câu 5. Cho tam giác ABC có AC = 3cm, AB = 4cm, BC = 5cm. Vẽ đường tròn (C;CA). Khẳng định nào sau đây là đúng?
A. Đường thẳng BC cắt đường tròn (C;CA) tại một điểm.
B. AB là cát tuyến của đường tròn (C;CA).
C. AB là tiếp tuyến của (C;CA).
D. BC là tiếp tuyến của (C;CA).
Câu 6. Cho tam giác MNP có MN = 5cm, NP = 12cm, MP = 13cm. Vẽ đường tròn (M; MN). Khẳng
định nào sau đây là đúng?
A. NP là tiếp tuyến của (M; MN).
B. MP là tiếp tuyến của (M; MN). C. △MNP vuông tại M. D. △MNP vuông tại P.
Câu 7. Cho tam giác ABC cân tại A, đường cao AH và BK cắt nhau tại I. Khi đó đường thẳng nào sau
đây là tiếp tuyến của đường tròn đường kính AI? A. HK. B. IB. C. IC. D. AC.
Câu 8. Cho hình chữ nhật ABCD, H là hình chiếu của A trên BD. M, N lần lượt là trung điểm của
BH, CD. Đường thẳng nào sau đây là tiếp tuyến của đường tròn tâm A, bán kính AM? A. BN. B. MN. C. AB. D. CD.
Câu 9. Cho tam giác ABC vuông tại A, đường cao AH. Đường tròn đường kính BH cắt AB tại D,
đường tròn đường kính CH cắt AC tại E. Chọn khẳng định sai trong các khẳng định sau.
A. DE là cát tuyến của đường tròn đường kính BH.
B. DE là tiếp tuyến của đường tròn đường kính BH.
C. Tứ giác AEHD là hình chữ nhật. GV: Mạc Lê Chí Đạo – 0946820895 63 Chương 2. ĐƯỜNG TRÒN
D. DE ⊥ DI với I là trung điểm BH.
Câu 10. Cho đường tròn (O; 2cm) bán kính OB. Vẽ dây BC sao cho ‘
OBC = 60◦. Trên tia OB lấy điểm
M sao cho BM = 2cm. Khẳng định đúng là
A. MC là tiếp tuyến của (O).
B. MC là cát tuyến của (O). C. MC ⊥ BC. D. ’ MCB = 45◦.
Câu 11. Cho đường tròn (O; 2cm) bán kính OB. Vẽ dây BC sao cho ‘
OBC = 60◦. Trên tia OB lấy điểm
M sao cho BM = 2cm. Tính độ dài MC. √ √ √ A. MC = 2 2cm. B. MC = 3cm. C. MC = 2 3cm. D. MC = 4cm.
Câu 12. Từ một điểm A ở bên ngoài đường tròn(O; R), vẽ hai tiếp tuyến AB, AC với (O). Đường
thẳng vuông góc với OB tại O cắt tia AC tại N. Đường thẳng vuông góc với OC cắt tia AB tại M. Tứ giác AMON là hình gì? A. Hình bình hành. B. Hình thoi. C. Hình thang. D. Hình chữ nhật.
Câu 13. Từ một điểm A ở bên ngoài đường tròn(O; R), vẽ hai tiếp tuyến AB, AC với (O). Đường thẳng
vuông góc với OB tại O cắt tia AC tại N. Đường thẳng vuông góc với OC cắt tia AB tại M. Điểm A phải
cách O một khoảng là bao nhiêu để cho MN là tiếp tuyến của (O)? 3 4 A. OA = 2R. B. OA = R. C. OA = 3R. D. OA = R. 2 3
Câu 14. Cho đường tròn (O), dây AB khác đường kính. Qua O kẻ đường vuông góc với AB, cắt tiếp
tuyến tại A của đường tròn ở điểm C. Chọn khẳng định đúng.
A. BC là cát tuyến của (O).
B. BC là tiếp tuyến của (O). C. BC ⊥ AB. D. BC//AB.
Câu 15. Cho đường tròn (O), dây AB khác đường kính. Qua O kẻ đường vuông góc với AB, cắt tiếp
tuyến tại A của đường tròn ở điểm C. Cho bán kính của đường tròn bằng 15cm, AB = 24cm. Tính OC. A. OC = 35cm. B. OC = 20cm. C. OC = 25cm. D. OC = 15cm.
Câu 16. Cho đường tròn (O), dây MN khác đường kính. Qua O kẻ đường vuông góc với MN, cắt tiếp
tuyến tại M của đường tròn ở điểm P. Chọn khẳng định đúng.
A. PN là tiếp tuyến của (O) tại P. B. △MOP = △PON.
C. PN là tiếp tuyến của (O) tại N. D. ‘ ONP = 80◦.
Câu 17. Cho đường tròn (O), dây MN khác đường kính. Qua O kẻ đường vuông góc với MN, cắt tiếp
tuyến tại M của đường tròn ở điểm P. Cho bán kính của đường tròn bằng 10cm, MN = 12cm. Tính OP. A. OP = 12,5cm. B. OP = 17,5cm. C. OP = 25cm. D. OP = 15cm.
Câu 18. Cho tam giác ABC có hai đường cao BD, CE cắt nhau tại H. Xác định tâm F của đường tròn
đi qua bốn điểm A, D, H, E. A. F ≡ B.
B. F là trung điểm đoạn AD.
C. F là trung điểm đoạn AH.
D. F là trung điểm đoạn AE.
Câu 19. Cho tam giác ABC có hai đường cao BD, CE cắt nhau tại H. Gọi M là trung điểm của BC.
Đường tròn (F) ở trên nhận các đường thẳng nào dưới đây là tiếp tuyến? A. ME, MD. B. ME. C. MD. D. EC.
Câu 20. Cho nửa đường tròn đường kính AB, C là một điểm thuộc nửa đường tròn. Vẽ dây BD là
phân giác của góc ABC. BD cắt AC tại E, AD cắt BC tại G. H là điểm đối xứng với E qua D. Chọn đáp
án đúng nhất: AHGE là hình gì? A. Hình bình hành. B. Hình thoi. C. Hình vuông. D. Hình chữ nhật. 64
BÀI TẬP TRẮC NGHIỆM TOÁN 9
3. DẤU HIỆU NHẬN BIẾT TIẾP TUYẾN CỦA ĐƯỜNG TRÒN
Câu 21. Cho nửa đường tròn đường kính AB, C là một điểm thuộc nửa đường tròn. Vẽ dây BD là
phân giác của góc ABC. BD cắt AC tại E, AD cắt BC tại G. H là điểm đối xứng với E qua D. Khẳng định đúng là
A. AH là tiếp tuyến của đường tròn đường kính AB.
B. HG là tiếp tuyến của đường tròn đường kính AB. C. ‘ ADB = 90◦. D. Cả A và C đều đúng. Câu 22.
Cho hình vẽ bên. Biết ‘
BAC = 60◦, AO = 10cm. Độ dài bán kính B OB bằng√ √ √ A A. 4 3. B. 5. C. 5 3. D. 10 3. O C Câu 23.
Cho hình vẽ bên. Biết ‘
BAC = 60◦, AO = 10cm. Độ dài tiếp B tuyến AB bằng √ √ √ A A. 4 3. B. 5. C. 5 3. D. 10 3. O C Câu 24.
Cho hình vẽ bên. Biết AB và AC là hai tiếp tuyến của (O), B ‘
BAC = 120◦, AO = 8cm. Độ dài bán kính OB bằng √ √ A A. 4 3cm. B. 5cm. C. 4cm. D. 8 3cm. O C
Câu 25. Cho hình vẽ bên. Biết AB và AC là hai tiếp tuyến của (O), ‘
BAC = 120◦, AO = 8cm. Độ dài đoạn AB bằng √ √ A. 4 3cm. B. 5cm. C. 5 3cm. D. 4cm.
Câu 26. Cho nửa đường tròn (O; R), AB là đường kính. Dây BC có độ dài R. Trên tia đối của tia CB
lấy điểm D sao cho CD = 3R. Chọn khẳng định đúng.
A. AD là tiếp tuyến của đường tròn (O). B. ‘ ACB = 90◦.
C. AD cắt đường tròn (O; R) tại hai điểm phân biệt. D. Cả A, B đều đúng. Câu 27. Cho d
xOy, trên tia Ox lấy điểm P, trên tia Oy lấy điểm Q sao cho chu vi △POQ bằng 2a
không đổi. Chọn câu đúng. GV: Mạc Lê Chí Đạo – 0946820895 65 Chương 2. ĐƯỜNG TRÒN
A. PQ luôn tiếp xúc với một đường tròn cố định.
B. PQ không tiếp xúc với một đường tròn cố định nào. C. PQ = a. D. PQ = OP. BẢNG ĐÁP ÁN 1. A 2. B 3. C 4. B 5. C 6. A 7. A 8. B 9. A 10. A 11. C 12. B 13. A 14. B 15. C 16. C 17. A 18. C 19. A 20. B 21. D 22. B 24. A 25. D 26. D 27. A 66
BÀI TẬP TRẮC NGHIỆM TOÁN 9
4. VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN
§4. VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN A B
BÀI TẬP TRẮC NGHIỆM
Câu 1. Đường thẳng và đường tròn có nhiều nhất bao nhiêu điểm chung? A. 1. B. 2. C. 0. D. Vô số.
Câu 2. Nếu đường thẳng và đường tròn có duy nhất một điểm chung thì
A. đường thẳng tiếp xúc với đường tròn.
B. đường thẳng cắt đường tròn.
C. đường thẳng không cắt đường tròn. D. đáp án khác.
Câu 3. Nếu đường thẳng và đường tròn có hai điểm chung thì
A. đường thẳng tiếp xúc với đường tròn.
B. đường thẳng cắt đường tròn.
C. đường thẳng không cắt đường tròn. D. đáp án khác.
Câu 4. Nếu đường thẳng d là tiếp tuyến của đường tròn (O) tại A thì A. d//OA. B. d ≡ OA. C. d ⊥ OA tại A. D. d ⊥ OA tại O.
Câu 5. Cho đường tròn (O) và điểm A nằm trên đường tròn (O). Nếu đường thẳng d ⊥ OA tại A thì
A. d là tiếp tuyến của (O).
B. d cắt (O) tại hai điểm phân biệt.
C. d tiếp xúc với (O) tại O. D. Cả A, B, C đều sai.
Câu 6. Cho đường tròn (O) và đường thẳng d. Kẻ OH ⊥ d tại H, biết OH > R khi đó đường thẳng d và đường tròn (O) A. cắt nhau. B. không cắt nhau. C. tiếp xúc. D. đáp án khác.
Câu 7. Cho đường tròn (O) và đường thẳng d. Kẻ OH ⊥ d tại H, biết OH < R khi đó đường thẳng d và đường tròn (O) A. cắt nhau. B. không cắt nhau. C. tiếp xúc. D. đáp án khác.
Câu 8. Điền vào các vị trí (1), (2) trong bảng sau (R là bán kính của đường tròn, d là khoảng cách từ
tâm đến đường thẳng): R d
Vị trí tương đối của đường thẳng và đường tròn 5cm 4cm · · · (1) · · · 8cm · · · (2) · · · Tiếp xúc nhau A. (1): cắt nhau, (2): 8cm. B. (1): 9cm, (2): cắt nhau.
C. (1): không cắt nhau, (2): 8cm. D. (1): cắt nhau, (2): 6cm.
Câu 9. Điền vào các vị trí (1), (2) trong bảng sau (R là bán kính của đường tròn, d là khoảng cách từ
tâm đến đường thẳng): R d
Vị trí tương đối của đường thẳng và đường tròn 3cm 5cm · · · (1) · · · · · · (2) · · · 9cm Tiếp xúc nhau A. (1): cắt nhau, (2): 9cm.
B. (1): tiếp xúc nhau, (2): 8cm.
C. (1): không cắt nhau, (2): 9cm.
D. (1): không cắt nhau, (2): 10cm. GV: Mạc Lê Chí Đạo – 0946820895 67 Chương 2. ĐƯỜNG TRÒN
Câu 10. Trên mặt phẳng tọa độ Oxy, cho điểm A (4; 5). Hãy xác định vị trí tương đối của đường tròn
(A; 5) và các trục tọa độ.
A. Trục tung cắt đường tròn và trục hoành tiếp xúc với đường tròn.
B. Trục hoành cắt đường tròn và trục tung tiếp xúc với đường tròn.
C. Cả hai trục tọa độ đều cắt đường tròn.
D. Cả hai trục tọa độ đều tiếp xúc với đường tròn.
Câu 11. Trên mặt phẳng tọa độ Oxy, cho điểm A (−2; 3). Hãy xác định vị trí tương đối của đường
tròn (A; 2) và các trục tọa độ.
A. Trục tung cắt đường tròn và trục hoành tiếp xúc với đường tròn.
B. Trục hoành cắt đường tròn và trục tung tiếp xúc với đường tròn.
C. Cả hai trục tọa độ đều cắt đường tròn.
D. Cả hai trục tọa độ đều tiếp xúc với đường tròn.
Câu 12. Cho a, b là hai đường thẳng song song và cách nhau một khoảng 2,5cm. Lấy điểm I trên
đường thẳng a và vẽ đường tròn (I; 2,5cm). Khi đó đường tròn tâm I với đường thẳng b A. cắt nhau. B. không cắt nhau. C. tiếp xúc. D. đáp án khác.
Câu 13. Cho a, b là hai đường thẳng song song và cách nhau một khoảng 3cm. Lấy điểm I trên đường
thẳng a và vẽ đường tròn (I; 3,5cm). Khi đó đường tròn tâm I với đường thẳng b A. cắt nhau. B. không cắt nhau. C. tiếp xúc. D. đáp án khác. Ä Câu 14. Cho d xOy 0◦ < d
xOy < 180◦ä. Đường tròn (I) tiếp xúc với cả hai trục tọa độ Ox, Oy. Khi đó
điểm I di chuyển trên đường nào?
A. Đường thẳng vuông góc với Ox tại O. B. Tia phân giác của d xOy.
C. Tia Oz nằm giữa Ox và Oy.
D. Tia phân giác của góc d xOy trừ điểm O.
Câu 15. Cho đường tròn tâm O bán kính 3cm và một điểm A cách O là 5cm. Kẻ tiếp tuyến AB với
đường tròn (B là tiếp điểm). Tính độ dài AB. A. AB = 3cm. B. AB = 4cm. C. AB = 5cm. D. AB = 2cm.
Câu 16. Cho đường tròn tâm O bán kính 6cm và một điểm A cách O là 10cm. Kẻ tiếp tuyến AB với
đường tròn (B là tiếp điểm). Tính độ dài AB. A. AB = 12cm. B. AB = 4cm. C. AB = 6cm. D. AB = 8cm.
Câu 17. Cho đường tròn (O; R) và dây AB = 1,2R. Vẽ một tiếp tuyến song song với AB, cắt các tia
OA, OB lần lượt tại E và F. Tính diện tích tam giác OEF theo R. A. SOEF = 0,75R2. B. SOEF = 1,5R2. C. SOEF = 0,8R2. D. SOEF = 1,75R2.
Câu 18. Cho đường tròn (O; R) và dây AB = 9,6cm. Vẽ một tiếp tuyến song song với AB, cắt các tia
OA, OB lần lượt tại E và F. Tính diện tích tam giác OEF. A. SOEF = 36cm2. B. SOEF = 24cm2. C. SOEF = 48cm2. D. SOEF = 96cm2.
Câu 19. Cho đường tròn (O; R). Cát tuyến qua A ở ngoài (O) cắt (O) tại B và C. Biết AB = BC và kẻ
đường kính CD. Tính độ dài đoạn thẳng AD. R A. AD = R. B. AD = 2R. C. AD = . D. AD = 2R. 2
Câu 20. Cho đường tròn (O; 5cm). Cát tuyến qua A ở ngoài (O) cắt (O) tại B và C. Biết AB = BC và
kẻ đường kính CD. Tính độ dài đoạn thẳng AD. A. AD = 2,5cm. B. AD = 10cm. C. AD = 15cm. D. AD = 5cm.
Câu 21. Cho hai đường thẳng a và b song song với nhau, cách nhau một khoảng là h. Một đường tròn
(O) tiếp xúc với cả a và b. Hỏi tâm O di động trên đường nào? 68
BÀI TẬP TRẮC NGHIỆM TOÁN 9
4. VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN h
A. Đường thẳng c song song và cách đều a, b một khoảng . 2 2h
B. Đường thẳng c song song và cách đều a, b một khoảng . 3
C. Đường thẳng c đi qua O vuông góc với a, b.
D. Đường tròn (A; AB) với A, B lần lượt là tiếp điểm của a, b với (O). BẢNG ĐÁP ÁN 1. B 2. A 3. B 4. C 5. A 6. B 7. A 8. A 9. C 10. A 11. B 12. C 13. A 14. D 15. B 16. D 17. A 18. C 19. D 20. B 21. A GV: Mạc Lê Chí Đạo – 0946820895 69 Chương 2. ĐƯỜNG TRÒN
§5. TÍNH CHẤT CỦA HAI TIẾP TUYẾN CẮT NHAU A B
BÀI TẬP TRẮC NGHIỆM
Câu 1. Tâm đường tròn nội tiếp tam giác là
A. giao ba đường phân giác trong tam giác.
B. giao ba đường trung trực của tam giác. C. trọng tâm tam giác. D. trực tâm tam giác.
Câu 2. Số đường tròn nội tiếp của tam giác là A. 1. B. 2. C. 3. D. Vô số.
Câu 3. Mỗi một tam giác có bao nhiêu đường tròn bàng tiếp tam giác? A. 1. B. 2. C. 3. D. Vô số.
Câu 4. Tâm đường tròn bàng tiếp tam giác là
A. giao ba đường trung tuyến.
B. giao ba đường phân giác trong của tam giác.
C. giao của 1 đường phân giác trong và 2 đường phân giác góc ngoài của tam giác.
D. giao ba đường trung trực.
Câu 5. Cho hai tiếp tuyến của một đường tròn cắt nhau tại một điểm. Chọn khẳng định sai.
A. Khoảng cách từ điểm đó đến hai tiếp tuyến là bằng nhau.
B. Tia nối từ điểm đó tới tâm là tia phân giác của góc tạo bởi hai bán kính.
C. Tia nối từ tâm tới điểm đó là tia phân giác của góc tạo bởi hai bán kính.
D. Tia nối từ điểm đó tới tâm là tia phần giác của góc tạo bởi tiếp tuyến.
Câu 6. “Cho hai tiếp tuyến của một đường tròn cắt nhau tại một điểm. Tia nối từ điểm đó tới tâm là
tia phân giác của góc tạo bởi · · · Tia nối từ tâm tới điểm đó là tia phân giác của góc tạo bởi · · · ”. Hai
cụm từ thích hợp điền vào chỗ trống lần lượt là
A. hai tiếp tuyến, hai bán kính đi qua tiếp điểm. B. hai bán kính đi qua tiếp điểm, hai tiếp tuyến.
C. hai tiếp tuyến, hai dây cung.
D. hai dây cung, hai bán kính.
Câu 7. Hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A. Biết OB = 3cm, OA = 5cm. Khẳng định sai là 4 3 A. AC = AB = 4cm. B. ‘ BAO = ‘ CAO. C. sin ‘ OBA = . D. sin ‘ COA = . 5 5
Câu 8. Hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A. Biết OB = 3cm, OA = 5cm. Vẽ
đường kính CD của (O). Tính độ dài đoạn BD. A. BD = 2cm. B. BD = 4cm. C. BD = 1,8cm. D. BD = 3,6cm.
Câu 9. Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By với nửa đường tròn cùng
phía đối với AB. Từ điểm M trên nửa đường tròn (M khác A, B) vẽ tiếp tuyến với nửa đường tròn cắt
Ax, By lần lượt tại C và D. Khi đó MC · MD bằng A. OC2. B. OM2. C. OD2. D. OM.
Câu 10. Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By với nửa đường tròn
cùng phía đối với AB. Từ điểm M trên nửa đường tròn (M khác A, B) vẽ tiếp tuyến với nửa đường tròn
cắt Ax, By lần lượt tại C và D. Biết OD = BA = 2R. Tính AC và BD theo R. √ √ 2R √ √ A. BC = 2R, AC = . B. BC = 3R, AC = 2R. 2 √ √ 3R C. BC = 2R, AC = R. D. BC = 3R, AC = . 3 70
BÀI TẬP TRẮC NGHIỆM TOÁN 9
5. TÍNH CHẤT CỦA HAI TIẾP TUYẾN CẮT NHAU
Câu 11. Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại I. Đường thẳng qua I và vuông góc
với IA cắt OB tại K. Chọn khẳng định đúng. A. OI = OK = KI. B. KI = KO. C. OI = OK. D. IO = IK.
Câu 12. Cho đường tròn (O). Từ một điểm M ở ngoài (O), vẽ hai tiếp tuyến MA và MB sao cho góc √ Ä ä
AMB bằng 120◦. Biết chu vi tam giác MAB bằng 6 3 + 2 3 cm, tính độ dài dây AB. √ √ A. 18cm. B. 6 3cm. C. 12 3cm. D. 15cm.
Câu 13. Cho đường tròn (O). Từ một điểm M ở ngoài (O), vẽ hai tiếp tuyến MA và MB sao cho góc
AMB bằng 60◦. Biết chu vi tam giác AMB bằng 24cm, tính độ dài bán kính của đường tròn (O). √ 4 A. 8cm. B. 4 3cm. C. √ cm. D. 5cm. 3
Câu 14. Cho tam giác ABC cân tại A, I là tâm đường tròn nội tiếp, K là tâm đường tròn bàng tiếp
trong góc A. Gọi O là trung điểm của IK. Tâm của đường tròn đi qua bốn điểm B, I, C, K là A. Điểm O. B. Điểm H. C. Trung điểm AK. D. Trung điểm BK.
Câu 15. Cho tam giác ABC cân tại A, I là tâm đường tròn nội tiếp, K là tâm đường tròn bàng tiếp
trong góc A. Gọi O là trung điểm của IK. Tính bán kính đường tròn (O) biết AB = AC = 20cm, BC = 24cm. A. 18cm. B. 15cm. C. 12cm. D. 9cm.
Câu 16. Cho đường tròn (O), bán kính OA. Dây CD là đường trung trực của OA. Tứ giác OCAD là hình gì? A. Hình bình hành. B. Hình thoi. C. Hình chữ nhật. D. Hình thang cân.
Câu 17. Cho đường tròn (O), bán kính OA. Dây CD là đường trung trực của OA. Kẻ tiếp tuyến với
đường tròn tại C, tiếp tuyến này cắt đường thẳng OA tại I. Biết OA = R. Tính CI theo R. √ √ A. CI = 2R. B. CI = R. C. CI = R 2. D. CI = R 3.
Câu 18. Cho tam giác ABC cân tại A nội tiếp đường tròn (O). Gọi D là trung điểm cạnh AC, tiếp
tuyến của đường tròn (O) tại A cắt tia BD tại E. Chọn khẳng định đúng. A. AE//OD. B. AE//BC. C. AE//OC. D. AE//OB.
Câu 19. Cho tam giác ABC cân tại A nội tiếp đường tròn (O). Gọi D là trung điểm cạnh AC, tiếp
tuyến của đường tròn (O) tại A cắt tia BD tại E. Tứ giác ABCE là hình gì? A. Hình bình hành. B. Hình thang. C. Hình thoi. D. Hình thang cân.
Câu 20. Cho hai đường tròn (O), (O′) cắt nhau tại A, B trong đó O′ ∈ (O). Kẻ đường kính O′OC của
đường tròn (O). Chọn khẳng định sai. A. AC = CB. B. ’ CBO′ = 90◦.
C. CA, CB là hai tiếp tuyến của (O′).
D. CA, CB là hai cát tuyến của (O′).
Câu 21. Cho đường tròn (O; R). Từ một điểm M nằm ngoài đường tròn kẻ các tiếp tuyến ME, MF
đến đường tròn với (E, F là tiếp điểm). Đoạn OM cắt đường tròn (O; R) tại I. Kẻ đường kính ED của
(O; R). Hạ FK vuông góc với ED. Gọi P là giao điểm của MD và FK. Chọn khẳng định đúng.
A. Các điểm M, E, O, F cùng thuộc một đường tròn.
B. Điểm I là tâm đường tròn nội tiếp tam giác MEF.
C. Điểm I là tâm đường tròn ngoại tiếp tam giác MEF. D. Cả A, B, C đều đúng.
Câu 22. Cho đường tròn (O; R). Từ một điểm M nằm ngoài đường tròn kẻ các tiếp tuyến ME, MF
đến đường tròn với (E, F là tiếp điểm). Đoạn OM cắt đường tròn (O; R) tại I. Kẻ đường kính ED của
(O; R). Hạ FK vuông góc với ED. Gọi P là giao điểm của MD và FK. Biết FK = 4cm. Khi đó GV: Mạc Lê Chí Đạo – 0946820895 71 Chương 2. ĐƯỜNG TRÒN A. FP = PK = 2cm.
B. P là trọng tâm tam giác FDE. C. A, B đều đúng. D. A, B đều sai.
Câu 23. Cho đường tròn (O; R) và điểm A nằm ngoài (O). Từ A kẻ hai tiếp tuyến AB, AC với (O) (B,
C là các tiếp điểm). Gọi H là giao điểm của OA và BC. Lấy D đối xứng với B qua O. Gọi E là giao
điểm của đoạn thẳng AD với (O) (E không trùng với D). Chọn câu đúng nhất.
A. Bốn điểm A, B, O, C cùng thuộc một đường tròn đường kính AC.
B. BC là đường trung trực của OA. C. Cả A, B đều đúng. D. Cả A, B đều sai.
Câu 24. Cho đường tròn (O; R) và điểm A nằm ngoài (O). Từ A kẻ hai tiếp tuyến AB, AC với (O) (B,
C là các tiếp điểm). Gọi H là giao điểm của OA và BC. Lấy D đối xứng với B qua O. Gọi E là giao DE
điểm của đoạn thẳng AD với (O) (E không trùng với D). Tỉ số bằng BE DA BA BD BA A. . B. . C. . D. . BA DA BA BD
Câu 25. Cho đường tròn (O; R) và điểm A nằm ngoài (O). Từ A kẻ hai tiếp tuyến AB, AC với (O) (B,
C là các tiếp điểm). Gọi H là giao điểm của OA và BC. Lấy D đối xứng với B qua O. Gọi E là giao
điểm của đoạn thẳng AD với (O) (E không trùng với D). Số đo góc HEC là A. 60◦. B. 80◦. C. 45◦. D. 90◦.
Câu 26. Hai tiếp tuyến tại hai điểm B, C của đường tròn (O) cắt nhau tại A tạo thành ‘ BAC = 50◦. Số đo của ‘
BOC chắn cung nhỏ BC bằng A. 30◦. B. 40◦. C. 130◦. D. 310◦. BẢNG ĐÁP ÁN 1. A 2. A 3. C 4. C 5. B 6. A 7. D 8. D 9. B 10. D 11. B 12. A 13. C 14. A 15. B 16. B 17. D 18. B 19. A 20. D 21. D 22. A 23. D 24. C 25. D 26. C 72
BÀI TẬP TRẮC NGHIỆM TOÁN 9
6. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG TRÒN
§6. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG TRÒN A B
BÀI TẬP TRẮC NGHIỆM
Câu 1. Nếu hai đường tròn tiếp xúc nhau thì số điểm chung của hai đường tròn là A. 1. B. 2. C. 3. D. Vô số.
Câu 2. Nếu hai đường tròn không cắt nhau thì số điểm chung của hai đường tròn là A. 1. B. 2. C. 3. D. 0.
Câu 3. Cho hai đường tròn (O; R) và (O′; r) với R > r cắt nhau tại hai điểm phân biệt và OO′ = d. Chọn khẳng định đúng. A. d = R − r. B. d > R + r.
C. R − r < d < R + R. D. d < R + r.
Câu 4. Cho hai đường tròn tiếp xúc ngoài (O; R) và (O′; r) với R > r và OO′ = d. Chọn khẳng định đúng. A. d = R − r. B. d > R + r.
C. R − r < d < R + R. D. d = R + r.
Câu 5. Cho đoạn OO′ và điểm A nằm trên đoạn OO′ sao cho OA = 2O′A. Đường tròn (O) bán kính
OA và đường tròn (O′) bán kính O′A. Vị trí tương đối của hai đường tròn là A. Nằm ngoài nhau. B. Cắt nhau. C. Tiếp xúc ngoài. D. Tiếp xúc trong.
Câu 6. Cho đoạn OO′ và điểm A nằm trên đoạn OO′ sao cho OA = 2O′A. Đường tròn (O) bán kính
OA và đường tròn (O′) bán kính O′A. Dây AD của đường tròn lớn cắt đường tròn nhỏ tại C. Khi đó AD 1 AD A. = . B. = 3. C. OD//O′C. D. Cả A, B, C đều sai. AC 2 AC
Câu 7. Cho hai đường tròn (O1) và (O2) tiếp xúc ngoài tại A và một đường thẳng d tiếp xúc với (O1),
(O2) lần lượt tại B, C. Tam giác ABC là A. Tam giác cân. B. Tam giác đều. C. Tam giác vuông. D. Tam giác vuông cân.
Câu 8. Cho hai đường tròn (O1) và (O2) tiếp xúc ngoài tại A và một đường thẳng d tiếp xúc với (O1),
(O2) lần lượt tại B, C. Lấy M là trung điểm BC. Chọn khẳng định sai.
A. AM là tiếp tuyến chung của hai đường tròn (O1), (O2).
B. AM là đường trung bình của hình thang O1BCO2. C. AM = MC. 1 D. AM = BC. 2
Câu 9. Cho (O1; 3cm) tiếp xúc ngoài với (O2; 1cm). Vẽ bán kính O1B và O2C song song với nhau
cùng thuộc một nửa mặt phẳng bờ O1O2. Gọi D là giao điểm của BC và O1O2. Tính số đo ‘ BAC. A. 90◦. B. 60◦. C. 100◦. D. 80◦.
Câu 10. Cho (O1; 3cm) tiếp xúc ngoài với (O2; 1cm). Vẽ bán kính O1B và O2C song song với nhau
cùng thuộc một nửa mặt phẳng bờ O1O2. Gọi D là giao điểm của BC và O1O2. Tính độ dài O1D A. O1D = 4,5cm. B. O1D = 5cm. C. O1D = 8cm. D. O1D = 6cm.
Câu 11. Cho hai đường tròn (O; 20cm) và (O′; 15cm) cắt nhau tại A và B. Tính độ dài đoạn nối tâm
OO′. Biết rằng AB = 24cm và O, O′ nằm cùng phía đối với AB. A. OO′ = 7cm. B. OO′ = 8cm. C. OO′ = 9cm. D. OO′ = 25cm.
Câu 12. Cho hai đường tròn (O; 10cm) và (O′; 5cm) cắt nhau tại A và B. Tính độ dài đoạn nối tâm GV: Mạc Lê Chí Đạo – 0946820895 73 Chương 2. ĐƯỜNG TRÒN
OO′. Biết rằng AB = 8cm và O, O′ nằm cùng phía đối với AB. (làm tròn đến chữ số thập phân thứ nhất) A. OO′ ≈ 6,5cm. B. OO′ ≈ 6,1cm. C. OO′ ≈ 6,3cm. D. OO′ ≈ 6,2cm.
Câu 13. Cho nửa đường tròn (O), đường kính AB. Vẽ nửa đường tròn tâm O′ đường kính AO (cùng
phía với nửa đường tròn (O)). Một cát tuyến bất kì qua A cắt (O′), (O) lần lượt tại C, D. Chọn khẳng định sai.
A. C là trung điểm của AD.
B. Các tiếp tuyến tại C và D của các nửa đường tròn song song với nhau. C. O′C//OD.
D. Các tiếp tuyến tại C và D của các nửa đường tròn cắt nhau.
Câu 14. Cho nửa đường tròn (O), đường kính AB. Vẽ nửa đường tròn tâm O′ đường kính AO (cùng
phía với nửa đường tròn (O)). Một cát tuyến bất kì qua A cắt (O′), (O) lần lượt tại C, D. Nếu BC là tiếp
tuyến của nửa đường tròn (O′) thì tính BC theo R (với OA = R). √ √ √ A. BC = 2R. B. BC = 2R. C. BC = 3R. D. BC = 5R.
Câu 15. Cho hai đường tròn (O), (O′) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài MN với
M ∈ (O), N ∈ (O′). Gọi P là điểm đối xứng với M qua OO′, Q là điểm đối xứng với N qua OO′. Khi
đó tứ giác MNPQ là hình gì? A. Hình thang cân. B. Hình thang. C. Hình thang vuông. D. Hình bình hành.
Câu 16. Cho hai đường tròn (O), (O′) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài MN với
M ∈ (O), N ∈ (O′). Gọi P là điểm đối xứng với M qua OO′, Q là điểm đối xứng với N qua OO′. Khi đó MN + PQ bằng A. MP + NQ. B. MQ + NP. C. 2MP. D. OP + PQ.
Câu 17. Cho hai đường tròn (O; R) và (O′; R′) (R > R′) tiếp xúc ngoài tại A. Vẽ các bán kính
OB//O′D với B, D cùng phía nửa mặt phẳng bờ OO′. Đường thẳng DB và OO′ cắt nhau tại I. Tiếp
tuyến chung ngoài GH của (O) và (O′) với G, H nằm ở nửa mặt phẳng bờ OO′ không chứa B, D. Tính PI theo R và R′. R + R′ R − R′ R (R − R′) R (R + R′) A. OI = . B. OI = . C. OI = . D. OI = . R − R′ R + R′ R + R′ R − R′
Câu 18. Cho hai đường tròn (O; R) và (O′; R′) (R > R′) tiếp xúc ngoài tại A. Vẽ các bán kính
OB//O′D với B, D cùng phía nửa mặt phẳng bờ OO′. Đường thẳng DB và OO′ cắt nhau tại I. Tiếp
tuyến chung ngoài GH của (O) và (O′) với G, H nằm ở nửa mặt phẳng bờ OO′ không chứa B, D. Chọn khẳng định đúng.
A. BD, OO′ và GH đồng quy.
B. BD, OO′ và GH không đồng quy.
C. Không có ba đường nào đồng quy. D. Cả A, B, C đều sai.
Câu 19. Cho hai đường tròn (O; 8cm) và (O′; 6cm) cắt nhau tại A, B sao cho OA là tiếp tuyến của
(O′). Độ dài dây AB bằng A. AB = 8,6cm. B. AB = 6,9cm. C. AB = 4,8cm. D. AB = 9,6cm.
Câu 20. Cho hai đường tròn (O; 6cm) và (O′; 2cm) cắt nhau tại A, B sao cho OA là tiếp tuyến của
(O′). Độ dài dây AB bằng √ √ √ √ 6 10 3 10 10 A. AB = 3 10cm. B. AB = cm. C. AB = cm. D. AB = cm. 5 5 5
Câu 21. Cho hai đường tròn (O) và (O′) tiếp xúc ngoài tại A. Kẻ các đường kính AOB, AO′C. Gọi
DE là tiếp tuyến chung của hai đường tròn (D ∈ (O) ; E ∈ (O′)). Gọi M là giao điểm của BD và CE.
Tính diện tích tứ giác ADME biết ‘ DOA = 60◦ và OA = 6cm. √ A. 12 3cm2. B. 12cm2. C. 16cm2. D. 24cm2. 74
BÀI TẬP TRẮC NGHIỆM TOÁN 9
6. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG TRÒN
Câu 22. Cho hai đường tròn (O) và (O′) tiếp xúc ngoài tại A. Kẻ các đường kính AOB, AO′C. Gọi
DE là tiếp tuyến chung của hai đường tròn (D ∈ (O) ; E ∈ (O′)). Gọi M là giao điểm của BD và CE.
Tính diện tích tứ giác ADME biết ‘ DOA = 60◦ và OA = 8cm. √ 64 √ 32 √ A. 12 3cm2. B. 3cm2. C. 3cm2. D. 36cm2. 3 3
Câu 23. Cho hai đường tròn (O), (O′) cắt nhau tại A, B trong đó O′ ∈ (O). Kẻ đường kính O′OC của
đường tròn (O). Chọn khẳng định sai. A. AC = CB. B. ’ CBO′ = 90◦.
C. CA, CB là hai tiếp tuyến của (O′).
D. CA, CB là hai cát tuyến của (O′).
Câu 24. Cho hai đường tròn (O), (O′) cắt nhau tại A, B. Kẻ đường kính AC của đường tròn (O) và
đường kính AD của đường tròn (O′). Chọn khẳng định sai. A. OO′ DC . B. C, B, D thẳng hàng. 2 C. OO′ ⊥ AB. D. BC = BD.
Câu 25. Cho các đường tròn (A; 10cm), (B; 15cm), (C; 15cm) tiếp xúc ngoài với nhau đôi một. Hai
đường tròn (B) và (C) tiếp xúc với nhau tại A′. Đường tròn (A) tiếp xúc với đường tròn (B) và (C) lần
lượt tại C′ và B′. Chọn khẳng định đúng nhất.
A. AA′ là tiếp tuyến chung của đường tròn (B), (C). B. AA′ = 25cm. C. AA′ = 15cm. D. Cả A và B đều đúng.
Câu 26. Cho các đường tròn (A; 10cm), (B; 15cm), (C; 15cm) tiếp xúc ngoài với nhau đôi một. Hai
đường tròn (B) và (C) tiếp xúc với nhau tại A′. Đường tròn (A) tiếp xúc với đường tròn (B) .và (C) lần
lượt tại C′ và B′. Tính diện tích tam giác A′B′C′ A. 36cm2. B. 72cm2. C. 144cm2. D. 96cm2. BẢNG ĐÁP ÁN 1. A 2. D 3. C 4. D 5. C 6. C 7. C 8. B 9. A 10. D 11. A 12. D 13. D 14. B 15. A 16. A 17. D 18. A 19. D 20. B 21. A 22. B 23. D 24. D 25. A 26. B GV: Mạc Lê Chí Đạo – 0946820895 75
Document Outline
- I ĐẠI SỐ
- CĂN BẬC HAI – CĂN BẬC BA
- CĂN BẬC HAI
- BÀI TẬP TRẮC NGHIỆM
- Bảng đáp án
- CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC
- BÀI TẬP TRẮC NGHIỆM
- Bảng đáp án
- LIÊN HỆ GIỮA PHÉP NHÂN – CHIA VÀ PHÉP KHAI PHƯƠNG
- BÀI TẬP TRẮC NGHIỆM
- Bảng đáp án
- BIẾN ĐỔI ĐƠN GIẢN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI
- BÀI TẬP TRẮC NGHIỆM
- Bảng đáp án
- RÚT GỌN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI
- BÀI TẬP TRẮC NGHIỆM
- Bảng đáp án
- CĂN BẬC BA
- BÀI TẬP TRẮC NGHIỆM
- Bảng đáp án
- HÀM SỐ BẬC NHẤT
- NHẮC LẠI VÀ BỔ SUNG CÁC KHÁI NIỆM VỀ HÀM SỐ
- BÀI TẬP TRẮC NGHIỆM
- Bảng đáp án
- HÀM SỐ BẬC NHẤT
- BÀI TẬP TRẮC NGHIỆM
- Bảng đáp án
- ĐỒ THỊ HÀM SỐ BẬC NHẤT
- BÀI TẬP TRẮC NGHIỆM
- Bảng đáp án
- ĐƯỜNG THẲNG SONG SONG VÀ ĐƯỜNG THẲNG CẮT NHAU
- BÀI TẬP TRẮC NGHIỆM
- Bảng đáp án
- HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
- BÀI TẬP TRẮC NGHIỆM
- Bảng đáp án
- II HÌNH HỌC
- HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
- MỘT SỐ HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG
- BÀI TẬP TRẮC NGHIỆM
- Bảng đáp án
- TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
- BÀI TẬP TRẮC NGHIỆM
- Bảng đáp án
- MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG
- BÀI TẬP TRẮC NGHIỆM
- Bảng đáp án
- ỨNG DỤNG THỰC TẾ CÁC TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
- BÀI TẬP TRẮC NGHIỆM
- Bảng đáp án
- ĐƯỜNG TRÒN
- SỰ XÁC ĐỊNH ĐƯỜNG TRÒN. TÍNH CHẤT ĐỐI XỨNG CỦA ĐƯỜNG TRÒN
- BÀI TẬP TRẮC NGHIỆM
- Bảng đáp án
- ĐƯỜNG KÍNH VÀ DÂY CỦA ĐƯỜNG TRÒN
- BÀI TẬP TRẮC NGHIỆM
- Bảng đáp án
- DẤU HIỆU NHẬN BIẾT TIẾP TUYẾN CỦA ĐƯỜNG TRÒN
- BÀI TẬP TRẮC NGHIỆM
- Bảng đáp án
- VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN
- BÀI TẬP TRẮC NGHIỆM
- Bảng đáp án
- TÍNH CHẤT CỦA HAI TIẾP TUYẾN CẮT NHAU
- BÀI TẬP TRẮC NGHIỆM
- Bảng đáp án
- VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG TRÒN
- BÀI TẬP TRẮC NGHIỆM
- Bảng đáp án
- SỰ XÁC ĐỊNH ĐƯỜNG TRÒN. TÍNH CHẤT ĐỐI XỨNG CỦA ĐƯỜNG TRÒN
- MỘT SỐ HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG
- HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
- NHẮC LẠI VÀ BỔ SUNG CÁC KHÁI NIỆM VỀ HÀM SỐ
- CĂN BẬC HAI
- CĂN BẬC HAI – CĂN BẬC BA




