Bài tập trắc nghiệm ôn tập cuối kỳ các chương 3, 4, 5, 6 | Giải tích 2 | Đại học Bách Khoa Hà Nội

Bài tập trắc nghiệm ôn tập cuối kỳ các chương 3, 4, 5, 6 | Giải tích 2 | Đại học Bách Khoa Hà Nội. Tài liệu được biên soạn giúp các bạn tham khảo, củng cố kiến thức, ôn tập và đạt kết quả cao kết thúc học phần. Mời các bạn đọc đón xem!

19 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Giải tích 2

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

98 trang 1 tháng trước

Tác giả:

Profile Thùy Dương
BÁCH KHOA ĐẠI CƯƠNG MÔN PHÁI
BỘ TÀI LIỆU ÔN TẬP TR C NGHIẮ ỆM
GIẢI TÍCH II
____________________________________________________
Biên so n b i: Team GT2 ạ ở – BKĐCMP
Hà N ội, tháng 9 năm 2021
MỤC L C Ụ
Đề …..……………………………………………………………………..……1 bài
Lời gi i tham khả ảo……………………………………………………….………18
Tài li u tham khệ ảo……………………………………………………………….95
LỜI NÓI ĐẦU
Hiện nay i hình th i m i t thi t , vớ ức thi đổ ớ ừ ự luận sang thi tr c nghi m, chinh ắ ệ
vì v y nhi u bậ ề ạn sinh viên s g p khó ẽ ặ khăn trong việ ập. Trong tinh hình đó, c ôn t
nhôm “BK – Đại cương môn phai” đã biên soạn “BỘ TÀI LIỆU ÔN T P TRẬ ẮC
NGHIỆM MÔN GIẢI TÍCH II” để giúp các bạn thuận tiện hơn trong việc ôn tập.
Nhóm tác gi : Team Gi i Tích II BK- ả ả Đại cương môn phái
(Đỗ Tuấn Cường, Đinh Tiến Long, Phạm Thanh Tùng, Trần Trung Dũng, Đỗ Ngọc
Hiếu, Nguy n Thu Hi n, Nguy n Minh Hiễ ề ễ ếu)
Chịu trách nhi m nệ ội dung: Ph m Thanh Tùng ạ
Do quá trình so n b tài li u gạ ộ ệ ấp rút cùng v i nh ng h n ch nh v ớ ữ ạ ế nhất đị ề
kiến thức, dù đã cố gắng hết sức nhưng chắc chắn không th tránh kh i nh ng sai ể ỏ ữ
sót v tính toán, lề ỗi đánh máy, mọi ý ki n góp ý c a b c xin g ng ế ủ ạn đọ ửi qua đườ
link fb “fb.com/tungg810” hoặc email tungcrossroad@gmail.com.
Tài li u ch mang tính ch t tham kh o, không có tác d ng thay th các giáo ệ ỉ ấ ả ụ ế
trình, sách gi khoa chính tháo ống. Xin chân thành c ảm ơn!
1
I. Bài t p tr c nghi m Tích phân Euler ậ ắ ệ
Câu 1: Kết qu c a tích phânả ủ
4
5
0
x
x e dx
+
−
là:
A.
8
B.
2
C.
6
D.
6
Câu 2: Kết qu c a tích phân ả ủ
2
6 4
0
sin cosx xdx
là:
A.
7
512
B.
C.
512
D.
3
512
Câu 3: Biết
4
7/2
6
0
3
(ln3)
x
a
b
x dx
+
−
=
, ch n khọ ẳng định đúng:
A. C. 𝑎 − 𝑏 = −1 B. 𝑎 + 𝑏 = 10 𝑎 > 𝑏 𝑎.𝑏 < D. 100
Câu 4: Biểu di n tích phân ễ
2
4 4
0
(1 )
x
x
dx
+
+
theo hàm Gamma:
A.
( )
3 13
.
4 4
6. 4
B.
( )
3 1
.
4 4
4. 4
C.
( )
3 13
.
4 4
4. 4
D.
( )
3 5
.
4 4
4. 4
Câu 5: Tính tích phân
30
30
1
0
1
1
x
dx
−
A.
30sin
20
B.
30sin
30
C.
sin
30
D.
50sin
30
2
Câu 6: Tính tích phân
4
3 2
0
( 1)
x
x
dx
+
+
A.
4 3
27
B.
4 2
27
C.
2 2
27
D.
2 3
27
Câu 7: Tính tích phân
10
1
0
1
ln dx
x
A. 11! B.
10! C.
12! D.
9!
Câu 8: Tính tích phân
1
5 10
0
(ln )x x
dx
A.
11
10!
5
B.
11
10!
6
C.
11
11!
5
D.
11
11!
6
Câu 9: u di n tích phân Biể ễ
3 3
0
2
1
x
x
e
e dx
−
−
theo hàm Gamma:
A.
( )
2 4
.
3 3
2. 2
B.
( )
2 1
.
3 3
3. 2
C.
( )
2 1
.
3 3
9. 2
D.
( )
2 4
.
3 3
3. 2
Câu 10: Tính tích phân
2
7 5
0
sin cos
x x
dx
A.
5
128 2
B.
3
256 2
C.
256 2
D.
7
256 2
3
II. Bài t p tr c nghi ậ ắ ệm Tích phân đường
1. Tích phân đường loại I:
Câu 11: Tính tích phân
( )
L
x y ds+
với 𝐿 n th ng nlà đoạ ẳ ối điểm 𝑂
(
0;0
)
và 𝐴
(
4;3
)
A.
35
2
B.
35
4
C.
35
3
D.
35
6
Câu 12: Tính
( )
L
x y ds+
với 𝐿 là n ng tròn ửa đườ {
𝑥 = 2 + 2cos 𝑡
𝑦 = 2sin 𝑡
0 ≤ 𝑡 ≤𝜋
A.
4 8
+
B.
8 4
+
C.
4
D.
2 4
+
Câu 13: Tìm 𝑚để
( )
C
mx y ds−
=− 9 − 𝑥18 với 𝐶: 𝑦 = √
2
A. B. C. 𝑚 = 1 𝑚 = 2 𝑚 = 3 𝑚 = 4 D.
Câu 14: Với 𝐶 ng tròn tính là đườ 𝑥
2
+ 𝑦 = 2𝑥,
2
( )
C
x y ds−
A. 𝜋 B. C. D. 2𝜋 3𝜋 6𝜋
Câu 15: Tính
( )
C
x y ds+
với cung 𝐶: 𝑟 = cos 2𝜑,
2
4 4
−
A.
√
5 B.
√
6 C.
√
10 D.
√
2
Câu 16: Với 𝐶 ng cong trong góc phlà đườ 𝑥
2/3
+ 𝑦 = 1
2/3
ần tư thứ nhất nối
𝐴
(
1,0 0,1 ,
)
và 𝐵
( )
tính
2
( 1)
C
y ds+
A.
15
8
B.
15
9
C.
15
7
D.
15
4
Câu 17: Tính
C
yds
v ới 𝐶 là đườ đi từng 𝑥 = 𝑦
2
𝑂
(
0,0
)
đến 𝐴
(
1,1
)
A.
1
(5 5 1)
3
−
B.
1
(5 5 1)
12
−
C.
1
(5 5 1)
6
−
D.
1
(5 5 1)
2
−
4
Câu 18: Tính
L
xyds
với 𝐿 là chu tuy n c a hình ch ế ủ ữ nhật 𝐴𝐵𝐶𝐷 0,0 ;𝐵 4,0 , với 𝐴
( ) ( )
𝐶
(
4,2 , 𝐷 0,2
) ( )
A. B. C. D. 20 25 24 18
Câu 19: Tính
với 𝐶 là biên c a mi ủ ền
| |
𝑥
|
+ 𝑦
|
≤1
A. B. C. 1 4 2 D. 0
Câu 20: Tính
2 2
L
x y ds+
với 𝐿: 𝑥
2
+ 𝑦 = 2𝑥
2
A. C. 8 B. 6 4 D. 10
2. Tích phân đường loại II:
Câu 21: Tính
( 3 ) 2
AB
x y dx ydy− +
với 𝐴𝐵
⏜
là cung 𝑦 = 1 −𝑥
2
,𝐴
(
1,0
)
,𝐵
(
−1,0
)
A. C. 0 B. 2 4 6D.
Câu 22: Tính
4 3
5 4
ABC
y dx x dy−
với 𝐴𝐵𝐶 ng glà đườ ấp khúc đi qua các điểm
𝐴
(
0,1 ; 𝐵 1,0 ;𝐶 0,−1
) ( ) ( )
A. 2 B. 3 C. 5 D. 4
Câu 23: Tìm 𝑚 để
2
10
( ) .
3
C
x xy dx m x dy
−
+ + =
với 𝐶 là cung bé trên đường tròn
𝑥
2
+ 𝑦 =4 −2,0
2
đi từ 𝐴
( )
đến 𝐵
(
0,2
)
A. B. C. 2 3 0 D. 1
Câu 24: Tính
) ( sin )
y
x y dx xy e x y dy
−
+ + + − + − +
với 𝐿 là đường
𝑥
2
+ 𝑦 =2𝑥
2
theo chiều dương.
A. C. −3𝜋 B. 3𝜋 −2𝜋 4𝜋 D.
5
Câu 25: Tính
2
1 2
2y + + sin(y )
y
e dy
+
với 𝐿 là chu tuy n c a tam giácế ủ
𝐴𝐵𝐶 −1,0 ,𝐵 0,2 ,𝐶 2,0
có 𝐴
( ) ( ) ( )
chi u cùng chi ng h . ề ều kim đồ ồ
A. C. 1 B. 2 4 6 D.
Câu 26: Tính
10 2
( ) ( )
x
AB
xy e dx y x dy+ + −
với 𝐴𝐵
⏜
là cung 𝑦=
√
1 − 𝑥
2
đi từ điểm
𝐴
(
−1,0 1,0
)
đến 𝐵
( )
A.
2
1
2
e
e
−
B.
2
1e
e
−
C.
2
2
2
e
e
−
D.
2
3
e
Câu 27: Tính
2 4
(2 ) ( )
x y
C
e y dx x e dy+ + +
với 𝐶: 𝑦 = 1 − 𝑥
√
2
4
đi từ 𝐴
(
−1,0
)
đến
𝐵
(
1,0
)
A.
2
2
2
e
e
− +
B.
3
2 e
−
−𝑒 C.
3
2 e
−
D.
3
3
2
e
e
− +
Câu 28: Tính tích phân
( )
(3,0)
4 3 2 2 4
( 2, 1)
4 (6 5 )x xy dx x y y dy
− −
+ + −
A. 61 B. 62 C. D. 63 64
Câu 29: Tìm tích phân 𝑚để
2
2 2
2 ( . )
x y
L
e xy dx y m y dy e
+
+ + =
với 𝐿 là đường
𝑥 = 1 − 𝑦
2
đi từ 𝐴
(
1,0
)
đến 𝐵
(
0,1
)
A. 1 B. 2 C. 3 D. 4
Câu 30: Tính tích phân
2 2
2 2 2 2
2 1 1
( 1) ( 1)
L
y xy x x x
dx dy
y x y x
− + − + − −
+
− − − −
với 𝐿:𝑦 = 2𝑥+ 2
đi từ
𝐴
(
0,2
)
đến 𝐵
(
2,6
)
A. D. 4 B. 3 2 C. 1
Câu 31: Tìm 𝑎,𝑏 tích phân để
( )
( )
2
2 1 2
x
L
e x ay dx bx y dy
+ + + +
không ph ụ
thuộc vào đường đi
6
A.
{
𝑎 = 1
𝑏 = 0
B.
{
𝑎 = 0
𝑏 = 1
C.
{
𝑎 = 0
𝑏 = 0
D.
{
𝑎 = 1
𝑏 = 1
Câu 32:
Tìm hằng s u thố 𝑎,𝑏 để biể ức
[
𝑦
2
+ 𝑎𝑥𝑦+ 𝑦sin + 𝑏𝑥𝑦 +
(
𝑥𝑦
)]
𝑑𝑥 +
[
𝑥
2
𝑥sin
(
𝑥𝑦
)]
𝑑𝑦 là vi ph n toàn ph n c a mầ ầ ủ ộ ốt hàm s 𝑢
(
𝑥,𝑦
)
nào đó
A.
{
𝑎 = 1
𝑏 = 1
B.
{
𝑎 = 2
𝑏 = 2
C.
{
𝑎 = 2
𝑏 = 1
D.
{
𝑎 = 1
𝑏 = 2
Câu 33: Tính
( )
2 2 2 2
2
2
1
x y x y
L
xe dx ye dy
x y
+ +
+
− +
với
2
: 2L y x x= −
đi từ
𝑂
(
0,0
)
đến 𝐴
(
2,0
)
A. C. 1 B. 0 2 3D.
Câu 34: Cho tích phân 𝐼 =
2
(5 2 )
x y dy
y
− + +
+
với 𝐶 là biên c a hình ủ
phẳng 𝐷: 𝑥 + 𝑦 ≤ 9
2 2
, theo chi n ều dương, bạ 𝐴 l p luậ ận “Ta đặt
2 2
2 5x y
P
x y
−
=
+
và
2 2
5 2x y
Q
x y
+
=
+
,
' '
0
x y
Q P− =
, 𝐶 ng cong kín, chi i h n milà đườ ều dương, giớ ạ ền 𝐷 nên
𝐼 = 0”. Hỏi bạn 𝐴 làm vậy có đúng không? Nếu sai, thì sửa lại đáp án chính xác
A.
Đúng
B. Sai, 𝐼 = 10𝜋 C. Sai, 𝐼 = 𝜋 D. Sai, 𝐼 = 5𝜋
Câu 35: Tìm tích phân 𝑚để
( 3 ) 2 4
AB
x y dx ydy− + =
với
2
:AB y m x= −
và hai
điểm
(1,0), ( 1,0)A B −
A. 1 B. C. D. −1 2
−2
Câu 36: Tính
C
ydx zdy xdz+ +
v theo ới 𝐶:𝑥 = cos 𝑡,𝑦 = sin𝑡,𝑧 = 2𝑡, 0 ≤ 𝑡 ≤ 2𝜋
chiều tăng của 𝑡
A. C. 2𝜋 𝜋 B.
−𝜋 D. 3𝜋
Câu 37: Tính tích phân
(4,5,6)
(1,2,3)
( 1)
y y z
e dx xe dy z e dz+ + +
A.
4𝑒 + 6𝑒 − 𝑒 − 3𝑒
5 6 2 3
B.
4𝑒 + 6𝑒 − 𝑒 − 3𝑒
4 6 2 3
7
C.
4𝑒 + 6𝑒 − 2𝑒 − 3𝑒
4 6 2 3
D.
4𝑒 + 6𝑒 − 2𝑒 − 3𝑒
5 6 2 3
Câu 38:
Tìm hàm th v c a biế ị ủ ểu thức
(
𝑥
4
+ 4𝑥𝑦
3
) (
𝑑𝑥 + 6𝑥
2
𝑦
2
− 5𝑦
4
)
𝑑𝑦
A.
2 2 3 5
1
2
5
x x y y+ −
B.
2 2 3 5
2
2
5
x x y y+ −
C.
2 2 3 5
2
5
x x y y+ −
D.
2 2 3 5
1
5
x x y y+ −
Câu 39: Tính
(2 5) (2 3 )
L
xy dx x y dy− + +
với 𝐿 là biên c a miủ ền 𝐷 xác định bởi
các đườ ều dươngng 𝑦= 𝑥 ,𝑦 = 0,𝑥 = 1,
2
chi
A.
1
3
B.
1
4
C.
1
5
D.
1
6
Câu 40: Tính
2 2 3
2 3
2 2
3 3
4 1 4
C
x y dx x y dy
x y
+ + +
+ +
với 𝐶 ng cong là đườ
𝑦 = 1 − 𝑥
√
4
đi từ 𝐴
(
1,0
)
đến 𝐵
(
−1,0 .
)
A.
4
arctan 2
7
−
B.
4
2arctan2
7
−
C.
4
3arctan2
7
−
D.
4
2arctan2
7
+
3. ng d ng cỨ ụ ủa tích phân đường
Câu 41:
Tính di n tích c a miệ ủ ền D i h n bgiớ ạ ởi 𝐿:{
𝑥 = 2
(
𝑡 − sin 𝑡
)
𝑦 = 2 1 − cos𝑡
( )
với trục 𝑂𝑥
biế ằt r ng d𝑡 đi từ 2𝜋 ến 0
A.
13𝜋
(
đvdt
)
B.
12
𝜋
(
đvdt
)
C.
11 10
𝜋
(
đvdt
)
D. 𝜋
(
đvdt
)
Câu 42:
Tính công c a lủ ực 𝐹
=
(
𝑥+ 2𝑦 𝑖+ 3𝑥 + 4𝑦 𝑗
) ( )
làm d ch chuy n mị ể ột chất
đi
ể ừm t 𝐴
(
1,3 2,4
)
đến 𝐵
( )
dọc theo đoạn thẳng 𝐴𝐵. (đvc: đơn vị công)
A. 21 (đvc) B. 21,5 (đvc) 26 (đvc) 27 (đvc) C. D.
8
Câu 43:
Tính khối lượng c ng cong v t ch t ủa đườ ậ ấ 𝐿 có phương trình {
𝑥 = cos𝑡
𝑦 = sin𝑡
0≤ 𝑡 ≤ 𝜋/2
bi
ết hàm mật độ là 𝑝
(
𝑥,𝑦 = 𝑦
)
A.
1
(
đvkl
)
B.
2
(
đvkl
)
C.
3
(
đvkl
)
D.
5
(
đvkl
)
Câu 44:
Tính công làm d ch chuy n mị ể ột ch m t ất điể ừ A
(
0,1 1,0
)
đến B
( )
của lực
𝐹
=
[
8𝑥 − 2𝑦 1 +𝑥
3
ln
(
2
𝑦
2
)]
𝑖+ 5𝑦 − 2𝑥 1 + 𝑥
[
4
ln
(
2
𝑦
2
)]
𝑗
A. 1 (đvc) B. 2 (đvc) C. 5 (đvc) D. 4 (đvc)
Câu 45: Tính khối lượ ủa đường c ng cong v t ch t ậ ấ 𝐿 có phương trình 𝑥
2
+ 𝑦 = 1
2
bi
ết hàm mật độ là 𝑝
(
𝑥,𝑦 = 𝑥
)
2
A.
3𝜋
(
đvkl
)
B.
4𝜋
(
đvkl
)
C.
2𝜋
(
đvkl
)
D.
𝜋
(
đvkl
)
9
III. Bài t p tr c nghi m Tích phân m t ậ ắ ệ ặ
1. Tích phân m t lo i I: ặ ạ
Câu 46: Tính
S
xydS
v là mới 𝑆 ặt 𝑧= +𝑦 ,𝑧 ≤ 1,𝑥 ≥ 0
√
𝑥
2 2
A. B. 0 2 C. 1 3 D.
Câu 47: Tính
2
S
x dS
v là biên c a mi n gi i h n b i mới 𝑆 ủ ề ớ ạ ở ặt 𝑧 = + 𝑦 ,𝑧 = 1
√
𝑥
2 2
A.
(2 2)
4
+
B.
(2 3)
4
+
C.
(1 2)
4
+
D.
(1 3)
4
+
Câu 48: Tìm 𝑚 để
5 6
3
( )
S
x y mz dS =
+ +
với 𝑆 là mặt 2𝑥 + 4𝑦 +2𝑧 = 4 và u điề
kiện 𝑥 ≥ 0,𝑦 ≥ 0,𝑧 ≥ 0
A. C. D. 𝑚 = 0 B. 𝑚 = 1 𝑚 = −1 𝑚 = 2
Câu 49: Tính
S
xyzdS
với 𝑆 là mặt 𝑥− 2𝑦 + 3𝑧 − 4 = 0 i h n trong m t tr có giớ ạ ặ ụ
phương trình 2𝑥 + 3𝑦 =6
2 2
A. B. C. 1 0 2 D. 3
Câu 50: Biết
5 1
12
S
a
b
xdS
= +
biết 𝑆 là phần m t paraboloid ặ 𝑥 = 𝑦 + 𝑧
2 2
thỏa
mãn 𝑥 ≤ 1. Kết luận nào sau đây là chính xác?
A. 𝑎 +𝑏 < 70 B.
𝑎 − 𝑏 > 0 C.
𝑎.𝑏 < 70 D.
𝑎/𝑏 > 1
Câu 51: Tính
2 2
1
S
x y dS+ +
v là ph n m t ới 𝑆 ầ ặ 2𝑧 = 𝑥 + 𝑦 ,0 ≤𝑥,𝑦 ≤ 1
2 2
. Chọn
đáp án gần với kết qu c a tích phân nhả ủ ất.
A. D. 2 B. 3 4 C. 0
Câu 52: t Biế
S
dS
4
(33 3 2)
15
a b= − −
v là mới 𝑆 ặt
( )
3/2 3/2
2
3
z x y= +
v i ớ điều
kiện 0 ≤ 𝑥 ≤ 2,0 ≤ 𝑦 ≤ 1. Tìm kh ẳng định đúng?
10
A. 𝑎 <𝑏 B.
𝑎 + 𝑏 = 10 C.
𝑎 − 𝑏 = 5 D.
𝑎.𝑏 = 10
Câu 53: Tính
2
S
zy dS
v là ph n m t nón ới 𝑆 ầ ặ 𝑧 = +𝑦
√
𝑥
2 2
n m gi a hai mằ ữ ặt 𝑧 = 1
và 𝑧 = 2
A.
31 2
3
B.
31 2
10
C.
31 2
4
D.
31 2
5
Câu 54: Tính
2
S
yx dS
với 𝑆 là ph n m t nón ầ ặ 𝑦 = + 𝑧 , 1≤ 𝑦 ≤ 2
√
𝑥
2 2
A.
32 2
5
B.
31 2
5
C.
33 2
5
D.
34 2
5
Câu 55: Tính
S
xdS
v là m t tr n m gi a hai mới 𝑆 ặ ụ 𝑥
2
+ 𝑦 = 4
2
ằ ữ ặt 𝑧 =0 𝑧 = 6 và
A. C. 0 B. 1 2 3 D.
2. Tích phân m t lo i II: ặ ạ
Câu 56: Tính
(1 )
S
x z dzdx− −
v là m t trên c a mới 𝑆 ặ ủ ặt 𝑥+ 𝑦 +𝑧 = 1, 𝑥 ≥ 0,𝑦 ≥
0,𝑧 ≥ 0
A.
1
5
B.
2
3
C.
1
6
D.
4
3
Câu 57: Tính
2 2 2
( )
S
I x y z dxdy= + +
v là m t n a cới 𝑆 ặ ử ầu 𝑥
2
+ 𝑦 + 𝑧 = 1
2 2
phía
trên ng lên trên.𝑂𝑥𝑦, mặt 𝑆 hướ
A. B. C. D. 𝜋 −𝜋 2𝜋 3𝜋
Câu 58: Cho 𝐼 =
2
S
ydzdx z dxdy+
, là phía ngoài m𝑆 ặt 𝑥
2
+ 𝑦 + 𝑧
2 2
= 1 với điều
kiện 𝑥 ≥ 0,𝑦 ≥ 0,𝑧 ≥ 0.Chọn đáp án gần nhất với kết qu cả ủa 𝐼
A. B. C. 1 0 2 D. 3
Câu 59: Tính 𝐼 =
2
S
xdzdx z dxdy+
v là phía ngoài mới 𝑆 ặt 𝑧 = 𝑥 + 𝑦
2 2
với điều
kiện 0≤ 𝑧 ≤ 2,𝑦 ≥ 0
11
A.
4
5
−
B.
7
3
−
C.
5
3
−
D.
4
3
−
Câu 60: Tính
2 2 2
4 9
S
xz dydz yx dzdx zy dxdy+ +
v i mớ ặt 𝑆:4𝑥 + 9𝑦 + 𝑧 =1
2 2 2
,
hướng ra ngoài.
A.
4
15
B.
2
15
C.
2
13
D.
2
19
Câu 61: Biết 𝐼 =
2 2
2 ( ) (4 )
S
a
xydydz x y dzdx x y dxdy
b
+ + + + =
với m là biên cặt 𝑆 ủa
miền 𝑉:𝑥 + 𝑦 +𝑧 ≤ 1, 𝑥 ≥ 0,𝑦 ≥ 0,𝑧 ≥ 0 hướng ra ngoài. Tìm khẳng định đúng
A. C. 𝑎− 𝑏 = 7 B. 𝑎. 𝑏 = 7 𝑎 +𝑏 = 7 D.
𝑎/𝑏 = 7
Câu 62: Tính 𝐼 =
2 3 3 2
( 2 ) ( 2 )
S
xy z dydz z y dzdx x zdxdy+ + + +
v là n a mới 𝑆 ử ặt
cầu 𝑥
2
+ 𝑦 + 𝑧 = 1,𝑧 ≥ 0
2 2
hướng ra ngoài m t cặ ầu.
A.
8
5
B.
8
3
C.
6
7
D.
8
7
Câu 63: Tính 𝐼 =
3 2 2
( 2 ) (3 ) (6 )
S
x yz dydz x y y dzdx y z xy dxdy+ + + + +
với 𝑆 là mặt
𝑧 = 𝑥 + 𝑦
2 2
v ng xuới 𝑧 ≤ 1, hướ ống dưới.
A. 1 0 2 8 B. C. D.
Câu 64: Tính
2 2
1
( )
1
S
xdydz ydzdx dxdy
x y
− − +
+ +
với 𝑆 là mặt 2𝑧 = 𝑥 + 𝑦 ,
2 2
𝑧 ≤ 2 theo chi u âm c a trề ủ ục 𝑂𝑥
A.
(2 10 5)
3
+
B.
(2 5)
3
+
C.
( 2 10 5)
3
− +
D.
( 2 5)
3
− +
12
Câu 65: Biết
S
a
b
xdydz zdxdy
=
+
với 𝑆 là ph n trên c a m t nón ầ ủ ặ có phương
trình 𝑧 = − +𝑦
√
𝑥
2 2
,−1 ≤ 𝑧 ≤ 0 khi nhìn t chiừ ều dương trục 𝑂𝑧. Tính 2𝑎 + 𝑏
A. 1 B. 9 C. 0 D. 5
Câu 66: Tính
zdz+
d ng tròn ọc theo đườ 𝐶:𝑥 + 𝑦 = 1,𝑧 = 0
2 2
chiều dương giới hạn mặt cầu 𝑧= 1 − 𝑥 − 𝑦
√
2 2
A.
6
B.
4
−
C.
7
D.
8
−
Câu 67: Tính tích phân 𝐼 =
2 2
1
( 2 2 )
1 4 4
S
xdydz ydzdx dxdy
x y
− − +
+ +
v là ới 𝑆
mặt có phương trình 𝑧 = 𝑥
2
+ 𝑦 ,0 ≤ 𝑧 ≤ 4
2
theo chiều 𝑧 ≥ 0
A.
(17 17 1)
7
−
B.
(17 17 1)
6
−
C.
(17 16 1)
6
−
D.
(17 17 1)
6
+
Câu 68: Tính tích phân 𝐼 =
3 3
(6 9 ) (3 2 ) (3 3 )
S
z y dydz x z dzdx y x dxdy− + − + −
với
𝑆 là mặt 𝑥
2
+ 3𝑦 + 𝑧 = 1,𝑧 ≥ 0,
2 4
hướng lên trên.
A. C. D. 2 B. 3 0 1
Câu 69: Tính
2
(2 ) ( 2 ) (1 6 )
S
x xy dydz y xz dzdx z z dxdy+ + + + + +
với 𝑆 là m t nặ ằm
trong c a n a c
ủ ử ầu 𝑧 = − +𝑦 + 𝑧
√
16 −
(
𝑥
2 2 2
)
A.
( )
80 190−
√
2 𝜋
B. (80 192−
√
2)𝜋
C.
( )
80 193−
√
2 𝜋
D.
( )
80 194−
√
2 𝜋
Câu 70: Tính
S
xydydz yzdzdx zxdxdy+ +
biết 𝑆 là m t ngoài c a t ặ ủ ứ diện 𝑂𝐴𝐵𝐶 với
𝑂
(
0,0,0 , 𝐴 1,0,0 ,𝐵 0,1,0 ,𝐶 0,0,1
) ( ) ( ) ( )
13
A.
1
7
B.
1
8
C.
1
9
D.
1
10
Câu 71: Biết
2 2 2
2 dyd
S
x z y dzdx z dxdy a b
+ − = +
, S mlà ặt ngoài c n giủa miề ới
hạn bởi 𝑦 = 0,𝑦 = √1 −𝑧
2
,𝑥 = 0,𝑥 = 2 n kh chọ ẳng định đúng
A. 𝑎 + 3𝑏 = 12
B. 3𝑎 + 6𝑏 = 16
C. −𝑎 + 3𝑏 = 0
D. 𝑎 + 𝑏 = 4
Câu 72: Biết
( ) ( ) ( )
S
a
I x z dydz y x dzdx z y dxdy
b
= + + + + + =
với 𝑆 là m t trong ặ
của parabol 𝑧 = 𝑥 + 𝑦 𝑥 + 𝑧 = 2
2 2
n i mằm dướ ặt Tính . 𝑎− 𝑏
A. B. C. D. 50 49 52 47
3. Ứng dụng của tích phân mặt:
Câu 73: Tính di n tích m ệ ặt 𝑆:𝑧 = 2 + + 𝑦
√
𝑥
2 2
,𝑧 ≤ 3
A.
7
(đvdt) B.
3
(đvdt) C.
2
(đvdt) D.
5
(đvdt)
Câu 74: Tính di n tích m t cong vệ ặ 𝑆 ới 𝑆 là ph n m t nón ầ ặ 𝑦 = + 𝑧
√
𝑥
2 2
với điều
kiện 1≤𝑦 ≤ 2,𝑧 ≥ 0
A.
3 2
2
(đvdt) B.
3 3
2
(đvdt) C.
3
2
(đvdt)
D.
3
3
(đvdt)
Câu 75: Tính di n tích m t paraboloid n m phía trên mệ ặ 𝑧 = 4𝑥− 𝑥 − 𝑦
2 2
ằ ặt 𝑂𝑥𝑦 là
( 17 1)a
b
−
, tính 𝑎 + 𝑏
A. 20 B. 23 C. 19 D. 15
Câu 76: Tính di n tích ph n m t paraboloid a mãn ệ ầ ặ 𝑥 = 𝑦 + 𝑧
2 2
thỏ 𝑥 ≤ 1
A.
(5 5 1)
6
−
B.
6
2
C.
(3 6 1)
6
−
D.
( 6 1)
6
−
Câu 77: Tính di n tích m ệ ặt 𝑆:𝑧 = + 𝑦
√
𝑥
2 2
,𝑧 ≤ 3
A. 9𝜋
√
2
B.
8𝜋
√
5 C.
9𝜋
√
8 D.
7𝜋 3
√
14
IV.Bài t p trậ ắc nghi m Lý thuy ệ ết trường
1. Trường vô hướng:
Câu 78:
Tính đạo hàm theo hướng 𝑙
=
(
1,2,−2
)
của 𝑢 = 𝑒
𝑥
(
𝑦
2
+ 𝑧 − 2
)
𝑥𝑦𝑧
3
tại
𝐴
(
0,1,2
)
A.
11
4
−
B.
11
3
−
C.
15
4
−
D.
15
2
−
Câu 79:
Cho Tính 𝑢
(
𝑥,𝑦,𝑧 = 𝑥 + 3𝑦𝑥 + 2𝑦𝑧 .
)
3 2 2
u
n
với 𝑛
󰇍
là vecto pháp tuyến
hư
ớng ra ngoài c a mủ ặt cầu 𝑥
2
+ 𝑦 + 𝑧 = 3,𝑧 ≤ 0
2 2
tại điểm 𝐴
(
1,1,−1
)
A. −6
√
3 B. −6
√
2 C. −2
√
3 D. −2 6
√
Câu 80:
Biết nhiệt độ ại điể trong không gian đượ t m
(
𝑥,𝑦,𝑧
)
c cho b i hàm ở
𝑇
(
𝑥,𝑦,𝑧
)
=
80
1 + 𝑥 + 2𝑦 + 3𝑧
2 2 2
ở đó 𝑇 có đơn vị là và ℃ 𝑥,𝑦,𝑧 là mét. Theo hướng nào thì nhi ệt độ tăng nhanh
nh
ất tại điểm 𝐴
(
1,1,−2
)
A.
5 5 15
; ;
8 4 4
B.
5 15 15
; ;
8 4 4
C.
5 5 15
; ;
8 4 4
− −
D.
5 5 15
; ;
8 4 4
−
Câu 81: Tính góc gi a hai vecto ữ 𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑧 (đơn vị: radian) của các trường vô hướng
sau
𝑧
1
=
√
𝑥
2
+ 𝑦
2
,𝑧
2
=𝑥− 3𝑦 +
√
3𝑥𝑦 tại 𝑀
(
3,4
)
(Chọn đáp án gần đúng nhất)
A. B. D. 2 1 C. 3 4
Câu 82:
Cho Tính 𝑢
(
𝑥,𝑦,𝑧 (1 + 𝑥 + 𝑒 ),𝑂 0,0,0 ,𝐴 1,−2,2 .
)
= ln
2 𝑦−𝑧
( ) ( )
u
l
theo
hướng 𝑂𝐴
󰇍
󰇍
󰇍
󰇍
󰇍
A.
2
5
−
B.
2
3
−
C.
1
3
−
D.
1
5
−
15
Câu 83: Theo hướng nào thì s n thiên c a hàm ự biế ủ 𝑢 = 𝑥 sin𝑧 − 𝑦 cos𝑧 t i g c tạ ố ọa
độ là lớn nhất
A.
𝑙
=
(
0,1,0
)
B. 𝑙
=
(
0,−1,0
)
C.
𝑙
=
(
0,−2,0
)
D.
𝑙
=
(
0,−3,0
)
Câu 84:
Cho điểm 𝐴
(
2,−1,0 , 𝐵 1,1,3
) ( )
. Tính đạo hàm của hàm 𝑢 = 𝑥 + 3𝑦 +
3 2
𝑒
𝑧
+ 𝑥𝑦𝑧
2
tại điểm 𝐴 theo hướng 𝐴𝐵
󰇍
󰇍
󰇍
󰇍
󰇍
A.
14
3
B.
14
2
C.
3 14
2
−
D.
2 14
3
−
Câu 85: Tính góc giữa 𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑢,
2 2 2
x
u
x y z
=
+ +
t và
ại điểm 𝐴
(
1,2,2
)
𝐵
(
−3,1,0
)
A.
8
arccos
9
−
B.
1
arccos
9
−
C.
1
arccos
9
D.
7
arccos
9
−
2.Trường Vecto:
Câu 86:
Cho 𝐹
=𝑥 𝑖+ 3𝑥𝑦 𝑧𝑗+ 𝑚𝑥𝑦𝑧 𝑘
2
𝑦𝑧
2 2
󰇍
v là tham s c. Tìm
ới 𝑚 ố thự 𝑚 để 𝐹
là
trường ống.
A. 𝑚 = 4 B.
𝑚 = −4 C.
𝑚 = 5 D.
𝑚 = −5
Câu 87: Xác đị ững điể ải điểm xoáy trong trườnh nh m không ph ng vecto
𝐹
=
(
𝑧
2
+ 2 𝑖+ 3𝑥 − 2 𝑗 − 𝑧 𝑘𝑥𝑦
) (
2
𝑦𝑧
)
2
󰇍
A.
(
1,0,0
)
B.
( ) (
0,0,1 C. 0,0,0
)
D.
(
0,1,0
)
Câu 88:
Biết 𝐹
= 𝑒
𝑥
2
+𝑦 +𝑧
2 2
[
(
2𝑥
2
𝑦𝑧 𝑦𝑧+
)
𝑖+ 2𝑦 𝑗+ 2𝑧 𝑘
(
2
𝑥𝑧 𝑥𝑧+
) (
2
𝑦𝑥+ 𝑥𝑦
)
󰇍
]
là
trường thế. Tìm hàm th v . ế ị
A.
2 2 2
x y z
u e xyz C
+ +
= +
B.
2 2 2
x y z
u e xy C
+ +
= +
C.
2 2
x y z
u e xy C
+ +
= +
D.
2 2
y z
u e xyz C
+
= +
Câu 89:
Biết 𝐹
=
(
3𝑥 − 3𝑦 𝑖+ arctan𝑧 − 6 𝑗+
2 2
𝑧
) (
𝑥𝑦𝑧
)
(
𝑦
1+𝑧
2
+ 3𝑥𝑦
2
)𝑘
󰇍
là trường
thế, tìm hàm th vế ị.
A.
2
arctan 3u x y z xy z C= + + +
B.
2
3 arctan 3u x y z xy z C= + + +
C.
2
arctan 3u y z xy z C= + +
D.
3 2
arctan 3u x y z xy z C= + + +
16
Câu
90: Biết 𝐹
=
(
3𝑥 𝑖 + 6𝑦 𝑗+ + 𝑒
2
+ 𝑦𝑧
) (
2
+ 𝑥𝑧
) (
𝑧
2
+ 𝑥𝑦
𝑧
)
𝑘
󰇍
ng th , tìm là trườ ế
hàm th v ế ị
A.
3
3 3
2
3
z
z
u x y e xyz C= + + + + +
B.
3
3 3
3
3
z
z
u x y e xyz C= + + + + +
C.
3
3 3
2
3
z
z
u x y e xy C= + + + + +
D.
3
3 3
2
3
xz
z
u x y e xyz C= + + + + +
Câu
91: Tính thông lượng của 𝐹
= 𝑥𝑖+ +2𝑧 𝑗+ 3𝑥 𝑧 − 𝑥 𝑘
(
𝑦
3
) (
2
)
󰇍
qua m t cặ ầu
𝑆: 𝑥
2
+ 𝑦 + 𝑧 = 1
2 2
ng ra ngoài. hướ
A.
54
15
B.
57
15
C.
47
15
D.
44
15
Câu
92: Tính thông lượng của 𝐹
= 𝑥𝑦 𝑖− 𝑧𝑒 𝑗+ 𝑧+ sin𝑦 𝑘
2 𝑥
(
𝑥
2
)
󰇍
qua là m 𝑆 ặt
𝑧 = 𝑥 + 𝑦 ,𝑧 ≤ 4,
2 2
ng ra ngoài. hướ (Chọn kết qu gả ần đúng nhất)
A. −17 B.
−15 C.
−10 D.
−14
Câu 93
: Tính thông lượng của 𝐹
=
(
𝑥
2
− 2𝑦 +𝑧 𝑖− + 2 𝑗+ 𝑥𝑘
) (
𝑧
2
𝑥𝑦
)
󰇍
qua phía
trên m t nón ặ 𝑧= 1 + + 𝑦
√
𝑥
2 2
c t b i hai m t ph ng ắ ở ặ ẳ 𝑧 = 2,𝑧 = 5
A. 25 B. 16 C. 0 D. 20
Câu 94:
Tính thông ng c ng vecto lượ ủa trườ 𝐹
=2𝑥 𝑖 + 𝑦 𝑗− 𝑧 𝑘
2 2 2
󰇍
qua mS là ặt
ngoài c a mi n gi i h n bủ ề ớ ạ ởi 𝑦 = 0,𝑦 = √1− 𝑧 ,𝑥 = 0,𝑥 = 2
2
A.
8
4
3
+
B.
8
3
3
+
C.
8
3
+
D.
8
4
5
+
Câu 95
: Tính thông lượ ủa trường c ng vecto 𝐹
= 𝑥 𝑖+ 𝑦 𝑗 +
3 2
𝑧
2
2
𝑘
󰇍
qua biên 𝑆 là
ngoài c a
ủ miền 𝑉: 𝑥− 𝑦 ≤ 1, 𝑦− 𝑧 ≤ 1, 𝑧 +𝑥 ≤ 1
| | | | | |
A. D. 5 B. 4 0 C. 3
Câu 96: Cho trường vô hướng 𝑢 = .𝑥𝑦 𝑥𝑧+ 𝑦𝑧+ cTính lưu số ủa trường vecto
𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑢
d n th ng n i t ọc theo đoạ ẳ ố ừ 𝐴
(
−1,−1,−1 2,4,1
)
đến 𝐵
( )
A. 11 B. 12 C. 16 D. 14
Câu 97
: Tính lưu số của 𝐹
=𝑥 𝑖+𝑗+ 𝑧𝑘
2
𝑦
3
󰇍
d ng tròn ọc theo đườ có phương trình
17
𝐶:𝑥 + 𝑦 = 1, 𝑧 =0
2 2
i h n m t cgiớ ạ ặ ầu 𝑧 = 1 −𝑥 − 𝑦
√
2 2
A.
6
−
B.
8
−
C.
7
−
D.
9
−
Câu 98
: Tính lưu số của 𝐹
=
(
𝑦𝑒 +3𝑦+ 𝑧 𝑖+ 𝑥𝑒 +𝑦− 5𝑧 𝑗 + 1 + 2𝑥 𝑘
𝑥𝑦
) (
𝑥𝑦
) ( )
󰇍
dọc
theo đường cong 𝐿 là giao c a mủ ặt 𝑥
2
+ 𝑦 + 𝑧 = 4
2 2
và mặt 𝑥− 𝑦 + 𝑧 = 0 ng hướ
ngược chi ng h n u nhìn t chiều kim đồ ồ ế ừ ều dương trục 𝑂𝑧.
A.
3
√
3𝜋
B.
6
√
3𝜋
C.
4
√
3𝜋 D.
√
3𝜋
Câu 99
: Tính lưu số của 𝐹
=
(
𝑦
2
+ 𝑧
2
)
𝑖+ + 𝑧
(
𝑥
2 2
)
𝑗+ + 𝑦
(
𝑥
2 2
)
𝑘
󰇍
d ng ọc theo đườ
cong 𝐶 trong đó 𝐶 là giao c a m t củ ặ ầu 𝑥
2
+ 𝑦 + 𝑧 = 4
2 2
và mặt nón có phương
trình v ng cùng chi ng h khi nhìn t g c O. 𝑧 = − +(𝑦 − 1)
√
𝑥
2 2
ới hướ ều kim đồ ồ ừ ố
A. 3 B. 0 C. 1 D. 5
Câu 100:
Tính thông lượng của 𝐹
= (6𝑧− 2𝑦 )𝑖+ 2𝑥− 3𝑧 𝑗+ 2𝑦 − 4𝑥 𝑘
3
( ) (
3
)
󰇍
qua
mặt cong 2 𝑆: 𝑥
2
+ 𝑦 +3𝑧 = 1, 𝑧 ≥ 0
4 2
hướng lên trên.
A. C. 3 B. 0 2 1 D.
18
V. L oời giải tham khả
Tích phân Euler:
Câu 1: Kết qu c a tích phânả ủ
4
5
0
x
x e dx
+
−
là:
Đáp án: A.
8
Giải:
Đặt
3 3
4
2 1/2
4
4
du
x dx du x dx
x u
x u
= =
=
=
⇒ ∫ 𝑥
5
+∞
0
𝑒
−𝑥
4
𝑑𝑥 =
1
4
∫ 𝑢
1/2
𝑒
−𝑢
𝑑𝑢 =
1
4
∫ 𝑢
3
2
−1
𝑒
−𝑢
𝑑𝑢 =
+∞
0
1
4
Γ(
3
2
)=
√
𝜋
8
+∞
0
Câu 2: Kết qu c a tích phân ả ủ
2
6 4
0
sin cosx xdx
là:
Đáp án: D.
3
512
Giải:
∫
sin
6
𝑥cos
4
𝑥
𝜋
2
0
𝑑𝑥 = ∫
(
sin𝑥
)
2.
7
2
−1
.
(
cos𝑥
)
2.
5
2
−1
𝑑𝑥
𝜋
2
0
=
1
2
𝐵(
7
2
,
5
2
)
=
1
2
.
Γ(
7
2
).Γ(
5
2
)
Γ(6)
=
1
2
.
45
32
.
Γ(
1
2
).Γ(
1
2
)
5!
=
3𝜋
512
Câu 3: Biết
4
7/2
6
0
3
(ln3)
x
a
b
x dx
+
−
=
, ch n khọ ẳng định đúng:
Đáp án: A. 𝑎 − 𝑏 = −1
19
Giải:
Đặt
2
3
6
3
2ln3.
2 ln3.
ln3.
(ln3)
du
xdx du dx
u
x u
u
x
= =
=
=
⇒ ∫ 𝑥
6
.3
−𝑥
2
𝑑𝑥
𝜋
2
0
= ∫
𝑢
3
(
ln3
)
3
.
𝑒
−𝑢
2
√
ln3.𝑢
𝑑𝑢
𝜋
2
0
=
1
2
∫
(
ln3
)
−
7
2
.𝑢
5
2
.𝑒
−𝑢
𝑑𝑢
𝜋
2
0
=
(ln3)
−7/2
2
.∫𝑢
7
2
−1
.𝑒
−𝑢
𝑑𝑢
𝜋
2
0
=
(ln3)
−7/2
2
.Γ(
7
2
)=
15
√
𝜋
16
(ln3)
7
2
⇒𝑎 = ,𝑏 =15 16
Câu 4: Biểu di n tích phân ễ
2
4 4
0
(1 )
x
x
dx
+
+
theo hàm Gamma:
Đáp án: C.
( )
3 13
.
4 4
4. 4
Giải:
Đặt
3 2
4
1/4
1/4
4
4
du
x dx du x dx
x u
u
x u
= =
=
=
⇒
∫
𝑥
2
(
1 + 𝑥
4
)
4
𝑑𝑥
+∞
0
=
1
4
∫
𝑢
−1
4
𝑑𝑢
(1 + 𝑢)
4
+∞
0
=
1
4
𝐵(
3
4
,
13
4
)=
1
4
.
Γ(
3
4
).Γ(
13
4
)
Γ
(
4
)
Câu 5: Tính tích phân
3030
1
0
1
1
x
dx
−
20
Đáp án: B.
30sin
30
Giải:
Đặt
29
30
29/30
1/30
30
30.
du
du x dx dx
u x
u
x u
= =
=
=
⇒
∫
1
√1 − 𝑥
30
30
𝑑𝑥
1
0
=
1
30
∫
𝑢
−
29
30
√
1 − 𝑢
30
𝑑𝑢
1
0
=
1
30
∫𝑢
1
30
−1
.
(
1 − 𝑢
)
29
30
−1
𝑑𝑢
1
0
=
1
30
𝐵(
1
30
,
29
30
)
=
1
30
𝜋
sin
(
𝜋
30
)
Câu 7: Tính tích phân
10
1
0
1
ln dx
x
Đáp án: B.
10!
Giải:
Đặt
1 1
1
ln
1
u
u
dx du dx du
x e
u
x
e
x
− −
= =
=
=
⇒
∫(ln
1
𝑥
)
10
𝑑𝑥
1
0
=− ∫
𝑢
10
.𝑒
−𝑢
𝑑𝑢
0
+∞
= ∫
𝑢
11−1
.𝑒
−𝑢
𝑑𝑢
+∞
0
=Γ
(
11 10
)
= !
Câu 8: Tính tích phân
1
5 10
0
(ln )x x
dx
Đáp án: B.
11
10!
6
Giải:
21
Đặt
5 5
1
ln
u
u
dx du dx e du
x u
x
x e
= =
=
=
⇒ ∫𝑥
5
(ln𝑥)
10
𝑑𝑥
1
0
= ∫
𝑒
6𝑢
.𝑢
10
𝑑𝑢
0
−∞
Đặt
10
10
10
6 ,
6 6
dt t
u t du u
−
= − = =
Đổ ậi c n: 𝑢 = 0 ⇒−𝑡 = 𝑢 →−∞ ⇒ 0, −𝑡 → +∞
⇒ ∫𝑒
6𝑢
.𝑢
10
𝑑𝑢
0
−∞
=
1
6
11
∫ 𝑒
−𝑡
.𝑡
10
𝑑𝑡
+∞
0
=
1
6
11
.Γ
(
11
)
=
10!
6
11
Câu 9: u di n tích phân Biể ễ
3 3
0
2
1
x
x
e
e dx
−
−
theo hàm Gamma:
Đáp án: C.
( )
2 1
.
3 3
9. 2
và D.
( )
2 4
.
3 3
3. 2
Giải:
Đặt 𝐼 =
3 3
0
2
1
xx
ee dx
−
−
Đặt 𝑢 = 𝑒
3𝑥
⇒ 𝑑𝑢 = 3𝑒
3𝑥
𝑑𝑥 𝑑𝑥⇒ =
𝑑𝑢
3𝑒
3𝑥
=
𝑢
−1
𝑑𝑢
3
Với 𝑥 = 0 ⇒ 𝑢 = 1,𝑥 = −∞ ⇒ 𝑢 = 0
⇒𝐼 =
1
3
∫𝑢
2
3
( )
1 − 𝑢
1
3
1
0
𝑢
−1
𝑑𝑢 =
1
3
∫𝑢
−
1
3
( )
1 − 𝑢
1
3
1
0
𝑑𝑢 =
1
3
𝐵(
2
3
,
4
3
)=
1
3
Γ(
2
3
)Γ(
4
3
)
Γ(2)
Mà
Γ(
4
3
)=
1
3
Γ(
1
3
)⇒ 𝐼 =
1
9
Γ(
2
3
)Γ(
1
3
)
Γ(2)
=
1
9
2
√
3
𝜋
1!
=
2
9
√
3
𝜋
22
Câu 10: Tính tích phân
2
7 5
0
sin cos
x x
dx
Đáp án: A.
5
128 2
Giải:
∫
(
sin𝑥
)
7
2
( )
cos𝑥
5
2
𝑑𝑥
𝜋
2
0
= ∫
(
sin𝑥
)
2.
9
4
−1
(
cos𝑥
)
2.
7
4
−1
𝑑𝑥
𝜋
2
0
=
1
2
.𝐵(
9
4
,
7
4
)=
1
2
Γ(
9
4
)Γ(
7
4
)
Γ(4)
Mà
{
Γ(
9
4
)=
5
4
Γ(
5
4
)=
5
4
.
1
4
.Γ(
1
4
)=
5
16
Γ(
1
4
)
Γ(
7
4
)=
3
4
Γ(
3
4
)
⇒
𝑇𝑃 =
1
2
.𝐵(
9
4
,
7
4
)=
1
2
.
15
64
.
Γ(
1
4
)Γ(
3
4
)
Γ(4)
=
15
128
2
√
2
𝜋
3!
=
5𝜋
128
√
2
Tích phân đường
Câu 11: Tính tích phân
( )
L
x y ds+
với 𝐿 n th ng nlà đoạ ẳ ối điểm 𝑂
(
0;0
)
và 𝐴
(
4;3
)
Đáp án: A.
35
2
Giải:
Phương trình ạn
đo 𝑂𝐴 là {
𝑦 =
3
4
𝑥
0≤ 𝑥 ≤ 4
⇒𝑦
′
(
𝑥
)
=
3
4
⇒ 𝑑𝑠 =
√
1 +
9
16
𝑑𝑥 =
5
4
𝑑𝑥
⇒ ∫(𝑥+ 𝑦)𝑑𝑠
𝐿
= ∫
(𝑥+
3
4
𝑥)
5
4
𝑑𝑥
4
0
=
35
2
Câu 12: Tính
( )
L
x y ds+
với 𝐿 là n ng tròn ửa đườ {
𝑥 = 2 +2cos𝑡
𝑦 = 2sin𝑡
0≤ 𝑡 ≤ 𝜋
23
Đáp án: B.
8 4
+
Giải:
Đường 𝐶: {
𝑥 = 2 +2 cos𝑡
𝑦 = 2sin𝑡
0≤ 𝑡 ≤ 𝜋
⇒ {
𝑥
′
(
𝑡
)
=−2sin𝑡
𝑦
′
(
𝑡
)
=2cos𝑡
⇒ 𝑑𝑠 =
√
𝑥
′
2
(
𝑡
)
+ 𝑦 (𝑡)
′
2
𝑑𝑡 𝑑𝑡= 2
⇒
∫
(
𝑥+ 𝑦
)
𝑑𝑠
𝐶
=2 2 + 2cos𝑡 + 2sin𝑡∫
(
)
𝑑𝑡
𝜋
0
=8 + 4𝜋
Câu 13: Tìm 𝑚 để
( )
C
mx y ds−
= −18 với 𝐶: 𝑦 =
√
9 − 𝑥
2
Đáp án: C. 𝑚 = 3
Giải:
N
ửa đường tròn 𝐶: {
𝑥
2
+ 𝑦
2
=9
𝑦 ≥ 0
. Tham s hóa ố 𝐶
Đặt {
𝑥 = 3cos𝑡
𝑦 = 3sin𝑡
0≤ 𝑡 ≤ 𝜋
⇒ {
𝑥
′
(
𝑡
)
=−3sin𝑡
𝑦
′
(
𝑡
)
=3cos𝑡
⇒ 𝑑𝑠 =
√
𝑥
′
2
(
𝑡
)
+ 𝑦
′
2
(𝑡)𝑑𝑡 = 3
⇒
∫
(
𝑚𝑥 −𝑦
)
𝑑𝑠
𝐶
=3 3𝑚 cos𝑡− 3sin 𝑡∫
(
)
𝑑𝑡
𝜋
0
=−18 ⇒ 𝑚 = 3
Câu 14: Với 𝐶 ng tròn tính là đườ 𝑥
2
+ 𝑦 = 2𝑥,
2
( )
C
x y ds−
Đáp án: B. 2𝜋
Giải:
𝐶:𝑥 + 𝑦 = 2𝑥 ⇔ 𝑥 − 1
2 2
( )
2
+ 𝑦 = 1
2
Đặt {
𝑥 = 1 + cos𝑡
𝑦 = sin𝑡
0≤ 𝑡 ≤ 2𝜋
⇒ {
𝑥
′
(
𝑡
)
=−sin𝑡
𝑦
′
(
𝑡
)
=cos𝑡
⇒ 𝑑𝑠 =
√
𝑥
′
2
(
𝑡
)
+ 𝑦
′
2
(𝑡)𝑑𝑡 𝑑𝑡=
∫
(
𝑥− 𝑦
)
𝑑𝑠
𝐶
= ∫
(
1 + cos𝑡− sin𝑡
)
𝑑𝑡
2𝜋
0
=2𝜋
24
Câu 15: Tính
( )
C
x y ds+
với cung 𝐶: 𝑟 = cos 2𝜑,
2
4 4
−
Đáp án:
D.
√
2
Giải:
Cung 𝐶:
{
𝑟
2
= cos 2𝜑
−𝜋
4
≤𝜑 ≤
𝜋
4
⇔ {
𝑟 = cos2𝜑
√
−𝜋
4
≤ 𝜑 ≤
𝜋
4
⇒𝑟
′
=
−sin2𝜑
√
cos2𝜑
⇒
𝑑𝑠 =
√
𝑟
2
(
𝜑
)
+ 𝑟
′
2
(𝜑)𝑑𝜑 =
√
cos2𝜑 +
sin
2
2𝜑
cos2𝜑
𝑑𝜑 = √
1
cos2𝜑
𝑑𝜑
Đặ
t {
𝑥 = 𝑟cos 𝜑
𝑦 = 𝑟sin𝜑
⇒
∫𝑟
(
cos𝜑 + sin 𝜑
)
√
1
cos2𝜑
𝑑𝜑
𝜋
4
−𝜋
4
= ∫
√
cos2𝜑
(
cos𝜑+ sin𝜑
)
√
1
cos2𝜑
𝑑𝜑
𝜋
4
−𝜋
4
=
√
2
Câu 16: Với 𝐶 ng cong trong góc ph t nlà đườ 𝑥
2/3
+ 𝑦 = 1
2/3
ần tư thứ nhấ ối
𝐴
(
1,0 0,1 ,
)
và 𝐵
( )
tìm 𝑚để
2
( 1)
C
y ds+
Đáp án: A.
15
8
Giải:
Ta
có 𝐶: 𝑥
2
3
+ 𝑦
2
3
=1 ⇔ (𝑥
1
3
)
2
+ (𝑦
1
3
)
2
=1
Tham số hóa:
{
𝑥
1
3
=cos𝑡
𝑦
1
3
=sin𝑡
⇒ {
𝑥 = cos
3
𝑡
𝑦 = sin
3
𝑡
⇒
{
𝑥
′
(
𝑡
)
= −3sin 𝑡cos
2
𝑡
𝑦
′
(
𝑡
)
=3cos𝑡 sin
2
𝑡
⇒
𝑑𝑠 =
√
𝑥
′
2
(
𝑡
)
+ 𝑦 (𝑡)
′
2
𝑑𝑡 =
√
9sin
2
𝑡cos 𝑡 + 9cos 𝑡sin = 3sin𝑡 cos𝑡
4 2 4
𝑡 𝑑𝑡 𝑑𝑡
T
ại 𝐴
(
1,0
)
: {
𝑥 = cos
3
𝑡 = 1
𝑦 = sin 𝑡 = 0
3
⇔𝑡 = 0, 0,1 tại 𝐵
( )
: {
𝑥 = cos
3
𝑡 = 1
𝑦 = sin 𝑡 =0
3
⇔𝑡 =𝜋/2
25
⇒
∫
(
𝑦
2
+ 1
)
𝐶
𝑑𝑠 = 3 sin∫
(
6
𝑡 + 1
)
𝜋
2
0
sin𝑡cos𝑡 = 3 sin𝑑𝑡 ∫
(
7
𝑡 + sin 𝑡
)
𝜋
2
0
𝑑
(
sin𝑡
)
=3
∫
(
𝑢
7
+ 𝑢
)
1
0
𝑑𝑢 =
15
8
Câu 17: Tính
C
yds
v ới 𝐶 là đườ đi từng 𝑥 = 𝑦
2
𝑂
(
0,0
)
đến 𝐴
(
1,1
)
Đáp án: B.
1
(5 5 1)
12
−
Giải:
Đư
ờng 𝐶: {
𝑥 = 𝑦
2
0≤ 𝑦 ≤ 1
⇒ 𝑥
′
(
𝑦
)
= 2𝑦 ⇒ 1+ 𝑥 (𝑦)𝑑𝑠 =
√
′
2
𝑑𝑦 =
√1 + 4𝑦
2
𝑑𝑦
⇒ ∫ 𝑦𝑑𝑠
𝐶
= ∫
𝑦
1
0
√
1 + 4𝑦
2
𝑑𝑦 =
1
2
∫√
1 + 4𝑦
2
𝑑
(
𝑦
2
)
1
0
=
1
2
∫√1 + 4𝑢𝑑𝑢
1
0
=
1
12
(5
√
5 − 1)
Câu 18: Tính
L
xyds
v
ới 𝐿 là chu tuy n c a hình ch vế ủ ữ nhật 𝐴𝐵𝐶𝐷 ới 𝐴
(
0,0 ;𝐵 4,0 ;
) ( )
𝐶
(
4,2 , 𝐷 0,2
) ( )
Đáp án: C. 24
Giải:
26
Ta có:∫ 𝑥𝑦𝑑𝑠
𝐿
= ∫
𝑥𝑦𝑑𝑠
𝐴𝐵
+ ∫
𝑥𝑦𝑑𝑠
𝐵𝐶
+ ∫
𝑥𝑦𝑑𝑠
𝐶𝐷
+ ∫
𝑥𝑦𝑑𝑠
𝐷𝐴
Phương trình
𝐴𝐵: {
𝑦= 0 ⇒ 1 + 0𝑑𝑠 =
√
𝑑𝑥 𝑑𝑥=
0≤ 𝑥 ≤ 4
Phương trình
𝐵𝐶 {
𝑥 = 4 ⇒ 1 + 0𝑑𝑠 =
√
𝑑𝑦 𝑑𝑦=
0≤ 𝑦 ≤ 2
Phương trình
𝐶𝐷{
𝑦 = 2 ⇒ 1 + 0𝑑𝑠 =
√
𝑑𝑥 𝑑𝑥=
0≤ 𝑥 ≤ 4
Phương trình
𝐷𝐴:{
𝑥 = 0 ⇒ 1 + 0𝑑𝑠 =
√
𝑑𝑦 𝑑𝑦=
0≤ 𝑦 ≤ 2
⇒
{
∫
𝑥𝑦𝑑𝑠
𝐴𝐵
= ∫
𝑥.0 = 0𝑑𝑥
4
0
∫
𝑥𝑦𝑑𝑠
𝐵𝐶
= ∫
4𝑦𝑑𝑦 = 8
2
0
∫
𝑥𝑦𝑑𝑠
𝐶𝐷
= ∫
2𝑥𝑑𝑥
4
0
= 16
∫
𝑥𝑦𝑑𝑠
𝐷𝐴
= ∫
0.𝑦𝑑𝑦
2
0
= 0
⇒ ∫ 𝑥𝑦𝑑𝑠
𝐿
= 24
Câu 19: Tính
v
ới 𝐶 là biên c a mi ủ ền
|
𝑥
|
+
|
𝑦
|
≤ 1
Đáp án: D. 0
27
Giải:
Đư
ờng 𝐶:
|
𝑥
|
+
|
𝑦
|
= 1
Phương trình
𝐴𝐵: {
𝑦 = 1 −𝑥
0 ≤ 𝑥 ≤ 1
Phương trình
𝐵𝐶: {
𝑦 = 𝑥− 1
0≤ 𝑥 ≤ 1
Phương trình
𝐶𝐷: {
𝑦 = −𝑥 − 1
−1 ≤ 𝑥 ≤ 0
Phương trình
𝐷𝐴: {
𝑦 = 𝑥 + 1
−1 ≤ 𝑥 ≤ 0
∮ 𝑥𝑦𝑑𝑠
𝐶
=∫ 𝑥𝑦𝑑𝑠
𝐴𝐵
+ ∫ 𝑥𝑦𝑑𝑠
𝐵𝐶
+ ∫ 𝑥𝑦𝑑𝑠
𝐶𝐷
+ ∫ 𝑥𝑦𝑑𝑠
𝐷𝐴
Xét ∫ 𝑥𝑦𝑑𝑠
𝐴𝐵
,ta có 𝑑𝑠 =
√
1 + 𝑦
′
2
(
𝑥
)
𝑑𝑥 = √2𝑑𝑥 ⇒ ∫ 𝑥𝑦𝑑𝑠
𝐴𝐵
=
√
2∫𝑥 1 − 𝑥 𝑑𝑥
( )
1
0
=
√
2
6
Xét ∫ 𝑥𝑦𝑑𝑠
𝐵𝐶
,ta 𝑑𝑠 =có
√
1 + 𝑦
′
2
(
𝑥
)
𝑑𝑥 = √2𝑑𝑥 ⇒ ∫𝑥𝑦𝑑𝑠
𝐵𝐶
=
√
2∫𝑥 𝑥 − 1 𝑑𝑥
( )
1
0
=
−
√
2
6
Xét ∫ 𝑥𝑦𝑑𝑠
𝐶𝐷
,ta 𝑑𝑠 =có
√
1 + 𝑦
′
2
(
𝑥
)
𝑑𝑥 = √2𝑑𝑥 ⇒ ∫ 𝑥𝑦𝑑𝑠
𝐶𝐷
=
√
2 ∫𝑥 −1 − 𝑥 𝑑𝑥
( )
0
−1
=
√
2
6
Xét ∫ 𝑥𝑦𝑑𝑠
𝐴𝐵
,ta có 𝑑𝑠 =
√
1 + 𝑦
′
2
(𝑥)𝑑𝑥 =
√
2𝑑𝑥 ⇒∫ 𝑥𝑦𝑑𝑠
𝐷𝐴
=
√
2 ∫𝑥 𝑥 +1 𝑑𝑥
( )
0
−1
=
−
√
2
6
⇒ ∮ 𝑥𝑦𝑑𝑠
𝐶
= ∫ 𝑥𝑦𝑑𝑠
𝐴𝐵
+ ∫ 𝑥𝑦𝑑𝑠
𝐵𝐶
+ ∫ 𝑥𝑦𝑑𝑠
𝐶𝐷
+ ∫ 𝑥𝑦𝑑𝑠
𝐷𝐴
= 0
Câu 20: Tính
2 2
L
x y ds+
với 𝐿: 𝑥
2
+ 𝑦 = 2𝑥
2
Đáp án: A. 8
Giải:
28
Đặ𝑡
{
𝑥 = 𝑟 cos𝜑
𝑦 = 𝑟 sin𝜑
⇒ Đường cong 𝐿: {
𝑟 = 2cos𝜑
−
𝜋
2
≤𝜑 ≤
𝜋
2
⇒
𝑑𝑠 =
√
𝑟
2
(
𝜑
)
+ 𝑟
′
2
(𝜑)𝑑𝜑 = √
4cos
2
𝜑 + 4 sin
2
𝜑
𝑑𝜑 𝑑𝜑= 2
∫√
𝑥
2
+ 𝑦
2
𝑑𝑠
𝐿
= ∫
√
𝑟
2
.2𝑑𝜑
𝜋
2
−𝜋
2
=2 𝑟𝑑𝜑∫
𝜋
2
−𝜋
2
=2 2 cos𝜑∫ 𝑑𝜑
𝜋
2
−𝜋
2
=8
Câu 21: Tính
( 3 ) 2
AB
x y dx ydy− +
với 𝐴𝐵
⏜
là cung 𝑦 = 1 − 𝑥
2
,𝐴
(
1,0
)
,𝐵
(
−1,0
)
Đáp án: 4C.
Giải:
Cung 𝐴𝐵
⏜
: {
𝑦 = 1 − 𝑥
2
⇒ 𝑑𝑦 = −2𝑥𝑑𝑥
Đi
từ 𝐴
(
1,0 →𝐵
) (
−1,0
)
⇒
∫
(
𝑥− 3𝑦
)
𝑑𝑥 + 2𝑦𝑑𝑦
𝐴𝐵
⏜
= ∫
[
𝑥− 3
(
1 − 𝑥
2
)]
−1
1
𝑑𝑥 + ∫ 2
(
1 − 𝑥
2
) (
. −2𝑥
)
𝑑𝑥
−1
1
=4
Câu 22: Tính
4 3
5 4
ABC
y dx x dy−
với 𝐴𝐵𝐶 ng glà đườ ấp khúc đi qua các điểm
𝐴
(
0,1 ;𝐵 1,0 ;𝐶 0,−1
) ( ) ( )
Đáp áp: A. 2
Giải:
29
∫
5𝑦
4
𝑑𝑥 − 4𝑥
3
𝑑𝑦
𝐴𝐵𝐶
= ∫
5𝑦
4
𝑑𝑥 − 4𝑥
3
𝑑𝑦
𝐴𝐵
+ ∫
5𝑦
4
𝑑𝑥 − 4𝑥
3
𝑑𝑦
𝐵𝐶
=𝐼
1
+ 𝐼
2
Đo
ạ ẳn th ng 𝐴𝐵: {
𝑦 = 1 − 𝑥 ⇒ = −𝑑𝑦 𝑑𝑥
Đi
từ 𝐴
(
0,1
)
đến 𝐵
(
1,0
)
⇒𝐼
1
= ∫
5
(
1 − 𝑥
)
4
𝑑𝑥
1
0
+ ∫
(−4𝑥
3
).(−𝑑𝑥)
1
0
=2
Đo
ạ ẳn th ng 𝐵𝐶:{
𝑦 = 𝑥 − 1 ⇒ 𝑑𝑦 𝑑𝑥=
Đi
từ 𝐵
(
1,0
)
đến 𝐶
(
0,−1
)
⇒𝐼
2
= ∫
5
(
𝑥 − 1
)
4
𝑑𝑥
0
1
+ ∫
(
−4𝑥
3
)
.𝑑𝑥
0
1
=0
⇒ ∫ 5𝑦
4
𝑑𝑥 − 4𝑥
3
𝑑𝑦
𝐴𝐵𝐶
=𝐼
1
+ 𝐼
2
= 2
Câu 23: Tìm 𝑚 để
2
10
( ) .
3
C
x xy dx m x dy
−
+ + =
với 𝐶 là cung bé trên đường tròn
𝑥
2
+ 𝑦 =4 −2,0
2
đi từ 𝐴
( )
đến 𝐵
(
0,2
)
Đáp án: D. 1
Giải:
Đặ
t {
𝑥 = 2cos𝑡
𝑦 = 2sin𝑡
với 𝑡 y t chạ ừ 𝜋 đến 𝜋/2. Đặt 𝐼 =
2
( ) .
C
x xy dx m x dy+ +
𝐼 = 2cos𝑡+ 4cos 𝑡sin𝑡 −2 sin𝑡 + 𝑚. cos𝑡 2cos𝑡
∫
[( )( ) ( )
2
( )]
𝑑𝑡
𝜋
2
𝜋
=
∫
(
−4cos𝑡sin 𝑡 − 8cos𝑡 sin 𝑡+ 2𝑚cos
2 3
𝑡
)
𝑑𝑡
𝜋
2
𝜋
30
=
∫
(
−4sin𝑡− 8sin 𝑡 + 2𝑚 cos cos𝑡
2 2
𝑡
)
𝑑𝑡
𝜋
2
𝜋
=
∫
(
−4sin𝑡− 8sin 𝑡 + 2𝑚− 2𝑚sin cos𝑡
2 2
𝑡
)
𝑑𝑡
𝜋
2
𝜋
=
∫
[
−4sin𝑡− 8+ 2𝑚 sin 𝑡 + 2 sin 𝑡
( )
2
]
𝑑
( )
𝜋
2
𝜋
= ∫
[
−4𝑢 −
(
8 + 2𝑚
)
𝑢
2
+ 2
]
𝑑𝑢
1
0
=
−10
3
⇒𝑚 =1
Câu 24: Tính
) ( sin )
y
x y dx xy e x y dy
−
+ + + − + − +
với 𝐿 là đường
𝑥
2
+ 𝑦 = 2𝑥
2
theo chi ều dương.
Đáp án: A. −3𝜋
Giải:
Đặt 𝐼 =
) ( sin )
y
x y dx xy e x y dy
−
+ + + − + − +
Đặt: 𝑃 = + 𝑒 sin𝑥+ 𝑥 + 𝑦,𝑄 = − + 𝑒 − 𝑥 + sin𝑦𝑥𝑦
𝑥
𝑥𝑦
−𝑦
⇒𝑃
𝑦
′
=𝑥+ 1,𝑄
𝑥
′
=−𝑦 − 1 𝑃.
𝑦
′
,𝑄
𝑥
′
liên t c v . ụ ới 𝑥,𝑦 ∈ 𝑅
Đường cong 𝐿kín hướng dương, giới hạn miền 𝐷:𝑥 + 𝑦
2 2
≤ 2𝑥
31
Áp d ng công th c Green, ta có: ụ ứ
𝐼 = (−𝑦 − 𝑥 − 2)𝑑𝑥𝑑𝑦∬
𝐷
Nhận xét: hàm s là hàm l v i bi n y, miố 𝑓
(
𝑥,𝑦 =−𝑦
)
ẻ ớ ế ền 𝐷 đố ứi x ng qua trục Ox
⇒ ∬−𝑦𝑑𝑥𝑑𝑦
𝐷
=0 ⇒ 𝐼 = (−𝑥 −2)𝑑𝑥𝑑𝑦∬
𝐷
Đặ
t: {
𝑥 = 1 + 𝑟 cos𝜑
𝑦 = 𝑟sin𝜑
|
𝐽
|
= 𝑟. Miền
( )
𝐷 :{
0≤ 𝑟 ≤ 1
0≤ 𝜑 < 2𝜋
𝐼 = ∫ 𝑑𝜑
2𝜋
0
∫
( )
−𝑟cos𝜑−3 𝑟𝑑𝑟
1
0
= ∫
(
−1
3
cos𝜑 −
3
2
)𝑑𝜑
2𝜋
0
=−3𝜋
Câu 25: Tính
2
1 2
2y + + sin(y )
y
e dy
+
với 𝐿 là chu tuy n c a tam ế ủ
giác
𝐴𝐵𝐶 có 𝐴
(
−1,0 , 𝐵 0,2 ,𝐶 2,0
) ( ) ( )
chi u cùng chi ng h . ề ều kim đồ ồ
Đáp án: B. 2
Giải:
Đặt 𝐼 =
2
1 2
2y + + sin(y )
y
e dy
+
Đặ
t {
𝑃 = 2𝑥
𝑄 = −
[
𝑥+ 2𝑦 + 𝑒 + sin
𝑦
2
+1
(
𝑦
2
)
]
⇒ {
𝑃
𝑦
′
= 0
𝑄
𝑥
′
=−2𝑥
,𝑃
𝑦
′
,𝑄
𝑥
′
liên t c vụ ới 𝑥,𝑦 ∈ 𝑅
32
Gọi 𝐷 là mi c gi i hền đượ ớ ạn b i chu tuyở ến ∆𝐴𝐵𝐶
𝐷
được gi i h n bớ ạ ởi các đường: {
𝐴𝐵: 𝑦 = 2𝑥+ 2
𝐵𝐶:𝑦 = −𝑥 + 2
𝐶𝐴
:𝑦 = 0
⇒
(
𝐷
)
:{
(
𝑦 − 2
)
/2≤ 𝑥 ≤ 2− 𝑦
0≤ 𝑦 ≤ 2
𝐿 là đường cong kín, hướng âm, gi i h n miớ ạ ền 𝐷. Áp d ng công th c Green:ụ ứ
𝐼 = − −2𝑥𝑑𝑥𝑑𝑦∬
𝐷
= ∬
2𝑥𝑑𝑥𝑑𝑦
𝐷
= ∫
𝑑𝑦
2
0
∫
2𝑥𝑑𝑥
2−𝑦
𝑦−2
2
=2
Câu 26: Tính
10 2
( ) ( )
x
AB
xy e dx y x dy+ + −
với 𝐴𝐵
⏜
là cung 𝑦 =
√
1 − 𝑥
2
đi từ điểm
𝐴
(
−1,0 1,0
)
đến 𝐵
( )
Đáp án: B.
2
1e
e
−
Giải:
Đặt 𝐼 =
10 2
( ) ( )
x
AB
xy e dx y x dy+ + −
Cung 𝐴𝐵
⏜
⇔ {
𝑥
2
+ 𝑦
2
= 1
𝑦 ≥ 0
đi từ 𝐴
(
−1,0
)
đến 𝐵
(
1,0
)
33
B
ổ sung thêm đoạn BA {
𝑦= 0
đi
từ 𝐵 đến 𝐴(−1,0)
(
1,0
)
Ta có: đường 𝐴𝐵
⏜
∪ 𝐵𝐴 cong kín gi i h n milà đường ớ ạ ền
( )
𝐷 :𝑥
2
+ 𝑦
2
≤ 1, 𝑦≥ 0, có
chiều âm
Đặ
t {
𝑃 = + 𝑒𝑥𝑦
𝑥
𝑄 = 𝑦 − 𝑥
10 2
⇒
{
𝑃
𝑦
′
=𝑥
𝑄
𝑥
′
=−2𝑥
⇒𝑃
𝑦
′
,𝑄
𝑥
′
liên t c vụ ới 𝑥,𝑦 ∈ 𝑅
𝐼 =
∮
(
𝑥𝑦+ 𝑒
𝑥
)
𝑑𝑥 + (𝑦 − 𝑥
10 2
)𝑑𝑦
𝐴𝐵
⏜
∪𝐵𝐴
− ∫
(
𝑥𝑦 + 𝑒
𝑥
) (
𝑑𝑥 + 𝑦
10
− 𝑥
2
)
𝑑𝑦
𝐵𝐴
=𝐼
1
− 𝐼
2
Áp d ng công th c Green cho ụ ứ 𝐼
1
ta có:
𝐼
1
= − −3𝑥∬
𝐷
𝑑𝑥𝑑𝑦 = 3𝑥∬
𝐷
𝑑𝑥𝑑𝑦
Đặ
t {
𝑥 = 𝑟cos𝜑
𝑦 = 𝑟sin𝜑
|
𝐽
|
= 𝑟. Miền
( )
𝐷 :{
0≤𝑟 ≤1
0≤ 𝜑 ≤ 𝜋
⇒𝐼
1
= ∫
𝑑𝜑
𝜋
0
∫
3𝑟cos𝜑 𝑟𝑑𝑟
1
0
= ∫
cos𝜑𝑑𝜑
𝜋
0
=0
(Ho c có th s dặ ể ử ụng tính đố ứng đểi x ra giá trị bằng 0 ngay)
𝐼
2
= ∫
(
𝑥𝑦+ 𝑒
𝑥
)
𝑑𝑥 +
(
𝑦
10
− 𝑥
2
)
𝑑𝑦
𝐵𝐴
Đo
ạn 𝐵𝐴 {
𝑦 = 0 ⇒ = 0𝑑𝑦
đi
từ 𝐵 đến 𝐴
(
1,0
) (
−1,0
)
⇒𝐼
2
= ∫
(
𝑥.0 + 𝑒
𝑥
)
𝑑𝑥 = 𝑒
𝑥
|
−1
1
=𝑒
−1
− 𝑒 =
1 − 𝑒
2
𝑒
−1
1
⇒𝐼 = 𝐼
1
− 𝐼
2
= 0−
1 − 𝑒
2
𝑒
=
𝑒
2
− 1
𝑒
Câu 27: Tính
2 4
(2 ) ( )
x y
C
e y dx x e dy+ + +
với 𝐶:𝑦 = √1 − 𝑥
2
4
đi từ 𝐴
(
−1,0
)
đến
𝐵
(
1,0
)
34
Đáp án: A.
2
2
2
e
e
− +
Giải:
𝐶:𝑦 = 1 − 𝑥
√
2
4
ng cong h là đườ ở đi từ 𝐴
(
−1,0 1,0
)
đến 𝐵
( )
B
ổ sung thêm đoạn 𝐵𝐴: {
𝑦 = 0
Đi
từ 𝐵
(
1,0 →𝐴
) (
−1,0
)
𝐼 =
∫
(
2𝑒 + 𝑦
𝑥 2
)
𝑑𝑥
𝐶∪
𝐵𝐴
+
(
𝑥
4
+ 𝑒
𝑦
) (
𝑑𝑦 − ∫ 2𝑒
𝑥
+ 𝑦
2
)
𝑑𝑥
𝐵𝐴
+
(
𝑥
4
+ 𝑒
𝑦
)
𝑑𝑦 = 𝐼
1
− 𝐼
2
Áp d ng công th c Green cho ụ ứ 𝐼
1
Đặ
t {
𝑃
(
𝑥,𝑦
)
=2𝑒
𝑥
+ 𝑦
2
𝑄
(
𝑥,𝑦 = 𝑥 + 𝑒
)
4 𝑦
⇒ {
𝑃
𝑦
′
= 2𝑦
𝑄
𝑥
′
=4𝑥
3
liên tục với ∀𝑥,𝑦 ∈ 𝑅
Ta có ng cong kín, có chi u âm, gi i h n mi
𝐶 ∪ 𝐵𝐴 là đườ ề ớ ạ ền 𝐷: {
0≤ 𝑦 ≤
√
1 − 𝑥
2
4
−1≤ 𝑥 ≤ 1
⇒𝐼
1
= − 4𝑥 − 2𝑦 𝑑𝑥𝑑𝑦∬
(
3
)
𝐷
= ∫
𝑑𝑥
1
−1
∫
(
−4𝑥
3
+ 2𝑦
)
𝑑𝑦
√
1−𝑥
2
4
0
=
∫(
−4𝑥
3
.
√
1 − 𝑥
2
4
+
√
1 − 𝑥
2
)
𝑑𝑥
1
−1
Hàm 𝑓
(
𝑥
)
=−4𝑥 1 − 𝑥
3
.
√
2
4
là hàm số lẻ ⇒ ∫ −4𝑥 1 − 𝑥
3
.
√
2
4
𝑑𝑥
1
−1
⇒𝐼
1
= ∫
√
1 − 𝑥
2
𝑑𝑥
1
−1
Đặt 𝑥 = sin𝑡 ⇒ = cos𝑡𝑑𝑥 𝑑𝑥
⇒𝐼
1
= ∫
√
1 − 𝑥
2
𝑑𝑥
1
−1
= ∫
cos𝑡cos𝑡 𝑑𝑡
𝜋
2
−
𝜋
2
= ∫
cos
2
𝑡 𝑑𝑡
𝜋
2
−
𝜋
2
=
𝜋
2
35
Đo
ạn 𝐵𝐴:{
𝑦 = 0 ⇒ = 0𝑑𝑦
đi
từ 𝐵 đến 𝐴
(
1,0
) (
−1,0
)
⇒𝐼
2
= ∫
2𝑒
𝑥
𝑑𝑥
−1
1
=2
(
𝑒
−1
− 𝑒
)
V
ậy 𝐼 =𝜋/2 −2 − 𝑒
(
𝑒
−1
)
Câu 28: Tính tích phân
( )
(3,0)
4 3 2 2 4
( 2, 1)
4 (6 5 )x xy dx x y y dy
− −
+ + −
Đáp án: B. 62
Giải:
Đặt 𝐼 =
( )
(3,0)
4 3 2 2 4
( 2, 1)
4 (6 5 )x xy dx x y y dy
− −
+ + −
Đặ
t 𝑃 = +4𝑥𝑦
(
𝑥
4 3
)
,𝑄 = 6𝑥 − 5𝑦
(
2
𝑦
2 4
)
⇒ 𝑃
𝑦
′
= 𝑄
𝑥
′
= 12𝑥𝑦
2
⇒𝐼 không ph thuụ ộc
đường đi
Cách 1: Dùng đườ là đường thay thế ng g p khúc: ấ
Chọn đường đi là đường gấp khúc 𝐴𝐶𝐵
𝐼 = ∫ 𝑃𝑑𝑥 + 𝑄𝑑𝑦
𝐴𝐶𝐵
= ∫
𝑃𝑑𝑥+ 𝑄𝑑𝑦
𝐴𝐶
+ ∫
𝑃𝑑𝑥+ 𝑄𝑑𝑦
𝐶𝐵
=𝐼
1
+ 𝐼
2
Đo
ạn 𝐴𝐶: {
𝑦 = −1 ⇒ = 0𝑑𝑦
đi
từ 𝐴 đến 𝐶
(
−2,−1
) (
3,−1
)
36
⇒𝐼
1
= ∫
(
𝑥
4
− 4𝑥
)
𝑑𝑥
3
−2
= 45
Đo
ạn 𝐶𝐵: {
𝑥 = 3 ⇒ = 0𝑑𝑥
đi
từ 𝐶 đến 𝐵
(
3,−1
) (
3,0
)
⇒ 𝐼
2
= ∫
(
6.9.𝑦
2
− 5𝑦
4
)
𝑑𝑦
0
−1
= 17
⇒𝐼 = 𝐼
1
+ 𝐼
2
= 62
Cách 2: Dùng đường thay th ng th ế là đườ ẳng
Phương trình đường thẳng đi qua 𝐴,𝐵 là 𝑦 = 𝑥/5 − 3/5
Đo
ạn : 𝐴𝐵 {
𝑦 =
𝑥
5
−
3
5
⇒ 𝑑𝑦 =
𝑑𝑥
5
Đi
𝑡ừ 𝐴
(
−2,−1 → 𝐵
) (
3,0
)
⇒𝐼 = +4𝑥(
∫[𝑥
4
𝑥
5
−
3
5
)
3
]𝑑𝑥 + [
6𝑥
2
(
𝑥
5
−
3
5
)
2
− 5(
𝑥
5
−
3
5
)
4
].
𝑑𝑥
5
3
−2
=
∫[𝑥
4
+ 4𝑥 (
𝑥
5
−
3
5
)
3
+
6𝑥
2
5
(
𝑥
5
−
3
5
)
2
− (
𝑥
5
−
3
5
)
4
]𝑑𝑥
3
−2
=⋯ = 62
Cách 3: Dùng hàm th v ế ị
Đặ
t 𝑃 = +4𝑥𝑦
(
𝑥
4 3
)
,𝑄 = 6𝑥 − 5𝑦
(
2
𝑦
2 4
)
⇒ 𝑃
𝑦
′
= 𝑄
𝑥
′
= 12𝑥𝑦
2
⇒𝐼 không ph thuụ ộc
đường đi
là vi phân toàn ph n c a hàm ⇒ 𝑃𝑑𝑥 + 𝑄𝑑𝑦 ầ ủ
𝑢
(
𝑥,𝑦 𝑃(𝑡,𝑦
)
= ∫
0
)𝑑𝑡
𝑥
𝑥
0
+ ∫
𝑄(𝑥,𝑡)𝑑𝑡
𝑦
𝑦
0
Chọn 𝑥 = 𝑦
0 0
= 0
⇒𝑢 𝑥,𝑦 + 4𝑡.0
( )
= ∫
(
𝑡
4 3
)
𝑑𝑡
𝑥
0
+ ∫
(
6𝑥
2
𝑡
2
− 5𝑡
4
)
𝑑𝑡
𝑦
0
37
𝑢
(
𝑥,𝑦
)
=
1
5
𝑡
5
|
𝑥
0
+ (6𝑥
2
.
1
3
𝑡
3
− 𝑡
5
)|
𝑦
0
=
1
5
𝑥
5
+ 2𝑥
2
𝑦
3
− 𝑦
5
⇒𝐼 = 𝑢 3,0 −𝑢 −2, −1
( ) ( )
=
243
5
− (
−67
5
)= 62
Câu 29: Tìm tích phân 𝑚để
2
2 2
2 ( . )
x y
L
e xy dx y m y dy e
+
+ + =
với 𝐿 ng là đườ
𝑥 = 1 − 𝑦
2
đi từ 𝐴
(
1,0
)
đến 𝐵
(
0,1
)
Đáp án: B. 2
Giải:
Đặt 𝐼 =
2
2 2
2 ( . )
x y
L
e xy dx y m y dy e
+
+ + =
Đặ
t 𝑃 = 𝑒 .2𝑥𝑦 ,𝑄 = 𝑒 + 2𝑦 ⇒𝑃
𝑥
2
+𝑦 2 𝑥
2
+𝑦
.
(
𝑦
2
)
𝑦
′
= 𝑄
𝑥
′
=
(
4𝑥𝑦+ 2𝑥𝑦
2
)
𝑒
𝑥
2
+𝑦
Tích phân không ph thu⇒ ụ ộc đường đi
Cách 1: Chọn đường đi là đường gấp khúc
Chọn đường đi là đường gấp khúc 𝐴𝑂𝐵
𝐼 =
∫𝑒
𝑥
2
+𝑦
[
2𝑥𝑦
2
𝑑𝑥 𝑑𝑦+ +
(
𝑦
2
𝑚𝑦
) ]
𝐴𝑂
+ ∫
𝑒
𝑥
2
+𝑦
[
2𝑥𝑦
2
𝑑𝑥 +
(
𝑦
2
+ 𝑚𝑦
)
𝑑𝑦
]
𝑂𝐵
= 𝐼
1
+ 𝐼
2
38
Đo
ạn : 𝐴𝑂 {
𝑦 = 0 ⇒ = 0𝑑𝑦
Đi
từ 𝐴
(
1,0 → 𝑂
) (
0,0
)
⇒𝐼
1
= ∫
0𝑑𝑥
0
1
=0
Đo
ạn : 𝑂𝐵 {
𝑥 = 0 ⇒ = 0𝑑𝑥
Đi
từ 𝑂
(
0,0 →𝐵
) (
0,1
)
⇒ 𝐼
2
= ∫
𝑒
𝑦
(
𝑦
2
+ 𝑚𝑦
)
𝑑𝑦
1
0
=𝐼 = 𝑒 ⇒ 𝑚 = 2
Tích phân trên phải dùng tích phân từng phần hai lần, tương đối dài.
Cách 2: Chọn đường đi là một đường cong
Nhận xét: Tích phân 𝐼 phức tạp là do biểu thức vì để làm đơn giả𝑒
𝑥
2
+𝑦
n tích phân
𝐼 cần khử biểu thức này iến ⇒ B 𝑒
𝑥
2
+𝑦
=𝐶 ⇒ 𝑥
2
+ 𝑦 = 𝐶 𝐶 hằng
(
là số
)
Do tích phân 𝐼 không phụ thuộc đường đi nên sẽ chọn đường đi mới thỏa mãn
𝑥
2
+ 𝑦 = 𝐶
Để
tìm ta d𝐶, ựa vào điểm đầu 𝐴
(
1,0
)
và điểm cu ối 𝐵
(
0,1
)
Đường cong mới
𝐿
′
: 𝑥
2
+ 𝑦 = 𝐶 đi qua 𝐴,𝐵 ⇒ {
1
2
+ 0 = 𝐶
0
2
+ 1 = 𝐶
⇒𝐶 = 1
Chọn đường đi
𝐿
′
:𝑦 = 1 − 𝑥
2
đi từ 𝐴
(
1,0
)
đến 𝐵
(
0,1 =−2𝑥𝑑𝑥
)
⇒ 𝑑𝑦
⇒𝐼 = 𝑒 ( 2𝑥 1 − 𝑥
∫
[
(
2
)
2
]
𝑑𝑥 + ∫
[(
1 − 𝑥
2
)
2
+ 𝑚
(
1 − 𝑥
2
)](
−2𝑥
)
𝑑𝑥
0
1
0
1
)= 𝑒 ⇒ 𝑚 = 2
Câu 30: Tính tích phân
2 2
2 2 2 2
2 1 1
( 1) ( 1)
L
y xy x x x
dx dy
y x y x
− + − + − −
+
− − − −
với 𝐿:𝑦 = 2𝑥+ 2
đi từ
𝐴
(
0,2
)
đến 𝐵
(
2,6
)
Đáp án: C. 2
Giải:
Đặt 𝐼 =
2 2
2 2 2 2
2 1 1
( 1) ( 1)
L
y xy x x x
dx dy
y x y x
− + − + − −
+
− − − −
Đặt
{
𝑃
(
𝑥,𝑦
)
=
−𝑦+ 2𝑥𝑦 − 𝑥
2
+ 1
( )
𝑦 − 𝑥
2
− 1
2
𝑄
(
𝑥,𝑦
)
=
𝑥 − 𝑥
2
− 1
( )
𝑦 − 𝑥
2
− 1
2
⇒𝑃
𝑦
′
=𝑄
𝑥
′
=
−2𝑥
3
+ 3𝑥
2
− 2 − 2𝑥 + 𝑦− 1𝑥𝑦
( )
𝑦 − 𝑥
2
− 1
3
39
⇒ 𝐼 không phụ thuộc vào đường đi
Tích phân phức tạp do biểu thức
(
𝑦− 𝑥 − 1
2
)
2
⇒ Chọn đường đi mới khử biểu
thức này
Chọn đường đi mới dạng
𝐿
′
: 𝑦 − 𝑥
2
− 1= 𝐶 ( 𝐶 là hằng số)
𝐿
′
đi qua 𝐴
(
0,2 , 𝐵 2,6
) ( )
⇒ {
2 − 0
2
− 1 = 𝐶
6 − 2 −1 = 𝐶
2
⇒ 𝐶 = 1
Chọn đường đi
𝐿
′
:{
𝑦 = 𝑥
2
+ 2 ⇒ = 2𝑥𝑑𝑥𝑑𝑦
Đi
từ 𝐴
(
0,2 → 𝐵
) (
2,6
)
⇒𝐼 =
∫
−
(
𝑥
2
+ 2
)
+ 2𝑥
(
𝑥
2
+ 2
)
− 𝑥
2
+ 1
1
2
𝑑𝑥
2
0
+ ∫
𝑥− 𝑥
2
− 1
1
2
.2𝑥𝑑𝑥
2
0
=
26
3
−
20
3
=2
Câu 31: Tìm 𝑎,𝑏 tích phân để
( )
( )
2
2 1 2
x
L
e x ay dx bx y dy
+ + + +
không ph ụ
thuộc vào đường đi
Đáp án:
A. {
𝑎 = 1
𝑏 = 0
Giải:
Đặ
t 𝑃 = 𝑒
𝑥
(
2𝑥+ 𝑎𝑦 + 1 , 𝑄 = 𝑒
2
)
𝑥
(
𝑏𝑥+ 2𝑦
)
Để tích phân không phụ thuộc đường đi ⇔ 𝑃
𝑦
′
= 𝑄
𝑥
′
⇔2𝑎𝑒 𝑦 = 𝑒 .2𝑦 + 𝑒 + 𝑏𝑒 ⇔ 𝑎 = 1,𝑏 = 0
𝑥 𝑥 𝑥
.𝑏𝑥
𝑥
Câu 32: Tìm hằng s u thố 𝑎,𝑏 để biể ức
[ [
𝑦
2
+ 𝑎𝑥𝑦+ 𝑦 sin
(
𝑥𝑦
)]
𝑑𝑥 + 𝑥
2
+ 𝑏𝑥𝑦+
𝑥sin
(
𝑥𝑦
)]
𝑑𝑦 là vi ph toàn ph n c a m t hàm s ần ầ ủ ộ ố 𝑢
(
𝑥,𝑦
)
nào đó
Đáp án: B.
{
𝑎 = 2
𝑏 = 2
Giải:
Đặ
t 𝑃 = + 𝑎𝑥𝑦 + 𝑦 sin ,𝑄 = 𝑥 +𝑏𝑥𝑦+ 𝑥sin
[
𝑦
2
(
𝑥𝑦
)]
2
(
𝑥𝑦
)
Để ể ứ
bi u th c
[
𝑦
2
+ 𝑎𝑥𝑦+ 𝑦 sin +𝑏𝑥𝑦+ 𝑥sin
(
𝑥𝑦
)]
𝑑𝑥 +
[
𝑥
2
(
𝑥𝑦
)]
𝑑𝑦 là vi phần toàn
phần c a mủ ột hàm số 𝑢
(
𝑥,𝑦
)
nào đó ⇔ 𝑃
𝑦
′
= 𝑄
𝑥
′
⇔2𝑦+ + sin cos = 2𝑥 + + sin cos
𝑎𝑥
(
𝑥𝑦 𝑥𝑦
)
+
(
𝑥𝑦
)
𝑏𝑦
(
𝑥𝑦 𝑥𝑦
)
+
(
𝑥𝑦
)
40
⇔
{
𝑎 = 2
𝑏 = 2
Câu 3 3: Tính
( )
2 2 2 2
2
2
1
x y x y
L
xe dx ye dy
x y
+ +
+
− +
với
2
: 2L y x x= −
đi từ
𝑂
(
0,0
)
đến 𝐴
(
2,0
)
Đáp án: B. 0
Giải:
𝐿:𝑦 = 2𝑥− 𝑥
√
2
⇔ {
𝑦
2
= 2𝑥 − 𝑥
2
𝑦 ≥ 0
⇔ {
𝑥
2
− 2𝑥 + 1 + 𝑦
2
= 1
𝑦 ≥ 0
⇔
{
(
𝑥− 1
)
2
+ 𝑦
2
= 1
𝑦 ≥ 0
𝑦 = 2𝑥 − 𝑥
√
2
⇒ 𝑑𝑦 =
2 − 2𝑥
2
2
√
2𝑥− 𝑥
2
𝑑𝑥 =
1 − 𝑥
2
√
2𝑥− 𝑥
2
𝑑𝑥
∫
𝑥𝑒
𝑥
2
+𝑦
2
𝑑𝑥 +𝑦𝑒
𝑥
2
+𝑦
2
𝑑𝑦
( )
𝑥− 1
2
+ 𝑦
2
𝐿
= ∫
𝑥𝑒
2𝑥
1
2
0
𝑑𝑥 + ∫
√2𝑥− 𝑥
2
𝑒
2𝑥
1
2
0
1 − 𝑥
2
√
2𝑥− 𝑥
2
𝑑𝑥
=∫𝑥𝑒
2𝑥
2
0
𝑑𝑥 + ∫ 𝑒
2𝑥
(
1 − 𝑥
2
)
2
0
𝑑𝑥 = 0
Câu 34: Cho tích phân 𝐼 =
2
(5 2 )
x y dy
y
− + +
+
với 𝐶 là biên c a hình ủ
phẳng 𝐷:𝑥 + 𝑦 ≤ 9
2 2
, theo chi n ều dương, bạ 𝐴 l p luậ ận “Ta đặt
2 2
2 5x y
P
x y
−
=
+
và
2 2
5 2x y
Q
x y
+
=
+
,
' '
0
x y
Q P− =
, 𝐶 ng cong kín, chi i hlà đườ ều dương, giớ ạn miền 𝐷 nên
𝐼 = 0”. Hỏi bạn 𝐴 làm vậy có đúng không? Nếu sai, thì sửa lại đáp án chính xác
Đáp án: B. Sai, 𝐼 =10𝜋
Giải:
41
Ta có:
2 2
'
2 2 2
2 2
'
2 2 2
5( ) 2 (2 5 )
( )
5( ) 2 (5 2 )
( )
y
x
x y y x y
P
x y
x y x x y
Q
x y
− + − −
=
+
+ − +
=
+
gián đoạ ại điể
n t m 𝑂
(
0,0 ∈𝐷:𝑥 + 𝑦 ≤ 9
)
2 2
⇒ Không s dử ụng được công th c Green ứ
Đặ
t
{
𝑥 = 3cos 𝑡
𝑦 = 3sin 𝑡
, 𝑡 y t chạ ừ 0 đến 2𝜋 ⇒ {
𝑑𝑥 = −3sin𝑡 𝑑𝑡
𝑑𝑦 𝑑𝑡= 3 cos𝑡
2
2
0
(5 2 ) (2.3cos 5.3sin )( 3sin ) (5.3cos 2.3sin )(3cos )
9
x y dy t t t t t t
dt
y
− + + − − + +
=
+
= 10𝜋
Câu 35: Tìm tích phân 𝑚để
( 3 ) 2 4
AB
x y dx ydy− + =
với
2
:AB y m x= −
và hai
điểm
(1,0), ( 1,0)A B −
Đáp án: A. 1
Giải:
Cung 𝐴𝐵
⏜
: {
𝑦 = 𝑚 −𝑥
2
⇒ 𝑑𝑦 = −2𝑥𝑑𝑥
Đi
từ 𝐴
(
1,0 →𝐵
) (
−1,0
)
⇒
∫
(
𝑥− 3𝑦
)
𝑑𝑥 + 2𝑦𝑑𝑦
𝐴𝐵
⏜
= ∫
[
𝑥− 3
(
𝑚− 𝑥
2
)]
−1
1
𝑑𝑥 + ∫ 2
(
𝑚− 𝑥
2
) (
. −2𝑥
)
𝑑𝑥
−1
1
=4
⇒𝑚 =1
Câu 36: Tính
C
ydx zdy xdz+ +
v theo ới 𝐶:𝑥 = cos 𝑡,𝑦 = sin𝑡,𝑧 = 2𝑡,0 ≤ 𝑡 ≤2𝜋
chiều tăng của 𝑡
Đáp án: C.
−𝜋
Giải:
𝐶:
{
𝑥 = cos𝑡
𝑦 = sin𝑡
𝑧 = 2𝑡
⇒ {
𝑥
′
= − sin𝑡
𝑦
′
=cos𝑡
𝑧
′
=2
42
∫
𝑦𝑑𝑥 + 𝑧𝑑𝑦 + 𝑥𝑑𝑧
𝐶
= ∫
(
−sin𝑡.sin𝑡 + 2𝑡.cos𝑡 + cos 𝑡.2
)
𝑑𝑡
2𝜋
0
=⋯ = −𝜋
Câu 37: Tính tích phân
(4,5,6)
(1,2,3)
( 1)
y y z
e dx xe dy z e dz+ + +
Đáp án: A. 4𝑒 + 6𝑒 − 𝑒 − 3𝑒
5 6 2 3
Giải:
Đặ
t {
𝑃 = 𝑒
𝑦
𝑄 = 𝑥𝑒
𝑦
𝑅 = 𝑧 + 1
( )
𝑒
𝑧
⇒ {
𝑃
𝑧
′
=0,𝑃
𝑦
′
=𝑒
𝑦
𝑄
𝑧
′
= 0, 𝑄
𝑥
′
=𝑒
𝑦
𝑅
𝑥
′
= 0, 𝑅
𝑦
′
=0
⇒ 𝑅′
𝑦
− 𝑄′
𝑧
= 𝑃′
𝑧
− 𝑅′
𝑥
=𝑄′
𝑥
− 𝑃′
𝑦
=0
⇒ Tích phân
(4,5,6)
(1,2,3)
( 1)
y y z
e dx xe dy z e dz+ + +
không ph thuụ ộc vào đường đi
Cách 1: Dùng hàm th v ế ị
Hàm th v ế ị
𝑢 = 𝑡, 𝑦
∫𝑃
(
0
,𝑧
0
)
𝑑𝑡
𝑥
𝑥
0
+ ∫
𝑄
(
𝑥,𝑡,𝑧
0
)
𝑑𝑡
𝑦
𝑦
0
+ ∫
𝑅
(
𝑥,𝑦,𝑡
)
𝑑𝑡
𝑧
𝑧
0
+ 𝐶
Chọn 𝑥 =𝑦
0 0
= 𝑧
0
= 0
𝑢 = ∫1𝑑𝑡
𝑥
0
+ ∫
𝑥𝑒
𝑡
𝑑𝑡
𝑦
0
+ ∫
(
𝑡 + 1
)
𝑒
𝑡
𝑑𝑡
𝑧
0
+ 𝐶
=𝑥+ 𝑥𝑒
𝑦
− 𝑥+𝑒 − 1 + 𝑧𝑒 − 1 + 𝐶 =𝑥𝑒 + 𝑧𝑒 + 𝐶
𝑧 𝑧
−
(
𝑒
𝑧
)
𝑦 𝑧
(4,5,6)
(1,2,3)
( 1)
y y z
e dx xe dy z e dz+ + +
=𝑢 4,5,6 − 𝑢 1,2,3 = 4𝑒 + 6𝑒 − 𝑒 − 3𝑒
( ) ( )
5 6 2 3
Cách 2: Chọn đường đi là đường thẳng
Đặ
t 𝐴
(
1,2,3 , 𝐵 4,5,6
) ( )
Đo
ạn : 𝐴𝐵 {
vecto ỉ phương ch 𝐴𝐵
󰇍
󰇍
󰇍
󰇍
󰇍
=
(
3,3,3
)
Đi
qua 𝐴
(
1,2,3
)
⇒ 𝐴𝐵:
𝑥 − 1
3
=
𝑦 − 2
3
=
𝑧 − 3
3
=𝑡
43
⇒ 𝐴𝐵: {
𝑥 = 3𝑡 +1
𝑦 = 3𝑡 +2
𝑧 = 3𝑡 + 3
,với 𝑡 từ 0 đến 1 ⇒ 𝑥đi
′
=𝑦 = 𝑧 = 3
′ ′
⇒
∫ 𝑒
𝑦
𝑑𝑥 +𝑥𝑒
𝑦
𝑑𝑦 +
(
𝑧+ 1
)
𝑒
𝑧
𝑑𝑧
( )
4,5,6
(
1,2,3
)
=3 3𝑡+ 1 3𝑡 +4
∫
[
𝑒
3𝑡+2
+
( )
𝑒
3𝑡+2
+
( )
𝑒
3𝑡+3
]
𝑑𝑡
1
0
= ⋯ =4𝑒
5
+ 6𝑒
6
− 𝑒
2
− 3𝑒
3
Câu 38:
Tìm hàm th v cế ị ủa bi u thể ức
(
𝑥
4
+ 4𝑥𝑦
3
)
𝑑𝑥 + 6𝑥 − 5𝑦
(
2
𝑦
2 4
)
𝑑𝑦
Đáp án: A.
2 2 3 5
1
2
5
x x y y+ −
Giải:
Đặ
t 𝑃 = + 4𝑥𝑦
(
𝑥
4 3
)
,𝑄 = 6𝑥 − 5𝑦
(
2
𝑦
2 4
)
⇒ 𝑃
𝑦
′
=𝑄
𝑥
′
= 12𝑥𝑦
2
⇒ 𝑃𝑑𝑥+ 𝑄𝑑𝑦 là vi phân toàn ph n c a hàm ầ ủ
𝑢
(
𝑥,𝑦 𝑃(𝑡,𝑦
)
= ∫
0
)𝑑𝑡
𝑥
𝑥
0
+ ∫
𝑄(𝑥,𝑡)𝑑𝑡
𝑦
𝑦
0
Chọn 𝑥 = 𝑦
0 0
= 0
⇒𝑢 𝑥,𝑦 + 4𝑡.0
( )
= ∫
(
𝑡
4 3
)
𝑑𝑡
𝑥
0
+ ∫
(
6𝑥
2
𝑡
2
− 5𝑡
4
)
𝑑𝑡
𝑦
0
𝑢
(
𝑥,𝑦
)
=
1
5
𝑡
5
|
𝑥
0
+ (6𝑥
2
.
1
3
𝑡
3
− 𝑡
5
)|
𝑦
0
=
1
5
𝑥
5
+ 2𝑥
2
𝑦
3
− 𝑦
5
Câu 39: Tính
(2 5) (2 3 )
L
xy dx x y dy− + +
với 𝐿 là biên c a miủ ền 𝐷 nh bxác đị ởi
các đườ ều dươngng 𝑦= 𝑥 ,𝑦 = 0,𝑥 = 1,
2
chi
Đáp án: D.
1
6
Giải:
44
Đặ
t {
𝑃 = 2 − 5𝑥𝑦
𝑄 = 2𝑥 + 3𝑦
⇒
{
𝑃
𝑦
′
= 2𝑥
𝑄
𝑥
′
=2
liên t ục
Ta có ng cong kín, chi
𝐿là đườ ều dương, giới hạn miền 𝐷:{
0≤ 𝑥 ≤ 1
0≤ 𝑦 ≤ 𝑥
2
Áp d ng công th c Green: ụ ứ
∫
(
2𝑥𝑦 − 5 2𝑥+ 3𝑦
)
𝑑𝑥 +
( )
𝑑𝑦
𝐿
= ∬
(
2 − 2𝑥
)
𝑑𝑥𝑑𝑦
𝐷
= ∫
𝑑𝑥
1
0
∫
(
2 − 2𝑥
)
𝑑𝑦
𝑥
2
0
=
1
6
Câu 40: Tính
2 2 3
2 3
2 2
3 3
4 1 4
C
x y dx x y dy
x y
+ + +
+ +
với 𝐶 ng cong là đườ
𝑦 = 1 − 𝑥
√
4
đi từ 𝐴
(
1,0
)
đến 𝐵
(
−1,0 .
)
Đáp án: B.
4
2arctan2
7
−
𝑥
𝑦
𝑦 = 𝑥
2
𝑥 = 1
45
Giải:
Đặt 𝐼 =
2 2 3
2 3
2 2
3 3
4 1 4
C
x y dx x y dy
x y
+ + +
+ +
𝐿:𝑦 = 1 − 𝑥
√
4
ng cong h là đườ ở đi từ 𝐴
(
1,0 −1,0
)
đến 𝐵
( )
B
ổ sung thêm đoạn 𝐵𝐴: {
𝑦 = 0
Đi
từ 𝐵
(
−1,0 →𝐴 1,0
) ( )
Đặt
{
𝑃
(
𝑥,𝑦 = 3𝑥
)
2
𝑦
2
+
2
4𝑥 + 1
2
𝑄
(
𝑥,𝑦 = 3𝑥
)
3
𝑦+
2
𝑦
3
+ 4
⇒ {
𝑃
𝑦
′
= 6𝑥
2
𝑦
𝑄
𝑥
′
=9𝑥
2
𝑦
liên tục với ∀𝑥,𝑦 ∈ 𝑅
𝐼 = ∮ 𝑃𝑑𝑥 + 𝑄𝑑𝑦
𝐿∪
𝐵𝐴
− ∫
𝑃𝑑𝑥 + 𝑄𝑑𝑦
𝐵𝐴
=𝐼
1
− 𝐼
2
Áp d ng công th c Green cho ụ ứ 𝐼
1
Đặt
{
𝑃
(
𝑥,𝑦 = 3𝑥
)
2
𝑦
2
+
2
4𝑥 + 1
2
𝑄
(
𝑥,𝑦 = 3𝑥
)
3
𝑦+
2
𝑦
3
+ 4
⇒ {
𝑃
𝑦
′
= 6𝑥
2
𝑦
𝑄
𝑥
′
=9𝑥
2
𝑦
liên tục với ∀𝑥,𝑦 ∈ 𝑅
Ta có ng cong kín, có chi i h n mi𝐿 ∪ 𝐵𝐴 là đườ ều dương, giớ ạ ền
𝐷:
{
0 ≤ 𝑦 ≤
√
1 − 𝑥
4
−1≤ 𝑥 ≤ 1
46
⇒𝐼
1
= ∬
3𝑥
2
𝑦𝑑𝑥𝑑𝑦
𝐷
= ∫
𝑑𝑥
1
−1
∫
3𝑥
2
𝑦𝑑𝑦
√
1−𝑥
4
0
=
3
2
∫𝑥
2
(
1 − 𝑥
4
)
𝑑𝑥
1
−1
=
4
7
Đo
ạn 𝐵𝐴:{
𝑦 = 0 ⇒ = 0𝑑𝑦
đi
từ 𝐵 đến 𝐴
(
−1,0
) (
1,0
)
⇒𝐼
2
= ∫
2
4𝑥 + 1
2
𝑑𝑥
1
−1
= 2arctan2
Vậy 𝐼 =4/7 − 2arctan2
Câu :
41 Tính di n tích cệ ủa miền D i h n bgiớ ạ ởi 𝐿:{
𝑥 = 2
(
𝑡 − sin𝑡
)
𝑦 = 2 1 − cos𝑡
( )
với trục 𝑂𝑥
biế ằt r ng d𝑡 đi từ 2𝜋 ến 0
Đáp án: B.
12
𝜋
(
đvdt
)
Giải:
Ta có: 𝜕𝐷 = 𝐿∪ 𝑂𝑥
⇒𝑆
(
𝐷
)
= ∫
𝑥𝑑𝑦
𝐿∪
𝑂𝑥
= ∫
𝑥𝑑𝑦
𝐿
+ ∫
𝑥𝑑𝑦
𝑂𝑥
= ∫
𝑥𝑑𝑦
𝐿
= ∫
2
(
𝑡 − sin 𝑡
)
.2sin𝑡 𝑑𝑡 = 12𝜋
0
2𝜋
Câu
42: Tính công c a lủ ực 𝐹
=
(
𝑥 + 2𝑦 𝑖+ 3𝑥 + 4𝑦 𝑗
) ( )
làm dịch chuyển một
ch
ất điểm từ 𝐴
(
1,3
) )
đến 𝐵
(
2,4 d n th ng ọc theo đoạ ẳ 𝐴𝐵. (đvc: đơn vị công)
Đáp án: D. 27 (đvc)
Giải:
Công c a l
ủ ực 𝐹
là:
W ( 2 ) (3 4 )
L
x y dx x y dy= + + +
Đo
ạ ẳn th ng AB: {
𝑦 = 𝑥 + 2 ⇒ 𝑑𝑦 𝑑𝑥=
đi
từ 𝐴 đến 𝐵
(
1,3
) (
2,4
)
⇒𝑊 = (𝑥+ 2𝑥 +4 + 3𝑥+ 4𝑥+ 8)∫ 𝑑𝑥
2
1
= 27
(
đơn vị công
)
Câu
43: Tính kh ng cối lượ ủa đường cong vật chất 𝐿có phương trình {
𝑥 = cos𝑡
𝑦 = sin𝑡
0≤ 𝑡 ≤ 𝜋/2
bi
ết hàm mật độ là 𝑝
(
𝑥,𝑦 = 𝑦
)
47
Đáp án: A.
1
(
đvkl
)
Giải:
Khối lượng của đường cong v t ch ậ ất 𝐿 được tính theo công th ức:
𝑚 = 𝑝(𝑥,𝑦)∫ 𝑑𝑠
𝐿
= ∫
𝑦𝑑𝑠
𝐿
{
𝑥 = cos𝑡
𝑦 = sin𝑡
0≤ 𝑡 ≤ 𝜋/2
⇒ {
𝑥
′
=−sin𝑡
𝑦
′
=cos𝑡
0≤ 𝑡 ≤ 𝜋/2
⇒ 𝑑𝑠 =
√
𝑥
′
2
(
𝑡
)
+ 𝑦
′
2
(𝑡)𝑑𝑡 𝑑𝑡=
⇒ 𝑚 = ∫𝑦𝑑𝑠
𝐿
= ∫sin𝑡𝑑𝑡
𝜋
2
0
= 1
(
đvkl
)
Câu
44: Tính công làm d ch chuy n m t ch m t ị ể ộ ất điể ừ A
(
0,1
)
đến B
(
1,0
)
của lực
𝐹
=
[
8𝑥 − 2𝑦 1 +𝑥
3
ln
(
2
𝑦
2
)]
𝑖+ 5𝑦 − 2𝑥 1 + 𝑥
[
4
ln
(
2
𝑦
2
)]
𝑗
Đáp án: A. 1 (đvc)
Giải:
Công c a l
ủ ực 𝐹
𝑊 = 8𝑥 − 2𝑦 1 + 𝑥
∫
[
3
ln
(
2
𝑦
2
)]
𝑑𝑥 +
𝐿
[
5𝑦
4
− 2𝑥 1 + 𝑥ln
(
2
𝑦
2
)]
𝑑𝑦
Với 𝐿 là đường đi từ 𝐴đến 𝐵 t hình d(chưa biế ạng)
Đặ
t {
𝑃 =
[
8𝑥
3
− 2𝑦 1 + 𝑥ln
(
2
𝑦
2
)]
𝑄 = 5𝑦 − 2𝑥 1 + 𝑥
[
4
ln
(
2
𝑦
2
)]
⇒𝑃
𝑦
′
=𝑄
𝑥
′
=−2 1 + 𝑥ln
(
2
𝑦
2
)
−
4𝑥
2
𝑦
2
1 + 𝑥
2
𝑦
2
⇒ Tích phân 𝑊 không ph thuụ ộc vào đường đi
Chọn đường đi là đường gấp khúc 𝐴𝑂𝐵 v và ới 𝐴
(
0,1
)
𝐵
(
1,0 ,𝑂 0,0
) ( )
48
𝑊 = ∫ 𝑃𝑑𝑥 +
𝐴𝑂𝐵
𝑄𝑑𝑦 =∫ 𝑃𝑑𝑥 +
𝐴𝑂
𝑄𝑑𝑦 + 𝑃𝑑𝑥 +∫
𝑂𝐵
𝑄𝑑𝑦
𝐴𝑂
:{
𝑥 = 0 ⇒ = 0𝑑𝑥
Đi
từ A
(
0,1 → 𝑂
) (
0,0
)
⇒
∫
𝑃𝑑𝑥 +
𝐴𝑂
𝑄𝑑𝑦 = 5𝑦∫
4
𝑑𝑦
0
1
=−1
𝑂𝐵
: {
𝑦 = 0 ⇒ = 0𝑑𝑦
Đi
từ O
(
0,0 →𝐵
) (
1,0
)
⇒ ∫ 𝑃𝑑𝑥 +
𝑂𝐵
𝑄𝑑𝑦 = 8𝑥∫
3
𝑑𝑥
1
0
=2
⇒𝑊 = ∫ 𝑃𝑑𝑥+
𝐴𝑂𝐵
𝑄𝑑𝑦 =∫ 𝑃𝑑𝑥 +
𝐴𝑂
𝑄𝑑𝑦 + 𝑃𝑑𝑥 +∫
𝑂𝐵
𝑄𝑑𝑦 = 1
(
đvc
)
Câu 45: Tính kh ng c ng cong v ối lượ ủa đườ ật 𝐿 chất có phương trình 𝑥
2
+ 𝑦 = 1
2
bi
ết hàm mật độ là 𝑝
(
𝑥,𝑦 = 𝑥
)
2
Đáp án: D. 𝜋
Giải:
Khối lượng:
L
m xds
=
Tham s hóa:
ố {
𝑥 = 𝑐𝑜𝑠𝑡
𝑦 = sin𝑡
,0 ≤ 𝑡 ≤ 2𝜋 ⇒
{
𝑥
′
= − sin𝑡
𝑦
′
=cos𝑡
⇒ 𝑑𝑠 =
√
(
𝑥
′
)
2
+
(
𝑦
′
)
2
𝑑𝑡 𝑑𝑡=
⇒𝑚 =∫𝑥
2
𝑑𝑠
𝐿
= ∫
(
cos𝑡
)
2
𝑑𝑡
2𝜋
0
=𝜋
(
đvkl
)
49
Tích phân mặt
Câu 46: Tính
S
xydS
v là mới 𝑆 ặt 𝑧= + 𝑦 ,𝑧 ≤ 1,𝑥 ≥ 0
√
𝑥
2 2
Đáp án: A. 0
Giải:
Ta có: 𝑧 = √𝑥
2
+ 𝑦 ⇒
2
{
𝑧
𝑥
′
=
𝑥
√𝑥
2
+ 𝑦
2
𝑧
𝑦
′
=
𝑦
√
𝑥
2
+ 𝑦
2
⇒
𝑑𝑆 =
√
1 +
(
𝑧
𝑥
′
)
2
+ (
𝑧
𝑦
′
)
2
𝑑𝑥𝑑𝑦 = 2𝑑𝑥𝑑𝑦
√
Hình chi u c a mế ủ ặt 𝑆 lên là: 𝑂𝑥𝑦 𝐷:𝑥 + 𝑦 ≤ 1,𝑥 ≥ 0
2 2
⇒ ∬𝑥𝑦𝑑𝑆
𝑆
=
√
2∬
𝑥𝑦𝑑𝑥𝑑𝑦
𝐷
Đặ
t {
𝑥 = 𝑟 cos𝜑
𝑦 = 𝑟sin𝜑
,𝐽 = 𝑟 ⇒ 𝐷: {
0≤ 𝑟 ≤ 1
−𝜋/2≤ 𝜑 ≤ 𝜋/2
50
⇒ ∬𝑥𝑦𝑑𝑆
𝑆
=
√
2 ∫
𝑑𝜑
𝜋
2
−𝜋
2
∫
𝑟
2
cos𝜑sin𝜑 .𝑟𝑑𝑟
1
0
=
√
2
4
∫cos𝜑 sin𝜑𝑑𝜑
𝜋
2
−𝜋
2
=0
Câu 47: Tính
2
S
x dS
v là biên c a mi n gi i h n b i mới 𝑆 ủ ề ớ ạ ở ặt 𝑧 = + 𝑦 ,𝑧 = 1
√
𝑥
2 2
Đáp án: C.
(1 2)
4
+
Giải:
𝑆 là biên c a miủ ền 𝑉: + 𝑦
√
𝑥
2 2
≤𝑧 ≤ 1 ⇒ g m hai m𝑆 ồ ặt
{
𝑆
1
:{
𝑧 = 1
𝑥
2
+ 𝑦 ≤ 1
2
𝑆
2
: {
𝑧 = √𝑥
2
+ 𝑦
2
0 ≤ 𝑧 ≤ 1
⇒ ∬𝑥
2
𝑑𝑆
𝑆
= ∬
𝑥
2
𝑑𝑆
𝑆
1
+ ∬
𝑥
2
𝑑𝑆
𝑆
2
Xét m
ặt 𝑆
1
: {
𝑧 = 1
𝑥
2
+ 𝑦 ≤ 1
2
⇒ 𝑧
𝑥
′
= 𝑧
𝑦
′
= 0 ⇒ = 𝑑𝑥𝑑𝑦𝑑𝑆
Hình chi u c a mế ủ ặt 𝑆
2
lên là: 𝑂𝑥𝑦 𝐷: 𝑥 + 𝑦 ≤ 1
2 2
51
⇒ ∬ 𝑥
2
𝑑𝑆
𝑆
1
= ∬
𝑥
2
𝑑𝑥𝑑𝑦
𝐷
Đặ
t {
𝑥 = 𝑟cos𝜑
𝑦 = 𝑟sin𝜑
,𝐽 = 𝑟 ⇒ 𝐷:
{
0 ≤ 𝑟 ≤ 1
0≤ 𝜑 ≤ 2𝜋
∬
𝑥
2
𝑑𝑥𝑑𝑦
𝐷
= ∫
𝑑𝜑
2𝜋
0
∫
𝑟
2
cos
2
𝜑𝑟𝑑𝑟
1
0
=⋯ =
𝜋
4
Xét mặt 𝑆
2
:
Có: 𝑧 = √𝑥
2
+ 𝑦
2
⇒
{
𝑧
𝑥
′
=
𝑥
√𝑥
2
+ 𝑦
2
𝑧
𝑦
′
=
𝑦
√
𝑥
2
+ 𝑦
2
⇒ 𝑑𝑆 =
√
1 +
(
𝑧
𝑥
′
)
2
+ (
𝑧
𝑦
′
)
2
𝑑𝑥𝑑𝑦 = 2𝑑𝑥𝑑𝑦
√
Hình chiếu của mặt 𝑆
2
lên là: 𝑂𝑥𝑦 𝐷:𝑥 + 𝑦 ≤ 1,𝑥 ≥ 0
2 2
⇒ ∬𝑥
2
𝑑𝑆
𝑆
2
=
√
2∬
𝑥
2
𝑑𝑥𝑑𝑦
𝐷
Đặ
t {
𝑥 = 𝑟cos𝜑
𝑦 = 𝑟sin𝜑
,𝐽 = 𝑟 ⇒ 𝐷:
{
0 ≤ 𝑟 ≤ 1
0≤ 𝜑 ≤ 2𝜋
⇒ ∬𝑥
2
𝑑𝑆
𝑆
2
=
√
2∫
𝑑𝜑
2𝜋
0
∫
𝑟
2
cos
2
𝜑.𝑟𝑑𝑟
1
0
=⋯ =
𝜋
√
2
4
⇒ ∬𝑥
2
𝑑𝑆
𝑆
= ∬
𝑥
2
𝑑𝑆
𝑆
1
+ ∬
𝑥
2
𝑑𝑆
𝑆
2
=
𝜋(
1 +
√
2
)
4
Câu 48: Tìm 𝑚 để
5 6
3
( )
S
x y mz dS =
+ +
với 𝑆 là mặt 2𝑥+ 4𝑦 + 2𝑧 = 4 u và điề
kiện 𝑥 ≥ 0,𝑦 ≥ 0,𝑧 ≥ 0
Đáp án: B. 𝑚= 1
52
Giải:
Mặt 𝑆:
{
𝑧 = 2 − 2𝑦 − 𝑥
𝑥,𝑦,𝑧 ≥ 0
⇒
{
𝑧
𝑥
′
= −1
𝑧
𝑦
′
= −2
⇒ 𝑑𝑆 =
√
1 + 𝑧
(
𝑥
′
)
2
+ (
𝑧
𝑦
′
)
2
𝑑𝑥𝑑𝑦 = 6𝑑𝑥𝑑𝑦
√
Hình chi u c
ế ủa 𝑆 lên là mi𝑂𝑥𝑦 ền 𝐷 đượ ớc gi i h n bạ ởi {
2𝑥 + 4𝑦 = 4
𝑥 ≥ 0,𝑦 ≥ 0
⇒𝐷:
{
0 ≤ 𝑥 ≤ 2
0≤ 𝑦 ≤ 1 − 𝑥/2
⇒
∬
(
𝑥+ 𝑦 +
𝑚𝑧
)
𝑑𝑆
𝑆
=
√
6∬
(
𝑥+ 𝑦 + 2𝑚 −2𝑚𝑦 𝑚𝑥−
)
𝑑𝑥𝑑𝑦
𝐷
=
√
6∫
𝑑𝑥
2
0
∫
( )
𝑥+ 𝑦 + 2𝑚 −2𝑚𝑦 𝑚𝑥− 𝑑𝑦
1−
𝑥
2
0
=
5
√
6
3
⇒𝑚 = 1
Câu 49: Tính
S
xyzdS
với 𝑆 là mặ ạ ặt 𝑥 −2𝑦 + 3𝑧− 4 = 0 i hgiớ n trong m t trụ có
phương trình 2𝑥 + 3𝑦 =6
2 2
Đáp án: B. 0
Giải:
Mặt 𝑧 =
4 − 𝑥+ 2𝑦
3
⇒ 𝑑𝑆 =
√
1 + (𝑧
𝑥
′
)
2
+ (𝑧
𝑦
′
)
2
𝑑𝑥𝑑𝑦 =
√
14
3
𝑑𝑥𝑑𝑦
Hình chi u c a mế ủ ặt 𝑆 lên 𝑂𝑥𝑦 là 𝐷:2𝑥 + 3𝑦
2 2
≤ 6
⇒𝐼 = 𝑥𝑦𝑧𝑑𝑆∬
𝑆
=
√
14
3
∬𝑥𝑦
4 − 𝑥+ 2𝑦
3
𝑑𝑥𝑑𝑦
𝐷
=
√
14
9
∬𝑥𝑦
(
4 − 𝑥 + 2𝑦
)
𝑑𝑥𝑑𝑦
𝐷
53
{
Miền 𝐷 đối xứ qua ng 𝑂𝑥 𝑂𝑦,
𝑓
(
𝑥,𝑦,𝑧 =4
)
𝑥𝑦 lẻ với biến 𝑥
𝑔
(
𝑥,𝑦,𝑧 = −𝑥
)
2
𝑦 lẻ với biến 𝑦
ℎ
(
𝑥,𝑦,𝑧 =2𝑥𝑦
)
2
lẻ với biến 𝑥
⇒
∬
4𝑥𝑦𝑑𝑥𝑑𝑦
𝐷
+ ∬
−𝑥
2
𝑦𝑑𝑥𝑑𝑦
𝐷
+ ∬
2𝑥𝑦
2
𝑑𝑥𝑑𝑦
𝐷
=0
⇒𝐼 = 0
Câu 50: Biết
5 1
12
S
a
b
xdS
= +
biết 𝑆 n m t paraboloid là phầ ặ 𝑥 = 𝑦 + 𝑧
2 2
thỏa
mãn t lu𝑥 ≤ 1. Kế ận nào sau đây là chính xác?
Đáp án: A. 𝑎 + 𝑏 < 70
Giải:
M
ặt 𝑥 = 𝑦 + 𝑧
2 2
⇒ {
𝑥
𝑦
′
=2𝑦
𝑥
𝑧
′
=2𝑧
54
⇒
𝑑𝑆 =
√
1 +
(𝑥
𝑦
′
)
2
+
(
𝑥
𝑧
′
)
2
𝑑𝑥𝑑𝑧 = 1+ 4√
(
𝑦
2
+ 𝑧
2
)
𝑑𝑦𝑑𝑧
Hình chi u cế ủa 𝑆 lên là 𝑂𝑦𝑧 𝐷:𝑦 + 𝑧 ≤ 1
2 2
𝐼 = 𝑥𝑑𝑆∬
𝑆
= ∬
(
𝑦
2
+ 𝑧
2
)
𝐷
√
1 + 4
(
𝑦
2
+ 𝑧
2
)
𝑑𝑦𝑑𝑧
Đặ
t {
𝑦 = 𝑟 cos𝜑
𝑧 = 𝑟 sin𝜑
,𝐽 = 𝑟 ⇒ 𝐷:
{
0 ≤ 𝑟 ≤ 1
0≤ 𝜑 ≤ 2𝜋
⇒𝐼 = ∫ 𝑑𝜑
2𝜋
0
∫
𝑟
2
√
1 + 4𝑟
2
.𝑟𝑑𝑟
1
0
=
1
2
∫ 𝑑𝜑
2𝜋
0
∫
𝑟
2
√
1 + 4𝑟
2
𝑑
(
𝑟
2
)
1
0
=
1
2
∫ 𝑑𝜑
2𝜋
0
∫
𝑢
√
1 + 4𝑢𝑑𝑢
1
0
Đặ𝑡 𝑡 =
√
1 + 4𝑢 ⇒ 𝑑𝑡 =
2
√
1 + 4𝑢
𝑑𝑢 =
2
𝑡
𝑑𝑢 𝑑𝑢⇒ =
𝑡
2
𝑑𝑡
⇒ ∫𝑢
√
1 + 4𝑢𝑑𝑢
1
0
= ∫
𝑡
2
− 1
4
.𝑡.
𝑡
2
𝑑𝑡
√
5
1
=
5
√
5
12
+
1
60
⇒𝐼 =
1
2
.(
5
√
5
12
+
1
60
).∫ 𝑑𝜑
2𝜋
0
=(
5
√
5
12
+
1
60
)𝜋 ⇒ 𝑎 =5,𝑏 = 60
Câu 51: Tính
2 2
1
S
x y dS+ +
v là ph n m t ới 𝑆 ầ ặ 2𝑧 = 𝑥 + 𝑦 ,0 ≤𝑥,𝑦 ≤ 1
2 2
. Chọn
đáp án gần với kết qu c a tích phân nh ả ủ ất.
Đáp án: A. 2
Gi i:ả
Mặt 𝑆:𝑧 =
𝑥
2
+ 𝑦
2
2
⇒ 𝑑𝑆 =
√
1 +
(
𝑧
𝑥
′
)
2
+ (
𝑧
𝑦
′
)
2
𝑑𝑥𝑑𝑦 = 1+ 𝑥√
2
+ 𝑦
2
𝑑𝑥𝑑𝑦
Hình chi u c
ế ủa 𝑆 lên 𝑂𝑥𝑦 𝐷: là {
0≤ 𝑥 ≤ 1
0≤ 𝑦 ≤ 1
55
∬√
1 + 𝑥
2
+ 𝑦
2
𝑑𝑆
𝑆
= ∬
(
1 + 𝑥
2
+ 𝑦
2
)
𝑑𝑥𝑑𝑦
𝐷
= ∫
𝑑𝑥
1
0
∫
(
1 + 𝑥
2
+ 𝑦
2
)
𝑑𝑦
1
0
=⋯ =
5
3
Câu 52: t Biế
S
dS
4
(33 3 2)
15
a b= − −
v là mới 𝑆 ặt
( )
3/2 3/2
2
3
z x y= +
v i ớ điều
kiện 0 ≤ 𝑥 ≤ 2,0 ≤ 𝑦 ≤ 1. Tìm kh ? ẳng định đúng
Đáp án: C.
𝑎 − 𝑏 = 5
Gi i:ả
Hình chi u c a mế ủ ặt 𝑧 =
2
3
(
𝑥
3/2
+ 𝑦
3/2
)
với 0 ≤ 𝑥 ≤ 2,0 ≤ 𝑦 ≤ 1 𝑂𝑥𝑦 lên là miền
𝐷:
{
0 ≤ 𝑥 ≤ 2
0≤ 𝑦 ≤ 1
Ta có:
𝑧
𝑥
′
=
√
𝑥,𝑧
𝑦
′
=
√
𝑦 ⇒ 1 + 𝑧𝑑𝑆 =
√
(
𝑥
′
)
2
+ (
𝑧
𝑦
′
)
2
𝑑𝑥𝑑𝑦 = 1+ 𝑥+ 𝑦𝑑𝑥𝑑𝑦
√
∬
𝑑𝑆
𝑆
= ∬
√
1 + 𝑥+ 𝑦𝑑𝑥𝑑𝑦
𝐷
= ∫
𝑑𝑦
1
0
∫
√
1 + 𝑥+ 𝑦𝑑𝑥
2
0
=
2
3
∫[
(
3 + 𝑦
)
3
2
−
(
1 + 𝑦
)
3
2
]
𝑑𝑦
1
0
=
4
15
(33 − 9
√
3 − 4
√
2)
⇒𝑎 = 9,𝑏 = 4
Câu 53: Tính
2
S
zy dS
v là ph n m t nón ới 𝑆 ầ ặ 𝑧 = + 𝑦
√
𝑥
2 2
n m gi a hai mằ ữ ặt 𝑧 = 1
và 𝑧 = 2
Đáp án: D.
31 2
5
Giải:
𝑧 = + 𝑦√𝑥
2 2
⇒
{
𝑧
𝑥
′
=
𝑥
√
𝑥
2
+ 𝑦
2
𝑧
𝑦
′
=
𝑦
√
𝑥
2
+ 𝑦
2
⇒𝑑𝑆=
√
1 +
(
𝑧
𝑥
′
)
2
+ (
𝑧
𝑦
′
)
2
𝑑𝑥𝑑𝑦 = 𝑑𝑥𝑑𝑦
√
2
Hình chi u c a mế ủ ặt 𝑆 lên là 𝑂𝑥𝑦 𝐷:1 ≤ 𝑥 + 𝑦 ≤ 4
2 2
56
Đặ
t {
𝑥 = 𝑟 cos𝜑
𝑦 = 𝑟 sin𝜑
,𝐽 = 𝑟 ⇒ 𝐷:{
1 ≤ 𝑟 ≤ 2
0 ≤ 𝜑 ≤ 2𝜋
∬𝑧𝑦
2
𝑑𝑆
𝑆
=
√
2∬
√
𝑥
2
+ 𝑦
2
.𝑦
2
𝑑𝑥𝑑𝑦
𝐷
=
√
2∫ 𝑑𝜑
2𝜋
0
∫𝑟.𝑟
2
.sin
2
𝜑 .𝑟𝑑𝑟
2
1
=
31
√
2𝜋
5
Câu 54: Tính
2
S
yx dS
với 𝑆 là phần m t nón ặ 𝑦= + 𝑧 ,1 ≤ 𝑦 ≤ 2
√
𝑥
2 2
Đáp án: B.
31 2
5
Giải:
𝑦 = + 𝑧
√
𝑥
2 2
⇒
{
𝑦
𝑥
′
=
𝑥
√
𝑥
2
+ 𝑧
2
𝑦
𝑧
′
=
𝑧
√
𝑥
2
+ 𝑧
2
⇒𝑑𝑆=√
1 +
(
𝑦
𝑥
′
)
2
+
(
𝑦
𝑧
′
)
2
𝑑𝑥𝑑𝑧 = 𝑑𝑥𝑑𝑧
√
2
Hình chi u c a mế ủ ặt 𝑆 lên là 𝑂𝑥𝑧 𝐷:1 ≤ 𝑥 + 𝑧 ≤ 4
2 2
Đặ
t {
𝑧 = 𝑟 cos𝜑
𝑥 = 𝑟sin𝜑
,𝐽 = 𝑟 ⇒ 𝐷:{
1 ≤ 𝑟 ≤ 2
0 ≤ 𝜑 ≤ 2𝜋
∬𝑦𝑥
2
𝑑𝑆
𝑆
=
√
2∬
√
𝑥
2
+ 𝑧
2
.𝑥
2
𝑑𝑥𝑑𝑧
𝐷
=
√
2∫ 𝑑𝜑
2𝜋
0
∫𝑟.𝑟
2
.sin
2
𝜑 .𝑟𝑑𝑟
2
1
=
31
√
2𝜋
5
Câu 55: Tính
S
xdS
v là m t tr n m gi a hai mới 𝑆 ặ ụ 𝑥
2
+ 𝑦 = 4
2
ằ ữ ặt 𝑧 = 0 𝑧 = 6 và
Đáp án: A. 0
Giải:
Chia m t tr thành hai m
ặ ụ ặt 𝑆
1
:{
𝑥 = 4 − 𝑦
√
2
0 ≤ 𝑧 ≤ 6
và 𝑆
2
:{
𝑥 = − 4 − 𝑦
√
2
0≤ 𝑧 ≤ 6
Hình chi u c
ế ủa 𝑆
1
và 𝑆
2
lên là 𝑂𝑦𝑧 𝐷: {
−2≤𝑦 ≤ 2
0≤ 𝑧 ≤ 6
∬𝑥𝑑𝑆
𝑆
= ∬𝑥𝑑𝑆
𝑆
1
+ ∬𝑥𝑑𝑆
𝑆
2
57
Xét mặt
'
2
' 2 ' 2
2
1
2
'
| |
4
: ( ) ( )4
0 6
4
0
y
y z
z
y
x
y dydz
x y
S dS x x dydz
y
z
y
x
−
=
= −
= + =
−
−
=
∬𝑥𝑑𝑆
𝑆
1
= ∬
√
4 − 𝑦
2
.
|
𝑦
|
√
4 − 𝑦
2
𝑑𝑦𝑑𝑧
𝐷
= ∫𝑑𝑧
6
0
∫
|
𝑦
|
2
−2
𝑑𝑦 = 24
Xét mặt
'
2
' 2 ' 2
2
2
2
'
| |
4
: ( ) ( )4
0 6
4
0
y
y z
z
y
x
y dydz
x y
S dS x x dydzy
z
y
x
=
= − −
= + =
−
−
=
∬𝑥𝑑𝑆
𝑆
2
= ∬− 4− 𝑦
√
2
.
|
𝑦
|
√
4 − 𝑦
2
𝑑𝑦𝑑𝑧
𝐷
= −∫ 𝑑𝑧
6
0
∫
|
𝑦
|
2
−2
𝑑𝑦 = −24
⇒ ∬𝑥𝑑𝑆
𝑆
=
∬
𝑥𝑑𝑆
𝑆
1
+
∬
𝑥𝑑𝑆
𝑆
2
= 0
Câu 56: Tính
(1 )
S
x z dzdx− −
v là m t trên c a mới 𝑆 ặ ủ ặt 𝑥+ 𝑦 +𝑧 = 1, 𝑥 ≥ 0,𝑦 ≥
0,𝑧 ≥ 0
Đáp án: C.
1
6
Giải:
M
ặt 𝑆:𝑦 = 1 − 𝑥 − 𝑧,𝑥 ≥ 0,𝑦 ≥ 0, 𝑧≥0, 𝑛
(
󰇍
,
𝑂𝑦
)
<𝜋/2
58
Hình chi u c a m
ế ủ ặt 𝑆 lên 𝑂𝑥𝑧 là 𝐷: {
0≤ 𝑥 ≤ 1
0≤ 𝑧 ≤ 1 − 𝑥
⇒
∬
(
1 − 𝑥− 𝑧
)
𝑑𝑧𝑑𝑥
𝑆
=+ 1 −𝑥 − 𝑧 𝑑𝑧𝑑𝑥∬
(
)
𝐷
= ∫
𝑑𝑥
1
0
∫
( )
1 − 𝑥− 𝑧 𝑑𝑧
1−𝑥
0
=⋯ =
1
6
Câu 57: Tính
2 2 2
( )
S
I x y z dxdy= + +
v là m t n a cới 𝑆 ặ ử ầu 𝑥
2
+ 𝑦 + 𝑧 = 1
2 2
phía
trên ng lên trên.𝑂𝑥𝑦, mặt 𝑆 hướ
Đáp án: A. 𝜋
Giải:
M
ặt 𝑆:𝑧 = 1 − 𝑥 −𝑦
√
2 2
, hướng lên trên,
(
𝑛
󰇍
,
𝑂𝑧
)
< 𝜋/2
Hình chi u c a m lên là
ế ủ ặt 𝑆 𝑂𝑥𝑦
(
𝐷
)
:𝑥 + 𝑦 ≤ 1
2 2
⇒
∬
(
𝑥
2
+ 𝑦 + 𝑧
2 2
)
𝑑𝑥𝑑𝑦
𝑆
=+∬
(
𝑥
2
+ 𝑦
2
+ 1 − 𝑥
2
− 𝑦
2
)
𝑑𝑥𝑑𝑦
𝐷
= ∬
1𝑑𝑥𝑑𝑦
𝐷
=𝑆
(
𝐷
)
= 𝜋𝑅
2
= 𝜋
Câu 58: Cho 𝐼 =
2
S
ydzdx z dxdy+
, là phía ngoài m𝑆 ặt 𝑥
2
+ 𝑦 + 𝑧
2 2
= 1 với điều
kiện 𝑥 ≥ 0,𝑦 ≥ 0,𝑧 ≥ 0.Chọn đáp án gần nhất với kết quả của 𝐼
Đáp án: 1 A.
Giải:
59
𝐼 = 𝑦𝑑𝑧𝑑𝑥∬
𝑆
+ ∬
𝑧
2
𝑑𝑥𝑑𝑦
𝑆
=𝐼
1
+ 𝐼
2
Xét 𝐼
1
, mặt 𝑆:𝑦 = 1 − 𝑥 − 𝑧
√
2 2
,𝑥 ≥ 0,𝑧 ≥ 0, 𝑛
(
󰇍
,
𝑂𝑦
)
< 𝜋/2
Hình chi u c a mế ủ ặt 𝑆 lên là 𝑂𝑥𝑧 𝐷
𝑥𝑧
: 𝑥
2
+ 𝑧
2
≤ 1,𝑥 ≥ 0,𝑧 ≥ 0
⇒𝐼
1
= ∬
𝑦𝑑𝑧𝑑𝑥
𝑆
= ∬
√
1 − 𝑥
2
− 𝑧
2
𝑑𝑥𝑑𝑧
𝐷
𝑥𝑧
Đặ
t {
𝑧= 𝑟 cos𝜑
𝑥 = 𝑟 sin𝜑
𝐽 = 𝑟. Miền 𝐷
𝑥𝑧
: {
0 ≤ 𝑟 ≤ 1
0≤ 𝜑 ≤ 𝜋/2
⇒𝐼
1
= ∫
𝑑𝜑
𝜋
2
0
∫
√
1 − 𝑟
2
.𝑟𝑑𝑟
1
0
=
1
2
∫ 𝑑𝜑
𝜋
2
0
∫
√
1 − 𝑟
2
.𝑑
(
𝑟
2
)
1
0
=
1
2
∫𝑑𝜑
𝜋
2
0
∫
√1 − 𝑢.𝑑𝑢
1
0
=
1
6
𝜋
Xét 𝐼
2
, mặt 𝑆:𝑧 = 1 − 𝑥 − 𝑦
√
2 2
,𝑥 ≥ 0,𝑦 ≥ 0, 𝑛
(
󰇍
,
𝑂𝑧
)
< 𝜋/2
Hình chi u c a mế ủ ặt 𝑆 lên là 𝑂𝑥𝑧 𝐷
𝑥𝑦
: 𝑥
2
+ 𝑦
2
≤ 1,𝑥 ≥ 0,𝑦 ≥ 0
⇒𝐼
2
= ∬
𝑧
2
𝑑𝑥𝑑𝑦
𝑆
= ∬
(
1 − 𝑥
2
− 𝑦
2
)
𝑑𝑥𝑑𝑦
𝐷
𝑥𝑦
Đặt
{
𝑥 = 𝑟 cos𝜑
𝑦 = 𝑟 sin𝜑
𝐽 = 𝑟. ền 𝐷Mi
𝑥𝑦
: {
0≤𝑟 ≤1
0≤ 𝜑 ≤
𝜋
2
⇒𝐼
2
= ∫
𝑑𝜑
𝜋
2
0
∫
(
1 − 𝑟
2
)
.𝑟𝑑𝑟
1
0
=
1
8
𝜋
60
Vậy 𝐼 = 𝐼
1
+ 𝐼
2
=
7
24
𝜋
Câu 59: Tính 𝐼 =
2
S
xdzdx z dxdy+
v là phía ngoài mới 𝑆 ặt 𝑧 = 𝑥 + 𝑦
2 2
với điều
kiện 0 ≤𝑧 ≤ 2,𝑦 ≥ 0
Đáp án: D.
Giải:
𝐼 = 𝑥𝑑𝑧𝑑𝑥+ 𝑧 𝑑𝑥𝑑𝑦∬
2
𝑆
= ∬
𝑥𝑑𝑧𝑑𝑥
𝑆
+ ∬
𝑧
2
𝑑𝑥𝑑𝑦
𝑆
=𝐼
1
+ 𝐼
2
Xét 𝐼
1
, mặt 𝑆:𝑧 = 𝑥 + 𝑦 𝑛
2 2
,
(
󰇍
,
𝑂𝑦
)
< 𝜋/2
Hình chi u c
ế ủa 𝑆 lên là 𝑂𝑥𝑧 𝐷
𝑥𝑧
: {
𝑥
2
≤𝑧 ≤ 2
−
√
2 ≤ 𝑥 ≤
√
2
⇒𝐼
1
= ∬
𝑥𝑑𝑧𝑑𝑥
𝑆
= ∬
𝑥𝑑𝑧𝑑𝑥
𝐷
𝑥𝑧
= ∫
𝑑𝑥
√
2
−
√
2
∫
𝑥
2
𝑥
2
𝑑𝑧 = ∫ 𝑥
(
2 − 𝑥
2
)
𝑑𝑥
√
2
−
√
2
=0
Xét 𝐼
2
, mặt 𝑆:𝑧 = 𝑥 + 𝑦 𝑛
2 2
,
(
󰇍
,
𝑂𝑧
)
> 𝜋/2
Hình chi u cế ủa 𝑆 lên là 𝑂𝑥𝑦 𝐷
𝑥𝑦
:𝑥
2
+ 𝑦
2
≤ 2,𝑦 ≥ 0
Đặ
t {
𝑥 = 𝑟cos𝜑
𝑦 = 𝑟sin𝜑
𝐽 = 𝑟. Miền
( )
𝐷 :{
0≤𝑟 ≤
√
2
0≤ 𝜑 ≤ 𝜋
61
⇒𝐼
2
= ∬
𝑧
2
𝑑𝑥𝑑𝑦
𝑆
=− (𝑥∬
2
+ 𝑦
2
)
2
𝑑𝑥𝑑𝑦
𝐷
𝑥𝑦
=−∫
𝑑𝜑
𝜋
0
∫
𝑟
4
.𝑟𝑑𝑟
√
2
0
=
−4
3
𝜋
Vậy 𝐼 = 𝐼
1
+ 𝐼
2
=
−4𝜋
3
Câu 60: Tính
2 2 2
4 9
S
xz dydz yx dzdx zy dxdy+ +
v i mớ ặt 𝑆:4𝑥 + 9𝑦 + 𝑧 = 1
2 2 2
,
hướng ra ngoài.
Đáp án: B.
2
15
Giải:
Mặt 𝑆 là mặt trơn kín giới hạn miền 𝑉: 4𝑥
2
+ 9𝑦 + 𝑧 ≤ 1,
2 2
h ng pháp tuyướ ến
ngoài.
Đặ
t {
𝑃 = 𝑥𝑧
2
𝑄 = 4𝑦𝑥
2
𝑅 = 9𝑧𝑦
2
⇒ {
𝑃
𝑥
′
= 𝑧
2
𝑄
𝑦
′
=4𝑥
2
𝑅
𝑧
′
=9𝑦
2
,𝑃
𝑥
′
,𝑄
𝑦
′
,𝑅
𝑧
′
liên t ục
Áp d ng công th c Ostrogradsky: ụ ứ
𝐼 = 𝑑𝑦𝑑𝑧∬ 𝑥𝑧
2
𝑆
+ 4𝑦𝑥
2
𝑑𝑧𝑑𝑥+ 9𝑧𝑦
2
𝑑𝑥𝑑𝑦 = 4𝑥∭
(
2
+ 9𝑦
2
+ 𝑧
2
)
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
Đặt{
2𝑥 = 𝑟 sin𝜃cos𝜑
3𝑦 = 𝑟sin 𝜃sin𝜑
𝑧 = 𝑟 cos𝜃
⇔
{
𝑥 =
1
2
𝑟sin𝜃 cos𝜑
𝑦 =
1
3
𝑟sin𝜃 sin𝜑
𝑧 = 𝑟 cos𝜃
|
𝐽
|
=
1
6
𝑟
2
sin𝜃.Miền 𝑉: {
0≤ 𝑟 ≤ 1
0≤ 𝜃 ≤ 𝜋
0≤ 𝜑 ≤ 2𝜋
⇒𝐼 =
1
6
∫ 𝑑𝜑
2𝜋
0
∫
𝑑𝜃
𝜋
0
∫
𝑟
2
.𝑟
2
sin𝜃 𝑑𝑟
1
0
=
2
15
𝜋
Câu 61: t Biế 𝐼 =
2 2
2 ( ) (4 )
S
a
xydydz x y dzdx x y dxdy
b
+ + + + =
với m là biên cặt 𝑆 ủa
miền 𝑉:𝑥 + 𝑦 +𝑧 ≤ 1, 𝑥 ≥ 0,𝑦 ≥ 0,𝑧 ≥ 0 hướng ra ngoài. Tìm kh ẳng định đúng
Đáp án: C. 𝑎 + 𝑏 = 7
62
Giải:
Mặt 𝑆 kín gi i h n miớ ạ ền 𝑉: 𝑥+ 𝑦 +𝑧 ≤ 1, 𝑥 ≥ 0,𝑦 ≥ 0,𝑧 ≥ 0
⇔𝑉:
{
0 ≤ 𝑥 ≤ 1
0≤ 𝑦 ≤ 1 − 𝑥
0≤ 𝑧 ≤ 1 − 𝑥 − 𝑦
hướng ra ngoài.
Đặ
t {
𝑃 = 2𝑥𝑦
𝑄 = 𝑥 +𝑦
2
𝑅 = 4𝑥 + 𝑦
2
⇒
{
𝑃
𝑥
′
= 2𝑦
𝑄
𝑦
′
=2𝑦
𝑅
𝑧
′
=0
,𝑃
𝑥
′
,𝑄
𝑦
′
,𝑅
𝑧
′
liên t ục.
Áp d ng công th Ostrogradsky: ụ ức
𝐼 = 4𝑦𝑑𝑥𝑑𝑦𝑑𝑧∭
𝑉
= ∫
𝑑𝑥
1
0
∫
𝑑𝑦
1−𝑥
0
∫
4𝑦𝑑𝑧
1−𝑥−𝑦
0
=⋯ =
1
6
⇒𝑎 = 1,𝑏 = 6
Câu 62: Tính 𝐼 =
2 3 3 2
( 2 ) ( 2 )
S
xy z dydz z y dzdx x zdxdy+ + + +
v là n a mới 𝑆 ử ặt
cầu 𝑥
2
+ 𝑦 + 𝑧 = 1,𝑧 ≥ 0
2 2
hướng ra ngoài m t cặ ầu.
Đáp án: A.
8
5
Giải:
B
ổ sung thêm mặt 𝑆
′
:{
𝑧 = 0
𝑥
2
+ 𝑦 ≤ 1
2
ng xuhướ ống dưới
M
ặt 𝑆 ∪ 𝑆
′
là m t cong kín, gi i h n miặ ớ ạ ền 𝑉:{
𝑥
2
+ 𝑦
2
+ 𝑧
2
≤1
𝑧 ≥ 0
ng pháp tuyhướ ến
ngoài.
63
Đặ
t {
𝑃 = 𝑥𝑦
2
+ 2𝑧
3
𝑄 = 𝑧 + 2𝑦
3
𝑅 = 𝑥
2
𝑧
⇒
{
𝑃
𝑥
′
= 𝑦
2
𝑄
𝑦
′
=2
𝑅
𝑧
′
=𝑥
2
,𝑃
𝑥
′
,𝑄
𝑦
′
,𝑅
𝑧
′
liên t c ụ
𝐼 =∯𝑃𝑑𝑦𝑑𝑧 +𝑄𝑑𝑧𝑑𝑥+ 𝑅𝑑𝑥𝑑𝑦
𝑆∪𝑆
′
− ∬
𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦
𝑆
=𝐼
1
− 𝐼
2
Áp d ng công th c Ostrogradsky cho ụ ứ 𝐼
1
⇒𝐼
1
= ∭
(
𝑥
2
+ 𝑦
2
+ 2
)
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∭
(
𝑥
2
+ 𝑦
2
)
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
+ 2𝑉
(
𝑉
)
Đặt {
𝑥 = 𝑟sin𝜃 cos𝜑
𝑦 = 𝑟sin𝜃 sin𝜑
𝑧 = 𝑟 cos𝜃
|
𝐽
|
=𝑟
2
sin𝜃. Miền
(
𝑉
)
:{
0≤𝑟 ≤1
0≤ 𝜃 ≤
𝜋
2
0≤ 𝜑 ≤ 2𝜋
∭
(
𝑥
2
+ 𝑦
2
)
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∫
𝑑𝜑
2𝜋
0
∫
𝑑𝜃
𝜋
2
0
∫
𝑟
2
( )
sin𝜃
2
.𝑟
2
sin𝜃 𝑑𝑟
1
0
=
4
15
𝜋
⇒𝐼
1
=
4
15
𝜋 +
4
3
𝜋 =
8
5
𝜋
Mặt 𝑆
′
:{
𝑧 = 0 ⇒ = 0𝑑𝑧
𝑥
2
+ 𝑦
2
≤1
,
(
𝑛
󰇍
,
𝑂𝑧
)
>
𝜋
2
,có chi hình ếu lên 𝑂𝑥𝑦 𝐷: 𝑥là
2
+ 𝑦 ≤ 1
2
⇒𝐼
2
= − .0𝑑𝑥𝑑𝑦∬
𝑥
2
𝐷
=0 ⇒ 𝐼 = 𝐼
1
− 𝐼
2
=
8
5
𝜋
64
Câu 63: Tính 𝐼 =
3 2 2
( 2 ) (3 ) (6 )
S
x yz dydz x y y dzdx y z xy dxdy+ + + + +
với 𝑆 là m ặt
𝑧 = 𝑥 + 𝑦
2 2
v ng xuới 𝑧 ≤ 1, hướ ống dưới.
Đáp án: B. 0
Giải:
B
ổ sung thêm mặt 𝑆
′
:
{
𝑧 = 1
𝑥
2
+ 𝑦 ≤ 1
2
, hướng lên trên
Mặt 𝑆 ∪ 𝑆
′
là mặt cong trơn kín, giớ , hưới hạn miền 𝑉:𝑥 + 𝑦 ≤ 𝑧 ≤ 1
2 2
ng pháp
tuyến ngoài
Đặ
t {
𝑃 = 𝑥
3
+ 2𝑦𝑧
𝑄 = 3𝑥 𝑦 +𝑦
2
𝑅 = 6𝑦 𝑧 +
2
𝑥𝑦
⇒
{
𝑃
𝑥
′
= 3𝑥
2
𝑄
𝑦
′
=3𝑥
2
+ 1
𝑅
𝑧
′
=6𝑦
2
,𝑃
𝑥
′
,𝑄
𝑦
′
,𝑅
𝑧
′
liên t c ụ
𝐼 =∯𝑃𝑑𝑦𝑑𝑧 +𝑄𝑑𝑧𝑑𝑥+ 𝑅𝑑𝑥𝑑𝑦
𝑆∪𝑆
′
− ∬
𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦
𝑆
′
=𝐼
1
− 𝐼
2
Áp d ng công th c Ostrogradsky cho ụ ứ 𝐼
1
⇒𝐼
1
= ∭
(
6𝑥
2
+ 6𝑦
2
+ 1
)
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
65
Hình chi u cế ủa 𝑉 lên là 𝑂𝑥𝑦 𝐷: 𝑥
2
+ 𝑦 ≤1
2
Đặt
{
𝑥 = 𝑟 cos𝜑
𝑦 = 𝑟sin𝜑
𝑧 = 𝑧
𝐽 = 𝑟. ền 𝑉:Mi {
0≤ 𝑟 ≤ 1
0≤ 𝜑 ≤ 2𝜋
𝑟
2
≤𝑧 ≤ 1
⇒ 𝐼
1
= ∫
𝑑𝜑
2𝜋
0
∫
𝑑𝑟
1
0
∫
(6𝑟
2
+ 1)𝑟𝑑𝑧
1
𝑟
2
= ∫
𝑑𝜑
2𝜋
0
∫
𝑟
(
6𝑟
2
+ 1 1 − 𝑟
)(
2
)
𝑑𝑟
1
0
=
3𝜋
2
M
ặt 𝑆
′
:{
𝑧= 1 ⇒ = 0𝑑𝑧
𝑥
2
+ 𝑦
2
≤1
,
(
𝑛
󰇍
,
𝑂𝑧
)
< 𝜋/2.
Hình chi u cế ủa 𝑆
′
lên là 𝑂𝑥𝑦 𝐷: 𝑥
2
+ 𝑦 ≤ 1
2
⇒𝐼
2
= ∬
(
6𝑦
2
+ 𝑥𝑦
)
𝑑𝑥𝑑𝑦
𝑆
′
= ∬
(
6𝑦
2
+ 𝑥𝑦
)
𝑑𝑥𝑑𝑦
𝐷
= ∫
𝑑𝜑
2𝜋
0
∫
𝑟
[
6𝑟
2
( )
sin𝜑
2
+
sin2𝜑
2
]𝑑𝑟
1
0
=
3𝜋
2
⇒ 𝐼 = 𝐼
1
− 𝐼
2
= 0
Câu 64: Tính
2 2
1
( )
1
S
xdydz ydzdx dxdy
x y
− − +
+ +
với 𝑆 là mặt 2𝑧 = 𝑥 + 𝑦 ,
2 2
𝑧 ≤ 2 theo chi u âm c a tr ề ủ ục 𝑂𝑥
Đáp án: C.
( 2 10 5)
3
− +
Giải:
66
B
ổ sung thêm mặt 𝑆
′
:{
𝑧 = 2
𝑥
2
+ 𝑦 ≤ 4
2
, hướ ống dướng lên xu i
Mặt 𝑆 ∪ 𝑆
′
là mặt cong trơn kín, giới hạn miền 𝑉: + 𝑦
(
𝑥
2 2
)
/2≤ 𝑧 ≤ 2, hướng
pháp tuy n trong ế
Đặt
{
𝑃 =
−𝑥
√𝑥
2
+ 𝑦 + 1
2
𝑄 =
−𝑦
√𝑥
2
+ 𝑦 + 1
2
𝑅 =
1
√
𝑥
2
+ 𝑦 + 1
2
⇒
{
𝑃
𝑥
′
=
−𝑦
2
− 1
( )
𝑥
2
+ 𝑦
2
+ 1
√
𝑥
2
+ 𝑦
2
+ 1
𝑄
𝑦
′
=
−𝑥
2
− 1
( )
𝑥
2
+ 𝑦
2
+ 1
√
𝑥
2
+ 𝑦
2
+ 1
𝑅
𝑧
′
=0
,𝑃
𝑥
′
,𝑄
𝑦
′
,𝑅
𝑧
′
𝐼 =∯𝑃𝑑𝑦𝑑𝑧 +𝑄𝑑𝑧𝑑𝑥+ 𝑅𝑑𝑥𝑑𝑦
𝑆∪𝑆
′
− ∬
𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦
𝑆
′
=𝐼
1
− 𝐼
2
Áp d ng công th c Ostrogradsky cho ụ ứ 𝐼
1
⇒𝐼
1
= −∭
−𝑥
2
− 𝑦
2
− 2
( )
𝑥
2
+ 𝑦
2
+ 1
√
𝑥
2
+ 𝑦
2
+ 1
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
Hình chi u cế ủa 𝑉 lên là 𝑂𝑥𝑦 𝐷: 𝑥 + 𝑦 ≤ 4
2 2
Đặ
t {
𝑥 = 𝑟cos𝜑
𝑦 = 𝑟sin𝜑
𝑧 = 𝑧
,𝐽 = 𝑟 ⇒ 𝑉: {
0 ≤ 𝑟 ≤ 2
0≤ 𝜑 ≤ 2𝜋
𝑟
2
/2≤ 𝑧 ≤ 2
⇒𝐼
1
= −∫
𝑑𝜑
2𝜋
0
∫
𝑑𝑟
2
0
∫
−𝑟
2
− 2
( )
𝑟
2
+ 1
√
𝑟
2
+ 1
2
𝑟
2
2
.𝑟𝑑𝑧
= ∫ 𝑑𝜑
2𝜋
0
∫
(
𝑟
2
+ 2 𝑟
)
( )
𝑟
2
+ 1
√
𝑟
2
+ 1
.(2 −
𝑟
2
2
)𝑑𝑟
2
0
= 2𝜋
∫
(
𝑟
2
+ 2
)
𝑟
( )
𝑟
2
+ 1
√
𝑟
2
+ 1
.(2 −
𝑟
2
2
)𝑑𝑟
2
0
= 𝜋 ∫
(
𝑟
2
+ 2
)
( )
𝑟
2
+ 1
√
𝑟
2
+ 1
.(2 −
𝑟
2
2
)𝑑
(
𝑟
2
)
2
0
= 𝜋
∫
(
𝑢+ 2
)
( )
𝑢 + 1
√
𝑢+ 1
.
(
2 −
𝑢
2
)𝑑𝑢
2
0
=
𝜋
2
∫
(
𝑢 + 2 4 − 𝑢
)( )
( )
𝑢 + 1
√
𝑢+ 1
𝑑𝑢
2
0
67
Đặt
√
𝑢 + 1 = 𝑡 ⇒𝑢+ 1= 𝑡 = 2
2
⇒ 𝑑𝑢 𝑡𝑑𝑡
⇒𝐼
1
=
𝜋
2
∫
(
𝑡
2
+ 1 5 − 𝑡
)(
2
)
𝑡
3
2𝑡𝑑𝑡
√
5
1
=
𝜋
2
(
8
√
5
3
+
8
3
) = 𝜋 (
4
√
5
3
+
4
3
)
M
ặt 𝑆
′
:{
𝑧= 2 ⇒ = 0𝑑𝑧
𝑥
2
+ 𝑦
2
≤4
,
(
𝑛
󰇍
,
𝑂𝑧
)
> 𝜋/2.
Hình chi u cế ủa 𝑆
′
lên là 𝑂𝑥𝑦 𝐷:𝑥 + 𝑦
2 2
≤ 4
⇒𝐼
2
= ∬
𝑑𝑥𝑑𝑦
√1 + 𝑥 + 𝑦
2 2
𝑆
′
= ∬
−𝑑𝑥𝑑𝑦
√1 + 𝑥 + 𝑦
2 2
𝐷
=−∫
𝑑𝜑
2𝜋
0
∫
𝑟𝑑𝑟
√
1 + 𝑟
2
= ⋯ = −2𝜋(
√5 − 1)
2
0
⇒ 𝐼 = 𝐼
1
− 𝐼
2
=
(−2 + 10
√
5
)
𝜋
3
Câu 65: Biết
S
a
b
xdydz zdxdy
=
+
với 𝑆 là ph n trên cầ ủa mặt nón có phương
trình 𝑧 = − +𝑦
√
𝑥
2 2
,−1 ≤ 𝑧 ≤ 0 khi nhìn t chiừ ều dương trục 𝑂𝑧. Tính 2𝑎 + 𝑏
Đáp án: A. 1
Giải:
B
ổ sung thêm mặt 𝑆
′
: {
𝑧 = −1
𝑥
2
+ 𝑦 ≤1
2
ng xu i hướ ống dướ
Mặt kín 𝑆∪ 𝑆
′
giới hạn miền 𝑉: − 1≤ 𝑧 ≤ −
√
𝑥
2
+ 𝑦
2
68
Đặ
t {
𝑃 = 𝑥
𝑄 = 0
𝑅 = 𝑧
⇒ {
𝑃
𝑥
′
= 1
𝑄
𝑦
′
=0
𝑅
𝑧
′
=1
.𝑃
𝑥
′
,𝑄
𝑦
′
,𝑅
𝑧
′
liên t ục.
∬
𝑥𝑑𝑦𝑑𝑧 + 𝑦𝑑𝑥𝑑𝑦
𝑆
= ∯
𝑥𝑑𝑦𝑑𝑧 + 𝑧𝑑𝑥𝑑𝑦
𝑆∪𝑆
′
− ∬
𝑥𝑑𝑦𝑑𝑧 + 𝑧𝑑𝑥𝑑𝑦
𝑆
′
=𝐼
1
− 𝐼
2
Áp d ng công th c Ostrogradsky cho ụ ứ 𝐼
1
𝐼
1
= ∭
2𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
=2𝑉
(𝑉)
= 2.
1
3
𝜋𝑅
2
.ℎ =
2𝜋
3
(
Thể tích hình nón
)
M
ặt 𝑆
′
: {
𝑧 = −1 ⇒ = 0𝑑𝑧
𝑥
2
+ 𝑦
2
≤1
,
(
𝑛
󰇍
,𝑂𝑧
)
> 𝜋/2 có hình chi u lên là ế 𝑂𝑥𝑦 𝐷:𝑥 + 𝑦 ≤ 1
2 2
𝐼
2
= − −1𝑑𝑥𝑑𝑦∬
𝐷
= ∬
𝑑𝑥𝑑𝑦
𝐷
=𝑆
(
𝐷
)
=𝜋𝑅
2
=𝜋
⇒𝐼 = 𝐼
1
− 𝐼
2
=
2𝜋
3
− 𝜋 =
−𝜋
3
⇒𝑎 = −1, 𝑏= 3
Câu 66: Tính
zdz+
d ng tròn ọc theo đườ 𝐶:𝑥 + 𝑦 = 1,𝑧 = 0
2 2
chiều dương giới hạn mặt cầu 𝑧 = 1 − 𝑥 −𝑦
√
2 2
Đáp án: D.
8
−
Giải:
Đường cong i h n ph n m t c u 𝐶 giớ ạ ầ ặ ầ 𝑆: 𝑧 =
√
1 − 𝑥 − 𝑦
2 2
ng lên trên hướ
69
Áp d ng công th c Stoke: ụ ứ
∮
𝑥
2
𝑦
3
𝑑𝑥 𝑑𝑦+ + 𝑧𝑑𝑧
𝐶
= ∬
−3𝑥
2
𝑦
2
𝑑𝑥𝑑𝑦
𝑆
Hình chi u c a mế ủ ặt 𝑆 lên là 𝑂𝑥𝑦 𝐷: 𝑥 + 𝑦 ≤ 1
2 2
Đặ
t {
𝑥 = 𝑟cos𝜑
𝑦 = sin𝜑
,𝐽 = 𝑟 ⇒ 𝐷:
{
0 ≤ 𝑟 ≤ 1
0≤ 𝜑 ≤ 2𝜋
⇒ ∬−3𝑥
2
𝑦
2
𝑑𝑥𝑑𝑦
𝑆
=−3∫
𝑑𝜑
2𝜋
0
∫
𝑟
2
sin
2
𝜑𝑟
2
cos
2
𝜑.𝑟𝑑𝑟
1
0
=⋯ =
−𝜋
8
Câu 67: Tính tích phân 𝐼 =
2 2
1
( 2 2 )
1 4 4
S
xdydz ydzdx dxdy
x y
− − +
+ +
v là ới 𝑆
mặt có phương trình 𝑧 = 𝑥
2
+ 𝑦 ,0 ≤ 𝑧 ≤ 4
2
theo chiều 𝑧 ≥ 0
Đáp án: B.
(17 17 1)
6
−
Giải:
Đặ
t 𝐹
(
𝑥,𝑦,𝑧
)
= 𝑧− 𝑥 − 𝑦
2 2
Do
(
𝑛
󰇍
,
𝑂𝑧
)
< 𝜋/2
nên 𝑛
󰇍
=
(𝐹
𝑥
′
,𝐹
𝑦
′
,𝐹
𝑧
′
)
=
(
−2𝑥,−2𝑦,1 𝑛
)
⇒
|
󰇍
|
=
√1 + 4𝑥 + 4𝑦
2 2
⇒cos𝛼 =
−2𝑥
√
1 + 4𝑥 + 4𝑦
2 2
,cos𝛽 =
−2𝑦
√
1 + 4𝑥 + 4𝑦
2 2
,cos𝛾 =
1
√1 + 4𝑥 + 4𝑦
2 2
Áp d ng công th c liên h a tích phân m t lo i I và i II ụ ứ ệ giữ ặ ạ loạ
𝐼 = 𝑃. cos𝛼 + 𝑄.cos𝛽 + 𝑅.cos𝛾
∬
(
)
𝑑𝑆
𝑆
=⋯ = 1.∬ 𝑑𝑆
𝑆
70
M
ặt 𝑆: 𝑧 = 𝑥
2
+ 𝑦 ⇒ 𝑧
2
𝑥
′
= 2𝑥,𝑧
𝑦
′
= 2𝑦 ⇒ 1 + 4𝑥 + 4𝑦𝑑𝑆 =
√
2 2
𝑑𝑥𝑑𝑦
Hình chi u cế ủa 𝑆 lên là 𝑂𝑥𝑦 𝐷:𝑥 + 𝑦 ≤ 4
2 2
⇒𝐼 = 1 + 4𝑥 + 4𝑦∬√
2 2
𝑑𝑥𝑑𝑦
𝐷
Đặ
t {
𝑥 = 𝑟cos𝜑
𝑦 = 𝑟sin𝜑
,𝐽 = 𝑟 ⇒ 𝐷:
{
0 ≤ 𝑟 ≤ 2
0≤ 𝜑 ≤ 2𝜋
⇒𝐼 = ∫ 𝑑𝜑
2𝜋
0
∫
√
1 + 4𝑟
2
.𝑟𝑑𝑟
2
0
=
2𝜋
2
∫
√
1 + 4𝑟
2
𝑑
(
𝑟
2
)
2
0
=𝜋 1 + 4𝑢∫
√
𝑑𝑢
4
0
=
(17
√
17 − 1)𝜋
6
Câu 68: Tính tích phân 𝐼 =
3 3
(6 9 ) (3 2 ) (3 3 )
S
z y dydz x z dzdx y x dxdy− + − + −
với
𝑆 là m t ặ 𝑥
2
+ 3𝑦 + 𝑧 = 1,𝑧 ≥ 0,
2 4
hướng lên trên.
Đáp án: C. 0
Giải:
Đặ
t 𝐹
(
𝑥,𝑦,𝑧
)
= 𝑥 + 3𝑦 + 𝑧 − 1
2 2 4
C. 0
Vecto pháp tuyến 𝑛
󰇍
=
(𝐹
𝑥
′
,𝐹
𝑦
′
,𝐹
𝑧
′
)
=
(
2𝑥,6𝑦,4𝑧
3
)
(do
(
𝑛
󰇍
,
𝑂𝑧
)
<𝜋/2)
|
𝑛
󰇍
|
= √
4𝑥
2
+ +36𝑦
2
16𝑧
6
= 2 + 9𝑦 + 4𝑧√𝑥
2 2 6
⇒
{
cos𝛼 =
𝑛
𝑥
|
𝑛
󰇍
|
=
𝑥
√𝑥
2
+ 4𝑦 + 4𝑧
2 6
cos𝛽 =
𝑛
𝑦
|
𝑛
󰇍
|
=
3𝑦
√𝑥
2
+ 9𝑦 + 4𝑧
2 6
cos𝛾 =
𝑛
𝑧
|
𝑛
󰇍
|
=
2𝑧
3
√𝑥
2
+ 9𝑦 + 4𝑧
2 6
Áp d ng công th c liên h a tích phân m t lo i I và lo i II ụ ứ ệ giữ ặ ạ ạ
∬
𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦
𝑆
= ∬
(
𝑃.cos𝛼 + 𝑄.cos𝛽 + 𝑅.cos𝛾
)
𝑑𝑆
𝑆
71
⇒𝐼 =
∬
𝑥
(
6𝑧
3
− 9𝑦
)
+ 3𝑦
(
3𝑥 − 2𝑧
3
)
+ 2𝑧
3
(
3𝑦 − 3𝑥
)
√𝑥
2
+ 9𝑦 + 4𝑧
2 6
𝑆
𝑑𝑆 = 0
Câu 69: Tính
2
(2 ) ( 2 ) (1 6 )
S
x xy dydz y xz dzdx z z dxdy+ + + + + +
với 𝑆 là m t nặ ằm
trong c a n a c
ủ ử ầu 𝑧 = − + 𝑦 + 𝑧
√
16 −
(
𝑥
2 2 2
)
Đáp án: B. (
80 192−
√
2
)
𝜋
Giải:
B
ổ sung thêm mặt 𝑆
′
:
{
𝑧 = 0
𝑥
2
+ 𝑦
2
≤ 16
hướng theo chi u âm trề ục 𝑂𝑧.
Mặt 𝑆 ∪ 𝑆
′
t o thành m ng pháp tuy n trong gi i h n miạ ặt cong kín, hướ ế ớ ạ ền
𝑉:−
√
16 − 𝑥
2
− 𝑦
2
2
≤𝑧 ≤0
Đặt 𝐼 =
2
(2 ) ( 2 ) (1 6 )
S
x xy dydz y xz dzdx z z dxdy+ + + + + +
Đặ
t {
𝑃 = 2𝑥 + 𝑥𝑦
𝑄 = 𝑦 +2𝑥𝑧
𝑅 = 1 + 6𝑧 +𝑧
2
⇒
{
𝑃
𝑥
′
= 2 + 𝑦
𝑄
𝑦
′
=1
𝑅
𝑧
′
=6 + 2𝑧
liên t c ụ
𝐼 =∯𝑃𝑑𝑦𝑧 +𝑄𝑑𝑧𝑑𝑥+ 𝑅𝑑𝑥𝑑𝑦
𝑆∪𝑆
′
− ∬
𝑃𝑑𝑦𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦
𝑆
′
=𝐼
1
− 𝐼
2
Áp d ng công th c Ostrgradsky cho tích phân ụ ứ 𝐼
1
𝐼
1
= − 2 + 𝑦 + 1+ 6+2𝑧 𝑑𝑥𝑑𝑦𝑑𝑧∭
(
)
𝑉
=− 9+𝑦 + 2𝑧 𝑑𝑥𝑑𝑦𝑑𝑧∭
(
)
𝑉
Do
𝑓
(
𝑥,𝑦,𝑧 = 𝑦
)
là hàm l v i bi ẻ ớ ến 𝑦,miền 𝑉 đố ứi x ng qua 𝑂𝑥𝑧
⇒ ∭𝑦𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
=0 ⇒ 𝐼
1
= − 9 + 2𝑧 𝑑𝑥𝑑𝑦𝑑𝑧∭
(
)
𝑉
Hình chi u cế ủa 𝑉 lên là 𝑂𝑥𝑦 𝐷:𝑥 + 𝑦
2 2
≤ 16
Đặ
t {
𝑥 = 𝑟cos𝜑
𝑦 = 𝑟sin𝜑
𝑧 = 𝑧
,𝐽 = 𝑟 ⇒ 𝑉:{
0 ≤ 𝑟 ≤4
0≤ 𝜑 ≤ 2𝜋
−
√
(
16 − 𝑟
2
)
/2 ≤ 𝑧 ≤ 0
72
𝐼
2
= −∫
𝑑𝜑
2𝜋
0
∫
𝑑𝑟
4
0
∫
(
9 + 2𝑧
)
0
−
√
(
16−𝑟
2
)
2
=⋯ = −192
√
2𝜋 + 64𝜋
Xét tích phân 𝐼
2
M
ặtn 𝑆
′
:{
𝑧 = 0 ⇒ = 0𝑑𝑧
𝑥
2
+ 𝑦
2
≤ 16
ng theo chi u âm trhướ ề ục 𝑂𝑧,
(
𝑛
󰇍
,
𝑂𝑧
)
> 𝜋, 2 có hình
chiếu lên 𝑂𝑥𝑦 là 𝐷: 𝑥
2
+ 𝑦
2
≤ 16
⇒𝐼
2
= − 1𝑑𝑥𝑑𝑦∬
𝐷
=−16𝜋
⇒𝐼 = 𝐼
1
− 𝐼
2
= (
80 192−
√
2)
𝜋
Câu 70: Tính
S
xydydz yzdzdx zxdxdy+ +
biết 𝑆 là m t ngoài c a t ặ ủ ứ diện 𝑂𝐴𝐵𝐶 với
𝑂
(
0,0,0 , 𝐴 1,0,0 ,𝐵 0,1,0 ,𝐶 0,0,1
) ( ) ( ) ( )
Đáp án: B.
1
8
Giải:
𝑆
là m t i h n mi n kín ặ giớ ạ ề 𝑉:{
0 ≤ 𝑥 ≤ 1
0≤ 𝑦 ≤ 1 − 𝑥
0≤ 𝑧 ≤ 1 − 𝑥 − 𝑦
,vecto pháp tuyến hướng ra ngoài.
Đặt {
𝑃 = 𝑥𝑦
𝑄 = 𝑦𝑧
𝑅 =
𝑧𝑥
⇒ {
𝑃
𝑥
′
= 𝑦
𝑄
𝑦
′
=𝑧
𝑅
𝑧
′
=𝑥
liên t c ụ
Áp d ng công th c Ostrogradsky ụ ứ
∬
𝑥𝑦𝑑𝑦𝑑𝑧 + 𝑦𝑧𝑑𝑧𝑑𝑥 + 𝑧𝑥𝑑𝑥𝑑𝑦
𝑆
= ∭
(
𝑥+ 𝑦 + 𝑧
)
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
=∫𝑑𝑥
1
0
∫
𝑑𝑦
1−𝑥
0
∫
( )
𝑥+ 𝑦 + 𝑧 𝑑𝑧
1−𝑥−𝑦
0
=
1
8
Câu 71: Biết
2 2 2
2 dyd
S
x z y dzdx z dxdy a b
+ − = +
, ch n khọ ẳng định đúng
Đáp án: A. 𝑎 + 3𝑏 = 12
Giải:
73
Mặt 𝑆 kín gi i h n miớ ạ ển 𝑉:0 ≤ 𝑦 ≤ √1 − 𝑧
2
,0 ≤𝑥 ≤ 2, ng pháp tuy n ngoài hướ ế
Đặ
t 𝑃 = 2𝑥 ,𝑄 = 𝑦 ,𝑅 = −𝑧 ⇒𝑃
2 2 2
𝑥
′
=4𝑥,𝑄
𝑦
′
=2𝑦,𝑅
𝑧
′
=−2𝑧 liên t ục.
Áp d ng công th c Ostrogradsky: ụ ứ
𝐼 = 2𝑥 𝑑𝑦𝑑𝑧+ 𝑦 𝑑𝑧𝑑𝑧 −𝑧 𝑑𝑥𝑑𝑦∬
2 2 2
𝑆
= ∭
(
4𝑥+ 2𝑦 − 2𝑧
)
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
Đặ
t {
𝑦= 𝑟 cos𝜑
𝑧 = 𝑟 sin𝜑
𝑥 = 𝑥
,𝐽 = 𝑟 ⇒ Miền 𝑉: {
0 ≤ 𝑟 ≤ 1
−𝜋/2≤ 𝜑 ≤ 𝜋/2
0≤ 𝑥 ≤ 2
𝐼 = 2 ∫ 𝑑𝜑
𝜋
2
−𝜋
2
∫
𝑑𝑟
1
0
∫
(
2𝑥+ 𝑟cos𝜑 .𝑟𝑑𝑥
)
2
0
=2 ∫
𝑑𝜑
𝜋
2
−𝜋
2
∫
(
4𝑟 + 2𝑟
2
cos𝜑
)
𝑑𝑟
1
0
=4𝜋+
8
3
⇒ 𝑎 = 4, 𝑏=
8
3
Câu 72: Biết
( ) ( ) ( )
S
a
I x z dydz y x dzdx z y dxdy
b
= + + + + + =
với 𝑆 là m t trong ặ
của parabol 𝑧 = 𝑥 + 𝑦 𝑥 + 𝑧 = 2
2 2
n i mằm dướ ặt Tính . 𝑎− 𝑏
Đáp án: B. 49
Giải:
Bổ sung thêm mặt 𝑆
′
:𝑥+ 𝑧 = 2 ng theo chi u âm trhướ ề ục 𝑂𝑧 n m trong mằ ặt
parabol 𝑧 = 𝑥 +𝑦
2 2
Ta có mặt 𝑆 ∪ 𝑆
′
là m ng pháp tuy n trong, gi i h n mi ặt kín, hướ ế ớ ạ ền
𝑉:𝑥 + 𝑦 ≤ 𝑧 ≤ 2 − 𝑥
2 2
Đặ
t {
𝑃 = 𝑥 + 𝑧
𝑄 = 𝑦 +𝑥
𝑅 = 𝑧 +𝑦
⇒
{
𝑃
𝑥
′
= 1
𝑄
𝑦
′
=1
𝑅
𝑧
′
=1
liên t c ụ
𝐼 =∯𝑃𝑑𝑦𝑑𝑧 +𝑄𝑑𝑧𝑑𝑥+ 𝑅𝑑𝑥𝑑𝑦
𝑆∪𝑆
′
− ∬
𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦
𝑆
=𝐼
1
− 𝐼
2
Áp d ng công th c Ostrogradsky cho tích phân ụ ứ 𝐼
1
74
𝐼
1
= − 3𝑑𝑥𝑑𝑦𝑑𝑧∭
𝑉
Hình chi u cế ủa 𝑉 lên là 𝑂𝑥𝑦 𝐷: 𝑥 + 1/2
( )
2
+ 𝑦 = 9/4
2
⇒𝐼
1
= −3 𝑑𝑥𝑑𝑦∬
𝐷
∫
𝑑𝑧
2−𝑥
𝑥
2
+𝑦
2
=−3 2 − 𝑥 − 𝑥∬
(
2
− 𝑦
2
)
𝑑𝑥𝑑𝑦
𝐷
= 3
∬
(
−2 + 𝑥+ 𝑥
2
+ 𝑦
2
)
𝑑𝑥𝑑𝑦
𝐷
=3 (𝑥 +∬[
1
2
)
2
+ 𝑦
2
−
9
4
]
𝑑𝑥𝑑𝑦
𝐷
Đặ
t {
𝑥 = −1/2 + 𝑟 cos𝜑
𝑦 = 𝑟 sin𝜑
,𝐽 = 𝑟 ⇒ 𝐷:{
0 ≤ 𝑟 ≤ 3/2
0≤ 𝜑 ≤ 2𝜋
𝐼
1
= 3 ∫
𝑑𝜑
2𝜋
0
∫
(𝑟
2
−
9
4
).𝑟𝑑𝑟
3
2
0
=⋯ =
−243𝜋
32
Xét tích phân 𝐼
2
Mặt 𝑆
′
:𝑥 + 𝑧 = 2 ng theo chi u âm trhướ ề ục 𝑂𝑧 có hình chi u lên là ế 𝑂𝑥𝑦
𝐷: 𝑥 + 1/2
( )
2
+ 𝑦 = 9/4,
2
vecto pháp tuyến 𝑛
󰇍
=
(
−1,0,−1 𝑛
)
,
|
󰇍
|
= 1/
√
2
Áp d ng công th c liên h a tích phân m t lo i I và lo i II ụ ứ ệ giữ ặ ạ ạ
𝐼
2
=
1
√
2
∬
[
−1.
(
𝑥+ 𝑧
)
+ 0.
(
𝑦 + 𝑥
)
− 1.
(
𝑧 + 𝑦
)]
𝑑𝑆
𝑆
′
=
−1
√
2
∬
(
𝑥+ 𝑦 + 2𝑧
)
𝑆
′
𝑑𝑆
V
ới 𝑆
′
:𝑧 = 2 − 𝑥 ⇒ 1 + 𝑧𝑑𝑆 =
√
(
𝑥
′
)
2
+ (
𝑧
𝑦
′
)
2
𝑑𝑥𝑑𝑦 = 2𝑑𝑥𝑑𝑦
√
⇒𝐼
2
= − 𝑥 +𝑦+ 4 − 2𝑥∬
(
)
𝐷
𝑑𝑥𝑑𝑦 = 𝑥 − 𝑦− 4∬
(
)
𝐷
𝑑𝑥𝑑𝑦
= ∫ 𝑑𝜑
2𝜋
0
∫
(−
1
2
+ 𝑟cos 𝜑 − 𝑟 sin𝜑 − 4).𝑟𝑑𝑟
3
2
0
=⋯ =
−81𝜋
8
75
𝐼 = 𝐼
1
− 𝐼
2
=
81𝜋
32
⇒𝑎 = 81 32,𝑏 =
Câu 73: Tính di n tích m ệ ặt 𝑆:𝑧 = 2 + + 𝑦
√
𝑥
2 2
,𝑧 ≤ 3
Đáp án:
C.
√
2 𝜋
(
đvdt
)
Giải:
Mặt 𝑧 = 2 + ⇒ √𝑥
2
+ 𝑦
2
𝑑𝑆 =
√
1 + (𝑧
𝑥
′
)
2
+ (𝑧
𝑦
′
)
2
𝑑𝑥𝑑𝑦 = 2𝑑𝑥𝑑𝑦
√
Hình chi u cế ủa 𝑆 lên là 𝑂𝑥𝑦 𝐷: 𝑥
2
+ 𝑦 ≤ 1
2
Diện tích m là: ặt 𝑆
𝑆
(
𝑆
)
= ∬
𝑑𝑆
𝑆
=
√
2∬
𝑑𝑥𝑑𝑦
𝐷
=
√
2.𝑆
(
𝐷
)
=
√
2𝜋
Câu 74: Tính di n tích m t cong vệ ặ 𝑆 ới 𝑆 là ph n m t nón ầ ặ 𝑦 = +𝑧
√
𝑥
2 2
với điều
kiện 1≤𝑦 ≤ 2,𝑧 ≥ 0
Đáp án: A.
3 2
2
(đvdt)
Giải:
76
Mặt 𝑆: 𝑦 =
√
𝑥
2
+ 𝑧
2
⇒
{
𝑦
𝑥
′
=
𝑥
√𝑥
2
+ 𝑦
2
𝑦
𝑧
′
=
𝑧
√
𝑥
2
+ 𝑦
2
⇒ 𝑑𝑆 =
√
1 +
(
𝑦
𝑥
′
)
2
+
(
𝑦
𝑧
′
)
2
𝑑𝑥𝑑𝑧 = 2𝑑𝑥𝑑𝑧
√
Hình chi u cế ủa 𝑆 lên là 𝑂𝑥𝑧 𝐷:1 ≤ 𝑥 + 𝑧 ≤ 4
2 2
Đặ
t {
𝑧= 𝑟 cos𝜑
𝑥 = 𝑟 sin𝜑
,𝐽 = 𝑟 ⇒𝐷:
{
1 ≤ 𝑟 ≤ 2
−𝜋/2≤ 𝜑 ≤ 𝜋/2
Diện tích m t cong là: ặ 𝑆
𝑆
(
𝑆
)
= ∬
𝑑𝑆
𝑆
=
√
2∬
𝑑𝑥𝑑𝑧
𝐷
=
√
2 ∫ 𝑑𝜑
𝜋
2
−𝜋
2
∫
𝑟𝑑𝑟
2
1
=
3
√
2
2
𝜋
(
đvdt
)
Câu 75: Tính di n tích m t paraboloid n m phía trên mệ ặ 𝑧 = 4𝑥 − 𝑥 − 𝑦
2 2
ằ ặt 𝑂𝑥𝑦 là
( 17 1)a
b
−
, tính 𝑎 + 𝑏
Đáp án: B. 23
Giải:
M
ặt 𝑧 = 4𝑥 − 𝑥 − 𝑦
2 2
⇒ {
𝑧
𝑥
′
=4 − 2𝑥
𝑧
𝑦
′
= −2𝑦
Hình chi u c a m
ế ủ ặt 𝑆 lên là 𝑂𝑥𝑦 𝐷: 𝑥 − 2
( )
2
+ 𝑦 ≤ 4
2
Diện tích m ặt
𝑆 = ∬𝑑𝑆
𝑆
= ∬
√
1 +
(
𝑧
𝑥
′
)
2
+ (
𝑧
𝑦
′
)
2
𝑑𝑥𝑑𝑦
𝐷
= ∬√
1 + 4
(
𝑥− 2
)
2
+ 4𝑦
2
𝑑𝑥𝑑𝑦
𝐷
Đặ
t {
𝑥 = 2 + 𝑟 cos𝜑
𝑦 = 𝑟 sin𝜑
,𝐽 = 𝑟 ⇒ 𝐷:{
0 ≤ 𝑟 ≤ 2
0≤ 𝜑 ≤ 2𝜋
𝑆 = ∫ 𝑑𝜑
2𝜋
0
∫
𝑟. 1 +4𝑟
√
2
𝑑𝑟
2
0
=
(
17 17
√
− 1 𝜋)
6
⇒𝑎 = 17,𝑏 = 6
Câu 76: Tính di n tích ph n m t paraboloid a mãn ệ ầ ặ 𝑥 = 𝑦 + 𝑧
2 2
thỏ 𝑥 ≤ 1
77
Đáp số: A.
(5 5 1)
6
−
Giải:
M
ặt 𝑥 =𝑦 + 𝑧
2 2
⇒ {
𝑥
𝑦
′
=2𝑦
𝑥
𝑧
′
=2𝑧
Hình chi u c a mế ủ ặt 𝑆 lên là 𝑂𝑦𝑧 𝐷: 𝑦 + 𝑧 ≤ 1
2 2
Diện tích m ặt
𝑆 = ∬𝑑𝑆
𝑆
= ∬
√
1 +
(
𝑥
𝑦
′
)
2
+
(
𝑥
𝑧
′
)
2
𝑑𝑦𝑑𝑧
𝐷
= ∬√
1 + 4𝑦
2
+ 4𝑧
2
𝑑𝑦𝑑𝑧
𝐷
Đặ
t {
𝑦= 𝑟 cos𝜑
𝑧 = 𝑟 sin𝜑
,𝐽 = 𝑟 ⇒ 𝐷:
{
0 ≤ 𝑟 ≤ 1
0≤ 𝜑 ≤ 2𝜋
𝑆 = ∫ 𝑑𝜑
2𝜋
0
∫
𝑟. 1 +4𝑟
√
2
𝑑𝑟
1
0
=
(
5
√
5 − 1 𝜋)
6
Câu 77: Tính di n tích m ệ ặt 𝑆:𝑧 = + 𝑦
√
𝑥
2 2
, 𝑧≤3
Đáp án:
Giải:
Mặt 𝑧 = ⇒ √𝑥
2
+ 𝑦
2
𝑑𝑆 =
√
1 + (𝑧
𝑥
′
)
2
+ (𝑧
𝑦
′
)
2
𝑑𝑥𝑑𝑦 = 2𝑑𝑥𝑑𝑦
√
Hình chi u cế ủa 𝑆 lên là n tích m𝑂𝑥𝑦 𝐷: 𝑥
2
+ 𝑦 ≤ 9
2
. Diệ ặt 𝑆 là:
𝑆
(
𝑆
)
= ∬
𝑑𝑆
𝑆
=
√
2∬
𝑑𝑥𝑑𝑦
𝐷
=
√
2.𝑆
(
𝐷
)
=9 2𝜋
√
Lý thuyết trường:
Câu 78:
Tính đạo hàm theo hướng 𝑙
=
(
1,2,−2
)
của 𝑢 = 𝑒
𝑥
(
𝑦
2
+ 𝑧 − 2
)
𝑥𝑦𝑧
3
tại
𝐴
(
0,1,2
)
Đáp án: B.
11
3
−
78
Giải:
Ta có:
𝑢 = 𝑒
𝑥
(
𝑦
2
+ 𝑧 − 2
)
𝑥𝑦𝑧
3
⇒ {
𝑢
𝑥
′
=𝑒
𝑥
(
𝑦
2
+ 𝑧 − 2𝑦𝑧
)
3
𝑢
𝑦
′
= 2𝑒
𝑥
𝑦 − 2𝑥𝑧
3
𝑢
𝑧
′
=𝑒
𝑥
− 6𝑥𝑦𝑧
2
⇒ {
𝑢
𝑥
′
(
𝐴
)
=−13
𝑢
𝑦
′
(
𝐴
)
=2
𝑢
𝑧
′
(
𝐴
)
=1
𝑙
=
(
1,2,−2 ⇒ cos𝛼 =
)
1
3
,cos𝛽 =
2
3
,cos𝛾 =
−2
3
⇒
𝜕𝑢
𝜕𝑙
( ( )
𝐴
)
= −13 .
1
3
+ 2.
2
3
+ 1.
−2
3
=
−11
3
Câu 79:
Cho Tính 𝑢
(
𝑥,𝑦,𝑧 = 𝑥 + 3𝑦𝑥 + 2𝑦𝑧 .
)
3 2 2
u
n
với 𝑛
󰇍
là vecto pháp tuyến
hư
ớng ra ngoài c a mủ ặt cầu 𝑥
2
+ 𝑦 + 𝑧 = 3,𝑧 ≤ 0
2 2
tại điểm 𝐴
(
1,1,−1
)
Đáp án: A. −6
√
3
Giải:
Xét
𝐹
(
𝑥,𝑦,𝑧
)
= 𝑥 + 𝑦 + 𝑧 − 3
2 2 2
⇒ Vecto pháp tuy ng ra ngoài c a nến hướ ủ ửa cầu 𝑥
2
+ 𝑦 + 𝑧 = 3
2 2
phía dưới 𝑂𝑥𝑦
t
ại 𝐴
(
1,1,−1
)
là 𝑛
󰇍
=− 𝐹
(
𝑥
′
(
𝐴
)
,𝐹
𝑦
′
( )
𝐴 ,𝐹
𝑧
′
( ( (
𝐴
)
) = − 2,2,−2
)
= −2,−2,2
)
𝑢
(
𝑥,𝑦,𝑧 =𝑥 + 3𝑦𝑥 + 2𝑦𝑧
)
3 2 2
⇒ {
𝑢
𝑥
′
=3𝑥
2
+ 6𝑦𝑥
𝑢
𝑦
′
=3𝑥
2
+ 2𝑧
2
𝑢
𝑧
′
=4𝑦𝑧
⇒ {
𝑢
𝑥
′
(
𝐴
)
=9
𝑢
𝑦
′
(
𝐴
)
=5
𝑢
𝑧
′
(
𝐴
)
=−4
𝑛
󰇍
=
(
−2,−2,2 𝑛
)
⇒
|
󰇍
|
=2
√
3 ⇒ cos 𝛼 =
−1
√
3
,cos𝛽 =
−1
√
3
,cos𝛾 =
1
√
3
⇒
𝜕𝑢
𝜕𝑛
󰇍
(
𝐴
)
=9.
−1
√
3
+ 5.
−1
√
3
+
(
−4
)
1
√
3
=−6√3
Câu 80:
Biết nhiệt độ ại điể trong không gian đượ t m
(
𝑥,𝑦,𝑧
)
c cho bởi hàm
𝑇
(
𝑥,𝑦,𝑧
)
=
80
1 + 𝑥 + 2𝑦 + 3𝑧
2 2 2
ở đó 𝑇 có đơn vị là và ℃ 𝑥,𝑦,𝑧 là mét. Theo hướng nào thì nhi ệt độ tăng nhanh
nh
ất tại điểm 𝐴
(
1,1,−2
)
79
Đáp án: C.
5 5 15
; ;
8 4 4
− −
Giải:
Xét vecto 𝑙
, o hàm cđạ ủa 𝑇 ng theo hướ 𝑙
t là: ại 𝐴
(
1,1,−2
)
𝜕𝑇
𝜕𝑙
(
𝐴
)
=𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑢
(
𝐴
)
.
𝑙
|
𝑙
|
Để nhiệt độ tăng nhanh nhất ⇔
T
l
l n nhớ ất
⇔𝑙
⇈ 𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑢
(
𝐴
)
⇔𝑙
= 𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑢
(
𝐴
)
𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑢 = (
−160𝑥
(
1 + 𝑥
2
+ 2𝑦
2
+ 3𝑧
2
)
2
,
−320𝑦
(
1 + 𝑥
2
+ 2𝑦
2
+ 3𝑧
2
)
2
,
−480𝑧
(
1 + 𝑥
2
+ 2𝑦
2
+ 3𝑧
2
)
2
)
⇒𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑢
(
𝐴
)
=(
−5
8
,
−5
4
,
15
4
)⇒ 𝑙
= (
−5
8
,
−5
4
,
15
4
)
Vậy theo nhiệt độ tăng nhanh ất theo 𝑙
nh hướng
= (
−5
8
,
−5
4
,
15
4
)
Câu 81: Tính góc gi hai vecto ữa 𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑧 (đơn vị: radian) c a các ủ trường vô hướng
sau
𝑧
1
=
√
𝑥
2
+ 𝑦
2
,𝑧
2
= 𝑥 − 3𝑦 +
√
3𝑥𝑦 tại 𝑀
(
3,4
)
(Chọn đáp án gần đúng nhất)
Đáp án: A. 2
Giải:
𝑧
1
= √
𝑥
2
+ 𝑦
2
⇒
{
𝑧
1𝑥
′
=
𝑥
√𝑥
2
+ 𝑦
2
𝑧
1𝑦
′
=
𝑦
√
𝑥
2
+ 𝑦
2
⇒ 𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑧
1
= (
𝑥
√
𝑥
2
+ 𝑦
2
,
𝑦
√
𝑥
2
+ 𝑦
2
)
⇒𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑧
1
(
𝑀
)
= (
3
5
,
4
5
)
𝑧
2
= 𝑥 − 3𝑦 +
√
3𝑥𝑦 ⇒
{
𝑧
2𝑥
′
=1 +
√
3𝑦
2
√
𝑥
𝑧
2𝑦
′
=−3 +
√
3𝑥
2
√
𝑦
⇒𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑧
2
= (1 +
√
3𝑦
2
√
𝑥
,−3 +
√
3𝑥
2
√
𝑦
)
80
⇒𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑧
2
(
𝑀
)
= (2,
−9
5
)
⇒cos 𝑔𝑟𝑎𝑑(
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑧
1
( )
𝑀 ,𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑧
2
( )
𝑀 )=
𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑧
1
(
𝑀
)
.𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑧
2
(
𝑀
)
|
𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑧
1
( )
𝑀 |.|
𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑧
2
( )
𝑀 |
=
−12
5
√
145
⇒ (𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑧
1
,𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑧
2
)
≈ 1, radian77
( )
Câu 82:
Cho Tính 𝑢
(
𝑥,𝑦,𝑧 (1 + 𝑥 + 𝑒 ),𝑂 0,0,0 ,𝐴 1,−2,2 .
)
= ln
2 𝑦−𝑧
( ) ( )
u
l
theo
hướng 𝑂𝐴
󰇍
󰇍
󰇍
󰇍
󰇍
Đáp án: B.
2
3
−
Giải:
𝑢
(
𝑥,𝑦,𝑧
)
= ln(1 + 𝑥 + 𝑒 ) ⇒
2 𝑦−𝑧
{
𝑢
𝑥
′
=
2𝑥
1 + 𝑥 + 𝑒
2 𝑦−𝑧
𝑢
𝑦
′
=
𝑒
𝑦−𝑧
1 + 𝑥 + 𝑒
2 𝑦−𝑧
𝑢
𝑧
′
=
−𝑒
𝑦−𝑧
1 + 𝑥 + 𝑒
2 𝑦−𝑧
⇒
{
𝑢
𝑥
′
(
𝑂
)
=0
𝑢
𝑦
′
(
𝑂
)
=
1
2
𝑢
𝑧
′
(
𝐴
)
=
−1
2
𝑂𝐴
󰇍
󰇍
󰇍
󰇍
󰇍
=
(
1,−2,2
)
⇒ |𝑂𝐴
󰇍
󰇍
󰇍
󰇍
󰇍
|
=3 ⇒ cos𝛼 =
1
3
,cos𝛽 =
−2
3
,cos𝛾 =
2
3
⇒
𝜕𝑢
𝜕𝑂𝐴
󰇍
󰇍
󰇍
󰇍
󰇍
(
𝑂
)
=0.
1
3
+
1
2
.
−2
3
−
1
2
.
2
3
=
−2
3
Câu 83: Theo hướng nào thì s n thiên c a hàm ự biế ủ 𝑢 = 𝑥 sin𝑧 − 𝑦 cos𝑧 t i g c tạ ố ọa
độ là lớn nhất
Đáp án:
B. 𝑙
=
(
0,−1,0
)
Giải:
𝑢
(
𝑥,𝑦,𝑧 =𝑥 sin𝑧− 𝑦 cos𝑧 ⇒
)
{
𝑢
𝑥
′
=sin𝑧
𝑢
𝑦
′
=−cos𝑧
𝑢
𝑧
′
=𝑥 cos𝑧 + 𝑦 sin𝑧
⇒𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑢 = sin𝑧,−cos𝑧 ,𝑥 cos𝑧+ 𝑦 sin𝑧
( )
Để t ốc độ biến thiên c tủa 𝑢 ại 𝑂
(
0,0,0
)
là l n nh t thì cớ ấ ần theo hướng
81
𝑙
=𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑢
(
𝑂
)
=
(
0,−1,0
)
Câu 84:
Cho điểm 𝐴
(
2,−1,0 ,𝐵 1,1,3
) ( )
. Tính đạo hàm của hàm 𝑢 = 𝑥 + 3𝑦 +
3 2
𝑒
𝑧
+ 𝑥𝑦𝑧
2
tại điểm 𝐴 theo hướng 𝐴𝐵
󰇍
󰇍
󰇍
󰇍
󰇍
Đáp án: C.
3 14
2
−
Giải:
𝑢
(
𝑥,𝑦,𝑧 =𝑥 + 3𝑦 +𝑒
)
3 2 𝑧
+ 𝑥𝑦𝑧
2
⇒ {
𝑢
𝑥
′
=3𝑥
2
+ 𝑦𝑧
2
𝑢
𝑦
′
=6𝑦+ 𝑥𝑧
2
𝑢
𝑧
′
=𝑒
𝑧
+ 2𝑥𝑦𝑧
⇒ {
𝑢
𝑥
′
(
𝐴
)
= 12
𝑢
𝑦
′
(
𝐴
)
=−6
𝑢
𝑧
′
(
𝐴
)
=1
𝐴𝐵
󰇍
󰇍
󰇍
󰇍
󰇍
=
(
−1,2,3
)
⇒ |𝐴𝐵
󰇍
󰇍
󰇍
󰇍
󰇍
|
= √14 ⇒ cos 𝛼 =
−1
√
14
,cos𝛽 =
2
√
14
,cos𝛾 =
3
√
14
⇒
𝜕𝑢
𝜕𝐴𝐵
󰇍
󰇍
󰇍
󰇍
󰇍
(
𝐴
)
= 12.
−1
√
14
+
(
−6
)
.
2
√
14
+
3
√
14
=
−3
√
14
2
Câu 85: Tính góc giữa 𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑢,
2 2 2
x
u
x y z
=
+ +
t và
ại điểm 𝐴
(
1,2,2
)
𝐵
(
−3,1,0
)
Đáp án: A.
8
arccos
9
−
Giải:
𝑢 =
𝑥
𝑥
2
+ 𝑦 + 𝑧
2 2
⇒
{
𝑢
𝑥
′
=
−𝑥
2
+ 𝑦
2
+ 𝑧
2
(
𝑥
2
+ 𝑦
2
+ 𝑧
2
)
2
𝑢
𝑦
′
=
−2𝑥𝑦
(
𝑥
2
+ 𝑦
2
+ 𝑧
2
)
2
𝑢
𝑧
′
=
−2𝑥𝑧
(
𝑥
2
+ 𝑦
2
+ 𝑧
2
)
2
⇒𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑢 = (
−𝑥
2
+ 𝑦
2
+ 𝑧
2
(
𝑥
2
+ 𝑦
2
+ 𝑧
2
)
2
,
−2𝑥𝑦
(
𝑥
2
+ 𝑦
2
+ 𝑧
2
)
2
,
−2𝑥𝑧
(
𝑥
2
+ 𝑦
2
+ 𝑧
2
)
2
)
⇒𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑢
(
𝐴
)
=(
7
81
,
−4
81
,
−4
81
);𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑢
(
𝐵
)
=(
−2
25
,
3
50
,0)
⇒𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑧
2
(
𝑀
)
= (2,
−9
5
)
82
⇒cos 𝑔𝑟𝑎𝑑(
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑢
(
𝐴
)
,𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑢
(
𝐵
)
) =
𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑧
1
( )
𝑀 .𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑧
2
(
𝑀
)
|
𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑧
1
(
𝑀
)
|.|
𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑧
2
( )
𝑀 |
=
−8
9
⇒ (𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑧
1
,𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑧
2
)
= arccos
−8
9
Câu 86:
Cho 𝐹
=𝑥 𝑖+ 3𝑥𝑦 𝑧𝑗+ 𝑚𝑥𝑦𝑧 𝑘
2
𝑦𝑧
2 2
󰇍
v là tham s c. Tìm
ới 𝑚 ố thự 𝑚 để 𝐹
là
trường ống.
Đáp án: B.
𝑚 = −4
Giải:
Đặ
t {
𝑃 = 𝑥
2
𝑦𝑧
𝑄 = 3𝑥𝑦 𝑧
2
𝑅 = 𝑚𝑥𝑦𝑧
2
⇒
{
𝑃
𝑥
′
= 2𝑥𝑦𝑧
𝑄
𝑦
′
=6𝑥𝑦𝑧
𝑅
𝑧
′
=2𝑚𝑥𝑦𝑧
⇒ 𝑑𝑖𝑣𝐹
= 𝑃
𝑥
′
+ 𝑄
𝑦
′
+ 𝑅
𝑧
′
=
(
8 + 2𝑚
)
𝑥𝑦𝑧
Để
𝐹
là trường ống ⇔ 𝑑𝑖𝑣𝐹
= 0 ⇔ 𝑚 = −4
Câu 87: Xác định nh m không phững điể ải điểm xoáy trong trường vecto
𝐹
=
(
𝑧
2
+ 2 𝑖+ 3𝑥 − 2 𝑗 − 𝑧 𝑘𝑥𝑦
) (
2
𝑦𝑧
)
2
󰇍
Đáp án:
C.
(
0,0,0
)
Giải:
Đặ
t {
𝑃 = 𝑧
2
+ 2𝑥𝑦
𝑄 = 3𝑥 − 2
2
𝑦𝑧
𝑅 = −𝑧
2
⇒
{
𝑃
𝑦
′
= 2𝑦,𝑃
𝑧
′
= 2𝑧
𝑄
𝑥
′
=6𝑥,𝑄
𝑧
′
=−2𝑦
𝑅
𝑥
′
= 0,𝑅
𝑦
′
= 0
⇒𝑟𝑜𝑡
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝐹
= (
𝜕𝑅
𝜕𝑦
−
𝜕𝑄
𝜕𝑧
;
𝜕𝑃
𝜕𝑧
−
𝜕𝑅
𝜕𝑥
;
𝜕𝑄
𝜕𝑥
−
𝜕𝑃
𝜕𝑦
)=
(
2𝑦;2𝑧;6𝑥 − 2𝑦
)
Điểm xoáy ng vecto th a mãn 𝑀 trong trườ ỏ
𝑟𝑜𝑡
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝐹
(
𝑀
)
=0
󰇍
⇔
{
2𝑦 = 0
2𝑧 = 0
6𝑥− 2𝑦 = 0
⇔ {
𝑥 = 0
𝑦 = 0
𝑧 = 0
V
ậy điểm không xoáy là 𝑀
(
0,0,0
)
Câu 88:
Biết 𝐹
= 𝑒
𝑥
2
+𝑦 +𝑧
2 2
[
(
2𝑥
2
𝑦𝑧 𝑦𝑧+
)
𝑖+ 2𝑦 𝑗+ 2𝑧 𝑘
(
2
𝑥𝑧 𝑥𝑧+
) (
2
𝑦𝑥+ 𝑥𝑦
)
󰇍
]
là
trường thế. Tìm hàm th v . ế ị
83
Đáp án: A.
2 2 2
x y z
u e xyz C
+ +
= +
Giải:
Hàm th v ế ị
𝑢 = 𝑡, 𝑦
∫𝑃
(
0
,𝑧
0
)
𝑑𝑡
𝑥
𝑥
0
+ ∫
𝑄
(
𝑥,𝑡,𝑧
0
)
𝑑𝑡
𝑦
𝑦
0
+ ∫
𝑅
(
𝑥,𝑦,𝑡
)
𝑑𝑡
𝑧
𝑧
0
+ 𝐶
Chọn 𝑥
0
= 𝑦
0
= 𝑧
0
= 0
⇒𝑢 = .0∫𝑒
𝑡
2
𝑑𝑡
𝑥
0
+ ∫
𝑒
𝑥
2
+𝑡
2
.0𝑑𝑡
𝑦
0
+ ∫
𝑒
𝑥
2
+𝑦
2
+𝑡
2
(
2𝑥𝑦𝑡
2
+ 𝑥𝑦
)
𝑑𝑡
𝑧
0
+ 𝐶
=
𝑥𝑦∫𝑒
𝑥
2
+𝑦
2
+𝑡
2
(
2𝑡 + 1
2
)
𝑑𝑡
𝑧
0
+ 𝐶
= 2𝑥𝑦 ∫𝑒
𝑥
2
+𝑦
2
+𝑡
2
.𝑡
2
𝑑𝑡
𝑧
0
+ 𝑥𝑦∫𝑒
𝑥
2
+𝑦
2
+𝑡
2
𝑑𝑡
𝑧
0
+ 𝐶
Đặt
{
𝑡 = 𝑢
𝑒
𝑥
2
+𝑦
2
+𝑡
2
.𝑡𝑑𝑡 = 𝑑𝑣
⇒
{
𝑑𝑢 = 𝑑𝑡
𝑣 =
1
2
𝑒
𝑥
2
+𝑦
2
+𝑡
2
⇒2 .𝑡𝑥𝑦 ∫𝑒
𝑥
2
+𝑦
2
+𝑡
2
2
𝑑𝑡
𝑧
0
=2𝑥𝑦 (
𝑡
2
𝑒
𝑥
2
+𝑦 +𝑡
2 2
|
𝑧
0
− ∫
1
2
𝑒
𝑥
2
+𝑦
2
+𝑡
2
𝑑𝑡
𝑧
0
)
=𝑥𝑦𝑧𝑒
𝑥
2
+𝑦
2
+𝑡
2
− 𝑥𝑦∫𝑒
𝑥
2
+𝑦
2
+𝑡
2
𝑑𝑡
𝑧
0
⇒𝑢 = 𝑥𝑦𝑧𝑒
𝑥
2
+𝑦
2
+𝑡
2
− 𝑥𝑦 ∫𝑒
𝑥
2
+𝑦
2
+𝑡
2
𝑑𝑡
𝑧
0
+ 𝑥𝑦∫𝑒
𝑥
2
+𝑦
2
+𝑡
2
𝑑𝑡
𝑧
0
=𝑥𝑦𝑧𝑒
𝑥
2
+𝑦
2
+𝑡
2
+ 𝐶
Câu 89:
Biết 𝐹
=
(
3𝑥 − 3𝑦 𝑖+ arctan𝑧 − 6 𝑗+
2 2
𝑧
) (
𝑥𝑦𝑧
)
(
𝑦
1+𝑧
2
+ 3𝑥𝑦
2
)𝑘
󰇍
là trường
thế, tìm hàm th v . ế ị
Đáp án: D.
3 2
arctan 3u x y z xy z C= + + +
Giải:
84
Hàm th v ế ị
𝑢 = 𝑡, 𝑦
∫𝑃
(
0
,𝑧
0
)
𝑑𝑡
𝑥
𝑥
0
+ ∫
𝑄
(
𝑥,𝑡,𝑧
0
)
𝑑𝑡
𝑦
𝑦
0
+ ∫
𝑅
(
𝑥,𝑦,𝑡
)
𝑑𝑡
𝑧
𝑧
0
+ 𝐶
Chọn 𝑥
0
= 𝑦
0
= 𝑧
0
= 0
⇒𝑢 = 3𝑡∫
2
𝑑𝑡
𝑥
0
+ ∫
0𝑑𝑡
𝑦
0
+ ∫
𝑦
1 + 𝑡
2
+ 3𝑥𝑦
2
𝑑𝑡
𝑧
0
+ 𝐶 = 𝑥
3
+ 𝑦arctan𝑧+ 3𝑥𝑦
2
+ 𝐶
Câu 90:
Biết 𝐹
=
(
3𝑥 𝑖+ 6𝑦 𝑗 + +𝑒
2
+ 𝑦𝑧
) (
2
+ 𝑥𝑧
) (
𝑧
2
+ 𝑥𝑦
𝑧
)
𝑘
󰇍
ng th , tìm là trườ ế
hàm th v ế ị
Đáp án: A.
3
3 3
2
3
z
z
u x y e xyz C= + + + + +
Giải:
Hàm th v ế ị
𝑢 = 𝑡, 𝑦
∫𝑃
(
0
,𝑧
0
)
𝑑𝑡
𝑥
𝑥
0
+ ∫
𝑄
(
𝑥,𝑡,𝑧
0
)
𝑑𝑡
𝑦
𝑦
0
+ ∫
𝑅
(
𝑥,𝑦,𝑡
)
𝑑𝑡
𝑧
𝑧
0
+ 𝐶
Chọn 𝑥 =𝑦
0 0
= 𝑧
0
= 0
⇒𝑢 = 3𝑡 𝑡∫
2
𝑥
0
+ ∫
6𝑡
2
𝑑𝑡
𝑦
0
+ ∫
(
𝑡
2
+ 𝑥𝑦 + 𝑒
𝑡
)
𝑑𝑡
𝑧
0
+ 𝐶
= 𝑡
3
|
𝑥
0
+ 2𝑡
3
|
𝑦
0
+ (
𝑡
3
3
+ 𝑥𝑦𝑡+ 𝑒
𝑡
)|
𝑧
0
+ 𝐶
= 𝑥
3
+ 2𝑦
3
+
𝑧
3
3
+ 𝑥𝑦𝑧 + 𝑒 −1 + 𝐶
𝑧
= 𝑥
3
+ 2𝑦
3
+
𝑧
3
3
+ 𝑥𝑦𝑧 + 𝑒 +𝐶
𝑧
Vậy hàm ế vị 𝑢 = 𝑥
th là
3
+ 2𝑦
3
+
𝑧
3
3
+ 𝑥𝑦𝑧+𝑒
𝑧
+ 𝐶
Câu 91:
Tính thông lượng của 𝐹
= 𝑥𝑖+ + 2𝑧 𝑗+ 3𝑥 𝑧 − 𝑥 𝑘
(
𝑦
3
) (
2
)
󰇍
qua m t cặ ầu
85
𝑆: 𝑥
2
+ 𝑦 + 𝑧 = 1
2 2
ng ra ngoài. hướ
Đáp án: D.
44
15
Giải:
Đặt 𝑃 = 𝑥, 𝑄 = 𝑦 + 2𝑧, 𝑅 = 3𝑥 𝑧 − 𝑥
3 2
Thông lượng cần tính là:
Φ= 𝑥𝑑𝑦𝑑𝑧+ (𝑦 + 2𝑧)𝑑𝑧𝑑𝑥+ 3𝑥 𝑧 − 𝑥 𝑑𝑥𝑑𝑦
∬
3
(
2
)
𝑆
Mặt 𝑆 là m t cong kín gi i hặ ớ ạn miền
( )
𝑉 𝑥
2
+ 𝑦
2
+ 𝑧
2
≤ 1 ng pháp tuy n ra hướ ế
ngoài.
𝑃
𝑥
′
= 1, 𝑄
𝑦
′
=3𝑦
2
,𝑅
𝑧
′
= 3𝑥
2
liên t c v ụ ới 𝑥,𝑦,𝑧 ∈ 𝑅
Áp d ng công th c Ostrogradsky: ụ ứ
Φ= 1 + 3𝑥 + 3𝑦
∭
(
2 2
)
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∭
(
3𝑥
2
+ 3𝑦
2
)
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
+ 𝑉
(
𝑉
)
= 𝐼+ 𝑉
(
𝑉
)
Đặt {
𝑥 = 𝑟sin𝜃 cos𝜑
𝑦 = 𝑟sin𝜃 sin𝜑
𝑧 = 𝑟 cos𝜃
. Miền
(
𝑉
)
: {
0 ≤ 𝑟 ≤ 1
0≤ 𝜃 ≤ 𝜋
0≤ 𝜑 ≤ 2𝜋
|
𝐽
|
=𝑟
2
sin𝜃
𝐼 = ∫ 𝑑𝜑
2𝜋
0
∫
𝑑𝜃
𝜋
0
∫
3𝑟
2
( )
sin𝜃
2
𝑟
2
sin𝜃 𝑑𝑟
1
0
=
3
5
∫ 𝑑𝜑
2𝜋
0
∫
( )
sin𝜃
3
𝑑𝜃
𝜋
0
=
8
5
𝜋
⇒Φ = 𝐼 + 𝑉
(
𝑉
)
=
8
5
𝜋 +
4
3
𝜋 =
44
15
𝜋
Câu 92:
Tính thông lượng của 𝐹
= 𝑥𝑦 𝑖 − 𝑧𝑒 𝑗+ 𝑧+ sin𝑦 𝑘
2 𝑥
(
𝑥
2
)
󰇍
qua là m 𝑆 ặt
𝑧 = 𝑥 + 𝑦 ,𝑧 ≤ 4,
2 2
ng ra ngoài. hướ (Chọn kết qu gả ần đúng nhất)
86
Đáp án: A. −17
Giải:
Thông lượng cần tính:
Φ= 𝑥𝑦 𝑑𝑦𝑑𝑧− 𝑧𝑒 𝑑𝑧𝑑𝑥+ 𝑧+ sin𝑦 𝑑𝑥𝑑𝑦
∬
2 𝑥
(
𝑥
2
)
𝑆
B
ổ sung thêm mặt 𝑆
′
:{
𝑧 = 4
𝑥
2
+ 𝑦 ≤ 4
2
ng lên trên hướ
Mặt 𝑆 ∪ 𝑆′ là mặt cong kín, hướng pháp tuyến ngoài gi i h n miớ ạ ền
( )
𝑉 : 𝑥
2
+ 𝑦
2
≤𝑧 ≤ 4
Đặ
t 𝑃 = 𝑥𝑦 , 𝑄 = −𝑧𝑒 ,𝑅 = 𝑥 𝑧 + cos𝑦 ⇒ 𝑃
2 𝑥 2
𝑥
′
= 𝑦
2
,𝑄
𝑦
′
=0,𝑅
𝑧
′
= 𝑥
2
liên t c vụ ới
𝑥,𝑦,𝑧 ∈ 𝑅
Ta có:
Φ=∯𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥+ 𝑅𝑑𝑥𝑑𝑦
𝑆∪𝑆
′
− ∬
𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦
𝑆
′
=𝐼
1
− 𝐼
2
Áp d ng công th c Ostrogradsky cho ụ ứ 𝐼
1
, ta có:
𝐼
1
= ∭
(𝑥
2
+ 𝑦
2
)𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
Hình chi u cế ủa 𝑉 lên 𝑂𝑥𝑦 là 𝐷: 𝑥
2
+ 𝑦 ≤4
2
.
87
Đặ
t {
𝑥 = 𝑟cos𝜑
𝑦 = 𝑟sin𝜑
𝑧 = 𝑧
𝐽= 𝑟. Miền
( )
𝑉 :{
0 ≤ 𝑟 ≤ 2
0≤ 𝜑 ≤ 2𝜋
𝑟
2
≤ 𝑧 ≤ 4
⇒𝐼
1
= ∫
𝑑𝜑
2𝜋
0
∫
𝑑𝑟
2
0
∫
𝑟
2
.𝑟𝑑𝑧
4
𝑟
2
= ∫
𝑑𝜑
2𝜋
0
∫
𝑟
3
(4 − 𝑟
2
)𝑑𝑟
2
0
=
32
3
𝜋
𝑆
′
:{
𝑧 = 4 ⇒ 𝑑𝑧 = 0
𝑥
2
+ 𝑦
2
≤4
,
(
𝑛
󰇍
,
𝑂𝑧
)
< 𝜋/2, hình chi u c lên ế ủa 𝑆
′
𝑂𝑥𝑦 là 𝐷: 𝑥
2
+ 𝑦 ≤ 4
2
⇒𝐼
2
= ∬
(
𝑥
2
𝑧 + sin 𝑦
)
𝑑𝑥𝑑𝑦
𝑆
′
= ∬
(
4𝑥
2
+ sin𝑦 𝑑𝑥𝑑𝑦
)
𝐷
= ∬
4𝑥
2
𝑑𝑥𝑑𝑦
𝐷
= 4 ∫ 𝑑𝜑
2𝜋
0
∫
𝑟
2
(cos𝜑)
2
𝑟𝑑𝑟
2
0
= 16∫ (cos𝜑)
2
𝑑𝜑
2𝜋
0
= 16𝜋
(∬sin𝑦 𝑑𝑥𝑑𝑦
𝐷
=0 tính ất đối xứ của ền 𝐷,hàm 𝑓 = sin𝑦 lẻ với 𝑦)do ch ng mi
(
𝑥,𝑦
)
⇒ Φ = 𝐼
1
− 𝐼
2
=
−16
3
𝜋
Câu 93
: Tính thông lượng của 𝐹
=
(
𝑥
2
− 2𝑦 +𝑧 𝑖− + 2 𝑗+ 𝑥𝑘
) (
𝑧
2
𝑥𝑦
)
󰇍
qua phía
trên m t nón ặ 𝑧= 1 + + 𝑦
√
𝑥
2 2
c t b i hai m t ph ng ắ ở ặ ẳ 𝑧 = 2,𝑧 = 5
Đáp án: C. 0
Giải:
Thông lượng cần tính:
Φ= − 2𝑦 + 𝑧 𝑑𝑦𝑑𝑧− + 2 𝑑𝑧𝑑𝑥+ 𝑥𝑑𝑥𝑑𝑦
∬
(
𝑥
2
) (
𝑧
2
𝑥𝑦
)
𝑆
Bổ sung thêm hai mặt:
𝑆
′
: {
𝑧 = 2
𝑥
2
+ 𝑦 ≤ 1
2
ng lên trên, hướ 𝑆
′′
: {
𝑧 = 5
𝑥
2
+ 𝑦
2
≤ 16
hướng xuống dưới
88
Mặt 𝑆 ∪ 𝑆 ∪𝑆
′ ′′
là m ng pháp tuy n trong, gi i hặt cong kín, hướ ế ớ ạn miền
𝑉:
{
𝑧 ≥ 1 +
√
𝑥
2
+ 𝑦
2
2≤ 𝑧 ≤ 5
Đặ
t 𝑃 = 𝑥 − 2𝑦 + 𝑧,𝑄 = − + 2 , 𝑅 = 𝑥 ⇒ 𝑃
2
(
𝑧
2
𝑥𝑦
)
𝑥
′
=2𝑥,𝑄
𝑦
′
=−2𝑥,𝑅
𝑧
′
= 0 liên t ục.
Φ= …∯
𝑆∪𝑆 ∪𝑆
′ ′′
− ∬
…
𝑆
′
− ∬
…
𝑆
′′
=𝐼
1
− 𝐼
2
− 𝐼
3
Áp d ng công th c Ostrogradsky cho ụ ứ 𝐼
1
⇒𝐼
1
= − 2𝑥 − 2𝑥 + 0 𝑑𝑥𝑑𝑦𝑑𝑧∭
(
)
𝑉
=0
𝑆
′
: {
𝑧 = 2 ⇒ 𝑑𝑧 = 0
𝑥
2
+ 𝑦
2
≤1
,
(
𝑛
󰇍
,𝑂𝑧
)
< 𝜋/2, hình chi u c lên là ế ủa 𝑆
′
𝑂𝑥𝑦 𝐷
′
: 𝑥
2
+ 𝑦 ≤1
2
⇒𝐼
2
= ∬
𝑥𝑑𝑥𝑑𝑦
𝑆
′
= ∬
𝑥𝑑𝑥𝑑𝑦
𝐷
=0 Dùng tính ất đối xứ
(
ch ng
)
𝑆
′′
: {
𝑧 = 5 ⇒ 𝑑𝑧 = 0
𝑥
2
+ 𝑦
2
≤ 16
,
(
𝑛
󰇍
,𝑂𝑧
)
> 𝜋/2, hình chi u c lên là ế ủa 𝑆
′′
𝑂𝑥𝑦 𝐷
′′
: 𝑥
2
+ 𝑦
2
≤ 16
⇒𝐼
3
= ∬
𝑥𝑑𝑥𝑑𝑦
𝑆
′′
= ∬
𝑥𝑑𝑥𝑑𝑦
𝐷
=0 Dùng tính ất đối xứ
(
ch ng
)
89
Vậy Φ = 𝐼
1
− 𝐼
2
− 𝐼
3
= 0
Câu 94:
Tính thông lượ ủa trường c ng vecto 𝐹
= 2𝑥 𝑖+ 𝑦 𝑗−𝑧 𝑘
2 2 2
󰇍
qua mS là ặt
ngoài c a mi n gi i h n bủ ề ớ ạ ởi 𝑦 = 0,𝑦 = √1 − 𝑧 ,𝑥 = 0, 𝑥= 2
2
Đáp án: A.
8
4
3
+
Giải:
Thông lượng cần tính là:
Φ= 2𝑥 𝑑𝑦𝑑𝑧 + 𝑦 𝑑𝑧𝑑𝑥− 𝑧 𝑑𝑥𝑑𝑦∬
2 2 2
𝑆
Mặt 𝑆 kín gi i h n miớ ạ ển 𝑉:0 ≤ 𝑦 ≤ √1 − 𝑧
2
,0 ≤𝑥 ≤ 2, ng pháp tuy n ngoài hướ ế
Đặ
t 𝑃 = 2𝑥 ,𝑄 = 𝑦 ,𝑅 = −𝑧 ⇒𝑃
2 2 2
𝑥
′
=4𝑥,𝑄
𝑦
′
=2𝑦,𝑅
𝑧
′
=−2𝑧 liên t ục.
Áp d ng công th c Ostrogradsky: ụ ứ
Φ = 2𝑥 𝑑𝑦𝑑𝑧 + 𝑦 𝑑𝑧𝑑𝑧 − 𝑧 𝑑𝑥𝑑𝑦∬
2 2 2
𝑆
= ∭
(
4𝑥+ 2𝑦 − 2𝑧
)
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
Đặ
t {
𝑦= 𝑟 cos𝜑
𝑧 = 𝑟 sin𝜑
𝑥 = 𝑥
,𝐽 = 𝑟 ⇒ Miền 𝑉: {
0 ≤ 𝑟 ≤ 1
−𝜋/2≤ 𝜑 ≤ 𝜋/2
0≤ 𝑥 ≤ 2
90
Φ= 2 ∫ 𝑑𝜑
𝜋
2
−𝜋
2
∫
𝑑𝑟
1
0
∫
( )
2𝑥+ 𝑟cos𝜑 .𝑟𝑑𝑥
2
0
=2 ∫
𝑑𝜑
𝜋
2
−𝜋
2
∫
(
4𝑟 + 2𝑟
2
cos𝜑
)
𝑑𝑟
1
0
=4𝜋+
8
3
Câu 95:
Tính thông lượ ủa trường c ng vecto 𝐹
=𝑥 𝑖+ 𝑦 𝑗+
3 2
𝑧
2
2
𝑘
󰇍
qua biên 𝑆 là
ngoài c a
ủ miền 𝑉: 𝑥 −𝑦 ≤ 1, 𝑦 − 𝑧 ≤1, 𝑧 + 𝑥 ≤ 1
| | | | | |
Đáp án: D. 3
Giải:
Thông lượng c n tínhầ
Φ= 𝑑𝑦𝑑𝑧 + 𝑦 𝑑𝑧𝑑𝑧 +
∬𝑥
3 2
𝑧
2
2
𝑑𝑥𝑑𝑦
𝑆
Mặt 𝑆 kín gi i h n miớ ạ ển 𝑉: 𝑥 − 𝑦 ≤ 1, 𝑦− 𝑧 ≤ 1, 𝑧 + 𝑥 ≤ 1
| | | | | |
ng pháp tuyhướ ến
ngoài
Đặ
t 𝑃 = 𝑥 ,𝑄 = 𝑦 ,𝑅 = 𝑧 /2 ⇒ 𝑃
3 2 2
𝑥
′
= 3𝑥
2
,𝑄
𝑦
′
=2𝑦,𝑅
𝑧
′
= 𝑧 liên tục.
Áp d ng công th c Ostrogradsky: ụ ứ
Φ= 3𝑥 + 2𝑦+𝑧 𝑑𝑥𝑑𝑦𝑑𝑧
∭
(
2
)
𝑉
Đặ
t {
𝑢 = 𝑥 − 𝑦
𝑣 = 𝑦− 𝑧
𝑤 = 𝑧 +𝑥
⇒ {
𝑥 =
(
𝑢 + 𝑣 + 𝑤
)
/2
𝑦 = (𝑣 + 𝑤 − 𝑢)/2
𝑧 = (𝑤− 𝑢 − 𝑣)/2
,𝐽 = 1/2
Miền 𝑉
𝑢𝑣𝑤
:−1 ≤ 𝑢 ≤ 1,−1 ≤ 𝑣 ≤ 1,−1 ≤ 𝑤 ≤ 1
⇒Φ =
1
2
∭[
3
(
𝑢+ 𝑣 + 𝑤
)
2
4
+
(
𝑣 + 𝑤 −𝑢
)
+
𝑤 − 𝑢− 𝑣
2
]𝑑𝑢𝑑𝑣𝑑𝑤
𝑉
𝑢𝑣𝑤
= ⋯ = 3
Câu 96: Cho trường vô hướng 𝑢 = .𝑥𝑦 𝑥𝑧+ 𝑦𝑧 + Tính lưu số ủa trườ c ng vecto
𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑢
d n th ng n i t ọc theo đoạ ẳ ố ừ 𝐴
(
−1,−1,−1
)
đến 𝐵
(
2,4,1
)
Đáp án: A. 11
Giải:
91
𝑔𝑟𝑎𝑑
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
𝑢 = (𝑢
𝑥
′
,𝑢
𝑦
′
,𝑢
𝑧
′
)
=
(
𝑦 + 𝑧,𝑥 + 𝑧,𝑥 + 𝑦 𝑦 + 𝑧 𝑖+ 𝑥+ 𝑧 𝑗+ 𝑥+ 𝑦 𝑘
)
=
( ) ( ) ( )
󰇍
Đo
ạn : 𝐴𝐵 {
vecto ỉ phương ch AB
󰇍
󰇍
󰇍
󰇍
󰇍
=
(
3,5,2
)
đi
qua A
(
−1,−1,−1
)
⇒ 𝐴𝐵:
𝑥+ 1
3
=
𝑦 + 1
5
=
𝑧 + 1
2
=𝑡
⇒
𝐴𝐵: {
𝑥 = 3𝑡 −1
𝑦 = 5𝑡 −1
𝑧 = 2𝑡 − 1
v y t . ới 𝑡 chạ ừ 0 đến 1
Lưu số cần tìm:
𝐶 =
∫
(
𝑦 + 𝑧
)
𝑑𝑥
𝐴𝐵
+ +
(
𝑥+ 𝑧
)
𝑑𝑦
(
𝑥+ 𝑦
)
𝑑𝑧
=
∫
[(
5𝑡− 1 + 2𝑡 − 1
)
.3 +
(
3𝑡 − 1+ 2𝑡 − 1
)
.5 +
(
3𝑡 − 1+ 5𝑡 −1
)
.2
]
𝑑𝑡
1
0
= 11
Câu 97:
Tính lưu số của 𝐹
=𝑥 𝑖+𝑗+ 𝑧𝑘
2
𝑦
3
󰇍
d ng tròn ọc theo đườ có phương trình
𝐶:𝑥 + 𝑦 = 1, 𝑧 =0
2 2
i h n m t cgiớ ạ ặ ầu 𝑧 = 1 −𝑥 − 𝑦
√
2 2
Đáp án:
Giải:
Lưu số cần tính là:
𝐶 = + 𝑧𝑑𝑧∮𝑥
2
𝑦
3
𝑑𝑥 𝑑𝑦+
𝐶
Đường cong i h n ph n m t c u 𝐶 giớ ạ ầ ặ ầ 𝑆: 𝑧 =
√1 − 𝑥 − 𝑦
2 2
ng lên trên hướ
92
(Đề bài không nói gì v chi u thì hi ng cong cho chiề ề ều là đườ ều dương).
Áp dụng công thức Stoke:
𝐶 = −3𝑥 𝑑𝑥𝑑𝑦∬
2
𝑦
2
𝑆
Hình chi u c a mế ủ ặt 𝑆 lên là 𝑂𝑥𝑦 𝐷: 𝑥 + 𝑦 ≤ 1
2 2
Đặ
t {
𝑥 = 𝑟cos𝜑
𝑦 = sin𝜑
,𝐽 = 𝑟 ⇒ 𝐷:
{
0 ≤ 𝑟 ≤ 1
0≤ 𝜑 ≤ 2𝜋
⇒𝐶 = −3𝑥 𝑑𝑥𝑑𝑦∬
2
𝑦
2
𝑆
=−3∫
𝑑𝜑
2𝜋
0
∫
𝑟
2
sin
2
𝜑𝑟
2
cos
2
𝜑.𝑟𝑑𝑟
1
0
=⋯ =
−𝜋
8
Câu 98:
Tính lưu số của 𝐹
=
(
𝑦𝑒 +3𝑦+ 𝑧 𝑖+ 𝑥𝑒 +𝑦−5𝑧 𝑗 + 1 + 2𝑥 𝑘
𝑥𝑦
) (
𝑥𝑦
) ( )
󰇍
dọc
theo đường cong 𝐿 là giao c a mủ ặt 𝑥
2
+ 𝑦 + 𝑧 = 4
2 2
và mặt 𝑥 − 𝑦 + 𝑧 = 0 ng hướ
ngược chi ng h n u nhìn t chiều kim đồ ồ ế ừ ều dương trục 𝑂𝑧.
Đáp án: C.
4
√
3𝜋
Giải:
Lưu số cần tính là:
𝐶 = 𝑦𝑒 + 3𝑦 +𝑧 𝑥𝑒 + 𝑦 − 5𝑧 1 + 2𝑥
∮
(
𝑥𝑦
)
𝑑𝑥 +
(
𝑥𝑦
)
𝑑𝑦 +
( )
𝑑𝑧
𝐿
Đường cong kín chi𝐿 ều dương giới hạn phần mặt phẳng 𝑆: 𝑥− 𝑦 + 𝑧 = 0 nằm
trong c u, mầ ặt hướng lên, có vecto pháp tuy n h p tr ế ợ ục 𝑂𝑧 < 𝜋/2
93
Áp d ng công th c Stoke: ụ ứ
𝐶 = 5𝑑𝑦𝑑𝑧 − 𝑑𝑧𝑑𝑥 −3𝑑𝑥𝑑𝑦∬
𝑆
Vecto pháp tuy n c là ế ủa 𝑆 𝑛
󰇍
=
(
1,−1,1 ⇒ cos 𝛼=
)
1
√
3
,cos𝛽 =
−1
√
3
,cos𝛾 =
1
√
3
⇒𝐶 = (5.
∬
1
√
3
+ 1.
1
√
3
− 3.
1
√
3
)𝑑𝑆
𝑆
=
√
3∬
𝑑𝑆
𝑆
=
√
3𝑆
𝑆
= 4 3𝜋
√
(𝑆 là hình tròn qua tâm c ầu)
Câu 99:
Tính lưu số của 𝐹
=
(
𝑦
2
+ 𝑧
2
)
𝑖+ + 𝑧
(
𝑥
2 2
)
𝑗+ + 𝑦
(
𝑥
2 2
)
𝑘
󰇍
d ng ọc theo đườ
cong 𝐶 trong đó 𝐶 là giao c a m t củ ặ ầu 𝑥
2
+ 𝑦 + 𝑧 = 4
2 2
và m t nón có ặ phương
trình v ng cùng chi ng h khi nhìn t g c O. 𝑧 = − +(𝑦 − 1)
√
𝑥
2 2
ới hướ ều kim đồ ồ ừ ố
Đáp án: B. 0
Giải:
Lưu số cần tính:
𝐶 = + 𝑧
∮
(
𝑦
2 2
)
𝑑𝑥 +
(
𝑥
2
+ 𝑧
2
)
𝑑𝑦 +
(
𝑥
2
+ 𝑦
2
)
𝑑𝑧
𝐶
Đường cong kín chi u âm là biên c a ph n m t cong c a c u n m trong nón 𝐶 ề ủ ầ ặ ủ ầ ằ
𝑆:
{
𝑥
2
+ 𝑦
2
+ 𝑧
2
≤ 4
𝑧 ≤ 0
ng xu ng theo chi u âm hướ ố ề 𝑂𝑧
Áp d ng công th c Stoke: ụ ứ
𝐶 = − 2𝑦 −2𝑧 𝑑𝑦𝑑𝑧
∬
(
)
𝑆
+
(
2𝑧 − 2𝑥 𝑑𝑧𝑑𝑥+ (2𝑥 − 2𝑦)𝑑𝑥𝑑𝑦
)
Vecto pháp tuy n c a mế ủ ặt 𝑆 là 𝑛
󰇍
=− 2𝑥,2𝑦,2𝑧
( )
⇒
|
𝑛
󰇍
|
= √
(
2𝑥
)
2
+
( )
2𝑦
2
+
( )
2𝑧
2
=4
(Dấu " − " do
(
𝑛
󰇍
,
𝑂𝑧
)
>𝜋/2)
⇒cos𝛼 =
−2𝑥
4
=
−𝑥
2
,cos𝛽 =
−2𝑦
4
=
−𝑦
2
,cos𝛾 =
−2𝑧
4
=
−𝑧
2
94
Áp d ng công th c liên h a tích phân m t lo i II và tích phân m t loụ ứ ệ giữ ặ ạ ặ ại I:
⇒𝐶 =
∬[
𝑥
2
(
2𝑦− 2𝑧
)
+
𝑦
2
(
2𝑧 − 2𝑥
)
+
𝑧
2
( )
2𝑥− 2𝑦 ]𝑑𝑆
𝑆
=0
Câu 100:
Tính thông lượng của 𝐹
= (6𝑧− 2𝑦 )𝑖+ 2𝑥−3𝑧 𝑗+ 2𝑦 − 4𝑥 𝑘
3
( ) (
3
)
󰇍
qua
mặt cong 2 𝑆: 𝑥
2
+ 𝑦 +3𝑧 = 1,𝑧 ≥ 0
4 2
hướng lên trên.
Đáp án:
Giải:
Thông lượng cần tính:
Φ= (6𝑧 −2𝑦 )𝑑𝑦𝑑𝑧 + 2𝑥 − 3𝑧 𝑑𝑧𝑑𝑧+ 2𝑦 − 4𝑥 𝑑𝑥𝑑𝑦
∬
3
( ) (
3
)
𝑆
Đặ
t 𝐹
(
𝑥,𝑦,𝑧 =2𝑥 + 𝑦 + 3𝑧 − 1
)
2 4 2
Vecto pháp tuyến 𝑛
󰇍
=
(𝐹
𝑥
′
,𝐹
𝑦
′
,𝐹
𝑧
′
)
=
(
4𝑥,4𝑦 ,6𝑧
3
)
(do
(
𝑛
󰇍
,
𝑂𝑧
)
< 𝜋/2)
|
𝑛
󰇍
|
= √
4𝑥
2
+ +16𝑦
6
36𝑧
2
= 2 + 4𝑦 + 9𝑧√𝑥
2 4 2
⇒
{
cos𝛼 =
𝑛
𝑥
|
𝑛
󰇍
|
=
2𝑥
√𝑥
2
+ 4𝑦 + 9𝑧
4 2
cos𝛽 =
𝑛
𝑦
|
𝑛
󰇍
|
=
2𝑦
3
√𝑥
2
+ 4𝑦 + 9𝑧
4 2
cos𝛾 =
𝑛
𝑧
|
𝑛
󰇍
|
=
3𝑧
√𝑥
2
+ 4𝑦 + 9𝑧
4 2
Áp d ng công th c liên h a tích phân m t lo i I và lo i II ụ ứ ệ giữ ặ ạ ạ
∬
𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦
𝑆
= ∬
(
𝑃.cos𝛼 + 𝑄.cos𝛽 + 𝑅.cos𝛾
)
𝑑𝑆
𝑆
⇒Φ =
∬
2𝑥
(
6𝑧− 2𝑦
3
)
+ 2𝑦
3
(
2𝑥− 3𝑧
)
+ 3𝑧
(
2𝑦
3
− 4𝑥
)
√𝑥
2
+ 4𝑦 + 9𝑧
4 2
𝑆
𝑑𝑆 = 0
95
Tài li u tham kh o: ệ ả
− Bài gi ng môn Gi i tích II, th y Bùi Xuân Diả ả ầ ệu.
− Bài t p gi i s n Gi i tích 2 (Tóm t t lý thuy t và chậ ả ẵ ả ắ ế ọn l c), th y Trọ ầ ần Bình.
− Bài t p Toán h c cao c p, t p hai: Gi i tích, GS.TS Nguyậ ọ ấ ậ ả ễn Đình Trí (chủ
biên), PGS.TS. Tr n Vi , PGS.TS. Trầ ệt Dũng ần Xuân Hiền, PGS.TS Nguyễn
Xuân Thảo.
− Bộ đề cương Giải tích II, Vi n Toán ng d ng và Tin h ệ ứ ụ ọc.
− Bộ đề thi Gi a kì và Cu i kì môn Giữ ố ải tích II Trường ĐH Bách Khoa Hà Nội.
| 1/98
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

BÁCH KHOA ĐẠI CƯƠNG MÔN PHÁI
BỘ TÀI LIỆU ÔN TẬP TRẮC NGHIỆM GIẢI TÍCH II
____________________________________________________ Biên so n b ạ
ởi: Team GT2 – BKĐCMP
Hà Nội, tháng 9 năm 2021
MỤC LỤC
Đề bài…..……………………………………………………………………..……1
Lời giải tham khảo……………………………………………………….………18
Tài liệu tham khảo……………………………………………………………….95
LỜI NÓI ĐẦU
Hiện nay, với hình thức thi đổi mới từ thi tự luận sang thi trắc nghiệm, chinh
vì vậy nhiều bạn sinh viên sẽ gặp khó khăn trong việc ôn tập. Trong tinh hình đó,
nhôm “BK – Đại cương môn phai” đã biên soạn “BỘ TÀI LIỆU ÔN TẬP TRẮC
NGHIỆM MÔN GIẢI TÍCH II” để giúp các bạn thuận tiện hơn trong việc ôn tập.
Nhóm tác giả: Team Giải Tích II BK- Đại cương môn phái
(Đỗ Tuấn Cường, Đinh Tiến Long, Phạm Thanh Tùng, Trần Trung Dũng, Đỗ Ngọc
Hiếu, Nguyễn Thu Hiền, Nguyễn Minh Hiếu)
Chịu trách nhiệm nội dung: Phạm Thanh Tùng
Do quá trình soạn bộ tài liệu gấp rút cùng với những hạn chế nhất định về
kiến thức, dù đã cố gắng hết sức nhưng chắc chắn không thể tránh khỏi những sai
sót về tính toán, lỗi đánh máy, mọi ý kiến góp ý của bạn đọc xin gửi qua đường
link fb “fb.com/tungg810” hoặc email tungcrossroad@gmail.com.
Tài liệu chỉ mang tính chất tham khảo, không có tác dụng thay thế các giáo trình, sách giá
o khoa chính thống. Xin chân thành cảm ơn! I. Bài t p tr ậ c nghi ắ ệm Tích phân Euler + 4
Câu 1: Kết quả của tích phân 5 −x x e dx  là: 0     A. B. C. D. 8 2 6 6  2
Câu 2: Kết quả của tích phân 6 4 sin xcos xdx  là: 0 7  3 A. 2 B. C. D. 512 512 512 512 + 4 −  Câu 3: Biết 6 x 3 x a dx = 
, chọn khẳng định đúng: 7/2 b(ln 3) 0
A. 𝑎 − 𝑏 = −1
B. 𝑎 + 𝑏 = 10
C. 𝑎 > 𝑏
D. 𝑎. 𝑏 < 100 + 2 x
Câu 4: Biểu diễn tích phân dx  theo hàm Gamma: 4 4 (1 + x ) 0  3  13  3  13 .        .       4    4   4   4 A. C. 6. (4) 4. (4)  3   1  3   5 .          .     B.  4   4   4   4  D. 4. (4 ) 4. (4 ) 1 1
Câu 5: Tính tích phân dx 30 30 0 1 − x     A. B. C. D.             30sin   30sin   sin   50sin    20   30  30   30  1 + 4
Câu 6: Tính tích phân x dx  3 2 (x +1) 0 4 3 4 2 2 2 2 3 A. B. C. D. 27 27 27 27 1 10  1
Câu 7: Tính tích phân ln dx    0  x A. 11! B. 10! C. 12! D. 9! 1
Câu 8: Tính tích phân 5 10
x (ln x) dx  0 10! 10! 11! 11! A. B. C. D. 11 5 11 6 11 5 11 6 0
Câu 9: Biểu diễn tích phân 2x 3 3 e 1 x −e dx  theo hàm Gamma: −  2   4  2   1 .        .       3    3   3   3 A.   C. 2. (2 ) 9.(2)  2   1  2   4 .       .      3     3   3   3 B.   D. 3.(2) 3.(2) 2
Câu 10: Tính tích phân 7 5 sin xcos xdx  0 5 3  7 A. B. C. D. 128 2 256 2 256 2 256 2 2 II. Bài t p tr ậ c nghi ắ
ệm Tích phân đườn g
1. Tích phân đường loại I:
Câu 11: Tính tích phân (x + y)ds
với 𝐿 là đoạn thẳng nối điểm 𝑂(0; 0) và 𝐴(4; 3) L 35 35 35 35 A. B. C. D. 2 4 3 6 𝑥 = 2 + 2 cos 𝑡
Câu 12: Tính (x + y)ds
với 𝐿 là nửa đường tròn { 𝑦 = 2 sin 𝑡 L 0 ≤ 𝑡 ≤ 𝜋 A. 4+ 8 B. 8 + 4 C. 4 D. 2 + 4
Câu 13: Tìm 𝑚 để (mx − ) y ds
= −18 với 𝐶: 𝑦 = √9 − 𝑥2 C A. 𝑚 = 1 B. 𝑚 = 2 C. 𝑚 = 3 D. 𝑚 = 4
Câu 14: Với 𝐶 là đường tròn 𝑥2 + 𝑦2 = 2𝑥, tính (x − y)dsC A. 𝜋 B. 2𝜋 C. 3𝜋 D. 6𝜋 − 
Câu 15: Tính (x + y)ds
với cung 𝐶: 𝑟2 = cos 2𝜑,    4 4 C A. √5 B. √6 C. √10 D. √2
Câu 16: Với 𝐶 là đường cong 𝑥2/3 + 𝑦2/3 = 1 trong góc phần tư thứ nhất nối 𝐴(1,0) và 𝐵(0,1), tính 2 ( y +1)dsC 15 15 15 15 A. B. C. D. 8 9 7 4
Câu 17: Tính yds
 với 𝐶 là đường 𝑥 = 𝑦2 đi từ 𝑂(0,0) đến 𝐴(1,1) C 1 1 1 1 A. (5 5 −1) B. (5 5 −1) C. (5 5 −1) D. (5 5 1 − ) 3 12 6 2 3
Câu 18: Tính xyds
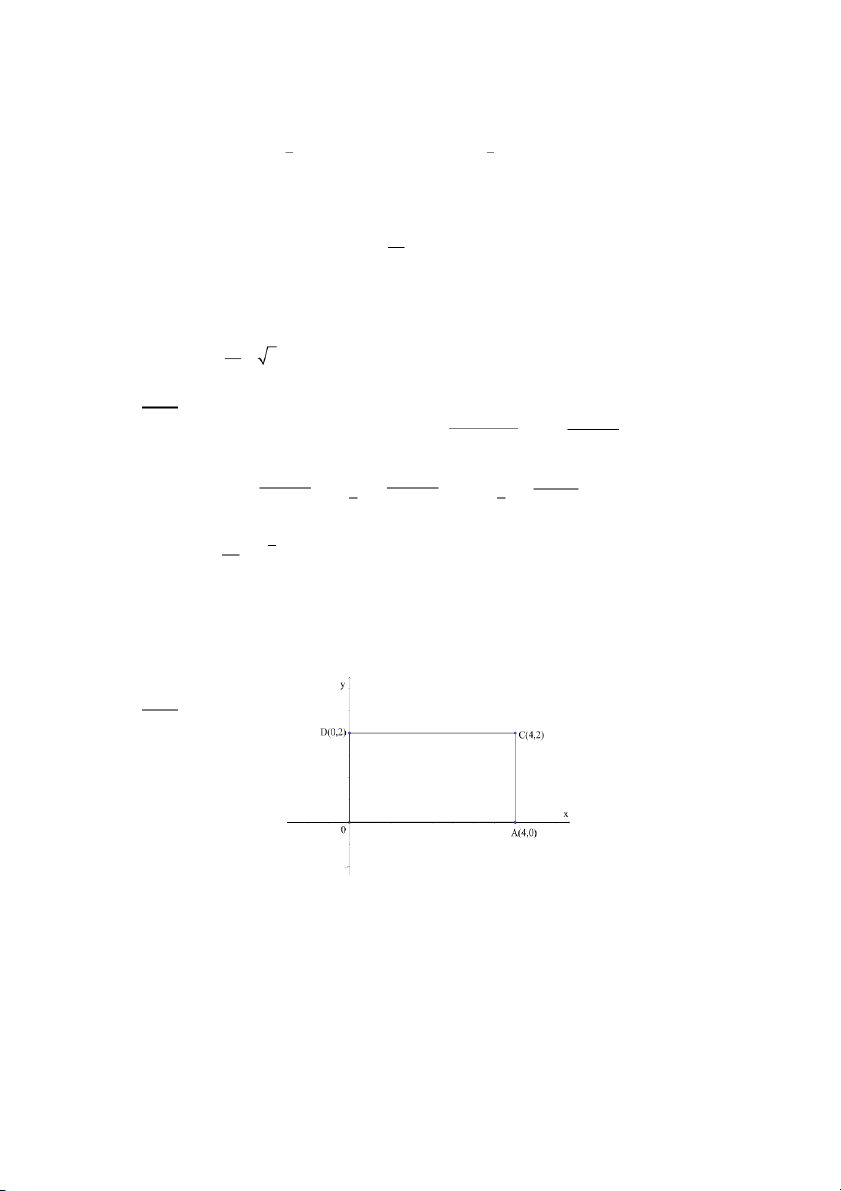
với 𝐿 là chu tuyến của hình chữ nhật 𝐴𝐵𝐶𝐷 với 𝐴(0,0); 𝐵(4,0), L 𝐶(4,2), 𝐷(0,2) A. 20 B. 25 C. 24 D. 18 Câu 19: Tính
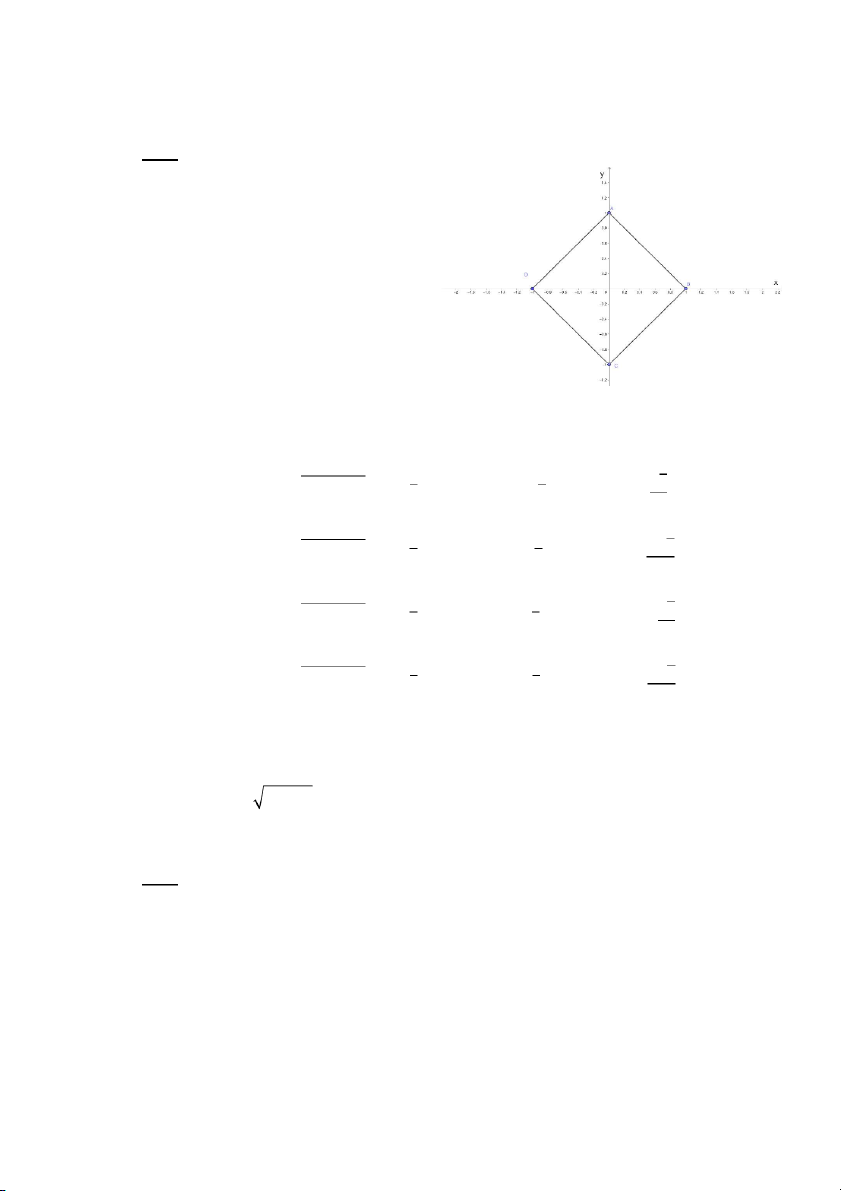
với 𝐶 là biên của miền |𝑥| + |𝑦| ≤ 1 A. 1 B. 4 C. 2 D. 0 Câu 20: Tính 2 2 x + y ds
với 𝐿: 𝑥2 + 𝑦2 = 2𝑥 L A. 8 B. 6 C. 4 D. 1 0
2. Tích phân đường loại II:
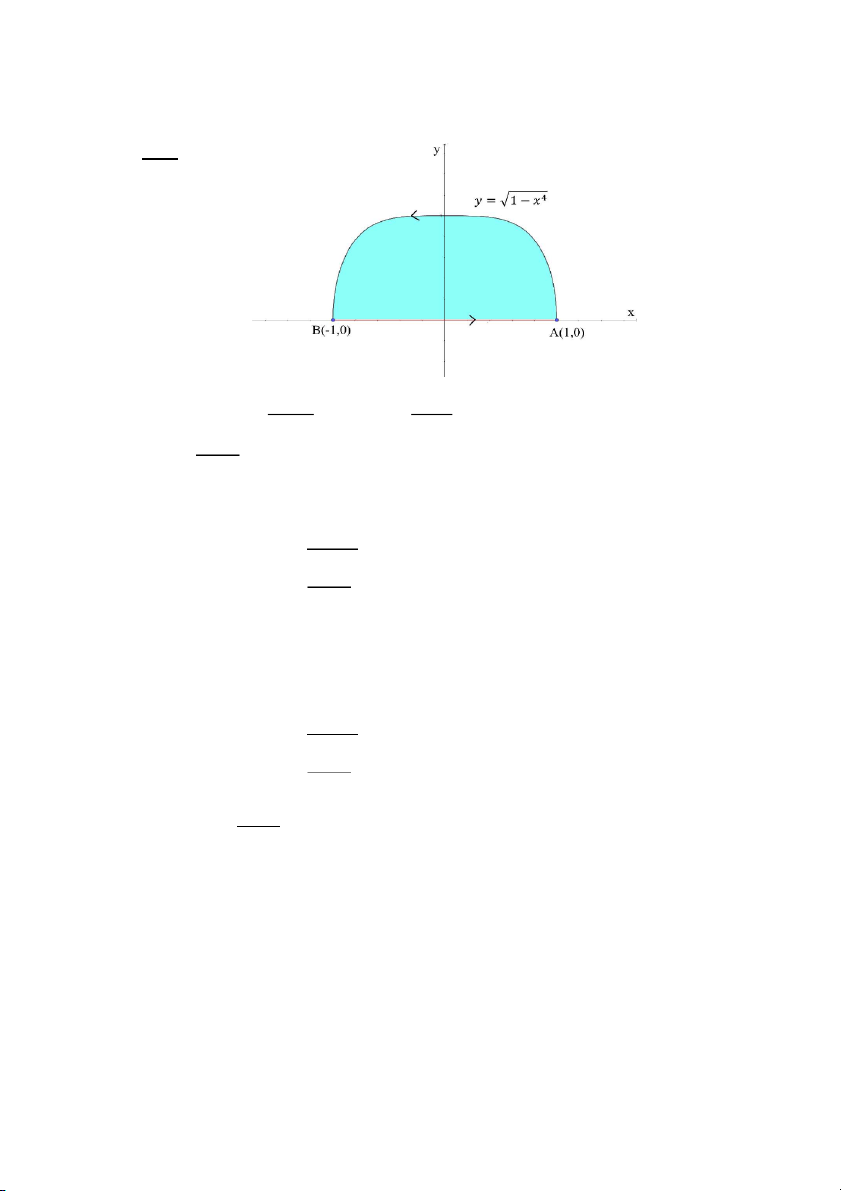
Câu 21: Tính (x − 3y)dx + 2ydy  với 𝐴𝐵
⏜ là cung 𝑦 = 1 − 𝑥2,𝐴(1,0),𝐵(−1,0) AB A. 0 B. 2 C. 4 D. 6 Câu 22: Tính 4 3 5 y dx −4 x dy
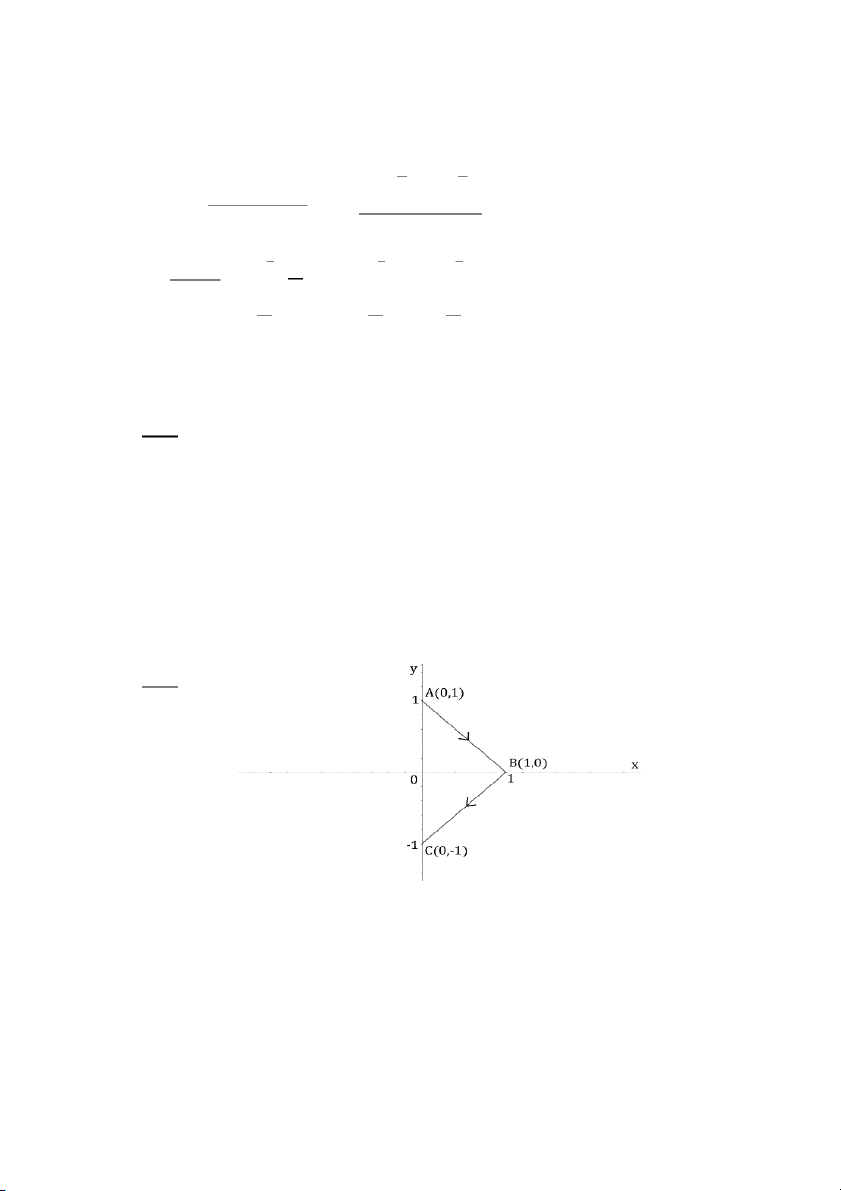
với 𝐴𝐵𝐶 là đường gấp khúc đi qua các điểm ABC
𝐴(0,1); 𝐵(1,0); 𝐶(0, −1) A. 2 B. 3 C. 5 D. 4 −
Câu 23: Tìm 𝑚 để 2 10 ( x + x ) y dx + . m x dy = 
với 𝐶 là cung bé trên đường tròn 3 C
𝑥2 + 𝑦2 = 4 đi từ 𝐴(−2,0) đến 𝐵(0,2) A. 2 B. 3 C. 0 D. 1 Câu 24: Tính + + ) + ( − y x y dx
−xy + e − x + sin y)dy với 𝐿 là đường
𝑥2 + 𝑦2 = 2𝑥 theo chiều dương. A. −3𝜋 B. 3𝜋 C. −2𝜋 D. 4𝜋 4 Câu 25: Tính 2 y +1 2 2y + e + sin(y )dy
 với 𝐿 là chu tuyến của tam giác
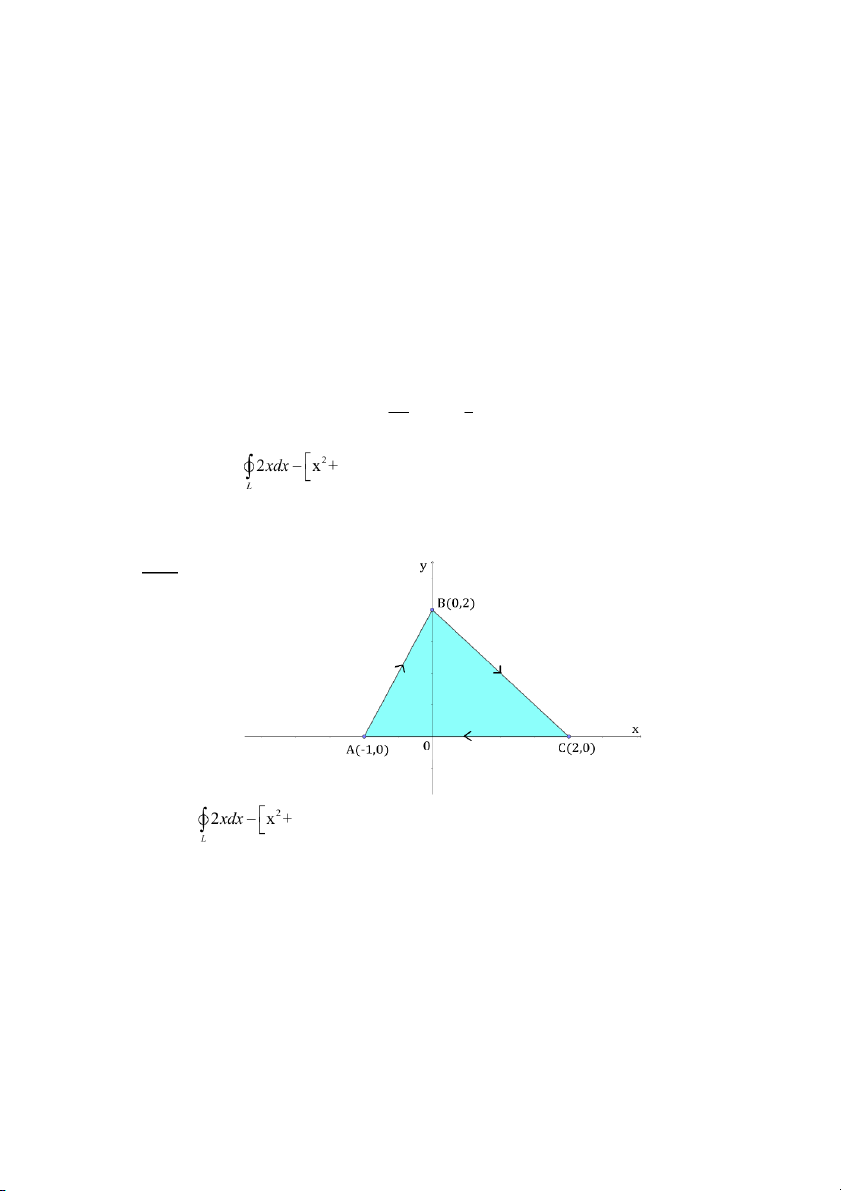
𝐴𝐵𝐶 có 𝐴(−1,0), 𝐵(0,2), 𝐶(2,0) chiều cùng chiều kim đồng hồ. A. 1 B. 2 C. 4 D. 6 Câu 26: Tính x 10 2
(xy + e )dx + (y − x )dy  với 𝐴𝐵
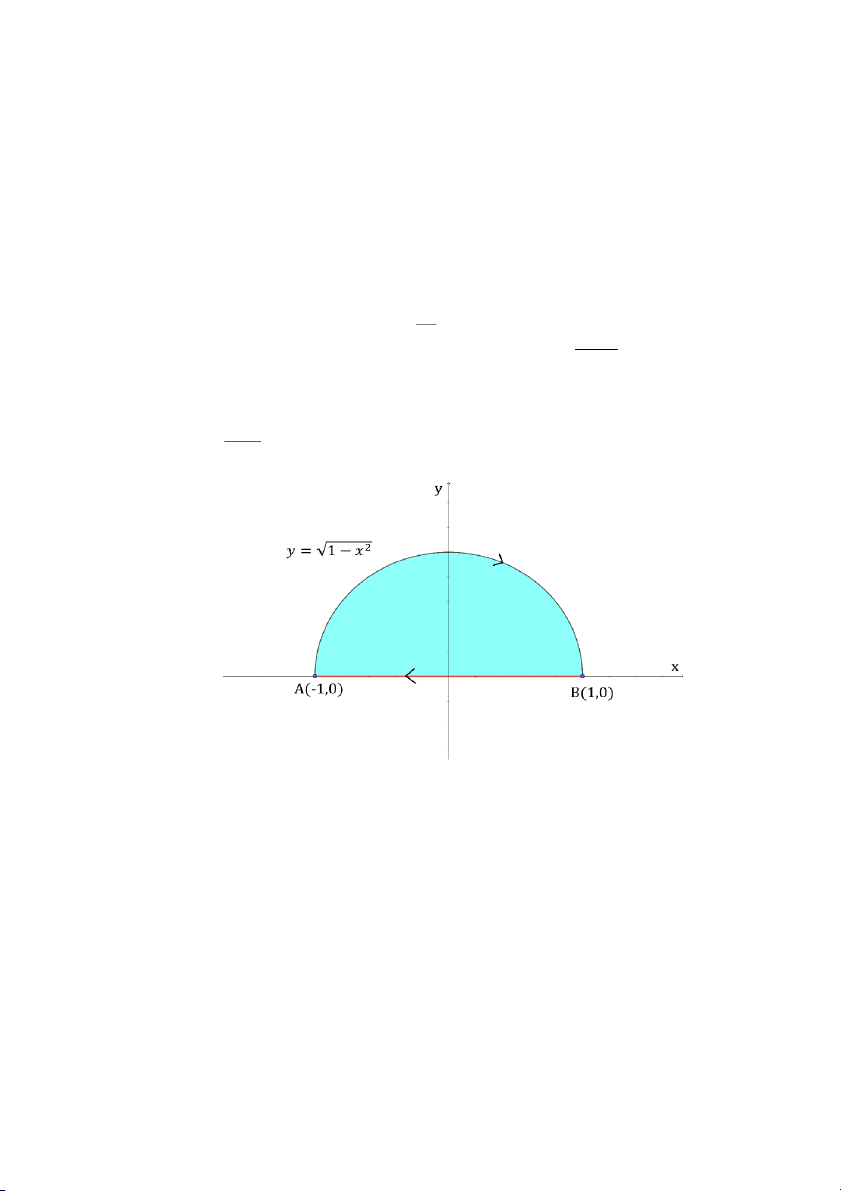
⏜ là cung 𝑦 = √1 − 𝑥2 đi từ điểm AB 𝐴(−1,0) đến 𝐵(1,0) 2 e −1 2 e −1 2 e − 2 2 A. e B. C. D. 2e e 2e 3 Câu 27: Tính x 2 4 (2 4
e + y )dx + ( y x + e )dy
với 𝐶: 𝑦 = √1 − 𝑥2 đi từ 𝐴(−1,0) đến C 𝐵(1,0)  2  3  3  3
A. − + 2e B. − −𝑒 C. − D. − +3e 2 e 2 e 2 e 2 e (3,0)
Câu 28: Tính tích phân  ( 4 3 x + 4xy ) 2 2 4
dx + (6x y − 5y )dy ( 2 − , 1 − ) A. 61 B. 62 C. 63 D. 64
Câu 29: Tìm 𝑚 để tích phân 2 x + y 2 2 e
2xy dx + (y + .
m y)dy  = e    với 𝐿 là đường L
𝑥 = 1 − 𝑦2 đi từ 𝐴(1,0) đến 𝐵(0,1) A. 1 B. 2 C. 3 D. 4 2 2
−y + 2xy − x +1 x − x −1
Câu 30: Tính tích phân +  với 𝐿: 𝑦 = 2𝑥 + 2 2 2 dx 2 2 dy ( y − x −1) ( y − x −1) L
đi từ 𝐴(0,2) đến 𝐵(2,6) A. 4 B. 3 C. 2 D. 1
Câu 31: Tìm 𝑎, 𝑏 để tích phân x e   ( 2
2x + ay +1)dx + (bx + 2y)dy không phụ L thuộc vào đường đi 5 A. {𝑎 = 1 𝑏 = 0 B. {𝑎 = 0 𝑏 = 1 C. {𝑎 = 0 𝑏 = 0 D. {𝑎 = 1 𝑏 = 1
Câu 32: Tìm hằng số 𝑎, 𝑏 để biểu thức [𝑦2 + 𝑎𝑥𝑦 + 𝑦 sin(𝑥𝑦)]𝑑𝑥 + [𝑥2 + 𝑏𝑥𝑦 +
𝑥 sin(𝑥𝑦)]𝑑𝑦 là vi phần toàn phần của một hàm số 𝑢(𝑥, 𝑦) nào đó A. {𝑎 = 1 𝑏 = 1 B. {𝑎 = 2 𝑏 = 2 C. {𝑎 = 2 𝑏 = 1 D. {𝑎 = 1 𝑏 = 2 2 2 2 2 x + y x + y +
Câu 33: Tính xe dx ye dy  với 2
L : y = 2x − x đi từ 𝑂(0,0) đến 𝐴(2,0) x − + y L ( )2 2 1 A. 1 B .0 C. 2 D. 3 − + (5x + 2y)
Câu 34: Cho tích phân 𝐼 =
dy với 𝐶 là biên của hình 2 + y 2x − 5
phẳng 𝐷: 𝑥2 + 𝑦2 ≤ 9 y
, theo chiều dương, bạn 𝐴 lập luận “Ta đặt P = và 2 2 x + y 5x + 2y Q = , ' '
Q − P = 0 , 𝐶 là đường cong kín, chiều dương, giới hạn miền 𝐷 nên 2 2 x + y x y
𝐼 = 0”. Hỏi bạn 𝐴 làm vậy có đúng không? Nếu sai, thì sửa lại đáp án chính xác A. Đúng B. Sai, 𝐼 = 10𝜋 C. Sai, 𝐼 = 𝜋 D. Sai, 𝐼 = 5𝜋
Câu 35: Tìm 𝑚 để tích phân (x −3y)dx + 2ydy = 4  với 2
AB : y = m − x và hai AB điểm ( A 1,0), B( 1 − ,0) A. 1 B. −1 C. 2 D. −2
Câu 36: Tính ydx + zdy + xdz
với 𝐶: 𝑥 = cos 𝑡 , 𝑦 = sin 𝑡 , 𝑧 = 2𝑡, 0 ≤ 𝑡 ≤ 2𝜋 theo C chiều tăng của 𝑡 A. 2𝜋 B. 𝜋 C. −𝜋 D. 3𝜋 (4,5,6)
Câu 37: Tính tích phân y y + + ( +1) z e dx xe dy z e dz  (1,2,3)
A. 4𝑒5 + 6𝑒6 − 𝑒2 − 3𝑒3
B. 4𝑒4 + 6𝑒6 − 𝑒2 − 3𝑒3 6
C. 4𝑒4 + 6𝑒6 − 2𝑒2 − 3𝑒3
D. 4𝑒5 + 6𝑒6 − 2𝑒2 − 3𝑒3
Câu 38: Tìm hàm thế vị của biểu thức (𝑥4 + 4𝑥𝑦3)𝑑𝑥 + (6𝑥2𝑦2 − 5𝑦4)𝑑𝑦 1 2 A. 2 2 3 5
x + 2x y − y C. 2 2 3 5
x + x y − y 5 5 2 1 B. 2 2 3 5 2 2 3 5
x + 2x y − y
D. x + x y − y 5 5
Câu 39: Tính (2 xy 5
− ) dx +(2 x +3 ) y dy
với 𝐿 là biên của miền 𝐷 xác định bởi L
các đường 𝑦 = 𝑥2, 𝑦 = 0, 𝑥 = 1, chiều dương 1 1 1 1 A. B. C. D. 3 4 5 6  2   2  Câu 40: Tính 2 2 3 3x y + dx + 3x y + dy 
với 𝐶 là đường cong 2   3   4x +1  y + 4  C
𝑦 = √1 − 𝑥4 đi từ 𝐴(1,0) đến 𝐵(−1,0). 4 4
A. − arctan 2
C. − 3arctan 2 7 7 4 4
B. − 2arctan 2 D. + 2arctan 2 7 7
3. Ứng dụng của tích phân đường
Câu 41: Tính diện tích của miền D giới hạn bởi 𝐿: { 𝑥 = 2(𝑡 − sin 𝑡)
𝑦 = 2(1 − cos 𝑡) với trục 𝑂𝑥
biết rằng 𝑡 đi từ 2𝜋 dến 0
A. 13𝜋 (đvdt)
B. 12𝜋 (đvdt)
C. 11𝜋 (đvdt) D. 10𝜋 (đvdt)
Câu 42: Tính công của lực 𝐹 = (𝑥 + 2𝑦)𝑖 + (3𝑥 + 4𝑦)𝑗 làm dịch chuyển một chất
điểm từ 𝐴(1,3) đến 𝐵(2,4) dọc theo đoạn thẳng 𝐴𝐵. (đvc: đơn vị công) A. 21 (đvc) B. 21,5 (đvc) C. 26 (đvc) D. 27 (đvc) 7 𝑥 = cos 𝑡
Câu 43: Tính khối lượng của đường cong vật chất 𝐿 có phương trình { 𝑦 = sin 𝑡 0 ≤ 𝑡 ≤ 𝜋/2
biết hàm mật độ là 𝑝(𝑥, 𝑦) = 𝑦 A. 1 (đvkl) B. 2 (đvkl) C. 3 (đvkl) D. 5 (đvkl)
Câu 44: Tính công làm dịch chuyển một chất điểm từ A(0,1) đến B(1,0) của lực
𝐹 = [8𝑥3 − 2𝑦 ln(1 + 𝑥2𝑦2)]𝑖 + [5𝑦4 − 2𝑥 ln(1 + 𝑥2𝑦2)]𝑗 A. 1 (đvc) B. 2 (đvc) C. 5 (đvc) D. 4 (đvc)
Câu 45: Tính khối lượng của đường cong vật chất 𝐿 có phương trình 𝑥2 + 𝑦2 = 1
biết hàm mật độ là 𝑝(𝑥, 𝑦) = 𝑥2
A. 3𝜋 (đvkl)
B. 4𝜋 (đvkl)
C. 2𝜋 (đvkl) D. 𝜋 (đvkl) 8 III. Bài t p tr ậ c nghi ắ
ệm Tích phân mặt
1. Tích phân mặt loại I:
Câu 46: Tính xydS 
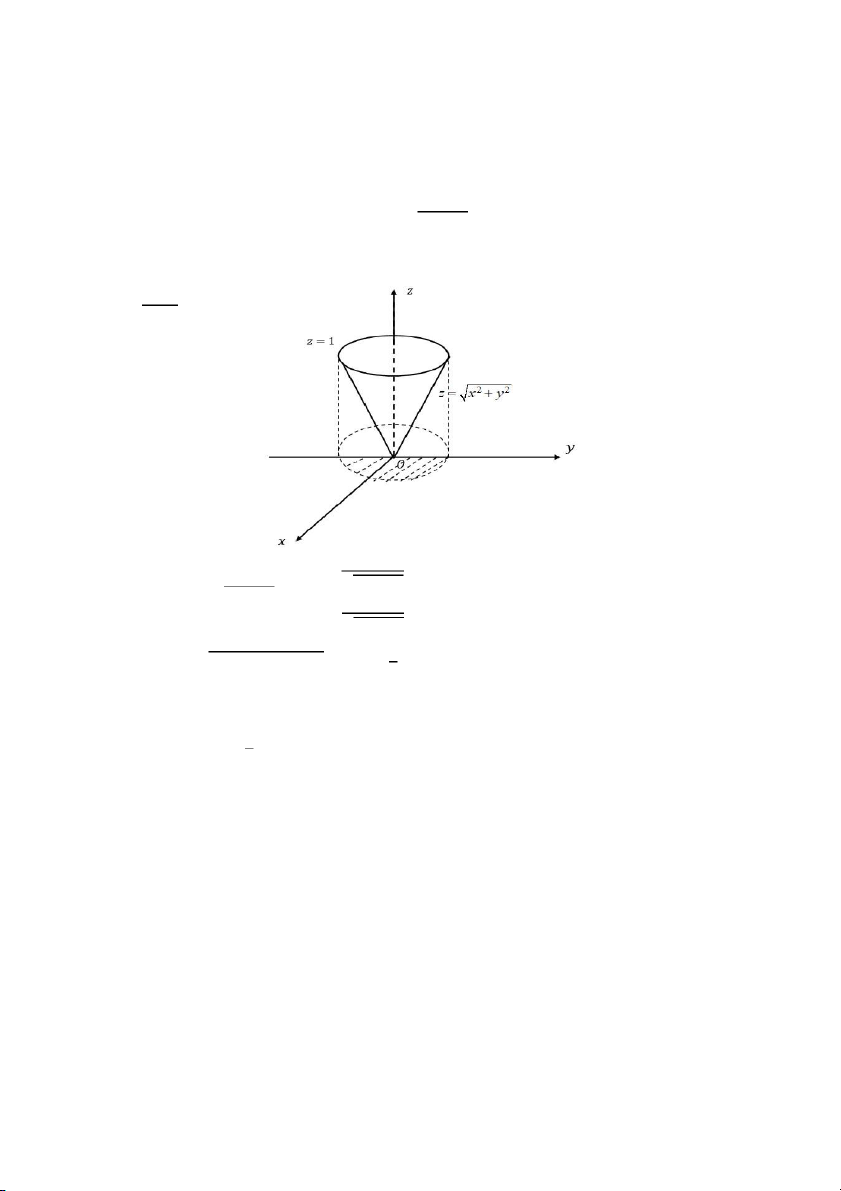
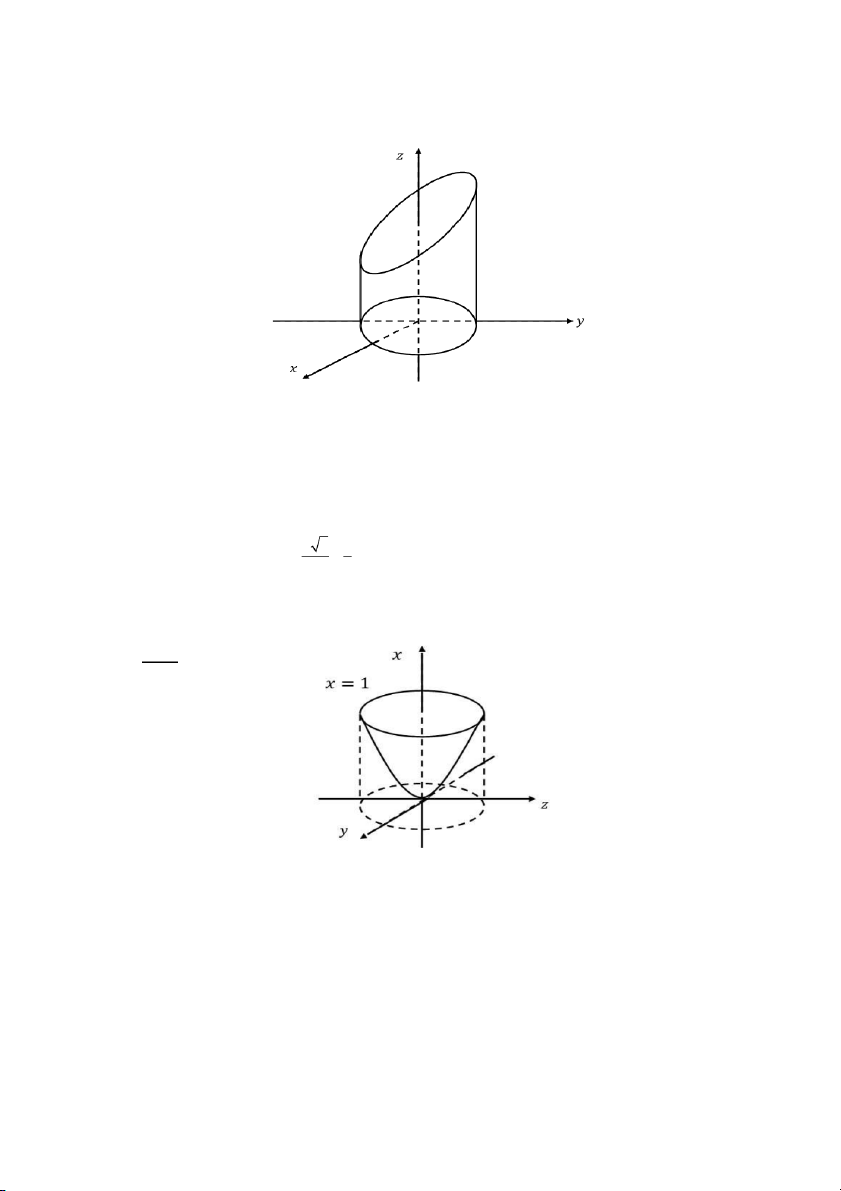
với 𝑆 là mặt 𝑧 = √𝑥2 + 𝑦2, 𝑧 ≤ 1, 𝑥 ≥ 0 S A. 0 B. 2 C. 1 D. 3 Câu 47: Tính 2 x dS 
với 𝑆 là biên của miền giới hạn bởi mặt 𝑧 = √𝑥2 + 𝑦2, 𝑧 = 1 S (2 + 2)  (2 + 3) (1 + 2) (1+ 3) A. B. C. D. 4 4 4 4 5 6
Câu 48: Tìm 𝑚 để (x + y +mz)dS = 
với 𝑆 là mặt 2𝑥 + 4𝑦 + 2𝑧 = 4 và điều 3 S
kiện 𝑥 ≥ 0, 𝑦 ≥ 0, 𝑧 ≥ 0 A. 𝑚 = 0 B. 𝑚 = 1 C. 𝑚 = −1 D. 𝑚 = 2
Câu 49: Tính xyzdS 
với 𝑆 là mặt 𝑥 − 2𝑦 + 3𝑧 − 4 = 0 giới hạn trong mặt trụ có S
phương trình 2𝑥2 + 3𝑦2 = 6 A. 1 B. 0 C. 2 D. 3   Câu 50: Biết a 5 1 xdS =  +   2 2 
biết 𝑆 là phần mặt paraboloid 𝑥 = 𝑦 + 𝑧 thỏa 12 b S  
mãn 𝑥 ≤ 1. Kết luận nào sau đây là chính xác?
A. 𝑎 + 𝑏 < 70
B. 𝑎 − 𝑏 > 0
C. 𝑎. 𝑏 < 70 D. 𝑎/𝑏 > 1 Câu 51: Tính 2 2 1+ x + y dS 
với 𝑆 là phần mặt 2𝑧 = 𝑥2 + 𝑦2, 0 ≤ 𝑥, 𝑦 ≤ 1. Chọn S
đáp án gần với kết quả của tích phân nhất. A. 2 B. 3 C. 4 D. 0 4 Câu 52: Biết 2 dS
 = (33− a 3 −b 2) với 𝑆 là mặt z = ( 3/2 3/2 x + y ) với điều 15 3 S
kiện 0 ≤ 𝑥 ≤ 2, 0 ≤ 𝑦 ≤ 1. Tìm khẳng định đúng? 9 A. 𝑎 < 𝑏
B. 𝑎 + 𝑏 = 10
C. 𝑎 − 𝑏 = 5
D. 𝑎. 𝑏 = 10 Câu 53: Tính 2 zy dS 
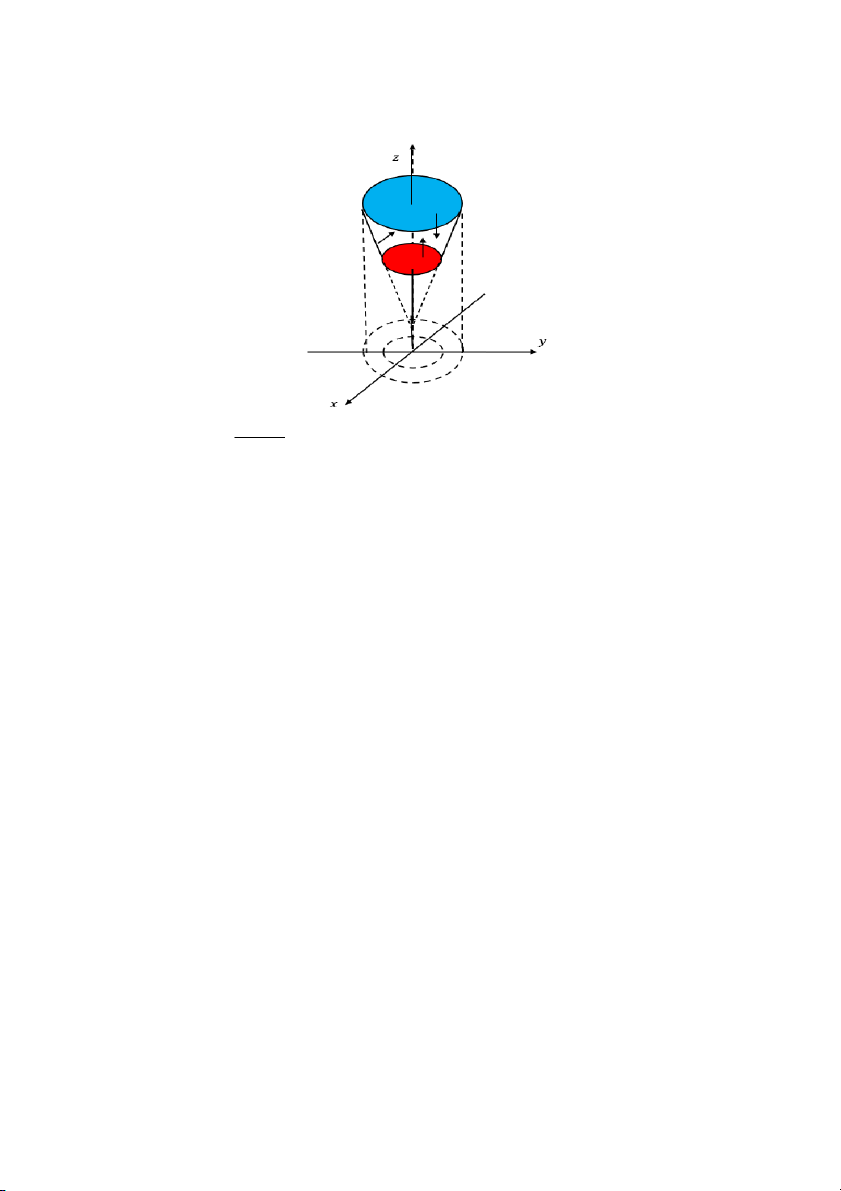
với 𝑆 là phần mặt nón 𝑧 = √𝑥2 + 𝑦2 nằm giữa hai mặt 𝑧 = 1 S và 𝑧 = 2 31 2 31 2 31 2 31 2 A. B. C. D. 3 10 4 5 Câu 54: Tính 2 yx dS 
với 𝑆 là phần mặt nón 𝑦 = √𝑥2 + 𝑧2, 1 ≤ 𝑦 ≤ 2 S 32 2 31 2 33 2 34 2 A. B. C. D. 5 5 5 5
Câu 55: Tính xdS 
với 𝑆 là mặt trụ 𝑥2 + 𝑦2 = 4 nằm giữa hai mặt 𝑧 = 0 và 𝑧 = 6 S A. 0 B. 1 C. 2 D. 3
2. Tích phân mặt loại II:
Câu 56: Tính (1− x − z)dzdx 
với 𝑆 là mặt trên của mặt 𝑥 + 𝑦 + 𝑧 = 1, 𝑥 ≥ 0, 𝑦 ≥ S 0, 𝑧 ≥ 0 1 2 1 4 A. B. C. D. 5 3 6 3 Câu 57: Tính 2 2 2 I =
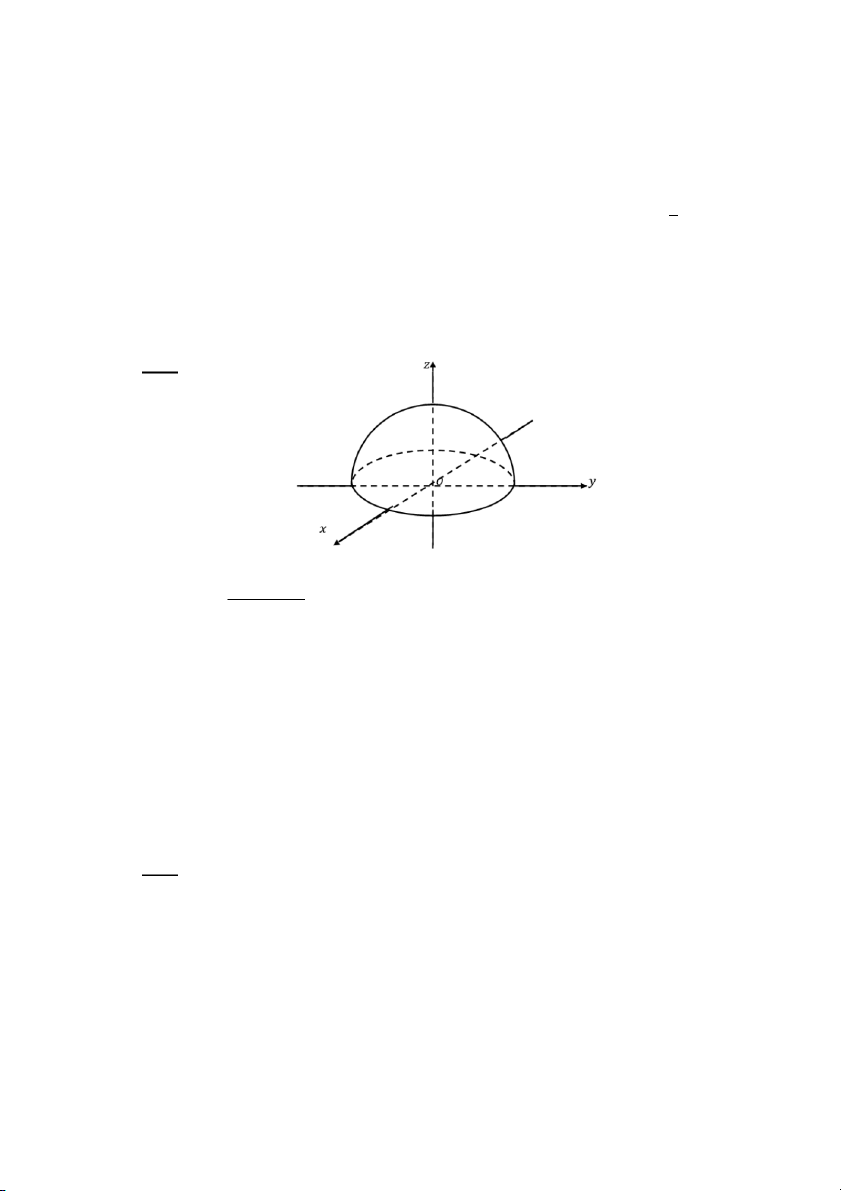
(x + y + z )dxdy 
với 𝑆 là mặt nửa cầu 𝑥2 + 𝑦2 + 𝑧2 = 1 phía S
trên 𝑂𝑥𝑦, mặt 𝑆 hướng lên trên. A. 𝜋 B. −𝜋 C. 2𝜋 D. 3𝜋 Câu 58: Cho 𝐼 = 2 ydzdx + z dxdy 
, 𝑆 là phía ngoài mặt 𝑥2 + 𝑦2 + 𝑧2 = 1 với điều S
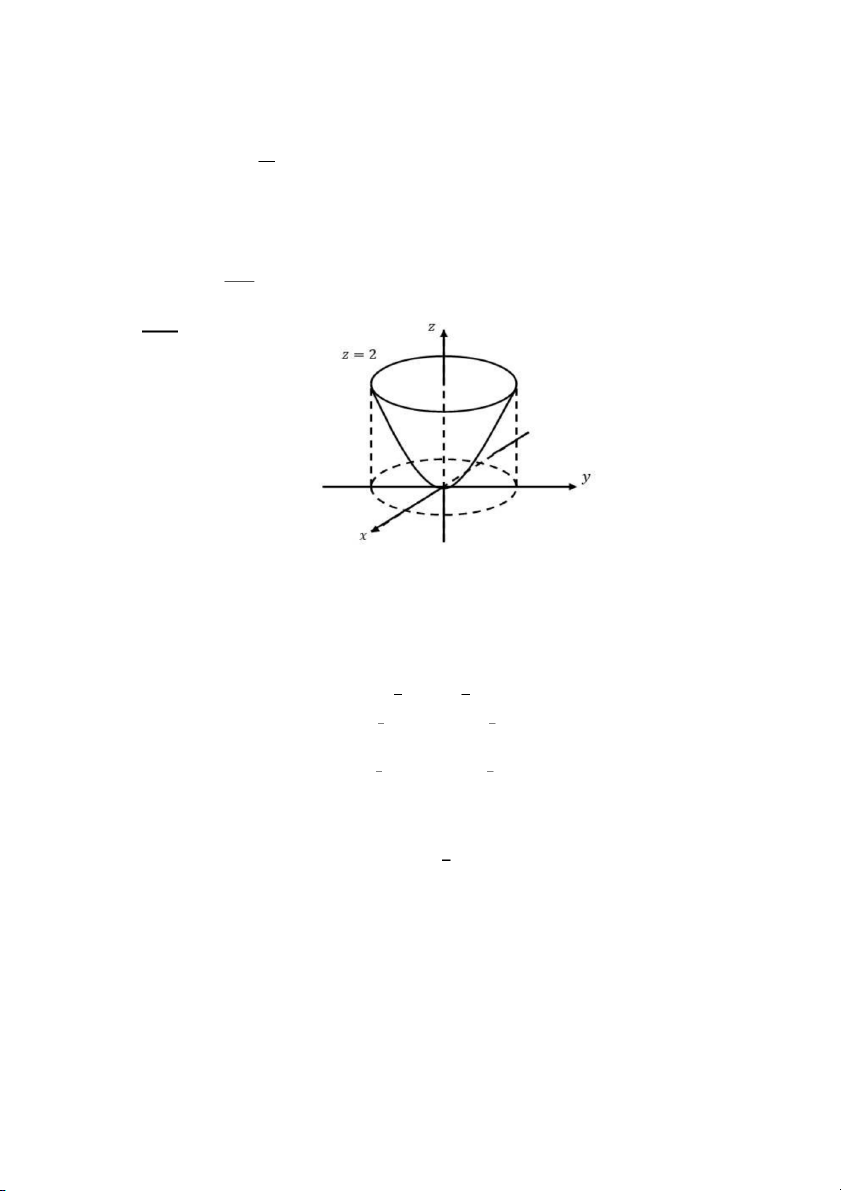
kiện 𝑥 ≥ 0, 𝑦 ≥ 0, 𝑧 ≥ 0. Chọn đáp án gần nhất với kết quả của 𝐼 A. 1 B. 0 C. 2 D. 3 Câu 59: Tính 𝐼 = 2 xdzdx + z dxdy 
với 𝑆 là phía ngoài mặt 𝑧 = 𝑥2 + 𝑦2 với điều S
kiện 0 ≤ 𝑧 ≤ 2, 𝑦 ≥ 0 10 4 −  7 −  −5 4 −  A. B. C. D. 5 3 3 3 Câu 60: Tính 2 2 2 2 2 2
xz dydz + 4yx dzdx + 9zy dxdy 
với mặt 𝑆: 4𝑥 + 9𝑦 + 𝑧 = 1, S hướng ra ngoài. 4 2 2 2 A. B. C. D. 15 15 13 19 Câu 61: Biết 𝐼 = 2 2 2 +( + ) +(4 + ) a xydydz x y dzdx x y dxdy = 
với mặt 𝑆 là biên của b S
miền 𝑉: 𝑥 + 𝑦 + 𝑧 ≤ 1, 𝑥 ≥ 0, 𝑦 ≥ 0, 𝑧 ≥ 0 hướng ra ngoài. Tìm khẳng định đúng
A. 𝑎 − 𝑏 = 7
B. 𝑎. 𝑏 = 7
C. 𝑎 + 𝑏 = 7 D. 𝑎/𝑏 = 7 Câu 62: Tính 𝐼 = 2 3 3 2
(xy + 2z )dydz + (z + 2y)dzdx + x zdxdy  với 𝑆 là nửa mặt S
cầu 𝑥2 + 𝑦2 + 𝑧2 = 1, 𝑧 ≥ 0 hướng ra ngoài mặt cầu. 8 8 6 8 A. B. C. D. 5 3 7 7 Câu 63: Tính 𝐼 = 3 2 2 (x +2 y )
z dydz + (3x y + )
y dzdx + (6 y z + x ) y dxdy  với 𝑆 là mặt S
𝑧 = 𝑥2 + 𝑦2 với 𝑧 ≤ 1, hướng xuống dưới. A. 1 B. 0 C. 2 D. 8 1 Câu 64: Tính
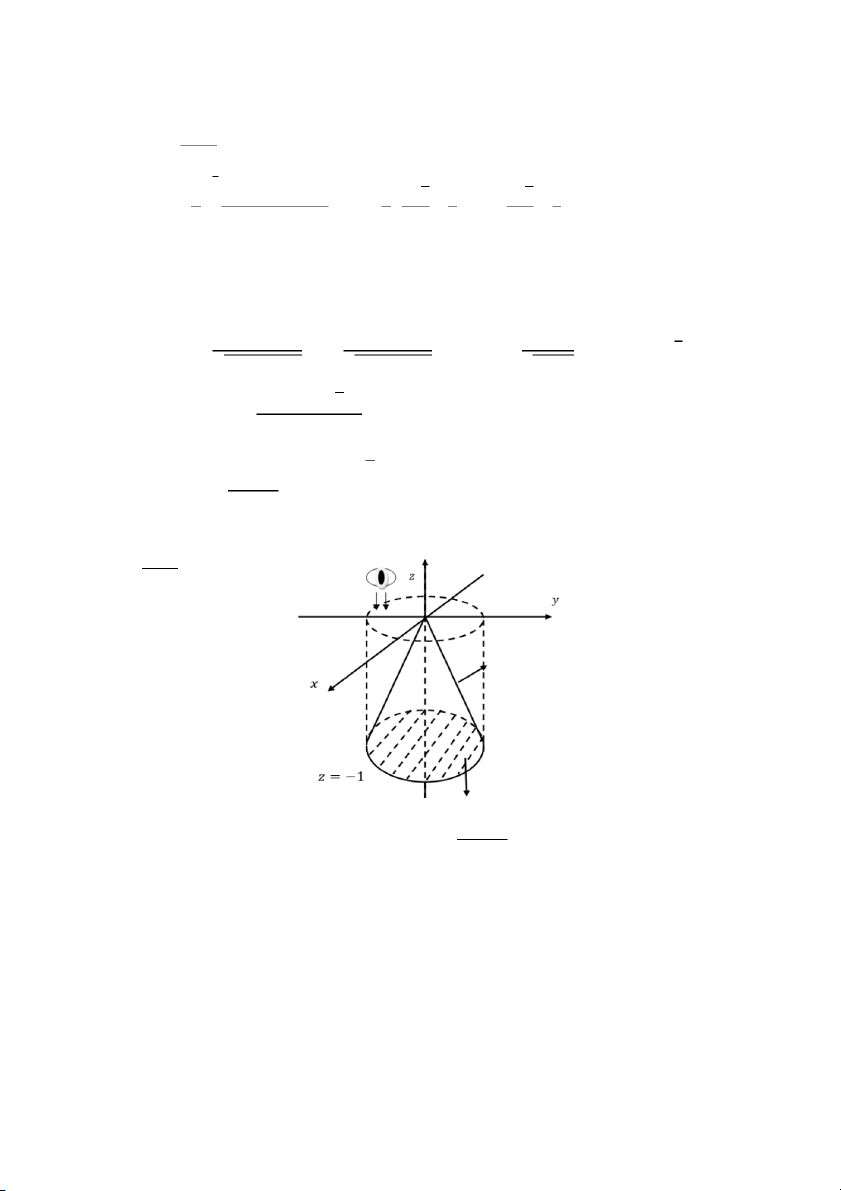
(−xdydz − ydzdx + dxdy) 
với 𝑆 là mặt 2𝑧 = 𝑥2 + 𝑦2, 2 2 S 1+ x + y
𝑧 ≤ 2 theo chiều âm của trục 𝑂𝑥 (2 +10 5) ( 2 − +10 5) A. C. 3 3 (2 + 5) ( 2 − + 5) B. D. 3 3 11 Câu 65: Biết a
xdydz + zdxdy =  
với 𝑆 là phần trên của mặt nón có phương b S
trình 𝑧 = −√𝑥2 + 𝑦2 , −1 ≤ 𝑧 ≤ 0 khi nhìn từ chiều dương trục 𝑂𝑧. Tính 2𝑎 + 𝑏 A. 1 B. 9 C. 0 D. 5 Câu 66: Tính + 2 2
zdz dọc theo đường tròn 𝐶: 𝑥 + 𝑦 = 1, 𝑧 = 0
chiều dương giới hạn mặt cầu 𝑧 = √1 − 𝑥2 − 𝑦2  −  − A. B. C. D. 6 4 7 8
Câu 67: Tính tích phân 𝐼 = 1 ( 2
− xdydz−2 ydzdx+ dxd ) y  với 𝑆 là 2 2 + + S 1 4x 4y
mặt có phương trình 𝑧 = 𝑥2 + 𝑦2, 0 ≤ 𝑧 ≤ 4 theo chiều 𝑧 ≥ 0 (17 17 −1) (17 16 −1) A. C. 7 6 (17 17 −1) (17 17 +1) B. D. 6 6
Câu 68: Tính tích phân 𝐼 = 3 3
(6z −9y)dydz + (3x − 2z )dzdx + (3y −3x)dxdy  với S
𝑆 là mặt 𝑥2 + 3𝑦2 + 𝑧4 = 1,𝑧 ≥ 0, hướng lên trên. A. 2 B. 3 C. 0 D. 1 Câu 69: Tính 2 (2x + x )
y dydz +( y + 2x )
z dzdx +(1+6 z + z )dxdy  với 𝑆 là mặt nằm S
trong của nửa cầu 𝑧 = −√16 − (𝑥2 + 𝑦2 + 𝑧2)
A. (80 − 190√2)𝜋
C. (80 − 193√2)𝜋
B. (80 − 192√2)𝜋
D. (80 − 194√2)𝜋
Câu 70: Tính xydydz + yzdzdx + zxdxdy 
biết 𝑆 là mặt ngoài của tứ diện 𝑂𝐴𝐵𝐶 với S
𝑂(0,0,0), 𝐴(1,0,0), 𝐵(0,1,0), 𝐶(0,0,1) 12 1 1 1 1 A. B. C. D. 7 8 9 10 Câu 71: Biết 2 2 2
2x dydz + y dzdx − z dxdy = a + b 
, S là mặt ngoài của miền giới S
hạn bởi 𝑦 = 0, 𝑦 = √1 − 𝑧2, 𝑥 = 0, 𝑥 = 2 chọn khẳng định đúng A. 𝑎 + 3𝑏 = 12 C. −𝑎 + 3𝑏 = 0 B. 3𝑎 + 6𝑏 = 16 D. 𝑎 + 𝑏 = 4 Câu 72: a Biết I =
(x + z)dydz + ( y + x)dzdx + (z + y)dxdy =   với 𝑆 là mặt trong b S
của parabol 𝑧 = 𝑥2 + 𝑦2 nằm dưới mặt 𝑥 + 𝑧 = 2 . Tí nh 𝑎 − 𝑏 A. 50 B. 49 C. 52 D. 47
3. Ứng dụng của tích phân mặt:
Câu 73: Tính diện tích mặt 𝑆: 𝑧 = 2 + √𝑥2 + 𝑦2 , 𝑧 ≤ 3 A. 7 (đvdt) B. 3 (đvdt) C. 2 (đvdt) D. 5 (đvdt)
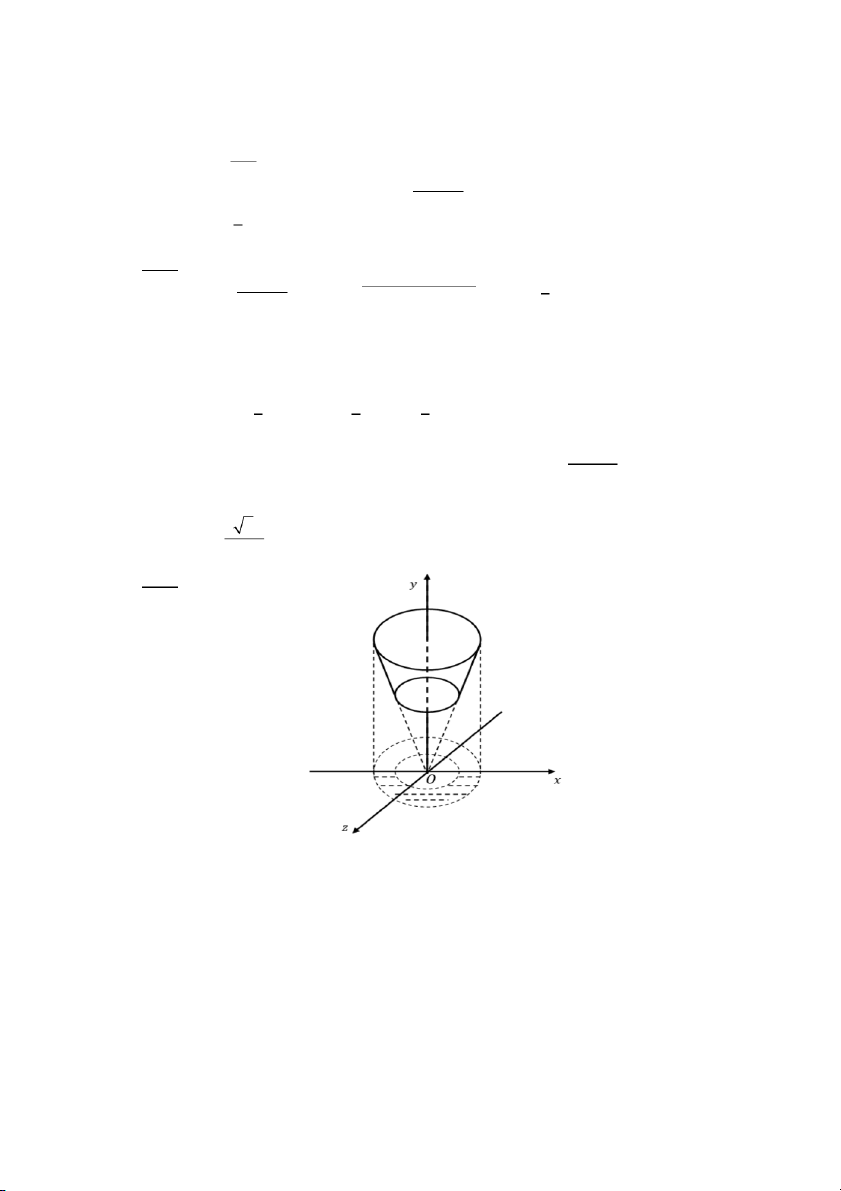
Câu 74: Tính diện tích mặt cong 𝑆 với 𝑆 là phần mặt nón 𝑦 = √𝑥2 + 𝑧2 với điều
kiện 1 ≤ 𝑦 ≤ 2, 𝑧 ≥ 0 3 2 3 3 3 3 A. (đvdt) B. (đvdt) C. (đvdt) D. (đvdt) 2 2 2 3
Câu 75: Tính diện tích mặt paraboloid 𝑧 = 4𝑥 − 𝑥2 − 𝑦2 nằm phía trên mặt 𝑂𝑥𝑦 là
(a 17 −1) , tính 𝑎 + 𝑏 b A. 20 B. 23 C. 19 D. 15
Câu 76: Tính diện tích phần mặt paraboloid 𝑥 = 𝑦2 + 𝑧2 thỏa mãn 𝑥 ≤ 1    A.  6 (5 5 −1) − D. ( 6 −1) 6 B. C. (3 6 1) 2 6 6
Câu 77: Tính diện tích mặt 𝑆: 𝑧 = √𝑥2 + 𝑦2 , 𝑧 ≤ 3 A. 9𝜋√2 B. 8𝜋√5 C. 9𝜋√8 D. 7𝜋√3 13 IV.Bài t p tr ậ
ắc nghiệm Lý thuyết trườn g
1. Trường vô hướng:
Câu 78: Tính đạo hàm theo hướng 𝑙 = (1,2, −2) của 𝑢 = 𝑒𝑥(𝑦2 + 𝑧) − 2𝑥𝑦𝑧3 tại 𝐴(0,1,2) −11 −11 −15 −15 A. B. C. D. 4 3 4 2
Câu 79: Cho 𝑢(𝑥, 𝑦, 𝑧) = 𝑥3 + 3𝑦𝑥2 + 2𝑦𝑧2. Tính u
với 𝑛󰇍 là vecto pháp tuyến n
hướng ra ngoài của mặt cầu 𝑥2 + 𝑦2 + 𝑧2 = 3, 𝑧 ≤ 0 tại điểm 𝐴(1,1, −1) A. −6√3 B. −6√2 C. −2√3 D. −2√6
Câu 80: Biết nhiệt độ tại điểm (𝑥, 𝑦, 𝑧) trong không gian được cho bởi hàm 80 𝑇(𝑥, 𝑦, 𝑧) = 1 + 𝑥2 + 2𝑦2 + 3𝑧2
ở đó 𝑇 có đơn vị là ℃ và 𝑥, 𝑦, 𝑧 là mét. Theo hướng nào thì nhiệt độ tăng nhanh
nhất tại điểm 𝐴(1,1, −2) 5 5 15   5 − 5 − 15  A. ; ;   C. ; ;   8 4 4   8 4 4  5 15 15 5 −5 15 B.   ; ;  D. ; ; 8 4 4      8 4 4 
Câu 81: Tính góc giữa hai vecto 𝑔󰇍𝑟𝑎𝑑
󰇍󰇍󰇍󰇍𝑧 (đơn vị: radian) của các trường vô hướng
sau 𝑧1 = √𝑥2 + 𝑦2, 𝑧2 = 𝑥 − 3𝑦 + √3𝑥𝑦 tại 𝑀(3,4) (Chọn đáp án gần đúng nhất) A. 2 B. 1 C. 3 D. 4
Câu 82: Cho 𝑢(𝑥, 𝑦, 𝑧) = l (
n 1 + 𝑥2 + 𝑒𝑦−𝑧) , 𝑂(0,0,0), 𝐴(1, −2,2). Tính u  theo l  hướng 𝑂 󰇍󰇍𝐴 󰇍 −2 −2 −1 −1 A. B. C. D. 5 3 3 5 14
Câu 83: Theo hướng nào thì sự biến thiên của hàm 𝑢 = 𝑥 sin 𝑧 − 𝑦 cos 𝑧 tại gốc tọa độ là lớn nhất
A. 𝑙 = (0,1,0)
B. 𝑙 = (0, −1,0)
C. 𝑙 = (0, −2,0)
D. 𝑙 = (0, −3,0)
Câu 84: Cho điểm 𝐴(2, −1,0), 𝐵(1,1,3). Tính đạo hàm của hàm 𝑢 = 𝑥3 + 3𝑦2 +
𝑒𝑧 + 𝑥𝑦𝑧2 tại điểm 𝐴 theo hướng 𝐴󰇍𝐵 󰇍󰇍 14 14 3 − 14 −2 14 A. B. C. D. 3 2 2 3
Câu 85: Tính góc giữa 𝑔󰇍𝑟𝑎𝑑 󰇍󰇍󰇍󰇍󰇍𝑢, x u =
tại điểm 𝐴(1,2,2) và 𝐵(−3,1,0) 2 2 2 x + y + z  8 −  −1 1  7 − A.     arccos B. arccos C. arccos D. arccos 9           9   9   9 
2.Trường Vecto:
Câu 86: Cho 𝐹 = 𝑥2𝑦𝑧𝑖 + 3𝑥𝑦2𝑧𝑗 + 𝑚𝑥𝑦𝑧2𝑘󰇍 với 𝑚 là tham số thực. Tìm 𝑚 để 𝐹 là trường ống. A. 𝑚 = 4 B. 𝑚 = −4 C. 𝑚 = 5 D. 𝑚 = −5
Câu 87: Xác định n ữ
h ng điểm không phải điểm xoáy trong trường vecto
𝐹 = (𝑧2 + 2𝑥𝑦)𝑖+ (3𝑥2 − 2𝑦𝑧)𝑗 − 𝑧2𝑘󰇍 A. (1,0,0) B. (0,0,1) C. (0,0,0) D. (0,1,0)
Câu 88: Biết 𝐹 = 𝑒𝑥2+𝑦2+𝑧2[(2𝑥2𝑦𝑧 + 𝑦𝑧)𝑖 + (2𝑦2𝑥𝑧 + 𝑥𝑧)𝑗 + (2𝑧2𝑦𝑥 + 𝑥𝑦)𝑘󰇍] là
trường thế. Tìm hàm thế vị. A. 2 2 2 x + y + z 2 2 x+ y + z u = e xyz+ C C. u = e xy+ C B. 2 2 2 x + y +z 2 2 y +z u = e xy+ C D. u = e xyz+ C
Câu 89: Biết 𝐹 = (3𝑥2 − 3𝑦2𝑧)𝑖 + (arctan 𝑧 − 6𝑥𝑦𝑧)𝑗 + ( 𝑦 + 3𝑥𝑦2) 𝑘󰇍 là trường 1+𝑧2
thế, tìm hàm thế vị. A. 2 2
u = x + y arctan z + 3xy z + C
C. u = yarctan z + 3xy z + C B. 2 3 2
u = 3x + y arctan z + 3xy z + C
D. u = x + y arctan z + 3xy z + C 15
Câu 90: Biết 𝐹 = (3𝑥2 + 𝑦𝑧)𝑖 + (6𝑦2 + 𝑥𝑧)𝑗 + (𝑧2 + 𝑥𝑦 + 𝑒𝑧)𝑘󰇍 là trường thế, tìm hàm thế vị 3 3 A. 3 3 z z z 3 3 z
u = x + 2y +
+ e + xyz + C
C. u = x + 2y +
+ e + xy + C 3 3 3 3 B. 3 3 z z z 3 3 xz
u = x + 3y +
+ e + xyz + C
D. u = x + 2y +
+ e + xyz + C 3 3
Câu 91: Tính thông lượng của 𝐹 = 𝑥𝑖 + (𝑦3 + 2𝑧)𝑗 + (3𝑥2𝑧 − 𝑥)𝑘󰇍 qua mặt cầu
𝑆: 𝑥2 + 𝑦2 + 𝑧2 = 1 hướng ra ngoài. 54 57 47 44 A. B. C. D. 15 15 15 15
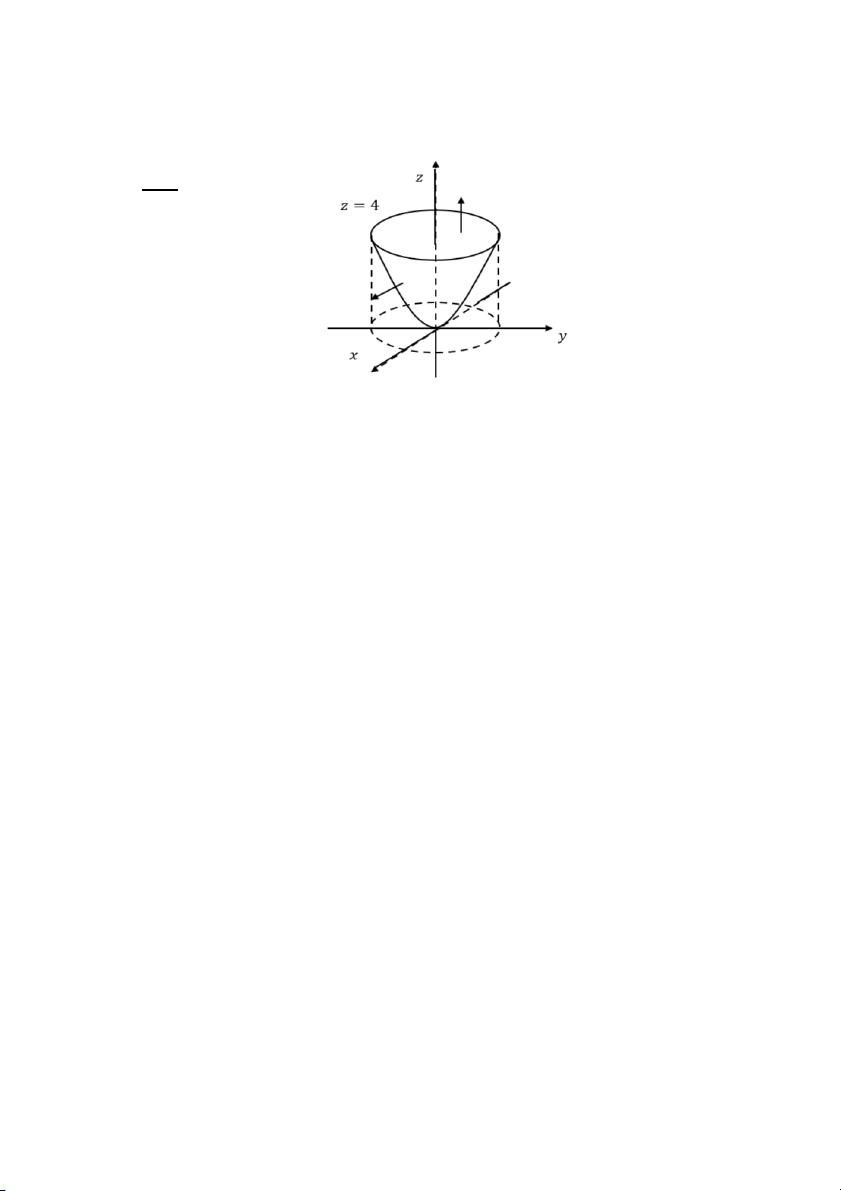
Câu 92: Tính thông lượng của 𝐹 = 𝑥𝑦2𝑖 − 𝑧𝑒𝑥𝑗 + (𝑥2𝑧 + sin 𝑦)𝑘󰇍 qua 𝑆 là mặt
𝑧 = 𝑥2 + 𝑦2, 𝑧 ≤ 4, hướng ra ngoài. (Chọn kết quả gần đúng nhất) A. −17 B. −15 C. −10 D. −14
Câu 93: Tính thông lượng của 𝐹 = (𝑥2 − 2𝑦 + 𝑧)𝑖 − (𝑧2 + 2𝑥𝑦)𝑗 + 𝑥𝑘󰇍 qua phía
trên mặt nón 𝑧 = 1 + √𝑥2 + 𝑦2 cắt bởi hai mặt phẳng 𝑧 = 2, 𝑧 = 5 A. 25 B. 16 C. 0 D. 2 0
Câu 94: Tính thông lượng của trường vecto 𝐹 = 2𝑥2𝑖 + 𝑦2𝑗 − 𝑧2𝑘󰇍 qua S là mặt
ngoài của miền giới hạn bởi 𝑦 = 0, 𝑦 = √1 − 𝑧2, 𝑥 = 0, 𝑥 = 2 8 8 8 8 A. 4 + B. 3 + C.  + D. 4 + 3 3 3 5
Câu 95: Tính thông lượng của trường vecto 𝐹 = 𝑥3𝑖 + 𝑦2𝑗 + 𝑧2 𝑘󰇍 qua 𝑆 là biên 2
ngoài của miền 𝑉: |𝑥 − 𝑦| ≤ 1, |𝑦 − 𝑧| ≤ 1, |𝑧 + 𝑥| ≤ 1 A. 5 B. 4 C. 0 D. 3
Câu 96: Cho trường vô hướng 𝑢 = 𝑥𝑦 + 𝑦𝑧 + 𝑥𝑧. Tính lưu số của trường vecto 𝑔󰇍𝑟𝑎𝑑
󰇍 󰇍 󰇍 𝑢 dọc theo đoạn thẳng nối từ 𝐴(−1,−1,−1) đến 𝐵(2,4,1) A. 11 B. 12 C. 16 D. 1 4
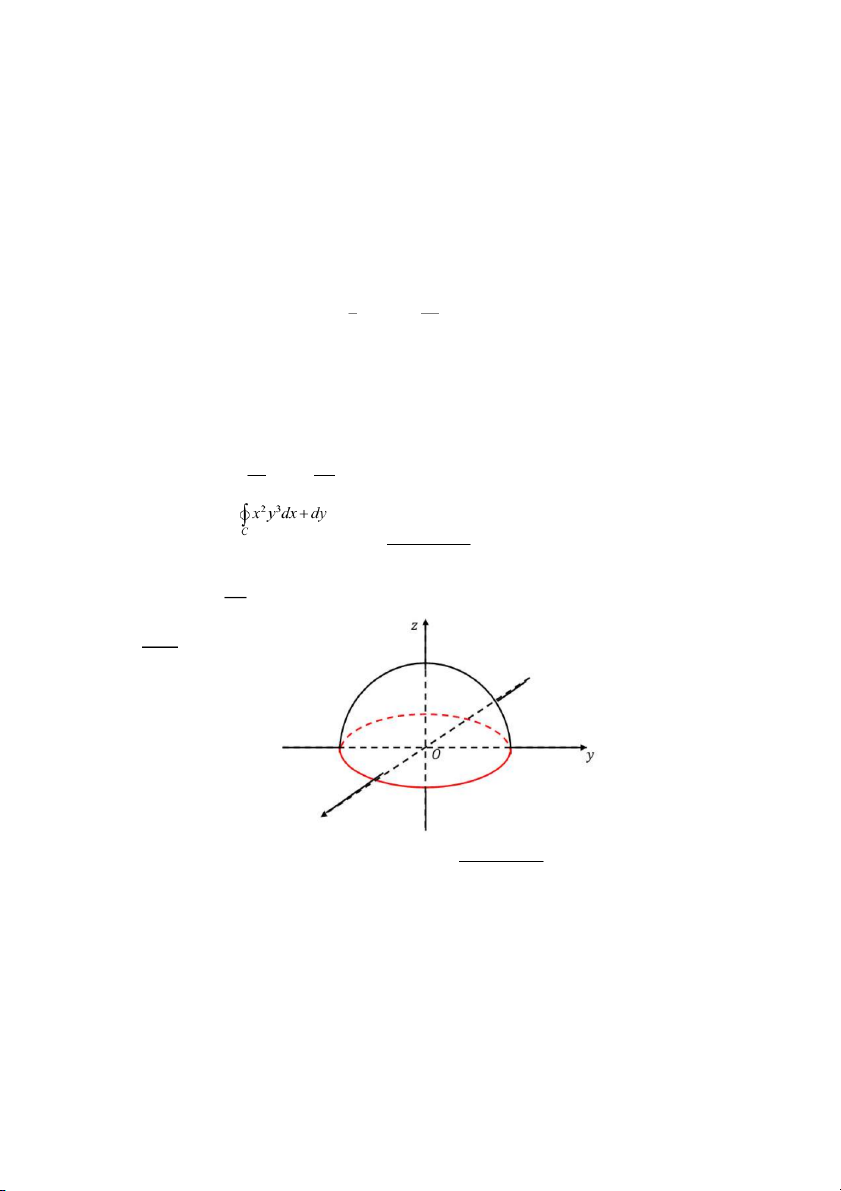
Câu 97: Tính lưu số của 𝐹 = 𝑥2𝑦3𝑖 + 𝑗 + 𝑧𝑘󰇍 dọc theo đường tròn có phương trình 16
𝐶: 𝑥2 + 𝑦2 = 1, 𝑧 = 0 giới hạn mặt cầu 𝑧 = √1 − 𝑥2 − 𝑦2 − − − − A. B. C. D. 6 8 7 9
Câu 98: Tính lưu số của 𝐹 = (𝑦𝑒𝑥𝑦 + 3𝑦 + 𝑧)𝑖 + (𝑥𝑒𝑥𝑦 + 𝑦 − 5𝑧)𝑗 + (1 + 2𝑥)𝑘󰇍 dọc
theo đường cong 𝐿 là giao của mặt 𝑥2 + 𝑦2 + 𝑧2 = 4 và mặt 𝑥 − 𝑦 + 𝑧 = 0 hướng
ngược chiều kim đồng hồ nếu nhìn từ chiều dương trục 𝑂𝑧. A. 3√3𝜋 B. 6√3𝜋 C. 4√3𝜋 D. √3𝜋
Câu 99: Tính lưu số của 𝐹 = (𝑦2 + 𝑧2)𝑖 + (𝑥2 + 𝑧2)𝑗 + (𝑥2 + 𝑦2)𝑘󰇍 dọc theo đường
cong 𝐶 trong đó 𝐶 là giao của mặt cầu 𝑥2 + 𝑦2 + 𝑧2 = 4 và mặt nón có phương
trình 𝑧 = −√𝑥2 + (𝑦 − 1)2 với hướng cùng chiều kim đồng hồ khi nhìn từ gốc O. A. 3 B. 0 C. 1 D. 5
Câu 100: Tính thông lượng của 𝐹 = (6𝑧 − 2𝑦3)𝑖 + (2𝑥 − 3𝑧)𝑗 + (2𝑦3 − 4𝑥)𝑘󰇍 qua
mặt cong 𝑆: 2𝑥2 + 𝑦4 + 3𝑧2 = 1, 𝑧 ≥ 0 hướng lên trên. A. 3 B. 0 C. 2 D. 1 17
V. Lời giải tham khảo Tích phân Euler: +
Câu 1: Kết quả củ 4 a tích phân 5 −x x e dx  là: 0  Đáp án: A. 8 Giải:  3 3 4 du
x dx = du x dx = Đặt 4 x = u   4 2 1/2  x = u  +∞ 1 +∞ 1 +∞ 3 1 3
⇒ ∫ 𝑥5 𝑒−𝑥4𝑑𝑥 = 2−1𝑒−𝑢𝑑𝑢 = 0
4 ∫ 𝑢1/2𝑒−𝑢𝑑𝑢 = 0 4 ∫ 𝑢 0 4 Γ (2) = √𝜋 8  2
Câu 2: Kết quả của tích phân 6 4 sin xcos xdx  là: 0 3 Đáp án: D. 512 Giải: 𝜋 𝜋 2 2 1 7 5
∫ sin6 𝑥 cos4 𝑥 𝑑𝑥 = ∫(sin 𝑥)2.72−1. (cos 𝑥)2.52−1𝑑𝑥 = 2𝐵(2, 2) 0 0 1 Γ (7 1 45 Γ (1 3𝜋 = 2) . Γ (52) 2) . Γ (12) 2 . Γ(6) = 2 . 32 . 5! = 512 + 4 −  Câu 3: Biết 6 x 3 x a dx = 
, chọn khẳng định đúng: 7/2 b(ln 3) 0
Đáp án: A. 𝑎 − 𝑏 = −1 18 Giải: 2ln3. du
xdx = du dx =  2 ln3.u Đặt 2
ln 3.x = u   3 6 ux = 3  (ln3)  𝜋 𝜋 𝜋 2 2 2 𝑒−𝑢 5
⇒ ∫ 𝑥6. 3−𝑥2𝑑𝑥 𝑢3 1 = ∫ (ln3)3 . 𝑑𝑢 = 2. 𝑒−𝑢𝑑𝑢 2√ln 3 . 𝑢 2 ∫(ln 3)−72. 𝑢 0 0 0 𝜋 2 (ln 3)−7/2 7 (ln 3)−7/2 7 15 = √𝜋 2−1 2
. ∫ 𝑢 . 𝑒−𝑢𝑑𝑢 = 2 . Γ (2) = 7 0 16(ln 3)2 ⇒ 𝑎 = 15, 𝑏 = 16 + 2 x
Câu 4: Biểu diễn tích phân dx  theo hàm Gamma: 4 4 (1+ x ) 0  3  13 .       
Đáp án: C.  4   4  4. (4) Giải:  3 2 du
4x dx = du x dx = Đặt 4 1/4 x = u   4u 1/4  x = u  +∞ +∞ −1 𝑥2 1 4 1 3 13 1 Γ (3 ⇒ ∫ 𝑢 𝑑𝑢 4) . Γ (13 4 ) ( = =
1 + 𝑥4)4 𝑑𝑥 4 ∫ (1 + 𝑢)4 4 𝐵 (4 , 4 ) = 4 . Γ(4) 0 0 1 1
Câu 5: Tính tích phân dx  30 30 0 1 − x 19  Đáp án: B.    30sin    30  Giải:  29  = 30 du du x dx dx = Đặt 30 29/30 u = x   30.u 1/30  x = u 1 1 1 1 1 1 1 29 1 ⇒ ∫ 1 29 = 𝑢−29 30 =
30−1. (1 − 𝑢)30−1𝑑𝑢 = √ 30 𝑑𝑥 1 − 𝑥30 30 ∫ √ 30 𝑑𝑢 1 − 𝑢 30 ∫ 𝑢 30 𝐵 (30 ,30) 0 0 0 1 𝜋 = 30 sin ( 𝜋30) 1 10  1
Câu 7: Tính tích phân ln dx     x  0 Đáp án: B. 10! Giải: −1 −1
dx = du dx = du  1  u   Đặt x e ln = u      x  1 u  = e  x 1 0 +∞ 1 10 ⇒ ∫ (ln = − ∫ = ∫ ) 𝑥) 𝑑𝑥 𝑢10. 𝑒−𝑢𝑑𝑢
𝑢11−1. 𝑒−𝑢𝑑𝑢 = Γ(11 = 10! 0 +∞ 0 1
Câu 8: Tính tích phân 5 10
x (ln x) dx  0 10! Đáp án: B. 11 6 Giải: 20 1 u
dx = du dx = e du
Đặt lnx = u  x 5 5ux = e  1 0
⇒ ∫ 𝑥5(ln 𝑥)10𝑑𝑥 = ∫ 𝑒6𝑢.𝑢10𝑑𝑢 0 −∞ 10 − Đặt dt 10 6 = −  = , t u t du u = 10 6 6
Đổi cận: 𝑢 = 0 ⇒ −𝑡 = 0, 𝑢 → −∞ ⇒ −𝑡 → +∞ 0 +∞ 1 1 10!
⇒ ∫ 𝑒6𝑢. 𝑢10𝑑𝑢= 6 =
11 ∫ 𝑒−𝑡. 𝑡10𝑑𝑡 611 . Γ(11) = 611 −∞ 0 0
Câu 9: Biểu diễn tích phân 2x 3 3 e 1 x −e dx  theo hàm Gamma: −  2   1  2   4 .          .    
Đáp án: C.  3   3   3   3  và D. 9.( 2) 3.(2) Giải: 0 Đặt 𝐼 = 2x 3 3 e 1 x − e dx − 𝑑𝑢 𝑢−1𝑑𝑢
Đặt 𝑢 = 𝑒3𝑥 ⇒ 𝑑𝑢 = 3𝑒3𝑥𝑑𝑥 ⇒ 𝑑𝑥 = 3𝑒3𝑥 = 3
Với 𝑥 = 0 ⇒ 𝑢 = 1, 𝑥 = −∞ ⇒ 𝑢 = 0 1 1 1 2 1 1 1 1 2 4 1 Γ (2 ⇒ 𝐼 = 3) Γ (43)
3 ∫ 𝑢3(1 − 𝑢)3 𝑢−1𝑑𝑢 = 3 ∫ 𝑢−13(1 − 𝑢)3 𝑑𝑢 = 3 𝐵 (3 ,3) = 3 Γ(2) 0 0 2 4 1 1 1 Γ (2 1 𝜋 2 Mà Γ ( 3) Γ (13) √3
3) = 3 Γ (3) ⇒ 𝐼 = 9 Γ(2) = 9 1! = 𝜋 9√3 21 2
Câu 10: Tính tích phân 7 5 sin xcos xdx  0 5 Đáp án: A. 128 2 Giải: 𝜋 𝜋 2 2 7 5 1 9 7 1 Γ (9
∫(sin 𝑥)2(cos𝑥)2𝑑𝑥 = ∫(sin 𝑥)2.94−1(cos 𝑥)2.74−1𝑑𝑥 = 4) Γ (74) 2 . 𝐵 (4 , 4) = 2 Γ(4) 0 0 9 5 5 5 1 1 5 1 Γ (
Mà { 4) = 4 Γ (4) = 4 . 4 . Γ (4) = 16 Γ (4) 7 3 3 Γ (4) = 4Γ(4) 2 1 9 7 1 15 Γ (1 15 𝜋 5𝜋 ⇒ 𝑇𝑃 = 4) Γ (34) √2 2 . 𝐵 (4 , 4) = 2 . 64 . Γ(4) = 128 3! = 128√2 Tích phân đường
Câu 11: Tính tích phân (x + y)ds
với 𝐿 là đoạn thẳng nối điểm 𝑂(0; 0) và 𝐴(4; 3) L 35 Đáp án: A. 2 Giải: 3 3 9 5
Phương trình đoạn 𝑂𝐴 là { 𝑦 =4𝑥 ⇒ 𝑦′(𝑥) = 0 ≤ 𝑥 ≤ 4
4 ⇒ 𝑑𝑠 = √1 + 16 𝑑𝑥 = 4 𝑑𝑥 4 3 5 35
⇒ ∫(𝑥 + 𝑦)𝑑𝑠 = ∫ (𝑥 + 4𝑥)4𝑑𝑥 = 2 𝐿 0 𝑥 = 2 + 2 cos 𝑡
Câu 12: Tính (x + y)ds
với 𝐿 là nửa đường tròn { 𝑦 = 2 sin 𝑡 L 0 ≤ 𝑡 ≤ 𝜋 22 Đáp án: B. 8 + 4 Giải: 𝑥 = 2 + 2 cos 𝑡
Đường 𝐶: { 𝑦 = 2 sin 𝑡 ⇒ {𝑥′(𝑡) = −2 sin 𝑡 ′2 𝑑𝑡 = 2𝑑𝑡 0 ≤ 𝑡 ≤ 𝜋
𝑦′(𝑡) = 2 cos 𝑡⇒ 𝑑𝑠 = √𝑥′2(𝑡) + 𝑦 (𝑡) 𝜋
⇒ ∫(𝑥 + 𝑦)𝑑𝑠 = 2 ∫(2 + 2 cos 𝑡 + 2 sin 𝑡)𝑑𝑡 = 8 + 4𝜋 𝐶 0
Câu 13: Tìm 𝑚 để (mx − y)ds
= −18 với 𝐶: 𝑦 = √9 − 𝑥2 C Đáp án: C. 𝑚 = 3 Giải:
Nửa đường tròn 𝐶: {𝑥2 + 𝑦2 = 9
𝑦 ≥ 0 . Tham số hóa 𝐶 𝑥 = 3 cos 𝑡
Đặt {𝑦 = 3 sin 𝑡 ⇒ {𝑥′(𝑡) = −3 sin 𝑡 0 ≤ 𝑡 ≤ 𝜋
𝑦′(𝑡) = 3 cos 𝑡⇒ 𝑑𝑠 = √𝑥′2(𝑡) + 𝑦′2(𝑡)𝑑𝑡 = 3 𝜋
⇒ ∫(𝑚𝑥 − 𝑦)𝑑𝑠 = 3 ∫(3𝑚 cos 𝑡 − 3 sin 𝑡)𝑑𝑡 = −18 ⇒ 𝑚 = 3 𝐶 0
Câu 14: Với 𝐶 là đường tròn 𝑥2 + 𝑦2 = 2𝑥, tính (x − y)dsC Đáp án: B. 2𝜋 Giải:
𝐶: 𝑥2 + 𝑦2 = 2𝑥 ⇔ (𝑥 − 1)2 + 𝑦2 = 1 𝑥 = 1 + cos 𝑡
Đặt { 𝑦 = sin 𝑡 ⇒ {𝑥′(𝑡) = − sin 𝑡 = 0 ≤ 𝑡 ≤ 2𝜋
𝑦′(𝑡) = cos 𝑡 ⇒ 𝑑𝑠 = √𝑥′2(𝑡) + 𝑦′2(𝑡)𝑑𝑡 𝑑𝑡 2𝜋
∫(𝑥 − 𝑦)𝑑𝑠 = ∫ (1 + cos 𝑡 − sin 𝑡)𝑑𝑡 = 2𝜋 𝐶 0 23 − 
Câu 15: Tính (x + y)ds
với cung 𝐶: 𝑟2 = cos 2𝜑,    4 4 C Đáp án: D. √2 Giải: 𝑟2 = cos 2𝜑 𝑟 = √cos2𝜑 − sin 2𝜑 Cung 𝐶: {−𝜋 𝜋 ⇔ {−𝜋 𝜋 ⇒ 𝑟′ = 4 ≤ 𝜑 ≤ 4 4 ≤ 𝜑 ≤ 4 √cos 2𝜑 sin2 2𝜑 1
⇒ 𝑑𝑠 = √𝑟2(𝜑) + 𝑟′2(𝜑)𝑑𝜑 = √cos 2𝜑 + cos2𝜑 𝑑𝜑 = √cos2𝜑𝑑𝜑 𝑥 = 𝑟 cos 𝜑 Đặt {𝑦 = 𝑟sin𝜑 𝜋 𝜋 4 4 1
⇒ ∫ 𝑟(cos 𝜑 + sin 𝜑)√ 1
cos 2𝜑 𝑑𝜑 = ∫ √cos 2𝜑 (cos 𝜑 + sin 𝜑)√ cos 2𝜑 𝑑𝜑 = √2 −𝜋 −𝜋 4 4
Câu 16: Với 𝐶 là đường cong 𝑥2/3 + 𝑦2/3 = 1 trong góc phần tư thứ nhất nối
𝐴(1,0) và 𝐵(0,1), tìm 𝑚 để 2 ( y 1 + ) dsC 15 Đáp án: A. 8 Giải: 2 2 1 2 1 2
Ta có 𝐶: 𝑥3 + 𝑦 3 = 1 ⇔ (𝑥3) + (𝑦 3) = 1 1
Tham số hóa: {𝑥3 = cos 𝑡 1 ⇒ {𝑥 = cos3 𝑡 𝑦3 = sin 𝑡
𝑦 = sin3 𝑡 ⇒ {𝑥′(𝑡) = −3 sin 𝑡 cos2 𝑡
𝑦′(𝑡) = 3 cos 𝑡 sin2 𝑡
⇒ 𝑑𝑠 = √𝑥′2(𝑡) + 𝑦′2(𝑡)𝑑𝑡 = √9 sin2 𝑡 cos4 𝑡 + 9 cos2 𝑡 sin4 𝑡 𝑑𝑡 = 3 sin 𝑡 cos 𝑡 𝑑𝑡
Tại 𝐴(1,0): {𝑥 = cos3 𝑡 = 1
𝑦 = sin3 𝑡 = 0 ⇔ 𝑡 = 0, tại 𝐵(0,1): {𝑥 = cos3 𝑡 = 1
𝑦 = sin3 𝑡 = 0 ⇔ 𝑡 = 𝜋/2 24 𝜋 𝜋 2 2
⇒ ∫(𝑦2 + 1) 𝑑𝑠 = 3 ∫(sin6 𝑡 + 1) sin 𝑡 cos 𝑡 𝑑𝑡 = 3 ∫(sin7 𝑡 + sin 𝑡)𝑑(sin 𝑡) 𝐶 0 0 1 15
= 3 ∫(𝑢7 + 𝑢)𝑑𝑢 = 8 0
Câu 17: Tính yds
 với 𝐶 là đường 𝑥 = 𝑦2 đi từ 𝑂(0,0) đến 𝐴(1,1) C 1 Đáp án: B. (5 5 −1) 12 Giải: Đường 𝐶: { 𝑥 = 𝑦2 ′2
0 ≤ 𝑦 ≤ 1 ⇒ 𝑥′(𝑦) = 2𝑦 ⇒ 𝑑𝑠 = √1 + 𝑥 (𝑦)𝑑𝑦 = √1 + 4𝑦2𝑑𝑦 1 1 1 1 1
⇒ ∫ 𝑦𝑑𝑠 = ∫ 𝑦 √1 + 4𝑦2𝑑𝑦 = 2∫√1 +4𝑦2𝑑(𝑦2) = 2∫√1+ 4𝑢𝑑𝑢 𝐶 0 0 0 1 = 12(5√5 −1)
Câu 18: Tính xyds
với 𝐿 là chu tuyến của hình chữ nhật 𝐴𝐵𝐶𝐷 với 𝐴(0,0); 𝐵(4,0); L 𝐶(4,2), 𝐷(0,2) Đáp án: C. 24 Giải: 25
Ta có: ∫ 𝑥𝑦𝑑𝑠 = ∫ 𝑥𝑦𝑑𝑠+ ∫ 𝑥𝑦𝑑𝑠 + ∫ 𝑥𝑦𝑑𝑠 + ∫ 𝑥𝑦𝑑𝑠 𝐿 𝐴𝐵 𝐵𝐶 𝐶𝐷 𝐷𝐴
Phương trình 𝐴𝐵: {𝑦 = 0 ⇒ 𝑑𝑠 = √1 + 0𝑑𝑥 = 𝑑𝑥 0 ≤ 𝑥 ≤ 4
Phương trình 𝐵𝐶 {𝑥 = 4 ⇒ 𝑑𝑠 = √1 + 0𝑑𝑦 = 𝑑𝑦 0 ≤ 𝑦 ≤ 2
Phương trình 𝐶𝐷 {𝑦 = 2 ⇒ 𝑑𝑠 = √1 + 0𝑑𝑥 = 𝑑𝑥 0 ≤ 𝑥 ≤ 4
Phương trình 𝐷𝐴: {𝑥 = 0 ⇒ 𝑑𝑠 = √1 + 0𝑑𝑦 = 𝑑𝑦 0 ≤ 𝑦 ≤ 2 4
∫ 𝑥𝑦𝑑𝑠= ∫ 𝑥. 0𝑑𝑥 = 0 𝐴𝐵 0 2
∫ 𝑥𝑦𝑑𝑠= ∫ 4𝑦𝑑𝑦 = 8 ⇒ 𝐵𝐶 0 = 24 4 ⇒ ∫ 𝑥𝑦𝑑𝑠
∫ 𝑥𝑦𝑑𝑠= ∫ 2𝑥𝑑𝑥 = 16 𝐿 𝐶𝐷 02
∫ 𝑥𝑦𝑑𝑠= ∫ 0. 𝑦𝑑𝑦 = 0 {𝐷𝐴 0 Câu 19: Tính
với 𝐶 là biên của miền |𝑥| + |𝑦| ≤ 1 Đáp án: D. 0 26 Giải:
Đường 𝐶: |𝑥| + |𝑦| = 1
Phương trình 𝐴𝐵: {𝑦 = 1 − 𝑥 0 ≤ 𝑥 ≤ 1
Phương trình 𝐵𝐶: {𝑦 = 𝑥 − 1 0 ≤ 𝑥 ≤ 1
Phương trình 𝐶𝐷: {𝑦 = −𝑥 − 1 −1 ≤ 𝑥 ≤ 0
Phương trình 𝐷𝐴: { 𝑦 = 𝑥 + 1 −1 ≤ 𝑥 ≤ 0
∮ 𝑥𝑦𝑑𝑠 =∫ 𝑥𝑦𝑑𝑠 + ∫ 𝑥𝑦𝑑𝑠 + ∫ 𝑥𝑦𝑑𝑠 + ∫ 𝑥𝑦𝑑𝑠 𝐶 𝐴𝐵 𝐵𝐶 𝐶𝐷 𝐷𝐴 1
Xét ∫ 𝑥𝑦𝑑𝑠, ta có 𝑑𝑠 = √1 + 𝑦 √2
′2(𝑥)𝑑𝑥 = √2𝑑𝑥 ⇒ ∫ 𝑥𝑦𝑑𝑠 = √2 ∫ 𝑥(1 − 𝑥)𝑑𝑥 = 6 𝐴𝐵 𝐴𝐵 0 1 −
Xét ∫ 𝑥𝑦𝑑𝑠, ta c 𝑑𝑠 ó
= √1 + 𝑦′2(𝑥)𝑑𝑥 = √2𝑑𝑥 ⇒ ∫ 𝑥𝑦𝑑𝑠 = √2
√2 ∫ 𝑥(𝑥 − 1)𝑑𝑥 = 6 𝐵𝐶 𝐵𝐶 0 0
Xét ∫ 𝑥𝑦𝑑𝑠, ta c 𝑑𝑠 ó
= √1 + 𝑦′2(𝑥)𝑑𝑥 = √2𝑑𝑥 ⇒ ∫ 𝑥𝑦𝑑𝑠 = √2 ∫ 𝑥(−1 − 𝑥)𝑑𝑥 = √26 𝐶𝐷 𝐶𝐷 −1 0 − Xét ∫ 𝑥𝑦𝑑𝑠 √2
, ta có 𝑑𝑠 = √1 + 𝑦′2(𝑥)𝑑𝑥 = √2𝑑𝑥 ⇒∫ 𝑥𝑦𝑑𝑠 = √2 ∫ 𝑥(𝑥 + 1)𝑑𝑥 = 6 𝐴𝐵 𝐷𝐴 −1
⇒ ∮ 𝑥𝑦𝑑𝑠 = ∫ 𝑥𝑦𝑑𝑠+ ∫ 𝑥𝑦𝑑𝑠 + ∫ 𝑥𝑦𝑑𝑠 + ∫ 𝑥𝑦𝑑𝑠 = 0 𝐶 𝐴𝐵 𝐵𝐶 𝐶𝐷 𝐷𝐴 Câu 20: Tính 2 2 x + y ds
với 𝐿: 𝑥2 + 𝑦2 = 2𝑥 L Đáp án: A. 8 Giải: 27 𝑥 = 𝑟 cos 𝜑 𝑟 = 2 cos 𝜑
Đặ𝑡 {𝑦 = 𝑟sin𝜑 ⇒ Đường cong 𝐿: { 𝜋 𝜋 − 2 ≤ 𝜑 ≤ 2
⇒ 𝑑𝑠 = √𝑟2(𝜑) + 𝑟′2(𝜑)𝑑𝜑 = √4 cos2 𝜑 + 4 sin2 𝜑 𝑑𝜑 = 2𝑑𝜑 𝜋 𝜋 𝜋 2 2 2
∫ √𝑥2 + 𝑦2𝑑𝑠 = ∫ √𝑟2.2𝑑𝜑 = 2 ∫ 𝑟𝑑𝜑 = 2 ∫ 2 cos 𝜑 𝑑𝜑 = 8 𝐿 −𝜋 −𝜋 −𝜋 2 2 2
Câu 21: Tính (x − 3y)dx + 2 ydy  với 𝐴𝐵
⏜ là cung 𝑦 = 1 − 𝑥2,𝐴(1,0),𝐵(−1,0) AB Đáp án: C. 4 Giải: Cung 𝐴𝐵
⏜ : {𝑦 = 1 − 𝑥2 ⇒ 𝑑𝑦 = −2𝑥𝑑𝑥
Đi từ 𝐴(1,0) → 𝐵(−1,0) −1 −1
⇒ ∫(𝑥 − 3𝑦)𝑑𝑥 + 2𝑦𝑑𝑦 = ∫ [𝑥 − 3(1 − 𝑥2)]𝑑𝑥 + ∫ 2(1 − 𝑥2). (−2𝑥)𝑑𝑥 = 4 𝐴𝐵 ⏜ 1 1 Câu 22: Tính 4 3 5 y dx − 4x dy
với 𝐴𝐵𝐶 là đường gấp khúc đi qua các điểm ABC
𝐴(0,1); 𝐵(1,0); 𝐶(0, −1) Đáp áp: A. 2 Giải: 28
∫ 5𝑦4𝑑𝑥 − 4𝑥3𝑑𝑦= ∫ 5𝑦4𝑑𝑥 − 4𝑥3𝑑𝑦 + ∫ 5𝑦4𝑑𝑥 − 4𝑥3𝑑𝑦 = 𝐼1 + 𝐼2 𝐴𝐵𝐶 𝐴𝐵 𝐵𝐶 𝑑𝑦 𝑑𝑥
Đoạn thẳng 𝐴𝐵: {𝑦 = 1 − 𝑥 ⇒ = −
Đi từ 𝐴(0,1) đến 𝐵(1,0) 1 1
⇒ 𝐼1 = ∫ 5(1 − 𝑥)4𝑑𝑥 + ∫(−4𝑥3).(−𝑑𝑥) = 2 0 0 =
Đoạn thẳng 𝐵𝐶: { 𝑦 = 𝑥 − 1 ⇒ 𝑑𝑦 𝑑𝑥
Đi từ 𝐵(1,0) đến 𝐶(0, −1) 0 0
⇒ 𝐼2 = ∫ 5(𝑥 − 1)4𝑑𝑥 + ∫(−4𝑥3). 𝑑𝑥 = 0 1 1
⇒ ∫ 5𝑦4𝑑𝑥 − 4𝑥3𝑑𝑦= 𝐼1 + 𝐼2 = 2 𝐴𝐵𝐶 −
Câu 23: Tìm 𝑚 để 2 10
(x + xy)dx + . m x dy = 
với 𝐶 là cung bé trên đường tròn 3 C
𝑥2 + 𝑦2 = 4 đi từ 𝐴(−2,0) đến 𝐵(0,2) Đáp án: D. 1 Giải: Đặt {𝑥 = 2 cos 𝑡
𝑦 = 2 sin 𝑡 với 𝑡 chạy từ 𝜋 đến 𝜋/2. Đặt 𝐼 = 2
(x + xy)dx + . m x dyC 𝜋 2
𝐼 = ∫[(2 cos 𝑡 + 4 cos 𝑡 sin 𝑡)(−2 sin 𝑡) + 𝑚. (cos 𝑡)2(2 cos 𝑡)]𝑑𝑡 𝜋 𝜋2
= ∫(−4 cos 𝑡 sin 𝑡 − 8 cos 𝑡 sin2 𝑡 + 2𝑚 cos3 𝑡)𝑑𝑡 𝜋 29 𝜋2
= ∫(−4 sin 𝑡 − 8 sin2 𝑡 + 2𝑚 cos2 𝑡) cos 𝑡 𝑑𝑡 𝜋 𝜋2
= ∫(−4 sin 𝑡 − 8 sin2 𝑡 + 2𝑚 − 2𝑚 sin2 𝑡) cos 𝑡 𝑑𝑡 𝜋 𝜋2 1 −10
= ∫[−4 sin 𝑡 − (8 + 2𝑚) sin2 𝑡 + 2]𝑑(sin 𝑡) = ∫[−4𝑢 − (8 + 2𝑚)𝑢2 + 2]𝑑𝑢 = 3 𝜋 0 ⇒ 𝑚 = 1 Câu 24: Tính − + + ) + ( y x y dx
−xy + e − x + sin y)dyvới 𝐿 là đường
𝑥2 + 𝑦2 = 2𝑥 theo chiều dương.
Đáp án: A. −3𝜋 Giải: Đặt 𝐼 = + + ) + ( − y x y dx
−xy + e − x +sin y)dy
Đặt: 𝑃 = 𝑥𝑦 + 𝑒𝑥 sin 𝑥 + 𝑥 + 𝑦, 𝑄 = −𝑥𝑦 + 𝑒−𝑦 − 𝑥 + sin 𝑦 ⇒ 𝑃′ ′ ′ ′
𝑦 = 𝑥 + 1, 𝑄𝑥 = −𝑦 − 1. 𝑃𝑦, 𝑄𝑥 liên tục với 𝑥, 𝑦 ∈ 𝑅.
Đường cong 𝐿 kín hướng dương, giới hạn miền 𝐷: 𝑥2 + 𝑦2 ≤ 2𝑥 30
Áp dụng công thức Green, ta có:
𝐼 = ∬(−𝑦 − 𝑥 − 2)𝑑𝑥𝑑𝑦 𝐷
Nhận xét: hàm số 𝑓(𝑥, 𝑦) = −𝑦 là hàm lẻ với biến y, miền 𝐷 đối xứng qua trục Ox
⇒ ∬ −𝑦𝑑𝑥𝑑𝑦 = 0 ⇒ 𝐼 = ∬(−𝑥 − 2)𝑑𝑥𝑑𝑦 𝐷 𝐷
Đặt: {𝑥 = 1 + 𝑟 cos 𝜑
𝑦 = 𝑟 sin 𝜑 |𝐽| = 𝑟. Miền (𝐷): { 0 ≤ 𝑟 ≤ 1 0 ≤ 𝜑 < 2𝜋 2𝜋 1 2𝜋 3
𝐼 = ∫ 𝑑𝜑∫(−𝑟 cos 𝜑 − 3)𝑟𝑑𝑟 −1
= ∫ ( 3 cos𝜑 − 2)𝑑𝜑 = −3𝜋 0 0 0 Câu 25: Tính 2 y 1 + 2 2y + e + sin(y ) dy
 với 𝐿 là chu tuyến của tam
giác 𝐴𝐵𝐶 có 𝐴(−1,0), 𝐵(0,2), 𝐶(2,0) chiều cùng chiều kim đồng hồ. Đáp án: B. 2 Giải: Đặt 2 𝐼 = y 1 + 2 2y + e + sin(y ) dy  𝑃 = 2𝑥 𝑃′ = 0 Đặt { 𝑦 ′ ′
𝑄 = −[𝑥 + 2𝑦 + 𝑒𝑦2+1 + sin(𝑦2)] ⇒ { liên tục với 𝑄′ , 𝑄𝑥 𝑥, 𝑦 ∈ 𝑅 𝑥 = −2𝑥 , 𝑃𝑦 31
Gọi 𝐷 là miền được giới hạn bởi chu tuyến ∆𝐴𝐵𝐶 𝐴𝐵: 𝑦 = 2𝑥 + 2
𝐷 được giới hạn bởi các đường: {𝐵𝐶: 𝑦 = −𝑥 + 2⇒ (𝐷): {(𝑦 − 2)/2 ≤ 𝑥 ≤ 2 − 𝑦 𝐶𝐴: 𝑦 = 0 0 ≤ 𝑦 ≤ 2
𝐿 là đường cong kín, hướng âm, giới hạn miền 𝐷. Áp dụng công thức Green: 2 2−𝑦
𝐼 = − ∬ −2𝑥𝑑𝑥𝑑𝑦 = ∬ 2𝑥𝑑𝑥𝑑𝑦 = ∫ 𝑑𝑦 ∫ 2𝑥𝑑𝑥 = 2 𝐷 𝐷 0 𝑦−2 2 Câu 26: Tính x 10 2
(xy + e )dx + ( y − x )dy  với 𝐴𝐵
⏜ là cung 𝑦 = √1 − 𝑥2 đi từ điểm AB 𝐴(−1,0) đến 𝐵(1,0) 2 e −1 Đáp án: B. e Giải: Đặt 𝐼 = x 10 2
(xy + e )dx + ( y − x )dyAB Cung 𝐴𝐵 ⏜ ⇔ {𝑥2 + 𝑦2 = 1
𝑦 ≥ 0 đi từ 𝐴(−1,0) đến 𝐵(1,0) 32 Bổ sung thêm đoạn BA { 𝑦 = 0
đi từ 𝐵(1,0) đến 𝐴(−1,0) Ta có: đường 𝐴𝐵
⏜ ∪ 𝐵𝐴 là đường cong kín giới hạn miền (𝐷):𝑥2 + 𝑦2 ≤ 1,𝑦 ≥ 0, có chiều âm 𝑥𝑦 𝑥 ′ = 𝑥 Đặt { 𝑃 = + 𝑒 ′ ′
𝑄 = 𝑦10 − 𝑥2 ⇒ { 𝑃𝑦 liên tục với 𝑄′ , 𝑄𝑥 𝑥, 𝑦 ∈ 𝑅 𝑥 = −2𝑥 ⇒ 𝑃𝑦
𝐼 = ∮ (𝑥𝑦 + 𝑒𝑥)𝑑𝑥 + (𝑦10 − 𝑥2)𝑑𝑦 − ∫(𝑥𝑦 + 𝑒𝑥)𝑑𝑥 + (𝑦10 − 𝑥2)𝑑𝑦 = 𝐼1 − 𝐼2 𝐴𝐵 ⏜ ∪𝐵𝐴 𝐵𝐴
Áp dụng công thức Green cho 𝐼1 ta có:
𝐼1 = − ∬ −3𝑥 𝑑𝑥𝑑𝑦 = ∬ 3𝑥 𝑑𝑥𝑑𝑦 𝐷 𝐷 𝑥 = 𝑟 cos 𝜑
Đặt {𝑦 = 𝑟sin𝜑 |𝐽| = 𝑟. Miền (𝐷):{0 ≤ 𝑟 ≤ 1 0 ≤ 𝜑 ≤ 𝜋 𝜋 1 𝜋
⇒ 𝐼1 = ∫ 𝑑𝜑 ∫ 3𝑟 cos 𝜑 𝑟𝑑𝑟 = ∫ cos 𝜑 𝑑𝜑 = 0 0 0 0
(Hoặc có thể sử dụng tính đối xứng để ra giá trị bằng 0 ngay)
𝐼2 = ∫(𝑥𝑦 + 𝑒𝑥)𝑑𝑥 + (𝑦10 − 𝑥2)𝑑𝑦 𝐵𝐴 Đoạn 𝐵𝐴 { 𝑦 = 0 ⇒ 𝑑𝑦 = 0
đi từ 𝐵(1,0)đến 𝐴(−1,0) −1 1 − 𝑒2
⇒ 𝐼2 = ∫ (𝑥. 0 + 𝑒𝑥)𝑑𝑥 = 𝑒𝑥 |−1 1 = 𝑒−1 − 𝑒 = 𝑒 1 1 − 𝑒2 ⇒ 𝐼 = 𝐼 𝑒2 − 1 1 − 𝐼2 = 0 − 𝑒 = 𝑒 Câu 27: Tính x 2 4 (2 4
e + y )dx + ( y x + e )dy
với 𝐶: 𝑦 = √1 − 𝑥2 đi từ 𝐴(−1,0) đến C 𝐵(1,0) 33  2
Đáp án: A. − + 2e 2 e Giải:
𝐶: 𝑦 = √41 − 𝑥2 là đường cong hở đi từ 𝐴(−1,0) đến 𝐵(1,0)
Bổ sung thêm đoạn 𝐵𝐴: { 𝑦 = 0
Đi từ 𝐵(1,0) → 𝐴(−1,0)
𝐼 = ∫ (2𝑒𝑥 + 𝑦2)𝑑𝑥 + (𝑥4 + 𝑒𝑦)𝑑𝑦 − ∫(2𝑒𝑥 + 𝑦2)𝑑𝑥 + (𝑥4 + 𝑒𝑦)𝑑𝑦 = 𝐼1 − 𝐼2 𝐶∪𝐵𝐴 𝐵𝐴
Áp dụng công thức Green cho 𝐼1 𝑃′ = 2𝑦
Đặt {𝑃(𝑥, 𝑦) = 2𝑒𝑥 + 𝑦2 𝑦
𝑄(𝑥, 𝑦) = 𝑥4 + 𝑒𝑦 ⇒ {𝑄′𝑥 = 4𝑥3 liên tục với ∀𝑥,𝑦 ∈ 𝑅 4
Ta có 𝐶 ∪ 𝐵𝐴 là đường cong kín, có chiều âm, giới hạn miền 𝐷: {0 ≤ 𝑦 ≤ √1 − 𝑥2 −1 ≤ 𝑥 ≤ 1 1 √ 4 1−𝑥2 ⇒ 𝐼 3
1 = − ∬(4𝑥 − 2𝑦)𝑑𝑥𝑑𝑦 = ∫ 𝑑𝑥 ∫ (−4𝑥3 + 2𝑦)𝑑𝑦 𝐷 −1 0 1
= ∫ (−4𝑥3. √41 − 𝑥2 + √1 − 𝑥2) 𝑑𝑥 −1 1
Hàm 𝑓(𝑥) = −4𝑥3. √
4 1 − 𝑥2 là hàm số lẻ ⇒ ∫ −4𝑥3. √41 − 𝑥2 𝑑𝑥 −1 1
⇒ 𝐼1 = ∫ √1 − 𝑥2𝑑𝑥 −1
Đặt 𝑥 = sin 𝑡 ⇒ 𝑑𝑥 = cos 𝑡 𝑑𝑥 𝜋 𝜋 1 2 2 𝜋
⇒ 𝐼1 = ∫ √1 − 𝑥2𝑑𝑥= ∫ cos 𝑡 cos 𝑡 𝑑𝑡 = ∫ cos2 𝑡 𝑑𝑡 = 2 −1 −𝜋2 −𝜋2 34 −1 Đoạn 𝐵𝐴: { 𝑦 = 0 ⇒ 𝑑𝑦 = 0
đi từ 𝐵(1,0) đến 𝐴(−1,0) ⇒ 𝐼2 = ∫ 2𝑒𝑥𝑑𝑥 = 2(𝑒−1 − 𝑒) 1
Vậy 𝐼 = 𝜋/2 − 2(𝑒−1 − 𝑒) (3,0)
Câu 28: Tính tích phân  ( 4 3 x + 4xy ) 2 2 4
dx + (6x y − 5y )dy (−2,−1)
Đáp án: B. 62 Giải: (3,0) Đặt 𝐼 =  ( 4 3 x +4xy ) 2 2 4
dx +(6x y −5y )dy (−2,−1)
Đặt 𝑃 = (𝑥4 + 4𝑥𝑦3), 𝑄 = (6𝑥2𝑦2 − 5𝑦4) ⇒ 𝑃′ ′
𝑦 = 𝑄𝑥 = 12𝑥𝑦2 ⇒ 𝐼 không phụ thuộc đường đi
Cách 1: Dùng đường thay thế là đường gấp khúc:
Chọn đường đi là đường gấp khúc 𝐴𝐶𝐵
𝐼 = ∫ 𝑃𝑑𝑥 + 𝑄𝑑𝑦 = ∫ 𝑃𝑑𝑥 + 𝑄𝑑𝑦 + ∫ 𝑃𝑑𝑥 + 𝑄𝑑𝑦 = 𝐼1 + 𝐼2 𝐴𝐶𝐵 𝐴𝐶 𝐶𝐵 𝑑𝑦 Đoạn 𝐴𝐶: { 𝑦 = −1 ⇒ = 0
đi từ 𝐴(−2, −1) đến 𝐶(3, −1) 35 3
⇒ 𝐼1 = ∫(𝑥4 − 4𝑥)𝑑𝑥= 45 −2 Đoạn 𝐶𝐵: { 𝑥 = 3 ⇒ 𝑑𝑥 = 0
đi từ 𝐶(3, −1) đến 𝐵(3,0) 0
⇒ 𝐼2 = ∫(6.9. 𝑦2 − 5𝑦4)𝑑𝑦= 17 −1
⇒ 𝐼 = 𝐼1 + 𝐼2 = 62
Cách 2: Dùng đường thay thế là đường thẳn g
Phương trình đường thẳng đi qua 𝐴, 𝐵 là 𝑦 = 𝑥/5 − 3/5 𝑥 3 𝑑𝑥
Đoạn 𝐴𝐵: { 𝑦 = 5 −5 ⇒ 𝑑𝑦 = 5
Đi 𝑡ừ 𝐴(−2, −1) → 𝐵(3,0) 3 3 3 𝑥 3 2 𝑥 3 4 𝑑𝑥 ⇒ 𝐼 = ∫ [𝑥4 𝑥
+ 4𝑥 (5 − 5) ]𝑑𝑥 + [6𝑥2 ( 5 − 5) − 5 (5 − 5) ] . 5 −2 3 𝑥 3 3 6𝑥2 𝑥 3 2 𝑥 3 4 = ∫ [𝑥4 + 4𝑥 ( − ( 5 − 5) + 5 (5 − 5)
5 − 5) ] 𝑑𝑥= ⋯ = 62 −2
Cách 3: Dùng hàm thế vị
Đặt 𝑃 = (𝑥4 + 4𝑥𝑦3), 𝑄 = (6𝑥2𝑦2 − 5𝑦4) ⇒ 𝑃′ ′
𝑦 = 𝑄𝑥 = 12𝑥𝑦2 ⇒ 𝐼 không phụ thuộc đường đi
⇒ 𝑃𝑑𝑥 + 𝑄𝑑𝑦 là vi phân toàn phần của hàm 𝑥 𝑦
𝑢(𝑥, 𝑦) = ∫ 𝑃(𝑡, 𝑦0)𝑑𝑡+ ∫ 𝑄(𝑥,𝑡)𝑑𝑡 𝑥0 𝑦0 Chọn 𝑥0 = 𝑦0 = 0 𝑥 𝑦
⇒ 𝑢(𝑥, 𝑦) = ∫(𝑡4 + 4𝑡. 03)𝑑𝑡 + ∫(6𝑥2𝑡2 − 5𝑡4)𝑑𝑡 0 0 36 1 𝑥 𝑦 1 𝑢(𝑥, 𝑦) = 1 5 𝑡5 | + (6𝑥2. = 0
3 𝑡3 − 𝑡5) | 0 5𝑥5 + 2𝑥2𝑦3 − 𝑦5 243 −67
⇒ 𝐼 = 𝑢(3,0) − 𝑢(−2, −1) = 5 − ( 5 ) = 62
Câu 29: Tìm 𝑚 để tích phân 2 x +y 2 2 e
2xy dx + (y + m.y)dy  =e    với 𝐿 là đường L
𝑥 = 1 − 𝑦2 đi từ 𝐴(1,0) đến 𝐵(0,1) Đáp án: B. 2 Giải: Đặt 𝐼 = 2 x + y 2 2 e
2xy dx + (y + m.y)dy = e    L
Đặt 𝑃 = 𝑒𝑥2+𝑦. 2𝑥𝑦2, 𝑄 = 𝑒𝑥2+𝑦. (𝑦2 + 2𝑦) ⇒ 𝑃′ ′
𝑦 = 𝑄𝑥 = (4𝑥𝑦 + 2𝑥𝑦2)𝑒𝑥2+𝑦
⇒ Tích phân không phụ thuộc đường đi
Cách 1: Chọn đường đi là đường gấp khúc
Chọn đường đi là đường gấp khúc 𝐴𝑂𝐵
𝐼 =∫ 𝑒𝑥2+𝑦[2𝑥𝑦2𝑑𝑥 + (𝑦2 + 𝑚𝑦)𝑑𝑦] + ∫ 𝑒𝑥2+𝑦[2𝑥𝑦2𝑑𝑥 + (𝑦2 + 𝑚𝑦)𝑑𝑦] 𝐴𝑂 𝑂𝐵 = 𝐼1 + 𝐼2 37 0
Đoạn 𝐴𝑂: { 𝑦 = 0 ⇒ 𝑑𝑦 = 0
Đi từ 𝐴(1,0) → 𝑂(0,0) ⇒ 𝐼1 = ∫ 0𝑑𝑥 = 0 1 1
Đoạn 𝑂𝐵: { 𝑥 = 0 ⇒ 𝑑𝑥 = 0
Đi từ 𝑂(0,0) → 𝐵(0,1) ⇒ 𝐼2 = ∫ 𝑒𝑦(𝑦2 + 𝑚𝑦)𝑑𝑦 = 𝐼 = 𝑒 ⇒ 𝑚 = 2 0
Tích phân trên phải dùng tích phân từng phần hai lần, tương đối dài.
Cách 2: Chọn đường đi là một đường cong
Nhận xét: Tích phân 𝐼 phức tạp là do biểu thức 𝑒𝑥2+𝑦 vì để làm đơn giản tích phân
𝐼 cần khử biểu thức này ⇒ Biến 𝑒𝑥2+𝑦 = 𝐶 ⇒ 𝑥2 + 𝑦 = 𝐶 (𝐶 l àhằng số)
Do tích phân 𝐼 không phụ thuộc đường đi nên sẽ chọn đường đi mới thỏa mãn 𝑥2 + 𝑦 = 𝐶
Để tìm 𝐶, ta dựa vào điểm đầu 𝐴(1,0) và điểm cuối 𝐵(0,1)
Đường cong mới 𝐿′: 𝑥2 + 𝑦 = 𝐶 đi qua 𝐴, 𝐵 ⇒ {12 + 0 = 𝐶 02 + 1 = 𝐶 ⇒ 𝐶 = 1
Chọn đường đi 𝐿′: 𝑦 = 1 − 𝑥2 đi từ 𝐴(1,0) đến 𝐵(0,1) ⇒ 𝑑𝑦 = −2𝑥𝑑𝑥 0 0
⇒ 𝐼 = 𝑒 (∫[2𝑥(1 − 𝑥2)2]𝑑𝑥 + ∫[(1 − 𝑥2)2 + 𝑚(1 − 𝑥2)](−2𝑥)𝑑𝑥) = 𝑒 ⇒ 𝑚 = 2 1 1 2 2
−y + 2xy − x +1 x − x −1
Câu 30: Tính tích phân dx + dy  với 𝐿: 𝑦 = 2𝑥 + 2 2 2 2 2 ( y − x −1) ( y − x −1) L
đi từ 𝐴(0,2) đến 𝐵(2,6) Đáp án: C. 2 Giải: 2 2
− y + 2xy − x + 1 x − x − 1 Đặt 𝐼 = dx + dy  2 2 2 2 ( y − x 1 − ) ( y − x 1 − ) L
−𝑦 + 2𝑥𝑦 − 𝑥2 + 1 𝑃(𝑥, 𝑦) = 2
−2𝑥3 + 3𝑥2 − 2𝑥𝑦 − 2𝑥 + 𝑦 − 1 Đặt (𝑦 − 𝑥2 − 1) ′ ′ 𝑥 − 𝑥2 − 1 ⇒ 𝑃𝑦 = 𝑄𝑥 = (𝑦 − 𝑥2 − 1)3 𝑄(𝑥, 𝑦) = { (𝑦 − 𝑥2 − 1)2 38
⇒ 𝐼 không phụ thuộc vào đường đi
Tích phân phức tạp do biểu thức (𝑦 − 𝑥2 − 1)2 ⇒ Chọn đường đi mới khử biểu thức này
Chọn đường đi mới dạng 𝐿′: 𝑦 − 𝑥2 − 1 = 𝐶 (𝐶 là hằng số)
𝐿′ đi qua 𝐴(0,2), 𝐵(2,6) ⇒ {2 − 02 − 1 = 𝐶
6 − 22 − 1 = 𝐶 ⇒ 𝐶 = 1
Chọn đường đi 𝐿′: {𝑦 = 𝑥2 + 2 ⇒ 𝑑𝑦 = 2𝑥𝑑𝑥
Đi từ 𝐴(0,2) → 𝐵(2,6) 2 2
−(𝑥2 + 2) + 2𝑥(𝑥2 + 2) − 𝑥2 + 1 26 20 ⇒ 𝐼 = ∫ 𝑥 − 𝑥2 − 1 12 𝑑𝑥 + ∫ 12 . 2𝑥𝑑𝑥 = 3 − 3 = 2 0 0
Câu 31: Tìm 𝑎, 𝑏 để tích phân x e   ( 2
2x + ay + 1)dx + (bx + 2y)dy   không phụ L thuộc vào đường đi Đáp án: A. {𝑎 = 1 𝑏 = 0 Giải:
Đặt 𝑃 = 𝑒𝑥(2𝑥 + 𝑎𝑦2 + 1), 𝑄 = 𝑒𝑥(𝑏𝑥 + 2𝑦)
Để tích phân không phụ thuộc đường đi ⇔ 𝑃′ ′ 𝑦 = 𝑄𝑥
⇔ 2𝑎𝑒𝑥𝑦 = 𝑒𝑥. 2𝑦 + 𝑒𝑥. 𝑏𝑥 + 𝑏𝑒𝑥 ⇔ 𝑎 = 1, 𝑏 = 0
Câu 32: Tìm hằng số 𝑎, 𝑏 để biểu thức [𝑦2 + 𝑎𝑥𝑦 + 𝑦 sin(𝑥𝑦)]𝑑𝑥 + [𝑥2 + 𝑏𝑥𝑦 +
𝑥 sin(𝑥𝑦)]𝑑𝑦 là vi phần toàn phần của một hàm số 𝑢(𝑥, 𝑦) nào đó Đáp án: B. {𝑎 = 2 𝑏 = 2 Giải:
Đặt 𝑃 = [𝑦2 + 𝑎𝑥𝑦 + 𝑦 sin(𝑥𝑦)], 𝑄 = 𝑥2 + 𝑏𝑥𝑦 + 𝑥 sin(𝑥𝑦) Để b ể
i u thức [𝑦2 + 𝑎𝑥𝑦 + 𝑦 sin(𝑥𝑦)]𝑑𝑥 + [𝑥2 + 𝑏𝑥𝑦 + 𝑥 sin(𝑥𝑦)]𝑑𝑦 là vi phần toàn
phần của một hàm số 𝑢(𝑥, 𝑦) nào đó ⇔ 𝑃′ ′ 𝑦 = 𝑄𝑥
⇔ 2𝑦 + 𝑎𝑥 + sin(𝑥𝑦) + 𝑥𝑦 cos(𝑥𝑦) = 2𝑥 + 𝑏𝑦 + sin(𝑥𝑦) + 𝑥𝑦 cos(𝑥𝑦) 39 ⇔ {𝑎 = 2 𝑏 = 2 2 2 2 2 x + y x + y +
Câu 33: Tính xe dx ye dy  với 2
L : y = 2x − x đi từ 𝑂(0,0) đến 𝐴(2,0) x − + y L ( )2 2 1 Đáp án: B. 0 Giải:
𝐿: 𝑦 = √2𝑥 − 𝑥2 ⇔ {𝑦2 = 2𝑥 − 𝑥2 𝑦 ≥ 0
⇔ {𝑥2 − 2𝑥 + 1 + 𝑦2 = 1 𝑦 ≥ 0
⇔ {(𝑥 − 1)2 + 𝑦2 = 1 𝑦 ≥ 0 2 − 2𝑥2 1 − 𝑥2
𝑦 = √2𝑥 − 𝑥2 ⇒ 𝑑𝑦 = 𝑑𝑥 = 𝑑𝑥 2√2𝑥 − 𝑥2 √2𝑥 − 𝑥2 2 2
𝑥𝑒𝑥2+𝑦2𝑑𝑥 + 𝑦𝑒𝑥2+𝑦2𝑑𝑦 𝑥𝑒2𝑥
√2𝑥 − 𝑥2𝑒2𝑥 1 − 𝑥2 ∫ ( = ∫ 𝑥 − 1) 𝑑𝑥 + ∫ 𝑑𝑥 2 + 𝑦2 1 1 √2𝑥 − 𝑥2 𝐿 0 0 2 2
= ∫ 𝑥𝑒2𝑥 𝑑𝑥 + ∫ 𝑒2𝑥(1 − 𝑥2) 𝑑𝑥 = 0 0 0 − + (5x + 2y)
Câu 34: Cho tích phân 𝐼 =
dy với 𝐶 là biên của hình 2 + y 2x − 5y
phẳng 𝐷: 𝑥2 + 𝑦2 ≤ 9, theo chiều dương, bạn 𝐴 lập luận “Ta đặt P = và 2 2 x + y 5x + 2y Q = , ' '
Q − P = 0 , 𝐶 là đường cong kín, chiều dương, giới hạn miền 𝐷 nên 2 2 x y x + y
𝐼 = 0”. Hỏi bạn 𝐴 làm vậy có đúng không? Nếu sai, thì sửa lại đáp án chính xác
Đáp án: B. Sai, 𝐼 = 10𝜋 Giải: 40 2 2 
−5(x + y ) − 2y(2x − 5y ) ' P =  y 2 2 2  (x + y ) Ta có: 
gián đoạn tại điểm 𝑂(0,0) ∈ 𝐷: 𝑥2 + 𝑦2 ≤ 9 2 2 
5(x + y ) − 2x(5x + 2y) ' Q = x 2 2 2  (x + y )
⇒ Không sử dụng được công thức Green Đặt {𝑥 = 3 cos 𝑡
𝑦 = 3 sin 𝑡, 𝑡 chạy từ 0 đến 2𝜋 ⇒ {𝑑𝑥 = −3 sin 𝑡 𝑑𝑡
𝑑𝑦 = 3 cos 𝑡 𝑑𝑡 2 (5  −
+ x + 2y)dy
(2.3cost − 5.3sint )(−3sint ) + (5.3cost + 2.3sint )(3cost ) = dt  2 + y 9 0 = 10𝜋
Câu 35: Tìm 𝑚 để tích phân (x −3y)dx + 2ydy = 4  với 2
AB : y = m − x và hai AB điểm ( A 1,0), B( 1 − ,0) Đáp án: A. 1 Giải: Cung 𝐴𝐵
⏜ : {𝑦 = 𝑚 − 𝑥2 ⇒ 𝑑𝑦 = −2𝑥𝑑𝑥
Đi từ 𝐴(1,0) → 𝐵(−1,0) −1 −1
⇒ ∫(𝑥 − 3𝑦)𝑑𝑥 + 2𝑦𝑑𝑦 = ∫ [𝑥 − 3(𝑚 − 𝑥2)]𝑑𝑥 + ∫ 2(𝑚 − 𝑥2). (−2𝑥)𝑑𝑥 = 4 𝐴𝐵 ⏜ 1 1 ⇒ 𝑚 = 1
Câu 36: Tính ydx + zdy + xdz
với 𝐶: 𝑥 = cos 𝑡 , 𝑦 = sin 𝑡 , 𝑧 = 2𝑡, 0 ≤ 𝑡 ≤ 2𝜋 theo C chiều tăng của 𝑡
Đáp án: C. −𝜋 Giải: 𝑥 = cos 𝑡 𝑥′ = − sin 𝑡
𝐶: {𝑦 = sin 𝑡⇒ { 𝑦′ = cos 𝑡 𝑧 = 2𝑡 𝑧′ = 2 41 2𝜋
∫ 𝑦𝑑𝑥 + 𝑧𝑑𝑦 + 𝑥𝑑𝑧 = ∫ (− sin 𝑡 . sin 𝑡 + 2𝑡. cos 𝑡 + cos 𝑡 . 2)𝑑𝑡 = ⋯ = −𝜋 𝐶 0 (4,5,6)
Câu 37: Tính tích phân y y + + ( +1) z e dx xe dy z e dz  (1,2,3)
Đáp án: A. 4𝑒5 + 6𝑒6 − 𝑒2 − 3𝑒3 Giải: 𝑃 = 𝑒𝑦 𝑃′ ′ 𝑧 = 0, 𝑃𝑦 = 𝑒𝑦 Đặt { 𝑄 = 𝑥𝑒𝑦 ⇒ {𝑄′ ′
𝑧 = 0, 𝑄𝑥 = 𝑒𝑦 ⇒ 𝑅′𝑦 − 𝑄′𝑧 = 𝑃′𝑧 − 𝑅′𝑥 = 𝑄′𝑥 − 𝑃′𝑦 = 0 𝑅 = (𝑧 + 1)𝑒𝑧 𝑅′ ′ 𝑥 = 0, 𝑅𝑦 = 0 (4,5,6) ⇒ Tích phân y y + + ( + 1) z e dx xe dy z e dz
không phụ thuộc vào đường đi (1,2,3)
Cách 1: Dùng hàm thế vị Hàm thế vị 𝑥 𝑦 𝑧
𝑢 = ∫ 𝑃(𝑡, 𝑦0, 𝑧0)𝑑𝑡+ ∫ 𝑄(𝑥,𝑡, 𝑧0)𝑑𝑡 + ∫ 𝑅(𝑥,𝑦,𝑡)𝑑𝑡 + 𝐶 𝑥0 𝑦0 𝑧0
Chọn 𝑥0 = 𝑦0 = 𝑧0 = 0 𝑥 𝑦 𝑧
𝑢 = ∫ 1𝑑𝑡 + ∫ 𝑥𝑒𝑡𝑑𝑡 + ∫(𝑡 + 1)𝑒𝑡𝑑𝑡 + 𝐶 0 0 0
= 𝑥 + 𝑥𝑒𝑦 − 𝑥 + 𝑒𝑧 − 1 + 𝑧𝑒𝑧 − (𝑒𝑧 − 1) + 𝐶 = 𝑥𝑒𝑦 + 𝑧𝑒𝑧 + 𝐶 (4,5,6) y y + + ( + 1) z e dx xe dy z e dz
= 𝑢(4,5,6) − 𝑢(1,2,3) = 4𝑒5 + 6𝑒6 − 𝑒2 − 3𝑒3 (1,2,3)
Cách 2: Chọn đường đi là đường thẳng
Đặt 𝐴(1,2,3), 𝐵(4,5,6) 𝑥 − 1
Đoạn 𝐴𝐵: {vecto chỉ phương 𝐴 󰇍󰇍 𝐵 󰇍 = (3,3,3) 𝑦 − 2 𝑧 − 3 Đi qua 𝐴(1,2,3)
⇒ 𝐴𝐵: 3 = 3 = 3 = 𝑡 42 𝑥 = 3𝑡 + 1
⇒ 𝐴𝐵: {𝑦 = 3𝑡 + 2, với 𝑡 đi từ 0 đến 1 ⇒ 𝑥′ = 𝑦′ = 𝑧′ = 3 𝑧 = 3𝑡 + 3 (4,5,6)
⇒ ∫ 𝑒𝑦𝑑𝑥 + 𝑥𝑒𝑦𝑑𝑦 + (𝑧 + 1)𝑒𝑧𝑑𝑧 (1,2,3) 1
= 3 ∫[𝑒3𝑡+2 + (3𝑡 + 1)𝑒3𝑡+2 + (3𝑡 + 4)𝑒3𝑡+3]𝑑𝑡 = ⋯ = 4𝑒5 + 6𝑒6 − 𝑒2 − 3𝑒3 0
Câu 38: Tìm hàm thế vị của biểu thức (𝑥4 + 4𝑥𝑦3)𝑑𝑥 + (6𝑥2𝑦2 − 5𝑦4)𝑑𝑦 1 Đáp án: A. 2 2 3 5
x + 2x y − y 5 Giải:
Đặt 𝑃 = (𝑥4 + 4𝑥𝑦3), 𝑄 = (6𝑥2𝑦2 − 5𝑦4) ⇒ 𝑃′ ′ 𝑦 = 𝑄𝑥 = 12𝑥𝑦2
⇒ 𝑃𝑑𝑥 + 𝑄𝑑𝑦 là vi phân toàn phần của hàm 𝑥 𝑦
𝑢(𝑥, 𝑦) = ∫ 𝑃(𝑡, 𝑦0)𝑑𝑡+ ∫ 𝑄(𝑥,𝑡)𝑑𝑡 𝑥0 𝑦0 Chọn 𝑥0 = 𝑦0 = 0 𝑥 𝑦
⇒ 𝑢(𝑥, 𝑦) = ∫(𝑡4 + 4𝑡. 03)𝑑𝑡 + ∫(6𝑥2𝑡2 − 5𝑡4)𝑑𝑡 0 0 1 𝑥 𝑦 1 𝑢(𝑥, 𝑦) = 1 5 𝑡5 | + (6𝑥2. = 0
3 𝑡3 − 𝑡5) | 0 5𝑥5 + 2𝑥2𝑦3 − 𝑦5
Câu 39: Tính (2xy − 5)dx + (2x + 3y)dy
với 𝐿 là biên của miền 𝐷 xác định bởi L
các đường 𝑦 = 𝑥2, 𝑦 = 0, 𝑥 = 1, chiều dương 1 Đáp án: D. 6 Giải: 43 𝑦 𝑦 = 𝑥2 𝑥 = 1 𝑥 ′ = 2𝑥 Đặ 𝑥𝑦 t {𝑃 = 2 − 5
𝑄 = 2𝑥 + 3𝑦 ⇒ {𝑃𝑦 ụ 𝑄′ c 𝑥 = 2 liên t
Ta có 𝐿 là đường cong kín, chiều dương, giới hạn miền 𝐷: { 0 ≤ 𝑥 ≤ 1 0 ≤ 𝑦 ≤ 𝑥2
Áp dụng công thức Green: 1 𝑥2 1
∫(2𝑥𝑦 − 5)𝑑𝑥 + (2𝑥 + 3𝑦)𝑑𝑦 = ∬(2 − 2𝑥)𝑑𝑥𝑑𝑦 = ∫ 𝑑𝑥 ∫ (2 − 2𝑥)𝑑𝑦 = 6 𝐿 𝐷 0 0  2   2  Câu 40: Tính 2 2 3 3x y + dx + 3x y + dy 
với 𝐶 là đường cong 2   3   4x +1  y + 4  C
𝑦 = √1 − 𝑥4 đi từ 𝐴(1,0) đến 𝐵(−1,0). 4
Đáp án: B. − 2arctan 2 7 44 Giải:  2   2  Đặt 𝐼 = 2 2 3 3x y + dx + 3x y + dy  2   3   4x +1  y + 4  C
𝐿: 𝑦 = √1 − 𝑥4 là đường cong hở đi từ 𝐴(1,0) đến 𝐵(−1,0)
Bổ sung thêm đoạn 𝐵𝐴: { 𝑦 = 0
Đi từ 𝐵(−1,0) → 𝐴(1,0) 2
𝑃(𝑥, 𝑦) = 3𝑥2𝑦2 + 2 ′ = 6𝑥2𝑦 Đặt 4𝑥 + 1⇒ {𝑃𝑦′
liên tục với ∀𝑥, 𝑦 ∈ 𝑅 ) 3 2 𝑄𝑥 = 9𝑥2𝑦
{ 𝑄(𝑥, 𝑦 = 3𝑥 𝑦 + 𝑦3 + 4
𝐼 = ∮ 𝑃𝑑𝑥 + 𝑄𝑑𝑦 − ∫ 𝑃𝑑𝑥 + 𝑄𝑑𝑦 = 𝐼1 − 𝐼2 𝐿∪𝐵𝐴 𝐵𝐴
Áp dụng công thức Green cho 𝐼1 2
𝑃(𝑥, 𝑦) = 3𝑥2𝑦2 + 2 ′ = 6𝑥2𝑦 Đặt 4𝑥 + 1⇒ {𝑃𝑦′
liên tục với ∀𝑥, 𝑦 ∈ 𝑅 ) 3 2 𝑄𝑥 = 9𝑥2𝑦
{ 𝑄(𝑥, 𝑦 = 3𝑥 𝑦 + 𝑦3 + 4
Ta có 𝐿 ∪ 𝐵𝐴 là đường cong kín, có chiều dương, giới hạn miền
𝐷: {0 ≤ 𝑦 ≤ √1 − 𝑥4 −1 ≤ 𝑥 ≤ 1 45 1 √1−𝑥4 1 ⇒ 𝐼 3 4
1 = ∬ 3𝑥2𝑦𝑑𝑥𝑑𝑦 = ∫ 𝑑𝑥 ∫
3𝑥2𝑦𝑑𝑦 = 2 ∫𝑥2(1− 𝑥4)𝑑𝑥= 7 𝐷 −1 0 −1 1 2 Đoạn 𝐵𝐴: { 𝑦 = 0 ⇒ 𝑑𝑦 = 0
đi từ 𝐵(−1,0) đến 𝐴(1,0) ⇒ 𝐼2 = ∫4𝑥2 + 1 𝑑𝑥= 2arctan2 −1
Vậy 𝐼 = 4/7 − 2 arctan 2 Câu 4 :
1 Tính diện tích của miền D giới hạn bởi 𝐿: { 𝑥 = 2(𝑡 − sin 𝑡)
𝑦 = 2(1 − cos 𝑡) với trục 𝑂𝑥
biết rằng 𝑡 đi từ 2𝜋 dến 0
Đáp án: B. 12𝜋 (đvdt) Giải:
Ta có: 𝜕𝐷 = 𝐿 ∪ 𝑂𝑥 0
⇒ 𝑆(𝐷) = ∫ 𝑥𝑑𝑦= ∫ 𝑥𝑑𝑦 + ∫ 𝑥𝑑𝑦= ∫ 𝑥𝑑𝑦 = ∫ 2(𝑡 − sin 𝑡).2 sin 𝑡 𝑑𝑡 = 12𝜋 𝐿∪𝑂𝑥 𝐿 𝑂𝑥 𝐿 2𝜋
Câu 42: Tính công của lực 𝐹 = (𝑥 + 2𝑦)𝑖 + (3𝑥 + 4𝑦)𝑗 làm dịch chuyển một
chất điểm từ 𝐴(1,3) đến 𝐵(2,4) dọc theo đoạn thẳng 𝐴𝐵. (đvc: đơn vị công)
Đáp án: D. 27 (đvc) Giải:
Công của lực 𝐹 là: W = (x + 2y)dx + (3x + 4y)dyL =
Đoạn thẳng AB: { 𝑦 = 𝑥 + 2 ⇒ 𝑑𝑦 𝑑𝑥
đi từ 𝐴(1,3) đến 𝐵(2,4) 2
⇒ 𝑊 = ∫(𝑥 + 2𝑥 + 4 + 3𝑥 + 4𝑥 + 8)𝑑𝑥 = 27 (đơn vị công) 1 𝑥 = cos 𝑡
Câu 43: Tính khối lượng của đường cong vật chất 𝐿 có phương trình { 𝑦 = sin 𝑡 0 ≤ 𝑡 ≤ 𝜋/2
biết hàm mật độ là 𝑝(𝑥, 𝑦) = 𝑦 46
Đáp án: A. 1 (đvkl) Giải:
Khối lượng của đường cong vật chất 𝐿 được tính theo công thức :
𝑚 = ∫ 𝑝(𝑥, 𝑦)𝑑𝑠 = ∫ 𝑦𝑑𝑠 𝐿 𝐿 𝑥 = cos 𝑡 𝑥′ = − sin 𝑡
{ 𝑦 = sin 𝑡 ⇒ { 𝑦′ = cos 𝑡 ⇒ 𝑑𝑠 = √𝑥′2(𝑡) + 𝑦′2(𝑡)𝑑𝑡 = 𝑑𝑡 0 ≤ 𝑡 ≤ 𝜋/2 0 ≤ 𝑡 ≤ 𝜋/2 𝜋 2
⇒ 𝑚 = ∫ 𝑦𝑑𝑠 = ∫ sin 𝑡 𝑑𝑡 = 1 (đvkl) 𝐿 0
Câu 44: Tính công làm dịch chuyển một chất điểm từ A(0,1) đến B(1,0) của lực
𝐹 = [8𝑥3 − 2𝑦 ln(1 + 𝑥2𝑦2)]𝑖+ [5𝑦4 − 2𝑥 ln(1 + 𝑥2𝑦2)]𝑗 Đáp án: A. 1 (đvc) Giải: Công của lực 𝐹
𝑊 = ∫[8𝑥3 − 2𝑦 ln(1 + 𝑥2𝑦2)]𝑑𝑥 + [5𝑦4 − 2𝑥 ln(1 + 𝑥2𝑦2)]𝑑𝑦 𝐿
Với 𝐿 là đường đi từ 𝐴 đến 𝐵 (chưa biết hình dạng) Đặ ln( 2𝑦2)] t {𝑃 = [8𝑥3 − 2𝑦 1 + 𝑥
𝑄 = [5𝑦4 − 2𝑥 ln(1 + 𝑥2𝑦2)] 4𝑥2𝑦2 ⇒ 𝑃′ ′ 2
𝑦 = 𝑄𝑥 = −2 ln(1 + 𝑥 𝑦2) − 1 + 𝑥2𝑦2
⇒ Tích phân 𝑊 không phụ thuộc vào đường đi
Chọn đường đi là đường gấp khúc 𝐴𝑂𝐵 với 𝐴(0,1) và 𝐵(1,0), 𝑂(0,0) 47
𝑊 = ∫ 𝑃𝑑𝑥 + 𝑄𝑑𝑦 =∫ 𝑃𝑑𝑥 + 𝑄𝑑𝑦 + ∫ 𝑃𝑑𝑥 + 𝑄𝑑𝑦 𝐴𝑂𝐵 𝐴𝑂 𝑂𝐵 0
𝐴𝑂: { 𝑥 = 0 ⇒ 𝑑𝑥 = 0 4
Đi từ A(0,1) → 𝑂(0,0) ⇒ ∫ 𝑃𝑑𝑥 +𝑄𝑑𝑦 = ∫ 5𝑦 𝑑𝑦 = −1 𝐴𝑂 1 1
𝑂𝐵: { 𝑦 = 0 ⇒ 𝑑𝑦 = 0 3
Đi từ O(0,0) → 𝐵(1,0) ⇒ ∫ 𝑃𝑑𝑥 +𝑄𝑑𝑦 = ∫ 8𝑥 𝑑𝑥 = 2 𝑂𝐵 0
⇒ 𝑊 = ∫ 𝑃𝑑𝑥 + 𝑄𝑑𝑦 =∫ 𝑃𝑑𝑥 + 𝑄𝑑𝑦 + ∫ 𝑃𝑑𝑥 + 𝑄𝑑𝑦 = 1(đvc) 𝐴𝑂𝐵 𝐴𝑂 𝑂𝐵
Câu 45: Tính khối lượng của đường cong vật 𝐿 chất có phương trình 𝑥2 + 𝑦2 = 1
biết hàm mật độ là 𝑝(𝑥, 𝑦) = 𝑥2 Đáp án: D. 𝜋 Giải:
Khối lượng: m = xdsL
Tham số hóa: {𝑥 = 𝑐𝑜𝑠𝑡
𝑦 = sin 𝑡 , 0 ≤ 𝑡 ≤ 2𝜋 ⇒ {𝑥′ = − sin 𝑡
𝑦′ = cos 𝑡 ⇒ 𝑑𝑠 = √(𝑥′)2 + (𝑦′)2𝑑𝑡 = 𝑑𝑡 2𝜋
⇒ 𝑚 = ∫ 𝑥2𝑑𝑠 = ∫ (cos 𝑡)2𝑑𝑡 = 𝜋 (đvkl) 𝐿 0 48
Tích phân mặt
Câu 46: Tính xydS 
với 𝑆 là mặt 𝑧 = √𝑥2 + 𝑦2, 𝑧 ≤ 1, 𝑥 ≥ 0 S Đáp án: A. 0 Giải: 𝑥 𝑧′𝑥 = √𝑥2 +𝑦2
Ta có: 𝑧 = √𝑥2 + 𝑦2 ⇒ 𝑦 𝑧′𝑦 = { √𝑥2 + 𝑦2
⇒ 𝑑𝑆 = √1 + (𝑧𝑥′)2 + (𝑧𝑦′)2𝑑𝑥𝑑𝑦 = √2𝑑𝑥𝑑𝑦
Hình chiếu của mặt 𝑆 lên 𝑂𝑥𝑦 là: 𝐷: 𝑥2 + 𝑦2 ≤ 1, 𝑥 ≥ 0
⇒ ∬ 𝑥𝑦𝑑𝑆 = √2 ∬ 𝑥𝑦𝑑𝑥𝑑𝑦 𝑆 𝐷 𝑥 = 𝑟 cos 𝜑
Đặt {𝑦 = 𝑟sin𝜑 ,𝐽 = 𝑟 ⇒ 𝐷: { 0 ≤ 𝑟 ≤ 1 −𝜋/2 ≤ 𝜑 ≤ 𝜋/2 49 𝜋 𝜋 2 1 2 √2
⇒ ∬ 𝑥𝑦𝑑𝑆 = √2 ∫ 𝑑𝜑 ∫ 𝑟2 cos 𝜑 sin 𝜑 . 𝑟𝑑𝑟 = 4 ∫cos𝜑sin𝜑𝑑𝜑 = 0 𝑆 −𝜋 0 −𝜋 2 2 Câu 47: Tính 2 x dS 
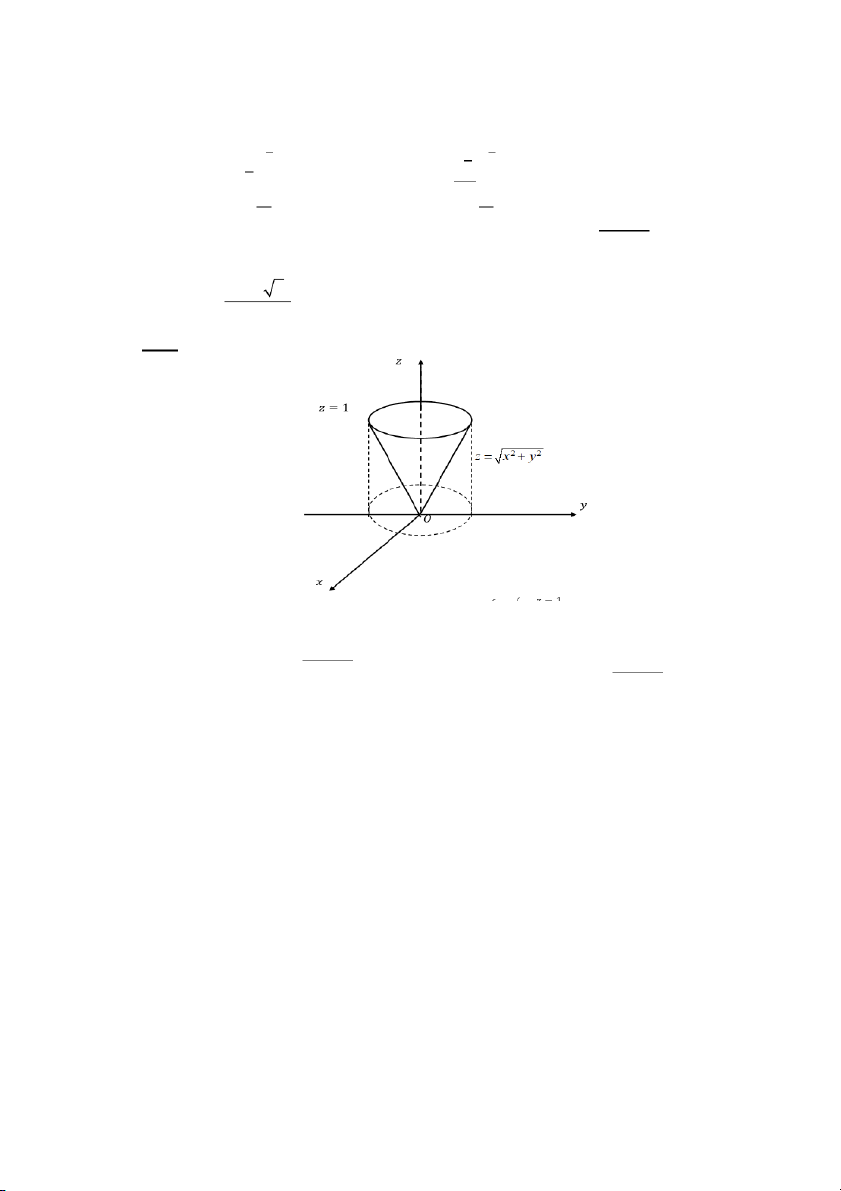
với 𝑆 là biên của miền giới hạn bởi mặt 𝑧 = √𝑥2 + 𝑦2, 𝑧 = 1 S  (1 + 2) Đáp án: C. 4 Giải: 𝑆1: { 𝑧 = 1 𝑥2 + 𝑦2 ≤ 1
𝑆 là biên của miền 𝑉: √𝑥2 + 𝑦2 ≤ 𝑧 ≤ 1 ⇒ 𝑆 gồm hai mặt
{𝑆2: {𝑧 = √𝑥2 + 𝑦2 0 ≤ 𝑧 ≤ 1
⇒ ∬ 𝑥2𝑑𝑆 = ∬ 𝑥2𝑑𝑆 + ∬ 𝑥2𝑑𝑆 𝑆 𝑆1 𝑆2 Xét mặt 𝑆 ′ ′ 1 : { 𝑧 = 1
𝑥2 + 𝑦2 ≤ 1 ⇒ 𝑧𝑥 = 𝑧𝑦 = 0 ⇒ 𝑑𝑆 = 𝑑𝑥𝑑𝑦 Hình chiếu của mặt 𝑆 2 2
2 lên 𝑂𝑥𝑦 là: 𝐷: 𝑥 + 𝑦 ≤ 1 50
⇒ ∬ 𝑥2𝑑𝑆 = ∬ 𝑥2𝑑𝑥𝑑𝑦 𝑆1 𝐷 𝑥 = 𝑟 cos 𝜑
Đặt {𝑦 = 𝑟sin𝜑 ,𝐽 = 𝑟 ⇒ 𝐷: { 0 ≤ 𝑟 ≤ 1 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 1 𝜋
∬ 𝑥2𝑑𝑥𝑑𝑦 = ∫ 𝑑𝜑∫ 𝑟2 cos2 𝜑 𝑟𝑑𝑟 = ⋯ = 4 𝐷 0 0 Xét mặt 𝑆2: 𝑥 𝑧′𝑥 = √𝑥2 +𝑦2
Có: 𝑧 = √𝑥2 + 𝑦2 ⇒ 𝑦
⇒ 𝑑𝑆 = √1 + (𝑧𝑥′)2 + (𝑧𝑦′)2𝑑𝑥𝑑𝑦 = √2𝑑𝑥𝑑𝑦 𝑧′𝑦 = { √𝑥2 + 𝑦2 Hình chiếu của mặt 𝑆 2 2
2 lên 𝑂𝑥𝑦 là: 𝐷: 𝑥 + 𝑦 ≤ 1, 𝑥 ≥ 0
⇒ ∬ 𝑥2𝑑𝑆 = √2 ∬ 𝑥2𝑑𝑥𝑑𝑦 𝑆2 𝐷 𝑥 = 𝑟 cos 𝜑
Đặt {𝑦 = 𝑟sin𝜑 ,𝐽 = 𝑟 ⇒ 𝐷: { 0 ≤ 𝑟 ≤ 1 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 1 𝜋
⇒ ∬ 𝑥2𝑑𝑆 = √2 ∫ 𝑑𝜑 ∫ 𝑟2 cos2 𝜑 . 𝑟𝑑𝑟 = ⋯ = √2 4 𝑆2 0 0 𝜋(1 + ⇒ ∬ 𝑥2𝑑𝑆 = ∬ √2)
𝑥2𝑑𝑆 + ∬ 𝑥2𝑑𝑆 = 4 𝑆 𝑆1 𝑆2 5 6
Câu 48: Tìm 𝑚 để (x + y + mz)dS = 
với 𝑆 là mặt 2𝑥 + 4𝑦 + 2𝑧 = 4 và điều 3 S
kiện 𝑥 ≥ 0, 𝑦 ≥ 0, 𝑧 ≥ 0
Đáp án: B. 𝑚 = 1 51 Giải: ′ = −1
Mặt 𝑆: {𝑧 = 2 − 2𝑦 − 𝑥
𝑥, 𝑦, 𝑧 ≥ 0 ⇒ {𝑧𝑥𝑧′ ( √
𝑦 = −2 ⇒ 𝑑𝑆 = √1 + 𝑧𝑥′)2 + (𝑧𝑦′)2𝑑𝑥𝑑𝑦 = 6𝑑𝑥𝑑𝑦
Hình chiếu của 𝑆 lên 𝑂𝑥𝑦 là miền 𝐷 được giới hạn bởi {2𝑥 + 4𝑦 = 4 𝑥 ≥ 0, 𝑦 ≥ 0 ⇒ 𝐷: { 0 ≤ 𝑥 ≤ 2 0 ≤ 𝑦 ≤ 1 − 𝑥/2
⇒ ∬(𝑥 + 𝑦 + 𝑚𝑧)𝑑𝑆 = √6 ∬(𝑥 + 𝑦 + 2𝑚 − 2𝑚𝑦 − 𝑚𝑥)𝑑𝑥𝑑𝑦 𝑆 𝐷 2 1−𝑥2 5
= √6 ∫ 𝑑𝑥 ∫ (𝑥 + 𝑦 + 2𝑚 − 2𝑚𝑦 − 𝑚𝑥)𝑑𝑦 = √6 3 ⇒ 𝑚 = 1 0 0
Câu 49: Tính xyzdS 
với 𝑆 là mặt 𝑥 − 2𝑦 + 3𝑧 − 4 = 0 giới hạn trong mặt trụ có S
phương trình 2𝑥2 + 3𝑦2 = 6 Đáp án: B. 0 Giải: 4 − 𝑥 + 2𝑦 Mặt 𝑧 = √14 3
⇒ 𝑑𝑆 = √1 + (𝑧𝑥′)2 + (𝑧𝑦′)2𝑑𝑥𝑑𝑦 = 3 𝑑𝑥𝑑𝑦
Hình chiếu của mặt 𝑆 lên 𝑂𝑥𝑦 là 𝐷: 2𝑥2 + 3𝑦2 ≤ 6 √14 4 − 𝑥 + 2𝑦 √14
⇒ 𝐼 = ∬ 𝑥𝑦𝑧𝑑𝑆 = 3 ∬𝑥𝑦 3
𝑑𝑥𝑑𝑦 = 9 ∬𝑥𝑦(4− 𝑥 + 2𝑦)𝑑𝑥𝑑𝑦 𝑆 𝐷 𝐷 52
Miền 𝐷 đối xứng qua 𝑂𝑥, 𝑂𝑦
𝑓(𝑥, 𝑦, 𝑧) = 4𝑥𝑦 lẻ với biến 𝑥
𝑔(𝑥, 𝑦, 𝑧) = −𝑥2𝑦 lẻ với biến 𝑦 ⇒ ∬ 4𝑥𝑦𝑑𝑥𝑑𝑦 + ∬ −𝑥2𝑦𝑑𝑥𝑑𝑦 + ∬ 2𝑥𝑦2𝑑𝑥𝑑𝑦 = 0
{ ℎ(𝑥,𝑦,𝑧) = 2𝑥𝑦2 lẻ với biến 𝑥 𝐷 𝐷 𝐷 ⇒ 𝐼 = 0  a 5 1 
Câu 50: Biết xdS =  +   2 2 
biết 𝑆 là phần mặt paraboloid 𝑥 = 𝑦 + 𝑧 thỏa 12 b S  
mãn 𝑥 ≤ 1. Kết luận nào sau đây là chính xác?
Đáp án: A. 𝑎 + 𝑏 < 70 Giải: 𝑥′ = 2𝑦
Mặt 𝑥 = 𝑦2 + 𝑧2 ⇒ { 𝑦 𝑥′𝑧 = 2𝑧 53
⇒ 𝑑𝑆 = √1 + (𝑥′𝑦)2 + (𝑥𝑧′)2𝑑𝑥𝑑𝑧 = √1 + 4(𝑦2 + 𝑧2)𝑑𝑦𝑑𝑧
Hình chiếu của 𝑆 lên 𝑂𝑦𝑧 là 𝐷: 𝑦2 + 𝑧2 ≤ 1
𝐼 = ∬ 𝑥𝑑𝑆 = ∬(𝑦2 + 𝑧2) √1 + 4(𝑦2 + 𝑧2)𝑑𝑦𝑑𝑧 𝑆 𝐷 𝑦 = 𝑟 cos 𝜑
Đặt {𝑧 = 𝑟 sin𝜑 ,𝐽 = 𝑟 ⇒ 𝐷: { 0 ≤ 𝑟 ≤ 1 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 1 2𝜋 1 1
⇒ 𝐼 = ∫ 𝑑𝜑 ∫ 𝑟2√1 + 4𝑟2. 𝑟𝑑𝑟 = 2∫ 𝑑𝜑∫𝑟2√1 + 4𝑟2𝑑(𝑟2) 0 0 0 0 2𝜋 1 1
= 2∫ 𝑑𝜑∫𝑢√1 + 4𝑢𝑑𝑢 0 0 2 2 𝑡
Đặ𝑡 𝑡 = √1 + 4𝑢 ⇒ 𝑑𝑡 = 𝑑𝑢 = ⇒ = √1 + 4𝑢
𝑡 𝑑𝑢 𝑑𝑢 2 𝑑𝑡 1 √5 𝑡2 −1 𝑡 5√5 1
⇒ ∫ 𝑢√1 + 4𝑢𝑑𝑢 = ∫ 4 . 𝑡. 2 𝑑𝑡 = 12+ 60 0 1 2𝜋 1 5√5 1 5√5 1
⇒ 𝐼 = 2.( 12+ 60).∫ 𝑑𝜑 = ( 12+ 60)𝜋 ⇒ 𝑎 = 5,𝑏 = 60 0 Câu 51: Tính 2 2 1+ x + y dS 
với 𝑆 là phần mặt 2𝑧 = 𝑥2 + 𝑦2, 0 ≤ 𝑥, 𝑦 ≤ 1. Chọn S
đáp án gần với kết quả của tích phân nhất. Đáp án: A. 2 Giải: 𝑥2 + 𝑦2 Mặt 𝑆: 𝑧 = 2 2
⇒ 𝑑𝑆 = √1 + (𝑧𝑥′)2 + (𝑧𝑦′)2𝑑𝑥𝑑𝑦 = √1 + 𝑥 + 𝑦2𝑑𝑥𝑑𝑦
Hình chiếu của 𝑆 lên 𝑂𝑥𝑦 là 𝐷: {0 ≤ 𝑥 ≤ 1 0 ≤ 𝑦 ≤ 1 54 1 1 5
∬ √1 + 𝑥2 + 𝑦2𝑑𝑆 = ∬(1 + 𝑥2 + 𝑦2)𝑑𝑥𝑑𝑦 = ∫ 𝑑𝑥∫(1 + 𝑥2 + 𝑦2)𝑑𝑦 = ⋯ = 3 𝑆 𝐷 0 0 4 Câu 52: Biết 2 dS
 = (33− a 3 −b 2) với 𝑆 là mặt z = ( 3/2 3/2 x + y ) với điều 15 3 S
kiện 0 ≤ 𝑥 ≤ 2, 0 ≤ 𝑦 ≤ 1. Tìm khẳng định đúng?
Đáp án: C. 𝑎 − 𝑏 = 5 Giải:
Hình chiếu của mặt 𝑧 = 2 (𝑥3/2 + 𝑦3/2) với 0 ≤ 𝑥 ≤ 2,0 ≤ 𝑦 ≤ 1 lên 𝑂𝑥𝑦 là miền 3 𝐷: {0 ≤ 𝑥 ≤ 2 0 ≤ 𝑦 ≤ 1 Ta có: 𝑧′ ′
𝑥 = √𝑥, 𝑧𝑦 = √𝑦 ⇒ 𝑑𝑆 = √1 + (𝑧𝑥′)2 + (𝑧𝑦′)2𝑑𝑥𝑑𝑦 = √1 + 𝑥 + 𝑦𝑑𝑥𝑑𝑦 1 2
∬ 𝑑𝑆 = ∬ √1 + 𝑥 + 𝑦𝑑𝑥𝑑𝑦 = ∫ 𝑑𝑦∫ √1 + 𝑥 + 𝑦𝑑𝑥 𝑆 𝐷 0 0 1 2 3 3 4
= 3∫[(3 +𝑦)2 − (1+ 𝑦)2]𝑑𝑦 = 15(33− 9√3 − 4√2) 0 ⇒ 𝑎 = 9, 𝑏 = 4 Câu 53: Tính 2 zy dS 
với 𝑆 là phần mặt nón 𝑧 = √𝑥2 + 𝑦2 nằm giữa hai mặt 𝑧 = 1 S và 𝑧 = 2 31 2 Đáp án: D. 5 Giải: 𝑧′𝑥 = 𝑥 √𝑥2 + 𝑦2 𝑧 = √𝑥2 + 𝑦2 ⇒
⇒ 𝑑𝑆 = √1 + (𝑧𝑥′)2 + (𝑧𝑦′)2𝑑𝑥𝑑𝑦 = √2𝑑𝑥𝑑𝑦 𝑧′𝑦 = 𝑦 { √𝑥2 + 𝑦2
Hình chiếu của mặt 𝑆 lên 𝑂𝑥𝑦 là 𝐷: 1 ≤ 𝑥2 + 𝑦2 ≤ 4 55 𝑥 = 𝑟 cos𝜑
Đặt {𝑦 = 𝑟 sin𝜑 ,𝐽 = 𝑟 ⇒ 𝐷:{ 1 ≤ 𝑟 ≤ 2 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 2 31
∬ 𝑧𝑦2𝑑𝑆 = √2 ∬ √𝑥2 + 𝑦2. 𝑦2𝑑𝑥𝑑𝑦 √2𝜋
= √2 ∫ 𝑑𝜑 ∫ 𝑟. 𝑟2.sin2 𝜑 . 𝑟𝑑𝑟 = 5 𝑆 𝐷 0 1 Câu 54: Tính 2 yx dS 
với 𝑆 là phần mặt nón 𝑦 = √𝑥2 + 𝑧2, 1 ≤ 𝑦 ≤ 2 S 31 2 Đáp án: B. 5 Giải: 𝑦′𝑥 = 𝑥 √ 𝑦 = √𝑥2 + 𝑧2 ⇒
𝑥2 + 𝑧2 ⇒ 𝑑𝑆 = √1 + (𝑦𝑥′)2 + (𝑦𝑧′)2𝑑𝑥𝑑𝑧 = √2𝑑𝑥𝑑𝑧 𝑦′ = 𝑧 { 𝑧 √𝑥2 + 𝑧2
Hình chiếu của mặt 𝑆 lên 𝑂𝑥𝑧 là 𝐷: 1 ≤ 𝑥2 + 𝑧2 ≤ 4 𝑧 = 𝑟 cos 𝜑
Đặt {𝑥 = 𝑟 sin 𝜑 , 𝐽 = 𝑟 ⇒ 𝐷:{ 1 ≤ 𝑟 ≤ 2 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 2 ∬ 𝑦𝑥2𝑑𝑆 31 = √2𝜋
√2 ∬ √𝑥2 + 𝑧2. 𝑥2𝑑𝑥𝑑𝑧 = √2 ∫ 𝑑𝜑 ∫ 𝑟. 𝑟2.sin2 𝜑 . 𝑟𝑑𝑟 = 5 𝑆 𝐷 0 1
Câu 55: Tính xdS 
với 𝑆 là mặt trụ 𝑥2 + 𝑦2 = 4 nằm giữa hai mặt 𝑧 = 0 và 𝑧 = 6 S Đáp án: A. 0 Giải:
Chia mặt trụ thành hai mặt 𝑆 √ 2 √ 2 1: {𝑥 = 4 − 𝑦 và 𝑆 0 ≤ 𝑧 ≤ 6 2: {𝑥 = − 4 − 𝑦 0 ≤ 𝑧 ≤ 6
Hình chiếu của 𝑆1 và 𝑆2 lên 𝑂𝑦𝑧 là 𝐷: {−2 ≤ 𝑦 ≤ 2 0 ≤ 𝑧 ≤ 6
∬ 𝑥𝑑𝑆 = ∬ 𝑥𝑑𝑆 + ∬ 𝑥𝑑𝑆 𝑆 𝑆1 𝑆2 56   − ' y 2 = x = 4 x −  y y | y | Xét mặt 2 ' 2 ' 2 S :   
4 − y dS = (x ) + (x ) dydz = 1 dydz y z 2  0  z  6  4 − '   = 0 y xz | 6 2 𝑦|
∬ 𝑥𝑑𝑆 = ∬ √4 − 𝑦2.
𝑑𝑦𝑑𝑧 = ∫ 𝑑𝑧 ∫|𝑦|𝑑𝑦 = 24 √4 − 𝑦2 𝑆1 𝐷 0 −2   ' y 2 = x = − 4 x −  y y | y| dydz Xét mặt 2 ' 2 ' 2 S :   
4 − y dS = ( x ) + ( x ) = 2 dydz y z 2  0  z  6  − ' 4 y x = 0   z | 6 2 ∬ 𝑥𝑑𝑆 𝑦| = ∬ −√4 − 𝑦2.
𝑑𝑦𝑑𝑧 = − ∫ 𝑑𝑧 ∫|𝑦|𝑑𝑦 = −24 √4 − 𝑦2 𝑆2 𝐷 0 −2
⇒ ∬ 𝑥𝑑𝑆 = ∬ 𝑥𝑑𝑆 + ∬ 𝑥𝑑𝑆 = 0 𝑆 𝑆1 𝑆2
Câu 56: Tính (1− x − z)dzdx 
với 𝑆 là mặt trên của mặt 𝑥 + 𝑦 + 𝑧 = 1, 𝑥 ≥ 0, 𝑦 ≥ S 0, 𝑧 ≥ 0 1 Đáp án: C. 6 Giải:
Mặt 𝑆: 𝑦 = 1 − 𝑥 − 𝑧, 𝑥 ≥ 0, 𝑦 ≥ 0, 𝑧 ≥ 0, (𝑛󰇍, 𝑂𝑦  ) < 𝜋/2 57
Hình chiếu của mặt 𝑆 lên 𝑂𝑥𝑧 là 𝐷: { 0 ≤ 𝑥 ≤ 1 0 ≤ 𝑧 ≤ 1 − 𝑥 1 1−𝑥 1
⇒ ∬(1 − 𝑥 − 𝑧)𝑑𝑧𝑑𝑥 = + ∬(1 − 𝑥 − 𝑧)𝑑𝑧𝑑𝑥 = ∫ 𝑑𝑥 ∫ (1 − 𝑥 − 𝑧)𝑑𝑧 = ⋯ = 6 𝑆 𝐷 0 0 Câu 57: Tính 2 2 2 I =
(x + y + z )dxdy 
với 𝑆 là mặt nửa cầu 𝑥2 + 𝑦2 + 𝑧2 = 1 phía S
trên 𝑂𝑥𝑦, mặt 𝑆 hướng lên trên. Đáp án: A. 𝜋 Giải:
Mặt 𝑆: 𝑧 = √1 − 𝑥2 − 𝑦2, hướng lên trên, (𝑛󰇍, 𝑂𝑧) < 𝜋/2 Hình chiếu c a m ủ
ặt 𝑆 lên 𝑂𝑥𝑦 là (𝐷):𝑥2 + 𝑦2 ≤ 1
⇒ ∬(𝑥2 + 𝑦2 + 𝑧2)𝑑𝑥𝑑𝑦 = + ∬(𝑥2 + 𝑦2 + 1 − 𝑥2 − 𝑦2)𝑑𝑥𝑑𝑦 = ∬ 1𝑑𝑥𝑑𝑦 𝑆 𝐷 𝐷
= 𝑆(𝐷) = 𝜋𝑅2 = 𝜋 Câu 58: Cho 𝐼 = 2 ydzdx + z dxdy 
, 𝑆 là phía ngoài mặt 𝑥2 + 𝑦2 + 𝑧2 = 1 với điều S
kiện 𝑥 ≥ 0, 𝑦 ≥ 0, 𝑧 ≥ 0. Chọn đáp án gần nhất với kết quả của 𝐼 Đáp án: A. 1 Giải: 58
𝐼 = ∬ 𝑦𝑑𝑧𝑑𝑥 + ∬ 𝑧2𝑑𝑥𝑑𝑦 = 𝐼1 + 𝐼2 𝑆 𝑆
Xét 𝐼1, mặt 𝑆: 𝑦 = √1 − 𝑥2 − 𝑧2, 𝑥 ≥ 0,𝑧 ≥ 0, (𝑛󰇍, 𝑂𝑦) < 𝜋/2
Hình chiếu của mặt 𝑆 lên 𝑂𝑥𝑧 là 𝐷𝑥𝑧: 𝑥2 + 𝑧2 ≤ 1, 𝑥 ≥ 0, 𝑧 ≥ 0
⇒ 𝐼1 = ∬ 𝑦𝑑𝑧𝑑𝑥 = ∬ √1 − 𝑥2 − 𝑧2𝑑𝑥𝑑𝑧 𝑆 𝐷𝑥𝑧 𝑧 = 𝑟 cos 𝜑
Đặt {𝑥 = 𝑟 sin𝜑 𝐽 = 𝑟. Miền 𝐷𝑥𝑧: { 0 ≤ 𝑟 ≤ 1 0 ≤ 𝜑 ≤ 𝜋/2 𝜋 𝜋 𝜋 2 1 2 1 2 1 1 1 1
⇒ 𝐼1 = ∫ 𝑑𝜑 ∫ √1 − 𝑟2.𝑟𝑑𝑟 = 2∫𝑑𝜑∫√1− 𝑟2.𝑑(𝑟2) = 2∫𝑑𝜑∫√1 −𝑢.𝑑𝑢 = 6𝜋 0 0 0 0 0 0
Xét 𝐼2, mặt 𝑆:𝑧 = √1 − 𝑥2 − 𝑦2, 𝑥 ≥ 0, 𝑦 ≥ 0, (𝑛󰇍, 𝑂𝑧) < 𝜋/2
Hình chiếu của mặt 𝑆 lên 𝑂𝑥𝑧 là 𝐷𝑥𝑦: 𝑥2 + 𝑦2 ≤ 1, 𝑥 ≥ 0, 𝑦 ≥ 0
⇒ 𝐼2 = ∬ 𝑧2𝑑𝑥𝑑𝑦 = ∬(1 − 𝑥2 − 𝑦2)𝑑𝑥𝑑𝑦 𝑆 𝐷𝑥𝑦 𝜋 2 1 𝑥 = 𝑟 cos 𝜑 0 ≤ 𝑟 ≤ 1 Đặt { 1
𝑦 = 𝑟 sin 𝜑 𝐽 = 𝑟. Miền 𝐷𝑥𝑦: { 𝜋
0 ≤ 𝜑 ≤ ⇒ 𝐼2 = ∫ 𝑑𝜑∫(1 − 𝑟2). 𝑟𝑑𝑟 = 2 8 𝜋 0 0 59 7
Vậy 𝐼 = 𝐼1 + 𝐼2 = 24𝜋 Câu 59: Tính 𝐼 = 2 xdzdx + z dxdy 
với 𝑆 là phía ngoài mặt 𝑧 = 𝑥2 + 𝑦2 với điều S
kiện 0 ≤ 𝑧 ≤ 2, 𝑦 ≥ 0 4 −  Đáp án: D. 3 Giải:
𝐼 = ∬ 𝑥𝑑𝑧𝑑𝑥 + 𝑧2𝑑𝑥𝑑𝑦 = ∬ 𝑥𝑑𝑧𝑑𝑥 + ∬ 𝑧2𝑑𝑥𝑑𝑦 = 𝐼1 + 𝐼2 𝑆 𝑆 𝑆 Xét 𝐼 2 2
1, mặt 𝑆: 𝑧 = 𝑥 + 𝑦 , (𝑛󰇍, 𝑂𝑦) < 𝜋/2
Hình chiếu của 𝑆 lên 𝑂𝑥𝑧 là 𝐷𝑥𝑧 : { 𝑥2 ≤ 𝑧 ≤ 2 −√2 ≤ 𝑥 ≤ √2 √2 2 √2
⇒ 𝐼1 = ∬ 𝑥𝑑𝑧𝑑𝑥 = ∬ 𝑥𝑑𝑧𝑑𝑥= ∫ 𝑑𝑥 ∫ 𝑥 𝑑𝑧 = ∫ 𝑥(2 − 𝑥2)𝑑𝑥 = 0 𝑆 𝐷𝑥𝑧 −√2 𝑥2 −√2 Xét 𝐼 2 2
2, mặt 𝑆: 𝑧 = 𝑥 + 𝑦 , (𝑛󰇍, 𝑂𝑧) > 𝜋/2
Hình chiếu của 𝑆 lên 𝑂𝑥𝑦 là 𝐷𝑥𝑦: 𝑥2 + 𝑦2 ≤ 2, 𝑦 ≥ 0 𝑥 = 𝑟 cos 𝜑
Đặt {𝑦 = 𝑟sin𝜑 𝐽 = 𝑟. Miền (𝐷):{0 ≤ 𝑟 ≤ √2 0 ≤ 𝜑 ≤ 𝜋 60 𝜋 √2 ⇒ 𝐼 2 −4
2 = ∬ 𝑧2𝑑𝑥𝑑𝑦 = − ∬(𝑥 + 𝑦2)2𝑑𝑥𝑑𝑦= − ∫ 𝑑𝜑 ∫ 𝑟4. 𝑟𝑑𝑟 = 3 𝜋 𝑆 𝐷𝑥𝑦 0 0 −4𝜋
Vậy 𝐼 = 𝐼1 + 𝐼2 = 3 Câu 60: Tính 2 2 2
xz dydz + 4yx dzdx + 9zy dxdy 
với mặt 𝑆: 4𝑥2 + 9𝑦2 + 𝑧2 = 1, S hướng ra ngoài. 2 Đáp án: B. 15 Giải:
Mặt 𝑆 là mặt trơn kín giới hạn miền 𝑉: 4𝑥2 + 9𝑦2 + 𝑧2 ≤ 1, hướng pháp tuyến ngoài. 𝑃 = 𝑥𝑧2 𝑃′𝑥 = 𝑧2
Đặt {𝑄 = 4𝑦𝑥2 ⇒ {𝑄′ ′ ′ ′
𝑦 = 4𝑥2 , 𝑃𝑥, 𝑄𝑦 , 𝑅𝑧 liên tục 𝑅 = 9𝑧𝑦2 𝑅′𝑧 = 9𝑦2
Áp dụng công thức Ostrogradsky:
𝐼 = ∬ 𝑥𝑧2𝑑𝑦𝑑𝑧 + 4𝑦𝑥2𝑑𝑧𝑑𝑥 + 9𝑧𝑦2𝑑𝑥𝑑𝑦 = ∭(4𝑥2 + 9𝑦2 + 𝑧2)𝑑𝑥𝑑𝑦𝑑𝑧 𝑆 𝑉 1 2𝑥 = 𝑟 sin 𝜃 cos 𝜑 𝑥 = 2𝑟sin𝜃cos𝜑 1 0 ≤ 𝑟 ≤ 1
Đặt {3𝑦 = 𝑟 sin 𝜃 sin 𝜑⇔ 1 |𝐽| = 0 ≤ 𝜃 ≤ 𝜋 𝑧 = 𝑟 cos 𝜃 𝑦 =
6 𝑟2 sin 𝜃 . Miền 𝑉: { 3 𝑟 sin 𝜃 sin 𝜑 0 ≤ 𝜑 ≤ 2𝜋 { 𝑧 = 𝑟 cos 𝜃 2𝜋 𝜋 1 1 2
⇒ 𝐼 = 6∫ 𝑑𝜑∫𝑑𝜃∫𝑟2.𝑟2 sin𝜃𝑑𝑟 = 15𝜋 0 0 0 Câu 61: Biết 𝐼 = 2 2 2 +( + ) +(4 + ) a xydydz x y dzdx x y dxdy = 
với mặt 𝑆 là biên của b S
miền 𝑉: 𝑥 + 𝑦 + 𝑧 ≤ 1, 𝑥 ≥ 0, 𝑦 ≥ 0, 𝑧 ≥ 0 hướng ra ngoài. Tìm khẳng định đúng
Đáp án: C. 𝑎 + 𝑏 = 7 61 Giải:
Mặt 𝑆 kín giới hạn miền 𝑉: 𝑥 + 𝑦 + 𝑧 ≤ 1, 𝑥 ≥ 0, 𝑦 ≥ 0, 𝑧 ≥ 0 0 ≤ 𝑥 ≤ 1
⇔ 𝑉: { 0 ≤ 𝑦 ≤ 1 − 𝑥 hướng ra ngoài.
0 ≤ 𝑧 ≤ 1 − 𝑥 − 𝑦 𝑃 = 2𝑥𝑦 𝑃′𝑥 = 2𝑦
Đặt {𝑄 = 𝑥 + 𝑦2 ⇒ {𝑄′𝑦 = 2𝑦 , 𝑃′ ′ ′
𝑥, 𝑄𝑦 , 𝑅𝑧 liên tục. 𝑅 = 4𝑥 + 𝑦2 𝑅′𝑧 = 0
Áp dụng công thức Ostrogradsky: 1 1−𝑥 1−𝑥−𝑦 1
𝐼 = ∭ 4𝑦𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝑥 ∫ 𝑑𝑦 ∫ 4𝑦𝑑𝑧 = ⋯ = 6 ⇒ 𝑎 = 1,𝑏 = 6 𝑉 0 0 0 Câu 62: Tính 𝐼 = 2 3 3 2
(xy + 2z )dydz + (z + 2 ) y dzdx + x zdxdy  với 𝑆 là nửa mặt S
cầu 𝑥2 + 𝑦2 + 𝑧2 = 1, 𝑧 ≥ 0 hướng ra ngoài mặt cầu. 8 Đáp án: A. 5 Giải:
Bổ sung thêm mặt 𝑆′: { 𝑧 = 0
𝑥2 + 𝑦2 ≤ 1 hướng xuống dưới
Mặt 𝑆 ∪ 𝑆′ là mặt cong kín, giới hạn miền 𝑉: {𝑥2 + 𝑦2 + 𝑧2 ≤ 1 hướng pháp tuyến 𝑧 ≥ 0 ngoài. 62 𝑃 = 𝑥𝑦2 + 2𝑧3 𝑃′𝑥 = 𝑦2
Đặt { 𝑄 = 𝑧3 + 2𝑦 ⇒ {𝑄 ′ ′ ′ ′
𝑦 = 2 , 𝑃𝑥, 𝑄𝑦 , 𝑅𝑧 liên tục 𝑅 = 𝑥2𝑧 𝑅′𝑧 = 𝑥2
𝐼 = ∯ 𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦 − ∬ 𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦 = 𝐼1 − 𝐼2 𝑆∪𝑆′ 𝑆
Áp dụng công thức Ostrogradsky cho 𝐼1
⇒ 𝐼1 = ∭(𝑥2 + 𝑦2 + 2)𝑑𝑥𝑑𝑦𝑑𝑧 = ∭(𝑥2 + 𝑦2)𝑑𝑥𝑑𝑦𝑑𝑧 + 2𝑉(𝑉) 𝑉 𝑉 𝑥 = 𝑟 sin 𝜃 cos 𝜑 0 ≤ 𝑟 ≤ 1
Đặt {𝑦 = 𝑟 sin 𝜃 sin 𝜑 |𝐽| = 𝑟2 sin 𝜃. Miền (𝑉): { 0 ≤ 𝜃 ≤ 𝜋 2 𝑧 = 𝑟 cos 𝜃 0 ≤ 𝜑 ≤ 2𝜋 𝜋 2𝜋 2 1 4
∭(𝑥2 + 𝑦2)𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝜃 ∫ 𝑟2(sin 𝜃)2.𝑟2 sin 𝜃 𝑑𝑟 = 15𝜋 𝑉 0 0 0 4 4 8
⇒ 𝐼1 = 15𝜋 + 3𝜋 = 5𝜋
Mặt 𝑆′: {𝑧 = 0 ⇒ 𝑑𝑧 = 0 𝜋 2 2
𝑥2 + 𝑦2 ≤ 1 , (𝑛󰇍 , 𝑂𝑧) > 2 , có hình chiếu lên 𝑂𝑥𝑦 l à𝐷: 𝑥 + 𝑦 ≤ 1 8
⇒ 𝐼2 = −∬ 𝑥2. 0𝑑𝑥𝑑𝑦 = 0 ⇒ 𝐼 = 𝐼1 − 𝐼2 = 5𝜋 𝐷 63 Câu 63: Tính 𝐼 = 3 2 2 (x +2 y )
z dydz + (3x y + )
y dzdx +(6 y z + x ) y dxdy  với 𝑆 là mặt S
𝑧 = 𝑥2 + 𝑦2 với 𝑧 ≤ 1, hướng xuống dưới. Đáp án: B. 0 Giải:
Bổ sung thêm mặt 𝑆′: { 𝑧 = 1
𝑥2 + 𝑦2 ≤ 1, hướng lên trên
Mặt 𝑆 ∪ 𝑆′ là mặt cong trơn kín, giới hạn miền 𝑉: 𝑥2 + 𝑦2 ≤ 𝑧 ≤ 1, hướng pháp tuyến ngoài 𝑃 = 𝑥3 + 2𝑦𝑧 𝑃′𝑥 = 3𝑥2
Đặt {𝑄 = 3𝑥2𝑦 + 𝑦 ⇒ {𝑄′ ′ ′ ′
𝑦 = 3𝑥2 + 1 , 𝑃𝑥, 𝑄𝑦 , 𝑅𝑧 liên tục 𝑅 = 6𝑦2𝑧 + 𝑥𝑦 𝑅′𝑧 = 6𝑦2
𝐼 = ∯ 𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦 − ∬ 𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦 = 𝐼1 − 𝐼2 𝑆∪𝑆′ 𝑆′
Áp dụng công thức Ostrogradsky cho 𝐼1
⇒ 𝐼1 = ∭(6𝑥2 + 6𝑦2 + 1)𝑑𝑥𝑑𝑦𝑑𝑧 𝑉 64
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 1 𝑥 = 𝑟 cos 𝜑 0 ≤ 𝑟 ≤ 1
Đặt {𝑦 = 𝑟 sin 𝜑 𝐽 = 𝑟. Miền 𝑉: {0 ≤ 𝜑 ≤ 2𝜋 𝑧 = 𝑧 𝑟2 ≤ 𝑧 ≤ 1 2𝜋 1 1 2𝜋 1 3𝜋 ⇒ 𝐼 2
1 = ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫(6𝑟2 + 1)𝑟𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑟(6𝑟2 + 1)(1 − 𝑟 )𝑑𝑟 = 2 0 0 𝑟2 0 0
Mặt 𝑆′: {𝑧 = 1 ⇒ 𝑑𝑧 = 0
𝑥2 + 𝑦2 ≤ 1 , (𝑛󰇍, 𝑂𝑧) < 𝜋/2.
Hình chiếu của 𝑆′ lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 1 2𝜋 1 sin 2𝜑 ⇒ 𝐼 2
2 = ∬(6𝑦2 + 𝑥𝑦)𝑑𝑥𝑑𝑦 = ∬(6𝑦2 + 𝑥𝑦)𝑑𝑥𝑑𝑦 = ∫ 𝑑𝜑 ∫ 𝑟 [6𝑟2(sin 𝜑) + 2 ] 𝑑𝑟 𝑆′ 𝐷 0 0 3𝜋 = 2
⇒ 𝐼 = 𝐼1 − 𝐼2 = 0 1 Câu 64: Tính
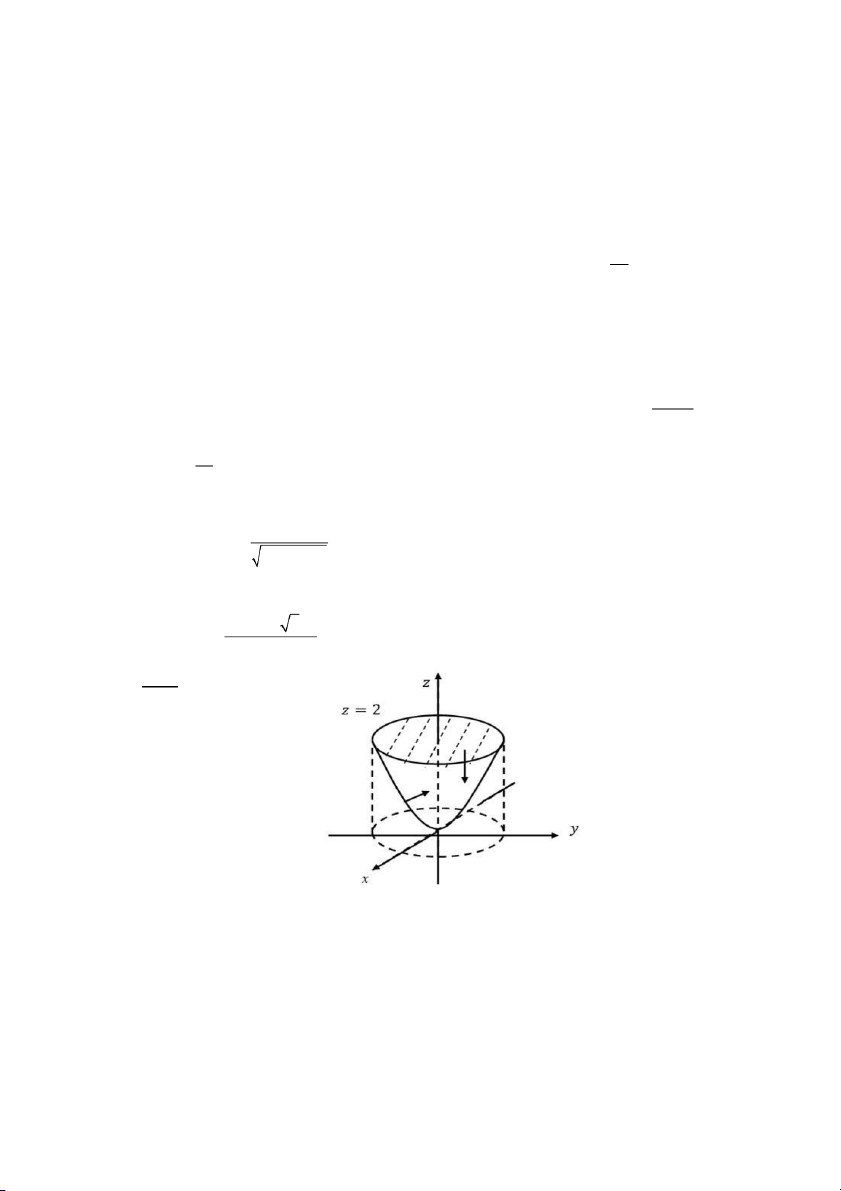
(−xdydz − ydzdx + dxdy) 
với 𝑆 là mặt 2𝑧 = 𝑥2 + 𝑦2, 2 2 + + S 1 x y
𝑧 ≤ 2 theo chiều âm của trục 𝑂𝑥 ( 2 − +10 5) Đáp án: C. 3 Giải: 65
Bổ sung thêm mặt 𝑆′: { 𝑧 = 2
𝑥2 + 𝑦2 ≤ 4, hướng lên xuống dưới
Mặt 𝑆 ∪ 𝑆′ là mặt cong trơn kín, giới hạn miền 𝑉: (𝑥2 + 𝑦2)/2 ≤ 𝑧 ≤ 2, hướng pháp tuyến trong −𝑥 𝑃 = −𝑦2 − 1 √𝑥2 + 𝑦2 + 1 𝑃′𝑥 = −𝑦
(𝑥2 + 𝑦2 + 1)√𝑥2 + 𝑦2 + 1 Đặt 𝑄 = ′ ′ ′ √𝑥2 + 𝑦2 + 1 ⇒ −𝑥2 − 1 , 𝑃 , 𝑄 , 𝑅 𝑄′ = 𝑥 𝑦 𝑧 1 𝑦
(𝑥2 + 𝑦2 + 1)√𝑥2 + 𝑦2 + 1 𝑅 = ′ { √𝑥2 + 𝑦2 + 1 { 𝑅𝑧 = 0
𝐼 = ∯ 𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦 − ∬ 𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦 = 𝐼1 − 𝐼2 𝑆∪𝑆′ 𝑆′
Áp dụng công thức Ostrogradsky cho 𝐼1 −𝑥2 − 𝑦2 − 2 ⇒ 𝐼1 = −∭ 𝑑𝑥𝑑𝑦𝑑𝑧
(𝑥2 + 𝑦2 + 1)√𝑥2 + 𝑦2 + 1 𝑉
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 4 𝑥 = 𝑟 cos 𝜑 0 ≤ 𝑟 ≤ 2
Đặt {𝑦 = 𝑟 sin 𝜑, 𝐽 = 𝑟 ⇒ 𝑉: { 0 ≤ 𝜑 ≤ 2𝜋 𝑧 = 𝑧 𝑟2/2 ≤ 𝑧 ≤ 2 2𝜋 2 2 −𝑟2 − 2
⇒ 𝐼1 = −∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ . 𝑟𝑑𝑧 (𝑟2 + 1)√𝑟2 + 1 0 0 𝑟2 2 2𝜋 2 (𝑟2 + 2)𝑟 = ∫ 𝑑𝜑 ∫ 𝑟2 . (2 − (𝑟2 + 1)√𝑟2 + 1 2 ) 𝑑𝑟 0 0 2 ( 2 𝑟2 + 2)𝑟 ( = 2𝜋 ∫ 𝑟2 𝑟2 + 2) 𝑟2 . (2 − = 𝜋 ∫ . (2 − (𝑟2 + 1)√𝑟2 + 1 2 ) 𝑑𝑟 (𝑟2 + 1)√𝑟2 + 1 2 ) 𝑑(𝑟2) 0 0 2 ( 2 𝑢 + 2) 𝜋 ( )( ) = 𝜋 ∫ 𝑢 𝑢 + 2 4 − 𝑢 . (2 − = 𝑑𝑢 (𝑢 + 1)√𝑢 + 1
2) 𝑑𝑢 2 ∫ (𝑢 + 1)√𝑢 + 1 0 0 66
Đặt √𝑢 + 1 = 𝑡 ⇒ 𝑢 + 1 = 𝑡2 ⇒ 𝑑𝑢 = 2𝑡𝑑𝑡 √5 𝜋 (𝑡2 + 1)(5 − 𝑡2) 𝜋 ⇒ 𝐼 8√5 8 4√5 4 1 = 2 ∫ 𝑡3
2𝑡𝑑𝑡 = 2( 3 + 3) = 𝜋( 3 + 3) 1
Mặt 𝑆′: {𝑧 = 2 ⇒ 𝑑𝑧 = 0
𝑥2 + 𝑦2 ≤ 4 , (𝑛󰇍, 𝑂𝑧) > 𝜋/2.
Hình chiếu của 𝑆′ lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 4 2𝜋 2 𝑑𝑥𝑑𝑦 −𝑑𝑥𝑑𝑦 𝑟𝑑𝑟 ⇒ 𝐼2 = ∬ = ∬ = − ∫ 𝑑𝜑 ∫ = ⋯ = −2𝜋(√5 − 1) √1 + 𝑥2 + 𝑦2 √1 + 𝑥2 + 𝑦2 √1 + 𝑟2 𝑆′ 𝐷 0 0 (−2 + 10 ⇒ 𝐼 = 𝐼 √5)𝜋 1 − 𝐼2 = 3 Câu 65: Biết a
xdydz + zdxdy =  
với 𝑆 là phần trên của mặt nón có phương b S
trình 𝑧 = −√𝑥2 + 𝑦2 , −1 ≤ 𝑧 ≤ 0 khi nhìn từ chiều dương trục 𝑂𝑧. Tính 2𝑎 + 𝑏 Đáp án: A. 1 Giải:
Bổ sung thêm mặt 𝑆′ : { 𝑧 = −1
𝑥2 + 𝑦2 ≤ 1 hướng xuống dưới
Mặt kín 𝑆 ∪ 𝑆′ giới hạn miền 𝑉: − 1 ≤ 𝑧 ≤ −√𝑥2 + 𝑦2 67 𝑃 = 𝑥 𝑃′𝑥 = 1
Đặt {𝑄 = 0 ⇒ {𝑄′𝑦 = 0 . 𝑃′ ′ ′
𝑥, 𝑄𝑦 , 𝑅𝑧 liên tục. 𝑅 = 𝑧 𝑅′𝑧 = 1
∬ 𝑥𝑑𝑦𝑑𝑧 + 𝑦𝑑𝑥𝑑𝑦 = ∯ 𝑥𝑑𝑦𝑑𝑧 + 𝑧𝑑𝑥𝑑𝑦 − ∬ 𝑥𝑑𝑦𝑑𝑧 + 𝑧𝑑𝑥𝑑𝑦 = 𝐼1 − 𝐼2 𝑆 𝑆∪𝑆′ 𝑆′
Áp dụng công thức Ostrogradsky cho 𝐼1 1 2𝜋
𝐼1 = ∭ 2𝑑𝑥𝑑𝑦𝑑𝑧 = 2𝑉(𝑉) = 2.3𝜋𝑅2.ℎ = 3 (Thể tích hình nón) 𝑉
Mặt 𝑆′: {𝑧 = −1 ⇒ 𝑑𝑧 = 0 2 2
𝑥2 + 𝑦2 ≤ 1 , (𝑛󰇍, 𝑂𝑧) > 𝜋/2 có hình chiếu lên 𝑂𝑥𝑦 là 𝐷: 𝑥 + 𝑦 ≤ 1
𝐼2 = −∬ −1𝑑𝑥𝑑𝑦 = ∬ 𝑑𝑥𝑑𝑦 = 𝑆(𝐷) = 𝜋𝑅2 = 𝜋 𝐷 𝐷 2𝜋 ⇒ 𝐼 = 𝐼 −𝜋
1 − 𝐼2 = 3 − 𝜋 = 3 ⇒ 𝑎 = −1, 𝑏 = 3 Câu 66: Tính + 2 2
zdz dọc theo đường tròn 𝐶: 𝑥 + 𝑦 = 1, 𝑧 = 0
chiều dương giới hạn mặt cầu 𝑧 = √1 − 𝑥2 − 𝑦2 − Đáp án: D. 8 Giải:
Đường cong 𝐶 giới hạn phần mặt cầu 𝑆: 𝑧 = √1 − 𝑥2 − 𝑦2 hướng lên trên 68
Áp dụng công thức Stoke:
∮ 𝑥2𝑦3𝑑𝑥 + 𝑑𝑦 + 𝑧𝑑𝑧 = ∬ −3𝑥2𝑦2𝑑𝑥𝑑𝑦 𝐶 𝑆
Hình chiếu của mặt 𝑆 lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 1 𝑥 = 𝑟 cos 𝜑
Đặt {𝑦 = sin𝜑,𝐽 = 𝑟 ⇒ 𝐷: { 0 ≤ 𝑟 ≤ 1 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 1 −𝜋
⇒ ∬ −3𝑥2𝑦2𝑑𝑥𝑑𝑦 = −3 ∫ 𝑑𝜑 ∫ 𝑟2sin2 𝜑 𝑟2cos2 𝜑 . 𝑟𝑑𝑟 = ⋯ = 8 𝑆 0 0 1
Câu 67: Tính tích phân 𝐼 = ( 2
− xdydz−2 ydzdx+ dxd ) y  với 𝑆 là 2 2 + + S 1 4x 4y
mặt có phương trình 𝑧 = 𝑥2 + 𝑦2, 0 ≤ 𝑧 ≤ 4 theo chiều 𝑧 ≥ 0 (17 17 −1) Đáp án: B. 6 Giải:
Đặt 𝐹(𝑥, 𝑦, 𝑧) = 𝑧 − 𝑥2 − 𝑦2
Do (𝑛󰇍, 𝑂𝑧) <
 𝜋/2 nên 𝑛󰇍= (𝐹′ ′ ′
𝑥, 𝐹𝑦, 𝐹𝑧 ) = (−2𝑥, −2𝑦, 1) ⇒ |𝑛󰇍| = √1 + 4𝑥2 + 4𝑦2 −2𝑥 −2𝑦 1 ⇒ cos 𝛼 = , cos 𝛽 = , cos 𝛾 = √1 + 4𝑥2 + 4𝑦2 √1 + 4𝑥2 + 4𝑦2 √1 + 4𝑥2 + 4𝑦2
Áp dụng công thức liên hệ giữa tích phân mặt loại I và loại II
𝐼 = ∬(𝑃. cos 𝛼 + 𝑄. cos 𝛽 + 𝑅. cos 𝛾)𝑑𝑆 = ⋯ = ∬ 1. 𝑑𝑆 𝑆 𝑆 69
Mặt 𝑆: 𝑧 = 𝑥2 + 𝑦2 ⇒ 𝑧′ ′ 2 2
𝑥 = 2𝑥, 𝑧𝑦 = 2𝑦 ⇒ 𝑑𝑆 = √1 + 4𝑥 + 4𝑦 𝑑𝑥𝑑𝑦
Hình chiếu của 𝑆 lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 4
⇒ 𝐼 = ∬ √1 + 4𝑥2 + 4𝑦2𝑑𝑥𝑑𝑦 𝐷 𝑥 = 𝑟 cos 𝜑
Đặt {𝑦 = 𝑟sin𝜑 ,𝐽 = 𝑟 ⇒ 𝐷: { 0 ≤ 𝑟 ≤ 2 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 2 2 4 2𝜋
⇒ 𝐼 = ∫ 𝑑𝜑 ∫ √1 + 4𝑟2. 𝑟𝑑𝑟 = 2 ∫√1 +4𝑟2𝑑(𝑟2) = 𝜋∫√1+ 4𝑢𝑑𝑢 0 0 0 0 (17√17 − 1)𝜋 = 6
Câu 68: Tính tích phân 𝐼 = 3 3
(6z −9y)dydz + (3x − 2z )dzdx +(3y −3x)dxdy  với S
𝑆 là mặt 𝑥2 + 3𝑦2 + 𝑧4 = 1, 𝑧 ≥ 0, hướng lên trên. Đáp án: C. 0 Giải:
Đặt 𝐹(𝑥, 𝑦, 𝑧) = 𝑥2 + 3𝑦2 + 𝑧4 − 1 C. 0
Vecto pháp tuyến 𝑛󰇍 = (𝐹′ ′ ′ 
𝑥, 𝐹𝑦, 𝐹𝑧) = (2𝑥, 6𝑦, 4𝑧3) (do (𝑛󰇍, 𝑂𝑧) < 𝜋/2)
|𝑛󰇍| = √4𝑥2 + 36𝑦2 + 16𝑧6 = 2√𝑥2 + 9𝑦2 + 4𝑧6 𝑛 𝑥 cos 𝛼 = 𝑥
|𝑛󰇍| = √𝑥2 + 4𝑦2 + 4𝑧6 𝑛𝑦 3𝑦
⇒ cos 𝛽 = |𝑛󰇍| = √𝑥2 + 9𝑦2 + 4𝑧6 𝑛 2𝑧3 cos 𝛾 = 𝑧 {
|𝑛󰇍| = √𝑥2 + 9𝑦2 + 4𝑧6
Áp dụng công thức liên hệ giữa tích phân mặt loại I và loại II
∬ 𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦 = ∬(𝑃.cos 𝛼 + 𝑄. cos 𝛽 + 𝑅.cos 𝛾)𝑑𝑆 𝑆 𝑆 70
𝑥(6𝑧3 − 9𝑦) + 3𝑦(3𝑥 − 2𝑧3) + 2𝑧3(3𝑦 − 3𝑥) ⇒ 𝐼 = ∬ 𝑑𝑆 = 0 √𝑥2 + 9𝑦2 + 4𝑧6 𝑆 Câu 69: Tính 2 (2x + x )
y dydz +( y + 2x )
z dzdx + (1+ 6z + z )dxdy  với 𝑆 là mặt nằm S
trong của nửa cầu 𝑧 = −√16 − (𝑥2 + 𝑦2 + 𝑧2)
Đáp án: B. (80 − 192√2)𝜋 Giải:
Bổ sung thêm mặt 𝑆′: { 𝑧 = 0
𝑥2 + 𝑦2 ≤ 16 hướng theo chiều âm trục 𝑂𝑧.
Mặt 𝑆 ∪ 𝑆′ tạo thành mặt cong kín, hướng pháp tuyến trong giới hạn miền
𝑉: −√16 − 𝑥2 − 𝑦2 2 ≤ 𝑧 ≤ 0 Đặt 𝐼 = 2
(2x + xy)dydz + (y + 2xz)dzdx + (1+ 6z + z )dxdy  S 𝑃 = 2𝑥 + 𝑥𝑦 𝑃′𝑥 = 2 + 𝑦
Đặt { 𝑄 = 𝑦 + 2𝑥𝑧 ⇒ { 𝑄′𝑦 = 1 liên tục 𝑅 = 1 + 6𝑧 + 𝑧2 𝑅′𝑧 = 6 + 2𝑧
𝐼 = ∯ 𝑃𝑑𝑦𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦 − ∬ 𝑃𝑑𝑦𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦 = 𝐼1 − 𝐼2 𝑆∪𝑆′ 𝑆′
Áp dụng công thức Ostrgradsky cho tích phân 𝐼1
𝐼1 = − ∭(2 + 𝑦 + 1 + 6 + 2𝑧)𝑑𝑥𝑑𝑦𝑑𝑧 = − ∭(9 + 𝑦 + 2𝑧)𝑑𝑥𝑑𝑦𝑑𝑧 𝑉 𝑉
Do 𝑓(𝑥, 𝑦, 𝑧) = 𝑦 là hàm lẻ với biến 𝑦, miền 𝑉 đối xứng qua 𝑂𝑥𝑧
⇒ ∭ 𝑦𝑑𝑥𝑑𝑦𝑑𝑧 = 0 ⇒ 𝐼1 = −∭(9 + 2𝑧)𝑑𝑥𝑑𝑦𝑑𝑧 𝑉 𝑉
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 16 𝑥 = 𝑟 cos 𝜑 0 ≤ 𝑟 ≤ 4
Đặt {𝑦 = 𝑟 sin 𝜑, 𝐽 = 𝑟 ⇒ 𝑉: { 0 ≤ 𝜑 ≤ 2𝜋 𝑧 = 𝑧
−√(16 − 𝑟2)/2 ≤ 𝑧 ≤ 0 71 2𝜋 4 0
𝐼2 = −∫ 𝑑𝜑 ∫ 𝑑𝑟
∫ (9 + 2𝑧)= ⋯ = −192√2𝜋 + 64𝜋 0 0 −√(16−𝑟2) 2 Xét tích phân 𝐼2
Mặtn 𝑆′: {𝑧 = 0 ⇒ 𝑑𝑧 = 0
𝑥2 + 𝑦2 ≤ 16 hướng theo chiều âm trục 𝑂𝑧, (𝑛󰇍, 𝑂𝑧) > 𝜋, 2 có hình
chiếu lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 16
⇒ 𝐼2 = −∬ 1𝑑𝑥𝑑𝑦 = −16𝜋 𝐷
⇒ 𝐼 = 𝐼1 − 𝐼2 = (80 − 192√2)𝜋
Câu 70: Tính xydydz + yzdzdx + zxdxdy 
biết 𝑆 là mặt ngoài của tứ diện 𝑂𝐴𝐵𝐶 với S
𝑂(0,0,0), 𝐴(1,0,0), 𝐵(0,1,0), 𝐶(0,0,1) 1 Đáp án: B. 8 Giải: 0 ≤ 𝑥 ≤ 1
𝑆 là mặt giới hạn miền kín 𝑉:{ 0 ≤ 𝑦 ≤ 1 − 𝑥 ,vecto pháp tuyến hướng ra ngoài.
0 ≤ 𝑧 ≤ 1 − 𝑥 − 𝑦 𝑃 = 𝑥𝑦 𝑃′𝑥 = 𝑦
Đặt {𝑄 = 𝑦𝑧 ⇒ {𝑄′𝑦 = 𝑧 liên tục 𝑅 = 𝑧𝑥 𝑅′𝑧 = 𝑥
Áp dụng công thức Ostrogradsky
∬ 𝑥𝑦𝑑𝑦𝑑𝑧 + 𝑦𝑧𝑑𝑧𝑑𝑥 + 𝑧𝑥𝑑𝑥𝑑𝑦 = ∭(𝑥 + 𝑦 + 𝑧)𝑑𝑥𝑑𝑦𝑑𝑧 𝑆 𝑉 1 1−𝑥 1−𝑥−𝑦 1
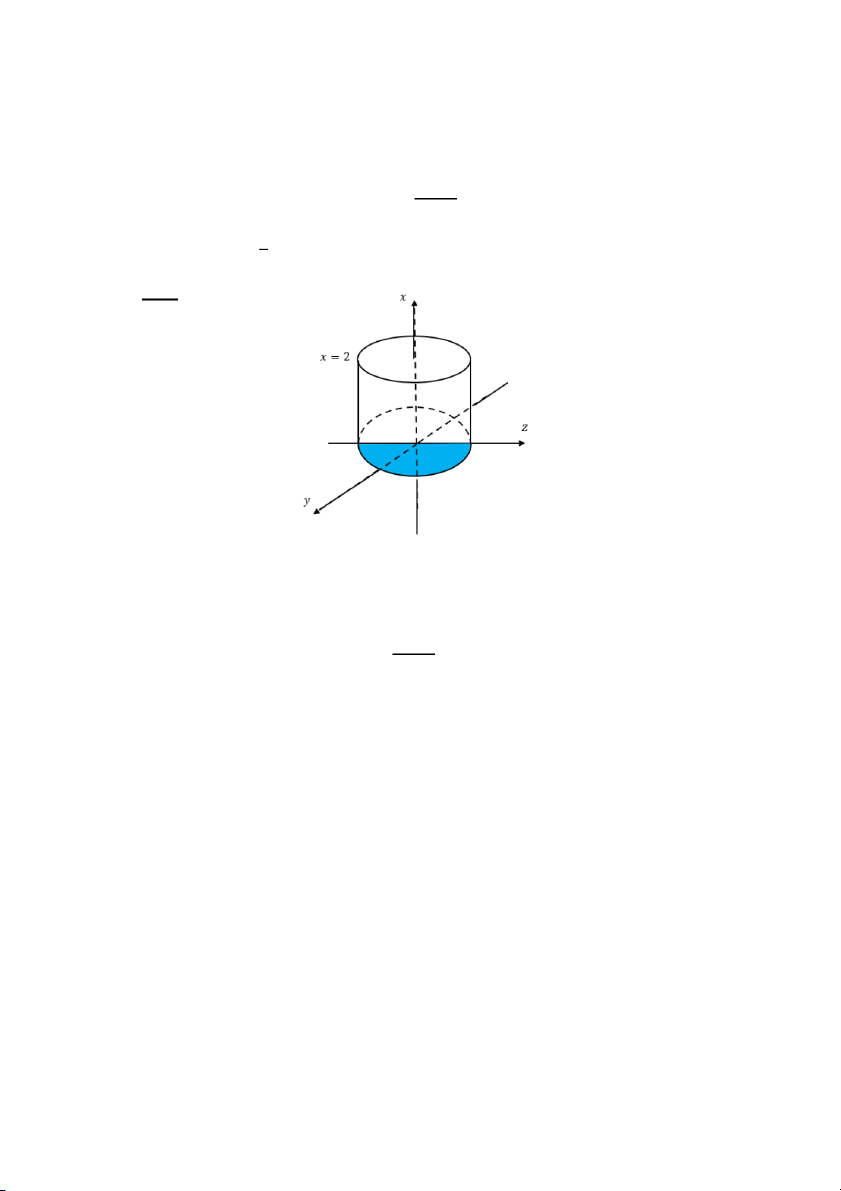
= ∫ 𝑑𝑥 ∫ 𝑑𝑦 ∫ (𝑥 + 𝑦 + 𝑧)𝑑𝑧 = 8 0 0 0 Câu 71: Biết 2 2 2
2x dydz + y dzdx − z dxdy = a + b 
, chọn khẳng định đúng S
Đáp án: A. 𝑎 + 3𝑏 = 12 Giải: 72
Mặt 𝑆 kín giới hạn miển 𝑉: 0 ≤ 𝑦 ≤ √1 − 𝑧2, 0 ≤ 𝑥 ≤ 2, hướng pháp tuyến ngoài
Đặt 𝑃 = 2𝑥2, 𝑄 = 𝑦2, 𝑅 = −𝑧2 ⇒ 𝑃′ ′ ′
𝑥 = 4𝑥, 𝑄𝑦 = 2𝑦, 𝑅𝑧 = −2𝑧 liên tục.
Áp dụng công thức Ostrogradsky:
𝐼 = ∬ 2𝑥2𝑑𝑦𝑑𝑧 + 𝑦2𝑑𝑧𝑑𝑧 − 𝑧2𝑑𝑥𝑑𝑦 = ∭(4𝑥 + 2𝑦 − 2𝑧)𝑑𝑥𝑑𝑦𝑑𝑧 𝑆 𝑉 𝑦 = 𝑟 cos 𝜑 0 ≤ 𝑟 ≤ 1
Đặt {𝑧 = 𝑟 sin 𝜑, 𝐽 = 𝑟 ⇒ Miền 𝑉: { −𝜋/2 ≤ 𝜑 ≤ 𝜋/2 𝑥 = 𝑥 0 ≤ 𝑥 ≤ 2 𝜋 𝜋 2 1 2 2 1 8
𝐼 = 2 ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫(2𝑥 + 𝑟 cos 𝜑). 𝑟𝑑𝑥= 2 ∫ 𝑑𝜑 ∫(4𝑟 + 2𝑟2 cos 𝜑)𝑑𝑟 = 4𝜋 + 3 −𝜋 0 0 −𝜋 0 2 2 8 ⇒ 𝑎 = 4, 𝑏 = 3 Câu 72: Biết = ( + ) + ( + ) + ( + ) a I x z dydz y x dzdx z y dxdy =   với 𝑆 là mặt trong b S
của parabol 𝑧 = 𝑥2 + 𝑦2 nằm dưới mặt 𝑥 + 𝑧 = 2 . Tí nh 𝑎 − 𝑏 Đáp án: B. 49 Giải:
Bổ sung thêm mặt 𝑆′: 𝑥 + 𝑧 = 2 hướng theo chiều âm trục 𝑂𝑧 nằm trong mặt parabol 𝑧 = 𝑥2 + 𝑦2
Ta có mặt 𝑆 ∪ 𝑆′ là mặt kín, hướng pháp tuyến trong, giới hạn miền
𝑉: 𝑥2 + 𝑦2 ≤ 𝑧 ≤ 2 − 𝑥 𝑃 = 𝑥 + 𝑧 𝑃′𝑥 = 1
Đặt {𝑄 = 𝑦 + 𝑥 ⇒ {𝑄′𝑦 = 1 liên tục 𝑅 = 𝑧 + 𝑦 𝑅′𝑧 = 1
𝐼 = ∯ 𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦 − ∬ 𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦 = 𝐼1 − 𝐼2 𝑆∪𝑆′ 𝑆
Áp dụng công thức Ostrogradsky cho tích phân 𝐼1 73
𝐼1 = − ∭ 3𝑑𝑥𝑑𝑦𝑑𝑧 𝑉
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là 𝐷: (𝑥 + 1/2)2 + 𝑦2 = 9/4 2−𝑥 ⇒ 𝐼 2 1 = −3 ∬ 𝑑𝑥𝑑𝑦
∫ 𝑑𝑧 = −3 ∬(2 − 𝑥 − 𝑥 − 𝑦2)𝑑𝑥𝑑𝑦 𝐷 𝑥2+𝑦2 𝐷 1 2 9
= 3 ∬(−2 + 𝑥 + 𝑥2 + 𝑦2)𝑑𝑥𝑑𝑦 = 3 ∬ [(𝑥 +
2) + 𝑦2 − 4] 𝑑𝑥𝑑𝑦 𝐷 𝐷
Đặt {𝑥 = −1/2 + 𝑟 cos 𝜑 𝑦 = 𝑟 sin 𝜑
, 𝐽 = 𝑟 ⇒ 𝐷: {0 ≤ 𝑟 ≤ 3/2 0 ≤ 𝜑 ≤ 2𝜋 3 2𝜋 2 𝐼 9 −243𝜋
1 = 3 ∫ 𝑑𝜑 ∫ (𝑟2 − 4). 𝑟𝑑𝑟 = ⋯ = 32 0 0 Xét tích phân 𝐼2
Mặt 𝑆′: 𝑥 + 𝑧 = 2 hướng theo chiều âm trục 𝑂𝑧 có hình chiếu lên 𝑂𝑥𝑦 là
𝐷: (𝑥 + 1/2)2 + 𝑦2 = 9/4, vecto pháp tuyến 𝑛󰇍 = (−1,0, −1), |𝑛󰇍| = 1/√2
Áp dụng công thức liên hệ giữa tích phân mặt loại I và loại II 1 𝐼 −1 2 =
∬[−1. (𝑥 + 𝑧) + 0. (𝑦 + 𝑥) − 1. (𝑧 + 𝑦)]𝑑𝑆=
∬(𝑥 + 𝑦 + 2𝑧)𝑑𝑆 √2 √2 𝑆′ 𝑆′
Với 𝑆′: 𝑧 = 2 − 𝑥 ⇒ 𝑑𝑆 = √1 + (𝑧𝑥′)2 + (𝑧𝑦′)2𝑑𝑥𝑑𝑦 = √2𝑑𝑥𝑑𝑦
⇒ 𝐼2 = −∬(𝑥 + 𝑦 + 4 − 2𝑥) 𝑑𝑥𝑑𝑦 = ∬(𝑥 − 𝑦 − 4) 𝑑𝑥𝑑𝑦 𝐷 𝐷 3 2𝜋 2 1 −81𝜋
= ∫ 𝑑𝜑 ∫ (− 2 + 𝑟cos𝜑 − 𝑟sin𝜑 −4).𝑟𝑑𝑟 = ⋯ = 8 0 0 74 81𝜋
𝐼 = 𝐼1 − 𝐼2 = 32⇒ 𝑎 = 81,𝑏 = 32
Câu 73: Tính diện tích mặt 𝑆: 𝑧 = 2 + √𝑥2 + 𝑦2 , 𝑧 ≤ 3
Đáp án: C. √2 𝜋 (đvdt) Giải:
Mặt 𝑧 = 2 + √𝑥2 + 𝑦2 ⇒ 𝑑𝑆 = √1 + (𝑧𝑥′)2 + (𝑧𝑦′)2𝑑𝑥𝑑𝑦 = √2𝑑𝑥𝑑𝑦
Hình chiếu của 𝑆 lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 1 Diện tích mặt 𝑆 là:
𝑆(𝑆) = ∬ 𝑑𝑆 = √2 ∬ 𝑑𝑥𝑑𝑦 = √2.𝑆(𝐷) = √2𝜋 𝑆 𝐷
Câu 74: Tính diện tích mặt cong 𝑆 với 𝑆 là phần mặt nón 𝑦 = √𝑥2 + 𝑧2 với điều
kiện 1 ≤ 𝑦 ≤ 2, 𝑧 ≥ 0 3 2 Đáp án: A. (đvdt) 2 Giải: 75 𝑥 𝑦′𝑥 = √𝑥2 +𝑦2
Mặt 𝑆: 𝑦 = √𝑥2 + 𝑧2 ⇒ 𝑧
⇒ 𝑑𝑆 = √1 + (𝑦𝑥′)2 + (𝑦𝑧′)2𝑑𝑥𝑑𝑧 = √2𝑑𝑥𝑑𝑧 𝑦′𝑧 = { √𝑥2 + 𝑦2
Hình chiếu của 𝑆 lên 𝑂𝑥𝑧 là 𝐷: 1 ≤ 𝑥2 + 𝑧2 ≤ 4 𝑧 = 𝑟 cos 𝜑
Đặt {𝑥 = 𝑟 sin𝜑 ,𝐽 = 𝑟 ⇒ 𝐷: { 1 ≤ 𝑟 ≤ 2 −𝜋/2 ≤ 𝜑 ≤ 𝜋/2
Diện tích mặt cong 𝑆 là: 𝜋 2 2 3 𝑆 √2
(𝑆) = ∬ 𝑑𝑆 = √2 ∬ 𝑑𝑥𝑑𝑧 = √2 ∫ 𝑑𝜑 ∫ 𝑟𝑑𝑟 = 2 𝜋 (đvdt) 𝑆 𝐷 −𝜋 1 2
Câu 75: Tính diện tích mặt paraboloid 𝑧 = 4𝑥 − 𝑥2 − 𝑦2 nằm phía trên mặt 𝑂𝑥𝑦 là
(a 17 −1) , tính 𝑎 + 𝑏 b
Đáp án: B. 23 Giải: ′ = 4 − 2𝑥
Mặt 𝑧 = 4𝑥 − 𝑥2 − 𝑦2 ⇒ {𝑧𝑥𝑧′𝑦 = −2𝑦
Hình chiếu của mặt 𝑆 lên 𝑂𝑥𝑦 là 𝐷: (𝑥 − 2)2 + 𝑦2 ≤ 4 Diện tích mặt
𝑆 = ∬ 𝑑𝑆 = ∬ √1 + (𝑧𝑥′)2 + (𝑧𝑦′)2𝑑𝑥𝑑𝑦 = ∬ √1 + 4(𝑥 − 2)2 + 4𝑦2𝑑𝑥𝑑𝑦 𝑆 𝐷 𝐷
Đặt {𝑥 = 2 + 𝑟 cos 𝜑
𝑦 = 𝑟 sin 𝜑 , 𝐽 = 𝑟 ⇒ 𝐷: { 0 ≤ 𝑟 ≤ 2 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 2
𝑆 = ∫ 𝑑𝜑∫ 𝑟. √1 + 4𝑟2𝑑𝑟 (17√17 − 1)𝜋 = 6 ⇒ 𝑎 = 17, 𝑏 = 6 0 0
Câu 76: Tính diện tích phần mặt paraboloid 𝑥 = 𝑦2 + 𝑧2 thỏa mãn 𝑥 ≤ 1 76 
Đáp số: A. (5 5 −1) 6 Giải: 𝑥′ = 2𝑦
Mặt 𝑥 = 𝑦2 + 𝑧2 ⇒ { 𝑦 𝑥′𝑧 = 2𝑧
Hình chiếu của mặt 𝑆 lên 𝑂𝑦𝑧 là 𝐷: 𝑦2 + 𝑧2 ≤ 1 Diện tích mặt
𝑆 = ∬ 𝑑𝑆 = ∬ √1 + (𝑥𝑦′ )2 + (𝑥𝑧′)2𝑑𝑦𝑑𝑧 = ∬ √1 + 4𝑦2 + 4𝑧2𝑑𝑦𝑑𝑧 𝑆 𝐷 𝐷 𝑦 = 𝑟 cos 𝜑
Đặt {𝑧 = 𝑟 sin𝜑 ,𝐽 = 𝑟 ⇒ 𝐷:{ 0 ≤ 𝑟 ≤ 1 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 1 (5 ) 𝑆 = ∫ 𝑑𝜑∫ √5 − 1 𝜋 𝑟. √1 + 4𝑟2𝑑𝑟 = 6 0 0
Câu 77: Tính diện tích mặt 𝑆: 𝑧 = √𝑥2 + 𝑦2 , 𝑧 ≤ 3 Đáp án: Giải:
Mặt 𝑧 = √𝑥2 + 𝑦2 ⇒ 𝑑𝑆 = √1 + (𝑧𝑥′)2 + (𝑧𝑦′)2𝑑𝑥𝑑𝑦 = √2𝑑𝑥𝑑𝑦
Hình chiếu của 𝑆 lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 9. Diện tích mặt 𝑆 là:
𝑆(𝑆) = ∬ 𝑑𝑆 = √2 ∬ 𝑑𝑥𝑑𝑦 = √2. 𝑆(𝐷) = 9√2𝜋 𝑆 𝐷
Lý thuyết trường:
Câu 78: Tính đạo hàm theo hướng 𝑙 = (1,2, −2) của 𝑢 = 𝑒𝑥(𝑦2 + 𝑧) − 2𝑥𝑦𝑧3 tại 𝐴(0,1,2) −11 Đáp án: B. 3 77 Giải: 𝑢′ 3 ′
𝑥 = 𝑒𝑥(𝑦2 + 𝑧) − 2𝑦𝑧 𝑢𝑥(𝐴) = −13
Ta có: 𝑢 = 𝑒𝑥(𝑦2 + 𝑧) − 2𝑥𝑦𝑧3 ⇒ { 𝑢′ ′
𝑦 = 2𝑒𝑥𝑦 − 2𝑥𝑧3 ⇒ { 𝑢𝑦(𝐴) = 2 𝑢′ ′
𝑧 = 𝑒𝑥 − 6𝑥𝑦𝑧2 𝑢𝑧(𝐴) = 1 2 −2 𝑙 = (1,2, −2) 1
⇒ cos 𝛼 = 3,cos𝛽 = 3,cos𝛾 = 3 𝜕𝑢 1 2 −2 −11 ⇒ (𝐴) = (−13). 𝜕𝑙 3 + 2. 3 + 1. 3 = 3 
Câu 79: Cho 𝑢(𝑥, 𝑦, 𝑧) = 𝑥3 + 3𝑦𝑥2 + 2𝑦𝑧2. Tính u
với 𝑛󰇍 là vecto pháp tuyến n
hướng ra ngoài của mặt cầu 𝑥2 + 𝑦2 + 𝑧2 = 3, 𝑧 ≤ 0 tại điểm 𝐴(1,1, −1) Đáp án: A. −6√3 Giải:
Xét 𝐹(𝑥, 𝑦, 𝑧) = 𝑥2 + 𝑦2 + 𝑧2 − 3
⇒ Vecto pháp tuyến hướng ra ngoài của nửa cầu 𝑥2 + 𝑦2 + 𝑧2 = 3 phía dưới 𝑂𝑥𝑦
tại 𝐴(1,1, −1) là 𝑛󰇍 = − (𝐹′ ′ ′
𝑥(𝐴), 𝐹𝑦(𝐴), 𝐹𝑧(𝐴)) = −(2,2, −2) = (−2, −2,2) 𝑢′ ′ 𝑥 = 3𝑥2 + 6𝑦𝑥 𝑢𝑥 (𝐴) = 9
𝑢(𝑥, 𝑦, 𝑧) = 𝑥3 + 3𝑦𝑥2 + 2𝑦𝑧2 ⇒ {𝑢′ ′
𝑦 = 3𝑥2 + 2𝑧2⇒ { 𝑢𝑦(𝐴) = 5 𝑢′ ′ 𝑧 = 4𝑦𝑧 𝑢𝑧(𝐴) = −4 −1 −1 1
𝑛󰇍 = (−2, −2,2) ⇒ |𝑛󰇍| = 2√3 ⇒ cos 𝛼 = , cos 𝛽 = , cos 𝛾 = √3 √3 √3 𝜕𝑢 −1 ⇒ −1 𝜕𝑛󰇍(𝐴) = 9. + 5. + (−4) 1 = −6√3 √3 √3 √3
Câu 80: Biết nhiệt độ tại điểm (𝑥, 𝑦, 𝑧) trong không gian được cho bởi hàm 80
𝑇(𝑥, 𝑦, 𝑧) = 1+ 𝑥2 +2𝑦2 + 3𝑧2
ở đó 𝑇 có đơn vị là ℃ và 𝑥, 𝑦, 𝑧 là mét. Theo hướng nào thì nhiệt độ tăng nhanh
nhất tại điểm 𝐴(1,1, −2) 78  5 − 5 − 15  Đáp án: C.  ; ;   8 4 4  Giải:
Xét vecto 𝑙, đạo hàm của 𝑇 theo hướng 𝑙 tại 𝐴(1,1, −2) là:
𝜕𝑇 (𝐴) = 𝑔󰇍𝑟𝑎𝑑 󰇍󰇍󰇍 󰇍 𝑙 𝑢(𝐴). 𝜕𝑙 |𝑙|
Để nhiệt độ tăng nhanh nhất ⇔ T lớn nhất l
⇔ 𝑙 ⇈ 𝑔󰇍󰇍𝑟𝑎𝑑
󰇍󰇍󰇍󰇍 𝑢(𝐴) ⇔ 𝑙 = 𝑔󰇍𝑟𝑎𝑑
󰇍󰇍󰇍 󰇍 𝑢(𝐴) −160𝑥 𝑔󰇍𝑟𝑎𝑑 󰇍 󰇍 󰇍  −320𝑦 −480𝑧
𝑢 = ((1+ 𝑥2 +2𝑦2 + 3𝑧2)2,(1+ 𝑥2 +2𝑦2 + 3𝑧2)2, (1+ 𝑥2 +2𝑦2 + 3𝑧2)2) −5 −5 15 −5 −5 15 ⇒ 𝑔󰇍𝑟𝑎𝑑
󰇍 󰇍󰇍𝑢(𝐴) = ( 8 , 4 , 4 ) ⇒ 𝑙= ( 8 , 4 , 4 ) −5 −5 15
Vậy theo nhiệt độ tăng nhanh n ấ
h t theo hướn g𝑙 = ( 8 , 4 , 4 )
Câu 81: Tính góc giữa hai vecto 𝑔󰇍𝑟𝑎𝑑
󰇍󰇍󰇍󰇍𝑧 (đơn vị: radian) của các trường vô hướng
sau 𝑧1 = √𝑥2 + 𝑦2, 𝑧2 = 𝑥 − 3𝑦 + √3𝑥𝑦 tại 𝑀(3,4) (Chọn đáp án gần đúng nhất) Đáp án: A. 2 Giải: 𝑥 𝑧′1𝑥 = √𝑥2 +𝑦2 𝑥 𝑦 𝑧1 = √𝑥2 + 𝑦2 ⇒ ⇒ 𝑔𝑟𝑎𝑑
󰇍󰇍󰇍󰇍󰇍𝑧1 = ( , ) 𝑧′ 𝑦 √𝑥2 + 𝑦2 √ 1𝑦 = 𝑥2 + 𝑦2 { √𝑥2 + 𝑦2 3 4 ⇒ 𝑔󰇍𝑟𝑎𝑑
󰇍 󰇍󰇍𝑧1(𝑀) = (5,5) √3𝑦 𝑧′2𝑥 = 1 + √3𝑦 𝑧 2√𝑥 󰇍󰇍󰇍󰇍 󰇍
2 = 𝑥 − 3𝑦 + √3𝑥𝑦 ⇒ , −3 + √3𝑥
√3𝑥 ⇒ 𝑔𝑟𝑎𝑑 𝑧2 = (1 + ) 𝑧′ = −3 + 2√𝑥 2√𝑦 { 2𝑦 2√𝑦 79 −9 ⇒ 𝑔󰇍𝑟𝑎𝑑
󰇍 󰇍󰇍𝑧2(𝑀) = (2, 5 ) 𝑔󰇍𝑟𝑎𝑑 󰇍 󰇍󰇍󰇍 𝑧 󰇍󰇍󰇍 󰇍󰇍 𝑧 −12 ⇒ cos (𝑔󰇍𝑟𝑎𝑑 󰇍󰇍󰇍󰇍𝑧 󰇍󰇍󰇍󰇍󰇍
1(𝑀). 𝑔𝑟𝑎𝑑 2(𝑀)
1(𝑀), 𝑔𝑟𝑎𝑑𝑧2(𝑀)) = = |𝑔󰇍𝑟𝑎𝑑 󰇍󰇍󰇍󰇍𝑧 󰇍󰇍󰇍󰇍 󰇍
1(𝑀)|. |𝑔𝑟𝑎𝑑𝑧2(𝑀)| 5√145 ⇒ (𝑔󰇍󰇍𝑟𝑎𝑑
󰇍󰇍󰇍󰇍 𝑧1,𝑔󰇍𝑟𝑎𝑑
󰇍󰇍󰇍󰇍𝑧2) ≈ 1,77 (radian)
Câu 82: Cho 𝑢(𝑥, 𝑦, 𝑧) = l (
n 1 + 𝑥2 + 𝑒𝑦−𝑧) , 𝑂(0,0,0), 𝐴(1, −2,2). Tính u  theo l  hướng 𝑂 󰇍󰇍𝐴 󰇍 −2 Đáp án: B. 3 Giải: 2𝑥 𝑢′ ′ 𝑥 = (𝑂) = 0 1 + 𝑥2 + 𝑒𝑦−𝑧 𝑢𝑥 ′ 1
𝑢(𝑥, 𝑦, 𝑧) = ln(1 + 𝑥2 + 𝑒𝑦−𝑧) ⇒ 𝑒𝑦−𝑧 𝑢′ 𝑢𝑦(𝑂) = 𝑦 = ⇒ 1 + 𝑥 2 + 𝑒𝑦−𝑧 2 ′ −1 ′ −𝑒𝑦−𝑧 𝑢𝑧(𝐴) = {𝑢𝑧 = { 1 + 𝑥2 + 𝑒𝑦−𝑧 2 1 𝑂󰇍𝐴 󰇍  −2 2
= (1, −2,2) ⇒ |𝑂󰇍󰇍𝐴
󰇍| = 3 ⇒ cos 𝛼 = 3,cos𝛽 = 3 ,cos𝛾 = 3 𝜕𝑢 1 1 −2 1 2 −2 ⇒ (𝑂) = 0. 𝜕𝑂󰇍𝐴 󰇍
3 + 2 . 3 − 2 . 3 = 3
Câu 83: Theo hướng nào thì sự biến thiên của hàm 𝑢 = 𝑥 sin 𝑧 − 𝑦 cos 𝑧 tại gốc tọa độ là lớn nhất
Đáp án: B. 𝑙 = (0, −1,0) Giải: 𝑢′𝑥= sin 𝑧
𝑢(𝑥, 𝑦, 𝑧) = 𝑥 sin 𝑧 − 𝑦 cos 𝑧 ⇒ { 𝑢′𝑦 = − cos 𝑧
𝑢′𝑧 = 𝑥 cos 𝑧 + 𝑦 sin 𝑧 ⇒ 𝑔󰇍𝑟𝑎𝑑
󰇍 󰇍󰇍𝑢 = (sin 𝑧 , − cos 𝑧 , 𝑥 cos 𝑧 + 𝑦 sin 𝑧)
Để tốc độ biến thiên của 𝑢 tại 𝑂(0,0,0) là lớn nhất thì cần theo hướng 80 𝑙 = 𝑔󰇍𝑟𝑎𝑑
󰇍󰇍󰇍󰇍𝑢(𝑂) = (0, −1,0)
Câu 84: Cho điểm 𝐴(2, −1,0), 𝐵(1,1,3). Tính đạo hàm của hàm 𝑢 = 𝑥3 + 3𝑦2 +
𝑒𝑧 + 𝑥𝑦𝑧2 tại điểm 𝐴 theo hướng 𝐴󰇍𝐵 󰇍󰇍 3 − 14 Đáp án: C. 2 Giải: 𝑢′ ′ 𝑥 = 3𝑥2 + 𝑦𝑧2 𝑢𝑥(𝐴) = 12
𝑢(𝑥, 𝑦, 𝑧) = 𝑥3 + 3𝑦2 + 𝑒𝑧 + 𝑥𝑦𝑧2 ⇒ { 𝑢′ ′
𝑦 = 6𝑦 + 𝑥𝑧2 ⇒ {𝑢𝑦(𝐴) = −6 𝑢′ ′
𝑧 = 𝑒𝑧 + 2𝑥𝑦𝑧 𝑢𝑧(𝐴) = 1 −1 𝐴󰇍𝐵 󰇍 2 3 = (−1,2,3) ⇒ |𝐴󰇍𝐵
󰇍| = √14 ⇒ cos 𝛼 = , cos 𝛽 = , cos 𝛾 = √14 √14 √14 𝜕𝑢 −1 ⇒ (𝐴) = 12. 2 3 −3 + (−6). + = √14 𝜕𝐴󰇍𝐵 󰇍 √14 √14 √14 2
Câu 85: Tính góc giữa 𝑔󰇍󰇍𝑟𝑎𝑑 󰇍 󰇍󰇍󰇍𝑢, x u =
tại điểm 𝐴(1,2,2) và 𝐵(−3,1,0) 2 2 2 x + y + z  8 −  Đáp án: A. arccos 9    Giải: −𝑥2 + 𝑦2 + 𝑧2
𝑢′𝑥 = (𝑥2 +𝑦2 +𝑧2)2 𝑥 𝑢 = ′ −2𝑥𝑦
𝑥2 + 𝑦2 + 𝑧2 ⇒ 𝑢𝑦 = (𝑥 2 + 𝑦2 + 𝑧2)2 ′ −2𝑥𝑧
{𝑢𝑧 = (𝑥2 + 𝑦2 + 𝑧2)2 −𝑥2 + 𝑦2 + 𝑧2 −2𝑥𝑦 −2𝑥𝑧 ⇒ 𝑔󰇍𝑟𝑎𝑑
󰇍 󰇍󰇍𝑢 = ((𝑥2 +𝑦2 +𝑧2)2,(𝑥2 +𝑦2 +𝑧2)2, (𝑥2 +𝑦2 +𝑧2)2) 7 −2 ⇒ 𝑔󰇍𝑟𝑎𝑑 󰇍 󰇍󰇍 −4 −4 3 𝑢(𝐴) = ( 󰇍󰇍󰇍󰇍󰇍
81 , 81 , 81) ; 𝑔𝑟𝑎𝑑 𝑢(𝐵) = (25 ,50 , 0) −9 ⇒ 𝑔󰇍𝑟𝑎𝑑
󰇍 󰇍󰇍𝑧2(𝑀) = (2, 5 ) 81 𝑔󰇍𝑟𝑎𝑑
󰇍󰇍 󰇍 𝑧 𝑀 .𝑔󰇍󰇍𝑟𝑎𝑑 󰇍 󰇍󰇍󰇍𝑧 −8 ⇒ cos (𝑔󰇍𝑟𝑎𝑑
󰇍󰇍󰇍󰇍𝑢(𝐴),𝑔󰇍𝑟𝑎𝑑
󰇍󰇍󰇍󰇍𝑢(𝐵)) = 1( ) 2(𝑀) = |𝑔󰇍𝑟𝑎𝑑 󰇍󰇍󰇍 󰇍𝑧 󰇍󰇍󰇍 󰇍  9
1(𝑀)|. |𝑔𝑟𝑎𝑑𝑧2(𝑀)| −8 ⇒ (𝑔󰇍󰇍𝑟𝑎𝑑
󰇍󰇍󰇍󰇍 𝑧 󰇍󰇍󰇍󰇍󰇍
1, 𝑔𝑟𝑎𝑑𝑧2) = arccos 9
Câu 86: Cho 𝐹 = 𝑥2𝑦𝑧𝑖 + 3𝑥𝑦2𝑧𝑗 + 𝑚𝑥𝑦𝑧2𝑘󰇍 với 𝑚 là tham số thực. Tìm 𝑚 để 𝐹 là trường ống.
Đáp án: B. 𝑚 = −4 Giải: 𝑃 = 𝑥2𝑦𝑧 𝑃′𝑥 = 2𝑥𝑦𝑧
Đặt {𝑄 = 3𝑥𝑦2𝑧 ⇒ { 𝑄 ′ ′ ′
𝑦 = 6𝑥𝑦𝑧 ⇒ 𝑑𝑖𝑣𝐹 = 𝑃′𝑥 + 𝑄𝑦 + 𝑅𝑧 = (8 + 2𝑚)𝑥𝑦𝑧 𝑅 = 𝑚𝑥𝑦𝑧2
𝑅′𝑧 = 2𝑚𝑥𝑦𝑧
Để 𝐹 là trường ống ⇔ 𝑑𝑖𝑣𝐹 = 0 ⇔ 𝑚 = −4
Câu 87: Xác định những điểm không phải điểm xoáy trong trường vecto
𝐹 = (𝑧2 + 2𝑥𝑦)𝑖+ (3𝑥2 − 2𝑦𝑧)𝑗 − 𝑧2𝑘󰇍
Đáp án: C. (0,0,0) Giải: 𝑃 = 𝑧2 + 2𝑥𝑦 𝑃′ ′ 𝑦 = 2𝑦, 𝑃𝑧 = 2𝑧
Đặt {𝑄 = 3𝑥2 − 2𝑦𝑧 ⇒ {𝑄′ ′
𝑥 = 6𝑥, 𝑄𝑧 = −2𝑦 𝑅 = −𝑧2 𝑅′ ′ 𝑥 = 0, 𝑅𝑦 = 0
𝜕𝑅 𝜕𝑄 𝜕𝑃 𝜕𝑅 𝜕𝑄 𝜕𝑃 ⇒ 𝑟𝑜𝑡
󰇍󰇍󰇍𝐹 = (𝜕𝑦 − 𝜕𝑧 ; 𝜕𝑧 − 𝜕𝑥 ; 𝜕𝑥 − 𝜕𝑦) = (2𝑦;2𝑧;6𝑥 −2𝑦)
Điểm xoáy 𝑀 trong trường vecto thỏa mãn 2𝑦 = 0 𝑥 = 0 𝑟𝑜𝑡
󰇍 󰇍󰇍𝐹(𝑀) = 0󰇍 ⇔ { 2𝑧 = 0 ⇔ {𝑦 = 0 6𝑥 − 2𝑦 = 0 𝑧 = 0
Vậy điểm không xoáy là 𝑀(0,0,0)
Câu 88: Biết 𝐹 = 𝑒𝑥2+𝑦2+𝑧2[(2𝑥2𝑦𝑧 + 𝑦𝑧)𝑖 + (2𝑦2𝑥𝑧 + 𝑥𝑧)𝑗 + (2𝑧2𝑦𝑥 + 𝑥𝑦)𝑘󰇍] là
trường thế. Tìm hàm thế vị. 82 Đáp án: A. 2 2 2 x + y + z u = e xyz + C Giải: Hàm thế vị 𝑥 𝑦 𝑧
𝑢 = ∫ 𝑃(𝑡, 𝑦0, 𝑧0)𝑑𝑡+ ∫ 𝑄(𝑥,𝑡, 𝑧0)𝑑𝑡 + ∫ 𝑅(𝑥,𝑦,𝑡)𝑑𝑡 + 𝐶 𝑥0 𝑦0 𝑧0
Chọn 𝑥0 = 𝑦0 = 𝑧0 = 0 𝑥 𝑦 𝑧
⇒ 𝑢 = ∫ 𝑒𝑡2. 0𝑑𝑡 + ∫ 𝑒𝑥2+𝑡2. 0𝑑𝑡 + ∫ 𝑒𝑥2+𝑦2+𝑡2(2𝑥𝑦𝑡2 + 𝑥𝑦)𝑑𝑡 + 𝐶 0 0 0 𝑧
= 𝑥𝑦 ∫ 𝑒𝑥2+𝑦2+𝑡2(2𝑡2 + 1)𝑑𝑡 + 𝐶 0 𝑧 𝑧
= 2𝑥𝑦 ∫ 𝑒𝑥2+𝑦2+𝑡2. 𝑡2𝑑𝑡 + 𝑥𝑦 ∫ 𝑒𝑥2+𝑦2+𝑡2𝑑𝑡 + 𝐶 0 0 𝑑𝑢 = 𝑑𝑡 Đặt { 𝑡 = 𝑢 1
𝑒𝑥2+𝑦2+𝑡2. 𝑡𝑑𝑡 = 𝑑𝑣 ⇒ {𝑣 = 2𝑒𝑥2+𝑦2+𝑡2 𝑧 𝑧 𝑧
⇒ 2𝑥𝑦 ∫ 𝑒𝑥2+𝑦2+𝑡2. 𝑡2𝑑𝑡 𝑡 = 2𝑥𝑦 ( 2 2 1
2 𝑒𝑥2+𝑦 +𝑡 | − ∫ 2 𝑒𝑥2+𝑦2+𝑡2𝑑𝑡 ) 0 0 0 𝑧
= 𝑥𝑦𝑧𝑒𝑥2+𝑦2+𝑡2 − 𝑥𝑦 ∫ 𝑒𝑥2+𝑦2+𝑡2𝑑𝑡 0 𝑧 𝑧
⇒ 𝑢 = 𝑥𝑦𝑧𝑒𝑥2+𝑦2+𝑡2 − 𝑥𝑦 ∫ 𝑒𝑥2+𝑦2+𝑡2𝑑𝑡 + 𝑥𝑦 ∫ 𝑒𝑥2+𝑦2+𝑡2𝑑𝑡 = 𝑥𝑦𝑧𝑒𝑥2+𝑦2+𝑡2 + 𝐶 0 0
Câu 89: Biết 𝐹 = (3𝑥2 − 3𝑦2𝑧)𝑖 + (arctan 𝑧 − 6𝑥𝑦𝑧)𝑗 + ( 𝑦
1+𝑧2 + 3𝑥𝑦2) 𝑘󰇍 là trường thế, tìm hàm thế vị. Đáp án: D. 3 2
u = x + y arctan z + 3xy z + C Giải: 83 Hàm thế vị 𝑥 𝑦 𝑧
𝑢 = ∫ 𝑃(𝑡, 𝑦0, 𝑧0)𝑑𝑡+ ∫ 𝑄(𝑥,𝑡, 𝑧0)𝑑𝑡 + ∫ 𝑅(𝑥,𝑦,𝑡)𝑑𝑡 + 𝐶 𝑥0 𝑦0 𝑧0
Chọn 𝑥0 = 𝑦0 = 𝑧0 = 0 𝑥 𝑦 𝑧
⇒ 𝑢 = ∫ 3𝑡2𝑑𝑡 + ∫ 0𝑑𝑡 𝑦
+ ∫ 1+ 𝑡2 +3𝑥𝑦2𝑑𝑡 +𝐶 = 𝑥3 + 𝑦arctan𝑧 +3𝑥𝑦2 + 𝐶 0 0 0
Câu 90: Biết 𝐹 = (3𝑥2 + 𝑦𝑧)𝑖 + (6𝑦2 + 𝑥𝑧)𝑗 + (𝑧2 + 𝑥𝑦 + 𝑒𝑧)𝑘󰇍 là trường thế, tìm hàm thế vị 3 Đáp án: A. 3 3 z z
u = x + 2y +
+ e + xyz + C 3 Giải: Hàm thế vị 𝑥 𝑦 𝑧
𝑢 = ∫ 𝑃(𝑡, 𝑦0, 𝑧0)𝑑𝑡+ ∫ 𝑄(𝑥,𝑡, 𝑧0)𝑑𝑡 + ∫ 𝑅(𝑥,𝑦,𝑡)𝑑𝑡 + 𝐶 𝑥0 𝑦0 𝑧0
Chọn 𝑥0 = 𝑦0 = 𝑧0 = 0 𝑥 𝑦 𝑧
⇒ 𝑢 = ∫ 3𝑡2𝑡 + ∫ 6𝑡2𝑑𝑡 + ∫(𝑡2 + 𝑥𝑦 + 𝑒𝑡)𝑑𝑡 + 𝐶 0 0 0 𝑥 𝑦 𝑧 = 𝑡3 | + 2𝑡3 | 𝑡3 + ( + 𝐶 0 0
3 + 𝑥𝑦𝑡 + 𝑒𝑡) | 0 𝑧3 = 𝑥3 + 2𝑦3 + 𝑧
3 + 𝑥𝑦𝑧 + 𝑒 − 1 + 𝐶 𝑧3 = 𝑥3 + 2𝑦3 + 𝑧
3 + 𝑥𝑦𝑧 + 𝑒 + 𝐶 𝑧3
Vậy hàm thế vị l à𝑢 = 𝑥3 + 2𝑦3 + 3 +𝑥𝑦𝑧 + 𝑒𝑧 +𝐶
Câu 91: Tính thông lượng của 𝐹 = 𝑥𝑖 + (𝑦3 + 2𝑧)𝑗 + (3𝑥2𝑧 − 𝑥)𝑘󰇍 qua mặt cầu 84
𝑆: 𝑥2 + 𝑦2 + 𝑧2 = 1 hướng ra ngoài. 44 Đáp án: D. 15 Giải:
Đặt 𝑃 = 𝑥, 𝑄 = 𝑦3 + 2𝑧, 𝑅 = 3𝑥2𝑧 − 𝑥
Thông lượng cần tính là:
Φ = ∬ 𝑥𝑑𝑦𝑑𝑧 + (𝑦3 + 2𝑧)𝑑𝑧𝑑𝑥 + (3𝑥2𝑧 − 𝑥)𝑑𝑥𝑑𝑦 𝑆
Mặt 𝑆 là mặt cong kín giới hạn miền (𝑉) 𝑥2 + 𝑦2 + 𝑧2 ≤ 1 hướng pháp tuyến ra ngoài. 𝑃′ ′ ′
𝑥 = 1, 𝑄𝑦 = 3𝑦2, 𝑅𝑧 = 3𝑥2 liên tục với 𝑥, 𝑦, 𝑧 ∈ 𝑅
Áp dụng công thức Ostrogradsky:
Φ = ∭(1 + 3𝑥2 + 3𝑦2)𝑑𝑥𝑑𝑦𝑑𝑧 = ∭(3𝑥2 + 3𝑦2)𝑑𝑥𝑑𝑦𝑑𝑧 + 𝑉(𝑉) = 𝐼 + 𝑉(𝑉) 𝑉 𝑉 𝑥 = 𝑟 sin 𝜃 cos 𝜑 0 ≤ 𝑟 ≤ 1
Đặt {𝑦 = 𝑟 sin 𝜃 sin 𝜑. Miền (𝑉): { 0 ≤ 𝜃 ≤ 𝜋 |𝐽| = 𝑟2 sin𝜃 𝑧 = 𝑟 cos 𝜃 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 𝜋 1 2𝜋 𝜋
𝐼 = ∫ 𝑑𝜑∫ 𝑑𝜃 ∫ 3 8
3𝑟2(sin 𝜃)2𝑟2 sin 𝜃 𝑑𝑟 = 3
5 ∫ 𝑑𝜑∫(sin 𝜃) 𝑑𝜃 = 5 𝜋 0 0 0 0 0 8 4 44
⇒ Φ = 𝐼 + 𝑉(𝑉) = 5𝜋 + 3𝜋 = 15𝜋
Câu 92: Tính thông lượng của 𝐹 = 𝑥𝑦2𝑖 − 𝑧𝑒𝑥𝑗 + (𝑥2𝑧 + sin 𝑦)𝑘󰇍 qua 𝑆 là mặt
𝑧 = 𝑥2 + 𝑦2, 𝑧 ≤ 4, hướng ra ngoài. (Chọn kết quả gần đúng nhất) 85 Đáp án: A. −17 Giải: Thông lượng cần tính:
Φ = ∬ 𝑥𝑦2𝑑𝑦𝑑𝑧 − 𝑧𝑒𝑥𝑑𝑧𝑑𝑥 + (𝑥2𝑧 + sin 𝑦)𝑑𝑥𝑑𝑦 𝑆
Bổ sung thêm mặt 𝑆′: { 𝑧 = 4
𝑥2 + 𝑦2 ≤ 4 hướng lên trên
Mặt 𝑆 ∪ 𝑆′ là mặt cong kín, hướng pháp tuyến ngoài giới hạn miền
(𝑉): 𝑥2 + 𝑦2 ≤ 𝑧 ≤ 4
Đặt 𝑃 = 𝑥𝑦2, 𝑄 = −𝑧𝑒𝑥, 𝑅 = 𝑥2𝑧 + cos 𝑦 ⇒ 𝑃′ ′ ′
𝑥 = 𝑦2, 𝑄𝑦 = 0, 𝑅𝑧 = 𝑥2 liên tục với 𝑥, 𝑦, 𝑧 ∈ 𝑅 Ta có:
Φ = ∯ 𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦 − ∬ 𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦 = 𝐼1 − 𝐼2 𝑆∪𝑆′ 𝑆′
Áp dụng công thức Ostrogradsky cho 𝐼1, ta có:
𝐼1 = ∭(𝑥2 + 𝑦2)𝑑𝑥𝑑𝑦𝑑𝑧 𝑉
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 4. 86 𝑥 = 𝑟 cos 𝜑 0 ≤ 𝑟 ≤ 2
Đặt {𝑦 = 𝑟 sin 𝜑 𝐽 = 𝑟. Miền (𝑉): {0 ≤ 𝜑 ≤ 2𝜋 𝑧 = 𝑧 𝑟2 ≤ 𝑧 ≤ 4 2𝜋 2 4 2𝜋 2 32
⇒ 𝐼1 = ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ 𝑟2.𝑟𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑟3(4 − 𝑟2)𝑑𝑟 = 3 𝜋 0 0 𝑟2 0 0
𝑆′: {𝑧 = 4 ⇒ 𝑑𝑧 = 0 2
𝑥2 + 𝑦2 ≤ 4 , (𝑛󰇍, 𝑂𝑧) < 𝜋/2, hình chiếu của 𝑆′ lên 𝑂𝑥𝑦 l à 𝐷: 𝑥2 + 𝑦 ≤ 4
⇒ 𝐼2 = ∬(𝑥2𝑧 + sin 𝑦)𝑑𝑥𝑑𝑦= ∬(4𝑥2 + sin 𝑦)𝑑𝑥𝑑𝑦 = ∬ 4𝑥2𝑑𝑥𝑑𝑦 𝑆′ 𝐷 𝐷 2𝜋 2 2𝜋
= 4 ∫ 𝑑𝜑 ∫ 𝑟2(cos 𝜑)2𝑟𝑑𝑟 = 16 ∫ (cos 𝜑)2𝑑𝜑 = 16𝜋 0 0 0
(∬ sin 𝑦 𝑑𝑥𝑑𝑦 = 0 do tính chất đối xứn gcủa miền 𝐷,hàm 𝑓(𝑥, 𝑦) = sin 𝑦 lẻ với 𝑦) 𝐷 −16
⇒ Φ = 𝐼1 − 𝐼2 = 3 𝜋
Câu 93: Tính thông lượng của 𝐹 = (𝑥2 − 2𝑦 + 𝑧)𝑖 − (𝑧2 + 2𝑥𝑦)𝑗 + 𝑥𝑘󰇍 qua phía
trên mặt nón 𝑧 = 1 + √𝑥2 + 𝑦2 cắt bởi hai mặt phẳng 𝑧 = 2, 𝑧 = 5 Đáp án: C. 0 Giải: Thông lượng cần tính:
Φ = ∬(𝑥2 − 2𝑦 + 𝑧)𝑑𝑦𝑑𝑧 − (𝑧2 + 2𝑥𝑦)𝑑𝑧𝑑𝑥 + 𝑥𝑑𝑥𝑑𝑦 𝑆 Bổ sung thêm hai mặt: 𝑆′: { 𝑧 = 2
𝑥2 + 𝑦2 ≤ 1 hướng lên trên, 𝑆′ : { 𝑧 = 5
𝑥2 + 𝑦2 ≤ 16 hướng xuống dưới 87
Mặt 𝑆 ∪ 𝑆′ ∪ 𝑆′ là mặt cong kín, hướng pháp tuyến trong, giới hạn miền
𝑉: {𝑧 ≥ 1 + √𝑥2 + 𝑦2 2 ≤ 𝑧 ≤ 5
Đặt 𝑃 = 𝑥2 − 2𝑦 + 𝑧, 𝑄 = −(𝑧2 + 2𝑥𝑦), 𝑅 = 𝑥 ⇒ 𝑃′ ′ ′
𝑥 = 2𝑥, 𝑄𝑦 = −2𝑥, 𝑅𝑧 = 0 liên tục.
Φ = ∯ …− ∬ … − ∬ …= 𝐼1 − 𝐼2 − 𝐼3 𝑆∪𝑆′∪𝑆′ 𝑆′ 𝑆′
Áp dụng công thức Ostrogradsky cho 𝐼1
⇒ 𝐼1 = −∭(2𝑥 − 2𝑥 + 0)𝑑𝑥𝑑𝑦𝑑𝑧 = 0 𝑉
𝑆′: {𝑧 = 2 ⇒ 𝑑𝑧 = 0 2
𝑥2 + 𝑦2 ≤ 1 , (𝑛󰇍, 𝑂𝑧) < 𝜋/2, hình chiếu của 𝑆′ lên 𝑂𝑥𝑦 là 𝐷′: 𝑥2 + 𝑦 ≤ 1
⇒ 𝐼2 = ∬ 𝑥𝑑𝑥𝑑𝑦 = ∬ 𝑥𝑑𝑥𝑑𝑦 = 0 (Dùng tính chất đối xứng) 𝑆′ 𝐷
𝑆′ : {𝑧 = 5 ⇒ 𝑑𝑧 = 0
𝑥2 + 𝑦2 ≤ 16 , (𝑛󰇍, 𝑂𝑧) > 𝜋/2, hình chiếu của 𝑆′ lên 𝑂𝑥𝑦 là 𝐷′ : 𝑥2 + 𝑦2 ≤ 16
⇒ 𝐼3 = ∬ 𝑥𝑑𝑥𝑑𝑦= ∬ 𝑥𝑑𝑥𝑑𝑦 = 0 (Dùng tính chất đối xứng) 𝑆′ 𝐷 88
Vậy Φ = 𝐼1 − 𝐼2 − 𝐼3 = 0
Câu 94: Tính thông lượng của trường vecto 𝐹 = 2𝑥2𝑖 + 𝑦2𝑗 − 𝑧2𝑘󰇍 qua S là mặt
ngoài của miền giới hạn bởi 𝑦 = 0, 𝑦 = √1 − 𝑧2, 𝑥 = 0, 𝑥 = 2 8
Đáp án: A. 4 + 3 Giải:
Thông lượng cần tính là:
Φ = ∬ 2𝑥2𝑑𝑦𝑑𝑧 + 𝑦2𝑑𝑧𝑑𝑥 − 𝑧2𝑑𝑥𝑑𝑦 𝑆
Mặt 𝑆 kín giới hạn miển 𝑉: 0 ≤ 𝑦 ≤ √1 − 𝑧2, 0 ≤ 𝑥 ≤ 2, hướng pháp tuyến ngoài
Đặt 𝑃 = 2𝑥2, 𝑄 = 𝑦2, 𝑅 = −𝑧2 ⇒ 𝑃′ ′ ′
𝑥 = 4𝑥, 𝑄𝑦 = 2𝑦, 𝑅𝑧 = −2𝑧 liên tục.
Áp dụng công thức Ostrogradsky:
Φ = ∬ 2𝑥2𝑑𝑦𝑑𝑧 + 𝑦2𝑑𝑧𝑑𝑧 − 𝑧2𝑑𝑥𝑑𝑦 = ∭(4𝑥 + 2𝑦 − 2𝑧)𝑑𝑥𝑑𝑦𝑑𝑧 𝑆 𝑉 𝑦 = 𝑟 cos 𝜑 0 ≤ 𝑟 ≤ 1
Đặt {𝑧 = 𝑟 sin 𝜑, 𝐽 = 𝑟 ⇒ Miền 𝑉: { −𝜋/2 ≤ 𝜑 ≤ 𝜋/2 𝑥 = 𝑥 0 ≤ 𝑥 ≤ 2 89 𝜋 𝜋 2 1 2 2 1 8
Φ = 2 ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫(2𝑥 + 𝑟 cos 𝜑).𝑟𝑑𝑥 = 2 ∫ 𝑑𝜑 ∫(4𝑟 + 2𝑟2 cos 𝜑)𝑑𝑟 = 4𝜋 + 3 −𝜋 0 0 −𝜋 0 2 2
Câu 95: Tính thông lượng của trường vecto 𝐹 = 𝑥3𝑖 + 𝑦2𝑗 + 𝑧2 𝑘󰇍 qua 𝑆 là biên 2
ngoài của miền 𝑉: |𝑥 − 𝑦| ≤ 1, |𝑦 − 𝑧| ≤ 1, |𝑧 + 𝑥| ≤ 1 Đáp án: D. 3 Giải: Thông lượng cần tính
Φ = ∬ 𝑥3𝑑𝑦𝑑𝑧 + 𝑦2 𝑧2
𝑑𝑧𝑑𝑧 + 2 𝑑𝑥𝑑𝑦 𝑆
Mặt 𝑆 kín giới hạn miển 𝑉: |𝑥 − 𝑦| ≤ 1, |𝑦 − 𝑧| ≤ 1, |𝑧 + 𝑥| ≤ 1 hướng pháp tuyến ngoài
Đặt 𝑃 = 𝑥3, 𝑄 = 𝑦2, 𝑅 = 𝑧2/2 ⇒ 𝑃′ ′ ′
𝑥 = 3𝑥2, 𝑄𝑦 = 2𝑦, 𝑅𝑧 = 𝑧 liên tục.
Áp dụng công thức Ostrogradsky:
Φ = ∭(3𝑥2 + 2𝑦 + 𝑧)𝑑𝑥𝑑𝑦𝑑𝑧 𝑉 𝑢 = 𝑥 − 𝑦 𝑥 = (𝑢 + 𝑣 + 𝑤)/2
Đặt {𝑣 = 𝑦 − 𝑧 ⇒ {𝑦 = (𝑣 + 𝑤 − 𝑢)/2 , 𝐽 = 1/2 𝑤 = 𝑧 + 𝑥
𝑧 = (𝑤 − 𝑢 − 𝑣)/2
Miền 𝑉𝑢𝑣𝑤: −1 ≤ 𝑢 ≤ 1, −1 ≤ 𝑣 ≤ 1, −1 ≤ 𝑤 ≤ 1 1 3(𝑢 + 𝑣 + 𝑤)2 𝑤 − 𝑢 − 𝑣 ⇒ Φ = 2 ∭[ 4 + (𝑣 + 𝑤 − 𝑢) + 2
] 𝑑𝑢𝑑𝑣𝑑𝑤= ⋯ = 3 𝑉𝑢𝑣𝑤
Câu 96: Cho trường vô hướng 𝑢 = 𝑥𝑦 + 𝑦𝑧 + 𝑥𝑧. Tính lưu số của trường vecto 𝑔󰇍𝑟𝑎𝑑
󰇍 󰇍 󰇍 𝑢 dọc theo đoạn thẳng nối từ 𝐴(−1,−1,−1) đến 𝐵(2,4,1) Đáp án: A. 11 Giải: 90 𝑔󰇍𝑟𝑎𝑑
󰇍 󰇍 󰇍 𝑢 = (𝑢′ ′ ′ 𝑥, 𝑢 󰇍
𝑦 , 𝑢𝑧) = (𝑦 + 𝑧, 𝑥 + 𝑧, 𝑥 + 𝑦) = (𝑦 + 𝑧)𝑖 + (𝑥 + 𝑧)𝑗 + (𝑥 + 𝑦)𝑘
Đoạn 𝐴𝐵: {vecto chỉ phương A 󰇍󰇍 B 󰇍 = (3,5,2) 𝑥 + 1 𝑦 + 1 𝑧 + 1 đi qua A(−1, −1, −1)
⇒ 𝐴𝐵: 3 = 5 = 2 = 𝑡 𝑥 = 3𝑡 − 1
⇒ 𝐴𝐵: {𝑦 = 5𝑡 − 1 với 𝑡 chạy từ 0 đến 1. 𝑧 = 2𝑡 − 1 Lưu số cần tìm:
𝐶 =∫(𝑦 + 𝑧)𝑑𝑥 + (𝑥 + 𝑧)𝑑𝑦 + (𝑥 + 𝑦)𝑑𝑧 𝐴𝐵 1
= ∫[(5𝑡 − 1 + 2𝑡 − 1). 3 + (3𝑡 − 1 + 2𝑡 − 1). 5 + (3𝑡 − 1 + 5𝑡 − 1). 2]𝑑𝑡 = 11 0
Câu 97: Tính lưu số của 𝐹 = 𝑥2𝑦3𝑖 + 𝑗 + 𝑧𝑘󰇍 dọc theo đường tròn có phương trình
𝐶: 𝑥2 + 𝑦2 = 1, 𝑧 = 0 giới hạn mặt cầu 𝑧 = √1 − 𝑥2 − 𝑦2 Đáp án: Giải: Lưu số cần tính là:
𝐶 = ∮ 𝑥2𝑦3𝑑𝑥 + 𝑑𝑦 + 𝑧𝑑𝑧 𝐶
Đường cong 𝐶 giới hạn phần mặt cầu 𝑆: 𝑧 = √1 − 𝑥2 − 𝑦2 hướng lên trên 91
(Đề bài không nói gì về chiều thì hiều là đường cong cho chiều dương).
Áp dụng công thức Stoke:
𝐶 = ∬ −3𝑥2𝑦2𝑑𝑥𝑑𝑦 𝑆
Hình chiếu của mặt 𝑆 lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 1 𝑥 = 𝑟 cos 𝜑
Đặt {𝑦 = sin𝜑,𝐽 = 𝑟 ⇒ 𝐷: { 0 ≤ 𝑟 ≤ 1 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 1 −𝜋
⇒ 𝐶 = ∬ −3𝑥2𝑦2𝑑𝑥𝑑𝑦 = −3 ∫ 𝑑𝜑 ∫ 𝑟2sin2 𝜑 𝑟2cos2 𝜑 . 𝑟𝑑𝑟 = ⋯ = 8 𝑆 0 0
Câu 98: Tính lưu số của 𝐹 = (𝑦𝑒𝑥𝑦 + 3𝑦 + 𝑧)𝑖 + (𝑥𝑒𝑥𝑦 + 𝑦 − 5𝑧)𝑗 + (1 + 2𝑥)𝑘󰇍 dọc
theo đường cong 𝐿 là giao của mặt 𝑥2 + 𝑦2 + 𝑧2 = 4 và mặt 𝑥 − 𝑦 + 𝑧 = 0 hướng
ngược chiều kim đồng hồ nếu nhìn từ chiều dương trục 𝑂𝑧.
Đáp án: C. 4√3𝜋 Giải: Lưu số cần tính là:
𝐶 = ∮(𝑦𝑒𝑥𝑦 + 3𝑦 + 𝑧)𝑑𝑥 + (𝑥𝑒𝑥𝑦 + 𝑦 − 5𝑧)𝑑𝑦 + (1 + 2𝑥)𝑑𝑧 𝐿
Đường cong kín 𝐿 chiều dương giới hạn phần mặt phẳng 𝑆: 𝑥 − 𝑦 + 𝑧 = 0 nằm
trong cầu, mặt hướng lên, có vecto pháp tuyến hợp trục 𝑂 𝑧 < 𝜋/2 92
Áp dụng công thức Stoke:
𝐶 = ∬ 5𝑑𝑦𝑑𝑧 − 𝑑𝑧𝑑𝑥 − 3𝑑𝑥𝑑𝑦 𝑆
Vecto pháp tuyến của 𝑆 là 𝑛󰇍 = (1, −1,1) ⇒ cos 𝛼 = 1 , cos 𝛽 = −1 , cos 𝛾 = 1 √3 √3 √3 1 1 1 ⇒ 𝐶 = ∬ (5. + 1.
− 3. ) 𝑑𝑆 = √3 ∬ 𝑑𝑆 = √3𝑆 √ √3 √3 √3 𝑆 = 4 3𝜋 𝑆 𝑆
(𝑆 là hình tròn qua tâm cầu)
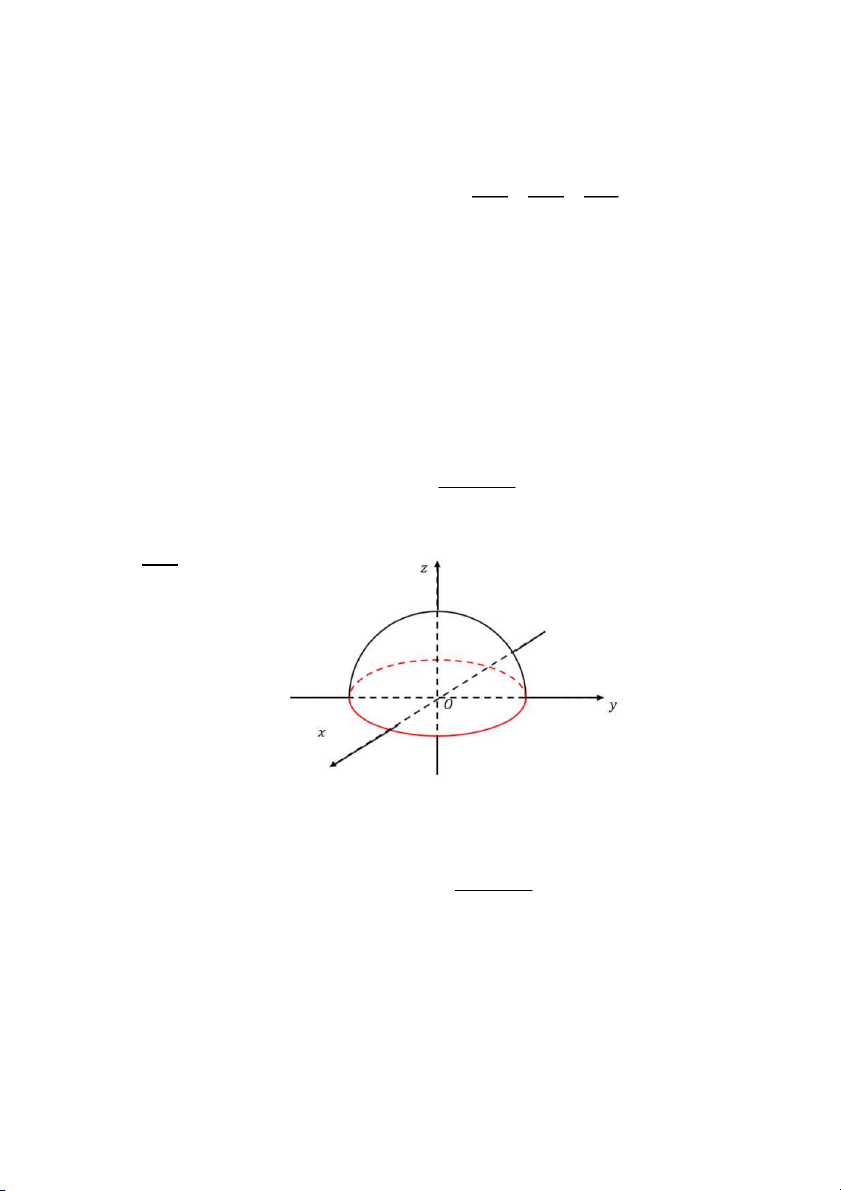
Câu 99: Tính lưu số của 𝐹 = (𝑦2 + 𝑧2)𝑖 + (𝑥2 + 𝑧2)𝑗 + (𝑥2 + 𝑦2)𝑘󰇍 dọc theo đường
cong 𝐶 trong đó 𝐶 là giao của mặt cầu 𝑥2 + 𝑦2 + 𝑧2 = 4 và mặt nón có phương
trình 𝑧 = −√𝑥2 + (𝑦 − 1)2 với hướng cùng chiều kim đồng hồ khi nhìn từ gốc O. Đáp án: B. 0 Giải: Lưu số cần tính:
𝐶 = ∮(𝑦2 + 𝑧2)𝑑𝑥 + (𝑥2 + 𝑧2)𝑑𝑦 + (𝑥2 + 𝑦2)𝑑𝑧 𝐶
Đường cong kín 𝐶 chiều âm là biên của phần mặt cong của cầu nằm trong nón
𝑆: {𝑥2 + 𝑦2 + 𝑧2 ≤ 4hướ ố ề 𝑧 ≤ 0
ng xu ng theo chi u âm 𝑂𝑧
Áp dụng công thức Stoke:
𝐶 = − ∬(2𝑦 − 2𝑧)𝑑𝑦𝑑𝑧 + (2𝑧 − 2𝑥)𝑑𝑧𝑑𝑥 + (2𝑥 − 2𝑦)𝑑𝑥𝑑𝑦 𝑆
Vecto pháp tuyến của mặt 𝑆 là 𝑛󰇍 = −(2𝑥, 2𝑦, 2𝑧)
⇒ |𝑛󰇍| = √(2𝑥)2 + (2𝑦)2 + (2𝑧)2 = 4
(Dấu " − " do (𝑛󰇍, 𝑂𝑧 ) > 𝜋/2) −2𝑥 −𝑥 −2𝑦 −𝑦 −2𝑧 −𝑧
⇒ cos 𝛼 = 4 = 2 ,cos𝛽 = 4 = 2 ,cos𝛾 = 4 = 2 93
Áp dụng công thức liên hệ giữa tích phân mặt loại II và tích phân mặt loại I: 𝑥 𝑧 ⇒ 𝐶 = ∬ [ ( 𝑦 ( (2𝑥 − 2𝑦)] 𝑑𝑆
2 2𝑦 − 2𝑧) + 2 2𝑧 − 2𝑥) + 2 = 0 𝑆
Câu 100: Tính thông lượng của 𝐹 = (6𝑧 − 2𝑦3)𝑖 + (2𝑥 − 3𝑧)𝑗 + (2𝑦3 − 4𝑥)𝑘󰇍 qua
mặt cong 𝑆: 2𝑥2 + 𝑦4 + 3𝑧2 = 1, 𝑧 ≥ 0 hướng lên trên. Đáp án: Giải: Thông lượng cần tính:
Φ = ∬(6𝑧 − 2𝑦3)𝑑𝑦𝑑𝑧 + (2𝑥 − 3𝑧)𝑑𝑧𝑑𝑧 + (2𝑦3 − 4𝑥)𝑑𝑥𝑑𝑦 𝑆
Đặt 𝐹(𝑥, 𝑦, 𝑧) = 2𝑥2 + 𝑦4 + 3𝑧2 − 1
Vecto pháp tuyến 𝑛󰇍 = (𝐹′ ′ ′ 3 
𝑥, 𝐹𝑦, 𝐹𝑧) = (4𝑥, 4𝑦 , 6𝑧) (do (𝑛󰇍 , 𝑂𝑧) < 𝜋/2)
|𝑛󰇍| = √4𝑥2 + 16𝑦6 + 36𝑧2 = 2√𝑥2 + 4𝑦4 + 9𝑧2 𝑛 2𝑥 cos 𝛼 = 𝑥
|𝑛󰇍| = √𝑥2 + 4𝑦4 + 9𝑧2 𝑛 2𝑦3 ⇒ cos 𝛽 = 𝑦 |𝑛󰇍| = √𝑥2 + 4𝑦4 + 9𝑧2 𝑛 3𝑧 cos 𝛾 = 𝑧 {
|𝑛󰇍| = √𝑥2 + 4𝑦4 + 9𝑧2
Áp dụng công thức liên hệ giữa tích phân mặt loại I và loại II
∬ 𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦 = ∬(𝑃.cos 𝛼 + 𝑄. cos 𝛽 + 𝑅.cos 𝛾)𝑑𝑆 𝑆 𝑆
2𝑥(6𝑧 − 2𝑦3) + 2𝑦3(2𝑥 − 3𝑧) + 3𝑧(2𝑦3 − 4𝑥) ⇒ Φ = ∬ 𝑑𝑆 = 0 √𝑥2 + 4𝑦4 + 9𝑧2 𝑆 94
Tài liệu tham kh o: ả
− Bài giảng môn Giải tích II, thầy Bùi Xuân Diệu.
− Bài tập giải sẵn Giải tích 2 (Tóm tắt lý thuyết và chọn lọc), thầy Trần Bình.
− Bài tập Toán học cao cấp, tập hai: Giải tích, GS.TS Nguyễn Đình Trí (chủ
biên), PGS.TS. Trần Việt Dũng, PGS.TS. Trần Xuân Hiền, PGS.TS Nguyễn Xuân Thảo.
− Bộ đề cương Giải tích II, Viện Toán ứng dụng và Tin học.
− Bộ đề thi Giữa kì và Cuối kì môn Giải tích II Trường ĐH Bách Khoa Hà Nội. 95