Bài tập trắc nghiệm thể tích khối chóp – Trần Đình Cư Toán 12

Tài liệu bài tập trắc nghiệm thể tích khối chóp do thầy Trần Đình Cư biên soạn và gửi tặng các em học sinh nhân dịp Giáng sinh 2016.Mời các bạn đón xem.

43 22 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

68 trang 8 tháng trước

Tác giả:

Profile Lan Tường
TRẦN ĐÌNH CƯ
THỂ TÍCH KHỐI
CHÓP
QUÀ
TẶNG
GIÁNG
SINH
HUẾ, 24/12/2016
1
MỤC LỤC
CHUYÊN ĐỀ 2. THỂ TÍCH KHỐI CHÓP...................................................... 2
DẠNG 1. KHỐI CHÓP CÓ CẠNH BÊN VUÔNG GÓC ĐÁY ............... 2
DẠNG 2. KHỐI CHÓP CÓ HÌNH CHIẾU CỦA ĐỈNH LÊN MẶT
PHẲNG ĐÁY .............................................................................................. 17
DẠNG 3. KHỐI CHÓP CÓ MẶT BÊN VUÔNG GÓC VỚI ĐÁY ....... 33
DẠNG 4. KHỐI CHÓP ĐỀU ..................................................................... 45
DẠNG 5. TỈ LỆ THỂ TÍCH ........................................................................ 54
2
CHUYÊN ĐỀ 2. THỂ TÍCH KHỐI CHÓP
Công thức chung:
Trong đó:
B
là diện tích đáy, h là chiều cap
DẠNG 1. KHỐI CHÓP CÓ CẠNH BÊN VUÔNG GÓC ĐÁY
Một số chú ý khi giải toán
Mt hình chóp có mt cnh bên vuông góc vnh bên
ng cao.
Mt hình chóp có hai mt bên k nhau cùng vuông góc v
thì cnh bên là giao tuyn ca hai m
Câu 1. Cho hình chóp S.ABC ABC a. SA vuông
ABCSB ABC)

0
. Tính theo a S.ABC .
A.
3
a 13
V
2
B.
3
a
V
12
C.
3
3a 13
V
2
D.
3
5a 13
V
2
Hướng dẫn giải
Ta có góc SB 
ABC) là
SBA 30
.
;
3
S.ABC ABC
1a
V S .SA
3 12

.
Vậy chọn đáp án A.
Câu 2. Cho hình chóp S.ABCD có chiu cao SA bng a. MABCD là
hình thoi cnh a, góc
ABC
bng 60
0
. Tính th tích khi chóp S.ABCD theo
a.
A.
21
a
15
B.
23
a
14
C.
21
a
14
D.
21
a
4
Hướng dẫn giải
2
1 3 3
..
2 2 4
ABC
aa
Sa
3
tan .
3
a
SA SBA AB
30
0
a
S
A
B
C
3
Tam giác ABC u cnh a nên
2
ABC
3
Sa
4
Di
2
3
ABCD ABC
2
S 2.S a
Th tích khi chóp:
3
2
3 a 3
V a .a
22

Câu 3. 
S.ABCD

ABCD

a2
AC
2

SAABCDSB 
ABCD
S.ABCD
A.
3
a3
24
B.
3
3a 3
24
C.
3
a3
8
D.
3
3a 3
8
Hướng dẫn giải
Ta có:
AB
là hình chiu ca
SB
lên
mt phng
ABCD
nên
0
SB, ABCD SBA 60
;
SA ABCD
SA
là chiu cao ca
khi chóp
S.ABCD

2
ABCD
a a 3 a
AB ;SA ;S
2 2 4
3
S.ABCD ABCD
1 a 3
V .SA.S
3 24


Vậy chọn đáp án A.
Câu 4. Cho t din OABC OBC là tam giác vuông ti O, OB = a, OC =
a3
, (a ng cao OA =
a3
. Tính th tích khi t din theo a.
A.
3
a
V
2
B.
3
a
V
3
C.
3
a
V
6
D.
3
a
V
12
Hướng dẫn giải
Ta có:
60
0
a
D
A
B
C
S
60
0
a
2
2
D
A
B
C
S
4
2
OBC
1 1 a 3
S OB.OC a(a 3)
2 2 2
Th tích khi t din
23
OBC
1 1 a 3 a
V S .OA ( )(a 3)
3 3 2 2
.
Vậy chọn đáp án A.
Câu 5. Cho hình chóp S.ABCD ABCD là hình thoi cnh a,
0
ABC 60
cnh SA vuông góc vSC to vt góc 60
0
. Tính theo a th
tích khi chóp S.ABCD.
A.
3
a
V
2
B.
3
a
V
3
C.
3
2a
V
3
D.
3
a
V
9
Hướng dẫn giải
Ta có
ABC
u nên
AC a.
Có:
22
BD AB AD 2AB.AD.cos120
BD a 3
Suy ra
2
ABCD
1 a 3
S AC.BD
22

Mt khác
SA AC.tan60 a 3.

Vy
3
S.ABCD ABCD
1a
V SA.S
32

.
Vậy ta chọn đáp án A.
Câu 6. Cho hình chóp S.ABCD ABCD là hình thoi có cnh bng
a3
,
0
BAD 120
và cnh bên SA vuông góc vt mt phng (SBC) và
ng 60
0
. Tính theo a th tích khi chóp S.ABCD.
A.
3
a3
V
4
B.
3
3.a 3
V
4
C.
3
3.a
V
4
D.
3
3.a 3
V
5
Hướng dẫn giải
a
a
60
0
60
0
D
A
B
C
S
5
ABCD
0
BAD 120
ABC
ADC
a3
HBC
AH
BCSA
BC
BC
SH

0
SBC ; ABCD AH;SH
SHA 60


0
3a
SA AH.tan60
2


2
2
ABCD ABC
a 3 3
3a 3
S 2S 2
42
.

3
S.ABCD ABCD
1 3a 3
V SA.S
34

Vậy chọn đáp án B.
Câu 7. Cho hình chóp
S.ABC
 
ABC
là tam giác vuông ti
B
,
0
AB 2a, BAC 60
. Cnh bên
SA
vuông góc vi mt phng
(ABC)
và
SA a 3
. Tính theo
a
th tích khi chóp
S.ABC
.
A.
3
V 2a
B.
3
V 3a
C.
3
Va
D.
3
V 4a
Hướng dẫn giải
Xét tam giác ABC có:
02
ABC
BC AB.tan60 2a 3 S 2a 3
3
SABC ABC
1
V S .SA 2a
3
Chọn đáp án A
Câu 8. Cho hình chóp
S.ABC
ABC là tam giác vuông ti B có góc
0
BAC 30
,
, SA a
,
0
SCA 45
và SA vuông góc v

S.ABC
là V. T s
3
V
a
gn giá tr nào nht trong các giá tr sau:
A.
0,01
B.
0,05
C.
0,08
D.
1
a
3
60
0
120
0
H
B
A
D
C
S
60
0
2a
a
3
S
A
B
C
6
Hướng dẫn giải
Ta có
0
SCA 45
AC SA.tanSCA a
0
3a
AB AC.cosBAC a.cos30
2
ABC
2
1
S AB.ACsinBAC
2
1 a. 3.a 1 a 3
..
2 2 2 8


Vy
23
S.ABC ABC
1 1 a 3 a 3
V .S .SA .a
3 3 8 24
3
V
0,072
a

Chọn đáp án C
Câu 9. Cho hình chóp
S.ABCD
, 
ABCD
là hình ch nht có
AB 2a,AD a
. Hai
mt phng
SAB
và
SAD
vuông góc v  a hai mt
phng
SAB
và
SBD
bng 45
0
. Th tích khi chóp
S.ABCD
là V. T s
3
V
a
gn nht giá tr 
A.
0,25
B.
0,5
C.
0,75
D.
1,5
Hướng dẫn giải
Ta có:
2
ABCD
S AB.AD 2a
SAB ABCD
và
SAD ABCD
SAB SAD SA
SA ABCD
Ta có:
AD AB,AD SA AD SAB
AD SB
. K
AH SB
SB AHD
SB HD
.
C
S
A
D
B
H
45
30
S
A
C
B
7
Ta có:
AH SB,HD SB
SAB SBD SB


0
SAB , SBD AHD 45
AH AD a
Xét tam giác SAB vuông ti S có:
2 2 2
2 2 2 2
1 1 1 AB.AH 2a.a 2a 3
SA
3
AH SA AB
AB AH 4a a

Vy
3
2
S.ABCD ABCD
1 1 2a 3 4a 3
V .S .SA .2a .
3 3 3 9
3
V 4 3
0,77
9
a
Chọn đáp án C
Câu 10. S.ABCSAABa
ACa
0
BAC 120
SBC

S.ABC
A.
3
a 21
V
14
B.
3
a 21
V
13
C.
3
2a 21
V
13
D.
3
3.a 21
V
14
Hướng dẫn giải



SF BC

0
SBC , ABC SFA 60
2
ABC
1 a 3
S .AB.AC.sinBAC
22
a 21 3a 7
BC=a 7, AF , SA
77


23
SABC ABC
1 1 a 3 3a 7 a 21
V .S .SA . .
3 3 2 7 14
Vậy chọn đáp án A.
Câu 11. S.ABCDaSA ABCD
SB a 3
S.AB
A.
3
a2
3
B.
3
a2
3
C.
3
a2
5
D.
3
a2
3
2a
120
0
a
S
A
B
C
F
8
Hướng dẫn giải
 
Chọn đáp án D.
Câu 12. Cho hình chóp S.ABCD ABCD là hình ch nht có AB = 3a,
AD = 4a.
SA (ABCD)
, SC to v 45
0
. Tính th tích khi chóp
S.ABCD.
A.
3
V 20a
B.
3
V 20a 2
C.
3
V 30a
D.
3
V 22a
Hướng dẫn giải
Do
SA (ABCD)
nên AC là hình chiu c
0
SC, ABCD SCA 45
. Suy ra:
0
SA AC.tan45 5a
Suy ra:
3
S.ABCD ABCD
1
V SA.S 20a
3

. Vậy chọn đáp án A.
Câu 13. Cho t din ABCD có AD vuông góc vi mt phng
ABC
và AB
= 3a, BC = 4a, AC = 5a. AD = 6a. Th tích khi t din ABCD là:
A.
3
6a
B.
3
12a
C.
3
18a
D.
3
36a
Hướng dẫn giải
Tam giác ABC có:
22
2 2 2 2
AB BC 3a 4a 25a AC
ABC
vuông
ti B
2
ABC
11
S AB.BC 3a.4a 6a
22
23
ABCD ABC
11
V S AD .6a .6a 12a
33
Chọn đáp án B
Câu 14. Cho t din SABC có
SA
vuông góc vi mt phng
ABC
, hai
mt phng
SAB
và
SBC
vuông góc vi nhau,
SB a 3
,
o
BSC 45
,
o
ASB 30
. Th tích t din SABC là V. T s
3
a
V
là:
A.
8
3
B.
83
3
C.
23
3
D.
4
3
Hướng dẫn giải
2 2 2 2
SB AB 3a a a 2
3
ABCD
1 a . 2
V S .SA
33

9
+ Ta có:
SA ABC SAB ABC
SBC SAB , ABC SAB
SBC ABC BC
BC SAB



ABC, SBC
là các tam giác vuông ti
B
Xét
SAB
vuông ti A có :
a3
AB SB.sinASB
2

,
3a
SA SB.cosASB
2

Xét
SBC
vuông ti B có :
BC SB.tanBSC a 3
2
ABC
1 1 a 3 3a
S AB.BC . .a 3
2 2 2 4
Vy
23
S.ABC ABC
1 1 3a 3a 3a
V .S .SA . .
3 3 4 2 8
3
a8
V3

Chọn đáp án A
Tổng quát: Cho t din SABC có
SA
vuông góc vi mt phng
ABC
, hai
mt phng
SAB
và
SBC
vuông góc vi nhau,
BSC 
,
ASB 
. Th tích
t din SABC là:
3
S.ABC
SB .sin2 .tan .
V
12

Thật vậy
Xét
SAB
vuông ti A có :
AB SB.sin
,
SA SB.cos
Xét
SBC
vuông ti B có :
BC SB.tan
2
ABC
11
S AB.BC .SB .sin .tan
22
Vy
3
2
S.ABC ABC
1 1 1 SB .sin2 .tan
V .S .SA . .SB .sin .tan .SB.cos
3 3 2 12

Câu 15. Cho hình chóp S.ABCD  ABCD là hình thang vuông ti A và
D, cnh bên SD vuông góc v
AB AD a
,
CD 3a,SA a 3
.
Th tích khi chóp S.ABCD là:
30
45
B
C
A
S
10
A.
3
2a
3
B.
3
4a
3
C.
3
a2
3
D.
3
2a 2
3
Hướng dẫn giải
+
2
ABCD
AB CD .AD a 3a .a
S 2a
22

+
2 2 2 2
SD SA AD 3a a a 2
Vy
3
2
S.ABCD ABCD
1 1 2a 2
V .S .SD .2a .a 2
3 3 3
Chọn đáp án D
Câu 16. Cho hình chóp
S.ABCD
, 
ABCD
là hình vuông cnh a. Hai mt
phng
SAB
và
SAD
vuông góc va hai mt phng
SBC
và
ABCD
bng 30
0
. Th tích khi chóp
S.ABCD
là V. T s
3
3V
a
là:
A.
3
3
B.
3
C.
3
2
D.
3
6
Hướng dẫn giải
0
SBC , ABCD SBA 30
a3
SA AB.tanSBA
3
Vy
3
2
S.ABCD ABCD
1 1 a 3 a 3
V .S .SA .a .
3 3 3 9
3
3V 3
3
a

Chọn đáp án A
Câu 17. Cho hình chóp
S.ABCD
, 
ABCD
là hình ch nht có
AB a, BC 3a
. Hai mt phng
SAB
và
SAD
vuông góc vi
nh SC hp vt góc 60
0
. Th tích khi chóp
S.ABCD
là:
A.
3
a
B.
3
2a
C.
3
3a
D.
3
2 3a
Hướng dẫn giải
A
C
D
S
B
11
Ta có:
2
ABCD
S AB.BC a 3
SAB ABCD
và
SAD ABCD
SAB SAD SA
SA ABCD
Xét tam giác SAC vuông ti S có:
2 2 0
SA AC.tanSCA
AB BC .tan60 2 3a
Vy
23
S.ABCD ABCD
11
V .S .SA a 3.2 3 2a
33
Chọn đáp án B
Câu 18. Cho hình chóp
S.ABC
có tam giác
ABC
vuông ti
B
,
0
ACB, 0AB a 6
, cnh bên
SA
vuông góc vi mt ph
SB
to
vi mt góc bng 45
0
. Th tích khi chóp
S.ABC
là:
A.
3
a3
6
B.
3
a3
18
C.
3
a3
9
D.
3
a3
12
Hướng dẫn giải
*
ABC
vuông ti B nên
0
a3
BC AB.cotACB a.cot60
3
2
ABC
1 1 a 3 a 3
S BA.BC a.
2 2 3 6
* Ta có
AB
là hình chiu vuông góc ca
SB
trên
ABC
o
SB, ABC SB,AB SBA 45
SAB
vuông ti A nên
o
SA AB.tanSBA AB.tan45 a
Vy
23
S.ABC ABC
1 1 a . 3 a 3
V S .SA .a
3 3 6 18
Chọn đáp án B
60
C
S
A
D
B
45
60
B
C
A
S
12
Câu 19. Cho t din ABCD có ABC là tam u cnh a, AD vuông góc
vi mt phng
ABC
, góc gia BD và mt phng
DAC
là 30
0

 din
ABCD
là V. T s
3
a6
V
là:
A.
1
B.
3
C.
4
D.
12
Hướng dẫn giải
Ta có ABC u
2
ABC
a3
S
4

Gi M m AC
Ta có
BM AC,BM DA BM DAC
0
BD, DAC BDM 30
Xét
BMD
vuông ti M có :
0
a 3 3a
DM BM.cot30 . 3
22
Xét
DAM
vuông ti A có :
22
2 2 2
9a a
DA DM AM a 2
44
Vy
23
ABCD ABC
1 1 a 3 a 6
V .S .DA . . 2a
3 3 4 12
3
a6
12
V

Chọn đáp án D
Câu 20. Cho hình chóp
S.ABCD
có c nh
bng 20cm, cnh SA = 30cm và vuông góc vi B’, D’ lt là
hình chiu vuông góc ca A lên SB và SD. Mt phng
AB'D'
ct SC t
Th tích khi chóp
S.AB'C'D'
gn nht giá tr 
A.
3
1466cm
B.
C.
D.
3
15400cm
Hướng dẫn giải
30
D
A
C
B
M
13
Do
S.ABCD ABCD
23
1
V SA.S
3
1
.30.20 4000cm
3

22
2 2 2
2
222
SC' SA SA
SC
SC SA AC
30 9
17
30 20 20



2 2 2
2 2 2 2 2
SD' SA SA 30 9
SD 13
SD SA AD 30 20

Ta có:
S.AB'C' D' SAC'D'
S.ABCD SACD
V 2V
SA SC' SD' SC' SD'
. . .
V 2V SA SC SD SC SD
3
S.AB'C'D' S.ABCD
9 9 81 324000
V . V .4000 1466cm
17 13 221 221
Câu 21. Cho hình chóp S.ABC ABC là tam giác vuông cân ti A, cnh
BC a 2
, cnh bên SA vuông góc vi mt pht bên
SBC
to
vi mt góc bng 45
0
. Th tích khi chóp S.ABC bng V. Giá tr
3
6V
a
là:
A.
1
B.
3
C.
2
2
D.
32
2
Hướng dẫn giải
Gi M m BC
1 a 2
AM BC
22
2
2
ABC
1 1 a
S AM.BC BC
2 4 2
+ Ta có
SA ABC
SA BC
và
BC AM
nên
BC SAM
BC AM
AM
BC ( vì
ABC cân ti A)
B
D
A
S
C
C'
B'
D'
45
S
A
C
B
M
14
o
SBC , ABC (SM,AM) SMA 45
Ta có
SAM
vuông ti A
a2
SA AM.tanSMA AM
2
Vy
23
S.ABC ABC
1 1 a a 2 a 2
V .S .SA . .
3 3 2 2 12
Chọn đáp án C
Câu 22. Cho hình chóp S.ABC có SA = SB = SC = a,
0
ASB 90 ,
0
BSC 120 ,
0
ASC 90
. Th tích khi chóp S.ABC là:
A.
3
a
2
B.
3
a
6
C.
3
a3
4
D.
3
a3
12
Hướng dẫn giải
Ta có
SA AB,SA AC
SA SBC
0
SBC
2
2
1
S SB.SB.sin120
2
1 3 a 3
a.
2 2 4

S.ABC A.SBC SBC
1
V V S .SA
3
23
1 a 3 a 3
. .a
3 4 12

Đáp án D
Câu 22. Cho hình chóp
SABC
có tam giác
SBC
u cnh
a
,
CA a
. Hai
mt
ABC
và
ASC
cùng vuông góc vi (SBC). Th tích hình chóp là
A.
3
a3
12
B.
3
a3
2
C.
3
a3
4
D.
3
a
12
Hướng dẫn giải
(ABC) (SBC)
(ASC) (SBC)
AC (SBC)

23
SBC
1 1 a 3 a 3
V S .AC a
3 3 4 12
Vậy chọn đáp án A.
120
B
C
S
A
_
\
/
/
a
B
S
C
A
15
Câu 23. Ci B vi
AC = a bit SA vuông góc vp vt góc 60
o
. Th
tích hình chóp là
A.
3
a
24
B.
3
a6
24
C.
3
a6
12
D.
3
a
12
Hướng dẫn giải
Ta có:
SA (ABC) AB



o
SAB 60
.
ABC
vuông cân nên BA = BC =
a
2
;
ABC
2
S
1a
BA.BC
24
o
a6
SA AB.tan60
2

.
Vy
23
ABC
1 1 a a 6 a 6
V S .SA
3 3 4 2 24
. Vậy chọn đáp án B
Câu 24. Cho hình chóp
S.ABC

ABC
u cnh
a
bit
SA
vuông góc v
ABC
và
SBC
hp vi
ABC
mt góc 60
o
. Th
tích hình chóp là
A.
3
a
8
B.
3
a3
4
C.
3
a3
8
D.
3
3a 3
8
Hướng dẫn giải
m cu nên AM
BC
SA
BC

) .
Vy góc[(SBC);(ABC)] =
o
SMA 60
.
Ta có V =
ABC
11
B.h S .SA
33
o
3a
SAM SA AMtan60
2
a
o
60
S
C
B
A
a
o
60
M
C
B
A
S
16
Vy V =
3
ABC
1 1 a 3
B.h S .SA
3 3 8

. Vậy chọn đáp án C.
Câu 25. Cho hình chóp
S.ABCD

ABCD
là hình vuông có cnh
a
và
SA

ABCD
và mt bên
SCD
hp vt góc 60
o
.
Th tích hình chóp
S.ABCD
là
A.
3
a
8
B.
3
a
3
C.
3
3a 3
8
D.
3
a3
3
Hướng dẫn giải
Ta có
SA (ABC)
và
CD AD CD SD
(1)

o
SCD , ABCD SDA 60 .

SAD
vuông nên SA = AD.tan60
o
=
a3

2
3
ABCD
a
1 1 a 3
V S .SA a 3
3 3 3
Vậy chọn đáp án D.
H
a
D
C
B
A
S
o
60
17
DẠNG 2. KHỐI CHÓP CÓ HÌNH CHIẾU CỦA ĐỈNH LÊN MẶT
PHẲNG ĐÁY
Câu 1. Cho hình chóp S.ABCD ABCD AB = a,
BC a 3
, H ABSHC) và
(SHDSD 
góc 60
0
a.
A.
3
a 13
V
2
B.
3
a 13
V
3
C.
3
3a 13
V
2
D.
3
5a 13
V
2
Hướng dẫn giải
Ta có:
(SHC) (ABCD)
(SHD) (ABCD)
(SHC) (SHD) SH

SH (ABCD)
SH là chiu cao ca hình chóp
S.ABCD.
Ta có HD là hình chiu vuông góc ca SD lên (ABCD)
SD,ABCD SD,HD
0
SDH 60
0
SH HD.tan60
a 39
2
Vy
S.ABCD ABCD
1
V S .SH
3
1
AB.AD.SH
3
. Vậy
chọn đáp án A.
Câu 2. Cho hình chóp S.ABC u cnh 2a, hình chiu
vuông góc ca S trên mt phng (ABCm c n AB, góc
ging thng SC và mt phng (ABC)bng
0
60
. Tính theo a th tích
khi chóp S.ABC .
A.
3
Va
B.
3
V a 3
C.
3
V 2a
D.
3
V 3.a 3
Hướng dẫn giải
60
0
a
3
a
H
D
A
B
C
S
3
1 39 13
. 3.
3 2 2
aa
aa
18
Ta có:
0
SC, ABC SCH 60
0
2a 3
SH CHtan60 . 3 3a
2
2
2
ABC
2a 3
S a 3
4

.
23
S.ABC ABC
11
V SH.S .3a.a 3 a 3
33
Vậy chọn đáp án B.
Câu 3. Cho hình chóp S.ABC có góc gia SC và mng 45
0
ABC
là tam giác vuông ti A có
AB 2a
, góc
0
ABC 60
và hình chiu ca S lên
mt phng (ABCm AB. Tính theo a th tích khi chóp S.ABC.
A.
3
2.a 39
V
3
B.
3
a 39
V
3
C.
3
2.a 37
V
3
D.
3
4.a 39
V
3
Hướng dẫn giải
 :
AC 2a 3
2
ABC
1
S AB.AC 2a 3
2

 :
HC a 13
0
SCH SC, ABC 45
.
Xét tam giác SHC vuông ti H :
SH HC a 13
.
3
S.ABC
2a 39
V
3
Vậy chọn đáp án A.
Câu 4. S.ABCABCBABa
ACaABC
HACSAABC

S.ABC
60
0
2a
H
C
B
A
S
45
0
2a
60
0
H
C
B
A
S
19
A.
3
V 3a
B.
3
Va
C.
3
V 4a
D.
3
V 3a 5
Hướng dẫn giải

SH (ABC)
SAABC
0
SAH 60
0
SH AH.tan60 2a 3
22
BC AC AB 2a 3
2
ABC
1
S AB.AC 2a 3
2

3
SABC ABC
1
V .SH.S 4a
3

Chọn đáp án C.
Câu 5. S.ABCDABCDABa
ADaABM
a
AM
2
ACMDH
 SH ABCD 
SH a
 
S. HCD
A.
3
4a
V
5
B.
3
a
V
15
C.
3
4a
V
15
D.
3
2a
V
15
Hướng dẫn giải
AMDDAC

AM AD 1
AD DC 2



ADH DCH

00
ADH HDC 90 DHC 90
ADCD
2 2 2
AC AD DC AC a 5

ADCDHACDADC
2a
4a
60
0
H
B
C
A
S
2a
a
H
M
B
A
D
C
S
20

DC.DA 2a
DH
AC
5

DHCH
22
4a
HC DC DH
5


HCD
2
HCD
1 4a
S DH.HC
25

S.HCD
3
S.HCD HCD
1 4a
V SH.S
3 15


Vậy chọn đáp án C.
Câu 6. S.ABC ABC  B
AB a 3

0
ACB 60
SABC
 ABC  E   AC 
SE a 3
  
S.ABC
A.
3
a . 78
V
18
B.
3
5a . 78
V
18
C.
3
a . 77
V
18
D.
3
7a . 78
V
18
Hướng dẫn giải


SG ABC


AB
AC 2a
sinACB


AB
BC a
tanBCA


BE a
GE
33


2
ABC
1 a 3
S AB.BC
22


2
2 2 2
a a 26
SG SE GE 3a
93

23
S.ABC ABC
1 1 a 26 a 3 a 78
V SG.S . .
3 3 3 2 18
Chọn đáp án A.
a
3
a
3
60
0
E
N
G
A
B
C
S
21
Câu 7. Cho ABCD là hình vuông cnh bng 1, gi M m AB. Qua
M dng thng vuông góc
ABCD
m S sao cho
5
SM
3
. Th tích khi chóp S.ADCM, khi chóp S.BCM và khi chóp
S.BCD lt là x, y, z. Giá tr
2 2 2
1 1 2
150
x y z
là:
A.
17,2
B.
247,6
C.
8,4
D.
5,2
Hướng dẫn giải
+ Ta có:
ADCM
AM CD .AD
3
S
24

S.ADCM ADCM
1
V .SM.S
3
1 5 3 5
..
3 3 4 12


2
55
xx
12 144
BCM
BM.BC 1
S
24

S.BCM BCM
1 1 5 1 5
V .SM.S . .
3 3 3 4 36
2
55
yy
36 1296
+
BCD
BC.CD 1
S
22

S.BCD BCD
1 1 5 1 5
V .SM.S . .
3 3 3 2 18
2
55
zy
36 324
Vy
2 2 2
1 1 2 42
150 8,4
5
x y z
Chọn đáp án C
Câu 8. Cho hình chóp S.ABC ABC là tam giác vuông ti B,
AB a 3
,
0
ACB 60
, hình chiu vuông góc ca S lên mt phng
ABC
là trng
tâm tam giác ABC, gi E m AC, góc gia SE và mt ph
là 30
0
. Th tích khi chóp S.ABC là:
B
D
A
S
C
M
22
A.
3
a
6
B.
3
a
18
C.
3
a
9
D.
3
12
a
Hướng dẫn giải
Gi G là trng tâm tam giác ABC
SG ABC
Xét tam giác ABC vuông ti B có
2
sin

AB
AC a
ACB
,
22
BC AC AB a
,
2
13
.
22
ABC
a
S AB BC
Do ABC vuông ti B nên:
2

AC
BE a
33
BE a
GE
0
, 30SE ABC SEG
0
3
.tan tan30
39
aa
SG GE SEG
Vy
23
.
1 1 3 3
. . .
3 3 9 2 18
S ABC ABC
a a a
V SG S
Đáp án B
Câu 9. Cho hình chóp S.ABCD ABCD là hình vuông cnh a, mt bên
SAB  u, mt bên SCD là tam giác vuông cân ti S. Th tích
khi chóp
.S ABCD
là V. T s
3
a
V
gn nht giá tr 
A.
5
B.
7
C.
8
D.
9
Hướng dẫn giải
2
ABCD
Sa
.
Gi M, N l   m AB và
CD.
K
SH MN
Ta có:
CD MN,CD SN
30
G
S
C
B
A
E
B
D
A
S
C
N
M
H
23
CD SMN
CD SH
mà
SH MN
SH ABCD
+ Ta có SAB u, SCD là tam giác vuông cân ti S
a3
SM
2

,
CD a
SN
22

Tam giác SMN có:
2
2
2 2 2 2
a 3 a
SM SN a MN
22







Tam giác SMN vuông ti S
2
a 3 a
.
SM.SN a 3
22
SH
MN 4
a
Do vy
3
2
S.ABCD ABCD
1 1 a 3 a 3
V .S .SH .a .
3 3 4 12
3
a
4 2 6,93
V
Chọn đáp án B
Câu 10. Cho hình chóp
S. ABCD
 
ABCD
là hình thoi cnh a,
0
BAC 60
, hình chiu vuông góc ca S trên mt phng
ABCD
trùng vi
trng tâm ca tam giác
ABC.
Mt phng
SAC
hp vi mt phng
ABCD
góc 45
0
. Th tích khi chóp
S. ABCD
bng V. Giá tr
3
6V
a
là:
A.
3
2
B.
1
6
C.
1
2
D.
2
2
Hướng dẫn giải
Ta có
0
BAC 60
nên tam giác ABC u
2
ABCD ABC
a3
S 2.S
2
Gi
O AC BD
.
Ta có
AC BD,AC SG
AC SBD
AC SO
. Mt khác
OB AC
60
O
C
S
A
D
B
G
24
0
SAC , ABCD SOB 45
Xét tam giác SOG vuông ti G:
0
1 a 3
SG OG.tanSOB OG.tan45 BO
36
Vy
23
S.ABCD ABCD
1 1 a 3 a 3 a
V SG.S . .
3 3 6 2 12
Đáp án C
Câu 11. Cho hình chóp S.ABCD  nht cnh AB = 2a, AD =
a. Hình chiu vuông góc ca S lên mt phng
ABCD
m H ca
AB. Cnh SC to vt góc bng 30
0
. Th tích khi chóp S.ABCD là V
thì t s
3
V
a
gn giá tr nào nht trong các giá tr sau:
A.
0,5
B.
1
C.
1,5
D.
2
Hướng dẫn giải
Ta có
2
ABCD
S AD.AD 2a
HC là hình chiu vuông góc ca SC
lên
ABCD
0
SC, ABCD SCH 30
Xét tam giác BHC vuông ti B có:
22
HC BH BC a 2
-Xét tam giác SHC vuông ti H có :
0
a6
SH HC.tanSCH HC.tan30
2
Vy
3
3
SABCD ABCD
1 1 a 6 a 6
V S .SH .2a. 0,82a
3 3 2 3
Chọn đáp án B
Câu 12. Cho hình chóp S.ABCD   ABCD là hình ch nht tâm O,
AB a;AD a 3.
Hình chiu ca S trên mt phng (ABCD) trùng vi
m H ca OA. Bit góc gia SC và mt phng (ABCD) bng 60
0
. Th
tích khi chóp S.ABCD là
30
B
D
A
S
C
H
25
A.
3
3
Va
2
B.
3
3
Va
5
C.
3
1
Va
2
D.
3
3
V a 3
2
Hướng dẫn giải
Ta có:
(SC,(ABCD)) (SC,AC) SCA

3 3a
AC 2a;SH
2

23
ABCD S.ABCD ABCD
13
S 3a ; V SH.V a .
32
Chọn đáp án A.
Câu 13. Cho hình chóp S.ABCD ABCD là hình vuông cnh a, hình
chiu vuông góc ca S trên mt phng (ABCDm H thuc cnh AD
sao cho HD = 2HA. Bit góc gia SB và mt phng (ABCD) bng 30
0
. Tính
theo a th tích ca khi chóp S.ABCD là
A.
3
a 30
V
27
B.
3
a 30
V
7
C.
3
a3
V
27
D.
3
5a 30
V
27
Hướng dẫn giải
Ta có
a 2a
AH ,DH
33

, do
SH (ABCD)
SH là chiu cao ca
khi chóp S.ABCD và góc gia SB vi
mt phng (ABCD) là góc
0
SBH 30
;
0
SH
tanSHB tan30
HB

2
0 2 2 0 2
a 1 a 30
SH HB.tan30 AB AH .tan30 a .
99
3

S.ABCD ABCD
1
V .SH.S
3
,vi
a 30
SH
9
,
3
22
ABCD S.ABCD
1 a 30 a 30
S a V . .a
3 9 27
.
Chọn đáp án A.
a
60
0
a
3
H
O
B
A
D
C
S
30
0
a
H
O
B
A
D
C
S
26
Câu 14. Cho hình chóp S.ABCD  nht tâm I,AB= 2a
3
,
BC = 2a.ng cao H h t nh S xum
DI. Cnh bên SB to v
0
. Tính th tích khi chóp S.ABCD
A.
3
V 12a
B.
3
V 11a
C.
3
V 10a
D.
3
V 9a
Hướng dẫn giải
0
SBH 60
SABCD ABCD
11
V S .SH AB.BC.SH
33

3
1
.2a 3.2a.3a 3 12a
3

Chọn đáp án A.
Câu 15. Cho hình chóp S.ABCD ABCD 
S ABCDO 
AC và BD
SA a 2
,
AC 2a
,
a5
SM
2
M là trung
AB. Tính theo a S.ABCD.
A.
3
a5
V
3
B.
3
a
V
3
C.
3
2a 3
V
3
D.
3
a3
V
3
Hướng dẫn giải

22
SO (ABCD) SO AC,OA a,
SO SA OA a
OSM
O:
22
1
OM SM SO a
2
Ta có:
ABC
B:
22
BC 2MO a,AB AC BC a 3
3
S.ABCD
13
V AB.BC.SO a
33

. Chọn đáp án D.
Câu 16.nh a. Hình
chiu ca S lên mt phng ABCD trùng vi trng tâm ca tam giác ABD.
2a
3
60
0
2a
H
I
B
A
D
C
S
O
M
D
A
B
C
S
27
Mt bên SAB to vt góc 60
0
. Tính theo a th tích khi chóp
SABCD
A.
3
a3
V
9
B.
3
a
V
9
C.
3
a3
V
3
D.
3
a3
V
7
Hướng dẫn giải
Gi G là trong tâm tam giác ABD, E
là hình chiu ca G lên AB
Ta có
0
0
AB (SGE) SEG 60
SG GE.tan60

Mà
3
SABCD
1 a 3
GE BC V
39
Chọn đáp án A.
Câu 17.            i A,
AB AC a
m ca SC, hình chiu vuông góc cnh S trên
mm H ca cnh BC, mt phng (SAB) to vi m
mt góc bng 60
0
. Tính th tích khi chóp S.ABC theo a
A.
3
a3
V
12
B.
3
a3
V
2
C.
3
a 3 3
V
12
D.
3
a
V
12
Hướng dẫn giải
Gm caAB
Vì SH (ABC)nên SH AB (2)
T (1) và (2) suy ra AB SK
a mp(SAB)vng góc
gia SK và HK và bng
Ta có
60
0
a
G
O
D
A
B
C
S
E
HK AB (1)
0
SKH 60

3
HS HK.tan SKH
2
a
a
60
0
a
K
H
B
C
A
S
28
Chọn đáp án A.
Câu 18. Cho hình chóp S.ABC  ABC u cnh a . Hình
chiu vuông góc cnh S trên mt phng (ABC) là m H thuc cnh BC
sao cho HC = 2HB , góc gia SA vi mABC) bng
0
45
. Tính theo a
th tích khi chóp S.ABC
A.
3
a 21
V
36
B.
3
2a 21
V
36
C.
3
a 21
V
6
D.
3
a 21
V
3
Hướng dẫn giải
Áp dnh lí côsin trong tam giác AHB có:
2 2 2 0
7a
AH HB AB 2HB.AB.cos60
9
a7
AH
3

Góc
ging thng SA và mp (ABC) là góc
0
SAH 45
.
Tam giác SAH vuông
cân ti H nên
a7
SH AH
3

Th tích khi chóp S.ABC là
3
ABC
1 a 21
V S .AH
3 36

Chọn đáp án A.
Bài toán 19.  nht,vi AB
= 2a, BD =
a6
. Hình chiu vuông góc ca S lên (ABCD) trùng vi trng
tâm G ca tam giác ca tam giác BCD, góc to bi SC và mng 60
0
.
Th tích khi chóp S.ABCD là
A.
3
a
V
3
B.
3
4a
V
3
C.
3
2a
V
3
D.
3
4a
V
5
Hướng dẫn giải
S.ABC S.ABC
3
1
Vaäy V .S .SH
3
1 1 3
. .AB.AC.SH
3 2 12
a

45
0
a
H
S
B
C
A
29

60
0
.
+ AD =
a2
=> SABCD = 2a.
a2
=
2
2 2a
+
2 a 6
GC AC
33

0
;SG GC.tan60 a 2
3
2
S.ABCD ABCD
1 1 4a
V .SG.S .a 2.2 2a
3 3 3
Chọn đáp án B.
Câu 20. uông ti A, cnh AC
= a,
AB 2a
,
SC a 5
ng cao h t n mt phng
ABC
trùng vm ca cnh AB. Tính theo a th tích khi chóp S.ABC
A.
3
a
V
3
B.
3
4a
V
3
C.
3
2a
V
3
D.
3
4a
V
5
Hướng dẫn giải

SH ABC

S.ABC ABC
1
V S .SH
3

2
ABC
11
S .AB.AC 2a.a a
22

Xét tam giác HA
2 2 2 2 2 2
CH HA AC a a 2a

2 2 2 2 2 2
SH SC CH 5a 2a 3a SH a 3
3
2
S.ABC ABC
1 1 a 3
V S .SH .a .a 3
3 3 3

Chọn đáp án A.
Câu 21.  nht có AB = a, BC
m cnh AB, SH vuông góc vi mt phnh bên
a5
SA
2
. Tính th tích hình chóp S.ABCD
60
0
O
M
C
B
A
D
S
G
a
a
5
2a
H
B
C
A
S
30
A.
3
a
V
3
B.
3
2a
V
3
C.
3
2a
V
13
D.
3
2a
V
5
Hướng dẫn giải
SH
(ABCD). Tam giác SHA vuông

22
SH SA HA a
3
S.ABCD ABCD
1 2a
V S .SH
33


Chọn đáp án B.
Câu 22. Cho hình chóp
S.ABCD
nh a,
3a
SD
2
.
Hình chiu vuông góc H cnh S lên mt phng (ABCDm
cn
AB
. Tính theo a th tích khi chóp
S.ABCD
A.
3
a
V
3
B.
3
2a
V
3
C.
3
2a
V
13
D.
3
2a
V
5
Hướng dẫn giải

SH

chóp S.ABCD và
2 2 2 2 2
2 2 2
SH SD HD SD (AH AD )
3a a
( ) ( ) a a
22
ABCD là
2
a
,
3
2
S.ABCD ABCD
1 1 a
V SH.S a.a
3 3 3
Chọn đáp án D.
Câu 23. Cho hình chóp S.ABCD ABCD 
S lên mp(ABCDO 
chéo AC và BD
5
SA a 2,AC 2a,SM a
2
M 
AB. Tính theo a S.ABCD
a
5
2
a
2a
O
H
C
B
A
D
S
3a
2
a
O
H
C
B
A
D
S
31
A.
3
a3
V
2
B.
3
a3
V
3
C.
3
a3
V
7
D.
3
5a 3
V
3
Hướng dẫn giải

SO (ABCD) SO AC, OA a
,
22
SO SA OA a
22
1
OSM O:OM SM SO a
2
Ta có
22
ABC B: BC 2MO a,
AB AC BC 3a
3
S.ABCD
13
V AB.BC.SO a
33

Chọn đáp án B.
Câu 24. i A và
D. Có AD = DC = a và AB = 2a. Hình chiu vuông góc ca S trên mt phng
  m ca AB và góc to bi hai mt phng ( SBC) và
(ABCD ) bng 60
0
. Tính th tích kh
A.
3
a6
V
4
B.
3
3a 6
V
4
C.
3
a6
V
2
D.
3
5a 6
V
4
Hướng dẫn giải

SH (ABCD)
HI BC(I BC)
,

BC (SHI) BC SI
. Suy ra góc
0
SIH 60
.
Ta có
2
ABCD
(AB DC).AD (2a a).a 3a
S
2 2 2

Ta có AH = HB = a , suy ra ADCH là hình vuông
22
CH AH a BC CH HB a 2
BC a 2
HI
22
(
BCH vuông cân)
O
M
C
B
A
D
S
a
a
I
H
A
D
C
B
S
32

0
a 2 a 6
SH HI.tanSIH .tan 60
22
3
S.ABCD ABCD
1 a 6
V SH.S
34

Chọn đáp án A.
Câu 25. ng ti A và
B. Hình chiu ca S lên mt phng (ABCD) trùng vm I ca AC
và BC. Mt bên (SAB) hp v  t góc
0
60
. Bit rng
AB BC a, AD 3a
. Tính th tích khi chóp S.ABCD
A.
3
a3
4
B.
3
a3
2
C.
3
3a 3
2
D.
3
a3
3
Hướng dẫn giải

Suy ra
0
SKI 60
.
Do
KI BI
IK / /AD
AD BD

.
Mà
BI BC a 1 BI 1 BI 1
ID AD 3a 3 BI ID 4 BD 4
Suy ra
KI 1 3a 3a 3
KI SI
AD 4 4 4
3
S.ABCD ABCD
1 1 3a 3 1 a 3
V SI.S . . a 3a .a
3 3 4 2 2
Vậy chọn đáp án B.
a
60
0
3a
I
B
A
D
C
S
33
DẠNG 3. KHỐI CHÓP CÓ MẶT BÊN VUÔNG GÓC VỚI ĐÁY
Để xác định đường cao hình chóp ta vận dụng định lí sau
( ) ( )
( ) ( ) d
a ( )
a ( )
ad

Câu 1. Cho hình chóp S.ABC ABC là tam giác vB, BA=3a,
BC=4aSBCABC
SB 2a 3
và
0
SBC 30
S.ABC.
A.
3
V a . 3
B.
3
Va
C.
3
V 3a . 3
D.
3
V 2a . 3
Hướng dẫn giải
SH vuông góc BC suy ra SH
vuông góc mp(ABC);
SH=SB.
sinSBC a 3
2
ABC
1
S BA.BC 6a
2

;
3
S.ABC ABC
1
V S .SH 2a 3
3

Vậy chọn đáp án D.
Câu 2. Cho hình chóp S.ABCD nh vuông cnh bng 4, mt bên
SAB u và nm trong mt phng vuông góc vi M, N,
P l    m ca các cnh SD, CD, BC. Th tích khi chóp
S.ABPN là x, th tích khi t din CMNP là y. Giá tr x, y tho mãn bt
ng thc nà
A.
22
x 2xy y 160
B.
22
x 2xy 2y 109
C.
24
x xy y 145
D.
24
x xy y 125
Hướng dẫn giải
4a
3a
2a
3
30
0
C
A
B
S
H
34
Gi H m AB. Do
ABC
u và
SAB ABCD
SH ABCD
Xét
ABC
u:
3AB
SH 2 3
2

Ta có:
ABPN ABCD ADN CNP
S S S S
2
2
AD.DN CN.CP
AB
22
4.2 2.2
4 10
22
S.ABPN ABPN
1 1 20 3
V .S .SH .10.2 3
3 3 3
20 3
x
3

Gi
AN HD K
ta có MK  ng trung bình ca
DHS
1
HK SH
2

CNCMNP P
1 1 1 1 1 2.2 2 3 2 3
V .S .MK . .CN.CP. .SH .
3 3 2 2 3 2 2 3
23
y
3


Chọn đáp án C.
Câu 3. nh a. Mt
bu nm trong mt phng vuông góc v
Th tích khi chóp S. ABCD là
A.
3
a3
3
B.
3
a3
6
C.
3
a
6
D.
3
a3
Hướng dẫn giải

SAB

SH AB
mà
(SAB) (ABCD) SH (ABCD)
       
chóp.

a3
2
K
B
D
A
S
C
H
N
P
M
a
H
D
C
B
A
S
35
Suy ra
3
ABCD
1 a 3
V S .SH
36

. Vậy chọn đáp án B.
Câu 4. Cho t diu, BCD là tam giác vuông
cân ti D , (ABC)
(BCD) và AD hp vi (BCD) mt góc 60
o
, AD=a. Th
tích t din ABCD là
A.
3
a
9
B.
3
a3
6
C.
3
a3
9
D.
3
a3
3
Hướng dẫn giải

ABC

(BCD) ,
ABC BCD
ABC BCD BC AH BCD
AH BC
Suy ra:
0
AD, BCD ADH 60
Ta có AH
HD
AH = AD.tan60
o
=
a3
& HD = AD.cot60
o
=
a3
3
BCD
BC = 2HD =
2a 3
3
. Suy ra
3
BCD
V
1 1 1 a 3
S .AH . BC.HD.AH
3 3 2 9

. Vậy chọn đáp án C.
Câu 5. i B, có
BC = a. Mt bên SAC vuông góc vt bên còn lu to vi
mt góc 45
0
. Tính th tích khi chóp SABC
A.
3
a
12
B.
3
a3
9
C.
3
3a
12
D.
3
a3
3
Hướng dẫn giải
a
60
0
H
A
B
C
D
36
 BC vì mp(SAC) mp(ABC)
nên SH      
      SI
AB, SJ    
0
SIH SJK 45
Ta có:
 
giác HIBJ là hình thoi nên BH là
   
ABC
 

HI = HJ = SH =
VSABC= . Vậy chọn đáp án A.
Câu 6. u cnh a, tam giác SBC vuông
cân ti S và nm trong mt phng vuông góc vi (ABC). Tính th tích khi
chóp SABC.
A.
3
a
9
B.
3
a3
9
C.
3
a3
16
D.
3
a
16
Hướng dẫn giải

Ta có:
SBC ABC
SBC ABC BC SH ABC
SH BC
a
SH
2
23
ABC
1 1 a a 3 a 3
V SH.S . .
3 2 2 4 16
. Vậy chọn đáp án C.
Câu 7. T diu lt nm
trong hai mt phng vuông góc vi nhau bit AD = a. Tính th tích t din.
HJHISHJSHI
2
a
12
.
3
1
3
a
SHS
ABC
45
I
J
H
A
C
B
S
a
a
a
H
S
c
B
A
37
A.
3
6a
9
B.
3
a3
9
C.
3
a3
36
D.
3
a6
36
Hướng dẫn giải
Ta có:
ABC BCD
ABC BCD BC AH BCD
AH BC

ABC DBC AH DH

Suy ra:
a
AH
2
mà
a
2.
BC 3 2AH a 2
2
AH BC
2
3 3 3

2
3
1 a a 2 3
. . .
3 2 4
3
a3
V
36




. Vậy chọn đáp án C.
Câu 8. Cho hình chóp S.ABC có
oo
BAC ABC90 ; 30
; SBC là tam giác
u cnh a và (SBC)
(ABC). Tính th tích khi chóp S.ABC
A.
3
a
6
B.
3
a
16
C.
3
a
3
D.
3
a
9
Hướng dẫn giải
Ta có:
0
0
BC a
a3
AB BCcos30
2
a
AC BCsin30
2


2
ABC
1 a 3 a a 3
S . .
2 2 2 8

30
0
H
S
B
C
A
a
H
A
B
C
D
38

23
1 a 3 a 3 a
V . .
3 2 8 16

. Vậy chọn đáp án B.
Câu 9. i M là trung
m ca AB. Tam giác SAB cân ti S và nm trong mt phng vuông góc
v
ABCD
, bit
SD 2a 5
, SC to vi m
ABCD
mt góc
0
60
. Tính theo a th tích khi chóp S.ABCD
A.
3
4a 15
3
B.
3
a 15
3
C.
3
4a
3
D.
3
a
3
Hướng dẫn giải

SM ABCD

ABCD
nên
     
ABCD
là
0
SCM 60
Trong tam giác vuông SMC và SMD ta có:
2 2 0
SM SD MD MC.tan60
mà ABCD
là hình vuông nên
MC MD
2 2 2
SD MC 3MC MC a 5
SM a 15

Li có
2
2
2 2 2
ABCD
AB 5BC
MC BC BC 2a S 4a
24



Vy
3
S.ABCD ABCD
1 4a 15
V SM.S
33

. Vậy chọn đáp án A.
Câu 10. i A, mt bên
    u nm trong mt phng vuông góc vi mt phng
ABC
. Bit
AB a, BC a 3
. Tính th tích khi chóp S.ABC
A.
3
a6
6
B.
3
a
12
C.
3
a6
12
D.
3
a6
4
Hướng dẫn giải
2a
5
60
0
M
D
A
B
C
S
39

SH AB
Do
SAB ABC
nên
SH ABC
        
a3
SH
2
,
22
AC BC AB a 2

3
S.ABC ABC
1 1 a 6
V SH.S SH.AB.AC
3 6 12
Vậy chọn đáp án C.
Câu 11.  nht,
AB a, AD 2a
.
Tam giác SAB cân ti S và nm trong mt phng vuông góc v
ging thng SC và mt phng (ABCD) bng
0
45
. Tính theo a th tích
ca khi chóp S.ABCD
A.
3
a 17
9
B.
3
a 17
3
C.
3
a 17
6
D.
3
a 17
3
Hướng dẫn giải
     AB
SH ABCD
     

0
SCH 45
2
ABCD
S 2a
2
2
3
2
S.ABCD ABCD
a a 17
SH HC 4a
42
1 1 a 17 a 17
V SH.S . .2a
3 3 2 3
Vậy chọn đáp án D.
Câu 12. nh a. SAB là
tam giác vuông cân ti S và nm trong mt phng vuông góc v
gia cnh SC và mt phng (ABCD) bng
0
60
, cnh
AC a
. Tính theo a
th tích khi chóp S.ABCD
a
3
a
H
S
A
B
C
2a
a
45
0
M
D
A
B
C
S
40
A.
3
a3
4
B.
3
a3
2
C.
3
a3
3
D.
3
a3
9
Hướng dẫn giải

SI AB, SAB ABCD SI ABCD
nên
0
a3
SCI SC; ABCD 60 , CI
2
0
3a
SI CItan60
2
         
 
a 3 a 3
AM IN
24
Ta có:
2 2 3
ABCD ABC S.ABCD
a 3 1 a 3 3a a 3
S 2S V . .
2 3 2 2 4
.
Vậy chọn đáp án A.
Câu 13. nh a. Mt bên SAB
là tam giác vuông ti S và nm trong mt phng vuông góc v
chiu vuông góc cng thm H thun AB sao
cho
BH 2AH
. Tính th tích khi chóp S.ABCD
A.
3
a3
3
B.
3
a2
3
C.
3
a2
9
D.
3
a3
9
Hướng dẫn giải
Ta có:
2
2
2a a 2
SH HA.HB SH
93
3
2
S.ABCD ABCD
1 1 a 2 a 2
V SH.S . .a
3 3 3 9
Vậy chọn đáp án C.
60
0
M
C
B
A
D
S
a
H
C
B
A
D
S
41
Câu 14. u và
nm trong mt phng vuông góc vi mt phng (ABCD). Bit
AC 2a, BD 4a
, tính theo a th tích khi chóp S.ABCD
A.
3
a3
15
B.
3
a 15
3
C.
3
2a 15
3
D.
3
a 15
2
Hướng dẫn giải

O AC BD

ra
SH AB
.
Do
AB SAB ABCD
và
SAB ABCD
nên
SH ABCD
Ta có:
AC 2a
OA a
22
BD 4a
OB 2a
22
2 2 2 2
2
ABCD
AB 3 a 15
AB OA OB a 4a a 5; SH
22
11
S AC.BD 2a.4a 4a
22
Th tích khi chóp S.ABCD là
3
2
ABCD
1 1 a 15 2a 15
V SH.S . .4a
3 3 2 3
.
Vậy chọn đáp án C.
Câu 15. i B,
BA 3a
,
BC 4a
, mt phng (SBC) vuông góc vi mt phng (ABC). Bit
SB 2a 3
và
0
SBC 30
. Tính th tích khi chóp S.ABC
A.
3
a
B.
3
a3
C.
3
2a 3
D.
3
2a
Hướng dẫn giải
O
H
C
B
A
D
S
42

Vì
SBC ABC
nên
SH ABC
Ta có
SH a 3

3
S.ABC ABC
1
V SH.S 2a 3
3

Vậy chọn đáp án C
Câu 16.           i A,
AB a, AC 2a
. Mt phng (SBC) vuông góc v   t phng
(SAB) và (SAC) cùng to vi mt ph
0
60
. Tính th tích khi
chóp S.ABC theo a.
A.
3
a3
3
B.
3
2a 3
9
C.
3
a3
9
D.
3
4a 3
9
Giải


ra
SH ABC
và
nên AH là

BAC
.
Ta có:
AB BC BH AB
11
HF HC HC AC
AB.AC 2a
HF
AB AC 3
Suy ra
0
2a 3
SH HF.tan60
3

2
ABC
1
S AB.AC a
2

. Vy
3
S.ABC
2a 3
V
9
. Vậy chọn đáp án B.
Câu 17. nh bng a,
SD a 2
,
SA SB a
, và mt phng (SBD) vuông góc vi mt phng
(ABCD). Tính theo a th tích khi chóp S.ABCD
A
C
B
H
S
A
C
B
H
S
F
E
43
A.
3
a2
4
B.
3
a2
6
C.
3
a2
2
D.
3
a2
8
Hướng dẫn giải

AS AB AD OS OB OD
hay
SBD

2 2 2 2
BD SB SD a 2a a 3
3
2 2 2
3a a
AO AB OB a
42
      

3
S.ABD A.SBD SBD
1 1 1 a a 2
V V S .AO SB.SD.AO a.a 2.
3 6 6 2 12
3
S.ABCD S.ABD
a2
V 2V
6
. Vy ch
Câu 18.         hình vuông cnh 2a,
SA a
,
SB a 3
và mt phng (SAB) vuông góc vi mt phi
M, N lm ca các cnh AB, BC. Tính theo a th tích ca
khi chóp S.BMDN
A.
3
a3
3
B.
3
a
3
C.
3
a2
2
D.
3
a2
3
Hướng dẫn giải
          
SH ABCD
        
S.BMDN
Ta có:
2 2 2 2 2
SA SB a 3a AB SAB
vuôn
AB
SM a
2

a3
SH
2
a
a
a
a
O
C
B
A
D
S
a
a
3
N
O
M
D
A
B
C
S
H
44
Din tích t giác BMDN là:
2
BMDN ABCD
1
S S 2a
2

Th tích khi chóp S.BMDN:
3
BMDN
1 a 3
V SH.S
33


Vậy chọn đáp án A.
Câu 19. Cho hình chóp S.u cnh a, tam giác
SAC cân ti S,
0
SBC 60
, mt phng (SAC) vuông góc vi (ABC). Tính
theo a th tích ca khi chóp S.ABC
A.
3
a
8
B.
3
3a 2
8
C.
3
a2
6
D.
3
a2
8
Hướng dẫn giải
       
SH AC SH ABC

SH h
.
Ta có:
2
2 2 2 2
a
SC HS HC h
4
,
2
2 2 2 2
3a
SB HS HB h
4
Mà
2 2 2 0
SC BS BC 2BS.BC.cos60
2 2 2
2 2 2 2
a 3a 3a 1
h h a 2a h .
4 4 4 2
3
ha
2

Ta có:
2 2 3
ABC S.ABC
a 3 1 3 a 3 a 2
S V .a .
4 3 2 4 8
.
Vậy chọn đáp án D.
60
0
H
A
B
C
S
45
DẠNG 4. KHỐI CHÓP ĐỀU
1. Định nghĩa: Mc gu na
nó là mu và các cnh bên bng nhau
2. Kết quả: u
ng cao hình chóp qua tâm c
Các cnh bên to vng nhau
Các mt bên to vng nhau
Chú ý:
u (t u) ta hiu là hình
u
u khác v
u  u thì b 
u và các cnh bên bng nhau, nói mt cách khác, hình
u
c l
Hình chóp t áy là hình vuông
Câu 1. u S.ABC có cng a, góc gia
cnh bên và mng 60
0
. Tính th tích khi chóp S.ABC.
A.
3
5a . 3
V
12
B.
3
a . 3
V
12
C.
3
a . 5
V
12
D.
3
a . 3
V
10
Hướng dẫn giải
S.ABCABC
G
SG ABC
S.ABC ABC
1
V SG.S
3

ABCa
2
ABC
a3
S
4
AGASABCSA
SA,AG
SAG 60

SG AG SAG

60
0
N
G
A
B
C
S
46
GABC
2 a 3
AG AN
33

SAG
SG AG.tan60 a

23
S.ABC
1 a 3 a 3
V .a.
3 4 12

Chọn đáp án B.
Câu 2. Cho hình chóp t u S.ABCD,  ABCD có din tích là 16cm
2
,
din tích mt mt bên là
2
8 3cm
. Th tích khi chóp S.ABCD là:
A.
3
32 2
cm
3
B.
3
32 13
cm
3
C.
3
32 11
cm
3
D.
3
4cm
Hướng dẫn giải
Ta có
2
ABCD
S 16cm
CD 4cm
22
SCD
1
S 8 3cm SH.CD 8 3cm
2
SH 4 3cm
Xét
SOH
vuông ti O có:
22
2
2
SO SH OH
4 3 2 cm 2 11cm

Vy:
33
S.ABCD ABCD
1 1 32 11
V S .SO .16.2 11cm cm
3 3 3
Vậy chọn đáp án C.
Câu 3. u S.ABC có các cnh bên bng
3
và to
vi mt ph
0
. Th tích khi chóp S.ABC là:
A.
93
32
B.
33
32
C.
3
32
D.
93
16
Hướng dẫn giải
O
B
D
A
S
C
H
47
+ Gi G là trng tâm
ABC
SG ABC
Xét
SGA
vuông ti G có :
0
3
SG SA.sin60
2

0
3
AG SA.cos60
2

3 3 3
AM AG
24
ABC
u
3
AM AB
2

23
AB AM
2
3
2
ABC
AB 3 9 3
S
4 16
Vy
SABC ABC
1 1 9 3 3 9 3
V .S .SM . .
3 3 16 2 32
Chọn đáp án A
Câu 4. u
S.ABC
có cng a. Gi G là
trng tâm tam giác ABC, góc gia SG và mt phng
SBC
là 30
0
. Th tích
khi chóp
S.ABC
là:
A.
3
a3
4
B.
3
a3
8
C.
3
a3
12
D.
3
a3
24
Hướng dẫn giải
- Do
ABC
u nên
2
ABC
a3
S
4
.
- Do
S.ABC
    u
SG ABC
SG BC
, mà
BC AM
BC SAM
SBC SAM
B
S
A
C
M
G
30
C
A
S
B
M
G
48
a
2a
H
O
C
B
A
S
SBC SAM SM
SBC SAM ,SG SAD


nên hình chiu vuông góc ca SG lên
SBC
là
SM
o
SG, SBC SG,SM GSM 30
-Xét tam giác
SGM
vuông ti M có:
0
1 1 a 3 a
SG GM.cotGSM .AM.cot30 . . 3
3 3 2 2
Do vy
23
S.ABC ABC
1 1 a 3 a a 3
V .S .SG . .
3 3 4 3 24
Chọn đáp án D
Câu 5. u SABC cng a và cnh bên bng
2a. Tính th u SABC
A.
3
a 11
12
B.
3
a 12
11
C.
3
a
12
D.
3
a
11
Hướng dẫn giải
Dng SO
(ABC) Ta có SA = SB = SC suy ra OA = OB = OC
Vy O là tâm cu ABC.
u nên
AO =
2 2 a 3 a 3
AH
3 3 2 3

2
2 2 2
11a
SAO SO SA OA
3
a 11
SO
3

.Vy
3
ABC
1 a 11
V S .SO
3 12

Vậy chọn đáp án A.
Câu 6. Cho khi t diu ABCD cnh bng a. Tính th tích khi t din
u ABCD.
A.
3
2a
12
B.
3
3a
12
C.
3
2a
6
D.
3
a
6
Hướng dẫn giải
49
O
C
D
B
A
S
    
,
Vậy chọn đáp án B.
Câu 7. Cho hình chóp t u S.ABCD có c bng 2a, cnh bên
bng
a3
. Tính th tích khi chóp S.ABCD.
A.
3
8a
3
B.
3
a3
3
C.
3
4a
3
D.
3
2a
3
Hướng dẫn giải

    , tâm O; SO
(ABCD);
SA=SB=SC=SD=
a3

AC = 2a.
2
AC 2a 2
AO= a 2
22

2
2
ABCD
S 2a 4a
;
SAO vuông ti O có
22
SO SA AO a
Th tích khi chóp S.ABCD:
3
2
S.ABCD ABCD
1 1 4a
V .S .SA .4a .a
3 3 3
.
Vậy chọn đáp án C.
Câu 8. Cho khi chóp t giác S. ABCD có tt c các c dài bng a .
Tính th tích khi chóp S.ABCD.
ABC
()DO ABC
2
3
4
ABC
a
S
23
33
a
OC CI
22
ô ó :DOC vu ngc DO DC OC
6
3
a
23
1 3 6 2
.
3 4 3 12
a a a
V
O
I
D
A
B
C
50
A.
3
a2
3
B.
3
a2
6
C.
3
a2
9
D.
3
a2
12
Hướng dẫn giải
Dng SO (ABCD). Ta có SA = SB = SC = SD nên OA = OB =OC = OD
ABCD
ng tròn gnoi tip nên ABCD là hình vuông .
Ta có:
22
a2
SO SD DO
2
. Vy
3
a2
V
6
.
Vậy chọn đáp án B.
Câu 9. u S.ABC có cnh ng a, các cnh
u to vt góc 60
o
. Tính th tích ca khi chóp
S.ABC.
A.
3
a2
3
B.
3
a2
6
C.
3
a2
9
D.
3
a2
12
Hướng dẫn giải
      


lên mp(ABC) nên g(SAH) = 60
o
Ta có:
AE =
a3
2
, AH =
a3
3
, HE =
a3
6
SH = AH.tan 60
o
=
a3
. 3 a
3
. Vy VSABC =
23
1 a 3 a 3
.a
3 4 12
.
Vậy chọn đáp án A.
Câu 10. u S. ABC có cnh bên bng a hp v
mt góc 60
o
. Tính th tích hình chóp.
3
2
1 1 2 2
.
3 3 2 6
ABCD
aa
V S SO a
H
F
E
A
C
B
S
51
60
0
a
H
S
A
B
C
O
A.
3
3a
32
B.
3
3a
13
C.
3
3a
23
D.
3
a
32
Hướng dẫn giải
ABC
1
V SH.S
3

AH

Đs:
3
3a
V
32
.
Vậy chọn đáp án A.
Câu 11. Cho u S.ABC có ct bên hp
vt góc 60
o
. Tính th tích hình chóp S.ABC.
A.
3
a3
12
B.
3
a2
24
C.
3
a3
24
D.
3
a
24
Hướng dẫn giải
0
(SAB);(ABC) SHC 60
Tính SO thông qua OH.
Đs:
3
a3
V
24
Vậy chọn đáp án C
Câu 12. ng cao h hp vi mt mt bên mt
góc 30
o
. Tính th tích hình chóp.
A.
3
h
3
B.
3
2h 3
3
C.
3
2h
3
D.
3
h3
3
Hướng dẫn giải
60
0
a
H
S
A
B
C
O
52
60
0
h
a
a
O
A
D
C
B
S

Ta có:
SO (SBC) S
SBC SAH BC
AH SBC
AH BC



0
SO,(SBC) HSO 30
.
ĐÁP SỐ:
3
h3
V
3
. Vậy chọn đáp án D.
Câu 13. Cho hình chóp t u SABCD có chiu cao h , góc nh ca
mt bên bng 60
o
. Tính th tích hình chóp.
A.
3
3h
2
B.
3
h
3
C.
3
2h
3
D.
3
h3
3
Hướng dẫn giải

2
ABCD
11
V SO.S h.a
33

Trong tam giác vuông
SOB
thì
2
2 2 2 2 2 2 2
a2
SB SO OB a h a 2h
2




3
2h
V
3
. Vậy chọn đáp án C.
Câu 14. Cho hình chóp t u có cnh bên bng a hp vt góc
60
o
. Tính th tích hình chóp.
A.
2
a3
B.
3
a2
12
C.
3
a
12
D.
3
a3
12
Hướng dẫn giải
30
0
H
S
A
B
C
O
53
a
60
0
O
S
A
D
C
B
ABCD
1
V SO.S
3
Tính DO
DB
.

Đs:
3
a3
V
12
.
Vậy chọn đáp án D.
54
DẠNG 5. TỈ LỆ THỂ TÍCH
Vic tính th tích ca mt khng hc sinh gii b nhiu sai sót,
 thi li yêu cu hc sinh tính th tích ca mt khi
a khc sinh có th thc hin các cách
sau:
+ Cách 1:
o 
o   ng cao ( phi ch  ng cao
vuông gi vi mt ph
o Tính th tích khi chóp theo công thc
+ Cách 2
o 
o Tình các t s dài c ng cao (n
c ding cao)
ca kht lun
th tích khi cn tìm bng k ln th tích kh
+ Cách 3: dùng t s th tích (Ch áp dng cho khi chóp (t din))
Hai khi chóp S.MNK và
nh S và góc
nh S
Ta có :
S.MNK
S.ABC
V
SM SN SK
..
V SA SB SC
n
B
C
A
S
N
K
M
55
G
M
N
I
C
B
A
S
Câu 1. Cho hình chóp S.ABC có tam giác ABC vuông cân B,
AC a 2
,
SA vuông góc v ABC ,
SA a
.
Gi G là trng tâm tam giác ABC,
mt phng ( ) qua AG và song song vi BC ct SC, SB lt ti M, N.
Tính th tích ca khi chóp S.AMN
A.
3
2a
27
B.
3
a
27
C.
3
a2
27
D.
3
a3
27
Hướng dẫn giải
Ta có: và
Vy:
Gm BC. G là trng tâm, ta có :
// BC MN// BC
Vy: . Vậy chọn đáp án A.
.
1
.
3
S ABC ABC
V S SA
SA a
â ó : 2ABCc n c AC a AB a
2
1
2
ABC
Sa
3
2
11
..
3 2 6
SABC
a
V a a
2
3
SG
SI
2
3
SM SN SG
SB SC SI
4
.
9
SAMN
SABC
V
SM SN
V SB SC
3
42
9 27
SAMN SABC
a
VV
56
Câu 2. Cho tam giác ABC vuông cân A và ng thng
qua C và vuông góc vi mt phng (ABC) lm D sao cho .
Mt phng qua C vuông góc vi BD, ct BD ti F và ct AD ti E.
Tính th tích khi t din CDEF.
A.
3
a3
12
B.
3
a
36
C.
3
a
12
D.
3
a3
36
Hướng dẫn
Tính
3
ABCD ABC
1a
V S .CD
36

Tacó:
Ta có:
Tính :Ta có:
Mà , chia cho
:
T(*) .Vy . Vậy chọn đáp án B.
AB a
CD a
,AB AC AB CD
()AB ACD
AB EC
DB EC
()EC ABD
EFDC
V
. (*)
DCEF
DABC
V
DE DF
V DA DB
2
.DE DA DC
2
DA
22
22
1
22
DE DC a
DA DA a
22
2 2 2
1
3
DF DC a
DB DB DC CB
1
6
DCEF
DABC
V
V

3
1
6 36
DCEF ABCD
a
VV
a
a
F
E
B
A
C
D
57
N
S
O
M
B
D
C
A
Câu 3. Cho khi chóp t u SABCD. Mt mt phng qua A, B và
trunm M ca SC . Tính t s th tích ca hai phn khi chóp b phân
chia bi mt ph
Hướng dẫn giải
     thì hình thang


S.ANB
S.ANB S.ADB
S.ADB
V
SN 1 1
VV
V SD 2 2
Mà VSABMN = VSANB + VSBMN = .

S.ABCD S.MNAB MNAB.ABCD
MNAB.ABCD S.ABCD S.MNAB S.ABCD S.ABCD S. ABCD
V V V
35
V V V V V V
88
 . C
Câu 4. Cho hình chóp t nh a, cnh
bên to v . Gm SC. Mt ph
và song song vi BD, ct SB ti E và ct SD ti F. Tính th tích khi chóp
S.AEMF
A.
3
a3
12
B.
3
a6
6
C.
3
a6
9
D.
3
a6
18
Hướng dẫn giải
)(
)SD
SABCDSBCDSBMN
SBCD
SBMN
VVV
SD
SN
SC
SM
V
V
8
1
4
1
4
1
2
1
.
2
1
.
SABCD
V
8
3
5
3
.
ABCDABMN
SABMN
V
V
60
58
 . Ta có (AEMF)
//BD EF // BD

SOA
có :
Phân chia chóp t giác ta có:
S.AMF
S.AMF S.AME
S.AME
V
SA SM SF SB
. . 1 V V
V SA SM SE SD
 = VSAMF + VSAME =2VSAMF; = 2VSACD = 2 VSABC
Xét khi chóp S.AMF và S.ACD
; có trng tâm I, EF // BD nên:
. Vậy chọn đáp án D.
I SO AM
. D D
1
.
3
S ABC ABC
V S SO
2
DABC
Sa
6
.tan60
2
a
SO AO

3
.D
6
6
S ABC
a
V
. EMFSA
V
.S ABCD
V
1
2
SM
SC

SAC
2
3
SI SF
SO SD
D
1
.
3
SAMF
SAC
V
SM SF
V SC SD
3
DD
1 1 6
3 6 36
SAMF SAC SAC
a
V V V
33
. EMF
66
2
36 18
SA
aa
V
59
Câu 5.         nh a, SA
 . Gu ca A lt lên SB,
SD. Mt pht SC t Tính th tích kh
A.
3
2a 2
9
B.
3
2a 3
9
C.
3
a2
9
D.
3
a3
9
Hướng dẫn
Ta có:
Ta có ;
.
Suy ra: nên AB'
  
AD'
SC.
Vy SC
(AB'D')
Tính
Tính : Ta có:
vuông cân nên
Ta có:
T
Ta có:
S.AC'B'
S.AC'B' S.AC'D'
S.AC'D'
V
SB' SB
1 B'D'/ / BD V V
V SD' SD
2SA a
3
.
12
.
33
S ABCD ABCD
a
V S SA
( ) 'BC SAB BC AB
'SB AB
' ( )AB SBC
. ' ' 'S AB C D
V
. ' 'S AB C
V
''
''
. (*)
SAB C
SABC
V
SB SC
V SB SC
SAC
'1
2
SC
SC
2 2 2
2 2 2 2
' 2 2 2
33
SB SA a a
SB SB SA AB a
''
1
(*)
3
SAB C
SABC
V
V

33
''
1 2 2
.
3 3 9
SAB C
aa
V
60
I
C'
C"
S
I
O
D'
B'
B
D
C
A
. Vậy chọn đáp án A.
Câu 6. Cho kh
lm ca SB và SD. Mt pht SC t
s th tích ca hai kh
A.
1
2
B.
1
4
C.
1
6
D.
1
8
Hướng dẫn giải
Gi O =
AC BD
ng quy tm ca
SO .
K       
nên
SC' 1
SC 3
.
Ta có
SAB'C' SAB'C'
SABC SABCD
VV
SB' SC' 1 1 1 1
..
V SB SC 2 3 6 V 12
 
SAC'D'
SABCD
V
1
V 12
Vy
SAb'C'D' SAB'C' SAC 'D'
SABCD SABCD
V V V
1 1 1
V V 12 12 6
.Vậy chọn đáp án C.
Câu 7. Cho khnh a, SA vuông góc
vi mt ph 2a.Gt là hình chiu ca A lên SB
và SD. Mt pht SC t tích kh
A.
3
4a
45
B.
3
8a
45
C.
3
a
45
D.
3
16a
45
3
. ' ' ' . ' '
22
2
9
S AB C D S AB C
a
VV
61
Hướng dẫn giải


CB

(SBC)

SC (a)
 
SC
(b)
T (a) và (b) suy ra
SC
(AB'C'D') SC AC'
i xng, ta có V = 2V
2 2 2 2
S.AB'C'
2 2 2 2 2 2
S.ABC
V
SB' SC' SB'.SB SC'.SC SA SA 4a 4a 8
. . . .
V SB SC 15
SB SC SB SC 5a 6a
VSABC =
2 3 3 3
SAB'C'
1 a a 8 a 8a
. .2a V .
3 2 3 15 3 45
Vy V =
3
16a
45
. Vậy chọn đáp án D.
Câu 8. Cho hình chóp S.ABC có
SA SB a
,
2SC a
,
60
o
ASB BSC
,
90
o
ASC
. Th tích ca khi chóp S.ABC bng V. T s
3
6V
a
là :
A.
46
3
B.
2
C.
3
D.
3
3
Hướng dẫn giải
A
n
B
D'
O
S
C'
B'
D
C
62
Gi M m SC , ta có
SM a
SAM
vuông cân ti S. Gi H là
 m ca AM . Ta có
22
2 AM SA SM a
12
22
a
SH AM
Ta có SM = BM = a và
60
o
BSC
BSM
u
BM a
BSM
u
Ta có AB = BM = a
ABM
cân ti B .
Mt khác:
2 2 2
2AB BM a
và
22
2AM a
2 2 2
AB BM AM
ABM
vuông cân ti B (định lý pitago đảo)
12
22
a
BH AM
.
Ta có
22
2 2 2
22
22
aa
SH BH a
2 2 2 2
SH BH SB a
SHB
vuông cân ti H (định lý pitago đảo)
Ta có
,SH AM SH HB
SH ABM
2
1
.
22

ABM
a
S AB BM
23
.
1 1 2 2
.
3 3 2 2 12
S ABM ABM
a a a
V SH S
.
3
.
..
.
2
22
6
S ABC
S ABC S ABM
S ABM
V
SC a
VV
V SM
3
6
2
V
a
Chọn đáp án B
* Cách khác: S dng công thc gii nhanh
Tổng quát: Cho chóp S.ABC có
,, SA a SB b SC c
và
,, ASB BSC ASC
.
60
60
B
C
A
S
M
H
63
Th tích khi chóp S.ABC là:
2 2 2
.
12
6
S ABC
abc
V cos cos cos cos cos cos
Áp dc:
3
2 0 2 0 2 0 0 0 0
.
. .2 2
1 60 60 90 2 60 60 90
66
S ABC
a a a a
V cos cos cos cos cos cos
3
6
2
V
a
Chọn đáp án B.
Câu 9. Cho hình chóp t u
.S ABCD
ABCD
cnh a, góc gia mt bên và mt ph
tho mãn
cos =
1
3
. Mt
phng
P
qua AC và vuông góc vi mt phng
SAD
chia khi chóp
.S ABCD
thành hai khn. T l th tích hai khn là gn nht
vi giá tr nào trong các giá tr sau:
A.
0,11
B.
0,13
C.
0,7
D.
0,9
Hướng dẫn giải
.S ABCD
là hình chóp t  u
SO ABCD
. Gi N là trung
m CD
,

CD SN CD ON
SCD ABCD CD
,SCD ABCD SNO
K
CM SD
. Ta có

AC BD
AC SBD AC SD
AC SO
SD ACM ACM SAD
nên mt phng
P
là
ACM
O
B
D
A
S
C
N
M
64
Xét tam giác SON vuông ti N có :
3
2
1
2
cos
3
a
ON a
SN
SNO
22
22
3
2
22
aa
SO SN ON a
Xét tam giác SOD vuông ti O có :
2
2
22
2 10
2
22




aa
SD SO OD a
Ta có
11
..
22

SCD
S CM SD SN CD
3
.
. 3 10
2
10
10
2
a
a
SN CD a
CM
SD
a
Xét tam giác MCD vuông ti M có :
2
2 2 2
3 10 10
10 10




aa
DM CD CM a
Ta có :
10
1 1 1 1
10
. . . . .
2. 2 2 2 10
10
2
MACD MACD
SABCD SACD
a
VV
DM DA DC DM
V V DS DA DA DS
a
1
10

MACD SABCD
VV
. Mt phng
P
chia khi chóp S.ABCD thành 2
khi
MACD
và
SABCM
SABCD MACD SABCM
V V V
9
10

SABCM SABCD
VV

1
0,11
9

MACD
SABCM
V
V
Chọn đáp án A
Tổng quát: Cho hình chóp t  u
.S ABCD
   nh vuông
ABCD cnh a, góc gia mt bên và mt ph
. Mt phng
P
65
qua AC và vuông góc vi mt phng
SAD
chia khi chóp
.S ABCD
thành hai khn. T l th tích hai khn là
2
1
2
cos
V
V
Chứng minh:
Ta có:
2 2 2 2
2
2
2
1
.
cos
1
1 cos 1
2 2.cos
cos
SD SN ND ON ND
SNO
aa
Ta có :
11
..
22

SCD
S CM SD SN CD
2
2
1
.
.
2 cos
1 cos
cos 1
2.cos
a
a
SN CD a
CM
a
SD
2
2 2 2
2
2
.cos
1 cos
1 cos
aa
DM CD CM a
2
2
2
2
11
. . . .
2. 2 2
.cos
1 cos
1 cos
2
1 cos
1 cos
2.cos

MACD MACD
SABCD SACD
VV
DM DA DC DM
V V DS DA DA DS
a
a
2
2
2
22
cos
1 cos
cos 1
1
1 cos 1 cos





MACD SABCD
SABCM SABCD SABCD
VV
V V V

Do vy :
2
cos
MACD
SABCM
V
V
.
66
Câu 10. u
.S ABC
có cng a. Gi
G là trng tâm tam giác ABC, góc gia SG và mt phng
SBC
là
30
0
. Mt phng
P
cha BC và vuông góc vi SA chia khi chóp
.S ABC
thành hai phn. T s th tích hai phn là:
A.
1
6
B.
1
7
C.
6
7
D.
2
3
Hướng dẫn giải
Do
.S ABC
u
SG ABC
SG BC
,
mà
BC AM
BC SAM
SBC SAM
,


SBC SAM SM
SBC SAM SG SAD
nên hình
chiu vuông góc ca SG lên
SBC
là
SM
, , 30
o
SG SBC SG SM GSM
K
MN SA
, ta có
BC SAM SA BC
SA NBC
nên mt
phng
P
là
NBC
.
Xét tam giác
SGM
vuông ti M có:
0
1 1 3
.cot . .cot30 . . 3
3 3 2 2
aa
SG GM GSM AM
23
.
23
3
cos
SG a a
SM
GSM
Xét tam giác
SGA
vuông ti G có:
2
2
22
2 3 21
.
2 3 2 6







a a a
SA SG AG
B
S
A
C
M
G
N
67
11
..
22

SAM
S MN SA SG AM
3
.
. 3 7
22
14
21
6
aa
SG AM a
MN
SA
a
Xét tam giác
SNM
vuông ti N có:
22
22
3 3 7 21
3 14 42
a a a
SN SM MN
Ta có:
21
1
42
..
7
21
6
SNBC
SABC
a
V
SN SB SC SN
V SA SB SC SA
a
1
7

SNBC SABC
VV
.
Mt phng
P
chia khi chóp thành 2 khi
SNBC
và
NABC
SABC SNBC NABC
V V V
6
7

NABC SABC
VV
Do vy
1
6
SNBC
NABC
V
V
Chọn đáp án A.
| 1/68
| | Tải xuống

Có thể bạn quan tâm:

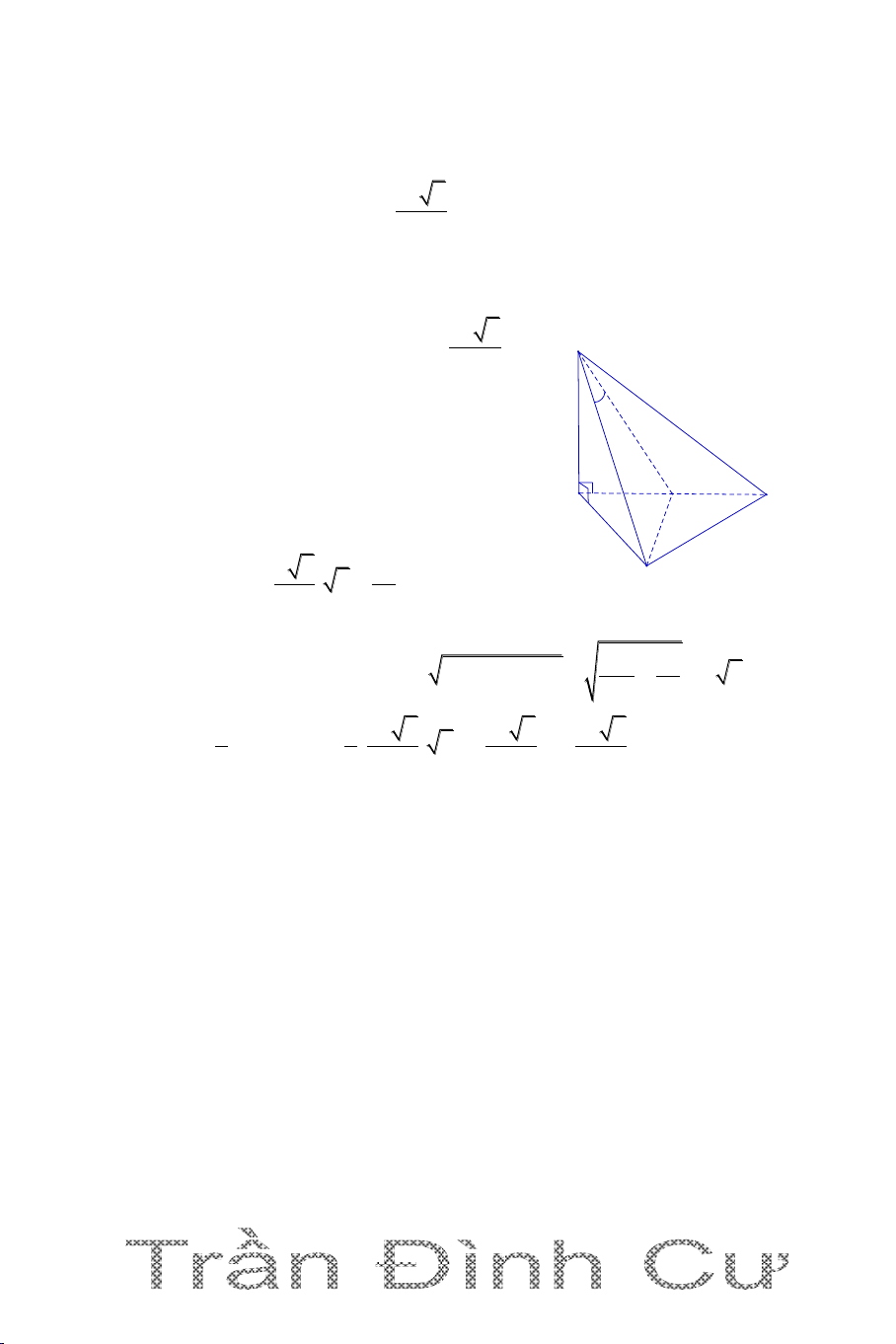
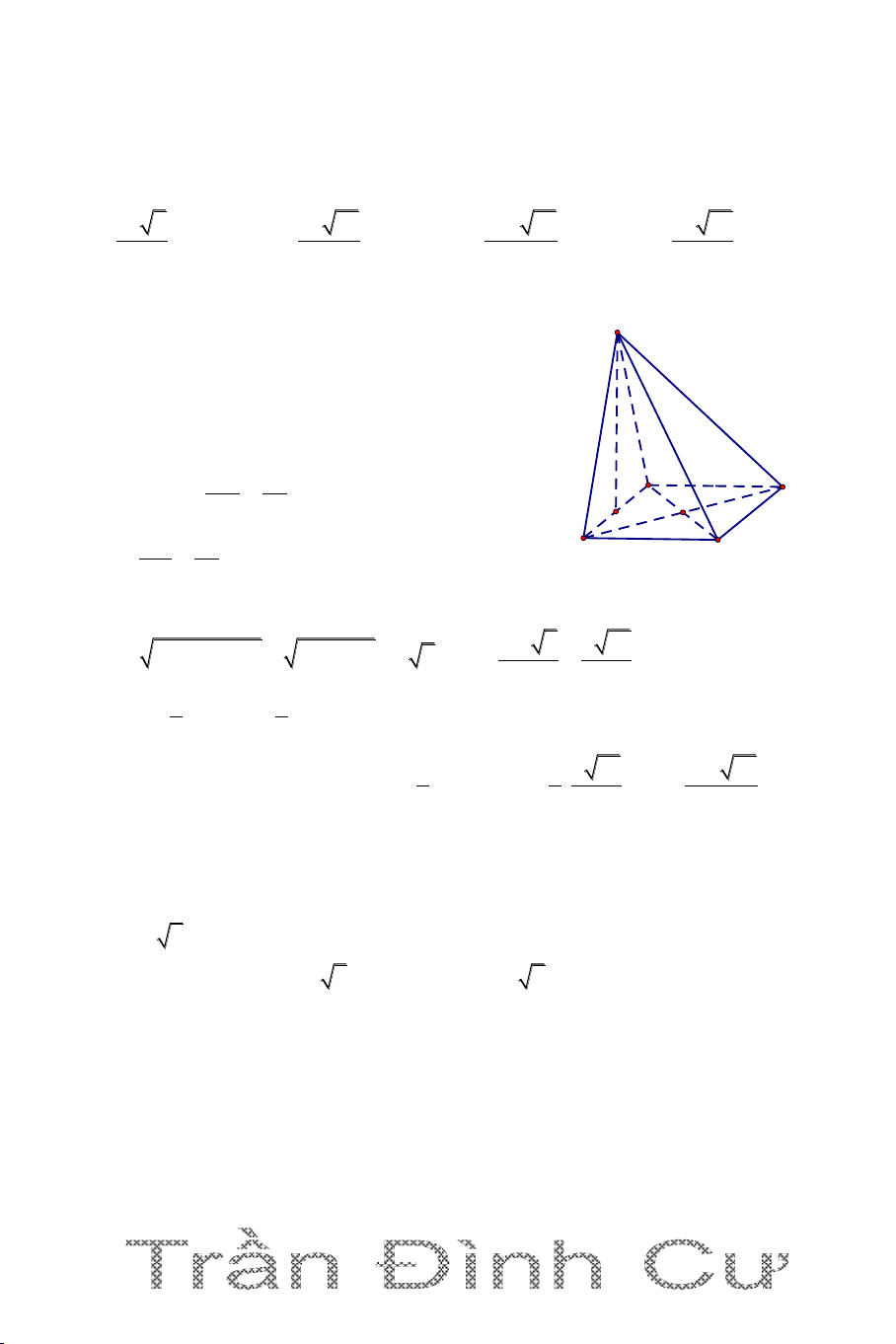
Preview text:

TRẦN ĐÌNH CƯ THỂ TÍCH KHỐI CHÓP QUÀ TẶNG GIÁNG SINH HUẾ, 24/12/2016 MỤC LỤC
CHUYÊN ĐỀ 2. THỂ TÍCH KHỐI CHÓP...................................................... 2
DẠNG 1. KHỐI CHÓP CÓ CẠNH BÊN VUÔNG GÓC ĐÁY ............... 2
DẠNG 2. KHỐI CHÓP CÓ HÌNH CHIẾU CỦA ĐỈNH LÊN MẶT
PHẲNG ĐÁY .............................................................................................. 17
DẠNG 3. KHỐI CHÓP CÓ MẶT BÊN VUÔNG GÓC VỚI ĐÁY ....... 33
DẠNG 4. KHỐI CHÓP ĐỀU ..................................................................... 45
DẠNG 5. TỈ LỆ THỂ TÍCH ........................................................................ 54 1
CHUYÊN ĐỀ 2. THỂ TÍCH KHỐI CHÓP 1
Công thức chung: V  Bh 3
Trong đó: B là diện tích đáy, h là chiều cap
DẠNG 1. KHỐI CHÓP CÓ CẠNH BÊN VUÔNG GÓC ĐÁY
Một số chú ý khi giải toán
 Một hình chóp có một cạnh bên vuông góc với đáy thì cạnh bên
đó chính là đường cao.
 Một hình chóp có hai mặt bên kề nhau cùng vuông góc với đáy
thì cạnh bên là giao tuyến của hai mặt đó vuông góc với đáy.
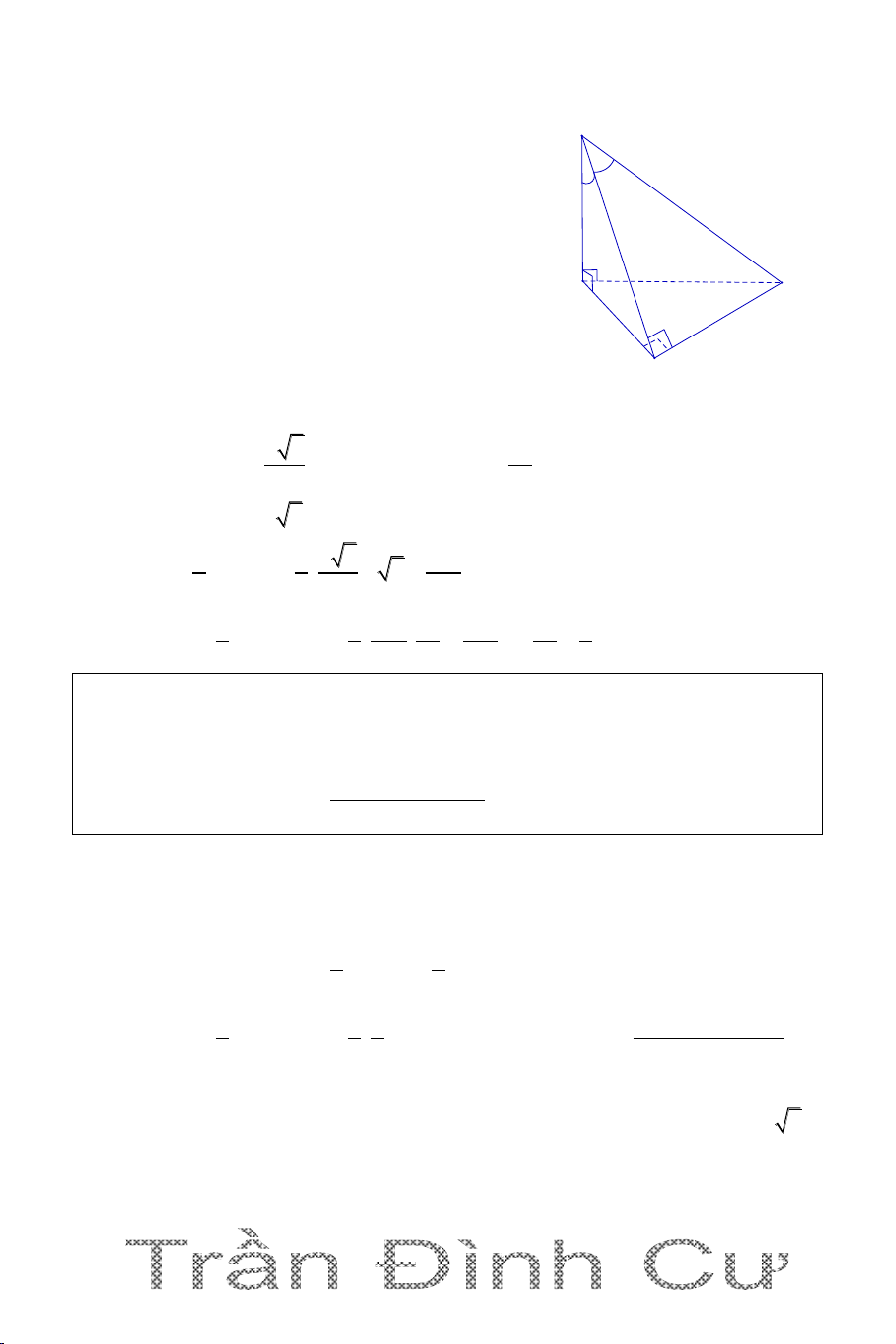
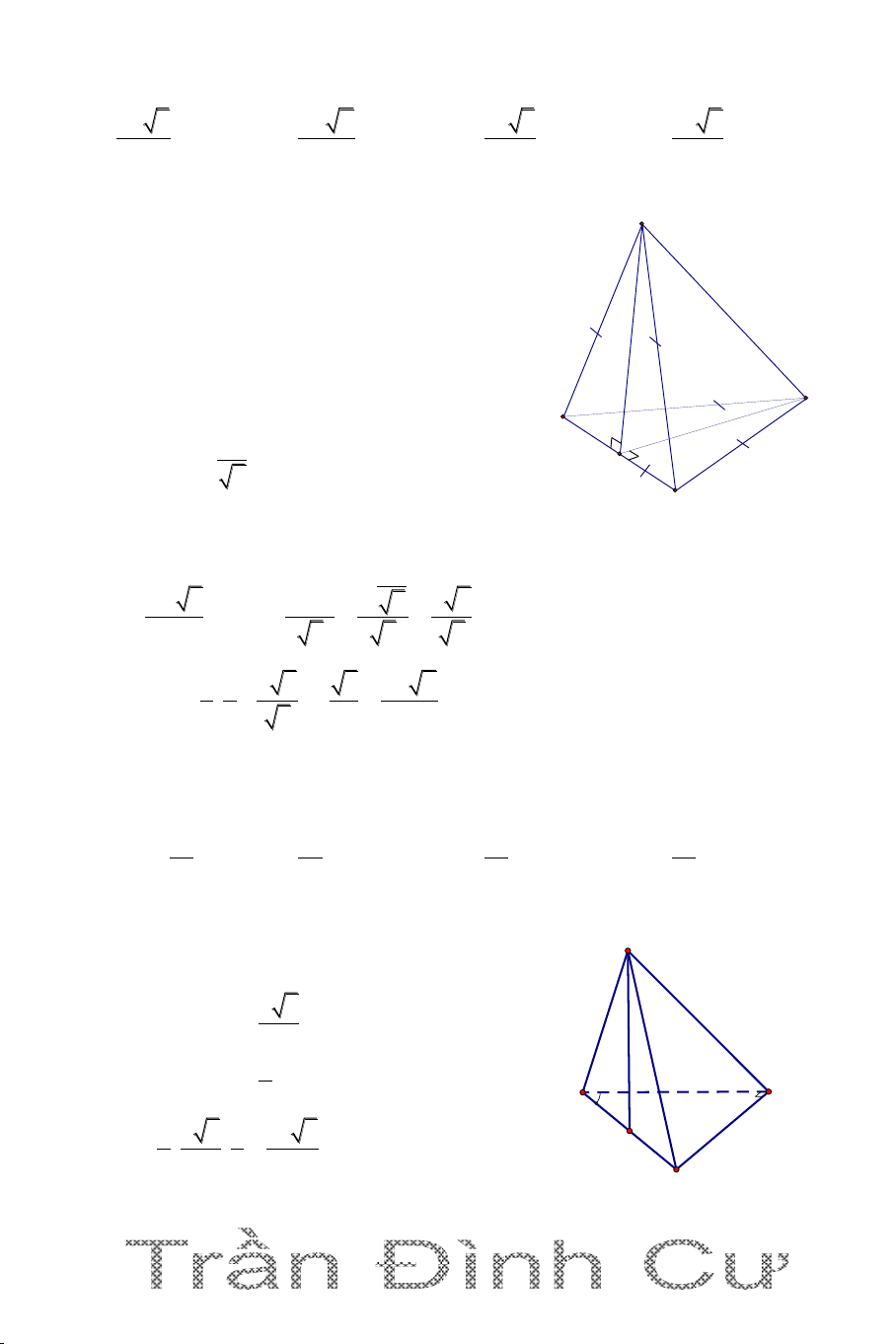
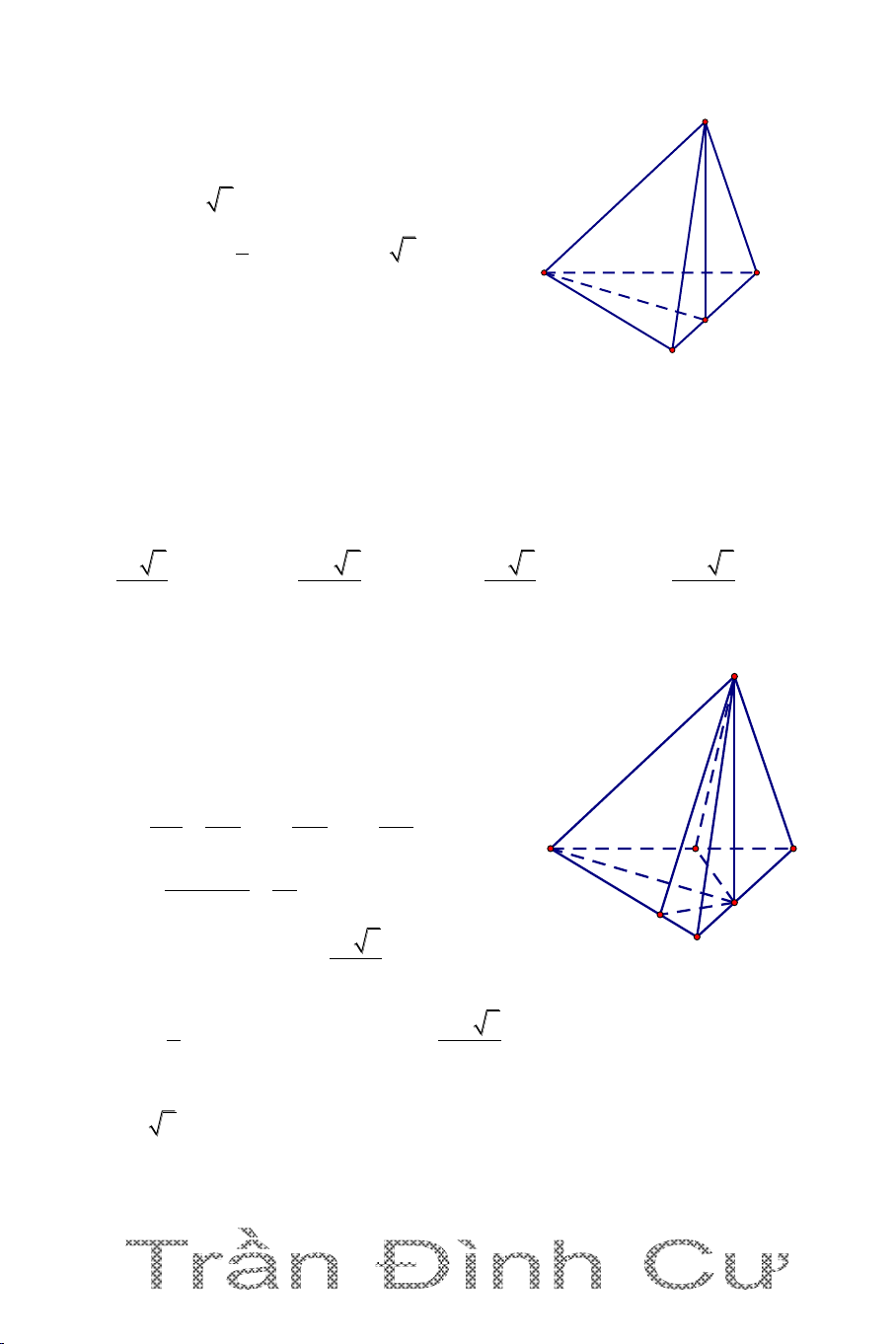
Câu 1. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. SA vuông
góc với mặt phẳng (ABC). Góc giữa đường thẳng SB và mặt phẳng (ABC)
bằng 300. Tính theo a thể tích khối chóp S.ABC . 3 a 13 3 a 3 3a 13 3 5a 13 A. V  B. V  C. V  D. V  2 12 2 2 Hướng dẫn giải
Ta có góc giữa đường thẳng SB và mặt S phẳng (ABC) là  SBA  30 . 2 1 a 3 a 3 S  . .a ; ABC 2 2 4 a 3 SA  tan SB . A AB 3 A C 3 1 a 300 a V  S .SA  . S.ABC ABC 3 12 B
Vậy chọn đáp án A.
Câu 2. Cho hình chóp S.ABCD có chiều cao SA bằng a. Mặt đáy ABCD là
hình thoi cạnh a, góc ABC bằng 600. Tính thể tích khối chóp S.ABCD theo a. 21 23 21 21 A. a B. a C. a D. a 15 14 14 4 Hướng dẫn giải 2
Tam giác ABC đều cạnh a nên S 2 3 S  a ABC 4 Diện tích đáy: 2 3 S  2.S  a ABCD ABC 2 A D Thể tích khối chóp: 3 600 2 3 a 3 V  a .a  B a C 2 2 a 2
Câu 3. Cho hình chóp S.ABCDcó đáy ABCD là hình vuông với AC  . 2
Cạnh bên SA vuông góc với mặt phẳng (ABCD), cạnh bên SB hợp với mặt
phẳng (ABCD) một góc 600. Tính thể tích khối chóp S.ABCD. 3 a 3 3 3a 3 3 a 3 3 3a 3 A. B. C. D. 24 24 8 8 Hướng dẫn giải
Ta có: AB là hình chiếu của SB lên S mặt phẳng ABCD nên    0 SB, ABCD  SBA  60 ;
SA  ABCD  SA là chiều cao của A D 600 a 2 khối chóp S.ABCD 2 B C 2 a a 3 a Tính được AB  ; SA  ; S  ABCD 2 2 4 3 1 a 3 V  .SA.S  (đvtt) S.ABCD ABCD 3 24
Vậy chọn đáp án A.
Câu 4. Cho tứ diện OABC có đáy OBC là tam giác vuông tại O, OB = a, OC =
a 3 , (a > 0) và đường cao OA = a 3 . Tính thể tích khối tứ diện theo a. 3 a 3 a 3 a 3 a A. V  B. V  C. V  D. V  2 3 6 12 Hướng dẫn giải Ta có: 3 2 1 1 a 3 S  OB.OC  a(a 3)  OBC 2 2 2 2 3 1 1 a 3 a
Thế tích khối tứ diện V  S .OA  ( )(a 3)  . OBC 3 3 2 2
Vậy chọn đáp án A.
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, 0 ABC  60
cạnh SA vuông góc với đáy và SC tạo với đáy một góc 600. Tính theo a thể
tích khối chóp S.ABCD. 3 a 3 a 3 2a 3 a A. V  B. V  C. V  D. V  2 3 3 9 Hướng dẫn giải Ta có A  BC đều nên AC  a. S Có: 2 2 
BD  AB  AD  2AB.AD.cos120  BD  a 3 2 A 1 a 3 D Suy ra S  AC.BD  a ABCD 600 2 2 600 B a C 3 1 a Mặt khác 
SA  AC.tan60  a 3. Vậy V  SA.S  . S.ABCD ABCD 3 2
Vậy ta chọn đáp án A.
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình thoi có cạnh bằng a 3 , 0
BAD  120 và cạnh bên SA vuông góc với đáy. Biết mặt phẳng (SBC) và
đáy bằng 600. Tính theo a thể tích khối chóp S.ABCD. 3 a 3 3 3.a 3 3 3.a 3 3.a 3 A. V  B. V  C. V  D. V  4 4 4 5 Hướng dẫn giải 4
Do dáy ABCD là hình thoi có S 0
BAD  120 nên các tam giác ABC,
ADC đều cạnh a 3 .
Gọi H là trung điểm của BC, ta có:
AH BC, SA BC BC SHA B
SBC;ABCD  AH;SH 600 Do đó: 1200 H 0  SHA  60 D a 3 C Tam giác SAH vuông tại A: 0 3a SA  AH.tan 60  2 a 32 3 2 3a 3 Ta có: S  2S  2  . ABCD ABC 4 2 3 1 3a 3 Suy ra: V  SA.S 
. Vậy chọn đáp án B. S.ABCD ABCD 3 4
Câu 7. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , 0
AB  2a, BAC 60 . Cạnh bên SA vuông góc với mặt phẳng (ABC) và
SA  a 3 . Tính theo a thể tích khối chóp S.ABC . A. 3 V  2a B. 3 V  3a C. 3 V  a D. 3 V  4a Hướng dẫn giải
Xét tam giác ABC có: S 0 2 BC  AB.tan60  2a 3  S  2a 3 ABC 1 a 3 3  V  S .SA  2a SABC A  BC 3 Chọn đáp án A A 600 C 2a B
Câu 8. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B có góc 0 BAC  30 , , SA  a , 0
SCA  45 và SA vuông góc với đáy. Thể tích khối V chóp S.ABC là V. Tỉ số
gần giá trị nào nhất trong các giá trị sau: 3 a A. 0,01 B. 0,05 C. 0,08 D. 1 5 Hướng dẫn giải Ta có 0 SCA  45 S  AC  SA.tanSCA  a 0 3a
AB  AC.cosBAC  a.cos30  2 1  45 S  AB.ACsin BAC A  BC A C 2 30 2 1 a. 3.a 1 a 3  . .  2 2 2 8 B 2 3 1 1 a 3 a 3 Vậy V  .S .SA  .a  S.ABC ABC 3 3 8 24 V 
 0,072  Chọn đáp án C 3 a
Câu 9. Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật có
AB  2a,AD  a . Hai
mặt phẳng SAB và SAD c ng vuông góc với đáy, góc giữa hai mặt
phẳng SAB và SBD bằng 450. Thể tích khối chóp S.ABCD là V. Tỉ số
V gần nhất giá trị nào dưới đây: 3 a A. 0,25 B. 0,5 C. 0,75 D. 1,5 Hướng dẫn giải Ta có: 2 S  AB.AD  2a S ABCD
SAB  ABCD và SAD  ABCD
SABSAD  SA SA ABCD H Ta có:
AD  AB,AD  SA  AD  SAB A D
 AD  SB. Kẻ AH  SB  SB  AHD  SB  HD . B C 6 AH  SB,HD   SB Ta có:       0 SAB , SBD  AHD  45 SAB  SBD   SB  AH  AD  a
Xét tam giác SAB vuông tại S có: 1 1 1 AB.AH 2a.a 2a 3    SA    2 2 2 2 2 2 2 AH SA AB 3 AB  AH 4a  a 3 1 1 2a 3 4a 3 V 4 3 Vậy 2 V  .S .SA  .2a .     0,77  S.ABCD ABCD 3 3 3 9 3 a 9
Chọn đáp án C
Câu 10. Cho hình chóp S.ABC có cạnh bên SA vuông góc với đáy và AB = a, AC = 2a, 0
BAC  120 . Mặt phẳng (SBC) tạo với đáy một góc 600. Tính thể
tích của khối chóp S.ABC. 3 a 21 3 a 21 3 2a 21 3 3.a 21 A. V  B. V  C. V  D. V  14 13 13 14 Hướng dẫn giải
Gọi F là hình chiếu vuông góc của A S lên BC. Khi đó SF  BC , suy ra     0 SBC , ABC  SFA  60 2 1 a 3 S .AB.AC.sin BAC A 2a A    BC 2 2 C 1200 a a 21 3a 7 F BC=a 7 , AF  , SA  7 7 B 2 3 1 1 a 3 3a 7 a 21 V  .S .SA  . .  . SABC A  BC 3 3 2 7 14
Vậy chọn đáp án A.
Câu 11. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA  (ABCD),
SB  a 3 . Tính theo a thể tích khối chóp S.ABCD . 3 a 2 3 a 2 3 a 2 3 a 2 A. B. C. D. 3 3 5 3 7 Hướng dẫn giải Ta có: SA = 2 2 2 2 SB  AB  3a  a  a 2 , SABCD = a2 3 1 a . 2 V  S .SA  Chọn đáp án D. ABCD 3 3
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB = 3a,
AD = 4a. SA  (ABCD) , SC tạo với đáy góc 450. Tính thể tích khối chóp S.ABCD. A. 3 V  20a B. 3 V  20a 2 C. 3 V  30a D. 3 V  22a Hướng dẫn giải
Do SA  (ABCD) nên AC là hình chiếu của SC lên đáy.    0
SC, ABCD  SCA  45 . Suy ra: 0 SA  AC.tan 45  5a 1 Suy ra: 3 V  SA.S
 20a . Vậy chọn đáp án A. S.ABCD ABCD 3
Câu 13. Cho tứ diện ABCD có AD vuông góc với mặt phẳng ABC và AB
= 3a, BC = 4a, AC = 5a. AD = 6a. Thể tích khối tứ diện ABCD là: A. 3 6a B. 3 12a C. 3 18a D. 3 36a Hướng dẫn giải 2 2 Tam giác ABC có: 2 2        2 2 AB BC 3a 4a  25a  AC  A  BC vuông tại B 1 1 2 1 1 S 2 3   AB.BC  3a.4a  6a  V  S AD  .6a .6a  12a ABC  2 2 ABCD ABC 3 3
Chọn đáp án B
Câu 14. Cho tứ diện SABC có SA vuông góc với mặt phẳng ABC , hai
mặt phẳng SAB và SBC vuông góc với nhau, SB  a 3 , o BSC  45 , 3 o a
ASB  30 . Thể tích tứ diện SABC là V. Tỉ số là: V 8 4 A. 8 3 2 3 B. C. D. 3 3 3 3 Hướng dẫ n giải 8 + Ta có: S
SA  ABC  SAB  ABC  45
SBC  SAB ,ABC   SAB 30 SBC  ABC   BC  BC  SAB A C  A  BC, S
 BC là các tam giác vuông tại B B Xét S
 AB vuông tại A có : a 3 3a AB  SB.s in ASB  , SA  SB.cos ASB  Xét S
 BC vuông tại B có : 2 2 BC  SB.tan BSC a 3 2 1 1 a 3 3a  S  AB.BC  . .a 3  ABC  2 2 2 4 2 1 1 3a 3a 3 3a 3 a 8 Vậy V  .S .SA  . .   
Chọn đáp án A S.ABC A  BC 3 3 4 2 8 V 3
Tổng quát: Cho tứ diện SABC có SA vuông góc với mặt phẳng ABC , hai
mặt phẳng SAB và SBC vuông góc với nhau, BSC   , ASB   . Thể tích 3 SB .sin 2 .  tan .  tứ diện SABC là: V  S.ABC 12 Thật vậy Xét S
 AB vuông tại A có : AB  SB.sin  , SA  SB.cos Xét S
 BC vuông tại B có : 1 1 BC  SB.tan 2  S  AB.BC  .SB .sin .  tan ABC  2 2 3 1 1 1 SB .sin 2.tan Vậy 2 V  .S
.SA  . .SB .sin.tan .SB.cos  S.ABC ABC 3 3 2 12
Câu 15. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và
D, cạnh bên SD vuông góc với đáy, cho AB  AD  a , CD  3a,SA  a 3 .
Thể tích khối chóp S.ABCD là: 9 3 2a 3 4a 3 a 2 3 2a 2 A. B. C. D. 3 3 3 3 Hướng dẫ n giải
ABCD.AD a  3a.a S + 2 S    2a ABCD 2 2 + 2 2 2 2
SD  SA  AD  3a  a  a 2 Vậy C D 3 1 1 2 2a 2 V  .S .SD  .2a .a 2  S.ABCD ABCD 3 3 3 A B
Chọn đáp án D
Câu 16. Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Hai mặt
phẳng SAB và SAD c ng vuông góc với đáy, góc giữa hai mặt phẳng  3V
SBC và ABCD bằng 300. Thể tích khối chóp S.ABCD là V. Tỉ số là: 3 a 3 B. 3 3 3 A. C. D. 3 2 6 Hướng dẫ n giải     0 a 3
SBC , ABCD  SBA  30  SA  AB.tan SBA  3 1 3 1 a 3 a 3 3V 3 Vậy 2 V  .S .SA  .a .    S.ABCD ABCD 3 3 3 9 3 a 3
Chọn đáp án A
Câu 17. Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật có
AB  a, BC  3a . Hai mặt phẳng SAB và SAD c ng vuông góc với
đáy, cạnh SC hợp với đáy một góc 600. Thể tích khối chóp S.ABCD là: A. 3 a B. 3 2a C. 3 3a D. 3 2 3a Hướng dẫn giải 10 Ta có: 2 S  AB.BC  a 3 S ABCD
SAB  ABCD và SAD  ABCD
SABSAD  SA SA ABCD
Xét tam giác SAC vuông tại S có: A D 60 SA  AC.tan SCA 2 2 0  B C AB  BC .tan 60  2 3a 1 1 Vậy 2 3 V  .S .SA  a 3.2 3  2a S.ABCD ABCD 3 3
Chọn đáp án B
Câu 18. Cho hình chóp S.ABC có tam giác ABC vuông tại B , 0 AB  a,ACB  0 6
, cạnh bên SA vuông góc với mặt phẳng đáy và SB tạo
với mặt đáy một góc bằng 450 . Thể tích khối chóp S.ABC là: 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 6 18 9 12 Hướng dẫ n giải * A
 BC vuông tại B nên S 0 a 3
BC  AB.cot ACB  a.cot 60  3 2 1 1 a 3 a 3  S  BA.BC  a.  ABC  2 2 3 6 A C
* Ta có AB là hình chiếu vuông góc của 45 60 SB trên ABC B      o SB, ABC SB,AB  SBA  45 S
 AB vuông tại A nên o
SA  AB.tanSBA  AB.tan 45  a 2 3 1 1 a . 3 a 3 Vậy V  S .SA  .a  S.ABC ABC 3 3 6 18
Chọn đáp án B 11
Câu 19. Cho tứ diện ABCD có ABC là tam giác đều cạnh a, AD vuông góc
với mặt phẳng ABC , góc giữa BD và mặt phẳng DAC là 300. Thể tích 3 a 6
khối tứ diện ABCD là V. Tỉ số là: V A. 1 B. 3 C. 4 D. 12 Hướng dẫn giải 2 a 3
Ta có ABC là tam giác đều  S  D ABC  4
Gọi M là trung điểm AC 30
Ta có BM  AC,BM  DA  BM  DAC     0 BD, DAC  BDM  30 M A C Xét B
 MD vuông tại M có : 0 a 3 3a DM  BM.cot 30  . 3  B 2 2 2 2 Xét D
 AM vuông tại A có : 2 2 2 9a a DA  DM  AM    a 2 4 4 2 3 1 1 a 3 a 6 3 a 6 Vậy V  .S .DA  . . 2a    12 ABCD ABC 3 3 4 12 V
Chọn đáp án D
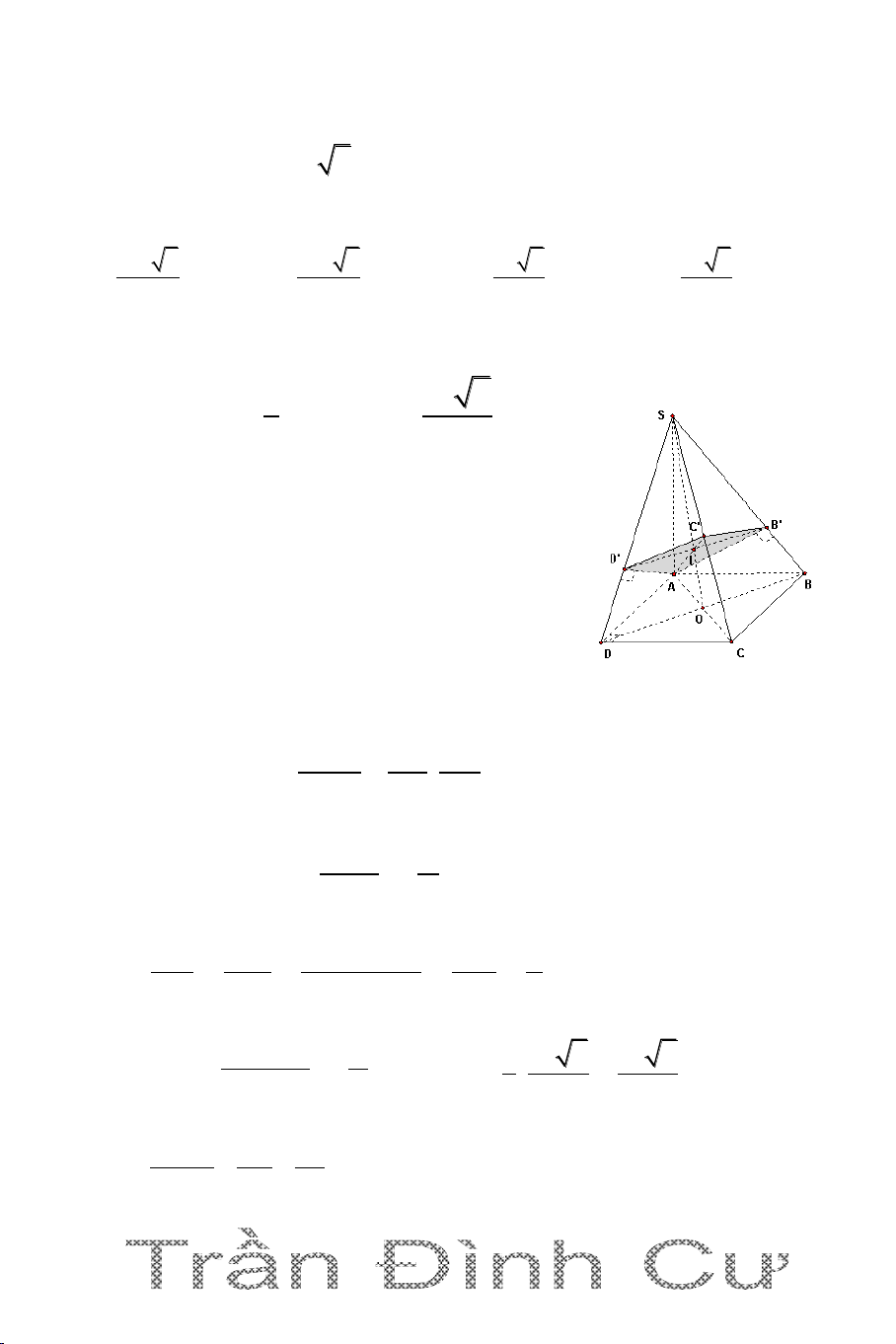
Câu 20. Cho hình chóp S.ABCD có cạnh đáy ABCD là hình vuông cạnh
bằng 20cm, cạnh SA = 30cm và vuông góc với đáy . Gọi B’, D’ lần lượt là
hình chiếu vuông góc của A lên SB và SD. Mặt phẳng AB'D' cắt SC tại C’.
Thể tích khối chóp S.AB'C' D' gần nhất giá trị nào dưới đây: A. 3 1466cm B. 3 1500cm C. 3 1400cm D. 3 15400cm Hướng dẫn giải 12 Do S 1 V  SA.S S.ABCD ABCD 3 1 C' D' 2 3  .30.20  4000cm 3 B' 2 2 SC' SA SA   2 2 2 SC D SC SA  AC A 2 30 9   2 2 2 30  20  20 17 B C 2 2 2 SD' SA SA 30 9     2 2 2 2 2 SD SD SA  AD 30  20 13 V 2V SA SC' SD' SC' SD' Ta có: S.AB'C'D' SAC' D'   . .  . V 2V SA SC SD SC SD S.ABCD SACD 9 9 81 324000 3 V  . V  .4000   1466cm S.AB'C' D' S.ABCD 17 13 221 221
Câu 21. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, cạnh
BC  a 2 , cạnh bên SA vuông góc với mặt phẳng đáy, mặt bên SBC tạo
với mặt đáy một góc bằng 450 . Thể tích khối chóp S.ABC bằng V. Giá trị 6V là: 3 a A. 1 B. 3 2 3 2 C. D. 2 2
Hướng dẫn giải
Gọi M là trung điểm BC S 1 a 2  AM  BC  2 2 2 1 1 2 a  S  AM.BC  BC  ABC  2 4 2
+ Ta có SA  ABC  SA  BC và A 45 C
BC  AM nên BC  SAM  BC  AM M B
AM  BC ( vì  ABC cân tại A) 13      o
SBC , ABC  (SM,AM)  SMA  45 a 2 Ta có S
 AM vuông tại A  SA  AM.tanSMA  AM  2 2 3 1 1 a a 2 a 2 Vậy V  .S .SA  . . 
Chọn đáp án C S.ABC ABC 3 3 2 2 12
Câu 22. Cho hình chóp S.ABC có SA = SB = SC = a, 0 ASB  90 , 0 BSC  120 , 0
ASC  90 . Thể tích khối chóp S.ABC là: 3 a 3 a 3 a 3 3 a 3 A. B. C. D. 2 6 4 12
Hướng dẫ n giải Ta có SA  AB,SA  AC A  SA  SBC 1 0 S SB.SB.sin120 SB   C 2 2 1 S C 2 3 a 3  120 a .  2 2 4 B 1 2 3  1 a 3 a 3 V  V  S .SA  . .a   Đáp án D S.ABC A.SBC S  BC 3 3 4 12
Câu 22. Cho hình chóp SABC có tam giác SBC đều cạnh a , CA  a . Hai
mặt ABC và ASC cùng vuông góc với (SBC). Thể tích hình chóp là 3 a 3 3 a 3 3 a 3 3 a A. B. C. D. 12 2 4 12 Hướng dẫ n giải (  ABC)  (SBC) A    (ASC)  AC (SBC) (SBC)  a _ Do đó 2 3 1 1 a 3 a 3 B C V  S   / SBC.AC a 3 3 4 12 / \
Vậy chọn đáp án A. S 14
Câu 23. Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B với
AC = a biết SA vuông góc với đáy ABC và SB hợp với đáy một góc 60o. Thể tích hình chóp là 3 a 3 a 6 3 a 6 3 a A. B. C. D. 24 24 12 12 Hướng dẫ n giải
Ta có: SA  (ABC)  AB là hình chiếu S của SB trên (ABC). Vậy góc [SB,(ABC)] = o SAB  60 . a A
 BCvuông cân nên BA = BC = ; C 2 A a 2 o 1 a 60 S  BA.BC  ABC 2 4 B o a 6 SA  AB.tan60  . 2 2 3 1 1 a a 6 a 6 Vậy V  S   ABC.SA
. Vậy chọn đáp án B 3 3 4 2 24
Câu 24. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a biết
SA vuông góc với đáy ABC và SBC hợp với ABC một góc 60o. Thể tích hình chóp là 3 a 3 a 3 3 a 3 3 3a 3 A. B. C. D. 8 4 8 8
Hướng dẫ n giải
M là trung điểm của BC, vì tam giác ABC đều nên AM  BC  SA  BC (đl3  ) . S Vậy góc[(SBC);(ABC)] = o SMA  60 . 1 1 Ta có V = B.h  SABC.SA 3 3 C o 3a A S  AM  SA  AMtan60  o 2 60 a M B 15 3 1 1 a 3 Vậy V = B.h  S  ABC.SA
. Vậy chọn đáp án C. 3 3 8
Câu 25. Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh a
và SA vuông góc đáy ABCD và mặt bên SCD hợp với đáy một góc 60o.
Thể tích hình chóp S.ABCD là 3 a 3 a 3 3a 3 3 a 3 A. B. C. D. 8 3 8 3
Hướng dẫ n giải Ta có SA  (ABC) và S CD  AD CD  SD (1) H Vậy góc      o
SCD , ABCD   SDA  60 .  o A 60 D S
 ADvuông nên SA = AD.tan60o = a 3 B a Vậy C 3 1 1 2 a 3 V  S   ABCD.SA a a 3 3 3 3
Vậy chọn đáp án D. 16
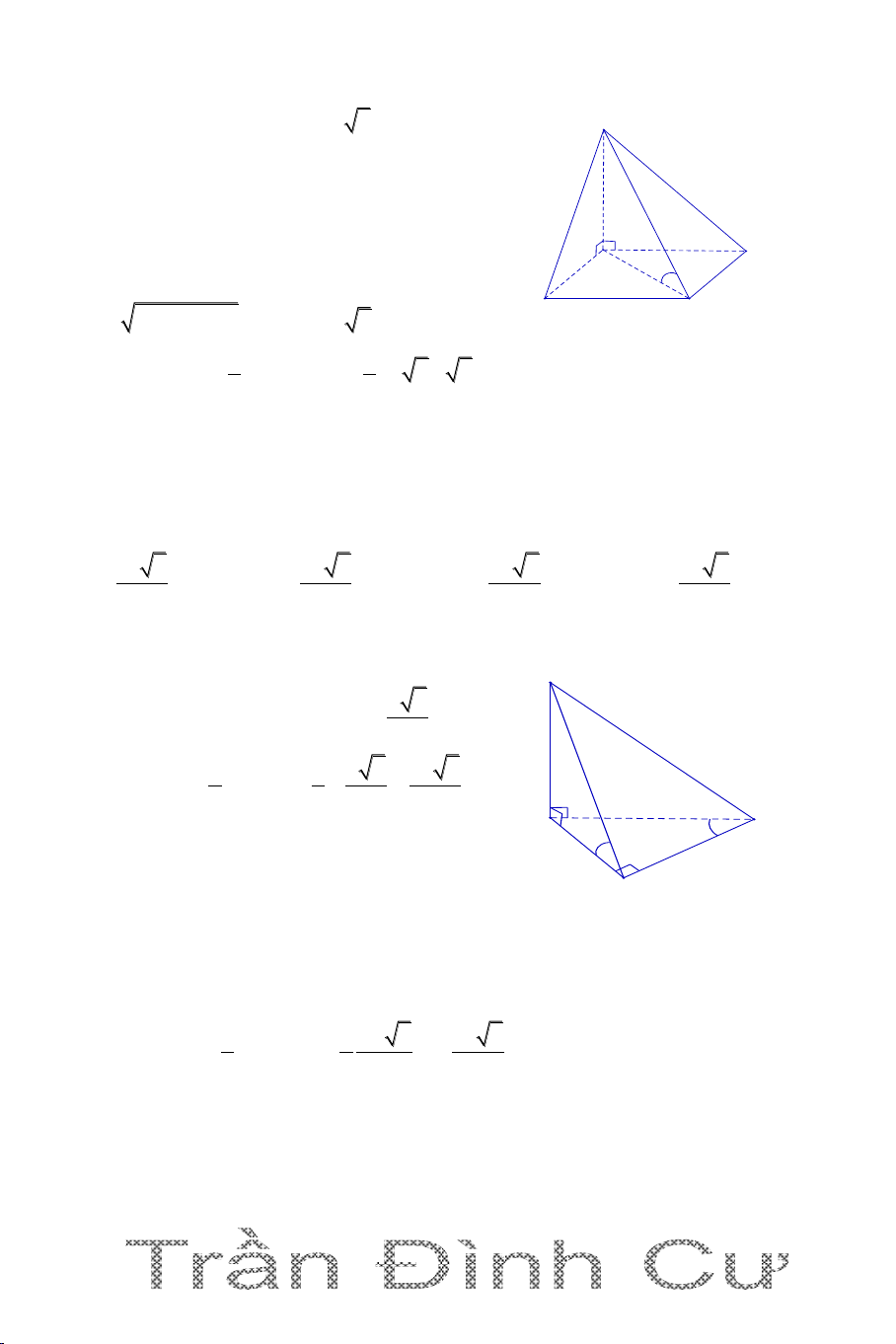
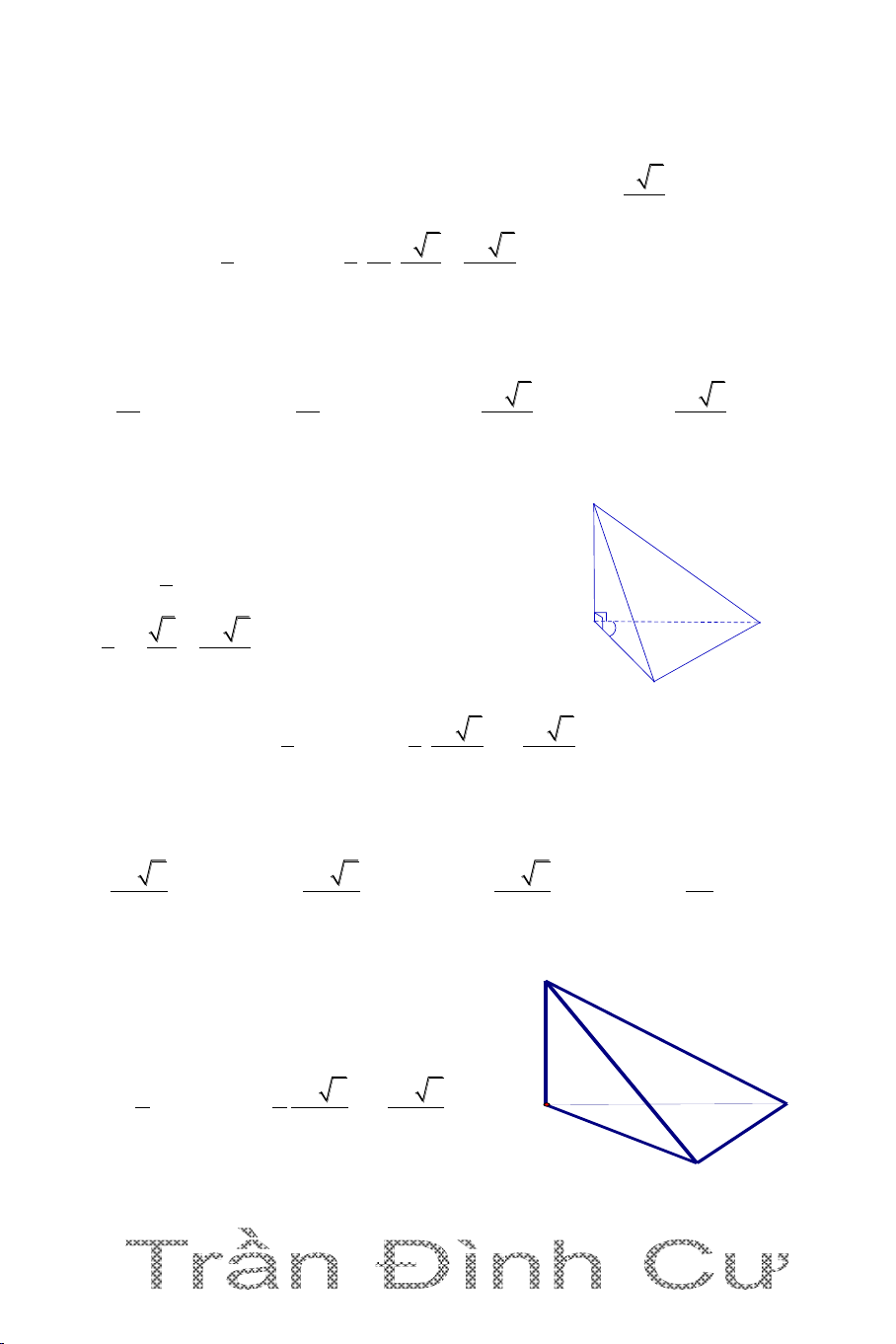
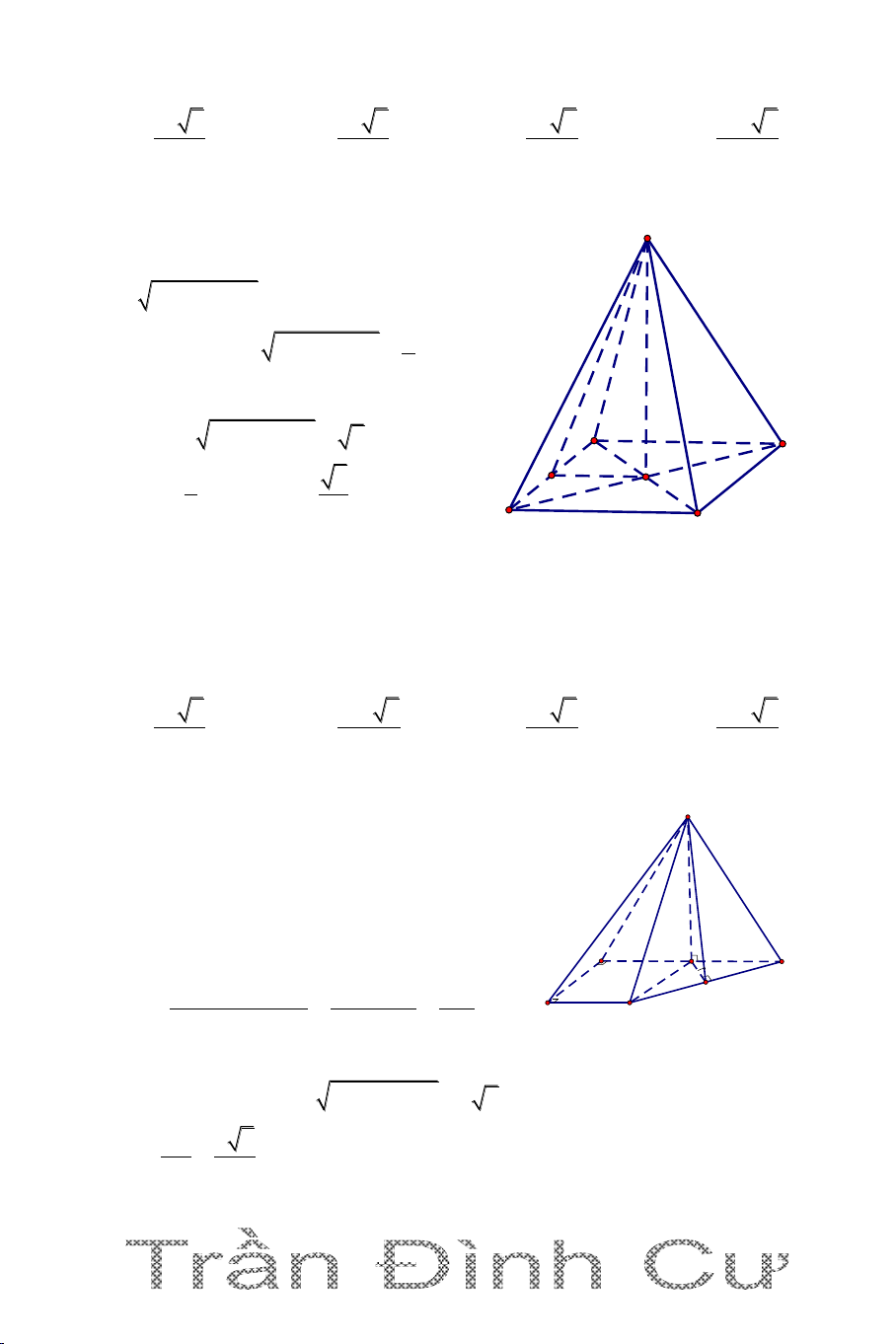
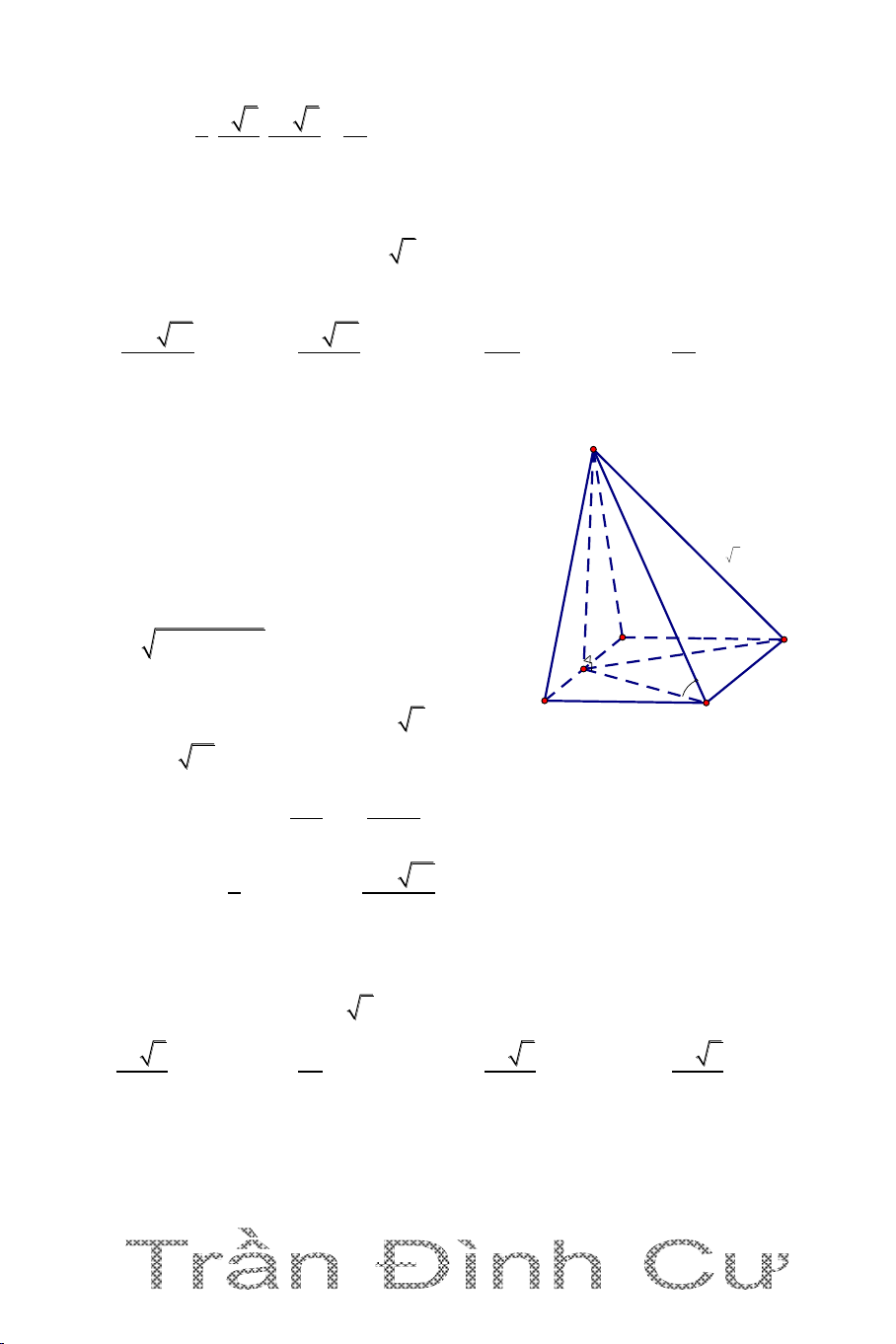
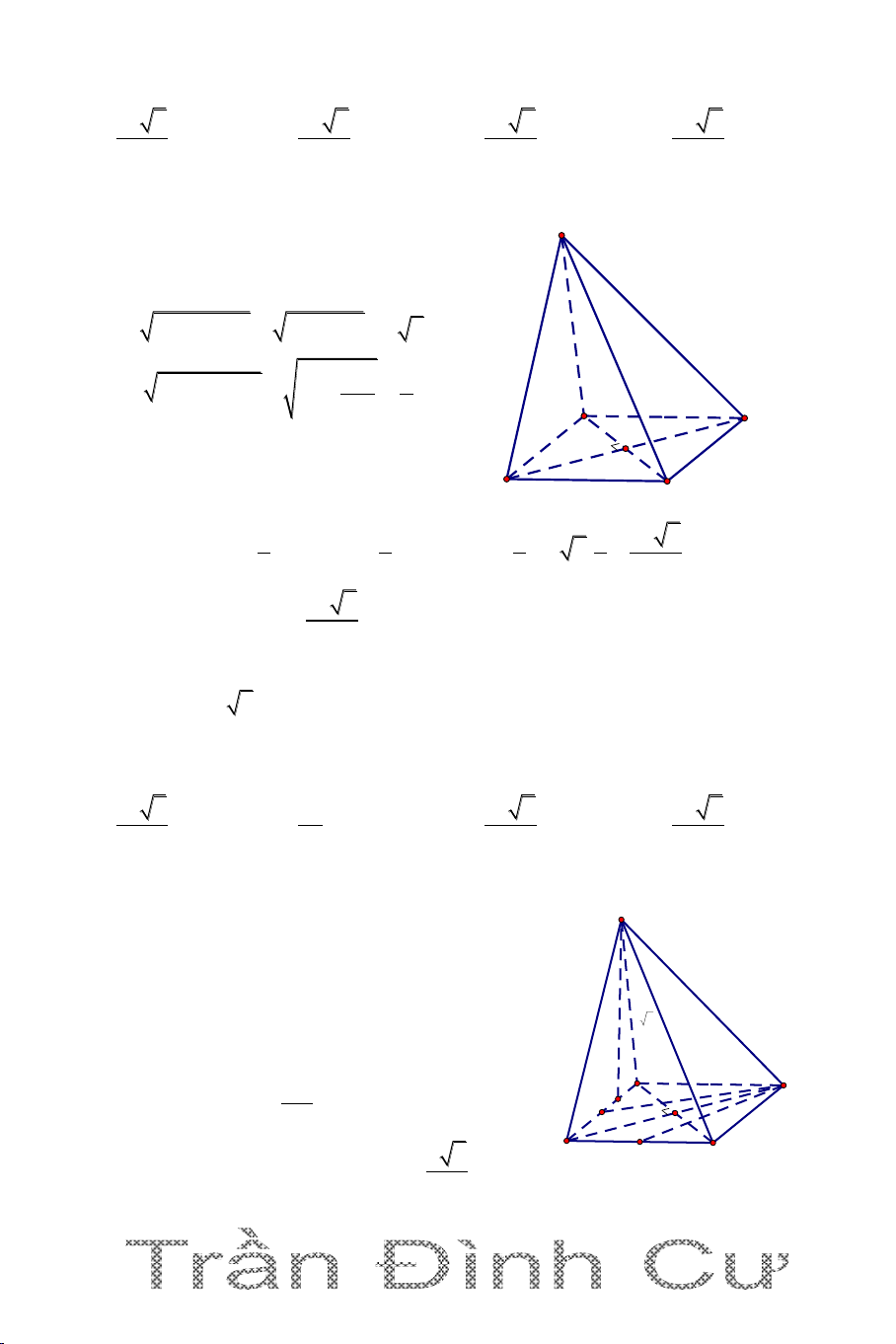
DẠNG 2. KHỐI CHÓP CÓ HÌNH CHIẾU CỦA ĐỈNH LÊN MẶT PHẲNG ĐÁY
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB = a,
BC  a 3 , H là trung điểm của cạnh AB. Biết hai mặt phẳng (SHC) và
(SHD) c ng vuông góc với mặt đáy, đường thẳng SD tạo với mặt đáy một
góc 600. Tính thể tích của khối chóp a. 3 a 13 3 a 13 3 3a 13 3 5a 13 A. V  B. V  C. V  D. V  2 3 2 2 Hướng dẫn giải (  SHC)  (ABCD) S  Ta có: (  SHD)  (ABCD) (SHC)(SHD)  SH   SH  (ABCD)
SH là chiều cao của hình chóp A 600 D S.ABCD. a H B a 3 C
Ta có HD là hình chiếu vuông góc của SD lên (ABCD)
 SD,ABCD  SD,HD 0  SDH  60  0 SH  a 39 HD.tan60  2 1 3 1 a 39 a 13 Vậy V  1 S .SH  AB.AD.SH  . a a 3.  . Vậy S.ABCD ABCD 3 3 3 2 2 chọn đáp án A.
Câu 2. Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a, hình chiếu
vuông góc của S trên mặt phẳng (ABC) là trung điểm của đoạn AB, góc
giữa đường thẳng SC và mặt phẳng (ABC)bằng 0
60 . Tính theo a thể tích khối chóp S.ABC . A. 3 V  a B. 3 V  a 3 C. 3 V  2a D. 3 V  3.a 3 Hướng dẫn giải 17 Ta có:    0 SC, ABC  SCH  60 S 0 2a 3 SH  CHtan 60  . 3  3a 2 2a2 3 2 S   a 3 . ABC 4 600 2a A C H B 1 1 2 3 V  SH.S  .3a.a 3  a 3 S.ABC A  BC 3 3
Vậy chọn đáp án B.
Câu 3. Cho hình chóp S.ABC có góc giữa SC và mặt đáy bằng 450, đáy ABC
là tam giác vuông tại A có AB  2a , góc 0
ABC  60 và hình chiếu của S lên
mặt phẳng (ABC) là trung điểm AB. Tính theo a thể tích khối chóp S.ABC. 3 2.a 39 3 a 39 3 2.a 37 3 4.a 39 A. V  B. V  C. V  D. V  3 3 3 3 Hướng dẫn giải
Tam giác ABC vuông tại A : S AC  2a 3 1 2 S AB.AC 2a 3 A    BC 2
Tam giác AHC vuông tại H : HC  a 13 450     0 A C SCH SC, ABC  45 . 2a 600 H B
Xét tam giác SHC vuông tại H : SH  HC  a 13 . 3 2a 39 V 
. Vậy chọn đáp án A. S.ABC 3
Câu 4. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B; AB = 2a,
AC = 4a. Hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABC) là trung
điểm H của đoạn AC. Góc giữa cạnh bên SA và mp(ABC) bằng 600. Tính thể
tích khối chóp S.ABC. 18 A. 3 V  3a B. 3 V  a C. 3 V  4a D. 3 V  3a 5 Hướng dẫn giải Ta có: SH  (ABC) S
 góc giữa SA và (ABC) là 0 SAH  60 0  SH  AH.tan60  2a 3 2 2 BC  AC  AB  2a 3 1 2  S  AB.AC  2a 3 ABC 2 1 Vậy 3 V  .SH.S  4a 600 2a SABC ABC B 3 A Chọn đáp án C. H 4a C
Câu 5. Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, biết AB = 2a , a
AD = a . Trên cạnh AB lấy điểm M sao cho AM 
, cạnh AC cắt MD tại H . 2
Biết SH vuông góc với mặt phẳng (ABCD) và SH  a . Tính thể tích khối chóp S. HCD. 3 4a 3 a 3 4a 3 2a A. V  B. V  C. V  D. V  5 15 15 15 Hướng dẫn giải
Hai tam giác vuông AMD và DAC S AM AD 1 có   nên đồng dạng, AD DC 2 Suy ra ADH  DCH , mà 0 0
ADH  HDC  90  DHC  90
ADC vuông tại D: A M B 2 2 2 a
AC  AD  DC  AC  a 5 H D 2a C
Hệ thức lượng  ADC: DH.AC = DA.DC 19 DC.DA 2a Suy ra: DH   AC 5
DHC vuông tại H: 2 2 4a HC  DC  DH  5 . 2 1 4a
Do đó diện tích  HCD: S  DH.HC  HCD 2 5 3 1 4a
Thể tích khối chóp S.HCD: V  SH.S  . S.HCD HCD 3 15
Vậy chọn đáp án C.
Câu 6. Cho hình chóp S.ABC có ABC là tam giác vuông tại B, AB  a 3 , 0
ACB  60 , hình chiếu vuông góc của S lên mặt phẳng (ABC) là trọng tâm
tam giác ABC, gọi E là trung điểm AC biết SE  a 3 . Tính thể tích khối chóp S.ABC. 3 a . 78 3 5a . 78 3 a . 77 3 7a . 78 A. V  B. V  C. V  D. V  18 18 18 18 Hướng dẫn giải
Gọi G là trọng tâm tam giác ABC S
Theo giả thiết có SG  ABC
Xét tam giác ABC vuông tại B AB a 3 Có AC   2a , sin ACB E AB BE a C BC   a , GE   A 600 tan BCA 3 3 G a 3 N 2 1 a 3 Ta có S  AB.BC  ABC 2 2 B 2
Xét tam giác SGE vuông tại G có 2 2 2 a a 26 SG  SE  GE  3a   9 3
Vậy thể tích khối chóp S.ABC là 2 3 1 1 a 26 a 3 a 78 V  SG.S  . .  S.ABC ABC 3 3 3 2 18 Chọn đáp án A. 20
Câu 7. Cho ABCD là hình vuông cạnh bằng 1, gọi M là trung điểm AB. Qua
M dựng đường thẳng vuông góc ABCD và trên đó lấy điểm S sao cho 5 SM 
. Thể tích khối chóp S.ADCM, khối chóp S.BCM và khối chóp 3 1 1 2
S.BCD lần lượt là x, y, z. Giá trị    150 là: 2 2 2 x y z A. 1  7,2 B. 2  47,6 C. 8,4 D. 5,2 Hướng dẫn giải + Ta có: S AM  CD.AD 3 S   ADCM 2 4 1  V  .SM.S S.ADCM ADCM 3 1 5 3 5 DA . .  3 3 4 12 M 5 2 5 C x   x  B 12 144 BM.BC 1 S   BCM 2 4 1 1 5 1 5  5 5 V  .SM.S  . .  2  y   y  S.BCM BCM 3 3 3 4 36 36 1296 BC.CD 1 1 1 5 1 5 + S    V  .SM.S  . .  BCD 2 2 S.BCD BCD 3 3 3 2 18 5 2 5  z   y  36 324 1 1 2 42 Vậy    150 
 8,4  Chọn đáp án C 2 2 2 x y z 5
Câu 8. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB  a 3 , 0
ACB  60 , hình chiếu vuông góc của S lên mặt phẳng ABC là trọng
tâm tam giác ABC, gọi E là trung điểm AC, góc giữa SE và mặt p hẳng đáy
là 300 . Thể tích khối chóp S.ABC là: 21 3 a 3 a 3 a 3 a A. B. C. D. 6 18 9 12 Hướng dẫ n giả i
Gọi G là trọng tâm tam giác ABC S
SG  ABC
Xét tam giác ABC vuông tại B có  AB AC  2a , sin ACB 30 E 2 2  A C
BC AC AB a , G 2 1 a 3  SA . B BC   ABC B 2 2 AC BE a
Do ABC vuông tại B nên: BE   a GE   2 3 3  a a SE ABC 0 ,  SEG  30 0 3  SG G .
E tanSEG  tan 30  3 9 2 3 1 1 a 3 a 3 a Vậy VS . G S  . .  S.ABC 3 ABC 3 9 2 18  Đáp án B
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên
SAB là tam giác đều, mặt bên SCD là tam giác vuông cân tại S. Thể tích 3 a khối chóp .
S ABCDlà V. Tỉ số
gần nhất giá trị nào dưới đây: V A. 5 B. 7 C. 8 D. 9 Hướng dẫn giải 2 S  a . S ABCD
Gọi M, N lần lượt là trung điểm AB và CD. A D Kẻ SH  MN M N
Ta có: CD  MN,CD  SN H B C 22  CD  SMN
 CD  SH mà SH  MN  SH  ABCD a 3
+ Ta có SAB là tam giác đều, SCD là tam giác vuông cân tại S  SM  , 2 CD a SN   2 2 2 2  a 3   a  Tam giác SMN có: 2 2 2 2 SM  SN        a  MN  2     2  a 3 a .  SM.SN a 3
Tam giác SMN vuông tại S 2 2  SH    2 MN a 4 3 1 1 a 3 a 3 3 a Do vậy 2 V  .S .SH  .a .    4 2  6,93  S.ABCD ABCD 3 3 4 12 V
Chọn đáp án B
Câu 10. Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a, 0
BAC  60 , hình chiếu vuông góc của S trên mặt phẳng ABCD trùng với
trọng tâm của tam giác ABC. Mặt phẳng SAC hợp với mặt phẳng  6V
ABCD góc 450 . Thể tích khối chóp S. ABCD bằng V. Giá trị là: 3 a 3 1 1 2 A. B. C. D. 2 6 2 2
Hướng dẫn giải Ta có 0
BAC  60 nên tam giác ABC đều S 2 a 3  S  2.S  ABCD ABC 2 Gọi O  AC  BD . A D
Ta có AC  BD,AC  SG  AC  SBD 60 O G B C
 AC  SO . Mặt khác OB  AC 23      0 SAC , ABCD  SOB  45
Xét tam giác SOG vuông tại G: 0 1 a 3
SG  OG.tan SOB  OG.tan 45  BO  3 6 2 3 1 1 a 3 a 3 a Vậy V  SG.S  . . 
Đáp án C S.ABCD ABCD 3 3 6 2 12
Câu 11. Cho hình chóp S.ABCD có đáy là hình chữ nhật cạnh AB = 2a, AD =
a. Hình chiếu vuông góc của S lên mặt phẳng ABCD là trung điểm H của
AB. Cạnh SC tạo với đáy một góc bằng 300. Thể tích k
hối chóp S.ABCD là V V thì tỉ số
gần giá trị nào nhất trong các giá trị sau: 3 a A. 0,5 B. 1 C. 1,5 D. 2 Hướng dẫn giải Ta có 2 S  AD.AD  2a S ABCD
HC là hình chiếu vuông góc của SC lên ABCD     0 SC, ABCD  SCH  30 A
Xét tam giác BHC vuông tại D B có: 2 2 HC  BH  BC  a 2 H 30 B C
-Xét tam giác SHC vuông tại H có : 0 a 6
SH  HC.tan SCH  HC.tan 30  2 3 1 1 a 6 a 6 Vậy 3 V  S .SH  .2a.   0,82a SABCD ABCD 3 3 2 3
Chọn đáp án B
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O,
AB  a; AD  a 3. Hình chiếu của S trên mặt phẳng (ABCD) trùng với
trung điểm H của OA. Biết góc giữa SC và mặt phẳng (ABCD) bằng 600. Thể
tích khối chóp S.ABCD là 24 3 3 1 3 A. 3 V  a B. 3 V  a C. 3 V  a D. 3 V  a 3 2 5 2 2 Hướng dẫn giải
Ta có: (SC,(ABCD))  (SC,AC)  SCA S 3 3a
Tính được AC  2a;SH  2 2 1 3 3 S  3a ; V  SH.V  a . ABCD S.ABCD ABCD 3 2 A a B a 3 H Chọn đáp án A. 600 O D C
Câu 13. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, hình
chiếu vuông góc của S trên mặt phẳng (ABCD) là điểm H thuộc cạnh AD
sao cho HD = 2HA. Biết góc giữa SB và mặt phẳng (ABCD) bằng 300. Tính
theo a thể tích của khối chóp S.ABCD là 3 a 30 3 a 30 3 a 3 3 5a 30 A. V  B. V  C. V  D. V  27 7 27 27 Hướng dẫn giải a 2a S Ta có AH  ,DH  , do 3 3
SH  (ABCD)  SH là chiều cao của
khối chóp S.ABCD và góc giữa SB với mặt phẳng (ABCD) là góc 0 SBH  30 ; A 300 B 0 SH tan SHB  tan 30  H O HB D a C 2 0 2 2 0 2 a 1 a 30
SH  HB.tan 30  AB  AH .tan 30  a  .  9 3 9 1 a 30 Khi đó V  .SH.S ,với SH  , S.ABCD ABCD 3 9 3 2 1 a 30 2 a 30 S  a  V  . .a  . ABCD S.ABCD 3 9 27 Chọn đáp án A. 25
Câu 14. Cho hình chóp S.ABCD có đáy là hình chữ nhật tâm I,AB= 2a 3 ,
BC = 2a.Chân đường cao H hạ từ đỉnh S xuống đáy tr ng với trung điểm
DI. Cạnh bên SB tạo với đáy góc 600. Tính thể tích khối chóp S.ABCD A. 3 V  12a B. 3 V  11a C. 3 V  10a D. 3 V  9a Hướng dẫn giải 0 SBH  60 S 1 1 V  S .SH  AB.BC.SH SABCD ABCD 3 3 1 3  .2a 3.2a.3a 3  12a 3 A 2a 3 600 B Chọn đáp án A. 2a I H D C
Câu 15. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, hình chiếu
vuông góc của đỉnh S lên mặt phẳng (ABCD) tr ng với giao điểm O của hai a 5
đường chéo AC và BD. Biết SA  a 2 , AC  2a , SM  , với M là trung 2
điểm cạnh AB. Tính theo a thể tích khối chóp S.ABCD. 3 a 5 3 a 3 2a 3 3 a 3 A. V  B. V  C. V  D. V  3 3 3 3 Hướng dẫn giải Từ giả thiết S
SO  (ABCD)  SO  AC,OA  a, 2 2 SO  SA  OA  a O  SM vuông tại O: 2 2 1 OM  SM  SO  a A D 2 Ta có: A  BC vuông tại B: M O 2 2 B
BC  2MO  a,AB  AC  BC  a 3 C 1 3 3 V  AB.BC.SO 
a . Chọn đáp án D. S.ABCD 3 3
Câu 16.Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a. Hình
chiếu của S lên mặt phẳng ABCD trùng với trọng tâm của tam giác ABD. 26
Mặt bên SAB tạo với đáy một góc 600. Tính theo a thể tích khối chóp SABCD 3 a 3 3 a 3 a 3 3 a 3 A. V  B. V  C. V  D. V  9 9 3 7 Hướng dẫn giải
Gọi G là trong tâm tam giác ABD, E S
là hình chiếu của G lên AB Ta có 0 AB  (SGE)  SEG  60 0  SG  GE.tan60 A 3 1 a 3 D E 600 G Mà GE  BC  V  SABCD 3 9 O Chọn đáp án A. a B C
Câu 17. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A,
AB  AC  a , I là trung điểm của SC, hình chiếu vuông góc của đỉnh S trên
mặt đáy là trung điểm H của cạnh BC, mặt phẳng (SAB) tạo với mặt đáy
một góc bằng 600 . Tính thể tích khối chóp S.ABC theo a 3 a 3 3 a 3 3 a 3 3 D. A. V  B. V  C. V  12 2 12 3 a V  12 Hướng dẫn giải
Gọi K là trung điểm củaAB S  HK  AB (1)
Vì SH  (ABC)nên SH  AB (2)
Từ (1) và (2) suy ra AB  SK
Do đó góc giữa mp(SAB)với đáy bằng góc giữa SK và HK và bằng  0 SKH 60 a 600 a B Ta có   3 HS HK.tan SKH A 2 K a H C 27 1 Vaäy V  .S .SH S.ABC S.ABC 3 3 1 1 a 3  . .AB.AC.SH  3 2 12 Chọn đáp án A.
Câu 18. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Hình
chiếu vuông góc của đỉnh S trên mặt phẳng (ABC) là điểm H thuộc cạnh BC
sao cho HC = 2HB , góc giữa SA với mặt đáy (ABC) bằng 0 45 . Tính theo a
thể tích khối chóp S.ABC 3 a 21 3 2a 21 3 a 21 3 a 21 A. V  B. V  C. V  D. V  36 36 6 3 Hướng dẫn giải
Áp dụng định lí côsin trong tam giác AHB có: S 2 2 2 0 7a
AH  HB  AB  2HB.AB.cos60  9 Góc a 7  AH  3
giữa đường thẳng SA và mp (ABC) là góc B 0 450 S  AH  45 . A H Tam giác SAH vuông a a 7 C
cân tại H nên SH  AH  3 3 1 a 21
Thể tích khối chóp S.ABC là V  S .AH  ABC 3 36 Chọn đáp án A.
Bài toán 19. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,với AB
= 2a, BD = a 6 . Hình chiếu vuông góc của S lên (ABCD) trùng với trọng
tâm G của tam giác của tam giác BCD, góc tạo bởi SC và mặt đáy bằng 600.
Thể tích khối chóp S.ABCD là 3 a 3 4a 3 2a 3 4a A. V  B. V  C. V  D. V  3 3 3 5 Hướng dẫn giải 28
+ Góc tạo bởi SC và (ABCD) là góc SCG bằng S 600.
+ AD = a 2 => SABCD = 2a. a 2 = 2 2 2a 2 a 6 + GC  AC  0 ;SG  GC.tan60  a 2 3 3 B 600 C 3 1 1 2 4a V  .SG.S  .a 2.2 2a  G S.ABCD ABCD 3 3 3 O M A Chọn đáp án B. D
Câu 20. Cho hình chóp SABC có đáy ABC là tam giác vuông tại A, cạnh AC
= a, AB  2a , SC  a 5 . Chân đường cao hạ từ S đến mặt phẳng ABC
trùng với trung điểm của cạnh AB. Tính theo a thể tích khối chóp S.ABC 3 a 3 4a 3 2a 3 4a A. V  B. V  C. V  D. V  3 3 3 5 Hướng dẫn giải
Gọi H là trung điểm của AB S
 SH  ABC  SH là chiều cao 1 V  S .SH S.ABC A  BC 3 1 1 Với 2 S .AB.AC 2a.a a a 5 ABC     (đvdt) 2 2 2a
Xét tam giác HAC vuông tại A : B A H 2 2 2 2 2 2
CH  HA  AC  a  a  2a a
Xét tam giác SHC vuông tại H: C 2 2 2 2 2 2
SH  SC  CH  5a  2a  3a  SH  a 3 3 1 1 2 a 3  V  S .SH  .a .a 3  (đvtt) S.ABC A  BC 3 3 3 Chọn đáp án A.
Câu 21. Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật có AB = a, BC
= 2a. H là trung điểm cạnh AB, SH vuông góc với mặt phẳng đáy, cạnh bên a 5 SA 
. Tính thể tích hình chóp S.ABCD 2 29 3 a 3 2a 3 2a 3 2a A. V  B. V  C. V  D. V  3 3 13 5 Hướng dẫn giải
SH  (ABCD). Tam giác SHA vuông S tại H. 2 2 SH  SA  HA  a 3 1 2a a 5 V  S .SH  (đvTT). 2 S.ABCD ABCD 3 3 B Chọn đáp án B. C H a O 2a A D 3a
Câu 22. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SD  . 2
Hình chiếu vuông góc H của đỉnh S lên mặt phẳng (ABCD) là trung điểm
của đoạn AB . Tính theo a thể tích khối chóp S.ABCD 3 a 3 2a 3 2a 3 2a A. V  B. V  C. V  D. V  3 3 13 5 Hướng dẫn giải
Từ giả thiết ta có SH là đường cao của hình S chóp S.ABCD và 2 2 2 2 2
SH  SD  HD  SD  (AH  AD ) 3a 3a 2 a 2 2  ( )  ( )  a  a 2 2 2 B
Diện tích của hình vuông ABCD là 2 a , C H 3 1 1 a O 2 a V  SH.S  a.a  S.ABCD ABCD 3 3 3 A D Chọn đáp án D.
Câu 23. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, hình chiếu
vuông góc của đỉnh S lên mp(ABCD) tr ng với giao điểm O của hai đường 5
chéo AC và BD. Biết SA  a 2 ,AC  2a,SM 
a , với M là trung điểm 2
cạnh AB. Tính theo a thể tích khối chóp S.ABCD 30 3 a 3 3 a 3 3 a 3 3 5a 3 A. V  B. V  C. V  D. V  2 3 7 3 Hướng dẫn giải Từ giả thiết S
SO  (ABCD)  SO  AC, OA  a , 2 2 SO  SA  OA  a 2 2 1 O
 SM  O :OM  SM  SO  a 2 A
 BC  B : BC  2MO  a, Ta có 2 2 B AB  AC  BC  3a C M 1 3 3 V  AB.BC.SO  a O S.ABCD 3 3 A D Chọn đáp án B.
Câu 24. Cho hình chóp S.ABCD, đáy ABCD là hình thang vuông tại A và
D. Có AD = DC = a và AB = 2a. Hình chiếu vuông góc của S trên mặt phẳng
(ABCD) là trung điểm của AB và góc tạo bởi hai mặt phẳng ( SBC) và
(ABCD ) bằng 600. Tính thể tích khối chóp S.ABCD đã cho 3 a 6 3 3a 6 3 a 6 3 5a 6 A. V  B. V  C. V  D. V  4 4 2 4 Hướng dẫn giải
Gọi H là trung điểm của AB, suy ra S
SH  (ABCD) . Dựng HI  BC(I BC) ,
khi đó BC  (SHI)  BC  SI . Suy ra góc
tạo bởi (SBC) và (ABCD) là 0 SIH  60 . Ta có A H B a 2 (AB  DC).AD (2a  a).a 3a I S    D a ABCD C 2 2 2
Ta có AH = HB = a , suy ra ADCH là hình vuông 2 2
 CH  AH  a  BC  CH  HB  a 2 BC a 2  HI   (  BCH vuông cân) 2 2 31 a 2 a 6 Khi đó 0 SH  HI.tan SIH  .tan 60  2 2 3 1 a 6
Thể tích khối chóp S.ABCD là: V  SH.S  S.ABCD ABCD 3 4 Chọn đáp án A.
Câu 25. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và
B. Hình chiếu của S lên mặt phẳng (ABCD) trùng với giao điểm I của AC
và BC. Mặt bên (SAB) hợp với đáy một góc 0 60 . Biết rằng
AB  BC  a, AD  3a . Tính thể tích khối chóp S.ABCD 3 a 3 3 a 3 3 3a 3 3 a 3 A. B. C. D. 4 2 2 3 Hướng dẫn giải
Gọi K là hình chiếu của I lên AB. S Suy ra 0 SKI  60 . KI BI Do IK / /AD   . AD BD BI BC a 1 BI 1 BI 1 Mà        B C 600 ID AD 3a 3 BI  ID 4 BD 4 a I KI 1 3a 3a 3 Suy ra   KI   SI  A 3a D AD 4 4 4 1 1 3a 3 1      3 a 3 V SI.S . . a 3a .a  S.ABCD ABCD 3 3 4 2 2
Vậy chọn đáp án B. 32
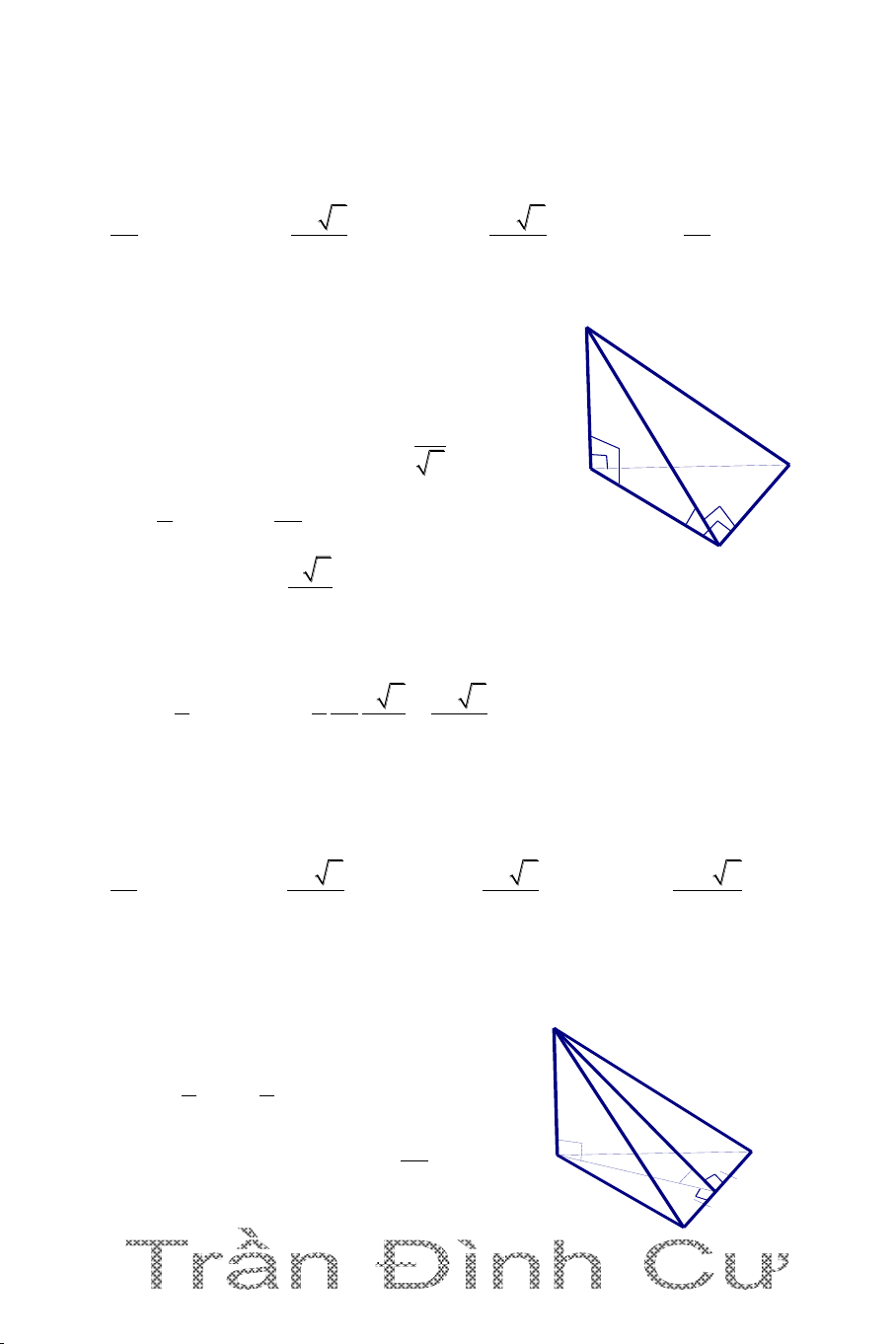
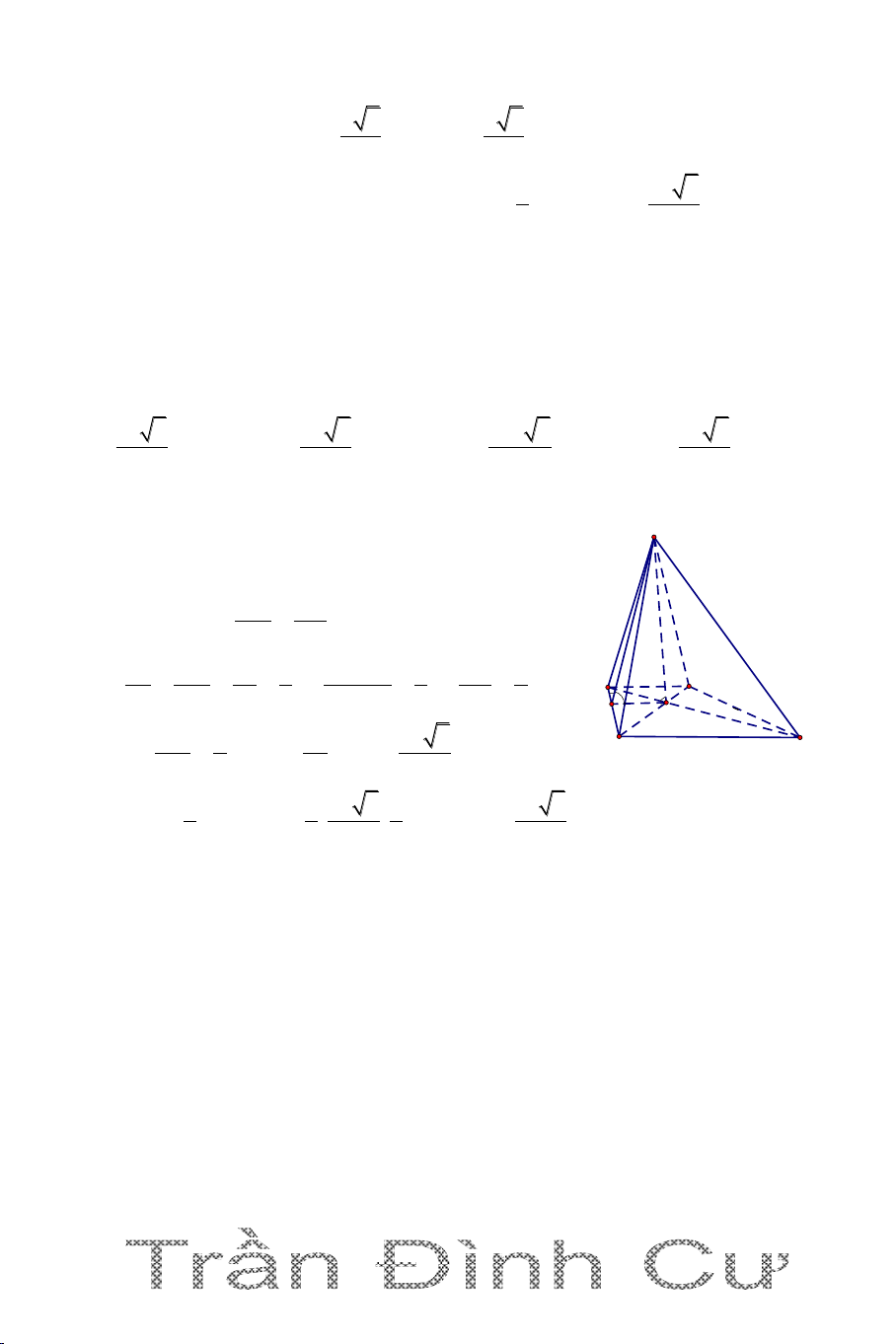
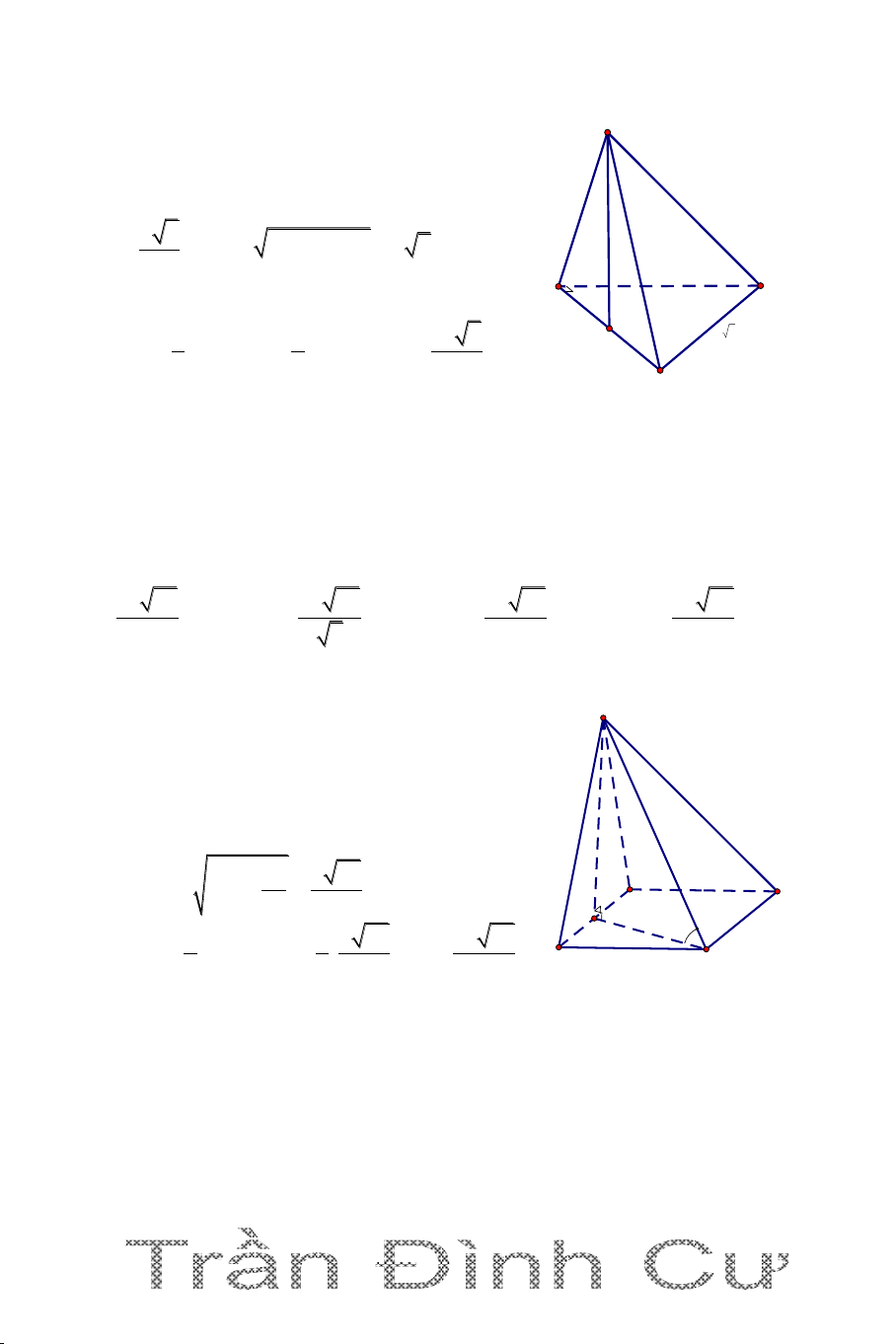
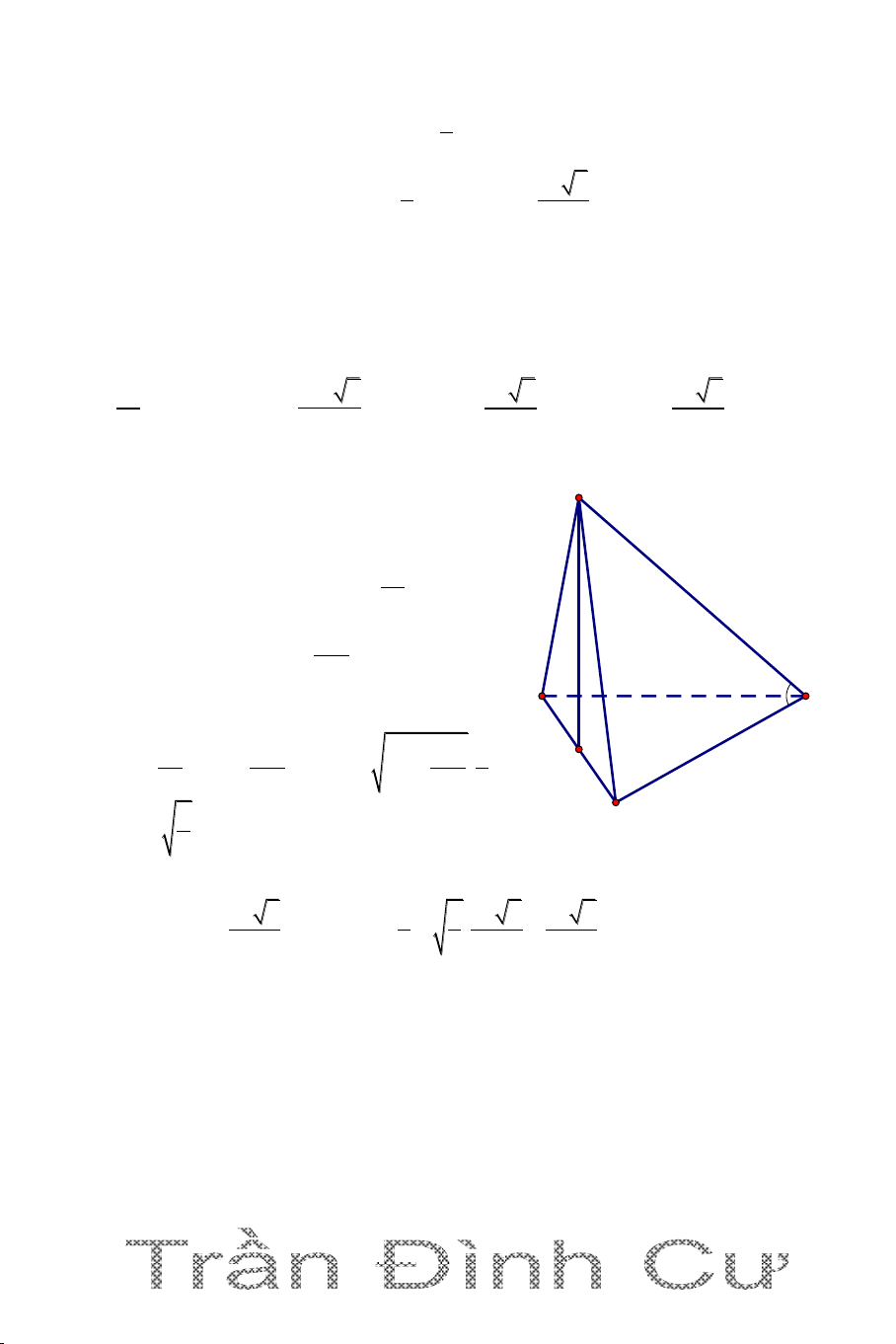
DẠNG 3. KHỐI CHÓP CÓ MẶT BÊN VUÔNG GÓC VỚI ĐÁY
Để xác định đường cao hình chóp ta vận dụng định lí sau ()  ( )    ()  ( )
  d a ( ) a  ()  a  d 
Câu 1. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BA=3a,
BC=4a; mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Biết SB  2a 3 và 0
SBC  30 . Tính thể tích khối chóp S.ABC. A. 3 V  a . 3 B. 3 V  a C. 3 V  3a . 3 D. 3 V  2a . 3 Hướng dẫn giải
Kẻ SH vuông góc BC suy ra SH S vuông góc mp(ABC);
SH=SB. sinSBC  a 3 2a 3 1 2 S BA.BC 6a ABC    ; 2 300 1 3 V  S .SH  2a 3 4a S.ABC A  BC 3 B C H 3a
Vậy chọn đáp án D. A
Câu 2. Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 4, mặt bên
SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M, N,
P lần lượt là trung điểm của các cạnh SD, CD, BC. Thể tích khối chóp
S.ABPN là x, thể tích khối tứ diện CMNP là y. Giá trị x, y thoả mãn bất
đẳng thức nào dưới đây: A. 2 2 x  2xy  y  160 B. 2 2 x  2xy  2y  109 C. 2 4 x  xy  y  145 D. 2 4 x  xy  y  125 Hướng dẫn giải 33
Gọi H là trung điểm AB. Do A  BC đều và S
SAB ABCD SH ABCD M 3AB Xét A  BC đều: SH   2 3 2 A Ta có: S  S  S  S D ABPN ABCD ADN CNP K 2 AD.DN CN.CP  H N AB   2 2 B P C 2 4.2 2.2  4    10 2 2 1 1 20 3  V  .S .SH  .10.2 3  20 3  x  S.ABPN ABPN 3 3 3 3 Gọi AN  HD   
K ta có MK là đường trung bình của D  HS 1  HK  SH 2 1 1 1 1 1 2.2 2 3 2 3  V  .S .MK  . .CN.CP. .SH  .  2 3  y  CMNP CNP 3 3 2 2 3 2 2 3 3
Thay vào các đáp án  Chọn đáp án C.
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh a. Mặt
bên SAB là tam giác đều nằm trong mặt phẳng vuông góc với đáy ABCD
Thể tích khối chóp S. ABCD là 3 a 3 3 a 3 3 a D. 3 a 3 A. B. C. 3 6 6 Hướng dẫn giải
Gọi H là trung điểm của AB. S S  AB đều SH  AB mà
(SAB)  (ABCD)  SH  (ABCD) D A
Vậy H là chân đường cao của khối H chóp. B a C a 3
Ta có tam giác SAB đều nên SA = 2 34 3 1 a 3 Suy ra V  S  ABCD.SH
. Vậy chọn đáp án B. 3 6
Câu 4. Cho tứ diện ABCD có ABC là tam giác đều, BCD là tam giác vuông
cân tại D , (ABC)  (BCD) và AD hợp với (BCD) một góc 60o , AD=a. Thể tích tứ diện ABCD là 3 a 3 a 3 3 a 3 3 a 3 A. B. C. D. 9 6 9 3 Hướng dẫn giải
Gọi H là trung điểm của BC. Ta có tam giác A ABC đều nên AH  (BCD) ,  a ABC  BCD   
ABC  BCD  BC  AH  BCD  600 AH  BC  B  D Suy ra:    0 AD, BCD  ADH  60 H C a 3
Ta có AH  HD  AH = AD.tan60o = a 3 & HD = AD.cot60o = 3 2a 3 B  CD BC = 2HD = . Suy ra 3 3 1 1 1 a 3 V  S   BCD.AH . BC.HD.AH
. Vậy chọn đáp án C. 3 3 2 9
Câu 5. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, có
BC = a. Mặt bên SAC vuông góc với đáy, các mặt bên còn lại đều tạo với
mặt đáy một góc 450. Tính thể tích khối chóp SABC 3 a 3 a 3 3 a 3 3 a 3 A. B. C. D. 12 9 12 3 Hướng dẫn giải 35
Kẽ SH  BC vì mp(SAC)  mp(ABC) S
nên SH  mp(ABC). Gọi I, J là hình
chiếu của H trên AB và BC  SI  AB, SJ  BC, theo giả thiết 0 SIH  SJK  45 Ta có: H A 45 C SHI S
HJ HI HJ . Tứ
giác HIBJ là hình thoi nên BH là I J đường phân giác của A  BCtừ đó
suy ra H là trung điểm của AC. B a 1 3 a HI = HJ = SH = V S .SH  SABC= ABC
. Vậy chọn đáp án A. 2 3 12
Câu 6. Cho hình chóp SABC có đáy ABC đều cạnh a, tam giác SBC vuông
cân tại S và nằm trong mặt phẳng vuông góc với (ABC). Tính thể tích khối chóp SABC. 3 a 3 a 3 3 a 3 3 a A. B. C. D. 9 9 16 16 Hướng dẫn giải
Gọi H là trung điểm của BC. S Ta có: SBC  ABC   
SBC  ABC  BC  SH  ABC  SH  BC  a A c a SH  a 2 H a B 2 3 1 1 a a 3 a 3 V  SH.S  . . 
. Vậy chọn đáp án C. ABC 3 2 2 4 16
Câu 7. Tứ diện ABCD có ABC và BCD là hai tam giác đều lần lượt nằm
trong hai mặt phẳng vuông góc với nhau biết AD = a. Tính thể tích tứ diện. 36 3 a 6 3 a 3 3 a 3 3 a 6 A. B. C. D. 9 9 36 36 Hướng dẫn giải Ta có: A ABC  BCD    ABC BC 
D  BC  AH  BCD  a AH  BC  Ta để ý: A  BC  D  BC  AH  DH
Do đó tam giác AHD vuông cân tại H. B D a Suy ra: AH  mà H 2 C a 2. BC 3 2AH 2 a 2 AH   BC    2 3 3 3 2   3 1 a a 2 3 a 3 Do đó: V  . .  . 
. Vậy chọn đáp án C. 3 2    3 4 36 
Câu 8. Cho hình chóp S.ABC có o o
BAC  90 ; ABC  30 ; SBC là tam giác
đều cạnh a và (SBC)  (ABC). Tính thể tích khối chóp S.ABC 3 a 3 a 3 a 3 a A. B. C. D. 6 16 3 9 Hướng dẫn giải Ta có: S BC  a 0 a 3 AB  BCcos 30  2 0 a AC  BCsin 30  B 2 A 300 2 1 a 3 a a 3 S  . .  H ABC 2 2 2 8 C 37 2 3 1 a 3 a 3 a Do đó: V  . . 
. Vậy chọn đáp án B. 3 2 8 16
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, gọi M là trung
điểm của AB. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc
với đáy ABCD , biết SD  2a 5 , SC tạo với mặt đáy ABCD một góc 0
60 . Tính theo a thể tích khối chóp S.ABCD 3 4a 15 3 a 15 3 4a 3 a A. B. C. D. 3 3 3 3 Hướng dẫn giải
Theo giả thiết ta có SM  ABCD S
MC là hình chiếu của SC trên ABCD nên
góc giữa SC với mặt phẳng ABCD là 0 2a 5 SCM  60
Trong tam giác vuông SMC và SMD ta có: A 2 2 0 D
SM  SD  MD  MC.tan60 mà ABCD M
là hình vuông nên MC  MD 600 2 2 2
 SD  MC  3MC  MC  a 5 B C  SM  a 15 2 2  AB  5BC Lại có 2 2 2 MC  BC    BC  2a  S    4a ABCD  2  4 3 1 4a 15 Vậy V  SM.S 
. Vậy chọn đáp án A. S.ABCD ABCD 3 3
Câu 10. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, mặt bên
SAB là tam giác đều nằm trong mặt phẳng vuông góc với mặt phẳng
ABC. Biết AB a, BC a 3 . Tính thể tích khối chóp S.ABC 3 a 6 3 a 3 a 6 3 a 6 A. B. C. D. 6 12 12 4 Hướng dẫn giải 38
Gọi H là trung điểm của AB  SH  AB S
Do SAB  ABC nên SH  ABC
Do SAB là tam giác đều cạnh a nên a 3 SH  , 2 2 AC  BC  AB  a 2 2 a C
Thể tích khối chóp S.ABC là A 3 1 1 a 6 a 3 H V  SH.S  SH.AB.AC  S.ABC ABC 3 6 12 B
Vậy chọn đáp án C.
Câu 11. Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB  a, AD  2a .
Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc
giữa đường thẳng SC và mặt phẳng (ABCD) bằng 0 45 . Tính theo a thể tích của khối chóp S.ABCD 3 a 17 3 a 17 3 a 17 3 a 17 A. B. C. D. 9 3 6 3 Hướng dẫn giải Gọi H là trung điểm của AB S
 SH  ABCD , suy ra HC là hình chiếu của SC lên (ABCD) 0  SCH  45 2 S  2a ABCD 2 2 a a 17 A SH  HC  4a   2a D 4 2 M 3 450 1 1 a 17 a 2 a 17 V  SH.S  . .2a  S.ABCD ABCD 3 3 2 3 B C
Vậy chọn đáp án D.
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. SAB là
tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy, góc
giữa cạnh SC và mặt phẳng (ABCD) bằng 0
60 , cạnh AC  a . Tính theo a
thể tích khối chóp S.ABCD 39 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 4 2 3 9 Hướng dẫn giải
Gọi I là trung điểm của đoạn AB S
 SI  AB, SAB  ABCD  SI  ABCD nên     0 a 3 SCI SC; ABCD  60 , CI  B 2 600 C M 0 3a  SI  CItan60  2 A D
Gọi M là trung điểm của đoạn BC, N là
trung điểm của đoạn BM. a 3 a 3 AM   IN  2 4 2 2 3 a 3 1 a 3 3a a 3 Ta có: S  2S   V  . .  . ABCD A  BC S.ABCD 2 3 2 2 4
Vậy chọn đáp án A.
Câu 13. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Mặt bên SAB
là tam giác vuông tại S và nằm trong mặt phẳng vuông góc với đáy, hình
chiếu vuông góc của S trên đường thẳng AB là điểm H thuộc đoạn AB sao
cho BH  2AH. Tính thể tích khối chóp S.ABCD 3 a 3 3 a 2 3 a 2 3 a 3 A. B. C. D. 3 3 9 9 Hướng dẫn giải 2 S Ta có: 2 2a a 2 SH  HA.HB   SH  9 3 3 1 1 a 2 2 a 2 V  SH.S  . .a  S.ABCD ABCD 3 3 3 9
Vậy chọn đáp án C. a B C H A D 40
Câu 14. Cho hình chóp S.ABCD có đáy là hình thoi, tam giác SAB đều và
nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Biết
AC  2a, BD 4a , tính theo a thể tích khối chóp S.ABCD 3 a 3 3 a 15 3 2a 15 3 a 15 A. B. C. D. 15 3 3 2 Hướng dẫn giải
Gọi O  AC  BD , H là trung điểm của AB, suy S ra SH  AB .
Do AB  SAB ABCD và
SAB ABCD nên SH ABCD AC 2a B Ta có: OA    a C 2 2 H O BD 4a OB    2a A D 2 2 2 2 2 2 AB 3 a 15
AB  OA  OB  a  4a  a 5; SH   2 2 1 1 2 S  AC.BD  2a.4a  4a ABCD 2 2 3 1 1 a 15 2a 15
Thể tích khối chóp S.ABCD là 2 V  SH.S  . .4a  . ABCD 3 3 2 3
Vậy chọn đáp án C.
Câu 15. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BA  3a
, BC  4a , mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Biết SB  2a 3 và 0
SBC  30 . Tính thể tích khối chóp S.ABC A. 3 a B. 3 a 3 C. 3 2a 3 D. 3 2a Hướng dẫn giải 41
Gọi H là hình chiếu của S trên BC. S
Vì SBC  ABC nên SH  ABC Ta có SH  a 3 1 Do đó 3 V  SH.S  2a 3 S.ABC ABC 3 A C
Vậy chọn đáp án C H B
Câu 16. Cho hình chóp S.ABC có đáy là tam giác vuông tại A,
AB  a, AC  2a . Mặt phẳng (SBC) vuông góc với đáy, hai mặt phẳng
(SAB) và (SAC) cùng tạo với mặt phẳng đáy góc 0 60 . Tính thể tích khối chóp S.ABC theo a. 3 a 3 3 2a 3 3 a 3 3 4a 3 A. B. C. D. 3 9 9 9 Giải
Gọi H là hình chiếu của S lên BC; E, F lần S
lượt là hình chiếu của H lên AB, AC suy
ra SH  ABC và HE  HF nên AH là phân giác của góc BAC . AB BC BH AB Ta có:   1  1 HF HC HC AC A C F AB.AC 2a  HF   AB  AC 3 H E Suy ra 0 2a 3 SH  HF.tan 60  B 3 1 3 2 2a 3 S AB.AC a V 
. Vậy chọn đáp án B. ABC    . Vậy 2 S.ABC 9
Câu 17. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng a,
SD  a 2 , SA  SB  a , và mặt phẳng (SBD) vuông góc với mặt phẳng
(ABCD). Tính theo a thể tích khối chóp S.ABCD 42 3 a 2 3 a 2 3 a 2 3 a 2 A. B. C. D. 4 6 2 8 Hướng dẫn giải Mặt khác S
AS  AB  AD  OS  OB  OD hay S
 BD là tam giác vuông tại S. 2 2 2 2
BD  SB  SD  a  2a  a 3 3 2 2 2 3a a AO  AB  OB  a   4 2 a B C a
Suy ra thể tích khối chóp S.ABD a O được tính bởi: a A D 3 1 1 1 a a 2 V  V  S
.AO  SB.SD.AO  a.a 2.  S.ABD A.SBD SBD 3 6 6 2 12 3 a 2  V  2V  . Vậy chọn đáp án B. S.ABCD S.ABD 6
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a,
SA  a , SB  a 3 và mặt phẳng (SAB) vuông góc với mặt phẳng đáy. Gọi
M, N lần lượt là trung điểm của các cạnh AB, BC. Tính theo a thể tích của khối chóp S.BMDN 3 a 3 3 a 3 a 2 3 a 2 A. B. C. D. 3 3 2 3 Hướng dẫn giải
Gọi H là hình chiếu của S trên AB, suy ra S SH  ABCD
Do đó SH là đường cao của hình chóp S.BMDN a 3 a Ta có: 2 2 2 2 2
SA  SB  a  3a  AB  S  AB A AB D vuông tại S  SM   a M H 2 O a 3 N B C
Do tam giác SMA đều, suy ra SH  2 43 1
Diện tích tứ giác BMDN là: 2 S  S  2a BMDN ABCD 2 3 1 a 3
Thể tích khối chóp S.BMDN: V  SH.S  (đvtt). BMDN 3 3
Vậy chọn đáp án A.
Câu 19. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, tam giác SAC cân tại S, 0
SBC  60 , mặt phẳng (SAC) vuông góc với (ABC). Tính
theo a thể tích của khối chóp S.ABC 3 a 3 3a 2 3 a 2 3 a 2 A. B. C. D. 8 8 6 8 Hướng dẫn giải
Gọi H là trung điểm của AC thì S
SH  AC  SH  ABC . Đặt SH  h . 2 Ta có: 2 2 2 2 a SC  HS  HC  h  , 4 2 2 2 2 2 3a SB  HS  HB  h  4 600 A B Mà 2 2 2 0
SC  BS  BC  2BS.BC.cos60 2 2 2 2 a 2 3a 2 2 3a 1  h   h   a  2a h  . H 4 4 4 2 3  C h  a 2 2 2 3 a 3 1 3 a 3 a 2 Ta có: S V .a . A      . BC S.ABC 4 3 2 4 8 Vậy chọn đáp án D. 44
DẠNG 4. KHỐI CHÓP ĐỀU
1. Định nghĩa: Một hình chóp được gọi là hình chóp đều nếu đáy của
nó là một đa giác đều và các cạnh bên bằng nhau
2. Kết quả: Trong hình chóp đều
 Đường cao hình chóp qua tâm của đa giác đáy
 Các cạnh bên tạo với đáy các góc bằng nhau
 Các mặt bên tạo với đáy các góc bằng nhau Chú ý:
 Đề bài cho hình chóp tam giác đều (tứ giác đều) ta hiểu là hình chóp đều
 Hình chóp tam giác đều khác với hình chóp có đáy là đa giác
đều vì hình chóp tam giác đều thì bản thân nó có đáy là tam
giác đều và các cạnh bên bằng nhau, nói một cách khác, hình
chóp tam giác đều thì suy ra hình chóp có đáy là tam giác đều
nhưng điều ngược lại là không đúng
 Hình chóp tứ giác đều là hình chóp đều có đáy là hình vuông
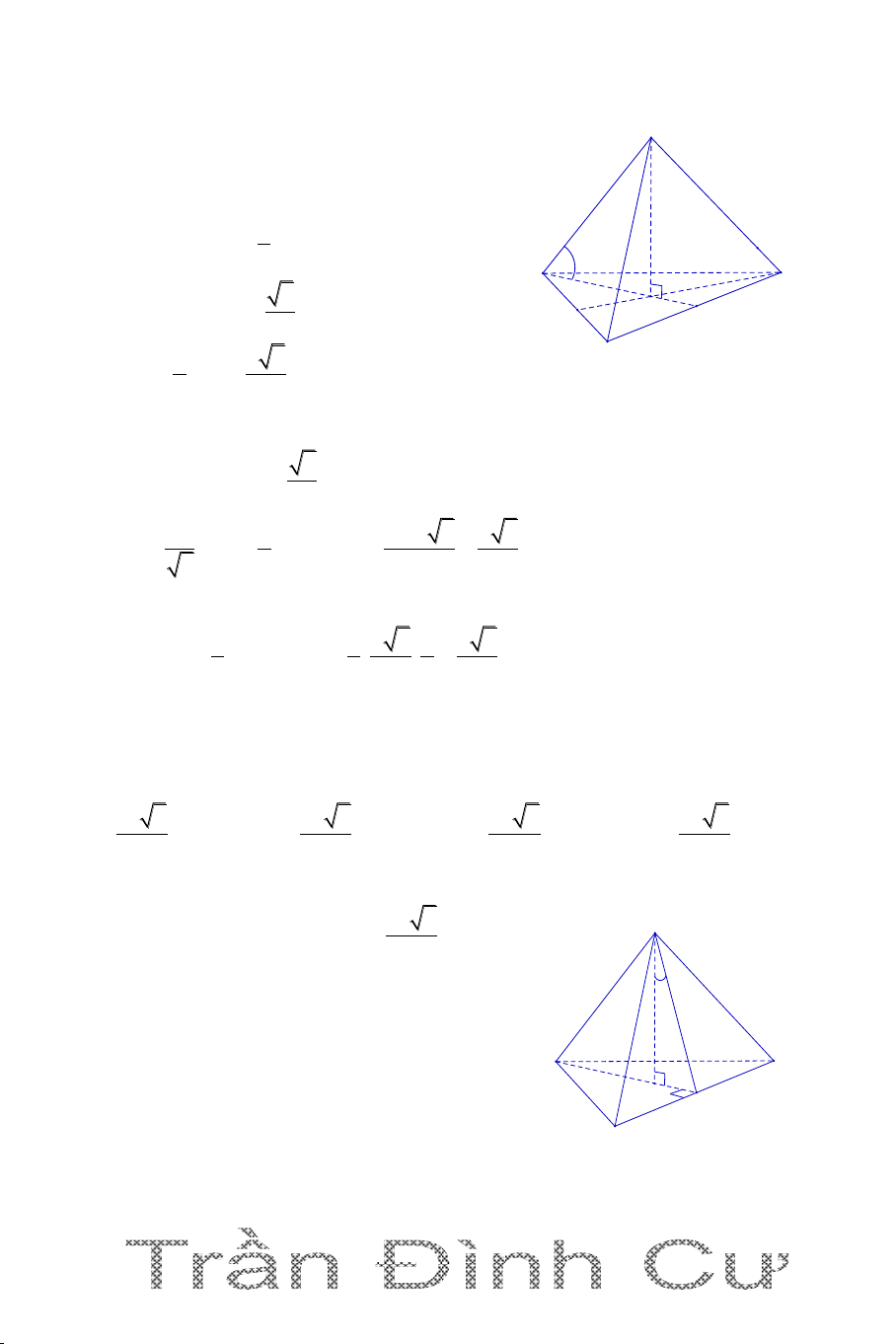
Câu 1. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa
cạnh bên và mặt đáy bằng 600. Tính thể tích khối chóp S.ABC. 3 5a . 3 3 a . 3 3 a . 5 3 a . 3 A. V  B. V  C. V  D. V  12 12 12 10 Hướng dẫn giải
Vì S.ABC là hình chóp đều nên ABC là tam S
giác đều tâm G và SG  ABC 1  V  SG.S S.ABC ABC 3 2 a 3
Tam giác ABC đều cạnh a nên S  600 C ABC 4 A G N B
Có AG là hình chiếu của AS trên (ABC) nên góc giữa cạnh bên SA với đáy là
(SA,AG) = SAG  60 (vì SG  AG  SAG nhọn) 45 2 a 3
Vì G là trọng tâm tam giác ABC nên AG  AN  . 3 3
Trong tam giác SAG có SG  AG.tan60  a 2 3 1 a 3 a 3 Vậy V  .a.  . Chọn đáp án B. S.ABC 3 4 12
Câu 2. Cho hình chóp tứ giác đều S.ABCD, đáy ABCD có diện tích là 16cm2,
diện tích một mặt bên là 2
8 3cm . Thể tích khối chóp S.ABCD là: 32 2 32 13 32 11 D. 3 4cm A. 3 cm B. 3 cm C. 3 cm 3 3 3 Hướng dẫn giải Ta có 2 S  16cm   S ABCD CD 4cm 2 1 2 S 8 3cm SH.CD 8 3cm S     CD 2  SH  4 3cm Xét S  OHvuông tại O có: A D 2 2 SO  SH  OH H O  4 32 2  2 cm  2 11cm B C 1 1 32 11 Vậy: 3 3 V  S .SO  .16.2 11cm  cm S.ABCD ABCD 3 3 3
Vậy chọn đáp án C.
Câu 3. Cho hình chóp tam giác đều S.ABC có các cạnh bên bằng 3 và tạo
với mặt phẳng đáy góc 600 . Thể tích khối chóp S.ABC là: 9 3 3 3 3 9 3 A. B. C. D. 32 32 32 16
Hướng dẫn giải 46 + Gọi G là trọng tâm A  BC S  SG  ABC Xét S  GA vuông tại G có : 0 3 SG  SA.sin 60  2 A C 0 3 AG  SA.cos60  G 2 M 3 3 3  B AM  AG  2 4 3 A  BC đều  AM  AB 2 2 3 2  AB 3 9 3 AB  AM   S   ABC  3 2 4 16 1 1 9 3 3 9 3 Vậy V  .S .SM  . . 
Chọn đáp án A SABC ABC 3 3 16 2 32
Câu 4. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a. Gọi G là
trọng tâm tam giác ABC, góc giữa SG và mặt phẳng SBC là 300. Thể tích khối chóp S.ABC là: 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 4 8 12 24 Hướng dẫ n giải 2 a 3 S - Do ABC đều nên S ABC   . 4
- Do S.ABC là hình chóp tam giác đều 30
 SG  ABC  SG  BC , mà BC  AM  BC  SAM C A  SBC  SAM G M B 47 SBCSAM   SM 
nên hình chiếu vuông góc của SG lênSBC SBC  SAM,SG   SAD là SM
  G,SBC SG,SM o S   GSM 30
-Xét tam giác SGM vuông tại M có: 1 0 1 a 3 a
SG  GM.cot GSM  .AM.cot 30  . . 3  3 3 2 2 2 3 1 1 a 3 a a 3 Do vậy V  .S .SG  . . 
Chọn đáp án D S.ABC ABC 3 3 4 3 24
Câu 5. Cho chóp tam giác đều SABC cạnh đáy bằng a và cạnh bên bằng
2a. Tính thể tích chóp đều SABC 3 a 11 3 a 12 3 a 3 a A. B. C. D. 12 11 12 11
Hướng dẫn giải
Dựng SO  (ABC) Ta có SA = SB = SC suy ra OA = OB = OC
Vậy O là tâm của tam giác đều ABC. S
Ta có tam giác ABC đều nên 2a 2 2 a 3 a 3 AO = AH   3 3 2 3 2 C A 2 2 2 11a SAO  SO  SA  OA  3 3 a O H a 11  1 a 11 SO  .Vậy V  S .SO  3 ABC 3 12 B
Vậy chọn đáp án A.
Câu 6. Cho khối tứ diện đều ABCD cạnh bằng a. Tính thể tích khối tứ diện đều ABCD. 3 a 2 3 a 3 3 a 2 3 a A. B. C. D. 12 12 6 6 Hướng dẫ n giải 48 Gọi O là tâm của ABCD
DO  (ABC) 2 a 3 a S  2 3 OC CI ABC , 4 3 3 2 2 DOC v ô u ng ó c :DO DC OC A C 2 3 a 6 1 a 3 a 6 a 2  V  .  O I 3 3 4 3 12
Vậy chọn đáp án B. B
Câu 7. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, cạnh bên
bằng a 3 . Tính thể tích khối chóp S.ABCD. 3 8a 3 a 3 3 4a 3 2a A. B. C. D. 3 3 3 3 Hướng dẫ n giải
S.ABCD là hình chóp tứ giác đều ABCD là S
hình vuông cạnh 2a , tâm O; SO  (ABCD); SA=SB=SC=SD= a 3
Diện tích hình vuông ABCD  AC = 2a. 2 A B  AC 2a 2 AO=   a 2 2 2 O D C  S  2a2 2  4a    ABCD ;  SAO vuông tại O có 2 2 SO SA AO a 3 1 1 4a
Thể tích khối chóp S.ABCD: 2 V  .S .SA  .4a .a  . S.ABCD ABCD 3 3 3
Vậy chọn đáp án C.
Câu 8. Cho khối chóp tứ giác S. ABCD có tất cả các cạnh có độ dài bằng a .
Tính thể tích khối chóp S.ABCD. 49 3 a 2 3 a 2 3 a 2 3 a 2 A. B. C. D. 3 6 9 12 Hướng dẫ n giải
Dựng SO  (ABCD). Ta có SA = SB = SC = SD nên OA = OB =OC = OD  ABCD
là hình thoi có đường tròn gnoại tiếp nên ABCD là hình vuông . Ta có: 2 2 a 2 SO  SD  DO  2 3 3 1 1 a 2 a 2  2 a 2 V S .SO aABCD . Vậy V  . 3 3 2 6 6
Vậy chọn đáp án B.
Câu 9. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, các cạnh
bên SA, SB, SC đều tạo với đáy một góc 60o. Tính thể tích của khối chóp S.ABC. 3 a 2 3 a 2 3 a 2 3 a 2 A. B. C. D. 3 6 9 12 Hướng dẫ n giải
Gọi H là hình chiếu của S lên S
mp(ABC), ta có H là trọng tâm tam
giác ABC, AH là hình chiếu của SA
lên mp(ABC) nên g(SAH) = 60o Ta có: A a 3 a 3 a 3 C AE = , AH = , HE = H 2 3 6 F E B a 3 2 3 1 a 3 a 3 SH = AH.tan 60o = . 3  a . Vậy VSABC = .a  . 3 3 4 12
Vậy chọn đáp án A.
Câu 10. Cho hình chóp đều S. ABC có cạnh bên bằng a hợp với đáy ABC
một góc 60o . Tính thể tích hình chóp. 50 3 3a 3 3a 3 3a 3 a A. B. C. D. 32 13 23 32 Hướng dẫ n giải 1 S V  SH.S
Tính AO. Từ đó suy ra được ABC 3 AH a
 cạnh của tam giác đáy đều. 3 3a 600 C Đs: V  . A 32 O
Vậy chọn đáp án A. H B
Câu 11. Cho hình chóp tam giác đều S.ABC có cạnh đáy a và mặt bên hợp
với đáy một góc 60o. Tính thể tích hình chóp S.ABC. 3 a 3 3 a 2 3 a 3 3 a A. B. C. D. 12 24 24 24 Hướng dẫ n giải   0 S
(SAB);(ABC)  SHC  60 Tính SO thông qua OH. 3 a 3 Đs: V  24 A C 600
Vậy chọn đáp án C a O H B
Câu 12. Cho chóp tam giác đều có đường cao h hợp với một mặt bên một
góc 30o . Tính thể tích hình chóp. 3 h 3 2h 3 3 2h 3 h 3 A. B. C. D. 3 3 3 3 Hướng dẫ n giải 51
Đường cao hình chóp là SO. S
Ta có: SO (SBC)  S 300
SBC SAH  BCAHSBC AH  BC  C A Do đó:   0 SO,(SBC)  HSO  30 . O H 3 h 3 B ĐÁP SỐ: V 
. Vậy chọn đáp án D. 3
Câu 13. Cho hình chóp tứ giác đều SABCD có chiều cao h , góc ở đỉnh của
mặt bên bằng 60o. Tính thể tích hình chóp. 3 3h 3 h 3 2h 3 h 3 A. B. C. D. 2 3 3 3
Hướng dẫ n giải
Giả sử hình vuông ABCD có cạnh là a. S 1 1 2 600 V  SO.S  h.a ABCD 3 3 a h
Trong tam giác vuông SOB thì 2  a 2  A B 2 2 2 2 2 2 2
SB  SO  OB  a  h     a  2h  2    a O 3 D 2h C V 
. Vậy chọn đáp án C. 3
Câu 14. Cho hình chóp tứ giác đều có cạnh bên bằng a hợp với đáy một góc
60o. Tính thề tích hình chóp. A. 2 a 3 3 a 2 3 a 3 a 3 B. C. D. 12 12 12 Hướng dẫ n giải 52 S 1 V  SO.S Tính DO  DB . ABCD 3
Từ đó suy ra cạnh của hình vuông 3 a a 3 Đs: V  . 12 A B
Vậy chọn đáp án D. 600 O D C 53
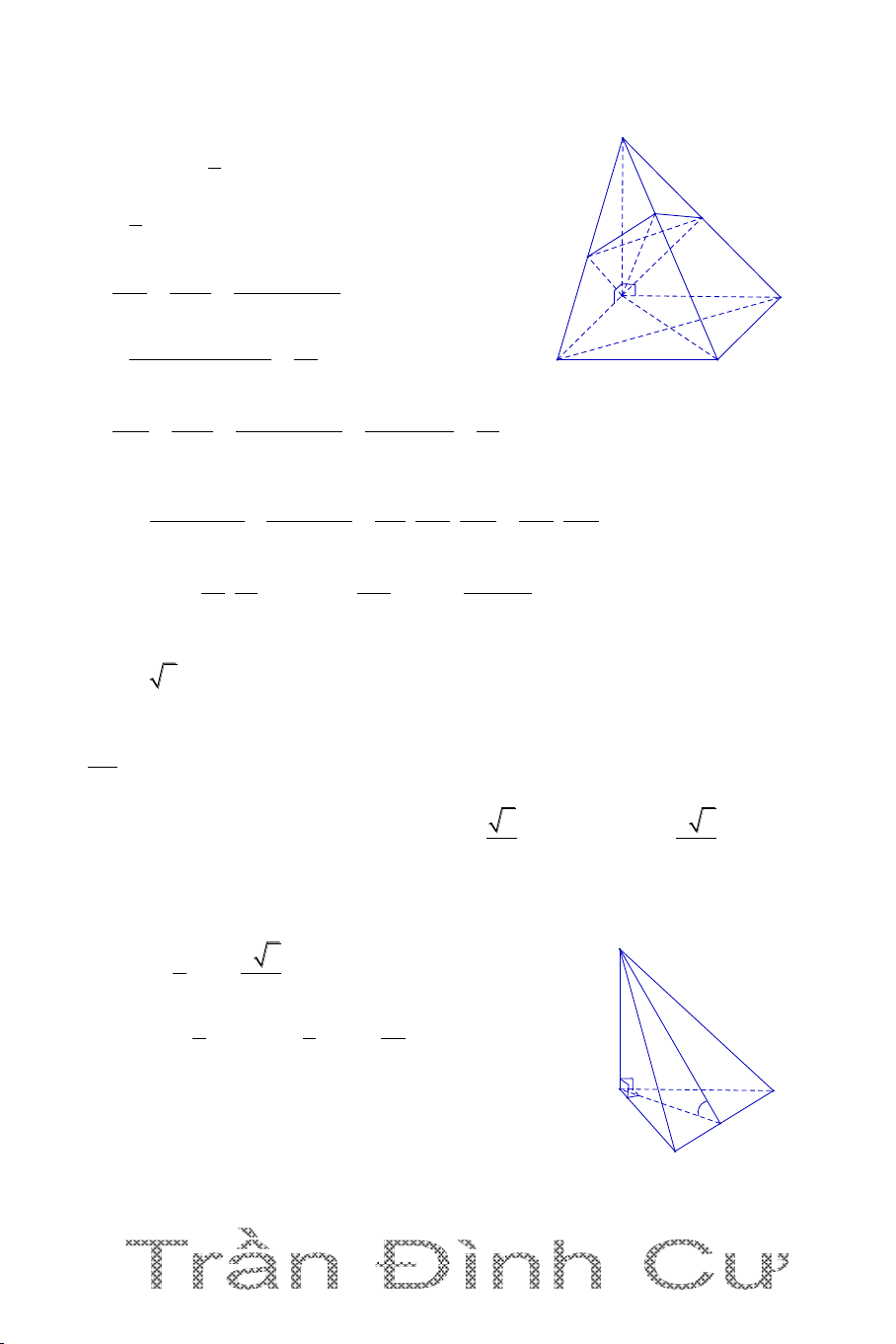
DẠNG 5. TỈ LỆ THỂ TÍCH
Việc tính thể tích của một khối chóp thường học sinh giải bị nhiều sai sót,
Tuy nhiên trong các đề thi lại yêu cầu học sinh tính thể tích của một khối
chóp “nhỏ” của khối chóp đã cho. Khi đó học sinh có thể thực hiện các cách sau: + Cách 1:
o Xác định đa giác đáy
o Xác định đường cao ( phải chứng minh đường cao
vuông gới với mặt phẳng đáy)
o Tính thể tích khối chóp theo công thức + Cách 2
o Xác định đa giác đáy
o Tình các tỷ số độ dài của đường cao (nếu c ng đa
giác đáy) hoặc diện tích đáy (nếu c ng đường cao)
của khối chóp “nhỏ” và khối chóp đã cho và kết luận
thể tích khối cần tìm bằng k lần thể tích khối đã cho
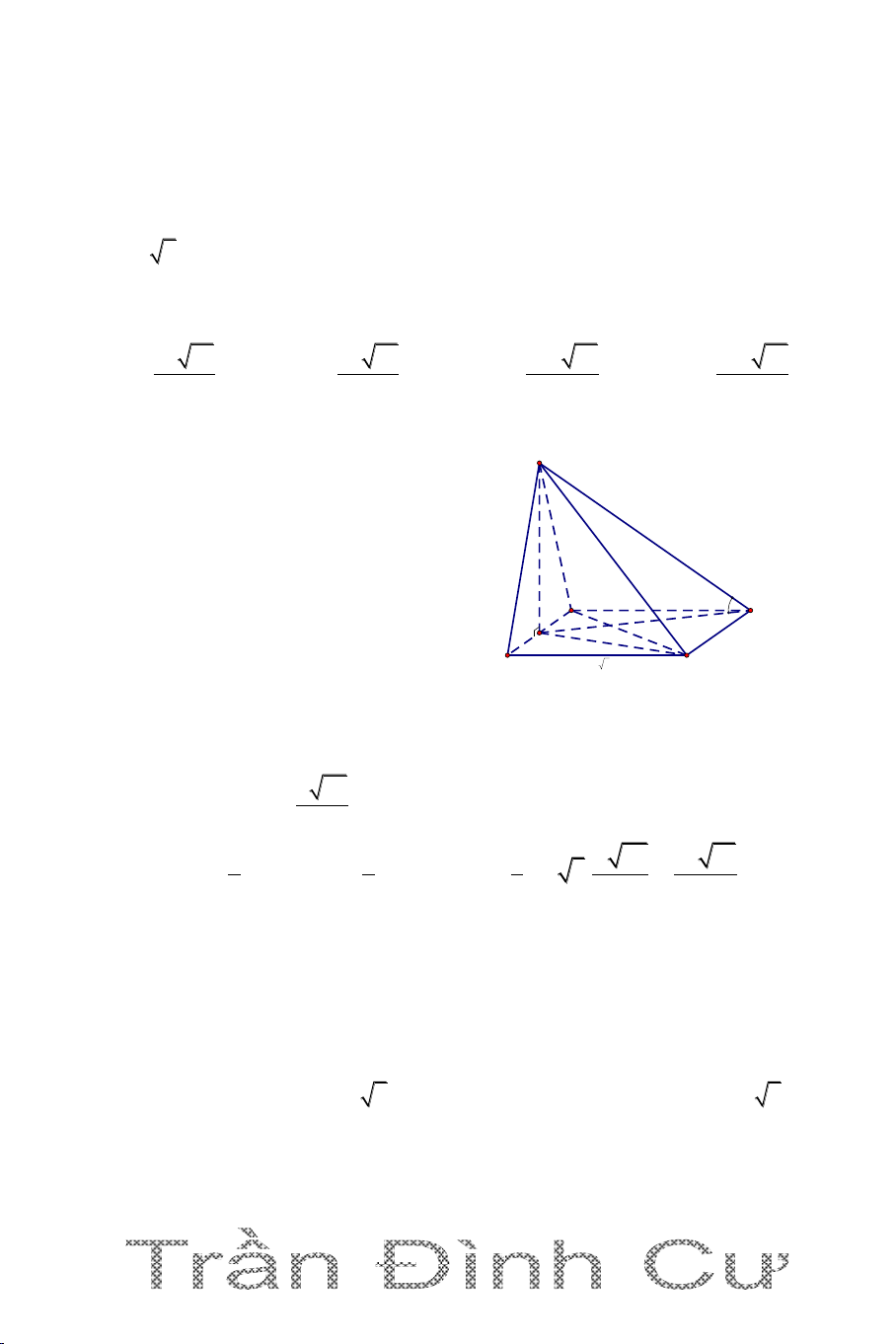
+ Cách 3: dùng tỷ số thể tích (Chỉ áp dụng cho khối chóp (tứ diện)) S Hai khối chóp S.MNK và M K
S.ABC có chung đỉnh S và góc n ở đỉnh S N A V SM SN SK C Ta có : S.MNK  . . V SA SB SC S.ABC B 54
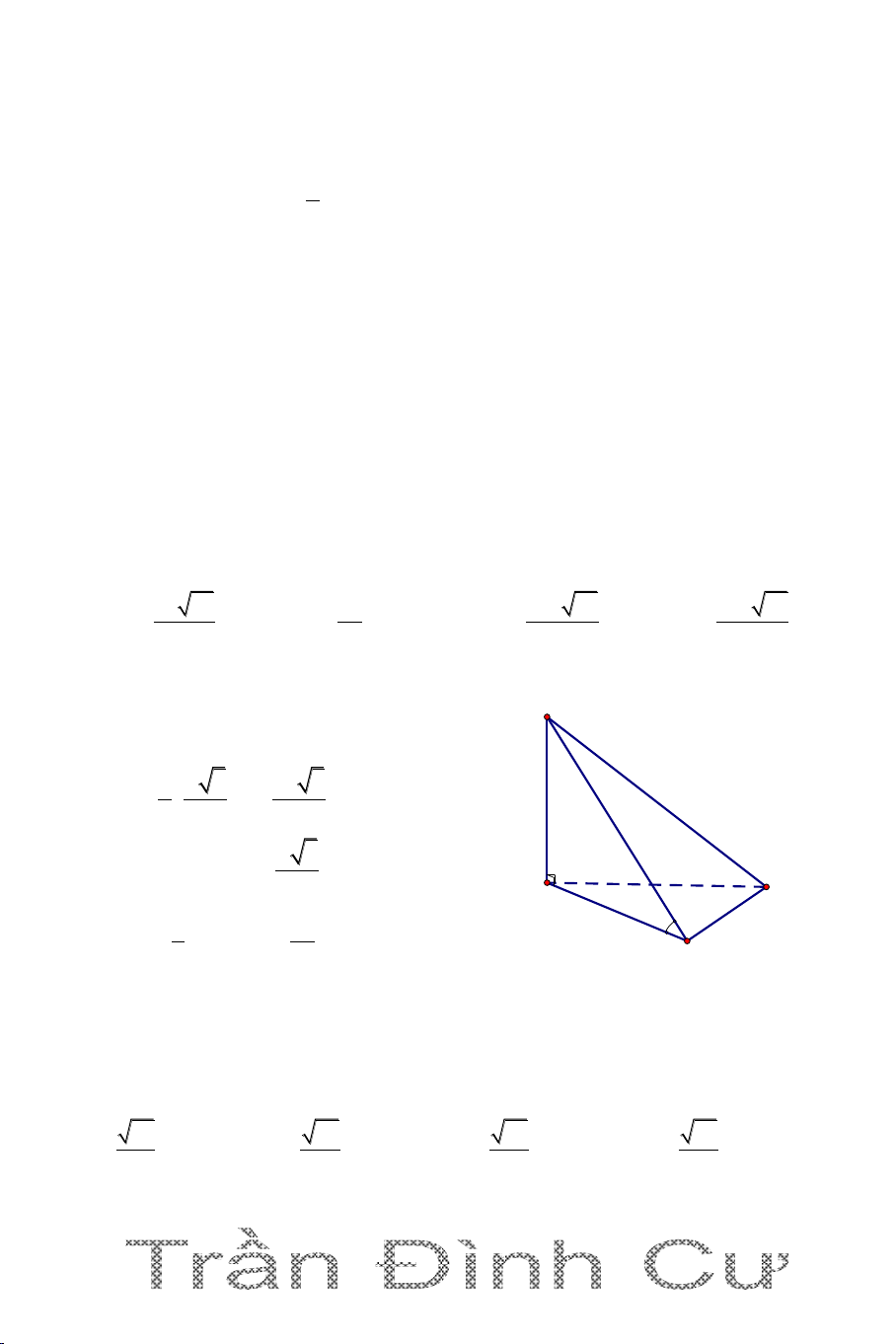
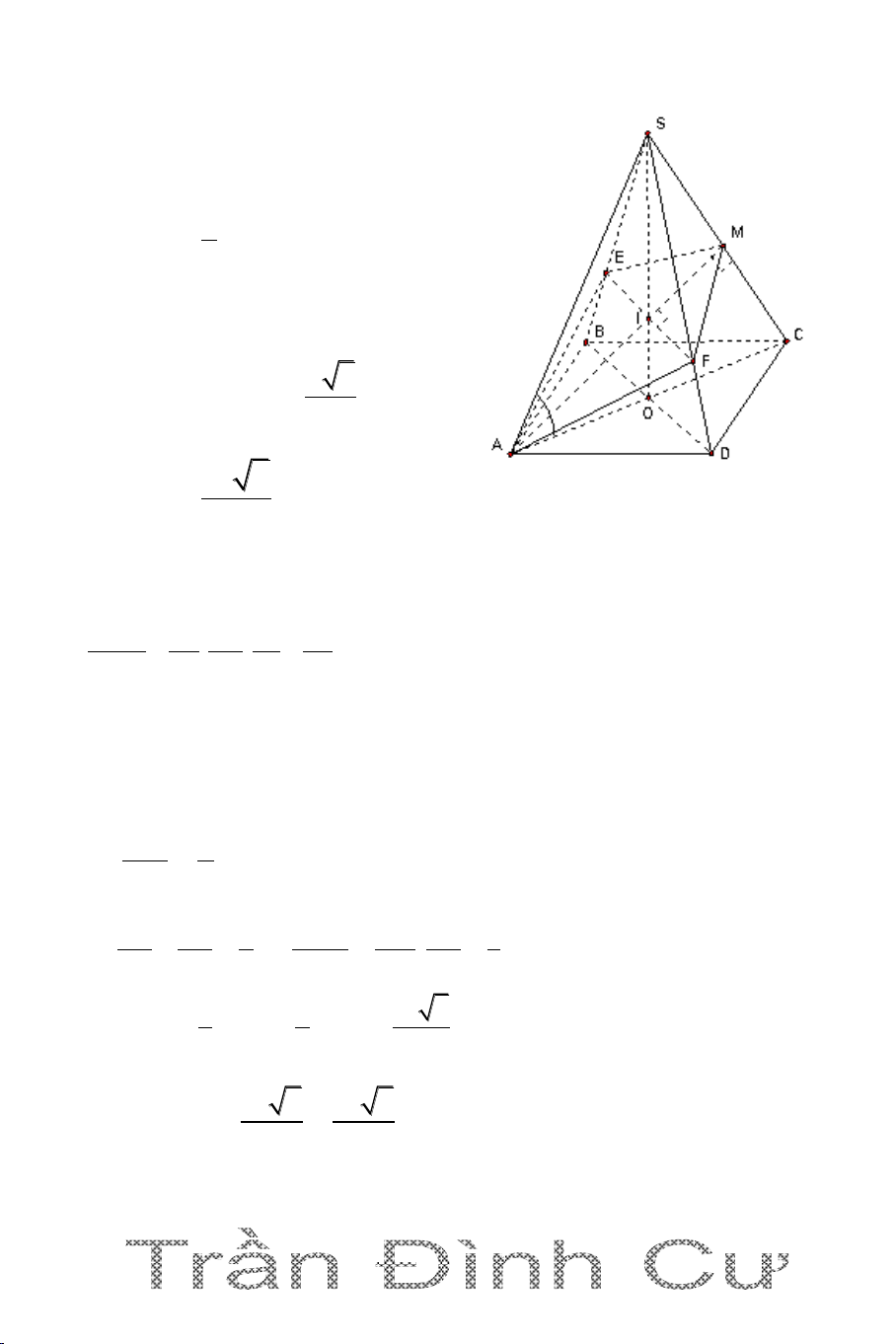
Câu 1. Cho hình chóp S.ABC có tam giác ABC vuông cân ở B, AC  a 2 ,
SA vuông góc với đáy ABC , SA  a . Gọi G là trọng tâm tam giác ABC,  mặt phẳng (
) qua AG và song song với BC cắt SC, SB lần lượt tại M, N.
Tính thể tích của khối chóp S.AMN 3 2a 3 a 3 a 2 3 a 3 A. B. C. D. 27 27 27 27 Hướng dẫn giải 1 S  Ta có: V S .SA S . ABC ABC và 3 SA a N ABC â c n ó
c : AC a 2  AB a G C A M 1 2 ISa ABC B 2 3 1 1 a 2 Vậy: V  . a .a SABC 3 2 6 SG 2 
Gọi I là trung điểm BC. G là trọng tâm, ta có : SI 3  // BC  MN// BC SM SN SG 2 V SM SN SAMN     4   .  SB SC SI 3 V SB SC 9 SABC 3 4 2a Vậy: VVSAMN SABC
. Vậy chọn đáp án A. 9 27 55
Câu 2. Cho tam giác ABC vuông cân ở A và AB a . Trên đường thẳng
qua C và vuông góc với mặt phẳng (ABC) lấy điểm D sao cho CD a .
Mặt phẳng qua C vuông góc với BD, cắt BD tại F và cắt AD tại E.
Tính thể tích khối tứ diện CDEF. 3 a 3 3 a 3 a 3 a 3 A. B. C. D. 12 36 12 36 Hướng dẫn 3 1 a Tính V  S .CD ABCD ABC  3 6 D F
Tacó: AB AC, AB CD aAB  (AC ) D EAB EC B C
Ta có: DB EC a
EC  ( AB ) D A Tính V EF DC :Ta có: V DE DF DCEF  . (*) V DA DB DABC 2 2 DE DC a 1 2 Mà D .
E DA DC , chia cho 2 DA     2 2 DA DA 2a 2 2 2 DF DC a 1 Tương tự:    2 2 2 DB DB DC CB 3 V 1 3 1 a DCEF   Từ(*) .VậyVVDCEF ABCD
. Vậy chọn đáp án B. V 6 6 36 DABC 56
Câu 3. Cho khối chóp tứ giác đều SABCD. Một mặt phẳng ( ) qua A, B và
trung điểm M của SC . Tính tỉ số thể tích của hai phần khối chóp bị phân
chia bởi mặt phẳng đó. Hướng dẫn giải
Kẻ MN // CD (N  SD) thì hình thang S
ABMN là thiết diện của khối chóp khi cắt
bởi mặt phẳng (ABM). N V SN 1 1 S.ANB    V  V S.ANB S.ADB M V SD 2 2 D S.ADB A O V SM SN 1 1 1 1 1 SBMN  .  .  VVV SBMN SBCD SABCD V SC SD 2 2 4 4 8 SBCD B C 3
Mà VSABMN = VSANB + VSBMN = VSABCD . 8 V  V  V S.ABCD S.MNAB MNAB.ABCD 3 5  V  V  V  V  V  V MNAB.ABCD S.ABCD S.MNAB S.ABCD S.ABCD S.ABCD 8 8 V 3 Do đó : SABMN  . C V 5 ABMN . ABCD
Câu 4. Cho hình chóp tứ giác đều S.ABCD, đáy là hình vuông cạnh a, cạnh 
bên tạo với đáy góc 60 . Gọi M là trung điểm SC. Mặt phẳng đi qua AM
và song song với BD, cắt SB tại E và cắt SD tại F. Tính thể tích khối chóp S.AEMF 3 a 3 3 a 6 3 a 6 3 a 6 A. B. C. D. 12 6 9 18 Hướng dẫn giải 57
Gọi I SO AM . Ta có (AEMF) //BD  EF // BD 1 VS .SO S . AB D C AB D C với 3 2 Sa D ABC S  OA có :  a 6 SO A . O tan 60  2 3 a 6 VS . AB D C 6
Phân chia chóp tứ giác ta có: V SA SM SF SB S.AMF  . .  1 V  V S.AMF S.AME V SA SM SE SD S.AME Do đó: V V S . E
A MF = VSAMF + VSAME =2VSAMF;
S . ABCD = 2VSACD = 2 VSABC
Xét khối chóp S.AMF và S.ACD SM 1   ; S
AC có trọng tâm I, EF // BD nên: SC 2 SI SF 2    V SM SF 1 SAMF   .  SO SD 3 V SC SD 3 SA D C 3 1 1 a 6 VVVSAMF SA D C SA D C 3 6 36 3 3 a 6 a 6 V  2  S . E A MF
. Vậy chọn đáp án D. 36 18 58
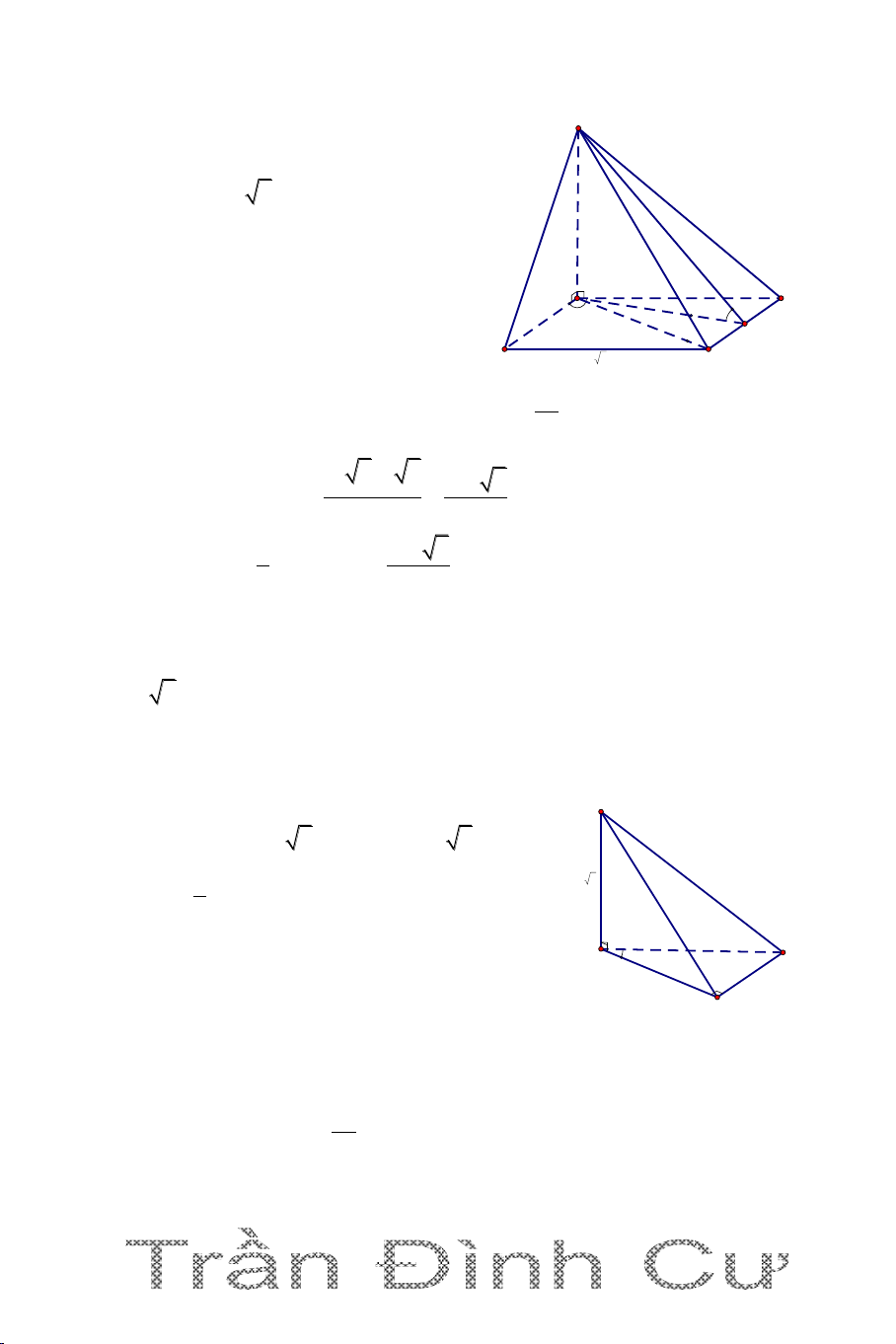
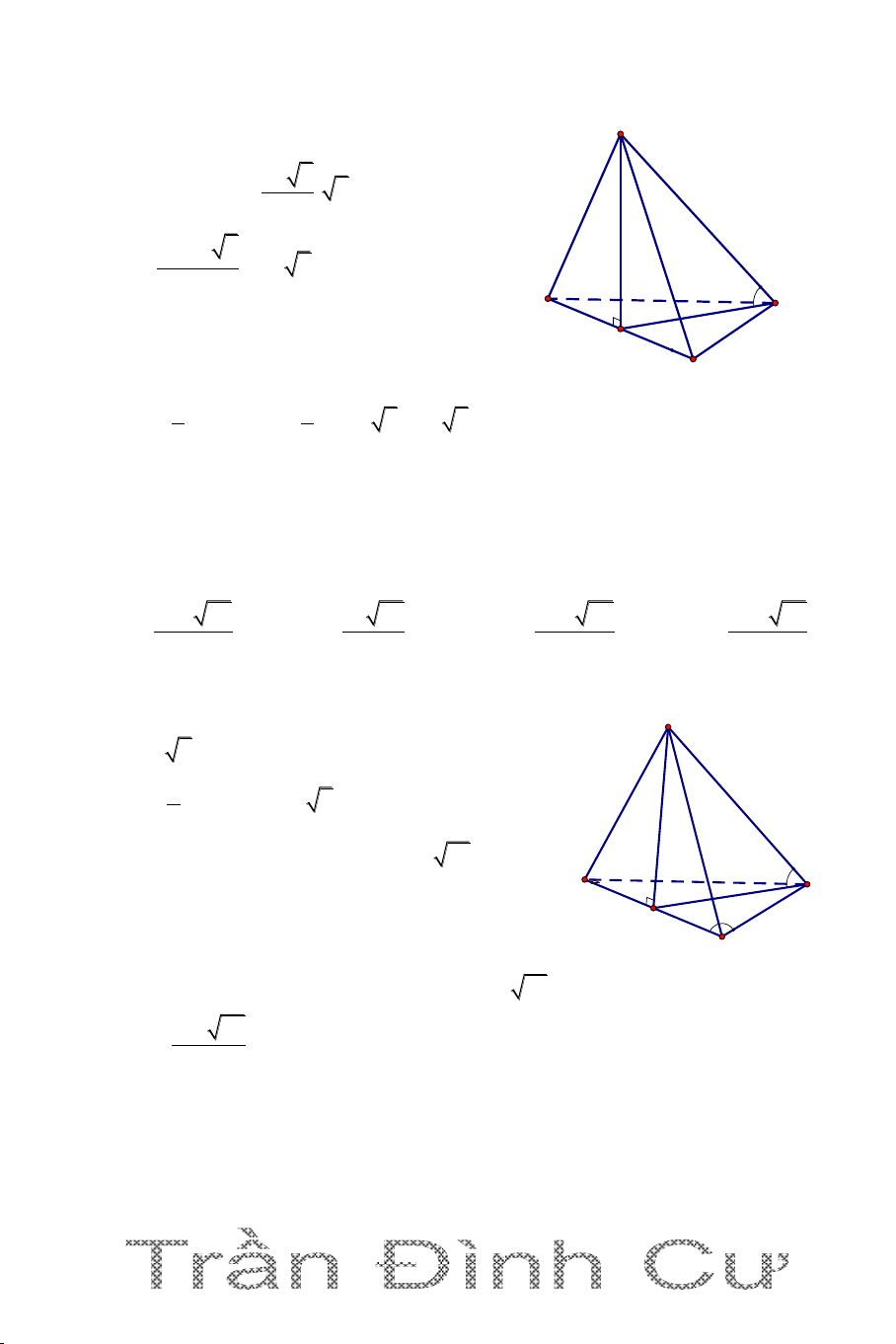
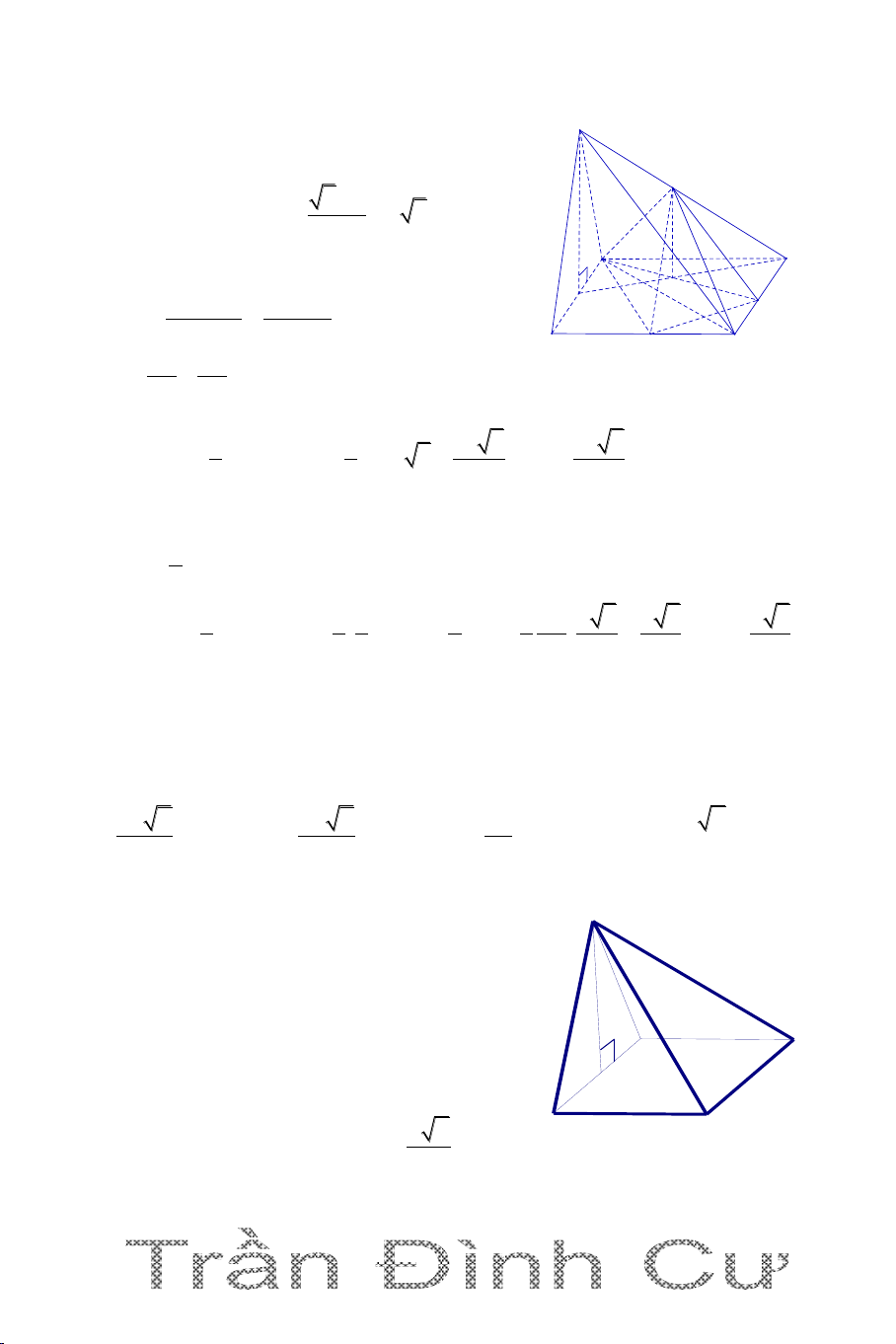
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA
vuông góc đáy, SA a 2 . Gọi B’, D’ là hình chiếu của A lần lượt lên SB,
SD. Mặt phẳng (AB’D’) cắt SC tại C’. Tính thể tích khối chóp S.AB’C’D’ 3 2a 2 3 2a 3 3 a 2 3 a 3 A. B. C. D. 9 9 9 9 Hướng dẫn 3 1 a 2   Ta có: V S .SA S . ABCD ABCD 3 3
Ta có BC  (SA )
B BC AB ' ; SB AB ' .
Suy ra: AB '  (SBC) nên AB'  SC . Tương tự AD'  SC. Vậy SC  (AB'D')
Tính VS.AB'C'D' V SB ' SC ' SAB C  Tính V ' ' . (*)
S . AB 'C ' : Ta có: V SB SC SABC SC S  ' 1 AC vuông cân nên  SC 2 2 2 2 SB ' SA 2a 2a 2     Ta có: 2 2 2 2 SB SB SA AB 3a 3 V 1 SAB 'C '   3 3 1 a 2 a 2 Từ (*) V  .  SAB 'C ' V 3 SABC 3 3 9 V SB' SB Ta có: S.AC'B'     1 B'D'/ / BD  V  V S.AC'B' S.AC'D' V SD' SD S.AC'D' 59 3 2a 2   V 2V
S . A B 'C ' D '
S .A B 'C '
. Vậy chọn đáp án A. 9
Câu 6. Cho khối chóp SABCD có đáy ABCD là hình bình hành. Gọi B’, C’
lần lượt là trung điểm của SB và SD. Mặt phẳng AB’D’cắt SC tại C’.Tính tỉ
số thể tích của hai khối chóp SAB’C’D’ và SABCD. 1 1 1 1 A. B. C. D. 2 4 6 8 Hướng dẫn giải
Gọi O = AC  BD .Ta có AC’, B’D’, SO đồng quy tại I và I là trung điểm của SO . S
Kẻ OC” // AC’ .Ta có SC’ = C’C” = C”C, SC' 1  C' D' nên SC 3 . I I B' Ta có A D C" V SB' SC' 1 1 1 V 1 SAB'C' SAB'C'  .  .    V SB SC 2 3 6 V 12 SABC SABCD O C V 1 B
Tương tự ta cũng có: SAC'D'  V 12 SABCD V V  V 1 1 1 Vậy SAb'C'D' SAB'C' SAC'D'     V V
12 12 6 .Vậy chọn đáp án C. SABCD SABCD
Câu 7. Cho khối chóp SABCD có đáy là hình vuông cạnh a, SA vuông góc
với mặt phẳng đáy và SA = 2a.Gọi B’, D’lần lượt là hình chiếu của A lên SB
và SD. Mặt phẳng (AB’D’) cắt SC tại C’. Tính thể tích khối chóp SAB’C’D’. 3 4a 3 8a 3 a 3 16a A. 45 B. 45 C. 45 D. 45 60 Hướng dẫn giải
Ta có AB’  SB, AB’  CB  AB’  (SBC) S  AB’  SC (a) D' C' Tương tự AD’  SC (b) B' Từ (a) và (b) suy ra D A
SC  (AB'C'D')  SC  AC' n O B C
Do tính đối xứng, ta có VSAB’C’D’ = 2VSAB’C’ 2 2 2 2 V SB' SC' SB'.SB SC'.SC SA SA 4a 4a 8 S.AB'C'  .  .  .  .  2 2 2 2 2 2 V SB SC SB SC SB SC 5a 6a 15 S.ABC 2 3 3 3 1 a a 8 a 8a VSABC = . .2a   V  .  SAB'C' 3 2 3 15 3 45 3 16a
Vậy VSAB’C’D’ = 45 . Vậy chọn đáp án D.
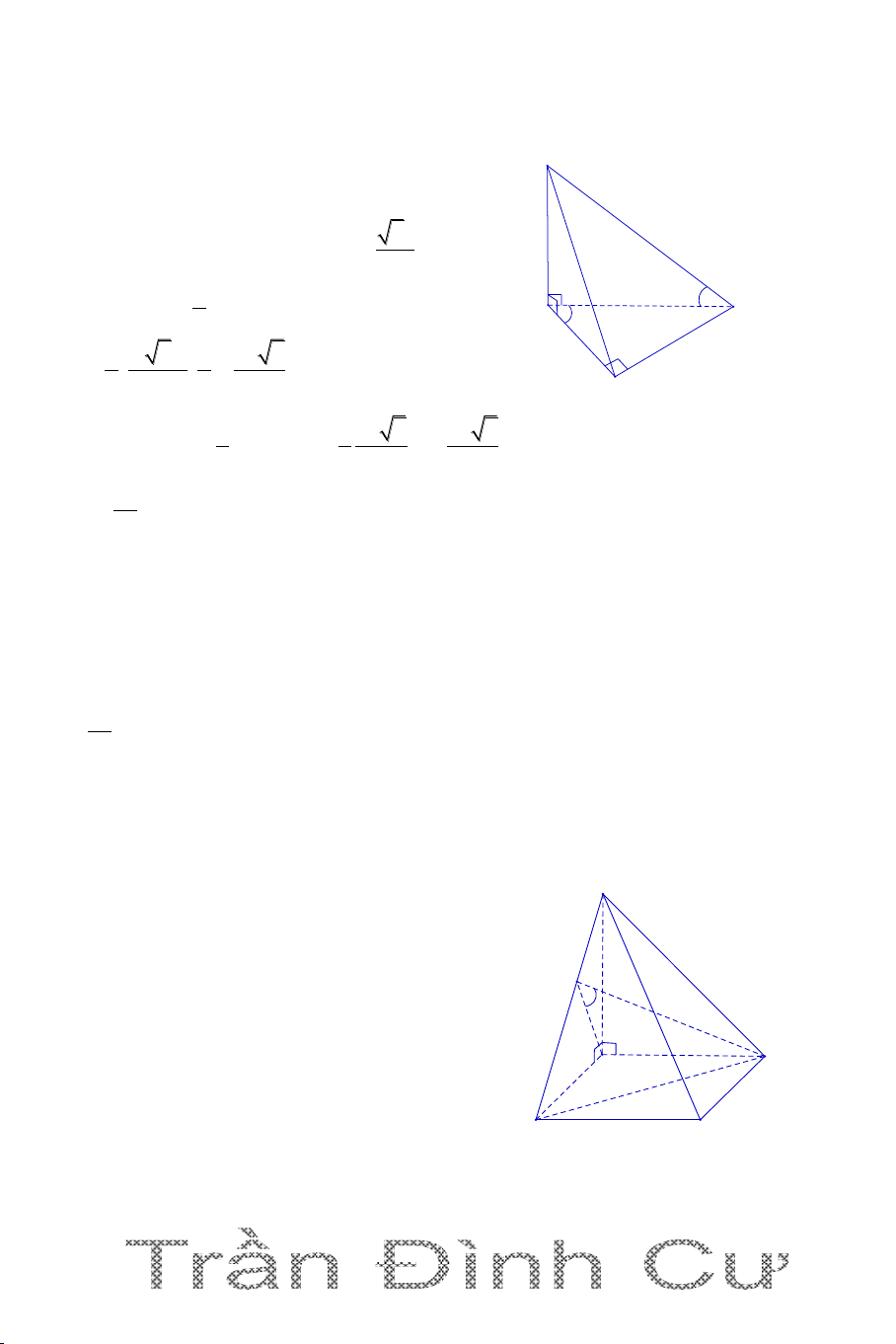
Câu 8. Cho hình chóp S.ABC có SA SB a , SC  2a ,   60o ASB BSC ,  6V 90o ASC
. Thể tích của khối chóp S.ABC bằng V. Tỉ số là : 3 a 4 6 B. 2 C. 3 3 A. D. 3 3 Hướng dẫn giải 61
Gọi M là trung điểm SC , ta có SM a S
 SAM vuông cân tại S. Gọi H là
trung điểm của AM . Ta có 60 2 2
AM SA SM a 2 60 M 1 2    a SH AM 2 2 H
Ta có SM = BM = a và  60o BSC C A
 BSMđều  BM a  BSM đều B
Ta có AB = BM = a  ABM cân tại B . Mặt khác: 2 2 2
AB BM  2a và 2 2 AM  2a 2 2 2
AB BM AM 1   2
ABM vuông cân tại B (định lý pitago đảo)    a BH AM . 2 2 2 2
a 2   a 2  Ta có 2 2 2
SH BH         a 2 2 2 2
SH BH SB a 2   2     
 SHB vuông cân tại H (định lý pitago đảo)
Ta có SH AM,SH HB SH   ABM 2 1 a 1 2 3 1 a 2 a a 2 SA . B BM   VSH S    . . ABM 2 2 S.ABM 3 ABM 3 2 2 12 3 V SC a 2 6V S.ABC   2  V  2V    2 S.ABC S.ABM V SM 6 3 a S.ABM
Chọn đáp án B
* Cách khác: Sử dụng công thức giải nhanh Tổng quát: Cho chóp S.ABC có
SA a,SB b,SC c và
ASB   , BSC   , ASC   . 62 Thể tích khối chóp S.ABC là: abc 2 2 2 V
1 cos   cos   cos   2coscoscosS.ABC 6
Áp dụng vào bài này ta được: 3 . a . a 2a 2 0 2 0 2 0 0 0 0 a 2 V
1 cos 60  cos 60  cos 90  2co 6 s 0 co 6 s 0 co 9 s 0  S.ABC 6 6 6
V  2 Chọn đáp án B. 3 a
Câu 9. Cho hình chóp tứ giác đều .
S ABCDcó đáy là hình vuông ABCD 1
cạnh a, góc giữa mặt bên và mặt phẳng đáy là  thoả mãn cos = . Mặt 3
phẳng P qua AC và vuông góc với mặt phẳng SAD chia khối chóp .
S ABCD thành hai khối đa diện. Tỉ lệ thể tích hai khối đa diện là gần nhất
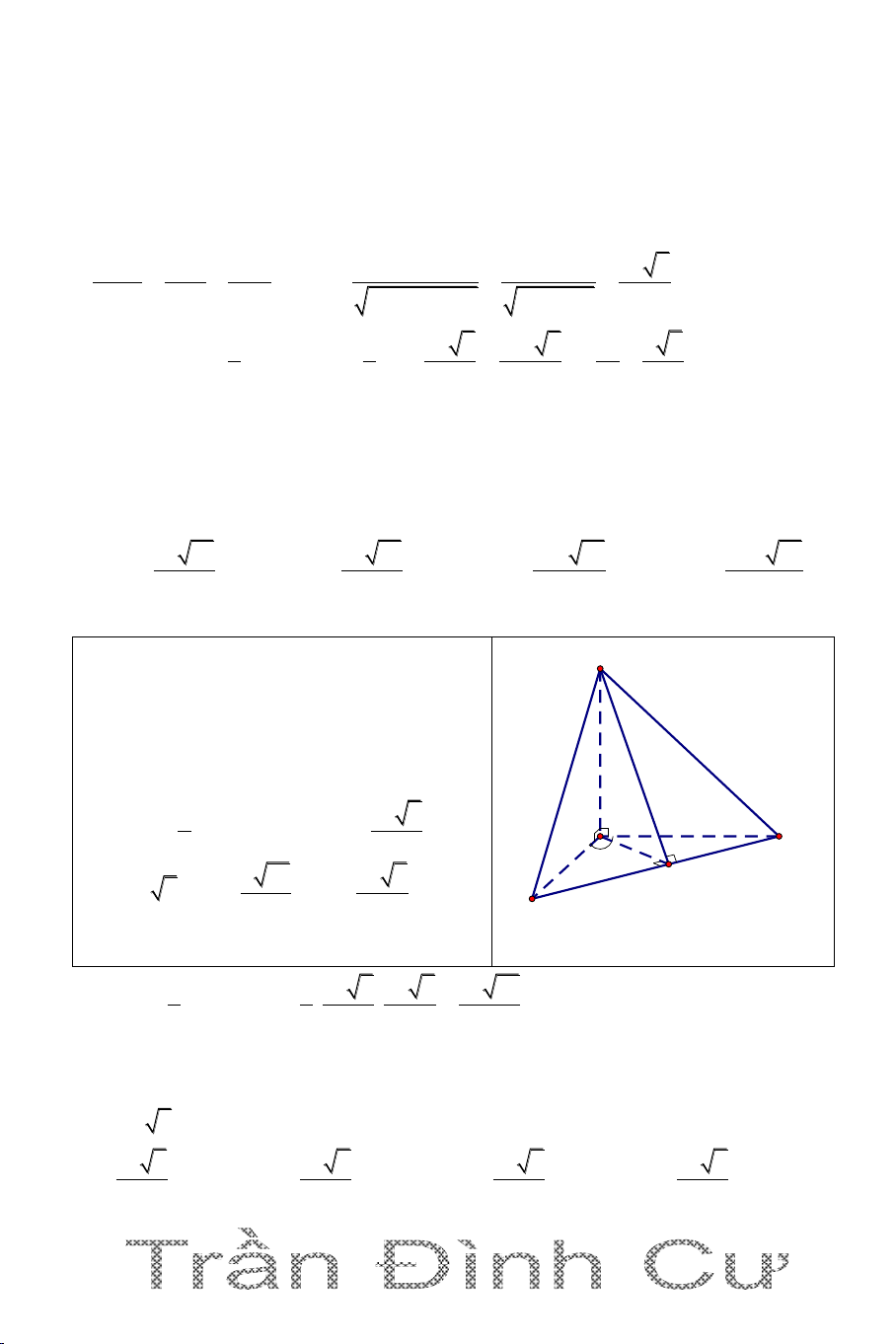
với giá trị nào trong các giá trị sau: A. 0,11 B. 0,13 C. 0,7 D. 0,9 Hướng dẫn giải .
S ABCD là hình chóp tứ giác đều S
SO   ABCD . Gọi N là trung điểm CD
CD SN,CD   ON   M
SCD  ABCD   CD
 SCD,ABCD SNO A D
Kẻ CM SD . Ta có O NAC BD
AC  SBD  AC B C AC SDSO
SD  ACM  ACM  SAD
nên mặt phẳng P là  ACM63 a ON 3a
Xét tam giác SON vuông tại N có : 2 SN    1 cos SNO 2 3 2 2  a   a 2 2 3
SO SN ON        a 2  2   2 
Xét tam giác SOD vuông tại O có :
SD SO OD  a  2 2   2 2 a 2 a 10 2      2  2   3a 1 1 .a SN.CD 3a 10 Ta có S
CM.SD SN. 2  CM     CD SCD 2 2 SD a 10 10 2
Xét tam giác MCD vuông tại M có : 2   2 2 2 3a 10 a 10
DM CD CM a      10  10   a 10 V V 1 DM DA DC 1 DM 1 1 Ta có : MACD MACD 10   . . .  .  .  V 2.V 2 DS DA DA 2 DS 2 SABCD SACD a 10 10 2 1  VV
. Mặt phẳng P chia khối chóp S.ABCD thành 2 MACD 10 SABCD
khối MACD và SABCM  9 VVVVV SABCD MACD SABCM SABCM 10 SABCD V 1 Do đó : MACD
 0,11  Chọn đáp án A V 9 SABCM
Tổng quát: Cho hình chóp tứ giác đều .
S ABCDcó đáy là hình vuông
ABCD cạnh a, góc giữa mặt bên và mặt phẳng đáy là  . Mặt phẳng P64
qua AC và vuông góc với mặt phẳng SAD chia khối chóp . S ABCD V
thành hai khối đa diện. Tỉ lệ thể tích hai khối đa diện là 1 2  cos  V2 Chứng minh: Ta có: 2 2 2 1 2
SD SN ND ON .  ND 2 cos SNO a 1 a 2   1  cos   1 2 2 cos  2.cos 1 1 Ta có : S
CM.SD SN.  CD SCD 2 2 a 1 .a SN.CD 2 cos      a CM 2 SD a 2 1   cos cos 1   2.cos 2  2 2 2 a . a cos
DM CD CM a   2 2 1 cos  1 cos  V V 1 DM DA DC 1 DM MACD MACD  . . .  . V 2.V 2 DS DA DA 2 DS SABCD SACD  . a cos 2 2 1 1  cos  cos    2 2 a   2 1 cos 1  cos  2.cos 2 cos   VV MACD 2 1  cos SABCD  2  cos   1  VV V SABCM 1   2 SABCD 2 1  cos  1    cos SABCDV Do vậy : MACD 2  cos  . VSABCM 65
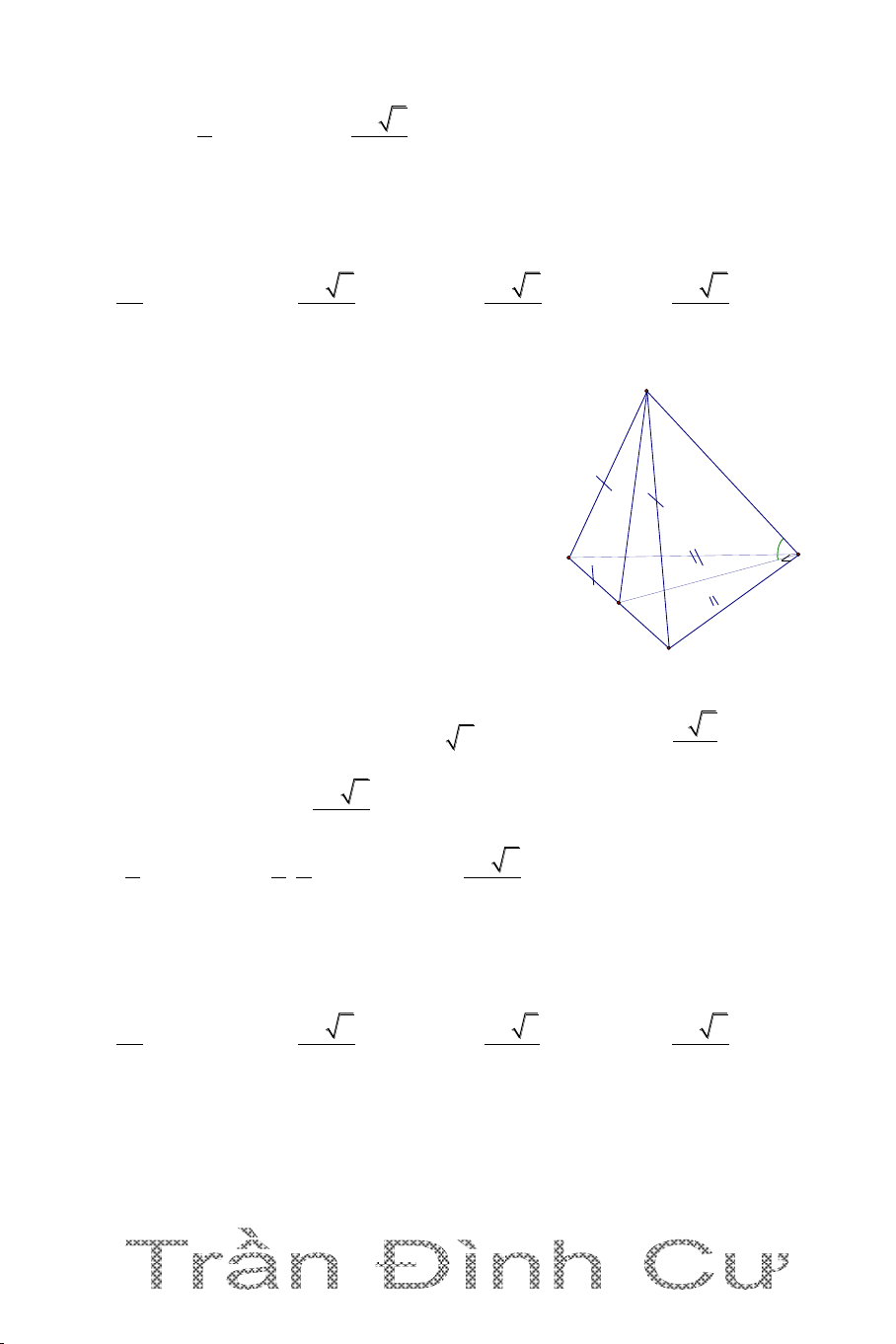
Câu 10. Cho hình chóp tam giác đều .
S ABC có cạnh đáy bằng a. Gọi
G là trọng tâm tam giác ABC, góc giữa SG và mặt phẳng SBC là
300. Mặt phẳng P chứa BC và vuông góc với SA chia khối chóp .
S ABC thành hai phần. Tỉ số thể tích hai phần là: 1 1 6 2 A. B. C. D. 6 7 7 3
Hướng dẫn gi ải Do .
S ABC là hình chóp tam giác đều S
SG  ABC SG N BC ,
mà BC AM BC  SAM
 SBC  SAMA CG
SBCSAM   SM M  nên hình B
SBC  SAM ,SG   SAD
chiếu vuông góc của SG lên SBC là SM
 SG, SBC   SG,SMo    GSM  30
Kẻ MN SA , ta có BC  SAM  SA BC SA  NBC nên mặt
phẳng P là NBC. Xét tam giác SGM vuông tại M có: 1 1 a 3 a 0
SG GM.cot GSM  .AM.cot 30  . . 3  3 3 2 2 SG a 2 a 3  SM   .  2 cosGSM 3 3 Xét tam giác SGA vuông tại G có: 2 2  a    2 2 2 a 3 a 21
SA SG AG      .   2  3 2    6   66 a a 3 1 1 . . SG AM 3a 7 S
MN.SA S . 2 2  MN     G AM SAM 2 2 SA a 21 14 6 Xét tam giác SNM vuông tại N có: 2 2     2 2 a 3 3a 7 a 21
SN SM MN         3   14  42     a 21 V SN SB SC SN 1 1 Ta có: SNBC 42  . .     VV . V SA SB SC SA SNBC 7 SABC SABC a 21 7 6
Mặt phẳng P chia khối chóp thành 2 khối SNBC và NABC  6 VVVVV SABC SNBC NABC NABC 7 SABC V 1 Do vậy SNBC
Chọn đáp án A. V 6 NABC 67