Bài tập trắc nghiệm thể tích khối đa diện và khoảng cách có lời giải chi tiết – Phạm Văn Huy Toán 12

Tài liệu gồm 120 trang, với các bài toán trắc nghiệm thuộc chuyên đề thể tích khối đa diện và khoảng cách, các bài toán có đáp án và lời giải chi tiết.Mời các bạn đón xem.

36 18 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

120 trang 7 tháng trước

Tác giả:

Profile Lan Tường
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
BÀI TẬP TRẮC NGHIỆM CHUYÊN
ĐỀ THỂ TÍCH KHỐI ĐA DIỆN
VÀ KHOẢNG CÁCH
CÓ LỜI GIẢI CHI TIẾT
BẠN NÀO CẦN FILE WORD LIÊN HỆ
0934286923
NGƯỜI BUỒN CẢNH CÓ VUI ĐÂU BAO GIỜ
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH
LUYỆN THI THPT QUỐC GIA 2016 - 2017
CHỦ ĐỀ 1: THỂ TÍCH
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a. Cạnh bên SA vuông góc
với mặt phẳng đáy, SC tạo với mặt phẳng đáy một góc 45 và SC = 2
2a
. Thể tích khối chóp
S.ABCD bằng:
A.
3
2
3
a
B.
3
23
3
a
C.
3
3
a
D.
3
3
3
a
Câu 2: Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hai mặt (SAB) và (SAC) cùng
vuông góc với đáy. Tính thể tích khối chóp biết SC = a
3
?
A.
3
26
9
a
B.
C.
3
3
4
a
D.
3
3
2
a
Câu 3: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B với AC = a biết SA vuông góc với
đáy ABC và SB hợp với đáy một góc 60. Tính thể tích khối chóp:
A.
B.
3
3
24
a
C.
D.
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh a và SA vuông góc với đáy
ABCD và mặt bên (SCD) hợp với đáy một góc 60. Tính thể tích hình chóp S.ABCD
A.
3
3
3
a
B.
3
23
3
a
C.
3
3
6
a
D.
3
3a
Câu 5: Cho khối chóp S.ABC có đáy ABC là tam giác cân tại A với BC = 2a, BAC 120
0
, biết SA
(ABC) và mặt (SBC) hợp với đáy một góc 45. Tính thể tích khối chóp S.ABC
A.
3
9
a
B.
3
3
a
C.
3
2a
D.
3
2
a
Câu 6: Cho khối chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B biết AB = BC = a, AD
= 2a, SA (ABCD) và (SCD) hợp với đáy một góc 60. Tính thể tích khối chóp S.ABCD
A.
B.
3
3
3
a
C.
D.
3
2
a
Câu 7: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật biết rằng SA (ABCD), SC hợp với
đáy một góc 45 và AB = 3a, BC = 4a. Tính thể tích khối chóp:
A.
3
40a
B.
3
10a
C.
3
10 3
3
a
D.
3
20a
Câu 8: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật AD = 2a, AB = a. Gọi H là trung điểm
của AD, biết SH ( ABCD) . Tính thể tích khối chóp biết SA =
5a
.
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
3
23
3
a
B.
3
43
3
a
C.
3
4
3
a
D.
3
2
3
a
Câu 9: Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A, G là trọng tâm tam giác ABC, SG
(ABC). Biết góc giữa SM và mặt phẳng (ABC) bằng 30
0
(với M là trung điểm của BC), BC 2a và
AB = 5a. Tính
3
9V
a
với V là thể tích khối chóp S.ABC:
A.
82
B.
83
C.
85
D.
87
Câu 10: Cho hình chóp S.ABC. có đáy ABC là tam giác đều cạnh 8a, SA ( ABC) . Biết góc giữa hai
mặt phẳng (SBC) và (ABC) bằng 45
0
. Tính
3
5V
a
, với V là thể tích khối chóp S.ABC?
A. 280 B. 320 C. 360 D. 400
Câu 11: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = 8a, SA (ABC). Biết
góc giữa hai mặt phẳng (SBC) và (ABC) bằng 30
0
. Tính,
3
93V
a
với V là thể tích khối chóp S.ABC.
A. 768 B. 769 C. 770 D. 771
Câu 12: Cho hình chóp S.ABCD có đáy là hình vuông cạnh 8a, SA (ABCD). Biết góc giữa SC và
mặt phẳng (ABCD) bằng 45
0
. Tính
3
3
512
V
a
, với V là thể tích khối chóp S ABC . .
A.
3
B. 3 C.
2
D. 2
Câu 13: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AC = a, SA (ABC). Biết
thể tích khối chóp S.ABC là
3
6
24
a
(đơn vị thể tích). Tính góc giữa SB và mặt phẳng (ABC).
A. 60
0
B. 45
0
C. 30
0
D. 90
0
Câu 14: Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = a, SC = 2a
2
, SA (ABCD).
Biết góc giữa SC và mặt phẳng (ABCD) bằng 30
0
. Tính theo a thể tích khối chóp S.ABCD.
A.
3
10
3
a
B.
3
10
5
a
C.
3
5
10
a
D.
3
5
3
a
Câu 15: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 8a, SA (ABC). Biết góc giữa hai
mặt phẳng (SBC) và (ABC) bằng 45
0
. Tính theo a thể tích khối chóp S.ABC.
A. 56a
3
B. 64a
3
C. 72a
3
D. 80a
3
Câu 16: Cho hình chóp tam giác đều S.ABC có cạnh AB bằng a. Các cạnh bên SA, SB, SC tạo với
đáy một góc 60
0
. Gọi D là giao điểm của SA với mặt phẳng qua BC và vuông góc với SA. Tính theo a
thể tích khối chóp S.DBC.
A.
3
5
96
a
B.
3
52
96
a
C.
3
53
96
a
D.
3
55
96
a
Câu 17: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB là tam giác đều
và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích khối chóp S.ABCD.
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
3
3
6
a
B.
3
3
5
a
C.
3
3
4
a
D.
3
3
3
a
Câu 18: Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA = 2a và SA
(ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC.
Tính
3
50 3V
a
, với V là thể tích khối chóp A.BCNM
A. 9 B. 10 C. 11 D. 12
Câu 19: Cho tứ diện ABCD có các cạnh AB; AC; AD đôi một vuông góc với nhau biết AC = a; AD
=
3a
và khoảng cách từ A đến mặt phẳng BCD bằng
21
7
a
. Thể tích khối chóp đã cho là:
A.
3
3
2
a
B.
3
3
6
a
C.
3
33
4
a
D.
3
3
3
a
Câu 20: Cho khối chóp S.ABCD có đáy là hình vuông, SA ABCD và SA=h. Biết SC tạo với đáy
một góc 45
0
. Thể tích khối chóp đá cho tính theo h là:
A.
B.
3
3
h
C.
3
3
6
h
D.
3
6
h
Câu 21: Cho hình chóp S.ABCD có đáy là hình thoi ABCD tâm I cạnh a, SI ABCD . Biết tam
giác ABC đều và SB =
2a
. Thể tích khối chóp đã cho là:
A.
3
46
3
a
B.
3
15
4
a
C.
3
15
12
a
D.
3
43
3
a
Câu 22: Cho khối chóp S.ABCD có đáy là hình chữ nhật ABCD có AB = 1; AD 2. Hình chiếu
vuông góc của S xuống mặt đáy là trung điểm của AD. Khoảng cách từ A đến mặt phẳng SBC bằng
2
2
. Thể tích khối chóp đã cho là:
A.
1
3
B. 1 C.
2
3
D.
2
3
Câu 23: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D có AD 2; AB = BC 1, SA
ABCD , đường thẳng SC tạo với đáy một góc 45
0
. Thể tích khối chóp đã cho là:
A.
22
B. 2 C.
2
D. 1
Câu 24: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 1, SA ABC, khoảng cách từ A đến
mặt phẳng SBC bằng
21
7
. Thể tích khối chóp đã cho là
A.
3
2
B.
3
4
C.
3
3
D.
3
12
Câu 25: Cho hình chóp tứ giác đều S.ABCD có đường cao bằng h và mặt bên tạo với đáy một góc
60
0
. Thể tích khối chóp đã cho tính theo h là:
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
3
2
3
h
B.
3
4
3
h
C.
3
4h
D.
3
4
9
h
Câu 26: Cho hình chóp S.ABCD có đáy là hình chữ nhật có AB = 4, AC = 5 và SA (ABCD biết
mặt phẳng SCD tạo với đáy một góc 60
0
. Thể tích khối chóp đã cho là:
A.
12 3
B.
43
C.
63
D.
20 3
Câu 27. Cho hình chóp tam giác đều S.ABC có đáy là tam giác đều cạnh
3a
, góc giữa SC và mặt
phẳng (ABC) bằng
0
60
. Tính theo
a
thể tích khối chóp S.ABC
A.
3
3
4
a
B.
3
4
a
C.
3
3
5
a
D.
3
5
a
Câu 28. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng
a
, cạnh bên bằng 2
a
. Biết khoảng
cách từ A đến mặt phẳng (SBC) bằng
3
6
a
. Tính
3
12V
a
, với V là thể tích khối chóp S.ABC
A. 10 B. 11 C.
10
D.
11
Câu 29. Cho hình chóp tam giác đều S.ABC có đáy là tam giác đều cạnh
a
, góc giữa mặt bên và mặt
đáy bằng
0
45
. Tính theo
a
thể tích khối chóp S.ABC
A.
3
3
6
a
B.
3
3
8
a
C.
3
6
a
D.
3
8
a
Câu 30. Cho hình chóp tam giác đều S.ABC có đường cao SH bằng h, góc hợp với SH với một mặt
bên bằng
0
30
. Tính theo h thể tích khối chóp S.ABC
A.
3
3
3
h
B.
3
3
9
h
C.
3
2
9
h
D.
3
2
h
Câu 31. Cho hình chóp đều tam giác S.ABC có đáy là tam giác đều cạnh
3a
, góc giữa hai mặt
phẳng (SAB) và (ABC) bằng
0
45
. Tính theo
a
thể tích khối chóp S.ABC
A.
3
3
6
a
B.
3
3
8
a
C.
3
3
4
a
D.
3
3
2
a
Câu 32. Cho hình chóp tứ giác đều S.ABCD có đường cao SH bằng h, góc ở đỉnh của mặt bên bằng
0
60
. Tính
0
3
3 sin30V
h
, với V là thể tích khối chóp S.ABCD
A.
3
B. 3 C. 2 D. 1
Câu 33. Cho hình chóp tứ giác đều, mặt bên hợp với mặt đáy một góc
0
45
và khoảng cách từ chân
đường cao của hình chóp đến các mặt bên bằng
a
. Tính theo
a
thể tích khối chóp.
A.
3
83
3
a
B.
3
3
3
a
C.
3
82
3
a
D.
3
2
3
a
Câu 34. Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh
0
a
. Biết thể tích khối chóp S.ABC là
3
3
36
a
V
. Tính góc giữa SA và mặt phẳng (ABC)
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
0
20
B.
0
30
C.
0
45
D.
0
60
Câu 35. Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh
3a
, khoảng cách từ A đến mặt
phẳng (SBC) bằng
32
4
a
. Tính theo
a
thể tích khối chóp S.ABC
A.
3
3
6
a
B.
3
3
8
a
C.
3
3
4
a
D.
3
3
2
a
Câu 36. Cho hình chóp tam giác đều S.ABC với
2,SA a AB a
. Gọi H là hình chiếu vuông góc của
A lên SC. Thể tích khối chóp S.ABH là:
A.
3
7 11
96
a
B.
3
3 11
87
a
C.
3
37
39
a
D.
3
37
11
a
Câu 37. Cho hình chóp tam giác đều S.ABC có cạnh bên bằng
a
và nghiêng đều với đáy ABC một
góc
0
60
. Thể tích khối chóp S.ABC là:
A.
3
6
a
B.
3
3
32
a
C.
3
3
16
a
D.
3
11
21
a
Câu 38. Cho hình chóp tứ giác đều có mặt bên hợp với đáy một góc
0
45
và khoảng cách từ chân
đường cao của hình chóp đến các mặt bằng
a
. Thể tích khối chóp đó là :
A.
B.
3
2
6
a
C.
3
82
3
a
D.
3
33
2
a
Câu 39. Cho hình chóp đều S.ABCD có cạnh đáy bằng
a
, góc giữa mặt bên với đáy bằng
0
45
. Gọi
,,M N P
lần lượt là trung điểm của
,,SA SB CD
. Thể tích khối tứ diện AMNP là:
A.
3
16
a
B.
3
24
a
C.
3
6
a
D.
3
48
a
Câu 40. Cho hình chóp tứ giác đều S.ABCD, đáy là hình vuông cạnh
a
, cạnh bên tạo với đáy một góc
0
60
. Gọi M là trung điểm của SC. Mặt phẳng đi qua AM và song song với BD, cắt SB tại P và cắt SD
tại Q. Thể tích khối chóp S.AMNQ là V. Tỉ số
3
18V
a
là:
A.
2
B.
6
C.
3
D. 1
Câu 41. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng
26
cm, đường cao
1SO cm
. Gọi
M, N lần lượt là trung điểm AC, AB. Thể tích khói chóp S.AMN tính bằng
3
cm
là:
A.
2
2
B. 1 C.
5
2
D.
3
2
Câu 42. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng
a
. Thể tích khối chóp đó là :
A.
3
3
3
a
B.
3
3
2
a
C.
3
3
6
a
D.
3
2
6
a
Câu 43. Cho hình chóp tam giác đều S.ABC có cạnh dáy bằng
3a
và cạnh bên bằng
2a
. Thể tích
khối chóp S.ABC theo
a
là:
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
3
3
6
a
B.
3
3
3
a
C.
3
3
4
a
D.
3
3
4
a
Câu 44. Cho hình chóp tam giác đều S.ABC có cạnh bên bằng
a
hợp với đáy một góc
0
60
. Thể tính
khối chóp S.ABC là:
A.
3
3
16
a
B.
3
6
a
C.
3
3
32
a
D.
3
12
a
Câu 45. Cho hình chóp tam giác đều S.ABC có cạnh bên bằng
a
, góc giữa mặt bên với mặt đáy là
0
45
. Thể tích khối chóp S.ABC là:
A.
3
12
a
B.
3
3
5
a
C.
3
15
25
a
D.
3
16
a
Câu 46. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
,
0
60ASB
. Thể tích khối chóp là:
A.
3
3
4
a
B.
3
2
6
a
C.
3
2
3
a
D.
3
3
3
a
Câu 47. Cho hình chóp tứ giác đều có mặt bên hợp với đáy một góc
0
45
và khoảng cách từ chân
đường cao của hình chóp đến mặt bên bằng
a
. Thể tích khối chóp đó là:
A.
3
3
4
a
B.
3
3
6
a
C.
3
3
9
a
D.
3
82
3
a
Câu 48. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với
,2AB a AD a
, cạnh SA
vuông góc với mặt phẳng (ABCD). Tính độ dài đoạn SA để khoảng cách từ D đến mặt phẳng (SBM)
bằng
2
33
a
với M là trung diểm của đoạn CD.
A.
a
B.
2a
C.
3a
D.
4a
Câu 49. Tính
3
12V
a
, với V là thể tích khối chóp tứ diện đều có cạnh bằng
a
.
A.
3
B. 3 C.
2
D. 2
Câu 50. Cho tứ diện ABCD với M,N lần lượt là trung điểm của AB, AC. Tính tỉ lệ thể tích của khối tứ
diện AMND và ABCD
A.
1
4
B. 1 C.
1
2
D.
2
5
Câu 51. Cho khối chóp S.ABCD có đáy là hình bình hành, M là trung điểm của CD, I là giao điểm
của AC và BM. Tính tỷ số thể tích (theo thứ tự) các khối chóp S.ICM và S.ABCD
A.
1
2
B.
1
4
C.
1
2
D.
1
12
Câu 52. Cho khối chóp S.ABCD có đáy là hình bình hành, gọi
'B
và
'D
theo thứ tự là trung điểm các
cạnh SB, SD. Mặt phẳng (AB’D’) cắt cạnh SC tại C’. Tính tỷ số thể tích của hai khối chóp được chia
ra bởi mặt phẳng (AB’D’)
A.
1
2
B.
1
12
C.
1
5
D.
1
6
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 53. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B,
,2AB BC a AD a
, cạnh SA vuông góc với phặt phẳng đáy và
2SA a
. Gọi M,N lần lượt là
trung điểm của SA, SD. Tính thể tích khối chóp S.BCNM theo
a
.
A.
3
3
a
B.
3
2
a
C.
3
a
D.
3
2a
Câu 54. Cho tứ diện ABCD có thể tích bằng V. Gọi B’ và D’ lần lượt là trung điểm của cạnh AB và
AD. Mặt phẳng (CB’D’) chia khối tứ diện thành hai phần. Tính theo V thể tích khối chóp C.B’D’DB
A.
3
2
V
B.
4
V
C.
2
V
D.
3
4
V
Câu 55. Cho hình chóp tứ giác đều có diện tích đáy bằng 4 và diện tích mặt bên bằng
2
. Tính thể
tích khối chóp S.ABCD
A.
4
3
B. 4 C.
43
3
D.
42
3
Câu 56. Cho hình chóp S.ABCD có đáy là hình thoi tâm với
0
120BAD
và
BD a
. Cạnh bên SA
vuông góc với đáy. Góc giữa mặt (SBC) và đáy bằng
0
60
. Mặt phẳng (P) đi qua BD và vuông góc với
cạnh SC. Tính tỉ số thể tích giữa hai phần của hình chóp do mặt phẳng (P) tạo ra khi cắt hình chóp.
A. 10 B. 11 C. 12 D. 13
Câu 57. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng
a
, cạnh bên hợp với đáy góc
0
60
.
Gọi M là điểm đối xứng với C qua D và N là trung điểm của SC. Tính tỉ số thể tích giữa hai phần của
hình chóp do mặt phẳng (BMN) tạo ra khi cắt hình chóp.
A.
5
7
B.
5
8
C.
5
9
D.
5
11
Câu 58. Cho hình chóp tứ giác đều S.ABC có cạnh đáy bằng
a
, cạnh bên hợp với đáy góc
0
60
. Mặt
phẳng (P) qua BC và vuông góc với SA. SA cắt (P) tại D. Tính tỉ số thể tích giữa hai khối chóp S.BDC
và S.ABC
A.
5
7
B.
5
8
C.
5
9
D.
5
11
Câu 59. Cho tứ diện ABCD có thể tích bằng V. Gọi B’ và D’ lần lượt là trung điểm của cạnh AB và
AD. Mặt phẳng (CB’D’) chia khối tứ diện thành hai phần. Tính theo V thể tích khối chóp C.AB’D’
A.
3
2
V
B.
4
V
C.
2
V
D.
3
4
V
Câu 60. Cho tứ diện ABCD có thể tích bằng V. Gọi B’ và D’ lần lượt là trung điểm của cạnh AB và
AD. Mặt phẳng (CB’D’) chia khối tứ diện thành hai phần. Tính tỉ số thể tích hai phần đó.
A.
1
6
B.
1
9
C.
1
12
D.
1
3
Câu 61. Cho hình chóp S.ABC có các cạnh lần lượt là
;;SA a SB b SC c
. Trên
,,SA SB SC
lấy
các điểm M,N,P sao cho
1
1; 2;
2
SM SN SP
. Tỷ số thể tích giữa khối chóp S.ABC và S.MNP là:
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
1
abc
B.
3
abc
C.
abc
D.
3
abc
Câu 62. Cho hình chóp tam giác S.ABC và một điểm M nằm trong tam giác ABC. Đường thẳng qua
M song song với SA cắt mặt phẳng (BCS) tại A’. Tỷ số thể tích giữa khối chóp M.BCS và S.ABC là:
A.
'MA
SM
B.
'
'
MA
SA
C.
'MA
SA
D.
'
SM
SA
Câu 63. Cho hình chóp S.ABCD có đáy là hình vuông ABCD,
SA ABCD
. Mặt phẳng qua AB cắt
SC và SD lần lượt tại M và N sao cho
SM
x
SC
. Tìm
x
biết
.
.
11
200
S ABMN
S ABCD
V
V
A. 0,25 B. 0,2 C. 0,3 D. 0,1
Câu 64. Cho hình chóp S.ABCD có đáy là hình vuông cạnh
,a SA ABCD
và
2SA a
. Gọi
M,N,P lần lượt là trung điểm của SB,BC và CD. Thể tích khối chóp C.MNP là:
A.
3
32
a
B.
3
12
a
C.
3
16
a
D.
3
24
a
Câu 65. Cho hình chóp S.ABC có đáy là tam giác đều cạnh
,a SA ABC
và
2SA a
. Gọi
,,M N P
lần lượt là trung điểm của SB, BC và SC. Thể tích khối chóp A.MNP là:
A.
B.
2
3
12
a
C.
2
3
8
a
D.
3
24
a
Câu 66. Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh
a
. Hai mặt phẳng (SAB) và
(SAD) cùng vuông góc với đáy. Tính thể tích khối chóp S.ABCD biết rằng
3SC a
A.
3
.
3
9
S ABCD
a
V
B.
3
.
3
3
S ABCD
a
V
C.
3
.S ABCD
Va
D.
3
.
3
S ABCD
a
V
Câu 67. Cho khối chóp S.ABCD có ABCD là hình chữ nhật;
2;AD a AB a
. Gọi H là trung điểm
AD, biết SH vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết
5SA a
A.
3
.
23
3
S ABCD
a
V
B.
3
.
43
3
S ABCD
a
V
C.
3
.
4
3
S ABCD
a
V
D.
3
.
2
3
S ABCD
a
V
Câu 68. Cho khối chóp S.ABCD có ABCD là hình vuông cạnh
2a
. Gọi H là trung điểm AB, biết SH
vuông góc với mặt phẳng. Tính thể tích khối chóp S.ABCD biết tam giác SAB đều
A.
3
.
23
3
S ABCD
a
V
B.
3
.
43
3
S ABCD
a
V
C.
3
.
6
S ABCD
a
V
D.
3
.
3
S ABCD
a
V
Câu 69. Cho khối chóp S.ABC có tam giác ABC vuông tại B,
3 ; 6AB a AC a
. Hình chiếu của S
trên mặt phẳng (ABC) là điểm H thuộc đoạn AB sao cho
2AH HB
. Biết SC hợp với (ABC) một góc
bằng
0
60
. Tính thể tích khối chóp S.ABC
A.
3
.
21
3
S ABC
a
V
B.
3
.
97
S ABC
Va
C.
3
.
7
S ABC
Va
D.
3
.
21
6
S ABC
a
V
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 70. Cho khối chóp S.ABC có đáy là tam giác đều, cạnh bằng
a
. Gọi I là trung điểm AB. Hình
chiếu của S trên mặt phẳng (ABC) là trung điểm H thuộc đoạn CI. Góc giữa SA và (ABC) bằng
0
45
.
Tính thể tích khối chóp S.ABC
A.
3
.
21
16
S ABC
a
V
B.
3
.
7
48
S ABC
a
V
C.
3
.
7
36
S ABC
a
V
D.
3
.
21
48
S ABC
a
V
Câu 71. Cho khối chóp S.ABCD có ABCD là hình vuông tâm O, cạnh bằng
2a
. Hình chiếu của S
trên mặt phẳng (ABCD) là trung điểm H thuộc đoạn AO. Góc giữa SD và (ABCD) bằng
0
45
. Tính
thể tích khối chóp S.ABCD
A.
3
.
2
3
S ABCD
a
V
B.
3
.
2
S ABCD
Va
C.
3
.
3
3
S ABCD
a
V
D.
3
.
5
3
S ABCD
a
V
Câu 72. Cho khối chóp S.ABC có
SA ABC
;
ABC
là tam giác đều cạnh
a
. Góc giữa mặt phẳng
SBC
và
ABC
bằng
0
60
. Tính thể tích khối chóp S.ABC
A.
3
.
3
4
S ABC
a
V
B.
3
.
3
8
S ABC
a
V
C.
3
.
6
S ABC
a
V
D.
3
.
12
S ABC
a
V
Câu 73. Cho khối chóp
.S ABC
có
SA ABC
; tam giác ABC vuông tại A, biết
3;BC a AB a
.
Góc giữa mặt phẳng (SBC) và (ABC) bằng
0
45
. Tính thể tích khối chóp
.S ABC
A.
3
.
2
2
S ABC
a
V
B.
3
.
2
6
S ABC
a
V
C.
3
.
4
9
S ABC
a
V
D.
3
.
2
9
S ABC
a
V
Câu 74. Cho khối chóp S.ABCD có ABCD là hình chữ nhật;
SA ABCD
;
24AC AB a
. Tính
thể tích khối chóp S.ABCD biết rằng góc giữa mặt phẳng (SBC) và (ABCD) bằng
0
30
.
A.
3
.
2
3
S ABCD
a
V
B.
3
.
2
S ABCD
Va
C.
3
.
23
3
S ABCD
a
V
D.
3
.
8
3
S ABCD
a
V
Câu 75. Cho khối chóp S.ABC có
SA ABC
; tam giác ABC vuông tại B,
;3AB a AC a
.
Tính thể tích khối chóp S.ABC biết rằng
5SB a
A.
3
.
2
3
S ABC
a
V
B.
3
.
6
4
S ABC
a
V
C.
3
.
6
6
S ABC
a
V
D.
3
.
15
6
S ABC
a
V
Câu 76. Cho khối chóp S.ABC có
SA ABC
; tam giác ABC vuông tại B;
;3AB a AC a
. Tính
thể tích khối chóp S.ABC biết rằng
6SB a
A.
3
.
10
6
S ABC
a
V
B.
3
.
6
2
S ABC
a
V
C.
3
.
6
3
S ABC
a
V
D.
3
.
15
6
S ABC
a
V
Câu 77. Cho khối chóp
.S ABC
có đáy ABC là tam giác đều cạnh
a
. Hai mặt phẳng (SAB) và (SAC)
cùng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết rằng
3SC a
A.
3
.
26
9
S ABC
a
V
B.
3
.
6
12
S ABC
a
V
C.
3
.
3
4
S ABC
a
V
D.
3
.
3
2
S ABC
a
V
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 78. Cho khối chóp S.ABCD có ABCD là hình chữ nhật tâm O;
22AC AB a
; SA vuông góc
với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết rằng
5SD a
A.
3
.
5
3
S ABCD
a
V
B.
3
.
15
3
S ABCD
a
V
C.
3
.
6
S ABCD
Va
D.
3
.
6
3
S ABCD
a
V
Câu 79. Cho khối chóp đều S.ABCD có cạnh đáy bằng
3a
. Tính thể tích khối chóp S.ABCD biết
mặt bên là tam giác đều
A.
3
.
3
6
S ABCD
a
V
B.
3
.
3
3
S ABCD
a
V
C.
3
.
36
2
S ABCD
a
V
D.
3
.
6
2
S ABCD
a
V
Câu 80. Cho khối chóp đều S.ABC có cạnh đáy bằng
a
. Tính thể tích khối chóp S.ABC biết mặt bên
là tam giác đều.
A.
3
.
2
36
S ABC
a
V
B.
3
.
2
12
S ABC
a
V
C.
3
.
7
12
S ABC
a
V
D.
3
.
7
36
S ABC
a
V
Câu 81. Cho khối chóp S.ABC có
SA ABC
; tam giác ABC vuông tại B,
;3AB a AC a
. Tính
thể tích khối chóp S.ABC biết rằng góc giữa SB và (ABC) bằng
0
30
A.
3
.
6
9
S ABC
a
S
B.
3
.
6
6
S ABC
a
S
C.
3
.
6
18
S ABC
a
S
D.
3
.
26
3
S ABC
a
S
Câu 82. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh
a
. Hai mặt phẳng (SAB) và (SAC)
cùng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết rằng SB hợp với đáy một góc
0
30
A.
3
.
3
6
S ABC
a
V
B.
3
.
3
12
S ABC
a
V
C.
3
.
4
S ABC
a
V
D.
3
.
12
S ABC
a
V
Câu 83. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh
a
. Hai mặt phẳng (SAB) và (SAC)
cùng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết rằng SM hợp với đáy một góc
0
60
, với
M là trung điểm BC.
A.
3
.
6
8
S ABC
a
V
B.
3
.
3
4
S ABC
a
V
C.
3
.
3
8
S ABC
a
V
D.
3
.
6
24
S ABC
a
V
Câu 84. Cho khối chóp S.ABC có
SA ABC
; tam giác ABC vuông tại A,
2. 2BC AB a
. Tính
thể tích khối chóp S.ABC biết SC hợp với (ABC) một góc bằng
0
45
.
A.
3
.
2
S ABC
a
V
B.
3
.
3
2
S ABC
a
V
C.
3
.
33
2
S ABC
a
V
D.
3
.
6
S ABC
a
V
Câu 85. Cho khối chóp S.ABC có
SA ABC
; tam giác ABC vuông tại A,
22BC AB a
. Tính
thể tích khối chóp S.ABC biết SM hợp với đáy một góc bằng
0
60
, với M là trung điểm BC
A.
3
.
2
S ABC
a
V
B.
3
.
3
6
S ABC
a
V
C.
3
.
33
2
S ABC
a
V
D.
3
.
6
S ABC
a
V
Câu 86. Cho khối chóp S.ABCD có ABCD là hình chữ nhật tâm O;
22AC AB a
; SA vuông góc
với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết góc giữa SC và (ABCD) bằng
0
45
.
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
3
.
23
3
S ABCD
a
V
B.
3
.
43
3
S ABCD
a
V
C.
3
.S ABCD
Va
D.
3
.
3
S ABCD
a
V
Câu 87. Cho khối chóp S.ABCD có ABCD là hình chữ nhật tâm O;
22AC AB a
; SA vuông góc
với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết góc giữa SO và (ABCD) bằng
0
60
A.
3
.
23
3
S ABCD
a
V
B.
3
.
3
3
S ABCD
a
V
C.
3
.S ABCD
Va
D.
3
.
3
S ABCD
a
V
Câu 88. Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh
a
. Hai mặt phẳng (SAB) và
(SAD) cùng vuông góc với đáy. Tính thể tích khối chóp S.ABCD biết rằng góc giữa SC và (ABCD)
bằng
0
45
A.
3
.
2
6
S ABCD
a
V
B.
3
.
2
3
S ABCD
a
V
C.
3
.
6
S ABCD
a
V
D.
3
.
3
S ABCD
a
V
Câu 89. Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh
a
. Hai mặt phẳng (SAB) và
(SAD) cùng vuông góc với đáy. Tính thể tích khối chóp S.ABCD biết rằng góc giữa SM và (ABCD)
bằng
0
60
, với M là trung điểm BC
A.
3
.
15
6
S ABCD
a
V
B.
3
.
15
3
S ABCD
a
V
C.
3
.
6
S ABCD
a
V
D.
3
.
3
S ABCD
a
V
Câu 90. Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh
2a
. Gọi H là trung điểm AB, biết
SH vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết góc giữa SC và (ABCD) bằng
0
60
A.
3
.
2 15
3
S ABCD
a
V
B.
3
.
4 15
3
S ABCD
a
V
C.
3
.
6
S ABCD
a
V
D.
3
.
3
S ABCD
a
V
Câu 91. Cho khối chóp S.ABCD có ABCD là hình chữ nhật;
2;AD a AB a
. Gọi H là trung điểm
AD, biết SH vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết góc giữa SD và
(ABCD) bằng
0
45
A.
3
.
3
2
S ABCD
a
V
B.
3
.
3
S ABCD
Va
C.
3
.
2
3
S ABCD
a
V
D.
3
.
3
S ABCD
a
V
Câu 92. Cho khối chóp S.ABCD có ABCD là hình chữ nhật.
SA ABCD
;
24AC AB a
. Tính
thể tích khối chóp S.ABC biết rằng góc giữa mặt phẳng (SBD) và (ABCD) bằng
0
30
A.
3
.
4
9
S ABCD
a
V
B.
3
.
8
9
S ABCD
a
V
C.
3
.
23
3
S ABCD
a
V
D.
3
.
46
9
S ABCD
a
V
Câu 93. Cho khối chóp S.ABC có ABCD là hình vuông cạnh
a
;
SA ABCD
. Góc giữa mặt phẳng
(SBD) và (ABCD) bằng
0
30
. Tính thể tích khối chóp S.ABCD
A.
3
.
3
3
S ABCD
a
V
B.
3
.
2
3
S ABCD
a
V
C.
3
.
6
18
S ABCD
a
V
D.
3
.
6
9
S ABCD
a
V
Câu 94. Cho khối chóp S.ABC có ABCD là hình thoi, cạnh bằng
3a
;
;SA ABCD
0
120BAD
.
Tính thể tích khối chóp S.ABC biết rằng góc giữa mặt phẳng (SBD) và (ABCD) bằng
0
60
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
3
.
33
8
S ABCD
a
V
B.
3
.
3
6
S ABCD
a
V
C.
3
.
6
8
S ABCD
a
V
D.
3
.
6
4
S ABCD
a
V
Câu 95. Cho khối chóp S.ABCD có ABCD là hình thoi, cạnh bằng
3;a SA ABCD
;
0
120BAC
.
Tính thể tích khối chóp S.ABCD biết rằng góc giữa mặt phẳng (SCD) và (ABCD) bằng
0
30
A.
3
.
3
4
S ABCD
a
V
B.
3
.
33
4
S ABCD
a
V
C.
3
.
3
8
S ABCD
a
V
D.
3
.
3
4
S ABCD
a
V
Câu 96. Cho khối chóp S.ABC có ABCD là hình thoi,
6 ; 8AC a BD a
. Hai mặt phẳng
SAC
và
(SBD) cùng vuông góc với đáy. Góc giữa mặt phẳng (SBC) và (ABCD) bằng
0
30
. Tính thể tích khối
chóp S.ABCD
A.
3
.
32 3
5
S ABCD
a
V
B.
3
.
16 3
5
S ABCD
a
V
C.
3
.
32
5
S ABCD
a
V
D.
3
.
32
15
S ABCD
a
V
Câu 97. Cho khối chóp đều
.S ABC
D có cạnh đáy bằng
. Mặt bên hợp với đáy một góc
0
45
.
Tính thể tích khối chóp
.S ABCD
A.
3
.
82
S ABCD
Va
B.
3
.
3
S ABCD
a
V
C.
3
.
2
3
S ABCD
a
V
D.
3
.
82
3
S ABCD
a
V
Câu 98. Cho khối chóp đều S.ABCD có cạnh đáy bằng
2a
. Mặt bên hợp với đáy một góc
0
60
. Tính
thể tích khối chóp S.ABC
A.
3
.
3
3
S ABC
a
V
B.
3
.
22
3
S ABC
a
V
C.
3
.
4
9
S ABC
a
V
D.
3
.
2
9
S ABC
a
V
Câu 99. Cho khối chóp S.ABC có ABCD là hình chữ nhật;
8 ; 6AB a AD a
. Gọi H là trung điểm
AB, biết SH vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết rằng góc giữa mặt
phẳng (SCD) và (ABCD) bằng
0
60
A.
3
.
32 3
S ABCD
Va
B.
3
.
32
S ABCD
Va
C.
3
.
96
S ABCD
Va
D.
3
.
96 3
S ABCD
Va
Câu 100. Cho khối chóp S.ABC có đáy ABCD là hình chữ nhật;
8 ; 6AB a AD a
. Gọi H là trung
điểm AB, biết SH vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABC biết rằng góc giữa
mặt phẳng (SBD) và (ABCD) bằng
0
60
A.
3
.
56
S ABCD
Va
B.
3
.
192 5
5
S ABCD
a
V
C.
3
.
28 5
5
S ABCD
a
V
D.
3
.
28
S ABCD
Va
Câu 101. Cho khối chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng
2a
. Hình chiếu của
S trên mặt phẳng (ABCD) là trung điểm H thuộc đoạn AO. Góc giữa mặt phẳng (SCD) và (ABCD)
bằng
0
60
. Tính thể tích khối chóp S.ABCD
A.
3
.
2
S ABCD
Va
B.
3
.
3
S ABCD
a
V
C.
3
.
3
S ABCD
Va
D.
3
.
23
S ABCD
Va
Câu 102. Cho khối chóp S.ABCD có ABCD là hình vuông cạnh bằng
2a
; SAD là tam giác cân tại S
và nằm trong mặt phẳng vuông góc với đáy. Gọi M là trung điểm của CD. Góc giữa hai mặt phẳng
(SBM) và (ABCD) bằng
0
60
. Tính thể tích khối chóp S.ABCD.
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
3
.
63
S ABCD
Va
B.
3
.
4 15
5
S ABCD
a
V
C.
3
.
2 15
5
S ABCD
a
V
D.
3
.
23
S ABCD
Va
Câu 103. Cho khối chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D;
2;AB AD a CD a
. Góc giữa hai mặt phẳng (SBC) và (ABCD) bằng
0
60
. Gọi I là trung điểm của
AD
. Biết 2 mặt phẳng (SBI) và (SCI) cùng vuông góc với mặt phẳng (ABCD). Tính thể tích khối
chóp S.ABCD.
A.
3
.
63
S ABCD
Va
B.
3
.
6 15
5
S ABCD
a
V
C.
3
.
3 15
5
S ABCD
a
V
D.
3
.
6
S ABCD
Va
Câu 104. Cho khối lăng trụ đứng
1 1 1
.ABC A BC
có đáy ABC là tam giác vuông cân tại A, cạnh
2BC a
. Tính thể tích khối lăng trụ
1 1 1
.ABC A BC
biết
1
3A B a
A.
1 ! 1
3
.
2
3
ABC A BC
a
V
B.
1 ! 1
3
.
2
ABC A BC
Va
C.
1 ! 1
3
.
3
2
ABC A BC
a
V
D.
1 ! 1
3
.
63
ABC A BC
Va
Câu 105. Cho khối lăng trụ đứng
1 1 1
.ABC A BC
có đáy ABC là tam giác vuông cân tại A, cạnh
2BC a
. Tính thể tích khối lăng trụ
1 1 1
.ABC A BC
biết
1
AC
tạo với đáy một góc
0
60
.
A.
1 ! 1
3
.
33
2
ABC A BC
a
V
B.
1 ! 1
3
.
33
ABC A BC
Va
C.
1 ! 1
3
.
3
2
ABC A BC
a
V
D.
1 ! 1
3
.
63
ABC A BC
Va
Câu 106. Cho khối chóp S.ABCD có ABCD là hình chữ nhật
2;AD a AB a
. Gọi H là trung điểm
AD, biết SH vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết góc giữa SC và
(ABCD) bằng
0
60
.
A.
3
.
46
3
S ABCD
a
V
B.
3
.
26
3
S ABCD
a
V
C.
3
.
6
S ABCD
a
V
D.
3
.
3
S ABCD
a
V
Câu 107. Cho khối chóp đều S.ABCD có cạnh đáy bằng
3a
. Tính thể tích khối chóp S.ABCD biết
cạnh bên bằng
2a
.
A.
3
.
10
2
S ABCD
a
V
B.
3
.
10
4
S ABCD
a
V
C.
3
.
3
6
S ABCD
a
V
D.
3
.
12
3
S ABCD
a
V
Câu 108. Cho khối chóp đều S.ABCD có cạnh đáy bằng . Tính thể tích khối chóp S.ABCD biết góc
giữa cạnh bên và mặt đáy bằng
0
60
.
A.
3
.
32
2
S ABCD
a
V
B.
3
.
32
4
S ABCD
a
V
C.
3
.
36
2
S ABCD
a
V
D.
3
.
6
3
S ABCD
a
V
Câu 109. Cho khối chóp S.ABC có cạnh đáy bằng
a
. Tính thể tích khối chóp S.ABC biết cạnh bên
bằng
2a
.
A.
3
.
11
12
S ABC
a
V
B.
3
.
3
6
S ABCD
a
V
C.
3
.
12
S ABCD
a
V
D.
3
.
4
S ABCD
a
V
Câu 110. Cho khối chóp đều S.ABC có cạnh đáy bằng
a
. Tính thể tích khối chóp S.ABC biết góc
giữa cạnh bên và mặt đáy bằng
0
45
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
3
.
3
12
S ABC
a
V
B.
3
.
3
6
S ABCD
a
V
C.
3
.
12
S ABCD
a
V
D.
3
.
4
S ABCD
a
V
Câu 111. Cho khối chóp đều S.ABC có cạnh đáy bằng
3a
. Tính thể tích khối chóp S.ABC biết mặt
bên là tam giác vuông cân ?
A.
3
.
21
36
S ABC
a
V
B.
3
.
21
12
S ABCD
a
V
C.
3
.
6
8
S ABCD
a
V
D.
3
.
6
4
S ABCD
a
V
Câu 112. Cho khối chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B. Hai mặt phẳng
(SAB) và (SAD) cùng vuông góc với đáy. Biết
22AD BC a
và
5BD a
. Tính thể tích khối
chóp S.ABCD biết rằng góc giữa SB và (ABCD) bằng
0
30
A.
3
.
3
6
S ABCD
a
V
B.
3
.
4 21
9
S ABCD
a
V
C.
3
.
2 21
3
S ABCD
a
V
D.
3
.
3
8
S ABCD
a
V
Câu 113. Cho khối chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B. Hai mặt phẳng
(SAB) và (SAD) cùng vuông góc với đáy. Biết
22AD BC a
và
5BD a
.Tính thể tích khối chóp
S.ABCD biết rằng góc giữa SO và (ABCD) bằng
0
45
, với O là giao điểm của AC và BD
A.
3
.
3
S ABCD
Va
B.
3
.
22
3
S ABCD
a
V
C.
3
.
2
3
S ABCD
a
V
D.
3
.
3
2
S ABCD
a
V
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Đáp án
01-A
02-B
03-A
04-A
05-B
06-A
07-D
08-C
09-B
10-B
11-A
12-C
13-A
14-A
15-B
16-C
17-A
18-A
19-B
20-D
21-C
22-C
23-C
24-D
25-D
26-A
27A
28C
29C
30A
31B
32D
33A
34B
35B
36A
37B
38C
39D
40A
41D
42D
43D
44C
45C
46B
47D
48A
49C
50. A
51. D
52. C
53. A
54. D
55. A
56. C
57. A
58. B
59.B
60. D
61. C
62. C
63. D
64. D
65. A
66. D
67. C
68. B
69. B
70. D
71. D
72. B
73. C
74. D
75. A
76. A
77. B
78. D
79. D
80. B
81. C
82. D
83. C
84. A
85. A
86. A
87. C
88. B
89. A
90. B
91. C
92. C
93. C
94. A
95. C
96. A
97. D
98. A
99. D
100. B
101. D
102. B
103. C
104. B
105. C
106. B
107. A
108. A
109. A
110. C
111. C
112. A
113. C
LỜI GIẢI CHI TIẾT
Hướng dẫn giải
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a. Cạnh bên SA vuông góc
với mặt phẳng đáy, SC tạo với mặt phẳng đáy một góc 45 và SC = 2
2a
. Thể tích khối chóp
S.ABCD bằng:
A.
3
2
3
a
B.
3
23
3
a
C.
3
3
a
D.
3
3
3
a
HD: Ta có
0
, 45SC ABCD SCA
22
2
2
a
SA AC a
Ta có
22
3BC AC AB a
2
.3
ABCD
S AB BC a
3
2
.
1 1 2
. .2 .a 3
33
3
S ABCD ABCD
a
V SA S a
Câu 2: Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hai mặt (SAB) và (SAC) cùng
vuông góc với đáy. Tính thể tích khối chóp biết SC = a
3
?
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
3
26
9
a
B.
C.
3
3
4
a
D.
3
3
2
a
HD: Ta có:
SAB ABC
SA ABC
SAC ABC

Ta có
22
2SA SC AC a
23
.
1 1 3 6
. 2.
3 3 4 12
S ABC ABC
aa
V SAS a
Câu 3: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B
với AC = a biết SA vuông góc với đáy ABC và SB hợp với đáy một
góc 60. Tính thể tích khối chóp:
A.
B.
3
3
24
a
C.
D.
HD: Ta có
0
; 60SB ABC SBA
Tam giác ABC có
2
a
AB BC
6
.tan
2
a
SA AB SBA
Ta có
2
11
. . .
2 2 4
22
ABC
a a a
S AB AC
23
1 1 6 6
. . .
3 3 2 4 24
SABC ABC
a a a
V SA S
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh a và SA vuông góc với đáy
ABCD và mặt bên (SCD) hợp với đáy một góc 60. Tính thể tích hình chóp S.ABCD
A.
3
3
3
a
B.
3
23
3
a
C.
3
3
6
a
D.
3
3a
HD: Ta có
0
, 60SCD ABCD ADS
.tan 3SA AD ADS a
Ta có
2
.
ABCD
S AB BC a
3
2
1 1 3
. . 3.
3 3 3
SABCD ABCD
a
V SAS a a
Câu 5: Cho khối chóp S.ABC có đáy ABC là tam giác cân tại
A với BC = 2a, BAC 120
0
, biết SA (ABC) và mặt (SBC)
hợp với đáy một góc 45. Tính thể tích khối chóp S.ABC
A.
3
9
a
B.
3
3
a
C.
3
2a
D.
3
2
a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
HD: Ta có
0
; 45SBC ABCD SMA
Ta có
2
;AM
33
aa
AB 
.tan
3
a
SA AM SMA
Ta có
2
11
.BC . .2
22
33
ABC
aa
S AM a
23
11
. . .
3 3 9
33
SABC ABC
a a a
V SA S
Câu 6: Cho khối chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B biết AB = BC = a, AD
= 2a, SA (ABCD) và (SCD) hợp với đáy một góc 60. Tính thể tích khối chóp S.ABCD
A.
B.
3
3
3
a
C.
D.
3
2
a
HD: ta có
0
, 60SCD ABCD SCA
Ta có
22
2AC AB BC a
.tan 6SA AC SCA a
Ta có
2
1 1 3
.3
2 2 2
ABCD
a
S AB AD BC a a
23
1 1 3 6
. .a 6.
3 3 2 2
SABD ABCD
aa
V SA S
Câu 7: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật biết rằng SA (ABCD), SC hợp với
đáy một góc 45 và AB = 3a, BC = 4a. Tính thể tích khối chóp:
A.
3
40a
B.
3
10a
C.
3
10 3
3
a
D.
3
20a
HD: Ta có
0
; 45SC ABCD SCA
Ta có
22
5AC AB BC a
.tan 5SA AC SCA a
Ta có
2
. 12
ABCD
S AB BC a
23
11
. .5a.12a 20
33
SABCD ABCD
V SA S a
Câu 8: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật AD = 2a, AB = a. Gọi H là trung điểm
của AD, biết SH ( ABCD) . Tính thể tích khối chóp biết SA =
5a
.
A.
3
23
3
a
B.
3
43
3
a
C.
3
4
3
a
D.
3
2
3
a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
HD: Ta có
22
2SH SA AH a
Và
2
.2
ABCD
S AB BC a
3
2
1 1 4
.S .2 .2
3 3 3
SABCD ABCD
a
V SA a a
Câu 9: Cho hình chóp S.ABC có đáy ABC là tam giác cân tại
A, G là trọng tâm tam giác ABC, SG (ABC). Biết góc giữa
SM
và mặt phẳng (ABC) bằng 30
0
(với M là trung điểm của BC), BC 2a và AB = 5a. Tính
3
9V
a
với V là
thể tích khối chóp S.ABC:
A.
82
B.
83
C.
85
D.
87
HD: Ta có
22
26
26
3
a
AM AB BM a GM
Do đó
0
22
tan30
3
a
SG GM
Khi đó
3
1 1 2 2 1 8 3
.S . . .2 6.2
3 3 3 2 9
ABC
aa
V SG a a
Vậy
3
9
83
V
a
.
Câu 10: Cho hình chóp S.ABC. có đáy ABC là tam giác đều cạnh 8a, SA ( ABC) . Biết góc giữa hai
mặt phẳng (SBC) và (ABC) bằng 45
0
. Tính
3
5V
a
, với V là thể tích khối chóp S.ABC?
A. 280 B. 320 C. 360 D. 400
HD: Dựng
AM BC
, lại có
SA BC
suy ra
SAM BC
Vậy
0
; 45SBC ABC SMA
Lại có
83
4 3 4 3
2
a
AM a SA AM a
Do đó
3
15
. 64 320
3
ABC
V
V SA S
a
Câu 11: Cho hình chóp S.ABC có đáy ABC là tam giác
vuông cân tại B, AB = 8a, SA (ABC). Biết góc giữa hai mặt
phẳng (SBC) và (ABC) bằng 30
0
. Tính,
3
93V
a
với V là thể
tích
khối chóp S.ABC.
A. 768 B. 769 C. 770 D. 771
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
HD: Ta có
22
1
32
2
ABC
S AB a
. Lại có
0
; 30SBC ABC SBA
Do vậy
0
8
tan30
3
a
SA AB
suy ra
3
1 256
..
3
33
ABC
a
V SA S
Do đó
3
93
768
V
a
Chọn A
Câu 12: Cho hình chóp S.ABCD có đáy là hình vuông cạnh 8a, SA (ABCD).
Biết góc giữa SC và mặt phẳng (ABCD) bằng 45
0
. Tính
3
3
512
V
a
, với V là thể
tích khối chóp S ABC . .
A.
3
B. 3 C.
2
D. 2
HD: Ta có
0
8 2 tan45 8 2AC a SA AC a
Do đó
3
1 521 2
.
33
ABCD
a
V SA S
Vậy
3
3
2
512
V
a
Chọn C
Câu 13: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AC = a, SA (ABC). Biết
thể tích khối chóp S.ABC là
3
6
24
a
(đơn vị thể tích). Tính góc giữa SB và mặt phẳng (ABC).
A. 60
0
B. 45
0
C. 30
0
D. 90
0
HD: Ta có
.tanSA AB
(với
là góc giữa SB và mp(ABC) )
Mặt khác
22
AC a
AB BC
Khi đó
23
.
1 1 6
. . .tan .
3 3 4 24
2
S ABC ABC
a a a
V SA S
Do vậy
0
tan 3 60

Chọn A
Câu 14: Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB =
a, SC = 2a
2
, SA (ABCD). Biết góc giữa SC và mặt phẳng
(ABCD) bằng 30
0
. Tính theo a thể tích khối chóp S.ABCD.
A.
3
10
3
a
B.
3
10
5
a
C.
3
5
10
a
D.
3
5
3
a
HD: Ta có
0
26
cos30 6
2
a
AC SC a
0
sin30 2SA SC a
. Khi đó
22
5BC AC AB a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Do vậy
3
.
1 10
.
33
S ABCD ABCD
a
V SAS
Chọn A
Câu 15: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 8a, SA (ABC). Biết góc giữa hai
mặt phẳng (SBC) và (ABC) bằng 45
0
. Tính theo a thể tích khối chóp S.ABC.
A. 56a
3
B. 64a
3
C. 72a
3
D. 80a
3
HD: Gọi M là trung điểm của BC. Khi đó
BC SA
BC SAM
BC AM

Do vậy
0
; 45SBC ABC SMA
Mặt khác
0
83
4 3 tan45 4 3
2
a
AM a SA AM a
Do đó
2
3
.
1 1 64 3
. .4 3. 64
3 3 4
S ABC ABC
a
V SA S a a
. Chọn B
Câu 16: Cho hình chóp tam giác đều S.ABC có cạnh AB bằng a. Các
cạnh bên SA, SB, SC tạo với đáy một góc 60
0
. Gọi D là giao điểm của
SA với mặt phẳng qua BC và vuông góc với SA. Tính theo a thể tích khối chóp S.DBC.
A.
3
5
96
a
B.
3
52
96
a
C.
3
53
96
a
D.
3
55
96
a
HD: Gọi M là trung điểm của BC khi đó
3
2
a
AM
. Gọi H là trọng tâm tam giác ABC suy ra
0
; 60SH ABC SAH
Dễ thấy
BC AM
BC SA
BC SH

. Dựng
BD SA
Khi đó
2
0
1 1 3
, . .sin60 .
2 2 8
BCD
a
BCD SA S DM BC AM BC
00
3 2 3
.cos60 ; cos60
43
aa
AD AM SA AH SA
Do vậy
53
12
a
SD SA AD
Suy ra
3
.
1 5 3
.
3 96
S DBC BCD
a
V SD S
Chọn C
Cách 2:
.
.
S DBC
S ABC
V
SD
V SA
Câu 17: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB là tam giác đều
và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích khối chóp S.ABCD.
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
3
3
6
a
B.
3
3
5
a
C.
3
3
4
a
D.
3
3
3
a
HD: Gọi H là trung điểm của AB.
Khi đó
SH AB
, mặt khác
SAB ABCD
Do vậy
3
;
2
a
SH ABCD SH
Do đó
3
.
13
.
36
S ABCD ABCD
a
V SH S
. Chọn A
Câu 18: Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA = 2a và SA
(ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC.
Tính
3
50 3V
a
, với V là thể tích khối chóp A.BCNM
A. 9 B. 10 C. 11 D. 12
HD: Tam giác SAB vuông tại A có đường cao AM
Khi đó
2
2
2
4
.
5
SA SM SM
SA SM SB
SB SB SB
. Tương tự
4
5
SN
SC
Lại có
23
.
1 1 3 3
. .2 .
3 3 4 6
S ABC ABC
aa
V SA S a
Mặt khác
.
..
.
16 9
..
25 25
S AMN
A BCNM S ABC
S ABC
V
SA SM SN
VV
V SA SB SC
Do đó
33
.
3
9 3 3 3 50 3
.9
25 6 50
A BCNM
a a V
V
a
. Chọn A
Câu 19: Cho tứ diện ABCD có các cạnh AB; AC; AD đôi một vuông góc với nhau biết AC = a; AD
=
3a
và khoảng cách từ A đến mặt phẳng BCD bằng
21
7
a
. Thể tích khối chóp đã cho là:
A.
3
3
2
a
B.
3
3
6
a
C.
3
33
4
a
D.
3
3
3
a
HD: Từ A kẻ AH vuông góc với CD tại H.
Ta có
BA ACD BA CD
mà
AH CD CD BAH
Kẻ
,AK BH K BH
do đó:
AK BH
AK BCD
AK CD

Hay
21
;
7
a
d A BCD AK
. Lại có
2 2 2
1 1 1
AK AB AH

Do đó:
2 2 2 2 2
1 1 1 1 1
AB a
AB AK AC AD a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Vậy
3
1 1 3
. . . . .
3 6 6
ABCD ACD
a
V AB S AB AC AD
. Chọn B
Câu 20: Cho khối chóp S.ABCD có đáy là hình vuông, SA ABCD và SA=h. Biết SC tạo với đáy
một góc 45
0
. Thể tích khối chóp đá cho tính theo h là:
A.
B.
3
3
h
C.
3
3
6
h
D.
3
6
h
HD: Ta có AC là hình chiếu của SC lên mặt phẳng đáy.
Do đó
0
; ; 45SC ABCD SC AC SCA
Nên tam giác SAC là tam giác vuông cân tại A
AC h
Đặt
AB x
, ta có
2 2 2 2 2
2
2
h
AB BC AC x h x
Khi đó
2
3
.
11
. . .h.
3 3 6
2
S ABCD ABCD
hh
V SA S



. Chọn D
Câu 21: Cho hình chóp S.ABCD có đáy là hình thoi ABCD tâm I
cạnh a, SI ABCD . Biết tam giác ABC đều và SB =
2a
. Thể tích
khối chóp đã cho là:
A.
3
46
3
a
B.
3
15
4
a
C.
3
15
12
a
D.
3
43
3
a
HD: Gọi I là tâm của hình thoi ABCD nên I là trung điểm của AC.
Tam giác ABC đều nên
2
2 2 2
3
42
aa
IB BC IC a
Xét
SIB
vuông tại I, có
2
2 2 2
35
2
44
aa
SI SB IB a
Do
23
.
1 1 2 5 3 15
. . . .2. . .
3 3 3 2 4 12
S ABCD ABCD ABC
a a a
V SI S SI S
Chọn C
Câu 22: Cho khối chóp S.ABCD có đáy là hình chữ nhật ABCD có AB = 1; AD 2. Hình chiếu
vuông góc của S xuống mặt đáy là trung điểm của AD. Khoảng cách từ A đến mặt phẳng SBC bằng
2
2
. Thể tích khối chóp đã cho là:
A.
1
3
B. 1 C.
2
3
D.
2
3
HD: Gọi I là trung điểm của AD, theo giả thiết, ta có
SI ABCD
Ta có
||AD BC
nên
|| , ,AD SBC d A SBC d I SBC
Gọi H là trung điểm của BC suy ra
IH BC
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Từ I kẻ IK vuông góc với SH tại K.
Khi đó
2
,
2
IK SH
IK SBC d I SBC IK
IK BC
Mà
2
2 2 2 2 2
1 1 1 1 1 1
1
1
2
2
SA
SA IH IK SA



Do đó
.
1 1 2
. . . . .
3 3 3
S ABCD ABCD
V SAS SA AB AD
. Chọn C
Câu 23: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D có AD 2; AB = BC 1, SA
ABCD , đường thẳng SC tạo với đáy một góc 45
0
. Thể tích khối chóp đã cho là:
A.
22
B. 2 C.
2
D. 1
HD: Ta có AC là hình chiếu của SC lên mặt phẳng đáy
Do đó
0
; ; 45SC ABCD SC AC SCA
Nên tam giác SAC là tam giác vuông cân tại A
AC SA
Gọi M là trung điểm của
1
2
AD
AD AM
Lại có
1AB BC
và
|| BCAM
nên ABCM là hình vuông
Khi đó
22
AC 2AM MC
nên
2SA AC
Vậy
.
1 1 2
. . .SA.AB.
3 6 2
S ABCD ABCD
V SAS AD BC
. Chọn C
Câu 24: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 1, SA ABC, khoảng cách từ A đến
mặt phẳng SBC bằng
21
7
. Thể tích khối chóp đã cho là
A.
3
2
B.
3
4
C.
3
3
D.
3
12
HD: Gọi M là trung điểm của BC, ta có
AM BC
Mà
SA BC ABC
và
AM BC BC SAM
Từ A kẻ
AH SM
tại H nên
,AH SBC d A SBC AH
Xét tam giác SAM vuông tại A, có
2 2 2
1 1 1
AH SA AM

2
22
2
1 1 1
1 1 1
21 3
72
SA SA
SA
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Vậy
.
1 1 3 3
. . .1.
3 3 4 12
S ABC ABC
V SA S
(đvtt). Chọn D
Câu 25: Cho hình chóp tứ giác đều S.ABCD có đường cao bằng h và mặt bên tạo với đáy một góc
60
0
. Thể tích khối chóp đã cho tính theo h là:
A.
3
2
3
h
B.
3
4
3
h
C.
3
4h
D.
3
4
9
h
HD: Gọi O là tâm của hình vuông ABCD, ta có
SO ABCD
Gọi M là trung điểm của BC, ta có
OM BC
Do đó
BC SOM
mà
SOM ABCD OM
SOM SBC SM
ABCD SBC BC



Nên ta có được
0
, , 60SBC ABCD SM OM SMO
Xét tam giác SOM vuông tại O, có
tan
SO
SMO
MO
0
2
2.
tan60
33
SO h h
MO AB MO
Vậy
3
.
1 1 4
. . . .
3 3 9
S ABCD ABCD
h
V SO S SO AB BC
. Chọn D
Câu 26: Cho hình chóp S.ABCD có đáy là hình chữ nhật có AB = 4, AC = 5 và SA (ABCD biết
mặt phẳng SCD tạo với đáy một góc 60
0
. Thể tích khối chóp đã cho là:
A.
12 3
B.
43
C.
63
D.
20 3
HD: tam giác ABC vuông tại B, có
22
3BC AC AB
Ta có
SA ABCD SA CD
mà
CD AD
nên
CD SAD
SCD SAD SD
ABCD SAD AD
SCD ABCD CD



nên
,,SCD ABCD SD AD SDA
Xét
DSA
vuông tại A, có
0
tan tan60 .AD 3 3
SA
SDA SA
AD
Vậy
.
11
. .S .3 3.3.4 12 3
33
S ABCD ABCD
V SA
. Chọn A
Câu 27. Ta có
0
, 60SC ABC SCH
.
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Ta có
3. 3 3 2
2 2 3
aa
CM CH AM a
0
.tan60 3SH CH a
Ta có
2
2
33
33
44
ABC
a
a
S 
23
.
1 1 3 3 3
. 3.
3 3 4 4
S ABC ABC
aa
V SH S a
Chọn A
Câu 28. Ta có
, 3 ,d A SBC d H SBC
3
,
18
a
d H SBC
.
Ta có
BC HN
BC SHN BC HK
BC SH
Mà
3
18
a
HK SN HK SBC HK
Ta có
3 1 3
2 3 6
aa
AN HN AN
. Lại có
2 2 2
1 1 1 6
24
a
SH
HK HS HN
.
Ta có
2 2 3
.
3 1 1 6 3 2
. . .
4 3 3 24 4 96
ABC S ABC ABC
a a a a
S V SH S
3
12 2
8
V
a

.
Chọn D
Câu 29. Gọi N là trung điểm của BC.
Ta có
BC HN
BC SHN BC SN
BC SH
0
, 45SBC ABC SNB
Ta có
3 1 3
.
2 3 6
aa
AN HN AN
0
3
.tan45
6
a
SH AN
.
Ta có
2 2 3
.
3 1 1 3 3
. . .
4 3 3 6 4 24
ABC S ABC ABC
a a a a
S V SH S
Chọn C
Câu 30. Gọi N là trung điểm của BC, kẻ
HK SN
.
Ta có
BC HN
BC SHN BC HK
BC SH
Mà
HK SN HK SBC
,,SH SBC SH SK
0
30HSK
.
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Ta có
tan
3
HN h
HSK HN
SH
3AN h
3
22
.
1 1 3
3 . . 3
3 3 3
ABC S ABC ABC
h
S h V SH S h h
Chọn A
Câu 31. Gọi M là trung điểm của AB
Ta có
AB HM
AB SHM AB SM
AB SH
0
, 45SAB ABC SMH
Ta có
3
2 2 2
a a a
CM HM SH HM
Lại có
2
2
33
33
44
ABC
a
a
S 
33
.
1 1 3 3 3
. . .
3 3 2 4 8
S ABC ABC
a a a
V SH S
Chọn B
Câu 32. Gọi M là trung điểm của CD
Ta có
CD OM
CD SOM CD SM
CD SO
Do
0
60CSD SCD
là tam giác đều
SC SD CD x
3
2
x
SM
và
2
x
OM
Ta có
22
2 2 2 2
3
44
xx
SO OM SM h
2
2
2
2
x
h x h
3
22
.
12
2 .2
33
ABCD S ABCD
h
S h V h h
0
3
3 sin30
1
V
h

Chọn D
Câu 33. Gọi M là trung điểm của CD, kẻ
OH SM
Ta có
CD OM
CD SOM CD SM
CD SO
0
, 45SCD ABCD SMO
Do
SD SOM CD OH
mà
OH SM
,OH SCD OH d O SCD a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
2
2
2 2 2 8
ABCD
SO OM a S a a
3
2
.
1 1 8 2
. 2.8
3 3 3
S ABCD ABCD
a
V SO S a a
Chọn C
Câu 34. Gọi H là trọng tâm tam giác đều
ABC SH ABC
Gọi M là trung điểm của
BC
ta có:
33
;
23
aa
AM AH
Mặt khác
33
1 1 3 3
. . .
3 3 4 36 3
ABC
a a a
V SH S SH SH
Khi đó
1
tan
3
SH
SAH
AH

00
30 ; 30SAH SA ABC
Chọn B
Câu 35. Gọi G là trọng tâm tam giác đều ABC và M là trung điểm
của AB
Khi đó
;SG ABC
Do
AB SG
AB HM
AB CM

Lại có
22
3
;
2
a
CM SG SC CG
2
2
11
4
3
3
aa
a SG
Suy ra
. 11
4
SG CM a
HM
SC

22
4
a
CH CM HM
Khi đó
3
7 1 7 11
.
4 3 96
HBC
aa
SH V SH S
Chọn A
Cách 2:
2 2 2
77
cos cos
2. . 8 4
SA SC AC a
ASC SH SA S
SASC

Khi đó
.
.
7
..
8
S HAB
S ABC
V
SA SB SH
V SA SB SC

Câu 36. Gọi G là trọng tâm tam giác đều ABC và M là trung điểm của AB
Khi đó
SG ABC
; Do
AB SG
AB HM
AB CM

Lại có:
22
3
;
2
a
CM SG SC CG
2
2
11
4
3
3
aa
a SG
Suy ra
. 11
4
SG CM a
HM
SC

22
4
a
CH CM HM
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Khi đó
3
7 1 7 11
.
4 3 96
HBC
aa
SH V SH S
Chọn A
Cách 2:
2 2 2
77
cos cos
2. . 84 4
SA SC AC a
ASC SH SA S
SASC

Khi đó
.
.
7
..
8
S HAB
S ABC
V
SA SB SH
V SA SB SC

Câu 37. Gọi H là trọng tâm tam giác đều
ABC SH ABC
.
Gọi M là trung điểm của BC.
Ta có:
0
3
cos60
24
aa
AH SA AM
;
0
3
sin60
2
a
SH SA
Đặt
3 3 3
2 4 2
x a a
AB x AM x
Do đó
2 2 3
3 3 3 1 3
.
4 16 3 32
ABC ABC
x a a
S V SH S
Chọn B
Câu 38. Gọi H là tâm của đáy khi đó
SH ABCD
.
Dựng
;HE CD HK SE
. Khi đó
0
45CD SHE SEH
; 2 2d H SCD HK a HE a SH HE a
Mặt khác
3
1 8 2
2 2 2 .
33
ABCD
a
AD HE a V SH S
Chọn C
Câu 39. Gọi H là tâm của đáy khi đó
SH ABCD
Dựng
0
45HP CD CD SPH SPH
Khi đó
0
tan45
22
aa
HP SH HP
Do vậy
23
.
2 12
ABP S APB
aa
SV
Mặt khác
3
.
.
.
1
..
4 48
S MNP
S MNP
S ABP
V
SM SN SP a
V
V SA SB SP
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Do vậy
3
..
48
A MNP S MNP
a
VV
(do
;;d S MNP d A MNP
Chọn D
Câu 40. Gọi H là tâm của đáy khi đó
SH ABCD
Lại có
0
26
tan60 . 3
22
aa
SH HA
3
.
16
.
36
S ABCD ABCD
a
V SH S
Mặt khác gọi
G SH AM G
là trọng tâm tam giác SAC
Do đó
2
3
SG
SH
. Qua G dựng đường thẳng song song với
BD
cắt
SB, SD lần lượt tại P và Q.
Khi đó
.
.
2 1 1
..
3 2 3
S ABM
S ABC
V
SP SM
V SB SC
từ đó suy ra
.
.
1
3
S APMQ
S ABCD
V
V
Do vậy
3
.
3
6 18
6
18
S APMQ
aV
V
a
Chọn B
Câu 41. Ta có
2
63
33
6
2 4 2
AMN
AB
AM S
Do vậy
.
13
.
32
S AMN AMN
V SO S
Chọn D
Câu 42. Gọi H là tâm hình vuông ABCD
SH ABCD
22
22
2 2 2
AC a a
HA SH SA HA
3
.
.
2
36
ABCD
S ABCD
SH S
a
V
Chọn D
Câu 43. Gọi H là tâm của tam giác ABC
SH ABC
;
22
3HA a SH SA HA a
3
.
.
3
34
ABC
S ABCD
SH S
a
V
Chọn D
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 44. Gọi H là tâm của tam giác ABC
SH ABC
3
.cos
22
aa
AH SH SAH SH
3 2 3 3
2 2 2
3
a AH a
SH AB



3
.
.
3
3 32
ABC
S ABC
SH S
a
V
Chọn C
Câu 45. Gọi H là tâm của ta giác ABC, M là trung điểm AB.
Dễ dàng xác định
0
, 45SAB ABC SMH
Đặt
; 2 3 3SH x HM x SM x CM HM x
3
2 3 3
3
CM
AB x AM x
2 2 2 2 2 2 2
2 3 5
5
a
SA SM AM a x x x x
33
.
.
3 15
3 25
55
ABC
S ABC
SH S
aa
V
Chọn C
Câu 46. Gọi H là tâm của hình vuông ABCD. M là trung
điểm AB.
Tam giác SAB đều nên
3
,
22
aa
SM HM
22
2
2
a
SH SM HM
3
.
2
6
S ABCD
a
V
Chọn B
Câu 47. Hình chóp đều là S.ABCD. Gọi H là tâm của hình
vuông ABCD. M là trung điểm AB, K là hình chiếu của H lên
SM.
Xác định nhanh:
0
, 45SAB ABCD SMH
và
,d H SAB HK a
Như vậy tam giác SMH vuông cân tại H nên:
2 2 2SH MH a AB a
3
.
.
82
33
ABCD
S ABCD
SH S
a
V
.
Chọn D
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 48. Gọi P là giao điểm của BM và AD. H là hình
chiếu của A lên BM, K là hình chiếu của A lên SH.
Vì
SA BM AH BM SAH
BM AK
. Mà
AK SH
AK SBM
,d A SBM AK
.
Vì
2AP DP
nên:
,
,
2
d A SBM
d D SBM
24
2
33 33
AK a a
AK
Tính:
22
2. 4
sin . .
17
4.
AP AD a
AH AB ABH AB AB
BP
AB AD
Sử dụng
2 2 2
1 1 1
SA a
SA HA AK
Chọn A
Câu 49. Gọi M là trung điểm của CD, O là giao điểm AC và BD
Ta có
CD OM
CD SOM CD SM
CD SO
Ta có
22
32
22
aa
SM SO SM OM
3
2
.
1 1 2 2
. . .
3 3 2 12
S ABCD ABCD
aa
V SO S a
3
12
2
V
a

Chọn C
Câu 50. Ta có
1
,
3
AMND AMN
V d D ABC S
Lại có
1
,
3
ABCD ABC
V d D ABC S
Mà
11
44
AMND
AMN ABC
ABCD
V
SS
V
Chọn A
Câu 51. Ta có
.
1
,.
3
S ICM ICM
V d S ABCD S
Lại có
.
1
,.
3
S ABCD ABCD
V d S ABCD S
Ta có
1
4
BCM ABCD
SS
mà
1
4
ICM BCM
SS
.
.
11
12 12
S ICM
ICM ABCD
S ABCD
V
SS
V
Chọn D
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 52. Gọi O là tâm của hình bình hành ABCD. SO cắt B’D’ tại I. Nối AI cắt SC tại C’ nên A, B’,
C’, D’ đồng phẳng.
Đặt
. . .
2
S ABCD S ACD S ABC
V
V V V V
Ta có
. ' '
.
''
.
S AC D
S ACD
V
SC SD
V SC SD
và
. ' '
.
''
.
S AC B
S ACB
V
SC SB
V SC SB
.
Do đó
. ' ' . ' ' . ' ' '
..
' 1 ' 1
.
26
S AC B S AC D S AB C D
S ACB S ACD
V V V
SC SC
V V SC V SC
Vậy
. ' ' '
. ' ' ' ' ' '.
15
6 6 6 6
S AB C D
S AB C D AB C D ABCD
V
V V V
V V V
V
Hay tỷ số thể tích của hai khối chóp được chia ra bởi (AB’D’) là:
. ' ' '
' ' '.
51
:
6 6 5
S AB C D
AB C D ABCD
V
VV
V

Chọn C
Câu 53. Ta có MN là đường trung bình của tam giác SAD
Suy ra MN song song với AD và
1
2
MN BC
MN AD
MN BC

Do đó BCNM là hình bình hành mặt khác
CB BM
Nên BCNM là hình chữ nhật nên
..
22
BCNM BCM S BCNM S BCM
S S V V
3
.
1 1 1
. . .2 .
3 6 6 3
S BCM SBM SAB
a
V BC S BC S a a a

Chọn A
Câu 54. Áp dụng công thức tính tỉ số thể tích, ta có:
. ' '
. ' '
.
' ' 1
..
44
A B CD
A B CD
A BCD
V
AB AC AD V
V
V AB AC AD
Mà
. . ' ' . ' ' . ' '
3
44
A BCD A B CD C BDD B C BDD B
VV
V V V V V
Chọn D
Câu 55. Gọi H là tâm của hình vuông ABCD.
Vì
SA SB SC SD
nên
SH ABCD
Đặt
AB x
, khi đó
2
42xx
. Gọi M là trung điểm của
AB.
Xét tam giác SAB cân tại S, có
1
. . 2 2
2
SAB
S SM AB SM
Xét tam giác SHM vuông tại H, có
22
1SH SM MH
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Vậy thể tích khối chóp là
.
14
..
33
S ABCD ABCD
V SH S
Chọn A
Câu 56. Gọi O là tâm của đáy ABCD, M là trung điểm của BC.
Từ O kẻ OH vuông góc với SC, ta có
SC BDH
Ta có
..
..
,
S AHD S AHB
S ACD S ACB
VV
SH SH
V SC V SC

mà
. . .
1
22
S ACD S ACB S ABCD
V
V V V
Nên
. . .
2
2
S AHD S AHB S ABHD
V V V
SH SH
V
SC V SC
Có
BC SAM
nên
0
; 60SBC ABCD SMA
3
2
a
SA
Mặt khác
13
CH CO a
CAS CHO CH
CA SA
Suy ra
.
11 11
1
13 13
S ABHD
SH SC HC HC
VV
SC SC SC
Do đó
..
11 2
12 13
H BCD S ABHD
V V V V V V
Chọn D
Câu 57. Gọi Q là trung điểm của AD. Và MN cắt SD tại P.
Suy ra P là trọng tâm của tam giác SMC nên
2
3
SP
SD
Gọi h là độ dài đường cao của tứ diện, do đó
; , ;
32
hh
d P ABCD d N ABCD
.
Ta có
2
.
1
. ; .
36
N BCM BCM
ah
V d N ABCD S

và
2
.
1
;.
3 36
P MQD MQD
ah
V d P ABCD S

. Nên
2 2 2 2 2 2
.
5 5 7
6 36 36 3 36 36
NBC PQD SABNPQ
a h a h a h a h a h a h
VV
Vậy tỉ số thể tích giữa hai phần của hình chóp tạo bởi mặt phẳng
(BMN) là
.
5
7
NBC PQD
SABNPQ
V
V
Chọn A
Câu 58. Gọi M là trung điểm của BC, H là tâm của đáy ABC.
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Ta có
SH ABC SH BC
và
SM BC
nên
BC SAM
.
Từ M kẻ MD vuông góc với SA tại D nên
SA DBC P
Lại có
0
; ; 60SA ABC SA AH SAH
Do đó
0
2
cos
cos60
3
AH AH a
SAH SA
SA
Xét tam giác SAB cân tại A, có đường cao BD, gọi K là trung điểm của AB suy ra
13
..
4
a
SK AB BD SA BD
. Khi đó
2
2
22
2 13 5 3
4 12
3
a a a
SD SB BD







Vậy
.
.
5
..
8
S BDC
S ABC
V
SD SB SC
V SA SB SC

Chọn B
Câu 159. Áp dụng công thức thể tích, ta có
. ' '
. ' '
.
' ' 1 1 1
..
2 2 4 4
S B CD
S AB D
S BCD
V
AB AD V
V
V AB AD
Chọn B
Câu 60. Áp dụng công thức thể tích, ta có
. ' '
. ' '
.
' ' 1 1 1
..
2 2 4 4
S B CD
C AB D
S BCD
V
AB AD V
V
V AB AD
và
. ' '
3
4
C BB D B
V
V
. Suy ra
. ' '
. ' '
31
:
4 4 3
C AB D
S BB D B
V
VV
V

Chọn D
Câu 61. Áp dụng công thức tỷ số thể tích, ta có
.
.
1 2 1 1
. . . .
2
S MNP
S ABC
V
SM SN SP
V SA SB SC a b c abc
.
.
S ABC
S MNP
V
abc
V

Chọn C.
Câu 62. Kẻ AM cắt BC tại N.
Từ M kẻ MA’ song song với SA, với
'A SN
Xét
'
'
MA MN
NMA NAS
SA NA
Ta có
..
.
1
;.
3
1
;.
3
M BCS S MBC MBC
S ABC
V V d S ABC S
V d S ABC S ABC


.
.
M BCS MBC
S ABC ABC
VS
VS

Mà
;
'
;
MBC
ABC
d M BC
S
MN MA
S d A BC AN SA
.
.
'
M BCS
S ABC
V
MA
V SA

Chọn C
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 63. Kẻ MN//CD, với
N SD
nên
SM SN
x
SC SD

Ta có
. . .
11
22
S ACB S ACD S ABCD
V V V V
Và
2
..
..
.,
S AMN S AMB
S ACD S ACB
VV
SM SN SM
xx
V SC SD V SC
Do
2
2
. . .
. . .
2
S AMN S AMB S ABMN
S ACD S ACB S ABCD
V V V
xx
xx
V V V
2
11
2 200
xx

2
1 0 0
0,1
100 100 11 0
x
xx

Chọn D
Câu 64. M là trung điểm của SB nên
; 2 ;d S ABCD s M ABCD
Do đó
..
;
23
C MNP M PCN PCN
SA a
d M ABCD a V V S
Mà
2
11
..
2 8 8
PCN
a
S CN CP CBCD
Vậy thể tích khói chóp S.MNP là
23
.
.
3 8 24
C MNP
a a a
V 
Chọn D
Câu 65. Vì M, P, N lần lượt là trung điểm của SB, SC, BC.
Nên
11
; ; ; .2
22
d M ABC d P ABC d S ABC a a
Và
2
13
28
ABN ANC ABC
a
S S S
2
..
3
24
M ABN P ANC
a
VV
Mà
3
.
.
.
13
;
4 24
S AMP
S AMP
S ABC
V
SM SP a
V
V SB SC
Do đó
3 3 3
. . . .
3 3 3
6 8 24
A MNP S ABC M ABN P ANC
a a a
V V V V
Chọn A
Câu 66 Ta có
SAB ABCD
SAD ABCD
và
SAB SAD SA ABCD
Ta có
22
2AC AB BC a
22
SA SC AC a
Ta có
2
ABCD
Sa
.
3
2
.
11
..
3 3 3
S ABCD ABCD
a
V SA S a a
Chọn D
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 67. Ta có
22
22AD a HA HD a SH SA HA a
Ta có
2
.2
ABCD
S AD AB a
.
1
.
3
S ABCD ABCD
V SH S
3
2
14
2 .2
33
a
aa
Chọn C
Câu 68. Do
đều nên
23
3
2
a
SH a
Ta có
22
4
ABCD
S AB a
2
.
11
. 3.4
33
S ABCD ABCD
V SH S a a
3
43
3
a
Chọn B
Câu 69. Do
ABC
vuông tại B
22
33BC AC AB a
Ta có
22
1
27
3
HB AB a CH HB BC a
Ta có
0
, 60SC ABC SCH
0
2 7.tan60 2 21SH a a
Mà
2
1 1 9 3
. 3 .3 3
2 2 2
ABC
a
S AB BC a a
2
3
.
1 1 9 3
. 2 21. 9 7
3 3 2
S ABC ABC
a
V SH S a a
Chọn B
Câu 70. Ta có
0
, 45SA ABC SAH
Ta có
33
24
aa
CI HI
22
7
4
a
AH AI HI
7
.tan
4
a
SH AH SAH
Ta có
2
3
4
ABC
a
S
23
.
1 1 7 3 21
. . .
3 3 4 4 48
S ABC ABC
a a a
V SH S
Chọn D
Câu 71. Ta có
0
, 45SD ABCD SDH
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Lại có
2 2 2
5
2 4 2
AD DO AO a
DH
5
.tan
2
a
SH DH SDH
.Ta có
22
2
ABCD
S AB a
3
2
.
1 1 5 5
. . .2
3 3 2 3
S ABCD ABCD
aa
V SH S a
Chọn D
Câu 72. Gọi M là trung điểm của BC
Ta có
BC AM
BC SAM
BC SA

0
, 60SBC ABC SMA
Ta có
33
.tan
22
aa
AM SA AM SMA
Lại có
2
3
4
ABC
a
S
2
.
1 1 3 3
. . .
3 3 2 4
S ABC ABC
aa
V SA S
3
3
8
a
Chọn B
Câu 73. Kẻ
AH BC
Ta có
,
BC AH
BC SAH SBC ABC
BC SA
0
45SHA
Ta có
22
22AC BC AB a
2 2 2 2
1 1 1 9
8AH AB AC a
2 2 2 2
33
aa
AH SA
Ta có
2
11
. .2 2 2
22
ABC
S AB AC a a a
2
.
1 1 2 2
. . 2
3 3 3
S ABC ABC
a
V SA S a
Chọn C
Câu 74. Ta có :
AB BC
BC SBA
SA BC

Do vậy
0
; 30SBC ABC SBA
Mặt khác
22
23BC AC AC a
Lại có
0
2
tan30
3
a
SA AB
Do vậy
3
.
1 1 2 8
. . .2 .2 3
3 3 3
3
S ABCD ABCD
aa
V SA S a a
Chọn D
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 75. Ta có tam giác ABC vuông tại B nên
22
2BC AC AB a
Mặt khác
22
2SA SB AB a
Do vậy
23
.
1 1 2 2
. 2 .
3 3 2 3
S ABC ABC
aa
V SA S a
Chọn A
Câu 76. Ta có tam giác ABC vuông tại B nên
22
2BC AC AB a
Mặt khác
22
5SA SB AB a
Do vậy
23
.
1 1 2 10
. 5.
3 3 2 6
S ABC ABC
aa
V SA S a
Chọn A
Câu 77. Do
SAB ABC
SAC ABC
SA ABC
SA SAB SAC



Mặt khác
2
22
3
2;
4
ABC
a
SA SC AC a S
Do vậy
23
.
1 1 3 6
. 2.
3 3 4 12
S ABC ABC
aa
V SAS a
Chọn B
Câu 78. Ta có
22
3BC AC AB a
Mặt khác
2 2 2 2
3SA SD AD SD BC a
Do vậy
3
.
1 1 6
. . 3. 2.
3 3 3
S ABCD ABCD
a
V SA S a a a
Chọn D
Câu 79. Gọi O là tâm của hình đáy ABCD khi đó
SO ABCD
Ta có:
6
26
2
a
AC AB a OC
Mặt khác mặt bên của khối chóp là tam giác đều nên
22
6
3
2
a
SC CD SD a SO SC OC
Do vậy
3
.
16
.
32
S ABCD ABCD
a
V SO S
Chọn D
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 80. Gọi G là trọng tâm tam giác đều ABC khi đó
SG ABC
Gọi M là trung điểm của BC khi đó
3
2
a
AM
Suy ra
23
33
a
GA AM
. Mặt khác mặt bên của chóp là tam
giác
đều nên
22
6
3
a
SA AB SB a SG SA GA
Do đó
23
.
1 1 6 3 2
. . .
3 3 3 4 12
S ABC ABC
a a a
V SG S
Chọn B
Câu 81. Ta có tam giác ABC vuông tại B nên
22
2BC AC AB a
Mặt khác
00
; 30 30SB ABC SBA
Do đó
0
tan30
3
a
SA AB
Khi đó
23
.
1 1 2 6
. . .
3 3 2 18
3
S ABC ABC
a a a
V SA S
Chọn C
Câu 82. Từ
SAB ABC
SAC ABC SA ABC
SAB SAC SA

0
; 30SB ABC SBA SBA
0
1
tan30
3 3 3
SA AB a
SA
AB
3
0
.
1 1 1
. . . . .sin60
3 3 2 12
3
S ABC ABC
aa
V SA S a a
Chọn D
Câu 83. Từ
SAB ABC
SAC ABC SA ABC
SAB SAC SA

0
; 60SM ABC SMA SMA
0
33
tan60 3 3 . 3
22
SA AB a
SA AM
AM
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
3
0
.
1 1 3 1 3
. . . . sin60
3 3 2 2 8
S ABC ABC
aa
V SA S a a
Chọn C
Câu 84. Từ
0
; 45SA ABC SC ABC SCA SCA
2 2 2 2
43SA AC BC AB a a a
3
.
1 1 1 3
. 3. . . . 3
3 3 2 6 2
S ABC ABC
aa
V SAS a AB AC a a
Chọn A
Câu 85. Từ
0
; 60SA ABC SM ABC SMA SMA
0
1
tan60 3 3 3 3
2
SA
SA AM BC a
AM
Cạnh
2 2 2 2
43AC BC AB a a a
3
.
1 1 1 3
. 3. . . . 3
3 3 2 6 2
S ABC ABC
aa
V SA S a AB AC a a
Chọn A
Câu 86. Cạnh
2 2 2 2
43BC AC AB a a a
Từ
0
; 45SA ABCD SC ABCD SCA SCA
2sA AC a
3
.
1 1 2 3
. 2 . . 3
3 3 3
S ABCD ABCD
a
V SAS a a a
Chọn A
Câu 87. Cạnh
2 2 2 2
43BC AC AB a a a
Từ
0
; 60SA ABCD SO ABCD SOA SOA
0
tan60 3 3 3 3
2
SA AC
SA OA a
OA
3
.
11
. 3. . 3
33
S ABCD ABCD
V SA S a a a a
Chọn C
Câu 88. Từ
SAB ABC
SAD ABC SA ABCD
SAB SAD SA

CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
;SC ABCD SCA
0
45 2SCA SC AC a
3
2
.
1 1 2
. 2.
3 3 3
S ABCD ABCD
a
V SA S a a
Chọn B
Câu 89. Từ
SAB ABC
SAD ABC SA ABCD
SAB SAD SA

;SM ABCD SMA
00
60 tan60 3 3
SA
SMA SA AM
AM
Cạnh
2
2 2 2
5 15
2 2 2
a a a
AM AB BM a SA



3
2
.
1 1 15 15
..
3 3 2 6
S ABCD ABCD
aa
V SAS a
Chọn A
Câu 90. Ta có
.
1
.
3
S ABCD ABCD
SH ABCD V SH S
Và HC là hình chiếu của SC trên mặt phẳng (ABCD)
Do đó
0
; ; 60SC ABCD SC HC SCH
Xét
SCH
vuông, có
0
tan tan 60 . 3.
SH
SCH SH HC HC
HC
Mà
2 2 2 2
45HC BC BH a a a
nên
15SH a
Vậy thể tích khối chóp
.S ABCD
là
3
.
4 15
3
S ABCD
a
V
Chọn B
Câu 91. Ta có
.
1
.
3
S ABCD ABCD
SH ABCD V SH S
Và HD là hình chiếu của SD trên mặt phẳng (ABCD)
Do đó
0
; ; 45SD ABCD SD HC SDH
Xét
SDH
vuông cân tại H, có
SH HD
mà
2
AD
HD a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Nên
SH a
. Vậy thể tích
3
.
12
.2 .
33
S ABCD
a
V a a a
(đvtt)
Chọn C
Câu 92. Ta có
.
1
.
3
S ABC ABC
SA ABCD V SA S
Từ A kẻ AH vuông góc với BD,
H BD BD SAH
Có
,
SAH SBD SH
SBD ABCD
SAH ABCD AH


0
30SHA
Mà
2 2 2 2
16 4 2 3BC AC AB a a a
Nên
2 2 2 2 2 2
1 1 1 1 1 1
4 12 3AH AB AD a a a
3AH a
Do đó
0
tan tan30 .
SH
SHA SH AH a
AH
Vậy thể tích
3
.
1 1 2 3
. 2 .2 3
3 2 3
S ABC
a
V a a a
(đvtt)
Chọn C
Câu 93. Ta có
.
1
.
3
S ABCD ABCD
SA ABCD V SA S
Từ A kẻ AH vuông góc với BD,
H BD BD SAH
Có
,
SAH SBD SH
SBD ABCD
SAH ABCD AH


0
30SHA
Mà H là trung điểm của AC suy ra
2
2
AC a
AH 
Do đó
0
tan tan30 .
6
SH a
SHA SH AH
AH
Vậy thể tích
3
2
.
16
.
3 18
6
S ABCD
aa
Va
(đvtt)
Chọn C
Câu 94. Ta có
.
1
.
3
S ABCD ABCD
SA ABCD V SA S
Gọi H là tâm của hình thoi ABCD nên
AH BD
Mà
SA BD ABCD BD SAH
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Có
,
SAH SBD SH
SBD ABCD
SAH ABCD AH


0
60SHA
Mặt khác
0
33
tan60 .
2 2 2
AC a a
AH SH AH
Vậy thể tích
3
.
1 3 1 3 3 3
. . 3. 3.
3 2 2 2 8
S ABCD
aa
V a a
(đvtt)
Chọn A
Câu 95. Ta có
.
1
.
3
S ABCD ABCD
SA ABCD V SA S
Gọi H là trung điểm của CD, tam giác ACD đều nên
AH CD
Mà
SA CD ABCD CD SAH
Có
,
SAH SBD SH
SBD ABCD
SAH ABCD AH


0
30SHA
Mặt khác
0
3 3 3
3. tan30 .
2 2 2
aa
AH a SH AH
Vậy thể tích
23
.
1 3 3 3 3
..
3 2 4 8
S ABCD
a a a
V 
(đvtt)
Chọn C
Câu 96. Gọi O là tâm của hình thoi ABCD, do đó
SO ABCD
Gọi H là hình chiếu của O trên BC,
H BC OH BC
Do đó
BC SOH
và
,
SOH SBD SH
SBC ABCD
SOH ABCD OH


0
; 30SO HO SHO
Mà
2 2 2 2
1 1 1 25 12 12
144 5
53
aa
OH SH
OH OB OC a
Vậy thể tích
3
.
1 12 1 32 3
. . .6 .8
3 2 5
53
S ABCD
aa
V a a
(đvtt)
Chọn A
Câu 97. Gọi O là tâm của hình vuông ABCD, do đó
SO ABCD
Gọi H là hình chiếu của O trên BC,
H BC OH BC
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Do đó
BC SOH
và
SOH SBC SH
SOH ABCD OH


0
; ; 45SBC ABCD SO HO SHO
Mà H là trung điểm của BC nên
22
2
BC
OH a SO a
Vậy thể tích
3
2
.
1 8 2
. 2. 2 2
33
S ABCD
a
V a a
(đvtt)
Chọn D
Câu 98. +) Gọi H là tâm của tam giác đều
ABC SH ABC
. Lấy M là trung điểm BC. Ta có
SH BC AM SAM BC
SBC ABC
và
SAM
cắt hai mặt phẳng này tại 2 giao tuyến SM và AM
0
, 60SBC ABC SMH
+)
33
3
2 3 3
AB AM a
AM a HM
3SH HM a
3
.
.
3
33
ABC
S ABC
SH S
a
V
Chọn A
Câu 99. +) Gọi K là trung điểm CD. Vì
SH CD HK CD SHK
.
(SHK) vuông góc với giao tuyến CD của (SCD) và
(ABCD), đồng thời cắt 2 mặt phẳng này tại các giao tuyến
SK và HK
0
, 60SCD ABCD SKH
+)
6 3 6 3HK AD a SH HK a
3
.
.
..
96 3
33
ABCD
S ABCD
SH S
SH AB AD
Va
Chọn D
Câu 100. +) Gọi K là hình chiếu vuông góc của H lên
cạnh BD. Vì
SH BD HK SHK BD SBD ABCD
, và
SHK
cắt 2 mặt phẳng này tại các giao
tuyến
SK
và HK
0
, 60SBD ABCD SKH
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
+)
22
12
10 ;
5
HK BH a
BD AD AB a HK
AD BD
.
.
12 3
3
53
ABCD
S ABCD
SH S
a
SH HK V
3
. . 192 3
35
SH AB AD a

Chọn B
Câu 101. +) Gọi M là hình chiếu vuông góc của H lên
CD. Vì
HM CD SH SHM CD SCD ABCD
Và (SHM) cắt hai mặt phẳng này tại các giao tuyến SM và HM nên suy ra
0
, 60SCD ABCD SMH
+)
3 3 3 3
3
4 2 2
HM CH a a
HM SH HM
AD CA
2
3
.
.
.
23
33
ABCD
S ABCD
SH S
SH AB
Va
Chọn D
Câu 102. +) Gọi H là hình chiếu của S lên (ABCD). Vì tam
giác SAD cân tại S và nằm trong mặt phẳng vuông góc
đáy nên H là trung điểm AD. Gọi K là giao điểm HC và
BM.
+)
..CHD BMC c g c
CHD BMC
. Lại
có:
00
90 90CHD DCH BMC DCH
CH BM
. Nên
SH BM HC BM SHK
. Mặt phẳng (SHK) vuông góc với BM là giao
tuyến của (SBM) và (ABCD), đồng thời cắt 2 mặt phẳng này tại các giao tuyến SK và HK, suy ra
0
, 60SBM ABCD SKH
.
+)
22
5CH CD HD a
;
23
55
CK CM a a
CK HK CH CK
CD CH
33
3
5
a
SH HK
3
.
.
4 15
35
ABCD
S ABCD
SH S
a
V
Chọn B
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 103. +)
SBI SCI SI
SBI ABCD SCI


SI ABCD
Lấy E là điểm đối xứng với D qua C, suy ra tứ giác ABED là hình vuông. Gọi K là giao điểm của IE
và BC.
+)
..EID BCE c g c EID BCE
. Lại có:
00
90 90EID DEI BCE DEI EI BC
Nên
SI BC IE BC SIK
.
Mặt phẳng (SIK) vuông góc với BC là giao tuyến của (SBC) và (ABCD), đồng thời cắt 2 mặt phẳng
này tại các giao tuyến
SK
và IK, suy ra
0
, 60SBC ABCD SKI
+)
22
5IE ED ID a
;
23
55
EK EC a a
EK IK IE KE
ED EI
33
3
5
a
SI IK
3
.
.
.
3 15
3 6 5
ABCD
S ABCD
SI AB CD AD
SI S
a
V
Chọn C
Câu 104. +)
2
BC
AB AC a
. Khối
. ' ' 'ABC A B C
là lăng trụ
đứng
nên A là hình chiếu của A’ lên mặt phẳng
ABC
22
' ' 2 2AA A B AB a
+)
3
. ' ' '
'. .
'. 2
2
ABC A B C ABC
AA AB AC
V AA S a
Chọn B
Câu 105.
2
BC
AB AC a
. Khối
. ' ' 'ABC A B C
là lăng trụ đứng
nên A
là hình chiếu của A’ lên mặt phẳng (ABC)
0
' , ' 60A C ABC A CA
3
. ' ' '
3
' 3 3 '.
2
ABC A B C ABC
a
AA AC a V AA S
Chọn C
Câu 106. Do
2AD a HA HD a
Ta có
22
2HC HD CD a
Ta có
0
, 60SC ABCD SCH
.tan 6SH HC SCH a
Ta có
2
.2
ABCD
S AB BC a
2
.
11
. 6.2
33
S ABCD ABCD
V SH S a a
3
26
3
a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Chọn B
Câu 107. Ta có
22
6AC AD CD a
6
2
a
OA OC
22
10
2
a
SO SA OA
Ta có
22
3
ABCD
S AB a
3
2
.
1 1 10 10
. . .3
3 3 2 2
S ABCD ABCD
aa
V SO S a
Chọn A
Câu 108. Ta có
0
, 60SA ABCD SAO
Ta có
22
6AC AD CD a
6
2
a
OA OC
32
.tan
2
a
SO OA SAO
Ta có
22
3
ABCD
S AB a
2
.
1 1 3 2
. . .3
3 3 2
S ABCD ABCD
a
V SO S a
3
32
2
a
Chọn A
Câu 109. Ta có
3 2 3
2 3 3
aa
CM CH CM
22
33
3
a
SH SC CH
Ta có
2
3
4
ABC
a
S
23
.
1 1 33 3 11
. . .
3 3 3 4 2
S ABC ABC
a a a
V SH S
Chọn A
Câu 110. Ta có
0
, 45SC ABC SCH
Ta có
3 2 3
2 3 3
aa
CM CH CM
3
.tan
3
a
SH CH SCH
Ta có
2
3
4
ABC
a
S
23
.
1 1 3 3
. . .
3 3 3 4 12
S ABC ABC
a a a
V SH S
Chọn C
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 111. Do
vuông cân tại
13
22
a
S SM AB
Ta có
3. 3 3 1
2 2 3 2
a a a
CM HM CM
22
2
2
a
SH SM HM
Ta có
2
2
33
33
44
ABC
a
a
S 
33
.
1 1 2 3 3 6
. . .
3 3 2 4 8
S ABC ABC
a a a
V SH S
Chọn C
Câu 112. Ta có
22
AB BD AD a
Ta có
0
, 30SB ABCD SBA
3
.tan
3
a
SA AB SBA
Ta có
2
1 1 3
2
2 2 2
ABCD
a
S AB AD BC a a a
23
.
1 1 3 3 3
. . .
3 3 3 2 6
S ABCD ABCD
a a a
V SAS
Chọn A
Câu 113. Ta có
22
AB BD AD a
Ta có
0
, 45SO ABCD SOA
Ta có
22
2AC AB BC a
2 2 2
33
a
AO AC
22
.tan
3
a
SA AO SOA
Ta có
2
1 1 3
2
2 2 2
ABCD
a
S AB AD BC a a a
23
.
1 1 2 2 3 2
. . .
3 3 3 2 3
S ABCD ABCD
a a a
V SA S
Chọn C
CHỦ ĐỀ 2: KHOẢNG CÁCH
VẤN ĐỀ 1: KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT MẶT PHẲNG
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc
0
60ABC
. Mặt phẳng (SAB)
và (SAD) cùng vuông góc với mặt phẳng đáy. Trên cạnh SC lấy điểm M sao cho
2MC MS
. Khoảng
cách từ điểm M đến mặt phẳng (SAB) bằng:
A.
3
a
B.
3
6
a
C.
2
3
a
D.
3
3
a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 2: Cho hình chóp S.ABCD có đáy là hình bình hành với

0
2, 60BC a ABC
. Tam giác SAB
nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ điểm D đến mặt phẳng (SAB)
bằng:
A.
6
2
a
B.
2
2
a
C.
2a
D.
26
3
a
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc
0
60ABC
. Cạnh SA vuông
góc với mặt phẳng đáy. Trên cạnh BC và CD lần lượt lấy hai điểm M và N sao cho
MB MC
và
2NC ND
. Gọi P là giao điểm của AC và MN. Khoảng cách từ điểm P đến mặt phẳng (SAB) bằng:
A.
3
8
a
B.
C.
D.
Câu 4: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,
,3AB a BC a
. Hình chiếu
vuông góc của S trên mặt đáy là trung điểm của cạnh AC. Biết
2SB a
. Tính theo a khoảng cách từ
điểm H đến mặt phẳng (SAB)
A.
B.
C.
3 21
7
a
D.
7 21
3
a
Câu 5: Cho hình chóp S.ABCD có đáy là hình chữ nhật, diện tích tứ giác ABCD bằng
2
66a
. Cạnh
10
3
SA a
và vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SC và mặt phẳng đáy bằng 30
0
.
Khoảng cách từ điểm B đến mặt phẳng (SAC) gần nhất với giá trị nào sau đây:
A.
13
10
a
B.
7
5
a
C.
3
2
a
D.
8
5
a
Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D,
22AD AB BC
,
22CD a
. Hình chiếu vuông góc của S trên mặt đáy là trung điểm M của cạnh CD. Khoảng cách từ
điểm B đến mặt phẳng (SAM) bằng:
A.
3 10
10
a
B.
3 10
5
a
C.
3 10
2
a
D.
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D,
22AD AB BC
,
22CD a
. Hình chiếu vuông góc của S trên mặt đáy là trung điểm M của cạnh CD. Khoảng cách từ
trọng tâm G của tam giác SAD đến mặt phẳng (SBM) bằng:
A.
4 10
15
a
B.
3 10
5
a
C.
D.
3 10
15
a
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có diện tích bằng
2
2a
,
2, 2AB a BC a
. Gọi M là trung điểm của CD. Hai mặt phẳng (SBD) và (SAM) cùng vuông góc
với đáy. Khoảng cách từ điểm B đến mặt phẳng (SAM) bằng
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
4 10
15
a
B.
3 10
5
a
C.
2 10
5
a
D.
3 10
15
a
Câu 9: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a,
0
120ADC
. Hình chiếu vuông
góc của S trên mặt đáy là trọng tâm của tam giác ABC. Khoảng cách từ điểm C đến mặt phẳng (SAG)
bằng
A.
7
3
a
B.
C.
D.
3
7
a
Câu 10: Cho hình chóp S.ABC có đáy ABC là tam giác đều có cạnh bằng a. Gọi M là trung điểm của
AC. Hình chiếu của S trên mặt đáy là điểm H thuộc đoạn BM sao cho
2HM HB
. Khoảng cách từ
điểm A đến mặt phẳng (SHC) bằng
A.
27
14
a
B.
7
14
a
C.
37
14
a
D.
27
7
a
Câu 11: Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác cân có
3AC BC a
. Đường thẳng
A'C tạo với đáy một góc 60
0
. Trên cạnh A'C lấy điểm M sao cho
'2A M MC
. Biết rằng
' 31A B a
. Khoảng cách từ M đến mặt phẳng (ABB'A') là:
A.
32
4
a
B.
42
3
a
C.
32a
D.
22a
Câu 12: Cho khối chóp S.ABCD có đáy là hình chữ nhật ABCD với
AB a
. Hình chiếu vuông góc
của đỉnh S lên mặt đáy trùng với trọng tâm tam giác ABD. Biết
22SC a
và tạo với đáy một góc
45
0
. Khoảng cách từ trung điểm của SD đến mặt phẳng (SAC) là:
A.
2
3
a
B.
3
3
a
C.
2
3
a
D.
Câu 13: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có
3AD a
. Tam giác SAB là tam
giác đều và thuộc mặt phẳng vuông góc với đáy. Gọi M là trung điểm của AD. Biết rằng
2SD a
.
Khoảng cách từ A đến mặt phẳng (SHM) là:
A.
2
4
a
B.
3
4
a
C.
2
2
a
D.
3
2
a
Câu 14: Cho khối chóp S.ABC có đáy là tam giác vuông tại A có
AC a
. Tam giác SAB vuông tại S
và hình chiếu vuông góc của đỉnh S trên mặt đáy là điểm H thuộc cạnh AB sao cho
2HB SA
. Biết
22SH a
, khoảng cách từ B đến mặt phẳng (SHC) là:
A.
2
5
a
B.
5
a
C.
4
5
a
D.
3
5
a
Câu 15: Cho hình lăng trụ ABCD.A'B'C'D' có đáy là hình chữ nhật với
3AD a
. Tam giác A'AC
vuông cân tại A' và thuộc mặt phẳng vuông góc với đáy. Biết rằng
'2A A a
. Khoảng cách từ D'
đến mặt phẳng (A'ACC') là:
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
3
4
a
B.
2
2
a
C.
2
4
a
D.
3
2
a
Câu 16: Cho hình hộp ABCD.A'B'C'D' có đáy là hình vuông, tam giác A'AC vuông cân tại A,
'A C a
. Tính khoảng cách từ A đến mặt phẳng (BCD') theo a?
A.
3
3
a
B.
6
3
a
C.
2
2
a
D.
3
2
a
Câu 17: Cho hình chóp S.ABC có
3SA a
và
SA A BC
. Giả sử
2AB BC a
, góc
0
120ABC
. Tìm khoảng cách từ A đến mặt phẳng (SBC) ?
A.
2
a
B. a C.
3
2
a
D.
2a
Câu 18: Cho hình chóp S.ABC có đáy là tam giác vuông tại B,
3 , 4BA a BC a
, mặt phẳng (SBC)
vuông góc với mặt phẳng (ABC). Biết
23SB a
và góc
0
30SBC
. Tính khoảng cách từ B đến mặt
phẳng (SAC) theo a ?
A.
B.
56
4
a
C.
6
7
a
D.
6
7
a
Câu 19: Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật với
,3AB a AD a
. Hình
chiếu vuông góc của A' lên mặt phẳng (ABCD) trùng với trung điểm của AC và BD. Tính khoảng cách
từ B' đến mặt phẳng (A'BD) theo a ?
A.
3
2
a
B.
2
2
a
C.
3
3
a
D.
2
3
a
Câu 20: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,
,3AB a BC a
. Hình chiếu
vuông góc của S trên mặt đáy là trung điểm của cạnh AC. Biết
2SB a
. Tính theo a khoảng cách từ
điểm H đến mặt phẳng (SBC).
A.
3
5
a
B.
23
5
a
C.
5
5
a
D.
25
5
a
Câu 21: Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng
2,a SAB
là tam giác vuông cân
nằm trong mặt phẳng vuông góc với đáy. Khoảng cách từ trung điểm H của AB đến mặt phẳng (SBD)
là ?
A.
3
3
a
B. a C.
3
2
a
D.
Câu 22: Cho hình chóp S.ABCD có đáy là hình thoi cạnh bằng a, góc
0
60BAD
. Gọi H là hình
chiếu vuông góc của S xuống mặt đáy (ABCD) và
H AC
sao cho
1
3
AH AC
. Khoảng cách từ A
đến mặt phẳng (SBC) bằng bao nhiêu nếu biết
0
; 60SA ABCD
.
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
3
4
a
B.
3
4
a
C. a D.
3
2
a
Câu 23: Cho hình chóp S.ABC có
3SA a
và
SA A BC
. Biết
0
2 , 120AB BC a ABC
. Tính
khoảng cách từ A đến (SBC) ?
A.
2a
B.
2
a
C. a D.
3
2
a
Câu 24: Cho hình chóp S.ABCD có đáy là hình vuông có đường chéo bằng
2a
. Mặt bên
SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách h từ A đến mặt phẳng
(SCD) là:
A.
21
3
a
h
B.
21
14
a
h
C.
21
21
a
h
D.
21
7
a
h
Câu 25: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A,

0
3, 30AC a ABC
, góc giữa
SC và mặt phẳng (ABC) bằng 60
0
. Cạnh bên SA vuông góc với đáy. Khoảng cách từ A đến mặt phẳng
(SBC) bằng
A.
6
35
a
B.
3
35
a
C.
3
5
a
D.
23
35
a
Câu 26: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A,

0
3, 30AC a ABC
, góc giữa
SC và mặt phẳng (ABC) bằng 60
0
. Cạnh bên SA vuông góc với đáy. Khoảng cách từ trọng tâm G của
tam giác SAC đến mặt phẳng (SBC) bằng
A.
3
5
a
B.
5
a
C.
6
5
a
D.
2
5
a
Câu 27: Cho hình lăng trụ đứng ABC.A'B'C' có
. ' ' 'ABC A B C
có

0
, 120 ,AC a BAC
góc
0
30ABC
, mặt bên BCB'C' có diện tích bằng
2
2a
. Gọi M là trung điểm của BC. Khoảng cách từ C
đến mặt phẳng (C'AM) bằng
A.
23
3
a
B.
2
5
a
C.
2 57
19
a
D.
23
5
a
Câu 28: Cho hình lăng trụ ABC.A'B'C' có
00
3, 30 , 60AB a ABC ACB
. Hình chiếu vuông góc
của A' trên mặt đáy là trung điểm của BC. Thể tích khối chóp A'AC bằng
3
6
a
. Khoảng cách từ C đến
mặt phẳng (A'AB) bằng
A.
6
6
a
B.
2
7
a
C.
6
4
a
D.
6
12
a
Câu 29: Cho hình chóp đều S.ABC có
AB a
, góc giữa mặt bên và mặt đáy bằng 60
0
. Tính
4d
a
, biết
d là khoảng c cách từ điểm A đến mặt phẳng (SBC).
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
3a
B.
5a
C.
7a
D.
9a
Câu 30: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
,SA ABCD SA AB a
và
.AD x a
. Gọi E là trung điểm cạnh SC. Tìm x, biết khoảng cách từ điểm E đến mặt phẳng (SBD) là
3
a
d
A.
1x
B.
2x
C.
3x
D.
4x
Câu 31: Cho hình chóp S.ABCD, ABCD là hình vuông cạnh
AB a
. Mặt phẳng chứa tam giác đều
SAB vuông góc với mặt phẳng đáy (ABCD). Khoảng cách từ điểm A đến mặt phẳng (SCD) là:
A.
B.
C.
7
a
D.
2
7
a
Câu 32: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
,3SA ABCD SA a
. Tính theo
a khoảng cách từ điểm O đến mặt phẳng (SBC).
A.
2
a
B.
3
4
a
C.
5
6
a
D.
7
8
a
Câu 33: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
,SA ABCD
SA AB a
và
2AD a
. Gọi F là trung điểm cạnh CD. Tính
33d
a
, biết d là khoảng cách từ điểm A đến mặt phẳng
(SBF)
A.
2 33a
B.
4 33a
C.
2 11a
D.
4 11a
Câu 34: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với
2AD a
. Hình chiếu vuông góc
của S trên mặt đáy là điểm H
H AB
thỏa mãn
2HA HB
. Biết
.SA x a
và
SH a
. Tìm x biết
khoảng cách từ điểm C đến mặt phẳng (SHD) là
32
2
a
d
A.
5x
B.
5x
C.
3x
D.
3x
Câu 35: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,
,3AB a BC a
. Hình chiếu
vuông góc của S trên mặt đáy là trung điểm của cạnh AC. Biết
2SB a
. Tính theo a khoảng cách từ
H đến mặt phẳng (SBC).
A.
3
5
a
B.
23
5
a
C.
5
5
a
D.
25
5
a
Câu 36: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
,3SA ABCD SA a
. Tính theo
a khoảng cách từ điểm O đến mặt phẳng (SBC).
A.
2
a
B.
3
4
a
C.
5
6
a
D.
7
8
a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 37: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
,SA ABCD
SA AB a
và
2AD a
. Gọi F là trung điểm cạnh CD. Tính
33d
a
, biết d là khoảng cách từ điểm A đến mặt phẳng
(SBF)
A.
2 33a
B.
4 33a
C.
2 11a
D.
4 11a
Câu 38: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với
2AD a
. Hình chiếu vuông góc
của S trên mặt đáy là điểm H
H AB
thỏa mãn
2HA HB
. Biết
.SA x a
và
SH a
. Tìm x biết
khoảng cách từ điểm C đến mặt phẳng (SHD) là
32
2
a
d
A.
5x
B.
5x
C.
3x
D.
3x
Câu 39: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,
,3AB a BC a
. Hình chiếu
vuông góc của S trên mặt đáy là trung điểm của cạnh AC. Biết
2SB a
. Tính theo a khoảng cách từ
H đến mặt phẳng (SBC).
A.
3
5
a
B.
23
5
a
C.
5
5
a
D.
25
5
a
Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
,SA ABCD
SA AB a
và
2AD a
Gọi E là trung điểm cạnh SC. Tính theo a khoảng cách từ điểm E
đến mặt phẳng (SBD)
A.
2
a
B.
3
a
C.
4
a
D.
5
a
Câu 41: Cho hình hộp đứng ABCD.A'B'C'D' có đáy là hình vuông, tam giác A'AC là tam giác vuông
cân,
'A C a
. Khoảng cách từ A đến mặt phẳng (BCD') là:
A.
6
3
a
B.
6
2
a
C.
6
a
D.
6
4
a
Câu 42: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông
góc với mặt phẳng đáy. Gọi M là trung điểm của SB. Tỷ số
SA
a
khi khoảng cách từ điểm M đến mặt
phẳng (SCD) bằng
5
a
là:
A.
2
B. 2 C.
3
2
D. 1
Câu 43: Cho hình chóp S.ABC có
SA A BC
và
4 , 3 , 4SA cm AB cm AC cm
và
5BC cm
.
Khoảng cách từ điểm A đến mp (SBC) bằng (đơn vị cm) :
A.
2
;
17
d A SBC
B.
72
;
17
d A SBC
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
C.
6 34
;
17
d A SBC
D.
3
;
17
d A SBC
Câu 44: Cho khối chóp S.ABCD có đáy là hình vuông cạnh 4cm. Hình chiếu vuông góc của S xuống
mặt đáy là trung điểm H của AB. Biết rằng
2SH cm
. Khoảng cách từ A đến mặt phẳng (SBD) là:
A. 1 cm B. 2 cm C. 3 cm D. 4 cm
Câu 45: Cho hình chóp S.ABC có đáy là tam giác đều. Hình chiếu vuông góc của đỉnh S lên mặt đáy
là điểm H thuộc cạnh AC sao cho
2HC HA
. Gọi M là trung điểm của SC và N là điểm thuộc cạnh
SB sao cho
3SB SN
. Khẳng định nào sau đây là sai:
A. Khoảng cách từ M đến mặt phẳng (ABC) bằng
4
3
lần khoảng cách từ N đến mặt phẳng (ABC).
B. Khoảng cách từ M đến mặt phẳng (SAB) bằng một nửa khoảng cách từ C đến mặt phẳng (SAB)
C. Khoảng cách từ N đến mặt phẳng (SAC) bằng
1
3
khoảng cách từ B đến mặt phẳng (SAC)
D. Khoảng cách từ M đến mặt phẳng (SAB) bằng
3
2
khoảng cách từ H đến mặt phẳng (SAB)
Câu 46: Cho hình chóp S.ABCD có đáy là hình chữ nhật có
9, 12AB AD
. Hình chiếu vuông góc
của đỉnh S xuống mặt đáy trùng với trọng tâm H của tam giác ABC. Biết
6SH
, khoảng cách từ A
đến mặt phẳng (SCD) là:
A.
36
5
B.
24
5
C.
12
5
D.
4
5
Câu 47: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD. Tam giác SAD cân tại S và thuộc
mặt phẳng vuông góc với đáy. Gọi M là điểm thoã mãn
20SM CM
. Tỷ số khoảng cách D đến mặt
phẳng (SAB) và từ M đến mặt phẳng (SAB) là:
A.
2
3
B.
3
2
C.
1
2
D. 2
Câu 48: Cho hình chóp S.ABCD có đáy là hình thoi. Tam giác SAB cân tại S và thuộc mặt phẳng
vuông góc với đáy , biết tam giác ABC đều cạnh 20 cm và mặt phẳng (SCD) tạo với đáy một góc 60
0
.
Khoảng cách từ A đến (SCD) là:
A. 20 cm B. 10 cm C. 15 cm D. 30 cm
Câu 49: Cho hình lăng trụ ABC.A'B'C', hình chiếu vuông góc của A' xuống mặt đáy (ABC) trùng với
trung điểm H của AB. Gọi h là khoảng cách từ A đến mặt phẳng (A'BC). Gọi M là trung điểm của
A'C' và N thuộc cạnh CC' sao cho
'2NC NC
. Tính khoảng cách từ M và N đến mặt phẳng (A'BC)
A.
2
3
2
h
B.
2
6
h
C.
2
2
3
h
D.
6
h
Câu 50: Cho hình lăng trụ ABCD.A'B'C'D' có đáy là hình chữ nhật ABCD có
3; 4AB AD
. Tam
giác A'BD cân tại A' và thuộc mặt phẳng vuông góc với đáy và
'5AA
. Gọi M là trung điểm của
A'D'. Khoảng cách từ M đến mặt phẳng (A'AC) là:
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
12
5
B.
6
5
C.
3
5
D.
4
5
Câu 51: Cho hình chóp đều S.ABCD có SAC là tam giác đều. Gọi d
A
là khoảng cách từ A đến mặt
phẳng (SCD) và d
B
là khoảng cách từ B đến mặt phẳng (SAC). Tỷ lệ
A
B
d
d
bằng:
A. 2 B.
21
7
C.
3
D.
Câu 52: Cho hình chóp S.ABC có tam giác ABC vuông tại A,
,AB AC a
I là trung điểm của SC,
hình chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm H của BC, mặt phẳng (SAB) tạo với
đáy 1 góc bằng 60
0
. Khoảng cách từ điểm I đến mặt phẳng (SAB).
A.
3
4
a
B.
39
3
a
C.
3
2
a
D.
3
4
a
Câu 53: Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh 2a. Mặt phẳng (A'BC) tạo
với mặt đáy (ABC) một góc 60
0
. Khoảng cách từ B đến mặt phẳng (B'AC) là:
A.
3
2
a
B.
2
3
a
C.
9
4
a
D.
2
a
Câu 54: Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác cân tại A,
0
2 , 120AB AC a CAB
.
Góc giữa (A'BC) và (ABC) là 45
0
. Khoảng cách từ B' đến mặt phẳng (ABC) là:
A.
2a
B.
22a
C. a D.
2
4
a
Câu 55: Cho lăng trụ tứ giác đều ABCD.A'B'C'D' với cạnh đáy
23dm
. Biết rằng mặt phẳng (BDC')
hợp với đáy một góc 30
0
. Khoảng cách từ A đến mặt phẳng (BDC') là:
A.
6
2
dm
B.
3
2
dm
C.
2
3
dm
D.
6
3
dm
Câu 56: Cho hình chóp S.ABCD có đáy là tam giác vuông tại A,
2 , 3AB a AC a
. Hình chiếu
vuông góc của S lên mặt phẳng (ABC) là trung điểm H của cạnh AB. Cạnh bên SC hợp với đáy 1 góc
60
0
. Khoảng cách từ A đến mặt phẳng (SBC) là:
A.
4 29
29
a
B.
C.
4 87
29
a
D.
4
29
a
Câu 57: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,

0
, 60BC a ACB
,
SA A BC
và M là điểm nằm trên cạnh AC sao cho
2MC MA
. Biết (SBC) tạo với đáy góc 30
0
.
Khoảng cách từ M đến mặt phẳng (SBC) là:
A.
3
2
a
B.
3
3
a
C.
3
6
a
D.
2
9
a
Câu 58: Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng 2a, cạnh bên bằng 3a. Gọi O là tâm đáy,
M, N là trung điểm của AB, BC. Khoảng cách từ O đến mặt phẳng (SMN) là:
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
279
69
a
B.
279
23
a
C.
23
279
a
D.
23
279
a
Câu 59: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a,
,3SA ABCD SA a
. Gọi G là trọng tâm
SAC
. Từ G kẻ đường thẳng song song với SB cắt OB
tại I. Khoảng cách từ I đến mặt phẳng (SBC) là:
A.
2
2
a
B.
2
6
a
C.
3
6
a
D.
6
3
a
Câu 60: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều
cạnh a và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của AB, E là trung điểm của
BC. Khoảng cách từ I đến mặt phẳng (SED) là:
A.
2
2
a
B.
2
6
a
C.
2
4
a
D.
32
8
a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Đáp án
1-B
2-A
3-C
4-B
5-B
6-B
7-A
8-C
9-B
10-D
11-B
12-A
13-B
14-C
15-D
16-B
17-C
18-D
19-B
20-C
21-A
22-B
23-D
24-D
25-C
26-B
27-C
28-B
29-A
30-B
31-A
32-B
33-B
34-A
35-C
36-B
37-B
38-A
39-C
30-B
41-C
42-B
43-C
44-B
45-A
46-A
47-B
48-C
9-B
50-B
51-D
52-D
53-A
54-C
55-A
56-C
57-B
58-D
59-C
60-D
Hướng dẫn giải
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc
0
60ABC
. Mặt phẳng (SAB)
và (SAD) cùng vuông góc với mặt phẳng đáy. Trên cạnh SC lấy điểm M sao cho
2MC MS
. Khoảng
cách từ điểm M đến mặt phẳng (SAB) bằng:
A.
3
a
B.
3
6
a
C.
2
3
a
D.
3
3
a
HD: Ta có:

SAB ABC
SA ABCD
SAD ABC
Dựng
CH AB CH SAB
Do

;
3
2
;
d C SAB
CS
MS
d M SAB
2 2 2 3 3
; ; .
3 3 3 2 6
aa
d M SAB d C SAB CH
Chọn B
Câu 2: Cho hình chóp S.ABCD có đáy là hình bình hành với

0
2, 60BC a ABC
. Tam giác SAB
nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ điểm D đến mặt phẳng (SAB)
bằng:
A.
6
2
a
B.
2
2
a
C.
2a
D.
26
3
a
HD: Dựng
SH AB
Do
DDSAB ABC SH ABC
Dựng
CK AB
, có
SCK H CK SAB
Do
D/ / ; ;C AB d D SAB d C SAB CK
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
0
36
sin60 3.
22
a
BC a
. Chọn A
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc
0
60ABC
. Cạnh SA vuông
góc với mặt phẳng đáy. Trên cạnh BC và CD lần lượt lấy hai điểm M và N sao cho
MB MC
và
2NC ND
. Gọi P là giao điểm của AC và MN. Khoảng cách từ điểm P đến mặt phẳng (SAB) bằng:
A.
3
8
a
B.
C.
D.
HD: Dựng
CH AB CH SAB
Giả sử MN cắt AD tại F. theo định lý Talet ta có:
1
2 2 4
DF ND MC a
DF
MC NC
Khi đó
57
25
PA AF CA
PC MC PA
Do đó

55
;;
77
d P SAB d C SAB CH

5 3 5 3
.
7 2 14
aa
. Chọn C
Câu 4: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,
,3AB a BC a
. Hình chiếu
vuông góc của S trên mặt đáy là trung điểm của cạnh AC. Biết
2SB a
. Tính theo a khoảng cách từ
điểm H đến mặt phẳng (SAB)
A.
B.
C.
3 21
7
a
D.
7 21
3
a
HD:
22
2
2
AC
AC AB BC a BH a
Do vậy
22
SH SB BH a
. Dựng
;HE AB HF SE
Ta có
22
3 . 21
;
2 2 7
BC a SH HE a
HE d H SAB
SH HE
Chọn B.
Câu 5: Cho hình chóp S.ABCD có đáy là hình chữ nhật, diện tích tứ giác ABCD bằng
2
66a
. Cạnh
10
3
SA a
và vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SC và mặt phẳng đáy bằng 30
0
.
Khoảng cách từ điểm B đến mặt phẳng (SAC) gần nhất với giá trị nào sau đây:
A.
13
10
a
B.
7
5
a
C.
3
2
a
D.
8
5
a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
HD: Dựng
BH AC
, lại có
SBH A BH SAC
Có
D;SA ABC SA ABC SCA
Ta có:
0
110
tan30 110
3
AC SA a AC a
Do vậy
2
2S
6a 6 7
1,4a
5
110
ABC
BH a
AC
. Chọn B
Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D,
22AD AB BC
,
22CD a
. Hình chiếu vuông góc của S trên mặt đáy là trung điểm M của cạnh CD. Khoảng cách từ
điểm B đến mặt phẳng (SAM) bằng:
A.
3 10
10
a
B.
3 10
5
a
C.
3 10
2
a
D.
HD:
Gọi E là trung điểm của AD ta có
2 2 2CD a CE ED a
Do vậy
4 ;BD 2aAD a
. Gọi N là trung điểm của AB suy ra
2
1
MN 3a,S . 3
2
MAB
NM AB a
22
10MA AN NM a
. Dựng
2
3 10
;
5
ABM
S
a
BK AM d B SAM BK
AM
Chọn B.
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D,
22AD AB BC
,
22CD a
. Hình chiếu vuông góc của S trên mặt đáy là trung điểm M của cạnh CD. Khoảng cách từ
trọng tâm G của tam giác SAD đến mặt phẳng (SBM) bằng:
A.
4 10
15
a
B.
3 10
5
a
C.
D.
3 10
15
a
HD:
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Gọi E là trung điểm của AD ta có
CE AB ED
. Có
2 2 2CD a CE ED a
Do vậy
4 ;BD 2aAD a
. Gọi N là trung điểm của AB suy ra
2
1
MN 3a,S . 3
2
MAB
NM AB a
.
22
10MA AN NM a MB
Gọi L là trung điểm của DE ta có
3aLA
là L là trung điểm của AP.
Khi đó
3 4 ; 6LP a EP a AP a
.
;
6 3 3
, ; ;
4 2 2
;
d A SBM
d E SBM d G SBM
d E SBM
Do đó
4 4 4 3 10 4 10
; ; .
9 9 9 5 15
aa
d G SBM d A SMB AF
. Chọn A.
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có diện tích bằng
2
2a
,
2, 2AB a BC a
. Gọi M là trung điểm của CD. Hai mặt phẳng (SBD) và (SAM) cùng vuông góc
với đáy. Khoảng cách từ điểm B đến mặt phẳng (SAM) bằng
A.
4 10
15
a
B.
3 10
5
a
C.
2 10
5
a
D.
3 10
15
a
HD: Gọi
DH AM B
Ta có

DSB ABC
SH ABC
SAM ABC
Lại có
1
2 ; ;
D2
HB AB
d D SAM d B SAM
H DM
2
D D D
11
2 4 2
A M A C ABC
a
S S S
Ta có
0
D
12
D.DM.sinD sin 45
22
AM
S A D D
Do vậy
2 2 0
10
2 . .cos45
2
AM AD DM AD DM a
Do vậy
2.
2 10
5
10
ADM
S
aa
DK
AM
. Chọn C
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 9: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a,
0
120ADC
. Hình chiếu vuông
góc của S trên mặt đáy là trọng tâm của tam giác ABC. Khoảng cách từ điểm C đến mặt phẳng (SAG)
bằng
A.
7
3
a
B.
C.
D.
3
7
a
HD: Dựng
CH AG CH SAG
Ta có:
sin
CH OG
GAO
CA AG
. Dễ thấy tam giác ABC đều
Trong đó
2 3 2
2 2. 2 3;
2 6 3
a a a
CA OA a OG
Do vậy

22
21
.
7
OG a
CH CA
OG OA
. Chọn B
Câu 10: Cho hình chóp S.ABC có đáy ABC là tam giác đều có cạnh bằng a. Gọi M là trung điểm của
AC. Hình chiếu của S trên mặt đáy là điểm H thuộc đoạn BM sao cho
2HM HB
. Khoảng cách từ
điểm A đến mặt phẳng (SHC) bằng
A.
27
14
a
B.
7
14
a
C.
37
14
a
D.
27
7
a
HD:
; 2 ;d A SCH d M SHC
. Dựng
MK CH
Khi đó
;2d A SCH MK
Mặt khác
3 2 3
;
2 3 3 2
a a a
BM MH BM MC
Suy ra

22
.
7
MH HC a
MK
MH MC
do đó

27
2
7
a
d MK
. Chọn D
Câu 11: Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác cân
có
3AC BC a
. Đường thẳng A'C tạo với đáy một góc 60
0
. Trên cạnh A'C lấy điểm M sao cho
'2A M MC
. Biết rằng
' 31A B a
. Khoảng cách từ M đến mặt phẳng (ABB'A') là:
A.
32
4
a
B.
42
3
a
C.
32a
D.
22a
HD: Ta có

0
' tan60 3 3A A AC a
Suy ra
22
' ' 2AB A B AA a
Do vậy
22
22CH AC AH a
2 2 4 2
; ' ' ; ' '
3 3 3
a
d M ABB A d C ABB A CH
. Chọn B
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 12: Cho khối chóp S.ABCD có đáy là hình chữ nhật ABCD với
AB a
. Hình chiếu vuông góc
của đỉnh S lên mặt đáy trùng với trọng tâm tam giác ABD. Biết
22SC a
và tạo với đáy một góc
45
0
. Khoảng cách từ trung điểm của SD đến mặt phẳng (SAC) là:
A.
2
3
a
B.
3
3
a
C.
2
3
a
D.
HD: Ta có
2a 2 2a 3aSC GC AC
Khi đó
D 2a 2C
suy ra
2a 2
3
DH
Do vậy

12
;
23
a
d M SAC DH
Câu 13: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có
3AD a
. Tam giác SAB là tam
giác đều và thuộc mặt phẳng vuông góc với đáy. Gọi M là trung điểm của AD. Biết rằng
2SD a
.
Khoảng cách từ A đến mặt phẳng (SHM) là:
A.
2
4
a
B.
3
4
a
C.
2
2
a
D.
3
2
a
HD: Ta có:
22
DDSA S A a AB
Khi đó

22
.3
4
AH AM a
AK
AH AM
Câu 14: Cho khối chóp S.ABC có đáy là tam giác vuông tại A có
AC a
. Tam giác SAB vuông tại S
và hình chiếu vuông góc của đỉnh S trên mặt đáy là điểm H thuộc cạnh AB sao cho
2HB SA
. Biết
22SH a
, khoảng cách từ B đến mặt phẳng (SHC) là:
A.
2
5
a
B.
5
a
C.
4
5
a
D.
3
5
a
HD: Ta có

22
.2SH HA HB HA
Suy ra
22
8 2 2aa HA HA
Do vậy
2a 4a
2A
55
c
AM d M
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 15: Cho hình lăng trụ ABCD.A'B'C'D' có đáy là hình chữ nhật với
3AD a
. Tam giác A'AC
vuông cân tại A' và thuộc mặt phẳng vuông góc với đáy. Biết rằng
'2A A a
. Khoảng cách từ D'
đến mặt phẳng (A'ACC') là:
A.
3
4
a
B.
2
2
a
C.
2
4
a
D.
3
2
a
HD:
Ta có
3
' 2 2a D ; '
2
a
AC A A C a d D A AC DH
(do
DD'/ /AA'
)
Câu 16: Cho hình hộp ABCD.A'B'C'D' có đáy là hình vuông, tam giác A'AC vuông cân tại A,
'A C a
. Tính khoảng cách từ A đến mặt phẳng (BCD') theo a?
A.
3
3
a
B.
6
3
a
C.
2
2
a
D.
3
2
a
HD:
+) kẻ
' ; D' ; 'AP A B d A BC d A A BC AP
+)
'A AC
vuông cân tại A
'C 2a
'2
22
A
A A AC a
Tứ giác ABCD là hình vuông
2 2 2 2 2 2
1 1 1 1 1 3
' 2 2a
2
AC
AB a
AP A A AB a a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
2 6 6
; D'
33
3
a a a
AP d A BC
Câu 17: Cho hình chóp S.ABC có
3SA a
và
SA A BC
. Giả sử
2AB BC a
, góc
0
120ABC
. Tìm khoảng cách từ A đến mặt phẳng (SBC) ?
A.
2
a
B. a C.
3
2
a
D.
2a
HD:
+) Trên mặt phẳng đáy , qua A kẻ một đường thẳng vuông góc với
AC, đường thẳng này cắt BC tại P.
;;d A SBC d A SPC h
,
Đặt
tứ diện vuông
2 2 2 2
1 1 1 1
.S APC
h AS AC AP
+)
ABP
đều




2 2 2 2 2
0
2
2
1 1 1 1 4 3
2
9 12 4 9
tan60 3
23
AP AB a
AP a
a
h
AC
h a a a a
AC a
AP
Câu 18: Cho hình chóp S.ABC có đáy là tam giác vuông tại B,
3 , 4BA a BC a
, mặt phẳng (SBC)
vuông góc với mặt phẳng (ABC). Biết
23SB a
và góc
0
30SBC
. Tính khoảng cách từ B đến mặt
phẳng (SAC) theo a ?
A.
B.
56
4
a
C.
6
7
a
D.
6
7
a
HD:
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
+) Kẻ
0
3
cos30
2
BH
SH BC H BC SH ABC
SB
;
3 2 3. 3 4
34
2 2 4 3
;
d B SAC
SB a BC a
BH a
HC a a
d H SHC
+) Kẻ
, ; ; 4HK AC HP SK d H SAC HP d B SAC HP
+)

2 2 2 2
.CH 3 .a 3
~
5
9 16
HK CH AB a a
CKH CBA HK
AB CA
AB BC a a
Ta có
0
2 2 2 2 2 2
1 1 1 1 1 1 28
sin30 3
22
3 9 9
25
SH SB
SH a
SB
HP HS HK a a a
3 12 6
;4
28 28 7
a a a
HP d B SAC HP
Câu 19: Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật với
,3AB a AD a
. Hình
chiếu vuông góc của A' lên mặt phẳng (ABCD) trùng với trung điểm của AC và BD. Tính khoảng cách
từ B' đến mặt phẳng (A'BD) theo a ?
A.
3
2
a
B.
2
2
a
C.
3
3
a
D.
2
3
a
HD:
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
+) Gọi
'OO AC BC A ABCD
+)
'. ' . 'AB '.ABD '
11
'; ' . ' .
33
B A BD D A A A BD ABD
V V V d B A BD S A O S
22
'BD
1
'O. . .
'.
. 3 3
2
'; '
1
2
3
' .BD
2
ABD
A
A AB AD
A O S
AB AD aa a
d B A BD
S BD
aa
AO
Câu 20: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,
,3AB a BC a
. Hình chiếu
vuông góc của S trên mặt đáy là trung điểm của cạnh AC. Biết
2SB a
. Tính theo a khoảng cách từ
điểm H đến mặt phẳng (SBC).
A.
3
5
a
B.
23
5
a
C.
5
5
a
D.
25
5
a
HD:
+) Kẻ
,;HK BC HP SK d H SBC HP
Từ
1
//
2 2 2
HK BC
HK CH AB a
HK AB HK
AB CA
AB BC
+)
ABC
vuông tại B có H là trung điểm của cạnh AC
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
2 2 2 2 2 2 2 2
1 1 1
3 S 2a
2 2 2
HB AC AB BC a a a H SB HB a a
2 2 2 2 2
1 1 1 1 4 5 5
;
55
S
aa
HP d H SBC
HP H HK a a
Câu 21: Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng
2,a SAB
là tam giác vuông cân
nằm trong mặt phẳng vuông góc với đáy. Khoảng cách từ trung điểm H của AB đến mặt phẳng (SBD)
là ?
A.
3
3
a
B. a C.
3
2
a
D.
HD: vì
SAB
là tam giác vuông cân tại S nên
DSH ABC
Từ H kẻ
DHI B
, từ H kẻ
SIHK
với
I BD,K SI
Ta có
SH BD
BD SHI BD HK HK SBD
HI BD
Do đó
,d H SBD HK
. Mặt khác

2 2 2
1 1 1
HI SH HK
Mà

1
,
2
2
a
HI d A BD
và

2
AB
SH a
Nên



2 2 2 2
1 1 1 3
3
2
a
HK
HK a a
a
. Chọn A.
Câu 22: Cho hình chóp S.ABCD có đáy là hình thoi cạnh bằng a, góc
0
60BAD
. Gọi H là hình
chiếu vuông góc của S xuống mặt đáy (ABCD) và
H AC
sao cho
1
3
AH AC
. Khoảng cách từ A
đến mặt phẳng (SBC) bằng bao nhiêu nếu biết
0
; 60SA ABCD
.
A.
3
4
a
B.
3
4
a
C. a D.
3
2
a
HD: Ta có AH là hình chiếu của SA lên mặt phẳng (ABCD)
Do đó
0
, D ; 60SA ABC SA AH SAH
Từ H kẻ
HI BC
, kẻ
SHK I
với
,I BC K SI
Ta có
SH BC
BC SHI BC HK HK SBC
HI BC
Do đó
,d H SBD HK
. Mặt khác

2 2 2
1 1 1
HI SH HK
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Mà
0
tan60 .
3
AC
SH AH a
và
2 2 3
.d , .
3 3 2
3
aa
HI A BC
Khi đó
2 2 2 2
1 1 3 4
2
a
HK
HK a a a
Vậy
3 3 3
; .HK .
2 2 2 4
aa
d A SBC
. Chọn B
Câu 23: Cho hình chóp S.ABC có
3SA a
và
SA A BC
. Biết
0
2 , 120AB BC a ABC
. Tính
khoảng cách từ A đến (SBC) ?
A.
2a
B.
2
a
C. a D.
3
2
a
HD: Từ A kẻ
AH BC
, kẻ
AK SH
với
,K BC K SH
Ta có
SA BC
BC SAH BC AK AK SBC
AH BC
Do đso
;d A SBC AK
thỏa mãn

2 2 2
1 1 1
SA AH AK
Mà
3SA a
và
0
3
sin60 . .2 3
2
AH AB a a
Nên
2 2 2 2
1 1 1 4 3 3
;
22
9 3 9
aa
AK d A SBC
AK a a a
Chọn D.
Câu 24: Cho hình chóp S.ABCD có đáy là hình vuông có đường chéo bằng
2a
. Mặt bên
SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách h từ A đến mặt phẳng
(SCD) là:
A.
21
3
a
h
B.
21
14
a
h
C.
21
21
a
h
D.
21
7
a
h
HD:
Chọn D.
Câu 25: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A,

0
3, 30AC a ABC
, góc giữa
SC và mặt phẳng (ABC) bằng 60
0
. Cạnh bên SA vuông góc với đáy. Khoảng cách từ A đến mặt phẳng
(SBC) bằng
A.
6
35
a
B.
3
35
a
C.
3
5
a
D.
23
35
a
HD: Kẻ
E , S ,A BC AK E E BC K SE
Chứng minh
;AK SBC AK d A SBC
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Xét tam giác SAE vuông tại A ta có:
22
.SA AE
AK
SA AE
Tính SA, AE:
Xét hai tam giác vuông ABC và SAC:
3AB SA a
Xét tam giác vuông ABC:
3
2
a
AE
3
;
5
a
d A SBC HK
. Chọn C.
Câu 26: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A,

0
3, 30AC a ABC
, góc giữa
SC và mặt phẳng (ABC) bằng 60
0
. Cạnh bên SA vuông góc với đáy. Khoảng cách từ trọng tâm G của
tam giác SAC đến mặt phẳng (SBC) bằng
A.
3
5
a
B.
5
a
C.
6
5
a
D.
2
5
a
HD: Kẻ
E , S ,A BC AK E E BC K SE
Chứng minh
;AK SBC AK d A SBC
Xét tam giác SAE vuông tại A ta có:
22
.SA AE
AK
SA AE
Tính SA, AE:
Xét hai tam giác vuông ABC và SAC:
3AB SA a
Xét tam giác vuông ABC:
3
2
a
AE
3
;
5
a
d A SBC HK
.
1
,,
3
5
a
d G SBC d A SBC
. Chọn B
Câu 27: Cho hình lăng trụ đứng ABC.A'B'C' có
. ' ' 'ABC A B C
có

0
, 120 ,AC a BAC
góc
0
30ABC
, mặt bên BCB'C' có diện tích bằng
2
2a
. Gọi M là trung điểm của BC. Khoảng cách từ C
đến mặt phẳng (C'AM) bằng
A.
23
3
a
B.
2
5
a
C.
2 57
19
a
D.
23
5
a
HD: Ta có
3
, 3,
2
a
AB AC a BC a CM
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com

22
.'
,'
'
CM CC
d C AMC CK
CM CC
Lại có:
2
''
2 57
. ' 2 ' 2
19
BCC B
a
S BC CC a CC a CK
. Chọn C
Câu 28: Cho hình lăng trụ ABC.A'B'C' có
00
3, 30 , 60AB a ABC ACB
. Hình chiếu vuông góc
của A' trên mặt đáy là trung điểm của BC. Thể tích khối chóp A'AC bằng
3
6
a
. Khoảng cách từ C đến
mặt phẳng (A'AB) bằng
A.
6
6
a
B.
2
7
a
C.
6
4
a
D.
6
12
a
HD: Gọi E là trung điểm của AB.
Ta có
0
.tan30
2
a
AC AB a HE
3
'.
1
' . 'H
36
3
A ABC ABC
aa
V A H S A
Kẻ
' , '
7
a
HK A E HK d H A AB
2a
, ' 2d , '
7
d C A AB H A AB
. Chọn B
Câu 29: Cho hình chóp đều S.ABC có
AB a
, góc giữa mặt bên và mặt đáy
bằng 60
0
. Tính
4d
a
, biết d là khoảng c cách từ điểm A đến mặt phẳng (SBC).
A.
3a
B.
5a
C.
7a
D.
9a
HD: Gọi O là tâm của tam giác ABC và H là trung điểm của BC.
Có
;;
SO BC
BC SAH SBC ABC SH AH SHA
AH BC
Kẻ
OK SH
suy ra
; SBCOK SBC d O OK
Xét
OKH
vuông tại K, có
0
33
sin60 . . . .AH
2 6 4
a
OK OH OH
Do đó
34
, 3 , 3
4
ad
d A SBC d H SBC d
a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 30: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
,SA ABCD SA AB a
và
.AD x a
. Gọi E là trung điểm cạnh SC. Tìm x, biết khoảng cách từ điểm E đến mặt phẳng (SBD) là
3
a
d
A.
1x
B.
2x
C.
3x
D.
4x
HD: Ta có
1 2a
, , , D
2 3 3
a
d E SBD d A SBC d A SB
Gọi H là hình chiếu của A lên BD. Và K là hình chiếu của A lên SH. Ta được
2a
D , D
3
AK SB AK d A SB
Mà

2
2 2 2 2 2
. D .
. D . D
D
AB A x a
AH B AB A AH
AB B a x a
Do đó
2 2 2
2 2 2 2 2 2 4
1 1 1 9 1
4a
a x a
AK SA AH a x a
2
2
2
51
42
4
x
xx
x
vì
0x
. Chọn B.
Câu 31: Cho hình chóp S.ABCD, ABCD là hình vuông cạnh
AB a
. Mặt phẳng chứa tam giác đều
SAB vuông góc với mặt phẳng đáy (ABCD). Khoảng cách từ điểm A đến mặt phẳng (SCD) là:
A.
B.
C.
7
a
D.
2
7
a
HD: Chọn A
Câu 32: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
,3SA ABCD SA a
. Tính theo
a khoảng cách từ điểm O đến mặt phẳng (SBC).
A.
2
a
B.
3
4
a
C.
5
6
a
D.
7
8
a
HD: Ta có
, 2d ,d A SBC O SBC
Gọi H là hình chiếu của A lên SB.
Ta có
SA BC
BC SAB BC AH AH SBC
AB BC
Mà
2 2 2 2 2 2
1 1 1 1 1 4 3
2
33
a
AH
AH SA AB a a a
Do đó
1 1 3
;,
2 2 4
a
d O SBC d A SBC AH
. Chọn B
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 33: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
,SA ABCD
SA AB a
và
2AD a
. Gọi F là trung điểm cạnh CD. Tính
33d
a
, biết d là khoảng cách từ điểm A đến mặt phẳng
(SBF)
A.
2 33a
B.
4 33a
C.
2 11a
D.
4 11a
HD: Gọi H là hình chiếu của A lên BF. Và K là hình chiếu của A lên SH.
Ta có
SA BF
BF SAH BF AK AK SBF
AH BF
Do đó
,d d A SBF AK
. Mà
22
17
2
a
BF BC CF
Nên
2
. 2 4
..
17 17
2
AB AD a a
AH BF AD AB AH
BF
a
Khi đó
2 2 2 2 2 2
1 1 1 1 17 33 4
16 16
33
a
AK
AK SA AH a a a
Vậy

4
33.
33
33
4 33
a
d
aa
. Chọn B
Câu 34: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với
2AD a
. Hình chiếu vuông góc
của S trên mặt đáy là điểm H
H AB
thỏa mãn
2HA HB
. Biết
.SA x a
và
SH a
. Tìm x biết
khoảng cách từ điểm C đến mặt phẳng (SHD) là
32
2
a
d
A.
5x
B.
5x
C.
3x
D.
3x
HD: Kẻ
32
D,
2
a
CK H CK d C SHD CK
Giả sử
3AB b
. Ta có

11
.DH
22
CHD ABCD
S S CK
2 2 2 2
32
2 .3 4 4 2 2 2
2
a
a b a b ab a a b
2 2 2 2 2 4 2 2
4 2 2 3a b a a b a a b a b AB a
22
2 5 5AH a SA SH AH a x
. Chọn A
Câu 35: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,
,3AB a BC a
. Hình chiếu
vuông góc của S trên mặt đáy là trung điểm của cạnh AC. Biết
2SB a
. Tính theo a khoảng cách từ
H đến mặt phẳng (SBC).
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
3
5
a
B.
23
5
a
C.
5
5
a
D.
25
5
a
HD: Kẻ
,,HE BC HF SE HF d H SBC
Ta có
22
1
2
2
AC AB BC a BH AC a
Ta có
22
SH SB BH a
Xét
SHE
ta có
2 2 2 2
1 1 1 5
HF HS HE a

5
5
a
HF
. Chọn C
Câu 36: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
,3SA ABCD SA a
. Tính theo
a khoảng cách từ điểm O đến mặt phẳng (SBC).
A.
2
a
B.
3
4
a
C.
5
6
a
D.
7
8
a
HD: Ta có
1
,,
2
d O SBC d A SBC
Kẻ
,AH SB AH d A SBC
Ta có
2 2 2 2
1 1 1 4
3AH AS AB a
33
,
24
aa
AH d O SBC
. Chọn B
Câu 37: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
,SA ABCD
SA AB a
và
2AD a
. Gọi F là trung điểm cạnh CD. Tính
33d
a
, biết d là khoảng cách từ điểm A đến mặt phẳng
(SBF)
A.
2 33a
B.
4 33a
C.
2 11a
D.
4 11a
HD: Kẻ
,,AH BF AK SH AK d A SBF
Ta có

11
.BF
22
ABF ABCD
S S AH



2
2
4 17
AB.BC AH.BF 2a.a AH. 4
2 17
aa
a AH
Ta có
2 2 2 2
1 1 1 33
16AK AH AS a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
4 4 33
4 33
33 33
a a d
AK d
a
. Chọn B
Câu 38: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với
2AD a
. Hình chiếu vuông góc
của S trên mặt đáy là điểm H
H AB
thỏa mãn
2HA HB
. Biết
.SA x a
và
SH a
. Tìm x biết
khoảng cách từ điểm C đến mặt phẳng (SHD) là
32
2
a
d
A.
5x
B.
5x
C.
3x
D.
3x
HD: Kẻ
32
D,
2
a
CK H CK d C SHD CK
Giả sử
3AB b
. Ta có

11
.DH
22
CHD ABCD
S S CK
2 2 2 2
32
2 .3 4 4 2 2 2
2
a
a b a b ab a a b
2 2 2 2 2 4 2 2
4 2 2 3a b a a b a a b a b AB a
22
2 5 5AH a SA SH AH a x
. Chọn A
Câu 39: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,
,3AB a BC a
. Hình chiếu
vuông góc của S trên mặt đáy là trung điểm của cạnh AC. Biết
2SB a
. Tính theo a khoảng cách từ
H đến mặt phẳng (SBC).
A.
3
5
a
B.
23
5
a
C.
5
5
a
D.
25
5
a
HD: Kẻ
,,HE BC HF SE HF d H SBC
Ta có
22
1
2
2
AC AB BC a BH AC a
Ta có
22
SH SB BH a
Xét
SHE
ta có
2 2 2 2
1 1 1 5
HF HS HE a

5
5
a
HF
. Chọn C
Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
,SA ABCD
SA AB a
và
2AD a
Gọi E là trung điểm cạnh SC. Tính theo a khoảng cách từ điểm E đến mặt phẳng (SBD)
A.
2
a
B.
3
a
C.
4
a
D.
5
a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
HD: ta có

11
, D , D , D
22
d E SB d C SB d A SB
Ta có
22
5
5
2
a
AC AB BC a AO
Ta có
2 2 2 2
1 1 1 9
5AH AS AO a
55
,
36
aa
AH d E SBD
. Chọn B
Câu 41: Cho hình hộp đứng ABCD.A'B'C'D' có đáy là hình
vuông, tam giác A'AC là tam giác vuông cân,
'A C a
. Khoảng cách từ A đến mặt phẳng (BCD') là:
A.
6
3
a
B.
6
2
a
C.
6
a
D.
6
4
a
HD:
; ' ; 'd A BCD d D BCD
Hình hộp đứng
. ' ' ' ' 'ABCD A B C D D D BCD
Kẻ
' ' ; 'AP CD P CD d D BCD DP
; ' ; 'd D BCD DP d A BCD DP
+) hình hộp đứng
. ' ' ' ' 'ABCD A B C D A A AC
 'ACA
vuông cân thì chỉ có thể vuông cân tại A.


''
'
2
A'A AC
22
2
2
a
D D A A
A C a
AC a
DC
+)
2 2 2 2 2
1 1 1 2 4
;'
'
66
aa
DP d A BCD
DP D D DC a a
. Chọn C
Câu 42: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông
góc với mặt phẳng đáy. Gọi M là trung điểm của SB. Tỷ số
SA
a
khi khoảng cách từ điểm M đến mặt
phẳng (SCD) bằng
5
a
là:
A.
2
B. 2 C.
3
2
D. 1
HD: +)

11
; D ; D ; D
22
d M SC d B SC d A SC
+) Kẻ
;AP SD P SD d A SCD AP
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
12
;
2
55
aa
AP d M SCD AP
+)
2 2 2 2 2 2
1 1 1 5 1 1
2
44
SA
a
AS AP AD a a a
. Chọn B
Câu 43: Cho hình chóp S.ABC có
SA A BC
và
4 , 3 , 4SA cm AB cm AC cm
và
5BC cm
.
Khoảng cách từ điểm A đến mp (SBC) bằng (đơn vị cm) :
A.
2
;
17
d A SBC
B.
72
;
17
d A SBC
C.
6 34
;
17
d A SBC
D.
3
;
17
d A SBC
HD: +) Ta có
2 2 2 2 2
3 4 2 5AB AC BC
ABC
vuông tại A.
+) Kẻ
,AK BC K BC AP SK P SK
;d A SBC AP
+)
2 2 2 2 2 2
1 1 1 1 1 1
AP AS AK AS AB AC
2 2 2
1 1 1 17 6 34
72 17
434
AP

6 34
;
17
d A SBC
. Chọn C
Câu 44: Cho khối chóp S.ABCD có đáy là hình vuông cạnh 4cm. Hình chiếu vuông góc của S xuống
mặt đáy là trung điểm H của AB. Biết rằng
2SH cm
. Khoảng cách từ A đến mặt phẳng (SBD) là:
A. 1 cm B. 2 cm C. 3 cm D. 4 cm
HD: +
; D 2d ; Dd A SB H SB
+) Kẻ
D D ,HK B K B HP SK P SK
; ; 2d H SBD HP d A SBD HP
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
+)
HBK
vuông cân tại K
2
2
BH
HK
+)
2 2 2
1 1 1 1 1
1
22
HP
HP HS HK
; D 2d A SB
. Chọn B
Câu 45: Cho hình chóp S.ABC có đáy là tam giác đều. Hình chiếu vuông góc của đỉnh S lên mặt đáy
là điểm H thuộc cạnh AC sao cho
2HC HA
. Gọi M là trung điểm của SC và N là điểm thuộc cạnh
SB sao cho
3SB SN
. Khẳng định nào sau đây là sai:
A. Khoảng cách từ M đến mặt phẳng (ABC) bằng
4
3
lần khoảng cách từ N đến mặt phẳng (ABC).
B. Khoảng cách từ M đến mặt phẳng (SAB) bằng một nửa khoảng cách từ C đến mặt phẳng (SAB)
C. Khoảng cách từ N đến mặt phẳng (SAC) bằng
1
3
khoảng cách từ B đến mặt phẳng (SAC)
D. Khoảng cách từ M đến mặt phẳng (SAB) bằng
3
2
khoảng cách từ H đến mặt phẳng (SAB)
HD:
; N;
12
;
23
;;
d M ABC d ABC
MC NB
SC SB
d S ABC d S ABC
;
1 2 3
:
2 3 4
;
d M ABC
A
d N ABC
sai
+)
;
1
2
C;
d M SAB
MS
B
CS
d SAB
đúng
+)
;
1
3
B;
d N SAC
NS
C
BS
d SAC
đúng
+)

1
;;
2
;
3
H;
d M SAB d C SAB
D
d C SAB
CA
HA
d SAB
đúng
Câu 46: Cho hình chóp S.ABCD có đáy là hình chữ nhật có
9, 12AB AD
. Hình chiếu vuông góc
của đỉnh S xuống mặt đáy trùng với trọng tâm H của tam giác ABC. Biết
6SH
, khoảng cách từ A
đến mặt phẳng (SCD) là:
A.
36
5
B.
24
5
C.
12
5
D.
4
5
HD: +)
; D ; Dd A SC d B SC
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
+) Gọi
, , ,O AC BD B H O D
thẳng hàng
;
2 1 3
3 3 2
;
d B SAC
BD
BH BO BD
HD
d H SAC
3
; ; ;
2
d A SCD d B SCD d H SAC
+) Kẻ
,HK CD K CD HP SK P SK
3
;;
2
d H SCD HP d A SCD HP
+)
2 2 2
, / / .12 8
3 3 3
HK DB
HK CD BC CD HK BC HK BC
BC DB
+)
2 2 2 2 2
1 1 1 1 1 25 24 3 24 36
;.
576 5 2 5 5
68
HP d A SCD
HP HS HK
. Chọn A.
Câu 47: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD. Tam giác SAD cân tại S và thuộc
mặt phẳng vuông góc với đáy. Gọi M là điểm thoã mãn
20SM CM
. Tỷ số khoảng cách D đến mặt
phẳng (SAB) và từ M đến mặt phẳng (SAB) là:
A.
2
3
B.
3
2
C.
1
2
D. 2
HD: +) Từ
20SM CM M
thuộc đoạn thẳng SC và
2SM MC
+)

;
S2
S3
C;
d M SAB
M
C
d SAB
22
; C; D;
33
d M SAB d SAB d SAB

D;
3
2
;
d SAB
d M SAB
. Chọn B.
Câu 48: Cho hình chóp S.ABCD có đáy là hình thoi. Tam
giác SAB cân tại S và thuộc mặt phẳng vuông góc với đáy ,
biết tam giác ABC đều cạnh 20 cm và mặt phẳng (SCD) tạo với đáy một góc 60
0
. Khoảng cách từ A
đến (SCD) là:
A. 20 cm B. 10 cm C. 15 cm D. 30 cm
HD: +)_ Kẻ
D,HK C K CD HP SK P SK


0
;;
; 60
d A SCD d H SCD HP
SCD ABCD SKH
0
3
; sin60
2
d A SCD HP HK HK
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
+)
0
1
2 2. .20.20.sin60 200 3
2
11
. . 20 20
22
ABCD ABC
abcd
SS
S HK AB CD HK
3
20 200 3 10 3 ; .10 3 15
2
HK HK d A SCD cm
. Chọn C
Câu 49: Cho hình lăng trụ ABC.A'B'C', hình chiếu vuông góc của A' xuống mặt đáy (ABC) trùng với
trung điểm H của AB. Gọi h là khoảng cách từ A đến mặt phẳng (A'BC). Gọi M là trung điểm của
A'C' và N thuộc cạnh CC' sao cho
'2NC NC
. Tính khoảng cách từ M và N đến mặt phẳng (A'BC)
A.
2
3
2
h
B.
2
6
h
C.
2
2
3
h
D.
6
h
HD: +) Dựng hình lăng trụ BCD.B'C'D; như hình vẽ
+)

1
1
; ' ; '
2
d d M A BC d C A BC

2
1
N; ' ; '
3
d d A BC d C A BC
+)
' / / ' '; ' ; 'C D A B d C A BC d D A BC
2
12
;'
2 3 6
h h h
d A A BC h d d
. Chọn B
Câu 50: Cho hình lăng trụ ABCD.A'B'C'D' có đáy là hình chữ nhật ABCD có
3; 4AB AD
. Tam
giác A'BD cân tại A' và thuộc mặt phẳng vuông góc với đáy và
'5AA
. Gọi M là trung điểm của
A'D'. Khoảng cách từ M đến mặt phẳng (A'AC) là:
A.
12
5
B.
6
5
C.
3
5
D.
4
5
HD: Gọi
D ' DH AC B A H ABC
+)
1
; ' '; '
2
d M A AC d D A AC
1
;'
2
d D A AC
+) kẻ
A
'
DP AC
DP AC P C
DP A H
' ; 'DP A AC d D A AC DP
+)
2
2 2 2 2
1 1 1 1 1 25 12 12
;'
3 144 5 5
4
DP d D A AC
DP DA DC
1 12 6
; ' .
2 5 5
d M A AC
. Chọn B
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 51: Cho hình chóp đều S.ABCD có SAC là tam giác đều. Gọi d
A
là khoảng cách từ A đến mặt
phẳng (SCD) và d
B
là khoảng cách từ B đến mặt phẳng (SAC). Tỷ lệ
A
B
d
d
bằng:
A. 2 B.
21
7
C.
3
D.
HD: +) Hình chóp đều
. D DS ABC ABC
là hình vuông
Đặt
D 0 D 2AB BC C DA x AC B x
+) Gọi
S
BH AC
H AC BC
BH H
D 2 2
22
2
b
Bx
BH SAC d BH
+)
2d H; D
A
d SC
Kẻ
D,HP SHK C K P SK
;2
A
d H SCD HP d HP
SAC
đều
3 3 6
2
2 2 2
x
SH AC x
Ta có
2 2 2 2 2 2
1 1 1 1 4 4 14 3
2 2 14
63
x
HK BC HP x
HP HS HK x x x
3 3 3 2 21
2 2 : 2
14 14 7 7
2
A
A
B
d
x
d x x
d
. Chọn D
Câu 52: Cho hình chóp S.ABC có tam giác ABC vuông tại A,
,AB AC a
I là trung điểm của SC,
hình chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm H của BC, mặt phẳng (SAB) tạo với
đáy 1 góc bằng 60
0
. Khoảng cách từ điểm I đến mặt phẳng (SAB).
A.
3
4
a
B.
39
3
a
C.
3
2
a
D.
3
4
a
HD: +)

1
, ; ;
2
d I SAB d C SAB d H SAB
Kẻ
A , SHK AB K B HP K P SK
;;d H SAB HP d I SAB HP
+)

0
; 60SAB ABC SKH
0
3
sin60
2
HP HK HK
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
+)
1
//
2
HK AB
HK BH
HK CA
CA BC
CA AB
1 3 3 3
.;
2 2 2 2 4 4
a a a a
HK CA HP d I SAB
. Chọn D
Câu 53: Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh 2a. Mặt phẳng (A'BC) tạo
với mặt đáy (ABC) một góc 60
0
. Khoảng cách từ B đến mặt phẳng (B'AC) là:
A.
3
2
a
B.
2
3
a
C.
9
4
a
D.
2
a
HD: +) Lăng trụ đứng
. ' ' ' 'ABC A B C A A ABC
Kẻ
EA BC E BC
0
' ; ' A 60A BC ABC A E
0
3
' Etan60 3 . 3 3
2
AB
A A A AE a
+)
, ' 'BK AC K AC BP B K P B K
;'d B B AC BP
+)
2 2 2 2 2 2
3 1 1 1 1 1 4
3
2
' 9 3 9
AB
BK a
BP B B BK a a a
33
;'
22
aa
BP d B B AC
. Chọn A.
Câu 54: Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác cân tại A,
0
2 , 120AB AC a CAB
.
Góc giữa (A'BC) và (ABC) là 45
0
. Khoảng cách từ B' đến mặt phẳng (ABC) là:
A.
2a
B.
22a
C. a D.
2
4
a
HD: Ta có:
', ' 'd B ABC BB AA
Gọi H là trung điểm của
BC AH BC
Do đó

'
'
AH BC
BC AA H
AA BC
Suy ra

0
' , ' 45A BC ABC A HA
Do đó tam giác A'AH vuông cân tại A
Mà
cos
AH
CAH AH a
AC
Nên ta được
' ',AH AA a d B ABC a
. Chọn C
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 55: Cho lăng trụ tứ giác đều ABCD.A'B'C'D' với cạnh đáy
23dm
. Biết rằng mặt phẳng (BDC')
hợp với đáy một góc 30
0
. Khoảng cách từ A đến mặt phẳng (BDC') là:
A.
6
2
dm
B.
3
2
dm
C.
2
3
dm
D.
6
3
dm
HD: Gọi O là tâm
D D D 'ABC OC B B OCC
Suy ra

0
D ' , D ' 30B C ABC COC
Kẻ
' , D ' , D 'CH OC d A B C d C B C CH
Do đó
0
6
sin sin30 . 6
2
CH
HOC CH
OC
Vậy
6
, D '
2
d A B C dm
Câu 56: Cho hình chóp S.ABCD có đáy là tam giác vuông tại A,
2 , 3AB a AC a
. Hình chiếu
vuông góc của S lên mặt phẳng (ABC) là trung điểm H của cạnh AB. Cạnh bên SC hợp với đáy 1 góc
60
0
. Khoảng cách từ A đến mặt phẳng (SBC) là:
A.
4 29
29
a
B.
C.
4 87
29
a
D.
4
29
a
HD: Kẻ
,,HO BC HK SO d H SBC HK
Ta có
OBH
đồng dạng vsơi
ABC
. 21
7
AC BH a
OH
BC
Mà
0
, 60 tan .SC ABC SCH SH SCH CH
22
2 2 3CH HA AC a SH a
Có
2 2 2 2
1 1 1 29 2 87
29
12
HK a
HK HO SH a
Mà

4 87
, 2 ,
29
a
d A SBC d H SBC
. Chọn C
Câu 57: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,

0
, 60BC a ACB
,
SA A BC
và M là điểm nằm trên cạnh AC sao cho
2MC MA
. Biết (SBC) tạo với đáy góc 30
0
.
Khoảng cách từ M đến mặt phẳng (SBC) là:
A.
3
2
a
B.
3
3
a
C.
3
6
a
D.
2
9
a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
HD: Kẻ
S,AH B d A SBC AH
Ta có
22
,,
33
MC
d M SBC d A SBC
AC
Ta có
BC SAB
và


SAB ABC AB
SAB SBC SB
Nên góc giữa (SBC) và (ABC) là
0
30SBA
Do đó
.tanSA AB SBA a
vì
.tanAB BC ACB
Nên
2 2 2
1 1 1 3
2
a
AH
AH SA AB

3
;
3
a
d M SBC
. Chọn B
Câu 58: Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng 2a, cạnh bên bằng 3a. Gọi O là tâm đáy,
M, N là trung điểm của AB, BC. Khoảng cách từ O đến mặt phẳng (SMN) là:
A.
279
69
a
B.
279
23
a
C.
23
279
a
D.
23
279
a
HD: Kẻ
,SOH MN OK H
với
,K SHH MN
Suy ra
d,O SMN OK
Ta có
OMN
cân tại O có

0
3
6
tan60
MH a
OH
SMA
vuông tại M
22
22SM SA MA a
SMO
vuông tại O
22
69
3
a
SO SM MO
Do đó
2 2 2 2
1 1 1 279 23
279
23
OK a
OK OH OS a
. Chọn D
Câu 59: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a,
,3SA ABCD SA a
. Gọi G là trọng tâm
SAC
. Từ G kẻ đường thẳng song song với SB cắt OB
tại I. Khoảng cách từ I đến mặt phẳng (SBC) là:
A.
2
2
a
B.
2
6
a
C.
3
6
a
D.
6
3
a
HD: Ta có GI song song SB nên

1
3
OG OI
OS OB
Mà O là trung điểm AC nên I là trọng tâm
ABC
Do đó
1
,,
3
d I SBC d A SBC
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Kẻ
,AH SB H SB d A SBC AH
Xét
vuông tại A, có:
2 2 2
1 1 1 3
2
a
AH
AH SA AB
Suy ra
3
,
6
a
d I SBC
. Chọn C.
Câu 60: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều
cạnh a và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của AB, E là trung điểm của
BC. Khoảng cách từ I đến mặt phẳng (SED) là:
A.
2
2
a
B.
2
6
a
C.
2
4
a
D.
32
8
a
HD: Kẻ
,,IH DE IK SH d I SED IK
Tam giác SAB đều cạnh a nên
3
2
a
SI
.
Ta có
2
3
2
8
IDE ABCD AID IBE
a
S S S S
Mà
1 3 5
.
2 10
IDE
a
S IH DE IH
Do đó
2
2 2 2
1 1 1 32 3 2
98
aa
IK
IK IH SI
. Chọn D
VẤN ĐỀ 2: KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG
Câu 1: Cho khối chóp
.S ABCD
có đáy là hình vuông cạnh 4
.cm
Biết
3SA
,cm
khoảng cách giữa
2 đường thẳng
SA
và
BC
là:
A.
1
5
cm B. 1 cm C.
2
5
cm D.
4
5
cm
Câu 2: Cho khối chóp đều S.ABC có đáy là tam giác đều cạnh 3 cm. Biết SA tạo với đáy một góc
0
60
.
Khoảng cách giữa 2 đường thẳng SA và BC là:
A. 3 cm B.
9
4
cm C. 2 cm D.
3
2
cm
Câu 3: Cho khối chóp S.ABCD có
()SA ABCD
có đáy ABCD là hình chữ nhật có
3; 4.AB AD
Biết
13.SC
Khoảng cách giữa 2 đường thẳng SB và AD là:
A.
4
17
B.
12
17
C.
2
17
D.
3
17
Câu 4: Cho khối chóp
.S ABCD
có đáy là hình vuông cạnh 2a. Biết hình chiếu vuông góc của S lên
mặt đáy trùng với trung điểm của AB và
0
; 60SCD ABCD
Khoảng cách giữa 2 đường thẳng SD
và BC là:
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
4 39
13
a
B.
43
13
a
C.
23
13
a
D.
43
39
a
Câu 5: Cho hình chóp
.S ABC
có đáy ABC là tam giác vuông tại A ,
3AB a

AC a
tam giác
SBC là tam giác vuông cân tại đỉnh S và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC). Tính
khoảng cách giữa 2 đường thẳng SB và AC.
A.
3
7
a
B.
3
7
a
C.
D.
2 21
7
a
Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình vuông,
23
SB SC
a
.
Cạnh
()SA ABCD
khoảng cách từ điểm A đến mặt phẳng (SCD) bằng:
A.
6
a
B.
3
a
C.
3
a
D.
2
a
Câu 7: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S trên
mặt phẳng (ABC) là trung điểm H của AB. Diện tích tam giác SAB bằng
2
2
a
. Khoảng cách từ điểm B
đến mặt phẳng (SAC) bằng:
A.
6
35
a
B.
3
35
a
C.
26
35
a
D.
23
35
a
Câu 8: Cho hình chóp S.ABC có đáy là ABC là tam giác đều cạnh a. Tam giác SAB cân tại S và nằm
trong mặt phẳng vuông góc với mặt phẳng (ABC). Góc giữa đường thẳng SC và mặt phẳng (ABC)
bằng
0
45
. Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng
A.
B.
C.
D.
Câu 9: Cho tứ điện đều ABCD cạnh
3a
. Độ dài khoảng cách giữa hai đường thẳng AB và CD là ?
A.
6
4
a
B.
6
2
a
C.
3
2
a
D.
6
3
a
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2a và (SAD) nằm trong mặt
phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng AD và SB? Biết SAD là tam
giác đều.
A.
2 21
7
a
B.
2 14
7
a
C.
D.
Câu 11: Cho hình hộp đứng ABCD.A’B’C’D có đáy là hình thoi cạnh
3a
,
0
60BAD
, góc của
đường chéo A’C và mặt phẳng đáy bằng
0
60
. Khoảng cách giữa hai đường A’C và BB’ là?
A.
2
a
B.
3
2
a
C.
2
2
a
D.
.a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc đáy, góc giữa
đường thẳng SC và mặt phẳng (ABCD) bằng
0
45
. Khoảng cách giữa hai đường thẳng SB, AC là:
A.
5
a
B.
C.
5
a
D.
.a
Câu 13: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B. Biết
, , 3 , 2.AB a BC a AD a SA a
Khi
( ),SA ABCD
khoảng cách giữa hai đường thẳng SA, CD là:
A.
5
a
B.
5
a
C.
2
5
a
D.
3
5
a
Câu 14: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B. Biết
, , 3 , 2.AB a BC a AD a SA a
Khi
( ),SA ABCD
khoảng cách giữa hai đường thẳng SC và AD
là:
A.
3
a
B.
6
2
a
C.
6
3
a
D.
2
3
a
Câu 15: Cho hình chóp S.ABCD có đáy ABCD là hình vuông và
.
23
SB SC
a
Cạnh
( ),SA ABCD
khoảng cách từ điểm A đến mặt phẳng (SCD) bằng:
A.
6
a
B.
3
a
C.
3
a
D.
2
a
Câu 16: Cho tứ điện đều ABCD cạnh
3a
. Độ dài khoảng cách giữa hai đường thẳng AB và CD là?
A.
6
4
a
B.
6
2
a
C.
3
2
a
D.
6
.
3
a
Câu 17: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2a và (SAD) nằm trong mặt
phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng AD và SB? Biết SAD là tam
giác đều.
A.
2 21
7
a
B.
2 14
7
a
C.
D.
14
.
3
a
Câu 18: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B có
, , 6, 2.AB a BC a CD a SA a
Khi
()SA ABCD
thì khoảng cách giữa AD và SC là?
A.
5
3
a
B.
5
2
a
C.
6
3
a
D.
6
.
2
a
Câu 19: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B,
2,SA AC a
SA vuông
góc với mặt phẳng đáy. Khoảng cách giữa 2 đường thẳng SA và BC là:
A.
2a
B.
22a
C.
2
2
a
D.
2
4
a
Câu 20: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B,
2,SA AC a
SA vuông
góc với mặt phẳng đáy. Khoảng cách giữa 2 đường thẳng SC và AB là:
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
3a
B.
3
2
a
C.
3
a
D.
2
3
a
Câu 21: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B có
,AB a
BC a,CD a 6, 2SA a
. Khi
SA ABCD
thì khoảng cách từ giữa AD và SC là ?
A.
5
3
a
B.
5
2
a
C.
6
3
a
D.
6
2
a
Câu 22: Cho hình chóp S.ABC có đáy tam giác đều ABC cạnh là a, cạnh bên
,SA a
SA A BC
, I
là trung điểm của BC. Khoảng cách giữa hai đường thẳng SI và AB là?
A.
B.
57
19
a
C.
23
7
a
D.
Câu 23: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, SA vuông góc với mặt
phẳng đáy, góc tạo bởi SC với (SAB) là 30
0
. Gọi E, F lần lượt là trung điểm của BC và SD. Khoảng
cách giữa hai đường thẳng chéo nhau DE và CF là ?
A.
B.
3 17
11
a
C.
D.
3 31
31
a
Câu 24: Hình chóp S.ABC có đáy ABC là tam giác vuông tại C. Có
,CA a CB b
, cạnh
SA h
vuông góc với đáy. Gọi D là trung điểm cạnh AB. Khoảng cách giữa hai đường thẳng AC và SD là ?
A.
22
ah
ah
B.
22
4
bh
bh
C.
22
4
ah
bh
D.
22
2
ah
bh
Câu 25: Cho khối lăng trụ ABC.A'B'C' có đáy là tam giác ABC cân tại A có
2;AB AC a
23BC a
. Tam giác A'BC vuông cân tại A' và nằm trong mặt phẳng vuông góc với đáy (ABC).
Khoảng cách giữa 2 đường thẳng AA' và BC là:
A.
3a
B.
2
2
a
C.
5
2
a
D.
3
2
a
Câu 26: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A và SA vuông góc với mặt phẳng
(ABC),
2AB AC SA a
. Gọi I là trung điểm của BC. Tính theo a khoảng cách giữa hai đường
thẳng SI, AC
A.
2 10
5
a
B.
25
5
a
C.
D.
5
5
a
Câu 27: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAD)
cùng vuông góc với đáy. Góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng 60
0
. Tính theo a
khoảng cách giữa 2 đường thẳng SB, AD.
A.
3a
B.
3
2
a
C.
3
3
a
D.
3
5
a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 28: Cho hình chóp S.ABCD có đáy là hình bình hành ABCD tâm O tam giác ABC vuông cân tại
A có
,AB AC a SA ABCD
. Đường thẳng SD tạo với đáy một góc 45
0
. Khoảng cách giữa 2
đường thẳng AD và SB là:
A.
3
2
a
B.
5
5
a
C.
D.
Câu 29: Cho khối chóp S.ABCD có đáy là hình vuông cạnh a,
SA ABCD
. Gọi M là trung điểm
cạnh BC và
3
2
a
SM
. Khoảng cách giữa 2 đường thẳng SM và AD là :
A.
3
2
a
B. a C.
2
a
D.
2a
Câu 30: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có
3,AB a
2,AD a
SA ABCD
. Gọi M là trung điểm của AD. Khoảng cách giữa 2 đường thẳng CM và SA là
A.
6
13
a
B.
3
10
a
C.
2
5
a
D.
6
10
a
Câu 31: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B. Cạnh bên
, 4 , 2 , 3SA ABCD AD a AB BC a SA a
. Khoảng cách giữa hai đường thẳng SB và CD
bằng:
A.
56a
B.
30
5
a
C.
5
6
a
D.
6
5
a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Đáp án
1-D
2-B
3-B
4-A
5-D
6-D
7-C
8-B
9-B
10-A
11-B
12-B
13-D
14-C
15-D
16-B
17-A
18-C
19-A
20-D
21-C
22-B
23-C
24-B
25-D
26-B
27-B
28-D
29-C
30-B
31-B
Hướng dẫn giải
Câu 1: Cho khối chóp
.S ABCD
có đáy là hình vuông cạnh 4
.cm
Biết
3SA
,cm
khoảng cách giữa
2 đường thẳng
SA
và
BC
là:
A.
1
5
cm B. 1 cm C.
2
5
cm D.
4
5
cm
HD: Ta có
22OA
(O là tâm hình vuông).
22
1SO SA OA cm
4
; ; 2 ;
5
d SA BC d BC SAD d O SAD
. Chọn D
Câu 2: Cho khối chóp đều S.ABC có đáy là tam giác đều cạnh 3 cm. Biết SA tạo với đáy một góc
0
60
.
Khoảng cách giữa 2 đường thẳng SA và BC là:
A. 3 cm B.
9
4
cm C. 2 cm D.
3
2
cm
HD: Gọi O là trọng tâm tam giác ABC. Ta có:

2 3 3
.3
32
OA
. Kẻ
//Ax BC
suy ra
//Ax SOA
.
0
3 3 9
; ; ; . sin60
2 2 4
d SA BC d BC SAx d O SAx OA
. Chọn B
Câu 3: Cho khối chóp S.ABCD có
()SA ABCD
có đáy ABCD là hình chữ nhật có
3; 4.AB AD
Biết
13.SC
Khoảng cách giữa 2 đường thẳng SB và AD là:
A.
4
17
B.
12
17
C.
2
17
D.
3
17
HD: Ta có:
22
5 12AC SA SC AC
12
; D D; ;
17
d SB A d A SBC d A SBC
. Chọn B
Câu 4: Cho khối chóp
.S ABCD
có đáy là hình vuông cạnh 2a. Biết hình chiếu vuông góc của S lên
mặt đáy trùng với trung điểm của AB và
0
; 60SCD ABCD
Khoảng cách giữa 2 đường thẳng SD
và BC là:
A.
4 39
13
a
B.
43
13
a
C.
23
13
a
D.
43
39
a
HD: Dựng
00
60 , tan60 2 3HK CD SKH SH HK a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com

4 39
;BC ; 2 ;
13
a
d SD d BC SAD d H SAD
. Chọn A
Câu 5: Cho hình chóp
.S ABC
có đáy ABC là tam giác vuông tại A ,
3AB a

AC a
tam giác
SBC là tam giác vuông cân tại đỉnh S và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC). Tính
khoảng cách giữa 2 đường thẳng SB và AC.
A.
3
7
a
B.
3
7
a
C.
D.
2 21
7
a
HD: H là trung điểm BC. Ta có:
22
1
2a
2
BC AB AC SH BC a
Dựng
2a 21
x / / ; ; x ; x 2d ; x
7
B AC d AC SB d AC SB d C SB H SB
. Chọn D
Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình vuông,
23
SB SC
a
.
Cạnh
()SA ABCD
khoảng cách từ điểm A đến mặt phẳng (SCD) bằng:
A.
6
a
B.
3
a
C.
3
a
D.
2
a
HD: Kẻ
SD , DAH AH d A SC
Ta có
BC AB
BC SAB BC SB
BC SA
22
BC SC SB a
. Mà
22
SA SB AB a
Ta có
2 2 2 2
1 1 1 2
,
2
a
AH d A SCD
AH AS AD a
. Chọn D
Câu 7: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S trên
mặt phẳng (ABC) là trung điểm H của AB. Diện tích tam giác SAB bằng
2
2
a
. Khoảng cách từ điểm B
đến mặt phẳng (SAC) bằng:
A.
6
35
a
B.
3
35
a
C.
26
35
a
D.
23
35
a
HD: Ta có
, 2d ,d B SAC H SAC
Kẻ
, , 2HK SN HK d H SAC d B SAC HK
Ta có

2
2
SAB
S
SH a
AB
Và

13
24
a
HN BM
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Ta có
2 2 2 2
1 1 1 35 6
6
35
a
HK
HK HN HS a
26
,2
35
a
d B SAC HK
. Chọn C
Câu 8: Cho hình chóp S.ABC có đáy là ABC là tam giác đều cạnh a. Tam giác SAB cân tại S và nằm
trong mặt phẳng vuông góc với mặt phẳng (ABC). Góc giữa đường thẳng SC và mặt phẳng (ABC)
bằng
0
45
. Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng
A.
B.
C.
D.
HD: Ta có
, 2d ,d A SBC H SBC
Kẻ
, , 2HK SN HK d H SBC d A SBC HK
Ta có

0
3
.tan45
2
a
SH CH
Và

13
24
a
HN AM
Ta có
2 2 2 2
1 1 1 20 15
10
3
a
HK
HK HS HN a
2 15
,2
5
a
d A SBC HK
. Chọn B
Câu 9: Cho tứ điện đều ABCD cạnh
3a
. Độ dài khoảng cách giữa hai đường thẳng AB và CD là ?
A.
6
4
a
B.
6
2
a
C.
3
2
a
D.
6
3
a
HD: Ta có

AB CM
AB CDM
AB SH
Kẻ
MN CD AB MN
do
AB CDM
=> MN là khoảng cách giữa hai đường thẳng AB và CD
Ta có

3. 3 3
22
aa
CM
Và

13
22
a
CN CD
22
66
,
22
aa
MN CM NC d AB CD
. Chọn B
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2a và (SAD) nằm trong mặt
phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng AD và SB? Biết SAD là tam
giác đều.
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
2 21
7
a
B.
2 14
7
a
C.
D.
HD: Do
D/ /A BC
, , ,d AD SB d AD SBC d H SBC
Kẻ
,,HE SK HE d H SBC d AD SB
Ta có

23
3
2
a
SH a
Ta có
2 2 2 2
1 1 1 7 2 21
7
12
a
HE
HE HS HK a

2 21
,
7
a
d AD SB
. Chọn A
Câu 11: Cho hình hộp đứng ABCD.A’B’C’D có đáy là hình thoi cạnh
3a
,
0
60BAD
, góc của
đường chéo A’C và mặt phẳng đáy bằng
0
60
. Khoảng cách giữa hai đường A’C và BB’ là?
A.
2
a
B.
3
2
a
C.
2
2
a
D.
.a
HD: Có
' ' 'A C AA C C
mà BB' song song (AA'C'C)
Nên
'C, ' ', ' 'C)d A BB d BB AA C
Gọi O là tâm hình thoi ABCD
Ta có

''
'
BO AC
BO AA C C
BO AA
Suy ra
3
, ' '
22
BD a
d O AA C C BO
Do đó

3
' , ' , ' '
2
a
d A C BB d O AA C C
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc đáy, góc giữa
đường thẳng SC và mặt phẳng (ABCD) bằng
0
45
. Khoảng cách giữa hai đường thẳng SB, AC là:
A.
5
a
B.
C.
5
a
D.
.a
HD: Ta có

0
, D 45SC ABC SCA
Kẻ đường thẳng d qua B và song song với AC.
Kẻ
dAH
với
. Kẻ
SAK H
Lại có
SA BH
BH SAH BH AK
AH BH
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Do đó
,AK SHB d SB AC AK
Tam giác SAH vuông tại A, có
SAK H
Nên
2 2 2 2
1 1 1 5 10
5
2a
a
AK
AK SH AH
Vậy
10
,AC
5
a
d SB
. Chọn B
Câu 13: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B. Biết
, , 3 , 2.AB a BC a AD a SA a
Khi
( ),SA ABCD
khoảng cách giữa hai đường thẳng SA, CD là:
A.
5
a
B.
5
a
C.
2
5
a
D.
3
5
a
HD: kẻ
DAH C
mà
,DSA AH AH d SA C
Ta có

D
11
. D . D
22
AC
S AB A AH C
. D .3a 3a
D
55
AB A a
AH
C
a

3a
,D
5
d SA C
. Chọn D
Câu 14: Cho hình chóp S.ABCD có đáy ABCD là hình
thang vuông tại A, B. Biết
, , 3 , 2.AB a BC a AD a SA a
Khi
( ),SA ABCD
khoảng cách giữa
hai đường thẳng SC và AD là:
A.
3
a
B.
6
2
a
C.
6
3
a
D.
2
3
a
HD: Kẻ
S,AH B H SB
. Ta có
||SC SBC AD
, ; ,d AD SC d AD SBC d A SBC
Ta có
BC AB
BC SAB BC AH
BC SA
Mà
AH SB
nên
AH SBC
Do đó
2 2 2 2
1 1 1 3 6
3
2
a
AH
AH SA AB a
. Chọn C
Câu 15: Cho hình chóp S.ABCD có đáy ABCD là hình vuông và
.
23
SB SC
a
Cạnh
( ),SA ABCD
khoảng cách từ điểm A đến mặt phẳng (SCD) bằng:
A.
6
a
B.
3
a
C.
3
a
D.
2
a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
HD: Kẻ
,AH SD AH d A SCD
Ta có
BC AB
BC SAB BC SB
BC SA
22
BC SC SB a
. Mà
22
SA SB AB a
Ta có
2 2 2 2
1 1 1 2
AH AS AD a
,
2
a
AH d A SCD
. Chọn D
Câu 16: Cho tứ điện đều ABCD cạnh
3a
. Độ dài khoảng cách giữa hai đường thẳng AB và CD là?
A.
6
4
a
B.
6
2
a
C.
3
2
a
D.
6
.
3
a
HD: Ta có

SH
AB CM
AB CDM
AB
Kẻ
MN CD AB MN
do
AB CDM
=> MN là khoảng cách giữa hai đường thẳng AB và CD
Ta có

3. 3 3
22
aa
CM
và

13
22
a
CN CD
22
66
,
22
aa
MN CM CN d AB CD
. Chọn B
Câu 17: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2a và (SAD) nằm trong mặt
phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng AD và SB? Biết SAD là tam
giác đều.
A.
2 21
7
a
B.
2 14
7
a
C.
D.
14
.
3
a
HD: Do
D/ /A BC
D,SB D, ,d A d A SBC d H SBC
Kẻ
S , ,HE K HE d H SBC d AD SB
Ta có

23
3
2
a
SH a
Ta có
2 2 2 2
1 1 1 7 2 21
7
12
a
HE
HE HS HK a

2 21
,
7
a
d AD SB
. Chọn A
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 18: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B có
, , 6, 2.AB a BC a CD a SA a
Khi
()SA ABCD
thì khoảng cách giữa AD và SC là?
A.
5
3
a
B.
5
2
a
C.
6
3
a
D.
6
.
2
a
HD: Do
//AD BC
, ; ,d AD SC d AD SBC d A SBC
Kẻ
AH SB
Ta có
BC AB
BC SAB BC AH
BC SA
,AH SB AH SBC AH d A SBC
ta có
2 2 2 2
1 1 1 3 6
3
2
a
AH
AH SA AB a

6
D,SC
3
a
dA
. Chọn C
Câu 12: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B,
2,SA AC a
SA vuông
góc với mặt phẳng đáy. Khoảng cách giữa 2 đường thẳng SA và BC là:
A.
2a
B.
22a
C.
2
2
a
D.
2
4
a
HD: Ta có
SA AB
AB
BC AB
là đoạn vuông góc chung
Do đó
,d SA BC AB
Tam giác ABC vuông cân tại B
Nên
2
2 , 2
22
AC a
AB a d SA BC a
Chọn A.
Câu 13: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân
tại B,
2,SA AC a
SA vuông góc với mặt phẳng đáy. Khoảng
cách giữa 2 đường thẳng SC và AB là:
A.
3a
B.
3
2
a
C.
3
a
D.
2
3
a
HD: Từ C kẻ
||Cx AB
. Kẻ
,AH Cx H Cx
Kẻ
,SCAK SH AK SHC d AB AK
Ta có
2 2 2 2 2 2
1 1 1 1 1 3
4 2 4AK SA AH a a a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Do đó
22
,
33
aa
AK d AB SC
. Chọn D
Câu 21: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B có
,AB a
BC a,CD a 6, 2SA a
. Khi
SA ABCD
thì khoảng cách từ giữa AD và SC là ?
A.
5
3
a
B.
5
2
a
C.
6
3
a
D.
6
2
a
HD: Do
//AD BC
, ; ,d AD SC d AD SBC d A SBC
Kẻ
AH SB
Ta có
BC AB
BC SAB BC AH
BC SA
Mà
,AH SB AH SBC AH d A SBC
ta có
2 2 2 2
1 1 1 3 6
3
2
a
AH
AH SA AB a

6
D,SC
3
a
dA
. Chọn C
Câu 22: Cho hình chóp S.ABC có đáy tam giác đều ABC cạnh là a, cạnh bên
,SA a
SA ABC
, I
là trung điểm của BC. Khoảng cách giữa hai đường thẳng SI và AB là?
A.
B.
57
19
a
C.
23
7
a
D.
HD: Kẻ
//IJ AB
, , ,d SI AB d AB SIJ d A SIJ
Kẻ
,AH SD AH d A SIJ
Ta có

13
24
a
AD MC
Ta có
2 2 2 2
1 1 1 19 57
19
3
a
AH
AH AS AD a

57
,
19
a
d SI AB
. Chọn B
Câu 23: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, SA vuông góc với mặt
phẳng đáy, góc tạo bởi SC với (SAB) là 30
0
. Gọi E, F lần lượt là trung điểm của BC và SD. Khoảng
cách giữa hai đường thẳng chéo nhau DE và CF là ?
A.
B.
3 17
11
a
C.
D.
3 31
31
a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
HD: Ta có
,,d DE CF d DE FCK

1
,,
2
d D FCK d H FCK
Kẻ
,HI CK HJ FI
1
,,
2
HJ d H FCK d DE CF HJ
Ta có
25
5
a
HI
Ta có
0
, 30 3SC SAB BSC SB a
22
2
2
2
a
SA SB AB a HF
Ta có
2 2 2 2
1 1 1 13 2 13 13
,
13 13
4
aa
HJ d DE CF
HJ HI HF a
. Chọn C
Câu 24: Hình chóp S.ABC có đáy ABC là tam giác vuông tại C. Có
,CA a CB b
, cạnh
SA h
vuông góc với đáy. Gọi D là trung điểm cạnh AB. Khoảng cách giữa hai đường thẳng AC và SD là ?
A.
22
ah
ah
B.
22
4
bh
bh
C.
22
4
ah
bh
D.
22
2
ah
bh
HD: Dựng hình bình hành
; ; ;ACKD d AC SD d AC SDK d A SDK d
+) Kẻ
2 2 2
1 1 1
AP DK
d SA AP
+) Gọi
M BC DK ACMP
là hình chữ nhật
2
b
AP CM
2 2 2
22
1 1 4
4
bh
d
d h b
bh
=> Chọn B
Câu 25: Cho khối lăng trụ ABC.A'B'C' có đáy là tam giác ABC cân tại A có
2;AB AC a
23BC a
. Tam giác A'BC vuông cân tại A' và nằm trong mặt phẳng vuông góc với đáy (ABC).
Khoảng cách giữa 2 đường thẳng AA' và BC là:
A.
3a
B.
2
2
a
C.
5
2
a
D.
3
2
a
HD: +) Gọi H là trung điểm của cạnh BC
' ' 'A H ABC A H HC HC HA
+)
ABC
cân tại A
'
HC HA
AH HC
HC HA
''HC A AH BC A AH
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
+) Kẻ
''HP A A P A A BC HP
=> HP là đường vuông góc chung của A'A và BC
' ;BCd A A HP
+)
'A BC
vuông cân tại
' ' 3
2
BC
A A H a
+) Cạnh
2 2 2 2
43HA AB BH a a a
2 2 2 2 2 2
1 1 1 1 1 4 3 3
';
22
' 3 3
aa
HP d A A BC
HP A H AH a a a
Câu 26: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A và SA vuông góc với mặt phẳng
(ABC),
2AB AC SA a
. Gọi I là trung điểm của BC. Tính theo a khoảng cách giữa hai đường
thẳng SI, AC
A.
2 10
5
a
B.
25
5
a
C.
D.
5
5
a
HD: +) Gọi E là trung điểm của cạnh
/ / IE AC/ /AB AC SEI
; ; ;d AC SI d AC SEI d A SEI
+)

//AC IE
IE AE
AC AE
, kẻ
;;AP SE P SE d A SEI AP d AC SI AP
Ta có
2 2 2 2 2 2
1 1 1 1 1 5 2 5 2 5
;
55
44
aa
AP d AC SI
AP SA AE a a a
Câu 27: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAD)
cùng vuông góc với đáy. Góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng 60
0
. Tính theo a
khoảng cách giữa 2 đường thẳng SB, AD.
A.
3a
B.
3
2
a
C.
3
3
a
D.
3
5
a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
HD: +)

SAB SAD SA
SAB ABCD SA ABCD
SAD ABCD
0
; 60SB ABCD SBA
+)
/ / / /AD BC AD SBC
; ; ;d AD SB d AD SBC d A SBC
+) Ta có
AB BC
, kẻ
AP SB P SB
; ;SBd A SBC AP d AD AP
+)
0
3 3 3 3
sin sin60 ;
2 2 2 2
AP a a
ABP AP AB d AD SB
AB
. Chọn B
Câu 28: Cho hình chóp S.ABCD có đáy là hình bình hành ABCD tâm O tam giác ABC vuông cân tại
A có
,AB AC a SA ABCD
. Đường thẳng SD tạo với đáy một góc 45
0
. Khoảng cách giữa 2
đường thẳng AD và SB là:
A.
3
2
a
B.
5
5
a
C.
D.
HD: Lấy M là trung điểm BC, H là hình chiếu của A lên SM. Xác định
0
, 45AD ABCD SDA
SA BC AM BC SAM BC AH
,AH SM AH SBC d A SBC AH
Vì
//AD SBC
chứa BC nên
, , ,d SB AD d AD ABC d A SBC AH
Tính:
2,
2
a
SA AD a AM
2 2 2
1 1 1 2
5
AH a
AH AS AM
. Chọn D
Câu 29: Cho khối chóp S.ABCD có đáy là hình vuông cạnh a,
SA ABCD
. Gọi M là trung điểm
cạnh BC và
3
2
a
SM
. Khoảng cách giữa 2 đường thẳng SM và AD là :
A.
3
2
a
B. a C.
2
a
D.
2a
HD: Lấy H là hình chiếu của A lên SB.
AB BC SA BC SAB BC AH
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
,AH SB AH SBC d A SBC AH
Ta có: Vì
//AD SBC
chứa SM
, , ,d AD SM d AD SAB d A SAB AH
Tính:
2 2 2 2
5
2
a
AM BA BM SA SM AM a
2 2 2
1 1 1
2
a
AH
AH AS AB
. Chọn C
Câu 30: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có
3,AB a
2,AD a
SA ABCD
. Gọi M là trung điểm của AD. Khoảng cách giữa 2 đường thẳng CM và SA là
A.
6
13
a
B.
3
10
a
C.
2
5
a
D.
6
10
a
HD: Lấy H là hình chiếu của A lên MC
,MC AH SA d SA CM AH
Tính
22
10CM DM DC a
.MC AM.AC.sin . .
CD
AH MAC AM AC
AC

3
10
a
AH
. Chọn B
Câu 31: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B. Cạnh bên
, 4 , 2 , 3SA ABCD AD a AB BC a SA a
. Khoảng cách giữa hai đường thẳng SB và CD
bằng:
A.
56a
B.
30
5
a
C.
5
6
a
D.
6
5
a
HD: Kẻ
/ / / /BM CD CD SBM SB
, , ,d CD SB d CD SBM d A SBM
Kẻ
,,AE BM AK SE E BM K SE
,AK SBM AK d A SBM
Ta có
2
2
AC
AE a
Ta có
2 2 2
1 1 1 30
5
a
AK
AK SA AE
. Chọn B
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
CHỦ ĐỀ 3: MẶT TRỤ – HÌNH TRỤ – KHỐI TRỤ
Câu 1. Cho hình trụ (T) có chiều cao h, độ dài đường sinh
l
, bán kính đáy r. Ký hiệu
xq
S
là diện tích
xung quanh của (T). Công thức nào sau đây là đúng?
A.
xq
S rh
B.
2
xq
S rl
C.
2
2
xq
S r h
D.
xq
S rl
Câu 2. Cho hình trụ (T) có chiều cao h, độ dài đường sinh
l
, bán kính đáy r. Ký hiệu
tp
S
là diện tích
toàn phần của (T). Công thức nào sau đây là đúng?
A.
tp
S rl
B.
2
tp
S rl r


C.
2
tp
S rl r


D.
2
22
tp
S rl r


Câu 3. Cho hình trụ (T) có chiều cao h, độ dài đường sinh
l
, bán kính đáy r. Ký hiệu
T
V
là thể tích
khối trụ (T). Công thức nào sau đây là đúng?
A.
1
3
T
V rh
B.
2
T
V r h
C.
2
N
V rl
D.
2
2
N
V r h
Câu 4. Một hình trụ có bán kính đáy
5r cm
, chiều cao
7h cm
. Diện tích xung quanh của hình trụ
này là:
A.
2
35 cm
B.
2
70 cm
C.
2
70
3
cm
D.
2
35
3
cm
Câu 5. Một hình trụ có bán kính đáy
ra
, đồ dài đường sinh
2la
. Diện tích toàn phần của hình
trụ này là:
A.
2
6 a
B.
2
2 a
C.
2
4 a
D.
2
5 a
Câu 6. Quay hình vuông ABCD cạnh
a
xung quanh một cạnh. Thể tích của khối trụ được tạo thành
là:
A.
3
1
3
a
B.
3
2 a
C.
3
a
D.
3
3 a
Câu 7. Cho hình vuông ABCD cạnh 8cm. Gọi M, N lần lượt là trung điểm của
AB
và
CD
. Quay
hình vuông ABCD xung quanh MN. Diện tích xung quanh của hình trụ tạo thành là:
A.
2
64 cm
B.
2
32 cm
C.
2
96 cm
D.
2
126 cm
Câu 8. Một hình trụ (T) có diện tích toàn phần là
2
120 cm
và có bán kính đáy bằng 6cm. Chiều cao
của (T) là:
A. 6cm B. 5cm C. 4cm D. 3cm
Câu 9. Một khối trụ (T) có thể tích bằng
3
81 cm
và có dường sinh gấp ba lấn bán kính đáy. Độ dài
đường sinh của (T) là:
A. 12cm B. 3cm C. 6cm D. 9cm
Câu 10. Cho hình chữ nhật ABCD có
AB a
và góc
0
30BDC
. Quay hình chữ nhật này xung
quanh cạnh AD. Diện tích xung quanh của hình trụ được tạo thành là:
A.
2
3 a
B.
2
23a
C.
2
2
3
a
D.
2
a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 11. Cho hình lập phương
. ' ' ' 'ABCD A B C D
có cạnh bằng
a
. Gọi (C) và (C’) lần lượt là hai
đường tròn ngoại tiếp hình vuông ABCD và
' ' ' 'A B C D
. Hình trụ có hai đáy là (C) và (C’) có thể
tích là:
A.
3
1
3
a
B.
3
2 a
C.
3
a
D.
3
2
a
Câu 12. Cắt hình trụ (T) bằng một mặt phẳng đi qua trục được thiết diện là một hình chữ nhật có diện
tích bằng
2
30cm
và chu vi bằng
26cm
. Biết chiều dài của hình chữ nhật lớn hơn đường kính mặt đáy
của hình trụ (T). Diện tích toàn phần của (T) là:
A.
2
69
2
cm
B.
2
69 cm
C.
2
23 cm
D.
2
23
2
cm
Câu 13. Cắt hình trụ (T) bằng một mặt phẳng song song với trục và cách trục một khoảng bằng 2cm
được thiết diện là một hình vuông có diện tích bằng
2
16cm
. Thể tích của (T) là:
A.
3
32 cm
B.
3
16 cm
C.
3
64 cm
D.
3
8 cm
Câu 14. Một hình trụ có tỉ số giữa diện tích toàn phần và diện tích xung quanh bằng 4. Khẳng định
nào sau đây là đúng :
A. Đường sinh bằng bán kính đáy. B. Bán kính đáy bằng ba lần đường sinh
C. Đường sinh bằng ba lần bán kính đáy D. Đường sinh bằng bốn lần bán kính đáy
Câu 15. Trong không gian, cho hình chữ nhật ABCD có
1AB
và
2AD
. Gọi M,N lần lượt là trung
điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích
toàn phần
tp
S
của hình trụ đó.
A.
4
tp
S
B.
2
tp
S
C.
6
tp
S
D.
10
tp
S
Câu 16. Khi quay hình chữ nhật ABCD quanh đường thẳng AB thì hình chữ nhật ABCD tạo thành
hình tròn xoay là:
A. Hình trụ B. Khối trụ C. Mặt trụ D. Hai hình trụ
Câu 17. Khối nón có chiều cao
3h cm
và bán kính đáy
2r cm
thì có thể tích bằng:
A.
3
4 cm
B.
3
4
3
cm
C.
2
16 cm
D.
2
4 cm
Câu 18. Khối trụ có chiều cao
3h cm
và bán kính đáy
2r cm
thì có thể tích bằng:
A.
3
12 cm
B.
3
4 cm
C.
3
6 cm
D.
2
12 cm
Câu 19. Diện tích xung quanh của hình trụ có bán kính bằng 7 và chiều cao bằng 9 là:
A.
62
B.
63
C.
126
D.
128
Câu 20. Hình trụ có bán kính bằng 5, khoảng cách giữa hai đáy bằng 7. Diện tích toàn phần của hình
trụ bằng:
A.
10
B.
85
C.
95
D.
120
Câu 21. Một hình trụ có diện tích đáy bằng
2
4 m
. Khoảng cách giữa trục và đường sinh của mặt
xung quanh hình trụ đó bằng:
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A. 4m B. 3m C. 2m D. 1m
Câu 22. Bên trong một lon sữa hình trụ có đường kính đáy bằng chiều cao và bằng 1 dm. Thể tích
thực của lon sữa đó bằng:
A.
3
2 dm
B.
3
2
dm
C.
3
4
dm
D.
3
dm
Câu 23. Một hình vuông cạnh
a
quay xung quanh một cạnh tạo thành một hình tròn xoay có diện tích
toàn phần bằng:
A.
2
4a
B.
2
6a
C.
2
2a
D.
2
3a
Câu 24. Cho hình vuông ABCD có cạnh 2 cm, biết O và O’ lần lượt là trung điểm của AB và CD. Khi
quay hình vuông ABCD quanh trục OO’ thì khối trụ tròn xoay được tạo thành có thể tích bằng:
A.
3
2 cm
B.
3
4 cm
C.
3
6 cm
D.
3
8 cm
Câu 25. Một khối cầu bán kính R, một khối trụ có bán kính R, chiều cao 2R. Tỉ số thể tích giữa khối
cầu và khối trụ bằng:
A.
1
2
B.
2
3
C.
3
2
D. 2
Câu 26. Cho hình lập phương
. ' ' ' 'ABCD A B C D
cạnh
a
và một hình trụ có 2 đáy nội tiếp trong 2
hình vuông ABCD và A’B’C’D’. Tỉ số giữa diện tích xung quanh hình trụ và diện tích toàn phần của
hình lập phương bằng:
A.
1
2
B.
2
C.
6
D.
Câu 27. Một hình trụ có đường kính đáy bằng chiều cao nội tiếp trong mặt cầu bán kính R. Diện tích
xung quanh của hình trụ bằng:
A.
2
22R
B.
2
2R
C.
2
2 R
D.
2
R
Câu 28. Cho lăng trụ tam giác đều có tất cả các cạnh bằng
a
. Một hình trụ tròn xoay có hai đáy là hai
hình tròn ngoại tiếp hai đáy của lăng trụ. Thể tích của khối trụ tròn xoay bằng:
A.
3
a
B.
3
9
a
C.
3
3 a
D.
3
3
a
Câu 29. Một hình trụ có diện tích xung quanh bằng
4
và có thiết diện qua trục là hình vuông. Thể
tích khối trụ tương ứng bằng:
A.
2
B.
C.
3
D.
4
Câu 30. Một hình trụ có diện tích xung quanh bằng
4
và có thiết diện qua trục là hình vuông. Diện
tích toàn phần của hình trụ bằng:
A.
12
B.
10
C.
8
D.
6
Câu 31. Một hình trụ có bán kính đáy bằng 4cm, thiết diện qua trục là hình vuông. Diện tích xung
quanh của hình trụ bằng:
A.
2
16 cm
B.
2
64 cm
C.
2
32 cm
D.
2
24 cm
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 32. Một hình trụ có bán kính đáy bằng
2cm
, thiết diện qua trục là hình vuông. Thể tích của khối
trụ tương ứng bằng:
A.
2
12 cm
B.
2
16 cm
C.
2
20 cm
D.
2
24 cm
Câu 33. Hình trụ có bán kính đáy R, thiết diện qua trục là hình vuông. Thể tích của khối lăng trụ tứ
giác đều có hai đáy nội tiếp trong hai đường tròn đáy của hình trụ bằng:
A.
3
2R
B.
3
3R
C.
3
4R
D.
3
5R
Câu 34. Trong một chiếc hộp hình trụ người ta bỏ vào đó ba quả banh tennis, biết rằng đáy của hình
trụ bằng hình tròn lớn trên quả banh và chiều cao của hình trụ bằng 3 lần đường kính của quả banh.
Gọi
1
S
là tổng diện tích của ba quả banh và
2
S
là diện tích xung quanh của hình trụ. Tỉ số
1
2
S
S
bằng:
A. 1 B. 2 C. 3 D.
1
2
Câu 35. Khối trụ có chiều cao
23a
, bán kính đáy
3a
. Thể tích khối cầu ngoại tiếp khối trụ bằng:
A.
3
86a
B.
3
63a
C.
3
46
3
a
D.
3
43a
Câu 36. Một hình tứ diện đều ABCD cạnh
a
. Xét hình trụ có 1 đáy là đường tròn nội tiếp tam giác
ABC và có chiều cao bằng chiều cao hình tứ diện. Diện tích xung quanh của hình trụ đó bằng:
A.
2
3
3
a
B.
2
2
2
a
C.
2
2
3
a
D.
2
3
2
a
Câu 37. Một hình trụ có bán kính đáy bằng
a
, chiều cao
'3OO a
. Hai điểm A, B lần lượt nằm
trên 2 đáy (O), (O’) sao cho góc giữa OO’ và AB bằng
0
30
. Khoảng cách giữa AB và OO’ bằng:
A.
3
3
a
B.
3
2
a
C.
23
3
a
D.
3a
Câu 38. Một hình trụ có bán kính đáy bằng chiều cao và bằng
a
. Một hình vuông ABCD có AB, CD
lần lượt là 2 dây cung của 2 đường tròn đáy và mặt phẳng (ABCD) không vuông góc với đáy. Diện
tích hình vuông đó bằng:
A.
2
5
2
a
B.
2
5a
C.
2
52
2
a
D.
2
52a
Câu 39. Hình trụ có bán kính đáy 3cm và khoảng cách giữa hai đáy bằng 10cm thì có diện tích toàn
phần là:
A.
2
78 cm
B.
2
60 cm
C.
2
18 cm
D.
2
69 cm
Câu 40. Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng
a
. Gọi S là diện tích xung quanh của
hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông ABCD và A’B’C’D’. Diện tích S là:
A.
2
a
B.
2
2a
C.
2
3a
D.
2
2
2
a
ĐÁP ÁN TRẮC NGHIỆM
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
01. B
02. D
03. B
04. B
05. A
06. C
07. A
08. C
09. D
10. C
11. D
12. A
13. A
14. B
15. A
16. A
17. A
18. D
19. C
20. D
21. C
22. C
23. A
24. A
25. B
26. C
27. C
28. D
29. A
30. D
31. B
32. B
33. C
34. A
35. A
36. C
37. B
38. A
39. A
40. B
GIẢI CHI TIẾT
Câu 1. Với hình trụ ta có
22
xq
h l S rh rl

. Chọn D
Câu 2. Ta có:
22
2.
2 2 2 2
tp xq d
S S S rh r rl r
. Chọn D
Câu 3. Ta có:
2
.
d
T
V S h r h

. Chọn B
Câu 4. Ta có:
2
2 2 .5.7 70
xq
S rh cm
. Chọn B
Câu 5. Ta có:
2 2 2 2 2
2.
2 2 2 2 4 2 6
tp xq d
S S S rh r rl r a a a
. Chọn A
Câu 6. Khi quay hình vuông cạnh
a
quanh 1 cạnh ta được khối trụ có
r h a
Ta có:
23
.
d
T
V S h r h a

. Chọn C
Câu 7. Quay hình vuông ABCD xung quanh MN ta được hình trụ như
hình vẽ.
Khi đó
2
4; 8 . 2 64
2
xq d
AB
r h AD S C h rh cm

Chọn A
Câu 8. Ta có:
2
2.
2 2 12 72 120 4
tp xq d
S S S rh r h h cm
. Chọn C
Câu 9. Ta có:
2
2 2 3
. 81 729 9
3
d
T
l
V S h r h r l l l l



. Chọn D
Câu 10. Khi quay hình chữ nhật này xung quanh cạnh AD ta được hình trụ
như hình vẽ. Ta có:
0
; tan30r AB a h BC CD
.
Suy ra
2
2
2
33
xq
aa
h S rh
.
Chọn C
Câu 11. Ta có bán kính đáy hình trụ là
' ' 2
22
A C a
r 
Đường cao là
ha
.
Khi đó
3
2
2
a
V r h

Chọn D
Câu 12. Giả sử thiết diện là hình chữ nhật ABCD như hình vẽ khi đó
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
AD CD
. Ta có
13
2 26
. 30
. 30
AD CD
AD CD
ADCD
ADCD


Với
AD CD
giải hệ trên ta được
10 ; 3 2AD h CD r
3
2
r
. Khi đó
22
3 9 69
2 2 2 .10 2
2 4 2
tp
S rh r cm
Chọn A
Câu 13. Giả sử thiết diện là hình vuông
MNPQ
như hình vẽ
Với
'2OH
và
2
16 4
MNPQ
S PQ PQ
ta có
2
2
' ' 2 2
2
PQ
O Q O H



mà
23
4 . .8.4 32
d
t
h MQ V S h r h cm
Chọn A
Câu 14. Gọi bán kính đáy bằng r, độ dài đường sinh bằng
l
và
h
là độ dài đường cao của hình trụ.
Theo giả thiết, ta có
2
22
4 3 3
2
tp
xq
S
r rh r h
r h l
S rh h


Nếu bán kính đáy bằng ba lần độ dài đường sinh. Chọn B
Câu 15. Quay hình chữ nhật xung quanh trục MN, ta được hình trục có bán kính đáy là AM và đường
cao là MN. Với
1, 1
2
AD
AM MN AB
nên
2 2 .1.2 4
tp
S r r h
.
Chọn A
Câu 16. Vì ABCD là hình chữ nhật nên khi quay quanh đường thẳng AB ta sẽ được một hình trụ.
Chọn A
Câu 17. Thể tích của khối nón là
22
11
.2 .3 4
33
V r h
. Chọn A
Câu 18. Thể tích của khối trụ là
22
.2 .3 12V r h
. Chọn D
Câu 19. Diện tích xung quanh của hình trụ là
2 2 .7.9 126
xq
S rh
. Chọn C
Câu 20. Diện tích toàn phần của hình trụ là
2 2 5. 5 7 120
tp
S r r h
. Chọn D
Câu 21. Diện tích toàn phần của hình trụ là
2 2 .5 5 7 120
tp
S r r h
. Chọn D
Câu 22. Thể tích thực của lon sữa hình trụ là
2
2
1
.1
24
V r h




. Chọn C
Câu 23. Diện tích toàn phần hình trụ là
2
2 2 .2 4
tp
S r r h a a a
.Chọn A
Câu 24. Thể tích của hình trụ là
22
.1 .2 2V r h
. Chọn A
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 25. Thể tích của hình trụ là
2 2 3
. .2 2
ht
V r h R R R
Thể tích của khối cầu là
3
4
.
3
mc
VR
Suy ra
3
3
4
2
3
23
mc
ht
R
V
VR

. Chọn B
Câu 26. Diện tích toàn phần của hình lập phương cạnh
a
bằng
2
6
tp
Va
Diện tích xung quanh hình trụ là
2
2 2 . .
2
xq
a
V rh a a
. Suy ra
6
xq
tp
V
V
. Chọn C
Câu 27. Gọi r là bán kính đáy của hình trụ, theo giả thiết, ta có
2hr
Gọi ABCD là thiết diện qua trụ của hình trụ, O là tâm của hình chữ nhật ABCD
Ta có bán kính mặt cầu
2
2
22
22
2
AC h R
R AO r r R r h R



Diện tích xung quanh hình trụ là
2
2 2 . . 2 2
2
xq
R
V rh R R
. Chọn C
Câu 28. Gọi R, h là bán kính đáy và chiều cao của hình trụ. Ta có
ha
(cùng đường cao với lăng trụ)
là
3
3
a
R
vì R cũng là bán kính đường tròn ngoại tiếp đáy lăng trụ
3
2
3
a
V R h
. Chọn D
Câu 29. Thiết diện qua trục là hình vuông nên
2hR
Ta có:
22
2
4 2 2
1
xq
h
S Rh h V R h
R
. Chọn A
Câu 30. Thiết diện qua trục là hình vuông nên
2hR
Ta có:
22
2
4 2 2 2 6
1
xq tp
h
S Rh h S Rh R
R
. Chọn D
Câu 31. Thiết diện qua trục là hình vuông nên
2 8 2 64
xq
h R S Rh

. Chọn B
Câu 32. Thiết diện qua trục là hình vuông nên
2
2 4 16h R V R h

. Chọn B
Câu 33. Thiết diện qua trục là hình vuông nên
2hR
. Lăng trụ có cùng chiều cao với hình trụ, và có
đáy là hình vuông với bán kính đường tròn ngoại tiếp là
R
Diện tích đáy lăng trụ:
2
2
22S R R
Thể tích lăng trụ:
3
4V Sh R
.Chọn C
Câu 34. Gọi R là bán kính 1 quả banh
Tổng diện tích 3 quả banh:
22
1
3 4 12S R R

Chiếc hộp có bán kính đáy cũng bằng R và chiều cao bằng
6hR
Diện tích xung quanh hình trụ
2
1
2
2
2 12 1
S
S Rh R
S

.Chọn A
Câu 35. Tâm khối cầu ngoại tiếp khối trụ là trung điểm của đoạn nối tâm 2 mặt đáy khối trụ
2
3
23
0
0
4
6 8 6
23
R
h
R R a V a



. Chọn A
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 36. Gọi O là tâm của tam giác ABC và M là trung điểm BC
Chiều cao tứ diện
22
6
3
a
h DO DA AO
Bán kính đường tròn nội tiếp đáy ABC:
3
36
AM a
R 
2
2
2
3
xq
a
S Rh
. Chọn C
Câu 37. Trên (O) lấy điểm C sao cho BC//OO’. Khi đó:
0
30ABC AC a
Gọi H là hình chiếu của O lên AC. Suy ra
', ',d OO AB d OO AC OH
Tam giác OAC là tam giác đều nên
3
2
a
OH
. Chọn B
Câu 38. Gọi M, N lần lượt là trung điểm của AB, CD và O, O’ là tâm của 2 đáy hình trụ chứa AB,
CD. Ta có:
2 2 2 2
2 2 2AB AM OA OM a OM
và
2
2 2 2
'
24
2
OO
MN OM a OM



Vì tứ giác ABCD là hình vuông nên
AB MN
hay
2 2 2 2
6
24
4
a
a OM a OM OM
10
2
a
AB
Diện tích hình vuông:
2
2
5
2
a
AB
.Chọn A
Câu 39.
3R
và
2
10 2 2 78
tp
h S Rh R
. Chọn A
Câu 40. Chiều cao hình trụ là chiều cao (hay cạnh) của hình lập phương:
ha
Bán kính đáy hình trụ là bán kính đường tròn ngoại tiếp hình vuông ABCD cạnh
a
2
a
R
2
22
xq
S Rh a

. Chọn B
CHỦ ĐỀ 4: MẶT CẦU – HÌNH CẦU – KHỐI CẦU
Câu 1. Một khối cầu tiếp xúc với tất cả các mặt của hình lập phương. Tỉ số thể tích giữa khối cầu và
khối lập phương đó bằng:
A.
3
B.
6
C.
2
3
D.
2
3
Câu 2. Mặt cầu ngoại tiếp hình lập phương cạnh
a
thì có diện tích bằng:
A.
3
a
B.
3
4
3
a
C.
2
3 a
D.
2
12 3a
Câu 3. Cho hình lập phương cạnh
a
nội tiếp trong một mặt cầu. Bán kính đường tròn lớn của mặt
cầu đó bằng:
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
3a
B.
2a
C.
3
2
a
D.
2
2
a
Câu 4. Cho mặt cầu
S
có tâm A đường kình
10cm
và mặt phẳng (P) cách tâm một khoảng
4cm
.
Kết luận nào sau đây sai ?
A. (P) cắt (S)
B. (P) cắt (S) theo một đường tròn bán kính 3cm
C. (P) tiếp xúc với (S)
D. (P) và (S) có vô số điểm chung
Câu 5. Tỉ số thể tích giữa khối lập phương và khối cầu ngoại tiếp khối lập phương đó là:
A.
23
3
B.
3
23
C.
3
2
D.
2
3
Câu 6. Một hình hộp chữ nhật có 3 kích thước 20cm,
20 3
cm, 30cm. Thể tích khối cầu ngoại tiếp
hình hộp đó bằng:
A.
3
32
3
dm
B.
3
62,5
3
dm
C.
3
625000
3
dm
D.
3
3200
3
cm
Câu 7. Hình hộp chữ nhật
. ' ' ' 'ABCD A B C D
có
' 2 3BB cm
,
' ' 3C B cm
, diện tích mặt đáy bằng
2
6cm
. Thể tích khối cầu ngoại tiếp hình hộp trên bằng:
A.
3
500
3
cm
B.
3
125
6
cm
C.
3
100 cm
D.
3
100
3
cm
Câu 8. Cho mặt cầu (S) tâm O bán kính R và điểm A nằm trên (S). Mặt phẳng (P) qua A tạo với OA
một góc
0
60
và cắt (S) theo một đường tròn có diện tích bằng:
A.
B.
2
2
R
C.
2
3
2
R
D.
2
4
R
Câu 9. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt phẳng
(ABC) và cạnh
10SA AB cm
. Diện tích mặt cầu ngoại tiếp hình chóp bằng:
A.
12 dm
B.
1200 dm
C.
2
1200 dm
D.
2
12 dm
Câu 10. Cho hình chóp S.ABC
,3SA ABC AB cm
, góc giữa SB và đáy bằng
0
60
. Thể tích khối
cầu ngoại tiếp hình chóp bằng:
A.
3
36 cm
B.
3
43cm
C.
2
36 cm
D.
2
43cm
Câu 11. Hình lăng trụ đứng
. ' ' 'ABC A B C
có đáy ABC là tam giác vuông tại B,
'2AA AC a
.
Diện tích mặt cầu ngoại tiếp hình lăng trụ bằng:
A.
2
8 a
B.
2
4 a
C.
2
12 a
D.
2
10 a
Câu 12. Cho hình chóp S.ABCD có đáy là hình vuông,
SA ABCD
và
22SA AC a
. Diện
tích mặt cầu ngoại tiếp hình chóp bằng:
A.
2
16
3
a
B.
2
32
3
a
C.
2
16 a
D.
2
8 a
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 13. Cho hình hộp chữ nhật
. ' ' ' 'ABCD A B C D
có diện tích các mặt
, ' ', 'ABCD ABB A ADD A
lần
lượt bằng
2 2 2
20 ,28 ,35cm cm cm
. Bán kính mặt cầu ngoại tiếp hình hộp bằng:
A.
3 10
2
cm
B.
6 10cm
C.
3 10cm
D.
30cm
Câu 14. Cho hình chóp S.ABC có tam giác ABC đều cạnh
3a cm
,
SA ABC
và
2SA a
. Tính
thể tích khối cầu ngoại tiếp hình chóp bằng:
A.
3
32 3cm
B.
3
16 3cm
C.
3
3
8
33
a
cm
D.
3
3
4
3
a
cm
Câu 15. Cho hình chóp S.ABC có tam giác ABC vuông tại A, cạnh
3 , 3 3BC m SA
và
SA ABC
. Thể tích khối cầu ngoại tiếp hình chóp bằng:
A.
3
18 m
B.
3
36 m
C.
3
16 m
D.
3
12 3m
Câu 16. Cho hình lăng trụ đều
. ' ' 'ABC A B C
có cạnh đáy bằng
a
, cạnh bên
2
'
3
a
AA
. Thể tích khối
cầu ngoại tiếp tứ diện
''ACB C
bằng:
A.
3
4
81
a
B.
3
4
27
a
C.
3
4
9
a
D.
3
16
27
a
Câu 17. Hình hộp chữ nhật ABCD.A’B’C’D’ nội tiếp trong mặt cầu bán kính
3R cm
. Tam giác
ABC cân và có diện tích bằng
2
2cm
. Diện tích toàn phần của hình hộp đó bằng:
A.
2
8cm
B.
2
24cm
C.
2
8 26cm
D.
2
8 1 26 cm
Câu 18. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng
a
. Bán kính của mặt cầu
ngoại tiếp hình chóp nói trên bằng:
A.
2
4
a
R
B.
2
2
a
R
C.
2
3
a
R
D.
3
2
a
R
Câu 19. Một mặt cầu có đường kính bằng
2a
thì có diện tích bằng:
A.
2
8 a
B.
2
4
3
a
C.
2
4 a
D.
2
16 a
Câu 20. Một đường thẳng cắt mặt cầu tâm O tại hai điểm A, B sao cho tam giác OAB vuông cân tại O
và
2AB a
. Thể tích khối cầu là:
A.
3
4Va
B.
3
Va
C.
3
4
3
Va
D.
3
2
3
Va
Câu 21. Cho mặt cầu (S) có tâm I bán kính
5R
và mặt phẳng (P) cắt (S) theo một đường tròn (C) có
bán kính
3r
. Kết luận nào sau đây là sai ?
A. Tâm của (C) là hình chiếu vuông góc của I trên (P)
B. (C) là giao tuyến của (S) và (P)
C. Khoảng cách từ I đến (P) bằng 4
D. (C) là đường tròn giao tuyến lớn nhất của (P) và (S)
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 22. Cho tứ diện OABC có OA, OB, OC đôi một vuông góc nhau và
, 2 , 3OA a OB a OC a
.
Diện tích của mặt cầu (S) ngoại tiếp hình chóp S.ABC bằng:
A.
2
14Sa
B.
2
8Sa
C.
2
12Sa
D.
2
10Sa
Câu 23. Thể tích V của một mặt cầu có bán kính R được xác định bởi công thức nào sau đây:
A.
3
VR
B.
3
4VR
C.
3
3
R
V
D.
3
4
3
R
V
Câu 24. Cho tứ diện ABCD có
5DA a
và vuông góc với (ABC),
ABC
vuông tại B và
3 , 4AB a BC a
. Bán kính của mặt cầu nói trên bằng:
A.
52
2
a
R
B.
53
3
a
R
C.
52
3
a
R
D.
53
2
a
R
Câu 25. Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại A,
SA ABC
,
;SA a AB b
;
AC c
. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là:
A.
2 2 2
2R a b c
B.
2 2 2
2
3
abc
R

C.
2 2 2
R a b c
D.
2 2 2
1
2
R a b c
Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy. Bán kính
R của mặt cầu ngoại tiếp hình chóp S.ABCD bằng:
A.
1
2
R AC
B.
1
2
R SB
C.
1
2
R SC
D.
1
2
R SA
Câu 27. Trong các khẳng định sau, khẳng định nào sai ?
A. Mặt phẳng (P) tiếp xúc với mặt cầu (S) tâm O tại điểm H thì OH là khoảng cách ngắn nhất từ O đến
một điểm bất kỳ nằm trong mặt phẳng (P)
B. Chỉ có duy nhất hai mặt phẳng vuông góc với mặt phẳng cho trước và tiếp xúc với mặt cầu (S).
C. Mặt phẳng cắt mặt cầu (S) theo đường tròn (C) , tâm của đường tròn (C) là hình chiếu của tâm mặt
cầu (S) xuống mặt phẳng (P)
D. Tại điểm H nằm trên mặt cầu chỉ có 1 tiếp tuyến duy nhất.
Câu 28. Trong các mệnh đề sau đây, mệnh đề nào sai ?
A. Bất kì một hình tứ diện nào cũng có mặt cầu ngoại tiếp
B. Bất kì một hình hộp chữ nhật nào cũng có một mặt cầu ngoại tiếp
C. Bất kì một hình hộp nào cũng có một mặt cầu ngoại tiếp
D. Bất kì một hình chóp đều nào cũng có một mặt cầu ngoại tiếp
Câu 29. Một mặt cầu có bán kính
3R
. Diện tích mặt cầu bằng:
A.
2
8 R
B.
2
12 R
C.
2
4 R
D.
2
12 3 R
Câu 30. Mặt cầu có bán kính r thì có diện tích là:
A.
4 r
B.
2
4 r
C.
2
4
3
r
D.
3
4
3
r
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Câu 31. Khối cầu có bán kính r thì có thể tích là:
A.
3
4 r
B.
2
4 r
C.
2
4
3
r
D.
3
4
3
r
Câu 32. Khối cầu có bán kính 3cm thì có thể tích là:
A.
3
9 cm
B.
3
36 cm
C.
3
27 cm
D.
3
12 cm
Câu 33. Mặt cầu có bán kính 4cm thì có diện tích là:
A.
2
64 cm
B.
2
16 cm
C.
2
64
3
cm
D.
2
256
3
cm
Câu 34. Mặt cầu (S) có diện tích bằng
2
100 cm
thì có bán kính là:
A. 3 (cm) B. 4 (cm) C. 5 (cm) D.
5
(cm)
Câu 35. Khối cầu (S) có thể tích bằng
3
288 cm
thì có bán kính là:
A.
62cm
B. 6(cm) C.
66cm
D.
6 cm
Câu 36. Khối cầu (S) có diện tích bằng
2
16 , 0aa
thì có thể tích là:
A.
33
32
3
a cm
B.
33
32 a cm
C.
33
16 a cm
D.
33
16
3
a cm
Câu 37. Khối cầu
1
S
có thể tích bằng
3
36 cm
và có bán kính gấp 3 lần bán kính khối cầu
2
S
.
Thể tích của khối cầu
2
S
là:
A.
3
4 cm
B.
3
4
3
cm
C.
3
297 cm
D.
3
324 cm
Câu 38. Cắt mặt cầu (S) bằng một mặt phẳng đi qua tâm được thiết diện là một hình tròn có chu vi
bằng
4
. Diện tích và thể tích của (S) lần lượt là:
A.
16
và
32
3
B.
16
và
32
C.
8
và
32
3
D.
8
và
32
Câu 39. Cắt mặt cầu (S) bằng một mặt phẳng cách tâm một khoảng 4cm được thiết diện là một hình
tròn có bán kính bằng 3cm. Bán kính của mặt cầu (S) là:
A. 5cm B. 7cm C. 12cm D. 10cm
Câu 40. Cắt mặt cầu (S) có bán kính 10 cm bằng một mặt phẳng cách tâm một khoảng 6 cm được thiết
diện là hình tròn (C). Diện tích của (C) là:
A.
2
16 cm
B.
2
32 cm
C.
2
64 cm
D.
2
128 cm
Câu 41. Cắt mặt cầu (S) bằng một mặt phẳng cách tâm một khoảng 4cm được thiết diện là hình tròn
có diện tích
2
9 cm
. Thể tích của (S) là:
A.
3
250
3
cm
B.
3
1372
3
cm
C.
3
2304 cm
D.
3
500
3
cm
Câu 42. Mặt cầu ngoại tiếp hình lập phương cạnh
2a
có thể tích là:
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
A.
33
3 a cm
B.
33
3
2
a cm
C.
33
3 a cm
D.
33
43a cm
Câu 43. Mặt cầu nội tiếp hình lập phương cạnh
a
có thể tích là:
A.
3
3
a
B.
3
6
a
C.
3
4
3
a
D.
3
4
9
a
Câu 44. Mặt cầu ngoại tiếp hình chóp tứ giác đều có tất cả các cạnh bằng
2a
thì có bán kính là:
A.
2
2
a
B.
2a
C.
a
D.
3
2
a
ĐÁP ÁN TRẮC NGHIỆM
01. B
02. C
03. C
04. C
05. A
06. B
07. B
08. D
09. D
10. A
11. B
12. C
13. A
14. A
15. B
16. A
17. D
18. B
19. C
20. C
21. D
22. A
23. D
24. A
25.D
26. C
27. D
28. C
29. B
30. B
31. C
32. B
33. A
34. C
35. B
36. A
37. B
38. A
39. A
40. C
41.D
42.D
43. B
44. B
GIẢI CHI TIẾT
Câu 1. Giả sử cạnh của hình lập phương trình
a
, khi đó bán kính khối cầu là
2
a
Thể tích của khối cầu là
3
3
1
4
3 2 6
aa
V




Thể tích hình lập phương trình
3
2
Va
. Ta có
1
2
6
V
V
.Chọn B
Câu 2. Ta có
2
2
33
43
22
aa
R S a





.Chọn C
Câu 3. Ta có bán kính đường tròn lớn là
3
2
a
. Chọn C
Câu 4. Bán kính đường tròn là 5cm, mà
,4d I P cm
. Chọn C
Câu 5. Giả sử cạnh của hình lập phương trình
a
, khi đó bán kính khối cầu là
3
2
a
Thể tích khối lập phương là
3
1
Va
Thể tích khối cầu ngoại tiếp khối lập phương là
3
3
2
4 3 3
3 2 2
aa
V





. Ta có
1
2
23
3
V
V
. Chọn A
Câu 6. Đường kính khối cầu ngoại tiếp là
2
22
20 20 3 30 50cm
bán kính
25 2,5R cm dm
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Thể tích khối cầu là
3
3
4 62,5
2,5
33
V dm

. Chọn B
Câu 7. Ta có
6
' ' 2
3
A B cm
đường kính khối cầu ngoại tiếp là
2
22
2 3 3 2 5 2,5cm R cm
Thể tích khối cầu ngoại tiếp hình hộp là
3
3
4 125
2,5
36
V cm

. Chọn B
Câu 8. Bán kính đường tròn là
2
2
0
.cos60
2 2 4
R R R
r R S



. Chọn D
Câu 9. Ta có
BC AB
BC SAB BC SB
BC SA
Gọi I là trung điểm của SC
IS IC IA IB
(do
0
90SAC SBC
)
Ta có:
2
2 2 2
10 10 2 10 3 5 3SC SA AC IA
2
22
4 5 3 1200 12
mc
S cm dm
. Chọn D
Câu 10. Chọn A
Câu 11. Gọi M,N lần lượt là trung điểm của AC, A’C’ , I là trung điểm của
MN
I là tâm mặt cầu ngoại tiếp hình lăng trụ.
Ta có
2
,
2
a
IM IN AB BC a
2 2 2
'4
mc
R IA IN NA a S a
. Chọn B
Câu 12. Gọi I là trung điểm của
SC IA IB IC ID IS
Ta có
22
42SC SA AC a IA a
2
2
4 2 16
mc
S a a

.
Chọn C
Câu 13. Giả sử
, , 'AB a AD b AA c
ta có
20, 28, 35 7, 5, 4ab ac bc c b a
. Đường kính mặt cầu ngoại tiếp là
2 2 2
3 10
3 10
2
a b c cm R cm
. Chọn A
Câu 14. Gọi G là trọng tâm của
ABC
Qua G kẻ
//Gx SA Gx ABC
Gọi M là trung điểm của SA, qua M kẻ đường thẳng song song với SA cắt
Gx tại I
IA IB IC IS
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Ta có tứ giác MIGA là hình chữ nhật
23
.3
32
a
IM AG cm
3
2 2 3
4
2 3 2 3 32 3
3
AI MA MI cm V cm

. Chọn A
Câu 15. Gọi M là trung điểm của BC, qua M kẻ đường thẳng
//Mx SA Mx ABC
Gọi N là trung điểm của SA, qua N kẻ đường thẳng vuông góc với SA
cắt Mx tại
I
IA IB IC IS
Do tứ giác AMIN là hình chữ nhật
3
2
NI AM cm
2 2 3 3
4
3 .3 36
3
IA AN NI cm V cm

. Chọn B
Câu 16. Dễ thấy mặt cầu ngoại tiếp hình lăng trụ đều cũng chính là mặt
cầu ngoại tiếp tứ diện ACB’C’
+) Gọi G là trọng tâm tam giác đều ABC, trục đường trong ngoại tiếp
ABC
cắt mặt phẳng trung trực của AA’ tại O suy ra O là tâm
mặt
cầu ngoại tiếp khối lăng trụ
Ta có:
3
;
33
aa
AG OG IA
+)
22
22
2
3 9 3
a a a
R GA OG
Do đó
33
4 32
3 81
Ra
V


. Chọn A
Câu 17. Tam giác ABC vuông tại B suy ra nó vuông cân tại B
Khi đó gọi I là tâm của hình vuông ABCD
Ta có
2
22
2
ABC
AB
S AB
. Do vậy
22
2 9 2 7
2
AC
IC OI R IC
Do đó chiều cao của khối hộp là
2 2 7h OI
8 8.2 7 8 1 28
tp d xq
S S S
. Chọn D
Câu 18. Dựng hình như hình vẽ ta có O là tâm mặt cầu ngoại tiếp của
hình chóp. Ta có:
2
2
2
a
BD a ED
Khi đó
2
SO SK SO SD
SKO SED
SD SE SD SE
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Do đó
22
2
2
2
2
2
2
SD a a
SO R
SE
a
a



. Chọn B
Câu 19. Ta có:
22
2 4 4
2
d
d a R a S R a

(với d là đường kính của mặt cầu).
Chọn C
Câu 20. Dễ thấy
33
2 2 2 2
44
2
33
Ra
OA OB R R R AB a R a V

.
Chọn C.
Câu 21. Ta có:
2 2 2
R r d
(trong đó
;d d I P
suy ra
22
4d R r
. D sai vì đường giao
tuyến lớn nhất của (P) và (S) phải đi qua tâm I. Chọn D
Câu 22. Gọi M là trung điểm của BC. Khi đó M là tâm đường tròn
ngoại tiếp tam giác OBC.
Từ M dựng đường thẳng d song song với OA. Trong mặt phẳng
;OA d
dựng đường thẳng trung trực của OA cắt d tại E. Khi đó
E là
tâm mặt cầu ngoại tiếp của khối chóp.
Ta có:
22
13
2 2 2
BC OB OC a
OM
22
14
2 2 2
OA a a
EM OI R EM OM
Do vậy
22
4 14S R a


.Chọn A
Câu 23. Công thức thể tích khối cầu là
3
4
3
R
V
. Chọn D
Câu 24. Gọi I là trung điểm của AC. Khi đó I là tâm đường trong
ngoại tiếp tam giác ABC vuông tại B.
Đường thẳng qua I vuông góc với mp(ABC) cắt CD tại O. Khi đó dễ
thấy
1
2
OA OC OD CD
Khi đó
22
22
CD DA AC
R

2 2 2
52
22
DA AB BC a

. Chọn A
Câu 25. Gọi M là trung điểm của BC. Khi đó M là tâm đường tròn
ngoại tiếp tam giác ABC. Từ M dựng đường thẳng d song song với
SA. Trong mặt phẳng (SA;d) dựng đường thẳng trung trực SA cắt d
tại O. Khi đó O là tâm mặt cầu ngoại tiếp của khối chóp.
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Ta có:
22
22
11
2 2 2
bc
MA BC AB AC
Lại có:
1
22
a
OM IA SA
. Do vậy
2 2 2
22
2
abc
OA OM MA

. Chọn D
Câu 26. Gọi I là tâm hình chữ nhật ABCD. Từ I dựng đường
thẳng song song với SA cắt SC tại O.
Khi đó
OA OB OC OD
. Mặt khác O là trung điểm
của
cạnh huyền SC trong tam giác vuông SAC nên
SO OC OA O
là tâm mặt cầu ngoại tiếp của hình
chóp
do vậy
2
SC
R
. Chọn C
Câu 27. D sai vì tại một điểm H bất kì nằm trên mặt cầu có vô số
tiếp tuyến đi qua điểm đó. Chọn D
Câu 28. Đáp án C sai vì chỉ có hình hộp chữ nhật mới có mặt cầu ngoại tiếp. Hình hộp xiên hoặc hình
hộp có đáy là hình bình hành thì không có mặt cầu ngoại tiếp. Chọn C
Câu 29. Ta có
2
4 3 12SR


. Chọn B
Câu 30. Công thức diện tích mặt cầu bán kính
r
là
2
4Sr
. Chọn B
Câu 31. Công thức thể tíc khối cầu là
3
4
3
r
V
. Chọn D
Câu 32. Ta có:
3
4
36
3
VR


. Chọn B.
Câu 33. Ta có:
2
4 64SR


. Chọn A.
Câu 34. Ta có:
2
4 100 5S R R

. Chọn C.
Câu 35. Ta có:
3
4
288 6
3
V R R

. Chọn A
Câu 36. Ta có:
3
2 2 3
4 32
4 16 2
33
a
S R a R a V R
. Chọn A.
Câu 37. Ta có:
1
3
4
3
S
R
V
và
2
3
3
4
14
3
.
3 27 3
S
R
R
V




1
4
27 3
S
V

. Chọn B
Câu 38. Ta có:
2 4 2C r r

(với r là bán kính đường tròn thiết diện)
Do thiết diện qua tâm nên
32
4 32
2 ; 4 16
33
R r V R S R
. Chọn A
Câu 39. Ta có:
2 2 2 2 2 2
4 3 5R r d R R
. Chọn A
Câu 40. Ta có:
2 2 2 2 2 2
10 6 8R r d r r
(với r là bán kính đường tròn (C))
Khi đó
2
64
C
SR


. Chọn C
Câu 41. Gọi r là bán kính hình tròn là thiết diện của mặt phẳng và mặt cầu (S)
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
ĐT: 0934286923 Email: emnhi1990@gmail.com
Ta có:
2
93rr

. Mặt khác
2 2 2 3
4 500
5
33
R r d R V R

. Chọn D
Câu 42. Bán kính mặt cầu ngoại tiếp hình lập phương cạnh
2a
là
23
3
2
a
Ra
Do đó
33
4
43
3
V R a


. Chọn D
Câu 43. Bán kính đường tròn nội tiếp hình lập phương là
3
3
4
2 3 6
nt
aa
r V r
.Chọn B
Câu 44. Dựng hình như hình vẽ ta có:
SKO SED g g
Do vậy
2
22
SK SO SD SO SD
R SO
SE SD SE SD SE
Mặt khác
22
22SD AB a SE SD ED
Do vậy
2Ra
. Chọn B
| 1/120
| | Tải xuống

Có thể bạn quan tâm:

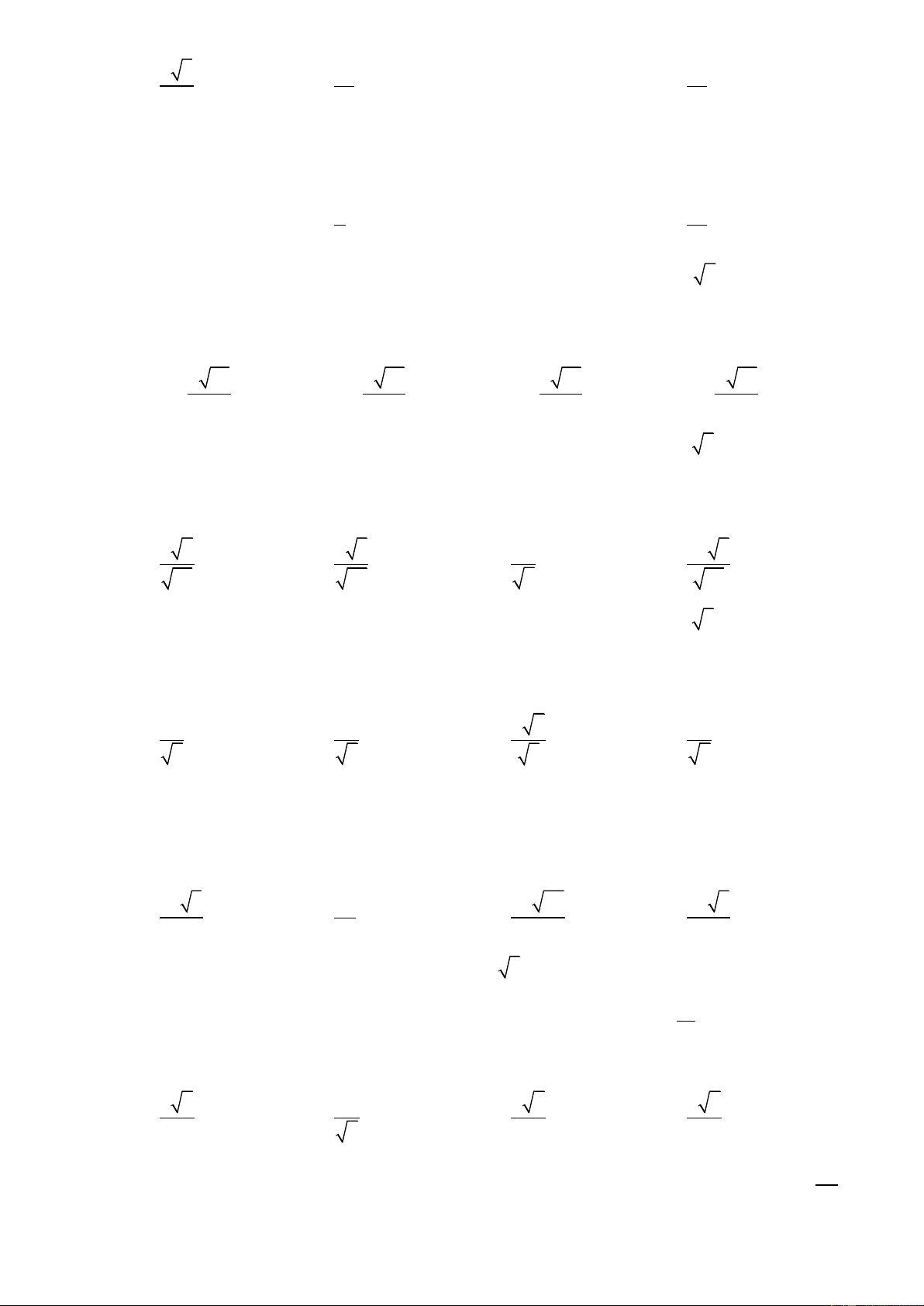
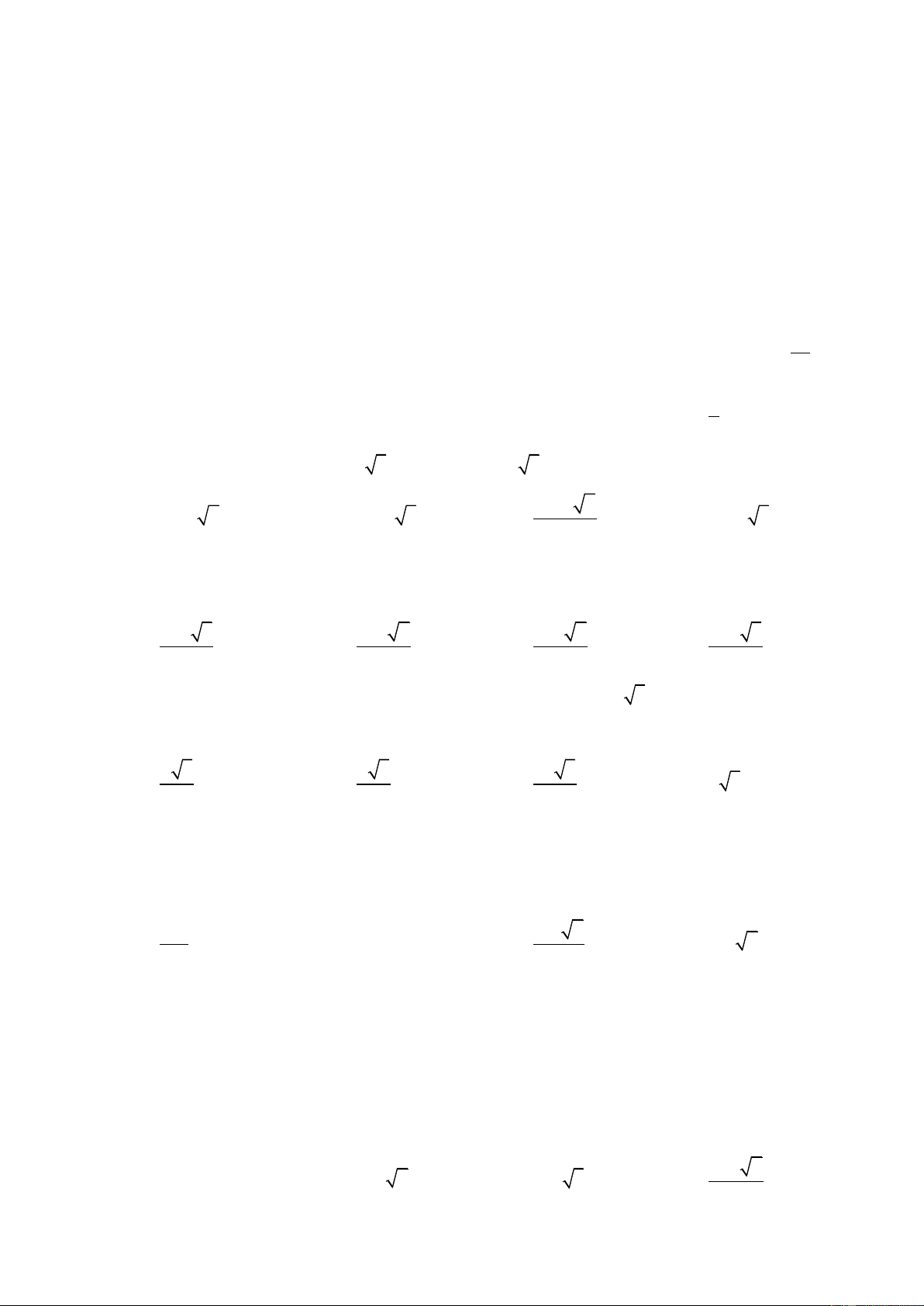
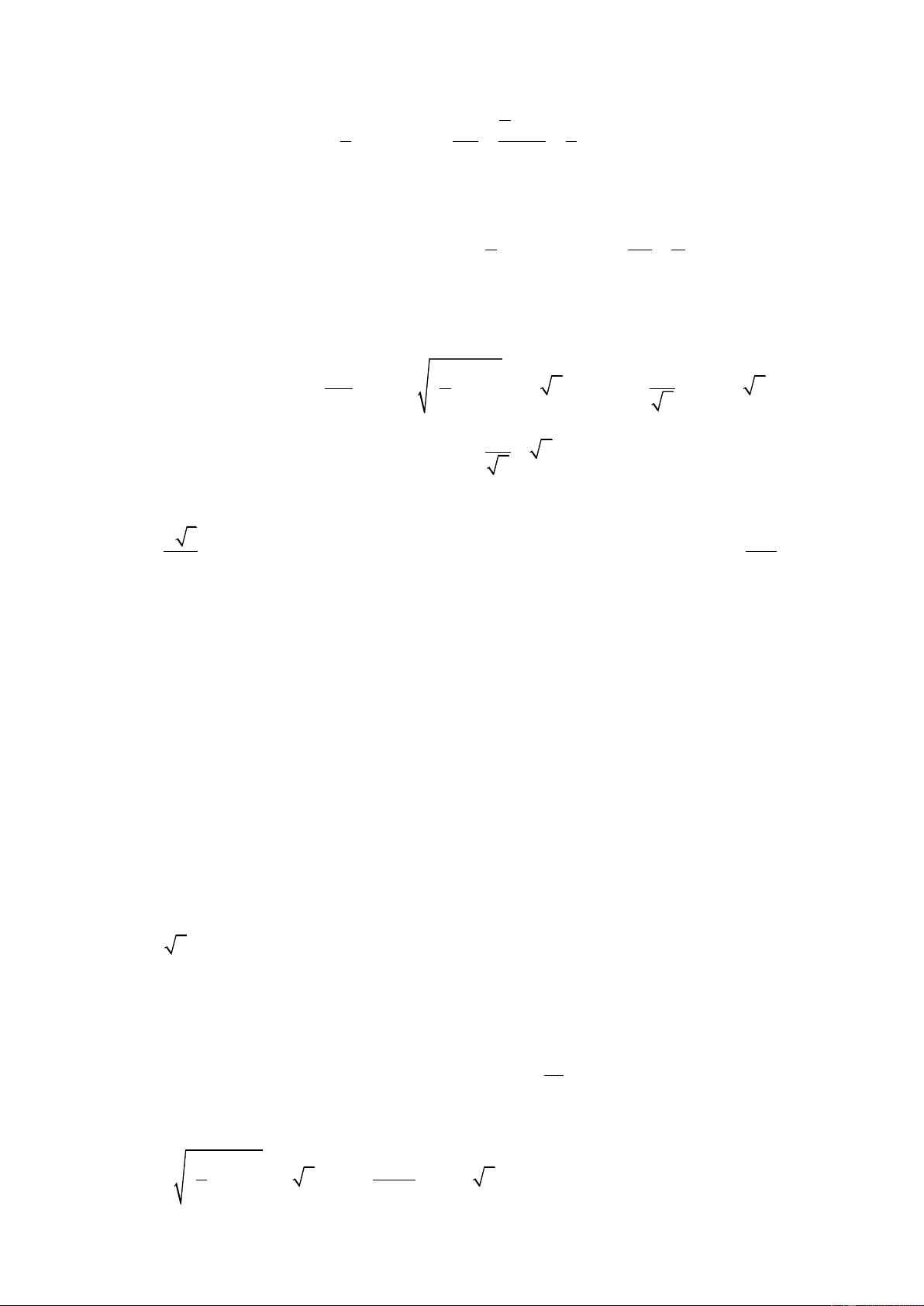
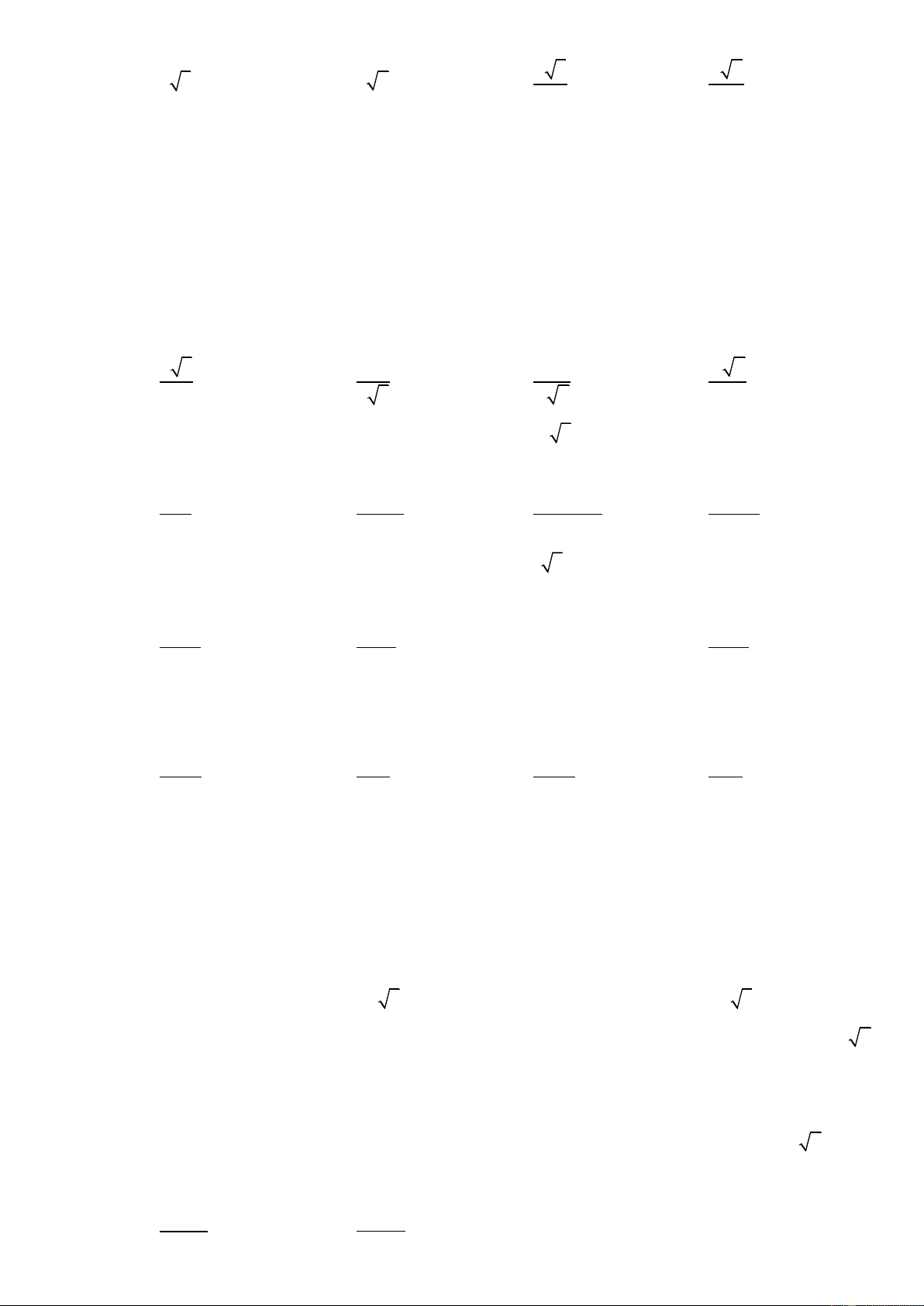
Preview text:

CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
BÀI TẬP TRẮC NGHIỆM CHUYÊN
ĐỀ THỂ TÍCH KHỐI ĐA DIỆN VÀ KHOẢNG CÁCH CÓ LỜI GIẢI CHI TIẾT
BẠN NÀO CẦN FILE WORD LIÊN HỆ 0934286923
NGƯỜI BUỒN CẢNH CÓ VUI ĐÂU BAO GIỜ ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH
LUYỆN THI THPT QUỐC GIA 2016 - 2017
CHỦ ĐỀ 1: THỂ TÍCH
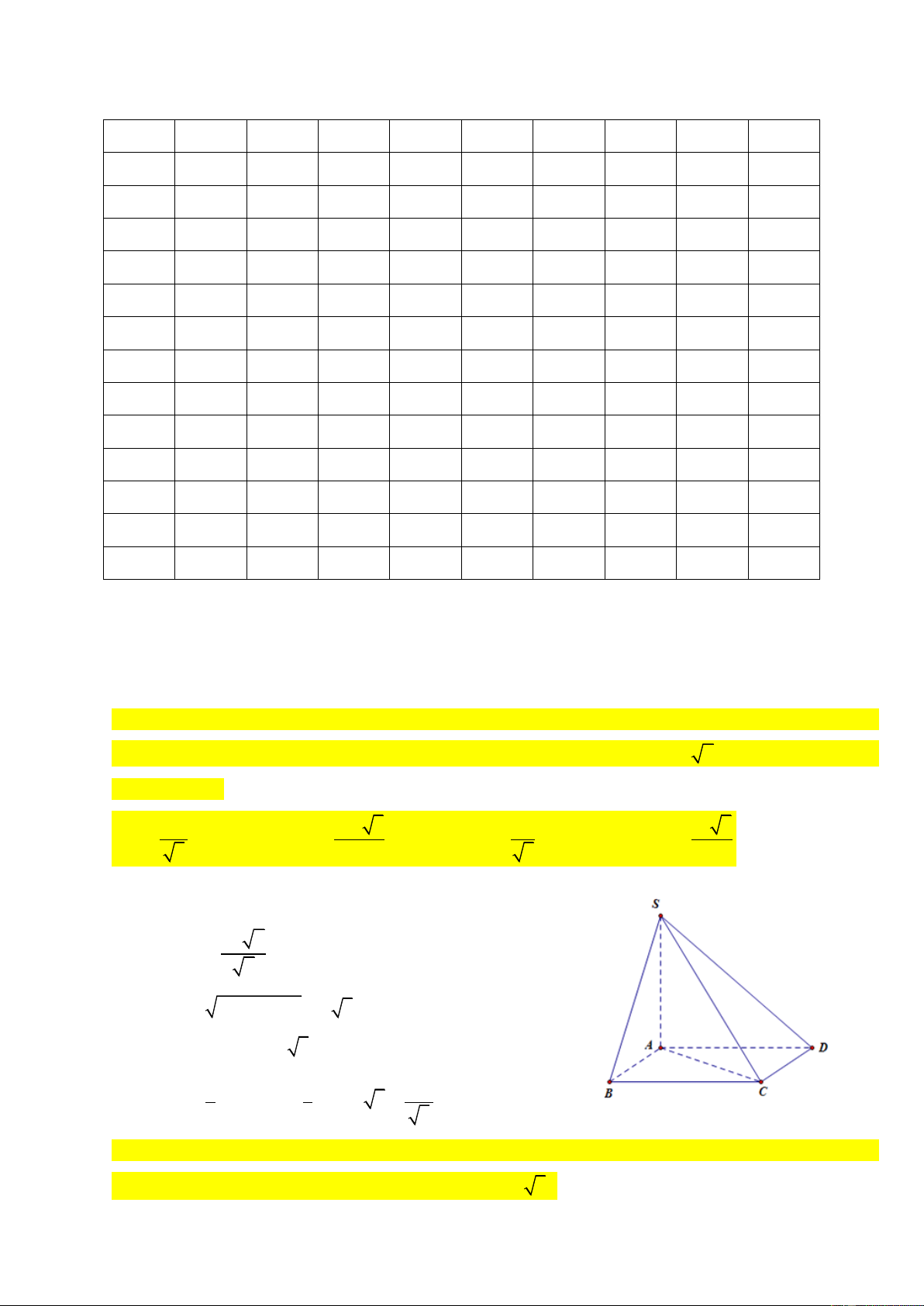
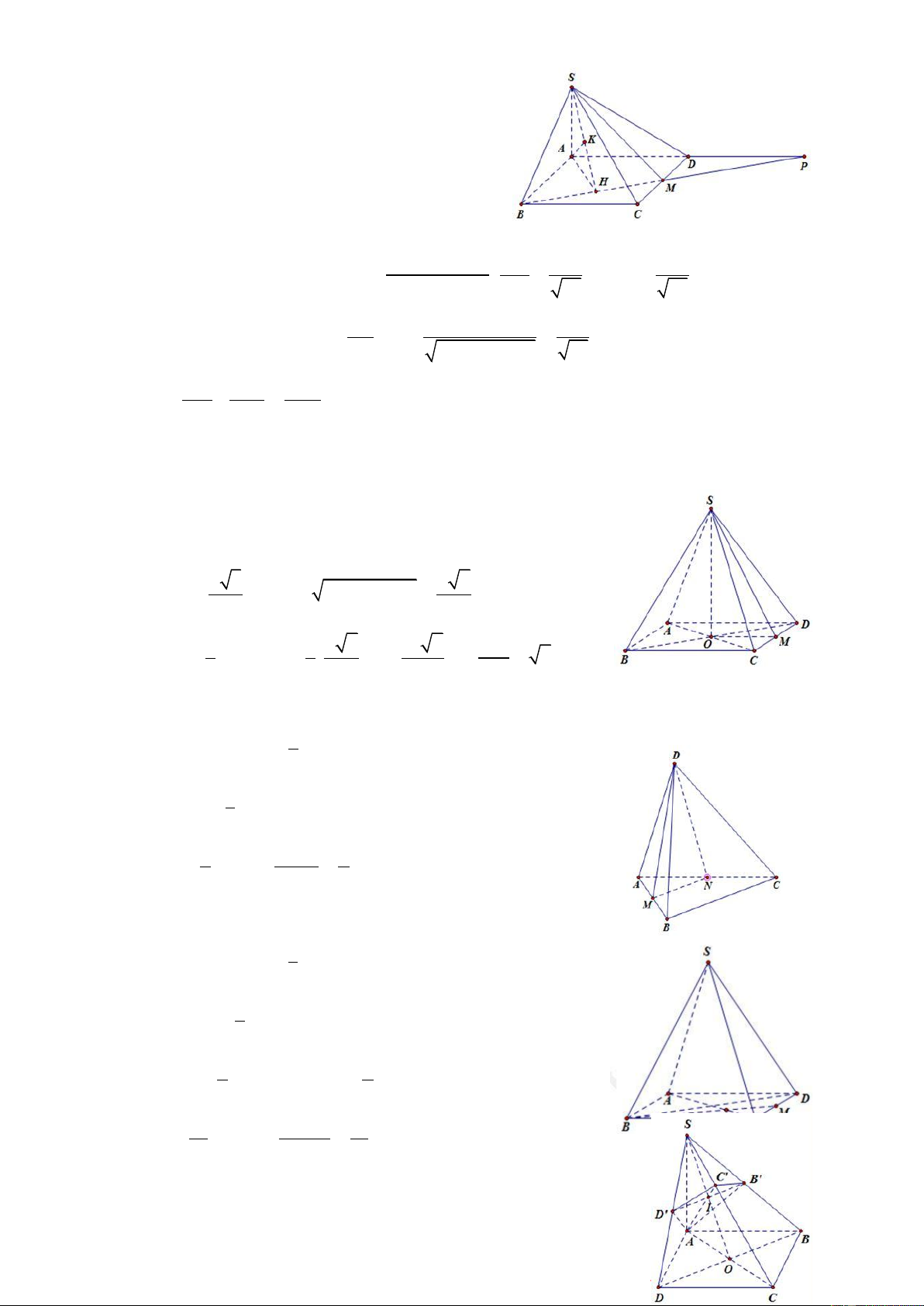
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a. Cạnh bên SA vuông góc
với mặt phẳng đáy, SC tạo với mặt phẳng đáy một góc 45 và SC = 2 a 2 . Thể tích khối chóp S.ABCD bằng: 3 2a 3 a 2 3 3 a 3 a 3 A. B. C. D. 3 3 3 3
Câu 2: Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hai mặt (SAB) và (SAC) cùng
vuông góc với đáy. Tính thể tích khối chóp biết SC = a 3 ? 3 2a 6 3 a 6 3 a 3 3 a 3 A. B. C. D. 9 12 4 2
Câu 3: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B với AC = a biết SA vuông góc với
đáy ABC và SB hợp với đáy một góc 60. Tính thể tích khối chóp: 3 a 6 3 a 3 3 a 6 3 a 6 A. B. C. D. 24 24 8 48
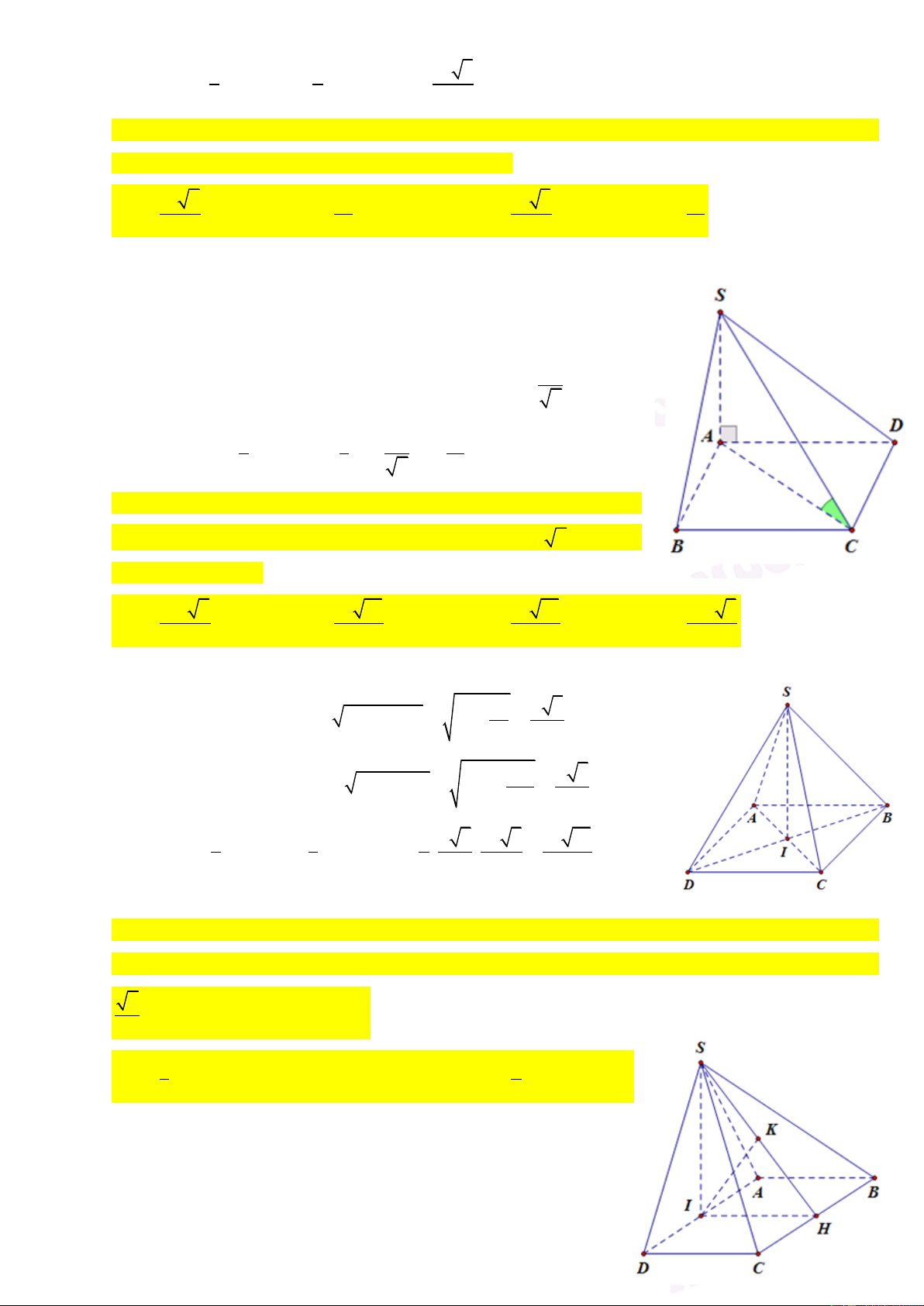
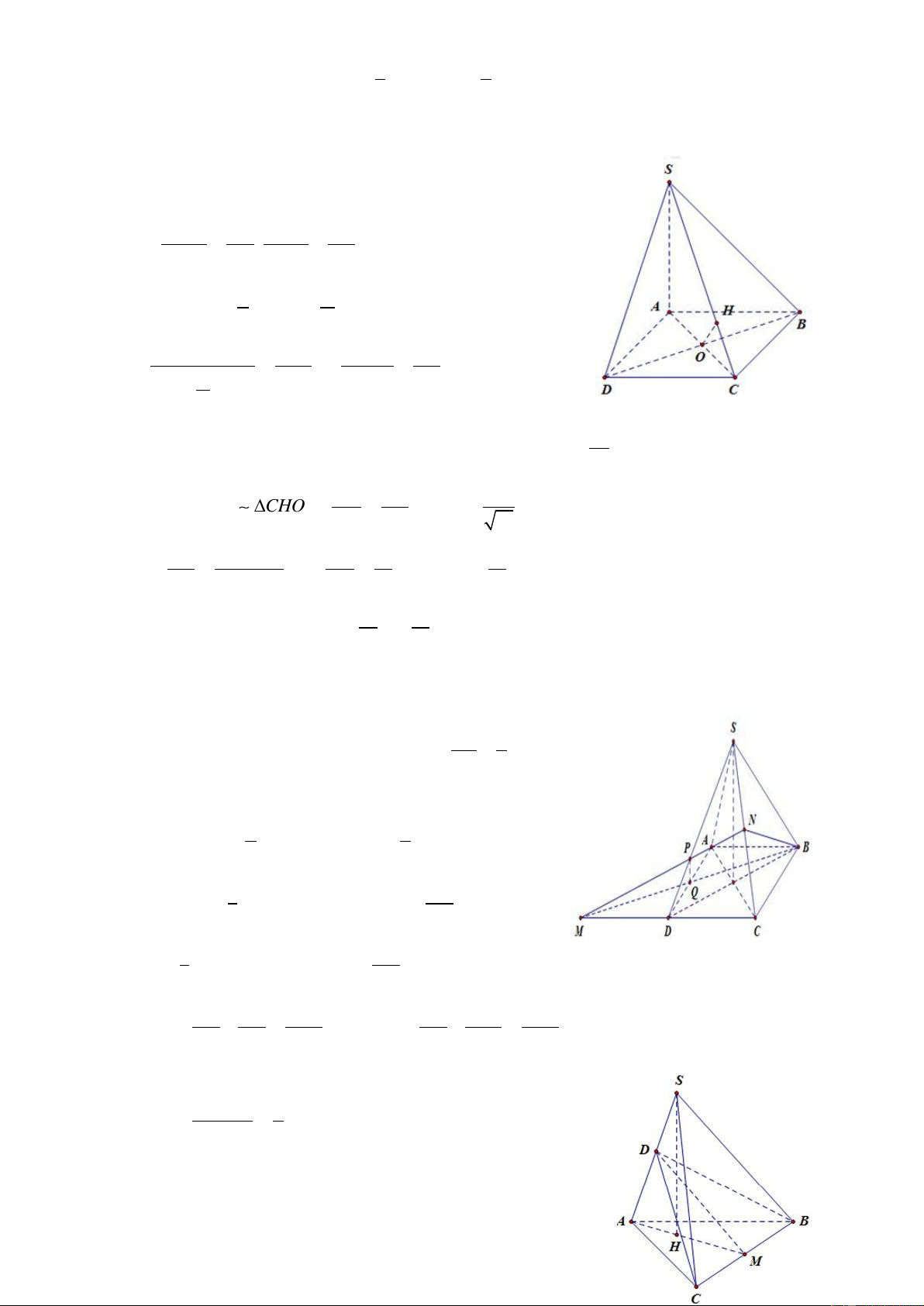
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh a và SA vuông góc với đáy
ABCD và mặt bên (SCD) hợp với đáy một góc 60. Tính thể tích hình chóp S.ABCD 3 a 3 3 2a 3 3 a 3 A. B. C. D. 3 a 3 3 3 6
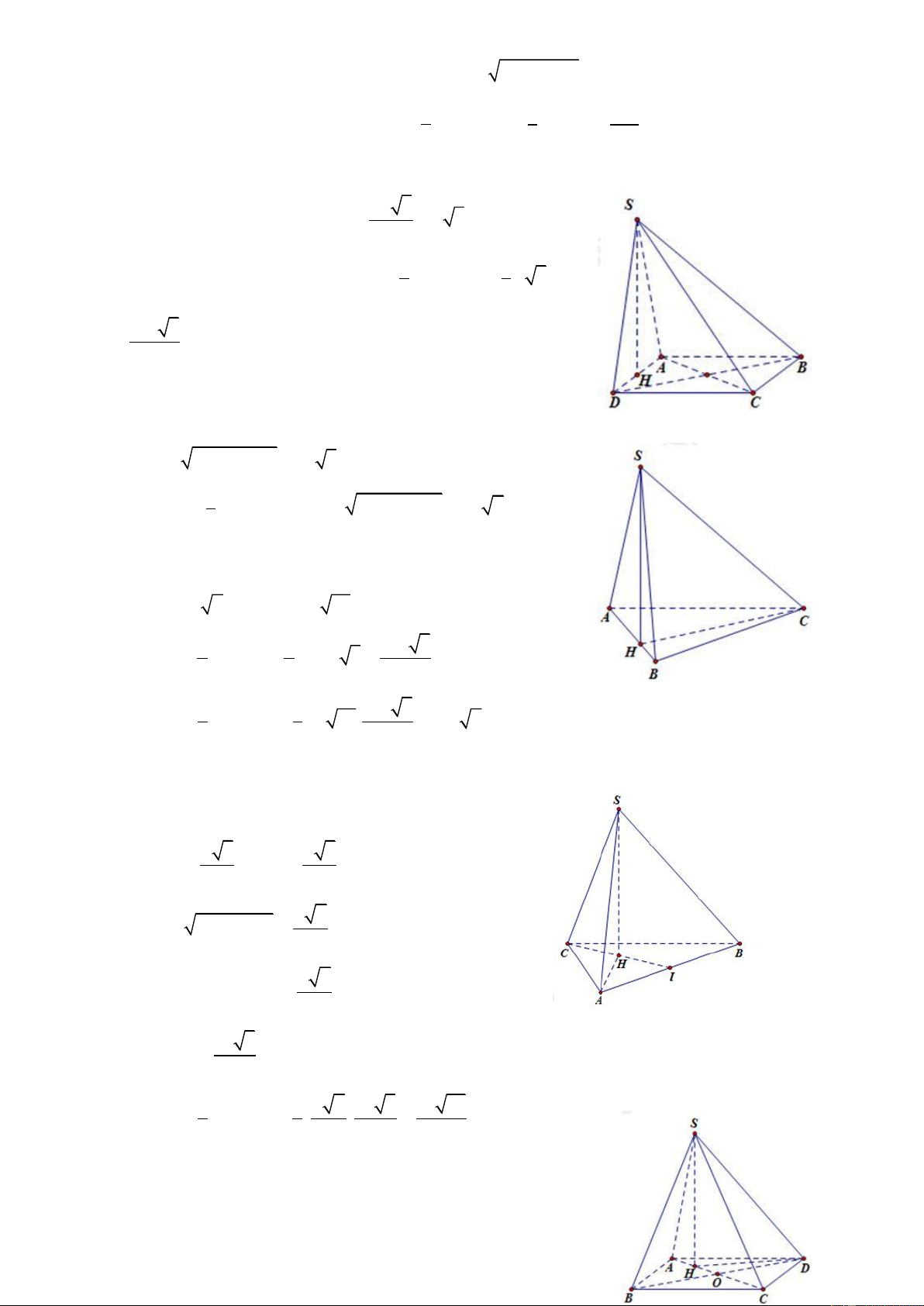
Câu 5: Cho khối chóp S.ABC có đáy ABC là tam giác cân tại A với BC = 2a, BAC  1200, biết SA 
(ABC) và mặt (SBC) hợp với đáy một góc 45. Tính thể tích khối chóp S.ABC 3 a 3 a 3 a A. B. C. 3 a 2 D. 9 3 2
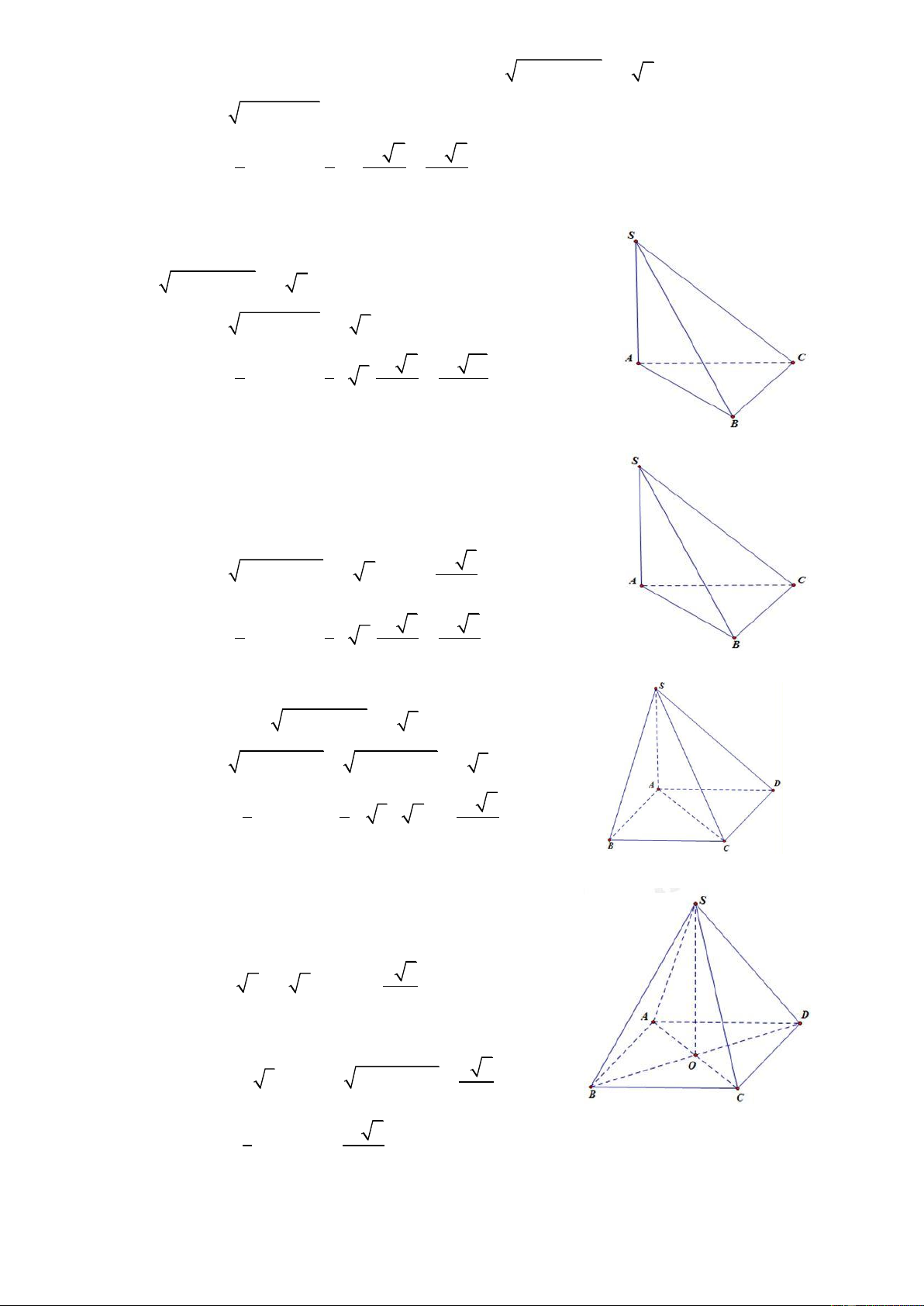
Câu 6: Cho khối chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B biết AB = BC = a, AD
= 2a, SA  (ABCD) và (SCD) hợp với đáy một góc 60. Tính thể tích khối chóp S.ABCD 3 a 6 3 a 3 3 a 6 3 a A. B. C. D. 2 3 6 2
Câu 7: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật biết rằng SA  (ABCD), SC hợp với
đáy một góc 45 và AB = 3a, BC = 4a. Tính thể tích khối chóp: 3 10a 3 A. 3 40a B. 3 10a C. D. 3 20a 3
Câu 8: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật AD = 2a, AB = a. Gọi H là trung điểm
của AD, biết SH  ( ABCD) . Tính thể tích khối chóp biết SA = a 5 . ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 3 2a 3 3 4a 3 3 4a 3 2a A. B. C. D. 3 3 3 3
Câu 9: Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A, G là trọng tâm tam giác ABC, SG 
(ABC). Biết góc giữa SM và mặt phẳng (ABC) bằng 300 (với M là trung điểm của BC), BC  2a và 9V AB = 5a. Tính
với V là thể tích khối chóp S.ABC: 3 a A. 8 2 B. 8 3 C. 8 5 D. 8 7
Câu 10: Cho hình chóp S.ABC. có đáy ABC là tam giác đều cạnh 8a, SA  ( ABC) . Biết góc giữa hai 5V
mặt phẳng (SBC) và (ABC) bằng 450. Tính
, với V là thể tích khối chóp S.ABC? 3 a A. 280 B. 320 C. 360 D. 400
Câu 11: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = 8a, SA  (ABC). Biết 9V 3
góc giữa hai mặt phẳng (SBC) và (ABC) bằng 300. Tính,
với V là thể tích khối chóp S.ABC. 3 a A. 768 B. 769 C. 770 D. 771
Câu 12: Cho hình chóp S.ABCD có đáy là hình vuông cạnh 8a, SA  (ABCD). Biết góc giữa SC và 3V
mặt phẳng (ABCD) bằng 450. Tính
, với V là thể tích khối chóp S ABC . . 3 512a A. 3 B. 3 C. 2 D. 2
Câu 13: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AC = a, SA  (ABC). Biết 3 a 6
thể tích khối chóp S.ABC là
(đơn vị thể tích). Tính góc giữa SB và mặt phẳng (ABC). 24 A. 600 B. 450 C. 300 D. 900
Câu 14: Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = a, SC = 2a 2 , SA  (ABCD).
Biết góc giữa SC và mặt phẳng (ABCD) bằng 300. Tính theo a thể tích khối chóp S.ABCD. 3 a 10 3 a 10 3 a 5 3 a 5 A. B. C. D. 3 5 10 3
Câu 15: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 8a, SA  (ABC). Biết góc giữa hai
mặt phẳng (SBC) và (ABC) bằng 450. Tính theo a thể tích khối chóp S.ABC. A. 56a3 B. 64a3 C. 72a3 D. 80a3
Câu 16: Cho hình chóp tam giác đều S.ABC có cạnh AB bằng a. Các cạnh bên SA, SB, SC tạo với
đáy một góc 600. Gọi D là giao điểm của SA với mặt phẳng qua BC và vuông góc với SA. Tính theo a
thể tích khối chóp S.DBC. 3 5a 3 5a 2 3 5a 3 3 5a 5 A. B. C. D. 96 96 96 96
Câu 17: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB là tam giác đều
và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích khối chóp S.ABCD. ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 6 5 4 3
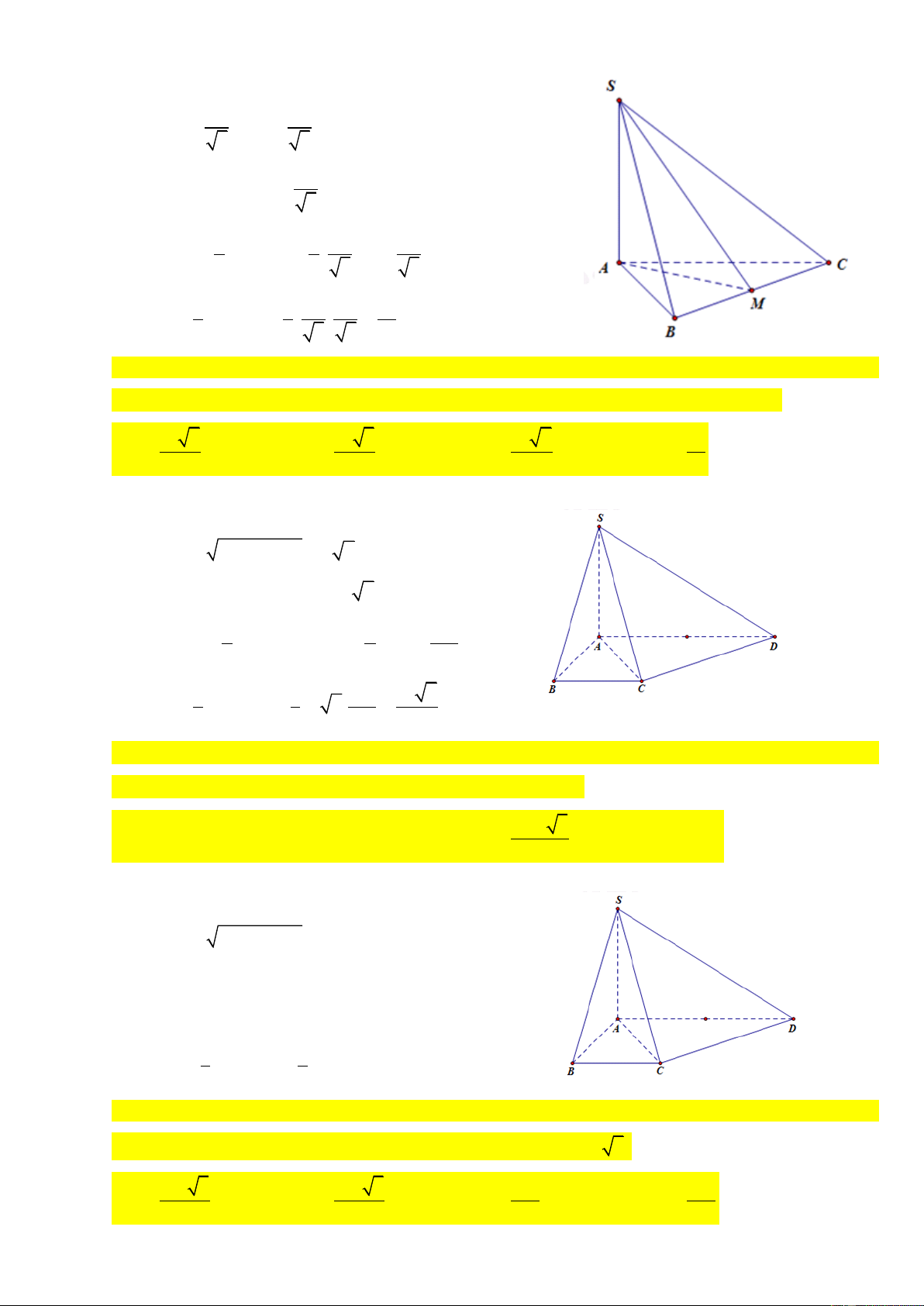
Câu 18: Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA = 2a và SA 
(ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. 50V 3 Tính
, với V là thể tích khối chóp A.BCNM 3 a A. 9 B. 10 C. 11 D. 12
Câu 19: Cho tứ diện ABCD có các cạnh AB; AC; AD đôi một vuông góc với nhau biết AC = a; AD a 21
= a 3 và khoảng cách từ A đến mặt phẳng BCD bằng
. Thể tích khối chóp đã cho là: 7 3 a 3 3 a 3 3 3a 3 3 a 3 A. B. C. D. 2 6 4 3
Câu 20: Cho khối chóp S.ABCD có đáy là hình vuông, SA  ABCD và SA=h. Biết SC tạo với đáy
một góc 450. Thể tích khối chóp đá cho tính theo h là: 3 h 2 3 h 3 h 3 3 h A. B. C. D. 6 3 6 6
Câu 21: Cho hình chóp S.ABCD có đáy là hình thoi ABCD tâm I cạnh a, SI  ABCD . Biết tam
giác ABC đều và SB = a 2 . Thể tích khối chóp đã cho là: 3 4a 6 3 a 15 3 a 15 3 4a 3 A. B. C. D. 3 4 12 3
Câu 22: Cho khối chóp S.ABCD có đáy là hình chữ nhật ABCD có AB = 1; AD  2. Hình chiếu
vuông góc của S xuống mặt đáy là trung điểm của AD. Khoảng cách từ A đến mặt phẳng SBC bằng
2 . Thể tích khối chóp đã cho là: 2 1 2 2 A. B. 1 C. D. 3 3 3
Câu 23: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D có AD  2; AB = BC  1, SA
 ABCD , đường thẳng SC tạo với đáy một góc 450. Thể tích khối chóp đã cho là: A. 2 2 B. 2 C. 2 D. 1
Câu 24: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 1, SA  ABC, khoảng cách từ A đến 21 mặt phẳng SBC bằng
. Thể tích khối chóp đã cho là 7 3 3 3 3 A. B. C. D. 2 4 3 12
Câu 25: Cho hình chóp tứ giác đều S.ABCD có đường cao bằng h và mặt bên tạo với đáy một góc
600. Thể tích khối chóp đã cho tính theo h là: ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 3 2h 3 4h 3 4h A. B. C. 3 4h D. 3 3 9
Câu 26: Cho hình chóp S.ABCD có đáy là hình chữ nhật có AB = 4, AC = 5 và SA  (ABCD biết
mặt phẳng SCD tạo với đáy một góc 600. Thể tích khối chóp đã cho là: A. 12 3 B. 4 3 C. 6 3 D. 20 3
Câu 27. Cho hình chóp tam giác đều S.ABC có đáy là tam giác đều cạnh a 3 , góc giữa SC và mặt phẳng (ABC) bằng 0
60 . Tính theo a thể tích khối chóp S.ABC 3 3a 3 a 3 3a 3 a A. B. C. D. 4 4 5 5
Câu 28. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a , cạnh bên bằng 2 a . Biết khoảng a 3 12V
cách từ A đến mặt phẳng (SBC) bằng . Tính
, với V là thể tích khối chóp S.ABC 6 3 a A. 10 B. 11 C. 10 D. 11
Câu 29. Cho hình chóp tam giác đều S.ABC có đáy là tam giác đều cạnh a , góc giữa mặt bên và mặt đáy bằng 0
45 . Tính theo a thể tích khối chóp S.ABC 3 a 3 3 a 3 3 a 3 a A. B. C. D. 6 8 6 8
Câu 30. Cho hình chóp tam giác đều S.ABC có đường cao SH bằng h, góc hợp với SH với một mặt bên bằng 0
30 . Tính theo h thể tích khối chóp S.ABC 3 h 3 3 h 3 3 h 2 3 h A. B. C. D. 3 9 9 2
Câu 31. Cho hình chóp đều tam giác S.ABC có đáy là tam giác đều cạnh a 3 , góc giữa hai mặt
phẳng (SAB) và (ABC) bằng 0
45 . Tính theo a thể tích khối chóp S.ABC 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 6 8 4 2
Câu 32. Cho hình chóp tứ giác đều S.ABCD có đường cao SH bằng h, góc ở đỉnh của mặt bên bằng 0 3V sin 30 0 60 . Tính
, với V là thể tích khối chóp S.ABCD 3 h A. 3 B. 3 C. 2 D. 1
Câu 33. Cho hình chóp tứ giác đều, mặt bên hợp với mặt đáy một góc 0
45 và khoảng cách từ chân
đường cao của hình chóp đến các mặt bên bằng a . Tính theo a thể tích khối chóp. 3 8a 3 3 a 3 3 8a 2 3 a 2 A. B. C. D. 3 3 3 3
Câu 34. Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh 0
a . Biết thể tích khối chóp S.ABC là 3 a 3 V
. Tính góc giữa SA và mặt phẳng (ABC) 36 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 A. 0 20 B. 0 30 C. 0 45 D. 0 60
Câu 35. Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a 3 , khoảng cách từ A đến mặt 3a 2 phẳng (SBC) bằng
. Tính theo a thể tích khối chóp S.ABC 4 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 6 8 4 2
Câu 36. Cho hình chóp tam giác đều S.ABC với SA  2a, AB a . Gọi H là hình chiếu vuông góc của
A lên SC. Thể tích khối chóp S.ABH là: 3 7a 11 3 3 11a 3 3 7a 3 3 7a A. B. C. D. 96 87 39 11
Câu 37. Cho hình chóp tam giác đều S.ABC có cạnh bên bằng a và nghiêng đều với đáy ABC một góc 0
60 . Thể tích khối chóp S.ABC là: 3 a 3 3a 3 3a 3 11a A. B. C. D. 6 32 16 21
Câu 38. Cho hình chóp tứ giác đều có mặt bên hợp với đáy một góc 0
45 và khoảng cách từ chân
đường cao của hình chóp đến các mặt bằng a . Thể tích khối chóp đó là : 3 a 2 3 a 2 3 8a 2 3 3a 3 A. B. C. D. 3 6 3 2
Câu 39. Cho hình chóp đều S.ABCD có cạnh đáy bằng a , góc giữa mặt bên với đáy bằng 0 45 . Gọi
M , N, P lần lượt là trung điểm của S ,
A SB,CD . Thể tích khối tứ diện AMNP là: 3 a 3 a 3 a 3 a A. B. C. D. 16 24 6 48
Câu 40. Cho hình chóp tứ giác đều S.ABCD, đáy là hình vuông cạnh a , cạnh bên tạo với đáy một góc 0
60 . Gọi M là trung điểm của SC. Mặt phẳng đi qua AM và song song với BD, cắt SB tại P và cắt SD 18V
tại Q. Thể tích khối chóp S.AMNQ là V. Tỉ số là: 3 a A. 2 B. 6 C. 3 D. 1
Câu 41. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2 6 cm, đường cao SO  1cm . Gọi
M, N lần lượt là trung điểm AC, AB. Thể tích khói chóp S.AMN tính bằng 3 cm là: 2 5 3 A. B. 1 C. D. 2 2 2
Câu 42. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a . Thể tích khối chóp đó là : 3 a 3 3 a 3 3 a 3 3 a 2 A. B. C. D. 3 2 6 6
Câu 43. Cho hình chóp tam giác đều S.ABC có cạnh dáy bằng a 3 và cạnh bên bằng 2a . Thể tích
khối chóp S.ABC theo a là: ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 3 a 3 3 a 3 3 a 3 3 3a A. B. C. D. 6 3 4 4
Câu 44. Cho hình chóp tam giác đều S.ABC có cạnh bên bằng a hợp với đáy một góc 0 60 . Thể tính khối chóp S.ABC là: 3 3a 3 a 3 3a 3 a A. B. C. D. 16 6 32 12
Câu 45. Cho hình chóp tam giác đều S.ABC có cạnh bên bằng a , góc giữa mặt bên với mặt đáy là 0
45 . Thể tích khối chóp S.ABC là: 3 a 3 3a 3 15a 3 a A. B. C. D. 12 5 25 16
Câu 46. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , 0
ASB  60 . Thể tích khối chóp là: 3 a 3 3 a 2 3 a 2 3 a 3 A. B. C. D. 4 6 3 3
Câu 47. Cho hình chóp tứ giác đều có mặt bên hợp với đáy một góc 0
45 và khoảng cách từ chân
đường cao của hình chóp đến mặt bên bằng a . Thể tích khối chóp đó là: 3 a 3 3 a 3 3 a 3 3 8a 2 A. B. C. D. 4 6 9 3
Câu 48. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a, AD  2a , cạnh SA
vuông góc với mặt phẳng (ABCD). Tính độ dài đoạn SA để khoảng cách từ D đến mặt phẳng (SBM) 2a bằng
với M là trung diểm của đoạn CD. 33 A. a B. 2a C. 3a D. 4a 12V Câu 49. Tính
, với V là thể tích khối chóp tứ diện đều có cạnh bằng a . 3 a A. 3 B. 3 C. 2 D. 2
Câu 50. Cho tứ diện ABCD với M,N lần lượt là trung điểm của AB, AC. Tính tỉ lệ thể tích của khối tứ diện AMND và ABCD 1 1 2 A. B. 1 C. D. 4 2 5
Câu 51. Cho khối chóp S.ABCD có đáy là hình bình hành, M là trung điểm của CD, I là giao điểm
của AC và BM. Tính tỷ số thể tích (theo thứ tự) các khối chóp S.ICM và S.ABCD 1 1 1 1 A. B. C. D. 2 4 2 12
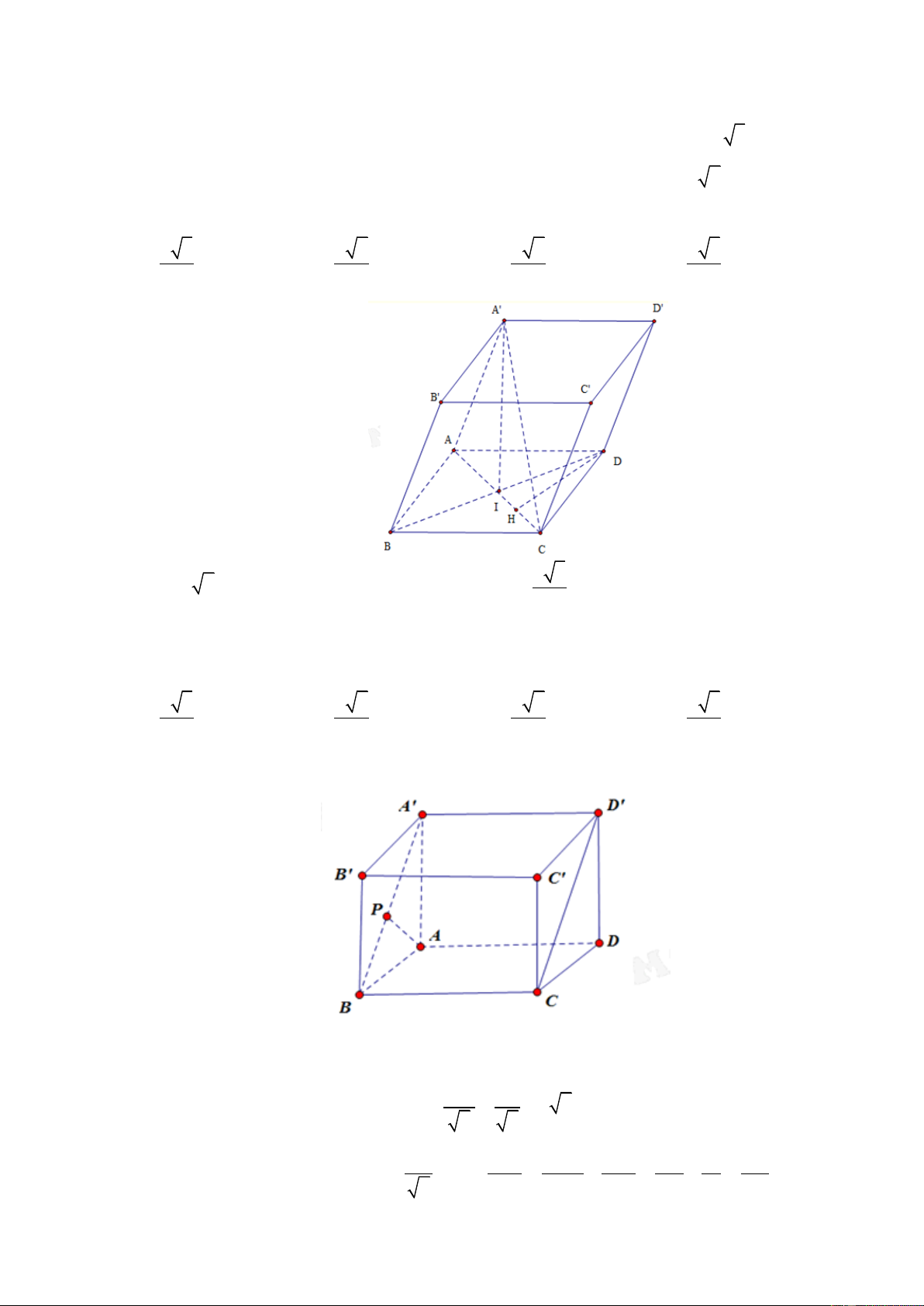
Câu 52. Cho khối chóp S.ABCD có đáy là hình bình hành, gọi B ' và D ' theo thứ tự là trung điểm các
cạnh SB, SD. Mặt phẳng (AB’D’) cắt cạnh SC tại C’. Tính tỷ số thể tích của hai khối chóp được chia
ra bởi mặt phẳng (AB’D’) 1 1 1 1 A. B. C. D. 2 12 5 6 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 53. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B,
AB BC a, AD  2a , cạnh SA vuông góc với phặt phẳng đáy và SA  2a . Gọi M,N lần lượt là
trung điểm của SA, SD. Tính thể tích khối chóp S.BCNM theo a . 3 a 3 a A. B. C. 3 a D. 3 2a 3 2
Câu 54. Cho tứ diện ABCD có thể tích bằng V. Gọi B’ và D’ lần lượt là trung điểm của cạnh AB và
AD. Mặt phẳng (CB’D’) chia khối tứ diện thành hai phần. Tính theo V thể tích khối chóp C.B’D’DB 3V V V 3V A. B. C. D. 2 4 2 4
Câu 55. Cho hình chóp tứ giác đều có diện tích đáy bằng 4 và diện tích mặt bên bằng 2 . Tính thể tích khối chóp S.ABCD 4 4 3 4 2 A. B. 4 C. D. 3 3 3
Câu 56. Cho hình chóp S.ABCD có đáy là hình thoi tâm với 0
BAD  120 và BD a . Cạnh bên SA
vuông góc với đáy. Góc giữa mặt (SBC) và đáy bằng 0
60 . Mặt phẳng (P) đi qua BD và vuông góc với
cạnh SC. Tính tỉ số thể tích giữa hai phần của hình chóp do mặt phẳng (P) tạo ra khi cắt hình chóp. A. 10 B. 11 C. 12 D. 13
Câu 57. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , cạnh bên hợp với đáy góc 0 60 .
Gọi M là điểm đối xứng với C qua D và N là trung điểm của SC. Tính tỉ số thể tích giữa hai phần của
hình chóp do mặt phẳng (BMN) tạo ra khi cắt hình chóp. 5 5 5 5 A. B. C. D. 7 8 9 11
Câu 58. Cho hình chóp tứ giác đều S.ABC có cạnh đáy bằng a , cạnh bên hợp với đáy góc 0 60 . Mặt
phẳng (P) qua BC và vuông góc với SA. SA cắt (P) tại D. Tính tỉ số thể tích giữa hai khối chóp S.BDC và S.ABC 5 5 5 5 A. B. C. D. 7 8 9 11
Câu 59. Cho tứ diện ABCD có thể tích bằng V. Gọi B’ và D’ lần lượt là trung điểm của cạnh AB và
AD. Mặt phẳng (CB’D’) chia khối tứ diện thành hai phần. Tính theo V thể tích khối chóp C.AB’D’ 3V V V 3V A. B. C. D. 2 4 2 4
Câu 60. Cho tứ diện ABCD có thể tích bằng V. Gọi B’ và D’ lần lượt là trung điểm của cạnh AB và
AD. Mặt phẳng (CB’D’) chia khối tứ diện thành hai phần. Tính tỉ số thể tích hai phần đó. 1 1 1 1 A. B. C. D. 6 9 12 3
Câu 61. Cho hình chóp S.ABC có các cạnh lần lượt là SA  ; a SB  ;
b SC c . Trên S , A SB, SC lấy các điể 1
m M,N,P sao cho SM  1; SN  2; SP
. Tỷ số thể tích giữa khối chóp S.ABC và S.MNP là: 2 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 1 abc 3 A. B. C. abc D. abc 3 abc
Câu 62. Cho hình chóp tam giác S.ABC và một điểm M nằm trong tam giác ABC. Đường thẳng qua
M song song với SA cắt mặt phẳng (BCS) tại A’. Tỷ số thể tích giữa khối chóp M.BCS và S.ABC là: MA ' MA ' MA ' SM A. B. C. D. SM SA ' SA SA '
Câu 63. Cho hình chóp S.ABCD có đáy là hình vuông ABCD, SA   ABCD . Mặt phẳng qua AB cắt SM V 11
SC và SD lần lượt tại M và N sao cho
x . Tìm x biết S.ABMN SC V 200 S . ABCD A. 0,25 B. 0,2 C. 0,3 D. 0,1
Câu 64. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA   ABCD và SA  2a . Gọi
M,N,P lần lượt là trung điểm của SB,BC và CD. Thể tích khối chóp C.MNP là: 3 a 3 a 3 a 3 a A. B. C. D. 32 12 16 24
Câu 65. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA   ABC  và SA  2a . Gọi
M , N, P lần lượt là trung điểm của SB, BC và SC. Thể tích khối chóp A.MNP là: 2 a 3 2 a 3 2 a 3 3 a A. B. C. D. 24 12 8 24
Câu 66. Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Hai mặt phẳng (SAB) và
(SAD) cùng vuông góc với đáy. Tính thể tích khối chóp S.ABCD biết rằng SC a 3 3 a 3 3 a 3 3 a A. V B. V C. 3 Va D. VS . ABCD 9 S . ABCD 3 S . ABCD S . ABCD 3
Câu 67. Cho khối chóp S.ABCD có ABCD là hình chữ nhật; AD  2 ;
a AB a . Gọi H là trung điểm
AD, biết SH vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết SA a 5 3 2a 3 3 4a 3 3 4a 3 2a A. VB. VC. VD. VS . ABCD 3 S . ABCD 3 S .ABCD 3 S .ABCD 3
Câu 68. Cho khối chóp S.ABCD có ABCD là hình vuông cạnh 2a . Gọi H là trung điểm AB, biết SH
vuông góc với mặt phẳng. Tính thể tích khối chóp S.ABCD biết tam giác SAB đều 3 2a 3 3 4a 3 3 a 3 a A. VB. VC. VD. VS . ABCD 3 S . ABCD 3 S . ABCD 6 S . ABCD 3
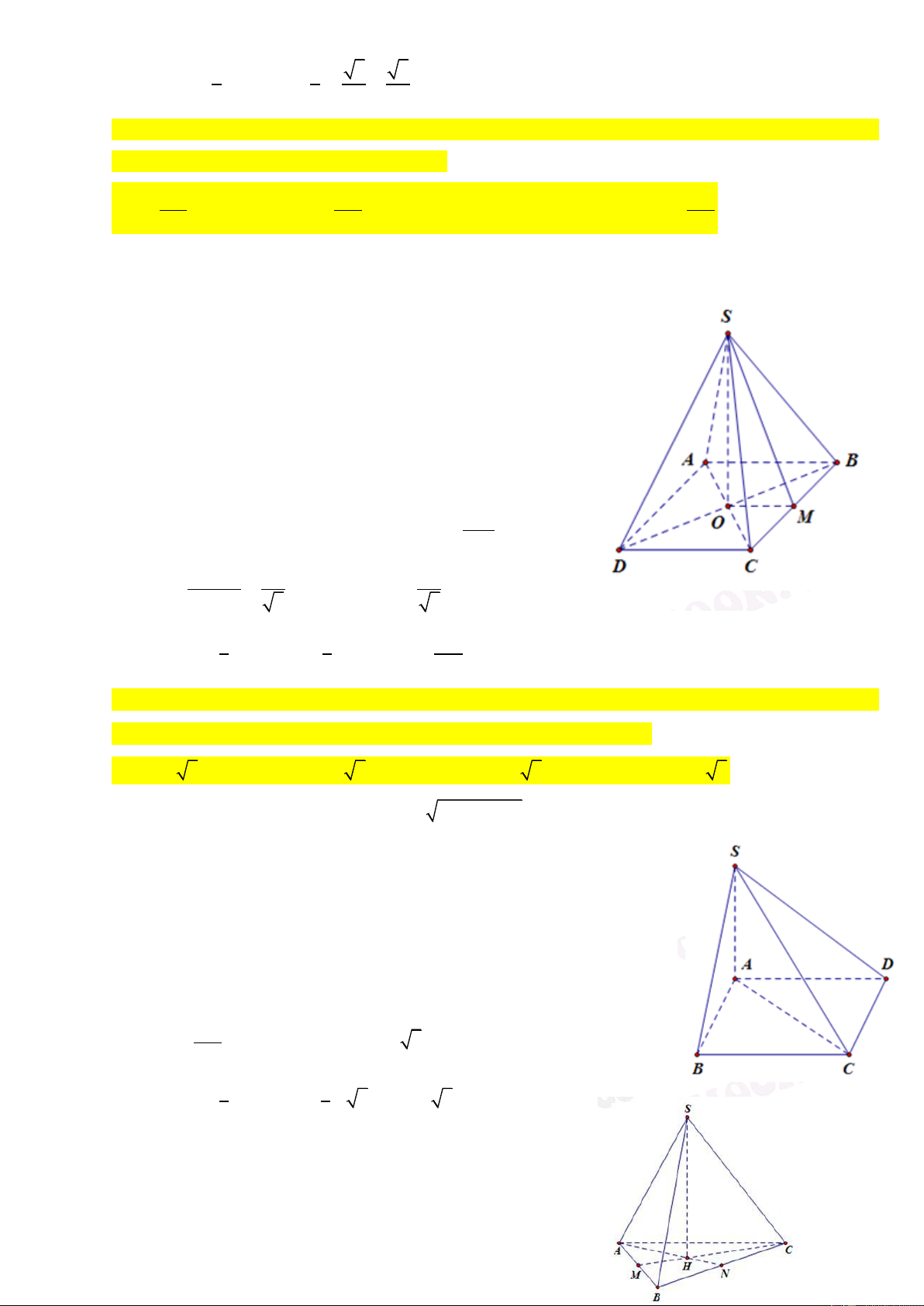
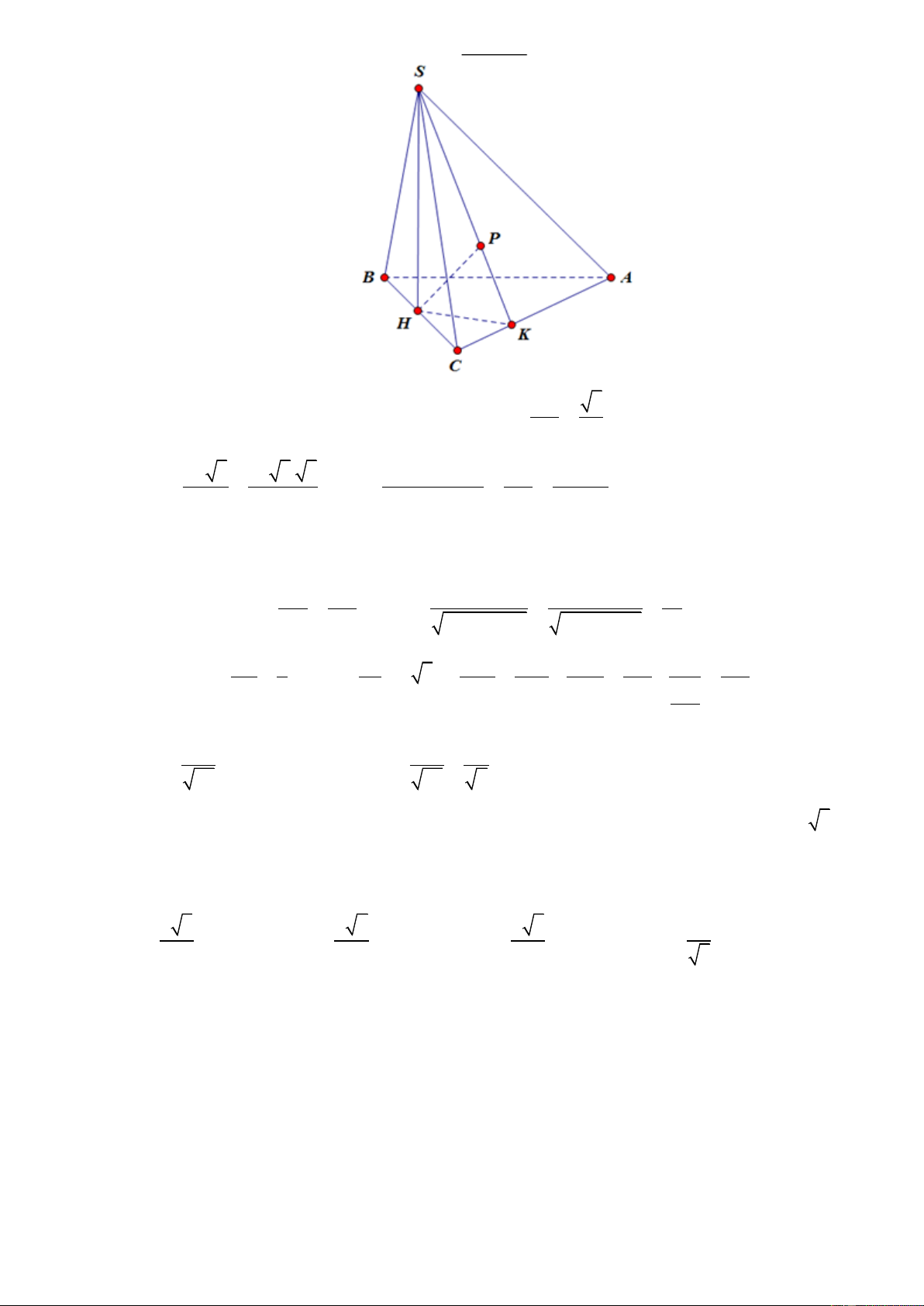
Câu 69. Cho khối chóp S.ABC có tam giác ABC vuông tại B, AB  3 ;
a AC  6a . Hình chiếu của S
trên mặt phẳng (ABC) là điểm H thuộc đoạn AB sao cho AH  2HB . Biết SC hợp với (ABC) một góc bằng 0
60 . Tính thể tích khối chóp S.ABC 3 a 21 3 a 21 A. VB. 3 V  9a 7 C. 3 Va 7 D. VS . ABC 3 S . ABC S . ABC S . ABC 6 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 70. Cho khối chóp S.ABC có đáy là tam giác đều, cạnh bằng a . Gọi I là trung điểm AB. Hình
chiếu của S trên mặt phẳng (ABC) là trung điểm H thuộc đoạn CI. Góc giữa SA và (ABC) bằng 0 45 .
Tính thể tích khối chóp S.ABC 3 a 21 3 a 7 3 a 7 3 a 21 A. VB. VC. VD. VS . ABC 16 S . ABC 48 S . ABC 36 S . ABC 48
Câu 71. Cho khối chóp S.ABCD có ABCD là hình vuông tâm O, cạnh bằng a 2 . Hình chiếu của S
trên mặt phẳng (ABCD) là trung điểm H thuộc đoạn AO. Góc giữa SD và (ABCD) bằng 0 45 . Tính
thể tích khối chóp S.ABCD 3 2a 3 a 3 3 a 5 A. V B. 3 V  2a C. V D. VS .ABCD 3 S . ABCD S . ABCD 3 S . ABCD 3
Câu 72. Cho khối chóp S.ABC có SA   ABC  ; ABC là tam giác đều cạnh a . Góc giữa mặt phẳng
SBC và ABC bằng 0
60 . Tính thể tích khối chóp S.ABC 3 a 3 3 a 3 3 a 3 a A. VB. VC. VD. VS . ABC 4 S . ABC 8 S . ABC 6 S . ABC 12
Câu 73. Cho khối chóp S.ABC có SA   ABC  ; tam giác ABC vuông tại A, biết BC  3 ; a AB a .
Góc giữa mặt phẳng (SBC) và (ABC) bằng 0
45 . Tính thể tích khối chóp S.ABC 3 a 2 3 a 2 3 4a 3 2a A. VB. VC. VD. VS . ABC 2 S . ABC 6 S .ABC 9 S .ABC 9
Câu 74. Cho khối chóp S.ABCD có ABCD là hình chữ nhật; SA   ABCD ; AC  2AB  4a . Tính
thể tích khối chóp S.ABCD biết rằng góc giữa mặt phẳng (SBC) và (ABCD) bằng 0 30 . 3 2a 3 2a 3 3 8a A. VB. 3 V  2a C. VD. VS .ABCD 3 S . ABCD S . ABCD 3 S . ABCD 3
Câu 75. Cho khối chóp S.ABC có SA   ABC  ; tam giác ABC vuông tại B, AB  ; a AC a 3 .
Tính thể tích khối chóp S.ABC biết rằng SB a 5 3 a 2 3 a 6 3 a 6 3 a 15 A. VB. VC. VD. VS . ABC 3 S . ABC 4 S . ABC 6 S . ABC 6
Câu 76. Cho khối chóp S.ABC có SA   ABC  ; tam giác ABC vuông tại B; AB  ;
a AC a 3 . Tính
thể tích khối chóp S.ABC biết rằng SB a 6 3 a 10 3 a 6 3 a 6 3 a 15 A. VB. VC. VD. VS . ABC 6 S . ABC 2 S . ABC 3 S . ABC 6
Câu 77. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a . Hai mặt phẳng (SAB) và (SAC)
cùng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết rằng SC a 3 3 2a 6 3 a 6 3 a 3 3 a 3 A. VB. VC. VD. VS .ABC 9 S . ABC 12 S . ABC 4 S . ABC 2 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 78. Cho khối chóp S.ABCD có ABCD là hình chữ nhật tâm O; AC  2AB  2a ; SA vuông góc
với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết rằng SD a 5 3 a 5 3 a 15 3 a 6 A. VB. VC. 3 Va 6 D. VS . ABCD 3 S . ABCD 3 S . ABCD S . ABCD 3
Câu 79. Cho khối chóp đều S.ABCD có cạnh đáy bằng a 3 . Tính thể tích khối chóp S.ABCD biết
mặt bên là tam giác đều 3 a 3 3 a 3 3 3a 6 3 a 6 A. VB. VC. VD. VS . ABCD 6 S . ABCD 3 S . ABCD 2 S . ABCD 2
Câu 80. Cho khối chóp đều S.ABC có cạnh đáy bằng a . Tính thể tích khối chóp S.ABC biết mặt bên là tam giác đều. 3 a 2 3 a 2 3 a 7 3 a 7 A. VB. VC. VD. VS . ABC 36 S . ABC 12 S . ABC 12 S . ABC 36
Câu 81. Cho khối chóp S.ABC có SA   ABC  ; tam giác ABC vuông tại B, AB  ;
a AC a 3 . Tính
thể tích khối chóp S.ABC biết rằng góc giữa SB và (ABC) bằng 0 30 3 a 6 3 a 6 3 a 6 3 2a 6 A. SB. SC. SD. SS . ABC 9 S . ABC 6 S . ABC 18 S . ABC 3
Câu 82. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a . Hai mặt phẳng (SAB) và (SAC)
cùng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết rằng SB hợp với đáy một góc 0 30 3 a 3 3 a 3 3 a 3 a A. VB. VC. VD. VS . ABC 6 S . ABC 12 S . ABC 4 S . ABC 12
Câu 83. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a . Hai mặt phẳng (SAB) và (SAC)
cùng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết rằng SM hợp với đáy một góc 0 60 , với M là trung điểm BC. 3 a 6 3 a 3 3 a 3 3 a 6 A. VB. VC. VD. VS . ABC 8 S . ABC 4 S . ABC 8 S . ABC 24
Câu 84. Cho khối chóp S.ABC có SA   ABC  ; tam giác ABC vuông tại A, BC  2.AB  2a . Tính
thể tích khối chóp S.ABC biết SC hợp với (ABC) một góc bằng 0 45 . 3 a 3 a 3 3 3a 3 3 a A. VB. VC. VD. VS . ABC 2 S . ABC 2 S . ABC 2 S . ABC 6
Câu 85. Cho khối chóp S.ABC có SA   ABC  ; tam giác ABC vuông tại A, BC  2AB  2a . Tính
thể tích khối chóp S.ABC biết SM hợp với đáy một góc bằng 0
60 , với M là trung điểm BC 3 a 3 a 3 3 3a 3 3 a A. VB. VC. VD. VS . ABC 2 S . ABC 6 S . ABC 2 S . ABC 6
Câu 86. Cho khối chóp S.ABCD có ABCD là hình chữ nhật tâm O; AC  2AB  2a ; SA vuông góc
với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết góc giữa SC và (ABCD) bằng 0 45 . ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 3 2a 3 3 4a 3 3 a A. V B. V C. 3 Va D. VS . ABCD 3 S . ABCD 3 S . ABCD S . ABCD 3
Câu 87. Cho khối chóp S.ABCD có ABCD là hình chữ nhật tâm O; AC  2AB  2a ; SA vuông góc
với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết góc giữa SO và (ABCD) bằng 0 60 3 2a 3 3 a 3 3 a A. VB. VC. 3 Va D. VS . ABCD 3 S . ABCD 3 S . ABCD S . ABCD 3
Câu 88. Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Hai mặt phẳng (SAB) và
(SAD) cùng vuông góc với đáy. Tính thể tích khối chóp S.ABCD biết rằng góc giữa SC và (ABCD) bằng 0 45 3 a 2 3 a 2 3 a 3 a A. VB. VC. VD. VS . ABCD 6 S . ABCD 3 S . ABCD 6 S . ABCD 3
Câu 89. Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Hai mặt phẳng (SAB) và
(SAD) cùng vuông góc với đáy. Tính thể tích khối chóp S.ABCD biết rằng góc giữa SM và (ABCD) bằng 0
60 , với M là trung điểm BC 3 a 15 3 a 15 3 a 3 a A. VB. VC. VD. VS . ABCD 6 S . ABCD 3 S . ABCD 6 S . ABCD 3
Câu 90. Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a . Gọi H là trung điểm AB, biết
SH vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết góc giữa SC và (ABCD) bằng 0 60 3 2a 15 3 4a 15 3 a 3 a A. VB. VC. VD. VS . ABCD 3 S . ABCD 3 S . ABCD 6 S . ABCD 3
Câu 91. Cho khối chóp S.ABCD có ABCD là hình chữ nhật; AD  2 ;
a AB a . Gọi H là trung điểm
AD, biết SH vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết góc giữa SD và (ABCD) bằng 0 45 3 a 3 3 2a 3 a A. VB. 3 Va 3 C. VD. VS . ABCD 2 S. ABCD S .ABCD 3 S . ABCD 3
Câu 92. Cho khối chóp S.ABCD có ABCD là hình chữ nhật. SA   ABCD ; AC  2AB  4a . Tính
thể tích khối chóp S.ABC biết rằng góc giữa mặt phẳng (SBD) và (ABCD) bằng 0 30 3 4a 3 8a 3 2a 3 3 4a 6 A. VB. VC. VD. VS .ABCD 9 S . ABCD 9 S . ABCD 3 S .ABCD 9
Câu 93. Cho khối chóp S.ABC có ABCD là hình vuông cạnh a ; SA   ABCD . Góc giữa mặt phẳng (SBD) và (ABCD) bằng 0
30 . Tính thể tích khối chóp S.ABCD 3 a 3 3 a 2 3 a 6 3 a 6 A. VB. VC. VD. VS . ABCD 3 S . ABCD 3 S . ABCD 18 S . ABCD 9
Câu 94. Cho khối chóp S.ABC có ABCD là hình thoi, cạnh bằng a 3 ; SA   ABCD; 0 BAD  120 .
Tính thể tích khối chóp S.ABC biết rằng góc giữa mặt phẳng (SBD) và (ABCD) bằng 0 60 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 3 3a 3 3 a 3 3 a 6 3 a 6 A. VB. VC. VD. VS . ABCD 8 S . ABCD 6 S . ABCD 8 S . ABCD 4
Câu 95. Cho khối chóp S.ABCD có ABCD là hình thoi, cạnh bằng a 3; SA   ABCD ; 0 BAC  120 .
Tính thể tích khối chóp S.ABCD biết rằng góc giữa mặt phẳng (SCD) và (ABCD) bằng 0 30 3 a 3 3 3a 3 3 3a 3 3a A. VB. VC. VD. VS . ABCD 4 S . ABCD 4 S . ABCD 8 S . ABCD 4
Câu 96. Cho khối chóp S.ABC có ABCD là hình thoi, AC  6 ;
a BD  8a . Hai mặt phẳng SAC  và
(SBD) cùng vuông góc với đáy. Góc giữa mặt phẳng (SBC) và (ABCD) bằng 0 30 . Tính thể tích khối chóp S.ABCD 3 32a 3 3 16a 3 3 32a 3 32a A. VB. VC. VD. VS . ABCD 5 S . ABCD 5 S .ABCD 5 S .ABCD 15
Câu 97. Cho khối chóp đều S.ABC D có cạnh đáy bằng 2a 2 . Mặt bên hợp với đáy một góc 0 45 .
Tính thể tích khối chóp S.ABCD 3 a 3 2a 3 8a 2 A. 3 V  8a 2 B. VC. VD. VS . ABCD S . ABCD 3 S .ABCD 3 S . ABCD 3
Câu 98. Cho khối chóp đều S.ABCD có cạnh đáy bằng 2a . Mặt bên hợp với đáy một góc 0 60 . Tính
thể tích khối chóp S.ABC 3 a 3 3 2a 2 3 4a 3 2a A. VB. VC. VD. VS . ABC 3 S .ABC 3 S .ABC 9 S .ABC 9
Câu 99. Cho khối chóp S.ABC có ABCD là hình chữ nhật; AB  8 ;
a AD  6a . Gọi H là trung điểm
AB, biết SH vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết rằng góc giữa mặt
phẳng (SCD) và (ABCD) bằng 0 60 A. 3 V  32a 3 B. 3 V  32a C. 3 V  96a D. 3 V  96a 3 S . ABCD S. ABCD S. ABCD S . ABCD
Câu 100. Cho khối chóp S.ABC có đáy ABCD là hình chữ nhật; AB  8 ;
a AD  6a . Gọi H là trung
điểm AB, biết SH vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABC biết rằng góc giữa
mặt phẳng (SBD) và (ABCD) bằng 0 60 3 192a 5 3 28a 5 A. 3 V  56a B. VC. VD. 3 V  28a S. ABCD S .ABCD 5 S . ABCD 5 S. ABCD
Câu 101. Cho khối chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng 2a . Hình chiếu của
S trên mặt phẳng (ABCD) là trung điểm H thuộc đoạn AO. Góc giữa mặt phẳng (SCD) và (ABCD) bằng 0
60 . Tính thể tích khối chóp S.ABCD 3 a A. 3 V  2a B. VC. 3 Va 3 D. 3 V  2a 3 S . ABCD S . ABCD 3 S. ABCD S . ABCD
Câu 102. Cho khối chóp S.ABCD có ABCD là hình vuông cạnh bằng 2a ; SAD là tam giác cân tại S
và nằm trong mặt phẳng vuông góc với đáy. Gọi M là trung điểm của CD. Góc giữa hai mặt phẳng (SBM) và (ABCD) bằng 0
60 . Tính thể tích khối chóp S.ABCD. ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 3 4a 15 3 2a 15 A. 3 V  6a 3 B. V C. V D. 3 V  2a 3 S . ABCD S . ABCD 5 S . ABCD 5 S . ABCD
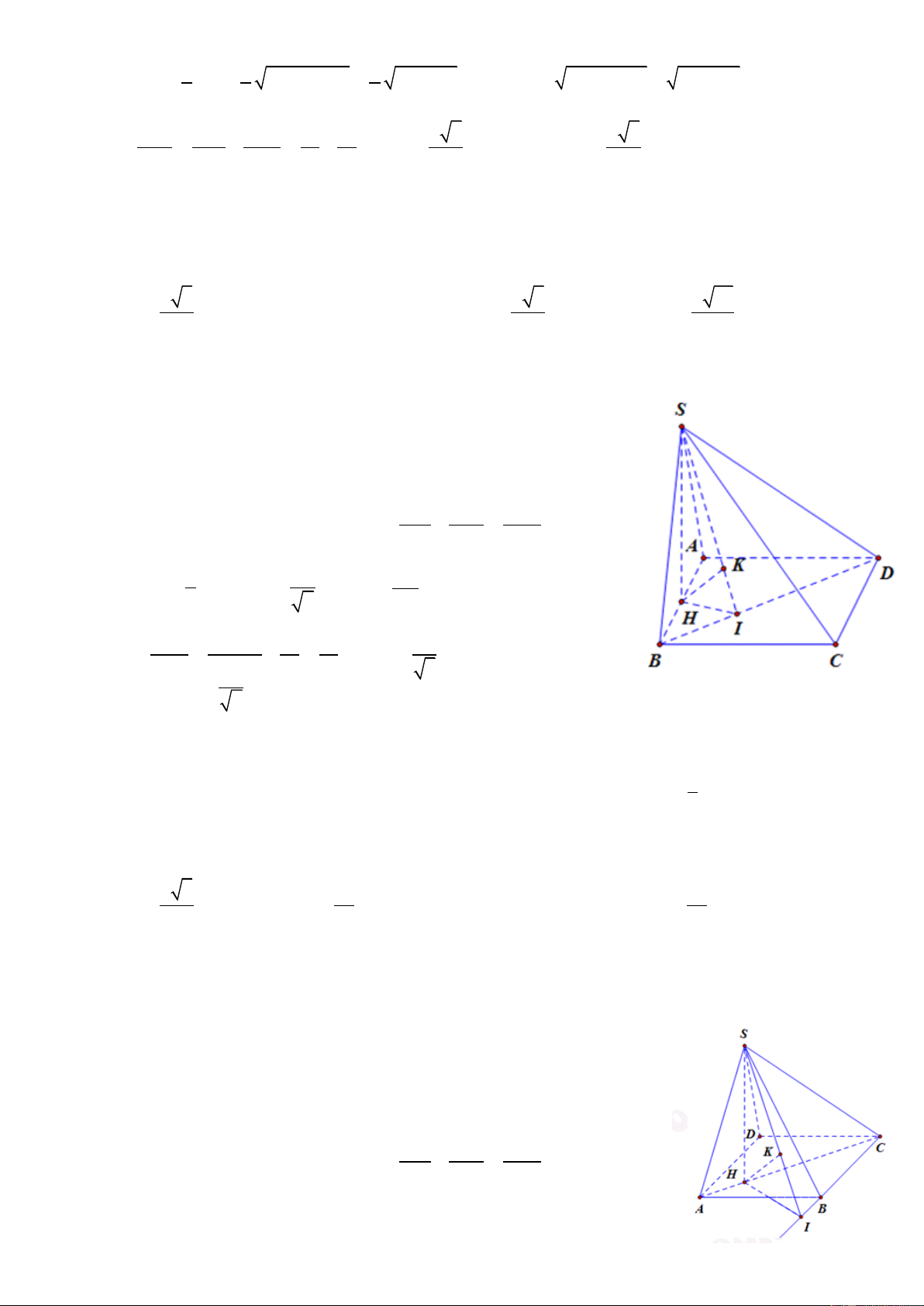
Câu 103. Cho khối chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D;
AB AD  2 ;
a CD a . Góc giữa hai mặt phẳng (SBC) và (ABCD) bằng 0
60 . Gọi I là trung điểm của
AD . Biết 2 mặt phẳng (SBI) và (SCI) cùng vuông góc với mặt phẳng (ABCD). Tính thể tích khối chóp S.ABCD. 3 6a 15 3 3a 15 A. 3 V  6a 3 B. VC. VD. 3 V  6a S . ABCD S . ABCD 5 S . ABCD 5 S . ABCD
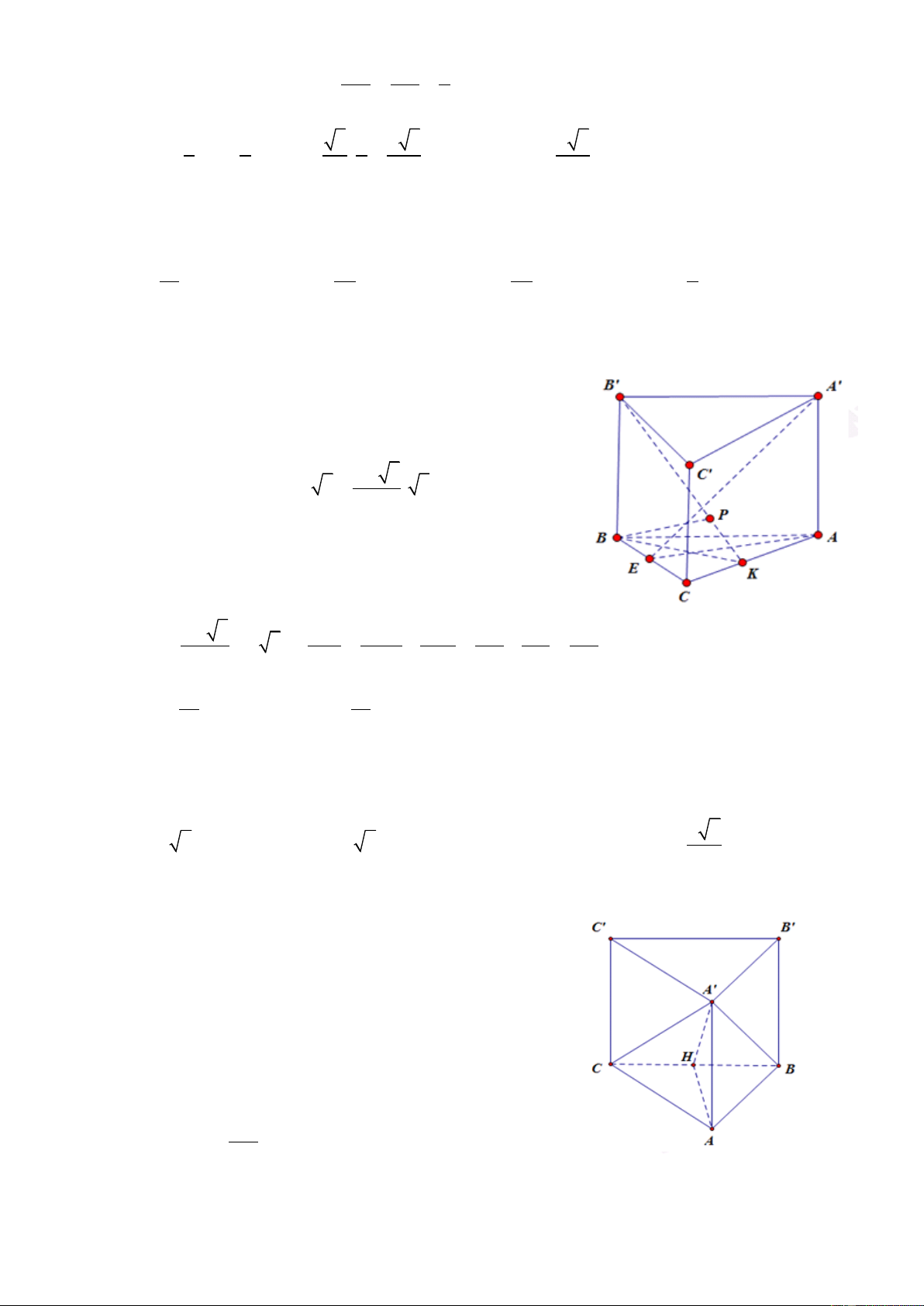
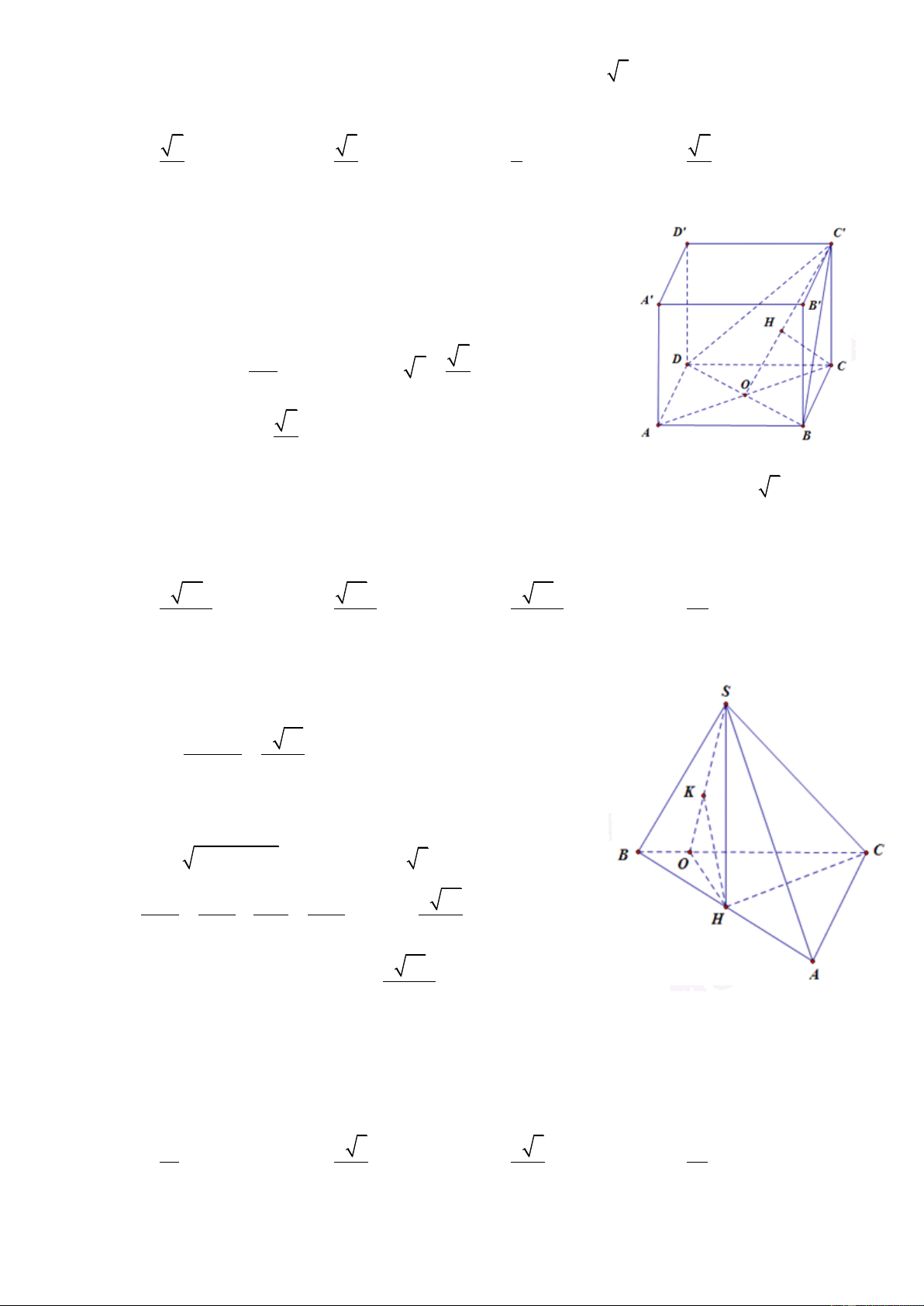
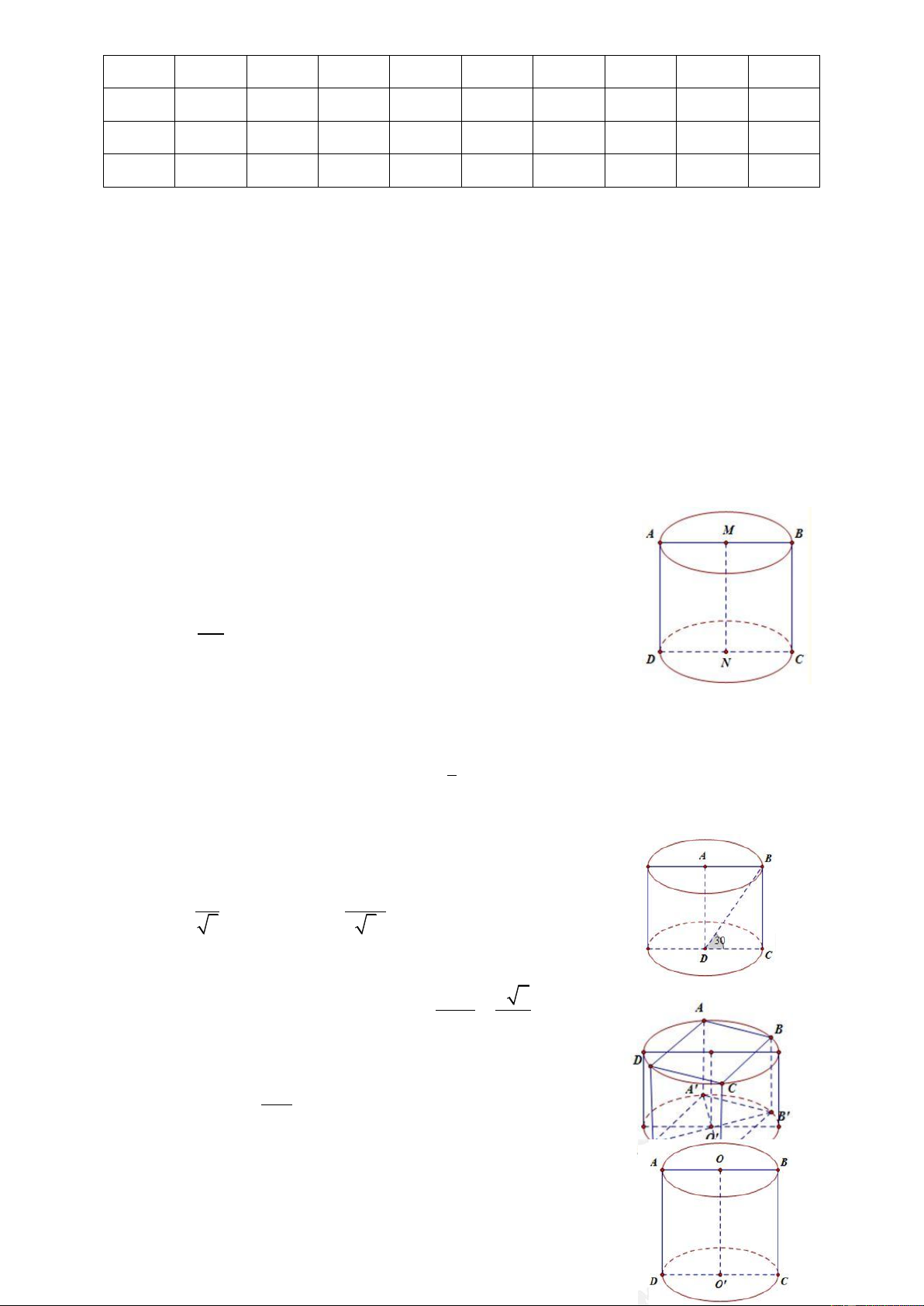
Câu 104. Cho khối lăng trụ đứng AB .
C A B C có đáy ABC là tam giác vuông cân tại A, cạnh 1 1 1
BC a 2 . Tính thể tích khối lăng trụ AB .
C A B C biết A B  3a 1 1 1 1 3 a 2 3 a 3 A.V B. 3 Va 2 C. VD. 3 V  6a 3 ABC. ABC. A BC ABC. A BC 1 A ! B 1 C 3 1 ! 1 ABC. 1 A ! B 1 C 2 1 ! 1
Câu 105. Cho khối lăng trụ đứng AB .
C A B C có đáy ABC là tam giác vuông cân tại A, cạnh 1 1 1
BC a 2 . Tính thể tích khối lăng trụ AB .
C A B C biết A C tạo với đáy một góc 0 60 . 1 1 1 1 3 3a 3 3 a 3 A.VB. 3 V
 3a 3 C. VD. 3 V  6a 3 ABC. ABC. A BC ABC. A BC 1 A ! B 1 C 2 1 ! 1 ABC. 1 A ! B 1 C 2 1 ! 1
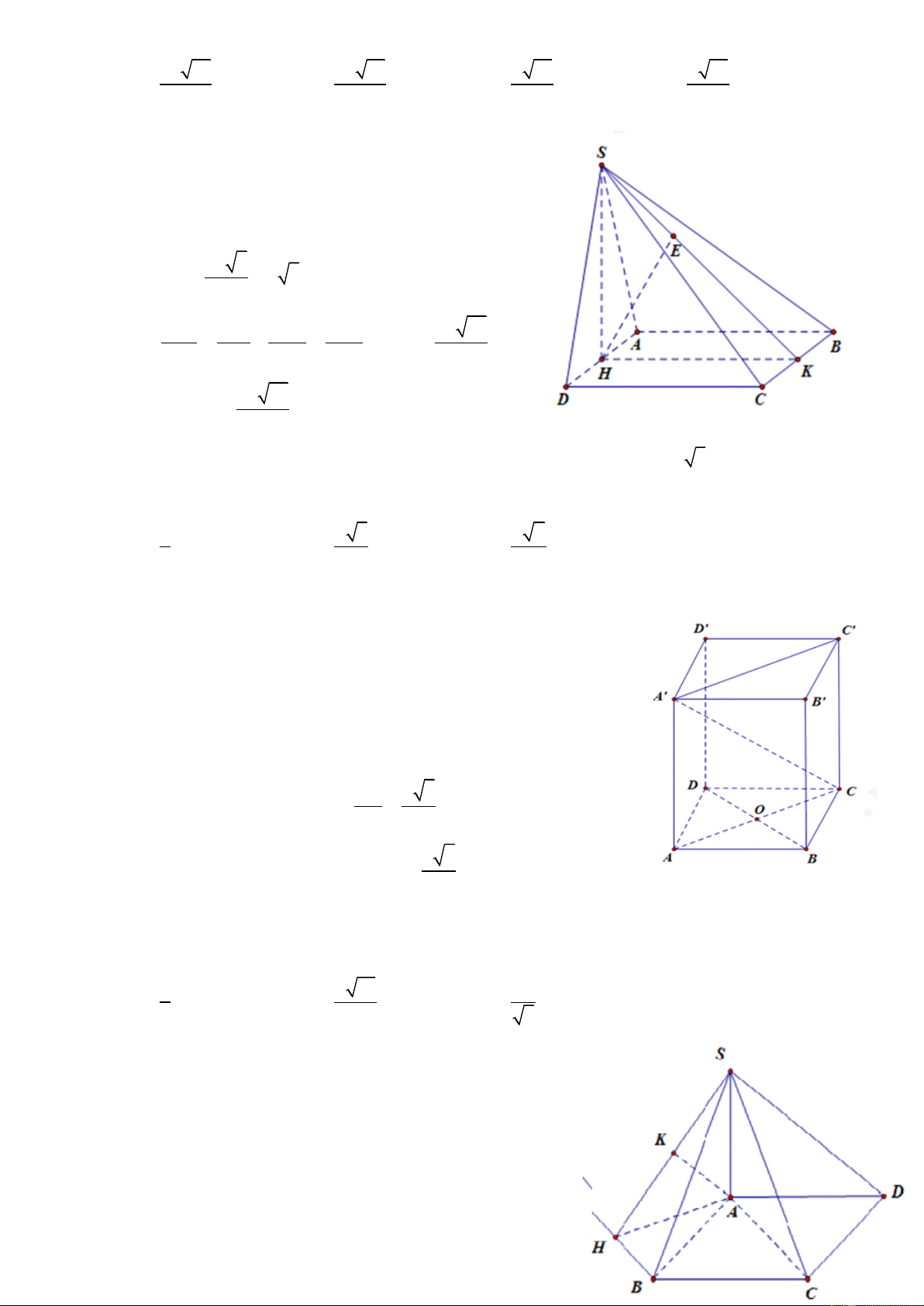
Câu 106. Cho khối chóp S.ABCD có ABCD là hình chữ nhật AD  2 ;
a AB a . Gọi H là trung điểm
AD, biết SH vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết góc giữa SC và (ABCD) bằng 0 60 . 3 4a 6 3 2a 6 3 a 3 a A. VB. VC. VD. VS .ABCD 3 S .ABCD 3 S . ABCD 6 S . ABCD 3
Câu 107. Cho khối chóp đều S.ABCD có cạnh đáy bằng a 3 . Tính thể tích khối chóp S.ABCD biết
cạnh bên bằng 2a . 3 a 10 3 a 10 3 a 3 3 a 12 A. V B. V C. V D. VS . ABCD 2 S . ABCD 4 S . ABCD 6 S . ABCD 3
Câu 108. Cho khối chóp đều S.ABCD có cạnh đáy bằng . Tính thể tích khối chóp S.ABCD biết góc
giữa cạnh bên và mặt đáy bằng 0 60 . 3 3a 2 3 3a 2 3 3a 6 3 a 6 A.VB. VC. VD. VS . ABCD 2 S . ABCD 4 S . ABCD 2 S . ABCD 3
Câu 109. Cho khối chóp S.ABC có cạnh đáy bằng a . Tính thể tích khối chóp S.ABC biết cạnh bên bằng 2a . 3 a 11 3 a 3 3 a 3 a A. V B. V C. V D. VS . ABC 12 S . ABCD 6 S . ABCD 12 S . ABCD 4
Câu 110. Cho khối chóp đều S.ABC có cạnh đáy bằng a . Tính thể tích khối chóp S.ABC biết góc
giữa cạnh bên và mặt đáy bằng 0 45 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 3 a 3 3 a 3 3 a 3 a A. VB. VC. VD. VS . ABC 12 S . ABCD 6 S . ABCD 12 S . ABCD 4
Câu 111. Cho khối chóp đều S.ABC có cạnh đáy bằng a 3 . Tính thể tích khối chóp S.ABC biết mặt
bên là tam giác vuông cân ? 3 a 21 3 a 21 3 a 6 3 a 6 A. VB. VC. VD. VS . ABC 36 S . ABCD 12 S . ABCD 8 S . ABCD 4
Câu 112. Cho khối chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B. Hai mặt phẳng
(SAB) và (SAD) cùng vuông góc với đáy. Biết AD  2BC  2a và BD a 5 . Tính thể tích khối
chóp S.ABCD biết rằng góc giữa SB và (ABCD) bằng 0 30 3 a 3 3 4a 21 3 2a 21 3 a 3 A. VB. VC. VD. VS . ABCD 6 S . ABCD 9 S . ABCD 3 S . ABCD 8
Câu 113. Cho khối chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B. Hai mặt phẳng
(SAB) và (SAD) cùng vuông góc với đáy. Biết AD  2BC  2a và BD a 5 .Tính thể tích khối chóp
S.ABCD biết rằng góc giữa SO và (ABCD) bằng 0
45 , với O là giao điểm của AC và BD 3 2a 2 3 a 2 3 a 3 A. 3 Va 3 B. VC. VD. VS. ABCD S .ABCD 3 S . ABCD 3 S . ABCD 2 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 Đáp án 01-A 02-B 03-A 04-A 05-B 06-A 07-D 08-C 09-B 10-B 11-A 12-C 13-A 14-A 15-B 16-C 17-A 18-A 19-B 20-D 21-C 22-C 23-C 24-D 25-D 26-A 27A 28C 29C 30A 31B 32D 33A 34B 35B 36A 37B 38C 39D 40A 41D 42D 43D 44C 45C 46B 47D 48A 49C 50. A 51. D 52. C 53. A 54. D 55. A 56. C 57. A 58. B 59.B 60. D 61. C 62. C 63. D 64. D 65. A 66. D 67. C 68. B 69. B 70. D 71. D 72. B 73. C 74. D 75. A 76. A 77. B 78. D 79. D 80. B 81. C 82. D 83. C 84. A 85. A 86. A 87. C 88. B 89. A 90. B 91. C 92. C 93. C 94. A 95. C 96. A 97. D 98. A 99. D 100. B 101. D 102. B 103. C 104. B 105. C 106. B 107. A 108. A 109. A 110. C 111. C 112. A 113. C
LỜI GIẢI CHI TIẾT Hướng dẫn giải
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a. Cạnh bên SA vuông góc
với mặt phẳng đáy, SC tạo với mặt phẳng đáy một góc 45 và SC = 2 a 2 . Thể tích khối chóp S.ABCD bằng: 3 2a 3 a 2 3 3 a 3 a 3 A. B. C. D. 3 3 3 3
HD: Ta có SC ABCD 0 ,  SCA  45 2a 2
SA AC   2a 2 Ta có 2 2 BC
AC AB a 3 2  SA . B BC a 3 ABCD 3 1 1 2a 2  VS . A S  .2 . a a 3  S . ABCD 3 ABCD 3 3
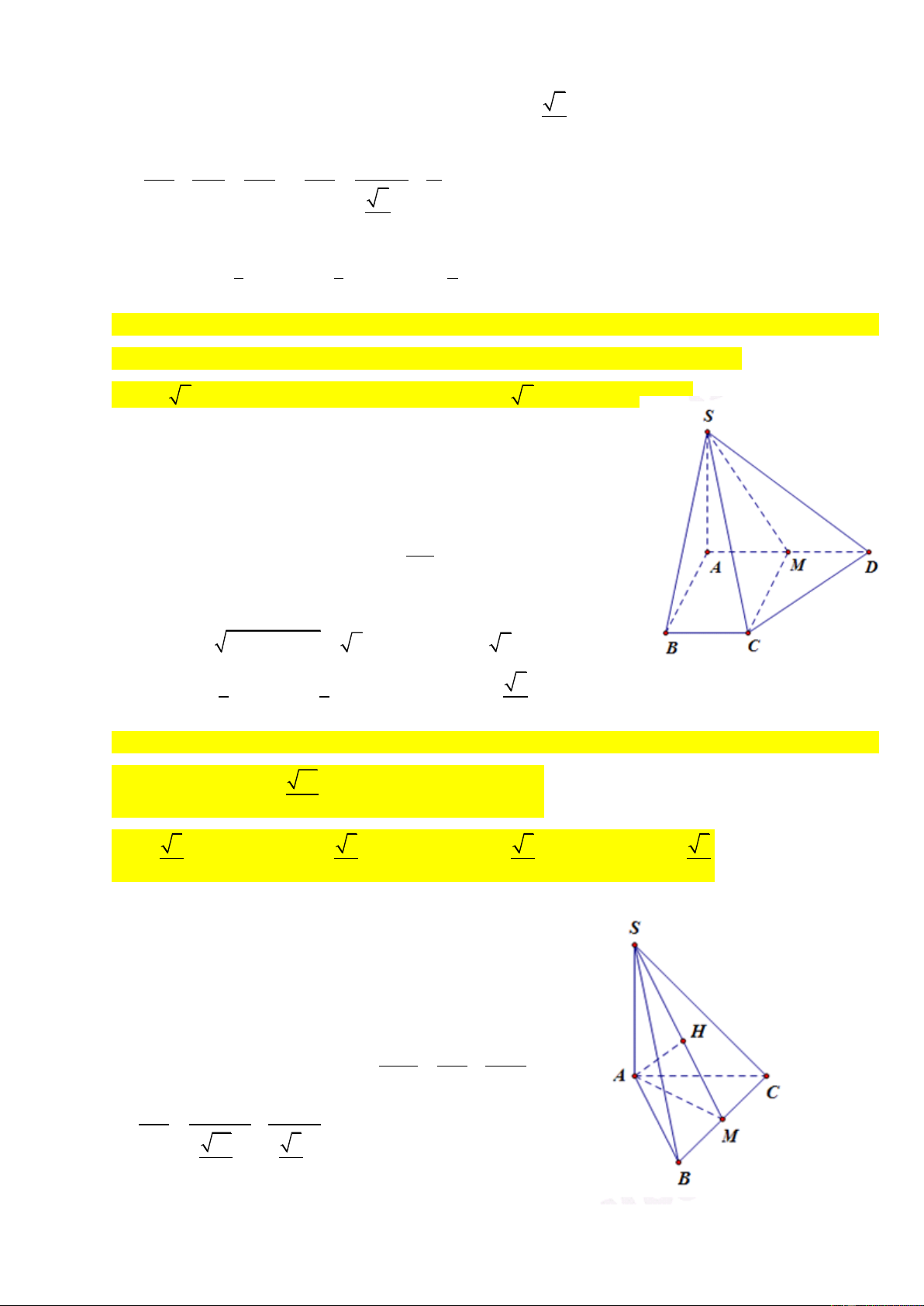
Câu 2: Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hai mặt (SAB) và (SAC) cùng
vuông góc với đáy. Tính thể tích khối chóp biết SC = a 3 ? ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 3 2a 6 3 a 6 3 a 3 3 a 3 A. B. C. D. 9 12 4 2   SAB     ABCHD: Ta có: 
SA   ABC   SAC     ABC Ta có 2 2 SA
SC AC a 2 2 3 1 1 a 3 a 6 VS . A Sa 2.  S . ABC 3 ABC 3 4 12
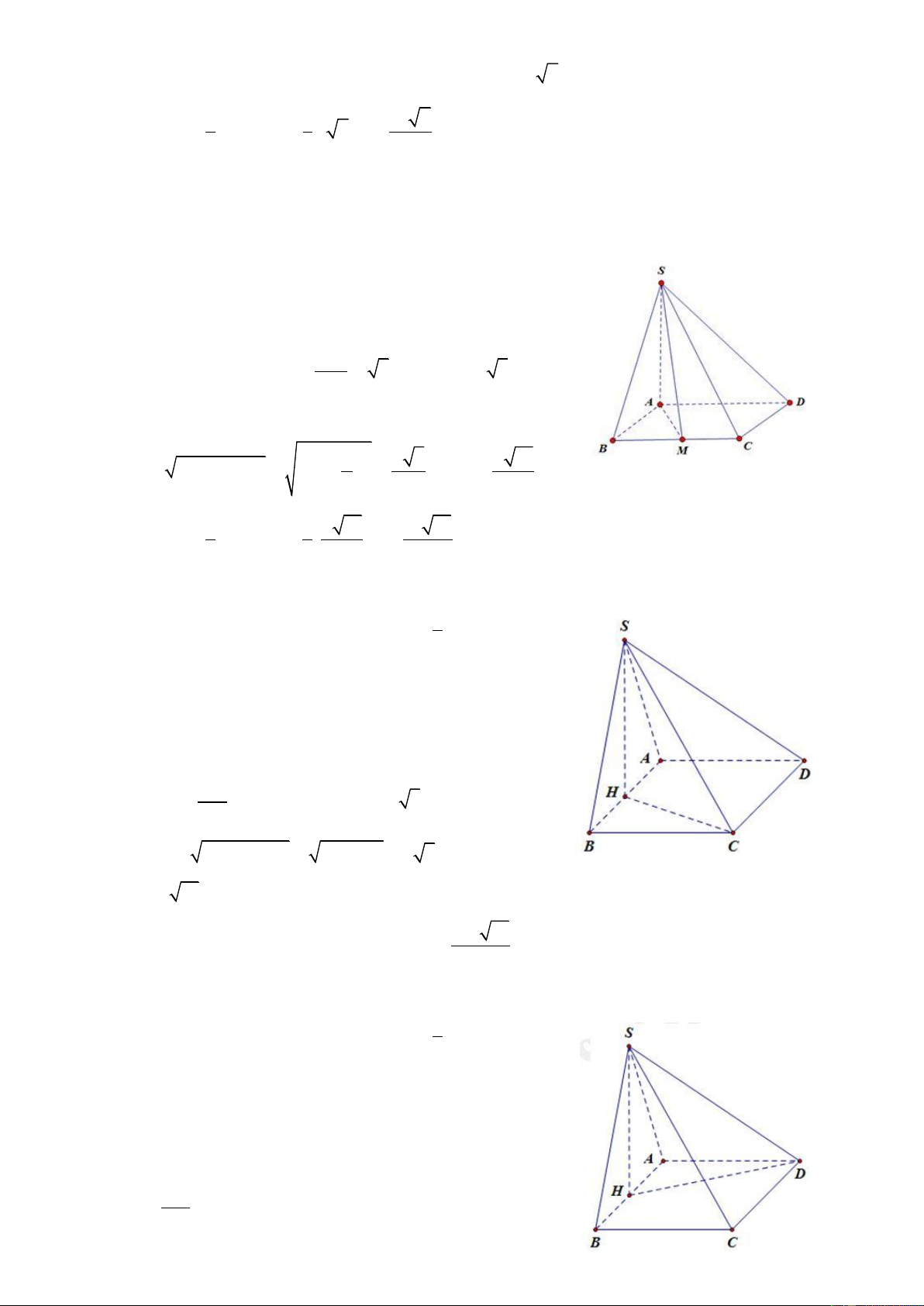
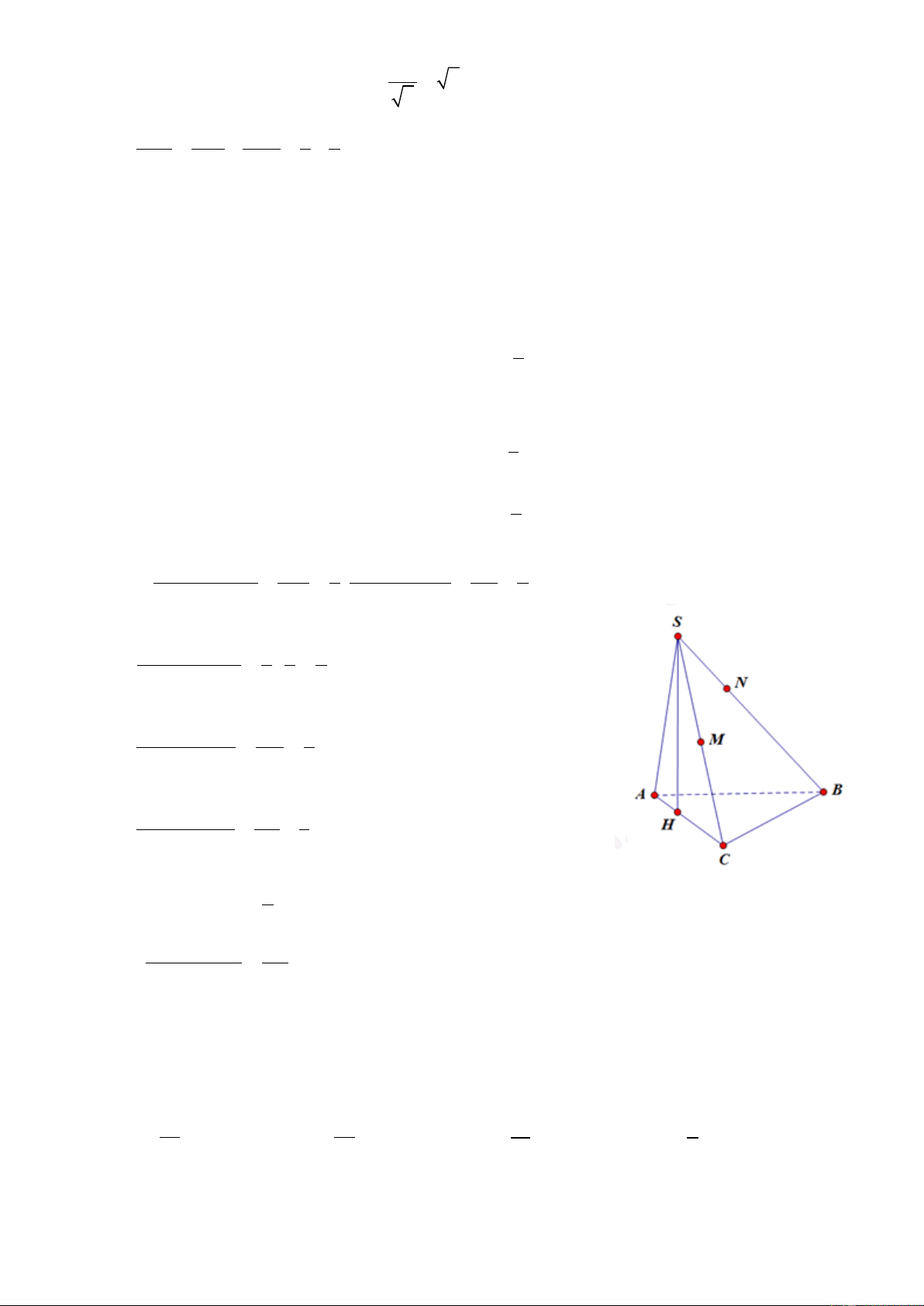
Câu 3: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B
với AC = a biết SA vuông góc với đáy ABC và SB hợp với đáy một
góc 60. Tính thể tích khối chóp: 3 a 6 3 a 3 3 a 6 3 a 6 A. B. C. D. 24 24 8 48
HD: Ta có SB ABC 0 ;  SBA  60 a
Tam giác ABC có AB BC  2 a 6  SA A . B tan SBA  2 2 1 1 a a a Ta có SA . B AC  . .  ABC 2 2 2 2 4 2 3 1 1 a 6 a a 6  V  .S . A S  .  SABC 3 ABC 3 2 4 24
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh a và SA vuông góc với đáy
ABCD và mặt bên (SCD) hợp với đáy một góc 60. Tính thể tích hình chóp S.ABCD 3 a 3 3 2a 3 3 a 3 A. B. C. D. 3 a 3 3 3 6
HD: Ta có SCD  ABCD 0 ,  ADS  60  SA A .
D tan ADS a 3 Ta có 2 SA . B BC a ABCD 3 1 1 a 3 2 VS . A S  .a 3.a SABCD 3 ABCD 3 3
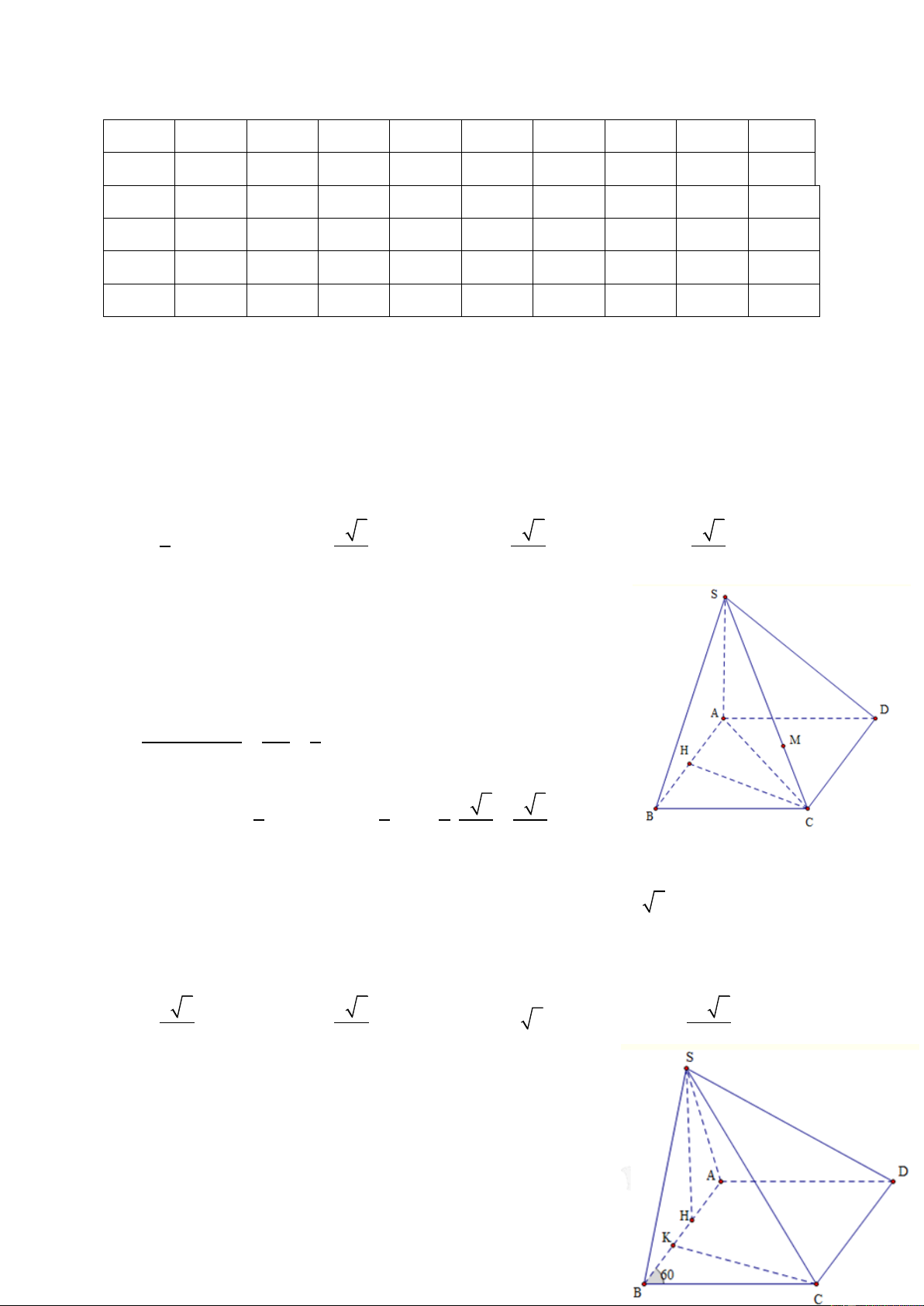
Câu 5: Cho khối chóp S.ABC có đáy ABC là tam giác cân tại
A với BC = 2a, BAC  1200, biết SA  (ABC) và mặt (SBC)
hợp với đáy một góc 45. Tính thể tích khối chóp S.ABC 3 a 3 a 3 a A. B. C. 3 a 2 D. 9 3 2 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
HD: Ta có SBC  ABCD 0 ;  SMA  45 2a a Ta có AB  ; AM  3 3 a
SA AM.tan SMA  3 2 1 1 a a Ta có SAM.BC  . .2a ABC 2 2 3 3 2 3 1 1 a a aVS . A S  . .  SABC 3 ABC 3 3 3 9
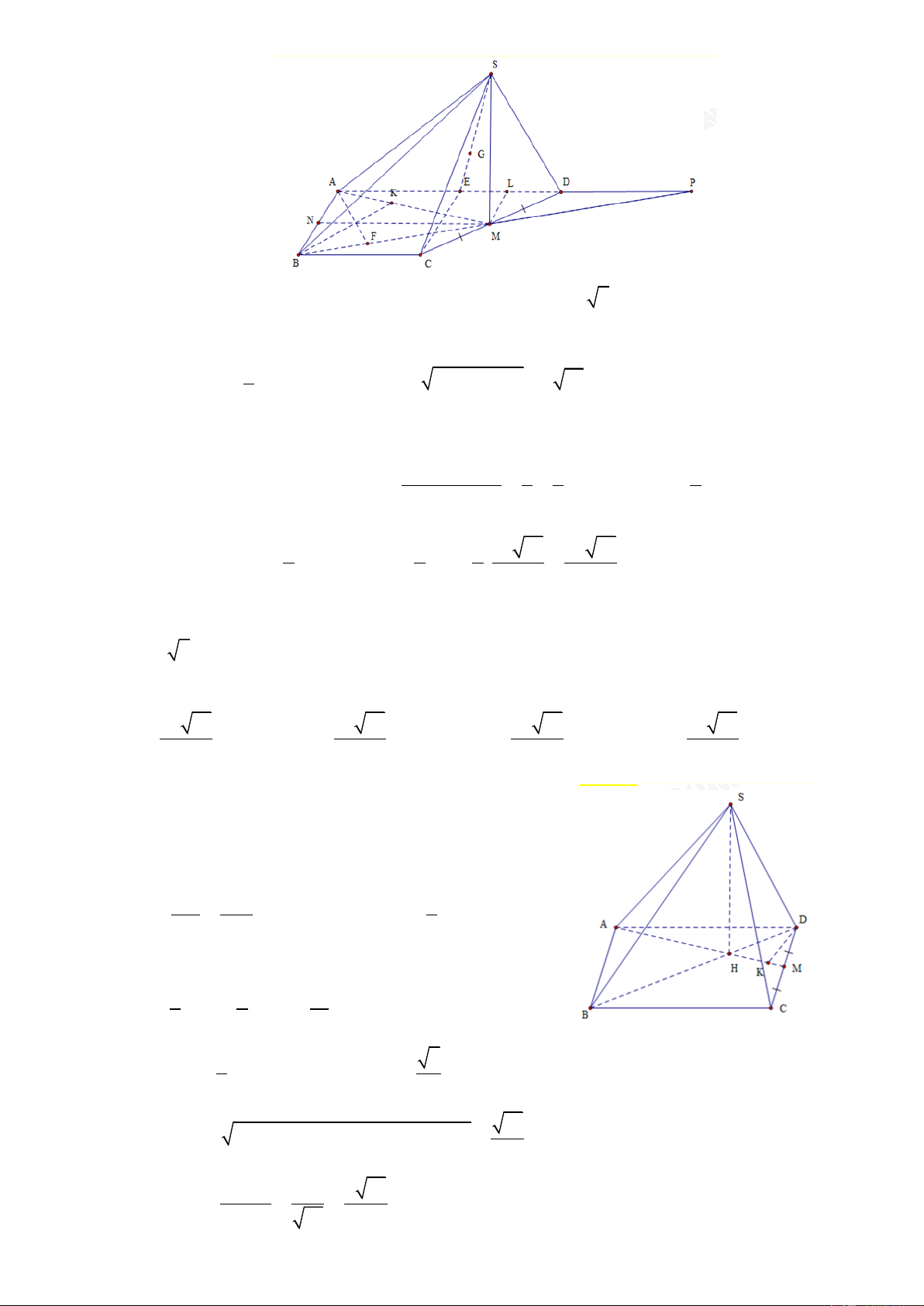
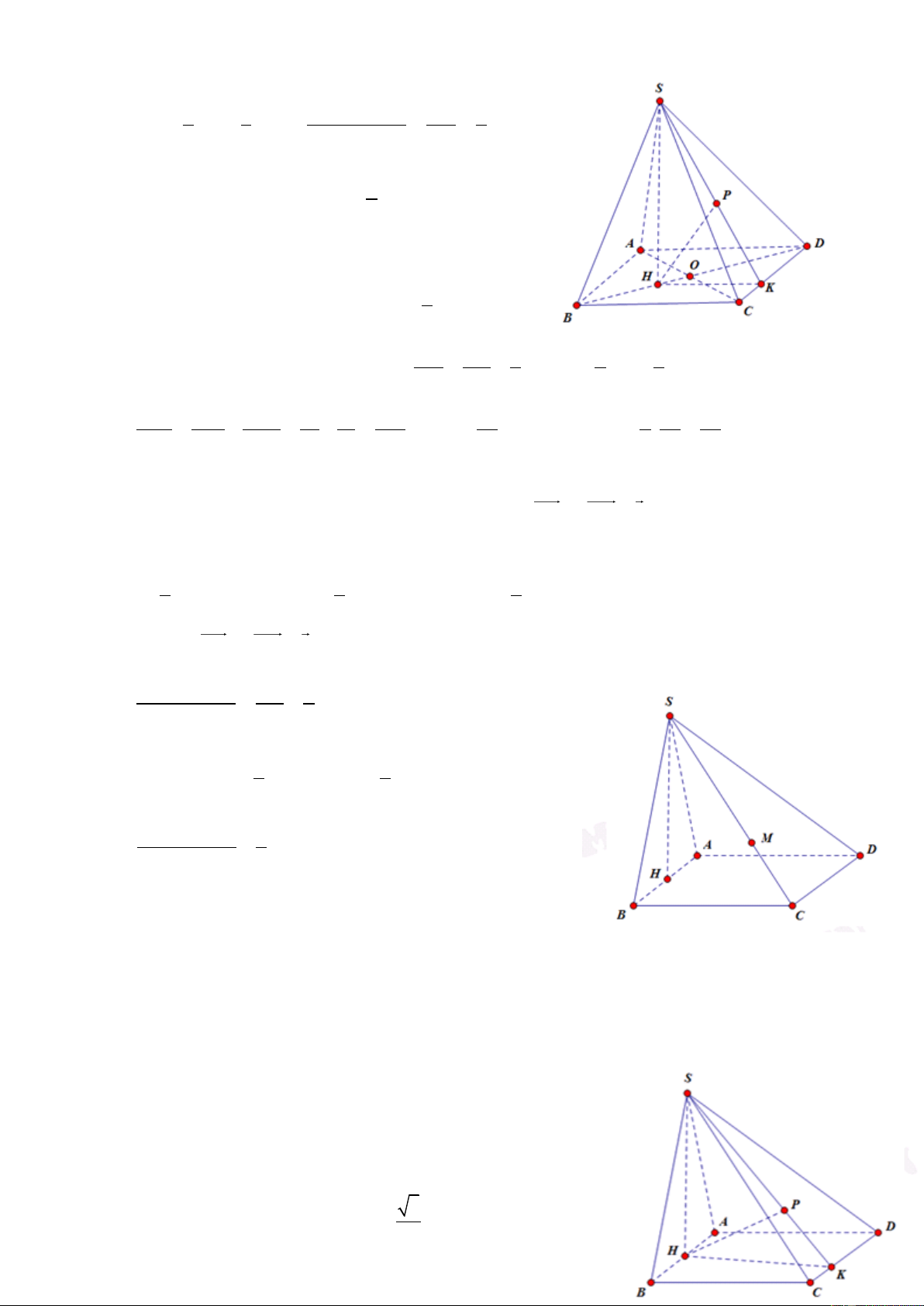
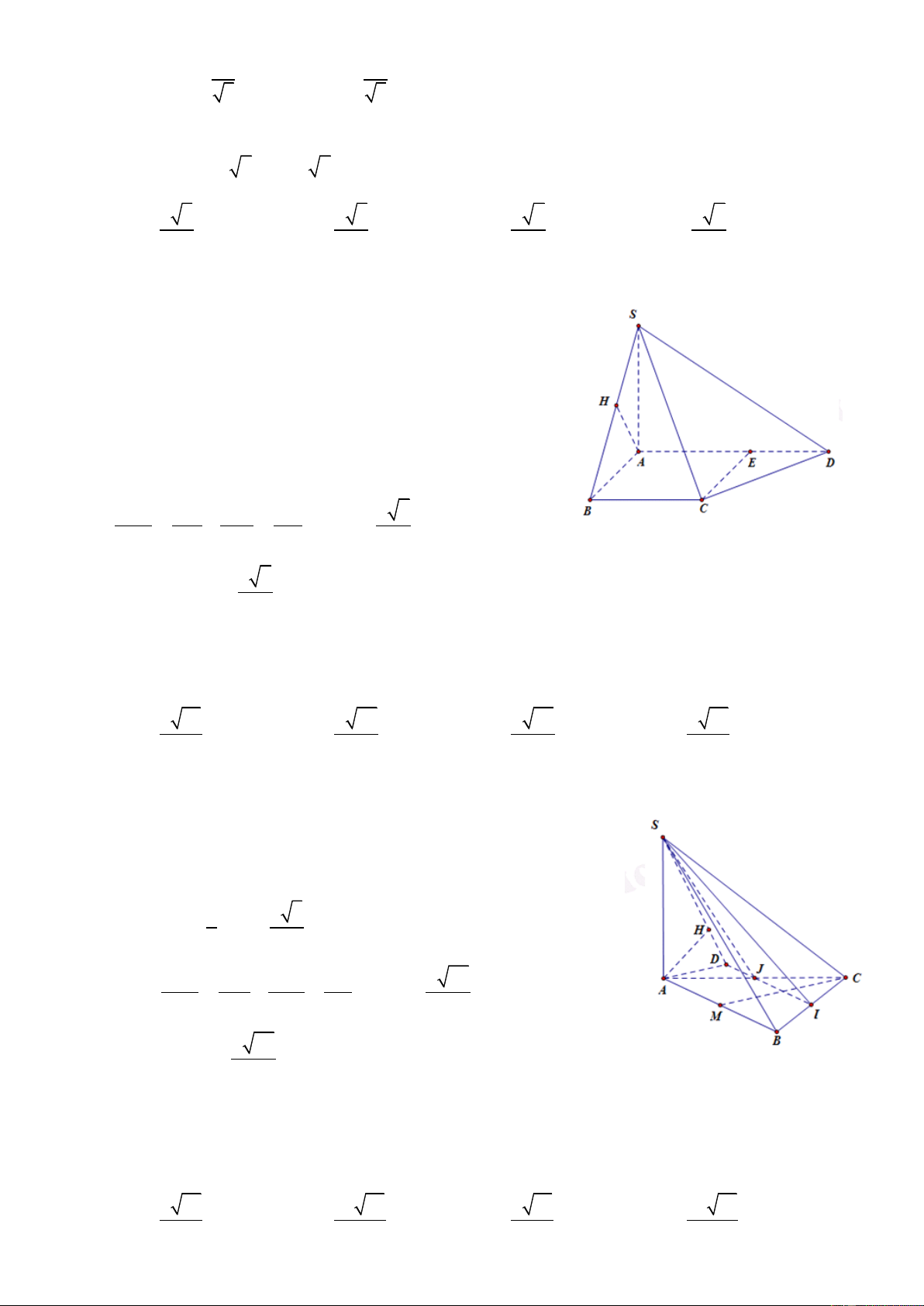
Câu 6: Cho khối chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B biết AB = BC = a, AD
= 2a, SA  (ABCD) và (SCD) hợp với đáy một góc 60. Tính thể tích khối chóp S.ABCD 3 a 6 3 a 3 3 a 6 3 a A. B. C. D. 2 3 6 2
HD: ta có SCD  ABCD 0 ,  SCA  60 Ta có 2 2 AC
AB BC a 2
SA AC.tan SCA a 6 a Ta có S
AB AD BC a a ABCD   2 1 1 3 .3 2 2 2 2 3 1 1 3a a 6 VS . A S  .a 6.  SABD 3 ABCD 3 2 2
Câu 7: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật biết rằng SA  (ABCD), SC hợp với
đáy một góc 45 và AB = 3a, BC = 4a. Tính thể tích khối chóp: 3 10a 3 A. 3 40a B. 3 10a C. D. 3 20a 3
HD: Ta có SC ABCD 0 ;  SCA  45 Ta có 2 2 AC
AB BC  5aSA A .
C tan SCA  5a Ta có 2 SA . B BC  12a ABCD 1 1 2 3  VS . A S  .5a.12a  20a SABCD 3 ABCD 3
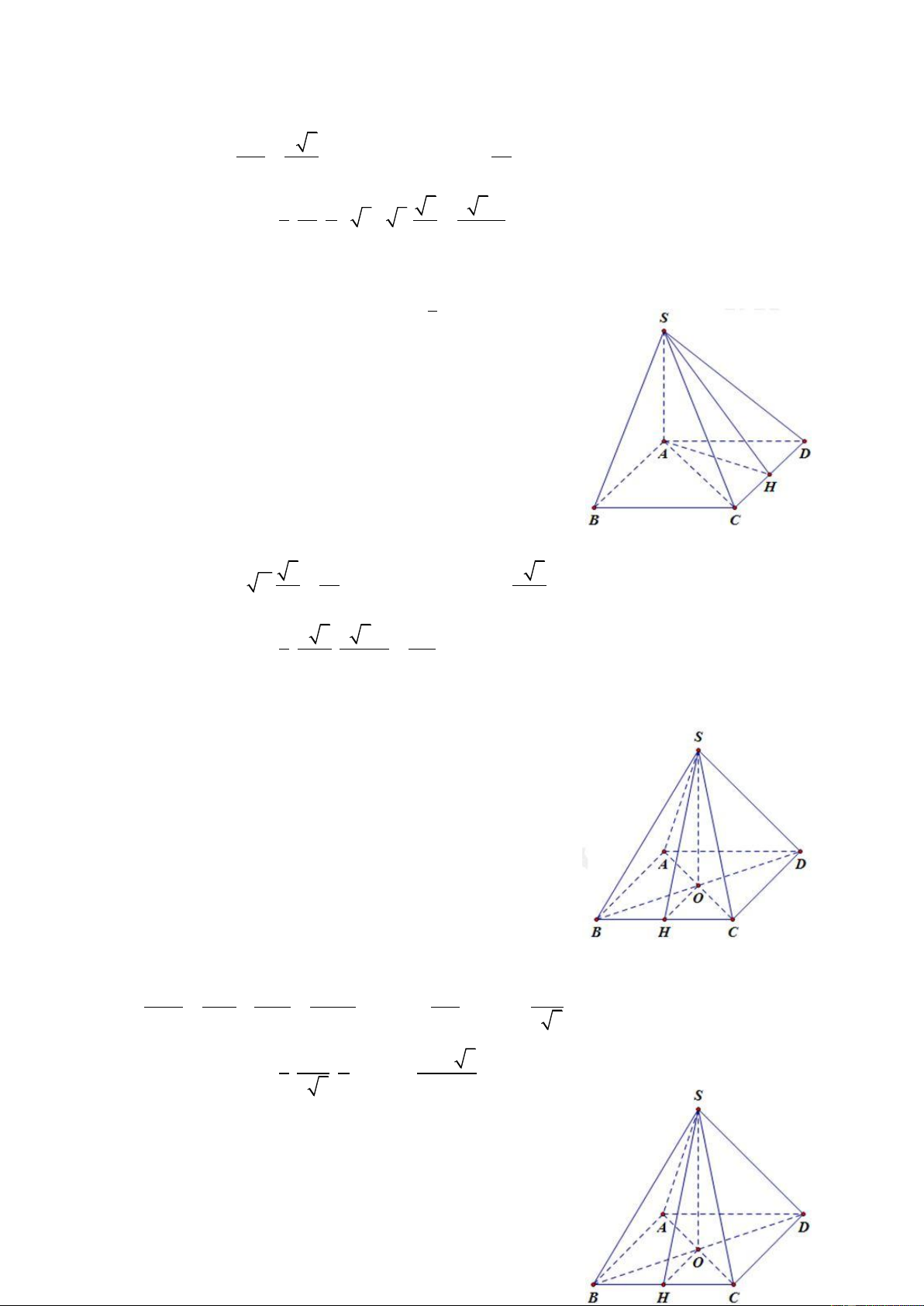
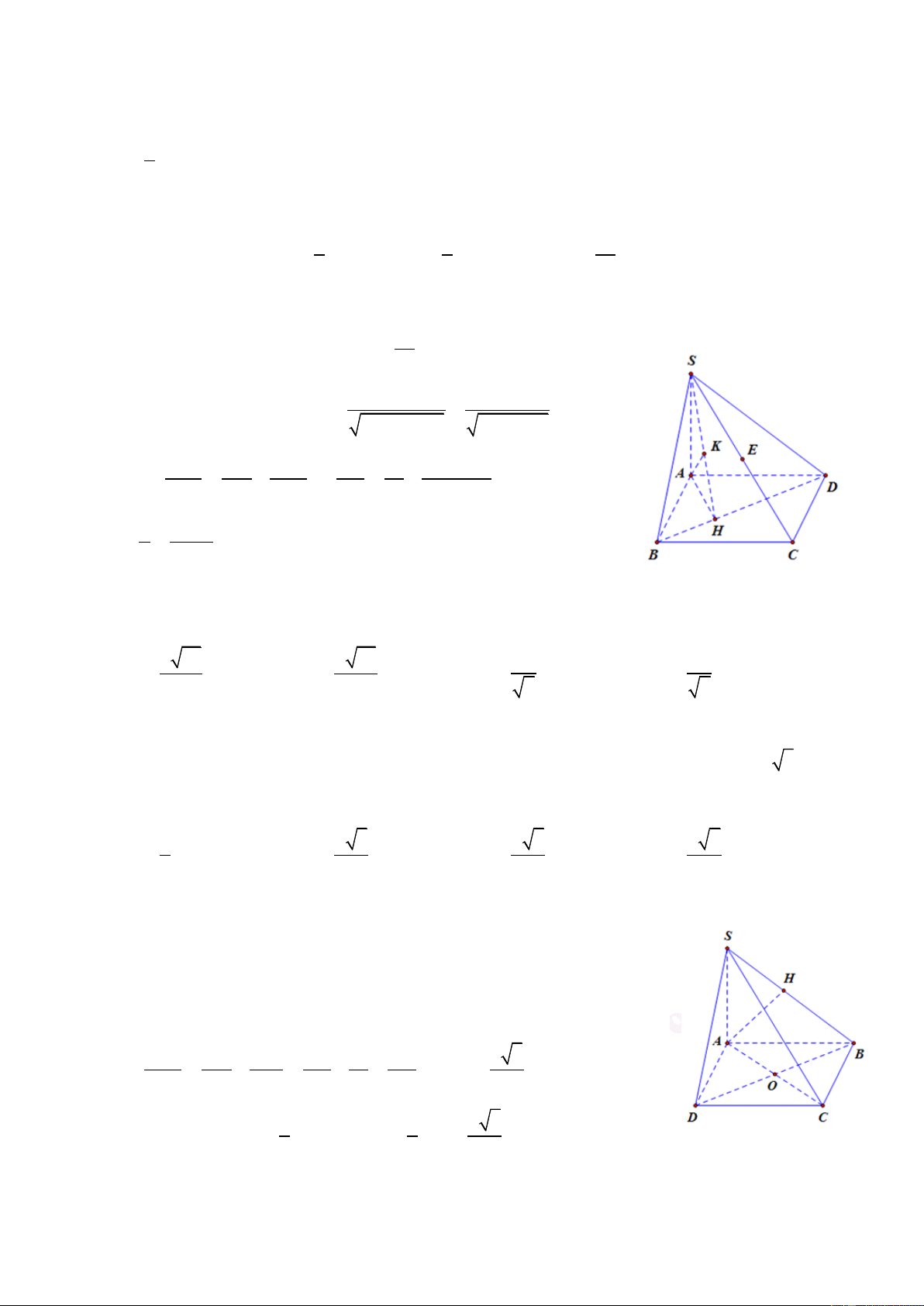
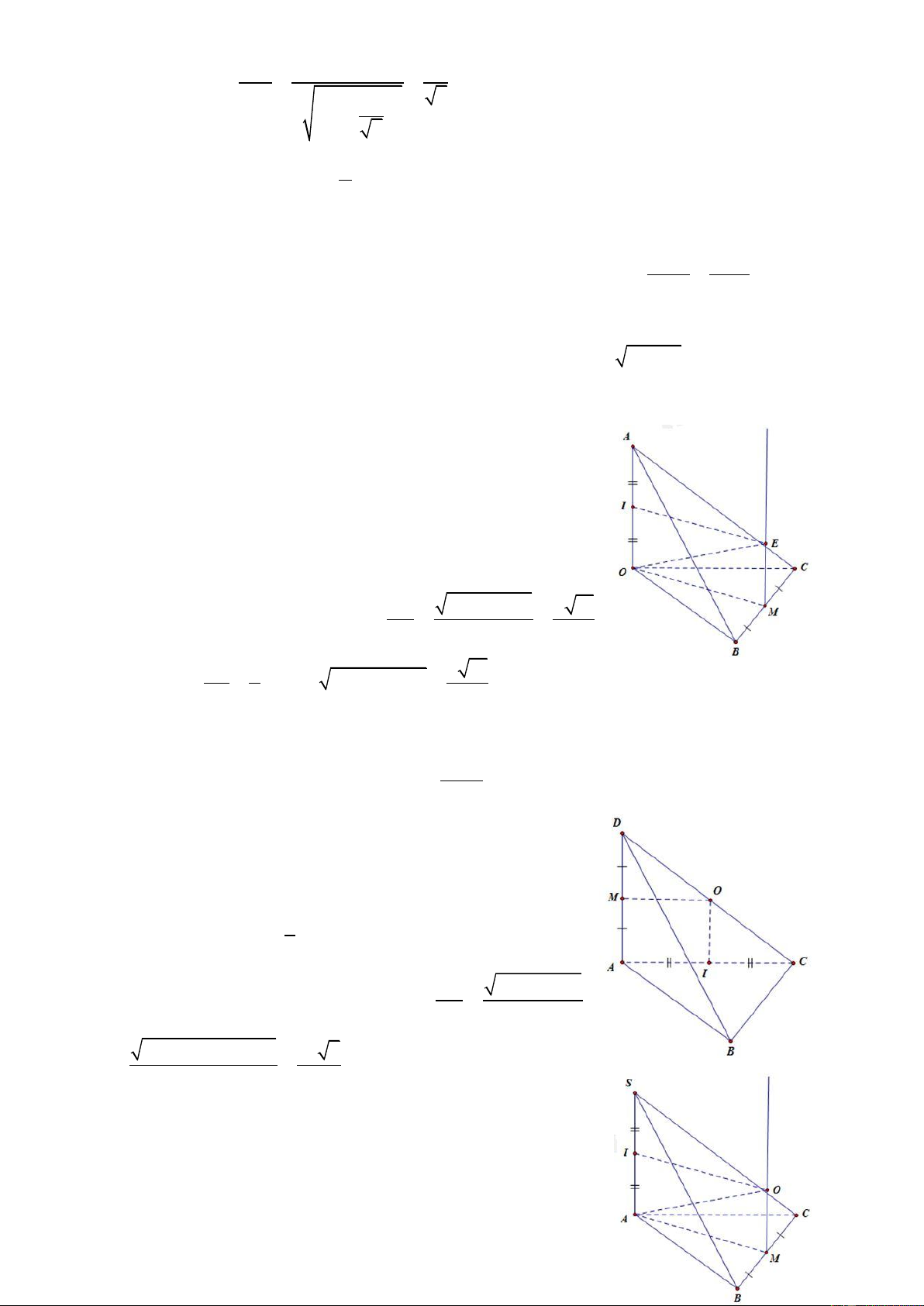
Câu 8: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật AD = 2a, AB = a. Gọi H là trung điểm
của AD, biết SH  ( ABCD) . Tính thể tích khối chóp biết SA = a 5 . 3 2a 3 3 4a 3 3 4a 3 2a A. B. C. D. 3 3 3 3 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 HD: Ta có 2 2 SH
SA AH  2a Và 2 SA . B BC  2a ABCD 3 1 1 4a 2 VS . A S  .2 . a 2a SABCD 3 ABCD 3 3
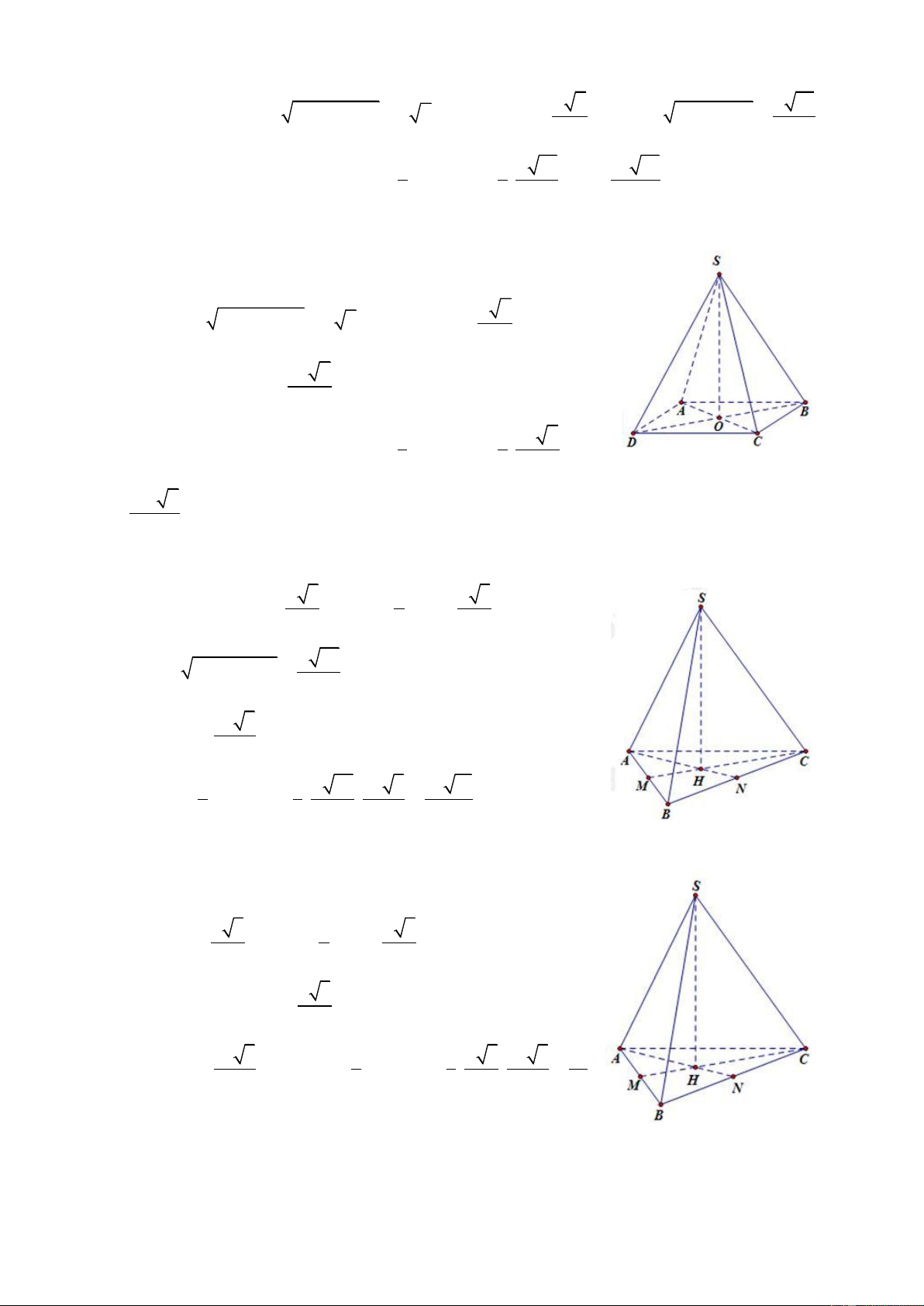
Câu 9: Cho hình chóp S.ABC có đáy ABC là tam giác cân tại
A, G là trọng tâm tam giác ABC, SG  (ABC). Biết góc giữa SM 9V
và mặt phẳng (ABC) bằng 300 (với M là trung điểm của BC), BC  2a và AB = 5a. Tính với V là 3 a
thể tích khối chóp S.ABC: A. 8 2 B. 8 3 C. 8 5 D. 8 7 2a 6 HD: Ta có 2 2 AM
AB BM  2a 6  GM  3 Do đó 2a 2 0
SG GM tan 30  3 3 Khi đó 1 1 2a 2 1 8 3a V S . G S  . . .2a 6.2a  3 ABC 3 3 2 9 9V Vậy  8 3 . 3 a
Câu 10: Cho hình chóp S.ABC. có đáy ABC là tam giác đều cạnh 8a, SA  ( ABC) . Biết góc giữa hai 5V
mặt phẳng (SBC) và (ABC) bằng 450. Tính
, với V là thể tích khối chóp S.ABC? 3 a A. 280 B. 320 C. 360 D. 400
HD: Dựng AM BC , lại có SA BC suy ra SAM   BC
Vậy SBC   ABC  0 ; SMA  45 8a 3 Lại có AM
 4a 3  SA AM  4a 3 2 Do đó 1 5V V S . A S  64   320 3 3 ABC a
Câu 11: Cho hình chóp S.ABC có đáy ABC là tam giác
vuông cân tại B, AB = 8a, SA  (ABC). Biết góc giữa hai mặt 9V 3
phẳng (SBC) và (ABC) bằng 300. Tính, với V là thể tích 3 a khối chóp S.ABC. A. 768 B. 769 C. 770 D. 771 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 1 HD: Ta có 2 2 S
AB  32a . Lại có SBC  ABC 0 ;  SBA  30 ABC 2 8a 3 1 256a Do vậy 0
SA AB tan 30 
suy ra V  .S . A SABC 3 3 3 3
Do đó 9V 3  768 Chọn A 3 a
Câu 12: Cho hình chóp S.ABCD có đáy là hình vuông cạnh 8a, SA  (ABCD). 3V
Biết góc giữa SC và mặt phẳng (ABCD) bằng 450. Tính , với V là thể 3 512a tích khối chóp S ABC . . A. 3 B. 3 C. 2 D. 2 HD: Ta có 0
AC  8a 2  SA AC tan 45  8a 2 3 Do đó 1 521a 2 V S . A S  3 ABCD 3 3V Vậy  2 Chọn C 3 512a
Câu 13: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AC = a, SA  (ABC). Biết 3 a 6
thể tích khối chóp S.ABC là
(đơn vị thể tích). Tính góc giữa SB và mặt phẳng (ABC). 24 A. 600 B. 450 C. 300 D. 900
HD: Ta có SA A .
B tan (với  là góc giữa SB và mp(ABC) ) AC a
Mặt khác AB BC   2 2 2 3 Khi đó 1 1 a a a 6 V  . SA S  . . tan .  S . ABC 3 ABC 3 2 4 24 Do vậy 0
tan   3    60 Chọn A
Câu 14: Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB =
a, SC = 2a 2 , SA  (ABCD). Biết góc giữa SC và mặt phẳng
(ABCD) bằng 300. Tính theo a thể tích khối chóp S.ABCD. 3 a 10 3 a 10 3 a 5 3 a 5 A. B. C. D. 3 5 10 3 2a 6 HD: Ta có 0
AC SC cos 30   a 6 2 0
SA SC sin 30  a 2 . Khi đó 2 2 BC
AC AB a 5 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 3 1 a 10 Do vậy VS . A SChọn A S . ABCD 3 ABCD 3
Câu 15: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 8a, SA  (ABC). Biết góc giữa hai
mặt phẳng (SBC) và (ABC) bằng 450. Tính theo a thể tích khối chóp S.ABC. A. 56a3 B. 64a3 C. 72a3 D. 80a3 BC SA
HD: Gọi M là trung điểm của BC. Khi đó 
BC  SAM  BC AM
Do vậy SBC   ABC  0 ; SMA  45 8a 3 Mặt khác 0 AM
 4a 3  SA AM tan 45  4a 3 2 2 Do đó 1 1 64a 3 3 VS . A S  .4a 3.
 64a . Chọn B S .ABC 3 ABC 3 4
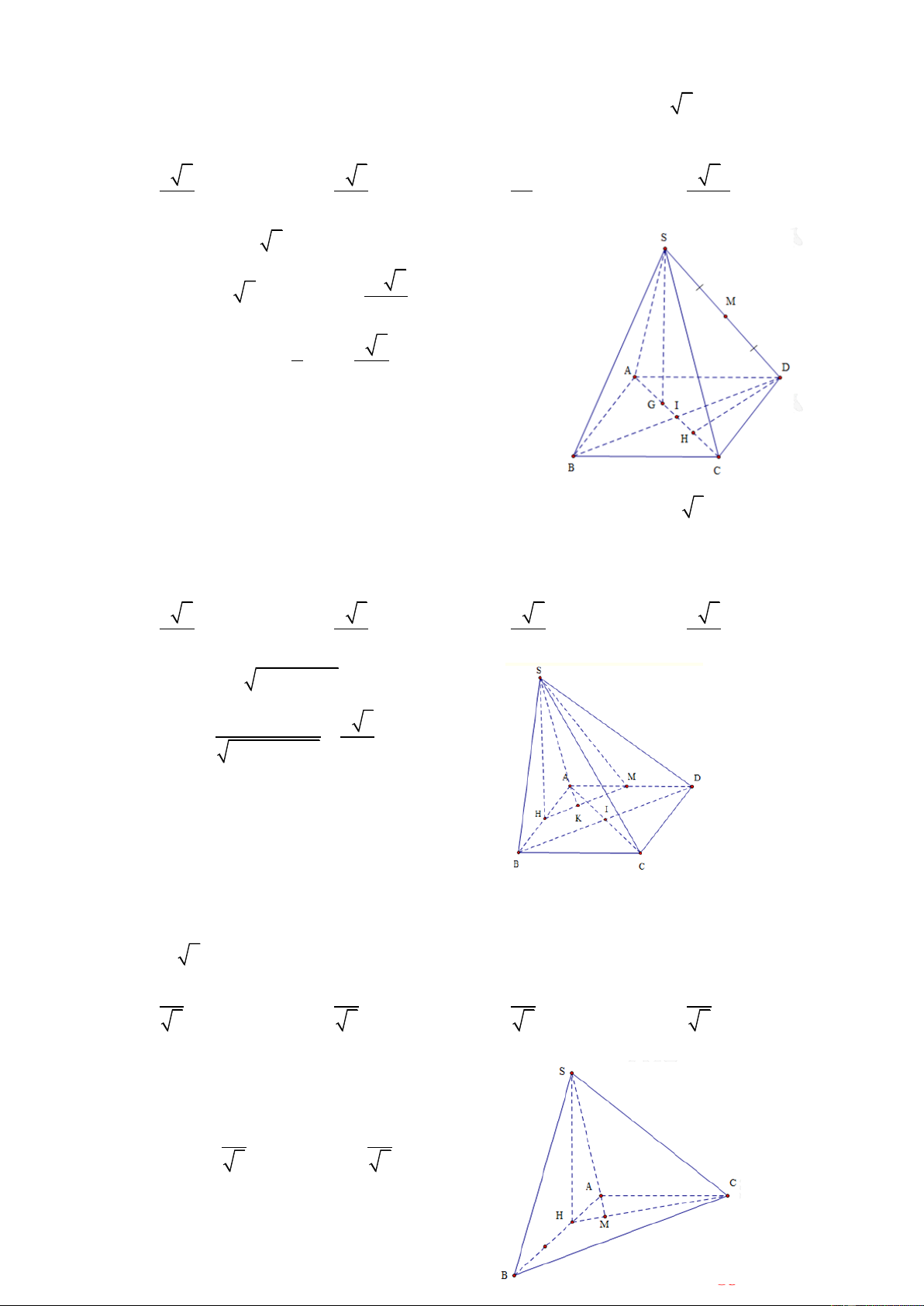
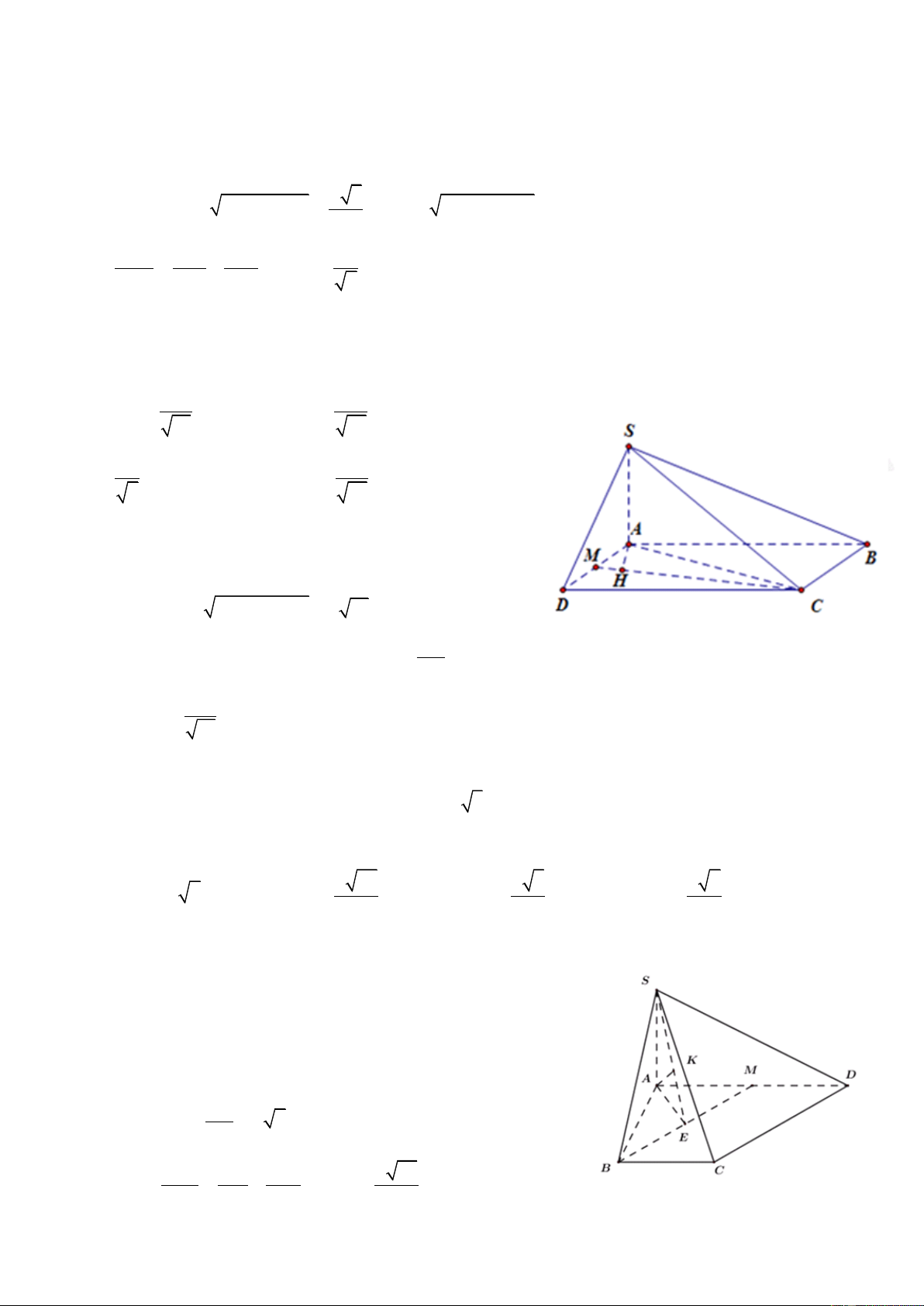
Câu 16: Cho hình chóp tam giác đều S.ABC có cạnh AB bằng a. Các
cạnh bên SA, SB, SC tạo với đáy một góc 600. Gọi D là giao điểm của
SA với mặt phẳng qua BC và vuông góc với SA. Tính theo a thể tích khối chóp S.DBC. 3 5a 3 5a 2 3 5a 3 3 5a 5 A. B. C. D. 96 96 96 96 a
HD: Gọi M là trung điểm của BC khi đó 3 AM
. Gọi H là trọng tâm tam giác ABC suy ra 2
SH   ABC  0 ; SAH  60 BC AM Dễ thấy 
BC SA . Dựng BD SABC SH Khi đó BCD 2 1 1 3a 0  S , A S
DM.BC AM.sin 60 .BC BCD 2 2 8 a 3 2a 3 0 0
AD AM .cos 60 
; SAcos 60  AH SA  4 3 5a 3
Do vậy  SD SA AD  12 3 1 5a 3 Suy ra VS . D SChọn C S .DBC 3 BCD 96 V SD
Cách 2: S.DBC V SA S . ABC
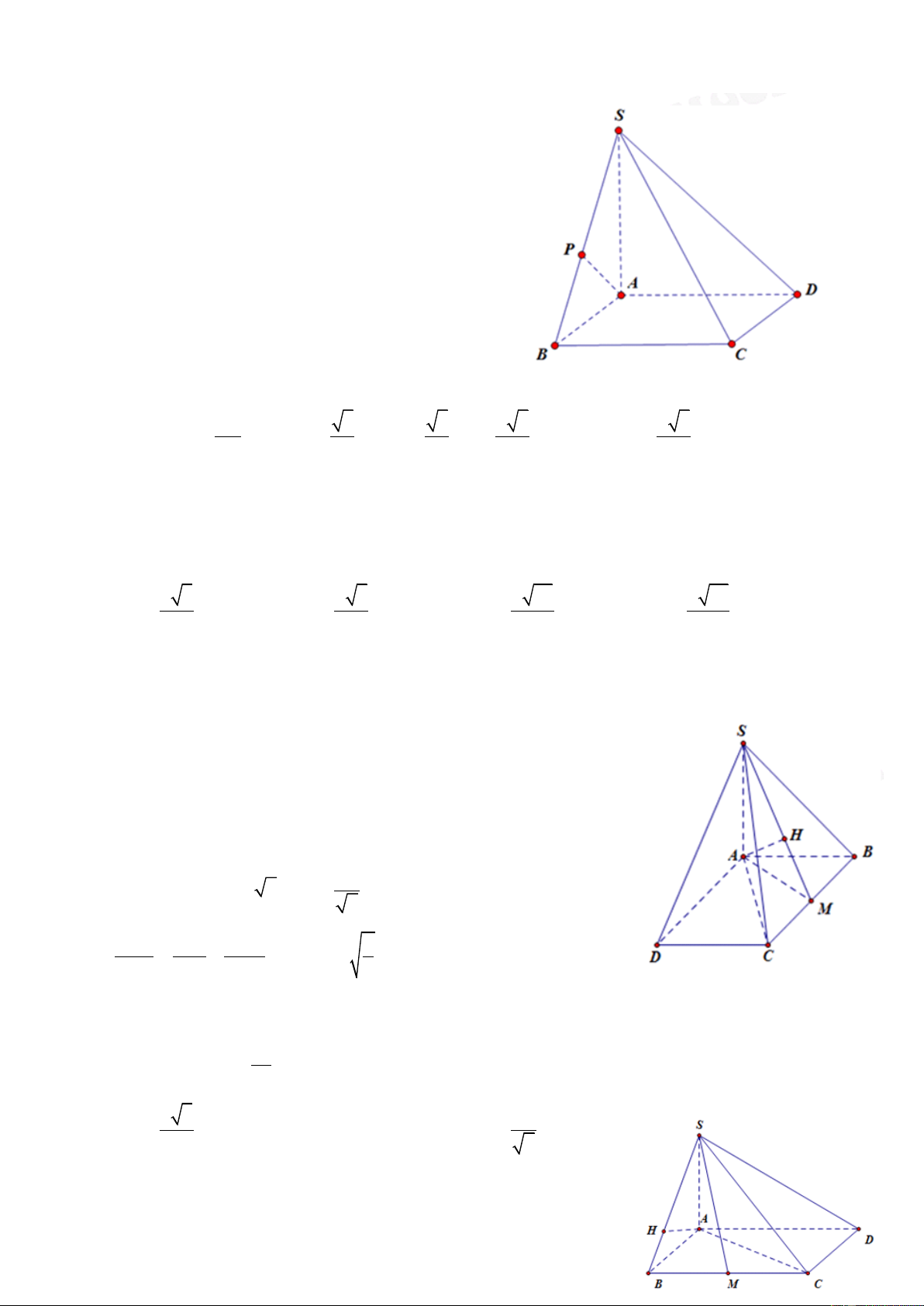
Câu 17: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB là tam giác đều
và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích khối chóp S.ABCD. ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 6 5 4 3
HD: Gọi H là trung điểm của AB.
Khi đó SH AB , mặt khác SAB   ABCDa
Do vậy SH   ABCD  3 ;SH  2 3 Do đó 1 a 3 VSH.S  . Chọn A S .ABCD 3 ABCD 6
Câu 18: Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA = 2a và SA 
(ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. 50V 3 Tính
, với V là thể tích khối chóp A.BCNM 3 a A. 9 B. 10 C. 11 D. 12
HD: Tam giác SAB vuông tại A có đường cao AM 2 Khi đó SA SM SM 4 SN 2
SA SM .SB     . Tương tự 4  2 SB SB SB 5 SC 5 2 3 1 1 a 3 a 3 Lại có VS . A S  .2 . aS . ABC 3 ABC 3 4 6 V SA SM SN 16 9
Mặt khác S.AMN  . .   VV . A BCNM S . V SA SB SC 25 25 ABC S .ABC 3 3 Do đó 9 a 3 3a 3 50V 3 V  .    9 . Chọn A . A BCNM 3 25 6 50 a
Câu 19: Cho tứ diện ABCD có các cạnh AB; AC; AD đôi một vuông góc với nhau biết AC = a; AD a 21
= a 3 và khoảng cách từ A đến mặt phẳng BCD bằng
. Thể tích khối chóp đã cho là: 7 3 a 3 3 a 3 3 3a 3 3 a 3 A. B. C. D. 2 6 4 3
HD: Từ A kẻ AH vuông góc với CD tại H.
Ta có BA   ACD  BA CD mà AH CD CD   BAH  AK BH
Kẻ AK BH , K BH do đó: 
AK  BCD AK CD a 1 1 1
Hay d A BCD 21 ;  AK  . Lại có   7 2 2 2 AK AB AH Do đó: 1 1 1 1 1      AB a 2 2 2 2 2 AB AK AC AD a ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 3 1 1 a 3 Vậy V  .A . B S
 .AB.AC.AD  . Chọn B ABCD  3 ACD 6 6
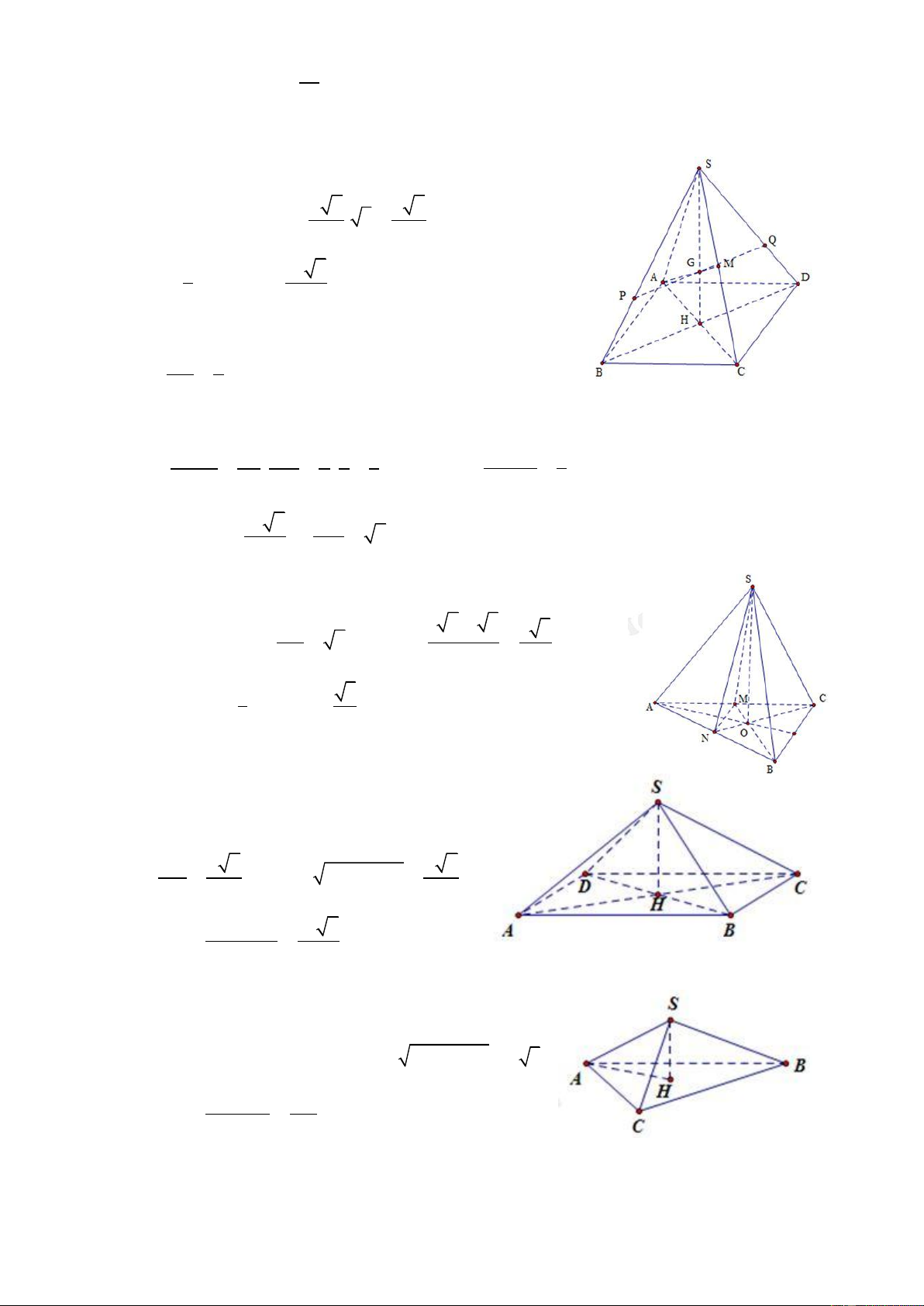
Câu 20: Cho khối chóp S.ABCD có đáy là hình vuông, SA  ABCD và SA=h. Biết SC tạo với đáy
một góc 450. Thể tích khối chóp đá cho tính theo h là: 3 h 2 3 h 3 h 3 3 h A. B. C. D. 6 3 6 6
HD: Ta có AC là hình chiếu của SC lên mặt phẳng đáy.
Do đó SC ABCD  SC AC 0 ; ;  SCA  45
Nên tam giác SAC là tam giác vuông cân tại A  AC h Đặ h
t AB x , ta có 2 2 2 2 2
AB BC AC  2x h x  2 2 3   Khi đó 1 1 h h V  .S . A S  .h.  . Chọn D S . ABCD   3 ABCD 3  2  6
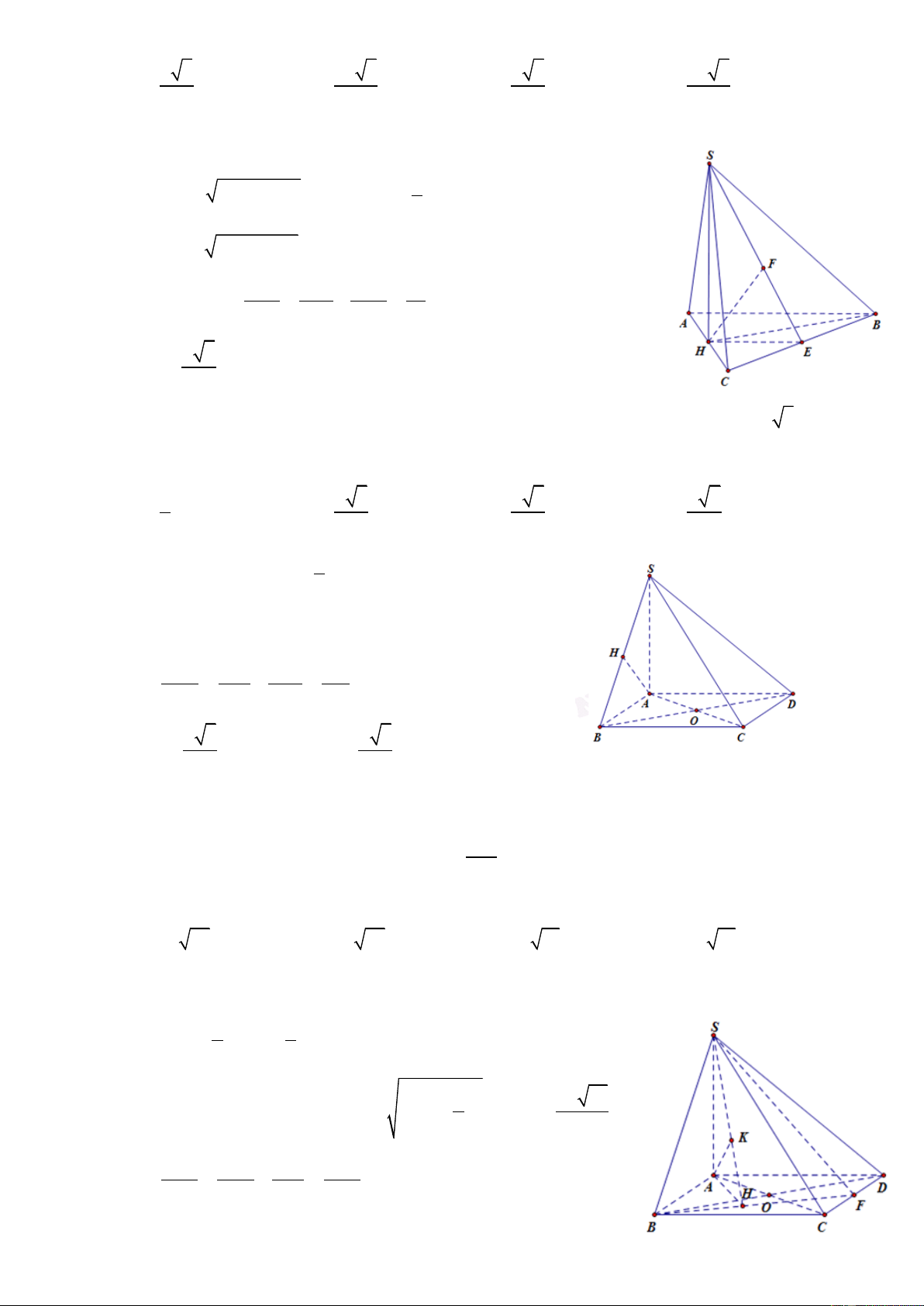
Câu 21: Cho hình chóp S.ABCD có đáy là hình thoi ABCD tâm I
cạnh a, SI  ABCD . Biết tam giác ABC đều và SB = a 2 . Thể tích khối chóp đã cho là: 3 4a 6 3 a 15 3 a 15 3 4a 3 A. B. C. D. 3 4 12 3
HD: Gọi I là tâm của hình thoi ABCD nên I là trung điểm của AC. 2 Tam giác ABC đề a a 3 u nên 2 2 2 IB BC IC a   4 2 2 3a a 5 Xét S
IB vuông tại I, có 2 2 2 SI SB IB  2a   4 4 2 3 1 1 2 a 5 a 3 a 15 Do V  .SI.S  .SI.2.S  . .  S .ABCD  3 ABCD 3 ABC 3 2 4 12 Chọn C
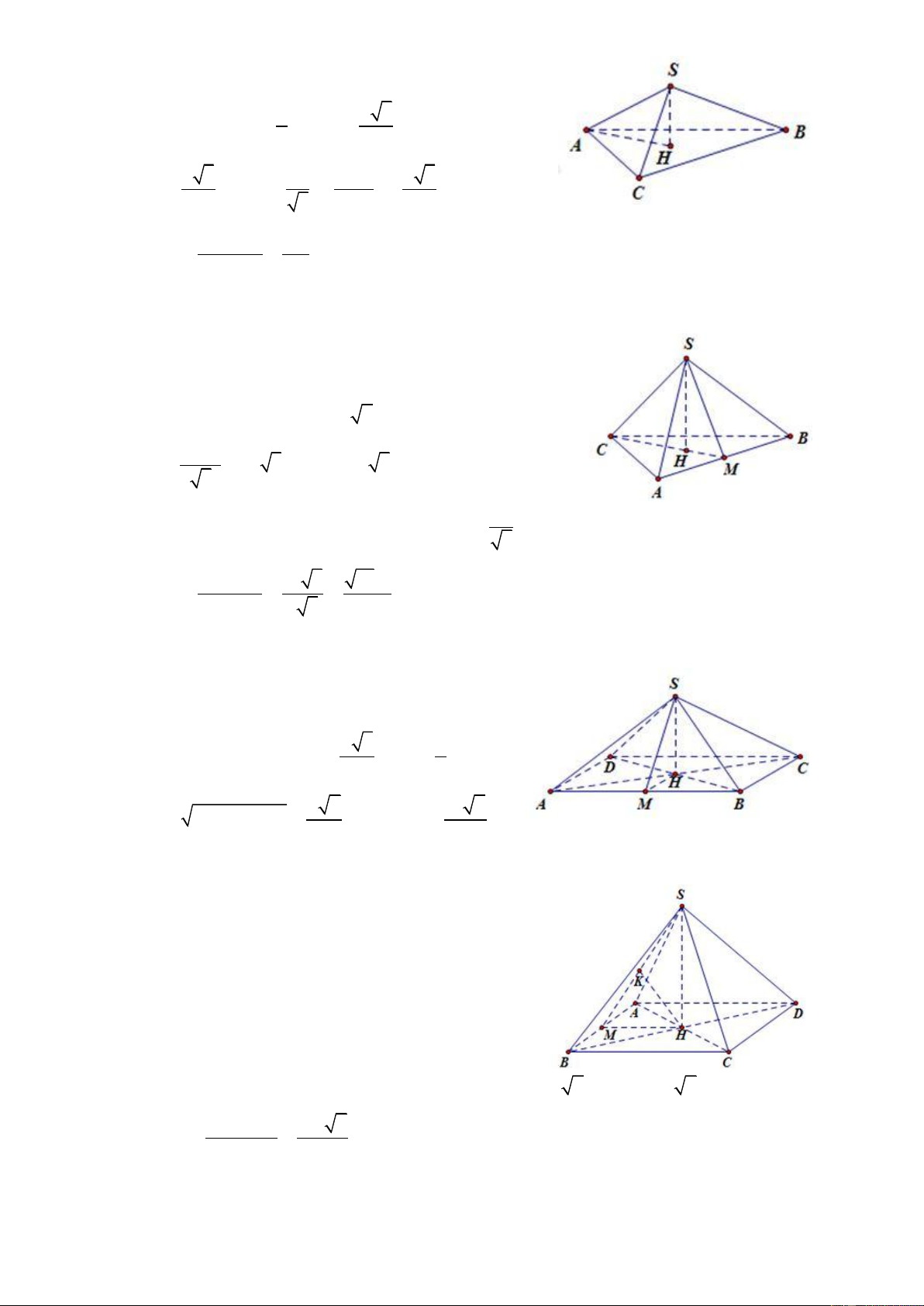
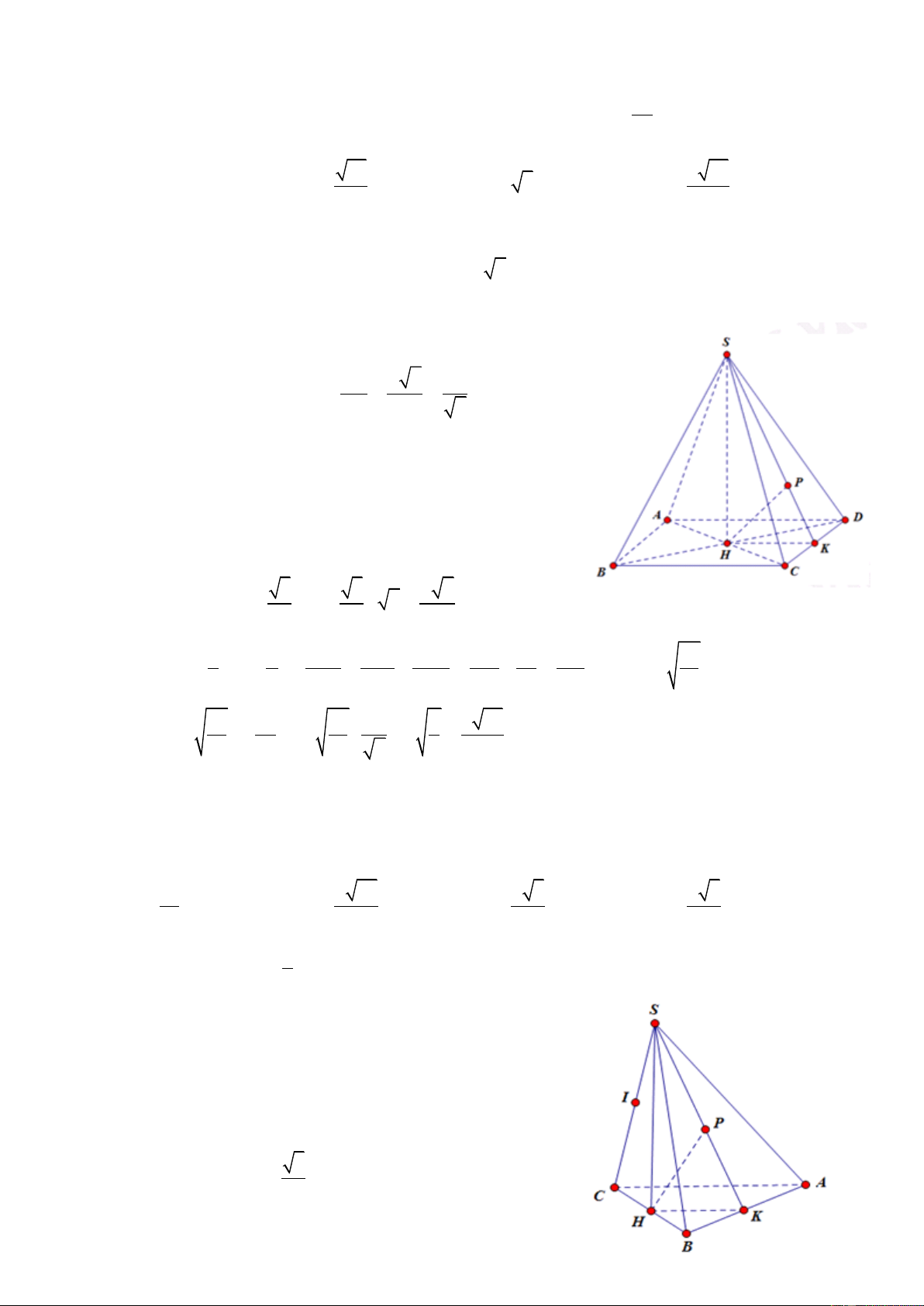
Câu 22: Cho khối chóp S.ABCD có đáy là hình chữ nhật ABCD có AB = 1; AD  2. Hình chiếu
vuông góc của S xuống mặt đáy là trung điểm của AD. Khoảng cách từ A đến mặt phẳng SBC bằng
2 . Thể tích khối chóp đã cho là: 2 1 2 2 A. B. 1 C. D. 3 3 3
HD: Gọi I là trung điểm của AD, theo giả thiết, ta có SI   ABCD
Ta có AD || BC nên AD || SBC   d  ,
A SBC   d I,SBC 
Gọi H là trung điểm của BC suy ra IH BC ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Từ I kẻ IK vuông góc với SH tại K. IK SH Khi đó 
IK  SBC  d I SBC 2 ,  IK  IK BC 2 1 1 1 1 1 1 Mà       SA  1 2 2 2 2 2 2 SA IH IK SA   1 2   2   Do đó 1 1 2 V  .S . A S  .S . A A . B AD  . Chọn C S . ABCD 3 ABCD 3 3
Câu 23: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D có AD  2; AB = BC  1, SA
 ABCD , đường thẳng SC tạo với đáy một góc 450. Thể tích khối chóp đã cho là: A. 2 2 B. 2 C. 2 D. 1
HD: Ta có AC là hình chiếu của SC lên mặt phẳng đáy
Do đó SC ABCD  SC AC 0 ; ;  SCA  45
Nên tam giác SAC là tam giác vuông cân tại A  AC SA AD
Gọi M là trung điểm của AD AM   1 2
Lại có AB BC  1 và AM || BC nên ABCM là hình vuông Khi đó 2 2 AC 
AM MC  2 nên SA AC  2 1 1 2 Vậy V  .S . A S
 .SA.AB. AD BC  . Chọn C S .ABCD ABCD   3 6 2
Câu 24: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 1, SA  ABC, khoảng cách từ A đến 21 mặt phẳng SBC bằng
. Thể tích khối chóp đã cho là 7 3 3 3 3 A. B. C. D. 2 4 3 12
HD: Gọi M là trung điểm của BC, ta có AM BC
Mà SA BC   ABC  và AM BC BC  SAM
Từ A kẻ AH SM tại H nên
AH  SBC   d  ,
A SBC   AH 1 1 1
Xét tam giác SAM vuông tại A, có   2 2 2 AH SA AM 1 1 1 2   
 1  SA  1  SA  1 2 2 2 SA  21   3      7 2     ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 1 1 3 3 Vậy V  .S . A S  .1.  (đvtt). Chọn D S .ABC  3 ABC 3 4 12
Câu 25: Cho hình chóp tứ giác đều S.ABCD có đường cao bằng h và mặt bên tạo với đáy một góc
600. Thể tích khối chóp đã cho tính theo h là: 3 2h 3 4h 3 4h A. B. C. 3 4h D. 3 3 9
HD: Gọi O là tâm của hình vuông ABCD, ta có
SO   ABCD
Gọi M là trung điểm của BC, ta có OM BC
SOM   ABCD  OM
Do đó BC  SOM  mà 
SOM  SBC  SM   ABCD
SBC  BC
Nên ta có được SBC  ABCD  SM OM  0 , ,  SMO  60 SO
Xét tam giác SOM vuông tại O, có tan SMO MO SO h 2hMO  
AB  2.MO  0 tan 60 3 3 3 1 1 4h Vậy V  .S . O S
SO.AB.BC  . Chọn D S .ABCD 3 ABCD 3 9
Câu 26: Cho hình chóp S.ABCD có đáy là hình chữ nhật có AB = 4, AC = 5 và SA  (ABCD biết
mặt phẳng SCD tạo với đáy một góc 600. Thể tích khối chóp đã cho là: A. 12 3 B. 4 3 C. 6 3 D. 20 3
HD: tam giác ABC vuông tại B, có 2 2 BC AC AB  3
Ta có SA   ABCD  SA CD mà CD AD nên CD  SAD 
SCD SAD  SD  
ABCD SAD  AD nên SCD, ABCD  S ,
D AD  SDA   SCD
ABCD  CD Xét D SA  vuông tại A, có SA 0 tan SDA
SA  tan 60 .AD  3 3 AD 1 1 Vậy V  . . SA S
 .3 3.3.4  12 3 . Chọn A S . ABCD 3 ABCD 3
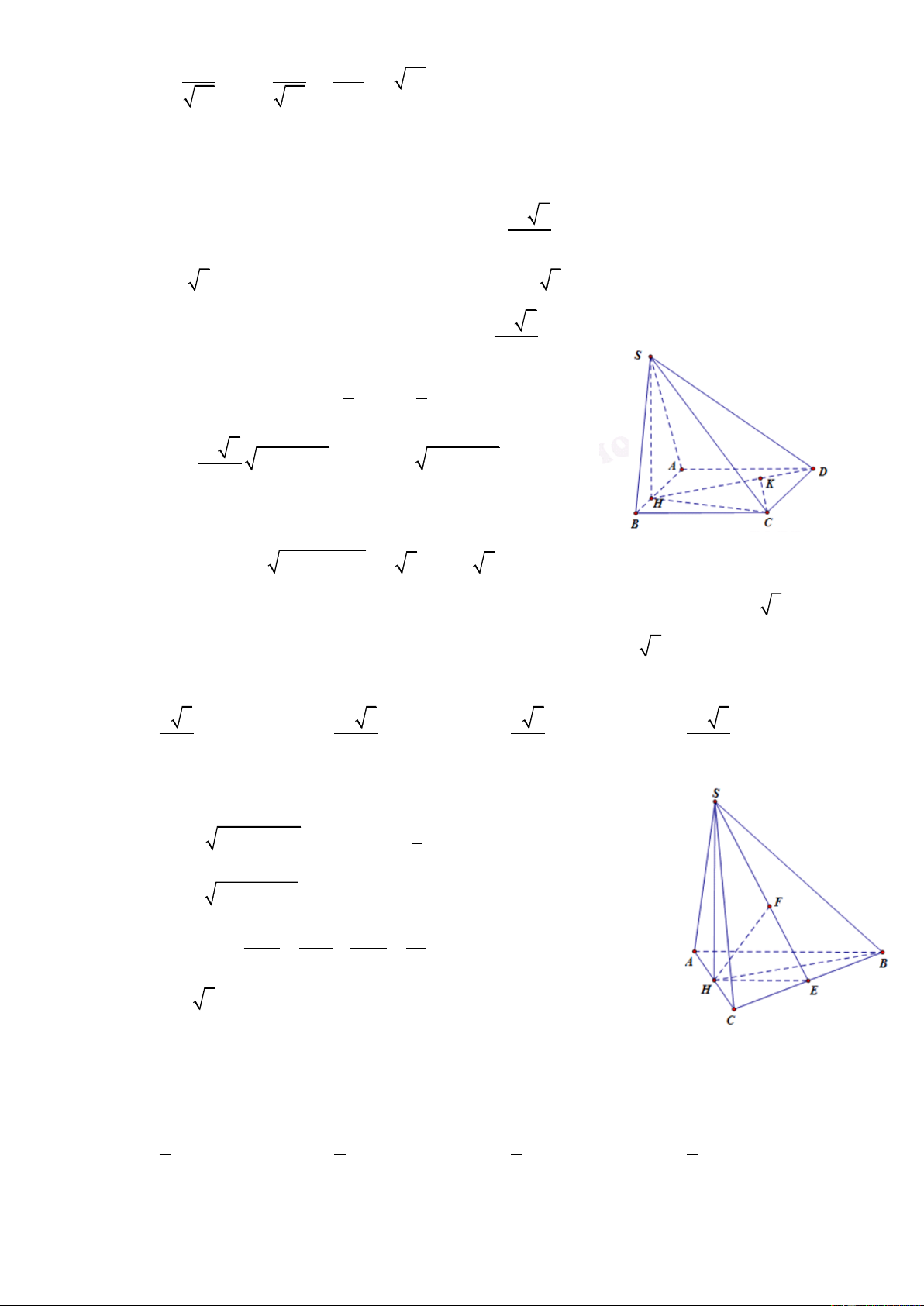
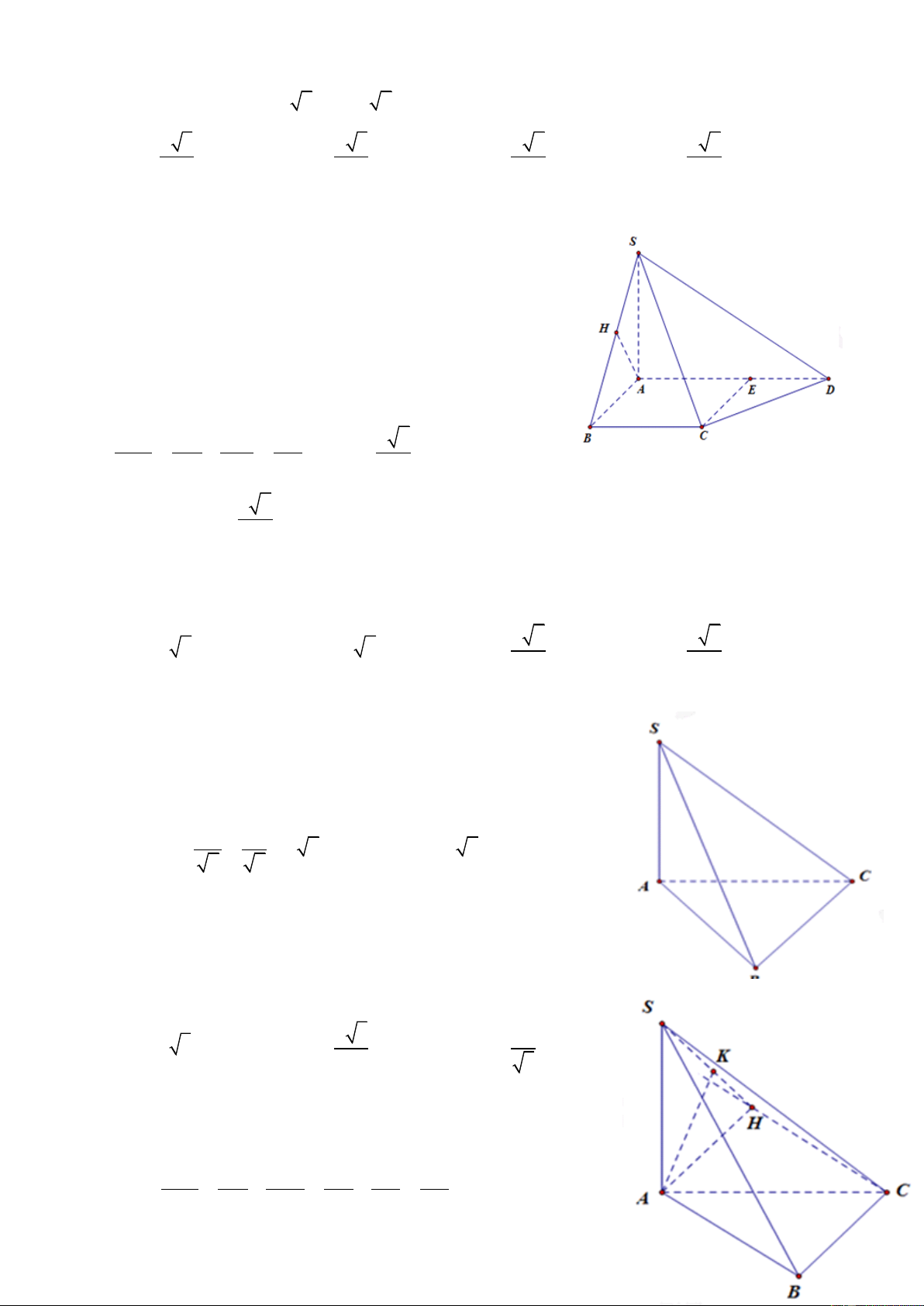
Câu 27. Ta có SC ABC 0 ,  SCH  60 . ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 a 3. 3 3a 2 Ta có CM  
CH AM a 0
SH CH.tan 60  a 3 2 2 3 a 2 2 3 3 3a 3 2 3 1 1 3a 3 3a Ta có S    VSH.Sa 3.  ABC 4 4 S . ABC 3 ABC 3 4 4  Chọn A
Câu 28. Ta có d  ,
A SBC   3d H,SBC 
d H SBC a 3 ,  . 18 BC HN Ta có 
BC  SHN   BC HKBC SH a
Mà HK SN HK  SBC  3  HK  18 a 3 1 a 3 Ta có AN
HN AN  . Lại có 2 3 6 1 1 1 a 6    SH  . 2 2 2 HK HS HN 24 2 2 3 a 3 1 1 a 6 a 3 a 2 12V 2 Ta có S   VSH.S  . .    . ABC S . 4 ABC 3 ABC 3 24 4 96 3 a 8  Chọn D
Câu 29. Gọi N là trung điểm của BC. BC HN Ta có 
BC  SHN   BC SNBC SH
 SBC  ABC 0 ,  SNB  45 a 3 1 a 3 Ta có AN
HN  .AN  2 3 6 a 3 0
SH AN.tan 45  . 6 2 2 3 a 3 1 1 a 3 a 3 a Ta có S   VSH.S  . .  ABC S . 4 ABC 3 ABC 3 6 4 24  Chọn C
Câu 30. Gọi N là trung điểm của BC, kẻ HK SN . BC HN Ta có 
BC  SHN   BC HKBC SH
Mà HK SN HK  SBC   SH,SBC  SH, SK  0  HSK  30 . ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 HN h Ta có tan HSK   HN   AN h 3 SH 3 3 1 1 h 3 2 2  Sh 3 VSH.S  . h h 3  ABC S . ABC 3 ABC 3 3 Chọn A
Câu 31. Gọi M là trung điểm của AB AB HM Ta có 
AB  SHM   AB SMAB SH
 SAB  ABC 0 ,  SMH  45 3a a a Ta có CM
HM   SH HM  2 2 2 a 2 2 3 3 3a 3 Lại có S   ABC 4 4 3 3 1 1 a 3a 3 a 3  VSH.S  . .  S . ABC 3 ABC 3 2 4 8 Chọn B
Câu 32. Gọi M là trung điểm của CD CD   OM Ta có 
CD  SOM   CD SMCD SO Do 0
CSD  60  SCD là tam giác đều  x x
SC SD CD  3 x SM  và OM  2 2 2 2 x 3x Ta có 2 2 2 2
SO OM SM h   4 4 2 x 2  h   x h 2 2 3 1 2h 0 3V sin 30 2 2  S  2h V  . h 2h   1 ABCD S .ABCD 3 3 3 h Chọn D
Câu 33. Gọi M là trung điểm của CD, kẻ OH SM CD   OM Ta có 
CD  SOM   CD SMCD SO
 SCD  ABCD 0 ,  SMO  45
Do SD  SOM   CD OH mà OH SM
OH  SCD  OH d O,SCD  a ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 3  1 1 8a 2
SO OM aS   a 2 2 2 2 2  8a 2 VS . O Sa 2.8a ABCD S . ABCD 3 ABCD 3 3 Chọn C
Câu 34. Gọi H là trọng tâm tam giác đều ABC SH   ABC a 3 a 3
Gọi M là trung điểm của BC ta có: AM  ; AH  2 3 3 3 1 1 a 3 a 3 a Mặt khác V SH.S  .SH.   SH  3 ABC 3 4 36 3 Khi đó SH 1 tan SAH   0  SAH
 SA ABC 0 30 ;  30 AH 3 Chọn B
Câu 35. Gọi G là trọng tâm tam giác đều ABC và M là trung điểm của AB  AB SG
Khi đó SG   ABC; Do   AB HMAB CM a 3 Lại có 2 2 CM  ; SG SC CG 2 2 a a 11 2  4a   SG  3 3 S . G CM a 11 a Suy ra HM   2 2
CH CM HM SC 4 4 3 Khi đó 7a 1 7a 11 SH
V SH.S  4 3 HBC 96 Chọn A 2 2 2
SA SC AC 7 7a
Cách 2: cos ASC
  SH SAcos S  2.S . A SC 8 4 Khi đó V SA SB SH 7 S .HAB  . .  V SA SB SC 8 S . ABC
Câu 36. Gọi G là trọng tâm tam giác đều ABC và M là trung điểm của AB  AB SG
Khi đó SG   ABC ; Do   AB HMAB CM a 3 Lại có: 2 2 CM  ; SG SC CG 2 2 a a 11 2  4a   SG  3 3 S . G CM a 11 a Suy ra HM   2 2
CH CM HM SC 4 4 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 3 Khi đó 7a 1 7a 11 SH
V SH.S  4 3 HBC 96 Chọn A Cách 2: 2 2 2
SA SC AC 7 7a cos ASC  
SH SAcos S  2.S . A SC 84 4 Khi đó V SA SB SH 7 S .HAB  . .  V SA SB SC 8 S . ABC
Câu 37. Gọi H là trọng tâm tam giác đều
ABC SH   ABC  .
Gọi M là trung điểm của BC. a 3a Ta có: 0
AH SA cos 60   AM  ; 2 4 a 3 0
SH SAsin 60  2 Đặ x 3 3a a 3
t AB x AM    x  2 4 2 2 2 3 Do đó x 3 3a 3 1 3a S  
V SH.SABC 4 16 3 ABC 32 Chọn B
Câu 38. Gọi H là tâm của đáy khi đó SH   ABCD .
Dựng HE C ;
D HK SE . Khi đó
CD  SHE  0  SEH  45
d H;SCD  HK a HE a 2  SH HE a 2 3 1 8a 2
Mặt khác AD  2HE  2a 2  V SH.S  3 ABCD 3 Chọn C
Câu 39. Gọi H là tâm của đáy khi đó SH   ABCD
Dựng HP CD CD  SPH  0  SPH  45 Khi đó a a 0 HP
SH HP tan 45  2 2 2 3 a a Do vậy S  VABP S . 2 APB 12 3 V SM SN SP 1 a
Mặt khác S.MNP  . .   VS . V SA SB SP 4 MNP 48 S . ABP ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 3 a Do vậy VV
(do d S;MNP  d  ; A MNP . A MNP S .MNP 48 Chọn D
Câu 40. Gọi H là tâm của đáy khi đó SH   ABCDa 2 a 6 Lại có 0
SH HA tan 60  . 3  2 2 3 1 a 6 VSH.SS . ABCD 3 ABCD 6
Mặt khác gọi G SH AM G là trọng tâm tam giác SAC Do đó SG 2
 . Qua G dựng đường thẳng song song với BD cắt SH 3
SB, SD lần lượt tại P và Q. V Khi đó V SP SM 2 1 1 S APMQ 1 S . ABM  .  .  từ đó suy ra .  V SB SC 3 2 3 V 3 S . ABC S . ABCD 3 a 6 18V Do vậy V    6 S .APMQ 3 18 a Chọn B AB  2 6 3 3 3
Câu 41. Ta có AM   6  S   2 AMN 4 2 1 3 Do vậy VS . O SS . AMN 3 AMN 2 Chọn D
Câu 42. Gọi H là tâm hình vuông ABCD
SH   ABCDAC a 2 a 2 2 2 HA  
SH SA HA  2 2 2 3 SH.S a 2 ABCDV   S . ABCD 3 6 Chọn D
Câu 43. Gọi H là tâm của tam giác ABC
SH   ABC; 2 2
HA a SH
SA HA a 3 3 SH.S 3a ABCV   S . ABCD 3 4 Chọn D ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 44. Gọi H là tâm của tam giác ABC  SH   ABC a a 3
AH SH.cos SAH   SH  2 2 a 3 2  3AH a 3  SH   AB      2 3  2  2 3 SH.S 3a ABCV   S . ABC 3 32 Chọn C
Câu 45. Gọi H là tâm của ta giác ABC, M là trung điểm AB.
Dễ dàng xác định SAB  ABC 0 ,  SMH  45
Đặt SH x HM  ;
x SM x 2  CM  3HM  3x 3CMAB
 2x 3  AM x 3 3 a 2 2 2 2 2 2 2
SA SM AM a  2x  3x  5x x  5 3 3 SH.S a 3 15a ABCV    S . ABC 3 5 5 25 Chọn C
Câu 46. Gọi H là tâm của hình vuông ABCD. M là trung điểm AB. Tam giác SAB đề a 3 a u nên SM  , HM  2 2 a 2 3 a 2 2 2
SH SM HM   V  2 S . ABCD 6 Chọn B
Câu 47. Hình chóp đều là S.ABCD. Gọi H là tâm của hình
vuông ABCD. M là trung điểm AB, K là hình chiếu của H lên SM.
Xác định nhanh: SAB  ABCD 0 ,  SMH  45 và
d H,SAB  HK a
Như vậy tam giác SMH vuông cân tại H nên: SH MH a 2  AB  2a 2 3 SH.S 8a 2 ABCDV   . S . ABCD 3 3 Chọn D ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 48. Gọi P là giao điểm của BM và AD. H là hình
chiếu của A lên BM, K là hình chiếu của A lên SH.
Vì SA BM AH BM  SAH
BM AK . Mà AK SH AK  SBM   d  ,
A SBM   AK . d  , A SBM AK a a
Vì AP  2DP nên: d D,SBM     2 4   AK  2 2 33 33 AP 2.AD 4a
Tính: AH AB sin ABH A . BA . B  2 2 BP AB  4.AD 17 1 1 1 Sử dụng    SA a 2 2 2 SA HA AK Chọn A
Câu 49. Gọi M là trung điểm của CD, O là giao điểm AC và BD CD   OM Ta có 
CD  SOM   CD SMCD SO a 3 a 2 Ta có 2 2 SM
SO SM OM  2 2 3 1 1 a 2 a 2 12V 2 VS . O S  . .a    2 S . ABCD 3 ABCD 3 2 12 3 aChọn C 1
Câu 50. Ta có Vd D ABC S AMND  ,  3 AMN 1 Lại có Vd D ABC S ABCD  ,  3 ABC 1 V 1 Mà AMND SS   AMN 4 ABC V 4 ABCD Chọn A 1
Câu 51. Ta có V
d S, ABCD .S S .ICM    3 ICM 1 Lại có V
d S, ABCD .S S . ABCD    3 ABCD 1 1 Ta có SS mà SS BCM 4 ABCD ICM 4 BCM 1 V 1 S .ICMSS   ICM 12 ABCD V 12 S . ABCD Chọn D ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 52. Gọi O là tâm của hình bình hành ABCD. SO cắt B’D’ tại I. Nối AI cắt SC tại C’ nên A, B’, C’, D’ đồng phẳng. Đặ V t VV VVS . ABCD S . ACD S. ABC 2 V SC ' SD ' V SC ' SB '
Ta có S.AC'D'  . và
S . AC ' B '  . . V SC SD V SC SB S . ACD S . ACB Do đó V V SC ' V 1 SC ' 1
S . AC ' B '
S . AC ' D '
S . AB 'C ' D '     .  V V SC V 2 SC 6 S . ACB S . ACD V 1 V V 5V
Vậy S.AB'C' D'   V   VV  
S . AB'C' D'
AB 'C ' D'. V 6 6 ABCD 6 6
Hay tỷ số thể tích của hai khối chóp được chia ra bởi (AB’D’) là: V V 5V 1
S . AB 'C ' D '  :  V 6 6 5
AB 'C ' D '. ABCD Chọn C
Câu 53. Ta có MN là đường trung bình của tam giác SAD 1  MN BC
Suy ra MN song song với AD và MN AD   2 MN BC
Do đó BCNM là hình bình hành mặt khác CB BM
Nên BCNM là hình chữ nhật nên S  2SV  2V BCNM BCM S.BCNM S.BCM 3 1 1 1 a VBC.SBC.S  . a 2 . a a S .BCM   3 SBM 6 SAB 6 3 Chọn A
Câu 54. Áp dụng công thức tính tỉ số thể tích, ta có: V AB ' AC AD ' 1 V . A B 'CD '  . .   V  . A B 'CD ' V AB AC AD 4 4 . A BCD V 3V Mà VVVVV   . A BCD . A B 'CD '
C.BDD ' B '
C.BDD ' B ' 4 4 Chọn D
Câu 55. Gọi H là tâm của hình vuông ABCD.
Vì SA SB SC SD nên SH   ABCD
Đặt AB x , khi đó 2
x  4  x  2 . Gọi M là trung điểm của AB.
Xét tam giác SAB cân tại S, có 1 S
 .SM.AB  2  SM  2 SAB 2
Xét tam giác SHM vuông tại H, có 2 2 SH SM MH  1 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 1 4
Vậy thể tích khối chóp là V  .SH.SS . ABCD 3 ABCD 3 Chọn A
Câu 56. Gọi O là tâm của đáy ABCD, M là trung điểm của BC.
Từ O kẻ OH vuông góc với SC, ta có SC   BDH V SH V SH Ta có S.AHD S .  , AHB  mà V SC V SC S . ACD S . ACB 1 V VVVS . ACD S . ACB S . 2 ABCD 2 VV 2SH V SH Nên S.AHD S .AHB S .ABHD    V SC V SC 2 a
Có BC  SAM  nên SBC  ABCD 0 ;  SMA  3 60  SA  2 CH CO a Mặt khác CAS CHO    CH CA SA 13 SH SC HC HC 11 11 Suy ra  1   VV S . SC SC SC 13 ABHD 13 Do đó 11 2 VV VV V V H .BCD S . ABHD 12 13 Chọn D
Câu 57. Gọi Q là trung điểm của AD. Và MN cắt SD tại P. SP 2
Suy ra P là trọng tâm của tam giác SMC nên  SD 3
Gọi h là độ dài đường cao của tứ diện, do đó  h h d ;
P ABCD  , d N; ABCD  . 3 2 1 a h Ta có V  .d N ABCD S  và N BCM  ;  2 . .  3 BCM 6 1 a h Vd P ABCD S  . Nên P MQD  ;  2 . .  3 MQD 36 2 2 2 2 2 2 a h a h 5a h a h 5a h 7a h V    V    NBC.PQD 6 36 36 SABNPQ 3 36 36
Vậy tỉ số thể tích giữa hai phần của hình chóp tạo bởi mặt phẳng V
(BMN) là NBC.PQD 5  V 7 SABNPQ Chọn A
Câu 58. Gọi M là trung điểm của BC, H là tâm của đáy ABC. ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Ta có SH   ABC   SH BC và SM BC nên BC  SAM  .
Từ M kẻ MD vuông góc với SA tại D nên SA   DBC    P
Lại có SA ABC  SA AH  0 ; ;  SAH  60 Do đó AH AH 2a cos SAH   SA   0 SA cos 60 3
Xét tam giác SAB cân tại A, có đường cao BD, gọi K là trung điểm của AB suy ra 2 2 a 13  2a   a 13  5a 3
SK.AB B . D SA BD  . Khi đó 2 2 SD SB BD          4  3  4 12   V SD SB SC 5 Vậy S.BDC  . .  V SA SB SC 8 S . ABC Chọn B V AB ' AD ' 1 1 1 V
Câu 159. Áp dụng công thức thể tích, ta có S.B'CD'  .  .   V
S . AB ' D ' V AB AD 2 2 4 4 S .BCD Chọn B V AB ' AD ' 1 1 1 V
Câu 60. Áp dụng công thức thể tích, ta có S.B'CD'  .  .   V  và
C. AB ' D ' V AB AD 2 2 4 4 S .BCD 3V V V 3V 1 V
. Suy ra C.AB'D'  : 
C.BB ' D ' B 4 V 4 4 3
S .BB ' D ' B Chọn D V SM SN SP 1 2 1 1
Câu 61. Áp dụng công thức tỷ số thể tích, ta có S.MNP  . .  . .  V SA SB SC a b 2c abc S .ABC VS.ABC   abc VS.MNP Chọn C.
Câu 62. Kẻ AM cắt BC tại N.
Từ M kẻ MA’ song song với SA, với A' SN MA ' MN Xét NMA' NAS    SA NA  1 VV
d S; ABC .SM.BCS S .MBC      3 MBC V S Ta có  M .BCS MBC   1  V S V
d S; ABC .S ABCS . ABC ABC S . ABC     3 S d M BC MN MA V MA' MBC  ;  ' Mà    M .BCS   S d A BC AN SA V SA ABC   ;  S . ABC Chọn C ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 SM SN
Câu 63. Kẻ MN//CD, với N SD nên   x SC SD 1 1 Ta có VVVV S . ACB S . ACD S . 2 ABCD 2 V SM SN V SM Và S.AMN 2 S .  .  x , AMB   x V SC SD V SC S .ACD S . ACB 2 V V V x x Do S.AMN S .AMB 2 S .ABMN   x x   V V V 2 S . ACD S . ACB S . ABCD 2 x x 11      1 0 0    x  0,1 2 200 2 10
 0x 100x 11  0 Chọn D
Câu 64. M là trung điểm của SB nên
d S; ABCD  2s M ; ABCD Do đó  SA a
d M ; ABCD   a VVS C.MNP M .  2 PCN 3 PCN 2 1 1 a Mà S
CN.CP C . B CD PCN 2 8 8 2 3 a a a
Vậy thể tích khói chóp S.MNP là V  .  C.MNP 3 8 24 Chọn D
Câu 65. Vì M, P, N lần lượt là trung điểm của SB, SC, BC. 1 1
Nên d M ; ABC   d  ;
P ABC   d S; ABC   .2a a 2 2 2 1 a 3 2 a 3 Và SSS   VVABN ANC  2 ABC 8 M . ABN P.ANC 24 3 V SM SP 1 a 3 Mà S.AMP  ;   VS . V SB SC 4 AMP 24 S . ABC 3 3 3 Do đó a 3 a 3 a 3 VVVV    . A MNP S . ABC M .ABN P.ANC 6 8 24 Chọn A
SAB   ABCDCâu 66 Ta có  và  SAD    ABCD
SABSAD  SA  ABCD Ta có 2 2 AC
AB BC a 2 2 2
SA SC AC a 3 1 1 a Ta có 2 Sa . 2 VS . A S  . a a ABCD S . ABCD 3 ABCD 3 3 Chọn D ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 Câu 67. Ta có 2 2
AD  2a HA HD a SH
SA HA  2a 1 3 1 4a Ta có 2 SA .
D AB  2a VSH.S 2  2 . a 2a ABCD S . ABCD 3 ABCD 3 3 Chọn C 2a 3 Câu 68. Do S
AB đều nên SH   a 3 2 1 1 Ta có 2 2 SAB  4a 2  VSH.Sa 3.4a ABCD S . ABCD 3 ABCD 3 3 4a 3  3 Chọn B Câu 69. Do ABC  vuông tại B 2 2
BC AC AB  3a 3 1 Ta có 2 2 HB
AB a CH
HB BC  2a 7 3
Ta có SC ABC 0 ,  SCH  60 0
SH  2a 7.tan 60  2a 21 2 1 1 9a 3 Mà SA . B BC  3 . a 3a 3  ABC 2 2 2 2 1 1 9a 3 3 VSH.S  2a 21.  9a 7 S . ABC 3 ABC 3 2 Chọn B
Câu 70. Ta có SA ABC 0 ,  SAH  45 a 3 a 3 Ta có CI   HI  2 4 a 7 2 2
AH AI HI  4 a 7
SH AH.tan SAH  4 2 a 3 Ta có SABC 4 2 3 1 1 a 7 a 3 a 21 VSH.S  . .  S . ABC 3 ABC 3 4 4 48 Chọn D
Câu 71. Ta có SD ABCD 0 ,  SDH  45 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 2 2 2 AD DO AO a 5 a Lại có DH    5
SH DH.tan SDH  .Ta có 2 2 SAB  2a 2 4 2 2 ABCD 3 1 1 a 5 a 5 2  VSH.S  . .2a S . ABCD 3 ABCD 3 2 3 Chọn D
Câu 72. Gọi M là trung điểm của BC BC AM Ta có 
BC  SAM   BC SA
 SBC  ABC 0 ,  SMA  60 a 3 3a Ta có AM
SA AM.tan SMA  2 2 2 a 3 2 1 1 3a a 3 Lại có S  VS . A S  . . ABC 4 S . ABC 3 ABC 3 2 4 3 a 3  8 Chọn B
Câu 73. Kẻ AH BCBC AH Ta có 
BC  SAH   SBC, ABC  BC SA 0  SHA  45 Ta có 2 2 AC
BC AB  2a 2 1 1 1 9    2a 2 2a 2  AH   SA  2 2 2 2 AH AB AC 8a 3 3 1 1 1 1 2a 2 3 4a Ta có 2 SA . B AC  .2 a a 2  a 2 2  VS . A S  . a 2  ABC 2 2 S .ABC 3 ABC 3 3 9 Chọn C AB BC Câu 74. Ta có : 
BC  SBA  SA BC
Do vậy SBC   ABC  0 ; SBA  30 Mặt khác 2 2 BC
AC AC  2a 3 2a Lại có 0
SA AB tan 30  3 3 1 1 2a 8a Do vậy VS . A S  . .2 .2 a a 3  S .ABCD 3 ABCD 3 3 3 Chọn D ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 75. Ta có tam giác ABC vuông tại B nên 2 2 BC
AC AB a 2 Mặt khác 2 2 SA
SB AB  2a 2 3 1 1 a 2 a 2 Do vậy VS . A S  2 . aS . ABC 3 ABC 3 2 3 Chọn A
Câu 76. Ta có tam giác ABC vuông tại B nên 2 2 BC
AC AB a 2 Mặt khác 2 2 SA
SB AB a 5 2 3 1 1 a 2 a 10 Do vậy VS . A Sa 5.  S . ABC 3 ABC 3 2 6 Chọn A
 SAB   ABC 
Câu 77. Do  SAC    ABC   SA   ABC
SA  SAB  SAC 2 a 3 Mặt khác 2 2 SA
SC AC a 2; SABC 4 2 3 1 1 a 3 a 6 Do vậy VS . A Sa 2.  S . ABC 3 ABC 3 4 12 Chọn B Câu 78. Ta có 2 2 BC
AC AB a 3 Mặt khác 2 2 2 2 SA SD AD
SD BC a 3 3 1 1 a 6 Do vậy VS . A S
 .a 3.a 2.a S .ABCD 3 ABCD 3 3 Chọn D
Câu 79. Gọi O là tâm của hình đáy ABCD khi đó
SO   ABCDa 6
Ta có: AC AB 2  a 6  OC  2
Mặt khác mặt bên của khối chóp là tam giác đều nên a 6 2 2
SC CD SD a 3  SO SC OC  2 3 1 a 6 Do vậy VS . O SS . ABCD 3 ABCD 2 Chọn D ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 80. Gọi G là trọng tâm tam giác đều ABC khi đó
SG   ABC a
Gọi M là trung điểm của BC khi đó 3 AM  2 2 a 3 Suy ra GA AM
. Mặt khác mặt bên của chóp là tam giác 3 3 đề a 6 u nên 2 2
SA AB SB a SG SA GA  3 2 3 Do đó 1 1 a 6 a 3 a 2 VS . G S  . .  S .ABC 3 ABC 3 3 4 12 Chọn B
Câu 81. Ta có tam giác ABC vuông tại B nên 2 2 BC
AC AB a 2
Mặt khác SB ABC 0 0 ;  30  SBA  30 Do đó a 0
SA AB tan 30  3 2 3 Khi đó 1 1 a a 2 a 6 V  . SA S  . .  S . ABC 3 ABC 3 3 2 18 Chọn C
 SAB   ABC 
Câu 82. Từ  SAC    ABC   SA   ABC    SAB
SAC  SA
 SB ABC 0 ;
SBA SBA  30 SA 1 AB a 0  tan 30    SA   AB 3 3 3 3 1 1 a 1 a 0  VS . A S  . . . a . a sin 60  S . ABC 3 ABC 3 3 2 12 Chọn D
 SAB   ABC 
Câu 83. Từ  SAC    ABC
SA   ABC   SAB
SAC  SA
 SM ABC 0 ;
SMA SMA  60 SA AB 3 3a 0  tan 60 
 3  SA AM 3  . 3  AM 2 2 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 3 1 1 3a 1 a 3 0 VS . A S  . . . a a sin 60  S . ABC 3 ABC 3 2 2 8 Chọn C
Câu 84. Từ SA   ABC  SC ABC 0 ;
SCA SCA  45 2 2 2 2
SA AC BC AB  4a a a 3 3 1 1 1 a 3 aVS . A Sa 3. A . B AC  . . a a 3  S .ABC 3 ABC 3 2 6 2 Chọn A
Câu 85. Từ SA   ABC  SM ABC 0 ;
SMA SMA  60 SA 1 0  tan 60 
 3  SA AM 3  BC 3  a 3 AM 2 Cạnh 2 2 2 2 AC
BC AB  4a a a 3 3 1 1 1 a 3 aVS . A Sa 3. A . B AC  . . a a 3  S .ABC 3 ABC 3 2 6 2 Chọn A Câu 86. Cạnh 2 2 2 2 BC
AC AB  4a a a 3
Từ SA   ABCD  SC ABCD 0 ;
SCA SCA  45
sA AC  2a 3 1 1 2a 3 VS . A S  2 . a . a a 3  S . ABCD 3 ABCD 3 3 Chọn A Câu 87. Cạnh 2 2 2 2 BC
AC AB  4a a a 3 Từ
SA   ABCD  SO ABCD 0 ;
SOA SOA  60 SA AC 0  tan 60 
 3  SA OA 3  3  a 3 OA 2 1 1 3  VS . A Sa 3. . a a 3  a S . ABCD 3 ABCD 3 Chọn C
 SAB   ABC 
Câu 88. Từ  SAD   ABC
SA   ABCD   SAB
SAD  SA ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
 SC; ABCD  SCA 0
SCA  45  SC AC a 2 3 1 1 a 2 2  VS . A Sa 2.a S . ABCD 3 ABCD 3 3 Chọn B
 SAB   ABC 
Câu 89. Từ  SAD   ABC   SA   ABCD   SAB
SAD  SA
 SM; ABCD  SMA SA 0 0
SMA  60  tan 60 
 3  SA AM 3 AM Cạnh 2  a a 5 a 15 2 2 2 AM AB BM a    SA     2  2 2 3 1 1 a 15 a 15 2 VS . A S  . a S . ABCD 3 ABCD 3 2 6 Chọn A 1
Câu 90. Ta có SH   ABCD  VSH.S S . ABCD 3 ABCD
Và HC là hình chiếu của SC trên mặt phẳng (ABCD)
Do đó SC ABCD  SC HC 0 ; ;  SCH  60 Xét SCH vuông, có SH 0 tan SCH
SH  tan 60 .HC  3.HC HC Mà 2 2 2 2 HC
BC BH  4a a a 5 nên SH a 15 3 4a 15
Vậy thể tích khối chóp S.ABCD là VS . ABCD 3 Chọn B 1
Câu 91. Ta có SH   ABCD  VSH.S S . ABCD 3 ABCD
Và HD là hình chiếu của SD trên mặt phẳng (ABCD)
Do đó SD ABCD  SD HC 0 ; ;  SDH  45 Xét S
DH vuông cân tại H, có SH HD mà AD HD   a 2 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 3 1 2a
Nên SH a . Vậy thể tích V  . a 2 . a a  (đvtt) S . ABCD 3 3 Chọn C 1
Câu 92. Ta có SA   ABCD  VS . A S S . ABC  3 ABC
Từ A kẻ AH vuông góc với BD,
H BD BD  SAH
 SAH  SBD  SH Có    SAH   ABCD
SBD,ABCD  AH 0  SHA  30 Mà 2 2 2 2 BC
AC AB  16a  4a  2 3a 1 1 1 1 1 1 Nên       AH a 3 2 2 2 2 2 2 AH AB AD 4a 12a 3a Do đó SH 0 tan SHA
SH  tan 30 .AH a AH 3 1 1 2a 3 Vậy thể tích V  . a 2 . a 2a 3  (đvtt) S . ABC 3 2 3 Chọn C 1
Câu 93. Ta có SA   ABCD  VS . A S S . ABCD  3 ABCD
Từ A kẻ AH vuông góc với BD, H BD BD  SAH
 SAH  SBD  SH Có    SAH   ABCD
SBD,ABCD  AH 0  SHA  30 Mà H là trung điể AC a
m của AC suy ra AH   2 2 Do đó SH a 0 tan SHA
SH  tan 30 .AH AH 6 3 1 a a 6 Vậy thể tích 2 V  . a  (đvtt) S . ABCD 3 6 18 Chọn C 1
Câu 94. Ta có SA   ABCD  VS . A S S . ABCD  3 ABCD
Gọi H là tâm của hình thoi ABCD nên AH BD
Mà SA BD   ABCD  BD  SAH ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
 SAH  SBD  SH Có 0     SHA  60  SAH   ABCD
SBD,ABCD  AH AC a 3 3a Mặt khác 0 AH  
SH  tan 60 .AH  2 2 2 3 1 3a 1 3 3 3a Vậy thể tích V  . . a 3.a 3.  (đvtt) S . ABCD 3 2 2 2 8 Chọn A 1
Câu 95. Ta có SA   ABCD  VS . A S S . ABCD  3 ABCD
Gọi H là trung điểm của CD, tam giác ACD đều nên AH CD
Mà SA CD   ABCD  CD  SAH  Có
 SAH  SBD  SH 0     SHA  30  SAH   ABCD
SBD,ABCD  AH 3 3a a 3 Mặt khác 0 AH a 3. 
SH  tan 30 .AH  2 2 2 2 3 1 a 3 3 3a 3a Vậy thể tích V  . .  (đvtt) S . ABCD 3 2 4 8 Chọn C
Câu 96. Gọi O là tâm của hình thoi ABCD, do đó
SO   ABCD
Gọi H là hình chiếu của O trên BC, H BC OH BC
Do đó BC  SOH  và
 SOH  SBD  SH     SOH   ABCD
SBC,ABCD  OH  SO HO 0 ;  SHO  30 1 1 1 25 12a 12a Mà     OH   SH  2 2 2 2 OH OB OC 144a 5 5 3 3 1 12a 1 32a 3 Vậy thể tích V  . . .6 .8 a a  (đvtt) S . ABCD 3 5 3 2 5 Chọn A
Câu 97. Gọi O là tâm của hình vuông ABCD, do đó
SO   ABCD
Gọi H là hình chiếu của O trên BC, H BC OH BC ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
 SOH  SBC  SH
Do đó BC  SOH  và 
 SBC  ABCD  SO HO 0 ; ;  SHO  45  SOH
 ABCD  OH Mà H là trung điể BC m của BC nên OH
a 2  SO a 2 2 1 8a 2 Vậy thể tích V  .a 2. a  (đvtt) S ABCD 2 2 3 2 . 3 3 Chọn D
Câu 98. +) Gọi H là tâm của tam giác đều
ABC SH   ABC  . Lấy M là trung điểm BC. Ta có
SH BC AM  SAM   BC  SBC    ABC  và
SAM  cắt hai mặt phẳng này tại 2 giao tuyến SM và AM
 SBC  ABC 0 ,  SMH  60 AB 3 AM a 3 +) AM
a 3  HM  
SH HM 3  a 2 3 3 3 SH.S a 3 ABCV   S . ABC 3 3 Chọn A
Câu 99. +) Gọi K là trung điểm CD. Vì
SH CD HK CD  SHK  .
(SHK) vuông góc với giao tuyến CD của (SCD) và
(ABCD), đồng thời cắt 2 mặt phẳng này tại các giao tuyến
SK và HK  SCD  ABCD 0 ,  SKH  60
+) HK AD  6a SH HK 3  6a 3 SH.S SH.A . B AD ABCD 3  V    96a 3 S . ABCD 3 3 Chọn D
Câu 100. +) Gọi K là hình chiếu vuông góc của H lên cạnh BD. Vì
SH BD HK  SHK   BD  SBD   ABCD , và SHK  cắt 2 mặt phẳng này tại các giao
tuyến SK và HK  SBD  ABCD 0 ,  SKH  60 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 HK BH 12a +) 2 2 BD
AD AB  10 ; a   HK AD BD 5 12a 3 SH.S 3  SH.A . B AD 192a 3 SH HK 3 ABCD  V    S . 5 ABCD 3 3 5 Chọn B
Câu 101. +) Gọi M là hình chiếu vuông góc của H lên CD. Vì
HM CD SH  SHM   CD  SCD   ABCD
Và (SHM) cắt hai mặt phẳng này tại các giao tuyến SM và HM nên suy ra
SCD ABCD 0 ,  SMH  60 HM CH 3 3a 3a 3 +)    HM
SH HM 3  AD CA 4 2 2 2 SH.S SH.AB ABCD 3 V    2a 3 S . ABCD 3 3 Chọn D
Câu 102. +) Gọi H là hình chiếu của S lên (ABCD). Vì tam
giác SAD cân tại S và nằm trong mặt phẳng vuông góc
đáy nên H là trung điểm AD. Gọi K là giao điểm HC và BM. +) CHD B
MC  .cg.c  CHD BMC . Lại có: 0 0
CHD DCH  90  BMC DCH  90
CH BM . Nên SH BM HC BM  SHK  . Mặt phẳng (SHK) vuông góc với BM là giao
tuyến của (SBM) và (ABCD), đồng thời cắt 2 mặt phẳng này tại các giao tuyến SK và HK, suy ra
SBM  ABCD 0 ,  SKH  60 . CK CM 2a 3a +) 2 2
CH CD HD a 5 ;   CK
HK CH CK CD CH 5 5 3a 3
SH HK 3  5 3 SH.S 4a 15 ABCDV   S . ABCD 3 5 Chọn B ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
 SBI  SCI   SI Câu 103. +) 
SI   ABCD  SBI
   ABCD  SCI
Lấy E là điểm đối xứng với D qua C, suy ra tứ giác ABED là hình vuông. Gọi K là giao điểm của IE và BC. +) EID BCE
 .cg.c  EID BCE . Lại có: 0 0
EID DEI  90  BCE DEI  90  EI BC
Nên SI BC IE BC  SIK  .
Mặt phẳng (SIK) vuông góc với BC là giao tuyến của (SBC) và (ABCD), đồng thời cắt 2 mặt phẳng
này tại các giao tuyến SK và IK, suy ra SBC  ABCD 0 ,  SKI  60 EK EC 2a 3a a +) 2 2 IE
ED ID a 5 ;   EK
IK IE KE  3 3
SI IK 3  ED EI 5 5 5 SI.S SI AB CD AD a ABCD   3 . 3 15  V    S .ABCD 3 6 5 Chọn C BC
Câu 104. +) AB AC
a . Khối AB .
C A' B 'C ' là lăng trụ đứng 2
nên A là hình chiếu của A’ lên mặt phẳng  ABC  2 2
AA'  A' B AB  2a 2 AA'.A . B AC +) 3 VAA'.S   a 2
ABC. A' B 'C ' ABC 2 Chọn B BC
Câu 105. AB AC
a . Khối AB .
C A' B 'C ' là lăng trụ đứng nên A 2
là hình chiếu của A’ lên mặt phẳng (ABC)
  A C ABC 0 ' ,  A'CA  60 3 a 3
AA'  AC 3  a 3  VAA'.S
ABC. A' B 'C ' ABC 2 Chọn C
Câu 106. Do AD  2a HA HD a Ta có 2 2 HC
HD CD a 2
Ta có SC ABCD 0 ,  SCH  60
SH HC.tan SCH a 6 Ta có 2 SA . B BC  2a ABCD 1 1 3 2a 6 2  VSH.Sa 6.2a S . ABCD 3 ABCD 3 3 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 Chọn B a a 10 Câu 107. Ta có 2 2 AC AD CD  6
a 6  OA OC  2 2
SO SA OA  2 2 3 1 1 a 10 a 10 Ta có 2 2 SAB  3a 2 VS . O S  . .3a ABCD S . ABCD 3 ABCD 3 2 2 Chọn A
Câu 108. Ta có SA ABCD 0 ,  SAO  60 a Ta có 2 2 AC AD CD  6
a 6  OA OC  2 3a 2  SO O . A tan SAO  2 1 1 3a 2 Ta có 2 2 SAB  3a 2 VS . O S  . .3a ABCD S . ABCD 3 ABCD 3 2 3 3a 2  2 Chọn A a 3 2 a 3
Câu 109. Ta có CM
CH CM  2 3 3 a 33 2 2
SH SC CH  3 2 a 3 Ta có SABC 4 2 3 1 1 a 33 a 3 a 11  VSH.S  . .  S .ABC 3 ABC 3 3 4 2 Chọn A
Câu 110. Ta có SC ABC 0 ,  SCH  45 a 3 2 a 3 Ta có CM
CH CM  2 3 3 a 3
SH CH.tan SCH  3 2 a 3 2 3 1 1 a 3 a 3 a Ta có S   VSH.S  . .  ABC 4 S . ABC 3 ABC 3 3 4 12 Chọn C ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 1 a 3 Câu 111. Do S
AB vuông cân tại S SM AB  2 2 a 3. 3 3a 1 a Ta có CM  
HM CM  2 2 3 2 a 2 2 2
SH SM HM  2 a 2 2 3 3 3a 3 Ta có S   ABC 4 4 3 3 1 1 a 2 3a 3 a 6 VSH.S  . .  S . ABC 3 ABC 3 2 4 8 Chọn C Câu 112. Ta có 2 2 AB
BD AD a
Ta có SB ABCD 0 ,  SBA  30 a 3  SA A . B tan SBA  3 a Ta có S
AB AD BC a a a ABCD     2 1 1 3 2 2 2 2 2 3 1 1 a 3 3a a 3 VS . A S  . .  S . ABCD 3 ABCD 3 3 2 6 Chọn A Câu 113. Ta có 2 2 AB
BD AD a
Ta có SO ABCD 0 ,  SOA  45 a Ta có 2 2 AC AB BC  2 2 2 a 2  AO AC  3 3 2a 2  SA A . O tan SOA  3 a 2 3 1 1 2a 2 3a a 2 Ta có S
AB AD BC a a a   VS . A S  . .  ABCD     2 1 1 3 2 2 2 2 S . ABCD 3 ABCD 3 3 2 3 Chọn C
CHỦ ĐỀ 2: KHOẢNG CÁCH
VẤN ĐỀ 1: KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT MẶT PHẲNG
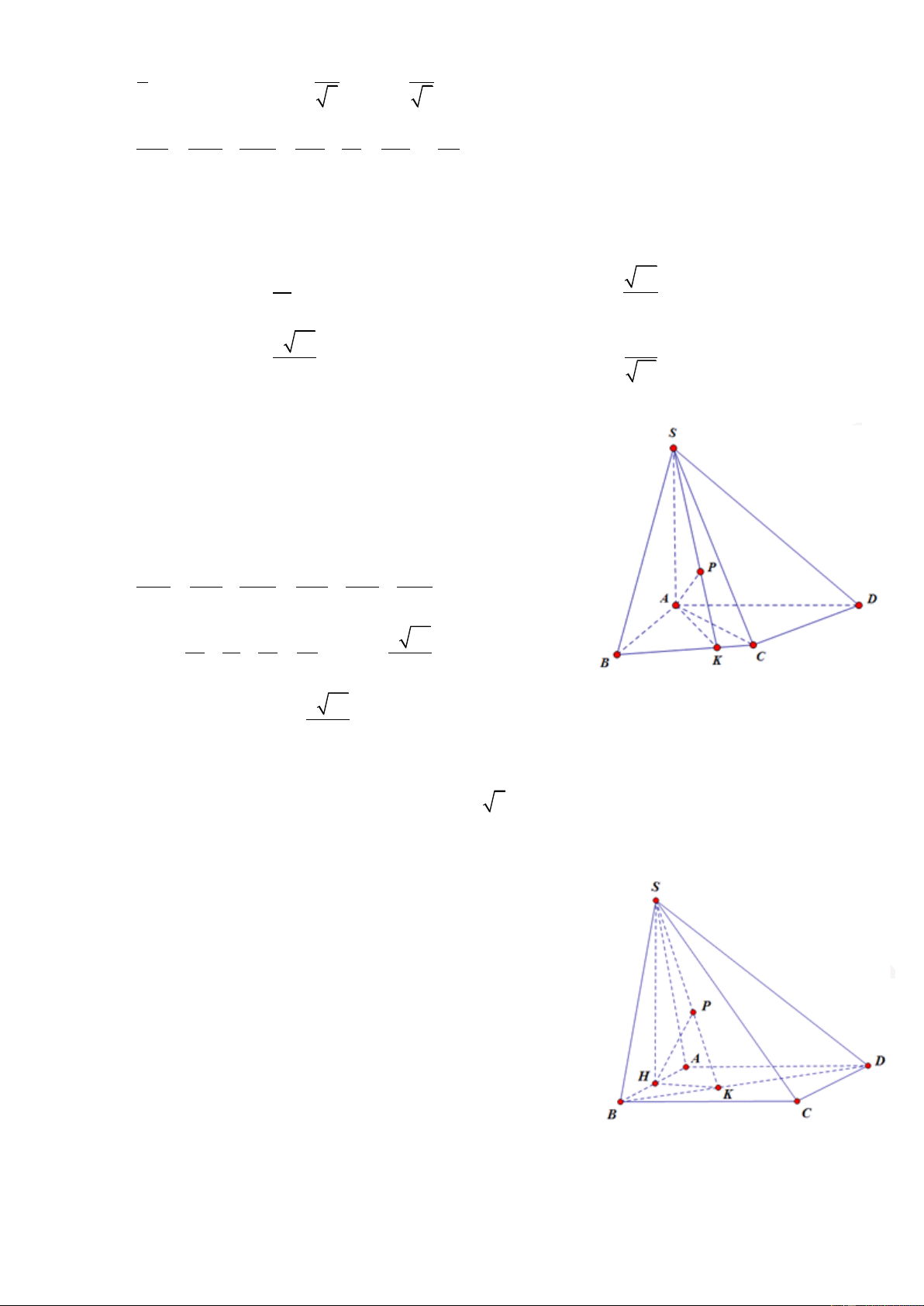
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc ABC  0 60 . Mặt phẳng (SAB)
và (SAD) cùng vuông góc với mặt phẳng đáy. Trên cạnh SC lấy điểm M sao cho MC  2MS . Khoảng
cách từ điểm M đến mặt phẳng (SAB) bằng: a a 3 a 2 a 3 A. 3 B. 6 C. 3 D. 3 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 2: Cho hình chóp S.ABCD có đáy là hình bình hành với BC a ABC  0 2, 60 . Tam giác SAB
nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ điểm D đến mặt phẳng (SAB) bằng: a 6 a 2 2a 6 A. a 2 B. 2 C. 2 D. 3
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc ABC  0 60 . Cạnh SA vuông
góc với mặt phẳng đáy. Trên cạnh BC và CD lần lượt lấy hai điểm M và N sao cho MB MC và
NC  2ND . Gọi P là giao điểm của AC và MN. Khoảng cách từ điểm P đến mặt phẳng (SAB) bằng: a 3 5a 3 5a 3 3a 3 A. 8 B. 12 C. 4 D. 10
Câu 4: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB  ,
a BC a 3 . Hình chiếu
vuông góc của S trên mặt đáy là trung điểm của cạnh AC. Biết SB a 2 . Tính theo a khoảng cách từ
điểm H đến mặt phẳng (SAB) a 21 a 21 3a 21 7a 21 A. 3 B. 7 C. 7 D. 3 2
Câu 5: Cho hình chóp S.ABCD có đáy là hình chữ nhật, diện tích tứ giác ABCD bằng 6a 6 . Cạnh 10
SA a 3 và vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SC và mặt phẳng đáy bằng 300.
Khoảng cách từ điểm B đến mặt phẳng (SAC) gần nhất với giá trị nào sau đây: 13a 7a 3a 8a A. 10 B. 5 C. 2 D. 5
Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AD  2AB  2BC ,
CD  2a 2 . Hình chiếu vuông góc của S trên mặt đáy là trung điểm M của cạnh CD. Khoảng cách từ
điểm B đến mặt phẳng (SAM) bằng: 3a 10 3a 10 3a 10 a 10 A. 10 B. 5 C. 2 D. 3
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AD  2AB  2BC ,
CD  2a 2 . Hình chiếu vuông góc của S trên mặt đáy là trung điểm M của cạnh CD. Khoảng cách từ
trọng tâm G của tam giác SAD đến mặt phẳng (SBM) bằng: 4a 10 3a 10 a 10 3a 10 A. 15 B. 5 C. 5 D. 15 2
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có diện tích bằng 2a ,
AB a 2,BC  2a . Gọi M là trung điểm của CD. Hai mặt phẳng (SBD) và (SAM) cùng vuông góc
với đáy. Khoảng cách từ điểm B đến mặt phẳng (SAM) bằng ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 4a 10 3a 10 2a 10 3a 10 A. 15 B. 5 C. 5 D. 15
Câu 9: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a, ADC  0 120 . Hình chiếu vuông
góc của S trên mặt đáy là trọng tâm của tam giác ABC. Khoảng cách từ điểm C đến mặt phẳng (SAG) bằng a 7 a 21 a 21 a 3 A. 3 B. 7 C. 3 D. 7
Câu 10: Cho hình chóp S.ABC có đáy ABC là tam giác đều có cạnh bằng a. Gọi M là trung điểm của
AC. Hình chiếu của S trên mặt đáy là điểm H thuộc đoạn BM sao cho HM  2HB . Khoảng cách từ
điểm A đến mặt phẳng (SHC) bằng 2a 7 a 7 3a 7 2a 7 A. 14 B. 14 C. 14 D. 7
Câu 11: Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác cân có AC BC  3a . Đường thẳng
A'C tạo với đáy một góc 600. Trên cạnh A'C lấy điểm M sao cho A' M  2MC . Biết rằng
A'B a 31 . Khoảng cách từ M đến mặt phẳng (ABB'A') là: 3a 2 4a 2 A. a a 4 B. 3 C. 3 2 D. 2 2
Câu 12: Cho khối chóp S.ABCD có đáy là hình chữ nhật ABCD với AB a . Hình chiếu vuông góc
của đỉnh S lên mặt đáy trùng với trọng tâm tam giác ABD. Biết SC  2a 2 và tạo với đáy một góc
450. Khoảng cách từ trung điểm của SD đến mặt phẳng (SAC) là: a 2 a 3 2a 4 2a A. 3 B. 3 C. 3 D. 3
Câu 13: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có AD a 3 . Tam giác SAB là tam
giác đều và thuộc mặt phẳng vuông góc với đáy. Gọi M là trung điểm của AD. Biết rằng SD  2a .
Khoảng cách từ A đến mặt phẳng (SHM) là: a 2 a 3 a 2 a 3 A. 4 B. 4 C. 2 D. 2
Câu 14: Cho khối chóp S.ABC có đáy là tam giác vuông tại A có AC a . Tam giác SAB vuông tại S
và hình chiếu vuông góc của đỉnh S trên mặt đáy là điểm H thuộc cạnh AB sao cho HB  2SA . Biết
SH  2a 2 , khoảng cách từ B đến mặt phẳng (SHC) là: 2a a 4a 3a A. B. C. D. 5 5 5 5
Câu 15: Cho hình lăng trụ ABCD.A'B'C'D' có đáy là hình chữ nhật với AD a 3 . Tam giác A'AC
vuông cân tại A' và thuộc mặt phẳng vuông góc với đáy. Biết rằng A ' A a 2 . Khoảng cách từ D'
đến mặt phẳng (A'ACC') là: ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 a 3 a 2 a 2 a 3 A. 4 B. 2 C. 4 D. 2
Câu 16: Cho hình hộp ABCD.A'B'C'D' có đáy là hình vuông, tam giác A'AC vuông cân tại A,
A'C a . Tính khoảng cách từ A đến mặt phẳng (BCD') theo a? a 3 a 6 a 2 a 3 A. 3 B. 3 C. 2 D. 2
Câu 17: Cho hình chóp S.ABC có SA  3a và SA   ABC . Giả sử AB BC  2a , góc ABC  0
120 . Tìm khoảng cách từ A đến mặt phẳng (SBC) ? a 3a A. 2 B. a C. 2 D. 2a
Câu 18: Cho hình chóp S.ABC có đáy là tam giác vuông tại B, BA  3 ,
a BC  4a , mặt phẳng (SBC)
vuông góc với mặt phẳng (ABC). Biết SB  2a 3 và góc SBC  0
30 . Tính khoảng cách từ B đến mặt phẳng (SAC) theo a ? 3a 3 5a 6 6a 6a A. 2 B. 4 C. 7 D. 7
Câu 19: Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật với AB  ,
a AD a 3 . Hình
chiếu vuông góc của A' lên mặt phẳng (ABCD) trùng với trung điểm của AC và BD. Tính khoảng cách
từ B' đến mặt phẳng (A'BD) theo a ? a 3 a 2 a 3 2a A. 2 B. 2 C. 3 D. 3
Câu 20: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB  ,
a BC a 3 . Hình chiếu
vuông góc của S trên mặt đáy là trung điểm của cạnh AC. Biết SB a 2 . Tính theo a khoảng cách từ
điểm H đến mặt phẳng (SBC). a 3 2a 3 a 5 2a 5 A. 5 B. 5 C. 5 D. 5
Câu 21: Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2 ,
a SAB là tam giác vuông cân
nằm trong mặt phẳng vuông góc với đáy. Khoảng cách từ trung điểm H của AB đến mặt phẳng (SBD) là ? a 3 a 3 a 10 A. 3 B. a C. 2 D. 2
Câu 22: Cho hình chóp S.ABCD có đáy là hình thoi cạnh bằng a, góc BAD  0 60 . Gọi H là hình 1
chiếu vuông góc của S xuống mặt đáy (ABCD) và H AC sao cho AH AC 3 . Khoảng cách từ A
đến mặt phẳng (SBC) bằng bao nhiêu nếu biết SA ABCD  0 ; 60 . ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 a 3 3a 3a A. 4 B. 4 C. a D. 2
Câu 23: Cho hình chóp S.ABC có SA  3a và SA   ABC . Biết AB BC a ABC  0 2 , 120 . Tính
khoảng cách từ A đến (SBC) ? a 3a A. 2a B. 2 C. a D. 2
Câu 24: Cho hình chóp S.ABCD có đáy là hình vuông có đường chéo bằng a 2 . Mặt bên
SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách h từ A đến mặt phẳng (SCD) là: a 21 a 21 a 21 a 21 A. h h h h 3 B.  14 C.  21 D.  7
Câu 25: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AC a ABC  0 3, 30 , góc giữa
SC và mặt phẳng (ABC) bằng 600. Cạnh bên SA vuông góc với đáy. Khoảng cách từ A đến mặt phẳng (SBC) bằng a 6 a 3 3a 2a 3 A. B. C. D. 35 35 5 35
Câu 26: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AC a ABC  0 3, 30 , góc giữa
SC và mặt phẳng (ABC) bằng 600. Cạnh bên SA vuông góc với đáy. Khoảng cách từ trọng tâm G của
tam giác SAC đến mặt phẳng (SBC) bằng 3a a a 6 2a A. B. C. D. 5 5 5 5
Câu 27: Cho hình lăng trụ đứng ABC.A'B'C' có AB .
C A'B'C' có AC a BAC  0 , 120 , góc ABC  0 30 2
, mặt bên BCB'C' có diện tích bằng 2a . Gọi M là trung điểm của BC. Khoảng cách từ C
đến mặt phẳng (C'AM) bằng 2a 3 2a 2a 57 2a 3 A. 3 B. 5 C. 19 D. 5 0 0
Câu 28: Cho hình lăng trụ ABC.A'B'C' có AB a 3, ABC  30 , ACB  60 . Hình chiếu vuông góc 3 a
của A' trên mặt đáy là trung điểm của BC. Thể tích khối chóp A'AC bằng 6 . Khoảng cách từ C đến mặt phẳng (A'AB) bằng a 6 2a a 6 a 6 A. 6 B. C. D. 7 4 12 4d
Câu 29: Cho hình chóp đều S.ABC có AB a , góc giữa mặt bên và mặt đáy bằng 600. Tính a , biết
d là khoảng c cách từ điểm A đến mặt phẳng (SBC).
ĐT: 0934286923 Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 A. 3a B. 5a C. 7a D. 9a
Câu 30: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA   ABCD,SA AB a và AD  .
x a . Gọi E là trung điểm cạnh SC. Tìm x, biết khoảng cách từ điểm E đến mặt phẳng (SBD) là a d  3 A. x  1 B. x  2 C. x  3 D. x  4
Câu 31: Cho hình chóp S.ABCD, ABCD là hình vuông cạnh AB a . Mặt phẳng chứa tam giác đều
SAB vuông góc với mặt phẳng đáy (ABCD). Khoảng cách từ điểm A đến mặt phẳng (SCD) là: a 21 a 14 a 2a A. 7 B. 7 C. D. 7 7
Câu 32: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA   ABCD,SA a 3 . Tính theo
a khoảng cách từ điểm O đến mặt phẳng (SBC). a a 3 a 5 a 7 A. 2 B. 4 C. 6 D. 8
Câu 33: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA   ABCD, SA AB a và AD 33d
 2a . Gọi F là trung điểm cạnh CD. Tính a , biết d là khoảng cách từ điểm A đến mặt phẳng (SBF) A. 2a 33 B. 4a 33 C. 2a 11 D. 4a 11
Câu 34: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AD  2a . Hình chiếu vuông góc
của S trên mặt đáy là điểm H H AB thỏa mãn HA  2HB . Biết SA  .
x a và SH a . Tìm x biết 3a 2
khoảng cách từ điểm C đến mặt phẳng (SHD) là d  2 A. x  5 B. x  5 C. x  3 D. x  3
Câu 35: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB  ,
a BC a 3 . Hình chiếu
vuông góc của S trên mặt đáy là trung điểm của cạnh AC. Biết SB a 2 . Tính theo a khoảng cách từ H đến mặt phẳng (SBC). a 3 2a 3 a 5 2a 5 A. 5 B. 5 C. 5 D. 5
Câu 36: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA   ABCD,SA a 3 . Tính theo
a khoảng cách từ điểm O đến mặt phẳng (SBC). a a 3 a 5 a 7 A. 2 B. 4 C. 6 D. 8 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 37: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA   ABCD, SA AB a và AD 33d
 2a . Gọi F là trung điểm cạnh CD. Tính a , biết d là khoảng cách từ điểm A đến mặt phẳng (SBF) A. 2a 33 B. 4a 33 C. 2a 11 D. 4a 11
Câu 38: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AD  2a . Hình chiếu vuông góc
của S trên mặt đáy là điểm H H AB thỏa mãn HA  2HB . Biết SA  .
x a và SH a . Tìm x biết 3a 2
khoảng cách từ điểm C đến mặt phẳng (SHD) là d  2 A. x  5 B. x  5 C. x  3 D. x  3
Câu 39: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB  ,
a BC a 3 . Hình chiếu
vuông góc của S trên mặt đáy là trung điểm của cạnh AC. Biết SB a 2 . Tính theo a khoảng cách từ H đến mặt phẳng (SBC). a 3 2a 3 a 5 2a 5 A. 5 B. 5 C. 5 D. 5
Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA   ABCD, SA AB a và
AD  2a Gọi E là trung điểm cạnh SC. Tính theo a khoảng cách từ điểm E đến mặt phẳng (SBD) a a a a A. 2 B. 3 C. 4 D. 5
Câu 41: Cho hình hộp đứng ABCD.A'B'C'D' có đáy là hình vuông, tam giác A'AC là tam giác vuông
cân, A'C a . Khoảng cách từ A đến mặt phẳng (BCD') là: a 6 a 6 a a 6 A. 3 B. 2 C. D. 6 4
Câu 42: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông SA
góc với mặt phẳng đáy. Gọi M là trung điểm của SB. Tỷ số a khi khoảng cách từ điểm M đến mặt a phẳng (SCD) bằng là: 5 3 A. 2 B. 2 C. 2 D. 1
Câu 43: Cho hình chóp S.ABC có SA   ABC  và SA  4 , cm AB  3 ,
cm AC  4cm và BC  5cm .
Khoảng cách từ điểm A đến mp (SBC) bằng (đơn vị cm) : 2 72 A. d  ; A SBC  d  ; A SBC   17 B.   17 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 6 34 3 C. d  ;
A SBC  d  ; A SBC   17 D.   17
Câu 44: Cho khối chóp S.ABCD có đáy là hình vuông cạnh 4cm. Hình chiếu vuông góc của S xuống
mặt đáy là trung điểm H của AB. Biết rằng SH  2 cm . Khoảng cách từ A đến mặt phẳng (SBD) là: A. 1 cm B. 2 cm C. 3 cm D. 4 cm
Câu 45: Cho hình chóp S.ABC có đáy là tam giác đều. Hình chiếu vuông góc của đỉnh S lên mặt đáy
là điểm H thuộc cạnh AC sao cho HC  2HA . Gọi M là trung điểm của SC và N là điểm thuộc cạnh
SB sao cho SB  3SN . Khẳng định nào sau đây là sai: 4
A. Khoảng cách từ M đến mặt phẳng (ABC) bằng 3 lần khoảng cách từ N đến mặt phẳng (ABC).
B. Khoảng cách từ M đến mặt phẳng (SAB) bằng một nửa khoảng cách từ C đến mặt phẳng (SAB) 1
C. Khoảng cách từ N đến mặt phẳng (SAC) bằng 3 khoảng cách từ B đến mặt phẳng (SAC) 3
D. Khoảng cách từ M đến mặt phẳng (SAB) bằng 2 khoảng cách từ H đến mặt phẳng (SAB)
Câu 46: Cho hình chóp S.ABCD có đáy là hình chữ nhật có AB  9, AD  12 . Hình chiếu vuông góc
của đỉnh S xuống mặt đáy trùng với trọng tâm H của tam giác ABC. Biết SH  6 , khoảng cách từ A
đến mặt phẳng (SCD) là: 36 24 12 4 A. 5 B. 5 C. 5 D. 5
Câu 47: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD. Tam giác SAD cân tại S và thuộc
mặt phẳng vuông góc với đáy. Gọi M là điểm thoã mãn SM  2CM  0 . Tỷ số khoảng cách D đến mặt
phẳng (SAB) và từ M đến mặt phẳng (SAB) là: 2 3 1 A. 3 B. 2 C. 2 D. 2
Câu 48: Cho hình chóp S.ABCD có đáy là hình thoi. Tam giác SAB cân tại S và thuộc mặt phẳng
vuông góc với đáy , biết tam giác ABC đều cạnh 20 cm và mặt phẳng (SCD) tạo với đáy một góc 600.
Khoảng cách từ A đến (SCD) là: A. 20 cm B. 10 cm C. 15 cm D. 30 cm
Câu 49: Cho hình lăng trụ ABC.A'B'C', hình chiếu vuông góc của A' xuống mặt đáy (ABC) trùng với
trung điểm H của AB. Gọi h là khoảng cách từ A đến mặt phẳng (A'BC). Gọi M là trung điểm của
A'C' và N thuộc cạnh CC' sao cho NC '  2NC . Tính khoảng cách từ M và N đến mặt phẳng (A'BC) 3 2 2 2 h 2h h A. h 2 B. 6 C. 3 D. 6
Câu 50: Cho hình lăng trụ ABCD.A'B'C'D' có đáy là hình chữ nhật ABCD có AB  3; AD  4 . Tam
giác A'BD cân tại A' và thuộc mặt phẳng vuông góc với đáy và AA'  5 . Gọi M là trung điểm của
A'D'. Khoảng cách từ M đến mặt phẳng (A'AC) là:
ĐT: 0934286923 Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 12 6 3 4 A. 5 B. 5 C. 5 D. 5
Câu 51: Cho hình chóp đều S.ABCD có SAC là tam giác đều. Gọi dA là khoảng cách từ A đến mặt d
phẳng (SCD) và dB là khoảng cách từ B đến mặt phẳng (SAC). Tỷ lệ A d bằng: B 21 2 21 A. 2 B. 7 C. 3 D. 7
Câu 52: Cho hình chóp S.ABC có tam giác ABC vuông tại A, AB AC  ,
a I là trung điểm của SC,
hình chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm H của BC, mặt phẳng (SAB) tạo với
đáy 1 góc bằng 600. Khoảng cách từ điểm I đến mặt phẳng (SAB). 3a a 39 a 3 a 3 A. 4 B. 3 C. 2 D. 4
Câu 53: Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh 2a. Mặt phẳng (A'BC) tạo
với mặt đáy (ABC) một góc 600. Khoảng cách từ B đến mặt phẳng (B'AC) là: 3a 2a 9a a A. 2 B. 3 C. 4 D. 2
Câu 54: Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác cân tại A, AB AC a CAB  0 2 , 120 .
Góc giữa (A'BC) và (ABC) là 450. Khoảng cách từ B' đến mặt phẳng (ABC) là: a 2 A. a 2 B. 2a 2 C. a D. 4
Câu 55: Cho lăng trụ tứ giác đều ABCD.A'B'C'D' với cạnh đáy 2 3 dm . Biết rằng mặt phẳng (BDC')
hợp với đáy một góc 300. Khoảng cách từ A đến mặt phẳng (BDC') là: 6 3 2 6 A. dm dm dm dm 2 B. 2 C. 3 D. 3
Câu 56: Cho hình chóp S.ABCD có đáy là tam giác vuông tại A, AB  2 ,
a AC a 3 . Hình chiếu
vuông góc của S lên mặt phẳng (ABC) là trung điểm H của cạnh AB. Cạnh bên SC hợp với đáy 1 góc
600. Khoảng cách từ A đến mặt phẳng (SBC) là: 4 29a 87a 4 87a 4a A. 29 B. 29 C. 29 D. 29
Câu 57: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BC a ACB  0 , 60 ,
SA  ABC và M là điểm nằm trên cạnh AC sao cho MC  2MA. Biết (SBC) tạo với đáy góc 300.
Khoảng cách từ M đến mặt phẳng (SBC) là: 3a a 3 a 3 2a A. 2 B. 3 C. 6 D. 9
Câu 58: Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng 2a, cạnh bên bằng 3a. Gọi O là tâm đáy,
M, N là trung điểm của AB, BC. Khoảng cách từ O đến mặt phẳng (SMN) là:
ĐT: 0934286923 Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 a 279 a 279 a 23 23 A. a 69 B. 23 C. 279 D. 279
Câu 59: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a,
SA  ABCD,SA a 3 . Gọi G là trọng tâm SAC . Từ G kẻ đường thẳng song song với SB cắt OB
tại I. Khoảng cách từ I đến mặt phẳng (SBC) là: a 2 a 2 a 3 a 6 A. 2 B. 6 C. 6 D. 3
Câu 60: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều
cạnh a và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của AB, E là trung điểm của
BC. Khoảng cách từ I đến mặt phẳng (SED) là: a 2 a 2 a 2 3a 2 A. 2 B. 6 C. 4 D. 8 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 Đáp án 1-B 2-A 3-C 4-B 5-B 6-B 7-A 8-C 9-B 10-D 11-B 12-A 13-B 14-C 15-D 16-B 17-C 18-D 19-B 20-C 21-A 22-B 23-D 24-D 25-C 26-B 27-C 28-B 29-A 30-B 31-A 32-B 33-B 34-A 35-C 36-B 37-B 38-A 39-C 30-B 41-C 42-B 43-C 44-B 45-A 46-A 47-B 48-C 9-B 50-B 51-D 52-D 53-A 54-C 55-A 56-C 57-B 58-D 59-C 60-D Hướng dẫn giải
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc ABC  0 60 . Mặt phẳng (SAB)
và (SAD) cùng vuông góc với mặt phẳng đáy. Trên cạnh SC lấy điểm M sao cho MC  2MS . Khoảng
cách từ điểm M đến mặt phẳng (SAB) bằng: a a 3 a 2 a 3 A. 3 B. 6 C. 3 D. 3 SAB   ABCHD: Ta có:  SA ABCD
 SAD   ABC    
Dựng CH AB CH  SAB
d C;SAB CS 3 Do
d M;SAB   MS 2 2 2 2 a 3 a 3
d M;SAB  d C;SAB  CH  .  3 3 3 2 6 Chọn B
Câu 2: Cho hình chóp S.ABCD có đáy là hình bình hành với BC a ABC  0 2, 60 . Tam giác SAB
nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ điểm D đến mặt phẳng (SAB) bằng: a 6 a 2 2a 6 A. a 2 B. 2 C. 2 D. 3
HD: Dựng SH AB
Do SAB   AB D
C   SH  AB D C
Dựng CK AB , có CK  SH CK  SAB Do D
C / / AB d  ;
D SAB  d  ;
C SAB  CK ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 a  0 3 6
BC sin60  a 3.  2 2 . Chọn A
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc ABC  0 60 . Cạnh SA vuông
góc với mặt phẳng đáy. Trên cạnh BC và CD lần lượt lấy hai điểm M và N sao cho MB MC và
NC  2ND . Gọi P là giao điểm của AC và MN. Khoảng cách từ điểm P đến mặt phẳng (SAB) bằng: a 3 5a 3 5a 3 3a 3 A. 8 B. 12 C. 4 D. 10
HD: Dựng CH AB CH  SAB
Giả sử MN cắt AD tại F. theo định lý Talet ta có: DF ND 1 MC a    DF   MC NC 2 2 4 PA AF 5 CA 7 Khi đó     PC MC 2 PA 5 5 5 Do đó d  ;
P SAB  d  ;
C SAB  CH 7 7 5 a 3 5a 3  .  7 2 14 . Chọn C
Câu 4: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB  ,
a BC a 3 . Hình chiếu
vuông góc của S trên mặt đáy là trung điểm của cạnh AC. Biết SB a 2 . Tính theo a khoảng cách từ
điểm H đến mặt phẳng (SAB) a 21 a 21 3a 21 7a 21 A. 3 B. 7 C. 7 D. 3 2 2 AC HD: AC
AB BC  2a BH   a 2 2 2 Do vậy SH
SB BH a . Dựng HE A ; B HF SE Ta có BC a 3 SH.HE a 21 HE  
d H;SAB   2 2 2 SH  2 7 HE Chọn B. 2
Câu 5: Cho hình chóp S.ABCD có đáy là hình chữ nhật, diện tích tứ giác ABCD bằng 6a 6 . Cạnh 10
SA a 3 và vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SC và mặt phẳng đáy bằng 300.
Khoảng cách từ điểm B đến mặt phẳng (SAC) gần nhất với giá trị nào sau đây: 13a 7a 3a 8a A. 10 B. 5 C. 2 D. 5 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
HD: Dựng BH AC , lại có BH  SA BH  SAC
Có SA   AB D
C   S ;AABC  SCA 0 110
Ta có: AC tan 30  SA aAC a 110 3 2 2S 6a 6 7 Do vậy  ABC BH   1,4a  a AC . Chọn B 110 5
Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AD  2AB  2BC ,
CD  2a 2 . Hình chiếu vuông góc của S trên mặt đáy là trung điểm M của cạnh CD. Khoảng cách từ
điểm B đến mặt phẳng (SAM) bằng: 3a 10 3a 10 3a 10 a 10 A. 10 B. 5 C. 2 D. 3 HD:
Gọi E là trung điểm của AD ta có CD  2a 2  CE ED  2a Do vậy AD  4 ;
a BD  2a. Gọi N là trung điểm của AB suy ra 1 MN  3a,S  NM.AB  2 3a MAB 2 2S MA 3a 10  2 AN  2
NM a 10 . Dựng BK AM d  ;
B SAM  BK ABM AM 5 Chọn B.
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AD  2AB  2BC ,
CD  2a 2 . Hình chiếu vuông góc của S trên mặt đáy là trung điểm M của cạnh CD. Khoảng cách từ
trọng tâm G của tam giác SAD đến mặt phẳng (SBM) bằng: 4a 10 3a 10 a 10 3a 10 A. 15 B. 5 C. 5 D. 15 HD: ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Gọi E là trung điểm của AD ta có CE AB ED . Có CD  2a 2  CE ED  2a Do vậy AD  4 ;
a BD  2a. Gọi N là trung điểm của AB suy ra 1 MN  3a,S  NM.AB  2 3a 2 2 MA AN NM a 10 MB MAB 2 .    
Gọi L là trung điểm của DE ta có LA  3a là L là trung điểm của AP. d  ;
A SBM 6 3 3
Khi đó LP  3a EP  4 ;
a AP  6a . d
  ,d E; SBM   d  ; G SBM E;SBM    4 2 2 4 4 4 3a 10 4a 10 Do đó d  ;
G SBM  d  ;
A SMB  AF  .  9 9 9 5 15 . Chọn A. 2
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có diện tích bằng 2a ,
AB a 2,BC  2a . Gọi M là trung điểm của CD. Hai mặt phẳng (SBD) và (SAM) cùng vuông góc
với đáy. Khoảng cách từ điểm B đến mặt phẳng (SAM) bằng 4a 10 3a 10 2a 10 3a 10 A. 15 B. 5 C. 5 D. 15
HD: Gọi H AM  D B S D B    ABC Ta có  SH ABC
 SAMABC     HB AB 1 Lại có   2  d  ;
D SAM  d  ; B SAM D H DM 2 2 1 1 a SSS  D A M D A C AB D 2 4 C 2 1 2 Ta có S  D.
A DM.sinD  sin D   D  0 45 D A M 2 2 2 2 0 10 Do vậy AM
AD DM  2A . D DM.cos45  a 2 2.S 2a a 10 Do vậy DK ADM   AM . Chọn C 10 5 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 9: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a, ADC  0 120 . Hình chiếu vuông
góc của S trên mặt đáy là trọng tâm của tam giác ABC. Khoảng cách từ điểm C đến mặt phẳng (SAG) bằng a 7 a 21 a 21 a 3 A. 3 B. 7 C. 3 D. 7
HD: Dựng CH AG CH  SAG Ta có: sin CH OG GAO   CA
AG . Dễ thấy tam giác ABC đều 2a 3 2a a
Trong đó CA  2OA  2.  2a 3;OG   2 6 3 OG a 21 Do vậy CH  .CA  . Chọn B 2 OG  2 7 OA
Câu 10: Cho hình chóp S.ABC có đáy ABC là tam giác đều có cạnh bằng a. Gọi M là trung điểm của
AC. Hình chiếu của S trên mặt đáy là điểm H thuộc đoạn BM sao cho HM  2HB . Khoảng cách từ
điểm A đến mặt phẳng (SHC) bằng 2a 7 a 7 3a 7 2a 7 A. 14 B. 14 C. 14 D. 7 HD: d  ;
A SCH  2d M;SHC . Dựng MK CH Khi đó d  ;
A SCH  2MK a 3 2 a 3 a Mặt khác BM
MH BM  ; MC  2 3 3 2 MH.HC a 2a 7 Suy ra MK  
do đó d  2MK  . Chọn D 2 MH  2 MC 7 7
Câu 11: Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác cân
có AC BC  3a . Đường thẳng A'C tạo với đáy một góc 600. Trên cạnh A'C lấy điểm M sao cho
A' M  2MC . Biết rằng A'B a 31 . Khoảng cách từ M đến mặt phẳng (ABB'A') là: 3a 2 4a 2 A. a a 4 B. 3 C. 3 2 D. 2 2 0
HD: Ta có A ' A AC tan 60  3a 3 2 2 Suy ra AB
A'B AA'  2a 2 2 Do vậy CH
AC AH  2a 2
d M ABB A  2 2 4a 2 ;
' '  d C;ABB' A'  CH  3 3 3 . Chọn B ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 12: Cho khối chóp S.ABCD có đáy là hình chữ nhật ABCD với AB a . Hình chiếu vuông góc
của đỉnh S lên mặt đáy trùng với trọng tâm tam giác ABD. Biết SC  2a 2 và tạo với đáy một góc
450. Khoảng cách từ trung điểm của SD đến mặt phẳng (SAC) là: a 2 a 3 2a 4 2a A. 3 B. 3 C. 3 D. 3
HD: Ta có SC  2a 2  GC  2a  AC  3a 2a 2 Khi đó D
C  2a 2 suy ra DH  3 1 a 2
Do vậy d M;SAC  DH  2 3
Câu 13: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có AD a 3 . Tam giác SAB là tam
giác đều và thuộc mặt phẳng vuông góc với đáy. Gọi M là trung điểm của AD. Biết rằng SD  2a .
Khoảng cách từ A đến mặt phẳng (SHM) là: a 2 a 3 a 2 a 3 A. 4 B. 4 C. 2 D. 2 2 2
HD: Ta có: SA  D S  D Aa AB AH.AM a 3 Khi đó AK   2 AH  2 4 AM
Câu 14: Cho khối chóp S.ABC có đáy là tam giác vuông tại A có AC a . Tam giác SAB vuông tại S
và hình chiếu vuông góc của đỉnh S trên mặt đáy là điểm H thuộc cạnh AB sao cho HB  2SA . Biết
SH  2a 2 , khoảng cách từ B đến mặt phẳng (SHC) là: 2a a 4a 3a A. B. C. D. 5 5 5 5 2 2
HD: Ta có SH H . A HB  2HA 2 2
Suy ra 8a  2HA HA  2a 2a 4a Do vậy AM
d  2AM  5 c 5 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 15: Cho hình lăng trụ ABCD.A'B'C'D' có đáy là hình chữ nhật với AD a 3 . Tam giác A'AC
vuông cân tại A' và thuộc mặt phẳng vuông góc với đáy. Biết rằng A ' A a 2 . Khoảng cách từ D'
đến mặt phẳng (A'ACC') là: a 3 a 2 a 2 a 3 A. 4 B. 2 C. 4 D. 2 HD: Ta có a 3
AC A' A 2  2a  D
C a d  ;
D A' AC  DH  2 (do DD'/ /AA')
Câu 16: Cho hình hộp ABCD.A'B'C'D' có đáy là hình vuông, tam giác A'AC vuông cân tại A,
A'C a . Tính khoảng cách từ A đến mặt phẳng (BCD') theo a? a 3 a 6 a 2 a 3 A. 3 B. 3 C. 2 D. 2 HD:
+) kẻ AP A ' B d  ; A B D
C '  d  ;
A A'BC  AP A'C 2a
+) A' AC vuông cân tại A  A ' A AC    a 2 2 2 AC 1 1 1 1 1 3
Tứ giác ABCD là hình vuông  AB   a       2 2 2 2 2 2 2 AP A' A AB 2a a 2a ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 a 2 a 6 a 6  AP    d  ; A B D C '  3 3 3
Câu 17: Cho hình chóp S.ABC có SA  3a và SA   ABC . Giả sử AB BC  2a , góc ABC  0
120 . Tìm khoảng cách từ A đến mặt phẳng (SBC) ? a 3a A. 2 B. a C. 2 D. 2a HD:
+) Trên mặt phẳng đáy , qua A kẻ
một đường thẳng vuông góc với
AC, đường thẳng này cắt BC tại P. Đặt d  ;
A SBC  d  ;
A SPC  h , tứ diện vuông 1 1 1 1 S.APC     2 2 2 2 h AS AC AP +) ABP đều
AP AB  2a  AP  2a 1 1 1 1 4 3a   AC         h  0 tan 60    3  2 2 2 2 2 AC  2a 3 h 9a 12a 4a 9a 2  AP
Câu 18: Cho hình chóp S.ABC có đáy là tam giác vuông tại B, BA  3 ,
a BC  4a , mặt phẳng (SBC)
vuông góc với mặt phẳng (ABC). Biết SB  2a 3 và góc SBC  0
30 . Tính khoảng cách từ B đến mặt phẳng (SAC) theo a ? 3a 3 5a 6 6a 6a A. 2 B. 4 C. 7 D. 7 HD: ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 0 BH 3
+) Kẻ SH BC H BC  SH   ABC  cos30   SB 2 d  ; 3 2 3. 3 B SAC SB a  BC 4aBH  
 3a dH;SHC    4 2 2
HC 4a  3a
+) Kẻ HK AC, HP SK d H;SAC  HP d  ;
B SAC  4HP HK CH . AB CH 3 . a a 3a
+) CKH ~ CBA    HK    2 AB CA AB  2 2 BC a  2 5 9 16a SH 1 SB 1 1 1 1 1 28 Ta có 0 sin30    SH   a 3       2 2 2 2 2 2 SB 2 2 HP HS HK 3a 9a 9a 25 3a 12a 6aHP   d  ;
B SAC  4HP   28 28 7
Câu 19: Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật với AB  ,
a AD a 3 . Hình
chiếu vuông góc của A' lên mặt phẳng (ABCD) trùng với trung điểm của AC và BD. Tính khoảng cách
từ B' đến mặt phẳng (A'BD) theo a ? a 3 a 2 a 3 2a A. 2 B. 2 C. 3 D. 3 HD: ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
+) Gọi O AC BC A 'O   ABCD 1 1 +) VVVd B A BD S A O S B A BD D A A  '; '  .  ' . '. ' . 'AB '.ABD A' 3 BD 3 ABD 1 A'O. .A . ' . B AD A O S A . B AD aa 3 a 3
d B A BD  ABD  2 '; '    S 1 2 BD A a  2 2 'BD 3 ' .BD a A O 2
Câu 20: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB  ,
a BC a 3 . Hình chiếu
vuông góc của S trên mặt đáy là trung điểm của cạnh AC. Biết SB a 2 . Tính theo a khoảng cách từ
điểm H đến mặt phẳng (SBC). a 3 2a 3 a 5 2a 5 A. 5 B. 5 C. 5 D. 5 HD:
+) Kẻ HK BC, HP SK d H;SBC  HPHK BC HK CH 1 AB a Từ 
HK / / AB     HK   AB BC AB CA 2 2 2
+) ABC vuông tại B có H là trung điểm của cạnh AC ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 1 1 1
HB AC  2 AB  2 BC  2 a  2 3a a  S H  2 SB  2 HB  2 2a  2 a a 2 2 2 1 1 1 1 4 a 5 a 5       HP
d H;SBC  2 2 2 2 2 HP S H HK a a 5 5
Câu 21: Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2 ,
a SAB là tam giác vuông cân
nằm trong mặt phẳng vuông góc với đáy. Khoảng cách từ trung điểm H của AB đến mặt phẳng (SBD) là ? a 3 a 3 a 10 A. 3 B. a C. 2 D. 2
HD: vì SAB là tam giác vuông cân tại S nên SH   ABCD Từ H kẻ HI  D
B , từ H kẻ HK  SI với IBD,K SISH BD Ta có 
BD  SHI   BD HK HK  SBD HI BD 1 1 1
Do đó d H,SBD  HK . Mặt khác   2 2 2 HI SH HK 1 a AB Mà HI d  , A BD  SH a 2 và   2 2 1 1 1 3 a Nên     HK  . Chọn A. 2 HK  2 2 2 a a a 3    2 
Câu 22: Cho hình chóp S.ABCD có đáy là hình thoi cạnh bằng a, góc BAD  0 60 . Gọi H là hình 1
chiếu vuông góc của S xuống mặt đáy (ABCD) và H AC sao cho AH AC 3 . Khoảng cách từ A
đến mặt phẳng (SBC) bằng bao nhiêu nếu biết SA ABCD  0 ; 60 . a 3 3a 3a A. 4 B. 4 C. a D. 2
HD: Ta có AH là hình chiếu của SA lên mặt phẳng (ABCD)
Do đó SA ABC   SA AH  SAH  0 , D ; 60
Từ H kẻ HI BC , kẻ HK  SI với I BC, K SISH BC Ta có 
BC  SHI   BC HK HK  SBC HI BC 1 1 1
Do đó d H,SBD  HK . Mặt khác   2 2 2 HI SH HK ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 0 AC 2 2 a 3 a
Mà SH  tan 60 .AH
a và HI  .d  , A BC  .  3 3 3 2 3 1 1 3 4 a Khi đó     HK  2 2 2 2 HK a a a 2 3 3 a 3a Vậy d  ;
A SBC  .HK  .  2 2 2 4 . Chọn B
Câu 23: Cho hình chóp S.ABC có SA  3a và SA   ABC . Biết AB BC a ABC  0 2 , 120 . Tính
khoảng cách từ A đến (SBC) ? a 3a A. 2a B. 2 C. a D. 2
HD: Từ A kẻ AH BC , kẻ AK SH với K BC, K SHSA BC Ta có 
BC  SAH  BC AK AK  SBC AH BC 1 1 1 Do đso d  ;
A SBC  AK thỏa mãn   2 2 2 SA AH AK 0 3
Mà SA  3a và AH  sin 60 .AB  .2a a 3 2 1 1 1 4 3a 3a Nên     AK   d  ;
A SBC  2 2 2 2 AK 9a 3a 9a 2 2 Chọn D.
Câu 24: Cho hình chóp S.ABCD có đáy là hình vuông có đường chéo bằng a 2 . Mặt bên
SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách h từ A đến mặt phẳng (SCD) là: a 21 a 21 a 21 a 21 A. h h h h 3 B.  14 C.  21 D.  7 HD: Chọn D.
Câu 25: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AC a ABC  0 3, 30 , góc giữa
SC và mặt phẳng (ABC) bằng 600. Cạnh bên SA vuông góc với đáy. Khoảng cách từ A đến mặt phẳng (SBC) bằng a 6 a 3 3a 2a 3 A. B. C. D. 35 35 5 35 HD: Kẻ E
A BC, AK  SE E BC,K SE
Chứng minh AK  SBC  AK d  ; A SBC ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 . SA AE
Xét tam giác SAE vuông tại A ta có: AK  2 SA  2 AE Tính SA, AE:
Xét hai tam giác vuông ABC và SAC: AB SA  3a 3a
Xét tam giác vuông ABC: AE  2 3ad  ;
A SBC  HK  . Chọn C. 5
Câu 26: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AC a ABC  0 3, 30 , góc giữa
SC và mặt phẳng (ABC) bằng 600. Cạnh bên SA vuông góc với đáy. Khoảng cách từ trọng tâm G của
tam giác SAC đến mặt phẳng (SBC) bằng 3a a a 6 2a A. B. C. D. 5 5 5 5 HD: Kẻ E
A BC, AK  SE E BC,K SE
Chứng minh AK  SBC  AK d  ; A SBC . SA AE
Xét tam giác SAE vuông tại A ta có: AK  2 SA  2 AE Tính SA, AE:
Xét hai tam giác vuông ABC và SAC: AB SA  3a 3a
Xét tam giác vuông ABC: AE  2 3ad  ;
A SBC  HK  . 5 1 a
d G,SBC  d A,SBC  3 . Chọn B 5
Câu 27: Cho hình lăng trụ đứng ABC.A'B'C' có AB .
C A'B'C' có AC a BAC  0 , 120 , góc ABC  0 30 2
, mặt bên BCB'C' có diện tích bằng 2a . Gọi M là trung điểm của BC. Khoảng cách từ C
đến mặt phẳng (C'AM) bằng 2a 3 2a 2a 57 A. 3 B. 5 C. 19 2a 3 D. 5 a 3
HD: Ta có AB AC  ,
a BC a 3,CM  2 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
d C AMC  CM.CC ' , '  CK  2 CM  2 CC ' 2 2a 57 Lại có: S
BC.CC '  2a CC '  2a CK BCC'B' 19 . Chọn C 0 0
Câu 28: Cho hình lăng trụ ABC.A'B'C' có AB a 3, ABC  30 , ACB  60 . Hình chiếu vuông góc 3 a
của A' trên mặt đáy là trung điểm của BC. Thể tích khối chóp A'AC bằng 6 . Khoảng cách từ C đến mặt phẳng (A'AB) bằng a 6 2a a 6 a 6 A. 6 B. C. D. 7 4 12
HD: Gọi E là trung điểm của AB. a Ta có AC  0 A .
B tan30  a HE  2 3 1 a a VA'H.S   A'H  A'.ABC 3 ABC 6 3 a
Kẻ HK A ' E HK d H, A' AB  7 2a
d C,A' AB  2dH,A' AB  . Chọn B 7
Câu 29: Cho hình chóp đều S.ABC có AB a , góc giữa mặt bên và mặt đáy 4d
bằng 600. Tính a , biết d là khoảng c cách từ điểm A đến mặt phẳng (SBC). A. 3a B. 5a C. 7a D. 9a
HD: Gọi O là tâm của tam giác ABC và H là trung điểm của BC. SO BC Có 
BC  SAH  SBC ; ABC SH; AH SHAAH BC     
Kẻ OK SH suy ra OK  SBC  d  ;
O SBC  OK 0 3 3 a
Xét OKH vuông tại K, có OK  sin 60 .OH  .OH.  .AH  2 6 4 3a 4d Do đó d  ,
A SBC  3d H,SBC   d   3 4 a ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 30: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA   ABCD,SA AB a và AD  .
x a . Gọi E là trung điểm cạnh SC. Tìm x, biết khoảng cách từ điểm E đến mặt phẳng (SBD) là a d  3 A. x  1 B. x  2 C. x  3 D. x  4 1 a 2a
HD: Ta có d E,SBD  d  ,
A SBC   d  , A S D B   2 3 3
Gọi H là hình chiếu của A lên BD. Và K là hình chiếu của A lên SH. Ta được 2a AK  S D
B   AK d  , A S D B   3 2 . AB D A x.a Mà AH. D B  . AB AD  AH   2 AB  2 2 D B a  2 2 x a 2 1 1 1 9 1 a  2 2 x a Do đó      2 2 2 2 2 2 4 AK SA AH 4a a x a 5 1 2 x    2
x  4  x  2 vì x  0. Chọn B. 2 4 x
Câu 31: Cho hình chóp S.ABCD, ABCD là hình vuông cạnh AB a . Mặt phẳng chứa tam giác đều
SAB vuông góc với mặt phẳng đáy (ABCD). Khoảng cách từ điểm A đến mặt phẳng (SCD) là: a 21 a 14 a 2a A. 7 B. 7 C. D. 7 7 HD: Chọn A
Câu 32: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA   ABCD,SA a 3 . Tính theo
a khoảng cách từ điểm O đến mặt phẳng (SBC). a a 3 a 5 a 7 A. 2 B. 4 C. 6 D. 8
HD: Ta có d  ,
A SBC  2dO,SBC
Gọi H là hình chiếu của A lên SB. SA BC Ta có 
BC  SAB  BC AH AH  SBC AB BC 1 1 1 1 1 4 a 3 Mà       AH  2 2 2 2 2 2 AH SA AB 3a a 3a 2 1 1 a 3 Do đó d  ;
O SBC  d  ,
A SBC  AH  2 2 4 . Chọn B ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 33: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA   ABCD, SA AB a và AD 33d
 2a . Gọi F là trung điểm cạnh CD. Tính a , biết d là khoảng cách từ điểm A đến mặt phẳng (SBF) A. 2a 33 B. 4a 33 C. 2a 11 D. 4a 11
HD: Gọi H là hình chiếu của A lên BF. Và K là hình chiếu của A lên SH. SA BF Ta có 
BF  SAH  BF AK AK  SBF AH BF a
Do đó d d  ,
A SBF  AK 2 2 17 . Mà BF BC CF  2 2 . AB AD 2a 4a
Nên AH.BF AD.AB AH    BF a 17 17 2 1 1 1 1 17 33 4a Khi đó       AK  2 2 2 2 2 2 AK SA AH a 16a 16a 33 4 33. a 33d 33 Vậy   4 33 a a . Chọn B
Câu 34: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AD  2a . Hình chiếu vuông góc
của S trên mặt đáy là điểm H H AB thỏa mãn HA  2HB . Biết SA  .
x a và SH a . Tìm x biết 3a 2
khoảng cách từ điểm C đến mặt phẳng (SHD) là d  2 A. x  5 B. x  5 C. x  3 D. x  3 3a 2
HD: Kẻ CK  DH CK d C,SHD  CK  2 1 1
Giả sử AB  3b . Ta có SSCK.DH CHD 2 ABCD 2 3a 2  2 .3 a b  2 4a  2 4b  2ab  2 a 2a  2 2b 2  2 2 a b  2 a  2 a  2 b   4 a  2 2 4 2 2
a b a b AB  3a
AH a SA  2 SH  2 2
AH a 5  x  5 . Chọn A
Câu 35: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB  ,
a BC a 3 . Hình chiếu
vuông góc của S trên mặt đáy là trung điểm của cạnh AC. Biết SB a 2 . Tính theo a khoảng cách từ H đến mặt phẳng (SBC). ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 a 3 2a 3 a 5 2a 5 A. 5 B. 5 C. 5 D. 5
HD: Kẻ HE BC, HF SE HF d H,SBC Ta có AC  2 AB  2 1
BC  2a BH AC a 2 2 2 Ta có SH
SB BH a 1 1 1 5 Xét SHE ta có    2 2 2 2 HF HS HE a a 5
HF  5 . Chọn C
Câu 36: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA   ABCD,SA a 3 . Tính theo
a khoảng cách từ điểm O đến mặt phẳng (SBC). a a 3 a 5 a 7 A. 2 B. 4 C. 6 D. 8 1
HD: Ta có d O,SBC  d  , A SBC 2
Kẻ AH SB AH d  , A SBC 1 1 1 4 Ta có    2 2 2 2 AH AS AB 3a a 3 a 3  AH
d O,SBC  2 4 . Chọn B
Câu 37: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA   ABCD, SA AB a và AD 33d
 2a . Gọi F là trung điểm cạnh CD. Tính a , biết d là khoảng cách từ điểm A đến mặt phẳng (SBF) A. 2a 33 B. 4a 33 C. 2a 11 D. 4a 11
HD: Kẻ AH BF, AK SH AK d  , A SBF 1 1 Ta có SSAH.BF ABF 2 ABCD 2 2  a 2 4a 17
 AB.BC  AH.BF  2a.a  AH. 4a   AH     2  17 1 1 1 33 Ta có    2 2 2 2 AK AH AS 16a ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 4a 4a 33dAK   d    4 33 33 33 a . Chọn B
Câu 38: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AD  2a . Hình chiếu vuông góc
của S trên mặt đáy là điểm H H AB thỏa mãn HA  2HB . Biết SA  .
x a và SH a . Tìm x biết 3a 2
khoảng cách từ điểm C đến mặt phẳng (SHD) là d  2 A. x  5 B. x  5 C. x  3 D. x  3 3a 2
HD: Kẻ CK  DH CK d C,SHD  CK  2 1 1
Giả sử AB  3b . Ta có SSCK.DH CHD 2 ABCD 2 3a 2  2 .3 a b  2 4a  2 4b  2ab  2 a 2a  2 2b 2  2 2 a b  2 a  2 a  2 b   4 a  2 2 4 2 2
a b a b AB  3a
AH a SA  2 SH  2 2
AH a 5  x  5 . Chọn A
Câu 39: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB  ,
a BC a 3 . Hình chiếu
vuông góc của S trên mặt đáy là trung điểm của cạnh AC. Biết SB a 2 . Tính theo a khoảng cách từ H đến mặt phẳng (SBC). a 3 2a 3 a 5 2a 5 A. 5 B. 5 C. 5 D. 5
HD: Kẻ HE BC, HF SE HF d H,SBC 2 2 1 Ta có AC
AB BC  2a BH AC a 2 2 2 Ta có SH
SB BH a 1 1 1 5 Xét SHE ta có    2 2 2 2 HF HS HE a a 5
HF  5 . Chọn C
Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA   ABCD, SA AB a và
AD  2a Gọi E là trung điểm cạnh SC. Tính theo a khoảng cách từ điểm E đến mặt phẳng (SBD) a a a a A. 2 B. 3 C. 4 D. 5 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 1 1
HD: ta có d E,S D
B   d C,S D
B   d  , A S D B  2 2 2 2 a 5 Ta có AC
AB BC a 5  AO  2 1 1 1 9 Ta có    2 2 2 2 AH AS AO 5a a 5 a 5  AH
d E,SBD  3 6 . Chọn B
Câu 41: Cho hình hộp đứng ABCD.A'B'C'D' có đáy là hình
vuông, tam giác A'AC là tam giác vuông cân, A'C a . Khoảng cách từ A đến mặt phẳng (BCD') là: a 6 a 6 a a 6 A. 3 B. 2 C. D. 6 4 HD: d  ;
A BCD'  d  ; D BCD'
Hình hộp đứng ABCD.A ' B 'C ' D '  D ' D  BCD
Kẻ AP CD 'P CD '  d  ;
D BCD'  DPd  ;
D BCD'  DP d  ;
A BCD'  DP
+) hình hộp đứng ABC .
D A'B'C'D'  A' A AC
 A'AC vuông cân thì chỉ có thể vuông cân tại A.  ' a
D D A' A   A'C a       2 A'A AC  2 2  AC a DC    2 2 1 1 1 2 4 a a +)      DP   d  ;
A BCD'  2 2 2 2 2 . Chọn C DP D 'D DC a a 6 6
Câu 42: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông SA
góc với mặt phẳng đáy. Gọi M là trung điểm của SB. Tỷ số a khi khoảng cách từ điểm M đến mặt a phẳng (SCD) bằng là: 5 3 A. 2 B. 2 C. 2 D. 1 1 1
HD: +) d M;S D
C   d  ; B S D
C   d  ; A S D C  2 2
+) Kẻ AP SD P SD  d  ;
A SCD  AP ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 1 a 2a
AP d M;SCD   AP  2 5 5 1 1 1 5 1 1 SA +)        2 . Chọn B 2 2 2 2 2 2 AS AP AD 4a a 4a a
Câu 43: Cho hình chóp S.ABC có SA   ABC  và SA  4 , cm AB  3 ,
cm AC  4cm và BC  5cm .
Khoảng cách từ điểm A đến mp (SBC) bằng (đơn vị cm) : 2 72 A. d  ; A SBC  d  ; A SBC   17 B.   17 6 34 3 C. d  ;
A SBC  d  ; A SBC   17 D.   17 2 2 2 2 2
HD: +) Ta có AB AC  3  4  25  BC
 ABC vuông tại A.
+) Kẻ AK BC K BC, AP SK P SK   d  ;
A SBC  AP 1 1 1 1 1 1 +)      2 2 2 2 2 2 AP AS AK AS AB AC 1 1 1 17 6 34      AP  2 2 2 4 3 4 72 17 6 34  d  ;
A SBC  17 . Chọn C
Câu 44: Cho khối chóp S.ABCD có đáy là hình vuông cạnh 4cm. Hình chiếu vuông góc của S xuống
mặt đáy là trung điểm H của AB. Biết rằng SH  2 cm . Khoảng cách từ A đến mặt phẳng (SBD) là: A. 1 cm B. 2 cm C. 3 cm D. 4 cm HD: + d  ; A S D
B   2dH;S D B  +) Kẻ HK  D B K  D
B ,HP SK P SK
d H;SBD  HP d  ;
A SBD  2HP ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 BH
+) HBK vuông cân tại K  HK   2 2 1 1 1 1 1 +)      HP  1 2 2 2 HP HS HK 2 2  d  ; A S D
B   2 . Chọn B
Câu 45: Cho hình chóp S.ABC có đáy là tam giác đều. Hình chiếu vuông góc của đỉnh S lên mặt đáy
là điểm H thuộc cạnh AC sao cho HC  2HA . Gọi M là trung điểm của SC và N là điểm thuộc cạnh
SB sao cho SB  3SN . Khẳng định nào sau đây là sai: 4
A. Khoảng cách từ M đến mặt phẳng (ABC) bằng 3 lần khoảng cách từ N đến mặt phẳng (ABC).
B. Khoảng cách từ M đến mặt phẳng (SAB) bằng một nửa khoảng cách từ C đến mặt phẳng (SAB) 1
C. Khoảng cách từ N đến mặt phẳng (SAC) bằng 3 khoảng cách từ B đến mặt phẳng (SAC) 3
D. Khoảng cách từ M đến mặt phẳng (SAB) bằng 2 khoảng cách từ H đến mặt phẳng (SAB)
d M;ABC d N; 1 ABC MC  NB 2
HD: d ;SABC   ; SC
2 d S;ABC   SB 3
d M;ABC 1 2 3   A sai
d N;ABC  :   2 3 4
d M;SAB MS 1 +) đúng d B C;SAB    CS 2
d N;SAC NS 1 +) đúng d C B;SAC    BS 3
dM SAB 1 ;  
d C;SAB  2 +)   ;   D d C SAB đúng  CA
d H;SAB   3  HA
Câu 46: Cho hình chóp S.ABCD có đáy là hình chữ nhật có AB  9, AD  12 . Hình chiếu vuông góc
của đỉnh S xuống mặt đáy trùng với trọng tâm H của tam giác ABC. Biết SH  6 , khoảng cách từ A
đến mặt phẳng (SCD) là: 36 24 12 4 A. 5 B. 5 C. 5 D. 5 HD: +) d  ; A S D
C   d  ; B S D C  ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
+) Gọi O AC BD  , B H, , O D thẳng hàng d  ; 2 1
B SAC BD 3
BH BO BD  3 3
d H;SAC   HD 2 3  d  ;
A SCD  d  ;
B SCD  d H;SAC 2
+) Kẻ HK CD K CD,HP SK P SK  3
d H;SCD  HP d  ;
A SCD  HP 2 HK DB 2 2 2
+) HK CD, BC CD HK / / BC  
  HK BC  .12  8 BC DB 3 3 3 1 1 1 1 1 25 24 3 24 36 +)       HP   d  ;
A SCD  .  . Chọn A. 2 2 2 2 2 HP HS HK 6 8 576 5 2 5 5
Câu 47: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD. Tam giác SAD cân tại S và thuộc
mặt phẳng vuông góc với đáy. Gọi M là điểm thoã mãn SM  2CM  0 . Tỷ số khoảng cách D đến mặt
phẳng (SAB) và từ M đến mặt phẳng (SAB) là: 2 3 1 A. 3 B. 2 C. 2 D. 2
HD: +) Từ SM  2CM  0  M thuộc đoạn thẳng SC và SM  2MC
d M;SAB MS 2 +)
d C;SAB   S C 3 2 2
d M;SAB  d C;SAB  d D;SAB 3 3
d D;SAB 3  . Chọn B.
d M;SAB  2
Câu 48: Cho hình chóp S.ABCD có đáy là hình thoi. Tam
giác SAB cân tại S và thuộc mặt phẳng vuông góc với đáy ,
biết tam giác ABC đều cạnh 20 cm và mặt phẳng (SCD) tạo với đáy một góc 600. Khoảng cách từ A đến (SCD) là: A. 20 cm B. 10 cm C. 15 cm D. 30 cm
HD: +)_ Kẻ HK  D
C K CD,HP SK P SK
d  ;ASCD  d H;SCD   HP
  SCD;ABCD 0    SKH  60
d A SCD  HP  0 3 ; HK sin60  HK 2 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017  1 S  2S  0 2. .20.20.sin 60   200 3  ABCD ABC 2 +)  1 1 SHK. AB CD HK abcd     .20  20  2 2 3
 20HK  200 3  HK  10 3  d  ;
A SCD  .10 3  15cm 2 . Chọn C
Câu 49: Cho hình lăng trụ ABC.A'B'C', hình chiếu vuông góc của A' xuống mặt đáy (ABC) trùng với
trung điểm H của AB. Gọi h là khoảng cách từ A đến mặt phẳng (A'BC). Gọi M là trung điểm của
A'C' và N thuộc cạnh CC' sao cho NC '  2NC . Tính khoảng cách từ M và N đến mặt phẳng (A'BC) 3 2 h 2 2h h A. 2 h 2 B. 6 C. 3 D. 6
HD: +) Dựng hình lăng trụ BCD.B'C'D; như hình vẽ 1 +)
d d M;A'BC  d ; C A'BC 1    2 1
d d N;A'BC  d ; C A'BC 2    3
+) C ' D / / A ' B d C '; A'BC  d  ;
D A'BC 2 h h hd  ;
A A'BC  h d d   1 2 2 3 6 . Chọn B
Câu 50: Cho hình lăng trụ ABCD.A'B'C'D' có đáy là hình chữ nhật ABCD có AB  3; AD  4 . Tam
giác A'BD cân tại A' và thuộc mặt phẳng vuông góc với đáy và AA'  5 . Gọi M là trung điểm của
A'D'. Khoảng cách từ M đến mặt phẳng (A'AC) là: 12 6 3 4 A. 5 B. 5 C. 5 D. 5
HD: Gọi H AC  D
B A' H   AB D C  1
+) d M; A' AC  d D'; A' AC 2 1  d  ;
D A' AC 2 DP AC +) kẻ DP
AC P AC    
 DP A'H
DP  A' AC  d  ;
D A' AC  DP 2 1 1 1 1 1 25 12 12 +)       DP   d ; D A' AC 2 2 2 2     DP DA DC 4 3 144 5 5 1 12 6
d M;A' AC  .  2 5 5 . Chọn B ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 51: Cho hình chóp đều S.ABCD có SAC là tam giác đều. Gọi dA là khoảng cách từ A đến mặt d
phẳng (SCD) và dB là khoảng cách từ B đến mặt phẳng (SAC). Tỷ lệ A d bằng: B 21 2 21 A. 2 B. 7 C. 3 D. 7
HD: +) Hình chóp đều . S AB D C AB D C là hình vuông
Đặt AB BC  D
C DA x  0  AC  D B x 2 BH AC
+) Gọi H AC BC  BH  SH D B x 2 2
BH  SAC  d BH    b 2 2 2
+) d  2d H;S D C A  Kẻ HK  D
C ,HP  SK P SK
d H;SCD  HP d  2HP A 3 3 x 6
SAC đều  SH AC x 2  2 2 2 1 x 1 1 1 4 4 14 3 Ta có HK BC         HP x 2 2 2 2 2 2 2 2 HP HS HK 6x x 3x 14 3 d 3 x 3 2 21  d  2xA  2x :  2  A 14 d 14 . Chọn D B 2 7 7
Câu 52: Cho hình chóp S.ABC có tam giác ABC vuông tại A, AB AC  ,
a I là trung điểm của SC,
hình chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm H của BC, mặt phẳng (SAB) tạo với
đáy 1 góc bằng 600. Khoảng cách từ điểm I đến mặt phẳng (SAB). 3a a 39 a 3 a 3 A. 4 B. 3 C. 2 D. 4 1
HD: +) d I,SAB  d C;SAB  d H;SAB 2
Kẻ HK AB K  AB, HP  SK P SK
d H;SAB  HP d I;SAB  HP
+)  SAB  ABC  SKH  0 ; 60  HP  0 3 HK sin60  HK 2 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 HK AB HK BH 1 +)   HK / /CA    CA AB CA BC 2 1 a 3 a a 3 a 3
HK CA   HP  . 
d I;SAB  2 2 2 2 4 4 . Chọn D
Câu 53: Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh 2a. Mặt phẳng (A'BC) tạo
với mặt đáy (ABC) một góc 600. Khoảng cách từ B đến mặt phẳng (B'AC) là: 3a 2a 9a a A. 2 B. 3 C. 4 D. 2
HD: +) Lăng trụ đứng ABC.A ' B 'C '  A ' A   ABC  Kẻ E
A BC E BC
  A BC ABC  A E  0 ' ; ' A 60 ABA A  0 3 ' E
A tan60  AE 3  . 3  3a 2
+) BK AC K AC ,BP B ' K P B ' K   d  ;
B B' AC  BP AB 3 1 1 1 1 1 4 +) BK   a 3       2 2 2 2 2 2 2 BP B'B BK 9a 3a 9a 3a 3aBP   d  ;
B B' AC  2 2 . Chọn A.
Câu 54: Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác cân tại A, AB AC a CAB  0 2 , 120 .
Góc giữa (A'BC) và (ABC) là 450. Khoảng cách từ B' đến mặt phẳng (ABC) là: a 2 A. a 2 B. 2a 2 C. a D. 4
HD: Ta có: d B', ABC  BB'  AA'
Gọi H là trung điểm của BC AH BC AH BC Do đó 
BC  AA'H AA'  BC
Suy ra  A BC  ABC  A HA  0 ' , ' 45
Do đó tam giác A'AH vuông cân tại A Mà cos AH CAH   AH a AC
Nên ta được AH AA'  a d B',ABC  a . Chọn C ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 55: Cho lăng trụ tứ giác đều ABCD.A'B'C'D' với cạnh đáy 2 3 dm . Biết rằng mặt phẳng (BDC')
hợp với đáy một góc 300. Khoảng cách từ A đến mặt phẳng (BDC') là: 6 3 2 6 A. dm dm dm dm 2 B. 2 C. 3 D. 3
HD: Gọi O là tâm AB D C OC  D B  D B  OCC'
Suy ra  B C   ABC   COC  0 D ' , D ' 30
Kẻ CH OC '  d  , A  D
B C '  d C, D
B C '  CH CH Do đó HOC   CH  0 6 sin sin30 . 6  OC 2 6
Vậy d A,BDC '  dm 2
Câu 56: Cho hình chóp S.ABCD có đáy là tam giác vuông tại A, AB  2 ,
a AC a 3 . Hình chiếu
vuông góc của S lên mặt phẳng (ABC) là trung điểm H của cạnh AB. Cạnh bên SC hợp với đáy 1 góc
600. Khoảng cách từ A đến mặt phẳng (SBC) là: 4 29a 87a 4 87a 4a A. 29 B. 29 C. 29 D. 29
HD: Kẻ HO BC, HK SO d H,SBC  HK
Ta có OBH đồng dạng vsơi ABC AC.BH a 21  OH   BC 7 0
Mà SC, ABC  SCH  60  SH  tan SCH.CHCH  2 HA  2
AC  2a SH  2a 3 1 1 1 29 2 87 Có     HK a 2 2 2 2 HK HO SH 12a 29 4 87a Mà d  ,
A SBC  2d H,SBC  29 . Chọn C
Câu 57: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BC a ACB  0 , 60 ,
SA  ABC và M là điểm nằm trên cạnh AC sao cho MC  2MA. Biết (SBC) tạo với đáy góc 300.
Khoảng cách từ M đến mặt phẳng (SBC) là: 3a a 3 a 3 2a A. 2 B. 3 C. 6 D. 9 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
HD: Kẻ AH  SB d  ,
A SBC  AH MC 2 2 Ta có
  d M,SBC  d  , A SBCAC 3 3
SABABC   AB
Ta có BC  SAB và SABSBC SB
Nên góc giữa (SBC) và (ABC) là SBA  0 30
Do đó SA A .
B tan SBA a vì AB BC.tan ACB 1 1 1 a 3 Nên    AH  2 2 2 AH SA AB 2 a 3
d M;SBC  3 . Chọn B
Câu 58: Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng 2a, cạnh bên bằng 3a. Gọi O là tâm đáy,
M, N là trung điểm của AB, BC. Khoảng cách từ O đến mặt phẳng (SMN) là: a 279 a 279 a 23 23 A. a 69 B. 23 C. 279 D. 279
HD: Kẻ OH MN,OK  SH với H MN,K  SH
Suy ra d O,SMN   OK MH a 3
Ta có OMN cân tại O có OH   0 tan 60 6 SMA 2 2
vuông tại M  SM
SA MA  2 2a aSMO 2 2 69
vuông tại O  SO SM MO  3 1 1 1 279 23 Do đó     OK a 2 2 2 2 OK OH OS 23a 279 . Chọn D
Câu 59: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a,
SA  ABCD,SA a 3 . Gọi G là trọng tâm SAC . Từ G kẻ đường thẳng song song với SB cắt OB
tại I. Khoảng cách từ I đến mặt phẳng (SBC) là: a 2 a 2 a 3 a 6 A. 2 B. 6 C. 6 D. 3 OG OI 1
HD: Ta có GI song song SB nên   OS OB 3
Mà O là trung điểm AC nên I là trọng tâm ABC 1
Do đó d I,SBC  d  , A SBC 3 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Kẻ AH SB H SB  d  ,
A SBC  AH
Xét SAB vuông tại A, có: 1 1 1 a 3    AH  2 2 2 AH SA AB 2 a 3
Suy ra d I,SBC  6 . Chọn C.
Câu 60: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều
cạnh a và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của AB, E là trung điểm của
BC. Khoảng cách từ I đến mặt phẳng (SED) là: a 2 a 2 a 2 3a 2 A. 2 B. 6 C. 4 D. 8
HD: Kẻ IH DE, IK SH d I,SED  IK a 3
Tam giác SAB đều cạnh a nên SI  2 . 2 3a Ta có SS  2SS  IDE ABCDAIDIBE 8 1 3 5a Mà S
IH.DE IH  IDE 2 10 2 1 1 1 32a 3 2a Do đó     IK  2 2 2 IK IH SI 9 8 . Chọn D
VẤN ĐỀ 2: KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG
Câu 1: Cho khối chóp S.ABCD có đáy là hình vuông cạnh 4 .
cm Biết SA  3 ,
cm khoảng cách giữa
2 đường thẳng SA và BC là: 2 A. 1 cm B. 1 cm C. cm D. 4 cm 5 5 5
Câu 2: Cho khối chóp đều S.ABC có đáy là tam giác đều cạnh 3 cm. Biết SA tạo với đáy một góc 0 60 .
Khoảng cách giữa 2 đường thẳng SA và BC là: 9 3 A. 3 cm B. cm C. 2 cm D. cm 4 2
Câu 3: Cho khối chóp S.ABCD có SA  ( ABCD) có đáy ABCD là hình chữ nhật có AB  3; AD  4.
Biết SC  13. Khoảng cách giữa 2 đường thẳng SB và AD là: 4 12 2 3 A. B. C. D. 17 17 17 17
Câu 4: Cho khối chóp S.ABCD có đáy là hình vuông cạnh 2a. Biết hình chiếu vuông góc của S lên
mặt đáy trùng với trung điểm của AB và SCD ABCD 0 ;
 60 Khoảng cách giữa 2 đường thẳng SD và BC là: ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 4a 39 4a 3 a 4a 3 A. B. C. 2 3 D. 13 13 13 39
Câu 5: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , AB a 3  AC a tam giác
SBC là tam giác vuông cân tại đỉnh S và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC). Tính
khoảng cách giữa 2 đường thẳng SB và AC. 3a a 3 a 21 2a 21 A. B. C. D. 7 7 7 7 SB SC Câu 6: Cho hình chóp S.ABCD
có đáy ABCD là hình vuông,   a . 2 3
Cạnh SA  ( ABCD) khoảng cách từ điểm A đến mặt phẳng (SCD) bằng: a a a a A. B. C. D. 6 3 3 2
Câu 7: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S trên 2 a
mặt phẳng (ABC) là trung điểm H của AB. Diện tích tam giác SAB bằng
. Khoảng cách từ điểm B 2
đến mặt phẳng (SAC) bằng: a 6 a 3 2a 6 2a 3 A. B. C. D. 35 35 35 35
Câu 8: Cho hình chóp S.ABC có đáy là ABC là tam giác đều cạnh a. Tam giác SAB cân tại S và nằm
trong mặt phẳng vuông góc với mặt phẳng (ABC). Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 0
45 . Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng a 15 a 15 a 15 a 15 A. B. C. D. 10 5 6 3
Câu 9: Cho tứ điện đều ABCD cạnh a 3 . Độ dài khoảng cách giữa hai đường thẳng AB và CD là ? a 6 a 6 a 3 a 6 A. B. C. D. 4 2 2 3
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2a và (SAD) nằm trong mặt
phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng AD và SB? Biết SAD là tam giác đều. 2a 21 2a 14 a 14 a 14 A. B. C. D. 7 7 7 3
Câu 11: Cho hình hộp đứng ABCD.A’B’C’D có đáy là hình thoi cạnh a 3 , 0
BAD  60 , góc của
đường chéo A’C và mặt phẳng đáy bằng 0
60 . Khoảng cách giữa hai đường A’C và BB’ là? a a 3 a 2 A. B. C. D. . a 2 2 2 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc đáy, góc giữa
đường thẳng SC và mặt phẳng (ABCD) bằng 0
45 . Khoảng cách giữa hai đường thẳng SB, AC là: a a 10 a A. B. C. D. . a 5 5 5
Câu 13: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B. Biết
AB a, BC a, AD  3a,SA a 2. Khi SA  ( ABCD), khoảng cách giữa hai đường thẳng SA, CD là: a a 2a 3a A. B. C. D. 5 5 5 5
Câu 14: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B. Biết
AB a, BC a, AD  3a,SA a 2. Khi SA  ( ABCD), khoảng cách giữa hai đường thẳng SC và AD là: a a 6 a 6 2a A. B. C. D. 3 2 3 3 Câu 15: Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SB SC   .
a Cạnh SA  ( ABCD), khoảng cách từ điểm A đến mặt phẳng (SCD) bằng: 2 3 a a a a A. B. C. D. 6 3 3 2
Câu 16: Cho tứ điện đều ABCD cạnh a 3 . Độ dài khoảng cách giữa hai đường thẳng AB và CD là? a 6 a 6 a 3 a 6 A. B. C. D. . 4 2 2 3
Câu 17: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2a và (SAD) nằm trong mặt
phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng AD và SB? Biết SAD là tam giác đều. 2a 21 2a 14 a 14 a 14 A. B. C. D. . 7 7 7 3
Câu 18: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B có
AB a, BC a,CD a 6, SA a 2. Khi SA  ( ABCD) thì khoảng cách giữa AD và SC là? a a 5 a 6 a 6 A. 5 B. C. D. .  3 2 3 2
Câu 19: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA AC  2 , a SA vuông
góc với mặt phẳng đáy. Khoảng cách giữa 2 đường thẳng SA và BC là: a 2 a 2 A. a 2 B. 2a 2 C. 2 D. 4
Câu 20: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA AC  2 , a SA vuông
góc với mặt phẳng đáy. Khoảng cách giữa 2 đường thẳng SC và AB là: ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 a 3 a 2a A. a 3 B. 2 C. D. 3 3
Câu 21: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B có AB  , a
BC  a,CD  a 6,SA a 2 . Khi SA  ABCD thì khoảng cách từ giữa AD và SC là ? a 5 a 5 a 6 a 6 A. 3 B. 2 C. 3 D. 2
Câu 22: Cho hình chóp S.ABC có đáy tam giác đều ABC cạnh là a, cạnh bên SA  ,
a SA  ABC, I
là trung điểm của BC. Khoảng cách giữa hai đường thẳng SI và AB là? a 17 a 57 a 23 a 17 A. 4 B. 19 C. 7 D. 7
Câu 23: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, SA vuông góc với mặt
phẳng đáy, góc tạo bởi SC với (SAB) là 300. Gọi E, F lần lượt là trung điểm của BC và SD. Khoảng
cách giữa hai đường thẳng chéo nhau DE và CF là ? a 21 3a 17 a 13 3a 31 A. 21 B. 11 C. 13 D. 31
Câu 24: Hình chóp S.ABC có đáy ABC là tam giác vuông tại C. Có CA  ,
a CB b , cạnh SA h
vuông góc với đáy. Gọi D là trung điểm cạnh AB. Khoảng cách giữa hai đường thẳng AC và SD là ? ah bh ah ah A. B. C. D. 2 a  2 h 2 b  2 4h 2 b  2 4h 2 b  2 2h
Câu 25: Cho khối lăng trụ ABC.A'B'C' có đáy là tam giác ABC cân tại A có AB AC  2 ; a
BC  2a 3 . Tam giác A'BC vuông cân tại A' và nằm trong mặt phẳng vuông góc với đáy (ABC).
Khoảng cách giữa 2 đường thẳng AA' và BC là: a 2 a 5 a 3 A. a 3 B. 2 C. 2 D. 2
Câu 26: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A và SA vuông góc với mặt phẳng
(ABC), AB AC SA  2a . Gọi I là trung điểm của BC. Tính theo a khoảng cách giữa hai đường thẳng SI, AC 2a 10 2a 5 a 10 a 5 A. 5 B. 5 C. 5 D. 5
Câu 27: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAD)
cùng vuông góc với đáy. Góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng 600. Tính theo a
khoảng cách giữa 2 đường thẳng SB, AD. a 3 a 3 a 3 A. a 3 B. 2 C. 3 D. 5 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 28: Cho hình chóp S.ABCD có đáy là hình bình hành ABCD tâm O tam giác ABC vuông cân tại
A có AB AC  ,
a SA  ABCD. Đường thẳng SD tạo với đáy một góc 450. Khoảng cách giữa 2
đường thẳng AD và SB là: a 3 a 5 a 10 a 10 A. 2 B. 5 C. 10 D. 5
Câu 29: Cho khối chóp S.ABCD có đáy là hình vuông cạnh a, SA   ABCD . Gọi M là trung điểm 3a
cạnh BC và SM  2 . Khoảng cách giữa 2 đường thẳng SM và AD là : a 3 a A. a 2 B. a C. D. 2 2
Câu 30: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có AB  3 , a AD  2 , a
SA  ABCD . Gọi M là trung điểm của AD. Khoảng cách giữa 2 đường thẳng CM và SA là 6a 3a 2a 6a A. B. C. D. 13 10 5 10
Câu 31: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B. Cạnh bên
SA  ABCD, AD  4 ,
a AB BC  2 ,
a SA a 3 . Khoảng cách giữa hai đường thẳng SB và CD bằng: a 30 a 5 a 6 A. 5a 6 B. 5 C. 6 D. 5 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 Đáp án 1-D 2-B 3-B 4-A 5-D 6-D 7-C 8-B 9-B 10-A 11-B 12-B 13-D 14-C 15-D 16-B 17-A 18-C 19-A 20-D 21-C 22-B 23-C 24-B 25-D 26-B 27-B 28-D 29-C 30-B 31-B Hướng dẫn giải
Câu 1: Cho khối chóp S.ABCD có đáy là hình vuông cạnh 4 .
cm Biết SA  3 ,
cm khoảng cách giữa
2 đường thẳng SA và BC là: 2 A. 1 cm B. 1 cm C. cm D. 4 cm 5 5 5 2 2
HD: Ta có OA  2 2 (O là tâm hình vuông). SO SA OA  1cm d SA BC 4 ;
d BC;SAD  2d  ;
O SAD  . Chọn D 5
Câu 2: Cho khối chóp đều S.ABC có đáy là tam giác đều cạnh 3 cm. Biết SA tạo với đáy một góc 0 60 .
Khoảng cách giữa 2 đường thẳng SA và BC là: 9 3 A. 3 cm B. cm C. 2 cm D. cm 4 2 2 3 3
HD: Gọi O là trọng tâm tam giác ABC. Ta có: OA  .  3 Ax BC Ax / / SOA 3 2 . Kẻ / / suy ra   . d SA BC 3 3 9 ;  d B ;
C SAx  d  ;
O SAx  0 .OAsin60  2 2 4 . Chọn B
Câu 3: Cho khối chóp S.ABCD có SA  ( ABCD) có đáy ABCD là hình chữ nhật có AB  3; AD  4.
Biết SC  13. Khoảng cách giữa 2 đường thẳng SB và AD là: 4 12 2 3 A. B. C. D. 17 17 17 17 2 2
HD: Ta có: AC  5  SA SC AC  12 d SB A  12 ; D  d  D;
A SBC  d  ;
A SBC  . Chọn B 17
Câu 4: Cho khối chóp S.ABCD có đáy là hình vuông cạnh 2a. Biết hình chiếu vuông góc của S lên
mặt đáy trùng với trung điểm của AB và SCD ABCD 0 ;
 60 Khoảng cách giữa 2 đường thẳng SD và BC là: 4a 39 4a 3 a 4a 3 A. B. C. 2 3 D. 13 13 13 39 0 0
HD: Dựng HK CD SKH  60 , SH HK tan 60  2a 3 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 d SD  4a 39
;BC  d BC;SAD  2d H;SAD  13 . Chọn A
Câu 5: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , AB a 3  AC a tam giác
SBC là tam giác vuông cân tại đỉnh S và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC). Tính
khoảng cách giữa 2 đường thẳng SB và AC. 3a a 3 a 21 2a 21 A. B. C. D. 7 7 7 7
HD: H là trung điểm BC. Ta có: BC  2 AB  2 1
AC  2a  SH BC a 2 2a 21 Dựng x
B / / AC d AC;SB  d AC;S x
B   d C;S x
B   2dH;S x
B   7 . Chọn D SB SC Câu 6: Cho hình chóp S.ABCD
có đáy ABCD là hình vuông,   a . 2 3
Cạnh SA  ( ABCD) khoảng cách từ điểm A đến mặt phẳng (SCD) bằng: a a a a A. B. C. D. 6 3 3 2
HD: Kẻ AH  SD  AH d  , A S D C  BC AB Ta có 
BC  SAB  BC SBBC SA   2  2 BC SC SB a 2 2 . Mà SA
SB AB a 1 1 1 2 a Ta có     AH   d , A SCD 2 2 2 2
  . Chọn D AH AS AD a 2
Câu 7: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S trên 2 a
mặt phẳng (ABC) là trung điểm H của AB. Diện tích tam giác SAB bằng
. Khoảng cách từ điểm B 2
đến mặt phẳng (SAC) bằng: a 6 a 3 2a 6 2a 3 A. B. C. D. 35 35 35 35
HD: Ta có d  ,
B SAC  2dH,SAC
Kẻ HK SN HK d H,SAC  d B,SAC  2HK 2S Ta có SH SAB a 2 AB 1 a 3 Và HN BM  2 4 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 1 1 1 35 a 6 Ta có     HK  2 2 2 2 HK HN HS 6a 35 2a 6
d B,SAC  2HK  . Chọn C 35
Câu 8: Cho hình chóp S.ABC có đáy là ABC là tam giác đều cạnh a. Tam giác SAB cân tại S và nằm
trong mặt phẳng vuông góc với mặt phẳng (ABC). Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 0
45 . Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng a 15 a 15 a 15 a 15 A. B. C. D. 10 5 6 3
HD: Ta có d  ,
A SBC  2dH,SBC
Kẻ HK SN HK d H,SBC  d  ,
A SBC  2HK 0 a 3
Ta có SH CH.tan 45  2 1 a 3 Và HN AM  2 4 1 1 1 20 a 15 Ta có     HK  2 2 2 2 HK HS HN 3a 10 2a 15  d  ,
A SBC  2HK  5 . Chọn B
Câu 9: Cho tứ điện đều ABCD cạnh a 3 . Độ dài khoảng cách giữa hai đường thẳng AB và CD là ? a 6 a 6 a 3 a 6 A. B. C. D. 4 2 2 3 AB CM HD: Ta có 
AB  CDM AB SH
Kẻ MN CD AB MN do AB  CDM
=> MN là khoảng cách giữa hai đường thẳng AB và CD a 3. 3 3a Ta có CM   2 2 1 a 3 Và CN CD  2 2 a aMN  2 CM  2 6 6 NC
d AB,CD  2 2 . Chọn B
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2a và (SAD) nằm trong mặt
phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng AD và SB? Biết SAD là tam giác đều. ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 2a 21 2a 14 a 14 a 14 A. B. C. D. 7 7 7 3 HD: Do D A / /BC
d AD,SB  d AD,SBC  d H,SBC
Kẻ HE SK HE d H,SBC  d AD,SB 2a 3 Ta có SH   a 3 2 1 1 1 7 2a 21 Ta có     HE  2 2 2 2 HE HS HK 12a 7 2a 21
d AD,SB  7 . Chọn A
Câu 11: Cho hình hộp đứng ABCD.A’B’C’D có đáy là hình thoi cạnh a 3 , 0
BAD  60 , góc của
đường chéo A’C và mặt phẳng đáy bằng 0
60 . Khoảng cách giữa hai đường A’C và BB’ là? a a 3 a 2 A. B. C. D. . a 2 2 2
HD: Có A 'C   AA'C 'C  mà BB' song song (AA'C'C)
Nên d A'C,BB'  d BB', AA'C 'C)
Gọi O là tâm hình thoi ABCD BO AC Ta có 
BO  AA'C'C BO AA' BD a 3
Suy ra d O, AA'C 'C  BO   2 2 a 3
Do đó d A'C,BB'  d O,AA'C 'C  2
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc đáy, góc giữa
đường thẳng SC và mặt phẳng (ABCD) bằng 0
45 . Khoảng cách giữa hai đường thẳng SB, AC là: a a 10 a A. B. C. D. . a 5 5 5
HD: Ta có SC ABC   SCA  0 , D 45
Kẻ đường thẳng d qua B và song song với AC.
Kẻ AH  d với H d . Kẻ AK  SH SA BH Lại có 
BH  SAH  BH AKAH BH ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Do đó AK  SHB  d SB, AC  AK
Tam giác SAH vuông tại A, có AK  SH 1 1 1 5 a 10 Nên     AK  2 2 2 2 AK SH AH 2a 5 a 10
Vậy d SB,AC  5 . Chọn B
Câu 13: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B. Biết
AB a, BC a, AD  3a,SA a 2. Khi SA  ( ABCD), khoảng cách giữa hai đường thẳng SA, CD là: a a 2a 3a A. B. C. D. 5 5 5 5
HD: kẻ AH  D
C mà SA AH AH d  , SA D C  1 1 Ta có SA . B D A AH. D C  D AC 2 2 A . B D A . a 3a 3a  AH    D C a 5 5 3a  d SA, D C   . Chọn D 5
Câu 14: Cho hình chóp S.ABCD có đáy ABCD là hình
thang vuông tại A, B. Biết AB  , a BC  , a AD  3 ,
a SA a 2. Khi SA  ( ABCD), khoảng cách giữa
hai đường thẳng SC và AD là: a a 6 a 6 2a A. B. C. D. 3 2 3 3
HD: Kẻ AH  SB, H SB . Ta có SC  SBC  || AD
d AD,SC  d A ;
D SBC  d  , A SBC BC AB Ta có 
BC  SAB  BC AHBC SA
Mà AH SB nên AH  SBC 1 1 1 3 a 6 Do đó     AH  2 2 2 2 AH SA AB 2a 3 . Chọn C Câu 15: Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SB SC   .
a Cạnh SA  ( ABCD), khoảng cách từ điểm A đến mặt phẳng (SCD) bằng: 2 3 a a a a A. B. C. D. 6 3 3 2 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
HD: Kẻ AH SD AH d  , A SCD BC AB Ta có 
BC  SAB  BC SBBC SA   2  2 BC SC SB a 2 2 . Mà SA
SB AB a 1 1 1 2 Ta có    2 2 2 2 AH AS AD a aAH   d  ,
A SCD. Chọn D 2
Câu 16: Cho tứ điện đều ABCD cạnh a 3 . Độ dài khoảng cách giữa hai đường thẳng AB và CD là? a 6 a 6 a 3 a 6 A. B. C. D. . 4 2 2 3 AB CM HD: Ta có 
AB  CDM AB  SH
Kẻ MN CD AB MN do AB  CDM
=> MN là khoảng cách giữa hai đường thẳng AB và CD a 3. 3 3a 1 a 3 Ta có CM   CN CD 2 2 và   2 2 a aMN  2 CM  2 6 6 CN
d AB,CD  2 2 . Chọn B
Câu 17: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2a và (SAD) nằm trong mặt
phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng AD và SB? Biết SAD là tam giác đều. 2a 21 2a 14 a 14 a 14 A. B. C. D. . 7 7 7 3 HD: Do D A / /BCd  D
A ,SB  d  D
A ,SBC  d H,SBC
Kẻ HE  SK HE d H,SBC  d AD,SB 2a 3 Ta có SH   a 3 2 1 1 1 7 2a 21 Ta có     HE  2 2 2 2 HE HS HK 12a 7 2a 21
d AD,SB  7 . Chọn A ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 18: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B có
AB a, BC a,CD a 6, SA a 2. Khi SA  ( ABCD) thì khoảng cách giữa AD và SC là? a a 5 a 6 a 6 A. 5 B. C. D. . 3 2 3 2
HD: Do AD / / BC
d AD,SC  d A ;
D SBC  d  , A SBC Kẻ AH SBBC AB Ta có 
BC  SAB  BC AHBC SA
AH SB AH  SBC  AH d  ,
A SBC ta có 1 1 1 3 a 6     AH  2 2 2 2 AH SA AB 2a 3 a 6  d  D
A ,SC  3 . Chọn C
Câu 12: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA AC  2 , a SA vuông
góc với mặt phẳng đáy. Khoảng cách giữa 2 đường thẳng SA và BC là: a 2 a 2 A. a 2 B. 2a 2 C. 2 D. 4 SA AB HD: Ta có 
AB là đoạn vuông góc chung BC AB Do đó d S , A BC   AB
Tam giác ABC vuông cân tại B AC 2a Nên AB  
a 2  d S , A BC   a 2 2 2 Chọn A.
Câu 13: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân
tại B, SA AC  2 ,
a SA vuông góc với mặt phẳng đáy. Khoảng
cách giữa 2 đường thẳng SC và AB là: a 3 a 2a A. a 3 B. 2 C. D. 3 3
HD: Từ C kẻ Cx || AB . Kẻ AH Cx, H Cx
Kẻ AK SH AK  SHC   d AB,SC  AK 1 1 1 1 1 3 Ta có      2 2 2 2 2 2 AK SA AH 4a 2a 4a ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 Do đó 2a    SC  2a AK d AB,  . Chọn D 3 3
Câu 21: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B có AB  , a
BC  a,CD  a 6,SA a 2 . Khi SA  ABCD thì khoảng cách từ giữa AD và SC là ? a 5 a 5 a 6 a 6 A. 3 B. 2 C. 3 D. 2
HD: Do AD / / BC
d AD,SC  d A ;
D SBC  d  , A SBC Kẻ AH SBBC AB Ta có 
BC  SAB  BC AHBC SA
Mà AH SB AH  SBC  AH d  ,
A SBC ta có 1 1 1 3 a 6     AH  2 2 2 2 AH SA AB 2a 3 a 6  d  D
A ,SC  3 . Chọn C
Câu 22: Cho hình chóp S.ABC có đáy tam giác đều ABC cạnh là a, cạnh bên SA  ,
a SA  ABC, I
là trung điểm của BC. Khoảng cách giữa hai đường thẳng SI và AB là? a 17 a 57 a 23 a 17 A. 4 B. 19 C. 7 D. 7
HD: Kẻ IJ / / AB
d SI, AB  d A ,
B SIJ  d  , A SIJ
Kẻ AH SD AH d  , A SIJ 1 a 3 Ta có AD MC  2 4 1 1 1 19 a 57 Ta có     AH  2 2 2 2 AH AS AD 3a 19 a 57
d SI, AB  19 . Chọn B
Câu 23: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, SA vuông góc với mặt
phẳng đáy, góc tạo bởi SC với (SAB) là 300. Gọi E, F lần lượt là trung điểm của BC và SD. Khoảng
cách giữa hai đường thẳng chéo nhau DE và CF là ? a 21 3a 17 a 13 3a 31 A. 21 B. 11 C. 13 D. 31 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
HD: Ta có d DE,CF  d DE,FCK  1
d D,FCK  d H,FCK 2
Kẻ HI CK, HJ FI 1
HJ d H,FCK  d DE,CF  HJ 2 2a 5 Ta có HI  5 0
Ta có SC,SAB  BSC  30  SB a 3 aSA  2 SB  2 2
AB a 2  HF  2 1 1 1 13 2a 13 a 13 Ta có     HJ
d DE,CF  2 2 2 2 . Chọn C HJ HI HF 4a 13 13
Câu 24: Hình chóp S.ABC có đáy ABC là tam giác vuông tại C. Có CA  ,
a CB b , cạnh SA h
vuông góc với đáy. Gọi D là trung điểm cạnh AB. Khoảng cách giữa hai đường thẳng AC và SD là ? ah bh ah ah A. B. C. D. 2 a  2 h 2 b  2 4h 2 b  2 4h 2 b  2 2h
HD: Dựng hình bình hành ACKD d A ;
C SD  d A ;
C SDK  d  ;
A SDK  d 1 1 1
+) Kẻ AP DK    2 2 2 d SA AP b
+) Gọi M BC DK ACMP là hình chữ nhật  AP CM  2 1 1 4 bh     d  2 2 2 => Chọn B 2 d h b b  2 4h
Câu 25: Cho khối lăng trụ ABC.A'B'C' có đáy là tam giác ABC cân tại A có AB AC  2 ; a
BC  2a 3 . Tam giác A'BC vuông cân tại A' và nằm trong mặt phẳng vuông góc với đáy (ABC).
Khoảng cách giữa 2 đường thẳng AA' và BC là: a 2 a 5 a 3 A. a 3 B. 2 C. 2 D. 2
HD: +) Gọi H là trung điểm của cạnh BC
A' H   ABC  A'H HC HC HA' HC HA
+) ABC cân tại A  AH HC  HC HA'
HC  A' AH   BC  A' AH ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
+) Kẻ HP A ' A P A' A  BC HP
=> HP là đường vuông góc chung của A'A và BC  d A' ; A BC  HP BC
+) A' BC vuông cân tại A '  A ' H   a 3 2 2 2 2 2 +) Cạnh HA
AB BH  4a  3a a 1 1 1 1 1 4 a 3 a 3        HP   d A' ; A BC  2 2 2 2 2 2 HP A'H AH 3a a 3a 2 2
Câu 26: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A và SA vuông góc với mặt phẳng
(ABC), AB AC SA  2a . Gọi I là trung điểm của BC. Tính theo a khoảng cách giữa hai đường thẳng SI, AC 2a 10 2a 5 a 10 a 5 A. 5 B. 5 C. 5 D. 5
HD: +) Gọi E là trung điểm của cạnh AB AC / / IE  AC/ / SEI   d A ;
C SI   d A ;
C SEI   d  ; A SEI  AC / /IE +) 
IE AE , kẻ AP SE PSE  d  ;
A SEI   AP d A ; C SI   APAC AE 1 1 1 1 1 5 2a 5 2a 5 Ta có       AP
d AC;SI   2 2 2 2 2 2 AP SA AE 4a a 4a 5 5
Câu 27: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAD)
cùng vuông góc với đáy. Góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng 600. Tính theo a
khoảng cách giữa 2 đường thẳng SB, AD. a 3 a 3 a 3 A. a 3 B. 2 C. 3 D. 5 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
SABSAD  SA  HD: +) 
SAB   ABCD
SA  ABCD SAD   ABCD
 SB ABCD  SBA  0 ; 60
+) AD / / BC AD / / SBC   d A ;
D SB  d A ;
D SBC  d  ; A SBC
+) Ta có AB BC , kẻ AP SB P SB  d  ;
A SBC  AP d A ; D SB  AP AP 0 3 3 a 3 a 3 +) sin ABP   sin 60   AP AB   d A ; D SB  AB 2 2 2 2 . Chọn B
Câu 28: Cho hình chóp S.ABCD có đáy là hình bình hành ABCD tâm O tam giác ABC vuông cân tại
A có AB AC  ,
a SA  ABCD. Đường thẳng SD tạo với đáy một góc 450. Khoảng cách giữa 2
đường thẳng AD và SB là: a 3 a 5 a 10 a 10 A. 2 B. 5 C. 10 D. 5
HD: Lấy M là trung điểm BC, H là hình chiếu của A lên SM. Xác định  AD ABCD 0 ,  SDA  45
SA BC AM BC  SAM   BC AH
AH SM AH  SBC   d  ,
A SBC   AH
Vì AD / / SBC  chứa BC nên
d SB, AD  d A ,
D ABC   d  ,
A SBC   AH a
Tính: SA AD a 2, AM  2 1 1 1 2    AH a . Chọn D 2 2 2 AH AS AM 5
Câu 29: Cho khối chóp S.ABCD có đáy là hình vuông cạnh a, SA   ABCD . Gọi M là trung điểm 3a
cạnh BC và SM  2 . Khoảng cách giữa 2 đường thẳng SM và AD là : a 3 a A. a 2 B. a C. D. 2 2
HD: Lấy H là hình chiếu của A lên SB.
AB BC SA BC  SAB  BC AH ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
AH SB AH  SBC   d  ,
A SBC   AH
Ta có: Vì AD / / SBC  chứa SM
d AD,SM   d AD,SAB  d  ,
A SAB  AH a 5 Tính: 2 2 2 2 AM BA BM
SA SM AM a 2 1 1 1 a    AH  . Chọn C 2 2 2 AH AS AB 2
Câu 30: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có AB  3 , a AD  2 , a
SA  ABCD . Gọi M là trung điểm của AD. Khoảng cách giữa 2 đường thẳng CM và SA là 6a 3a A. B. C. 13 10 2a 6a D. 5 10
HD: Lấy H là hình chiếu của A lên MC
MC AH SA d S , A CM   AH Tính 2 2 CM
DM DC a 10 CD
AH.MC  AM.AC.sin MAC AM .AC. AC 3aAH  . Chọn B 10
Câu 31: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B. Cạnh bên
SA  ABCD, AD  4 ,
a AB BC  2 ,
a SA a 3 . Khoảng cách giữa hai đường thẳng SB và CD bằng: a 30 a 5 a 6 A. 5a 6 B. 5 C. 6 D. 5
HD: Kẻ BM / /CD CD / / SBM   SBd C ,
D SB  d CD,SBM   d  , A SBM 
Kẻ AE BM , AK SE E BM , K SE
AK  SBM   AK d  , A SBM  AC Ta có AE   a 2 2 1 1 1 a 30 Ta có    AK  . Chọn B 2 2 2 AK SA AE 5 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
CHỦ ĐỀ 3: MẶT TRỤ – HÌNH TRỤ – KHỐI TRỤ
Câu 1. Cho hình trụ (T) có chiều cao h, độ dài đường sinh l , bán kính đáy r. Ký hiệu S là diện tích xq
xung quanh của (T). Công thức nào sau đây là đúng? A. S   rh B. S  2rl C. 2 S  2 r h D. S  rl xq xq xq xq
Câu 2. Cho hình trụ (T) có chiều cao h, độ dài đường sinh l , bán kính đáy r. Ký hiệu S là diện tích tp
toàn phần của (T). Công thức nào sau đây là đúng?
A. S   rl
B. S   rl  2 r C. 2
S   rl   r D. 2
S  2 rl  2 r tp tp tp tp
Câu 3. Cho hình trụ (T) có chiều cao h, độ dài đường sinh l , bán kính đáy r. Ký hiệu  V là thể tích T
khối trụ (T). Công thức nào sau đây là đúng? 1 A.   2 2 2  V rh B. V   r h C. V   rl D. V  2 r h T  T  N  N 3
Câu 4. Một hình trụ có bán kính đáy r  5cm , chiều cao h  7cm . Diện tích xung quanh của hình trụ này là: 70 35 A.   2 35 cm B.   2 70 cm C.   2 cm D.   2 cm  3 3
Câu 5. Một hình trụ có bán kính đáy r a , đồ dài đường sinh l  2a . Diện tích toàn phần của hình trụ này là: A. 2 6 a B. 2 2 a C. 2 4 a D. 2 5 a
Câu 6. Quay hình vuông ABCD cạnh a xung quanh một cạnh. Thể tích của khối trụ được tạo thành là: 1 A. 3  a B. 3 2 a C. 3  a D. 3 3 a 3
Câu 7. Cho hình vuông ABCD cạnh 8cm. Gọi M, N lần lượt là trung điểm của AB và CD . Quay
hình vuông ABCD xung quanh MN. Diện tích xung quanh của hình trụ tạo thành là: A.   2 64 cm B.   2 32 cm C.   2 96 cm D.   2 126 cm
Câu 8. Một hình trụ (T) có diện tích toàn phần là   2 120
cm  và có bán kính đáy bằng 6cm. Chiều cao của (T) là: A. 6cm B. 5cm C. 4cm D. 3cm
Câu 9. Một khối trụ (T) có thể tích bằng   3 81
cm  và có dường sinh gấp ba lấn bán kính đáy. Độ dài đường sinh của (T) là: A. 12cm B. 3cm C. 6cm D. 9cm
Câu 10. Cho hình chữ nhật ABCD có AB a và góc 0
BDC  30 . Quay hình chữ nhật này xung
quanh cạnh AD. Diện tích xung quanh của hình trụ được tạo thành là: 2 A. 2 3 a B. 2 2 3 a C. 2  a D. 2  a 3 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 11. Cho hình lập phương ABC .
D A' B 'C ' D ' có cạnh bằng a . Gọi (C) và (C’) lần lượt là hai
đường tròn ngoại tiếp hình vuông ABCD và  A' B 'C ' D ' . Hình trụ có hai đáy là (C) và (C’) có thể tích là: 1 3  a A. 3  a B. 3 2 a C. 3  a D. 3 2
Câu 12. Cắt hình trụ (T) bằng một mặt phẳng đi qua trục được thiết diện là một hình chữ nhật có diện tích bằng 2
30cm và chu vi bằng 26cm . Biết chiều dài của hình chữ nhật lớn hơn đường kính mặt đáy
của hình trụ (T). Diện tích toàn phần của (T) là: 69 23 A.  2 cm B.   2 69 cm C.   2 23 cm D.  2 cm  2 2
Câu 13. Cắt hình trụ (T) bằng một mặt phẳng song song với trục và cách trục một khoảng bằng 2cm
được thiết diện là một hình vuông có diện tích bằng 2
16cm . Thể tích của (T) là: A.   3 32 cm B.   3 16 cm C.   3 64 cm D.   3 8 cm
Câu 14. Một hình trụ có tỉ số giữa diện tích toàn phần và diện tích xung quanh bằng 4. Khẳng định nào sau đây là đúng :
A. Đường sinh bằng bán kính đáy.
B. Bán kính đáy bằng ba lần đường sinh
C. Đường sinh bằng ba lần bán kính đáy
D. Đường sinh bằng bốn lần bán kính đáy
Câu 15. Trong không gian, cho hình chữ nhật ABCD có AB  1 và AD  2 . Gọi M,N lần lượt là trung
điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần S của hình trụ đó. tp A. S  4 B. S  2 C. S  6 D. S  10 tp tp tp tp
Câu 16. Khi quay hình chữ nhật ABCD quanh đường thẳng AB thì hình chữ nhật ABCD tạo thành hình tròn xoay là: A. Hình trụ B. Khối trụ C. Mặt trụ D. Hai hình trụ
Câu 17. Khối nón có chiều cao h  3cm và bán kính đáy r  2cm thì có thể tích bằng: 4 A.   3 4 cm B.   3 cm C.   2 16 cm D.   2 4 cm  3
Câu 18. Khối trụ có chiều cao h  3cm và bán kính đáy r  2cm thì có thể tích bằng: A.   3 12 cm B.   3 4 cm C.   3 6 cm D.   2 12 cm
Câu 19. Diện tích xung quanh của hình trụ có bán kính bằng 7 và chiều cao bằng 9 là: A. 62 B. 63 C. 126 D. 128
Câu 20. Hình trụ có bán kính bằng 5, khoảng cách giữa hai đáy bằng 7. Diện tích toàn phần của hình trụ bằng: A. 10 B. 85 C. 95 D. 120
Câu 21. Một hình trụ có diện tích đáy bằng   2 4
m  . Khoảng cách giữa trục và đường sinh của mặt
xung quanh hình trụ đó bằng: ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 A. 4m B. 3m C. 2m D. 1m
Câu 22. Bên trong một lon sữa hình trụ có đường kính đáy bằng chiều cao và bằng 1 dm. Thể tích
thực của lon sữa đó bằng:   A.   3 2 dm B.  3 dm C.  3 dm D.   3 dm  2 4
Câu 23. Một hình vuông cạnh a quay xung quanh một cạnh tạo thành một hình tròn xoay có diện tích toàn phần bằng: A. 2 4a B. 2 6a C. 2 2a D. 2 3a
Câu 24. Cho hình vuông ABCD có cạnh 2 cm, biết O và O’ lần lượt là trung điểm của AB và CD. Khi
quay hình vuông ABCD quanh trục OO’ thì khối trụ tròn xoay được tạo thành có thể tích bằng: A.   3 2 cm B.   3 4 cm C.   3 6 cm D.   3 8 cm
Câu 25. Một khối cầu bán kính R, một khối trụ có bán kính R, chiều cao 2R. Tỉ số thể tích giữa khối
cầu và khối trụ bằng: 1 2 3 A. B. C. D. 2 2 3 2
Câu 26. Cho hình lập phương ABC .
D A' B 'C ' D ' cạnh a và một hình trụ có 2 đáy nội tiếp trong 2
hình vuông ABCD và A’B’C’D’. Tỉ số giữa diện tích xung quanh hình trụ và diện tích toàn phần của hình lập phương bằng: 1   A. B. C. D.  2 2 6
Câu 27. Một hình trụ có đường kính đáy bằng chiều cao nội tiếp trong mặt cầu bán kính R. Diện tích
xung quanh của hình trụ bằng: A. 2 2 R 2 B. 2  R 2 C. 2 2 R D. 2  R
Câu 28. Cho lăng trụ tam giác đều có tất cả các cạnh bằng a . Một hình trụ tròn xoay có hai đáy là hai
hình tròn ngoại tiếp hai đáy của lăng trụ. Thể tích của khối trụ tròn xoay bằng: 3  a 3  a A. 3  a B. C. 3 3 a D. 9 3
Câu 29. Một hình trụ có diện tích xung quanh bằng 4 và có thiết diện qua trục là hình vuông. Thể
tích khối trụ tương ứng bằng: A. 2 B. C. 3 D. 4
Câu 30. Một hình trụ có diện tích xung quanh bằng 4 và có thiết diện qua trục là hình vuông. Diện
tích toàn phần của hình trụ bằng: A. 12 B. 10 C. 8 D. 6
Câu 31. Một hình trụ có bán kính đáy bằng 4cm, thiết diện qua trục là hình vuông. Diện tích xung
quanh của hình trụ bằng: A. 2 16 cm B. 2 64 cm C. 2 32 cm D. 2 24 cm ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 32. Một hình trụ có bán kính đáy bằng 2cm , thiết diện qua trục là hình vuông. Thể tích của khối trụ tương ứng bằng: A.   2 12 cm B.   2 16 cm C.   2 20 cm D.   2 24 cm
Câu 33. Hình trụ có bán kính đáy R, thiết diện qua trục là hình vuông. Thể tích của khối lăng trụ tứ
giác đều có hai đáy nội tiếp trong hai đường tròn đáy của hình trụ bằng: A. 3 2R B. 3 3R C. 3 4R D. 3 5R
Câu 34. Trong một chiếc hộp hình trụ người ta bỏ vào đó ba quả banh tennis, biết rằng đáy của hình
trụ bằng hình tròn lớn trên quả banh và chiều cao của hình trụ bằng 3 lần đường kính của quả banh. S
Gọi S là tổng diện tích của ba quả banh và S là diện tích xung quanh của hình trụ. Tỉ số 1 bằng: 1 2 S2 1 A. 1 B. 2 C. 3 D. 2
Câu 35. Khối trụ có chiều cao 2a 3 , bán kính đáy a 3 . Thể tích khối cầu ngoại tiếp khối trụ bằng: 3 4 a 6 A. 3 8 a 6 B. 3 6 a 3 C. D. 3 4 a 3 3
Câu 36. Một hình tứ diện đều ABCD cạnh a . Xét hình trụ có 1 đáy là đường tròn nội tiếp tam giác
ABC và có chiều cao bằng chiều cao hình tứ diện. Diện tích xung quanh của hình trụ đó bằng: 2  a 3 2  a 2 2  a 2 2  a 3 A. B. C. D. 3 2 3 2
Câu 37. Một hình trụ có bán kính đáy bằng a , chiều cao OO '  a 3 . Hai điểm A, B lần lượt nằm
trên 2 đáy (O), (O’) sao cho góc giữa OO’ và AB bằng 0
30 . Khoảng cách giữa AB và OO’ bằng: a 3 a 3 2a 3 A. B. C. D. a 3 3 2 3
Câu 38. Một hình trụ có bán kính đáy bằng chiều cao và bằng a . Một hình vuông ABCD có AB, CD
lần lượt là 2 dây cung của 2 đường tròn đáy và mặt phẳng (ABCD) không vuông góc với đáy. Diện
tích hình vuông đó bằng: 2 5a 2 5a 2 A. B. 2 5a C. D. 2 5a 2 2 2
Câu 39. Hình trụ có bán kính đáy 3cm và khoảng cách giữa hai đáy bằng 10cm thì có diện tích toàn phần là: A.   2 78 cm B.   2 60 cm C.   2 18 cm D.   2 69 cm
Câu 40. Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a . Gọi S là diện tích xung quanh của
hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông ABCD và A’B’C’D’. Diện tích S là: 2  a 2 A. 2  a B. 2  a 2 C. 2 a 3 D. 2
ĐÁP ÁN TRẮC NGHIỆM ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 01. B 02. D 03. B 04. B 05. A 06. C 07. A 08. C 09. D 10. C 11. D 12. A 13. A 14. B 15. A 16. A 17. A 18. D 19. C 20. D 21. C 22. C 23. A 24. A 25. B 26. C 27. C 28. D 29. A 30. D 31. B 32. B 33. C 34. A 35. A 36. C 37. B 38. A 39. A 40. B GIẢI CHI TIẾT
Câu 1. Với hình trụ ta có h l S
 2rh  2rl . Chọn D xq
Câu 2. Ta có: S S S
 2 rh  2  r   rl   r . Chọn D d  2 2 2 2 tp xq 2. Câu 3. Ta có: 2     V S h r h . Chọn B T  . d
Câu 4. Ta có: S   rh      2 2 2 .5.7 70 cm . Chọn B xq
Câu 5. Ta có: S S S
 2 rh  2  r   rl   r a   a   a  . Chọn A d  2 2 2 2 2 2 2 4 2 6 tp xq 2.
Câu 6. Khi quay hình vuông cạnh a quanh 1 cạnh ta được khối trụ có r h a Ta có: 2 3       V S h r h a . Chọn C T  . d
Câu 7. Quay hình vuông ABCD xung quanh MN ta được hình trụ như hình vẽ. Khi đó AB r
h AD   S C h   rh    2 4; 8 . 2 64 cm  2 xq d Chọn A
Câu 8. Ta có: S S S
 2 rh  2  r   h   
  h cm . Chọn C d  2 12 72 120 4 tp xq 2.    2  l Câu 9. Ta có: 2 2 3           V S h r h r l ll   l    . Chọn D T  . 81 729 9 d  3 
Câu 10. Khi quay hình chữ nhật này xung quanh cạnh AD ta được hình trụ như hình vẽ. Ta có: 0 r AB  ;
a h BC CD tan 30 . 2 a 2 a Suy ra h
S  2 rh  . xq 3 3 Chọn C A'C ' a 2
Câu 11. Ta có bán kính đáy hình trụ là r   2 2
Đường cao là h a . 3 a Khi đó 2
V   r h  2 Chọn D
Câu 12. Giả sử thiết diện là hình chữ nhật ABCD như hình vẽ khi đó ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
2 AD CD  26
AD CD 13
AD CD . Ta có     A . D CD  30  A . D CD  30 Với
AD CD giải hệ trên ta được AD  10  ; h CD  3  3 2rr  . Khi đó 2 3 9 69 2
S  2 rh  2 r  2 .10  2  cm tp  2 2 4 2 Chọn A
Câu 13. Giả sử thiết diện là hình vuông MNPQ như hình vẽ
Với O ' H  2 và 2 S
PQ 16  PQ  4 MNPQ 2  PQ  ta có 2
O 'Q O ' H   2 2    2  mà 2 h MQ
V S h   r h     cm t  3 4 . .8.4 32 d    Chọn A
Câu 14. Gọi bán kính đáy bằng r, độ dài đường sinh bằng l và h là độ dài đường cao của hình trụ. 2 S     tp 2 r 2 rh r h Theo giả thiết, ta có  
 4  r  3h  3l S 2 rh h xq
Nếu bán kính đáy bằng ba lần độ dài đường sinh. Chọn B
Câu 15. Quay hình chữ nhật xung quanh trục MN, ta được hình trục có bán kính đáy là AM và đường AD
cao là MN. Với AM
1, MN AB  1 nên S  2 r r h     . tp   2 .1.2 4 2 Chọn A
Câu 16. Vì ABCD là hình chữ nhật nên khi quay quanh đường thẳng AB ta sẽ được một hình trụ. Chọn A 1 1
Câu 17. Thể tích của khối nón là 2 2
V   r h   .2 .3  4 . Chọn A 3 3
Câu 18. Thể tích của khối trụ là 2 2
V   r h   .2 .3  12 . Chọn D
Câu 19. Diện tích xung quanh của hình trụ là S
 2rh  2.7.9 126 . Chọn C xq
Câu 20. Diện tích toàn phần của hình trụ là S  2 r r h  2 5.5  7  120 . Chọn D tp
Câu 21. Diện tích toàn phần của hình trụ là S  2 r r h  2.55  7  120 . Chọn D tp 2 1 
Câu 22. Thể tích thực của lon sữa hình trụ là 2 Vr h      .1    . Chọn C  2  4
Câu 23. Diện tích toàn phần hình trụ là S   r r h 2 2  2 .
a 2a  4 a .Chọn A tp
Câu 24. Thể tích của hình trụ là 2 2
V   r h   .1 .2  2 . Chọn A ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 25. Thể tích của hình trụ là 2 2 3
V   r h   .R .2R  2 R ht 4 3  R 4 V 2
Thể tích của khối cầu là 3 V
  R . Suy ra mc 3   . Chọn B mc 3 3 V 2 R 3 ht
Câu 26. Diện tích toàn phần của hình lập phương cạnh a bằng 2 V  6a tp a V
Diện tích xung quanh hình trụ là 2
V  2 rh  2 . .a   a . Suy ra xq  . Chọn C xq 2 V 6 tp
Câu 27. Gọi r là bán kính đáy của hình trụ, theo giả thiết, ta có h  2r
Gọi ABCD là thiết diện qua trụ của hình trụ, O là tâm của hình chữ nhật ABCD 2 ACh R Ta có bán kính mặt cầu 2 R   AO
r r 2  R r   h R 2   2  2  2 R
Diện tích xung quanh hình trụ là 2
V  2 rh  2 .
.R 2  2 R . Chọn C xq 2
Câu 28. Gọi R, h là bán kính đáy và chiều cao của hình trụ. Ta có h a (cùng đường cao với lăng trụ) a 3 3 a là R
vì R cũng là bán kính đường tròn ngoại tiếp đáy lăng trụ 2
V   R h  . Chọn D 3 3
Câu 29. Thiết diện qua trục là hình vuông nên h  2R h  2 Ta có: 2 2 S
 4  2 Rh   h  
V   R h  2 . Chọn A xqR 1
Câu 30. Thiết diện qua trục là hình vuông nên h  2R h  2 Ta có: 2 2 S
 4  2 Rh   h  
S  2 Rh  2 R  6 . Chọn D xqR 1 tp
Câu 31. Thiết diện qua trục là hình vuông nên h  2R  8  S
 2 Rh  64 . Chọn B xq
Câu 32. Thiết diện qua trục là hình vuông nên 2
h  2R  4  V   R h  16 . Chọn B
Câu 33. Thiết diện qua trục là hình vuông nên h  2R . Lăng trụ có cùng chiều cao với hình trụ, và có
đáy là hình vuông với bán kính đường tròn ngoại tiếp là R  Diện tích đáy lăng trụ: S  R 2 2 2
 2R  Thể tích lăng trụ: 3
V Sh  4R .Chọn C
Câu 34. Gọi R là bán kính 1 quả banh  Tổng diện tích 3 quả banh: 2 2
S  3 4 R  12 R 1
Chiếc hộp có bán kính đáy cũng bằng R và chiều cao bằng h  6R S
Diện tích xung quanh hình trụ 2 1
S  2 Rh  12 R  1 .Chọn A 2 S2
Câu 35. Tâm khối cầu ngoại tiếp khối trụ là trung điểm của đoạn nối tâm 2 mặt đáy khối trụ 2 3  h  4 R 2 0 3  R
R a 6  V
 8 a 6 . Chọn A 0    2  3 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 36. Gọi O là tâm của tam giác ABC và M là trung điểm BC a 6 Chiều cao tứ diện 2 2 h DO DA AO  3 Bán kính đườ AM a
ng tròn nội tiếp đáy ABC: 3 R   3 6 2  a 2
S  2 Rh  . Chọn C xq 3
Câu 37. Trên (O) lấy điểm C sao cho BC//OO’. Khi đó: 0
ABC  30  AC a Gọi H là hình chiếu của O lên AC. Suy ra
d OO ', AB  d OO ', AC   OH
Tam giác OAC là tam giác đề a 3 u nên OH  . Chọn B 2
Câu 38. Gọi M, N lần lượt là trung điểm của AB, CD và O, O’ là tâm của 2 đáy hình trụ chứa AB, CD. Ta có: 2  OO '  2 2 2 2
AB  2AM  2 OA OM  2 a OM và 2 2 2 MN  2
OM a  4OM    2  a 6
Vì tứ giác ABCD là hình vuông nên AB MN hay 2 2 2 2
2 a OM a  4OM OM  4 a 10 2  5a AB   Diện tích hình vuông: 2 AB  .Chọn A 2 2
Câu 39. R  3 và 2
h  10  S  2 Rh  2 R  78 . Chọn A tp
Câu 40. Chiều cao hình trụ là chiều cao (hay cạnh) của hình lập phương: h a Bán kính đáy hình trụ a
là bán kính đường tròn ngoại tiếp hình vuông ABCD cạnh a R  2 2
S  2 Rh   a 2 . Chọn B xq
CHỦ ĐỀ 4: MẶT CẦU – HÌNH CẦU – KHỐI CẦU
Câu 1. Một khối cầu tiếp xúc với tất cả các mặt của hình lập phương. Tỉ số thể tích giữa khối cầu và
khối lập phương đó bằng:    2 2 A. B. C. D. 3 6 3 3
Câu 2. Mặt cầu ngoại tiếp hình lập phương cạnh a thì có diện tích bằng: 3 4 a A. 3 a B. C. 2 3 a D. 2 12 a 3 3
Câu 3. Cho hình lập phương cạnh a nội tiếp trong một mặt cầu. Bán kính đường tròn lớn của mặt cầu đó bằng: ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 a 3 a 2 A. a 3 B. a 2 C. D. 2 2
Câu 4. Cho mặt cầu S  có tâm A đường kình 10cm và mặt phẳng (P) cách tâm một khoảng 4cm .
Kết luận nào sau đây sai ? A. (P) cắt (S)
B. (P) cắt (S) theo một đường tròn bán kính 3cm
C. (P) tiếp xúc với (S)
D. (P) và (S) có vô số điểm chung
Câu 5. Tỉ số thể tích giữa khối lập phương và khối cầu ngoại tiếp khối lập phương đó là: 2 3 3 3  2 A. C. D. 3 B. 2 3  2 3
Câu 6. Một hình hộp chữ nhật có 3 kích thước 20cm, 20 3 cm, 30cm. Thể tích khối cầu ngoại tiếp hình hộp đó bằng: 32 62, 5 625000 3200 A. 3 dm B. 3 dm C. 3 dm D. 3 cm 3 3 3 3
Câu 7. Hình hộp chữ nhật ABC .
D A' B 'C ' D ' có BB '  2 3cm , C ' B '  3cm , diện tích mặt đáy bằng 2
6cm . Thể tích khối cầu ngoại tiếp hình hộp trên bằng: 500 125 100 A.  3 cm B.  3 cm C.   3 100 cm D.  3 cm  3 6 3
Câu 8. Cho mặt cầu (S) tâm O bán kính R và điểm A nằm trên (S). Mặt phẳng (P) qua A tạo với OA một góc 0
60 và cắt (S) theo một đường tròn có diện tích bằng: 2 3 R 2  R 2 3 R 2  R A. B. C. D. 4 2 2 4
Câu 9. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt phẳng
(ABC) và cạnh SA AB  10cm . Diện tích mặt cầu ngoại tiếp hình chóp bằng:
A. 12 dm
B. 1200 dm C. 2 1200 dm D. 2 12 dm
Câu 10. Cho hình chóp S.ABC SA   ABC , AB  3cm , góc giữa SB và đáy bằng 0 60 . Thể tích khối
cầu ngoại tiếp hình chóp bằng: A. 3 36 cm B. 3 4 3cm C. 2 36 cm D. 2 4 3cm
Câu 11. Hình lăng trụ đứng AB .
C A' B 'C ' có đáy ABC là tam giác vuông tại B, AA '  AC a 2 .
Diện tích mặt cầu ngoại tiếp hình lăng trụ bằng: A. 2 8 a B. 2 4 a C. 2 12 a D. 2 10 a
Câu 12. Cho hình chóp S.ABCD có đáy là hình vuông, SA   ABCD và SA AC  2a 2 . Diện
tích mặt cầu ngoại tiếp hình chóp bằng: 2 16 a 2 32 a A. B. C. 2 16 a D. 2 8 a 3 3 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 13. Cho hình hộp chữ nhật ABC .
D A' B 'C ' D ' có diện tích các mặt ABC ,
D ABB ' A', ADD ' A lần lượt bằng 2 2 2
20cm , 28cm ,35cm . Bán kính mặt cầu ngoại tiếp hình hộp bằng: 3 10 A. cm B. 6 10cm C. 3 10cm D. 30cm 2
Câu 14. Cho hình chóp S.ABC có tam giác ABC đều cạnh a  3cm , SA   ABC  và SA  2a . Tính
thể tích khối cầu ngoại tiếp hình chóp bằng: 3 8a  3 4 a A. 3 32 3cm B. 3 16 3cm C. 3 cm D. 3 cm 3 3 3
Câu 15. Cho hình chóp S.ABC có tam giác ABC vuông tại A, cạnh BC  3 , m SA  3 3 và
SA   ABC  . Thể tích khối cầu ngoại tiếp hình chóp bằng: A. 3 18 m B. 3 36 m C. 3 16 m D. 3 12 3m 2a
Câu 16. Cho hình lăng trụ đều AB .
C A' B 'C ' có cạnh đáy bằng a , cạnh bên AA '  . Thể tích khối 3
cầu ngoại tiếp tứ diện ACB 'C ' bằng: 3 4 a 3 4 a 3 4 a 3 16 a A. B. C. D. 81 27 9 27
Câu 17. Hình hộp chữ nhật ABCD.A’B’C’D’ nội tiếp trong mặt cầu bán kính R  3cm . Tam giác
ABC cân và có diện tích bằng 2
2cm . Diện tích toàn phần của hình hộp đó bằng: A. 2 8cm B. 2 24cm C. 2 8 26cm D.    2 8 1 26 cm
Câu 18. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a . Bán kính của mặt cầu
ngoại tiếp hình chóp nói trên bằng: a 2 a 2 a 2 a 3 A. R B. R C. R D. R  4 2 3 2
Câu 19. Một mặt cầu có đường kính bằng 2a thì có diện tích bằng: 2 4 a A. 2 8 a B. C. 2 4 a D. 2 16 a 3
Câu 20. Một đường thẳng cắt mặt cầu tâm O tại hai điểm A, B sao cho tam giác OAB vuông cân tại O
và AB a 2 . Thể tích khối cầu là: 4 2 A. 3 V  4 a B. 3 V   a C. 3 V   a D. 3 V   a 3 3
Câu 21. Cho mặt cầu (S) có tâm I bán kính R  5 và mặt phẳng (P) cắt (S) theo một đường tròn (C) có
bán kính r  3 . Kết luận nào sau đây là sai ?
A. Tâm của (C) là hình chiếu vuông góc của I trên (P)
B. (C) là giao tuyến của (S) và (P)
C. Khoảng cách từ I đến (P) bằng 4
D. (C) là đường tròn giao tuyến lớn nhất của (P) và (S) ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 22. Cho tứ diện OABC có OA, OB, OC đôi một vuông góc nhau và OA a,OB  2a,OC  3a .
Diện tích của mặt cầu (S) ngoại tiếp hình chóp S.ABC bằng: A. 2 S  14 a B. 2 S  8 a C. 2 S  12 a D. 2 S  10 a
Câu 23. Thể tích V của một mặt cầu có bán kính R được xác định bởi công thức nào sau đây: 3  R 3 4 R A. 3 V   R B. 3 V  4 R C. V D. V  3 3
Câu 24. Cho tứ diện ABCD có DA  5a và vuông góc với (ABC), ABC  vuông tại B và
AB  3a, BC  4a . Bán kính của mặt cầu nói trên bằng: 5a 2 5a 3 5a 2 5a 3 A. R B. R C. R D. R  2 3 3 2
Câu 25. Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại A, SA   ABC  ,
SA a; AB b ; AC c . Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là:  2 2 2
2 a b c A. 2 2 2
R  2 a b c B. R  3 1 C. 2 2 2
R a b c D. 2 2 2 R
a b c 2
Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy. Bán kính
R của mặt cầu ngoại tiếp hình chóp S.ABCD bằng: 1 1 1 1 A. R AC B. R SB C. R SC D. R SA 2 2 2 2
Câu 27. Trong các khẳng định sau, khẳng định nào sai ?
A. Mặt phẳng (P) tiếp xúc với mặt cầu (S) tâm O tại điểm H thì OH là khoảng cách ngắn nhất từ O đến
một điểm bất kỳ nằm trong mặt phẳng (P)
B. Chỉ có duy nhất hai mặt phẳng vuông góc với mặt phẳng cho trước và tiếp xúc với mặt cầu (S).
C. Mặt phẳng cắt mặt cầu (S) theo đường tròn (C) , tâm của đường tròn (C) là hình chiếu của tâm mặt
cầu (S) xuống mặt phẳng (P)
D. Tại điểm H nằm trên mặt cầu chỉ có 1 tiếp tuyến duy nhất.
Câu 28. Trong các mệnh đề sau đây, mệnh đề nào sai ?
A. Bất kì một hình tứ diện nào cũng có mặt cầu ngoại tiếp
B. Bất kì một hình hộp chữ nhật nào cũng có một mặt cầu ngoại tiếp
C. Bất kì một hình hộp nào cũng có một mặt cầu ngoại tiếp
D. Bất kì một hình chóp đều nào cũng có một mặt cầu ngoại tiếp
Câu 29. Một mặt cầu có bán kính R 3 . Diện tích mặt cầu bằng: A. 2 8 R B. 2 12 R C. 2 4 R D. 2 12 3 R
Câu 30. Mặt cầu có bán kính r thì có diện tích là: 4 4 A. 4 r B. 2 4 r C. 2  r D. 3  r 3 3 ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017
Câu 31. Khối cầu có bán kính r thì có thể tích là: 4 4 A. 3 4 r B. 2 4 r C. 2  r D. 3  r 3 3
Câu 32. Khối cầu có bán kính 3cm thì có thể tích là: A.   3 9 cm B.   3 36 cm C.   3 27 cm D.   3 12 cm
Câu 33. Mặt cầu có bán kính 4cm thì có diện tích là: 64 256 A.   2 64 cm B.   2 16 cm C.   2 cm D.   2 cm  3 3
Câu 34. Mặt cầu (S) có diện tích bằng   2 100
cm  thì có bán kính là: A. 3 (cm) B. 4 (cm) C. 5 (cm) D. 5 (cm)
Câu 35. Khối cầu (S) có thể tích bằng   3 288
cm  thì có bán kính là:
A. 6 2 cm B. 6(cm) C. 6 6 cmD. 6 cm
Câu 36. Khối cầu (S) có diện tích bằng 2
16 a ,a  0 thì có thể tích là: 32 16 A. 3  a  3 cm B. 3   3 32 a cm C. 3   3 16 a cm D. 3  a  3 cm  3 3
Câu 37. Khối cầu  S có thể tích bằng   3 36
cm  và có bán kính gấp 3 lần bán kính khối cầu S . 2  1 
Thể tích của khối cầu  S là: 2  4 A.   3 4 cm B.   3 cm C.   3 297 cm D.   3 324 cm  3
Câu 38. Cắt mặt cầu (S) bằng một mặt phẳng đi qua tâm được thiết diện là một hình tròn có chu vi
bằng 4 . Diện tích và thể tích của (S) lần lượt là: 32 32 A. 16 và  B. 16 và 32 C. 8 và  D. 8 và 32 3 3
Câu 39. Cắt mặt cầu (S) bằng một mặt phẳng cách tâm một khoảng 4cm được thiết diện là một hình
tròn có bán kính bằng 3cm. Bán kính của mặt cầu (S) là: A. 5cm B. 7cm C. 12cm D. 10cm
Câu 40. Cắt mặt cầu (S) có bán kính 10 cm bằng một mặt phẳng cách tâm một khoảng 6 cm được thiết
diện là hình tròn (C). Diện tích của (C) là: A.   2 16 cm B.   2 32 cm C.   2 64 cm D.   2 128 cm
Câu 41. Cắt mặt cầu (S) bằng một mặt phẳng cách tâm một khoảng 4cm được thiết diện là hình tròn có diện tích   2 9
cm  . Thể tích của (S) là: 250 1372 500 A.   3 cm B.   3 cm C.   3 2304 cm D.   3 cm  3 3 3
Câu 42. Mặt cầu ngoại tiếp hình lập phương cạnh 2a có thể tích là: ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 3 A. 3   3 3 a cm B. 3  a  3 cm C. 3   3 3 a cm D. 3   3 4 3 a cm  2
Câu 43. Mặt cầu nội tiếp hình lập phương cạnh a có thể tích là: 3  a 3  a 3 4 a 3 4 a A. B. C. D. 3 6 3 9
Câu 44. Mặt cầu ngoại tiếp hình chóp tứ giác đều có tất cả các cạnh bằng 2a thì có bán kính là: a 2 a 3 A. B. a 2 C. a D. 2 2
ĐÁP ÁN TRẮC NGHIỆM 01. B 02. C 03. C 04. C 05. A 06. B 07. B 08. D 09. D 10. A 11. B 12. C 13. A 14. A 15. B 16. A 17. D 18. B 19. C 20. C 21. D 22. A 23. D 24. A 25.D 26. C 27. D 28. C 29. B 30. B 31. C 32. B 33. A 34. C 35. B 36. A 37. B 38. A 39. A 40. C 41.D 42.D 43. B 44. B GIẢI CHI TIẾT a
Câu 1. Giả sử cạnh của hình lập phương trình a , khi đó bán kính khối cầu là 2 3 3 4 aa
Thể tích của khối cầu là V      1   3  2  6 V
Thể tích hình lập phương trình 3
V a . Ta có 1  .Chọn B 2 V 6 2 2 a 3  a 3  Câu 2. Ta có 2 R   S  4    3 a   .Chọn C 2 2   a 3
Câu 3. Ta có bán kính đường tròn lớn là . Chọn C 2
Câu 4. Bán kính đường tròn là 5cm, mà d I,P  4cm . Chọn C a 3
Câu 5. Giả sử cạnh của hình lập phương trình a , khi đó bán kính khối cầu là 2
Thể tích khối lập phương là 3 V a 1 3 3 4  a 3   a 3 V 2 3
Thể tích khối cầu ngoại tiếp khối lập phương là V      . Ta có 1  . Chọn A 2   3 2 2   V 3 2
Câu 6. Đường kính khối cầu ngoại tiếp là   2 2 2 20 20 3
 30  50cm  bán kính
R  25cm  2,5dm ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 4 62, 5
Thể tích khối cầu là V   2,53 3  dm . Chọn B 3 3 6 Câu 7. Ta có A ' B '   2cm  đường kính khối cầu ngoại tiếp là 3  2 2 2 2 3
 3  2  5cm R  2,5cm 4 125
Thể tích khối cầu ngoại tiếp hình hộp là V   2,53 3  cm . Chọn B 3 6 2 2 R RR
Câu 8. Bán kính đường tròn là 0 r . R cos 60 S           . Chọn D 2  2  4 BC AB Câu 9. Ta có 
BC  SAB  BC SBBC SA
Gọi I là trung điểm của SC
IS IC IA IB (do 0
SAC SBC  90 ) Ta có: SC SA AC    2 2 2 2 10 10 2 10 3  IA  5 3  S    2 2 2 4 5 3
1200cm 12 dm . Chọn D mc
Câu 10. Chọn A
Câu 11. Gọi M,N lần lượt là trung điểm của AC, A’C’ , I là trung điểm của
MN  I là tâm mặt cầu ngoại tiếp hình lăng trụ. a 2 Ta có IM IN
, AB BC a 2 2 2 2
R IA'  IN NA a S  4 a . Chọn B mc
Câu 12. Gọi I là trung điểm của SC IA IB IC ID IS Ta có 2 2 SC
SA AC  4a IA  2a
S    a2 2 4 2  16 a . mc Chọn C Câu 13. Giả sử
AB a, AD  , b AA'  c ta có
ab  20, ac  28,bc  35  c  7,b  5, a  4 . Đường kính mặt cầu ngoại tiếp là 3 10 2 2 2
a b c  3 10 cm  R
cm. Chọn A 2
Câu 14. Gọi G là trọng tâm của ABC
Qua G kẻ Gx / /SA Gx   ABC
Gọi M là trung điểm của SA, qua M kẻ đường thẳng song song với SA cắt
Gx tại I  IA IB IC IS ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 2 a 3 Ta có tứ giác MIGA là hình chữ nhật
IM AG  .  3cm 3 2 4
AI MA MI  2 3cm V   2 33 2 2 3
 32 3cm . Chọn A 3
Câu 15. Gọi M là trung điểm của BC, qua M kẻ đường thẳng
Mx / /SA Mx   ABC
Gọi N là trung điểm của SA, qua N kẻ đường thẳng vuông góc với SA
cắt Mx tại I IA IB IC IS 3
Do tứ giác AMIN là hình chữ nhật  NI AM cm 2 4 2 2 3 3
IA AN NI 3cm V  .3  36cm . Chọn B 3
Câu 16. Dễ thấy mặt cầu ngoại tiếp hình lăng trụ đều cũng chính là mặt
cầu ngoại tiếp tứ diện ACB’C’
+) Gọi G là trọng tâm tam giác đều ABC, trục đường trong ngoại tiếp ABC
cắt mặt phẳng trung trực của AA’ tại O suy ra O là tâm mặt
cầu ngoại tiếp khối lăng trụ a 3 a Ta có: AG  ;OG IA  3 3 2 2 a a 2a +) 2 2
R GA OG    3 9 3 3 3   Do đó 4 R 32 a V   . Chọn A 3 81
Câu 17. Tam giác ABC vuông tại B suy ra nó vuông cân tại B
Khi đó gọi I là tâm của hình vuông ABCD 2 AB Ta có S   2  AB  2 . Do vậy ABC 2 AC 2 2 IC
 2  OI R IC  9  2  7 2
Do đó chiều cao của khối hộp là h  2OI  2 7
S S S
 8  8.2 7  81 28 . Chọn D tp d xq
Câu 18. Dựng hình như hình vẽ ta có O là tâm mặt cầu ngoại tiếp của a 2
hình chóp. Ta có: BD a 2  ED  2 Khi đó SO SK SO SD SKO SED     SD SE SD 2SE ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 2 2 Do đó SD a a SO R    . Chọn B 2 2SE 2  a  2 2 a     2  d Câu 19. Ta có: 2 2
d  2a R
a S  4 R  4 a (với d là đường kính của mặt cầu). 2 Chọn C 3 3 4 R 4 a Câu 20. Dễ thấy 2 2 2 2
OA OB R R R AB  2a R a V   . 3 3 Chọn C. Câu 21. Ta có: 2 2 2
R r d (trong đó d d I;P suy ra 2 2 d
R r  4 . D sai vì đường giao
tuyến lớn nhất của (P) và (S) phải đi qua tâm I. Chọn D
Câu 22. Gọi M là trung điểm của BC. Khi đó M là tâm đường tròn ngoại tiếp tam giác OBC.
Từ M dựng đường thẳng d song song với OA. Trong mặt phẳng O ;
A d  dựng đường thẳng trung trực của OA cắt d tại E. Khi đó E là
tâm mặt cầu ngoại tiếp của khối chóp. 2 2 BC OB OC a 13 Ta có: OM    2 2 2 OA a a 14 2 2 EM OI
  R EM OM  2 2 2 Do vậy 2 2
S  4 R  14 a .Chọn A 3 4 R
Câu 23. Công thức thể tích khối cầu là V  . Chọn D 3
Câu 24. Gọi I là trung điểm của AC. Khi đó I là tâm đường trong
ngoại tiếp tam giác ABC vuông tại B.
Đường thẳng qua I vuông góc với mp(ABC) cắt CD tại O. Khi đó dễ 1
thấy OA OC OD CD 2 2 2  Khi đó CD DA AC R   2 2 2 2 2
DA AB BC 5a 2   . Chọn A 2 2
Câu 25. Gọi M là trung điểm của BC. Khi đó M là tâm đường tròn
ngoại tiếp tam giác ABC. Từ M dựng đường thẳng d song song với
SA. Trong mặt phẳng (SA;d) dựng đường thẳng trung trực SA cắt d
tại O. Khi đó O là tâm mặt cầu ngoại tiếp của khối chóp. ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 2 2 1 1 b c Ta có: 2 2 MA BC AB AC  2 2 2 1 a 2 2 2
a b c
Lại có: OM IA SA  . Do vậy 2 2
OA OM MA  . Chọn D 2 2 2
Câu 26. Gọi I là tâm hình chữ nhật ABCD. Từ I dựng đường
thẳng song song với SA cắt SC tại O.
Khi đó OA OB OC OD . Mặt khác O là trung điểm của
cạnh huyền SC trong tam giác vuông SAC nên
SO OC OA O là tâm mặt cầu ngoại tiếp của hình chóp SC do vậy R  . Chọn C 2
Câu 27. D sai vì tại một điểm H bất kì nằm trên mặt cầu có vô số
tiếp tuyến đi qua điểm đó. Chọn D
Câu 28. Đáp án C sai vì chỉ có hình hộp chữ nhật mới có mặt cầu ngoại tiếp. Hình hộp xiên hoặc hình
hộp có đáy là hình bình hành thì không có mặt cầu ngoại tiếp. Chọn C
Câu 29. Ta có S   R 2 4 3 12 . Chọn B
Câu 30. Công thức diện tích mặt cầu bán kính r là 2
S  4 r . Chọn B 3 4 r
Câu 31. Công thức thể tíc khối cầu là V  . Chọn D 3 4 Câu 32. Ta có: 3 V
R  36 . Chọn B. 3 Câu 33. Ta có: 2
S  4 R  64 . Chọn A. Câu 34. Ta có: 2
S  4 R  100  R  5 . Chọn C. 4 Câu 35. Ta có: 3 V
R  288  R  6 . Chọn A 3 3 4 32 a Câu 36. Ta có: 2 2 3
S  4 R  16 a R  2a V   R  . Chọn A. 3 3 3  R  4 3   4 R 3  3  1 4 R VS 4 Câu 37. Ta có: 1  V  và V     .   . Chọn B SS2 1  3 3 27 3 27 3
Câu 38. Ta có: C  2 r  4  r  2 (với r là bán kính đường tròn thiết diện) 4 32
Do thiết diện qua tâm nên 3 2
R r  2  V   R
;S  4 R 16 . Chọn A 3 3 Câu 39. Ta có: 2 2 2 2 2 2
R r d R  4  3  R  5 . Chọn A Câu 40. Ta có: 2 2 2 2 2 2
R r d  10  r  6  r  8 (với r là bán kính đường tròn (C)) Khi đó 2 S       R 64 . Chọn C C
Câu 41. Gọi r là bán kính hình tròn là thiết diện của mặt phẳng và mặt cầu (S) ĐT: 0934286923
Email: emnhi1990@gmail.com
CHUYÊN ĐỀ THỂ TÍCH VÀ KHOẢNG CÁCH LUYỆN THI THPT QUỐC GIA 2016 - 2017 4 500 Ta có: 2
9   r r  3 . Mặt khác 2 2 2 3
R r d R  5  V   R   . Chọn D 3 3 2a 3
Câu 42. Bán kính mặt cầu ngoại tiếp hình lập phương cạnh 2a là R   a 3 2 Do đó 4 3 3 V
R  4 3 a . Chọn D 3 3 a 4 a
Câu 43. Bán kính đường tròn nội tiếp hình lập phương là 3 r
V  r  .Chọn B nt 2 3 6
Câu 44. Dựng hình như hình vẽ ta có: SKO S
EDg g 2 SK SO SD SO SD Do vậy     R SO SE SD 2SE SD 2SE Mặt khác 2 2
SD AB  2a SE SD ED  2
Do vậy R a 2 . Chọn B ĐT: 0934286923
Email: emnhi1990@gmail.com