Bài tập trắc nghiệm thể tích khối đa diện vận dụng cao

Tuyển chọn các bài tập trắc nghiệm thể tích khối đa diện vận dụng cao, có đáp án và lời giải chi tiết, giúp học sinh lớp 12 tham khảo khi học chương trình Toán 12 phần Hình học chương 1: Khối Đa Diện Và Thể Tích Của Chúng..Mời bạn đọc đón xem.

21 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

64 trang 8 tháng trước

Tác giả:

Profile Lan Tường
1
THỂ TÍCH
KHỐI ĐA DIỆN
Phần 1. Thể tích khối đa diện
Câu 1. Cho khối tứ diện
ABCD
có thể tích
.V
Gọi
V
là thể tích của khối tám mặt có
các đỉnh là trung điểm các cạnh của khối tứ diện
.
ABCD
Tỉ số
V
V
bằng
A.
1
.
2
B.
1
.
4
C.
3
.
4
D.
Câu 2. Cho hình chóp tam giác đều
.S ABC
có cạnh đáy bằng
1,
góc giữa cạnh bên và
mặt đáy bằng
60 .
Gọi
,,ABC

lần lượt là các điểm đối xứng của
,,ABC
qua
.S
Thể tích của khối bát diện
.ABC A B C

bằng
A.
3
.
2
B.
23
.
3
C.
43
.
3
D.
2 3.
Câu 3.
Cho khối chóp tứ giác đều
.,S ABCD
có đáy
ABCD
là
hình vuông cạnh bằng
,a
tâm
;O
cạnh bên bằng
3.
a
Gọi
M
là trung điểm của
,
CD
H
là điểm đối xứng của
O
qua
.
SM
Thể tích khối đa diện
ABCDSH
bằng
A.
3
10
.
12
a
B.
3
10
.
18
a
C.
3
10
.
24
a
D.
3
5 10
.
24
a
Câu 4.
Cho hình đa diện như hình vẽ, trong đó
.ABCD A B C D

là hình hộp chữ nhật với
2,AB AD a
,AA a
.S ABCD
là hình chóp
có các cạnh bên bằng nhau và bằng
3.
a
Thể
tích của khối tứ diện
SA BD
có thể tích bằng
A.
3
2.
a
B.
3
2
.
2
a
C.
3
2
.
3
a
D.
3
2
.
6
a
Câu 5. Cho khối lăng trụ
.ABC A B C

có thể tích là
Hai mặt phẳng
ACB
và
BA C

chia khối lăng trụ đã cho thành bốn phần. Thể tích của phần có thể tích lớn
nhất bằng
2
A.
1
.
2
V
B.
2
.
5
V
C.
3
.
5
V
D.
5
.
12
V
Câu 6. Cho hình lăng trụ đứng
.ABC A B C

có đáy
ABC
là tam giác đều cạnh
,.a AA a
Gọi
E
là trung điểm cạnh
,
AC
mặt phẳng
ABE

cắt
BC
tại
.F
Thể
tích khối đa diện
CABFE

bằng
A.
3
3
.
4
a
B.
3
3
.
8
a
C.
3
3
.
15
a
D.
3
3
.
16
a
Câu 7. Cho hình lăng trụ tam giác đều
.ABC A B C

có tất cả các cạnh bằng
.a
Gọi
,
MN
lần lượt là trung điểm của các cạnh
AB
và
.
BC

Mặt phẳng
A MN
cắt cạnh
BC
tại
.P
Thể tích khối đa diện
.MBPABN

bằng
A.
3
3
.
32
a
B.
3
73
.
32
a
C.
3
73
.
48
a
D.
3
73
.
96
a
Câu 8. Cho hình lăng trụ
.
ABC A B C

có thể tích
3
96 cm .
Gọi
G
là trọng tâm của
tam giác
ABC

và
là trung điểm của
.BC
Thể tích khối tứ diện
B GAH
bằng
A.
3
12 cm .
B.
3
16 cm .
C.
3
18 cm .
D.
3
24 cm .
Câu 9. Cho lăng trụ tam giác
.ABC A B C

có thể tích bằng
.V
Gọi
,,MNP
lần lượt
là trung điểm của các cạnh
,, .
A B BC CC

Mặt phẳng
MNP
chia khối lăng trụ
thành hai phần, phần chứa điểm
B
có thể tích là
1
.
V
Tỉ số
1
V
V
bằng
A.
1
.
3
B.
25
.
72
C.
49
.
144
D.
73
.
216
Câu 10. Cho hình lăng trụ
.ABC A B C

có thể tích bằng
.V
Gọi
,,MNP
lần lượt là
trung điểm của các cạnh
, ,.AB A C BB

Thể tích của khối tứ diện
CMNP
bằng
A.
.
3
V
B.
.
4
V
C.
5
.
24
V
D.
7
.
24
V
Câu 11. Cho tứ diện
ABCD
có
5, 34, 41.AB CD AC BD AD BC
Thể
tích của tứ diện
ABCD
bằng
A.
10.
B.
20.
C.
30.
D.
40.
Câu 12. Cho hình hộp
.ABCD A B C D

có thể tích
3
120 cm .
Gọi
,MN
lần lượt là
trung điểm
AB
và
.AD
Thể tích khối tứ diện
MNA C

bằng:
A.
3
15 cm .
B.
3
20 cm .
C.
3
24 cm .
D.
3
30 cm .
Câu 13. Cho tứ diện
ABCD
có
22
4 cm , 6 cm , 3cm.
ABC ABD
S S AB


Góc giữa hai
mặt phẳng
ABC
và
ABD
bằng
60 .
Thể tích của khối tứ diện đã cho bằng
A.
3
2 3 cm .
B.
3
23
cm .
3
C.
3
43
cm .
3
D.
3
83
cm .
3
Câu 14. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành và có thể tích
Gọi
E
là điểm trên cạnh
SC
sao cho
2.EC ES
Gọi
là mặt phẳng chứa đường
3
thẳng
AE
và song song với đường thẳng
,BD
cắt hai cạnh
,SB SD
lần lượt tại hai
điểm
,.
MN
Thể tích khối chóp
.
S AMEN
bằng
A.
.
6
V
B.
.
9
V
C.
.
12
V
D.
.
27
V
Câu 15. Cho hình chóp
.
S ABCD
có đáy là hình thoi,
SA
vuông góc với đáy. Mặt
phẳng
P
qua
A
vuông góc với
SC
cắt các cạnh
,,SB SC SD
lần lượt tại
,,.GFE
Biết rằng
P
chia khối chóp thành hai phần có thể tích bằng nhau. Tính
.
SF
k
SC
A.
13 1
.
4
k
B.
13 1
.
6
k
C.
17 1
.
4
k
D.
17 1
.
8
k
Câu 16. Cho khối lăng trụ
..
ABC A B C

Gọi
,MN
lần lượt là trung điểm của hai
cạnh
AA
và
.BB
Mặt phẳng
C MN
chia khối lăng trụ đã cho thành hai phần. Gọi
1
V
là thể tích khối
C MNB A

và
2
V
là thể tích khối
..ABC MNC
Khi đó tỷ số
1
2
V
V
bằng
A.
1
.
2
B.
1
.
3
C.
2
.
3
D.
3
.
4
Câu 17. Cho hình lăng trụ tam giác
.ABC A B C

có thể tích là
V
và có độ dài cạnh
bên
6.
AA
Trên cạnh
, ,
AA BB CC

lần lượt lấy các điểm
1 11
, ,A BC
sao cho
1
2,AA
1
,BB x
1
CC y
với
,xy
là các số thực dương thỏa mãn
12.xy
Biết rằng
thể tích của khối đa diện
111
.ABC A B C
bằng
1
.
2
V
Giá trị của
xy
bằng
A.
1.
B.
2.
C.
3.
D.
4.
Câu 18. Cho hình lập phương
.ABCD A B C D

có các cạnh bằng
,a
một mặt phẳng
cắt các cạnh
,,,
AA BB CC DD

lần lượt tại
, ,,.M N PQ
Biết
2
,.
35
aa
AM CP
Thể tích khối đa diện
.
ABCD MNPQ
bằng
A.
3
.
3
a
B.
3
2
.
3
a
C.
3
11
.
15
a
D.
3
11
.
30
a
Câu 19. Cho hình chóp đều
.S ABC
có đáy
ABC
là tam giác đều cạnh
.a
Gọi
,E
F
lần lượt là trung điểm của các cạnh
,SB
.SC
Biết mặt phẳng
AEF
vuông góc với
mặt phẳng
.SBC
Thể tích khối chóp
.S ABC
bằng
A.
3
5
.
8
a
B.
3
3
.
24
a
C.
3
5
.
24
a
D.
3
15
.
27
a
Câu 20. Cho hình chóp đều
.S ABC
có cạnh bên bằng
.a
Gọi
,E
F
lần lượt là trung
điểm của các cạnh
,SB
.SC
Biết mặt phẳng
AEF
vuông góc với mặt phẳng
.
SBC
Thể tích khối chóp
.S ABC
bằng
A.
3
5
.
8
a
B.
3
3
.
24
a
C.
3
5
.
24
a
D.
3
15
.
27
a
4
Câu 21. Cho hình chóp đều
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
.a
Gọi
M
là
trung điểm
.SA
Biết mặt phẳng
MCD
vuông góc với mặt phẳng
.SAB
Thể tích của
khối chóp
.S ABCD
bằng
A.
3
.
3
a
B.
3
5
.
2
a
C.
3
3
.
6
a
D.
3
5
.
6
a
Câu 22. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
.BC a
Cạnh
bên
SA
vuông góc với đáy, góc
0
45 ,BSC
mặt phẳng
SAC
tạo với mặt phẳng
SBC
một góc
0
60 .
Thể tích khối chóp
.S ABC
bằng
A.
3
6
.
15
a
B.
3
2
.
18
a
C.
3
3
.
24
a
D.
3
6
.
30
a
Câu 23. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
,
a
mặt bên
SAB
là
tam giác đều, mặt bên
SCD
là tam giác vuông cân tại
.S
Gọi
M
là điểm thuộc đường
thẳng
CD
sao cho
BM
vuông góc với
.SA
Thể tích của khối chóp
.S BDM
bằng
A.
3
3
.
16
a
B.
3
3
.
24
a
C.
3
3
.
32
a
D.
3
3
.
48
a
Câu 24. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
và hai tam giác
SAC
và
SBD
là những tam giác đều. Gọi
',A
lần lượt là trung điểm của
SA
và
.SC
Thể tích khối tứ diện
''A BC D
bằng
A.
3
3
.
16
a
B.
3
3
.
24
a
C.
3
6
.
24
a
D.
3
6
.
32
a
Câu 25. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
.a
Cạnh bên
SA
vuông góc với đáy,
3.SC a
Gọi
,M
,
N
,P
Q
lượt là trung điểm của
,SB
,SD
,
CD
.
BC
Thể tích của khối chóp
.A MNPQ
bằng
A.
3
.
3
a
B.
3
.
4
a
C.
3
.
8
a
D.
3
.
12
a
Câu 26. Cho lăng trụ
.ABC A B C

có đáy
ABC
là tam giác vuông tại
A
và góc
0
30 .ABC
Gọi
M
là trung điểm của
,
AB
tam giác
MA C
đều cạnh
a
và nằm trong
mặt phẳng vuông góc với đáy
.ABC
Thể tích khối lăng trụ đã cho bằng
A.
3
.
7
a
B.
3
2
.
7
a
C.
3
3
.
7
a
D.
3
5
.
7
a
Câu 27. Cho hình lăng trụ đều
..
ABC A B C

Biết khoảng cách từ điểm
C
đến mặt
phẳng
ABC
bằng
,
a
góc giữa hai mặt phẳng
ABC
và
BCC B

bằng
với
1
cos .
3
Thể tích khối lăng trụ
.ABC A B C

bằng
A.
3
3 15
.
10
a
B.
3
9 15
.
10
a
C.
3
3 15
.
20
a
D.
3
9 15
.
20
a
Câu 28. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang cân với
2
AD AB
2 2 2.BC CD a
Cạnh bên
SA
vuông góc với đáy. Gọi
,M
N
lần lượt là trung
5
điểm của
SB
và
.CD
Biết thể tích khối chóp
.S ABCD
bằng
3
3
.
4
a
Cosin góc giữa
MN
và
SAC
bằng
A.
5
.
10
B.
35
.
10
C.
310
.
20
D.
3 310
.
20
Câu 29. Cho khối chóp
.S ABC
có
6,SA
2,SB
4,
SC
2 10AB
và
SBC ASC
0
90 .
Thể tích khối chóp
.S ABC
bằng
A.
4 3.
B.
6 3.
C.
8 3.
D.
12 3.
Câu 30. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật với
1,AB
10;AD
,SA SB
.SC SD
Biết hai mặt phẳng
SAB
và
SCD
cùng vuông góc
với nhau và tổng diện tích hai tam giác
SAB
và
SCD
bằng
2.
Thể tích khối chóp
.S ABCD
bằng
A.
1
.
2
B.
1.
C.
3
.
2
D.
2.
Câu 31. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân đỉnh
,A
2,BC a
,SB SC
2SA a
và
SA
tạo với đáy một góc
60 .
Biết
H
là hình chiếu vuông góc của
đỉnh
S
trên mặt đáy
ABC
thuộc tam giác
.ABC
Thể tích khối chóp
.S AHC
bằng
A.
3
3
.
3
a
B.
3
3
.
6
a
C.
3
3
.
9
a
D.
3
3
.
12
a
Câu 32. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật tâm
, , 3;O AB a BC a
tam giác
SOA
cân tại
S
và mặt phẳng
SAD
vuông góc vói
mặt đáy
.ABCD
Biết góc giữa
SD
và mặt phẳng
ABCD
bằng
0
60 .
Thể tích khối
chóp
.S ABCD
bằng
A.
3
3
.
3
a
B.
3
23
.
3
a
C.
3
3
.
6
a
D.
3
3
.
9
a
Câu 33. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
.a
Các mặt bên
,
SAB SAC
lần lượt tạo với đáy các góc là
00
60 , 30 .
Hình chiếu vuông góc của
S
trên mặt phẳng
ABC
nằm trên cạnh
.BC
Thể tích khối chóp
.S ABC
bằng
A.
3
3
.
4
a
B.
3
3
.
12
a
C.
3
3
.
32
a
D.
3
3
.
64
a
Câu 34. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác với
5,AB AC a
6BC a
và các mặt bên cùng tạo với đáy các góc
60 .
Hình chiếu vuông góc của
S
trên mặt
phẳng
ABC
nằm bên trong tam giác
.ABC
Thể tích khối chóp
.S ABC
bằng
A.
3
2
.
3
a
B.
3
3.a
C.
3
6 3.a
D.
3
8.a
Câu 35. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật với
,AB a
2.AD a
Hình chiếu vuông góc của
S
xuống mặt phẳng
ABCD
thuộc đoạn
.BD
Hai mặt
6
phẳng
SBC
và
SCD
lần lượt hợp với đáy các góc
0
60
và
0
30 .
Thể tích khối chóp
.S ABCD
bằng
A.
3
3
.
5
a
B.
3
43
.
5
a
C.
3
3
.
15
a
D.
3
43
.
15
a
Câu 36. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thoi cạnh
a
và
0
60 .BAD
Các mặt phẳng
,SAB
SBD
và
SAD
cùng hợp với đáy
ABCD
một góc
60 .
Biết
hình chiếu vuông góc của
S
trên mặt đáy nằm ngoài tam giác
.ABD
Thể tích của
khối chóp
.S ABCD
bằng
A.
3
3
.
2
a
B.
3
3
.
4
a
C.
3
3
.
6
a
D.
3
3
.
12
a
Câu 37. Cho lăng trụ
.ABCD A B C D

có đáy
ABCD
là hình chữ nhật với
3,AB
7,AD
cạnh bên bằng
1.
Hai mặt bên
ABB A

và
ADD A

lần lượt tạo với đáy
những góc bằng
0
45
và
0
60 .
Thể tích khối lăng trụ đã cho bằng
A.
3.
B.
3 3.
C.
7.
D.
7 7.
Câu 38. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật với
6,AB
3,
AD
tam giác
SAC
nhọn và nằm trong mặt phẳng vuông góc với đáy. Biết hai
mặt phẳng
SAB
và
SAC
tạo với nhau góc
thỏa mãn
3
tan ;
4
cạnh
3.SC
Thể tích khối
.S ABCD
bằng
A.
4
.
3
B.
8
.
3
C.
3 3.
D.
53
.
3
Câu 39. Cho hình chóp
.S ABC
có
, 3, 2AB a AC a SB a
và
ABC BAS
BCS
90 .
Sin của góc giữa đường thẳng
SB
và mặt phẳng
SAC
bằng
11
.
11
Thể tích
khối chóp
.S ABC
bằng
A.
3
6
.
3
a
B.
3
6
.
6
a
C.
3
3
.
9
a
D.
3
23
.
9
a
Câu 40. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác cân tại
A
với
AB a
và
120 ,BAC 
90 .SBA SCA 
Biết góc giữa
SB
và mặt đáy
ABC
bằng
60 ,
thể tích
khối chóp
.S ABC
bằng
A.
3
.
4
a
B.
3
3
.
4
a
C.
3
3
.
4
a
D.
3
33
.
4
a
Câu 41. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
và
90 .SBA SCA 
Biết góc giữa hai mặt phẳng
SAB
và mặt đáy
ABC
bằng
60 ,
thể tích khối chóp
.S ABC
bằng
A.
3
3
.
4
a
B.
3
3
.
6
a
C.
3
3
.
12
a
D.
3
3
.
24
a
7
Câu 42. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác cân tại
A
với
AB a
và
120 ,
BAC 
90 .
SBA SCA 
Biết góc
giữa
SB
và mặt phẳng
SAC
thỏa mãn
3
sin ,
8
khoảng cách từ
S
đến mặt đáy
ABC
nhỏ hơn
2.a
Thể tích khối chóp
.S ABC
bằng
A.
3
3
.
4
a
B.
3
3
.
6
a
C.
3
3
.
12
a
D.
3
3
.
24
a
Câu 43. Cho lăng trụ tam giác
.ABC A B C

có độ dài cạnh bên bằng
4
và khoảng
cách từ điểm
A
đến các đường thẳng
,BB CC

lân lượt bằng
1
và
2.
Biết góc giữa hai
mặt phẳng
ABB A

và
ACC A

bằng
60 .
Tính thể tích khối lăng trụ
..ABC A B C

A.
3.
B.
2 3.
C.
3 3.
D.
4 3.
Câu 44. Cho khối lăng trụ

.,ABC A B C
khoảng cách từ
C
đến đường thẳng
BB
bằng
2,
khoảng cách từ
A
đến các đường thẳng
BB
và
CC
lần lượt bằng
1
và
3.
Hình chiếu vuông góc của
A
lên mặt phẳng

ABC
là trung điểm
M
của

BC
và
23
.
3
AM
Thể tích của khối lăng trụ đã cho bằng
A.
23
.
3
B.
1.
C.
3.
D.
2.
Câu 45. Cho khối lăng trụ

.,ABC A B C
khoảng cách từ
C
đến đường thẳng
BB
bằng
2,
khoảng cách từ
A
đến các đường thẳng
BB
và
CC
lần lượt bằng
1
và
3.
Hình chiếu vuông góc của
A
lên mặt phẳng

ABC
là trọng tâm
G
của tam giác

ABC
và

4
.
3
AG
Thể tích của khối lăng trụ đã cho bằng
A.
2
.
3
B.
4
.
3
C.
8
.
3
D.
2.
Phần 2. Tỷ số thể tích
Câu 1.
Cho hình chóp tứ giác đều
..
S ABCD
Gọi
là
hình hộp chữ nhật có bốn đỉnh là bốn trung điểm của các
cạnh bên
, , , SA SB SC SD
và bốn đỉnh còn lại nằm trong
mặt đáy
ABCD
(tham khảo hình vẽ). Biết thể tích khối
hộp
là
Thể tích của khối chóp đã cho bằng
A.
2.V
B.
6.V
C.
4
.
3
V
D.
8
.
3
V
8
Câu 2. Cho khối chóp
.S ABCD
có đáy là hình bình
hành
.ABCD
Gọi
, , ,M NPQ
lần lượt là trọng tâm
các tam giác
,,,.SAB SBC SCD SDA
Biết khối chóp
.S MNPQ
có thể tích là
khi đó thể tích của khối
chóp
.S ABCD
bằng
A.
9
.
4
V
B.
27
.
4
V
C.
81
.
4
V
D.
81
.
8
V
Câu 3. Cho khối tứ diện
ABCD
có thể tích
Gọi
, ,,M N PQ
lần lượt là trọng tâm
của các tam giác
,ABC
,ABD
,ACD
.BCD
Gọi
V
là thể tích của khối tứ diện
.MNPQ
Tỉ số
V
V
bằng
A.
1
.
27
B.
2
.
27
C.
4
.
27
D.
1
.
9
Câu 4. Cho lăng trụ tam giác
.ABC MNP
có thể tích
.
V
Gọi
1234
,,,GGGG
lần lượt là
trọng tâm của các tam giác
, ,,;ABC ACM AMB BCM
1
V
là thể tích khối tứ diện
1234
.GGGG
Khẳng định nào sau đây đúng ?
A.
1
9.VV
B.
1
27 .
VV
C.
1
81 .VV
D.
1
8 81 .VV
Câu 5. Cho khối tứ diện đều
ABCD
có thể tích
.
V
Gọi
,,MNP
lần lượt là trọng tâm
các tam giác
,,ABC ACD ADB
và
V
là thể tích khối tứ diện
.AMNP
Tỉ số
V
V
bằng
A.
4
.
9
B.
2
.
27
C.
4
.
27
D.
8
.
81
Câu 6.
Cho khối lập phương
.ABCD A B C D

có cạnh bằng
1.
Gọi
, , , MNPL
lần lượt là tâm của các hình vuông
,ABB A

,ABCD

ADD A

và
.CDD C

Gọi
Q
là trung điểm của
BL
(tham khảo hình vẽ bên). Thể tích khối tứ diện
MNPQ
bằng
A.
1
.
16
B.
1
.
24
C.
2
.
27
D.
3
.
27
Câu 7. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
,a
SA
vuông góc với
mặt đáy. Gọi
M
là trung điểm
.BC
Mặt phẳng
P
đi qua
A
và vuông góc với
SM
cắt
,SB SC
lần lượt tại
,.EF
Biết
1
.
4
SAEF SABC
VV
Thể tích khối chóp
.S ABC
bằng
A.
3
.
2
a
B.
3
2
.
5
a
C.
3
.
8
a
D.
3
.
12
a
9
Câu 8. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh bằng
1,
mặt bên
SAB
là tam giác cân tại
S
và nằm trong mặt phẳng vuông góc với mặt đáy
.ABC
Gọi
là hình chiếu vuông góc của
A
lên
.SC
Biết
.
.
16
.
19
S ABH
S ABC
V
V
Thể tích của khối
chóp
.S ABC
bằng
A.
3
.
2
B.
3
.
4
C.
3
.
6
D.
3
.
12
Câu 9. Cho hình chóp đều
..S ABC
Gọi
G
là trọng tâm tam giác
,ABC
góc giữa
SG
và
mặt phẳng
SBC
là
30 .
Mặt phẳng
P
chứa
BC
và vuông góc với
SA
chia khối
chóp
.S ABC
thành hai phần. Tỉ số thể tích hai phần bằng
A.
2
.
3
B.
1
.
6
C.
D.
6
.
7
Câu 10. Cho lăng trụ tam giác đều
.
ABC A B C

có cạnh đáy bằng
,a
chiều cao bằng
2.a
Mặt phẳng
P
qua
B
và vuông góc
AC
chia lăng trụ thành hai khối. Biết thể
tích của hai khối là
1
V
và
2
V
với
12
.VV
Tỉ số
1
2
V
V
bằng
A.
1
.
7
B.
1
.
11
C.
1
.
23
D.
1
.
47
Câu 11. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang,
, 2.AB CD AB CD
Gọi
,MN
lần lượt là trung điểm của
SA
và
.SD
Tỉ số
.
.
S BCNM
S BCDA
V
V
bằng
A.
B.
1
.
4
C.
D.
5
.
12
Câu 12. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
M
là điểm di
động trên cạnh
AB
và
là trung điểm của
.SD
Mặt phẳng
đi qua
,MN
và
song song với
BC
chia khối chóp
.S ABCD
thành hai khối có tỷ số thể tích
1
2
3
,
5
V
V
trong đó
1
V
là thể tích khối đa diện chứa đỉnh
,A
2
V
là thể tích khối đa diện chứa
đỉnh
.B
Tỉ số
AM
AB
bằng
A.
1
.
2
B.
1
.
3
C.
D.
Câu 13. Cho hình hộp
..ABCD A B C D

Gọi
M
là điểm thuộc đoạn
CC
thỏa mãn
3.CC CM
Mặt phẳng
AB M
chia khối hộp thành hai phần có thể tích là
12
,.VV
Gọi
1
V
là thể tích phần chứa điểm
.B
Tỉ số
1
2
V
V
bằng
A.
7
.
9
B.
13
.
20
C.
7
.
27
D.
13
.
41
10
Câu 14. Cho hình hộp
..
ABCD A B C D

Gọi
, , MNP
lần lượt là trung điểm của
,,.AA BC CD
Mặt phẳng
MNP
chia khối hộp thành hai phần có thể tích là
12
,.VV
Gọi
1
V
là thể tích phần chứa điểm
.C
Tỉ số
1
2
V
V
bằng
A.
3
.
4
B.
113
.
24
C.
119
.
25
D.
119
.
425
Câu 15. Cho hình lăng trụ tam giác đều
.ABC A B C

có tất cả các cạnh bằng
.a
Gọi
,
MN
lần lượt là trung điểm của các cạnh
AB
và
.BC

Mặt phẳng
A MN
cắt cạnh
BC
tại
.
P
Thể tích khối đa diện
.MBPABN

bằng
A.
3
3
.
12
a
B.
3
3
.
24
a
C.
3
73
.
32
a
D.
3
73
.
96
a
Câu 16. Cho hình hộp
.ABCD A B C D

có
,,MNP
lần lượt là trung điểm ba cạnh
,A B BB

và
.
DD
Mặt phẳng
MNP
cắt đường thẳng
AA
tại
.I
Biết thể tích khối
tứ diện
IANP
là
Thể tích khối hộp đã cho
.ABCD A B C D

bằng
A.
2.V
B.
4.V
C.
6.V
D.
12 .V
Câu 17. Cho lăng trụ tam giác đều
..
ABC A B C

Trên
AB

kéo dài lấy điểm
M
sao
cho
1
.
2
BM AB

Gọi
,NP
lần lượt là trung điểm của
,.
AC BB

Mặt phẳng
MNP
chia khối lăng trụ
.ABC A B C

thành hai khối đa diện, trong đó khối đa diện chứa
đỉnh
A
có thể tích
1
,V
khối đa diện chứa đỉnh
C
có thể tích
2
.
V
Tỉ số
1
2
V
V
bằng
A
97
.
59
B
49
.
95
C.
49
.
144
D.
95
.
144
Câu 18. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
,a
cạnh bên hợp với
đáy góc
o
60 .
Gọi
M
là điểm đối xứng của
C
qua
,DN
là trung điểm của
.SC
Mặt
phẳng
BMN
chia khối chóp
.
S ABCD
thành hai phần có thể tích là
12
,
VV
trong đó
1
V
là phần thể tích chứa đỉnh
Tỉ số
2
1
V
V
bằng
A.
7
.
5
B.
5
.
7
C.
12
.
5
D.
5
.
12
Câu 19. Cho khối chóp
.S ABC
có đáy
ABC
là tam giác vuông cân đỉnh
,B
4;AB
12.SA SB SC
Gọi
, MN
lần lượt là trung điểm
, .AC BC
Trên cạnh
,
SA SB
lần
lượt lấy điểm
, EF
sao cho
2
.
3
SE BF
SA BS

Thể tích khối tứ diện
MNEF
bằng
A.
4 34
.
3
B.
16 34
.
3
C.
4 17
.
9
D.
4 34
.
9
Câu 20. Cho hình lập phương
.ABCD A B C D

có độ dài cạnh bằng
1.
Gọi
, ,,M N PQ
lần lượt là trung điểm của
,,AB BC C D

và
.DD
Thể tích khối tứ diện
MNPQ
bằng
11
A.
1
.
8
B.
3
.
8
C.
1
.
12
D.
1
.
24
Câu 21. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành, thể tích là
Gọi
M
là một điểm trên cạnh
AB
sao cho
, 0 1.
AM
xx
AB

Mặt phẳng
qua
M
và
song song với
SBC
chia khối chóp
.S ABCD
thành hai phần, trong đó phần chứa
điểm
A
có thể tích bằng
4
.
27
V
Giá trị của biểu thức
1
1
x
P
x
bằng
A.
1
.
2
B.
1
.
3
C.
D.
Câu 22. Cho hình chóp tứ giác
..S ABCD
Mặt phẳng đi qua trọng tâm các tam giác
,,
SAB SAC SAD
chia khối chóp thành hai phần có thể tích là
1
V
và
2
V
12
.VV
Tỉ số
1
2
V
V
bằng
A.
8
.
19
B.
8
.
27
C.
16
.
75
D.
16
.
81
Câu 23. Cho tứ diện đều
ABCD
có cạnh bằng
.a
Gọi
,MN
lần lượt là trung điểm
,AB BC
và điểm
P
là điểm đối xứng với
B
qua
.D
Mặt phẳng
MNP
chia tứ diện
thành hai phần có tỉ số thể tích là
A.
1
.
2
B.
7
.
11
C.
7
.
18
D.
11
.
18
Câu 24. Cho tứ diện
,ABCD
trên các cạnh
, , BC BD AC
lần lượt lấy các điểm
, , MNP
sao cho
3,BC BM
3
,
2
BD BN
2.AC AP
Mặt phẳng
MNP
chia khối tứ
diện
ABCD
thành hai phần có thể tích là
1
V
và
2
.
V
Tỉ số
1
2
V
V
có giá trị bằng
A.
26
.
13
B.
3
.
19
C.
15
.
19
D.
26
.
19
Câu 25. Cho tứ diện
ABCD
và các điểm
,,MNP
lần lượt thuộc các cạnh
,,BC BD AC
sao cho
4 , 3, 2 .BC BM AC AP BD BN 
Tỉ số thể tích hai phần của
khối tứ diện
ABCD
được phân chia bởi mặt phẳng
MNP
bằng
A.
7
.
13
B.
8
.
13
C.
7
.
15
D.
8
.
15
Câu 26. Cho tứ diện đều
ABCD
có cạnh bằng
.a
Gọi
,MN
lần lượt là trọng tâm của
các tam giác
,ABD ABC
và
E
là điểm đối xứng với
B
qua điểm
D
. Mặt phẳng
MNE
chia khối tứ diện
ABCD
thành hai khối đa diện, thể tích khối đa diện chứa
đỉnh
A
bằng
A.
3
32
.
80
a
B.
3
2
.
96
a
C.
3
32
.
320
a
D.
3
92
.
320
a
12
Câu 27. Cho tứ diện đều
ABCD
có cạnh bằng
.a
Gọi
, MN
lần lượt là điểm trên
cạnh
,AB
AC
sao cho
1
,
2
AM
BM
2.
AN
CN
Mặt phẳng
chứa
MN
và song song với
AD
chia khối tứ diện thành hai phần. Thể tích khối đa diện chứa đỉnh
A
bằng
A.
3
42
.
81
a
B.
3
42
.
108
a
C.
3
52
.
108
a
D.
3
11 2
.
342
a
Câu 28. Cho khối chóp
.S ABC
có
, M SA N SB
sao cho
2 , 2.MA MS NS NB 
   
Mặt phẳng
đi qua hai điểm
,MN
và song song với
SC
chia khối chóp thành hai
khối đa diện. Tỉ số thể tích của hai khối đa diện đó bằng
A.
3
.
5
B.
4
.
5
C.
4
.
9
D.
5
.
9
Câu 29. Cho tứ diện đều
ABCD
có cạnh bằng
.a
Gọi
E
là điểm đối xứng của
A
qua
.D
Mặt phẳng qua
CE
và vuông góc với mặt phẳng
ABD
cắt cạnh
AB
tại điểm
.F
Thể tích của khối tứ diện
AECF
bằng
A.
3
2
.
15
a
B.
3
2
.
30
a
C.
3
2
.
40
a
D.
3
2
.
60
a
Câu 30. Cho hình chop
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
, MN
lần lượt
là trung điểm của
, .AD DC
Kéo dài
SD
một đoạn sao cho
D
là trung điểm của
.
SP
Thiết diện tạo bởi mặt phẳng
MNP
chia hình chóp thành hai khối lần lượt có thể
tích là
12
, VV
(trong đó
2
V
là thể tích của phần chứa điểm
S
). Tỉ số
1
2
V
V
bằng
A.
3
.
4
B.
71
.
49
C.
72
.
49
D.
71
.
120
Phần 3. Cực trị
Câu 1. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
A
,
SA
vuông
góc với đáy, khoảng cách từ
A
đến mặt phẳng
SBC
bằng
3
. Gọi
là góc giữa hai
mặt phẳng
SBC
và
ABC
, tính
cos
khi thể tích khối chóp
.S ABC
nhỏ nhất.
A.
2
cos .
2
B.
1
cos .
3
C.
3
cos .
3
D.
2
cos .
3
Câu 2. Trên đường thẳng qua
A
và vuông góc với mặt phẳng chứa tam giác đều
ABC
cạnh bằng
2,
lấy các điểm
M
và
N
không trùng với
A
sao cho
MBC
vuông
góc với
.NBC
Giá trị nhỏ nhất thể tích tứ diện
BCMN
bằng
A.
2.
B.
2 2.
C.
2 3.
D.
6.
Câu 3. Cho tam giác
OAB
đều cạnh
a
. Trên đường thẳng
d
qua
O
và vuông góc với
mặt phẳng
OAB
lấy điểm
M
sao cho
OM x
. Gọi
, EF
lần lượt là hình chiếu
13
vuông góc của
A
trên
MB
và
OB
. Gọi
là giao điểm của
EF
và
d
. Tìm
x
để thể
tích tứ diện
ABMN
có giá trị nhỏ nhất.
A.
2.xa
B.
2
.
2
a
x
C.
3
.
2
a
x
D.
6
.
12
a
x
Câu 4. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành, thể tích là
.V
Gọi
M
là trung điểm của cạnh
, SA N
là điểm nằm trên cạnh
SB
sao cho
2;SN NB
mặt
phẳng
di động qua các điểm
,
MN
và cắt các cạnh
, SC SD
lần lượt tại hai điểm
phân biệt
, PQ
. Thể tích lớn nhất của khối chóp
.S MNPQ
bằng
A.
.
2
V
B.
.
3
V
C.
2
.
3
V
D.
3
.
4
V
Câu 5. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành, thể tích là
Điểm
M
di động trên cạnh
,SC
đặt
.
MC
k
MS
Mặt phẳng
qua
, AM
và song song với
BD
cắt
,SB
SD
thứ tự tại
, .NP
Thể tích khối chóp
.C APMN
lớn nhất khi
A.
1.k
B.
2.k
C.
2.k
D.
3.k
Câu 6. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
,a
cạnh bên
SA y
0y
và vuông góc với đáy
.
ABCD
Trên cạnh
AD
lấy điểm
M
và đặt
AM x
0.xa

Biết
222
,xya
thể tích lớn nhất
max
V
của khối chóp
.S ABCM
bằng
A.
3
3
.
3
a
B.
3
33
.
3
a
C.
3
3
.
8
a
D.
3
3
.
24
a
Câu 7.
Từ hình vuông có cạnh bằng
6
người ta cắt bỏ
các tam giác vuông cân tạo thành hình tô đậm như hình
vẽ. Sau đó người ta gập thành hình hộp chữ nhật không
nắp. Thể tích lớn nhất của khối hộp bằng
A.
8 2.
B.
9 2.
C.
10 2.
D.
11 2.
Câu 8. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành với
4AD a
. Các
cạnh bên của hình chóp bằng nhau và bằng
6a
. Thể tích lớn nhất của khối chóp đã
cho bằng
A.
3
8
.
3
a
B.
3
46
.
3
a
C.
3
8.a
D.
3
46 .a
Câu 9. Cho tam giác
ABC
vuông tại
A
có
3, .AB a AC a
Gọi
Q
là mặt phẳng
chứa
BC
và vuông góc với mặt phẳng
.ABC
Điểm
D
di động trên
Q
sao cho tam
giác
DBC
nhọn và hai mặt phẳng
DAB
và
DAC
lần lượt hợp với mặt phẳng
ABC
hai góc phụ nhau. Thể tích lớn nhất của khối chóp
.D ABC
bằng
A.
3
3
.
4
a
B.
3
3
.
8
a
C.
3
32
.
10
a
D.
3
3
.
13
a
14
Câu 10. Cho lăng trụ đứng
.
ABC A B C

có đáy là tam giác đều. Tam giác
ABC
có
diện tích bằng
3
và nằm trong mặt phẳng tạo với đáy một góc nhọn bằng
.
Thể
tích khối lăng trụ
.ABC A B C

đạt giá trị lớn nhất khi
bằng
A.
1
arctan .
2
B.
1
arctan .
6
C.
arctan 2.
D.
arctan 6.
Câu 11. Trong tất cả các hình chóp tứ giác đều có
3d
là khoảng cách giữa hai
đường thẳng chéo nhau gồm một đường thẳng chứa một đường chéo của đáy và đường
thẳng còn lại chứa một cạnh bên hình chóp. Thể tích nhỏ nhất của khối chóp bằng
A.
3.
B.
9.
C.
9 3.
D.
27.
Câu 12. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ
nhật. Một mặt phẳng không qua
S
và song song với đáy
cắt các cạnh bên
,,,SA SB SC SD
lần lượt tại
, ,,.
M N PQ
Gọi
, ,,M NPQ

lần lượt là hình chiếu của
, ,,M N PQ
trên mặt phẳng đáy. Khi thể tích khối đa diện
.
MNPQ M N P Q

đạt giá trị lớn nhất, tỉ số
SM
SA
bằng
A.
1
.
2
B.
1
.
3
C.
2
.
3
D.
3
.
4
Câu 13. Cho hình chóp
.
S ABC
có
0 3,SA x x 
tất cả các cạnh còn lại đều
bằng
1
. Thể tích lớn nhất của khối chóp đã cho bằng
A.
1
.
4
B.
C.
1
.
12
D.
1
.
16
Câu 14. Cho hình chóp
.S ABC
có
,, 1.AB
SA x BC Sy AC SB C

Thể tích
khối chóp
.
S ABC
lớn nhất khi tổng
xy
bằng
A.
2
.
3
B.
4
.
3
C.
3.
D.
4 3.
Câu 15 . Cho hình vuông
ABCD
cạnh
,a
trên đường thẳng vuông góc với
ABCD
tại
A
ta lấy điểm
S
di động. Hình chiếu vuông góc của
A
lên
,SB SD
lần lượt là
,.HK
Thể tích lớn nhất của tứ diện
ACHK
bằng
A.
3
.
6
a
B.
3
2
.
12
a
C.
3
3
.
16
a
D.
3
6
.
32
a
Câu 16. Trong mặt phẳng
P
cho đường tròn
T
đường kính
2,AB r C
là một
điểm di dộng trên đường tròn
.T
Trên đường thẳng
d
vuông góc với
P
tại
A
lấy
điểm
S
sao cho
.SA r
Gọi
,HK
lần lượt là hình chiếu vuông góc của
A
lên
SC
và
.SB
Khi
C
chạy trên đường tròn, thể tích lớn nhất của tứ diện
.S AHK
bằng
A.
3
.
3
r
B.
3
5
.
3
r
C.
3
5
.
25
r
D.
3
5
.
75
r
15
Câu 17. Cho khối chóp
.S ABC
có đáy là tam giác vuông cân tại
Khoảng cách từ
A
đến mặt phẳng
SBC
bằng
2,
a
0
90 .SAB SCB
Xác định độ dài cạnh
AB
để khối
chóp
.S ABC
có thể tích nhỏ nhất.
A.
10
.
2
a
AB
B.
3.AB a
C.
2.AB a
D.
3 5.
AB a
Câu 18. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2.
a
Tam giác
SAB
vuông tại
S
và nằm trong mặt phẳng vuông góc với đáy. Gọi
là góc tạo bởi đường
thẳng
SD
và mặt phẳng
SBC
với
30 . 
Giá trị lớn nhất của thể tích khối chóp
.S ABCD
bằng
A.
3
4
.
3
a
B.
3
42
.
3
a
C.
3
82
.
9
a
D.
3
83
.
9
a
Câu 19. Cho khối chóp
.
S ABC
có
,SA SB SC a

60 ,ASB 
90 ,BSC 
120 .
CSA 
Gọi
, MN
lần lượt là các điểm trên cạnh
AB
và
SC
sao cho
.
CN AM
CS AB
Khi khoảng
cách giữa
M
và
nhỏ nhất thì thể tích của khối chóp
.
S AMN
bằng
A.
3
2
.
72
a
B.
3
52
.
72
a
C.
3
52
.
432
a
D.
3
2
.
432
a
Câu 20. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
,a
2SA a
và
vuông góc với mặt đáy
.ABCD
Gọi
M
là điểm di động trên cạnh
CD
và
là hình
chiếu vuông góc của
S
lên đường thẳng
.BM
Khi điểm
M
di động trên cạnh
,CD
thể
tích khối chóp
.S ABH
có giá trị lớn nhất bằng
A.
3
2
.
6
a
B.
3
2
.
8
a
C.
3
2
.
12
a
D.
3
2
.
15
a
Câu 21. Cho tứ diện
.
ABCD
Hai điểm
,MN
lần lượt di động trên hai đoạn thẳng
,BC BD
(
,
MN
không trùng
B
) sao cho
2 3 10.
BC BD
BM BN

Gọi
12
,
VV
lần lượt là thể
tích của các khối tứ diện
ABMN
và
.ABCD
Giá trị nhỏ nhất của
1
2
V
V
bằng
A.
25
.
3
B.
3
.
8
C.
3
.
25
D.
6
.
25
Câu 22. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Hai điểm
,MN
lần lượt trên các đoạn thẳng
,AB AD
(
,MN
không trùng
A
) sao cho
2 4.
AB AD
AM AN

Kí hiệu
1
,VV
lần lượt là thể tích của các khối chóp
.S ABCD
và
..S MBCDN
Giá trị lớn
nhất của tỉ số
1
V
V
bằng
A.
2
.
3
B.
3
.
4
C.
1
.
6
D.
17
.
14
16
Câu 23. Cho tứ diện đều
ABCD
có cạnh bằng
1.
Gọi
, MN
là hai điểm thay đổi lần
lượt thuộc cạnh
,BC BD
sao cho
AMN
luôn vuông góc với
.BCD
Tổng giá trị lớn
nhất và giá trị nhỏ nhất của thể tích khối tứ diện
ABMN
bằng
A.
2
.
12
B.
17 2
.
72
C.
17 2
.
144
D.
17 2
.
216
Câu 24. Cho tứ diện
OABC
có
, , OA OB OC
đôi một vuông góc và
2,OA OB
1.OC
Hai điểm
, MN
lần lượt di động trên hai cạnh
, AC BC
sao cho
OMN
vuông góc với
.ABC
Thể tích khối đa diện
ABOMN
có giá trị lớn nhất bằng
A.
1
.
4
B.
1
.
9
C.
2
.
9
D.
1
.
12
Câu 25. Cho hình chóp
.S ABC
có
1, 2, 3.SA SB SC
Gọi
G
là trọng tâm tam giác
.ABC
Mặt phẳng
đi qua trung điểm
I
của
SG
cắt các cạnh
,,SA SB SC
lần lượt
tại
, ,.
MNP
Giá trị nhỏ nhất của biểu thức
2 22
1 11
T
SM SN SP

bằng
A.
2
.
7
B.
3
.
7
C.
18
.
7
D.
6.
1
THỂ TÍCH
KHỐI ĐA DIỆN
Phần 1. Thể tích khối đa diện
Phần 2. Tỷ số thể tích
Phần 3. Cực trị
2
Phần 1. Thể tích khối đa diện
Câu 1. Cho khối tứ diện
ABCD
có thể tích
.
V
Gọi
V
là thể tích của khối tám mặt có
các đỉnh là trung điểm các cạnh của khối tứ diện
.
ABCD
Tỉ số
V
V
bằng
A.
1
.
2
B.
1
.
4
C.
3
.
4
D.
Lời giải. Ta có
.
1
.. .
8
A MNP
V
AM AN AP
V AB AC AD

Suy ra
.
.
8
A MNP
V
V
Tương tự, ta có
...
.
8
B MSQ C NQR D PSR
V
VVV
Từ đó suy ra
2
V
V
nên
1
.
2
V
V
Chọn A.
Câu 2. Cho hình chóp tam giác đều
.S ABC
có cạnh đáy bằng
1,
góc giữa cạnh bên và
mặt đáy bằng
60 .
Gọi
,,ABC

lần lượt là các điểm đối xứng của
,,ABC
qua
.S
Thể tích của khối bát diện
.ABC A B C

bằng
A.
3
.
2
B.
23
.
3
C.
43
.
3
D.
2 3.
Lời giải. Dễ dàng tính được
.
3
.
12
S A BC
V
Thể tích khối bát diện
..
.
23
2 2.4 8 .
3
B ACS S ABC
B ACA C
VV V V


Chọn B.
Câu 3.
Cho khối chóp tứ giác đều
.,S ABCD
có đáy
ABCD
là
hình vuông cạnh bằng
,a
tâm
;O
cạnh bên bằng
3.a
Gọi
M
là trung điểm của
,CD
H
là điểm đối xứng của
O
qua
.SM
Thể tích khối đa diện
ABCDSH
bằng
A.
3
10
.
12
a
B.
3
10
.
18
a
C.
3
10
.
24
a
D.
3
5 10
.
24
a
Lời giải. Khối đa diện
ABCDSH
được chia thành hai khối chóp
.S ABCD
và
..H SCD
3
22
.
1 1 10
. ..
33 6
S ABCD ABCD ABCD
a
V SO S SB OB S 
Vì
H
là điểm đối xứng của
O
qua
SM
nên
,,d O SCD d H SCD


3
.
1 10
.
4 24
HSCD OSCD S ABCD
a
VV V 
3
Vậy thể tích khối đa diện cần tính bằng
3
..
5 10
24
S ABCD H SCD
a
VV

. Chọn D.
Câu 4. Cho hình đa diện như hình vẽ, trong đó
.ABCD A B C D

là hình hộp chữ nhật với
2,AB AD a
,AA a
.S ABCD
là hình chóp
có các cạnh bên bằng nhau và bằng
3.a
Thể
tích của khối tứ diện
SA BD
có thể tích bằng
A.
3
2.a
B.
3
2
.
2
a
C.
3
2
.
3
a
D.
3
2
.
6
a
Lời giải. Gọi
,.
O AC BD I SA AC
 
Ta thấy
.
..
S DBI
S A BD A DBI
V VV


Tính được
22DB a 
2OB a
và
22
.SO SB OB a A A

Suy ra
..
..
2.
S DBI S DBI
S A BD A DBI
V VV V


Ta có
2
1
.
4
DBI ABCD
S Sa

Vậy
3
2
.
.
1 22
2 2. . . .
3 33
S DBI DBI
S A BD
a
V V S SO a a

Chọn C.
Câu 5. Cho khối lăng trụ
.ABC A B C

có thể tích là
Hai mặt phẳng
ACB
và
BA C

chia khối lăng trụ đã cho thành bốn phần. Phần lớn nhất có thể tích bằng
A.
1
.
2
V
B.
2
.
5
V
C.
3
.
5
V
D.
5
.
12
V
Lời
giải.
Gọi
,.I A B AB J B C BC

 
Ta tính được
1 11
;.
3 4 12
B BAC BJIB B BAC
V VV V V


Suy ra
11 1
.
3 12 4
ABCJI
A B C JI
V V V VV


Vậy
11 5
.
3 4 12
ACC A JI
V VVV V


Chọn D.
Câu 6. Cho hình lăng trụ đứng
.ABC A B C

có đáy
ABC
là tam giác đều cạnh
,.a AA a
Gọi
E
là trung điểm cạnh
,AC
mặt phẳng
ABE

cắt
BC
tại
.F
Thể
tích khối đa diện
CABFE

bằng
A.
3
3
.
4
a
B.
3
3
.
8
a
C.
3
3
.
15
a
D.
3
3
.
16
a
4
Lời giải. Dễ dàng xác định được
F
là trung điểm của
.BC
Kéo dài
AE
cắt
CC
tại
.
I
Khi đó
2.CI a
Ta có
3
.
..
3
.
16
I EFC
CABFE I ABC C ABC
a
V V VV
  

Chọn D.
Câu 7. Cho hình lăng trụ tam giác đều
.ABC A B C

có tất cả các cạnh bằng
.
a
Gọi
,MN
lần lượt là trung điểm của các cạnh
AB
và
.BC

Mặt phẳng
A MN
cắt cạnh
BC
tại
.P
Thể tích khối đa diện
.MBPABN

bằng
A.
3
3
.
32
a
B.
3
73
.
32
a
C.
3
73
.
48
a
D.
3
73
.
96
a
Lời giải. Chia khối đa diện
.MBPABN

thành
2
phần gồm: chóp tam giác
.M ABN

và chóp tứ giác
.M BB NP
(như hình vẽ).
Ta có
..
1
. ..
3
M A B N M BB NP A B N BB NP
V V V AA S MP S
 

Trong đó
2 22
1 3 3 13
, , .. .
2 8 4 224 8
ABC
A B N BB NP
a a a aa
S S MP S a


Vậy
33
3 33 7 3
.
3 8 32 96
aa
V



Chọn D.
Câu 8. Cho hình lăng trụ
.ABC A B C

có thể tích
3
96 cm .
Gọi
G
là trọng tâm của
tam giác
ABC

và
là trung điểm của
.BC
Thể tích khối tứ diện
B GAH
bằng
A.
3
12 cm .
B.
3
16 cm .
C.
3
18 cm .
D.
3
24 cm .
Lời giải. Gọi
H
là trung điểm của của
BC

,,H GA


thẳng hàng.
Ta có
..
1
..
3
B ABH A B H ABH
VV

Suy ra
3
. ..
21
. 32 cm .
33
B AHH A ABH A B H ABC A B C
VV V
 

Do
3
..
11
16 cm .
22
GAH
AHH A B GAH B AHH A
SS V V
 

Chọn B.
Câu 9. Cho lăng trụ tam giác
.ABC A B C

có thể tích bằng
.V
Gọi
,,MNP
lần lượt
là trung điểm của các cạnh
,, .A B BC CC

Mặt phẳng
MNP
chia khối lăng trụ
thành hai phần, phần chứa điểm
B
có thể tích là
1
.V
Tỉ số
1
V
V
bằng
A.
1
.
3
B.
25
.
72
C.
49
.
144
D.
73
.
216
5
Lời giải. Kéo dài
NP
cắt
,
BB B C

lần lượt tại
,.RQ
Gọi
,.
K AB MR J A C MQ


Vì
1
.
2
PNC PQC g c g C Q CN BC


Gọi
h
và
S
lần lượt là chiều cao và diện tích đáy lăng trụ.
Ta có
.
31 3 13 3 3
. .. .
22 4 3 2 4 8
MB Q R MB Q
hV
S SS V S


.
11 1 1 1
. .. .
2 6 12 3 2 12 72
KBN R KBN
hV
S SSV S 
.'
11 1 1 1
. .. .
4 2 8 3 2 8 48
P JC Q
JQC
hV
S SS V S

Suy ra
1.
..
49
.
144
R KBN
R MB Q P C JQ
VV V V V


Chọn C.
Câu 10. Cho hình lăng trụ
.
ABC A B C

có thể tích bằng
.V
Gọi
,,MNP
lần lượt là
trung điểm của các cạnh
, ,.
AB A C BB

Thể tích của khối tứ diện
CMNP
bằng
A.
.
3
V
B.
.
4
V
C.
5
.
24
V
D.
7
.
24
V
Lời giải. Gọi
E
là trung điểm của
.AC
Gọi
G
là trọng tâm của tam giác
,ABC
gọi
I
là giao điểm của
NP
và
.EB
Dễ dàng chứng minh được
5
.
2
IG GB
Suy ra
..
55 5 5
.
2 4 4 12
IMC MBC ABC N IMC N ABC
SS S V V V


Ta có
.
..
.
1 15
..
2 2 24
N MCP
N MCP N MCI
N MCI
V
NP V
VV
V NI

Chọn C.
Câu 11. Cho tứ diện
ABCD
có
5, 34, 41.AB CD AC BD AD BC
Thể
tích của tứ diện
ABCD
bằng
A.
10.
B.
20.
C.
30.
D.
40.
Lời giải. Cho tứ diện
ABCD
gần đều có
,,AB CD a AC BD b
.AD BC c
Khi đó
 
222222222
2
.
12
ABCD
V a b cb c aa c b   
Áp dụng:
 
2
25 34 41 34 41 25 25 41 34 20.
12
ABCD
V  
Chọn B.
Cách 2. Đặt
5, 34, 41.a AB CD b AC BD c AD BC
6
Dựng tứ diện
AMNP
với
,,BC D
là trung điểm của
, ,.MN MP NP
Ta có
,,
2 22
MN MP NP
AB AC AD


các tam giác
,,AMN ANP AMP
đều vuông tại đỉnh
A
,,AM AN AP 
đôi một vuông góc.
Khi đó
2 2 22
2 22
2 2 2 2 222
2 22
2 2 22
2
4
42
4
2
AM a b c
AM AN a
AN AP c AN b c a
AM AP b
AM c a b










Vậy
222222222
1
. . 20.
33 3 2
ABCD
a b cb c aa c b
V
 

Câu 12. Cho hình hộp
.ABCD A B C D

có thể tích
3
120 cm .
Gọi
,MN
lần lượt là
trung điểm
AB
và
.AD
Thể tích khối tứ diện
MNA C

bằng:
A.
3
15 cm .
B.
3
20 cm .
C.
3
24 cm .
D.
3
30 cm .
Lời giải. Gọi
,,hSV
lần lượt là chiều cao, diện tích đáy, thể
tích của hình hộp
..ABCD A B C D

Khi đó
..
V hS
Ta có
11
. .sin , . . .sin , .
22
S AC BD AC BD V h AC BD AC BD 
Vì
,MN
là trung điểm của
,AB AD
nên ta có
, ,.MN BD MN AC BD AC 
Lại có
,d MN A C h


1
.. ,.sin,.
6
MNA C
V MN A C d MN A C MN A C

  
Vậy
3
11 1
. . . .sin , 20 cm .
62 6
MNA C
V BD AC h MN AC V


Chọn B.
Câu 13. Cho tứ diện
ABCD
có
22
4 cm , 6 cm , 3cm.
ABC ABD
S S AB


Góc giữa hai
mặt phẳng
ABC
và
ABD
bằng
60 .
Thể tích của khối tứ diện đã cho bằng
A.
3
2 3 cm .
B.
3
23
cm .
3
C.
3
43
cm .
3
D.
3
83
cm .
3
Lời giải. Cho tứ diện
,ABCD
biết diện tích hai mặt bên là
1
S
và
2
;S
Độ dài giao
tuyến của hai mặt là
;
Góc giữa hai mặt bên là
.
Khi đó
12
.
2. . .sin
.
3
S ABC
SS
V
Áp dụng:
3
.
2.4.6sin 60 8 3
cm .
3.3 3
S ABC
V

Chọn D.
Cách 2. Kẻ
.CK AB K AB
Ta có
18
. cm.
23
ABC
S AB CK CK

7
Gọi
H
là chân đường cao của hình chóp hạ từ đỉnh
.
C
Xét tam giác vuông
,
CHK
ta có
43
.sin .
3
CH CK CKH

Vậy thể tích khối tứ diện
3
1 83
. cm .
33
ABD
V S CH

Chọn D.
Câu 14. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành và có thể tích
Gọi
E
là điểm trên cạnh
SC
sao cho
2.EC ES
Gọi
là mặt phẳng chứa đường
thẳng
AE
và song song với đường thẳng
,BD
cắt hai cạnh
,SB SD
lần lượt tại hai
điểm
,.
MN
Thể tích khối chóp
.S AMEN
bằng
A.
.
6
V
B.
.
9
V
C.
.
12
V
D.
.
27
V
Lời giải.
Kẻ
OF
song song
,IE
suy ra
11
.
22
SI SE SM SN
SO SF SB SD

Khi đó
1, 3
.
2, 2
SA SC
ac
SA SE
SB SD
bd
SM SN


Áp dụng công thức tính nhanh
.
.
4
S MNPQ
S ABCD
V
abcd
V abcd
ac bd


ta được
.
.
1
.
6
S AMEN
S ABCD
V
V
Chọn A.
Câu 15. Cho hình chóp
.S ABCD
có đáy là hình thoi,
SA
vuông góc với đáy. Mặt
phẳng
P
qua
A
vuông góc với
SC
cắt các cạnh
,,SB SC SD
lần lượt tại
,,.GFE
Biết rằng
P
chia khối chóp thành hai phần có thể tích bằng nhau. Tính
.
SF
k
SC
A.
13 1
.
4
k
B.
13 1
.
6
k
C.
17 1
.
4
k
D.
17 1
.
8
k
Lời giải. Đặt
, , 0.
SB SD SC
x y xy
SG SE SF

Áp dụng công thức tính nhanh
.
2
.
12
4
1
S AEFG
S ABCD
V
yx
V
yx
xx y


0
2
1 2 2 2 17 1
.
2 12
1
y
y
y
yy
yy

 
Từ đó ta tính được
1 17 1
.
8
SF
k
SC y

Chọn D.
8
Câu 16. Cho khối lăng trụ
..
ABC A B C

Gọi
,MN
lần lượt là trung điểm của hai
cạnh
AA
và
.BB
Mặt phẳng
C MN
chia khối lăng trụ đã cho thành hai phần. Gọi
1
V
là thể tích khối
C MNB A

và
2
V
là thể tích khối
..ABC MNC
Khi đó tỷ số
1
2
V
V
bằng
A.
1
.
2
B.
1
.
3
C.
2
.
3
D.
3
.
4
Lời giải. Ta có
1
0; .
2
CC AM BN
CC AA BB



Áp dụng công thức giải nhanh:
.
1 11 1
0.
3 22 3
C MNB A
CAB C A B
V
V





Suy ra
1
2
1
.
2
V
V
Chọn A.
Câu 17. Cho hình lăng trụ tam giác
.ABC A B C

có thể tích là
V
và có độ dài cạnh
bên
6.AA
Trên cạnh
, ,AA BB CC

lần lượt lấy các điểm
1 11
, ,A BC
sao cho
1
2,AA
1
,BB x
1
CC y
với
,xy
là các số thực dương thỏa mãn
12.xy
Biết rằng
thể tích của khối đa diện
111
.ABC A B C
bằng
1
.
2
V
Giá trị của
xy
bằng
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải. Ta có
11 1
1
, , .
36 6
AA BB CC
xy
AA BB CC


Áp dụng công thức giải nhanh:
111
.
.
11 1
.
33 6 6 2
ABC A B C
ABC A B C
V
xy
V




Suy ra
7.xy

Kết hợp với giải thiết
12xy
ta được
3; 4
1.
4; 3
xy
xy
xy



Chọn A.
Câu 18. Cho hình lập phương
.ABCD A B C D

có các cạnh bằng
,a
một mặt phẳng
cắt các cạnh
,,,
AA BB CC DD

lần lượt tại
, ,,.M N PQ
Biết
2
,.
35
aa
AM CP
Thể tích khối đa diện
.ABCD MNPQ
bằng
A.
3
.
3
a
B.
3
2
.
3
a
C.
3
11
.
15
a
D.
3
11
.
30
a
Lời giải. Thể tích hình lập phương
.ABCD A B C D

là
3
.
.
ABCD A B C D
Va

Ta có
12
,
35
.
,
AM CP
ac
AA CC
BN DQ
bd
BB DD




9
Áp dụng công thức giải nhanh:
.
.
1
4
MNPQ A D C B
ABCD A D C B
V
abcd
V
ac bd




Suy ra
.
.
1 11
2 30
MNPQ A D C B
ABCD A D C B
V
ac
V



3
..
11 11
.
30 30
MNPQ A D C B ABCD A D C B
a
VV
 

Chọn D.
Câu 19. Cho hình chóp đều
.
S ABC
có đáy
ABC
là tam giác đều cạnh
.a
Gọi
,E
F
lần lượt là trung điểm của các cạnh
,SB
.SC
Biết mặt phẳng
AEF
vuông góc với
mặt phẳng
.SBC
Thể tích khối chóp
.S ABC
bằng
A.
3
5
.
8
a
B.
3
3
.
24
a
C.
3
5
.
24
a
D.
3
15
.
27
a
Lời giải. Gọi
M
là trung điểm
,BC
O
là trọng tâm tam giác
.ABC
Suy ra
.SO ABC
Gọi
SN EF
N SM EF
AN EF

nên
0
90 , .AEF SBC SNA
Xét tam giác
,SAM
có
AN
là đường trung tuyến và
cũng là đường cao nên tam giác
SAM
cân tại
A
3
.
2
a
SA AM 
Tam giác vuông
,SAO
có
22
5
.
23
a
SO SA AO

Vậy
3
.
15
..
3 24
S ABC ABC
a
V S SO

Chọn C.
Câu 20. Cho hình chóp đều
.S ABC
có cạnh bên bằng
.a
Gọi
,E
F
lần lượt là trung
điểm của các cạnh
,SB
.
SC
Biết mặt phẳng
AEF
vuông góc với mặt phẳng
.SBC
Thể tích khối chóp
.S ABC
bằng
A.
3
5
.
8
a
B.
3
3
.
24
a
C.
3
5
.
24
a
D.
3
15
.
27
a
Lời giải. Tương tự như bài trên, ta có
.AM SA a
Suy ra
2
2
3
3
2
5
3
3
ABC
a
a
S
AB BC CA
a
a
AO
SO








nên
3
.
15
.
27
S ABC
a
V
Chọn D.
Câu 21. Cho hình chóp đều
.S ABCD
có đáy
ABCD
là hình vuông cạnh
.a
Gọi
M
là
trung điểm
.SA
Biết mặt phẳng
MCD
vuông góc với mặt phẳng
.SAB
Thể tích của
khối chóp
.S ABCD
bằng
A.
3
.
3
a
B.
3
5
.
2
a
C.
3
3
.
6
a
D.
3
5
.
6
a
Lời giải. Gọi
,N MCD SB
suy ra
là trung điểm
.SB
10
Gọi
, , PQR
lần lượt là trung điểm
, , MN CD AB
SP MN
QP MN

nên
0
90 , .MCD SAB QPS
Xét tam giác
,SQR
có
QP
là đường trung tuyến và
cũng là đường cao nên tam giác
SQR
cân tại
Q
.SQ QR a 
Tam giác vuông
,SQO
có
22
3
.
2
a
SO SQ QO 
Vậy
3
2
.
13
..
36
S ABCD ABCD
a
V S SO
Chọn C.
Câu 22. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
.BC a
Cạnh
bên
SA
vuông góc với đáy, góc
0
45 ,BSC
mặt phẳng
SAC
tạo với mặt phẳng
SBC
một góc
0
60 .
Thể tích khối chóp
.S ABC
bằng
A.
3
6
.
15
a
B.
3
2
.
18
a
C.
3
3
.
24
a
D.
3
6
.
30
a
Lời giải. Gọi
là hình chiếu vuông góc của
B
trên mặt phẳng
.SAC
Suy ra
H AC
và
.BH AC
Gọi
E
là hình chiếu vuông góc của
H
trên
.SC
Suy ra
BE SC
và
0
60 , .SAC SBC HEB

Tam giác
SBC
vuông cân tại
B
suy ra
E
là trung điểm
.
SC
Ta có
2 2,SC BC a

suy ra
12
.
22
a
BE SC
Tam giác
BHE
có
6
sin .
4
a
BH BE HEB
Từ đó tính được
15 2 10 10
, , .
5 55
a aa
AB AC SA
Vậy
3
.
16
..
3 30
S ABC ABC
a
V S SA

Chọn D.
Câu 23. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
,a
mặt bên
SAB
là
tam giác đều, mặt bên
SCD
là tam giác vuông cân tại
.S
Gọi
M
là điểm thuộc đường
thẳng
CD
sao cho
BM
vuông góc với
.SA
Thể tích của khối chóp
.S BDM
bằng
A.
3
3
.
16
a
B.
3
3
.
24
a
C.
3
3
.
32
a
D.
3
3
.
48
a
Lời giải. Gọi
,EF
lần lượt là trung điểm của
,AB CD
EF 
là trung trực của
.AB
11
Kẻ
,
SH ABCD H ABCD

mà
SA SB a

HA HB
nên
H EF
Suy ra
HC HD SD SC SDC

vuông cân tại
.S
Trong tam giác
SEF
có
3
;; .
2 22
a CD a
SE EF a SF 
Nhận thấy
22 2
SE SF EF SEF

vuông cân tại
S
2
33
; ; .
44 4
SE a a a
EH FH SH
EF

Kéo dài
AH
cắt
BC
tại
3
2.
2
a
BK EH 
Từ giả thiết
,
BM SA
suy ra
.BM AK
Từ đó ta chứng minh được
3
.
22
aa
ABK BCM g c g CM BK DM 
Vậy
3
.
1 11 3
.. .
3 3 2 48
S BDM BDM
a
V S SH BC DM SH



Chọn D.
Câu 24. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
và hai tam giác
SAC
và
SBD
là những tam giác đều. Gọi
',A
lần lượt là trung điểm của
SA
và
.SC
Thể tích khối tứ diện
''A BC D
bằng
A.
3
3
.
16
a
B.
3
3
.
24
a
C.
3
6
.
24
a
D.
3
6
.
32
a
Lời giải. Gọi
H
là tâm hình vuông
.ABCD
Từ giải thiết suy ra
.
SA SB SC SD
SH ABCD

Suy ra
.S ABCD
là hình chóp đều nên
' ' . ''
2.
A BC D B HA C
VV
Ta có
' '.BH SAC BH HA C 
Do đó
3
' ' ''
1 21 6
2. . . .
3 3 4 24
A BC D HA C SAC
a
V S BH S BH




Chọn C.
Câu 25. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
.a
Cạnh bên
SA
vuông góc với đáy,
3.SC a
Gọi
,
M
,N
,P
Q
lượt là trung điểm của
,SB
,SD
,CD
.BC
Thể tích của khối chóp
.A MNPQ
bằng
A.
3
.
3
a
B.
3
.
4
a
C.
3
.
8
a
D.
3
.
12
a
12
Lời giải. Gọi
.
I AC PQ

Ta có
MN PQ
MN PQ
NP PQ

MNPQ
là hình chữ nhật nên
..
2.
A MNPQ M APQ
VV
Ta có
1
,,
2
d M APQ SA


mà
22
1
, ..
22
a
SA SC AC a d M APQ SA



Tính được
2
1 13 1 3
. .. .. .
2 24 2 8
APQ
a
S AI PQ AC BD

Từ đó suy ra
3
.
.
16
M APQ
a
V
Vậy
3
..
2.
8
A MNPQ M APQ
a
VV

Chọn C.
Câu 26. Cho lăng trụ
.
ABC A B C

có đáy
ABC
là tam giác vuông tại
A
và góc
0
30 .ABC
Gọi
M
là trung điểm của
,AB
tam giác
MA C
đều cạnh
a
và nằm trong
mặt phẳng vuông góc với đáy
.ABC
Thể tích khối lăng trụ đã cho bằng
A.
3
.
7
a
B.
3
2
.
7
a
C.
3
3
.
7
a
D.
3
5
.
7
a
Lời giải. Gọi
H
là trung điểm
.
CM
Suy ra
3
2
a
AH
và
.A H ABC
Đặt
,AC x
suy ra
2BC x
và
3.AB x
Pitago trong
CAM
tìm được
2
.
7
a
x
Vậy
3
.'''
13
. .. .
27
ABC A B C A BC
a
V S A H AB AC A H


Chọn C.
Câu 27. Cho hình lăng trụ đều
..ABC A B C

Biết khoảng cách từ điểm
C
đến mặt
phẳng
ABC
bằng
,a
góc giữa hai mặt phẳng
ABC
và
BCC B

bằng
với
1
cos .
3
Thể tích khối lăng trụ
.ABC A B C

bằng
A.
3
3 15
.
10
a
B.
3
9 15
.
10
a
C.
3
3 15
.
20
a
D.
3
9 15
.
20
a
Lời giải. Gọi
M
là trung điểm của
,AB
là hình chiếu của
C
lên
.CM
Suy ra
CH ABC
và
.CH a
Gọi
N
là hình chiếu của
C
lên
,BC
khi đó
,.BC CHN BC NH ABC BCC CNH


13
Đặt
3
.
2
x
AB AC BC x CM 
Trong tam giác vuông
CHN
có
32
.
sin 4
CH a
CN

Trong hai tam giác vuông
C CB
và
C CM
lần lượt có
2 2 22 2 2
1 1 11 1 1
;.
C C CN BC C C CH CM
 

2 2 2 2 22 2 2
1 1 1 1 8114 3
3.
2
93
a
x a CM
CN BC CH CM a x a x
  
Từ đó ta tính được
35
5
a
CC
và
2
33
.
4
ABC
a
S
Vậy
3
.
9 15
..
20
ABC
ABC A B C
a
V CC S


Chọn D.
Câu 28. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang cân với
2AD AB
2 2 2.
BC CD a
Cạnh bên
SA
vuông góc với đáy. Gọi
,
M
N
lần lượt là trung
điểm của
SB
và
.CD
Biết thể tích khối chóp
.S ABCD
bằng
3
3
.
4
a
Cosin góc giữa
MN
và
SAC
bằng
A.
5
.
10
B.
35
.
10
C.
310
.
20
D.
3 310
.
20
Lời giải. Ta có
3
.
1 13 3 3
. . , .. .
3 2 3 22 4
S ABCD
AD BC a a a
V SA d AD BC SA SA a

Gọi
P
là trung điểm
,AB
khi đó
.MP ABCD
Gọi
.K NP AC
Dựng
HK ABCD
với
.H MN
Khi đó
.H SAC
Ta có
3, , 2AC a CD a AD a 
suy ra
.NC AC
Khi đó
cos , cos
HC
MN SAC NHC
NH

22
3 310
.
2 20
HK KC
MN

Chọn C.
Câu 29. Cho khối chóp
.S ABC
có
6,SA
2,SB
4,SC
2 10AB
và
SBC ASC
0
90 .
Thể tích khối chóp
.S ABC
bằng
A.
4 3.
B.
6 3.
C.
8 3.
D.
12 3.
Lời giải.
Pitago trong tam giác
SBC
ta được
2 3;BC
trong tam giác
SAC
ta được
2 13.AC
Kiểm tra thấy
22 2
AB BC AC

tam giác
ABC
vuông tại
Ta có
.
BC SB
BC SAB ABC SAB
BC AB

14
Do đó nếu gọi
là chân đường cao hạ từ
S
trong tam giác
SAB
thì ta có
SH ABC
và
22
.6
.
10
SA SB
SH
SA SB

Vậy
.
1
. . 4 3.
3
S ABC ABC
V S SH

Chọn A.
Câu 30. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật với
1,
AB
10;AD
,SA SB
.SC SD
Biết hai mặt phẳng
SAB
và
SCD
cùng vuông góc với nhau và
tổng diện tích hai tam giác
SAB
và
SCD
bằng
2.
Thể tích khối chóp
.S ABCD
bằng
A.
1
.
2
B.
1.
C.
3
.
2
D.
2.
Lời giải. Gọi
H
là hình chiếu vuông góc của
S
trên
mặt đáy
.ABCD
Do
SA SB
suy ra
H
thuộc đường
trung trực của
;AB
tương tự
thuộc đường trung
trực của
.CD
Suy ra
H MN
(như hình vẽ).
Ta có
gia thiet 0
90 .
;
SAB SCD Sx
MSN
SM Sx SN Sx



Đặt
,
SM x
SN y
ta có hệ
22 2
22 22
10
10 10
.
11
43
. .2
22
x y MN
xy xy
x y xy
x AB y CD



 








Khi đó
22
3
.
10
xy
SH
xy

Vậy
.
1
. 1.
3
S ABCD ABCD
V S SH
Chọn B.
Câu 31. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân đỉnh
,
A
2,BC a
,SB SC
2SA a
và
SA
tạo với đáy một góc
60 .
Biết
H
là hình chiếu vuông góc của
đỉnh
S
trên mặt đáy
ABC
thuộc tam giác
.ABC
Thể tích khối chóp
.S AHC
bằng
A.
3
3
.
3
a
B.
3
3
.
6
a
C.
3
3
.
9
a
D.
3
3
.
12
a
Lời giải. Ta có
SB SC
suy ra
H
thuộc trung trực của đoạn
.BC
Tam giác
ABC
vuông cân tại
A
nên
nằm trên đường thẳng đi qua hai điểm
A
và
M
(
M
là
trung điểm
BC
nên
1
2
AM BC a
). Hình chiếu vuông góc của
SA
trên mặt phẳng
ABC
là
HA
nên
0
60 , , .SA ABC SA HA SAH 
Xét tam giác vuông
,SAH
ta có
.cosAH SA SAH a AM 
. Do đó
.HM
Trong tam giác vuông cân
ABC
có
2.
2
BC
AB AC a
Trong tam giác vuông
SHA
có
.sin 3.SH SA SAH a
Ta có
2
1 11
..
2 22 2
AHC ABC
a
S S AB AC




Vậy
3
.
13
..
36
S AHC AHC
a
V S SH

Chọn B.
15
Câu 32. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật tâm
, , 3;O AB a BC a
tam giác
SOA
cân tại
S
và mặt phẳng
SAD
vuông góc vói
mặt đáy
.ABCD
Biết góc giữa
SD
và mặt phẳng
ABCD
bằng
0
60 .
Thể tích khối
chóp
.S ABCD
bằng
A.
3
3
.
3
a
B.
3
23
.
3
a
C.
3
3
.
6
a
D.
3
3
.
9
a
Lời giải. Tam giác
SOA
cân tại
S
nên
SO SA
suy ra
thuộc trung trực đoạn
;
OA
mặt phẳng
SAD
vuông
góc với mặt đáy
ABCD
nên
thuộc giao tuyến
AD
.
Từ đó suy ra
H
là giao điểm của trung trực đoạn
OA
với cạnh
.AD
Ta có
22
2AC BD AB BC a
.
Suy ra
AO BO AB a
nên tam giác
ABO
đều cạnh
,a
suy ra
0
30 .ABI
Gọi
I
là trung điểm của
,AO
suy ra đường trung trực đoạn
OA
đi qua hai điểm
, IB
.
Suy ra
.H BI AD
Khi đó
0
60 , , .SD ABCD SD HD SDH 
Tính được
,
3
a
AH
suy ra
2
.tan 2 .
3
a
HD AD AH SH HD SDH a 
Vậy
3
.
1 23
..
33
S ABCD ABCD
a
V S SH
Chọn B.
Câu 33. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
.a
Các mặt bên
,
SAB SAC
lần lượt tạo với đáy các góc là
00
60 , 30 .
Hình chiếu vuông góc của
S
trên mặt phẳng
ABC
nằm trên cạnh
.BC
Thể tích khối chóp
.S ABC
bằng
A.
3
3
.
4
a
B.
3
3
.
12
a
C.
3
3
.
32
a
D.
3
3
.
64
a
Lời giải. Kẻ
, HE AB E AB HF AC F AC
(tham khảo hình vẽ).
Từ hình vẽ, suy ra
60 .cot 60
.
.cot 30
30
SEH HE SH
HF SH
SFH








Ta có
2
11 3
..
22 4
ABH ACH ABC
a
S S S AB HE AC HF


2
1 33
. . . cot 60 cot 30 .
2 48
aa
a SH SH 
Vậy
3
.
13
.. .
3 32
S ABC ABC
a
V SH S

Chọn C.
Câu 34. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác với
5,AB AC a
6BC a
và các mặt bên cùng tạo với đáy các góc
60 .
Hình chiếu vuông góc của
S
trên mặt
phẳng
ABC
nằm bên trong tam giác
.ABC
Thể tích khối chóp
.S ABC
bằng
16
A.
3
2
.
3
a
B.
3
3.a
C.
3
6 3.a
D.
3
8.a
Lời giải. Kẻ
, ,.HE AB E AB HF AC F AC HI BC I BC

Từ hình vẽ, suy ra
60 .cot 60 .SEH SFH SIH HI HE HF SH 
Ta có
ABH ACH BCH ABC
SSSS


2
2
111
. . . 12
222
1 33
.16 . .cot 60 12 .
22
AB HE AC HF BC HI a
a
a SH a SH


Vậy
3
.
1
. 6 3.
3
S ABC ABC
V S SH a

Chọn C.
Câu 35. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật với
,AB a
2.
AD a
Hình chiếu vuông góc của
S
xuống mặt phẳng
ABCD
thuộc đoạn
.BD
Hai mặt
phẳng
SBC
và
SCD
lần lượt hợp với đáy các góc
0
60
và
0
30 .
Thể tích khối chóp
.S ABCD
bằng
A.
3
3
.
5
a
B.
3
43
.
5
a
C.
3
3
.
15
a
D.
3
43
.
15
a
Lời giải. Ta có
BCD BHC CHD
SSS


2 00
1 1 23
. cot 60 . cot 30 .
22 5
a
a BC SH CD SH SH
Khi đó
3
.
1 43
..
3 15
S ABCD ABCD
a
V S SH

Chọn D.
Câu 36. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi cạnh
a
và
0
60 .BAD
Các mặt phẳng
,SAB
SBD
và
SAD
cùng hợp với đáy
ABCD
một góc
60 .
Biết
hình chiếu vuông góc của
S
trên mặt đáy nằm ngoài tam giác
.ABD
Thể tích của
khối chóp
.S ABCD
bằng
A.
3
3
.
2
a
B.
3
3
.
4
a
C.
3
3
.
6
a
D.
3
3
.
12
a
Lời giải.
Từ giả thiết suy ra chân đường cao của hình chóp
.S ABCD
là tâm đường tròn bàng tiếp tam giác đều
.ABD
Do ba đường tròn bàng tiếp của tam giác đều
ABD
có bán
kính bằng nhau nên chỉ cần xét một trường hợp
là tâm
đường tròn bàng tiếp ứng với đỉnh
Dễ thấy
C
là tâm đường tròn bàng tiếp cần tìm và bán
kính bằng
3
2
a
CO
3
.tan 60 .
2
a
SC CO 
17
Vậy
3
.
13
.. .
34
S ABCD ABCD
a
V S SC

Chọn B.
Câu 37. Cho lăng trụ
.ABCD A B C D

có đáy
ABCD
là hình chữ nhật với
3,AB
7,AD
cạnh bên bằng
1.
Hai mặt bên
ABB A

và
ADD A

lần lượt tạo với đáy
những góc bằng
0
45
và
0
60 .
Thể tích khối lăng trụ đã cho bằng
A.
3.
B.
3 3.
C.
7.
D.
7 7.
Lời giải.
Gọi
là hình chiếu vuông góc của
A
xuống mặt đáy
.ABCD
Đặt
.AH h
Ta có
00
cot 45 ; cot 60MHh NHh
và
22 2
1.AH AA h h

Từ
22 2
3
.
7
MH NH AH h 
Suy ra
.
. 3.
ABCD
ABCD A B C D
V S AH


Chọn A.
Câu 38. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật với
6,AB
3,AD
tam giác
SAC
nhọn và nằm trong mặt phẳng vuông góc với đáy. Biết hai
mặt phẳng
SAB
và
SAC
tạo với nhau góc
thỏa mãn
3
tan ;
4
cạnh
3.SC
Thể tích khối
.S ABCD
bằng
A.
4
.
3
B.
8
.
3
C.
3 3.
D.
53
.
3
Lời giải. Đặt
,.AH x SH y
Có
6, 3 3.AB AD AC 
Ta có
2
2 2 2 22
3 3 6 0.SC HC SH x y x y x

1
Gọi
,2M AC BM AC BM 
và
2.AM
Kẻ
,.MN SA N SA SAB SAC 
Ta có:
3 42
tan .
43
BM
MN
MN

Mặt khác:
22
,
2
42
3
xy
d H SA
xy
AH x
MN AM

suy ra
2
16
.
3
yx
2
Từ
1, 2
suy ra
2 42
,
33
xy
nên
.
8
.
3
S ABCD
V
Chọn B.
18
Câu 39. Cho hình chóp
.S ABC
có
, 3, 2
AB a AC a SB a
và
ABC BAS
BCS
90 .
Sin của góc giữa đường thẳng
SB
và mặt phẳng
SAC
bằng
11
.
11
Thể tích
khối chóp
.
S ABC
bằng
A.
3
6
.
3
a
B.
3
6
.
6
a
C.
3
3
.
9
a
D.
3
23
.
9
a
Lời giải. Gọi
O
là trung điểm
,
AC
D
đối xứng của
B
qua
Suy ra
, ,.d B SAC d D SAC


Ta có
.
AB AD
AB SD
AB SA

Tương tự có
.BC SD
Từ đó suy ra
.
SD ABCD
Đặt
0SD x x

22 2
31 .
SB a
SB x a x a

Vì
,
11 11 11
sin , , .
11 11 11
d B SAC
SB SAC d D SAC SB
SB

2
Lại có
2 2 2 22 2
2
1 1 1 1 11 1
.
2
,
SD DC DA x a a
d D SAC

3
Từ
1,2
và
3
ta có phương trình
4 22 4
2 22 2
11 1 3
3 11 6 0 3.
32
xa
x xa a x a
x ax a

Vậy
3
.
16
..
36
S ABC ABC
a
V S SD

Chọn B.
Câu 40. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác cân tại
A
với
AB a
và
120 ,BAC 
90 .SBA SCA

Biết góc giữa
SB
và mặt đáy
ABC
bằng
60 ,
thể tích
khối chóp
.S ABC
bằng
A.
3
.
4
a
B.
3
3
.
4
a
C.
3
3
.
4
a
D.
3
33
.
4
a
Lời giải.
Chọn
D ABC
sao cho
90 .
DBA DCA 
Suy ra
DBC
đều nên
3.DB DC BC a 
Tương tự như bài trên ta chứng minh được
.SD ABCD
Suy ra
60 , .SB ABC SBD
Khi đó ta tính được
.tan 3 .SD DB SBD a
Vậy
3
.
13
..
34
S ABC ABC
a
V S SD

Chọn B.
Câu 41. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
và
90 .SBA SCA 
Biết góc giữa hai mặt phẳng
SAB
và mặt đáy
ABC
bằng
60 ,
thể tích khối chóp
.S ABC
bằng
19
A.
3
3
.
4
a
B.
3
3
.
6
a
C.
3
3
.
12
a
D.
3
3
.
24
a
Lời giải.
Chọn
D ABC
sao cho
90 .DBA DCA

Ta chứng minh được
.
SD ABCD
Suy ra
60 , .SAB ABC SBD
Tính được
3
.tan
3
a
BD AB BAD
và
.tan .SD BD SBD a
Vậy
3
.
13
..
3 12
S ABC ABC
a
V S SD

Chọn C.
Câu 42. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác cân tại
A
với
AB a
và
120 ,BAC

90 .
SBA SCA 
Biết góc
giữa
SB
và mặt phẳng
SAC
thỏa mãn
3
sin ,
8
khoảng cách từ
S
đến mặt đáy
ABC
nhỏ hơn
2.a
Thể tích khối chóp
.S ABC
bằng
A.
3
3
.
4
a
B.
3
3
.
6
a
C.
3
3
.
12
a
D.
3
3
.
24
a
Lời giải.
Chọn
D ABC
sao cho
90 .DBA DCA

Suy ra
DBC
đều nên
3.DB DC BC a 
Ta chứng minh được
.SD ABCD
Đặt
22
0 2 3.SD x x a SB x a 
Gọi
.I DB AC

Trong tam giác vuông
,DCI
có
23
cos 60
DC
DI a
nên
B
là trung điểm của
DI
1
, ., .
2
d B SAC d D SAC



1
Ta có
22
,
3. 3
sin , .sin .
8
d B SAC
xa
d B SAC SB
SB






2
Kẻ
DK SC K SC
2 2 22
.3
,.
3
SD DC xa
d D SAC DK
SD DC x a




3
Từ
1, 2
và
3
suy ra
22
02
22
3 3. 3
.
4
3
xa
xa x a
xa
xa


Vậy
3
.
13
..
3 12
S ABC ABC
a
V S SD

Chọn C.
Câu 43. Cho lăng trụ tam giác
.ABC A B C

có độ dài cạnh bên bằng
4
và khoảng
cách từ điểm
A
đến các đường thẳng
,BB CC

lân lượt bằng
1
và
2.
Biết góc giữa hai
mặt phẳng
ABB A

và
ACC A

bằng
60 .
Tính thể tích khối lăng trụ
..ABC A B C

20
A.
3.
B.
2 3.
C.
3 3.
D.
4 3.
Lời giải.
Kẻ
AE BB
tại
;E
AF CC
tại
.F
Khi đó
, ,.ABB A ACC A AE AF

Trường hợp 1.
cosin
60 3.
EAF EF 
Ta có
2 22
.AF AE EF AE EF 
Suy ra
.
AE BCC B

..
3 31 31
. . . . . 2 3.
2 23 23
ABC A B C A BCC B BCC B
V V S AE BB EF AE
 









Trường hợp 2.
cosin
120 7.EAF EF 
Ta có
1 1 . .sin120 21
. . .sin120 , . , .
22 7
AEF
AE AF
S AE AF d A EF EF d A EF
EF

Ta có
..
3 3 1 1 21
. . . , . . 7.4 2 3.
2 23 2 7
ABC A B C A BCC B
V V BB EF d A EF


Chọn B.
Câu 44. Cho khối lăng trụ

.,ABC A B C
khoảng cách từ
C
đến đường thẳng
BB
bằng
2,
khoảng cách từ
A
đến các đường thẳng
BB
và
CC
lần lượt bằng
1
và
3.
Hình chiếu vuông góc của
A
lên mặt phẳng

ABC
là trung điểm
M
của

BC
và
23
.
3
AM
Thể tích của khối lăng trụ đã cho bằng
A.
23
.
3
B.
1.
C.
3.
D.
2.
Lời giải. Gọi
,EF
lần lượt là hình chiếu của
A
lên đường thẳng
,.BB CC

Ta có
,.
.
do
,,
BB EF d C BB EF
BB AE
BB AF BB CC
AEF BCC B d A BB C C d A EF











Tam giác
AEF
có
1, 3 , 2AE AF EF
nên vuông tại
Suy ra
3
,.
2
d A EF
Gọi
N
là trung điểm
BC
và
.
H EF MN
Suy ra
H
là trung điểm
EF
nên
1
1.
2
AH EF
Trong tam
AMN
vuông tại
có
23
43
.
3
3
1
AN A M
BB MN
AH


Vậy
..
3 31
. . , 2.
2 23
ABC A B C A BCC B
V V BB EF d A EF




Chọn D.
Cách 2. Ta có
AEF BB
nên
ABC
có hình chiếu vuông góc lên
AEF
là
.AEF
Mà
, ,.
MN AEF
AEF ABC MN AM AMN
AM ABC

21
Do đó
..
cos
AEF
ABC AEF
S
MN
SS
AMN AM


Vậy
.
. . 2.
ABC AEF
ABC A B C
V AM S MN S



Cách 3. Ta chứng minh được
.
AA AEF
Khi đó thể tích lăng trụ đã cho bằng thể
tích của khối lăng trụ
T
có đáy là tam giác
AEF
và chiều cao là
AA
(chỉ cần cắt
khối đa diện
ABCFE
ghép xuống dưới khối

ABCAEF
ta sẽ thu được lăng trụ đứng).
Do đó
.
. 2.
AEF
ABC A B C
V AA S


Câu 45. Cho khối lăng trụ

.,ABC A B C
khoảng cách từ
C
đến đường thẳng
BB
bằng
2,
khoảng cách từ
A
đến các đường thẳng
BB
và
CC
lần lượt bằng
1
và
3.
Hình chiếu vuông góc của
A
lên mặt phẳng

ABC
là trọng tâm
G
của tam giác

ABC
và

4
.
3
AG
Thể tích của khối lăng trụ đã cho bằng
A.
2
.
3
B.
4
.
3
C.
8
.
3
D.
2.
Lời giải. Tương tự như bài trên
..
AEF
V AA S
Gọi
G
là trọng tâm
22
.
33
AEF AG AH 
Vì
AA AEF AA AG


nên
,.d G AA AG
Mà
AA GG

nên
2
,, .
3
d G AA d G AA AG


Tam giác vuông
AG A

có
24
, ,
33
d G AA A G


nên
tính được
8
.
33
AA
Vậy
4
.
3
V
Chọn B.
22
Phần 2. Tỷ số thể tích
Câu 1.
Cho hình chóp tứ giác đều
..
S ABCD
Gọi
là
hình hộp chữ nhật có bốn đỉnh là bốn trung điểm của các
cạnh bên
, , ,
SA SB SC SD
và bốn đỉnh còn lại nằm trong
mặt đáy
ABCD
(tham khảo hình vẽ). Biết thể tích khối
hộp
là
Thể tích của khối chóp đã cho bằng
A.
2.V
B.
6.V
C.
4
.
3
V
D.
8
.
3
V
Lời giải. Chiều cao của khối chóp gấp hai lần chiều cao khối hộp và diện tích mặt đáy
khối chóp gấp
4
lần diện tích mặt đáy khối hộp. Do đó
8
.
3
SABCD
VV
Chọn D.
Câu 2. Cho khối chóp
.S ABCD
có đáy là hình bình
hành
.ABCD
Gọi
, , ,
M N PQ
lần lượt là trọng tâm
các tam giác
,,,.SAB SBC SCD SDA
Biết khối chóp
.
S MNPQ
có thể tích là
khi đó thể tích của khối
chóp
.S ABCD
bằng
A.
9
.
4
V
B.
27
.
4
V
C.
81
.
4
V
D.
81
.
8
V
Lời giải. Ta có
3
,,
2
d S ABCD d S MNPQ


và
2
39
2 2. .
22
ABCD IJHK MNPQ MNPQ
SS S S



Do đó
..
27
.
4
S ABCD S MNPQ
VV
Chọn B.
Câu 3. Cho khối tứ diện
ABCD
có thể tích
Gọi
, ,,M N PQ
lần lượt là trọng tâm
của các tam giác
,ABC
,ABD
,ACD
.BCD
Gọi
V
là thể tích của khối tứ diện
.MNPQ
Tỉ số
V
V
bằng
A.
1
.
27
B.
2
.
27
C.
4
.
27
D.
1
.
9
23
Lời giải. Ta có
MNP DCB∽
theo tỉ số
1
3
k
nên
1
9
MNP DCB
SS

=
và
1
,,
3
d Q MNP d A DCB


nên
1
.
27
V
V
Chọn A.
Câu 4. Cho lăng trụ tam giác
.ABC MNP
có thể tích
.V
Gọi
1234
,,,
GGGG
lần lượt là
trọng tâm của các tam giác
, ,,;ABC ACM AMB BCM
1
V
là thể tích khối tứ diện
1234
.GGGG
Khẳng định nào sau đây đúng ?
A.
1
9.VV
B.
1
27 .VV
C.
1
81 .VV
D.
1
8 81 .VV
Lời giải. Tương tự như bài trên và chú ý rằng đây là thể tích lăng trụ. Chọn C.
Câu 5. Cho khối tứ diện đều
ABCD
có thể tích
.
V
Gọi
,,MNP
lần lượt là trọng tâm
các tam giác
,,ABC ACD ADB
và
V
là thể tích khối tứ diện
.AMNP
Tỉ số
V
V
bằng
A.
4
.
9
B.
2
.
27
C.
4
.
27
D.
8
.
81
Lời giải. Xác định được thiết diện là tam giác
EFH
(tham khảo hình vẽ). Ta có
•
2
, , ,.
3
d A MNP d A EGH d A BCD



•
2
1 12 1
..
4 43 9
MNP EFH BCD BCD
S S SS




Suy ra
2
27
AMNP ABCD
VV
nên
2
.
27
V
V
Chọn B.
Câu 6. Cho khối lập phương
.ABCD A B C D

có cạnh bằng
1.
Gọi
, , , MNPL
lần lượt là tâm của các hình vuông
,ABB A

,ABCD

ADD A

và
.CDD C

Gọi
Q
là trung điểm của
BL
(tham khảo hình vẽ bên). Thể tích khối tứ diện
MNPQ
bằng
A.
1
.
16
B.
1
.
24
C.
2
.
27
D.
3
.
27
24
Lời giải. Ta có
, , MNP
lần lượt là trung điểm của
,AB
,BD

AD
nên suy ra
1
.
4
MNP
AB D
SS

1
Lại có
,Q BC D
mà
BC D AB D

nên
, , ,.
d Q AB D d B AB D d A AB D
 
  

 
 
2
Từ
1
và
2
11 1
.
4 4 24
MNPQ
BAB D A AB D
VV V
 

Chọn B.
Câu 7. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
,a
SA
vuông góc với
mặt đáy. Gọi
M
là trung điểm
.BC
Mặt phẳng
P
đi qua
A
và vuông góc với
SM
cắt
,SB SC
lần lượt tại
,.EF
Biết
1
.
4
SAEF SABC
VV
Thể tích khối chóp
.S ABC
bằng
A.
3
.
2
a
B.
3
2
.
5
a
C.
3
.
8
a
D.
3
.
12
a
Lời giải. Kẻ
.AH SM H SM
Ta có
.
BC AM
BC SM
BC SA

Do
P
đi qua
A
vuông góc với
SM
cắt
,SB SC
tại
,EF
nên
EF
đi qua
và song song với
BC
.
SE SH SF
SB SM SC

Trong tam giác vuông
,SAM
có
2
2
2
..
SH SA
SH SM SA
SM
SM

Ta có
2
2
2
2
2
11
.
44
3
4
SAEF
SABC
V
SE SF SH SA
V SB SC SM
a
SA





22
33
.
42
a
SA a SA 
Vậy thể tích khối chóp
.S ABC
là
23
13 3
.. .
32 4 8
aa a
V 
Chọn C.
Câu 8. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh bằng
1,
mặt bên
SAB
là tam giác cân tại
S
và nằm trong mặt phẳng vuông góc với mặt đáy
.ABC
Gọi
là hình chiếu vuông góc của
A
lên
.SC
Biết
.
.
16
.
19
S ABH
S ABC
V
V
Thể tích của khối
chóp
.S ABC
bằng
25
A.
3
.
2
B.
3
.
4
C.
3
.
6
D.
3
.
12
Lời giải. Gọi
O
là trung điểm của
AB
.SO ABC 
Ta có
.
SC AH
SC AHB
SC AB

Suy ra
.SC OH
Trong tam giác vuông
,SOC
có
2
2
2
..
SH SO
SH SC SO
SC
SC

Ta có
22
.
2
2
.
16 16 16 16
2.
3
19 19 19 19
4
S AHB
S ACB
V
SH SO SO
SO
V SC
SC
SO
   
Vậy
1 133
. .2. .
3 34 6
ABC
V S SO

Chọn C.
Câu 9. Cho hình chóp đều
..S ABC
Gọi
G
là trọng tâm tam giác
,ABC
góc giữa
SG
và
mặt phẳng
SBC
là
30 .
Mặt phẳng
P
chứa
BC
và vuông góc với
SA
chia khối
chóp
.S ABC
thành hai phần. Tỉ số thể tích hai phần bằng
A.
2
.
3
B.
1
.
6
C.
D.
6
.
7
Lời giải. Ta chứng minh được
.BC SA
Trong mặt phẳng
,SAM
kẻ
MN SA
với
.
N SA
Khi đó thiết diện tạo bởi mp
P
và khối chóp là
NBC
(hình a).
Dễ dàng xác định được:
30 , , .
SG SBC SG SM GSM
hình a hình b
Ta có
.
.
.
S NBC
S ABC
V
SN
V SA
Ta tính được
1
7
SN
SA
(hình b). Suy ra
1
.
6
SNBC
NABC
V
V
Chọn B.
Câu 10. Cho lăng trụ tam giác đều
.ABC A B C

có cạnh đáy bằng
,a
chiều cao bằng
2.a
Mặt phẳng
P
qua
B
và vuông góc
AC
chia lăng trụ thành hai khối. Biết thể
tích của hai khối là
1
V
và
2
V
với
12
.VV
Tỉ số
1
2
V
V
bằng
A.
1
.
7
B.
1
.
11
C.
1
.
23
D.
1
.
47
Lời giải. Gọi
H
là trung điểm của
,AC

suy ra
BH AC

nên
.BH P
26
Trong mặt phẳng
,ACC A

kẻ
HK A C
với
.K AA
Suy ra
.HK P
Do đó thiết diện tạo bởi mặt phẳng
P
và khối lăng trụ là tam giác
.
HKB
hình a hình b
Ta có
1
2
ABH A BC
SS
 

và tính được
1
.
8
KA AA

Do đó
1
..
2
11
.
48 47
K ABH ABCDABCD
V
VV
V
 

Chọn D.
Câu 11. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang,
, 2.AB CD AB CD
Gọi
,MN
lần lượt là trung điểm của
SA
và
.SD
Tỉ số
.
.
S BCNM
S BCDA
V
V
bằng
A.
B.
1
.
4
C.
D.
5
.
12
Lời giải. Vì hình thang
ABCD
có
2
AB CD
nên
2.
ABD BCD
SS

Ta có
. ..
.
S BCMN S BCN S BNM
V VV
•
.
...
.
1 11
. ..
2 26
S BCN
S BCN S BCD S ABCD
S BCD
V
SN
VVV
V SD

•
.
. ..
.
1 11
..
4 46
S BNM
S MBN S ABD S ABCD
S BDA
V
SN SM
V VV
V SD SA

Suy ra
..
1
3
S BCMN S ABCD
VV
nên
.
.
1
.
3
S BCMN
S BCDA
V
V
Chọn A.
Câu 12. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
M
là điểm di
động trên cạnh
AB
và
là trung điểm của
.SD
Mặt phẳng
đi qua
,MN
và
song song với
BC
chia khối chóp
.S ABCD
thành hai khối có tỷ số thể tích
1
2
3
,
5
V
V
trong đó
1
V
là thể tích khối đa diện chứa đỉnh
,A
2
V
là thể tích khối đa diện chứa
đỉnh
.
B
Tỉ số
AM
AB
bằng
A.
1
.
2
B.
1
.
3
C.
D.
Lời giải. Gọi
,PQ
lần lượt là giao điểm của
với
, .CD S A
Đặt
0;1 .
AM
x
AB

27
Ta có
1. . . . .
..
S ADPM S QNPM S ABCD S QNP S QMP
AM
VV V V V V
AB

•
... .
11 1
;
48 8
S QNP S ADP S ADPM S ABCD
V V V xV

•
.. . .
11 1
.
24 4
S QMP S AMP S ADPM S ABCD
V V V xV
Suy ra
1. 2 .
55
1.
88
S ABCD S ABCD
V xV V x V



Theo đề, ta có
5
33
8
.
5
55
1
8
x
x
x

Chọn C.
Câu 13. Cho hình hộp
..
ABCD A B C D

Gọi
M
là điểm thuộc đoạn
CC
thỏa mãn
3.CC CM
Mặt phẳng
AB M
chia khối hộp thành hai phần có thể tích là
12
,.VV
Gọi
1
V
là thể tích phần chứa điểm
.B
Tỉ số
1
2
V
V
bằng
A.
7
.
9
B.
13
.
20
C.
7
.
27
D.
13
.
41
Lời giải. Vì
BAB CKM
nên
1
.
3
IK IC IM
IA IB IB

Ta có
.
'
11
.. .
27 27
IKCM
IKCM
B A BI
IABB
V
IK IC IM
VV
V IA IB IB

Suy ra
1
.
26
.
27
B A BI
VV
Mà
.''' '
.
1 1 31
', . ', . .
3 3 44
ABI ABCD ABCD A B C D
B ABI
V d B ABCD S d B ABCD S V
 

 
Vậy
1
1 .''' ' .''' '
2
26 1 13 13
..
27 4 54 41
ABCD A B C D ABCD A B C D
V
VV V
V

Chọn D.
Câu 14. Cho hình hộp
..ABCD A B C D

Gọi
, , MNP
lần lượt là trung điểm của
,,.AA BC CD
Mặt phẳng
MNP
chia khối hộp thành hai phần có thể tích là
12
,.VV
Gọi
1
V
là thể tích phần chứa điểm
.C
Tỉ số
1
2
V
V
bằng
A.
3
.
4
B.
113
.
24
C.
119
.
25
D.
119
.
425
Lời giải. Ta có
28
•
.
1
,.
3
R BNF BNF
V d R ABCD S


.
11 1 1
., . ;
3 3 9 27
AEF M AEF
d M ABCD S V



•
.
1
,.
3
Q DEP DEP
V d Q ABCD S


.
11 1 1
., . .
3 3 9 27
AEF M AEF
d M ABCD S V



Suy ra
2 ..
1 1 25
1.
27 27 27
M AEF M AEF
V VV



Mà
. .''' '
1 11 9 3
,. .,. .
3 3 2 8 16
M AEF AEF ABCD ABCD A B C D
V d M ABCD S d A ABCD S V



Vậy
1
2 .''' ' .''' '
2
25 3 25 119
..
27 16 144 25
ABCD A B C D ABCD A B C D
V
VV V
V

Chọn C.
Câu 15. Cho hình lăng trụ tam giác đều
.ABC A B C

có tất cả các cạnh bằng
.a
Gọi
, MN
lần lượt là trung điểm của các cạnh
AB
và
.BC

Mặt phẳng
A MN
cắt cạnh
BC
tại
.P
Thể tích khối đa diện
.MBPABN

bằng
A.
3
3
.
12
a
B.
3
3
.
24
a
C.
3
73
.
32
a
D.
3
73
.
96
a
Lời giải. Ta có
''
111 1
. . .. .
' ' 222 8
IMBP
IA B N
V
IM IB IP
V IA IB IN

Suy ra
'' ''
.
17
1.
88
IA B N IA B N
MBP A B N
V VV




Mà
'' ''
1
, ' ' '.
3
IABN ABN
V dI ABC S


''' .'''
1 11
.2 , ' ' ' . .
3 23
ABC ABCABC
dB ABC S V



Vậy
3
.''' .'''
.
71 7 7 3
..
8 3 24 96
ABC A B C ABC A B C
MBP A B N
V VV a


Chọn D.
Câu 16. Cho hình hộp
.
ABCD A B C D

có
,,MNP
lần lượt là trung điểm ba cạnh
,A B BB

và
.DD
Mặt phẳng
MNP
cắt đường thẳng
AA
tại
.I
Biết thể tích khối
tứ diện
IANP
là
Thể tích khối hộp đã cho
.ABCD A B C D

bằng
A.
2.
V
B.
4.V
C.
6.V
D.
12 .
V
29
Lời giải. Gọi
.
Q MNP A D


Theo tính chất của giao
tuyến suy ra
MQ NP
nên
Q
là trung điểm của
.AD

Suy
ra
,MQ
lần lượt là trung điểm
,.
IN IP
Ta có
.
.
111 1
. . .. .
3 2 2 12 12
I A MQ
I A MQ
IANP
V
IA IM IQ V
V
V IA IN IP

Mặt khác
.
1
,.
3
I A MQ A MQ
V d I ABCD S





.
11 1 1
., . .
3 2 8 48
ABCD ABCDABCD
d A ABCD S V
 



Từ đó suy ra
.
4.
ABCD A B C D
VV

Chọn B.
Câu 17. Cho lăng trụ tam giác đều
..
ABC A B C

Trên
AB

kéo dài lấy điểm
M
sao
cho
1
.
2
BM AB

Gọi
,NP
lần lượt là trung điểm của
,.AC BB

Mặt phẳng
MNP
chia khối lăng trụ
.ABC A B C

thành hai khối đa diện, trong đó khối đa diện chứa
đỉnh
A
có thể tích
1
,V
khối đa diện chứa đỉnh
C
có thể tích
2
.
V
Tỉ số
1
2
V
V
bằng
A
97
.
59
B
49
.
95
C.
49
.
144
D.
95
.
144
Lời giải. Gọi các giao điểm như hình vẽ. Ta chứng
minh được
J
là trung điểm
;MN
là trung điểm
.AB
Ta có
.
.
.
.
111 1
. . ..
3 2 3 18
.
111 1
. . ..
333 27
M PJB
M SNA
S ALK
S A NM
V
MP MJ MB
V MS MN MA
V
SA SK SL
V SA SM SN


Suy ra
1
1 1 49
1.
18 27 54
MA NS MA NS
V VV




Mà
.
.
1 133 3
. . .. .
3 324 8
S A NM MNA
ABC ABC ABC
VS
SA
V SA S

 

Suy ra
1
.
49
144
ABC A B C
VV

nên
1
2
49
.
95
V
V
Chọn B.
Câu 18. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
,a
cạnh bên hợp với
đáy góc
o
60 .
Gọi
M
là điểm đối xứng của
C
qua
,DN
là trung điểm của
.SC
Mặt
phẳng
BMN
chia khối chóp
.S ABCD
thành hai phần có thể tích là
12
,
VV
trong đó
1
V
là phần thể tích chứa đỉnh
Tỉ số
2
1
V
V
bằng
A.
7
.
5
B.
5
.
7
C.
12
.
5
D.
5
.
12
30
Lời giải. Dễ thấy
DE
là đường trung
bình của tam giác
,MBC
suy ra
1
;
2
ME
MB
F
là trọng tâm của tam giác
,SMC
suy ra
2
.
3
MF
MN
Ta có
.
.
112 1
. . ..
223 6
M DEF
M CBN
V
MD ME MF
V MC MB MN

Suy ra
2 ..
15
1.
66
M CBN M CBN
V VV



Mà
.
.. .
.
11
. .2 1 .
22
C BNM
C BNM C BSD S ABCD
C BSD
V
CN CM
VV V
V CS CD

Vậy
2
2.
1
51 5
..
62 7
S ABCD
V
VV
V

Chọn B.
Câu 19. Cho khối chóp
.S ABC
có đáy
ABC
là tam giác vuông cân đỉnh
,B
4;
AB
12.
SA SB SC
Gọi
, MN
lần lượt là trung điểm
, .AC BC
Trên cạnh
, SA SB
lần
lượt lấy điểm
, EF
sao cho
2
.
3
SE BF
SA BS

Thể tích khối tứ diện
MNEF
bằng
A.
4 34
.
3
B.
16 34
.
3
C.
4 17
.
9
D.
4 34
.
9
Lời giải. Gọi
là trung điểm của
SE
và
I
.EF AB
Suy ra
E
là trung điểm của
IF
và
IA KF
1
3
AB
nên
11
.
46
IMN ABC FIMN SABC
S S VV


Mà
.
11
.
22
FEMN
FEMN FIMN
FIMN
V
FE
VV
V FI

Vậy
1 1 16
..
12 12
43
39
34 4
FEMN SABC
VV

Chọn D.
Câu 20. Cho hình lập phương
.ABCD A B C D

có độ dài cạnh bằng
1.
Gọi
, ,,M N PQ
lần lượt là trung điểm của
,,AB BC C D

và
.DD
Thể tích khối tứ diện
MNPQ
bằng
A.
1
.
8
B.
3
.
8
C.
1
.
12
D.
1
.
24
Lời giải.
Gọi
.E PQ CD
Khi đó ta có
Q
là trung điểm
của
PE
và
1
.
2
DE
Tính được
11
.
22
MNE ABCD
SS

Ta có
.
..
.
11
22
P QMN
P QMN P EMN
P EMN
V
PQ
VV
V PE

31
11 11 1 1
.. , . ..1. .
23 23 2 12
MNE
d P MNE S



Chọn C.
Câu 21. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành, thể tích là
Gọi
M
là một điểm trên cạnh
AB
sao cho
, 0 1.
AM
xx
AB

Mặt phẳng
qua
M
và
song song với
SBC
chia khối chóp
.S ABCD
thành hai phần, trong đó phần chứa
điểm
A
có thể tích bằng
4
.
27
V
Giá trị của biểu thức
1
1
x
P
x
bằng
A.
1
.
2
B.
1
.
3
C.
D.
Lời giải.
Tham khảo hình vẽ bên.
Từ giả thiết suy ra
;
AQ AM
x
AS AB

1;
AF
x
AD

.
DF
x
DA
Do đó
.
2
.
1;
Q AMEF
S ABCD
V
xx
V

3
.
.
.
P FEND
S ABCD
V
x
V
Ta có
2
.. .
33
1.
22
AMQ FED Q AMEF S AB CD
V V x xV 
Theo giả thiết:
2 3 01
.. .
43 4 1
1
27 2 27 3
x
AMQ FED P FEND S ABCD
V V V x xx x


nên
1
.
2
P
Chọn A.
Câu 22. Cho hình chóp tứ giác
..S ABCD
Mặt phẳng đi qua trọng tâm các tam giác
,,
SAB SAC SAD
chia khối chóp thành hai phần có thể tích là
1
V
và
2
V
12
.VV
Tỉ số
1
2
V
V
bằng
A.
8
.
19
B.
8
.
27
C.
16
.
75
D.
16
.
81
Lời giải.
Gọi
123
,,GGG
lần lượt là trọng tâm
các tam giác
,,.SAB SAD SAC
Gọi
,IJ
lần lượt là trung điểm của
,AB AC
thì
3
1
13 13
2
.
3
SG
SG
G G IJ G G ABC
SI SJ


Chứng minh tương tự ta có
23
.G G ABC
Suy ra
123
.G G G ABCD
Gọi các giao điểm của
123
GGG
với các cạnh bên
như hình vẽ, ta tìm được thiết diện của hình chóp
.S ABCD
khi cắt bởi
123
GGG
là tứ
giác
.MNPQ
32
Ta có
.
..
.
.. 8 8
;
. . 27 27
S MNP
S MNP S ABC
S ABC
V
SM SN SP
VV
V SA SB SC

Tương tự
..
8
.
27
S MPQ S ACD
VV
Suy ra
. . . .. .
88
27 27
S MNPQ S MNP S MPQ S ABC S ACD S ABCD
V V V VV V
nên
1
2
8
.
19
V
V
Chọn A.
Câu 23. Cho tứ diện đều
ABCD
có cạnh bằng
.a
Gọi
,MN
lần lượt là trung điểm
,AB BC
và điểm
P
là điểm đối xứng với
B
qua
.D
Mặt phẳng
MNP
chia tứ diện
thành hai phần có tỉ số thể tích là
A.
1
.
2
B.
7
.
11
C.
7
.
18
D.
11
.
18
Lời giải. Do
, EF
lần lượt là trọng tâm các tam giác
, ABP BCP
nên
1
.
3
DE DF
DA DC

Ta có
11 1
. . . .2
22 2
11 1
. . . .1
33 9
BMNP
BACD
DEFP
DACB
V
BM BN BP
V BA BC BD
V
DE DF DP
V DA DC DB


11 7
2 9 18
BMNDEF
DACB
V
V

nên
7
.
11
BDMNFE
ACMNFE
V
V
Chọn B.
Câu 24. Cho tứ diện
,ABCD
trên các cạnh
, , BC BD AC
lần lượt lấy các điểm
, , MNP
sao cho
3,BC BM
3
,
2
BD BN
2.AC AP
Mặt phẳng
MNP
chia khối tứ
diện
ABCD
thành hai phần có thể tích là
1
V
và
2
.
V
Tỉ số
1
2
V
V
có giá trị bằng
A.
26
.
13
B.
3
.
19
C.
15
.
19
D.
26
.
19
Lời giải. Gọi
I PM AB
và
.R NI AD
Ta cần tính
..
APRI
ACDB
V
AP AR AI
V AC AD AB
và
. ..
BMNI
BCDA
V
BM BN BI
V BC BD BA
Theo Menelaus, ta có
•
. . 1 2;
PC IA MB IA
PA IB MC IB

•
1
.. 1 .
4
RD IA NB RD
RA IB ND RA

Từ đó suy ra
14 4
. .2
25 5
APRI
ACDB
V
V

và
12 2
. .1 .
33 9
BMNI
BCDA
V
V

Suy ra
4 2 26
5 9 45
APRBMN ACDB ACDB
V VV



nên
1
2
26
.
19
V
V
Chọn D.
33
Câu 25. Cho tứ diện
ABCD
và các điểm
,,MNP
lần lượt thuộc các cạnh
,,BC BD AC
sao cho
4 , 3, 2 .BC BM AC AP BD BN 
Tỉ số thể tích hai phần của
khối tứ diện
ABCD
được phân chia bởi mặt phẳng
MNP
bằng
A.
7
.
13
B.
8
.
13
C.
7
.
15
D.
8
.
15
Lời giải. Gọi
I MN DC
và
.K AD PI
Ta cần tính
..
CMPI
CBAD
V
CM CP CI
V CB CA CD
và
...
DNKI
DBAC
V
DN DK DI
V DB DA DC
Theo Menelaus, ta có
•
. . 1 3;
IC ND MB IC
ID NB MC ID

•
2
.. 1 .
3
KD PA IC KD
KA PC ID KA

Từ đó suy ra
323 3
..
432 4
CMPI
CBAD
V
V

và
121 1
.. .
2 5 2 10
DNKI
DBAC
V
V

Suy ra
3 1 13
4 10 20
MCPNDK ACDB ACDB
V VV



nên tỉ số cần tính bằng
7
.
13
Chọn A.
Câu 26. Cho tứ diện đều
ABCD
có cạnh bằng
.
a
Gọi
,MN
lần lượt là trọng tâm của
các tam giác
,ABD ABC
và
E
là điểm đối xứng với
B
qua điểm
D
. Mặt phẳng
MNE
chia khối tứ diện
ABCD
thành hai khối đa diện, thể tích khối đa diện chứa
đỉnh
A
bằng
A.
3
32
.
80
a
B.
3
2
.
96
a
C.
3
32
.
320
a
D.
3
92
.
320
a
Lời giải. Thể tích khối tứ diện đều cạnh
a
là:
3
2
.
12
ABCD
a
V
Gọi các giao điểm như hình vẽ. Menelaus cho
•
,AID
ta có
. . 1 3.
ED MI QA QA
EI MA QD QD

• Tương tự ta cũng có
3.
PA
PC
•
,ABI
ta có
2
.. 1 .
3
EI TB MA TB
EB TA MI TA

Ta có
3 3 3 27
. . ..
5 4 4 80
ATPQ
ABCD
V
AT AP AQ
V AB AC AD

33
27 2 9 2
..
80 12 320
ATPQ
aa
V 
Chọn D.
34
Câu 27. Cho tứ diện đều
ABCD
có cạnh bằng
.a
Gọi
, MN
lần lượt là điểm trên
cạnh
,AB
AC
sao cho
1
,
2
AM
BM
2.
AN
CN
Mặt phẳng
chứa
MN
và song song với
AD
chia khối tứ diện thành hai phần. Thể tích khối đa diện chứa đỉnh
A
bằng
A.
3
42
.
81
a
B.
3
42
.
108
a
C.
3
52
.
108
a
D.
3
11 2
.
342
a
Lời giải. Thể tích khối tứ diện đều cạnh
a
là:
3
2
.
12
ABCD
a
V
Kẻ
MQ AD
với
;Q BD
NP AD
với
.P CD
Gọi
.
E PQ BC
Suy ra
2
3
BQ BM
BD BA

và
1
.
3
CP CN
CD CA

Menelaus cho
,
BCD
ta có
1
.. 1 .
4
EC QB PD EC
EB QD PC EB

Ta có
242 16
. . ..
333 27
111 1
. . ..
333 27
BMEQ
BACD
CNEP
CABD
V
BM BE BQ
V BA BC BD
V
CN CE CP
V CA CB CD


16 1 5
27 27 9
BMQCNP
ABCD
V
V

nên thể tích cần tính bằng
3
42
.
9 27
ABCD
a
V
Chọn B.
Câu 28. Cho khối chóp
.S ABC
có
, M SA N SB
sao cho
2 , 2.MA MS NS NB 
   
Mặt phẳng
đi qua hai điểm
,MN
và song song với
SC
chia khối chóp thành hai
khối đa diện. Tỉ số thể tích của hai khối đa diện đó bằng
A.
3
.
5
B.
4
.
5
C.
4
.
9
D.
5
.
9
Lời giải. Hoàn toàn tương tự như bài trên, ta được đáp án B.
Câu 29. Cho tứ diện đều
ABCD
có cạnh bằng
.a
Gọi
E
là điểm đối xứng của
A
qua
.D
Mặt phẳng qua
CE
và vuông góc với mặt phẳng
ABD
cắt cạnh
AB
tại điểm
.F
Thể tích của khối tứ diện
AECF
bằng
A.
3
2
.
15
a
B.
3
2
.
30
a
C.
3
2
.
40
a
D.
3
2
.
60
a
Lời giải. Gọi
G
là trọng tâm tam giác
,ABD
suy ra
.CG ABD
Do đó mặt phẳng cần dựng là
.CEG
Gọi
.F EG AB
Gọi
M
là trung điểm
,AD
áp dụng Menelaus cho
,ABM
ta có
2
.. 1 .
3
FA GB FM FA
FB GM FA FB

35
Ta có
3
24 4 2
. . 2.1. .
5 5 5 15
AECF
AECF ADCB
ADCB
V
AE AC AF a
VV
V AD AC AB

Chọn A.
Câu 30. Cho hình chop
.
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
, MN
lần lượt
là trung điểm của
, .AD DC
Kéo dài
SD
một đoạn sao cho
D
là trung điểm của
.SP
Thiết diện tạo bởi mặt phẳng
MNP
chia hình chóp thành hai khối lần lượt có thể
tích là
12
, VV
(trong đó
2
V
là thể tích của phần chứa điểm
S
). Tỉ số
1
2
V
V
bằng
A.
3
.
4
B.
71
.
49
C.
72
.
49
D.
71
.
120
Lời giải. Tham khảo hình vẽ. Menelaus cho
•
,
SCD
có
. . 1 2.
PD RS NC RS
PS RC ND RC

• Tượng tự ta cũng có
2.
QS
QA
•
,SBD
có
2
.. 1 .
3
PD TS HB TS
PS TB HD TB

Ta có
.
..
.
.
..
.
. ..
84
..
45 45
84
.. .
99
11 1
do
48 4
S QTR
S QTR S ABCD
S ABC
S QPR
S QPR S ABCD
S ADC
P DMN S DAC S A BCD DMN DAC
V
SQ ST SR
VV
V SA SB SC
V
SQ SP SR
VV
V SA SD SC
V VV S S






Suy ra
1
2. . . .
2
49 71
.
120 49
S QTR S QPR P DM N S ABCD
V
VV V V V
V

Chọn B.
36
Phần 3. Cực trị
Câu 1. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông cân tại
A
,
SA
vuông
góc với đáy, khoảng cách từ
A
đến mặt phẳng
SBC
bằng
3
. Gọi
là góc giữa hai
mặt phẳng
SBC
và
ABC
, tính
cos
khi thể tích khối chóp
.S ABC
nhỏ nhất.
A.
2
cos .
2
B.
1
cos .
3
C.
3
cos .
3
D.
2
cos .
3
Lời giải. Đặt
;AB AC x SA y
. Khi đó
2
.
1
.
6
S ABC
V xy
Vì
, , AB AC AS
đôi một vuông góc nên
3
2 2 2 42
2
1 1 111 1
3.
9
,
x x y xy
d A SBC



Suy ra
22
1 27 3
81 3 .
62
SABC
xy V xy 
Dấu
""
xảy ra
3 3.
xy
Khi đó
3
cos cos .
3
SMA 
Chọn C.
Câu 2. Trên đường thẳng qua
A
và vuông góc với mặt phẳng chứa tam giác đều
ABC
cạnh bằng
2,
lấy các điểm
M
và
N
không trùng với
A
sao cho
MBC
vuông
góc với
.NBC
Giá trị nhỏ nhất thể tích tứ diện
BCMN
bằng
A.
2.
B.
2 2.
C.
2 3.
D.
6.
Lời giải.
Ta có
MBC
vuông góc với
NBC
khi tam giác
MHN
vuông tại
.H
Đặt
, .MA x NA y
Ta có
2
. 3.MA NA AH xy 
Áp dụng công thức thể tích đặc biệt:
1
sin
6
V abd
ta có
0
11
. . .sin , .2. 3.sin 90 .
66
BCMN
V MN BC AH MN BC x y 
Theo BĐT Côsi:
2 2 3.x y xy
Do đó
3
2.
3
BCMN
V xy 
Dấu
'' ''
xảy ra khi
3
.
2
xy
Chọn A.
Câu 3. Cho tam giác
OAB
đều cạnh
a
. Trên đường thẳng
d
qua
O
và vuông góc với
mặt phẳng
OAB
lấy điểm
M
sao cho
OM x
. Gọi
, EF
lần lượt là hình chiếu
vuông góc của
A
trên
MB
và
OB
. Gọi
là giao điểm của
EF
và
d
. Tìm
x
để thể
tích tứ diện
ABMN
có giá trị nhỏ nhất.
A.
2.xa
B.
2
.
2
a
x
C.
3
.
2
a
x
D.
6
.
12
a
x
37
Lời giải. Do tam giác
OAB
đều cạnh
,a
suy ra
F
là trung điểm
.
2
a
OB OF

Ta có
.
AF OB
AF MOB AF MB
AF MO
 
Lại có
MB AE
nên suy ra
.MB AEF MB EF

Suy ra
OBM ONF∽
nên
2
.
.
2
OB ON OB OF a
ON
OM OF OM x

Ta có
ABMN ABOM ABON
V VV
2 23
1 36
.
3 12 2 12
OAB
a aa
S OM ON x
x



Đẳng thức xảy ra khi và chỉ khi
2
2
22
aa
xx
x

. Chọn B.
Câu 4. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành, thể tích là
.V
Gọi
M
là trung điểm của cạnh
,
SA N
là điểm nằm trên cạnh
SB
sao cho
2;SN NB
mặt
phẳng
di động qua các điểm
, MN
và cắt các cạnh
, SC SD
lần lượt tại hai điểm
phân biệt
, PQ
. Thể tích lớn nhất của khối chóp
.S MNPQ
bằng
A.
.
2
V
B.
.
3
V
C.
2
.
3
V
D.
3
.
4
V
Lời giải. Gọi
0 1.
SP
aa
SC

Vì mặt phẳng
di động đi qua các điểm
,
MN
và
cắt các cạnh
, SC SD
lần lượt tại hai điểm phân biệt
, PQ
nên ta có đẳng thức
13 2
2.
22
SA SC SB SD SD SD a
SM SP SN SQ a SQ SQ a

Áp dụng công thức tính nhanh
2
.
.
312
2
2
22
.
312
36
4.2. . .
22
S MNPQ
S ABCD
a
V
aa
aa
a
Va
aa


Xét hàm
21
32
a
fa
a

trên đoạn
0;1 ,
ta được
0;1
1
max 1 .
3
fa f
Chọn B.
Câu 5. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành, thể tích là
Điểm
M
di động trên cạnh
,SC
đặt
.
MC
k
MS
Mặt phẳng
qua
, AM
và song song với
BD
cắt
,SB
SD
thứ tự tại
, .NP
Thể tích khối chóp
.
C APMN
lớn nhất khi
A.
1.k
B.
2.k
C.
2.k
D.
3.k
Lời giải. Từ giả thiết
MC
k
MS
suy ra
.MC kMS
Khi đó
1.
SC SM MC
k
SM SM

38
Áp dụng Menelaus cho
,SOC
có
.. 1 ,
2
AC IO MS IO k
AO IS MC IS

suy ra
2
.
2
SO k
SI
Vì
NP BD
nên suy ra
2
.
2
SB SD SO k
SN SP SI

Ta có

.
22
11
2
22
.
22
12
4.1. 1 . .
22
S ANMP
kk
k
V
kk
V kk
k





Lại có
.
.
1
.
S ANMP
C ANMP
V
SM
V CM k

Suy ra

.
2
.
12
C ANMP
kV
V
kk

Xét
2
32
k
fk
kk

trên
0; ,

có
0;
max 2 3 2 2.fk f


Chọn C.
Chú ý: Ta có thể tính theo cách khác:
. . . ..
.
C ANMP S ABCD S ANMP P ACD N ABC
V V V VV 
Câu 6. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
,a
cạnh bên
SA y
0y
và vuông góc với đáy
.ABCD
Trên cạnh
AD
lấy điểm
M
và đặt
AM x
0.xa
Biết
222
,xya
thể tích lớn nhất
max
V
của khối chóp
.S ABCM
bằng
A.
3
3
.
3
a
B.
3
33
.
3
a
C.
3
3
.
8
a
D.
3
3
.
24
a
Lời giải. Từ
2 2 2 22
.xya y ax

Diện tích
..
22
ABCM
BC AM a x
S AB a










Thể tích khối chóp
.
1
.
3
S ABCM ABCM
V S SA
22 22
1
.. .
32 6
ax a
aax axax



Xét hàm
22
fx a x a x
trên
0; ,a
ta được
2
0;
33
max .
24
a
aa
fx f



Suy ra
3
max
3
8
a
V
. Chọn C.
Câu 7. Từ hình vuông có cạnh bằng
6
người ta cắt bỏ
các tam giác vuông cân tạo thành hình tô đậm như hình
vẽ. Sau đó người ta gập thành hình hộp chữ nhật không
nắp. Thể tích lớn nhất của khối hộp bằng
A.
8 2.
B.
9 2.
C.
10 2.
D.
11 2.
39
Lời giải. Gọi độ dài các cạnh của hình hộp chữ nhật không
nắp là
,ab
(như hình vẽ).
Suy ra hình chữ nhật có đáy là hình vuông cạnh
,b
chiều
cao là
a
2
.
hh
V ab 
Ta tính được cạnh của hình vuông ban đầu là
2 2.
ba
Theo đề suy ra
2 2 6 32 .ba a b 
Khi đó ta có
22
32 .
hh
V ab b b

Xét hàm
23
32
fb b b
trên
0;3 2 ,
ta được
0;3 2
max 2 2 8 2.fx f
Chọn A.
Câu 8. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành với
4AD a
. Các
cạnh bên của hình chóp bằng nhau và bằng
6a
. Thể tích lớn nhất của khối chóp đã
cho bằng
A.
3
8
.
3
a
B.
3
46
.
3
a
C.
3
8.a
D.
3
46 .a
Lời giải. Do
6SA SB SC SD a
nên hình chiếu vuông góc của
S
trên mặt
phẳng
ABCD
trùng với tâm đường tròn ngoại tiếp đáy. Do đó tứ giác
ABCD
là hình
chữ nhật. Gọi
,
H AC BD
suy ra
SH ABCD
.
Đặt
0,AB x
suy ra
2222
16 .AC AD AB x a 
Tam giác vuông
,SHA
có
2 22
2
8
.
42
AC a x
SH SA

Khi đó
.
11
. ..
33
S ABCD ABCD
V S SH AB AD SH
22 3
22 2 22
18 8
. .4 . 2 8 8 .
3 23 3 3
ax a a a
xa xax x ax

Chọn A.
Câu 9. Cho tam giác
ABC
vuông tại
A
có
3, .
AB a AC a
Gọi
Q
là mặt phẳng
chứa
BC
và vuông góc với mặt phẳng
.ABC
Điểm
D
di động trên
Q
sao cho tam
giác
DBC
nhọn và hai mặt phẳng
DAB
và
DAC
lần lượt hợp với mặt phẳng
ABC
hai góc phụ nhau. Thể tích lớn nhất của khối chóp
.D ABC
bằng
A.
3
3
.
4
a
B.
3
3
.
8
a
C.
3
32
.
10
a
D.
3
3
.
13
a
Lời giải. Kẻ
DH BC
với
.H BC
Suy ra
.DH ABC
Vì diện tích tam giác
ABC
không đổi nên thể tích khối chóp
.D ABC
lớn nhất khi
DH
lớn nhất.
Kẻ
HM AB
với
,M AB
HN AC
với
.N AC
Khi đó theo giả thiết, ta có
,DAB ABC DMH 
và
, 90 .DAC ABC DNH 
40
Ta có
AHC AHB ABC
SSS
2
1 13
. cot 90 . . cot .3
2 22
a
DH a DH a 
tan
2
3 3.
.
tan 3cot
3
x
a ax
DH
x


Xét
2
3
x
fx
x
trên
0; ,

được
0;
3
max 3 .
6
fx f


Khi đó
max
3
2
a
DH
và
3
max
3
.
4
a
V
Chọn A.
Câu 10. Cho lăng trụ đứng
.ABC A B C

có đáy là tam giác đều. Tam giác
ABC
có
diện tích bằng
3
và nằm trong mặt phẳng tạo với đáy một góc nhọn bằng
.
Thể
tích khối lăng trụ
.ABC A B C

đạt giá trị lớn nhất khi
bằng
A.
1
arctan .
2
B.
1
arctan .
6
C.
arctan 2.
D.
arctan 6.
Lời giải. Đặt
0.AB x
Gọi
M
là trung điểm của
AB
3
2
.
,
x
MC
ABC ABC CMC



Suy ra
3
.
2 cos
x
MC
Theo giải thiết:
1
. 3 2 cos .
2
MC AB x

Khi đó
2
.
3
. .8cos cos .tan 3sin cos 3 cos 1 cos .
8
ABC
ABC A B C
V S CC  


Xét hàm
2
1ft t t

trên
0;1 ,
ta được
0;1
23
max
9
t
ft
khi
1
.
3
t
Vậy
max
23V
khi
1
cos tan 2 arctan 2.
3
 
Chọn C.
Câu 11. Trong tất cả các hình chóp tứ giác đều có
3d
là khoảng cách giữa hai
đường thẳng chéo nhau gồm một đường thẳng chứa một đường chéo của đáy và đường
thẳng còn lại chứa một cạnh bên hình chóp. Thể tích nhỏ nhất của khối chóp bằng
A.
3.
B.
9.
C.
9 3.
D.
27.
Lời giải. Xét hình chóp tứ giác đều
..S ABCD
Đặt
2
.
1
, .
3
S ABCD
AB x SO h V hx 
Ta cần đánh giá
2
1
3
hx
hằng số.
Ta tính được
2
x
OA
nên theo giả thiết ta có
2 2 2 2 22
1 1 1 1 12
OH SO OA d h x

2
3
22 222 24
112 111 11
3 . 27.
3
AM GM
hx
hx hxx hx

41
Dấu
'' ''
xảy ra
3.xh
Khi đó
min
9.V
Chọn B.
Câu 12.
Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ
nhật. Một mặt phẳng không qua
S
và song song với đáy
cắt các cạnh bên
,,,
SA SB SC SD
lần lượt tại
, ,,.M N PQ
Gọi
, ,,M NPQ

lần lượt là hình chiếu của
, ,,M N PQ
trên mặt phẳng đáy. Khi thể tích khối đa diện
.MNPQ M N P Q

đạt giá trị lớn nhất, tỉ số
SM
SA
bằng
A.
1
.
2
B.
1
.
3
C.
2
.
3
D.
3
.
4
Lời giải. Đặt
0 1.
SM
xx
SA

Suy ra
MN NP PQ SM
x
AB BC CD SA

và
1.
MA
x
SA

Do
MNPQ
đồng dạng với
ABCD
theo tỉ số
x
nên
2
.
MNPQ
ABCD
S
x
S
Ta có
.
2
.
.,
3. 3 1 .
1
.,
3
MNPQ
MNPQ M N P Q MNPQ
S ABCD ABCD
ABCD
S d M ABCD
V
S
MA
xx
V S SA
S d A ABCD






Suy ra
2
.
.
31 . .
S ABCD
MNPQ M N P Q
V x xV


Xét
2 32
31 3 3fx x x x x 
trên
0;1 ,
ta được
0;1
24
max .
39
fx f



Chọn C.
Câu 13. Cho hình chóp
.S ABC
có
0 3,
SA x x 
tất cả các cạnh còn lại đều
bằng
1
. Thể tích lớn nhất của khối chóp đã cho bằng
A.
1
.
4
B.
C.
1
.
12
D.
1
.
16
Lời giải. Ta có tam giác
ABC
và
SBC
là những tam giác đều cạnh bằng
1
.
Gọi
N
là trung điểm
3
.
2
BC SN 
Trong tam giác
SAN
, kẻ
SH AN
.
1
Ta có
BC AN
BC SAN BC SH
BC SN
 
.
2
Từ
1
và
2
, suy ra
SH ABC
.
Khi đó
.
1 1 133 1
. . .. .
3 3 34 2 8
S ABC ABC A BC
V S SH S SN


Dấu
'' ''
xảy ra
.HN
Chọn B.
Cách 2. Gọi
M
là trung điểm
,.
NM SA
SA d SA BC MN
NM BC
 
Tam giác
SNA
cân tại
,N
có
3
2
SN AN
nên suy ra
2
3
.
2
x
MN
42
Khi đó
2
.
1 31
. . , .sin , .
6 12 8
S ABC
xx
V SA BC d SA BC SA BC

Dấu
'' ''
xảy ra
2
6
3.
2
x xx 
Câu 14. Cho hình chóp
.
S ABC
có
,, 1.
ABSA x BC
S
y AC SB C


Thể tích
khối chóp
.S ABC
lớn nhất khi tổng
xy
bằng
A.
2
.
3
B.
4
.
3
C.
3.
D.
4 3.
Lời giải.
Tương tự như bài trên ta được
22
.
1
1
64
S ABC
xy
V xy

22 2 2
3
22 22
1
4
12
1 4 23
.
12 3 27
xy x y
xy xy





Dấu
""
xảy ra
2 2 22
23
4.
3
x y x y xy

Vậy
4
.
3
xy
Chọn B.
Câu 15. Cho hình vuông
ABCD
cạnh
,a
trên đường thẳng vuông góc với
ABCD
tại
A
ta lấy điểm
S
di động. Hình chiếu vuông góc của
A
lên
,SB SD
lần lượt là
,.HK
Thể tích lớn nhất của tứ diện
ACHK
bằng
A.
3
.
6
a
B.
3
2
.
12
a
C.
3
3
.
16
a
D.
3
6
.
32
a
Lời giải. Tham khảo hình vẽ. Ta sẽ sử dụng công thức
1
.. ,.sin,.
6
V abd ab ab
Đặt
0.SA x x
Tính được
2
22
2
,
xa
KH
ax
2
22
.
ax
IH
ax
Chứng minh được
,HI d KH AC
và
.AC HK
Khi đó
1
..
6
ACHK
V AC KH HI
2 2 43
2222 2
22
12
. 2. . . .
63
xa ax a x
a
axax
ax


Xét hàm
3
2
22
x
fx
x a
trên
0; ,
ta có
0;
33
max
16
fx
a

khi
3.xa
Suy ra thể tích khối tứ diện lớn nhất bằng
3
max
3
.
16
a
V
Chọn C.
Câu 16. Trong mặt phẳng
P
cho đường tròn
T
đường kính
2,AB r C
là một
điểm di dộng trên đường tròn
.T
Trên đường thẳng
d
vuông góc với
P
tại
A
lấy
43
điểm
S
sao cho
.SA r
Gọi
,HK
lần lượt là hình chiếu vuông góc của
A
lên
SC
và
.SB
Khi
C
chạy trên đường tròn, thể tích lớn nhất của tứ diện
.S AHK
bằng
A.
3
.
3
r
B.
3
5
.
3
r
C.
3
5
.
25
r
D.
3
5
.
75
r
Lời giải. Chuẩn hóa, chọn
1,r
đặt
0 2.AC x x 
Khi đó
2
4.BC x
Trong hai tam giác vuông
,SAC SAB
lần lượt có
2
22
1
1
SH SA
SC
SC x

và
2
2
1
.
5
SK SA
SB
SB

Ta có
.
2
.
1
.
51
S AKH
S ABC
V
SK SH
V SB SC
x

2
..
22
2
2
4 56
15 1
1
15 1
1
S AHK S AHK
xx
VV
x
x
x


Có
2
22 2
2
5 6 4 1 34
15 .
5 55
11
1
xx
x






Dấu
""
xảy ra khi
2
13 6
.
53
1
x
x

Vậy
3
.
5
max .
75
S AHK
r
V
Dấu
""
xảy ra khi
6
.
3
r
AC
Chọn D.
Câu 17. Cho khối chóp
.
S ABC
có đáy là tam giác vuông cân tại
Khoảng cách từ
A
đến mặt phẳng
SBC
bằng
2,a
0
90 .SAB SCB

Xác định độ dài cạnh
AB
để khối
chóp
.S ABC
có thể tích nhỏ nhất.
A.
10
.
2
a
AB
B.
3.AB a
C.
2.
AB a
D.
3 5.AB a
Lời giải. Gọi
D
là điểm sao cho
ABCD
là hình vuông.
Ta có
0
90
AB AD
AB SAD AB SD
SAB AB SA
 

.
Tương tự, ta cũng có
BC SD
. Từ đó suy ra
SD ABDC
.
Kẻ
.DH SC H SC DH SBC 
Khi đó
,,.d A SBC d D SBC DH



Đặt
0.AB x
Trong tam giác vuông
,SDC
có
22 2 222
1 1 1 1 11
.
2
DH SD DC SD x
a
 
Suy ra
22
2
.
2
ax
SD
xa
Thể tích khối chóp
33
..
22 22
1 122
. ..
26 6
22
S ABC S ABCD
ax a x
VV
xa xa


44
Xét
3
22
2
x
fx
xa
trên
2; ,
a 
được
2
2;
min 3 3 3 .
a
fx fa a


Chọn B.
Câu 18. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2.a
Tam giác
SAB
vuông tại
S
và nằm trong mặt phẳng vuông góc với đáy. Gọi
là góc tạo bởi đường
thẳng
SD
và mặt phẳng
SBC
với
30 . 
Giá trị lớn nhất của thể tích khối chóp
.S ABCD
bằng
A.
3
4
.
3
a
B.
3
42
.
3
a
C.
3
82
.
9
a
D.
3
83
.
9
a
Lời giải. Lấy điểm
K
thỏa mãn
.
SK AD
 
Ta chứng minh được
.SA SBC DK SBC 
Do đó
,.SD SBC KSD SDA 
Tam giác
SAD
vuông nên ta có
tan 2 tan .SA AD a
Trong tam giác vuông
,SAB
có
22
. 2 tan .SA AH AB AH a 
Suy ra
22 2 2
2 tan 1 tan .
SH SA AH a


Khi đó
3
22
.
18
. tan 1 tan .
33
S ABCD ABCD
a
V S SH 
Xét hàm
42
fx x x
trên
1
0; ,
3

ta được
1
0;
3
12
max .
9
3
fx f




Suy ra
3
.
82
max .
9
S ABCD
a
V
Chọn C.
Câu 19. Cho khối chóp
.S ABC
có
,SA SB SC a
60 ,ASB 
90 ,BSC 
120 .CSA

Gọi
, MN
lần lượt là các điểm trên cạnh
AB
và
SC
sao cho
.
CN AM
CS AB
Khi khoảng
cách giữa
M
và
nhỏ nhất thì thể tích của khối chóp
.S AMN
bằng
A.
3
2
.
72
a
B.
3
52
.
72
a
C.
3
52
.
432
a
D.
3
2
.
432
a
Lời giải. Tính được
, 2, 3AB a BC a CA a
suy ra
ABC
vuông tại
Gọi
H
là trung điểm
.
SA SB SC
AC SH ABC


Khi đó
3
.
2
.
12
S A BC
a
V
Đặt
0 1.
CN AM
xx
CS AB

Ta có
. 1.
.
. 1. .
CN x CS SN x SC
AM x AB SM x SA x SB


   
    
Suy ra
1. . 1..NM x SA x SB x SC 
   
Suy ra
2
2
2 22 2
5 11 11
3 53 3 .
6 12 12
a
MN a x x a x








Dấu
""
xảy ra khi
5
.
6
x
45
Ta có
.
3
.
..
.
.
1
6
5 52
.
36 432
5
.
6
S AMN
S AMC
S AMN S ABC
A SCM
A SCB
V
SN
V SC
a
VV
V
AM
V AB



Chọn C.
Cách khác. Kẻ
MP AC
với
.P BC
Dùng định lý hàm số cosin trong tam giác
MNP
tính được độ dài
2 22
3 5 3.MN a x x 
Câu 20. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
,a
2SA a
và
vuông góc với mặt đáy
.ABCD
Gọi
M
là điểm di động trên cạnh
CD
và
là hình
chiếu vuông góc của
S
lên đường thẳng
.BM
Khi điểm
M
di động trên cạnh
,CD
thể
tích khối chóp
.S ABH
có giá trị lớn nhất bằng
A.
3
2
.
6
a
B.
3
2
.
8
a
C.
3
2
.
12
a
D.
3
2
.
15
a
Lời giải. Lấy điểm
N BC
sao cho
.BN CM
Dễ dàng chứng minh được
.AN BM
Gọi
.H AN BM
Ta có
BM AN
BM SAH BM SH
BM SA
 
nên
là hình
chiếu vuông góc của
S
lên đường thẳng
.BM
Đặt
,0 .BN CM x x a
Trong tam giác vuông
ABN
có
BH
là đường cao, suy ra
22
,
ax
BH
xa
2
22
.
a
AH
xa
Ta có
3
22
1
. ..
22
ABH
ax
S AH BH
xa

Thể tích khối chóp
4 43
Cosi
.
22
1 2 22
.. . .
3 6 6 2 12
S ABH ABH
a x a xa
V S SA
ax
xa

Dấu
""
xảy ra khi
xa
hay
, .N CM D

Chọn C.
Câu 21. Cho tứ diện
.ABCD
Hai điểm
,MN
lần lượt di động trên hai đoạn thẳng
,BC BD
(
, MN
không trùng
B
) sao cho
2 3 10.
BC BD
BM BN

Gọi
12
,VV
lần lượt là thể
tích của các khối tứ diện
ABMN
và
.ABCD
Giá trị nhỏ nhất của
1
2
V
V
bằng
A.
25
.
3
B.
3
.
8
C.
3
.
25
D.
6
.
25
Lời giải. Đặt
, , 1.
BC BD
x y xy
BM BN

Theo giả thiết:
10 2 3 2 10 3 .xy x y 
Do
8
12 2103 2 .
3
x x yy  
46
Ta có
1
2
11 1 2
. . . .1 .
10 3
V
BM BN BA
V BC BD BA x y xy y y

Xét
10 3fy y y
trên
8
1; ,
3




được
16 25
;.
33
fy




Suy ra
1
2
63
;.
25 8
V
V





Chọn D.
Cách khác: Ta có
Cosi
25
10 2 3 2 6 .
6
x y xy xy 
Câu 22. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành. Hai điểm
,
MN
lần lượt trên các đoạn thẳng
,AB AD
(
,MN
không trùng
A
) sao cho
2 4.
AB AD
AM AN

Kí hiệu
1
,VV
lần lượt là thể tích của các khối chóp
.S ABCD
và
..S MBCDN
Giá trị lớn
nhất của tỉ số
1
V
V
bằng
A.
2
.
3
B.
3
.
4
C.
1
.
6
D.
17
.
14
Lời giải. Đặt
, , 1.
AB AD
x y xy
AM AN

Theo giả thiết:
2424.xy y x 
Do
1 2 2 4 2 2.y y xx 
Ta có
.
1
.1
1 1 1.
2 2. 4
S AMN AMN
ABD
VV S
V
AM AN
V V S AB AD x x
  
Xét
1
4
fx
xx
trên
1; 2 ,
ta được
11
;.
43
fx




Suy ra
1
23
;.
34
V
V




Chọn B.
Câu 23. Cho tứ diện đều
ABCD
có cạnh bằng
1.
Gọi
, MN
là hai điểm thay đổi lần
lượt thuộc cạnh
,BC BD
sao cho
AMN
vuông góc với
.BCD
Tổng giá trị lớn nhất
và giá trị nhỏ nhất của thể tích khối tứ diện
ABMN
bằng
A.
2
.
12
B.
17 2
.
72
C.
17 2
.
144
D.
17 2
.
216
Lời giải. Gọi
H
là tâm đường tròn ngoại tiếp
.BCD
Khi đó
MN
luôn đi qua
.H
Ta có
3 3 3.
BC BD BC BD
BC BD BH BM BN BH
BM BN BM BN

     
Đặt
, , 1 .
BC BD
x y xy
BM BN

Suy ra
3.xy
Ta có
1
..
ABMN
ABCD
V
BM BN
V BC BD xy

Tương tự như các bài trên, ta được
1 41
;.
92xy




Suy ra
41
;.
92
ABMN ABCD ABCD
V VV




Vậy
12
17 17 2
.
18 216
ABCD
VV V
Chọn D.
47
Câu 24. Cho tứ diện
OABC
có
, , OA OB OC
đôi một vuông góc và
2,
OA OB
1.
OC
Hai điểm
, MN
lần lượt di động trên hai cạnh
, AC BC
sao cho
OMN
vuông góc với
.ABC
Thể tích khối đa diện
ABOMN
có giá trị lớn nhất bằng
A.
1
.
4
B.
1
.
9
C.
2
.
9
D.
1
.
12
Lời giải. Thể tích
ABOMN
có giá trị lớn nhất khi
.
COMN
COAB
V
CM CN
V CA CB
nhỏ nhất.
Gọi
K
là trung điểm
,AB
suy ra
OK AB
và
1
1.
2
OK AB
Kẻ
,
OI CK
suy ra
I
là trung điểm
.CK
Ta chứng minh được
.OI ABC
Do
OMN ABC
suy ra
MN
đi qua
.I
Ta có
2 4 4.
CA CB CA CB
CA CB CK CM CN CK
CM CN CM CN

     
Đặt
, , 1 .
CA CB
x y xy
CM CN

Suy ra
4.xy

Ta có
1
..
COMN
COAB
V
CM CN
V CA CB xy

Tương tự như các bài trên, ta được
1 11
;.
43xy




Suy ra
1 3 32 1
min max . .
4 4 46 4
COMN COAB ABOMN COAB
VV V V

Chọn A.
Câu 25. Cho hình chóp
.S ABC
có
1, 2, 3.SA SB SC
Gọi
G
là trọng tâm tam giác
.ABC
Mặt phẳng
đi qua trung điểm
I
của
SG
cắt các cạnh
,,SA SB SC
lần lượt
tại
, ,.
MNP
Giá trị nhỏ nhất của biểu thức
2 22
1 11
T
SM SN SP

bằng
A.
2
.
7
B.
3
.
7
C.
18
.
7
D.
6.
Lời giải. Do
G
là trọng tâm
.ABC
Ta có
1
3
SG SA SB SC 
   
1
. . ..
3
1
. . ..
6
SG SA SB SC
SI SM SN SP
SI SM SN SP
SA SB SC
SI SM SN SP
SM SN SP






   
   
Do
, ,,IMNP
đồng phẳng nên
1
1 6.
6
SA SB SC SA SB SC
SM SN SP SM SN SP

 

Áp dụng BĐT Bunhiacopxki, ta có
2
22 2
2 22
1 11
.
SA SB SC
SA SB SC
SM SN SP
SM SN SP









48
Suy ra
22 2
36 18
.
7
T
SA SB SC


Chọn C.
| 1/64
| | Tải xuống

Có thể bạn quan tâm:

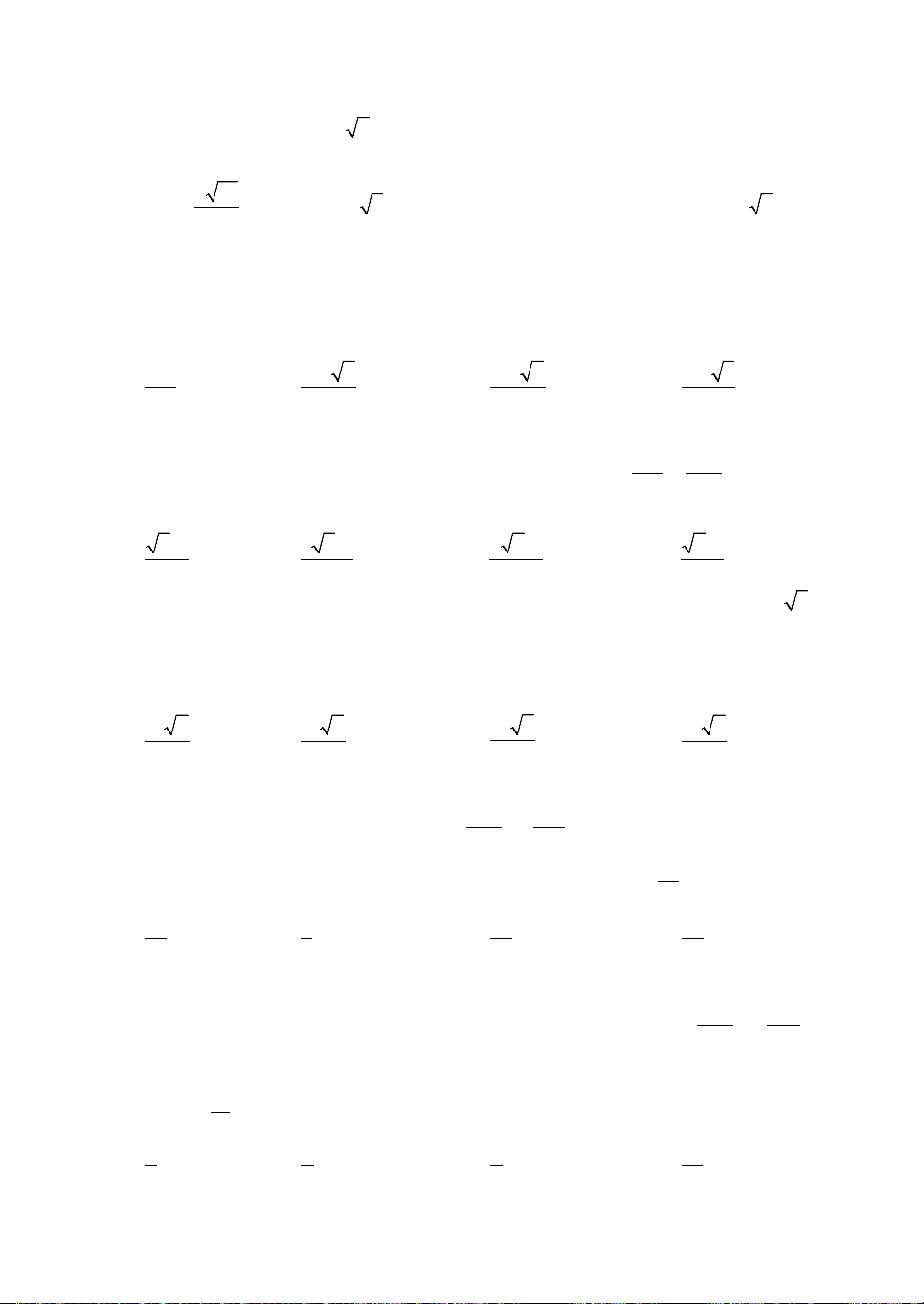
Preview text:

THỂ TÍCH KHỐI ĐA DIỆN
Phần 1. Thể tích khối đa diện
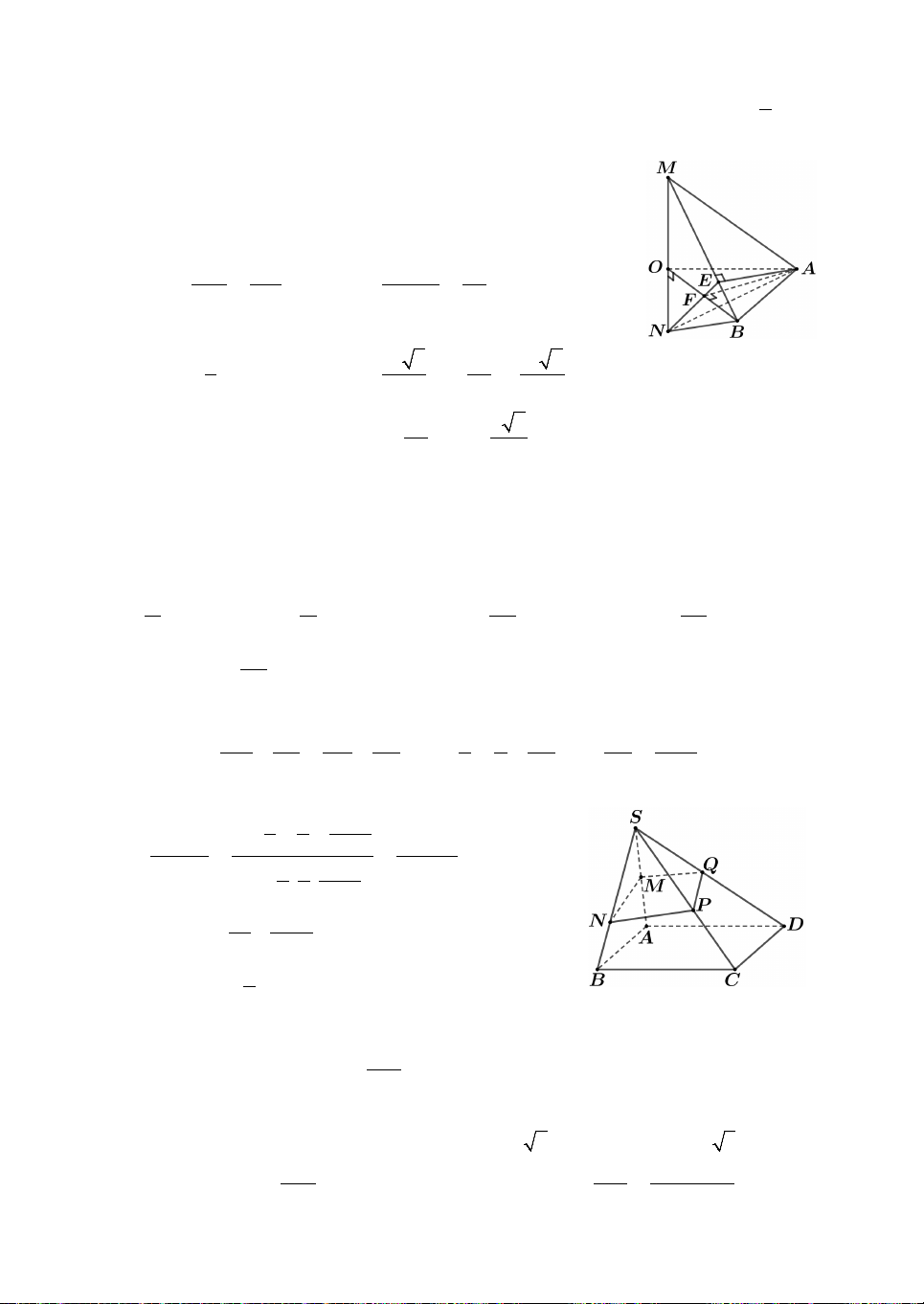
Câu 1. Cho khối tứ diện ABCD có thể tích V. Gọi V  là thể tích của khối tám mặt có 
các đỉnh là trung điểm các cạnh của khối tứ diện ABCD. Tỉ số V bằng V A. 1 . B. 1 . C. 3 . D. 1 . 2 4 4 8
Câu 2. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 1, góc giữa cạnh bên và
mặt đáy bằng 60. Gọi A , B , C  lần lượt là các điểm đối xứng của ,
A B, C qua S.
Thể tích của khối bát diện ABC.AB C   bằng A. 3 . B. 2 3 . C. 4 3 . D. 2 3. 2 3 3
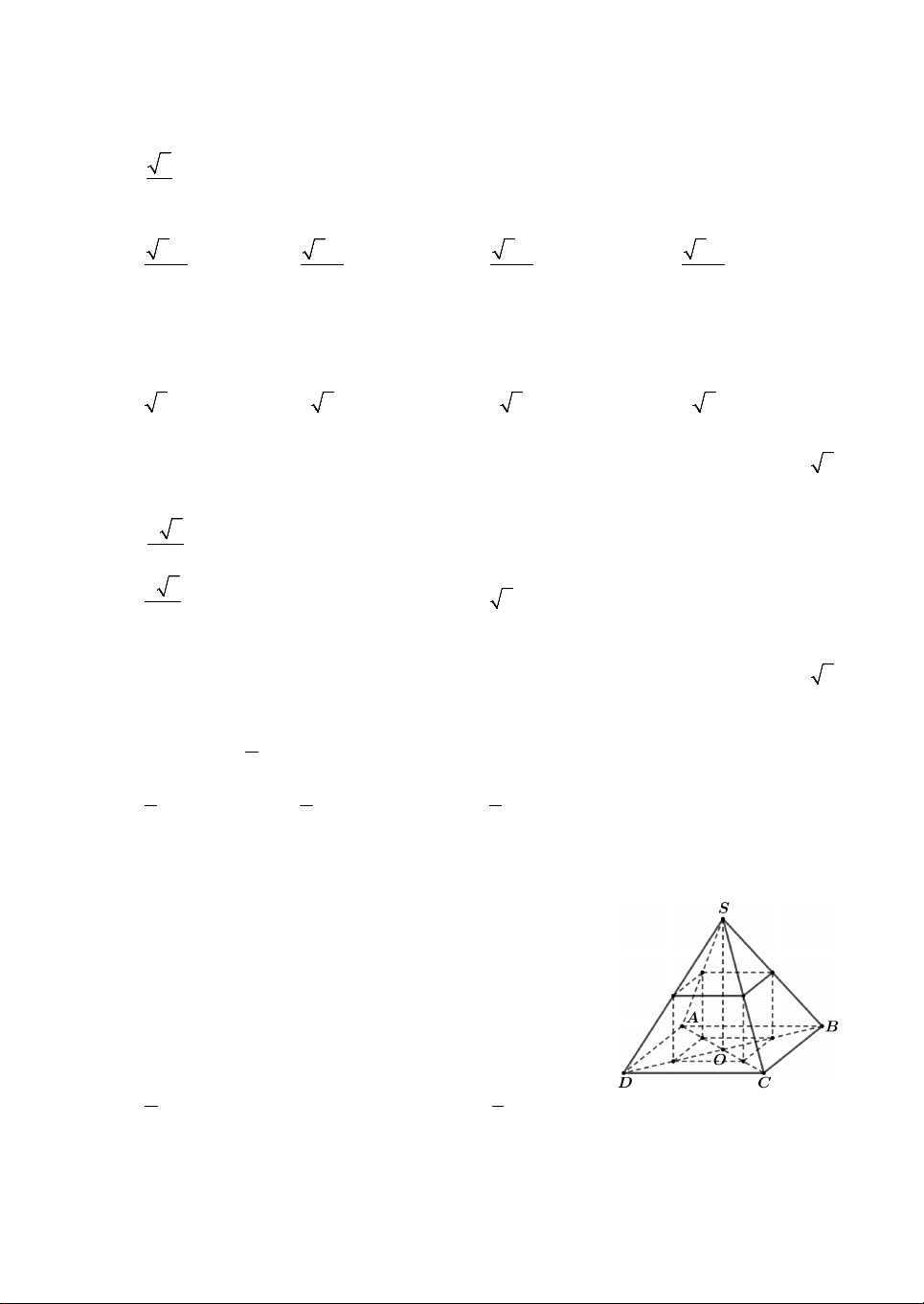
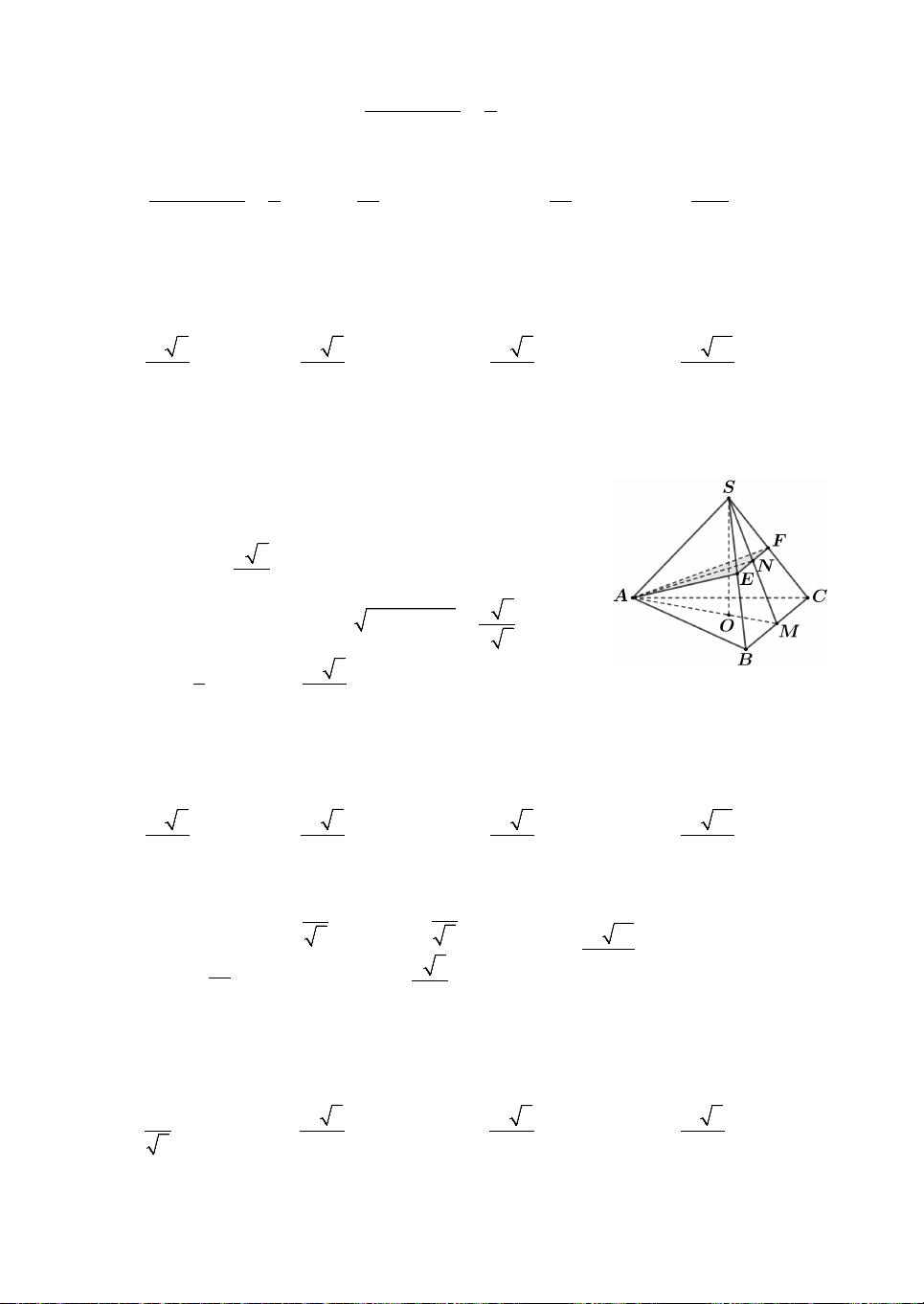
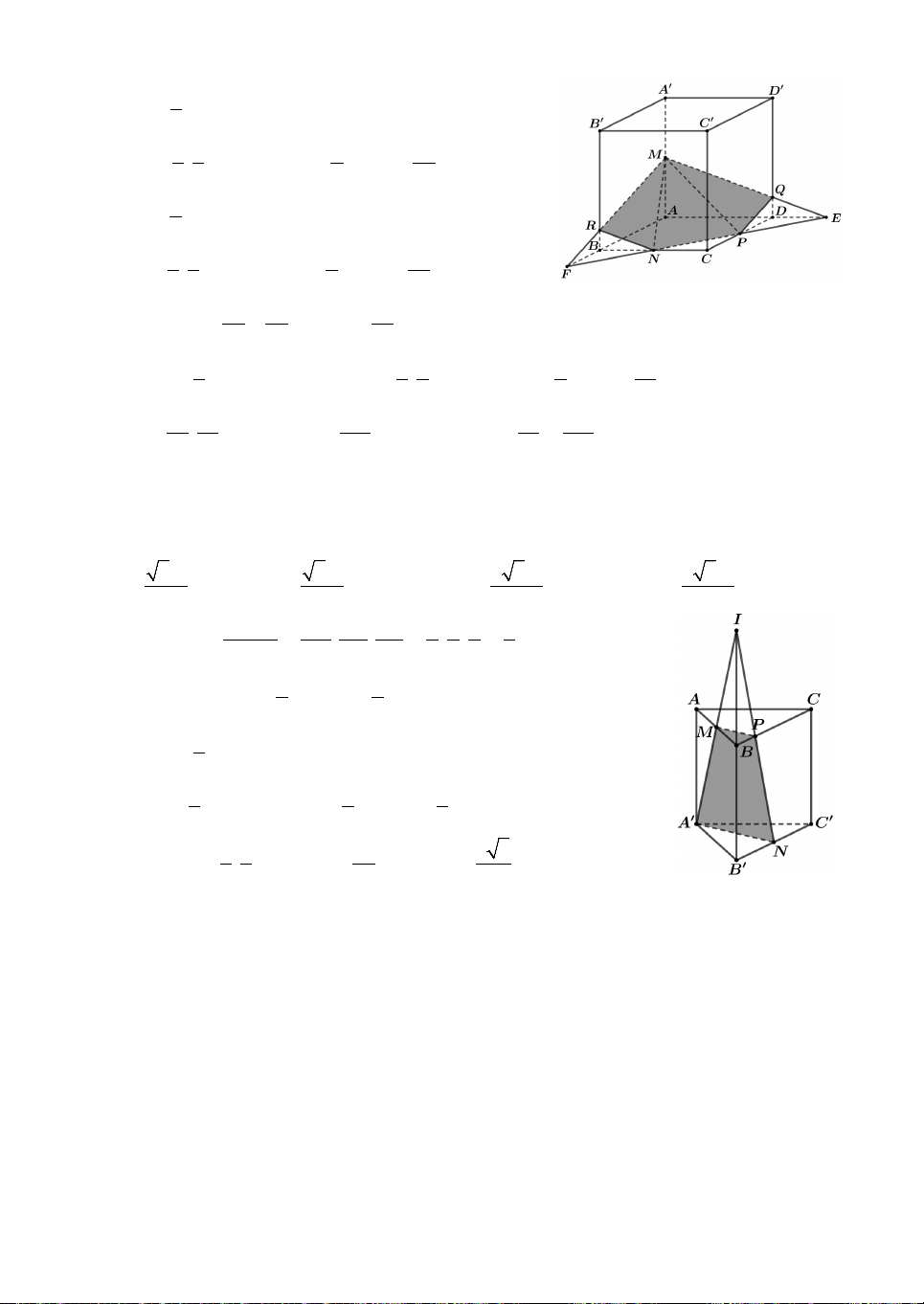
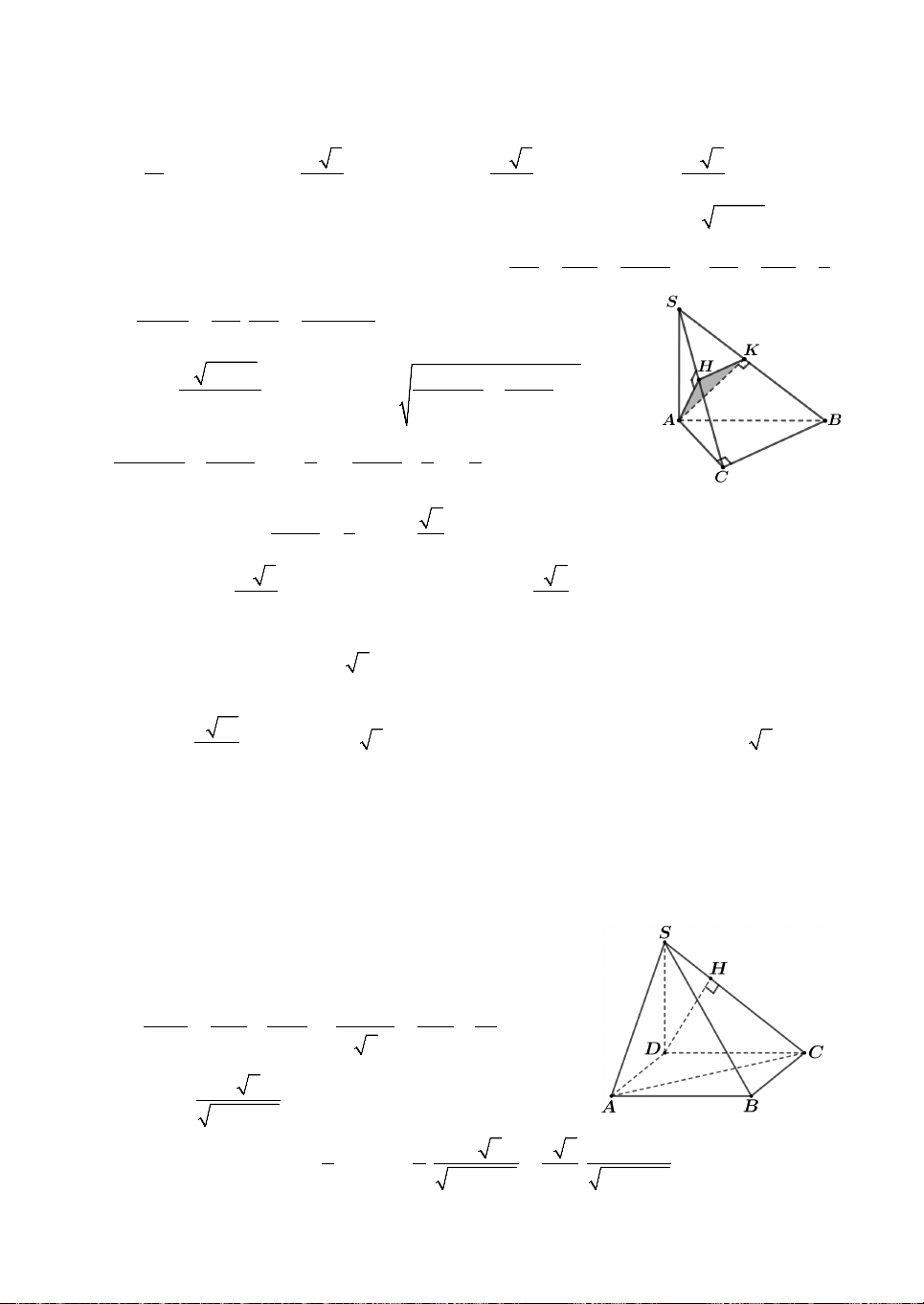
Câu 3. Cho khối chóp tứ giác đều S.ABCD, có đáy ABCD là hình vuông cạnh bằng ,
a tâm O; cạnh bên bằng a 3. Gọi M
là trung điểm của CD, H là điểm đối xứng của O qua SM.
Thể tích khối đa diện ABCDSH bằng 3 3 3 3 A. a 10 a 10 a 10 5a 10 . B. . C. . D. . 12 18 24 24
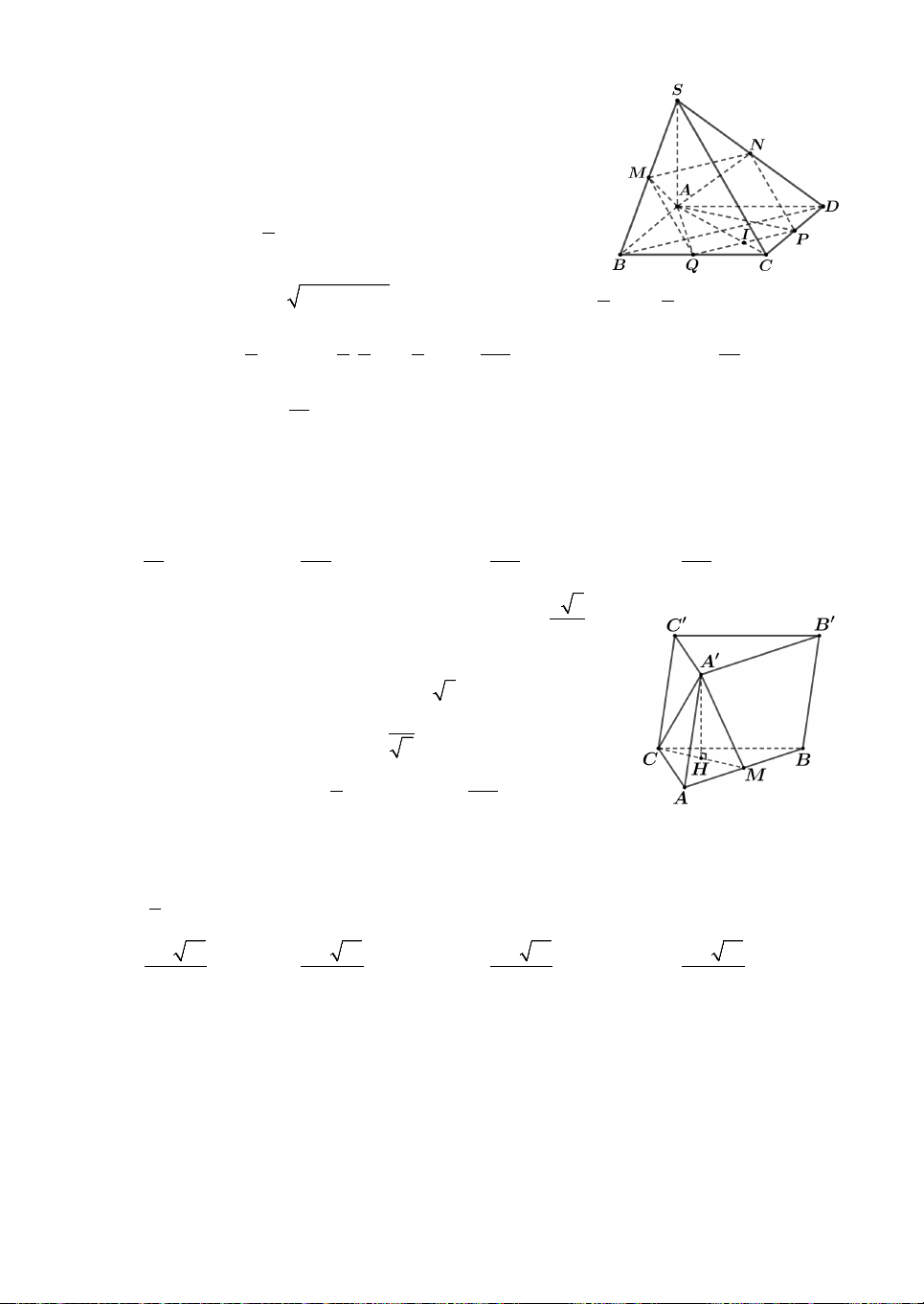
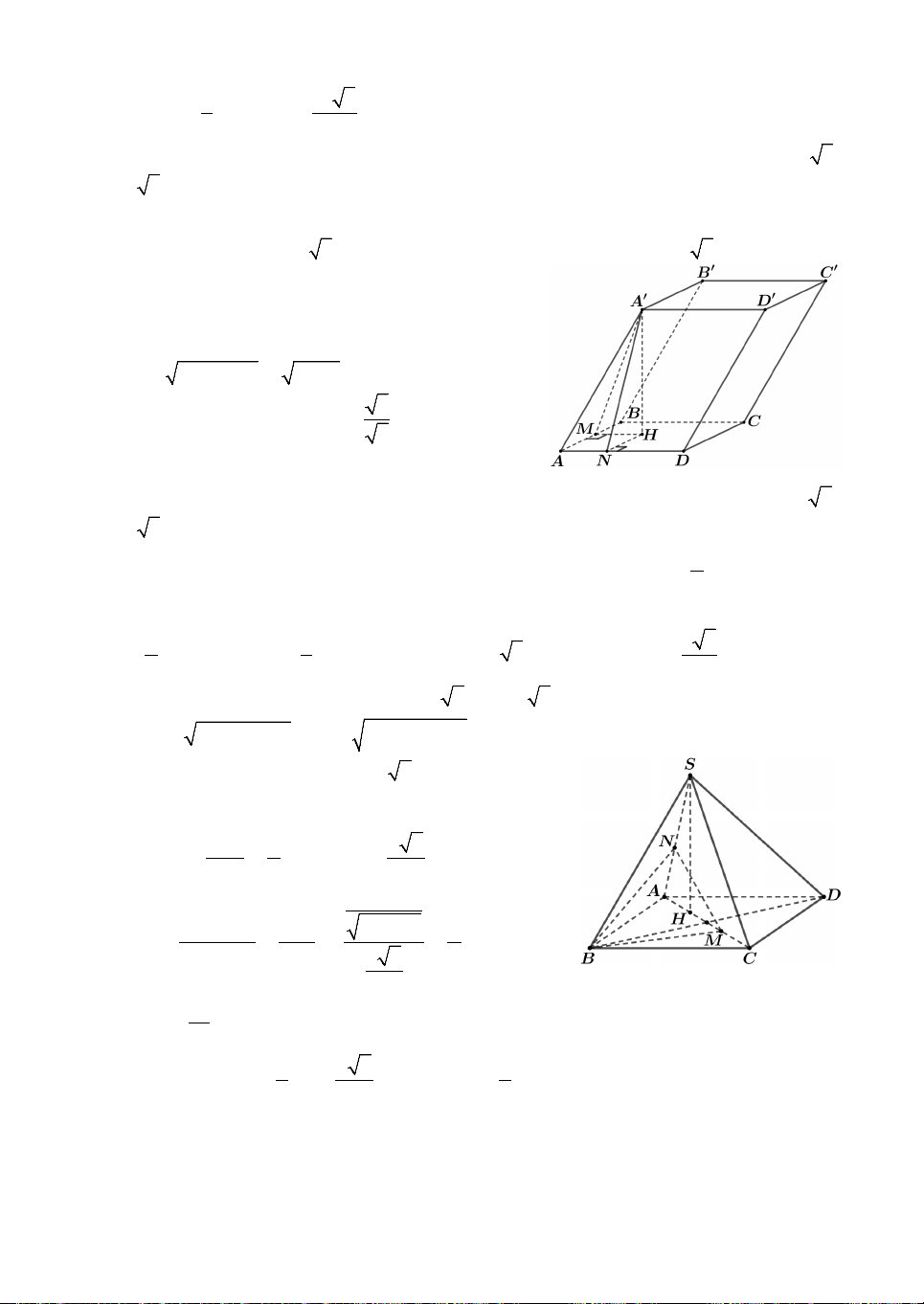
Câu 4. Cho hình đa diện như hình vẽ, trong đó
ABCD.AB CD
  là hình hộp chữ nhật với
AB AD  2 , a AA  ,
a S.ABCD là hình chóp
có các cạnh bên bằng nhau và bằng a 3. Thể
tích của khối tứ diện SABD có thể tích bằng 3 A. a 2 3 2a . B. . 2 3 3 C. 2a a 2 . D. . 3 6
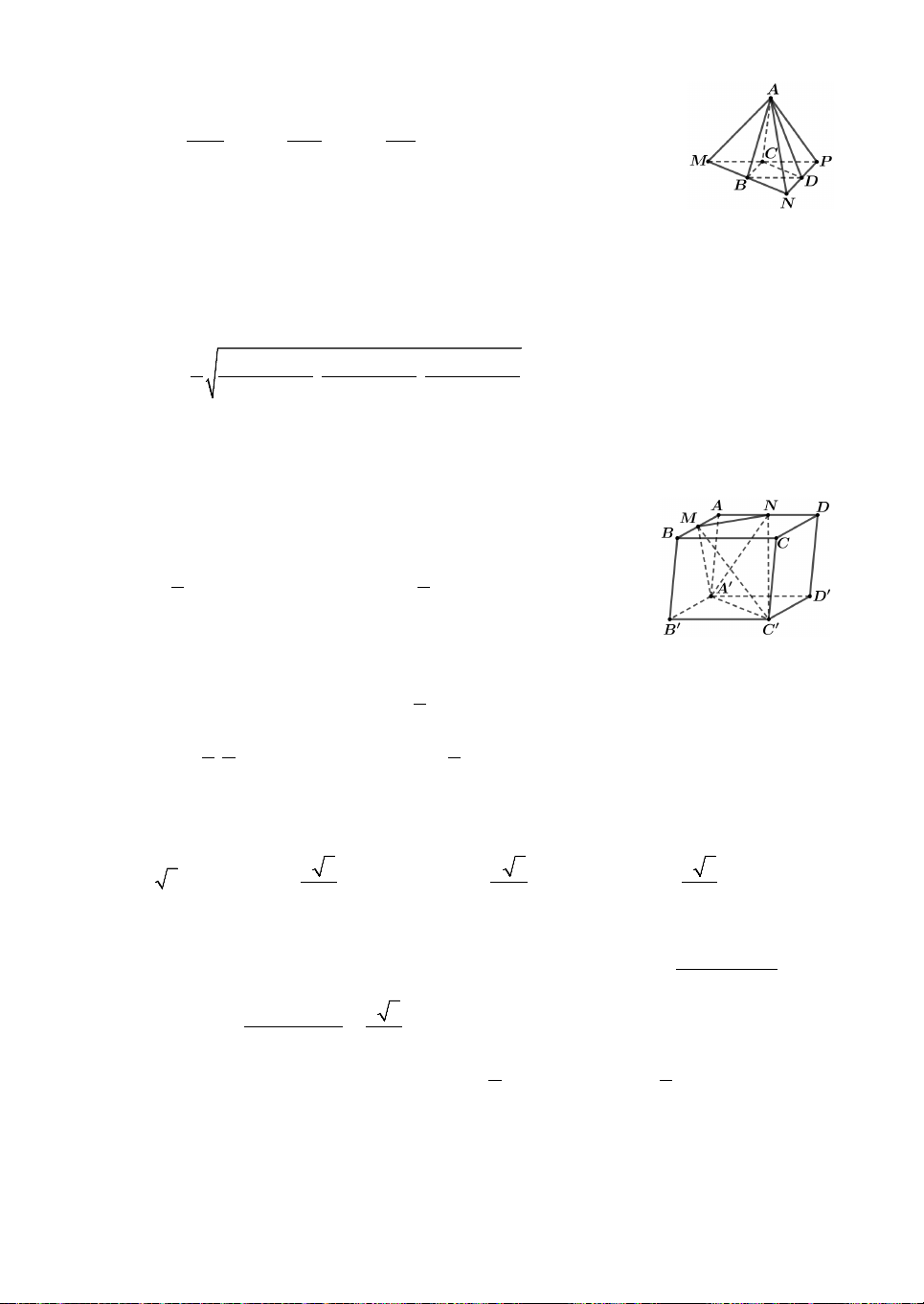
Câu 5. Cho khối lăng trụ ABC.AB C
  có thể tích là V. Hai mặt phẳng ACB và
BAC  chia khối lăng trụ đã cho thành bốn phần. Thể tích của phần có thể tích lớn nhất bằng 1 A. 1V. B. 2V. C. 3V. D. 5 V. 2 5 5 12
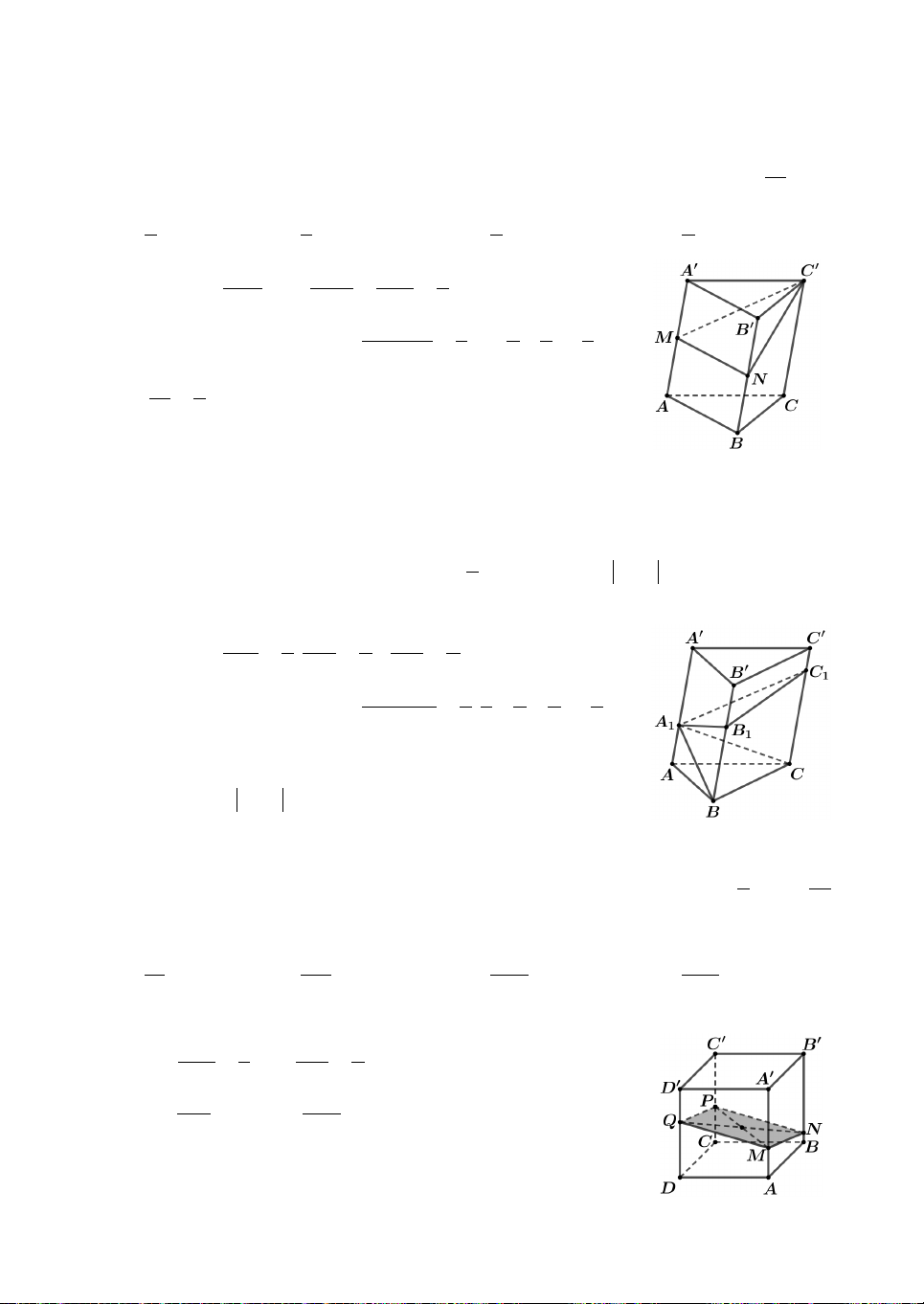
Câu 6. Cho hình lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác đều cạnh , a AA  .
a Gọi E là trung điểm cạnh AC, mặt phẳng AB E
  cắt BC tại F. Thể
tích khối đa diện CAB FE bằng 3 3 3 3 A. a 3 a 3 a 3 a 3 . B. . C. . D. . 4 8 15 16
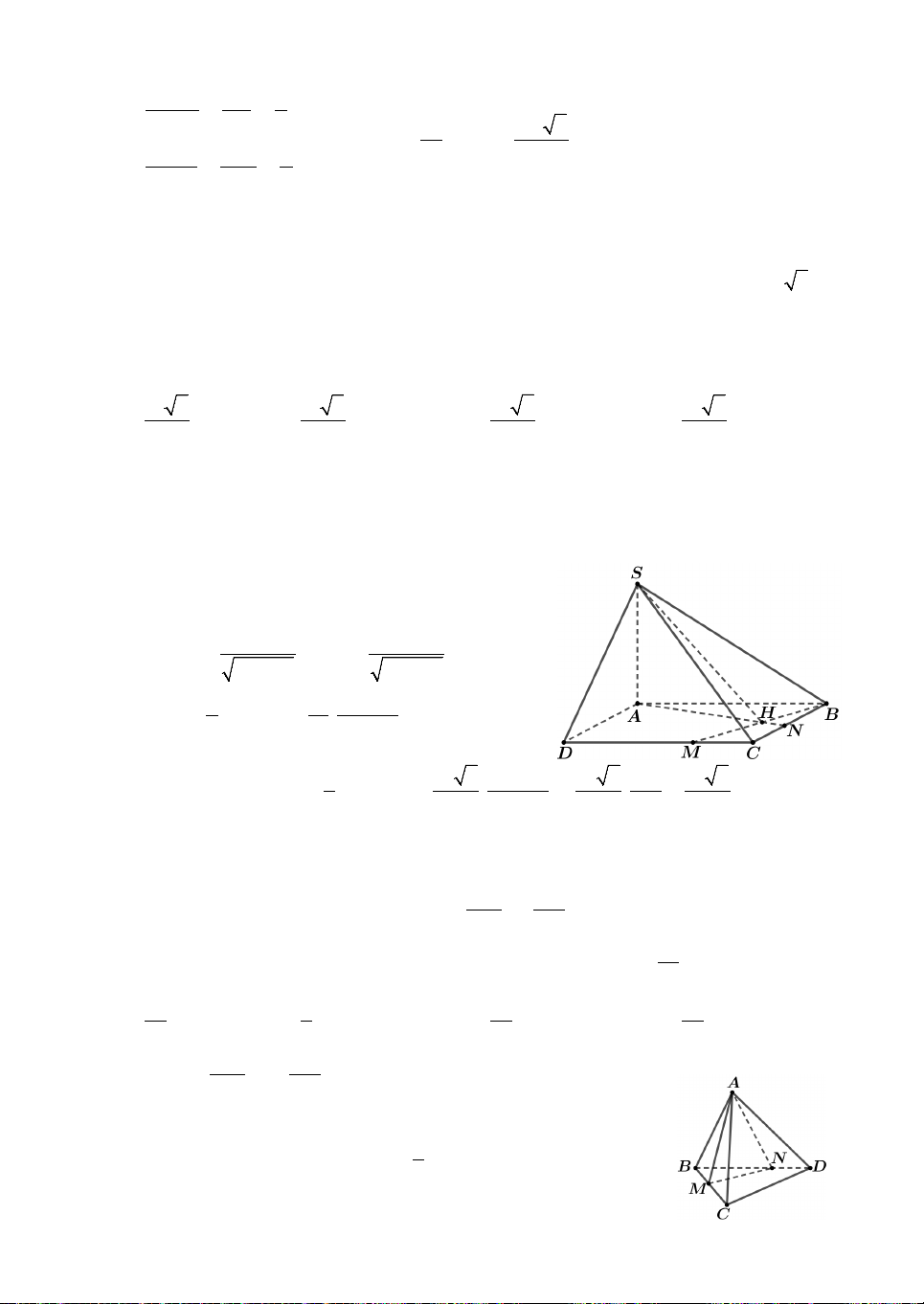
Câu 7. Cho hình lăng trụ tam giác đều ABC.AB C
  có tất cả các cạnh bằng . a Gọi
M , N lần lượt là trung điểm của các cạnh AB và B C
 . Mặt phẳng AMN  cắt cạnh
BC tại P. Thể tích khối đa diện MBP.AB N  bằng 3 3 3 3 A. a 3 7a 3 7a 3 7a 3 . B. . C. . D. . 32 32 48 96
Câu 8. Cho hình lăng trụ ABC.AB C   có thể tích 3
96 cm . Gọi G là trọng tâm của
tam giác AB C
  và H là trung điểm của BC. Thể tích khối tứ diện B GAH bằng A. 3 12 cm . B. 3 16 cm . C. 3 18 cm . D. 3 24 cm .
Câu 9. Cho lăng trụ tam giác ABC.AB C
  có thể tích bằng V. Gọi M , N, P lần lượt
là trung điểm của các cạnh AB , BC, CC . Mặt phẳng MNP chia khối lăng trụ
thành hai phần, phần chứa điểm V
B có thể tích là V . Tỉ số 1 bằng 1 V A. 1. B. 25. C. 49 . D. 73 . 3 72 144 216
Câu 10. Cho hình lăng trụ ABC.AB C
  có thể tích bằng V. Gọi M , N, P lần lượt là
trung điểm của các cạnh AB, AC , BB . Thể tích của khối tứ diện CMNP bằng A. V V V V . B. . C. 5 . D. 7 . 3 4 24 24
Câu 11. Cho tứ diện ABCD có AB CD  5, AC BD  34, AD BC  41. Thể
tích của tứ diện ABCD bằng A. 10. B. 20. C. 30. D. 40.
Câu 12. Cho hình hộp ABCD.AB CD   có thể tích 3
120 cm . Gọi M , N lần lượt là
trung điểm AB và AD. Thể tích khối tứ diện MNAC  bằng: A. 3 15 cm . B. 3 20 cm . C. 3 24 cm . D. 3 30 cm .
Câu 13. Cho tứ diện ABCD có 2 2 S  4 cm , S
 6 cm , AB  3cm. Góc giữa hai ABC ABD
mặt phẳng ABC và ABD bằng 60. Thể tích của khối tứ diện đã cho bằng A. 2 3 4 3 8 3 3 2 3 cm . B. 3 cm . C. 3 cm . D. 3 cm . 3 3 3
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích V.
Gọi E là điểm trên cạnh SC sao cho EC  2ES. Gọi  là mặt phẳng chứa đường 2
thẳng AE và song song với đường thẳng BD,  cắt hai cạnh SB, SD lần lượt tại hai
điểm M, N. Thể tích khối chóp S.AMEN bằng A. V V V V . B. . C. . D. . 6 9 12 27
Câu 15. Cho hình chóp S.ABCD có đáy là hình thoi, SA vuông góc với đáy. Mặt
phẳng P qua A vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại G, F, E. Biết rằng  SF
P  chia khối chóp thành hai phần có thể tích bằng nhau. Tính k  . SC A. 13 1    k  . B. 13 1 k  . C. 17 1 k  . D. 17 1 k  . 4 6 4 8
Câu 16. Cho khối lăng trụ ABC.AB C
 . Gọi M , N lần lượt là trung điểm của hai
cạnh AA và BB . Mặt phẳng C MN
 chia khối lăng trụ đã cho thành hai phần. Gọi V
V là thể tích khối C MNB A
  và V là thể tích khối ABC.MNC . Khi đó tỷ số 1 bằng 1 2 V2 A. 1 . B. 1. C. 2 . D. 3 . 2 3 3 4
Câu 17. Cho hình lăng trụ tam giác ABC.AB C
  có thể tích là V và có độ dài cạnh
bên AA  6. Trên cạnh A , A B B  , C C
 lần lượt lấy các điểm A , B , C sao cho 1 1 1
A A  2, B B x, C C y với x, y là các số thực dương thỏa mãn xy  12. Biết rằng 1 1 1
thể tích của khối đa diện ABC.A B C bằng 1V. Giá trị của x y bằng 1 1 1 2 A. 1. B. 2. C. 3. D. 4.
Câu 18. Cho hình lập phương ABCD.AB CD
  có các cạnh bằng , a một mặt phẳng  a a
 cắt các cạnh AA , BB , CC , DD lần lượt tại M , N, P, Q. Biết 2 AM  , CP  . 3 5
Thể tích khối đa diện ABCD.MNPQ bằng 3 3 3 3 A. a 2a 11a 11a . B. . C. . D. . 3 3 15 30
Câu 19. Cho hình chóp đều S.ABC có đáy ABC là tam giác đều cạnh .
a Gọi E, F
lần lượt là trung điểm của các cạnh SB, SC. Biết mặt phẳng AEF  vuông góc với
mặt phẳng SBC. Thể tích khối chóp S.ABC bằng 3 3 3 3 A. a 5 a 3 a 5 a 15 . B. . C. . D. . 8 24 24 27
Câu 20. Cho hình chóp đều S.ABC có cạnh bên bằng .
a Gọi E, F lần lượt là trung
điểm của các cạnh SB, SC. Biết mặt phẳng AEF  vuông góc với mặt phẳng SBC.
Thể tích khối chóp S.ABC bằng 3 3 3 3 A. a 5 a 3 a 5 a 15 . B. . C. . D. . 8 24 24 27 3
Câu 21. Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh . a Gọi M là trung điểm .
SA Biết mặt phẳng MCD vuông góc với mặt phẳng SAB. Thể tích của
khối chóp S.ABCD bằng 3 3 3 3 A. a a 5 a 3 a 5 . B. . C. . D. . 3 2 6 6
Câu 22. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BC  . a Cạnh
bên SA vuông góc với đáy, góc  0
BSC  45 , mặt phẳng SAC  tạo với mặt phẳng SBC một góc 0
60 . Thể tích khối chóp S.ABC bằng 3 3 3 3 A. a 6 a 2 a 3 a 6 . B. . C. . D. . 15 18 24 30
Câu 23. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh ,
a mặt bên SAB là
tam giác đều, mặt bên SCD là tam giác vuông cân tại S. Gọi M là điểm thuộc đường
thẳng CD sao cho BM vuông góc với .
SA Thể tích của khối chóp S.BDM bằng 3 3 3 3 A. a 3 a 3 a 3 a 3 . B. . C. . D. . 16 24 32 48
Câu 24. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và hai tam giác
SAC và SBD là những tam giác đều. Gọi A', C ' lần lượt là trung điểm của SA và
SC. Thể tích khối tứ diện A' BC ' D bằng 3 3 3 3 A. a 3 a 3 a 6 a 6 . B. . C. . D. . 16 24 24 32
Câu 25. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh .
a Cạnh bên SA
vuông góc với đáy, SC a 3. Gọi M , N, P, Q lượt là trung điểm của SB, SD, CD,
BC. Thể tích của khối chóp . A MNPQ bằng 3 3 3 3 A. a a a a . B. . C. . D. . 3 4 8 12
Câu 26. Cho lăng trụ ABC.AB C
  có đáy ABC là tam giác vuông tại A và góc  0
ABC  30 . Gọi M là trung điểm của AB, tam giác MAC đều cạnh a và nằm trong
mặt phẳng vuông góc với đáy ABC. Thể tích khối lăng trụ đã cho bằng 3 3 3 3 A. a 2a 3a 5a . B. . C. . D. . 7 7 7 7
Câu 27. Cho hình lăng trụ đều ABC.AB C
 . Biết khoảng cách từ điểm C đến mặt
phẳng ABC  bằng ,
a góc giữa hai mặt phẳng ABC  và BCC B
  bằng với 1
cos  . Thể tích khối lăng trụ ABC.AB C   bằng 3 3 3 3 3 A. 3a 15 9a 15 3a 15 9a 15 . B. . C. . D. . 10 10 20 20
Câu 28. Cho hình chóp S.ABCD có đáy ABCD là hình thang cân với AD  2AB
 2BC  2CD  2 .
a Cạnh bên SA vuông góc với đáy. Gọi M , N lần lượt là trung 4 3 điểm của a 3
SB và CD. Biết thể tích khối chóp S.ABCD bằng . Cosin góc giữa 4
MN và SAC  bằng A. 5 . B. 3 5 . C. 310 . D. 3 310 . 10 10 20 20
Câu 29. Cho khối chóp S.ABC có SA  6, SB  2, SC  4, AB  2 10 và   SBC ASC 0
 90 . Thể tích khối chóp S.ABC bằng A. 4 3. B. 6 3. C. 8 3. D. 12 3.
Câu 30. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  1,
AD  10; SA SB, SC SD. Biết hai mặt phẳng SAB và SCD cùng vuông góc
với nhau và tổng diện tích hai tam giác SAB và SCD bằng 2. Thể tích khối chóp
S.ABCD bằng A. 1 . B. 1. C. 3 . D. 2. 2 2
Câu 31. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh ,
A BC  2a,
SB SC, SA  2a và SA tạo với đáy một góc 60. Biết H là hình chiếu vuông góc của
đỉnh S trên mặt đáy ABC thuộc tam giác ABC. Thể tích khối chóp S.AHC bằng 3 3 3 3 A. a 3 a 3 a 3 a 3 . B. . C. . D. . 3 6 9 12
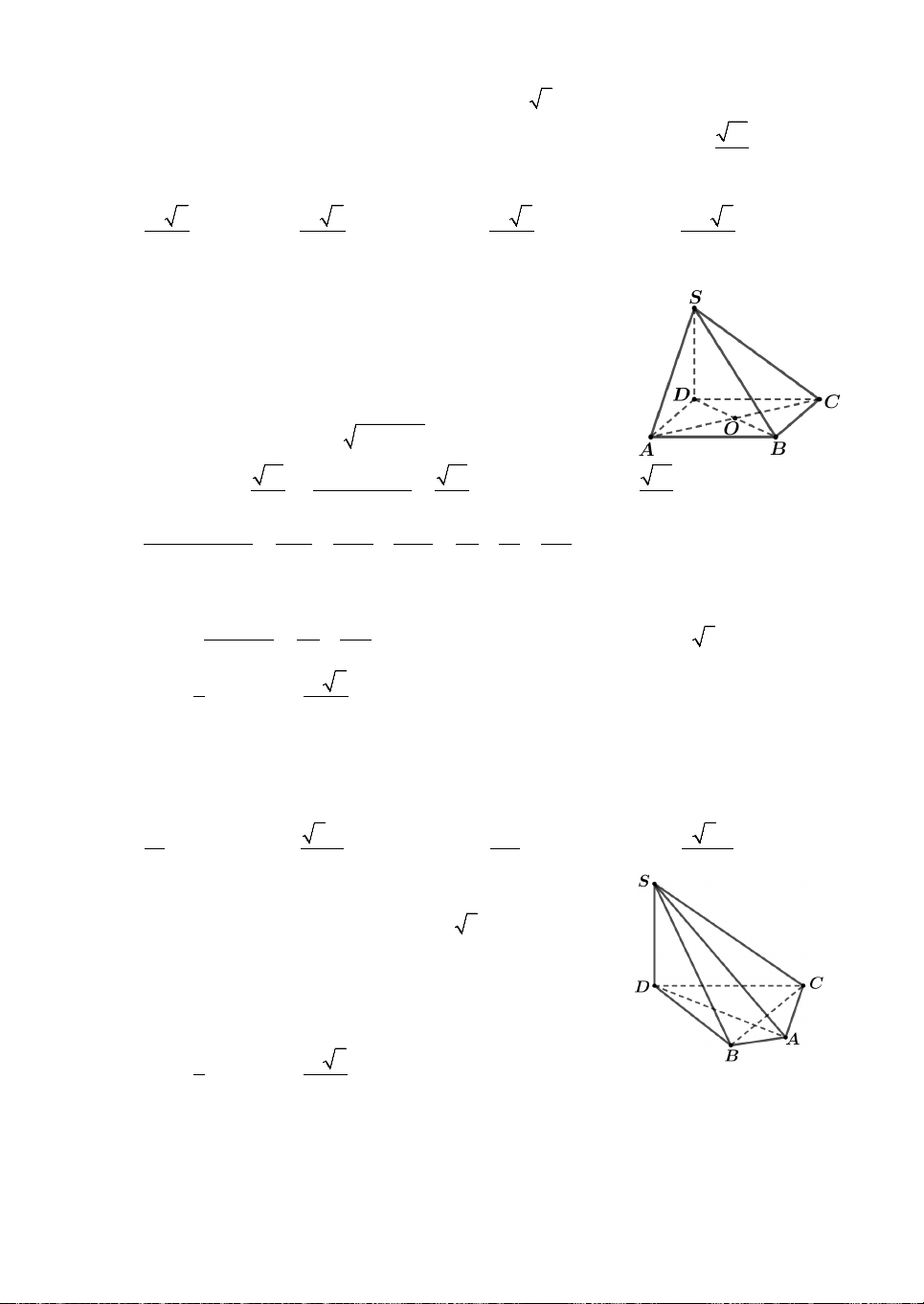
Câu 32. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, AB  , a
BC a 3; tam giác SOA cân tại S và mặt phẳng SAD vuông góc vói
mặt đáy ABCD. Biết góc giữa SD và mặt phẳng ABCD bằng 0 60 . Thể tích khối
chóp S.ABCD bằng 3 3 3 3 A. a 3 2a 3 a 3 a 3 . B. . C. . D. . 3 3 6 9
Câu 33. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh . a Các mặt bên
SAB, SAC lần lượt tạo với đáy các góc là 0 0
60 , 30 . Hình chiếu vuông góc của S
trên mặt phẳng ABC nằm trên cạnh BC. Thể tích khối chóp S.ABC bằng 3 3 3 3 A. a 3 a 3 a 3 a 3 . B. . C. . D. . 4 12 32 64
Câu 34. Cho hình chóp S.ABC có đáy ABC là tam giác với AB AC  5 ,
a BC  6a
và các mặt bên cùng tạo với đáy các góc 60. Hình chiếu vuông góc của S trên mặt
phẳng ABC nằm bên trong tam giác ABC. Thể tích khối chóp S.ABC bằng 3 A. 2a . B. 3 a 3. C. 3 6a 3. D. 3 8a . 3
Câu 35. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  , a AD  2 . a
Hình chiếu vuông góc của S xuống mặt phẳng ABCD thuộc đoạn BD. Hai mặt 5
phẳng SBC và SCD lần lượt hợp với đáy các góc 0 60 và 0 30 . Thể tích khối chóp S.ABCD bằng 3 3 3 3 A. a 3 4a 3 a 3 4a 3 . B. . C. . D. . 5 5 15 15
Câu 36. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và  0 BAD  60 .
Các mặt phẳng SAB, SBD và SAD cùng hợp với đáy ABCD một góc 60. Biết
hình chiếu vuông góc của S trên mặt đáy nằm ngoài tam giác ABD. Thể tích của
khối chóp S.ABCD bằng 3 3 3 3 A. a 3 a 3 a 3 a 3 . B. . C. . D. . 2 4 6 12
Câu 37. Cho lăng trụ ABCD.AB CD
  có đáy ABCD là hình chữ nhật với AB  3,
AD  7, cạnh bên bằng 1. Hai mặt bên ABB A   và ADD A
  lần lượt tạo với đáy những góc bằng 0 45 và 0
60 . Thể tích khối lăng trụ đã cho bằng A. 3. B. 3 3. C. 7. D. 7 7.
Câu 38. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  6,
AD  3, tam giác SAC nhọn và nằm trong mặt phẳng vuông góc với đáy. Biết hai
mặt phẳng SAB và SAC tạo với nhau góc thỏa mãn 3
tan  ; cạnh SC  3. 4
Thể tích khối S.ABCD bằng A. 4 . B. 8 . C. 3 3. D. 5 3 . 3 3 3
Câu 39. Cho hình chóp S.ABC có AB  ,
a AC a 3, SB  2a và   ABC BAS   BCS
 90. Sin của góc giữa đường thẳng SB và mặt phẳng SAC  bằng 11 . Thể tích 11
khối chóp S.ABC bằng 3 3 3 3 A. a 6 a 6 a 3 2a 3 . B. . C. . D. . 3 6 9 9
Câu 40. Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A với AB a và  BAC  120 ,   
SBA SCA  90. Biết góc giữa SB và mặt đáy ABC  bằng 60 , thể tích
khối chóp S.ABC bằng 3 3 3 3 A. a 3a 3a 3 3a . B. . C. . D. . 4 4 4 4
Câu 41. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và  
SBA SCA  90. Biết góc giữa hai mặt phẳng SAB và mặt đáy ABC  bằng 60 ,
thể tích khối chóp S.ABC bằng 3 3 3 3 A. 3a 3a 3a 3a . B. . C. . D. . 4 6 12 24 6
Câu 42. Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A với AB a và  BAC  120 ,   
SBA SCA  90. Biết góc giữa SB và mặt phẳng SAC  thỏa mãn 3 sin
, khoảng cách từ S đến mặt đáy ABC  nhỏ hơn 2 .
a Thể tích khối chóp 8
S.ABC bằng 3 3 3 3 A. 3a 3a 3a 3a . B. . C. . D. . 4 6 12 24
Câu 43. Cho lăng trụ tam giác ABC.AB C
  có độ dài cạnh bên bằng 4 và khoảng
cách từ điểm A đến các đường thẳng BB , CC  lân lượt bằng 1 và 2. Biết góc giữa hai mặt phẳng ABB A   và ACC A
  bằng 60. Tính thể tích khối lăng trụ ABC.AB C  . A. 3. B. 2 3. C. 3 3. D. 4 3.
Câu 44. Cho khối lăng trụ ABC.ABC , khoảng cách từ C đến đường thẳng BB
bằng 2, khoảng cách từ A đến các đường thẳng BB và CC  lần lượt bằng 1 và 3.
Hình chiếu vuông góc của A lên mặt phẳng ABC  là trung điểm M của BC  và A 2 3 M
. Thể tích của khối lăng trụ đã cho bằng 3 A. 2 3 . B. 1. C. 3. D. 2. 3
Câu 45. Cho khối lăng trụ ABC.ABC , khoảng cách từ C đến đường thẳng BB
bằng 2, khoảng cách từ A đến các đường thẳng BB và CC  lần lượt bằng 1 và 3.
Hình chiếu vuông góc của A lên mặt phẳng ABC  là trọng tâm G của tam giác 4
ABC  và AG  . Thể tích của khối lăng trụ đã cho bằng 3 A. 2 . B. 4 . C. 8 . D. 2. 3 3 3
Phần 2. Tỷ số thể tích
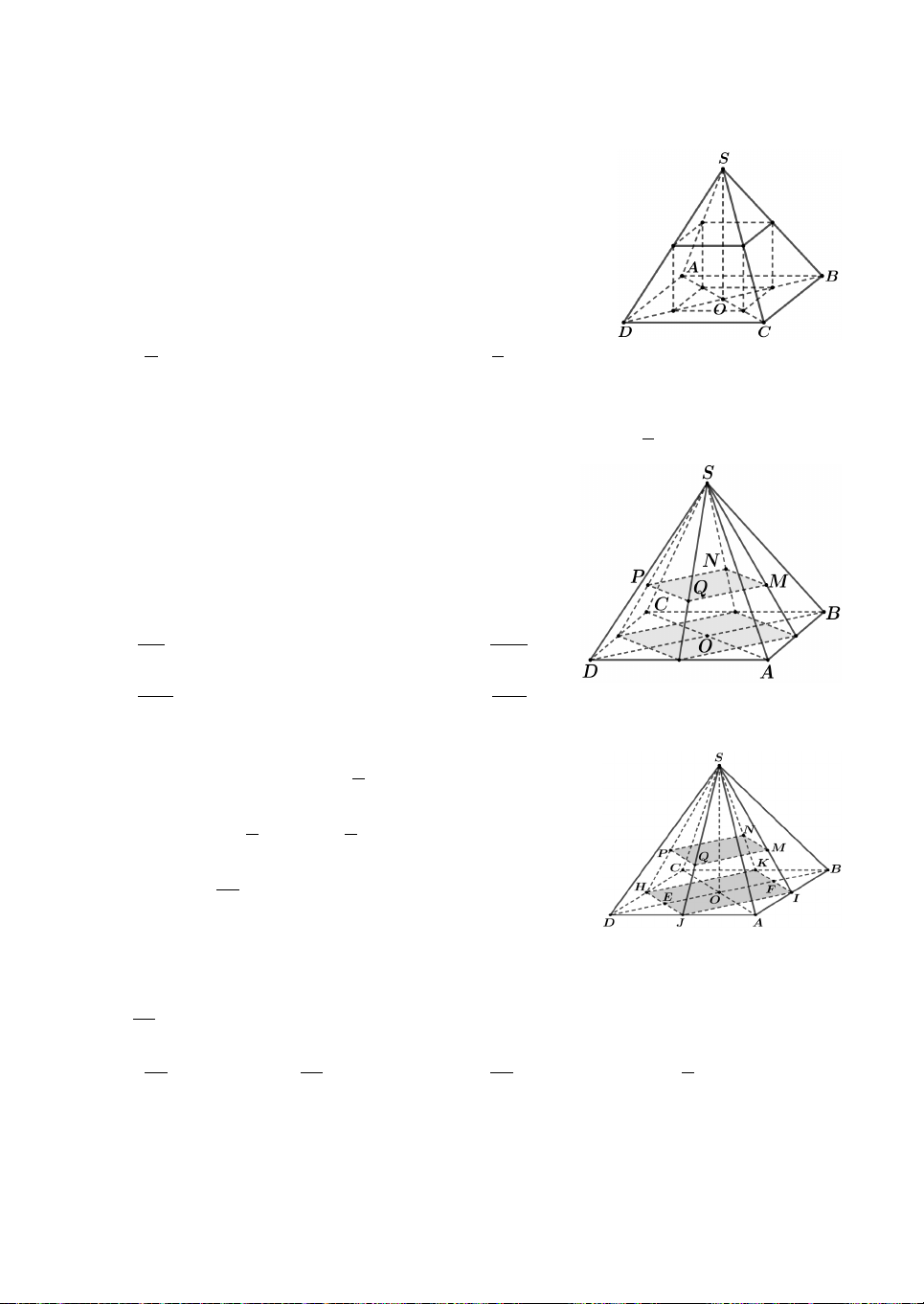
Câu 1. Cho hình chóp tứ giác đều S.ABCD. Gọi H là
hình hộp chữ nhật có bốn đỉnh là bốn trung điểm của các cạnh bên , SA SB, SC,
SD và bốn đỉnh còn lại nằm trong
mặt đáy ABCD (tham khảo hình vẽ). Biết thể tích khối
hộp H là V. Thể tích của khối chóp đã cho bằng A. 2V. B. 6V. C. 4V. D. 8V. 3 3 7
Câu 2. Cho khối chóp S.ABCD có đáy là hình bình
hành ABCD. Gọi M,
N, P, Q lần lượt là trọng tâm
các tam giác SAB, SBC, SCD, .
SDA Biết khối chóp
S.MNPQ có thể tích là V , khi đó thể tích của khối
chóp S.ABCD bằng A. 9V V . B. 27 . 4 4 C. 81V V . D. 81 . 4 8
Câu 3. Cho khối tứ diện ABCD có thể tích V. Gọi M, N, P, Q lần lượt là trọng tâm
của các tam giác ABC, ABD, ACD, BCD. Gọi V  là thể tích của khối tứ diện MNPQ.  Tỉ số V bằng V A. 1 . B. 2 . C. 4 . D. 1 . 27 27 27 9
Câu 4. Cho lăng trụ tam giác ABC.MNP có thể tích V. Gọi G , G , G , G lần lượt là 1 2 3 4
trọng tâm của các tam giác ABC, ACM , AMB, BCM ; V là thể tích khối tứ diện 1
G G G G . Khẳng định nào sau đây đúng ? 1 2 3 4
A. V  9V .
B. V  27V .
C. V  81V .
D. 8V  81V . 1 1 1 1
Câu 5. Cho khối tứ diện đều ABCD có thể tích V. Gọi M , N, P lần lượt là trọng tâm 
các tam giác ABC, ACD, ADB và V  là thể tích khối tứ diện AMNP. Tỉ số V bằng V A. 4 . B. 2 . C. 4 . D. 8 . 9 27 27 81
Câu 6. Cho khối lập phương ABCD.AB CD
  có cạnh bằng 1. Gọi
M , N, P, L lần lượt là tâm của các hình vuông ABB A  , AB CD  , ADD A   và CDD C
 . Gọi Q là trung điểm của BL
(tham khảo hình vẽ bên). Thể tích khối tứ diện MNPQ bằng A. 1 . B. 1 . C. 2 . D. 3 . 16 24 27 27
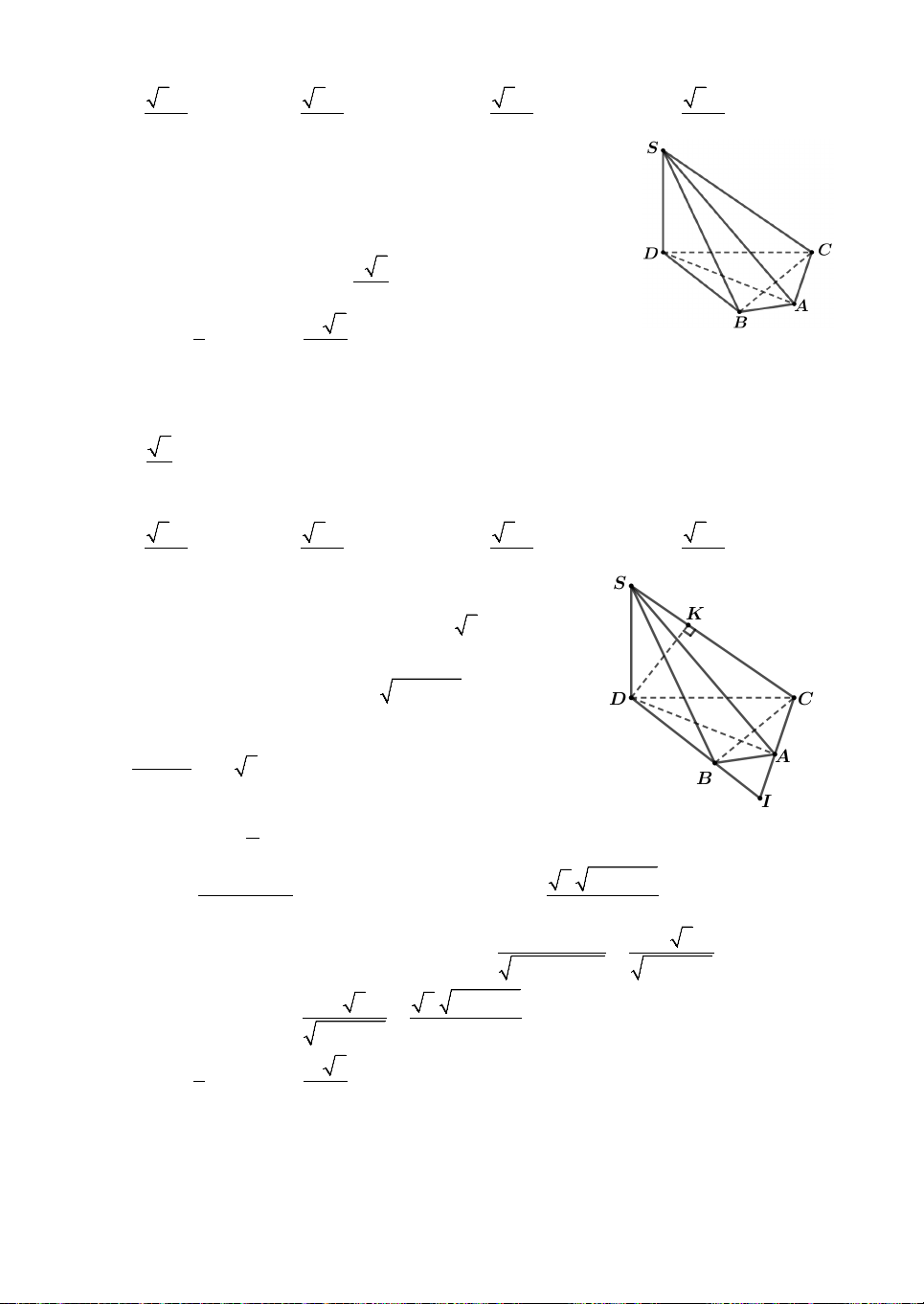
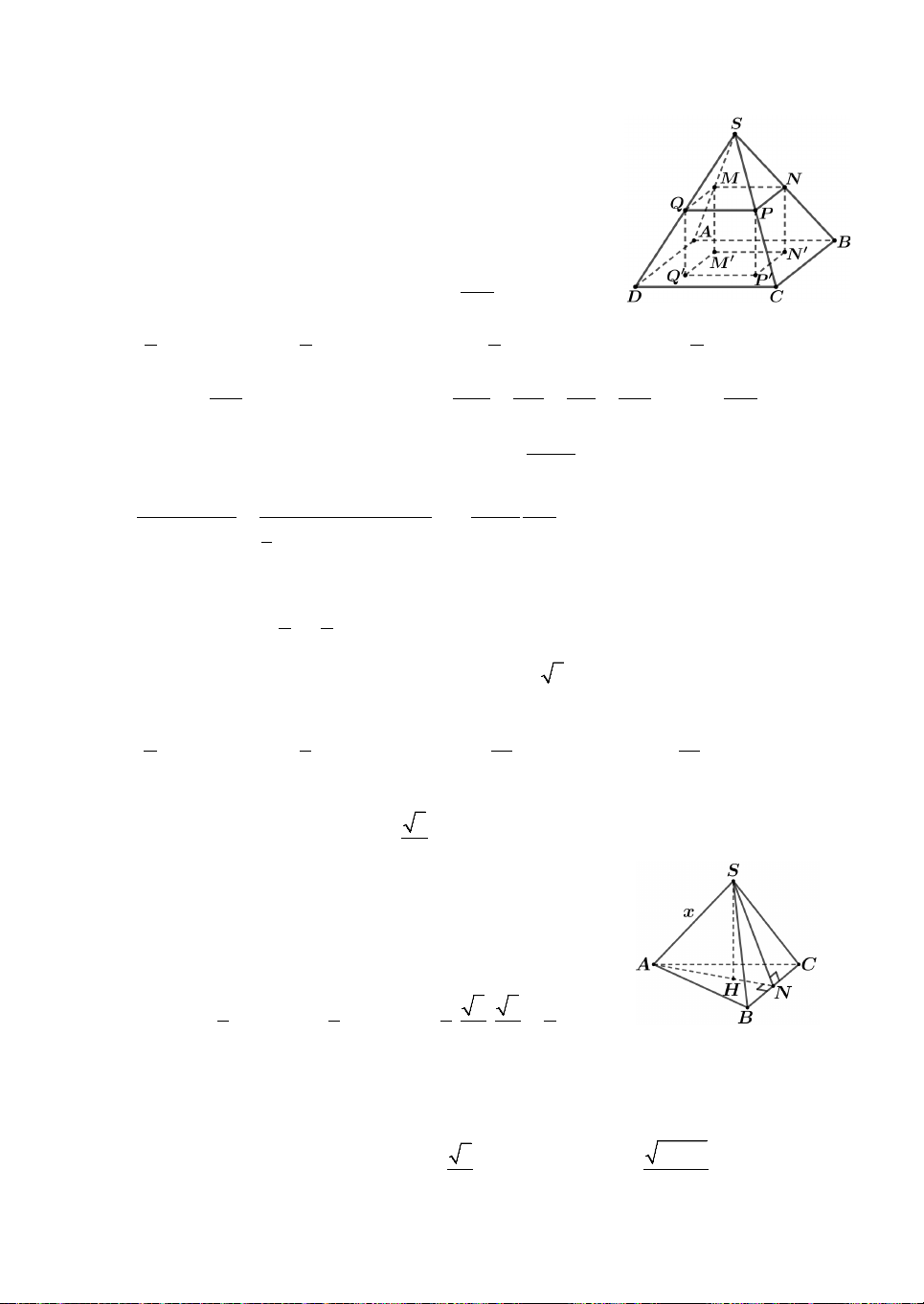
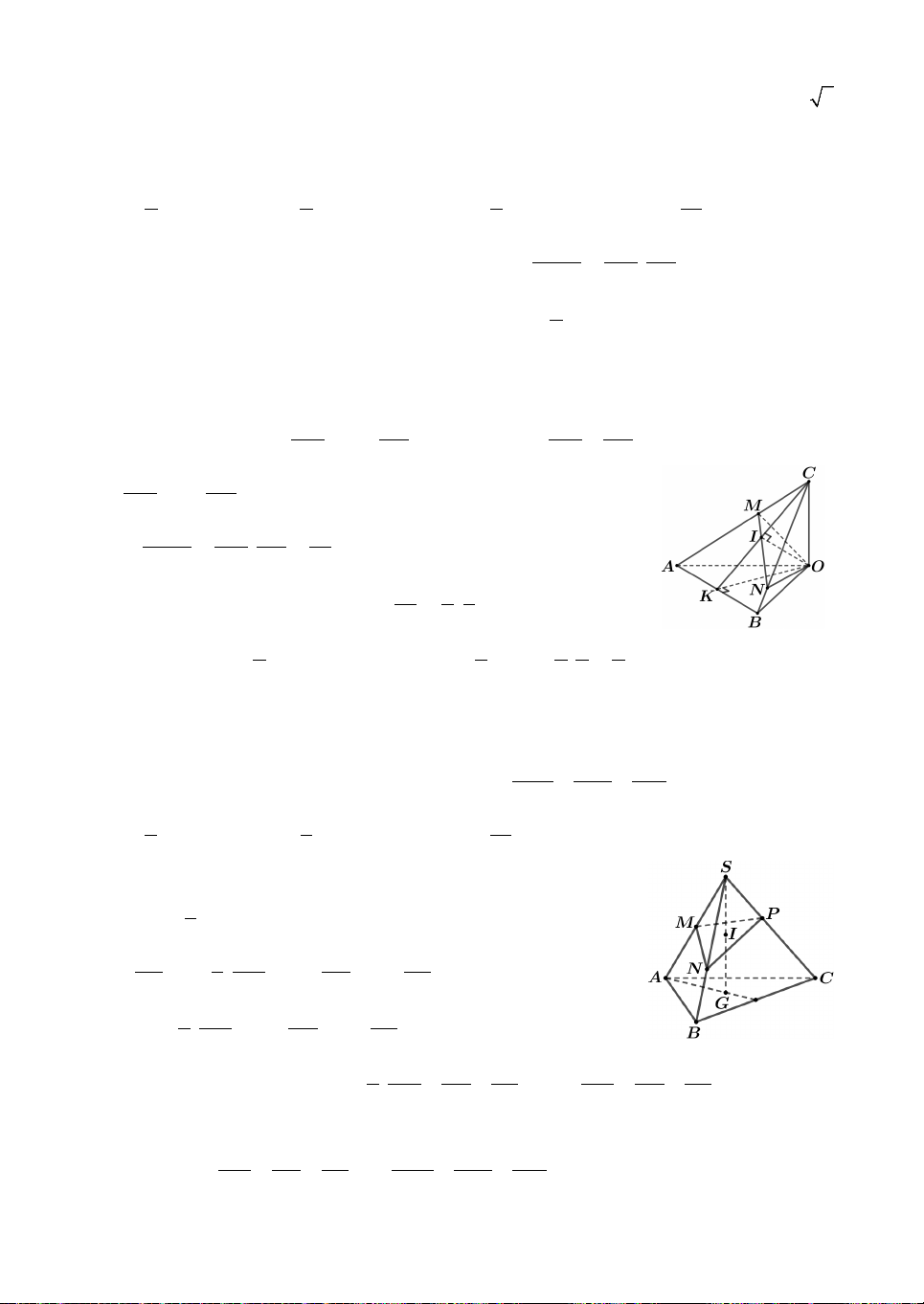
Câu 7. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh ,
a SA vuông góc với
mặt đáy. Gọi M là trung điểm BC. Mặt phẳng P đi qua A và vuông góc với SM
cắt SB, SC lần lượt tại E, F. Biết 1 VV
. Thể tích khối chóp S.ABC bằng SAEF 4 SABC 3 3 3 3 A. a 2a a a . B. . C. . D. . 2 5 8 12 8
Câu 8. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên
SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy ABC . Gọi V 16
H là hình chiếu vuông góc của A lên SC. Biết S.ABH  . Thể tích của khối V 19 S.ABC
chóp S.ABC bằng A. 3 . B. 3 . C. 3 . D. 3 . 2 4 6 12
Câu 9. Cho hình chóp đều S.ABC. Gọi G là trọng tâm tam giác ABC, góc giữa SG và
mặt phẳng SBC là 30. Mặt phẳng P chứa BC và vuông góc với SA chia khối
chóp S.ABC thành hai phần. Tỉ số thể tích hai phần bằng A. 2 . B. 1 . C. 1 . D. 6 . 3 6 7 7
Câu 10. Cho lăng trụ tam giác đều ABC.AB C
  có cạnh đáy bằng , a chiều cao bằng 2 .
a Mặt phẳng P qua B và vuông góc AC chia lăng trụ thành hai khối. Biết thể tích của hai khối là V
V và V với V V . Tỉ số 1 bằng 1 2 1 2 V2 A. 1 . B. 1 . C. 1 . D. 1 . 7 11 23 47
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB CD, AB  2CD. Gọi V
M , N lần lượt là trung điểm của SA và SD. Tỉ số S.BCNM bằng VS.BCDA A. 1. B. 1 . C. 3. D. 5 . 3 4 8 12
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm di
động trên cạnh AB và N là trung điểm của SD. Mặt phẳng  đi qua M, N và song song với V 3
BC chia khối chóp S.ABCD thành hai khối có tỷ số thể tích 1  , V 5 2
trong đó V là thể tích khối đa diện chứa đỉnh ,
A V là thể tích khối đa diện chứa 1 2
đỉnh B. Tỉ số AM bằng AB A. 1 . B. 1. C. 3. D. 3. 2 3 5 7
Câu 13. Cho hình hộp ABCD.AB CD
 . Gọi M là điểm thuộc đoạn CC  thỏa mãn
CC   3CM. Mặt phẳng AB M
  chia khối hộp thành hai phần có thể tích là V , V . 1 2 Gọi V
V là thể tích phần chứa điểm B. Tỉ số 1 bằng 1 V2 A. 7 . B. 13 . C. 7 . D. 13 . 9 20 27 41 9
Câu 14. Cho hình hộp ABCD.AB CD  . Gọi M , N,
P lần lượt là trung điểm của
AA , BC, CD. Mặt phẳng MNP chia khối hộp thành hai phần có thể tích là V , V . 1 2 Gọi V
V là thể tích phần chứa điểm C. Tỉ số 1 bằng 1 V2 A. 3 . B. 113. C. 119 . D. 119 . 4 24 25 425
Câu 15. Cho hình lăng trụ tam giác đều ABC.AB C
  có tất cả các cạnh bằng . a Gọi
M , N lần lượt là trung điểm của các cạnh AB và B C
 . Mặt phẳng AMN  cắt cạnh
BC tại P. Thể tích khối đa diện MBP.AB N  bằng 3 3 3 3 A. 3a 3a 7 3a 7 3a . B. . C. . D. . 12 24 32 96
Câu 16. Cho hình hộp ABCD.AB CD
  có M , N, P lần lượt là trung điểm ba cạnh
AB , BB và D D
 . Mặt phẳng MNP cắt đường thẳng AA tại I. Biết thể tích khối
tứ diện IANP là V. Thể tích khối hộp đã cho ABCD.AB CD   bằng A. 2V. B. 4V. C. 6V. D. 12V.
Câu 17. Cho lăng trụ tam giác đều ABC.AB C
 . Trên AB kéo dài lấy điểm M sao cho 1 B M
AB . Gọi N, P lần lượt là trung điểm của AC , B B
 . Mặt phẳng MNP 2
chia khối lăng trụ ABC.AB C
  thành hai khối đa diện, trong đó khối đa diện chứa đỉnh V
A có thể tích V , khối đa diện chứa đỉnh C  có thể tích V . Tỉ số 1 bằng 1 2 V2 A 97 . B 49 . C. 49 . D. 95 . 59 95 144 144
Câu 18. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng ,
a cạnh bên hợp với đáy góc o
60 . Gọi M là điểm đối xứng của C qua D, N là trung điểm của SC. Mặt
phẳng BMN  chia khối chóp S.ABCD thành hai phần có thể tích là V , V trong đó 1 2 V
V là phần thể tích chứa đỉnh .
A Tỉ số 2 bằng 1 V1 A. 7 . B. 5. C. 12 . D. 5 . 5 7 5 12
Câu 19. Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh B, AB  4;
SA SB SC  12. Gọi M , N lần lượt là trung điểm AC, BC. Trên cạnh , SA SB lần lượt lấy điểm SE BF E, F sao cho 2 
 . Thể tích khối tứ diện MNEF bằng SA BS 3 A. 4 34 . B. 16 34 . C. 4 17 . D. 4 34 . 3 3 9 9
Câu 20. Cho hình lập phương ABCD.AB CD
  có độ dài cạnh bằng 1. Gọi M , N, P, Q
lần lượt là trung điểm của AB, BC, C D
  và DD . Thể tích khối tứ diện MNPQ bằng 10 A. 1 . B. 3. C. 1 . D. 1 . 8 8 12 24
Câu 21. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, thể tích là V. Gọi AM
M là một điểm trên cạnh AB sao cho
x, 0  x 1. Mặt phẳng  qua M và AB
song song với SBC chia khối chóp S.ABCD thành hai phần, trong đó phần chứa điểm  x
A có thể tích bằng 4 V . Giá trị của biểu thức 1 P  bằng 27 1 x A. 1 . B. 1. C. 1. D. 3. 2 3 5 5
Câu 22. Cho hình chóp tứ giác S.ABCD. Mặt phẳng đi qua trọng tâm các tam giác
SAB, SAC, SAD chia khối chóp thành hai phần có thể tích là V và V V V . Tỉ số 1 2  1 2 V1 bằng V2 A. 8 . B. 8 . C. 16 . D. 16 . 19 27 75 81
Câu 23. Cho tứ diện đều ABCD có cạnh bằng .
a Gọi M , N lần lượt là trung điểm
AB, BC và điểm P là điểm đối xứng với B qua D. Mặt phẳng MNP chia tứ diện
thành hai phần có tỉ số thể tích là A. 1 . B. 7 . C. 7 . D. 11. 2 11 18 18
Câu 24. Cho tứ diện ABCD, trên các cạnh BC, BD,
AC lần lượt lấy các điểm M , N,
P sao cho BC  3BM , 3
BD BN, AC  2AP. Mặt phẳng MNP chia khối tứ 2 diện V
ABCD thành hai phần có thể tích là V và V . Tỉ số 1 có giá trị bằng 1 2 V2 A. 26 . B. 3 . C. 15 . D. 26 . 13 19 19 19
Câu 25. Cho tứ diện ABCD và các điểm M , N, P lần lượt thuộc các cạnh
BC, BD, AC sao cho BC  4BM , AC  3AP, BD  2BN. Tỉ số thể tích hai phần của
khối tứ diện ABCD được phân chia bởi mặt phẳng MNP bằng A. 7 . B. 8 . C. 7 . D. 8 . 13 13 15 15
Câu 26. Cho tứ diện đều ABCD có cạnh bằng .
a Gọi M , N lần lượt là trọng tâm của
các tam giác ABD, ABC và E là điểm đối xứng với B qua điểm D . Mặt phẳng
MNE chia khối tứ diện ABCD thành hai khối đa diện, thể tích khối đa diện chứa đỉnh A bằng 3 3 3 3 A. 3a 2 a 2 3a 2 9a 2 . B. . C. . D. . 80 96 320 320 11
Câu 27. Cho tứ diện đều ABCD có cạnh bằng .
a Gọi M , N lần lượt là điểm trên cạnh AM AN AB, AC sao cho 1  ,
 2. Mặt phẳng  chứa MN và song song với BM 2 CN
AD chia khối tứ diện thành hai phần. Thể tích khối đa diện chứa đỉnh A bằng 3 3 3 3 A. 4 2a 4 2a 5 2a 11 2a . B. . C. . D. . 81 108 108 342    
Câu 28. Cho khối chóp S.ABC có M  ,
SA N SB sao cho MA  2MS, NS  2NB.
Mặt phẳng  đi qua hai điểm M, N và song song với SC chia khối chóp thành hai
khối đa diện. Tỉ số thể tích của hai khối đa diện đó bằng A. 3. B. 4 . C. 4 . D. 5 . 5 5 9 9
Câu 29. Cho tứ diện đều ABCD có cạnh bằng .
a Gọi E là điểm đối xứng của A qua
D. Mặt phẳng qua CE và vuông góc với mặt phẳng ABD cắt cạnh AB tại điểm F.
Thể tích của khối tứ diện AECF bằng 3 3 3 3 A. 2a 2a 2a 2a . B. . C. . D. . 15 30 40 60
Câu 30. Cho hình chop S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt
là trung điểm của AD,
DC. Kéo dài SD một đoạn sao cho D là trung điểm của SP.
Thiết diện tạo bởi mặt phẳng MNP chia hình chóp thành hai khối lần lượt có thể tích là V
V , V (trong đó V là thể tích của phần chứa điểm S ). Tỉ số 1 bằng 1 2 2 V2 A. 3 . B. 71 . C. 72 . D. 71 . 4 49 49 120 Phần 3. Cực trị
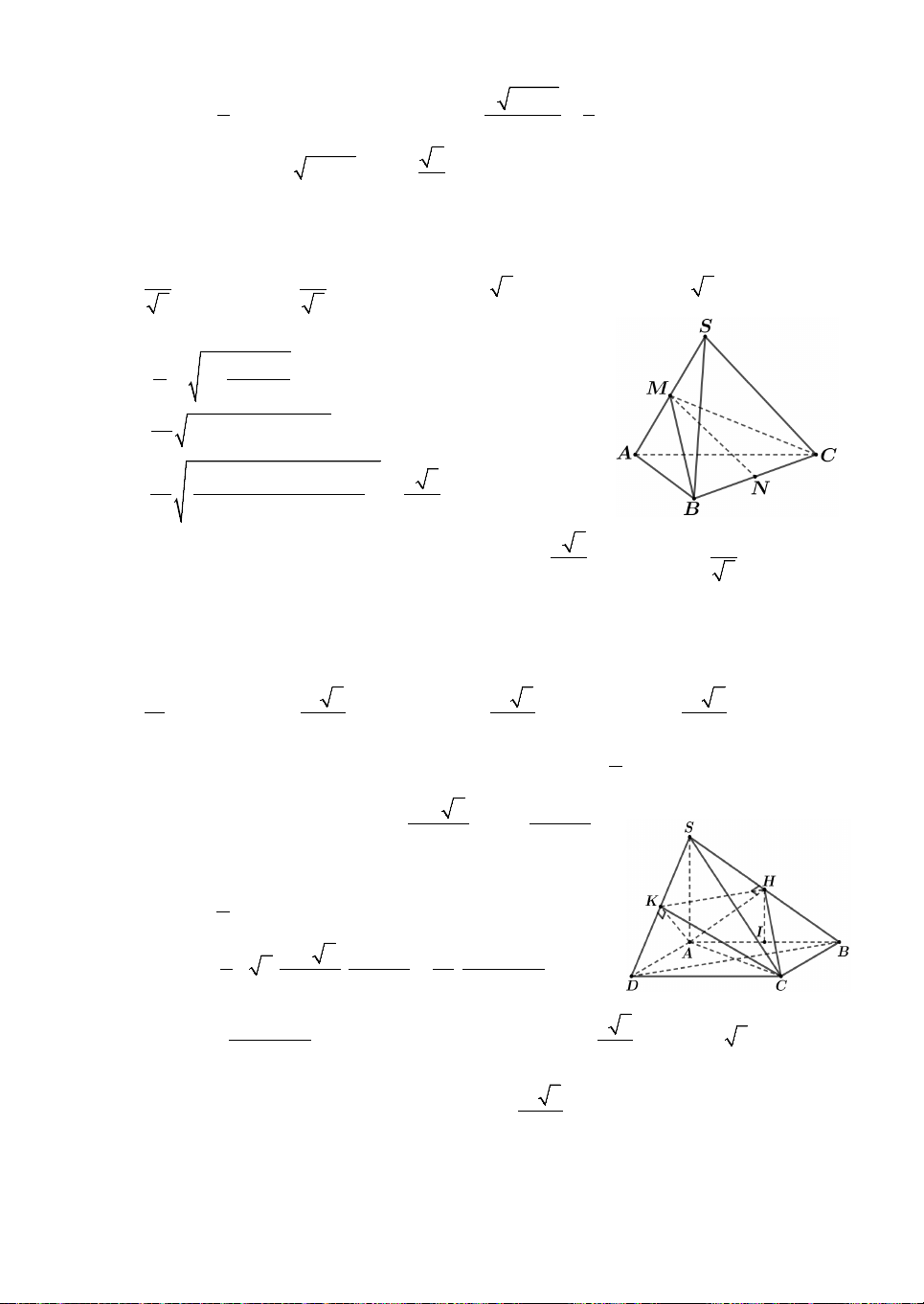
Câu 1. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , SA vuông
góc với đáy, khoảng cách từ A đến mặt phẳng SBC bằng 3 . Gọi là góc giữa hai
mặt phẳng SBC và ABC, tính cos khi thể tích khối chóp S.ABC nhỏ nhất. A. 2 cos  . B. 1 cos  . C. 3 cos  . D. 2 cos  . 2 3 3 3
Câu 2. Trên đường thẳng qua A và vuông góc với mặt phẳng chứa tam giác đều
ABC cạnh bằng 2, lấy các điểm M và N không trùng với A sao cho MBC  vuông
góc với NBC. Giá trị nhỏ nhất thể tích tứ diện BCMN bằng A. 2. B. 2 2. C. 2 3. D. 6.
Câu 3. Cho tam giác OAB đều cạnh a . Trên đường thẳng d qua O và vuông góc với
mặt phẳng OAB lấy điểm M sao cho OM x . Gọi E, F lần lượt là hình chiếu 12
vuông góc của A trên MB và OB . Gọi N là giao điểm của EF và d . Tìm x để thể
tích tứ diện ABMN có giá trị nhỏ nhất. A. a a a x a 2. B. 2 x  . C. 3 x  . D. 6 x  . 2 2 12
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, thể tích là V. Gọi
M là trung điểm của cạnh ,
SA N là điểm nằm trên cạnh SB sao cho SN  2NB; mặt
phẳng  di động qua các điểm M, N và cắt các cạnh SC, SD lần lượt tại hai điểm
phân biệt P, Q . Thể tích lớn nhất của khối chóp S.MNPQ bằng A. V V V V . B. . C. 2 . D. 3 . 2 3 3 4
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, thể tích là V. Điểm MC
M di động trên cạnh SC, đặt
k. Mặt phẳng  qua ,
A M và song song với MS
BD cắt SB, SD thứ tự tại N, P. Thể tích khối chóp C.APMN lớn nhất khi A. k  1. B. k  2. C. k  2. D. k  3.
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh ,
a cạnh bên SA y
y  0 và vuông góc với đáy ABCD. Trên cạnh AD lấy điểm M và đặt AM x
0  x a. Biết 2 2 2
x y a , thể tích lớn nhất V
của khối chóp S.ABCM bằng max 3 3 3 3 A. a 3 3a 3 a 3 a 3 . B. . C. . D. . 3 3 8 24
Câu 7. Từ hình vuông có cạnh bằng 6 người ta cắt bỏ
các tam giác vuông cân tạo thành hình tô đậm như hình
vẽ. Sau đó người ta gập thành hình hộp chữ nhật không
nắp. Thể tích lớn nhất của khối hộp bằng A. 8 2. B. 9 2. C. 10 2. D. 11 2.
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành với AD  4a . Các
cạnh bên của hình chóp bằng nhau và bằng a 6 . Thể tích lớn nhất của khối chóp đã cho bằng 3 A. 8a 4 6 . B. 3 a . C. 3 8a . D. 3 4 6 a . 3 3
Câu 9. Cho tam giác ABC vuông tại A có AB  3 , a AC  .
a Gọi Q là mặt phẳng
chứa BC và vuông góc với mặt phẳng ABC. Điểm D di động trên Q sao cho tam
giác DBC nhọn và hai mặt phẳng DAB và DAC lần lượt hợp với mặt phẳng
ABC hai góc phụ nhau. Thể tích lớn nhất của khối chóp D.ABC bằng 3 3 3 3 A. a 3 3a 3a 2 3a . B. . C. . D. . 4 8 10 13 13
Câu 10. Cho lăng trụ đứng ABC.AB C
  có đáy là tam giác đều. Tam giác ABC  có
diện tích bằng 3 và nằm trong mặt phẳng tạo với đáy một góc nhọn bằng . Thể
tích khối lăng trụ ABC.AB C
  đạt giá trị lớn nhất khi bằng A. 1  arctan . B. 1  arctan .
C.  arctan 2.
D.  arctan 6. 2 6
Câu 11. Trong tất cả các hình chóp tứ giác đều có d  3 là khoảng cách giữa hai
đường thẳng chéo nhau gồm một đường thẳng chứa một đường chéo của đáy và đường
thẳng còn lại chứa một cạnh bên hình chóp. Thể tích nhỏ nhất của khối chóp bằng A. 3. B. 9. C. 9 3. D. 27.
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình chữ
nhật. Một mặt phẳng không qua S và song song với đáy cắt các cạnh bên ,
SA SB, SC, SD lần lượt tại M , N, P, Q.
Gọi M , N , P , Q lần lượt là hình chiếu của M , N, P, Q
trên mặt phẳng đáy. Khi thể tích khối đa diện MNPQ.M NPQ
  đạt giá trị lớn nhất, tỉ số SM bằng SA A. 1 . B. 1. C. 2 . D. 3 . 2 3 3 4
Câu 13. Cho hình chóp S.ABC có SA x 0  x  3, tất cả các cạnh còn lại đều
bằng 1. Thể tích lớn nhất của khối chóp đã cho bằng A. 1 . B. 1 . C. 1 . D. 1 . 4 8 12 16
Câu 14. Cho hình chóp
S.ABC có SA x, BC
y, AB AC SB SC  1. Thể tích
khối chóp S.ABC lớn nhất khi tổng x y bằng A. 2 . B. 4 . C. 3. D. 4 3. 3 3
Câu 15. Cho hình vuông ABCD cạnh ,
a trên đường thẳng vuông góc với ABCD tại
A ta lấy điểm S di động. Hình chiếu vuông góc của A lên SB, SD lần lượt là H , K.
Thể tích lớn nhất của tứ diện ACHK bằng 3 3 3 3 A. a a 2 a 3 a 6 . B. . C. . D. . 6 12 16 32
Câu 16. Trong mặt phẳng P cho đường tròn T  đường kính AB  2r, C là một
điểm di dộng trên đường tròn T . Trên đường thẳng d vuông góc với P tại A lấy
điểm S sao cho SA r. Gọi H, K lần lượt là hình chiếu vuông góc của A lên SC và
SB. Khi C chạy trên đường tròn, thể tích lớn nhất của tứ diện S.AHK bằng 3 3 3 3 A. r r 5 r 5 r 5 . B. . C. . D. . 3 3 25 75 14
Câu 17. Cho khối chóp S.ABC có đáy là tam giác vuông cân tại B. Khoảng cách từ A
đến mặt phẳng SBC bằng a 2,   0
SAB SCB  90 . Xác định độ dài cạnh AB để khối
chóp S.ABC có thể tích nhỏ nhất. A. a 10 AB
. B. AB a 3. C. AB  2 . a
D. AB  3a 5. 2
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 .
a Tam giác SAB
vuông tại S và nằm trong mặt phẳng vuông góc với đáy. Gọi là góc tạo bởi đường
thẳng SD và mặt phẳng SBC với  30. Giá trị lớn nhất của thể tích khối chóp
S.ABCD bằng 3 3 3 3 A. 4a 4a 2 8a 2 8a 3 . B. . C. . D. . 3 3 9 9
Câu 19. Cho khối chóp S.ABC có SA SB SC  , a ASB  60 ,   BSC  90 ,   CSA  120. Gọi CN AM
M , N lần lượt là các điểm trên cạnh AB và SC sao cho  . Khi khoảng CS AB
cách giữa M và N nhỏ nhất thì thể tích của khối chóp S.AMN bằng 3 3 3 3 A. 2a 5 2a 5 2a 2a . B. . C. . D. . 72 72 432 432
Câu 20. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh ,
a SA a 2 và
vuông góc với mặt đáy ABCD. Gọi M là điểm di động trên cạnh CD và H là hình
chiếu vuông góc của S lên đường thẳng BM. Khi điểm M di động trên cạnh CD, thể
tích khối chóp S.ABH có giá trị lớn nhất bằng 3 3 3 3 A. a 2 a 2 a 2 a 2 . B. . C. . D. . 6 8 12 15
Câu 21. Cho tứ diện ABCD. Hai điểm M , N lần lượt di động trên hai đoạn thẳng BC BD
BC, BD ( M , N không trùng B ) sao cho 2 3
 10. Gọi V , V lần lượt là thể BM BN 1 2
tích của các khối tứ diện V
ABMN và ABCD. Giá trị nhỏ nhất của 1 bằng V2 A. 25. B. 3. C. 3 . D. 6 . 3 8 25 25
Câu 22. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Hai điểm M , N
lần lượt trên các đoạn thẳng AB AD
AB, AD ( M , N không trùng A ) sao cho  2  4. AM AN
Kí hiệu V , V lần lượt là thể tích của các khối chóp S.ABCD và S.MBCDN. Giá trị lớn 1
nhất của tỉ số V1 bằng V A. 2 . B. 3 . C. 1 . D. 17 . 3 4 6 14 15
Câu 23. Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N là hai điểm thay đổi lần
lượt thuộc cạnh BC, BD sao cho AMN  luôn vuông góc với BCD. Tổng giá trị lớn
nhất và giá trị nhỏ nhất của thể tích khối tứ diện ABMN bằng A. 2 . B. 17 2 . C. 17 2 . D. 17 2 . 12 72 144 216
Câu 24. Cho tứ diện OABC có O , A OB,
OC đôi một vuông góc và OA OB  2,
OC  1. Hai điểm M , N lần lượt di động trên hai cạnh AC, BC sao cho OMN
vuông góc với ABC. Thể tích khối đa diện ABOMN có giá trị lớn nhất bằng A. 1 . B. 1 . C. 2 . D. 1 . 4 9 9 12
Câu 25. Cho hình chóp S.ABC có SA  1, SB  2, SC  3. Gọi G là trọng tâm tam giác
ABC. Mặt phẳng  đi qua trung điểm I của SG cắt các cạnh ,
SA SB, SC lần lượt tại 1 1 1
M , N, P. Giá trị nhỏ nhất của biểu thức T    bằng 2 2 2 SM SN SP A. 2 . B. 3. C. 18 . D. 6. 7 7 7 16 THỂ TÍCH KHỐI ĐA DIỆN
Phần 1. Thể tích khối đa diện
Phần 2. Tỷ số thể tích Phần 3. Cực trị 1
Phần 1. Thể tích khối đa diện
Câu 1. Cho khối tứ diện ABCD có thể tích V. Gọi V  là thể tích của khối tám mặt có 
các đỉnh là trung điểm các cạnh của khối tứ diện ABCD. Tỉ số V bằng V A. 1 . B. 1 . C. 3 . D. 1 . 2 4 4 8
Lời giải. Ta có V AM AN AP 1 A.MNP  . .  . V AB AC AD 8 Suy ra V V  . A.MNP 8 Tương tự, ta có V VVV  . B.MSQ C .NQR D.PSR 8  Từ đó suy ra V V V   nên 1  . Chọn A. 2 V 2
Câu 2. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 1, góc giữa cạnh bên và
mặt đáy bằng 60. Gọi A , B , C  lần lượt là các điểm đối xứng của ,
A B, C qua S.
Thể tích của khối bát diện ABC.AB C   bằng A. 3 . B. 2 3 . C. 4 3 . D. 2 3. 2 3 3
Lời giải. Dễ dàng tính được 3 V  . S.ABC 12
Thể tích khối bát diện 2 3 V  2V  2.4     V 8V . B.ACA C B.ACS S.ABC 3 Chọn B.
Câu 3. Cho khối chóp tứ giác đều S.ABCD, có đáy ABCD là hình vuông cạnh bằng ,
a tâm O; cạnh bên bằng a 3. Gọi M
là trung điểm của CD, H là điểm đối xứng của O qua SM.
Thể tích khối đa diện ABCDSH bằng 3 3 3 3 A. a 10 a 10 a 10 5a 10 . B. . C. . D. . 12 18 24 24
Lời giải. Khối đa diện ABCDSH được chia thành hai khối chóp S.ABCD và H.SCD. 3 1 1 a 10  2 2 VSO.S
SB OB .S  . S.ABCD 3 ABCD 3 ABCD 6
 Vì H là điểm đối xứng của O qua SM nên d O
 ,SCD  d H,SCD     3 1 a 10  V  VV  . HSCD OSCD S. 4 ABCD 24 2 3
Vậy thể tích khối đa diện cần tính bằng 5a 10 VV  . Chọn D. S.ABCD H .SCD 24
Câu 4. Cho hình đa diện như hình vẽ, trong đó
ABCD.AB CD
  là hình hộp chữ nhật với
AB AD  2 , a AA  ,
a S.ABCD là hình chóp
có các cạnh bên bằng nhau và bằng a 3. Thể
tích của khối tứ diện SABD có thể tích bằng 3 A. a 2 3 2a . B. . 2 3 3 C. 2a a 2 . D. . 3 6
Lời giải. Gọi O AC BD, I SA  AC. Ta thấy V    V V S.A BD S.DBI A.DBI
Tính được DB  2 2a 
OB  2a và 2 2
SO SB OB a A . A Suy ra V     V V 2  V . S.A BD S.DBI A .DBI S.DBI Ta có 1 2 SSa . DBI  4 ABCD 3 Vậy 1 2 2 2 a V  2     V 2. S .SO a .a . S.A BD S.DBI 3 DBI  3 3 Chọn C.
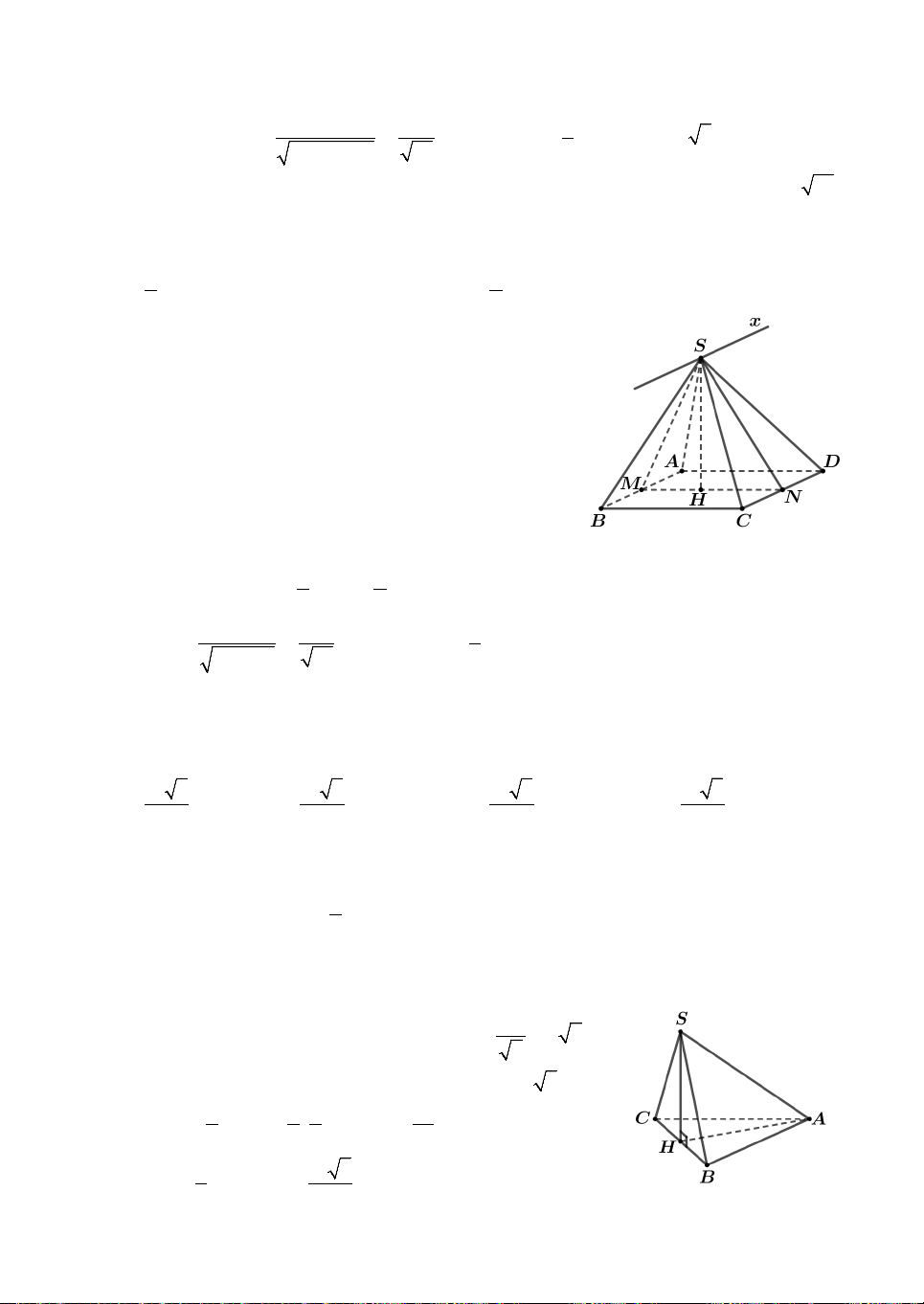
Câu 5. Cho khối lăng trụ ABC.AB C
  có thể tích là V. Hai mặt phẳng ACB và
BAC  chia khối lăng trụ đã cho thành bốn phần. Phần lớn nhất có thể tích bằng A. 1V. B. 2V. C. 3V. D. 5 V. 2 5 5 12
Lời giải. Gọi I AB AB , J B C   BC . Ta tính được 1 1 1 V     V ; VV V . B BAC 3 BJIB 4 B BAC 12 Suy ra 1 1 1 VV       V V V . ABCJI A B C JI 3 12 4 Vậy 1 1 5 V     Chọn D.   V V V V . ACC A JI 3 4 12
Câu 6. Cho hình lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác đều cạnh , a AA  .
a Gọi E là trung điểm cạnh AC, mặt phẳng AB E
  cắt BC tại F. Thể
tích khối đa diện CAB FE bằng 3 3 3 3 A. a 3 a 3 a 3 a 3 . B. . C. . D. . 4 8 15 16 3
Lời giải. Dễ dàng xác định được F là trung điểm của BC.
Kéo dài AE cắt CC  tại I. Khi đó C I  2 . a 3 Ta có a 3 V     Chọn D.   V    V V . CA B FE I .A B C I .EFC
C .AB C   16
Câu 7. Cho hình lăng trụ tam giác đều ABC.AB C
  có tất cả các cạnh bằng . a Gọi
M , N lần lượt là trung điểm của các cạnh AB và B C
 . Mặt phẳng AMN  cắt cạnh
BC tại P. Thể tích khối đa diện MBP.AB N  bằng 3 3 3 3 A. a 3 7a 3 7a 3 7a 3 . B. . C. . D. . 32 32 48 96
Lời giải. Chia khối đa diện MBP.AB N
 thành 2 phần gồm: chóp tam giác M.AB N
và chóp tứ giác M.BB NP  (như hình vẽ). Ta có 1 V V       VAA .S   MP.S . M .A B N M .BB NPA B N BB NP   3 Trong đó 2 2 2 1 a 3 a 3 a 1 a 3a S          S , MP , S . .   a . A B N 2 ABC 8 4 BB NP 2 2 4 8 3 3   Vậy a 3 3 3   7a 3 V        . Chọn D. 3  8 32  96
Câu 8. Cho hình lăng trụ ABC.AB C   có thể tích 3
96 cm . Gọi G là trọng tâm của
tam giác AB C
  và H là trung điểm của BC. Thể tích khối tứ diện B GAH bằng A. 3 12 cm . B. 3 16 cm . C. 3 18 cm . D. 3 24 cm .
Lời giải. Gọi H  là trung điểm của của B C   
H , G, A thẳng hàng. Ta có 1 V  .  V . B .ABH AB H  . 3 ABH Suy ra 2 1 3 V       V .    V 32 cm . B .AHH A ABH .A B H ABC . 3 3 AB C   Do 1 1 3 SS     Chọn B.    V V 16 cm . GAH AHH A B .GAH B . 2 2 AHH A  
Câu 9. Cho lăng trụ tam giác ABC.AB C
  có thể tích bằng V. Gọi M , N, P lần lượt
là trung điểm của các cạnh AB , BC, CC . Mặt phẳng MNP chia khối lăng trụ
thành hai phần, phần chứa điểm V
B có thể tích là V . Tỉ số 1 bằng 1 V A. 1. B. 25. C. 49 . D. 73 . 3 72 144 216 4
Lời giải. Kéo dài NP cắt BB , B C   lần lượt tại , R Q.
Gọi K AB  ,
MR J AC   MQ. Vì PNC   PQ
C  g c g 1  C Q
  CN BC. 2
Gọi h và S lần lượt là chiều cao và diện tích đáy lăng trụ. Ta có 3 1 3 1 3h 3 3V S  .       S S V . .  S . MB Q R. 2 2 4 MB Q 3 2 4 8 1 1 1 1 h 1 V S  . S S  V   . . S  . KBN R. 2 6 12 KBN 3 2 12 72 1 1 1 1 h 1 V S  .       S S V . . S . JQC P.JC ' 4 2 8 Q 3 2 8 48 Suy ra 49 V V    Chọn C. V V V . 1 R.MB Q R.KBN P.C JQ 144
Câu 10. Cho hình lăng trụ ABC.AB C
  có thể tích bằng V. Gọi M , N, P lần lượt là
trung điểm của các cạnh AB, AC , BB . Thể tích của khối tứ diện CMNP bằng A. V V V V . B. . C. 5 . D. 7 . 3 4 24 24
Lời giải. Gọi E là trung điểm của AC. Gọi G là trọng tâm của tam giác ABC, gọi I
là giao điểm của NP và EB.
Dễ dàng chứng minh được 5 IG GB. 2 Suy ra 5 5 5 5 SSS  V   VV . IMC MBC ABC N .IMC N . 2 4 4 ABC 12 Ta có V NP 1 1 5V N .MCP    V   .V  . Chọn C. N .MCP N . V NI 2 2 MCI 24 N .MCI
Câu 11. Cho tứ diện ABCD có AB CD  5, AC BD  34, AD BC  41. Thể
tích của tứ diện ABCD bằng A. 10. B. 20. C. 30. D. 40.
Lời giải. Cho tứ diện ABCD gần đều có AB CD  ,
a AC BD b, AD BC c. Khi đó 2 V
a b c
b c a
a c b ABCD
 2 2 2 2 2 2 2 2 2. 12 Áp dụng: 2 V         Chọn B. ABCD 25 34  41 34 41  25 25 41 34 20. 12
Cách 2. Đặt a AB CD  5, b AC BD  34, c AD BC  41. 5
Dựng tứ diện AMNP với B, C, D là trung điểm của MN, MP, NP. Ta có MN MP NP AB  , AC  , AD  2 2 2 
 các tam giác AMN, ANP, AMP đều vuông tại đỉnh A 
AM , AN, AP đôi một vuông góc. 2   AM  2    4   2 2 2 2 2 2
a b c AM AN a      Khi đó  2 2 2  2
AN AP  4c  AN  2 2 2 2
b c a     2 2 2      2 AM AP 4b  AM  2   2 2 2
c a b   2 2 2 2 2 2 2 2 2 Vậy
1 a b c b c a a c b V  . .  20. ABCD 3 3 3 2
Câu 12. Cho hình hộp ABCD.AB CD   có thể tích 3
120 cm . Gọi M , N lần lượt là
trung điểm AB và AD. Thể tích khối tứ diện MNAC  bằng: A. 3 15 cm . B. 3 20 cm . C. 3 24 cm . D. 3 30 cm . Lời giải. Gọi ,
h S, V lần lượt là chiều cao, diện tích đáy, thể
tích của hình hộp ABCD.AB CD
 . Khi đó V  . h S. Ta có 1 S AC BDAC BD 1 . .sin , V  .
h AC.BD.sinAC,BD. 2 2
Vì M , N là trung điểm của AB, AD nên ta có MN BD  MN AC   BD AC  , , . Lại có 1
d MN, AC   h   V         
MN.A C .d MN A C MN A C MNA C  , .sin , . 6 Vậy 1 1 V  .   Chọn B.   BD.AC. . h sin MN AC V MNA C  ,  1 3 20 cm . 6 2 6
Câu 13. Cho tứ diện ABCD có 2 2 S  4 cm , S
 6 cm , AB  3cm. Góc giữa hai ABC ABD
mặt phẳng ABC và ABD bằng 60. Thể tích của khối tứ diện đã cho bằng A. 2 3 4 3 8 3 3 2 3 cm . B. 3 cm . C. 3 cm . D. 3 cm . 3 3 3
Lời giải. Cho tứ diện ABCD, biết diện tích hai mặt bên là S và S ; Độ dài giao 1 2 tuyến của hai mặt là
2.S .S .sin
; Góc giữa hai mặt bên là . Khi đó 1 2 V  . S.ABC 3 Áp dụng: 2.4.6 sin 60 8 3 3 V   cm . Chọn D. S.ABC 3.3 3
Cách 2. Kẻ CK AB K AB. Ta có 1 8 SAB.CK  CK  cm. ABC 2 3 6
Gọi H là chân đường cao của hình chóp hạ từ đỉnh C.
Xét tam giác vuông CHK, ta có  4 3
CH CK.sinCKH  . 3
Vậy thể tích khối tứ diện 1 8 3 3 V S .CH  cm . Chọn D. 3 ABD 3
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích V.
Gọi E là điểm trên cạnh SC sao cho EC  2ES. Gọi  là mặt phẳng chứa đường
thẳng AE và song song với đường thẳng BD,  cắt hai cạnh SB, SD lần lượt tại hai
điểm M, N. Thể tích khối chóp S.AMEN bằng A. V V V V . B. . C. . D. . 6 9 12 27
Lời giải. Kẻ OF song song IE, suy ra SI SE 1 SM SN 1       . SO SF 2 SB SD 2  SA SC a    1, 3 c    Khi đó  SA SE  .  SB SD b    2, d   2  SM SN V  S.MNPQ
a b c d  
Áp dụng công thức tính nhanh  V 1 V 4abcd
ta được S.AMEN  . Chọn A. S.ABCDV 6 a
 c b d S.ABCD 
Câu 15. Cho hình chóp S.ABCD có đáy là hình thoi, SA vuông góc với đáy. Mặt
phẳng P qua A vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại G, F, E. Biết rằng  SF
P  chia khối chóp thành hai phần có thể tích bằng nhau. Tính k  . SC A. 13 1    k  . B. 13 1 k  . C. 17 1 k  . D. 17 1 k  . 4 6 4 8
Lời giải. Đặt SB SD SC   x ,
y x, y  0. SG SE SF
Áp dụng công thức tính nhanh V  1 y  2x S.AEFG    2 V  4 yx S.ABCD
x x y1  1 2 y  2 2  y 17 1 0       y  . 2 yy  2 1 yy   1 2 Từ đó ta tính được SF 1 17 1 k    . Chọn D. SC y 8 7
Câu 16. Cho khối lăng trụ ABC.AB C
 . Gọi M , N lần lượt là trung điểm của hai
cạnh AA và BB . Mặt phẳng C MN
 chia khối lăng trụ đã cho thành hai phần. Gọi V
V là thể tích khối C MNB A
  và V là thể tích khối ABC.MNC . Khi đó tỷ số 1 bằng 1 2 V2 A. 1 . B. 1. C. 2 . D. 3 . 2 3 3 4    
Lời giải. Ta có C C A M B N 1  0;   . C CAA B B  2  
Áp dụng công thức giải nhanh: V    1 1 1 1 C MNB A  0      . V 3  2 2 3 CAB.C A  B Suy ra V 1 1  . Chọn A. V 2 2
Câu 17. Cho hình lăng trụ tam giác ABC.AB C
  có thể tích là V và có độ dài cạnh
bên AA  6. Trên cạnh A , A B B  , C C
 lần lượt lấy các điểm A , B , C sao cho 1 1 1
A A  2, B B x, C C y với x, y là các số thực dương thỏa mãn xy  12. Biết rằng 1 1 1
thể tích của khối đa diện ABC.A B C bằng 1V. Giá trị của x y bằng 1 1 1 2 A. 1. B. 2. C. 3. D. 4.
Lời giải. Ta có AA 1 BB x CC y 1 1 1  ,  ,  . AA 3 BB 6 CC  6  
Áp dụng công thức giải nhanh: V    1 1 x y 1
ABC .A B C         . V 3 3 6 6  2 ABC . 1 A 1 B 1 C
Suy ra x y  7. Kết hợp với giải thiết xy  12 ta được
x  3; y  4  
x y  1. Chọn A.
x  4; y  3 
Câu 18. Cho hình lập phương ABCD.AB CD
  có các cạnh bằng , a một mặt phẳng  a a
 cắt các cạnh AA , BB , CC , DD lần lượt tại M , N, P, Q. Biết 2 AM  , CP  . 3 5
Thể tích khối đa diện ABCD.MNPQ bằng 3 3 3 3 A. a 2a 11a 11a . B. . C. . D. . 3 3 15 30
Lời giải. Thể tích hình lập phương ABCD.AB CD   là 3 V      a . ABCD.A B C D  AM 1 CP 2 a    , c    Ta có  AA 3 CC  5  .  BN DQ b   , d   BBDD 8 V
 MNPQ.AD CB 1 
 a b c d
Áp dụng công thức giải nhanh: V 4
ABCD.AD CB  
ac bd  V 3
Suy ra MNPQ.AD CB 1 11 11a
 a c 11   V   .   Chọn D.     V V 2 30 MNPQ.A D C B ABCD. 30 AD CB   30
ABCD.AD CB  
Câu 19. Cho hình chóp đều S.ABC có đáy ABC là tam giác đều cạnh .
a Gọi E, F
lần lượt là trung điểm của các cạnh SB, SC. Biết mặt phẳng AEF  vuông góc với
mặt phẳng SBC. Thể tích khối chóp S.ABC bằng 3 3 3 3 A. a 5 a 3 a 5 a 15 . B. . C. . D. . 8 24 24 27
Lời giải. Gọi M là trung điểm BC, O là trọng tâm tam giác ABC. S  N EF
Suy ra SO  ABC. Gọi N SM EF      nên 0
90  AEF ,SBC     . SNA AN EF 
Xét tam giác SAM , có AN là đường trung tuyến và
cũng là đường cao nên tam giác SAM cân tại A a 3  SA AM  . 2 Tam giác vuông a 5 SAO, có 2 2
SO SA AO  . 2 3 3 Vậy 1 a 5 VS .SO  . Chọn C. S.ABC 3 ABC 24
Câu 20. Cho hình chóp đều S.ABC có cạnh bên bằng .
a Gọi E, F lần lượt là trung
điểm của các cạnh SB, SC. Biết mặt phẳng AEF  vuông góc với mặt phẳng SBC.
Thể tích khối chóp S.ABC bằng 3 3 3 3 A. a 5 a 3 a 5 a 15 . B. . C. . D. . 8 24 24 27
Lời giải. Tương tự như bài trên, ta có AM SA  . a 2  2a  a
AB BC CA S     ABC   3 Suy ra  3  3 a 15    nên V  . Chọn D.  2aS.ABC   a 5 27 AO SO    3    3
Câu 21. Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh . a Gọi M là trung điểm .
SA Biết mặt phẳng MCD vuông góc với mặt phẳng SAB. Thể tích của
khối chóp S.ABCD bằng 3 3 3 3 A. a a 5 a 3 a 5 . B. . C. . D. . 3 2 6 6
Lời giải. Gọi N  MCDSB, suy ra N là trung điểm SB. 9
Gọi P, Q, R lần lượt là trung điểm MN, CD, AB SP   MN    nên 0
90  MCD,SAB    QPS. QP MN  Xét tam giác SQ ,
R có QP là đường trung tuyến và
cũng là đường cao nên tam giác SQR cân tại Q 
SQ QR  . a Tam giác vuông a 3 SQO, có 2 2
SO SQ QO  . 2 3 Vậy 1 a 3 2 VS .SO  . Chọn C. S.ABCD 3 ABCD 6
Câu 22. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BC  . a Cạnh
bên SA vuông góc với đáy, góc  0
BSC  45 , mặt phẳng SAC  tạo với mặt phẳng SBC một góc 0
60 . Thể tích khối chóp S.ABC bằng 3 3 3 3 A. a 6 a 2 a 3 a 6 . B. . C. . D. . 15 18 24 30
Lời giải. Gọi H là hình chiếu vuông góc của B trên mặt phẳng SAC. Suy ra
H AC và BH AC. Gọi E là hình chiếu vuông góc của H trên SC. Suy ra BE SC và 0
60  SAC ,SBC     HEB.
Tam giác SBC vuông cân tại B suy ra E là trung điểm SC. Ta có a
SC BC 2  a 2, suy ra 1 2 BE SC  . 2 2 Tam giác a BHE có  6
BH BE sin HEB  . 4 Từ đó tính được a 15 2a 10 a 10 AB  , AC  , SA  . 5 5 5 3 Vậy 1 a 6 VS .SA  . Chọn D. S.ABC 3 ABC 30
Câu 23. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh ,
a mặt bên SAB là
tam giác đều, mặt bên SCD là tam giác vuông cân tại S. Gọi M là điểm thuộc đường
thẳng CD sao cho BM vuông góc với .
SA Thể tích của khối chóp S.BDM bằng 3 3 3 3 A. a 3 a 3 a 3 a 3 . B. . C. . D. . 16 24 32 48
Lời giải. Gọi E, F lần lượt là trung điểm của AB, CD 
EF là trung trực của AB. 10
Kẻ SH  ABCD H ABCD, mà SA SB a HA HB nên H EF
Suy ra HC HD SD SC   SDC  vuông cân tại S. Trong tam giác a CD a SEF có 3 SE
; EF a; SF   . 2 2 2 Nhận thấy 2 2 2
SE SF EF   SE
F vuông cân tại S 2 SE 3a a a 3   EH   ; FH  ; SH  . EF 4 4 4 Kéo dài 3a
AH cắt BC tại K 
BK  2EH  . 2
Từ giả thiết BM  ,
SA suy ra BM AK.
Từ đó ta chứng minh được        3a a ABK BCM g c
g CM BK    DM  . 2 2 3   Vậy 1 1 1 a 3 VS
.SH   BC.DM SH  . Chọn D. S.BDM 3 BDM  3 2  48
Câu 24. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và hai tam giác
SAC và SBD là những tam giác đều. Gọi A', C ' lần lượt là trung điểm của SA và
SC. Thể tích khối tứ diện A' BC ' D bằng 3 3 3 3 A. a 3 a 3 a 6 a 6 . B. . C. . D. . 16 24 24 32
Lời giải. Gọi H là tâm hình vuông ABCD. SA 
SB SC SD
Từ giải thiết suy ra  . SH    ABCD 
Suy ra S.ABCD là hình chóp đều nên V  2V .
A ' BC ' D B.HA 'C '
Ta có BH  SAC BH  HA'C '. 3   Do đó 1 2 1 a 6 V  2. S .BH   S .BH  . Chọn C.
A ' BC ' D HA  'C ' 3 3 4 SAC  24
Câu 25. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh .
a Cạnh bên SA
vuông góc với đáy, SC a 3. Gọi M , N, P, Q lượt là trung điểm của SB, SD, CD,
BC. Thể tích của khối chóp . A MNPQ bằng 3 3 3 3 A. a a a a . B. . C. . D. . 3 4 8 12 11 MN PQLời giải. Gọi 
I AC PQ. Ta có MN PQ
NP PQ  
MNPQ là hình chữ nhật nên V  2V . A.MNPQ M .APQ
Ta có d M APQ 1 ,   , SA   mà 2 1 2 2 a
SA SC AC a 
d M ,APQ  .SA  .   2 2 2 3 Tính được 1 1 3 1 3a a S
AI.PQ  . .AC. .BD  . Từ đó suy ra V  . APQ 2 2 4 2 8 M .APQ 16 3 Vậy a V  2V  . Chọn C. A.MNPQ M .APQ 8
Câu 26. Cho lăng trụ ABC.AB C
  có đáy ABC là tam giác vuông tại A và góc  0
ABC  30 . Gọi M là trung điểm của AB, tam giác MAC đều cạnh a và nằm trong
mặt phẳng vuông góc với đáy ABC. Thể tích khối lăng trụ đã cho bằng 3 3 3 3 A. a 2a 3a 5a . B. . C. . D. . 7 7 7 7 Lời giải. Gọi a
H là trung điểm CM. Suy ra 3 AH  và 2
AH  ABC .
Đặt AC x, suy ra BC  2x và AB x 3. Pitago trong a CAM tìm được 2 x  . 7 3 Vậy 1 3a VS
.AH AB.AC.AH  . Chọn C.
ABC .A ' B 'C ' ABC 2 7
Câu 27. Cho hình lăng trụ đều ABC.AB C
 . Biết khoảng cách từ điểm C đến mặt
phẳng ABC  bằng a, góc giữa hai mặt phẳng ABC  và BCC B
  bằng với 1
cos  . Thể tích khối lăng trụ ABC.AB C   bằng 3 3 3 3 3 A. 3a 15 9a 15 3a 15 9a 15 . B. . C. . D. . 10 10 20 20
Lời giải. Gọi M là trung điểm của AB, H là hình chiếu của C lên C M  .
Suy ra CH  ABC  và CH  . a
Gọi N là hình chiếu của C lên BC , khi đó
BC   CHN   BC   NH 
ABC  BCC    ,  CNH  . 12 Đặt x 3
AB AC BC x  CM  . 2 Trong tam giác vuông CH a CHN có 3 2 CN   . sin 4
Trong hai tam giác vuông C CB  và C CM  lần lượt có 1 1 1 1 1 1   ;   . 2 2 2 2 2 2 C CCN BC C CCH CM 1 1 1 1 8 1 1 4 3a          
x a 3  CM  . 2 2 2 2 2 2 2 2 CN BC CH CM 9a x a 3x 2 2 Từ đó ta tính được 3a 5 3a 3 CC   và S  . 5 ABC 4 3 Vậy 9a 15 V    Chọn D.    CC .S . ABC .A B C ABC 20
Câu 28. Cho hình chóp S.ABCD có đáy ABCD là hình thang cân với AD  2AB
 2BC  2CD  2 .
a Cạnh bên SA vuông góc với đáy. Gọi M , N lần lượt là trung 3 điểm của a 3
SB và CD. Biết thể tích khối chóp S.ABCD bằng . Cosin góc giữa 4
MN và SAC  bằng A. 5 . B. 3 5 . C. 310 . D. 3 310 . 10 10 20 20 3 Lời giải. Ta có 1 AD BC 1 3a a 3 a 3 V  . SA .d AD, BC  . SA .   SA  . a S.ABCD   3 2 3 2 2 4
Gọi P là trung điểm AB, khi đó MP  ABCD.
Gọi K NP AC.
Dựng HK  ABCD với H MN. Khi đó H SAC.
Ta có AC a 3, CD  , a
AD  2a suy ra NC AC. Khi đó
MN SAC  HC cos ,  cos NHC NH 2 2 3 HK KC 310   . Chọn C. 2MN 20
Câu 29. Cho khối chóp S.ABC có SA  6, SB  2, SC  4, AB  2 10 và   SBC ASC 0
 90 . Thể tích khối chóp S.ABC bằng A. 4 3. B. 6 3. C. 8 3. D. 12 3.
Lời giải. Pitago trong tam giác SBC ta được BC  2 3;
trong tam giác SAC ta được AC  2 13. Kiểm tra thấy 2 2 2
AB BC AC   tam giác ABC vuông tại B. BC SB Ta có 
BC  SAB  ABC   SAB. BC AB  13
Do đó nếu gọi H là chân đường cao hạ từ S trong tam giác SAB thì ta có . SA SB 6 1
SH  ABC  và SH   . Vậy VS
.SH.  4 3. Chọn A. 2 2 S.ABC ABC SA SB 10 3
Câu 30. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  1, AD  10;
SA SB, SC SD. Biết hai mặt phẳng SAB và SCD cùng vuông góc với nhau và
tổng diện tích hai tam giác SAB và SCD bằng 2. Thể tích khối chóp S.ABCD bằng A. 1 . B. 1. C. 3 . D. 2. 2 2
Lời giải. Gọi H là hình chiếu vuông góc của S trên
mặt đáy ABCD. Do SA SB suy ra H thuộc đường
trung trực của AB; tương tự H thuộc đường trung
trực của CD. Suy ra H MN (như hình vẽ). 
 SABSCD Sx Ta có  gia thiet  0 
 MSN  90 . SM 
Sx; SN Sx 2 2 2  SM
x y MN  10   x 2 2 2 2       Đặt  x y 10 x y  10  , ta có hệ         . SN   y 1 1 
 x.AB  .yCD  2 x y  4 xy  3   2 2   Khi đó xy 3 1 SH   . Vậy VS
.SH  1. Chọn B. 2 2 S.ABCD ABCD x y 10 3
Câu 31. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh ,
A BC  2a,
SB SC, SA  2a và SA tạo với đáy một góc 60. Biết H là hình chiếu vuông góc của
đỉnh S trên mặt đáy ABC thuộc tam giác ABC. Thể tích khối chóp S.AHC bằng 3 3 3 3 A. a 3 a 3 a 3 a 3 . B. . C. . D. . 3 6 9 12
Lời giải. Ta có SB SC suy ra H thuộc trung trực của đoạn BC. Tam giác ABC
vuông cân tại A nên H nằm trên đường thẳng đi qua hai điểm A và M ( M là trung điểm BC nên 1
AM BC a ). Hình chiếu vuông góc của SA trên mặt phẳng 2
ABC là HA nên 0 60  , SA ABC      , SA HA SAH.
Xét tam giác vuông SAH, ta có  AH  .
SA cosSAH a AM . Do đó H M. Trong tam giác vuông cân BC
ABC có AB AC   a 2. 2
Trong tam giác vuông SHA có  SH  .
SA sin SAH a 3. 2   Ta có 1 1 1 a SS
  AB.AC  . AHC 2 ABC 2 2  2 3 Vậy 1 a 3 VS .SH  . Chọn B. S.AHC 3 AHC 6 14
Câu 32. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, AB  , a
BC a 3; tam giác SOA cân tại S và mặt phẳng SAD vuông góc vói
mặt đáy ABCD. Biết góc giữa SD và mặt phẳng ABCD bằng 0 60 . Thể tích khối
chóp S.ABCD bằng 3 3 3 3 A. a 3 2a 3 a 3 a 3 . B. . C. . D. . 3 3 6 9
Lời giải. Tam giác SOA cân tại S nên SO SA suy ra
H thuộc trung trực đoạn O ;
A mặt phẳng SAD vuông
góc với mặt đáy ABCD nên H thuộc giao tuyến AD .
Từ đó suy ra H là giao điểm của trung trực đoạn OA với cạnh AD. Ta có 2 2
AC BD AB BC  2a .
Suy ra AO BO AB a nên tam giác ABO đều cạnh a, suy ra  0 ABI  30 .
Gọi I là trung điểm của AO, suy ra đường trung trực đoạn OA đi qua hai điểm I, B .
Suy ra H BI AD. Khi đó 0
60  SD,ABCD   
SD, HD SDH. Tính được a 2a AH  , suy ra 
HD AD AH  
SH HD.tan SDH  2 . a 3 3 3 Vậy 1 2a 3 VS .SH  . Chọn B. S.ABCD 3 ABCD 3
Câu 33. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh . a Các mặt bên
SAB, SAC lần lượt tạo với đáy các góc là 0 0
60 , 30 . Hình chiếu vuông góc của S
trên mặt phẳng ABC nằm trên cạnh BC. Thể tích khối chóp S.ABC bằng 3 3 3 3 A. a 3 a 3 a 3 a 3 . B. . C. . D. . 4 12 32 64
Lời giải. Kẻ HE AB E AB, HF AC F AC (tham khảo hình vẽ).  SEH  60
HE SH.cot 60 Từ hình vẽ, suy ra      . 
HF SH.cot 30 SFH 30      2 Ta có 1 1 a 3 SSS
AB.HE AC.HF ABH ACH ABC 2 2 4 2 1  a SH     a 3 3a . . . cot 60 cot 30   SH  . 2 4 8 3 Vậy 1 a 3 V  .SH.S  . Chọn C. S.ABC 3 ABC 32
Câu 34. Cho hình chóp S.ABC có đáy ABC là tam giác với AB AC  5 ,
a BC  6a
và các mặt bên cùng tạo với đáy các góc 60. Hình chiếu vuông góc của S trên mặt
phẳng ABC nằm bên trong tam giác ABC. Thể tích khối chóp S.ABC bằng 15 3 A. 2a . B. 3 a 3. C. 3 6a 3. D. 3 8a . 3
Lời giải. Kẻ HE AB E AB, HF AC F AC, HI BC I BC. Từ hình vẽ, suy ra   
SEH SFH SIH  60 
HI HE HF SH.cot 60. Ta có SSSS ABH ACH BCH ABC 1 1 1 2
AB.HE AC.HF BC.HI  12a 2 2 2 1 3a 3 2  .16 .
a SH.cot 60  12a  SH  . 2 2 Vậy 1 3 VS
.SH  6a 3. Chọn C. S.ABC 3 ABC
Câu 35. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  , a AD  2 . a
Hình chiếu vuông góc của S xuống mặt phẳng ABCD thuộc đoạn BD. Hai mặt
phẳng SBC và SCD lần lượt hợp với đáy các góc 0 60 và 0 30 . Thể tích khối chóp S.ABCD bằng 3 3 3 3 A. a 3 4a 3 a 3 4a 3 . B. . C. . D. . 5 5 15 15
Lời giải. Ta có SSS BCD BHC CHD 1 1 2a 3 2 0 0
a BC.SH cot 60  CD.SH cot 30  SH  . 2 2 5 3 Khi đó 1 4a 3 VS .SH  . Chọn D. S.ABCD 3 ABCD 15
Câu 36. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và  0 BAD  60 .
Các mặt phẳng SAB, SBD và SAD cùng hợp với đáy ABCD một góc 60. Biết
hình chiếu vuông góc của S trên mặt đáy nằm ngoài tam giác ABD. Thể tích của
khối chóp S.ABCD bằng 3 3 3 3 A. a 3 a 3 a 3 a 3 . B. . C. . D. . 2 4 6 12
Lời giải. Từ giả thiết suy ra chân đường cao của hình chóp
S.ABCD là tâm đường tròn bàng tiếp tam giác đều ABD.
Do ba đường tròn bàng tiếp của tam giác đều ABD có bán
kính bằng nhau nên chỉ cần xét một trường hợp H là tâm
đường tròn bàng tiếp ứng với đỉnh . A
Dễ thấy C là tâm đường tròn bàng tiếp cần tìm và bán kính bằng a 3 3a CO  
SC CO.tan 60  . 2 2 16 3 Vậy 1 a 3 V  .S .SC  . Chọn B. S.ABCD 3 ABCD 4
Câu 37. Cho lăng trụ ABCD.AB CD
  có đáy ABCD là hình chữ nhật với AB  3,
AD  7, cạnh bên bằng 1. Hai mặt bên ABB A   và ADD A
  lần lượt tạo với đáy những góc bằng 0 45 và 0
60 . Thể tích khối lăng trụ đã cho bằng A. 3. B. 3 3. C. 7. D. 7 7.
Lời giải. Gọi H là hình chiếu vuông góc của A
xuống mặt đáy ABCD.
Đặt AH  . h Ta có 0 0
MH h cot 45 ; NH h cot 60 và 2 2 2
AH AA h  1h . Từ 3 2 2 2
MH NH AH  h  . 7 Suy ra V    Chọn A.     S .A H 3. ABCD.A B C D ABCD
Câu 38. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  6,
AD  3, tam giác SAC nhọn và nằm trong mặt phẳng vuông góc với đáy. Biết hai
mặt phẳng SAB và SAC tạo với nhau góc thỏa mãn 3
tan  ; cạnh SC  3. 4
Thể tích khối S.ABCD bằng A. 4 . B. 8 . C. 3 3. D. 5 3 . 3 3 3
Lời giải. Đặt AH x, SH  .
y Có AB  6, AD  3   AC  3.
Ta có SC HC SH     x2 2 2 2 2 2 3 3  y 
x y 6x  0.   1
Gọi M AC, BM AC 
BM  2 và AM  2.
Kẻ MN SA N SA 
SAB SAC   ,  . Ta có: BM 3 4 2 tan     MN  . MN 4 3 xy d H SA 2 2 , Mặt khác: AH x y x    MN AM 4 2 2 3 suy ra 16 2 y x. 2 3 Từ   8 1 , 2 suy ra 2 4 2 x  , y  nên V  . Chọn B. 3 3 S.ABCD 3 17
Câu 39. Cho hình chóp S.ABC có AB  ,
a AC a 3, SB  2a và   ABC BAS   BCS
 90. Sin của góc giữa đường thẳng SB và mặt phẳng SAC  bằng 11 . Thể tích 11
khối chóp S.ABC bằng 3 3 3 3 A. a 6 a 6 a 3 2a 3 . B. . C. . D. . 3 6 9 9
Lời giải. Gọi O là trung điểm AC, D đối xứng của B qua O.
Suy ra d B,SAC  d D,SAC.     AB AD Ta có   AB SD. AB SA 
Tương tự có BC SD. Từ đó suy ra SD  ABCD.
Đặt SD x x  0 2 2       SB2 3 1 a SB x a  x  . a 11
d B, SAC  Vì
SB SAC   11    
d D SAC 11 sin , ,  SB. 2 11 SB 11 11 Lại có 1 1 1 1 1 1 1       .   3 2
d D,SAC 2 2 2 2 2 2 SD DC DA x a 2a Từ   1 ,2 và   3 ta có phương trình 11 1 3 4 2 2 4    3 11
 6  0 xa x x a a   x a 3. 2 2 2 2 x  3a x 2a 3 Vậy 1 a 6 VS .SD  . Chọn B. S.ABC 3 ABC 6
Câu 40. Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A với AB a và  BAC  120 ,   
SBA SCA  90. Biết góc giữa SB và mặt đáy ABC  bằng 60 , thể tích
khối chóp S.ABC bằng 3 3 3 3 A. a 3a 3a 3 3a . B. . C. . D. . 4 4 4 4
Lời giải. Chọn D ABC sao cho  
DBA DCA  90. Suy ra DBC
đều nên DB DC BC a 3.
Tương tự như bài trên ta chứng minh được SD  ABCD.
Suy ra   SB ABC   60 ,  SBD. Khi đó ta tính được 
SD DB.tan SBD  3 . a 3 Vậy 1 a 3 VS .SD  . Chọn B. S.ABC 3 ABC 4
Câu 41. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và  
SBA SCA  90. Biết góc giữa hai mặt phẳng SAB và mặt đáy ABC  bằng 60 ,
thể tích khối chóp S.ABC bằng 18 3 3 3 3 A. 3a 3a 3a 3a . B. . C. . D. . 4 6 12 24
Lời giải. Chọn D ABC sao cho  
DBA DCA  90.
Ta chứng minh được SD  ABCD. Suy ra   
SAB ABC   60 ,  SBD. Tính được  a 3
BD AB.tan BAD  và 
SD BD.tan SBD  . a 3 3 Vậy 1 a 3 VS .SD  . Chọn C. S.ABC 3 ABC 12
Câu 42. Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A với AB a và  BAC  120 ,   
SBA SCA  90. Biết góc giữa SB và mặt phẳng SAC  thỏa mãn 3 sin
, khoảng cách từ S đến mặt đáy ABC  nhỏ hơn 2 .
a Thể tích khối chóp 8
S.ABC bằng 3 3 3 3 A. 3a 3a 3a 3a . B. . C. . D. . 4 6 12 24
Lời giải. Chọn D ABC sao cho  
DBA DCA  90. Suy ra DBC
đều nên DB DC BC a 3.
Ta chứng minh được SD  ABCD.
Đặt SD x   x a 2 2 0 2 
SB x 3a .
Gọi I DB AC. Trong tam giác vuông DCI, có DC DI
 2a 3 nên B là trung điểm của DI cos 60 
d B SAC  1 ,
  .d D,SAC.   2     1
d B SAC  2 2 , Ta có     
d B SAC  3. x 3a sin ,
  SB.sin . 2 SB     8 Kẻ SD.DC xa 3
DK SC K SC  
d D,SAC   DK   .     3 2 2 2 2 SD DC x  3a 2 2 Từ   xa 3 3. x  3a 1 , 2 và   3 suy ra 0x2a    x  . a 2 2 x  3 4 a 3 Vậy 1 a 3 VS .SD  . Chọn C. S.ABC 3 ABC 12
Câu 43. Cho lăng trụ tam giác ABC.AB C
  có độ dài cạnh bên bằng 4 và khoảng
cách từ điểm A đến các đường thẳng BB , CC  lân lượt bằng 1 và 2. Biết góc giữa hai mặt phẳng ABB A   và ACC A
  bằng 60. Tính thể tích khối lăng trụ ABC.AB C  . 19 A. 3. B. 2 3. C. 3 3. D. 4 3.
Lời giải. Kẻ AE BB tại E; AF CC  tại F. Khi đó ABB A   ACC A     ,  AE, AF.
Trường hợp 1.  cosin EAF  60   EF  3. Ta có 2 2 2
AF AE EF 
AE EF . Suy ra AE  BCC B  . 3 3 1  3 1  V                   V .   S .   AE . BB .EF.AE 2 3. ABC .A B C A. 2 BCC B 2 3 BCC B  2 3 
Trường hợp 2.  cosin
EAF  120   EF  7. Ta có 1 1 AE AFSAE AF
  d A EF EF  d A EF   AEF     . .sin120 21 . . .sin120 , . , . 2 2 EF 7 Ta có 3 3 1 1 21 V      Chọn B.    V .   BB .EF.d , A EF . . 7.4 2 3. ABC .A B C A.BCC B   2 2 3 2 7
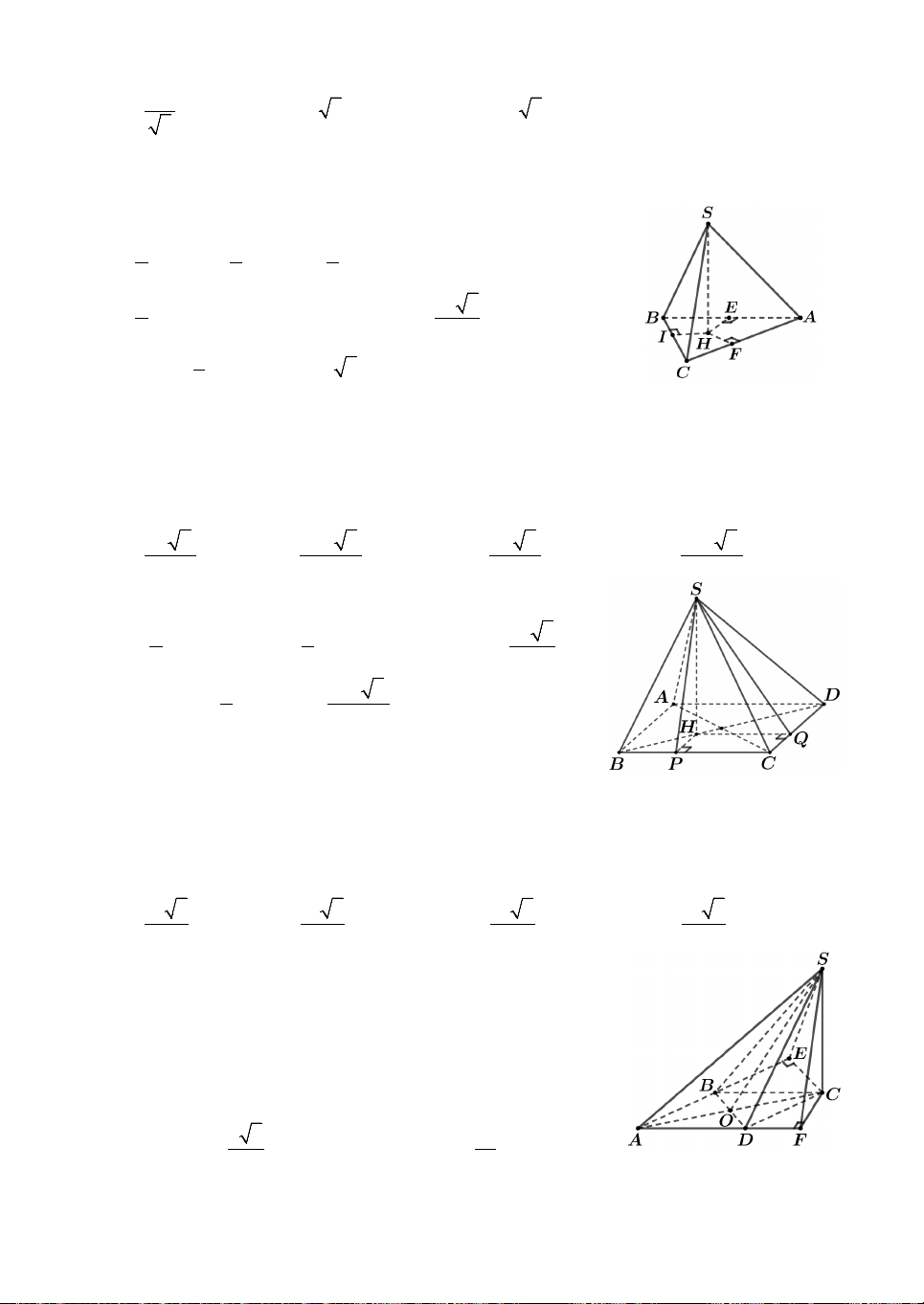
Câu 44. Cho khối lăng trụ ABC.ABC , khoảng cách từ C đến đường thẳng BB
bằng 2, khoảng cách từ A đến các đường thẳng BB và CC  lần lượt bằng 1 và 3.
Hình chiếu vuông góc của A lên mặt phẳng ABC  là trung điểm M của BC  và A 2 3 M
. Thể tích của khối lăng trụ đã cho bằng 3 A. 2 3 . B. 1. C. 3. D. 2. 3
Lời giải. Gọi E, F lần lượt là hình chiếu của A lên đường thẳng BB , CC .
BB  AE
BB  EF  d  
C,BB EF. Ta có     BB  AF
BB  CC  . do   
AEF   BCC B    d  , A   BB CC    d     , A EF  
Tam giác AEF có AE  1, AF  3, EF  2 nên vuông tại .
A Suy ra d A EF  3 ,  . 2
Gọi N là trung điểm BC và H EF MN.
Suy ra H là trung điểm EF nên 1
AH EF  1. 2
Trong tam AMN vuông tại , A có  2 3
AN AM  4 3 
3  BB  MN  .  3 AH 1    Vậy 3 3 1 V          Chọn D.    V  
BB .EF.d , A EF 2. ABC .A B C A.BCC B   2 2 3 
Cách 2. Ta có AEF   BB nên ABC có hình chiếu vuông góc lên AEF  là AEF.
MN  AEF  Mà 
 AEF  ABC     ,
MN, AM AMN.
AM ABC  20 Do đó SMN AEF S   .S . Vậy V       AM.S MN.S 2. ABC cos AEF AMN AM ABC .A B C ABC AEF
Cách 3. Ta chứng minh được AA  AEF . Khi đó thể tích lăng trụ đã cho bằng thể
tích của khối lăng trụ T  có đáy là tam giác AEF và chiều cao là AA (chỉ cần cắt
khối đa diện ABCFE ghép xuống dưới khối ABC AEF ta sẽ thu được lăng trụ đứng). Do đó V       AA .S 2. ABC .A B C AEF
Câu 45. Cho khối lăng trụ ABC.ABC , khoảng cách từ C đến đường thẳng BB
bằng 2, khoảng cách từ A đến các đường thẳng BB và CC  lần lượt bằng 1 và 3.
Hình chiếu vuông góc của A lên mặt phẳng ABC  là trọng tâm G của tam giác 4
ABC  và AG  . Thể tích của khối lăng trụ đã cho bằng 3 A. 2 . B. 4 . C. 8 . D. 2. 3 3 3
Lời giải. Tương tự như bài trên V AA .S . AEF Gọi G là trọng tâm 2 2 AE
F AG AH  . 3 3
Vì AA  AEF  AA  AG nên d G, AA  AG.
Mà AA  GG nên d GAA  d G AA 2 , ,  AG  . 3 Tam giác vuông AG A
  có d GAA 2 4 ,
 , AG  nên 3 3 tính được 8 AA  . Vậy 4
V  . Chọn B. 3 3 3 21
Phần 2. Tỷ số thể tích
Câu 1. Cho hình chóp tứ giác đều S.ABCD. Gọi H là
hình hộp chữ nhật có bốn đỉnh là bốn trung điểm của các cạnh bên , SA SB, SC,
SD và bốn đỉnh còn lại nằm trong
mặt đáy ABCD (tham khảo hình vẽ). Biết thể tích khối
hộp H là V. Thể tích của khối chóp đã cho bằng A. 2V. B. 6V. C. 4V. D. 8V. 3 3
Lời giải. Chiều cao của khối chóp gấp hai lần chiều cao khối hộp và diện tích mặt đáy
khối chóp gấp 4 lần diện tích mặt đáy khối hộp. Do đó 8 V
V. Chọn D. SABCD 3
Câu 2. Cho khối chóp S.ABCD có đáy là hình bình
hành ABCD. Gọi M,
N, P, Q lần lượt là trọng tâm
các tam giác SAB, SBC, SCD, .
SDA Biết khối chóp
S.MNPQ có thể tích là V , khi đó thể tích của khối
chóp S.ABCD bằng A. 9V V . B. 27 . 4 4 C. 81V V . D. 81 . 4 8
Lời giải. Ta có d S ABCD 3 ,   d S  ,MNPQ   2   và 2 3 9 S  2S  2.    SS . ABCD IJHK 2 MNPQ  2 MNPQ Do đó 27 VV . Chọn B. S.ABCD S. 4 MNPQ
Câu 3. Cho khối tứ diện ABCD có thể tích V. Gọi M , N, P, Q lần lượt là trọng tâm
của các tam giác ABC, ABD, ACD, BCD. Gọi V  là thể tích của khối tứ diện MNPQ.  Tỉ số V bằng V A. 1 . B. 2 . C. 4 . D. 1 . 27 27 27 9 22
Lời giải. Ta có MNP ∽ DCB theo tỉ số 1 k  3 nên 1 1 S = S
và d Q,MNP  d  , A DCB MNP  9 DCB   3    nên V 1  . Chọn A. V 27
Câu 4. Cho lăng trụ tam giác ABC.MNP có thể tích V. Gọi G , G , G , G lần lượt là 1 2 3 4
trọng tâm của các tam giác ABC, ACM, AMB, BCM ; V là thể tích khối tứ diện 1
G G G G . Khẳng định nào sau đây đúng ? 1 2 3 4
A. V  9V .
B. V  27V .
C. V  81V .
D. 8V  81V . 1 1 1 1
Lời giải. Tương tự như bài trên và chú ý rằng đây là thể tích lăng trụ. Chọn C.
Câu 5. Cho khối tứ diện đều ABCD có thể tích V. Gọi M, N, P lần lượt là trọng tâm 
các tam giác ABC, ACD, ADB và V  là thể tích khối tứ diện AMNP. Tỉ số V bằng V A. 4 . B. 2 . C. 4 . D. 8 . 9 27 27 81
Lời giải. Xác định được thiết diện là tam giác EFH (tham khảo hình vẽ). Ta có
• d A MNP  d A EGH  2 , ,   d  , A BCD.     3   2   • 1 1 2 1 SS  .    SS . MNP 4 EFH 4 3 BCD  9 BCD  Suy ra 2 V VV nên 2  . Chọn B. AMNP 27 ABCD V 27
Câu 6. Cho khối lập phương ABCD.AB CD
  có cạnh bằng 1. Gọi
M , N, P, L lần lượt là tâm của các hình vuông ABB A  , AB CD  , ADD A   và CDD C
 . Gọi Q là trung điểm của BL
(tham khảo hình vẽ bên). Thể tích khối tứ diện MNPQ bằng A. 1 . B. 1 . C. 2 . D. 3 . 16 24 27 27 23
Lời giải. Ta có M , N,
P lần lượt là trung điểm của AB , B D
 , AD nên suy ra 1 SS .   1 MNP  4 ABD  
Lại có Q BC D  , mà BC D    AB D   nên d Q,  AB D
   d B,    AB D
   d A ,    AB D  .   2 Từ   1 1 1 1 và 2  V   V   Chọn B.   V . MNPQ 4 BAB D 4 AAB D 24
Câu 7. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh ,
a SA vuông góc với
mặt đáy. Gọi M là trung điểm BC. Mặt phẳng P đi qua A và vuông góc với SM
cắt SB, SC lần lượt tại E, F. Biết 1 VV
. Thể tích khối chóp S.ABC bằng SAEF 4 SABC 3 3 3 3 A. a 2a a a . B. . C. . D. . 2 5 8 12
Lời giải. Kẻ AH SM H SM . BC AM Ta có  
BC SM. BC SA 
Do P đi qua A vuông góc với SM cắt SB, SC tại E, F
nên EF đi qua H và song song với BC SE SH SF     . SB SM SC 2 Trong tam giác vuông SH SA SAM , có 2
SH.SM SA    . 2 SM SM 2     2  2      Ta có V 1 SE SF SH SA 3 a 3        1 SAEF .      2 2    
SA a  SA  . 2 V 4 SB SCSM   a  4 2 SABC 2 3  4 SA    4  2 3
Vậy thể tích khối chóp 1 a 3 a 3 a
S.ABC là V  . .  . Chọn C. 3 2 4 8
Câu 8. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên
SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy ABC . Gọi V 16
H là hình chiếu vuông góc của A lên SC. Biết S.ABH  . Thể tích của khối V 19 S.ABC
chóp S.ABC bằng 24 A. 3 . B. 3 . C. 3 . D. 3 . 2 4 6 12
Lời giải. Gọi O là trung điểm của AB 
SO  ABC . SC   AH Ta có 
SC  AHB. Suy ra SC OH. SC   AB  2 Trong tam giác vuông SH SO SOC, có 2
SH.SC SO    . 2 SC SC 2 2 Ta có V 16 SH 16 SO 16 SO 16 S.AHB         SO  2. 2 V 19 SC 19 SC 19 2 3 19 S.ACB SO  4 Vậy 1 1 3 3 V S .SO  .2.  . Chọn C. 3 ABC 3 4 6
Câu 9. Cho hình chóp đều S.ABC. Gọi G là trọng tâm tam giác ABC, góc giữa SG và
mặt phẳng SBC là 30. Mặt phẳng P chứa BC và vuông góc với SA chia khối
chóp S.ABC thành hai phần. Tỉ số thể tích hai phần bằng A. 2 . B. 1 . C. 1 . D. 6 . 3 6 7 7
Lời giải. Ta chứng minh được BC  .
SA Trong mặt phẳng SAM , kẻ MN SA với N  .
SA Khi đó thiết diện tạo bởi mp P và khối chóp là NBC  (hình a).
Dễ dàng xác định được:   SG SBC  SG SM    30 , ,  GSM. hình a hình b Ta có V SN SN V S.NBC  . Ta tính được 1  (hình b). Suy ra 1
SNBC  . Chọn B. V SA SA 7 V 6 S.ABC NABC
Câu 10. Cho lăng trụ tam giác đều ABC.AB C
  có cạnh đáy bằng , a chiều cao bằng 2 .
a Mặt phẳng P qua B và vuông góc AC chia lăng trụ thành hai khối. Biết thể tích của hai khối là V
V và V với V V . Tỉ số 1 bằng 1 2 1 2 V2 A. 1 . B. 1 . C. 1 . D. 1 . 7 11 23 47
Lời giải. Gọi H là trung điểm của AC , suy ra B H
  AC nên B H  P. 25
Trong mặt phẳng ACC A
 , kẻ HK AC với K AA . Suy ra HK P.
Do đó thiết diện tạo bởi mặt phẳng P và khối lăng trụ là tam giác HKB . hình a hình b Ta có 1 S  và tính được 1
KA  AA .    S A B H 2 A  B C   8 Do đó 1 V 1 1 V     Chọn D.   V . K .A B H ABCD. 48 AB CD   V 47 2
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB CD, AB  2CD. Gọi V
M , N lần lượt là trung điểm của SA và SD. Tỉ số S.BCNM bằng VS.BCDA A. 1. B. 1 . C. 3. D. 5 . 3 4 8 12
Lời giải. Vì hình thang ABCD có AB  2CD nên S  2S . ABD BCD Ta có VVV . S.BCMN S.BCN S.BNM • V SN 1 1 1 S.BCN    V   .V  .V . S.BCN S.BCD S. V SD 2 2 6 ABCD S.BCD • V SN SM 1 1 1 S.BNM  .   V   VV . S.MBN S.ABD S. V SD SA 4 4 6 ABCD S.BDA Suy ra 1 V 1 VV
nên S.BCMN  . Chọn A. S.BCMN S. 3 ABCD V 3 S.BCDA
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm di
động trên cạnh AB và N là trung điểm của SD. Mặt phẳng  đi qua M, N và song song với V 3
BC chia khối chóp S.ABCD thành hai khối có tỷ số thể tích 1  , V 5 2
trong đó V là thể tích khối đa diện chứa đỉnh ,
A V là thể tích khối đa diện chứa 1 2
đỉnh B. Tỉ số AM bằng AB A. 1 . B. 1. C. 3. D. 3. 2 3 5 7 Lời giải. Gọi AM
P, Q lần lượt là giao điểm của  với CD, S . A Đặt  x 0;  1 . AB 26 Ta có AM V V V   .VVV . 1 S.ADPM S.QNPM S.ABCDS.QNP S.QMP AB • 1 1 1 VVVxV ; S.QNP S.ADP S.ADPM S. 4 8 8 ABCD • 1 1 1 VVVxV . S.QMP S.AMP S.ADPM S. 2 4 4 ABCD   Suy ra 5 5 V xV  V   1   x V  . 1 S.ABCD 2 S. 8  8 ABCD  5 x Theo đề, ta có 8 3 3  
x  . Chọn C. 5 5 5 1 x 8
Câu 13. Cho hình hộp ABCD.AB CD
 . Gọi M là điểm thuộc đoạn CC  thỏa mãn
CC   3CM. Mặt phẳng AB M
  chia khối hộp thành hai phần có thể tích là V , V . 1 2 Gọi V
V là thể tích phần chứa điểm B. Tỉ số 1 bằng 1 V2 A. 7 . B. 13 . C. 7 . D. 13 . 9 20 27 41 Lời giải. Vì  IK IC IM
BABCKM  nên 1    . IA IB IB 3 Ta có V IK IC IM 1 1 IKCM  . .   V   V . IKCM B . V IA IB IB 27 27 ABI IABB ' Suy ra 26 V V . 1 . 27 B ABI Mà 1 1 3 1 V        
d B ', ABCD .S
d B ', ABCD . S V . B .ABI   ABI   ABCD
ABCD.A ' B 'C ' D ' 3   3   4 4 Vậy 26 1 13 V 13 1 V  . VV    . Chọn D. 1
ABCD.A ' B 'C ' D '
ABCD.A ' B 'C ' D ' 27 4 54 V 41 2
Câu 14. Cho hình hộp ABCD.AB CD  . Gọi M , N,
P lần lượt là trung điểm của
AA , BC, CD. Mặt phẳng MNP chia khối hộp thành hai phần có thể tích là V , V . 1 2 Gọi V
V là thể tích phần chứa điểm C. Tỉ số 1 bằng 1 V2 A. 3 . B. 113. C. 119 . D. 119 . 4 24 25 425 Lời giải. Ta có 27 • 1 Vd  , R ABCD .S R.BNF   3 BNF    1 1 
d M ABCD 1 1 . , . SV ; AEF M . 3 3   9 27 AEF • 1 V
d Q, ABCD .S Q.DEP   3 DEP   1 1 
d M ABCD 1 1 . , . SV . AEF M . 3 3   9 27 AEF   Suy ra 1 1 25 V  1    V   V . 2 M .AEF M .  27 27 27 AEF Mà 1 1 1 9 3 V
d M , ABCD .S
 . d A , ABCD . SV . M .AEF   AEF   ABCD
ABCD.A ' B 'C ' D ' 3   3 2   8 16 Vậy 25 3 25 V 119 1 V  . VV    . Chọn C. 2
ABCD.A ' B 'C ' D '
ABCD.A ' B 'C ' D ' 27 16 144 V 25 2
Câu 15. Cho hình lăng trụ tam giác đều ABC.AB C
  có tất cả các cạnh bằng . a Gọi
M , N lần lượt là trung điểm của các cạnh AB và B C
 . Mặt phẳng AMN  cắt cạnh
BC tại P. Thể tích khối đa diện MBP.AB N  bằng 3 3 3 3 A. 3a 3a 7 3a 7 3a . B. . C. . D. . 12 24 32 96
Lời giải. Ta có V IM IB IP 1 1 1 1 IMBP  . .  . .  . V
IA' IB ' IN 2 2 2 8
IA ' B ' N   Suy ra 1 7 V  1         V V . MBP.A B N
IA ' B ' N IA ' B '  8 8 N Mà 1 V
d I, A' B 'C ' .S
IA ' B ' N   A  ' B ' 3 N   1 
d B A B C  1 1 .2 , ' ' ' . SV . A  ' B 'C '
ABC .A ' B 'C ' 3   2 3 Vậy 7 1 7 7 3 3 V  .   Chọn D.   V V a . MBP.A B N
ABC .A ' B 'C '
ABC .A ' B 'C ' 8 3 24 96
Câu 16. Cho hình hộp ABCD.AB CD
  có M , N, P lần lượt là trung điểm ba cạnh
AB , BB và D D
 . Mặt phẳng MNP cắt đường thẳng AA tại I. Biết thể tích khối
tứ diện IANP là V. Thể tích khối hộp đã cho ABCD.AB CD   bằng A. 2V. B. 4V. C. 6V. D. 12V. 28
Lời giải. Gọi Q  MNP AD . Theo tính chất của giao
tuyến suy ra MQ NP nên Q là trung điểm của AD . Suy
ra M, Q lần lượt là trung điểm IN, IP. V
Ta có I.AMQ IA IM IQ 1 1 1 1 V  . .  . .   V   . I . V IA IN IP 3 2 2 12 AMQ 12 IANP Mặt khác 1 V        
d I, A B C D .S I .A MQ    3   A  MQ 1 1 
d A ABCD 1 1 . , . SV  4 Chọn B.     V .     V .   Từ đó suy ra A B C D ABCD. 3 2 8 48 AB CD   ABCD.A B C D
Câu 17. Cho lăng trụ tam giác đều ABC.AB C
 . Trên AB kéo dài lấy điểm M sao cho 1 B M
AB . Gọi N, P lần lượt là trung điểm của AC , B B
 . Mặt phẳng MNP 2
chia khối lăng trụ ABC.AB C
  thành hai khối đa diện, trong đó khối đa diện chứa đỉnh V
A có thể tích V , khối đa diện chứa đỉnh C  có thể tích V . Tỉ số 1 bằng 1 2 V2 A 97 . B 49 . C. 49 . D. 95 . 59 95 144 144
Lời giải. Gọi các giao điểm như hình vẽ. Ta chứng
minh được J là trung điểm MN; K là trung điểm AB. V   MP MJ MB 1 1 1 1 M .PJB   . .  . .  V     MS MN MA 3 2 3 18 Ta có  M.SNA  .  V SA SK SL 1 1 1 1  S.ALK   . .  . .  V    SA SM SN 3 3 3 27  S.A NM    Suy ra 1 1 49 V  1 SA S  1 3 3 3 V  1    V   Mà S.A NM  . . MNA  . .  .  V . 1  18 27 MA NS  54 MANS V 3    SA S 3 2 4 8 ABC .A B C A  B C   Suy ra 49 V 49 V V nên 1  . Chọn B. 1 .
144 ABC AB C V 95 2
Câu 18. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng ,
a cạnh bên hợp với đáy góc o
60 . Gọi M là điểm đối xứng của C qua D, N là trung điểm của SC. Mặt
phẳng BMN  chia khối chóp S.ABCD thành hai phần có thể tích là V , V trong đó 1 2 V
V là phần thể tích chứa đỉnh .
A Tỉ số 2 bằng 1 V1 A. 7 . B. 5. C. 12 . D. 5 . 5 7 5 12 29
Lời giải. Dễ thấy DE là đường trung bình của tam giác ME MBC, suy ra 1  ; MB 2
F là trọng tâm của tam giác SMC, suy ra MF 2  . Ta có MN 3 V MD ME MF 1 1 2 1 M .DEF  . .  . .  V MC MB MN 2 2 3 6 M .CBN   Suy ra 1 5 V  1   V   V . 2 M .CBN M .  6 6 CBN Mà V CN CM 1 1 C .BNM  .  .2  1 VVV . C .BNM C .BSD S. V CS CD 2 2 ABCD C .BSD Vậy 5 1 V 5 2 V  . V    . Chọn B. 2 S. 6 2 ABCD V 7 1
Câu 19. Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh B, AB  4;
SA SB SC  12. Gọi M , N lần lượt là trung điểm AC, BC. Trên cạnh , SA SB lần lượt lấy điểm SE BF E, F sao cho 2 
 . Thể tích khối tứ diện MNEF bằng SA BS 3 A. 4 34 . B. 16 34 . C. 4 17 . D. 4 34 . 3 3 9 9
Lời giải. Gọi K là trung điểm của SE và I
EF AB. Suy ra E là trung điểm của IF và IA KF 1  AB nên 1 1 SS  V   V . 3 IMN 4 ABC FIMN 6 SABC Mà V FE 1 1 FEMN .    V   V . V FI 2 FEMN 2 FIMN FIMN Vậy 1 1 16 34 4 34 VV  .  . Chọn D. FEMN 12 SABC 12 3 9
Câu 20. Cho hình lập phương ABCD.AB CD
  có độ dài cạnh bằng 1. Gọi M , N, P, Q
lần lượt là trung điểm của AB, BC, C D
  và DD . Thể tích khối tứ diện MNPQ bằng A. 1 . B. 3. C. 1 . D. 1 . 8 8 12 24
Lời giải. Gọi E PQ CD. Khi đó ta có Q là trung điểm của PE và 1 DE  . 2 Tính được 1 1 SS  . MNE  2 ABCD 2 V Ta có P.QMN PQ 1 1    V   V P.QMN P. V PE 2 2 EMN P.EMN 30 1 1 
d P MNE 1 1 1 1 . . , .S  . .1.  . 2 3 MNE    Chọn C. 2 3 2 12
Câu 21. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, thể tích là V. Gọi AM
M là một điểm trên cạnh AB sao cho
x, 0  x 1. Mặt phẳng  qua M và AB
song song với SBC chia khối chóp S.ABCD thành hai phần, trong đó phần chứa điểm  x
A có thể tích bằng 4 V . Giá trị của biểu thức 1 P  bằng 27 1 x A. 1 . B. 1. C. 1. D. 3. 2 3 5 5
Lời giải. Tham khảo hình vẽ bên. Từ giả thiết suy ra AQ AM AF DF   x;  1 x;  x. AS AB AD DA V Do đó Q.AMEF V 2
x 1 x; P.FEND 3  x . V V S.ABCD S.ABCD Ta có 3 3 2 VVx 1 x V . AMQ.FED Q.AMEF   S. 2 2 ABCD Theo giả thiết: 4 3 4 x 1 2 VVVxx x
 x  nên AMQ FED P FEND S ABCD 1  3 0 1 . . . 27 2 27 3 1
P  . Chọn A. 2
Câu 22. Cho hình chóp tứ giác S.ABCD. Mặt phẳng đi qua trọng tâm các tam giác
SAB, SAC, SAD chia khối chóp thành hai phần có thể tích là V và V V V . Tỉ số 1 2  1 2 V1 bằng V2 A. 8 . B. 8 . C. 16 . D. 16 . 19 27 75 81
Lời giải. Gọi G , G , G lần lượt là trọng tâm 1 2 3
các tam giác SAB, SAD, SAC.
Gọi I, J lần lượt là trung điểm của AB, AC thì SG 2 SG 1 3  
G G IJ 
G G ABC . 1 3 1 3   SI 3 SJ
Chứng minh tương tự ta có G G ABC . 2 3  
Suy ra G G G ABCD . 1 2 3   
Gọi các giao điểm của G G G với các cạnh bên 1 2 3 
như hình vẽ, ta tìm được thiết diện của hình chóp S.ABCD khi cắt bởi G G G là tứ 1 2 3  giác MNPQ. 31 Ta có V SM.SN.SP 8 8 8 S.MNP    V   V ; Tương tự VV . S.MNP S. V . SA SB.SC 27 27 ABC S.MPQ S. 27 ACD S.ABC Suy ra 8 8 V 8 VVVVVV nên 1  . Chọn A. S.MNPQ S.MNP S.MPQS.ABC S.ACD S. 27 27 ABCD V 19 2
Câu 23. Cho tứ diện đều ABCD có cạnh bằng .
a Gọi M , N lần lượt là trung điểm
AB, BC và điểm P là điểm đối xứng với B qua D. Mặt phẳng MNP chia tứ diện
thành hai phần có tỉ số thể tích là A. 1 . B. 7 . C. 7 . D. 11. 2 11 18 18 Lời giải. Do DE DF
E, F lần lượt là trọng tâm các tam giác ABP, BCP nên 1   . DA DC 3 V  BM BN BP 1 1 1 BMNP   . .  . .2  V BA BC BD 2 2 2 Ta có  BACDVDE DF DP 1 1 1  DEFP   . .  . .1  V  DA DC DB 3 3 9  DACB V 1 1 7 V BMNDEF      nên 7 BDMNFE  . Chọn B. V 2 9 18 V 11 DACB ACMNFE
Câu 24. Cho tứ diện ABCD, trên các cạnh BC, BD,
AC lần lượt lấy các điểm M , N,
P sao cho BC  3BM , 3
BD BN, AC  2AP. Mặt phẳng MNP chia khối tứ 2 diện V
ABCD thành hai phần có thể tích là V và V . Tỉ số 1 có giá trị bằng 1 2 V2 A. 26 . B. 3 . C. 15 . D. 26 . 13 19 19 19
Lời giải. Gọi I PM AB và R NI AD. Ta cần tính V AP AR AI V BM BN BI APRI  . . và BMNI  . . . V AC AD AB V BC BD BA ACDB BCDA Theo Menelaus, ta có • PC IA MB IA . .  1    2; PA IB MC IB • RD IA NB RD 1 . .  1    . RA IB ND RA 4 Từ đó suy ra V 1 4 4 V APRI  . .2  và 1 2 2 BMNI  . .1  . V 2 5 5 V 3 3 9 ACDB BCDA   Suy ra 4 2 26 V 26 V    V   V nên 1  . Chọn D. APRBMN 5 9 ACDB  45 ACDB V 19 2 32
Câu 25. Cho tứ diện ABCD và các điểm M, N, P lần lượt thuộc các cạnh
BC, BD, AC sao cho BC  4BM , AC  3AP, BD  2BN. Tỉ số thể tích hai phần của
khối tứ diện ABCD được phân chia bởi mặt phẳng MNP bằng A. 7 . B. 8 . C. 7 . D. 8 . 13 13 15 15
Lời giải. Gọi I MN DC và K AD PI. Ta cần tính V CM CP CI V DN DK DI CMPI  . . và DNKI  . . . V CB CA CD V DB DA DC CBAD DBAC Theo Menelaus, ta có • IC ND MB IC . .  1    3; ID NB MC ID • KD PA IC KD 2 . .  1    . KA PC ID KA 3 Từ đó suy ra V 3 2 3 3 V CMPI  . .  và 1 2 1 1 DNKI  . .  . V 4 3 2 4 V 2 5 2 10 CBAD DBAC   Suy ra 3 1 13 V    V   V
nên tỉ số cần tính bằng 7 . Chọn A. MCPNDK 4 10 ACDB  20 ACDB 13
Câu 26. Cho tứ diện đều ABCD có cạnh bằng .
a Gọi M , N lần lượt là trọng tâm của
các tam giác ABD, ABC và E là điểm đối xứng với B qua điểm D . Mặt phẳng
MNE chia khối tứ diện ABCD thành hai khối đa diện, thể tích khối đa diện chứa đỉnh A bằng 3 3 3 3 A. 3a 2 a 2 3a 2 9a 2 . B. . C. . D. . 80 96 320 320 3
Lời giải. Thể tích khối tứ diện đều cạnh a 2 a là: V  . ABCD 12
Gọi các giao điểm như hình vẽ. Menelaus cho • ED MI QA QA AID  , ta có . .  1    3. EI MA QD QD
• Tương tự ta cũng có PA  3. PC • EI TB MA TB ABI  , ta có 2 . .  1    . EB TA MI TA 3 V 3 3 Ta có ATPQ AT AP AQ 3 3 3 27 27 a 2 9a 2  . .  . .   V   .  . Chọn D. V AB AC AD 5 4 4 80 ATPQ 80 12 320 ABCD 33
Câu 27. Cho tứ diện đều ABCD có cạnh bằng .
a Gọi M , N lần lượt là điểm trên cạnh AM AN AB, AC sao cho 1  ,
 2. Mặt phẳng  chứa MN và song song với BM 2 CN
AD chia khối tứ diện thành hai phần. Thể tích khối đa diện chứa đỉnh A bằng 3 3 3 3 A. 4 2a 4 2a 5 2a 11 2a . B. . C. . D. . 81 108 108 342 3
Lời giải. Thể tích khối tứ diện đều cạnh a 2 a là: V  . ABCD 12
Kẻ MQ AD với Q BD; NP AD với P CD. Gọi E PQ BC. Suy ra BQ BM 2 CP CN   và 1   . BD BA 3 CD CA 3 Menelaus cho EC QB PD EC BCD, ta có 1 . .  1    . EB QD PC EB 4 V  BMEQ BM BE BQ 2 4 2 16   . .  . .  V  BA BC BD 3 3 3 27 Ta có  BACDV  CN CE CP 1 1 1 1 CNEP   . .  . .  V  CA CB CD 3 3 3 27  CABD V 3 BMQCNP 16 1 5 4 a 2    
 nên thể tích cần tính bằng V  . Chọn B. V 27 27 9 9 ABCD 27 ABCD    
Câu 28. Cho khối chóp S.ABC có M  ,
SA N SB sao cho MA  2MS, NS  2NB.
Mặt phẳng  đi qua hai điểm M, N và song song với SC chia khối chóp thành hai
khối đa diện. Tỉ số thể tích của hai khối đa diện đó bằng A. 3. B. 4 . C. 4 . D. 5 . 5 5 9 9
Lời giải. Hoàn toàn tương tự như bài trên, ta được đáp án B.
Câu 29. Cho tứ diện đều ABCD có cạnh bằng .
a Gọi E là điểm đối xứng của A qua
D. Mặt phẳng qua CE và vuông góc với mặt phẳng ABD cắt cạnh AB tại điểm F.
Thể tích của khối tứ diện AECF bằng 3 3 3 3 A. 2a 2a 2a 2a . B. . C. . D. . 15 30 40 60
Lời giải. Gọi G là trọng tâm tam giác ABD, suy ra CG  ABD.
Do đó mặt phẳng cần dựng là CEG. Gọi
F EG AB.
Gọi M là trung điểm AD, áp dụng Menelaus cho ABM  , ta có FA GB FM FA 2 . .  1    . FB GM FA FB 3 34 3 Ta có V AE AC AF 2 4 4 2a AECF  . .  2.1.   V   V  . Chọn A. V AD AC AB 5 5 AECF 5 ADCB 15 ADCB
Câu 30. Cho hình chop S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt
là trung điểm của AD,
DC. Kéo dài SD một đoạn sao cho D là trung điểm của SP.
Thiết diện tạo bởi mặt phẳng MNP chia hình chóp thành hai khối lần lượt có thể tích là V
V , V (trong đó V là thể tích của phần chứa điểm S ). Tỉ số 1 bằng 1 2 2 V2 A. 3 . B. 71 . C. 72 . D. 71 . 4 49 49 120
Lời giải. Tham khảo hình vẽ. Menelaus cho • PD RS NC RS SCD, có . .  1    2. PS RC ND RC
• Tượng tự ta cũng có QS  2. QA • PD TS HB TS SBD  , có 2 . .  1    . PS TB HD TB 3 Ta có V  S.QTR SQ ST SR 8 4   . .   V   V S.QTR S. V  SA SB SC 45 45 ABCD S.ABC VS.QPR SQ SP SR 8 4   . .   V   V . S.QPR S. VSA SD SC 9 9 ABCDS.ADC  1 1  1  V   VV do  SS  P.DMN S.DAC S.  4 8 ABCD DMN   4 DAC   Suy ra 49 V 71 1 V VV V   V    . Chọn B. 2 S.QTR S.QPR P.DMN S. 120 ABCD V 49 2 35 Phần 3. Cực trị
Câu 1. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , SA vuông
góc với đáy, khoảng cách từ A đến mặt phẳng SBC bằng 3 . Gọi là góc giữa hai
mặt phẳng SBC và ABC, tính cos khi thể tích khối chóp S.ABC nhỏ nhất. A. 2 cos  . B. 1 cos  . C. 3 cos  . D. 2 cos  . 2 3 3 3 Lời giải. Đặt 1
AB AC x; SA y . Khi đó 2 Vx . y S.ABC 6 Vì AB, AC,
AS đôi một vuông góc nên 1 1 1 1 1 1      33 . 2 9 d  , A SBC  2 2 2 4 2  x x y x y   Suy ra 1 27 3 2 2
x y  81 3  V   x y  . SABC 6 2
Dấu "  " xảy ra  x y  3 3. Khi đó  3
cos  cosSMA  . Chọn C. 3
Câu 2. Trên đường thẳng qua A và vuông góc với mặt phẳng chứa tam giác đều
ABC cạnh bằng 2, lấy các điểm M và N không trùng với A sao cho MBC  vuông
góc với NBC. Giá trị nhỏ nhất thể tích tứ diện BCMN bằng A. 2. B. 2 2. C. 2 3. D. 6.
Lời giải. Ta có MBC vuông góc với NBC khi tam giác
MHN vuông tại H.
Đặt MA x, NA  . y Ta có 2 M .
A NA AH xy  3.
Áp dụng công thức thể tích đặc biệt: 1
V abd sin ta có 6 1 VMN BC AH MN BC x y BCMN   1 . . .sin ,   0 .2. 3.sin 90 . 6 6
Theo BĐT Côsi: x y  2 xy  2 3. Do đó 3 V
x y  Dấu ''  '' xảy ra khi 3
x y  . Chọn A. BCMN   2. 3 2
Câu 3. Cho tam giác OAB đều cạnh a . Trên đường thẳng d qua O và vuông góc với
mặt phẳng OAB lấy điểm M sao cho OM x . Gọi E, F lần lượt là hình chiếu
vuông góc của A trên MB và OB . Gọi N là giao điểm của EF và d . Tìm x để thể
tích tứ diện ABMN có giá trị nhỏ nhất. A. a a a x a 2. B. 2 x  . C. 3 x  . D. 6 x  . 2 2 12 36
Lời giải. Do tam giác a OAB đều cạnh ,
a suy ra F là trung điểm OB OF  . 2 AF OB Ta có  
AF  MOB  AF MB. AF MO 
Lại có MB AE nên suy ra MB  AEF  MB EF. Suy ra OBM ∽ ONF nên 2 OB ON OB.OF a   ON   . OM OF OM 2x Ta có VVV ABMN ABOM ABON 2 2 3   1 a a   aS OM ON  x    OAB   3 6 . 3 12  2x  12 2
Đẳng thức xảy ra khi và chỉ khi a a 2 x   x  . Chọn B. 2x 2
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, thể tích là V. Gọi
M là trung điểm của cạnh ,
SA N là điểm nằm trên cạnh SB sao cho SN  2NB; mặt
phẳng  di động qua các điểm M, N và cắt các cạnh SC, SD lần lượt tại hai điểm
phân biệt P, Q . Thể tích lớn nhất của khối chóp S.MNPQ bằng A. V V V V . B. . C. 2 . D. 3 . 2 3 3 4 Lời giải. Gọi SP a   0  a  
1 . Vì mặt phẳng  di động đi qua các điểm M , N và SC
cắt các cạnh SC, SD lần lượt tại hai điểm phân biệt P, Q nên ta có đẳng thức SA SC SB SD 1 3 SD SD 2  a     2       . SM SP SN SQ a 2 SQ SQ 2a
Áp dụng công thức tính nhanh 3 1 2  a 2    2 VS.MNPQ 2 a 2 2 a a a   . V 3 1 2  a 3a  6 S.ABCD 4.2. . . 2 a 2a
Xét hàm f a 2a 1   trên đoạn 0;  1 , ta được 3 a  2
f a  f   1 max 1  . Chọn B. 0  ;1 3
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, thể tích là V. Điểm MC
M di động trên cạnh SC, đặt
k. Mặt phẳng  qua ,
A M và song song với MS
BD cắt SB, SD thứ tự tại N, P. Thể tích khối chóp C.APMN lớn nhất khi A. k  1. B. k  2. C. k  2. D. k  3.
Lời giải. Từ giả thiết MC SC SM MC
k suy ra MC kMS. Khi đó   1 k. MS SM SM 37 Áp dụng Menelaus cho AC IO MS IO k SOk SOC, có . .  1    , suy ra 2  . AO IS MC IS 2 SI 2 Vì SB SD SOk
NP BD nên suy ra 2    . SN SP SI 2   
  k 2 k 2 k 1 1   Ta có V 2 S.ANMP 2 2   . Vkk 4.1.1 k 2 2
1 k2  k . . 2 2 Lại có V SM 1 2kV S.ANMP   . Suy raV  . V CM k C .ANMP
1 k2  kC .ANMP Xét   k f k
trên 0;, có max f k f  2 32 2. Chọn C. 2 k  3k  2 0;
Chú ý: Ta có thể tính theo cách khác: VV VVV  . C .ANMP S.ABCD S.ANMP P.ACD N .ABC
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh ,
a cạnh bên SA y
y  0 và vuông góc với đáy ABCD. Trên cạnh AD lấy điểm M và đặt AM x
0  x a. Biết 2 2 2
x y a , thể tích lớn nhất V
của khối chóp S.ABCM bằng max 3 3 3 3 A. a 3 3a 3 a 3 a 3 . B. . C. . D. . 3 3 8 24 Lời giải. Từ 2 2 2 2 2
x y a y a x .       Diện tích BC AM a x S     .AB        . a ABCM  2   2  Thể tích khối chóp 1 VS .SA S.ABCM 3 ABCM    1 a x 2 2 a  .
.a a x  a x 2 2 a x . 3  2  6 2   Xét hàm   a 3 3a     2 2 f x a x
a x trên 0;a, ta được max f x  f      . 0;a 2 4 3 Suy ra a 3 V  . Chọn C. max 8
Câu 7. Từ hình vuông có cạnh bằng 6 người ta cắt bỏ
các tam giác vuông cân tạo thành hình tô đậm như hình
vẽ. Sau đó người ta gập thành hình hộp chữ nhật không
nắp. Thể tích lớn nhất của khối hộp bằng A. 8 2. B. 9 2. C. 10 2. D. 11 2. 38
Lời giải. Gọi độ dài các cạnh của hình hộp chữ nhật không nắp là ,
a b (như hình vẽ).
Suy ra hình chữ nhật có đáy là hình vuông cạnh b, chiều cao là a 2  V   ab . hh
Ta tính được cạnh của hình vuông ban đầu là b 2  a 2.
Theo đề suy ra b 2  a 2  6  a  3 2  . b Khi đó ta có 2 V ab   b 2 3 2 b . hh
Xét hàm f b 2 3
 3 2b b trên 0;3 2, ta được max f x f 2 2 8 2. Chọn A. 0;3 2
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành với AD  4a . Các
cạnh bên của hình chóp bằng nhau và bằng a 6 . Thể tích lớn nhất của khối chóp đã cho bằng 3 A. 8a 4 6 . B. 3 a . C. 3 8a . D. 3 4 6 a . 3 3
Lời giải. Do SA SB SC SD a 6 nên hình chiếu vuông góc của S trên mặt
phẳng ABCD trùng với tâm đường tròn ngoại tiếp đáy. Do đó tứ giác ABCD là hình
chữ nhật. Gọi H AC BD, suy ra SH  ABCD.
Đặt AB x  0, suy ra 2 2 2 2
AC AD AB x 16a . 2 2 2 Tam giác vuông AC 8a x S , HA có 2 SH SA   . 4 2 Khi đó 1 1 VS
.SH AB.AD.SH S.ABCD 3 ABCD 3 2 2 1 8a x a a a  .x.4 . a
 2x 8a x  3 8 2 2   2 2 2
x  8a x  . Chọn A. 3 2 3 3 3
Câu 9. Cho tam giác ABC vuông tại A có AB  3 , a AC  .
a Gọi Q là mặt phẳng
chứa BC và vuông góc với mặt phẳng ABC. Điểm D di động trên Q sao cho tam
giác DBC nhọn và hai mặt phẳng DAB và DAC lần lượt hợp với mặt phẳng
ABC hai góc phụ nhau. Thể tích lớn nhất của khối chóp D.ABC bằng 3 3 3 3 A. a 3 3a 3a 2 3a . B. . C. . D. . 4 8 10 13
Lời giải. Kẻ DH BC với H BC. Suy ra DH  ABC. Vì diện tích tam giác ABC
không đổi nên thể tích khối chóp D.ABC lớn nhất khi DH lớn nhất.
Kẻ HM AB với M AB, HN AC với N AC. Khi đó theo giả thiết, ta có
DAB ABC   ,
DMH và DAC  ABC    ,  DNH  90 . 39 Ta có SSS AHC AHB ABC 2 1  DH   1 3a . cot 90 .a  .DH cot . 3a  2 2 2 tan 3 x a 3 . a xDH   . 2
tan 3cot x  3 Xét   x 3 f x
trên0;, được max f x f  3 . 2 x  3 0; 6 3 Khi đó a 3 a 3 DH  và V  . Chọn A. max 2 max 4
Câu 10. Cho lăng trụ đứng ABC.AB C
  có đáy là tam giác đều. Tam giác ABC  có
diện tích bằng 3 và nằm trong mặt phẳng tạo với đáy một góc nhọn bằng . Thể
tích khối lăng trụ ABC.AB C
  đạt giá trị lớn nhất khi bằng A. 1  arctan . B. 1  arctan .
C.  arctan 2.
D.  arctan 6. 2 6
Lời giải. Đặt AB x  0. Gọi M là trung điểm của AB  x 3 MC   x   2 . Suy ra 3 MC   .  2 cos   
ABC ,ABC    CMC  
Theo giải thiết: 1 MC .AB  3 
x 2 cos. 2 Khi đó 3 V          S .CC .8 cos 
cos.tan 3sin cos3 cos ABC A B C ABC  2 1 cos . .  8 Xét hàm 2 3
f t t  2
1t  trên 0; 
1 , ta được max f t  khi 1 t  . t   0  ;1 9 3 Vậy V  2 3 khi 1 cos  tan  2 
arctan 2. Chọn C. max 3
Câu 11. Trong tất cả các hình chóp tứ giác đều có d  3 là khoảng cách giữa hai
đường thẳng chéo nhau gồm một đường thẳng chứa một đường chéo của đáy và đường
thẳng còn lại chứa một cạnh bên hình chóp. Thể tích nhỏ nhất của khối chóp bằng A. 3. B. 9. C. 9 3. D. 27.
Lời giải. Xét hình chóp tứ giác đều S.ABCD. Đặt 1 1 2 AB x,
SO h  V
hx . Ta cần đánh giá 2 hx  hằng số. S.ABCD 3 3 Ta tính được x OA
nên theo giả thiết ta có 2 1 1 1 1 1 2      2 2 2 2 2 2 OH SO OA d h x 1 1 2 1 1 1 1 1 2        3  3 .  hx  27. 2 2 2 2 2 2 4 3 h x h x x h x AM GM  40
Dấu ''  '' xảy ra  x h  3. Khi đó V  9. Chọn B. min
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình chữ
nhật. Một mặt phẳng không qua S và song song với đáy cắt các cạnh bên ,
SA SB, SC, SD lần lượt tại M , N, P, Q.
Gọi M , N , P , Q lần lượt là hình chiếu của M, N, P, Q
trên mặt phẳng đáy. Khi thể tích khối đa diện MNPQ.M NPQ
  đạt giá trị lớn nhất, tỉ số SM bằng SA A. 1 . B. 1. C. 2 . D. 3 . 2 3 3 4
Lời giải. Đặt SM MA
x 0  x   1 . Suy ra MN NP PQ SM     x và  1 x. SA AB BC CD SA SA S
Do MNPQ đồng dạng với ABCD theo tỉ số x nên MNPQ 2  x . SABCD V S
.d M , ABCD      S MNPQ.M N P Q MNPQ   Ta có   MNPQ MA 2   3.
 3x 1 x. V 1 S SA S.ABCD S .d  , A ABCD ABCD   ABCD 3   Suy ra 2 V  3  Xét f x 2
x   x 3 2 3 1
 3x 3x trên 0;  1 ,     x 1 x .V . MNPQ.M N P Q   S.ABCD   ta được f x 2 4 max  f  
   . Chọn C. 0  ;1 3 9
Câu 13. Cho hình chóp S.ABC có SA x 0  x  3, tất cả các cạnh còn lại đều
bằng 1. Thể tích lớn nhất của khối chóp đã cho bằng A. 1 . B. 1 . C. 1 . D. 1 . 4 8 12 16
Lời giải. Ta có tam giác
ABC và SBC là những t am giác đều cạnh bằng 1.
Gọi N là trung điểm 3 BC  SN  . 2
Trong tam giác SAN , kẻ SH AN .   1 BC AN Ta có  
BC  SAN  
BC SH . 2 BC SN  Từ  
1 và 2 , suy ra SH  ABC . Khi đó 1 1 1 3 3 1 VS .SH S .SN  . .  . S.ABC 3 ABC 3 ABC 3 4 2 8
Dấu ''  '' xảy ra  H N. Chọn B. NM SA
Cách 2. Gọi M là trung điểm SA     d  ,
SA BC   MN. NM BC  2 Tam giác 3 x
SNA cân tại N, có 3 SN AN  nên suy ra MN  . 2 2 41 Khi đó 1 xx VSA BC d SA BC SA BC   S ABC    2 3 1 . . , .sin , . . 6 12 8 Dấu 6 ''  '' xảy ra 2
x  3 x x  . 2
Câu 14. Cho hình chóp S.ABC có SA x, BC y, AB AC SB SC  1. Thể tích
khối chóp S.ABC lớn nhất khi tổng x y bằng A. 2 . B. 4 . C. 3. D. 4 3. 3 3
Lời giải. Tương tự như bài trên ta được 2 2 1 x y Vxy 1 S.ABC 6 4 1 2 2  x y  2 2
4  x y  12 3 2 2 2 2
1  x y  4  x y  2 3       . 12  3  27 Dấu 2 3 "  " xảy ra 2 2 2 2
x y  4  x y   x y  . Vậy 4 x y  . Chọn B. 3 3
Câu 15. Cho hình vuông ABCD cạnh ,
a trên đường thẳng vuông góc với ABCD tại
A ta lấy điểm S di động. Hình chiếu vuông góc của A lên SB, SD lần lượt là H , K.
Thể tích lớn nhất của tứ diện ACHK bằng 3 3 3 3 A. a a 2 a 3 a 6 . B. . C. . D. . 6 12 16 32
Lời giải. Tham khảo hình vẽ. Ta sẽ sử dụng công thức 1 V  . a .
b d a,b.sina,b. 6 2 2 Đặt x a 2 a x
SA x x  0. Tính được KH  , IH  . 2 2 a x 2 2 a x
Chứng minh được HI d KH, AC và AC HK. Khi đó 1 V
AC.KH.HI ACHK 6 2 2 4 3 1 x a 2 a x a x  .a 2. .  . . 2 2 2 2 6
a x a x
3 a x 2 2 2 3 Xét hàm   x 3 3 f x
trên 0;, ta có max f x khi x a 3. x a 2 2 2 0; 16a 3
Suy ra thể tích khối tứ diện lớn nhất bằng a 3 V  . Chọn C. max 16
Câu 16. Trong mặt phẳng P cho đường tròn T  đường kính AB  2r, C là một
điểm di dộng trên đường tròn T . Trên đường thẳng d vuông góc với P tại A lấy 42
điểm S sao cho SA r. Gọi H, K lần lượt là hình chiếu vuông góc của A lên SC và
SB. Khi C chạy trên đường tròn, thể tích lớn nhất của tứ diện S.AHK bằng 3 3 3 3 A. r r 5 r 5 r 5 . B. . C. . D. . 3 3 25 75
Lời giải. Chuẩn hóa, chọn r  1, đặt AC x 0  x  2. Khi đó 2
BC  4  x . 2 2 Trong hai tam giác vuông SH SA 1 SK SA 1
SAC, SAB lần lượt có   và   . 2 2 SC SC x 1 2 SB SB 5 Ta có V SK SH 1 S.AKH  .  V SB SC S ABC 5 2 . x   1 2 x 4  x 5 6 V   15V   1 S.AHK 15 2 x   S. 1 AHK  2x  2 2 x 1 1 2    Có 5 6 4 1 3 4  1  5     .   2 2 2 2 1 5  1 5 5 1 x x x Dấu 1 3 6 "  " xảy ra khi   x  . 2 x 1 5 3 3 Vậy r 5 r maxV  . Dấu "  " xảy ra khi 6 AC  . Chọn D. S.AHK 75 3
Câu 17. Cho khối chóp S.ABC có đáy là tam giác vuông cân tại B. Khoảng cách từ A
đến mặt phẳng SBC bằng a 2,   0
SAB SCB  90 . Xác định độ dài cạnh AB để khối
chóp S.ABC có thể tích nhỏ nhất. A. a 10 AB
. B. AB a 3. C. AB  2 . a
D. AB  3a 5. 2
Lời giải. Gọi D là điểm sao cho ABCD là hình vuông. AB AD Ta có  .  
AB  SAD   AB SD 0 SAB
 90  AB SA
Tương tự, ta cũng có BC SD . Từ đó suy ra SD  ABDC .
Kẻ DH SC H SC 
DH  SBC  . Khi đó d  ,
A SBC   d D,SBC   DH.    
Đặt AB x  0. Trong tam giác vuông SDC, có 1 1 1 1 1 1      . 2 2 2 DH SD DC  22 2 2 SD x a Suy ra ax 2 SD  . 2 2 x 2a 3 3 Thể tích khối chóp 1 1 ax 2 a 2 x VV  .  . . S.ABC S.ABCD 2 2 2 2 2 6 x 2 6 a x 2a 43 3 Xét   x f x  trên a 2; 
 , được min f x  f a 3 2
 3 3a . Chọn B. 2 2 x 2aa 2;
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 .
a Tam giác SAB
vuông tại S và nằm trong mặt phẳng vuông góc với đáy. Gọi là góc tạo bởi đường
thẳng SD và mặt phẳng SBC với  30. Giá trị lớn nhất của thể tích khối chóp
S.ABCD bằng 3 3 3 3 A. 4a 4a 2 8a 2 8a 3 . B. . C. . D. . 3 3 9 9  
Lời giải. Lấy điểm K thỏa mãn SK AD.
Ta chứng minh được SA  SBC 
DK  SBC . Do đó SD SBC     ,
KSD SDA  .
Tam giác SAD vuông nên ta có SA AD tan 2a tan .
Trong tam giác vuông SAB, có 2 2
SA AH.AB AH  2a tan . Suy ra 2 2 2
SH SA AH a  2 2 tan 1 tan . 3 Khi đó 1 8a 2 VS .SH  tan S ABCD ABCD  2 1 tan . .  3 3     Xét hàm   1 2 4 2
f x  x x trên 1 0; ,   
ta được max f x    f  .  3      1     3  9 0;  3 3 Suy ra 8a 2 maxV  . Chọn C. S.ABCD 9
Câu 19. Cho khối chóp S.ABC có SA SB SC  , a ASB  60 ,   BSC  90 ,   CSA  120. Gọi CN AM
M , N lần lượt là các điểm trên cạnh AB và SC sao cho  . Khi khoảng CS AB
cách giữa M và N nhỏ nhất thì thể tích của khối chóp S.AMN bằng 3 3 3 3 A. 2a 5 2a 5 2a 2a . B. . C. . D. . 72 72 432 432
Lời giải. Tính được AB  , a BC a 2,
CA a 3 suy ra ABC  vuông tại B. 3 Gọi a 2 H là trung điểm
SASBSC
AC SH  ABC . Khi đó V  . S.ABC 12 Đặt CN AM
x 0  x   1 . Ta có CS AB     CN
  x.CS SN 1x.SC     .
AM x.AB SM 1x.SAx.SB     
Suy ra NM  1 x.SA x.SB 1 x.SC. 2   2   Suy ra 5 11 11 2 2   2 a MN
a 3x 5x   2 3  a 3  x       .  Dấu "  " xảy ra khi 5 x  .  6 12 12   6 44 V  SN 1 S.AMN     3 VSC 6 Ta có  S.AMC 5 5a 2   V   V  . Chọn C. S.AMN S. VAM 5 36 ABC 432  A.SCM    . V AB 6  A.SCB
Cách khác. Kẻ MP AC với P BC. Dùng định lý hàm số cosin trong tam giác MNP tính được độ dài 2 2 MN a  2 3x 5x   3 .
Câu 20. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh ,
a SA a 2 và
vuông góc với mặt đáy ABCD. Gọi M là điểm di động trên cạnh CD và H là hình
chiếu vuông góc của S lên đường thẳng BM. Khi điểm M di động trên cạnh CD, thể
tích khối chóp S.ABH có giá trị lớn nhất bằng 3 3 3 3 A. a 2 a 2 a 2 a 2 . B. . C. . D. . 6 8 12 15
Lời giải. Lấy điểm N BC sao cho BN CM. Dễ dàng chứng minh được AN BM. BM AN
Gọi H AN BM. Ta có 
BM  SAH   BM SH nên H là hình BM SA 
chiếu vuông góc của S lên đường thẳng BM.
Đặt BN CM x, 0  x  .
a Trong tam giác vuông
ABN có BH là đường cao, suy ra ax 2 a BH  , AH  . 2 2 x a 2 2 x a 3 Ta có 1 a x SAH.BH  . . ABH 2 2 2 2 x a 4 4 3 Cosi Thể tích khối chóp 1 a 2 x a 2 x a 2 VS .SA  .  .  . S.ABH ABH 2 2 3 6 x a 6 2ax 12
Dấu "  " xảy ra khi x a hay N C,
M D. Chọn C.
Câu 21. Cho tứ diện ABCD. Hai điểm M , N lần lượt di động trên hai đoạn thẳng BC BD
BC, BD ( M , N không trùng B ) sao cho 2 3
 10. Gọi V , V lần lượt là thể BM BN 1 2
tích của các khối tứ diện V
ABMN và ABCD. Giá trị nhỏ nhất của 1 bằng V2 A. 25. B. 3. C. 3 . D. 6 . 3 8 25 25
Lời giải. Đặt BC BDx,
y x, y   1 . BM BN
Theo giả thiết: 10  2x 3y  2x  103 . y Do 8
x 1  2x  2  10 3y  2  y  . 3 45 Ta có V BM BN BA 1 1 1 2 1  . .  . .1   . V BC BD BA x y xy y 10 3y 2         Xét V 6 3
f y  y103y trên 8 1; 
, được f y 16 25   ; . Suy ra 1   ; . Chọn D.  3    3 3    V 25 8 2  Cosi Cách khác: Ta có 25
10  2x  3y  2 6xy   xy  . 6
Câu 22. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Hai điểm M , N
lần lượt trên các đoạn thẳng AB AD
AB, AD ( M , N không trùng A ) sao cho  2  4. AM AN
Kí hiệu V , V lần lượt là thể tích của các khối chóp S.ABCD và S.MBCDN. Giá trị lớn 1
nhất của tỉ số V1 bằng V A. 2 . B. 3 . C. 1 . D. 17 . 3 4 6 14
Lời giải. Đặt AB ADx,
y x, y   1 . AM AN
Theo giả thiết: x  2y  4  2y  4  x.
Do y 1  2y  2  4  x  2  x  2. Ta có V V VSAM.AN 1 1 S.AMN   1 AMN   1  1 . V V 2S 2AB.AD xx ABD 4      Xét V 2 3 f x 1 
trên 1;2, ta được f x 1 1
  ; . Suy ra 1   ; . Chọn B. x 4  x  4 3   V 3 4  
Câu 23. Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N là hai điểm thay đổi lần
lượt thuộc cạnh BC, BD sao cho AMN  vuông góc với BCD. Tổng giá trị lớn nhất
và giá trị nhỏ nhất của thể tích khối tứ diện ABMN bằng A. 2 . B. 17 2 . C. 17 2 . D. 17 2 . 12 72 144 216
Lời giải. Gọi H là tâm đường tròn ngoại tiếp B
CD. Khi đó MN luôn đi qua H.       Ta có BC BD BC BD
BC BD  3BH BM
BN  3BH     3. BM BN BM BN Đặt BC BDx,  y x, y  
1 . Suy ra x y  3. BM BN Ta có V BM BN 1 ABMN  .  . V BC BD xy ABCD  
Tương tự như các bài trên, ta được 1 4 1   ; . xy  9 2     Suy ra 4 1 17 17 2 V   V ; V
. Vậy V V V  . Chọn D. ABMN
 9 ABCD 2 ABCD    1 2 18 ABCD 216 46
Câu 24. Cho tứ diện OABC có O , A OB,
OC đôi một vuông góc và OA OB  2,
OC  1. Hai điểm M , N lần lượt di động trên hai cạnh AC, BC sao cho OMN
vuông góc với ABC. Thể tích khối đa diện ABOMN có giá trị lớn nhất bằng A. 1 . B. 1 . C. 2 . D. 1 . 4 9 9 12
Lời giải. Thể tích V CM CN
ABOMN có giá trị lớn nhất khi COMN  . nhỏ nhất. V CA CB COAB
Gọi K là trung điểm AB, suy ra OK AB và 1
OK AB  1. 2
Kẻ OI CK, suy ra I là trung điểm CK. Ta chứng minh được OI  ABC.
Do OMN   ABC suy ra MN đi qua I.       Ta có CA CB CA CB
CA CB  2CK CM
CN  4CK     4. CM CN CM CN Đặt CA CBx,  y x, y  
1 . Suy ra x y  4. CM CN Ta có V CM CN 1 COMN  .  . V CA CB xy COAB  
Tương tự như các bài trên, ta được 1 1 1   ; . xy  4 3   Suy ra 1 3 3 2 1 minVV  maxVV  .  . Chọn A. COMN 4 COAB ABOMN 4 COAB 4 6 4
Câu 25. Cho hình chóp S.ABC có SA  1, SB  2, SC  3. Gọi G là trọng tâm tam giác
ABC. Mặt phẳng  đi qua trung điểm I của SG cắt các cạnh ,
SA SB, SC lần lượt tại 1 1 1
M , N, P. Giá trị nhỏ nhất của biểu thức T    bằng 2 2 2 SM SN SP A. 2 . B. 3. C. 18 . D. 6. 7 7 7
Lời giải. Do G là trọng tâm ABC  .     Ta có 1
SG  SASB SC 3 SG  1  SA 
SB  SC   .SI   .SM  .SN  .SP     SI 3 SM SN SP  1  SA 
SB  SC   SI   .SM  .SN  .SP. 6 SM SN SP    Do SA SB SC SA SB SC
I, M , N, P đồng phẳng nên 1        1     6. 6 SM SN SP  SM SN SP
Áp dụng BĐT Bunhiacopxki, ta có 2  SA SB SC   1 1 1                    2 2 2
SA SB SC . 2 2 2  SM SN SPSM SN SP  47 Suy ra 36 18 T   . Chọn C. 2 2 2
SA SB SC 7 48
Document Outline

  • DE
  • 1 Thể tích
  • 2 Tỷ số
  • 3 Cực trị