lOMoAR cPSD| 49519085
ÔN TẬP PHẦN THỐNG KÊ 1.
Một hãng sản xuất vòng găng cho ộng cơ ô tô cho biết ường kính vòng găng có phân bố chuẩn
với ộ lệch chuẩn là 0,015 mm. Người ta chọn ngẫu nhiên 13 vòng găng thì o ược ường kính trung bình là 74,035 mm.
Hãy tìm khoảng tin cậy hai phía 95% cho ường kính trung bình của vòng găng. 2.
Một vùng có 2000 hộ gia ình. Để iều tra nhu cầu tiêu dùng một loại hàng nào ó, người ta chọn
ngẫu nhiên 100 hộ và thấy có 70 hộ có nhu cầu về loại hàng trên. Với ộ tin cậy 95% hãy ước
lượng bằng khoảng tin cậy ối xứng cho tỷ lệ hộ gia ình có nhu cầu về loại hàng trên. 3.
Để iều tra thời gian hoàn thành sản phẩm của công nhân người ta chọn ngẫu nhiên 100 công
nhân và thu ược kết quả sau:
Thời gian (phút) 12-13 13-14 14-15 15-16 16-17 17-18 18-19 19-20 Số công nhân 6 10 15 23 19 16 7 4
a) Với ộ tin cậy 95%, hãy ước lượng khoảng cho thời gian trung bình ể công nhân hoàn thành xong một sản phẩm.
b) Có người nói thời gian trung bình hoàn thành sản phẩm của công nhân vào khoảng 15 phút.
Với mức ý nghĩa 5%, hãy kiểm tra iều ó úng hay sai. 4.
Chiều cao của sinh viên ại học là ại lượng ngẫu nhiên có phân bố chuẩn. Kiểm tra một nhóm
gồm 25 sinh viên thì thấy ộ cao trung bình là 1,67 m với ộ lệch chuẩn hiệu chỉnh mẫu là 0,08
m. Hãy xây ựng khoảng tin cậy 95% cho chiều cao trung bình của toàn bộ sinh viên. 5.
Người ta thống kê giá bán căn hộ chung cư ở một thành phố và thu ược kết quả sau: Giá bán (triệu) 550 480 980 1000 500 490 750 540 368 Số nhà 3 4 8 1 9 5 3 1 8
Hãy ước lượng giá bán căn hộ trung bình với ộ tin cậy 95%. 6.
Điều tra lương trung bình của một nhóm 26 công nhân của công ty A thấy lương trung bình
là 2,4 triệu( ). Biết lương công nhân tuân theo luật phân bố chuẩn với ộ lệch chuẩn hiệu chỉnh
mẫu là 1,2 triệu( ). Hãy xây dựng khoảng tin cậy 95% cho mức lương trung bình của toàn bộ
công nhân của công ty A. 7.
Một kỹ sư về lốp nghiên cứu tuổi thọ của lốp ối với một hỗn hợp cao su mới, ông chế tạo 15
chiếc và em chúng thử nghiệm trên ường cho ến hỏng.Trung bình mẫu và ộ lệch chuẩn mẫu
là 60139 và 3645 (km). Giả thiết tuổi thọ của lốp tuân theo luật phân bố chuẩn. Tìm khoảng
tin cậy 95% cho tuổi thọ lốp trung bình. 8.
Quá trình sản xuất vòng bi ược coi là bình thường nếu khối lượng vòng bi có phân phối chuẩn
với khối lượng trung bình là 5(ounce) và ộ lệch chuẩn là 0,1 (ounce). Do nghi ngờ khối lượng
vòng bi ã tăng lên, người ta lấy ngẫu nhiên 15 vòng bi ể kiểm tra thì thấy khối lượng trung
bình là 5,04 (ounce). Với mức ý nghĩa 0,05 có thể xem khối lượng trung bình của vòng bi ã
thực sự tăng lên hay chưa? 9.
Vì sự cố kỹ thuật, một máy óng chai ã óng thiếu khá nhiều trong một ca sản xuất. Kiểm tra
ngẫu nhiên 78 chai thì thấy có tới 21 chai bị óng thiếu. Tính khoảng tin cậy 90% cho tỷ lệ chai
ã bị óng thiếu trong ca sản xuất nói trên. Cho Z0,05 = 1,645 .
10. Để ước lượng mức xăng tiêu hao trung bình cho một loại ôtô chạy từ A ến B, người ta quan
sát mức xăng tiêu hao (X lít) của 30 chuyến xe và thu ược kết quả như sau: 1 lOMoAR cPSD| 49519085
Giả sử X tuân theo luật chuẩn.
a) Với ộ tin cậy 95% mức xăng tiêu hao trung bìnhh nằm trong khoảng nào?
b) Có người cho rằng mức xăng tiêu hao trung bình lớn hơn 9,4 lít. Với mức 5%, hãy kiểm ịnh
xem khẳng ịnh trên úng hay sai?
11. Để ước lượng iểm thi ại học trung bình môn toán của học sinh trường A, người ta theo dõi iểm
thi (X) của 50 học sinh và thu ược kết quả sau: Điểm
(0,2] (2,4] (4,6] (6.8] (9,10] Số học sinh 4 6 13 17 10
Giả sử X tuân theo luật chuẩn.
a) Hãy ước lượng iểm thi trung bình.
b) Với ộ tin cậy 95%, iểm thi trung bìnhh nằm trong khoảng nào? Muốn giảm ộ rộng khoảng
tin cậy còn một nửa thì cần theo dõi bao nhiêu học sinh?
12. Để ước lượng chiều cao trung bình của sinh viên, người ta o chiều cao của 100 sinh viên ã thu ược kết quả sau: X
[1,60; 1,65 ) [1,65; 1,70) [1,70; 1,75) [1,75; 1,80) Số sinh viên 15 40 35 10
Giả sử chiều cao của sinh viên là biến ngẫu nhiên X có phân bố chuẩn.
a) Với ộ tin cậy 95% chiều cao trung bình nằm trong khoảng nào?
b) Có người cho rằng chiều cao trung bình lớn hơn 1,7 m. Với mức 5% hãy kiểm ịnh xem
khẳng ịnh trên úng hay sai.
13. Tiến hành 30 quan sát về biến ngẫu nhiên X có phân bố chuẩn, người ta thu ược số liệu và tính ược:
X =5.52, S= 2.05 EX
a) Hãy tìm khoảng tin cậy 0.95 % cho . EX
b) Với mức ý nghĩa = 0.025 có thể nói 5.5 ược không?
14. Để kiểm tra khối lượng của trứng ( ơn vị gam), người ta chọn ngẫu nhiên 100 quả và thu ược kết quả như sau:
Khối lượng [140;145) [145;150) [150;155) [155;160) [160;165) [165;170) [170;175) Số quả 8 10 17 23 19 16 7
a) Với = 5% , hãy ước lượng khối lượng trung bình của trứng.
b) Trứng là loại I nếu khối lượng từ 160 gam trở lên. Với = 5% , hỏi có thể chấp nhận giả
thuyết: tỷ lệ trứng loại I là 40% hay không?
15. Điều tra mức chi tiêu hàng năm của 100 công nhân ở một công ty thu ược số liệu sau: Mức chi tiêu (triệu ồng/năm)
15,6 16,0 16,4 16,8 17,2 17,6 18,0 Số công nhân 10 14 26 28 12 8 2 2 lOMoAR cPSD| 49519085
a) Với ộ tin cậy 95% hãy ước lượng: số công nhân của công ty có mức chi tiêu hằng năm dưới
16 triệu ồng, biết công ty có 1000 công nhân.
b) Nếu năm trước mức chi tiêu trung bình mỗi công nhân là16 triệu ồng/năm thì với mức ý
nghĩa 0,05 có thể nói mức chi tiêu trung bình của mỗi công nhân năm nay cao hơn năm trước không?
16. Để ước lượng tuổi thọ trung bình của một loại bóng èn, người ta kiểm tra ngẫu 16 bóng và
tính ược tuổi thọ trung bình của chúng là X=1200giờ với ộ lệch tiêu chuẩn mẫu iều chỉnh 26,094 giờ.
a) Hãy ước lượng tuổi thọ trung bình của bóng èn bằng khoảng tin cậy ối xứng với ộ tin cậy
0,95. Giả sử tuổi thọ của bóng èn là biến ngẫu nhiên có phân bố chuẩn.
b) Với = 5%, ể ộ rộng khoảng tin cậy còn một nửa thì cần kiểm tra bao nhiêu bóng èn.
17. Năng suất một giống cây ăn quả tại vùng A là ại lượng ngẫu nhiên có phân phối chuẩn. Trên
cơ sở số liệu iều tra như sau: Năng suất (kg/cây) 22 24 26 28 30 Số cây thu hoạch 10 15 30 25 20
Hãy ước lượng năng suất trung bình tối a của giống cây ăn quả nói trên với ộ tin cậy 95%.
18. Một trại chăn nuôi gà, tỷ lệ gà bị cúm A là 30%. Sau một thời gian iều trị, kiểm tra 100 con
gà thì thấy 20 con mắc cúm A. Với mức ý nghĩa 0,05 có thể kết luận sự iều trị trên có hiệu quả không
19. Tại một thành phố người ta thông kê 88073 cháu mới sinh trong 1 năm thì có 45682 cháu trai.
Với mức ý nghĩa 1% có thể kết luận tỷ lệ trai lớn hơn tỷ lệ con gái không?
20. Mức tiêu hao nhiên liệu của một loại xe tải là BNN tuân theo quy luật chuẩn. Do tình hình
ường xá ã ược cải thiện, ể thay ổi mức tiêu hao nhiên liệu, người ta ã theo dõi ngẫu nhiên 100
chuyến xe và thu ược các số liệu sau: Mức tiêu hao(lít/100 km) 35-40 40-45 45-50 50-55 55-60 Số chuyến xe 14 20 36 22 8
a) Hãy ước lượng mức tiêu hao nhiên liệu trung bình với ộ tin cậy 95%.
b) Xe cần ưa vào kiểm tra kĩ thuật là xe có mức tiêu hao nhiên liệu trên 55 lít/100 km. Hãy ước
lượng tỷ lệ xe cần ưa vào kiểm tra kỹ thuật với ộ tin cậy 95% dựa trên cơ sở số liệu ã iều tra.
21. Để ánh giá chất lượng của hai loại máy trộn bê tông về mặt thời gian, người ta cho vận hành
hai loại máy trên trong những iều kiện giống hệt nhau và thu ược kết quả sau: Thời gian
5,0 [5,0; 5,5) [5,5; 6,0) [6,0; 6,5) [6,5; 7,0) 7,0 Số tấn (máy loại 1) 2 4 15 13 10 6 Số tấn (máy loại 2) 1 5 12 18 4 7
Biết thời gian trộn trung bình một tấn bê tông của máy là biến ngẫu nhiên có phân bố chuẩn với
cùng phương sai. Hãy so sánh chất lượng hai loại máy trên với mức 5%. Biết t0,05(95) =1,66.
22. Điều tra mức chi tiêu hàng năm của 100 công nhân ở một công ty thu ược số liệu sau:
Mức chi tiêu (triệu ồng/năm) 15,6 16,0 16,4 16,8 17,2 17,6 18,0 Số công nhân 10 14 26 28 12 8 2 3 lOMoAR cPSD| 49519085
a) Với ộ tin cậy 95% hãy ước lượng: số công nhân của công ty có mức chi tiêu hàng năm dưới
16 triệu ồng, biết công ty có 2000 công nhân.
b) Nếu năm trước mức chi tiêu trung bình mỗi công nhân là 16 triệu ồng/năm thì với mức ý
nghĩa 0,05 có thể nói mức chi tiêu trung bình của mỗi công nhân năm nay cao hơn năm
trước không? Giả thiết mức chi tiêu của công nhân có phân bố chuẩn.
23. Một loại hạt giống có tỷ lệ nảy mầm là 90%. Do iều kiện thời tiết thay ổi người ta kiểm tra lai
bằng cách gieo 200 hạt thì thấy có 160 hạt nảy mầm. Với mức ý nghĩa =0,01 kiểm tra xem
thời tiết có ảnh hưởng xấu ến tỷ lệ nảy mầm của hạt giống hay không?
24. Để ánh giá hiệu quả của một loại thức ăn gia súc mới, người ta theo dõi hai lô con giống sau
hai tháng chăn nuôi và ược kết quả như sau: Lô 1: Dùng thức ăn mới
Cân nặng (kg) 30-35 35-40 40-45 45-50 50-55 55-60 60-65 Số con 1 4 9 17 6 5 3 Lô 2: Dùng thức ăn cũ
Cân nặng (kg) 30-35 35-40 40-45 45-50 50-55 55-60 60-65 Số con 3 6 4 19 5 7 1
Từ số liệu trên, với ộ tin cậy mức ý nghĩa 0.05 hãy ánh giá hiệu quả của loại thức ăn gia súc mới.
Giả sử cân nặng của lợn là biến ngẫu nhiên có phân bố chuẩn.
25. Quá trình sản xuất xà phòng tắm óng chai ược coi là bình thường về mặt khối lượng nếu khối
lượng trung bình các chai hoàn chỉnh là 20 (ounce). Mẫu 9 chai ược kiểm tra cho kết quả khối lượng là 21,4; 19,7; 19,7; 20,6; 20,8; 20,1; 19,7; 20,3; 20,9.
Giả sử rằng khối lượng của chai xà phòng có phân bố chuẩn. Hãy kiểm tra xem quá trình sản
suất có bình thường không? Với mức ý nghĩa =0,05.
26. Để ánh giá chất lượng của hai loại máy trộn bê tông về mặt thời gian, người ta cho vận hành
hai loại máy trên trong những iều kiện giống hệt nhau và thu ược kết quả sau: Thời gian
5,0 [5,0; 5,5) [5,5; 6,0) [6,0; 6,5) [6,5; 7,0) 7,0 Số tấn (máy loại 1) 2 4 15 13 10 6 Số tấn (máy loại 2) 1 5 312 18 4 7
Biết thời gian trộn trung bình một tấn bê tông của máy là biến ngẫu nhiên có phân bố chuẩn
với cùng phương sai. Hãy so sánh chất lượng hai loại máy trên với mức ý nghĩa 5%.
27. Người ta iều tra mức thu nhập hàng tháng của một số người dân trong một vùng và ược số liệu sau ây:
Mức thu nhập (triệu) [0; 1) [1; 2) [2; 3) [3; 4) [4; 5) [5; 6] Số người 3 8 12 14 9 4 a)
Với ộ tin cậy 95%, hãy ước lượng mức thu nhập trung bình hàng tháng của người dân ở vùng ó. b)
Có người nói rằng mức thu nhập trung bình hàng tháng của người dân vùng ó là 3.5
triệu. Với mức ý nghĩa 5%, hãy kiểm tra xem người ó nói có úng không? 4 lOMoAR cPSD| 49519085
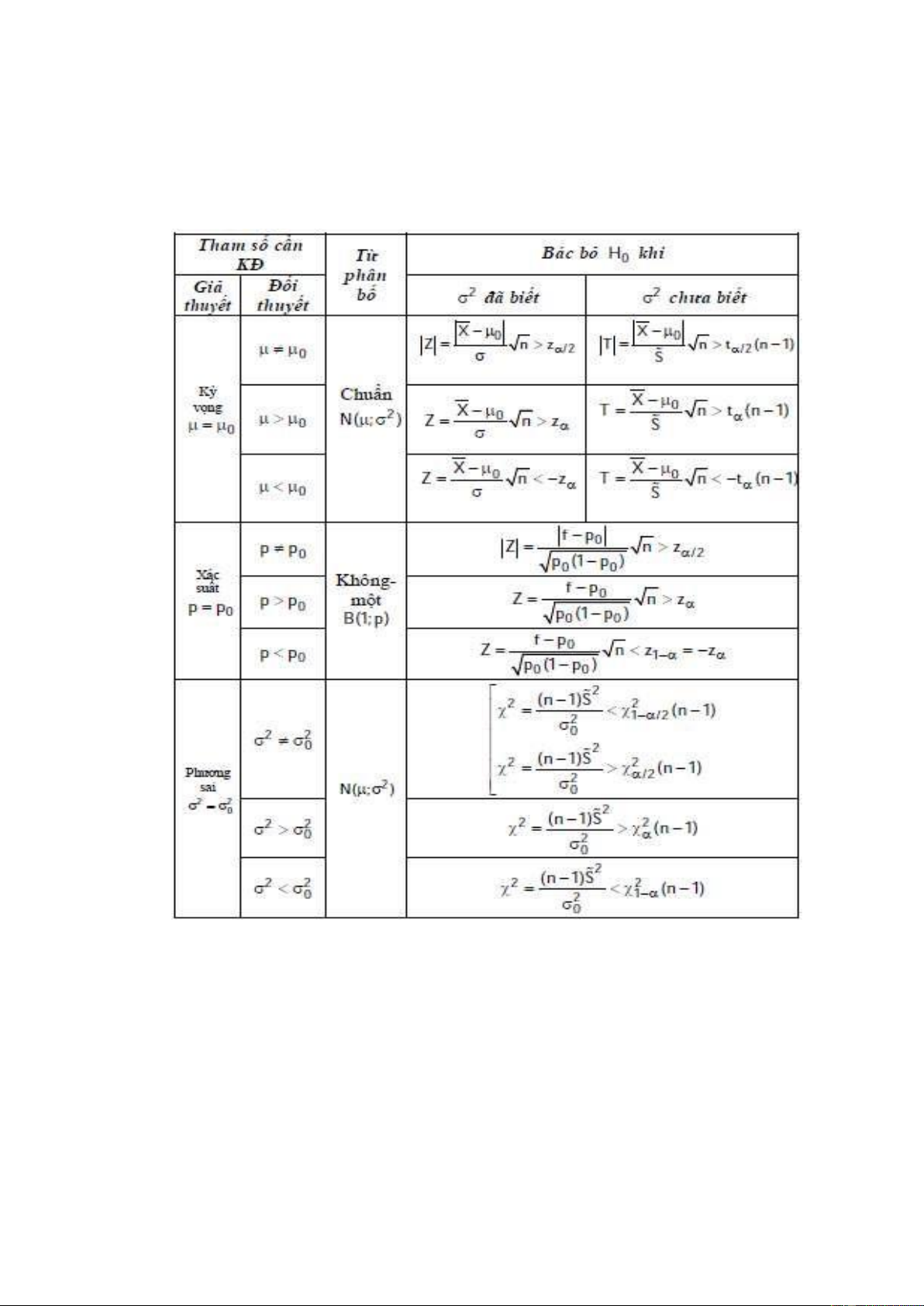
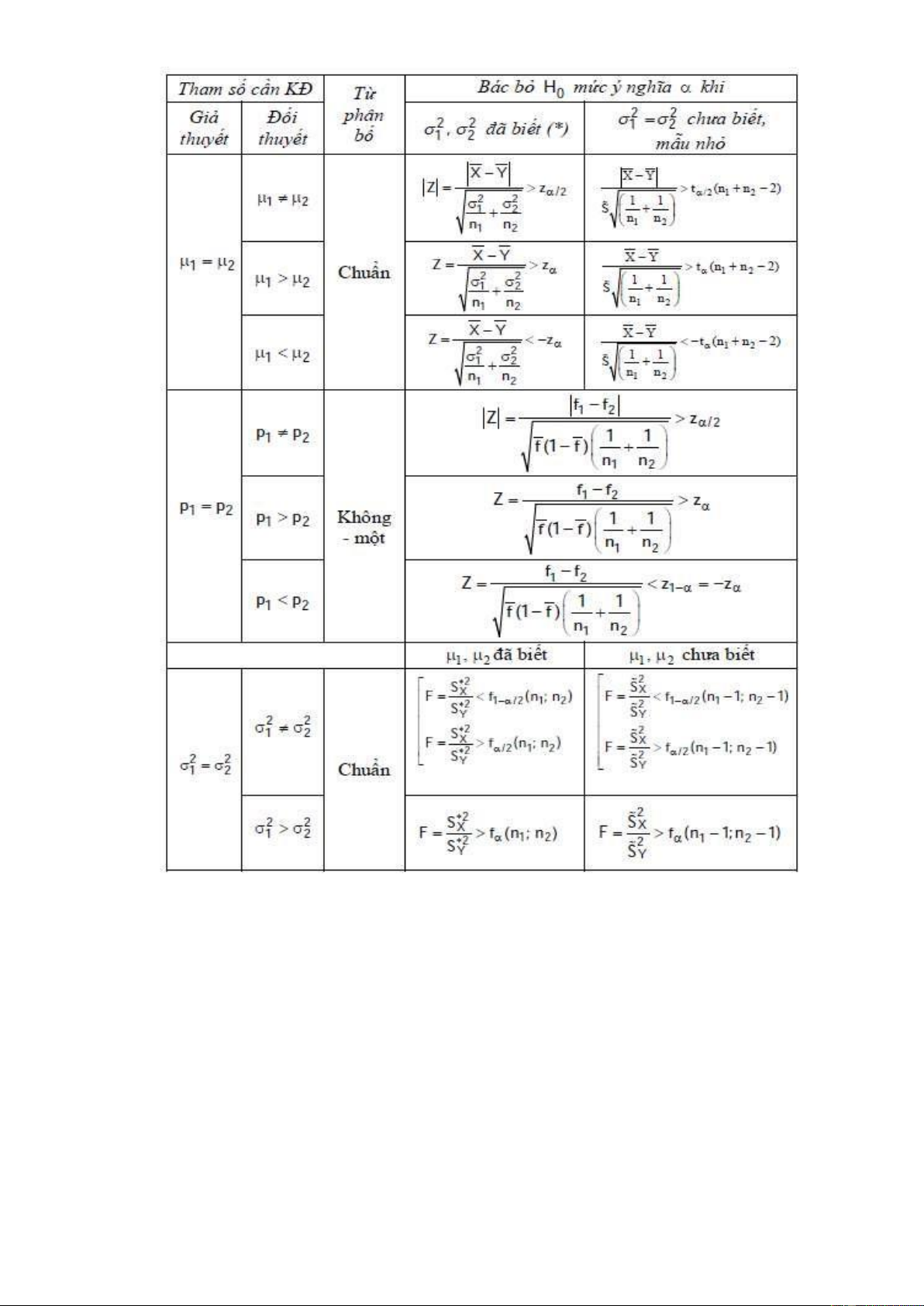
• Bảng kiểm ịnh tham số
• Bảng tóm tắt so sánh kỳ vọng và so sánh phương sai 5 lOMoAR cPSD| 49519085 6