Lý thuyết chương 1: các kiến thức bổ trợ | Môn xác suất thống kê

lOMoAR cPSD| 47207194 GV:
Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU
Chương 0. Các kiến thức bổ trợ 0.1 Hoán vị
1) Định nghĩa: Cho tập hợp A có n (n 1) phần tử. Khi sắp xếp n phần tử này theo một
thứ tự, ta ược một hoán vị của A.
Ví dụ. Các hoán vị của tập hợp A = {a, b, c} là (a, b, c), (a, c, b), (b, a, c), (b, c, a), (c, a, b), (c, b, a).
2) Số các hoán vị: Số các hoán vị của một tập hợp gồm có n phần tử, ký hiệu là Pn, là Pn = n!
Ví dụ. Tập hợp A = {a, b, c} có 3! = 6 hoán vị. 0.2 Chỉnh hợp 1)
Định nghĩa. Cho tập hợp A gồm n phần tử và số nguyên k với 1 k n . Khi lấy
ra k phần tử khác nhau của A và sắp xếp chúng theo một thứ tự, ta ược một chỉnh hợp
một chỉnh hợp chập k của A.
Ví dụ. Cho tập hợp A = {a, b, c}. Các chỉnh hợp chập 2 của A là: (a, b), (b, a), (a, c), (c, a), (b, c), (c, b). 2)
Số các chỉnh hợp: Số các chỉnh hợp chập k của một tập hợp gồm có n phần tử (1 k n) là: Akn n(n 1)(n 2)...(n k1)
Ví dụ. Từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9 có thể lập ược bao nhiêu số tự nhiên có 5 chữ số khác nhau? 1 lOMoAR cPSD| 47207194 GV:
Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU
Giải. Mỗi cách sắp xếp 5 chữ số trong 9 chữ số ã cho cho ta một số tự nhiên gồm 5 chữ
số. Như vậy, mỗi số tự nhiên gồm 5 chữ số ó có thể coi là một chỉnh hợp chập 5
của tập hợp gồm 9 số ã cho. Vậy có A59 9.8.7.6.5 15120 số tự nhiên gồm 5 chữ số ược
lập từ 9 chữ số ã cho.
Chú ý. Từ ịnh nghĩa ta thấy một hoán vị của tập hợp n phần tử là một chỉnh hợp chập n của tập ó nên Ann Pn n!
0.3 Chỉnh hợp lặp 1)
Định nghĩa. Cho tập A có n phần tử và số nguyên dương k. Một chỉnh hợp lặp
chập k của A là một bộ gồm k phần tử ược lấy từ n phần tử của A, trong ó các phần tử
có thể lấy lặp lại và ược sắp xếp theo một thứ tự. Như vậy, ây là một bộ gồm k phần tử,
trong ó các phần tử có thể giống nhau và ược sắp xếp theo thứ tự.
Ví dụ. Cho tập hợp A = {1, 2, 3, 4, 5, 6, 7, 8, 9}. Các chỉnh hợp lặp chập 5 của A có thể
là: 43255, 22222, 44118, 39476, … 2)
Số các chỉnh hợp lặp: Số các chỉnh hợp lặp chập k của một tập hợp n phần tử bằng: Akn nk
Ví dụ. Từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9 có thể lập ược bao nhiêu số tự nhiên có 5 chữ số?
Giải. Theo giả thiết các chữ số của một số tự nhiên gồm 5 chữ số ược lập từ 9 chữ số ã
cho có thể trùng nhau. Vì vậy, mỗi số gồm 5 chữ số ược lập từ 9 chữ số ã cho có thể coi
là một chỉnh hợp lặp chập 5 của tập hợp gồm 9 phần tử. Vậy số chữ số gồm 5
chữ số lập từ 9 số ã cho ã cho là: A59 95 59049 số. 0.4 Tổ hợp 2 lOMoAR cPSD| 47207194 GV:
Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU
1) Định nghĩa: Cho tập A có n phần tử và số nguyên k với 1 k n . Mỗi tập con của A
có k phần tử ược gọi là một tổ hợp chập k của A.
Chú ý. Số k trong ịnh nghĩa trên cần thỏa mãn iều kiện 1 k n . Tuy vậy, ta quy ước tổ
hợp chập không (tức k = 0) của n phần tử là tập rỗng.
Ví dụ. Cho tập hợp A = {a, b, c, d}. Các tổ hợp chập 3 của tập A là {a, b, c}, {a, b, d}, {a, c, d}, {b, c, d}.
2) Số các tổ hợp: Số các tổ hợp chập k của một tập hợp có n phần tử (0 k n) là: k n! Cn k!(n k)!
Ví dụ. Một tổ có 10 người gồm 6 nam và 4 nữ. Cần lập một oàn ại biểu gồm có 5 người. Hỏi:
a) Có tất cả bao nhiêu cách lập?
b) Có bao nhiêu cách lập oàn ại biểu, trong ó có ba nam, hai nữ? Giải. a) C 5 10 252 b) C .C3 2 6 120 4 3) Tính chất a) Ck n Cn kn (0 k n) b) Ck 1n 1 Ckn 1 C (1nk k n) 3 lOMoAR cPSD| 47207194 GV:
Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU
Phần 1. Lý thuyết Xác suất
Chương 1. Biến cố và xác suất của biến cố
1.1 Khái niệm phép thử và biến cố
1.1.1 Định nghĩa. Phép thử ược hiểu như làm một thí nghiệm ể quan sát một hiện
tượng nào ó có xảy ra hay không.
Còn hiện tượng có thể xảy ra trong kết quả của phép thử ó ược gọi là biến cố.
Ví dụ 1. Tung một ồng tiền xu: ây là một phép thử.
Các biến cố của phép thử này là: "Xuất hiện mặt sấp" và "Xuất hiện mặt ngửa".
Ví dụ 2. Một hộp sản phẩm gồm a chính phẩm và b phế phẩm (a;b N;a,b 2) .
Lấy ngẫu nhiên ra 2 sản phẩm: ây là một phép thử
Các biến cố của phép thử này là: “Lấy ược 2 chính phẩm”; “Lấy ược 2 phế
phẩm”; và “Lấy ược 1 chính phẩm và 1 phế phẩm”.
1.1.2 Phân loại các loại biến cố:
a) Biến cố không thể có: là biến cố nhất ịnh không xảy ra khi thực hiện phép thử.
Biến cố này ược ký hiệu là V.
b) Biến cố chắc chắn: là biến cố chắc chắn xảy ra khi thực hiện phép thử.
Biến cố này ược ký hiệu là U.
c) Biến cố ngẫu nhiên: là biến cố có thể xảy ra hoặc không xảy ra khi phép thử thực hiện.
Các biến cố này ược ký hiệu là A, B, C… 4 lOMoAR cPSD| 47207194 GV:
Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU
Ví dụ 3. Các biến cố trong các phép thử ở VD1 và VD2 là loại biến cố nào?
Ví dụ 4. Tung một con xúc xắc: Đó là một phép thử
V = "Xuất hiện mặt có 7 chấm"- Đây một biến cố nhưng biến cố này không thể
xảy ra khi phép thử ược thực hiện. Biến cố này là biến cố không thể có.
U = "Xuất hiện mặt có số chấm 1và 6". Đây cũng là một biến cố. Biến cố
này luôn xảy ra khi ta tung một con xúc xắc. Biến cố này ược gọi là biến cố chắc chắn. A
= "Xuất hiện mặt có 2 chấm". Đây cũng là một biến cố. Khi ta
tung một con xúc xắc, biến cố này có thể xảy ra cũng có thể không xảy ra, biến
cố này là biến cố ngẫu nhiên. B
= "Xuất hiện mặt có số chấm chẵn". Biến cố này là biến cố ngẫu
nhiên. 1.2 Mối quan hệ giữa các biến cố
1.2.1 Tổng của các biến cố:
1) Định nghĩa. Tổng của hai biến cố A và B là một biến cố, kí hiệu là A + B hay A B,
sao cho biến cố tổng A + B xảy ra khi và chỉ khi có ít nhất một trong hai biến cố A, B xảy ra. n
Định nghĩa này cũng mở rộng cho tổng của nhiều biến cố: A ,i Ai . i 1 i 1
Ví dụ 5. Tung một con xúc xắc. Gọi A là biến cố " Xuất hiện mặt 6 chấm", B là biến cố
"Xuất hiện mặt 5 chấm", A + B = " Xuất hiện mặt có số chấm lớn hơn hoặc bằng 5". 5 lOMoAR cPSD| 47207194 GV:
Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU
Ví dụ 6. Ba xạ thủ mỗi người bắn một viên ạn vào một bia. Gọi Ai là biến cố "Xạ thủ
thứ i bắn trúng bia", i = 1,2,3. Vậy A1 + A2 + A3 = “Có ít nhất một xạ thủ bắn trúng bia”
(hay A1 + A2 + A3 = “Bia bị trúng ạn”). 2) Tính chất
Tính chất giao hoán: A + B = B + A
Tính chất kết hợp: (A + B) + C = A + (B + C) A + A = A; A + U = U; A + V = A
1.2.2 Tích của các biến cố:
1) Định nghĩa. Tích của hai biến cố A và B là một biến cố, kí hiệu là A.B hoặc A B,
sao cho biến cố tích A.B xảy ra khi và chỉ khi A và B cùng ồng thời xảy ra. n
Định nghĩa này cũng mở rộng cho tích nhiều biến cố: A ,i Ai i 1 i 1
Ví dụ 7. Với A, B là 2 biến cố trong VD5 thì AB = V.
Ví dụ 8. Với A1, A2, A3 là 3 biến cố trong VD6 thì A1A2A3 = “Cả ba xạ thủ ều bắn trúng
bia”; A1A2 + A2A3 + A3A1 = “Có ít nhất hai xạ thủ bắn trúng bia”. 2) Tính chất:
Tính chất giao hoán: AB = BA
Tính chất kết hợp: A(BC) = (AB)C
Tính chất phân phối: A(B + C) = AB + AC 6 lOMoAR cPSD| 47207194 GV:
Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU
A + (BC) = (A + B)(A + C)
Chứng minh. A + (BC) = (A + B)(A + C)
Giả sử A + BC xảy ra thì hoặc A xảy ra hoặc BC xảy ra. Nếu A xảy ra thì A + B và A
+ C xảy ra, do ó (A+B)(A+C) xảy ra. Nếu BC xảy ra thì B xảy ra và C xảy ra nên
A + B và A + C xảy ra, do ó (A+B)(A+C) xảy ra.
Ngược lại, nếu (A + B)(A + C) xảy ra thì A + B xảy ra và A + C xảy ra. Nếu A
xảy ra thì hiển nhiên A + (BC) xảy ra. Còn nếu A không xảy ra thì do A + B xảy ra và A
+ C xảy ra nên B xảy ra và C xảy ra, do ó BC xảy ra. Do ó A + BC xảy ra. A.A = A; A.U = A; A.V = V
1.2.3 Các biến cố xung khắc
Định nghĩa 1. Hai biến cố A và B ược gọi là xung khắc với nhau nếu chúng không thể
ồng thời xảy ra trong một phép thử (tức là A.B = V).
Ví dụ 9. Hai biến cố A và B trong ví dụ 5 không thể ồng thời xảy ra nên hai biến cố này xung khắc với nhau.
Ví dụ 10. Hai xạ thủ mỗi người bắn một viên ạn vào một bia. Gọi A là biến cố "Xạ thủ
thứ nhất bắn trúng bia", B là biến cố "Xạ thủ thứ hai bắn trúng bia". Hai biến cố A và B
có thể ồng thời xảy ra nên chúng không xung khắc với nhau.
Định nghĩa 2. n biến cố A1, A2, …, An ược gọi là xung khắc từng ôi nếu hai biến cố bất
kỳ trong n biến cố này cũng xung khắc với nhau.
A1, A2, …, An xung khắc từng ôi AiAj = V (i ≠ j; i, j = 1, 2, …, n).
Ví dụ 11. Ba biến cố trong ví dụ 2 là xung khắc với nhau từng ôi.
1.2.4 Hai biến cố ối lập: 7 lOMoAR cPSD| 47207194 GV:
Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU
a) Định nghĩa. Hai biến cố A và A ược gọi là hai biến cố ối lập với nhau nếu
ỏa mãn ồng thời hai iều kiện:
i) A vµ A xung kh¾c víi nhau trong phép chúng th ii) A+A =U
thử xảy ra nột và chỉ một trong hai biến cố A và A .
Ví dụ 12. Một hộp sản phẩm gồm a chính phẩm và b phế phẩm (a;b N;a,b 2) . Lấy
ngẫu nhiên lần lượt 2 sản phẩm từ hộp. Gọi A = “Lấy ược ít nhất 1 chính phẩm” thì
A = “Cả 2 sản phẩm lấy ược ều là phế phẩm”.
Ví dụ 13. Với A1, A2, A3 là 3 biến cố trong VD6 thì A A
1 2 A3 = “Cả ba xạ thủ ều bắn trượt” = A1 A2 A 3 . A A A A A A A AA 1 2 3 1 2 3
1 2 3 = “Chỉ có một xạ thủ bắn trúng bia”.
A A A1 2 3 = “Chỉ có xạ thủ thứ 3 bắn trúng bia”. b) Tính chất
+) A B A.B; A B+C A.B.C; Tổng quát: n A n i Ai i 1 i 1 +) AB A B; ABC A B C; Tổng quát: n A n i Ai i 1 i 1 +) A A.
1.3 Xác suất của một biến cố 8 lOMoAR cPSD| 47207194 GV:
Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU
Một biến cố ngẫu nhiên xảy ra hay không xảy ra khi thực hiện một phép thử là
không thể oán trước ược. Tuy nhiên, ta có thể nhận thấy các biến cố ngẫu nhiên khác
nhau có những khả năng xảy ra khác nhau. Hơn nữa, khi lặp i lặp lại nhiều lần cùng một
phép thử trong những iều kiện như nhau, người ta thấy tính chất ngẫu nhiên của biến cố
dần mất i và khả năng xảy ra của biến cố sẽ ược thể hiện theo một quy luật nhất ịnh. Từ
ó, ta thấy có thể o lường khả năng xuất hiện một biến cố nào ó. Khái niệm xác suất ược
hình thành ể nghiên cứu vấn ề này.
Định nghĩa. Xác suất của biến cố A, ký hiệu là P(A), là một con số o lường khả năng
xuất hiện biến cố A khi thực hiện phép thử.
Chú ý rằng, ây là khả năng khách quan, do những iều kiện xảy ra của phép thử
quy ịnh chứ không tuỳ thuộc vào ý muốn chủ quan của con người.
Để tính xác suất của một biến cố, người ta xây dựng các ịnh nghĩa sau ây:
1.3.1 Định nghĩa cổ iển về xác suất: 1)
Ví dụ mở ầu. Giả sử thực hiện một phép thử là tung một con xúc xắc ối xứng và
ồng chất. Ta thấy có 6 trường hợp có thể xảy ra là: Xuất hiện mặt 1 chấm, 2 chấm, …, 6
chấm. Những trường hợp này thoả mãn 2 iều kiện: Trước hết chúng duy nhất, tức là
trong kết quả của phép thử xảy ra một và chỉ một trong các trường hợp ó. Sau nữa, ây là
những trường hợp có khả năng xảy ra như nhau. Các trường hợp thoả mãn
hai iều kiện nói trên ược gọi là các kết cục ồng khả năng.
Gọi A là biến cố “Xuất hiện mặt có số chấm chẵn”. Trong số 6 kết cục ồng khả
năng ó ta thấy chỉ có 3 kết cục mà nếu xảy ra thì biến cố A sẽ xảy ra, ó là những kết cục
ược mặt 2 chấm, 4 chấm và 6 chấm. Những kết cục này ược gọi là các kết cục thuận lợi cho biến cố A. 2)
Định nghĩa. Xác suất của biến cố A trong một phép thử là tỉ số giữa số kết cục
thuận lợi cho biến cố A và số các kết cục ồng khả năng khi thực hiện phép thử ó.
Nếu m là số kết cục thuận lợi cho biến cố A, n là số các kết cục ồng khả năng 9 lOMoAR cPSD| 47207194 GV:
Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU
khi thực hiện phép thử thì: P(A) Sè kÕt côc thuËn lîi cho A m . Sè kÕt côc ®ång kh¶ n¨ng n
Ví dụ. Xác suất ể khi tung một con xúc xắc xuất hiện mặt có số chấm chẵn là:P(A) = 3/6 = 0,5
Chú ý. Khi áp dụng ịnh nghĩa cổ iển về xác suất òi hỏi hai giả thiết sau thỏa mãn:
+) Các kết cục có thể xảy ra trong phép thử là hữu hạn
+) Các kết cục có thể xảy ra trong phép thử là ồng khả năng. Thường thì tính ồng
khả năng của các kết cục suy ra từ tính ối xứng. Chẳng hạn khi tung một con xúc xắc ta
giả thiết rằng nó ối xứng và ồng chất.
Nếu các kết cục có thể xảy ra trong phép thử không ồng khả năng thì ta không
thể tính xác suất bằng ịnh nghĩa cổ iển ược. Khi ó, ta có thể tính xác suất bằng ịnh nghĩa sau ây:
1.3.2 Định nghĩa thống kê về xác suất:
Giả sử một phép thử ược thực hiện lặp i lặp lại n lần trong những iều kiện như
nhau. Nếu trong n lần thực hiện phép thử ó biến cố A xuất hiện k lần thì tỉ số k/n ược
gọi là tần suất xuất hiện biến cố A trong n phép thử ã cho, ký hiệu là f(A): f(A) = k/n. Chú ý. 0 f(A) 1
Ví dụ. Để nghiên cứu khả năng xuất hiện mặt sấp khi tung một ồng xu, Buffon và
Pearson ã tiến hành tung ồng xu nhiều lần và ược kết quả sau ây: 10 lOMoAR cPSD| 47207194 GV:
Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU
Người làm thí nghiệm Số lần tung (n) Số lần xuất hiện Tần suất mặt sấp (k) f(A) k n Buffon 4040 2048 0,5069 Pearson 12000 6019 0,5016 Pearson 24000 12012 0,5005
Ta thấy khi số lần tung ồng xu tăng lên thì tần suất xuất hiện mặt sấp sẽ dao ộng
ngày càng ít hơn xung quanh giá trị không ổi là 0,5.
Khi số lần thực hiện phép thử ó thay ổi (n thay ổi), tần suất xuất hiện biến cố A
cũng thay ổi nhưng nó luôn dao ộng xung quanh một số cố ịnh nào ó. Khi n càng lớn thì
tần suất xuất hiện biến cố A càng gần số cố ịnh ó. Số cố ịnh ấy ược gọi là xác suất của
biến cố A theo nghĩa thống kê.
Vậy, xác suất xuất hiện mặt sấp khi tung ồng xu cân ối và ồng chất là 0,5.
Chú ý. Trên thực tế khi n ủ lớn, ta có thể xấp xỉ P(A) bởi f(A): P(A) f(A).
1.3.3 Định nghĩa hình học về xác suất: Định nghĩa hình học về xác suất có thể sử dụng
khi xác suất ể một iểm rơi vào một phần nào ó của một miền cho trước tỷ lệ với ộ o của
miền ó ( ộ dài, diện tích hay thể tích tương ứng miền ó là oạn thẳng, miền phẳng hay
khối không gian) và không phụ thuộc vào vị trí và dạng thức của miền ó.
Định nghĩa. Nếu ộ o hình học của toàn bộ miền cho trước là S, còn ộ o hình học của
một phần H nào ó của nó là SH thì xác suất ể iểm ngẫu nhiên rơi vào phần H sẽ
bằng: p SH . S 11 lOMoAR cPSD| 47207194 GV:
Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU
Ví dụ. Điểm A ược lấy ngẫu nhiên trên miền D {(x;y):0 x 2; 0 y 2}. Tính xác suất
ể giá trị tuyệt ối của hiệu hai tọa ộ của A nhỏ hơn 1.
Giải. Ta có S = S(D) = 2.2 = 4, H {A(x;y):|y-x| 1} S(H) = 3.
Xác suất ể giá trị tuyệt ối của hiệu hai tọa ộ của A nhỏ hơn 1 là p = 3/4 = 0,75.
Ngoài ra còn có ịnh nghĩa tiên ề về xác suất. 1.3.3 Tính chất: 1) 0 P(A) 1.
Chứng minh. Thật vậy, vì số kết cục thuận lợi cho một biến cố ngẫu nhiên luôn luôn thỏa mãn 0 m n. Do ó: 0 m 1 hay 0 PA( ) 1 . n 2) P U( ) 1.
Chứng minh. Thật vậy, nếu U là biến cố chắc chắn thì tất cả các kết cục duy nhất ồng
khả năng có thể xảy ra trong phép thử ều thuận lợi cho biến cố xảy ra. Do ó m = n và ta có: P(U) m n 1 n n
3) P V( ) 0 .
Chứng minh. Nếu V là biến cố không thể có thì trong số các kết cục duy nhất ồng khả
năng có thể xảy ra trong phép thử không có kết cục nào thuận lợi cho biến cố xảy 0
ra. Do ó m = 0 và ta có:P(V) 0. n 12 lOMoAR cPSD| 47207194 GV:
Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU
Bài tập. Các phát biểu sau là úng hay sai:
a) Nếu một biến cố có xác suất bằng 0 thì là biến cố không thể có.
b) Nếu một biến cố có xác suất bằng 1 thí là biến cố chắc chắn.
Giải. a) Sai vì biến cố có xác suất bằng 0 vẫn có thể xảy ra.
b) Sai vì biến cố có xác suất bằng 1 vẫn có thể không xảy ra.
Chẳng hạn, cho một miền G có diện tích SG ủ lớn và một iểm M trong miền ó. Ném một
iểm vào miền G. Gọi A là biến cố iểm ó rơi úng iểm M, B là biến cố iểm ó không rơi úng iểm M. Ta có: P A( ) SM
0 0 song A vẫn có thể xảy ra SG SG P B( ) S S S G
M G 1 song B vẫn có thể không xảy ra SG SG
1.3.4 Các phương pháp tính xác suất bằng ịnh nghĩa cổ iển:
1) Phương pháp suy luận trực tiếp
Nếu số các kết cục trong phép thử là khá nhỏ và việc suy oán là khá ơn giản thì
ta sử dụng phương pháp suy luận trực tiếp.
Ví dụ 1. Một hộp có a quả cầu trắng và b quả cầu en. Lấy ngẫu nhiên một quả cầu.
Tìm xác suất ể lấy ược quả cầu trắng.
Giải. Gọi A = “Lấy ược quả cầu trắng”.
Số kết cục ồng khả năng là a + b.
Số kết cục thuận lợi cho biến cố A là a. 13 lOMoAR cPSD| 47207194 GV:
Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU Vậy, P(A) = a . a b
2) Phương pháp dùng sơ ồ Ven
Khi số kết cục là khá lớn và việc suy oán phức tạp hơn thì có thể dùng sơ ồ Ven. a) Sơ ồ hình cây
Ví dụ 2. Một xạ thủ bắn liên tiếp ba phát vào một chiếc bia, biết rằng xác suất bắn trúng
và không bắn trúng bia là như nhau. Tìm xác suất ể xạ thủ ó có úng hai lần bắn trúng bia.
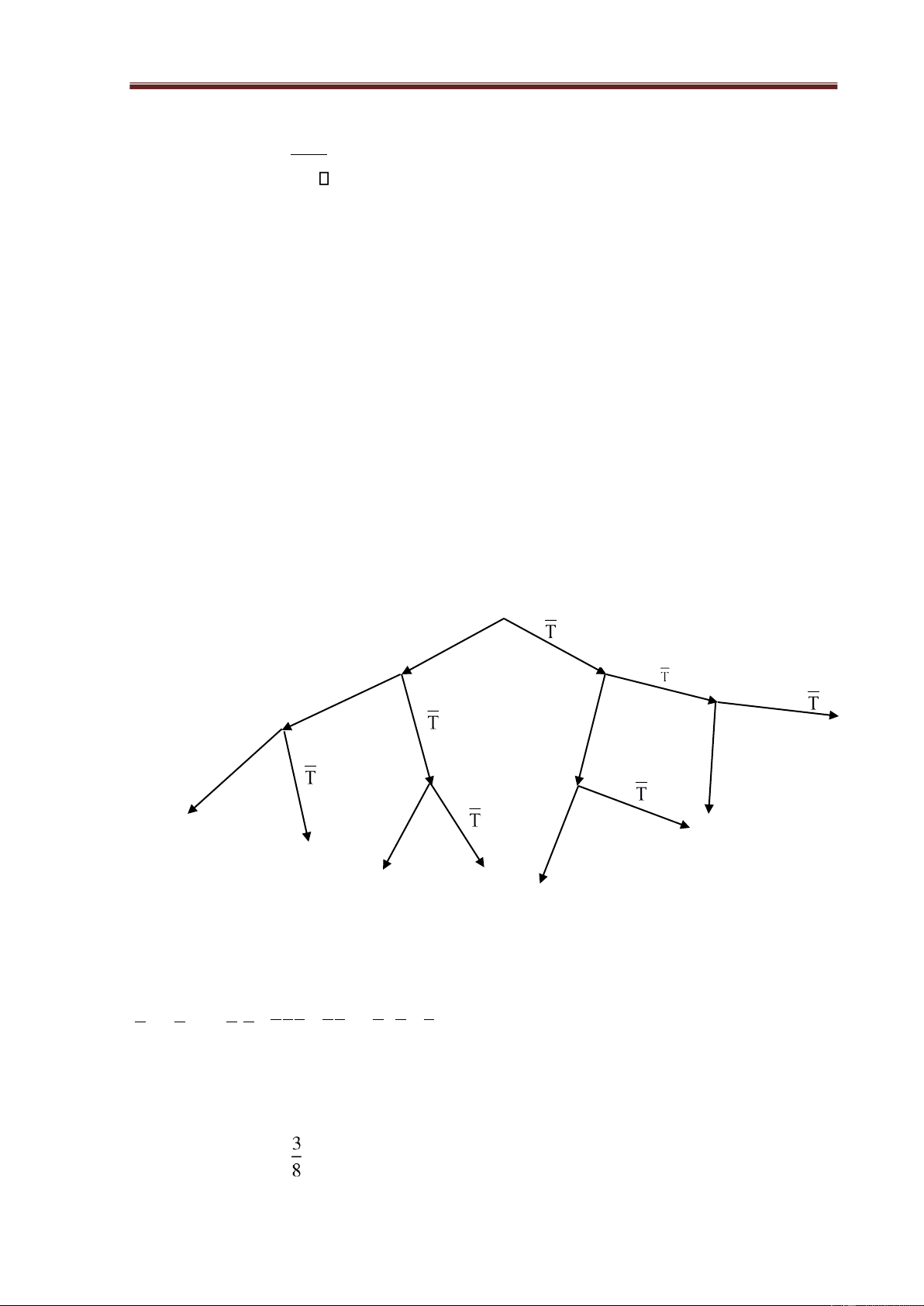
Giải.Ta có sơ ồ sau: L ầ n b ắ n 1 T L ầ n b ắ n 2 T L ầ n b ắ n 3 T T T T T
Gọi T = “xạ thủ bắn trúng bia”; A = “xạ thủ có úng hai lần bắn trúng bia”
Khi xạ thủ ó bắn 3 lần liên tiếp thì số kết cục ồng khả năng là n = 8: TTT, TT
T, TTT, TT T, TTT , TTT , TTT , TTT.
Số kết cục thuận lợi cho A là m = 3. Vậy, P(A) = . 14 lOMoAR cPSD| 47207194 GV:
Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU
b) Sơ ồ dạng bảng
Ví dụ 3. Tung ồng thời hai con xúc xắc ối xứng và ồng chất. Tìm xác suất ể ược hai mặt
có tổng số chấm bằng 7.
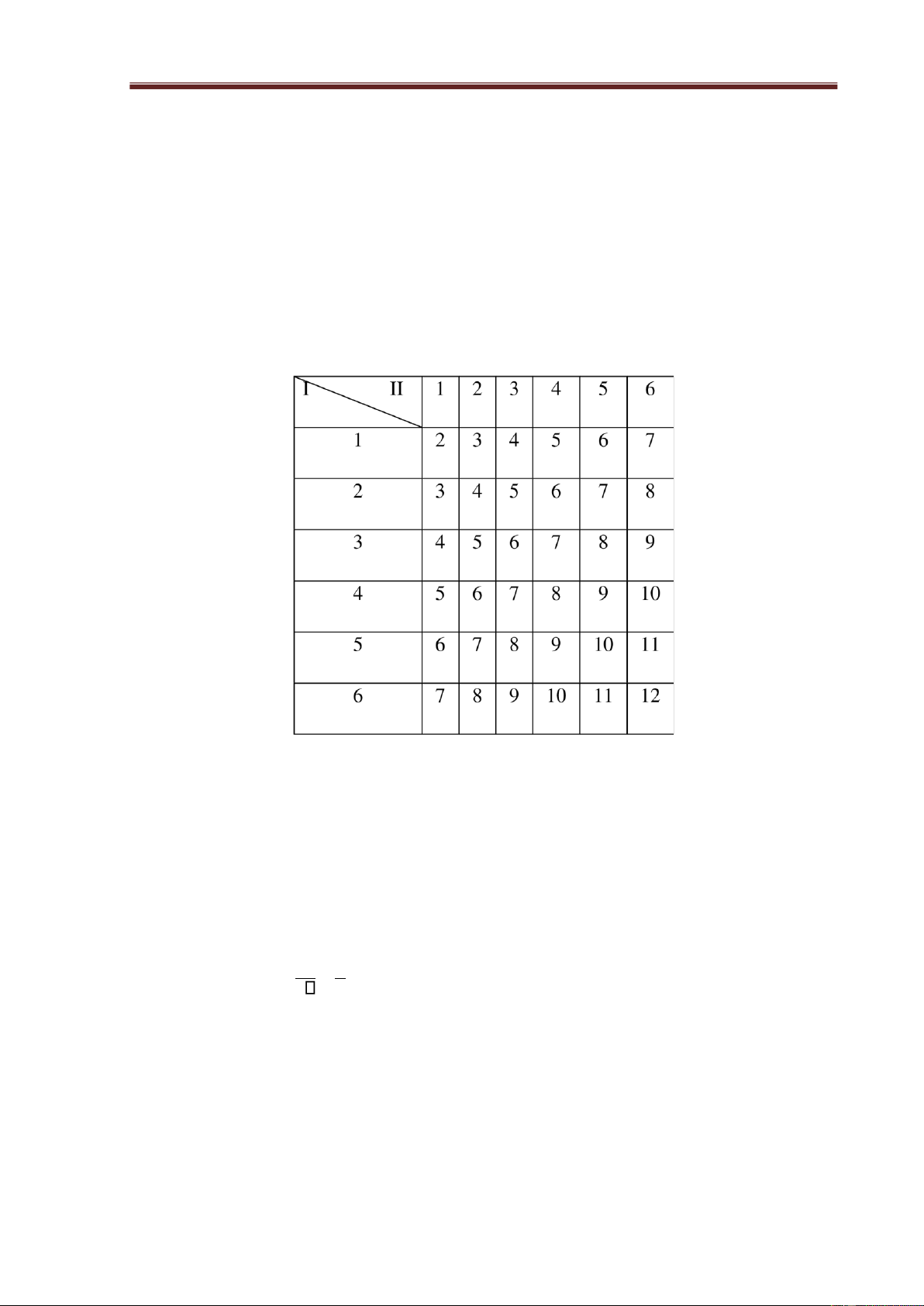
Giải. Phép thử có thể mô tả bằng bảng dưới ây
Gọi A = “hai mặt có tổng số chấm bằng 7”.
Số kết cục ồng khả năng khi phép thử thực hiện là 36.
Số kết cục thuận lợi cho A là 6. Vậy, P(A) = 6 1. 36 6
c) Sơ ồ dạng tập hợp
Ví dụ 4. Trong một lớp có 50 học sinh, trong ó có 20 người biết chơi àn Piano, 15 15 lOMoAR cPSD| 47207194 GV:
Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU
người biết chơi àn Organ, 10 người biết chơi àn Ghita, 7 người vừa biết chơi àn Piano
vừa biết chơi àn Organ, 5 người vừa biết chơi àn Piano vừa biết chơi àn Ghita, 3 người
vừa biết chơi àn Organ vừa biết chơi àn Ghita, 1 người vừa biết chơi àn Piano vừa biết
chơi àn Organ vừa biết chơi àn Ghita. Lấy ngẫu nhiên một học sinh. Tìm xác xuất ể học
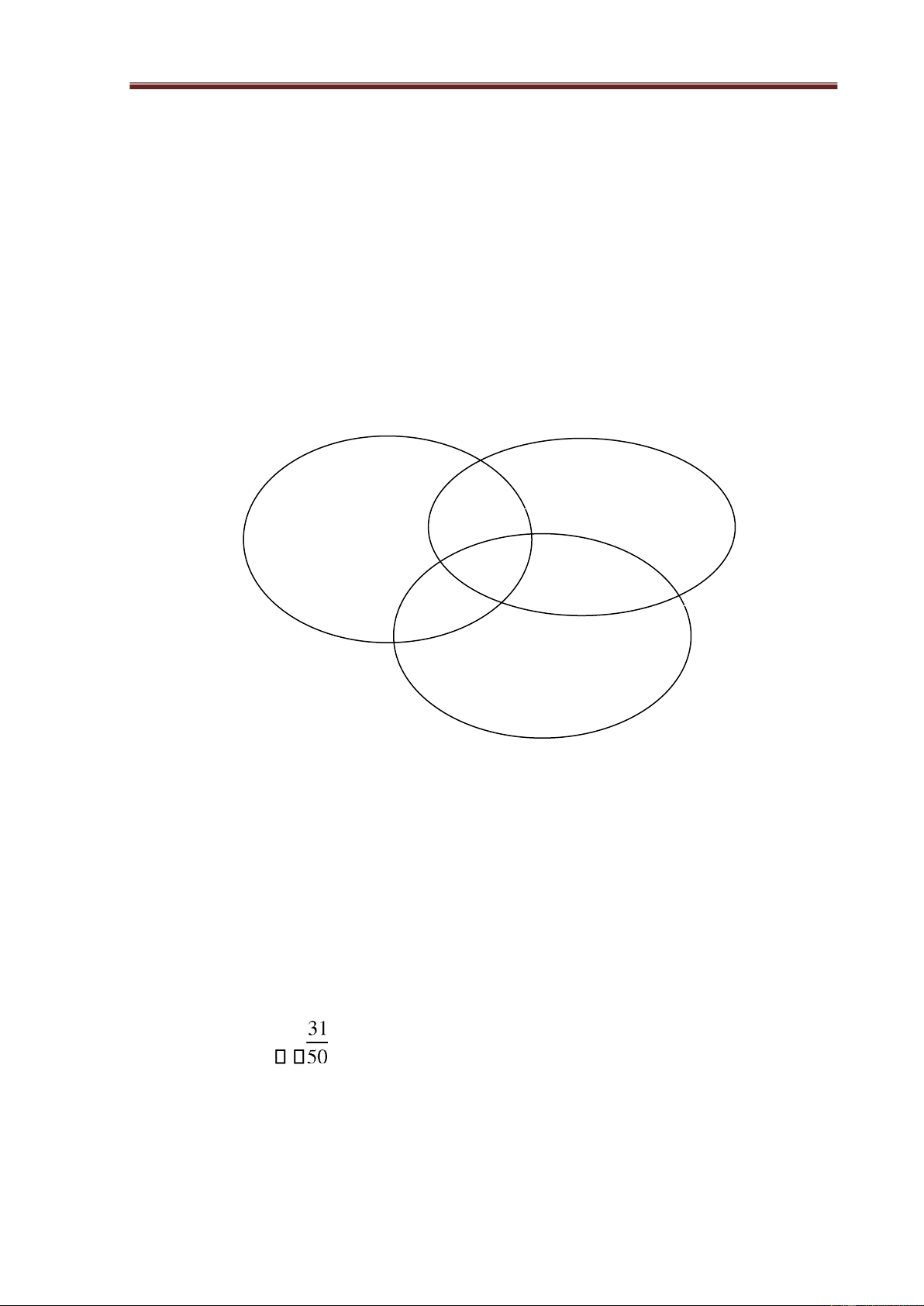
sinh ó biết chơi ít nhất một loại àn. Giải. Piano Organ 6 9 6 1 2 4 Ghita 3
Gọi A = “Lấy ngẫu nhiên một học sinh thì học sinh ó biết chơi ít nhất một một
loại àn". Trong n = 50 kết cục duy nhất ồng khả năng thì số kết cục thuận lợi cho biến cố A là
9 + 6 + 3 + 6 + 4 + 2 + 1 = 31 Vậy, P(A) 0,62 .
3) Phương pháp dùng các công thức của giải tích tổ hợp 16 lOMoAR cPSD| 47207194 GV:
Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU
Ví dụ 5. Rút ngẫu nhiên từ bộ bài tú lơ khơ gồm 52 quân bài ra 4 quân bài. Tìm xác suất
sao cho trong 4 quân bài rút ra ta có:
a) 1 quân màu ỏ, 3 quân màu en
b) 2 quân Cơ, 1 quân Rô, 1 quân Pic c) 2 quân At
Giải. Phép thử của ta là rút ngẫu nhiên 4 quân bài. Số kết cục ồng khả năng là 4 52! 52.51.50.49 C52 270725. 4!48! 24
Gọi A = “trong 4 quân bài rút ra có 1 quân màu ỏ, 3 quân màu en” Tương tự
B, C là các biến cố tương ứng với các câu b, c.
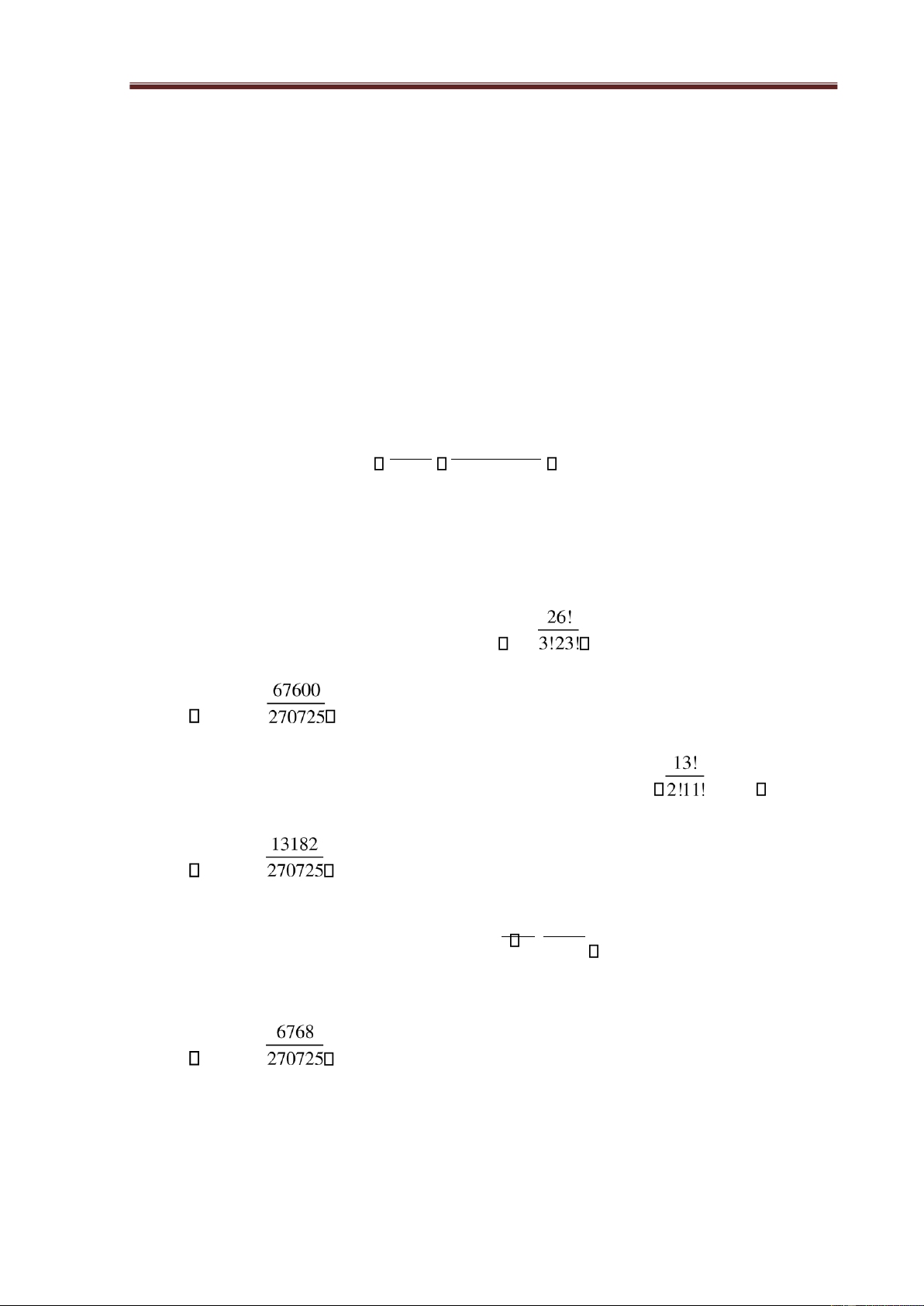
Số kết cục thuận lợi cho A là: C .C1 3 26 26 26. 67600 P(A) = 0,2497
Số kết cục thuận lợi cho B là:C .C .C 2 1 1 13 13 13 .13.13 13182 P(B) = 0,0487
Số kết cục thuận lợi cho C là: C .C 4! 2 2 4 48 . 48! 6768 2!2! 2!46! P(C) = 0,025
Ví dụ 6. Số iện thoại ở thành phố A là một số gồm 7 chữ số, bắt ầu bằng số 8. Giả sử ta
chọn ngẫu nhiên một số iện thoại của thành phố. Tìm xác suất ể chọn ược một số iện thoại: 17 lOMoAR cPSD| 47207194 GV:
Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU
a) có 6 chữ số còn lại khác nhau. b) là số chia hết cho 5.
c) có 7 chữ số khác nhau, số cuối cùng chẵn.
Giải. Ta thấy 6 chữ số còn lại của một số iện thoại của thành phố A ều ược lấy từ tập
hợp 10 chữ số: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 mà các chữ số trong 6 chữ số này có thể
trùng nhau. Do ó Số kết cục ồng khả năng là A 6 10 106 .
a) Gọi A = “Chọn ược số iện thoại có có 6 chữ số còn lại khác nhau”. Số kết cục thuận lợi cho A là A 6 10 . P(A) A106 10.9.8.7.6.5 0,1512 106 106
b) Gọi B = “Chọn ược số iện thoại là số chia hết cho 5”. Một số iện thoại là số chia hết
cho 5 nếu chữ số cuối cùng của nó có thể là 1 trong 2 chữ số là 0 và 5. Các chữ số trong
5 chữ số còn lại của số iện thoại ó có thể trùng nhau. Do ó, số kết cục thuận lợi cho B là: A 5 10 .2 10 .25 10 .25 10 P(B) 0,2. 6
c) Gọi C = “Chọn ược số iện thoại có có 7 chữ số khác nhau, số cuối cùng chẵn”. Vì chữ
số ầu tiên của số iện thoại ó là 8, nên chữ số cuối cùng của số iện thoại ó chỉ có thể là 1
trong 4 chữ số 0, 2, 4, 6. 5 chữ số còn lại của số iện thoại ó khác nhau,
khác 8 và khác chữ số cuối. Do
ó, số kết cục thuận lợi cho C là A .4 5 8 8.7.6.5.4.4 26880 18 lOMoAR cPSD| 47207194 GV:
Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU 26880 P(C) 0,2688 6 10
Ví dụ 7. Một oàn tàu gồm 9 toa tiến vào một sân ga, ở ó ang có 5 hành khách chờ lên
tàu. Giả sử mỗi toa còn ít nhất 5 chỗ trống. Tìm xác suất ể:
a) Tất cả cùng lên toa 2
b) Tất cả cùng lên một toa
c) 5 người lên 5 toa khác nhau d) 3 người lên toa 2
e) 5 người lên 4 toa khác nhau
Giải. Mỗi hành khách ều có 9 khả năng ể lên 9 toa của oàn tàu. Do ó số kết cục
ồng khả năng là n A5995 59049.
a) Gọi A = “Tất cả cùng lên toa 2”. Số kết cục thuận lợi cho A là m = 1. Vậy, P(A) 0,000017
b) Gọi B = “Tất cả cùng lên một toa”. Số kết cục thuận lợi cho B là m = 9. Vậy, P(B) 0,000152
c) Gọi C = “5 người lên 5 toa khác nhau”. Số trường hợp thuận lợi cho C là m A59 9.8.7.6.5 15120. Vậy, P(C) 0,256
d) Gọi D = “3 người lên toa 2”.
Số cách ghép 3 hành khách trong số 5 hành khách lên toa 2 là C35 10 19 lOMoAR cPSD| 47207194 GV:
Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU
2 hành khách còn lại, mỗi hành khách có 8 cách chọn lên 8 toa còn lại, do vậy 2
hành khách còn lại có số cách chọn là: A 2 8 82 64.
Vậy, số trường hợp thuận lợi cho D là m = 10.64 = 640. P(D) 6405 0,011 9
e) Gọi E = “5 người lên 4 toa khác nhau”.
Theo giả thiết thì có hai khách cùng lên một toa. Ta có thể coi hai hành khách này
là 1 hành khách. Khi ó, bài toán quy về 4 hành khách lên 4 toa khác nhau, nên số cách sẽ là A 4 9
9.8.7.6 3024. Nhứng số cách ghép 2 hành khách trong 5 hành khách lên cùng một toa là C 2 5
10. Vậy, số trường hợp thuận lợi cho E là m = 3024.10 = 30240. P(E) 0,512
Ví dụ 8. Một tổ gồm 10 người tổ chức buổi liên hoan ngồi quanh bàn tròn. Mọi người
ngồi vào chỗ một cách ngẫu nhiên. Tìm xác suất ể cho A và B ngồi cạnh nhau.
Giải. Số kết cục ồng khả năng là P10 10!
A có thể ngồi một trong 10 chỗ, 2 chỗ bên cạnh giành cho B, 8 chỗ còn lại giành
cho 8 người kia. Vậy số thuận lợi là 10.2.8!
Vậy xác suất cần tìm là 10.2.8! 2 10! 9
Ví dụ 9. Có 12 người, trong ó có 7 nam và 5 nữ xếp ngẫu nhiên thành một hàng ngang. Tìm xác suất ể: 20