Bài tập tỷ số thể tích khối đa diện – Lê Bá Bảo Toán 12

Tài liệu gồm 15 trang trình bày phương pháp, ví dụ mẫu có lời giải chi tiết và bài tập rèn luyện về dạng toán tỷ số thể tích khối đa diện.Mời các bạn đón xem.

34 17 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

15 trang 7 tháng trước

Tác giả:

Profile Lan Tường
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 1 CLB Giáo viên trẻ TP Huế
TỶ SỐ THỂ TÍCH KHỐI ĐA DIỆN
Giáo viên: LÊ BÁ BẢO Trường THPT Đặng Huy Trứ, Huế
SĐT: 0935.785.115 Địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế
I- PHƯƠNG PHÁP
Kết quả 1:
Cho tam gi¸c trªn c¹nh chän trªn c¹nh chän , ' , ' .OAB OA A O OB B O
Lóc ®ã:
''
''
.
OA B
OAB
S
OA OB
S OA OB
Chøng minh:
11
22
Gäi H, H' lÇn lît l¯ h×nh chiÕu vu«ng gãc cña A v¯ A' lªn OB.
Lóc ®ã: v¯
''
' '. ' .
OA B OAB
S A H OB S AH OB
Suy ra:
§Þnh lý thales
''
' ' ' ' '
..
OA B
OAB
S
A H OB OA OB
S AH OB OA OB

H'
H
B'
B
A
O
Kết quả 2:
Cho h×nh chãp trªn c¹nh chän trªn c¹nh chän trªn c¹nh S chän . , ' , ' ' .S ABC SA A O SB B O C C O
Lóc ®ã:
.
. ' ' '
.
' ' '
.
S A B C
S ABC
V
SA SB SC
V SA SB SC
Chøng minh:
Gäi H, H' lÇn lît l¯ h×nh chiÕu vu«ng gãc cña A v¯ A' lªn mp .
Lóc ®ã:
()SBC
11
33
v¯ V
. ' ' ' ' ' .
' '. .
S A B C SB C S ABC SBC
V A H S AH S
Suy ra:
. §Þnh lý thales
V
. ' ' ' ' '
.
' ' ' ' '
..
S A B C SB C
S ABC SBC
VS
A H SA SB SC
AH S SA SB SC

H'
H
C'
B'
A'
C
B
A
S
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 2 CLB Giáo viên trẻ TP Huế
II- BÀI TẬP TRẮC NGHIỆM MINH HỌA
Ví dụ 1: Cho hình lăng trụ
. ' ' 'ABC A B C
. Tỉ số thể tích của khối
' ' 'AA B C
và khối
'ABCC
là
A.
1.
B.
1
2
. C.
1
3
.
D.
2
3
.
Lời giải
Ta có:
1
3
1
3
' ' '
' ' '
'
; ' ' ' .
;.
A B C
AA B C
C ABC
ABC
d A A B C S
V
V
d C ABC S
(1)
Do
' ' 'ABC A B C
SS
và
; ' ' ' ;d A A B C d C ABC
nên (1):
1
' ' '
'
AA B C
C ABC
V
V
.
Chọn đáp án A.
A'
B'
C'
B
C
A
Ví dụ 2: Cho hình chóp tứ giác đều
.S ABCD
. Gọi
,MN
lần lượt là trung điểm của
,SB SD
. Mặt
phẳng
AMN
cắt
SC
tại
E
. Gọi
2
V
là thể tích của khối chóp
.S AMEN
và
1
V
là thể tích khối
chóp
.S ABCD
. Khẳng định nào sau đây đúng?
A.
21
1
3
.VV
B.
21
1
4
.VV
C.
21
1
8
.VV
D.
21
1
6
.VV
Lời giải
1
2
SM SN SI
SB SD SO
Qua O dựng OK // AE.
Xét
AEC
:
1
2
//OK AE
OK AE
. Suy ra:
K
là trung
điểm
EC
.
Xét
SOK
:
1
2
//IE OK
IE OK
. Suy ra:
E
là trung
điểm
SK
. Vậy
1
3
SE
SC
Ta có:
2
1 1 1
2 2 3 6
..
..
. . .
S AMEN S AME
S ABCD S ABC
VV
SA SM SE
V V SA SB SC
1
6
..S AMEN S ABCD
VV
hay
21
1
6
.VV
K
I
O
E
M
N
S
D
C
B
A
Chọn đáp án D.
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 3 CLB Giáo viên trẻ TP Huế
Ví dụ 3: Cho tứ diện đều ABCD. Điểm
M
là trung điểm
AB
và
N
trên cạnh
CD
sao cho
2CN ND
. Tỉ số thể tích của khối ABCD và khối
MNBC
bằng
A.
3.
B.
3
2
.
C.
1
3
.
D.
4
3
.
Lời giải
Ta có:
1 2 1
2 3 3
1
3
3
;.
.
BMCN BACN BMCN BACN
BACN BACD BACN BACD
BMCN BACD
BACD BMCN
V V V V
V V V V
VV
VV
Chọn đáp án A.
D
A
B
C
M
N
Ví dụ 4: Cho hình chóp
.S ABC
. Gọi
,MN
lần lượt thuộc các cạnh
,SB SC
sao cho
2 ,.SM MB SN CN
Mặt phẳng
AMN
chia khối chóp thành hai phần, gọi
1 .S AMN
VV
và
2 ABCNM
VV
. Khẳng định nào sau đây đúng?
A.
12
.VV
B.
12
1
3
.VV
C.
12
1
2
.VV
D.
12
2
3
.VV
Lời giải
Ta có:
1 2 1
2 3 3
.
.
. . .
S AMN
S ABC
V
SM SN
V SB SC
12
33
. . .S AMN S ABC ABCNM S ABC
V V V V
Vậy
12
1
2
.VV
Chọn đáp án C.
N
M
C
B
A
S
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 4 CLB Giáo viên trẻ TP Huế
Ví dụ 5: Cho hình chóp tam giác đều
.S ABC
. Gọi
,MN
lần lượt là trung điểm của
,BC SM
. Mặt
phẳng
ABN
cắt
SC
tại
E
.Gọi
2
V
là thể tích của khối chóp
.S ABE
và
1
V
là thể tích khối chóp
.S ABC
. Khẳng định nào sau đây đúng?
A.
21
1
3
.VV
B.
21
1
4
.VV
C.
21
1
8
.VV
D.
21
1
6
.VV
Lời giải
Qua M dựng MK // BE. Xét tam giác
BEC
:
1
2
//MK BE
MK BE
. Suy ra:
K
là trung điểm
EC
.
Xét tam giác
SMK
:
1
2
//NE MK
NE MK
. Suy ra:
E
là
trung điểm
SK
. Vậy
1
3
SE
SC
Ta có:
11
33
.
..
.
..
S ABE
S ABE S ABC
S ABC
V
SA SB SE
VV
V SA SB SC
hay
21
1
3
.VV
Chọn đáp án A.
K
E
N
M
C
B
A
S
Ví dụ 6: Cho hình lăng trụ
. ' ' '.ABC A B C
Gọi
,EF
lần lượt là trung điểm của các cạnh
'AA
và
'.BB
Đường thẳng
CE
cắt đường thẳng
''CA
tại
'.E
Đường thẳng
CF
cắt đường thẳng
''BC
tại
'.F
Gọi
2
V
là thể tích khối chóp
.C ABFE
và
1
V
là thể tích khối lăng trụ
. ' ' '.ABC A B C
Khẳng định nào
sau đây đúng?
A.
21
1
3
.VV
B.
21
1
4
.VV
C.
21
1
8
.VV
D.
21
1
6
.VV
Lời giải
Hình chóp
. ' ' 'C A B C
và lăng trụ
. ' ' 'ABC A B C
có
đường cao và đáy bằng nhau nên
1 1 1
1 1 2
3 3 3
. ' ' ' . ' ' ' . ' '
.
C A B C ABC A B C C ABB A
V V V V V V
Do
EF
là đường trung bình của hình bình hành
1
1 1 1
2 2 3
' ' . . ' '
''
ABFE ABB A C ABFE C ABB A
ABB A S S V V V
hay
21
1
3
.VV
Chọn đáp án A.
E'
F'
F
E
A'
B'
C'
C
B
A
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 5 CLB Giáo viên trẻ TP Huế
Ví dụ 7: Cho hình chóp S.ABC, trên AB, BC, SC lần lượt lấy các điểm M, N, P sao cho
2 ,AM MB
4 ,BN NC SP PC
. Tỉ lệ thể tích hai khối chóp
.S BMN
và
.A CPN
là:
A.
4
3
.
B.
5
6
.
C.
8
3
.
D.
1.
Lời giải
+
1 4 4
3 5 15
..
..
. . .
S BMN B MNS
S ABC B ACS
VV
BM BN BS
V V BA BC BS
+
1 1 1
5 2 10
..
..
. . .
A CPN C ANP
S ABC C ABS
VV
CA CN CP
V V CA CB CS
4 1 8
15 10 3
.
.
:
S BMN
A CNP
V
V
P
N
M
B
A
S
C
Chọn đáp án C.
Ví dụ 8: (Đề minh họa Bộ GD&ĐT) Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông
góc với nhau;
6AB a
,
7AC a
và
4AD a
. Gọi M, N, P tương ứng là trung điểm các cạnh BC,
CD, DB. Tính thể tích V của tứ diện AMNP.
A.
3
7
2
.Va
B.
3
14 .Va
C.
3
28
3
.Va
D.
3
7 .Va
Lời giải
Ta có:
3
1
28
6
. . .
ABCD
V AB AC AD a
Dễ thấy
MNP
được tạo nên bởi các đường trung
bình của
BCD
chúng đồng dạng với nhau theo tỉ
số
3
1 1 1 1 1
7
2 2 2 4 4
..
AMNP MNP
AMNP ABCD
ABCD BCD
VS
V V a
VS
Chọn đáp án D.
M
N
P
D
A
B
C
Ví dụ 9: Cho hình hộp
. ' ' ' 'ABCD A B C D
. Gọi
O
là tâm của
ABCD
;
,MN
lần lượt là trung điểm
của
''AB
và
''AD
. Tỉ số thể tích của khối
'A ABD
và khối
' ' 'OMND C B
bằng
A.
4
9
.
B.
4
7
. C.
5
7
.
D.
3
7
.
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 6 CLB Giáo viên trẻ TP Huế
Lời giải
Do
' ' ' ' ' ' ' ' ' 'B'ABD A B D MND C B B C D MND
S S S S S
'B'ABD MND
SS
Mặt khác ta có:
1 3 3
4 4 4
'
'B' ' ' '
' ' '
A MN
MND A B D ABD
A B D
S
S S S
S
Suy ra:
7
4
' ' 'MND C B ABD
SS
.
Ta có:
1
3
1
3
'
' ' '
' ' '
'; .
; ' ' ' ' .
ABD
A ABD
OMND C B
MND C B
d A ABCD S
V
V
d O A B C D S
4
7
' ' '
.
ABD
MND C B
S
S

Chọn đáp án B.
O
N
M
A'
B'
D'
C'
D
A
B
C
Ví dụ 10: Cho hình chóp
.S ABC
có
SA
vuông góc với mặt đáy,
,SA a ABC
đều cạnh
2 .a
Gọi
,MN
lần lượt thuộc các cạnh
,SB SC
sao cho
2 ,.SM MB SN CN
Tính thể tích khối
.AMNCB
A.
3
23
9
.
a
B.
3
3
9
.
a
C.
3
43
9
.
a
D.
3
23
3
.
a
Lời giải
Ta có:
2
3
2
32
13
3
4 3 3
.
..
ABC S ABC ABC
a
a
S a V SA S

Ta có:
1 2 1
2 3 3
.
.
. . .
S AMN
S ABC
V
SM SN
V SB SC
3
1 2 2 3
3 3 9
. . .
.
S AMN S ABC ABCNM S ABC
a
V V V V
Chọn đáp án A.
2a
a
S
A
B
C
M
N
Ví dụ 11: Cho hình chóp
.S ABCD
có đáy là hình bình hành. Gọi
M
là trung điểm cạnh
.SA
Mặt
phẳng
qua
M
và song song với
ABCD
, cắt các cạnh
,,SB SC SD
lần lượt tại
, , .N P Q
Gọi
1 .S ABCD
VV
và
2 .S MNPQ
VV
. Khẳng định nào sau đây đúng?
A.
12
8 .VV
B.
12
6 .VV
C.
12
16 .VV
D.
12
4 .VV
Lời giải
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 7 CLB Giáo viên trẻ TP Huế
Dễ thấy,
,,N P Q
lần lượt là trung điểm các cạnh
, , .SB SC SD
Ta có:
12
2
2
2
1 1 1 1
2 2 2 2 8
8
..
.
.
.
..
. . . . .
.
S MNPQ S MNP
S ABCD ABC
S MNPQ
S MNP
S ABCD S ABC
VV
VV
V
V
SM SN SP
V V SA SB SC
VV

Chọn đáp án A.
Q
P
N
M
S
D
C
A
B
Ví dụ 12: Cho hình chóp
.S ABCD
có đáy là hình bình hành. Gọi
M
là trung điểm cạnh
.SC
Mặt
phẳng
chứa
AM
và song song với
BD
, cắt các cạnh
,SB SD
lần lượt tại
,.NP
Gọi
1 .S ANMP
VV
và
2 ABCDPMN
VV
. Khẳng định nào sau đây đúng?
A.
21
3 .VV
B.
21
3
2
.VV
C.
21
2 .VV
D.
21
7
2
.VV
Lời giải
Gọi
;.BD AC O AM SO I
Suy ra
I
là
trọng tâm
SAC
và
.SBD
Qua
I
dựng
//PN BD
Thiết diện là tứ giác
.ANMP
Ta có:
1
2
2 1 1
2 3 2 3
.
..
..
S ANM
S ABCD S ABC
V
V
SN SM
V V SB SC
1 2 2 1
12
2
33
..
.
S ABCD S ABCD
V V V V V V
Chọn đáp án C.
I
O
B
A
C
D
S
M
N
P
Ví dụ 13: Cho hình chóp tứ giác đều
.S ABCD
có tất cả các cạnh đều bằng
.a
Gọi
, , ,M N P Q
lần
lượt thuộc các cạnh
, , ,SA SB SC SD
sao cho
1
23
3
; ; ; .SM MA SN NB SP PC SQ SD
Tính thể
tích khối
.SMNPQ
A.
3
32
16
.
a
B.
3
2
48
.
a
C.
3
2
16
.
a
D.
3
2
32
.
a
Lời giải
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 8 CLB Giáo viên trẻ TP Huế
Ta có:
1 2 3 1
2 3 4 4
.
.
. . . .
S MNP
S ABC
V
SM SN SP
V SA SB SC
11
48
. . .
.
S MNP S ABC S ABCD
V V V
Tương tự:
1 3 1 1
2 4 3 8
.
.
. . . .
S MPQ
S ACD
V
SM SP SQ
V SA SC SD
11
8 16
. . .
.
S MPQ S ACD S ABCD
V V V
Vậy
3
16
. . .SMNPQ S MNP S MPQ S ABCD
V V V V
33
3 2 2
16 6 32
..
aa

Chọn đáp án D.
Q
P
N
M
S
D
C
A
B
O
Ví dụ 14: Cho hình lăng trụ
. ' ' '.ABC A B C
Gọi
1 . ' ' 'A A B C
VV
và
2 . ' ' 'ABC A B C
VV
. Khẳng định nào sau
đây đúng?
A.
12
3
4
.VV
B.
12
1
2
.VV
C.
12
1
3
.VV
D.
12
2
3
.VV
Lời giải
Ta có:
1
3
. ' ' ' ' ' '
; ' ' ' .
A A B C A B C
V d A A B C S
và
. ' ' ' ' ' '
; ' ' ' . .
ABC A B C A B C
V d A A B C S
Suy ra:
1
2
1
3
.
V
V
Chọn đáp án C.
B'
C'
A'
A
B
C
Ví dụ 15: Cho hình lăng trụ
. ' ' '.ABC A B C
Điểm
M
trên cạnh
'AA
sao cho:
2 '.AM MA
Gọi
1 . ' 'M BCC B
VV
và
2 . ' ' 'ABC A B C
VV
. Khẳng định nào sau đây đúng?
A.
12
3
4
.VV
B.
12
1
2
.VV
C.
12
1
3
.VV
D.
12
2
3
.VV
Lời giải
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 9 CLB Giáo viên trẻ TP Huế
Do
. ' ' . ' '
'/ / ' ' .
M BCC B A BCC B
AA BCC B V V
Ta có:
12
33
. ' ' ' . ' ' ' . ' ' . ' ' '
.
A A B C ABC A B C A BCC B ABC A B C
V V V V
Suy ra:
1
2
2
3
.
V
V
Chọn đáp án D.
M
C
B
A
A'
C'
B'
Nhận xét: Điểm
M
có vẻ như có thể nằm bất kì trên đường thẳng
'?AA
Kết quả tỉ số thể tích trên vẫn
đúng!
Ví dụ 16: Cho hình hộp
. ' ' ' '.ABCD A B C D
Gọi
1 'BACB
VV
và
2 . ' ' ' 'ABCD A B C D
VV
. Khẳng định nào sau
đây đúng?
A.
12
5
9
.VV
B.
12
1
6
.VV
C.
12
1
3
.VV
D.
12
2
3
.VV
Lời giải
Ta có:
1
3
. ' '
; ' .
B ACB BCB
V d A BCB S
11
32
11
66
''
' ' . ' ' ' '
; ' ' .
; ' ' . .
BCB C
BCB C ABCD A B C D
d A BCB C S
d A BCB C S V

Suy ra:
1
2
1
6
.
V
V
Chọn đáp án B.
D
A
B
C
D'
A'
B'
C'
Ví dụ 17: Cho hình hộp
. ' ' ' '.ABCD A B C D
Gọi
M
là trung điểm cạnh
.AB
Gọi
1 'MBCB
VV
và
2 . ' ' ' 'ABCD A B C D
VV
. Khẳng định nào sau đây đúng?
A.
12
5
12
.VV
B.
12
1
6
.VV
C.
12
1
12
.VV
D.
12
2
3
.VV
Lời giải
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 10 CLB Giáo viên trẻ TP Huế
Ta có:
1 1 1 1
2 2 6 12
' ' . ' ' ' ' . ' ' ' '
.
MBCB ABCB ABCD A B C D ABCD A B C D
V V V V
Chọn đáp án C.
M
C'
B'
A'
D'
C
B
A
D
Ví dụ 18: Cho khối lăng trụ tam giác
' ' 'ABCA B C
, đường thẳng đi qua trọng tâm tam giác
ABC
song song với
BC
cắt
AB
tại
D
, cắt
AC
tại
E
. Mặt phẳng đi qua
', ,A D E
chia khối lăng trụ thành
hai phần, tỉ số thể tích (số bé chia cho số lớn) của chúng bằng:
A.
2
.
3
B.
4
.
23
C.
4
.
9
D.
4
.
27
Lời giải
Ta có:
2 2 4
. . .
3 3 9
ADE
ABC
S
AD AE
S AB AC
Mặt khác:
'
1 1 4
'; . '; .
3 3 9
A ADE ADE ABC
V d A ADE S d A ABC S


. ' ' '
44
'; . .
27 27
ABC ABC A B C
d A ABC S V

'
' ' ' . ' ' '
' ' '
23 4
.
27 23
A ADE
A B C CEDB ABC A B C
A B C CEDB
V
VV
V
Chọn đáp án B.
E
D
G
M
A'
B'
C'
C
B
A
Ví dụ 19: Xét khối chóp tứ giác đều
SABCD
, mặt phẳng chứa đường thẳng
AB
đi qua điểm
'C
của
cạnh
SC
chia khối chóp thành hai phần có thể tích bằng nhau. Tính tỉ số
'
.
SC
SC
A.
1
.
2
B.
2
.
3
C.
51
.
2
D.
4
.
5
Lời giải
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 11 CLB Giáo viên trẻ TP Huế
Đặt
'
; 0 1 .
SC
xx
SC
Ta có:
2
22
. ' '
. ' ' . .
.
''
..
2
S AD C
S AD C S ADC S ABCD
S ADC
V
SD SC x
x V x V V
V SD SC
và
.'
. ' . .
.
'
.
2
S ABC
S ABC S ABC S ABCD
S ABC
V
SC x
x V xV V
V SC
2
. ' ' . ' . ' ' .
..
2
S ABC D S ABC S AC D S ABCD
xx
V V V V
Theo đề bài ta suy ra
2
. ' ' .
11
2 2 2
S ABC D S ABCD
xx
VV
2
15
1 0 .
2
x x x

Chọn đáp án C.
S
O
C'
D'
D
A
B
C
Ví dụ 20: Cho khối hộp
. ' ' ' 'ABCD A B C D
có thể tích
.V
Tính thể tích khối chóp
. ' '.ACB D
A.
.
3
V
B.
.
2
V
C.
2
.
3
V
D.
3
.
4
V
Lời giải
Hình hộp đã cho là hợp của khối chóp đang xét với 4
khối chóp
'. ' '; . ' ; '. ' '; . 'A AB D B AB C C B CD D ACD
; 4
khối cuối này cùng có thể tích bằng
6
V
nên thể tích cần
tìm bằng
4
.
63
VV
V 
Chọn đáp án A.
Nhận xét: Hoàn toàn có thể "thử" trường hợp đặc biệt, khi
hình hộp đặc biệt trở thành hình lập phương cạnh
a
thì dễ
thấy thể tích khối lập phương là
3
a
, còn khối
. ' 'ACB D
là
khối tứ diện đều cạnh
2a
thể tích tương ứng là
3
3
22
.
12 3
a
a
So sánh ta đưa ra kết quả.
D'
A'
B'
C'
A
B
C
D
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 12 CLB Giáo viên trẻ TP Huế
Ví dụ 21: Cho hình chóp
.,S ABCD
đáy là hình chữ nhật
ABCD
có
2,BC AB SA
vuông góc với
đáy. Gọi
M
là điểm trên cạnh
AD
sao cho
.AM AB
Gọi
12
,VV
lần lượt là thể tích của hai khối
chóp
.S ABM
và
..S ABC
Tính
1
2
.
V
V
A.
1
.
8
B.
1
.
6
C.
1
.
4
D.
1
.
2
Lời giải
Ta có:
..
1 1 1
. . . .
2 2 4 4
ABM ABCD S ABM S ABCD
AD
S AB S V V
Mặt khác:
1
..
2
11
.
22
S ABC S ABCD
V
VV
V
Chọn đáp án D.
M
D
C
B
A
S
í dụ 22: Cho hình chóp đều
.S ABC
có cạnh đáy bằng
,a
góc giữa đường thẳng
SA
và mặt đáy
bằng
0
60 .
Gọi
'; '; 'A B C
tương ứng là điểm đối xứng của
;;A B C
qua
.S
Tính thể tích khối bát
diện có các mặt
; ' ' '; ' ; ' ; ' ; ' '; ' '; ' '.ABC A B C A BC B CA C AB AB C BC A CA B
A.
3
2 3 .a
B.
3
3
.
2
a
C.
3
23
.
3
a
D.
3
43
.
3
a
Lời giải
Thể tích khối bát diện đã cho là
' ' ' '.
1
2 2.4 8. . . .
3
A B C BC A SBC SBC
V V V SG S
Ta có:
0
; 60 .SA ABC SAG
Xét
SGA
vuông tại
:G
tan .tan .
SG
SAG SG SA SAG a
SA
Vậy
23
1 1 3 2 3
8. . . 8. . . .
3 3 4 3
ABC
aa
V SG S a
Chọn đáp án C.
60
0
a
C'
B'
A'
G
A
C
B
S
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 13 CLB Giáo viên trẻ TP Huế
III- BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 1. Cho hình chóp tứ giác đều
.S ABCD
có tất cả các cạnh đều bằng
.a
Gọi
, , ,M N P Q
lần
lượt thuộc các cạnh
, , ,SA SB SC SD
sao cho
1
23
3
; ; ; .SM MA SN NB SP PC SQ SD
Tính tỉ số thể tích giữa khối
SMNPQ
và khối
..S ABCD
A.
3
16
.
B.
3
8
.
C.
3
32
.
D.
1
12
.
Câu 2. Cho hình lăng trụ
. ' ' '.ABC A B C
Gọi
1 . ' 'A BCC B
VV
và
2 . ' ' 'ABC A B C
VV
. Khẳng định nào sau
đây đúng?
A.
12
3
4
.VV
B.
12
1
2
.VV
C.
12
1
3
.VV
D.
12
2
3
.VV
Câu 3. Cho tứ diện
ABCD
. Gọi
'B
và
'C
lần lượt là trung điểm của
AB
và
.AC
Khi đó tỉ số thể
tích của khối tứ diện
''AB C D
và khối tứ diện
ABCD
bằng:
A.
1
2
.
B.
1
4
.
C.
1
6
.
D.
1
8
.
Câu 4. Cho hình lăng trụ ngũ giác
. ' ' ' ' '.ABCDE A B C D E
Gọi
, , , ,A B C D E
lần lượt là trung
điểm của
', ', ', ', 'AA BB CC DD EE
. Khi đó tỉ số thể tích của khối lăng trụ
..ABCDE A B C D E
và khối lăng trụ
. ' ' ' ' '.ABCDE A B C D E
bằng:
A.
1
2
.
B.
1
4
.
C.
1
8
.
D.
1
10
.
Câu 5. Cho hình chóp tứ giác
.S ABCD
có thể tích bằng
V
. Lấy điểm
'A
trên cạnh
SA
sao cho
1
3
'SA SA
. Mặt phẳng qua
'A
và song song với đáy của hình chóp cắt các cạnh
,,SB SC SD
lần lượt tại
', ', 'B C D
. Khi đó thể tích khối chóp
. ' ' ' 'S A B C D
bằng:
A.
3
.
V
B.
9
.
V
C.
27
.
V
D.
81
.
V
Câu 6. Cho hình chóp
.S ABC
có
'A
và
'B
lần lượt là trung điểm của các cạnh
,.SA SB
Tỉ số thể thể
tích
.
. ' '
S ABC
S A B C
V
V
bằng:
A.
1
2
.
B.
1
4
.
C.
4.
D.
2.
Câu 7. Cho hình chóp
.S ABC
. Gọi
'A
và
'B
lần lượt là trung điểm của
SA
và
.SASB
Khi đó tỉ số
thể tích của hai khối chóp
. ' 'S A B C
và
.S ABC
bằng:
A.
1
2
.
B.
1
3
.
C.
1
4
.
D.
1
8
.
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 14 CLB Giáo viên trẻ TP Huế
Câu 8. Cho hình chóp
.S ABCD
. Gọi
', ', ', 'A B C D
lần lượt là trung điểm của
, , , .SA SB SC SD
Khi
đó tỉ số thể tích của hai khối chóp
. ' ' ' 'S A B C D
và
.S ABCD
bằng:
A.
1
2
B.
1
4
C.
1
8
D.
1
16
Câu 9. Cho hình hộp
. ' ' ' 'ABCD A B C D
. Tỉ số thể tích của khối tứ diện
''ACB D
và khối hộp
. ' ' ' 'ABCD A B C D
bằng:
A.
1
2
.
B.
1
3
.
C.
1
4
.
D.
1
6
.
Câu 10. Cho hình hộp
. ' ' ' 'ABCD A B C D
, gọi
O
là giao điểm của
AC
và
BD
. Tỉ số thể tích của
khối chóp
. ' ' ' 'O A B C D
và khối hộp
. ' ' ' 'ABCD A B C D
bằng:
A.
1
2
.
B.
1
3
.
C.
1
4
.
D.
1
6
.
Câu 11. Cho hình chóp
.S ABCD
có đáy là hình vuông tâm
O
. Khi đó, tỉ số
.
.
S ABC
S ABCD
V
V
bằng
A.
1
2
.
B.
1
4
.
C.
1
6
.
D.
1
8
.
Câu 12. Cho hình chóp
.S ABCD
có đáy là hình vuông tâm
O
. Khi đó, tỉ số
.
.
S OAB
S ABCD
V
V
bằng
A.
1
2
.
B.
1
4
.
C.
1
6
.
D.
1
8
.
Câu 13. Cho hình chóp
.S ABCD
có đáy là hình vuông tâm
O
. Khi đó, tỉ số
.
.
S OAB
S ABC
V
V
bằng
A.
1
2
.
B.
1
4
.
C.
1
6
.
D.
1
8
.
Câu 14. Cho tứ diện
SABC
. Gọi
,,M N P
lần lượt là trung điểm các cạnh
,,AB BC AC
. Gọi
1 .S ABC
VV
,
2 .S MNP
VV
. Lựa chọn kết luận đúng trong các kết luận sau:
A.
12
2 .VV
B.
12
8 .VV
C.
12
4 .VV
D.
12
6 .VV
Câu 15. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
,MN
lần lượt là trung
điểm của
SA
và
.SB
Tính tỉ số thể tích
.
.
.
S CDMN
S CDAB
V
V
A.
1
4
.
B.
5
8
.
C.
3
8
.
D.
1
2
.
Câu 16. Cho hình chóp
.S ABC
có
9; 4; 8SA SB SC
và đôi một vuông góc. Các điểm
'; '; 'A B C
thỏa mãn
2 '; 3 '; 4 '.SA SA SB SB SC SC
Tính thể tích khối chóp
. ' ' '.S A B C
A.
24.
B.
16.
C.
2.
D.
12.
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 15 CLB Giáo viên trẻ TP Huế
Câu 17. Cho hình lập phương
. ' ' ' 'ABCD A B C D
có cạnh bằng
.a
Tính thể tích khối tứ diện
' '.ACD B
A.
3
3
.
a
B.
3
2
3
.
a
C.
3
4
.
a
D.
3
6
4
.
a
| 1/15
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

[...Chuyên đề Trắc nghiệm Toán 12...]
Luyện thi THPT Quốc gia 2018
TỶ SỐ THỂ TÍCH KHỐI ĐA DIỆN
Giáo viên: LÊ BÁ BẢO Trường THPT Đặng Huy Trứ, Huế
SĐT: 0935.785.115 Địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế I- PHƯƠNG PHÁP
Kết quả 1: Cho tam gi¸c OA ,
B trªn c¹nh OA chän A'  O, trªn c¹nh O
B chän B'  O . S OA' OB' Lóc ®ã: OA' B'  . S OA OB OAB Chøng minh:
Gäi H, H' lÇn l­ît l¯ h×nh chiÕu vu«ng gãc cña A v¯ A' lªn OB. A 1 1 A' Lóc ®ã: S
A' H '.OB' v¯ SAH.OB OA' B' 2 OAB 2 Suy ra: O S
A' H ' OB' OA' OB' B OA' B'  .  . §Þnh lý thales B' H' H S AH OB OA OB OAB Kết quả 2: Cho h×nh chãp .
S ABC, trªn c¹nh SA chän A'  O, trªn c¹nh S
B chän B'  O trªn c¹nh SC chän C'  O . V
SA' SB' SC ' Lóc ®ã:
S.A' B'C'  . . V SA SB SC S.ABC Chøng minh:
Gäi H, H' lÇn l­ît l¯ h×nh chiÕu vu«ng gãc cña A v¯ A' lªn mp(SBC . ) A Lóc ®ã: A' 1 1 V
A'H'.S v¯ V  AH.S
S.A'B'C' 3 SB'C' S.ABC 3 SBC Suy ra: B' B S V A' H ' S
SA' SB' SC '
S.A' B'C' SB'C'  .  H' H . . §Þnh lý thales C' V AH S SA SB SC C S.ABC SBC
Giáo viên: LÊ BÁ BẢO...0935.785.115... 1
CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
II- BÀI TẬP TRẮC NGHIỆM MINH HỌA
Ví dụ 1: Cho hình lăng trụ AB .
C A' B'C' . Tỉ số thể tích của khối AA' B'C ' và khối ABCC ' là 1 1 2 A. 1. B. . C. . D. . 2 3 3 Lời giải
1 dA;A'B'C'.S A C A' B'C' V
Ta có: AA'B'C' 3  (1) V 1 C' ABC
d C; ABC.S B 3 ABC Do SS và d ;
A A' B'C'  dC;ABC ABC A'B'C' V C'
nên (1): AA'B'C'  1. A' VC'ABC B'
Chọn đáp án A.
Ví dụ 2: Cho hình chóp tứ giác đều .
S ABCD . Gọi M, N lần lượt là trung điểm của SB, SD . Mặt
phẳng  AMN cắt SC tại E . Gọi V là thể tích của khối chóp .
S AMEN và V là thể tích khối 2 1 chóp .
S ABCD. Khẳng định nào sau đây đúng? 1 1 1 1
A. V V . B. V V . C. V V . D. V V . 2 1 3 2 1 4 2 1 8 2 1 6 Lời giải SM SN SI 1      S
Qua O dựng OK // AE. SB SD SO 2 OK  / / AEE Xét AEC :  . Suy ra: K là trung 1 OK AE  2 N điểm EC . I M KIE / /OK  Xét SOK :  . Suy ra: E là trung 1 D IE OKC  2 O SE 1 A điểm SK . Vậy  B SC 3 V 2V SA SM SE 1 1 1 Ta có: S.AMEN S.AME   . .  .  V 2V SA SB SC 2 3 6 S.ABCD S.ABC 1  1 VV hay V V . S.AMEN 6 S.ABCD 2 1 6
Chọn đáp án D.
Giáo viên: LÊ BÁ BẢO...0935.785.115... 2 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Ví dụ 3: Cho tứ diện đều ABCD. Điểm M là trung điểm AB và N trên cạnh CD sao cho  
CN  2ND . Tỉ số thể tích của khối ABCD và khối MNBC bằng 3 1 4 A. 3. B. . C. . D. . 2 3 3 Lời giải Ta có: A V 1 V 2 V V 1 BMCN  ; BACN BMCN   . BACN V 2 V 3 V V 3 BACN BACD BACN BACD V 1 V M BMCN BACD     3. V 3 V BACD BMCN
Chọn đáp án A. D B N C
Ví dụ 4: Cho hình chóp .
S ABC . Gọi M, N lần lượt thuộc các cạnh SB, SC sao cho  
SM MB, SN  2
CN. Mặt phẳng AMN chia khối chóp thành hai phần, gọi V V và 1 S.AMN V V
. Khẳng định nào sau đây đúng? 2 ABCNM 1 1 2 A. V V . B. V V . C. V V . D. V V . 1 2 1 2 3 1 2 2 1 2 3 Lời giải V SM SN 1 2 1
Ta có: S.AMN  .  .  . S V SB SC 2 3 3 S.ABC 1 2  VVVV S.AMN 3 S.ABC ABCNM 3 S.ABC 1 M Vậy V V . N 1 2 2
Chọn đáp án C. C A B
Giáo viên: LÊ BÁ BẢO...0935.785.115... 3 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Ví dụ 5: Cho hình chóp tam giác đều .
S ABC . Gọi M, N lần lượt là trung điểm của BC, SM . Mặt
phẳng  ABN cắt SC tại E .Gọi V là thể tích của khối chóp .
S ABE và V là thể tích khối chóp 2 1 .
S ABC . Khẳng định nào sau đây đúng? 1 1 1 1
A. V V . B. V V . C. V V . D. V V . 2 1 3 2 1 4 2 1 8 2 1 6 Lời giải 
Qua M dựng MK // BE. Xét tam giác BEC : SMK / /BE  
. Suy ra: K là trung điểm EC . E 1 MK BE  2 NE / /MKK N
Xét tam giác SMK : 
. Suy ra: E là 1 NE MK  2 C SE 1
trung điểm SK . Vậy  A SC 3 M V SA SB SE 1 1
Ta có: S.ABE  . .   VV V SA SB SC 3 S.ABE 3 S.ABC S.ABC B 1
hay V V .  Chọn đáp án A. 2 1 3
Ví dụ 6: Cho hình lăng trụ AB .
C A' B'C'. Gọi E, F lần lượt là trung điểm của các cạnh AA' và BB'.
Đường thẳng CE cắt đường thẳng C ' A' tại E'. Đường thẳng CF cắt đường thẳng B'C ' tại F '.
Gọi V là thể tích khối chóp .
C ABFE và V là thể tích khối lăng trụ AB .
C A' B'C'. Khẳng định nào 2 1 sau đây đúng? 1 1 1 1
A. V V . B. V V . C. V V . D. V V . 2 1 3 2 1 4 2 1 8 2 1 6 Lời giải Hình chóp .
C A' B'C' và lăng trụ AB .
C A' B'C' có A C
đường cao và đáy bằng nhau nên B 1 1 2 VVV
V V V .
C.A' B'C'
ABC.A'B'C' C.ABB' A' 1 1 1 3 3 3 E
Do EF là đường trung bình của hình bình hành F 1 1 1
ABB' A'  SSVVV E' C' ABFE ABB' A' C.ABFE C.ABB' A' 1 2 2 3 A' 1 B'
hay V V .  Chọn đáp án A. 2 1 3 F'
Giáo viên: LÊ BÁ BẢO...0935.785.115... 4 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Ví dụ 7: Cho hình chóp S.ABC, trên AB, BC, SC lần lượt lấy các điểm M, N, P sao cho AM  2M , B   BN 4NC,SP
PC . Tỉ lệ thể tích hai khối chóp . S BMN và . A CPN là: 4 5 8 A. . B. . C. . D.1. 3 6 3 Lời giải V V BM BN BS S 1 4 4 + S.BMN B.MNS   . .  .  V V BA BC BS 3 5 15 S.ABC B.ACS P V V CA CN CP 1 1 1 + A.CPN C.ANP   . .  .  V V CA CB CS 5 2 10 S.ABC C.ABS A V C 4 1 8 S.BMN   :  V 15 10 3 N A.CNP M B
Chọn đáp án C.
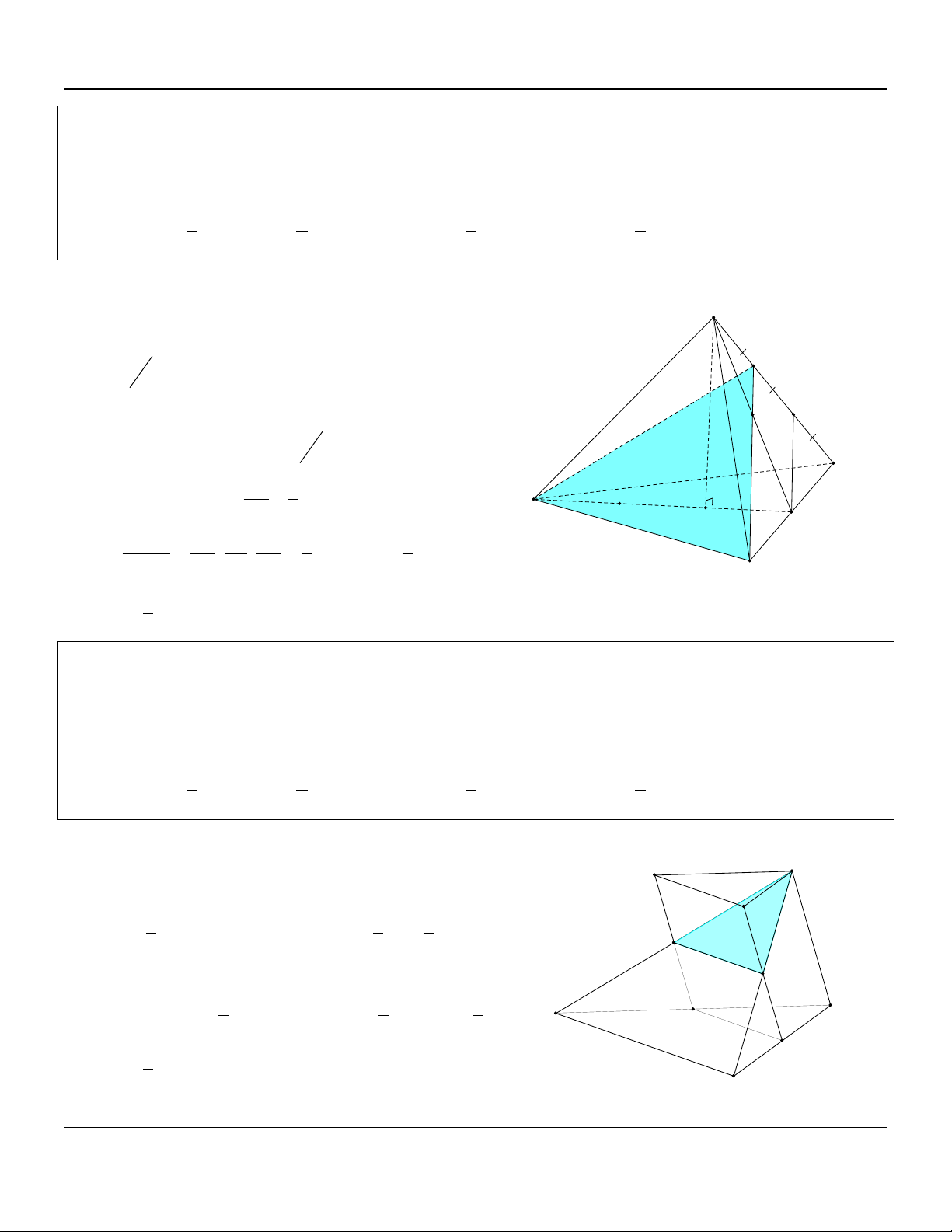
Ví dụ 8: (Đề minh họa Bộ GD&ĐT) Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông
góc với nhau; AB  6a , AC  7a và AD  4a . Gọi M, N, P tương ứng là trung điểm các cạnh BC,
CD, DB. Tính thể tích V của tứ diện AMNP. 7 28 A. 3 V a . B. 3 V  14a . C. 3 V a . D. 3 V  7a . 2 3 Lời giải 1 Ta có: 3 VA .
B AC.AD  28a . D ABCD 6 Dễ thấy M
NP được tạo nên bởi các đường trung N bình của B
CD chúng đồng dạng với nhau theo tỉ số P 1 V S 1 1 1 1 AMNP MNP 3    .   VV  7a . 2 V S 2 2 4 AMNP 4 ABCD ABCD BCD A C
Chọn đáp án D. M B
Ví dụ 9: Cho hình hộp ABC .
D A' B'C' D' . Gọi O là tâm của ABCD ; M, N lần lượt là trung điểm
của A' B' và A' D' . Tỉ số thể tích của khối A' ABD và khối OMND'C 'B' bằng 4 4 5 3 A. . B. . C. . D. . 9 7 7 7
Giáo viên: LÊ BÁ BẢO...0935.785.115... 5 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018 Lời giải Do SSSSS ABD A'B'D' MND'C'B' B'C'D' MND'B' B CSS ABD MND'B' O S 1 3 3 A
Mặt khác ta có: A'MN   SSS D S 4 MND'B' 4 A'B'D' 4 ABD A' B' D' 7 Suy ra: SS . B' C' MND'C'B' 4 ABD M
1 dA';ABCD.SABD V A' Ta có: A' ABD 3  N D' V 1
OMND'C' B'
d O; A' B'C' D'.S 3 MND'C' B' S 4 ABD
 . Chọn đáp án B. S 7 MND'C' B'
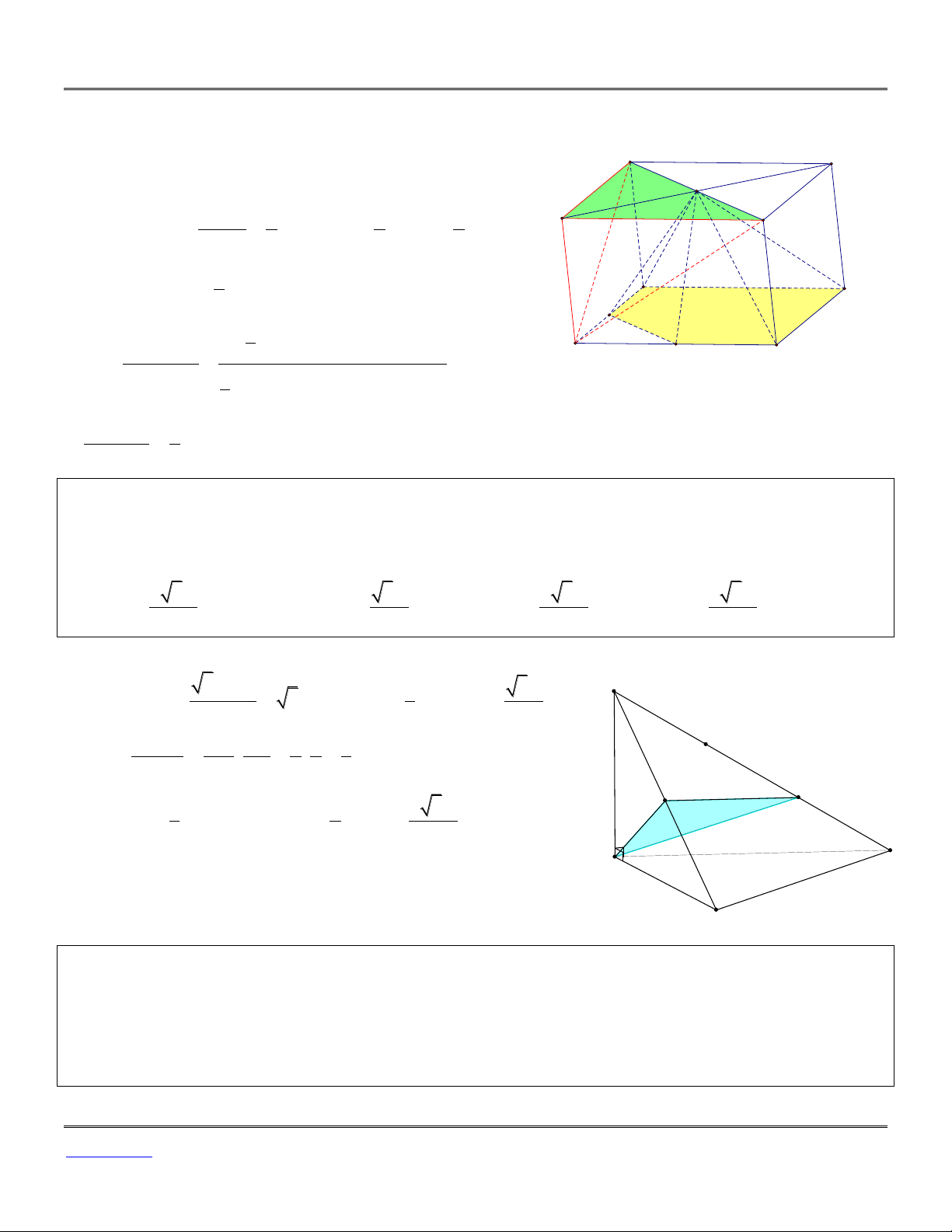
Ví dụ 10: Cho hình chóp .
S ABC có SA vuông góc với mặt đáy, SA a, A
BC đều cạnh 2 . a Gọi  
M, N lần lượt thuộc các cạnh SB, SC sao cho SM MB, SN  2
CN. Tính thể tích khối AMNC . B 3 2 3a 3 3a 3 4 3a 3 2 3a A. . B. . C. . D. . 9 9 9 3 Lời giải 3 2a2 3 1 3a S Ta có: 2 S   3a VS . A S  . ABC  4 S.ABC 3 ABC 3 V SM SN 1 2 1
Ta có: S.AMN  .  .  . V SB SC 2 3 3 S.ABC a M N 3 1 2 2 3aVVVV  . S.AMN 3 S.ABC ABCNM 3 S.ABC 9  C
Chọn đáp án A. A 2a B
Ví dụ 11: Cho hình chóp .
S ABCD có đáy là hình bình hành. Gọi M là trung điểm cạnh . SA Mặt
phẳng   qua M và song song với  ABCD , cắt các cạnh S ,
B SC, SD lần lượt tại N, P, . Q Gọi V V và V V
. Khẳng định nào sau đây đúng? 1 S.ABCD 2 S.MNPQ A. V  8V . B. V  6V . C. V  16V . D. V  4V . 1 2 1 2 1 2 1 2 Lời giải
Giáo viên: LÊ BÁ BẢO...0935.785.115... 6 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Dễ thấy, N, P, Q lần lượt là trung điểm các cạnh S S ,
B SC, S . D Ta có: QPV  2V S.MNPQ S.MNP  V  2VM S.ABCD ABC N V 2 D C S.MNPQ V SM SN SP 1 1 1 1 S.MNP    . .  . .  . V 2V SA SB SC 2 2 2 8 S.ABCD S.ABCV  8V . 1 2 A
Chọn đáp án A. B
Ví dụ 12: Cho hình chóp .
S ABCD có đáy là hình bình hành. Gọi M là trung điểm cạnh SC. Mặt
phẳng   chứa AM và song song với BD , cắt các cạnh SB, SD lần lượt tại N, . P Gọi V V và V V
. Khẳng định nào sau đây đúng? 1 S.ANMP 2 ABCDPMN 3 7 A. V  3V . B. V V . C. V  2V . D. V V . 2 1 2 1 2 2 1 2 1 2 Lời giải
Gọi BD AC   
O ; AM SO  I. Suy ra I là S trọng tâm SAC và SB .
D Qua I dựng
PN / /BD  Thiết diện là tứ giác ANM . P V 2V SN SM 2 1 1 M Ta có: 1 S.ANM   .  .  V 2V SB SC 3 2 3 S.ABCD S.ABC P 1 2  I V VV VV  2V . 1 S.ABCD 2 S.ABCD 2 1 N 3 3 C D
Chọn đáp án C. O A B
Ví dụ 13: Cho hình chóp tứ giác đều .
S ABCD có tất cả các cạnh đều bằng .
a Gọi M, N, P, Q lần     1
lượt thuộc các cạnh SA, S ,
B SC, SD sao cho SM M ;
A SN  2N ;
B SP  3PC; SQ S . D Tính thể 3 tích khối SMNP . Q 3 3 2a 3 2a 3 2a 3 2a A. . B. . C. . D. . 16 48 16 32 Lời giải
Giáo viên: LÊ BÁ BẢO...0935.785.115... 7 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018 V SM SN SP 1 2 3 1
Ta có: S.MNP  . .  . .  S V SA SB SC 2 3 4 4 S.ABC 1 1  VVV . S.MNP 4 S.ABC 8 S.ABCD Q VS.MPQ SM SP SQ 1 3 1 1 M Tương tự:  . .  . .  P V SA SC SD 2 4 3 8 S.ACD N 1 1  C VVV . S.MPQ 8 S.ACD 16 S.ABCD D 3 O Vậy VVVV SMNPQ S.MNP S.MPQ 16 S.ABCD A B 3 3 3 2a 2a  .  . 16 6 32
Chọn đáp án D.
Ví dụ 14: Cho hình lăng trụ AB .
C A' B'C'. Gọi V V và V V . Khẳng định nào sau 1
A.A'B'C' 2
ABC.A'B'C' đây đúng? 3 1 1 2 A. V V . B. V V . C. V V . D. V V . 1 2 4 1 2 2 1 2 3 1 2 3 Lời giải 1 Ta có: Vd ;
A A' B'C ' .S A C
A.A'B'C'     3 A'B'C' và Vd ;
A A' B'C ' .S .
ABC.A' B'C'  
 A'B'C' B V 1 Suy ra: 1  . V 3 2
Chọn đáp án C. A' C' B'
Ví dụ 15: Cho hình lăng trụ AB .
C A' B'C'. Điểm M trên cạnh AA' sao cho: AM  2MA'. Gọi V V và V V
. Khẳng định nào sau đây đúng? 1 M.BCC'B' 2
ABC.A'B'C' 3 1 1 2 A. V V . B. V V . C. V V . D. V V . 1 2 4 1 2 2 1 2 3 1 2 3 Lời giải
Giáo viên: LÊ BÁ BẢO...0935.785.115... 8 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Do AA'/ / BCC' B'  VV . M.BCC' B' A.BCC'B' A C 1 2 Ta có: VVVV .
A.A'B'C'
3 ABC.A'B'C' A.BCC'B'
3 ABC.A'B'C' B V 2 Suy ra: 1  . V 3 2 M
Chọn đáp án D. A' C' B'
Nhận xét: Điểm M có vẻ như có thể nằm bất kì trên đường thẳng AA'? Kết quả tỉ số thể tích trên vẫn đúng!
Ví dụ 16: Cho hình hộp ABC .
D A' B'C' D'. Gọi V V và V V . Khẳng định nào sau 1 BACB' 2
ABCD.A'B'C'D' đây đúng? 5 1 1 2 A. V V . B. V V . C. V V . D. V V . 1 2 9 1 2 6 1 2 3 1 2 3 Lời giải 1 D Ta có: Vd ; A BCB' .S C B.ACB'     3 BCB' B 1
dA;BCB'C' 1 . S A  3 2 BCB'C' 1
dA;BCB'C' 1 .SV .  6 BCB'C'
6 ABCD.A'B'C'D' D' C' V 1 Suy ra: 1  . V 6 2 A' B'
Chọn đáp án B.
Ví dụ 17: Cho hình hộp ABC .
D A' B'C' D'. Gọi M là trung điểm cạnh .
AB Gọi V V và 1 MBCB' V V
. Khẳng định nào sau đây đúng? 2
ABCD.A'B'C'D' 5 1 1 2 A. V V . B. V V . C. V V . D. V V . 1 2 12 1 2 6 1 2 12 1 2 3 Lời giải
Giáo viên: LÊ BÁ BẢO...0935.785.115... 9 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018 Ta có: D C 1 1 1 1 VV  . VV MBCB' 2 ABCB'
2 6 ABCD.A'B'C'D'
12 ABCD.A'B'C'D' BA
Chọn đáp án C. M D' C' A' B'
Ví dụ 18: Cho khối lăng trụ tam giác ABCA' B'C' , đường thẳng đi qua trọng tâm tam giác ABC
song song với BC cắt AB tại D , cắt AC tại E . Mặt phẳng đi qua A', D, E chia khối lăng trụ thành
hai phần, tỉ số thể tích (số bé chia cho số lớn) của chúng bằng: 2 4 4 4 A. . B. . C. . D. . 3 23 9 27 Lời giải S AD AE 2 2 4 Ta có: ADE  .  .  . E A C S AB AC 3 3 9 ABC G M Mặt khác: D B 1 1 4 V
d A'; ADE .S
d A'; ABC . S A' ADE    ADE    3 3 9 ABC 4 
dA ABC 4 '; .SV . ABC
ABC.A'B'C' 27 27 23 V 4 A' ADEVV   .
A' B'C'CEDB
ABC.A' B'C' 27 V 23
A' B'C'CEDB A' C'
Chọn đáp án B. B'
Ví dụ 19: Xét khối chóp tứ giác đều SABCD , mặt phẳng chứa đường thẳng AB đi qua điểm C ' của SC '
cạnh SC chia khối chóp thành hai phần có thể tích bằng nhau. Tính tỉ số . SC 1 2 5  1 4 A. . B. . C. . D. . 2 3 2 5 Lời giải
Giáo viên: LÊ BÁ BẢO...0935.785.115... 10 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018 SC ' S Đặt
x; 0  x   1 . SC Ta có: 2 V SD' SC ' x S.AD'C' 2 2  .  x Vx VV . S.AD'C' S.ADC S. V SD SC 2 ABCD S.ADC C' V SC ' x và S.ABC'   x VxVV . S.ABC' S.ABC S. V SC 2 ABCD D' S.ABC B C 2 x xVVV  .V . S.ABC' D' S.ABC' S.AC' D' S. 2 ABCD O 2 1 x x 1 A D
Theo đề bài ta suy ra VV   S.ABC' D' S. 2 ABCD 2 2   2 1 5
x x 1  0  x  . 2
Chọn đáp án C.
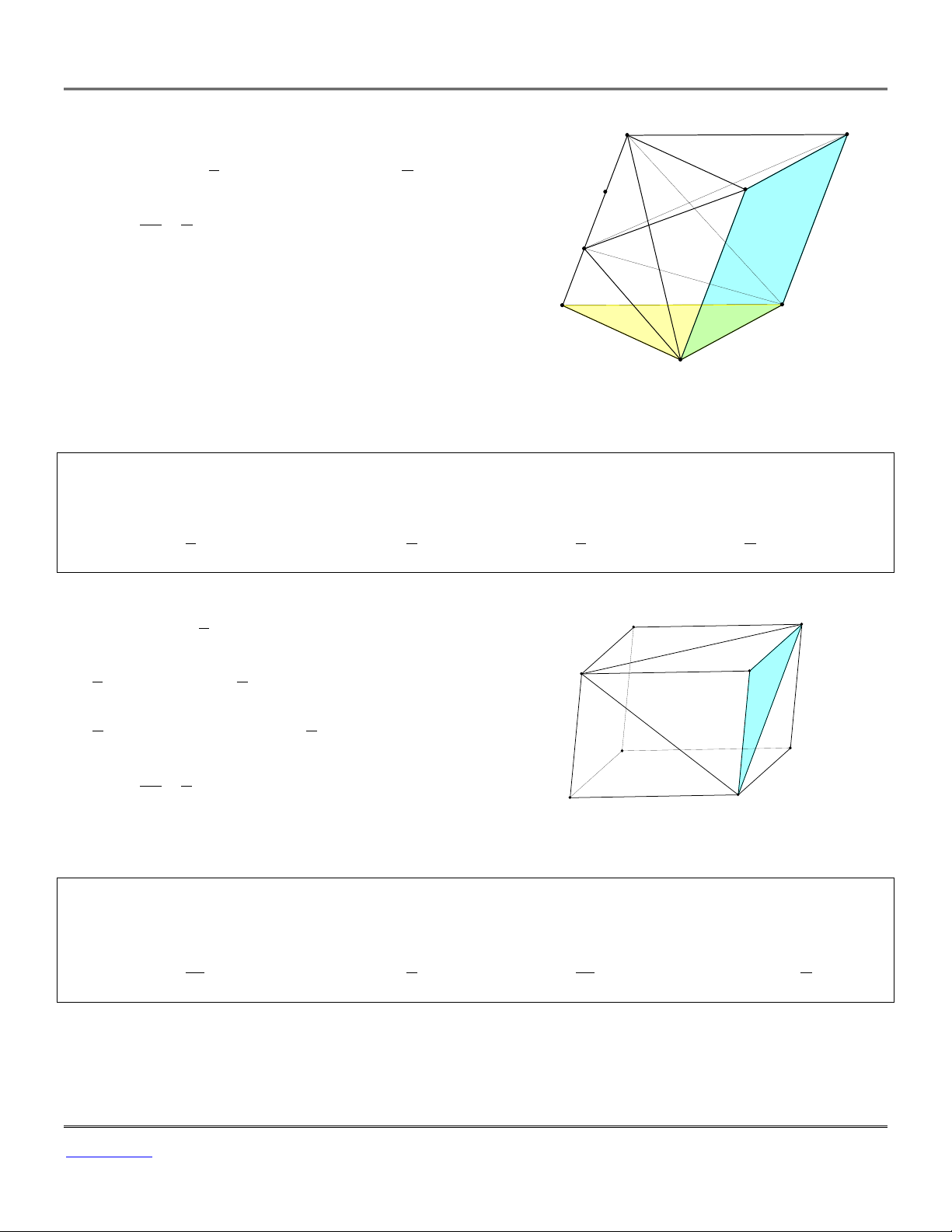
Ví dụ 20: Cho khối hộp ABC .
D A' B'C' D' có thể tích V . Tính thể tích khối chóp . A CB' D'. V V 2V 3V A. . B. . C. . D. . 3 2 3 4 Lời giải
Hình hộp đã cho là hợp của khối chóp đang xét với 4 D C
khối chóp A'.AB' D'; .
B AB'C; C'.B'CD'; . D ACD' ; 4 V
khối cuối này cùng có thể tích bằng nên thể tích cần A B 6 4V V tìm bằng V   . 6 3
Chọn đáp án A. C' D'
Nhận xét: Hoàn toàn có thể "thử" trường hợp đặc biệt, khi
hình hộp đặc biệt trở thành hình lập phương cạnh a thì dễ A' B'
thấy thể tích khối lập phương là 3 a , còn khối .
A CB' D' là
khối tứ diện đều cạnh a 2  thể tích tương ứng là 2 a 2 3 3 a
. So sánh ta đưa ra kết quả. 12 3
Giáo viên: LÊ BÁ BẢO...0935.785.115... 11 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Ví dụ 21: Cho hình chóp .
S ABCD, đáy là hình chữ nhật ABCD có BC  2A ,
B SA vuông góc với
đáy. Gọi M là điểm trên cạnh AD sao cho AM A .
B Gọi V , V lần lượt là thể tích của hai khối 1 2 V chóp . S ABM và . S AB . C Tính 1 . V2 1 1 1 1 A. . B. . C. . D. . 8 6 4 2 Lời giải Ta có: S 1 AD 1 1 S  .A . B  .SVV . ABM ABCD S.ABM S. 2 2 4 4 ABCD 1 V 1 Mặt khác: 1 VV   . S.ABC S. 2 ABCD V 2 2
Chọn đáp án D. A M D B C
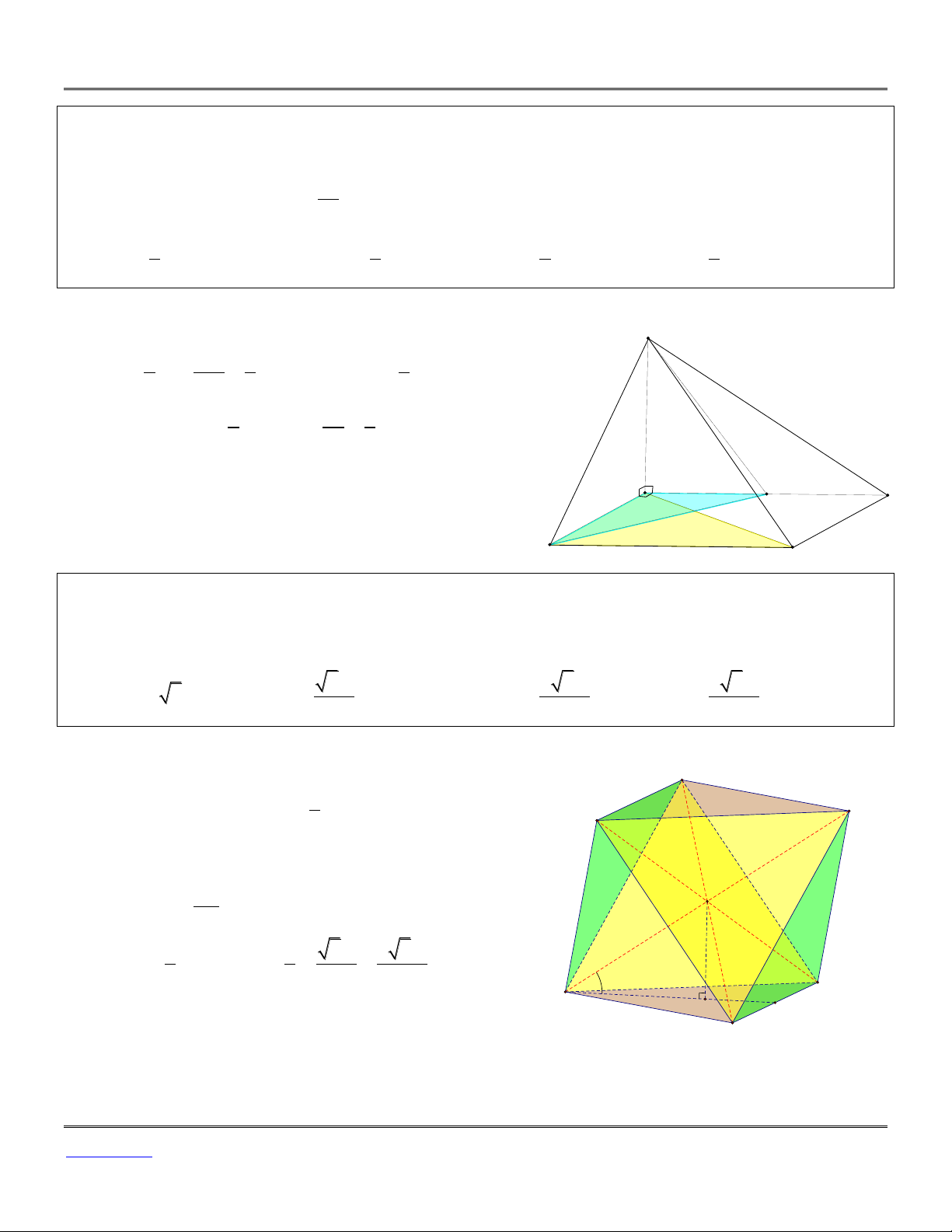
í dụ 22: Cho hình chóp đều .
S ABC có cạnh đáy bằng a, góc giữa đường thẳng SA và mặt đáy bằng 0
60 . Gọi A'; B'; C' tương ứng là điểm đối xứng của ; A ; B C qua .
S Tính thể tích khối bát
diện có các mặt ABC; A' B'C'; A' B ; C B'C ; A C' A ;
B AB'C'; BC' A'; CA' B'. 3 3a 3 2 3a 3 4 3a A. 3 2 3a . B. . C. . D. . 2 3 3 Lời giải
Thể tích khối bát diện đã cho là B' 1 V  2V  2.4V  8. .S . G S .
A'B'C' BC A'.SBC A' 3 SBC C'
Ta có: SA ABC  0 ;
SAG  60 . Xét SGA vuông tại  SGS G : tanSAG   SG S . A tanSAG  . a SA 2 3 1 1 3a 2 3a
Vậy V  8. .S . G S  8. . . a  . 3 ABC 3 4 3 600 C A
Chọn đáp án C. a G B
Giáo viên: LÊ BÁ BẢO...0935.785.115... 12 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
III- BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 1. Cho hình chóp tứ giác đều .
S ABCD có tất cả các cạnh đều bằng .
a Gọi M, N, P, Q lần     1
lượt thuộc các cạnh SA, SB, SC, SD sao cho SM M ;
A SN  2N ;
B SP  3PC; SQ S . D 3
Tính tỉ số thể tích giữa khối SMNPQ và khối . S ABC . D 3 3 3 1 A. . B. . C. . D. . 16 8 32 12
Câu 2. Cho hình lăng trụ AB .
C A' B'C'. Gọi V V và V V . Khẳng định nào sau 1 A.BCC 'B' 2
ABC.A'B'C' đây đúng? 3 1 1 2 A. V V . B. V V . C. V V . D. V V . 1 2 4 1 2 2 1 2 3 1 2 3
Câu 3. Cho tứ diện ABCD . Gọi B' và C ' lần lượt là trung điểm của AB và AC. Khi đó tỉ số thể
tích của khối tứ diện AB'C' D và khối tứ diện ABCD bằng: 1 1 1 1 A. . B. . C. . D. . 2 4 6 8
Câu 4. Cho hình lăng trụ ngũ giác ABCD .
E A' B'C' D' E'. Gọi A , B , C , D , E lần lượt là trung
điểm của AA', BB', CC', DD', EE' . Khi đó tỉ số thể tích của khối lăng trụ ABCD . E AB  C  D  E
 . và khối lăng trụ ABCD .
E A' B'C' D' E'. bằng: 1 1 1 1 A. . B. . C. . D. . 2 4 8 10
Câu 5. Cho hình chóp tứ giác .
S ABCDcó thể tích bằng V . Lấy điểm A' trên cạnh SA sao cho 1
SA'  SA . Mặt phẳng qua A' và song song với đáy của hình chóp cắt các cạnh 3 S ,
B SC, SD lần lượt tại B', C', D' . Khi đó thể tích khối chóp .
S A' B'C' D' bằng: V V V V A. . B. . C. . D. . 3 9 27 81
Câu 6. Cho hình chóp .
S ABC có A' và B' lần lượt là trung điểm của các cạnh SA, S .
B Tỉ số thể thể V tích S.ABC bằng:
VS.A'B'C 1 1 A. . B. . C. 4. D. 2. 2 4
Câu 7. Cho hình chóp .
S ABC . Gọi A' và B' lần lượt là trung điểm của SA và SAS . B Khi đó tỉ số
thể tích của hai khối chóp .
S A' B'C và . S ABC bằng: 1 1 1 1 A. . B. . C. . D. . 2 3 4 8
Giáo viên: LÊ BÁ BẢO...0935.785.115... 13 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Câu 8. Cho hình chóp .
S ABCD. Gọi A', B', C', D' lần lượt là trung điểm của SA, S ,
B SC, S . D Khi
đó tỉ số thể tích của hai khối chóp .
S A' B'C' D' và . S ABCD bằng: 1 1 1 1 A. B. C. D. 2 4 8 16
Câu 9. Cho hình hộp ABC .
D A' B'C' D' . Tỉ số thể tích của khối tứ diện ACB' D' và khối hộp ABC .
D A' B'C' D' bằng: 1 1 1 1 A. . B. . C. . D. . 2 3 4 6
Câu 10. Cho hình hộp ABC .
D A' B'C' D' , gọi O là giao điểm của AC và BD . Tỉ số thể tích của khối chóp .
O A' B'C' D' và khối hộp ABC .
D A' B'C' D' bằng: 1 1 1 1 A. . B. . C. . D. . 2 3 4 6 V
Câu 11. Cho hình chóp .
S ABCD có đáy là hình vuông tâm O . Khi đó, tỉ số S.ABC bằng VS.ABCD 1 1 1 1 A. . B. . C. . D. . 2 4 6 8 V
Câu 12. Cho hình chóp .
S ABCD có đáy là hình vuông tâm O . Khi đó, tỉ số S.OAB bằng VS.ABCD 1 1 1 1 A. . B. . C. . D. . 2 4 6 8 V
Câu 13. Cho hình chóp .
S ABCD có đáy là hình vuông tâm O . Khi đó, tỉ số S.OAB bằng VS.ABC 1 1 1 1 A. . B. . C. . D. . 2 4 6 8
Câu 14. Cho tứ diện SABC . Gọi M, N, P lần lượt là trung điểm các cạnh A ,
B BC, AC . Gọi V V , V V
. Lựa chọn kết luận đúng trong các kết luận sau: 1 S.ABC 2 S.MNP A. V  2V . B. V  8V . C. V  4V . D. V  6V . 1 2 1 2 1 2 1 2
Câu 15. Cho hình chóp .
S ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung V điểm của SA và .
SB Tính tỉ số thể tích S.CDMN . VS.CDAB 1 5 3 1 A. . B. . C. . D. . 4 8 8 2
Câu 16. Cho hình chóp .
S ABC có SA  9; SB  4; SC  8 và đôi một vuông góc. Các điểm      
A'; B'; C' thỏa mãn SA  2SA'; SB  3SB'; SC  4SC '. Tính thể tích khối chóp .
S A' B'C'. A. 24. B. 16. C. 2. D. 12.
Giáo viên: LÊ BÁ BẢO...0935.785.115... 14 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Câu 17. Cho hình lập phương ABC .
D A' B'C' D' có cạnh bằng .
a Tính thể tích khối tứ diện ACD' B'. 3 a 3 2a 3 a 3 6a A. . B. . C. . D. . 3 3 4 4
Giáo viên: LÊ BÁ BẢO...0935.785.115... 15 CLB Giáo viên trẻ TP Huế