Bài tập về tính năng lượng , fourier, laplace, biến đổi z, tổng chập, tích chập môn Tín hiệu và hệ thống | Học viện Công Nghệ Bưu Chính Viễn Thông

BÀI TẬP
Môn học: Tín hiệu và hệ thống
Bài 1: Tính giá trị trung bình và rms của tín hiệu. Hãy cho biết đây là tín hiệu năng lượng
hay tín hiệu công suất. Tính năng lượng/ công suất trung bình của tín hiệu. a) x(t) = (1 + t2)cos2(5t) b) x(t) = e–2tsin(2t)
c) x(t) = e t v ớ i 0 < t < 1 d) x(n) = 6( – 1) n ( 3 ) ! 0 ≤ 𝑛 ≤ 10 e) 𝑥 𝑛 = 𝑒 ! ! " ! ! ! !
f) 𝑥 𝑛 = 2 11 ≤ 𝑛 ≤ 15
0 𝑛 𝑐 ò 𝑛 𝑙 ạ 𝑖
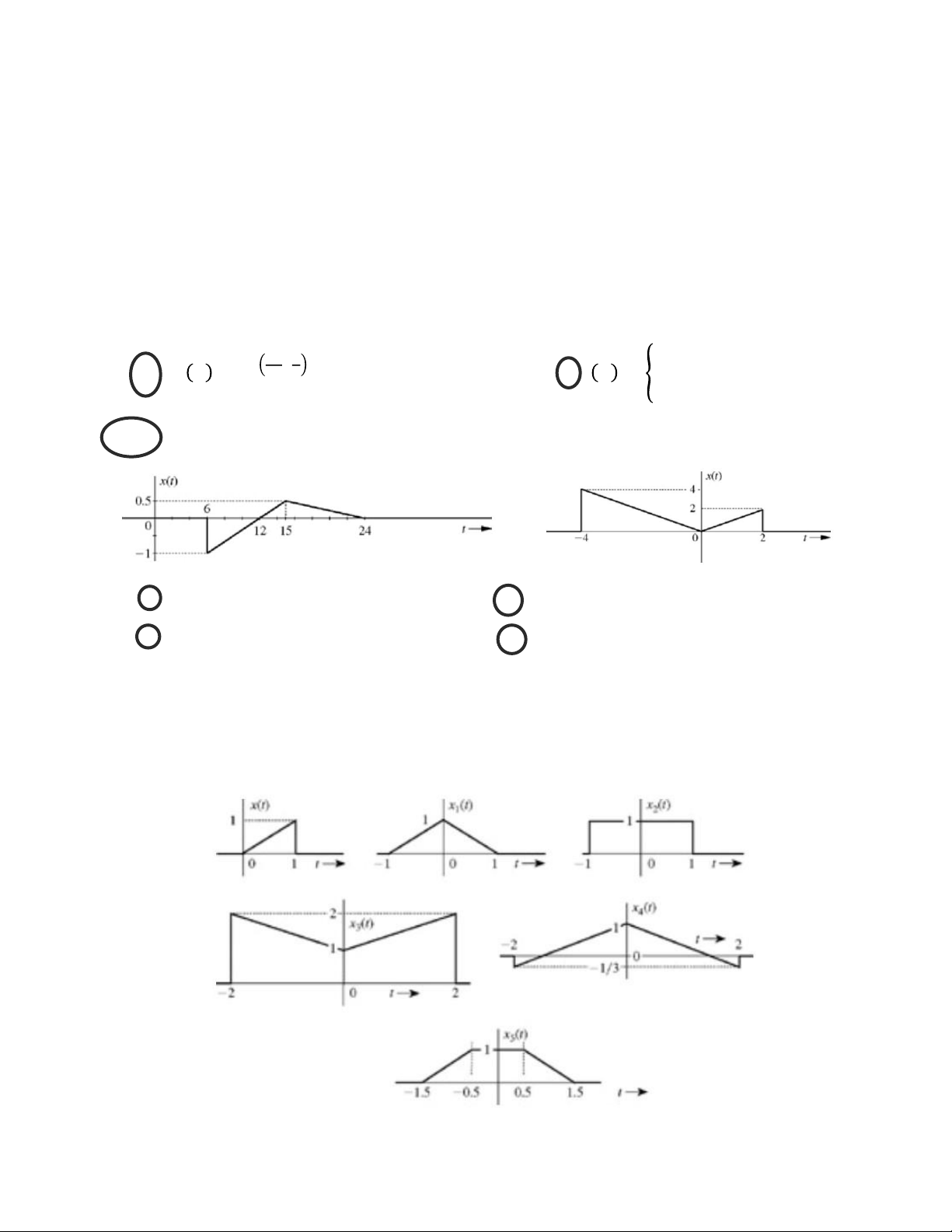
Bài 2: Cho tín hi ệ u x(t) nh ư hình v ẽ , v ẽ các tín hi ệ u trong các tr ư ờ ng h ợ p sau a) x( – t) b) x(t + 6) c) x( – t/2 + 2) d) x(2t – 4 ) Bài 3:
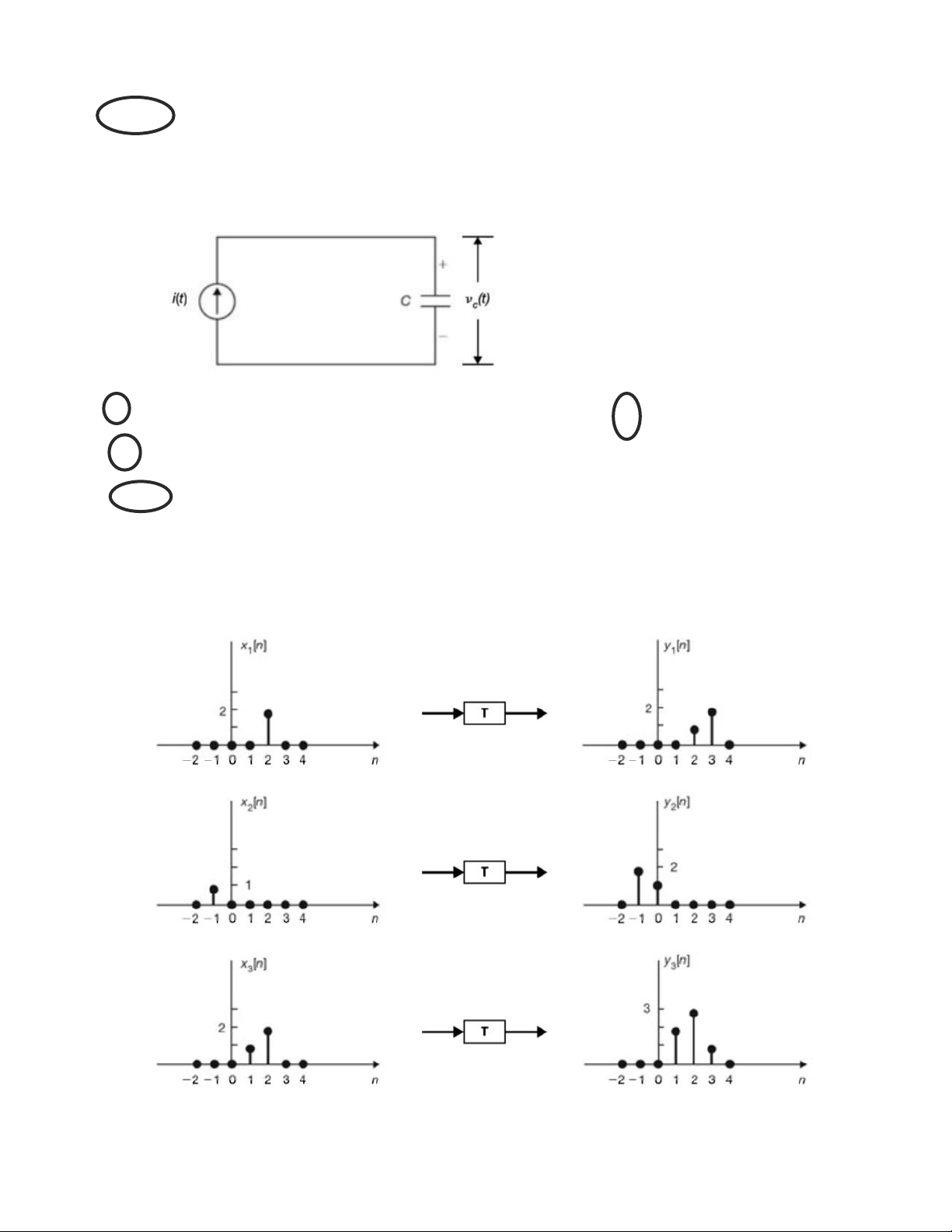
Cho x(t), x1(t), x2(t), x3(t), x4(t) và x5(t) như trong hình vẽ dưới đây. Hãy viết phtr biểu diễn
x1(t), x2(t), x3(t), x4(t) và x5(t) qua x(t) có sử dụng các phép toán cơ bản của tín hiệu. Bài 4:
Xác định mối quan hệ giữa đầu vào và đầu ra của các hệ thống sau (nếu cần). Hãy cho biết
các hệ thống có tuyến tính, bất biến, nhân quả, có nhớ và ổn định không? a) b) y ( ) t = T { x} = x ( t) 2
c) y(n) = T { x} = nx(n )
d) y(n) = T { x} = x*(n ) Bài 5:
Hệ thống rời rạc theo thời gian được đặc trưng bởi hàm truyền đạt T bất biến theo thời
gian. Biết rằng các tín hiệu đầu vào hệ thống lần lượt là x1(n), x2(n) và x3(n) sẽ thu được
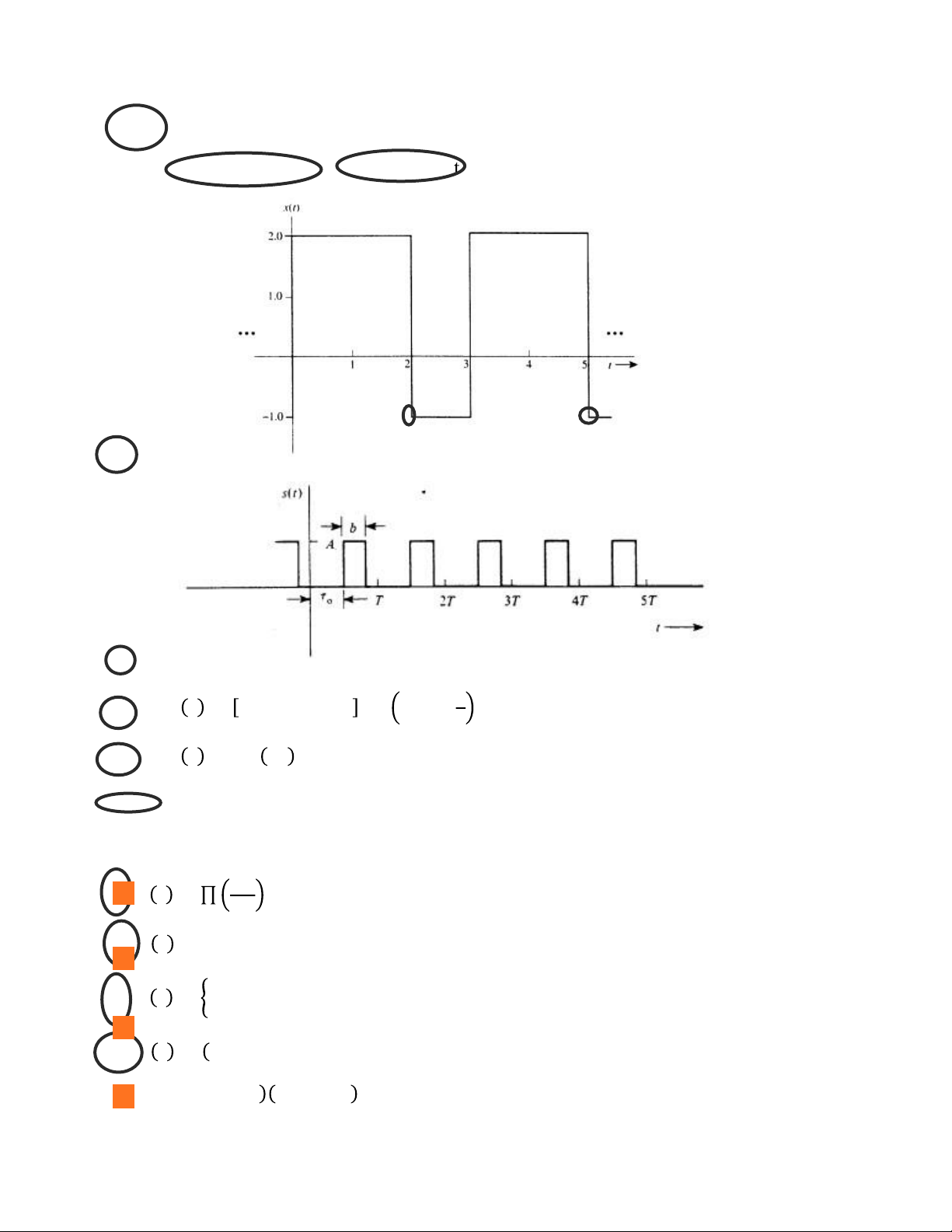
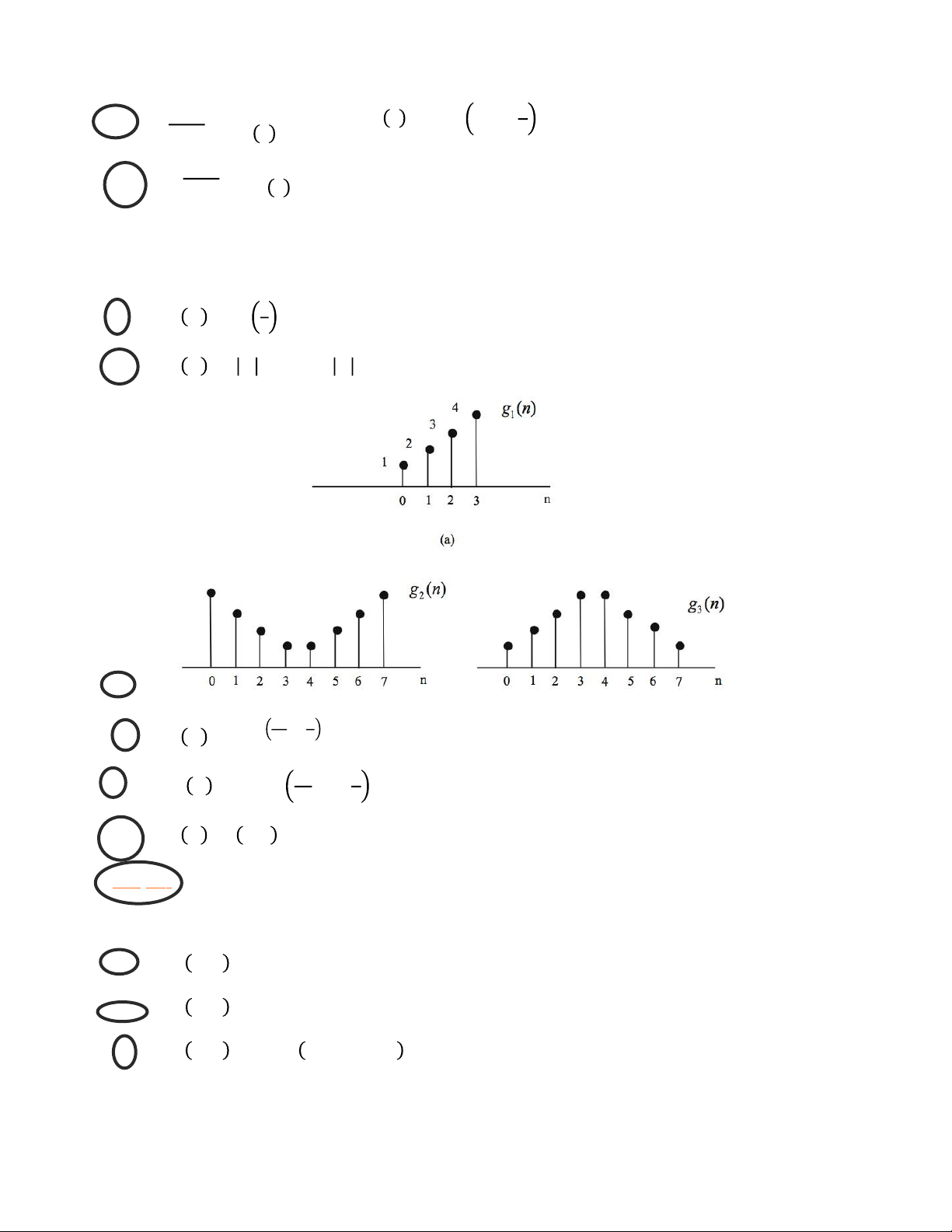
các tín hiệu đầu ra lần lượt là y1(n), y2(n) và y3(n) như trong hình vẽ dưới đây. Hãy cho biết
hệ thống có tuyến tính không? Vì sao? Bài 6 :
Tìm chu ỗ i Fourier và tính công su ấ t cho các chu ỗ i tín hi ệ u liên t ụ c sau T=3 a) b) c)
𝑥 𝑡 = 1 + 𝑐𝑜𝑠 ( 2 𝜋𝑡 ) 𝑠𝑖𝑛 5 𝜋𝑡 + ! ! P=3/4 d)
𝑥 𝑡 = 𝑠𝑖𝑛 2 𝑡 𝑣 ớ 𝑖 0 < 𝑡 < 𝜋 / 2 P=1/2 Bài 7:
Thực hiện biến đổi Fourier cho các tín hiệu liên tục sau:
a) 𝑤 𝑡 = !!! +8𝑠𝑖𝑛 (6𝜋𝑡) !"
b) 𝑤 𝑡 =5−5𝑒!!!𝑢(𝑡)
𝐴𝑡, 𝑣ớ𝑖 0< 𝑡 <𝑇 c) 𝑤 𝑡 = !
0 𝑣ớ𝑖 𝑡 𝑐ò𝑛 𝑙ạ𝑖
d) 𝑤 𝑡 = 𝑠𝑖𝑛2𝜋𝑓!𝑡 𝑐𝑜𝑠2𝜋𝑓!𝑡
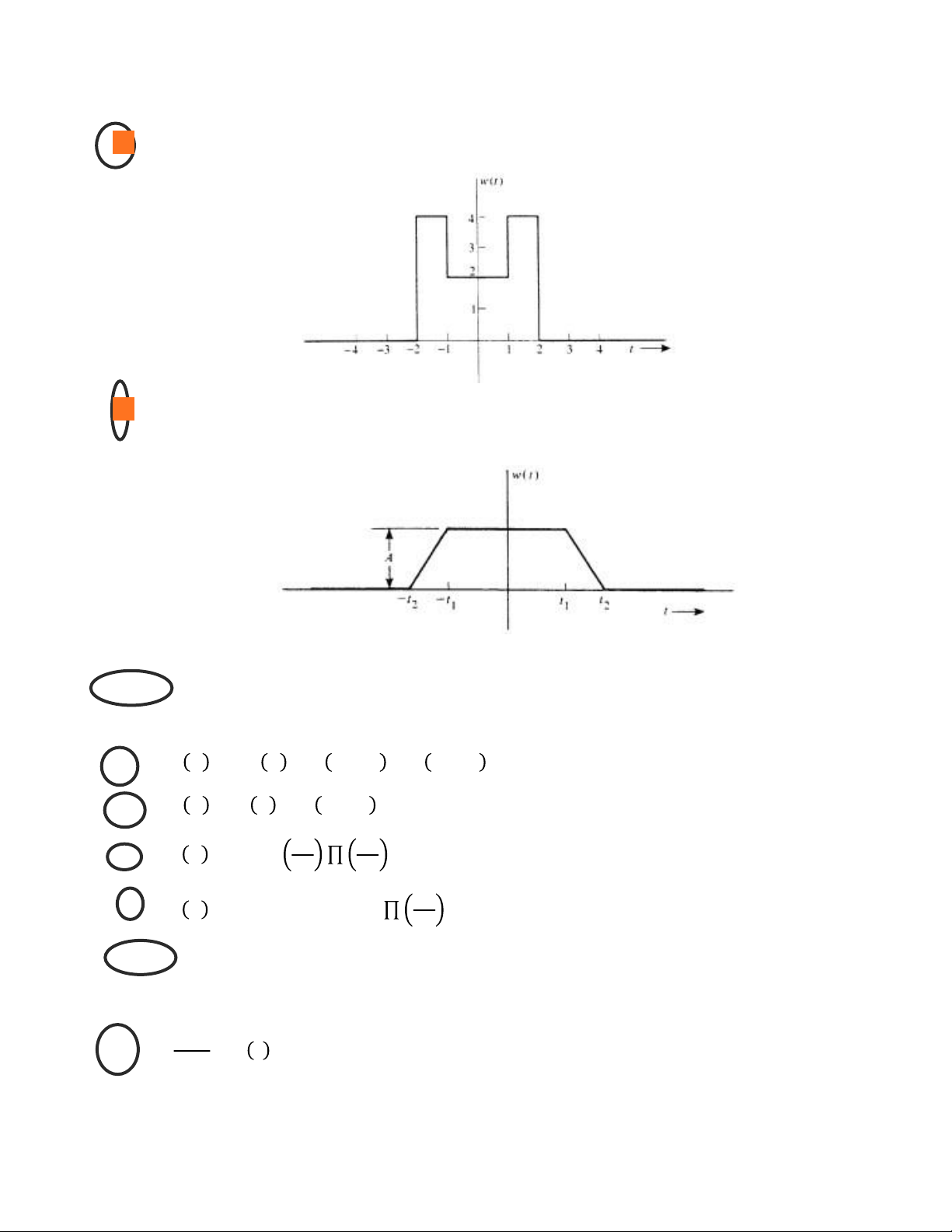
e) w(t) được mô tả bởi
f) w(t) được mô tả bởi Bài 8:
Thực hiện biến đổi Fourier ngược cho các tín hiệu sau a)
𝑋 𝑓 = 2 𝛿 𝑓 + 𝛿 𝑓 − 2 + 𝛿 𝑓 + 2 b)
𝑋 𝑓 = 𝑢 𝑓 − 𝑢 𝑓 − 2 c) ! !
𝑍 𝑓 = 𝐴𝑐𝑜𝑠 " ! ! ! ! d)
𝑍 𝑓 = − 𝑗𝐴𝑠𝑖𝑛 ( 𝜋𝑓 / 2 𝑊 ) ! ! ! Bài 9 :
Xác định đáp ứng đầu ra của hệ thống được biểu diễn bởi phtr vi phân sau a) ! " ( ! ) ! "
+𝑦 𝑡 = 𝑒!!! +𝑒!!!
+2𝑦 𝑡 = 2−3𝑠𝑖𝑛 𝑡 +𝑐𝑜𝑠 2𝑡+! b) ! " ( ! ) ! " ! ! " ( !) ! " c) 2 +3𝑦 𝑡 = 𝛿(𝑡) Bài 10:
Thực hiện biến đổi Fourier của các tín hiệu rời rạc sau: ! a) 𝑥 𝑛 = 𝑛 ! ! b)
𝑥 𝑛 = 𝑎 ! 𝑠𝑖𝑛𝜔𝑛 , 𝑎 < 1 c) d) 𝑥 𝑛 = 2 𝑒 ! ! ! ! ! ! ! ! e)
𝑥 𝑛 = 2 𝑐𝑜𝑠 ! ! ! 𝑛 + ! ! f)
𝑥 𝑛 = 0 ,6 ! 𝑢 ( 𝑛 − 2 ) Bài 11 :
Th ự c hi ệ n bi ế n đ ổ i Fourier ng ư ợ c c ủ a các tín hi ệ u sau: a)
𝐻 𝑒 ! " = 1 + 4 𝑐𝑜𝑠𝜔 + 3 𝑐𝑜𝑠 2 𝜔 b)
𝐻 𝑒 ! " = 𝑒 ! ! " / ! c)
𝐻 𝑒 ! " = 𝑒 ! ! " 1 + 4 𝑐𝑜𝑠𝜔 Bài 12:
Xác định đáp ứng đầu ra hoặc đáp ứng xung của hệ thống được biểu diễn bởi phtr sai phân sau a)
𝑦 𝑛 −!𝑦 𝑛−1 = 𝑥 𝑛 +!𝑥 𝑛−1
với 𝑥 𝑛 =𝑐𝑜𝑠𝑛 ! ! b)
𝑦 𝑛 = 𝑥 𝑛 +!𝑦 𝑛−1 với 𝑥 𝑛 =𝑐𝑜𝑠 𝑛−! 𝑢(𝑛) ! ! c)
𝑦 𝑛 = 3𝑥 𝑛 −2𝑥 𝑛−1 +3𝑥 𝑛−2 + ! 𝑦 𝑛−1 − ! 𝑦 𝑛−2 !" !" với 𝑥 𝑛 =𝑢(𝑛) ! ! d)
𝑦 𝑛 = 𝑥 𝑛 +!!𝑦 𝑛−1 − ! 𝑦 𝑛−2 ! !" !" Bài 13:
Tính tích chập cho các tín hiệu sau:
1, 𝑡 <𝑇! 𝑣à 𝑤! 𝑡 = 𝑇!−2 𝑡 , 𝑡 < !!𝑇!
a) 𝑤! 𝑡 = 0, 𝑡 𝑒𝑙𝑠𝑒𝑤ℎ𝑒𝑟𝑒0, 𝑡 𝑒𝑙𝑠𝑒𝑤ℎ𝑒𝑟𝑒
b) 𝑤! 𝑡 =Π !! 𝑣à 𝑤! 𝑡 = 𝐴𝑠𝑖𝑛𝜔!𝑡 c) 𝑤! 𝑡 =2Π ! ! !
𝑣à 𝑤 𝑡 = 0𝐴,, 𝑡 𝑒𝑙𝑠𝑒𝑤 𝑡ℎ≥𝑒𝑟𝑒4 ! ! ! ! d) 𝑤! 𝑡 =2Π ! ! !
𝑣à 𝑤 𝑡 = 0𝑒,! ! ! , 𝑡 𝑒𝑙𝑠𝑒𝑤 𝑡ℎ>𝑒𝑟𝑒0 Bài 14:
Tính tổng chập cho các tín hiệu sau:
a) 𝑥 𝑛 = 𝛼!𝑢 𝑛 𝑣à ℎ 𝑛 = 𝛽!𝑢 𝑛
b) 𝑥 𝑛 = 𝛼!𝑢 𝑛 𝑣à ℎ 𝑛 = 𝛼!!𝑢 −𝑛 𝑣ớ𝑖 0<𝛼<1
c) 𝑥 𝑛 , 𝑛=0, 1, 2 = 4, 2, 1 𝑣à ℎ 𝑛 , 𝑛=0, 1, = −2, −3
d) 𝑥 𝑛 , 𝑛=−2, −1,0, = 2, −1,4, 𝑣à ℎ 𝑛 , 𝑛=3,4,5,6 = 2,1,4,3 Bài 15:
Thực hiện biến đổi Laplace và vẽ giản đồ cực - không cho các tín hiệu liên tục sau
!!!𝑠𝑖𝑛 2𝑡 𝑢(𝑡) a) 𝑥 𝑡 = 𝑒 b)
𝑥 𝑡 =2𝑡!𝑢(𝑡−2) c)
𝑥 𝑡 =3𝑡(𝑢 𝑡−2 −𝑢(𝑡−4)) d)
𝑥 𝑡 =𝑒!!𝑢 𝑡 +𝑒!!! 𝑢(−𝑡) Bài 16:
Thực hiện biến đổi Laplace ngược cho các tín hiệu sau a)
𝑋 𝑠 = ! ! ! ! " ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! b) 𝑋 𝑠 = ! ! ! ! ! ! ! ! ! ! c) 𝑋 𝑠 = ! ! ! ! ! ! ! d) 𝑋 𝑠 = ! ! ! ! " ! ( ! ! ! ! ! ! ! " ) Bài 17 : với Re(s) > −1
Tìm đáp ứng xung và đầu ra của hệ thống được đặc trưng bởi phtr vi phân tuyến tính sau
nhờ biến đổi Laplace y’’(t) + 6y’(t) + 8y(t) = x’(t) + x(t) y’’(t) + 6y’(t) + 8y(t) = a) 2x’(t) + 3x(t) b)
với điều kiện ban đầu y(0–) = 2, y’(0–) = 3 và x(t) = u(t)
y’’(t) + 2y’(t) + y(t) = x(t) c)
với điều kiện ban đầu y(0–) = 2, y’(0–) = –3 và x(t) = e–2tu(t)
y’’(t) + 5y’(t) + 6y(t) = x(t) d)
với điều kiện ban đầu y(0–) = –1, y’(0–) = –3 và x(t) = tu(t)
Bài 18 : Thực hiện biến đổi z và vẽ giản đồ cực – không cho các tín hiệu rời rạc sau a)
𝑥 𝑛 = 1 / 3 ! ! ! − 𝑢 ( 𝑛 − 1 ) b) 𝑥 𝑛 = 𝑠𝑖𝑛 ! ! ! 𝑛 − ! ! 𝑢 ( 𝑛 − 1 ) ! c) 𝑥 𝑛 = 𝑛 + 0 ,5 ! 𝑢 𝑛 − 1 − ! ! ! 𝛿 ( 𝑛 − 3 ) d)
𝑥 𝑛 = 4 ! ! ! − 3 2 ! ! ! Bài 19:
Thực hiện biến đổi z ngược cho các tín hiệu sau a)
𝑋 𝑧 = ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! b) 𝑋 𝑧 = ! ! ! ! ! ! ! ! ! ! !
c) 𝑋 𝑧 = ! ! ! ! ! ! ! ! ! ! ! ! ! ! d) 𝑋 𝑧 = ! ! ! ! ! ! ( ! ! ! ! ) Bài 20 : với |𝑧| <1
Tìm đáp ứng xung và đáp ứng đầu ra của hệ thống được mô tả bởi phtr sai phân tuyến tính sau nhờ biến đổi z a)
y(n) = x(n) + 2x(n – 1) + x(n – 2) + 3y(n – 1) – 2y(n – 2) b)
y(n) = 2x(n) – x(n – 1) + x(n – 2) + (7/6)y(n – 1) – (1/3)y(n – 2)
với điều kiện ban đầu y(–1) = 2, y(–2) = –3 và x(n) = u(n) c)
y(n) = x(n) + 2x(n – 1) – x(n – 2) + (5/4)y(n – 1) – (3/8)y(n –
2) với điều kiện ban đầu y(–1) = 2, y(–2) = 1 và x(n) = (–1)nu(n) y(n) d)
= 3x(n) – 3x(n – 1) + x(n – 2) + (7/12)y(n – 1) – (1/12)y(n – 2)
với điều kiện ban đầu y(–1) = 1, y(–2) = 2 và x(n) = nu(n)