Bài tập Xác suất & Thống kê | Đại học Kinh tế kỹ thuật công nghiệp

lOMoAR cPSD| 45315597
Bộ môn Toán- Khoa KHCB Bài tập xác suất thống kê, học kỳ 2 (19-20)
Phần 1: Tính Xác suất.
Câu 1. Cho hệ đầy đủ ba biến cố {A,B,C} với P(A)=2P(B)=2P(C). Biết biến cố F thỏa mãn:
P(F/A)=0,05; P(F/B)=0,15 và P(F/C)=0,45
1/. Tính xác suất P(F). 2/. Tính xác suất
Câu 2. Cho hai biến cố A và B độc lập nhau. Biết rằng P(A + B) = 0,82 ; P(B) = 0,5
1/. Tìm xác suất P(A)
2/. Đặt T=A+B+C, biết biến cố C xung khắc với biến cố {A+B} và P(C)=0,001. Tính:
Câu 3. Cho hai biến cố A và B. Biết P(A)=0,6; P(B)=0,7 và P(A+B)=0,9.
1/. Chứng minh rằng A và B phụ thuộc nhau. 2/. Tính xác suất:
Câu 4. Cho hệ đầy đủ ba biến cố {A,B,C} với P(A)=0,3; P(B)=2P(A). Biết biến cố F thỏa mãn:
P(F/A)=0,02; P(F/B)=0,35 và P(F/C)=0,5. Tính các xác suất sau: 1/. Xác suất P(F) 2/. Xác suất:
Câu 5. Cho hai biến cố A và B độc lập nhau. Biết: P(A + B) = 0,88; P(A) = 0,8.
1/. Tính P(B).
2/. Tìm xác suất để chỉ có một trong hai biến cố A, B xảy ra.
Câu 6. Cho hệ đầy đủ ba biến cố {A,B,C} với P(A)=0,2; P(C)=0,5. Biết biến cố F thỏa mãn:
P(F/A)=0,25; P(F/B)=0,15 và P(F/C)=0,35. Tính các xác suất sau: 1/. Xác suất P(F) 2/. Xác suất:
Câu 7. Cho hệ đầy đủ ba biến cố {A,B,C} với P(A)=P(B)=2P(C). Biết biến cố F thỏa mãn:
P(F/A)=0,2; P(F/B)=0,3 và P(F/C)=0,4
1/. Tính xác suất P(F).
2/. Tính xác suất: P[(A+B)*(A+B+C)].
Câu 8. Cho hai biến cố A và B độc lập nhau. Biết: P(A + B) = 0,83; P(A) = 0,5 và P(B)=a 1/.
Tìm giá trị của a=?
2/. Cho biến cố D = A+B+C có P(D)=0,45 ; và giả sử A,B, C độc lập, hãy tính xác suất P(C)?
Câu 9.Cho hai biến cố A, B. Biết P(A+B) = 0,6; P(A) = 0,3; P(B) =0,4.
1/. Tìm xác suất P(AB).
2/. Đặt C=A+B, tính xác suất: P(A|C)
Câu 10. Cho hai biến cố A, B. Biết P(A) = 0,3; P(B) =0,5; P(A|B)=0,2.
1/. Tìm xác suất: P(AB).
2/. Tìm xác suất: P(A+B+C), với C ⊂ A
Phần 2: Đại lượng ngẫu nhiên và các quy luật phân phối
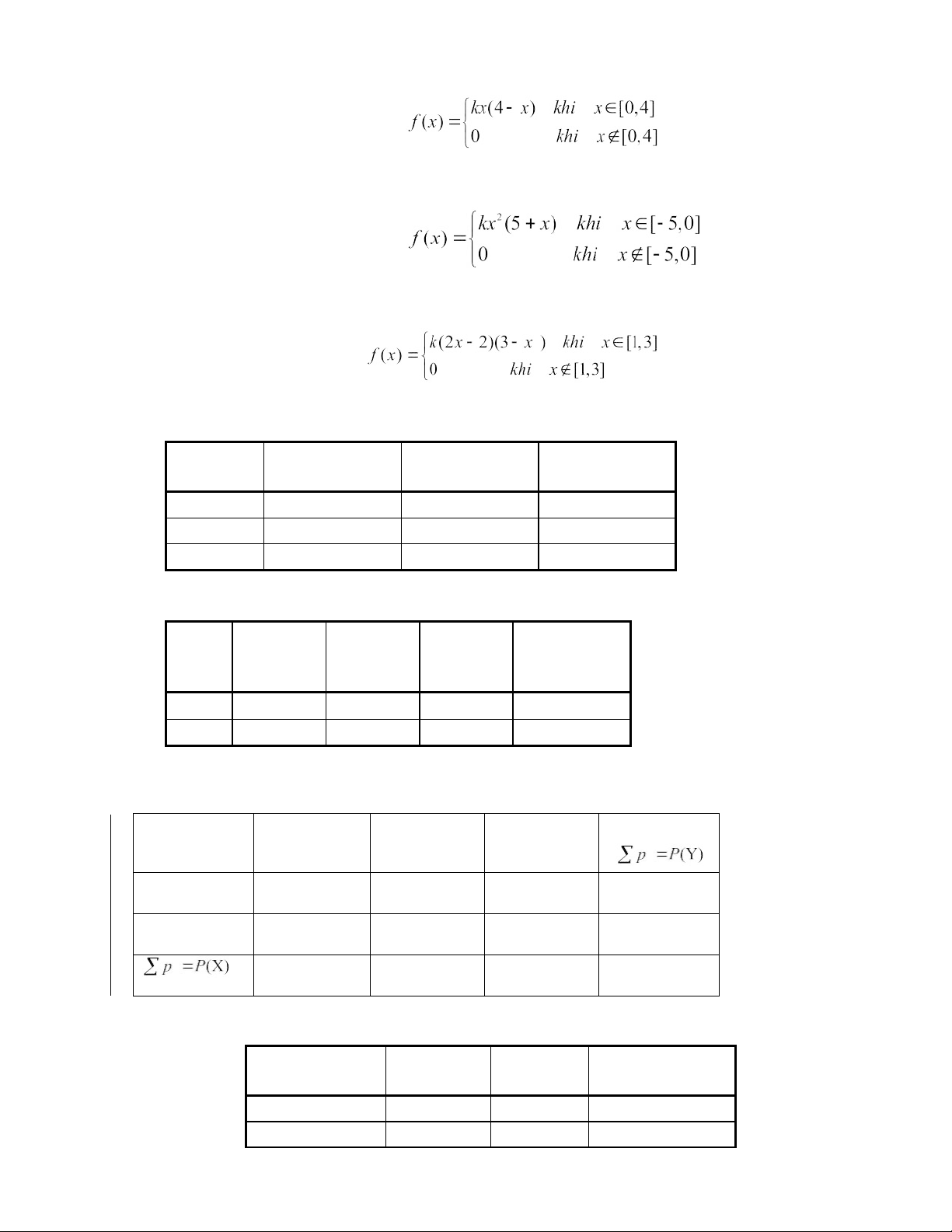
1/. Cho hàm mật độ của biến ngẫu nhiên X:
a) Tìm k để f(x) là hàm mật độ. b) Tính giá trị của ModX.
2/. Cho hàm mật độ của biến ngẫu nhiên X: lOMoAR cPSD| 45315597
Bộ môn Toán- Khoa KHCB Bài tập xác suất thống kê, học kỳ 2 (19-20)
a) Tìm k để f(x) là hàm mật độ. b) Tính E(3 - 2X) và P(X > 2).
3/.Cho hàm mật độ của biến ngẫu nhiên X:
a) Tìm k để f(x) là hàm mật độ. b) Tính xác suất P(X
4/. Cho hàm mật độ của biến ngẫu nhiên X:
a) Tìm k để f(x) là hàm mật độ. b) Tính giá trị của E(4X-2020).
5/. Cho biến ngẫu nhiên X và Y có bảng phân phối đồng thời như sau : Y -3 3 6 X -2 a 0,5a a 2 0,05 a 1,5a 3 0,15 0,1 0,2
a). Tìm hệ số a từ bảng phân phối. b). Tính MedZ với Z=2X-Y. 6/.
Cho biến ngẫu nhiên X và Y có bảng phân phối đồng thời như sau : -3 -2 2 3 Y X -3 a 2a 4a 4a 3 4a a 3a a a). Tìm hệ số a từ
bảng phân phối. b). Tính MedZ với Z=X+Y. 7/. Cho biến ngẫu nhiên X
và Y có bảng phân phối đồng thời như sau : X 0 1 2 Y 2 0.05 0.4 4 0.2 0.2 0.5 1
a). Điền các giá trị còn thiếu vào bảng. b). Tính MedZ với Z=X-Y. 8/.
Cho biến ngẫu nhiên X và Y có bảng phân phối đồng thời như sau : Y -2 0 2 X -2 a 0,5a a 0 0,05 a 1,5a lOMoAR cPSD| 45315597
Bộ môn Toán- Khoa KHCB Bài tập xác suất thống kê, học kỳ 2 (19-20) 2 0,15 0,1 0,2
a). Tìm hệ số a từ bảng phân phối. b). Tính xác suất P(X-Y< 0,1).
9/. Một sinh viên đi thi chỉ thuộc 30 câu trong 50 câu ở đề cương. Mỗi đề thi có 10 câu hỏi thuộc để
cương, gọi Y là số câu hỏi sinh viên đó thuộc. Biết X ~ N(4,2; 0,9); đặt Z = X+Y-modX
a). Hãy tính giá trị của E(Z). b). Tính P(X2 < 4).
10/. Cho X ~ N(3; 1); Y ~ B(6; 0,2) và đặt T = X + Y – modX.modY.
a) Hãy tính giá trị của E(T). b) Tính xác suất P(X2 -2X < 8).
11/. Trong một lô 100 sản phẩm có 65 sản phẩm loại I. Lấy ngẫu nhiên 45 sản phẩm để kiểm tra, gọi
X là số sản phẩm loại I gặp được khi kiểm tra. Biết Y ~ N(4; 2).
a) Hãy tính giá trị của E(2X+Y). b) Tính xác suất P(Y2-3Y+2<0).
12/. Cho Cho X ~ N(3; 0,4); Y ~ H(30; 8; 0,6). Đ t ặ Z =X+Y
a). Hãy tính giá trị của E(2020Z). b). Tính P(X2+4X+3<0)
13/. Một sinh viên đi thi chỉ thuộc 30 câu trong 40 câu ở đề cương. Mỗi đề thi có 5 câu hỏi thuộc để
cương, gọi X là số câu hỏi sinh viên đó thuộc. Biết Y ~ N(5,5; 0,6),
a) Hãy tính giá trị của E(X+Y-2020). b) Tính xác suất P(Y2 -2Y < 4). 14/.
Cho X và Y độc lập, X ~ N(3; 1); Y ~ B( 10; 0,3). Cho Z = X+Y-modX-modY
a). Hãy tính giá trị của E(Z). b). Tính P(X2-4X+3<0).
15/. Trong lượng của một gói chè Ô long là biến ngẫu nhiên phân phối chuẩn X (đơn vị: gram) với
trọng lượng trung bình là 255 gram và độ lệch chuẩn là 2,5 gram.
a) Tính D(10X+5). b) Tính xác suất P(X > 250).
Phần 3: Thống kê 1-mẫu
Câu 1.Mức tiêu hao nhiên liệu của một loại máy xúc Komatsu trong một ca làm việc, là biến ngẫu
nhiên có phân bố chuẩn, với số liệu như sau: cỡ mẫu=38 ca; trung bình mẫu=160,2 (lít); độ lệch
hiệu chỉnh=8,3 (lít); trong đó có 12 ca máy hoạt động quá tải so với quy định.
1/. Hãy ước lượng mức tiêu hao trung bình cho loại máy xúc Komatsu với độ tin cậy 95%.
2/. Hãy ước lượng tỷ lệ ca làm việc quá tải với độ tin cậy 90%.
3/. Khi ước lượng tỷ lệ ca làm việc quá tải với yêu càu độ chính xác là 0,05 và độ tin cậy là 99% thì
cần khảo sát thêm bao nhiêu mẫu nữa.
Câu 2. Doanh thu/tuần (x: triệu đồng) của một số cửa hàng kinh doanh mặt hàng A ở vùng x là ĐLNN
có phân bố chuẩn. Điều tra trên một mẫu với n=60, ta thu được trung bình mẫu =190,5 (triệu); độ lệch
mẫu hiệu chỉnh là 2,01(triệu) và có 12 cửa hàng có doanh thu trên 200(triệu) . 1/. Hãy ước lượng
doanh thu/tuần trung bình của các của hàng ở vùng x với độ tin cậy 99%.
2/. Khi ước lượng doanh thu/tuần trung bình của các của hàng ở vùng x với độ chính xác là 0,16 và độ
tin cậy cần đảm bảo là 95% thì cần điều tra mẫu thêm bao nhiêu phần tử nữa.
3/. Có báo cáo khẳng định rằng, tỷ lệ cửa hàng có doanh thu trên 200(triệu) đạt ít nhất là 25% , với
mức ý nghĩa 10% hãy cho kết luận?
Câu 3. Trọng lượng (gam) của một loại sản phẩm của một dây chuyền sản xuất là BNN có phân bố
chuẩn. Điều tra trên một mẫu 100 sản phẩm, ta thu được trọng lượng trung bình mẫu là 1805g và
độ lệch mẫu hiệu chỉnh là 55g. lOMoAR cPSD| 45315597
Bộ môn Toán- Khoa KHCB Bài tập xác suất thống kê, học kỳ 2 (19-20)
1/. Hãy ước lượng trọng lượng trung bình của sản phẩm của dây chuyền với độ tin cậy 99%. 2/.
Khi ước lượng trọng lượng trung bình của sản phẩm của dây chuyền với độ chính xác là 11g thì độ tin cậy bằng bao nhiêu.
3/. Quản đốc dây chuyền khẳng định rằng trọng lượng trung bình của sản phẩm là 1850g, hãy cho kết
luận với mức ý nghĩa 5%.
Câu 4.Số cuộc gọi đến/ngày ở một cửa hàng bảo dưỡng điều hòa vào mùa hè là đại lượng tuân theo
quy luật chuẩn. Theo dõi số cuộc gọi đến/ngày, ta có kết quả sau: cỡ mẫu=36 ngày; trung bình
mẫu=16,2 và độ lệch hiệu chỉnh=2,3. Trong đó có 8 ngày cửa hàng không đáp ứng hết yêu cầu gọi đến.
1/. Hãy ước lượng tỷ lệ của những ngày không đáp ứng hết yêu cầu gọi đến với độ tin cậy 95%.
2/. Hãy ước lượng số cuộc gọi trung bình đến cửa hàng với độ tin cậy 90%
3/. Khi ước lượng số cuộc gọi trung bình đến cửa hàng bảo dưỡng điều hòa với yêu cầu độ chính xác
là 1,1 thì độ tin cậy bằng bao nhiêu.
Câu 5. Năng suất Hồ tiêu tại vùng X là các biến ngẫu nhiên có phân phối chuẩn. Có kết quả điều
tra: cỡ mẫu=100 ha; trung bình mẫu=16,2 (tạ) và độ lệch hiệu chỉnh=2,3. Trong đó có 18 ha có năng suất cao.
1/. Với độ tin cậy 90% hãy ước lượng năng suất Hồ tiêu trung bình.
2/. Khi ước lượng tỷ lệ số ha có năng suất cao với độ tin cậy 90% và độ chính xác 0,025 thì cần điều
tra thêm bao nhiêu điểm thu hoạch nữa.
3/. Nếu lấy số liệu trên để ước lượng cho năng suất Hồ tiêu trung bình với yêu cầu độ chính xác là 0,21
thì độ tin cậy tương ứng là bao nhiêu.
Câu 6. Một xí nghiệp đưa ra thị trường một sản phẩm mới. Để xem đánh giá của người tiêu dùng
đối với loại sản phẩm mới này như thế nào, người ta phát cho mỗi người mua hàng một phiếu thăm
dò. Kết quả xí nghiệp nhận được 300 phiếu thăm dò, trong đó có 90 phiếu tỏ ra thích thú loại sản phẩm này.
1/. Hãy ước lượng tỷ lệ khách hàng thích loại sản phẩm này với độ tin cậy 95%?
2/. Muốn nhận được ước lượng khoảng cho tỷ lệ thực trên với độ tin cậy 99% và độ chính xác là 0,03
thì cần thăm dò thêm bao nhiêu phiếu nữa?
3/. Khi thiết kế tính năng của sản phẩm mới xí nghiệp đưa ra mục tiêu sẽ thu hút được ít nhất 50%
lượng khách hàng tham gia sử dụng yêu thích sản phẩm. Hãy đưa ra kết luận với mức ý nghĩa 5%?
Câu 7. Một khu rừng có diện tích rất lớn. Căn cứ vào kết quả điều tra ngẫu nhiên trên 31 ô, mỗi ô có
diện tích 0,1 ha ta tính được thể tích gỗ trung bình trên mỗi ô là 10,2 m3 và sai số tiêu chuẩn là 1,45
m3. Giả thiết thể tích gỗ X tuân theo luật chuẩn.
1/. Hãy ước lượng thể tích gỗ trung bình của khu rừng đó với độ tin cậy 95% ?
2/. Khi ước lượng thể tích gỗ trung bình của khu rừng với độ chính xác là 0,5 m3 thì độ tin cậy bằng bao nhiêu?
3/. Theo số liệu điều tra của năm trước thì thể tích gỗ trung bình của khu rừng đó là 15 m3. Vậy có
thể kết luận thể tích gỗ của khu rừng giảm đi với mức ý nghĩa 5% không?
Câu 8.Bột mỳ được đóng bao bằng máy tự động với trọng lượng theo quy định là 16 kg. Lấy ngẫu
nhiên 35 bao bột để kiểm tra, ta tính được trung bình là 16,6 kg và độ lệch hiệu chỉnh là 1 kg. Biết
trọng lượng của bao bột mỳ là biến ngẫu nhiên X tuân theo quy luật chuẩn lOMoAR cPSD| 45315597
Bộ môn Toán- Khoa KHCB Bài tập xác suất thống kê, học kỳ 2 (19-20)
1/. Hãy ước lượng tỷ lệ bao bột mỳ có trọng lượng trên 17kg với độ tin cậy 90%, biết trong 35 bao đã
kiểm tra thì có 7 bao có trọng lượng trên 17kg.
2/. Nếu muốn độ chính xác khi ước lượng cho trọng lượng trung bình là 0,5 kg thì độ tin cậy đạt được là bao nhiêu.
3/. Với mức ý nghĩa 5%, có cần dừng máy để điều chỉnh không? Biết rằng nếu máy đóng bao với trọng
lượng không đúng quy định thì phải điều chỉnh. Phần 4: Tương quan và hồi quy tuyến tính đơn
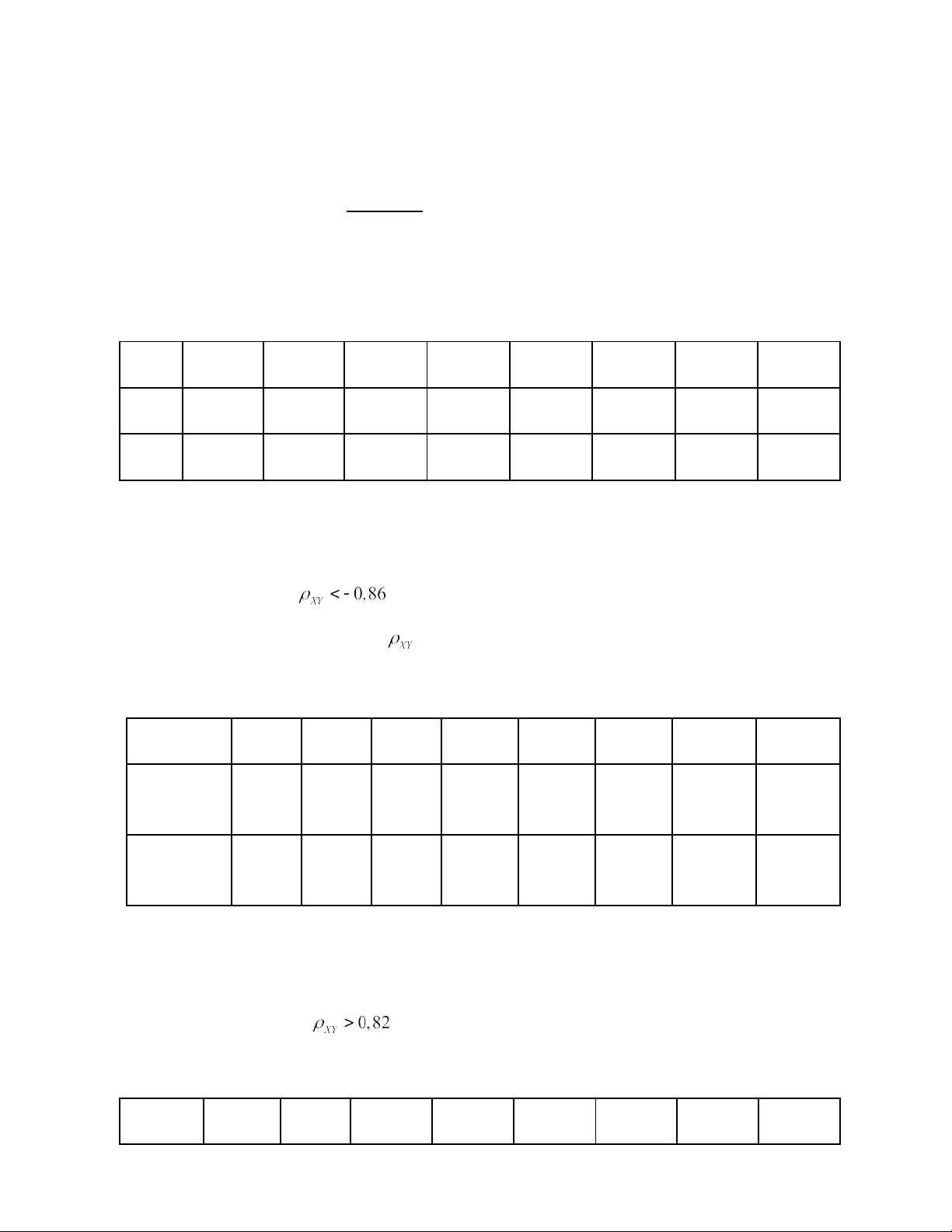
Câu 1. Khảo sát chỉ số chất lượng không khí y (đơn vị:AQI), và số lượng cây xanh trên đầu người
x (m2/người) tại một số thành phố lớn khu vực Đông Nam Á, người ta thu được mẫu số liệu như sau: xi 60 55 42 35 28 20 11 5 yi 25 75 124 180 250 300 350 400 ni 3 5 2 6 4 3 5 2
Với biến BNN X về lượng cây xanh và Y chỉ số chất lượng không khí đều tuân theo luật chuẩn.
1/. Lập phương trình hồi quy tuyến tính thực nghiệm, và cho biết sai số về chỉ số chất lượng không
khí AQI khi khảo sát chất lượng không khí ở thành phố có lượng cây xanh 42 (m2/người) giữa số
liệu thực tế và qua hàm hồi quy.
2/. Có giả thiết cho rằng
, hãy đưa ra kết luận với mức ý nghĩa 1%.
3/. Hãy ước lượng hệ số tương quan
với độ tin cậy 90%.
Câu 2.Theo dõi về lượng khách vào cửa hàng (người/ngày) và doanh thu trong ngày của cửa hàng đó
(triệu/ngày) ta có số liệu thống kê như sau: xi 22 24 26 28 30 32 34 36 yi 12,5 14 15 15, 17 18 18,5 20 5 Số 3 5 7 6 8 4 5 2 ngày
Với BNN X về lượng khách trong ngày; Y về doanh thu trong ngày của cửa hàng.
1/. Lập phương trình hồi quy tuyến tính thực nghiệm? và cho biết nếu lượng khách vào cửa hàng là
40 (người/ngày) thì doanh thu là bao nhiêu?
2/. Hãy ước lượng hệ số tương quan ρxy với độ tin cậy 99%.
3/. Có giả thiết cho rằng
, hãy đưa ra kết luận với mức ý nghĩa 1%.
Câu 3. Nghiên cứu về mối liên hệ giữa tuổi nghề và năng suất lao động (NSLĐ) của một số công nhân
ở một phân xưởng ta có số liệu sau: xi 1 2 3 4 5 6 7 8 lOMoAR cPSD| 45315597
Bộ môn Toán- Khoa KHCB Bài tập xác suất thống kê, học kỳ 2 (19-20) yi 6,5 8 10 11 13,5 15 18 20 Số CN 3 5 8 10 7 5 3 2
Với biến BNN X là tuổi nghề (năm) và Y là NSLĐ (kg/giờ).
1/. Lập phương trình hồi quy tuyến tính biểu diễn mối quan hệ giữa X và Y và cho biết nếu tuổi nghề
là 10 năm thì NSLĐ là bao nhiêu?
2/. Có giả thiết cho rằng
, hãy đưa ra kết luận với mức ý nghĩa 5%.
Câu 4. Để tìm hiểu mối liên hệ giữa kết quả học tập ở phổ thông và ở năm thứ nhất bậc đại học, ta
thống kê kết quả của 40 sinh viên. Gọi X là kết quả thi tốt nghiệp THPT về môn toán, Y là điểm thi
môn toán ở năm thứ nhất tương ứng: xi 6 6 7 7 7 8 9 9 yi 4 6 4 6 7 4 6 7 ni 8 3 2 6 3 1 4 13
Với biến ngẫu nhiên X ;Y đều tuân theo luật chuẩn.
1/. Lập phương trình hồi quy tuyến tính thực nghiệm? và cho biết sai số về điểm thi môn toán
năm thứ nhất của những sinh viên có kết quả thi tốt nghiệp THPT được 9 điểm giữa số liệu thực tế và qua hàm hồi quy?
2/. Có giả thiết cho rằng
> 0,5, hãy đưa ra kết luận với mức ý nghĩa 5%?
Câu 5. Khảo sát về tổng thu nhập X (triệu VNĐ/tháng) và tỷ lệ chi cho giáo dục Y (%) của một số gia
đình ở một địa phương ta có bảng số liệu sau: xi 10 15 20 25 30 35 40 45 yi 10 12 13 15 16 18 20 21 ni 7 8 10 15 8 7 3 2
Với biến ngẫu nhiên X, Y đều tuân theo luật chuẩn
1/. Lập phương trình hồi quy tuyến tính mẫu và cho biết tỷ lệ chi cho giáo dục là bao nhiêu nếu gia
đình có tổng thu nhập 43 triệu VNĐ/tháng?
2/. Với mức ý nghĩa 5%, có thể cho rằng không?
---------------------------------------------------------- Hết-----------------------------------------------------