Bài toán chứng minh các đường thẳng đồng quy

1
Chủ đề 6: Chứng minh các đường thẳng đồng quy
ủ đề 6 CÁC BÀI TOÁN CHỨNG MINH Ch ĐỒNG QUY
F. CÁC BÀI TOÁN CHỨNG MINH ĐỒNG QUY MỤC LỤC
F. CÁC BÀI TOÁN CHỨNG MINH ĐỒNG QUY ............................................................. 1
Bài tập có giải ............................................................................................................................. 2
Một số bài tập tự rèn: .............................................................................................................. 16
CÁC PHƯƠNG PHÁP THƯỜNG ĐƯỢC SỬ DỤNG
Cách 1. Lợi dụng định lí về các đường đồng quy trong tam giác
 Sử dụng định lí ba đường cao của tam giác đồng quy tại một điểm
 Sử dụng định lí ba đường trung tuyến của tam giác đồng quy tại một điểm. Điểm đó gọi
là trọng tâm của tam giác.
 Sử dụng các định lí: 1.Ba đường phân giác của tam giác đồng quy tại một điểm.
 Giao điểm của hai đường phân giác ngoài nằm trên đường phân giác trong của góc thứ ba.
 Sử dụng định lí ba đường trung trực của tam giác đồng quy tại một điểm.
Cách 2. Sử dụng tính chất các đường chéo cắt nhau tai trung điểm mỗi đường của của hình
bình hành, hình chữ nhật, hình thoi, hình vuông.
Cách 3. Lùi về quen thuộc, chứng minh ba điểm thẳng hàng hoặc giao điểm của hai đường
nằm trên đường thẳng thứ ba.
Chúc các em học sinh học tập tốt!
Toán Họa: 0986 915 960 – Tổng hợp. 2
Chủ đề 6: Chứng minh các đường thẳng đồng quy Bài tập có giải
Sử dụng tính chất các đường chéo cắt nhau tai trung điểm mỗi đường của của hình
bình hành, hình chữ nhật, hình thoi, hình vuông.
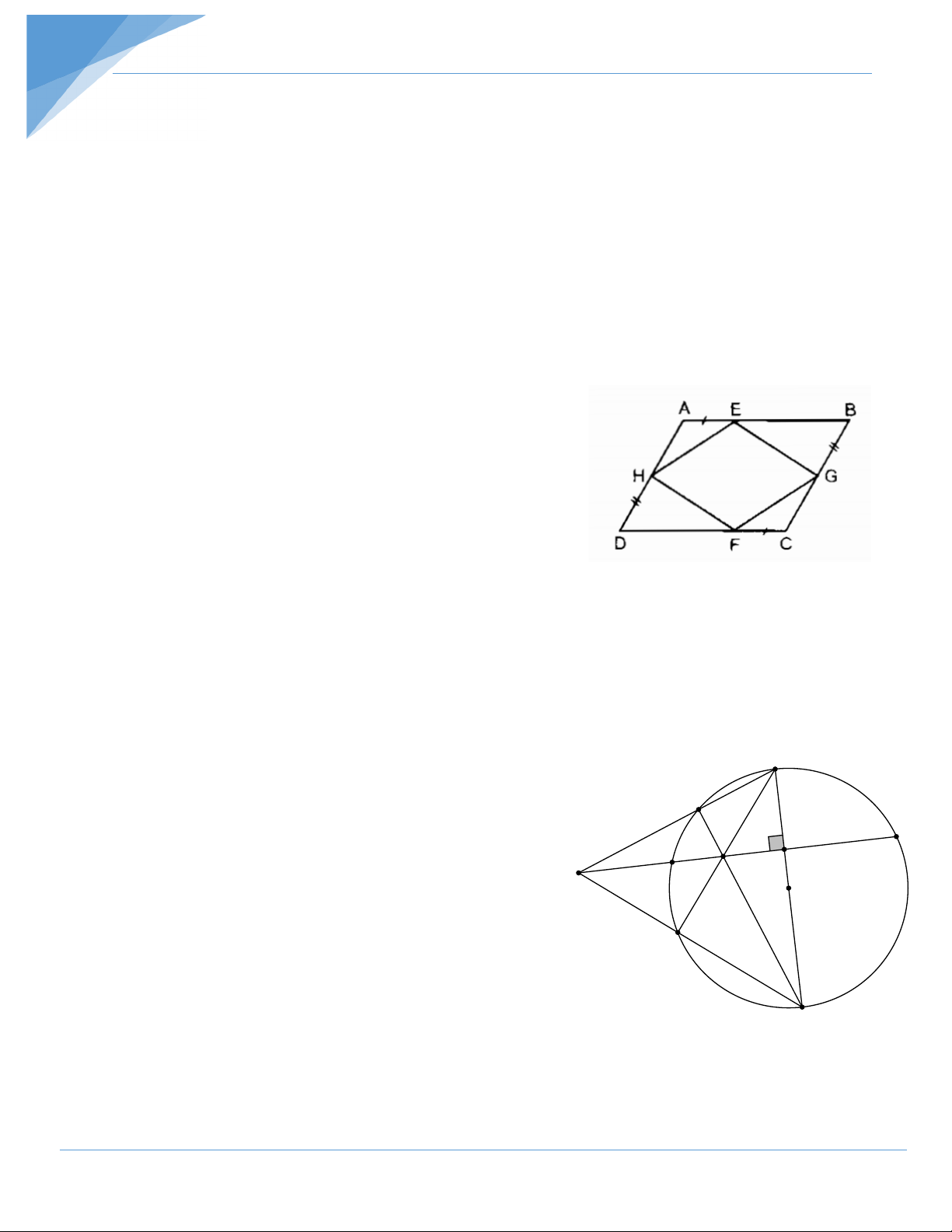
Bài 1: Trên hình vẽ bên, cho ABCD là hình bình hành. Chứng minh rằng:
a) EFGH là hình bình hành.
b) Các đường thẳng AC, BD, EF,GH đồng quy. Hướng dẫn giải
a) Chứng minh rằng EG = HF;EH = GF .
b) Gọi O là giao điểm của AC và EF . Tứ giác AECF
có AE = CF, AE / /CF nên là hình bình hành.. Suy ra O
là trung điểm của AC, EF .
ABCD là hình bình hành, O là trung điểm của AC
nên O là trung điểm của BD .
EGHF là hình bình hành, O là trung điểm của EF nên O là trung điểm của GH .
Vậy AC, BD, EF,GH đồng quy tại O .
Lợi dụng các đường đồng quy trong tam giác: đồng quy tại trực tâm, trọng tâm, tâm
đường tròn nội tiếp, tâm đường tròn ngoại tiếp tam giác.
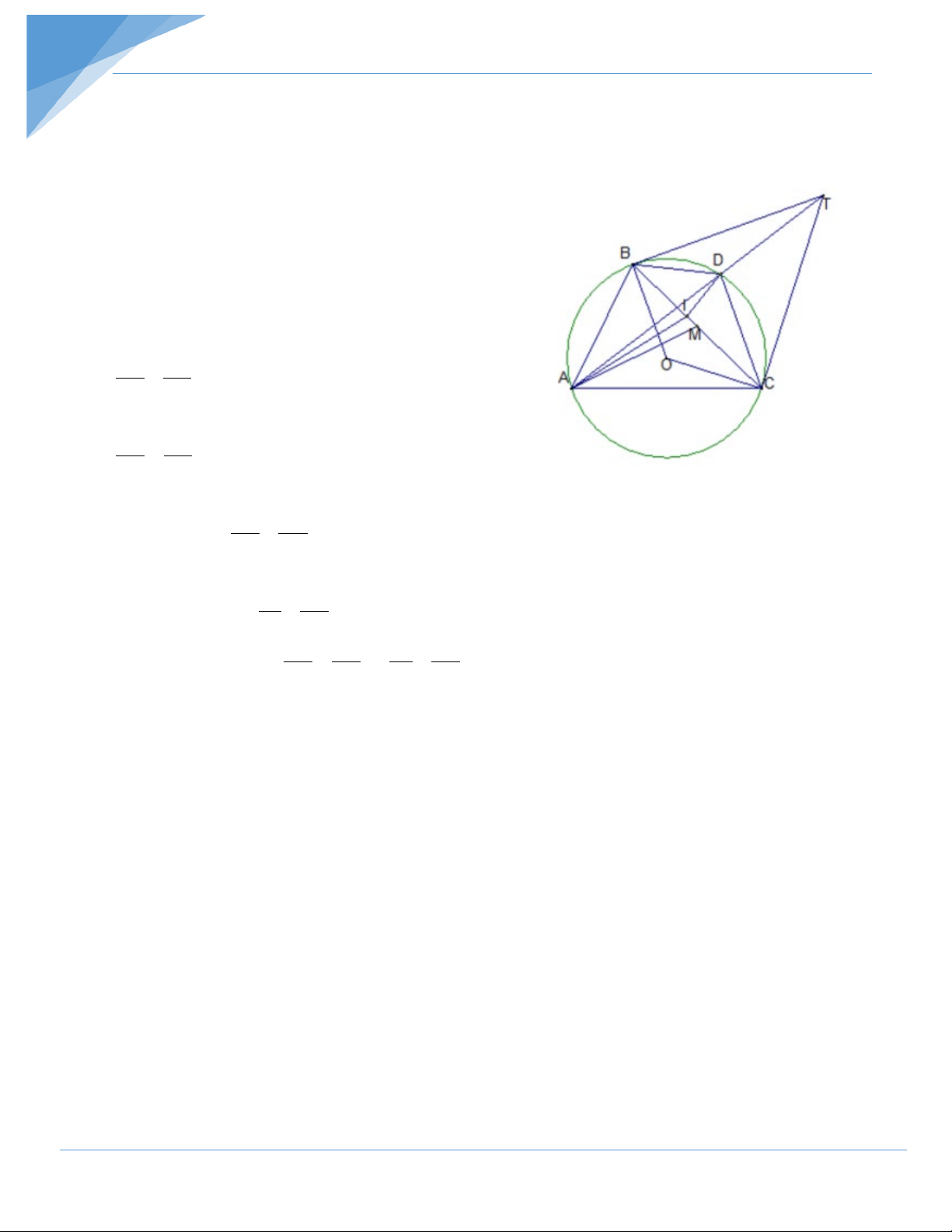
Bài 2: Từ một điểm C ở ngoài đường tròn (O) kẻ I
các tuyến CBA . Gọi IJ là đường kính vuông góc
với AB . Các đường thẳng CI,CJ theo thứ tự cắt M A
đường tròn (O) tại M , N . Chứng minh rằng
IN, JM , AB đồng quy tại một điểm D . D C B O Hướng dẫn giải N
M thuộc đường tròn đường kính IJ nên 
JMI = 90° hay JM ⊥ CI J
Tương tự IN ⊥ CJ
Tam giác CIJ có 3 đường cao C ,
A JM , IN đồng quy tại D .
Vậy IN, JM , AB đồng quy tại một điểm D .
Toán Họa: 0986 915 960 – Tổng hợp. 3
Chủ đề 6: Chứng minh các đường thẳng đồng quy
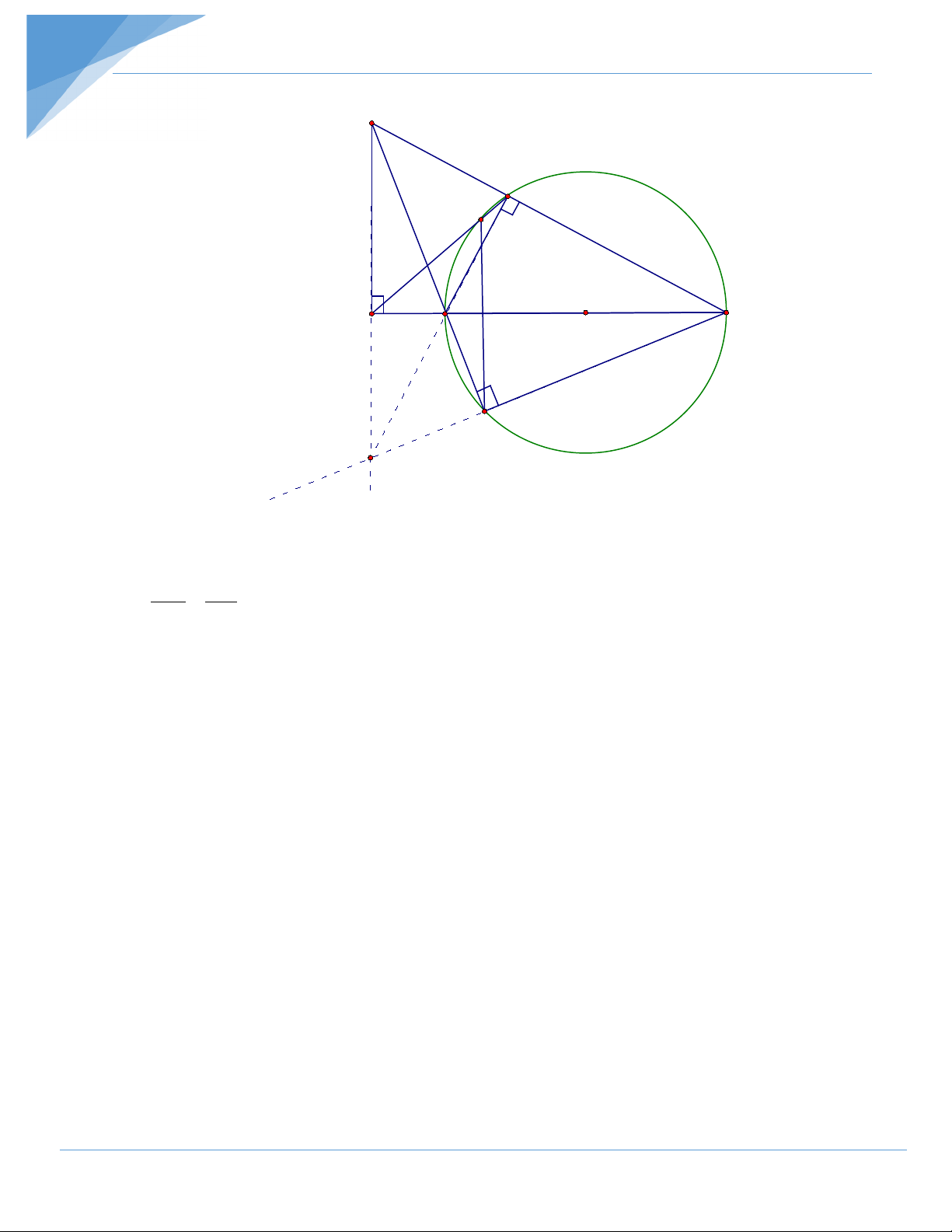
Bài 3: Cho tam giác ABC vuông ở A. Trên cạnh AC lấy điểm M, dựng đường tròn (O)
có đường kính MC. đường thẳng BM cắt đường tròn (O) tại. D. đường thẳng AD cắt đường tròn (O) tại S.
1. Chứng minh ABCD là tứ giác nội tiếp.
2. Chứng minh CA là tia phân giác của góc SCB.
3. Gọi E là giao điểm của BC với đường tròn (O). Chứng minh rằng các đường thẳng BA, EM, CD đồng quy.
4. Chứng minh DM là tia phân giác của góc ADE.
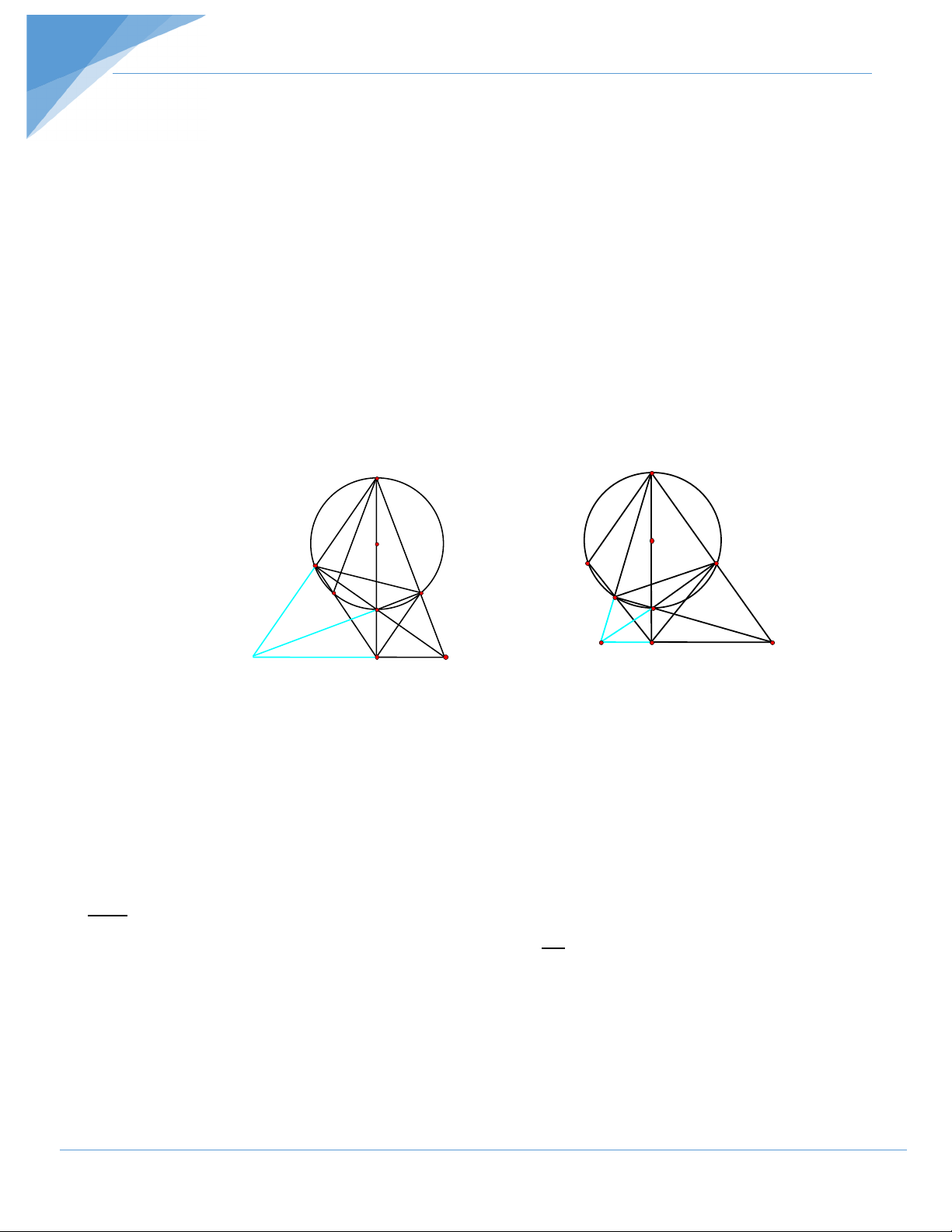
5. Chứng minh điểm M là tâm đường tròn nội tiếp tam giác ADE. Hướng dẫn giải C C 2 1 1 2 3 O O 3 D E S 2 1 1 S 2 M E D 2 M 1 1 2 2 1 2 2 3 1 3 1 F A F A B B H×nh a H×nh b 1. Ta có  0
CAB = 90 ( vì tam giác ABC vuông tại A);  0
MDC = 90 ( góc nội tiếp chắn nửa đường tròn ) =>  0
CDB = 90 như vậy D và A cùng nhìn BC dưới một góc bằng 900 nên
A và D cùng nằm trên đường tròn đường kính BC => ABCD là tứ giác nội tiếp.
2. ABCD là tứ giác nội tiếp =>  = 
D C ( nội tiếp cùng chắn cung AB). 1 3  = 
D C =>  =  SM EM =>  =  C
C (hai góc nội tiếp đường tròn (O) chắn hai cung bằng 1 3 2 3
nhau) => CA là tia phân giác của góc SCB. TH2 (Hình b)  =  ABC CME (cùng phụ  ACB );  =  ABC CDS (cùng bù  ADC ) =>  =  CME CDS =>  =  ⇒  =  CE CS SM EM =>  =  SCM
ECM => CA là tia phân giác của góc SCB.
3. Xét ∆CMB Ta có BA⊥CM; CD ⊥ BM; ME ⊥ BC như vậy BA, EM, CD là ba đường cao
của tam giác CMB nên BA, EM, CD đồng quy. 4. Theo trên Ta có  =  SM EM =>  = 
D D => DM là tia phân giác của góc ADE.(1) 1 2
Toán Họa: 0986 915 960 – Tổng hợp. 4
Chủ đề 6: Chứng minh các đường thẳng đồng quy 5. Ta có  0
MEC = 90 (nội tiếp chắn nửa đường tròn (O)) =>  0 MEB = 90 . Tứ giác AMEB có  0 MAB = 90 ;  0
MEB = 90 =>  +  0
MAB MEB = 180 mà đây là hai góc
đối nên tứ giác AMEB nội tiếp một đường tròn =>  =  A . B 2 2
Tứ giác ABCD là tứ giác nội tiếp =>  = 
A B ( nội tiếp cùng chắn cung CD) 1 2 =>  =  1 A
A => AM là tia phân giác của góc DAE (2) 2
Từ (1) và (2) ta có M là tâm đường tròn nội tiếp tam giác ADE.
Bài 4: Cho đường tròn (O) đường kính AB. Trên đoạn thẳng OB lấy điểm H bất kì ( H
không trùng O, B); trên đường thẳng vuông góc với OB tại H, lấy một điểm M ở ngoài
đường tròn; MA và MB thứ tự cắt đường tròn (O) tại C và.
D. Gọi I là giao điểm của AD và BC.
1. Chứng minh MCID là tứ giác nội tiếp.
2. Chứng minh các đường thẳng AD, BC, MH đồng quy tại I.
3. Gọi K là tâm đường tròn ngoại tiếp tứ giác MCID, Chứng minh KCOH là tứ giác nội Hướng dẫn giải M 1.  C =  0
BCA BDA=90 ( nội tiếp chắn nửa đường tròn ) …. K =>  +  0
MCI IDM = 180 mà đây là hai góc đối của tứ giác I D
MCID nên MCID là tứ giác nội tiếp.
2. AD, MC, MH là ba đường cao của tam giác BAM nên A B O H đồng quy tại I.
3. Chỉ ra KCI là tam giác cân, từ đó  =  =  =  CIK HIB CAB ACO  +  =  +  0
ACO OCI KCI OCI = 90 . Từ đó chỉ ra  0
OCK = 90 …. (tự chứng minh)
Bài 5: Cho tam giác nhọn ABC nội tiếp đường tròn (O;R). Tiếp tuyến tại B và C của
đường tròn (O;R) cắt nhau tại T, đường thẳng AT cắt đường tròn tại điểm thứ hai là D khác A. 1.Chứng minh rằng A ∆ BT” ∆ BDT.
2. Chứng minh rằng : AB.CD = BD.AC
3. Chứng minh rằng hai đường phân giác góc BAC; BDC và đường thẳng BC đồng quy tại một điểm
Toán Họa: 0986 915 960 – Tổng hợp. 5
Chủ đề 6: Chứng minh các đường thẳng đồng quy Hướng dẫn giải
1. Xét tam giác ABT và tam giác BDT có:  BTD chung  = 
BAT TBD (góc nội tiếp và góc tạo bởi tiếp
tuyến và dây cùng chắn cung BD). => A ∆ BT” ∆ BDT. (g-g) 2. Có A ∆ BT” ∆ BDT. (g-g) AB AT => = (1) BD BT Chứng minh được A ∆ CT ” CD ∆ T (g-g) AC AT => = (2) CD CT
Tiếp tuyến tại B và C cắt nhau tại T nên BT = CT (3)
Từ (1), (2), (3) có AB AC = => A . B CD = B . D AC BD CD
3. Phân giác góc BAC cắt BC tại I, theo tính chất phân giác trong tam giác ta có: IB AB = IC AC Từ AB.CD = BD.AC AB BD IB BD => = => = AC CD IC CD
=> DI là phân giác góc BDC
Do đó hai đường phân giác góc BAC và BDC và đường thẳng BC đồng quy.
Bài 6: Cho nửa đường tròn ( O) đường kính AB. Vẽ 2 tiếp tuyến Ax và By. Lấy M trên
đường tròn sao cho AM < BM. AM cắt By tại F, BM cắt Ax tại E. a. Chứng minh: 2 AB = . AE BF
b. Tiếp tuyến của đường tròn tại M cắt AE, BF tại C và D. Chứng minh C và D là trung điểm của AE và BF.
c. Chứng minh các đường thẳng AB, CD, EF đồng quy. Hướng dẫn giải a. Ta có 
AMB = 90º (góc nội tiếp chắn nửa đường tròn)⇒AM ⊥BE Xét ∆EAB và ∆ABF có:    = 
EAB=ABF; AEB FAB (cùng phụ với  EAM )
Toán Họa: 0986 915 960 – Tổng hợp. 6
Chủ đề 6: Chứng minh các đường thẳng đồng quy Suy ra ∆EAB ~ ∆ABF ( g.g) ⇒ AB AE = ⇔ AB2 = AE. BF BF AB
b. CA = CM và CO là tia phân giác của  ACM
⇒ ∆AMC cân tại C và CO là đường cao ⇒ CO ⊥AM
Do đó trong ∆ABE có OA=OB, OC//BE nên CA=CE.
c. Gọi giao điểm của AB và EF là S. Ta sẽ chứng minh S, C, D thằng hàng.
Giả sử SC cắt BF tại D’. Vì AE // BF nên theo định lí Ta-let, có: AC BD' =
=1 ⇒ D’ là trung điểm của BF CE D'F
⇒ D trùng với D’ hay S, C, D thẳng hàng.
Vậy ba đường thẳng AB, EF, CD đồng quy tại S.
Bài 7: Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O;R). H là trực
tâm của tam giác ABC . Vẽ đường kính AD của đường tròn (O); vẽ OM  BC tại M . a) Chứng minh rằng 1 OM  AH 2
b) Gọi G là trọng tâm của tam giác ABC . Chứng minh rằng H,G,O thẳng hàng và HG  2GO .
c) Gọi B ,C  lần lượt là trung điểm của các cạn ,
CA AB . Đường thẳng d qua M song 1
song với OA , đường thẳng d qua B song song với OB , đường thẳng d qua C  2 3 song song với OC .
Chứng minh rằng các đường thẳng d ,d ,d đồng qui. d 1 2 3 1 A Hướng dẫn giải N
a) HB  AC (H là trực tâm của A  BC ) G O H
AD là đường kính nên  0
ACD  90 BH  AC, DC  AC  BH  DC B M C
Chứng minh tương tự có: CH  DB D
Do đó tứ giác BHCD là hình bình hành
Toán Họa: 0986 915 960 – Tổng hợp. 7
Chủ đề 6: Chứng minh các đường thẳng đồng quy Ta có: O A   BC
 M là trung điểm của HD
OM là đường trung bình của AHD  nên 1 OM  AH 2 b) A
 BC có AM là đường trung tuyến, G thuộc đoạn thẳng AM và 2 AG  AM nên 3
G là trọng tâm của tam giác AHD . HO là đường trung tuyến nên HO đi qua G và HG  2GO
Gọi N là giao điểm của d với AH 1 HAD 
có MN  AD , M là trung điểm của HD
 N là trung điểm của AH Ta có: 1
NH  OM( AH ), NH OM 2
Do đó HNOM là hình bình hành.
 d đi qua trung điểm I của OH 1
Chứng minh tương tự có d ,d đi qua I 2 3
Vậy các đường thẳng d ,d ,d đồng quy 1 2 3
Bài 8: Trên các cạnh AB,BC của tam giác ABC dựng ra phía ngoài tam giác các hình
vuông ACAA và BCB B . Chứng minh rằng các đường thẳng AB ,AB,A B đồng quy. 1 2 1 2 1 1 2 2 B1 Hướng dẫn giải
Trường hợp 1: C  0
90 . Rõ ràng AB ,A B,A B đồng quy tại C . 1 1 2 2 A2 C Trường hợp 2:  0 C  90 B2
Các đường tròn ngoại tiếp hình vuông ACAA và BCB B 1 2 1 2 A2
Có điểm chung c sẽ cắt nhau tại M (khác C ) A B Ta có:  0
AMA  45 (góc nội tiếp chắn cung một phần tư đường tròn) 2   0
A MC  A AC  90 (góc nội tiếp chắn nửa đường tròn) 2 2 Tương tự:  0 CMB  45 1
Vì tia MA nằm giữa hai tia MA và MC ,tia MC nằm giữa hai tia MB và MA 2 2 nên    0 0 0 0
AMA  A MC CMB  45  90  45  180 2 2 1
Toán Họa: 0986 915 960 – Tổng hợp. 8
Chủ đề 6: Chứng minh các đường thẳng đồng quy hay ,
A M, B thẳng hàng.
Chứng minh tương tự A ,M,B và A ,M,B thẳng hàng 1 2 2
Vậy AB ,AB và A B cùng đi qua M 1 1 2 2
Hay AB ,AB và A B đồng quy. 1 1 2 2
Bài 9: Cho đường tròn ( ;
O R) , đường kính BC , A là điểm trên đường tròn ( A khác B
và C ). Kẻ AH vuông góc với BC ( H thuộc BC ). Đường tròn tâm I đường kính AH
cắt AB, AC và đường tròn (O) tại D, E, F
a) Chứng minh tứ giác BDEC nội tiếp
b) Chứng minh OA vuông góc với DE
c) Chứng minh các đường thẳng AF, DE, BC đồng quy d) Cho biết sđ 
AB = 60°. Tính theo R diện tích tứ giác BDEC Hướng dẫn giải A F E I D S B C H O
a) Chứng minh tứ giác BDEC nội tiếp: Ta có:  = 
ADH AEH = 90° (góc nội tiếp chắn nửa đường tròn) Ta lại có:  = 
ADE AHE (góc nội tiếp cùng chắn cung AE )  = 
AHE ACB (cùng phụ với  EHC )
Vậy tứ giác BDEC nội tiếp (góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện)
Toán Họa: 0986 915 960 – Tổng hợp. 9
Chủ đề 6: Chứng minh các đường thẳng đồng quy
b) Chứng minh OA ⊥ DE : Ta có: OA ∆
B cân tại O (OA = OB = R ) ⇒  =  OAB OBA . Mà  + 
OBA ACB = 90° ( A
∆ BC vuông tại A )  =  AHE ACB ⇒  + 
OAB ADE = 90° hay OA ⊥ DE
c) Chứng minh các đường thẳng AF, DE, BC đồng quy:
Gọi S là giao điểm của AF và BC S
∆ AO có: AH ⊥ BC (gt)
OI ⊥ AS (tính chất đường nối tâm của 2 đtr cắt nhau)
⇒ SI ⊥ OA (đường cao thứ ba trong S ∆ AO )
Mà OA ⊥ DE (câu b)
⇒ S, D, I, E thẳng hàng hay đường thẳng DE qua S .
Vậy các đường thẳng AF, DE, BC đồng quy
d) Tính theo R diện tích tứ giác BDEC : Ta có: A sd AB
∆ BC vuông tại A ,   60 ACB ° = = = 30° 2 2 AB = BC.sin 30° 1 = 2 . R = R ; 3
AC = BC.cos30° = 2 . R = R 3 2 2
AH.BC = A . B AC A . B AC . R R 3 R 3 ⇒ AH = = = BC 2R 2 Ta lại có: A
∆ DE đồng dạng A ∆ CB   2 2 2 S  BC   BC   R   R  ACB 2 4 16 ⇒ = = =   = = S   DE     AH    ADE 
 R 3   R 3  3  2    S S S − S S 2 ACB 13. ADE ACB ADE BDEC ⇒ = = = S AB AC R R R ACB 13 . 13 . 3 13 3 ⇒ S = = ⋅ = ⋅ = 16 3 16 − 3 13 BDEC 16 16 2 16 2 32
Toán Họa: 0986 915 960 – Tổng hợp. 10
Chủ đề 6: Chứng minh các đường thẳng đồng quy
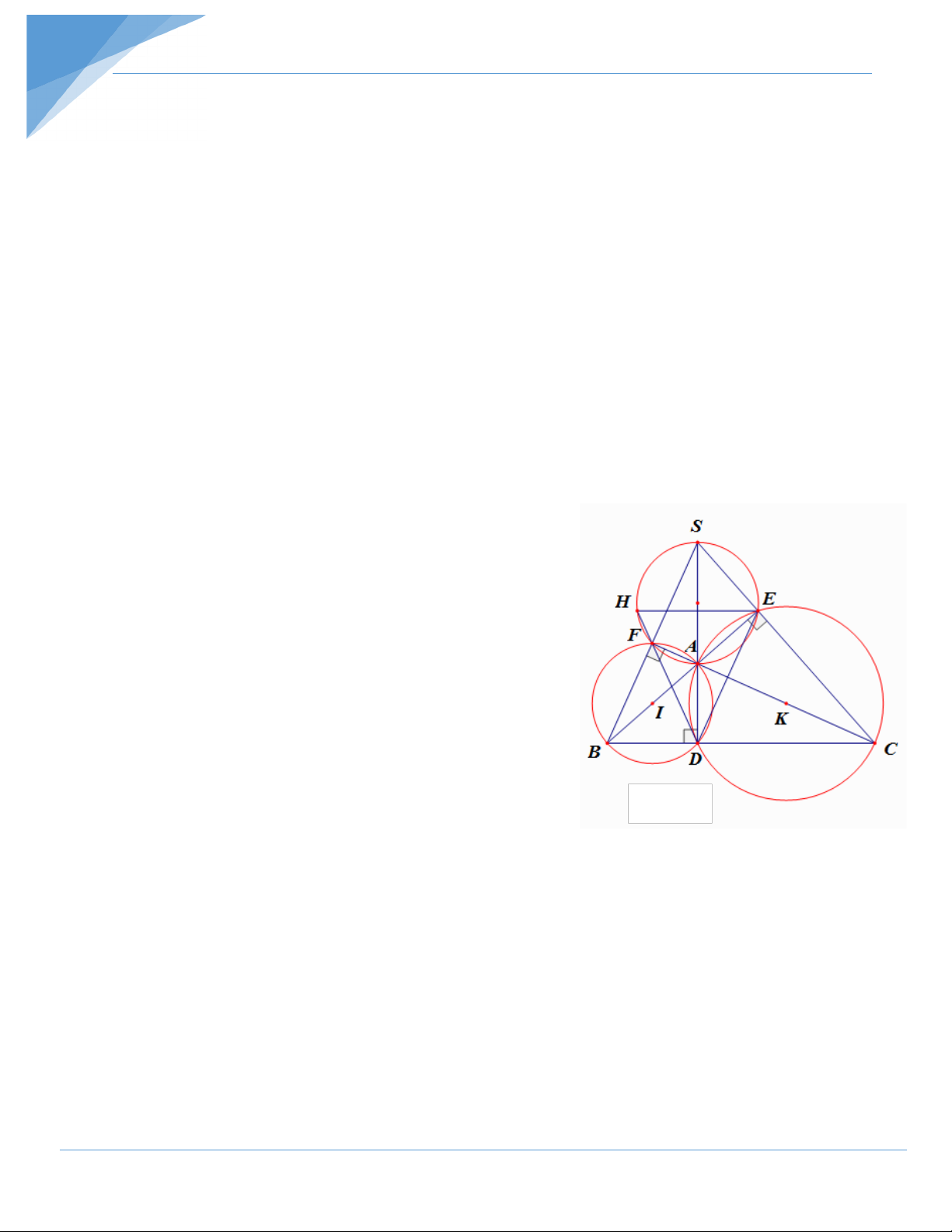
Bài 10: Cho tam giác ABC vuông tại A , I là một điểm trên cạnh AC . Đường tròn đường
kính IC cắt BC ở E và cắt BI ở D .
a) Chứng minh tứ giác ABCD nội tiếp được trong đường tròn.
b) Chứng minh DB là phân giác của góc ADE .
c) Chứng minh I là tâm đường tròn nội tiếp tam giác ADE .
d) Chứng minh AB,CD, EI đồng qui. Hướng dẫn giải
a) Chứng minh tứ giác ABCD nội tiếp được trong đường tròn. Ta có C 
BDC = 90°(góc nội tiếp chắn nửa đường tròn). 
CAB = 90° ( tam giác ABC vuông tại A ). E
Mặt khác hai đỉnh D, A cùng nhìn BC dưới một góc D 90°. I
Vậy tứ giác ABCD nội tiếp được trong đường tròn.
b) Chứng minh DB là phân giác của góc ADE . K A B
Do tứ giác ABCD nội tiếp được trong đường tròn. Nên  = 
ADB ACB (cùng chắn cung AB ).  = 
IDE ACB (cùng chắn cung IE của đường tròn đường kính IC ). ⇒  =  ADB BDE .
Vậy DB là phân giác của góc  ADE .
c) Chứng minh I là tâm đường tròn nội tiếp tam giác ADE .
Chứng minh được tứ giác ABEI nội tiếp được trong đường tròn. ⇒  = 
CAE CBD (cùng chắn cung IE ).
Mặt khác vì tứ giác ABCD nội tiếp được trong đường tròn.
Toán Họa: 0986 915 960 – Tổng hợp. 11
Chủ đề 6: Chứng minh các đường thẳng đồng quy Nên  = 
CAD CBD (cùng chắn cung CD ). ⇒  = 
CAE CAD ⇒ AC là phân giác của góc DAE .
Mà DB cắt AC tại I . Do đó I là tâm đường tròn nội tiếp tam giác ADE .
d) Chứng minh AB,CD, EI đồng qui.
Gọi K là giao điểm của AB và CD . Ta có 
BDC = 90°(góc nội tiếp chắn nửa đường tròn) ⇒ BD ⊥ KC . 
CAB = 90° ( tam giác ABC vuông tại A )⇒ CA ⊥ KB . CKB ∆
có BD và CA là hai đường cao cắt nhau tại I nên I là trực tâm của CKB ∆
⇒ KE là đường cao của CKB ∆
⇒ KE ⊥ BC(1). Mặt khác 
IEC = 90°(góc nội tiếp chắn nửa đường tròn) ⇒ IE ⊥ CE ⇒ IE ⊥ BC(2) .
Từ (1),(2) suy ra E, I, K thẳng hàng.
Vậy AB,CD, EI đồng qui tại K .
Bài 11: Cho tam giác ABC vuông tại A . Trên cạnh AC lấy điểm M không trùng với A
và C . Vẽ đường tròn đường kính MC , cắt cạnh BC tại D . Các đường thẳng BM và
AD lần lượt cắt đường tròn tại các điểm E, F . Chứng minh rằng: a) A ∆ BC ∽ D
∆ MC . Suy ra A .
B MC = BC.DM .
b) Các tứ giác ABDM và AECB nội tiếp c) AB//EF .
d) Các đường thẳng AB,CE,MD đồng quy. Hướng dẫn giải
Toán Họa: 0986 915 960 – Tổng hợp. 12
Chủ đề 6: Chứng minh các đường thẳng đồng quy B D F A M C E I a) Vì  =  BAC MDC = 90°và 
BCA chung nên A ∆ BC ∽ D ∆ MC . Do đó AB BC = ⇒ A .
B MC = BC.DM . DM MC b) Vì  + 
BAM MDB =180° nên tứ giác AMDB nội tiếp. Vì  = 
BAC BEC = 90° nên tứ giác AECB nội tiếp. c) Ta có:  = 
ABM ADM ( cùng chắn  AM )  = 
MEF ADM ( cùng chắn  MF ) Suy ra  = 
ABM MEF ⇒ AB//EF .
d) Giả sử AB cắt EC tại I . Ta có C ,
A BE là đường cao của tam giác BIC .
⇒ M là trực tâm của B
∆ IC ⇒ IM ⊥ BC .
Mà MD ⊥ BC ⇒ I, M , D thẳng hàng. Vậy AB, EC,MD đồng quy tại M .
Toán Họa: 0986 915 960 – Tổng hợp. 13
Chủ đề 6: Chứng minh các đường thẳng đồng quy
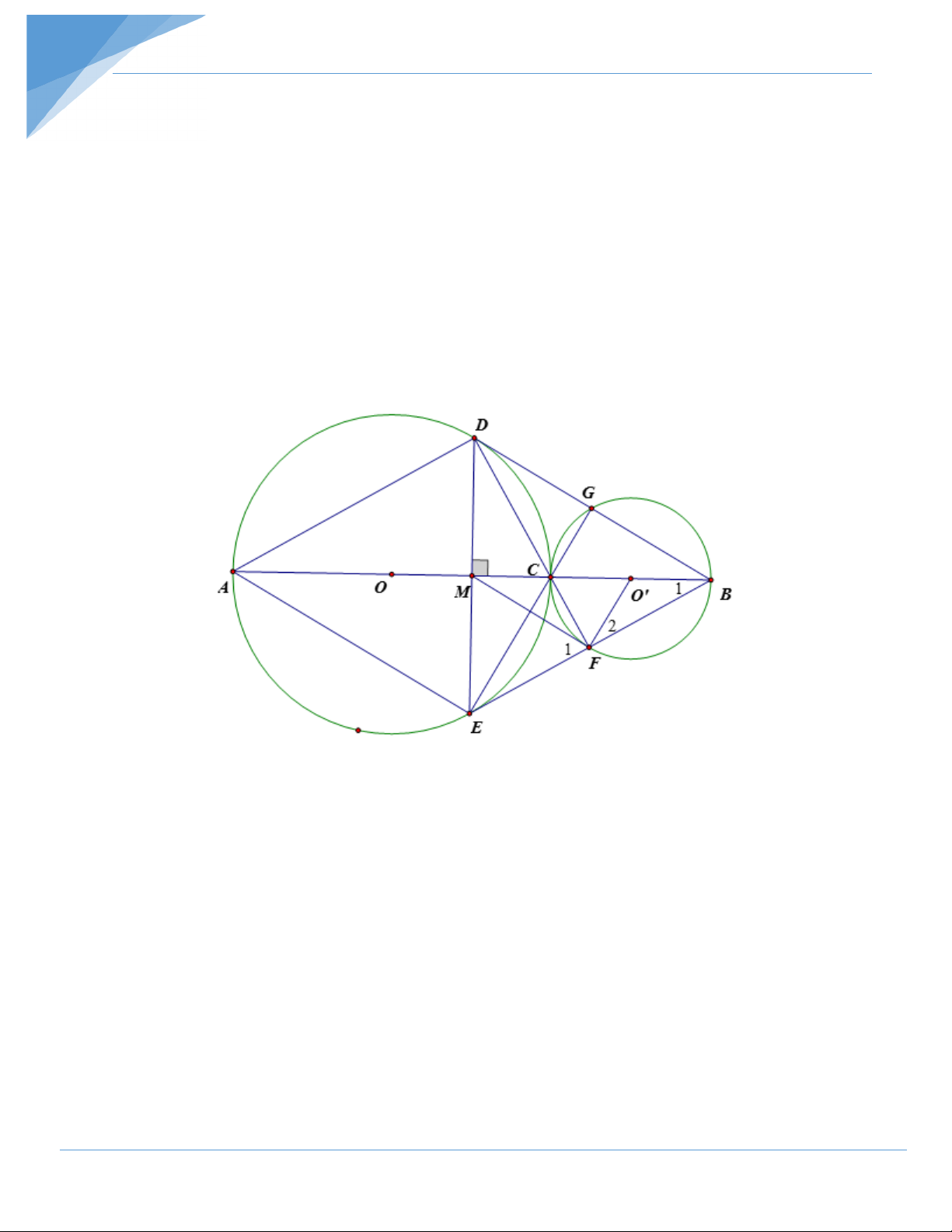
Bài 12: Hai đường tròn ( ;
O R) và (O';r) tiếp xúc ngoài tại C (R > r) gọi AC và BC là hai
đường kính đi qua C của đường tròn (O) và (O') . DE là dây cung của đường tròn (O)
vuông góc với AB tại trung điểm M của AB. Tia DC cắt đường tròn (O') tại điểm thứ 2 là F
a) Tứ giác ADBE là hình gì? Vì sao?
b) Chứng minh ba điểm B, F, E thẳng hàng
c) DB cắt đường tròn (O') tại điểm thứ hai là G. Chứng minh DF, EG và AB đồng quy
d) Chứng minh MF là tiếp tuyến của (O') Hướng dẫn giải
a) Tứ giác ADBE là hình thoi vì AM = MB; MD = ME và DE ⊥ AB
b) Ta có BE / /DA . Nối BF ta có  =  0
ADF BFD = 90 ⇒ BF / /DA. Như vậy BE / /DA và
BF / /DA mà qua B chỉ có duy nhất một đường thẳng song song với DA do đó 3 điểm B, F, E phải thẳng hàng
c) Ta có CG vuông góc với DB, mặt khác EC vuông góc với DB. Nhưng qua C chỉ tồn
tại duy nhất một đường vuông góc với DB nên E, C , G phải thẳng hàng và DF, EG,
AB phải đồng quy tại điểm C, chính là trực tâm tam giác EDB d) Nhận thấy  =  MEF F và  = 
O ' BF F mà  +  0
MEF O 'BF = 90 nên  +  0 F F = 90 , suy ra 1 2 1 2  0
MFO ' = 90 . Vậy MF là tia tiếp tuyến của đường tròn tâm O’.
Toán Họa: 0986 915 960 – Tổng hợp. 14
Chủ đề 6: Chứng minh các đường thẳng đồng quy
Bài 13: Cho ∆ABC (AC > AB,  0
BAC = 90 ). Gọi I, K theo thứ tự là trung điểm của AB,
AC. Các đường tròn đường kính AB, AC cắt nhau tại điểm thứ hai D; tia BA cắt
đường tròn (K) tại điểmt hứ hai E; tia CA cắt đường tròn (I) tại điểm thứ hai F
a) Chứng minh B, C, D thẳng hàng
b) Chứng minh tứ giác BFEC nội tiép
c) Chứng minh ba đường thẳng AD, BF, CE đồng quy.
d) Gọi H là giao điểm thứ hai của tia DF với đường tròn ngoại tiếp tam giác AEF, hãy so sánh DH và DE. Hướng dẫn giải
a) ) Áp dụng định lý góc nội tiếp chắn nửa đường tròn, ta có : ADB � = 900; ADC � = 900 . Suy ra  +  0 ADB ADC = 1 80 . Vậy B, D, C thẳng hàng.
b) Áp dụng định lý góc nội tiếp
chắn nửa đường tròn, ta có: BFA � = 900; CEA � = 900; suy ra   BFC = BEC ( 0 = 90 ). Khi đó ;
E F là hai đỉnh liên
tiếp cùng nhìn BC dưới một góc bằng nhau.
Vậy tứ giác BFEC nội tiếp.
c) Xét tam giác ABC có AD ⊥ BC; BF ⊥ AC;CE ⊥ AB .
Suy ra AD,BF,CE là ba đường cao. Vậy chúng cắt nhau tại một điểm S .
d) Ta có AEHF nội tiếp nên  
EHF = FAB mặt khác    
FAB = FDB ⇒ EHF = FDB
⇒ HE / / BC ⇒ AD ⊥ HE. (1)
Vận dụng góc nội tiếp, tứ giác nội tiếp ta có:    
FDA = FBA = FCE = ADE
⇒ DA là đường phân giác  EDF (2)
Từ (1) và (2) suy ra DEH cân tại D suy ra DE = DH .
Toán Họa: 0986 915 960 – Tổng hợp. 15
Chủ đề 6: Chứng minh các đường thẳng đồng quy
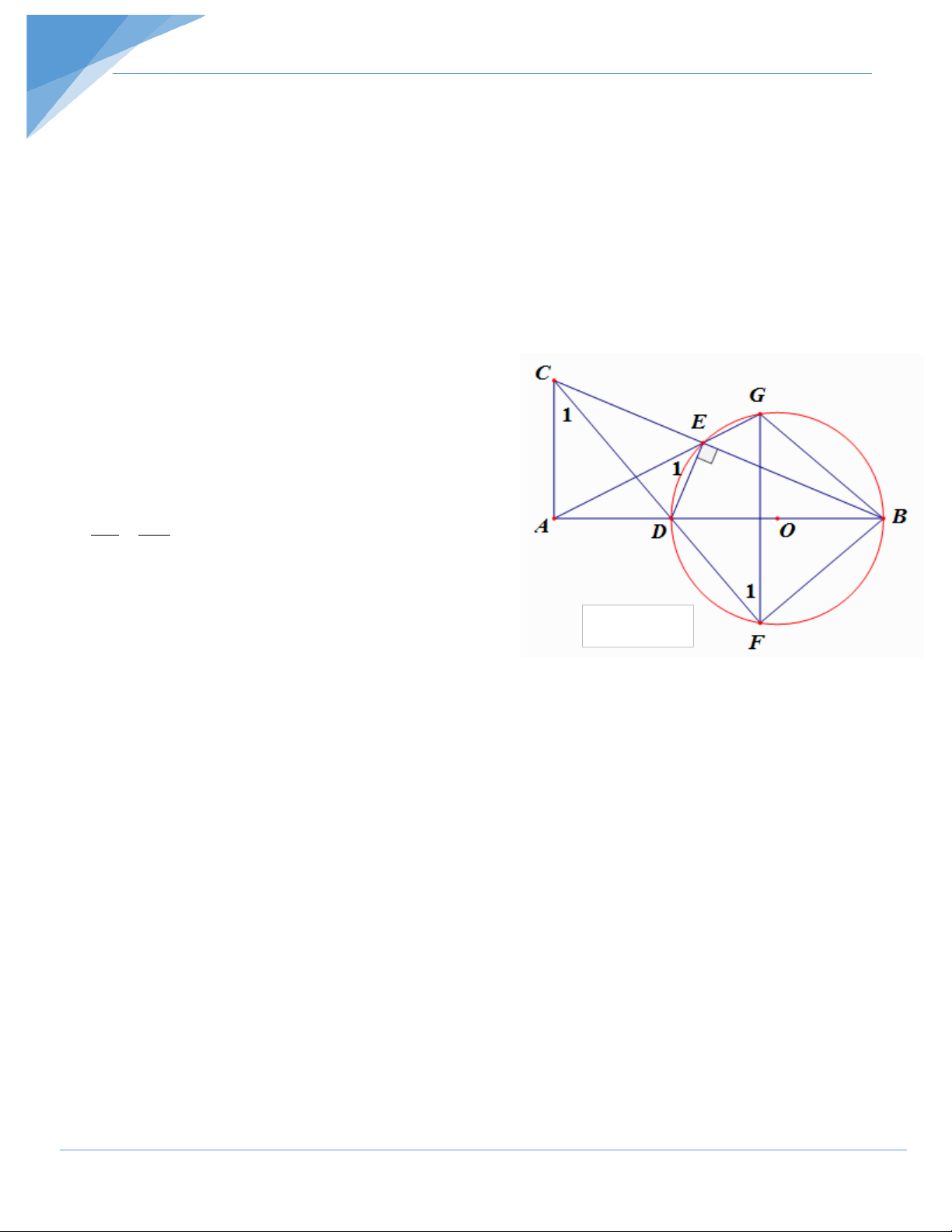
Bài 14: Cho tam giác ABC vuông tại A và một điểm D nằm giữa A và B. Đường tròn
(O) đường kính BD cắt BC tại E. Các đường thẳng CD, AE lần lượt cắt đường tròn (O)
tại các điểm thứ hai là F, G. Chứng minh rằng :
a) Các tứ giác ADEC và AFBC nội tiếp b) AD.AB = AG.AE c) AC//FG d) AC, DE và BF đồng quy. Hướng dẫn giải a)  0  0
CAD = 90 ,CED = 90 ⇒ tứ giác ADEC nội tiếp.  0  0
CAB = 90 ,CFB = 90 ⇒ tứ giác AFBC nội tiếp.
b) Ta có ∆AED” ∆ABG( .gg) ⇒ AE AD = ⇒ . AD AB = . AE . AG AB AG
c) Tứ giác ACED nội tiếp ⇒   C = E . 1 1
Tứ giác DFGE nội tiếp ⇒   F = E . 1 1 Suy ra  
C = F ⇒ AC / /GF . 1 1 d) B
∆ CD có CA,BF,DE là đường cao ⇒ CA,BF,DE đồng quy.
Toán Họa: 0986 915 960 – Tổng hợp. 16
Chủ đề 6: Chứng minh các đường thẳng đồng quy
Một số bài tập tự rèn:
Bài 1: Cho hai đường tròn (O) và ( O') cắt nhau tại A, B. Kẻ đường kính AC của (O) cắt
đường tròn (O') tại F. Kẻ đường kính AE của ( O') cắt đường tròn (O) tạo G. Chứng minh:
a) Tứ giác GFEC nội tiếp ; b) GC, FE, AB đồng quy.
Bài 2: Cho đường tròn (O) đường kính AB, gọi I là trung điểm của OA, dây CD vuông
góc với AB tại I. Lấy K tùy ý trên dây cung BC nhỏ, AK cắt CD tại H.
a. Chứng minh tứ giác BIHK nội tiếp.
b. Chứng minh AH.AK có giá trị không phụ thuộc vị trí điểm K
c. Kẻ DN  CB, DM  AC. Chứng minh các đường thẳng MN, AB, CD đồng quy.
Bài 3: Cho đường tròn (O) đường kính AB, gọi I là trung điểm của OA, dây CD vuông
góc với AB tại I. Lấy K tùy ý trên dây cung BC nhỏ, AK cắt CD tại H.
a) Chứng minh tứ giác BIHK nội tiếp.
b) Chứng minh AH.AK có giá trị không phụ thuộc vị trí điểm K
c) Kẻ DN  CB, DM  AC. Chứng minh các đường thẳng MN, AB, CD đồng quy
Bài 4: Cho đường tròn (O) đường kính AB, Gọi I là trung điểm OA. Dây CD vuông góc
với AB tại I. Lấy K tùy ý trên cung BC nhỏ. AK cắt CD tại H
a, Chứng minh tứ giác BIHK nội tiếp
b, Chứng minh AH.AK có giá trị không phụ thuộc vào vị trí điểm K .
c, kẻ DN  CB, DM  AC . chứng minh MN,AB, CD đồng quy .
d, Cho BC = 25cm . Hãy tính diện tích xung quanh hình trụ tạo thành khi cho tứ giác MCND quay quanh MD.
Chúc các em học sinh học tập tốt!
Toán Họa: 0986 915 960 – Tổng hợp.
Document Outline

• HCD6_DongQuy
  • F. CÁC BÀI TOÁN CHỨNG MINH ĐỒNG QUY
  • Bài tập có giải
  • Một số bài tập tự rèn: