































Preview text:
CHỦ ĐỀ 19: BÀI TOÁN CỰC TRỊ TỌA ĐỘ KHÔNG GIAN
I. LÝ THUYẾT TRỌNG TÂM
II. CÁC DẠNG TOÁN TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Tìm điểm M thuộc (P) sao cho u = aMA + bMB + cMC có u đạt min. Phương pháp giải:
ax + bx + cx A B C x = 1 a + b + c
+Tìm điểm I thõa mãn hệ thức + +
aIB + bIB + cIC = 0 tọa độ điểm I là: ay by cy A B C y = 1 a + b + c
az + bz + cz A B C z = 1 a + b + c
Phân tích u = aMA + bMB + cMC = (a + b + c) MI + (aIA+bIB + cIC) = (a +b + c)MI
Khi đó u = a + b + c MI ⇒ u
⇔ M là hình chiếu vuông góc của I lên (P). min
Viết phương trình đường thẳng IM đi qua I và vuông góc với (P) ⇒ u = n IM (P)
Khi đó M = (P) ∩(IM ).
Ví dụ 1: Cho các điểm A(2;1;− ) 1 ; B( 0;3; )
1 và (P) : x+ y− z+ 3 = 0 . Tìm điểm M thuộc (P) sao cho a) MA + MB . min b) 2MA − MB . min Lời giải
a) Gọi I (1;2;0) là trung điểm của AB thì IA+ IB = 0
Ta có: MA + MB = 2MI nhỏ nhất ⇔ MI ⇔ là M là hình chiếu của điểm I trên (P) min x =1+ t
Phương trình đường thẳng MI là: y = 2 + t ⇒ M (1+ t;2 + t; t − ) z = t−
Cho M ∈(P) ⇒1+ t + 2 + t + t + 3 = 0 ⇔ t = 2 − ⇒ M ( 1; − 0;2). 2x − x A B x = = 4 1 2 −1
b) Gọi I là điểm thỏa mãn 2 2 − IA − IB = 0 y y A B ⇒ y = = 1 − 1 2 −1 2z − z A B z = = 3 − 1 2 −1
Ta có: 2MA − MB = 2MI + 2IA − (MI + IB) = MI = MI nhỏ nhất ⇔ M là hình chiếu của điểm I trên x = 4 + t
(P). Phương trình đường thẳng MI là: y = 1
− + t ⇒ M (4 + t; 1 − + t; 3 − − t) z = 3 − − t
Cho M ∈(P) ⇒ 4 + t −1+ t + 3+ t + 3 = 0 ⇔ t = 3 − ⇒ M (1; 4 − ;0).
Ví dụ 2: Cho các điểm A(1;0;− ) 1 ; B( 2; 2 − )
;1 C (0;− ;10) và (P) : x− 2 y+ 2z+ 6 = 0 . Tìm điểm M thuộc (P) sao cho
a) MA + MB + MC . min
b) 2MA − 4MB + 3MC . min Lời giải G (0;1; 2 − )
a) Gọi G là trọng tâm tam giác ABC ⇒ . GA + GB + GC = 0
Ta có: MA + MB + MC = 3MG = 3MG ⇔ M là hình chiếu của G trên mặt phẳng (P). x = t
Phương trình đường thẳng MG khi đó là: y = 1
− − 2t ⇒ M (t; 1 − − 2t; 2 − + 2t) z = 2 − + 2t
Cho M ∈(P) ⇒ t + 4t − 2 + 4t − 4 + 6 = 0 ⇔ t = 0 ⇒ M (0;1; 2 − ) .
2x − x + x A 4 B 3 C x = = 6 − 1 2 − 4 + 3
b) Gọi I là điểm thỏa mãn
2y − y + y A 4 B 3
2IA − 4IB + 3IC = 0 C ⇒ y = = 5 1 2 − 4 + 3
2z − z + z A 4 B 3 C z = = 6 − 1 2 − 4 + 3 x = 6 − + t
Phương trình đường thẳng MI khi đó là: y = 5− 2t ⇒ M ( 6
− + t;5 − 2t; 6 − + 2t) z = 6 − + 2t Cho 22 32 89 10 M (P)
6 t 4t 10 4t 12 6 0 t M − ; ; ∈
⇒ − + + − + − + = ⇔ = ⇒ − . 9 9 9 9
Ví dụ 3: Cho các điểm A(4;1;− ) 1 ; B( 2;3; 2 − )C (6;3; 1
− 2) và (P) : x+ 2 y− z+1 = 0 . Tìm điểm M thuộc (P)
sao cho 2MA + 3MB − MC
. Độ dài đoạn thẳng OM là: min A. OM = 5 . B. OM = 3 . C. OM = 3. D. OM = 9 . Lời giải
2x + x − x A 3 B C x = = 2 1 2 + 3−1
Gọi I là điểm thỏa mãn
2y + y − y A 3
2IA + 3IB − IC = 0 B C ⇒ y = = 2 1 2 + 3−1
2z + z − z A 3 B C z = = 1 1 2 + 3−1 x = 2 + t
Phương trình đường thẳng MI khi đó là: y = 2 + 2t ⇒ M (2 + t;2 + 2t;1−t) z =1− t
Cho M ∈(P) ⇒ 2 + t + 4t + 4 + t −1+1 = 0 ⇔ t = 1
− ⇒ M (1;0;2) ⇒ OM = 5 . Chọn A.
Ví dụ 4: Trong không gian tọa độ Oxyz cho tam giác ABC có A( 1 − ;2;3); B( 3;0;− ) 1 C (1;4;7) và
(P) : x− 2 y+ 2z+ 6 = 0 . Gọi M (a; ;
b c) là điểm thuộc mặt phẳng (P) sao cho 2 2 2
MA + MB + MC nhỏ nhất. Giá trị biểu thức 2 2 2
T = a + b + c là. A. T =10 . B. T =17 . C. T = 21. D. T = 26. Lời giải:
Gọi G (1;2;3) là trọng tâm tam giác ABC thì GA+ GB + GC = 0. Ta có: 2 2 2 2 2 2
MA + MB + MC = MA + MB + MC = (MG +GA)2 +(MG +GB)2 +(MG +GC)2
2
= MG + MG (GA+GB +GC) 2 2 2 3 2
+ GA + GB + GC = 2 2 2 2
3MG + GA + GB + GC nhỏ nhất khi M là hình chiếu của G trên mặt phẳng (P)
Phương trình MG: x −1 y − 2 z − 3 = =
suy ra M = MG ∩ (P) ⇒ M(0;4;1) 1 2 − 2 Do đó 2 2 2
T = a + b + c =17 . Chọn B.
Ví dụ 5: Trong không gian tọa độ Oxyz cho mặt phẳng cho 3 điểm A(0; 3 − ; ) 1 ; B( 2;7; ) 1 và C (1;0;3) và
mặt phẳng (P) có phương trình x+ y− z− 3 = 0 . Gọi M (a; ;
b c) trên (P) sao cho MA + MB + 2MC nhỏ
nhất. Tính giá trị của T = a + 2b − 3c . A. T = 0 . B. T = 4. C. T = 3. D. T = 1 − . Lời giải: x + x + x A B 2 C x = = 1 1 1+1+ 2
Gọi I là điểm thỏa mãn y + y + y A B 2
IA + IB = IA + IB + 2IC = 0 C ⇒ y = = 2 ⇔ I 1;1;2 . 1 ( ) 1+1+ 2 z + z + z A B 2 C z = = 2 1 1+1+ 2
Khi đó MA + 2MB + 3MC = MI + IA + MI + IA + 2MI + 2IC = 4MI
Khi đó MA + MB + 2MC nhỏ nhất ⇔ MI ⇔ M là hình chiếu của điểm I trên mặt phẳng (P). min Ta có: x −1 y z −1 IM : = =
⇒ M = MI ∩ (P) ⇒ M(2;1;0)T = 4 . Chọn B. 1 1 1 −
Dạng 2: Tìm điểm M thuộc (P) sao cho 2 2 2
T = aMA + bMB + cMC đạt max hoặc min. Phương pháp giải:
+) Tìm điểm I thỏa mãn hệ thức aIA + bIB + cIC = 0 +) Phân tích 2 2 2 2 2 2
T = aMA + bMB + cMC = a(MI + IA) +b(MI + IB) + c(MI + IC)
⇒ (a + b + c) 2
MI + MI (aIA+bIB + cIC) 2 2 2 2
+ aIA + bIB + cIC 2 2 2 2
= (a + b + c)MI + aIA + bIB + cIC .
+) Nếu a + b + c > 0 thì T đặt min; a + b + c < 0 thì T đặt max.
Khi đó T T ⇔ MI → M là hình chiếu vuông góc của I lên (P). max ; min min
Ví dụ 1: Cho các điểm A( 3 − ;5; 5 − ); B( 5; 3
− ;7)C (1;0;3) và (P) : x+ y+ z = 0 . Tìm điểm M thuộc (P) sao cho a) 2 2
T = MA + MB đạt giá trị nhỏ nhất. b) 2 2
T = MA − 2MB đạt giá trị lớn nhất. Lời giải:
a) Gọi I là trung điểm của AB thì IA + IB = 0 . Ta có: 2 2 2 2 2
T = MA + MB = 2MI + IA + IB đạt giá trị nhỏ nhất ⇔ M là hình chiếu vuông góc của I x =1+ t
lên (P). Khi đó phương trình IM là: y =1+ t ⇒ M (1+ t;1+ t;1+ t) z =1+ t
Cho M ∈(P) ⇒ 3(1+ t) = 0 ⇔ t = 1 − ⇒ M (0;0;0) . x − x A 2 B x = =13 1 1− 2
b) Gọi I là điểm thỏa mãn y − y A 2 IA − 2IB = 0 B ⇒ y = = 11 − 1 1− 2 z − z A 2 B z = = 19 1 1− 2 Ta có: 2 2 2 2
T = MA − 2MB = MA − 2MB = (MI + IA)2 − 2(MI + IB)2 = 2 2 2
−MI + 2MI(IA − 2IB) + IA − 2IB = 2 2 2
−MI + IA − 2IB . Do 2 2
IA − 2IB không đổi nên 2
T ⇔ −MI lớn nhất khi đó MI ⇔ M là hình chiếu vuông góc của I max min x =13 + t
lên (P). Khi đó phương trình IM là: y = 11
− + t ⇒ M (13+ t; 11
− + t;19 + t). z =19+ t
Cho M ∈(P) ⇒ 21+ 3t = 0 ⇔ t = 7 − ⇒ M (6; 18 − ;12).
Ví dụ 2: Cho các điểm A(1;4;5); B( 0;3; ) 1 C (2; 1
− ;0) và (P) :3x− 3y− 2z −15 = 0 . Tìm điểm M thuộc (P) sao cho a) 2 2 2
T = MA + MB + MC đạt giá trị nhỏ nhất. b) 2 2 2
T = MA + MB − 4MC đạt giá trị lớn nhất. Lời giải: G (1;2;2)
a) Gọi G là trọng tâm của tam giác ABC ⇒ GA + GB + GC = 0 Ta có: 2 2 2
T = MA + MB + MC = (MG +GA)2 +(MG +GB)2 +(MG +GC)2
2 2 2 2 2 2 2 2
= 3MG + 2MG(GA + GB + GC) + GA + GB + GC = 3MG + GA + GB + GC Do đó T ⇔ M
⇔ M là hình chiếu vuông góc của G lên (P). min min x =1+ 3t
Khi đó phương trình MG là: y = 2 −3t ⇒ M (1+ 3t;2 −3t;2 −t) . z = 2− 2t
Giải M ∈(P) ⇒ 9t + 3+ 9t − 6 + 4t − 4 −15 = 0 ⇔ t =1⇒ M (4; 1 − ;0) .
x + x − x A 2 B 4 C x = = 7 1 1+ 2 − 4
b) Gọi I là điểm thỏa mãn
y + y − y A 2 B 4 IA + 2IB − 4 C IC ⇒ y = = 14 − 1 1+ 2 − 4
z + z − z A 2 B 4 C z = = 7 − 1 1+ 2 − 4 Biến đổi 2 2 2 2
T = −MI + IA + 2IB − 4IC đạt giá trị lớn nhất ⇔ MI ⇔ M là hình chiếu vuông góc của I min x = 7 + 3t
lên (P). Khi đó phương trình MI là: y = 14
− − 3t ⇒ M (7 + 3t; 14 − − 3t; 7 − − 2t) . z = 7 − − 2t Giải 31 − 16 61 − 15 M (P)
9t 21 9t 42 4t 14 15 0 t M ; ; − ∈ ⇒ + + + + + − = ⇔ = ⇒ − . 11 11 11 11
Ví dụ 3: Cho các điểm A(1;1;− ) 1 ; B( 2;0; ) 1 C (1; 1; − − )
1 và (P) : x+ 3y+ z + 2 = 0 . Biết điểm M thuộc (P) sao cho 2 2 2
T = MA + 2MB − MC đạt giá trị nhỏ nhất. Tính độ dài OM. A. OM = 6 . B. OM = 3 . C. OM = 2 . D. OM = 2 . Lời giải:
x + x − x A 2 B C x = = 1 1 1+ 2 −1
Gọi điểm I là điểm thỏa mãn
y + y − y A 2
IA + 2IB − IC = 0 B C ⇒ y = = 1 1 1+ 2 −1
z + z − z A 2 B C z = = 1 1 1+ 2 −1 Biến đổi 2 2 2 2
T = 2MI + IA − 2IB + IC đạt gía trị nhỏ nhất ⇔ MI ⇔ M là hình chiếu vuông góc của I min x = 2 + t
lên (P). Khi đó phương trình MI là: y =1+ t ⇒ M (2 + t;1+ t;1+ t) . z =1+ t
Giải M ∈(P) ⇒ 3t + 4 + 2 = 0 ⇔ t = 2 − ⇒ M (0; 1 − ;− )
1 ⇒ OM = 2 . Chọn C.
Ví dụ 4: Cho các điểm A(0;4; 2 − ); B( 1;2;− )
1 và (P) : x+ y+ z +1 = 0 . Biết điểm M thuộc (P) sao cho biểu thức 2 2
MA − 2MB đạt giá trị lớn nhất. Tính OM. A. OM = 6 . B. OM = 3 . C. OM = 2 . D. OM = 2 . Lời giải:
Gọi I là điểm thỏa mãn IA − 2IB = 0 ⇒ I (2;0;0). Biến đổi 2 2 2 2 2
MA − 2MB = −MI + IA − 2IB đạt giá trị lớn nhất khi M là hình chiếu vuông góc của I lên x = 2 + t
(P). Khi đó phương trình MI là: y = t −
⇒ M (2 + t; t − ;t) . z = t
Cho M ∈(P) ⇒ 2 + t + t + t +1 = 0 ⇔ t = 1 − ⇒ M (1;1;− )
1 ⇒ OM = 3 . Chọn B.
Ví dụ 5: Trong không gianOxyz , cho hai điểm A(1;2; ) 1 ; B( 2; 1;
− 3). Điểm M trên mặt phẳng (O sao xyz ) cho 2 2
MA − 2MB lớn nhất. Khi đó T = x + y có giá trị là M M A. T =1. B. T = 0 . C. T = 1 − . D. T = 2. Lời giải:
Gọi M là điểm thỏa mãn IA − 2IB = 0 ⇔ IA = 2IB ⇔ I (3; 4 − ;5) .
Khi đó MA − MB = (MI + IA)2 − (MI + IB)2 2 2 2 2 2 2
= −MI + 2MI(IA − 2IB) + IA − 2IB 2 2 2
= −MI + IA − 2IB lớn nhất ⇔ MI nhỏ nhất ⇔ M là hình chiếu của I trên mặt phẳng ( O ) xy Suy ra M (3; 4 − ;0) ⇒ T = 1 − . Chọn C.
Ví dụ 6: Trong không gian Oxyz ,cho 3 điểm A(4;1;5); B( 3;0 )
;1 ;C (− ;12;0) và mặt phẳng
(P) :3x− 3y+ 2z + 37 = 0 . Điểm M (a;b;c) thuộc (P) sao cho S = . MA MB + .
MB MC + MC.MA nhỏ nhất. Tính a+b+c. A. a+b+c=13. B. a+b+c=9. C. a+b+c=11. D. a+b+c=1. Lời giải: Gọi 7 1 1 3 3 5 D
; ;3;E 1;1; ;F ; ;
lần lượt là trung điểm của AB, BC và AC. 2 2 2 2 2 2
Ta có: = ( + )( + ) =( + )( − ) 2 2 2 2 . AB MA MB MD DA MD DB
MD DA MD DA = MD − AD = MD − 4 2 2 2 Suy ra 2 2 2 AB BC AC S MD ME MF + + = + + − nhỏ nhất 2 2 2
⇔ MD + ME + MF nhỏ nhất. 4
Gọi G (2;1;2) là trọng tâm tam giác DEF 2 2 2 2 2 2 2
⇒ MD + ME + MF = 3MG + GD + GE + GF nhỏ nhất x = 2 + 3t
⇔ MG ⇔ M là hình chiếu của G trên (P) MG : ⇒ y = 1− 3t min z = 2+ 2t
Suy ra M = MG ∩ (P) ⇒ M( 4; − 7; 2
− ) ⇒ a+ b+ c =1. Chọn D.
Dạng 3: Tìm điểm M thuộc (P) sao cho (MA+ MB) hoặc MA− MB min max Phương pháp giải:
+) Kiểm tra vị trí tương đối của các điểm A và B so với mặt phẳng (P).
+) Nếu A và B cùng phía (P) thì bài toán (MA+ MB) phải lấy đối xứng A qua (P) khi đó min
MA + MB = MA′ + MB ≥ A′B dấu bằng xảy ra ⇔ A ,′ M , B thẳng hàng hay M = A′B ∩ (P) .
Bài toán tìm MA − MB , ta có MA − MB ≤ AB ⇒ M là giao điểm trực tiếp của đường thẳng AB và max (P).
+) Nếu A và B khác phía (P) thì bài toán MA − MB phải lấy đối xứng A qua (P) bài toán max
tìm(MA+ MB) ⇒M là giao điểm trực tiếp của đường thẳng AB và (P). min
Ví dụ 1: Trong không gian hệ tọa độOxyz , cho 2 điểm A( 1 − ;3; 2 − ); B( 3 − ;7; 1 − 8) và mặt phẳng
(P) : 2x − y + z +1 = 0 . Tìm điểm M thuộc (P) sao cho MA + MB nhỏ nhất. Lời giải:
Đặt f = 2x − y + z +1 = 0 ta có: f ( A). f (B) > 0 ⇒ A,B cùng phía với mặt phẳng (P). Gọi + − +
A′ là điểm đối xứng của A qua (P) : 2x − y + z +1 = 0
x 1 y 3 z 2 ⇒ AA′: = = 2 1 − 1 Gọi I ( 1
− + 2t;3− t; 2
− + t) = AA′∩ (P) suy ra 2( 1
− + 2t) − (3− t) − 2 + t +1 = 0
⇔ t =1⇒ I(1;2; 1 − ) ⇒ ( A 3;1;0) .
Khi đó MA + MB = MA′ + MB ≥ A′B dấu bằng xảy ra ⇔ A ,′ M , B thẳng hàng. x = 3 + u
Phương trình đường thẳng A′B y =1−u ⇒ M = A B
′ ∩ (P) ⇒ M(3+ u;1− u;3u) z = 3u
Giải M ∈(P) ⇒ u = 1 − ⇒ M(2;2; 3) − .
Ví dụ 2: Trong không gian hệ tọa độOxyz cho mặt phẳng (P) : x − y + 2z − 2 = 0 và 2 điểm A(2;3;0); B(2; 1
− ;2) . Tìm điểm M thuộc mặt phẳng (P) sao cho MA − MB lớn nhất. Lời giải:
Kí hiệu f = x − y + 2z − 2 = 0 . Ta có f ( A). f (B) < 0 nên A,B nằm khác phía so với mặt phẳng (P).
Gọi A′ là điểm đối xứng của A qua (P). Ta có: x 2 y 3 : z AA − − ′ = = 1 1 − 2 Khi đó 1
I = AA′∩ (P) ⇒ (2 + t;3− t;2t) ⇒ t+ 2 + t− 3+ 4 t− 2 = 0 ⇒ t = 2 5 5 ⇒ I ; ;1 ⇒ A (′3;2;2) 2 2
Lại có MA − MB = MA′ − MB ≤ A′B dấu bằng xảy ra ⇔ A ,′ M , B thẳng hàng. x = 3 + u Khi đó 9 13
A′B y = 2 + 3u ⇒ M = A B∩(P) ⇒ M ; ;2 ′ . 2 2 z = 2
Ví dụ 3: : Trong không gian hệ tọa độOxyz cho điểm A(3;1;0); B( 9;
− 4;9) và mặt phẳng (P) có phương
trình (P) : 2x − y + z +1 = 0 . Gọi I (a;b;c) là điểm thuộc mặt phẳng (P) sao cho IA − IB đạt giá trị lớn nhất.
Khi đó tổng a +b +c bằng
A. a + b + c = 22 .
B. a + b + c = 4 − .
C. a + b + c = 13 − .
D. a + b + c =13. Lời giải: f (x y z = A; A; A ) 6 Đặt f ( ;
x y; z) = 2x − y + z +1⇒ ⇒ f ( )
A . f (B) = 7 − 2 < 0 . f (x ; y ;z ) = 1 − 2 B B B
Do đó hai điểm A, B nằm khác phía so với mặt phẳng (P).
Gọi B′ là điểm đối xứng của B qua mặt phẳng (P) ⇒ (BB′) x + 9 y − 4 z −9 : = = . 2 1 − 1
Điểm H ∈(BB )′ ⇒ H(2t −9;4 −t;t + 9)∈(P) → 2(2t −9) − (4 −t) + t + 9 +1 = 0 ⇒ t = 2
Ta có IA − IB = IA − IB′ ≤ A′B ⇒ IA − IB
= AB′ ⇒ I là giao điểm của AB′và mặt phẳng (P). max Lại có ′ = (− − ) x − 3 y −1 4; 1;13 z AB ⇒ u = − ⇒ ′ = = . AB′ (4;1; 13) (AB ) : ( ) 4 1 13 −
Điểm I ∈(AB )′ ⇒ I (4t + 3;t +1; 1
− 3t)∈(P) → I(7;2; 1
− 3) ⇒ a + b + c = 4 − . Chọn B
Ví dụ 4: Trong không gian hệ tọa độOxyz cho mặt phẳng (P) có phương trình (P) : x − y + 2z + 2 = 0 và 2 điểm A(0;1; 2 − ); B(2;0; 3
− ) . Gọi M (a;b;c) là điểm thuộc mặt phẳng (P) sao cho MA + MB nhỏ nhất. Tính giá trị của T= a+b+c. A. T = 5 − . B. 1 T = − . C. T = 1 − . D. 1 T = . 5 5 Lời giải:
Kí hiệu f = x − y + 2z + 2 ta có f ( A). f (B) > 0 ⇒ nên A,B nằm cùng phía với (P).
Gọi A′ là điểm đối xứng của A qua mặt phẳng (P).
Khi đó MA + MB = MA′ + MB′ ≥ A′B dấu bằng xảy ra ⇔ A ,′ M , B thẳng hàng. Phương trình x y −1 z + 2 AA′: = =
. Gọi H = AA′∩(P),H(t;1−t; 2 − + 2t) 4 1 − 2 Cho H ∈(P) 1 1 1
⇒ t + t −1+ 4t − 4 + 2 = 0 ⇐ t = ⇒ H ; ; 1 − ⇒ A (′1;0;0) . 2 2 2 x =1+ t
Khi đó A′B y =
⇒ M = A′B ∩(P) 8 9 1 : 0 ⇒ M ;0;− ⇒
a + b + c = − . Chọn B. 5 5 5 z = 3 − t
Dạng 4: Bài toán lập phương trình mặt phẳng, đường thẳng có yếu tố cực trị Phương pháp đại số:
• Gọi véc tơ pháp tuyến hoặc véc tơ chỉ phương của mặt phẳng (hoặc đường thẳng) cần lập là 2 2 2 (a;b;c),(a + b + c ) > 0
• Thiết lập một phương trình quy ẩn (a theo b,c hoặc ngược lại) từ một dữ kiện về mặt phẳng chứa
đường, song song hoặc vuông góc. Giả sử phương trình thu gọn ẩn là a = f ( ; b c) .
• Thiết lập phương trình khoảng cách mà đề bài yêu cầu, thay a = f ( ;
b c) vào ta được một phương trình hai ẩn b;c.
• Xét hàm khoảng cách d = g ( ; b c)
+ Nếu c = 0 thì b ≠ 0 → d = d lưu lại giá trị khoảng cách d này. 1 1 + Nếu 0 b ≠ ⇒ = = ( ); b c d g g t t = c c
Khảo sát hàm g (t) ta thu được kết quả. Chú ý:
Ax + By + Cz + D
• Công thức khoảng cách từ một điểm đến một mặt phẳng d ( ;( A P)) 0 0 0 = 2 2 2 A + B + C u ∆ ; AM
• Công thức khoảng cách từ một điểm đến một đường thẳng d ( ; A ) ∆ = ; với M thuộc ∆ . u∆
u ∆ ; u∆ M .M
• Công thức khoảng cách giữa hai đường thẳng d ( ; ) 1 2 1 2 ∆ ∆ = 1 2 u ∆ ; u 1 ∆2
Phương pháp hình học:
Bài toán 1: Lập phương trình mặt phẳng (P) chứa đường thẳng d sao cho khoảng cách từ M đến (P) lớn
nhất, với M là điểm không thuộc d. Phương pháp giải:
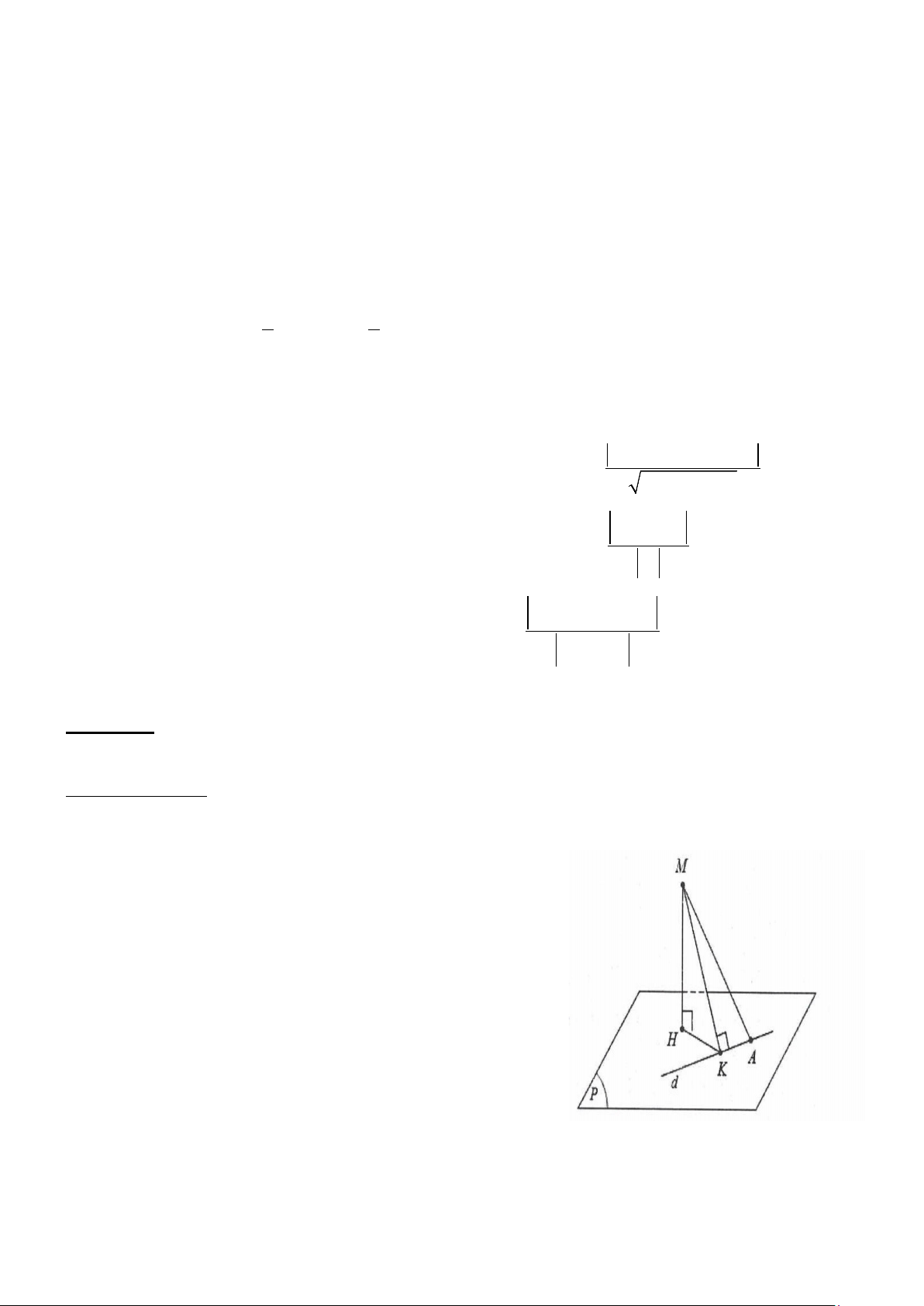
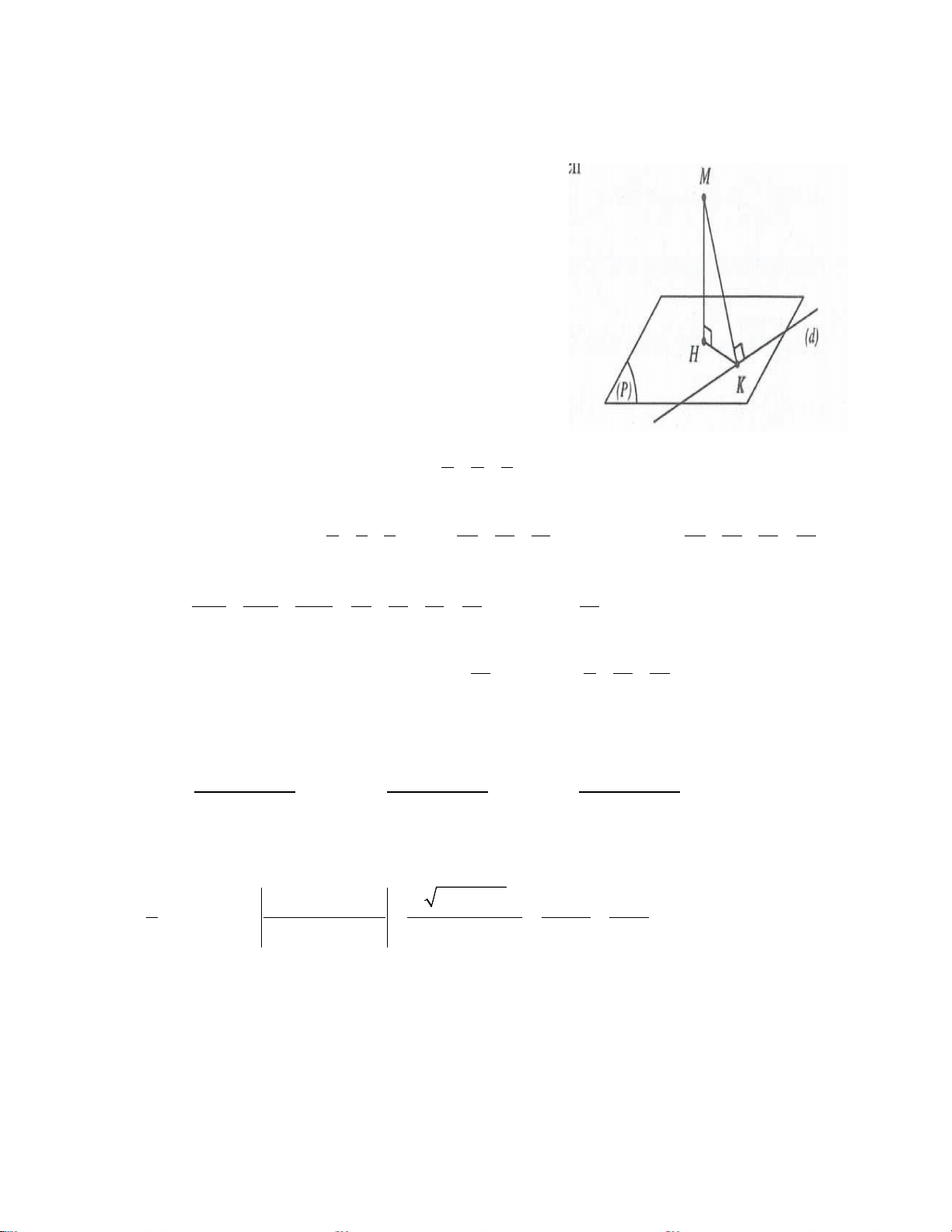
Đường thẳng d xác định đi qua điểm A và có véc tơ chỉ phương là u . d
Kẻ MH ⊥ (P);MK ⊥ d ⇒ MH = d (M;(P))và điểm K cố định.
Ta có d (M;(P)) = MH ≤ MK d ⊂ (P) Suy ra d = MK . Khi đó max ( P
) ⊥ (M ;d )
Gọi (α ) là mặt phẳng chứa M và d ta có: n ⊥ u (P) d
⇒ n = u u ;MA (P) d d n ⊥ n = α u ;MA (P) d
Khi đó (P) đi qua A và có véc tơ pháp tuyến là: n = u u ;MA (P) d d
Ví dụ 1: Trong không gian hệ tọa độ − −
Oxyz cho các điểm M (2;5;3) và đường thẳng x 1 y z 2 d : = = . 2 1 2
Lập (P) chứa d sao cho khoảng cách từ M đến (P) đạt giá trị lớn nhất. Lời giải:
Đường thẳng d xác định đi qua điểm A và có véc tơ chỉ phương là u d ( 2;1; 2)
Kẻ MH ⊥ (P);MK ⊥ d ⇒ MH = d (M;(P))và điểm K cố định.
Ta có d (M;(P)) = MH ≤ MK d ⊂ (P) Suy ra d = MK . Khi đó max ( P
) ⊥ (M ;d ) ≡ (α ) n ⊥ u (P) d
⇒
⇒ n = u u ;MA (P) d d n ⊥ n = α u ;MA (P) d
Ta có: MA(1; 5 − ;− )
1 ⇒ n = u ;u ;MA = 9 − (1; 4 − ;1) (P) d d
Do đó mặt phẳng (P) cần tìm đi qua A(1;0;2) và có n (1; 4
− ;1) ⇒ (P) : x − 4y + z − 3 = 0. (P)
Ví dụ 2: Trong không gian hệ tọa độ − + −
Oxyz cho các điểm M (5;1;6) và đường thẳng
x 1 y 1 z 2 d : = = . 2 1 5
Lập (P) chứa d sao cho khoảng cách từ M đến (P) đạt giá trị lớn nhất. Lời giải:
Đường thẳng d xác định đi qua điểm A(1; 1;
− 2) và có véc tơ chỉ phương là u . d ( 2;1; 5)
Kẻ MH ⊥ (P);MK ⊥ d ⇒ MH = d (M;(P))và điểm K cố định.
Ta có d (M;(P)) = MH ≤ MK d ⊂ (P) Suy ra d = MK . Khi đó max ( P
) ⊥ (M ;d ) ≡ (α ) n ⊥ u (P) d
⇒
⇒ n = u ;u ;MA (P) d d n ⊥ n = α u ;MA (P) d
Ta có: MA( 4; − 2; − 4 − ) = 2
− (2;1;2) ⇒ n = u ;u ;MA = 30(2;1; 1 − ) . (P) d d
Do đó mặt phẳng (P) cần tìm đi qua A(1;2;− ) 1 và có n (2;1; 1
− ) ⇒ (P) : 2x + y − z +1 = 0. (P)
Ví dụ 3: Trong không gian hệ tọa độOxyz cho các điểm M (1;2; 3 − ) và đường thẳng
x +1 y − 2 z −1 d : = =
. Mặt phẳng (P) chứa đường thẳng d đồng thời cách điểm M một khoảng lớn 4 3 − 2
nhất. Khi đó khoảng cách từ O đến (P) bằng: A. d = 3. B. d = 3. C. 3 d = . D. d = 5. 5 Lời giải:
Gọi H, K lần lượt là hình chiếu của điểm M lên mặt phẳng (P) và đường thẳng d .
Đường thẳng d đi qua A( 1; − 2; ) 1
Ta có: d (M;(P)) = MH ≤ MK Khi đó Suy ra d = MK . max d ⊂ (P) Khi đó ( P
) ⊥ (M ;d ) ≡ (α ) n ⊥ u (P) d
⇒
⇒ n = u ;u ;MA (P) d d n ⊥ n = α u ;MA (P) d Ta có: u = − = − d (4; 3;2);MA ( 2;0;4)
⇒ u ;MA = 2
− 6;10;3 ⇒ n = u ;u ;MA = ( 29 − ;0;58) = 29( − 1;0; 2) − d ( ) (P) d d
Khi đó (P) − + = ⇒ (O (P)) 3 : x 2z 3 0 d ; = . Chọn C. 5
Ví dụ 4: Trong không gian hệ tọa độ Oxyz cho ba điểm M ( 1 − ;2;4); (
A 0;2;1); B(1;0;2) . Mặt phẳng
(P)chứa đường thẳng AB đồng thời cách điểm M một khoảng lớn nhất cắt các trục tọa dộ tại các điểm
N, P,Q . Thể tích V của khối chóp . O NPQ là: A. 9 V = . B. 3 V = . C. V = 9. D. V = 27. 2 2 Lời giải: Giả sử
Ta có: Ta có d (M;(P)) = MH ≤ MK d ⊂ (P) Suy ra d = MK . Khi đó max ( P
) ⊥ (M ;d ) ≡ (α ) n ⊥ u (P) d
⇒
⇒ n = u ;u ;MA (P) d d n ⊥ n = α u ;MA (P) d Ta có: u = − = − . d (1; 2; ) 1 ;MA (1;0; 3)
⇒ u ;MA = 2 3;2;1 ⇒ n = u ;u ;MA = ( 4; − 2;8) = 2 − (2; 1 − ; 4 − ) d ( ) (P) d d Khi đó (P)
− y − + = ⇒ N (− ) ( ) 3 1 9 : 2 x 4z 6 0 3;0;0 ;P 0;6;0 ;Q 0;0; ⇒ V = OM OP OQ = O . . . .NPQ 2 6 2 Chọn A.
Ví dụ 5: Trong không gian hệ tọa độOxyz cho các điểm A(1;4;2) và đường thẳng x 1 y 2 : z d − + = = . 1 − 1 2
Mặt phẳng (P) chứa đường thẳng d đồng thời cách điểm M một khoảng lớn nhất. Khi đó khoảng cách từ
O đến (P) bằng: A. 210 d = . B. 210 d = . C. 21 d = . D. 21 d = . 10 30 5 10 Lời giải:
Đường thẳng d xác định đi qua điểm B(1; 2
− ;0) và có véc tơ chỉ phương là u − . d ( 1;1; 2) Ta có: AB(0; 6; − 2 − ) = 2 − (0;3; ) 1 .
Áp dụng công thức nhanh ta có: n = u ;u ;MA = 2 5;13; 4 − (P) d d ( ) ⇒ (P) + − − = ⇒ (O (P)) 21 210 :5x 13y 4z 21 0 d ; = = . Chọn A. 2 2 2 5 +13 + 4 10
Bài toán 2: Lập phương trình đường thẳng d nằm trong mặt phẳng (P) , đi qua điểm A sao cho khoảng
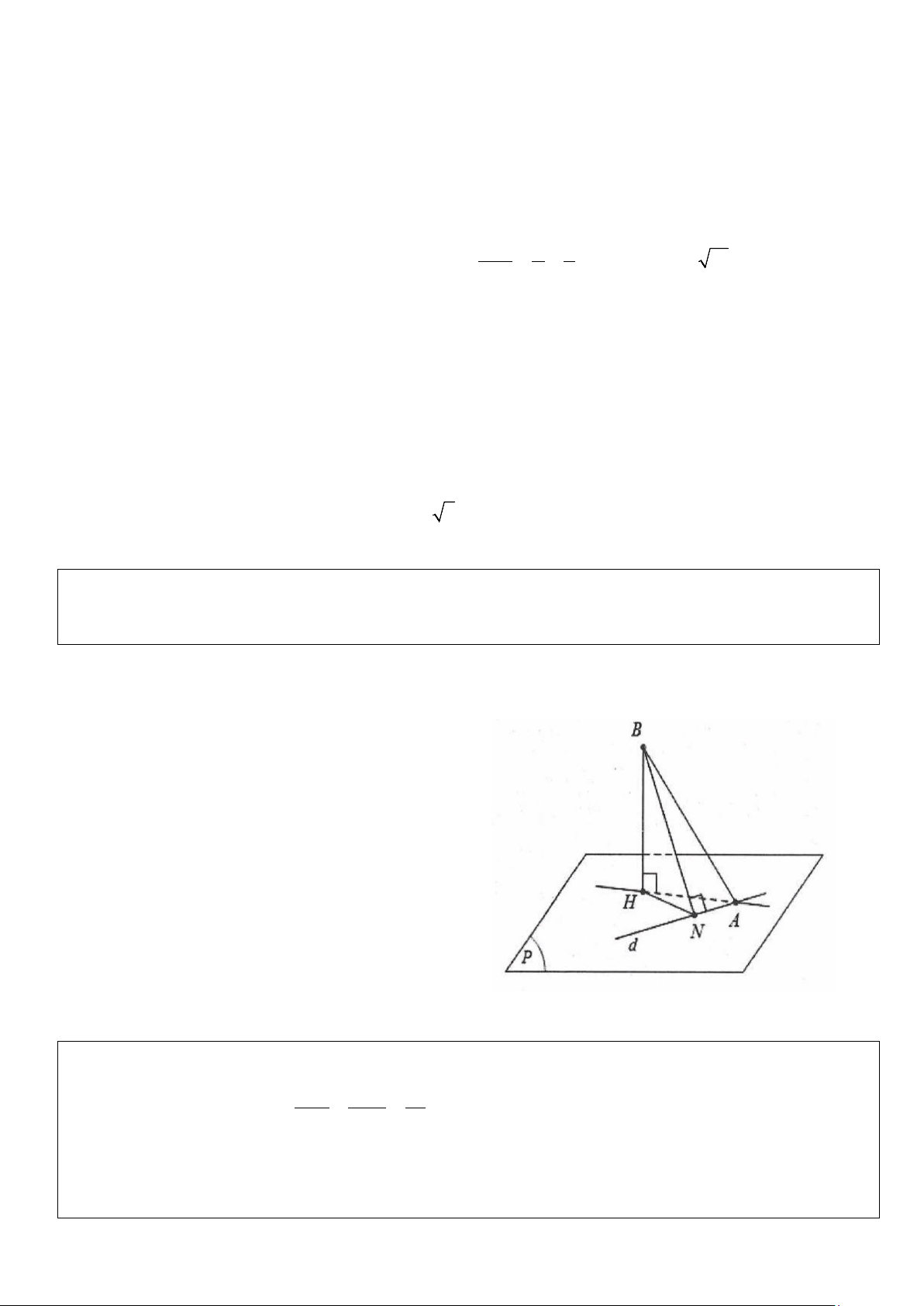
cách từ điểm M đến d lớn nhất, nhỏ nhất? Phương pháp giải:
+ Kẻ MK ⊥ d;MK ⊥ (P) ⇒ MK = d (M;d)và điểm H cố định.
+ Kẻ MK ⊥ d;MH ⊥ (P);⇒ MK = d (M;d) = d và điểm H cố định.
Ta có: MH ≤ MK ≤ MA ⇔ MH ≤ d ≤ MA.
+) Ta có MK ≤ MA ⇒ d (M;d ) = MA ⇔ K ≡ . A max
Khi đó đường thẳng d nằm trong (P) , đi qua A và vuông góc với đường thẳng AM , suy ra d có một
véc tơ chỉ phương là u = n d (P);MA
+) Mặt khác, lại có MK ≥ MH ⇒ d (M;d ) = MH ⇔ H ≡ K . min
Khi đó đường thẳng d nằm trong (P) , đi qua A và đi qua hình chiếu H của M. Suy ra
d = (P) ∩(MHA) . Trong đó n( = n MHA ) (P);MA
Khi đó đường thẳng d có một véc tơ chỉ phương là u = n ;n P ; MA d (P)
(Chú ý: Trong trường hợp d thì d chính là hình chiếu vuông góc của MA trên mặt phẳng (P) ). min
Ví dụ 1: Cho các điểm M (1;0;0); ( A 0;2; 3)
− và (P) : x + 2y − z −1 = 0. Lập phương trình đường thẳng d
nằm trong mặt phẳng (P) , đi qua A và cách M một khoảng lớn nhất, nhỏ nhất?` Lời giải: Ta có: n (1;2; 1 − );MA = 1; 2 − ;3 . (P) ( )
+) Kẻ MK ⊥ d;MK ⊥ (P) ⇒ MK = d (M;d) = d và điểm H cố định.
Ta có: MH ≤ MK ≤ MA ⇔ MH ≤ d ≤ MA.
+) Ta có MK ≤ MA ⇒ d (M;d ) = MA ⇔ K ≡ . A max
Khi đó đường thẳng d nằm trong (P) , đi qua A và vuông góc với đường thẳng AM , suy ra d có một véc tơ chỉ phương là x y z u = n = − ⇒ d − = = và d = MA = 14 . d ;MA 4 P ( 1;1; ) 1 ( ) 1 : 1 − 1 1 max
+) Mặt khác, lại có MK ≥ MH ⇒ d (M;d ) = MH ⇔ H ≡ K . min
Khi đó đường thẳng d nằm trong (P) , đi qua A và đi qua hình chiếu H của M. Suy ra
d = (P) ∩(MHA) . Trong đó n( = n = − − MHA ) ;MA 4 P (1; 1; ) ( ) 1
Khi đó đường thẳng d có một véc tơ chỉ phương là u = n ;n = − P ; MA 12 1;0;1 d (P) ( ) x =1+ t
Suy ra d : y = 0 và d = MH = d M; P = 6 . min ( ( )) z = t
Ví dụ 2: Cho các điểm A(1;2;4); ( A 1;2; 2
− ) và (P) : x + y − z +1 = 0. Lập phương trình đường thẳng d nằm
trong mặt phẳng (P) , đi qua A và cách B một khoảng lớn nhất, nhỏ nhất?` Lời giải: Ta có: n (1;1; 1 − );AB = 0;0; 6 − = 6 − (0;0;1). (P) ( )
Gọi H; N lần lượt là hình chiếu của B trên (P) và d. Khi đó d ( ;
B (d )) = BN
Ta có: BH ≤ BN ≤ BA ⇔ BH ≤ d ≤ BA. +) d ⇔ u = n ;AB = 6 − 1; 1; − 0 . max d P ( ) ( )
⇒ d :{x =1+ t; y = 2 − t; z = } 4 .
+) d ⇔ u = n ;n ;AB = 6 1;1;2 . min d (P) P ( ) ( )
⇒ d :{x =1+ t; y = 2 + t; z = 4 + 2t}.
Ví dụ 3: [Đề luyện thi đại học Vinh 2017] Trong không gian hệ tọa độOxyz cho hai điểm M ( 1; − 2; ) 1 ; A(1;2; 3 − ) và đường thẳng x 1 y 5 : z d + − = =
vec tơ chỉ phương u của đường thẳng ∆ đi qua M, vuông 2 2 1 −
góc với đường thẳng d đồng thời cách điểm A một khoảng lớn nhất. A. u = (4; 3 − ;2). B. u = (1;0;2). C. u = (2;0; 4 − ).
D. u = (2;2;− ) 1 . Lời giải:
Phương trình mặt phẳng đi qua M và vuông góc với d
là: (P) = 2x + 2y − z −1 = 0 khi đó (P) chứa ∆ . Gọi
H là hình chiếu vuông góc của A xuống (P) và N là
hình chiếu vủa A xuống ∆ . Ta có: AH ≤ AN ≤ AM . Khi đó AN ⇔ N ≡ M max Do
∆ ⊥ d;∆ ⊥ AM ⇒ u = = − − .Chọn ∆ u AM d ; ( 8;6; 4) A.
Ví dụ 4: Trong không gian hệ tọa độOxyz cho hai điểm A(1;1;− ) 1 ; B(0;2; )
1 và mặt phẳng (P) có phương
trình (P) : 2x − y − z = 0 . Gọi d là đường thẳng đi qua A nằm trong mặt phẳng (P) , và cách điểm B một
khoảng lớn nhất. Đường thẳng d cắt mặt phẳng (O tại điểm. xy ) A. Q(0;4;0). B. Q(1; 2 − ;0). C. Q(0; 2; − 0). D. Q(1;4;0). Lời giải: Ta có: d ( ; B d ) − − + ⇔ u = n AB = (− − )
x 1 y 1 z 1 1; 3;1 ⇒ d : = = d ; max (P) 1 − 3 − 1
Mặt phẳng (O có phương trình z = 0 ⇒ d ∩ (O = Q − . Chọn C. xy ) (0; 2;0) xy )
Ví dụ 5: Trong không gian hệ tọa độ − +
Oxyz cho đường thẳng x y 1 z 2 d : = =
và hai điểm A(1;1; 2 − ) ; 1 5 − 1 − B( 1;
− 0;2) . Viết phương trình đường thẳng ∆ đi qua A, vuông góc với đường thẳng d sao cho khoảng cách
từ B đến ∆ là nhỏ nhất.
A. x −1 y −1 z + 2 − − + = = .
B. x 1 y 1 z 2 = = . 2 5 8 − 2 5 − 8 −
C. x −1 y −1 z + 2 − − + = = .
D. x 1 y 1 z 2 = = . 2 5 8 2 5 − 8 Lời giải:
Đường thẳng ∆ nằm trong mặt phẳng (P) đi qua điểm A(1;1; 2
− ) và n = u = (1;2; 1 − ) (P) d Ta có: AB( 2 − ; 1; − 4)
Áp dụng công thức nhanh ta có: d ⇔ u = n ;n ;AB = 4; 1 − 0; 1 − 6 = 2(2; 5 − ; 8 − ) . min d (P) (P) ( )
Phương trình đường thẳng − − +
∆ là: x 1 y 1 z 2 = = . Chọn B. 2 5 − 8 −
Ví dụ 6: Trong không gian hệ tọa độOxyz cho hai điểm A(1;2;− ) 1 ; B(3; 1 − ; 5 − ) và đường thẳng + + ∆ x 1 y z 1 : = =
. Gọi d là đường thẳng đi qua A và cắt đường thẳng sao cho khoảng cách từ B đến ∆ 2 3 1 −
là lớn nhất, đường thẳng d đi qua các điểm nào trong các điểm sau: A. E (2;4; 2 − ). B. F (2;3;0). C. G(2;4;0). D. N (2;0;0). Lời giải:
Gọi (P) là mặt phẳng đi qua A và chứa + + ∆ x 1 y z 1 : = = ; ∆ qua M ( 1; − 0;− ) 1 và u = − ∆ (2;3; )1 2 3 1 −
Ta có: n AM;u = − − ⊂ ∆ 2(1; 1; ) ( ) 1 ;d (P). P Khi đó ( ∆) x y z d B ⇔ u = AB n = − − ⇒ d − − + = = d P ( ) 1 2 1 ; ; 1;2; 1 : . max ( ) 2 2 1 − Suy ra E (2;4; 2
− )∈d.Chọn A.
Bài toán 3: Lập phương trình đường thẳng d nằm trong mặt phẳng (P), đi qua điểm A cho trước sao cho
khoảng cách giữa d và d’lớn nhất, với d’ là đường thẳng cho trước và cắt (P). Phương pháp giải:
+) Gọi I = d′∩ (P) , qua A dựng đường thẳng d′′ d′ ⇒ d′ (Q) , với (Q) là mặt phẳng chứa d và d′′.
Khi đó d(d;d′) = d (d ;′(Q)) = d (I;(Q))
+) Kẻ IH ⊥ (Q);IK ⊥ d′′ ⇒ IH = d (I;(Q))và điểm K cố định.
+) Ta có H ≤ IK ⇒ d (I;(Q)) = IK ⇔ H ≡ K. Khi đó đường thẳng d nằm trong (P), đi qua A và max
vuông góc với đường thẳng IK, suy ra d có một véc tơ chỉ phương là u = n IK d (P);
Gọi A′ là hình chiếu vuông góc của A lên d’ , suy ra AA′ IK , khi đó u = n ′ d (P);AA
Vậy đường thẳng d cần lập đi qua điểm A và có véc tơ chỉ phương là u = n ′ d (P);AA
Ví dụ 1: Trong không gian hệ tọa độOxyz cho hai điểm A(1;0; ) 1 ; và đường thẳng x − 2 y −1 d : z = =
và (P) = x − y + z − 2 = 0 . Lập phương trình đường thẳng d đi qua A, nằm trong (P) 2 1 − 1 −
sao cho khoảng cách giữa d và d′ lớn nhất? Lời giải:
Gọi A′(2 + 2t;1−t; t
− ) là hình chiếu vuông góc của điểm A trên d′
Ta có: AA′(1+ 2t;1−t; t − − ) 1 và 1
AA .′u = t + + t − + t + = ⇔ t = − d 4 2 1 1 0 3 Suy ra 1 4 2 1 AA ′ ; ;− = (1;4; 2 − ). Lại có: n = − P (1; 1; ) 1 . 3 3 3 3 ( )
Khi đó d (d;d′) ⇔ u = n AA′ = − d ; P ( 2;3;5) max ( ) Suy ra x −1 y z −1 d : = = . 2 − 3 5
Ví dụ 2: Trong không gian hệ tọa độ − + + −
Oxyz cho hai đường thẳng x 1 y 1 d : z = = và x y 1 z 1 d′: = = . 1 2 − 1 2 2 − 1 −
Lập phương trình đường ∆ đi qua O(0;0;0) vuông góc với d và cách d′ một khoảng lớn nhất? Lời giải:
Mặt phẳng (P) đi qua O(0;0;0) và vuông góc với d có VTPT là u = u = − P d (1; 2; ) ( ) 1 .
Khi đó d ⊂ (Q) . Gọi O′(2t; 1
− − 2t;1− t)∈d′ là hình chiếu vuông góc của O trên d′
Ta có: OO′(2t; 2 − t− t; t − + ) 1 1 2 7 10 ⇒ OO .u ′ = + + + − = ⇔ = − ⇒ ′ − − ′ t t t t OO d 4 4 2 1 0 ; ; 9 9 9 9 Khi đó ( ′) 1 ; max x y z d d d
⇔ u = OO′ n = ⇒ ∆ = = d ; P (13;12; ) ( ) 11 : . 9 13 12 11
Ví dụ 3: Trong không gian hệ tọa độ −
Oxyz cho điểm A(0;1;− ) 1 ;đường thẳng x 1 d : y z = = và 1 1 − 1 −
(P) : x − 2y + 2z = 0 . Lập phương trình đường ∆ đi qua A song song với (P) sao cho khoảng cách giữa ∆ và d lớn nhất? Lời giải:
Gọi (Q) là mặt phẳng qua A và song song với (P) : x − 2y + 2z = 0 ⇒ n = (1; 2 − ;2) ( ) . Q
Khi đó , d ⊂ (Q) Gọi A′(1+ t;− t; t
− )∈d là hình chiếu vuông góc của điểm A trên d . Ta có: AA′(t − +1; t − −1; t − + ) 1 ⇒ 1
AA .′u = + + + + − = ⇔ = ∆
t 1 t 1 t 11 0 t 3 Suy ra 2 2 − 4 2 AA′ ; ; = 2 (1; 1; − 2) ⇒ d ( ; ∆ d ) ⇔ u = ′ = − . ∆ AA ;n Q (2;0; ) 1 3 3 3 3 max ( ) 3 x = 2t Khi đó : ∆ y =1 . z = 1 − − t
Ví dụ 4: Trong không gian hệ tọa độOxyz , gọi d là đường thẳng đi qua A(0;2; ) 1 , song song với mặt phẳng ( −
P) : 2x + y + z +1 = 0 sao cho khoảng cách giữa d và x 1 ∆ : y z
= = lớn nhất. Đường thẳng d đi 1 2 1
qua điểm nào trong các điểm sau: A. M (1;9;10). B. N (1; 9 − ; 8 − ). C. P(1; 9 − ; 1 − 0). D. Q(1;9; 8 − ). Lời giải:
Gọi (Q) là mặt phẳng qua A và song song với (P) : 2x + y + z +1 = 0 ⇒ n = (2;1 ) ( ) ;1 . Q
Khi đó , d ⊂ (Q) Gọi A′(1+ t;2 t;t)∈∆ là hình chiếu vuông góc của điểm A trên ∆
Ta có: AA′(t +1;2t − 2;t − ) 1 ⇒ 2
AA .′u = + + − + − = ⇔ = ∆
t 1 4t 4 t 1 0 t 3 Suy ra 5 2 − 1 − 1 AA′ ; ; = 1 (5; 2 − ;− ) 1 ⇒
d (d;∆) ⇔ u = AA′ n = − − . d ; Q (1;7; 9) 3 3 3 3 max ( ) 3 Khi đó x y − 2 z −1 d : = = ⇒ Q(1;9; 8
− )∈d . Chọn D. 1 7 9 −
Bài toán 4: Lập phương trình đường thẳng d đi qua điểm A cho trước, d cắt d1 và khoảng cách giữa d và d2 lớn nhất Phương pháp giải:
Gọi (P) là mặt phẳng đi qua A và chứa d1 , suy ra d nằm trong (P). Khi đó quy về bài toán 3!
Ví dụ 1: Cho điểm A(0; 1; + − − 2) và đường thẳng x 1 y z 2 d : = = . 1 1 1 −
Lập phương trình đường ∆ đi qua A cắt d sao cho
a) Khoảng cách từ B(2;1;1) đến đường thẳng ∆ là lớn nhất.
b) Khoảng cách giữa − ∆ và x 5 d′: y z = = là lớn nhất. 1 2 − 1 Lời giải:
Đường thẳng d đi qua điểm M ( 1;
− 0;2) có VTCP là u = − , ta có: AM = ( 1; − 1;0) d (1;1; )1
Gọi (P) là mặt phẳng qua A và d ⇒ ∆ ⊂ (P) .
Ta có: n = u AM = và AB = (2;2;− ) 1 . P d ; ; (1;1;2) ( ) x = t
a) d (B;∆) ⇔ u = = − − ⇒ ∆ = − − ∆ n ; AB 5 y t P (1; 1;0) 1 . max ( ) z = 2
b) Gọi A′(5 + 2t; 2
− t;t) là hình chiếu vuông góc của A trên d′ .
Ta có: AA′(5 + 2t; 2
− t +1;t − 2) ⇒ 2
AA .′u = + + − + − = ⇔ = − ′ t t t t d 4 10 4 2 2 0 3 Suy ra 11 7 8 − 1 AA′ ; ; = (11;7; 8 − ) . 3 3 3 3 Khi đó (∆ ′) 2 x y + z d d ⇔ u − = ′ = − ⇒ ∆ = = ∆ AA n P ( ) 1 2 ; ; 11; 15;2 : . max ( ) 3 11 15 − 2
Ví dụ 2: Trong không gian hệ tọa độOxyz , phương trình đường thẳng d đi qua A(0; 1; − 2) , cắt đường thẳng x +1 y z − 2 d : − = =
, sao cho khoảng cách giữa d và x 5 d : y z =
= lớn nhất có một véc tơ chỉ 1 2 1 1 − 2 2 2 − 1 phương là: A. u = − B. u = − − d (29; 41; 4). d (29; 41;4). C. u = − D. u = − − d (14; 20; 2). d (14; 20;2). Lời giải:
Đường thẳng d1 đi qua điểm B( 1;
− 0;2) có VTCP là u = 2;1; 1 − ⇒ AB = 1; − 1;0 1 ( ) ( )
Gọi (P) = ( Ad ⇒ n = A ;
B u = − 1;1;3 ⇒ d ⊂ P . ; 1 ) P 1 ( ) ( ) ( )
Gọi A′(2 + 5t; 2
− t;t)∈d là hình chiếu vuông góc của A trên d ta có: 2 2
AA′ = ( + t − t + t − ) 2
5 2 ; 2 1; 2 ⇒ AA .′u = t + + t − + t − = ⇔ t = − d 4 10 4 2 2 0 2 3 Suy ra 11 7 8 AA − ′ ⇒ d ( 1 ; ; d;d
⇔ u = AA′ n = − . Chọn A. d ; 29; 41;4 2 ) P ( ) max ( ) 3 3 3 3
Ví dụ 2: Trong không gian hệ tọa độOxyz , phương trình đường thẳng d đi qua A(2; 1; − 2) , cắt đường thẳng
x −1 y +1 z −1 d : + = =
, sao cho khoảng cách giữa d và x 1 d : y z = =
lớn nhất có một véc tơ 1 2 1 1 − 2 2 2 − 3 − chỉ phương là: A. u = B. u = − − d (43; 8; 25). d (33;8;25). C. u = D. u = − d (41;68; 27). d (2;1 ) ;1 . Lời giải:
Đường thẳng d1 đi qua điểm B( 1; − 1; − )
1 có VTCP là u = 2;1;1 ⇒ AB = 1; − 0; 1 − 1 ( ) ( ) Gọi (P) = ( ;
A d ⇒ n = A ; B u = 1; 1; − 1
− ⇒ d ⊂ P . 1 ) P 1 ( ) ( ) ( ) Gọi A′( 1 − + t; 2 − t; 3
− t)∈d là hình chiếu vuông góc của A trên d ta có: 2 2
AA′ = (t − − t + − t − ) 1
3; 2 1; 3 2 ⇒ AA .′u = t − + t − + t + = ⇔ t = − d 3 4 2 9 6 0 . 2 14 43 − 8 25 − 1 ⇒ AA′ = = (− − ) ⇒ d ( 1 ; ; 43;16; 25 d;d
⇔ u = AA′ n = − Chọn D. d ; 41;68; 27 . 2 ) P ( ) max ( ) 14 7 14 14 14
Dạng 5: Bài toán tìm điểm M thuộc đường thẳng có yếu tố cực trị Phương pháp giải:
Tham số hóa điểm M theo phương trình đường thẳng.
Biến đổi giả thiết về dạng y = f (t) và tìm giá trị lớn nhất, nhỏ nhất của hàm số y = f (t) . Chú ý: Tam thức bậc hai: 2 y − −∆
= ax + bx + c(a ≠ 0) có đỉnh b I ; . 2a 4a
Bất đẳng thức véc tơ: Cho 2 véc tơ u = (a;b) và v = ( ;
c d ) ta có: u + v ≥ u + v Khi đó 2 2 2 2
a + b + c + d ≥ (a + c)2 + (b + d )2 dấu bằng xảy ra a b ⇔ = . c d
Ví dụ 1: Trong không gian hệ tọa độ − +
Oxyz cho đường thẳng x y 3 z 1 d : = =
và hai điểm A(2; 1; − ) 1 ; 1 1 − 2 B(0;1; 2
− ) . Tìm tọa độ điểm M thuộc đường thẳng d sao cho tam giác ABM có diện tích nhỏ nhất. Lời giải: x = t
Đường thẳng d có phương trình tham số d : y = 3−t z = 1 − + 2t
Gọi M là điểm cần tìm. Do nếu M thuộc d thì M nên M (t;3−t; 1 − + 2t) .
AM = (t − 2;4 −t;2t − 2)
Diện tích tam giác M được tính bởi 1
S= AM ; BM trong đó 2 AB = ( 2; − 2; 3 − ) Do đó 1 1 S = AM AB = − − t t − − = t + + t + + ABM ( ) 1 , 8 ; 2;4 ( 8)2 ( 2)2 16 2 2 2 1 = (t + ) 1 2 5 + 34 ≥ 34. Vậy 34 minS = t = 5 − ⇒ M ( 5; − 8; 1 − ) 1 . 2 2 2
Ví dụ 2: Trong không gian hệ tọa độOxyz cho ba điểm A(1;0;− )
1 ; B(0;2;3);C ( 1; − 1; ) 1 và đường thẳng x +1 y −1 d : z =
= Tìm điểm M trên d sao cho: 1 2 − 2 a) 2 2 2
MA + 2MB − 4MC đạt giá trị lớn nhất? b) AM + BC
đạt giá trị nhỏ nhất. min Lời giải: a) Gọi M ( 1
− + t;1− 2t;2t)∈d và I là điểm thỏa mãn IA + 2IB − 4IC = 0 ⇒ I ( 5; − 0;− ) 1 Biến đổi 2 2 2 2 2 2 2
MA + 2MB − 4MC = −MI + IA + 2MB − 4MC lớn nhất 2 ⇔ MI nhỏ nhất Lại có: 2 MI −
= (t + )2 + ( t − )2 + ( t + )2 2 4 2 1
2 1 = 9t + 8t +18 nhỏ nhất 4 13 17 8 t M − ; ; ⇔ = − ⇒ . 9 7 9 9
b) Ta có: AM (t − 2;1− 2t;2t + ) 1 ; BC = ( 1; − 1; − 2 − ) Khi đó AM + BC = (t − 3; 2 − t;2t − ) 1 = (t −3)2 2
+ 4t + (2t − )2 2
1 = 9t −10t +10 nhỏ nhất min b − 5 13 − 1 − 19 t M ; ; ⇔ = = ⇒ . 2a 9 9 9 9
Ví dụ 3: Trong không gian hệ tọa độOxyz cho hai điểm A(0;0;3); B(0;3;3) và đường thẳng d : x y z = = 1 1 1
Tìm điểm M trên d sao cho: a) 2 2
MA + 2MB đạt giá trị nhỏ nhất
b) MA + MB đạt giá trị nhỏ nhất. Lời giải:
a) Gọi M (t;t;t) ta có: 2 2 2 2
MA + MB = t + t −
+ t + (t − )2 2 2 2 ( 3) 2 2
3 = 9t − 30t + 45
đạt giá trị nhỏ nhất b − 5 5 5 5 t M ; ; = = ⇒ . 2a 3 3 3 3 b) Ta có: 2 MA + MB == t + (t − )2 2 2
3 + t + 2(t −3)2 = 3 ( (t − )2
1 + 2 + (t − 2)2 + 2) =
( (t− ) + + ( −t) + )≥ (t− + −t) +( + )2 2 2 2 3 1 2 2 2 3. 1 2 2 2 = 3 3. Dấu bằng xảy ra t −1 3 3 3 3 1 t M ; ; ⇔ = ⇔ = ⇒ . 2 − t 2 2 2 2
Ví dụ 4: Trong không gian hệ tọa độ − +
Oxyz , gọi là điểm thuộc x 2 y 1 d : z = = sao cho 1 1 − 2 2 2 2
A = 3a + 2b − c nhỏ nhất. Khi đó độ dài đoạn thẳng OM là. A. OM = 87. B. OM = 93. C. OM = 41. D. OM = 3 3. Lời giải: Gọi M(2 −t; 1
− − t;2t) khi đó 2 2 2
a + b − c = (t − )2 + (t + )2 2 3 3 3 2 2 1 − 4t 2
= t −8t +14 = (t − 4)2 − 2 ≥ 2 − . Do đó A = 2
− khi t = 4 ⇒ M ( 2 − ; 5; − 8) min
Khi đó OM = 93 . Chọn B.
Ví dụ 5: Trong không gian hệ tọa độOxyz cho ba điểm A( 1 − ;1;6); B( 3 − ; 2; − 4 − );C (1;2;− ) 1 D(2; 2; − 0) .
Gọi M(a;b;c) làm điểm thuộc đường thẳng CD sao cho tam giác ABM có chu vi nhỏ nhất. Tính S = a+ b+ c . A. S = 1. − B. S =1. C. S = 2. − D. S = 2. Lời giải: x = 2 + t Ta có: CD(1; 4 − ; )
1 . Phương trình đường thẳng CD là: CD : y = 2 − − 4t. z = t
Vì M ∈CD nên M (2 + t; 2 − − 4t;t).
Chu vi tam giác MAB là: P = AB + MA + MB Vì A,B cố định nên AB không đổi.
Ta có: P = AB + (t + )2 + ( t + )2 + (t − )2 + (t + )2 + ( t)2 + (t + )2 3 4 3 6 5 4 4 2 2 = 2 2 1 27 1 73 27 73
18t +18t +18 + 18t +18t + 41 = 18 t + + + 18t + + ≥ + 2 2 2 2 2 2 Dấu = xảy ra 1 3 1 3 1
⇔ t = − ⇒ M ;0;− ⇒ S = + 0 − = 1. Chọn B. 2 2 2 2 2
Ví dụ 6: Trong không gian hệ tọa độOxyz cho hai điểm A( 1; − 3; 2
− ); B(1;1;4) và đường thẳng D có
phương trình x +1 y + 2 z =
= . Gọi M là điểm thuộc đường thẳng d sao cho chu vi tam giác MAB nhỏ 2 1 − 2
nhất. Khi đó độ dài OM là.
A. OM = 3. B. OM = 3.
C. OM = 2. D. OM = 5. Lời giải: Gọi M ( 1 − + 2t; 2
− − t;2t) ta có: C
nhỏ nhất ⇔ P = MA + MB nhỏ nhất. ABC Khi đó 2
P = 4t + (t + 5)2 + (2t + 2)2 + (2t − 2)2 + (t + 3)2 + (2t − 4)2 2 2 2 2
= 9t +18t + 29 + 9t −18t + 29 = (3t + )2
1 + (2 5) + (1−3t)2 +(2 5)
Trong mặt phẳng tọa độ gọi u = (3t +1;2 5);v = (1−3t;2 5);
Ta có: u + v ≥ u + v ⇒ P ≥ + ( )2 2 2 4 5 Dấu bằng xảy ra 3t +1 ⇔
= 1 ⇔ t = 0 ⇒ M ( 1; − 2
− ;0) do đó OM = 5 . Chọn D. 1− 3t
Ví dụ 7: Trong không gian hệ tọa độ − − +
Oxyz , cho hai đường thẳng x y 1 ∆ : z = = và x 1 y z 2 ∆ : = = . 1 2 1 − 1 2 1 2 1
Một mặt phẳng (P) vuông góc với ∆ , cắt trục Oz tại A và cắt ∆ tại B. Tìm độ dài nhỏ nhất của đoạn 1 2 AB. A. 2 30 . B. 2 31 . C. 6. D. 24 . 5 5 5 5 Lời giải:
Gọi A(0;0;a) và B(b +1;2 ;
b b − 2) suy ra AB = (b +1;2 ;
b b − a − 2) .
Vì AB ⊂ (P) và vuông góc với(∆ ⇒ A . B u = ⇔ + − + − − = ⇔ = ∆ 0 2 b 1 2b b a 2 0 a . b 1 ) ( ) ( 1)
Khi đó AB = (a + a − ) ⇒ AB = AB = (a + )2 2 2 1;2 ; 2
1 + 4a + 4 = 5a + 2a + 5 2 1 24 24 2 30 2 30 = 5 a + + ≥ = ⇒ AB = min 5 5 5 5 5
Vậy độ dài nhỏ nhất của đoạn AB là 2 30 . Chọn A. 5
Dạng 6: Một số bài toán cực trị khoảng cách liên quan đến mặt cầu
Ví dụ 1: Trong không gian hệ tọa độOxyz cho ba điểm A(0;1; ) 1 ; B(0;0;− ) 1 ;C (1;2;− ) 1 D( 1 − ; 2; − 3 − ) và
mặt cầu (S) có phương trình (x − )2 2 1 + y + (z + )2
1 = 4 . Tìm điểm D trên mặt phẳng (S) sao cho thể tích tứ
diện ABCD lớn nhất. Lời giải:
Mặt cầu (S) có tâm I (1;0;− )
1 và bán kính R = 2. Ta có: 1 V = d D ABC S lớn nhất ⇔ d ( ;
D ( ABC)) lớn nhất ABCD ( ;( )). 3 ABC
Gọi D D là đường kính của mặt cầu (S) và vuông góc với mặt phẳng ( ABC) 1 2 Khi đó ⇔ d ( ;
D ( ABC)) ⇔ D trùng với 1 trong 2 điểm D hoặc D max 1 2
Đường thẳng D D qua I (1;0;− )
1 và có VTCP là n = n = A ; B AC = − − ABC ( 2;2; )1 1 2 ( )
Phương trình mặt phẳng( ABC) : 2x − 2y + z +1 = 0 . x =1+ 2t
Suy ra D D : y = 2
− t , tọa độ D ; D là nghiệm của hệ phương trình 1 2 1 2 z = 1 − + t x =1+ 2t 2 y 2 t t = = − 3 7 4 1 1 4 5 D D : D ; ; ; D ; ; ⇒ ⇒ − − − − − 1 2 1 1 z 1 t 2 − 3 3 3 3 3 3 = − + t = ( x − )2 2 1 + y + (z + )2 1 = 4 3 Do d ( 7 4 1 D ; ABC d D ; ABC D ; ; > ⇒ − − là điểm cần tìm. 1 ( )) ( 2 ( )) 3 3 3
Ví dụ 2: Trong không gian hệ tọa độOxyz cho điểm A(1;2; 3
− ) và mặt phẳng (P) : 2 x+ 2 y− z+ 9 = 0 .
Đường thẳng đi qua A và vuông góc với mặt phẳng (Q) :3x+ 4 y− 4z+ 5 = 0 cắt mặt phẳng (P) tại B. Điểm
M nằm trong mặt phẳng (P) sao cho M luôn nhìn đoạn AB dưới một góc vuông và độ dài MB lớn nhất. Độ dài MB là:
A. MB = 5. B. 5 MB = . C. 41 MB = . D. MB = 41. 2 2 Lời giải: x =1+ 3t
Đường thẳng d đi qua A(1;2; 3
− ) và vuông góc (Q) có phương trình là y = 2 + 4t . z = 3 − − 4t
Vì B = d ∩(P) ⇒ B(1+ 3t;2 + 4t; 3
− − 4t)∈(P) suy ra t = 1 − ⇒ B( 2; − 2; − ) 1 . M ∈(P) Ta có
⇒ M thuộc đường tròn giao tuyến của (P) và mặt cầu (S ) (tâm I, đường kính AB). MA ⊥ MB 1 2 2. − + 2.0 +1+ 9
Phương trình mặt cầu (S ) là 1 2 x 2 + + y + (z + )2 41 1 =
và d (I;(P)) = = 3. 2 4 3 Khi đó 2 2 5
BK = IB − d =
, với K là tâm đường tròn giao tuyến của (P) và (S ). 2
Để MB lớn nhất ⇔ MB là đường kính đường tròn giao tuyến ⇒ MB = 2BK = 5 . Chọn A.
Ví dụ 3: Trong không gian hệ tọa độOxyz cho điểm A(1;2; 3
− ) và mặt phẳng (P) : 2 x+ 2 y− z+ 9 = 0 .
Đường thẳng d đi qua A và có véc tơ chỉ phương u = (3;4; 4
− ) cắt (P) tại điểm B. Điểm M thay đổi trong
(P)sao cho M luôn nhìn đoạn AB dưới góc 90°. Khi độ dài MB lớn nhất, đường thẳng MB đi qua điểm nào trong các điểm sau? A. J ( 3 − ;2;7). B. K (3;0;15). C. H ( 2 − ; 1; − 3). D. I ( 1; − 2 − ;3). Lời giải:
Phương trình đường thẳng
x −1 y − 2 z + 3 d : = =
. Vì B ∈d ⇒ B(3b +1;4b + 2; 4 − b − 3). 3 4 4 −
Mà B = d ∩(P) suy ra 2(3b + )
1 + 2(4b + 2) + 4b + 3+ 9 = 0 ⇔ b = 1 − ⇒ B( 2; − 2; − ) 1 .
Gọi là hình chiếu của A trên (P)
x −1 y − 2 z + 3 ⇒ AA′: = = ⇒ A′( 3 − ; 2 − ;− ) 1 . 2 2 1 − Theo bài ra, ta có 2 2 2 2 2 2 2 2 2
MA + MB = AB ⇔ MB = AB − MA ≤ AB − AA′ = A′B . x = 2 − + t
Độ dài MB lớn nhất khi M ≡ A ⇒ MB : ′ y = 2 − ⇒ I ( 1; − 2
− ;3)∈ MB . Chọn D. z =1+ 2t
Ví dụ 4: Trong không gian hệ tọa độOxyz cho mặt cầu (S có tâm I (2;1 )
;1 bán kính bằng 4 và mặt cầu 1 )
(S có tâm J(2;1;5) bán kính bằng 2. (P)là mặt phẳng thay đổi tiếp xúc với hai mặt cầu (S , S . Đặt 1 ) ( 2 ) 2 )
M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của khoảng cách từ điểm O đến (P) . Giá trị M + m bằng
A. 8. B. 8 3. C. 9 D. 15. Lời giải:
Do IJ = 4 > R + R nên 2 mặt cầu cắt nhau. 1 2
Giả sử IJ cắt (P) tại M ta có MJ R2 =
= 2 ⇒ J là trung điểm của MI MI R1
Suy ra M (2;1;9) . Khi đó (P) a(x − ) + b( y − ) + c(z − ) = ( 2 2 2 : 2 1 9
0 a + b + c > 0) 8c 2c
Mặt khác d (I;(P)) = 4 ⇔ = 4 ⇔ = 1 2 2 2 2 2 2 a + b + c a + b + c Do đó c ≠ 0 chọn 2 2
c =1⇒ a + b = 3 2a + b + 9 2a + b + 9
2 3 sin t + 3 cot t + 9
Đặt a = 3 sin t;b = 3 cot t ⇒ d ( ; O (P)) = = = 2 2 2 a + b + c 2 2 9 − 15 15 + 9
Mặt khác − 12 + 3 ≤ 2 3 sin t + 3 cot t ≤ 12 + 3 ⇒ ≤ d ≤ ⇒ M + m = 9. 0 2 2 Chọn C.
Ví dụ 5: (Đề thi thử nghiệm Bộ GD&ĐT 2017) Trong không gian hệ tọa độOxyz cho mặt phẳng
(P) : x− 2 y+ 2z− 3 = 0 và mặt cầu (S ) 2 2 2
: x + y + z + 2 x− 4 y− 2z+ 5 = 0 . Giả sử điểm M ∈(P)và
N ∈(S ) sao cho MN cùng phương với véc tơ u (1;0; )
1 và khoảng cách giữa M và N lớn nhất. Tính MN. A. MN = 3. B. MN =1+ 2 2. C. MN = 3 2. D. MN =14. Lời giải:
Ta có: (P) : x− 2 y+ 2z− 3 = 0 và (S ) ( + )2 + ( − )2 + ( − )2 : x 1 y 2 z 1 =1 1+ 2 Gọi MN = k ( ) ⇒ MN (P) ( )= (u n = = ⇒ MN P = ° MN P ) 1 1;0;1 sin ; cos ; ;( ) 45 2. 3 2
Gọi H là hình chiếu của M trên (P) khi đó MN sin 45° = MH
Do đó MN = MH 2 lớn nhất ⇔ MH
= d I; P + R = 2 +1 = 3 max ( ( )) Suy ra MN = 3 2 . Chọn C. max
Ví dụ 6: Trong không gian hệ tọa độ Oxyz cho mặt phẳng (P) : x+ y− z− 3 = 0 và hai điểm A(1;1; ) 1 ; B( 3 − ; 3 − ; 3
− ) . Mặt cầu (S ) đi qua hai điểm A, B và tiếp xúc với (P) tại điểm C. Biết rằng C luôn
thuộc đường tròn cố định. Tính bán kính đường tròn đó. A. R = 4. B. R = 6. C. 2 33 R = . D. 2 11 R = . 3 3 Lời giải: x = t
Phương trình đường thẳng AB là: y = t. z = t
Suy ra M (3;3;3) là giao điểm của AB và mặt phẳng (P) khi đó MC là tiếp tuyến của mặt cầu (S ) .
Theo tính chất phương tích ta có: 2 2 .
MA MB = MC ⇒ MC = 2 3.6 3 = 36
Do đó tập hợp điểm C là đường tròn tâm M (3;3;3) bán kính R = 6. . Chọn B.
Ví dụ 7: Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P) : x+ 2 y+ 2z+18 = 0 , M là điểm di
chuyển trên mặt phẳng (P) ; N là điểm nằm trên tia OM sao cho OM.ON = 24 . Tìm giá trị nhỏ nhất của
khoảng cách từ N đến mặt phẳng (P) .
A. Min d N, (P) = 6.
B. Min d N, (P) = 4 .
C. Min d N, (P) = 2 .
D. Min d N, (P) = 0 . Lời giải: Gọi N (a; ; b c) thì 2 2 2
ON = a + b + c Nên 24 24 24 OM = ⇒ OM = .ON = a; ; b c 2 2 2 2 2 2 ( ) 2 2 2 a + b + c a + b + c a + b + c Lại có ∈( ) a 2b 2 ⇒ 24 c M P ( + + +18 = 0 2 2 2
a + b + c ) ( 2 2 2
a + b + c ) ( 2 2 2
a + b + c ) 2 2 2 4a 8b 8c ⇔ + + + + + = ⇒ ∈( ) 2 2 2 4x 8y 8 0 : z a b c N
S x + y + z + + + = 0; 3 3 3 3 3 3 2 − 4 − 4 I ; ; − ⇒ ; R =
2. Khi đó d (N;(P)) = d (N;(P)) − R = 2 . Chọn C. 3 3 3 min
Ví dụ 8: Cho mặt cầu (S ) ( − )2 + ( + )2 + ( − )2 : x 2 y 1
z 3 = 9 . Điểm M (1;0; )
1 di động trên (S ) . Tìm giá trị
nhỏ nhất của biểu thức P = 2x + 2y − z +16 . A. 6. B. 3. C. 24. D. 2. Lời giải:
Mặt cầu (S )có tâm I (2; 1;
− 3) , bán kính R = 3. Xét mặt phẳng (P) : 2x + 2y − z +16 = 0
Đường thẳng ∆ qua I và vuông góc với (P) có phương trình x = 2 + 2t, y = 1
− + 2t, z = 3− t
Cho ∆ ∩(S ) ⇒ ∆ và (S ) cắt nhau tại 2 điểm: A(0; 3 − ;4); B(4;1;2).
Ta có d (A,(P)) = 2,d (B,(P)) = 8
x + y − z +
Lấy M (x y z)∈(S ) ⇒ d (M (P)) 2 2 16 1 ; ; ; = = P 3 3
Ta có: (A;( )) ≤ (M;( )) ≤ ( ;( )) ⇔ 2 P d P d P d B P ≤
≤ 8 ⇔ 6 ≤ P ≤ 24. 3
Vậy P = 6 khi x = 0, y = 3,
− z = 4. Chọn A. min
Ví dụ 9: Trong không gian hệ tọa độ Oxyz , cho ba điểm A(0;1; ) 1 , B(3;0;− ) 1 ,C(0;21; 1 − 9)và mặt cầu
(S) ( − )2 +( − )2 +( − )2 : x 1 y 1
z 1 =1 . M (a;b;c) là điểm thuộc mặt cầu (S )sao cho biểu thức 2 2 2
T = 3MA + 2MB + MC đạt giá trị nhỏ nhất. Tính tổng a + b + c.
A. a + b + c = 0.
B. a + b + c =12. C. 12
a + b + c = . D. 14
a + b + c = . 5 5 Lời giải: Gọi I ( ;
x y; z) là điểm thỏa mãn 3IA + 2IB + IC = 0 3
(0 − x + 2 3− x + 0 − x = 0 1 ) ( 1 ) ( 1 ) Khi đó: 3
(1− y + 2 0 − y + 21− y = 0 ⇒ I 1;4; 3 − 1 ) ( 1 ) ( 1 ) ( ) 3 (1− z + 2 1 − − z + 19 − − z = 0 1 ) ( 1 ) ( 1 ) Ta có: 2 2 2 2 2 2
T = 3MA + 2MB + MC = 3MA + 2MB + MC
⇒ T = (MI + IA)2 + (MI + IB)2 +(MC + IC)2 2
= MI + MI ( IA+ IB + IC) 2 2 2 3 2 6 2 3 2
+ 3IA + 2IB + IC 2 2 2 2
= 6MI + 3IA + 2IB + IC nhỏ nhất ⇔ MI nhỏ nhất. 8 1 x =1 M 1; ; 1 5 5
Mặt cầu (S ) có tâm K (1;1; ) 1 I : ⇒
y = 1+ 3t . Cho KI ∩ (S ) ⇒ z 2 9 = 1− 4t M 1; ; 2 5 5
Tính M I = 4;M I = 6 ⇒ M là điểm thỏa mãn yêu cầu nên 14
a + b + c = . Chọn D. 1 2 1 5
Ví dụ 10: Trong không gian hệ tọa độ Oxyz , cho các điểm A(a;0;0), B(0;b;0),C(0;0;c) với
a ≥ 4,b ≥ 5,c ≥ 6 và mặt cầu (S ) có bán kính bằng 3 10 ngoại tiếp tứ diện OABC. Khi tổng 2
OA + OB + OC đạt giá trị nhỏ nhất thì mặt cầu (S ) tiếp xúc với mặt phẳng nào trong các mặt phẳng sau đây?
A. 2x + 2y + 2z + 3− 2 2 = 0.
B. 2x + 2y − 2z + 6 + 3 2 = 0 .
C. 2x + 2y − 2z + 3+ 2 2 = 0.
D. 2x + 2y + 2z + 7 − 2 2 = 0. Lời giải: 2 2 2
Bán kính mặt cầu ngoại tiếp tứ diện . + + O ABC là a b c 3 10 2 2 2 R = =
⇔ a + b + c = 90. 2 2
Ta có P = OA + OB + OC = a + b + c . Đặt m = a − 4 ≥ 0,n = b − 5 ≥ 0, p = c − 6 ≥ 0. Khi đó 2 2 2
a + b + c = (m + )2 + (n + )2 + ( p + )2 2 2 2 4 5
6 = m + n + p + 8m +10n +12 p + 77 = 90.
T = (m + n + p)2 + (m + n + p) 2 2 2 12
= m + n + p + 8m +10n +12 p + 2(mn + np + pm + 2m + n). Vì 2 2 2
m + n + p + 8m +10n +12 p =13 và , m ,
n p ≥ 0 nên (m + n + p)2 +12(m + n + p) −13 ≥ 0.
⇔ m + n + p ≥1 ⇔ a + b + c ≥16 ⇒ {OA + OB + OC} =16. Dấu “ = ” xảy ra ⇔ a = 4,b = 5,c = 7 . min
Tâm của mặt cầu (S ) là a b c 5 7 I I ⇒
⇒ d (I (P) = Chọn D. D ) 3 10 ; ; 2; ; ; . 2 2 2 2 2 2
Dạng 7: Bài toán cực trị liên quan đến góc Phương pháp đại số
• Gọi véc tơ pháp tuyến hoặc véc tơ chỉ phương của mặt phẳng (hoặc đường thẳng) cần lập là ( ; a ;c b ) trong đó 2 2 2
a + b + c > 0 .
• Thiết lập một phương trình quy ẩn (a theo b,c hoặc ngược lại) từ một dữ kiện về mặt phẳng chứa
đường, song song hoặc vuông góc. Giả sử phương trình thu gọn ẩn là a = f ( ; b c).
• Thiết lập phương trình về góc, thay a = f ( ;
b c). vào ta được một phương trình hai ẩn b,c. Chú ý: u .u
• Góc giữa hai đường thẳng cos(d ;d ) = cos(u ;u ) 1 2 = 1 2 1 2 u . u 1 2 n .n
• Góc giữa hai mặt phẳng cos( P) ;(P ) = cos n ;n = 1 ) ( ) 1 2 2 1 2 n . n 1 2 n u
• Góc giữa đường thẳng và mặt phẳng ( ( )) = (n u ) P . sin d; P cos ; d = P d n u P . d
• Ta biết rằng hàm sinϕ đồng biến khi 0 < ϕ < 90° , ngược lại hàm cosϕ nghịch biến .
Vậy khi hàm xét max, min là hàm sin thì góc lớn ứng với hàm max,, góc nhỏ ứng với hàm nhỏ. Còn
khi hàm xét max, min là hàm cosin thì ngược lại, đề bài yêu cầu tìm góc lớn thì hàm phải đạt min, góc
nhỏ thì hàm đạt max.
Phương pháp hình học
Bài toán 1: Lập phương trình mặt phẳng (Q) chứa ∆ sao cho mặt phẳng (Q) tạo với mặt phẳng
(P)cho trước một góc nhỏ nhất (hoặc tạo với đường thẳng d cho trước một góc lớn nhất) Phương pháp giải: - TH1: (P);(Q) ( ) min
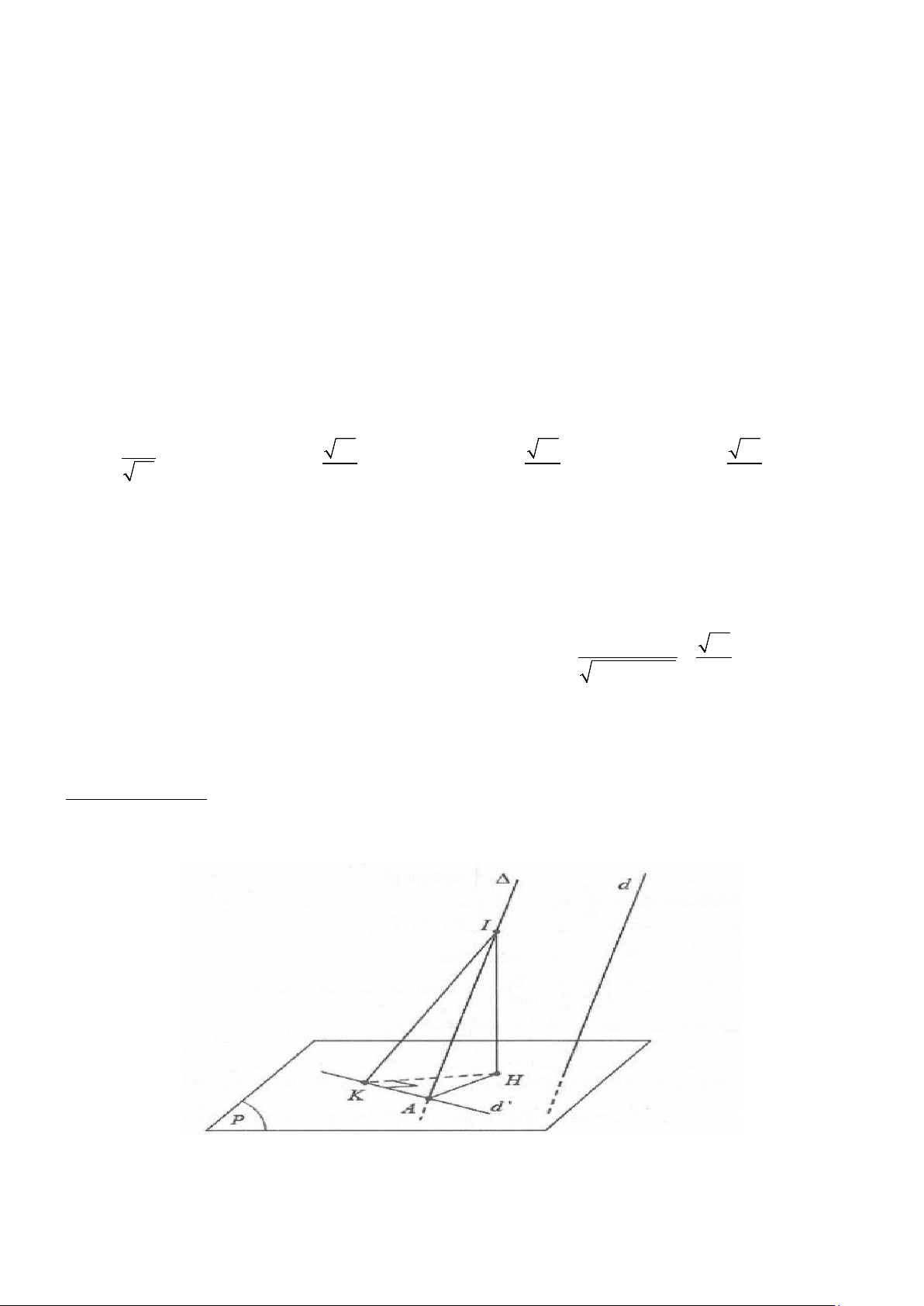
Gọi A = ∆ ∩(P);d = (P) ∩(Q)với (Q) là mặt phẳng (IAK ) trong hình vẽ. Lấy I ∈∆ ⇒ ;
A I cố định, dựng IH ⊥ d ⇒ (P) (Q) ( )= ; IKH = ϕ. Do ≥ ⇒ sin IH IH IA IK ϕ = ≥
⇒ ϕ khi K ≡ A tức là ∆ ⊥ d ⇔ ∆ ⊥ (P) ⇒ n = u ∆ u Q ; min IK IA d IA ⊥ d ∆ ⊥ d Mặt khác ⇔ ⇒ = d (P) d (P) u u∆ n d ; (P) ⊂ ⊂
Suy ra (P);(Q) (
)nhỏ nhất ⇔ ∆⊥giao tuyến d của (P)và (Q) ⇔ = ( n ) u ∆ ; u∆ ; n Q (P) -TH2: (Q) ( ;d) ⇔ = ( n u ∆ u∆ u Q) ; ; d max (
P);(Q) ( ) ⇔ = ( n
u∆ u∆ n Q) ; ; (P) Tổng kết: min (Q)
( ;d) ⇔ = ( n
u∆ u∆ u Q) ; ; d max Ví dụ 1: Cho x + 2 y + 2 z x + 2 y −1 : = = ; ′: z d d =
= ;(Q) : x + 2y + 2z − 3 = 0 1 2 1 − 2 1 − 2 Lập chứa d sao cho
a) Góc giữa (P) và (Q) nhỏ nhất.
b) Góc giữa (P) và d′ lớn nhất. Lời giải: a) Ta có: u =
− và n = (1;2;2 . Đường thẳng d đi qua M (1; 2 − ;0). Q ) d (1;2; )1 ( ) (
P);(Q) (
) ⇔ n =u u n = − − − =− P d ; d ; Q ( 3; 6; 15) 3(1;2;5) ( ) ( ) min
Mặt phẳng (P) đi qua điểm M và có véc tơ pháp tuyến n = (1;2;5) có phương trình là:
(P): x + 2y +5z +3 = 0 . b) Ta có: u = − d′ (2; 1;2). Để (P)
( ;d′) ⇔ n =u u u = − − =− − P d ; d ; d′ ( 14;2; 10) 2(7; 1;5) ( ) max
Mặt phẳng (P) đi qua điểm M và có véc tơ pháp tuyến n = (7; 1; − 5)
Phương trình mặt phẳng (P) : 7x − y + 5z −9 = 0 .
Ví dụ 2: Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P) : 2 x− y− 2z− 2 = 0 và đường thẳng x y +1 z − 2 ∆ : = =
. Gọi (Q) là mặt phẳng chứa ∆ và tạo với (P) một góc nhỏ nhất. Khoảng cách từ 1 − 2 1
gốc tọa độ O đến mặt phẳng (Q) bằng A. 3. B. 2 . C. 5. D. 1. 3 Lời giải: Ta có: n = (2; 1; − 2 − );u −
và đường thẳng ∆ đi qua A(0; 1; − 2). ∆ ( 1; 2; ) ( ) 1 P (
P);(Q) ( ) nhỏ nhất ⇔ = ( n ) u ∆ ; u∆ ; n Q (P) Ta có: u = u = −
suy ra n = u u = − − Q d ; ∆ 2(1;1; ) 1 ∆ n d ; 3 P (1;0; ) ( ) 1 ( )
Khi đó (Q) đi qua A(0; 1;
− 2) và n = (1;1;− )
1 (Q) : x + y − z + 3 = 0 ⇒ d ( ;
O (Q)) = 3. Chọn A.
Ví dụ 3: Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P) : 2 x− 2 y− z+1 = 0 và đường thẳng x −1 ∆ : y z = =
. Gọi (Q) là mặt phẳng chứa ∆ và tạo với (P) một góc nhỏ nhất. Tính cosin góc 1 1 − 2 −
ϕ giữa 2 mặt phẳng (P) và (Q) khi đó: A. 1 cosϕ = . ϕ = 3 B. 3 cosϕ = . C. 2 cosϕ = . D. 1 cos . 3 2 2 Lời giải: Ta có: u = − −
− − và đường thẳng ∆ đi qua M (1;0;0). ∆ (1; 1; 2);n (2; 2; ) ( ) 1 P
Để (P);(Q) (
) ⇔ n =u = − − = − − ∆ ; u∆ ; n ( 6;6; 6) 6(1; 1; ) ( ) ( ) 1 . Q P min 2.1+ 2 −1 Suy ra 3 cosϕ = = . Chọn B. 4 + 4 +1. 3 3
Ví dụ 4: Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P) : x+ 2 y− z+ 3 = 0 và đường thẳng
x +1 y +1 z − 3 d : = =
. Mặt phẳng (Q) chứa đường thẳng d và tạo với mặt phẳng (P) một góc nhỏ 2 1 1
nhất. Khoảng cách từ O đến (Q) bằng: A. 4 2. B. 2. C. 2. D. 2 2. Lời giải: Ta có: u = n
− và đường thẳng ∆ đi qua M ( 1; − 1; − 3). d (2;1; )1; P (1;2; ) ( ) 1
(P);(Q) (
) ⇔ n =u u n = − =− − Q d ; d ; P (0; 9;9) 9(0;1; ) ( ) ( ) 1 . min
Phương trình mặt phẳng (P) cần tìm đi qua điểm M ( 1; − 1;
− 3).và có véc tơ pháp tuyến n(Q) = (0;1;− ) 1
Suy ra (P) y − z + = ⇒ d (O Q) 4 : 4 0 ; = = 2 2. Chọn D. 2
Ví dụ 5: Trong không gian với hệ tọa độ − +
Oxyz , cho đường thẳng x 1 z 2 d : z =
= . Gọi (P) là mặt 1 − 1 2
phẳng chứa d và tạo với trục Oy một góc lớn nhất. Mặt phẳng (P) đi qua điểm nào trong các điểm sau: A. A(6; 3 − ;0). B. B(2; 3 − ;0). C. C (2;1;− ) 1 . D. D(2;1 ) ;1 . Lời giải: Ta có: u = − u
và đường thẳng d đi qua M (1; 2 − ;0). d ( 1;1;2); Oy (0;1;0)
Để (P)
( ;Oy) ⇔ n =u u u = − − =− − P d ; d ; Oy ( 1; 5;2) 1(1;5; 2) ( ) . max
Mặt phẳng (P) đi qua điểm M và có véc tơ pháp tuyến n = (1;5; 2 − )
Phương trình mặt phẳng (P) : x + 5y − 2z + 9 = 0 .
Do đó (P) đi qua điểm A(6; 3 − ;0). Chọn A.
Ví dụ 6: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A(1;2;− ) 1 ; B( 1;
− 1;2) . Gọi (Q) là phương
trình mặt phẳng đi qua 2 điểm A, B sao cho (Q) tạo với mặt phẳng(Oxy) một góc nhỏ nhất. Khoảng cách
từ gốc O đến mặt phẳng (Q) bằng: A. 7 d = . 35 B. 70 d = . C. 70 d = . D. 70 d = . 10 70 35 Lời giải: Ta có: AB = ( 2; − 1 − ;3);n (0;0; ) ( ) 1 . Oxy
Để (P)
( ;Oxy) ⇔ n =AB AB n = − − − =− Q ; ; Oxy ( 6; 3; 5) (6;3;5) ( ) . min
Phương trình mặt phẳng (Q) là: x + y + z − = ⇒ d (O (Q)) 7 70 6 3 5 7 0 ; = = .Chọn B. 2 2 2 6 + 3 + 5 10
Bài toán 2: Viết phương trình đường thẳng d′ qua A nằm trong(P) sao cho góc giữa 2 đường thẳng d và
d′ nhỏ nhất (hoặc tạo với mặt phẳng (Q) cho trước một góc lớn nhất) Phương pháp giải: - TH1: (d;d′) min
Qua A dựng đường thẳng ∆ d , trên ∆ lấy điểm I, hạ IH ⊥ (P) ⇒ ,
A I, H cố định, điểm K thay đổi (d d′)= (∆ d′)= ; ; IAK = α Mà sin IK IH α = ≥
(Do IK ≥ IH ) suy ra α
⇔ H ≡ K hay d′ qua A và H. IA IA min
Khi đó d′ là hình chiếu vuông góc của ∆ trên (P) .
Ta có:
(d;d′) ⇔u = = ′ n n n n u d (P); AIH (P); (P); d . min
- TH2: d;(Q) ( ) ⇔u = ′ n n n d (P); (P); Q . max (
d;d′ ) ⇔u = ′ n n u d (P); (P); d Tổng kết: min
d;(Q) ( ) ⇔u = ′ n n n d (P); (P); (Q) . max
Ví dụ 1: Trong không gian với hệ tọa độ Oxyz , cho điểm A(1; 1;
− 2) và mặt phẳng (P) : 2x − y − z + 3 = 0 .
Lập phương trình đường thẳng d đi qua A; song song với (P) đồng thời tạo với đường x +1 y −1 ∆ : z = = 1 2 − 2 một góc nhỏ nhất. Lời giải:
Gọi (α ) là mặt phẳng chứa A và song song với (P) ⇒ n = − − α (2; 1; ) ( ) 1 .
Khi đó d nằm trong (α ) sao cho góc giữa d và ∆ nhỏ nhất.
Ta có:
(d;∆) ⇔u = n = − − α u∆ n d ; ; α 2(1; 5;7) ( ) ( ) min
Phương trình đường thẳng d là:
x −1 y +1 z − 2 d : = = . 1 5 − 7
Ví dụ 2: Trong không gian với hệ tọa độ Oxyz , cho điểm A(1; 1; − 2) và hai đường
x −1 y − 2 z + 2
x − 3 y − 2 z + 3 d : = = ;d′: = =
. Lập phương trình đường thẳng ∆ đi qua A đồng thời cắt 2 1 1 − 1 − 2 2
đường d sao cho góc giữa ∆ và d′ nhỏ nhất? Lời giải:
Gọi (P) là mặt phẳng chứa A và d.
Đường thẳng d đi qua điểm A(1;2; 2
− )và có VTCP là u = − d (2;1; )1.
Khi đó n = AM ;u = −
. Đường thẳng ∆ ⊂ (P) . P d (1;0;2) ( )
Ta có:
( ;∆d′) ⇔u = = − − = − − ∆ n ; n ;u P P d′ (8; 10; 4) 2(4; 5; 2) ( ) ( ) . min
Phương trình đường thẳng là: x +1 y z +1 d : = = . 4 5 − 2 −
Ví dụ 3: Trong không gian với hệ tọa độ Oxyz , lập phương trình đường thẳng d đi qua A(1;0; 2 − ) và cắt
x −1 y +1 z − 2 ∆ : = =
sao cho góc giữa d và mặt phẳng (P) : 2 x− y + 2z −1 = 0 lớn nhất?. 3 2 2 − Lời giải:
Đường thẳng d nằm trong mặt phẳng (Q) chứa A và ∆ .
Đường thẳng ∆ đi qua điểm M (1; 1;
− 2) và có VTCP là u = − − ∆ (3;2; 2), AM (0; 1;4)
Ta có: n = AM ;u = − − ⇒ = − . ∆ ( 6;12;3) n ( 2;4; ) ( ) ( ) 1 Q Q
Để d;(P)
( ) ⇔u =n n n = − − − =− d ; ; Q Q P ( 30; 3; 48) 3(10;1;16) ( ) ( ) ( ) . max
Khi đó phương trình đường thẳng x −1 y z + 2 d : = = . 10 1 16
Ví dụ 4: Trong không gian với hệ tọa độ Oxyz , đường thẳng ∆ đi qua A(1;0; ) 1 , nằm trong mặt phẳng ( P) : 2 x − +
+ y − z −1 = 0 và tạo với đường thẳng x y 1 z 1 d : = =
một góc nhỏ nhất. Biết u = (5; ; b c) là 2 1 − 2
một véc tơ chỉ phương của đường thẳng ∆ . Tìm b + c.
A.b + c = 6. −
B. b + c = 6.
C. b + c = 3. −
D. b + c = 3. Lời giải: Ta có: n = − u = − P (2;1; ) 1 ; d (2; 1;2) ( ) .
Để ( ∆) ⇔u = = − − = − − ∆ n ; n ;u P P d ( 10;7; 13) 5 7 13 d; ( ) ( ) 2 ; ; . min 2 2 2 Do đó: 7 13 b = − ;c =
⇒ b + c = 3.Chọn D. 2 2
Ví dụ 5: Trong không gian với hệ tọa độ −
Oxyz , cho điểm A(3; 1; − ) 1 , đường thẳng x y 2 ∆ : z = = , mặt 1 2 2
phẳng (P) : x− y + z −5 = 0 . Gọi d là đường thẳng đi điểm qua A nằm trong (P) và tạo với ∆ một góc bé nhất là α . Tính sinα . A. 78 . B. 3 . C. 6 . D. 75 . 9 9 9 9 Lời giải: Ta có: n = (1; 1; − ) 1 ;u = ∆ (1;2;2) ( ) . P
Để
(d;∆) ⇔u = n n u = − − − = − d ; ; P P ∆ ( 2; 7; 5) (2;7;5) ( ) ( ) . min
Phương trình đường thẳng d là:
x − 3 y +1 z −1 d : = = . 2 7 5 2 +14 +10 Khi đó α = (u u = = ⇒ α = − α = Chọn B. ∆ d ) 78 2 3 cos cos ; . sin 1 cos . 2 2 2 3. 2 + 7 + 5 9 9
Ví dụ 6: Trong không gian với hệ tọa độ Oxyz , gọi d là đường thẳng song song với (P) : x− 2y + 2z −5 = 0
, đồng thời tạo với mặt phẳng (Oyz) một góc lớn nhất là ϕ . Tính P = sinϕ . A. P =1. B. 2 2 P = . C. 1 P = . D. 1 P = . 3 3 2 Lời giải:
Gọi Q ≡ (Oyz) ⇒ n = (1;0;0);n = (1; 2 − ;2) ( ) ( ) . Q P
Ta có ϕ = d;(Q) (
) ⇔u =n n n = − − =− − d ; ; P P Q ( 8; 2;2) 2(4;1; ) ( ) ( ) ( ) 1 . max Suy ra ϕ = (u n = = . Chọn B. d Q ) 4 2 2 sin cos ; ( ) 18 3
Ví dụ 7: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : 2x− y + z −1= 0, điểm A(2;3;0)
thuộc mặt phẳng (P) và đường thẳng x +1 y z −1 d : = =
. Đường thẳng d′ qua A nằm trong (P) sao cho 1 1 − 1
góc giữa 2 đường thẳng d và d′ nhỏ nhất đi qua điểm nào trong các điểm sau: A. (0;0; ) 1 . B. (2;4; ) 1 . C. (1;1;0) . D. (1;2; ) 1 . Lời giải: Ta có: n = − u = − P (2; 1; ) 1 ; d (1; 1; ) ( ) 1 .
Do đó ( ′) x − y − z ⇔ u = = − = − ⇒ ′ = = ′ n n u d ; ; P P d (2;2; 2) 2(1;1; ) 2 3 d;d ( ) ( ) 1 d : . min 1 1 1 −
Vậy d′ đi qua hai điểm (1;2; ) 1 . Chọn D.
Ví dụ 8: Cho mặt phẳng (P) : x− y + z − 2 = 0 điểm A(2;1 )
;1 thuộc mặt phẳng (P) và đường thẳng x −1 y z +1 d : = =
. Đường thẳng d′ qua A nằm trong (P) sao cho góc giữa 2 đường thẳng d và d′ nhỏ 1 − 2 2
nhất cắt mặt phẳng (Oyz) tại điểm E. Tính P = OE . A. P =14. B. P = 2 6. C. P =10. D. P = 14. Lời giải: Ta có: n = − u = − ⇒ n u = − P (1; 1; )1; d ( 1;2;2) ; P d (4;3; ) ( ) ( ) 1
Ta có: ( ′) x − y − z ⇔ u − = = − − − ⇒ ′ = = ′ n n u d ; ; P P d (2; 5; 7) 2 1 1 d;d ( ) ( ) d : . min 2 5 − 7 −
Vậy d′ cắt mặt phẳng x = 0 tại điểm E (0;6;8) ⇒ OE =10. Chọn C.
BÀI TẬP TỰ LUYỆN
Câu 1: Trong không gian Oxyz , cho hai điểm A(1;2;2),B(5;4;4) và mặt phẳng (P) : 2x + y − z + 6 = 0 .
Nếu M thay đổi thuộc (P) thì giá trị nhỏ nhất của 2 2 MA + MB là A. 60. B. 50. C. 200 . D. 2968. 3 25
Câu 2: Trong không gian với hệ trục tọa độOxyz , cho các điểm A( 5 − ;2;2),B( 1 − ;6;2) . Mặt phẳng
(P) : x + y − 2z − 5 = 0 . Gọi M(a;b;c) là điểm thuộc (P) thỏa mãn MA + 3MB nhỏ nhất, khi đó tính giá trị của tích abc. A. 20. − B. 0 . C. 12. D. 24 .
Câu 3: Trong không gian với hệ trụcOxyz , cho các điểm A(5;8; 1 − ) 1 ,B(3;5; 4 − );C (2;1; 6 − ) và mặt cầu
(x − )2 +( y − )2 +(z + )2 (S) : 4 2 1 = 9 . Gọi M(x
là điểm trên (S ) sao cho biểu thức
M ; yM ;zM )
MA − MB − MC đạt giá trị nhỏ nhất. Tính P = x + y . M M A. P = 4. B. P = 0. C. P = 2. − D. P = 2.
Câu 4: Trong không gian với hệ trục Oxyz , cho hai điểm A(1;0;2),B(0; 1; − 6) và mặt phẳng
(P) : x + 2y − 2z +12 = 0 . Gọi M là điểm di động trên mặt phẳng (P) . Tìm giá trị lớn nhất của MA− MB . A. 6 2. B. 10 . C. 3 2 . D. 2 10 .
Câu 5: Trong không gian với hệ trục Oxyz , cho hai điểm A(2; 1; − ) 1 ,B(1; 1; − 0) và đường thẳng
x −1 y −1 z −1 d : = =
. Gọi M là điểm thuộc đường thẳng d sao cho diện tích tam giác MAB nhỏ nhất. Tính 1 2 3 giá trị biểu thức 2 2 2 Q = x + + M y M z M A. Q = 29. B. 53 Q = . C. 49 Q = . D. 101 Q = . 18 18 36
Câu 6: Trong không gian vớihệ trục Oxyz , cho hai điểm M (0;1;3),B(10;6;0) và mặt phẳng (P) có
phương trình (P) : x − 2y + 2z −10 = 0. Điểm I( 1
− 0;a;b) thuộc mặt phẳng (P) sao cho IM − IN lớn nhất.
Tính tổng T = a + b. A. T = 6 . B. T = 5 . C. T =1. D. T = 2.
Câu 7: Trong không gian với hệ tọa độOxyz , cho mặt phẳng (α) : x + y + z + 3 = 0 và hai điểm A(3;1; )
1 ,B(7;3;9) . Gọi M(a;b;c) là điểm trên mặt phẳng (α ) sao cho MA+ MB đạt giá trị nhỏ nhất.
Tính S = a − 2b + 3c . A. S = 6 − . B. S =19 . C. S = 5. D. S = 6 .
Câu 8: Trong không gian với hệ tọa độOxyz , cho các điểm A( 3 − ;5; 5 − ),B(5; 3 − ;7) và mặt phẳng
(P) : x + y + z − 6 = 0 . Lấy điểm M(a;b;c) trên mặt phẳng (α ) sao cho 2 2
MA + MB đạt giá trị nhỏ nhất.
Tính S = a + b + c . A. S = 4 . B. S = 3. C. S = 5. D. S = 6 .
Câu 9: Trong không gian với hệ trục tọa độOxyz , cho điểm A(0; 2; − 3 − ),B( 4; − 4; − ) 1 ;C(2; 3 − ;3) . Tìm tọa
độ điểm M trong mặt phẳng Oxz sao cho 2 2 2
MA + MB + 2MC đạt giá trị nhỏ nhất. A. (0;0;3). B. (0;0;2) . C. (0;0; ) 1 . D. (0;0; ) 1 − .
Câu 10: Trong không gian với hệ trục Oxyz , cho các điểm A(2;0;− ) 1 ,B(1;0;− )
1 ,C (0;1;0) Gọi M là điểm
thuộc mặt phẳng Oxy sao cho 2 2 2
AM − 5BM + 2CM đạt giá trị lớn nhất. Tính độ dài đoạn thẳng OM. A. 13 . B. 29 . C. 26 . D. 6 . 2 2 2 2
Câu 11: Trong không gian với hệ tọa độOxyz , cho điểm A(3;1;0),B( 9; − 4;9) và mặt phẳng
(P) : 2x − y + z +1 = 0 . Gọi I (a;b;c) là điểm thuộc mặt phẳng (P) sao cho IA − IB đạt giá trị lớn nhất. Khi
đó tổng a + b + c là
A. a + b + c = 22 .
B. a + b + c = 4 − .
C. a + b + c = 13 − .
D. a + b + c =13.
Câu 12: Trong không gian với hệ tọa độOxyz , cho hai điểm A(2; 3
− ;2),B(3;5;4) . Tìm tọa độ điểm M trên trục Oz sao cho 2 2
MA + MB đạt giá trị nhỏ nhất. A. M (0;0;49) . B. M (0;0;0) . C. M (0;0;67) . D. M (0;0;3) .
Câu 13: Trong không gian Oxyz , cho A(1;2;3) và B(3;2; )
1 . Viết phương trình mặt phẳng đi qua A và cách
B một khoảng lớn nhất.
A. x − z − 2 = 0 .
B. 3x + 2y + z −10 = 0 .
C. x + 2y + 3z −10 = 0 .
D. x − z + 2 = 0 .
Câu 14: Trong không gian với hệ tọa độ Oxyz , mặt cầu
(x − )2 +( y − )2 +(z + )2 (S) : 4 7 1 = 36 và mặt phẳng
(P) :3x + y − z + m = 0 . Tìm m để mặt phẳng (P) cắt (S ) theo giao tuyến là một đường tròn có bán kính lớn nhất. A. m = 20 − . B. m = 6. C. m = 36 . D. m = 20 .
Câu 15: Cho mặt cầu 2 2 2
(S) : x + y + z − 2x − 4y + 6z −1 = 0 . Tìm tất cả các giá trị thực của tham số m để
mặt phẳng (P) : x + 3y − 2z − m = 0 cắt mặt cầu (S )theo một đường trong có chu vi lớn nhất. A. m =1. B. m = 13 − . C. m =13. D. m = 1 − .
Câu 16: Trong không gian với hệ tọa độ Oxyz ,viết phương trình mặt phẳng (P) đi qua điểm M (1;2;3) và cắt các tia Ox, Oy,
Oz lần lượt tại các điểm A, B, C sao cho 1 1 1 T = + +
đạt giá trị nhỏ nhất. 2 2 2 OA OB OC
A. (P) : x + 2y + 3z −14 = 0 .
B. (P) : 6x −3y + 2z − 6 = 0 .
C. (P) : 6x + 3y + 2z −18 = 0
D. (P) :3x + 2y + z −10 = 0 .
Câu 17: Trong không gian với hệ trục Oxyz , cho đường thẳng x 4 y 5 : z d − − =
= . Xét mặt phẳng (P) 1 2 3
chứa đường thẳng d sao cho khoảng cách từ M (0;0;0) đến (P) đạt giá trị lớn nhất. Xác định tọa độ giao
điểm N của (P) và trục Oz . A. N (0;0; 9 − ) . B. N (0;0;9). C. N (0;0;3) . D. N (0;0;6).
Câu 18: Trong không gian với hệ trục − −
Oxyz , cho đường thẳng x 1 y z 2 d : = =
và điểm M (1;7;3). Viết 2 1 2
phương trình mặt phẳng (P) chứa đường thẳng d sao cho khoảng cách từ M đến (P) đạt giá trị lớn nhất.
A. 2x − 6y + z − 4 = 0.
B. 2x + y − 2z −10 = 0.
C. x + y + 2z −15 = 0
D. x − 2y − z +1 = 0 .
Câu 19: Trong không gian với hệ trục Oxyz , viết phương trình mặt phẳng (P) đi qua điểm M (2;1;3)và cắt
các trục tọa độ Ox, Oy,
Oz lần lượt tại các điểm A, B, C không trùng với O sao cho biểu thức 1 1 1 + +
đạt giá trị nhỏ nhất. 2 2 2 OA OB OC
A. 2x + y + 3z −10 = 0 .
B. 2x − y + 3z −14 = 0.
C. 2x + y + 3z −14 = 0
D. 2x + y − 3z −14 = 0.
Câu 20: Cho ba tia Ox, Oy,
Oz đôi một vuông góc. Một điểm M cố định và khoảng cách từ điểm M đến các
mặt phẳng (Oxy), (Oyz) , (Oxz)
lần lượt là a, b, c. Biết tồn tại mặt phẳng (P) qua M và cắt các tia Ox, Oy,
Oz tại A, B, C sao cho thể tích khối tứ diện OABC nhỏ nhất. Tính giá trị nhỏ nhất đó. A. 9abc V = . B. abc V = .
C. V = 27abc . D. abc V = . min 2 min 6 min min 3
Câu 21: Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm M ( 2; − 2; − ) 1 , A(1;2; 3 − ) và đường thẳng x 1 y 5 : z d + − = =
.Tìm véc tơ chỉ phương u của đường thẳng ∆ đi qua M, vuông góc với đường thẳng d 2 2 1 −
đồng thời cách điểm A một khoảng bé nhất. A. u = (3;4; 4 − ) .
B. u = (2;2;− ) 1 . C. u = (2;1;6). D. u = (1;0;2).
Câu 22: Trong không gian với hệ trục Oxyz , cho các điểm M (2;2; 3 − ) và N ( 4; − 2; ) 1 . Viết phương trình
đường thẳng ∆ đi qua M, song song với mặt phẳng (P) : 2x + y + z = 0 sao cho khoảng cách từ N đến ∆ đạt giá trị nhỏ nhất. A.
x − 2 y − 2 z + 3 − − + ∆ : = = . B.
x 2 y 2 z 3 ∆ : = = . 3 2 − 4 − 1 1 − 1 − C.
x − 2 y − 2 z + 3 − − + ∆ : = = . D.
x 2 y 2 z 3 ∆ : = = . 5 2 − 8 − 2 − 7 3 −
Câu 23: Trong không gian với hệ tọa độOxyz , cho mặt phẳng (α) : a x + by + cz + d = 0 ( 2 2 2
a + b + c > 0) đi
qua hai điểm M (5;1;3) và N (1;6;2) . Biết rằng khoảng cách từ điểm P(5;0;4) đến mặt phẳng (α ) đạt giá
a + b + c + d
trị lớn nhất. Tính giá trị biểu thức S = 2 2 2 a + b + c A. 14 S = . B. 4 14 S = . C. 14 = . D. 10 14 S = . 2 7 7 7
LỜI GIẢI BÀI TẬP TỰ LUYỆN
Câu 1: Gọi I (3;3;3) là trung điểm của AB thì IA+ IB = 0 2 2 2 2
T = MA + MB = MA + MB = (MI + IA)2 +(MI + IB)2 2 2 2
= 2MI + IA + IB nhỏ nhất ⇔ MI min
Khi đó M là hình chiếu vuông góc của I trên (P) ⇒ IM ⊥ (P) 2 2.3+ 3− 3+ 6 Suy ra MI d M P T = = = ⇒ = + IA + IB = . Chọn A. in ( ;( )) 12 12 2 2 2. 60 m min 4 +1+1 6 6
Câu 2: Gọi I là điểm thỏa mãn IA + 3IB = 0 ⇒ I ( 2 − ;5;2)
Khi đó MA + 3MB = 4MI nhỏ nhất ⇔ MI ⇔ M là hình chiếu của I trên (P) . min x = 2 − + t
Phương trình đường thẳng IM qua I vuông góc với (P) là: y = 5+ t ⇒ M ( 2
− + t;5 + t;2 − 2t) z = 2− 2t
Cho M ∈(P) ⇒ t − 2 + 5 + 4t − 4 −5 = 0 ⇔ t =1⇒ M ( 1
− ;6;0) ⇒ abc = 0. Chọn B.
Câu 3: Gọi điểm G( ;
x y; z) sao cho GA − GB − GC = 0 ⇔ BA = GC ⇒ G(0; 2; − ) 1
Xét măt cầu (S ) (x − )2 + ( y − )2 + (z + )2 : 4 2 1 = 9 tâm I (4;2;− )
1 và bán kính R = 3. Ta có IG = ( − ) 2 ⇒ IG = + (− )2 2 4; 4;2 4
4 + 2 = 6 > R ⇒ G nằm ngoài mặt cầu (S ).
Ta có MA − MB − MC = −MG + GA − GB − GC = MG = MG ⇒ MG nhỏ nhất ⇔ I, M ,G thẳng x =
hàng hay M chính là trung điểm của IG ⇒ M ( ) M 2 2;0;0 ⇒
⇒ P = 2 . Chọn D. y = M 0
Câu 4: Kí hiệu f = x + 2y − 2z +12 . Ta có f ( A). f (B) < 0 nên A,B nằm khác phía so với mặt
phẳng (P) . Gọi là điểm đối xứng của A qua mặt phẳng (P) Ta có: x −1 y z − 2 AA′: = =
. Khi đó I = AA′∩(P) ⇒ I (1+ t;2t;2 − 2t)∈(P) 1 2 2
⇒ t +1+ 4t + 4t − 4 +12 = 0 ⇒ t = 1 − ⇒ I (0; 2; − 4) ⇒ A′( 1 − ; 4; − 6).
Lại có MA − MB = MA′ − MB ≤ A′B dấu bằng xảy ra ⇔ A ,′ M , B thẳng hàng. Vậy MA − MB
= A′B = 10 . Chọn B. max
Câu 5: Gọi M (1+ t;1+ 2t;1+ 3t)∈d ⇒ AM (t −1;2t + 2;3t); AB( 1; − 0;− ) 1 Ta có 1 1 S = AM AB =
− t − − t − t + = t + + t + + t + MAB ( ) 1 . 2 2; 2 1;2 2 (2 2)2 (2 )2 1 (2 2)2 2 2 2 1 2 − − − − =
12t + 20t + 9 nhỏ nhất 20 5 1 2 3 49 ⇔ t = = ⇒ M ; ; ⇒ Q = .Chọn C. 2 24 6 6 3 2 18
Câu 6: Đặt f = x − 2y + 2z −10 ⇒ f (M ). f (N ) > 0 ⇒ M , N nằm cùng phía với mặt phẳng (P)
Ta có: IM − IN ≤ MN ⇔ M , N, I thẳng hàng. x =10t
Phương trình đường thẳng MN là: y =1+ 5t ⇒ I = MN ∩(P) = ( 1 − 0; 4; − 6) z = 3− 3t
Suy ra T = a + b = 2 .Chọn D.
Câu 7: Gọi I (5;2;5) là trung điểm của AB
Ta có: MA + MB = 2MI nhỏ nhất ⇔ MI ⇔ M là hình chiếu vuông góc của I trên min x = 5 + t
(α ): x y z 3 0 MI : + + + = ⇒
y = 2 + t ⇒ M (5 + t;2 + t;5 + t) z = 5+ t
Cho M ∈(α ) ⇒ t + 5 + t + 2 + t + 5 + 3 = 0 ⇔ t = 5 − ⇒ M (0; 3
− ;0) ⇒ S = 6.Chọn A.
Câu 8: Gọi I (1;1; )
1 là trung điểm của AB Ta có: 2 2 2 2 2 2 2
MA + MB = 2MI + IA + IB = 2MI + 2IA nhỏ nhất ⇔ MI
⇔ M là hình chiếu min x =1+ t
vuông góc của I trên (P) : x y z 6 0 MI : + + − = ⇒
y = 1+ t ⇒ M (1+ t;1+ t;1+ t) z =1+ t
Giải M ∈(P) ⇒ t =1⇒ M (2;2;2) ⇒ S = 6.Chọn D
Câu 9: Gọi I là điểm thỏa mãn IA + IB + 2IC = 0 ⇒ I (0; 3 − ; ) 1 Biến đổi 2 2 2 2 2 2 2
MA + MB + 2MC = 4MI + IA + IB + 2IC nhỏ nhất ⇔ MI ⇔ M là hình chiếu min
vuông góc của I trên (Oxz) ⇒ M (0;0; ) 1 . Chọn C. Câu 10: Đặt 2 2 2
T = MA − 5MB + 2MC
Gọi I là điểm thỏa mãn 3
IA 5IB 2IC 0 I ; 1; 2 − + = ⇒ − − 2 Biến đổi 2 2 2 2 T = 2
− MI + IA − 5IB + 2IC lớn nhất ⇔ MI
⇔ M là hình chiếu vuông góc của I min trên 3 13 Oxy ⇒ M ; 1; − 0 ⇒ OM = . Chọn A. 2 2
Câu 11: Đặt f = 2x − y + z +1⇒ f ( A). f (B) < 0 ⇒ M , N nằm khác phía so với
(P): 2x − y + z +1= 0. Gọi x − y − z
A′ là điểm đối xứng của A qua mặt phẳng (P) ta có: 3 1 AA′: = = 2 1 − 1
Khi đó K = AA′∩(P) ⇒ K (3+ 2t;1−t;t)∈(P) : 4t + 6 + t −1+ t +1= 0 ⇒ t = 1 − Do đó K (1;2;− ) 1 ⇒ A′( 1; − 3; 2 − ).
Lại có IA − IB = IA′ − IB ≤ A′B dấu bằng xảy ra ⇔ A ,′I, B thẳng hàng. x = 1 − + 8u Khi đó A B : ′ y = 3 − u
⇒ I = A' B ∩ (P) ⇒ I (7;2; 13
− ) ⇒ a + b + c = 4. − Chọn B. z = 2 − − 11u
Câu 12: Gọi M ( t) 2 2
⇒ MA + MB = + + (t − )2 + + + (t − )2 2 0;0; 4 9 2 9 25
4 = 2t −12t + 67 nhỏ nhất b − 12 ⇔ t = =
= 3 ⇒ M (0;0;3).Chọn D. 2a 2.2
Câu 13: Gọi H là hình chiếu của B trên (α )
Ta có BH ≤ BA ⇒ BH
= AB . Dấu bằng xảy ra khi AB ⊥ (α ) max Lại có AB = (2;0; 2
− ) ⇒ Phương trình mặt phẳng (α ) là x − z + 2 = 0.Chọn D.
Câu 14: Mặt cầu (S )có tâm I (4;7;− ) 1 , bán kính R = 6 .
Gọi r là bán kính đường tròn giao tuyến 2 2 2
⇒ r = R − d (I;(P))
Để r ⇔ d I; P nhỏ nhất ⇔ (P) đi qua I ⇒ m = 20. − Chọn A. max ( ( ))
Câu 15: (S ) (x − )2 + ( y − )2 + (x + )2 : 1 2
3 =16 có tâm I (1;2; 3
− ) , bán kính R = 4 .
Yêu cầu bài toán ⇔ (P) đi qua tâm I ⇒1+ 3.2 − 2.( 3
− ) − m = 0 ⇔ m =13. Chọn C.
Câu 16: Gọi phương trình mặt phẳng ( ) : x y z P + + =1, với A( ; a 0;0), B(0; ;
b 0),C (0;0;c). a b c
Vì (P) đi qua M suy ra 1 2 3 1 1 1 = + + ⇔ ≤ + + ( 2 2 2 1 1 1 1 1 1 1 + 2 + 3 ⇔ + + ≥ 2 2 2 ) 2 2 2 a b c a b c a b c 14 Ta có 1 1 1 1 1 1 1 T = + + = + + ≥ . Suy ra 1 T ≥ . 2 2 2 2 2 2 OA OB OC a b c 14 14
Dấu bằng xảy ra khi và chỉ khi 14
a =14;b = 7;c = . Vậy ( ) x y 3 : z P + + =1. Chọn A. 3 14 7 14
Câu 17: Gọi H, K lần lượt là hình chiếu của M trên (P),(d ). Khi đó
d (M;(P)) = MH ≤ MK ⇒ d (M;(P)) = MK . max
Gọi (α ) là mặt phẳng đi qua M và chứa đường thẳng d. n ⊥ u Suy ra (P) d
= u MA với A(4;5;0)∈(d ) . d ; (n ⊥ n P) (α )
⇒ = ( n u u MA Mà P) d ; d ; . u = d (1;2;3) ⇒ n = − . P (1;1; )1 MA = (4;5;0) ( )
Do đó phương trình mặt phẳng (P) : x + y − z −9 = 0 .
Vậy N = P ∩Oz → N (0;0;9). Chọn B.
Câu 18: Gọi H, K lần lượt là hình chiếu của M trên (P),(d ) .
Khi đó d (M;(P)) = MH ≤ MK ⇒ d (M;(P)) = MK max
Gọi (α ) là mặt phẳng đi qua M và chứa đường thẳng d. n ⊥ u Suy ra (P) d
= u MA với A(1;0;2)∈(d ) . d ; (n ⊥ n P) (α )
⇒ = ( n u u MA P) d ; d ; . Mà u = d (2;1;2) ⇒ n = −
⇒ x − y + z − = . P (2; 6; )1 2 6 4 0 MA = (0; 7 − ;− ) ( ) 1 Chọn A.
Câu 19: Gọi phương trình mặt phẳng ( ) : x y z P + + =1, với A( ; a 0;0), B(0; ;
b 0),C (0;0;c). a b c
Vì (P) đi qua M suy ra 2 1 3 1 1 1 = + + ⇔ ≤ + + ( 2 2 2 1 1 1 1 1 1 2 +1 + 3 ⇔ + + ≥ 2 2 2 ) 2 2 2 a b c a b c a b c 14 Ta có 1 1 1 1 1 1 1 T = + + = + + ≥ . Suy ra 1 T ≥ . 2 2 2 2 2 2 OA OB OC a b c 14 14
Dấu bằng xảy ra khi và chỉ khi 14
a = 7;b =14;c = .. Vậy ( ) x y 3 : z P + + = 1. Chọn C. 3 7 14 14
Câu 20: Ta có M (a; ;
b c) . Phương trình mặt phẳng là: (P) : A(x − b) + B( y − c) + C (z − a) = 0
Khi đó Ab + Bc + Ca ;0;0,B0; Ab + Bc + Ca ;0,C0;0; Ab + Bc + Ca A A B C
Thể tích khối tứ diện OABC là:
( Ab + Bc +Ca)3 (3 ABC. 1 abc )3 3 27abc 9 = . . abc V OAOB OC = ≥ = = . Chọn A. 6 6ABC 6ABC 6 2
Câu 21: Gọi (P) là mặt phẳng đi qua M và vuông góc với d khi đó n = u = − P d (2;2; ) ( ) 1 .
Khi đó ∆ ⊂ (P) . Ta có: d (A;d) ⇔ u =
trong đó AM ( 3 − ; 4 − ;4). ∆ n ; AM ;n . min (P) (P)
Suy ra u = = Chọn D. ∆ n ; AM ;n 9(1;0;2) ( ) ( ) . P P
Câu 22: Gọi (Q) là mặt phẳng đi qua M , song song với mặt phẳng(P) : 2x + y + z = 0 suy ra n = n = (2;1 ) − = − − ( ) ( )
;1 . Khi đó ∆ ⊂ (Q) . Ta có: MN = ( 6;0;4) 2(3;0; 2). Q P
d (N;∆) ⇔ u = = − − − = − − − ∆ n ; MN;n 2 Q Q (10; 4; 16) 4(5; 2; 8). min ( ) ( )
Phương trình đường thẳng
x − 2 y − 2 z + 3 ∆ : = = .Chọn C. 5 2 − 8 −
Câu 23: Gọi phương trình đường thẳng MN là:
x − 5 y −1 z − 3 ∆ : = = . 4 5 − 1
Gọi H(5 + 4t;1−5t;3+ t)∈ MN là hình chiếu vuông góc của điểm P trên đường thẳng MN.
Khi đó: PH = (4t;1−5t; 1 − + t);u = − MN (4; 5 ) ;1 . Giải 1 4 2 6 PH.u t t t t PH − = + − + − = ⇔ = ⇒ MN 16 25 5 1 0 ; ; 7 7 7 7 Ta có: − d ( ; P (α )) 4 2 6 2
≤ PH , dấu bằng xảy ra ⇔ PH ⊥ (α ) ⇒ n = = = − α PH ; ; (2;1; 3) ( ) . 7 7 7 7
Phương trình mặt phẳng (α ) là: 2x + y −3z − 2 = 0 . Gọi I (1;1; ) 1
Khi đó S = d ( (α )) 2 14 I; = = .Chọn C. 14 7
Document Outline
- ITMTTL~1
- IIBITP~1
- IIILIG~1




