Bài toán khối đa diện và thể tích trong đề thi THPT môn Toán của Bộ GD&ĐT (2017 – 2021)

Tuyển tập các bài toán khối đa diện và thể tích khối đa diện trong các đề thi minh họa và đề thi chính thức THPT môn Toán của Bộ Giáo dục và Đào tạo giai đoạn từ năm 2017 đến năm 2021; các bài toán có đáp án và lời giải chi tiết.Mời bạn đọc đón xem.

16 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

61 trang 8 tháng trước

Tác giả:

Profile Lan Tường
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 1

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

CHƯƠNG 1: KHỐI ĐA DIỆN VÀ THỂ TÍCH KHỐI ĐA DIỆN
(CÂU HỎI TRẮC NGHIỆM TỔNG HỢP TỪ ĐỀ THI BGD)
ĐỀ BÀI
Câu 1: (Câu 36 - ĐTN - BGD&ĐT - Năm 2017) Hình đa diện nào dưới đây không có tâm đối xứng?
A. Tứ diện đều. B. Bát diện đều. C. Hình lập phương. D. Lăng trụ lục giác đều.
Câu 2: (Câu 20 - ĐTK - BGD&ĐT - Năm 2017) Hình đa diện trong hình vẽ có bao nhiêu mặt?
A.
6
B.
10
C.
12
D.
11
Câu 3: (Câu 25 - MĐ 102 - BGD&ĐT - Năm 2017) Mặt phẳng
chia khối lăng trụ
.ABC A B C
thành các khối đa diện nào?
A. Một khối chóp tam giác và một khối chóp ngũ giác.
B. Một khối chóp tam giác và một khối chóp tứ giác.
C. Hai khối chóp tam giác.
D. Hai khối chóp tứ giác.
Câu 4: (Câu 18 - MĐ 101 - BGD&ĐT - Năm 2017) Hình hộp chữ nhật có ba kích thước đôi một khác nhau
có bao nhiêu mặt phẳng đối xứng?
A. 4 mặt phẳng. B. 3 mặt phẳng. C. 6 mặt phẳng. D. 9 mặt phẳng.
Câu 5: (Câu 23 - MĐ 103 BGD&ĐT NĂM 2016-2017) Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng
đối xứng?
A.
4
mặt phẳng. B.
1
mặt phẳng. C.
2
mặt phẳng. D.
3
mặt phẳng.
Câu 6: Cho khối lăng trụ có diện tích đáy
2
3Ba=
và chiều cao
ha=
. Thể tích của khối lăng trụ đã cho bằng
A.
3
1
2
a
. B.
3
3a
. C.
3
3
2
a
. D.
3
a
.
Câu 7: (MĐ 103 - BGD&ĐT - Năm 2021) Cho khối chóp có diện tích đáy
2
7Ba=
và chiều cao
ha=
. Thể
tích của khối chóp đã cho bằng
A.
3
7
6
a
. B.
3
7
2
a
. C.
3
7
3
a
. D.
3
7a
.
Câu 8: (Câu 2 - MĐ 102 - BGD&ĐT - Năm 2021) Cho khối chóp có diện tích đáy
2
3Ba=
và chiều cao
ha=
. Thể tích của khối chóp đã cho bằng:
A.
3
3
2
a
. B.
3
3a
. C.
3
1
3
a
. D.
3
a
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 2

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Câu 9: (Câu 22 - MĐ 101 - BGD&ĐT - Năm 2021) Cho khối chóp có diện tích đáy
2
5Ba=
và chiều cao
ha=
. Thể tích của khối chóp đã cho bằng
A.
3
5
6
a
. B.
3
5
2
a
. C.
3
5a
. D.
3
5
3
a
.
Câu 10: (Câu 21 - Đề Tham Khảo BGD - 2021) Một khối chóp có diện tích đáy bằng
6
và chiều cao bằng
5
.
Thể tích của khối chóp đã cho bằng
A.
10
. B.
30
. C.
90
. D.
15
.
Câu 11: (Câu 12 - Đề - BGD - 2020 - Đợt 2 - Mã đề - 104– 2021) Cho khối chóp có diện tích đáy
2
3Ba=
và
chiều cao
6ha=
. Thể tích của khối chóp đã cho bằng
A.
3
3a
. B.
3
6a
. C.
3
9a
. D.
3
18a
.
Câu 12: (Câu 15 - BGD - Đợt 1 - Mã đề 104 - 2020) Cho khối chóp có diện tích đáy
3=B
, chiều cao
8=h
.
Thể tích của khối chóp đã cho bằng
A.
24
. B.
12
. C.
8
. D.
6
.
Câu 13: (Câu 12 - BGD - Đợt 1 - Mã đề 103 - 2020) Cho khối chóp có diện tích đáy
2B =
và chiều cao
3h =
. Thể tích của khối chóp đã cho bằng
A.
12.
B.
2.
C.
3.
D.
6.
Câu 14: (BGD - Đợt 1 - Mã đề 102 - 2020) Cho khối chóp có diện tích đáy
3B =
và chiều cao
2h =
. Thể tích
của khối chóp đã cho bằng.
A.
6
B.
12
C.
2
D.
3
Câu 15: (Câu 18 - ĐỀ BGD-MÃ 101-L1-2020) Cho khối chóp có diện tích đáy
6B =
và chiều cao
2h =
. Thể
tích của khối chóp đã cho bằng
A.
6
. B.
3
. C.
4
. D.
12
.
Câu 16: (ĐTK - BGD&ĐT - L1 - Năm 2020) Cho khối chóp có diện tích đáy
3B =
và chiều cao
4h =
. Thể
tích của khối chóp đã cho bằng
A.
6
. B.
12
. C.
36
. D.
4
.
Câu 17: (MĐ 103 - BGD&ĐT - Năm 2018) Cho khối lăng trụ có đáy là hình vuông cạnh
a
và chiều cao bằng
4a
. Thể tích của khối lăng trụ đã cho bằng
A.
3
4a
. B.
3
16
3
a
. C.
3
4
3
a
. D.
3
16a
Câu 18: (ĐTK-BGD&ĐT-Năm 2018) Thể tích của khối chóp có chiều cao bằng
h
và diện tích đáy bằng
B
là:
A.
V Bh=
1
3
B.
V Bh=
1
6
C.
V Bh=
D.
V Bh=
1
2
Câu 19: (MĐ 104 - BGD&ĐT - Năm 2021) Cho khối chóp có diện tích đáy
2
8Ba=
và chiều cao
ha=
. Thể
tích khối chóp đã cho bằng
A.
3
8a
B.
3
4
3
a
. C.
3
4a
. D.
3
8
3
a
.
Câu 20: (MĐ 104 BGD&ĐT NĂM 2016-2017) Cho hình bát diện đều cạnh . Gọi là tổng diện tích tất cả các
mặt của hình bát diện đó. Mệnh đề nào dưới đây đúng?
A. . B. . C. . D. .
Câu 21: (Đề TNTHPT 2020 - mã đề 103) Cho khối chóp có diện tích đáy
2
2Ba=
và chiều cao
9ha=
. Thể
tích của khối chóp đã cho bằng
A.
3
3a
. B.
3
6a
. C.
3
18a
. D.
3
9a
.
a
S
2
43Sa=
2
3Sa=
2
23Sa=
2
8Sa=
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 3

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Câu 22: (Câu 7 - Đề thi TNTHPT 2020 - mã đề 102) Cho khối chóp có diện tích đáy
2
6Ba=
và chiều cao
2ha=
. Thể tích khối chóp đã cho bằng:
A.
3
2a
. B.
3
4a
. C.
3
6a
. D.
3
12a
.
Câu 23: (Đề tốt nghiệp THPT đợt 2 năm 2020 - mã đề 101) Cho khối chóp có diện tích đáy
2
2Ba=
và chiều
cao
6ha=
. Thể tích của khối chóp đã cho bằng
A.
3
12a
. B.
3
4a
. C.
3
2a
. D.
3
6a
.
Câu 24: (Câu 16 - MĐ 103 BGD&ĐT NĂM 2016-2017) Cho khối chóp
.S ABC
có
SA
vuông góc với đáy,
4SA =
,
6AB =
,
10BC =
và
8CA =
. Tính thể tích khối chóp
.S ABC
.
A.
40V =
. B.
192
. C.
32V =
. D.
24V =
.
Câu 25: (Câu 36 - ĐTK - BGD&ĐT - Năm 2017) Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với mặt đáy,
SD
tạo với mặt phẳng
( )
SAB
một góc bằng
30
. Tính thể tích
V
của khối chóp
.S ABCD
.
A.
3
6
18
a
V =
B.
3
3Va=
C.
3
6
3
a
V =
D.
3
3
3
a
V =
Câu 26: (Câu 36 - ĐMH - BGD&ĐT - Năm 2017) Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
là hình
vuông cạnh
a
, cạnh bên
SA
vuông góc với mặt phẳng đáy và
2SA a=
. Tính thể tích
V
của khối chóp
.S ABCD
A.
3
2
6
a
V =
B.
3
2
4
a
V =
C.
3
2Va=
D.
3
2
3
a
V =
Câu 27: (Câu 37 - ĐMH - BGD&ĐT - Năm 2017) Cho tứ diện
DABC
có các cạnh
AB
,
AC
và
AD
đôi một
vuông góc với nhau;
6AB a=
,
7AC a=
và
4AD a=
. Gọi
M
,
N
,
P
tương ứng là trung điểm các cạnh
BC
,
CD
,
DB
. Tính thể tích
V
của tứ diện
AMNP
.
A.
3
7
2
Va=
B.
3
14Va=
C.
3
28
3
Va=
D.
3
7Va=
Câu 28: (Câu 27 - ĐTK - BGD&ĐT - Năm 2019) Cho khối chóp tứ giác đều có tất cả các cạnh bằng
2a
. Thể
tích của khối chóp đã cho bằng
A.
3
42
3
a
. B.
3
8
3
a
. C.
3
82
3
a
. D.
3
22
3
a
.
Câu 29: (MĐ 104 BGD&ĐT NĂM 2016-2017) Cho khối chóp tam giác đều
.S ABC
có cạnh đáy bằng
a
và
cạnh bên bằng
2a
. Tính thể tích
V
của khối chóp
.S ABC
A.
3
13
12
a
V =
. B.
3
11
12
a
V =
. C.
3
11
6
a
V =
. D.
3
11
4
a
V =
.
Câu 30: (Câu 21 - MĐ 101 - BGD&ĐT - Năm 2017) Cho khối chóp tứ giác đều có cạnh đáy bằng a, cạnh bên
gấp hai lần cạnh đáy. Tính tích V của khối chóp tứ giác đã cho.
A.
3
2
2
a
V =
B.
3
2
6
a
V =
C.
3
14
2
a
V =
D.
3
14
6
a
V =
Câu 31: (Câu 15 - MĐ 101 - BGD&ĐT - Năm 2018) Cho khối chóp có đáy là hình vuông cạnh
a
và chiều cao
bằng
2a
. Thể tích của khối chóp đã cho bằng
A.
3
4a
B.
3
2
3
a
C.
3
2a
D.
3
4
3
a
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 4

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Câu 32: (Câu 35 - ĐTN - BGD&ĐT - Năm 2017) Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
2a
và
thể tích bằng
3
a
. Tính chiều cao
h
của hình chóp đã cho.
A.
3
6
=
a
h
B.
3
2
=
a
h
C.
3
3
=
a
h
D.
3=ha
Câu 33: (MĐ 102 - BGD&ĐT - Năm 2018) Cho khối chóp có đáy là hình vuông cạnh
a
và chiều cao bằng
4a
. Thể tích khối chóp đã cho bằng
A.
3
4
3
a
. B.
3
16
3
a
. C.
3
4a
. D.
3
16a
Câu 34: (Câu 43 - Đề Tham Khảo BGD - 2021) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
cạnh bên
SA
vuông góc với mặt phẳng đáy, góc giữa
SA
và mặt phẳng
()SBC
bằng
0
45
(tham khảo
hình bên). Thể tích khối chóp
.S ABC
bằng
A.
3
8
a
. B.
3
3
8
a
. C.
3
3
12
a
. D.
3
4
a
.
Câu 35: (Câu 36 - MĐ 102 - BGD&ĐT - Năm 2017) Cho khối chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
AB a=
,
3AD a=
,
SA
vuông góc với mặt phẳng đáy và mặt phẳng
( )
SBC
tạo với đáy một góc
60
o
.
Tính thể tích
V
của khối chóp
.S ABCD
.
A.
3
3
a
V =
B.
3
3
3
a
V =
C.
3
Va=
D.
3
3Va=
Câu 36: (Câu 43 - MĐ 101 - BGD&ĐT - Năm 2017) Cho khối chóp S. ABCD có đáy là hình vuông cạnh a, SA
vuông góc với đáy và SC tạo với mặt phẳng một góc
30
. Tính thể tích V của khối chóp đã cho.
A.
3
6
3
a
V =
B.
3
2
3
a
V =
C.
3
2
3
a
V =
D.
3
2Va=
Câu 37: (Câu 45 - Đề thi TNTHPT 2020 - mã đề 102) Cho hình chóp đều
.S ABCD
có cạnh đáy bằng
4a
, cạnh
bên bằng
23a
và
O
là tâm của đáy. Gọi
,,M N P
và
Q
lần lượt là hình chiếu vuông góc của
O
trên
các mặt phẳng
( ),( ),( )SAB SBC SCD
và
()SDA
. Thể tích của khối chóp
.O MNPQ
bằng
A.
3
4
3
a
. B.
3
64
81
a
. C.
3
128
81
a
. D.
3
2
3
a
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 5

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Câu 38: (Đề tốt nghiệp THPT đợt 2 năm 2020 - mã đề 101) Cho hình chóp đều
.S ABCD
có cạnh đáy bằng
3a
, cạnh bên bằng
33
2
a
và
O
là tâm của đáy. Gọi
,,M N P
và
Q
lần lượt là hình chiếu vuông góc
của
O
trên các mặt phẳng
( )
SAB
,
( )
SBC
,
( )
SCD
và
( )
SDA
. Thể tích của khối chóp
.O MNPQ
bằng
A.
3
9
16
a
. B.
3
2
3
a
. C.
3
9
32
a
. D.
3
3
a
.
Câu 39: (Câu 50 - ĐTK - BGD&ĐT - Năm 2017) Cho khối tứ diện có thể tích bằng
V
. Gọi
V
là thể tích của
khối đa diện có các đỉnh là các trung điểm của các cạnh của khối tứ diện đã cho, tính tỉ số
V
V
.
A.
1
2
V
V
=
. B.
1
4
V
V
=
. C.
2
3
V
V
=
. D.
5
8
V
V
=
.
Câu 40: (Câu 37 - ĐTN - BGD&ĐT - Năm 2017) Cho tứ diện
ABCD
có thể tích bằng 12 và
G
là trọng tâm
của tam giác
BCD
. Tính thể tích
V
của khối chóp
.AGBC
A.
3V =
B.
4V =
C.
6V =
D.
5V =
Câu 41: (Câu 34 - MĐ 103 BGD&ĐT NĂM 2016-2017) Cho khối chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với đáy và khoảng cách từ
A
đến mặt phẳng
( )
SBC
bằng
2
2
a
. Tính thể tích
V
của khối chóp đã cho.
A.
3
2
=
a
V
. B.
3
=Va
. C.
3
3
9
=
a
V
. D.
3
3
=
a
V
.
Câu 42: (Câu 38 - ĐMH - BGD&ĐT - Năm 2017) Cho hình chóp tứ giác
.S ABCD
có đáy là hình vuông cạnh
bằng
2a
. Tam giác
SAD
cân tại
S
và mặt bên
( )
SAD
vuông góc với mặt phẳng đáy. Biết thể tích khối
chóp
.S ABCD
bằng
3
4
3
a
. Tính khoảng cách
h
từ
B
đến mặt phẳng
( )
SCD
A.
2
3
ha=
B.
4
3
ha=
C.
8
3
ha=
D.
3
4
ha=
Câu 43: (Đề TNTHPT 2020 - mã đề 103) Cho hình chóp đều
ABCD
có cạnh đáy bằng
a
, cạnh bên bằng
3
2
a
và
O
là tâm của đáy. Gọi
,,M N P
và
Q
lần lượt là hình chiếu vuông góc của
O
trên các mặt phẳng
( ) ( ) ( ) ( )
, , ,SAB SBC SCD SDA
. Thể tích của khối chóp
.O MNPQ
bằng
A.
3
48
a
. B.
3
2
81
a
. C.
3
81
a
. D.
3
96
a
.
Câu 44: (Câu 45 - BGD - Đợt 1 - Mã đề 104 - 2020) Cho hình chóp đều
.S ABCD
có tất cả các cạnh bằng
a
và
O
là tâm đáy. Gọi
, , ,M N P Q
lần lượt là các điểm đối xứng với
O
qua trọng tâm của các tam giác
, , ,SAB SBC SCD SDA
và
S
là điểm đỗi xứng với
S
qua
O
. Thể tích của khối chóp
.S MNPQ
bằng
A.
3
22
9
a
. B.
3
20 2
81
a
. C.
3
40 2
81
a
. D.
3
10 2
81
a
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 6

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Câu 45: (Câu 47 - BGD - Đợt 1 - Mã đề 103 - 2020) Cho hình chóp đều
.S ABCD
có cạnh đáy bằng
a
, cạnh
bên bằng
2a
và
O
là tâm của đáy. Gọi
M
,
N
,
P
,
Q
lần lượt là các điểm đối xúng với
O
qua trọng
tâm của các tam giác
SAB
,
SBC
,
SCD
,
SDA
và
S
là điểm đối xứng với
S
qua
O
. Thể tích của khối
chóp
.S MNPQ
.
A.
3
26
9
a
. B.
3
40 6
81
a
. C.
3
10 6
81
a
. D.
3
20 6
81
a
.
Câu 46: (BGD - Đợt 1 - Mã đề 102 - 2020) Cho hình chóp đều
.S ABCD
có cạnh đáy bằng
a
, cạnh bên bằng
3a
và
O
là tâm của đáy. Gọi
, , ,M N P Q
lần lượt là các điểm đối xứng với
O
qua trọng tâm của các
tam giác
, , ,SAB SBC SCD SDA
và
S
là điểm đối xứng với
S
qua
O
. Thể tích khối chóp
S MNPQ
bằng
A.
3
40 10
81
a
. B.
3
10 10
81
a
. C.
3
20 10
81
a
. D.
3
2 10
9
a
.
Câu 47: (Câu 47 - ĐỀ BGD-MÃ 101-L1-2020) Cho hình chóp đều
.S ABCD
có cạnh đáy bằng
a
, cạnh bên
bằng
2a
và
O
là tâm của đáy. Gọi
M
,
N
,
P
,
Q
lần lượt là các điểm đối xứng với
O
qua trọng tâm
của các tam giác
SAB
,
SBC
,
SCD
,
SDA
và
'S
là điểm đối xứng với
S
qua
O
. Thể tích của khối
chóp
'.S MNPQ
bằng
A.
3
20 14
81
a
. B.
3
40 14
81
a
. C.
3
10 14
81
a
. D.
3
2 14
9
a
.
Câu 48: (Câu 46 - Đề - BGD - 2020 - Đợt 2 - Mã đề - 104– 2021) Cho hình chóp đều
.S ABCD
có cạnh đáy
bằng
2a
, cạnh bên bằng
3a
và
O
là tâm đáy. Gọi
và
Q
lần lượt là hình chiếu vuông góc
của
O
trên các mặt phẳng
( )
SAB
,
( )
SBC
,
( )
SCD
và
( )
SDA
. Thể tích khối chóp
.O MNPQ
bằng
A.
3
8
81
a
. B.
3
6
a
. C.
3
12
a
. D.
3
16
81
a
.
Câu 49: (Câu 49 - ĐTK - BGD&ĐT - L1 - Năm 2020) Cho khối chóp
.S ABC
có đáy
ABC
là tam giác vuông
cân tại
, , 90 ,A AB a SBA SCA
góc giữa hai mặt phẳng
( )
SAB
và
( )
SAC
bằng
60
. Thể tích khối
chóp đã cho bằng
A.
3
a
. B.
3
3
a
. C.
3
2
a
. D.
3
6
a
.
Câu 50: (ĐTK - BGD&ĐT - Năm 2018) Cho hình vuông
ABCD
và
ABEF
có cạnh bằng
1
, lần lượt nằm trên
hai mặt phẳng vuông góc với nhau. Gọi
S
là điểm đối xứng của
B
qua đường thẳng
DE
. Thể tích của
khối đa diện
ABCDSEF
bằng
A.
7
6
B.
11
12
C.
2
3
D.
5
6
Câu 51: (Câu 44 - MĐ 103 BGD&ĐT NĂM 2016-2017) Xét khối chóp
.S ABC
có đáy là tam giác vuông cân
tại
A
,
SA
vuông góc với đáy, khoảng cách từ
A
đến mặt phẳng
( )
SBC
bằng
3
. Gọi
là góc giữa mặt
phẳng
( )
SBC
và
( )
ABC
, tính
cos
khi thể tích khối chóp
.S ABC
nhỏ nhất.
A.
1
cos .
3
=
B.
3
cos .
3
=
C.
2
cos .
2
=
D.
2
cos .
3
=
Câu 52: (Câu 49 - MĐ 102 - BGD&ĐT - Năm 2017) Xét khối tứ diện
ABCD
có cạnh
AB x=
và các cạnh
còn lại đều bằng
23
. Tìm
x
để thể tích khối tứ diện
ABCD
đạt giá trị lớn nhất.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 7

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

A.
6x =
B.
14x =
C.
32x =
D.
23x =
Câu 53: (MĐ 104 - BGD&ĐT - Năm 2021) Thể tích của khối lập phương cạnh
2a
bằng
A.
3
a
. B.
3
2a
. C.
3
8a
. D.
3
4a
.
Câu 54: (MĐ 103 - BGD&ĐT - Năm 2021) Thể tích khối lập phương cạnh
3a
bằng
A.
3
27a
. B.
3
3a
. C.
3
9a
. D.
3
a
.
Câu 55: (Câu 22 - Đề Tham Khảo BGD - 2021) Thể tích khối hộp chữ nhật có ba kích thước
2,3,7
bằng
A.
14.
B.
42.
C.
126.
D.
12.
Câu 56: (Câu 14 - BGD - Đợt 1 - Mã đề 104 - 2020) Cho khối hộp chữ nhật có ba kích thước
2
;
3
;
7
. Thể tích
của khối hộp đã cho bằng
A.
7
. B.
42
. C.
12
. D.
14
.
Câu 57: (Câu 11 - BGD - Đợt 1 - Mã đề 103 - 2020) Cho khối hộp chữ nhật có ba kích thước
2;6;7
. Thể tích
của khối hộp đã cho bằng
A.
28.
B.
14.
C.
15.
D.
84.
Câu 58: (BGD - Đợt 1 - Mã đề 102 - 2020) Cho khối hộp chữ nhật có kích thước
2;4;6
. Thể tích của khối hộp
đã cho bằng
A.
16
. B.
12
. C.
48
. D.
8
.
Câu 59: (Câu 5 - ĐỀ BGD-MÃ 101-L1-2020) Cho khối hộp chữ nhật có ba kích thước
3; 4; 5
. Thể tích của
khối hộp đã cho bằng
A.
10
. B.
20
. C.
12
. D.
60
.
Câu 60: (Câu 26 - MĐ 104 - BGD&ĐT - Năm 2019) Cho khối lăng trụ đứng
.ABC A B C
có đáy là tam giác
đều cạnh
a
và
2AA a
=
(minh họa như hình vẽ bên). Thể tích của khối lăng trụ đã cho bằng
A.
3
6
4
a
. B.
3
6
6
a
. C.
3
6
12
a
. D.
3
6
2
a
.
Câu 61: (Câu 25 - MĐ 103 - BGD&ĐT - Năm 2019) Cho khối lăng trụ đứng
.ABC A B C
có đáy là tam giác
đều cạnh
2a
và
3AA a
=
(minh họa như hình vẽ bên).
C
B
A
B'
C'
A'
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 8

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Thể tích của khối lăng trụ đã cho bằng
A.
3
23a
. B.
3
3a
. C.
3
63a
. D.
3
33a
.
Câu 62: (Câu 21 - MĐ 102-BGD&ĐT-Năm 2019) Cho khối lăng trụ đứng
.ABC A B C
có đáy là tam giác đều
cạnh bằng
a
và
2AA a
=
(minh họa như hình vẽ bên). Thể tích của khối lăng trụ đã cho bằng
A.
3
3
3
a
. B.
3
3
6
a
. C.
3
3a
. D.
3
3
2
a
.
Câu 63: (ĐTK - BGD&ĐT - L1 - Năm 2020) Cho khối lăng trụ đứng
.
ABCD A B C D
có đáy là hình thoi cạnh
,3a BD a=
và
4
=AA a
(minh họa như hình bên dưới). Thể tích của khối lăng trụ đã cho bằng
A.
3
2 3 .a
B.
3
4 3 .a
C.
3
23
.
3
a
D.
3
43
.
3
a
Câu 64: (Câu 22 - MĐ 101-BGD&ĐT-Năm 2019) Cho khối lăng trụ đứng
. ' ' 'ABC A B C
có đáy là tam giác
đều cạnh
a
và
'3AA a=
. Thể tích của lăng trụ đã cho bằng
A.
3
3
4
a
. B.
3
3
2
a
. C.
3
4
a
. D.
3
2
a
.
Câu 65: (Câu 18 - MĐ 102 - BGD&ĐT - Năm 2017) Cho khối lăng trụ đứng
.ABC A B C
có
BB a
=
, đáy
ABC
là tam giác vuông cân tại
B
và
2AC a=
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
Va=
B.
3
3
a
V =
C.
3
6
a
V =
D.
3
2
a
V =
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 9

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Câu 66: (Câu 1 - ĐTK - BGD&ĐT - Năm 2019) Thể tích của khối lập phương cạnh
2a
bằng
A.
3
8a
. B.
3
2a
. C.
3
a
. D.
3
6a
.
Câu 67: (Câu 35 - ĐMH - BGD&ĐT - Năm 2017) Tính thể tích
V
của khối lập phương
.ABCD A B C D
, biết
3AC a
=
.
A.
3
Va=
. B.
3
36
4
a
V =
. C.
3
33Va=
. D.
3
1
3
Va=
.
Câu 68: (Câu 9 - Đề - BGD - 2020 - Đợt 2 - Mã đề - 104– 2021) Cho khối lăng trụ có diện tích đáy
6B =
và
chiều cao
4h =
. Thể tích khối lăng trụ đã cho bằng
A.
24
. B.
4
. C.
8
. D.
12
.
Câu 69: (Câu 4 - MĐ 104 - BGD&ĐT - Năm 2019) Thể tích của khối lăng trụ có diện tích đáy
B
và chiều cao
h
là
A.
4
3
Bh
. B.
1
3
Bh
. C.
3Bh
. D.
Bh
.
Câu 70: (Câu 8 - MĐ 103 - BGD&ĐT - Năm 2019) Thể tích của khối lăng trụ có diện tích đáy
B
và chiều cao
h
là
A.
4
3
Bh
. B.
3Bh
. C.
1
3
Bh
. D.
Bh
.
Câu 71: (Câu 12 - MĐ 102-BGD&ĐT-Năm 2019) Thể tích của khối lăng trụ có diện tích đáy
B
và chiều cao
h
là
A.
3Bh
. B.
Bh
. C.
4
3
Bh
. D.
1
3
Bh
.
Câu 72: (Câu 12 - MĐ 101-BGD&ĐT-Năm 2019) Thể tích khối lăng trụ có diện tích đáy
B
và chiều cao
h
là
A.
3.Bh
B.
.Bh
C.
4
.
3
Bh
D.
1
.
3
Bh
Câu 73: (Câu 11 - MĐ 104 - BGD&ĐT - Năm 2018) Cho khối lăng trụ có đáy là hình vuông cạnh
a
và chiều
cao bằng
2a
. Thể tích của khối lăng trụ đã cho bằng
A.
3
2
3
a
B.
3
4
3
a
C.
3
2a
D.
3
4a
Câu 74: (Đề TNTHPT 2020 - mã đề 103) Cho khối lăng trụ có diện tích đáy
6B =
và chiều cao
3h =
. Thể
tích của khối lăng trụ đã cho bằng
A.
3.
B.
18.
C.
6.
D.
9.
Câu 75: (Câu 18 - Đề thi TNTHPT 2020 - mã đề 102) Cho khối lăng trụ có diện tích đáy
3B =
và chiều cao
2h =
. Thể tích khối lăng trụ đã cho bằng
A. 1. B. 3. C. 2. D. 6.
Câu 76: (Câu 19 - Đề thi TNTHPT 2020 - mã đề 102) Cho khối lăng trụ có diện tích đáy
3B =
và chiều cao
2h =
. Thể tích của khối lăng trụ đã cho bằng
A.
1
. B.
3
. C.
2
. D.
6
.
Câu 77: (Đề tốt nghiệp THPT đợt 2 năm 2020 - mã đề 101) Cho khối lăng trụ có diện tích đáy
3B =
và chiều
cao
6h =
. Thể tích của khối lăng trụ đã cho bằng
A.
9
. B.
18
. C.
3
. D.
6
.
Câu 78: (Đề tốt nghiệp THPT đợt 2 năm 2020 - mã đề 101) Cho khối trụ có bán kính đáy
4r =
và chiều cao
3h =
. Thể tích của khối trụ đã cho bằng
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 10

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

A.
48
. B.
4
. C.
16
. D.
24
.
Câu 79: (MĐ 104 - BGD&ĐT - Năm 2021) Cho khối hộp chữ nhật
.ABCD A B C D
có đáy là hình vuông
4BD a=
, góc giữa hai mặt phẳng
( )
A BD
và
( )
ABCD
bằng
0
60
. Thể tích của khối hộp chữ nhật đã
cho bằng
A.
3
48 3a
. B.
3
16 3
9
a
. C.
3
16 3
3
a
. D.
3
16 3a
.
Câu 80: (MĐ 103 - BGD&ĐT - Năm 2021) Cho khối hộp chữ nhật
.ABCD A B C D
có đáy là hình vuông,
2BD a=
, góc giữa hai mặt phẳng
( )
A BD
và
( )
ABCD
bằng
60
. Thể tích của khối hộp chữ nhật đã
cho bằng
A.
3
23
9
a
. B.
3
63a
. C.
3
23
3
a
. D.
3
23a
.
Câu 81: (Câu 44 - MĐ 102 - BGD&ĐT - Năm 2021) Cho khối hộp chữ nhật
. ' ' ' 'ABCD A B C D
có đáy là hình
vuông,
4BD a=
, góc giữa hai mặt phẳng
( )
'A BD
và
( )
ABCD
=
30
o
. Thể tích của khối hộp chữ nhật
đã cho bằng
A.
3
16 3
9
a
B.
3
48 3a
C.
3
16 3
3
a
D.
3
16 3a
Câu 82: (Câu 48 - MĐ 101 - BGD&ĐT - Năm 2021) Cho khối hộp chữ nhật
. ' ' ' 'ABCD A B C D
có đáy là hình
vuông,
2BD a=
, góc giữa hai mặt phẳng
( )
'A BD
và
( )
ABCD
bằng
0
30
. Thể tích của khối hộp chữ
nhật đã cho bằng
A.
3
63a
. B.
3
23
9
a
. C.
3
23a
. D.
3
23
3
a
.
Câu 83: (MĐ 101 BGD&ĐT NĂM 2021-L2) Cho khối lăng trụ tam giác đều
.ABC A B C
có cạnh bên bằng
2a
, góc giữa hai mặt phẳng
( )
'A BC
và
( )
ABC
bằng
30
. Thể tích của khối lăng trụ đã cho bằng
A.
3
83
9
a
. B.
3
83
3
a
. C.
3
83
27
a
. D.
3
83a
.
Câu 84: (MĐ 104 BGD&ĐT NĂM 2016-2017) Cho khối lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác
cân với
AB AC a==
,
120BAC =
. Mặt phẳng
( )
AB C

tạo với đáy một góc
60
. Tính thể tích
V
của
khối lăng trụ đã cho.
A.
3
3
8
a
V =
. B.
3
9
8
a
V =
. C.
3
8
a
V =
. D.
3
3
4
a
V =
.
Câu 85: (Câu 38 - ĐTN - BGD&ĐT - Năm 2017) Cho lăng trụ tam giác
.
ABC A B C
có đáy
ABC
là tam giác
vuông cân tại
A
, cạnh
22=AC
. Biết
AC
tạo với mặt phẳng
( )
ABC
một góc
60
và
4
=AC
. Tính
thể tích
V
của khối đa diện

ABCB C
.
A.
8
3
=V
B.
16
3
=V
C.
83
3
=V
D.
16 3
3
=V
Câu 86: (Câu 39 - MĐ 104 - BGD&ĐT - Năm 2018) Cho khối lăng trụ
.ABC A B C
, khoảng cách từ
C
đến
đường thẳng
BB
bằng
5
, khoảng cách từ
A
đến các đường thẳng
BB
và
CC
lần lượt bằng
1
và
2
, hình chiếu vuông góc của
A
lên mặt phẳng
( )
ABC
là trung điểm
M
của
BC

và
5AM
=
. Thể
tích của khối lăng trụ đã cho bằng
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 11

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

A.
25
3
B.
2 15
3
C.
5
D.
15
3
Câu 87: (MĐ 103 - BGD&ĐT - Năm 2018) Cho khối lăng trụ
. ' ' 'ABC A B C
, khoảng cách từ
C
đến đường
thẳng
'BB
bằng 2, khoảng cách từ
A
đến các đường thẳng
'BB
và
'CC
lần lượt bằng 1 và
3
, hình
chiếu vuông góc của
A
lên mặt phẳng
( ' ' ')A B C
là trung điểm
M
của
''BC
và
'2AM=
. Thể tích của
khối lăng trụ đã cho bằng
A.
3
. B.
2
. C.
23
3
. D.
1
Câu 88: (MĐ 102 - BGD&ĐT - Năm 2018) Cho khối lăng trụ
.ABC A'B'C'
, khoảng cách từ
C
đến
'BB
là
5
, khoảng cách từ
A
đến
'BB
và
'CC
lần lượt là
1; 2
. Hình chiếu vuông góc của
A
lên mặt phẳng
' ' 'A B C
là trung điểm
M
của
''BC
,
15
'
3
=AM
. Thể tích của khối lăng trụ đã cho bằng
A.
15
3
. B.
25
3
. C.
5
. D.
2 15
3
Câu 89: (Câu 42 - MĐ 101 - BGD&ĐT - Năm 2018) Cho khối lăng trụ
.ABC A B C
, khoảng cách từ
C
đến
đường thẳng
BB
bằng
2
, khoảng cách từ
A
đến các đường thẳng
BB
và
CC
lần lượt bằng
1
và
3
, hình chiếu vuông góc của
A
lên mặt phẳng
( )
ABC
là trung điểm
M
của
BC

và
23
3
AM
=
. Thể
tích của khối lăng trụ đã cho bằng
A.
2
B.
1
C.
3
D.
23
3
Câu 90: (ĐTK - BGD&ĐT - L1 - Năm 2020) Cho hình hộp
. ' ' ' 'ABCD A B C D
có chiều cao bằng
8
và diện tích
đáy bằng
9.
Gọi
,,M N P
và
Q
lần lượt là tâm của các mặt bên
' ', ' ', ' 'ABB A BCC B CDD C
và
''DAA D
. Thể tích của khối đa diện lồi có các đỉnh là các điểm
, , , , , ,A B C D M N P
và
Q
bằng
A. 27. B. 30. C. 18. D. 36
Câu 91: (Câu 46 - MĐ 104 - BGD&ĐT - Năm 2019) Cho hình lăng trụ
.ABC A B C
có chiều cao bằng
4
và
đáy là tam giác đều cạnh bằng
4
. Gọi
,MN
và
P
lần lượt là tâm của các mặt bên
ABB A
,
ACC A
và
BCC B
. Thể tích của khối đa diện lồi có các đỉnh là các điểm
, , , , ,A B C M N P
bằng
A.
14 3
3
. B.
83
. C.
63
. D.
20 3
3
.
Câu 92: (Câu 49 - MĐ 103 - BGD&ĐT - Năm 2019) Cho lăng trụ
. ' ' 'ABC A B C
có chiều cao bằng 6 và đáy
là tam giác đều cạnh bằng 4. Gọi M, N, P lần lượt là tâm của các mặt bên
' ', ' ', ' 'ABB A ACC A BCC B
.
Thể tích của khối đa diện lồi có các đỉnh là các điểm
, , , , ,A B C M N P
bằng
A.
93
. B.
10 3
. C.
73
. D.
12 3
.
Câu 93: (Câu 49 - MĐ 102-BGD&ĐT-Năm 2019) Cho lăng trụ
.ABC A B C
có chiều cao là
8
và đáy là tam
giác đều cạnh bằng
4
. Gọi
M
,
N
và
P
lần lượt là tâm của các mặt bên
ABB A

,
ACC A

và
BCC B

. Thể tích của khối đa diện lồi có các đỉnh là các điểm
A
,
B
,
C
,
M
,
N
,
P
bằng
A.
12 3
. B.
16 3
. C.
28 3
3
. D.
40 3
3
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 12

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Câu 94: (Câu 47 - MĐ 101-BGD&ĐT-Năm 2019) Cho lăng trụ
. ' ' 'ABC A B C
có chiều cao bằng
8
và đáy là
tam giác đều cạnh bằng
6
. Gọi
,MN
và
P
lần lượt là tâm của các mặt bên
''ABB A
,
''ACC A
và
''BCC B
. Thể tích của khối đa diện lồi có các đỉnh là các điểm
, , , , ,A B C M N P
bằng:
A.
27 3
. B.
21 3
. C.
30 3
. D.
36 3
.
Câu 95: (Câu 47 - ĐTK - BGD&ĐT - Năm 2019) Cho khối lăng trụ
.ABC A B C
có thể tích bằng 1. Gọi
,MN
lần lượt là trung điểm các đoạn thẳng
AA
và
BB
. Đường thẳng
CM
cắt đường thẳng
CA

tại
P
,
đường thẳng
CN
cắt đường thẳng
CB

tại
Q
. Thể tích của khối đa diện lồi
A MPB NQ

bằng
A.
1
. B.
1
3
. C.
1
2
. D.
2
3
.
Câu 96: (Câu 44 - MĐ 101 - BGD&ĐT - Năm 2017) Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt
là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng chia khối tứ diện
ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V. Tính V.
A.
3
72
216
a
V =
B.
3
11 2
216
a
V =
C.
3
13 2
216
a
V =
D.
3
2
18
a
V =
Câu 97: (MĐ 102 - BGD&ĐT - Năm 2018) Ông A dự định sử dụng hết
2
6,7m
kính để làm một bể cá bằng
kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước
không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm).
A.
3
1,57m
. B.
3
1,11m
. C.
3
1,23m
. D.
3
2,48m
Câu 98: (Câu 31 - MĐ 101 - BGD&ĐT - Năm 2018) Ông
A
dự định dùng hết
2
6,5m
kính để làm một bể cá
có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng. Bể cá có dung tích lớn nhất bằng
bao nhiêu.
A.
3
2,26 m
B.
3
1,61m
C.
3
1,33m
D.
3
1,50 m
Câu 99: (MĐ 103 - BGD&ĐT - Năm 2018) Ông A dự định sử dụng hết
2
5 m
kính để làm một bể cá bằng kính
có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng. Bể cá có dung tích lớn nhất bằng
bao nhiêu?
A.
3
1,01m
. B.
3
0,96 m
. C.
3
1,33m
. D.
3
1,51m
Câu 100: (Câu 32 - MĐ 104 - BGD&ĐT - Năm 2018) Ông A dự định sử dụng hết
2
5,5 m
kính để làm một bể
cá bắng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng. Bể cá có dung tích lớn
nhất bằng bao nhiêu?
A.
3
1,17 m
B.
3
1,01 m
C.
3
1,51 m
D.
3
1,40 m
HẾT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 13

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

BẢNG ĐÁP ÁN
1.A
2.D
3.B
4.B
5.A
6.B
7.C
8.D
9.D
10.A
11.B
12.C
13.B
14.C
15.C
16.D
17.A
18.A
19.D
20.C
21.B
22.B
23.B
24.C
25.D
26.D
27.D
28.A
29.B
30.D
31.B
32.D
33.A
34.A
35.C
36.B
37.D
38.C
39.A
40.B
41.D
42.B
43.D
44.B
45.D
46.C
47.A
48.C
49.D
50.D
51.B
52.C
53.C
54.A
55.B
56.B
57.D
58.C
59.D
60.A
61.D
62.D
63.A
64.A
65.D
66.A
67.A
68.A
69.D
70.D
71.B
72.B
73.C
74.B
75.D
76.D
77.B
78.A
79.D
80.D
81.C
82.D
83.D
84.A
85.D
86.B
87.B
88.D
89.A
90.B
91.C
92.A
93.A
94.A
95.D
96.B
97.A
98.D
99.A
100.A
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 14

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

CHƯƠNG 1: KHỐI ĐA DIỆN VÀ THỂ TÍCH KHỐI ĐA DIỆN
(CÂU HỎI TRẮC NGHIỆM TỔNG HỢP TỪ ĐỀ THI BGD)
HƯỚNG DẪN GIẢI CHI TIẾT
CHỦ ĐỀ: KHỐI ĐA DIỆN VÀ KHỐI ĐA DIỆN ĐỀU
Câu 1: (Câu 36 - ĐTN - BGD&ĐT - Năm 2017) Hình đa diện nào dưới đây không có tâm đối xứng?
A. Tứ diện đều. B. Bát diện đều. C. Hình lập phương. D. Lăng trụ lục giác đều.
Lời giải
Chọn A
Dễ dàng thấy hình bát diện đều, hình lập phương và hình lăng trục lục giác đều có tâm đối
xứng. Còn tứ diện đều không có tâm đối xứng.
Câu 2: (Câu 20 - ĐTK - BGD&ĐT - Năm 2017) Hình đa diện trong hình vẽ có bao nhiêu mặt?
A.
6
B.
10
C.
12
D.
11
Lời giải
Chọn D
Đếm đáy hình chóp có 5 mặt tam giác và 5 mặt tứ giác và 1 mặt ngũ giá C. Vậy có 11 mặt.
Câu 3: (Câu 25 - MĐ 102 - BGD&ĐT - Năm 2017) Mặt phẳng
( )
AB C

chia khối lăng trụ
.ABC A B C
thành các khối đa diện nào?
A. Một khối chóp tam giác và một khối chóp ngũ giác.
B. Một khối chóp tam giác và một khối chóp tứ giác.
C. Hai khối chóp tam giác.
D. Hai khối chóp tứ giác.
Lời giải
Chọn B
Mặt phẳng
( )
AB C

chia khối lăng trụ
.ABC A B C
thành hai khối chóp
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 15

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Chóp tam giác:
.A A B C
và chóp tứ giác:
.A BB C C

.
Câu 4: (Câu 18 - MĐ 101 - BGD&ĐT - Năm 2017) Hình hộp chữ nhật có ba kích thước đôi một khác
nhau có bao nhiêu mặt phẳng đối xứng?
A. 4 mặt phẳng. B. 3 mặt phẳng. C. 6 mặt phẳng. D. 9 mặt phẳng.
Lời giải
Chọn B
Câu 5: (Câu 23 - MĐ 103 BGD&ĐT NĂM 2016-2017) Hình lăng trụ tam giác đều có bao nhiêu mặt
phẳng đối xứng?
A.
4
mặt phẳng. B.
1
mặt phẳng. C.
2
mặt phẳng. D.
3
mặt phẳng.
Lời giải
Chọn A
Lăng trụ đều có
4
mặt phẳng đối xứng là:
Mặt phẳng cách đều
2
đáy.
3
mặt phẳng chứa
1
cạnh bên và trung điểm cạnh đáy.
THỂ TÍCH KHỐI CHÓP
Câu 6: Cho khối lăng trụ có diện tích đáy
2
3Ba=
và chiều cao
ha=
. Thể tích của khối lăng trụ đã cho bằng
A.
3
1
2
a
. B.
3
3a
. C.
3
3
2
a
. D.
3
a
.
Lời giải
Chọn B
Thể tích của khối lăng trụ đã cho là
23
. 3 . 3V B h a a a= = =
.
Câu 7: (MĐ 103 - BGD&ĐT - Năm 2021) Cho khối chóp có diện tích đáy
2
7Ba=
và chiều cao
ha=
.
Thể tích của khối chóp đã cho bằng
A.
3
7
6
a
. B.
3
7
2
a
. C.
3
7
3
a
. D.
3
7a
.
Lời giải
Chọn C
Áp dụng công thức tính thể tích ta được
3
17
33
V Bh a==
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 16

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Câu 8: (Câu 2 - MĐ 102 - BGD&ĐT - Năm 2021) Cho khối chóp có diện tích đáy
2
3Ba=
và chiều cao
ha=
. Thể tích của khối chóp đã cho bằng:
A.
3
3
2
a
. B.
3
3a
. C.
3
1
3
a
. D.
3
a
.
Lời giải
Chọn D
Công thức thể tích khối chóp là
23
11
. 3 .
33
V B h a a a= = =
.
Câu 9: (Câu 22 - MĐ 101 - BGD&ĐT - Năm 2021) Cho khối chóp có diện tích đáy
2
5Ba=
và chiều cao
ha=
. Thể tích của khối chóp đã cho bằng
A.
3
5
6
a
. B.
3
5
2
a
. C.
3
5a
. D.
3
5
3
a
.
Lời giải
Chọn D
Thể tích của khối chóp đã cho
23
1 1 5
. . .5 .
3 3 3
V B h a a a= = =
.
Câu 10: (Câu 21 - Đề Tham Khảo BGD - 2021) Một khối chóp có diện tích đáy bằng
6
và chiều cao bằng
5
. Thể tích của khối chóp đã cho bằng
A.
10
. B.
30
. C.
90
. D.
15
.
Lời giải
Chọn A
11
.6.5 10
33
V Bh= = =
.
Câu 11: (Câu 12 - Đề - BGD - 2020 - Đợt 2 - Mã đề - 104– 2021) Cho khối chóp có diện tích đáy
2
3Ba=
và chiều cao
6ha=
. Thể tích của khối chóp đã cho bằng
A.
3
3a
. B.
3
6a
. C.
3
9a
. D.
3
18a
.
Lời giải
Chọn B
Thể tích của khối chóp đã cho là
1
.
3
V B h=
23
1
3 .6 6
3
a a a==
.
Câu 12: (Câu 15 - BGD - Đợt 1 - Mã đề 104 - 2020) Cho khối chóp có diện tích đáy
3=B
, chiều cao
8=h
. Thể tích của khối chóp đã cho bằng
A.
24
. B.
12
. C.
8
. D.
6
.
Lời giải
Chọn C
Thể tích khối chóp:
1
.3.8 8
3
==V
.
Câu 13: (Câu 12 - BGD - Đợt 1 - Mã đề 103 - 2020) Cho khối chóp có diện tích đáy
2B =
và chiều cao
3h =
. Thể tích của khối chóp đã cho bằng
A.
12.
B.
2.
C.
3.
D.
6.
Lời giải
Chọn B
Thể tích của khối chóp đã cho là:
11
. . .2.3 2.
33
V B h= = =
Câu 14: (BGD - Đợt 1 - Mã đề 102 - 2020) Cho khối chóp có diện tích đáy
3B =
và chiều cao
2h =
. Thể
tích của khối chóp đã cho bằng.
A.
6
B.
12
C.
2
D.
3
Lời giải
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 17

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Ta có
11
. .3.2 2
33
V B h= = =
Câu 15: (Câu 18 - ĐỀ BGD-MÃ 101-L1-2020) Cho khối chóp có diện tích đáy
6B =
và chiều cao
2h =
.
Thể tích của khối chóp đã cho bằng
A.
6
. B.
3
. C.
4
. D.
12
.
Lời giải
Chọn C
Thể tích khối chóp là
11
.6.2 4
33
V Bh= = =
.
Câu 16: (ĐTK - BGD&ĐT - L1 - Năm 2020) Cho khối chóp có diện tích đáy
3B =
và chiều cao
4h =
.
Thể tích của khối chóp đã cho bằng
A.
6
. B.
12
. C.
36
. D.
4
.
Lời giải
Chọn D
Thể tích khối chóp đã cho là
11
. . .3.4 4
33
V B h= = =
.
Câu 17: (MĐ 103 - BGD&ĐT - Năm 2018) Cho khối lăng trụ có đáy là hình vuông cạnh
a
và chiều cao
bằng
4a
. Thể tích của khối lăng trụ đã cho bằng
A.
3
4a
. B.
3
16
3
a
. C.
3
4
3
a
. D.
3
16a
Lời giải
Chọn A
23
. .4 4
day
V S h a a a===
.
Câu 18: (ĐTK - BGD&ĐT - Năm 2018) Thể tích của khối chóp có chiều cao bằng
h
và diện tích đáy
bằng
B
là:
A.
V Bh=
1
3
B.
V Bh=
1
6
C.
V Bh=
D.
V Bh=
1
2
Lời giải
Chọn A
Thể tích của khối chóp có chiều cao bằng
h
và diện tích đáy bằng
B
là:
V Bh=
1
3
Câu 19: (- MĐ 104 - BGD&ĐT - Năm 2021) Cho khối chóp có diện tích đáy
2
8Ba=
và chiều cao
ha=
.
Thể tích khối chóp đã cho bằng
A.
3
8a
B.
3
4
3
a
. C.
3
4a
. D.
3
8
3
a
.
Lời giải
Chọn D
Thể tích khối chóp đã cho bằng
23
1 1 8
. . .8 . .
3 3 3
V B h a a a= = =
Câu 20: (MĐ 104 BGD&ĐT NĂM 2016-2017) Cho hình bát diện đều cạnh . Gọi là tổng diện tích tất
cả các mặt của hình bát diện đó. Mệnh đề nào dưới đây đúng?
A. . B. . C. . D. .
Lời giải
Chọn C
a
S
2
43Sa=
2
3Sa=
2
23Sa=
2
8Sa=
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 18

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Ta thấy hình bát diện đều có
8
mặt, mỗi mặt là một tam giác đều cạnh có diện tích là
2
3
4
a
.
Suy ra .
Câu 21: (Đề TNTHPT 2020 - mã đề 103) Cho khối chóp có diện tích đáy
2
2Ba=
và chiều cao
9ha=
.
Thể tích của khối chóp đã cho bằng
A.
3
3a
. B.
3
6a
. C.
3
18a
. D.
3
9a
.
Lời giải
Chọn B
Thể tích khối chóp đã cho là
23
1
. .2 .9 6
3
1
.
3
BV h a a a= ==
.
Câu 22: (Câu 7 - Đề thi TNTHPT 2020 - mã đề 102) Cho khối chóp có diện tích đáy
2
6Ba=
và chiều
cao
2ha=
. Thể tích khối chóp đã cho bằng:
A.
3
2a
. B.
3
4a
. C.
3
6a
. D.
3
12a
.
Lời giải
Chọn B
23
11
. 6 .2 4
33
V B h a a a= = =
Câu 23: (Đề tốt nghiệp THPT đợt 2 năm 2020 - mã đề 101) Cho khối chóp có diện tích đáy
2
2Ba=
và
chiều cao
6ha=
. Thể tích của khối chóp đã cho bằng
A.
3
12a
. B.
3
4a
. C.
3
2a
. D.
3
6a
.
Lời giải
Chọn B
Thể tích của khối chóp đã cho là:
1
3
V Bh=
23
1
.2 .6 4
3
a a a==
.
Câu 24: (Câu 16 - MĐ 103 BGD&ĐT NĂM 2016-2017) Cho khối chóp
.S ABC
có
SA
vuông góc với đáy,
4SA =
,
6AB =
,
10BC =
và
8CA =
. Tính thể tích khối chóp
.S ABC
.
A.
40V =
. B.
192
. C.
32V =
. D.
24V =
.
Lời giải
Chọn C
Ta có
2 2 2
AB AC BC+=
suy ra tam giác
ABC
vuông tại
A
,do đó diện tích tam giác
ABC
là:
11
. .6.8 24
22
S AB AC= = =
Có
11
. . .4.24 32
33
SABC ABC
V SA S= = =
.
Câu 25: (Câu 36 - ĐTK - BGD&ĐT - Năm 2017) Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
a
2
2
3
8. 2 3
4
a
Sa==
8
6
10
4
A
C
B
S
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 19

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

,
SA
vuông góc với mặt đáy,
SD
tạo với mặt phẳng
( )
SAB
một góc bằng
30
. Tính thể tích
V
của khối chóp
.S ABCD
.
A.
3
6
18
a
V =
B.
3
3Va=
C.
3
6
3
a
V =
D.
3
3
3
a
V =
Lời giải
Chọn D
Góc giữa SD và mp là
0
30DSA =
.
Ta có
0
3
tan30
AD
SA a==
.
3
2
13
.3
33
a
V a a==
.
Câu 26: (Câu 36 - ĐMH - BGD&ĐT - Năm 2017) Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
là hình
vuông cạnh
a
, cạnh bên
SA
vuông góc với mặt phẳng đáy và
2SA a=
. Tính thể tích
V
của
khối chóp
.S ABCD
A.
3
2
6
a
V =
B.
3
2
4
a
V =
C.
3
2Va=
D.
3
2
3
a
V =
Lời giải
Chọn D
Ta có
( )
SA ABCD SA⊥
là đưng cao của hình chóp
Thể tích khối chóp
.S ABCD
:
3
2
1 1 2
. . 2.
3 3 3
ABCD
a
V SAS a a= = =
.
Câu 27: (Câu 37 - ĐMH - BGD&ĐT - Năm 2017) Cho tứ diện
DABC
có các cạnh
AB
,
AC
và
AD
đôi
một vuông góc với nhau;
6AB a=
,
7AC a=
và
4AD a=
. Gọi
M
,
N
,
P
tương ứng là trung điểm
các cạnh
BC
,
CD
,
DB
. Tính thể tích
V
của tứ diện
AMNP
.
A.
3
7
2
Va=
B.
3
14Va=
C.
3
28
3
Va=
D.
3
7Va=
Lời giải
Chọn D
A
B
D
C
S
A
B
D
C
S
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 20

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Ta có
3
1 1 1
. . 6 .7 .4 28
3 2 6
ABCD
V AB AD AC a a a a= = =
Ta nhận thấy
3
1 1 1
7
2 4 4
MNP MNPD BCD AMNP ABCD
S S S V V a= = = =
.
Câu 28: (Câu 27 - ĐTK - BGD&ĐT - Năm 2019) Cho khối chóp tứ giác đều có tất cả các cạnh bằng
2a
.
Thể tích của khối chóp đã cho bằng
A.
3
42
3
a
. B.
3
8
3
a
. C.
3
82
3
a
. D.
3
22
3
a
.
Lời giải
Chọn A
Xét khối chóp tứ giác đều
.S ABCD
có đáy là hình vuông tâm
O
, suy ra
( )
SO ABCD⊥
.
Ta có:
+
22AC a=
2AO a=
;
22
SO SA AO=−
22
42aa=−
2a=
.
+
( )
2
2
24
ABCD
S a a==
.
Vậy
1
..
3
ABCD
V SO S=
2
1
. 2.4
3
aa=
3
42
3
a
=
.
Câu 29: (MĐ 104 BGD&ĐT NĂM 2016-2017) Cho khối chóp tam giác đều
.S ABC
có cạnh đáy bằng
a
và cạnh bên bằng
2a
. Tính thể tích
V
của khối chóp
.S ABC
A.
3
13
12
a
V =
. B.
3
11
12
a
V =
. C.
3
11
6
a
V =
. D.
3
11
4
a
V =
.
Lời giải
Chọn B
O
A
D
B
C
S
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 21

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Do đáy là tam giác đều nên gọi
I
là trung điểm cạnh
BC
, khi đó
AI
là đưng cao của tam
giác đáy. Theo định lý Pitago ta có
2
2
3
42
aa
AI a= − =
, và
2 2 3 3
3 3.2 3
aa
AO AI= = =
.
Trong tam giác
SOA
vuông tại
O
ta có
2
2
11
4
3
3
aa
SO a= − =
Vậy thể tích khối chóp
.S ABC
là
3
1 1 3 11 11
..
3 2 2 12
3
a a a
Va==
.
Câu 30: (Câu 21 - MĐ 101 - BGD&ĐT - Năm 2017) Cho khối chóp tứ giác đều có cạnh đáy bằng a, cạnh
bên gấp hai lần cạnh đáy. Tính tích V của khối chóp tứ giác đã cho.
A.
3
2
2
a
V =
B.
3
2
6
a
V =
C.
3
14
2
a
V =
D.
3
14
6
a
V =
Lời giải
Chọn D
.S ABCD
là khối chóp tứ giác đều
ABCD
là hình vuông và
( )
, SO ABCD O⊥
là tâm của
hình vuông.
2
2 2 2
1 2 2 14
;4
2 2 2 2
aa
OD BD SO SD OD a a

= = = − = − =



23
1 1 14 14
. . . .
3 3 2 6
ABCD
V SO S a a a= = =
Câu 31: (Câu 15 - MĐ 101 - BGD&ĐT - Năm 2018) Cho khối chóp có đáy là hình vuông cạnh
a
và
chiều cao bằng
2a
. Thể tích của khối chóp đã cho bằng
A.
3
4a
B.
3
2
3
a
C.
3
2a
D.
3
4
3
a
Lời giải
O
I
A
C
B
S
C
B
D
A
S
O
a
2a
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 22

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Chọn B
Khối chóp có đáy là hình vuông cạnh
a
nên có diện tích đáy:
2
đáy
Sa=
.
Chiều cao
2ha=
.
Vậy thể tích khối chóp đã cho là
1
..
3
đáy
V S h=
2
1
. .2
3
aa=
3
2
3
a=
.
Câu 32: (Câu 35 - ĐTN - BGD&ĐT - Năm 2017) Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
2a
và thể tích bằng
3
a
. Tính chiều cao
h
của hình chóp đã cho.
A.
3
6
=
a
h
B.
3
2
=
a
h
C.
3
3
=
a
h
D.
3=ha
Lời giải
Chọn D
Do đáy là tam giác đều cạnh
2a
nên
( )
2
2
23
3
4
==
ABC
a
Sa
.
Mà
1
.
3
ABC
V S h
=
3
2
33
3
3
ABC
Va
ha
S
a
= = =
Câu 33: (MĐ 102 - BGD&ĐT - Năm 2018) Cho khối chóp có đáy là hình vuông cạnh
a
và chiều cao
bằng
4a
. Thể tích khối chóp đã cho bằng
A.
3
4
3
a
. B.
3
16
3
a
. C.
3
4a
. D.
3
16a
Lời giải
Chọn A
Thể tích khối chóp:
1
.
3
V B h=
2
1
.4
3
aa=
3
4
3
a=
.
Câu 34: (Câu 43 - Đề Tham Khảo BGD - 2021) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
, cạnh bên
SA
vuông góc với mặt phẳng đáy, góc giữa
SA
và mặt phẳng
()SBC
bằng
0
45
(tham khảo hình bên). Thể tích khối chóp
.S ABC
bằng
A.
3
8
a
. B.
3
3
8
a
. C.
3
3
12
a
. D.
3
4
a
.
Lời giải
Chọn A
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 23

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Gọi
M
là trung điểm
BC
thì
AM BC⊥
và
SA BC⊥
nên
( ).BC SAM⊥
Kẻ
AH SM⊥
tại
H
thì
( )
AH SBC⊥
. Suy ra góc giữa
SA
và mặt phẳng
()SBC
bằng
45ASH ASM= =
. Do đó,
SAM
vuông cân ở
A
và
3
.
2
a
SA AM==
Suy ra
23
.
1 3 3
.
3 2 4 8
S ABC
a a a
V = =
Câu 35: (Câu 36 - MĐ 102 - BGD&ĐT - Năm 2017) Cho khối chóp
.S ABCD
có đáy
ABCD
là hình chữ
nhật,
AB a=
,
3AD a=
,
SA
vuông góc với mặt phẳng đáy và mặt phẳng
( )
SBC
tạo với đáy
một góc
60
o
. Tính thể tích
V
của khối chóp
.S ABCD
.
A.
3
3
a
V =
B.
3
3
3
a
V =
C.
3
Va=
D.
3
3Va=
Lời giải
Chọn.C
Ta có
2
3
ABCD
Sa=
.
Vì
( ) ( )
( )
( )
( ) ( )
( )
( )
,;
SBC ABCD BC
BC SB SBC SBC ABCD SB AB SBA
BC AB ABCD
=
⊥ = =
⊥
.
Vậy
60
o
SBA =
M
A
C
B
S
H
60
a
a
3
D
A
B
C
S
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 24

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Xét tam giác vuông
SAB
có:
tan60 .tan60 3
oo
SA
SA AB a
AB
= = =
Vậy
23
.
11
. 3. 3
33
S ABCD ABCD
V S SA a a a= = =
.
Câu 36: (Câu 43 - MĐ 101 - BGD&ĐT - Năm 2017) Cho khối chóp S. ABCD có đáy là hình vuông cạnh
a, SA vuông góc với đáy và SC tạo với mặt phẳng một góc
30
. Tính thể tích V của khối chóp
đã cho.
A.
3
6
3
a
V =
B.
3
2
3
a
V =
C.
3
2
3
a
V =
D.
3
2Va=
Lời giải
Chọn B
( )
( )
( )
⊥
⊥⊥
lµ hinh vu«ngBC BA ABCD
BC SA SA ABCD
( ) ( )
(
)
⊥ = =, 30BC SAB SC SAB BSC
SBC
vuông tại B:
0
0
tan30 3
tan30
BC BC
SB a
SB
= = =
SAB
vuông tại A:
2 2 2 2
32SA SB AB a a a= − = − =
23
1 1 2
. . 2 .
3 3 3
ABCD
V SA S a a a= = =
Câu 37: (Câu 45 - Đề thi TNTHPT 2020 - mã đề 102) Cho hình chóp đều
.S ABCD
có cạnh đáy bằng
4a
, cạnh bên bằng
23a
và
O
là tâm của đáy. Gọi
,,M N P
và
Q
lần lượt là hình chiếu vuông
góc của
O
trên các mặt phẳng
( ),( ),( )SAB SBC SCD
và
()SDA
. Thể tích của khối chóp
.O MNPQ
bằng
A.
3
4
3
a
. B.
3
64
81
a
. C.
3
128
81
a
. D.
3
2
3
a
.
Lời giải
Chọn D
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 25

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Gọi
, , ,E F K H
lần lượt là trung điểm của
, , ,AB BC CD DA
và
,,M N P
,
Q
lần lượt là hình chiếu
vuông góc của
O
trên
, , ,SE SF SK SH
,,M N P
,
Q
lần lượt là hình chiếu vuông góc của
O
trên các mặt phẳng
( ),( ),( )SAB SBC SCD
,
()SDA
.
Ta có
2 2 2 2
(2 3 ) (2 2 ) 2SO SD OD a a a OE OF OK OH= − = − = = = = =
các tam giác
, , ,SOE SOF SOK SOH
vuông cân tại
O
và bằng nhau nên
,,M N P
và
Q
lần
lượt là trung điểm của của
, , ,SE SF SK SH
MNPQ
là hình vuông cạnh
2a
Mặt khác ta có
2OM ON OP OQ a= = = =
.O MNPQ
là hình chóp đều có tất cả các cạnh
bằng
2a
nên có đưng cao bằng
2
2
1
( 2) . 2. 2
2
a a a

−=


.
Khi đó thể tích của khối chóp
.O MNPQ
bằng
3
2
12
. .( 2)
33
a
aa =
Câu 38: (Đề tốt nghiệp THPT đợt 2 năm 2020 - mã đề 101) Cho hình chóp đều
.S ABCD
có cạnh đáy
bằng
3a
, cạnh bên bằng
33
2
a
và
O
là tâm của đáy. Gọi
,,M N P
và
Q
lần lượt là hình chiếu
vuông góc của
O
trên các mặt phẳng
( )
SAB
,
( )
SBC
,
( )
SCD
và
( )
SDA
. Thể tích của khối chóp
.O MNPQ
bằng
A.
3
9
16
a
. B.
3
2
3
a
. C.
3
9
32
a
. D.
3
3
a
.
Lời giải
Chọn C
O
A
D
B
C
S
E
K
H
F
M
N
P
Q
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 26

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Gọi
, , ,E F G H
theo thứ tự là trung điểm của
, , ,AB BC CD DA
.
Ta có:
( ) ( ) ( )
AB SO
AB SOE SAB SOE
AB OE
⊥
⊥ ⊥
⊥
.
Mặt khác:
( ) ( )
=SAB SOE SE
đồng thi
M
là hình chiếu vuông góc của
O
lên mặt phẳng
( )
SAB
nên
OM SE⊥
tại
M
.
Ta có:
= − = − = =
22
22
3 3 3 2 3
2 2 2
a a a
SO SA OA OE
.
Khi đó tam giác
SOE
vuông cân tại
O
M
là trung điểm
SE
.
Chứng minh tương tự ta cũng có
,,N P Q
lần lượt là trung điểm của các cạnh
,,SF SG SH
.
Khi đó
13
( ,( )) ( ,( ))
24
= = =
a
d O MNPQ d S MNPQ SO
,
2
1 1 9
4 8 8
MNPQ EFGH ABCD
a
S S S= = =
.
Suy ra
23
.
1 1 3 9 9
. ( ,( )) .
3 3 4 8 32
= = =
O MNPQ MNPQ
a a a
V S d O MNPQ
.
Vậy
3
.
9
32
=
O MNPQ
a
V
.
Câu 39: (Câu 50 - ĐTK - BGD&ĐT - Năm 2017) Cho khối tứ diện có thể tích bằng
V
. Gọi
V
là thể tích
của khối đa diện có các đỉnh là các trung điểm của các cạnh của khối tứ diện đã cho, tính tỉ số
V
V
.
A.
1
2
V
V
=
. B.
1
4
V
V
=
. C.
2
3
V
V
=
. D.
5
8
V
V
=
.
Lời giải
Chọn A
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 27

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Cách 1. Đặc biệt hóa tứ diện cho là tứ diện đều cạnh
a
. Hình đa diện cần tính có được bằng
cách cắt
4
góc của tứ diện, mỗi góc cũng là một tứ diện đều có cạnh bằng
2
a
.
Do đó thể tích phần cắt bỏ là
4.
82
VV
V

==
.
Vậy
1
22
VV
V
V
= =
.
Cách 2. Khối đa diện là hai khối chóp tứ giác có cùng đáy là hình bình hành úp lại. Suy ra:
. . .
1 1 1
2 4. 4. 4. .
2 4 2
N MEPF N MEP P MNE
V V V V V V
= = = = =
Cách 3. Ta có
. . . .
'
AQEP B QMF C MNE D NPF
V V V V V
V
VV
− − − −
=
..
..
1
AQEP B QMF
C MNE D NPF
VV
VV
V V V V
= − − − −
1 1 1 1 1 1 1 1 1 1 1 1 1
1 . . . . . . . .
2 2 2 2 2 2 2 2 2 2 2 2 2
= − − − − =
.
Câu 40: (Câu 37 - ĐTN - BGD&ĐT - Năm 2017) Cho tứ diện
ABCD
có thể tích bằng 12 và
G
là trọng
tâm của tam giác
BCD
. Tính thể tích
V
của khối chóp
.AGBC
A.
3V =
B.
4V =
C.
6V =
D.
5V =
Lời giải
Chọn B
Cách 1:
Phân tích: tứ diện
ABCD
và khối chóp
.AGBC
có cùng đưng cao là khoảng cách từ
A
đến
mặt phẳng
( )
BCD
. Do
G
là trọng tâm tam giác
BCD
nên ta có
==
BGC BGD CGD
S S S
3

=
BCD BGC
SS
(xem phần chứng minh).
Áp dụng công thức thể tích hình chóp ta có:
Q
P
N
M
D
C
B
A
E
F
A
B
C
D
G
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 28

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

.
.
1
1
.
.
3
3
3
1
1
.
.
3
3
=
= = =
=
ABCD BCD
BCD
ABCD BCD
A GBC GBC
GBC
A GBC GBC
V h S
hS
VS
VS
hS
V h S
.
11
.12 4
33
= = =
A GBC ABCD
VV
.
Chứng minh: Đặt
;==DN h BC a
.
+)
11
//
2 2 2
= = = =
MF CM h
MF ND MF DN MF
DN CD
.
+)
2 2 2
// .
3 3 3 2 3
= = = = =
GE BG h h
GE MF GE MF
MF BM
+)
11
.
22
33
11
.
2 2 3

= = = =
BCD
BCD GBC
GBC
DN BC ha
S
SS
h
S
GE BC a
+) Chứng minh tương tự có
33
==
BCD GBD GCD
S S S
BGC BGD CGD
S S S
= =
Cách 2:
Ta có
( )
( )
( )
( )
( )
( )
( )
( )
;
11
;;
33
;
= = =
d G ABC
GI
d G ABC d D ABC
DI
d D ABC
.
Nên
( )
( )
.
11
; . . 4
33
G ABC ABC DABC
V d G ABC S V
= = =
Câu 41: (Câu 34 - MĐ 103 BGD&ĐT NĂM 2016-2017) Cho khối chóp
.S ABCD
có đáy là hình vuông
cạnh
a
,
SA
vuông góc với đáy và khoảng cách từ
A
đến mặt phẳng
( )
SBC
bằng
2
2
a
. Tính
thể tích
V
của khối chóp đã cho.
A.
3
2
=
a
V
. B.
3
=Va
. C.
3
3
9
=
a
V
. D.
3
3
=
a
V
.
Lời giải
Chọn D
Kẻ vuông góc .
Ta có nên chính là khoảng cách từ đến mp .
G
I
D
B
C
A
H
1
H
AH
SB
()⊥AH SBC
AH
A
( )
SBC
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 29

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Ta có .
Suy ra . Thể tích cần tính là .
Câu 42: (Câu 38 - ĐMH - BGD&ĐT - Năm 2017) Cho hình chóp tứ giác
.S ABCD
có đáy là hình vuông
cạnh bằng
2a
. Tam giác
SAD
cân tại
S
và mặt bên
( )
SAD
vuông góc với mặt phẳng đáy. Biết
thể tích khối chóp
.S ABCD
bằng
3
4
3
a
. Tính khoảng cách
h
từ
B
đến mặt phẳng
( )
SCD
A.
2
3
ha=
B.
4
3
ha=
C.
8
3
ha=
D.
3
4
ha=
Lời giải
Chọn B
Gọi
I
là trung điểm của
AD
. Tam giác
SAD
cân tại
S
SI AD⊥
Ta có
( ) ( )
( )
SI AD
SI ABCD
SAD ABCD
⊥
⊥
⊥
SI
là đưng cao của hình chóp.
Theo giả thiết
32
.
1 4 1
. . .2 2
3 3 3
S ABCD ABCD
V SI S a SI a SI a= = =
Vì
AB
song song với
( )
SCD
( )
( )
( )
( )
( )
( )
, , 2 ,d B SCD d A SCD d I SCD = =
Gọi
H
là hình chiếu vuông góc của
I
lên
SD
.
Mặt khác
SI DC
IH DC
ID DC
⊥
⊥
⊥
. Ta có
( ) ( )
( )
,
IH SD
IH SCD d I SCD IH
IH DC
⊥
⊥ =
⊥
Xt tam giác
SID
vuông tại
2 2 2 2 2
1 1 1 1 4 2
:
4 2 3
a
I IH
IH SI ID a a
= + = + =
( )
( )
( )
( )
( )
( )
4
, , 2 ,
3
d B SCD d A SCD d I SCD a = = =
.
Câu 43: (Đề TNTHPT 2020 - mã đề 103) Cho hình chóp đều
ABCD
có cạnh đáy bằng
a
, cạnh bên bằng
3
2
a
và
O
là tâm của đáy. Gọi
và
Q
lần lượt là hình chiếu vuông góc của
O
trên các
mặt phẳng
( ) ( ) ( ) ( )
, , ,SAB SBC SCD SDA
. Thể tích của khối chóp
.O MNPQ
bằng
A.
3
48
a
. B.
3
2
81
a
. C.
3
81
a
. D.
3
96
a
.
Lời giải
Chọn D
2 2 2 2 2 2 2
1 1 1 1 1 1 1
= + = − =
AH SA AB SA AH AB a
=SA a
3
1
..
33
==
a
V a a a
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 30

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Từ giả thiết ta có
22
22
2 3 2
,
2 4 4 2
a a a a
OA SO SA OA= = − = − =
.
Gọi
E
là trung điểm của
AB
, kẻ
( )
OM SE M SE⊥
( )
OM SAB⊥
.
Và
2
2
22
22
1
4
2
44
a
SM SO
aa
SE SO OE
= = =
+
+
M
là trung điểm của
SE
.
Chứng minh tương tự với các điểm
,,N P Q
.
Diện tích tứ giác
MNPQ
là
2
2
2
48
aa

=



và
( )
( )
1
;
24
a
d O MNPQ SO==
.
23
.
1
..
3 4 8 96
O MNPQ
a a a
V = =
.
Câu 44: (Câu 45 - BGD - Đợt 1 - Mã đề 104 - 2020) Cho hình chóp đều
.S ABCD
có tất cả các cạnh bằng
a
và
O
là tâm đáy. Gọi
, , ,M N P Q
lần lượt là các điểm đối xứng với
O
qua trọng tâm của
các tam giác
, , ,SAB SBC SCD SDA
và
S
là điểm đỗi xứng với
S
qua
O
. Thể tích của khối chóp
.S MNPQ
bằng
A.
3
22
9
a
. B.
3
20 2
81
a
. C.
3
40 2
81
a
. D.
3
10 2
81
a
.
Lời giải
Chọn B
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 31

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Ta có
.S ABCD
là hình chóp đều có tất cả các cạnh đều bằng
a
2
2
a
SO=
.
Gọi
,GI
lần lượt là trọng tâm các tam giác
,SDA SDC
.
Gọi
,EF
lần lượt là trung điểm
,DA DC
.
Ta có
2
,
3
GI EF=
12
22
a
EF AC==
2
3
a
GI=
.
Mà
,GI
lần lượt là trung điểm của
,OQ OP
22
2
3
a
QP GI = =
.
Từ giả thiết cho dễ dàng suy ra được
MNPQ
là hình vuông cạnh
22
3
a
PQ =
2
8
9
MNPQ
a
S=
.
Gọi
O
là tâm hình vuông
MNPQ
kẻ
( )
//GH QO H OO

H
là trung điểm
OO
(vì
G
là
trung điểm
OQ
).
Ta có
2 2 2 2
.
3 2 3
aa
QO
==
và
12
2 2. .
33
a
OO OH SO
= = =
Theo giả thiết
2
2
a
OS OS
==
2 2 5 2
2 3 6
a a a
S O S O OO
= + = + =
23
.
1 5 2 8 20 2
..
3 6 9 81
S MNPQ
a a a
V
==
.
Câu 45: (Câu 47 - BGD - Đợt 1 - Mã đề 103 - 2020) Cho hình chóp đều
.S ABCD
có cạnh đáy bằng
a
,
cạnh bên bằng
2a
và
O
là tâm của đáy. Gọi
M
,
N
,
P
,
Q
lần lượt là các điểm đối xúng với
O
qua trọng tâm của các tam giác
SAB
,
SBC
,
SCD
,
SDA
và
S
là điểm đối xứng với
S
qua
O
. Thể tích của khối chóp
.S MNPQ
.
A.
3
26
9
a
. B.
3
40 6
81
a
. C.
3
10 6
81
a
. D.
.
Lời giải
Chọn D
O'
H
N
M
P
G
I
O
B
F
E
A
D
C
S
Q
S'
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 32

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Gọi
1
G
,
2
G
,
3
G
,
4
G
lần lượt là trọng tâm các tam giác
SAB
,
SBC
,
SCD
,
SDA
.
E
,
F
,
I
,
K
lần lượt là trung điểm
AB
,
BC
,
CD
,
DA
.
Ta có:
1 2 3 4
2
4 16 1 8
4 4.
9 9 2 9
MNPQ G G G G EFIK ABCD
S S S S a= = = =
.
( )
2
2
2
2
26
22
2 2 2
a a a
SO a a

= − = − =



2 5 6
36
a
S H S O OH SO SO

= + = + =
.
3
2
.
1 5 6 8 20 6
3 6 9 81
S MNPQ
aa
Va
= =
(đvtt).
Câu 46: (BGD - Đợt 1 - Mã đề 102 - 2020) Cho hình chóp đều
.S ABCD
có cạnh đáy bằng
a
, cạnh bên
bằng
3a
và
O
là tâm của đáy. Gọi
, , ,M N P Q
lần lượt là các điểm đối xứng với
O
qua trọng
tâm của các tam giác
, , ,SAB SBC SCD SDA
và
S
là điểm đối xứng với
S
qua
O
. Thể tích khối
chóp
S MNPQ
bằng
A.
3
40 10
81
a
. B.
3
10 10
81
a
. C.
3
20 10
81
a
. D.
3
2 10
9
a
.
Lời giải
Chọn C
Gọi
1 2 3 4
, , ,G G G G
lần lượt là trọng tâm của
, , ,SAB SBC SCD SAD
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 33

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Do
1 2 3 4 1 2 3 4
1
// // ;
2
G G G G EF G G G G EF= =
Tứ giác
1 2 3 4
G G G G
là hình bình hành.
1 2 1 2
// // , 2MN PQ GG MN PQ G G = =
Tứ giác
MNPQ
là hình bình hành.
Gọi
H QN MP=
. Ta có:
1
3
SH
SO
=
.
Ta có:
( )
2
2
2 10
3
22
a
SO a a

= − =



Ta có:
1 2 3 4
3
. . . . .
2 80
5. 5.2 5.2. . .
3 27
S MNPQ S MNPQ S G G G G S EFIK S EFIK
V V V V V

= = = =


2
3
80 1 10 2 20 10
. . . .
27 3 2 2 81
a a a

==



Câu 47: (Câu 47 - ĐỀ BGD-MÃ 101-L1-2020) Cho hình chóp đều
.S ABCD
có cạnh đáy bằng
a
, cạnh
bên bằng
2a
và
O
là tâm của đáy. Gọi
M
,
N
,
P
,
Q
lần lượt là các điểm đối xứng với
O
qua
trọng tâm của các tam giác
SAB
,
SBC
,
SCD
,
SDA
và
'S
là điểm đối xứng với
S
qua
O
. Thể
tích của khối chóp
'.S MNPQ
bằng
A.
3
20 14
81
a
. B.
3
40 14
81
a
. C.
3
10 14
81
a
. D.
3
2 14
9
a
.
Lời giải
Chọn A
Gọi
1 2 3 4
, , ,G G G G
lần lượt là trọng tâm
, , ,SAB SBC SCD SDA
.
, , ,E F G H
lần lượt là trung điểm của các cạnh
, , ,AB BC CD DA
.
Ta có
1 2 3 4
2
4 4 1 8
4 4. 4. . .
9 9 2 9
MNPQ G G G G EFGH
a
S S S EG HF= = = =
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 34

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
1 2 3 4
, , ,
, 2 ,
2
,,
3
5 5 14
,
36
d S MNPQ d S ABCD d O MNPQ
d S ABCD d O G G G G
d S ABCD d S ABCD
a
d S ABCD

=+
=+
=+
==
Vậy
23
.
1 5 14 8 20 14
3 6 9 81
S MNPQ
a a a
V
= =
.
Câu 48: (Câu 46 - Đề - BGD - 2020 - Đợt 2 - Mã đề - 104– 2021) Cho hình chóp đều
.S ABCD
có cạnh
đáy bằng
2a
, cạnh bên bằng
3a
và
O
là tâm đáy. Gọi
và
Q
lần lượt là hình chiếu
vuông góc của
O
trên các mặt phẳng
( )
SAB
,
( )
SBC
,
( )
SCD
và
( )
SDA
. Thể tích khối chóp
.O MNPQ
bằng
A.
3
8
81
a
. B.
3
6
a
. C.
3
12
a
. D.
3
16
81
a
.
Lời giải
Chọn C
Do
.S ABCD
là hình chóp đều nên có
( )
SO ABCD⊥
.
Xét tam giác
SOA
vuông tại
O
có
( ) ( )
22
22
32SO SA OA a a a= − = − =
.
Gọi
, , ,G H I J
lần lượt là trung điểm của
, , ,AB BC CD DA
.
Ta có
( )
,AB GO AB SO AB SOG⊥ ⊥ ⊥
mà
( )
AB SAB⊥
nên
( ) ( )
SGO SAB⊥
do đó
M
là hình
chiếu vuông góc của
O
trên các mặt phẳng
( )
SAB
suy ra
và
OM SG⊥
.
Xét
SOG
vuông tại
O
có
SO OG a==
,
OM SG⊥
nên
M
là trung điểm của
SG
.
Hoàn toàn tương tự có
,,N P Q
lần lượt là trung điểm của
,,SH SI SJ
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 35

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Do đó dễ thấy
.O MNPQ
là chóp tứ giác đều có đưng cao
1
'
22
a
OO SO==
và cạnh đáy
1 1 2 2 2
2 4 4 2
aa
MN GH AC= = = =
.
Vậy thể tích khối chóp
.O MNPQ
bằng
2
3
1 1 2
'. .
.
3 3 2 2 12
a a a
V OO S
O MNPQ MNPQ

= = =



.
Câu 49: (Câu 49 - ĐTK - BGD&ĐT - L1 - Năm 2020) Cho khối chóp
.S ABC
có đáy
ABC
là tam giác
vuông cân tại
, , 90 ,A AB a SBA SCA
góc giữa hai mặt phẳng
( )
SAB
và
( )
SAC
bằng
60
.
Thể tích khối chóp đã cho bằng
A.
3
a
. B.
3
3
a
. C.
3
2
a
. D.
3
6
a
.
Lời giải
Chọn D
Cách 1:
Ta có
2
1
.
22
ABC
a
S AB AC
==
.
Gọi
D
là hình chiếu vuông góc của
S
lên mặt phẳng
( )
ABC
.
Ta có
( )
AB SB
AB SBD AB BD
AB SD
⊥
⊥ ⊥
⊥
.
Tương tự, ta có
AC CD⊥
ABDC
là hình vuông cạnh
a
.
Đăt
,0SD x x=
.
Gọi
H
là hình chiếu vuông góc của
D
lên
2 2 2 2
.DB DS ax
SB DH
DB DS a x
= =
++
.
Ta có
( ) ( )
( )
22
,
DH SB
ax
DH SAB d D SAB DH
DH AB
ax
⊥
⊥ = =
⊥
+
.
Lại có
( ) ( )
( )
( )
( )
// // , ,CD AB CD SAB d C SAB d D SAB DH = =
.
SCA
vuông tại
,C
có
22
,AC a SC x a= = +
.
Kẻ
22
2 2 2 2
..
2
CACS a x a
CK SA CK
CA CS x a
+
⊥ = =
++
.
Vì
( ) ( ) ( ) ( )
( )
( )
( )
( )
,
sin ,
,
d C SAB
DH
SAB SAC SA SAB SAC
d C SA CK
= = =
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 36

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

( ) ( )
22
22
2
2 2 2 2 2
22
22
22
32
sin60 3 4 2
2
2
ax
x x a
ax
x a x x a x a
xa
a x a
xa
+
+
= = + = + =
+
+
+
.
DH a=
.
Vậy
3
.
1
.
36
S ABC ABC
a
V S SD
==
.
Cách 2:
Dựng hình vuông
ABCD
( )
SD ABCD⊥
.
Đặt
,0SD x x=
.
Kẻ
( ) ( )
,DH SB H SB DH SAB⊥ ⊥
và
22
ax
DH
xa
=
+
.
Kẻ
( ) ( )
,DK SC K SC DK SAC⊥ ⊥
và
22
ax
DK
xa
=
+
.
Ta có
2 2 2 2
2 2 2 2 2 2 2
// . 2
SH SK SD x x x
HK BD HK BD a
SB SC
SB x a x a x a
= = = = =
+ + +
.
Ta có
( ) ( )
( )
2 2 2
cos , cos
2.
DH DK HK
SAB SAC HDK
DH DK
+−
==
( )
2 2 2 4
2 2 2
22
2
2 2 2 2
22
22
11
22
2
x a a x
xa
xa
a
xa
x a x a
xa
−
+
+
= = =
+
+
.
.SD a=
Lại có
2
1
.
22
ABC
a
S AB AC
==
.
Vậy
3
.
1
.
36
S ABC ABC
a
V S SD
==
.
Cách trình bày khác
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 37

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Hai tam giác vuông
SAB
và
SAC
bằng nhau chung cạnh huyền
SA
.
Kẻ
BI
vuông góc với
SA
suy ra
CI
cũng vuông góc với
SA
và
IB IC=
.
( )
,SA IC SA IB SA IBC⊥ ⊥ ⊥
tại
I
.
( )
. . .
1 1 1 1
3 3 3 3
S ABC A IBC S IBC IBC IBC IBC IBC
V V V S AI S SI S AI SI S SA
= + = + = + =
.
( ) ( )
( )
( ) ( )
00
, , , 60 60SAB SAC IB IC IB IC BIC= = =
hoặc
0
120BIC =
.
Ta có
IC IB AB a= =
mà
2BC a=
nên tam giác
IBC
không thể đều suy ra
0
120BIC =
.
Trong tam giác
IBC
đặt
( )
0IB IC x x= =
có:
( )
2
2
2 2 2
0
2
22
1 6 6
cos120
2 . 2 3 3
2
xa
IB IC BC a a
x IB IC
IB IC
x
−
+−
= − = = = =
.
Trong tam giác
ABI
vuông tại
I
có:
2
2 2 2
63
33
aa
AI AB IB a

= − = − =



.
Trong tam giác
SAB
vuông tại
B
đưng cao
BI
có:
22
2
.3
3
3
AB a
AB IA SA SA a
IA
a
= = = =
.
Vậy
2
3
0
.
1 1 1 1 6
. . sin a 3sin120
3 3 2 6 3 6
S ABC IBC
aa
V S SA IB IC SA BIC

== = = =



.
Cách trình bày khác
Gọi
H
là hình chiếu của
S
lên
( )
ABC
.
Theo bài ra, ta có
,HC CA HB BA ABHC⊥ ⊥
là hình vuông cạnh
a
.
Gọi
O HA BC=
,
E
là hình chiếu của
O
lên
SA
.
Ta dễ dàng chứng minh được
,EC SA EB SA⊥⊥
.
Từ đó, ta được: góc giữa
( )
SAC
và
( )
SAB
là góc giữa
EB
và
EC
.
a
a
2
A
B
C
S
I
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 38

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Vì
0
90CAB =
nên
00
90 120 .BEC BEC =
Ta dễ dàng chỉ ra được
0
60OEB OEC==
.
Đặt
22
22
.2
2
22
AO SH xa
SH x SA x a OE
SA
xa
= = + = =
+
.
0
22
22
tan60 : 3
2
22
OC a xa
xa
OE
xa
= = =
+
.
Vậy
3
2
..
1 1 1
. . .
2 2 3 6
S ABC S HBAC
a
V V a a= = =
.
Cách trình bày khác
Ta có
SAB SAC ⊥ = ⊥
và chung cạnh huyền SA. Kẻ
( ) ( )
BI SA CI SA⊥ ⊥
và góc giữa hai
mặt phẳng
( )
SAB
và
( )
SAC
là góc giữa hai đưng thẳng
BI
và
( )
; 60CI BI CI =
.
Có
2BC a=
,
BIC
cân tại I. Do
2BI CI AC a a BC= = =
nên
BIC
không đều
6
120
3
a
BIC BI CI
. Từ đó
3
3
a
AI =
;
2
. 3.AB AI SA SA a= =
Dựng hình vuông
ABDC
( )
SD ABDC⊥
.
Có:
3
2 2 2
.
1
; . .
36
ABC S ABC ABC
a
SD SA AD a S a V S SD

= − = = = =
HOẶC CÁCH KHÁC PPTHỂ TÍCH
( )
.
11
..
33
S ABC IBC IBC
V S SI AI S SA

= + =
.
Với
2 2 3
.
1 3 1 3
. . . 120 . . 3 .
2 6 3 6 6
IBC S ABC
a a a
S IB IC sin V a
= = = =
Câu 50: (ĐTK - BGD&ĐT - Năm 2018) Cho hình vuông
ABCD
và
ABEF
có cạnh bằng
1
, lần lượt nằm
trên hai mặt phẳng vuông góc với nhau. Gọi
S
là điểm đối xứng của
B
qua đưng thẳng
DE
.
Thể tích của khối đa diện
ABCDSEF
bằng
A.
7
6
B.
11
12
C.
2
3
D.
5
6
Lời giải
Chọn D
S
B
D
C
A
I
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 39

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Ta có:ADF.BCE là hình lăng trụ đứng có đáy là tam giác vuông cân
Dựa vào hình vẽ ta có:
. ....
2= + = + = −
ABCDSEF ADF BCE ADFS CDFE B CDFEBCE AD E B DEF ABC
V V V V V V V
.
1 1 1 1 1 5
. ; . 2.
2 3 6 2 6 6

= = = = = − =
ADF BCE BCE BADE ABE ABCDSEF
V AB S V AD S V
Câu 51: (Câu 44 - MĐ 103 BGD&ĐT NĂM 2016-2017) Xét khối chóp
.S ABC
có đáy là tam giác vuông
cân tại
A
,
SA
vuông góc với đáy, khoảng cách từ
A
đến mặt phẳng
( )
SBC
bằng
3
. Gọi
là
góc giữa mặt phẳng
( )
SBC
và
( )
ABC
, tính
cos
khi thể tích khối chóp
.S ABC
nhỏ nhất.
A.
1
cos .
3
=
B.
3
cos .
3
=
C.
2
cos .
2
=
D.
2
cos .
3
=
Lời giải
Chọn B
Gọi
M
là trung điểm
BC
,
H
là giao điểm của đưng thẳng qua
A
và vuông góc với
SM
. Ta
được:
Góc giữa mặt phẳng
( )
SBC
và
( )
ABC
là
SMA
.
3
;
sin
AM
3
cos
SA
=
;
1
.
2
AM BC=
Suy ra
2
.
2
19
..
3 sin .cos
S ABC
V AM SA

==
.
Thể tích khối chóp nhỏ nhất khi
2
sin .cos

lớn nhất.
Xét hàm số
( )
23
f sin .cos cos cosx x x x x= = −
với
0
2
x

( )
sin 3cos .sinf x x x x
= − +
,
sin 0
( ) 0
3
cos
3
x
fx
x
=
=
=
S
F
E
D
C
B
A
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 40

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Suy ra
2
sin .cos

lớn nhất khi
3
cos .
3
=
Câu 52: (Câu 49 - MĐ 102 - BGD&ĐT - Năm 2017) Xét khối tứ diện
ABCD
có cạnh
AB x=
và các cạnh
còn lại đều bằng
23
. Tìm
x
để thể tích khối tứ diện
ABCD
đạt giá trị lớn nhất.
A.
6x =
B.
14x =
C.
32x =
D.
23x =
Lời giải
Chọn C
Gọi
,MN
lần lượt là trung điểm của
CD
và
AB
.
Ta có
( )
CD MB CD MN
CD MAB
CD MA CD AB
⊥⊥

⊥

⊥⊥

.
Tam giác
MAB
cân tại
M
nên
MN AB⊥
.
( ) ( )
11
. . , .sin , .2 3. .sin90
66
ABCD
V AB CD d AB CD AB CD x MN= =
( )
22
2
22
36
1 3 3
.2 3. 3 . 36 . 3 3
6 2 6 6 2
xx
x
x x x

+−


= − = − =




.
Dấu
""=
xảy ra
2
36 3 2x x x = − =
.
Vậy với
32x =
thì
ABCD
V
đạt giá trị lớn nhất bằng
33
.
THỂ TÍCH KHỐI LĂNG TRỤ
Câu 53: (MĐ 104 - BGD&ĐT - Năm 2021) Thể tích của khối lập phương cạnh
2a
bằng
A.
3
a
. B.
3
2a
. C.
3
8a
. D.
3
4a
.
Lời giải
Chọn C
Ta có thể tích của khối lập phương cạnh
2a
là:
( )
3
3
2 8 .V a a==
Câu 54: (MĐ 103 - BGD&ĐT - Năm 2021) Thể tích khối lập phương cạnh
3a
bằng
A.
3
27a
. B.
3
3a
. C.
3
9a
. D.
3
a
.
Lời giải
Chọn A
33
(3 ) 27V a a==
.
Câu 55: (Câu 22 - Đề Tham Khảo BGD - 2021) Thể tích khối hộp chữ nhật có ba kích thước
2,3,7
bằng
A.
14.
B.
42.
C.
126.
D.
12.
Lời giải
Chọn B
2
3
2
3
2
3
2
3
2
3
x
M
N
A
D
C
B
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 41

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Thể tích khối hộp có ba kích thước
2,3,7
bằng
2.3.7 42V abc= = =
.
Câu 56: (Câu 14 - BGD - Đợt 1 - Mã đề 104 - 2020) Cho khối hộp chữ nhật có ba kích thước
2
;
3
;
7
. Thể
tích của khối hộp đã cho bằng
A.
7
. B.
42
. C.
12
. D.
14
.
Lời giải
Chọn B
Thể tích khối hộp chữ nhật có ba kích thước
2
;
3
;
7
là:
2.3.7 42V ==
.
Câu 57: (Câu 11 - BGD - Đợt 1 - Mã đề 103 - 2020) Cho khối hộp chữ nhật có ba kích thước
2;6;7
. Thể
tích của khối hộp đã cho bằng
A.
28.
B.
14.
C.
15.
D.
84.
Lời giải
Chọn D
Thể tích của khối hộp đã cho là:
2.6.7 84.=
Câu 58: (BGD - Đợt 1 - Mã đề 102 - 2020) Cho khối hộp chữ nhật có kích thước
2;4;6
. Thể tích của khối
hộp đã cho bằng
A.
16
. B.
12
. C.
48
. D.
8
.
Lời giải
Chọn C
Thể tích của khối hộp là
2.4.6 48V ==
.
Câu 59: (Câu 5 - ĐỀ BGD-MÃ 101-L1-2020) Cho khối hộp chữ nhật có ba kích thước
3; 4; 5
. Thể tích
của khối hộp đã cho bằng
A.
10
. B.
20
. C.
12
. D.
60
.
Lời giải
Chọn D
Thể tích của khối hộp đã cho là
3.4.5 60V ==
.
Câu 60: (Câu 26 - MĐ 104 - BGD&ĐT - Năm 2019) Cho khối lăng trụ đứng
.ABC A B C
có đáy là tam
giác đều cạnh
a
và
2AA a
=
(minh họa như hình vẽ bên). Thể tích của khối lăng trụ đã cho
bằng
A.
3
6
4
a
. B.
3
6
6
a
. C.
3
6
12
a
. D.
3
6
2
a
.
Lời giải
Chọn A
Ta có:
23
. ' ' '
36
'. 2.
44
ABC A B C ABC
aa
V AA S a= = =
.
Câu 61: (Câu 25 - MĐ 103 - BGD&ĐT - Năm 2019) Cho khối lăng trụ đứng
.ABC A B C
có đáy là tam
giác đều cạnh
2a
và
3AA a
=
(minh họa như hình vẽ bên).
C
B
A
B'
C'
A'
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 42

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Thể tích của khối lăng trụ đã cho bằng
A.
3
23a
. B.
3
3a
. C.
3
63a
. D.
3
33a
.
Lời giải
Chọn D
Thể tích khối lăng trụ là:
( )
2
3
23
. .3 3 3
4
ABC
a
V S AA a a
= = =
.
Câu 62: (Câu 21 - MĐ 102-BGD&ĐT-Năm 2019) Cho khối lăng trụ đứng
.ABC A B C
có đáy là tam giác
đều cạnh bằng
a
và
2AA a
=
(minh họa như hình vẽ bên). Thể tích của khối lăng trụ đã cho
bằng
A.
3
3
3
a
. B.
3
3
6
a
. C.
3
3a
. D.
3
3
2
a
.
Lời giải
Chọn D
Diện tích tam giác
ABC
là
2
3
4
ABC
a
S =
.
Thế tích khối lăng trụ đã cho bằng
23
.
33
2
42
ABC A B C ABC
aa
V S AA a
= = =
.
Câu 63: (ĐTK - BGD&ĐT - L1 - Năm 2020) Cho khối lăng trụ đứng
.
ABCD A B C D
có đáy là hình thoi
cạnh
,3a BD a=
và
4
=AA a
(minh họa như hình bên dưới). Thể tích của khối lăng trụ đã cho
bằng
A.
3
2 3 .a
B.
3
4 3 .a
C.
3
23
.
3
a
D.
3
43
.
3
a
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 43

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Lời giải
Chọn A
Vì
ABCD
là hình thoi cạnh
22
3
, 3 2 2
4
= = = − =a BD a AC AO a a a
Vậy
2
3
3
. 2 3
2
= = =
ABCD ABCD
a
S V AA S a
Câu 64: (Câu 22 - MĐ 101-BGD&ĐT-Năm 2019) Cho khối lăng trụ đứng
. ' ' 'ABC A B C
có đáy là tam
giác đều cạnh
a
và
'3AA a=
. Thể tích của lăng trụ đã cho bằng
A.
3
3
4
a
. B.
3
3
2
a
. C.
3
4
a
. D.
3
2
a
.
Lời giải
Chọn A
Ta có:
ABC
là tam giác đều cạnh
a
nên
2
3
4
ABC
a
S
=
.
Ta lại có
. ' ' 'ABC A B C
là khối lăng trụ đứng nên
'3AA a=
là đưng cao của khối lăng trụ.
Vậy thể tích khối lăng trụ đã cho là:
23
. ' ' '
33
'. 3.
44
ABC A B C ABC
aa
V AA S a
= = =
.
Câu 65: (Câu 18 - MĐ 102 - BGD&ĐT - Năm 2017) Cho khối lăng trụ đứng
.ABC A B C
có
BB a
=
, đáy
ABC
là tam giác vuông cân tại
B
và
2AC a=
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
Va=
B.
3
3
a
V =
C.
3
6
a
V =
D.
3
2
a
V =
Lời giải
Chọn D
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 44

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Tam giác
ABC
vuông cân tại
B
2
AC
AB BC a = = =
. Suy ra:
2
1
2
ABC
Sa=
.
Khi đó:
3
2
.
1
..
22
ABC A B C ABC
a
V S BB a a
= = =
Câu 66: (Câu 1 - ĐTK - BGD&ĐT - Năm 2019) Thể tích của khối lập phương cạnh
2a
bằng
A.
3
8a
. B.
3
2a
. C.
3
a
. D.
3
6a
.
Lời giải
Chọn A
Thể tích của khối lập phương cạnh
2a
bằng
( )
3
3
28aa=
.
Câu 67: (Câu 35 - ĐMH - BGD&ĐT - Năm 2017) Tính thể tích
V
của khối lập phương
.ABCD A B C D
, biết
3AC a
=
.
A.
3
Va=
. B.
3
36
4
a
V =
. C.
3
33Va=
. D.
3
1
3
Va=
.
Lời giải
Chọn A
Giả s khối lập phương có cạnh bằng
( )
;0xx
Xt tam giác
' ' 'A B C
vuông cân tại
'B
ta có:
2 2 2
' ' ' ' ' 'A C A B B C=+
2 2 2
2x x x= + =
' ' 2A C x=
Xt tam giác
''A AC
vuông tại
'A
ta có
2 2 2
' ' ' 'AC A A A C=+
2 2 2
32a x x = +
xa=
Thể tích của khối lập phương
.ABCD A B C D
là
3
Va=
.
Câu 68: (Câu 9 - Đề - BGD - 2020 - Đợt 2 - Mã đề - 104– 2021) Cho khối lăng trụ có diện tích đáy
6B =
và chiều cao
4h =
. Thể tích khối lăng trụ đã cho bằng
A.
24
. B.
4
. C.
8
. D.
12
.
Lời giải
Chọn A
a
a
2
C'
B'
A
B
C
A'
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 45

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Thể tích khối lăng trụ có diện tích đáy
6B =
và chiều cao
4h =
là:
. 6.4 24V B h= = =
.
Câu 69: (Câu 4 - MĐ 104 - BGD&ĐT - Năm 2019) Thể tích của khối lăng trụ có diện tích đáy
B
và chiều
cao
h
là
A.
4
3
Bh
. B.
1
3
Bh
. C.
3Bh
. D.
Bh
.
Lời giải
Chọn D
Thể tích của khối lăng trụ có diện tích đáy
B
và chiều cao
h
là:
Bh
.
Câu 70: (Câu 8 - MĐ 103 - BGD&ĐT - Năm 2019) Thể tích của khối lăng trụ có diện tích đáy
B
và chiều
cao
h
là
A.
4
3
Bh
. B.
3Bh
. C.
1
3
Bh
. D.
Bh
.
Lời giải
Chọn D
Câu 71: (Câu 12 - MĐ 102-BGD&ĐT-Năm 2019) Thể tích của khối lăng trụ có diện tích đáy
B
và chiều
cao
h
là
A.
3Bh
. B.
Bh
. C.
4
3
Bh
. D.
1
3
Bh
.
Lời giải
Chọn B
Thể tích
V
của khối lăng trụ có diện tích đáy
B
và chiều cao
h
là:
V Bh=
(đvtt).
Câu 72: (Câu 12 - MĐ 101-BGD&ĐT-Năm 2019) Thể tích khối lăng trụ có diện tích đáy
B
và chiều cao
h
là
A.
3.Bh
B.
.Bh
C.
4
.
3
Bh
D.
1
.
3
Bh
Lời giải
Chọn B
Câu 73: (Câu 11 - MĐ 104 - BGD&ĐT - Năm 2018) Cho khối lăng trụ có đáy là hình vuông cạnh
a
và
chiều cao bằng
2a
. Thể tích của khối lăng trụ đã cho bằng
A.
3
2
3
a
B.
3
4
3
a
C.
3
2a
D.
3
4a
Lời giải
Chọn C
Ta có:
.
langtru day
V S h=
2
.2aa=
3
2a=
.
Câu 74: (Đề TNTHPT 2020 - mã đề 103) Cho khối lăng trụ có diện tích đáy
6B =
và chiều cao
3h =
.
Thể tích của khối lăng trụ đã cho bằng
A.
3.
B.
18.
C.
6.
D.
9.
Lời giải
Chọn B
Thể tích của khối lăng trụ đã cho là:
. 6.3 18.V B h= = =
Câu 75: (Câu 18 - Đề thi TNTHPT 2020 - mã đề 102) Cho khối lăng trụ có diện tích đáy
3B =
và chiều
cao
2h =
. Thể tích khối lăng trụ đã cho bằng
A. 1. B. 3. C. 2. D. 6.
Lời giải
Chọn D
Thể tích khối lăng trụ
3.2 6V Bh= = =
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 46

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Câu 76: (Câu 19 - Đề thi TNTHPT 2020 - mã đề 102) Cho khối lăng trụ có diện tích đáy
3B =
và chiều
cao
2h =
. Thể tích của khối lăng trụ đã cho bằng
A.
1
. B.
3
. C.
2
. D.
6
.
Lời giải
Chọn D
Thể tích khối lăng trụ là
. 3.2 6V B h= = =
.
Câu 77: (Đề tốt nghiệp THPT đợt 2 năm 2020 - mã đề 101) Cho khối lăng trụ có diện tích đáy
3B =
và
chiều cao
6h =
. Thể tích của khối lăng trụ đã cho bằng
A.
9
. B.
18
. C.
3
. D.
6
.
Lời giải
Chọn B
Thể tích khối lăng trụ đã cho là:
. 3.6 18V B h= = =
.
Câu 78: (Đề tốt nghiệp THPT đợt 2 năm 2020 - mã đề 101) Cho khối trụ có bán kính đáy
4r =
và chiều
cao
3h =
. Thể tích của khối trụ đã cho bằng
A.
48
. B.
4
. C.
16
. D.
24
.
Lời giải
Chọn A
Thể tích của khối trụ đã cho là:
2
48V r h

==
.
Câu 79: (MĐ 104 - BGD&ĐT - Năm 2021) Cho khối hộp chữ nhật
.ABCD A B C D
có đáy là hình vuông
4BD a=
, góc giữa hai mặt phẳng
( )
A BD
và
( )
ABCD
bằng
0
60
. Thể tích của khối hộp chữ nhật
đã cho bằng
A.
3
48 3a
. B.
3
16 3
9
a
. C.
3
16 3
3
a
. D.
3
16 3a
.
Lời giải
Chọn D
Ta có đáy
ABCD
là hình vuông có
4 2 2BD a AB a= =
.
Gọi
I
trung điểm
.BD
Vì
42BD a BI AI a= = =
.
Tam giác
A AI
vuông tại
A
có:
0
tan60 2 3
AA
A A a
AI
= =
.
Thể tích của khối hộp chữ nhật đã cho bằng:
( )
2
3
. 2 2 .2 3 16 3
ABCD
V S A A a a a
= = =
.
Câu 80: (MĐ 103 - BGD&ĐT - Năm 2021) Cho khối hộp chữ nhật
.ABCD A B C D
có đáy là hình vuông,
2BD a=
, góc giữa hai mặt phẳng
( )
A BD
và
( )
ABCD
bằng
60
. Thể tích của khối hộp chữ
nhật đã cho bằng
A.
3
23
9
a
. B.
3
63a
. C.
3
23
3
a
. D.
3
23a
.
Lời giải
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 47

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Chọn D
+) Ta có
2 2 ; 2BD a AC a AB a= = =
.
+)
( )
2
2
22
ABCD
S a a==
.
+) Góc giữa hai mặt phẳng
( )
A BD
và
( )
ABCD
là góc
A OA
tan .tan60 3AA AO A OA a a

= = =
.
Vậy
23
.
. 3.2 2 3
ABCD A B C D ABCD
V AA S a a a
= = =
.
Câu 81: (Câu 44 - MĐ 102 - BGD&ĐT - Năm 2021) Cho khối hộp chữ nhật
. ' ' ' 'ABCD A B C D
có đáy là
hình vuông,
4BD a=
, góc giữa hai mặt phẳng
( )
'A BD
và
( )
ABCD
=
30
o
. Thể tích của khối hộp
chữ nhật đã cho bằng
A.
3
16 3
9
a
B.
3
48 3a
C.
3
16 3
3
a
D.
3
16 3a
Lời giải
Chọn C
Gọi
O
là trung điểm của
BD
. Ta có:
''A AB A AD =
suy ra
''A B A D=
suy ra
'A BD
cân.
Mà
( ) ( )
'
'
A BD ABCD BD
A O BD
AO BD
=
⊥
⊥
( ) ( )
(
)
, 30 .A BD ABCD A OA

= =
=
30
o
.
Xét
A OA
vuông tại
A
có:
tan30
2
22
o
A A A A A A A A
AC BD
AO a
= = = =
23
' 2 tan30
3
a
A A a= =
.
Xét hình vuông
ABCD
có:
2 2 2.BD AB AB a= =
Vậy thể tích của khối hình hộp chữ nhật bằng:
2
'.V A A AB=
=
( )
2
23
. 2 2
3
a
a
=
3
16 3
3
a
.
Câu 82: (Câu 48 - MĐ 101 - BGD&ĐT - Năm 2021) Cho khối hộp chữ nhật
. ' ' ' 'ABCD A B C D
có đáy là
hình vuông,
2BD a=
, góc giữa hai mặt phẳng
( )
'A BD
và
( )
ABCD
bằng
0
30
. Thể tích của khối
hộp chữ nhật đã cho bằng
A.
3
63a
. B.
3
23
9
a
. C.
3
23a
. D.
3
23
3
a
.
Lời giải
Chọn D
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 48

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Gọi
O
là tâm hình vuông
ABCD
. Vì
BD OA⊥
và
'BD AA⊥
nên
( )
''BD A OA BD OA⊥ ⊥
Lại có
( ) ( )
'A BD ABCD BD=
. Do đó
( ) ( )
( )
0
' , ' 30A BD ABCD A OA==
(Hình vẽ trên).
Vì tứ giác
ABCD
là hình vuông có
2BD a=
nên
OA a=
và
2AB AD a==
.
Xét tam giác
'A AO
vuông tại
A
có
OA a=
và
0
' 30A OA=
nên
0
3
' .tan30
3
a
AA OA==
.
Vậy thể tích khối hộp chữ nhật
3
3 2 3
. . ' a 2. 2.
33
a
V AB AD AA a a= = =
.
Câu 83: (MĐ 101 BGD&ĐT NĂM 2021-L2) Cho khối lăng trụ tam giác đều
.ABC A B C
có cạnh bên bằng
2a
, góc giữa hai mặt phẳng
( )
'A BC
và
( )
ABC
bằng
30
. Thể tích của khối lăng trụ đã cho bằng
A.
3
83
9
a
. B.
3
83
3
a
. C.
3
83
27
a
. D.
3
83a
.
Lời giải
Chọn D
Gọi
N
là trung điểm
BC
ta có:
( )
BC AN
BC AA N
BC AA
⊥
⊥
⊥
. Suy ra góc giữa hai mặt phẳng
( )
A BC
và
( )
ABC
là góc
30A NA
=
Xét tam giác vuông
AA N
ta có
2
tan 2 3
tan30
tan
AA AA a
A NA AN a
AN
A NA

= = = =
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 49

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Xét tam giác đều
ABC
ta có
3 2 2.2 3
4
2
33
AB AN a
AN AB a= = = =
Suy ra diện tích tam giác
ABC
bằng:
2
1
.4 .2 3 4 3
2
a a a=
.
Vậy thể tích khối lăng trụ
.ABC A B C
bằng:
23
. 2 .4 3 8 3
ABC
V AA S a a a
= = =
Câu 84: (MĐ 104 BGD&ĐT NĂM 2016-2017) Cho khối lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam
giác cân với
AB AC a==
,
120BAC =
. Mặt phẳng
( )
AB C

tạo với đáy một góc
60
. Tính thể
tích
V
của khối lăng trụ đã cho.
A.
3
3
8
a
V =
. B.
3
9
8
a
V =
. C.
3
8
a
V =
. D.
3
3
4
a
V =
.
Lời giải
Chọn A
Gọi
I
là trung điểm của
BC

.
Trong
2 2 2 2
: 2 . .cos 3A B C B C A B A C A B A C B A C a
= + − =
2
13
. .sin120
24
ABC
a
S a a
= =
;
2
23
2
23
ABC
S a a
AI
BC
a
= = =

Ta có :
( ) ( )
60
AB C A B C B C
AI B C AIA
A I B C
=
⊥ =
⊥
Trong tam giác vuông
AIA
có
3
.tan60
2
a
AA A I

= =
.
Vậy thể tích
23
3 3 3
.
4 2 8
a a a
V ==
.
Câu 85: (Câu 38 - ĐTN - BGD&ĐT - Năm 2017) Cho lăng trụ tam giác
.
ABC A B C
có đáy
ABC
là tam
giác vuông cân tại
A
, cạnh
22=AC
. Biết
AC
tạo với mặt phẳng
( )
ABC
một góc
60
và
4
=AC
. Tính thể tích
V
của khối đa diện

ABCB C
.
A.
8
3
=V
B.
16
3
=V
C.
83
3
=V
D.
16 3
3
=V
Lời giải
Chọn D
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 50

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Phân tích: Tính thể tích của khối đa diện

ABCB C
bằng thể tích khối của lăng trụ
.
ABC A B C
trừ đi thể tích của khối chóp
.
A A B C
.
Giả s đưng cao của lăng trụ là
CH
. Khi đó góc giữa
AC
mặt phẳng
( )
ABC
là góc
60
=C AH
.
Ta có:
sin60 2 3; 4
= = =
ABC
CH
C H S
AC
;
( )
2
.
1
. 2 3. . 2 2 8 3
2
= = =
ABC A B C ABC
V C H S
.
..
1 1 8 3
..
3 3 3
= = =
A A B C ABC ABC A B C
V C H S V
;
..
8 3 16 3
83
33
= − = − =
ABB C C ABC A B C A A B C
V V V
.
Câu 86: (Câu 39 - MĐ 104 - BGD&ĐT - Năm 2018) Cho khối lăng trụ
.ABC A B C
, khoảng cách từ
C
đến đưng thẳng
BB
bằng
5
, khoảng cách từ
A
đến các đưng thẳng
BB
và
CC
lần lượt
bằng
1
và
2
, hình chiếu vuông góc của
A
lên mặt phẳng
( )
ABC
là trung điểm
M
của
BC

và
5AM
=
. Thể tích của khối lăng trụ đã cho bằng
A.
25
3
B.
2 15
3
C.
5
D.
15
3
Lời giải
Chọn B
Gọi
J
,
K
lần lượt là hình chiếu vuông góc của
A
lên
BB
và
CC
,
H
là hình chiếu vuông góc
của
C
lên
BB
Ta có
( )
1AJ BB
⊥
.
( )
2AK CC AK BB

⊥ ⊥
.
Từ
( )
1
và
( )
2
suy ra
( )
BB AJK
⊥
BB JK
⊥
//JK CH
5JK CH = =
.
Xét
AJK
có
2 2 2
5JK AJ AK= + =
suy ra
AJK
vuông tại
A
.
Gọi
F
là trung điểm
JK
khi đó ta có
5
2
AF JF FK= = =
.
B’
B
A
C
H
C’
A’
4
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 51

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Gọi
N
là trung điểm
BC
, xét tam giác vuông
ANF
ta có:
cos
AF
NAF
AN
=
5
2
5
=
1
2
=
60NAF=
. (
5AN AM==
vì
//AN AM
và
AN AM=
).
Vậy ta có
1
.
2
AJK
S AJ AK
=
1
.1.2 1
2
==
.cos60
AJK ABC
SS

=
1
2
1
cos60
2
AJK
ABC
S
S
= = =
.
Xét tam giác
AMA
vuông tại
M
ta có
30MAA AMF
==
hay
.tan30AM A M
=
15
3
=
.
Vậy thể tích khối lăng trụ là
.
ABC
V AM S
=
15 2 15
.2
33
==
.
Câu 87: (MĐ 103 - BGD&ĐT - Năm 2018) Cho khối lăng trụ
. ' ' 'ABC A B C
, khoảng cách từ
C
đến đưng
thẳng
'BB
bằng 2, khoảng cách từ
A
đến các đưng thẳng
'BB
và
'CC
lần lượt bằng 1 và
3
, hình chiếu vuông góc của
A
lên mặt phẳng
( ' ' ')A B C
là trung điểm
M
của
''BC
và
'2AM=
. Thể tích của khối lăng trụ đã cho bằng
A.
3
. B.
2
. C.
23
3
. D.
1
Lời giải
Chọn B
Gọi
12
,AA
lần lượt là hình chiếu của
A
trên
'BB
,
'CC
. Theo đề ra
1 2 1 2
1; 3; 2.AA AA A A= = =
Do
2 2 2
1 2 1 2
AA AA A A+=
nên tam giác
12
AA A
vuông tại
A
.
Gọi
H
là trung điểm
12
AA
thì
12
1
2
AA
AH ==
.
Lại có
12
' ( )MH BB MH AA A MH AH ⊥ ⊥
suy ra
22
3MH AM AH= − =
.
nên
12
3
cos(( ),( )) cos( , ) cos .
2
MH
ABC AA A MH AM HMA
AM
= = = =
Suy ra
12
12
1.
cos(( ),( ))
AA A
ABC
S
S
ABC AA A
==
Thể tích lăng trụ là
2
ABC
V AM S= =
.
Nhận xét. Ý tưởng câu này là dùng diện tích hình chiếu
' cosSS
=
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 52

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Câu 88: (MĐ 102 - BGD&ĐT - Năm 2018) Cho khối lăng trụ
.ABC A'B'C'
, khoảng cách từ
C
đến
'BB
là
5
, khoảng cách từ
A
đến
'BB
và
'CC
lần lượt là
1; 2
. Hình chiếu vuông góc của
A
lên
mặt phẳng
' ' 'A B C
là trung điểm
M
của
''BC
,
15
'
3
=AM
. Thể tích của khối lăng trụ đã cho
bằng
A.
15
3
. B.
25
3
. C.
5
. D.
2 15
3
Lời giải
Chọn D
Kẻ
'⊥AI BB
,
'⊥AK CC
( hình vẽ ).
Khoảng cách từ
A
đến
'BB
và
'CC
lần lượt là
1; 2
1=AI
,
2=AK
.
Gọi
F
là trung điểm của
BC
.
15
'
3
=AM
15
3
=AF
Ta có
( )
'
'
'
⊥
⊥
⊥
AI BB
BB AIK
BB AK
'⊥BB IK
.
Vì
''CC BB
( , ') d C BB
( , ')= d K BB
= IK
5=
AIK
vuông tại
A
.
Gọi
E
là trung điểm của
IK
' EF BB
( )
⊥EF AIK
⊥EF AE
.
Lại có
( )
⊥AM ABC
. Do đó góc giữa hai mặt phẳng
( )
ABC
và
( )
AIK
là góc giữa
EF
và
AM
bằng góc
=AME FAE
. Ta có
cos =
AE
FAE
AF
5
2
15
3
=
3
2
=
30 = FAE
.
Hình chiếu vuông góc của tam giác
ABC
lên mặt phẳng
( )
AIK
là
AIK
nên ta có:
cos=
AIK ABC
S S EAF
3
1
2
=
ABC
S
2
3
=
ABC
S
.
F
E
K
I
A'
B'
M
C
B
A
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 53

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Xét
AMF
vuông tại
A
:
tan =
AF
AMF
AM
15
3
3
3
=AM
5=AM
.
Vậy
. ' ' '
2
5.
3
=
ABC A B C
V
2 15
3
=
.
Câu 89: (Câu 42 - MĐ 101 - BGD&ĐT - Năm 2018) Cho khối lăng trụ
.ABC A B C
, khoảng cách từ
C
đến đưng thẳng
BB
bằng
2
, khoảng cách từ
A
đến các đưng thẳng
BB
và
CC
lần lượt
bằng
1
và
3
, hình chiếu vuông góc của
A
lên mặt phẳng
( )
ABC
là trung điểm
M
của
BC

và
23
3
AM
=
. Thể tích của khối lăng trụ đã cho bằng
A.
2
B.
1
C.
3
D.
23
3
Lời giải
Chọn A
Cắt lăng trụ bởi một mặt phẳng qua
A
và vuông góc với
AA
ta được thiết diện là tam giác
11
A B C
có các cạnh
1
1AB
=
;
1
3AC
=
;
11
2BC =
.
Suy ra tam giác
11
A B C
vuông tại
A
và trung tuyến
AH
của tam giác đó bằng
1
.
Gọi giao điểm của
AM
và
AH
là
T
.
Ta có:
23
3
AM
=
;
1AH
=
1
3
MH=
. Suy ra
30MA H
=
.
Do đó
60MA A
=
4
3
cos
AM
AA
MA A
= =
.
Thể tích khối lăng trụ
.ABC A B C
bằng thể tích khối lăng trụ
1 1 2 2
.A BC AB C
và bằng
11
43
.2
2
3
A B C
V AA S
= = =
.
T
M
B
2
H
C
2
A'
C
1
A
B
1
A
A'
T
B'
C'
M
H
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 54

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Câu 90: (ĐTK - BGD&ĐT - L1 - Năm 2020) Cho hình hộp
. ' ' ' 'ABCD A B C D
có chiều cao bằng
8
và diện
tích đáy bằng
9.
Gọi
,,M N P
và
Q
lần lượt là tâm của các mặt bên
' ', ' ', ' 'ABB A BCC B CDD C
và
''DAA D
. Thể tích của khối đa diện lồi có các đỉnh là các điểm
, , , , , ,A B C D M N P
và
Q
bằng
A. 27. B. 30. C. 18. D. 36
Lời giải
Chọn B
Mặt
( )
MNPQ
cắt các cạnh
AA',BB',CC', DD'
tại
1 1 1 1
, , ,A B C D
. Thể tích khối đa diện cần tìm là
V
, thì:
1 1 1 1 1 1 1 1
. ' ' ' ' '. '. '. '.
8.9
4
2 24
30
A B C D A B C D A QMA B MNB C PNC D QPD
V V V V V V
V
V
= − − − −
= −
=
.
Câu 91: (Câu 46 - MĐ 104 - BGD&ĐT - Năm 2019) Cho hình lăng trụ
.ABC A B C
có chiều cao bằng
4
và đáy là tam giác đều cạnh bằng
4
. Gọi
,MN
và
P
lần lượt là tâm của các mặt bên
ABB A
,
ACC A
và
BCC B
. Thể tích của khối đa diện lồi có các đỉnh là các điểm
, , , , ,A B C M N P
bằng
A.
14 3
3
. B.
83
. C.
63
. D.
20 3
3
.
Lời giải
Chọn C
Cách 1:
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 55

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Chia đôi khối lăng trụ bằng mặt phẳng
( )
.MNP
Khi đó ta có
( )
MNP BB F
=
thì
..
1
2
ABC EFG ABC A B C
VV
=
Lại có
. . . . .ABC MNP ABC EFG B MPF A EMN C NPG
V V V V V= − − −
Dễ thấy
. . . . . .
1 1 1 1
.
4 4 2 8
B MPF A EMN C NPG ABC EFG ABC A B C ABC A B C
V V V V V V
= = = = =
Tức là
2
. . .
1 1 3 3 4.4 3
. 6 3.
2 8 8 8 4
ABC MNP ABC A B C ABC A B C
V V V

= − = = =


Cách 2
2
4 3
43
4
ABC
S ==
;
.ABC A B C
VV
=
Hạ
1 1 1
,,M N P
lần lượt vuông góc
,,AB AC BC
,
khi đó
1 1 1
,,M N P
lần lượt là trung điểm các cạnh
,,AB AC BC
Khi đó
1 1 1 1 1 1 1 1 1
. . . .ABCMNP MNP M N P B MPPM C NPPN A MNN M
V V V V V= + + +
Dễ thấy
1
4
MNP ABC
SS=
;
1
1
2
MM AA=
nên
1 1 1
..
11
88
MNP M N P ABC A B C
V V V
==
Do đáy là tam giác đều nên
1 1 1 1 1 1
. . .B MPPM C NPPN A MNN M
V V V==
Ta có
( )
( )
( )
( )
11
1
;;
2
d B MPPM d B ACC A=

;
11
1
4
MPPM ACC A
SS

=
nên
11
..
1 1 2 1
.
8 8 3 12
B MPPM B ACC A
V V V V

= = =
.
Do đó
1 1 1 1 3 3
.4.4 3 6 3
8 12 12 12 8 8
ABCMNP
V V V V V V= + + + = = =
.
Câu 92: (Câu 49 - MĐ 103 - BGD&ĐT - Năm 2019) Cho lăng trụ
. ' ' 'ABC A B C
có chiều cao bằng 6 và
đáy là tam giác đều cạnh bằng 4. Gọi M, N, P lần lượt là tâm của các mặt bên
' ', ' ', ' 'ABB A ACC A BCC B
. Thể tích của khối đa diện lồi có các đỉnh là các điểm
, , , , ,A B C M N P
bằng
A.
93
. B.
10 3
. C.
73
. D.
12 3
.
Lời giải
Chọn A
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 56

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

. ' ' '
3
6.16 24 3
4
ABC A B C
V ==
’
Thể tích cần tìm là
1 .MNP ' ' '.ABC A B C MNP
V V V==
2 '. '. 'A AMN B BMP C CNP
V V V V= = =
. ' ' ' 1 2
23
ABC A B C
V V V = +
' ' 2 '. ' ' . ' ' ' . ' ' '
1 1 1 1 1
.
4 4 4 3 12
AMN AB C A AB C ABC A B C ABC A B C
S S V V V V= = = =
. ' ' ' 1 . ' ' ' 1 . ' ' '
13
2 9 3
48
ABC A B C ABC A B C ABC A B C
V V V V V = + = =
Câu 93: (Câu 49 - MĐ 102-BGD&ĐT-Năm 2019) Cho lăng trụ
.ABC A B C
có chiều cao là
8
và đáy là
tam giác đều cạnh bằng
4
. Gọi
M
,
N
và
P
lần lượt là tâm của các mặt bên
ABB A

,
ACC A

và
BCC B

. Thể tích của khối đa diện lồi có các đỉnh là các điểm
A
,
B
,
C
,
M
,
N
,
P
bằng
A.
12 3
. B.
16 3
. C.
28 3
3
. D.
40 3
3
.
Lời giải
Chọn A
Cách 1:
Ta có
2
4 . 3
8. 32 3
4
ABCA B C
VV
= = =
, gọi
( )
( )
,h d A ABC
=
.
Ta có
1
..
3 2 6
MABC ABC
hV
VS==
.
C'
B'
A'
B
C
A
K
J
I
P
N
M
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 57

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

1
..
3 2 4 24
ABC
MNPC
S
hV
V ==
.
( )
( )
( )
( )
.
,
11
. , . .
3 3 2 4 8 12
BCC B A BCC B
MBCP PBC
d A BCC B
SV
V
V d M PBC S
= = = =
.
Tương tự
12
MNAC
V
V =
.
Vậy
3
12 3
8
MNPABC MABC MNAC MNPC MBCP
V
V V V V V= + + + = =
.
Cách 2:
Đặc biết hóa cho lăng trụ đứng.
Gọi
E
,
F
,
G
lần lượt là trung điểm của
AB
,
AC
,
BC
.
Ta có:
.
. 4 3
MNP EFG EFG
V ME S==
.
( )
( )
.
1 1 1 1 8 3
, . . . . . 3.4.2
3 3 2 3 3
B MEGP MEGP
V d B MEGP S BF ME EG= = = =
.
Tương tự:
..
83
3
A MNFE C PNFG
VV==
.
Vậy
. . . .
83
4 3 3. 12 3
3
MNPABC MNP EFG B MEGP A MNFE C PNFG
V V V V V= + + + = + =
.
Câu 94: (Câu 47 - MĐ 101-BGD&ĐT-Năm 2019) Cho lăng trụ
. ' ' 'ABC A B C
có chiều cao bằng
8
và đáy
là tam giác đều cạnh bằng
6
. Gọi
,MN
và
P
lần lượt là tâm của các mặt bên
''ABB A
,
''ACC A
và
''BCC B
. Thể tích của khối đa diện lồi có các đỉnh là các điểm
, , , , ,A B C M N P
bằng:
A.
27 3
. B.
21 3
. C.
30 3
. D.
36 3
.
Lời giải
Chọn A
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 58

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Gọi
1 1 1
,,A B C
lần lượt là trung điểm của các cạnh
', ', 'AA BB CC
.
Khối lăng trụ
1 1 1
.ABC ABC
có chiều cao là
4
là tam giác đều cạnh
6
.
Ba khối chóp
1
.A AMN
,
1
BB MP
,
1
CC NP
đều có chiều cao là 4 và cạnh là tam giác đều cạnh
3
Ta có:
( )
1 1 1 1 1 1
. . . . .ABC MNP ABC A B C A A MN B B MP C C NP
V V V V V= − + +
2
6 3 1 9 3
4 3 4 27 3
4 3 4
= − =
Câu 95: (Câu 47 - ĐTK - BGD&ĐT - Năm 2019) Cho khối lăng trụ
.ABC A B C
có thể tích bằng 1. Gọi
,MN
lần lượt là trung điểm các đoạn thẳng
AA
và
BB
. Đưng thẳng
CM
cắt đưng thẳng
CA

tại
P
, đưng thẳng
CN
cắt đưng thẳng
CB

tại
Q
. Thể tích của khối đa diện lồi
A MPB NQ

bằng
A.
1
. B.
1
3
. C.
1
2
. D.
2
3
.
Lời giải
Chọn D
+) Ta có
A
là trung điểm
PC
;
B
là trung điểm
QC
. Do đó
44
C PQ
C PQ C A B
C A B
S
SS
S
= =
.
+)
. . . .
14
. 4 4 .
33
C PQ
C C PQ C A B C C A B C ABC A B C
C A B
S
V V V V
S

= = = =


+) Mặt khác
. . .
1 1 1 1 2
. . 1 .
3 3 2 2 3
A B C MNC ABC A B C ABC A B C
A M B N C C
V V V
A A B B C C
= + + = + + =
+) Do đó
..
4 2 2
.
3 3 3
A MPB NQ C C PQ A B C MNC
V V V
= − = − =
Câu 96: (Câu 44 - MĐ 101 - BGD&ĐT - Năm 2017) Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N
lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng
N
M
A
C
B
A'
B'
C'
P
Q
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 59

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích
V. Tính V.
A.
3
72
216
a
V =
B.
3
11 2
216
a
V =
C.
3
13 2
216
a
V =
D.
3
2
18
a
V =
Lời giải
Chọn B
( )
MNE
chia khối tứ diện ABCD thành 2 khối đa diện
( )
1
:.AC MNPQ
và
( )
2
:.BD MNPQ
( )
MNE
cắt AD tại Q, cắt CD tại P.
. . .AC MNPQ E AMNC E ACPQ
V V V=−
( )
( )
( )
( )
( )
( )
( )
( )
( )


=
=−

=−


==
.
1
,.
3
1
,.
3
11
,.
34
1 3 3
.2. D, .
3 4 2
E AMNC AMNC
ABC BMN
ABC ABC
ABC ABCD
V d E AMNC S
d E ABC S S
d E ABC S S
d ABC S V
( )
( )
( )
( )
( )
( )
( )
.
1 1 1 8 8
, . B, . B, .
3 3 3 9 9
E ACPQ ACPQ ACD DPQ ACD ABCD
V d E ACPQ S d ACD S S d ACD S V
= = − = =
33
.
3 8 11 11 2 11 2
.
2 9 18 18 12 216
AC MNPQ ABCD ABCD ABCD
V V V V a a= − = = =
Câu 97: (MĐ 102 - BGD&ĐT - Năm 2018) Ông A dự định s dụng hết
2
6,7m
kính để làm một bể cá
bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép
có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn
đến hàng phần trăm).
A.
3
1,57m
. B.
3
1,11m
. C.
3
1,23m
. D.
3
2,48m
Lời giải
Chọn A
Gọi
x
là chiều rộng, ta có chiều dài là
2x
Do diện tích đáy và các mặt bên là
2
6,7m
nên có chiều cao
2
6,7 2
6
x
h
x
−
=
,
ta có
0h
nên
6,7
2
x
.
Thể tích bể cá là
( )
3
6,7 2
3
xx
Vx
−
=
và
( )
2
6,7 6
0
3
x
Vx
−
==
6,7
6
x=
Bảng biến thiên
A
B
C
D
Q
P
E
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 60

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Bể cá có dung tích lớn nhất bằng
3
1,57m
.
Câu 98: (Câu 31 - MĐ 101 - BGD&ĐT - Năm 2018) Ông
A
dự định dùng hết
2
6,5m
kính để làm một
bể cá có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng. Bể cá có dung tích
lớn nhất bằng bao nhiêu.
A.
3
2,26 m
B.
3
1,61m
C.
3
1,33m
D.
3
1,50 m
Lời giải
Chọn D
Giả s hình hộp chữ nhật có kích thước như hình vẽ. Ta có dung tích của bể cá:
=V abc
Mặt khác theo giả thiết ta có:
2 2 6,5
2
+ + =
=
ab bc ac
ab
2
2 6 6,5
2
+=
=
b bc
ab
2
6,5 2
6
2
−
=
=
b
c
b
ab
Khi đó
2
2
6,5 2
2.
6
−
=
b
Vb
b
3
6,5 2
3
−
=
bb
V
.
Xét hàm số:
( )
3
6,5 2
3
−
=
bb
fb
. Có BBT
Vậy bể cá có dung tích lớn nhất là:
3
39
1,50
6

=



fm
.
Câu 99: (MĐ 103 - BGD&ĐT - Năm 2018) Ông A dự định s dụng hết
2
5 m
kính để làm một bể cá bằng
kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng. Bể cá có dung tích
lớn nhất bằng bao nhiêu?
A.
3
1,01m
. B.
3
0,96 m
. C.
3
1,33m
. D.
3
1,51m
c
b
a
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – NĂM HỌC 2021 - 2022
https://www.facebook.com/groups/toanvd.vdc Trang 61

NHÓM
GIÁO VIÊN TOÁN VI
ỆT NAM

Lời giải
Chọn A
Gọi
,xy
lần lượt là chiều rộng và chiều cao của bể cá.
Ta có thể tích bể cá
2
2V x y=
.
Theo đề bài ta có:
2
2 2.2 2 5xy xy x+ + =
2
6 2 5xy x + =
2
52
6
x
y
x
−
=
23
2
5 2 5 2
2
63
x x x
Vx
x
−−
= =
2
56
3
x
V
−
=
2
0 5 6 0Vx
= − =
5
6
x=
3
max
5 30
1,01
27
V m =
.
Câu 100: (Câu 32 - MĐ 104 - BGD&ĐT - Năm 2018) Ông A dự định s dụng hết
2
5,5 m
kính để làm
một bể cá bắng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng. Bể
cá có dung tích lớn nhất bằng bao nhiêu?
A.
3
1,17 m
B.
3
1,01 m
C.
3
1,51 m
D.
3
1,40 m
Lời giải
Chọn A
Gọi
,2 ,x x h
lần lượt là chiều rộng, dài, cao của bể cá.
Ta có
( )
2
2 2 2 5,5x xh xh+ + =
2
5,5 2
6
x
h
x
−
=
.
Thể tích bể cá
2
23
5,5 2 1
2 . (5,5 2 )
63
x
V x x x
x
−
= = −
.
/2
1
(5,5 6 )
3
Vx=−
.
/
5,5
0
6
Vx= =
.
Lập BBT suy ra
3
max
11 33
1,17
54
Vm=
.
y
x
2
x
C
D
A
D'
B
C'
B'
A'
| 1/61
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
CHƯƠNG 1: KHỐI ĐA DIỆN VÀ THỂ TÍCH KHỐI ĐA DIỆN
(CÂU HỎI TRẮC NGHIỆM TỔNG HỢP TỪ ĐỀ THI BGD) ĐỀ BÀI Câu 1:
(Câu 36 - ĐTN - BGD&ĐT - Năm 2017) Hình đa diện nào dưới đây không có tâm đối xứng?     
A. Tứ diện đều.
B. Bát diện đều.
C. Hình lập phương.
D. Lăng trụ lục giác đều. Câu 2:
(Câu 20 - ĐTK - BGD&ĐT - Năm 2017) Hình đa diện trong hình vẽ có bao nhiêu mặt? NHÓ M GIÁO VI A. 6 B. 10 C. 12 D. 11 ÊN Câu 3:
(Câu 25 - MĐ 102 - BGD&ĐT - Năm 2017) Mặt phẳng ( AB C
 ) chia khối lăng trụ AB . C A BC  TO
thành các khối đa diện nào? ÁN
A. Một khối chóp tam giác và một khối chóp ngũ giác. VI
B. Một khối chóp tam giác và một khối chóp tứ giác. ỆT
C. Hai khối chóp tam giác. N
D. Hai khối chóp tứ giác. AM Câu 4:
(Câu 18 - MĐ 101 - BGD&ĐT - Năm 2017) Hình hộp chữ nhật có ba kích thước đôi một khác nhau
có bao nhiêu mặt phẳng đối xứng? 
A. 4 mặt phẳng.
B. 3 mặt phẳng.
C. 6 mặt phẳng. D. 9 mặt phẳng.  Câu 5:
(Câu 23 - MĐ 103 BGD&ĐT NĂM 2016-2017) Hình lăng trụ tam giác đều có bao nhiêu mặt phẳ  ng  đối xứng? 
A. 4 mặt phẳng.
B. 1 mặt phẳng.
C. 2 mặt phẳng. D. 3 mặt phẳng. Câu 6:
Cho khối lăng trụ có diện tích đáy 2
B = 3a và chiều cao h = a . Thể tích của khối lăng trụ đã cho bằng 1 3 A. 3 a . B. 3 3a . C. 3 a . D. 3 a . 2 2 Câu 7:
(MĐ 103 - BGD&ĐT - Năm 2021) Cho khối chóp có diện tích đáy 2
B = 7a và chiều cao h = a . Thể
tích của khối chóp đã cho bằng 7 7 7 A. 3 a . B. 3 a . C. 3 a . D. 3 7a . 6 2 3 Câu 8:
(Câu 2 - MĐ 102 - BGD&ĐT - Năm 2021) Cho khối chóp có diện tích đáy 2
B = 3a và chiều cao h = a
. Thể tích của khối chóp đã cho bằng: 3 1 A. 3 a . B. 3 3a . C. 3 a . D. 3 a . 2 3
https://www.facebook.com/groups/toanvd.vdc Trang 1
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 Câu 9:
(Câu 22 - MĐ 101 - BGD&ĐT - Năm 2021) Cho khối chóp có diện tích đáy 2
B = 5a và chiều cao
h = a . Thể tích của khối chóp đã cho bằng 5 5 5 A. 3 a . B. 3 a . C. 3 5a . D. 3 a . 6 2 3
Câu 10: (Câu 21 - Đề Tham Khảo BGD - 2021) Một khối chóp có diện tích đáy bằng 6 và chiều cao bằng 5 .
Thể tích của khối chóp đã cho bằng A. 10 . B. 30 . C. 90 . D. 15 .
Câu 11: (Câu 12 - Đề - BGD - 2020 - Đợt 2 - Mã đề - 104– 2021) Cho khối chóp có diện tích đáy 2 B = 3a và
chiều cao h = 6a . Thể tích của khối chóp đã cho bằng  A. 3 3a . B. 3 6a . C. 3 9a . D. 3 18a .  
Câu 12: (Câu 15 - BGD - Đợt 1 - Mã đề 104 - 2020) Cho khối chóp có diện tích đáy B = 3 , chiều cao h = 8 .
Thể tích của khối chóp đã cho bằng  A. 24 . B. 12 . C. 8 . D. 6 .
Câu 13: (Câu 12 - BGD - Đợt 1 - Mã đề 103 - 2020) Cho khối chóp có diện tích đáy B = 2 và chiều cao h = NHÓ 3
. Thể tích của khối chóp đã cho bằng A. 12. B. 2. C. 3. D. 6. M G
Câu 14: (BGD - Đợt 1 - Mã đề 102 - 2020) Cho khối chóp có diện tích đáy B = 3 và chiều cao h = 2 . Thể tíc IÁO h
của khối chóp đã cho bằng. A. 6 B. 12 C. 2 D. 3 VI ÊN
Câu 15: (Câu 18 - ĐỀ BGD-MÃ 101-L1-2020) Cho khối chóp có diện tích đáy B = 6 và chiều cao h = 2 . ThểT
tích của khối chóp đã cho bằng O ÁN A. 6 . B. 3 . C. 4 . D. 12 . VI
Câu 16: (ĐTK - BGD&ĐT - L1 - Năm 2020) Cho khối chóp có diện tích đáy B = 3 và chiều cao h = 4 . Th Ệể T
tích của khối chóp đã cho bằng N A. 6 . B. 12 . C. 36 . D. 4 . AM
Câu 17: (MĐ 103 - BGD&ĐT - Năm 2018) Cho khối lăng trụ có đáy là hình vuông cạnh a và chiều cao bằn g
4a . Thể tích của khối lăng trụ đã cho bằng  16 4 A. 3 4a . B. 3 a . C. 3 a . D. 3 16a  3 3  
Câu 18: (ĐTK-BGD&ĐT-Năm 2018) Thể tích của khối chóp có chiều cao bằng h và diện tích đáy bằng B  là:
A. V = 1 Bh
B. V = 1 Bh
C. V = Bh
D. V = 1 Bh 3 6 2
Câu 19: (MĐ 104 - BGD&ĐT - Năm 2021) Cho khối chóp có diện tích đáy 2
B = 8a và chiều cao h = a . Thể
tích khối chóp đã cho bằng 4 8 A. 3 8a B. 3 a . C. 3 4a . D. 3 a . 3 3
Câu 20: (MĐ 104 BGD&ĐT NĂM 2016-2017) Cho hình bát diện đều cạnh a . Gọi S là tổng diện tích tất cả các
mặt của hình bát diện đó. Mệnh đề nào dưới đây đúng? A. 2
S = 4 3a . B. 2 S = 3a . C. 2
S = 2 3a . D. 2 S = 8a .
Câu 21: (Đề TNTHPT 2020 - mã đề 103) Cho khối chóp có diện tích đáy 2
B = 2a và chiều cao h = 9a . Thể
tích của khối chóp đã cho bằng A. 3 3a . B. 3 6a . C. 3 18a . D. 3 9a .
https://www.facebook.com/groups/toanvd.vdc Trang 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
Câu 22: (Câu 7 - Đề thi TNTHPT 2020 - mã đề 102) Cho khối chóp có diện tích đáy 2
B = 6a và chiều cao
h = 2a . Thể tích khối chóp đã cho bằng: A. 3 2a . B. 3 4a . C. 3 6a . D. 3 12a .
Câu 23: (Đề tốt nghiệp THPT đợt 2 năm 2020 - mã đề 101) Cho khối chóp có diện tích đáy 2
B = 2a và chiều
cao h = 6a . Thể tích của khối chóp đã cho bằng A. 3 12a . B. 3 4a . C. 3 2a . D. 3 6a .
Câu 24: (Câu 16 - MĐ 103 BGD&ĐT NĂM 2016-2017) Cho khối chóp S.ABC có SA vuông góc với đáy,
SA = 4 , AB = 6, BC =10 và CA = 8 . Tính thể tích khối chóp S.ABC .
A. V = 40 . B. 192 .
C. V = 32 . D. V = 24 .  
Câu 25: (Câu 36 - ĐTK - BGD&ĐT - Năm 2017) Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA
vuông góc với mặt đáy, SD tạo với mặt phẳng (SAB) một góc bằng 30 . Tính thể tích V của khối c  hóp  S.ABCD . 3 3 3 6a 6a 3a A. V = B. 3 V = 3a C. V = D. V = NHÓ 18 3 3
Câu 26: (Câu 36 - ĐMH - BGD&ĐT - Năm 2017) Cho hình chóp tứ giác S.ABCD có đáy ABCD là M hình G
vuông cạnh a , cạnh bên SA vuông góc với mặt phẳng đáy và SA = a 2 . Tính thể tích V của khối c IÁO hóp S.ABCD 3 3 3 VI 2a 2a 2a A. V = B. V = C. 3 V = 2a D. V = ÊN 6 4 3 T O
Câu 27: (Câu 37 - ĐMH - BGD&ĐT - Năm 2017) Cho tứ diện D ABC
có các cạnh AB , AC và AD đôi mộÁNt
vuông góc với nhau; AB = 6a , AC = 7a và AD = 4a . Gọi M , N , P tương ứng là trung điểm các cạ VI nh
BC , CD , DB . Tính thể tích V của tứ diện AMNP . ỆT 7 28 N A. 3 V = a B. 3 V = 14a C. 3 V = a D. 3 V = 7a AM 2 3
Câu 28: (Câu 27 - ĐTK - BGD&ĐT - Năm 2019) Cho khối chóp tứ giác đều có tất cả các cạnh bằng 2a . Thể
tích của khối chóp đã cho bằng  3 4 2a 3 8a 3 8 2a 3 2 2aA. . B. . C. . D. .  3 3 3 3 
Câu 29: (MĐ 104 BGD&ĐT NĂM 2016-2017) Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a  và
cạnh bên bằng 2a . Tính thể tích V của khối chóp S.ABC 3 13a 3 11a 3 11a 3 11a A. V = . B. V = . C. V = . D. V = . 12 12 6 4
Câu 30: (Câu 21 - MĐ 101 - BGD&ĐT - Năm 2017) Cho khối chóp tứ giác đều có cạnh đáy bằng a, cạnh bên
gấp hai lần cạnh đáy. Tính tích V của khối chóp tứ giác đã cho. 3 2a 3 2a 3 14a 3 14a A. V = B. V = C. V = D. V = 2 6 2 6
Câu 31: (Câu 15 - MĐ 101 - BGD&ĐT - Năm 2018) Cho khối chóp có đáy là hình vuông cạnh a và chiều cao
bằng 2a . Thể tích của khối chóp đã cho bằng 2 4 A. 3 4a B. 3 a C. 3 2a D. 3 a 3 3
https://www.facebook.com/groups/toanvd.vdc Trang 3
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
Câu 32: (Câu 35 - ĐTN - BGD&ĐT - Năm 2017) Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a và thể tích bằng 3
a . Tính chiều cao h của hình chóp đã cho. 3 3 3 A. = a h B. = a h C. = a h
D. h = 3a 6 2 3
Câu 33: (MĐ 102 - BGD&ĐT - Năm 2018) Cho khối chóp có đáy là hình vuông cạnh a và chiều cao bằng 4a
. Thể tích khối chóp đã cho bằng 4 16 A. 3 a . B. 3 a . C. 3 4a . D. 3 16a 3 3
Câu 34: (Câu 43 - Đề Tham Khảo BGD - 2021) Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , 
cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa SA và mặt phẳng (SBC) bằng 0 45 (tham khả o
hình bên). Thể tích khối chóp S.ABC bằng    NHÓ M GIÁO VI ÊN T O ÁN 3 a 3 3a 3 3a 3 a VI A. . B. . C. . D. . Ệ 8 8 12 4 T N
Câu 35: (Câu 36 - MĐ 102 - BGD&ĐT - Năm 2017) Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhậ AMt,
AB = a , AD = a 3 , SA vuông góc với mặt phẳng đáy và mặt phẳng (SBC ) tạo với đáy một góc 60o .
Tính thể tích V của khối chóp S.ABCD . 3 3  a 3a A. V = C. 3 V = a D. 3 V = 3a V = B. 3 3  
Câu 36: (Câu 43 - MĐ 101 - BGD&ĐT - Năm 2017) Cho khối chóp S. ABCD có đáy là hình vuông cạnh a, SA
vuông góc với đáy và SC tạo với mặt phẳng một góc 30 . Tính thể tích V của khối chóp đã cho. 3 6a 3 2a 3 2a A. V = B. V = C. V = D. 3 V = 2a 3 3 3
Câu 37: (Câu 45 - Đề thi TNTHPT 2020 - mã đề 102) Cho hình chóp đều S.ABCD có cạnh đáy bằng 4a , cạnh
bên bằng 2 3a và O là tâm của đáy. Gọi M , N, P và Q lần lượt là hình chiếu vuông góc của O trên
các mặt phẳng (SAB), (SBC), (SCD) và (S )
DA . Thể tích của khối chóp . O MNPQ bằng 3 4a 3 64a 3 128a 3 2a A. . B. . C. . D. . 3 81 81 3
https://www.facebook.com/groups/toanvd.vdc Trang 4
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
Câu 38: (Đề tốt nghiệp THPT đợt 2 năm 2020 - mã đề 101) Cho hình chóp đều S.ABCD có cạnh đáy bằng 3 3a
3a , cạnh bên bằng
và O là tâm của đáy. Gọi ,
M N, P và Q lần lượt là hình chiếu vuông góc 2
của O trên các mặt phẳng (SAB) , (SBC ) , (SCD) và (SDA) . Thể tích của khối chóp . O MNPQ bằng 3 9a 3 2a 3 9a 3 a A. . B. . C. . D. . 16 3 32 3
Câu 39: (Câu 50 - ĐTK - BGD&ĐT - Năm 2017) Cho khối tứ diện có thể tích bằng V . Gọi V  là thể tích của V
khối đa diện có các đỉnh là các trung điểm của các cạnh của khối tứ diện đã cho, tính tỉ số . VV  1    = V 1 = V 2 = V 5 =  A. . B. . C. . D. . V 2 V 4 V 3 V 8  
Câu 40: (Câu 37 - ĐTN - BGD&ĐT - Năm 2017) Cho tứ diện ABCD có thể tích bằng 12 và G là trọng  tâm
của tam giác BCD . Tính thể tích V của khối chóp . A GBC
A. V = 3
B. V = 4
C. V = 6 D. V = 5 NHÓ
Câu 41: (Câu 34 - MĐ 103 BGD&ĐT NĂM 2016-2017) Cho khối chóp S.ABCD có đáy là hình vuông cạ Mnh a 2 G
a , SA vuông góc với đáy và khoảng cách từ A đến mặt phẳng (SBC ) bằng
. Tính thể tích V IÁO 2 của khối chóp đã cho. VI 3 3 3 3 Ê A. = a V . B. 3 V = a . C. = a V . D. = a V . N 2 9 3 T O ÁN
Câu 42: (Câu 38 - ĐMH - BGD&ĐT - Năm 2017) Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh
bằng 2a . Tam giác SAD cân tại S và mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết thể tích khốVI i Ệ 4 T
chóp S.ABCD bằng 3
a . Tính khoảng cách h từ B đến mặt phẳng (SCD) N 3 AM 2 4 8 3 A. h = a B. h = a C. h = a D. h = a 3 3 3 4  a 3
Câu 43: (Đề TNTHPT 2020 - mã đề 103) Cho hình chóp đều ABCD có cạnh đáy bằng a , cạnh bên bằng  2 
và O là tâm của đáy. Gọi M , N, P và Q lần lượt là hình chiếu vuông góc của O trên các mặt phẳ  ng 
(SAB),(SBC),(SCD),(SDA). Thể tích của khối chóp . O MNPQ bằng 3 a 3 2a 3 a 3 a A. . B. . C. . D. . 48 81 81 96
Câu 44: (Câu 45 - BGD - Đợt 1 - Mã đề 104 - 2020) Cho hình chóp đều S.ABCD có tất cả các cạnh bằng a
và O là tâm đáy. Gọi M , N, P, Q lần lượt là các điểm đối xứng với O qua trọng tâm của các tam giác
SAB, SBC, SC ,
D SDA và S là điểm đỗi xứng với S qua O . Thể tích của khối chóp S .MNPQ bằng 3 2 2a 3 20 2a 3 40 2a 3 10 2a A. . B. . C. . D. . 9 81 81 81
https://www.facebook.com/groups/toanvd.vdc Trang 5
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
Câu 45: (Câu 47 - BGD - Đợt 1 - Mã đề 103 - 2020) Cho hình chóp đều S.ABCD có cạnh đáy bằng a , cạnh
bên bằng a 2 và O là tâm của đáy. Gọi M , N , P , Q lần lượt là các điểm đối xúng với O qua trọng
tâm của các tam giác SAB , SBC , SCD , SDA và S là điểm đối xứng với S qua O . Thể tích của khối
chóp S .MNPQ . 3 2 6a 3 40 6a 3 10 6a 3 20 6a A. . B. . C. . D. . 9 81 81 81
Câu 46: (BGD - Đợt 1 - Mã đề 102 - 2020) Cho hình chóp đều S.ABCD có cạnh đáy bằng a , cạnh bên bằng
a 3 và O là tâm của đáy. Gọi M , N , P ,Q lần lượt là các điểm đối xứng với O qua trọng tâm của các
tam giác SAB , SBC , SCD , SDA và S là điểm đối xứng với S qua O . Thể tích khối chóp S MNP Q bằng  3 3 3 3  40 10a 10 10a 20 10a 2 10a A. . B. . C. . D. .  81 81 81 9 
Câu 47: (Câu 47 - ĐỀ BGD-MÃ 101-L1-2020) Cho hình chóp đều S.ABCD có cạnh đáy bằng a , cạnh bê n
bằng 2a và O là tâm của đáy. Gọi M , N , P , Q lần lượt là các điểm đối xứng với O qua trọng tâ NHÓ m
của các tam giác SAB , SBC , SCD , SDA và S ' là điểm đối xứng với S qua O . Thể tích của khối
chóp S '.MNPQ bằng M 3 3 3 3 G 20 14a 40 14a 10 14a 2 14a IÁO A. . B. . C. . D. . 81 81 81 9 VI
Câu 48: (Câu 46 - Đề - BGD - 2020 - Đợt 2 - Mã đề - 104– 2021) Cho hình chóp đều S.ABCD có cạnh đá Êy N
bằng 2a , cạnh bên bằng a 3 và O là tâm đáy. Gọi M , N, P và Q lần lượt là hình chiếu vuông T góc O
của O trên các mặt phẳng ( SAB) , (SBC ) , (SCD) và (SDA) . Thể tích khối chóp . O MNPQ bằng ÁN 3 8a 3 a 3 a 3 16a VI A. . B. . C. . D. . Ệ 81 6 12 81 T N
Câu 49: (Câu 49 - ĐTK - BGD&ĐT - L1 - Năm 2020) Cho khối chóp S.ABC có đáy ABC là tam giác AM vuông cân tại , A AB a, SBA SCA
90 , góc giữa hai mặt phẳng (SAB) và (SAC ) bằng 60 . Thể tích khố i chóp đã cho bằng 3 3 3  a a a A. 3 a . B. . C. . D. .  3 2 6  
Câu 50: (ĐTK - BGD&ĐT - Năm 2018) Cho hình vuông ABCD và ABEF có cạnh bằng 1, lần lượt nằm trê n
hai mặt phẳng vuông góc với nhau. Gọi S là điểm đối xứng của B qua đường thẳng DE . Thể tích củ a
khối đa diện ABCDSEF bằng 7 11 2 5 A. B. C. D. 6 12 3 6
Câu 51: (Câu 44 - MĐ 103 BGD&ĐT NĂM 2016-2017) Xét khối chóp S.ABC có đáy là tam giác vuông cân
tại A , SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng ( SBC ) bằng 3 . Gọi  là góc giữa mặt
phẳng (SBC ) và ( ABC ) , tính cos khi thể tích khối chóp S.ABC nhỏ nhất. 1 3 2 2 A. cos = . B. cos = . C. cos = . D. cos = . 3 3 2 3
Câu 52: (Câu 49 - MĐ 102 - BGD&ĐT - Năm 2017) Xét khối tứ diện ABCD có cạnh AB = x và các cạnh
còn lại đều bằng 2 3 . Tìm x để thể tích khối tứ diện ABCD đạt giá trị lớn nhất.
https://www.facebook.com/groups/toanvd.vdc Trang 6
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
A. x = 6
B. x = 14
C. x = 3 2 D. x = 2 3
Câu 53: (MĐ 104 - BGD&ĐT - Năm 2021) Thể tích của khối lập phương cạnh 2a bằng A. 3 a . B. 3 2a . C. 3 8a . D. 3 4a .
Câu 54: (MĐ 103 - BGD&ĐT - Năm 2021) Thể tích khối lập phương cạnh 3a bằng A. 3 27a . B. 3 3a . C. 3 9a . D. 3 a .
Câu 55: (Câu 22 - Đề Tham Khảo BGD - 2021) Thể tích khối hộp chữ nhật có ba kích thước 2, 3, 7 bằng A. 14. B. 42. C. 126. D. 12.
Câu 56: (Câu 14 - BGD - Đợt 1 - Mã đề 104 - 2020) Cho khối hộp chữ nhật có ba kích thước 2 ; 3 ; 7 . Thể tíc h
của khối hộp đã cho bằng  A. 7 . B. 42 . C. 12 . D. 14 .  
Câu 57: (Câu 11 - BGD - Đợt 1 - Mã đề 103 - 2020) Cho khối hộp chữ nhật có ba kích thước 2; 6; 7 . Thể tíc h
của khối hộp đã cho bằng A. 28. B. 14. C. 15. D. 84. NHÓ
Câu 58: (BGD - Đợt 1 - Mã đề 102 - 2020) Cho khối hộp chữ nhật có kích thước 2; 4; 6 . Thể tích của khối hộp đã cho bằng M A. 16 . B. 12 . C. 48 . D. 8 . G IÁO
Câu 59: (Câu 5 - ĐỀ BGD-MÃ 101-L1-2020) Cho khối hộp chữ nhật có ba kích thước 3; 4; 5 . Thể tích củ VIa khối hộp đã cho bằng ÊN A. 10 . B. 20 . C. 12 . D. 60 . T O
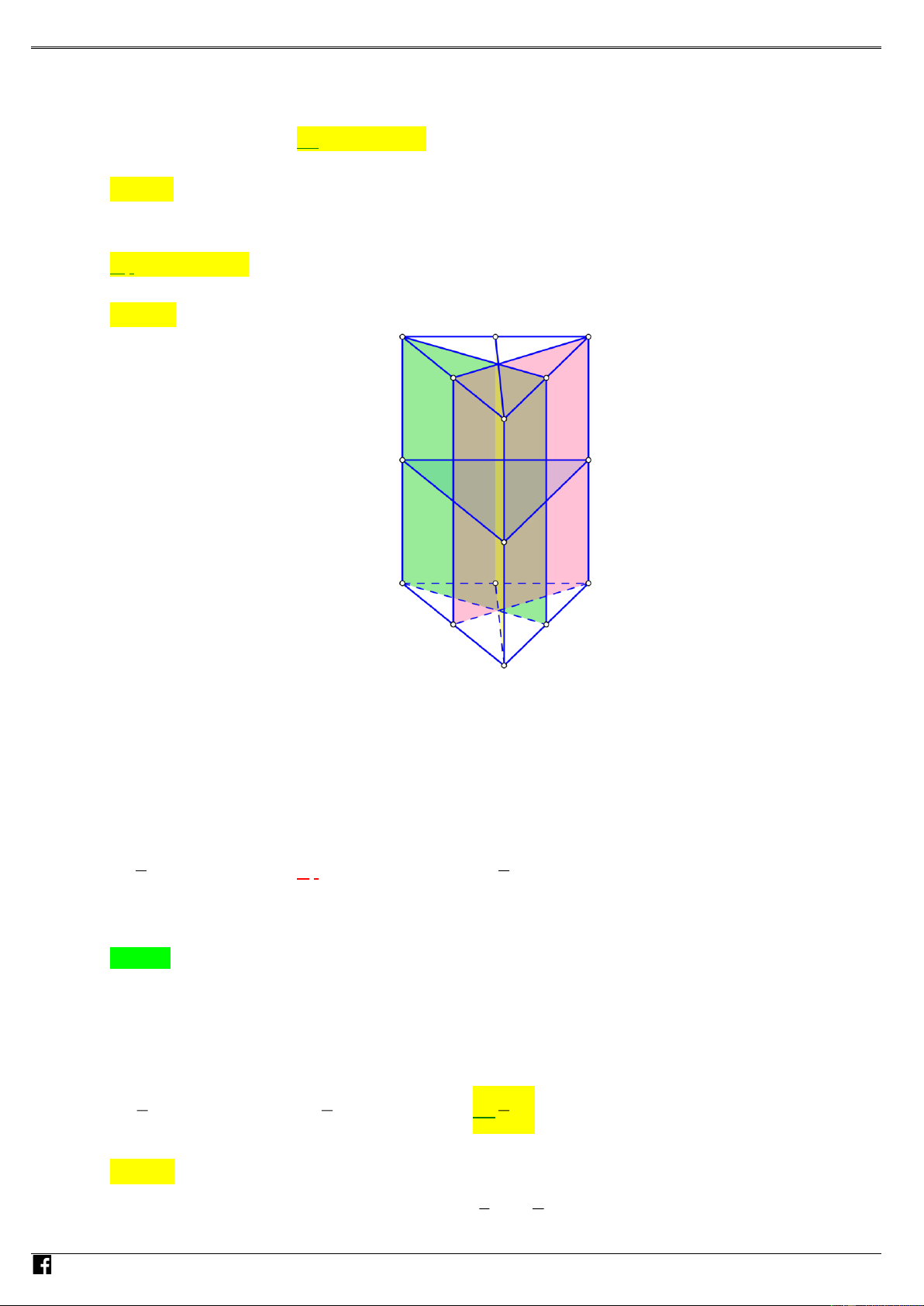
Câu 60: (Câu 26 - MĐ 104 - BGD&ĐT - Năm 2019) Cho khối lăng trụ đứng AB . C A BC   có đáy là tam ÁN giác
đều cạnh a và AA = 2a (minh họa như hình vẽ bên). Thể tích của khối lăng trụ đã cho bằng VI Ệ A' T C' N AM B'    A C   B 3 6a 3 6a 3 6a 3 6a A. . B. . C. . D. . 4 6 12 2
Câu 61: (Câu 25 - MĐ 103 - BGD&ĐT - Năm 2019) Cho khối lăng trụ đứng AB . C A BC
  có đáy là tam giác
đều cạnh 2a và AA = 3a (minh họa như hình vẽ bên).
https://www.facebook.com/groups/toanvd.vdc Trang 7
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
Thể tích của khối lăng trụ đã cho bằng A. 3 2 3a . B. 3 3a . C. 3 6 3a . D. 3 3 3a .
Câu 62: (Câu 21 - MĐ 102-BGD&ĐT-Năm 2019) Cho khối lăng trụ đứng AB . C A BC
  có đáy là tam giác đều
cạnh bằng a và AA = 2a (minh họa như hình vẽ bên). Thể tích của khối lăng trụ đã cho bằng      3 3 3 3a 3a 3a A. . B. . C. 3 3a . D. . 3 6 2 NHÓ
Câu 63: (ĐTK - BGD&ĐT - L1 - Năm 2020) Cho khối lăng trụ đứng ABC . DA B C 
D có đáy là hình thoi cạnh M ,
a BD = a 3 và A
A = 4a (minh họa như hình bên dưới). Thể tích của khối lăng trụ đã cho bằng GIÁO VI ÊN T O ÁN VI ỆT N AM 2 3 4 3 A. 3 2 3a . B. 3 4 3a . C. 3 a . D. 3 a . 3 3
Câu 64: (Câu 22 - MĐ 101-BGD&ĐT-Năm 2019) Cho khối lăng trụ đứng AB .
C A' B 'C ' có đáy là tam  giác 
đều cạnh a và AA' = 3a . Thể tích của lăng trụ đã cho bằng    3 3a 3 3a 3 a 3 a A. . B. . C. . D. . 4 2 4 2
Câu 65: (Câu 18 - MĐ 102 - BGD&ĐT - Năm 2017) Cho khối lăng trụ đứng AB . C A BC
  có BB = a , đáy
ABC là tam giác vuông cân tại B và AC = a 2 . Tính thể tích V của khối lăng trụ đã cho. 3 a 3 a 3 a A. 3 V = a B. V = C. V = D. V = 3 6 2
https://www.facebook.com/groups/toanvd.vdc Trang 8
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
Câu 66: (Câu 1 - ĐTK - BGD&ĐT - Năm 2019) Thể tích của khối lập phương cạnh 2a bằng A. 3 8a . B. 3 2a . C. 3 a . D. 3 6a .
Câu 67: (Câu 35 - ĐMH - BGD&ĐT - Năm 2017) Tính thể tích V của khối lập phương ABC . D A BCD   , biết AC = a 3 . 3 3 6a 1 A. 3 V = a . B. V = . C. 3
V = 3 3a . D. 3 V = a . 4 3
Câu 68: (Câu 9 - Đề - BGD - 2020 - Đợt 2 - Mã đề - 104– 2021) Cho khối lăng trụ có diện tích đáy B = 6 và
chiều cao h = 4 . Thể tích khối lăng trụ đã cho bằng A. 24 . B. 4 . C. 8 . D. 12 .  
Câu 69: (Câu 4 - MĐ 104 - BGD&ĐT - Năm 2019) Thể tích của khối lăng trụ có diện tích đáy B và chiều ca o h là  4 1  A. Bh . B. Bh . C. 3Bh . D. Bh . 3 3
Câu 70: (Câu 8 - MĐ 103 - BGD&ĐT - Năm 2019) Thể tích của khối lăng trụ có diện tích đáy B và chiều ca NHÓ o h là 4 1 M A. Bh . B. 3Bh . C. Bh . D. Bh . 3 3 G IÁO
Câu 71: (Câu 12 - MĐ 102-BGD&ĐT-Năm 2019) Thể tích của khối lăng trụ có diện tích đáy B và chiều ca VIo h là ÊN 4 1 A. 3Bh . B. Bh . C. Bh . D. Bh . T 3 3 O ÁN
Câu 72: (Câu 12 - MĐ 101-BGD&ĐT-Năm 2019) Thể tích khối lăng trụ có diện tích đáy B và chiều cao h VI là 4 1 A. 3 . Bh B. . Bh C. . Bh D. . Bh Ệ 3 3 T N
Câu 73: (Câu 11 - MĐ 104 - BGD&ĐT - Năm 2018) Cho khối lăng trụ có đáy là hình vuông cạnh a và chiề AMu
cao bằng 2a . Thể tích của khối lăng trụ đã cho bằng 2 4 A. 3 a B. 3 a C. 3 2a D. 3 4a 3 3  
Câu 74: (Đề TNTHPT 2020 - mã đề 103) Cho khối lăng trụ có diện tích đáy B = 6 và chiều cao h = 3 . Th ể 
tích của khối lăng trụ đã cho bằng  A. 3. B. 18. C. 6. D. 9.
Câu 75: (Câu 18 - Đề thi TNTHPT 2020 - mã đề 102) Cho khối lăng trụ có diện tích đáy B = 3 và chiều cao
h = 2 . Thể tích khối lăng trụ đã cho bằng A. 1. B. 3. C. 2. D. 6.
Câu 76: (Câu 19 - Đề thi TNTHPT 2020 - mã đề 102) Cho khối lăng trụ có diện tích đáy B = 3 và chiều cao
h = 2 . Thể tích của khối lăng trụ đã cho bằng A. 1. B. 3 . C. 2 . D. 6 .
Câu 77: (Đề tốt nghiệp THPT đợt 2 năm 2020 - mã đề 101) Cho khối lăng trụ có diện tích đáy B = 3 và chiều
cao h = 6 . Thể tích của khối lăng trụ đã cho bằng A. 9 . B. 18 . C. 3 . D. 6 .
Câu 78: (Đề tốt nghiệp THPT đợt 2 năm 2020 - mã đề 101) Cho khối trụ có bán kính đáy r = 4 và chiều cao
h = 3 . Thể tích của khối trụ đã cho bằng
https://www.facebook.com/groups/toanvd.vdc Trang 9
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 A. 48 . B. 4 . C. 16 . D. 24 .
Câu 79: (MĐ 104 - BGD&ĐT - Năm 2021) Cho khối hộp chữ nhật ABC . D A BCD
  có đáy là hình vuông
BD = 4a , góc giữa hai mặt phẳng ( ABD) và ( ABCD) bằng 0
60 . Thể tích của khối hộp chữ nhật đã cho bằng 16 3 16 3 A. 3 48 3a . B. 3 a . C. 3 a . D. 3 16 3a . 9 3
Câu 80: (MĐ 103 - BGD&ĐT - Năm 2021) Cho khối hộp chữ nhật ABC . D A BCD
  có đáy là hình vuông,
BD = 2a , góc giữa hai mặt phẳng ( A B
D) và ( ABCD) bằng 60. Thể tích của khối hộp chữ nhật đã cho bằng   2 3 2 3 A. 3 a . B. 3 6 3a . C. 3 a . D. 3 2 3a .  9 3  
Câu 81: (Câu 44 - MĐ 102 - BGD&ĐT - Năm 2021) Cho khối hộp chữ nhật ABC .
D A' B 'C ' D ' có đáy là hình
vuông, BD = 4a , góc giữa hai mặt phẳng ( A' BD) và ( ABCD) = 30o . Thể tích của khối hộp chữ nhậ t NHÓ đã cho bằng 16 3 16 3 A. 3 a B. 3 48 3a C. 3 a D. 3 16 3a M 9 3 GIÁO
Câu 82: (Câu 48 - MĐ 101 - BGD&ĐT - Năm 2021) Cho khối hộp chữ nhật ABC .
D A' B 'C ' D ' có đáy là hình vuông, =
, góc giữa hai mặt phẳng ( A' BD) và ( ABCD) bằng 0
30 . Thể tích của khối hộp ch VI BD 2a ữÊ nhật đã cho bằng N T 2 3 2 3 O 3 A. 3 6 3a . B. 3 a . C. 3 2 3a . D. a . ÁN 9 3 VI
Câu 83: (MĐ 101 BGD&ĐT NĂM 2021-L2) Cho khối lăng trụ tam giác đều AB . C A BC
  có cạnh bên bằ ỆTng
2a , góc giữa hai mặt phẳng ( A' BC ) và ( ABC ) bằng 30 . Thể tích của khối lăng trụ đã cho bằng N AM 8 3 8 3 8 3 A. 3 a . B. 3 a . C. 3 a . D. 3 8 3a . 9 3 27
Câu 84: (MĐ 104 BGD&ĐT NĂM 2016-2017) Cho khối lăng trụ đứng AB . C A BC
  có đáy ABC là tam  giác 
cân với AB = AC = a , BAC = 120 . Mặt phẳng ( AB C
 ) tạo với đáy một góc 60. Tính thể tích V củ a  khối lăng trụ đã cho.  3 3a 3 9a 3 a 3 3a A. V = . B. V = . C. V = . D. V = . 8 8 8 4
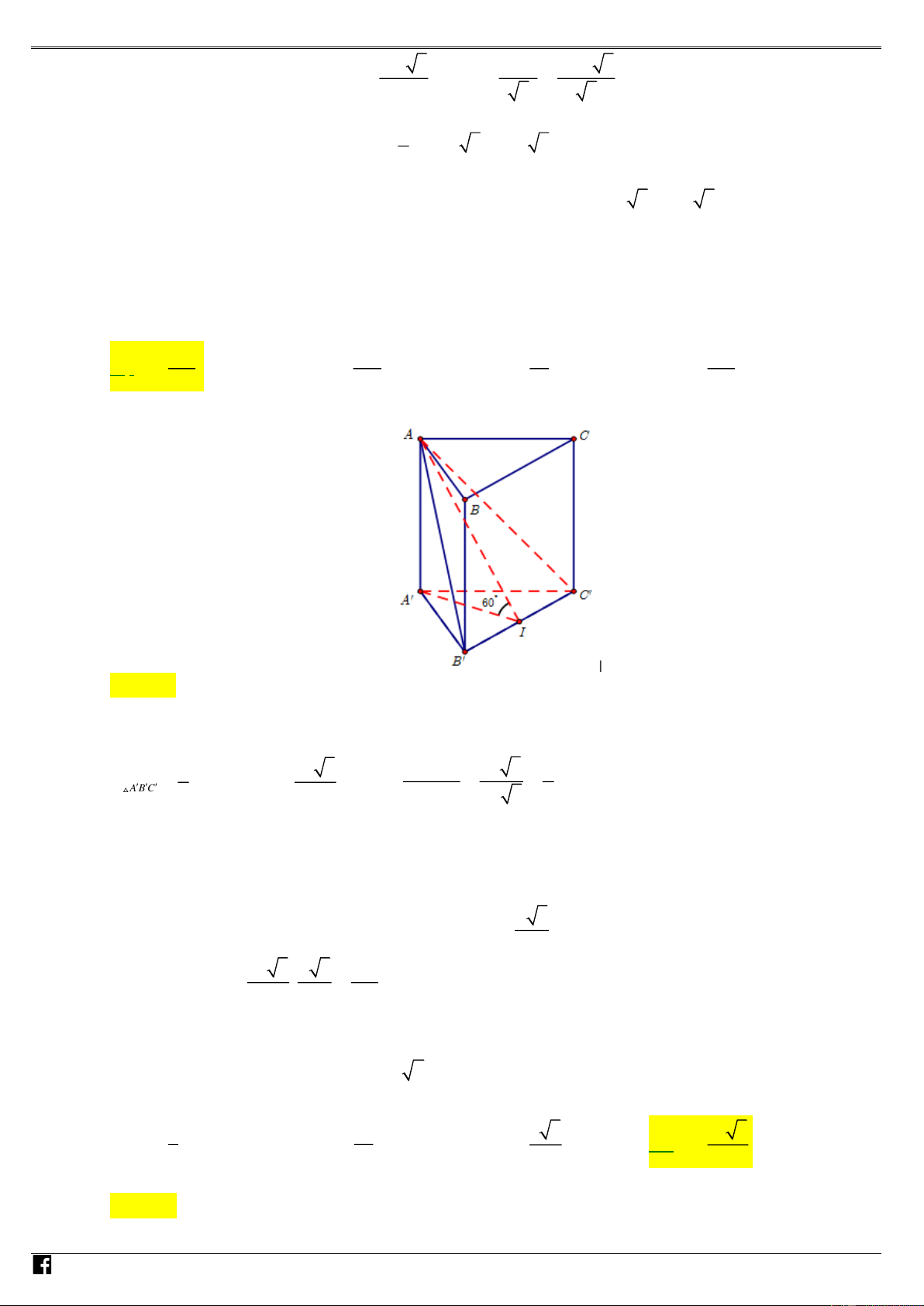
Câu 85: (Câu 38 - ĐTN - BGD&ĐT - Năm 2017) Cho lăng trụ tam giác AB . C A
B C có đáy ABC là tam giác
vuông cân tại A , cạnh AC = 2 2 . Biết AC tạo với mặt phẳng ( ABC ) một góc 60 và AC = 4 . Tính
thể tích V của khối đa diện ABC B C . 8 16 8 3 16 3 A. V = B. V = C. V = D. V = 3 3 3 3
Câu 86: (Câu 39 - MĐ 104 - BGD&ĐT - Năm 2018) Cho khối lăng trụ AB . C A BC
 , khoảng cách từ C đến
đường thẳng BB bằng 5 , khoảng cách từ A đến các đường thẳng BB và CC lần lượt bằng 1 và 2
, hình chiếu vuông góc của A lên mặt phẳng ( AB C
 ) là trung điểm M của B C   và A M  = 5 . Thể
tích của khối lăng trụ đã cho bằng
https://www.facebook.com/groups/toanvd.vdc Trang 10
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 2 5 2 15 15 A. B. C. 5 D. 3 3 3
Câu 87: (MĐ 103 - BGD&ĐT - Năm 2018) Cho khối lăng trụ AB .
C A' B 'C ' , khoảng cách từ C đến đường
thẳng BB ' bằng 2, khoảng cách từ A đến các đường thẳng BB ' và CC ' lần lượt bằng 1 và 3 , hình
chiếu vuông góc của A lên mặt phẳng ( A' B 'C ') là trung điểm M của B 'C ' và A' M = 2 . Thể tích của
khối lăng trụ đã cho bằng 2 3 A. 3 . B. 2 . C. . D. 1 3
Câu 88: (MĐ 102 - BGD&ĐT - Năm 2018) Cho khối lăng trụ AB .
C A'B'C' , khoảng cách từ C đến BB ' là 5 
, khoảng cách từ A đến BB ' và CC ' lần lượt là 1; 2 . Hình chiếu vuông góc của A lên mặt phẳ ng 15 
A' B 'C ' là trung điểm M của B 'C ' , A' M =
. Thể tích của khối lăng trụ đã cho bằng  3 15 2 5 2 15 A. . B. . C. 5 . D. 3 3 3 NHÓ
Câu 89: (Câu 42 - MĐ 101 - BGD&ĐT - Năm 2018) Cho khối lăng trụ AB . C A BC
 , khoảng cách từ C đế Mn
đường thẳng BB bằng 2 , khoảng cách từ A đến các đường thẳng BB và CC lần lượt bằng 1 và G3IÁO 2 3
, hình chiếu vuông góc của A lên mặt phẳng ( AB C
 ) là trung điểm M của B C
  và AM = . Thể 3 VI
tích của khối lăng trụ đã cho bằng ÊN 2 3 T A. 2 B. 1 C. 3 D. O 3 ÁN
Câu 90: (ĐTK - BGD&ĐT - L1 - Năm 2020) Cho hình hộp ABC .
D A' B 'C ' D ' có chiều cao bằng 8 và diện tíc VI h Ệ
đáy bằng 9. Gọi M , N, P và Q lần lượt là tâm của các mặt bên ABB ' A', BCC ' B ',CDD 'C ' và DAA' D T N'
. Thể tích của khối đa diện lồi có các đỉnh là các điểm ,
A B, C, D, M , N , P và Q bằng AM A. 27. B. 30. C. 18. D. 36
Câu 91: (Câu 46 - MĐ 104 - BGD&ĐT - Năm 2019) Cho hình lăng trụ AB .
C A B C có chiều cao bằng 4 và 
đáy là tam giác đều cạnh bằng 4 . Gọi M , N và P lần lượt là tâm của các mặt bên ABB A , ACC A
và BCC B . Thể tích của khối đa diện lồi có các đỉnh là các điểm ,
A B,C, M , N, P bằng   14 3 20 3  A. . B. 8 3 . C. 6 3 . D. . 3 3
Câu 92: (Câu 49 - MĐ 103 - BGD&ĐT - Năm 2019) Cho lăng trụ AB .
C A' B 'C ' có chiều cao bằng 6 và đáy
là tam giác đều cạnh bằng 4. Gọi M, N, P lần lượt là tâm của các mặt bên ABB ' A', ACC ' A', BCC ' B ' .
Thể tích của khối đa diện lồi có các đỉnh là các điểm ,
A B,C, M , N, P bằng A. 9 3 . B. 10 3 . C. 7 3 . D. 12 3 .
Câu 93: (Câu 49 - MĐ 102-BGD&ĐT-Năm 2019) Cho lăng trụ AB . C A BC
  có chiều cao là 8 và đáy là tam
giác đều cạnh bằng 4 . Gọi M , N và P lần lượt là tâm của các mặt bên ABB A  , ACC A   và BCC B  
. Thể tích của khối đa diện lồi có các đỉnh là các điểm A , B , C , M , N , P bằng 28 3 40 3 A. 12 3 . B. 16 3 . C. . D. . 3 3
https://www.facebook.com/groups/toanvd.vdc Trang 11
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
Câu 94: (Câu 47 - MĐ 101-BGD&ĐT-Năm 2019) Cho lăng trụ AB .
C A' B 'C ' có chiều cao bằng 8 và đáy là
tam giác đều cạnh bằng 6 . Gọi M , N và P lần lượt là tâm của các mặt bên ABB' A' , ACC ' A' và
BCC ' B ' . Thể tích của khối đa diện lồi có các đỉnh là các điểm ,
A B, C, M , N , P bằng: A. 27 3 . B. 21 3 . C. 30 3 . D. 36 3 .
Câu 95: (Câu 47 - ĐTK - BGD&ĐT - Năm 2019) Cho khối lăng trụ AB . C A BC
  có thể tích bằng 1. Gọi M , N
lần lượt là trung điểm các đoạn thẳng AA và BB . Đường thẳng CM cắt đường thẳng C A   tại P ,
đường thẳng CN cắt đường thẳng C B
  tại Q . Thể tích của khối đa diện lồi A MPB NQ bằng 1 1 2 A. 1. B. . C. . D. . 3 2 3  
Câu 96: (Câu 44 - MĐ 101 - BGD&ĐT - Năm 2017) Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt
là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua
D. Mặt phẳng chia khối tứ diệ n
ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V. Tính V.  3 3 3 3 7 2a 11 2a 13 2a 2a A. V = B. V = C. V = D. V = 216 216 216 18 NHÓ
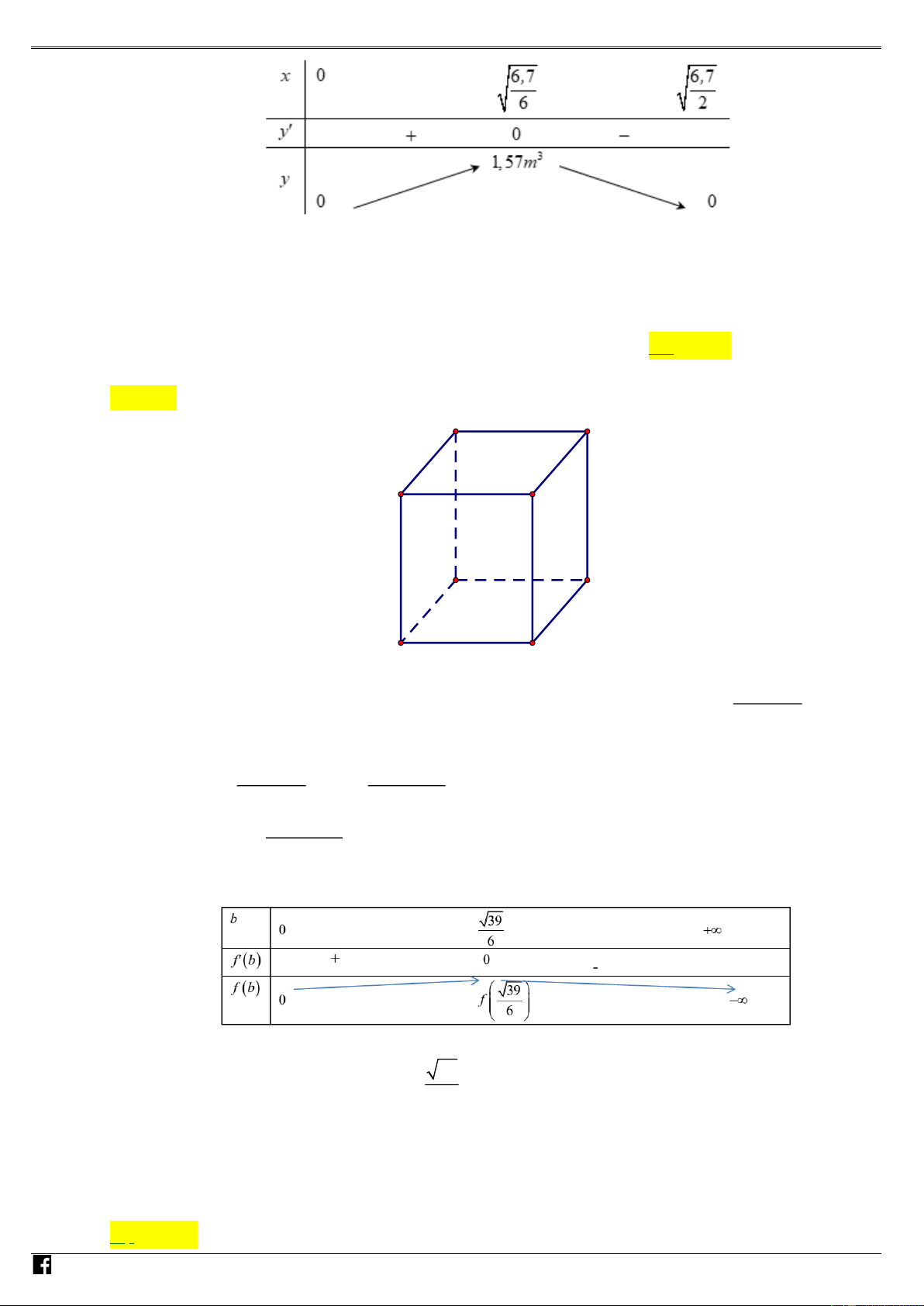
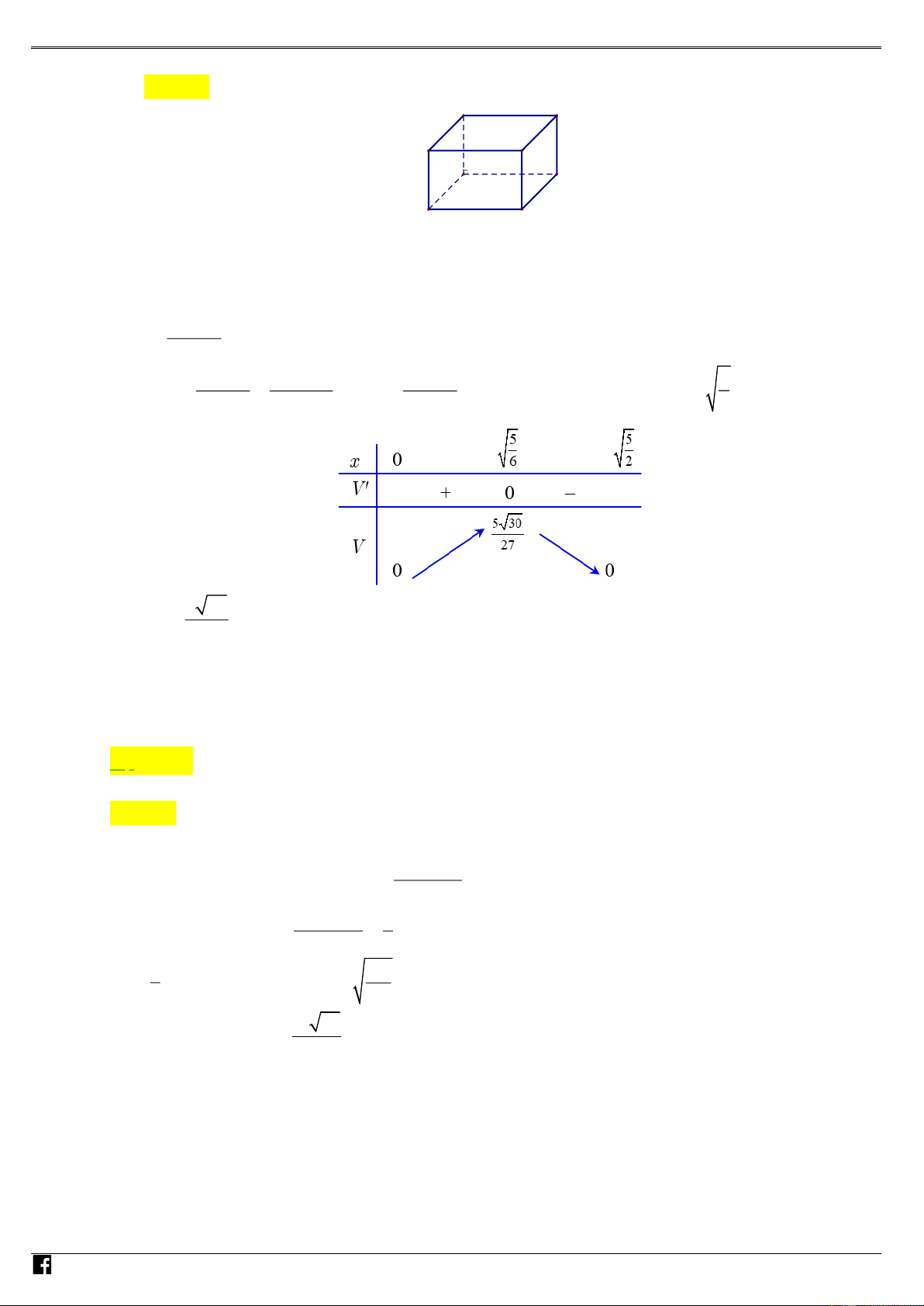
Câu 97: (MĐ 102 - BGD&ĐT - Năm 2018) Ông A dự định sử dụng hết 2
6, 7m kính để làm một bể cá bằng M
kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thướ Gc
không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm). IÁO A. 3 1,57m . B. 3 1,11m . C. 3 1, 23m . D. 3 2, 48m VI Ê
Câu 98: (Câu 31 - MĐ 101 - BGD&ĐT - Năm 2018) Ông A dự định dùng hết 2
6,5m kính để làm một bể c N á T
có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng. Bể cá có dung tích lớn nhất bằ O ng bao nhiêu. ÁN A. 3 2, 26 m B. 3 1, 61 m C. 3 1,33 m D. 3 1,50 m VI ỆT
Câu 99: (MĐ 103 - BGD&ĐT - Năm 2018) Ông A dự định sử dụng hết 2
5 m kính để làm một bể cá bằ N ng kính
có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng. Bể cá có dung tích lớn nhất bằ AM ng bao nhiêu? A. 3 1, 01 m . B. 3 0,96 m . C. 3 1,33 m . D. 3 1,51 m
Câu 100: (Câu 32 - MĐ 104 - BGD&ĐT - Năm 2018) Ông A dự định sử dụng hết 2
5,5 m kính để làm một b ể 
cá bắng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng. Bể cá có dung tích lớ n nhất bằng bao nhiêu?  A. 3 1,17 m B. 3 1, 01 m C. 3 1,51 m D. 3 1, 40 m HẾT
https://www.facebook.com/groups/toanvd.vdc Trang 12
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 BẢNG ĐÁP ÁN 1.A 2.D 3.B 4.B 5.A 6.B 7.C 8.D 9.D 10.A 11.B 12.C 13.B 14.C 15.C 16.D 17.A 18.A 19.D 20.C 21.B 22.B 23.B 24.C 25.D 26.D 27.D 28.A 29.B 30.D 31.B 32.D 33.A 34.A 35.C 36.B 37.D 38.C 39.A 40.B 41.D 42.B 43.D 44.B 45.D 46.C 47.A 48.C 49.D 50.D 51.B 52.C 53.C 54.A 55.B 56.B 57.D 58.C 59.D 60.A 61.D 62.D 63.A 64.A 65.D 66.A 67.A 68.A 69.D 70.D 71.B 72.B 73.C 74.B 75.D 76.D 77.B 78.A 79.D 80.D 81.C 82.D 83.D 84.A 85.D 86.B 87.B 88.D 89.A 90.B  91.C 92.A 93.A 94.A 95.D 96.B 97.A 98.D 99.A 100.A    NHÓ M GIÁO VI ÊN T O ÁN VI ỆT NAM     
https://www.facebook.com/groups/toanvd.vdc Trang 13
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
CHƯƠNG 1: KHỐI ĐA DIỆN VÀ THỂ TÍCH KHỐI ĐA DIỆN
(CÂU HỎI TRẮC NGHIỆM TỔNG HỢP TỪ ĐỀ THI BGD)
HƯỚNG DẪN GIẢI CHI TIẾT
CHỦ ĐỀ: KHỐI ĐA DIỆN VÀ KHỐI ĐA DIỆN ĐỀU
Câu 1: (Câu 36 - ĐTN - BGD&ĐT - Năm 2017) Hình đa diện nào dưới đây không có tâm đối xứng?     
A. Tứ diện đều.
B. Bát diện đều.
C. Hình lập phương. D. Lăng trụ lục giác đều. Lời giải NHÓ Chọn A M
Dễ dàng thấy hình bát diện đều, hình lập phương và hình lăng trục lục giác đều có tâm đố Gi
xứng. Còn tứ diện đều không có tâm đối xứng. IÁO
Câu 2: (Câu 20 - ĐTK - BGD&ĐT - Năm 2017) Hình đa diện trong hình vẽ có bao nhiêu mặt? VI ÊN T O ÁN VI Ệ A. 6 B. 10 C. 12 D. 11 T N Lời giải AM Chọn D
Đếm đáy hình chóp có 5 mặt tam giác và 5 mặt tứ giác và 1 mặt ngũ giá C. Vậy có 11 mặt.
Câu 3: (Câu 25 - MĐ 102 - BGD&ĐT - Năm 2017) Mặt phẳng ( AB C
 ) chia khối lăng trụ AB . C A BC   
thành các khối đa diện nào? 
A. Một khối chóp tam giác và một khối chóp ngũ giác. 
B. Một khối chóp tam giác và một khối chóp tứ giác. 
C. Hai khối chóp tam giác.
D. Hai khối chóp tứ giác. Lời giải Chọn B Mặt phẳng ( AB C
 ) chia khối lăng trụ AB . C A BC
  thành hai khối chóp
https://www.facebook.com/groups/toanvd.vdc Trang 14
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 Chóp tam giác: . A A BC
  và chóp tứ giác: . A BB CC  .
Câu 4: (Câu 18 - MĐ 101 - BGD&ĐT - Năm 2017) Hình hộp chữ nhật có ba kích thước đôi một khác
nhau có bao nhiêu mặt phẳng đối xứng?
A. 4 mặt phẳng.
B. 3 mặt phẳng.
C. 6 mặt phẳng. D. 9 mặt phẳng. Lời giải Chọn B
Câu 5: (Câu 23 - MĐ 103 BGD&ĐT NĂM 2016-2017) Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng?
A. 4 mặt phẳng.
B. 1 mặt phẳng.
C. 2 mặt phẳng. D. 3 mặt phẳng. Lời giải Chọn A     NHÓ M GIÁO VI ÊN T O ÁN
Lăng trụ đều có 4 mặt phẳng đối xứng là: VI Ệ
Mặt phẳng cách đều 2 đáy. T N
3 mặt phẳng chứa 1 cạnh bên và trung điểm cạnh đáy. AM
THỂ TÍCH KHỐI CHÓP
Câu 6: Cho khối lăng trụ có diện tích đáy 2
B = 3a và chiều cao h = a . Thể tích của khối lăng trụ đã cho bằng  1 3  A. 3 a . B. 3 3a . C. 3 a . D. 3 a . 2 2   Lời giải Chọn B
Thể tích của khối lăng trụ đã cho là 2 3 V = .
B h = 3a .a = 3a .
Câu 7: (MĐ 103 - BGD&ĐT - Năm 2021) Cho khối chóp có diện tích đáy 2
B = 7a và chiều cao h = a .
Thể tích của khối chóp đã cho bằng 7 7 7 A. 3 a . B. 3 a . C. 3 a . D. 3 7a . 6 2 3 Lời giải Chọn C 1 7
Áp dụng công thức tính thể tích ta được 3 V = Bh = a . 3 3
https://www.facebook.com/groups/toanvd.vdc Trang 15
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
Câu 8: (Câu 2 - MĐ 102 - BGD&ĐT - Năm 2021) Cho khối chóp có diện tích đáy 2
B = 3a và chiều cao
h = a . Thể tích của khối chóp đã cho bằng: 3 1 A. 3 a . B. 3 3a . C. 3 a . D. 3 a . 2 3 Lời giải Chọn D 1 1
Công thức thể tích khối chóp là 2 3 V = . B h =
3a .a = a . 3 3
Câu 9: (Câu 22 - MĐ 101 - BGD&ĐT - Năm 2021) Cho khối chóp có diện tích đáy 2
B = 5a và chiều cao
h = a . Thể tích của khối chóp đã cho bằng  5 5 5 A. 3 a . B. 3 a . C. 3 5a . D. 3 a .  6 2 3  Lời giải Chọn D  1 1 5
Thể tích của khối chóp đã cho 2 3 V = . .
B h = .5a .a = a . 3 3 3 NHÓ
Câu 10: (Câu 21 - Đề Tham Khảo BGD - 2021) Một khối chóp có diện tích đáy bằng 6 và chiều cao bằng
5 . Thể tích của khối chóp đã cho bằng M A. 10 . B. 30 . C. 90 . D. 15 . GIÁO Lời giải Chọn A VI 1 1 = = = Ê V Bh .6.5 10 . N 3 3 T
Câu 11: (Câu 12 - Đề - BGD - 2020 - Đợt 2 - Mã đề - 104– 2021) Cho khối chóp có diện tích đáy B = a O2 3 ÁN
và chiều cao h = 6a . Thể tích của khối chóp đã cho bằng A. 3 3a . B. 3 6a . C. 3 9a . D. 3 18a . VI Ệ Lời giải T N Chọn B AM 1 1
Thể tích của khối chóp đã cho là V = . B h 2 3
= 3a .6a = 6a . 3 3
Câu 12: (Câu 15 - BGD - Đợt 1 - Mã đề 104 - 2020) Cho khối chóp có diện tích đáy B = 3, chiều cao h = 8
. Thể tích của khối chóp đã cho bằng  A. 24 . B. 12 . C. 8 . D. 6 .  Lời giải Chọn C  1
Thể tích khối chóp: V = .3.8 = 8 . 3
Câu 13: (Câu 12 - BGD - Đợt 1 - Mã đề 103 - 2020) Cho khối chóp có diện tích đáy B = 2 và chiều cao
h = 3 . Thể tích của khối chóp đã cho bằng A. 12. B. 2. C. 3. D. 6. Lời giải Chọn B 1 1
Thể tích của khối chóp đã cho là: V = . . B h = .2.3 = 2. 3 3
Câu 14: (BGD - Đợt 1 - Mã đề 102 - 2020) Cho khối chóp có diện tích đáy B = 3 và chiều cao h = 2 . Thể
tích của khối chóp đã cho bằng. A. 6 B. 12 C. 2 D. 3 Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 16
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 1 1 Ta có V = . B h = .3.2 = 2 3 3
Câu 15: (Câu 18 - ĐỀ BGD-MÃ 101-L1-2020) Cho khối chóp có diện tích đáy B = 6 và chiều cao h = 2 .
Thể tích của khối chóp đã cho bằng A. 6 . B. 3 . C. 4 . D. 12 . Lời giải Chọn C 1 1
Thể tích khối chóp là V = Bh = .6.2 = 4 . 3 3
Câu 16: (ĐTK - BGD&ĐT - L1 - Năm 2020) Cho khối chóp có diện tích đáy B = 3 và chiều cao h = 4 .
Thể tích của khối chóp đã cho bằng   A. 6 . B. 12 . C. 36 . D. 4 .  Lời giải Chọn D  1 1 = = =
Thể tích khối chóp đã cho là V . . B h .3.4 4 . 3 3 NHÓ
Câu 17: (MĐ 103 - BGD&ĐT - Năm 2018) Cho khối lăng trụ có đáy là hình vuông cạnh a và chiều cao
bằng 4a . Thể tích của khối lăng trụ đã cho bằng M 16 4 A. 3 4a . B. 3 a . C. 3 a . D. 3 16a G 3 3 IÁO Lời giải VI Chọn A Ê 2 3 V = S
.h = a .4a = 4a . N day T O ÁN
Câu 18: (ĐTK - BGD&ĐT - Năm 2018) Thể tích của khối chóp có chiều cao bằng h và diện tích đáy bằng B là: VI Ệ = 1 = 1 = = 1 T A. V Bh B. V Bh C. V Bh D. V Bh N 3 6 2 AM Lời giải Chọn A
Thể tích của khối chóp có chiều cao bằng h và diện tích đáy bằng B là: V = 1 Bh  3 
Câu 19: (- MĐ 104 - BGD&ĐT - Năm 2021) Cho khối chóp có diện tích đáy 2
B = 8a và chiều cao h = a .
Thể tích khối chóp đã cho bằng  4 8  A. 3 8a B. 3 a . C. 3 4a . D. 3 a . 3 3 Lời giải Chọn D 1 1 8
Thể tích khối chóp đã cho bằng 2 3 V = . .
B h = .8a .a = a . 3 3 3
Câu 20: (MĐ 104 BGD&ĐT NĂM 2016-2017) Cho hình bát diện đều cạnh a . Gọi S là tổng diện tích tất
cả các mặt của hình bát diện đó. Mệnh đề nào dưới đây đúng? A. 2
S = 4 3a . B. 2 S = 3a . C. 2
S = 2 3a . D. 2 S = 8a . Lời giải Chọn C
https://www.facebook.com/groups/toanvd.vdc Trang 17
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 2 a 3
Ta thấy hình bát diện đều có 8 mặt, mỗi mặt là một tam giác đều cạnh a có diện tích là . 4 2 a 3 Suy ra 2 S = 8. = 2 3a . 4
Câu 21: (Đề TNTHPT 2020 - mã đề 103) Cho khối chóp có diện tích đáy 2
B = 2a và chiều cao h = 9a .
Thể tích của khối chóp đã cho bằng A. 3 3a . B. 3 6a . C. 3 18a . D. 3 9a . Lời giải Chọn B 1 1
Thể tích khối chóp đã cho là 2 3 V = . . B h =
.2a .9a = 6a .  3 3 
Câu 22: (Câu 7 - Đề thi TNTHPT 2020 - mã đề 102) Cho khối chóp có diện tích đáy 2
B = 6a và chiề u h = a  cao
2 . Thể tích khối chóp đã cho bằng:  A. 3 2a . B. 3 4a . C. 3 6a . D. 3 12a . Lời giải Chọn B NHÓ 1 1 2 3 V = . B h =
6a .2a = 4a 3 3 M
Câu 23: (Đề tốt nghiệp THPT đợt 2 năm 2020 - mã đề 101) Cho khối chóp có diện tích đáy 2
B = 2a v GIÁO à
chiều cao h = 6a . Thể tích của khối chóp đã cho bằng A. 3 12a . B. 3 4a . C. 3 2a . D. 3 6a . VI Lời giải ÊN Chọn B T 1 1 O
Thể tích của khối chóp đã cho là: V = Bh 2 3
= .2a .6a = 4a . ÁN 3 3 S ABC VI
Câu 24: (Câu 16 - MĐ 103 BGD&ĐT NĂM 2016-2017) Cho khối chóp .
có SA vuông góc với đáyỆ,
SA = 4 , AB = 6, BC =10 và CA = 8 . Tính thể tích khối chóp S.ABC . T N
A. V = 40 . B. 192 .
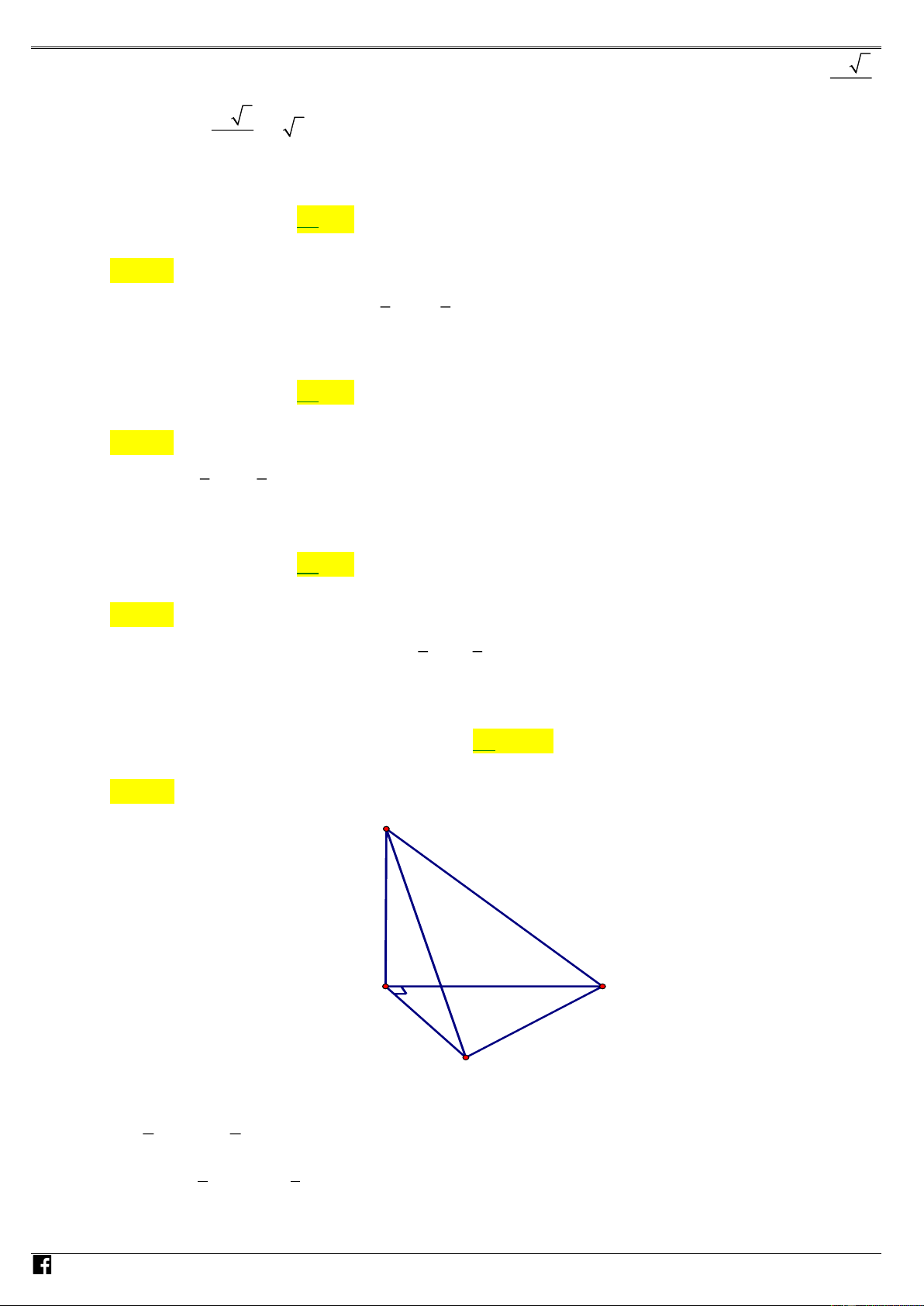
C. V = 32. D. V = 24 . AM Lời giải Chọn C S      4 8 A C 6 10 B Ta có 2 2 2
AB + AC = BC suy ra tam giác ABC vuông tại A ,do đó diện tích tam giác ABC là: 1 1 S = A . B AC = .6.8 = 24 2 2 1 1 Có V = .S . A S = .4.24 = 32. SABC 3 ABC 3
Câu 25: (Câu 36 - ĐTK - BGD&ĐT - Năm 2017) Cho hình chóp S.ABCD có đáy là hình vuông cạnh a
https://www.facebook.com/groups/toanvd.vdc Trang 18
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
, SA vuông góc với mặt đáy, SD tạo với mặt phẳng (SAB) một góc bằng 30 . Tính thể tích V
của khối chóp S.ABCD . 3 6a 3 6a 3 3a A. V = B. 3 V = 3a C. V = D. V = 18 3 3 Lời giải Chọn D SA B     D C
Góc giữa SD và mp là 0 DSA = 30 . NHÓ AD Ta có SA= = a 3 . 0 tan 30 M 3 1 a 3 G 2 V = a .a 3 = . IÁO 3 3
Câu 26: (Câu 36 - ĐMH - BGD&ĐT - Năm 2017) Cho hình chóp tứ giác S.ABCD có đáy ABCD là hìn VIh Ê
vuông cạnh a , cạnh bên SA vuông góc với mặt phẳng đáy và SA = a 2 . Tính thể tích V củ N a S ABCD T khối chóp . O 3 3 3 ÁN 2a 2a 2a A. V = B. V = C. 3 V = 2a D. V = 6 4 3 VI Ệ Lời giải T N Chọn D S AM    B A   D C
Ta có SA ⊥ ( ABCD)  SA là đường cao của hình chóp 3 1 1 a 2
Thể tích khối chóp S.ABCD : 2 V = S . A S = .a 2.a = . 3 ABCD 3 3
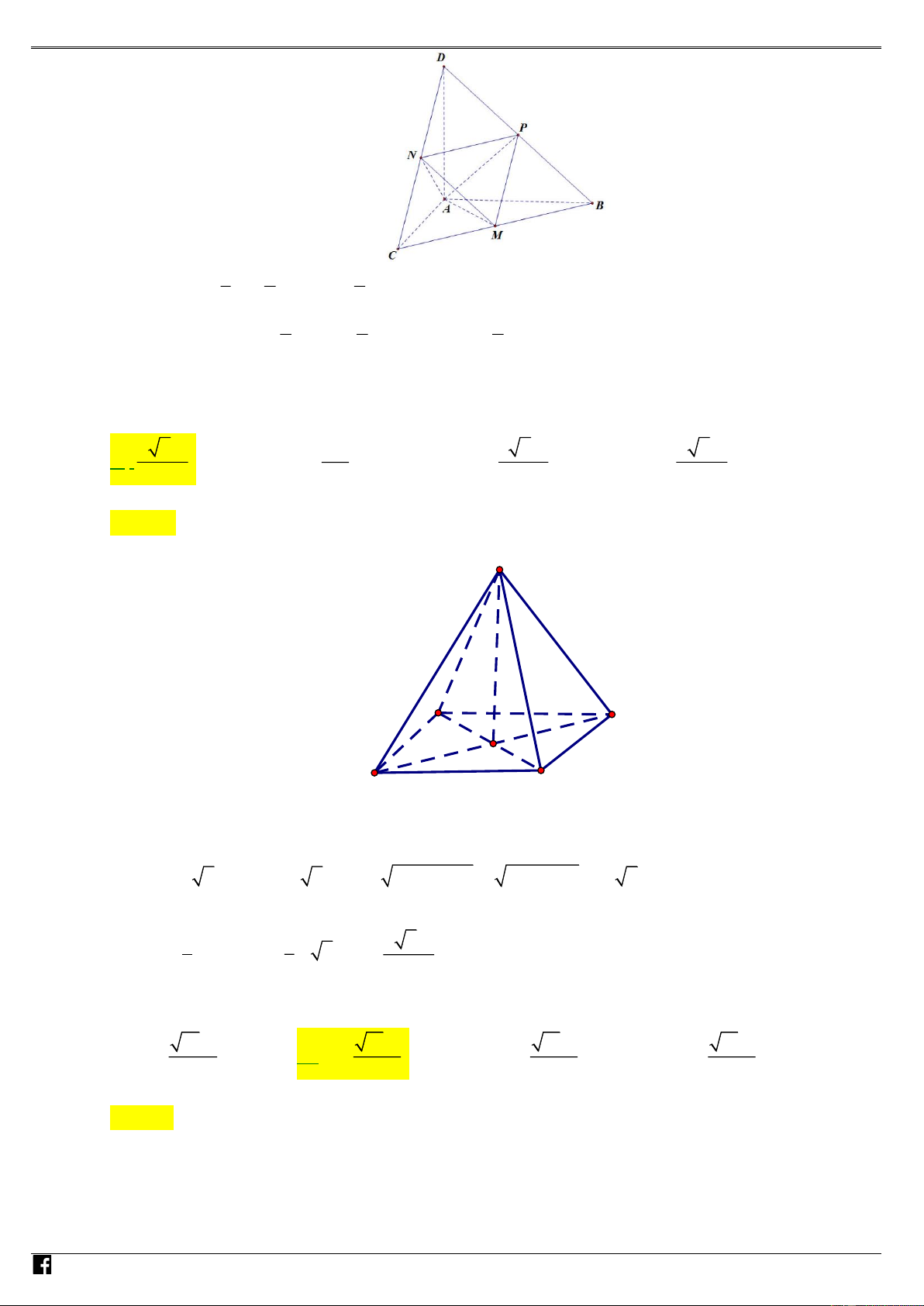
Câu 27: (Câu 37 - ĐMH - BGD&ĐT - Năm 2017) Cho tứ diện D ABC
có các cạnh AB , AC và AD đôi
một vuông góc với nhau; AB = 6a , AC = 7a và AD = 4a . Gọi M , N , P tương ứng là trung điểm
các cạnh BC , CD , DB . Tính thể tích V của tứ diện AMNP . 7 28 A. 3 V = a B. 3 V = 14a C. 3 V = a D. 3 V = 7a 2 3 Lời giải Chọn D
https://www.facebook.com/groups/toanvd.vdc Trang 19
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 1 1 1 Ta có 3 V = A . B A . D AC = 6 .7 a .4 a a = 28a ABCD 3 2 6  1 1 1  Ta nhận thấy 3 S = S = SV = V = 7a . MNP 2 MNPD 4 BCD AMNP 4 ABCD  
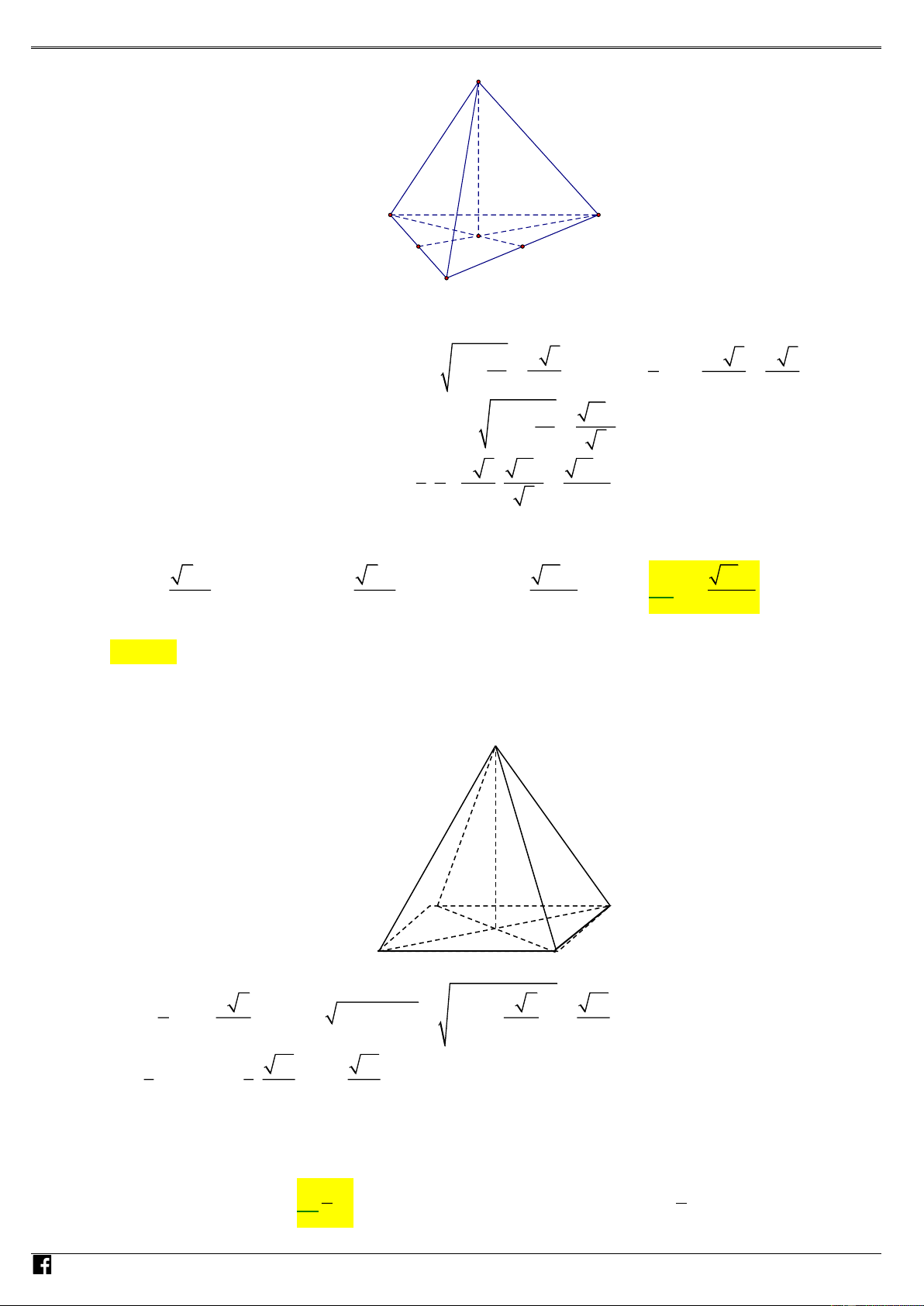
Câu 28: (Câu 27 - ĐTK - BGD&ĐT - Năm 2019) Cho khối chóp tứ giác đều có tất cả các cạnh bằng 2a .
Thể tích của khối chóp đã cho bằng 3 3 3 3 4 2a 8a 8 2a 2 2a NHÓ A. . B. . C. . D. . 3 3 3 3 M Lời giải G Chọn A IÁO S VI ÊN T O ÁN VI A Ệ D T N AM O B C
Xét khối chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O , suy ra SO ⊥ ( ABCD) .   Ta có: 
+ AC = 2a 2  AO = a 2 ; 2 2 SO = SA − AO 2 2
= 4a − 2a = a 2 .   + S = ( a)2 2 2 = 4a . ABCD 1 1 3 4 2a Vậy V = . . SO S 2 = .a 2.4a = . 3 ABCD 3 3
Câu 29: (MĐ 104 BGD&ĐT NĂM 2016-2017) Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a
và cạnh bên bằng 2a . Tính thể tích V của khối chóp S.ABC 3 13a 3 11a 3 11a 3 11a A. V = . B. V = . C. V = . D. V = . 12 12 6 4 Lời giải Chọn B
https://www.facebook.com/groups/toanvd.vdc Trang 20
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 S A C O I B
Do đáy là tam giác đều nên gọi I là trung điểm cạnh BC , khi đó AI là đường cao của tam  2  a a 3 2 = − = 2 2a 3 a 3 
giác đáy. Theo định lý Pitago ta có AI a , và AO = AI = = . 4 2 3 3.2 3  2 a 11a 2 SO = 4a − =
Trong tam giác SOA vuông tại O ta có 3 3 NHÓ 3 1 1 a 3 11a 11a
Vậy thể tích khối chóp S.ABC là V = . a . = . 3 2 2 3 12 M G
Câu 30: (Câu 21 - MĐ 101 - BGD&ĐT - Năm 2017) Cho khối chóp tứ giác đều có cạnh đáy bằng a, cạ IÁO nh
bên gấp hai lần cạnh đáy. Tính tích V của khối chóp tứ giác đã cho. 3 3 3 3 VI 2a 2a 14a 14a A. V = B. V = C. V = D. V = Ê 2 6 2 6 N T Lời giải O Chọn D ÁN
S.ABCD là khối chóp tứ giác đều  ABCD là hình vuông và SO ⊥( ABCD), O là tâm của VI Ệ hình vuông. T N S AM 2a     A D O a B C 2 1 a 2  a 2  14 2 2 2 OD = BD = ; SO = SD − OD = 4a −   = a 2 2  2  2   1 1 14 14 2 3 V = .S . O S = . . a a = a 3 ABCD 3 2 6
Câu 31: (Câu 15 - MĐ 101 - BGD&ĐT - Năm 2018) Cho khối chóp có đáy là hình vuông cạnh a và
chiều cao bằng 2a . Thể tích của khối chóp đã cho bằng 2 4 A. 3 4a B. 3 a C. 3 2a D. 3 a 3 3 Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 21
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 Chọn B
Khối chóp có đáy là hình vuông cạnh a nên có diện tích đáy: 2 S = đáy a .
Chiều cao h = 2a . 1 1 2
Vậy thể tích khối chóp đã cho là V = .S . 2 = 3 = đáy h .a .2a a . 3 3 3
Câu 32: (Câu 35 - ĐTN - BGD&ĐT - Năm 2017) Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a và thể tích bằng 3
a . Tính chiều cao h của hình chóp đã cho. 3 3 3 A. = a h B. = a h C. = a h
D. h = 3a 6 2 3 Lời giải Chọn D   (2a)2 3 2 S = = a 3 
Do đáy là tam giác đều cạnh 2a nên  . ABC 4  3 1 3V 3a Mà V = S .h  = = =  h 3a 3 ABC 2 Sa ABC 3 NHÓ
Câu 33: (MĐ 102 - BGD&ĐT - Năm 2018) Cho khối chóp có đáy là hình vuông cạnh a và chiều c M ao
bằng 4a . Thể tích khối chóp đã cho bằng GIÁO 4 16 A. 3 a . B. 3 a . C. 3 4a . D. 3 16a 3 3 VI Lời giải ÊN Chọn A T 1 1 4 2 3 O
Thể tích khối chóp: V = . B h = a .4a = a . ÁN 3 3 3 VI Ệ
Câu 34: (Câu 43 - Đề Tham Khảo BGD - 2021) Cho hình chóp S.ABC có đáy ABC là tam giác đều cạ T nh N
a , cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa SA và mặt phẳng (SBC) bằng 0 45 AM
(tham khảo hình bên). Thể tích khối chóp S.ABC bằng      3 a 3 3a 3 3a 3 a A. . B. . C. . D. . 8 8 12 4 Lời giải Chọn A
https://www.facebook.com/groups/toanvd.vdc Trang 22
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 S HA C    MB ⊥ ⊥ BC ⊥ SAM
Gọi M là trung điểm BC thì AM BC và SA BC nên ( ). NHÓ
Kẻ AH ⊥ SM tại H thì AH ⊥ (SBC ) . Suy ra góc giữa SA và mặt phẳng (SBC) bằng M a 3
ASH = ASM = 45 . Do đó, S
AM vuông cân ở A và SA = AM = . G 2 IÁO 2 3 1 a 3 a 3 a Suy ra V =   = . S .ABC VI 3 2 4 8 Ê
Câu 35: (Câu 36 - MĐ 102 - BGD&ĐT - Năm 2017) Cho khối chóp S.ABCD có đáy ABCD là hình ch N ữ T
nhật, AB = a , AD = a 3 , SA vuông góc với mặt phẳng đáy và mặt phẳng (SBC ) tạo với đá Oy ÁN
một góc 60o . Tính thể tích V của khối chóp S.ABCD . 3 3 VI a 3a A. V = B. V = C. 3 V = a D. 3 V = 3a Ệ 3 3 T N Lời giải AM Chọn.C S      a 60 B A a 3 D C Ta có 2 S = 3a . ABCD (
SBC)( ABCD) = BC
Vì BC ⊥ SB  (SBC )
 ((SBC),( ABCD)) = (SB; AB) = SBA. BC ⊥ AB   (ABCD) Vậy 60o SBA =
https://www.facebook.com/groups/toanvd.vdc Trang 23
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 SA
Xét tam giác vuông SAB có: tan 60o =  SA = A .
B tan 60o = a 3 AB 1 1 Vậy 2 3 V = S .SA = a 3.a 3 = a . S . ABCD 3 ABCD 3
Câu 36: (Câu 43 - MĐ 101 - BGD&ĐT - Năm 2017) Cho khối chóp S. ABCD có đáy là hình vuông cạnh
a, SA vuông góc với đáy và SC tạo với mặt phẳng một góc 30 . Tính thể tích V của khối chóp đã cho. 3 6a 3 2a 3 2a A. V = B. V = C. V = D. 3 V = 2a 3 3 3 Lời giải Chọn B     NHÓ M GIÁO VI ÊN T O ÁN BC ⊥ 
BA ( ABCD lµ hinh vu«ng)  VI BC ⊥  SA (SA ⊥  (ABCD)) ỆT N
BC ⊥ (SAB)  (S ,
C (SAB)) = BSC = 30 AM BC BC
SBC vuông tại B: 0 tan 30 =  SB = = 3a 0 SB tan 30
SAB vuông tại A: 2 2 2 2 SA = SB − AB = 3a − a = 2a   1 1 2 2 3 V = S . A S = . 2 . a a = a  3 ABCD 3 3 
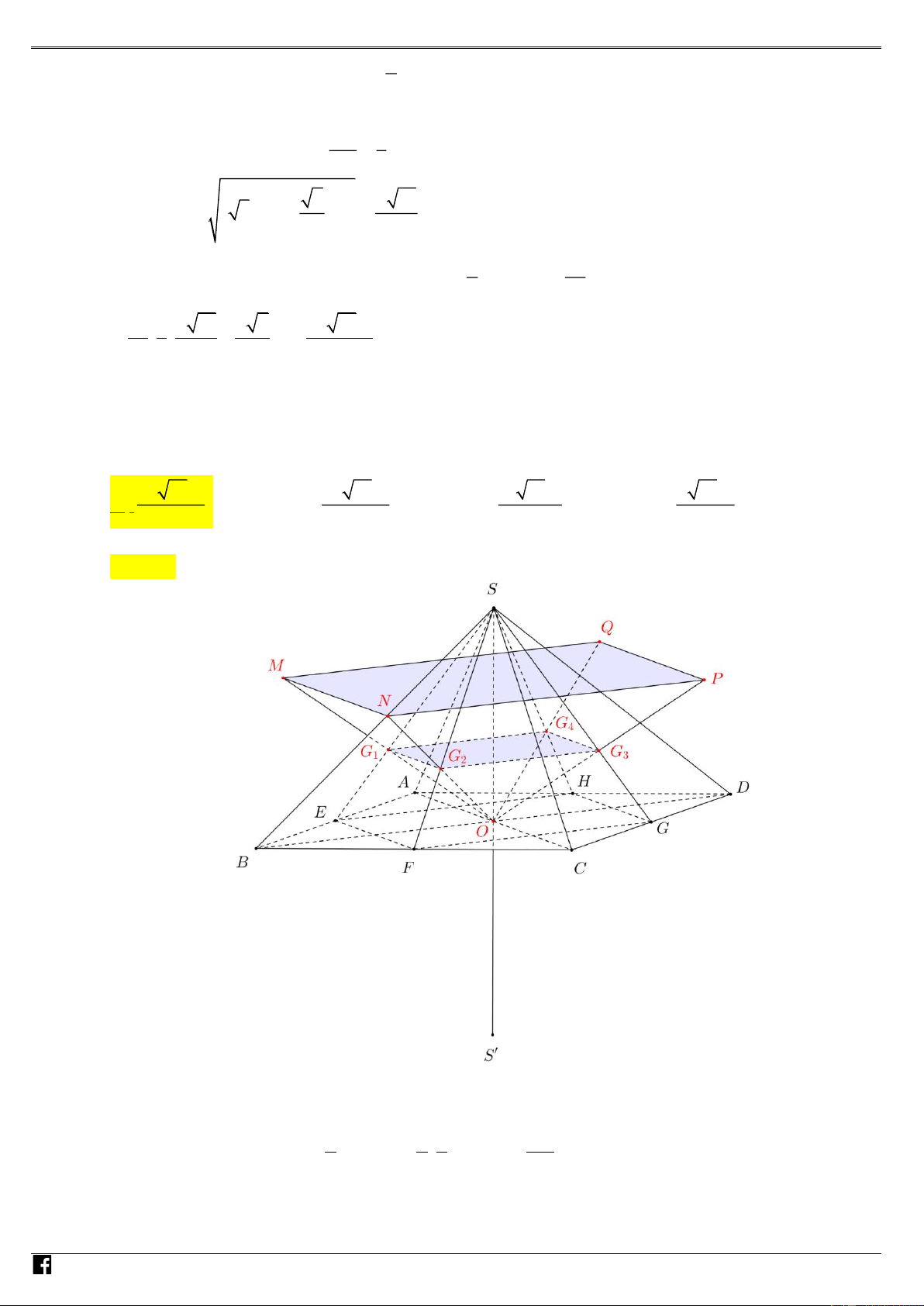
Câu 37: (Câu 45 - Đề thi TNTHPT 2020 - mã đề 102) Cho hình chóp đều S.ABCD có cạnh đáy bằng 4a
, cạnh bên bằng 2 3a và O là tâm của đáy. Gọi M , N, P và Q lần lượt là hình chiếu vuông
góc của O trên các mặt phẳng (SAB), (SBC), (SCD) và (S )
DA . Thể tích của khối chóp . O MNPQ bằng 3 4a 3 64a 3 128a 3 2a A. . B. . C. . D. . 3 81 81 3 Lời giải Chọn D
https://www.facebook.com/groups/toanvd.vdc Trang 24
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 S Q M P N A D HE O K   B C F  
Gọi E, F, K, H lần lượt là trung điểm của AB, BC,CD, DA và M , N, P , Q lần lượt là hình chiế u
vuông góc của O trên SE, SF, SK, SH M , N, P , Q lần lượt là hình chiếu vuông góc của O SAB SBC SCD SDA NHÓ trên các mặt phẳng ( ), ( ), ( ) , ( ) . Ta có 2 2 2 2 SO =
SD − OD = (2 3a) − (2 2a) = 2a = OE = OF = OK = OH M 
các tam giác SOE, SOF, SOK, SOH vuông cân tại O và bằng nhau nên M , N, P và Q lầ GIÁO n
lượt là trung điểm của của SE, SF, SK, SH MNPQ là hình vuông cạnh a 2 = = = = VI Mặt khác ta có OM ON OP OQ a 2  .
O MNPQ là hình chóp đều có tất cả các cạ Ê nh 2 N  1 
bằng a 2 nên có đường cao bằng 2 (a 2) − .a 2. 2 = a   . T  2  O ÁN 3 1 2a
Khi đó thể tích của khối chóp . O MNPQ bằng 2 . . a (a 2) = VI 3 3 Ệ
Câu 38: (Đề tốt nghiệp THPT đợt 2 năm 2020 - mã đề 101) Cho hình chóp đều S.ABCD có cạnh T N đáy 3 3a AM
bằng 3a , cạnh bên bằng
và O là tâm của đáy. Gọi ,
M N, P và Q lần lượt là hình chiếu 2
vuông góc của O trên các mặt phẳng (SAB) , (SBC ) , (SCD) và (SDA) . Thể tích của khối chóp . O MNPQ bằng  3 3 3 3  9a 2a 9a a A. . B. . C. . D. .  16 3 32 3  Lời giải Chọn C
https://www.facebook.com/groups/toanvd.vdc Trang 25
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022     
Gọi E, F, G, H AB BC CD DA .
theo thứ tự là trung điểm của , , , NHÓ AB ⊥ SO Ta có: 
AB ⊥ (SOE)  (SAB) ⊥ (SOE) . AB ⊥ OE M
Mặt khác: (SAB) (SOE) = SE đồng thời M là hình chiếu vuông góc của O lên mặt phẳng GIÁO
(SAB) nên OM ⊥ SE tại M . VI
 3a 3 2  3a 2 2 3a Ê Ta có: SO = 2 SA − 2 OA =   −   = = OE . N      2   2  2 T O
Khi đó tam giác SOE vuông cân tại O M là trung điểm SE . ÁN
Chứng minh tương tự ta cũng có N, P,Q lần lượt là trung điểm của các cạnh SF, SG, SH . VI 2 Ệ 1 3 1 1 9a ( , ( )) = ( , ( )) = = a d O MNPQ d S MNPQ SO S = S = S = T Khi đó , . MNPQ EFGH ABCD N 2 4 4 8 8 2 3 AM 1 1 3a 9a 9a Suy ra V =  S .d ( , O (MNPQ)) = .  = . O.MNPQ MNPQ 3 3 4 8 32 3 9a Vậy V = . O.MNPQ  32   
Câu 39: (Câu 50 - ĐTK - BGD&ĐT - Năm 2017) Cho khối tứ diện có thể tích bằng V . Gọi V  là thể tích 
của khối đa diện có các đỉnh là các trung điểm của các cạnh của khối tứ diện đã cho, tính tỉ s ố V  . V V  1 V  1 V  2 V  5 A. = . B. = . C. = . D. = . V 2 V 4 V 3 V 8 Lời giải Chọn A
https://www.facebook.com/groups/toanvd.vdc Trang 26
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 A Q P B E F D M N C  
Cách 1. Đặc biệt hóa tứ diện cho là tứ diện đều cạnh a . Hình đa diện cần tính có được bằng  a
cách cắt 4 góc của tứ diện, mỗi góc cũng là một tứ diện đều có cạnh bằng . 2  V V
Do đó thể tích phần cắt bỏ là V  = 4. = . 8 2  NHÓ V V 1 Vậy V  =  = . 2 V 2 M
Cách 2. Khối đa diện là hai khối chóp tứ giác có cùng đáy là hình bình hành úp lại. Suy ra: G 1 1 1 IÁO V  = 2V = 4.V = 4.V = 4. . V = V N .MEPF N .MEP P.MNE 2 4 2 VI ' V −V −V −V −V V Cách 3. Ta có . A QEP . B QMF C.MNE . D NPF = Ê V V N T V . A QEP V . B QMF C V .MNE V . D NPF O =1− − − − 1 1 1 1 1 1 1 1 1 1 1 1 1
=1− . . − . . − . . − . . = . ÁN V V V V 2 2 2 2 2 2 2 2 2 2 2 2 2
Câu 40: (Câu 37 - ĐTN - BGD&ĐT - Năm 2017) Cho tứ diện ABCD có thể tích bằng 12 và G là trọ VI ng Ệ
tâm của tam giác BCD . Tính thể tích V của khối chóp . A GBC T N
A. V = 3
B. V = 4
C. V = 6 D. V = 5 AM Lời giải A      B D G C Chọn B Cách 1:
Phân tích: tứ diện ABCD và khối chóp .
A GBC có cùng đường cao là khoảng cách từ A đến
mặt phẳng (BCD) . Do G là trọng tâm tam giác BCD nên ta có S = S =  S BGCBGDCGDS = 3  S (xem phần chứng minh). BCDBGC
Áp dụng công thức thể tích hình chóp ta có:
https://www.facebook.com/groups/toanvd.vdc Trang 27
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 1  1 V = . h S ABCDBCD .  h S 3   V 3 BCD S 1 1 ABCD    = = BCD = 3  V = V = .12 = 4 . 1 V 1 . A GBC ABCDS 3 3 . V = . A GBC h S . GBC h S .  GBC A GBC 3 GBC  3
Chứng minh: Đặt DN = ; h BC = a .    MF CM 1 1 h MF // ND  =
=  MF = DN MF =  +) . DN CD 2 2 2  GE BG 2 2 2 h h +) GE // MF  =
=  GE = MF = . = MF BM 3 3 3 2 3 1 1 NHÓ DN.BC ha S +) BCD 2 2 = = = 3  S = 3S S 1 1 BCDGBC h M GBC GE.BC a G 2 2 3 IÁO
+) Chứng minh tương tự có S = 3S = 3  = =  S S S S BCDGBDGCD BGC BGD CGD VI Cách 2: Ê
d (G;( ABC)) GI 1 1 N Ta có =
=  d (G; ABC ) = d ( ; D ( ABC )) . T d ( ; D ( ABC )) ( ) DI 3 3 O ÁN 1 1 Nên V
= d G; ABC .S = .V = 4 G. ABC ( ( )) ABC DABC VI 3 3 Ệ D T N AM G   A C H1HIB
Câu 41: (Câu 34 - MĐ 103 BGD&ĐT NĂM 2016-2017) Cho khối chóp S.ABCD có đáy là hình vuông a 2
cạnh a , SA vuông góc với đáy và khoảng cách từ A đến mặt phẳng (SBC ) bằng . Tính 2
thể tích V của khối chóp đã cho. 3 3 3 3 A. = a V . B. 3 V = a . C. = a V . D. = a V . 2 9 3 Lời giải Chọn D
Kẻ AH vuông góc SB .
Ta có AH ⊥ (SBC) nên AH chính là khoảng cách từ A đến mp (SBC ) .
https://www.facebook.com/groups/toanvd.vdc Trang 28
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 1 1 1 1 1 1 1 Ta có = +  = − = . 2 2 2 2 2 2 2 AH SA AB SA AH AB a 3 1
Suy ra SA = a . Thể tích cần tính là = . . = a V a a a . 3 3
Câu 42: (Câu 38 - ĐMH - BGD&ĐT - Năm 2017) Cho hình chóp tứ giác S.ABCD có đáy là hình vuông
cạnh bằng 2a . Tam giác SAD cân tại S và mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết 4
thể tích khối chóp S.ABCD bằng 3
a . Tính khoảng cách h từ B đến mặt phẳng (SCD) 3 2 4 8 3
A. h = a
B. h = a
C. h = a
D. h = a 3 3 3 4  Lời giảiChọn B    NHÓ M GIÁO VI
Gọi I là trung điểm của AD . Tam giác SAD cân tại S ÊN  SI ⊥ AD T  ⊥ O SI AD  ÁN Ta có (  ⊥  SAD
) ⊥ (ABCD) SI (ABCD) VI
SI là đường cao của hình chóp. ỆT 1 4 1 N Theo giả thiết 3 2 V = .SI.S
a = SI.2a SI = 2a S . ABCD ABCD AM 3 3 3
Vì AB song song với (SCD)
d (B,(SCD)) = d ( ,
A (SCD)) = 2d (I,(SCD)) 
Gọi H là hình chiếu vuông góc của I lên SD .  SI ⊥ DCIH ⊥ SD  Mặt khác 
IH ⊥ DC . Ta có 
IH ⊥ (SCD)  d (I,(SCD)) = IH  ID ⊥ DCIH ⊥ DC  1 1 1 1 4 2a
Xét tam giác SID vuông tại I : = + = +  IH = 2 2 2 2 2 IH SI ID 4a 2a 3
d (B (SCD)) = d ( A (SCD)) = d (I (SCD)) 4 , , 2 , = a . 3
Câu 43: (Đề TNTHPT 2020 - mã đề 103) Cho hình chóp đều ABCD có cạnh đáy bằng a , cạnh bên bằng
a 3 và O là tâm của đáy. Gọi M, N,P và Q lần lượt là hình chiếu vuông góc của O trên các 2
mặt phẳng (SAB),(SBC),(SCD),(SDA) . Thể tích của khối chóp . O MNPQ bằng 3 a 3 2a 3 a 3 a A. . B. . C. . D. . 48 81 81 96 Lời giải Chọn D
https://www.facebook.com/groups/toanvd.vdc Trang 29
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022      NHÓ 2 2 a 2 3a 2a a Từ giả thiết ta có 2 2 OA = , SO = SA − OA = − = . 2 4 4 2 M
OM ⊥ SE M SE OM ⊥ (SAB) G
Gọi E là trung điểm của AB , kẻ ( ) . IÁO 2 a 2 SM SO 1 VI Và 4 = =
=  M là trung điểm của SE . 2 2 2 2 Ê SE SO + OE a a 2 N + 4 4 T O
Chứng minh tương tự với các điểm N, P,Q . ÁN 2 2  a 2  a a VI
 Diện tích tứ giác MNPQ là   =  
và d (O (MNPQ)) 1 ; = SO = . 2 4 Ệ 4 8   T 2 3 N 1 a a a  = = AM V . . . O.MNPQ 3 4 8 96
Câu 44: (Câu 45 - BGD - Đợt 1 - Mã đề 104 - 2020) Cho hình chóp đều S.ABCD có tất cả các cạnh bằng
a và O là tâm đáy. Gọi M , N, P, Q lần lượt là các điểm đối xứng với O qua trọng tâm củ a
các tam giác SAB, SBC, SC ,
D SDA và S là điểm đỗi xứng với S qua O . Thể tích của khối c  hóp 
S .MNPQ bằng  3 2 2a 3 20 2a 3 40 2a 3 10 2aA. . B. . C. . D. . 9 81 81 81 Lời giải Chọn B
https://www.facebook.com/groups/toanvd.vdc Trang 30
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 S M Q N O' P G H I A B E O D F C    S'   a 2
Ta có S.ABCD là hình chóp đều có tất cả các cạnh đều bằng a SO = . 2 G I SDA SDC
Gọi , lần lượt là trọng tâm các tam giác , . NHÓ
Gọi E, F lần lượt là trung điểm D , A DC . 2 1 a 2 a 2 M Ta có GI = EF , EF = AC =  GI = . G 3 2 2 3 IÁO 2 2a
Mà G, I lần lượt là trung điểm của OQ,OP QP = 2GI = . VI 3 2 Ê 2 2a 8a N
Từ giả thiết cho dễ dàng suy ra được MNPQ là hình vuông cạnh PQ =  S = . MNPQ T 3 9 O
Gọi O là tâm hình vuông MNPQ kẻ GH / /QO(H OO)  H là trung điểm OO (vì G là ÁN trung điểm OQ ). VI Ệ 2 2a 2 2a 1 a 2 T Ta có QO = . =
và OO = 2OH = 2. .SO = N 3 2 3 3 3 AM a 2 a 2 a 2 5 2a
Theo giả thiết OS = OS =  S O   = S O  + OO = + = 2 2 3 6 2 3 1 5 2a 8a 20 2a V = =  . . .  S .MNPQ 3 6 9 81 
Câu 45: (Câu 47 - BGD - Đợt 1 - Mã đề 103 - 2020) Cho hình chóp đều S.ABCD có cạnh đáy bằng a , 
cạnh bên bằng a 2 và O là tâm của đáy. Gọi M , N , P , Q lần lượt là các điểm đối xúng với
O qua trọng tâm của các tam giác SAB , SBC , SCD , SDA và S là điểm đối xứng với S qua
O . Thể tích của khối chóp S .MNPQ . 3 2 6a 3 40 6a 3 10 6a 3 20 6a A. . B. . C. . D. . 9 81 81 81 Lời giải Chọn D
https://www.facebook.com/groups/toanvd.vdc Trang 31
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022    
Gọi G , G , G , G lần lượt là trọng tâm các tam giác SAB , SBC , SCD , SDA . 1 2 3 4
E , F , I , K lần lượt là trung điểm AB , BC , CD , DA . 4 16 1 8 2 NHÓ Ta có: S = 4S = 4. S =  S = a . MNPQ 1 G 2 G 3 G 4 G 9 EFIK 9 2 ABCD 9 M  a 2  a a 6 2 5a 6 SO = a 2 −   = 2a − =  S H  = S O
 + OH = SO + SO = G ( ) 2 2 2 2   . IÁO 2 2 2   3 6 3 1 5a 6 8 20a 6 VI 2 V =   =  a (đvtt). S .MNPQ Ê 3 6 9 81 N
Câu 46: (BGD - Đợt 1 - Mã đề 102 - 2020) Cho hình chóp đều S.ABCD có cạnh đáy bằng a , cạnh T O bên
bằng a 3 và O là tâm của đáy. Gọi M , N , P ,Q lần lượt là các điểm đối xứng với O qua trọn ÁNg
tâm của các tam giác SAB , SBC , SCD , SDA và S là điểm đối xứng với S qua O . Thể tích khốVI i chóp S MNPQ bằng ỆT 3 3 3 3 N 40 10a 10 10a 20 10a 2 10a A. . B. . C. . D. . AM 81 81 81 9 Lời giải Chọn C     
Gọi G ,G ,G ,G lần lượt là trọng tâm của SAB, SBC , SCD, SAD . 1 2 3 4
https://www.facebook.com/groups/toanvd.vdc Trang 32
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 1
Do G G //G G //EF;G G = G G =
EF  Tứ giác G G G G là hình bình hành. 1 2 3 4 1 2 3 4 2 1 2 3 4
MN//PQ//G G , MN = PQ = 2G G  Tứ giác MNPQ là hình bình hành. 1 2 1 2 SH 1
Gọi H = QN MP . Ta có: = . SO 3   a
Ta có: SO = ( a) 2 2 2 10 3 −  a  =   2 2   3  2  80 Ta có: V = = = =  5.V 5.2V 5.2. .V .V S .MNPQ S .MNPQ S .   1 G 2 G 3 G 4 G S .EFIK S .  3  27 EFIK 2  3
80 1 a 10  a 2  20 10a  = . . .  = .    27 3 2 2 81   
Câu 47: (Câu 47 - ĐỀ BGD-MÃ 101-L1-2020) Cho hình chóp đều S.ABCD có cạnh đáy bằng a , cạ  nh
bên bằng 2a và O là tâm của đáy. Gọi M , N , P , Q lần lượt là các điểm đối xứng với O qu a
trọng tâm của các tam giác SAB , SBC , SCD , SDA và S ' là điểm đối xứng với S qua O . Th NHÓ ể
tích của khối chóp S '.MNPQ bằng 3 20 14a 3 40 14a 3 10 14a 3 2 14a M A. . B. . C. . D. . 81 81 81 9 G IÁO Lời giải Chọn A VI ÊN T O ÁN VI ỆT NAM     
Gọi G ,G ,G ,G lần lượt là trọng tâm SAB, SBC, SCD, SDA . 1 2 3 4
E, F,G, H lần lượt là trung điểm của các cạnh AB, BC,CD, DA . 2 4 4 1 8a Ta có S = 4S = 4. S = 4. . E . G HF = . MNPQ 1 G 2 G 3 G 4 G 9 EFGH 9 2 9
https://www.facebook.com/groups/toanvd.vdc Trang 33
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
d (S ,(MNPQ)) = d (S ,( ABCD)) + d (O,(MNPQ))
= d (S,( ABCD)) + 2d (O,(G G G G 1 2 3 4 )) =
d (S ( ABCD)) 2 ,
+ d (S,( ABCD)) 3 5
= d (S ( ABCD)) 5a 14 , = 3 6 2 3 1 5a 14 8a 20a 14 Vậy V =   = . S .  MNPQ 3 6 9 81
Câu 48: (Câu 46 - Đề - BGD - 2020 - Đợt 2 - Mã đề - 104– 2021) Cho hình chóp đều S.ABCD có cạ  nh
đáy bằng 2a , cạnh bên bằng a 3 và O là tâm đáy. Gọi M , N, P và Q lần lượt là hình chiế u 
vuông góc của O trên các mặt phẳng (SAB) , (SBC ) , (SCD) và (SDA) . Thể tích khối c  hóp . O MNPQ bằng 3 3 3 3 8a a a 16a A. . B. . C. . D. . 81 6 12 81 NHÓ Lời giải M GIÁO VI ÊN T O ÁN VI ỆT NAM      Chọn C
Do S.ABCD là hình chóp đều nên có SO ⊥ ( ABCD) . 2 2
Xét tam giác SOA vuông tại O có 2 2 SO =
SA − OA = (a 3) − (a 2) = a .
Gọi G, H , I, J lần lượt là trung điểm của AB, BC,CD, DA .
Ta có AB ⊥ G ,
O AB ⊥ SO AB ⊥ (SOG) mà AB ⊥ (SAB) nên (SGO) ⊥ (SAB) do đó M là hình
chiếu vuông góc của O trên các mặt phẳng (SAB) suy ra M SG và OM ⊥ SG .
Xét SOG vuông tại O có SO = OG = a , OM ⊥ SG nên M là trung điểm của SG .
Hoàn toàn tương tự có N, P,Q lần lượt là trung điểm của SH , SI , SJ .
https://www.facebook.com/groups/toanvd.vdc Trang 34
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 1 a Do đó dễ thấy .
O MNPQ là chóp tứ giác đều có đường cao OO ' = SO = và cạnh đáy 2 2 1 1 2a 2 a 2 MN = GH = AC = = . 2 4 4 2 2 3 1 1 a a 2  a
Vậy thể tích khối chóp . O MNPQ bằng V = OO '.S = .  = . . O MNPQ   3 MNPQ 3 2 2 12  
Câu 49: (Câu 49 - ĐTK - BGD&ĐT - L1 - Năm 2020) Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân tại , A AB a, SBA SCA
90 , góc giữa hai mặt phẳng (SAB) và (SAC ) bằng 60 .
Thể tích khối chóp đã cho bằng 3 3 3  a a a A. 3 a . B. . C. . D. .  3 2 6  Lời giải   Chọn D Cách 1: NHÓ M GIÁO VI ÊN T O ÁN 2 1 a VI Ta có S = A . B AC = . ABC  Ệ 2 2 T N
Gọi D là hình chiếu vuông góc của S lên mặt phẳng ( ABC) . AM AB ⊥ SB Ta có 
AB ⊥ (SBD)  AB ⊥ BD . AB ⊥ SD
Tương tự, ta có AC ⊥ CD
ABDC là hình vuông cạnh a .  
Đăt SD = x, x  0 .  D . B DS ax  = = 
Gọi H là hình chiếu vuông góc của D lên SB DH . 2 2 2 2 DB + DS a + xDH ⊥ SB ax Ta có 
DH ⊥ (SAB)  d (D,(SAB)) = DH = .  ⊥ 2 2 DH AB a + x
Lại có CD // AB CD // (SAB)  d (C,(SAB)) = d ( ,
D (SAB)) = DH . S
CA vuông tại C, có 2 2
AC = a, SC = x + a . 2 2 C . A CS . a x + a
Kẻ CK ⊥ SA CK = = . 2 2 2 2 CA + CS x + 2a
d (C, SAB ) DH
Vì (SAB)  (SAC ) = SA  sin ((SAB),(SAC)) ( ) = = d (C, SA) CK
https://www.facebook.com/groups/toanvd.vdc Trang 35
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 ax 2 2 2 2 a + x 3 x x + 2a  sin 60 =  =  3(x + a )2 2 2 2 = 4x ( 2 2 x + 2ax = a . 2 2 ) 2 2 2 + x + a a x a 2 2 x + 2aDH = a . 3 1 a Vậy V = S .SD = . S.ABC  3 ABC 6 Cách 2:      NHÓ M  ⊥ G
Dựng hình vuông ABCD SD (ABCD). IÁO
Đặt SD = x, x  0 . VI ax
Kẻ DH ⊥ SB,( H SB)  DH ⊥ (SAB) và DH = . Ê 2 2 N x + a T ax O
Kẻ DK ⊥ SC,( K SC )  DK ⊥ (SAC ) và DK = . ÁN 2 2 x + a 2 2 2 2 VI SH SK SD x x x Ta có = = =
HK // BD HK = BD = .a 2 . Ệ 2 2 2 2 2 2 2 SB SC SB x + a x + a x + a T N
DH + DK − HK AM Ta có ((SAB) (SAC)) 2 2 2 cos , = cos HDK = 2DH.DK 2 2 2 4 2x a 2a x − 2 2 2  x + a + 1 ( 2 2 x a ) 2 1 a   =  =  x = a . 2 2 2 2  2 2x a 2 x + a  2 2 x + a   SD = . a 2 1 a Lại có S A . B AC ABC  = = . 2 2 3 1 a Vậy V = S .SD = . S.ABC  3 ABC 6
Cách trình bày khác
https://www.facebook.com/groups/toanvd.vdc Trang 36
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 S I A C a a 2 B
Hai tam giác vuông SAB và SAC bằng nhau chung cạnh huyền SA . 
Kẻ BI vuông góc với SA suy ra CI cũng vuông góc với SA và IB = IC .  
SA ⊥ IC, SA ⊥ IB SA ⊥ (IBC) tại I .  1 1 1 1 V = V +V = S AI + S SI = S AI + SI = S SA . S . ABC . A IBC S .IBC IBC IBC IBC ( ) IBC 3 3 3 3 =  =  = NHÓ
((SAB) (SAC)) (IB IC) (IB IC) 0 0 , , , 60 BIC 60 hoặc 0 BIC = 120 .
Ta có IC = IB AB = a mà BC = a 2 nên tam giác IBC không thể đều suy ra 0 BIC = 120 . M = = 
Trong tam giác IBC đặt IB IC x ( x 0) có: G IÁO 2x −
IB + IC − BC (a 2 1 )2 2 2 2 2 a 6 a 6 0 =  − =  =  = = VI cos120 x IB IC . 2 2I . B IC 2 2x 3 3 ÊN 2  a 6  a 3 T
Trong tam giác ABI vuông tại I có: 2 2 2 AI = AB − IB = a −   = . O   3 3 ÁN   2 2 AB a VI
Trong tam giác SAB vuông tại B đường cao BI có: 2 AB = I . A SA SA = = = a 3 . Ệ IA a 3 T N 3 AM 2 3 1 1 1 1  a 6  a 0 == = =   = Vậy V S SA I .
B IC.SAsin BIC a 3 sin120 . S . ABC    3 IBC 3 2 6 3 6   
Cách trình bày khác    
Gọi H là hình chiếu của S lên ( ABC) .
Theo bài ra, ta có HC ⊥ C ,
A HB ⊥ BA ABHC là hình vuông cạnh a .
Gọi O = HABC , E là hình chiếu của O lên SA .
Ta dễ dàng chứng minh được EC ⊥ S , A EB ⊥ SA .
Từ đó, ta được: góc giữa (SAC ) và (SAB) là góc giữa EB và EC .
https://www.facebook.com/groups/toanvd.vdc Trang 37
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 Vì 0 CAB = 90 nên 0 0
BEC  90  BEC = 120 .
Ta dễ dàng chỉ ra được 0
OEB = OEC = 60 . A . O SH xa 2 Đặt 2 2
SH = x SA =
x + 2a OE = = . 2 2 SA 2 x + 2a OC a 2 xa 2 0 tan 60 =  : = 3  x = a . 2 2 OE 2 2 x + 2a 3 1 1 1 a Vậy 2 V = V = . . . a a = . S. ABC S. 2 HBAC 2 3 6
Cách trình bày khác S     I D NHÓ C M GIÁO B A ⊥  ⊥ VI
Ta có  ⊥ SAB =  ⊥ SAC và chung cạnh huyền SA. Kẻ BI
(SA) CI (SA) và góc giữa hai Ê  =  N
mặt phẳng (SAB) và (SAC ) là góc giữa hai đường thẳng BI và CI (BI;CI) 60 . T BC = a
BI = CI AC = a a = BC  O Có
2 , BIC cân tại I. Do 2
nên BIC không đều ÁN a 6 a 3 BIC 120 BI CI . Từ đó AI = ; 2
AB = AI.SA SA = a 3. VI 3 3 Ệ  SD ⊥ ABDC T
Dựng hình vuông ABDC ( ) . N 3 1 a 2 2 2 AM
Có: SD = SA − AD = ; a S = a V = S .SD = . ABC S . ABC  3 ABC 6
HOẶC CÁCH KHÁC PPTHỂ TÍCH 1 1 V = S . SI + AI = S .SA . S .ABC IBC ( )   3 3 IBC  2 2 3 1 a 3 1 a 3 a  Với S = .I . B IC.s 1 in 20 = V = . .a 3 = . IBC S . ABC  2 6 3 6 6 
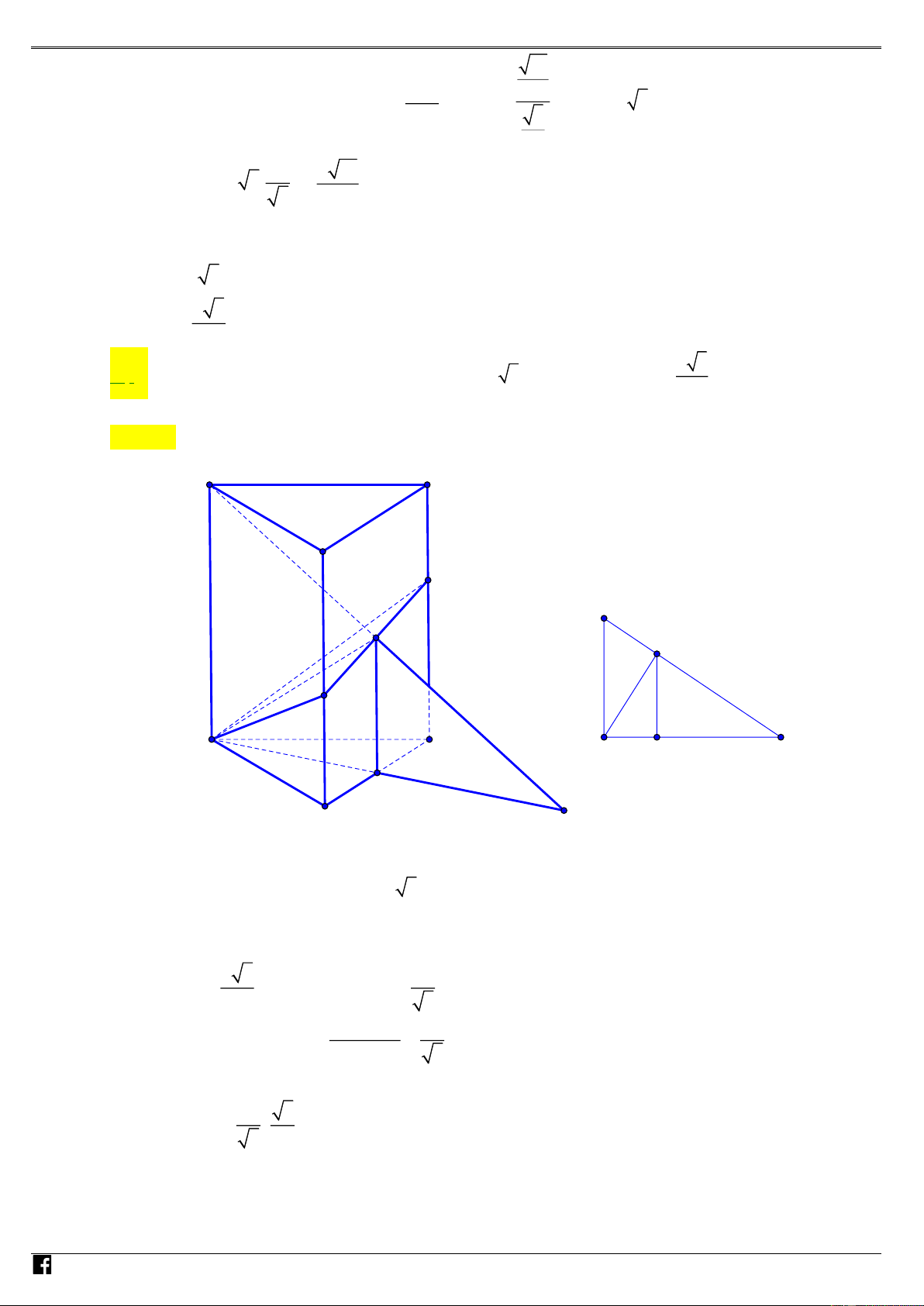
Câu 50: (ĐTK - BGD&ĐT - Năm 2018) Cho hình vuông ABCD và ABEF có cạnh bằng 1, lần lượt nằ m
trên hai mặt phẳng vuông góc với nhau. Gọi S là điểm đối xứng của B qua đường thẳng DE .
Thể tích của khối đa diện ABCDSEF bằng 7 11 2 5 A. B. C. D. 6 12 3 6 Lời giải Chọn D
https://www.facebook.com/groups/toanvd.vdc Trang 38
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 S F E D AC B  
Ta có:ADF.BCE là hình lăng trụ đứng có đáy là tam giác vuông cân  Dựa vào hình vẽ ta có:  V = V +V = V +V = V − 2 V ABCDSEF ADF .BCE S .CDFE ADF .BCE B.CDFE ADF . E BC B D A E NHÓ 1 1 1 1 1 5 V = A . B S = ;V = A . D S =  V = 2. − = ADF .BCEBCE BADE  2 3 ABE 6 ABCDSEF 2 6 6 M
Câu 51: (Câu 44 - MĐ 103 BGD&ĐT NĂM 2016-2017) Xét khối chóp S.ABC có đáy là tam giác v G uông
cân tại A , SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBC ) bằng 3 . Gọi  IÁO là
góc giữa mặt phẳng (SBC ) và ( ABC) , tính cos khi thể tích khối chóp S.ABC nhỏ nhất. VI Ê 1 3  = 2  = 2 N A. cos = . B. cos . C. cos . D. cos = . 3 3 2 3 T O Lời giải ÁN Chọn B VI ỆT NAM  
Gọi M là trung điểm BC , H là giao điểm của đường thẳng qua A và vuông góc với SM . Ta  được: 
Góc giữa mặt phẳng (SBC ) và ( ABC) là SMA . 3 3 1 AM ; SA = ; AM = BC. sin  cos 2 1 9 Suy ra 2 V = .AM .SA = . S . ABC 2 3 sin .cos
Thể tích khối chóp nhỏ nhất khi 2
sin .cos lớn nhất.  Xét hàm số ( x) 2 3 f = sin .
x cos x = cos x − cos x với 0  x  2 sin x = 0 
f ( x) = −sin x + 3cos .
x sin x , f (  x) = 0  3  cos x =   3
https://www.facebook.com/groups/toanvd.vdc Trang 39
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 3 Suy ra 2
sin .cos lớn nhất khi cos = . 3
Câu 52: (Câu 49 - MĐ 102 - BGD&ĐT - Năm 2017) Xét khối tứ diện ABCD có cạnh AB = x và các cạnh
còn lại đều bằng 2 3 . Tìm x để thể tích khối tứ diện ABCD đạt giá trị lớn nhất.
A. x = 6
B. x = 14
C. x = 3 2 D. x = 2 3 Lời giải Chọn C A2 3 Nx   2 32 3 B C 2 3 NHÓ 2 3 M M D G
Gọi M , N lần lượt là trung điểm của CD và AB . IÁO CD ⊥ MBCD  ⊥ MN Ta có
  CD ⊥ (MAB)   . VI CD ⊥ MACD  ⊥ AB ÊN
Tam giác MAB cân tại M nên MN ⊥ AB . T 1 1 O V = A . B . CD d AB CD AB CD = x MNABCD ( , ).sin( , ) .2 3. .sin 90 ÁN 6 6 2 2 2 VI  x + 36 −  1   3 3 x x 2 2 ( ) = . x 2 3. 3 − = . x 36 − x  .   = 3 3 . Ệ   T 6  2  6 6  2    N AM Dấu " = " xảy ra 2
x = 36 − x x = 3 2 .
Vậy với x = 3 2 thì V
đạt giá trị lớn nhất bằng 3 3 . ABCD   
THỂ TÍCH KHỐI LĂNG TRỤ
Câu 53: (MĐ 104 - BGD&ĐT - Năm 2021) Thể tích của khối lập phương cạnh 2a bằng A. 3 a . B. 3 2a . C. 3 8a . D. 3 4a . Lời giải Chọn C
Ta có thể tích của khối lập phương cạnh 2a là: V = ( a)3 3 2 = 8a .
Câu 54: (MĐ 103 - BGD&ĐT - Năm 2021) Thể tích khối lập phương cạnh 3a bằng A. 3 27a . B. 3 3a . C. 3 9a . D. 3 a . Lời giải Chọn A 3 3
V = (3a) = 27a .
Câu 55: (Câu 22 - Đề Tham Khảo BGD - 2021) Thể tích khối hộp chữ nhật có ba kích thước 2,3, 7 bằng A. 14. B. 42. C. 126. D. 12. Lời giải Chọn B
https://www.facebook.com/groups/toanvd.vdc Trang 40
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
Thể tích khối hộp có ba kích thước 2,3, 7 bằng V = abc = 2.3.7 = 42 .
Câu 56: (Câu 14 - BGD - Đợt 1 - Mã đề 104 - 2020) Cho khối hộp chữ nhật có ba kích thước 2 ; 3 ; 7 . Thể
tích của khối hộp đã cho bằng A. 7 . B. 42 . C. 12 . D. 14 . Lời giải Chọn B
Thể tích khối hộp chữ nhật có ba kích thước 2 ; 3 ; 7 là: V = 2.3.7 = 42 .
Câu 57: (Câu 11 - BGD - Đợt 1 - Mã đề 103 - 2020) Cho khối hộp chữ nhật có ba kích thước 2;6;7 . Thể
tích của khối hộp đã cho bằng A. 28. B. 14. C. 15. D. 84.  Lời giải Chọn D  = 
Thể tích của khối hộp đã cho là: 2.6.7 84. 
Câu 58: (BGD - Đợt 1 - Mã đề 102 - 2020) Cho khối hộp chữ nhật có kích thước 2; 4;6 . Thể tích của khố i hộp đã cho bằng A. 16 . B. 12 . C. 48 . D. 8 . NHÓ Lời giải Chọn C M
Thể tích của khối hộp là V = 2.4.6 = 48 . G IÁO
Câu 59: (Câu 5 - ĐỀ BGD-MÃ 101-L1-2020) Cho khối hộp chữ nhật có ba kích thước 3; 4; 5 . Thể tích
của khối hộp đã cho bằng VI Ê A. 10 . B. 20 . C. 12 . D. 60 . N Lời giải T O Chọn D ÁN
Thể tích của khối hộp đã cho là V = 3. 4. 5 = 60 . VI
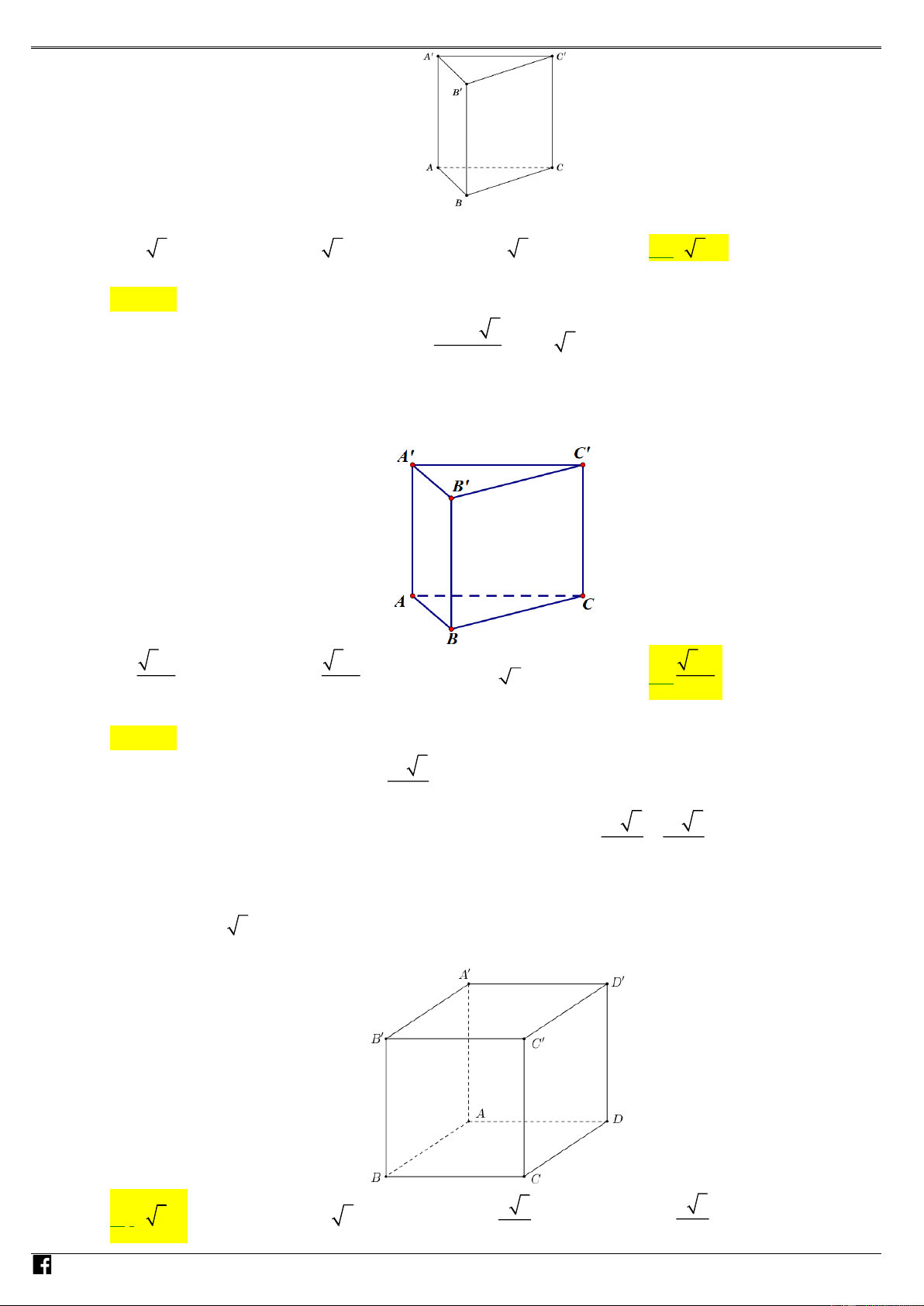
Câu 60: (Câu 26 - MĐ 104 - BGD&ĐT - Năm 2019) Cho khối lăng trụ đứng AB . C A BC
  có đáy là ta ỆTm
giác đều cạnh a và AA = 2a (minh họa như hình vẽ bên). Thể tích của khối lăng trụ đã c N ho AM bằng A' C'   B'    A C B 3 6a 3 6a 3 6a 3 6a A. . B. . C. . D. . 4 6 12 2 Lời giải Chọn A 2 3 a 3 a 6 Ta có: V = AA'.S = a 2. = .
ABC.A' B 'C ' ABC 4 4
Câu 61: (Câu 25 - MĐ 103 - BGD&ĐT - Năm 2019) Cho khối lăng trụ đứng AB . C A BC   có đáy là tam
giác đều cạnh 2a và AA = 3a (minh họa như hình vẽ bên).
https://www.facebook.com/groups/toanvd.vdc Trang 41
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
Thể tích của khối lăng trụ đã cho bằng A. 3 2 3a . B. 3 3a . C. 3 6 3a . D. 3 3 3a . Lời giải Chọn D   (2a)2 3
Thể tích khối lăng trụ là: 3 V = S .AA = .3a = 3 3a . ABC  4 
Câu 62: (Câu 21 - MĐ 102-BGD&ĐT-Năm 2019) Cho khối lăng trụ đứng AB . C A BC
  có đáy là tam gi  ác  =
đều cạnh bằng a và AA
2a (minh họa như hình vẽ bên). Thể tích của khối lăng trụ đã c ho bằng NHÓ M GIÁO VI ÊN T O 3 3 3 ÁN 3a 3a 3a A. . B. . C. 3 3a . D. . VI 3 6 2 Ệ Lời giải T N Chọn D AM 2 a 3
Diện tích tam giác ABC là S = . ABC 4 2 3 a 3 a 3 
Thế tích khối lăng trụ đã cho bằng V =   =  =    S AA 2a . ABC.A B C ABC  4 2 
Câu 63: (ĐTK - BGD&ĐT - L1 - Năm 2020) Cho khối lăng trụ đứng ABC . DA B C 
D có đáy là hình t  hoi = A  cạnh , a BD
a 3 và A = 4a (minh họa như hình bên dưới). Thể tích của khối lăng trụ đã cho bằng 2 3 4 3 A. 3 2 3a . B. 3 4 3a . C. 3 a . D. 3 a . 3 3
https://www.facebook.com/groups/toanvd.vdc Trang 42
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 Lời giải Chọn A      3
Vì ABCD là hình thoi cạnh 2 2
a, BD = a 3  AC = 2AO = 2 a − a = a 4 2 a 3 3 NHÓ Vậy S =
V = AA .S = 2 3a ABCD 2 ABCD
Câu 64: (Câu 22 - MĐ 101-BGD&ĐT-Năm 2019) Cho khối lăng trụ đứng AB .
C A' B 'C ' có đáy là ta M m G
giác đều cạnh a và AA' = 3a . Thể tích của lăng trụ đã cho bằng IÁO VI ÊN T O ÁN VI ỆT NAM 3 3 3 3 3a 3a a a A. . B. . C. . D. . 4 2 4 2  Lời giải   Chọn A  2 a 3 
Ta có: ABC là tam giác đều cạnh a nên S = . ABC  4 Ta lại có AB .
C A' B 'C ' là khối lăng trụ đứng nên AA' = 3a là đường cao của khối lăng trụ. 2 3 a 3 3a
Vậy thể tích khối lăng trụ đã cho là: V = AA'.S = a 3. = .
ABC.A' B 'C ' ABC 4 4
Câu 65: (Câu 18 - MĐ 102 - BGD&ĐT - Năm 2017) Cho khối lăng trụ đứng AB . C A BC
  có BB = a , đáy
ABC là tam giác vuông cân tại B và AC = a 2 . Tính thể tích V của khối lăng trụ đã cho. 3 a 3 a 3 a A. 3 V = a B. V = C. V = D. V = 3 6 2 Lời giải Chọn D
https://www.facebook.com/groups/toanvd.vdc Trang 43
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 A' C' a B' a 2 A C B AC 1
Tam giác ABC vuông cân tại B AB = BC = = a . Suy ra: 2 S = a . ABC  2 2  3 1 a 2  Khi đó: V =  = =    S .BB a .a ABC.A B C ABC  2 2 
Câu 66: (Câu 1 - ĐTK - BGD&ĐT - Năm 2019) Thể tích của khối lập phương cạnh 2a bằng A. 3 8a . B. 3 2a . C. 3 a . D. 3 6a . NHÓ Lời giải Chọn A M G
Thể tích của khối lập phương cạnh 2a bằng ( a)3 3 2 = 8a . IÁO VI
Câu 67: (Câu 35 - ĐMH - BGD&ĐT - Năm 2017) Tính thể tích V của khối lập phương ABC . D A BCD  Ê  = N , biết AC a 3 . T 3 3 6a 1 O A. 3 V = a . B. V = . C. 3
V = 3 3a . D. 3 V = a . ÁN 4 3 Lời giải VI Ệ Chọn A T N AM     
Giả sử khối lập phương có cạnh bằng ; x ( x  0)
Xét tam giác A' B 'C ' vuông cân tại B ' ta có: 2 2 2
A'C ' = A' B ' + B 'C ' 2 2 2
= x + x = 2x A'C ' = x 2
Xét tam giác A' AC ' vuông tại A' ta có 2 2 2
AC ' = A' A + A'C ' 2 2 2
 3a = x + 2x x = a
Thể tích của khối lập phương ABC . D A BCD   là 3 V = a .
Câu 68: (Câu 9 - Đề - BGD - 2020 - Đợt 2 - Mã đề - 104– 2021) Cho khối lăng trụ có diện tích đáy B = 6
và chiều cao h = 4 . Thể tích khối lăng trụ đã cho bằng A. 24 . B. 4 . C. 8 . D. 12 . Lời giải Chọn A
https://www.facebook.com/groups/toanvd.vdc Trang 44
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
Thể tích khối lăng trụ có diện tích đáy B = 6 và chiều cao h = 4 là: V = .
B h = 6.4 = 24 .
Câu 69: (Câu 4 - MĐ 104 - BGD&ĐT - Năm 2019) Thể tích của khối lăng trụ có diện tích đáy B và chiều cao h là 4 1 A. Bh . B. Bh . C. 3Bh . D. Bh . 3 3 Lời giải Chọn D
Thể tích của khối lăng trụ có diện tích đáy B và chiều cao h là: Bh .
Câu 70: (Câu 8 - MĐ 103 - BGD&ĐT - Năm 2019) Thể tích của khối lăng trụ có diện tích đáy B và chiều cao h là 4 1  A. Bh . B. 3Bh . C. Bh . D. Bh .  3 3  Lời giải Chọn D
Câu 71: (Câu 12 - MĐ 102-BGD&ĐT-Năm 2019) Thể tích của khối lăng trụ có diện tích đáy B và chiề u cao h là NHÓ 4 1 A. 3Bh . B. Bh . C. Bh . D. Bh . 3 3 M Lời giải G Chọn B IÁO
Thể tích V của khối lăng trụ có diện tích đáy B và chiều cao h là: V = Bh (đvtt). VI
Câu 72: (Câu 12 - MĐ 101-BGD&ĐT-Năm 2019) Thể tích khối lăng trụ có diện tích đáy B và chiều c Ê ao h N là T 4 1 A. 3 . Bh B. . Bh C. O . Bh D. . Bh 3 3 ÁN Lời giải VI Chọn B ỆT
Câu 73: (Câu 11 - MĐ 104 - BGD&ĐT - Năm 2018) Cho khối lăng trụ có đáy là hình vuông cạnh a v Nà AM
chiều cao bằng 2a . Thể tích của khối lăng trụ đã cho bằng 2 4 A. 3 a B. 3 a C. 3 2a D. 3 4a 3 3 Lời giải   Chọn C 2 3  Ta có: V
= S .h = a .2a = 2a . langtru day  
Câu 74: (Đề TNTHPT 2020 - mã đề 103) Cho khối lăng trụ có diện tích đáy B = 6 và chiều cao h = 3 .
Thể tích của khối lăng trụ đã cho bằng A. 3. B. 18. C. 6. D. 9. Lời giải Chọn B
Thể tích của khối lăng trụ đã cho là: V = . B h = 6.3 = 18.
Câu 75: (Câu 18 - Đề thi TNTHPT 2020 - mã đề 102) Cho khối lăng trụ có diện tích đáy B = 3 và chiều
cao h = 2 . Thể tích khối lăng trụ đã cho bằng A. 1. B. 3. C. 2. D. 6. Lời giải Chọn D
Thể tích khối lăng trụ V = Bh = 3.2 = 6
https://www.facebook.com/groups/toanvd.vdc Trang 45
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
Câu 76: (Câu 19 - Đề thi TNTHPT 2020 - mã đề 102) Cho khối lăng trụ có diện tích đáy B = 3 và chiều
cao h = 2 . Thể tích của khối lăng trụ đã cho bằng A. 1. B. 3 . C. 2 . D. 6 . Lời giải Chọn D
Thể tích khối lăng trụ là V = . B h = 3.2 = 6 .
Câu 77: (Đề tốt nghiệp THPT đợt 2 năm 2020 - mã đề 101) Cho khối lăng trụ có diện tích đáy B = 3 và
chiều cao h = 6 . Thể tích của khối lăng trụ đã cho bằng A. 9 . B. 18 . C. 3 . D. 6 . Lời giải Chọn B
Thể tích khối lăng trụ đã cho là: V = . B h = 3.6 = 18 . 
Câu 78: (Đề tốt nghiệp THPT đợt 2 năm 2020 - mã đề 101) Cho khối trụ có bán kính đáy r = 4 và chiề u 
cao h = 3. Thể tích của khối trụ đã cho bằng A. 48 . B. 4 . C. 16 . D. 24 . Lời giải NHÓ Chọn A
Thể tích của khối trụ đã cho là: 2
V =  r h = 48 . M GIÁO
Câu 79: (MĐ 104 - BGD&ĐT - Năm 2021) Cho khối hộp chữ nhật ABC . D A BCD
  có đáy là hình vuông
BD = 4a , góc giữa hai mặt phẳng ( ABD) và ( ABCD) bằng 0
60 . Thể tích của khối hộp chữ nhậVIt Ê đã cho bằng N 16 3 16 3 T A. 3 48 3a . B. 3 a . C. 3 a . D. 3 16 3a . O 9 3 ÁN Lời giải VI Chọn D ỆT NAM     
Ta có đáy ABCD là hình vuông có BD = 4a AB = 2 2a . Gọi I trung điểm .
BD Vì BD = 4a BI = AI = 2a . AA Tam giác A A
I vuông tại A có: 0 tan 60 =  A A  = 2 3a . AI
Thể tích của khối hộp chữ nhật đã cho bằng: V = S A A  = ( a)2 3 . 2 2 .2 3a = 16 3a . ABCD
Câu 80: (MĐ 103 - BGD&ĐT - Năm 2021) Cho khối hộp chữ nhật ABC . D A BCD
  có đáy là hình vuông,
BD = 2a , góc giữa hai mặt phẳng ( A B
D) và ( ABCD) bằng 60. Thể tích của khối hộp chữ nhật đã cho bằng 2 3 2 3 A. 3 a . B. 3 6 3a . C. 3 a . D. 3 2 3a . 9 3 Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 46
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 Chọn D
+) Ta có BD = 2a AC = 2 ; a AB = a 2 . +) S = (a )2 2 2 = 2a . ABCD  +) Góc giữa hai mặt phẳng ( A B
D) và ( ABCD) là góc A OA  
AA = AO tan A OA = .
a tan 60 = a 3 .  Vậy 2 3 V =  = =     AA .S a 3.2a 2 3a .  ABCD. A B C D ABCD
Câu 81: (Câu 44 - MĐ 102 - BGD&ĐT - Năm 2021) Cho khối hộp chữ nhật ABC .
D A' B 'C ' D ' có đáy là BD = a A' BD ABCD hình vuông,
4 , góc giữa hai mặt phẳng ( ) và (
) =30o. Thể tích của khối hộ NHÓ p chữ nhật đã cho bằng 16 3 16 3 M A. 3 a B. 3 48 3a C. 3 a D. 3 16 3a G 9 3 IÁO Lời giải Chọn C VI ÊN T O ÁN VI ỆT N AM
Gọi O là trung điểm của BD . Ta có: A  ' AB = A
 ' AD suy ra A'B = A'D suy ra A  ' BD cân. (
A' BD) ( ABCD) = BD
Mà A'O ⊥ BD  ((A B
D),( ABCD)) = A OA = 30 .  =30o .  AO ⊥ BD    A AA AA AA Aa o  Xét AO
A vuông tại A có: tan30 = = = =  2 3
A' A = 2a tan 30 = . AO AC BD 2a 3  2 2
Xét hình vuông ABCD có: BD = AB 2  AB = 2a 2. a 16 3
Vậy thể tích của khối hình hộp chữ nhật bằng: 2 V = A' . A AB = ( a )2 2 3 . 2 2 = 3 a . 3 3
Câu 82: (Câu 48 - MĐ 101 - BGD&ĐT - Năm 2021) Cho khối hộp chữ nhật ABC .
D A' B 'C ' D ' có đáy là
hình vuông, BD = 2a , góc giữa hai mặt phẳng ( A' BD) và ( ABCD) bằng 0 30 . Thể tích của khối
hộp chữ nhật đã cho bằng 2 3 2 3 A. 3 6 3a . B. 3 a . C. 3 2 3a . D. 3 a . 9 3 Lời giải Chọn D
https://www.facebook.com/groups/toanvd.vdc Trang 47
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
Gọi O là tâm hình vuông ABCD . Vì BD ⊥ OA và BD ⊥ AA' nên BD ⊥ ( A'OA)  BD ⊥ OA' 
Lại có ( A' BD) ( ABCD) = BD . Do đó (( A BD) ( ABCD)) 0 ' ,
= A'OA = 30 (Hình vẽ trên).  
Vì tứ giác ABCD là hình vuông có BD = 2a nên OA = a và AB = AD = a 2 .   a 3
Xét tam giác A' AO vuông tại A có OA = a và 0 A'OA = 30 nên 0 AA' = O . A tan 30 = . 3 a 3 2 3
Vậy thể tích khối hộp chữ nhật 3 V = A . B A . D AA' = a 2.a 2. = a . NHÓ 3 3    M
Câu 83: (MĐ 101 BGD&ĐT NĂM 2021-L2) Cho khối lăng trụ tam giác đều AB .
C A B C có cạnh bên bằn g G
2a , góc giữa hai mặt phẳng ( A' BC ) và ( ABC ) bằng 30 . Thể tích của khối lăng trụ đã cho bằng IÁO VI 8 3 8 3 8 3 A. 3 a . B. 3 a . C. 3 a . D. 3 8 3a . Ê 9 3 27 N T O Lời giải ÁN Chọn D VI ỆT NAM     
Gọi N là trung điểm BC ta có: BC ⊥ AN
BC ⊥ ( AA N
 ). Suy ra góc giữa hai mặt phẳng ( ABC) và ( ABC) là góc A NA = 30 BC ⊥ AAAAAA 2a
Xét tam giác vuông AA N  ta có tan A NA =  AN = = = 2a 3 AN tan A NA tan30
https://www.facebook.com/groups/toanvd.vdc Trang 48
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 Xét tam giác đề AB 3 2AN 2.2a 3
u ABC ta có AN =  AB = = = 4a 2 3 3 1
Suy ra diện tích tam giác ABC bằng: 2 .4 .2 a a 3 = 4a 3 . 2
Vậy thể tích khối lăng trụ AB . C A BC   bằng: 2 3 V = AA .  S = 2 . a 4a 3 = 8a 3 ABC
Câu 84: (MĐ 104 BGD&ĐT NĂM 2016-2017) Cho khối lăng trụ đứng AB . C A BC
  có đáy ABC là tam
giác cân với AB = AC = a , BAC = 120 . Mặt phẳng ( AB C
 ) tạo với đáy một góc 60. Tính th ể 
tích V của khối lăng trụ đã cho. 3 3 3 3  3a 9a a 3a A. V = . B. V = . C. V = . D. V = .  8 8 8 4  Lời giải NHÓ M GIÁO VI ÊN T O ÁN VI Chọn A Ệ
Gọi I là trung điểm của B C  . T N Trong 2 2 2 2 ABC  : B C   = A B   + A C   − 2A B  .A C  .cos B AC   = 3a AM 2 1 a 3 2 2S    a 3 a S =  = A B C  = = =    . a . a sin120 ; A I A B C 2 4 B C   2a 3 2 (  AB C
 )( AB C  ) = B C     
Ta có : AI ⊥ B C    AIA = 60 
A I ⊥ B C      a 3
Trong tam giác vuông AIA có AA = A I  .tan 60 = . 2 2 3 a 3 a 3 3a Vậy thể tích V = . = . 4 2 8
Câu 85: (Câu 38 - ĐTN - BGD&ĐT - Năm 2017) Cho lăng trụ tam giác AB . C A
B C có đáy ABC là tam
giác vuông cân tại A , cạnh AC = 2 2 . Biết AC tạo với mặt phẳng ( ABC ) một góc 60 và
AC = 4 . Tính thể tích V của khối đa diện ABC B C . 8 16 8 3 16 3 A. V = B. V = C. V = D. V = 3 3 3 3 Lời giải Chọn D
https://www.facebook.com/groups/toanvd.vdc Trang 49
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 B’ C’ A’ 4 B C H A
Phân tích: Tính thể tích của khối đa diện ABC
B C bằng thể tích khối của lăng trụ AB . C A B C 
trừ đi thể tích của khối chóp . A A B C .  
Giả sử đường cao của lăng trụ là CH . Khi đó góc giữa AC mặt phẳng ( ABC) là gó c CAH = 60 . CH 1 NHÓ Ta có: sin 60 =
CH = 2 3; S = 4 V = CH S = =  ; . ABCA BC . 2 3. . 2 2 8 3 . ABC ( )2 ACABC 2 M 1 1 8 3 8 3 16 3 V = CH S = V = ; V = V −V = − = .
ABBCC ABCA BCAA BC 8 3 AA BC . . ABC ABCA BC . . . . G 3 3 3 3 3 IÁO VI
Câu 86: (Câu 39 - MĐ 104 - BGD&ĐT - Năm 2018) Cho khối lăng trụ AB . C A BC
 , khoảng cách từ ÊC
đến đường thẳng BB bằng 5 , khoảng cách từ A đến các đường thẳng BB và CC lần lượ N t T
bằng 1 và 2 , hình chiếu vuông góc của A lên mặt phẳng ( AB C
 ) là trung điểm M của B C  O ÁN và A M
 = 5 . Thể tích của khối lăng trụ đã cho bằng VI 2 5 2 15 15 A. B. C. 5 D. Ệ 3 3 3 T N Lời giải AM Chọn B     
Gọi J , K lần lượt là hình chiếu vuông góc của A lên BB và CC , H là hình chiếu vuông góc
của C lên BB
Ta có AJ ⊥ BB ( ) 1 .
AK ⊥ CC  AK ⊥ BB (2) . Từ ( )
1 và (2) suy ra BB ⊥ ( AJK )  BB ⊥ JK JK //CH JK = CH = 5 . Xét AJK có 2 2 2
JK = AJ + AK = 5 suy ra A
JK vuông tại A . 5
Gọi F là trung điểm JK khi đó ta có AF = JF = FK = . 2
https://www.facebook.com/groups/toanvd.vdc Trang 50
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
Gọi N là trung điểm BC , xét tam giác vuông ANF ta có: 5 AF cos NAF = 2 = 1
=  NAF = 60 . ( AN = AM = 5 vì AN//AM và AN = AM ). AN 5 2 1 S Vậy ta có S = 1 AJ.AK = .1.2 = 1  S = 1 S .cos 60 AJKS  = = = 2 . AJK     2 2 AJK ABC ABC cos 60 1 2
Xét tam giác AMA vuông tại M ta có MAA = AMF = 30 hay AM = 15 A M  .tan 30 = . 3
Vậy thể tích khối lăng trụ là V = 15 2 15 AM.S = .2 = . ABC   3 3 
Câu 87: (MĐ 103 - BGD&ĐT - Năm 2018) Cho khối lăng trụ AB .
C A' B 'C ' , khoảng cách từ C đến đườ  ng BB BB CC  thẳng
' bằng 2, khoảng cách từ A đến các đường thẳng ' và
' lần lượt bằng 1 và 3
, hình chiếu vuông góc của A lên mặt phẳng (A' B 'C ') là trung điểm M của B 'C ' và A' M = 2
. Thể tích của khối lăng trụ đã cho bằng 2 3 NHÓ A. 3 . B. 2 . C. . D. 1 3 Lời giải M G Chọn B IÁO VI ÊN T O ÁN VI ỆT NAM     
Gọi A , A lần lượt là hình chiếu của A trên BB ' , CC ' . Theo đề ra AA = 1; AA = 3; A A = 2. 1 2 1 2 1 2 Do 2 2 2
AA + AA = A A nên tam giác AA A vuông tại A . 1 2 1 2 1 2 A A
Gọi H là trung điểm A A thì 1 2 AH = =1. 1 2 2
Lại có MH BB '  MH ⊥ (AA A )  MH ⊥ AH suy ra 2 2 MH = AM − AH = 3 . 1 2 MH 3
nên cos((ABC), (AA A )) = cos(MH , AM ) = cos HMA = = . 1 2 AM 2 SAA A Suy ra 1 2 S =
=1. Thể tích lăng trụ là V = AM S = 2 . ABC
cos(( ABC), ( AA A )) ABC 1 2
Nhận xét. Ý tưởng câu này là dùng diện tích hình chiếu S ' = S cos .
https://www.facebook.com/groups/toanvd.vdc Trang 51
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
Câu 88: (MĐ 102 - BGD&ĐT - Năm 2018) Cho khối lăng trụ AB .
C A'B'C' , khoảng cách từ C đến BB '
là 5 , khoảng cách từ A đến BB ' và CC ' lần lượt là 1; 2 . Hình chiếu vuông góc của A lên 15
mặt phẳng A' B 'C ' là trung điểm M của B 'C ' , A' M =
. Thể tích của khối lăng trụ đã cho 3 bằng 15 2 5 2 15 A. . B. . C. 5 . D. 3 3 3 Lời giải Chọn D AB    FI NHÓ E C M GIÁO VI Ê B' N A' T O ÁN K M VI ỆT NAM
Kẻ AI ⊥ BB' , AK ⊥ CC ' ( hình vẽ ).
Khoảng cách từ A đến BB ' và CC ' lần lượt là 1; 2  AI = 1, AK = 2 .  15 15 
Gọi F là trung điểm của BC . A' M =  AF = 3 3  
AI ⊥ BB '  BB' ⊥ AIK BB' ⊥ IK  Ta có ( ) . BB ' ⊥ AK
Vì CC ' BB '  d(C, BB ') = d (K, BB ') = IK = 5  AIK vuông tại A .
Gọi E là trung điểm của IK EF BB '  EF ⊥ ( AIK )  EF ⊥ AE .
Lại có AM ⊥ ( ABC ) . Do đó góc giữa hai mặt phẳng ( ABC ) và ( AIK ) là góc giữa EF và AM 5 bằng góc 2
AME = FAE . Ta có cos = AE FAE = 3 =  FAE = 30. AF 15 2 3
Hình chiếu vuông góc của tam giác ABC lên mặt phẳng ( AIK ) là AIK nên ta có: 3 2 S = S
cos EAF 1 = S  = S . AIK ABC ABC 2 ABC 3
https://www.facebook.com/groups/toanvd.vdc Trang 52
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 15 3
Xét AMF vuông tại A : tan = AF AMFAM =  AM = 5 . AM 3 3 2 2 15 Vậy V = 5. = .
ABC.A' B 'C ' 3 3
Câu 89: (Câu 42 - MĐ 101 - BGD&ĐT - Năm 2018) Cho khối lăng trụ AB . C A BC
 , khoảng cách từ C
đến đường thẳng BB bằng 2 , khoảng cách từ A đến các đường thẳng BB và CC lần lượt
bằng 1 và 3 , hình chiếu vuông góc của A lên mặt phẳng ( AB C
 ) là trung điểm M của B C   2 3  và AM =
. Thể tích của khối lăng trụ đã cho bằng  3  2 3  A. 2 B. 1 C. 3 D.  3 Lời giải Chọn A NHÓ A C2 M GIÁO B2 VI C' Ê A N T M M O ÁN VI B' ỆT N A' AM A' C1 H T H B1 T
Cắt lăng trụ bởi một mặt phẳng qua A và vuông góc với AA ta được thiết diện là tam g  iác  
A B C có các cạnh A B  =1; A C  = 3 ; B C = 2 . 1 1 1 1 1 1  Suy ra tam giác A B
C vuông tại A và trung tuyến A H
 của tam giác đó bằng 1. 1 1
Gọi giao điểm của AM và A H  là T . 2 3 1 Ta có: AM = ; A H  =1  MH = . Suy ra MA H  = 30. 3 3 A M  Do đó MA A  = 60 4  AA = = . cos MA A  3
Thể tích khối lăng trụ AB . C A BC
  bằng thể tích khối lăng trụ A B
C .AB C và bằng 1 1 2 2 4 3
V = AA .S =  =  2 . A 1 B 1 C 3 2
https://www.facebook.com/groups/toanvd.vdc Trang 53
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
Câu 90: (ĐTK - BGD&ĐT - L1 - Năm 2020) Cho hình hộp ABC .
D A' B 'C ' D ' có chiều cao bằng 8 và diện
tích đáy bằng 9. Gọi M , N, P và Q lần lượt là tâm của các mặt bên ABB ' A', BCC ' B ',CDD 'C '
và DAA' D' . Thể tích của khối đa diện lồi có các đỉnh là các điểm ,
A B, C, D, M , N , P và Q bằng A. 27. B. 30. C. 18. D. 36 Lời giải Chọn B      NHÓ M GIÁO VI
Mặt (MNPQ) cắt các cạnh AA', BB',CC', DD' tại A , B ,C , D . Thể tích khối đa diện cần tìm là 1 1 1 1 ÊN V , thì: T = − − − − O V V V V V V 1 A 1 B 1 C 1
D . A ' B ' C ' D ' A '.QM 1 A B '.M 1 NB C '.P 1 NC D '.QP 1 D ÁN 8.9 V = − 4 . VI 2 24 Ệ  = T V 30 N
Câu 91: (Câu 46 - MĐ 104 - BGD&ĐT - Năm 2019) Cho hình lăng trụ AB .
C A B C có chiều cao bằ AM ng
4 và đáy là tam giác đều cạnh bằng 4 . Gọi M , N và P lần lượt là tâm của các mặt bên ABB A
, ACC A và BCC B . Thể tích của khối đa diện lồi có các đỉnh là các điểm ,
A B,C, M , N, P bằng 14 3 20 3  A. . B. 8 3 . C. 6 3 . D. .  3 3  Lời giải Chọn C Cách 1:
https://www.facebook.com/groups/toanvd.vdc Trang 54
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
Chia đôi khối lăng trụ bằng mặt phẳng (MNP). Khi đó ta có (MNP)  BB = F thì 1 V = V ABC.EFG ABC.    2 A B C Lại có V =V −V −V −V ABC.MNP ABC.EFG B.MPF . A EMN C.NPG 1 1 1 1 Dễ thấy V = V = V = V = . V =    V B.MPF . A EMN C.NPG ABC.EFG ABC.A B C ABC.    4 4 2 8 A B C 2  1 1  3 3 4.4 3 Tức là V = − V = = =      V    . 6 3. ABC.MNP ABC. A B C ABC.  2 8  8 A B C 8 4 Cách 2      NHÓ 2 M 4 3 S = = 4 3 ; V =    V ABC ABC.A B C G 4 IÁO
Hạ M , N , P lần lượt vuông góc AB, AC, BC , 1 1 1 VI
khi đó M , N , P lần lượt là trung điểm các cạnh AB, AC, BC 1 1 1 ÊN Khi đó V =V +V +V +V ABCMNP MNP.M N P B.MPP M C.NPP N . A MNN M 1 1 1 1 1 1 1 1 1 T 1 1 1 1 O Dễ thấy S = S ; MM = AA nên V = V =    V ÁN MNP 4 ABC 1 2 MNP.M N P ABC. A B C 1 1 1 8 8 VI
Do đáy là tam giác đều nên V =V =V B.MPP M C.NPP N . A MNN M 1 1 1 1 1 1 Ệ 1 1 T Ta có d ( ; B (MPPM = d ; B ACC A   ; S = S nên 1 1 )) ( ( )) N   2 MPP M ACC A 1 1 4 AM 1 1 2 1 V = V = =   . V V . B.MPP M B. ACC A 1 1 8 8 3 12 1 1 1 1 3 3 Do đó V = V + V + V +
V = V = .4.4 3 = 6 3 .  ABCMNP 8 12 12 12 8 8 
Câu 92: (Câu 49 - MĐ 103 - BGD&ĐT - Năm 2019) Cho lăng trụ AB .
C A' B 'C ' có chiều cao bằng 6 v à 
đáy là tam giác đều cạnh bằng 4. Gọi M, N, P lần lượt là tâm của các mặt b ên
ABB ' A', ACC ' A', BCC ' B ' . Thể tích của khối đa diện lồi có các đỉnh là các điểm ,
A B,C, M , N, P bằng A. 9 3 . B. 10 3 . C. 7 3 . D. 12 3 . Lời giải Chọn A
https://www.facebook.com/groups/toanvd.vdc Trang 55
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 A C B N K I P M J C' A' B'   3 V = 6.16 = 24 3 ’ 
ABC. A' B 'C ' 4 
Thể tích cần tìm là V = V =V  1 ABC.MNP
A' B'C '.MNP V = V =V =V 2 A'. AMN B'.BMP C 'CNPV = 2V + 3V
ABC. A' B'C ' 1 2 NHÓ 1 1 1 1 1 S = SV = V = . V = V AMN AB 'C ' 2
A'. AB 'C '
ABC. A' B 'C '
ABC. A' B 'C ' 4 4 4 3 12 M 1 3 G  V = 2V + VV = V = 9 3
ABC. A' B 'C ' 1
ABC. A' B 'C ' 1
ABC. A'B 'C ' IÁO 4 8
Câu 93: (Câu 49 - MĐ 102-BGD&ĐT-Năm 2019) Cho lăng trụ AB . C A BC
  có chiều cao là 8 và đáy l VIà
tam giác đều cạnh bằng 4 . Gọi M , N và P lần lượt là tâm của các mặt bên ABB A  , ACC A  ÊN và BCC B
 . Thể tích của khối đa diện lồi có các đỉnh là các điểm A , B , C , M , N , P bằng T O 28 3 40 3 ÁN A. 12 3 . B. 16 3 . C. . D. . 3 3 VI Lời giải ỆT Chọn A N Cách 1: AM      2 4 . 3 Ta có V = V = =
h = d ( A , ABC )    8. 32 3 , gọi ( . ABCA B C 4 1 h V Ta có V = . .S = . MABC 3 2 ABC 6
https://www.facebook.com/groups/toanvd.vdc Trang 56
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 1 h S V V = . . ABC = . MNPC 3 2 4 24 1 d ABCC B   S   V    V V = .d ( 1 ( , ) M ,( PBC )) ( ) BCCB A . .S = . BCC B = = . MBCP 3 PBC 3 2 4 8 12 V Tương tự V = . MNAC 12 3V Vậy V = V +V +V +V = = 12 3 . MNPABC MABC MNAC MNPC MBCP 8 Cách 2:
Đặc biết hóa cho lăng trụ đứng.      NHÓ M GIÁO VI ÊN T O ÁN VI Ệ T
Gọi E , F , G lần lượt là trung điểm của AB , AC , BC . N AM Ta có: V = ME.S = 4 3 . MNP.EFG EFG 1 1 1 1 8 3 V
= d B, MEGP .S
= . BF.ME.EG = . 3.4.2 = . B.MEGP ( ( )) 3 MEGP 3 2 3 3  8 3  Tương tự: V =V = . . A MNFE C.PNFG  3  8 3  Vậy V =V +V +V +V = 4 3 + 3. =12 3 . MNPABC MNP.EFG B.MEGP . A MNFE C.PNFG 3
Câu 94: (Câu 47 - MĐ 101-BGD&ĐT-Năm 2019) Cho lăng trụ AB .
C A' B 'C ' có chiều cao bằng 8 và đáy
là tam giác đều cạnh bằng 6 . Gọi M , N và P lần lượt là tâm của các mặt bên ABB' A' , ACC ' A'
và BCC ' B ' . Thể tích của khối đa diện lồi có các đỉnh là các điểm ,
A B, C, M , N , P bằng: A. 27 3 . B. 21 3 . C. 30 3 . D. 36 3 . Lời giải Chọn A
https://www.facebook.com/groups/toanvd.vdc Trang 57
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
Gọi A , B ,C 1 1
1 lần lượt là trung điểm của các cạnh AA ', BB ', CC ' .   Khối lăng trụ AB . C A B C
1 1 1 có chiều cao là 4 là tam giác đều cạnh 6 .  . A A MN BB MP CC NPBa khối chóp 1 , 1 , 1
đều có chiều cao là 4 và cạnh là tam giác đều cạnh 3 Ta có : 2 6 3 1 9 3 V = V − V +V +V = 4 − 3  4 = 27 3 ABC.MNP ABC. 1 A 1 B 1 C
( .A 1AMN B. 1BMP C. 1CNP) 4 3 4 NHÓ
Câu 95: (Câu 47 - ĐTK - BGD&ĐT - Năm 2019) Cho khối lăng trụ AB . C A BC
  có thể tích bằng 1. Gọi M , N M
lần lượt là trung điểm các đoạn thẳng AA và BB . Đường thẳng CM cắt đường thẳ ng G C A
  tại P , đường thẳng CN cắt đường thẳng C B
  tại Q . Thể tích của khối đa diện lồIÁO i A MPB NQ bằng VI 1 1 2 A. 1. B. . C. . D. . Ê 3 2 3 N T Lời giải O ÁN Chọn D A C VI ỆT N B AM M NPA' C'    B' Q S
+) Ta có A là trung điểm 
PC ; B là trung điểm QC . Do đó S =  =  4 C PQ S    4 . C PQ C A B SC AB S   C PQ 1 4 +) V = = = =  .V    4V    4 V     . C.C PQ C. A B C C. A B C ABC .  S     3 A B C  3 C A B 1  A MB NC C   1  1 1  2 +) Mặt khác V = + + = + + =    . V      . 1 V      . A B C .MNC ABC.A B C ABC. 3  A AB BC C   3  2 2 A B C  3 4 2 2 +) Do đó V = − = − =   VV    . A MPB NQ C.C PQ A B C .MNC 3 3 3
Câu 96: (Câu 44 - MĐ 101 - BGD&ĐT - Năm 2017) Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N
lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua
D. Mặt phẳng
https://www.facebook.com/groups/toanvd.vdc Trang 58
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V. Tính V. 3 7 2a 3 11 2a 3 13 2a 3 2a A. V = B. V = C. V = D. V = 216 216 216 18 Lời giải Chọn B
(MNE) chia khối tứ diện ABCD thành 2 khối đa diện ( : A .
C MNPQ và ( : B . D MNPQ 2 ) 1 ) A Q E D B   P C NHÓ
(MNE) cắt AD tại Q, cắt CD tại P. V = V − V AC.MNPQ E. AMNC E. ACPQ M 1 G V
= d E, AMNC .S E. AMNC ( ( )) IÁO 3 AMNC 1 VI
= d (E, (ABC)).(S −  S ABCBMN ) Ê 3 N 1  1  T
= d (E, (ABC)). S −   S ABCABC  O 3  4  ÁN 1 3 3 VI
= .2.d (D, (ABC)). S =  V 3 4 ABC 2 ABCD ỆT 1 1 1 8 8 N V
= d E, ACPQ .S
= d B, ACD . S − S
= d B, ACD . S = V E. ACPQ ( ( )) ACPQ ( ( )) ( ACD DPQ ) ( ( ))  3 3 3 9 ACD 9 ABCD AM 3 8 11 11 2 11 2 3 3 V = V − V = V = . a = a AC. MNPQ 2 ABCD 9 ABCD 18 ABCD 18 12 216  
Câu 97: (MĐ 102 - BGD&ĐT - Năm 2018) Ông A dự định sử dụng hết 2
6, 7m kính để làm một bể c á
bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối gh  ép
có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm trò n đến hàng phần trăm). A. 3 1,57m . B. 3 1,11m . C. 3 1, 23m . D. 3 2, 48m Lời giải Chọn A
Gọi x là chiều rộng, ta có chiều dài là 2x 2 6, 7 − 2x
Do diện tích đáy và các mặt bên là 2
6, 7m nên có chiều cao h = , 6x 6, 7
ta có h  0 nên x  . 2 x − x − x
Thể tích bể cá là V ( x) 3 6, 7 2 = và V ( x) 2 6, 7 6 = = 6, 7 0  x = 3 3 6 Bảng biến thiên
https://www.facebook.com/groups/toanvd.vdc Trang 59
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022
Bể cá có dung tích lớn nhất bằng 3 1,57m .
Câu 98: (Câu 31 - MĐ 101 - BGD&ĐT - Năm 2018) Ông A dự định dùng hết 2
6,5m kính để làm một
bể cá có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng. Bể cá có dung tíc h
lớn nhất bằng bao nhiêu.  A. 3 2, 26 m B. 3 1, 61 m C. 3 1,33 m D. 3 1,50 m   Lời giải Chọn D a b c NHÓ M GIÁO VI ÊN T O ÁN
Giả sử hình hộp chữ nhật có kích thước như hình vẽ. Ta có dung tích của bể cá: V = abc 2 VI  −  6, 5 2b
ab + 2bc + 2ac = 6, 5 2
2b + 6bc = 6,5 c = Ệ
Mặt khác theo giả thiết ta có:      6b T a = 2ba = 2b N a = 2b AM 2 6,5 − 2 3 6,5 − 2 2 Khi đó = b V 2b .  = b b V . 6b 3 −  Xét hàm số: ( ) 3 6,5 2 = b b f b . Có BBT  3     39 
Vậy bể cá có dung tích lớn nhất là: 3 f   =1,50   m . 6  
Câu 99: (MĐ 103 - BGD&ĐT - Năm 2018) Ông A dự định sử dụng hết 2
5 m kính để làm một bể cá bằng
kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng. Bể cá có dung tích
lớn nhất bằng bao nhiêu? A. 3 1, 01 m . B. 3 0,96 m . C. 3 1,33 m . D. 3 1,51 m
https://www.facebook.com/groups/toanvd.vdc Trang 60
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TỔ 5 – NĂM HỌC 2021 - 2022 Lời giải Chọn A A' D' B' C' y 2 x A D x B C Gọi ,
x y lần lượt là chiều rộng và chiều cao của bể cá. Ta có thể tích bể cá 2 V = 2x y . Theo đề bài ta có: 2
2xy + 2.2xy + 2x = 5 2
 6xy + 2x = 5  2 5 − 2x   y =  6x  2 3 5 − 2x 5x − 2x 2 5 − 6x 5 2      V = 2x = V = 2
V = 0  5 − 6x = 0  x = 6x 3 3 6 NHÓ M GIÁO VI Ê 5 30 N 3  V = 1,01 m . max T 27 O ÁN
Câu 100: (Câu 32 - MĐ 104 - BGD&ĐT - Năm 2018) Ông A dự định sử dụng hết 2 5,5 m kính để VI làm Ệ
một bể cá bắng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng. B Tể N
cá có dung tích lớn nhất bằng bao nhiêu? AM A. 3 1,17 m B. 3 1, 01 m C. 3 1,51 m D. 3 1, 40 m Lời giải Chọn A
Gọi x, 2x, h lần lượt là chiều rộng, dài, cao của bể cá.  2 5,5 − 2x  Ta có 2
2x + 2( xh + 2xh) = 5,5  h = .  6x  2 5,5 − 2x 1 2 3
Thể tích bể cá V = 2x .
= (5,5x − 2x ) . 6x 3 1 5,5 / 2 V = (5, 5 − 6x ) . / V = 0  x = . 3 6 11 33 Lập BBT suy ra 3 V = 1,17 m . max 54
https://www.facebook.com/groups/toanvd.vdc Trang 61