30 trang 25 lượt tải

Bài toán tương giao giữa hai đồ thị Toán 12

49

Tài liệu gồm 30 trang, trình bày lý thuyết trọng tâm, các dạng toán trọng tâm kèm phương pháp giải và bài tập trắc nghiệm tự luyện chuyên đề bài toán tương giao giữa hai đồ thị, có đáp án và lời giải chi tiết; hỗ trợ học sinh lớp 12 trong quá trình học tập chương trình Toán 12 phần Giải tích chương 1.

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số 375 tài liệu

Môn: Toán 12 3.9 K tài liệu

Tác giả:

Profile

Mai Nguyệt

1 năm trước
Danh sách Quiz
/30
CHỦ ĐỀ 7: BÀI TOÁN TƯƠNG GIAO GIỮA HAI ĐỒ THỊ
I. LÝ THUYẾT TRỌNG TÂM
II. CÁC DẠNG TOÁN TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Tìm tọa độ giao điểm của hai đồ thị
Phương pháp giải:
Cho 2 hàm số
()y fx=
và
()y gx
=
có đồ thị lần lượt là
(
)
C
và
(
)
C
′
:
Lập phương trình hoành độ giao điểm của
( )
C
và
( )
C
′
là
( )
() ()f x gx= ∗
Giải phương trình tìm x thay vào
()fx
hoặc
()gx
để suy ra y và tọa độ giao điểm
Số nghiệm của phương trình
( )
∗
là số giao điểm của
( )
C
và
( )
C
′
22yx=−+
3
2yx x= ++
tại điểm duy nhất; ký hiệu
(
)
;
oo
xy
là tọa độ của điểm đó. Tìm
o
y
A.
4
o
y =
B.
0
o
y =
C.
2
o
y =
D.
1
o
y = −
Lời giải
Phương trình hoành độ giao điểm là:
33
22 2 30 0 2x xx x x x y− += ++⇔ + =⇔=⇒=
Vậy tọa độ giao điểm là
( )
0; 2 .
Chọn C.
Ví dụ 2: Biết rằng đồ thị hàm số
42
35yx x
=−+
và đường thẳng
9
y =
cắt nhau tại hai điểm phân biệt
( ) (
)
11 2 2
; ,B ; .Ax y x y
Tính
12
xx+
A.
12
3xx
+=
B.
12
0xx+=
C.
12
18xx+=
D.
12
5xx+=
Lời giải
Phương trình hoành độ giao điểm hai đồ thị là:
2
1
42 42 2
12
2
2
2
12
3 59 3 40 4 0
22
4
x
xx
xx xx x xx
xx
x
=
=−=
−+=⇔−−=⇔ ⇒=⇔ ⇒ ⇒+=
=−=−
=
Chọn B.
32
21yx x x= + −+
2
3yx x= −+
chung?
A. 0 B. 2 C. 1 D. 3
Lời giải
Phương trình hoành độ giao điểm đồ thị hai hàm số là
3 2 2 32
2 1 3 20x xx xx xx+ −+= −+⇔ + −=
( )
2
( 1) 2 2 0 1 0 1.x xx x x⇔ − + + = ⇔ −= ⇔ =
Suy ra hai đồ thị có một điểm chung. Chọn C.
32
31yx x=++
43
3yx x=+−
A. 1 B. 4 C. 3 D. 2
Lời giải
Phương trình hoành độ giao điểm đồ thị hai hàm số là
3 2 43 4 2
3 1 3 3 40x x xx x x+ += + −⇔ − − =
2
2
2
12
4
2
4
xx
x
x
x
=−=
⇔ ⇒=⇔ ⇒
= −
=
2 đồ thị hàm số có 2 giao điểm. Chọn D.
Ví dụ 5: Tìm số giao điểm của đồ thị hàm số
2
23
1
xx
y
x
−+
=
−
với đường thằng
36yx
= −
A. 3 B. 0 C. 1 D. 2
Lời giải
Phương trình hoành độ giao điểm của đồ thị
( )
C
và đường thẳng
( )
d
là
2
23
36
1
xx
x
x
−+
= −
−
( )
2 22 2
10 1 1
2 3 ( 1)(3 6) 2 3 3 9 6 2 7 3 0
x xx
xx x x xx xx xx
−≠ ≠ ≠

⇔ ⇔ ⇔∗

− += − − − += − + − +=

Hệ phương trình
( )
∗
có hai nghiệm phân biệt nên
( )
C
cắt
( )
d
tại hai điểm. Chọn D.
Ví dụ 6: Hoành độ các giao điểm của đồ thị hàm số
( )
21
2
x
yC
x
−
=
+
và đường thẳng
:2dy x
= −
là
A.
1
3
x
x
= −
=
B.
1
3
x
x
=
= −
C.
16
16
x
x
= +
= −
D.
1
3
x
x
= −
= −
Lời giải
Phương trình hoành độ giao điểm của đồ thị
( )
C
và
( )
d
là
2
2
21
2
2
21 4
x
x
x
x
xx
≠−
−
=−⇔
+
−= −
2
2
2
1
1
3
2 30
3
x
x
x
x
x
xx
x
≠−
≠−
= −
⇔ ⇔⇔
= −

=
− −=
=
. Chọn A.
Ví dụ 7: Biết đường thẳng
34
yx= +
cắt đồ thị hàm số
42
1
x
y
x
+
=
−
tại hai điểm phân biệt có tung độ
1
y
và
2
y
. Tính
12
yy+
A.
12
10yy+=
B.
12
11yy+=
C.
12
9yy+=
D.
12
1yy+=
Lời giải
Phương trình hoành độ giao điểm hai đồ thị là
2
1
20
42
34
2
1
1
x
xx
x
x
x
x
x
= −
−−=
+
= +⇔ ⇔
=
−
≠
Ta có:
11
12
22
11
11.
2 10
xy
yy
xy
=−=

⇒ ⇒+=

= =

Chọn B.
Ví dụ 8: Gọi A, B là giao điểm của hai đồ thị hàm số
3
1
x
y
x
−
=
−
và
1yx= −
. Diện tích tam giác OAB
bằng:
A.
32
2
B. 3 C.
3
2
D.
32
Lời giải
Phương trình hoành độ giao điểm:
2
1
12
3
1
21
1
20
≠
=−⇒ =
−
=−⇔ ⇔
=⇒=−
−
−−=
x
xy
x
x
xy
x
xx
Khi đó
9 9 32
AB = +=
và
( ) ( )
1
; ;: 10
2
dOAB dOd x y= + −= =
Do đó
( )
1 11 3
; . . .3 2
2 22
2
OAB
S d O AB AB= = =
. Chọn C.
Ví dụ 9: Đồ thị hàm số
2
yx x= −
và đồ thị hàm số
3
5y
x
= +
cắt nhau tại hai điểm A và B. Khi đó độ dài
AB là
A.
85AB =
B.
25AB =
C.
42AB
=
D.
10 2AB =
Lời giải
Phương trình hoành độ giao điểm đồ thị hai hàm số là
2
32
0
3
5
5 30
x
xx
x
xx x
≠
−=+ ⇔
− − −=
3 6 (3; 6)
42
1 2 ( 1; 2 )
xy A
AB
xyB
=⇒=

⇔ ⇒ ⇒=
=−⇒ = −

. Chọn C.
Ví dụ 10: Gọi M, N là giao điểm của đường thẳng
1
yx= +
và đường cong
24
1
x
y
x
+
=
−
. Khi đó hoành độ
trung điểm I của đoạn thẳng MN bằng
A.
5
2
B.
5
2
−
C. 1 D. 2
Lời giải
Phương trình hoành độ giao điểm là
2
16
24
1 2 50
1
16
x
x
x xx
x
x
= +
+
= +⇔ − −= ⇔
−
= −
16
1
16
M
I
N
x
x
x
= +
⇒ ⇒=
= −
. Chọn C.
32
3 21yx x x=− +−
2
31yx x=−+
Tính độ dài AB.
A.
3AB =
B.
22AB =
C.
2AB =
D.
1AB =
Lời giải
Phương trình hoành độ giao điểm hai đồ thị là
32 2 32
321 31 4520xxx xx xxx− + −= − +⇔ − + − =
( ) ( )
2
1 (1; 1)
1 20 1
2 (2; 1)
xA
x x AB
xB
= −

⇔− −=⇔ → ⇒ =
= −

. Chọn D.
Dạng 2: Sự tương giao của đồ thị hàm số phân thức bậc nhất trên bậc nhất
Phương pháp giải:
Xét sự tương giao giữa đồ thị
( )
:
ax b
Cy
cx d
+
=
+
và đường thẳng
:y= + d kx
Phương trình hoành độ giao điểm của d và
( )
C
là:
( )
2
() 0
≠−
+
= +⇔ ∗
+
= + +=
d
x
ax b
kx
c
cx d
g x Ax Bx C
Bài toán biện luận số giao điểm của hai đồ thị
Trường hợp 1: Xét
0
A = ⇒
Kết luận về số giao điểm.
Trường hợp 2: Xét
0A ≠
+) d cắt
( )
C
tại hai điểm phân biệt
(
)
0gx⇔=
hai nghiệm phân biệt
khác
2
2
40
. .0
B AC
d
d dd
c
g A BC
c cc
∆= − >
−
⇔
− −−
 
= + +≠
 
 
+) d cắt
(
)
C
tại điểm duy nhất
( )
gx⇔
có nghiệm kép khác
d
c
−
hoặc
( )
gx
có hai nghiệm phân
biệt trong đó có một nghiệm
()
()
0
0
0
0
gx
gx
d
g
c
d
x
c
d
g
c
∆=
−

≠


−
= ⇔
∆>
−

=


+) d không cắt
( )
C
( )
gx⇔
vô nghiệm hoặc có nghiệm kép bằng
()
()
0
0
0
gx
gx
d
c
d
g
c
∆<
∆=
−
⇔
−

=


Bài toán liên quan đến tính chất các giao điểm
Phần này, ta chỉ xét bài toán mà có liên quan đến d cắt
( )
C
tại hai điểm phân biệt.
Bước 1. Tìm điều kiện để d cắt
( )
C
tại hai điểm phân biệt
( )
0gx⇔=
có hai nghiệm phân biệt khác
( )
2
2
40
1
. .0
B AC
d
d dd
c
g A BC
c cc
∆= − >
−
⇔
− −−
 
= + +≠
 
 
Bước 2. Khi đó gọi
11 2 2
( ; ), ( ; )++A x kx B x kx
là tọa độ hai giao điểm
Với
12
,xx
là hai nghiệm của phương trình
() 0gx=
nên theo định lý Viet ta có
12
12
B
xx
A
C
xx
A
+=−
=
Bước 3. Theo yêu cầu bài toán, ta tìm giá trị của tham số chú ý đối chiếu với điều kiện (1) để chọn đáp án
đúng.
Chú ý:
•
( )
2
22
1 2 1 2 12
2
x x x x xx+= + −
•
( ) ( )
22
1 2 1 2 12
4x x x x xx−=+−
•
( ) (
)
22
AB AB
AB x x y y= − +−
•
( )
1
;.
2
IAB
S d I AB AB
=
• Tam giác IAB vuông tại
.0I IA IB
⇔=
 
• Trọng tâm tam giác IAB là
;
33
I A BI A B
xx xy y y
G
++ ++



( )
:2 0d x ym− +=
3
1
x
y
x
−
=
+
tại hai điểm phân biệt.
A.
3 42 3 42
22
m
−+
<<
B.
3 42 3 42m− < <+
C.
3 42
2
3 42
2
m
m
−
<
+
>
D.
3 42
3 42
m
m
<−
>+
Lời giải
Ta có:
:
22
xm
dy= +
. Phương trình hoành độ giao điểm là:
3
12
x xm
x
−+
=
+
( )
2
1
( 1) 6 0
x
gx x m x m
≠−
⇔
= + − + +=
Để d cắt đồ thị hàm số
3
1
x
y
x
−
=
+
tại 2 điểm phân biệt thì
() 0gx=
phải có 2 nghiệm phân biệt
khác
2
2
3 42
( 1) 4( 6) 0
1 6 23 0
( 1) 8 0
3 42
m
mm
mm
g
m
>+
∆= − − + >
−⇔ ⇔ − − > ⇔
−=≠
<−
. Chọn D.
1yx= +
2
1
xm
y
x
+
=
−
tại hai điểm phân biệt có hoành độ dương.
A.
21
m
− < <−
B.
1m <−
C.
1m <
D.
21
m
−< <
Lời giải
Điều kiện:
1x ≠
. Phương trình hoành độ giao điểm
( )
2
2
1 2 10
1
xm
x x xm
x
+
+= ⇔ − − −= ∗
−
Để cắt nhau tại hai điểm phân biệt có hoành độ dương thì phương trình (*) có hai nghiệm dương phân biệt
khác
0 1 10
2
0 20
1 12 1
0 10
2
22
m
m
S
mm
Pm
m
mm
′
∆> + + >

>−

>>

⇔ ⇔ ⇔ <− ⇔− < <−

> − −>

≠−

≠− ≠−

. Chọn A.
Ví dụ 3: Cho hàm số
(
)
1
1
x
yC
x
+
=
−
và đường thẳng
:dy x m= +
. Gọi S là tập hợp các giá trị của m để d
cắt
( )
C
tại 2 điểm phân biệt có hoành độ
12
;xx
thỏa mãn
22
12
9xx+=
. Tổng các phần tử của tập hợp S là:
A. – 2 B. 3 C. 2 D. – 1
Lời giải
Phương trình hoành độ giao điểm của
( )
C
và d là
( )
( )
2
1
1
1
( 2) x m 1 0
1
x
x
xm
gx x m
x
≠
+
=+⇔
= + − − −=
−
Để đồ thị
( )
C
cắt d tại 2 điểm phân biệt
() 0
gx⇔=
có 2 nghiệm phân biệt khác 1.
( )
2
( 2) 4( 1) 0
*
(1) 2 0
mm
g
∆= − + + >
⇔
=−≠
. Khi đó gọi
12
;xx
là nghiệm của PT
() 0gx=
Theo Viet ta có:
12
12
2
1
xx m
xx m
+=−
=−−
Ta có:
22 2 2 2
1 2 1 2 12
3
( ) 2 (2 ) 2( 1) 2 6 9
1
m
x x x x xx m m m m
m
=
+ = + − = − + + = − +=⇔
= −
(thỏa mãn (*))
Vậy
{ }
3; 1 2ST= −⇒=
.Chọn C.
Ví dụ 4: Cho hàm số:
21
()
1
x
yC
x
−
=
+
và đường thẳng
:2dy x m= +
. Gọi S là tập hợp các giá trị của m để
d cắt
(
)
C
tại 2 điểm phân biệt có hoành độ
12
;xx
thỏa mãn
12
1
2
xx−=
. Tổng các phần tử của tập hợp S
là:
A. 8 B. 9 C. 10 D. -1
Lời giải
Phương trình hoành độ giao điểm của
( )
C
và d:
2
1
21
2
1
() 2 1 0
x
x
xm
x
g x x mx m
≠−
−
= +⇔
+
= + + +=
Để đồ thị
( )
C
cắt d tại 2 điểm phân biệt
() 0gx⇔=
có 2 nghiệm phân biệt khác -1.
2
8( 1) 0
(*)
( 1) 3 0
mm
g
∆= − + >
⇔
−=≠
. Khi đó gọi
12
;xx
là nghiệm của PT
() 0
gx=
Theo Viet ta có:
12
12
2
1
2
m
xx
m
xx
−
+=
+
=
Khi đó
22
12 12 12 12
11 1
( ) ( )4
24 4
xx xx xx xx
−=⇔− =⇔+ − =
2
9
1
2( 1)
1
44
m
m
m
m
=
⇔ − +=⇔
= −
(t/m)
Vậy
{ }
9; 1 8ST= −⇒=
. Chọn A.
Ví dụ 5: Cho hàm số
1
()
2
x
yC
x
+
=
−
và đường thẳng
:dy x m= +
. Số các giá trị của tham số m để d cắt (C)
tại 2 điểm phân biệt A, B sao cho
42AB =
là
A. 2 B. 1 C. 0 D. 3
Lời giải
Phương trình hoành độ giao điểm của
( )
C
và d:
2
2
1
2
( ) ( 3) 2 1 0
x
x
xm
x
gxx m xm
≠
+
=+⇔
−
= + − − −=
(1)
Để đồ thị (C) cắt d tại 2 điểm phân biệt
() 0gx⇔=
có 2 nghiệm phân biệt khác 2.
( )
2
( 3) 4(2 1) 0
(2) 3 0
mm
g
∆= − + + >
⇔∗
=−≠
Khi đó gọi
11 2 2
( ; ); ( ; )Ax x m Bx x m++
là 2 tọa độ các giao điểm
Theo Viet ta có:
12
12
3
21
xx m
xx m
+=−
=−−
Ta có:
22 2 2
12 12 12 12 12
()()2()2()4AB xx xx xx xx xx

= − +− = − = + −

22 2
1
2 (3 ) 4( 2 1) 2( 2 13) 4 2 2 3 0 ( / )
3
m
m m mm mm tm
m
=

= − −−−= ++= ⇔+−=⇔

= −
Vậy
3; 1mm=−=
là các giá trị cần tìm. Chọn A.
Ví dụ 6: Cho hàm số
21
()
1
x
yC
x
+
=
+
và đường thẳng
:2
dy x m
= +
. Số các giá trị của m để d cắt (C) tại 2
điểm phân biệt A, B sao cho
. 10OA OB = −
 
trong đó O là gốc tọa độ.
A. 2 B. 1 C. 0 D. 3
Lời giải
Phương trình hoành độ giao điểm của
( )
C
và d:
2
1
21
2
1
() 2 1 0
x
x
xm
x
g x x mx m
≠−
+
= +⇔
+
= + + −=
(1)
Để đồ thị (C) cắt d tại 2 điểm phân biệt
() 0gx⇔=
có 2 nghiệm phân biệt khác -1.
( )
2
8(m 1) 0
( 1) 1 0
m
g
∆= − − >
⇔∗
−=≠
Khi đó gọi
11 2 2
( ;2 ); ( ;2 )Ax x m Bx x m++
là 2 tọa độ các giao điểm
Theo Viet ta có:
12
12
2
1
2
m
xx
m
xx
−
+=
−
=
Khi đó
( )
2 22
1 2 1 2 12 1 2
55
. . (2 )(2 ) 5 2 10
2
m
OA OB x x x m x m x x m x x m m m
−
= + + += + ++= −+=−
 
( )
3/m tm⇔=−
. Vậy
3
m = −
là các giá trị cần tìm. Chọn B.
Ví dụ 7: Cho hàm số
1
()
2
−
=
−
x
yC
x
và đường thẳng
:dy x m=−+
. Gọi m là giá trị để d cắt
( )
C
tại 2 điểm
phân biệt A, B sao cho trọng tâm tam giác OAB thuộc đường thẳng
0xy
+=
. Tính độ dài AB khi đó.
A.
22AB =
B.
10AB
=
C.
5AB
=
D.
10AB
=
Lời giải
Phương trình hoành độ giao điểm của
( )
C
và d:
2
2
1
2
( ) ( 1) 2 1 0
x
x
xm
x
gx x m x m
≠
−
=−+ ⇔
−
= − + + −=
(1)
Để đồ thị (C) cắt d tại 2 điểm phân biệt
() 0gx⇔=
có 2 nghiệm phân biệt khác 2.
( ) ( )
( )
2
1 42 1 0
(1) 1 0
mm
g
∆= + − − >
⇔∗
=−≠
Khi đó gọi
11 2 2
( ; ); ( ; )Ax x m Bx x m−+ −+
là 2 tọa độ các giao điểm
Theo Viet ta có:
12
12
1
21
xx m
xx m
+=+
= −
Gọi G là trọng tâm tam giác OAB ta có
12
12
0
1
11
33
;
0
1
33
33
G
G
xx
m
x
mm
G
x mx m
m
y
++
+
= =
+−

⇒

−+− ++
−

= =
Do điểm
0Gxy∈+ =
nên ta có:
(
)
11
0 0/
33
mm
m tm
+−
+ =⇔=
Khi đó
( )
( ) ( ) (
)
22 2
2
1 2 1 2 12
2 2 8 2 1 8 2 1 10 10AB x x x x x x m m AB= − = + − = + − −= ⇒ =
. Chọn D.
Ví dụ 8: Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số
22
1
mx m
y
x
+−
=
+
cắt đường
thẳng
:3dy x= +
tại hai điểm phân biệt A, B sao cho tam giác IAB có diện tích bằng 3, với
( 1; 1)I −
. Tính
tổng tất cả các phần tử của S.
A. 7 B. – 10 C. 3 D. 5
Lời giải
Phương trình hoành độ giao điểm là
( )
2
2( 2) 5 0
22
3
1
1
fx x m x m
mx m
x
x
x
= − − +− =
+−
=+⇔
+
≠−
Hai đồ thị có giao điểm khi và chỉ khi
( )
( ) (
)
( )
( )
2
0
25 0
10
12 2 5 0
mm
f
mm
′
∆>
− −− >

⇔∗

−≠
+ − +− ≠
Khi đó
( )
( )
22
2( 2)
2 2 8.
.5
AB
A B A B AB
AB
xx m
AB x x x x x x
xx m
+= −
⇒= − = + −
= −
2
8( 2) 8(5 )mm= −−−
Mặt khác
( )
( )
( )
2
2
2
113
11 1 1
; . ; 8( 2) 8(5 ).
22
22
11
∆
−−+
= = ⇒ = = −−−
+−
ABC
d Id S ABd Id m m
22 2
5
( 2) (5 ) 3 1 3 3 10 0
2
m
m m mm mm
m
=
= −−−= −−=⇔−−=⇔
= −
Kết hợp điều kiện (*) suy ra m = 5. Chọn D.
Ví dụ 9: Cho hàm số
21
1
x
y
x
+
=
−
và đường thằng
:2dy x m
= −
. Gọi S là tập hợp tất cả các giá trị thực của
tham số m để d cắt
( )
C
tại 2 điểm phân biệt A, B sao cho
5
4
OAB
S =
trong đó O là gốc tọa độ. Tính tổng tất
cả các phần tử của S.
A. 1 B. 0 C. 2 D. 3
Lời giải
Phương trình hoành độ giao điểm của
( )
C
và d:
2
1
21
2
1
( ) 2 ( 4) 1 0
x
x
xm
x
gx x m x m
≠
+
= −⇔
−
= − + + −=
(1)
Để đồ thị (C) cắt d tại 2 điểm phân biệt
() 0
gx
⇔=
có 2 nghiệm phân biệt khác 1.
( )
(
)
2
( 4) 8 1 0
(1) 3 0
mm
g
∆= + − − >
⇔∗
=−≠
Khi đó gọi
11 2 2
( ;2 ); ( ;2 )Ax x m Bx x m−−
là 2 tọa độ các giao điểm
Theo Viet ta có:
12
12
4
2
1
2
m
xx
m
xx
+
+=
−
=
Ta có:
( )
22 2 2 2
12 1 2 12 12 12
5
( )(2 2) 5( ) 5( )4 24
4
AB xx x x xx xx xx m

= −+− = − = +− = +

( )
O; AB
5
m
d =
. Khi đó:
( )
2
1 15
. O; AB 24
2 44
OAB
S AB d m m= = +=
(
)( )
(
) { }
42 2 2
24 25 1 25 0 1 / 1m m m m m tm S
⇔ + = ⇔ − + =⇔=± ⇒=±
. Chọn B.
Ví dụ 10: Cho hàm số
1
1
x
y
x
+
=
−
và đường thằng
2y xm=−+
. Tìm giá trị của tham số m để đồ thị hàm số
đã cho cắt nhau tại 2 điểm phân biệt A, B và trung điểm AB có hoành độ bằng
5
2
A. 8 B. 11 C. 9 D. 10
Lời giải
Phương trình hoành độ giao điểm của
(
)
C
và (d):
2
1
1
2
1
2 ( 1) 1 0
x
x
mx
x
x m xm
≠
+
=−⇔
−
− + + +=
(*)
Để đồ thị (C) cắt (d) tại 2 điểm phân biệt
(*)⇔
có hai nghiệm khác 1.
( )
2
7
( 1) 8 1 0
1
m
mm
m
>
⇔ + − + >⇔
<−
Khi đó gọi
,
AB
xx
là hoành độ của hai giao điểm A, B suy ra
(
)
1
5 9/
2
AB
m
x x m tm
+
+ == ⇒=
Chọn C.
Ví dụ 11: Tìm m để đường thẳng
:dy x m=−+
cắt đồ thị
( )
C
của hàm số
1
x
y
x
=
−
tại hai điểm phân biệt
A và B sao cho hai điểm A, B cách đều đường thẳng
:2 4 5 0xy∆ − +=
A.
3m =
B.
5m = −
C.
1m =
D.
5m =
Lời giải
Để A, B cách đều đường thẳng
:2 4 5 0xy∆ − +=
thì
AB ∆
hoặc trung điểm I của AB thuộc
∆
Do
AB d≡
không song song với
∆
nên bài toán thỏa mãn khi trung điểm của I của AB thuộc
∆
.
Phương trình hoành độ giao điểm hai đồ thị là
( )
2
0*
1
1
x mx m
x
xm
x
x
− +=
=−+ ⇔
−
≠
Hai đồ thị cắt nhau tại hai điểm khi và chỉ khi PT (*) có hai nghiệm phân biệt
1
x ≠
Suy ra
( )
(
)
2
;
(*) 0 4
40 ;
10 0
22
;
AA
A BA B
BB
Ax y
m
x xy y
mm I
mm m
Bx y
∆> >

++

⇒ − >⇔ ⇒ ⇒


−+≠ <


là trung điểm AB.
Hai điểm A, B cách đều đường thẳng
( ) ( )
:2 4 50 2 50
AB A B
xy I xx yy∆ − +=⇒∈∆⇒ + − + +=
( ) ( ) ( )
2 2 50 3 4 50 5 0 5
AB AB AB
xx xx m xx m m m⇔ + − − − + +=⇔ + − +=⇔− =⇔ =
Kết hợp với điều kiện
4
5
0
m
m
m
>
⇒=
<
. Chọn D.
Ví dụ 12: Số các giá trị nguyên của tham số
[ ]
20; 20m∈−
để đồ thị
( )
C
của hàm số
3
1
x
y
x
+
=
+
cắt đường
thẳng
:dy x m= −
tại hai điểm phân biệt A và B thỏa mãn
AOB
tù, với O là gốc tọa độ.
A. 22 B. 17 C. 16 D. 23
Lời giải
Phương trình hoành độ giao điểm
( )( )
2
1
1
3
13
1
() 3 0
x
x
x
xm
xmx x
x
g x x mx m
≠−
≠−
+
−= ⇔ ⇔

− +=+
+
= − − −=
Ta có d cắt
( )
C
tại 2 điểm phân biệt
()gx⇔
có 2 nghiệm phân biệt khác – 1.
( )
( ) (
) ( )
( )
( )
2
2
2
4 30
2 80
*
1 1 1 30
mm
m
m
m
g mm
∆= − − − >
+ +>

⇔ ⇔ ⇔∈

∈
− =− − −− −≠
Do
( ) ( )
11 2 2
, ; ,B ;AB d A x x m x x m∈⇒ − −
với
12
;xx
là 2 nghiệm của
() 0gx
=
Theo hệ thức Viet, ta có
12
12
3
xx m
xx m
+=
=−−
Khi đó:
( )
( )
( )
( )
11
12 1 1
22
;
..
;
OA x x m
OA OB x x x m x m
OB x x m
= −
⇒ = +− −
= −

 

2 22
12 1 2
2 ( ) 2( 3) 2( 3)xxmxxmmmmm= − ++=− +−+=− +
Do
AOB
tù nên
.
cos 0 . 0 2( 3) 0 3
.
OA OB
AOB OA OB m m
OA OB
= <⇔ <⇔− + <⇔ >−
 
 
Kết hợp
[ ]
20; 20
m
m
∈
⇒
∈−
có 23 giá trị của m. Chọn D.
Ví dụ 13: Cho hàm số
21
()
1
x
yC
x
−
=
+
và đường thẳng
:2dy x m
= +
. Gọi m là giá trị để d cắt
( )
C
tại 2
điểm phân biệt A, B sao cho tam giác ABC cân tại
3
;3
4
C



. Tính
( )
;
d Od
khi đó:
A.
9
5
d =
B.
3
5
d =
C.
2
5
d =
D.
1
5
d =
Lời giải
Phương trình hoành độ giao điểm của
d
và
( )
C
:
2
1
21
2
1
() 2 1 0
x
x
xm
x
g x x mx m
≠−
−
= +⇔
+
= + + +=
Để d cắt (C) tại 2 điểm phân biệt
( )
2
()
8 10
( 1) 3 0
gx
mm
g
∆ = − +>
⇔
−=≠
Khi đó gọi
11 2 2
( ;2 ); ( ;2 )Ax x m Bx x m++
theo Viet ta có:
12
12
2
1
2
m
xx
m
xx
+=−
+
=
Trung điểm I của AB là
12 1 2
222
;
22
xx x x m
I
+ ++



hay
;
42
mm
I
−



Giải
( )
3
.0 2309/
42
AB
mm
IC u m t m
+

=⇔ + − =⇔=


 
. Khi đó
( )
9
;
5
d Od =
. Chọn A.
Dạng 3: Sự tương giao của đồ thị hàm số trùng phương
Phương pháp giải:
Xét sự tương giao đồ thị
( ) (
)
42
:0C y ax bx c a=++ ≠
và trục hoành có phương trình
0
y
=
Phương trình hoành độ giao điểm
( )
C
và trục hoành là
( )
42
01ax bx c+ +=
Bài toán liên quan đến số giao điểm
Số giao điểm của đồ thị
( )
C
và trục hoành chính là số nghiệm của phương trình (1).
Đặt
2
0= ≥tx
thì (1) thành
2
0(2)at bt c+ +=
+)
( )
C
cắt trục hoành tại 4 điểm phân biệt
(2)⇔
có 2 nghiệm dương phân biệt
2
12
12
40
0
.0
b ac
b
tt
a
c
tt
a
∆= − >
⇔ +=−>
= >
+)
(
)
C
cắt trục hoành tại đúng 3 điểm phân biệt
(2)⇔
có 1 nghiệm dương và 1 nghiệm bằng 0.
( )
C
cắt trục hoành tại đúng 2 điểm phân biệt
(2)⇔
có nghiệm kép dương hoặc (2) có hai nghiệm trái
dấu.
+)
( )
C
cắt trục hoành tại điểm duy nhất
(2)⇔
có nghiệm kép bằng 0 hoặc (2) có một nghiệm bằng 0
hoặc một nghiệm âm.
+)
( )
C
không cắt trục hoành
(2)
⇔
vô nghiệm, có nghiệm kép âm hoặc có 2 nghiệm phân biệt đều âm
Một số bài toán có thể thay trục hoành thành
:dy m
=
hoặc
2
( ):P y mx n= +
, phương pháp giải hoàn
toàn tương tự như trên.
Bài toán liên quan đến tính chất giao điểm
Tìm điều kiện để
( )
42
( ): 0C y ax bx c a=++ ≠
cắt trục hoành tại bốn điểm phân biệt A, B, C, D thỏa
mãn điều kiện cho trước.
Bước 1: Tìm điều kiện để (1) có 4 nghiệm phân biệt
(2)⇔
có 2 nghiệm dương phân biệt
1
t
và
2
t
2
12
12
40
0
.0
b ac
b
tt
a
c
tt
a
∆= − >
⇔ +=−>
= >
(*)
Bước 2: Giả sử
12
0tt>>
khi đó các nghiệm của (1) sắp xếp theo thứ tự tăng dần là
1 2 21
; ;;t ttt−−
, xử lý điều kiện và tìm giá trị của tham số.
Đặc biệt: Khi hoành độ 4 điểm A, B, C, D lập thành cấp số cộng hoặc
AB BC CD= =
khi:
1 2 2 1 2 12
2 39
ttttttt− = ⇔ = ⇔=
42
8 52
yx x m= − +−
phân biệt là:
A. 9 B. 6 C. 7 D. 8
Lời giải
Phương trình hoành độ giao điểm là
42
8 52 0xx m− +− =
Đặt
( )
22
, 0 8 5 2 0*= ≥⇒ ⇔ − +− =t x t PT t t m
Phương trình ban đầu có 4 nghiệm phân biệt khi và chỉ khi (*) có hai nghiệm phân biệt thỏa mãn
12
0tt>>
Khi đó
12
12
(*) 0 16 (5 2 ) 0
11 5
0 80
22
52 0
.0
m
tt m
m
tt
′
∆ > −− >

+ > ⇔ > ⇔− < <


−>
>
Kết hợp
m ∈⇒
Có 8 giá trị của m. Chọn D.
( )
42
22 4yx m x=+− +
( )
m
C
tất cả các giá trị của tham số m để
( )
m
C
cắt Ox tại bốn điểm phân biệt
A.
( )
0; 2T =
B.
(
)
4;T = +∞
C.
( ) ( )
; 0 4;T = −∞ ∪ +∞
D.
( )
;0T = −∞
Lời giải
Phương trình hoành độ giao điểm là
( ) ( )
2
42 2
2 2 40 2 2 40(*)
tx
x mx t mt
=
+ − +=→+ − +=
Đồ thị hàm số và trục hoành có 4 giao điểm khi và chỉ khi PT hoành độ giáo điểm có 4 nghiệm phân biệt
(*)⇔
có hai nghiệm phân biệt
(
)
2
12
12
2 40
(*) 0
0 0 2( 2) 0
40
.0
m
t tt m
tt
− −>
′
∆>

>⇒ + > ⇔− − >


>
>
( )
0 ;0
mT⇒ < ⇒ = −∞
. Chọn D.
Ví dụ 3: Cho hàm số
( )
42
21y x mx m C= − ++
. Gọi S là tập hợp các giá trị của m để
( )
C
cắt trục Ox tại 4
điểm phân biệt có hoành độ
1234
,,,xxxx
thỏa mãn
4444
1 234
20xxxx+++=
. Tổng các phần tử của tập hợp (S)
là:
A. 1 B. – 1 C. 2 D. – 3
Lời giải
Phương trình hoành độ giao điểm của
( )
C
và Ox là
( )
42
2 1 01x mx m− + +=
Đặt
( ) ( )
22
:1 2 1 02t x t mt m= ⇒ − + +=
Để
( )
C
cắt trục Ox tại 4 điểm phân biệt
(2)⇔
có 2 nghiệm phân biệt
12
0
tt>>
( )
2
10
20 *
10
mm
Sm
Pm
′
∆= − − >
⇔=>
= +>
. Theo Viet:
12
12
2
.1
tt m
tt m
+=
= +
Khi đó phương trình (1) có 4 nghiệm
1 2 21
; ;;t ttt−−
Ta có: giả thiết bài toán
( )
2
2222 22
1221 12 12 12
20 10 2 10tttt tt tt tt⇔+++= ⇔+= ⇔ + − =
22
2
4 2 2 10 2 6 0
3
m
m m mm
m
=
⇔−−=⇔−−=⇔
= −
Kết hợp (*)
2m⇒=
là giá trị cần tìm. Chọn C.
( )
42
(2 1) 2yx m x C=−++
( )
C
điểm phân biệt có hoành độ
1234
,,,xxxx
thỏa mãn
4444
1 234
11115
2xxxx
+++=
A. 0 B. 1 C. 2 D. 3
Lời giải
Phương trình hoành độ giao điểm của
( )
C
và Ox là
(
)
42
(2 1) 2 0 1x mx
− + +=
Đặt
( ) (
)
22
: 1 ( 2 1) 2 0 2tx t m t= ⇒ − + +=
Để
(
)
C
cắt trục Ox tại 4 điểm phân biệt
(2)⇔
có 2 nghiệm phân biệt
12
0tt>>
( )
( )
2
2 1 80
2 10 *
20
m
Sm
P
∆= + − >
⇔ = +>
= >
. Theo Viet:
12
12
21
.2
tt m
tt
+= +
=
+) Khi đó phương trình (1) có 4 nghiệm
1 2 21
; ;;t ttt−−
ta có:
2222
1 234
11115
2tttt
+++=
(
)
( ) (
)
22
22
12
22
1 2 1 2 12
2 2 22
1 2 12
2
1
225 5
5 2 5 21 9
2
2 .2
tt
m
t t t t tt m
m
t t tt
+
=
⇔ + =⇔ =⇔+=⇔ + − =⇔ + =⇔
= −
Kết hợp (*)
1m
⇒=
là giá trị cần tìm. Chọn B.
Ví dụ 5: Cho hàm số:
( )
42
24y x mx m C= − ++
. Gọi S là tập hợp các giá trị của m để
(
)
C
cắt Ox tại 4
điểm phân biệt có hoành độ
1234
,,,xxxx
thỏa mãn:
1234
8xxxx+++=
. Tổng các phần tử của tập hợp S
là:
A. 5 B. 12 C. 17 D. – 17
Lời giải
Phương trình hoành độ giao điểm của
( )
C
và Ox là
( )
42
2 4 01x mx m− + +=
Đặt
( ) ( )
22
:1 2 4 02t x t mt m= ⇒ − + +=
Để
( )
C
cắt trục Ox tại 4 điểm phân biệt
(2)
⇔
có 2 nghiệm phân biệt
12
0tt
>>
( )
2
40
20 *
40
mm
Sm
Pm
′
∆= − − >
⇔=>
= +>
. Theo Viet:
12
12
2
.4
tt m
tt m
+=
= +
+) Khi đó phương trình (1) có 4 nghiệm
1 2 21
; ;;t ttt−−
Ta có: giả thiết
( )
1 2 2 1 12 12
82 8 4t t t t tt tt⇔− +− + + = ⇔ + = ⇔ + =
1 2 12
2
8
2 16 2 4 16 2 4 8 5
17 60 0
m
t t tt m m m m m
mm
≤
⇔++ = ⇔ += − ⇔ +=− ⇔ ⇔ =
− +=
Vậy m = 5 là giá trị cần tìm. Chọn A.
( )
42
y f x ax bx c
= =++
Tập hợp các giá trị thực của m để đường thẳng
:2
dy m=−+
cắt đồ thị
hàm số
( )
y fx=
tại bốn điểm phân biệt cách đều nhau là
A.
34 7
;
25 4



B.
34
25



C.
7
4



D.
{ }
1; 2
Lời giải
Dựa vào đồ thị hàm số, suy ra
( )
42
21y fx x x= =−+
PT hoành độ giao điểm hai đồ thị là
( )
2
42 2
2 1 2 2 1 0*
tx
x x m t tm
=
− + = − + → − + − =
Hai đồ thị có 4 giao điểm khi và chỉ khi PT (*) có hai nghiệm dương phân biệt
Suy ra
12
12
12
12
(*) 0 1 1 0
2
0 20 1 2
.1
10
.0
m
tt
tt m
tt m
m
tt
′
∆ > − +>
+=

⇔ + > ⇔ > ⇔< < ⇒

= −

−>
>
Giả sử
12
tt>
, 4 nghiệm của PT ban đầu theo thứ tự từ bé đến lớn sẽ là
1 2 21
; ;;t ttt
−−
Theo đề bài ta có
12
12
1 2 2 1 2 1 2 12
12
12
2
91
;
2 3 9.1
55
.1
9
tt
tt
t t t t t t t tt m
tt m
tt
+=
= =

− + =− ⇒ = ⇔ = ⇒ = −⇒


= −
=
9 34
1
25 25
mm⇒ −= ⇔ =
. Chọn B.
( )
4 22
2( 2 1) 4
y x m x mC=− ++
( )
C
hoành tại 4 điểm phân biệt có hoành độ
1234
,,,xxxx
thỏa mãn
2222
1 234
6
xxxx+++=
là
A.
1
4
m ≥−
B.
1
4
m = −
C.
1
m =
D.
1
4
m =
Lời giải
PT hoành độ giao điểm hai đồ thị là
( )
2
4 22 2 2
2(2 1) 4 0 2(2 1) 4 0 *
tx
x m x m t mtm
=
− ++=→− ++=
Đồ thị cắt trục hoành tại 4 điểm
(*)⇔
có 2 nghiệm dương phân biệt
12
12
0
0
.0
tt
tt
′
∆>
+>
>
22
22
11 2
22
13 4
2
(2 1) 4 0
1
2( 2 1) 0
4
0
40
mm
tx x
m
m
tx x
m
m
+− >
= =
>−

⇔ +> ⇔ ⇒

= =

≠
>
Khi đó
( )
2222
1 2 3 4 12
1
2( ) 4 2 1 6
4
xxxx tt m m
+++= += +=⇔=
thỏa mãn
1
4
0
m
m
>−
≠
. Chọn D.
( )
4 22
(4 2) 2 1yx m x m C=−+ ++
( )
C
thành 4 đoạn phân biệt có độ dài bằng nhau.
A. 0 B. 1 C. 2 D. 3
Lời giải
Phương trình hoành độ giao điểm của
( )
C
và Ox là
( )
4 22
(4 2) 2 1 0 1x mxm− + + +=
Đặt
( ) ( )
22 2
: 1 (4 2) 2 1 0 2
tx t m t m= ⇒ − + + +=
Để
( )
C
cắt trục Ox tại 4 điểm phân biệt
(2)⇔
có 2 nghiệm phân biệt
12
0tt>>
( )
( ) ( )
2
2
2
2
2 1 2 10
2 40
4 20 *
2 10
2 10
mm
mm
Sm
m
Pm
′
∆= + − − >
+>
⇔ = +> ⇔

+>
= +>
.
Theo định lý Viet ta có:
12
2
12
42
.2 1
tt m
tt m
+= +
= +
Khi đó PT (1) có 4 điểm A, B, C, D theo thứ tự hoành độ tăng dần là:
1 2 21
; ;;t ttt−−
Ta có:
1 2 2 1 2 12
;2 3 9AB CD t t BC t AB BC CD t t t t= = − = ⇒ = = ⇔ = ⇔=
Giải hệ:
(
)
( )
12
2
12
2
12
2
2
12
12
42
21 21
9. ,
9 9 2 1 25 2 1
55
.2 1
.2 1
tt m
mm
tt
tt m m
tt m
tt m
+= +
++
= =
= ⇔ ⇒ += +


= +
= +
( )
2
2
7 18 8 0 / (*)
4
7
m
m m tm
m
=
⇔ − +=⇔
=
. Vậy
4
2,
7
mm= =
là giá trị cần tìm. Chọn C.
Dạng 4: Sự tương giao của đồ thị hàm số bậc 3
Phương pháp giải:
Xét đồ thị
( )
( )
32
:0C y ax bx cx d a= + ++ ≠
và đường thẳng
: = +
d y kx
Hoành độ giao điểm của
y xm= +
và
( )
C
là nghiệm của phương trình
32 32
() 0
+++=+⇔++−+−=ax bx cx d kx ax bx x k x d
(1)
→
Số giao điểm của d và
( )
C
là nghiệm của phương trình (1).
Trường hợp 1: Phương trình (1) có một nghiệm đẹp
o
xx=
Khi đó (1) thành
( )
( )
2
2
.0
() 0
o
o
xx
x x Ax Bx C
g x Ax Bx C
=
− ++=⇔
= + +=
- Phương trình (1) có 3 nghiệm phân biệt
() 0gx⇔=
có 2 nghiệm phân biệt khác
()
0
()0
gx
o
o
x
gx
∆>
⇔
≠
Gọi
12
,xx
là nghiệm của phương trình
() 0gx=
khi đó tọa độ các giao điểm của d và
( )
C
là:
(
) (
) ( )
11 2 2
; ,B ; ,C ;
++ +
oo
A x kx x kx x kx
trong đó
12
12
.
B
xx
A
C
xx
A
−
+=
=
( Định lý Viet).
- Phương trình (1) có đúng 2 nghiệm phân biệt
() 0gx⇔=
có nghiệm kép khác
o
x
hoặc
() 0
gx
=
có hai
nghiệm phân biệt, trong đó 1 nghiệm bằng
o
x
và nghiệm còn lại khác
o
x
.
- Phương trình (1) có nghiệm duy nhất
() 0gx⇔=
vô nghiệm hoặc
() 0gx=
có nghiệm kép
o
xx=
.
Trường hợp 2: Phương trình (1) không có một nghiệm đẹp
o
xx=
nhưng cô lập được tham số.
Khi đó ta biến đổi (1) thành
() ( )
x hm
ϕ
=
.
Từ đó số nghiệm của (1) là số giao điểm của đồ thị hàm số
()
yx
ϕ
=
và
()
y hm=
Lập bảng biến thiên cho hàm số
()yx
ϕ
= ⇒
Kết luận.
Ví dụ 1: Cho hàm số
( )
32
231yx x C=−+
. Tìm giá trị của tham số m để
(
)
C
cắt đường thẳng
1
y mx= +
tại 3 điểm phân biệt.
A.
3
2
2
m
m
>
≠
B.
9
8
1
m
m
−
>
≠
C.
9
8
m
−
>
D.
9
8
0
m
m
>−
≠
Lời giải
Phương trình hoành độ giao điểm là
32 32
2
0
231 123 0
() 2 3 0
x
x x mx x x mx
gx x x m
=
− += +⇔ − − = ⇔
= − −=
ĐK cắt tại 3 điểm phân biệt
()
9
98 0
8
(0) 0
0
gx
m
m
gm
m
−
∆=+>
>
⇔⇔

=−≠
≠
. Chọn D.
Ví dụ 2: Tìm m để đồ thị hàm số
( ) ( )
22
2 21y x x m xm m

=− − + ++

cắt trục hoành tại ba điểm phân biệt.
A. Không tồn tại m B.
1m
<
hoặc
2m >
C.
1, 2mm≠≠
D.
m∀∈
Lời giải
Phương trình hoành độ giao điểm của đồ thị hàm số
( )
C
và trục hoành là
( ) ( )
( )
22
22
2
(1) 2 2 1 0
() 2 1 0
x
x x m xm m
fx x m x m m
=

⇔− − + + + =⇔

= − + + +=
Đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt
(1)⇔
có 3 nghiệm phân biệt
() 0
fx⇔=
có
hai nghiệm phân biệt
( )
( )
( )
2
2
2
10
214 0
01
21
(2) 0 2
4 22 1 0
2
m mm
m
xm
fm
m mm
m
>
+− +>
∆> ≠


≠⇔ ⇔ ⇔ ≠⇔

≠≠

− ++ +≠

≠
. Chọn C.
Ví dụ 3: Số các giá trị nguyên của tham số m để
[
]
10;10m
∈−
đường thẳng
45yx
= −
cắt đồ thị của hàm
số
3
( 2) 2 1
yx m x m=−+ + −
tại ba điểm phân biệt là
A. 10 B. 11 C. 12 D. 13
Lời giải
Phương trình hoành độ giao điểm là
33
( 2) 2 1 4 5 ( 6) 2 4 0(*)x m xm x x m xm−+ + −=+⇔−+ + +=
2
2
2
( 2)( 2 2) 0
() 2 2 0
x
x x xm
fx x x m
=
− + −− =⇔
= + − −=
Hai đồ thị có giao điểm khi và chỉ khi PT (*) có ba nghiệm phân biệt, khi đó PT
() 0fx=
có 2 nghiệm
phân biệt
0 1 20 3
2
(2) 0 4 4 2 0 6
mm
x
f mm
′
∆ > + + > >−

≠⇔ ⇔ ⇔

≠ +− −≠ ≠

Kết hợp
[ ]
10;10m
m
∈−
⇒
∈
có 12 giá trị của m. Chọn C.
Ví dụ 4: Tìm tất cả các giá trị của tham số m để đồ thị hàm số
(
) ( )
( )
2
: 22C y x x mx m=− −+
cắt trục
hoành tại ba điểm phân biệt có hoành độ dương.
A.
( )
4
1; \
3
m

∈ +∞


B.
( )
44
; 0 1; ;
33
m

∈ −∞ ∪ ∪ +∞


C.
( )
1;m
∈ +∞
D.
( )
0;m ∈ +∞
Lời giải
Phương trình hoành độ giao điểm là
( )
( )
2
2
2
22 0
() 2 0
x
x x mx m
f x x mx m
=
− − +=⇔
= − +=
( )
C
cắt trục hoành tại ba điểm phân biệt có hoành độ dương
⇔
PT
() 0fx=
có hai nghiệm
0, 2xx
>≠
Suy ra
( )
2
12
12
0
0
1
0
20
4
1; \
4
.0
3
0
3
(2) 0
44 0
mm
m
xx
m
m
xx
m
m
f
mm
′
∆>
−>
>
+>
>


⇔ ⇔ ⇔ ∈ +∞

>
≠
>



≠
− +≠
. Chọn A.
32
3 ( 2)y x x m xm=− ++ −
thị hàm số
22yx= −
có ba điểm chung phân biệt
A.
3
m <
B.
2m <
C.
3m >
D.
2
m >
Lời giải
Phương trình hoành độ giao điểm đồ thị hai hàm số là
( )
( )
( )
32 32 2
3 ( 2) 2 2 3 2 0 1 2 2 0 *x x m xm x x x mxm x x xm−++−=−⇔−+−+=⇔− −+−=
Đồ thị hai hàm số có ba điểm chung phân biệt khi và chỉ khi pt (*) có ba nghiệm phân biệt. Khi đó
( )
( )
2
2
1
1 2 20
() 2 2 0
x
x x xm
fx x x m
=
− − +− =⇔
= − + −=
Yêu cầu bài toán
()
(1) 1
12 2 0 3
3
0
1 20 3
fx
f
mm
m
mm
≠
−+ −≠ ≠

⇒ ⇔ ⇔ ⇒<

′
∆>
− +> <

. Chọn A.
Ví dụ 6: Cho hàm số
(
)
( )
( )
2
11
y x x mx C=− ++
. Số các giá trị của m thỏa mãn đồ thị
( )
C
cắt trục Ox tại
3 điểm phân biệt có hoành độ
123
;;xxx
thỏa mãn
222
1 23
10xxx++=
là
A. 1 B. 2 C. 0 D. 3
Lời giải
Phương trình hoành độ giao điểm của
( )
C
và trục Ox là:
( )
( )
( )
3
2
2
2
1 10 1
() 1 0
x
x x mx
f x x mx
=
− + +=⇔
= + +=
Đồ thị
( )
C
cắt trục Ox tại 3 điểm phân biệt
(1)⇔
có 3 nghiệm phân biệt
⇔
g( ) 0x =
có 2 nghiệm phân
biệt và 2 nghiệm đó khác 1
22
40 4
(1) 0 2 0
mm
gm

∆= − > >
⇔⇔

≠ +≠

Khi đó cho
3
1x =
và
12
;xx
là nghiệm của PT
() 0gx=
. Theo định lý Viet ta có:
12
12
.1
xx m
xx
+=−
=
Theo đề bài ta có:
( )
2
222 2
1 2 3 1 2 12
10 2 9 2 9xxx xx xx m+ + = ⇔ + − =⇔ −=
(
)
2
11 11 /m m tm⇔ =⇔=±
Vậy
11m = ±
là giá trị cần tìm . Chọn B.
( )
3
1y x mx m C= − +−
o
m
( )
C
phân biệt có hoành độ
123
;;xxx
thỏa mãn:
123
111
2
A
xxx
=++=
. Khi đó:
A.
( )
2; 0
o
m ∈−
B.
( )
0;3
o
m ∈
C.
( )
3; 5
o
m ∈
D.
( )
5; 7
o
m ∈
Lời giải
Phương trình hoành độ giao điểm của
( )
C
và trục Ox là:
3
10
x mx m− + −=
( )
3
32
2
1
1 ( 1) 0 ( 1)( 1 ) 0 1
() 1 0
x
x mx x x x m
gx x x m
=
−− − = ⇔ − + +− = ⇔
= + +− =
Để đồ thị
( )
C
cắt trục Ox tại 3 điểm phân biệt
(1)
⇔
có 3 nghiệm phân biệt
( )
1 4(1 ) 4 3 0
*
(1) 3 0
mm
gm
∆= − − = − >
⇔
=−≠
Khi đó gọi
3
1x =
và
12
;xx
là nghiệm của PT
() 0gx=
Theo Viet ta có:
12
12
1
.1
xx
xx m
+=−
= −
Do vậy
( )
12
1 2 12
11 1
1 1 12 2
1
xx
A m tm
x x xx m
+
−
= + += += += ⇔ =
−
Vậy m = 2 là giá trị cần tìm. Chọn B.
Cho hàm số
32
21y x mx
=−−
có đồ thị
( )
m
C
, với m là tham số thực. Hỏi có tất cả bao nhiêu giá
trị nguyên của m để
( )
m
C
cắt đường thẳng
:1dy x= −
tại ba điểm phân biệt có hoành độ
123
,,xx x
thỏa
mãn
222
1 23
20xxx++≤
A. 4 B. 6 C. 5 D. 3
Lời giải
Phương trình hoành độ giao điểm
( )
32 2
2
0
2 1 1 ( 2 1) 0 1
2 10
x
x mx x x x mx
x mx
=
− −= −⇔ − − = ⇔
− −=
Ta có d cắt
( )
m
C
tại 3 điểm phân biệt
(1)⇔
có 2 nghiệm phân biệt khác 0
2
2
10
0 2 .0 1 0
m
m
m
′
∆= + >
⇔ ⇔∈
− −≠
(*)
Giả sử
3
0x =
khi đó
12
;xx
là 2 nghiệm của (1), theo Viet có
12
12
2
.1
xx m
xx
+=
= −
Do đó
( )
2
222 2 2
1 2 3 1 2 12
93 3
20 2 20 4 2 20
2
22
xxx xx xx m m m++≤⇔+ − ≤⇔ +≤⇔ ≤⇔− ≤≤
Mà
{ }
2; 1; 0mm∈ ⇒ ∈± ±
. Chọn C
( )
3
y x xC= −
: ( 1)d y mx
= −
o
m
( )
C
cắt đường thẳng d tại 3 điểm phân biệt A; B; C sao cho điểm
1
;9
2
M

−−


là trung điểm của đoạn AB
trong đó
( )
1; 0C
. Khi đó:
A.
1
o
m <−
B.
(
)
0; 4
o
m
∈
C.
( )
4; 7
o
m ∈
D.
( )
7;
o
m ∈ +∞
Lời giải
Phương trình hoành độ giao điểm của
( )
C
và đường thẳng d là:
(
)
(
)
2
1 10
xx mx−− −=
( )
( )
( ) ( )
( )
22
2
1
1 10 1 0
() 0
x
x xxmx x xxm
gx x x m
=
⇔− +− −=⇔− +− =⇔
= +− =
Đồ thị
( )
C
cắt d tại 3 điểm phân biệt
(1)⇔
có 3 nghiệm phân biệt
() 0
gx⇔=
có 2 nghiệm phân biệt và
2 nghiệm đó khác 1
14 0 4 10
(*)
(1) 0 2 0
mm
gm
∆= + > + >

⇔⇔

≠ −≠

Khi đó gọi
12
;xx
là nghiệm của PT
() 0gx
=
. Theo định lý Viet ta có:
12
12
1
.
xx
xx m
+=−
= −
Ta có:
(
)
( )
(
)
(
)
11 21
;1;B;1
Axmx x mx−−
, trung điểm của AB là
(
) (
)
( )
12
1 2 12
1
22
11 2
3
2 22
M
M
xx
x
mx mx mx x m
m
y
+
−
= =
−+ − + −
−
= = =
Theo bài ra
1
;0
2
M

−


nên
(
)
3
96
2
m
m tm
−
=−⇔ =
Vậy m = 6 là giá trị cần tìm. Chọn C.
1y mx m= −+
cắt đồ thị của hàm số
32
32yx x x= − ++
tại ba điểm A, B, C phân biệt sao cho AB = BC.
A.
(
] [
)
; 0 4;
m ∈ −∞ ∪ +∞
B.
5
;
4
m

∈ − +∞


C.
( )
2;m ∈ − +∞
D.
m ∈
Lời giải
Phương trình hoành độ giao điểm là
( )
32
3 2 11x x x mx− ++= − +
( )
( )
2
2
1
1 21 0
() 2 1 0
x
x xx m
gx x x m
=
− − −− = ⇔
= − −− =
Giả thiết bài toán B là trung điểm của AC hay
() 0gx=
có 2 nghiệm phân biệt
11
;1xx≠
thỏa mãn
()
12
12
20
2 1 (1) 2 0 2
1
gx
AC B
m
x x x xx g m m
xx
′
∆ =+>
⇔ + = ⇔ + = ⇔ =− − ≠ ⇔ >−
+=
. Chọn C.
( ) ( )
3
2y x m x mC=++ −
: 21dy x= +
đồ thị
(
)
C
cắt đường
y xm= +
tại 3 điểm phân biệt có tung độ
123
,,yyy
thỏa mãn
222
1 23
83Ayyy=++≤
A. 9 B. 10 C. 11 D. 12
Lời giải
Phương trình hoành độ giao điểm của
( )
C
và đường thẳng d là:
3
10x mx m
+ − −=
(
)
( )
( )
33
2
2
13
1 10 1
() 1 0
xy
x xx m
gx x x m
=⇒=
⇔ − + +− = ⇔
= + +− =
Đồ thị
( )
C
cắt
y xm= +
tại 3 điểm phân biệt
( )
1⇔
có 3 nghiệm phân biệt
() 0gx⇔=
có 2 nghiệm
phân biệt và 2 nghiệm đó khác 1
3
1 4(1 ) 0 4 3 0
(*)
4
(1) 0 3 0
3
mm
m
gm
m
∆= − − > − >
≥

⇔ ⇔⇔

≠ −≠

≠
Khi đó cho
33
1; 3xy= =
và
12
;xx
là nghiệm của phương trình
() 0gx
=
Theo định lý Viet ta có:
12
12
1
.
xx
xx m
+=−
= −
Theo đề bài ta có:
(
) ( )
( )
( )
22
222 22
1 2 3 1 2 1 2 12
2 1 2 1 9 4 4 11
Ayyy x x xx xx=++= ++ ++= + + + +
( ) ( )
( )
2
12 12 12
4 2 4 11 4 1 2 1 4 11 8 3 83 10
A xx xx xx m m m


= + − + + + = − − −+ = +≤ ⇔ ≤


Kết hợp (*) và
m
∈⇒
có 9 giá trị của m. Chọn A.
Ví dụ 12: Cho hàm số:
( )
3
4y x mx C=+−
và đường thẳng
:2 4d y mx= +
. Gọi
o
m
là giá trị của m để d
cắt
( )
C
tại 3 điểm phân biệt A, B, C sao cho trọng tâm tam giác OAB là
2
;8
3
G

−


trong đó
( )
C
là điểm
có hoành độ
2
C
x =
và O là gốc tọa độ. Khi đó
A.
( )
5; 2
o
m ∈− −
B.
(
)
1; 3
o
m ∈−
C.
( )
3; 6
o
m ∈
D.
( )
6;
o
m ∈ +∞
Lời giải
Phương trình hoành độ giao điểm của
( )
C
và d là:
3
2 80x mx mx+ − −=
( )
(
)
( )
( )
(
)
( )
( )
22
2
2 2; 4 4
2 24 20 2 24 0 1
() 2 4 0
x Cm
x xx mx x xx m
gx x x m
=⇒+
⇔− +++ −=⇔− +++ =⇔
= + ++ =
Để đồ thị
( )
C
cắt đường thẳng d tại 3 điểm phân biệt
(1)⇔
có 3 nghiệm phân biệt
( )
14 3 0
(*)
2 12 0
mm
gm
′
∆=−− =−−>
⇔
=+≠
Khi đó gọi
12
;xx
là nghiệm của phương trình
() 0gx=
. Theo Viet ta có:
12
12
2
.4
xx
xx m
+=−
= +
Gọi
( ) ( )
11 2 2
;2 4 ;B ;2 4A x mx x mx++
ta có:
( )
12
12
12
0
2
33
28
2 42 40
33
o
o
xx
x
mx x
mx mx
y
++
−
= =
++
++ ++
= =
Do vậy
28 4
;
33
m
G
−

−


. Cho
84
8 4( )
3
m
m tm
−
=⇔=−
Vậy
4m = −
là giá trị cần tìm. Chọn A.
Ví dụ 2: Cho hàm số
32
(2 3) (6 7) 4 3y x x m xm m= − ++ +− −
và đường thẳng
:1dy x= +
. Gọi S là tập
hợp các giá trị thực của m để đường thẳng d cắt đồ thị hàm số tại ba điểm phân biệt A, B, C sao cho
1
A
x
=
và diện tích tam giác OBC bằng
5
, với O là gốc tọa độ. Tổng các phần tử của tập hợp S là:
A. T = 2 B. T = 4 C.
2T = −
D. T = 3
Lời giải
Phương trình hoành độ giao điểm hai đồ thị là
32
(2 3) (6 7) 4 3 1x x m xm m x− + + + − −=+
( ) ( )
32 2
(23) (66)440 1 22 440x m x m xm x x m xm

⇔−+ ++−−=⇔− −+++=

( )
( )
2
2
1
10
22 440
() 22 440(*)
A
x
x
x m xm
fx x m x m
=
−=
⇔⇔

− + + +=
= − + + +=
Hai đồ thị có ba giao điểm khi và chỉ khi (*) có hai nghiệm phân biệt
1x ≠
Suy ra
( )
( )
( )
(
)
2
3
12 24 4 0
21
2
(1) 0
3
(*) 0
1 4 10
.41
1
BC
BC
m
mm
xx m
f
m
mm
xx m
m
≠−
− −+ +≠
+= +
≠

⇔ ⇔⇒

>
′
∆>
+ − +>
= +
<−
Ta có
( ) ( ) ( ) ( )
22 2 2
2 2 8.
BC B C BC BC BC
BC xx yy xx xx xx= − +− = − = + −
( ) ( )
2
8 1 32 1mm= +− +
. Mặt khác
( )
( )
2
2
1
1
;
2
11
d Od = =
+−
Suy ra
( ) ( ) ( ) { }( )
2
2
11
; . 8 1 32 1 5 2; 4 /
4
2
22
OBC
m
S d O d BC m m m t m
m
∆
= −
= = + − + = ⇒ ⇒ ∈−
=
Vậy
2T =
. Chọn A.
BÀI TẬP TỰ LUYỆN
Câu 1: Có bao nhiêu số nguyên dương m sao cho đường thẳng
y xm= +
cắt đồ thị hàm số
21
1
x
y
x
−
=
+
tại
hai điểm phân biệt A, B và
4AB ≤
?
A. 7 B. 6 C. 1 D. 2
Câu 2: Tìm tất cả các giá trị thực của tham số m để đường thẳng
( ): 1d y mx m= −−
cắt đồ thị
( )
32
: 31Cyx x=−+
tại 3 điểm A, B, C phân biệt (B thuộc đoạn AC), sao cho tam giác AOC cân tại O (với
O là gốc tọa độ).
A.
2m = −
B.
2
m =
C.
1m = −
D.
1m =
Câu 3: Tìm tất cả các giá trị thực của tham số m để đường thẳng
2y xm=−+
cắt đồ thị
( )
H
của hàm số
23
2
x
y
x
+
=
+
tại hai điểm A, B phân biệt sao cho
2018 2018
12
Pk k= +
đạt giá trị nhỏ nhất, với
12
,kk
là hệ số góc
của tiếp tuyến tại A, B của đồ thị
( )
H
.
A.
3m
=
B.
2m =
C.
3m = −
D.
2m = −
Câu 4: Cho hàm số
3
1
x
y
x
+
=
+
có đồ thị
( )
C
.Tìm m sao cho đường thẳng
:dy x m= +
cắt
( )
C
tại hai điểm
phân biệt A và B thỏa mãn điều kiện
( )
2; 2G −
là trọng tâm của tam giác OAB.
A.
2m =
B.
5m =
C.
6m
=
D.
3m =
Câu 5: Cho hàm số
3
1
x
y
x
+
=
+
và đường thẳng
2y xm
= +
. Tìm giá trị của m để đồ thị hai hàm số đã cho
cắt nhau tại hai điểm A, B phân biệt sao cho độ dài đoạn AB nhỏ nhất.
A.
1m
= −
B.
3m =
C.
4m
=
D.
1m
=
Câu 6: Tìm giá trị thực của tham số m để đồ thị hàm số
32
32yx x=−+
cắt đường thẳng
( )
: ( 1)d y mx= −
tại ba điểm phân biệt hoành độ
123
,,xx x
thỏa mãn
222
1 23
5xxx++>
.
A.
3m ≥−
B.
2m ≥−
C.
3m >−
D.
2m >−
Câu 7: Cho hàm số
32
2 3( 1) 2y x mx m= − + −+
có đồ thị
( )
C
. Đường thẳng
:2dy x
=−+
cắt đồ thị
( )
C
tại
ba điểm phân biệt
(0; 2),AB
và C. Với
(3;1)M
, giá trị của tham số m để tam giác MBC có diện tích bằng
26
là
A.
1
m = −
B.
1m = −
hoặc
4m =
C.
4m =
D. Không tồn tại m
Câu 8: Cho hàm số
32
3yx x m=++
có đồ thị
( )
C
.Biết đồ thị
( )
C
cắt trục hoành tại 3 điểm phân biệt A,
B, C sao cho B là trung điểm của AC. Phát biểu nào sau đây đúng?
A.
( )
0;m ∈ +∞
B.
( )
;4m ∈ −∞ −
C.
( )
4; 0m∈−
D.
( )
4; 2m∈− −
Câu 9: Cho hàm số
3
3yx x= −
có đồ thị
( )
C
. Gọi S là tập hợp tất cả các giá trị thực của k để đường thẳng
: ( 1) 2d y kx= ++
cắt đồ thị
( )
C
tại ba điểm phân biệt M, N, P sao cho các tiếp tuyến của
(
)
C
tại N và P
vuông góc với nhau. Biết
( )
1; 2M −
, tính tích tất cả các phần tử của tập S.
A.
1
9
B.
2
9
−
C.
1
3
D.
1−
Câu 10: Đường thẳng
2
ym=
cắt đồ thị hàm số
42
10yx x=−−
tại hai điểm phân biệt A, B sao cho tam
giác OAB vuông với O là gốc tọa độ. Mệnh đề nào sau đây đúng?
A.
( )
2
5; 7m ∈
B.
( )
2
3; 5m ∈
C.
( )
2
1; 3m ∈
D.
( )
2
0;1m
∈
Câu 11: Gọi S là tập tất cả các giá trị của tham số m để đồ thị hàm số
32
3 92 1yx x x m=+ −+ +
và trục Ox
có đúng hai điểm chung phân biệt. Tính tổng T của các phần tử thuộc tập S.
A. T = 12 B. T = 10 C.
12
T
= −
D.
10T = −
Câu 12: Biết rằng đường thẳng
y xm= −
cắt đồ thị hàm số
32
3yx x= −
tại ba điểm phân biệt sao cho có
một giao điểm cách đều hai giao điểm còn lại. Khi đó m thuộc khoảng nào dưới đây?
A.
(
)
2; 4
B.
( )
2; 0−
C.
( )
0; 2
D.
( )
4; 6
Câu 13: Cho hàm số
32
31y x mx x=− ++
và
(1; 2 )M −
. Biết có 2 giá trị của m là
1
m
và
2
m
để đường thẳng
:1yx∆=+
cắt đồ thị tại 3 điểm phân biệt
(0;1)A
, B, C sao cho tam giác MBC có diện tích bằng
42
.
Hỏi tổng
22
12
mm+
thuộc khoảng nào trong các khoảng sau:
A.
( )
15;17
B.
( )
3; 5
C.
(
)
31;33
D.
( )
16;18
LỜI GIẢI BÀI TẬP TỰ LUYỆN
Câu 1: Ta có
( )
2
21
1 10
1
x
xm x m xm
x
−
= + ⇔ + − + +=
+
Để cắt nhau tại 2 điểm phân biệt thì
2
3 23
0 6 30
3 23
m
mm
m
>+
∆>⇔ − −>⇔
<−
Giả sử
( ) ( ) ( )
2
11 2 2 1 2
; ,; 2
A x x m B x x m AB x x+ +⇒ = −
Ta có
( )
( ) ( )
2 22
12 12 12 12
42 4 8 4 8AB xx xx xx xx≤⇔ − ≤⇔ − ≤⇔ − − ≤
22
( 1) 4( 1) 8 6 11 0 3 2 5 3 2 5m m mm m⇔ − − + ≤⇔ − − ≤⇔− ≤ ≤+
Do đó
3 23 3 25 7
mm+<≤+⇒=
. Chọn C
Câu 2:
(
)
32 2
2
1
3 1 1 ( 1)( 2 2) 0
2 20
x
x x mxm x x xm
gx x x m
=
− += −−⇔ − − −− =⇔
= − − −=
Để cắt nhai tại 3 điểm thì
( )
10
3
3
30
0
g
m
m
m
≠
≠
⇔ ⇔ >−

+>
′
∆>
Giả sử
(
)
( )
11 2 2
; 1, ; 1
A x mx m C x mx m
−− −−
với
1 2 12
2, 2x x xx m+ = =−−
Ta có
2 22 2
11 22
( 1) ( 1)OA OC x mx m x mx m= ⇔ + −− = + −−
2 22 2
1 2 12 12
( 1)( ) 2 ( 1)( ) 0 ( 1)( ) 2 ( 1) 0m x x mm x x m x x mm⇔+ −− + −=⇔+ +− +=
2
2( 1) 2 ( 1) 0 2 2 m 0 m 1.m mm⇔ +− + =⇔− =⇔ =
Chọn D.
Câu 3: Ta có
2
1
(x 2)
y
′
=
+
. Xét phương trình
2
23
2 2 ( 6) 2 3 0
2
x
xm x m x m
x
+
=− + ⇔ − − − +=
+
Để cắt nhau tại 2 điểm thì
22
0 ( 6) 8( 2 3) 0 4 12 0,
m m mm m
∆>⇔ − −− + >⇔ + + >∀
Ta có
2018 2018
12
4036 4036
12
11
(x 2) (x 2)
Pk k=+= +
++
Để đạt giá trị nhỏ nhất thì
4036 4036
12
11
(x 2) (x 2)
=
++
1 2 12
6
2 ( 2) 4 4 2.
2
m
x x xx m
−
⇔ + =− + ⇔ + =−⇔ =−⇔ =−
Chọn D.
Câu 4: Ta có
2
3
3 0.
1
x
xm x mxm
x
+
=− ⇔ − − −=
+
Giả sử
( )
11 2 2
; ,(; )Ax x m Bx x m−−
Do G là trọng tâm của
ABC∆
nên
12
12
22
33
6.
2
2
2
3
3
xx
m
m
xx m m
+
= =

⇔ ⇔=

+− −

= −
= −
Chọn C.
Câu 5: Ta có
2
3
2 2 ( 1) 3 0.
1
x
xm x m xm
x
+
= + ⇔ + + + −=
+
Giả sử
( ) ( )
11 2 2
;2 , ;2Ax x m Bx x m++
Ta có
( )
( )
2
22
1 2 1 2 12
13
5 5 45 4
22
mm
AB x x x x x x

+−


= −= +− = −






2
1 3 25
5
4 44
mm

= −+


nhỏ nhất khi
3.
2
b
m
a
−
= =
Chọn B.
Câu 6: Ta có
( )
32 2
2
1
3 2 1 ( 1)( 2 2) 0
2 20
x
x x mx x x x m
x xm
=
− += + ⇔ − − − − =⇔
− − −=
Giả sử
23
1
23
2
1
3
xx
x
xx m
+=
= ⇒
=−−
Ta có
( )
2
222 2
1 2 3 1 2 3 23
5 25
xxx x xx xx+ + >⇔ + + − >
2
1 2 2( 3) 5 3.mm⇔ + − − − > ⇔ >−
Chọn C.
Câu 7: Phương trình hoành độ giao điểm của (C) và d là
32
2 3( 1) 2 2x mx m x x+ + − + =−+
32 2
2
()
0
2 (3 2) 0 ( 2 3 2) 0
2 3 20
fx
x
x mx m x x x mx m
x mx m
=
⇔+ + − =⇔ + + −=⇔
+ + −=

Để (C) cắt d tại 3 điểm
() 0fx
⇔=
có hai nghiệm phân biệt khác 0
2
3 20
3 20
m
mm
−≠
⇔
− +>
( )
∗
Khi đó, gọi
11
(0;2), B(x ; )Ay
và
22
(x ; )Cy
là tọa độ giao điểm của (C) và d
Với
12
x ,x
thỏa mãn hệ thức Vi – et :
12
12
xx 2
xx 3 2
m
m
+=−
= −
Ta có
(
) ( ) ( )
1
; ; 2 ; . 43
2
MBC
d M BC d M d S d M d BC BC
∆
 
= =⇒ = ⇒=
 
Lại có
( )
2
2
21 21 21 21 12
(xx;xx) BC 2(xx)2xx 4xx 48
BC

= − −+ ⇒ = − = − − =

Suy ra
22
1
( 2 m) 4(3 2) 24 4 12 16 0
4
m
m mm
m
= −
− − −= ⇔ − −=⇔
=
(thỏa mãn
( )
∗
)
Vậy
1m = −
hoặc
4m =
là giá trị cần tìm. Chọn B.
Câu 8: Yêu cầu bài toán
⇔
Điểm uốn của đồ thị (C) thuộc trục hoành
Ta có
2
3 6 6 6; 0 1 ( 1) 2y x xy x y x y m
′ ′′ ′′
= + ⇒ = + = ⇔ =−⇒ − = +
Do đó, tọa độ điểm uốn là
1( 1; 2) 2 0 2.m Ox m m− + ∈ ⇒ +=⇔ =−
Chọn C.
Câu 9: Phương trình hoành độ giao điểm của (C) và d là
3
3 (x 1) 2x xk− = ++
32
2
()
1
3 2 (x 1) (x 1)(x 1) (x 1)
20
fx
x
xx k x k
x xk
= −
⇔ − −= +⇔+ −−= +⇔
−−−=

Để (C) cắt d tại 3 điểm phân biệt
( )
0fx⇔=
có 2 nghiệm phân biệt khác
0
1
9
4
k
k
≠
−⇔
>−
Khi đó, gọi
11
( 1; 2), (x ; y )MN−
và
22
P(x ; )y
là tọa độ giao điểm của (C) và d
Với thỏa mãn hệ thức Vi – et :
12
12
1
2
xx
xx k
+=
=−−
Theo bài ra, ta có
22
12 1 2
( ). ( ) 1 (3x 3)(3x 3) 1yx yx
′′
=−⇔ − − =−
( )
(
)
(
)
( )
2 22
22
12 1 2 12 1 2 12
9 9 10 0 9 9 9 2 10 0xx x x xx x x xx

⇔ − + +=⇔ − + − +=

( )
(
)
2
2
12
1
9 2 9 1 2 2 10 0 9 18 1 0 . .
9
k k k k kk

⇔ + − + + + = ⇔ + += ⇒ =

Chọn A.
Câu 10: Phương trình hoành độ giao điểm của (C) và d là
42 2
10 0xxm−− −=
( )
∗
Đặt
2
0,tx= ≥
khi đó
( )
22
10 0t tm∗⇔ −− − =
luôn có hai nghiệm thỏa mãn
12
2
12
1
10
tt
tt m
+=
=−−
Vì
2
12
10 0 0m tt
− − <⇒ <
nên giả sử
11
21
21
00
xt
tt
xt
=
<⇒>⇒
= −
Do đó tọa độ hai điểm A, B lần lượt là
( )
( )
22
11
; ;B ;A tm tm−
Ta có
( )
( )
( )
2 2 22 4
1 1 11 1
;, ; . . .OA t m OB t m OA OB t t m m t m
= =− ⇒ = − + =−+
   
Tam giác OAB vuông
44
11
.0 0OA OB t m t m⇒ = ⇒− + = ⇒ =
 
Thay
4
1
tm
=
vào phương trình ẩn t, ta được
422 2
10 0 1 11.mmm m−−−=⇒=+
Chọn B.
Câu 11: Phương trình hoành độ giao điểm của (C) và Ox là
32 32
39210 2 391 2 ()xxxm mxxx mfx− − + + = ⇔− = − − + ⇔− =
Xét hàm số
32
() 3 9 1fx x x x=− −+
có
2
1
() 3 6 9; () 0
3
x
fx x x fx
x
=
′′
= +− =⇔
= −
Lập bảng biến thiên hàm số
( )
fx
, để
( )
2m fx−=
có 2 nghiệm
2 28 14
24 2
mm
mm
−= =

⇔⇔

−=− =

Vậy tổng các giá trị của m là
12T
= −
. Chọn C.
Câu 12: Phương trình hoành độ giao điểm của (C) và d là
( )
32 32
3 30xxxmfxxxxm− =− ⇔ = − −+ =
Yêu cầu bài toán trở thành: Đồ thị
( )
y fx=
cắt trục Ox tại 3 điểm phân biệt và có một giao điểm cách hai
giao điểm còn lại
⇔
Đồ thị
( )
y fx=
có điểm uốn thuộc Ox
Xét hàm số
( )
32
3,fx x x x m= − −+
có
2
() 3 6 1; () 6 6fx x x f x x
′ ′′
= −− =−
Ta có
( )
() 0 1 1 3fx x f m
′′
=⇔=⇒ =−
nên tọa độ điểm uốn là
(1; 3)Im
−
Theo bài ra, ta có
3 0 3.mm−=⇔ =
Chọn A.
Câu 13: Phương trình hoành độ giao điểm của (C) và d là
32
31 1
x mx x x− + += +
( )
32 2
2
()
0
2 0 20
10
fx
x
x mx x x x mx
x mx
=
⇔− + =⇔ − +=⇔
− +=

Để (C) cắt d tại 3 điểm phân biệt
( )
0fx⇔=
có 2 nghiệm phân biệt khác
2
0 80m⇔ −>
Khi đó, gọi
11
(0;1), B(x ; )
Ay
và
22
(x ; )
Cy
là tọa độ giao điểm của (C) và d
Với
12
x ,x
thỏa mãn hệ thức Vi – et :
12
12
2
xx m
xx
+=
=
Khoảng cách từ điểm
M BC→
là
( )
; 22h d M BC

= =

Suy ra
( )
2
21
1
. 4 2 4 2 16
2
MBC
S h BC BC x x
∆
= = ⇒=⇒ −=
( )
2
2 2 22
2 1 12 1 2
4 8 8 8 16 32.x x xx m m m m
⇔ − − =⇔ −=⇔ = → + =
Chọn C.

Tài liệu khác của Toán 12

Preview text:

CHỦ ĐỀ 7: BÀI TOÁN TƯƠNG GIAO GIỮA HAI ĐỒ THỊ
I. LÝ THUYẾT TRỌNG TÂM
II. CÁC DẠNG TOÁN TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Tìm tọa độ giao điểm của hai đồ thị Phương pháp giải:
Cho 2 hàm số y = f (x) và y = g(x) có đồ thị lần lượt là (C) và (C′) :
 Lập phương trình hoành độ giao điểm của (C) và (C′) là f (x) = g(x)(∗)
 Giải phương trình tìm x thay vào f (x) hoặc g(x) để suy ra y và tọa độ giao điểm
 Số nghiệm của phương trình (∗) là số giao điểm của (C) và (C′)
Ví dụ 1: [Đề minh họa THPT QG năm 2017] Biết rằng đường thẳng y = 2
− x + 2 cắt đồ thị hàm số 3
y = x + x + 2 tại điểm duy nhất; ký hiệu (x y là tọa độ của điểm đó. Tìm y o ; o ) o A. y = B. y = C. y = D. y = − o 1 o 2 o 0 o 4 Lời giải
Phương trình hoành độ giao điểm là: 3 3 2
− x + 2 = x + x + 2 ⇔ x + 3x = 0 ⇔ x = 0 ⇒ y = 2
Vậy tọa độ giao điểm là (0;2). Chọn C.
Ví dụ 2: Biết rằng đồ thị hàm số 4 2
y = x − 3x + 5 và đường thẳng y = 9 cắt nhau tại hai điểm phân biệt
A(x ; y ,B x ; y . Tính x + x 1 1 ) ( 2 2) 1 2
A. x + x = 3
B. x + x = 0
C. x + x =18
D. x + x = 5 1 2 1 2 1 2 1 2 Lời giải
Phương trình hoành độ giao điểm hai đồ thị là: 2 x = 1 − x = 2 x = 2 4 2 4 2 2 1
x − 3x + 5 = 9 ⇔ x − 3x − 4 = 0 ⇔  ⇒ x = 4 ⇔ ⇒ ⇒   x + x = 0 1 2 2 x = 4 x = 2 − x = 2 − 2 Chọn B.
Ví dụ 3: Hỏi đồ thị của hàm số 3 2
y = x + 2x − x +1 và đồ thị hàm số 2
y = x − x + 3 có tất cả bao nhiêu điểm chung? A. 0 B. 2 C. 1 D. 3 Lời giải
Phương trình hoành độ giao điểm đồ thị hai hàm số là 3 2 2 3 2
x + 2x − x +1 = x − x + 3 ⇔ x + x − 2 = 0 ⇔ x − ( 2
( 1) x + 2x + 2) = 0 ⇔ x −1= 0 ⇔ x =1. Suy ra hai đồ thị có một điểm chung. Chọn C.
Ví dụ 4: Số giao điểm của đồ thị hai hàm số 3 2
y = x + 3x +1 và 4 3
y = x + x − 3 là A. 1 B. 4 C. 3 D. 2 Lời giải
Phương trình hoành độ giao điểm đồ thị hai hàm số là 3 2 4 3 4 2
x + 3x +1 = x + x − 3 ⇔ x − 3x − 4 = 0 2 x = 1 − x = 2 2 ⇔  ⇒ x = 4 ⇔
⇒ 2 đồ thị hàm số có 2 giao điểm. Chọn D. 2 x = 4  x = 2 − 2
Ví dụ 5: Tìm số giao điểm của đồ thị hàm số x − 2x + 3 y =
với đường thằng y = 3x − 6 x −1 A. 3 B. 0 C. 1 D. 2 Lời giải 2
Phương trình hoành độ giao điểm của đồ thị ( − +
C) và đường thẳng (d ) là x 2x 3 = 3x − 6 x −1 x −1 ≠ 0 x ≠ 1 x ≠ 1 ⇔  ⇔  ⇔  (∗) 2 2 2 2
x − 2x + 3 = (x −1)(3x − 6)
x − 2x + 3 = 3x − 9x + 6
2x − 7x + 3 = 0
Hệ phương trình (∗) có hai nghiệm phân biệt nên (C) cắt (d ) tại hai điểm. Chọn D.
Ví dụ 6: Hoành độ các giao điểm của đồ thị hàm số 2x −1 y =
(C) và đường thẳng d : y = x − 2 là x + 2 x = 1 − x =1 x =1+ 6 x = 1 − A.B.C.D.  x = 3 x = 3 − x =1− 6 x = 3 − Lời giải 2x −1 x ≠ 2 −
Phương trình hoành độ giao điểm của đồ thị (C) và (d ) là = x − 2 ⇔  2 x + 2
2x −1 = x − 4 x ≠ 2 − x ≠ 2 −  x = 1 − ⇔  ⇔ x = 1 − ⇔ . Chọn A. 2
x − 2x − 3 = 0   x = 3 x = 3
Ví dụ 7: Biết đường thẳng +
y = 3x + 4 cắt đồ thị hàm số 4x 2 y =
tại hai điểm phân biệt có tung độ y và x −1 1
y . Tính y + y 2 1 2
A. y + y =10
B. y + y =11
C. y + y = 9
D. y + y =1 1 2 1 2 1 2 1 2 Lời giải 2 4x + 2
x − x − 2 = 0 x = 1 −
Phương trình hoành độ giao điểm hai đồ thị là = 3x + 4 ⇔  ⇔ x −1 x ≠ 1  x = 2 x = 1 − y =1 Ta có: 1 1  ⇒ 
⇒ y + y =11. Chọn B. 1 2 x = 2 y =   10 2 2
Ví dụ 8: Gọi A, B là giao điểm của hai đồ thị hàm số x − 3 y =
và y =1− x . Diện tích tam giác OAB x −1 bằng: A. 3 2 B. 3 C. 3 D. 3 2 2 2 Lời giải x − 3 x ≠ 1 x = 1 − ⇒ y = 2
Phương trình hoành độ giao điểm: = 1− x ⇔  ⇔ 2 x −1
x − x − 2 = 0 
x = 2 ⇒ y = 1 −
Khi đó AB = 9 + 9 = 3 2 và d (O AB) = d (O d x + y − = ) 1 ; ; : 1 0 = 2 Do đó 1 S = d O AB AB = = . Chọn C. OAB ( ) 1 1 3 ; . . .3 2 2 2 2 2
Ví dụ 9: Đồ thị hàm số 2
y = x − x và đồ thị hàm số 3
y = 5 + cắt nhau tại hai điểm A và B. Khi đó độ dài x AB là A. AB = 8 5 B. AB = 25 C. AB = 4 2 D. AB =10 2 Lời giải 3 x ≠ 0
Phương trình hoành độ giao điểm đồ thị hai hàm số là 2
x − x = 5 + ⇔  3 2 x
x − x − 5x − 3 = 0
x = 3 ⇒ y = 6  ( A 3;6) ⇔ ⇒  
⇒ AB = 4 2 . Chọn C.x = 1 − ⇒ y = 2 B( 1; − 2)
Ví dụ 10: Gọi M, N là giao điểm của đường thẳng +
y = x +1 và đường cong 2x 4 y = . Khi đó hoành độ x −1
trung điểm I của đoạn thẳng MN bằng A. 5 B. 5 − C. 1 D. 2 2 2 Lời giải 2x + 4 x =1+ 6
Phương trình hoành độ giao điểm là 2
= x +1 ⇔ x − 2x − 5 = 0 ⇔  x −1 x =1− 6 x = + M 1 6 ⇒ 
⇒ x = . Chọn C. I 1 x = − N 1 6
Ví dụ 11: Đồ thị hàm số 3 2
y = x − 3x + 2x −1 cắt đồ thị hàm số 2
y = x − 3x +1 tại hai điểm phân biệt A, B. Tính độ dài AB. A. AB = 3 B. AB = 2 2 C. AB = 2 D. AB =1 Lời giải
Phương trình hoành độ giao điểm hai đồ thị là 3 2 2 3 2
x − 3x + 2x −1 = x − 3x +1 ⇔ x − 4x + 5x − 2 = 0 ⇔ (  =  −
x − )2 (x − ) x 1 ( A 1; 1) 1 2 = 0 ⇔ →  
⇒ AB =1 . Chọn D. x = 2 B(2; 1) −
Dạng 2: Sự tương giao của đồ thị hàm số phân thức bậc nhất trên bậc nhất
Phương pháp giải:
Xét sự tương giao giữa đồ thị ( ): ax + b C y =
và đường thẳng d : y = kx +  cx + dd ax + bx ≠ −
Phương trình hoành độ giao điểm của d và (C) là: = kx +  ⇔  c (∗) cx + d  2
g(x) = Ax + Bx + C = 0
Bài toán biện luận số giao điểm của hai đồ thị
Trường hợp 1: Xét A = 0 ⇒ Kết luận về số giao điểm.
Trường hợp 2: Xét A ≠ 0
+) d cắt (C) tại hai điểm phân biệt ⇔ g (x) = 0 hai nghiệm phân biệt 2
∆ = B − 4AC > 0 khác −d  2 ⇔   −d    . −d  = +   . −d c g A B + C ≠ 0   c   c c
+) d cắt (C) tại điểm duy nhất −
⇔ g (x) có nghiệm kép khác d hoặc g (x) có hai nghiệm phân c ∆ = g x 0 ( )    −d g  ≠   0 −d   c
biệt trong đó có một nghiệm x = ⇔  c ∆ > g x 0 ( )    −d g  =   0   c  ∆ < g x 0 ( )  −d ∆ = g x 0
+) d không cắt (C) ⇔ g (x) vô nghiệm hoặc có nghiệm kép bằng ( ) ⇔ c    −dg   =   0   c
Bài toán liên quan đến tính chất các giao điểm
Phần này, ta chỉ xét bài toán mà có liên quan đến d cắt (C) tại hai điểm phân biệt.
Bước 1. Tìm điều kiện để d cắt (C) tại hai điểm phân biệt 2
∆ = B − 4AC > 0 −
⇔ g (x) = 0 có hai nghiệm phân biệt khác d  2 ⇔   −d   −d  −d ( )1 cg =   . A +   . B + C ≠ 0   c   c c
Bước 2. Khi đó gọi (
A x ;kx + ), B(x ;kx + ) là tọa độ hai giao điểm 1 1 2 2  B x + x = −  1 2
Với x , x là hai nghiệm của phương trình g(x) = 0 nên theo định lý Viet ta có  A 1 2  Cx x = 1 2  A
Bước 3. Theo yêu cầu bài toán, ta tìm giá trị của tham số chú ý đối chiếu với điều kiện (1) để chọn đáp án đúng. Chú ý:
• x + x = (x + x )2 2 2 − 2x x 1 2 1 2 1 2
• (x − x )2 = (x + x )2 − 4x x 1 2 1 2 1 2
• AB = (x − x )2 + ( y − y )2 A B A B • 1 S = d I AB AB IAB ( ; ). 2  
• Tam giác IAB vuông tại I ⇔ . IA IB = 0  + + + +
• Trọng tâm tam giác IAB là x x x y y y I A B G ; I A B   3 3   
Ví dụ 1: Tìm tất cả các giá trị thực của tham số m để đường thẳng (d ): x − 2y + m = 0 cắt đồ thị hàm số x − 3 y =
tại hai điểm phân biệt. x +1 A. 3− 4 2 3+ 4 2 < m <
B. 3− 4 2 < m < 3+ 4 2 2 2  3− 4 2 m < m < 3− 4 2 C. 2  D.   3+ 4 2 m > 3+ 4 2 m >  2 Lời giải Ta có: : x m d y − + = +
. Phương trình hoành độ giao điểm là: x 3 x m = 2 2 x +1 2 x ≠ 1 − ⇔  g  ( x) 2
= x + (m −1)x + m + 6 = 0
Để d cắt đồ thị hàm số x − 3 y =
tại 2 điểm phân biệt thì g(x) = 0 phải có 2 nghiệm phân biệt x +1 2
∆ = (m −1) − 4(m + 6) > 0 m > 3+ 4 2 khác 2 1 − ⇔ 
⇔ m − 6m − 23 > 0 ⇔  . Chọn D.g( 1) − = 8 ≠ 0 m < 3− 4 2
Ví dụ 2: Tìm tập hợp tất cả các giá trị của tham số m để đường thẳng y = x +1 cắt đồ thị hàm số 2x + m y =
tại hai điểm phân biệt có hoành độ dương. x −1 A. 2 − < m < 1 − B. m < 1 − C. m <1 D. 2 − < m <1 Lời giải Điều kiện: +
x ≠ 1 . Phương trình hoành độ giao điểm 2x m 2 x +1 =
⇔ x − 2x − m −1 = 0(∗) x −1
Để cắt nhau tại hai điểm phân biệt có hoành độ dương thì phương trình (*) có hai nghiệm dương phân biệt ∆′ > 0 1  + m +1 > 0   m > 2 − S > 0 2 > 0 khác 1  ⇔  ⇔  ⇔ m < 1 − ⇔ 2 − < m < 1 − . Chọn A. P > 0 −m −1 > 0    m ≠ 2 − m ≠ 2 − m ≠ 2 −
Ví dụ 3: Cho hàm số x +1 y =
(C) và đường thẳng d : y = x + m . Gọi S là tập hợp các giá trị của m để d x −1
cắt (C)tại 2 điểm phân biệt có hoành độ x ; x thỏa mãn 2 2
x + x = 9 . Tổng các phần tử của tập hợp S là: 1 2 1 2 A. – 2 B. 3 C. 2 D. – 1 Lời giải x +1 x ≠1
Phương trình hoành độ giao điểm của (C) và d là = x + m ⇔ x −1  g  ( x) 1 2 ( )
= x + (m − 2) x− m−1 = 0
Để đồ thị (C) cắt d tại 2 điểm phân biệt ⇔ g(x) = 0 có 2 nghiệm phân biệt khác 1. 2
∆ = (m − 2) + 4(m +1) > 0 ⇔ 
(*) . Khi đó gọi x ;x là nghiệm của PT g(x) = 0 1 2 g(1) = 2 − ≠ 0
x + x = 2 − m Theo Viet ta có: 1 2  x x = −m −  1 1 2 m = 3 Ta có: 2 2 2 2 2
x + x = (x + x ) − 2x x = (2 − m) + 2(m +1) = m − 2m + 6 = 9 ⇔ (thỏa mãn (*)) 1 2 1 2 1 2  m = 1 − Vậy S = {3;− }
1 ⇒ T = 2 .Chọn C.
Ví dụ 4: Cho hàm số: 2x −1 y =
(C) và đường thẳng d : y = 2x + m . Gọi S là tập hợp các giá trị của m để x +1
d cắt (C) tại 2 điểm phân biệt có hoành độ x ; x thỏa mãn 1
x − x = . Tổng các phần tử của tập hợp S 1 2 1 2 2 là: A. 8 B. 9 C. 10 D. -1 Lời giải 2x −1 x ≠ 1 −
Phương trình hoành độ giao điểm của (C)và d: = 2x + m ⇔  2 x +1
g(x) = 2x + mx + m +1 = 0
Để đồ thị (C) cắt d tại 2 điểm phân biệt ⇔ g(x) = 0 có 2 nghiệm phân biệt khác -1. 2
∆ = m −8(m +1) > 0 ⇔ 
(*) . Khi đó gọi x ; x là nghiệm của PT g(x) = 0 1 2 g( 1) − = 3 ≠ 0  −m x + x =  1 2 Theo Viet ta có:  2  m +1 x x = 1 2  2 Khi đó 1 2 1 2 1
x − x = ⇔ (x − x ) = ⇔ (x + x ) − 4x x = 1 2 1 2 1 2 1 2 2 4 4 2 m 1 m = 9 ⇔ − 2(m +1) = ⇔ (t/m) 4 4  m = 1 − Vậy S = {9;− }
1 ⇒ T = 8 . Chọn A.
Ví dụ 5: Cho hàm số x +1 y =
(C) và đường thẳng d : y = x + m . Số các giá trị của tham số m để d cắt (C) x − 2
tại 2 điểm phân biệt A, B sao cho AB = 4 2 là A. 2 B. 1 C. 0 D. 3 Lời giải x +1 x ≠ 2
Phương trình hoành độ giao điểm của (C)và d: = x + m ⇔  (1) 2 x − 2
g(x) = x + (m − 3)x − 2m −1 = 0
Để đồ thị (C) cắt d tại 2 điểm phân biệt ⇔ g(x) = 0 có 2 nghiệm phân biệt khác 2. 2
∆ = (m − 3) + 4(2m +1) > 0 ⇔  (∗) g(2) = 3 − ≠ 0 Khi đó gọi (
A x ; x + m); B(x ; x + m) là 2 tọa độ các giao điểm 1 1 2 2
x + x = 3 − m Theo Viet ta có: 1 2  x x = 2 − m −  1 1 2 Ta có: 2 2 2 2
AB = (x − x ) + (x − x ) = 2 (x − x )  = 2 (x + x ) − 4x x  1 2 1 2  1 2   1 2 1 2  m =1 2 2 2
= 2 (3− m) − 4( 2
− m −1) = 2(m + 2m +13) = 4 2 ⇔ m + 2m − 3 = 0 ⇔    (t / m) m = 3 − Vậy m = 3
− ;m =1 là các giá trị cần tìm. Chọn A.
Ví dụ 6: Cho hàm số 2x +1 y =
(C) và đường thẳng d : y = 2x + m . Số các giá trị của m để d cắt (C) tại 2 x +1  
điểm phân biệt A, B sao cho . OAOB = 10
− trong đó O là gốc tọa độ. A. 2 B. 1 C. 0 D. 3 Lời giải 2x +1 x ≠ 1 −
Phương trình hoành độ giao điểm của (C)và d: = 2x + m ⇔  (1) 2 x +1
g(x) = 2x + mx + m −1 = 0
Để đồ thị (C) cắt d tại 2 điểm phân biệt ⇔ g(x) = 0 có 2 nghiệm phân biệt khác -1. 2
∆ = m −8(m−1) > 0 ⇔  (∗) g( 1) − = 1 ≠ 0 Khi đó gọi (
A x ;2x + m); B(x ;2x + m) là 2 tọa độ các giao điểm 1 1 2 2  −m x + x =  1 2 Theo Viet ta có:  2  m −1 x x = 1 2  2   Khi đó .
OAOB = x .x + (2x + m)(2x + m) = 5x x + 2m(x + x ) 2 5m − 5 2 2 + m = − m + m = 1 − 0 1 2 1 2 1 2 1 2 2 ⇔ m = 3
− (t / m) . Vậy m = 3
− là các giá trị cần tìm. Chọn B.
Ví dụ 7: Cho hàm số x −1 y =
(C) và đường thẳng d : y = −x + m . Gọi m là giá trị để d cắt (C) tại 2 điểm x − 2
phân biệt A, B sao cho trọng tâm tam giác OAB thuộc đường thẳng x + y = 0 . Tính độ dài AB khi đó. A. AB = 2 2 B. AB =10 C. AB = 5 D. AB = 10 Lời giải x −1 x ≠ 2
Phương trình hoành độ giao điểm của (C)và d:
= −x + m ⇔  (1) 2 x − 2
g(x) = x − (m +1)x + 2m −1 = 0
Để đồ thị (C) cắt d tại 2 điểm phân biệt ⇔ g(x) = 0 có 2 nghiệm phân biệt khác 2. ∆ = (m + )2 1 − 4(2m − ) 1 > 0 ⇔  (∗) g(1) = 1 − ≠ 0 Khi đó gọi (
A x ;−x + m); B(x ;−x + m) là 2 tọa độ các giao điểm 1 1 2 2
x + x = m +1 Theo Viet ta có: 1 2  x x = 2m −  1 1 2 
x + x + 0 m +1 1 2 x = =  G
Gọi G là trọng tâm tam giác OAB ta có  3 3  m +1 m −1  G  ;  ⇒ x m x m 0 m 1   3 3  − + − + + − 1 2 y  = = G  3 3 Do điểm + −
G ∈ x + y = 0 nên ta có: m 1 m 1 +
= 0 ⇔ m = 0(t / m) 3 3
Khi đó AB = 2(x − x )2 = 2(x + x )2 −8x x = 2(m + )2 2
1 −8 2m −1 =10 ⇒ AB = 10 . Chọn D. 1 2 1 2 1 2 ( )
Ví dụ 8: Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số 2mx + m − 2 y = cắt đường x +1
thẳng d : y = x + 3 tại hai điểm phân biệt A, B sao cho tam giác IAB có diện tích bằng 3, với I( 1; − 1) . Tính
tổng tất cả các phần tử của S. A. 7 B. – 10 C. 3 D. 5 Lời giải 2mx + m − 2  f (x) 2
= x − 2(m − 2)x + 5 − m = 0
Phương trình hoành độ giao điểm là = x + 3 ⇔ x 1  + x ≠ 1 − ∆′ >  (  m − )2 0 2 − (5 − m) > 0
Hai đồ thị có giao điểm khi và chỉ khi  ⇔  ∗  f  (− ) ( ) 1 ≠ 0 1  + 2 
(m − 2)+5− m ≠ 0
x + x = m − A B 2( 2) Khi đó 
⇒ AB = 2(x − x = x + x − x x A B )2 2( A B )2 8 A. x .x = 5 B −  m A B 2
= 8(m − 2) −8(5 − m) 1 − −1+ 3
Mặt khác d (I d ) 1 1 = = ⇒ S = AB d I d = m − − − m ∆ABC ( ) 1 2 1 ; . ; 8( 2) 8(5 ). + (− )2 2 2 2 2 2 1 1 m = 5 2 2 2
= (m − 2) − (5 − m) = m − 3m −1 = 3 ⇔ m − 3m −10 = 0 ⇔  m = 2 −
Kết hợp điều kiện (*) suy ra m = 5. Chọn D.
Ví dụ 9: Cho hàm số 2x +1 y =
và đường thằng d : y = 2x − m . Gọi S là tập hợp tất cả các giá trị thực của x −1
tham số m để d cắt (C) tại 2 điểm phân biệt A, B sao cho 5 S
= trong đó O là gốc tọa độ. Tính tổng tất OAB 4
cả các phần tử của S. A. 1 B. 0 C. 2 D. 3 Lời giải 2x +1 x ≠ 1
Phương trình hoành độ giao điểm của (C)và d:
= 2x − m ⇔  (1) 2 x −1
g(x) = 2x − (m + 4)x + m −1 = 0
Để đồ thị (C) cắt d tại 2 điểm phân biệt ⇔ g(x) = 0 có 2 nghiệm phân biệt khác 1. 2
∆ = (m + 4) −8(m − ) 1 > 0 ⇔  (∗) g(1) = 3 − ≠ 0 Khi đó gọi (
A x ;2x − m); B(x ;2x − m) là 2 tọa độ các giao điểm 1 1 2 2  m + 4 x + x =  1 2 Theo Viet ta có:  2  m −1 x x = 1 2  2 Ta có: 2 2 2 2 5
AB = (x − x ) + (2x − 2x ) = 5(x − x ) = 5(x + x ) − 4x x  =   ( 2 m + 24 1 2 1 2 1 2 1 2 1 2 ) 4 ( m d O;AB) = . Khi đó: 1 S = AB d = m m + = OAB ( ) 1 2 5 . O;AB 24 5 2 4 4 4 2 ⇔ m + m = ⇔ ( 2 m − )( 2 24 25
1 m + 25) = 0 ⇔ m = 1
± (t / m) ⇒ S = {± } 1 . Chọn B.
Ví dụ 10: Cho hàm số x +1 y =
và đường thằng y = 2
− x + m . Tìm giá trị của tham số m để đồ thị hàm số x −1
đã cho cắt nhau tại 2 điểm phân biệt A, B và trung điểm AB có hoành độ bằng 5 2 A. 8 B. 11 C. 9 D. 10 Lời giải x +1 x ≠ 1
Phương trình hoành độ giao điểm của (C)và (d):
= m − 2x ⇔  (*) 2 x −1
2x − (m +1)x + m +1 = 0
Để đồ thị (C) cắt (d) tại 2 điểm phân biệt ⇔ (*) có hai nghiệm khác 1. m > 7 2
⇔ (m +1) −8(m + ) 1 > 0 ⇔  m < 1 −
Khi đó gọi x x là hoành độ của hai giao điểm A, B suy ra m +1 x + x = = ⇒ m = t m A B 5 9( / ) A , B 2 Chọn C.
Ví dụ 11: Tìm m để đường thẳng d : y = −x + m cắt đồ thị (C) của hàm số x y =
tại hai điểm phân biệt x −1
A và B sao cho hai điểm A, B cách đều đường thẳng ∆ : 2x − 4y + 5 = 0 A. m = 3 B. m = 5 − C. m =1 D. m = 5 Lời giải
Để A, B cách đều đường thẳng ∆ : 2x − 4y + 5 = 0 thì AB  ∆ hoặc trung điểm I của AB thuộc ∆
Do AB ≡ d không song song với ∆ nên bài toán thỏa mãn khi trung điểm của I của AB thuộc ∆ . 2 x
x − mx + m = 0(*)
Phương trình hoành độ giao điểm hai đồ thị là = −x + m ⇔ x 1  − x ≠ 1
Hai đồ thị cắt nhau tại hai điểm khi và chỉ khi PT (*) có hai nghiệm phân biệt x ≠ 1 ∆(*) > 0 m > 4 A(x y A; A ) Suy ra 2  + +  m 4m 0 x x y y A B A B  ⇒ − > ⇔ ⇒   là trung điểm AB.  − + ≠  <  ( ⇒ I m m m B x y     B ; B ) ; 1 0 0 2 2
Hai điểm A, B cách đều đường thẳng ∆ : 2x − 4y + 5 = 0 ⇒ I ∈∆ ⇒ (x + x − y + y + = A B ) 2( A B ) 5 0
⇔ (x + x − −x − x + m + = ⇔ x + x − m + = ⇔ − m = ⇔ m = A B ) 2( A B 2 ) 5 0 3( A B ) 4 5 0 5 0 5 m > 4
Kết hợp với điều kiện ⇒ m =  5 . Chọn D.m < 0
Ví dụ 12: Số các giá trị nguyên của tham số m + ∈[ 20
− ;20] để đồ thị (C) của hàm số x 3 y = cắt đường x +1
thẳng d : y = x − m tại hai điểm phân biệt A và B thỏa mãn 
AOB tù, với O là gốc tọa độ. A. 22 B. 17 C. 16 D. 23 Lời giải
Phương trình hoành độ giao điểm x + 3 x ≠ 1 − x ≠ 1 − x − m = ⇔  ⇔ x +1 (  x − m  )(x + )  2 1 = x + 3
g(x) = x − mx − m − 3 = 0
Ta có d cắt (C) tại 2 điểm phân biệt ⇔ g(x) có 2 nghiệm phân biệt khác – 1. 2 ∆ = m − 4  (−m −3) > 0 (
 m + 2)2 +8 > 0 ⇔  ⇔  ⇔ m∈(*) g  (− ) 1 = (− )2 1 − m(− ) 1 − m − 3 ≠ 0 m∈ Do ,
A B ∈d ⇒ A(x ; x − m ,B x ; x − m với x ; x là 2 nghiệm của g(x) = 0 1 1 ) ( 2 2 ) 1 2
x + x = m
Theo hệ thức Viet, ta có 1 2  x x = −m −  3 1 2  OA  = (x ; x −  m 1 1 )   Khi đó:  ⇒ .
OAOB = x .x + x − m x − m 1 2 ( 1 )( 1 ) OB  = 
(x ;x − m 2 2 ) 2 2 2
= 2x x − m(x + x ) + m = 2
− (m + 3) − m + m = 2 − (m + 3) 1 2 1 2     Do  AOB tù nên  . cos OAOB AOB = < 0 ⇔ . OAOB < 0 ⇔ 2(
− m + 3) < 0 ⇔ m > 3 − . OAOB m∈ Kết hợp 
⇒ có 23 giá trị của m. Chọn D.m∈  [ 20 − ;20]
Ví dụ 13: Cho hàm số 2x −1 y =
(C) và đường thẳng d : y = 2x + m . Gọi m là giá trị để d cắt (C) tại 2 x +1
điểm phân biệt A, B sao cho tam giác ABC cân tại 3 C  ;3  . Tính d ( ; O d ) khi đó: 4    A. 9 d = B. 3 d = C. 2 d = D. 1 d = 5 5 5 5 Lời giải 2x −1 x ≠ 1 −
Phương trình hoành độ giao điểm của d và (C): = 2x + m ⇔  2 x +1
g(x) = 2x + mx + m +1 = 0 2 ∆ = m − m + > g x 8 1 0 ( ) ( )
Để d cắt (C) tại 2 điểm phân biệt ⇔  g( 1) − = 3 ≠ 0  m x + x = −  1 2 Khi đó gọi (
A x ;2x + m); B(x ;2x + m) theo Viet ta có:  2 1 1 2 2  m +1 x x = 1 2  2
Trung điểm I của AB là  x + x 2x + 2x + 2mm m 1 2 1 2 I ;    hay I −  ; 2 2      4 2    Giải m + 3 .  m IC u  = ⇔ + − = ⇔ m =  
t m . Khi đó d (O d ) 9 ; = . Chọn A. AB 0 2 3 0 9( / ) 4  2  5
Dạng 3: Sự tương giao của đồ thị hàm số trùng phương Phương pháp giải:
Xét sự tương giao đồ thị (C) 4 2
: y = ax + bx + c(a ≠ 0) và trục hoành có phương trình y = 0
Phương trình hoành độ giao điểm (C) và trục hoành là 4 2
ax + bx + c = 0( ) 1
Bài toán liên quan đến số giao điểm
Số giao điểm của đồ thị (C) và trục hoành chính là số nghiệm của phương trình (1). Đặt 2
t = x ≥ 0 thì (1) thành 2
at + bt + c = 0(2)
+) (C) cắt trục hoành tại 4 điểm phân biệt ⇔ (2) có 2 nghiệm dương phân biệt  2
∆ = b − 4ac > 0   b ⇔ t  + t = − > 0 1 2 a   . c t t = > 0  1 2  a
+) (C) cắt trục hoành tại đúng 3 điểm phân biệt ⇔ (2) có 1 nghiệm dương và 1 nghiệm bằng 0.
(C) cắt trục hoành tại đúng 2 điểm phân biệt ⇔ (2) có nghiệm kép dương hoặc (2) có hai nghiệm trái dấu.
+) (C) cắt trục hoành tại điểm duy nhất ⇔ (2) có nghiệm kép bằng 0 hoặc (2) có một nghiệm bằng 0 hoặc một nghiệm âm.
+) (C) không cắt trục hoành ⇔ (2) vô nghiệm, có nghiệm kép âm hoặc có 2 nghiệm phân biệt đều âm
Một số bài toán có thể thay trục hoành thành d : y = m hoặc 2
(P) : y = mx + n , phương pháp giải hoàn
toàn tương tự như trên.
Bài toán liên quan đến tính chất giao điểm Tìm điều kiện để 4 2
(C) : y = ax + bx + c(a ≠ 0) cắt trục hoành tại bốn điểm phân biệt A, B, C, D thỏa
mãn điều kiện cho trước.
Bước 1: Tìm điều kiện để (1) có 4 nghiệm phân biệt  2
∆ = b − 4ac > 0 
⇔ (2) có 2 nghiệm dương phân biệt t và t b ⇔ t
 + t = − > 0 (*) 1 2 1 2 a   . c t t = > 0  1 2  a
Bước 2: Giả sử t > t > 0 khi đó các nghiệm của (1) sắp xếp theo thứ tự tăng dần là 1 2
− t ;− t ; t ; t , xử lý điều kiện và tìm giá trị của tham số. 1 2 2 1
Đặc biệt: Khi hoành độ 4 điểm A, B, C, D lập thành cấp số cộng hoặc AB = BC = CD khi:
t − t = 2 t ⇔ t = 3 t ⇔ t = 9t 1 2 2 1 2 1 2
Ví dụ 1: Số giá trị nguyên của tham số m để đồ thị hàm số 4 2
y = x −8x + 5 − 2m cắt trục hoành tại 4 điểm phân biệt là: A. 9 B. 6 C. 7 D. 8 Lời giải
Phương trình hoành độ giao điểm là 4 2
x −8x + 5 − 2m = 0 Đặt 2 2
t = x ,t ≥ 0 ⇒ PT ⇔ t −8t + 5 − 2m = 0(*)
Phương trình ban đầu có 4 nghiệm phân biệt khi và chỉ khi (*) có hai nghiệm phân biệt thỏa mãn t > t > 0 1 2 ∆ (* ′ ) > 0 1
 6 − (5 − 2m) > 0 Khi đó   11 5 t  + t > 0 ⇔ 8  > 0 ⇔ − < m < 1 2 2 2 t   .t > 0 5  −  2m > 0 1 2
Kết hợp m∈ ⇒ Có 8 giá trị của m. Chọn D.
Ví dụ 2: Cho hàm số 4
y = x + (m − ) 2 2
2 x + 4 có đồ thị (C , với m là tham số thực. Tìm tập hợp T gồm m )
tất cả các giá trị của tham số m để (C cắt Ox tại bốn điểm phân biệt m ) A. T = (0;2) B. T = (4;+∞) C. T = ( ;
−∞ 0) ∪(4;+∞) D. T = ( ;0 −∞ ) Lời giải
Phương trình hoành độ giao điểm là x + (m − ) 2 4 2 t=x 2 2 2 x + 4 = 0 
→t + 2(m − 2)t + 4 = 0(*)
Đồ thị hàm số và trục hoành có 4 giao điểm khi và chỉ khi PT hoành độ giáo điểm có 4 nghiệm phân biệt ∆ (′*) > 0 (
m − 2)2 − 4 > 0 
⇔ (*) có hai nghiệm phân biệt t 0 t   t 0  > ⇒ + > ⇔  2( − m − 2) > 0 1 2 t  .t >  0 4 > 0 1 2 
⇒ m < 0 ⇒ T = ( ;0 −∞ ) . Chọn D.
Ví dụ 3: Cho hàm số 4 2
y = x − 2mx + m +1(C) . Gọi S là tập hợp các giá trị của m để (C) cắt trục Ox tại 4
điểm phân biệt có hoành độ x , x , x , x thỏa mãn 4 4 4 4
x + x + x + x = 20 . Tổng các phần tử của tập hợp (S) 1 2 3 4 1 2 3 4 là: A. 1 B. – 1 C. 2 D. – 3 Lời giải
Phương trình hoành độ giao điểm của (C) và Ox là 4 2
x − 2mx + m +1 = 0( ) 1 Đặt 2 t = x ( ) 2
: 1 ⇒ t − 2mt + m +1 = 0(2)
Để (C) cắt trục Ox tại 4 điểm phân biệt ⇔ (2) có 2 nghiệm phân biệt t > t > 0 1 2 2
∆′ = m − m −1 > 0  t  + t = 2m
⇔ S = 2m > 0 (*) . Theo Viet: 1 2  
t .t = m +  1 P = m +1 > 0 1 2 
Khi đó phương trình (1) có 4 nghiệm − t ;− t ; t ; t 1 2 2 1
Ta có: giả thiết bài toán ⇔ t + t + t + t = 20 ⇔ t + t =10 ⇔ (t + t )2 2 2 2 2 2 2 − 2t t =10 1 2 2 1 1 2 1 2 1 2 m = 2 2 2
⇔ 4m − 2m − 2 =10 ⇔ 2m − m − 6 = 0 ⇔  m = 3 −
Kết hợp (*) ⇒ m = 2 là giá trị cần tìm. Chọn C.
Ví dụ 4: Cho hàm số 4 2
y = x − (2m +1)x + 2(C). Gọi S là tập hợp các giá trị của m để (C) cắt trục Ox tại 4
điểm phân biệt có hoành độ x , x , x , x thỏa mãn 1 1 1 1 5 + + + = 1 2 3 4 4 4 4 4 x x x x 2 1 2 3 4
Số phần tử của tập hợp S là: A. 0 B. 1 C. 2 D. 3 Lời giải
Phương trình hoành độ giao điểm của (C) và Ox là 4 2
x − (2m +1)x + 2 = 0( ) 1 Đặt 2 t = x ( ) 2
: 1 ⇒ t − (2m +1)t + 2 = 0(2)
Để (C) cắt trục Ox tại 4 điểm phân biệt ⇔ (2) có 2 nghiệm phân biệt t > t > 0 1 2 ∆ = ( m + )2 2 1 −8 > 0  t  + t = 2m +1
⇔ S = 2m +1 > 0 (*) . Theo Viet: 1 2   t .t =  2 P = 2 > 0 1 2 
+) Khi đó phương trình (1) có 4 nghiệm − t ;− t ; t ; t ta có: 1 1 1 1 5 + + + = 1 2 2 1 2 2 2 2 t t t t 2 1 2 3 4 2 2 5 2( 2 2 t + t 1 2 ) 5 m =1 2 2 ⇔ + = ⇔
= ⇔ t + t = 5 ⇔ t + t
− 2t t = 5 ⇔ 2m +1 = 9 ⇔ 2 2 2 2 1 2 ( 1 2)2 1 2 ( )2 t t 2 t .t 2  m = 2 − 1 2 1 2
Kết hợp (*) ⇒ m =1 là giá trị cần tìm. Chọn B.
Ví dụ 5: Cho hàm số: 4 2
y = x − 2mx + m + 4(C). Gọi S là tập hợp các giá trị của m để (C) cắt Ox tại 4
điểm phân biệt có hoành độ x , x , x , x thỏa mãn: x + x + x + x = 8 . Tổng các phần tử của tập hợp S 1 2 3 4 1 2 3 4 là: A. 5 B. 12 C. 17 D. – 17 Lời giải
Phương trình hoành độ giao điểm của (C) và Ox là 4 2
x − 2mx + m + 4 = 0( ) 1 Đặt 2 t = x ( ) 2
: 1 ⇒ t − 2mt + m + 4 = 0(2)
Để (C) cắt trục Ox tại 4 điểm phân biệt ⇔ (2) có 2 nghiệm phân biệt t > t > 0 1 2 2
∆′ = m − m − 4 > 0  t  + t = 2m
⇔ S = 2m > 0 (*) . Theo Viet: 1 2  
t .t = m +  4 P = m + 4 > 0 1 2 
+) Khi đó phương trình (1) có 4 nghiệm − t ;− t ; t ; t 1 2 2 1
Ta có: giả thiết ⇔ − t + − t + t + t = 8 ⇔ 2 t + t = 8 ⇔ t + t = 4 1 2 2 1 ( 1 2 ) 1 2 m ≤ 8
⇔ t + t + 2 t t =16 ⇔ 2 m + 4 =16 − 2m ⇔ m + 4 = 8 − m ⇔  ⇔ m = 5 1 2 1 2 2
m −17m + 60 = 0
Vậy m = 5 là giá trị cần tìm. Chọn A.
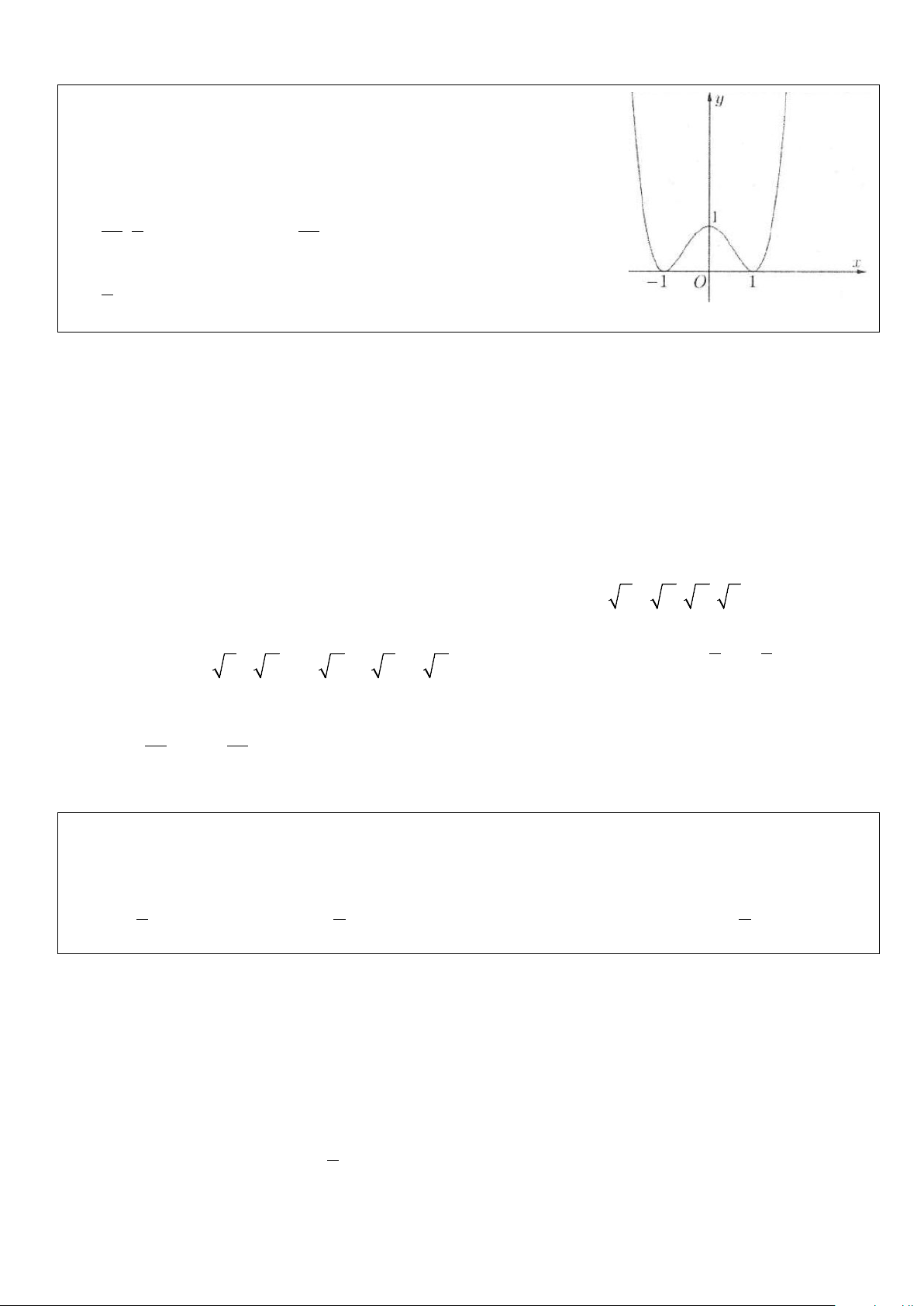
Ví dụ 2: Cho hàm số = ( ) 4 2
y f x = ax + bx + c có đồ thị như hình vẽ.
Tập hợp các giá trị thực của m để đường thẳng d : y = −m + 2 cắt đồ thị
hàm số y = f (x) tại bốn điểm phân biệt cách đều nhau là A. 34 7 ;     B. 34 25 4     25 C. 7  D. {1; } 2 4   Lời giải
Dựa vào đồ thị hàm số, suy ra y = f (x) 4 2 = x − 2x +1
PT hoành độ giao điểm hai đồ thị là 2 4 2 t=x 2
x − 2x +1 = −m + 2 
→t − 2t + m −1 = 0(*)
Hai đồ thị có 4 giao điểm khi và chỉ khi PT (*) có hai nghiệm dương phân biệt ∆ (′*) > 0 1  − m +1 > 0   t  + t = 2 Suy ra 1 2 ⇔ t
 + t > 0 ⇔ 2 > 0 ⇔ 1< m < 2 ⇒ 1 2 t  .t = m−    1 1 2 t  .t > 0 m −1 > 0 1 2
Giả sử t > t , 4 nghiệm của PT ban đầu theo thứ tự từ bé đến lớn sẽ là − t ;− t ; t ; t 1 2 1 2 2 1 t  + t = 2 1 2  9 1  t  = ;t = Theo đề bài ta có 1 2 − t + t = 2
− t ⇒ t = 3 t ⇔ t = 9t ⇒ t
 .t = m −1⇒ 1 2 2 1 2 1 2 1 2  5 5 t  =  9t t
 .t = m−1 1 2 1 2 9 34 ⇒ m −1 = ⇔ m = . Chọn B. 25 25
Ví dụ 7: Cho hàm số 4 2 2
y = x − 2(2m +1)x + 4m (C) . Các giá trị của tham số thực m để đồ thị (C) cắt trục
hoành tại 4 điểm phân biệt có hoành độ x , x , x , x thỏa mãn 2 2 2 2
x + x + x + x = 6 là 1 2 3 4 1 2 3 4 A. 1 m ≥ − B. 1 m = − C. m =1 D. 1 m = 4 4 4 Lời giải
PT hoành độ giao điểm hai đồ thị là 2 4 2 2 t=x 2 2
x − 2(2m +1)x + 4m = 0 
→t − 2(2m +1)t + 4m = 0(*) ∆′ > 0
Đồ thị cắt trục hoành tại 4 điểm ⇔ (*) có 2 nghiệm dương phân biệt t   + t > 0 1 2 t  .t >  0 1 2 2 2
(2m +1) − 4m > 0  1 2 2  m > − t  = x = x 1 1 2 ⇔ 2(2m +1) > 0 ⇔  4 ⇒  2 2   t  = >  ≠  x = x 2 1 3 4 m 0 4m 0  1 m > − Khi đó 2 2 2 2 1
x + x + x + x = 2(t + t ) = 4 2m +1 = 6 ⇔ m = thỏa mãn . Chọn D. 1 2 3 4 1 2 ( )  4 4 m ≠ 0
Ví dụ 8: Cho hàm số 4 2 2
y = x − (4m + 2)x + 2m +1(C). Có bao nhiêu giá trị của m để (C) chia trục hoành
thành 4 đoạn phân biệt có độ dài bằng nhau. A. 0 B. 1 C. 2 D. 3 Lời giải
Phương trình hoành độ giao điểm của (C) và Ox là 4 2 2
x − (4m + 2)x + 2m +1 = 0( ) 1 Đặt 2 t = x ( ) 2 2
: 1 ⇒ t − (4m + 2)t + 2m +1 = 0(2)
Để (C) cắt trục Ox tại 4 điểm phân biệt ⇔ (2) có 2 nghiệm phân biệt t > t > 0 1 2 ∆′ = (2m + )2 2 1 − 2m −1 > 0  2   + >
⇔ S = ( m + ) 2m 4m 0 4 2 > 0 ⇔  (*) .  2m +1 > 0 2 P = 2m +1 > 0  t
 + t = 4m + 2
Theo định lý Viet ta có: 1 2  2 t
 .t = 2m +1 1 2
Khi đó PT (1) có 4 điểm A, B, C, D theo thứ tự hoành độ tăng dần là: − t ;− t ; t ; t 1 2 2 1
Ta có: AB = CD = t − t ; BC = 2 t ⇒ AB = BC = CD ⇔ t = 3 t ⇔ t = 9t 1 2 2 1 2 1 2 t  + t = 4m + 2 1 2  2m +1 2m +1  t  = 9. ,t = Giải hệ: 1 2 t  = 9t ⇔  5 5 ⇒ 9(2m + )2 1 = 25( 2 2m +1 1 2 )   2 2 t  .t = 2m +1 t  .t = 2m +1 1 2 1 2 m = 2 2 7m 18m 8 0  ⇔ − + = ⇔
4 (t / m(*)) . Vậy 4
m = 2,m = là giá trị cần tìm. Chọn C.m = 7  7
Dạng 4: Sự tương giao của đồ thị hàm số bậc 3 Phương pháp giải:
Xét đồ thị (C) 3 2
: y = ax + bx + cx + d (a ≠ 0) và đường thẳng d : y = kx + 
Hoành độ giao điểm của y = x + m và (C) là nghiệm của phương trình 3 2 3 2
ax + bx + cx + d = kx +  ⇔ ax + bx + (x − k)x + d −  = 0 (1)
→ Số giao điểm của d và (C) là nghiệm của phương trình (1).
Trường hợp 1: Phương trình (1) có một nghiệm đẹp x = x ox = x
Khi đó (1) thành (x − x ).( 2
Ax + Bx + C) = 0 o ⇔ o  2
g(x) = Ax + Bx + C = 0 ∆ >  g x 0
- Phương trình (1) có 3 nghiệm phân biệt ⇔ g(x) = 0 có 2 nghiệm phân biệt khác ( ) x ⇔ o  g(x ≠ o ) 0
Gọi x , x là nghiệm của phương trình g(x) = 0 khi đó tọa độ các giao điểm của d và (C) là: 1 2  −B x + x =  1 2 A(x kx x kx x kx trong đó 
A ( Định lý Viet). o ; + o ),B( ; +  ,C ; + 1 1 ) ( 2 2 )   . C x x = 1 2  A
- Phương trình (1) có đúng 2 nghiệm phân biệt ⇔ g(x) = 0 có nghiệm kép khác x hoặc g(x) = 0 có hai o
nghiệm phân biệt, trong đó 1 nghiệm bằng x và nghiệm còn lại khác x . o o
- Phương trình (1) có nghiệm duy nhất ⇔ g(x) = 0 vô nghiệm hoặc g(x) = 0 có nghiệm kép x = x . o
Trường hợp 2: Phương trình (1) không có một nghiệm đẹp x = x nhưng cô lập được tham số. o
Khi đó ta biến đổi (1) thành ϕ(x) = h(m) .
Từ đó số nghiệm của (1) là số giao điểm của đồ thị hàm số y = ϕ(x) và y = h(m)
Lập bảng biến thiên cho hàm số y = ϕ(x) ⇒ Kết luận.
Ví dụ 1: Cho hàm số 3 2
y = 2x − 3x +1(C) . Tìm giá trị của tham số m để (C) cắt đường thẳng y = mx +1 tại 3 điểm phân biệt.  3  9 −  9  >  >  > − A. m m m  2 B.  8 C. 9 m − > D.  8  8 m ≠ 2 m ≠1 m ≠ 0 Lời giải
Phương trình hoành độ giao điểm là x = 0 3 2 3 2
2x − 3x +1 = mx +1 ⇔ 2x − 3x − mx = 0 ⇔  2
g(x) = 2x − 3x − m = 0  9 ∆ = + m − > g x 9 8 0 m >
ĐK cắt tại 3 điểm phân biệt ( ) ⇔  ⇔  8 . Chọn D.
g(0) = −m ≠ 0 m ≠ 0
Ví dụ 2: Tìm m để đồ thị hàm số y = (x − ) 2 x − ( m + ) 2 2 2
1 x + m + m 
 cắt trục hoành tại ba điểm phân biệt.
A. Không tồn tại m
B. m <1 hoặc m > 2
C. m ≠ 1,m ≠ 2 D. m ∀ ∈  Lời giải
Phương trình hoành độ giao điểm của đồ thị hàm số (C) và trục hoành là x = (1) ⇔ (x − 2) 2 2 x − (2m + ) 2
1 x + m + m = 0 ⇔    2
f (x) = x −  (2m + ) 2
1 x + m + m = 0
Đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt ⇔ (1) có 3 nghiệm phân biệt ⇔ f (x) = 0 có hai nghiệm phân biệt  > ∆ > 0 (  m+ )2 − ( 2 m + m) 1 0 2 1 4 > 0  m ≠ 1 x ≠ 2 ⇔  ⇔  ⇔ m ≠1 ⇔ . Chọn C.f (2) 0  ≠  −  ( m + ) 2 + + ≠  m ≠ 2 4 2 2 1 m m 0 m ≠  2
Ví dụ 3: Số các giá trị nguyên của tham số m để m∈[ 10
− ;10] đường thẳng y = 4x −5 cắt đồ thị của hàm số 3
y = x − (m + 2)x + 2m −1 tại ba điểm phân biệt là A. 10 B. 11 C. 12 D. 13 Lời giải
Phương trình hoành độ giao điểm là 3 3
x − (m + 2)x + 2m −1 = 4x + 5 ⇔ x − (m + 6)x + 2m + 4 = 0(*) x = 2 2
(x − 2)(x + 2x − m − 2) = 0 ⇔  2
f (x) = x + 2x − m − 2 = 0
Hai đồ thị có giao điểm khi và chỉ khi PT (*) có ba nghiệm phân biệt, khi đó PT f (x) = 0 có 2 nghiệm ∆′ > 0 1  + m + 2 > 0 m > 3 −
phân biệt x ≠ 2 ⇔  ⇔  ⇔  f (2) 0 4 4 m 2 0  ≠ + − − ≠ m ≠ 6 m∈[ 10 − ;10] Kết hợp 
⇒ có 12 giá trị của m. Chọn C. m∈
Ví dụ 4: Tìm tất cả các giá trị của tham số m để đồ thị hàm số (C) y = (x − )( 2 :
2 x − 2mx + m) cắt trục
hoành tại ba điểm phân biệt có hoành độ dương. A. m ( ) 4 1; \  ∈ +∞      B. m∈(−∞ ) 4 4 ;0 ∪1; ∪   ;+∞ 3     3   3  C. m∈(1;+∞) D. m∈(0;+∞) Lời giải x = 2
Phương trình hoành độ giao điểm là (x − 2)( 2
x − 2mx + m) = 0 ⇔  2
f (x) = x − 2mx + m = 0
(C) cắt trục hoành tại ba điểm phân biệt có hoành độ dương ⇔ PT f (x) = 0 có hai nghiệm x > 0, x ≠ 2 2 ∆′ > 0
m − m > 0   m >1 x + x > 0  > Suy ra 1 2 2m 0     ⇔  ⇔  4 ⇔ m∈( +∞) 4 1; \ . Chọn A. x .x 0   >  m > 0 m ≠ 3 1 2   3  f (2) ≠ 0
4−4m+ m ≠ 0
Ví dụ 5: Tìm tất cả các giá trị của tham số m sao cho đồ thị của hàm số 3 2
y = x − 3x + (m + 2)x − m và đồ
thị hàm số y = 2x − 2 có ba điểm chung phân biệt A. m < 3 B. m < 2 C. m > 3 D. m > 2 Lời giải
Phương trình hoành độ giao điểm đồ thị hai hàm số là 3 2 3 2
x − x + m + x − m = x − ⇔ x − x + mx − m + = ⇔ (x − )( 2 3 ( 2) 2 2 3 2 0
1 x − 2x + m − 2) = 0(*)
Đồ thị hai hàm số có ba điểm chung phân biệt khi và chỉ khi pt (*) có ba nghiệm phân biệt. Khi đó ( − ) x = x 1 ( 1 2
x − 2x + m − 2) = 0 ⇔  2
f (x) = x − 2x + m − 2 = 0  f (1) ≠ 1 1
 − 2 + m − 2 ≠ 0 m ≠ 3 Yêu cầu bài toán ⇒  ⇔  ⇔ 
⇒ m < 3 . Chọn A. ∆′ >  f x 0 ( ) 1  − m + 2 > 0 m < 3
Ví dụ 6: Cho hàm số y = (x − )( 2 1 x + mx + )
1 (C) . Số các giá trị của m thỏa mãn đồ thị (C) cắt trục Ox tại
3 điểm phân biệt có hoành độ x ; x ; x thỏa mãn 2 2 2
x + x + x =10 là 1 2 3 1 2 3 A. 1 B. 2 C. 0 D. 3 Lời giải
Phương trình hoành độ giao điểm của (C) và trục Ox là: x = 2 (x − ) 1 ( 2 x + mx + ) 3 1 = 0 ⇔  ( )1 2
f (x) = x + mx +1 = 0
Đồ thị (C)cắt trục Ox tại 3 điểm phân biệt ⇔ (1) có 3 nghiệm phân biệt ⇔ g(x) = 0 có 2 nghiệm phân 2 2 ∆ = − >  >
biệt và 2 nghiệm đó khác 1 m 4 0 m 4 ⇔  ⇔  g(1) ≠ 0 m + 2 ≠ 0
x + x = −m
Khi đó cho x =1 và x ; x là nghiệm của PT g(x) = 0 . Theo định lý Viet ta có: 1 2 3 1 2 x .x =  1 1 2
Theo đề bài ta có: x + x + x =10 ⇔ (x + x )2 2 2 2 2
− 2x x = 9 ⇔ m − 2 = 9 1 2 3 1 2 1 2 2
⇔ m =11 ⇔ m = ± 11(t / m)
Vậy m = ± 11 là giá trị cần tìm . Chọn B.
Ví dụ 7: Cho hàm số 3
y = x − mx + m −1(C) . Gọi m là giá trị của m để đồ thị (C) cắt trục Ox tại 3 điểm o
phân biệt có hoành độ x ; x ; x thỏa mãn: 1 1 1 A = + + = 2 . Khi đó: 1 2 3 x x x 1 2 3 A. m ∈ − B. m ∈ C. m ∈ D. m ∈ o (5;7) o (3;5) o (0;3) o ( 2;0) Lời giải
Phương trình hoành độ giao điểm của (C) và trục Ox là: 3
x − mx + m −1 = 0 x =1 3 2 3
x −1− m(x −1) = 0 ⇔ (x −1)(x + x +1− m) = 0 ⇔  ( )1 2
g(x) = x + x +1− m = 0
Để đồ thị (C) cắt trục Ox tại 3 điểm phân biệt ⇔ (1) có 3 nghiệm phân biệt
∆ = 1− 4(1− m) = 4m − 3 > 0 ⇔  (*)
g(1) = 3 − m ≠ 0
Khi đó gọi x =1 và x ; x là nghiệm của PT g(x) = 0 3 1 2 x + x = 1 − Theo Viet ta có: 1 2  x .x =1−  m 1 2 Do vậy 1 1 x + x 1 − 1 2 A = + +1 = +1 =
+1 = 2 ⇔ m = 2(tm) x x x x 1− m 1 2 1 2
Vậy m = 2 là giá trị cần tìm. Chọn B.
Ví dụ 8: Cho hàm số 3 2
y = x − 2mx −1có đồ thị (C , với m là tham số thực. Hỏi có tất cả bao nhiêu giá m )
trị nguyên của m để (C cắt đường thẳng d : y = x −1 tại ba điểm phân biệt có hoành độ x , x , x thỏa m ) 1 2 3 mãn 2 2 2
x + x + x ≤ 20 1 2 3 A. 4 B. 6 C. 5 D. 3 Lời giải
Phương trình hoành độ giao điểm x = 0 3 2 2
x − 2mx −1 = x −1 ⇔ x(x − 2mx −1) = 0 ⇔  ( )1 2
x − 2mx −1 = 0
Ta có d cắt (C tại 3 điểm phân biệt ⇔ (1) có 2 nghiệm phân biệt khác 0 m ) 2
∆′ = m +1> 0 ⇔  ⇔ m∈ (*) 2 0 − 2 .0 m −1 ≠ 0
x + x = 2m
Giả sử x = 0 khi đó x ; x là 2 nghiệm của (1), theo Viet có 1 2 3 1 2 x .x = 1 −  1 2
Do đó x + x + x ≤ ⇔ (x + x )2 2 2 2 2 2 9 3 3 20
− 2x x ≤ 20 ⇔ 4m + 2 ≤ 20 ⇔ m ≤ ⇔ − ≤ m ≤ 1 2 3 1 2 1 2 2 2 2
Mà m∈ ⇒ m∈{ 2 ± ; 1; ± } 0 . Chọn C
Ví dụ 9: Cho hàm số 3
y = x − x(C) và đường thẳng d : y = m(x −1) . Gọi m là giá trị của m để đồ thị o
(C) cắt đường thẳng d tại 3 điểm phân biệt A; B; C sao cho điểm 1 M  ; 9 − − 
là trung điểm của đoạn AB 2   
trong đó C (1;0) . Khi đó: A. m < − B. m ∈ C. m ∈ D. m ∈ +∞ o (7; ) o (4;7) o (0;4) o 1 Lời giải
Phương trình hoành độ giao điểm của (C) và đường thẳng d là: x( 2 x − ) 1 − m(x − ) 1 = 0 ⇔ ( − ) x = x 1 ( 1 2
x + x) − m(x − ) 1 = 0 ⇔ (x − ) 1 ( 2
x + x − m) = 0 ⇔  2
g(x) = x + x − m = 0
Đồ thị (C) cắt d tại 3 điểm phân biệt ⇔ (1) có 3 nghiệm phân biệt ⇔ g(x) = 0 có 2 nghiệm phân biệt và ∆ = 1+ 4m > 0 4m +1 > 0
2 nghiệm đó khác 1 ⇔  ⇔  (*) g(1) ≠ 0 2 − m ≠ 0 x + x = 1 −
Khi đó gọi x ; x là nghiệm của PT g(x) = 0 . Theo định lý Viet ta có: 1 2 1 2 x .x = −  m 1 2
Ta có: A(x ;m x −1 ;B x ;m x −1 , trung điểm của AB là 1 ( 1 )) ( 2 ( 1 ))  x + x 1 − 1 2 x = =  M  2 2 
m(x −1 + m x −1
m x + x − 2m 1 ) ( 2 ) ( 1 2) 3 −  m y = = = M  2 2 2 Theo bài ra 1 − M  ;0 − 3m  nên = 9
− ⇔ m = 6(tm) 2    2
Vậy m = 6 là giá trị cần tìm. Chọn C.
Ví dụ 10: [Đề thi THPT Quốc gia năm 2017] Tìm tất cả các giá trị thực của m để đường thẳng
y = mx − m +1 cắt đồ thị của hàm số 3 2
y = x − 3x + x + 2 tại ba điểm A, B, C phân biệt sao cho AB = BC. A. m∈( ; −∞ 0]∪[4;+∞) B. 5 m  ;  ∈ − +∞  4    C. m∈( 2; − +∞) D. m∈ Lời giải
Phương trình hoành độ giao điểm là 3 2
x − 3x + x + 2 = m(x − ) 1 +1 ( − ) x = x 1 ( 1 2
x − 2x −1− m) = 0 ⇔  2
g(x) = x − 2x −1− m = 0
Giả thiết bài toán B là trung điểm của AC hay g(x) = 0 có 2 nghiệm phân biệt x ; x ≠ 1 thỏa mãn 1 1 ∆′ = + m > g x 2 0 ( ) x x x x x  ⇔ + = ⇔ +
= ⇔ g = − − m ≠ ⇔ m > − . Chọn C. A C 2 B 1 (1) 2 0 2 1 2 x + x =1  1 2
Ví dụ 11: Cho hàm số: 3
y = x + (m + 2) x − m(C) và đường thẳng d : y = 2x +1. Số giá trị nguyên của m để
đồ thị (C) cắt đường y = x + m tại 3 điểm phân biệt có tung độ y , y , y thỏa mãn 2 2 2
A = y + y + y ≤ 83 1 2 3 1 2 3 A. 9 B. 10 C. 11 D. 12 Lời giải
Phương trình hoành độ giao điểm của (C) và đường thẳng d là: 3
x + mx − m −1 = 0 ⇔ ( − ) x = ⇒ y = x 1 ( 1 3 2
x + x +1− m) 3 3 = 0 ⇔  ( )1 2
g(x) = x + x +1− m = 0
Đồ thị (C) cắt y = x + m tại 3 điểm phân biệt ⇔ ( )
1 có 3 nghiệm phân biệt ⇔ g(x) = 0 có 2 nghiệm  3
∆ = 1− 4(1− m) > 0 4m − 3 > 0 m ≥
phân biệt và 2 nghiệm đó khác 1 ⇔  ⇔  ⇔  4 (*) g(1) ≠ 0 3  − m ≠ 0 m ≠ 3
Khi đó cho x =1; y = 3 và x ; x là nghiệm của phương trình g(x) = 0 3 3 1 2 x + x = 1 −
Theo định lý Viet ta có: 1 2  x .x = −  m 1 2
Theo đề bài ta có: A = y + y + y = (2x + )2 1 + (2x + )2 2 2 2 1 + 9 = 4( 2 2
x + x + 4 x + x +11 1 2 3 1 2 1 2 ) ( 1 2)
A = 4 (x + x )2 − 2x x  + 4 x + x +11 = 4 1
 − 2 1− m  − 4 +11 = 8m + 3 ≤ 83 ⇔ m ≤10 1 2 1 2 ( 1 2)    ( )
Kết hợp (*) và m∈ ⇒ có 9 giá trị của m. Chọn A.
Ví dụ 12: Cho hàm số: 3
y = x + mx − 4(C) và đường thẳng d : y = 2mx + 4 . Gọi m là giá trị của m để d o
cắt (C) tại 3 điểm phân biệt A, B, C sao cho trọng tâm tam giác OAB là 2 G  ;8 − 
trong đó (C) là điểm 3   
có hoành độ x = và O là gốc tọa độ. Khi đó C 2
A. m ∈ − − B. m ∈ − C. m ∈ D. m ∈ +∞ o (6; ) o (3;6) o ( 1;3) o ( 5; 2) Lời giải
Phương trình hoành độ giao điểm của (C) và d là: 3
x + mx − 2mx −8 = 0 ( x = ⇒ C m + ⇔ x − 2)( 2 2;4 4 2
x + 2x + 4) + m(x − 2) = 0 ⇔ (x − 2)( 2
x + 2x + 4 + m) ( ) = 0 ⇔  ( )1 2
g(x) = x + 2x + 4 + m = 0
Để đồ thị (C) cắt đường thẳng d tại 3 điểm phân biệt ⇔ (1) có 3 nghiệm phân biệt ∆′ = 
1− 4 − m = −m − 3 > 0 ⇔  g  ( ) (*) 2 =12 + m ≠ 0 x + x = 2 −
Khi đó gọi x ; x là nghiệm của phương trình g(x) = 0 . Theo Viet ta có: 1 2 1 2 x .x = 4+  m 1 2  x + x + 0 2 − 1 2 x = =  o
Gọi A(x ;2mx + 4 ;B x ;2mx + 4 ta có:  3 3 1 1 ) ( 2 2 ) 
2mx + 4 + 2mx + 4 + 
0 2m(x + x + 8 1 2 1 2 ) y = = o  3 3 Do vậy  2 8 4 ; m − G −  − m
. Cho 8 4 = 8 ⇔ m = 4( − tm) 3 3    3 Vậy m = 4
− là giá trị cần tìm. Chọn A.
Ví dụ 2: Cho hàm số 3 2
y = x − x (2m + 3) + x(6m + 7) − 4m − 3 và đường thẳng d : y = x +1 . Gọi S là tập
hợp các giá trị thực của m để đường thẳng d cắt đồ thị hàm số tại ba điểm phân biệt A, B, C sao cho x = A 1
và diện tích tam giác OBC bằng 5 , với O là gốc tọa độ. Tổng các phần tử của tập hợp S là: A. T = 2 B. T = 4 C. T = 2 − D. T = 3 Lời giải
Phương trình hoành độ giao điểm hai đồ thị là 3 2
x − x (2m + 3) + x(6m + 7) − 4m − 3 = x +1 3 2
⇔ x − m + x + m + x − m − = ⇔ (x − ) 2 (2 3) (6 6) 4 4 0
1 x − (2m + 2) x + 4m + 4 = 0   x −1 = 0 x = A 1 ⇔  ⇔ 2 x −  (2m + 2)  2 x + 4m + 4 = 0
f (x) = x − 
(2m + 2) x + 4m + 4 = 0(*)
Hai đồ thị có ba giao điểm khi và chỉ khi (*) có hai nghiệm phân biệt x ≠ 1  3 m ≠ −  f (1) ≠ 0 1
 − 2m − 2 + 4m + 4 ≠ 0    2
x + x = m + B C 2( )1 Suy ra  ⇔  ⇔  ⇒ ∆ (′*) > 0 (   m +  )2 1 − 4(m + ) 1 > 0 m > 3  x x = m +  B. C 4( )1  m < 1 −
Ta có BC = (x − x + y − y = x − x = x + x − x x B C )2 ( B C )2 ( B C )2 ( B C )2 2 2 8 B. C 1 = (m + )2 8 1 − 32(m + )
1 . Mặt khác d (O d ) 1 ; = = + (− )2 2 2 1 1 1 1 m = 2 − Suy ra S = = + − + = ⇒ ⇒ ∈ − ∆ d O d BC m mm t m OBC ( ; ). 8( )2 1 32( )1 5 { 2; } 4 ( / ) 2 2 2 m = 4
Vậy T = 2 . Chọn A.
BÀI TẬP TỰ LUYỆN
Câu 1: Có bao nhiêu số nguyên dương m sao cho đường thẳng −
y = x + m cắt đồ thị hàm số 2x 1 y = tại x +1
hai điểm phân biệt A, B và AB ≤ 4 ? A. 7 B. 6 C. 1 D. 2
Câu 2: Tìm tất cả các giá trị thực của tham số m để đường thẳng (d) : y = mx − m −1 cắt đồ thị (C) 3 2
: y = x − 3x +1 tại 3 điểm A, B, C phân biệt (B thuộc đoạn AC), sao cho tam giác AOC cân tại O (với O là gốc tọa độ). A. m = 2 − B. m = 2 C. m = 1 − D. m =1
Câu 3: Tìm tất cả các giá trị thực của tham số m để đường thẳng y = 2
− x + m cắt đồ thị (H ) của hàm số 2x + 3 y =
tại hai điểm A, B phân biệt sao cho 2018 2018 P = k + k
đạt giá trị nhỏ nhất, với k ,k là hệ số góc x + 2 1 2 1 2
của tiếp tuyến tại A, B của đồ thị (H ) .
A. m = 3
B. m = 2 C. m = 3 − D. m = 2 − Câu 4: Cho hàm số x + 3 y =
có đồ thị (C).Tìm m sao cho đường thẳng d : y = x + m cắt (C) tại hai điểm x +1
phân biệt A và B thỏa mãn điều kiện G (2; 2
− ) là trọng tâm của tam giác OAB.
A. m = 2 B. m = 5 C. m = 6 D. m = 3 Câu 5: Cho hàm số x + 3 y =
và đường thẳng y = 2x + m . Tìm giá trị của m để đồ thị hai hàm số đã cho x +1
cắt nhau tại hai điểm A, B phân biệt sao cho độ dài đoạn AB nhỏ nhất. A. m = 1 − B. m = 3 C. m = 4 D. m =1
Câu 6: Tìm giá trị thực của tham số m để đồ thị hàm số 3 2
y = x − 3x + 2 cắt đường thẳng (d ) : y = m(x −1)
tại ba điểm phân biệt hoành độ x , x , x thỏa mãn 2 2 2
x + x + x > 5 . 1 2 3 1 2 3 A. m ≥ 3 − B. m ≥ 2 − C. m > 3 − D. m > 2 − Câu 7: Cho hàm số 3 2
y = x − 2mx + 3(m −1) + 2 có đồ thị(C). Đường thẳng d : y = −x + 2 cắt đồ thị (C) tại ba điểm phân biệt (
A 0;2), B và C. Với M (3;1) , giá trị của tham số m để tam giác MBC có diện tích bằng 2 6 là A. m = 1 − B. m = 1 − hoặc m = 4 C. m = 4
D. Không tồn tại m Câu 8: Cho hàm số 3 2
y = x + 3x + m có đồ thị (C) .Biết đồ thị (C) cắt trục hoành tại 3 điểm phân biệt A,
B, C sao cho B là trung điểm của AC. Phát biểu nào sau đây đúng?
A. m∈(0;+∞) B. m∈( ; −∞ 4 − ) C. m∈( 4; − 0) D. m∈( 4; − 2 − ) Câu 9: Cho hàm số 3
y = x − 3x có đồ thị (C) . Gọi S là tập hợp tất cả các giá trị thực của k để đường thẳng
d : y = k(x +1) + 2 cắt đồ thị (C) tại ba điểm phân biệt M, N, P sao cho các tiếp tuyến của (C) tại N và P
vuông góc với nhau. Biết M ( 1;
− 2), tính tích tất cả các phần tử của tập S. A. 1 B. 2 − C. 1 D. 1 − 9 9 3
Câu 10: Đường thẳng 2
y = m cắt đồ thị hàm số 4 2
y = x − x −10 tại hai điểm phân biệt A, B sao cho tam
giác OAB vuông với O là gốc tọa độ. Mệnh đề nào sau đây đúng? A. 2 m ∈(5;7) B. 2 m ∈(3;5) C. 2 m ∈(1;3) D. 2 m ∈(0; ) 1
Câu 11: Gọi S là tập tất cả các giá trị của tham số m để đồ thị hàm số 3 2
y = x + 3x − 9x + 2m +1và trục Ox
có đúng hai điểm chung phân biệt. Tính tổng T của các phần tử thuộc tập S. A. T = 12 B. T = 10 C. T = 12 − D.T = 10 −
Câu 12: Biết rằng đường thẳng y = x − m cắt đồ thị hàm số 3 2
y = x − 3x tại ba điểm phân biệt sao cho có
một giao điểm cách đều hai giao điểm còn lại. Khi đó m thuộc khoảng nào dưới đây? A.(2;4) B. ( 2; − 0) C. (0;2) D. (4;6) Câu 13: Cho hàm số 3 2
y = x − mx + 3x +1 và M (1; 2
− ) . Biết có 2 giá trị của m là m và m để đường thẳng 1 2
∆ : y = x +1 cắt đồ thị tại 3 điểm phân biệt (
A 0;1) , B, C sao cho tam giác MBC có diện tích bằng 4 2 . Hỏi tổng 2 2
m + m thuộc khoảng nào trong các khoảng sau: 1 2 A.(15;17) B. (3;5) C. (31;33) D. (16;18)
LỜI GIẢI BÀI TẬP TỰ LUYỆN
Câu 1: Ta có 2x −1 2
= x + m ⇔ x + (m − ) 1 x + m +1 = 0 x +1 m > 3+ 2 3
Để cắt nhau tại 2 điểm phân biệt thì 2
∆ > 0 ⇔ m − 6m − 3 > 0 ⇔  m < 3− 2 3
Giả sử A(x ; x + m), B(x ; x + m) ⇒ AB = 2(x − x )2 1 1 2 2 1 2
Ta có AB ≤ 4 ⇔ 2(x − x )2 ≤ 4 ⇔ (x − x )2 ≤ 8 ⇔ (x − x )2 − 4x x ≤ 8 1 2 1 2 1 2 1 2 2 2
⇔ (m −1) − 4(m +1) ≤ 8 ⇔ m − 6m −11≤ 0 ⇔ 3− 2 5 ≤ m ≤ 3+ 2 5
Do đó 3+ 2 3 < m ≤ 3+ 2 5 ⇒ m = 7 . Chọn Cx =1 Câu 2: 3 2 2
x − 3x +1 = mx − m −1 ⇔ (x −1)(x − 2x − m − 2) = 0 ⇔  g  ( x) 2
= x − 2x − m − 2 = 0 g ( ) 1 ≠ 0 m ≠ 3
Để cắt nhai tại 3 điểm thì  ⇔  ⇔ m > 3 − ∆′ > 0 m + 3 > 0
Giả sử A(x ;mx − m −1 ,C x ;mx − m −1 với x + x = 2, x x = −m − 2 1 1 ) ( 2 2 ) 1 2 1 2 Ta có 2 2 2 2
OA = OC ⇔ x + (mx − m −1) = x + (mx − m −1) 1 1 2 2 2 2 2 2
⇔ (m +1)(x − x ) − 2m(m +1)(x − x ) = 0 ⇔ (m +1)(x + x ) − 2m(m +1) = 0 1 2 1 2 1 2 2
⇔ 2(m +1) − 2m(m +1) = 0 ⇔ 2 − 2m = 0 ⇔ m =1. Chọn D. Câu 3: Ta có 1 + y′ =
. Xét phương trình 2x 3 2 = 2
− x + m ⇔ 2x − (m − 6)x − 2m + 3 = 0 2 (x+ 2) x + 2
Để cắt nhau tại 2 điểm thì 2 2
∆ > 0 ⇔ (m − 6) −8( 2
− m + 3) > 0 ⇔ m + 4m +12 > 0, m ∀ Ta có 2018 2018 1 1 P = k + k = + 1 2 4036 4036 (x + 2) (x + 2) 1 2
Để đạt giá trị nhỏ nhất thì 1 1 = 4036 4036 (x + 2) (x + 2) 1 2 m − 6
⇔ x + 2 = −(x + 2) ⇔ x + x = 4 − ⇔ = 4 − ⇔ m = 2. − Chọn D. 1 2 1 2 2
Câu 4: Ta có x + 3 2
= x − m ⇔ x − mx − m − 3 = 0. Giả sử A(x ; x − m , B(x ; x − m) 1 1 ) x +1 2 2  x + xm 1 2 = 2 = 2  
Do G là trọng tâm của A ∆ BC nên  3  3  ⇔ 
⇔ m = 6. Chọn C.
x + x − 2m −m  1 2 = 2  − = 2 −  3  3
Câu 5: Ta có x + 3 2
= 2x + m ⇔ 2x + (m +1)x + m − 3 = 0. Giả sử A(x ;2x + m , B x ;2x + m 1 1 ) ( 2 2 ) x +1 2  +  −  Ta có AB =
(x − x )2 = (x + x )2 m 1 m 3 5 5 − 4x x  = 5 −   4 1 2 1 2 1 2     2  2    1 2 3 25 5 m m  − = − + b  nhỏ nhất khi m = = 3. Chọn B. 4 4 4    2ax =1 Câu 6: Ta có 3 2
x − 3x + 2 = m(x + ) 2
1 ⇔ (x −1)(x − 2x − m − 2) = 0 ⇔  2
x − 2x − m − 2 = 0 x + x = 2 Giả sử 2 3 x =1⇒
Ta có x + x + x > 5 ⇔ x + x + x − 2x x > 5 1 2 3 1 ( 2 3)2 2 2 2 2 1 x x = −m−  3 2 3 2 3 2
⇔ 1+ 2 − 2(−m − 3) > 5 ⇔ m > 3. − Chọn C.
Câu 7: Phương trình hoành độ giao điểm của (C) và d là 3 2
x + 2mx + 3(m −1)x + 2 = −x + 2 x = 0 3 2 2
⇔ x + 2mx + (3m − 2)x = 0 ⇔ x(x + 2mx + 3m − 2) = 0 ⇔  2
x + 2mx + 3m − 2 = 0     f (x) 3  m − 2 ≠ 0
Để (C) cắt d tại 3 điểm ⇔ f (x) = 0 có hai nghiệm phân biệt khác 0 ⇔  (∗) 2
m − 3m + 2 > 0 Khi đó, gọi (
A 0;2),B(x ; y ) và C(x ; y ) là tọa độ giao điểm của (C) và d 1 1 2 2 x + x = 2 − m
Với x , x thỏa mãn hệ thức Vi – et : 1 2 1 2 x x = 3m−  2 1 2
Ta có d M (BC) = d M (d ) 1 ; ;  = 2 ⇒ S =   ⇒ =     ∆ d M d BC BC MBC ;  ( ) . 4 3 2 
Lại có BC = (x − x ;− x + x ) ⇒ BC = 2(x − x ) = 2 (x − x )2 2 − 4 x x  = 48 2 1 2 1 2 1 2 1 1 2   m = 1 − Suy ra 2 2 ( 2
− m) − 4(3m − 2) = 24 ⇔ 4m −12m −16 = 0 ⇔  (thỏa mãn (∗) ) m = 4 Vậy m = 1
− hoặc m = 4 là giá trị cần tìm. Chọn B.
Câu 8: Yêu cầu bài toán ⇔ Điểm uốn của đồ thị (C) thuộc trục hoành Ta có 2
y′ = 3x + 6x ⇒ y′′ = 6x + 6; y′′ = 0 ⇔ x = 1 − ⇒ y( 1) − = m + 2
Do đó, tọa độ điểm uốn là 1( 1
− ;m + 2)∈Ox ⇒ m + 2 = 0 ⇔ m = 2. − Chọn C.
Câu 9: Phương trình hoành độ giao điểm của (C) và d là 3
x − 3x = k(x+1) + 2 x = 1 − 3 2
⇔ x − 3x − 2 = k(x+1) ⇔ (x+1)(x − x −1) = k(x+1) ⇔  2
x − x − k − 2 = 0     f (x) k ≠ 0
Để (C) cắt d tại 3 điểm phân biệt ⇔ f (x) = 0 có 2 nghiệm phân biệt khác 1  − ⇔  9 k > −  4 Khi đó, gọi M ( 1
− ;2), N(x ; y ) và P(x ; y ) là tọa độ giao điểm của (C) và d 1 1 2 2 x + x =1
Với thỏa mãn hệ thức Vi – et : 1 2  x x = −k −  2 1 2 Theo bài ra, ta có 2 2
y (′x ).y (′x ) = 1
− ⇔ (3x − 3)(3x − 3) = 1 − 1 2 1 2
⇔ 9(x x )2 − 9(x + x ) +10 = 0 ⇔ 9(x x )2 −99(x + x )2 2 2 − 2x x  +10 = 0 1 2 1 2 1 2 1 2 1 2   ⇔ (k + )2 −  +  (k + ) 2 1 9 2 9 1 2
2  +10 = 0 ⇔ 9k +18k +1 = 0 ⇒ k .k = .  Chọn A. 1 2 9
Câu 10: Phương trình hoành độ giao điểm của (C) và d là 4 2 2
x − x − m −10 = 0 (∗) t  + t =1 Đặt 2
t = x ≥ 0, khi đó (∗) 2 2
⇔ t − t − m −10 = 0 luôn có hai nghiệm thỏa mãn 1 2  2 t
 t = −m −10 1 2 x = t Vì 2
−m −10 < 0 ⇒ t t < 0 nên giả sử 1 1
t < 0 ⇒ t > 0 ⇒  1 2 2 1 x = − t  2 1
Do đó tọa độ hai điểm A, B lần lượt là A( 2 t ;m );B( 2 − t ;m 1 1 )     Ta có OA = ( 2
t ;m ),OB = ( 2 − t ;m ) ⇒ .
OAOB = t .(− t ) 2 2 4
+ m .m = t − + m 1 1 1 1 1   Tam giác OAB vuông 4 4 ⇒ . OAOB = 0 ⇒ t
− + m = 0 ⇒ t = m 1 1 Thay 4
t = m vào phương trình ẩn t, ta được 4 2 2 2
m − m − m −10 = 0 ⇒ m =1+ 11. Chọn B. 1
Câu 11: Phương trình hoành độ giao điểm của (C) và Ox là 3 2 3 2
x − 3x − 9x + 2m +1 = 0 ⇔ 2
− m = x − 3x − 9x +1 ⇔ 2
− m = f (x) x = 1 Xét hàm số 3 2
f (x) = x − 3x − 9x +1 có 2
f (′x) = 3x + 6x − 9; f (′x) = 0 ⇔  x = 3 −  2 − m = 28 m =14
Lập bảng biến thiên hàm số f (x) , để 2
− m = f (x) có 2 nghiệm ⇔ ⇔   2m 4  − = − m = 2
Vậy tổng các giá trị của m là T = 12 − . Chọn C.
Câu 12: Phương trình hoành độ giao điểm của (C) và d là 3 2
x − x = x − m ⇔ f (x) 3 2 3
= x − 3x − x + m = 0
Yêu cầu bài toán trở thành: Đồ thị y = f (x) cắt trục Ox tại 3 điểm phân biệt và có một giao điểm cách hai
giao điểm còn lại ⇔ Đồ thị y = f (x) có điểm uốn thuộc Ox
Xét hàm số f (x) 3 2
= x − 3x − x + , m có 2
f (′x) = 3x − 6x −1; f (
′′ x) = 6x − 6 Ta có f (
′′ x) = 0 ⇔ x =1⇒ f ( )
1 = m − 3 nên tọa độ điểm uốn là I(1;m − 3)
Theo bài ra, ta có m − 3 = 0 ⇔ m = 3. Chọn A.
Câu 13: Phương trình hoành độ giao điểm của (C) và d là 3 2
x − mx + 3x +1 = x +1 x = 0 3 2
⇔ x − mx + 2x = 0 ⇔ x( 2
x − mx + 2) = 0 ⇔  2 x − mx +1 = 0   f (x)
Để (C) cắt d tại 3 điểm phân biệt ⇔ f (x) = 0 có 2 nghiệm phân biệt khác 2 0 ⇔ m −8 > 0 Khi đó, gọi (
A 0;1),B(x ; y ) và C(x ; y ) là tọa độ giao điểm của (C) và d 1 1 2 2
x + x = m
Với x , x thỏa mãn hệ thức Vi – et : 1 2 1 2 x x =  2 1 2
Khoảng cách từ điểm M → BC là h = d M ;  (BC) = 2 2  Suy ra 1 S = = ⇒ = ⇒ − = ∆ h BC BC x x MBC . 4 2 4 2( )2 16 2 1 2 ⇔ (x − x )2 2 2 2 2
− 4x x = 8 ⇔ m −8 = 8 ⇔ m =16 → m + m = 32. Chọn C. 2 1 1 2 1 2
Document Outline

  • ITMTTL~1
  • IIBITP~1
  • IIILIG~1

Tài liệu liên quan: