Bài toán về phương trình mặt cầu Toán 12

Bài toán về phương trình mặt cầu Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

29 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Phương pháp tọa độ trong không gian

Môn: Toán 12

Thông tin:

27 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
CHỦ ĐỀ 17: BÀI TOÁN VỀ PHƯƠNG TRÌNH MẶT CẦU
Dạng 1: Lập phương trình mặt cầu
Phương pháp giải:
• Phương trình chính tắc của mặt cầu
( ) ( ) ( ) ( )
2 22
2
:S xa yb zc R− +− +− =
• Phương trình tổng quát của mặt cầu
( )
2 22
: 222S x y z ax by cz d++− − − +
với tâm
( )
;;I abc
bán kính
222
R abcd= ++−
.
Chú ý:
- Nếu A, B thuộc mặt cầu
(
)
S IA IB R⇒==
.
- Nếu
IA IB=
thì ta có:
22
22
2. . .
2
OB OA
AB OI OB OA AB OI
−
=−⇔ =
   
Chứng minh: Ta có:
( ) ( )
22
22
22
IA IB IA IB IA IB IO OA IO OB=⇔=⇔=⇔+ =+
     
.
- Với bài toán: Viết phương trình mặt cầu đi qua 4 điểm A, B, C, D ta sẽ làm như sau:
Gọi
( )
;;I xyz
là tâm mặt cầu thì:
IA IB IC ID
= = =
khi đó
( )
;;I xyz
là nghiệm của hệ phương trình:
22
22
22
.
2
.
2
.
2
OB OA
AB OI
IA IB
OC OA
IA IC AC OI
IA ID
OD OA
AD OI
−
=
=
−
= ⇔ = →


=
−
=
 
 
 
CASIO suy ra tọa độ điểm I.
Trong đó
( )
0; 0; 0O
là gốc tọa độ, giải hệ phương trình suy ra tọa độ điểm I.
Ví dụ 1: Lập phương trình của mặt cầu
( )
S
biết:
a) Tâm I thuộc Oy, đi qua
( )
( )
1;1; 3 ; 1; 3; 3AB−
.
b) Tâm I thuộc Oz, đi qua
( ) ( )
2;1;1 ; 4; 1; 1AB−−
.
Lời giải
a) Gọi
( )
0; ; 0Iy
ta có:
(
) ( )
22
22
1 1 9 1 3 9 2 14
IA IB y y y R IA= ⇔+ − +=+ − +⇔ =⇒ = =
Suy ra
( ) ( )
2
22
: 2 14Sx y z+− +=
.
b) Gọi
( )
0; 0;Iz
ta có:
( )
( )
22
22
41 1 161 1
IA IB z z= ⇔ ++ − = ++ +
( )
4 12 3 0;0; 3 ; 21z zI R⇔ =− ⇔ =−⇒ − =
.
Phương trình mặt cầu
( ) ( )
2
22
: 3 21Sx y z+++ =
Ví dụ 2: Lập phương trình mặt cầu
( )
S
biết:
a) Tâm I thuộc
1
:
2
xt
d yt
zt
= +
=
=
và đi qua
(
)
( )
3;0; 1 ; 1;4;1
AB−
.
b) Tâm I thuộc
21
:
1 12
x yz
d
−−
= =
−
và đi qua
( ) ( )
3;6; 1 ; 5; 4; 3AB−−
.
Lời giải
a) Gọi
( )
1 ; ;2I tt t+
là tâm mặt cầu ta có:
( ) ( ) ( ) ( )
2 2 22
22 2 2
2 21 4 21IA IB t t t t t t= ⇔−+++=+−+−
( )
12 12 1 2;1; 2 11t tI R⇔− =− ⇔ = ⇒ ⇒ =
.
Phương trình mặt cầu là:
( )
( ) ( )
22 2
2 1 2 11x yz− +− +− =
.
b) Gọi
( )
2 ;1 ;2I t tt−+
là tâm mặt cầu ta có:
( ) ( ) ( ) ( ) ( ) ( )
22 2 22 2
22
1 5 21 3 3 23IA IB t t t t t t= ⇔+ +− + + =+ +− + +
( )
16 0 0 2;1; 0 3 3ttI R⇔− = ⇔ = ⇒ ⇒ =
Phương trình mặt cầu là:
( ) ( )
22
2
2 1 27x yz− +− +=
.
Ví dụ 3: Lập phương trình mặt cầu
( )
S
biết
( )
S
a) Đi qua 4 điểm
( ) ( ) ( )
( )
2; 4; 1 ; 1; 4; 1 ; 2; 4;3 ; 2; 2; 1A B CD
− −− −
.
b) Đi qua 4 điểm
( ) ( ) ( ) ( )
3; 3; 0 ; 3; 0; 3 ; 0; 3; 3 ; 3; 3; 3ABCD−
.
Lời giải
Áp dụng:
IA IB IC ID= = =
thì
( )
;;I xyz
là nghiệm của hệ phương trình:
22
22
22
.
2
.
2
.
2
OB OA
AB OI
OC OA
AC OI
OD OA
AD OI
−
=
−
=
−
=
 
 
 
.
a) Gọi
( )
;;I xyz
là tâm mặt cầu ta có:
22
22
22
.
45
2
2
.1
2
3
.
2
OB OA
AB OI
x
IA IB
OC OA
IA IC AC OI z
IA ID y
OD OA
AD OI
−
=
−
=
=
−
=⇔ = ⇒=


= =

−
=
 
 
 
Phương trình mặt cầu:
( )
( )
2
22
45 2421
31
24
x yz

+ +− +− =


.
b) Gọi
( )
;;I xyz
là tâm mặt cầu ta có:
( )( )
( )( )
( )( )
3
2
0;3;3 ;; 0
3
3; 0; 3 ; ; 0
2
9
3
0; 0; 3 ; ;
2
2
x
xyz
xyz y
xyz
z
= −
−=
− =⇔=−



−=
= −
.
Phương trình mặt cầu:
2 22
3 3 3 171
2 2 24
xyz
 
+++++=
 
 
.
Ví dụ 4: Lập phương trình mặt cầu
( )
S
biết
a)
( )
S
đi qua
(
)
( )
(
)
2; 0;1 ; 1; 0; 0 ; 1;1; 1ABC
và
(
)
: 20
I Pxyz∈ ++−=
.
b)
( )
S
đi qua
(
) ( )
( )
2; 4;1 ; 3;1; 3 ; 5;0; 0ABC− −−
và
( )
:2 3 0I P xyz∈ +−+=
.
Lời giải
Gọi
( )
;;I xyz
là tâm mặt cầu
a) Ta có:
( )( )
( )( )
22
22
.
2
1;0;1 ;; 2
1
. 1;1; 0 ; ; 1 0
2
1
2
20
OB OA
AB OI
xyz
x
OC OA
AC OI x y z y
z
xyz
xyz
−
=
−− =−
=
−
= ⇔− =− ⇔ =


=
++=
++−=
 
 
.
Khi đó
( ) ( ) ( )
22
2
: 1 11Sx y z− + +− =
.
b) Ta có:
( )
( )
(
)( )
22
22
.
2
5;3;4 ;; 1
1
. 3;4;1 ;; 2 2
2
3
23
2 30
OB OA
AB OI
xyz
x
OC OA
AC OI x y z y
z
xyz
xyz
−
=
−− =−
=
−
= ⇔ −−− =⇔ =−


=
+−=−
+−+=
 
 
.
Khi đó
( ) ( )
( ) ( )
2 22
: 1 2 3 49Sx y z− ++ +− =
.
Ví dụ 5: [Đề thi THPT Quốc gia 2017] Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây
là phương trình mặt cầu đi qua ba điểm
(
) (
)
( )
2;3;3 ; 2; 1; 1 ; 2; 1;3MN P
−− −−
và có tâm thuộc mặt phẳng:
( )
:2 3 2 0x yz
α
+ −+=
.
A.
22
2 2 2 10 0xy xyz+−+ −−=
. B.
2 22
4 2 6 20xyz x yz
+ + − + − −=
.
C.
2 22
4 2 6 20xyz x yz
+ + + − + +=
. D.
2 22
2 2 2 20xyz x yz
+ + − + − −=
.
Lời giải
Giả sử mặt cầu có tâm
( )
;;I xyz
.
Ta có:
( )( )
( )
(
)
22
22
.
2
0;4;4 ;; 8
2
. 4; 4; 0 ; ; 4 1
2
3
22
2 3 20
ON OM
MN OI
xyz
x
OP OM
MP OI x y z y
z
xyz
x yz
−
=
−− =−
=
−
= ⇔ − − =−⇔ =−


=
+−=−
+ −+=
 
 
.
Phương trình mặt cầu là:
( ) ( ) ( )
222
2 1 3 16x yz−+++−=
hay
2 22
4 2 6 20xyz x yz+ + − + − −=
.
Chọn B.
Ví dụ 6: Trong không gian với hệ tọa độ Oxyz, cho các điểm
( ) ( )
( )
2; 4;0 , 0;0; 4 , 1;0;3A BC−−
. Phương
trình mặt cầu ngoại tiếp tứ diện OABC là:
A.
2 22
2440xyz x yz++−+ + =
. B.
2 22
4340xyz xyz
++−+− =
.
C.
2 22
6240xyz x yz++−+ − =
. D.
2 22
2440xyz x yz++−+ − =
.
Lời giải
Gọi
( )
;;
I xyz
là tâm mặt cầu ta có:
( )( )
( )( )
( )( )
2
2
2
.
2
2; 4; 0 ; ; 10
1
. 0;0; 4 ; ; 8 2
2
2
1; 0; 3 ; ; 5
.
2
OA
OI OA
xyz
x
OB
OI OI x y z y
z
xyz
OC
OC OI
=
−=
=
= ⇔ = ⇔=−


=
−=
=
 
 
 
Phương trình mặt cầu là:
( ) (
) ( )
2 22
1 2 29
xy z− ++ +− =
hay
2 22
2440
xyz x yz++−+ −=
. Chọn D.
Ví dụ 7: Trong không gian tọa độ Oxyz cho 2 điểm
( ) ( )
3; 2; 3 ; 1; 2;1AB− −−
và mặt phẳng
( )
:0Pxyz++=
. Viết phương trình mặt cầu
( )
S
có tâm I thuộc
( )
P
đi qua A, B sao cho tam giác OIA
vuông tại gốc tọa độ O.
A.
( )
( )
(
) ( )
2 22
: 5 6 1 84
Sx y z
+ +− ++ =
. B.
( )
( )
(
) (
)
2 22
: 5 6 1 84
Sx y z− ++ +− =
.
C.
( ) ( ) ( )
( )
2 22
: 5 6 1 42Sx y z+ +− ++ =
. D.
( ) ( ) ( ) ( )
2 22
: 5 6 1 42Sx y z− ++ +− =
.
Lời giải
Phương trình mặt phẳng trung trực của AB là:
(
)
: 20Qxyz+−−=
.
Gọi
(
)
( )
( )
1 ;1 ; 1
1
xt
d P Q d y t It t
z
=
= ∩ ⇒ =−⇒ − −
= −
.
Ta có:
( )
. 0 32230 5 5;6;1OI OA t t t I=⇔ +− +=⇔=−⇒ − −
 
.
Vậy PT mặt cầu
(
)
( ) ( ) ( )
2 22
: 5 6 1 84Sx y z+ +− ++ =
. Chọn A.
Ví dụ 8:
Trong không gian tọa độ Oxyz, phương trình mặt cầu đi qua 3 điểm
( ) ( ) ( )
3;1;1 ; 0;1;4 ;C 1; 3;1AB −−
và có tâm thuộc mặt phẳng
( )
: 2 40Pxy z+− +=
là:
A.
( )
(
) (
)
22 2
1129xyz
− ++ +− =
. B.
( )
(
) (
)
22 2
1 1 29
xyz+ +− ++ =
.
C.
(
) ( ) ( )
22 2
11281xyz− ++ +− =
. D.
( ) (
) ( )
22 2
1 1 2 81xyz+ +− ++ =
.
Lời giải
Gọi
( )
;;I xyz
là tâm mặt cầu
Ta có:
( )( )
( )( )
22
22
.
2
3; 0; 3 ; ; 3
1
. 4; 4;0 ; ; 0 1
2
2
24
2 40
OB OA
AB OI
xyz
x
OC OA
AC OI x y z y
z
xy z
xy z
−
=
−=
=
−
= ⇔ −− =⇔ =−


=
+− =−
+− +=
 
 
.
Khi đó phương trình mặt cầu là:
( ) ( ) ( )
22 2
1129xyz− ++ +− =
. Chọn A.
Ví dụ 9: Trong không gian với hệ tọa độ Oxyz, mặt phẳng
( )
:2 6 3 0P x yz+ +−=
cắt trục Oz và đường
thẳng
56
:
12 1
x yz
d
−−
= =
−
lần lượt tại A và B. Phương trình mặt cầu đường kính AB là
A.
( ) (
) ( )
222
2 1 59x yz− ++ +− =
. B.
( ) ( ) ( )
222
2 1 5 36x yz+ +− ++ =
.
C.
( ) ( ) ( )
222
2 1 5 36x yz− ++ +− =
. D.
( ) ( ) ( )
222
2 1 59x yz+ +− ++ =
.
Lời giải
Ta có
( )
0; 0;A Oz A a∈⇒
mà
( ) ( )
2.0 6.0 3 0 3 0;0;3AP a a A∈ ⇒ + +−=⇔ =⇒
.
Lại có
( )
5
:2
6
xt
dy tt
zt
= +
= ∈
= −
mà
( )
5; 2 ; 6B d Bt t t∈⇒ + −
.
Hơn nữa
( ) ( ) (
)
( )
2 5 6.2 6 3 0 13 13 0 1 4; 2;7BP t t t t t B∈ ⇒ + + + − − = ⇔ + = ⇔ =−⇒ −
.
Mặt cầu đường kính AB có tâm I là trung điểm của AB
( )
2; 1; 5I⇒−
.
Mặt cầu đường kính AB có bán kính
1
2
R AB=
.
Mà
(
)
( ) ( ) ( ) (
) (
)
2 222
22
4; 2; 4 4 2 4 6 3 : 2 1 5 9AB AB R S x y z=− ⇒ = +−+=⇒=⇒ − +++− =

.
Chọn A.
Dạng 2: Bài toán mặt cầu tiếp xúc với mặt phẳng
Có hai đặc điểm quan trọng của bài toán về trường hợp mặt phẳng tiếp xúc với mặt cầu
• Điều kiện tiếp xúc
( )
( )
;
dI P R=
.
• Tâm I sẽ nằm trên đường thẳng ∆ đi qua điểm tiếp xúc và vuông góc với mặt phẳng
( )
P
.
Ví dụ 1: Lập phương trình mặt cầu
( )
S
tiếp xúc
( )
:3 4 0
P xyz++−=
tại điểm
( )
1; 2; 3M −
và đi qua
( )
1; 0; 1A −
.
Lời giải
Do
(
)
S
tiếp xúc với
( )
P
tại
( )
1; 2; 3M −
nên
( )
IM P IM⊥⇒
qua
( )
1; 2; 3M −
và có vectơ chỉ phương
( )
( )
3;1;1
P
un= =

suy ra
13
:2
3
xt
IM y t
zt
= +
=−+
= +
Gọi
( )
1 3 ; 2 ;3I t tt+ −+ +
. Ta có
( ) ( )
( )
222
22 2
11 3 2 2 2IM IA t t t t= ⇔ = + +− ++
12 12 0 1tt
⇔ + = ⇔=−
.
Suy ra
( ) ( ) ( ) ( ) ( )
222
2; 3;2 ; 11 : 2 3 2 11I R IA S x y z−− = = ⇒ + + + + − =
.
Ví dụ 2: Lập phương trình mặt cầu
( )
S
tiếp xúc
( )
: 2 3 10 0Px y z+ ++=
tại điểm
( )
2;3;2M −−
và đi qua
( )
0; 1; 2A
.
Lời giải
Do
( )
S
tiếp xúc với
( )
P
tại
(
)
2;3;2M −−
nên
( )
IM P IM⊥⇒
qua
( )
2;3;2M −−
và có vectơ chỉ
phương
(
)
(
)
1; 2; 3
P
un
= =

suy ra
2
: 32
23
xt
IM y t
zt
= +
=−+
=−+
Gọi
( )
2 ;3 2;2 3It t t+ −+ −+
. Ta có
( ) ( ) ( )
222
22 2
14 2 2 4 3 4IM IA t t t t= ⇔ =+ +− +−
( )
36 36 0 1 3; 1;1 ; 14
t t I R IA⇔ − = ⇔=⇒ − = =
.
Phương trình mặt cầu
(
) (
) ( ) ( )
2 22
: 3 1 1 14
Sx y z
− ++ +− =
.
Ví dụ 3: Trong không gian Oxyz, phương trình nào dưới đây là phương trình mặt cầu có tâm
( )
1; 2; 1I −−
và tiếp xúc với mặt phẳng
(
)
:2 2 3 0P xy z−+ −=
?
A.
( ) ( ) ( )
2 22
1 2 13xy z− ++ +− =
. B.
( )
(
) (
)
2 22
1 2 19
xy z− ++ +− =
.
C.
( )
( )
(
)
2 22
1 2 13
xy z+ +− ++ =
. D.
(
) ( )
( )
2 22
1 2 19
xy z+ +− ++ =
.
Lời giải
Bán kính mặt cầu tâm I là:
(
)
(
)
( )
2. 1 2 2 3
;3
414
R dI P
−−−−
= = =
++
.
Do đó phương trình mặt cầu là:
( ) ( ) ( )
2 22
1 2 19xy z
+ +− ++ =
. Chọn D.
Ví dụ 4: Có bao nhiêu mặt phẳng song song với mặt phẳng
( )
:0xyz
α
++=
đồng thời tiếp xúc với mặt
cầu
( )
2 22
: 2220Sx y z x y z++−− − =
?
A. 1. B. 0. C. vô số. D. 2.
Lời giải
Mặt cầu có tâm
( )
1;1; 1 ; 3IR=
.
Mặt phẳng cầm tìm có dạng
( ) ( ) ( )
( )
: 0 Do / / 0Pxyzm P m
α
+++ = ⇒ ≠
.
Điều kiện tiếp xúc:
( )
( )
( )
0
3
;3
6
3
m loai
m
dI P R
m
=
+
=⇔=⇔
= −
. Chọn A.
Ví dụ 5: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
:1
xt
dy
zt
=
= −
= −
và hai mặt phẳng
( )
: 2 2 30Px y z+ + +=
và
( )
: 2 2 70Qx y z+ + +=
. Phương trình mặt cầu
( )
S
có
Id∈
và tiếp xúc với cả
hai mặt phẳng
( )
P
và
( )
Q
có phương trình là:
A.
( )
(
) (
)
222
9
313
4
x yz
− ++ ++ =
. B.
( )
(
) (
)
222
4
313
9
x yz
− ++ ++ =
.
C.
( ) ( ) ( )
222
9
313
4
x yz+ +− +− =
. D.
( ) ( ) ( )
222
4
313
9
x yz+ +− +− =
.
Lời giải
Gọi
( )
; 1; tIt d−− ∈
, do
( )
S
tiếp xúc với cả 2 mặt phẳng
( )
P
và
( )
Q
nên:
( )
( )
( )
( )
15
2
;; 3
33 3
tt
dI P dI Q R t R
−−
= = ⇔ = ⇔=⇒ =
.
Phương trình mặt cầu cần tìm là:
( ) ( ) ( )
222
4
313
9
x yz− ++ ++ =
. Chọn B.
Ví dụ 6: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
11
:
3 11
xyz
d
−+
= =
và mặt phẳng
( )
:2 2 2 0P xy z+− +=
. Phương trình mặt cầu
( )
S
có tâm thuộc đường thẳng d có bán kính nhỏ nhất, tiếp
xúc với
(
)
P
và đi qua điểm
( )
1; 1; 1
A −
là:
A.
( ) ( )
22
2
111x yz−++ +=
. B.
( ) ( )
22
2
11 4x yz−++ +=
.
C.
( ) ( )
22
2
111x yz+ +− +=
. D.
( ) ( )
22
2
11 4x yz+ +− +=
.
Lời giải
Do
Id∈
ta gọi
( )
1 3; 1 ;Ittt+ −+
khi đó
(
)
( )
;
IA d I P R= =
( )
(
)
2
22
01
53
11 2 1 9 11 2 5 3
24 77
3
37 37
tR
t
tt R ttt t
tR
=⇒=
+
⇔ −+= =⇔ −+= + ⇔
= ⇒=
Do
( )
S
có bán kính nhỏ nhất nên ta chọn
.
Chọn A.
Ví dụ 7: [Đề thi chuyên ĐH Vinh 2017] Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
( )
S
đi qua
điểm
( )
2; 2;5A −
và tiếp xúc với các mặt phẳng
( ) (
) ( )
: 1; : 1; : 1xy z
αβ γ
= =−=
. Bán kính của mặt cầu
( )
S
bằng:
A.
33
. B. 1. C.
32
. D. 3.
Lời giải
Gọi
( )
;;I abc
ta có:
( )
( )
( )
(
)
(
)
( )
;;;
dI dI dI
αβγ
= =
suy ra
111Ra b c
= −= +=−
.
Do điểm
( )
2; 2;5A −
thuộc miền
1; 1; 1xy z> <− >
nên
( )
;;I abc
cũng thuộc miền
1; 1; 1xy z> <− >
.
Khi đó
(
)
1; 1 ; 1
I R RR+ −− +
. Mặt khác
( )
(
) (
)
22
22
11 4 3
IA R R R R R R
=⇒ −+−+− = ⇔=
. Chọn D.
Dạng 3: Bài toán tương giao mặt cầu với mặt phẳng
Phương pháp giải:
Mặt cầu
( )
S
có tâm I và bán kính R cắt mặt phẳng
( )
P
theo giao tuyến là một đường tròn bán kính r
khi
( )
( )
;dI P R<
. Khi đó
( )
(
)
2 22
;
d IP r R+=
.
Tâm đường tròn giao tuyến của
( )
S
và
( )
P
và hình chiếu vuông góc xủa điểm I trên mặt phẳng
(
)
P
.
Ví dụ 1: Trong không gian tọa độ Oxyz, cho
( )
1; 2; 2I −
và
( )
:2 2 5 0P x yz+ ++=
.
Lập phương trình mặt cầu
( )
S
có tâm I sao cho giao tuyến của
( )
S
và
( )
P
là đường tròn có chu vi
8
π
.
Lời giải
Do chu vi đường tròn giao tuyến
28 4
C rrr
π
= = ⇒=
. Ta có:
( )
( )
2425
;3
441
dI P
+−+
= =
++
.
Bán kính mặt cầu là
2 2 22
43 5R rd
= + = +=
.
Phương trình mặt cầu là:
( ) ( ) ( ) ( )
2 22
:12225Sx y z− +− ++ =
.
Ví dụ 2: Cho mặt phẳng
( )
: 10xyz
α
+ −+=
và mặt cầu
( ) ( ) ( )
22
2
:1 29Sx y z− + ++ =
.
Lập phương trình mặt phẳng
( )
P
song song với
( )
α
và cắt
( )
S
theo giao tuyến là đường tròn có diện tích
bằng
6
π
.
Lời giải
Mặt cầu
( ) (
) (
)
22
2
:1 29Sx y z
− + ++ =
có tâm
( )
1; 0; 2I −
bán kính
3R =
.
Do diện tích đường tròn giao tuyến
( )
( )
2 22
6 6; 3S r r dI P R r
ππ
= = ⇒= ⇒ = − =
.
Mặt phẳng
( )
P
song song với
( )
α
( )
:0
PxyzD⇒ +−+ =
Ta có:
( )
( )
0
12
;3
6
3
D
D
dI P
D
=
++
= = ⇔
= −
.
Do đó
( )
:0Pxyz+−=
hoặc
60xyz+−+=
.
Ví dụ 3: Trong không gian tọa độ Oxyz, cho đường thẳng
3 21
:
21 2
xyz
d
−−−
= =
−
và mặt cầu
( )
2 22
: 2 2 4 19 0Sx y z x y z++−+ −−=
. Tìm tọa độ điểm M thuộc đường thẳng d sao cho mặt phẳng qua M
và vuông góc với d cắt mặt cầu
( )
S
theo một đường tròn có chu vi bằng
8
π
.
Lời giải
Mặt cầu
( )
S
có tâm
( )
1; 1; 2I −
, bán kính
5
R =
. Do
24C rr
π
= ⇒=
do vậy mặt phẳng qua M vuông
góc với d cắt
( )
S
theo 1 đường tròn có bán kính bằng 4.
VTCP của d là
(
)
2; 1; 2
d
u = −

khi đó
( )
3 2 ;2 ;1 2 tMd t t∈⇒ + + −
Phương trình mặt phẳng
( )
P
có dạng
( ) ( ) ( )
2 32 2 2 12 0x ty t z t−− + − − − −+ =
Hay
2 2 9 60xy z t+− − −=
Ta có:
( )
( )
22
0
99
; 33
2
3
t
t
dI P R r
t
=
+
= −=⇔ =⇔
= −
Từ đó suy ra
( ) ( )
3;2;1 , 1;0;5MM−
là các điểm cần tìm.
Ví dụ 4: Trong không gian cho mặt cầu có phương trình
(
)
( ) ( ) ( )
222
:3 5 74Sx y z++−+−=
và mặt phẳng
( )
: 40Pxyz−++=
. Biết mặt cầu
(
)
S
cắt mặt phẳng
( )
P
theo một đường tròn
( )
C
. Tính chu vi đường
tròn
( )
C
.
A.
8
π
. B.
4
π
. C.
2
π
. D.
42
π
.
Lời giải
Mặt cầu
( )
S
có tâm
( )
3; 5; 7I −
và bán kính
2R
=
.
Khoảng cách từ tâm I đến
( )
P
là:
3574
3
3
d
−− + +
= =
.
Bán kính đường tròn
( )
C
là:
22
431r Rd= − = −=
.
Chu vi đường tròn
( )
C
là:
22
Cr
ππ
= =
. Chọn C.
Ví dụ 5: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
( )
2 22
: 2 4 6 20Sx y z x y z
+ + − − − −=
. Viết
phương trình mặt phẳng
( )
α
chứa trục Oy và cắt mặt cầu
(
)
S
theo thiết diện là một đường tròn có chu vi
bằng
8
π
.
A.
30
xz+=
. B.
3 20xz++=
. C.
30xz−=
. D.
30xz−=
.
Lời giải
Ta có:
( ) ( )
( ) ( )
2 22
: 1 2 2 16
Sx y z− +− +− =
⇒
( )
S
có tâm
( )
1; 2; 3I
và bán kính
4R =
.
Bán kính của đường tròn là:
4
2
C
rR
π
= = =
⇒ đường tròn đi qua tâm của mặt cầu
( )
S
.
Vtcp của Oy là
( )
0; 1; 0u
, điểm
( )
0; 1; 0A Oy∈
.
Ta có:
( ) ( )
1;1; 3 ; 3; 0; 1IA n IA u

= ⇒= =−

 
.
Mặt phẳng
( )
α
đi qua O và nhận
n
làm vtpt suy ra phương trình mặt phẳng
( )
α
là:
( )
:3 0xz
α
−=
.
Chọn C.
Ví dụ 6: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
( )
S
có tâm I thuộc đường thẳng
3
Δ:
112
xy z+
= =
. Biết rằng mặt cầu
( )
S
có bán kính bằng
22
và cắt mặt phẳng
( )
Oxz
theo một đường
tròn có bán kính bằng 2. Tìm tọa độ tâm I.
A.
( ) ( )
1; 2; 2 ; 5;2;10II−
. B.
( ) ( )
1; 2; 2 ; 0; 3; 0II−−
.
C.
( ) ( )
5;2;10 ; 0; 3;0II−
. D.
( )
( )
1; 2; 2 ; 1; 2; 2II− −−
.
Lời giải
Khoảng cách từ tâm I đến mặt phẳng là
( )
Oxz
là
22
84 2d Rr= − = −=
.
Điểm
Id∈
suy ra
( ) ( )
( )
( )
( )
5; 2;10
5
; 3; 2 ; 3 2
1
1; 2; 2
I
t
I tt t d I P t
t
I
=
− ⇒ =−=⇒ ⇒
=
−
. Chọn A.
Ví dụ 7: Trong không gian với hệ tọa độ Oxyz, cho hai điểm
( )
0; 0;1S
. Hai điểm
( ) ( )
;0;0 ; 0; ;0Mm N n
thay đổi sao cho
1mn
+=
và
0; 0mn>>
. Biết rằng mặt phẳng
( )
SMN
luôn tiếp xúc với một mặt cầu cố
định. Bán kính mặt cầu đó bằng:
2R
=
.
A.
2R =
. B.
2R =
. C.
1R =
. D.
1
2
R =
.
Lời giải
Phương trình mặt phẳng
( )
SMN
theo đoạn chắn là:
1
xy
z
mn
+ +=
. Gọi
( )
0 00
;;
Px y z
Ta có:
( )
( )
00
0
22
1
;
11
1
xy
z
mn
d d P SMN
mn
+ +−
= =
++
.
Lại có
2 22 2
22
11112 2121
1 1 1 11
mn
m n m n mn mn mn mn mn mn
+

+ += + − += − += − += −


00
0
1
1
1
xy
z
mn
d
mn
+ +−
=
−
. Ta chọn
0
0
0
1
1
11
1
1
0
mn
x
mn
yd
z
mn
+
=
−
=⇒= =
−
=
với mọi
0; 0
mn>>
.
Do đó mặt cầu cần tìm là mặt cầu tâm
( )
0
1;1; 0P
bán kính
1R =
. Chọn C.
Dạng 4: Bài toán tương giao mặt cầu với đường thẳng
Phương pháp giải:
Xét sự tương giao của mặt cầu
(
)
S
có tâm I và bán kính R và đường thẳng ∆ ta có:
∆ tiếp xúc với mặt cầu
( ) ( )
;Δ
S dI R⇔=
.
∆ cắt mặt cầu
( )
S
tại 2 điểm phân biệt A, B khi
( )
;ΔdI R<
khi đó hình chiếu vuông góc của điểm I
trên ∆ là trung điểm của AB và
( )
2
22
;Δ
2
AB
dI R

+=


.
Ví dụ 1: Trong không gian tọa độ Oxyz, lập phương trình mặt cầu tâm
( )
2; 3; 1I −
cắt đường thẳng
12
:5
15 2
xt
dy t
zt
= +
=−+
=−−
tại A, B với
16AB =
.
Lời giải
Đường thẳng d đi qua điểm
( )
1;5;15M −−
và có vtcp là
( ) ( )
2;1;2; 1;8;14
d
u IM= − =−−−
 
.
Khi đó
(
)
( )
2
2 22
;
30; 30; 15
; 15 15 8 17
2; 1; 2 2
d
d
IM u
AB
d Id R d
u

−−


= = = ⇒= + = + =

−

 

.
Do đó phương trình mặt cầu cần tìm là:
( ) ( ) ( )
2 22
2 3 1 289xyz− +− ++ =
.
Ví dụ 2: Cho đường thẳng
( )
1
: 2 , : 10
2
xt
d y tPxyz
z
= +
=−− + + +=
= −
. Viết phương trình mặt cầu
( )
S
tiếp xúc với
( )
P
tại
(
)
1; 0; 2M −
và cắt d tại A, B sao cho
22
AB =
.
Lời giải
Đường thẳng d đi qua
( )
1;2;2
E −−
và có vectơ chỉ phương
( )
1; 1; 0
d
u −

.
Gọi I là tâm mặt cầu suy ra đường thẳng
( )
1
:
2
xt
IM P IM y t
zt
= +
⊥⇒ =
=−+
.
Khi đó gọi
( ) ( ) ( )
2
2 22 2
1 ;; 2 ; ; 2
2
AB
I tt t d Id R d Id IM

+ −+ ⇒ + = ⇔ + =


Trong đó
( )
( )
2
;
; ;2 2
6 84
;
22
d
d
IE u
ttt
tt
d Id
u

−− +
++

= = =
 

và
22
3IM t=
Suy ra
( )
22
3 4 2 2 3 1 0;1;3; 3t t t t I R IM+ + + = ⇔ =−⇒ − − = =
.
Phương trình mặt cầu
( )
S
là:
( ) ( )
22
2
1 33xy z++ ++ =
.
Ví dụ 3: Trong không gian tọa độ Oxyz, cho đường thẳng
11
:
12 1
x yz
d
+−
= =
−
và điểm
( )
2; 1; 0I
. Viết
phương trình mặt cầu
( )
S
tâm I và cắt d tại 2 điểm phân biệt A, B sao cho tam giác IAB vuông.
Lời giải
Ta có:
( )
1; 2; 1
d
u = −

, gọi H là trung điểm của AB ta có:
IH AB
⊥
.
Khi đó
( )
( )
1 ;2 ;1 3 ;2 1;1 . 0 3 4 2 1 0
d
H t t t IH t t t IH u t t t−+ − ⇒ −+ − − ⇒ = ⇔−++ − +−=
  
(
)
1 0; 2; 0tH
⇔=⇒
Tam giác IAB vuông cân tại I nên ta có:
2 2 4 1 10R IH= = +=
Do đó phương trình mặt cầu
( )
S
cần tìm là:
(
)
( )
22
2
2 1 10
x yz
− +− +=
.
Ví dụ 4: Trong không gian tọa độ Oxyz, cho đường thẳng
2 31
:
12 1
xyz
d
− −−
= =
−
và mặt cầu
( )
2 22
: 24 0Sx y z x y++−+ =
. Viết phương trình đường thẳng
Δ
qua
( )
1; 1; 0M −
cắt đường thẳng d đồng
thời cắt mặt cầu
( )
S
tại A, B sao cho
4AB
=
.
Lời giải
Ta có:
( )
1; 2; 0 , 5IR−=
. Gọi
( )
2 ;3 2 ;1N t tt−+ +
. Ta có:
( )
Δ
1 ;4 2 ;1u MN t t t= −+ +
 
Mặt khác
( ) ( )
2
22
;
Δ ;Δ 1
2
AB
d I R dI

+ =⇒=


( )
2
2
2
;
22
;Δ 1 4 16 16 0 2
6 16 18
IM MN
t
dI t t t
tt
MN

+

= = =⇔ + + = ⇔=−
++
 

Với
13
2 Δ: 1
xt
ty
zt
= +
=−⇒ =−
= −
là đường thẳng cần tìm.
Ví dụ 5: Trong không gian tọa độ Oxyz, cho mặt phẳng
( )
: 2 2 10 0Px y z−−+=
và 2 đường thẳng
1
21
Δ:
111
x yz−−
= =
và
2
23
Δ:
114
x yz
−+
= =
. Viết phương trình mặt cầu
( )
S
có tâm thuộc
1
Δ
đồng thời
tiếp xúc với
2
Δ
và
(
)
P
.
Lời giải
Gọi
( )
1
2 ; ;t 1 ΔI tt+ +∈
là tâm của mặt cầu.
2
Δ
xác định qua
( ) ( )
2
Δ
2; 0; 3 , 1;1; 4Mu−=

Ta có:
( ) ( )
( )
2
;
Δ;dI dI P=
. Khi đó
( )
( )
(
)
2 2 2 1 10
10 3
;
3
144
tt t
t
dI P
+− − + +
−
= =
++
.
(
) ( )
( )
2
2
2
Δ
2
Δ
;
23 4
34
; ;4 ;Δ
3
1116
IM u
t
t
IM t t t d I
u

−
−

−−−− ⇒ = = =
++
 


Cho
10 3 3 4
7 13 7 10
;;
3 3 3 333
tt
tI
−−

= ⇔= ⇒


Vậy phương trình mặt cầu
( )
22 2
13 7 10
:1
333
Sx y z
 
− +− +− =
 
 
.
Ví dụ 7: Trong không gian với hệ tọa độ Oxyz, cho điểm
( )
2; 4;5A −−
. Phương trình nào dưới đây là
phương trình của mặt cầu có tâm là A và cắt trục Oz tại hai điểm B, C sao cho tam giác ABC vuông.
A.
( )
( ) ( )
2 22
2 4 5 40xyz++++−=
. B.
( ) ( ) ( )
2 22
2 4 5 82xyz++++−=
.
C.
( ) ( ) (
)
2 22
2 4 5 58xyz++++−=
. D.
( ) ( ) ( )
2 22
2 4 5 90xyz++++−=
.
Lời giải
Gọi
(
)
0;0;5H
là hình chiếu vuông góc của A xuống trục Oz.
Khi đó tam giác OHB vuông cân tại H suy ra
2 2 10
2
R
OH R OH= ⇒= =
.
Suy ra
(
)
(
)
( )
( )
2 22
: 2 4 5 40Sx y z
++++−=
. Chọn A.
Ví dụ 8: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
2 11
:
22 1
x yz
d
− −+
= =
−
và điểm
( )
2; 1; 1
I −
. Viết phương trình mặt cầu có tâm I và cắt đường thẳng d tại hai điểm A, B sao cho tam giác IAB
vuông tại I.
A.
( ) ( ) ( )
2 22
2 1 19x yz− ++ +− =
. B.
( ) ( ) ( )
2 22
2 1 19x yz+ +− ++ =
.
C.
( ) ( ) ( )
2 22
2 1 18
x yz− ++ +− =
. D.
( ) ( ) ( )
2 22
80
2 11
9
x yz− ++ +− =
.
Lời giải
Gọi H là hình chiếu vuông góc của I lên đường thẳng d
( )
2 2; 2 1; 1Ht t t⇒ + + −−
. Đường thẳng d có
vecto pháp tuyến
( )
2; 2; 1
d
u = −

. Sử dụng
2 211
. 0 ;; 2
3 333
d
IH u t H IH

= ⇔=− ⇔ − − ⇒ =


 
.
Hoặc ta có
( )
0
;
;2
d
d
IM u
IH d I d
u


= = =
 

.
Tam giác IAB vuông cân tại I nên
2. 2 2R IA IH= = =
.
Suy ra phương trình mặt cầu là:
( ) ( ) ( )
2 22
2 1 18x yz− ++ +− =
. Chọn C.
Ví dụ 9: Trong không gian với hệ tọa độ Oxyz, cho các đường thẳng
52
: 6;Δ: 1
21
xt x t
dy t y t
zt z t
= = +


=−+ =+


= − =−−

và mặt
phẳng
( )
: 3 10Px yz+ −−=
. Mặt cầu
( )
S
có tâm I thuộc d, tiếp xúc với cả
Δ
và
( )
P
. Biết hoành độ điểm
I là số nguyên. Tung độ điểm I là
A. 2. B. 0. C. −4. D. −2.
Lời giải
Gọi
( )
; 6 ;2It t t−+ −
là tâm của mặt cầu và R là bán kính của mặt cầu
( )
S
.
Ta có
(
)
( )
(
) ( )
( )
( )
2
22
36 2 1
5 21
; 1
11
13 1
t tt
t
R dI P
+ −+ − − −
−
= = =
+ +−
.
Điểm
( ) ( ) ( )
5;1; 1 Δ 5; 7;3A AI t t t−∈ ⇒ = − − −

suy ra VTCP của
Δ
là
( )
2; 1; 1
u = −
.
Mặt khác
(
)
(
)
(
)
2
;
2 20 98
;
Δ 2
6
u AI
tt
R dI
u

−+

= = =

.
Từ (1), (2) ta được
2
5 21
2 20 98
22 4
11 6
II
t
tt
tx y
−
−+
= ⇒= ⇒ = ⇒ =−
. Chọn C.
Ví dụ 10: [Đề thi THPT Quốc gia năm 2018] Trong không gian Oxyz, cho mặt cầu
( ) ( ) ( ) ( )
2 22
: 1 1 19
Sx y z+++++=
và điểm
( )
2; 3; 1
A −
. Xét các điểm M thuộc
( )
S
sao cho đường thẳng
AM tiếp xúc với
( )
S
. M luôn thuộc mặt phẳng có phương trình là
A.
6 8 11 0xy+ +=
. B.
3 4 20xy+ +=
. C.
3 4 20xy+ −=
. D.
6 8 11 0
xy+ −=
.
Lời giải
Mặt cầu
( )
S
có tâm là
( )
1; 1; 1I −−−
, bán kính
3R =
.
Ta có:
( )
3; 4; 0 5IA IA= ⇒=

.
Vì AM là tiếp tuyến của mặt cầu nên ta có:
22
4AM IM AM IA IM⊥⇒ = − =
.
Gọi
( )
S
′
là mặt cầu tâm A, bán kính
4R
′
=
.
Ta có phương trình mặt cầu
( )
( ) ( ) (
)
2 22
: 2 3 1 16Sx y z
′
− +− ++ =
Vì
4AM =
nên điểm M luôn thuộc mặt cầu
( )
S
Vậy
( ) ( )
MS S
′
∈∩ ⇒
tọa độ điểm M là nghiệm của hệ:
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( )
( )
2 22
12
2 22
1 1 1 9 1
6 8 11 7 hay : 3 4 2 0
2 3 1 16 2
xyz
xy MPxy
xyz
−
+++++=
→ + − = − ∈ + − =
− +− ++ =
. Chọn C.
BÀI TẬP TỰ LUYỆN
Câu 1: Trong không gian với hệ tọa độ Oxyz, nếu mặt cầu
( )
S
tâm
( )
I a;b;c
bán kính bằng 1, tiếp xúc mặt
phẳng
( )
Oxz
thì
A.
1=a
B.
1=b
C.
1=c
D.
1
++=abc
Câu 2: Trong không gian với hệ tọa độ Oxyz, cho điểm
( )
1 23−A; ;
và đường d có phương trình
123
21 1
+−+
= =
−
xy z
. Tính đường kính của mặt cầu
( )
S
có tâm A và tiếp xúc với đường thẳng d.
A.
52
. B.
10 2
. C.
25
. D.
45
.
Câu 3: Trong không gian với hệ tọa độ Oxyz, nếu mặt cầu
( )
222
2 4 6 20+ + − − − −=S :x y z x y z
. Viết
phương trình mặt phẳng
( )
α
chứa trục Oy và cắt mặt cầu
( )
S
theo thiết diện là một đường tròn có chu vi
bằng
8
π
.
A.
30+=xz
. B.
3 20++=xz
. C.
30
−=xz
. D.
30
−=
xz
.
Câu 4: Trong không gian Oxyz, nếu mặt cầu
( )
S
tâm
( )
234I ;;
và cắt trục Ox tại hai điểm A, B sao cho diện
tích tam giác
IAB
bằng 10. Viết phương trình mặt cầu
( )
S
.
A.
( ) ( ) ( )
222
2 3 4 26− +− +− =
xyz
. B.
( ) ( ) (
)
222
2 3 4 50− +− +− =xyz
.
C.
( ) ( ) ( )
222
2 3 4 25− +− +− =xyz
. D.
( ) ( ) (
)
222
2 3 4 29− +− +− =xyz
.
Câu 5: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
( )
2 2 90− −+=P: x y z
và mặt cầu
( )
222
6 4 2 50+ + − + − +=S :x y z x y z
. Viết phương trình mặt phẳng
( )
Q
chứa trục Ox và cắt
( )
S
theo giao
tuyến là một đường tròn có bán kính bằng 2.
A.
( )
20−=Q: y z
. B.
( )
20+=
Q: y z
. C.
( )
0−=Q :y z
. D.
( )
20−=Q: x z
.
Câu 6: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
11
2 21
++
= =
−
xyz
d:
và mặt cầu
( )
222
2 4 2 30+ + − + − −=S :x y z x y z
. Viết phương trình mặt phẳng
( )
P
vuông góc với d,
( )
P
tiếp xúc với
( )
S
đồng thời
( )
P
cắt trục Oz tại điểm có cao độ dương.
A.
2 2 20− ++=x yz
B.
2 2 16 0− +− =x yz
C.
2 2 10 0− +− =x yz
D.
2 2 50
− +−=x yz
Câu 7: Trong không gian với hệ tọa độ Oxyz, mặt phẳng
( )
Oxy
cắt mặt cầu
( ) ( ) ( ) ( )
2 22
1 2 3 14−+−+−=S:x y z
theo giao tuyến là đường tròn tâm H, bán kính R. Tìm tọa độ tâm H và
tính bán kính R.
A.
(
)
120 5
H ; ; ,R =
B.
(
)
1 20 5
−− =
H ; ; ,R
C.
(
)
120 5=H ; ; ,R
D.
( )
102 5=H ; ; ,R
Câu 8: Trong không gian với hệ tọa độ Oxyz, cho điểm
( )
23 1−I ;;
và đường thẳng
797
21 2
+++
= =
−
xyz
d:
.
Viết phương trình mặt cầu tâm I và cắt đường thẳng d tại hai điểm A, B thỏa mãn
40=
AB
.
A.
(
)
( )
( )
2 22
2
2 3 1 25− +− ++ =
xyz
B.
( )
(
) (
)
222
2
2 3 4 25+ ++ ++ =xyz
C.
(
) (
)
22
2
2 1 25
− + ++ =
x yz
D.
( ) ( ) ( )
2 22
2 3 1 25− +− +− =xyz
Câu 9: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
( )
3 3 60+− +=P:x y z
và mặt cầu
( ) ( ) ( ) ( )
222
4 5 2 25− ++ ++ =S:x y z
. Mặt phẳng
( )
P
cắt mặt cầu
( )
S
theo giao tuyến là một đường tròn
bán kính r bằng bao nhiêu?
A.
5=r
B.
5=r
C.
6
=
r
D.
6
=
r
Câu 10: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
( ) ( ) ( )
22
2
1 1 25+− +− =S :x y z
và mặt phẳng
( )
2 2 50
+ + +=P :x y z
. Diện tích hình tròn thiết diện của
( )
P
và
( )
S
là.
A.
25
π
B.
9
π
C.
16
D.
16
π
Câu 11: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
( )
40
++−=P :x y z
và mặt cầu
( )
2 22
4 2 10 14 0++−− + +=S :x y z x y z
. Mặt phẳng
( )
P
cắt mặt cầu
( )
S
theo một đường tròn. Tính chu vi
đường tròn đó.
A.
2
π
B.
8
π
C.
4
π
D.
43
π
Câu 12: Trong không gian với hệ tọa độ Oxyz, cho các đường thẳng
6
2
=
=−+
= −
xt
d: y t
zt
và
52
1
1
= +
∆=+
=−−
xt
:y t
zt
và
mặt phẳng
( )
3 10+ −−=P :x y z
. Mặt cầu
( )
S
có tâm I thuộc d, tiếp xúc với cả
∆
và
( )
P
. Biết hoành độ
điểm I là số nguyên. Tung độ của điểm I là.
A. 2 B. 0 C. -4 D. -2
Câu 13: Trong không gian với hệ tọa độ Oxyz, cho các điểm
(
) ( )
200 040A ; ; ,B ; ;
và
( )
006C ;;
. Viết
phương trình mặt cầu ngoại tiếp tứ diện OABC.
A.
( ) ( ) ( )
2 22
1 2 3 56+++++=xy z
B.
( ) ( ) ( )
2 22
1 2 3 28+++++=xy z
C.
( ) ( ) (
)
2 22
1 2 3 14−+−+−=xy z
D.
( ) ( ) ( )
2 22
1 2 3 28−+−+−=xy z
Câu 14: Cắt mặt cầu
( )
S I,R
bởi mặt phẳng
( )
P
cách tâm I một khoảng
2
R
ta nhận được giao tuyến là
đường tròn có chu vi bằng bao nhiêu?
A.
3
R
π
B.
R
π
C.
2 R
π
D.
23R
π
Câu 15: Trong không gian với hệ tọa độ Oxyz, mặt phẳng
( )
α
cắt mặt cầu
(
)
S
tâm
( )
1 33−I; ;
theo giao
tuyến là đường tròn tâm
(
)
201H ;;
, bán kính
2
=r
. Phương trình của
( )
S
là
A.
(
)
( )
(
)
2 22
1 3 34
− ++ +− =
xyz
B.
(
)
( )
( )
2 22
1 3 34
+ +− ++ =
xyz
C.
( ) ( ) ( )
2 22
1 3 3 18− ++ +− =xy z
D.
( ) ( ) ( )
2 22
1 3 3 18+ +− ++ =xyz
Câu 16: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
( )
3 3 60+− +=P:x y z
và mặt cầu
( ) ( ) ( ) ( )
222
4 5 2 25− ++ ++ =S:x y z
. Mặt phẳng
( )
P
cắt mặt cầu
( )
S
theo giao tuyến là một đường tròn.
Tính bán kình r của đường tròn giao tuyến đó
A.
6
=
r
. B.
5
=r
. C.
6=
r
. D.
5=
r
.
Câu 17: Trong không gian với hệ trục tọa độ Oxyz, phương trình nào dưới đây là phương trình của mặt cầu
có tâm
( )
234−
I ;;
và tiếp xúc với mặt phẳng
( )
Oyz
?
A.
( ) ( )
( )
222
2 3 42+ +− +− =x yz
B.
( )
( ) ( )
222
2 3 44+ +− +− =x yz
C.
( ) (
) ( )
222
2 3 42− ++ ++ =xyz
D.
( )
( ) (
)
222
2 3 44
− +− ++ =xyz
Câu 18: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
(
) ( ) ( )
( )
2 22
1 2 34− ++ +− =
S:x y z
và điểm
( )
1 21−M; ;
. Viết phương trình mặt phẳng
( )
P
tiếp xúc với mặt cầu
( )
S
tại M.
A.
( )
3 1 30+ + +− =P :x y z
B.
( )
10−=P :z
C.
( )
2= −P :y
D.
( )
30+−=P:x y z
Câu 19: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
( ) ( ) (
) ( )
2 22
1 2 35− ++ +− =S:x y z
có tâm I và
một thời điểm
( )
0 21
−A; ;
. Một mặt phẳng
( )
P
cắt và vuông góc với đoạn thẳng IA và cắt mặt cầu
( )
S
theo
giao tuyến là một đường tròn có bán kính
2=r
. Viết phương trình của mặt phẳng
( )
P
.
A.
2 7 50+ −− =xz
. B.
2 7 50+ −− =xz
và
2 7 50+ −+ =xz
.
C.
2 7 50+ −+ =xz
. D.
2 3 50+ +− =xz
.
Câu 20: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
( ) ( ) ( ) ( )
2 22
2 1 14− +− +− =S:x y z
. Mặt phẳng
( )
P
cắt mặt cầu
( )
S
theo thiết diện là đường tròn lớn và cắt các trục Ox, Oy, Oz lần lượt tại các điểm
( ) ( ) ( )( )
00 0 0 003 0>A a; ; ,B ;b; ,C ; ; a,b
. Tính tổng
= +T ab
khi thể tích khối tứ diện OABC đạt giá trị nhỏ
nhất.
A.
18=T
. B.
9=
T
. C.
11=T
. D.
3
=
T
.
Câu 21: Trong không gian với hệ tọa độ Oxyz, cho điểm
( )
132−A ;;
và mặt phẳng
( )
36240+ − −=P: x y z
. Phương trình mặt cầu tâm A, tiếp xúc với mặt phẳng
( )
P
là
A.
( )
(
) (
)
222
1 3 27
+ +− +− =xyz
. B.
( ) ( ) (
)
222
1 3 21+ +− +− =xyz
.
C.
( ) ( ) ( )
222
1 3 2 49
+ +− +− =xyz
. D.
(
)
( )
( )
222
1
132
49
+ +− +− =xyz
.
Câu 22: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
( )
2 22
2440++−− − =S :x y z x y z
. Viết
phương trình mặt phẳng
( )
α
tiếp xúc với
( )
S
tại điểm
( )
343
A ;;
.
A.
( )
2 4 25 0+ +− =:x y z
α
. B.
( )
2 2 17 0+ +− =
:x y z
α
.
C.
( )
2 4 2 22 0+−−=:x y z
α
. D.
( )
10 0++− =:x y z
α
.
Câu 23: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
( )
2 22
10+ + + − +−=S :x y z x y z
cắt mặt
phẳng
( )
Oxy
theo giao tuyến là đường tròn. Tìm tọa độ tâm và bán kính của đường tròn này.
A.
11 6
0
22 2

−=


I ; ; ,r
. B.
11 6
0
22 3

−=


I ; ; ,r
.
C.
11 22
0
22 3

−=


I ; ; ,r
. D.
( )
6
110
2
−=
I ; ; ,r
.
Câu 24: Trong không gian với hệ trục tọa độ Oxyz, cho tứ diện ABCD với
( ) ( ) ( ) (
)
162 513 406 504A ;; ,B ;; ,C ;; ,D ;;
. Viết phương trình mặt cầu tâm D tiếp xúc với mặt phẳng
( )
ABC
.
A.
( ) ( )
22
2
2
54
223
− ++− =x yz
. B.
( ) ( )
22
2
4
54
446
− ++− =x yz
.
C.
( ) (
)
22
2
8
54
223
+ + ++ =x yz
. D.
( ) ( )
22
2
8
54
223
− ++− =x yz
Câu 25: Trong không gian với hệtọa độ Oxyz, cho mặt cầu
( )
S
có tâm I thuộc đường thẳng
3
112
+
= =
xy z
d:
. Biết rằng
( )
S
có bán kính
22=R
và cắt mặt phẳng Oxz theo một đường tròn có bán
kính bằng 2. Tìm tọa độ tâm I.
A.
( ) ( )
1 2 2 5 2 10−I ; ; ,I ; ;
. B.
( ) ( )
1 22 0 30−−I;;,I;;
.
C.
( ) (
)
5 2 10 0 3 0−I ; ; ,I ; ;
. D.
( ) (
)
1 22 12 2− −−I ; ; ,I ; ;
.
Câu 26: Trong hệ tọa độ Oxyz, viết phương trình mặt cầu
(
)
S
đi qua
( ) (
)
12 0 211−−A ; ; ,B ; ;
và có tâm nằm
trên trục Oz.
A.
2 22
50+ + −−=xyzz
. B.
2 22
50+ + +=
xyz
.
C.
2 22
50
+ + −−=xyzx
. D.
2 22
50+ + −−=xyzy
.
Câu 27: Viết phương trình mặt phẳng
( )
P
qua
( ) ( )
001 00 2−A ;; ,B ;;
và tiếp xúc với mặt cầu
( )
2 22
4 2 4 80
+ + + − + +=
S :x y z x y z
.
A.
43 0+=xy
. B.
43 0
0
+=
=
xy
z
. C.
43 0
0
+=
=
xy
y
. D.
0=z
.
Câu 28: Trong không gian với hệ trục Oxyz, cho điểm
( )
12 2−A ;;
và mặt phẳng
( )
2 2 50+ ++=P: x y z
.
Viết phương trình mặt cầu
( )
S
tâm A biết mặt phẳng
( )
P
cắt mặt cầu
( )
S
theo giao tuyến là đường tròn có
chu vi bằng
8
π
.
A.
( ) ( ) ( )
2 22
12225− +− ++ =xy z
. B.
( ) ( ) ( )
2 22
1225− +− ++ =xy z
.
C.
( )
( ) ( )
2 22
1229− +− ++ =xy z
. D.
( ) ( ) ( )
2 22
12216− +− ++ =xy z
.
Câu 29: Trong không gian với hệ trục Oxyz, cho hai mặt phẳng
( )
2 2 20+ − −=P :x y z
và
( )
2 2 40+ − +=
Q :x y z
. Phương trình nào dưới đây là phương trình mặt cầu
(
)
S
có tâm thuộc trục Ox và
tiếp xúc với hai mặt phẳng đã cho?
A.
( )
2
22
34− ++=x yz
. B.
( )
2
22
11−++=x yz
.
C.
( )
2
22
11+ ++=x yz
. D.
( )
2
22
19−++=x yz
.
Câu 30: Trong không gian với hệ trục Oxyz, cho các điểm
( ) ( ) ( )
12 4 1 31 2 23−−A ;; ,B ; ; ,C ;;
. Tính bán kính
mặt cầu
( )
S
đi qua A, B,C và có tâm thuộc mặt phẳng
( )
Oxy
.
A.
34
. B.
26
. C.
34
. D.
26
.
Câu 31: Trong không gian với hệ trục Oxyz, cho các điểm
( ) ( ) ( )
200 040 006A ;; ,B ;; ,C ;;
và
( )
246D ;;
.
Tìm tập hợp điểm M thỏa mãn
4+++ =
   
MA MB MC MD
A.
( )
( ) ( )
2 22
1 2 31−+−+−=xy z
. B.
( )
( ) ( )
2 22
1 2 31− ++ +− =
xy z
.
C.
( ) ( ) ( )
2 22
1 2 34−+−+−=
xy z
. D.
( ) ( ) ( )
2 22
1 2 31+++++=xy z
.
Câu 32: Trong không gian với hệ trục Oxyz, giả sử đường thẳng
2
2
= +
∆=+
= −
x mt
:y n t
z mt
cắt mặt cầu
( ) (
) (
)
22
2
2 29+− +− =S :x y z
tạ hai điểm A,B sao cho
6=
AB
. Tìm cặp số
( )
m;n
.
A.
( ) ( )
12=m;n ;
. B.
( )
( )
10
=m;n ;
. C.
( ) ( )
20=m;n ;
. D.
( )
(
)
02
=
m;n ;
.
Câu 33: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
( )
2 22
2220++−− − =S :x y z x y z
và điểm
( )
220A ;;
. Viết phương trình mặt phẳng
( )
OAB
, biết rằng điểm B thuộc mặt cầu
( )
S
, có hoành độ dương
và tam giác OAB đều.
A.
20−− =xy z
B.
0
−−=
xyz
C.
0−+=
xyz
D.
20−+ =xy z
LỜI GIẢI BÀI TẬP TỰ LUYỆN
Câu 1:
( )
( )
;1R d I Oxz b b= =⇒=
. Chọn B.
Câu 2: Ta có
( ) ( )
2; 1; 1 , 1; 2; 3
d
uM d= − −∈

. Ta có
( ) ( )
, 2; 14; 10 , 2; 4; 6
d
u AM AM

=−− =− −

  
Ta có
( )
( ) ( )
(
)
22
2
2
22
,
2 14 10
, 52
21 1
d
d
u AM
R d Md
u

+− +−

= = = =
+ +−
 

. Chọn A.
Câu 3: Mặt cầu
(
)
S
có tâm
( )
1; 2; 3I
, bán kính
4
R =
. Do
( )
α
chứa Oy nên
( )
:0ax cz
α
+=
Bán kính của thiết diện là
( ) ( )
4 qua 1; 2;3 3 0r R I ac
α
== ⇒ ⇒+ =⇒
chọn
3, 1ac= = −
Do đó phương trình mặt phẳng
( )
α
là
30
xz
−=
. Chọn C.
Câu 4: Giả sử
( )
(
)
;0;0 , ;0;0
Aa Bb
.
Ta có
( ) (
)
22
22 22
2 34 2 34 4IA IB a b b a= ⇔− ++=− ++ ⇔=−
Gọi M là trung điểm của AB
( )
2; 0; 0M⇒
.
Ta có
2
1 2.10
.4
25
IAB
IAB
S
S IM AB AB
IM
= ⇒= = =
Ta có
4
44242 2 29
0
a
AB a a R IA
a
=
=⇔− =⇔−=⇔ ⇒= =
=
Do đó phương trình mặt cầu là
( )
( )
( ) (
)
222
: 2 3 4 29Sx y z
− +− +− =
. Chọn D.
Câu 5: Mặt cầu
( )
S
có tâm
( )
3; 2;1I −
, bán kính
3R =
. Do
( )
Q
chứa Ox nên
( )
:0Q by cz+=
Ta có
( )
(
)
22 22
; 32 5
dI Q R r= −= −=
. Ta có
( )
( )
22
2
;5 5
bc
dI Q
bc
−+
=⇔=
+
22
440 2b bc c b c⇔ + + =⇔=− ⇒
chọn
( )
2, 1 : 2 0b c Q yz= =−⇒ − =
. Chọn A.
Câu 6: Mặt cầu
( )
S
có tâm
(
)
1; 2; 1
I −
, bán kính
3R =
. Đường thẳng d có
(
) (
)
2; 2;1 , 1; 1; 0
d
u Md= − −− ∈

Do
( )
P
vuông góc với d nên
( ) ( )
2; 2;1 : 2 2 0
Pd
n u P x yzm= = − ⇒ − ++ =
 
Do
( )
P
tiếp xúc với
( )
S
( )
( )
2
7
;3 3
16
3
m
m
dI P
m
=
+
⇒ =⇔=⇔
= −
Do
(
)
P
cắt Oz tại điểm có cao độ dương nên chọn
( )
16 : 2 2 16 0m P x yz=− ⇒ − +− =
. Chọn B.
Câu 7: Mặt cầu
( )
S
có tâm
( )
1; 2; 3I
, bán kính
14R
′
=
.
Ta có
( )
( )
( )
( )
22
;3 ; 5d I Oxy R R d I Oxy
′
=⇒= − =
Tâm H là hình chiếu của
( )
1; 2; 3I
lên
( ) ( )
1; 2; 0Oxy H⇒
. Chọn C.
Câu 8: Gọi H là trung điểm của
( )
;
AB IH AB IH d I d
⇒⊥⇒=
Ta có
( ) ( )
2;1;2, 7;9;7
d
uM d= − −−− ∈

. Ta có
( ) ( )
,
, 30; 30;15 ; 15
d
d
d
u IM
u IM d I d
u



=−⇒ = =

 
 

Bán kính mặt cầu
(
)
22 2 2
; 20 15 25
R AH d I d= + = +=
( ) ( ) ( ) (
)
2 22
2
: 2 3 1 25Sx y z⇒ − +− ++ =
. Chọn A.
Câu 9: Mặt cầu
( )
S
có tâm
( )
4;5;2I
−−
, bán kính
5R =
. Ta có
( )
( )
; 19dI P
=
Bán kính của giao tuyến là
( )
( )
22 2
, 5 19 6
r R d IP= − = −=
. Chọn D.
Câu 10: Mặt cầu
( )
S
có tâm
( )
0;1;1I
, bán kính
5
R =
. Ta có
( )
( )
;3dI P =
Bán kính thiết diện là
( )
( )
22
;4r R d IP=−=⇒
diện tích là
2
16
r
ππ
=
. Chọn A.
Câu 11: Mặt cầu
(
)
S
có tâm
( )
2; 1; 5I
−
, bán kính
4R =
. Ta có
( )
( )
; 23dI P =
Bán kính thiết diện là
( )
(
)
22
; 2 chu vi là 2 4
r R d IP r
ππ
=−=⇒ =
. Chọn C.
Câu 12: Do
(
)
; 6 ;2
I d It t t
∈ ⇒ −+ −
. Ta có
( )
( )
5 21
;
11
t
dI P
−
=
. Ta có
( ) ( )
Δ
2; 1; 1 , 5; 1; 1 ΔuM= − −∈

.
Ta có
( ) ( )
( ) ( ) ( )
22 2
2
Δ
419
2 20 98
, 4; 1; 9 ; Δ
66
tt
tt
u IM t t d I
− +− +−
−+

=−−−⇒ = =

 
Mà
( )
S
tiếp xúc với
Δ
và
( )
P
nên
( )
( )
( )
2
5 21
2 20 98
;;Δ
11 6
t
tt
dI P dI
−
−+
=⇔=
( )
(
)
( )
2
2
2
5 21
2 20 98
2; 4; 0
49
11 6
8
t
t
tt
I
tl
=
−
−+
⇔ = ⇔ ⇒−
=
. Chọn A.
Câu 13: Giả sử
( )
;;I xyz
là tâm mặt cầu.
Ta có
( )
( )
( )
2
2 22 22
2
2 22 2 2
2
22222
2
1
42
3
6
xyz x yz
IO IA x
IO IB x y z x y z y
IO IC z
xyzxy z
++=− ++
= =


= ⇔ ++=+− +⇔ =


= =

++=++−
Suy ra tâm
(
)
1; 2; 3I
, bán kính
(
) ( ) ( ) ( )
2 22
14 : 1 2 3 14R IO S x y z== ⇒ −+−+−=
. Chọn C.
Câu 14: Bán kính giao tuyến là
2
2
3
22
RR
rR

=−=⇒


chu vi là
23rR
ππ
=
. Chọn A.
Câu 15: Ta có
( ) ( )
2
22
1; 3; 2 1 3 2 14IH IH= − ⇒ = + +− =

( ) ( ) ( ) ( )
2 22
22
18 : 1 3 3 18R IH r S x y z⇒= + = ⇒ − + + +− =
. Chọn C.
Câu 16: Mặt cầu có tâm
( )
4;5;2
I −−
và bán kính
5R =
.
Ta có
(
)
(
)
(
)
(
)
2
2
2
3.4 5 3. 2 6
; 19 19 6
31 3
dI P r R
−− − +
= = ⇒= − =
++−
. Chọn C.
Câu 17:
(
) ( )
( )
( ) ( ) ( ) ( )
222
:0 ; 2 : 2 3 4 4
Oyz x R d I Oyz S x y z=⇒= =⇒ + + − +− =
. Chọn B.
Câu 18: Mặt cầu có tâm
( )
1; 2; 3I −
.
Mặt phẳng
( )
P
qua M và nhận
(
)
0; 0; 2
MI
=

là một VTPT
( ) ( )
:2 1 0 1 0Pz z⇒ − = ⇔ −=
. Chọn B.
Câu 19: Ta có
( ) ( )
1; 2; 3 1; 0; 2I AI− ⇒=

là một VTPT của
( ) ( )
:2 0P P x zm⇒ + +=
( )
( )
( )
2
22 2
3
3
; 45 3 5
5
5
m
m
dI P h h r R m
−
−
⇒ = = → + = ⇒ + = ⇔ = ±
. Chọn D.
Câu 20: Ta có
( )
:1
3
xyz
P
ab
++=
qua tâm
( )
211 21 2
2;1;1 1
33
I
ab ab
⇒++=⇔+=
.
Lại có
1 11
. . . .3
6 62
OABC
V OA OB OC a b ab
= = =
.
Ta có
2 2 1 21
2 . 18 9
3
OABC
ab V
a b ab
=+≥ ⇒ ≥ ⇒ ≥
.
Dấu “=” xảy ra
21
3
0
9
6
18
b
ab
ab
a
ab
=
= >
⇔ ⇔ ⇒+=

=
=
. Chọn B.
Câu 21: Ta có
( )
( )
( )
( )
( ) ( ) ( ) ( )
222
2
22
3. 1 6.3 2.2 4
; 1 : 1 3 21
36 2
R dAP S x y z
−+ − −
= = =⇒ + +− +− =
+ +−
. Chọn B.
Câu 22: Mặt cầu
( ) (
) ( ) (
)
2 22
:1 2 29Sx y z− +− +− =
có tâm
( )
1;2;2I
.
Mặt phẳng
( )
α
qua A và nhận
( )
2; 2;1IA =

là một VTPT
( ) ( ) ( ) ( )
: 2 3 2 4 3 0 2 2 17 0x y z x yz
α
⇒ −+ −+−=⇔ + +−=
. Chọn B.
Câu 23: Ta có
( )
:0Oxy z =
.
Mặt cầu
( )
2 22
1 1 17
:
2 2 24
Sx y z
 
+ +− ++ =
 
 
có tâm
11 1
;;
22 2
K

−−


và bán kính
7
2
R =
.
Ta có
( )
( )
22
16
;
22
h d I Oxy r R h= = ⇒= − =
.
Đường tròn cần tìm có tâm I là hình chiếu của
11 1
;;
22 2
K

−−


trên
( )
11
; ;0
22
Oxy I

⇒−


. Chọn A.
Câu 24: Ta có
( )
( )
( )
4; 5;1
; 14; 13; 9
3; 6; 4
AB
AB AC
AC
= −

⇒ =−−−

= −

 

là một VTPT của
( )
ABC
( )
14;13;9n⇒=
là một VTPT của
( )
ABC
(
)
( )
( ) ( )
:14 1 13 6 9 2 0 14 13 9 110 0ABC x y z x y z⇒ −+ − + − =⇔ + + − =
( )
( )
(
) (
) ( )
22
2
2 22
14.5 13.0 9.4 110
8
; :5 4
223
14 13 9
R d D ABC S x y z
+ +−
⇒= = ⇒ − + +− =
++
. Chọn D.
Câu 25: Ta có
( )
: 3 ; 3; 2
2
xt
d y t I tt t
zt
=
=−+⇒ −
=
.
Lại có
( ) ( )
( )
:0 ; 3Oxz y h d I Oxz t=⇒= =−
.
Ta có
( )
(
)
( )
2
2 22
1 1; 2; 2
2 8 34
5 5; 2;10
tI
Rh t
tI
=⇒−
= + ⇒= − +⇔
= ⇒
. Chọn A.
Câu 26: Ta có tâm
( )
( )
(
)
( )
2
2
5
1; 2;
0; 0;
2; 1; 1
15
AI t
AI t
I Oz I t
BI t
BI t
= +
= −

∈⇒ ⇒ ⇒

= −−
= −+



Ép cho
1 21
22
AI BI t R AI
= ⇒= ⇒ = =
(
)
2
22 222
1 21
: 50
24
Sxy z xyzz

⇒ ++− = ⇔++−−=


. Chọn A.
Câu 27: Gọi
( )
(
)
222
: 0 0P ax by cz d a b c+ + += + + >
.
Ta có
( ) ( )
0
, 0: 0
20
cd
A B P c d P ax by
cd
+=
∈ ⇒ ⇒= =⇒ + =
−+=
.
Mặt cầu
( )
( ) (
) ( ) ( )
22 2
: 2 1 2 1 2; 1; 2 , 1Sx y z I R
+ +− ++ =⇒− − =
.
Ta có
( )
( )
22 22
22
0
2
; 14 4
34
a
ab
dIP R ab abab
ab
ab
=
−+
= ==⇒ +− =+⇔
=
+
+) Với
( )
0 :0a Py=⇒=
.
+) Với
34ab=
, chọn
(
)
4 3 :4 3 0a b Pxy=⇒=⇒ + =
. Chọn C.
Câu 28: Đường tròn có bán kính
8
4
2
r
π
π
= =
.
Ta có
( )
( )
( ) ( ) ( ) ( )
2 22
22
2 22
2.1 2.2 2 5
; 3 345:12225
221
dAP R S x y z
+ −+
= =⇒= + =⇒ − + − ++ =
++
.
Chọn A.
Câu 29: Ta có tâm
( )
;0;0I Ox I t∈⇒
.
Ta có
( )
(
)
(
)
(
)
(
)
(
)
24
; ; 1 ;1
33
tt
dI P dI Q t R dI P
−+
= ⇔ = ⇔ =−⇒ = =
(
)
( )
2
22
:1 1Sx yz
⇒ + ++=
. Chọn C.
Câu 30: Gọi tâm
( )
( )
(
)
( )
( ) ( )
( ) ( )
( ) ( )
22
2
22
2
22
2
1 2 16
1; 2; 4
; ; 0 1; 3; 1 1 3 1
2; 2; 3
2 29
AI a b
AI a b
I a b BI a b BI a b
CI a b
CI a b
=− +− +
=−−

⇒ = − +− ⇒ = − + + +


= − −−
=−+−+




Ta có
20 4 10 6 1
26
17 2 13 4 2
IA IB b b b
R IA
IA IC a a a
= −=+ =

⇒ ⇔ ⇒= =

= −=− =−

. Chọn B.
Câu 31: Gọi
( )
(
)
( )
(
)
( )
2; ;
; 4;
;;
;; 6
2; 4; 6
AM x y z
BM x y z
M xyz
CM x y z
DM x y z
= −
= −
⇒
= −
=−−−




(
)
4 4;4 8;4 12
AM BM CM DM x y z⇒+++ =− − −
   
( )
( )
(
)
22 2
4 4 4 8 4 12 4
AM BM CM DM x y z⇒ +++ = −+−+− =
   
( ) ( ) ( )
2 22
1 2 31xy z⇔−+−+−=
. Chọn A.
Câu 32: Mặt cầu có bán kính
3
2
AB
R AB= = ⇒
qua tâm
(
)
0; 2; 2I
00
2 2 2 2 0; 2
22
0
0
mt mt
nt nt m n
mt
m
t
= + +=

⇒ =+ ⇔ +=⇒= =


= −
=
=
. Chọn D.
Câu 33: Mặt cầu
( )
S
có tâm
( )
1;1; 1I
, bán kính
3R =
. Ta thấy
( )
,OA S∈
Ta có
3 26
22
33
OAB
OA
OA R=⇒= =
. Gọi H là tâm tam giác đều OAB.
Do
( ) ( )
( )
22
3
,, ;
3
OAB
O A B S IH d I OAB R R∈⇒= = − =
Giả sử
( )
:0OAB ax by cz++=
do
( ) ( )
220 : 0A OAB a b a b OAB ax ay cz∈ ⇒ + = ⇔ =−⇒ − + =
Ta có
( )
( )
22
22
3
;
3
2
ac
c
d I OAB a c
ac
ac
=
= = ⇔=⇔
= −
+
Với
ac=
chọn
(
)
( )
1, 1 : 0 2; 2; 4a c Pxyz B= =⇒ −+=⇒ −
(loại)
Với
ac= −
chọn
( ) ( )
1, 1 : 0 2; 2; 4a c Pxyz B= =−⇒ − − = ⇒ −
. Chọn B.
| 1/27
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CHỦ ĐỀ 17: BÀI TOÁN VỀ PHƯƠNG TRÌNH MẶT CẦU
Dạng 1: Lập phương trình mặt cầu
Phương pháp giải:
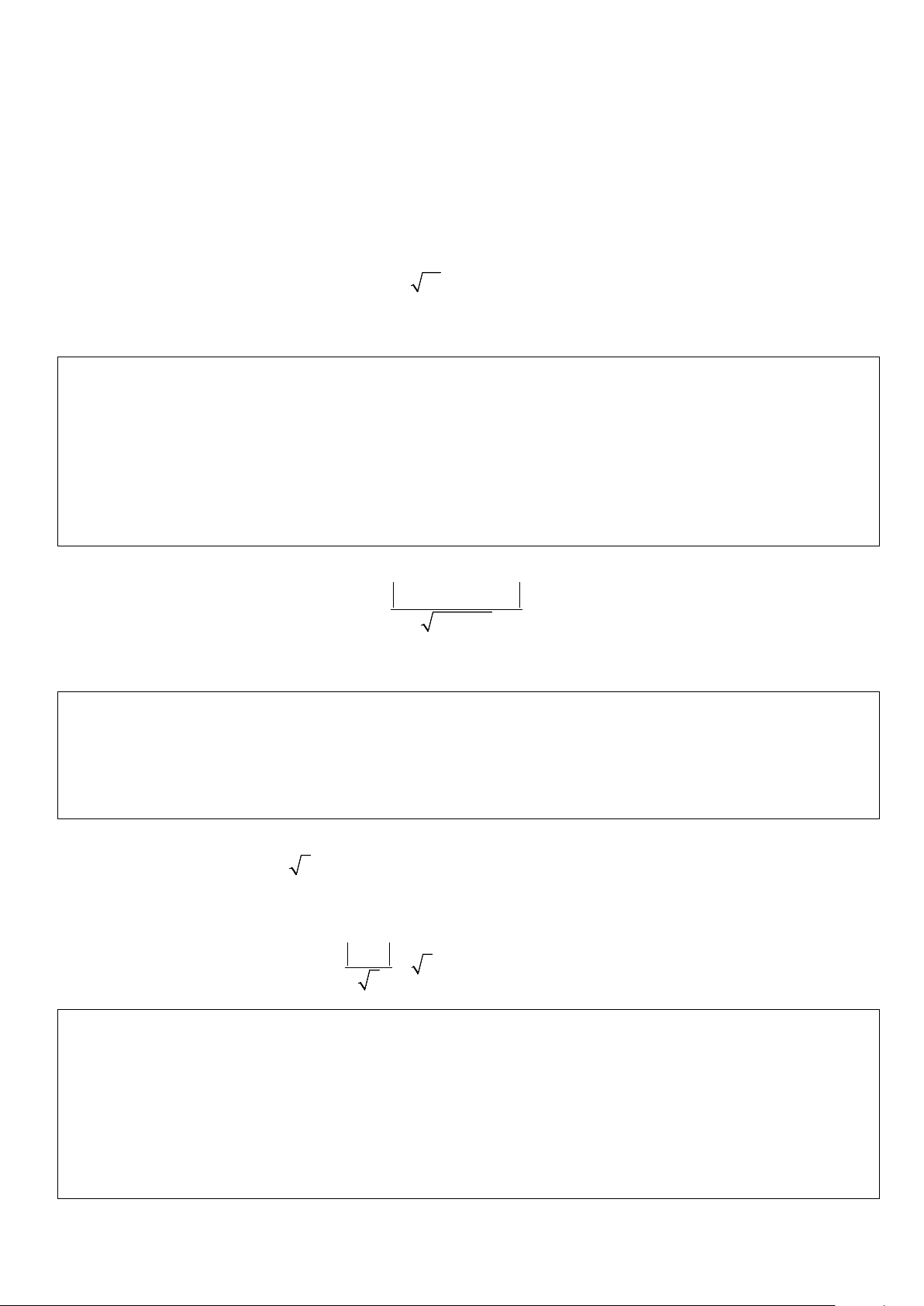
• Phương trình chính tắc của mặt cầu (S ) (x − a)2 + ( y − b)2 + (z − c)2 2 : = R
• Phương trình tổng quát của mặt cầu (S ) 2 2 2
: x + y + z − 2ax − 2by − 2cz + d với tâm I ( ; a ; b c) bán kính 2 2 2
R = a + b + c − d . Chú ý:
- Nếu A, B thuộc mặt cầu (S ) ⇒ IA = IB = R . 2 2    
- Nếu IA = IB thì ta có: 2 2 2. . . OB OA AB OI OB OA AB OI − = − ⇔ = 2       Chứng minh: Ta có: 2 2 2 2
IA = IB ⇔ IA = IB ⇔ IA = IB ⇔ (IO +OA)2 = (IO +OB)2
 ( ) 2 2   2 2 2 . . OB OA IO OB OA OB OA AB OI − ⇔ − = − ⇔ = . 2
- Với bài toán: Viết phương trình mặt cầu đi qua 4 điểm A, B, C, D ta sẽ làm như sau: Gọi I ( ;
x y; z) là tâm mặt cầu thì: IA = IB = IC = ID khi đó I ( ;
x y; z) là nghiệm của hệ phương trình: 2 2   . OB − OA AB OI =  2 IA = IB  2 2     = ⇔  . OC − OA IA IC AC OI = 
→ CASIO suy ra tọa độ điểm I. 2 IA ID  =  2 2   . OD − OA AD OI =   2
Trong đó O(0;0;0) là gốc tọa độ, giải hệ phương trình suy ra tọa độ điểm I.
Ví dụ 1: Lập phương trình của mặt cầu (S ) biết:
a) Tâm I thuộc Oy, đi qua A(1;1;3); B( 1; − 3;3) .
b) Tâm I thuộc Oz, đi qua A(2;1; ) 1 ; B(4; 1; − − ) 1 . Lời giải
a) Gọi I (0; y;0) ta có: 2 2
IA = IB ⇔ 1+ ( y − )2
1 + 9 =1+ ( y −3)2 + 9 ⇔ y = 2 ⇒ R = IA = 14 Suy ra (S ) 2 x + ( y − )2 2 : 2 + z =14 .
b) Gọi I (0;0; z) ta có: 2 2
IA = IB ⇔ 4 +1+ (z − )2 1 =16 +1+ (z + )2 1 ⇔ 4z = 1 − 2 ⇔ z = 3 − ⇒ I (0;0; 3 − ); R = 21 .
Phương trình mặt cầu (S ) 2 2
: x + y + (z + 3)2 = 21
Ví dụ 2: Lập phương trình mặt cầu (S ) biết: x =1+ t
a) Tâm I thuộc d : y = t và đi qua A(3;0;− ) 1 ; B(1;4; ) 1 . z =  2t
b) Tâm I thuộc x 2 y 1 : z d − − =
= và đi qua A(3;6;− ) 1 ; B(5;4; 3 − ). 1 − 1 2 Lời giải
a) Gọi I (1+ t;t;2t) là tâm mặt cầu ta có: 2 2
IA = IB ⇔ (t − )2 2 + t + ( t + )2 2 2
2 1 = t + (t − 4)2 + (2t − )2 1 ⇔ 12 − t = 12
− ⇔ t =1⇒ I (2;1;2) ⇒ R = 11 .
Phương trình mặt cầu là: (x − )2 + ( y − )2 + (z − )2 2 1 2 =11.
b) Gọi I (2 −t;1+ t;2t) là tâm mặt cầu ta có: 2 2
IA = IB ⇔ (t + )2
1 + (t −5)2 + (2t + )2
1 = (t + 3)2 + (t −3)2 + (2t + 3)2 ⇔ 1
− 6t = 0 ⇔ t = 0 ⇒ I (2;1;0) ⇒ R = 3 3
Phương trình mặt cầu là: (x − )2 + ( y − )2 2 2 1 + z = 27 .
Ví dụ 3: Lập phương trình mặt cầu (S ) biết (S )
a) Đi qua 4 điểm A(2;4;− ) 1 ; B(1; 4; − − )
1 ; C (2;4;3); D(2;2;− ) 1 .
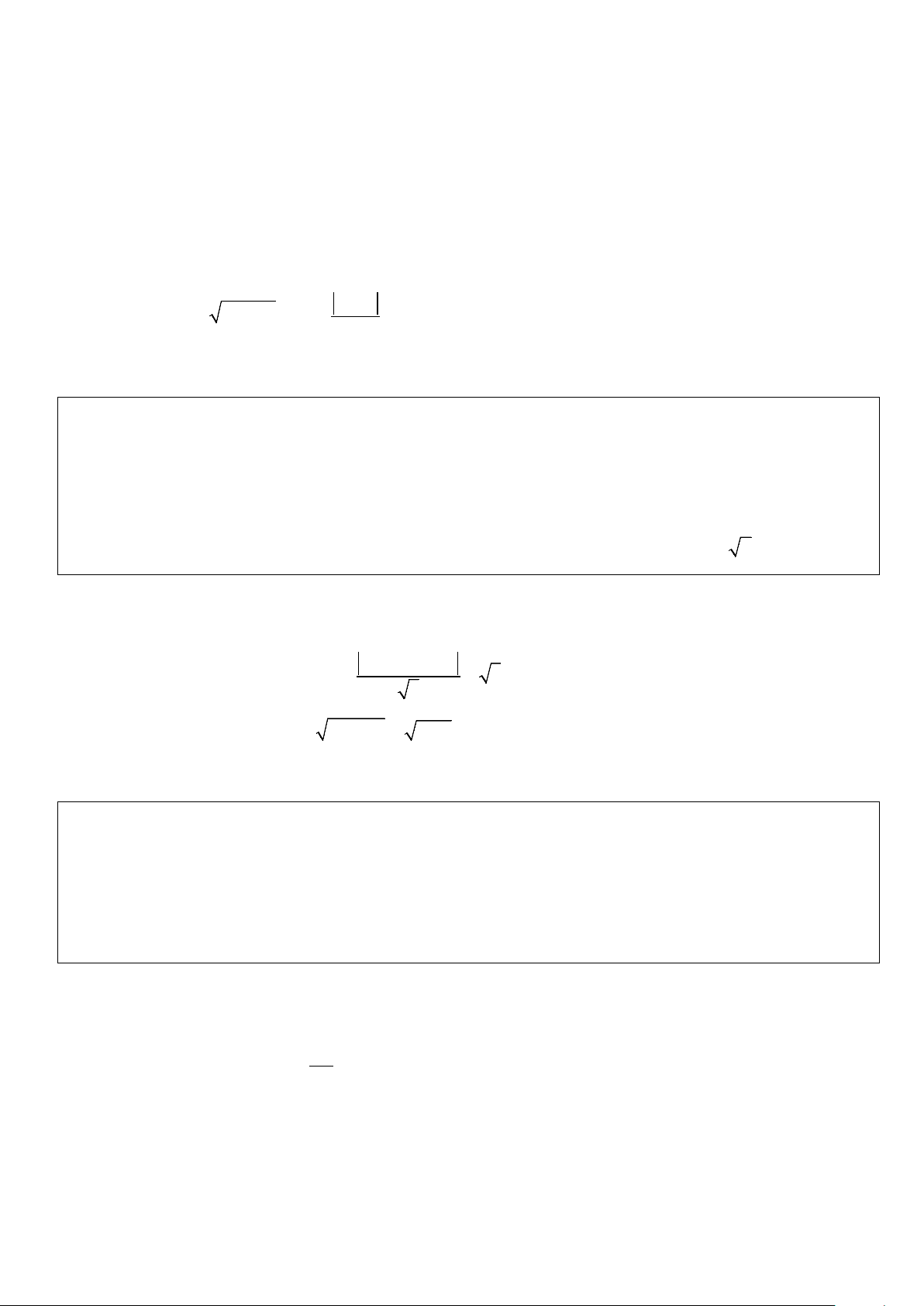
b) Đi qua 4 điểm A(3;3;0); B( 3;0;3); C ( 0;3;3); D( 3;3; 3 − ) . Lời giải 2 2   . OB − OA AB OI =  2  2 2   Áp dụng:  −
IA = IB = IC = ID thì I ( ;
x y; z) là nghiệm của hệ phương trình:  . OC OA AC OI = . 2  2 2   . OD − OA AD OI =   2 2 2    . OB − OA AB OI =  45 − 2 xIA = IB =   2 2 2    −  a) Gọi I ( ;
x y; z) là tâm mặt cầu ta có:  = ⇔  . OC OA IA IC AC OI = ⇒ z =1 2 IA ID   = =  2 2 y 3   −   . OD OA AD OI =  2  2
Phương trình mặt cầu:  45 x  + + 
( y − )2 +(z − )2 2421 3 1 =  .  2  4  3  x = −
(0; 3;3)( ;x y;z) 0   − = 2   b) Gọi I ( ;
x y; z) là tâm mặt cầu ta có: (  − )(x y z)  3
3;0;3 ; ; = 0 ⇔ y = − . 2   (  0;0; 3 − )( ; x y; z) 9 =  3 2 z = −   2 2 2 2
Phương trình mặt cầu:  3   3   3  171 x + +   y + +   z + =  . 2 2 2        4
Ví dụ 4: Lập phương trình mặt cầu (S ) biết
a) (S ) đi qua A(2;0; )
1 ; B(1;0;0);C (1;1; )
1 và I ∈(P) : x + y + z − 2 = 0 .
b) (S ) đi qua A( 2; − 4; ) 1 ; B(3;1; 3 − );C ( 5
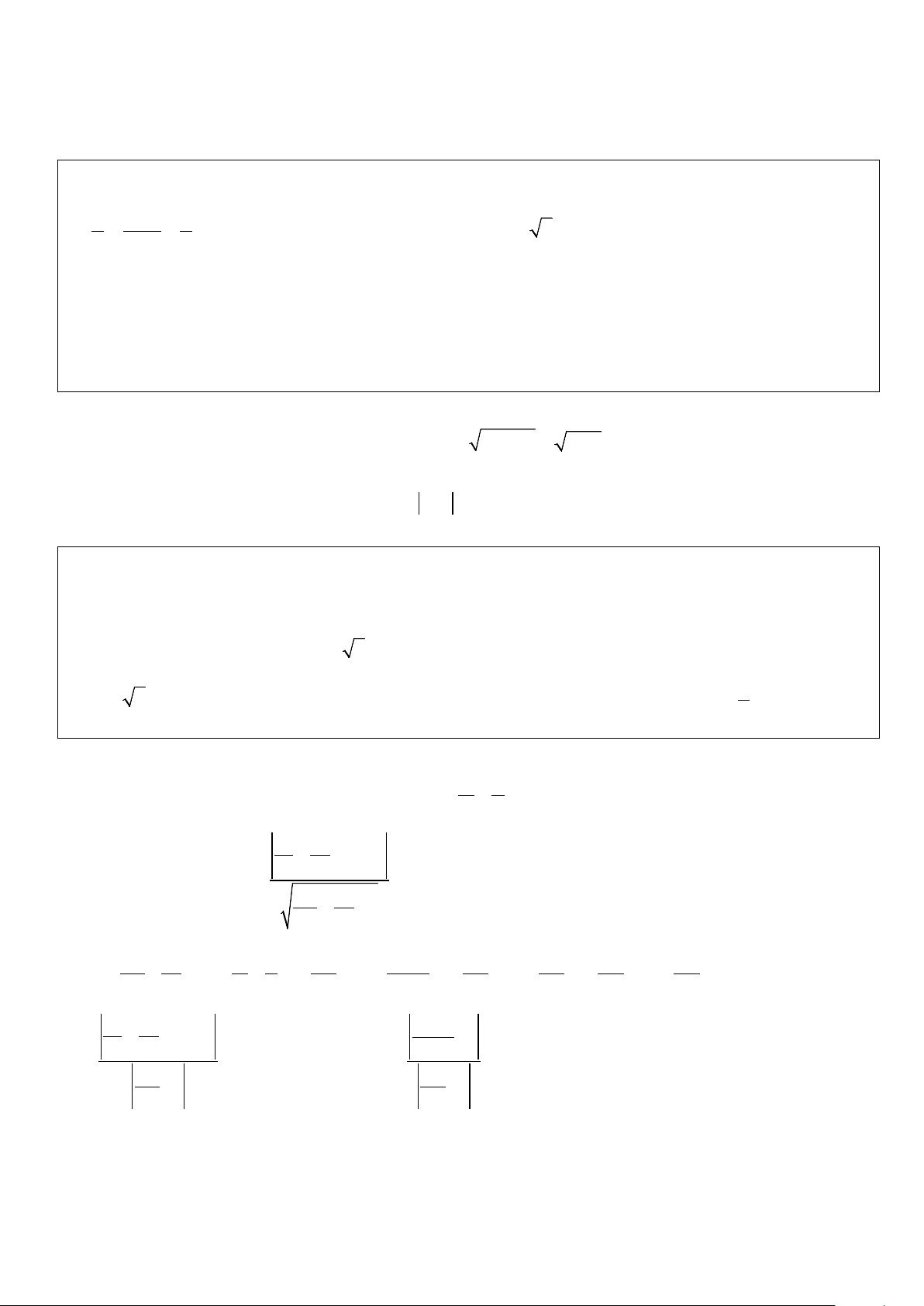
− ;0;0) và I ∈(P) : 2x + y − z + 3 = 0. Lời giải Gọi I ( ;
x y; z) là tâm mặt cầu 2 2   . OB − OA AB OI =  2  (  1 − ;0;− ) 1 ( ; x y; z) = 2 − x =1 2 2   −  a) Ta có:  . OC OA AC OI (  1;1;0)( ; x y; z) 1  = ⇔ − = − ⇔ y = 0 . 2 
x + y + z = 2  z = 1
x + y + z − 2 = 0   
Khi đó (S ) (x − )2 2 :
1 + y + (z − )2 1 =1. 2 2   . OB − OA AB OI =  2  (  5; 3 − ; 4 − )( ; x y; z) = 1 − x =1 2 2   −  b) Ta có:  . OC OA AC OI (  3; 4; ) 1 ( ; x y; z) 2  = ⇔ − − − = ⇔ y = 2 − . 2 
2x + y − z = 3  − z = 3
2x + y − z + 3 = 0   
Khi đó (S ) (x − )2 + ( y + )2 + (z − )2 : 1 2 3 = 49 .
Ví dụ 5: [Đề thi THPT Quốc gia 2017] Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây
là phương trình mặt cầu đi qua ba điểm M (2;3;3); N ( 2; 1 − ;− ) 1 ; P( 2; − 1
− ;3) và có tâm thuộc mặt phẳng:
(α ):2x +3y − z + 2 = 0. A. 2 2
x + y − 2x + 2y − 2z −10 = 0 . B. 2 2 2
x + y + z − 4x + 2y − 6z − 2 = 0 . C. 2 2 2
x + y + z + 4x − 2y + 6z + 2 = 0 . D. 2 2 2
x + y + z − 2x + 2y − 2z − 2 = 0 . Lời giải
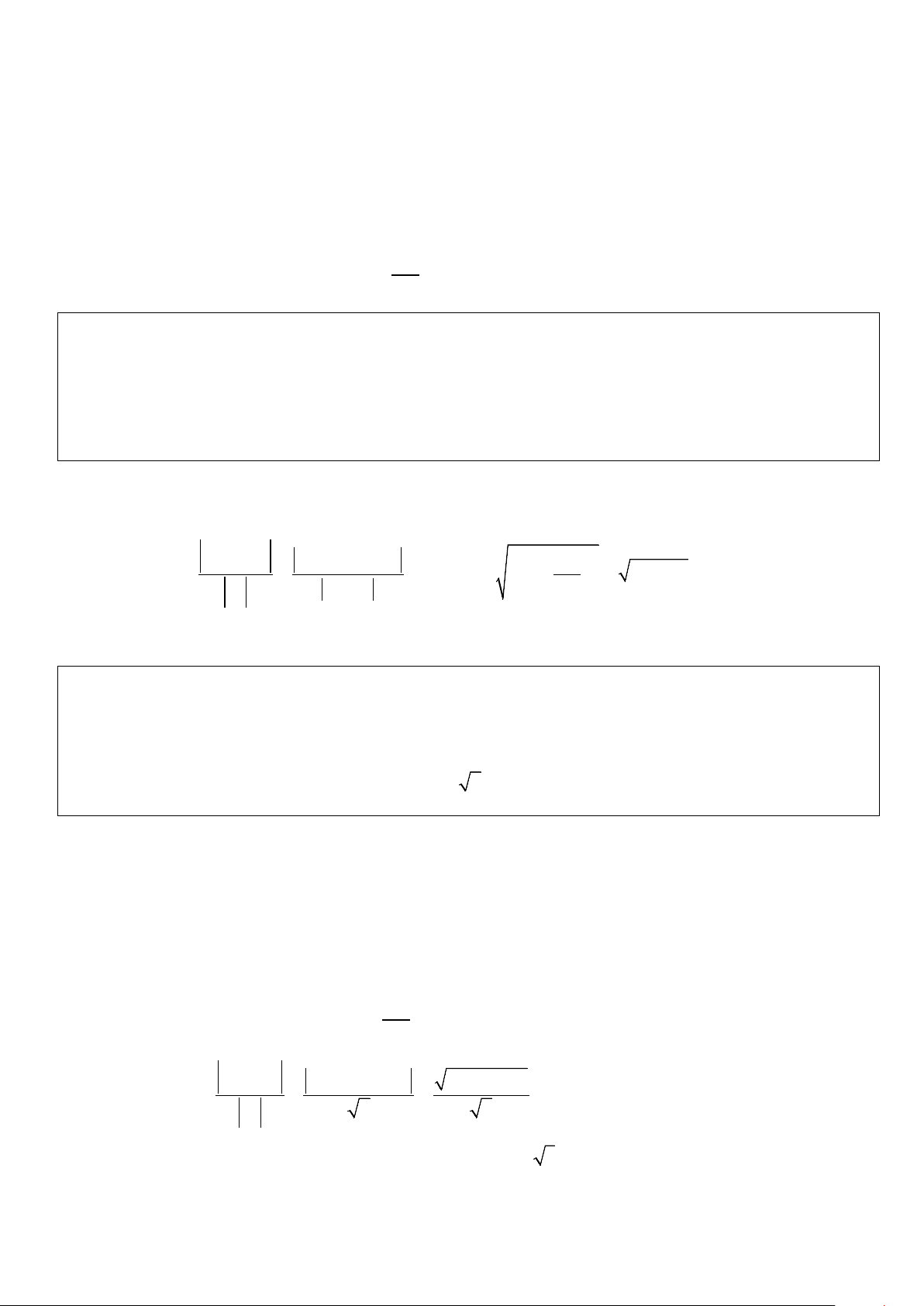
Giả sử mặt cầu có tâm I ( ; x y; z) . 2 2   . ON − OM MN OI =  2  (  0; 4 − ; 4 − )( ; x y; z) = 8 − x = 2 2 2   −  Ta có:  . OP OM MP OI (  4; 4;0)( ; x y; z) 4  = ⇔ − − = − ⇔ y = 1 − . 2 
2x + y − z = 2  − z = 3
2x + 3y − z + 2 = 0   
Phương trình mặt cầu là: (x − )2 + ( y + )2 + (z − )2 2 1 3 =16 hay 2 2 2
x + y + z − 4x + 2y − 6z − 2 = 0 . Chọn B.
Ví dụ 6: Trong không gian với hệ tọa độ Oxyz, cho các điểm A(2; 4;
− 0), B(0;0;4), C ( 1 − ;0;3) . Phương
trình mặt cầu ngoại tiếp tứ diện OABC là: A. 2 2 2
x + y + z − 2x + 4y + 4z = 0 . B. 2 2 2
x + y + z − 4x + 3y − 4z = 0 . C. 2 2 2
x + y + z − 6x + 2y − 4z = 0 . D. 2 2 2
x + y + z − 2x + 4y − 4z = 0. Lời giải 2   . OA OI OA =  2  (  2; 4; − 0)( ; x y; z) =10 x =1 2    Gọi I ( ;
x y; z) là tâm mặt cầu ta có:  . OB OI OI (  0;0;4)( ; x y; z) 8  = ⇔ = ⇔ y = 2 − 2    − = = 2   ( 1;0;3   )( ;x y;z) 5 z 2 . OC OC OI =   2
Phương trình mặt cầu là: (x − )2 + ( y + )2 + (z − )2 1 2 2 = 9 hay 2 2 2
x + y + z − 2x + 4y − 4z = 0. Chọn D.
Ví dụ 7: Trong không gian tọa độ Oxyz cho 2 điểm A(3;2; 3 − ); B( 1 − ; 2; − ) 1 và mặt phẳng
(P): x + y + z = 0. Viết phương trình mặt cầu (S) có tâm I thuộc (P) đi qua A, B sao cho tam giác OIA
vuông tại gốc tọa độ O.
A. (S ) (x + )2 + ( y − )2 + (z + )2 : 5 6 1 = 84 .
B. (S ) (x − )2 + ( y + )2 + (z − )2 : 5 6 1 = 84.
C. (S ) (x + )2 + ( y − )2 + (z + )2 : 5 6 1 = 42 .
D. (S ) (x − )2 + ( y + )2 + (z − )2 : 5 6 1 = 42 . Lời giải
Phương trình mặt phẳng trung trực của AB là: (Q) : x + y − z − 2 = 0 . x = t
Gọi d (P) (Q) d  = ∩
⇒ y =1−t ⇒ I (t;1−t;− ) 1 . z = 1 −   
Ta có: OI.OA = 0 ⇔ 3t + 2 − 2t + 3 = 0 ⇔ t = 5 − ⇒ I ( 5 − ;6;− ) 1 .
Vậy PT mặt cầu (S ) (x + )2 + ( y − )2 + (z + )2 : 5 6 1 = 84 . Chọn A.
Ví dụ 8: Trong không gian tọa độ Oxyz, phương trình mặt cầu đi qua 3 điểm A(3;1 ) ;1 ; B(0;1;4);C( 1 − ; 3 − )
;1 và có tâm thuộc mặt phẳng (P) : x + y − 2z + 4 = 0 là:
A. (x − )2 + ( y + )2 + (z − )2 1 1 2 = 9 .
B. (x + )2 + ( y − )2 + (z + )2 1 1 2 = 9 .
C. (x − )2 + ( y + )2 + (z − )2 1 1 2 = 81.
D. (x + )2 + ( y − )2 + (z + )2 1 1 2 = 81. Lời giải Gọi I ( ;
x y; z) là tâm mặt cầu 2 2   . OB − OA AB OI =  2  (  3 − ;0;3)( ; x y; z) = 3 x =1 2 2   −  Ta có:  . OC OA AC OI (  4; 4;0)( ; x y; z) 0  = ⇔ − − = ⇔ y = 1 − . 2 
x + y −2z = 4  − z = 2
x + y − 2z + 4 = 0   
Khi đó phương trình mặt cầu là: (x − )2 + ( y + )2 + (z − )2 1 1 2 = 9 . Chọn A.
Ví dụ 9: Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) : 2x + 6y + z −3 = 0 cắt trục Oz và đường thẳng
x − 5 y z − 6 d : = =
lần lượt tại A và B. Phương trình mặt cầu đường kính AB là 1 2 1 −
A. (x − )2 + ( y + )2 + (z − )2 2 1 5 = 9.
B. (x + )2 + ( y − )2 + (z + )2 2 1 5 = 36 .
C. (x − )2 + ( y + )2 + (z − )2 2 1 5 = 36.
D. (x + )2 + ( y − )2 + (z + )2 2 1 5 = 9 . Lời giải
Ta có A∈Oz ⇒ A(0;0;a) mà A∈(P) ⇒ 2.0 + 6.0 + a −3 = 0 ⇔ a = 3 ⇒ A(0;0;3). x = 5 + t
Lại có d : y = 2t (t ∈) mà B∈d ⇒ B(t + 5;2t;6 −t) . z = 6−  t
Hơn nữa B ∈(P) ⇒ 2(t + 5) + 6.2t + (6 −t) −3 = 0 ⇔ 13t +13 = 0 ⇔ t = 1 − ⇒ B(4; 2 − ;7).
Mặt cầu đường kính AB có tâm I là trung điểm của AB ⇒ I (2; 1; − 5) .
Mặt cầu đường kính AB có bán kính 1 R = AB . 2  Mà AB = ( − ) 2 ⇒ AB = + (− )2 2 4; 2;4 4
2 + 4 = 6 ⇒ R = 3 ⇒ (S ) :(x − 2)2 + ( y + )2 1 + (z −5)2 = 9. Chọn A.
Dạng 2: Bài toán mặt cầu tiếp xúc với mặt phẳng
Có hai đặc điểm quan trọng của bài toán về trường hợp mặt phẳng tiếp xúc với mặt cầu
• Điều kiện tiếp xúc d (I;(P)) = R .
• Tâm I sẽ nằm trên đường thẳng ∆ đi qua điểm tiếp xúc và vuông góc với mặt phẳng (P) .
Ví dụ 1: Lập phương trình mặt cầu (S ) tiếp xúc (P) :3x + y + z − 4 = 0 tại điểm M (1; 2 − ;3) và đi qua A( 1; − 0; ) 1 . Lời giải
Do (S ) tiếp xúc với (P) tại M (1; 2
− ;3) nên IM ⊥ (P) ⇒ IM qua M (1; 2
− ;3) và có vectơ chỉ phương x = 1+ 3t   u = n = (3;1 )  ( )
;1 suy ra IM : y = 2 − + t Pz = 3+  t
Gọi I (1+ 3t; 2
− + t;3+ t) . Ta có 2 2 2
IM = IA ⇔ 11t = (3t + 2)2 + (t − 2)2 + (t + 2)2
⇔ 12t +12 = 0 ⇔ t = 1 − .
Suy ra I (− − ) R = IA =
⇒ (S ) (x + )2 + ( y + )2 + (z − )2 2; 3;2 ; 11 : 2 3 2 =11.
Ví dụ 2: Lập phương trình mặt cầu (S ) tiếp xúc (P) : x + 2y + 3z +10 = 0 tại điểm M (2; 3 − ; 2 − ) và đi qua A(0;1;2) . Lời giải
Do (S ) tiếp xúc với (P) tại M (2; 3 − ; 2
− ) nên IM ⊥ (P) ⇒ IM qua M (2; 3 − ; 2 − ) và có vectơ chỉ x = 2 + t  
phương u = n = (1;2;3 suy ra IM : y = 3 − + 2t P ) ( ) z = 2 − +  3t
Gọi I (2 + t; 3 − + 2t; 2 − + 3t) . Ta có 2 2 2
IM = IA ⇔ 14t = (t + 2)2 + (2t − 4)2 + (3t − 4)2
⇔ 36 − 36t = 0 ⇔ t =1⇒ I (3; 1 − ; )
1 ; R = IA = 14 .
Phương trình mặt cầu (S ) (x − )2 + ( y + )2 + (z − )2 : 3 1 1 =14.
Ví dụ 3: Trong không gian Oxyz, phương trình nào dưới đây là phương trình mặt cầu có tâm I ( 1; − 2;− ) 1
và tiếp xúc với mặt phẳng (P) : 2x − y + 2z −3 = 0 ?
A. (x − )2 + ( y + )2 + (z − )2 1 2 1 = 3.
B. (x − )2 + ( y + )2 + (z − )2 1 2 1 = 9 .
C. (x + )2 + ( y − )2 + (z + )2 1 2 1 = 3 .
D. (x + )2 + ( y − )2 + (z + )2 1 2 1 = 9 . Lời giải 2. 1 − − 2 − 2 − 3
Bán kính mặt cầu tâm I là: R = d (I;(P)) ( ) = = 3 . 4 +1+ 4
Do đó phương trình mặt cầu là: (x + )2 + ( y − )2 + (z + )2 1 2 1 = 9 . Chọn D.
Ví dụ 4: Có bao nhiêu mặt phẳng song song với mặt phẳng (α ) : x + y + z = 0 đồng thời tiếp xúc với mặt cầu (S ) 2 2 2
: x + y + z − 2x − 2y − 2z = 0 ? A. 1. B. 0. C. vô số. D. 2. Lời giải
Mặt cầu có tâm I (1;1; ) 1 ; R = 3 .
Mặt phẳng cầm tìm có dạng (P) : x + y + z + m = 0 (Do (P) / /(α ) ⇒ m ≠ 0). m + 3 m = 0 loai
Điều kiện tiếp xúc: d (I;(P)) ( ) = R ⇔ = 3 ⇔  . Chọn A. 3 m = 6 − x = t
Ví dụ 5: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : y = 1 − và hai mặt phẳng z = t− 
(P): x + 2y + 2z +3 = 0 và (Q): x + 2y + 2z + 7 = 0 . Phương trình mặt cầu (S) có I ∈d và tiếp xúc với cả
hai mặt phẳng (P) và (Q) có phương trình là:
A. (x − )2 + ( y + )2 + (z + )2 9 3 1 3 = .
B. (x − )2 + ( y + )2 + (z + )2 4 3 1 3 = . 4 9
C. (x + )2 + ( y − )2 + (z − )2 9 3 1 3 = .
D. (x + )2 + ( y − )2 + (z − )2 4 3 1 3 = . 4 9 Lời giải Gọi I (t; 1;
− − t)∈d , do (S ) tiếp xúc với cả 2 mặt phẳng (P) và (Q) nên: − −
d (I (P)) = d (I (Q)) 1 t 5 t 2 ; ; = R ⇔ =
⇔ t = 3 ⇒ R = . 3 3 3
Phương trình mặt cầu cần tìm là: (x − )2 + ( y + )2 + (z + )2 4 3 1 3 = . Chọn B. 9
Ví dụ 6: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng x 1 y 1 : z d − + = = và mặt phẳng 3 1 1
(P):2x + y − 2z + 2 = 0 . Phương trình mặt cầu (S) có tâm thuộc đường thẳng d có bán kính nhỏ nhất, tiếp
xúc với (P) và đi qua điểm A(1; 1; − ) 1 là:
A. (x − )2 + ( y + )2 2 1 1 + z =1.
B. (x − )2 + ( y + )2 2 1 1 + z = 4.
C. (x + )2 + ( y − )2 2 1 1 + z =1.
D. (x + )2 + ( y − )2 2 1 1 + z = 4. Lời giải
Do I ∈d ta gọi I (1+ 3t; 1
− + t;t) khi đó IA = d (I;(P)) = R
t = 0 ⇒ R =1 5t + 3 2 11t 2t 1 R 9( 2 11t 2t t) (5t 3)2  ⇔ − + = = ⇔ − + = + ⇔ 24 77 3 t = ⇒ R =  37 37
Do (S ) có bán kính nhỏ nhất nên ta chọn t = R = ⇒ I ( − ) ⇒ (S ) (x − )2 + ( y + )2 2 0; 1 1; 1;1 : 1 1 + z =1. Chọn A.
Ví dụ 7: [Đề thi chuyên ĐH Vinh 2017] Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S ) đi qua điểm A(2; 2;
− 5) và tiếp xúc với các mặt phẳng (α ) : x =1; (β ) : y = 1; − (γ )
: z =1. Bán kính của mặt cầu (S) bằng: A. 33 . B. 1. C. 3 2 . D. 3. Lời giải Gọi I ( ; a ;
b c) ta có: d (I;(α )) = d (I;(β )) = d (I;(γ )) suy ra R = a −1 = b +1 = c −1 . Do điểm A(2; 2;
− 5) thuộc miền x >1; y < 1; − 1
z > nên I ( ; a ;
b c) cũng thuộc miền x >1; y < 1; − 1 z > .
Khi đó I (R +1; 1 − − ; R R + )
1 . Mặt khác IA = R ⇒ ( 2
R − ) + (R − )2 + (R − )2 2 1 1
4 = R ⇔ R = 3. Chọn D.
Dạng 3: Bài toán tương giao mặt cầu với mặt phẳng
Phương pháp giải:
 Mặt cầu (S ) có tâm I và bán kính R cắt mặt phẳng (P) theo giao tuyến là một đường tròn bán kính r
khi d (I;(P)) < R . Khi đó 2
d (I (P)) 2 2 ; + r = R .
 Tâm đường tròn giao tuyến của (S ) và (P) và hình chiếu vuông góc xủa điểm I trên mặt phẳng (P) .
Ví dụ 1: Trong không gian tọa độ Oxyz, cho I (1;2; 2
− ) và (P) : 2x + 2y + z + 5 = 0 .
Lập phương trình mặt cầu (S ) có tâm I sao cho giao tuyến của (S ) và (P) là đường tròn có chu vi 8π . Lời giải + − +
Do chu vi đường tròn giao tuyến C = 2π r = 8r ⇒ r = 4. Ta có: d (I (P)) 2 4 2 5 ; = = 3. 4 + 4 +1 Bán kính mặt cầu là 2 2 2 2
R = r + d = 4 + 3 = 5.
Phương trình mặt cầu là: (S ) (x − )2 + ( y − )2 + (z + )2 : 1 2 2 = 25 .
Ví dụ 2: Cho mặt phẳng (α ) : x + y − z +1= 0 và mặt cầu (S ) (x − )2 2 :
1 + y + (z + 2)2 = 9 .
Lập phương trình mặt phẳng (P) song song với (α ) và cắt (S ) theo giao tuyến là đường tròn có diện tích bằng 6π . Lời giải
Mặt cầu (S ) (x − )2 2 :
1 + y + (z + 2)2 = 9 có tâm I (1;0; 2
− ) bán kính R = 3.
Do diện tích đường tròn giao tuyến 2
S = π r = π ⇒ r =
⇒ d (I (P)) 2 2 6 6 ; = R − r = 3 .
Mặt phẳng (P) song song với (α ) ⇒ (P) : x + y − z + D = 0 1+ 2 + DD =
Ta có: d (I;(P)) 0 = = 3 ⇔ . 3  D = 6 −
Do đó (P) : x + y − z = 0 hoặc x + y − z + 6 = 0 .
Ví dụ 3: Trong không gian tọa độ Oxyz, cho đường thẳng
x − 3 y − 2 z −1 d : = = và mặt cầu 2 1 2 − (S) 2 2 2
: x + y + z − 2x + 2y − 4z −19 = 0 . Tìm tọa độ điểm M thuộc đường thẳng d sao cho mặt phẳng qua M
và vuông góc với d cắt mặt cầu (S ) theo một đường tròn có chu vi bằng 8π . Lời giải
Mặt cầu (S ) có tâm I (1; 1;
− 2) , bán kính R = 5. Do C = 2π r ⇒ r = 4 do vậy mặt phẳng qua M vuông
góc với d cắt (S ) theo 1 đường tròn có bán kính bằng 4. 
VTCP của d là u =
− khi đó M ∈d ⇒ (3+ 2t;2 + t;1− 2 t) d (2;1; 2)
Phương trình mặt phẳng (P) có dạng 2(x −3− 2t) + ( y − 2 −t) − 2(z −1+ 2t) = 0
Hay 2x + y − 2z − 9t − 6 = 0 9t + 9 t = 0
Ta có: d (I;(P)) 2 2
= R − r = 3 ⇔ = 3 ⇔ 3  t = 2 −
Từ đó suy ra M (3;2; ) 1 , M ( 1
− ;0;5) là các điểm cần tìm.
Ví dụ 4: Trong không gian cho mặt cầu có phương trình (S ) (x + )2 + ( y − )2 + (z − )2 : 3 5 7 = 4 và mặt phẳng
(P): x − y + z + 4 = 0 . Biết mặt cầu (S) cắt mặt phẳng (P) theo một đường tròn (C). Tính chu vi đường tròn (C). A. 8π . B. 4π . C. 2π . D. 4π 2 . Lời giải
Mặt cầu (S ) có tâm I ( 3
− ;5;7) và bán kính R = 2 . 3 − − 5 + 7 + 4
Khoảng cách từ tâm I đến (P) là: d = = 3 . 3
Bán kính đường tròn (C) là: 2 2
r = R − d = 4 − 3 =1.
Chu vi đường tròn (C) là: C = 2πr = 2π . Chọn C.
Ví dụ 5: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S ) 2 2 2
: x + y + z − 2x − 4y − 6z − 2 = 0 . Viết
phương trình mặt phẳng (α ) chứa trục Oy và cắt mặt cầu (S ) theo thiết diện là một đường tròn có chu vi bằng 8π .
A. 3x + z = 0 .
B. 3x + z + 2 = 0.
C. 3x − z = 0.
D. x − 3z = 0. Lời giải
Ta có: (S ) (x − )2 + ( y − )2 + (z − )2 : 1 2
2 =16 ⇒ (S ) có tâm I (1;2;3) và bán kính R = 4 .
Bán kính của đường tròn là: C r =
= 4 = R ⇒ đường tròn đi qua tâm của mặt cầu (S ) . 2π 
Vtcp của Oy là u (0;1;0) , điểm A(0;1;0)∈Oy .    
Ta có: IA = (1;1;3) ⇒ n =  ; IA u = ( 3 − ;0; ) 1   . 
Mặt phẳng (α ) đi qua O và nhận n làm vtpt suy ra phương trình mặt phẳng (α ) là: (α ) :3x − z = 0 . Chọn C.
Ví dụ 6: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S ) có tâm I thuộc đường thẳng x y + 3 Δ : z =
= . Biết rằng mặt cầu (S ) có bán kính bằng 2 2 và cắt mặt phẳng (Oxz) theo một đường 1 1 2
tròn có bán kính bằng 2. Tìm tọa độ tâm I. A. I (1; 2; − 2); I (5;2;10) . B. I (1; 2; − 2); I ( 0; 3 − ;0) .
C. I (5;2;10); I (0; 3 − ;0). D. I (1; 2 − ;2); I ( 1; − 2; 2 − ) . Lời giải
Khoảng cách từ tâm I đến mặt phẳng là (Oxz) là 2 2
d = R − r = 8 − 4 = 2 . t = 5 I 5;2;10
Điểm I ∈d suy ra I (t;t −3;2t) ⇒ d (I;(P)) ( ) = t − 3 = 2 ⇒ ⇒   . Chọn A. t = 1 I  (1; 2 − ;2)
Ví dụ 7: Trong không gian với hệ tọa độ Oxyz, cho hai điểm S (0;0; ) 1 . Hai điểm M ( ;0 m ;0); N (0; ;0 n )
thay đổi sao cho m + n =1 và m > 0;n > 0 . Biết rằng mặt phẳng (SMN ) luôn tiếp xúc với một mặt cầu cố
định. Bán kính mặt cầu đó bằng: R = 2 . A. R = 2 . B. R = 2 . C. R =1. D. 1 R = . 2 Lời giải
Phương trình mặt phẳng (SMN ) theo đoạn chắn là: x y
+ + z =1. Gọi P(x ; y ; z 0 0 0 ) m n x y 0 0 + + z −1 0 Ta có: = ( ;( )) m n d d P SMN = . 1 1 + +1 2 2 m n 2 2 2 2 Lại có 1 1  1 1  2  m + n  2  1  2  1 1   1   1   1  1 + + = + − + = − + = − + = − 2 2 m n m n mn mn mn mn mn mn          x y + 0 0 + + z −1  = 1 m n x −1 0 m n 0 d = . Ta chọn  =1 mn y ⇒ d =
= 1 với mọi m > 0;n > 0 . 1 0 −1 1 z =  0 −1 mn 0 mn
Do đó mặt cầu cần tìm là mặt cầu tâm P 1;1;0 bán kính R =1. Chọn C. 0 ( )
Dạng 4: Bài toán tương giao mặt cầu với đường thẳng Phương pháp giải:
Xét sự tương giao của mặt cầu (S ) có tâm I và bán kính R và đường thẳng ∆ ta có:
 ∆ tiếp xúc với mặt cầu (S ) ⇔ d (I;Δ) = R .
 ∆ cắt mặt cầu (S ) tại 2 điểm phân biệt A, B khi d (I;Δ) < R khi đó hình chiếu vuông góc của điểm I 2
trên ∆ là trung điểm của AB và 2
d (I )  AB  2 ;Δ + =   R .  2 
Ví dụ 1: Trong không gian tọa độ Oxyz, lập phương trình mặt cầu tâm I (2;3;− ) 1 cắt đường thẳng x =1+ 2t d : y = 5
− + t tại A, B với AB =16. z = 15 − −  2t
Lời giải  
Đường thẳng d đi qua điểm M (1; 5 − ; 1
− 5) và có vtcp là u = − IM = − − − . d (2;1; 2); ( 1; 8; 14)   IM;u d   30; 30 − ; 15 −
Khi đó d (I;d ) ( ) 2 2  AB  2 2 =  = =15 ⇒ R = d + = 15 + 8 =   17 . u 2;1; 2 −  2  d
Do đó phương trình mặt cầu cần tìm là: (x − )2 + ( y − )2 + (z + )2 2 3 1 = 289 . x =1+ t
Ví dụ 2: Cho đường thẳng d : y = 2
− − t ,(P) : x + y + z +1 = 0. Viết phương trình mặt cầu (S ) tiếp xúc với z = 2 − 
(P) tại M (1;0; 2
− ) và cắt d tại A, B sao cho AB = 2 2 .
Lời giải 
Đường thẳng d đi qua E (1; 2 − ; 2
− ) và có vectơ chỉ phương u − . d (1; 1; 0) x =1+ t
Gọi I là tâm mặt cầu suy ra đường thẳng IM (P) IM :  ⊥ ⇒ y = t . z = 2 − +  t 2
Khi đó gọi I ( + t t − + t) 2
⇒ d (I d )  AB  2 2 +
= R ⇔ d (I d ) 2 1 ; ; 2 ; ; + 2 =   IM  2    IE;u d   t − ; t − ;2t + 2
Trong đó d (I d ) ( ) 2 6t + 8t + 4 ; =  = = và 2 2 IM = 3t u 2 2 d Suy ra 2 2
3t + 4t + 2 + 2 = 3t ⇔ t = 1 − ⇒ I (0; 1 − ; 3
− ); R = IM = 3 .
Phương trình mặt cầu (S ) là: 2 x + ( y + )2 1 + (z + 3)2 = 3.
Ví dụ 3: Trong không gian tọa độ Oxyz, cho đường thẳng x +1 y z −1 d : = =
và điểm I (2;1;0). Viết 1 2 1 −
phương trình mặt cầu (S ) tâm I và cắt d tại 2 điểm phân biệt A, B sao cho tam giác IAB vuông. Lời giải  Ta có: u =
− , gọi H là trung điểm của AB ta có: IH ⊥ AB . d (1;2; )1    Khi đó H ( 1
− + t;2t;1− t) ⇒ IH ( 3
− + t;2t −1;1− t) ⇒ IH.u = ⇔ − + t + t − + t − = d 0 3 4 2 1 0
⇔ t =1⇒ H (0;2;0)
Tam giác IAB vuông cân tại I nên ta có: R = 2IH = 2 4 +1 = 10
Do đó phương trình mặt cầu (S ) cần tìm là: (x − )2 + ( y − )2 2 2 1 + z =10 .
Ví dụ 4: Trong không gian tọa độ Oxyz, cho đường thẳng
x − 2 y − 3 z −1 d : = = và mặt cầu 1 − 2 1 (S) 2 2 2
: x + y + z − 2x + 4y = 0. Viết phương trình đường thẳng Δ qua M (1; 1;
− 0) cắt đường thẳng d đồng
thời cắt mặt cầu (S ) tại A, B sao cho AB = 4 .
Lời giải   Ta có: I (1; 2
− ;0), R = 5 . Gọi N (2 − t;3+ 2t;1+ t). Ta có: u = MN 1− t;4 + 2t;1+ t Δ ( ) 2 Mặt khác  AB  2 + d (I ) 2
;Δ = R ⇒ d (I;Δ) =   1  2    IM;MN  2 d (I;Δ)   2t + 2 2 =  =
= 1 ⇔ 4t +16t +16 = 0 ⇔ t = 2 − 2 MN 6t +16t +18 x =1+ 3t Với t 2 Δ: = − ⇒ y = 1 −
là đường thẳng cần tìm. z = t− 
Ví dụ 5: Trong không gian tọa độ Oxyz, cho mặt phẳng (P) : x − 2y − 2z +10 = 0 và 2 đường thẳng x − 2 y z −1 Δ : − + = = và x 2 y z 3 Δ : = =
. Viết phương trình mặt cầu (S ) có tâm thuộc Δ đồng thời 1 1 1 1 2 1 1 4 1
tiếp xúc với Δ và (P) . 2 Lời giải 
Gọi I (2 + t;t;t+ )
1 ∈Δ là tâm của mặt cầu. Δ xác định qua M (2;0; 3 − ),u = 1;1;4 Δ ( ) 1 2 2
2 + t − 2t − 2 1+ t +10 10 − 3t
Ta có: d (I;Δ = d I; P . Khi đó d (I;(P)) ( ) = = . 2 ) ( ( )) 1+ 4 + 4 3   2   IM ;u  −   − IM ( t − t
− − − t) ⇒ d ( 2 3t 4 3t 4 ; ; 4 I;Δ =  = = 2 ) Δ2 ( ) u 1+1+16 3 Δ2 10 − 3t 3t − 4 Cho 7 13 7 10 t I  ; ;  = ⇔ = ⇒ 3 3 3 3 3 3    2 2 2
Vậy phương trình mặt cầu (S )  13   7   10 : x y z  − + − + − =       1.  3   3   3 
Ví dụ 7: Trong không gian với hệ tọa độ Oxyz, cho điểm A( 2; − 4;
− 5) . Phương trình nào dưới đây là
phương trình của mặt cầu có tâm là A và cắt trục Oz tại hai điểm B, C sao cho tam giác ABC vuông.
A. (x + )2 + ( y + )2 + (z − )2 2 4 5 = 40 .
B. (x + )2 + ( y + )2 + (z − )2 2 4 5 = 82 .
C. (x + )2 + ( y + )2 + (z − )2 2 4 5 = 58 .
D. (x + )2 + ( y + )2 + (z − )2 2 4 5 = 90 . Lời giải
Gọi H (0;0;5) là hình chiếu vuông góc của A xuống trục Oz.
Khi đó tam giác OHB vuông cân tại H suy ra R OH =
⇒ R = OH 2 = 2 10 . 2
Suy ra (S ) (x + )2 + ( y + )2 + (z − )2 : 2 4 5 = 40 . Chọn A.
Ví dụ 8: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
x − 2 y −1 z +1 d : = = và điểm 2 2 1 − I (2; 1; − )
1 . Viết phương trình mặt cầu có tâm I và cắt đường thẳng d tại hai điểm A, B sao cho tam giác IAB vuông tại I.
A. (x − )2 + ( y + )2 + (z − )2 2 1 1 = 9 .
B. (x + )2 + ( y − )2 + (z + )2 2 1 1 = 9 .
C. (x − )2 + ( y + )2 + (z − )2 2 1 1 = 8.
D. (x − )2 + ( y + )2 + (z − )2 80 2 1 1 = . 9 Lời giải
Gọi H là hình chiếu vuông góc của I lên đường thẳng d ⇒ H (2t + 2;2t +1; t − − )
1 . Đường thẳng d có    vecto pháp tuyến u = − . Sử dụng 2  2 1 1 IH.u t H  = ⇔ = − ⇔ − − ⇒   IH = . d 0 ; ; 2 d (2;2; )1 3  3 3 3    IM ;u
Hoặc ta có IH d (I;d ) 0 d   = =  = 2 . ud
Tam giác IAB vuông cân tại I nên R = IA = 2.IH = 2 2 .
Suy ra phương trình mặt cầu là: (x − )2 + ( y + )2 + (z − )2 2 1 1 = 8. Chọn C. x = tx = 5 + 2t
Ví dụ 9: Trong không gian với hệ tọa độ Oxyz, cho các đường thẳng d : y 6 t ;Δ :  = − +
y = 1+ t và mặt z 2 t  = − z = 1 − −   t
phẳng (P) : x + 3y − z −1 = 0 . Mặt cầu (S ) có tâm I thuộc d, tiếp xúc với cả Δ và (P) . Biết hoành độ điểm
I là số nguyên. Tung độ điểm I là A. 2. B. 0. C. −4. D. −2. Lời giải Gọi I (t; 6
− + t;2 − t) là tâm của mặt cầu và R là bán kính của mặt cầu (S ) . t + 3 6
− + t − 2 − t −1 5t − 21
Ta có R = d (I;(P = = )) ( ) ( ) ( )1 . 2 2 + + (− )2 11 1 3 1  Điểm A(5;1;− )
1 ∈(Δ) ⇒ AI = (t −5;t − 7;3−t) suy ra VTCP của Δ là u = (2;1;− ) 1 .   u; AI  2
Mặt khác R = d (I ( ))   2t − 20t + 98 ; Δ =  = (2) . u 6 2 5t − 21 Từ (1), (2) ta được 2t − 20t + 98 =
⇒ t = 2 ⇒ x = 2 ⇒ y = 4 − . Chọn C. 11 6 I I
Ví dụ 10: [Đề thi THPT Quốc gia năm 2018] Trong không gian Oxyz, cho mặt cầu
(S) (x + )2 +( y + )2 +(z + )2 : 1 1
1 = 9 và điểm A(2;3;− )
1 . Xét các điểm M thuộc (S ) sao cho đường thẳng
AM tiếp xúc với (S ) . M luôn thuộc mặt phẳng có phương trình là
A. 6x + 8y +11 = 0.
B. 3x + 4y + 2 = 0 .
C. 3x + 4y − 2 = 0.
D. 6x + 8y −11 = 0 . Lời giải
Mặt cầu (S ) có tâm là I ( 1; − 1; − − ) 1 , bán kính R = 3. 
Ta có: IA = (3;4;0) ⇒ IA = 5 .
Vì AM là tiếp tuyến của mặt cầu nên ta có: 2 2
AM ⊥ IM ⇒ AM = IA − IM = 4 .
Gọi (S′) là mặt cầu tâm A, bán kính R′ = 4.
Ta có phương trình mặt cầu (S′) (x − )2 + ( y − )2 + (z + )2 : 2 3 1 =16
Vì AM = 4 nên điểm M luôn thuộc mặt cầu (S )
Vậy M ∈(S ) ∩(S′) ⇒ tọa độ điểm M là nghiệm của hệ: (  x + )2 1 + ( y + )2 1 + (z + )2 1 =  ( ) 9 1 ( )1−(2) 
→6x + 8y −11 = 7
− hay M ∈(P) :3x + 4y − 2 = 0 . Chọn C. (  x − 2 
)2 +( y −3)2 +(z + )2 1 =16 (2)
BÀI TẬP TỰ LUYỆN
Câu 1: Trong không gian với hệ tọa độ Oxyz, nếu mặt cầu(S )tâm I (a;b;c) bán kính bằng 1, tiếp xúc mặt phẳng (Oxz) thì A. a =1 B. b =1 C. c =1
D. a + b + c =1
Câu 2: Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; 2
− ;3) và đường d có phương trình
x +1 y − 2 z + 3 = =
. Tính đường kính của mặt cầu (S )có tâm A và tiếp xúc với đường thẳng d. 2 1 1 − A. 5 2 . B.10 2 . C. 2 5 . D. 4 5 .
Câu 3: Trong không gian với hệ tọa độ Oxyz, nếu mặt cầu (S ) 2 2 2
: x + y + z − 2x − 4y − 6z − 2 = 0 . Viết
phương trình mặt phẳng (α ) chứa trục Oy và cắt mặt cầu (S )theo thiết diện là một đường tròn có chu vi bằng 8π .
A. 3x + z = 0 .
B. 3x + z + 2 = 0.
C. 3x − z = 0.
D. x − 3z = 0.
Câu 4: Trong không gian Oxyz, nếu mặt cầu(S )tâm I (2;3;4) và cắt trục Ox tại hai điểm A, B sao cho diện
tích tam giác IAB bằng 10. Viết phương trình mặt cầu (S ).
A. (x − )2 + ( y − )2 + (z − )2 2 3 4 = 26 .
B. (x − )2 + ( y − )2 + (z − )2 2 3 4 = 50.
C. (x − )2 + ( y − )2 + (z − )2 2 3 4 = 25.
D. (x − )2 + ( y − )2 + (z − )2 2 3 4 = 29 .
Câu 5: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) : 2x − 2y − z + 9 = 0 và mặt cầu (S) 2 2 2
: x + y + z − 6x + 4y − 2z + 5 = 0. Viết phương trình mặt phẳng (Q) chứa trục Ox và cắt (S ) theo giao
tuyến là một đường tròn có bán kính bằng 2.
A. (Q) : 2y − z = 0 .
B. (Q) : 2y + z = 0.
C. (Q) : y − z = 0 .
D. (Q) : 2x − z = 0.
Câu 6: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng x +1 y +1 = = z d : và mặt cầu 2 2 − 1 (S) 2 2 2
: x + y + z − 2x + 4y − 2z − 3 = 0 . Viết phương trình mặt phẳng (P) vuông góc với d, (P) tiếp xúc với
(S) đồng thời (P) cắt trục Oz tại điểm có cao độ dương.
A. 2x − 2y + z + 2 = 0
B. 2x − 2y + z −16 = 0
C. 2x − 2y + z −10 = 0
D. 2x − 2y + z − 5 = 0
Câu 7: Trong không gian với hệ tọa độ Oxyz, mặt phẳng (Oxy) cắt mặt cầu
(S) :(x − )2 +( y − )2 +(z − )2 1 2
3 =14 theo giao tuyến là đường tròn tâm H, bán kính R. Tìm tọa độ tâm H và tính bán kính R.
A. H (1;2;0) ,R = 5 B. H ( 1 − ; 2 − ;0) ,R = 5
C. H (1;2;0) ,R = 5
D. H (1;0;2) ,R = 5
Câu 8: Trong không gian với hệ tọa độ Oxyz, cho điểm I (2;3; ) 1 x + y + z + − và đường thẳng 7 9 7 d : = = . 2 1 2 −
Viết phương trình mặt cầu tâm I và cắt đường thẳng d tại hai điểm A, B thỏa mãn AB = 40 .
A. (x − )2 + ( y − )2 + (z + )2 2 2 3 1 = 25
B. (x + )2 + ( y + )2 + (z + )2 2 2 3 4 = 25 C. (x − )2 2 2 + y + (z + )2 1 = 25
D. (x − )2 + ( y − )2 + (z − )2 2 3 1 = 25
Câu 9: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) : 3x + y −3z + 6 = 0 và mặt cầu
(S) :(x − )2 +( y + )2 +(z + )2 4 5
2 = 25 . Mặt phẳng (P) cắt mặt cầu (S ) theo giao tuyến là một đường tròn
bán kính r bằng bao nhiêu? A. r = 5 B. r = 5 C. r = 6 D. r = 6
Câu 10: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S ) 2 : x + ( y − )2 1 + (z − )2 1 = 25 và mặt phẳng
(P) : x + 2y + 2z +5 = 0 . Diện tích hình tròn thiết diện của (P) và (S)là. A. 25π B. 9π C. 16 D. 16π
Câu 11: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) : x + y + z − 4 = 0 và mặt cầu (S) 2 2 2
: x + y + z − 4x − 2y +10z +14 = 0 . Mặt phẳng (P) cắt mặt cầu (S ) theo một đường tròn. Tính chu vi đường tròn đó. A. 2π B. 8π C. 4π D. 4 3π x = tx = 5 + 2t
Câu 12: Trong không gian với hệ tọa độ Oxyz, cho các đường thẳng  d :  y = 6
− + t và ∆ : y =1+ t và z = 2−   t z = 1 − −  t
mặt phẳng (P) : x + 3y − z −1 = 0 . Mặt cầu (S ) có tâm I thuộc d, tiếp xúc với cả ∆ và (P) . Biết hoành độ
điểm I là số nguyên. Tung độ của điểm I là. A. 2 B. 0 C. -4 D. -2
Câu 13: Trong không gian với hệ tọa độ Oxyz, cho các điểm A(2;0;0) ,B(0;4;0) và C (0;0;6). Viết
phương trình mặt cầu ngoại tiếp tứ diện OABC.
A. (x + )2 + ( y + )2 + (z + )2 1 2 3 = 56
B. (x + )2 + ( y + )2 + (z + )2 1 2 3 = 28
C. (x − )2 + ( y − )2 + (z − )2 1 2 3 =14
D. (x − )2 + ( y − )2 + (z − )2 1 2 3 = 28
Câu 14: Cắt mặt cầu S (I ,R) bởi mặt phẳng (P) cách tâm I một khoảng R ta nhận được giao tuyến là 2
đường tròn có chu vi bằng bao nhiêu? A. π R 3 B. π R C. 2π R D. 2π R 3
Câu 15: Trong không gian với hệ tọa độ Oxyz, mặt phẳng (α ) cắt mặt cầu (S ) tâm I (1; 3 − ;3) theo giao
tuyến là đường tròn tâm H (2;0; )
1 , bán kính r = 2 . Phương trình của (S ) là
A. (x − )2 + ( y + )2 + (z − )2 1 3 3 = 4
B. (x + )2 + ( y − )2 + (z + )2 1 3 3 = 4
C. (x − )2 + ( y + )2 + (z − )2 1 3 3 =18
D. (x + )2 + ( y − )2 + (z + )2 1 3 3 =18
Câu 16: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) : 3x + y −3z + 6 = 0 và mặt cầu
(S) :(x − )2 +( y + )2 +(z + )2 4 5
2 = 25 . Mặt phẳng (P) cắt mặt cầu (S ) theo giao tuyến là một đường tròn.
Tính bán kình r của đường tròn giao tuyến đó A. r = 6 . B. r = 5 . C. r = 6 . D. r = 5 .
Câu 17: Trong không gian với hệ trục tọa độ Oxyz, phương trình nào dưới đây là phương trình của mặt cầu có tâm I ( 2
− ;3;4) và tiếp xúc với mặt phẳng (Oyz) ?
A. (x + )2 + ( y − )2 + (z − )2 2 3 4 = 2
B. (x + )2 + ( y − )2 + (z − )2 2 3 4 = 4
C. (x − )2 + ( y + )2 + (z + )2 2 3 4 = 2
D. (x − )2 + ( y − )2 + (z + )2 2 3 4 = 4
Câu 18: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S ) : (x − )2 + ( y + )2 + (z − )2 1 2 3 = 4 và điểm M (1; 2 − ; )
1 . Viết phương trình mặt phẳng (P) tiếp xúc với mặt cầu (S ) tại M.
A. (P) : x + y + 3z +1− 3 = 0
B. (P) : z −1= 0
C. (P) : y = 2 −
D. (P) : 3x + y − z = 0
Câu 19: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S ) : (x − )2 + ( y + )2 + (z − )2 1 2 3 = 5 có tâm I và
một thời điểm A(0; 2 − ; )
1 . Một mặt phẳng (P) cắt và vuông góc với đoạn thẳng IA và cắt mặt cầu (S ) theo
giao tuyến là một đường tròn có bán kính r = 2 . Viết phương trình của mặt phẳng (P) .
A. x + 2z − 7 − 5 = 0 .
B. x + 2z − 7 − 5 = 0 và x + 2z − 7 + 5 = 0 .
C. x + 2z − 7 + 5 = 0 .
D. x + 2z + 3− 5 = 0.
Câu 20: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S ) : (x − )2 + ( y − )2 + (z − )2 2 1 1 = 4 . Mặt phẳng
(P) cắt mặt cầu (S) theo thiết diện là đường tròn lớn và cắt các trục Ox, Oy, Oz lần lượt tại các điểm
A(a;0;0) ,B(0;b;0) ,C (0;0;3)(a,b > 0) . Tính tổng T = a + b khi thể tích khối tứ diện OABC đạt giá trị nhỏ nhất. A. T =18 . B. T = 9 . C. T =11. D. T = 3.
Câu 21: Trong không gian với hệ tọa độ Oxyz, cho điểm A( 1
− ;3;2) và mặt phẳng
(P) :3x + 6y − 2z − 4 = 0. Phương trình mặt cầu tâm A, tiếp xúc với mặt phẳng (P) là
A. (x + )2 + ( y − )2 + (z − )2 1 3 2 = 7 .
B. (x + )2 + ( y − )2 + (z − )2 1 3 2 =1.
C. (x + )2 + ( y − )2 + (z − )2 1 3 2 = 49 .
D. (x + )2 + ( y − )2 + (z − )2 1 1 3 2 = . 49
Câu 22: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S ) 2 2 2
: x + y + z − 2x − 4y − 4z = 0 . Viết
phương trình mặt phẳng (α ) tiếp xúc với (S ) tại điểm A(3;4;3) .
A. (α ) : 2x + 4y + z − 25 = 0 .
B. (α ) : 2x + 2y + z −17 = 0 .
C. (α ) : 2x + 4y − 2z − 22 = 0.
D. (α ) : x + y + z −10 = 0 .
Câu 23: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S ) 2 2 2
: x + y + z + x − y + z −1 = 0 cắt mặt
phẳng (Oxy) theo giao tuyến là đường tròn. Tìm tọa độ tâm và bán kính của đường tròn này. A.  1 1  6
I − ; ;0 ,r =    . B. 1 1 6 I −  ; ;0 ,r = . 2 2     2  2 2  3 C.  1 1  2 2
I − ; ;0 ,r =  .
D. I (− ; ; ) 6 1 1 0 ,r = . 2 2    3 2
Câu 24: Trong không gian với hệ trục tọa độ Oxyz, cho tứ diện ABCD với
A(1;6;2) ,B(5 1
; ;3) ,C (4;0;6) ,D(5;0;4) . Viết phương trình mặt cầu tâm D tiếp xúc với mặt phẳng ( ABC). A. (x − )2 2 + y + (z − )2 2 5 4 = . B. (x − )2 2 + y + (z − )2 4 5 4 = . 223 446 C. (x + )2 2 + y + (z + )2 8 5 4 = . D. (x − )2 2 + y + (z − )2 8 5 4 = 223 223
Câu 25: Trong không gian với hệtọa độ Oxyz, cho mặt cầu (S )có tâm I thuộc đường thẳng x y + 3 = = z d :
. Biết rằng (S ) có bán kính R = 2 2 và cắt mặt phẳng Oxz theo một đường tròn có bán 1 1 2
kính bằng 2. Tìm tọa độ tâm I.
A. I (1; 2
− ;2) ,I (5;2 10 ; ) .
B. I (1; 2
− ;2) ,I (0; 3 − ;0).
C. I (5;2 10
; ) ,I (0; 3 − ;0) .
D. I (1; 2 − ;2) ,I ( 1 − ;2; 2 − ) .
Câu 26: Trong hệ tọa độ Oxyz, viết phương trình mặt cầu (S ) đi qua A( 1
− ;2;0) ,B( 2 − 1 ; ; ) 1 và có tâm nằm trên trục Oz. A. 2 2 2
x + y + z − z − 5 = 0. B. 2 2 2
x + y + z + 5 = 0 . C. 2 2 2
x + y + z − x − 5 = 0 . D. 2 2 2
x + y + z − y − 5 = 0 .
Câu 27: Viết phương trình mặt phẳng (P) qua A(0;0; )
1 ,B(0;0; 2
− ) và tiếp xúc với mặt cầu (S) 2 2 2
: x + y + z + 4x − 2y + 4z + 8 = 0 . 4x + 3y = 0 4x + 3y = 0
A. 4x + 3y = 0 . B.  . C.  . D. z = 0. z = 0  y = 0
Câu 28: Trong không gian với hệ trục Oxyz, cho điểm A(1;2; 2
− ) và mặt phẳng (P) : 2x + 2y + z + 5 = 0 .
Viết phương trình mặt cầu (S ) tâm A biết mặt phẳng (P) cắt mặt cầu (S ) theo giao tuyến là đường tròn có chu vi bằng 8π .
A. (x − )2 + ( y − )2 + (z + )2 1 2 2 = 25.
B. (x − )2 + ( y − )2 + (z + )2 1 2 2 = 5 .
C. (x − )2 + ( y − )2 + (z + )2 1 2 2 = 9 .
D. (x − )2 + ( y − )2 + (z + )2 1 2 2 =16 .
Câu 29: Trong không gian với hệ trục Oxyz, cho hai mặt phẳng (P) : x + 2y − 2z − 2 = 0 và
(Q) : x + 2y − 2z + 4 = 0 . Phương trình nào dưới đây là phương trình mặt cầu (S) có tâm thuộc trục Ox và
tiếp xúc với hai mặt phẳng đã cho? A. (x − )2 2 2 3 + y + z = 4. B. (x − )2 2 2 1 + y + z =1. C. (x + )2 2 2 1 + y + z =1. D. (x − )2 2 2 1 + y + z = 9.
Câu 30: Trong không gian với hệ trục Oxyz, cho các điểm A(1;2; 4 − ) ,B(1; 3 − ; )
1 ,C (2;2;3). Tính bán kính
mặt cầu (S ) đi qua A, B,C và có tâm thuộc mặt phẳng (Oxy). A. 34 . B. 26 . C. 34. D. 26 .
Câu 31: Trong không gian với hệ trục Oxyz, cho các điểm A(2;0;0) ,B(0;4;0) ,C (0;0;6) và D(2;4;6) .
   
Tìm tập hợp điểm M thỏa mãn MA + MB + MC + MD = 4
A. (x − )2 + ( y − )2 + (z − )2 1 2 3 =1.
B. (x − )2 + ( y + )2 + (z − )2 1 2 3 =1.
C. (x − )2 + ( y − )2 + (z − )2 1 2 3 = 4.
D. (x + )2 + ( y + )2 + (z + )2 1 2 3 =1.
x = m + t
Câu 32: Trong không gian với hệ trục Oxyz, giả sử đường thẳng 
∆ : y = n + 2t cắt mặt cầu z = 2−  mt (S) 2
: x + ( y − 2)2 + (z − 2)2 = 9 tạ hai điểm A,B sao cho AB = 6. Tìm cặp số (m;n) .
A. (m;n) = (1;2) .
B. (m;n) = (1;0) .
C. (m;n) = (2;0) .
D. (m;n) = (0;2) .
Câu 33: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S ) 2 2 2
: x + y + z − 2x − 2y − 2z = 0 và điểm
A(2;2;0). Viết phương trình mặt phẳng (OAB) , biết rằng điểm B thuộc mặt cầu (S ) , có hoành độ dương
và tam giác OAB đều.
A. x − y − 2z = 0
B. x − y − z = 0
C. x − y + z = 0
D. x − y + 2z = 0
LỜI GIẢI BÀI TẬP TỰ LUYỆN
Câu 1: R = d (I;(Oxz)) = b ⇒ b =1. Chọn B.    
Câu 2: Ta có u = M −
− ∈ d . Ta có u AM  = − − AM = − − d , (2; 14; 10), ( 2;4; 6) d (2;1; )1, ( 1;2; 3)       2 2 2 u AM d ,   2 + 14 − + 10 −
Ta có R = d (M ,d ) ( ) ( ) =  = = 5 2 . Chọn A. 2 2 ud 2 +1 + (− )2 1
Câu 3: Mặt cầu (S ) có tâm I (1;2;3) , bán kính R = 4 . Do (α ) chứa Oy nên (α ) : ax + cz = 0
Bán kính của thiết diện là r = 4 = R ⇒ (α ) qua I (1;2;3) ⇒ a + 3c = 0 ⇒ chọn a = 3,c = 1 −
Do đó phương trình mặt phẳng (α ) là 3x − z = 0. Chọn C.
Câu 4: Giả sử A( ;0 a ;0), B( ;0 b ;0) .
Ta có IA = IB ⇔ (a − )2 2 2 + + = (b − )2 2 2 2 3 4
2 + 3 + 4 ⇔ b = 4 − a
Gọi M là trung điểm của AB ⇒ M (2;0;0) . Ta có 1 2SIAB 2.10
S = IM AB ⇒ AB = = = IAB . 4 2 IM 5 a = 4
Ta có AB = 4 ⇔ 4 − 2a = 4 ⇔ 2 − a = 2 ⇔ ⇒ R = IA =  29 a = 0
Do đó phương trình mặt cầu là (S ) (x − )2 + ( y − )2 + (z − )2 : 2 3 4 = 29 . Chọn D.
Câu 5: Mặt cầu (S ) có tâm I (3; 2 − ; )
1 , bán kính R = 3. Do (Q) chứa Ox nên (Q) :by + cz = 0 2 − b + c
Ta có d (I (Q)) 2 2 2 2 ;
= R − r = 3 − 2 = 5 . Ta có d (I;(Q)) = 5 ⇔ = 5 2 2 b + c 2 2
⇔ b + 4bc + 4c = 0 ⇔ b = 2
− c ⇒ chọn b = 2,c = 1
− ⇒ (Q) : 2y − z = 0 . Chọn A. 
Câu 6: Mặt cầu (S ) có tâm I (1; 2 − ; )
1 , bán kính R = 3. Đường thẳng d có u = − M − − ∈ d d (2; 2; ) 1 , ( 1; 1;0)  
Do (P) vuông góc với d nên n = u = − ⇒ P
x − y + z + m = P d (2; 2; )1 ( ):2 2 0 m + 7 m =
Do (P) tiếp xúc với (S ) ⇒ d (I;(P)) 2 = 3 ⇔ = 3 ⇔ 3  m = 16 −
Do (P) cắt Oz tại điểm có cao độ dương nên chọn m = 16
− ⇒ (P) : 2x − 2y + z −16 = 0 . Chọn B.
Câu 7: Mặt cầu (S ) có tâm I (1;2;3) , bán kính R′ = 14 .
Ta có d (I (Oxy)) 2 2 ;
= 3 ⇒ R = R′ − d (I;(Oxy)) = 5
Tâm H là hình chiếu của I (1;2;3) lên (Oxy) ⇒ H (1;2;0) . Chọn C.
Câu 8: Gọi H là trung điểm của AB ⇒ IH ⊥ AB ⇒ IH = d (I;d )       u IM d , Ta có u = −
M − − − ∈d . Ta có u IM d I d     = − ⇒ =  = d , (30; 30;15) ( ; ) 15 d (2;1; 2), ( 7; 9; 7)   ud Bán kính mặt cầu 2 2
R = AH + d (I d ) 2 2 ; = 20 +15 = 25
⇒ (S ) (x − )2 + ( y − )2 + (z + )2 2 : 2 3 1 = 25 . Chọn A.
Câu 9: Mặt cầu (S ) có tâm I (4; 5 − ; 2
− ) , bán kính R = 5. Ta có d (I;(P)) = 19
Bán kính của giao tuyến là 2 2
r = R − d (I (P)) 2 ,
= 5 −19 = 6 . Chọn D.
Câu 10: Mặt cầu (S ) có tâm I (0;1 )
;1 , bán kính R = 5. Ta có d (I;(P)) = 3 Bán kính thiết diện là 2 2
r = R − d (I;(P)) = 4 ⇒ diện tích là 2
π r =16π . Chọn A.
Câu 11: Mặt cầu (S ) có tâm I (2;1; 5
− ) , bán kính R = 4 . Ta có d (I;(P)) = 2 3 Bán kính thiết diện là 2 2
r = R − d (I;(P)) = 2 ⇒ chu vi là 2πr = 4π . Chọn C. t − 
Câu 12: Do I ∈d ⇒ I (t; 6
− + t;2 − t). Ta có d (I (P)) 5 21 ; = . Ta có u = 2;1; 1 − , M 5;1; 1 − ∈Δ . Δ ( ) ( ) 11 2 2 2 2   4 −
+ t −1 + t − 9 Ta có 2t − 20t + 98
u , IM  = 4
− ;t −1;t − 9 ⇒ d I;Δ = = Δ ( ) ( ) ( ) ( ) ( )   6 6 2 5t − 21
Mà (S ) tiếp xúc với Δ và (P) nên d (I (P)) = d (I ) 2t − 20t + 98 ; ;Δ ⇔ = 11 6 (5t − )2 t = 2 2 21 2t − 20t + 98  ⇔ = ⇔ 49 ⇒ I − . Chọn A. 11 6 t = (l) (2; 4;0)  8
Câu 13: Giả sử I ( ;
x y; z) là tâm mặt cầu. 2 2 2
x + y + z =  = (x − 2)2 2 2 + y + z IO IAx =1  Ta có   2 2 2 2 IO IBx y z x ( y 4)2 2 z  = ⇔ + + = + − + ⇔ y = 2 IO IC   = 2 2 2 2 2
x + y + z = x + y + ( z − )2 z =   3 6 
Suy ra tâm I (1;2;3) , bán kính R = IO =
⇒ (S ) (x − )2 + ( y − )2 + (z − )2 14 : 1 2 3 =14 . Chọn C. 2
Câu 14: Bán kính giao tuyến là 2 R R 3 r R   = − = ⇒ 
chu vi là 2π r = π R 3 . Chọn A. 2    2 
Câu 15: Ta có IH = ( − ) 2 2
1;3; 2 ⇒ IH = 1 + 3 + ( 2 − )2 = 14 2 2
⇒ R = IH + r = 18 ⇒ (S ) :(x − )2
1 + ( y + 3)2 + (z −3)2 =18 . Chọn C.
Câu 16: Mặt cầu có tâm I (4; 5 − ; 2
− ) và bán kính R = 5. 3.4 − 5 − 3. 2 − + 6
Ta có d (I;(P)) ( ) 2 =
= 19 ⇒ r = R −19 = 6 . Chọn C. 2 3 +1+ ( 3 − )2
Câu 17: (Oyz) x = ⇒ R = d (I (Oyz)) = ⇒ (S) (x + )2 + ( y − )2 + (z − )2 : 0 ; 2 : 2 3 4 = 4 . Chọn B.
Câu 18: Mặt cầu có tâm I (1; 2 − ;3). 
Mặt phẳng (P) qua M và nhận MI = (0;0;2) là một VTPT ⇒ (P) : 2(z − )
1 = 0 ⇔ z −1 = 0 . Chọn B. 
Câu 19: Ta có I (1; 2
− ;3) ⇒ AI = (1;0;2) là một VTPT của (P) ⇒ (P) : x + 2z + m = 0 ( m − m − ⇒ d I;(P)) 3 ( 3)2 2 2 2 = = h 
→h + r = R ⇒
+ 4 = 5 ⇔ m = 3± 5 . Chọn D. 5 5
Câu 20: Ta có ( ) : x y z P + + = 1 qua tâm I ( ) 2 1 1 2 1 2 2;1;1 ⇒ + + =1 ⇔ + = . a b 3 a b 3 a b 3 Lại có 1 1 1 V
= OAOB OC = a b = ab . OABC . . . .3 6 6 2 Ta có 2 2 1 2 1 = + ≥ 2
. ⇒ ab ≥18 ⇒ V ≥ 9 . 3 OABC a b a b 2 1  = > 0 b  = 3
Dấu “=” xảy ra ⇔ a b ⇔ 
⇒ a + b = 9. Chọn B.  a = 6 ab = 18 3. 1 − + 6.3− 2.2 − 4
Câu 21: Ta có R = d ( ; A (P)) ( ) =
=1⇒ (S ) :(x + )2
1 + ( y −3)2 + (z − 2)2 =1. Chọn B. 2 2 3 + 6 + ( 2 − )2
Câu 22: Mặt cầu (S ) (x − )2 + ( y − )2 + (z − )2 : 1 2
2 = 9 có tâm I (1;2;2) . 
Mặt phẳng (α ) qua A và nhận IA = (2;2; ) 1 là một VTPT
⇒ (α ) : 2(x − 3) + 2( y − 4) + (z − 3) = 0 ⇔ 2x + 2y + z −17 = 0 . Chọn B.
Câu 23: Ta có (Oxy) : z = 0 . 2 2 2 Mặt cầu (S )  1   1   1  7 : x + +    y − +   z + =  có tâm 1 1 1 K  −  ; ;− và bán kính 7 R = . 2 2 2         4  2 2 2  2
Ta có h = d (I (Oxy)) 1 2 2 6 ;
= ⇒ r = R − h = . 2 2
Đường tròn cần tìm có tâm I là hình chiếu của 1 1 1 K  ; ;  − −   trên (Oxy) 1 1 ⇒ I  −  ; ;0 . Chọn A. 2 2 2      2 2   AB = (4; 5; −  )1  
Câu 24: Ta có  ⇒ A ; B AC = ( 14 − ; 13 − ; 9
− ) là một VTPT của ( ABC) AC  (3; 6;4)   = − 
⇒ n = (14;13;9) là một VTPT của ( ABC)
⇒ ( ABC) :14(x − )
1 +13( y − 6) + 9(z − 2) = 0 ⇔ 14x +13y + 9z −110 = 0 + + −
⇒ R = d (D ( ABC)) 14.5 13.0 9.4 110 =
⇒ (S ) (x − )2 2 + y + (z − )2 8 ; : 5 4 = . Chọn D. 2 2 2 14 +13 + 9 223 x = t
Câu 25: Ta có d : y = 3
− + t ⇒ I (t;t − 3;2t) . z =  2t
Lại có (Oxz) : y = 0 ⇒ h = d (I;(Oxz)) = t −3 .
t =1⇒ I 1; 2 − ;2 2 2 2 2 ( )
Ta có R = h + 2 ⇒ 8 = (t −3) + 4 ⇔  . Chọn A. t = 5 ⇒ I  (5;2;10)  AI = (1; 2 −  ;t)  2 AI = t + 5
Câu 26: Ta có tâm I ∈Oz ⇒ I (0;0;t) ⇒  ⇒  BI =  (2; 1; − t − ) 1
BI = (t − )2 1 + 5  Ép cho 1 21
AI = BI ⇒ t = ⇒ R = AI = 2 2 2 ⇒ (S ) 2 2  1  21 2 2 2
: x + y + z − =
⇔ x + y + z − z − 5 =   0 . Chọn A.  2  4
Câu 27: Gọi (P) ax + by + cz + d = ( 2 2 2 : 0 0
a + b + c > ). c + d = 0 Ta có ,
A B ∈(P) ⇒ 
⇒ c = d = 0 ⇒ (P) : ax + by = 0 .  2 − c + d = 0
Mặt cầu (S ) (x + )2 + ( y − )2 + (z + )2 : 2 1 2 =1⇒ I ( 2 − ;1; 2 − ), R =1. 2 − a + ba = 0
Ta có d (I;(P)) 2 2 2 2 =
= R =1⇒ 4a + b − 4ab = a + b ⇔  2 2 a + b 3a = 4b
+) Với a = 0 ⇒ (P) : y = 0 .
+) Với 3a = 4b , chọn a = 4 ⇒ b = 3 ⇒ (P) : 4x + 3y = 0. Chọn C.
Câu 28: Đường tròn có bán kính 8π r = = 4 . 2π 2.1+ 2.2 − 2 + 5 Ta có d ( ; A (P)) 2 2 =
= 3 ⇒ R = 3 + 4 = 5 ⇒ (S ) :(x − )2
1 + ( y − 2)2 + (z + 2)2 = 25 . 2 2 2 2 + 2 +1 Chọn A.
Câu 29: Ta có tâm I ∈Ox ⇒ I (t;0;0). t − 2 t + 4
Ta có d (I;(P)) = d (I;(Q)) ⇔ = ⇔ t = 1
− ⇒ R = d (I;(P)) =1 3 3 ⇒ (S ) (x + )2 2 2 :
1 + y + z =1. Chọn C. 
AI = (a −1;b − 2;4) 2
AI = (a − )2 1 + (b − 2)2 +16   
Câu 30: Gọi tâm I ( ; a ; b 0) 
⇒ BI = (a −1;b + 3;− )  2
1 ⇒ BI = (a − )2 1 + (b + 3)2 +1   CI = 
(a − 2;b − 2; 3 − ) 2 CI  
= (a − 2)2 + (b − 2)2 + 9  IA = IB
20 − 4b =10 + 6b b  = 1 Ta có  ⇒  ⇔ 
⇒ R = IA = 26 . Chọn B. IA = IC 17
 − 2a = 13 − 4aa = 2 − 
AM = (x − 2; y; z)  BM = ( ; x y −  4; z)
Câu 31: Gọi M ( ;
x y; z) ⇒  CM  = ( ; x y; z − 6)  DM = 
(x − 2; y − 4;z −6)
   
⇒ AM + BM + CM + DM = (4x − 4;4y −8;4z −12)
   
⇒ AM + BM + CM + DM = ( x − )2 + ( y − )2 + ( z − )2 4 4 4 8 4 12 = 4
⇔ (x − )2 + ( y − )2 + (z − )2 1 2 3 =1. Chọn A.
Câu 32: Mặt cầu có bán kính = 3 AB R =
⇒ AB qua tâm I (0;2;2) 2  0 m t  = + m + t = 0   2 n 2t  ⇒ = +
⇔ n + 2t = 2 ⇒ m = 0; 2 n = . Chọn D.  2 2 mt  = − m = 0  t = 0
Câu 33: Mặt cầu (S ) có tâm I (1;1; )
1 , bán kính R = 3 . Ta thấy O, A∈(S ) Ta có OA 3 2 6 OA = 2 2 ⇒ R = =
. Gọi H là tâm tam giác đều OAB. OAB 3 3
Do O A B ∈(S ) ⇒ IH = d (I (OAB)) 2 2 3 , , ; = R − R = OAB 3
Giả sử (OAB) : ax + by + cz = 0 do A∈(OAB) ⇒ 2a + 2b = 0 ⇔ a = b
− ⇒ (OAB) : ax − ay + cz = 0 ca = c
Ta có d (I;(OAB)) 3 2 2 = =
⇔ a = c ⇔  2 2 2a + c 3 a = −c
Với a = c chọn a =1,c =1⇒ (P) : x − y + z = 0 ⇒ B( 2; − 2;4) (loại)
Với a = −c chọn a =1,c = 1
− ⇒ (P) : x − y − z = 0 ⇒ B(2; 2; − 4) . Chọn B.
Document Outline

  • ITMTTL~1
  • IIBITP~1
  • IIILIG~1