1 trang 163 lượt tải

Bảng nguyên hàm đầy đủ | Toán 12

325

Nguyên hàm của các hàm số cấp Nguyên hàm của các hàm số  1.∫ dx= x+C 2. ∫ 1 1 x x dx α α α + = + +C 3. ∫ dx x = ln x +C 4. ∫ e xdx= ex+ C 5. ∫ axdx = ln x a a +C , (0 < a≠ 1) 6. ∫ cosx dx= sinx +C 7. ∫ sinxdx = -cosx +C 8. 2 cos dx x ∫ = tgx +C 9. 2 sin dx x ∫ =-cotgx+C. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem!        

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng 199 tài liệu

Môn: Toán 12 3.9 K tài liệu

Tác giả:

Profile

Phạm Thị Huyền

2 tháng trước
Danh sách Quiz
/1
BẢNG NGUYÊN HÀM ĐẦY ĐỦ
Nguyeân haøm cuûa caùc
haøm soá sô caáp
Nguyeân haøm cuûa caùc haøm
soá hôïp
1.
∫
dx= x+C
2.
∫
1
1
x
x dx
α
α
α
+
=
+
+C
3.
∫
dx
x
= ln
x
+C
4.
∫
e
x
dx= e
x
+ C
5.
∫
a
x
dx =
ln
x
a
a
+C , (0 < a
≠
1)
6.
∫
cosx dx= sinx +C
7.
∫
sinxdx = -cosx +C
8.
2
cos
dx
x
∫
= tgx +C
9.
2
sin
dx
x
∫
=-cotgx+C
10.
+C
11.
ln (
cos 2 4
dx x
tg
x
π
= +
∫
+C
12.
∫
tgxdx= -ln
cos x
+C
13.
∫
cotgxdx= ln
sin x
+C
14.
2 2
1
ln
2
dx x a
x a a x a
−
=
− +
∫
+C
15.
2 2
2 2
ln
dx
x x a
x a
= + ±
±
∫
+C
16.
2 2 2 2
2
x
x a dx x a± = ± ±
∫
2
2 2
ln
2
a
x x a± + ±
+C
17.
2 2
arcsin
dx x
C
a
a x
= +
−
∫
18.
2 2
1dx x
arctg C
a x a a
= +
+
∫
19.
2 2 2 2
2
x
a x dx a x− = − +
∫
2
arcsin
2
a x
C
a
+ +
1.
∫
du= u+C
2.
∫
1
1
u
u du
α
α
α
+
=
+
+C
3.
∫
du
u
= ln
u
+C
4.
∫
e
u
du= e
u
+ C
5.
∫
a
u
du =
ln
u
a
a
+C , (0 < a
≠
1)
6.
∫
cosudu= sinu +C
7.
∫
sinudu = -cosu +C
8.
2
cos
du
u
∫
= tgu +C
9.
2
sin
du
u
∫
=-cotgu+C
10.
+C
11.
ln (
cos 2 4
du u
tg
u
π
= +
∫
+C
12.
∫
tgudu= -ln
cosu
+C
13.
∫
cotgudu= ln
sin u
+C
14.
2 2
1
ln
2
du u a
u a a u a
−
=
− +
∫
+C
15.
2 2
2 2
ln
du
u u a
u a
= + ±
±
∫
+C
16.
2 2 2 2
2
u
u a du u a± = ± ±
∫
2
2 2
ln
2
a
u u a± + ±
+C
17.
2 2
arcsin
du u
C
a
a u
= +
−
∫
18.
2 2
1du u
arctg C
a u a a
= +
+
∫
19.
2 2 2 2
2
u
a u du a u− = − +
∫
2
arcsin
2
a u
C
a
+ +

Tài liệu khác của Toán 12

Preview text:

BẢNG NGUYÊN HÀM ĐẦY ĐỦ
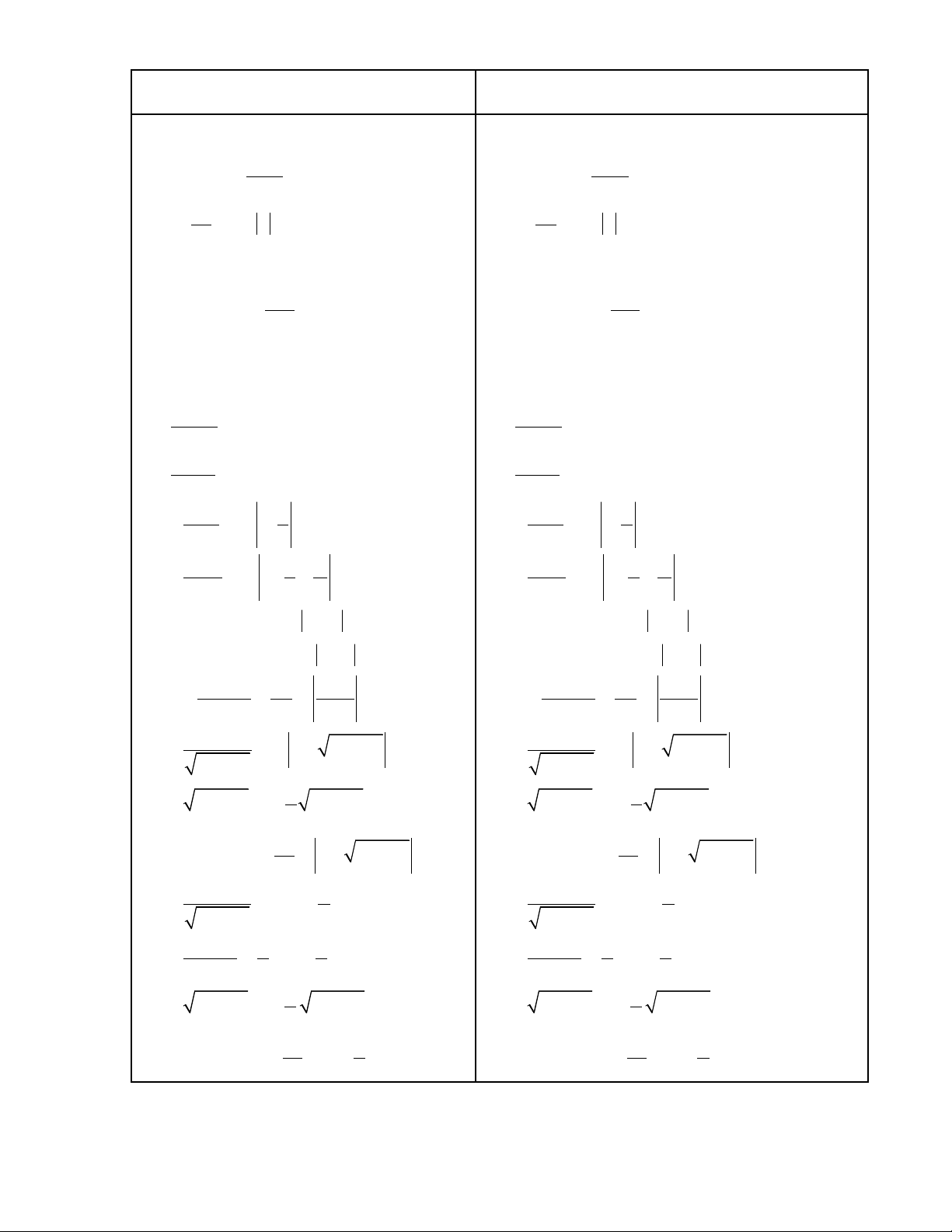
Nguyeân haøm cuûa caùc
Nguyeân haøm cuûa caùc haøm haøm soá sô caáp soá hôïp 1. ∫ dx= x+C 1. ∫ du= u+C + α + α xα α u 2. ∫ 1 x dx = +C 2. ∫ 1 = +C α u du +1 α +1
3. ∫ dx = ln x +C
3. ∫ du = ln u +C x u 4. ∫ exdx= ex+ C 4. ∫ eudu= eu+ C x a u a 5. ∫ axdx = +C , (0 < a ≠ 1) 5. ∫ audu = +C , (0 < a ≠ 1) ln a ln a 6. ∫ cosx dx= sinx +C 6. ∫ cosudu= sinu +C 7. ∫ sinxdx = -cosx +C 7. ∫ sinudu = -cosu +C dx du 8. ∫ = tgx +C 8. ∫ = tgu +C 2 cos x 2 cos u dx du 9. ∫ =-cotgx+C 9. ∫ =-cotgu+C 2 sin x 2 sin u dx x du u 10. = ln tg ∫ +C 10. = ln tg ∫ +C sin x 2 sin u 2 dx x π du u π 11. = ln tg( + ∫ +C 11. = ln tg( + ∫ +C cos x 2 4 cos u 2 4
12. ∫ tgxdx= -ln cos x +C
12. ∫ tgudu= -ln cosu +C
13. ∫ cotgxdx= ln sin x +C
13. ∫ cotgudu= ln sinu +C dx 1 x − a du 1 u − a 14. = ln ∫ +C 14. = ln ∫ +C 2 2 x − a 2a x + a 2 2 u − a 2a u + a dx du 2 2 2 2 15.
= ln x + x ± a ∫ +C 15.
= ln u + u ± a ∫ +C 2 2 x ± a 2 2 u ± a x u 16. 2 2 2 2 x ± a dx = x ± a ± ∫ 16. 2 2 2 2 u ± a du = u ± a ± ∫ 2 2 2 a 2 a 2 2 ±
ln x + x ± a +C 2 2 ±
ln u + u ± a +C 2 2 dx x du u 17. = arcsin + C ∫ 17. = arcsin + C ∫ 2 2 a a − x 2 2 a a − u dx 1 x du 1 u 18. = arctg + C ∫ 18. = arctg + C ∫ 2 2 a + x a a 2 2 a + u a a x u 19. 2 2 2 2 a − x dx = a − x + ∫ 19. 2 2 2 2 a − u du = a − u + ∫ 2 2 2 a x 2 + a u arcsin + C + arcsin + C 2 a 2 a

Tài liệu liên quan: