



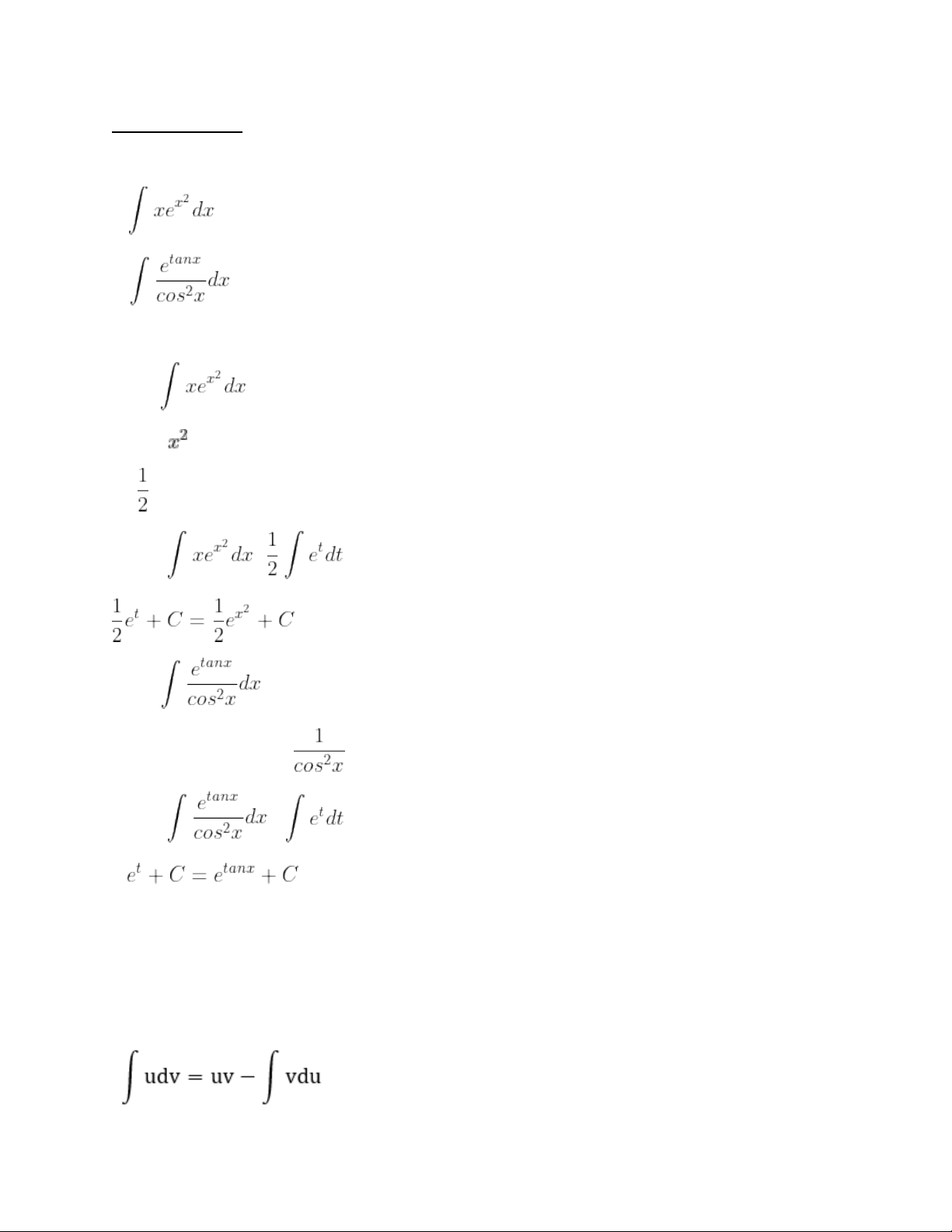





Preview text:
Các dạng bài tập Nguyên hàm thường gặp cùng cách giải chi tiết
1. Ôn la ̣i lý thuyết về nguyên hàm 1.1. Nguyên hàm
- Định nghĩa: Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F(x)
được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x ∈ K. - Định lí:
1) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì với mỗi hằng số C, hàm số G(x) =
F(x) + C cũng là một nguyên hàm của f(x) trên K.
2) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều
có dạng F(x) + C, với C là một hằng số.
Do đó F(x) + C, C ∈ R là họ tất cả các nguyên hàm của f(x) trên K. Ký hiệu = F(x) + C
1.2. Tính chất của nguyên hàm Tính chất 1: và + C Tính chất 2:
với k là hằng số khác 0. Tính chất 3: và
1.3. Sự tồn tại của nguyên hàm
Định lí: Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.
2. Phương pháp tính nguyên hàm
2.1. Phương pháp đổi biến số Định lí 1: Nếu
= F(u) + C và u = u(x) là hàm số có đạo hàm liên tục thì = F(u(x)) + C
Hệ quả: Nếu u = ax + b (a ≠ 0) thì ta có =
2.2. Phương pháp nguyên hàm từng phần
Định lí 2: Nếu hai hàm số u = u(x) và y = y(x) có đạo hàm liên tục trên K thì = u(x).v(x) - Hay = uv -
3. Các da ̣ng bài tâ ̣p nguyên hàm
Da ̣ng 1: Tìm nguyên hàm của hàm số
Phương pháp dùng định nghĩa vá tính chất
+ Biến đổi các hàm số dưới dấu nguyên hàm về dạng tổng, hiệu của các biểu thức chứa x.
+ Đưa các mỗi biểu thức chứa x về dạng cơ bản có trong bảng nguyên hàm.
+ Áp dụng các công thức nguyên hàm trong bảng nguyên hàm cơ bản.
Ví du ̣ minh hoa ̣: a, b,
Lời giải chi tiết:
Da ̣ng 2: Tìm nguyên hàm bằng phương pháp đổi biến số
Ví du ̣ minh hoa ̣:
Tìm các ho ̣ nguyên hàm sau đây: a, b,
Lời giải chi tiết: a, Xét Đăt t = , suy ra dt = 2xdx => dt = xdx Khi đó = b, Xét
Đă ̣t t = tanx, suy ra dt = dx Khi đó = =
Da ̣ng 3: Tim nguyên hàm bằng phương pháp từng phần
Với bài toán tìm nguyên hàm của các hàm số dạng tích (hoặc thương) của hai hàm số “khác lớp
hàm” ta thường sử dụng phương pháp nguyên hàm từng phần theo công thức
Dưới đây là một số trường hợp thường gặp như thế (với P(x) là một đa thức theo ẩn x)
Ví du ̣ minh hoa ̣: Tìm họ nguyên hàm của hàm số dx
Lời giải chi tiết: Xét dx
Đă ̣t u = ln(x+1) và dv = (4x-1)dx Khi đó dx = ( - x - 3)ln(x+1) - + 3x + C
Da ̣ng 4: Tìm nguyên hàm của số hữu tỉ
Nếu bâ ̣c của tử số P(x)≥ bâ ̣c của mẫu số Q(x) thì chia đa thức
Nếu bâ ̣c của tử số P(x) < bâ ̣c của mẫu số Q(x) thì Xem xét mẫu số và khi đó:
+ Nếu mẫu số phân tích được thành tích số, ta sẽ sử du ̣ng đồng nhất thức để đưa về da ̣ng tổng của các phân số.
Mô ̣t số trường hợp đồng nhất thức thường gă ̣p:
+ Nếu mẫu số không phân tích được thành tích số (biến đổi và đưa về da ̣ng lượng giác). Bài 1: f(x) = Lời giải chi tiết: Ta có: = = x + 2ln|x-1| + C
Bài 2: Tính nguyên hàm F(x) của hàm số:
Đáp án: -2ln|x-1| - ln|x+2| + C
Bài 3: Tính nguyên hàm F(x) của hàm số: I =
Đáp án: I = + 3x + 4ln|x-1| + C
Da ̣ng 5: Tìm nguyên hàm thoả mãn điều kiê ̣n cho trước
• Bước 1: Tìm nguyên hàm dựa vào những phương pháp đã biết:
- Sử dụng bảng nguyên hàm. - Đổi biến số - Nguyên hàm từng phần
• Bước 2: Dựa vào yêu cầu của bài toán tìm ra hằng số C tương ứng.
• Bước 3: Kết luận một nguyên hàm vừa tìm được.
Bài 1: Tìm một nguyên hàm F(x) của hàm số f(x) = (4x + 1) thỏa mãn điều kiện F(1) = e.
Đă ̣t u = 4x + 1 và dv = exdx suy ra du = 4dx và v =
⇒ ∫(4x + 1) dx = (x + 1) - = (4x + 1) - 4 + C = (4x - 3) + C
Mà F(1) = e ⇒ C = 0 nên F(x) = (4x - 3)
Bài 2: Cho F(x) là một nguyên hàm của hàm số f(x) =
thỏa mãn điều kiện F(0) = -1. Tính
tổng S các nghiệm của phương trình F(x) + x + 1 = 0. Đă ̣t u = x và dv = dx suy ra du = dx và v = - Khi đó F(x) =
Vì F(0) = -1 suy ra -1 + C = -1 => C = 0 => F(x) =
Phương trình F(x) + x + 1 = 0 <=> (x + 1) ( - 1) = 0 <=> x = -1 hoă ̣c
=1 suy ra x = -1 hoă ̣c x = 0 Vâ ̣y S = - 1 + 0 = -1.
Bài 3: Cho F(x) là một nguyên hàm của hàm số f(x) =
thỏa mãn F(0) = -ln2. Tìm tập
nghiệm S của phương trình F(x) + ln(ex+1) = 3
Các da ̣ng bài tâ ̣p nguyên hàm khác
Câu 1: Trong các khẳng định dưới đây, có bao nhiêu khẳng định đúng?
(1): Mọi hàm số liên tục trên [a; b] đều có đạo hàm trên [a; b] .
(2): Mọi hàm số liên tục trên [a; b] đều có nguyên hàm trên [a; b] .
(3): Mọi hàm số đạo hàm trên [a; b] đều có nguyên hàm trên [a; b] .
(4): Mọi hàm số liên tục trên [a; b] đều có giá trị lớn nhất và giá trị nhỏ nhất trên [a; b]
A. 2 khẳng đi ̣nh đúng
B. 3 khẳng đi ̣nh đúng
C. 1 khẳng đi ̣nh đúng
D. 4 khẳng đi ̣nh đúng
Câu 2: Cho hàm số f(x) xác định trên K . Khẳng định nào sau đây sai?
A. Nếu hàm số F(x) là một nguyên hàm của f(x) trên K thì với mỗi hằng số C , hàm số G(x) =
F(x) + C cũng là một nguyên hàm của f(x) trên K .
B. Nếu f(x) liên tục trên K thì nó có nguyên h àm trên K .
C. Hàm số F(x) được gọi là một nguyên hàm của f(x) trên K nếu (F'(x) = f(x) với mọi x thuô ̣c K
D. Nếu hàm số F(x) là một nguyên hàm của f(x) trên K thì hàm số F(−x) là một nguyên hàm của f(x) trên K Đáp án:
Câu 1 : Trong các khẳng định dưới đây, có bao nhiêu khẳng định đúng?
(1): Mọi hàm số liên tục trên [a; b] đều có đạo hàm trên [a; b]
(2): Mọi hàm số liên tục trên [a; b] đều có nguyên hàm trên [a; b]
(3): Mọi hàm số đạo hàm trên [a; b] đều có nguyên hàm trên [a; b] .
(4): Mọi hàm số liên tục trên [a; b] đều có giá trị lớn nhất và giá trị nhỏ nhất trên [a; b]
A. 2 khẳng đi ̣nh đúng
B. 3 khẳng đi ̣nh đúng
C. 1 khẳng đi ̣nh đúng
D. 4 khẳng đi ̣nh đúng Giải thích chi tiết:
- Khẳng định (1): Sai, vì hàm số y = |x| liện tục trên [-1; 1] nhưng không có đạo hàm tại x = 0
nên không thể có đạo hàm trên [-1; 1]
- Khẳng định (2): đúng vì mọi hàm số liên tục trên [a; b] đều có nguyên hàm trên [a; b].
- Khẳng định (3): Đúng vì mọi hàm số có đạo hàm trên [a; b] thì đều liên tục trên [a; b] nên đều có nguyên hàm trên [a; b]
- Khẳng định (4): Đúng vì mọi hàm số liên tục trên [a; b] đều có giá trị lớn nhất và giá trị nhỏ nhất trên [a; b] Câu 2:
Cho hàm số f(x) xác định trên K . Khẳng định nào sau đây sai?
A. Nếu hàm số F(x) là một nguyên hàm của f(x) trên K thì với mỗi hằng số C , hàm số G(x) =
F(x) + C cũng là một nguyên hàm của f(x) trên K .
B. Nếu f(x) liên tục trên K thì nó có nguyên h àm trên K .
C. Hàm số F(x) được gọi là một nguyên hàm của f(x) trên K nếu (F'(x) = f(x) với mọi x thuô ̣c K
D. Nếu hàm số F(x) là một nguyên hàm của f(x) trên K thì hàm số F(−x) là một nguyên hàm của f(x) trên K
Cho ̣n đáp án: D. Nếu hàm số F(x) là một nguyên hàm của f(x) trên K thì hàm số F(−x) là một
nguyên hàm của f(x) trên K




